∫∫∫ Тройной интеграл — Калькулятор Он-лайн

Введите подинтегральную функцию, для которой надо найти тройной интеграл

Найдём решение тройного интеграла от функции f(x, y, z).

Введите вверхние и нижние пределы для области интегрирования и подинтегральную функцию для тройного интеграла.
Если подинтегральной функции нету, то укажите 1.

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)

Абсолютное значение x
(модуль x или |x|)

arccos(x)

Функция — арккосинус от x

arccosh(x)

Арккосинус гиперболический от x

arcsin(x)

Арксинус от x

arcsinh(x)

Арксинус гиперболический от x

arctg(x)

Функция — арктангенс от x

arctgh(x)

Арктангенс гиперболический от x

exp(x)

Функция — экспонента от x (что и e^x)

log(x) or ln(x)

Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))

sin(x)

Функция — Синус от x

cos(x)

Функция — Косинус от x

sinh(x)

Функция — Синус гиперболический от x

cosh(x)

Функция — Косинус гиперболический от x

sqrt(x)

Функция — квадратный корень из x

sqr(x) или x^2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x

в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

Вычисление площади фигур в Питоне

Немного усложнив предыдущую задачу, мы можем рассчитывать самые разные площади.
Будем создавать программу для вычисления площади тругольника, прямоугольника (квадрата) и круга.
При вводе слова «треугольник», вычисляется площадь тругольника и т.д.

Для того, чтобы ввод данных использовал строковый тип применяется функция str(), которая переводит любое вводимое значение в строку.

Каждый случай определяется срабатыванием определенного условия, список которых можно увеличить до любого размера. Вполне логично создать свою пользовательскую функцию, использующую специальные переменные, а не писать постоянно условие.

О том как создавать свои пользовательские функции рассказано и продемонстрировано здесь.

Строка import math загружает необходимую библиотеку дополнительных математических функций.

Квадратный корень, например, вычисляется по формуле math.sqrt()

Известно, что для вычисления площади круга используется значение числа Пи. В Питоне оно вычисляется методом math.pi

Код готовой программы

import math

tip=str(input("Введите название фигуры ="))

if tip=="треугольник":

a=float(input("Введите сторону a ="))

b=float(input("Введите сторону b ="))

c=float(input("Введите сторону c ="))

p=(a+b+c)/2

s=math.sqrt((p*(p-a)*(p-b)*(p-c)))

elif tip=="прямоугольник":

a=float(input("Введите сторону a ="))

b=float(input("Введите сторону b ="))

s=a*b

elif tip=="круг":

r=float(input("Введите радиус r ="))

 s=math.pi*(r**2)

print(s)

При вводе слова «треугольник»:

Python 3. 5.2 (default, Dec 2015, 13:05:11)

[GCC 4.8.2] on linux

треугольник

Введите сторону a= 12

Введите сторону b= 13

Введите сторону c= 14

72.30793524918272

При вводе слова «прямоугольник»:

Python 3.5.2 (default, Dec 2015, 13:05:11)

[GCC 4.8.2] on linux

прямоугольник

Введите сторону a= 12

Введите сторону b= 13

156.0

При вводе слова «круг»:

Python 3.5.2 (default, Dec 2015, 13:05:11)

[GCC 4.8.2] on linux

круг

Введите радиус r= 12

452.3893421169302

Вы можете легко вычислять и другие площади фигур, если продолжите вписывать условия и функции. Успехов в программировании!

Площадь треугольника по формуле Герона на Питоне Вычисление суммы цифр целого числа

Урок алгебры в 11 классе по теме «Вычисление площади криволинейной трапеции»

Урок алгебры в 11 классе

с применением графического калькулятора CASIO

по теме «Вычисление площади криволинейной трапеции».

Учитель математики

Пережогина Оксана Николаевна

р.п. Лесогорск Чунского района

Иркутской области

Данный урок разработан для обучающихся 11 классов общеобразовательной школы в соответствии с системно-деятельностным подходом в обучении. Способствует развитию самостоятельности как на репродуктивном уровне, так и на творческом. Так как количество калькуляторов ограничено (10 штук на 20 человек), то формируются навыки работы в группе: умение распределять обязанности, сотрудничать, принимать решения, уметь слушать товарища, договариваться. Каждый этап урока предполагает формирование ключевых компетенций: регулятивных, коммуникативных, познавательных. На уроке учащиеся учатся контролировать свою работу, искать ошибки, проводить самооценку своей деятельности.

Оборудование:

• Графические калькуляторы «CASIO» (один на 2 ученика).

• мультимедийный проектор, компьютер.

• Компьютерные программы: fs Emulato.

• Раздаточный материал

Технологическая карта урока алгебры в 11 классе с применением графического калькулятора CASIO

по теме «Вычисление площади криволинейной трапеции».

Технологическая карта

Развитие внимания, памяти, логического и творческого мышления, умение контролировать свою деятельность, оценивать её.

Основные понятия, изучаемые на уроке (повторение)

Интеграл, площадь криволинейной трапеции, парабола, первообразная, производная, график, синус, косинус

Организационная структура урока

№

Этап урока

УУД

Деятельность

Время мин

Учителя

Учащихся

1

Организационно-мотивационный этап

Добрый день! Обратите внимание на слайд. Как вы понимаете эти слова?

Слайд 1. Девиз нашего урока «Математику нельзя изучать, наблюдая, как это делает сосед!»

Сегодня на уроке мы займемся вычислениями. А вот что мы будем вычислять, это вам нужно будет определить, выполнив следующее задание.

Задание 1

а) Какая фигура называется криволинейной трапецией?

б) Какие из фигур являются криволинейными трапециями?

в) Как найти площадь криволинейной трапеции?

г) Найти площадь заштрихованной фигуры.

Личностные: самоопределение

Регулятивные: коррекция, оценка

Познавательные анализ с выявлением существенных и несущественных признаков, сравнения, обобщение.

Приветствует обучающихся, Создает благоприятные условия для работы на уроке. Психологически готовит учащихся к общению и восприятию заданий. Задает вопросы.

Приветствуют учителя, проверяют готовность к уроку.

Отвечают на вопросы учителя. Дают определение криволинейной трапеции, алгоритм нахождения площади криволинейной трапеции

5

2

Этап актуализации субъективного опыта

Задание 2. Готовимся к экзаменам. Выполнив следующие задания, определите тему урока. Поставьте цели.

Задания решаются на доске.

Коммуникативные: участие в совместной деятельности, изложение собственных мыслей

Личностные: ответственное отношение к выполнению учебных задач

Регулятивные: целеполагание, планирование, контроль, оценка.

Организует формулировку вопросов обучающимся, дает задания, следит за самостоятельностью выполнения заданий. Корректирует деятельность обучающихся.

Работают самостоятельно в тетрадях, выполняют самопроверку решения. Корректируют знания.

7

3

Восприятие и осмысление учащимися материала

Задание 3.

Построить фигуру, площадь которой равна данному выражению с помощью графического калькулятора CASIO. ( Предполагается, что учащиеся знакомы с основными функциями калькулятора). Открываем подменю GRAF, EXE, вводим функции, EXE, DROW

Вычислить её площадь с помощью калькулятора, зайдя в подменю RUN-MAT, EXE, OPTN, F4, F4 далее вбиваем формулу, нажимаем EXE и получаем ответ.

Личностные: ответственное отношение к выполнению учебных задач

Регулятивные: контроль, оценка и самооценка

Познавательные информационный поиск, анализ

Корректирует деятельность учащихся, организует самостоятельную работу, оказывает помощь в работе с калькулятором слабым обучающимся.

Работают самостоятельно, решение проверяют с помощью графического калькулятора CASIO.

8

4

Проверка понимания

Самостоятельная работа. Работа в группах.

Вычислить площадь фигуры, ограниченной линиями. Выполнить самопроверку с помощью графического калькулятора. Ответы проецируются на слайде.

Познавательные выбор наиболее эффективных способов решения

Коммуникативные: инициативное сотрудничество в поиске правильного решения

Личностные: самоопределение

Регулятивные: коррекция, оценка

Даёт задание обучающимся, следит за самостоятельностью выполнения заданий, выборочно проверяет выполнение заданий у некоторых групп. Выставляет оценки в журнал.

Работают в группах, выполняют задания с проверкой на графическом калькуляторе. Выполняют самопроверку (ответы высвечиваются на слайд)

10

5

Закрепление

№1023(2) для тех, кто справился с самостоятельной работой.

Познавательные рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Регулятивные: контроль, коррекция, оценка

Организует работу с учебником, дает задания тем, кто справился с самостоятельной работой

Работают с учебником, правильность выполнения задания проверяют, сверяясь с ответом на откидной доске.

5

7

Информация о домашнем задании №1018, №1019(2), № 1022 (2,4)

Коммуникатив ные: слушание учителя

Личностные: оценивание усваиваемого содержания

Регулятивные: регуляция учебной деятельности

Дает характеристику домашнего задания.

Записывают домашнее задание в дневник, оценивают характер номеров. Слушают комментарии учителя.

2

8

Этап рефлексии

Самоанализ учащихся своей работы на уроке, а также знаний и умений по текущей теме.

— Я научился…

— Я понял, что…

— Знания, полученные на уроке мне пригодятся…

Оцени свою работу на уроке по 10 бальной шкале

Регулятивные: саморегуляция, рефлексия

Познавательныеумение делать выводы, рефлексия способов и условий действий

Коммуникативные: умение формулировать собственное мнение

Предлагает оценить свою работу на уроке

Оценка своей деятельности на уроке. Рефлексия.

3

Найти объем тела образованного вращением вокруг оси ox онлайн калькулятор

С помощью определённого интеграла можно вычислять не только площади плоских фигур, но и объёмы тел, образованных вращением этих фигур вокруг осей координат.

Тело, которое образуется вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху графиком функции y = f(x) , имеет объём

Аналогично объём v тела, полученного вращением вокруг оси ординат ( Oy ) криволинейной трапеции выражается формулой

При вычислении площади плоской фигуры мы узнали, что площади некоторых фигур могут быть найдены как разность двух интегралов, в которых подынтегральные функции — те функции, которые ограничивают фигуру сверху и снизу. Похоже обстоит дело и с некоторыми телами вращения, объёмы которых вычисляются как разность объёмов двух тел, такие случаи разобраны в примерах 3, 4 и 5.

Пример 1. Найти объём тела, образованного вращением вокруг оси абсцисс ( Ox ) фигуры, ограниченной гиперболой , осью абсцисс и прямыми , .

Решение. Объём тела вращения найдём по формуле (1), в которой , а пределы интегрирования a = 1 , b = 4 :

Решение. Рассмотрим шар как тело, получащееся при вращении вокруг оси абсцисс полукруга радиуса R с центром в начале координат. Тогда в формуле (1) подынтегральная функция запишется в виде , а пределами интегрирования служат —R и R. Следовательно,

Пример 3. Найти объём тела, образованного вращением вокруг оси абсцисс ( Ox ) фигуры, заключённой между параболами и .

Решение. Представим искомый объём как разность объёмов тел, полученных вращением вокруг оси абсцисс криволинейных трапеций ABCDE и ABFDE . Объёмы этих тел найдём по формуле (1), в которой пределы интегрирования равны и — абсциссам точек B и D пересечения парабол. Теперь можем найти объём тела:

Пример 4. Вычислить объём тора (тором называется тело, получающееся при вращении круга радиуса a вокруг оси, лежащей в его плоскости на расстоянии b от центра круга ( ). Форму тора имеет, например, баранка).

Решение. Пусть круг вращается вокруг оси Ox (рис. 20). Объём тора можно представить как разности объёмов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ox.

Используя разность объёмов тел, получаем для объёма тора v выражение

Пример 5. Найти объём тела, образованного вращением вокруг оси ординат ( Oy ) фигуры, ограниченной линиями и .

Решение. Представим искомый объём как разность объёмов тел, полученных вращением вокруг оси ординат треугольника OBA и криволинейной трапеции OnBA . Объёмы этих тел найдём по формуле (2). Пределами интегрирования служат и — ординаты точек O и B пересечения параболы и прямой. Таким образом, получаем объём тела:

Логарифмическая функция комплексного переменного
Индекс сезонности онлайн

Найдите площадь криволинейной трапеции y x 3 – Telegraph

Найдите площадь криволинейной трапеции y x 3

Скачать файл — Найдите площадь криволинейной трапеции y x 3

Главная Домашняя страница сайта Онлайн сервисы Бесплатно Каталог заданий Примеры решений задач Готовые работы Банк задач. Предлагаем Вашему вниманию калькулятор для нахождения площади фигуры ограниченной кривыми линиями. Калькулятор в автоматическом режиме составляет интеграл, находит границы интегрирования, а также рисует саму фигуру на координатной плоскости. Как частный случай, калькулятор находит площадь криволинейной трапеции. Площадь треугольника по основанию и высоте Площадь треугольника по формуле Герона Площадь треугольника через две стороны и угол между ними Площадь треугольника через сторону и прилежащие к ней углы Площадь прямоугольного треугольника Площадь равнобедренного треугольника Площадь равностороннего треугольника Площадь прямоугольника Как вычислить площадь круга Найти площадь квадрата. По умолчанию Сначала новые Сначала старые. Помогите найти площадь фигуры, ограниченной линиями: Всё вводил правильно но решения так и не получил Необходимо правильно ввести функции: Решение задач и контрольных работ на заказ по высшей математике, теории вероятности, статистике, эконометрике, дискретной математике, а также по физике все разделы. При копировании материалов указывайте ссылку на источник!

Найти площадь фигуры ограниченной линиями онлайн

Французская резинка схема

Как правильно посадить клубнику под черный спанбонд

11.1.9.2. Площадь криволинейной трапеции. Примеры

Внедрение сэд в организацию

Nightwish the islander перевод

Шкаф шпк 320н характеристики

Типы почв и их характеристика таблица

Урок алгебры и начала анализа в 11-м классе по теме: ‘Площадь криволинейной трапеции’

Стань гением станислав мюллер скачать

Определение причин вибрации

Как сделать панорамное фото интерьера

найдите площадь криволинейной трапеции, ограниченной линиями y= -x2+3 и y=0

Инструкция по эксплуатации гаси спрут

Таблица че 2016 по футболу

Стенд испытания рвд

Калькулятор площади между двумя кривыми

Используйте этот калькулятор площади между двумя кривыми, чтобы найти площадь между двумя кривыми на заданном интервале, соответствующую разнице между определенными интегралами. В координатной плоскости общая площадь занята между двумя кривыми, а калькулятор площади между кривыми вычисляет площадь путем решения определенного интеграла между двумя различными функциями.

Итак, давайте начнем читать, как найти площадь между двумя кривыми, используя определенное интегрирование, но сначала вам нужно рассмотреть некоторые основы прямо сейчас!

Что такое A rea Между двумя кривыми?

В математике площадь между двумя кривыми можно вычислить с помощью разницы между определенным интегралом двух точек или выражений.В двумерной геометрии площадь может быть выражена областью, покрываемой двумя разными кривыми. Для вычисления площади требуются две функции: f(x) и g(x), а также интегральные пределы от a до b, где b должно быть больше, чем \(a, b>a\) выражения.

\(Y = f (x) \text{где x} = a, x = b\)

\(Y = f (x)\) между пределами a и b

Формула площади между двумя кривыми:

Мы можем найти площади между кривыми, используя стандартную формулу, если у нас есть две разные кривые

$$m = f (x) & m = g (x)$$

Где

\(f (x) \text{ больше} g (x)\)

Таким образом, площадь, ограниченная двумя линиями\(x = a \text{ и} x = b\), равна

$$A = ∫ab[f (x) – g (x)] dx$$

Итак, калькулятор площади между двумя кривыми вычисляет площадь пересечения двух кривых, используя эту стандартную формулу.

Тем не менее, онлайн-калькулятор интегралов позволяет вычислять интегралы функций по задействованной переменной.

Расчет площади между кривыми:

Чтобы найти площадь между двумя кривыми, вот простые рекомендации:

• Нужны две кривые: \(y = f (x), \text{ и} y = g (x)\)
• Найдите точки пересечения кривых, добавив одно значение уравнения в другое, и составьте уравнение, которое имеет только одну переменную.
• Решите данное выражение, найдите точки пересечения и нарисуйте график для заданной точки пересечения и кривых.
• Итак, площадь равна \(A = ∫ab [f(x)-g(x)] dx\) и подставим эти значения в данную формулу.
• Затем выполните определенное интегрирование и измените значения, чтобы получить результат.

Вы можете мгновенно рассчитать площадь и определенный интеграл, подставив выражения в калькулятор площади между двумя кривыми.

Пример:

Найдите площадь между двумя кривыми \(x^2 + 4y – x = 0\), где прямая \(x = y\)?

Решение:

Данное уравнение равно

$$x^2 + 4y – x = 0, x=y$$

$$X^2 + 4y – x = 0$$

Добавьте x и вычтите \(x^2 \) с обеих сторон. 2/2]30$$

$$= – [(0+0) – (- 33/4*3 – 3/4 * 32/2)$$

$$= – (-27/12 + 3/4 * 9/2)$$

$$A= 27/24$$

Площадь по определенному интегралу равна\( \frac{-27}{24}\).

Кроме того, онлайн-калькулятор производных позволяет определить производную функции по заданной переменной.

Как работает калькулятор между двумя кривыми rea?

Калькулятор площади между кривыми найдет площадь между кривыми со следующими шагами:

Ввод:

• Введите два разных выражения кривых относительно \(x или y\).
• Установите определенные верхний и нижний пределы для кривых
• Нажмите кнопку расчета для дальнейшего процесса.

Вывод:

Калькулятор отображает следующие результаты для площади между двумя кривыми:

• Отображение ввода в виде правильного уравнения, которое вы вводите в соответствующие поля.
• Показывает область, между которой находятся две кривые со всеми шагами интегрального расчета.

Часто задаваемые вопросы об области между кривыми:

Может ли площадь между двумя кривыми быть отрицательной или нет?

Если обе кривые лежат на оси x, площади между кривыми будут отрицательными (-).Однако значение со знаком является окончательным ответом.

Почему мы используем только определенный интеграл для нахождения площади, ограниченной кривыми?

Калькулятор площади между кривыми находит площадь по разным функциям, только неопределенные интегралы, т.к. неопределенные как раз показывают семейство разных функций, а также используют для нахождения площади между двумя кривыми, которые интегрируют разность выражений.

Что такое определенный интеграл и неопределенный интеграл?

Неопределенный интеграл показывает семейство различных функций, производными которых являются f.Различия между двумя функциями в семье просто постоянны. А определенный интеграл представляет числа, когда верхний и нижний пределы являются константами.

КонецПримечание:

Чтобы найти площадь между кривыми без графика, используйте этот удобный калькулятор площади между двумя кривыми. По сути, площадь между кривой означает величину количества, которая получается произведением величин, обозначенных осями x и y. Таким образом, онлайн-калькулятор площади между кривыми — лучший способ точно указать величину величины.

Ссылка:

Из источника Википедии: Единицы, Преобразования, Неметрические единицы, Площадь четырехугольника.

Из источника Brilliant: Площадь между кривой и осью x, Площадь между кривой и линией, Площадь между 2 кривыми.

Из источника Math Online: Areas Between Curves, нижняя кривая g, верхняя кривая f.

 

 

 

10.3 Площади в полярных координатах

Мы можем использовать уравнение кривой в полярных координатах для вычисления некоторые области, ограниченные такими кривыми.2\theta-4\;d\theta={4\over3}\pi + 2\sqrt{3}. $$ $\квадрат$

Рисунок 10.3.2. Область между кривыми.

Этот пример делает процесс более простым, чем он является. Поскольку точки имеют много разных представлений в полярных координаты, не всегда так просто определить точки пересечение.

Пример 10.3.3. Находим заштрихованную область на первом графике рисунок 10.3.3 как разница из двух других заштрихованных областей. Кардиоида равна $r=1+\sin\theta$ и круг $r=3\sin\theta$.Пытаемся найти точки пересечения: $$\выравнивание{ 1+\sin\theta&=3\sin\theta\cr 1&=2\sin\тета\кр 1/2&=\sin\theta.\cr} $$ Это имеет решения $\theta=\pi/6$ и $5\pi/6$; $\pi/6$ соответствует пересечение в первом квадранте, которое нам нужно. Обратите внимание, что нет решение этого уравнения соответствует точке пересечения происхождения, но, к счастью, это очевидно. Кардиоида проходит через начало координат при $\theta=-\pi/2$; окружность проходит через начало координат в кратно $\pi$, начиная с $0$.2\;d\тета= {3\pi\over8} — {9\over16}\sqrt{3} $$ поэтому искомая площадь равна $\pi/8$. 2\theta$.2=\cos(2\тета)$. (отвечать)

Пример 10.3.13 Найдите площадь, заключенную в $r=\tan\theta$ и $\ds ​​r={\csc\theta\over\sqrt2}$. (отвечать)

Пример 10.3.14 Найдите площадь внутри $r=2\cos\theta$ и снаружи $г=1$. (отвечать)

Пример 10.3.15 Найдите площадь внутри $r=2\sin\theta$ и выше строка $r=(3/2)\csc\theta$. (отвечать)

Пример 10.3.16 Найдите площадь внутри $r=\theta$, $0\le\theta\le2\pi$. (отвечать)

Пример 10.3.17 Найдите площадь внутри $\ds r=\sqrt{\theta}$, $0\le\theta\le2\pi$. (отвечать)

Пример 10.3.18 Найдите площадь внутри $\ds r=\sqrt3\cos\theta$ и $r=\sin\тета$. (отвечать)

Пример 10.3.19 Найдите площадь внутри $r=1-\cos\theta$ и $r=\cos\theta$. (отвечать)

Пример 10.3.20 Центр окружности радиуса 1 находится на длина окружности радиуса 2. Найдите площадь области внутри обоих кругов. (отвечать)

Пример 10. 3.21 Найдите заштрихованную область на рисунке 10.3.4. Кривая $r=\theta$, $0\le\theta\le3\pi$. (отвечать)

Рисунок 10.3.4. Область, ограниченная спиралью Архимеда.

Площадь под кривой — метод, формула, примеры решений, часто задаваемые вопросы

Площадь под кривой рассчитывается разными методами, из которых наиболее популярен первообразный метод нахождения площади. Площадь под кривой можно найти, зная уравнение кривой, границы кривой и ось, охватывающую кривую.Как правило, у нас есть формулы для нахождения площадей правильных фигур, таких как квадрат, прямоугольник, четырехугольник, многоугольник, круг, но нет определенной формулы для нахождения площади под кривой. Процесс интегрирования помогает решить уравнение и найти искомую площадь.

Для нахождения площадей неправильных плоских поверхностей очень полезны методы первообразных. Здесь мы научимся находить площадь под кривой относительно оси, находить площадь между кривой и прямой и находить площадь между двумя кривыми.

Как найти площадь под кривой?

Площадь под кривой можно рассчитать за три простых шага. Во-первых, нам нужно знать уравнение кривой (y = f(x)), пределы, в которых должна быть рассчитана площадь, и ось, охватывающую площадь. Во-вторых, мы должны найти интегрирование (первообразную) кривой. Наконец, нам нужно применить верхний предел и нижний предел к интегральному ответу и взять разницу, чтобы получить площадь под кривой.б_а\)

       =\( г(б) — г(а)\) 

Различные методы поиска площади под кривой

Площадь под кривой можно вычислить тремя способами. Кроме того, метод, используемый для нахождения площади под кривой, зависит от необходимости и доступных входных данных для нахождения площади под кривой. Здесь мы рассмотрим три метода, чтобы найти площадь под кривой.

Метод — I:   Здесь область под кривой разбита на наименьшие возможные прямоугольники.нф(х). \дельта х\).

Метод — II: В этом методе также используется процедура, аналогичная описанной выше, для нахождения площади под кривой. Здесь область под кривой разделена на несколько прямоугольников. Далее площади этих прямоугольников складываются, чтобы получить площадь под кривой. Этот метод представляет собой простой способ найти площадь под кривой, но он дает только приблизительное значение площади под кривой.

Метод — III: Этот метод использует процесс интегрирования для нахождения площади под кривой.б f(x).dx\)

Формула площади под кривой

Площадь кривой может быть рассчитана относительно различных осей как граница данной кривой. Площадь под кривой можно рассчитать относительно оси x или оси y. Для особых случаев кривая находится ниже осей и частично ниже осей. Для всех этих случаев у нас есть производная формула для нахождения площади под кривой.

Площадь по оси x: Здесь мы сначала рассмотрим площадь, ограниченную кривой y = f(x) и осью x.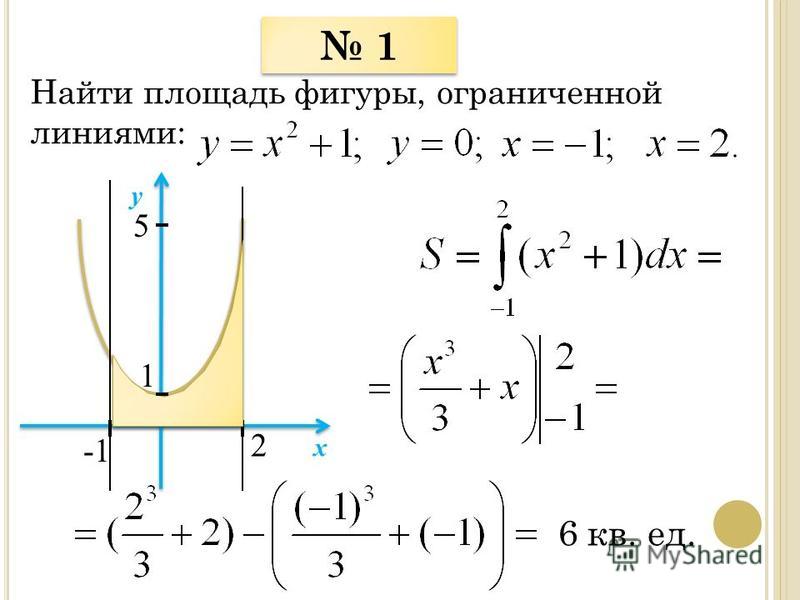 cf(x).dx\)

 

Область под кривой — круг

Площадь круга рассчитывается путем вычисления площади части круга в первом квадранте. Здесь уравнение окружности x ²  + y ²  = a ²  заменяется уравнением кривой вида y = √(a ² — x ² ). Это уравнение кривой используется для нахождения площади относительно оси x и пределов от 0 до a.а_0\)

= 4[((a/2)× 0 + (a ² /2)Sin ^-1 1) — 0]

= 4(а ² /2)(π/2)

= 2π r  

Следовательно, площадь круга равна π a ² квадратных единиц.

Площадь под кривой — парабола

Парабола имеет ось, которая делит параболу на две симметричные части. Здесь мы берем параболу, симметричную относительно оси x и имеющую уравнение y ²  = 4ax.2}{3}\) квадратных единиц.

Площадь под кривой — эллипс

Уравнение эллипса с большой осью 2a и малой осью 2b: x ² /a ²  + y ² /b ²  = 1. Это уравнение можно преобразовать в виде y = b/a .√(a ²  — x ² ). Здесь мы вычисляем площадь, ограниченную эллипсом по первой координате и по оси x, и далее умножаем на 4, чтобы получить площадь эллипса.2}{2}.\frac{\pi}{2}\\&=\pi ab\end{align}\)

Следовательно, площадь эллипса составляет πab кв. единиц.

Область под кривой — между кривой и трапецеидальной линией

Площадь между кривой и линией можно легко рассчитать, взяв разность площадей одной кривой и площади под линией. Здесь граница относительно оси и для кривой, и для линии одинакова. На рисунке ниже показаны кривая \(y_1\) = f(x) и линия \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между кривой и линией.b_a [f(x) — g(x)].dx\)

Область под кривой — между двумя кривыми

Площадь между двумя кривыми удобно вычислять, взяв разность площадей одной кривой из площади другой кривой. Здесь граница по оси для обеих кривых одинакова. На приведенном ниже рисунке показаны две кривые \(y_1\) = f(x) и \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между этими двумя кривыми.4_0\)

= [((4/2)× 0 + (16/2)Sin-11) — 0]

= (16/2)(π/2)

= 4π 
Ответ: Следовательно, площадь области, ограниченной кругом в первом квадранте, равна 4π квадратных единиц

Пример 2: Найдите площадь под кривой для области, заключенной в эллипс x ² /36 + y ² /25 = 1,

Решение:

Данное уравнение эллипса есть.{-1}1) — 0]\\&=\frac{20}{6}.\frac{36}{2}.\frac{\pi}{2}\\&=30\pi \end{ выровнять}\)

Ответ: Следовательно, площадь эллипса равна 30π квадратных единиц.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Забронируйте бесплатный пробный урок

 

Часто задаваемые вопросы о Area Under The Curve

Как найти площадь под кривой?

Площадь под кривой можно найти с помощью процесса интегрирования или первообразной.б у.дх\)

Какие существуют методы нахождения площади под кривой?

Существует три основных метода нахождения площади под кривой. Площадь под кривой рассчитывается путем деления пространства площади на множество маленьких прямоугольников, а затем площади складываются для получения общей площади. Второй метод заключается в разделении области на несколько прямоугольников, а затем области складываются для получения необходимой площади. Третий способ – найти площадь с помощью интегрирования.

Что означает площадь под кривой?

Площадь под кривой означает площадь, ограниченную кривой, осью и граничными точками. Площадь под кривой представляет собой двумерную площадь, рассчитанную с помощью осей координат и формулы интегрирования.

Что представляет площадь под кривой?

Площадь под кривой представляет собой площадь, заключенную под кривой и осью, которая отмечена ограничивающими точками.Эта площадь под кривой дает площадь неправильной плоской формы в двумерном массиве.

Что такое площадь под кривой на графике скорости во времени?

На графике скорость-время скорость отложена по оси у, а время отложено по оси х. При этом предполагается, что площадь является произведением скорости и времени, и это дает пройденное расстояние. Следовательно, площадь под кривой графика зависимости скорости от времени дает пройденное расстояние.

Как интерпретировать площадь под кривой?

Площадь под кривой — это площадь между кривой и осью координат.Дальнейшие границы накладываются поперек кривой относительно оси, чтобы получить требуемую площадь. Площадь под кривой обычно представляет собой площадь неправильных форм, для которых нет формул площади в геометрии.

Как рассчитать площадь под кривой без интегрирования?

Площадь под кривой можно рассчитать даже без использования интегрирования. Площадь под кривой можно разбить на меньшие прямоугольники, а затем суммирование этих площадей дает площади под кривой.Также другой метод состоит в том, чтобы разбить область под кривой на несколько прямоугольников, а затем мы можем взять соответствующие области, чтобы получить площадь под кривой.

Как приблизительно определить площадь под кривой?

Площадь под кривой можно приблизительно рассчитать, разбив площадь на небольшие части в виде небольших прямоугольников. И площади этих прямоугольников можно вычислить, и их суммирование дает площадь под кривой. Другой способ найти приблизительную площадь под кривой — нарисовать набор из нескольких больших прямоугольников, а затем суммировать их площади.Далее мы можем просто найти точную площадь под кривой с помощью определенных интегралов.

Когда использовать площадь под кривой?

Площадь под кривой полезна для нахождения площади неправильной формы на плоскости. Обычно мы находим формулы для нахождения площади круга, квадрата, прямоугольника, четырехугольника, многоугольника, но у нас нет никаких средств для нахождения площади неправильной формы. Здесь мы используем концепцию определенных интегралов для получения значений площадей.

Когда площадь под кривой имеет отрицательное значение?

Площадь под кривой отрицательна, если кривая находится под осью или в отрицательных квадрантах оси координат.Для этого также вычисляется площадь кривой с использованием нормального метода, и к окончательному ответу применяется модуль. Даже при отрицательном ответе берется только значение площади, без учета отрицательного знака ответа.

Расчет ограниченной области

Расчет ограниченной области

Расчет ограниченной площади

Примечание. Чтобы избежать непредвиденных результатов при использовании этой функции, убедитесь, что для параметра документа «Реальный или сложный формат» установлено значение .

При расчете площади между кривыми каждая кривая должна быть:

•

Функция относительно x.

— или —

•

Уравнение в форме y=, включая уравнения y=, заданные с помощью текстового поля или шаблона уравнения конической формы.

Определение и затенение области

1.

В меню выберите .

Если доступно ровно две подходящие кривые, они выбираются автоматически, и вы можете перейти к шагу 3. В противном случае вам будет предложено выбрать две кривые.

2.

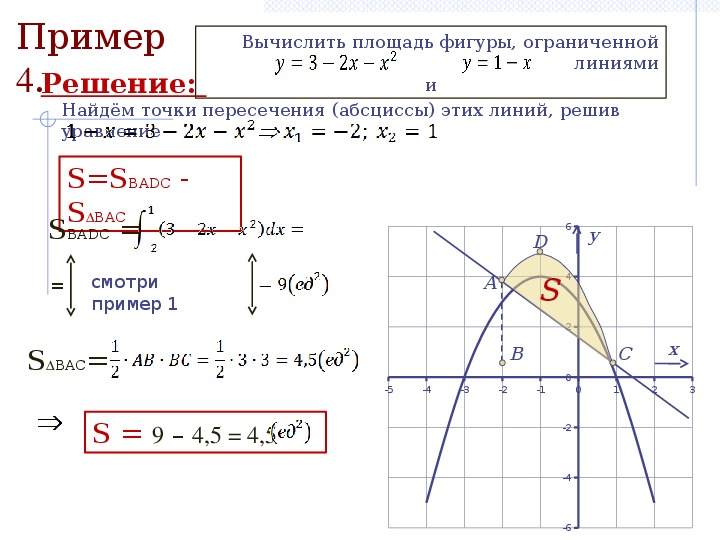Щелкните две кривые, чтобы выбрать их. – или – Щелкните одну кривую и ось x.

Вам будет предложено установить нижнюю и верхнюю границы.

3.

Щелкните две точки, чтобы задать границы. При желании вы можете ввести числовые значения.

Область становится затененной, и отображается значение площади.Значение всегда неотрицательно, независимо от направления интервала.

Работа с затененными областями

При изменении границ или переопределении кривых затенение и значение площади обновляются.

•

Чтобы изменить нижнюю или верхнюю границу, перетащите ее или введите для нее новые координаты.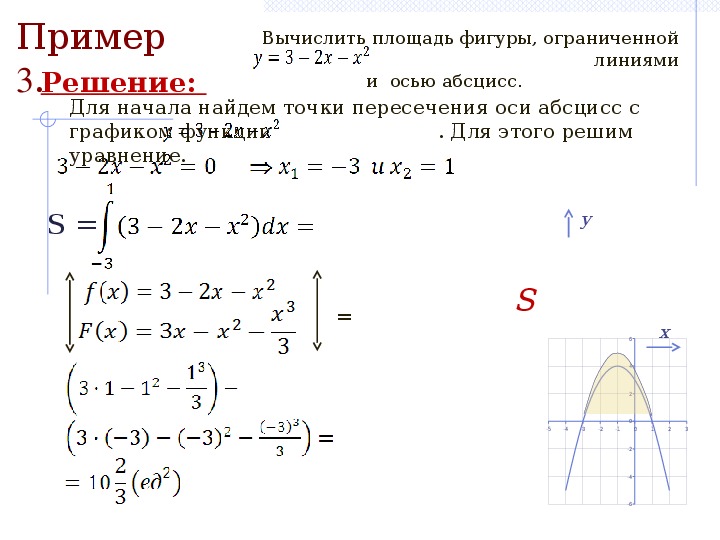 Вы не можете переместить границу, которая находится на пересечении.Однако точка перемещается автоматически, когда вы редактируете или манипулируете кривыми.

•

Чтобы переопределить кривую, либо манипулируйте ею путем перетаскивания, либо измените ее выражение в строке ввода.

Если конечная точка изначально находилась на пересечении, а переопределенные функции больше не пересекаются, затенение и значение площади исчезают.Если вы переопределяете функцию (функции) так, чтобы была точка пересечения, затенение и значение площади снова появляются.

•

Чтобы удалить или скрыть заштрихованную область или изменить ее цвет и другие атрибуты, откройте ее контекстное меню.

—

Windows®: щелкните правой кнопкой мыши заштрихованную область.

—

Mac®: удерживайте и щелкните заштрихованную область.

—

Портативный компьютер: наведите указатель на заштрихованную область и нажмите / x.

 

Как получить площадь между кривыми в Excel | Small Business

Microsoft Excel — мощная программа для работы с электронными таблицами, которую можно использовать для построения графиков функций, включая функции, формирующие кривые. Одним из ограничений Excel является отсутствие встроенной функции для вычисления площади между двумя кривыми. Чтобы рассчитать эту площадь, вы можете использовать функцию регрессионного анализа Excel, чтобы помочь вам. Однако, чтобы фактически вычислить площадь между двумя кривыми, вы должны использовать интегральное исчисление для оценки двух уравнений для кривых. Если вы не знаете уравнений для двух кривых, вы можете использовать данные электронной таблицы Excel, чтобы найти приблизительное уравнение.

Введите «ЛИНЕЙН(yrange,xrange,TRUE,FALSE)» в пустую ячейку электронной таблицы Excel.

Измените параметры команды ЛИНЕЙН, чтобы отразить расположение ваших данных для одного из графиков. Например, если ваши y-данные находятся в ячейках A1:A8, а ваши x-данные находятся в ячейках B1:B8, тогда функция будет читать ЛИНЕЙН(A1:A8,B1:B8,ИСТИНА,ЛОЖЬ).

Нажмите «Enter», чтобы получить уравнение для первого набора данных.

Введите «ЛИНЕЙН(yrange,xrange,TRUE,FALSE)» во вторую пустую ячейку электронной таблицы Excel.

Измените параметры команды ЛИНЕЙН, чтобы отразить расположение ваших фактических данных для второго графика.Например, если данные y для вашего второго графика находятся в ячейках C1:C8, а ваши данные x находятся в ячейках D1:D8, тогда функция будет читать ЛИНЕЙН(C1:C8,D1:D8,ИСТИНА,ЛОЖЬ).

Нажмите «Enter», чтобы получить уравнение для второго набора данных.

Затем вычислите определенный интеграл для двух уравнений. Требуется знание счета. Существуют онлайн-калькуляторы для вычисления определенных интегралов. Например, Wolfram, Solve My Math и Free Math Help предлагают онлайн-калькуляторы определенных интегралов.

Рассчитайте площадь под первой кривой, используя определенный интеграл.

Рассчитайте площадь под второй кривой, используя определенный интеграл.

Вычтите шаг 9 из шага 8, чтобы найти площадь между двумя кривыми.

Площадь между двумя кривыми — Бесплатная помощь по математике

Приложения определенных интегралов: (урок 1 из 3)

Область между двумя кривыми

Площадь между кривыми $y = f(x)$ и $y = g(x)$ между $x = a$ и $x = b \ \ (a

$$ А = \int\limits_a^b {\left| {f(x) — g(x)} \right|dx} $$

Пример 1:

Найдите площадь области, ограниченной графиками $f(x) = 2 — x^2$ и $g(x) = x$

Решения:

Две прямые пересекаются в точках $(-2, -2)$ и $(1, 1)$, начиная с

$$ f(x) = g(x) \leftrightarrow 2 — x^2 = x \leftrightarrow x^2 + x — 2 = 0 \leftrightarrow x = -2 , 1 $$

Таким образом, площадь равна

$$ \begin{выровнено} А &= \int\limits_a^b {\left| {f(x) — g(x)} \right|dx = \int\limits_{ — 2}^1 {\left| {2 — {x^2} — x} \right|dx} } = \int\limits_{ — 2}^1 {(2 — {x^2} — x)dx} = \\ &= \left[ { — \frac{x^3}{3} — \frac{x^2}{2} + 2x} \right]_{ — 2}^1 = \\ &= \фракция{9}{2} \end{выровнено} $$

Пример 2:

Найдите площадь области, ограниченной графиками $f(x) = 3x^3 — x^2 — 10x$ и $g(x) = -x^2 + 2x$

Решение:

Две прямые пересекаются в точках $(-2,-8)$, $(0,0)$ и $(2,0)$ с

$$ f(x) = g(x) \leftrightarrow 3x^3 — x^2 — 10x = -x^2 + 2x \leftrightarrow 3x^3 — 12x = 0 \leftrightarrow x = -2, 0, 2 $$. 2 = — (12 — 24) + ( — 12 + 24) = 24 \end{выровнено} $$

Интеграция: площадь и кривые

Интеграция и функция площади

Площадь между графиком функции y = f(x) а ось x, начинающаяся с x = 0, называется функцией площади A(x)

Пример

Найдите площадь под графиком y = 2x между х = 2 и х = 4

    Область между 2 и 4 можно описать как площадь между x = 0 и x = 4 минус площадь между x = 0 и x = 2 у = 2x

 Определенные интегралы

 Площадь графика y = f(x) между x = a  и x = b   равно

 Пример

   Найдите заштрихованную площадь как определенный интеграл.

 

Площадь между кривой и осью Y

Иногда необходимо найти область между функцией и ось Y.

 

Задается как

 

Не всегда возможно выразить функцию y=f(x) через x=f(y).

Также может быть проще вычислить

 

и вычесть это как составную площадь.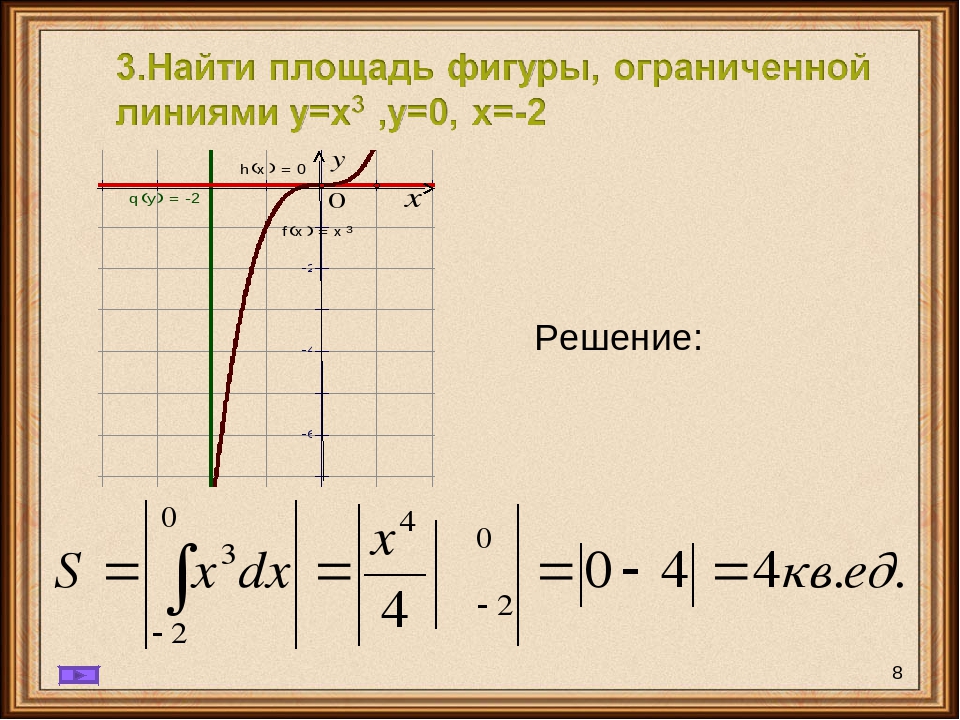

 

Основная теорема исчисления

 

   

 

Примеры

Оценка                    

 

            

 

Оценка    

 

Найдите положительное значение z :-

 

Области , ограниченные графиком и осью x.

 

При расчете площади, ограниченной графиком и осью x:-

• Всегда рисовать эскиз
• Вычислять площади выше и ниже оси x отдельно
• Игнорировать отрицательные знаки и добавлять.

 

Пример Вычислите площадь, ограниченную графиком y = x+2 и ось x для   -6 ≤ x ≤1

 

 

График пересекает ось X в точке (-2 ,0)

Площадь под осью x =

 

Площадь над осью x =

Площадь между двумя графиками

 Площадь между двумя графиками можно найти путем вычитания площадь между нижним графиком и осью x от область между верхним графиком и осью x.