Равнобедренный треугольник. Свойства, признаки, высота
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
| Равнобедренным называется треугольник, у которого две стороны равны. |
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.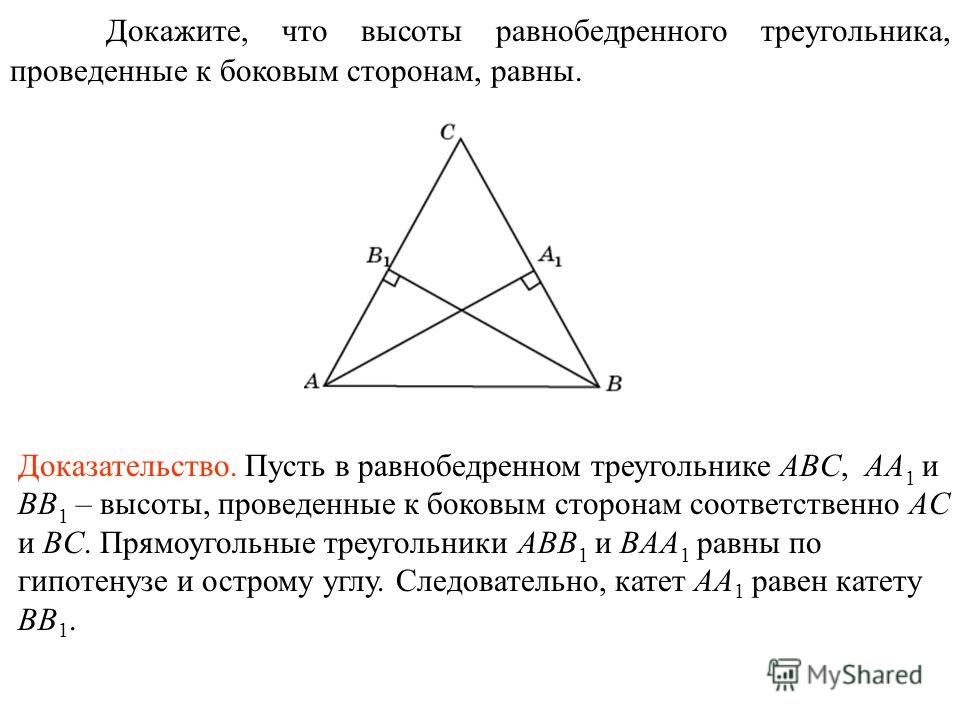
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.

Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Значит, ∠A = ∠C = 80°.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Ответ: ∠B = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
 2 )
2 )Равнобедренный треугольник
Определение равнобедренного треугольника
Равнобедренный треугольник — это треугольник, в котором длины двух его сторон равны между собой.Примечание. Из определения равнобедренного треугольника следует, что правильный треугольник также является равнобедренным. Однако, необходимо помнить, что обратное утверждение — неверно.
Свойства равнобедренного треугольника
Свойства, приведенные ниже, используются при решении задач. Поскольку они широко известны, то подразумевается, что они не нуждаются в пояснении. Поэтому в текстах задач ссылка на них опущена.- Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой.
- Биссектрисы, медианы и высоты, проведённые из углов, противолежащих равным сторонам треугольника, равны между собой.

- Биссектриса, медиана и высота, проведенные к основанию, совпадают между собой.
- Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане (они совпадают) проведенных к основанию.
- Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
Стороны в равнобедренном треугольнике могут быть вычислены с помощью формул, выражающих их длину через другие стороны и углы, величина которых известна.
Боковая сторона равнобедренного треугольника равна частному от деления основания на двойной косинус угла при основании (Формула 1). Данное тождество может быть получено путем несложных преобразований из теоремы косинусов.
Основание равнобедренного треугольника равно произведению боковой стороны на квадратный корень из удвоенной разности единицы и косинуса угла при вершине (Формула 2)
Основание равнобедренного треугольника равно удвоенному произведению боковой стороны на синус половины угла при вершине.
 (Формула 3)
(Формула 3)
Основание равнобедренного треугольника равно удвоенному произведению боковой стороны на косинус угла при его основании (Формула 4).
Радиус вписанной окружности в равнобедренный треугольник
Обозначения в формулах, можно посмотреть на рисунке выше. Радиус вписанной окружности для равнобедренного треугольника можно найти, исходя из величин основания и каждой стороны. (Формула 1)
Радиус вписанной окружности для равнобедренного треугольника можно определить,исходя из величин основания и высоты, проведенной к этому основанию (Формула 2)
Радиус вписанной в равнобедренный треугольник окружности можно также вычислить через длину боковой стороны и высоту, проведенную к основанию треугольника (Формула 3)
Знание величины угла между боковыми сторонами и длины основания также позволяет определить радиус вписанной окружности (Формула 4)
Аналогичная формула (5) позволяет определить радиус вписанной окружности через боковые стороны и угол между ними
Признаки равнобедренного треугольника
Треугольник, у которого присутствуют перечисленные ниже признаки, является равнобедренным.
- Два угла треугольника равны
- Высота совпадает с медианой
- Высота совпадает с биссектрисой
- Биссектриса совпадает с медианой
- Две высоты равны
- Две медианы равны
- Две биссектрисы равны
Площадь равнобедренного треугольника
Площадь равнобедренного треугольника находится по следующим формулам:
,
где
a — длина одной из двух равных сторон треугольника
b — длина основания
α — величина одного из двух равных углов при основанииβ — величина угла между равными сторонами треугольника и противолежащего его основанию.
См. также «Площадь треугольника».
Содержание главы:Площадь равнобедренного треугольника формула
В данной статье речь пойдет о том как найти площадь равнобедренного треугольника и формулы для решения.

Равнобедренный треугольник это такой треугольник у которого две параллельные основанию стороны равны. Он изображен на рисунке.Стоит заметить что буквы которыми обозначены стороны и углы, используются в формулах, для вашего удобства.
Заметка: Если вам нужна качественно выполненная курсовая или контрольная работа, без посредников. Тогда Вам на сайт tvoi5.ru. Так же Вы можете перейти по ссылке курсовая на заказ (http://tvoi5.ru/zakazat-kursovuyu-rabotu.html) и все подробности.Площадь равнобедренного треугольника формула.
Первая формула говорит о том что площадь находится, если нам известна только одна сторона и основа треугольника. Получили эту формула с помощью использования общей формулы. Когда основным является формула Герона и стороны фигуры равны, она сама по себе будет выглядеть проще.
Во второй формуле говориться о том что площадь находится через боковые стороны и угол находящийся между ними.
 Или sin угла находящийся между боковых сторон, умноженный на половину квадрата одной из боковых сторон. Когда проводим высоту на боковой стороне её длина равняется а*sin?. Так как длину стороны мы знаем, то и её высота нам известна. Соответственно, площадь равнобедренного треугольника будет половина от их выражения. Если быть точнее. то целая величина делает площадь треугольника. Разделяя высотой прямоугольник, получаем два не больших прямоугольных треугольника. Диагональю будет сторона треугольника, в свою очередь она делит фигуру на две равные части. Из чего следует что искомая нами величина находится как половина величины одной стороны умножаемая на высоту.
Или sin угла находящийся между боковых сторон, умноженный на половину квадрата одной из боковых сторон. Когда проводим высоту на боковой стороне её длина равняется а*sin?. Так как длину стороны мы знаем, то и её высота нам известна. Соответственно, площадь равнобедренного треугольника будет половина от их выражения. Если быть точнее. то целая величина делает площадь треугольника. Разделяя высотой прямоугольник, получаем два не больших прямоугольных треугольника. Диагональю будет сторона треугольника, в свою очередь она делит фигуру на две равные части. Из чего следует что искомая нами величина находится как половина величины одной стороны умножаемая на высоту.В третьей формуле площадь находится с помощью одной параллельной стороны, основания и угла находящегося на вершине. Другими словами можно сказать так: когда известен хоть один угол в равнобедренном треугольнике, с его помощью можно узнать и два других. Данная формула схожа со второй формулой, можно использовать и запомнить любую из них.
 Но из этой формулы выйдет пятая, которую опишу чуть ниже.
Но из этой формулы выйдет пятая, которую опишу чуть ниже.Четвертая формула показывает что найти площадь можно зная величину основания и угла при нем. Все углы у основания одинаковы и квадрат стороны основания разделенный на 4 tg пол угла, появившиеся от его боковых сторон. Когда внимательно разглядеть, можно понять, пол стороны основания b/2, при умножении tg (? /2) дает высоту. Которая в свою очередь играет роль медианы и биссектрисы, а значит tg (? /2)= (b/2)/h, из чего h=b/(2tg (? /2)) и сводиться к упрощенной формуле №5.
Итак пятая формула она гласит о том , что найти площадь можно с помощью высоты которая берет начало в вершине треугольника и заканчивается в его основании, при этом разделяя его на прямоугольные треугольники. А дальше как в третьей и четвертой формулах. Пол величины высоты умноженное на величину основания.
Шестая и заключительная формула. Она появляется в ходе решения площади треугольника через теорему Пифагора.
 Нам понадобиться высота, найденная в прошлой формуле. Она так же приходится катетом от прямоугольного треугольника, получившегося от боковой стороны, половины основания плюс высота. Гипотенузой будет боковая сторона, из квадрата гипотенузы (а) отнимем второй катет в квадрате. Так как он равняется полу — основания (b/2) значит квадрат = b2/4. Извлекая корень из полученного , найдем высоту.
Нам понадобиться высота, найденная в прошлой формуле. Она так же приходится катетом от прямоугольного треугольника, получившегося от боковой стороны, половины основания плюс высота. Гипотенузой будет боковая сторона, из квадрата гипотенузы (а) отнимем второй катет в квадрате. Так как он равняется полу — основания (b/2) значит квадрат = b2/4. Извлекая корень из полученного , найдем высоту.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:формул для равнобедренных треугольников — Какие формулы для равнобедренных треугольников? Примеры
В геометрии равнобедренный треугольник — это треугольник, у которого две стороны равны. Два угла, противоположные равным сторонам, равны и всегда остры. Ниже объясняются различные формулы для равнобедренных треугольников. Две важные формулы для равнобедренных треугольников — это площадь треугольника и периметр треугольника.
Что такое формулы для равнобедренных треугольников?
Равнобедренный треугольник имеет две стороны равной длины, и две равные стороны соединяются под одним углом к основанию i.
 е. третья сторона. Таким образом, в равнобедренном треугольнике высота перпендикулярна вершине, общей для равных сторон. Такие особые свойства равнобедренного треугольника помогают нам рассчитать его площадь и высоту с помощью формул равнобедренного треугольника.
е. третья сторона. Таким образом, в равнобедренном треугольнике высота перпендикулярна вершине, общей для равных сторон. Такие особые свойства равнобедренного треугольника помогают нам рассчитать его площадь и высоту с помощью формул равнобедренного треугольника.Формулы равнобедренного треугольника
Площадь равнобедренного треугольника: Это пространство, занимаемое треугольником. Здесь у нас есть три формулы, чтобы найти площадь треугольника на основе заданных параметров.{2}} {4}} \)
(Здесь a — равная сторона, а b — основание треугольника.)Площадь = 1/2 × abSinα
(Здесь a и b — длины двух сторон, а α — угол между этими сторонами.)- Площадь = 1/2 × abSinα
- Шаг 1. Проверьте параметр (площадь, периметр или высота), который нужно получить или рассчитать.
- Шаг 2: Определите сторону равнобедренного треугольника и введите значение в требуемую формулу — площадь, периметр или высоту.
- Площадь = 1/2 × Основание × Высота
- Площадь = \ (\ frac {b} {2} \ sqrt {a ^ {2} — \ frac {b ^ {2}} {4}} \)
- Площадь = 1/2 × abSinα
- Шаг 1: Определите стороны равнобедренного треугольника — две равные стороны a и основание b.
- Шаг 2: Введите значения в формулу периметра, P = 2a + b
- Шаг 3: Запишите полученное значение в соответствующей единице.
- Равносторонний : «равный» — боковой (боковой означает сторона), поэтому все равные стороны
- Равнобедренный : означает «равные ноги», а у нас две ноги , верно? Также i SOS celes имеет два равных «S ides», соединенных стороной « O dd».

- Scalene : означает «неровный» или «нечетный», поэтому нет равных сторон.
- «б» — расстояние по основанию
- «h» — высота (измеренная под прямым углом к основанию)
- Стороны равнобедренного треугольника: a = c
- Углы равнобедренного треугольника: A = C
- Высота равнобедренного треугольника: h a = h c
- Периметр равнобедренного треугольника: P = a + b + c = 2a + b
- Полупериметр равнобедренного треугольника: s = (a + b + c) / 2 = a + (b / 2)
- Площадь равнобедренного треугольника: K = (b / 4) * √ (4a 2 — b 2 )
- Высота a равнобедренного треугольника: h a = (b / 2a) * √ (4a 2 — b 2 )
- Высота b равнобедренного треугольника: h b = (1/2) * √ (4a 2 — b 2 )
- Высота c равнобедренного треугольника: h c = (b / 2a) * √ (4a 2 — b 2 )
- а и б известны; найти c, P, s, K, h a, h b и h c
- с = а
- P = 2a + b
- с = а + (b / 2)
- К = (b / 4) * √ (4a 2 — b 2 )
- ч a = (b / 2a) * √ (4a 2 — b 2 )
- ч b = (1/2) * √ (4a 2 — b 2 )
- ч c = (b / 2a) * √ (4a 2 — b 2 )
Периметр равнобедренного треугольника : У равнобедренного треугольника три стороны: две равные стороны и одно основание. Для вычисления периметра равнобедренного треугольника используется выражение 2a + b,
P = 2a + b
(Здесь длина равной стороны a, длина основания b)
Высота равнобедренного треугольника : В равнобедренном треугольнике его высота представляет собой перпендикулярное расстояние от вершины до основания. {2}} {4}} \)
{2}} {4}} \)
Давайте проверим несколько примеров, чтобы более четко понять использование формул для равнобедренных треугольников.
Разбивайте сложные концепции с помощью простых визуальных элементов.
Математика больше не будет сложным предметом, особенно если вы понимаете концепции посредством визуализации.
Забронируйте бесплатную пробную версию Класс
Примеры использования формул для равнобедренных треугольников
Пример 1: Определить площадь равнобедренного треугольника, у которого основание b составляет 8 единиц, а боковая сторона a — 5 единиц?
Решение: Применение теоремы Пифагора:
a 2 = (b / 2) 2 + h 2
h 2 = a 2 — (b / 2) 2 = 5 2 — 4 2 , что дает h = 3
Площадь A = (1/2) × b × h = (1/2) 8 × 3 = 12 шт. 2
2
Ответ: Площадь равнобедренного треугольника равна 12 единицам 2 .
Пример 2: Найти боковую сторону равнобедренного треугольника площадью 20 единиц 2 и основанием 10 единиц?
Решение: Используя формулу площади равнобедренного треугольника:
A = (1/2) b h = 20
Учитывая b = 10,
Найти: боковая сторона
ч = 40/10 = 4
Применение теоремы Пифагора:
a 2 = (b / 2) 2 + h 2 = √ (5 2 + 4 2 ) = √41
Ответ: Боковая сторона равнобедренного треугольника равна √41.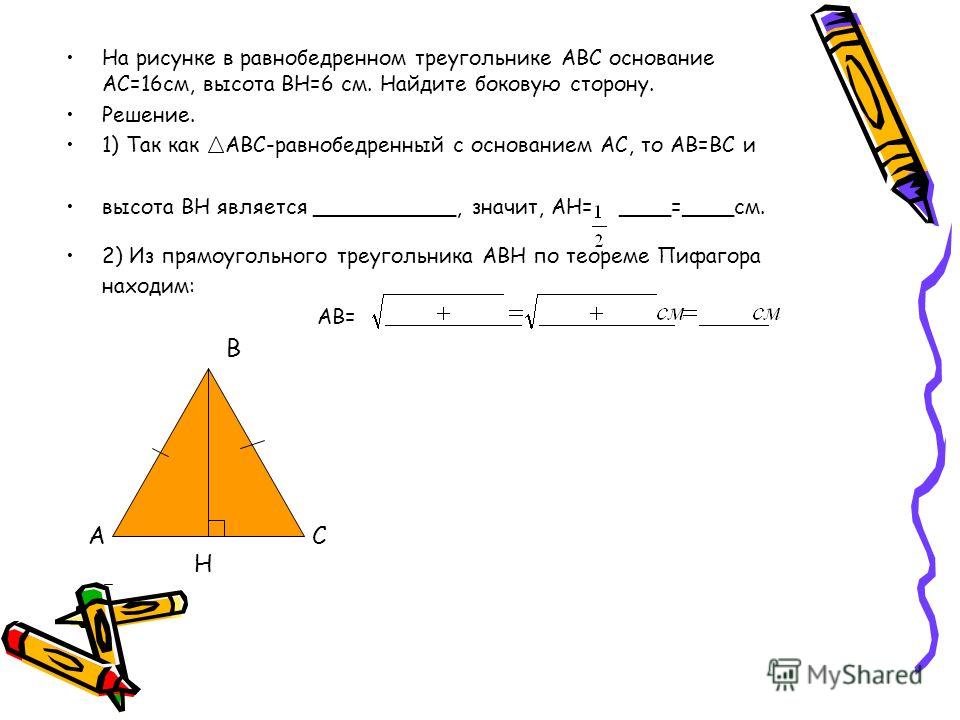
Пример 3: Вычислите площадь, высоту и периметр равнобедренного треугольника, если его две равные стороны имеют длину 6 единиц, а третья сторона — 8 единиц.
Решение:
Для a = b = 6 единиц, c = 8 единиц
Чтобы найти: площадь, высоту и периметр равнобедренного треугольника
Периметр равнобедренного треугольника,
P = 2 × a + b
П = 2 × 6 + 8
= 20 единиц
Высота равнобедренного треугольника,
h = √ (a 2 –b 2 /4)
h = √ (6 2 –8 2 /4)
ч = √ (36-16)
ч = √20 единиц
Площадь равнобедренного треугольника,
А = 1/2 × ш × в
= 1/2 × 8 × √20
= √20 / 4 квадратных единицы
Ответ:
Часто задаваемые вопросы по формулам равнобедренных треугольников
Что такое формула равнобедренного треугольника в геометрии?
В геометрии формулы равнобедренного треугольника определяются как формулы для вычисления площади и периметра равнобедренного треугольника. {2}} {4}} \)
{2}} {4}} \)
(Здесь a и b — длины двух сторон, а α — угол между этими сторонами.)
Как использовать формулу равнобедренного треугольника?
Мы можем использовать формулы равнобедренного треугольника следующим образом:
В случае, если указаны площадь, периметр или высота равнобедренного треугольника, вы можете найти меру стороны треугольника, приравняв данные значения к соответствующей формуле равнобедренного треугольника.
Что такое буква «а» в формуле равнобедренного треугольника?
В формуле равнобедренного треугольника, будь то площадь, периметр или высота, «а» означает меру равных сторон равнобедренного треугольника.
(Здесь a и b — длины двух сторон, а α — угол между этими сторонами. )
)
Как найти периметр треугольника по формуле равнобедренного треугольника?
Мы знаем, что периметр любой фигуры — это сумма всех ее сторон, таким образом,
Как найти высоту прямоугольного равнобедренного треугольника 45/45/90
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Равнобедренный треугольник
Равнобедренный треугольник — это треугольник, у которого есть как минимум две стороны равной длины. На рисунке ниже приведены два примера.
AB≅AC
Части равнобедренного треугольника
Для равнобедренного треугольника только с двумя конгруэнтными сторонами конгруэнтные стороны называются катетами.Третья сторона называется базой. Угол, противоположный основанию, называется углом при вершине, а углы, противоположные ногам, называются углами основания.
Длины равнобедренного треугольника
Высота равнобедренного треугольника — это отрезок перпендикулярной линии, проведенный от основания треугольника к противоположной вершине.
Используя теорему Пифагора, мы можем найти, что основание, катеты и высота равнобедренного треугольника имеют следующие отношения:
Базовые углы равнобедренного треугольника
Углы основания равнобедренного треугольника одинаковы по мере.См. Треугольник ABC ниже.
AB ≅AC, значит, треугольник ABC равнобедренный. ABC можно разделить на два равных треугольника, нарисовав отрезок AD, который также является высотой треугольника ABC.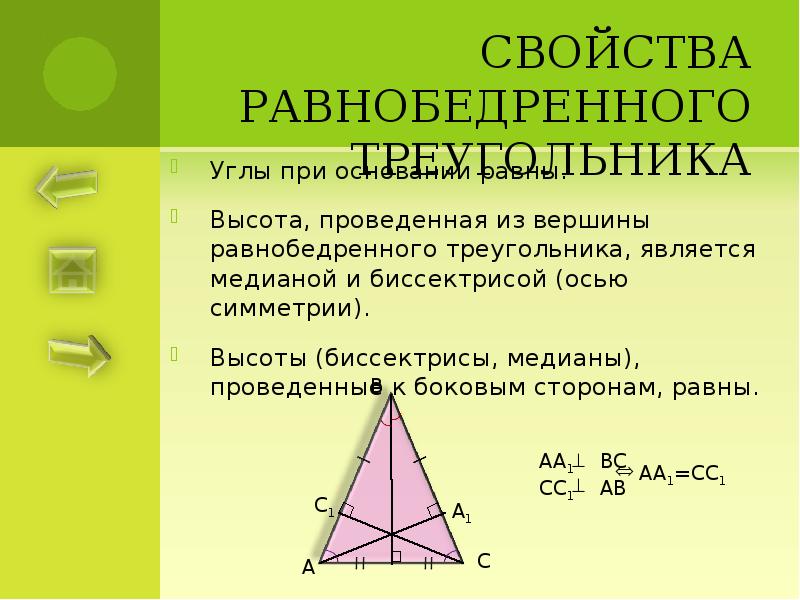
Используя теорему Пифагора, где l — длина ног,. На основании этого △ ADB≅ △ ADC по теореме Side-Side-Side для конгруэнтных треугольников, поскольку BD ≅CD, AB ≅ AC и AD ≅AD. Итак, ∠B≅∠C, поскольку соответствующие части конгруэнтных треугольников также конгруэнтны.
Симметрия в равнобедренном треугольнике
Высота равнобедренного треугольника также является линией симметрии.
Участок AB отражается на высоте AD в участок AC. Точно так же нога AC отражается в ногу AB. База BC отражается сама на себя, когда отражается на высоте.
45-45-90 треугольников
Когда углы основания равнобедренного треугольника составляют 45 °, треугольник представляет собой специальный треугольник, называемый треугольником 45 ° -45 ° -90 °. Длина основания, называемого гипотенузой треугольника, умножена на длину его катета.
Апофема правильного многоугольника
Апофема правильного многоугольника — это также высота равнобедренного треугольника, образованного центром и стороной многоугольника, как показано на рисунке ниже.
Для правильного пятиугольника ABCDE выше высота равнобедренного треугольника BCG является апофемой многоугольника.
треугольников — равносторонние, равнобедренные и чешуйчатые
c2ZWPA3kduw
Треугольник имеет три стороны и три угла | ||
Три угла всегда складываются в 180 ° |
Равносторонний, равнобедренный и чешуйчатый
Треугольникам даны три специальных названия, которые показывают, сколько сторон (или углов) равны.
Может быть 3 , 2 или Нет равных сторон / углов:
Равносторонний треугольник Три равных сторон | |
Равнобедренный треугольник Две равных сторон | |
Скаленовый треугольник Нет равных сторон |
Как запомнить? По алфавиту идут 3, 2, нет:
Какой тип угла?
Треугольники также могут иметь имена, которые сообщают вам, какой тип угла находится внутри :
Острый треугольникВсе углы меньше 90 ° | |
Прямой треугольникИмеет прямой угол (90 °) | |
Тупой треугольникИмеет угол более 90 ° |
Объединение имен
Иногда у треугольника будет два имени, например:Равнобедренный прямоугольный треугольникИмеет прямой угол (90 °), а также два равных угла. Вы можете угадать, каковы равные углы? |
Играй с ним.
 ..
..Попробуйте перетащить точки и составить разные треугольники:
геометрия / изображения / треугольник.js? режим = тип
Вы также можете поиграть с Интерактивным треугольником.
Уголки
Три внутренних угла всегда составляют 180 °
геометрия / изображения / треугольник.js? режим = углы
Периметр
Периметр — это расстояние по краю треугольника: просто сложите три стороны:
геометрия / изображения / треугольник.js? режим = перим
Площадь
Площадь составляет , половина базовой, умноженная на высоту .
Площадь = ½ × b × h
Формула работает для всех треугольников.
Примечание: более простой способ записать формулу — bh / 2
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Основание может быть любой стороной. Убедитесь, что высота измеряется под прямым углом к основанию. :
Убедитесь, что высота измеряется под прямым углом к основанию. :
геометрия / изображения / треугольник.js? mode = область
(Примечание: вы также можете рассчитать площадь, исходя из длин всех трех сторон, используя формулу Герона.)
Почему область «Половина bh»?
Представьте, что вы «удвоили» треугольник (перевернули его вокруг одного из верхних краев), чтобы получилась квадратная форма (параллелограмм), которая может быть преобразована в простой прямоугольник:
ЗАТЕМ вся площадь составляет bh , что соответствует обоим треугольникам, поэтому только один будет ½ × bh .
6702, 6708,720, 3134, 5032,627,723, 3132, 3133, 7502
Высота до основания равнобедренного треугольника делит основание пополам
В сегодняшнем уроке мы изучим простую стратегию доказательства того, что в равнобедренном треугольнике высота до основания делит основание пополам.
Доказав теорему об основных углах для равнобедренных треугольников с помощью конгруэнтности треугольников, мы знаем, что в равнобедренном треугольнике катеты равны, а углы при основании конгруэнтны.
Имея эти два факта в руках, будет легко показать некоторые другие свойства равнобедренных треугольников, используя тот же метод (конгруэнтность треугольников).
Начнем с доказательства того, что в равнобедренном треугольнике высота (или высота) до основания делит основание пополам.
Задача
Докажите, что в равнобедренном треугольнике ΔABC высота основания AD делит основание пополам.
Стратегия
Стратегия для этой и остальных аналогичных задач (показывающая, что высота до основания делит угол при вершине пополам, показывающая, что биссектриса угла перпендикулярна основанию, и т. Д…) будет так же.
У нас уже есть пара равных ребер (катеты согласно определению равнобедренного треугольника) и пара конгруэнтных углов (согласно теореме о базовых углах). Итак, мы найдем или построим другую пару конгруэнтных углов или другую пару равных сторон и воспользуемся одним из постулатов конгруэнтности треугольников, чтобы показать, что эти два треугольника конгруэнтны.
Итак, мы найдем или построим другую пару конгруэнтных углов или другую пару равных сторон и воспользуемся одним из постулатов конгруэнтности треугольников, чтобы показать, что эти два треугольника конгруэнтны.
Итак, мы знаем, что AD — это высота до основания. По определению это означает, что угол, который он образует с основанием (∠ADB), является прямым.И, как и ∠ADC, у нас есть вторая пара конгруэнтных углов.
Доказательство
(1) ΔABC равнобедренное // Дано
(2) AB = AC // Определение равнобедренного треугольника
(3) ∠ACB ≅ ∠ABC // Теорема об основных углах
(4) м ∠ADB = m∠ADC = 90 ° // Определение высоты до основания
(5) △ ABD≅ △ ACD // Угол-угол-сторона
(6) BD = DC // Соответствующие стороны в равных треугольниках (CPCTC )
Калькулятор равнобедренных треугольников
Форма равнобедренного треугольника
A = угол A
a = сторона a
B = угол B
b = сторона b
C = угол C
c = сторона c
А = С
а = с
ч а = ч в
K = площадь
P = периметр
См. Схему ниже:
Схему ниже:
h a = высота a
h b = высота b
h c = высота c
* Единицы длины приведены только для справки, поскольку значение результирующих длин всегда будет одинаковым, независимо от единиц.
Использование калькулятора
Равнобедренный треугольник — частный случай треугольник, в котором 2 стороны, a и c, равны, а 2 угла, A и C, равны.
В наших расчетах для прямоугольного треугольника мы учитываем только 2 известные стороны, чтобы вычислить остальные 7 неизвестных. Например, если мы знаем a и b, мы знаем c, поскольку c = a. Зная стороны a, b и c, мы можем вычислить периметр = P, полупериметр = s, площадь = K и высоту: h a, h b и h c. Сообщите нам, если у вас есть другие предложения!
Сообщите нам, если у вас есть другие предложения!
Формулы и расчеты для равнобедренного треугольника:
Расчет:
По заданным сторонам a и b найти сторону c, а также периметр, полупериметр, площадь и высоту.
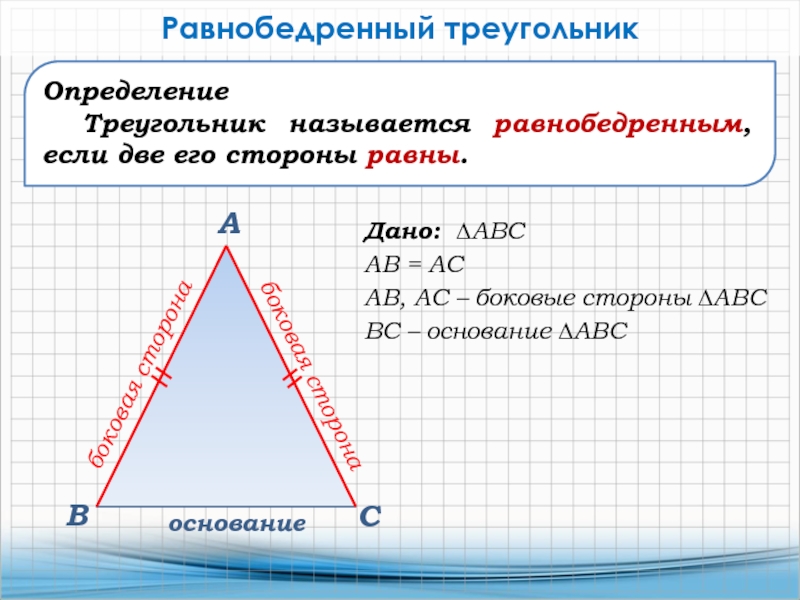
- ,
Подробнее о прямоугольных треугольниках см .:
Вайсштейн, Эрик В.»Равнобедренный треугольник.» От MathWorld — Интернет-ресурс Wolfram. Равнобедренный треугольник.
Решатель задач геометрии — Треугольники
Решатель задач геометрии
Треугольник
Они указывают на то, что некоторые проблемы могут быть решены автоматически, числовые значения не имеют значения в различных примерах.
равносторонний треугольник
равнобедренный треугольник
прямоугольный треугольник
разносторонний треугольник
вписанные и описанные треугольники
треугольников и p
Последние выпуски за 2013 год
равносторонний треугольник
Track 1
равносторонний треугольник со стороной 10 сантиметров.
Track 2
Вычислите периметр равностороннего треугольника, зная, что высота равна 10 см.
Track 3
Вычислите периметр и площадь равностороннего треугольника высотой 25,98 см.
Колея 4
Периметр равностороннего треугольника 99 см. Вычислите сторону треугольника.
Колея 5
Периметр равностороннего треугольника составляет 45 см. Насколько велика ваша территория?
Track 6
Чем нужно увеличить размер стороны равностороннего треугольника, равной 30 см, так, чтобы его периметр был равен 150 см?
Track 7
Затем вам нужно уменьшить периметр равностороннего треугольника размером 60 см так, чтобы его сторона была длиной 15 см.
Равнобедренный треугольник
Дорожка 8
Равнобедренный треугольник имеет основание 5 см, по наклонной стороне 0,3 дм. Вычислите периметр и площадь треугольника.
След 9
Равнобедренный треугольник имеет длину скошенной стороны 180 см и высоту 144 см. Рассчитайте периметр и площадь.
Track 10
Равнобедренный треугольник имеет основание 56 см и высоту 96 см. Рассчитайте размер периметра треугольника и площади.
Track 11
Вычислите периметр равнобедренного треугольника, зная, что длина основания составляет 5 см, а наклонная сторона составляет 4/5 от основания.
Дорожка 12
Равнобедренный треугольник имеет основание 60 см и высоту 2/3 основания. Рассчитайте размер скошенной стороны.
Колея 13
Сторона равнобедренного треугольника составляет 50 см, а основание равно его 6/5. Вычислите периметр и площадь треугольника.
Колея 14
Периметр равнобедренного треугольника составляет 52 см, а основание — 3/5 наклонной стороны. Вычислите размеры основания и стороны треугольника.
Вычислите размеры основания и стороны треугольника.
Колея 15
Разница между наклонной стороной и основанием составляет 20 см, а наклонная сторона составляет 5/4 от основания; вычислить периметр и площадь равнобедренного треугольника.
Track 16
В равнобедренном треугольнике сумма наклонной стороны и основания составляет 50 см, а их разность — 16 см. Calcolane размер сторон и периметр.
Направляющая 17
В равнобедренном треугольнике сумма основания и наклонной стороны составляет 41 см, а основание превышает 5 см наклонной стороны.Рассчитайте периметр.
Колея 18
Равнобедренный треугольник имеет периметр 35 см, а наклонная сторона в три раза больше основания. Рассчитайте размер основания и скошенной стороны.
Track 19
Вычисляет длину окружности и площадь равнобедренного треугольника, зная, что основание равно 2/5 наклонной стороны, а их сумма равна 49 см.
Дорожка 20
Угол при вершине равнобедренного треугольника равен 120 шириной. Вычислите периметр и площадь треугольника, зная, что его высота составляет 20 см.
Вычислите периметр и площадь треугольника, зная, что его высота составляет 20 см.
Track 21
Два равнобедренных треугольника ABC и PQR имеют одинаковый периметр размером 35 см, а каждая из наклонных сторон ABC в три раза больше основания. Насколько велика каждая из совпадающих сторон запроса предложения, зная, что основание превышает 4 см до ABC?
Трасса 22
Периметр равнобедренного треугольника составляет 17 дм, а основание превышает наклонную сторону на 20 см. Вычислите площадь треугольника.
Трасса 23
Периметр равнобедренного треугольника составляет 17 дм, а основание превышает наклонную сторону на 20 см. Зная, что измерение высоты 3,57 дм, вычисляем площадь треугольника.
Track 24
В равнобедренном треугольнике периметр составляет 120 см, а высота скошенной стороны основания составляет 50 см и 35,70 см соответственно. Вычислите площадь треугольника и высоту на наклонной стороне.
Трасса 25
В равнобедренном треугольнике с углом основания четвертая часть примыкает к внешней. Вычислите амплитуды трех внутренних углов треугольника.
Вычислите амплитуды трех внутренних углов треугольника.
Дорожка 26
Равнобедренный треугольник имеет площадь 432 см и основание 36 см. Рассчитайте периметр.
Дорожка 27
Периметр равнобедренного треугольника равен 64 см, основание и мера высоты соответственно 14 см и 24 см. Рассчитайте измерение высоты на наклонной стороне.
Дорожка 28
Высота равнобедренного треугольника равна 6/5 основания, а их сумма равна 44 см.Вычислите периметр и площадь треугольника.
Track 29
Периметр равнобедренного треугольника составляет 96 см, а длина основания — 36 см. Вычислите площадь треугольника.
Track 30
Равнобедренный треугольник имеет периметр 72 см в длину и длину каждой из наклонных сторон 26 см. Вычислите размер основания и площадь треугольника.
Track 31
Вычисляет протяженность сторон и площадь равнобедренного треугольника, зная, что длина периметра 72 см, а каждая из равных сторон превышает основание на 6 см.
Направляющая 32
Равнобедренный треугольник имеет основание длиной 36 см и длину каждой из наклонных сторон 30 см. Вычислите размер основания равнобедренного треугольника, подобного приведенному выше, со сторонами равными 15 см.
Track 33
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Рассчитайте периметр.
Track 34
В равнобедренном треугольнике, площадь которого составляет 432 см, основание составляет 3/2 высоты относительно него.Вычислите периметр треугольника.
Track 35
В равнобедренном треугольнике сумма наклонной стороны и основания составляет 50 см, а их разность — 16 см. Calcolane размер сторон и периметр.
Дорожка 36
Два равнобедренных треугольника имеют одинаковый периметр 96 см. Основание первого треугольника составляет 6/5 каждой из наклонных сторон. Основание второго треугольника равно 9/11 основания первого. Вычислите размер каждой из наклонных сторон и площадь треугольников.
Прямой треугольник
Дорожка 37
В прямоугольном треугольнике катет имеет длину 24 см, а другой катет — 7 см. Вычисляет длину гипотенузы.
Track 38
Прямоугольный треугольник имеет катет 4,6 дм и другой катет 58 см. Определяет его площадь и периметр.
Track 39
Постройте треугольник со сторонами соответственно 3 см, 5 см и 4 см. Что такое треугольник?
Track 40
В прямоугольном треугольнике катет проходит вдоль гипотенузы 1.5 м 3 м длиной. Вычисляет длину второго катета и относительную высоту гипотенузы.
Track 41
В прямоугольном треугольнике длина гипотенузы 25 см, длина катета 7 см. Вычисляет длину другого катета
Track 42
В прямоугольном треугольнике длина гипотенузы составляет 50 см, а длина катета — 30 см. Вычисляет площадь и периметр треугольника.
Дорожка 43
Прямоугольный треугольник имеет площадь 300 см, длина одного катета равна 2/3 другого катета.Рассчитайте длину двух коротких сторон.
Дорожка 44
Прямоугольный треугольник имеет площадь 300 см, длина одного катета равна 2/3 другого катета. Рассчитайте периметр.
Track 45
Разница между катетом и гипотенузой прямоугольного треугольника 2 м, их соотношение 5/3. Вычислите периметр и площадь треугольника.
Трасса 46
Сумма гипотенузы и катета прямоугольного треугольника равна 8 м; их соотношение составляет 5/3.Вычислите периметр и площадь треугольника.
Track 47
В прямоугольном треугольнике гипотенуза равна 180 см, а катет — ее 4/5. Вычислите периметр и площадь треугольника.
Track 48
Овощ имеет форму прямоугольного треугольника, длина гипотенузы которого равна 500 м, а катет равен 3/5 гипотенузы. Вы хотите огородить огород колючей проволокой. Сколько метров колючей проволоки нужно?
Дорожка 49
Прямоугольный треугольник имеет длинный катет 16.4 см и площадью 151,7 см. Вычисляет длину другого катета.
Колея 50
Площадь треугольника 600 см. Найдите периметр и гипотенузу высоты, зная, что больший катет имеет длину 40 см.
Найдите периметр и гипотенузу высоты, зная, что больший катет имеет длину 40 см.
Трасса 51
Площадь равнобедренного треугольника 200 дм. Рассчитайте протяженность двух катетов и периметр.
Track 52
В прямоугольном треугольнике гипотенуза составляет 50 см, а проекция катета на нее — 18 см.Вычисляет размер другого катета и площадь треугольника.
Track 53
В прямоугольном треугольнике катет — это 5/3 его проекции на гипотенузу, а разница двух измерений составляет 72 см. Определяет относительную высоту гипотенузы и периметра треугольника.
Дорожка 54
Катеты прямоугольного треугольника имеют длину 3 см и 4 см, найдите гипотенузу и высоту относительно нее
Дорожка 55
Гипотенуза прямоугольного треугольника имеет длину 5 см и катет 4 см. ; расположен другой катет, относительная высота гипотенузы и сегментов, на которые она делит гипотенузу.
Track 56
Площадь треугольника 6 см, длина катета 4 см. Найдите периметр и площадь двух треугольников, которые получаются при проведении медианы относительно большего катета.
Найдите периметр и площадь двух треугольников, которые получаются при проведении медианы относительно большего катета.
Track 57
Вычислите периметр и площадь равнобедренного треугольника с катетом длиной 20 см.
Track 58
Вычислите периметр и площадь прямоугольного треугольника, зная, что его размер составляет 2,4 дюйма, а высота составляет 3/4 проекции большего катета на гипотенузу.
Дорожка 59
Треугольник имеет площадь 600 квадратных сантиметров и длину гипотенузы высоты 24 см. Зная, что эта высота делит гипотенузу на две части, одну из 9/16 другой, вычислите периметр треугольника, периметр и площадь двух треугольников, в которых треугольник делится на гипотенузу высоты.
Track 60
Катет в прямоугольном треугольнике составляет 3/4 другого, а их разница составляет 10 см. Зная, что гипотенуза превышает катет более чем на 10 см, рассчитайте площадь и периметр треугольника.
Track 61
В прямоугольном треугольнике гипотенуза и катет размером 30 см, 40 см и 50 см соответственно. Вычислите меру гипотенузы и периметр.
Вычислите меру гипотенузы и периметр.
Track 62
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина гипотенузы составляет 10 см, а ширина острого угла — 30 см.
Track 63
В прямоугольном треугольнике гипотенуза размером 50 см и катет являются 3/4 другой. Зная, что периметр равен 120 см, рассчитываем протяженность коротких сторон и площадь треугольника.
Track 64
Прямоугольный треугольник имеет гипотенузу длиной 50 см и периметр 92 см. Вычисляет размер коротких сторон, которые составляют одну из 9/12 другой.
Track 65
В прямоугольном треугольнике гипотенуза и сумма катета размером 32 см 18 см и их разность. Вычислите периметр и площадь треугольника.
Дорожка 66
В прямоугольном треугольнике сумма двух коротких сторон размером 31 см 17 см и их разность.Вычислите периметр и площадь треугольника.
Track 67
Вычислите периметр и площадь прямоугольного треугольника с острыми углами 45 градусов, зная, что длина гипотенузы составляет 141,42 см.
Track 68
В прямоугольном треугольнике ABC AM — медиана на гипотенузе BC. Зная, что AM + AB = 31,18 см, AB -AM = 8,82 см и AB = 2AC, вычисляем периметр треугольника
Track 69
Вычислите меру гипотенузы прямоугольного треугольника, зная, что катет равен 40 см и 4/3 другого.Рассчитайте периметр и площадь.
Дорожка 70
В равнобедренном треугольнике длина коротких сторон составляет 10 см. Определяет длину гипотенузы, периметр и площадь.
Track 71
В прямоугольном треугольнике длина гипотенузы составляет 25 см, катет — 3/4 другой. Вычислите периметр и площадь треугольника.
Направляющая 72
Треугольник имеет периметр 120 см и две стороны 30 см и 40 см. Рассчитывает площадь.
Track 73
Прямоугольный треугольник имеет катет 10 см и гипотенузу 26 см.Рассчитайте проекцию катета на гипотенузу.
Track 74
Зная, что проекция катета меньше прямоугольного треугольника составляет 10,8 см, а проекция катета больше 19,2 см, вычислите площадь и периметр треугольника.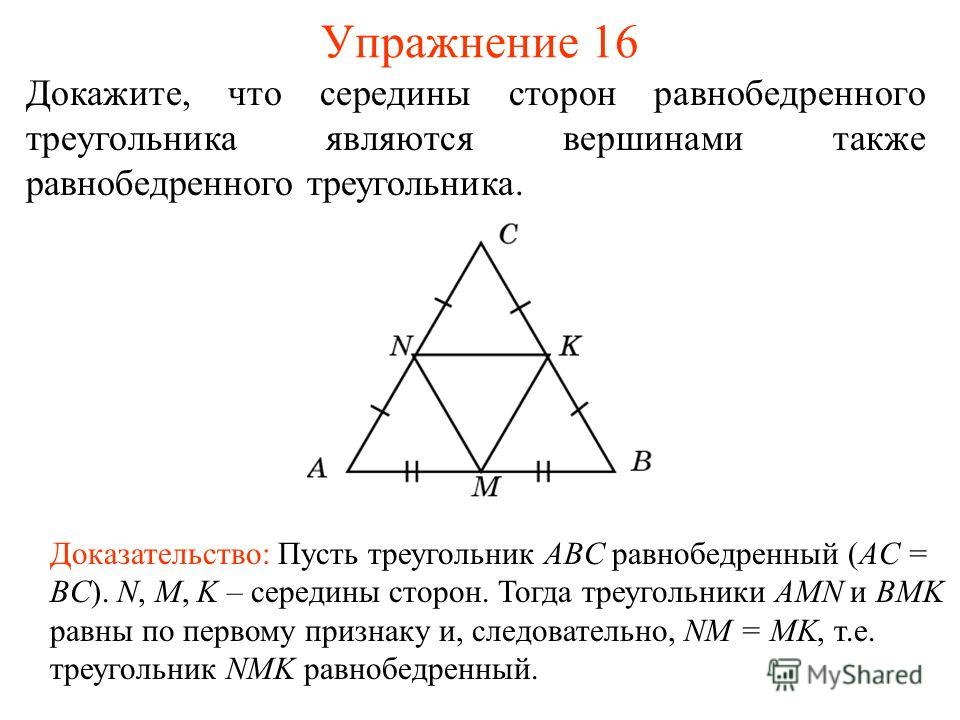
Track 75
Вычислите периметр и площадь прямоугольного треугольника, зная, что относительная высота гипотенузы составляет 2,4 см, а проекция катета, увеличивающая гипотенузу, равна 3.2 см.
Track 76
В прямоугольном треугольнике площадью 6 см гипотенуза равна 5 см. Вычислите периметр треугольника.
Колея 77
В равнобедренном треугольнике с периметром 34,14 см. Если гипотенуза размером 14,14 см, измеренная по катету?
Track 78
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина катета равна 5 см, а ширина острого угла — 60.
Track 79
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина катета равна 5 см, а ширина острого угла 30.
Track 80
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина большего катета составляет 8,66 см, а ширина острого угла — 30 см.
Track 81
Вычислите периметр и площадь прямоугольного треугольника, зная, что длина большего катета составляет 8,66 см, а ширина острого угла 60.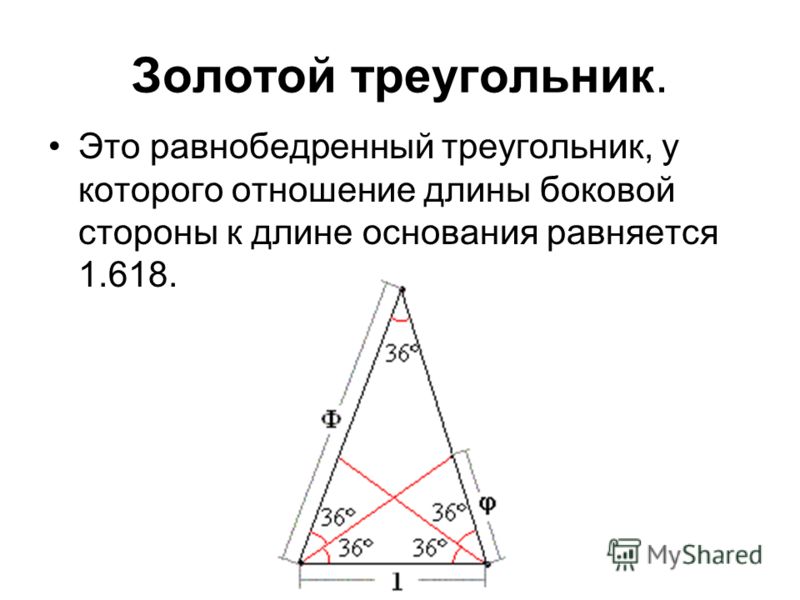
Track 82
Вычисляет малый катет прямоугольного треугольника, зная, что длина большего катета составляет 8,66 см, а ширина острого угла — 60.
Track 83
Вычисляет гипотенузу прямоугольного треугольника, зная, что длина большего катета составляет 8,66 см, а ширина острого угла — 60.
Track 84
Вычисляет гипотенузу прямоугольного треугольника, зная, что длина малого катета равна 5 см, а ширина острого угла — 60.
Track 85
Вычислите периметр прямоугольного треугольника, зная, что длина малого катета равна 5 см, а ширина острого угла — 60.
Track 86
Вычислите периметр и площадь прямоугольного треугольника с катетом длиной 18 см, который составляет 20/12 его проекции на гипотенузу.
Дорожка 87
Треугольник — это двойник прямоугольника. Вычислите площадь треугольника, зная, что разница в размере прямоугольника составляет 20 см, а основание — 3/5 высоты.
Track 88
В прямоугольном треугольнике гипотенуза 30 см, а высота гипотенузы 14,4 см. Зная, что выступ катета меньше 10,8 см и больше, чем у катета 19,2 см, вычислите площадь и периметр треугольника.
Зная, что выступ катета меньше 10,8 см и больше, чем у катета 19,2 см, вычислите площадь и периметр треугольника.
Track 89
Вычисляет относительную высоту гипотенузы прямоугольного треугольника, имеющего площадь 6 см и гипотенузу 5 см.Зная, что проекция катета меньшей протяженности на гипотенузу 1,8 см, вычисляем периметр данного треугольника.
Track 90
Вычисляет площадь и периметр прямоугольного треугольника, зная, что длина гипотенузы составляет 30 см и 5/3 меньшего катета.
Track 91
Из прямоугольного треугольника вы знаете, что больший катет, 24 см в длину, составляет 4/5 гипотенузы. Вычислите длину окружности и площадь треугольника.
Track 92
Из прямоугольного треугольника вы знаете, что катет больше вдоль гипотенузы — 24 см и его пять четвертей.Вычислите длину окружности и площадь треугольника.
Track 93
Из прямоугольного треугольника вы знаете, что катет больше на 24 см в длину, а другой катет — на 3/4.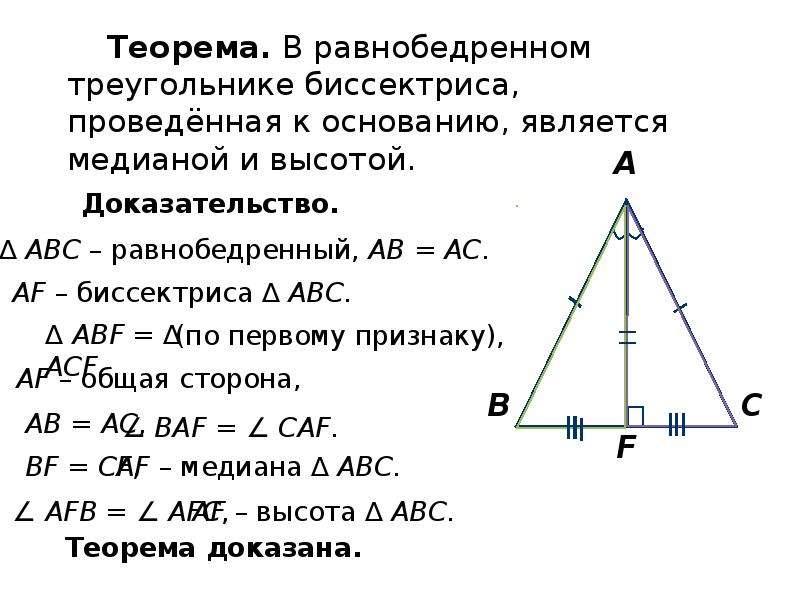 Вычислите длину окружности и площадь треугольника.
Вычислите длину окружности и площадь треугольника.
Track 94
Катет в прямоугольном треугольнике, гипотенуза составляет 24 см, и на 16 см больше другого катета. Рассчитайте периметр и площадь.
Track 95
В прямоугольном треугольнике гипотенуза составляет 50 см, а высота по отношению к ней — 24 см.Рассчитайте периметр, зная, что две короткие стороны составляют одну из 3/4 другой.
Track 96
Периметр прямоугольного треугольника составляет 60 см. Зная, что катет меньше пяти двенадцатых большей и 5/13 гипотенузы, вычислите площадь треугольника.
Дорожка 97
Сумма катетов прямоугольного треугольника равна 140 м, один из них равен 3/4 другого. Вычислите периметр, площадь и высоту гипотенузы треугольника.
разносторонний треугольник
Трасса 98
Нарисуйте треугольник со сторонами ABC в вершинах 300 см; 200 см; 150 см.
Track 99
Треугольник Scalene имеет сторону 50 см, длину второй стороны 40 см и длину третьей стороны 80 см. Вычислить периметр и площадь.
Вычислить периметр и площадь.
Колея 100
Основание треугольника составляет 20 см в длину. Высота треугольника 15 см. Вычислите площадь треугольника
Дорожка 101
Основание треугольника имеет длину 20 см, а площадь — 300 см.Рассчитайте высоту треугольника.
Track 102
В треугольнике внутренний угол равен 30, а угол превышает 40. Найдите амплитуду каждого внешнего угла.
Путь 103
Разносторонний треугольник имеет периметр 50 м, длина одной стороны 15 м, а другой — 12 м. Вычисляет длину третьей стороны.
Дорожка 104
Высота треугольника составляет 15 см в длину, а площадь — 300 см. Вычисляет основание треугольника.
Дорожка 105
В треугольнике основание составляет 2/3 высоты, разница между основанием и высотой составляет 120 см. Вычислите площадь треугольника.
Дорожка 106
Треугольник имеет основание 5 см, высота превышает основу на 0,2 дм. Вычислите площадь треугольника.
Дорожка 107
Сумма двух сторон треугольника размером 128 см, одна из которых равна 3/5 другой. Зная, что длина третьей стороны 40 см, вычислите размер каждой стороны треугольника и его периметра.
Зная, что длина третьей стороны 40 см, вычислите размер каждой стороны треугольника и его периметра.
Дорожка 108
Периметр треугольника 110 см, длина одной стороны 40 см. Вычислите размер двух сторон, зная, какая из них составляет 2/5 другой.
Дорожка 109
В треугольнике сумма основания и высоты составляет 40 см. Рассчитайте площадь, зная, что высота основания составляет 5/3.
Дорожка 110
Разница между основанием и высотой треугольника 81 см. Зная, что высота составляет 2/5 основания, определяется площадь треугольника.
Дорожка 111
Сумма основания и высоты треугольника составляет 120 см, а их разница составляет 20 см. Вычислите площадь треугольника.
Дорожка 112
В треугольнике ABC сторона AB составляет 20 см, сторона BC AB превышает 5 см, а сторона AC BC превышает 3 см. Вычислите периметр треугольника.
Дорожка 113
Вычислите площадь треугольника, зная, что основание составляет 50 м и имеет высоту 5/3
Дорожка 114
Разносторонний треугольник имеет периметр 65 см, длинную сторону 20 см и другую сторону. два один дубль другого.Вычисляет протяженность двух других сторон и площадь треугольника.
два один дубль другого.Вычисляет протяженность двух других сторон и площадь треугольника.
Дорожка 115
В треугольнике одна сторона равна 4/5 суммы двух других сторон, а последняя — одна из 3/2 другой. Зная, что размер периметра 90 см, рассчитайте размер каждой стороны.
Дорожка 116
Треугольник имеет периметр 260 см, разница между BC и AB составляет 5 см, разница между AC и BC составляет 10 см. Вычислите площадь треугольника.
Track 117
В треугольнике одна сторона размером 14 см, а вторая сторона превышает 8 см в три раза больше первой, зная, что периметр равен 112 см, вычисляется площадь.
Дорожка 118
В треугольнике одна сторона равна 10 см, вторая сторона превышает первые 14 см, а периметр равен 60 см. Вычислите размер третьей стороны.
Колея 119
Длина периметра треугольника 250 см, первая сторона равна 1/3 второй стороны. Третья сторона составляет 3/4 второй стороны.Вычислите три стороны треугольника.
Дорожка 120
Две стороны треугольника ABC превышают третью, соответственно, на 10 см и 20 см. Вычисляет длину трех сторон и площадь, зная, что периметр равен 120 см.
Track 121
Вычисляет длину сторон и площадь треугольника ABC с периметром 60 см, зная, что сторона AC превышает 14 см стороны AB, а сторона BC превышает сторону AC на 2 см.
Колея 122
Периметр треугольника 120 см.Зная, что вторая сторона превышает первую на 10 см, а третья превышает первые 20 см, вычисляет размеры трех сторон треугольника.
Track 123
У разностороннего треугольника два угла соответственно 45 и 60. Рассчитайте периметр и площадь, зная, что высота 20 см.
Вписанные и описанные треугольники
Трасса 124
Равнобедренный треугольник ABC вписан в круг с центром O. Учитывая, что длина окружности равна 275.69 см и что размер сегмента ОН равен 36,10 см, вычислите площадь и периметр треугольника.
Track 125
Вычислите площадь треугольника, зная, что основание составляет 20 см, а высота равна половине основания.
Дорожка 126
Диаметр окружности равен 3/5 стороны равностороннего треугольника, имеющего площадь 100 см. Вычисляет длину окружности.
Дорожка 127
Разносторонний треугольник имеет сторону 70 см, длину второй стороны 60 см и длину третьей стороны 80 см.Вычислите площадь круга, вписанного в треугольник.
Track 128
Вычислите длину описанной окружности в треугольнике, зная, что катет и его проекция на гипотенузу имеют размер dm и 1,8 дм 3 соответственно.
Track 129
Равнобедренный треугольник, вписанный в круг радиусом 43,90 см, имеет относительную высоту относительно основания 80 см. Вычислите периметр и площадь треугольника.
Колея 130
В круг диаметром 100 см вписанный равнобедренный треугольник ABC не содержит центра.Высота треугольника относительно стороны неравного размера 36 см. Вычислите длину периметра треугольника и его площадь.
Дорожка 131
Прямоугольный треугольник имеет стороны 18 см и 24 см. Рассчитайте длину радиуса описанной окружности.
Рассчитайте длину радиуса описанной окружности.
Track 132
Равнобедренный треугольник имеет основание 36 см и высоту 24 см. Вычислите периметр и длину радиуса описанной окружности треугольника.
Направляющая 133
Равнобедренный треугольник имеет основание 36 см и высоту 24 см.Вычислите периметр и длину радиуса круга, вписанного в треугольник.
Track 134
Равнобедренный треугольник имеет основание AB 36 см и высоту 24 см. Вычислить:
центральный угол, образованный хордой AB описанной окружности треугольника;
площадь кругового сектора;
— длина дуги, образуемой хордой AB;
расстояние веревки от центра круга.
Дорожка 135
Разносторонний треугольник имеет сторону 70 см, длину второй стороны 60 см и длину третьей стороны 80 см.Вычислить:
центральный угол, образованный хордой AB описанной окружности треугольника;
площадь кругового сектора;
— длина дуги, образуемой хордой AB;
расстояние веревки от центра круга.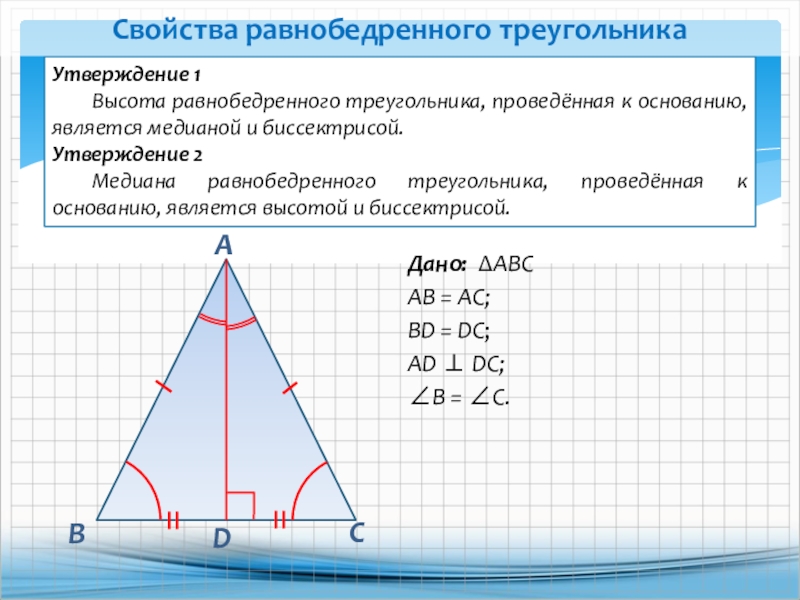
Track 136
Треугольник ABC вписан в окружность, его сторона AB конгруэнтна стороне вписанного квадрата, а сторона BC конгруэнтна стороне равностороннего треугольника, вписанного в ту же окружность.Вычислите величину углов треугольника.
треугольников и многоугольников
Дорожка 137
Окружность с центром O имеет радиус 10 см. Проведите из точки P вне окружности касательные PA и PB и соединив точку O с точками касания A и B, вы получите четырехугольник APBO. Зная, что периметр четырехугольника равен 100 см, рассчитайте размеры его сторон.
Колея 138
Окружность с центром O имеет радиус 10 см.Проведите из точки P вне окружности касательную PA и соединив точку O с точкой касания A и точкой P, мы получим треугольник APO. Зная, что отрезок РО составляет 40 см, рассчитайте площадь и периметр треугольника.
Дорожка 139
Окружность с центром O имеет радиус 10 см. Проведите из точки P вне окружности касательную PA и соединив точку O с точкой касания A и точкой P, мы получим треугольник APO. Зная, что сегмент PA равен 38,73 см, рассчитайте площадь и периметр треугольника.
Зная, что сегмент PA равен 38,73 см, рассчитайте площадь и периметр треугольника.
Дорожка 140
Хорда AB окружности составляет 90 см, а расстояние от центра — 40 см. Вычислите меру длины окружности и площади круга.
Дорожка 141
Хорда AB окружности составляет 90 см, а расстояние от центра — 40 см. Вычисляет длину периметра треугольника OBA и площадь треугольника.
Дорожка 142
Прямоугольник имеет основание и высоту соответственно 40 см в длину и 30 см; определяет площадь и периметр каждого из четырех треугольников, в которых он остается разделенным своими диагоналями.
Колея 143
Равносторонний треугольник имеет площадь 500 см и эквивалентен 2/3 равнобедренного треугольника. Вычисляет высоту равнобедренного треугольника, зная, что высота равностороннего треугольника размером 100 см и основанием равнобедренного треугольника в три раза больше, чем у равностороннего треугольника.
Дорожка 144
Треугольник имеет площадь, равную 2/5 площади прямоугольника с основанием 60 см и высотой 20 см. Вычислите высоту треугольника, зная, что его основание составляет 30 см
Вычислите высоту треугольника, зная, что его основание составляет 30 см
Дорожка 145
Прямоугольник с основанием 10 метров и высотой, равной шестерке основания, эквивалентен прямоугольному треугольнику. с одним катетом 30 метров. Вычислите периметр треугольника.
Дорожка 146
Треугольник имеет стороны соответственно 100 см, 60 см и 80 см. Вычислите периметр похожего на него треугольника с длинной стороной 200 см.
Дорожка 147
Размеры одного прямоугольника составляют 2/3 другого, а их разница составляет 3 см. Вычислите размер стороны равностороннего треугольника, периметр которого совпадает с периметром прямоугольника.
Колея 148
Сторона квадрата равна тройной стороне равностороннего треугольника с периметром 90 см. Вычислите периметр квадрата.
Колея 149
Периметр параллелограмма составляет 400 см, а одна сторона составляет 3/5 его ряда.Вычислите периметр и площадь равностороннего треугольника, длина стороны которого соответствует большей стороне параллелограмма.
Дорожка 150
Треугольник имеет основание 30 см и высоту 20 см. Найдите периметр квадрата, равный 4/3 треугольника.
Track 151
В прямоугольном треугольнике гипотенуза равна 5 дм катета и 4 дм. Найдите площадь квадрата, периметр которого равен 4/3 периметра треугольника.
Track 152
Найдите периметр квадрата, эквивалентного прямоугольному треугольнику, гипотенуза которого равна 76.Катет длиной 22 см и 2,5 дм.
Колея 153
Треугольник имеет площадь 1500 мм и длину основания 50 мм. Вычислите площадь треугольника, подобного заданному, зная, что его высота составляет 30 мм.
Дорожка 154
Прямоугольник эквивалентен квадрату с периметром 40 см. Учитывая, что высота прямоугольника составляет 1/4 от основания, вычисляется площадь изопериметрического ромба прямоугольника, совпадающая с высотой 3/5 стороны квадрата, а периметр равностороннего треугольника равен ромбу.
Track 155
В равнобедренном треугольнике периметр равен 170 см, а основание — 70 см. Вычисляет площадь и периметр квадрата, эквивалентные 2/25 треугольника.
Вычисляет площадь и периметр квадрата, эквивалентные 2/25 треугольника.
Track 156
Вычислите меру гипотенузы каждого из четырех треугольников, в которых ромб делится на диагонали, зная, что сумма диагонали 14 м составляет 3/4 другой.
Дорожка 157
Равнобедренный прямоугольный треугольник имеет короткие стороны 20 см в длину.Вычисляет периметр прямоугольника, эквивалентного треугольнику со сторонами одна 8/25 другой.
Track 158
Равнобедренный треугольник эквивалентен прямоугольнику с периметром 100 см. Вычислите размер основания треугольника, зная, что высота прямоугольника составляет 1/3 высоты треугольника, а их разница составляет 10 см.
Дорожка 159
В сумме диагоналей ромба размером 150 см, а — 1/2 другого.Вычислите:
— мера стороны квадрата, эквивалентной реву;
периметр прямоугольника, равный одной пятой бриллианта, зная, что его размер составляет 4/5 другого;
измерение трех высот разностороннего треугольника, эквивалентного 6/25 ромба, стороны которого составляют соответственно 30 см, 40 см и 50 см
Дорожка 160
В треугольнике ABC одна сторона имеет размер 15 см, вторая втрое больше первого, а третье — 4/5 секунды. Вычислите сторону равностороннего треугольника, периметр которого в четыре раза больше, чем у ABC.
Вычислите сторону равностороннего треугольника, периметр которого в четыре раза больше, чем у ABC.
Колея 161
Равносторонний треугольник имеет периметр 30 см. Равнобедренный треугольник, имеющий тот же периметр, что и равносторонний треугольник, имеет наклонные стороны, каждая из которых составляет 4/5 стороны данного треугольника; Рассчитайте размер основания.
Трасса 162
Периметр треугольника ABC составляет 160 см, сторона AB BC превышает 30 см, а сторона AC равна 5/4 BC. Вычислите периметр другого треугольника, каждая сторона которого соответственно равна 7/5, тройным и семи десятым сторон AB, BC и AC треугольника ABC.
Дорожка 163
В треугольнике ABC сторона AB равна 50 см, сторона BC — 3/5 стороны AB, а сторона AC — 3/2 стороны BC. Вычислите размер стороны равностороннего треугольника, периметр которого равен 3/5 периметра треугольника ABC.
Дорожка 164
Прямоугольник эквивалентен треугольнику с основанием 48 см и высотой 28 см. Зная, что размер прямоугольника 14 см, рассчитайте длину диагонали.
Зная, что размер прямоугольника 14 см, рассчитайте длину диагонали.
Track 165
Прямоугольник эквивалентен треугольнику с основанием 48 см и высотой 28 см.Зная, что размер прямоугольника 48 см, рассчитайте длину диагонали и периметр прямоугольника.
Дорожка 166
Стороны треугольника имеют размеры соответственно 300, 150 и 200 см. Вычисляет протяженность сторон треугольника, как если бы соотношение сходства было 1/10.
Дорожка 167
В разностороннем треугольнике, имеющем периметр 220 см, сумма двух сторон составляет 140 см, причем одна сторона равна 2/5 другой.Вычислите периметр равнобедренного треугольника, основание которого совпадает с большей стороной данного треугольника, а наклонная сторона в два раза больше меньшей стороны
Трасса 168
Трапеция образована квадратом и треугольником. Учитывая, что площадь треугольника составляет 6 см, а разница между основаниями трапеции составляет 4 см, рассчитайте площадь трапеции.
Дорожка 169
Пятиугольник образован квадратом и внешним по отношению к нему треугольником, основанием которого является сторона квадрата. Вычислите площадь пятиугольника, зная, что квадрат составляет 100 квадратных метров, а высота треугольника — 12 метров.
Вычислите площадь пятиугольника, зная, что квадрат составляет 100 квадратных метров, а высота треугольника — 12 метров.
Дорожка 170
Прямоугольник имеет периметр 160 см и длину основания 30 см. Вычисляет высоту треугольника, эквивалентного прямоугольнику, с основанием длиной 50 см.
Трасса 171
Периметр правильного пятиугольника равен 50 см, каков периметр равностороннего треугольника с длиной стороны, равной длине стороны пятиугольника?
Колея 172
Одна сторона равностороннего треугольника имеет длину 20 см.Какой должна быть сторона правильного шестиугольника, потому что у него такой же периметр?
Дорожка 173
Параллелограмм и треугольник имеют длину основания, 50 см и 40 см соответственно. Если две фигуры имеют одинаковую площадь и высота параллелограмма 30 см, вычисляется высота треугольника.
Колея 174
Равносторонний и равнобедренный треугольники имеют одинаковый периметр. Каждая из наклонных сторон равнобедренного треугольника составляет 5/6 основания, а сторона равностороннего треугольника составляет 32 см. Вычислите длину каждой стороны, площадь равнобедренного треугольника и площадь равностороннего треугольника.
Вычислите длину каждой стороны, площадь равнобедренного треугольника и площадь равностороннего треугольника.
Дорожка 175
Сумма основания и высоты треугольника составляет 60 см, а a — 1/2 другого. Вычисляет периметр квадрата, который имеет ту же площадь, что и треугольник.
Дорожка 176
Размеры сторон прямоугольного треугольника составляют 400 см и 30 дм, а периметр — 12 м. Определяет площадь и меру гипотенузы.Вычислить:
1) измеряет высоту и периметр прямоугольника, эквивалентного треугольнику и имеющего основание 25 дм;
2) Периметр квадрата равен 3/2 треугольника; 3) апофема пятиугольника, эквивалентного треугольнику;
4) периметр шестиугольника, равный 5/3 треугольника;
5) сторона семиугольника, имеющая тот же периметр треугольника; 6) апофема восьмиугольника, эквивалентного 7/8 треугольника;
7) периметр ennagono, эквивалентный треугольнику;
8) площадь десятиугольника, имеющего конгруэнтную боковую гипотенузу треугольника;
9) апофема endecagono, имеющая сторону, равную малому катету треугольника;
10) периметр двенадцатиугольника, сторона которого равна высоте относительно гипотенузы треугольника.
Дорожка 177
Периметр прямоугольника 68 см, размер — 5/12 другого. Вычислите площадь равностороннего треугольника с длиной стороны, равной диагонали прямоугольника.
Дорожка 178
Прямоугольник и квадрат являются изопериметрическими. Сумма длин диагонали и основания прямоугольника размером 98 см и равна 25/24 другого. Вычислите площадь равностороннего треугольника со стороной, равной диагонали квадрата.
Track 179
Вычисляет высоту треугольника с основанием 10 см, зная, что он эквивалентен другому треугольнику, сумма основания и высоты составляет 35 см, а их разница составляет 5 см.
Направляющая 180
Два одинаковых треугольника имеют длину основания соответственно 20 см и 40 см; зная, что в первом треугольнике относительная высота по отношению к основанию составляет 15 см, вычисляется соответствующая высота и площадь второго треугольника.
Дорожка 181
Ромб с диагональю 96 см эквивалентен двойному равнобедренному треугольнику с периметром 128 см и основанием 28 см. Определяет периметр алмаза.
Определяет периметр алмаза.
Дорожка 182
В равнобедренном треугольнике наклонная сторона равна 25 см, а периметр равен 64 см. Вычисляет периметр квадрата, площадь которого равна 50/21 площади треугольника.
Дорожка 183
В окружности с центром O и радиусом 30 см считается хордой AB, равной 36 см.Вычислите периметр и площадь треугольника ABO.
Track 184
Вычисляет длину хорды окружности с радиусом 30 см, зная, что это 24 см от центра. Вычисляет длину окружности и площадь круга. Вычислите периметр и площадь треугольника ABO.
Track 185
Вычисляет длину хорды круга диаметром 60 см, зная, что это 24 см от центра. Вычисляет длину окружности и площадь круга.Вычислите периметр и площадь треугольника ABO.
Дорожка 186
Равнобедренный треугольник, вершинами которого являются концы веревки и центр круга, имеет площадь 240 см. Зная, что расстояние от центра веревки составляет 24 см, рассчитайте длину радиуса круга.
Дорожка 187
Прямоугольный треугольник эквивалентен 3/4 параллелограмма с основанием и высотой 80 см, длиной и 40 см соответственно. Вычисляет размер катети, зная, что один составляет 3/4 от другого.
Колея 188
Диаметр круга равен стороне равностороннего треугольника, имеющего площадь 100 см. Вычисляет длину окружности.
Колея 189
Окружность соответствует равностороннему треугольнику с периметром 90 см. Вычисляет длину окружности.
Track 190
Прямоугольный треугольник с катетами соответственно 3 см и 4 см. Вычислите длину окружности, радиус которой равен гипотенузе треугольника.
Track 191
Прямоугольный треугольник с катетами соответственно 3 см и 4 см. Вычислите длину окружности, диаметр которой равен 3/4 гипотенузы треугольника.
Дорожка 192
Прямоугольный треугольник с катетами соответственно 3 см и 4 см. Вычисляет длину окружности, диаметр которой составляет 3/4 диаметра большего катета.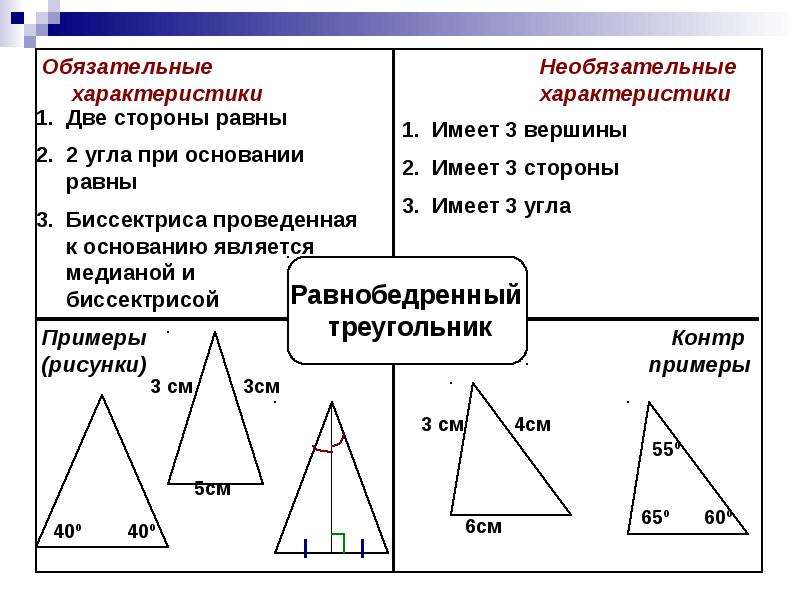
Track 193
Прямоугольный треугольник с катетами соответственно 3 см и 4 см. Вычислите длину круга, радиус которого на 3/4 диаметра катета больше.
Track 194
Прямоугольный треугольник имеет катетики соответственно 3 см и 4 см. Вычислите длину круга, радиус которого составляет 3/4 малого катета.
Track 195
Прямоугольный треугольник с катетами соответственно 3 см и 4 см. Вычисляет длину окружности, диаметр которой составляет 3/4 малого катета.
Track 196
Прямоугольный треугольник имеет площадь 6 см, а соотношение между двумя катетами составляет 3/4. Вычислите длину круга, диаметр которого меньше диаметра катета.
Track 197
Прямоугольный треугольник имеет площадь 6 см, а соотношение между двумя катетами составляет 3/4. Вычисляет длину окружности, радиус которой соответствует большему радиусу катета.
Последние выпуски за 2013 год.
Дорожка 198
В треугольнике ABC точка P представляет собой отрезок кривой PQ, перпендикулярный гипотенузе BC.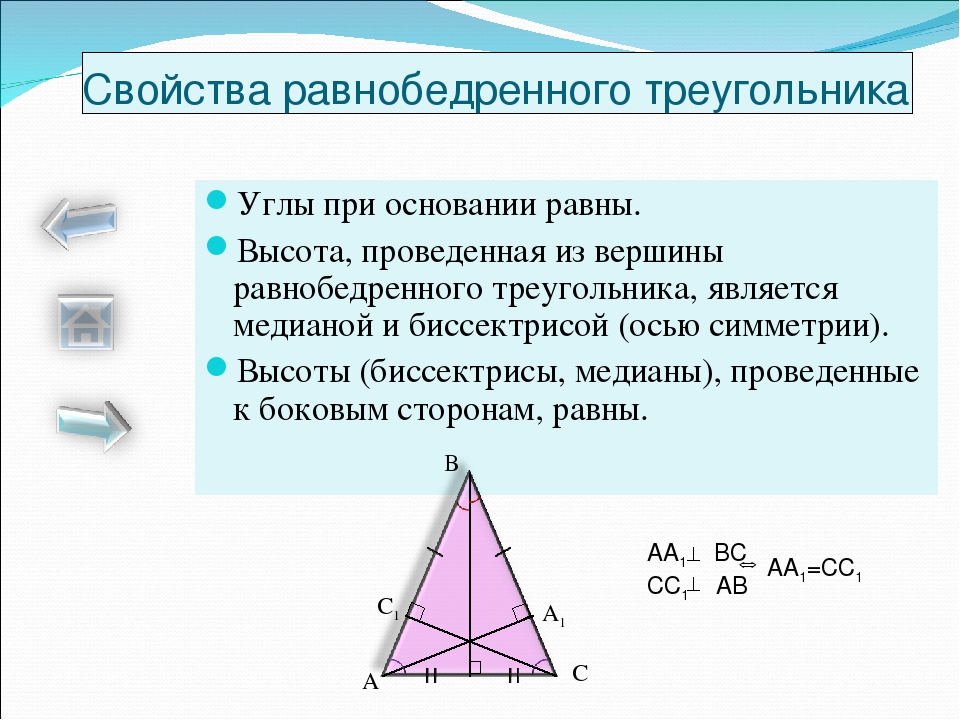 Докажите, что треугольник PQC подобен ABC. Зная, что ПК 15 см, 9 см и ПК 24 см. Найдите периметр треугольника ABC.
Докажите, что треугольник PQC подобен ABC. Зная, что ПК 15 см, 9 см и ПК 24 см. Найдите периметр треугольника ABC.
Track 199
В системе декартовых осей — это треугольник с вершинами A (3, -5), B (15, -5), C (-5, 5).
Track 200
В системе декартовых осей, имеющей единицей измерения см, является треугольник с вершинами A (3, -5), B (8, -5), C (-5, 5) .
Опишите его характеристики;
рассчитывает длину периметра;
вычисляет площадь;
вычисляет длину медианы.
Track 201
Равнобедренный треугольник имеет периметр 96 см и наклонную сторону 30 см.Вычислите высоту треугольника, зная, что площадь равна 432 см.
Дорожка 202
Треугольник из скалена имеет сторону 50 см, длину второй стороны 40 см и длину третьей стороны 80 см. Вычислите три медианы.
Трасса 203
Основание равнобедренного треугольника 36 м и высота 2/3. Вычисляет площадь и периметр треугольника, аналогичного заданному, с основанием 72 м.
Дорожка 204
Равносторонний треугольник со стороной 30 см эквивалентен прямоугольному треугольнику с катетом, равным одной трети стороны равностороннего треугольника.Вычислите периметр обоих треугольников.
Track 205
Вычислите количество сторон многоугольника, зная, что сумма внутренних углов равна 180.
Дорожка 206
Треугольник вписан в круг радиусом 10 см. Зная, что две короткие стороны равны соответственно 3/5 и 4/5 гипотенузы, вычислите площадь и периметр треугольника.
Track 207
Равнобедренный треугольник имеет основание 36 см и высоту 24 см.Вычислите периметр и площадь треугольника, как если бы зная, что он имеет высоту 6 см.
Колея 208
Основание равнобедренного треугольника составляет 6/5 наклонной стороны, а периметр — 96 см. Вычислите периметр равностороннего треугольника с длиной стороны 3/5 заданной наклонной стороны равнобедренного треугольника.
Колея 209
Основание равнобедренного треугольника составляет 6/5 наклонной стороны, а периметр — 96 см. Вычислите периметр равностороннего треугольника с длиной стороны, равной 5/3 основания данного равнобедренного треугольника.
Вычислите периметр равностороннего треугольника с длиной стороны, равной 5/3 основания данного равнобедренного треугольника.
Колея 210
Основание равнобедренного треугольника составляет 6/5 скошенной стороны, а периметр — 96 см. Вычислите периметр равностороннего треугольника с длиной стороны, равной основанию данного равнобедренного треугольника.
Колея 211
Основание равнобедренного треугольника составляет 6/5 наклонной стороны, а периметр — 96 см. Вычислите периметр равностороннего треугольника с длиной стороны, равной наклонной стороне данного равнобедренного треугольника.
Дорожка 212
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной 5/3 наклонной стороны данного равнобедренного треугольника.
Дорожка 213
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной 5/3 основания данного равнобедренного треугольника.
Дорожка 214
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см.Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной основанию данного равнобедренного треугольника.
Дорожка 215
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника с длиной стороны, равной наклонной стороне данного равнобедренного треугольника.
Дорожка 216
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника, высота которого равна наклонной стороне данного равнобедренного треугольника.
Дорожка 217
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника, высота которого равна 5/3 основания данного равнобедренного треугольника.
Дорожка 218
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см. Вычислите периметр и площадь равностороннего треугольника, высота которого равна 5/3 наклонной стороны заданного равнобедренного треугольника.
Вычислите периметр и площадь равностороннего треугольника, высота которого равна 5/3 наклонной стороны заданного равнобедренного треугольника.
Дорожка 219
Равнобедренный треугольник имеет площадь 432 см и высоту 24 см.Вычислите периметр и площадь равностороннего треугольника, высота которого равна основанию данного равнобедренного треугольника.
Колея 220
Треугольник имеет угол 30 и стороны, составляющие 6 см и 9 см; вычисляет периметр и площадь треугольника.
Дорожка 221
Прямоугольный треугольник имеет площадь 6 см и гипотенузу 5 см. Какая связь подобия с подобным треугольником, гипотенуза которого относительная высота 4.8 см?
Дорожка 222
Треугольник имеет угол 60, а катет, находящийся напротив него, имеет длину 8,66 см. Рассчитывает площадь и периметр.
Track 223
В прямоугольном треугольнике катет и его проекция на гипотенузу имеют размеры 30 см и 18 см. Рассчитайте периметр и площадь.
Track 224
Вычислите периметр и площадь прямоугольного треугольника, зная, что разница между гипотенузой и проекцией катета на нее составляет 32 см, а их соотношение составляет 25/9.
Track 225
Равнобедренный треугольник имеет основание 36 см и высоту 24 см. Вычислите периметр и площадь треугольника, аналогичного заданному, зная, что наклонная сторона второго треугольника составляет 7,5 см.
Колея 226
Равносторонний треугольник с длинной стороной 60 см и равнобедренный треугольник имеют одинаковый периметр. Основание равнобедренного треугольника составляет 80 см. Насколько велика наклонная сторона? Вычисляет, кроме того, площадь двух треугольников.
Track 227
Вычислите периметр и площадь прямоугольного треугольника, в котором один катет превышает 4 см, а другой катет, зная, что гипотенуза равна 20 см.
Колея 228
Площадь прямоугольного треугольника 600 см. Рассчитайте периметр, зная, что разница между двумя катетами составляет 10 см.
Дорожка 229
Вы хотите украсить фоторамки 10 в форме равностороннего треугольника со стороной 150 см. Сколько декаметров ленты нужно для декорирования?
Трасса 230
Радиус окружности конгруэнтен гипотенузе прямоугольного треугольника с двумя сторонами 3 см и 4 см.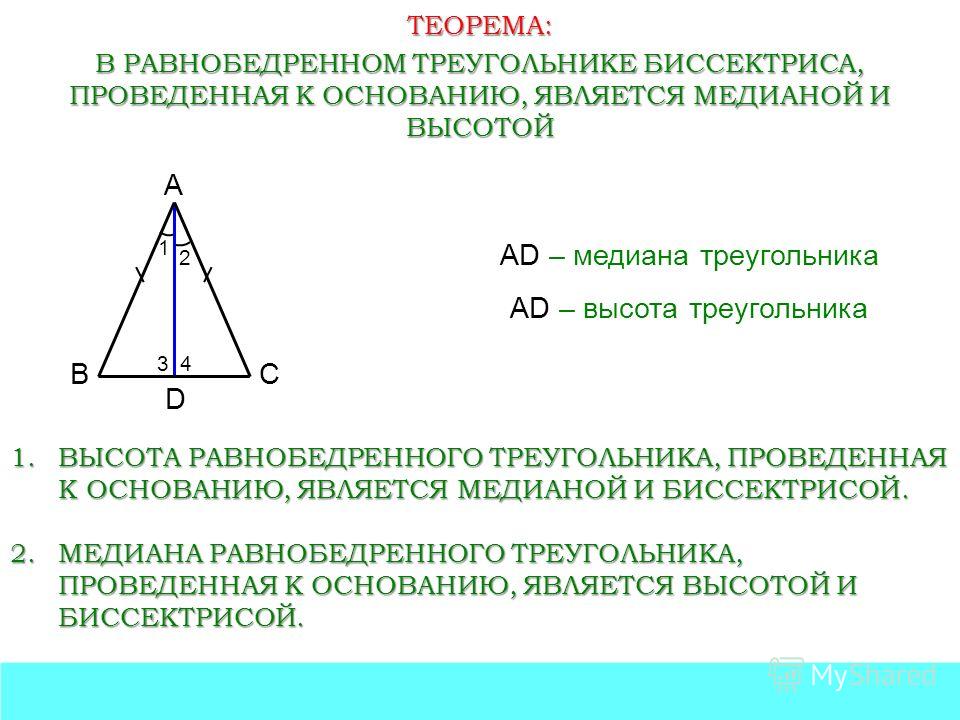

 2 )
2 )
 (Формула 3)
(Формула 3)


 Или sin угла находящийся между боковых сторон, умноженный на половину квадрата одной из боковых сторон. Когда проводим высоту на боковой стороне её длина равняется а*sin?. Так как длину стороны мы знаем, то и её высота нам известна. Соответственно, площадь равнобедренного треугольника будет половина от их выражения. Если быть точнее. то целая величина делает площадь треугольника. Разделяя высотой прямоугольник, получаем два не больших прямоугольных треугольника. Диагональю будет сторона треугольника, в свою очередь она делит фигуру на две равные части. Из чего следует что искомая нами величина находится как половина величины одной стороны умножаемая на высоту.
Или sin угла находящийся между боковых сторон, умноженный на половину квадрата одной из боковых сторон. Когда проводим высоту на боковой стороне её длина равняется а*sin?. Так как длину стороны мы знаем, то и её высота нам известна. Соответственно, площадь равнобедренного треугольника будет половина от их выражения. Если быть точнее. то целая величина делает площадь треугольника. Разделяя высотой прямоугольник, получаем два не больших прямоугольных треугольника. Диагональю будет сторона треугольника, в свою очередь она делит фигуру на две равные части. Из чего следует что искомая нами величина находится как половина величины одной стороны умножаемая на высоту. Но из этой формулы выйдет пятая, которую опишу чуть ниже.
Но из этой формулы выйдет пятая, которую опишу чуть ниже. Нам понадобиться высота, найденная в прошлой формуле. Она так же приходится катетом от прямоугольного треугольника, получившегося от боковой стороны, половины основания плюс высота. Гипотенузой будет боковая сторона, из квадрата гипотенузы (а) отнимем второй катет в квадрате. Так как он равняется полу — основания (b/2) значит квадрат = b2/4. Извлекая корень из полученного , найдем высоту.
Нам понадобиться высота, найденная в прошлой формуле. Она так же приходится катетом от прямоугольного треугольника, получившегося от боковой стороны, половины основания плюс высота. Гипотенузой будет боковая сторона, из квадрата гипотенузы (а) отнимем второй катет в квадрате. Так как он равняется полу — основания (b/2) значит квадрат = b2/4. Извлекая корень из полученного , найдем высоту. е. третья сторона. Таким образом, в равнобедренном треугольнике высота перпендикулярна вершине, общей для равных сторон. Такие особые свойства равнобедренного треугольника помогают нам рассчитать его площадь и высоту с помощью формул равнобедренного треугольника.
е. третья сторона. Таким образом, в равнобедренном треугольнике высота перпендикулярна вершине, общей для равных сторон. Такие особые свойства равнобедренного треугольника помогают нам рассчитать его площадь и высоту с помощью формул равнобедренного треугольника.