Как найти высоту трапеции. Запоминаем и применяем свойства трапеции
Трапецией называется такой четырехугольник, две стороны у которого параллельны (это основания трапеции, обозначенные на рисунке a и b), а другие две — нет (на рисунке АД и CB). Высота трапеции — это отрезок h, проведенный перпендикулярно к основаниям.
Как найти высоту трапеции при известных величинах площади трапеции и длин оснований?
Для вычисления площади S трапеции ABCD, воспользуемся формулой:
S = ((a+b) × h)/2.
Здесь отрезки a и b — это основания трапеции, h — это высота трапеции.
Преобразуя эту формулу, можем записать:
Используя эту формулу, получим значение h, если известны величина площади S и величины длин оснований a и b.
Пример
Если известно, что площадь трапеции S равна 50 см², длина основания a составляет 4 см, длина основания b составляет 6 см, то, чтобы найти высоту h, используем формулу:
Подставляем в формулу известные величины.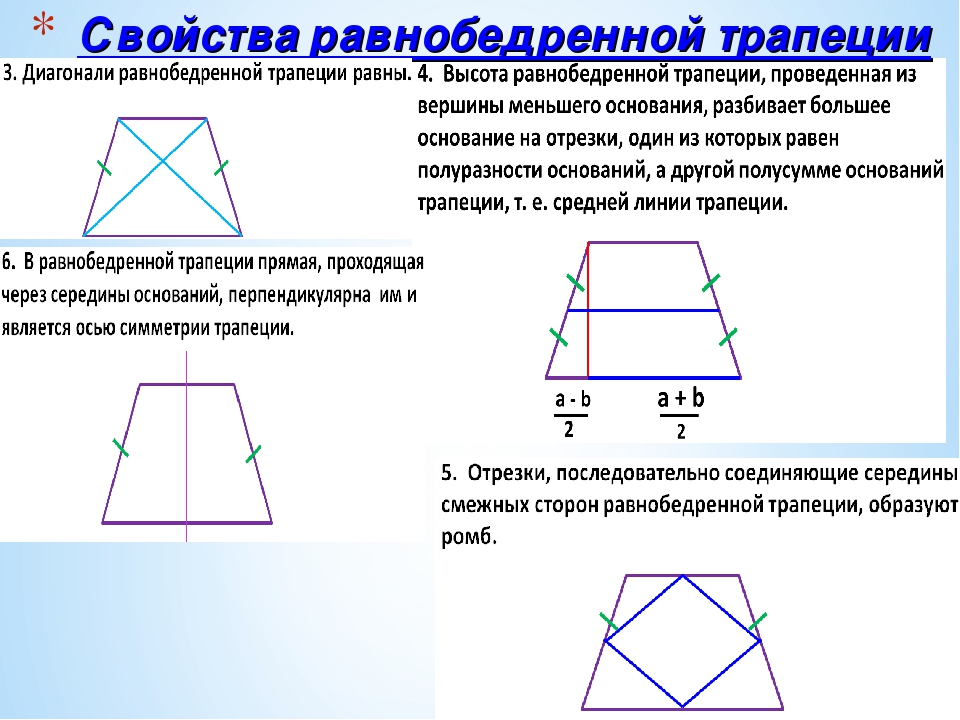
h = (2 × 50)/(4+6) = 100/10 = 10 см
Ответ: высота трапеции составляет 10 см.
Как находить высоту трапеции, если даны величины площади трапеции и длина средней линии?
Воспользуемся формулой вычисления площади трапеции:
Здесь m — средняя линия, h — высота трапеции.
Если возникает вопрос, как найти высоту трапеции, формула:
h = S/m, будет ответом.
Таким образом, можем найти величину высоты трапеции h, имея известные величины площади S и отрезка средней линии m.
Пример
Известна длина средней линии трапеции m, которая составляет 20 см, и площадь S, которая равна 200 см². Найдем значение величины высоты трапеции h.
Подставив значения S и m, получим:
h = 200/20 = 10 см
Ответ: высота трапеции составляет 10 см
Как найти высоту прямоугольной трапеции?
Если трапеция — это четырехугольник, с двумя параллельными сторонами (основаниями) трапеции. То диагональ — это отрезок, который соединяющий две противоположные вершины углов трапеции (отрезок АС на рисунке).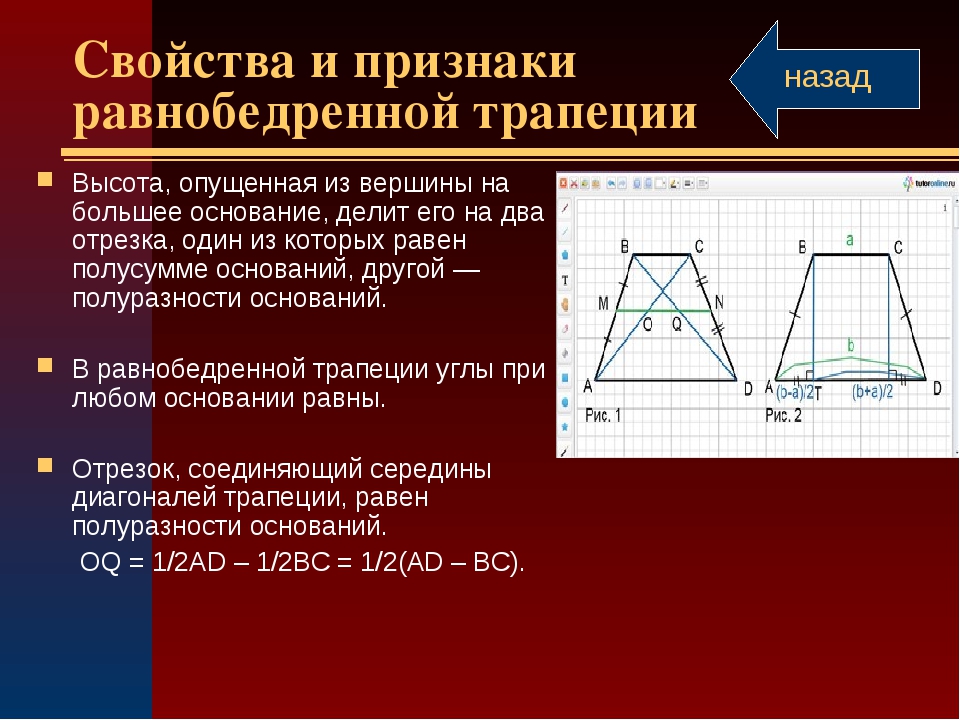 Если трапеция прямоугольная, с помощью диагонали, найдем величину высоты трапеции h.
Если трапеция прямоугольная, с помощью диагонали, найдем величину высоты трапеции h.
Прямоугольной трапецией называется такая трапеция, где одна из боковых сторон перпендикулярна основаниям. В этом случае ее длина (АД) совпадает с высотой h.
Итак, рассмотрим прямоугольную трапецию ABCD, где AD — это высота, DC — это основание, AC — это диагональ. Воспользуемся теоремой Пифагора. Квадрат гипотенузы AC прямоугольного треугольника ADC равен сумме квадратов его катетов AB и BC.
Тогда можно записать:
AC² = AD² + DC².
AD — это катет треугольника, боковая сторона трапеции и, в то же время, ее высота. Ведь отрезок АД перпендикулярен основаниям. Его длина составит:
AD = √(AC² — DC²)
Итак, имеем формулу для вычисления высоты трапеции h = AD
Пример
Если длина основания прямоугольной трапеции(DC) равна 14 см, а диагональ (AC) составляет 15 см, для получения значения высоты(AD -боковой стороны) воспользуемся теоремой Пифагора.
Пусть х — это неизвестный катет прямоугольного треугольника(AD), тогда
AC² = AD² + DC² можно записать
15² = 14² + х²,
х = √(15²-14²) = √(225-196) = √29 см
Ответ: высота прямоугольной трапеции (АВ) составит √29 см, что приблизительно составит, 5. 385 см
385 см
Как найти высоту равнобедренной трапеции?
Равнобедренной трапецией, называют трапецию, у которой длины боковых сторон равны между собой. Прямая, проведенная через середины оснований такой трапеции будет осью симметрии. Частным случаем является трапеция, диагонали которой перпендикулярны друг другу, тогда высота h, будет равна полусумме оснований.
Рассмотрим случай, если диагонали не перпендикулярны друг другу. В равнобочной (равнобедренной) трапеции равны углы при основаниях и длины диагоналей равны. Также известно, что все вершины равнобокой трапеции касаются линии окружности, проведенной вокруг этой трапеции.
Рассмотрим рисунок. ABCD- равнобедренная трапеция. Известно, что основания трапеции параллельны, значит, BC = b параллельно AD = a, сторона AB = CD = c, значит, углы при основаниях соответственно равны, можно записать угол BAQ = CDS = α, и угол ABC = BCD = β. Таким образом, делаем вывод о равенстве треугольника ABQ треугольнику SCD, значит, отрезок
AQ = SD = (AD — BC)/2 = (a — b)/2.
Имея по условию задачи величины оснований a и b, и длину боковой стороны с, найдем высоту трапеции h, равную отрезку BQ.
Рассмотрим прямоугольный треугольник ABQ. ВО — высота трапеции, перпендикулярна основанию AD, значит и отрезку AQ. Сторону AQ треугольника ABQ, найдем, воспользовавшись выведенной нами ранее формулой:
Имея значения двух катетов прямоугольного треугольника, найдем гипотенузу BQ= h. Используем теорему Пифагора.
AB²= AQ² + BQ²
Подставим данные задачи:
c² = AQ² + h².
Получим формулу для нахождения высоты равнобедренной трапеции:
h = √(c²-AQ²).
Пример
Дана равнобедренная трапеция ABCD, где основание AD = a = 10см, основание BC = b = 4см, а боковая сторона AB = c = 12см. При таких условиях, рассмотрим на примере, как найти трапеции высоту, равнобедренной трапеции АВСД.
Найдем сторону AQ треугольника ABQ, подставив известные данные:
AQ = (a — b)/2 = (10-4)/2=3см.
Теперь подставим значения сторон треугольника в формулу теоремы Пифагора.
h = √(c²- AQ²) = √(12²- 3²) = √135 = 11.6см.
Ответ. Высота h равнобедренной трапеции ABCD составляет 11.6 см.
Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди многообразия геометрических фигур отдельного внимания заслуживает и трапеция. Она представляет собой выпуклую фигуру с четырьмя сторонами, из которых две параллельны между собой. Последние называются основаниями, а оставшиеся две – боковыми сторонами. Отрезок, перпендикулярный основаниям и определяющий величину промежутка между ними, и будет высотой трапеции. Каким же образом можно вычислить его длину?
Найти высоту произвольной трапеции
Базируясь на исходных данных, определение высоты фигуры возможно несколькими способами.
Известна площадь
Если длина параллельных сторон известна, а также указана площадь фигуры, то для определения искомого перпендикуляра можно воспользоваться следующим соотношением:
S=h*(a+b)/2,
h – искомая величина (высота),
S – площадь фигуры,
a и b – стороны, параллельные друг другу.
Из приведенной формулы следует, что h=2S/(a+b).
Известна величина средней линии
Если среди исходных данных помимо площади трапеции (S) известна, и длина ее линии средины (l), то для вычислений пригодится другая формула. Прежде стоит уточнить, что такое средняя линия для данного вида четырехугольника. Термин определяет часть прямой, соединяющей средины боковых сторон фигуры.
Исходя из свойства трапеции l=(a+b)/2,
l – линия средины,
a, b – стороны-основания четырехугольника.
Поэтому h=2S/(a+b)=S/l.
Известны 4 стороны фигуры
В данном случае поможет теорема Пифагора. Опустив перпендикуляры на большую сторону-основание, воспользуйтесь ею для двух получившихся прямоугольных треугольников. Итоговое выражение будет иметь вид:
h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 ,
c и d – 2 другие стороны.
Углы в основании
При наличии данных об углах при основании, воспользуйтесь тригонометрическими функциями.
h = c* sinα = d*sinβ,
α и β – углы в основании четырехугольника,
c и d – его боковые стороны.
Диагонали фигуры и углы, которые пересекаясь они образуют
Длина диагонали – длина отрезка, соединяющего противоположные вершины фигуры. Обозначим данные величины символами d1 и d2, а углы между ними γ и φ. Тогда:
h = (d1*d2)/(a+b) sin γ = (d1*d2)/(a+b) sinφ,
h = (d1*d2)/2l sin γ = (d1*d2)/2l sinφ,
a и b – стороны-основания фигуры,
d1 и d2 – диагонали трапеции,
γ и φ – углы между диагоналями.
Высота фигуры и радиус окружности, которая в нее вписана
Как следует из определения такого рода окружности, она касается каждого основания в 1 точке, которые являются частью одной прямой. Поэтому расстояние между ними – диаметр – искомая высота фигуры. А так как диаметр – удвоенный радиус, то:
h = 2 * r,
r – радиус окружности, которую вписали в данную трапецию.
Найти высоту равнобедренной трапеции
- Как и следует из формулировки, отличительной характеристикой равнобедренной трапеции является равенство ее боковых сторон.
 Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Итак, если с = d, то h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 = √c 2 -(a-b) 2 /4,
a, b – стороны-основания четырехугольника,
c = d – его боковые стороны.
- При наличии величины углов, образованных двумя сторонами (основанием и боковой), высоту трапеции определяет следующее соотношение:
h = c* sinα,
h = с * tgα *cosα = с * tgα * (b – a)/2c = tgα * (b-a)/2,
α – угол в основании фигуры,
a, b (a
c = d – его боковые стороны.
- Если даны величины диагоналей фигуры, то выражение для нахождения высоты фигуры видоизменится, т.к. d1 = d2:
h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,
h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок.
 Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 . - Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке.
 Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .

- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .

- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам:
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне.
 Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ). - Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ .
 Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b.
 Радиус окружности можно вычислить по формуле: r = √ab .
Радиус окружности можно вычислить по формуле: r = √ab . - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.

- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
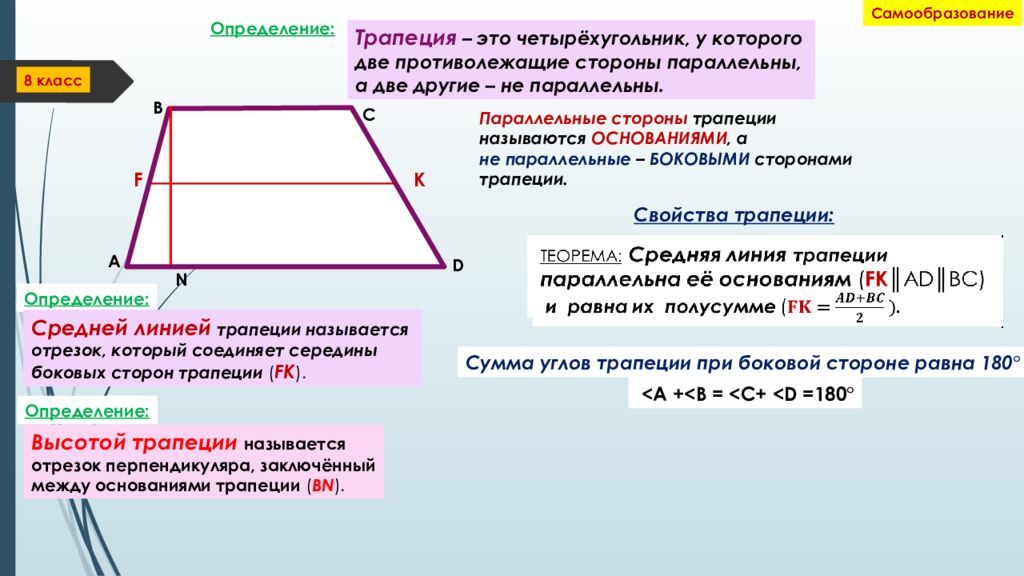
Трапеция
Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара противолежащих сторон параллельна.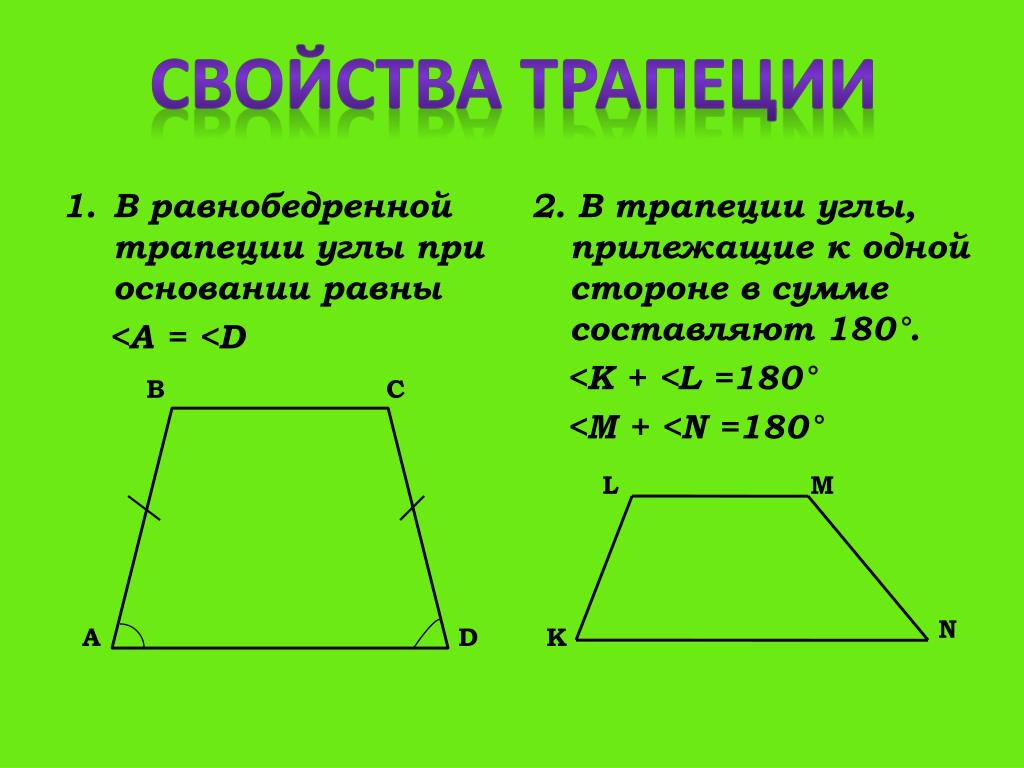
Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон трапеции.
Элементы трапеции
- Параллельные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
Виды трапеций
- Трапеция, у которой боковые стороны равны, называется равнобедренной.
- Трапеция, у которой один из углов «прямой», называется прямоугольной.
 2 \]
2 \]
Формулы длин сторон трапеции
Формула длины оснований трапеции через среднюю линию и другую основу:
\[ a = 2m — b , b = 2m — a \]
Формулы длины основ трапеции через высоту и углы при нижнем основании:
\[ a = b + h · (ctg \alpha + ctg \beta) , b = a — h · (ctg \alpha + ctg \beta)\]
Формулы длины основ трапеции через боковые стороны и углы при нижнем основании:
\[ a = b + c·cos \alpha + d·cos \beta, b = a — c·cos \alpha — d·cos \beta \]
Формулы боковых сторон трапеции через высоту и углы при нижнем основании:
\[ с = \dfrac{h}{sin \alpha } , d = \dfrac{h}{sin \beta } \]
Формулы длины средних линий трапеции
Формула определения длины средней линии через длины оснований:
\[ m = \dfrac{a + b}{2} \]
Формула определения длины средней линии через площадь и высоту:
\[ m = \dfrac{S}{h} \]
Формулы длины высоты трапеции
Формула высоты трапеции через сторону и прилегающий угол при основании:
\[ h = c·sin α = d·sin β \]
Формула высоты трапеции через диагонали и углы между ними:
\[ h = sin γ \cdot \dfrac{d_1\cdot d_2}{a + b} = sin δ \cdot \dfrac{d_1\cdot d_2}{a + b} \]
Формула высоты трапеции через диагонали, углы между ними и среднюю линию:
\[ h = sin γ \cdot \dfrac{d_1 \cdot d_2}{2m 2m} = sin δ · \dfrac{d_1}{d_2} \]
Формула высоты трапеции через площадь и длины оснований:
\[ h = \dfrac{2S}{a + b} \]
Формула высоты трапеции через площадь и длину средней линии:
\[ h = \dfrac{2S}{m} \]
Формулы длин диагоналей трапеции
Формулы длин диагоналей трапеции по теореме косинусов:
\[ d_1 = \sqrt{a^2 + d^2 — 2ad·cos β} \]
\[ d_2 = \sqrt{a^2 + c^2 — 2ac·cos β} \]
Формулы длин диагоналей трапеции через четыре стороны:
\[ d_1 = \sqrt{d^2 + ab — \dfrac{a(d^2 — c^2)}{a — b} } \]
\[ d_2 = \sqrt{c^2 + ab — \dfrac{ a(c^2 — d^2) }{a — b} } \]
Формулы длин диагоналей трапеции через высоту:
\[ d_1 = \sqrt{h^2 + (a — h · ctg β)^2} = \sqrt { h^2 + (b + h · ctg α)^2} \]
\[ d_2 = \sqrt{h^2 + (a — h · ctg α)^2} = \sqrt{h^2 + (b + h · ctg β)^2} \]
Формулы длин диагоналей трапеции через сумму квадратов диагоналей:
\[ d_1 = \sqrt{c^2 + d^2 + 2ab — d_2^2} \]
\[ d_2 = \sqrt{c^2 + d^2 + 2ab — d_1^2} \]
Формулы площади трапеции
Формула площади трапеции через основания и высоту:
\[ S = \dfrac{ (a + b) · h }{2} \]
Формула площади трапеции через среднюю линию и высоту:
\[ S = m · h \]
Формула площади трапеции через диагонали и угол между ними:
\[ S = \dfrac{d_1d_2}{2} · sin γ = \dfrac{d_1d_2}{2} · sin δ \]
Формула площади трапеции через четыре стороны:
\[ S = \dfrac{a + b}{2}\sqrt{c^2 — \left\lgroup\dfrac{(a — b)^2 + c^2 — d^2)}{2\cdot (a — b)} \right\rgroup ^2 } \]
Формула Герона для площади трапеции
\[ S = \frac{a + b}{\left|a-b\right| } \sqrt{(p — a)(p — b)(p — a — c)(p — a — d)} \]
где \( p = \dfrac{a + b + c + d}{2} \) — полупериметр трапеции.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Источник
Больше интересного в телеграм @calcsboxкак найти, если известны основания, стороны, площадь или радиус, формула расчета
Что такое трапеция
ОпределениеТрапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.
Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.
ОпределениеВысота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти высоту трапеции
Через стороны
Если нам известны стороны фигуры, мы можем найти ее высоту по формуле:
\(h=\sqrt{b^2-(\frac{{(a-d)}^2+d^2+c^2}{2\cdot(a-b)}})^2\)
Где h — высота, a — большее основание, b — меньшее основание, c и d — боковые стороны.

Через среднюю линию и площадь
Если в условии есть данные о величине средней линии и площади, можем использовать формулу:
\(h=\frac Sm\)
Где m — средняя линия трапеции.
Через боковую сторону и угол
Когда нам известна величина одной из боковых сторон и угол между этой стороной и большим основанием, используем формулу:
\(h=c\cdot\sin\left(\alpha\right)\)
Где \alpha — это угол между стороной c и большим основанием a.
Через диагонали, угол между ними и основания
Если нам известны длины обоих диагоналей трапеции, а также угол между ними, можем найти высоту следующим образом:
\(h=\frac{d_1d_2}{a+b}\cdot\sin\left(\gamma\right)\)
Где \(d_1\) и \(d_2\) — диагонали трапеции, а \(\gamma\) — угол между ними.
Через диагонали, угол и среднюю линию
В том случае, если нам известны сразу длины диагоналей, угол между ними и величина средней линии, мы можем узнать высоту трапеции по формуле:
\(h=\frac{d_1d_2}{2m}\cdot\sin\left(\gamma\right)\)
Через радиус вписанной окружности
Если в трапецию можно вписать окружность, то ее высота будет равна диаметру этой окружности, то есть d=h.
 \circ\right)=\frac63\cdot\frac12=1\) см.
\circ\right)=\frac63\cdot\frac12=1\) см.Ответ: h=1 см.
Трапеция Основные свойства трапеции Планиметрия 10 класс
Трапеция. Основные свойства трапеции. Планиметрия 10 класс
Трапеция • 1. Сумма внутренних углов трапеции равна 360 градусов. • 2. Сумма углов при боковых сторонах трапеции равна 180 градусов. • 3. Биссектрисы, проведенные из вершин односторонних углов А и В, пересекаются под углом в 90 градусов.
Трапеция • 4. Средняя линия MN трапеции параллельна основаниям BC и AD равна их полусумме
Трапеция • 5. Биссектриса, проведенная из вершины угла трапеции , отсекает равнобедренный треугольник
Трапеция • 6. Диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики.
Трапеция • 7.
 Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности основанийТрапеция • 8. Длина отрезка, параллельного основаниям трапеции, проходящего через точку пересечения диагоналей и соединяющего две точки на боковых сторонах, есть среднее гармоническое оснований трапеции.
Трапеция х = √(1/2(а 2 + b 2)) 10. Длина отрезка, делящего трапецию на две равновеликие, равна √((а 2 + b 2)/2) (среднему квадратичному длин оснований).
Равнобедренная трапеция • 1. В равнобедренной трапеции длины диагоналей равны; • 2. В равнобедренной трапеции углы при любом основании равны;
Равнобедренная трапеция АТ = TD = • 3. Проекция боковой стороны на основание равнобедренной трапеции, равна полуразности оснований, • 4. Проекция диагонали на основание – полусумме оснований (длине средней линии трапеции).
Равнобедренная трапеция • 5. Если в равнобедренную трапецию вписана окружность, то ее боковая сторона равна средней линии.

Равнобедренная трапеция • 6. Если диагонали равнобедренной трапеции взаимно перпендикулярны, то длина высоты трапеции равна длине средней линии, а площадь равна ДЛИНЕ высоты в квадрате.
Равнобедренная трапеция • 7. Если в равнобедренную трапецию можно вписать окружность, то высота есть среднее геометрическое оснований.
Равнобедренная трапеция • 8. Если около трапеции можно описать окружность, то такая трапеция — равнобедренная.
Какими свойствами обладает трапеция. Полезные свойства трапеции. Свойства средней линии трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .

Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.
 Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание . В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме .
Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16Ответ : 16 см
Задача .
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.Решение .
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — bТреугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2Ответ : площадь трапеции равна 80 см 2 .

С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции , которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
Вконтакте
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.
 е. пересекаются под углом 90° (как это показано на рис.1).
е. пересекаются под углом 90° (как это показано на рис.1).
Если сложить все градусные меры внутренних , то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей. Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:
Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см.
 Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, чтоПускай DF – будет . Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.
Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.

Разнобокая
Существует две формы: остроугольная и тупоугольная . ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.
- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.

- Вокруг любой правильной трапеции можно построить .
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции :
Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может, потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой. При этом, перпендикулярная сторона также будет являться и высотой.
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией. Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.

Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
Важно! Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур. Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции, следует определиться какие даны входные значения.
 Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.Рисунок 5. Решение задачи на поиск высоты трапеции
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда .
Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников.
 Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.Важно! В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.

(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как :
- средняя линия;
- площадь;
- высота;
- диагонали.
Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей.
 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.

- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .

- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.

- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже.
 Так и поймете быстрее, и запомните лучше.
Так и поймете быстрее, и запомните лучше.- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника.
 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.

- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны.
 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. - Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ.
 Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 .
 Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см.Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию.
 Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
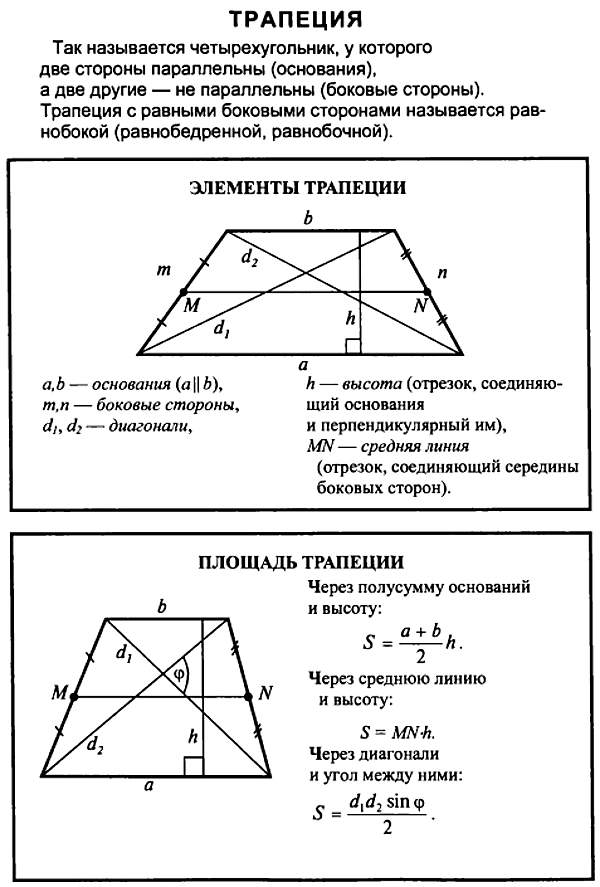
Трапеция — это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная .

— это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b — основания трапеции (a параллельно b ),
m, n — боковые стороны трапеции,
d 1 , d 2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b и высоту h : S = \frac{a + b}{2}\cdot h
- Через среднюю линию MN и высоту h : S = MN\cdot h
- Через диагонали d 1 , d 2 и угол (\sin \varphi ) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции , прилежащих к каждой боковой стороне, равна 180^{\circ} :
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликие треугольники трапеции
Равновеликими , то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC , образованные боковыми сторонами.
 {2}
.
{2}
.Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
Как найти высоту трапеции через радиус. Как найти высоту трапеции
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a = 3 см, b = 7 см и боковыми сторонами c = 5 см, d = 4 см. найдем площадь фигуры:Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a) – это значение первообразной функции f(x) в точке a , F(b) – значение этой же функции f(x) в точке b .
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x ={-8}, слева прямой x ={-10} и осью OX снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
По ней мы найдем значения первообразной в каждой из наших точек:Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Многоликая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.

Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.
По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии.
 А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin α.
В этом выражении можно легко заменить α на β. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность.
 И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:S = (4 * r 2) / sin γ.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками.
 После вычисления площадей этих фигур останется их только сложить.
После вычисления площадей этих фигур останется их только сложить.Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.

Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2).
 Задача решена.
Задача решена.Ответ: площадь трапеции равна 4,5 дм 2 .
№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.

Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ: S = 20 см 2 .
№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.
Решение. Пусть меньшее основание имеет обозначение ВС. Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ: Искомая площадь равна 45 см 2 .
№ 4. Условие. Имеется произвольная трапеция АВСД.
 На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест.
 Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.
Ответ : х = √ {(а 1 2 + 5 а 2 2) / 6}.
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.

В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).

Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались.
 Теперь о площади трапеции.
Теперь о площади трапеции.Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.

В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.

Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d.
 Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα .
 Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами.
 Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.

Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т.
 А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.

Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то2) Применение общей формулы площади четырехугольника .

Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать.
 Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.

1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Найти площадь трапеции (Мехмат МГУ, 1970г).Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .Трапеция и ее свойства с определением и примерами решения
Содержание:
Трапецией называют четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
На рисунке 66 изображена трапеция
Свойства трапеции
Рассмотрим некоторые свойства трапеции.
1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.

Так как то (как сумма внутренних односторонних углов). Аналогично
2. Трапеция является выпуклым четырехугольником.
Поскольку то Аналогично Следовательно, трапеция — выпуклый четырехугольник.
Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.
Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 — высота трапеции
Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 — прямоугольная трапеция Очевидно, что является меньшей боковой стороной прямоугольной трапеции и ее высотой.
Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 — равнобокая трапеция
Свойства равнобокой трапеции
Рассмотрим некоторые важные свойства равнобокой трапеции.
1. В равнобокой трапеции углы при основании равны.

Доказательство:
1) Пусть в трапеции Проведем высоты трапеции и из вершин ее тупых углов и (рис. 70). Получили прямоугольник Поэтому
2) (по катету и гипотенузе). Поэтому
3) Также Но поэтому и Следовательно,
2. Диагонали равнобокой трапеции равны.
Доказательство:
Рассмотрим рисунок 71. (как углы при основании равнобокой трапеции), — общая сторона треугольников и Поэтому (по двум сторонам и углу между ними). Следовательно,
Пример:
— точка пересечения диагоналей равнобокой трапеции с основаниями и (рис. 71). Докажите, что
Доказательство:
(доказано выше). Поэтому По признаку равнобедренного треугольника — равнобедренный. Поэтому Поскольку и то (так как ).
Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.
Доказательство:
1) Пусть в углы при большем основании равны (рис.
 70), то есть Проведем высоты и они равны.
70), то есть Проведем высоты и они равны.2) Тогда (по катету и противолежащему углу). Следовательно, Таким образом, трапеция равнобокая, что и требовалось доказать.
А еще раньше…
Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» — однокоренные).
В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.
Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие — не параллельны.
Свойство средней линии трапеции
Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.
Рассмотрим свойство средней линии трапеции.

Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство:
Пусть — данная трапеция, — ее средняя линия (рис. 109). Докажем, что и
1) Проведем луч до его пересечения с лучом Пусть — точка их пересечения. Тогда (как внутренние накрест лежащие при параллельных прямых и и секущей (как вертикальные), (по условию). Следовательно, (по стороне и двум прилежащим углам), откуда (как соответственные стороны равных треугольников).
2) Поскольку то — средняя линия треугольника Тогда, по свойству средней линии треугольника, а значит, Но так как то
3) Кроме того,
Пример:
Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.
Доказательство:
Пусть — средняя линия трапеции — точка пересечения и — точка пересечения и (рис.
 110). Пусть Докажем, что
110). Пусть Докажем, что 1) Так как и то, по теореме Фалеса, -середина — середина Поэтому — средняя линия треугольника — средняя линия треугольника
Тогда
2) — средняя линия трапеции, поэтому
3)
Пример:
В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции — 48 см.
Решение:
Пусть — данная трапеция, — ее средняя линия, (рис. 111).
1) Обозначим Тогда
2) (по условию). (как внутренние накрест лежащие при параллельных прямых и и секущей Поэтому Следовательно, — равнобедренный, у которого (по признаку равнобедренного треугольника). Но (по условию), значит,
3) Учитывая, что получим уравнение: откуда
4) Тогда
Ответ. 15 см.
А еще раньше…
То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в.
 до н. э.).
до н. э.).О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).
Калькулятор площади трапеции
Калькулятор площади трапеции быстро вычисляет площадь заданной трапеции, вводя заданные вами основание и высоту. Все, что вам нужно сделать, это ввести длину оснований трапеции и высоту, и калькулятор моментально рассчитает площадь и вернет ее вам. Помимо площади, калькулятор трапеций также может вычислить периметр и углы между сторонами трапеции.Кроме того, вы можете рассчитать площадь в различных единицах измерения, таких как квадратных сантиметра , квадратных метра , квадратных дюйма , квадратных фута и более.
Хотите изучить все аспекты пятиугольника и рассчитать его, воспользуйтесь нашим подробным калькулятором пятиугольника.
Что такое трапеция?Трапеция или трапеция — двумерная четырехугольная геометрическая фигура с четырьмя сторонами, из которых одна пара параллельна.
 Параллельные стороны называются основаниями, а непараллельные — катетами. Трапеция также может иметь параллельные стороны в некоторых случаях. Ноги могут быть ориентированы вертикально или горизонтально. Предположим, мы проводим прямую линию от одной стороны к противоположной. В этом случае мы называем это высотой ( перпендикулярного расстояния ) трапеции.
Параллельные стороны называются основаниями, а непараллельные — катетами. Трапеция также может иметь параллельные стороны в некоторых случаях. Ноги могут быть ориентированы вертикально или горизонтально. Предположим, мы проводим прямую линию от одной стороны к противоположной. В этом случае мы называем это высотой ( перпендикулярного расстояния ) трапеции.В зависимости от угла и длины сторон мы делим трапеции на 5 различных категорий:
1. Правая трапеция
Который имеет два угла по 90 градусов ( прямой угол ).
2. Равнобедренная трапеция
Который имеет противоположные стороны одинаковой длины
3. Несимметричная трапеция
Который не имеет ни равных сторон, ни равных углов.
4. Тупоугольная трапеция
У которого один внутренний угол больше 90 градусов
5.
 Острая трапеция
Острая трапеция У которого оба угла, образованные более длинным основанием и ножками, меньше 90 градусов.
Происхождение
В конце 1560-х годов термин «трапеция» впервые был внесен в английский словарь из греческого языка, что в исходном виде означает «столик, обеденный стол».
Трапеция в реальной жизни
Хорошо, мы уже знакомы с трапециями с математической точки зрения, но где мы можем найти трапеции в реальных сценариях? Если вы просто посмотрите вокруг себя, то обязательно найдете трапециевидные формы. Приведу несколько примеров:
Лампа
Прекрасный пример трапеции с парой параллельных и парой непараллельных сторон.
Ведро
Еще один прекрасный пример трапециевидной формы в реальной жизни — ведро.
Какими свойствами обладает трапеция?В координатной геометрии есть семь различных четырехугольников: параллелограмм, ромб, воздушный змей, прямоугольник, трапеция, квадрат и равнобедренная трапеция.
 Однако каждый из них отличается по своим свойствам. Итак, давайте упомянем некоторые из основных особенностей трапеции, которые выделяют ее среди других четырехугольников.
Однако каждый из них отличается по своим свойствам. Итак, давайте упомянем некоторые из основных особенностей трапеции, которые выделяют ее среди других четырехугольников.Особенности:
- Каждая трапеция имеет параллельные основания.
- Сумма углов, лежащих рядом друг с другом, равна 180 градусам.
- Если обе противоположные стороны трапеции параллельны, мы называем ее параллелограммом.
- Если обе пары противоположных сторон трапеции параллельны, все стороны имеют одинаковую длину и все углы прямые (90 градусов), мы называем ее квадратом.
- Если у нас есть две пары параллельных сторон, а противоположные стороны имеют одинаковую длину с прямыми углами на каждой стороне, мы называем это прямоугольником.
Площадь трапеции ( квадратных фута ) — это количество квадратных единиц, которые мы можем поместить в одну трапецию. Таким образом, число, которое мы получаем в результате расчета, в основном выражается в квадратных метрах, квадратных футах или квадратных дюймах.

пр. У нас есть 10 квадратных единиц, каждая длиной 1 метр — квадратные метры этой трапеции составляют 10 квадратных метров.
В двух словах, площадь трапеции равна среднему значению ее параллельных сторон и умножению этого числа на высоту трапеции , которая является расстоянием между двумя противоположными сторонами.
Как найти площадь трапеции?Нахождение площади трапеции очень похоже на нахождение площади других четырехугольников, таких как прямоугольники или треугольники. Во-первых, прежде чем мы покажем шаги по нахождению площади трапеции, нам нужно знать следующие параметры: длину обеих параллельных сторон и высоту трапеции.
Зная эти параметры, мы можем найти площадь трапеции в квадратных футах:
- Сложение длин двух противоположных сторон (сторона a + сторона b)
- Найти расстояние по перпендикуляру между стороной a и стороной b
- Умножить расстояние на сложение двух указанных сторон
- Полученные результаты из уравнения разделить на два, и он вернет квадратные метры трапеции.

Зная шаги нахождения площади трапеции, давайте посмотрим, что такое формула заданной площади в координатной геометрии.
Площадь трапеции формулаПринцип работы калькуляторов, включая наш калькулятор площади трапеции, основан на следующей формуле:
Формула площади = (основание 1 + основание 2) \ умножить на высоту \ деление 2база 1 – короткая база
база 2 – более длинная база
высота h – перпендикулярное расстояние между противоположными сторонами
Исключение: если обе стороны трапеции имеют одинаковую длину, то формула становится еще короче:
Формула площади = основание \ высотабаза – база 1 и база 2 (одинаковые)
высота
Проверяем, какие прямые параллельны данной трапеции, и находим их сумму.Это базовая точка при расчете его площади. Затем мы проводим линию между параллельными линиями, которая является высотой трапеции. Затем разделите это число на 2, и вы решите площадь трапеции.
Использование калькулятора площади трапеции: пример
Некоторые математические расчеты всегда проще объяснить на примере из жизни. Таким образом, в этом разделе давайте создадим сценарий и воспользуемся калькулятором площади трапеции, чтобы вычислить ее площадь в квадратных футах.
Сценарий: Вы находитесь на стройке и получаете задание осмотреть недавно построенный мост. Ферменный мост имеет свои размеры, а вам дана длина и высота его сторон. Ваша задача вычислить его площадь. Как мы подходим к этой задаче?
Более длинная сторона имеет длину 16 м, а более короткая сторона имеет длину 12 м. Расстояние между ними 4м. Для расчета используем формулу площади.
Примечание: Это только для примера, поэтому я рекомендую вам использовать для этого наш калькулятор.Это быстро и надежно. Помимо нахождения площади, вы также можете вычислить периметр трапеции и углы между сторонами и катетами.
A = (основание 1 + основание 2) \ умножить на высоту \ деление 2
A = (16 + 12) \× 4 \дел 2 = 56 квадратных метров
Альтернативный сценарий: если бы обе стороны были одинаковой длины (12 м), мы могли бы использовать более простую формулу:
А = 12 х 4 = 48 квадратных метров
Как найти периметр трапеции?Как правило, термин «периметр» обозначает площадь внутри конкретной геометрической фигуры.Он включает в себя все граничные линии (стороны) фигуры и дает вам их общую сумму. Теперь, применяя это определение к трапеции, мы можем сказать, что периметр трапеции — это общая сумма всех ее сторон. Поскольку у трапеции четыре стороны, периметр равен сумме ее четырех сторон. Давайте покажем это в формуле ниже:
Р = а + б + с + гП – периметр трапеции
а, б, в, г – трапециевидные стороны
Пример: Найдите периметр трапеции со сторонами a = 8 м, b = 6 м, c = 3 м, d = 4 м
P = 8 м + 6 м + 3 м + 4 м = 21 мОтношение площадей треугольников в трапеции
В сегодняшнем уроке мы будем использовать подобные треугольники и треугольники с одинаковой высотой, чтобы найти отношение между площадями треугольников, образованных пересечением диагоналей трапеции.

Диагонали трапеции образуют 2 подобных треугольника. и два других набора треугольников с одинаковым основанием и высотой. Это свойство используется во многих задачах геометрии, которые требуют, чтобы вы нашли отношение площадей этих треугольников или отношение сторон.
Вот один пример.
Задача
ABCD — трапеция (AB||CD). Его диагонали AC и BD пересекаются в точке O. Отношение площадей треугольников △ABO и △CDO равно 16:25. Найдите отношение площади △AOD к площади трапеции.
Стратегия
Задачи, требующие нахождения отношения площадей или отношения отрезков, часто основаны на использовании подобных треугольников и использовании того факта, что если ΔABC ∼ ΔDEF, то AB/DE=BC/EF=AC/DF.
В других случаях, если мы просто сравниваем площади треугольников, то часто пользуются тем, что отношение площадей треугольников с одинаковым основанием равно отношению их высот, а отношение площадей треугольников с одинаковым основанием высота равна отношению их оснований.
 Пример такой проблемы можно найти на этой странице.
Пример такой проблемы можно найти на этой странице.Так что в этой задаче — и то, и другое! Диагонали трапеции образуют два подобных треугольника (△ABO и △CDO) и несколько пар треугольников с одинаковым основанием (△ACD и △BDC; △DBA и △CAB) или одинаковой высотой (△ABO и △ADO; △BAO и △BOC).
И еще одна подсказка в условии задачи заключается в том, что отношение между двумя треугольниками △ABO и △CDO равно 16:25.
Это и намек на то, какие треугольники подобны (△ABO и △CDO), и каков масштабный коэффициент, поскольку мы знаем, что отношение площадей подобных треугольников равно квадрату масштабного коэффициента, а 16 и 25 равны квадраты целых чисел (4 и 5 соответственно).
Доказательство
(1) AB||CD //Дано
(2) ∠ACD≅ ∠CAB //Чередующиеся внутренние углы между двумя параллельными прямыми
(3) ∠ABD ≅ ∠BDC //Чередующиеся внутренние углы между двумя параллельными линии
(4) ∠BOA ≅ ∠DOC //Вертикальные углы
(5) ΔABO∼ ΔCDO //(2), (3), (4), Угол-Угол-Угол
(6) Площадь ABO /Площадь CDO =16/25 //Дано
(7) AO/OC=BO/OD=√(16/25)=⅘ //Отношение площадей подобных треугольников равно квадрату масштабного коэффициента
(8) Площадь ABO / Площадь ADO =⅘ //Отношение площадей треугольников одинаковой высоты равно отношению их оснований
(9) Площадь ABO / Площадь BOC =⅘ //Отношение площадей треугольников с одинаковой высотой одинаково s отношение их основанийSet Area ABO =16k.
 Тогда Area CDO = 25k, а Area ADO = Area BOC = 20k.
Тогда Area CDO = 25k, а Area ADO = Area BOC = 20k.(10) Область ABCD = Область ABO + Область ADO + Область CDO + Область BOC = 16k+20k+25k+20k=81k|
(11) Площадь AOD / Область ABCD =20k/81k=20/81Введение, формулы, свойства, примеры решения и часто задаваемые вопросы по форме трапеции или трапеции.Итак, давайте узнаем, что такое трапеция.
Четырехсторонняя двумерная фигура, одна из противоположных сторон которой параллельна, а две другие непараллельны, называется трапецией. Противоположные стороны называются основаниями, непараллельные стороны называются катетами трапеции, а перпендикулярное расстояние между двумя параллельными сторонами называется высотой или высотой трапеции.
Трапеции Определение
Четырехугольник, одна сторона которого параллельна, а две другие стороны не параллельны, называется трапецией.
 Трапецию также называют трапецией.
Трапецию также называют трапецией.Трапециевидные формы
После того, как мы поняли, что такое трапеция, теперь давайте посмотрим на трапециевидные формы. Математика форм трапеций поможет вам идентифицировать различные формы трапеций. Согласно определению трапеции, трапеция — это четырехсторонняя фигура с двумя параллельными сторонами и двумя непараллельными сторонами. Существуют разные формы трапеций или, по их форме, можно сказать, что трапеции бывают разных типов.
Различные формы трапеций Математика
Давайте сначала посмотрим на различные свойства трапеций и различных типов трапеций.Свойства трапеции помогут вам построить трапецию.
Свойства трапеции
Некоторые из основных свойств трапеции следующие:
Основания параллельны друг другу.
Угол нижнего основания и угол верхнего основания образуют линейную пару, т.
 е. 1800.
е. 1800.Медиана параллельна обоим основаниям. А длина медианы — это среднее длин двух оснований, т.е. m = a+b/2
В трапеции, если обе пары ее противоположных сторон параллельны, это будет параллелограмм.
В трапеции, если обе пары ее противоположных сторон параллельны и все ее стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то это квадрат
В трапеции, если обе пары ее противоположные стороны параллельны; его противоположные стороны имеют одинаковую длину и расположены под прямым углом друг к другу, то это прямоугольник.
Типы трапеций:
Различные типы трапеций:
- 0
- 0 0
INOSCELES Trapezoids
Scelene Trapezoids
правые трапециевии
углов называется прямоугольной трапецией.

Равнобедренные трапеции
В данной трапеции, если непараллельные стороны или катеты трапеции равны по длине, она называется равнобедренной трапецией.
Разносторонние трапеции
В данной трапеции, если ни стороны, ни углы трапеции не равны, мы называем ее разносторонней трапецией.
Площадь трапеции
Площадь трапеции вычисляется путем умножения среднего значения оснований на высоту трапеции.
Площадь трапеции = (a + b/2) x h, где a и b — два основания, а h — высота трапеции.
Площадь трапеции = ½ (a+ b) h
Периметр трапеции равен сумме всех сторон a Если a, b, c и d — все четыре стороны трапеции, то формула периметра определяется как:
a + b + c + d
Медиана трапеции
Медиана — это отрезок, проведенный из середины непараллельной стороны так, чтобы он был параллелен обоим основаниям.

Медиана вычисляется как среднее длин двух оснований:
м = a+b/2, где a и b площади длин оснований
Если медиана дана, мы можем вычислить даже площадь трапеции Формула
A = MXH
Median из трапеции = A + B / 2
Наклонная сторона правой трапеции
Здесь B и B являются основой правой трапеции , h — высота, l — наклонная сторона трапеции.2} \]
Решенные примеры
Пример 1. Дана трапеция с основаниями 6 м, 10 м и высотой 5 м. Найдите площадь трапеции.
Решение: имеем a = 6см, b = 10м и h = 5м 5
= 8 x 5
= 40 м2
Пример 2. Если основания трапеции равны 5 см, 8 см, 4 см и 6 см. Найдите периметр трапеции.
Решение: имеем a = 5 см, b = 8 см, c = 4 см и d = 6 см, тогда
По формуле периметра имеем
Периметр трапеции = a + b + c+ d
= 5 + 8 + 4 + 6
= 23 см
Викторина Время
Периметр равнобедренной трапеции равен 120 м, а основания 50 и 30 м.
 Вычислите площадь трапеции и длины непараллельных сторон.
Вычислите площадь трапеции и длины непараллельных сторон.Найдите площадь трапеции, если ее основания равны 12 см и 4 см соответственно.А высота трапеции 7см.
Трапеция | Математическая лексика
Свойства
Параллельные стороны трапеции называются основаниями трапеции. В общем случае, когда четырехугольник имеет только одну пару параллельных сторон, стороны называются короткое основание и длинное основание .
По своим свойствам трапеция также относится к семейству четырехугольников.
Формула
Площадь A трапеции с основаниями b и B и высотой h равна: \(A=\frac{(B +b) × h}{2}\).
Учебные заметки
Проблема с определениями заключается в том, что учащиеся часто склонны ограничивать их значение, а не понимать их с общей точки зрения.

Например, четырехугольник с парой параллельных сторон называется «трапецией», но это не означает, что у трапеции может быть только одна пара параллельных сторон.По этой причине указывается «по крайней мере одна пара параллельных сторон». В результате все параллелограммы являются трапециями. Если бы определение следовало понимать в самом строгом смысле, то четырехугольник с более чем одной парой параллельных сторон имел бы уже не одну пару и не был бы трапецией!
Парадокс!
Если рассматривать другие свойства трапеции, в том числе способ вычисления ее периметра и площади, то можно отметить, что эти свойства относятся и к параллелограммам.
Следует уточнить, что, хотя параллелограмм имеет конгруэнтные противоположные стороны, он не является равнобедренной трапецией, однако прямоугольник таков, поскольку он удовлетворяет определению равнобедренной трапеции, которое гласит, что равнобедренная трапеция симметрична относительно серединного перпендикуляра к его основания.
 Равнобедренную трапецию можно вписать в окружность, что является свойством, которым обладают не все параллелограммы.
Равнобедренную трапецию можно вписать в окружность, что является свойством, которым обладают не все параллелограммы.Говоря о трапециях вообще, мы не останавливаемся на частных случаях, таких как параллелограммы, ромбы, прямоугольники или квадраты, под которыми понимаются частные виды трапеций.
Следует отметить, что более ранние определения, такие как определение в Nouveau manuel complet d’architecture М. Туссена, опубликованное в 1837 году (стр. 32), указывают, что «трапеция имеет только две параллельные стороны […] ».
Разница между параллелограммом и трапецией
Параллелограмм и трапеция
Параллелограмм и трапеция (или трапеция) — два выпуклых четырехугольника. Несмотря на то, что это четырехугольники, геометрия трапеции существенно отличается от параллелограмма.
Параллелограмм
Параллелограмм можно определить как геометрическую фигуру с четырьмя сторонами, причем противоположные стороны параллельны друг другу.
 Точнее, это четырехугольник с двумя парами параллельных сторон. Эта параллельная природа придает параллелограммам множество геометрических характеристик.
Точнее, это четырехугольник с двумя парами параллельных сторон. Эта параллельная природа придает параллелограммам множество геометрических характеристик.Четырехугольник является параллелограммом, если обнаружены следующие геометрические характеристики.
• Две пары противоположных сторон имеют одинаковую длину.{\circ} = \пи рад[/латекс]
• Пара сторон, противолежащих друг другу, параллельна и имеет одинаковую длину. (AB = постоянный ток и AB∥DC)
• Диагонали делят друг друга пополам (AO = OC, BO = OD)
• Каждая диагональ делит четырехугольник на два равных треугольника. (∆ADB ≡ ∆BCD, ∆ABC ≡ ∆ADC)
Далее, сумма квадратов сторон равна сумме квадратов диагоналей. Иногда его называют законом параллелограмма , и он имеет широкое применение в физике и технике.(AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + BD 2 )
Каждая из вышеперечисленных характеристик может быть использована в качестве свойств, если установлено, что четырехугольник является параллелограммом.

Площадь параллелограмма можно вычислить произведением длины одной стороны и высоты противоположной стороны. Следовательно, площадь параллелограмма можно определить как
.Площадь параллелограмма = основание × высота = AB × h
Площадь параллелограмма не зависит от формы отдельного параллелограмма.Она зависит только от длины основания и высоты перпендикуляра.
Если стороны параллелограмма могут быть представлены двумя векторами, площадь может быть получена по величине векторного произведения (перекрестного произведения) двух соседних векторов.
Если стороны AB и AD представлены векторами ([latex]\overrightarrow{AB}[/latex]) и ([latex]\overrightarrow{AD}[/latex]) соответственно, площадь параллелограмма определяется как [латекс]\левый | \overrightarrow{AB}\times \overrightarrow{AD} \right | = AB\cdot AD \sin \alpha [/latex], где α — угол между [латекс]\overrightarrow{AB}[/латекс] и [латекс]\overrightarrow{AD}[/латекс].

Ниже приведены некоторые дополнительные свойства параллелограмма.
• Площадь параллелограмма вдвое больше площади треугольника, образованного любой из его диагоналей.
• Площадь параллелограмма делится пополам любой линией, проходящей через его середину.
• Любое невырожденное аффинное преобразование переводит параллелограмм в другой параллелограмм
• Параллелограмм имеет вращательную симметрию 2-го порядка
• Сумма расстояний от любой внутренней точки параллелограмма до сторон не зависит от положения точки
Трапеция
Трапеция (или Трапеция в британском английском) — выпуклый четырехугольник, у которого по крайней мере две стороны параллельны и неравны по длине.{2}}{b-a}}[/латекс]
Площадь трапеции можно рассчитать по следующей формуле
Площадь трапеции = [латекс]\фракция{а+b}{2}\умножить на час[/латекс]
В чем разница между параллелограммом и трапецией (трапецией)?
• И параллелограмм, и трапеция являются выпуклыми четырехугольниками.

• В параллелограмме обе пары противоположных сторон параллельны, а в трапеции параллельна только пара.
• Диагонали параллелограмма делят друг друга пополам (соотношение 1:1), а диагонали трапеции пересекаются с постоянным соотношением между сечениями.
• Площадь параллелограмма зависит от высоты и основания, а площадь трапеции зависит от высоты и середины отрезка.
• Два треугольника, образованные диагональю параллелограмма, всегда конгруэнтны, а треугольники трапеции могут быть либо конгруэнтны, либо нет.
Трапеции — Карьера сегодня
Что такое трапеции?
Четырехугольник, у которого две стороны параллельны, называется трапецией. В некоторых частях мира его также называют трапецией.
Стороны трапеции, параллельные друг другу, называются основаниями трапеции. Непараллельные стороны известны как ноги или боковые стороны.
 Расстояние между параллельными сторонами называется высотой.
Расстояние между параллельными сторонами называется высотой.Существуют некоторые разногласия по поводу определения трапеций. Одна школа математики считает, что трапеция может иметь одну и только одну пару параллельных сторон, а другая утверждает, что у трапеции может быть более одной пары параллельных сторон. Если рассматривать второе определение, то параллелограмм также является трапецией согласно этому. Но первое определение не считает параллелограмм трапецией.
Типы трапеций
Трапеции можно разделить на три группы:
- Прямоугольная трапеция имеет пару прямых углов.
- Если непараллельные стороны или стороны трапеции равны по длине, она называется равнобедренной трапецией.
- Когда ни стороны, ни углы трапеции не равны, мы называем ее разносторонней трапецией.
Площадь и периметр трапеций
Площадь трапеции можно вычислить, взяв среднее значение двух оснований и умножив его на высоту.
 Формула площади для трапеций задается как —
Формула площади для трапеций задается как —\(Площадь= \frac{a+b}{2}\times h\)
Трапециевидный периметр
Периметр трапеции равен сумме всех ее сторон.Следовательно, для трапеции со сторонами a, b, c и d формулу периметра можно записать в виде-
Периметр= a+b+c+d
Свойства трапеции
Существуют определенные свойства трапеций, которые идентифицируют их как трапеции-
- Углы при основании и диагонали равнобедренной трапеции равны.
- Если провести медиану трапеции, то она будет параллельна основаниям и ее длина будет равна средней длине оснований.{2}\)
Пример 2: Четыре стороны трапеции имеют длины 3 м, 5 м, 7 м и 4 м. Найдите его периметр. Решение:
Мы знаем, что периметр определяется суммой всех сторон.
Следовательно, периметр = 3+5+7+4
= 19 м
Пример 3: Является ли параллелограмм трапецией?
Решение: Нет, трапеция не является параллелограммом.

Согласно определению:
Параллелограмм имеет две пары параллельных сторон. пока
Трапеция имеет ровно две параллельные стороны.
Трапеции (ключевой этап 2)
Урок
Трапеция – это четырехсторонняя фигура с одной парой противоположных параллельных сторон.Оксфордский словарь английского языка определяет прямоугольник как «четырехугольник, у которого параллельны только две стороны.»
Части трапеции
- Параллельные стороны трапеции называются основаниями.
- Другие стороны трапеции называются катетами или боковыми сторонами.
Свойства трапеций
Периметр трапеции
Периметр трапеции находится по формуле:В этой формуле b 1 и b 2 — длины оснований трапеции, а l 1 и l 2 5 — длины катетов.

Площадь трапеции
Площадь трапеции находится по формуле:В этой формуле b 1 и b 2 — длины оснований трапеции, а h — высота трапеции.
Подробнее о том, как найти площадь трапецииИнтерактивный виджет
Вот интерактивный виджет, который поможет вам узнать о трапециях.Трапеция, Трапеция
Форма называется трапецией в Северной Америке. В англоязычных странах за пределами Северной Америки трапецию называют трапецией.Что в имени?
Трапеция и трапеция произошли от греческого слова «trapezion», что означает «маленький столик».Трапеция является многоугольником
Трапеция является разновидностью многоугольника. Многоугольник — это двумерная фигура с прямыми сторонами. Трапеция — это неправильный многоугольник. Неправильные многоугольники имеют разную длину сторон и разные углы.Трапеция является четырехугольником
Трапеция — это четырехугольник.
- 0
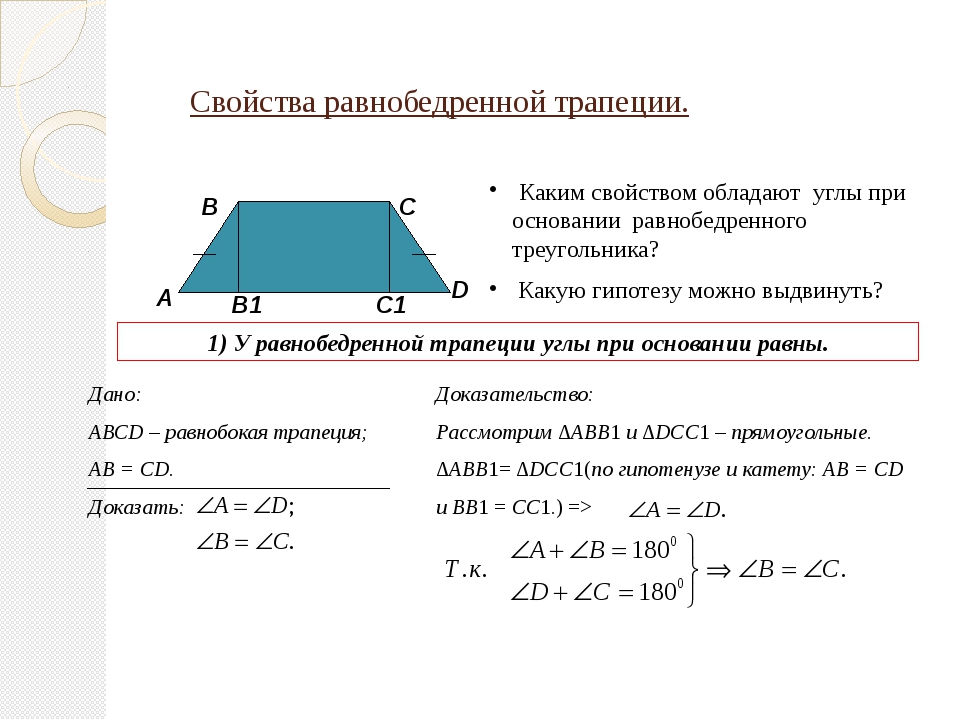 Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой для определения данной величины в случае, когда известны стороны трапеции. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .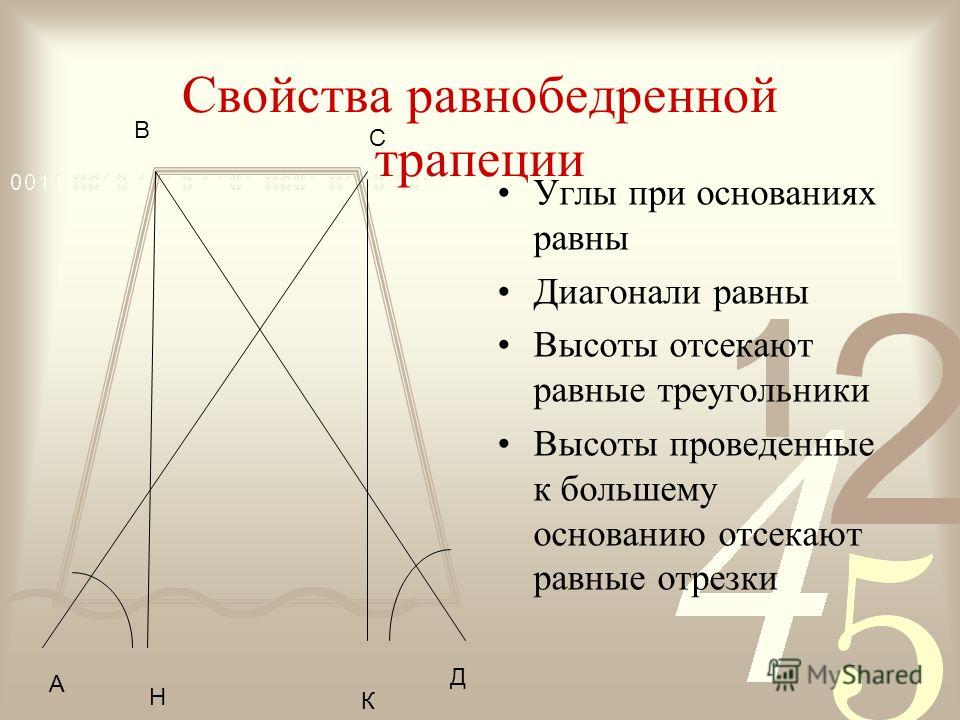 Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.


 Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ). Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. Радиус окружности можно вычислить по формуле: r = √ab .
Радиус окружности можно вычислить по формуле: r = √ab .
 2 \]
2 \]

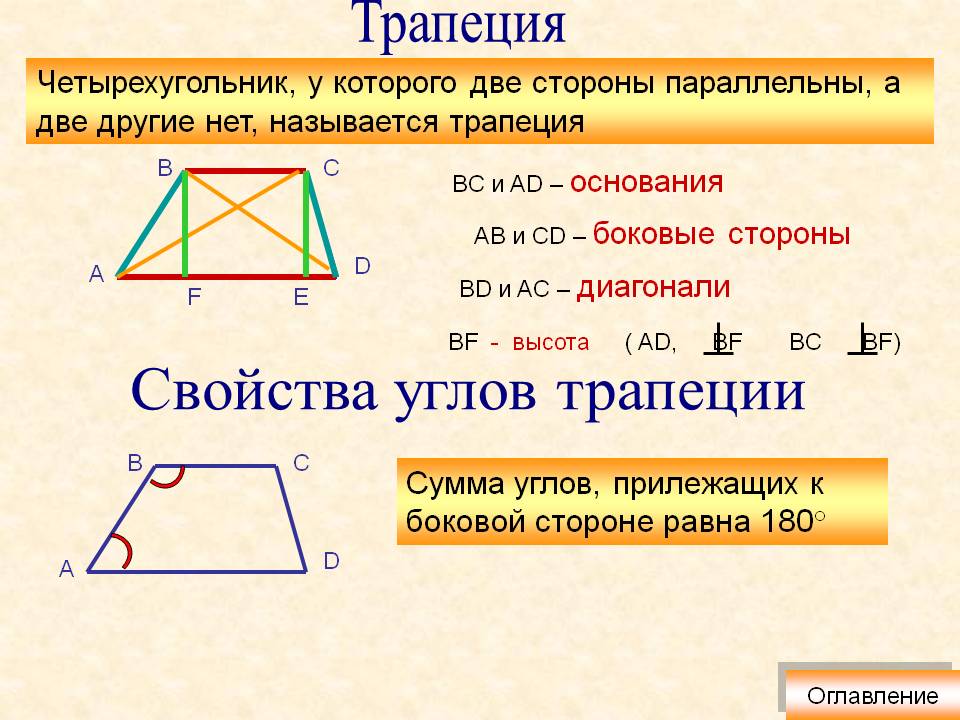
 \circ\right)=\frac63\cdot\frac12=1\) см.
\circ\right)=\frac63\cdot\frac12=1\) см. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований
Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований



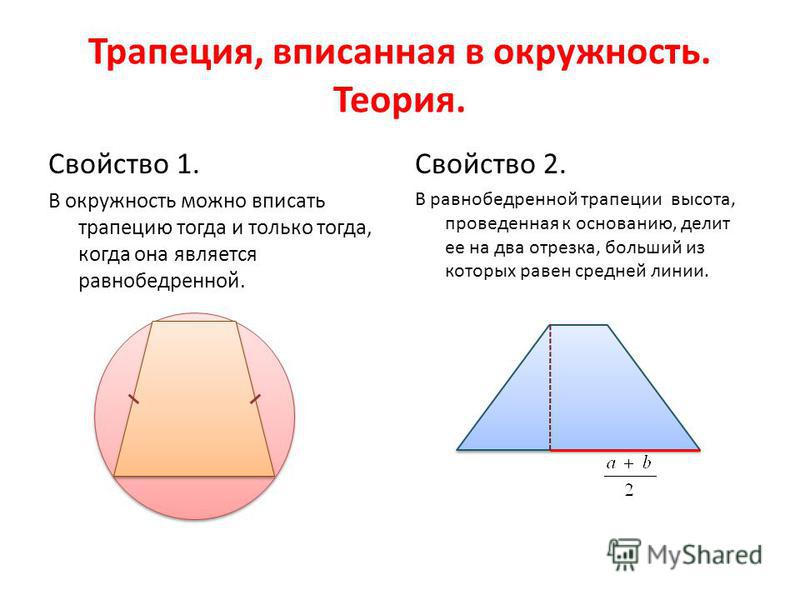 Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
 Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.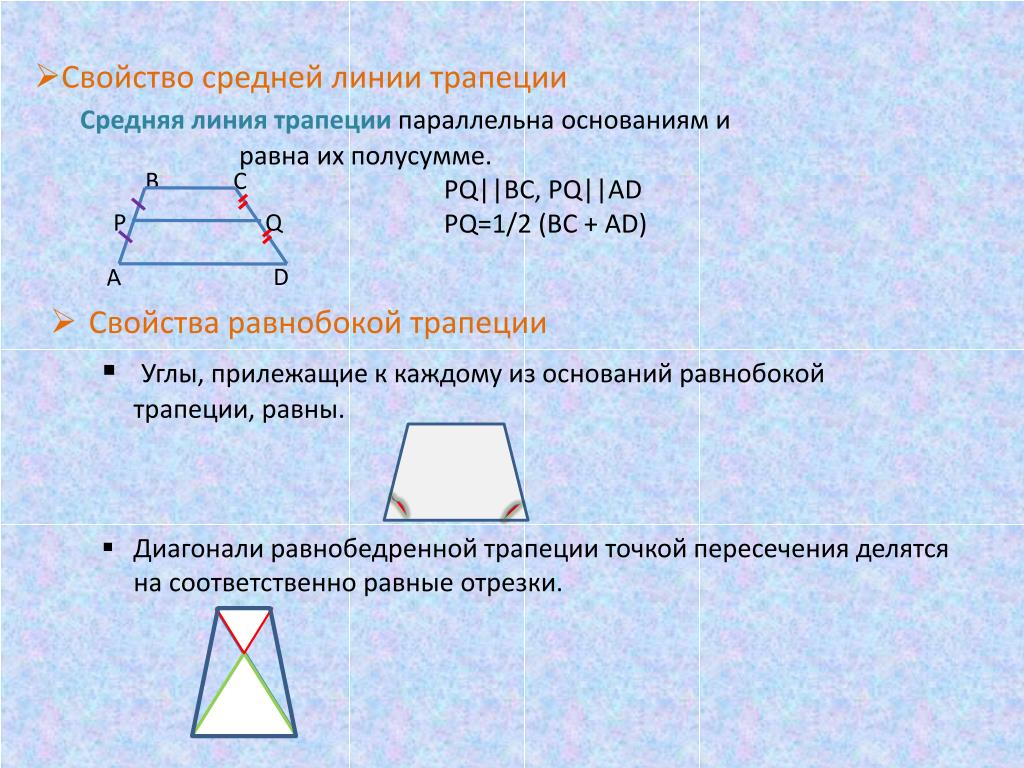
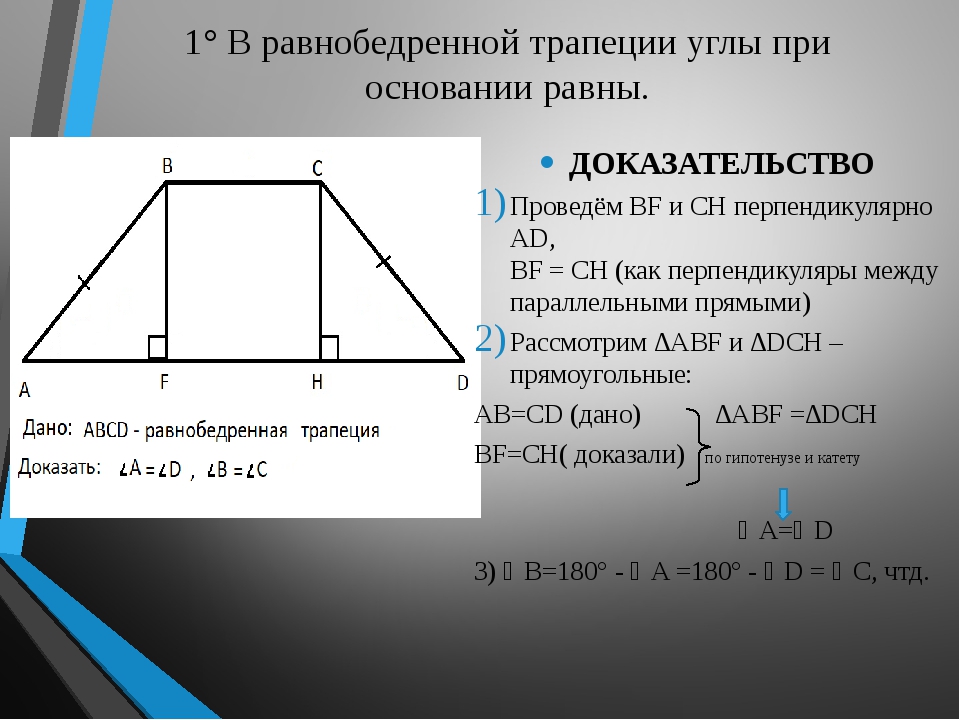 е. пересекаются под углом 90° (как это показано на рис.1).
е. пересекаются под углом 90° (как это показано на рис.1).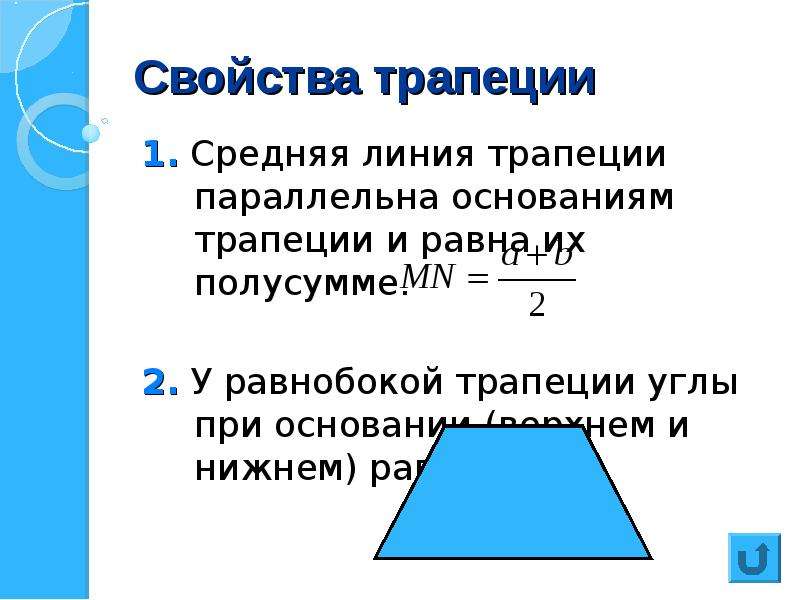 Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что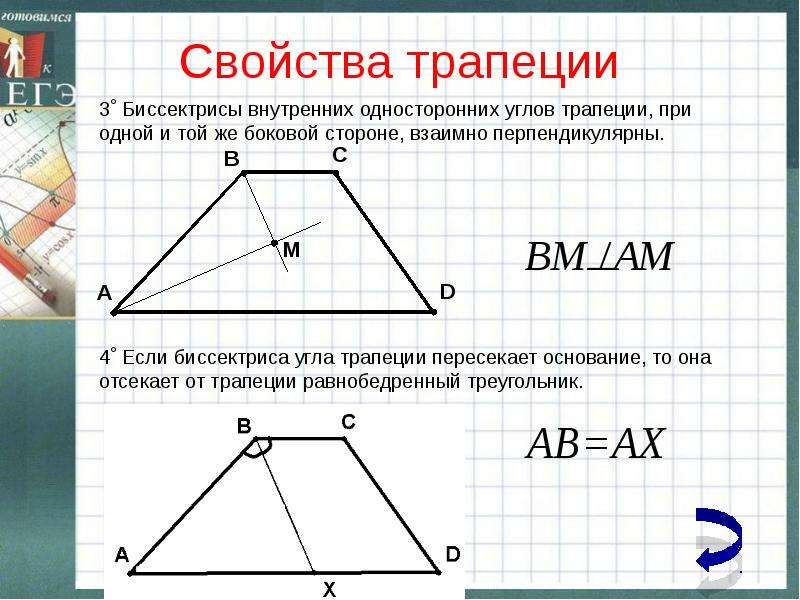


 Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно. Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.


 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
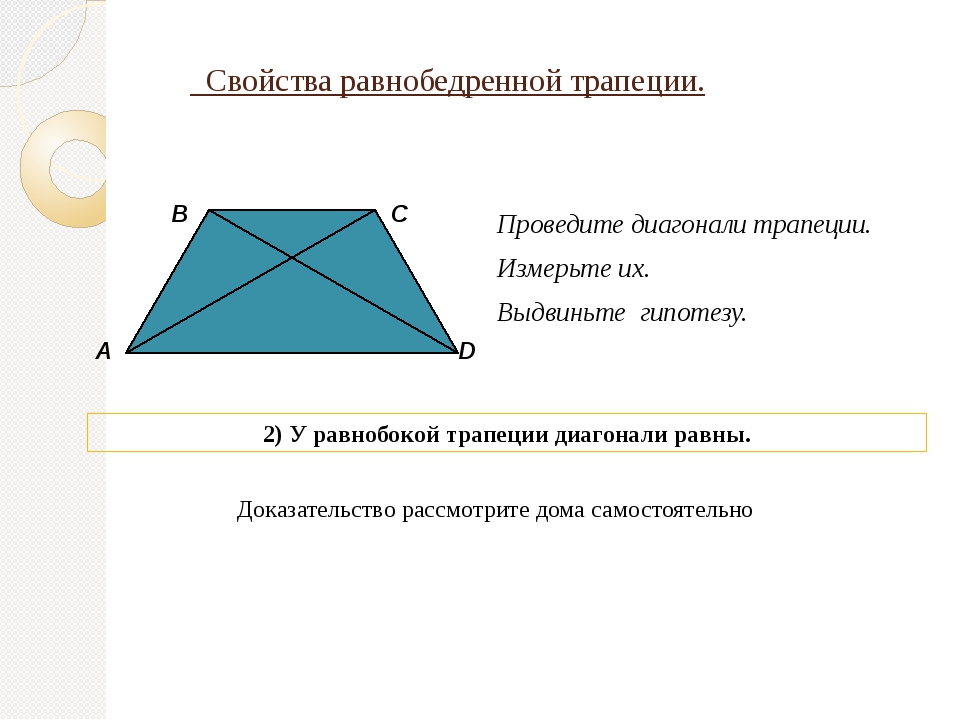
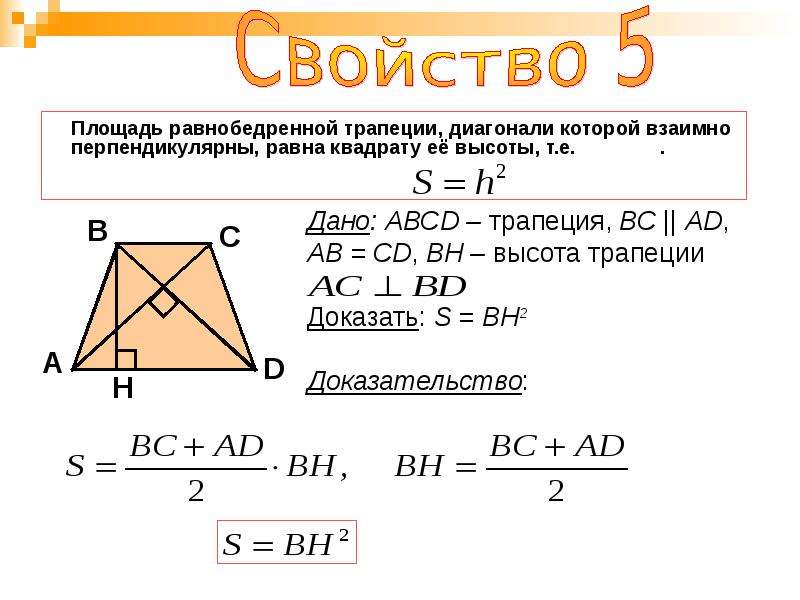
 Так и поймете быстрее, и запомните лучше.
Так и поймете быстрее, и запомните лучше.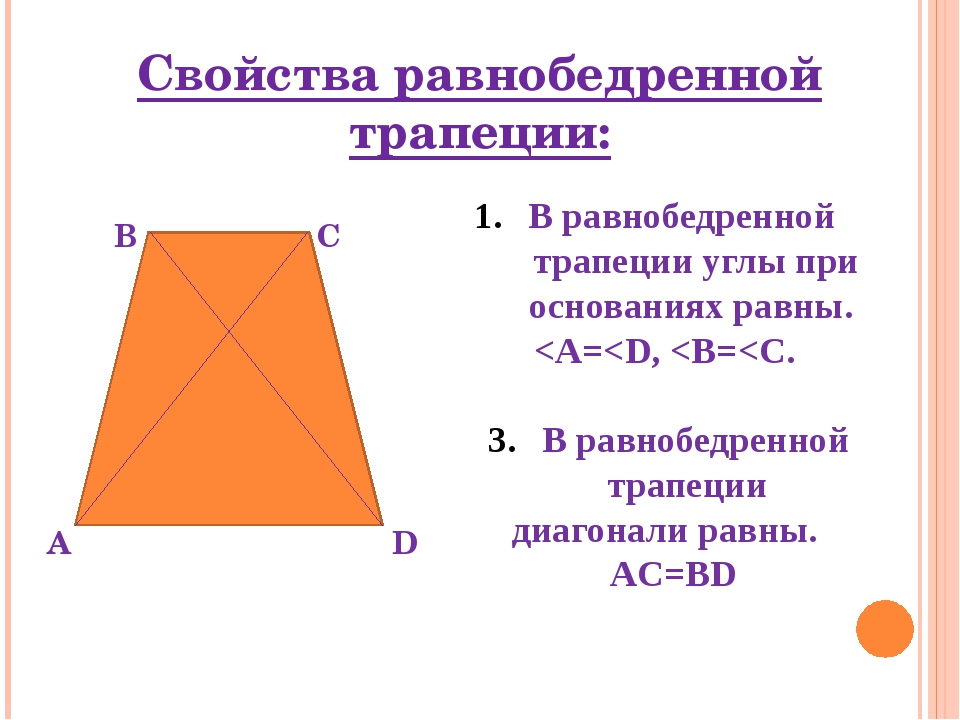 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
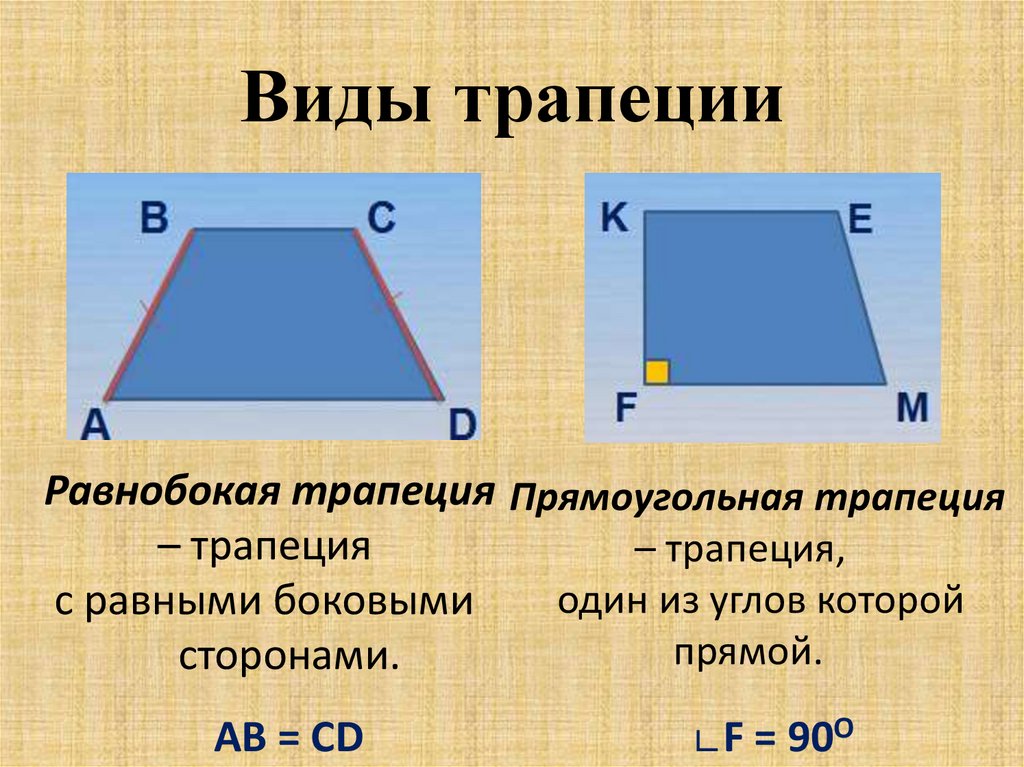 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).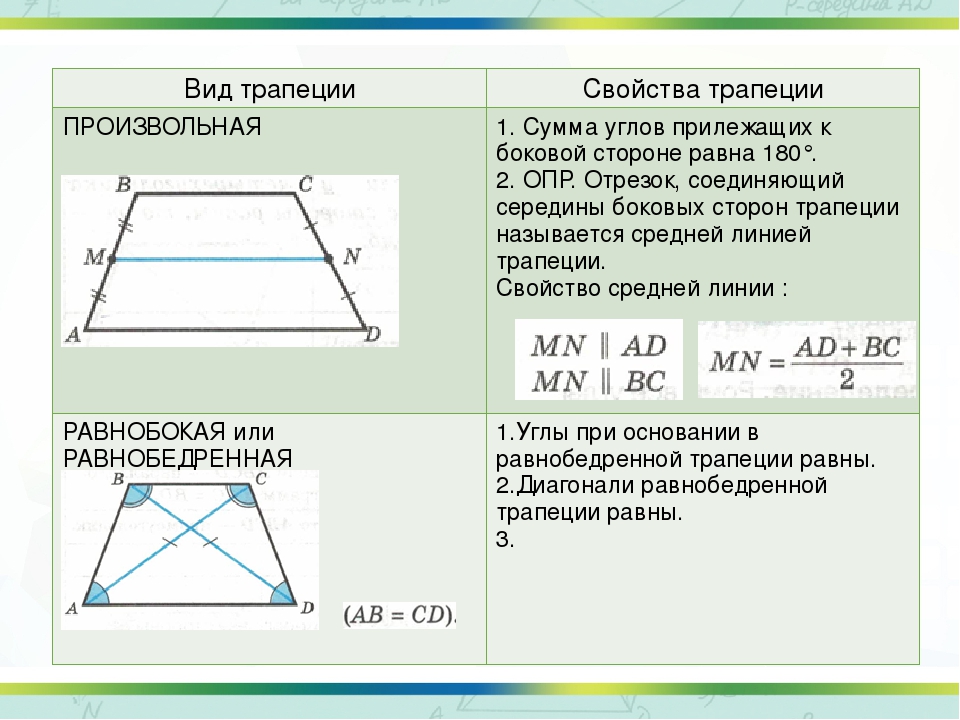 Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.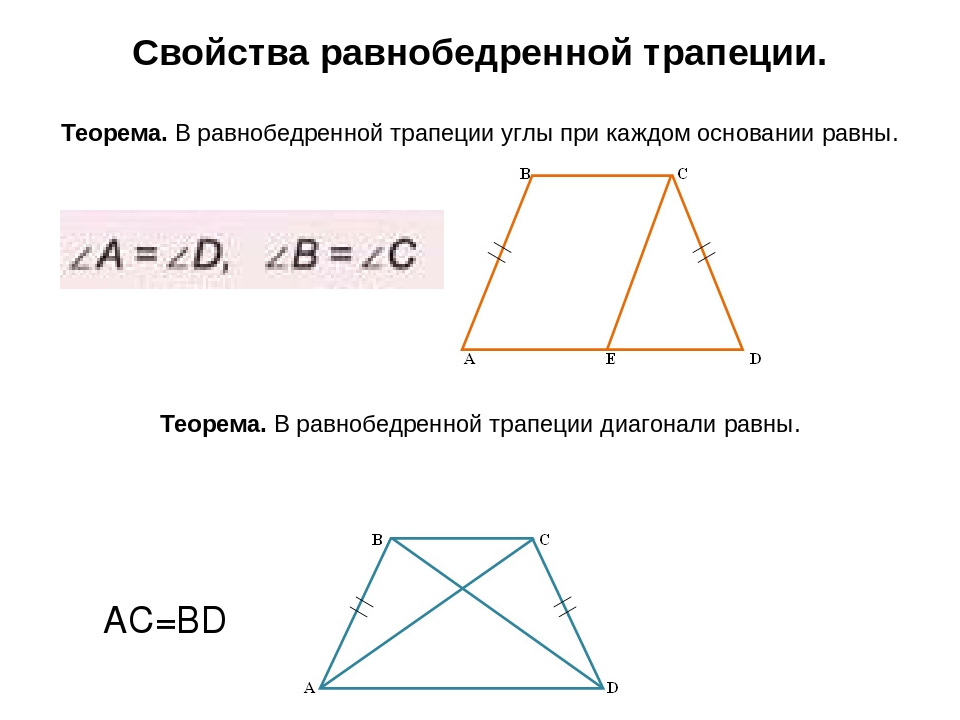


 {2}
.
{2}
.
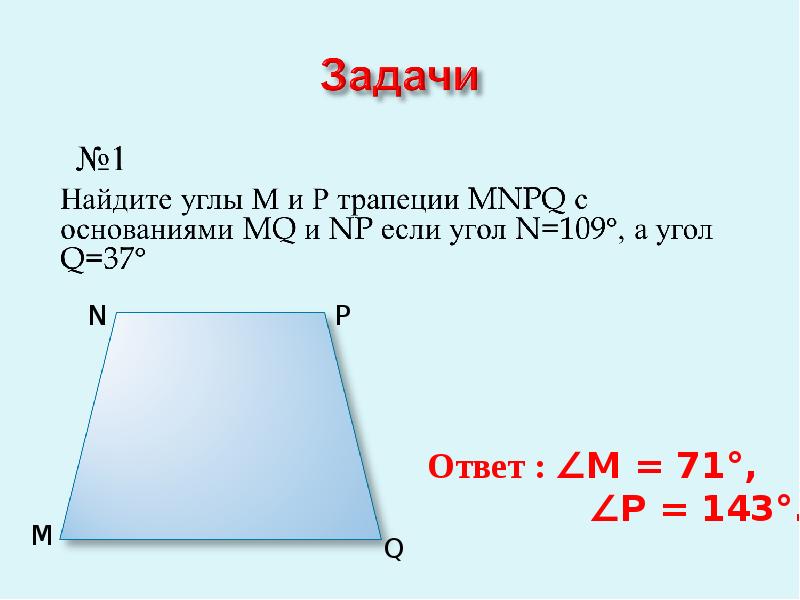
 По ней мы найдем значения первообразной в каждой из наших точек:
По ней мы найдем значения первообразной в каждой из наших точек:
 А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой: И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой: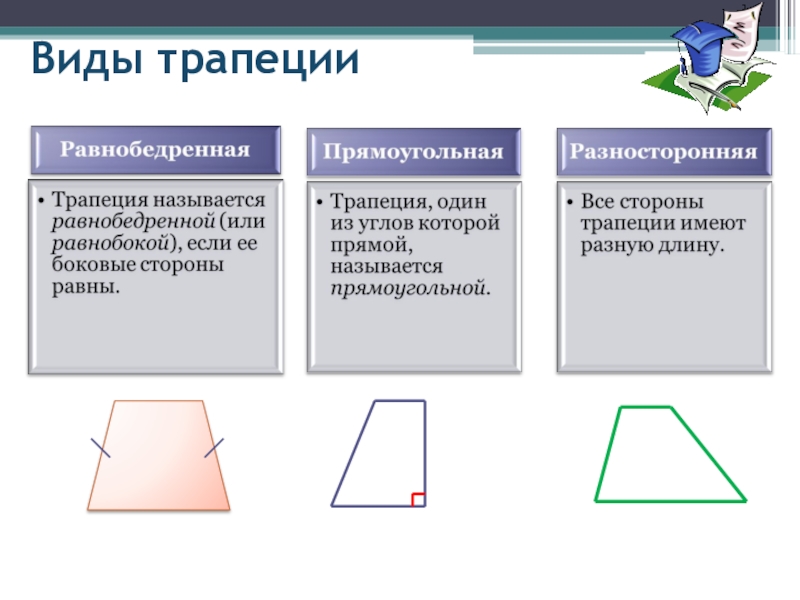 После вычисления площадей этих фигур останется их только сложить.
После вычисления площадей этих фигур останется их только сложить.
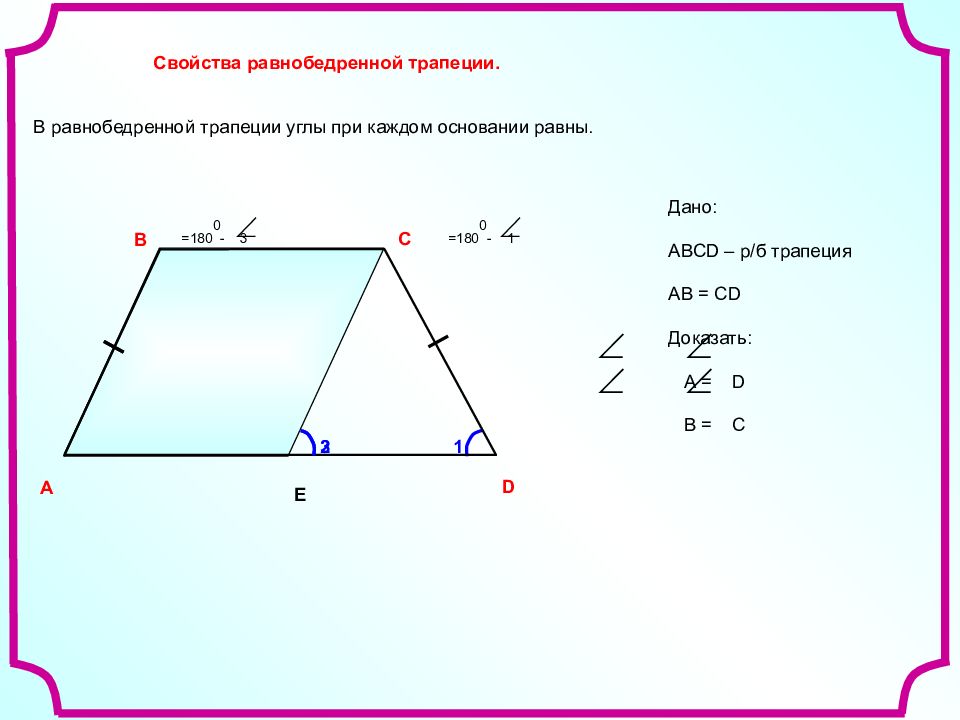 Задача решена.
Задача решена.
 На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.

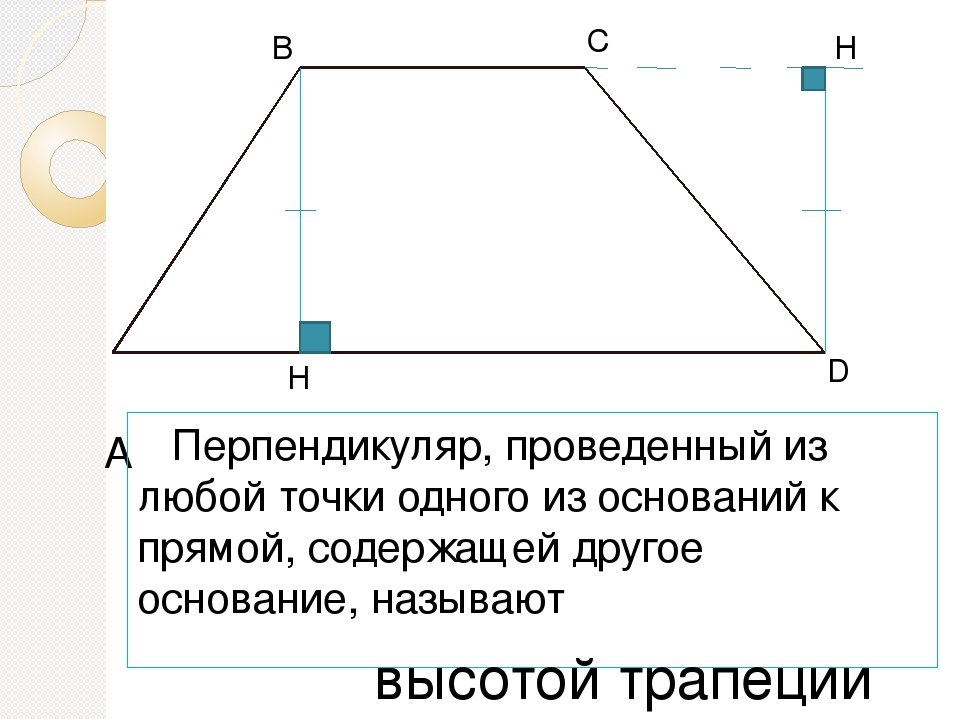 Теперь о площади трапеции.
Теперь о площади трапеции.

 Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .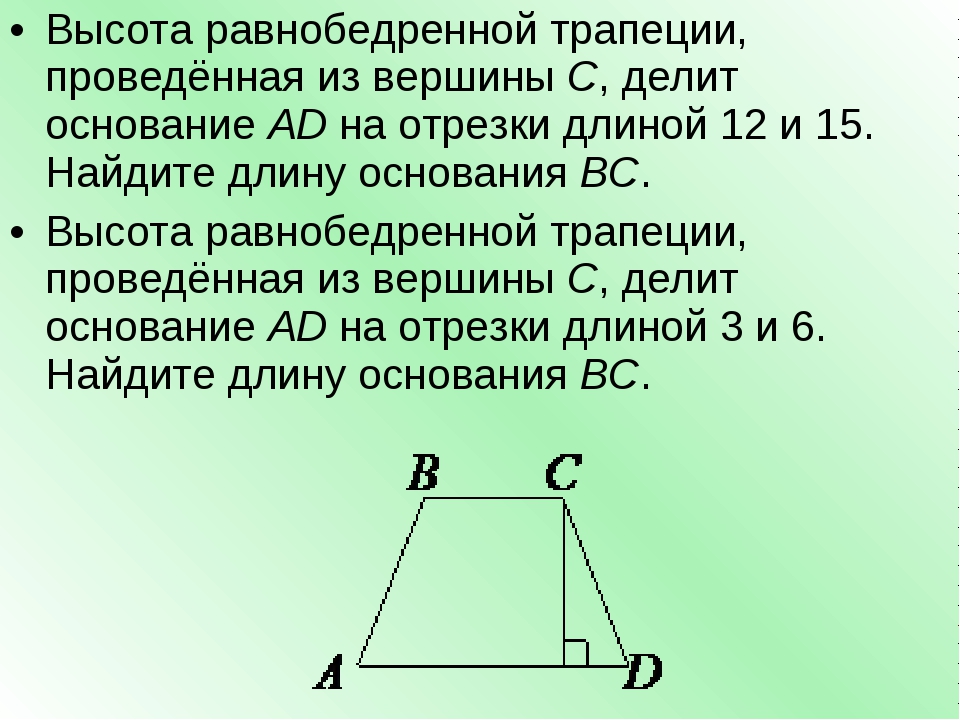 Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .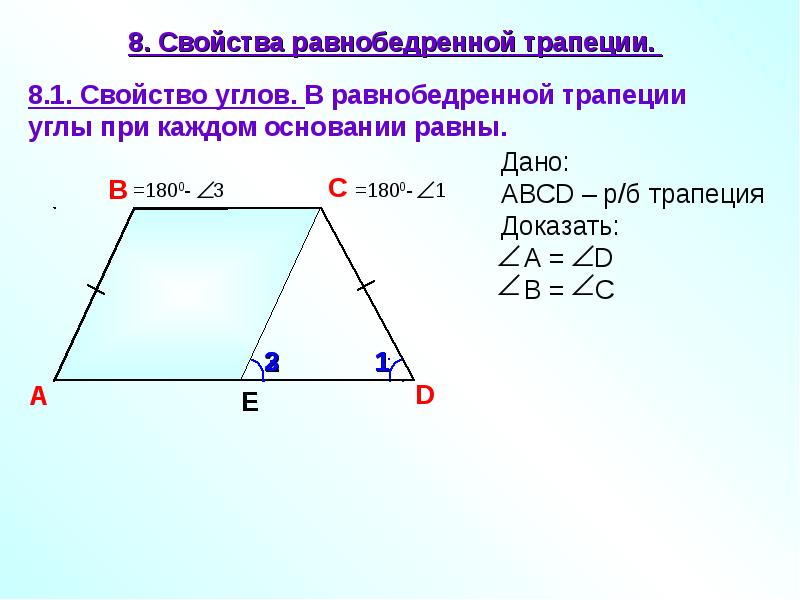 Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
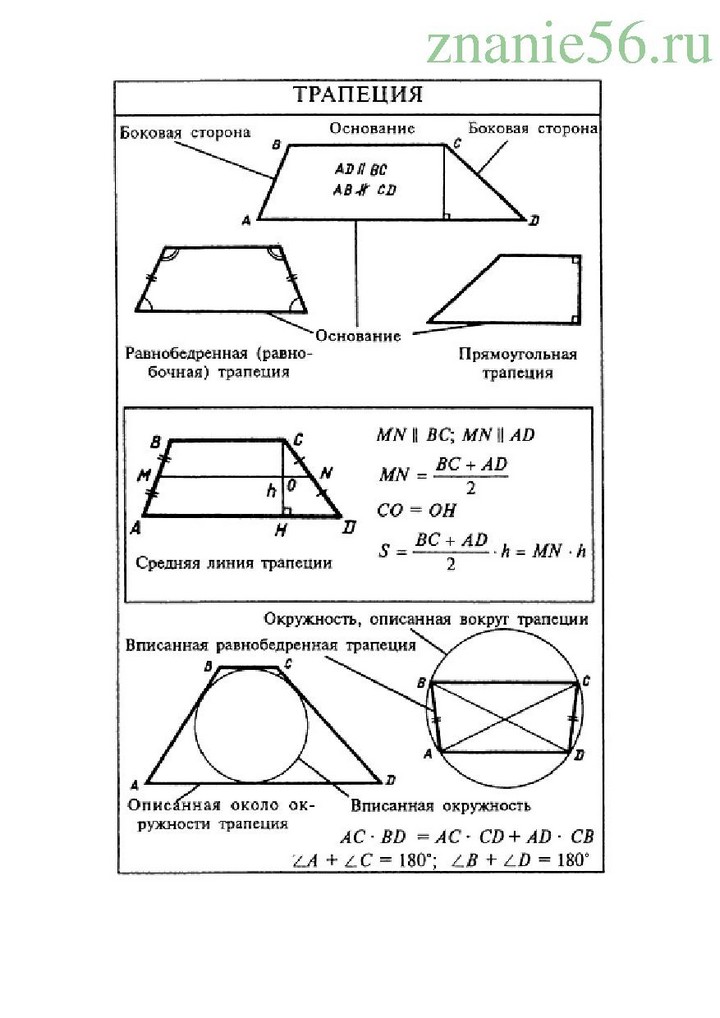 А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.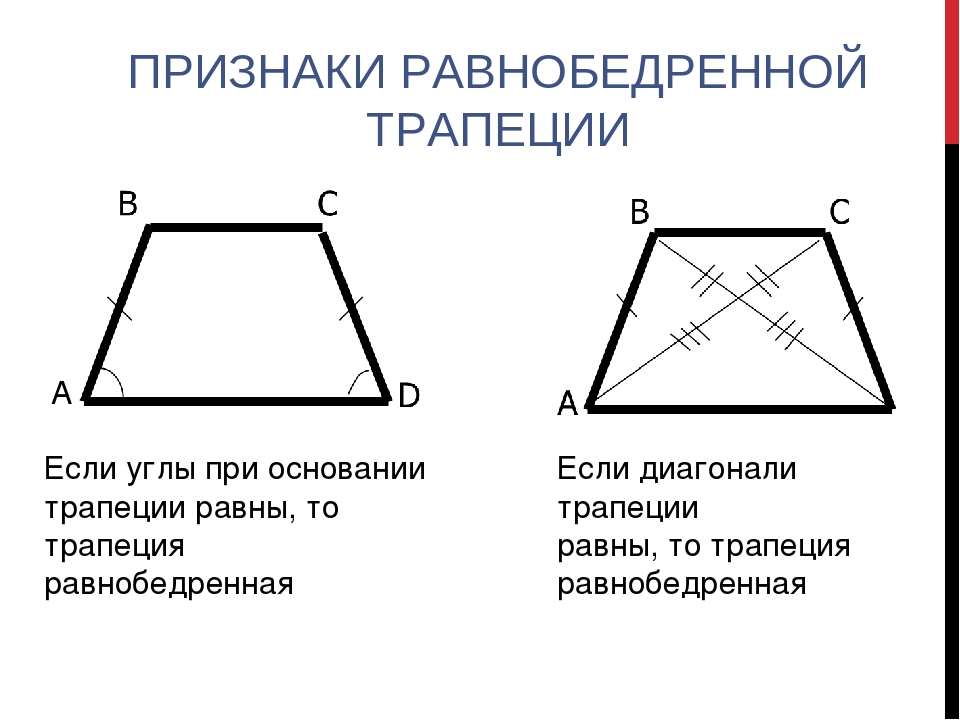

 В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем: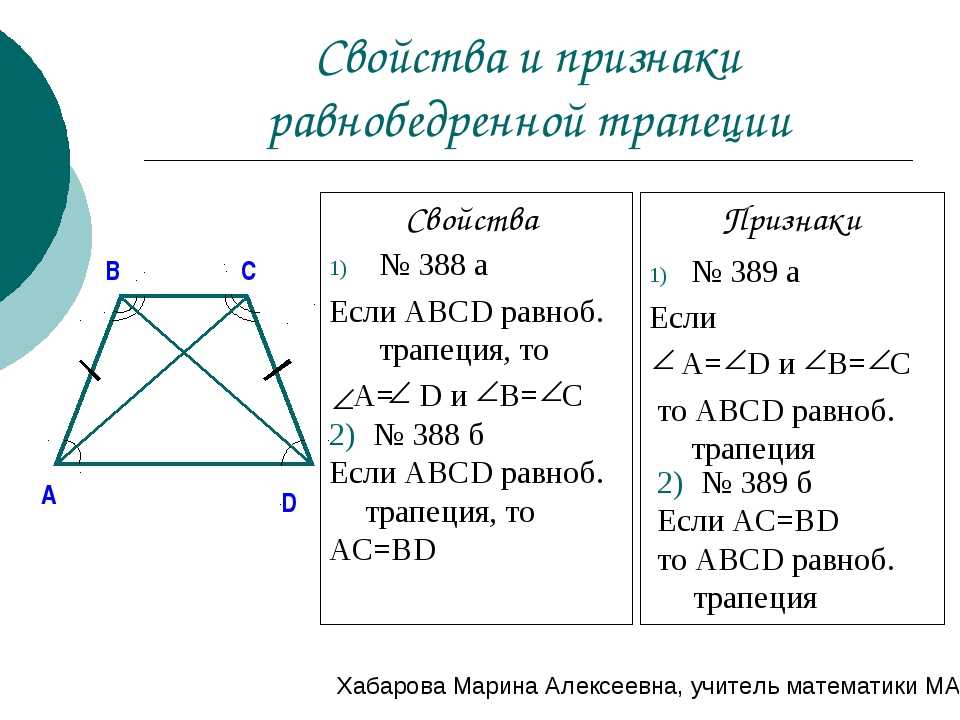 Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
 Найти площадь трапеции (Мехмат МГУ, 1970г).
Найти площадь трапеции (Мехмат МГУ, 1970г).

 70), то есть Проведем высоты и они равны.
70), то есть Проведем высоты и они равны.
 110). Пусть Докажем, что
110). Пусть Докажем, что  до н. э.).
до н. э.). Параллельные стороны называются основаниями, а непараллельные — катетами. Трапеция также может иметь параллельные стороны в некоторых случаях. Ноги могут быть ориентированы вертикально или горизонтально. Предположим, мы проводим прямую линию от одной стороны к противоположной. В этом случае мы называем это высотой ( перпендикулярного расстояния ) трапеции.
Параллельные стороны называются основаниями, а непараллельные — катетами. Трапеция также может иметь параллельные стороны в некоторых случаях. Ноги могут быть ориентированы вертикально или горизонтально. Предположим, мы проводим прямую линию от одной стороны к противоположной. В этом случае мы называем это высотой ( перпендикулярного расстояния ) трапеции.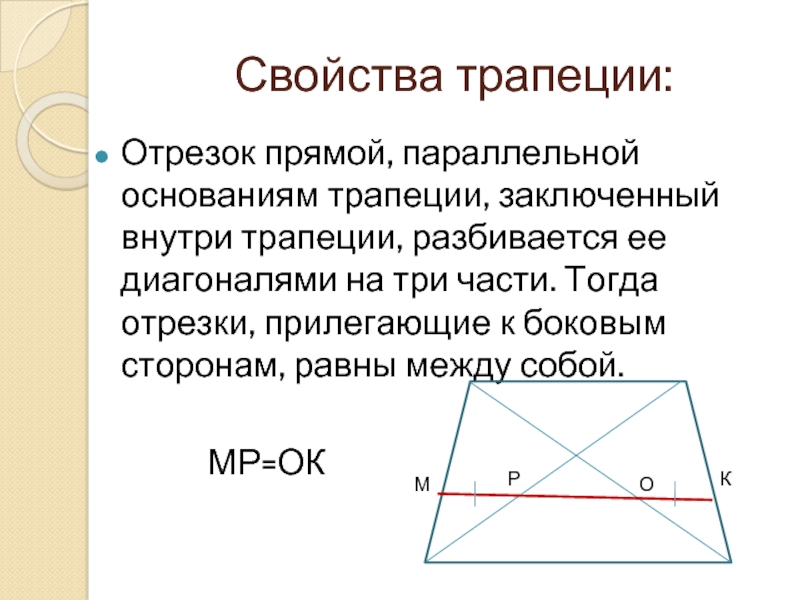 Острая трапеция
Острая трапеция 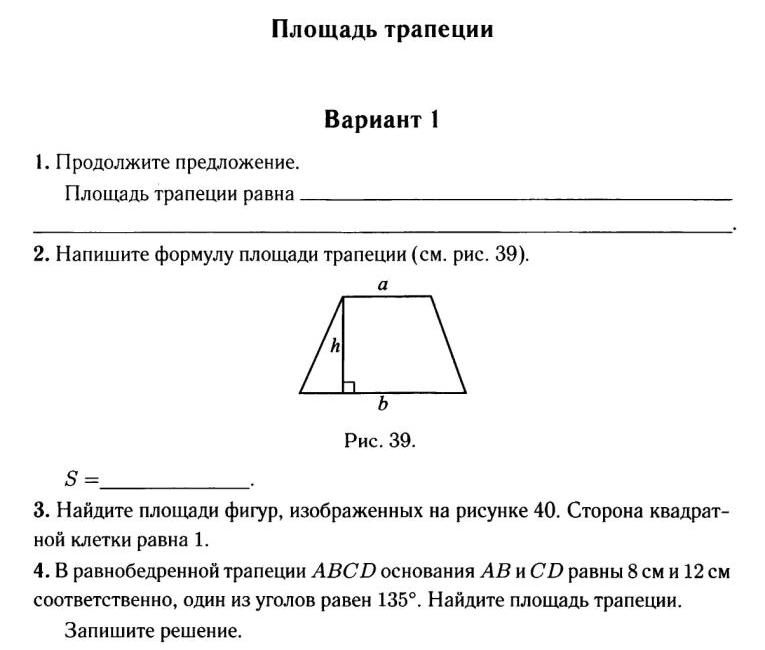 Однако каждый из них отличается по своим свойствам. Итак, давайте упомянем некоторые из основных особенностей трапеции, которые выделяют ее среди других четырехугольников.
Однако каждый из них отличается по своим свойствам. Итак, давайте упомянем некоторые из основных особенностей трапеции, которые выделяют ее среди других четырехугольников.

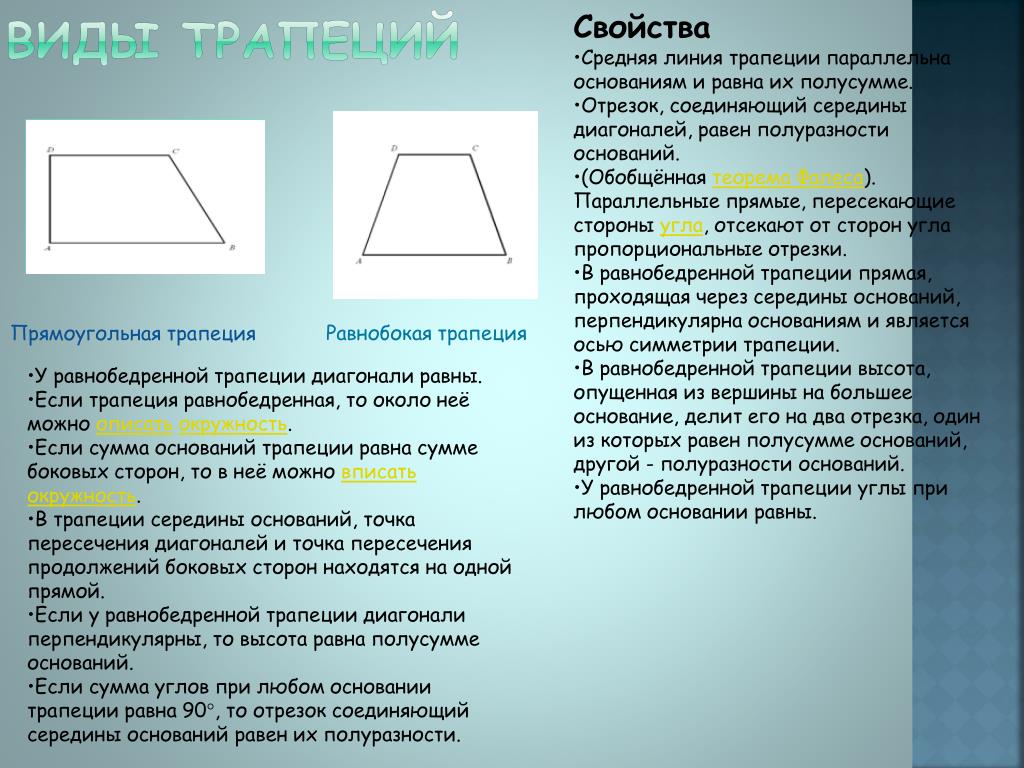
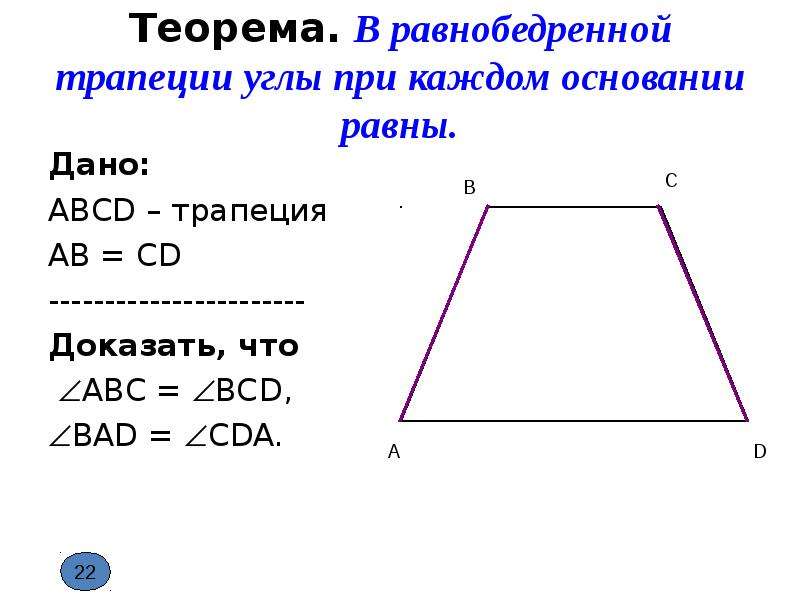

 Пример такой проблемы можно найти на этой странице.
Пример такой проблемы можно найти на этой странице. Тогда Area CDO = 25k, а Area ADO = Area BOC = 20k.
Тогда Area CDO = 25k, а Area ADO = Area BOC = 20k. Трапецию также называют трапецией.
Трапецию также называют трапецией. е. 1800.
е. 1800.

 Вычислите площадь трапеции и длины непараллельных сторон.
Вычислите площадь трапеции и длины непараллельных сторон.
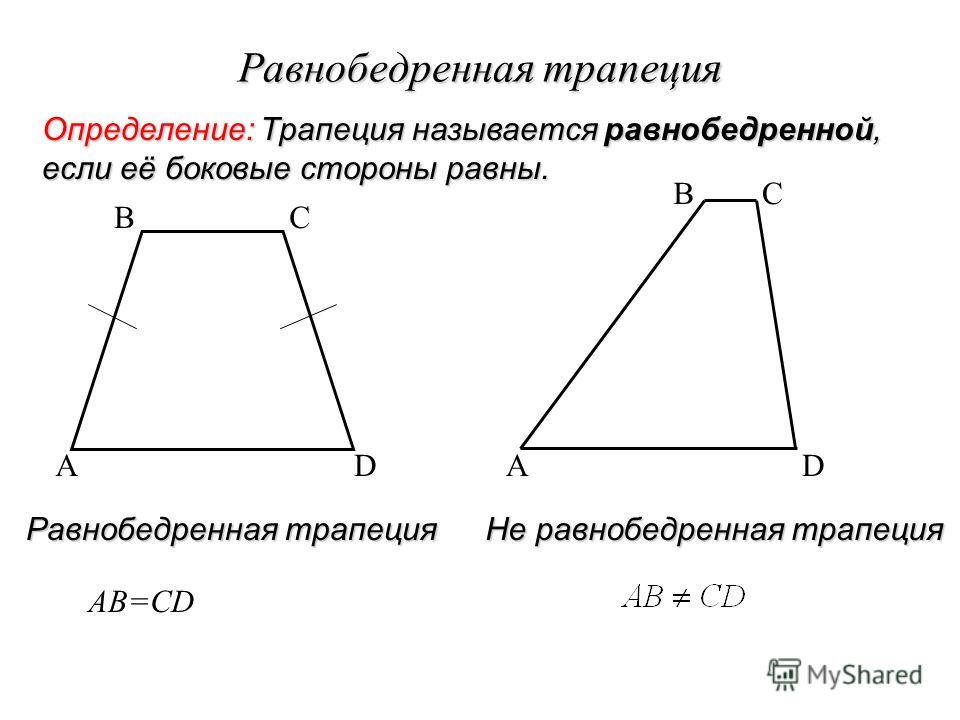 Равнобедренную трапецию можно вписать в окружность, что является свойством, которым обладают не все параллелограммы.
Равнобедренную трапецию можно вписать в окружность, что является свойством, которым обладают не все параллелограммы. Точнее, это четырехугольник с двумя парами параллельных сторон. Эта параллельная природа придает параллелограммам множество геометрических характеристик.
Точнее, это четырехугольник с двумя парами параллельных сторон. Эта параллельная природа придает параллелограммам множество геометрических характеристик.
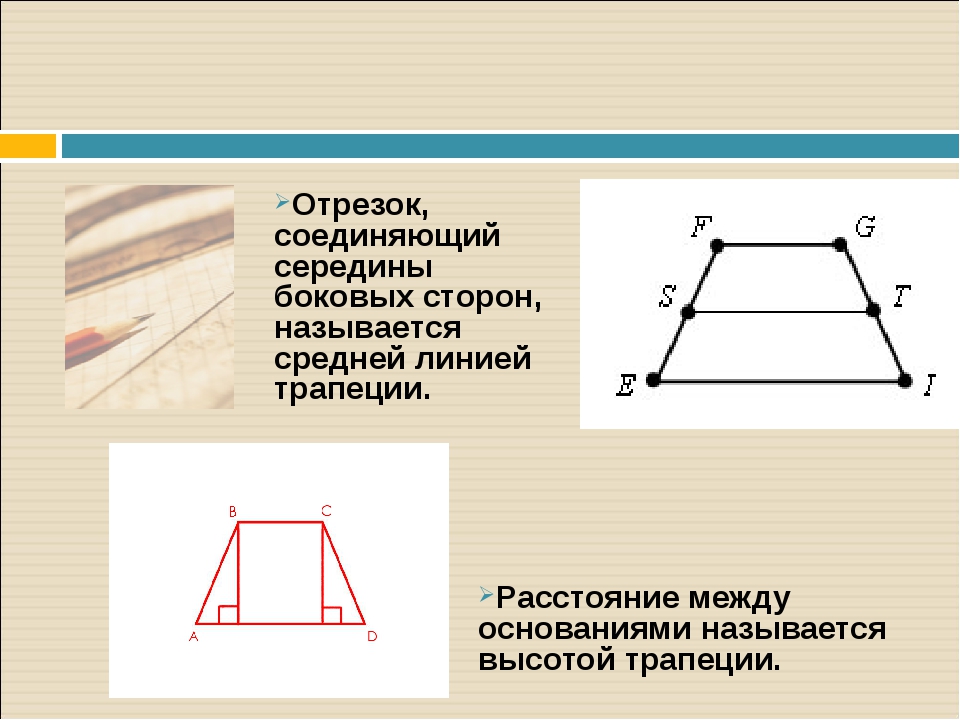

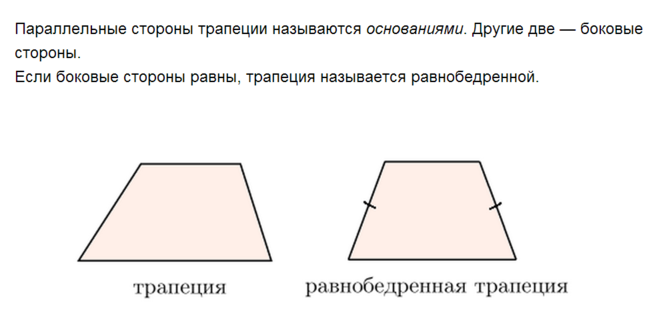 Расстояние между параллельными сторонами называется высотой.
Расстояние между параллельными сторонами называется высотой. Формула площади для трапеций задается как —
Формула площади для трапеций задается как —