свойства, признаки и формулы / Блог

Содержание:

1. Свойства равнобедренного треугольника.
2. Признаки равнобедренного треугольника.
3. Формулы равнобедренного треугольника:
   • формулы длины стороны;
   • формулы длины равных сторон;
   • формулы высоты, медианы, биссектрисы равнобедренного треугольника.

Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.

АВ = ВС — боковые стороны

АС — основание

 

Свойства равнобедренного треугольника

Свойства равнобедренного треугольника выражаются через 5 теорем:

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Рассмотрим равнобедренный Δ ABC с основанием АС.

Боковые стороны равны АВ = ВС,

Следовательно углы при основании ∠ BАC = ∠ BСA.

 

 

Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника

• Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
• Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
• Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Доказательство теоремы:

• Дан Δ ABC.
• Из точки В проведем высоту BD.
• Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
• Прямые АС и BD называются перпендикуляром.
• В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
• АВ = ВС — боковые стороны равны.
• Стороны АD = СD, т.к. точка D отрезок делит пополам.
• Следовательно Δ ABD = ΔBCD.
• Биссектриса, высота и медиана это один отрезок — BD

Вывод:

1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
3. Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.

• Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство теоремы:

Дано два Δ ABC и Δ A₁B₁C₁. Стороны AB = A₁B₁; BC = B₁C₁; AC = A₁C₁.

Доказательство от противного.

• Пусть треугольники не равны (а то треугольники были равны по первому признаку).
• Пусть Δ A₁B₁C₂ = Δ ABC, у которого вершина C₂ лежит в одной полуплоскости с вершиной C₁ относительно прямой A₁B₁. По предположению вершины C₁ и C₂ не совпадают. Пусть D – середина отрезка C₁C₂. Δ A₁C₁C₂ и Δ B₁C₁C₂ – равнобедренные с общим основанием C₁C₂. Поэтому их медианы A₁D и B₁D являются высотами. Значит, прямые A₁D и B₁D перпендикулярны прямой C₁C₂. A₁D и B₁D имеют разные точки A₁ и B₁, следовательно, не совпадают. Но через точку D прямой C₁C₂ можно провести только одну перпендикулярную ей прямую.
• Отсюда пришли к противоречию и теорему доказали.

 

Признаки равнобедренного треугольника

1. Если в треугольнике два угла равны.
2. Сумма углов треугольника 180°.
3. Если в треугольнике биссектриса является медианой или высотой.
4. Если в треугольнике медиана является биссектрисой или высотой.
5. Если в треугольнике высота является медианой или биссектрисой.

 

 

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

 

• b — сторона (основание)
• а — равные стороны
• a — углы при основании
• b — угол образованный равными сторонами

 

Формулы длины стороны (основания — b):

• b = 2a \sin( \beta /2)= a \sqrt { 2-2 \cos \beta }
• b = 2a \cos \alpha

Формулы длины равных сторон — (а):

• a=\frac { b } { 2 \sin(\beta /2) } = \frac { b } { \sqrt { 2-2 \cos \beta } }
• a=\frac { b } { 2 \cos\alpha }

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

• L — высота=биссектриса=медиана
• b — сторона (основание)
• а — равные стороны
• a — углы при основании
• b — угол образованный равными сторонами

 

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

• L = a sina
• L = \frac { b } { 2 } *\tg\alpha
• L = a \sqrt { (1 + \cos \beta)/2 } =a \cos (\beta)/2)

 

Формула высоты, биссектрисы и медианы, через стороны, (L):

• L = \sqrt { a^ { 2 } -b^ { 2 } /4 }

 

Площадь равнобедренного треугольника

• b — сторона (основание)
• а — равные стороны
• h — высота

 

Формула площади треугольника через высоту h и основание b, (S):

 

S=\frac { 1 } { 2 } *bh

---

 

Смотри также:

bingoschool.ru

Высота равнобедренного треугольника | Онлайн калькулятор

Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.

Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам — это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.

Рассмотрим каждый случай по отдельности.

Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой,

проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.


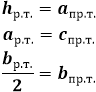
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:



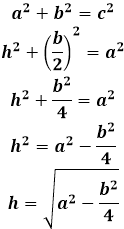
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.

Площадь любого треугольника можно найти несколькими способами — например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.

Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:



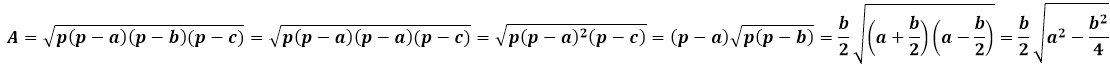
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне



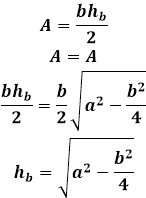
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.

Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sin⁡α

Формула через боковую сторону и угол напротив основания β: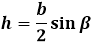

Формула через основание и угол при нем α: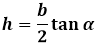

через основание и угол противолежащий ему β: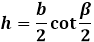

allcalc.ru

Как находить высоту в равнобедренном треугольнике? Формула нахождения, свойства высоты в равнобедренном треугольнике

Геометрия – это не только предмет в школе, по которому нужно получить отличную оценку. Это еще и знания, которые часто требуются в жизни. Например, при строительстве дома с высокой крышей необходимо рассчитать толщину бревен и их количество. Это несложно, если знать, как находить высоту в равнобедренном треугольнике. Архитектурные сооружения базируются на знании свойств геометрических фигур. Формы зданий зачастую визуально напоминают их. Египетские пирамиды, пакеты с молоком, художественная вышивка, северные росписи и даже пирожки – это все треугольники, окружающие человека. Как говорил Платон, весь мир базируется на треугольниках.



Равнобедренный треугольник

Чтобы было понятнее, о чем далее пойдет речь, стоит немного вспомнить азы геометрии.

Треугольник является равнобедренным, если он имеет две равных стороны. Их всегда называют боковыми. Сторона, размеры которой отличаются, получила название основания.

Основные понятия

Как и любая наука, геометрия имеет свои основные правила и понятия. Их достаточно много. Рассмотрим лишь те, без которых наша тема будет несколько непонятна.

Высота – это прямая линия, проведенная перпендикулярно к противоположной стороне.

Медиана – это отрезок, направленный из любой вершины треугольника исключительно к середине противоположной стороны.

Биссектриса угла – это луч, разделяющий угол пополам.

Биссектриса треугольника – это прямая, вернее, отрезок биссектрисы угла, соединяющий вершину с противоположной стороной.

Очень важно запомнить, что биссектриса угла – это обязательно луч, а биссектриса треугольника – это часть такого луча.

Углы при основании

Теорема гласит, что углы, расположенные при основании любого равнобедренного треугольника, всегда равны. Доказать эту теорему очень просто. Рассмотрим изображенный равнобедренный треугольник АВС, у которого АВ=ВС. Из угла АВС необходимо провести биссектрису ВД. Теперь следует рассмотреть два полученных треугольника. По условию АВ=ВС, сторона ВД у треугольников общая, а углы АВД и СВД равны, ведь ВД – биссектриса. Вспомнив первый признак равенства, можно смело заключить, что рассматриваемые треугольники равны. А следовательно, равны все соответствующие углы. И, конечно, стороны, но к этому моменту вернемся позже.



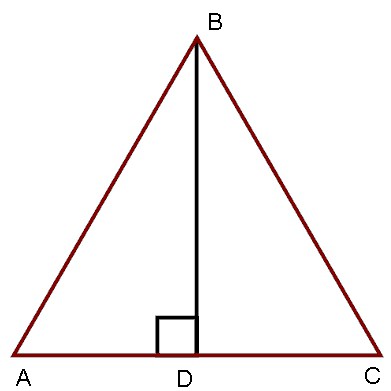
Высота равнобедренного треугольника

Основная теорема, на которой базируется решение практически всех задач, звучит так: высота в равнобедренном треугольнике является биссектрисой и медианой. Чтобы понять её практический смысл (или суть), следует сделать вспомогательное пособие. Для этого необходимо вырезать из бумаги равнобедренный треугольник. Легче всего это сделать из обычного тетрадного листка в клеточку.



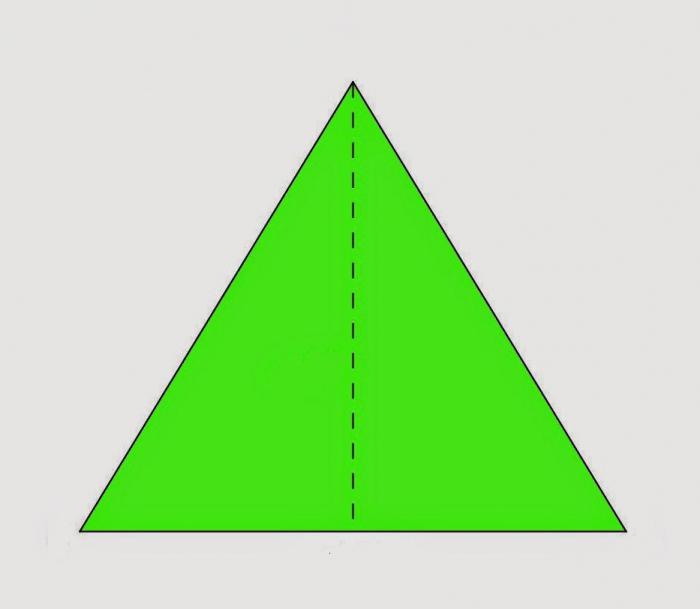
Согните полученный треугольник пополам, совместив боковые стороны. Что получилось? Два равных треугольника. Теперь следует проверить догадки. Разверните полученное оригами. Прочертите линию сгиба. При помощи транспортира проверьте угол между прочерченной линией и основанием треугольника. О чем говорит угол в 90 градусов? О том, что прочерченная линия – перпендикуляр. По определению – высота. Как находить высоту в равнобедренном треугольнике, мы разобрались. Теперь займемся углами при вершине. При помощи того же транспортира проверьте углы, образованные теперь уже высотой. Они равны. Значит, высота одновременно является и биссектрисой. Вооружившись линейкой, измерьте отрезки, на которые разбивает высота основание. Они равны. Следовательно, высота в равнобедренном треугольнике делит основание пополам и является медианой.

Доказательство теоремы

Наглядное пособие ярко демонстрирует истинность теоремы. Но геометрия – наука достаточно точная, поэтому требует доказательств.

Во время рассмотрения равенства углов при основании было доказано равенство треугольников. Напомним, ВД – биссектриса, а треугольники АВД и СВД равны. Вывод был таков: соответствующие стороны треугольника и, естественно, углы равны. Значит, АД = СД. Следовательно, ВД – медиана. Осталось доказать, что ВД является высотой. Исходя из равенства рассматриваемых треугольников, получается, что угол АДВ равен углу СДВ. Но эти два угла являются смежными, и, как известно, дают в сумме 180 градусов. Следовательно, чему они равны? Конечно, 90 градусам. Таким образом, ВД – это высота в равнобедренном треугольнике, проведенная к основанию. Что и требовалось доказать.



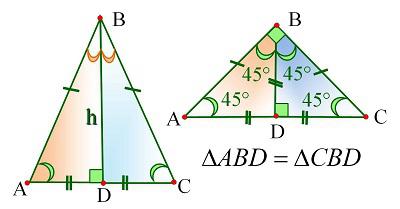
Основные признаки

• Чтобы успешно решать задачи, следует запомнить основные признаки равнобедренных треугольников. Они как бы обратны теоремам.
• Если в ходе решения задачи обнаруживается равенство двух углов, значит, вы имеете дело с равнобедренным треугольником.
• Если удалось доказать, что медиана является одновременно и высотой треугольника, смело заключайте – треугольник равнобедренный.
• Если биссектриса является и высотой, то, опираясь на основные признаки, треугольник относят к равнобедренным.
• И, конечно, если медиана выступает и в роли высоты, то такой треугольник — равнобедренный.

Формула высоты 1

Однако для большинства задач требуется найти арифметическую величину высоты. Именно поэтому рассмотрим, как находить высоту в равнобедренном треугольнике.

Вернемся к представленной выше фигуре АВС, у которой а – боковые стороны, в — основание. ВД – высота этого треугольника, она имеет обозначение h.



Что представляет собой треугольник АВД? Так как ВД – высота, то треугольник АВД – прямоугольный, катет которого необходимо найти. Воспользовавшись формулой Пифагора, получаем:

АВ² = АД² + ВД²

Определив из выражения ВД и подставив принятые ранее обозначения, получим:

Н² = а² – (в/2)².

Необходимо извлечь корень:

Н = √а² – в²/4.

Если вынести из под знака корня ¼ , то формула будет иметь вид:

Н = ½ √4а² – в².

Так находится высота в равнобедренном треугольнике. Формула вытекает из теоремы Пифагора. Даже если забыть эту символическую запись, то, зная метод нахождения, всегда можно её вывести.

Формула высоты 2

Формула, описанная выше, является основной и чаще всего используется при решении большинства геометрических задач. Но она не единственная. Иногда в условии, вместо основания, дано значение угла. При таких данных как находить высоту в равнобедренном треугольнике? Для решения подобных задач целесообразно использовать другую формулу:

Н = а/sin α,

где Н – высота, направленная к основанию,

а – боковая сторона,

α – угол при основании.

Если в задаче дано значение угла при вершине, то высота в равнобедренном треугольнике находится следующим образом:

Н = а/cos (β/2),

где Н – высота, опущенная на основание,,

β – угол при вершине,

а – боковая сторона.

Прямоугольный равнобедренный треугольник

Очень интересным свойством обладает треугольник, вершина которого равна 90 градусам. Рассмотрим прямоугольный треугольник АВС. Как и в предыдущих случаях, ВД – высота, направленная к основанию.



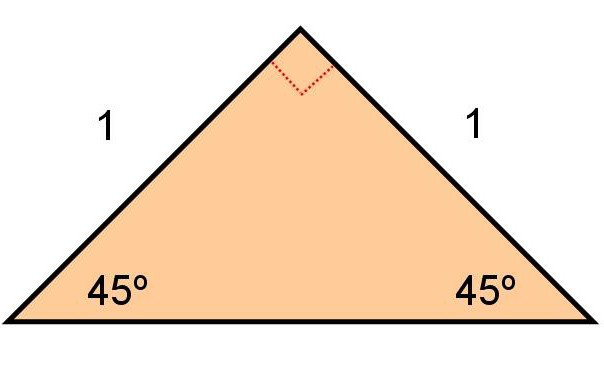
Углы при основании равны. Вычислить их большого труда не составит:

α = (180 – 90)/2.

Таким образом, углы, находящиеся при основании, всегда по 45 градусов. Теперь рассмотрим треугольник АДВ. Он также является прямоугольным. Найдем угол АВД. Путем несложных вычислений получаем 45 градусов. А, следовательно, этот треугольник не только прямоугольный, но и равнобедренный. Стороны АД и ВД являются боковыми сторонами и равны между собой.

Но сторона АД в то же время является половиной стороны АС. Получается, что высота в равнобедренном треугольнике равна половине основания, а если записать в виде формулы, то получим следующее выражение:

Н = в/2.

Следует не забывать, что данная формула является исключительно частным случаем, и может быть использована только для прямоугольных равнобедренных треугольников.



Золотые треугольники

Очень интересным является золотой треугольник. В этой фигуре отношение боковой стороны к основанию равняется величине, названной числом Фидия. Угол, расположенный при вершине — 36 градусов, при основании – 72 градуса. Этим треугольником восхищались пифагорейцы. Принципы золотого треугольника положены в основу множества бессмертных шедевров. Известная всем пятиконечная звезда построена на пересечении равнобедренных треугольников. Для многих творений Леонардо да Винчи использовал принцип «золотого треугольника». Композиция «Джоконды» основана как раз на фигурах, которые создают собой правильный звездчатый пятиугольник.

Картина «Кубизм», одно из творений Пабло Пикассо, завораживает взгляд положенными в основу равнобедренными треугольниками.

fb.ru

Как посчитать высоту равнобедренного треугольника

Чтобы посчитать чему равна высота равнобедренного треугольника просто воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор



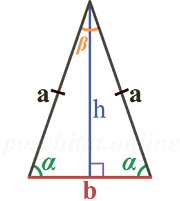
Чтобы вычислить высоту равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):

• длину двух равных сторон (a) и длину основания (b)
• длину двух равных сторон (a) и угол α
• длину двух равных сторон (a) и угол β
• длину основания (b) и угол α
• длину основания (b) и угол β

Введите их в соответствующие поля и получите результат.

Если известны длина стороны а и основания b

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и длина основания b?

Формула

h = √a² — (^b/₂)²

Пример

Если сторона a = 10 см, а сторона b = 5 см, то:

h = √10² — (⁵/₂)²

= √100 — 6.25 ≈ 9.68 см

Если известны длина стороны а и угол α

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол α?

Формула

h = a⋅sin α

Пример

Если сторона a = 5 см, а ∠α = 45°, то:

h = 5⋅sin 45 ≈ 3,53 см

Если известны длина стороны а и угол β

Чему равна высота h у равнобедренного треугольника если известны длина стороны a и угол β?

Формула

h = a⋅cos ^β/₂

Пример

Если сторона a = 5 см, а ∠β = 30°, то:

h = 5⋅cos ³⁰/₂ ≈ 4.83 см

Если известны длина стороны b и угол α

Чему равна высота h у равнобедренного треугольника если известны длина стороны b и угол α?

Формула

h = ^b/₂⋅tg α

Пример

Если сторона b = 20 см, а ∠α = 35°, то:

h = ²⁰/₂⋅tg 35 = 10⋅0.7 = 7 см

Если известны длина стороны b и угол β

Чему равна высота

h у равнобедренного треугольника если известны длина стороны b и угол β?

Формула

h = ^b/₂⋅ctg ^β/₂

Пример

Если сторона b = 15 см, а ∠β = 40°, то:

h = ¹⁵/₂⋅ctg ⁴⁰/₂ = 7.5⋅2.7474 ≈ 20.6 см

См. также

poschitat.online