ТЕМА 3. Системы линейных уравнений — Высшая математика: лекционный курс — ВЫСШАЯ МАТЕМАТИКА, ТВ и МС, МАТ. МЕТОДЫ — Учебно-методические материалы для студентов всех ВУЗов: — std72.ru
Пусть дана система n линейных уравнений с n неизвестными
 (1)
(1)
1. Правило Крамера
Пусть составленный из коэффициентов при неизвестных определитель:
 .
.
Тогда система (1) имеет единственное решение
 ,
,
где определитель Δk (k=1,2,…n) получен из определителя Δ путем замены k-го столбца столбцом свободных членов системы (1).
Пример. Решить систему линейных уравнений по правилу Крамера:

Решение. Вычислим определители Δ, Δ1 , Δ2 , Δ3.




Тогда  .
.
Ответ: х1=1, х2=0, х3= -1.
2. Метод Гаусса
Пусть дана система уравнений (1).
Предположим, что среди коэффициентов  при неизвестном х1 имеются коэффициенты, отличные от нуля. Пусть одним из таких коэффициентов является а11. Разделим первое уравнение системы (1) на а11, получим:
при неизвестном х1 имеются коэффициенты, отличные от нуля. Пусть одним из таких коэффициентов является а11. Разделим первое уравнение системы (1) на а11, получим:
 (2)
(2)
Это уравнение умножим на (–а21) и сложим его со вторым уравнением системы (1), затем уравнение (2) умножим на (-а31) и сложим его с третьим уравнением и т.д. С помощью таких операций исключим неизвестное х1 из всех уравнений системы, начиная со второго. Оставляем неизменным первое уравнение системы (1), а к оставшимся применяем тот же прием, т.е. в n-2 уравнениях исключаем неизвестное х2 и т.д.
Систему уравнений (1) приведем к треугольному виду:
 (3)
(3)
Пусть  . Из последнего уравнения системы (3) найдем хn. Подставляя затем это значение в предыдущее уравнение, найдем х n -1 и т.д. Продолжая эту процедуру, дойдем до первого уравнения, из которого путем подстановки уже найденных значений х2, х3, …, х n получим неизвестное х1.
. Из последнего уравнения системы (3) найдем хn. Подставляя затем это значение в предыдущее уравнение, найдем х n -1 и т.д. Продолжая эту процедуру, дойдем до первого уравнения, из которого путем подстановки уже найденных значений х2, х3, …, х n получим неизвестное х1.
Пример . Решить систему уравнений методом Гаусса:
 (4)
(4)
Решение. Заметим, что во втором уравнении системы коэффициент при х1 равен 1. Поменяв местами первое и второе уравнения, получим систему:
 (5)
(5)
Умножим первое уравнение системы (5) на (–2) и сложим его со вторым уравнением. Затем умножим первое уравнение на (–3) и сложим его с третьим уравнением. Получим следующую систему уравнений:
 (6)
(6)
Разделим второе уравнение системы (6) на (-5), затем полученное уравнение умножим на 9 и сложим с третьим уравнением системы (6). В результате придем к системе (7)
 (7)
(7)
Из третьего уравнения находим х3=-1. Подставим это значение во второе уравнение системы (7) и найдем х2:
 .
.
Подставляя полученные значения х2 = 0 и х3 = -1 в первое уравнение системы (7), найдем х1:
х1 + 2*0-1*(-1)=2, или х1 = 1.
Ответ: х1 = 1, х2= 0, х3 = -1.
3. Решение системы линейных уравнений с использованием обратной матрицы.
Введем для системы линейных уравнений (1) следующие матрицы:
 .
.
Систему (1) представим в матричной форме А* Х = В, которая эквивалентна исходной. Действительно, если перемножить матрицы А и Х и приравнять элементы матрицы-произведения к соответствующим элементам матрицы В, то получим систему уравнений (1).
Умножим обе части уравнения А*Х = В слева на матрицу А-1, получим А-1 * (А Х) = А-1 В или (А-1 А) Х= А-1 В.
Так как А-1 * А = Е, то Е*Х = А-1 * В или Х = А-1* В.
Эта формула дает решение системы в матричной форме.
Пример. Решить систему
 используя обратную матрицу.
используя обратную матрицу.
Решение. Найдем обратную матрицу к матрице системы  .
.
Определитель матрицы А: 
 .
.
Так как определитель матрицы А отличен от 0, то обратная матрица существует. Найдем ее по формуле  , вычислив предварительно алгебраические дополнения. Получим:
, вычислив предварительно алгебраические дополнения. Получим:
 .
.
Найдем матричное решение системы:
 .
.
Ответ: х1 = 1; х2 = 1; х3 = 1.
www.std72.ru
Решение систем линейных уравнений
Каталин Дэвид
Системы линейных уравнений имеют следующий общий вид:
$ \begin{cases} a_{1,1}\cdot x_{1} + a_{1,2}\cdot x_{2} + a_{1,3}\cdot x_{3} + \cdots a_{1,n} \cdot x_{n} =b_{1} \\ a_{2,1}\cdot x_{1} + a_{2,2}\cdot x_{2}+ a_{2,3}\cdot x_{3} + \cdots + a_{2,n}\cdot x_{n} = b_{2} \\ a_{3,1}\cdot x_{1} + a_{3,2}\cdot x_{2}+a_{3,3}\cdot x_{3}+ \cdots + a_{3,n}\cdot x_{n}=b_{3} \\ \cdots\\ a_{m,1}\cdot x_{1}+ a_{m,2}\cdot x_{2}+a_{m,3}\cdot x_{3}+\cdots + a_{m,n}\cdot x_{n} =b_{n} \end{cases}$
$ A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{m,1} & a_{m,2} & a_{m,3} & . & . & a_{m,n} \end{pmatrix}$ — матрица системы, а $b_{1}, b_{2},b_{3} \cdots b_{n}$ — свободные члены системы.
Если все свободные члены равны 0, то система однородна.
Матрица системы — квадратная (m=n)
Надо вычислить определитель матрицы системы.
$\Delta = \begin{vmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & a_{3,2} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$
Определитель матрицы системы не равен 0
Система называется невырожденной системой с единственным решением. Чтобы найти решение системы, используем метод Крамера.
Вычислим $ \Delta_{x_{1}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{1}$ столбцом свободных членов.
$\Delta_{x_{1}}= \begin{vmatrix} b_{1} & a_{1,2} & a_{1,3} & . & . & a_{1,n} \\ b_{2} & a_{2,2} & a_{2,3} & . & . & a_{2,n} \\ b_{3} & a_{3,2} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ b_{n} & a_{n,2} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$
Получаем $ x_{1} = \dfrac{\Delta_{x_{1}}}{\Delta}$
Вычислим $ \Delta_{x_{2}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{2}$ столбцом свободных членов.
$\Delta_{x_{2}}= \begin{vmatrix} a_{1,1} & b_{1} & a_{1,3} & . & . & a_{1,n} \\ a_{2,1} & b_{2} & a_{2,3} & . & . & a_{2,n} \\ a_{3,1} & b_{3} & a_{3,3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & b_{n} & a_{n,3} & . & . & a_{n,n} \end{vmatrix}$
Получаем $ x_{2} = \dfrac{\Delta_{x_{2}}}{\Delta}$
Вычислим $ \Delta_{x_{3}}$ — определитель матрицы, полученной заменой столбца с коэффициентами соответствующей переменной $x_{3}$ столбцом свободных членов.
$\Delta_{x_{3}}= \begin{vmatrix} a_{1,1} & a_{1,2} & b_{1} & . & . & a_{1,n} \\ a_{2,1} & a_{2,2} & b_{2} & . & . & a_{2,n} \\ a_{3,1} & a_{3,2} & b_{3} & . & . & a_{3,n} \\ \cdots \\ a_{n,1} & a_{n,2} & a_{n} & . & . & a_{n,n} \end{vmatrix}$
Получаем $ x_{3} = \dfrac{\Delta_{x_{3}}}{\Delta}$
Продолжаем делать это с остальными переменными, и в конце-концов записываем решение системы.
$x_{n}=\dfrac{\Delta_{x_{n}}}{\Delta}$
Пример 53
$\begin{cases} 2\cdot x + 3\cdot y -5\cdot z = \color{red}{-7}\\ -3 \cdot x + 2\cdot y + z = \color{red}{-9}\\ 4\cdot x — y + 2\cdot z = \color{red}{17} \end{cases}$
Матрица системы:
$ \begin{pmatrix} 2 & 3 & -5\\ -3 & 2 & 1\\ 4 & -1 & 2 \end{pmatrix}$
Вычисляем определитель матрицы и получаем $\Delta = 8 -15 + 12 +40 +2 + 18 = 65$
Вычисляем $ \Delta_{x}= \begin{vmatrix} \color{red}{-7} & 3 & -5\\ \color{red}{-9} & 2 & 1\\ \color{red}{17} & -1 & 2 \end{vmatrix}= -28 — 45 + 51 + 170 — 7 +54 = 195$
Вычисляем $ \Delta_{z}= \begin{vmatrix} 2 & 3 &\color{red}{-7}\\ -3 & 2 & \color{red}{-9}\\ 4 & -1 & \color{red}{17} \end{vmatrix}= 68 -21 -108 + 56 -18 + 153 =130$
Решение системы:
$x = \dfrac{\Delta_{x}}{\Delta} =\dfrac{195}{65} = 3$
$y = \dfrac{\Delta_{y}}{\Delta} = -\dfrac{65}{65}= -1$
$z = \dfrac{\Delta_{z}}{\Delta} =\dfrac{130}{65}= 2$
$S=\{3;-1;2\}$
Пример 54
$\begin{cases} 4\cdot x + 5\cdot y -2\cdot z = \color{red}{3}\\ -2 \cdot x + 3\cdot y — z = \color{red}{-3}\\ -1\cdot x — 2\cdot y + 3\cdot z = \color{red}{-5} \end{cases}$
Матрица системы: $ \begin{pmatrix} 4 & 5 & -2\\ -2 & 3 & -1\\ -1 & -2 & 3 \end{pmatrix}$
Вычисляем определитель матрицы и получаем $\Delta = 36 -8 + 5
www.math10.com
Лекция 6. Системы линейных уравнений
Системы линейных уравнений. Лекция 6.
Системы линейных уравнений.
Основные понятия.
Система видa
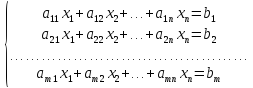
называется системой 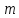 —
линейных уравнений с
—
линейных уравнений с 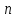 неизвестными.
неизвестными.
Числа 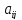
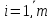 ,
, 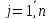 называются коэффициентами
системы.
называются коэффициентами
системы. Числа 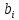 ,
, 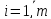 называются свободными
членами системы,
называются свободными
членами системы, 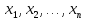 – переменными
системы.
Матрица
– переменными
системы.
Матрица
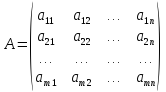
называется основной матрицей системы, а матрица

– расширенной матрицей системы
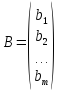 и
и 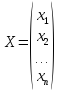 — соответственно матрицами
свободных членов и неизвестных системы.
Тогда в матричной форме систему уравнений
можно записать в виде
— соответственно матрицами
свободных членов и неизвестных системы.
Тогда в матричной форме систему уравнений
можно записать в виде 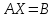 . Решением
системы называется
. Решением
системы называется 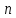 значений переменных
значений переменных 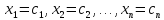 ,
при подстановке которых, все уравнения
системы обращаются в верные числовые
равенства. Всякое решение системы можно
представить в виде матрицы — столбца
,
при подстановке которых, все уравнения
системы обращаются в верные числовые
равенства. Всякое решение системы можно
представить в виде матрицы — столбца 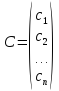 .
Тогда справедливо матричное равенство
.
Тогда справедливо матричное равенство 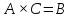
Система уравнений называется совместной если она имеет хотя бы одно решение и несовместной если не имеет ни одного решения.
Решить систему линейных уравнений это значит выяснить совместна ли она и в случае совместности найти её общее решение.
Система называется однородной если все её свободные члены равны нулю. Однородная система всегда совместна, так как имеет решение
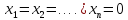 .
.
Теорема Кронекера – Копелли.
Ответ
на вопрос существования решений линейных
систем и их единственности позволяет
получить следующий результат, который
можно сформулировать в виде следующих
утверждений относительно системы 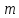
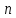 неизвестными
неизвестными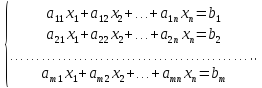 (1)
(1)
Теорема
2.
Система линейных уравнений (1) совместна
тогда и только тогда когда ранг основной
матрицы равен рангу расширенной ( .
.
Теорема 3. Если ранг основной матрицы совместной системы линейных уравнений равен числу неизвестных, то система имеет единственное решение.
Теорема 4. Если ранг основной матрицы совместной системы меньше числа неизвестных, то система имеет бесконечное множество решений.
Правила решения систем.
Находят ранги основной и расширенной матрицы и если
то система не совместна.
Если
 ,
то система совместна, в этом случае
находят какой-нибудь базисный минор
,
то система совместна, в этом случае
находят какой-нибудь базисный минор  — того порядка и берут соответствующие
ему
— того порядка и берут соответствующие
ему  — уравнений системы, отбрасывая остальные.
Те переменные, коэффициенты которых
входят в базисный минор, называются
главными, остальные
— уравнений системы, отбрасывая остальные.
Те переменные, коэффициенты которых
входят в базисный минор, называются
главными, остальные  переменных называют свободными.
Выражения со свободными переменными
переносят в правую часть.
переменных называют свободными.
Выражения со свободными переменными
переносят в правую часть.
3. Находят выражение главных переменных через свободные и получают общее решение системы.
4. Придавая свободным переменным произвольные значения получают все значения главных переменных.
Методы решения систем линейных уравнений.
Метод обратной матрицы.
Пусть
дана система 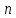 линейных уравнений с
линейных уравнений с 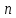 неизвестными
неизвестными
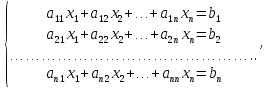
причем 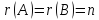 ,
т. е. система имеет единственное решение.
Запишем систему в матричном виде
,
т. е. система имеет единственное решение.
Запишем систему в матричном виде
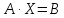 ,
,
где  ,
, 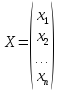 ,
, 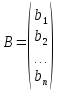 .
.
Умножим
обе части матричного уравнения слева
на матрицу 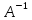
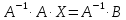 .
.
Так
как 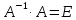 ,
то получаем
,
то получаем 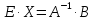 ,
откуда получаем равенство для нахождения
неизвестных
,
откуда получаем равенство для нахождения
неизвестных
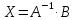 .
.
Пример
27. Методом
обратной матрицы решить систему линейных
уравнений 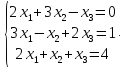
Решение.
Обозначим через 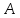 основную матрицу системы
основную матрицу системы
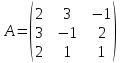 .
.
Пусть
,
тогда решение найдем по формуле 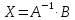 .
.
Вычислим 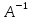 .
.
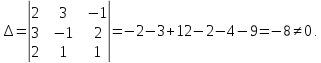
Так
как 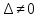 ,
то
,
то 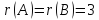 и система имеет единственное решение.
Найдем все алгебраические дополнения
и система имеет единственное решение.
Найдем все алгебраические дополнения
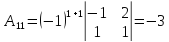 ,
, 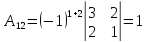 ,
,
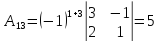 ,
, 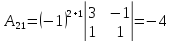 ,
,
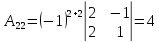 ,
, 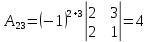 ,
,
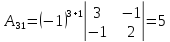 ,
, 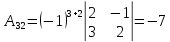 ,
,
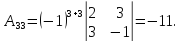
Таким образом
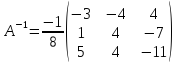 .
.
Сделаем проверку
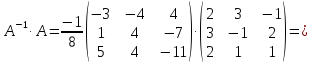
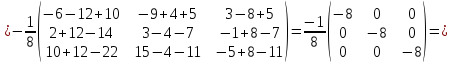
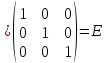 .
.
Обратная
матрица найдена верно. Отсюда по формуле 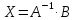 ,
найдем матрицу переменных
,
найдем матрицу переменных 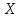 .
.
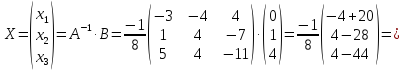
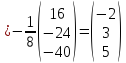 .
.
Сравнивая
значения матриц, получим ответ: 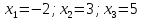 .
.
Метод Крамера.
Пусть
дана система 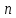 линейных уравнений с
линейных уравнений с 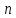 неизвестными
неизвестными
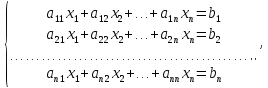
причем 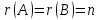 ,
т. е. система имеет единственное решение.
Запишем решение системы в матричном
виде
,
т. е. система имеет единственное решение.
Запишем решение системы в матричном
виде 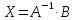 или
или
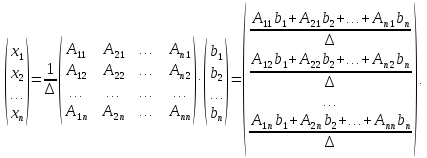
Отсюда
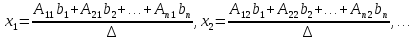
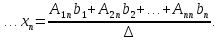
Обозначим
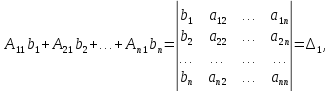
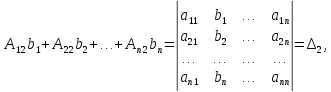
. . . . . . . . . . . . . . ,
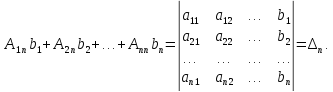
Таким образом, получаем формулы для нахождения значений неизвестных, которые называются формулами Крамера.
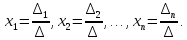
Пример
28. Решить
методом Крамера следующую систему
линейных уравнений 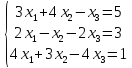 .
.
Решение. Найдем определитель основной матрицы системы
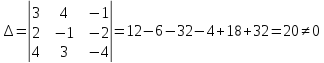 .
.
Так
как 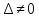 ,
то
,
то 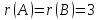 ,
система имеет единственное решение.
,
система имеет единственное решение.
Найдем остальные определители для формул Крамера
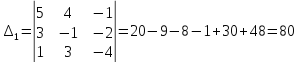 ,
,
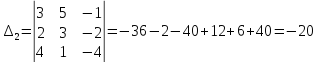 ,
,
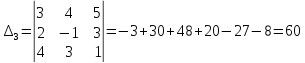 .
.
По формулам Крамера находим значения переменных
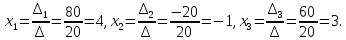
Ответ: 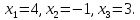
Метод Гаусса.
Метод заключается в последовательном исключении переменных.
Пусть
дана система 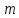 линейных уравнений с
линейных уравнений с 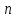 неизвестными.
неизвестными.
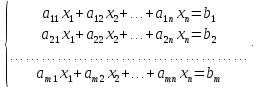
Процесс решения по методу Гаусса состоит из двух этапов:
На
первом этапе расширенная матрица системы 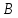 приводится с помощью элементарных
преобразований к ступенчатому виду
приводится с помощью элементарных
преобразований к ступенчатому виду
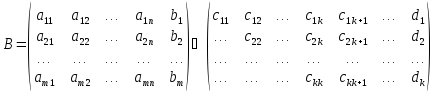 ,
,
где 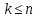 ,
которой соответствует система
,
которой соответствует система
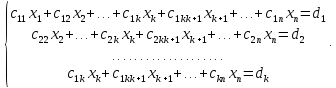
После
этого переменные 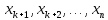 считаются свободными и в каждом уравнении
переносятся в правую часть.
считаются свободными и в каждом уравнении
переносятся в правую часть.
На
втором этапе из последнего уравнения
выражается переменная 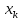 ,
полученное значение подставляется в
,
полученное значение подставляется в 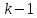 уравнение. Из этого уравнения
уравнение. Из этого уравнения
выражается
переменная 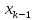 .
Этот процесс продолжается до первого
уравнения. В результате получается
выражение главных переменных
.
Этот процесс продолжается до первого
уравнения. В результате получается
выражение главных переменных 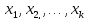 через
свободные переменные
через
свободные переменные 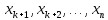 .
.
Пример 29. Решить методом Гаусса следующую систему
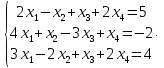
Решение. Выпишем расширенную матрицу системы и приведем ее к ступенчатому виду

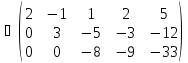 .
.
Так
как 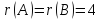 больше числа неизвестных, то система
совместна и имеет бесконечное множество
решений. Запишем систему для ступенчатой
матрицы
больше числа неизвестных, то система
совместна и имеет бесконечное множество
решений. Запишем систему для ступенчатой
матрицы
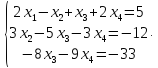
Определитель расширенной матрицы этой системы, составленный из трех первых столбцов не равен нулю, поэтому его считаем базисным. Переменные
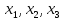 ,
будут базисными а переменная
,
будут базисными а переменная 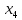 – свободной. Перенесем ее во всех
уравнениях в левую часть
– свободной. Перенесем ее во всех
уравнениях в левую часть
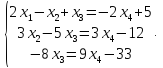
Из
последнего уравнения выражаем 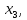
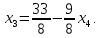
Подставив это значение в предпоследнее второе уравнение, получим
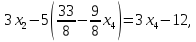
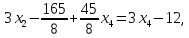 откуда
откуда 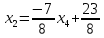 .
Подставив значения переменных
.
Подставив значения переменных 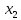 и
и 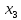 в первое уравнение, найдем
в первое уравнение, найдем 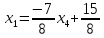 .
Ответ запишем в следующем виде
.
Ответ запишем в следующем виде
Ответ: 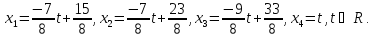
32
studfile.net
Система линейных уравнений | Математика
Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени.
В классическом варианте коэффициенты при переменных, свободные члены и неизвестные считаются вещественными числами, но все методы и результаты сохраняются (либо естественным образом обобщаются) на случай любых полей, например, комплексных чисел.
Решение систем линейных алгебраических уравнений — одна из классических задач линейной алгебры, во многом определившая её объекты и методы. Кроме того, линейные алгебраические уравнения и методы их решения играют важную роль во многих прикладных направлениях, в том числе в линейном программировании, эконометрике.
- $ \begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2\\ \dots\\ a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m \\ \end{cases} $
- $ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} = \begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_m \end{pmatrix} $
- $ Ax = b $.
- $ \bold{x} = A^\prime \bold{x} + \bold{b}^\prime $,
- $ \bold{x}_{n+1} = A^\prime \bold{x}_n + \bold{b}^\prime $.
- Основанные на расщеплении: $ (M-N)\bold{x}=\bold{b}\Leftrightarrow M\bold{x}=N\bold{x}+\bold{b} \Rightarrow M\bold{x}^{n+1}=N\bold{x}^n+\bold{b} $
- Вариационного типа: $ A\bold{x}=\bold{b}\Rightarrow \|A\bold{x}-\bold{b}\|\rightarrow \min $
- Проекционного типа: $ A\bold{x}=\bold{b}\Rightarrow (A\bold{x},\bold{m})=(\bold{b},\bold{m}) \forall\bold{m} $
Соглашения и определения
Общий вид системы линейных алгебраических уравнений:
Здесь $ m $ — количество уравнений, а $ n $ — количество переменных, $ x_1, x_2, \dots, x_n $ — неизвестные, которые надо определить, коэффициенты $ a_{11}, a_{12}, \dots, a_{mn} $ и свободные члены $ b_1, b_2, \dots, b_m $ предполагаются известными. Индексы коэффициентов в системах линейных уравнений ($ a_{ij} $) формируются по следующему соглашению: первый индекс ($ i $) обозначает номер уравнения, второй ($ j $) — номер переменной, при которой стоит этот коэффициент. Система называется однородной, если все её свободные члены равны нулю, в остальных случаях — неоднородной.
Квадратной называется такая СЛАУ, где количество уравнений совпадает с количеством переменных. Если переменных больше, чем уравнений, такая система называется прямоугольной или недоопределённой, если наоборот — переопределённой. Решение системы линейных алгебраических уравнений — совокупность $ n $ чисел $ c_1, c_2, \dots, c_n $, таких что их соответствующая подстановка вместо $ x_1, x_2, \dots, x_n $ в систему обращает все её уравнения в тождества.
Шаблон:ЯкорьСистема называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решения считаются различными, если хотя бы одно из значений переменных не совпадает. Совместная система с единственным решением называется определённой, при наличии более одного решения — недоопределённой.
Матричная запись
СЛАУ может быть представлена и в матричной форме:
или:
Здесь $ A $ — это матрица системы, $ x $ — столбец неизвестных, а $ b $ — столбец свободных членов. Если к матрице $ A $ приписать справа столбец свободных членов, то получившаяся матрица называется расширенной. Теорема Кронекера — Капелли устанавливает необходимое и достаточное условие совместности системы линейных алгебраических уравнений посредством свойств матричных представлений: система совместна тогда и только тогда, когда ранг её матрицы совпадает с рангом расширенной матрицы.
Эквивалентные системы линейных уравнений
Системы линейных уравнений называются эквивалентными, если множество их решений совпадает, то есть любое решение одной системы одновременно является решением другой, и наоборот. Также считается, что системы, не имеющие решений, эквивалентны.
Систему, эквивалентную данной, можно получить, в частности, заменив одно из уравнений на это уравнение, умноженное на любое отличное от нуля число. Эквивалентную систему можно получить также, заменив одно из уравнений суммой этого уравнения с другим уравнением системы. В общем, замена уравнения системы на линейную комбинацию уравнений даёт систему, эквивалентную исходной.
Система линейных алгебраических уравнений $ A \bold{x} \ = \bold{b} $ эквивалентна системе $ C A \bold{x} \ = C \bold{b} $, где $ C $ — невырожденная матрица. В частности, если сама матрица $ A $ — невырожденная, и для неё существует обратная матрица $ A^{-1} $, то решение системы уравнений можно формально записать в виде $ \bold{x} = A^{-1} \bold{b} $.
Методы решения
Прямые методы дают алгоритм, по которому можно найти точное решение систем линейных алгебраических уравнений. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.
Некоторые прямые методы:
Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения
эквивалентного начальной системе линейных алгебраических уравнений. При итерации $ \bold{x} $ в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:
Итерационные методы делятся на несколько типов, в зависимости от применяемого подхода:
Среди итерационных методов:
math.wikia.org
Решение систем линейных уравнений методом Крамера
Рассмотрим частный случай системы линейных уравнений, когда число уравнений системы совпадает с числом неизвестных, подлежащих нахождению, то есть когда .
Пусть дана система линейных уравнений с неизвестными:
Определитель, составленный из коэффициентов называется определителем системы:
Рассмотрим случай, когда – в этом случае система является определенной, то есть имеет единственное решение.
Напишем определитель, который будет отличаться от определителя только -м столбцом, который заменен столбцом свободных членов. Обозначив этот определитель через , будем иметь:
Систему уравнений можно решить по следующим формулам, придавая индексу значения :
Рассмотренный метод решения системы уравнений называется методом Крамера, а формулы – формулами Крамера.
Другие методы решения системы линейных алгебраических уравнений (СЛАУ):
100task.ru
Решение СЛАУ методами подстановки и сложения
Уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
Например, уравнение
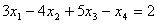 —
—
линейное, а уравнения
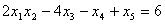 и
и
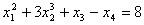 не являются линейными.
не являются линейными.
В общем виде система m линейных уравнений с n переменными записывается так:
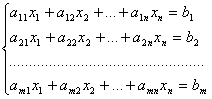 . (1)
. (1)
Числа 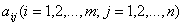
называются коэффициентами при переменных, а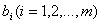 —
—
свободными членами.
Совокупность чисел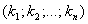
называется решением системы (1) линейных уравнений, если при подстановке их вместо переменных во все уравнения они обращаются в верные равенства.
Изучение систем линейных уравнений начинается в средней школе. В школьном курсе рассматриваются в основном системы двух линейных уравнений с двумя переменными и два метода их решения — метод подстановки и метод сложения. Эти методы являются основой изучаемого в курсе высшей математике метода Гаусса. (Принципиально иной метод — метод Крамера — основан на использовании определителей).
Чтобы последовательно двигаться от простому к ещё более простому (сложному), повторим два школьных метода.
Решение. При решении системы линейный уравнений методом подстановки сначала из какого-нибудь уравнения выражают одну переменную через другую (другие, если неизвестных больше двух). Полученное выражение подставляют в другие уравнения, в результате чего приходят к уравнению с одной переменной. Затем находят соответствующее значение второй (и третьей, если она есть) переменной.
Начнём со вполне школьного примера системы двух линейных уравнений с двумя переменными.
Пример 1. Решить систему линейных уравнений методом подстановки:
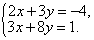
Выразим из первого уравнения 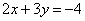 данной системы y через x (можно и наоборот) и получим:
данной системы y через x (можно и наоборот) и получим:
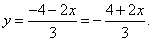
Подставив во второе уравнение данной системы вместо y выражение 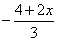 , получим систему
, получим систему
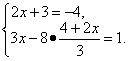
Данная и полученная системы равносильны. В последней системе второе уравнение содержит только одну переменную. Решим это уравнение:
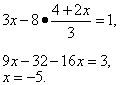
Соответствующее значение y найдём, подставив вместо x число -5 в выражение
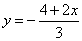 , откуда
, откуда 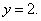
Пара (-5; 2) является решением системы линейных уравнений.
Методом подстановки можно решать и системы трёх линейных уравнений с тремя переменными.
Пример 2. Решить систему линейных уравнений методом подстановки:
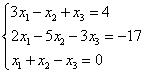
Из третьего уравнения системы выразим 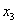 :
:
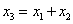 .
.
Подставим это выражение во второе уравнение данной системы:
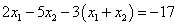 .
.
Произведём преобразования и выразим из этого уравнения 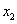 :
:
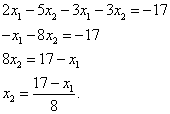
Полученные выражения для 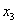 и
и 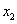 подставим в первое уравнение системы и получим
подставим в первое уравнение системы и получим
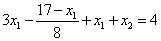 .
.
Вместо 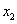 можно вновь подставить его выражение, тогда получим
уравнение с одним неизвестным:
можно вновь подставить его выражение, тогда получим
уравнение с одним неизвестным:
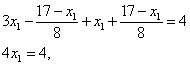
откуда
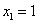 .
.
Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:
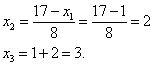
Итак, решение данной системы линейных уравнений:
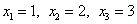 .
.
Пример 3. Решить систему линейных уравнений методом подстановки:
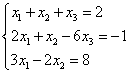
Из первого уравнения системы выразим 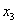 :
:
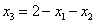 .
.
Подставим это выражение во второе уравнение данной системы, после чего выполним преобразования и получим:
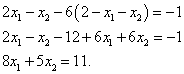
Из третьего уравнения выразим 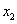 :
:
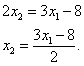
Полученное выражение для 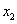 подставим в преобразованное второе уравнение системы и получим уравнение с одним неизвестным:
подставим в преобразованное второе уравнение системы и получим уравнение с одним неизвестным:
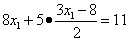 .
.
Произведём преобразования и найдём 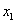 :
:
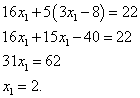
Теперь из ранее полученных выражений для остальных переменных найдём и эти переменные:
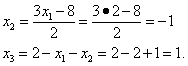
Итак, решение данной системы линейных уравнений:
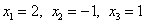 .
.
При решении систем линейных уравнений методом сложения уравнения системы почленно складывают, причём одно или оба (несколько) уравнений могут быть умножены на различные числа. В результате приходят к эквивалентной (равносильной) системе линейных уравнений, в которой одно из уравнений содержит только одну переменную.
Пример 4. Решить систему линейных уравнений методом сложения:
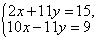
Решение. В уравнениях данной системы в этом примере системы коэффициенты при y — противоположные числа. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной:
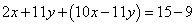 , или
, или 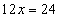 ,
, 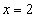 .
.
Заменим одно из уравнений исходной системы, например, первое, уравнением 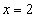 . Получим систему
. Получим систему
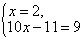
Решим полученную систему. Подставив значение 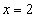 в уравнение
в уравнение 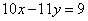 , получим уравнение с одной переменной y:
, получим уравнение с одной переменной y:
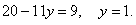
Пара (2; 1) является решением полученной системы линейных уравнений. Она является также решением исходной системы, так как эти две системы линейных уравнений равносильны.
Пример 5. Решить систему линейных уравнений методом сложения
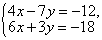
Почленное сложение уравнений системы не приводит к исключению одной из переменных. Но если умножить все члены первого уравнения на -3, а второго уравнения на 2, то коэффициенты при x в полученных уравнениях будут противоположными числами:
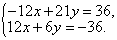
Почленное сложение уравнений полученной в результате преобразований системы приводит к уравнению с одной переменной:
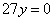 . Из этого уравнения находим, что
. Из этого уравнения находим, что 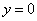 . Получили
. Получили
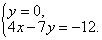
Решением полученной системы, а следовательно и исходной системы линейных уравнений является пара чисел (-3; 0).
Пример 6. Решить систему линейных уравнений методом сложения:
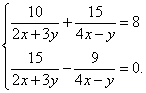
Решение. Для упрощения решения произведём замену переменных:
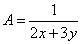 ,
, 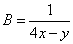 .
.
Приходим к системе линейных уравнений:
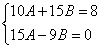
или
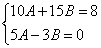
Умножим второе уравнение полученной системы на -2 и сложим с первым уравнением, получим
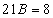 ,
,
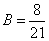 . Тогда
. Тогда 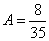 .
.
Следовательно, имеем систему уравнений
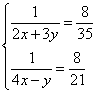
или
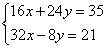
Умножим второе уравнение полученной системы на 3 и сложим с первым уравнением. Получим
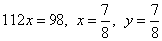 .
.
Решив задачи из примеров на решение систем линейных уравнений методом подстановки и методом сложения, мы научились производить элементарные преобразования, необходимые для решениях систем линейных уравнений в курсе высшей математики.

Продолжение темы «Системы уравнений и неравенств»
Начало темы «Линейная алгебра»
Поделиться с друзьями
function-x.ru
Решение систем линейных уравнений
Определение и формула решения систем линейных уравнений
Школьные методы решения систем описаны в статье (\textbf{ссылка на статью «Решение систем уравнений» выше}).
Метод Гаусса для решения систем линейных уравнений
Метод Гаусса — это метод последовательного исключения переменных, когда расширенная матрица системы с помощью элементарных преобразований над ее строками приводится к матрице (системе) треугольного вида, из которой последовательно, начиная с последней, находятся все остальные неизвестные системы. Метод назван в честь немецкого математика, механика, физика, астронома и геодезиста Иоганна Карла Фридриха Гаусса (1777-1855), хотя первое известное описание метода встречается уже в китайском трактате «Математика в девяти книгах» (10-2 в.в. до н.э.).
Метод Крамера для решения систем линейных уравнений
Матричный метод (метод обратной матрицы)
Матричный метод или метод обратной матрицы базируется на следующем алгоритме:
1. Система (1) записывается в матричной форме , где
2. Из матричного уравнения получаем, что
где матрица — это обратная матрица к матрице системы . Обратная матрица находится по формуле:
Матрица называется союзной матрицей к матрице , ее элементами есть алгебраические дополнения к соответствующим элементам матрицы .
Необходимым и достаточным условием применимости матричного метода является неравенство нулю определителя матрицы .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
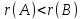
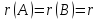 ,
то система совместна, в этом случае
находят какой-нибудь базисный минор
,
то система совместна, в этом случае
находят какой-нибудь базисный минор 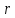 — того порядка и берут соответствующие
ему
— того порядка и берут соответствующие
ему 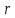 — уравнений системы, отбрасывая остальные.
Те переменные, коэффициенты которых
входят в базисный минор, называются
главными, остальные
— уравнений системы, отбрасывая остальные.
Те переменные, коэффициенты которых
входят в базисный минор, называются
главными, остальные 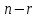 переменных называют свободными.
Выражения со свободными переменными
переносят в правую часть.
переменных называют свободными.
Выражения со свободными переменными
переносят в правую часть.