X 2 2x 3 решение: Mathway | Популярные задачи — Детская игровая комната «Волшебный лес»

Posted on 23.01.197017.06.2021 by alexxlab

3-2x+1 приведёт выражение к (x – 1)(x² +x +1).

Оператор expand раскроет скобки и разложит выражение, например expand (x – 1)(x2+x+1) приведёт выражение к x³ -2x +1.

Оператор partial fractions разложит отношение многочленов в сумму простейших дробей.

minimize минимизирует функцию, а maximize максимизирует

Число «Пи» записывается, как pi

Тригонометрические функции: sin, cos, tan, ctan, arcsin, arccos, arctan, arcctan

Команда series раскладывает функцию в ряд, например: taylor series sinx at x=0 даст нам разложение функции sin(x) в ряд Тейлора в точке x=0

Содержание

Производные и интегралы

Чтобы найти предел, необходимо в начале функции подставить lim

, а после записать саму функцию, в конце указать к чему стремится предел: as-> далее число (бесконечность записывается infinity).

2-2x-3) и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.

Функция состоит из трех квадратных трехчленов. разложим их на множители по формуле

ax² + bx + c = a(x — x₁)(x — x₂), где х₁ и х₂ — корни квадратных уравнений.

Все три квадратных уравнения приведенные. Это значит, что можно найти их корни по теореме Виета. Именно поэтому я сразу напишу разложения этих трехчленов на множители. Конечно, решать через дискриминант никто не запрещал и ошибкой это не будет.

Итак, после разложения на множители функция примет такой вид:

Видно невооруженным глазом, что скобки из знаменателя сокращаются со скобками из числителя. Это просто супер-пупер! Но надо обязательно оговориться, что знаменатель не может быть равен нулю, а значит, что x ≠ -1 и x ≠ 3. Эти исключения подразумевают выколотые точки на нашем будущем графике.

После сокращения раскрываем оставшиеся скобки.

О, чудо! Это квадратичная функция! График — парабола!

Ищем ее вершину О (m; n).

Первая координата m, которую мы будем отмечать на оси Ох, находится по формуле.

А чтобы найти вторую координату надо m подставить в упрощенную ранее функцию и посчитать.

В общем, вершина параболы имеет координаты (-0,5; -2,25).

Чертим координатную плоскость и отмечаем вершину.

Мастера по рисованию парабол могут ее начертить, не прибегая к таблице по нахождению координат других точек. А вот тем, кто не в очень теплых отношениях с параболами, придется ее рисовать.

Поскольку я мастер — обойдусь без таблицы 🙂

Не забываем про выколотые точки!

В условии задачи сказано, что некоторая прямая y = m должна иметь одну общую точку с параболой. Эта прямая будет параллельна оси Ох и одну общую точку она будет иметь в выколотых точках и вершине параболы.

Ответ: 10; -2; -2,25.

P.S. Бывает так, что график нарисован очень криво. 3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.

Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.

Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.

Пример.

Построить график функции y=x²+2x-3.

Решение:

y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д. ).

График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².

Пример.

Построить график функции y= -x²+2x+8.

Решение:

y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):

Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.

Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.

Построить график функции y=x²+5x+4.

Решение:

y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

то есть вершина параболы — точка (-2,5; -2,25).

Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).

В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).

Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:

Построить график функции y= -x²-3x.

Решение:

y= -x²-3x — квадратичная функция.

График — парабола ветвями вниз. Координаты вершины параболы

Вершина (-1,5; 2,25) — первая точка параболы.

В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.

При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.

Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.

Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.

Рубрика: |

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников.

Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

Пример 1. Изобразить график функции y = |x 2 – 4x + 3|

1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

x 2 – 4x + 3 = 0.

x 1 = 3, x 2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

y = 0 2 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2 , изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3

Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также

рис. 1 ).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

(рис. 3) .

Пример 3. Изобразить график функции y = log 2 |x|

Применяем схему, данную выше.

1) Строим график функции y = log 2 x (рис. 4) .

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.

1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1

можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x 2 + 2x – 1 (рис.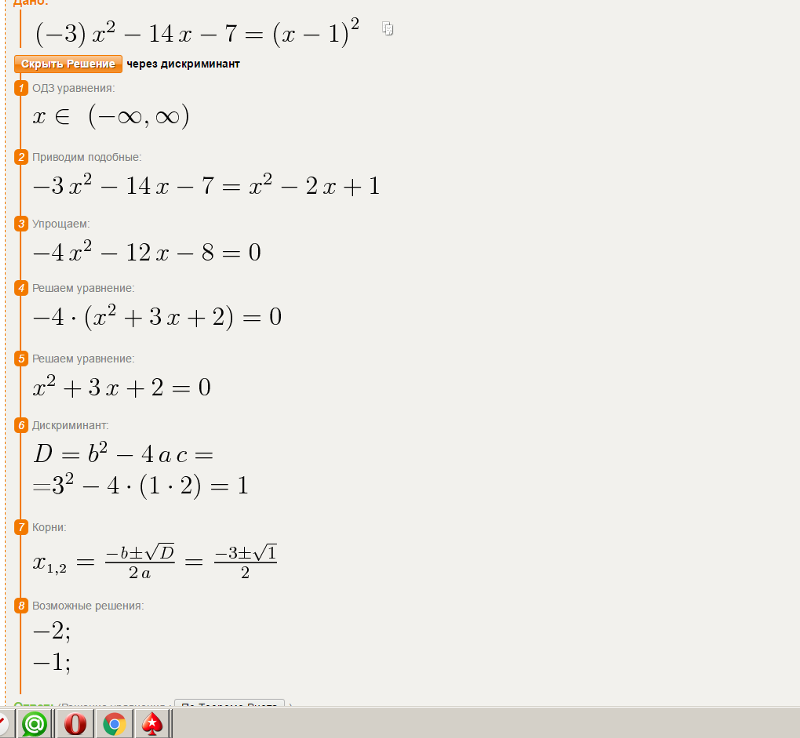 6) .

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7) .

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8) .

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11) .

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Разберем как строить график с модулем.

Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3

У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.

1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1

У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).

y=— (x-3)-(— (x+3))=-х+3+х+3=6

На интервале (-∞;-3) получился график линейной функции (прямой) у=6

2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3

У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.

y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x

На интервале (-3;3) получился график линейной функции (прямой) у=-2х

3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.

х=5
x-3=5-3=2 и x+3=5+3=8

У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).

y=+ (x-3)-(+ (x+3))=х-3-х-3=-6

На интервале (3;+∞) получился график линейной функции (прямой) у=-6

4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.

5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.

Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.

Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|.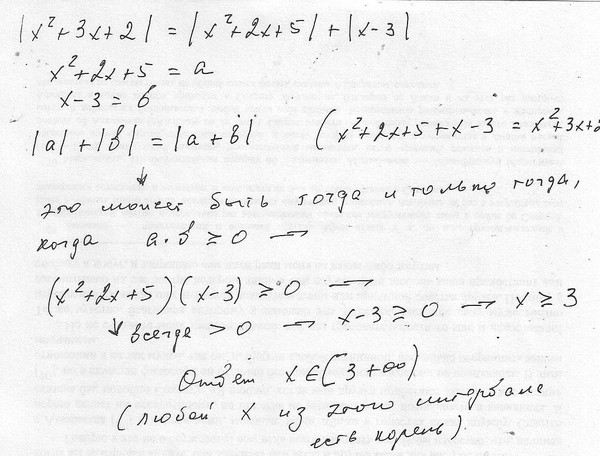 Этот вариант нам подходит.

Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.

Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.

Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.

Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.

Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }

Как построить параболу | Алгебра

Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.

График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле

для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ=xₒ²+bxₒ+c. От вершины (хₒ; yₒ ) строим параболу y=x².

Пример.

Построить график функции y=x²+2x-3.

Решение:

y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

y=x²+2x-3

Пример.

Построить график функции y= -x²+2x+8.

Решение:

y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

y= -x²+2x+8

Примеры.

Построить график функции y=x²+5x+4.

Решение:

y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы

то есть вершина параболы — точка (-2,5; -2,25).

Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).

В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).

y=x²+5x+4

Построить график функции y= -x²-3x.

Решение:

y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы

Вершина (-1,5; 2,25) — первая точка параболы.

При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.

y= -x²-3x

Построить график функции у=-x²+2x+8 (парабола) – решение и ответ

Формулировка задания: Построить график функции у = -x² + 2x + 8.

Решение:

Для построения графика параболы нужно построить таблицу значений x и y.

Для удобства начнем с точек, находящихся на осях Ox и Oy. Если точка лежит на оси Oy (x = 0), тогда:

x = 0 ⇒

y = -0² + 2 ⋅ 0 + 8 = 8

Если точка лежит на оси Ox (y = 0), нужно решить квадратное уравнение:

y = 0 ⇒

-x² + 2x + 8 = 0

a = -1, b = 2, c = 8

D = 2² – 4 ⋅ (-1) ⋅ 8 = 36

x₁ = (-2 + 6) / (-2) = -2

x₂ = (-2 – 6) / (-2) = 4

Таким образом, мы получили 3 точки пересечения с осями. Заполняем ими таблицу:

Возьмем еще пару точек, которые будет просто посчитать, например, x = 1 и x = -1:

x = 1 ⇒

y = -1² + 2 ⋅ 1 + 8 = 9

x = -1

y = -(-1)² + 2 ⋅ (-1) + 8 = 5

Таблица значений теперь выглядит следующим образом:

Отметим полученные точки на координатной плоскости:

Координату x вершины параболы можно определить по любым 2 точкам параболы, у которых равно значение y: она лежит точно между ними. Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):

(4 – (-2)) / 2 = 6 / 2 = 3

x_в = -2 + 3 = 1

Точка с таким значением x уже есть в таблице значений. Осталось построить график:

Поделитесь статьей с одноклассниками «Построить график функции у=-x²+2x+8 (парабола) – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.

Разложение на множители многочлена третьей степени

Пример 1. Разложить на множители многочлен x³ — 3x² — 4x + 6.

Решение.

Делители свободного члена: ±1, ±2, ±3, ±6. Значит, корни многочлена нужно искать среди них. Простой подстановкой убеждаемся, что корнем многочлена является число 1. Значит, исходный многочлен надо разделить на x — 1.

Воспользуемся схемой Горнера.

Таким образом, x³ — 3x² — 4x + 6 = (x — 1)(x² — 2x — 6). Чтобы найти оставшиеся 2 корня многочлена, решаем квадратное уравнение x² — 2x — 6 = 0.

Но обычно в разложении на множители нас не интересуют иррациональные корни (то есть, такое разложение квадратичного многочлена на множители

Ответ: x³ — 3x² — 4x + 6 = (x — 1)(x² — 2x — 6).

Пример 2. Разложить на множители многочлен -2x³ + 3x² — 4x — 9.

Решение.

Делители свободного члена: ±1, ±3, ±9. Делители старшего коэффициента: ±1, ±2.
Значит, корни исходного многочлена будем искать среди чисел: ±1, ±3, ±9,

Снова простой подстановкой убеждаемся, что -1 является корнем многочлена. С помощью схемы Горнера делим исходный многочлен на x + 1.

Таким образом, -2x³ + 3x² — 4x — 9 = (x + 1)(-2x² + 5x — 9).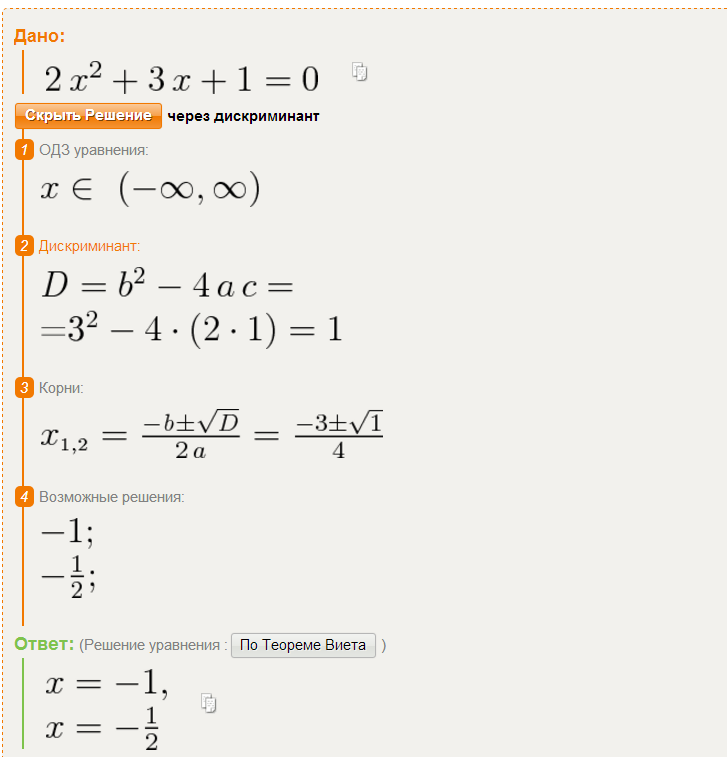 Решая квадратное уравнение -2x² + 5x — 9 = 0, получаем, что его дискриминант

Ответ: -2x³ + 3x² — 4x — 9 = (x + 1)(-2x² + 5x — 9).

Пример 3. Разложить на множители многочлен 2x³ — x² — 8x + 4.

Решение.

Простой подстановкой убеждаемся, что 2 является корнем многочлена. С помощью схемы Горнера делим исходный многочлен на x — 2.

Таким образом, 2x³ — x² — 8x + 4 = (x — 2)(2x² + 3x — 2).
Решая квадратное уравнение 2x² + 3x — 2 = 0, получаем,

Следовательно, 2x² + 3x — 2 = 2(x —

)(x + 2).

Ответ: 2x³ — x² — 8x + 4 = 2(x — 2)(x —

)(x + 2) = (2x — 1)(x — 2)(x + 2).

Разложение на множители многочлена третьей степени методом неопределенных коэффициентов

Еще один способ разложения на множители многочлена третьей степени — метод неопределенных коэффициентов. Он достаточно трудоемкий, но иногда бывает очень полезным, причем для разного рода задач, а не только в случае разложения на множители. Разложение на множители любого многочлена третьей степени можно представить следующим образом a(x) = (x-x₀)*(a₃x² + bx + c).

Раскрывая скобки, получим a(x) = a₃x³ + x²(b — a₃x₀) + x*(c — bx₀) — cx₀.

Приравнивая теперь коэффициенты при одинаковых степенях x и свободные члены в исходном многочлене и в многочлене a(x), получим систему из четырех уравнений и четырех неизвестных a₃,b,c и x₀. Рассмотрим применение метода неопределенных коэффициентов на примерах.

Пример 4. Разложить на множители многочлен x³ + 2x² — 5x — 6.

Решение.

Приравнивая соответствующие коэффициенты, получаем следующую систему уравнений

Выразим из первого уравнения x₀ = b — 2 и подставим в два оставшихся. Получим

Теперь из первого уравнения выразим переменную c и подставим во второе.

Раскрывая скобки во втором уравнении и решая его, находим b:

Если b=4, то c=3, x₀ = 2. Следовательно, x³ + 2x² — 5x — 6 = (x — 2)(x² — 4x + 3)=(x — 2)(x + 1)(x + 3).

Если b = 1, то c = -6, x₀ = -1. Следовательно, x³ + 2x² — 5x — 6 = (x + 1)(x² + x — 6)=(x + 1)(x + 3)(x — 2).

Если b = -1, то c = -2, x₀ = -3. Следовательно, x³ + 2x² — 5x — 6=(x + 3)(x² — x — 2) = (x + 3)(x — 2)(x + 1).

Ответ: x³ + 2x² — 5x — 6 = (x — 2)(x + 1)(x + 3).

Формулы сокращенного умножения

Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.

Предварительные навыки

Квадрат суммы двух выражений

Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)².

Выражение (2x + 3y)² это перемножение двух многочленов, каждый из которых равен (2x + 3y)

(2x + 3y)² = (2x + 3y)(2x + 3y)

Получили умножение многочлена на многочлен. Выполним его:

(2x + 3y)² = (2x + 3y)(2x + 3y) = 4x²+ 6xy + 6xy + 9y²= 4x²+ 12xy + 9y²

То есть выражение (2x + 3y)² равно 4x² + 12xy + 9y²

(2x + 3y)² = 4x²+ 12xy + 9y²

Решим аналогичный пример, который попроще:

(a + b)²

Выражение (a + b)² это перемножение двух многочленов, каждый из которых равен (a + b)

(a + b)² = (a + b)(a + b)

Выполним это умножение:

(a + b)² = (a + b)(a + b) = a²+ ab + ab + b² = a²+ 2ab + b²

То есть выражение (a + b)² равно a²+ 2ab + b²

(a + b)² = a²+ 2ab + b²

Оказывается, что случай (a + b)²можно распространить для любых a и b. Первый пример, который мы решили, а именно (2x + 3y)² можно решить с помощью тождества (a + b)² = a²+ 2ab + b². Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)². В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y

a = 2x

b = 3y

И далее можно воспользоваться тождеством (a + b)² = a²+ 2ab + b², но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:

(2x + 3y)² = (2x)² + 2 × 2x × 3y + (3y)² = 4x²+ 12xy + 9y²

Как и в прошлый раз получили многочлен 4x²+ 12xy + 9y². Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:

(2x + 3y)² = 4x²+ 12xy + 9y²

Тождество (a + b)² = a²+ 2ab + b² называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Рассмотрим выражение (2 + 3)². Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.

Первый способ:

(2 + 3)² = 5² = 25

Второй способ:

(2 + 3)² = 2² + 2 × 2 × 3 + 3² = 4 + 12 + 9 = 25

Пример 2. Преобразовать выражение (5a + 3)² в многочлен.

Воспользуемся формулой квадрата суммы двух выражений:

(a + b)² = a²+ 2ab + b²

(5a + 3)² = (5a)²+ 2 × 5a × 3 + 3² = 25a² + 30a + 9

Значит, (5a + 3)² = 25a² + 30a + 9.

Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:

(5a + 3)² = (5a + 3)(5a + 3) = 25a² + 15a + 15a + 9 = 25a² + 30a + 9

Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.

Например, площадь квадрата со стороной a будет равна a². Если увеличить сторону квадрата на b, то площадь будет равна (a + b)²

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b

Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:

Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.

Сначала можно вычислить квадрат со стороной a — его площадь будет равна a². Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b

В результате получается следующая сумма площадей:

a² + ab + ab + b²

Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a²+ 2ab + b², которое является правой частью формулы квадрата суммы двух выражений:

(a + b)² = a²+ 2ab + b²

Квадрат разности двух выражений

Формула квадрата разности двух выражений выглядит следующим образом:

(a − b)² = a²− 2ab + b²

Эту формулу можно прочитать так:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)² представляет собой произведение двух многочленов, каждый из которых равен (a − b)

(a − b)² = (a − b)(a − b)

Если выполнить это умножение, то получится многочлен a²− 2ab + b²

(a − b)² = (a − b)(a − b) = a²− ab − ab + b² = a²− 2ab + b²

Пример 1. Преобразовать выражение (7x − 5)² в многочлен.

Воспользуемся формулой квадрата разности двух выражений:

(a − b)² = a²− 2ab + b²

(7x − 5)² = (7x)²− 2 × 7x × 5 + 5² = 49x² − 70x + 25

Значит, (7x − 5)² = 49x² − 70x + 25.

Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:

(7x − 5)² = (7x − 5)(7x − 5) = 49x² − 35x − 35x + 25 = 49x² − 70x + 25.

Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a², то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)²

Рассмотрим следующий рисунок:

Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b

Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a² вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:

Тогда можно написать следующее выражение: старая площадь a² минус площадь ab минус площадь (a − b)b

a² − ab − (a − b)b

Раскроем скобки в выражении (a − b)b

a² − ab − ab + b²

Приведем подобные слагаемые:

a² − 2ab + b²

В результате получается выражение a² − 2ab + b², которое является правой частью формулы квадрата разности двух выражений:

(a − b)² = a²− 2ab + b²

Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.

Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.

Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.

Например, если дано выражение (5x − 2y)², и мы хотим воспользоваться формулой (a − b)² = a²− 2ab + b², то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.

(5x − 2y)²
a = 5x
b = 2y
(5x − 2y)² = (5x)² − 2 × 5x × 2y + (2y)² = 25x² − 20xy + 4y²

Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:

(5x − 2y)² = (5x + (−2y))²

и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:

(5x + (−2y)²
a = 5x
b = −2y
(5x + (−2y))² = (5x)² + 2 × 5x × (−2y) + (−2y)² = 25x² − 20xy + 4y²

Исключением могут быть выражения вида (x − (−y))². В данном случае, применяя формулу (a − b)² = a²− 2ab + b² вместо b следует подставить (−y)

(x − (−y))² = x² − 2 × x × (−y) + (−y)² = x² + 2xy + y²

Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)² и можно будет воспользоваться формулой квадрата суммы, а не разности:

(x + y)² = x² + 2xy + y²

Куб суммы и куб разности

Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:

(a + b)³ = a³+ 3a²b + 3ab²+ b³

(a − b)³ = a³− 3a²b + 3ab²− b³

Формулу куба суммы двух выражений можно прочитать так:

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

А формулу куба разности двух выражений можно прочитать так:

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.

Выведем формулу куба суммы самостоятельно:

(a + b)³

Выражение (a + b)³ представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)

(a + b)³ = (a + b)(a + b)(a + b)

Но выражение (a + b)³ также может быть записано как (a + b)(a + b)²

(a + b)³ = (a + b)(a + b)²

При этом сомножитель (a + b)² является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a²+ 2ab + b².

Тогда (a + b)³ можно записать как (a + b)(a²+ 2ab + b²).

(a + b)³ = (a + b)(a²+ 2ab + b²)

А это есть умножение многочлена на многочлен. Выполним его:

(a + b)³ = (a + b)(a²+ 2ab + b²) = a³ + 2a²b + ab² + a²b + 2ab² + b³ = a³+ 3a²b + 3ab²+ b³

Аналогично можно вывести формулу куба разности двух выражений:

(a − b)³ = (a − b)(a² − 2ab + b²) = a³ − 2a²b + ab² − a²b + 2ab² − b³ = a³− 3a²b + 3ab²− b³

Пример 1. Преобразуйте выражение (x + 1)³ в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b)³ = a³+ 3a²b + 3ab²+ b³

(x + 1)³ = x³ + 3 × x² × 1 + 3 × x × 1² + 1³ = x³ + 3x² + 3x + 1

Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:

(x + 1)³ = (x + 1)(x + 1)(x + 1) = (x + 1)(x² + 2x + 1) = x³ + 2x² + x + x² + 2x + 1 = x³ + 3x² + 3x + 1

Пример 2. Преобразовать выражение (6a²+ 3b³)³ в многочлен.

Воспользуемся формулой куба суммы двух выражений:

(a + b)³ = a³+ 3a²b + 3ab²+ b³

(6a² + 3b³)³= (6a²)³+ 3 × (6a²)² × 3b³ + 3 × 6a²× (3b³)² + (3b³)³ = 216a⁶ + 3 × 36a⁴ × 3b³+ 3 × 6a²× 9b⁶ + 27b⁹

Пример 3. Преобразовать выражение (n² − 3)³ в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b) = a³− 3a²b + 3ab²− b³

(n² − 3)³ = (n²)³ − 3 × (n²)² × 3 + 3 × n² × 3² − 3³ = n⁶ − 9n⁴ + 27n² − 27

Пример 4. Преобразовать выражение (2x²− x³)³ в многочлен.

Воспользуемся формулой куба разности двух выражений:

(a − b) = a³− 3a²b + 3ab²− b³

(2x²− x³)³= (2x²)³− 3 × (2x²)² × x³ + 3 × 2x²× (x³)²− (x³)³=
8x⁶ − 3 × 4x⁴ × x³ + 3 × 2x²× x⁶ − x⁹ =
8x⁶ − 12x⁷ + 6x⁸ − x⁹

Умножение разности двух выражений на их сумму

Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:

(a − b)(a + b)

В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:

(a − b)(a + b) = a² + ab − ab − b² = a² − b²

То есть выражение (a − b)(a + b) равно a² − b²

(a − b)(a + b) = a² − b²

Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.

Пример 1. Выполнить умножение (2x − 5)(2x + 5)

В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a² − b² имеем:

(2x − 5)(2x + 5) = (2x)² − 5²

Вычислим правую часть, получим 4x² − 25

(2x − 5)(2x + 5) = (2x)² − 5² = 4x² − 25

Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a²− b². У нас получится тот же результат 4x² − 25

(2x − 5)(2x + 5) = 4x²− 10x + 10x − 25 = 4x² − 25

Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a² − b²

(4x − 5y)(4x + 5y) = (4x)² − (5y)² = 16x² − 25y²

Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a² − b²

(2a + 3b)(2a − 3b) = (2a)² − (3b)² = 4a² − 9b²

В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a² − b² разность располагается раньше.

Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a² − b², поскольку от перестановки сомножителей произведение не меняется.

Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a²− 9b².

Пример 3. Выполнить умножение (7 + 3x)(3x − 7)

Воспользуемся формулой умножения разности двух выражений на их сумму:

(a − b)(a + b) = a² − b²

(7 + 3x)(3x − 7) = (3x)² − 7² = 9x² − 49

Пример 4. Выполнить умножение (x²− y³)(x²+ y³)

(a − b)(a + b) = a² − b²

(x²− y³)(x²+ y³) = (x²)² − (y³)² = x⁴ − y⁶

Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)

В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)

Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)² − (3y)²)

Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)². А это приведет к ошибке и изменению значения исходного выражения.

Далее вычисляем выражение в скобках:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)² − (3y)²) = −1(25x²− 9y²)

Теперь умножим −1 на выражение в скобках и получим окончательный результат:

(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)² − (3y)²) =
−1(25x²− 9y²) = −25x²+ 9y²

Умножение разности двух выражений на неполный квадрат их суммы

Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:

(a − b)(a² + ab + b²)

Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a² + ab + b²) является неполным квадратом суммы этих двух выражений.

Неполный квадрат суммы это многочлен вида a² + ab + b². Он похож на обычный квадрат суммы a² + 2ab + b² за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x² + 6xy + 9y² является неполным квадратом суммы выражений 2x и 3y.

Действительно, первый член выражения 4x² + 6xy + 9y², а именно 4x² является квадратом выражения 2x, поскольку (2x)² = 4x². Третий член выражения 4x² + 6xy + 9y², а именно 9y² является квадратом выражения 3y, поскольку (3y)² = 9y². Член находящийся в середине 6xy, является произведением выражений 2x и 3y.

Итак, умножим разность (a − b) на неполный квадрат суммы a² + ab + b²

(a − b)(a² + ab + b²) = a(a² + ab + b²) − b(a² + ab + b²) =
a³ + a²b + ab² − a²b − ab² − b³ = a³ − b³

То есть выражение (a − b)(a² + ab + b²) равно a³ − b³

(a − b)(a² + ab + b²) = a³ − b³

Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:

Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.

Пример 1. Выполнить умножение (2x − 3y)(4x² + 6xy + 9y²)

Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. Второй многочлен 4x² + 6xy + 9y² это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a² + ab + b²) = a³ − b³. В нашем случае умножение (2x − 3y)(4x² + 6xy + 9y²) можно заменить на разность кубов 2x и 3y

(2x − 3y)(4x² + 6xy + 9y²) = (2x)³ − (3y)³ = 8x³− 27y³

Попробуем решить этот же пример, не пользуясь формулой (a − b)(a²+ ab + b²) = a³− b³. У нас получится тот же результат, но решение станет длиннее:

(2x − 3y)(4x² + 6xy + 9y²) = 2x(4x² + 6xy + 9y²) − 3y(4x² + 6xy + 9y²) =
8x³ + 12x²y + 18xy² − 12x²y − 18xy² − 27y³ = 8x³ − 27y³

Пример 2. Выполнить умножение (3 − x)(9 + 3x + x²)

Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a² + ab + b²) = a³ − b³

(3 − x)(9 + 3x + x²) = 3³ − x³ = 27 − x³

Умножение суммы двух выражений на неполный квадрат их разности

Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:

(a + b)(a² − ab + b²)

Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a² − ab + b²) является неполным квадратом разности этих двух выражений.

Неполный квадрат разности это многочлен вида a² − ab + b². Он похож на обычный квадрат разности a² − 2ab + b² за исключением того, что в нём произведение первого и второго выражений не удваивается.

Например, выражение 4x² − 6xy + 9y² является неполным квадратом разности выражений 2x и 3y.

(2x)² − 2x × 3y + (3y)² = 4x² − 6xy + 9y²

Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a² − ab + b²

(a + b)(a² − ab + b²) = a(a² − ab + b²) + b(a² − ab + b²) =
a³ − a²b + ab² + a²b − ab² + b³ = a³ + b³

То есть выражение (a + b)(a² − ab + b²) равно a³ + b³

(a + b)(a² − ab + b²) = a³ + b³

Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:

Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.

Пример 1. Выполнить умножение (2x + 3y)(4x²− 6xy + 9y²)

Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y, а второй многочлен 4x² − 6xy + 9y² это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a² − ab + b²) = a³ + b³. В нашем случае умножение (2x + 3y)(4x² − 6xy + 9y²) можно заменить на сумму кубов 2x и 3y

(2x + 3y)(4x² − 6xy + 9y²) = (2x)³ + (3y)³ = 8x³+ 27y³

Попробуем решить этот же пример, не пользуясь формулой (a + b)(a²− ab + b²) = a³+ b³. У нас получится тот же результат, но решение станет длиннее:

(2x + 3y)(4x² − 6xy + 9y²) = 2x(4x² − 6xy + 9y²) + 3y(4x² − 6xy + 9y²) =
8x³ − 12x²y + 18xy² + 12x²y − 18xy² + 27y³ = 8x³ + 27y³

Пример 2. Выполнить умножение (2x + y)(4x² − 2xy + y²)

Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x² − 2xy + y²) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a²− ab + b²) = a³+ b³

(2x + y)(4x² − 2xy + y²) = (2x)³ + y³ = 8x³ + y³

(2x + y)(4x² − 2xy + y²) = 2x(4x² − 2xy + y²) + y(4x² − 2xy + y²) =
8x³ − 4x²y + 2xy² + 4x²y − 2xy² + y³ = 8x³ + y³

Задания для самостоятельного решения

Задание 1. Преобразуйте выражение (m + n)² в многочлен.

Решение:

(m + n)² = m² + 2mn + n²

Задание 2. Преобразуйте выражение (x + 8)² в многочлен.

Решение:

(x + 8)² = x² + 2 × x × 8 + 8² = x² + 16x + 64

Задание 3. Преобразуйте выражение (2x² + 3x³)² в многочлен.

Решение:

(2x² + 3x³)² = (2x²)² + 2 × 2x² × 3x³ + (3x³)² = 4x⁴ + 12x⁵ + 9x⁶

Задание 4. Преобразуйте выражение (5a + 5)² в многочлен.

Решение:

(5a + 5)² = (5a)² + 2 × 5a × 5 + 5² = 25a² + 50a + 25

Задание 5. Преобразуйте выражение (9 − x)² в многочлен.

Решение:

(9 − x)² = 9² − 2 × 9 × x + x² = 81 − 18x + x²

Задание 6. Преобразуйте выражение (x − 25)² в многочлен.

Решение:

(x − 25)² = x² − 2 × x × 25 + 25² = x² − 50x + 625

Задание 7. Преобразуйте выражение (3x² − y³)² в многочлен.

Решение:

(3x² − y³)² = (3x²)² − 2 × 3x² × y³ + ( y³)² = 9x⁴ − 6x²y³ + y⁶

Задание 8. Выполните умножение (x − y)(x + y)

Решение:

(x − y)(x + y) = x² − y²

Задание 9. Выполните умножение (2x − y)(2x + y)

Решение:

(2x − y)(2x + y) = (2x)² − y² = 4x² − y²

Задание 10. Выполните умножение (7 + 3y)(3y − 7)

Решение:

(7 + 3y)(3y − 7) = (3y)² − 7² = 9y² − 49

Задание 11. Выполните умножение (x² − 5)(x² + 5)

Решение:

(x² − 5)(x² + 5) = (x²)² − 5² = x⁴ − 25

Задание 12. Выполните умножение (a³ − b²)(a³ + b²)

Решение:

(a³ − b²)(a³ + b²) = (a³)² − (b²)² = a⁶ − b⁴

Задание 13. Выполните умножение (5a² + 2b³)(5a² − 2b³)

Решение:

(5a² + 2b³)(5a² − 2b³) = (5a²)² − (2b³)² = 25a⁴ − 4b⁶

Задание 14. Выполните умножение (9x − y²)(y² + 9x)

Решение:

(9x − y²)(y² + 9x) = (9x)² − (y²)² = 81x² − y⁴

Задание 15. Выполните умножение (2 − x)(4 + 2x + x²)

Решение:

(2 − x)(4 + 2x + x²) = 2³− x³ = 8 − x³

Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)

Решение:

(3 − 2)(9 + 6 + 4) = 3³− 2³ = 27 − 8 = 19

Задание 17. Выполните умножение (4x + 1)(16x² − 4x + 1)

Решение:

(4x + 1)(16x² − 4x + 1) = (4x)³+ 1³ = 64x³+ 1

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

2-2x-3 = 0 Tiger Algebra Solver

Пошаговое решение:

Шаг 1:

Попытка разложить на множители путем разделения среднего члена

1.1 Факторинг x ² -2x-3

Первый член равен , X ² его коэффициент равен 1.
Средний член равен -2x, его коэффициент равен -2.
Последний член, «константа», равен -3

Шаг-1: Умножьте коэффициент первого члена на константу 1 • -3 = -3

Шаг-2: Найдите два множителя -3, сумма которых равен коэффициенту среднего члена, равному -2.

-3

-2

Вот и все

Шаг 3: Перепишите полиномиальное разбиение среднего члена, используя два фактора, найденные в шаг 2 выше, -3 и 1
x ² — 3x + 1x — 3

Шаг 4: сложите первые 2 члена, вычитая одинаковые множители:
x • (x-3)
Сложите последнее 2 члена, извлекая общие множители:
1 • (x-3)
Шаг 5: сложите четыре члена из шага 4:
(x + 1) • (x-3)
Какая желаемая факторизация

Уравнение в конце шага 1:

 (x + 1) • (x - 3) = 0

Шаг 2:

Теория — Корни продукта:

2.1 Произведение нескольких членов равно нулю.

Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.

Теперь мы решим каждый член = 0 отдельно

Другими словами, мы собираемся решить столько уравнений, сколько членов содержится в произведении

Любое решение для члена = 0 также решает продукт = 0.

Решение уравнения с одной переменной:

2.2 Решите: x + 1 = 0

Вычтите 1 из обеих частей уравнения:
x = -1

Решение уравнения с одной переменной:

2.3 Решите: x-3 = 0

Добавьте 3 к обеим сторонам уравнения:
x = 3

Дополнение: Непосредственное решение квадратного уравнения

 Решение x ² -2x-3 = 0 напрямую

Ранее мы разложили этот многочлен на множители, разделив средний член. Давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу

Парабола, найдя вершину:

3.1 Найдите вершину y = x ² -2x-3

Параболы имеют наибольшее значение или самая низкая точка называется Вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (также известный как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).

Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.

Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.

Для любой параболы Ax ² + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна 1.0000

Подставляя в формулу параболы 1,0000 для x, мы можем вычислить координату y:
y = 1,0 * 1,00 * 1,00 — 2,0 * 1,00 — 3,0
или y = -4,000

Парабола, графическая вершина и пересечения по оси X:

Корневой график для: y = x ² -2x-3
Ось симметрии (пунктирная линия) {x} = {1.00}
Вершина в точке {x, y} = {1.00, -4.00}
x -Переходы ( Корни):
Корень 1 при {x, y} = {-1.00, 0.00}
Корень 2 при {x, y} = {3.00, 0.00}

Решите квадратное уравнение, заполнив квадрат

3.2 Решение x ² -2x-3 = 0, завершив Квадрат.

Добавьте 3 к обеим сторонам уравнения:
x ² -2x = 3

Теперь умный бит: возьмите коэффициент при x, равный 2, разделите его на два, получив 1, и возведите его в квадрат, получив 1

Добавьте 1 к обеим частям уравнения:
В правой части получим:
3 + 1 или, (3/1) + (1/1)
Общий знаменатель двух дробей равен 1 Сложение (3 / 1) + (1/1) дает 4/1
Таким образом, прибавляя к обеим сторонам, мы, наконец, получаем:
x ² -2x + 1 = 4

Добавление 1 завершило левую часть в идеальный квадрат:
x ² -2x + 1 =
(x-1) • (x-1) =
(x-1) ²
Вещи, которые равны одному и тому же, также равны друг другу.Поскольку
x ² -2x + 1 = 4 и
x ² -2x + 1 = (x-1) ²
, то согласно закону транзитивности
(x-1) ² = 4

Мы будем называть это уравнение уравнением. # 3.2.1

Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.

Обратите внимание, что квадратный корень из
(x-1) ² равен
(x-1) ^2/2 =
(x-1) ¹ =
x-1

Теперь, применяя Принцип квадратного корня для уравнения.# 3.2.1 получаем:
x-1 = √ 4

Добавьте 1 к обеим сторонам, чтобы получить:
x = 1 + √ 4

Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное
x ² — 2x — 3 = 0
имеет два решения:
x = 1 + √ 4
или
x = 1 — √ 4

Решите квадратное уравнение с помощью квадратичной формулы

3.3 Решение x ² -2x-3 = 0 по квадратичной формуле.

Согласно квадратичной формуле, x, решение для Ax ² + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:

— B ± √ B ² -4AC
x = ————————
2A

В нашем случае A = 1
B = -2
C = -3

Соответственно B ² — 4AC =
4 — (-12) =
16

Применение формулы квадратного уравнения:

2 ± √ 16
x = —————
2

Можно ли упростить √ 16?

Да! Разложение на простые множители 16 равно
2 • 2 • 2 • 2
Чтобы иметь возможность удалить что-либо из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).

√ 16 = √ 2 • 2 • 2 • 2 = 2 • 2 • √ 1 =
± 4 • √ 1 =
± 4

Итак, теперь мы смотрим на:
x = (2 ± 4) / 2

Два реальных решения:

x = (2 + √16) / 2 = 1 + 2 = 3.000

или:

x = (2-√16) / 2 = 1-2 = -1,000

Два были найдены решения:

x = 3
x = -1

Заполните квадрат x2-2x = 3

Учебное задание 1: ответьте на каждый вопрос, используя круговую диаграмму ниже.Пожалуйста, помогите мне сейчас, пожалуйста, тулунган, нё ако дито, друг тулунган, нё ако, пожалуйста

напишите, является ли каждый многоугольник правильным или неправильным

pa Ответ по требованию нa tnx

каково значение csc X? a.15 / 17b.15 / 8c.8 / 17d.17 / 15

Дано: ACAS, CS & gt; CA Prove; м м Доказательство: Заявления 1. БСПС, CS & gt; CA 2. Расширьте CA до точки T так, чтобы CT = CS. 3. CT CS и ACTS равнобедренный. 4 … . ZT CST (или m / TmZCST). 5. КТ & gt; CA 6. mzCST = mzCSA + m2AST.7. м mLCSA 8. m2T & gt; mzCSA 9. mzCAS & gt; mzT 10. mzCZAS & gt; mzCSA S Причины 1. 2. 3. Шаг 2, определение конгруэнтных отрезков и определение равнобедренного треугольника. 4. 5. Замена с использованием шага 1 (CS & gt; CA) и шага 2 (CT = CS) 6. 7. Определение угла 8. Замена, используя шаг 4 9. Теорема о внешнем угле. 10.

ЭТАПЫ ОБУЧЕНИЯ И УЧЕБНАЯ ДЕЯТЕЛЬНОСТЬ А. Ассимиляция (Временные рамки: 20 минут) Ответьте соответственно на следующие вопросы: 1. Опишите тип проблем, которые … требуют закона косинусов.2. Можно ли использовать закон косинусов для решения любого треугольника, для которого известны два угла и сторона. 3. Можете ли вы найти реальное применение закона косинусов? Опишите, как вы можете применить закон, дайте хотя бы две ситуации.

ОТВЕТ: В таблице показан результат, когда Майкл бросил кубик 100 раз. Ответьте на следующий вопрос: 1.OutcomeFrequency162.22022101. Что такое тео … теоретическая вероятность того, что кубик покажет «3»? 2. Какова теоретическая вероятность того, что на кубике будет четное число? 3.В эксперименте, проведенном Майклом, какова вероятность выпадения кубика на нечетное число? 4. Основываясь на частоте появления чисел на кубике, какова вероятность того, что он окажется больше 525. Когда Майкл бросил кубик 100 раз, какова вероятность того, что кубик выпадет? 344186145.Total100Учебное задание 2: Сделайте это простым! Взаимодействие с другими людьми

если бы эти стены ______ толще, мы не слышали бы шума снаружи

Давайте потренируемся! (Ответ на отдельных листах, предоставленных) Указания: Для пунктов 1–3 визуализируйте объем следующих сплошных цифр, считая их количество. … каждая из w многокубических единиц имеет Использовать 1 куб = 1 кубическая единица3.кубические единицы кубические единицы кубические единицы 2 Для пунктов с 4 по 5 нарисуйте кубы, чтобы визуализировать заданный объем сплошных фигур. Примечание: используйте куб того же размера.

Дано: ACAS, CS & gt; CA Prove; м м Доказательство: Заявления 1. БСПС, CS & gt; CA 2. Расширьте CA до точки T так, чтобы CT = CS. 3. CT CS и ACTS равнобедренный. 4 … . ZT CST (или m / TmZCST). 5. КТ & gt; CA 6. mzCST = mzCSA + m2AST. 7. м mLCSA 8. m2T & gt; mzCSA 9. mzCAS & gt; mzT 10. mzCZAS & gt; mzCSA S Причины 1. 2. 3. Шаг 2, определение конгруэнтных отрезков и определение равнобедренного треугольника.4. 5. Замена с использованием шага 1 (CS & gt; CA) и шага 2 (CT = CS) 6. 7. Определение угла 8. Замена, используя шаг 4 9. Теорема о внешнем угле. 10.

Алгебраическое решение уравнений

Содержание: Эта страница соответствует § 2.4 (с. 200) текста.

Предлагаемые задачи из текста:

с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87, 88, 95, 97

Квадратные уравнения
Уравнения с участием радикалов
Полиномиальные уравнения высшей степени
Уравнения, содержащие дробные выражения или абсолютные значения

Квадратные уравнения

Квадратное уравнение имеет вид ax ² + bx + c = 0, где a, b и c — числа, а a — не равно 0.

Факторинг

Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое. Для получения дополнительной информации о факторизации многочленов см. Обзорный раздел P.3 (p.26) текста.

Пример 1.

2x ² — 5x — 12 = 0.
(2x + 3) (x — 4) = 0.
2x + 3 = 0 или x — 4 = 0.
x = -3/2 или x = 4.

Принцип квадратного корня

Если x ² = k, то x = ± sqrt (k).

Пример 2.

x ² — 9 = 0.
x ² = 9.
x = 3 или x = -3.

Пример 3.

Пример 4.

x ² + 7 = 0.
х ² = -7.
х = ±.
Обратите внимание, что = =, так что решения
x = ±, два комплексных числа.

Завершение площади

Идея завершения квадрата состоит в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат корневой принцип.

Пример 5.

x ² + 6x — 1 = 0.
x ² + 6x = 1.
x ² + 6x + 9 = 1 + 9.
9, добавленное к обеим сторонам, получено из возведения в квадрат половины коэффициента при x, (6/2) ² = 9. Причина выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами). Поэтому эта процедура называется , завершение квадрата .[Заинтересованный читатель может видеть, что это верно, учитывая (x + a) ² = x ² + 2ax + a ². Чтобы получить «а» нужно всего лишь разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x ² + 2ax, нужно добавить ².]
(x + 3) ² = 10.
Теперь мы можем применить принцип квадратного корня и затем решить относительно x.
x = -3 ± sqrt (10).

Пример 6.

2x ² + 6x — 5 = 0.
2x ² + 6x = 5.
Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент (коэффициент x ²) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив обе части уравнения на 2.
x ² + 3x = 5/2.
Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат, (3/2) ² = 9/4. Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
x ² + 3x + 9/4 = 5/2 + 9/4.
Левая часть — квадрат (x + 3/2). [Проверьте это!]
(x + 3/2) ² = 19/4.
Теперь мы используем принцип квадратного корня и решаем относительно x.
x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2.
x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2

До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня могут быть перегруппированы и решены путем факторинга, как мы видим в следующем примере.

Пример 7.

x ² = 16.

x ² — 16 = 0.

(x + 4) (x — 4) = 0.

x = -4 или x = 4.

В некоторых случаях уравнение может быть решено путем факторизации, но факторизация не очевидна.

Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата, следующие: всегда одинаковы, поэтому их можно применить к общему квадратному уравнению

топор ² + bx + c = 0.

Результатом квадрата этого общего уравнения является формула для решений уравнения называется квадратной формулой.

Квадратичная формула

Решения уравнения ax ² + bx + c = 0:

Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае, где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу.

Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения. Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как сделай это!

Примеры использования квадратичной формулы:

Пример 8.

2x ² + 6x — 5 = 0.
В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратичную формулу, получаем
Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат.
Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика функции f (x) = 2x ² + 6x — 5.

Пример 9.

4x ² + 4x + 1 = 0
В этом примере a = 4, b = 4 и c = 1.
В этом примере следует обратить внимание на две вещи.
Есть только одно решение. С точки зрения графиков это означает, что существует только один пересечение по оси x.
Решение упрощено, поэтому квадратный корень не используется. Это означает, что уравнение могло быть решается факторингом. (Все квадратные уравнения могут быть решены путем разложения на множители ! Я имею в виду, что это могло быть решено легко факторингом.)
4x ² + 4x + 1 = 0.
(2x + 1) ² = 0.
х = -1/2.

Пример 10.

х ² + х + 1 = 0
а = 1, б = 1, с = 1
Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов. функции f (x) = x ² + x + 1. Таким образом, решения сложны, поскольку график y = x ² + x + 1 не имеет пересечений по x.

Выражение под радикалом в квадратичной формуле, b ² — 4ac, называется дискриминантом уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений.

1. Дискриминант> 0. Два реальных решения.
2. Дискриминант = 0. Одно реальное решение.
3. Дискриминант <0. Два сложных решения.

Примечания к проверке решений

Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример 3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения, потому что при решении уравнений очень легко сделать невнимательные ошибки.
Алгебраический метод, который заключается в подстановке числа обратно в уравнение и проверке того, что полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда решение предполагает радикальное.
Например, в нашем предпоследнем примере 4x ² + 4x + 1 = 0 мы нашли одно решение x = -1/2.
Алгебраическая проверка выглядит как
4 (-1/2) ² +4 (-1/2) + 1 = 0.
4 (1/4) — 2 + 1 = 0.
1-2 + 1 = 0.
0 = 0. Решение проверяет.
В предыдущем примере, 2x ² + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2. Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический проверить или использовать калькулятор для алгебраической проверки быстрее.
Сначала найдите десятичные приближения для двух предложенных решений.
(-3 + sqrt (19)) / 2 = 0,679449.
(-3 — sqrt (19)) / 2 = -3,679449.
Теперь используйте графическую утилиту для построения графика y = 2x ² + 6x — 5 и проследите график, чтобы приблизительно определить, где х-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения. Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно не точное решение.
Обратите внимание, что если вы начали с уравнения 2x ² + 6x — 5 = 0 и сразу перешли к графику утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя (алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень близко к найденным вами числам, значит, вы, наверное, правы!

Упражнение 1:

Решите следующие квадратные уравнения.
(а) 3x ² -5x — 2 = 0. Ответ
(б) (x + 1) ² = 3. Ответ
(в) x ² = 3x + 2. Ответ

Вернуться к содержанию

Уравнения с участием радикалов

Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения необходимо проверить.

Если в уравнении только один радикал, то перед возведением в степень вы должны договориться, чтобы радикальный член сам по себе на одной стороне уравнения.

Пример 11.

Теперь, когда мы изолировали радикальный член в правой части, возводим обе части в квадрат и решаем полученное уравнение для x.
Чек:
х = 0
Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно!
Итак, x = 0 не является решением .
х = 3
Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно раствор .
Решение : x = 3.
Примечание: Решением является x-координата точки пересечения графиков y = x и у = sqrt (х + 1) +1.

Посмотрите, что бы произошло, если бы мы возводили обе части уравнения в квадрат до , выделив радикал срок.

Это хуже, чем мы начали!

Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью возведение в степень один раз. Однако мы можем на уменьшить количество радикальных членов на , возведя их в степень.

Если уравнение включает более одного радикального члена, мы все равно хотим изолировать один радикал с одной стороны и возвести в степень. Затем мы повторяем этот процесс.

Пример 12.

Теперь возведите обе части уравнения в квадрат.
В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член, а затем возведите в квадрат снова обе стороны.
Чек:
Подстановка x = 5/4 в исходное уравнение дает
sqrt (9/4) + sqrt (1/4) = 2.
3/2 + 1/2 = 2.
Это утверждение верно, поэтому x = 5/4 является решением.

Примечание по проверке решений:

В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка имеет то преимущество, что показывает, что нет никаких решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение — координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1).

Упражнение 2:

Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ

Вернуться к содержанию

Полиномиальные уравнения высшей степени

Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) от одной переменной может быть решено с помощью Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее.Когда мы встречаемся такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать решения с графической утилитой.

Нулевая постоянная

Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий x, чтобы начать задачу.

Пример 13.

2x ³ + 3x ² -5x = 0.
x (2x ² + 3x -5) = 0.
Теперь у нас есть произведение x и квадратного многочлена, равного 0, так что у нас есть два более простых уравнения.
x = 0 или 2x ² + 3x -5 = 0.
Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение может быть решено факторингом. Примечание: Если бы мы не смогли разложить квадратичный коэффициент во втором уравнении, мы могли бы прибегнуть к к использованию квадратичной формулы.[Убедитесь, что вы получили те же результаты, что и ниже.]
x = 0 или (2x + 5) (x — 1) = 0.
Итак, есть три решения: x = 0, x = -5/2, x = 1.
Примечание: Решение находится при пересечении графиков f (x) = 2x ³ + 3x ² -5x.

Фактор по группировке

Пример 14.

x ³ -2x ² -9x +18 = 0.
Коэффициент при x ² в 2 раза больше, чем при x ³, и такое же соотношение существует между коэффициенты при третьем и четвертом членах. Группа слагает один и два, а также три и четыре.
x ² (x — 2) — 9 (x — 2) = 0.
Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить левую часть уравнения на множители.
(x — 2) (x ² — 9) = 0.
Всякий раз, когда мы находим продукт, равный нулю, мы получаем два более простых уравнения.
x — 2 = 0 или x ² — 9 = 0.
x = 2 или (x + 3) (x — 3) = 0.
Итак, есть три решения: x = 2, x = -3, x = 3.
Примечание: Эти решения находятся на пересечении графика f (x) = x ³ -2x ² -9x +18.

Квадратичная форма

Пример 15.

x ⁴ — x ² — 12 = 0.
Этот многочлен неквадратичный, у него четвертая степень. Однако его можно рассматривать как квадратичный по x ².
(x ²) ² — (x ²) — 12 = 0.
Это может помочь вам фактически заменить z на x ².
z ² — z — 12 = 0 Это квадратное уравнение относительно z.
(z — 4) (z + 3) = 0.
z = 4 или z = -3.
Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.Теперь заменим z на x ² и решите полученные уравнения.
x ² = 4.
х = 2, х = -2.
х ² = -3.
x = i , или x = — i.
Итак, есть четыре решения, два реальных и два комплексных.
Примечание: Эти решения находятся на пересечении графика f (x) = x ⁴ — х ² — 12.
График f (x) = x ⁴ — x ²-12 и масштабирование, показывающее его локальную экстремумы.

Упражнение 3:

Решите уравнение x ⁴ — 5x ² + 4 = 0. Ответ

Вернуться к содержанию

Уравнения, содержащие дробные выражения или абсолютные значения

Пример 16.

Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение.
Это уравнение квадратичное. Квадратичная формула дает решения
Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы убедитесь, что оба этих решения проверяют. Решением является координата x точки пересечения графиков. из y = 1 и y = 2 / x-1 / (x + 2).

Пример 17.

5 | х — 1 | = х + 11.
Ключ к решению уравнения с абсолютными значениями — помнить, что величина внутри абсолютного значения столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности, и все решения должны быть проверены.
Дело 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение
5 (x — 1) = x + 11.
5x — 5 = x + 11.
4x = 16.
x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11.
Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Этот точка часто сбивает студентов с толку, потому что кажется, что мы говорим, что абсолютное значение выражения отрицательно, но это не так.Выражение (x - 1) уже отрицательное, поэтому - (x - 1) положительное.
Теперь наше уравнение становится
-5 (x — 1) = x + 11.
-5x + 5 = x + 11.
-6x = 6.
x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11.
Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график
5 * abs (x — 1) — x — 11 и посмотрите на пересечения по оси x, или вы можете найти решение как координаты x точки пересечения графиков y = x + 11 и y = 5 * abs (x-1).

Упражнение 4:

(а) Решите уравнение Ответ
(b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ

Вернуться к содержанию

Решайте неравенства с помощью программы «Пошаговое решение математических задач»

В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах.Эти методы включают переписывание задач в виде символов. Например, заявленная проблема

«Найдите число, которое при добавлении к 3 дает 7»

можно записать как:

3+? = 7, 3 + n = 7, 3 + x = 1

и так далее, где символы?, N и x представляют число, которое мы хотим найти. Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1.Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.

РЕШЕНИЕ УРАВНЕНИЙ

Уравнения могут быть истинными или ложными, так же как словесные предложения могут быть истинными или ложными. Уравнение:

3 + х = 7

будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения.Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.

Пример 1 Определите, является ли значение 3 решением уравнения

4x — 2 = 3x + 1

Решение Мы подставляем значение 3 вместо x в уравнение и смотрим, равен ли левый член правому.

4 (3) — 2 = 3 (3) + 1

12 — 2 = 9 + 1

10 = 10

Отв.3 — это решение.

Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.

Пример 2 Найдите решение каждого уравнения путем осмотра.

а. х + 5 = 12
б. 4 · х = -20

Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИСЛЕНИЯ

В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам нужны некоторые математические «инструменты» для решения уравнений.

ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ

Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,

3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5

— эквивалентные уравнения, потому что 5 — единственное решение каждого из них. Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре.Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.

Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.

Если к обоим элементам прибавляется или вычитается одно и то же количество уравнения, полученное уравнение эквивалентно исходному уравнение.

в символах,

a — b, a + c = b + c и a — c = b — c

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

х + 3 = 7

путем вычитания 3 из каждого члена.

Решение Если вычесть 3 из каждого члена, получим

х + 3 — 3 = 7 — 3

или

х = 4

Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одинаково для обоих, а именно 4. В следующем примере показано, как мы можем сгенерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.

Пример 2 Напишите уравнение, эквивалентное

4x- 2-3x = 4 + 6

, объединив одинаковые термины, а затем добавив по 2 к каждому члену.

Объединение одинаковых терминов дает

х — 2 = 10

Добавление 2 к каждому члену дает

х-2 + 2 = 10 + 2

х = 12

Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.

Пример 3 Решить 2x + 1 = x — 2.

Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала добавим -1 (или вычтем 1 из) каждого члена, мы получим

2x + 1-1 = x — 2-1

2x = х — 3

Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим

2х-х = х — 3 — х

х = -3

, где решение -3 очевидно.

Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.

Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.

2 (-3) + 1 = (-3) — 2

-5 = -5

Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано

Если a = b, то b = a

Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,

Если 4 = x + 2, то x + 2 = 4

Если x + 3 = 2x — 5, то 2x — 5 = x + 3

Если d = rt, то rt = d

Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.

Пример 4 Решите 2x = 3x — 9. (1)

Решение Если мы сначала добавим -3x к каждому члену, мы получим

2x — 3x = 3x — 9 — 3x

-x = -9

, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решение равно 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем

2x-2x + 9 = 3x- 9-2x + 9

9 = х

, из которого решение 9 очевидно. При желании последнее уравнение можно записать как x = 9 по симметричному свойству равенства.

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ДЕЛЕНИЯ

Рассмотрим уравнение

3x = 12

Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения

, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.

Если оба члена уравнения делятся на одно и то же (ненулевое) количество, полученное уравнение эквивалентно исходному уравнению.

в символах,

— эквивалентные уравнения.

Пример 1 Напишите уравнение, эквивалентное

-4x = 12

, разделив каждый член на -4.

Решение Разделив оба элемента на -4, получим

При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.

Пример 2 Решите 3y + 2y = 20.

Сначала мы объединяем одинаковые термины, чтобы получить

5лет = 20

Тогда, разделив каждый член на 5, получим

В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.

Пример 3 Решить 4x + 7 = x — 2.

Решение

Сначала мы добавляем -x и -7 к каждому члену, чтобы получить

4x + 7 — x — 7 = x — 2 — x — 1

Далее, объединяя одинаковые термины, получаем

3x = -9

Наконец, мы разделим каждый член на 3, чтобы получить

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ УМНОЖЕНИЯ

Рассмотрим уравнение

Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения

, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.

Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.

в символах,

a = b и a · c = b · c (c ≠ 0)

— эквивалентные уравнения.

Пример 1 Запишите эквивалентное уравнение для

путем умножения каждого члена на 6.

Решение Умножение каждого члена на 6 дает

При решении уравнений мы используем указанное выше свойство для получения эквивалентных уравнений, не содержащих дробей.

Пример 2 Решить

Решение Во-первых, умножьте каждый член на 5, чтобы получить

Теперь разделите каждого члена на 3

Пример 3 Решить.

Решение Во-первых, упростите над дробной чертой, чтобы получить

Затем умножьте каждый член на 3, чтобы получить

Наконец, разделив каждого члена на 5, получим

ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ

Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.

Шаги по решению уравнений первой степени:

Объедините одинаковые члены в каждом члене уравнения.
Используя свойство сложения или вычитания, запишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
Объедините одинаковые термины в каждом элементе.
Используйте свойство умножения для удаления дробей.
Используйте свойство деления, чтобы получить коэффициент 1 для переменной.

Пример 1 Решите 5x — 7 = 2x — 4x + 14.

Решение Во-первых, мы объединяем одинаковые члены, 2x — 4x, чтобы получить

5x — 7 = -2x + 14

Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить

5x — 7 + 2x + 7 = -2x + 14 + 2x + 1

7x = 21

Наконец, мы разделим каждый член на 7, чтобы получить

В следующем примере мы упрощаем над дробной полосой перед применением свойств, которые мы изучали.

Пример 2 Решить

Решение Во-первых, мы объединяем одинаковые термины, 4x — 2x, чтобы получить

Затем мы добавляем -3 к каждому члену и упрощаем

Затем мы умножаем каждый член на 3, чтобы получить

Наконец, мы разделим каждый член на 2, чтобы получить

РЕШЕНИЕ ФОРМУЛ

Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами. Мы можем найти любую из переменных в формуле, если известны значения других переменных.Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.

Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.

Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть

d = RT

(24) = (3) т

8 = т

Часто бывает необходимо решить формулы или уравнения, в которых есть более одной переменной для одной из переменных в терминах других.Мы используем те же методы, что и в предыдущих разделах.

Пример 2 В формуле d = rt найдите t через r и d.

Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить

из которых по закону симметрии

В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.

Пример 3 В уравнении ax + b = c найдите x через a, b и c.

Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить

, затем разделив каждый член на a, мы получим

Математическая сцена — Уравнения III — Урок 2

Математическая сцена — Уравнения III — Урок 2 — Квадратные уравнения

2008 Rasmus ehf и Jhann sak Ptursson

Уравнения III

Урок 2 Уравнения кубической и четвертой степени

Как мы можем решить такие уравнения, как кубическое уравнение показано здесь?

x ³ — x ² 4x + 4 = 0

Существует чрезвычайно сложная формула решения кубические уравнения.Некоторые калькуляторы имеют встроенную формулу и поэтому могут использоваться для решения кубических уравнений.

Мы собираемся узнать, как эти уравнения могут быть решены с помощью факторизация. Если уравнение имеет решения, которые являются целыми числами a, b и c, то мы можем разложить уравнение на множители следующим образом:

x ³ — x ² 4x + 4 = (x — а) (х — б) (х — в) = 0

Умножая скобки, видим, что константа член 4 должен быть числом, которое мы получаем, когда мы умножаем a, b и c вместе.

abc = 4

Все решения a, b и c должны быть множителями 4, поэтому не так много целых чисел, которые нам нужно учитывать.

У нас есть только следующие возможности:

1, 2 и 4

Хорошо изучите каждое из этих чисел, чтобы найти, какие из них являются решениями уравнения.

f (1) = 1 ³ — 1 ² 4 × 1 + 4 = 0 1 — решение

f (-1) = (-1) ³ — (-1) ² 4 × (-1) + 4 = 6

f (2) = 2 ³ — 2 ² 4 × 2 + 4 = 0 2 — решение

f (−2) = (−2) ³ — (−2) ² 4 × (−2) + 4 = 0 −2 — решение

Мы нашли три решения, поэтому нам не нужно попробуйте 4 и −4 как кубический уравнение имеет максимум три решения.

Эти три числа дают нам значения a, b и c и мы можем факторизовать уравнение.

x ³ — x ² 4x + 4 = (x — 1) (x — 2) (x + 2) = 0

Этот метод включает поиск целых чисел, которые являются множителями (можно разделить на) постоянный член, а затем проверить, действительно ли эти целые числа являются решениями уравнения.
К сожалению, мы не можем предполагать, что решения уравнения третьей степени являются все целые числа.
Однако, если мы можем найти одно целочисленное решение, допустим, что это x = a, тогда по Теорема остатка, мы знаем, что (x — a) является фактором уравнения. Мы можно найти другой множитель, квадратичный множитель, делением. Затем мы можем решить квадратное уравнение, используя формула для решения квадратиков.

Пример 1

Решите уравнение x ³ — 3x ² 2x + 4 = 0

Ставим числа, кратные 4 в уравнение, чтобы увидеть, верны ли какие-либо из них.

f (1) = 1 ³ — 3 × 1 ² 2 × 1 + 4 = 0 1 — решение

f (−1) = (−1) ³ — 3 × (−1) ² 2 × (-1) + 4 = 2

f (2) = 2 ³ — 3 × 2 ² 2 × 2 + 4 = −4

f (−2) = (−2) ³ — 3 × (−2) ² 2 × (−2) + 4 = −12

f (4) = 4 ³ — 3 × 4 ² 2 × 4 + 4 = 12

f (−4) = (−4) ³ — 3 × (−4) ² 2 × (−4) + 4 = −100

Единственное целочисленное решение — x = 1.Когда мы нашли одно решение, нам действительно не нужно проверять другие числа, потому что теперь мы можем решить уравнение, разделив на (x — 1) и попытавшись решить квадратичный получаем из деления.

Теперь мы можем разложить наши выражение следующим образом:

x ³ — 3x ² 2x + 4 = (х — 1) (х ² — 2х — 4) = 0

Теперь нам остается решить квадратичную уравнение.

x ² — 2x — 4 = 0

Используем формулу квадратиков с a = 1, b = −2 и c = −4.

Мы нашли все три решения уравнение x ³ — 3x ² 2x + 4 = 0. Это: eftirfarandi:

х = 1

х = 1 + 5

x = 1- 5

Пример 2

Мы можем легко использовать тот же метод для решения уравнение четвертой степени или уравнения еще более высокой степени.Решите уравнение f (x) = x ⁴ — x ³ — 5x ² + 3x + 2 = 0.

Сначала мы находим целые множители постоянный член, 2. Целочисленные множители 2 равны 1 и 2.

f (1) = 1 ⁴ — 1 ³ — 5 × 1 ² + 3 × 1 + 2 = 0 1 — решение

f (−1) = (−1) ⁴ — (−1) ³ — 5 × (−1) ² + 3 × (−1) + 2 = −4

f (2) = 2 ⁴ — 2 ³ — 5 × 2 ² + 3 × 2 + 2 = −4

f (−2) = (−2) ⁴ — (−2) ³ — 5 × (−2) ² + 3 × (−2) + 2 = 0 ср. нашли вторую решение.

Два найденных нами решения 1 и −2 означают, что мы можем разделить на x — 1 и x + 2 и остатка не будет. Сделайте это в два этапа.
Сначала разделим на x + 2

Теперь разделите полученное кубический коэффициент по x — 1.

Теперь мы разложили на множители
f (x) = x ⁴ — x ³ — 5x ² + 3x + 2 в
f (x) = (x + 2) (x — 1) (x ² — 2x — 1) и только Осталось решить квадратное уравнение

x ² — 2x — 1 = 0.Мы используем формула с a = 1, b = −2 и c = −1.

Всего найдено четыре решения. Их:

х = 1

х = -2

х = 1 +

х = 1-

Иногда мы можем решить уравнение третьей степени, заключив в скобки члены два на два и найдя множитель что у них общего.Давайте посмотрим на это на примере.

Пример 3.

Решите уравнение x ³ — 2x ² — 4x + 8 = 0

x ³ — 2x ² — 4x + 8 = 0

(x ³ — 2x ² ) — (4x — 8) = 0

[x ² (x — 2) — 4 (x — 2)] = 0

(x — 2) [x ² — 4] = 0

(х — 2) (х — 2) (x + 2) = 0

Здесь скобка (x — 2) является общим множителем и может быть вынесена за пределы общая скобка.

Обратите внимание, что скоба (x — 2) происходит дважды, когда мы закончили факторизацию. x = 2 — это поэтому двойное решение, и у нас есть только два разных. Это:

х = 2 и х = -2 .

Лауснир: x = 2 или x = −2 .

Все примеры, которые мы рассмотрели до сих пор, уравнения, в которых член с наибольшей степенью имеет коэффициент 1.

Как нам иметь дело с уравнениями, где этот коэффициент — какое-то другое число?

Общая форма — f (x) = ax ³ + bx ² + cx + d, где a, b, c и d — целые числа.

Мы можем искать целочисленные решения в том же как и раньше, проверяя множители постоянного члена d. Если мы найдем целочисленное решение, тогда мы можем разделить и найти другие решения, как и раньше.

Если ни один из факторов d не дает нам решения затем мы ищем решения, которые являются дробями.
Предположим, есть дробное решение, и назовем его решение x = t / n.

Это означает, что x — t / n является фактором f (x), или, если мы умножаем на n, то xn — t является множителем.

Теперь предположим, что мы разделили f (x) на xn. — t и нашли квадратичный множитель, мы можем назвать его
Ax ² + Bx + C.

Теперь у нас есть результат, что

ax ³ + bx ² + cx + d = (xn — t) (Ax ² + Bx + C)

сравнение коэффициентов x ³ на обе стороны уравнения мы видим, что a = nA и, следовательно, n должно быть множителем а.
Аналогично, сравнивая постоянные члены, мы видим, что d = −tC и, следовательно, t является множителем d.

Мы заключаем, что любая дробь является решением кубическое уравнение ax ³ + bx ² + cx + d должен иметь вид t / n, где t — множитель числа d, а n — фактор числа a.

Обобщение для функции степени n:

ф (х) = a _n x ⁿ + a _{n − 1} x ^{n − 1} + × × × × + а ₁ х + ₀

с коэффициентами a ₀ , а ₁ , а ₂ , × × × × × а _{n − 2} , _{n − 1} и _n .

Если эта функция имеет рациональное решение, скажем, t / n, тогда t — коэффициент ₀ , а n — коэффициент _n .

Пример 4

Решите уравнение f (x) = 2x ³ — 7x ² + 4x + 3 = 0.

Возможные целые корни f (x) — это делители 3, они равны 1 и 3. Дроби, которые могут быть корнями, — это эти четыре числа, разделенные на множители 2.Итак, полный список рациональных чисел, которые нам нужно рассмотреть, — это , 1, ³ / ₂ и 3.

Сразу видно, что нам не нужно рассмотрите любые отрицательные значения, поскольку все они будут давать отрицательные значения для f (x), а не 0.

Теперь попробуем другие возможности

f () = 2 () ³ — 7 () ² + 4 × + 3 = 3

f (1) = 2 × 1 ³ — 7 × ² + 4 × 1 + 3 = 2

ф (³/₂) = 2 (³/₂) ³ — 7 (³/₂) ² + 4 × ³/₂ + 3 = 0, поэтому мы нашли решение.

x = ³/₂ — это решение, поэтому (x — ³/₂) является фактором. Разделение на (x — ³/₂) может быть трудным. Поэтому мы умножаем на 2 и вместо этого делим на (2x — 3). Если (x — ³/₂) является фактор

, то (2x — 3).

Теперь нам нужно решить уравнение x ² — 2x — 1 = 0.Мы уже решили это уравнение в примере 2. Решения: 1 + 2 og 1 — 2.

Итак, мы нашли три решения. Их:

x = ³/₂ = 1

х = 1 + 2

х = 1 — 2

Попробуйте пройти тест 2 по уравнениям III.

Не забудьте использовать контрольный список для следите за своей работой.

Квадратные неравенства — объяснение и примеры

Подобно тому, как уравнения имеют разные формы, неравенства также существуют в разных формах, и квадратное неравенство является одним из них.

Квадратичное неравенство — это уравнение второй степени, в котором вместо знака равенства используется знак неравенства.

Решения квадратного неравенства всегда дают два корня. Природа корней может быть разной и определяется дискриминантом (b ² — 4ac).

Общие формы квадратичных неравенств:

топор ² + bx + c <0

ах ² + bx + c ≤ 0

топор ² + bx + c> 0

топор ² + bx + c ≥ 0

Примеры квадратичных неравенств:

x ² — 6x — 16 ≤ 0, 2x ² — 11x + 12> 0, x ² + 4> 0, x ² — 3x + 2 ≤ 0 и т. Д.

Как решить квадратичные неравенства?

Примеры квадратичных неравенств: x ² — 6x — 16 ≤ 0, 2x ² — 11x + 12> 0, x ² + 4> 0, x ² — 3x + 2 ≤ 0 пр.

Решение квадратного неравенства в алгебре аналогично решению квадратного уравнения. Единственное исключение состоит в том, что в квадратных уравнениях вы приравниваете выражения к нулю, а в случае неравенств вам интересно знать, что находится по обе стороны от нуля i.е. отрицательные и положительные стороны.

Квадратные уравнения могут быть решены либо методом факторизации , либо с помощью квадратной формулы . Прежде чем мы научимся решать квадратные неравенства, давайте вспомним, как решаются квадратные уравнения, на нескольких примерах.

Как квадратные уравнения решаются методом факторизации?

Поскольку мы знаем, что можем решать квадратные неравенства аналогично квадратным уравнениям, полезно понять, как факторизовать данное уравнение или неравенство.

Давайте посмотрим здесь несколько примеров.

6x ² — 7x + 2 = 0

Решение

⟹ 6x ² — 4x — 3x + 2 = 0

Разложите выражение на множители;

⟹ 2x (3x — 2) — 1 (3x — 2) = 0

⟹ (3x — 2) (2x — 1) = 0

⟹ 3x — 2 = 0 или 2x — 1 = 0

⟹ 3x = 2 или 2x = 1

⟹ x = 2/3 или x = 1/2

Следовательно, x = 2/3, ½

Решить 3x ² — 6x + 4x — 8 = 0

Решение

Разложите выражение в левой части на множители.

⟹ 3x ² — 6x + 4x — 8 = 0

⟹ 3x (x — 2) + 4 (x — 2) = 0

⟹ (x — 2) (3x + 4) = 0

⟹ x — 2 = 0 или 3x + 4 = 0

⟹ x = 2 или x = -4/3

Следовательно, корни квадратного уравнения равны, x = 2, -4/3.

Решить 2 (x ² + 1) = 5x

Решение

2x ² + 2 = 5x

⟹ 2x ² — 5x + 2 = 0

⟹ 2x ² — 4x — x + 2 = 0

⟹ 2x (x — 2) — 1 (x — 2) = 0

⟹ (x — 2) (2x — 1) = 0

⟹ x — 2 = 0 или 2x — 1 = 0

⟹ x = 2 или x = 1/2

Следовательно, решения x = 2, 1/2.

(2x — 3) ² = 25

Решение

Разверните и разложите выражение на множители.

(2x — 3) ² = 25

⟹ 4x ² — 12x + 9-25 = 0

⟹ 4x ² — 12x — 16 = 0

⟹ x ² — 3x — 4 = 0

⟹ (x — 4) (x + 1) = 0

⟹ x = 4 или x = -1

Решить x ² + (4 — 3y) x — 12y = 0

Решение

Разверните уравнение;

x ² + 4x — 3xy — 12y = 0

Факторизация;

⟹ х (х + 4) — 3у (х + 4) = 0

х + 4) (х — 3y) = 0

⟹ x + 4 = 0 или x — 3y = 0

⟹ x = -4 или x = 3y

Таким образом, x = -4 или x = 3y

Чтобы решить квадратное неравенство, мы также применяем тот же метод, который проиллюстрирован в процедуре ниже:

Запишите квадратное неравенство в стандартной форме: ax ² + bx + c, где a, b и — коэффициенты, а a ≠ 0
Определите корни неравенства.
Запишите решение в виде неравенства или интервала.
Если квадратное неравенство имеет вид: (x — a) (x — b) ≥ 0, то a ≤ x ≤ b, а если оно имеет вид: (x — a) (x — b) ≤ 0 , когда a

Пример 1

Решите неравенство x ² — 4x> –3

Решение

Сначала сделайте одну сторону неравенства равной нулю, прибавив обе стороны по 3.

x ² — 4x> –3 ⟹ x ² — 4x + 3> 0

Учтите левую часть неравенства.

x ² — 4x + 3> 0 ⟹ (x — 3) (x — 1)> 0

Найти все нули неравенства;

Для, (x — 1)> 0 ⟹ x> 1 и для, (x — 3)> 0 ⟹ x> 3

Поскольку y положительно, мы выбираем значения x, при которых кривая будет выше оси x.
x <1 или x> 3

Пример 2

Решите неравенство x ² — x> 12.

Решение

Чтобы записать неравенство в стандартной форме, вычтите обе части неравенства на 12.

x ² — x> 12 ⟹ x ² — x — 12> 0.

Факторизуйте квадратное неравенство, чтобы добраться до;

( x -4) ( x + 3)> 0

Найти все нули неравенства;

Для, (x + 3)> 0 ⟹ x> -3

Для x — 4> 0 ⟹ x> 4

Значения x <–3 или x> 4, следовательно, являются решением этого квадратичного неравенства.

Пример 3

Решить 2x ² <9x + 5

Решение

Запишите неравенство в стандартной форме, приравняв одну сторону неравенства к нулю.

2x ² <9x + 5 ⟹ 2x ² — 9x — 5 <0

Разложите на множители левую часть квадратного неравенства.

2x ² — 9x — 5 <0 ⟹ (2x + 1) (x - 5) <0

Решить относительно всех нулей неравенства

Для, (x — 5) <0 ⟹ x <5 и для (2x + 1) <0 ⟹ x <-1/2

Поскольку y отрицателен для уравнения 2x ² — 9x — 5 <0, мы выбираем значения x, при которых кривая будет ниже оси x.

Следовательно, решение -1/2

Пример 4

Решить — x ² + 4 <0.

Решение

Поскольку неравенство уже имеет стандартную форму, мы факторизуем выражение.

-x ² + 4 <0 ⟹ (x + 2) (x - 2) <0

Решить относительно всех нулей неравенства

Для, (x + 2) <0 ⟹ x <-2 и для, (x - 2) <0 ⟹ x <2

Значение y для –x ² + 4 <0 отрицательно; поэтому мы выбираем значения x, при которых кривая будет ниже оси x: –2 2

Пример 5

Решить 2x ² + x — 15 ≤ 0.

Решение

Разложите квадратное уравнение на множители.

2x ² + x — 15 = 0

2x ² + 6x — 5x− 15 = 0

2x (x + 3) — 5 (x + 3) = 0

(2x — 5) (x + 3) = 0

Для, 2x — 5 = 0 ⟹ x = 5/2 и для, x + 3 = 0 ⟹ x = -3

Поскольку y для 2x ² + x — 15 ≤ 0 отрицательно, мы выбираем значения x, при которых кривая будет ниже оси x. Следовательно, x ≤ -3 или x ≥5 / 2 — решение.

Пример 6

Решить — x ² + 3x — 2 ≥ 0

Решение

Умножьте квадратное уравнение на -1 и не забудьте изменить знак.

x ² — 3x + 2 = 0

x ² — 1x — 2x + 2 = 0

х (х — 1) — 2 (х — 1) = 0

(х — 2) (х — 1) = 0

Для, x — 2 = 0 ⟹ x = 2 и для, x — 1 = 0 ⟹x = 1

Следовательно, решение квадратного неравенства 1 ≤ x ≤ 2

Пример 7

Решить x ² — 3x + 2> 0

Решение

Разложите выражение на множители, чтобы получить;

x ² — 3x + 2> 0 ⟹ (x — 2) (x — 1)> 0

Теперь найдите корни неравенства как;

(х — 2)> 0 ⟹ х> 2

(х — 1)> 0 ⟹x> 1

Кривая для x ² — 3x + 2> 0 имеет положительное значение y, поэтому выбираются значения x, при которых кривая будет выше оси x.Следовательно, решение x <1 или x> 2.

Пример 8

Решить −2x ² + 5x + 12 ≥ 0

Решение

Умножить все выражение на -1 и изменить знак неравенства

−2x ² + 5x + 12 ≥ 0 ⟹2x ² — 5x — 12 ≤ 0

Разложите выражение на множители, чтобы получить;

(2x + 3) (x — 4) ≤ 0.

Решите корни;

(2x + 3) ≤ 0 ⟹ x ≤ -3/2.

(x — 4) ≤ 0 ⟹ x ≤ 4.

Применяя правило; (x — a) (x — b) ≥ 0, тогда a ≤ x ≤ b, мы можем удобно записать решения этого квадратного неравенства в виде:

-3/2 ≤ x ≤ 4.

Пример 9

x ² — x — 6 <0

Решение

Разложить на множители x ² — x — 6 получить;

(x + 2) (x — 3) <0

Найдите корни уравнения как;

(x + 2) (x — 3) = 0

x = −2 или x = +3
Поскольку y отрицателен для x ² — x — 6 <0, то мы выбираем интервал, в котором кривая будет ниже оси x.Следовательно, -2

Практические вопросы

(x — 3) (x + 1) <0
x ² + 5x + 6 ≥ 0
(2x — 1) (3x + 4)> 0
10x ² — 19x + 6 ≤ 0
5 — 4x — x ²> 0
1 — x — 2x ² <0
(x — 3) (x + 2)> 0.
x ² −2x − 3 <0.

Ответы

-1 <х <3
x <−3 или x> −2
x <−4/3 или x> ½
2/5 ≤ х ≤ 3/2
−5 <х <1
x <−1 или x> ½
x <–2 или x> 3
−1≤ х ≤ 3

Предыдущий урок | Главная страница | Следующий урок

Как найти набор решений

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Производные и интегралы

Как построить параболу | Алгебра

Построить график функции у=-x²+2x+8 (парабола) – решение и ответ

Разложение на множители многочлена третьей степени

Разложение на множители многочлена третьей степени методом неопределенных коэффициентов

Формулы сокращенного умножения

Квадрат суммы двух выражений

Квадрат разности двух выражений

Куб суммы и куб разности

Умножение разности двух выражений на их сумму

Умножение разности двух выражений на неполный квадрат их суммы

Умножение суммы двух выражений на неполный квадрат их разности

Задания для самостоятельного решения

Навигация по записям

Пошаговое решение:

Шаг 1:

Попытка разложить на множители путем разделения среднего члена

Уравнение в конце шага 1:

Шаг 2:

Теория — Корни продукта:

Решение уравнения с одной переменной:

Решение уравнения с одной переменной:

Дополнение: Непосредственное решение квадратного уравнения

Парабола, найдя вершину:

Парабола, графическая вершина и пересечения по оси X:

Решите квадратное уравнение, заполнив квадрат

Решите квадратное уравнение с помощью квадратичной формулы

Два были найдены решения:

Заполните квадрат x2-2x = 3

Алгебраическое решение уравнений

Квадратные уравнения

Уравнения с участием радикалов

Полиномиальные уравнения высшей степени

Уравнения, содержащие дробные выражения или абсолютные значения

Квадратные уравнения

Факторинг

Принцип квадратного корня

Завершение площади

Квадратичная формула

Уравнения с участием радикалов

Полиномиальные уравнения высшей степени

Нулевая постоянная

Фактор по группировке

Квадратичная форма

Уравнения, содержащие дробные выражения или абсолютные значения

Решайте неравенства с помощью программы «Пошаговое решение математических задач»

РЕШЕНИЕ УРАВНЕНИЙ

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИСЛЕНИЯ

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ДЕЛЕНИЯ

РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ УМНОЖЕНИЯ

ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ

РЕШЕНИЕ ФОРМУЛ

Математическая сцена — Уравнения III — Урок 2

Уравнения III

Квадратные неравенства — объяснение и примеры

Как решить квадратичные неравенства?

Как квадратные уравнения решаются методом факторизации?

Как найти набор решений

Добавить комментарий Отменить ответ