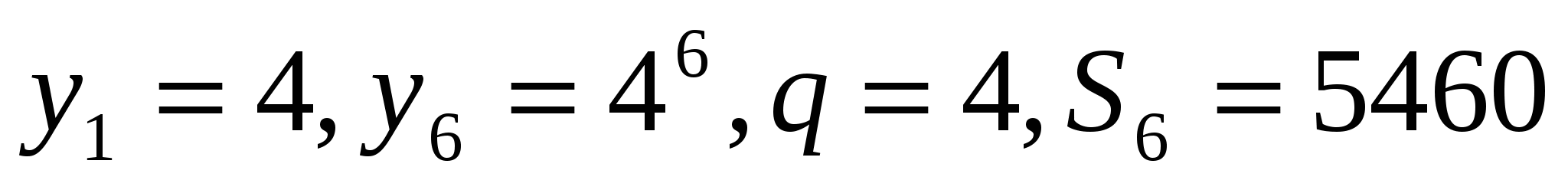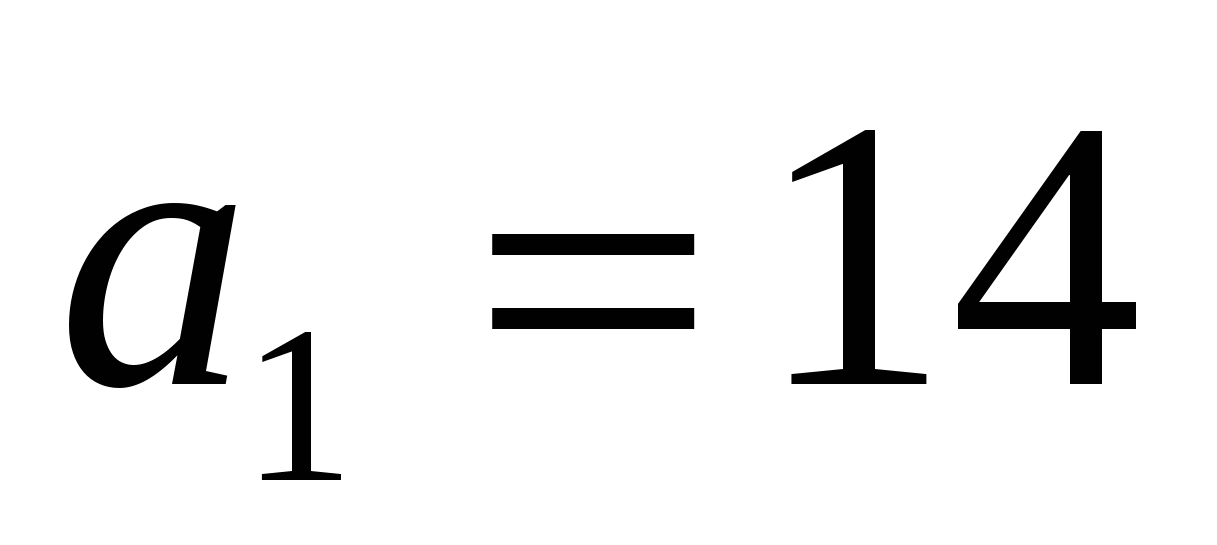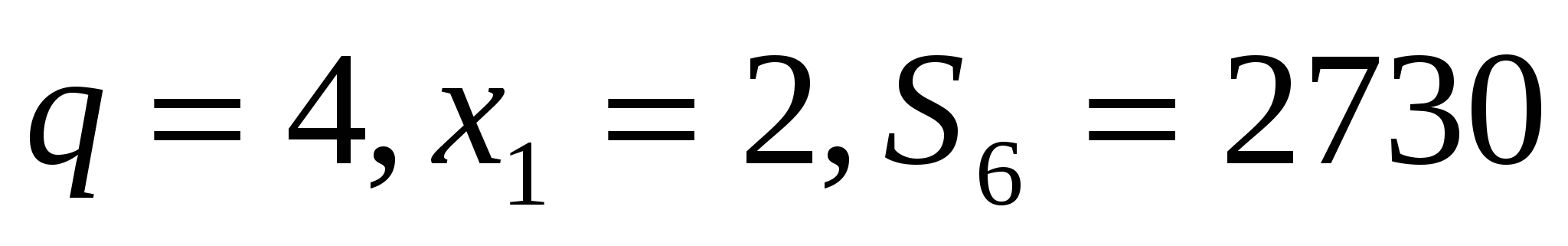Геометрическая прогрессия | Формулы с примерами
ОпределениеГеометрическая прогрессия — это числовая последовательность (bn), в
которой
 для любого натурального n, bn ? 0, q ? 0.
для любого натурального n, bn ? 0, q ? 0.q — знаменатель геометрической прогрессии (заданное число).
Пример| Дано | Геометрическая прогрессия | |
| 1. | b1 = 0,5; q = 2 | 0,5; 1; 2; 4; 8; 16; … |
| 2. | b1 = 7; q = -1 | 7; -7; 7; -7; 7; -7; … |
| 3. | b1 = 100; q = 0,2 | 100; 20; 4; 0,8; 0,16; 0,032; … |
Формула общего (n-го) члена геометрической прогрессии:

Формулы суммы Sn n первых членов геометрической прогрессии:

Где: S1 = b1. Sn = b1 + b2 + … + bn.
Пример решенияb1 = 12, b2 = -6. Найти b7 и сумму S8.
Знаменатель q = b2b1 = — 12.
Тогда b7 = b1 • q6 = 12 • (- 12)6 = 3 16 • S8 = b1(q8 — 1)q — 1 = 7 3132.
Характеристическое свойство геометрической прогрессии
Правило
formula-xyz.ru
Характеристическое свойство арифметической прогрессии. Видеоурок. Алгебра 9 Класс
На этом уроке мы познакомимся с характеристическим свойством арифметической прогрессии и решим ряд задач с его использованием.
Вначале вспомним, что такое числовая последовательность, арифметическая прогрессия, формулы n-го члена и суммы членов конечной прогрессии. Далее докажем прямую и обратную теоремы для арифметической прогрессии и сформулируем характеристическое свойство. В конце решим ряд задач на использование формулы характеристического свойства арифметической прогрессии.
Тема: Прогрессии
Урок: Характеристическое свойство арифметической прогрессии
Функцию  , где
, где  , называют функцией натурального аргумента, или числовой последовательностью.
, называют функцией натурального аргумента, или числовой последовательностью.
Числовая последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называется арифметической прогрессией, число d называется ее разностью: 
В арифметической прогрессии действуют определенные закономерности. Они выражены в следующих важных формулах.
Формула n-го члена арифметической прогрессии:
 .
.
Первая формула суммы первых n членов арифметической прогрессии:
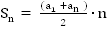 .
.
Вторая формула суммы первых n членов арифметической прогрессии:  .
.
Доказать, что каждый член арифметической прогрессии, начиная со второго, есть среднее арифметическое предыдущего и последующего членов.
Доказательство.
Из определения арифметической прогрессии следует, что

Значит,  ,
, 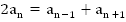 ,
, 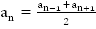 .
.
причем это свойство справедливо для всех n=2, 3,4, …
Таким образом, если мы имеем арифметическую прогрессию, то в ней справедливо доказанное характеристическое свойство.
Справедливо обратное утверждение, а именно: если в последовательности (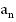 ) каждый член, начиная со второго, есть среднее арифметическое предыдущего и последующего членов, то последовательность (
) каждый член, начиная со второго, есть среднее арифметическое предыдущего и последующего членов, то последовательность (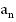
Действительно, из равенства 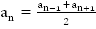 , получаем
, получаем 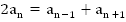
interneturok.ru
Показательно-геометрическая прогрессия и некоторые ее свойства
Как известно, числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с некоторым числом, называется арифметической прогрессией. А числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на некоторое отличное от нуля постоянное число, называется геометрической прогрессией. Из определения арифметической и геометрической прогрессий, мы видим, что данные прогрессии основаны на арифметических действиях суммы (разности) и умножения (деления). Возникает вопрос: существует ли прогрессия, которая основана на действии возведение в степень число. Отвечая на этот вопрос, автором был определен новый вид прогрессии — показательная прогрессия.
Определение 1 [1]. Пусть дана последовательность положительных чисел
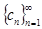
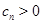
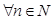 . (1)
. (1)
Последовательность (1), первый член которой отличен от единицы, называется показательной прогрессией, если ее каждый член, начиная со второго, равен предыдущему, возведенному в положительную степень 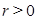
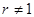 ).
).Таким образом,

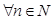 ,
, 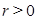 (
(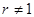 ), (2)
), (2)
где  и
и 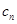 соответственно n— и n+1-й члены прогрессии; r — знаменатель показателя прогрессии, которая вычисляется по формуле
соответственно n— и n+1-й члены прогрессии; r — знаменатель показателя прогрессии, которая вычисляется по формуле
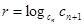 .
.
Показательную прогрессию будем обозначать следующим образом:
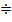
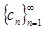 .
.В данной статье был определен новый вид числовой прогрессии — показательно-геометрическая прогрессия. Доказаны некоторые свойства введенной прогрессии, как общая формула 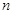 -го члена, формула нахождения знаменателя и знаменателя показателя прогрессии, характеристическое свойство, а также установлена связь с показательной прогрессией.
-го члена, формула нахождения знаменателя и знаменателя показателя прогрессии, характеристическое свойство, а также установлена связь с показательной прогрессией.
Прежде чем дать определение рассматриваемой прогрессии, хотелось бы поговорить о характеристическом свойстве показательной прогрессии. В [1] в качестве характеристического свойства взята следующая теорема.
Теорема. Для каждого члена показательной прогрессии, начиная со второго, выполняется равенство
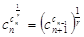 . (3)
. (3)
Хотя соотношение (3) и выражает связь между соседними тремя членами показательной прогрессии, оно связано со знаменателем показателя прогрессии r. Однако если вспомнить, характеристические свойства арифметической и геометрической прогрессий, которые не зависят соответственно от разности и знаменателя, можно сказать, что существует соотношение, которое будет связывать подряд идущих три члена показательной прогрессии, не завися от знаменателя показателя. Покажем ее с помощью следующей теоремы.
Теорема 1 (характеристическое свойство показательной прогрессии). Для каждого члена показательной прогрессии, начиная со второго, выполняется равенство
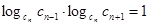 . (4)
. (4)
Доказательство. По определению показательной прогрессии
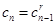
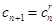 .
.Отсюда следует, что
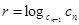 или
или 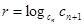
т. е.
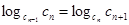

или

что и требовалось доказать.
Перейдем к основной части статьи.
Определение 2. Пусть дана последовательность положительных чисел
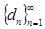

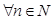 . (5)
. (5)
Последовательность (5), первый член которой отличен от единицы, называется показательно-геометрической прогрессией, если ее каждый член, начиная со второго, равен предыдущему, возведенному в одну и ту же положительную степень 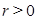 (
(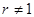 ) и умноженному на одно то же положительное число
) и умноженному на одно то же положительное число 
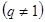 .
.
Таким образом,
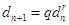
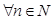 ,
, 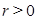 (
(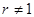 ),
), 
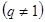 ,
, 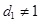 (6)
(6)
где 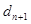 и
и 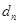 соответственно n— и n+1-й члены прогрессии; q — знаменатель, r — знаменатель показателя прогрессии, которая вычисляется по формуле.
соответственно n— и n+1-й члены прогрессии; q — знаменатель, r — знаменатель показателя прогрессии, которая вычисляется по формуле.
Показательную прогрессию будем обозначать следующим образом:
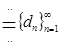 .
.
Пример 1. Следующая прогрессия является показательно-геометрической с 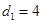 ,
, 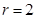 ,
, 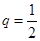 :
:
4, 8, 32, 512, 131072,….
Из определения 2 следуют замечания.
Замечание 1. Если в показатеьльно-геометрической прогрессии 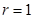 , то можно получить геометрическую прогрессию.
, то можно получить геометрическую прогрессию.
Замечание 2. Если в показатеьльно-геометрической прогрессии 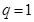 , то можно получить показательную прогрессию.
, то можно получить показательную прогрессию.
Определим знаменатель показателя показательно-геометрической прогрессии. По (6) запишем n+1-ый и n+2-ой члены прогрессии
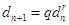 и
и  .
.
Разделим почленно данные равенства и прологарифмируем обе части получившегося равенства по основанию 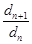 .
.
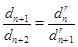 или
или 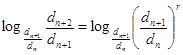 .
.
А от этого следует наше искомое равенство
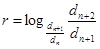 . (7)
. (7)
Замечание 3. Если 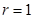 , то из (7) можно получить характеристическое свойство геометрическрй прогрессии, т. е.
, то из (7) можно получить характеристическое свойство геометрическрй прогрессии, т. е.
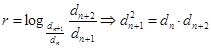 при
при 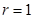 .
.
Рассмотрим следующие равенства
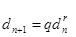 және
және 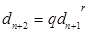 .
.
Отсюда следует, что

По свойству логарифмов
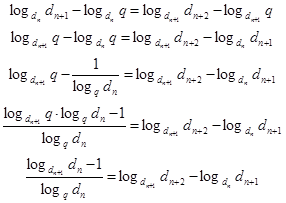
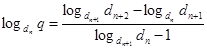 (8)
(8)
Итак, знаменатель показательно-геометрической прогрессии q можно найти по формуле (8).
Замечание 4. Если q=1, то из (8) можно получит характеристическое свойство показательной прогрессии.
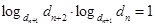 .
.
Формула (2) неудобна тем, что для вычисления п-го члена необходимо знать все предыдущие члены прогрессии. Выведем формулу общего члена показательно-геометрической прогрессии. По определению показательной прогрессии
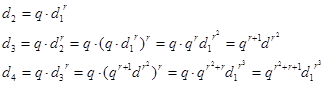
Мы видим, что здесь есть закономерность: индекс каждого члена прогрессии больше показателя степени  на единицу, и больше степени многочлена — показателя q на две единицы. Поэтому мы можем предположить, что n+1-й член прогрессии вычисляется по формуле
на единицу, и больше степени многочлена — показателя q на две единицы. Поэтому мы можем предположить, что n+1-й член прогрессии вычисляется по формуле

или
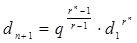 . (9)
. (9)
Доказательство данной формулы можно провети методом математической индукции.
Теорема 2.1. Пусть 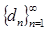 показательно-геометрическая прогрессия, тогда последовательность
показательно-геометрическая прогрессия, тогда последовательность 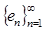 , n-член которой определяется следующим образом
, n-член которой определяется следующим образом
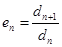 ,
,
будет показательной прогрессией.,
Для 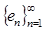 ее характеристическое свосйтво будет следующее равенство:
ее характеристическое свосйтво будет следующее равенство:
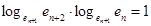 .
.
Если выполнить следующие замены:
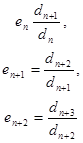
Тогда получим:
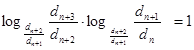 . (10)
. (10)
(10) формулу можно принять за харктеристическое свосйтво показательно-геометрической прогрессии.
Литература:
1. Н. К. Гульманов / Определение нового вида прогрессии, основанной на операции возведения в степень, и изучение ее основных свойств / Н. К. Гульманов, Н. А. Марчук // «Высокое качество и лидерство в образовании»: сборник докладов Международной научно-практической конференции (13–15 ноября 2013 года)/ АОО «Назарбаев Интеллектуальные школы». Часть 1. — Астана, 2013. — С. 120–124
moluch.ru
Геометрическая прогрессия Википедия
У этого термина существуют и другие значения, см. Прогрессия.Геометри́ческая прогре́ссия — последовательность чисел b1{\displaystyle b_{1}}, b2{\displaystyle b_{2}}, b3{\displaystyle b_{3}}, …{\displaystyle \ldots } (называемых членами прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q{\displaystyle q} (называемое знаменателем прогрессии), где b1≠0{\displaystyle b_{1}\neq 0}, q≠0{\displaystyle q\neq 0}: b1{\displaystyle b_{1}}, b2=b1q{\displaystyle b_{2}=b_{1}q}, b3=b2q{\displaystyle b_{3}=b_{2}q}, …{\displaystyle \ldots }, bn=bn−1q{\displaystyle b_{n}=b_{n-1}q}[1].
Любой член геометрической прогрессии может быть вычислен по формуле
- bn=b1qn−1.{\displaystyle b_{n}=b_{1}q^{n-1}.}
Если b1>0{\displaystyle b_{1}>0} и q>1
ruwikiorg.ru
Геометрическая прогрессия — это… Что такое Геометрическая прогрессия?
У этого термина существуют и другие значения, см. Прогрессия.Геометри́ческая прогре́ссия — последовательность чисел (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число (знаменатель прогрессии), где , : [1].
Описание
Любой член геометрической прогрессии может быть вычислен по формуле:
Если и , прогрессия является возрастающей последовательностью, если , — убывающей последовательностью, а при — знакочередующейся[2].
Своё название прогрессия получила по своему характеристическому свойству:
то есть каждый член равен среднему геометрическому его соседей.
Примеры
- Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата[3]:8-9.
- Последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
- 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из тринадцати членов.
- 50; −25; 12,5; −6,25; 3,125; … — бесконечно убывающая прогрессия со знаменателем -½.
- — геометрическая прогрессия со знаменателем 1 (и арифметическая прогрессия с шагом 0).
Свойства
Доказательство
Пусть — последовательность :
- Полученное соотношение является характеристическим для арифметической прогрессии.
Доказательство
- Произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
- ,
Доказательство
- Произведение членов геометрической прогрессии начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
Доказательство
- Сумма первых членов геометрической прогрессии:
Доказательство
- Через сумму:
Примечания
См. также
biograf.academic.ru
Геометрическая прогрессия Википедия
У этого термина существуют и другие значения, см. Прогрессия.Геометри́ческая прогре́ссия — последовательность чисел b1{\displaystyle b_{1}}, b2{\displaystyle b_{2}}, b3{\displaystyle b_{3}}, …{\displaystyle \ldots } (называемых членами прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q{\displaystyle q} (называемое знаменателем прогрессии), где b1≠0{\displaystyle b_{1}\neq 0}, q≠0{\displaystyle q\neq 0}: b1{\displaystyle b_{1}}, b2=b1q{\displaystyle b_{2}=b_{1}q}, b3=b2q{\displaystyle b_{3}=b_{2}q}, …{\displaystyle \ldots }, bn=bn−1q{\displaystyle b_{n}=b_{n-1}q}[1].
Описание
Любой член геометрической прогрессии может быть вычислен по формуле
- bn=b1qn−1.{\displaystyle b_{n}=b_{1}q^{n-1}.}
Если b1>0{\displaystyle b_{1}>0} и q>1{\displaystyle q>1}, прогрессия является возрастающей последовательностью, если 0<q<1{\displaystyle 0<q<1}, — убывающей последовательностью, а при q<0{\displaystyle q<0} — знакочередующейся[2], при q=1{\displaystyle q=1} — стационарной.
Своё название прогрессия получила по своему характеристическому свойству:
- |bn|=bn−1bn+1,{\displaystyle |b_{n}|={\sqrt {b_{n-1}b_{n+1}}},}
то есть модуль каждого члена равен среднему геометрическому его соседей.
Примеры
Получение новых квадратов путём соединения середин сторон предыдущих квадратов- Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата[3]:8—9.
- Геометрической является последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
- 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — геометрическая прогрессия со знаменателем 2 из тринадцати членов.
- 50; 25; 12,5; 6,25; 3,125; … — бесконечно убывающая геометрическая прогрессия со знаменателем 1/2.
- 4; 6; 9 — геометрическая прогрессия из трёх элементов со знаменателем 3/2.
- π{\displaystyle \pi }, π{\displaystyle \pi }, π{\displaystyle \pi }, π{\displaystyle \pi } — стационарная геометрическая прогрессия со знаменателем 1 (и стационарная арифметическая прогрессия с разностью 0).
- 3; -6; 12; -24; 48; … — знакочередующаяся геометрическая прогрессия со знаменателем -2.
- 1; -1; 1; -1; 1; … — знакочередующаяся геометрическая прогрессия со знаменателем -1.
Свойства
- Формула знаменателя геометрической прогрессии:
- q=bn+1bn{\displaystyle q={\frac {b_{n+1}}{b_{n}}}}
Доказательство
По определению геометрической прогрессии.
Доказательство
log(bn)=log(b1qn−1)=log(b1)+(n−1)⋅log(q){\displaystyle \log(b_{n})=\log(b_{1}q^{n-1})=\log(b_{1})+(n-1)\cdot \log(q)}
Формула общего члена арифметической прогрессии:
an=a1+(n−1)⋅d{\displaystyle a_{n}=a_{1}+(n-1)\cdot d}.
В нашем случае
a1=log(b1){\displaystyle a_{1}=\log(b_{1})},
d=log(q){\displaystyle d=\log(q)}.
- bn2=bn−ibn+i{\displaystyle b_{n}^{2}=b_{n-i}b_{n+i}}, если 1<i<n{\displaystyle 1<i<n}.
Доказательство
bn2=bnbn=b1qn−1b1qn−1=b1qn−1−ib1qn−1+i=bn−ibn+i.{\displaystyle b_{n}^{2}=b_{n}b_{n}=b_{1}q^{n-1}b_{1}q^{n-1}=b_{1}q^{n-1-i}b_{1}q^{n-1+i}=b_{n-i}b_{n+i}.}
- Произведение первых n членов геометрической прогрессии можно рассчитать по формуле
- Pn=(b1⋅bn)n2.{\displaystyle P_{n}=(b_{1}\cdot b_{n})^{\frac {n}{2}}.}
Доказательство
- Произведение членов геометрической прогрессии начиная с k-го члена, и заканчивая n-м членом, можно рассчитать по формуле
- Pk,n=PnPk−1.{\displaystyle P_{k,n}={\frac {P_{n}}{P_{k-1}}}.}
Доказательство
Pk,n=∏i=knbi=∏i=1nbi∏j=1k−1bj=PnPk−1.{\displaystyle P_{k,n}=\prod _{i=k}^{n}b_{i}={\frac {\prod _{i=1}^{n}b_{i}}{\prod _{j=1}^{k-1}b_{j}}}={\frac {P_{n}}{P_{k-1}}}.}
- Сумма n{\displaystyle n} первых членов геометрической прогрессии
- Sn={∑i=1nbi=b1−b1qn1−q=b1(1−qn)1−q,if q≠1nb1,if q=1{\displaystyle S_{n}={\begin{cases}\sum \limits _{i=1}^{n}b_{i}={\frac {b_{1}-b_{1}q^{n}}{1-q}}={\frac {b_{1}\left(1-q^{n}\right)}{1-q}},&{\mbox{if }}q\neq 1\\\\nb_{1},&{\mbox{if }}q=1\end{cases}}}
Доказательство
- Сумма всех членов убывающей прогрессии:
- |q|<1{\displaystyle \left|q\right|<1}, то bn→0{\displaystyle b_{n}\to 0} при n→+∞{\displaystyle n\to +\infty }, и
- Sn→b11−q{\displaystyle S_{n}\to {\frac {b_{1}}{1-q}}} при n→+∞{\displaystyle n\to +\infty }.
Доказательство
Примечания
См. также
wikiredia.ru
Обучающий модуль по алгебре на тему «Арифметическая и геометрическая прогрессия»
Арифметическая и геометрическая прогрессии
Теоретический материал
1. Понятие прогрессии
Арифметической прогрессией называется такая последовательность, в которой каждый следующий ее член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом. Число, которое прибавляется к предыдущему члену прогрессии для получения следующего, называется разностью арифметической прогрессии. Обозначается d.
Пример: (аn):2;4;6;8;… аn+1= аn + 2 , d=2
(хn):17; 15,5; 14; 12,5;… хn+1 = хn — 1,5, d= -1,5
аn+1= аn +d
Рекуррентная формула арифметической прогрессии
Геометрической прогрессией называется такая последовательность, в которой каждый следующий ее член, начиная со второго, равен предыдущему, умноженному на одно и то же число. Число, на которое умножается предыдущий член прогрессии для получения следующего, называется знаменателем геометрической прогрессии. Обозначается q.
Пример: (bn):2;4;8;16;… bn+1= 2bn , q=2
(yn):5; -5; 5; -5;… yn+1 = -yn , q= -1
bn+1= bnq
Рекуррентная формула геометрической прогрессии
2. Формула n-го члена арифметической и геометрической прогрессии.
Выведем формулу n-го члена арифметической и геометрической прогрессии.
Пусть (аn)-некоторая арифметическая прогрессия. Пусть(bn)-некоторая геометрическая прогрессия
Значит аn+1= аn +d , т.е. Значит bn+1= bnq , т.е

b2= b1 q
b3= b2 q= b1 q2
b4= b3 q= b1 q3
bn= bn-1 q= b1 qn-1

а2= а1 +d
а3= а2 +d= а1 +2d
а4= а3 +d= а1 +3d
аn= аn-1 +d= а1 +(n-1)d
аn= а1 +(n-1)d
bn= b1 qn-1
Примеры.
Составим формулу n-го члена последовательности (аn):5;3;1;-1;…
Заметим, что данная последовательность является арифметической прогрессией, т.к. аn+1= аn -2, в которой а1 =5, d=-2. Значит формула n -го члена этой последовательности имеет вид аn= 5 +(n-1)(-2). Преобразовав данное выражение, получим: аn= -2n+7.
Составим формулу n-го члена последовательности (хn):1;0,5;0,25;0,125;…
Данная последовательность является геометрической прогрессией, т.к. хn+1= 0,5хn , в которой х1 =1, q=-0,5. Значит формула n -го члена этой последовательности имеет вид хn= 1 0,5n-1. Преобразовав данное выражение, получим: хn= 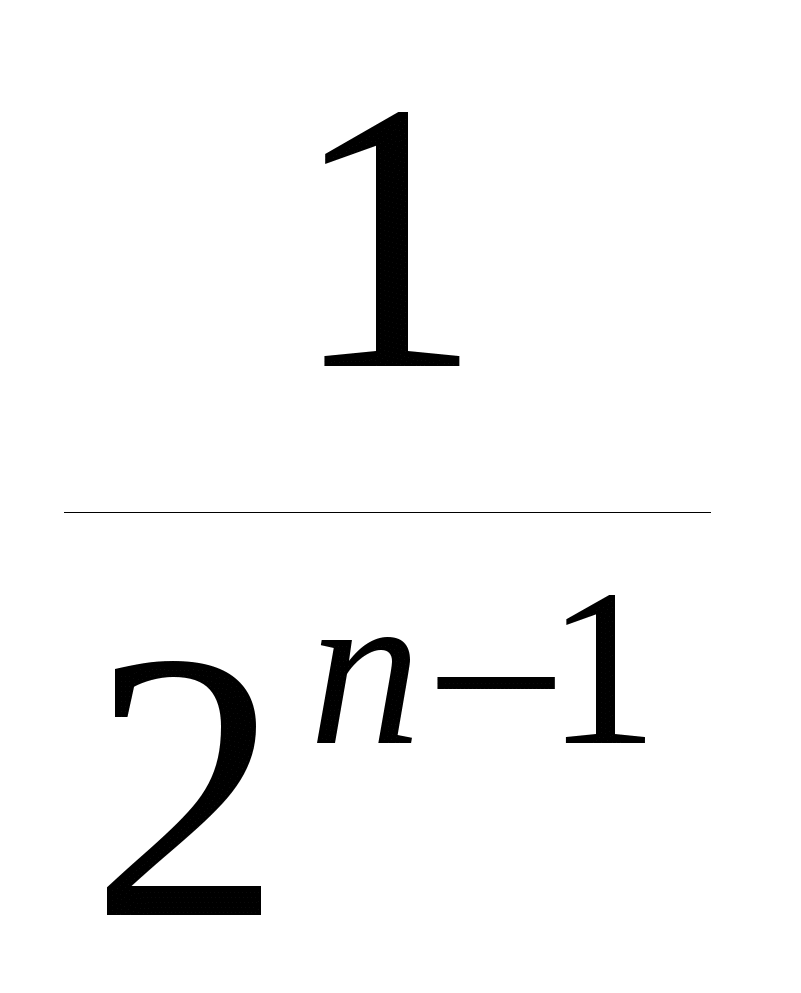 .
.
3. Характеристическое свойство членов прогрессии
□ Легко доказать что:
любой член арифметической прогрессии, начиная со второго, равен среднему арифметическому равноотстоящих от него членов этой прогрессии, т.е.
 .
.любой член геометрической прогрессии, начиная со второго, равен среднему геометрическому равноотстоящих от него членов этой прогрессии, т.е.
 .
.
Также можно доказать, что  , а
, а  . ( Проверьте эти равенства самостоятельно!)
. ( Проверьте эти равенства самостоятельно!)
Арифметическая и геометрическая прогрессии
Задания для разработки темы
Необходимо знать: определение арифметической и геометрической прогрессии
рекуррентное задание арифметической и геометрической прогрессии
формулу n-го члена арифметической и геометрической прогрессии
характеристическое свойство членов арифметической и геометрической прогрессии
Источник информации: учебник Алгебры, 9 кл., под ред. С.А.Теляковского, п.16,18.
Из приведенных ниже последовательностей выпишите те, которые являются а)арифметической прогрессией; б)геометрической прогрессией. Запишите рекуррентную формулу каждой из них Укажите ее первый член и разность или знаменатель:
1 (хn): 10;20;30;… 3 (хn):  5 (хn): 0,3; 0,03; 0,003;…
5 (хn): 0,3; 0,03; 0,003;…
2 (хn): 1;2;4;7;11;… 4 (хn): 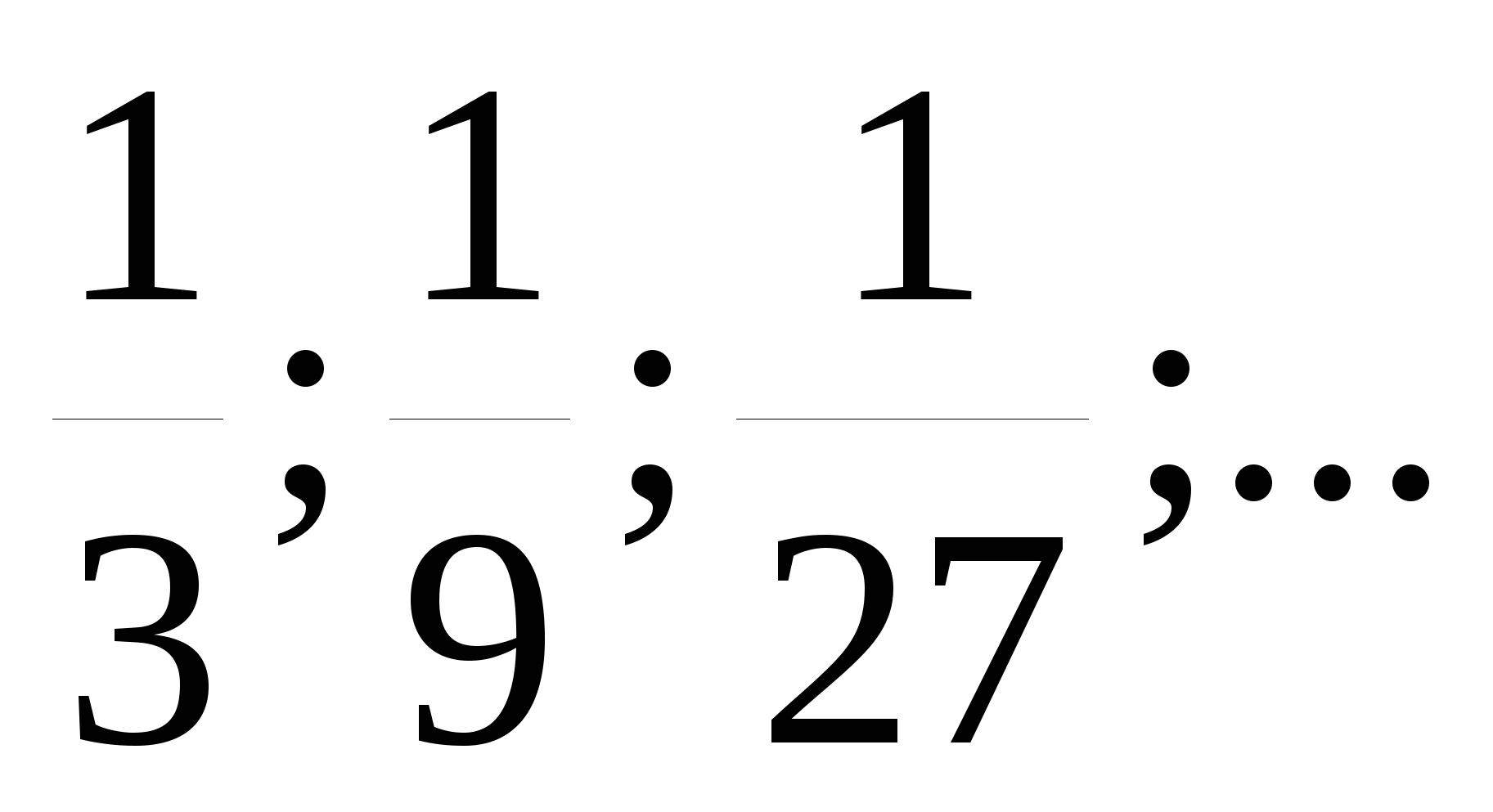 6 (хn):
6 (хn): 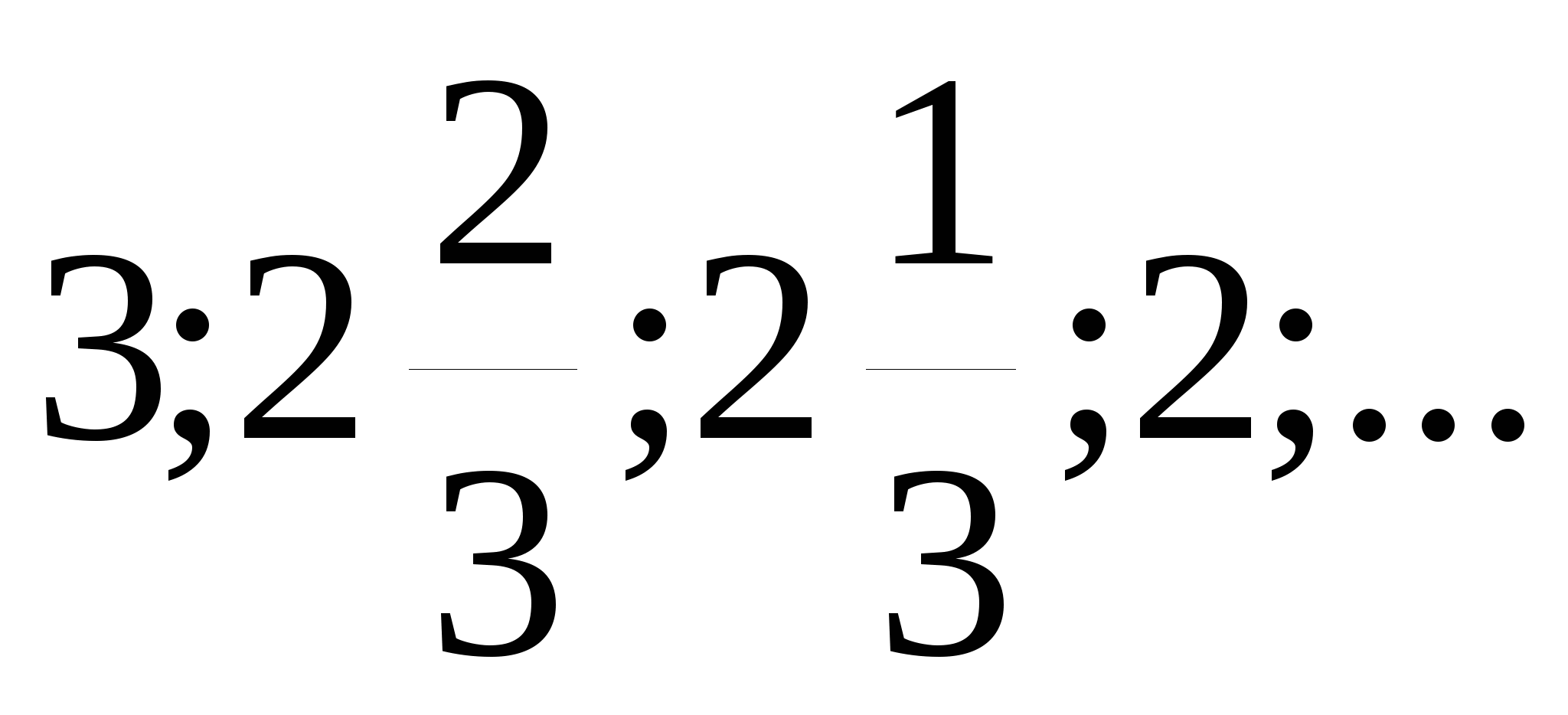
Запишите первые пять членов арифметической прогрессии, в которой а)а1=2, d=-3; б) а1=-3, d=2. Составьте формулу n-го члена и найдите а10, а20 , а100..
Запишите первые пять членов геометрической прогрессии, в которой а)с1=2, q=-3; б) c1=-3, q=2. Составьте формулу n-го члена и найдите с6.
Найдите члены арифметической прогрессии, обозначенные буквами:
-6; -4; х3; х4; х5;…
х1; 3; 7; х4, х5;…
х1; х2; 3; х4; 7;…
3; х2; х3; х4; -13;…
Найдите члены геометрической прогрессии, обозначенные буквами:
3; 1; у3; у4; у5;…
у1; 2; 8; у4, у5;…
у1; 4; у3; у4; 0,032;…
5; у2; у3; у4; 0,3125;…
(сn) – арифметическая прогрессия. Найдите:
с1, если d=5 с7=2
d, если с1=4 с15=48
с1, если с5=2 с11=3
(уn) – геометрическая прогрессия. Найдите:
у1, если q=-2 y6=50
q, если y3=4 y5=8.
Вставьте между числами 2 и 3 три таких числа, чтобы вместе с данными они составляли арифметическую прогрессию.
Ключ для проверки
Арифметической прогрессией является первая и последняя последовательность, причем для первой справедливо: хn+1=xn+10, x1=10, d=10,а для последней — хn+1=xn —
 , x1=3,d =
, x1=3,d = .
.
Геометрической прогрессией является четвертая и пятая последовательность. для четвертой последовательности выполняется: хn+1=xn ,x1=
,x1= ,q=
,q= .
.
для пятой последовательности справедливо: хn+1= 0,1 xn ,x1=0,3,q=0,1.
a) 2; 1; -4; -7; -10;… аn=-3n+5 a10=-25, a20=-55, a100=-295
б)-3; -1; 1; 3; 5;… аn=2n-5 a10=15, a20=35, a100=195
а) 2; -6; 18; -54; 162;… cn=2(-3)n-1c6=-486
б)-3; — 6; -12; -24; -48;… cn=-32n-1c6=-96
-6; -4; -2; 0; 2;… -1; 3; 7; 11; 15;… -1; 1; 3; 5; 7;… 3; -1; -5; -9; -13;…

 20; 4; 0,8; 0,16;0,032;… 5; ±2,5; 1,25; ±0,625; 0,3125;…
20; 4; 0,8; 0,16;0,032;… 5; ±2,5; 1,25; ±0,625; 0,3125;…с1=с7-6d=-28 d=
 d=
d= c1=c5-4d=
c1=c5-4d=


2; 2,25; 2,5; 2,75; 3
Выполните задания для самостоятельной учебной деятельности
По учебнику ∆
□
Ответьте на вопросы.
Какая последовательность называется арифметической прогрессией? Приведите примеры.
Что такое разность арифметической прогрессии? Объясните, как найти ее, зная а1 и а2; а8 и а9; а1 и а8; а3 и а12?
Объясните, как в арифметической прогрессии найти первый ее член, зная пятый и разность прогрессии; пятый и двенадцатый ее член?
Объясните на примере последовательности (хn): 3; 7; 11;…, как составить формулу ее n-го члена.
Поясните, при каких условия арифметическая прогрессия является возрастающей, а при каких – убывающей. Приведите примеры.
Объясните на примере характеристическое свойство членов арифметической прогрессии.
Какая последовательность называется геометрической прогрессией? Приведите примеры.
Что такое знаменатель геометрической прогрессии? Объясните, как найти его, зная а1 и а2; а8 и а9; а1 и а4; а10 и а12?
Объясните, как в геометрической прогрессии найти первый ее член, зная пятый член и знаменатель прогрессии; пятый и седьмой ее член?
Объясните на примере последовательности (хn): 3; 6; 12;…, как составить формулу ее n-го члена.
Поясните, при каких условиях геометрическая прогрессия является возрастающей, а при каких – убывающей. Приведите примеры.
Объясните на примере характеристическое свойство членов геометрической прогрессии
Арифметическая и геометрическая прогрессии
Проверочная работа
А1
Составьте формулу n-го члена арифметической прогрессии (аn) и найдите а11, если а1=2,4; d=-0.8
Составьте формулу n-го члена геометрической прогрессии (хn):3; -6;…
Найдите разность арифметической прогрессии (сn), если с1=-1,2; с5=-0,4
В геометрической прогрессии (уn) у3=
 , у5=
, у5= . Найдите у2 и у6.
. Найдите у2 и у6.Найдите первый член арифметической прогрессии (аn), если а6=23; а11=48..
А2
Составьте формулу n-го члена арифметической прогрессии (аn):-2,4;-1,6;… и найдите а11.
Составьте формулу n-го члена геометрической прогрессии (хn), если х1=81;q=
 :.
:.Найдите разность арифметической прогрессии (сn), если с1=-2,7; с4=-1,8
В геометрической прогрессии (уn) у3=
 , у5=
, у5= . Найдите у4 и у7.
. Найдите у4 и у7.Найдите первый член арифметической прогрессии (аn), если а4=4; а12=36..
Б1
Дана арифметическая прогрессия (аn): -22,5;-21;… Составьте рекуррентную формулу и формулу n-го члена этой прогрессии.
Найдите седьмой член геометрической прогрессии (bn), если b3=
 ,q=
,q= .
.Найдите первый член и разность арифметической прогрессии (аn), если а4=1,8; а7=0,6.
Найдите номер члена арифметической прогрессии, равного 22, если а3=-2; d=3.
Между числами
 и 9 вставьте три таких числа, чтобы вместе с данными они составляли геометрическую прогрессию.
и 9 вставьте три таких числа, чтобы вместе с данными они составляли геометрическую прогрессию.
Б2
Дана геометрическая прогрессия (аn): 30,-3;… Составьте рекуррентную формулу и формулу n-го члена этой прогрессии.
Найдите семнадцатый член арифметической прогрессии (bn), если b3= -25,d=0,7.
Найдите первый член и разность арифметической прогрессии (аn), если а3= -2,3; а8= -0,8.
Найдите номер члена арифметической прогрессии, равного 47, если а4= -3; d=5.
Между числами 16 и
 вставьте три таких числа, чтобы вместе с данными они составляли геометрическую прогрессию.
вставьте три таких числа, чтобы вместе с данными они составляли геометрическую прогрессию.
В1
Найдите семнадцатый член арифметической прогрессии (аn), если а5=-9,1; а12=-7.
Найдите шестой и n-й члены геометрической прогрессии (сn), если с1=8 с4; с5=
 .
.Докажите, что последовательность, заданная формулой xn=11n-78, является арифметической прогрессией. Опишите свойства этой прогрессии. Найдите ее первый положительный член.
Найдите значения х, при которых числа х+1, 4х и 16х-12 составляют геометрическую прогрессию.
В2
Найдите седьмой член геометрической прогрессии (аn), если а4= -4; а6= -8.
Найдите n-й член арифметической прогрессии (сn), если с3 с4=80;
 ..
..Докажите, что последовательность, заданная формулой xn=n2+2n, не является арифметической прогрессией. Опишите свойства этой последовательности. Найдите ее наименьший и наибольший член.
Найдите значения х, при которых числа х+1, 2х+1 и х2-3 составляют арифметическую прогрессию.
Ключ для проверки
А1
1. аn= -0.8n+32, a11= -5.6
2. bn=3(-2)n
3. d=0.2
4. y2=±2/3, y6=±1/24
5. a1=2
Б1
1. an+1=an+1.5, a1= -22.5,
an=1.5n-24
2. b7=1
3. d= -0.4, a1=3
4. n=11
5. ±1/3; 1; ±3
B1
1. a17= -4.3
2. c6=3/32, cn=3/2n-1
3. c a8>0, a8=10
4. x=3; 4;12;36
A2
1. аn= -3.2+0.8n, a11= 5.6
2. bn=81/3n-1
3. d=0.3
4. y2=±2/3, y6=16/3
5. a1= -8
Б2
1. an+1=an(-0.1)n-1, a1= 30,
an=30(-0.1)n-1
2. b17= —15.2
3. d= 0.3, a1= -2.9
4. n=14
5. ±4; 1; ±1/4
B2
1. a7= 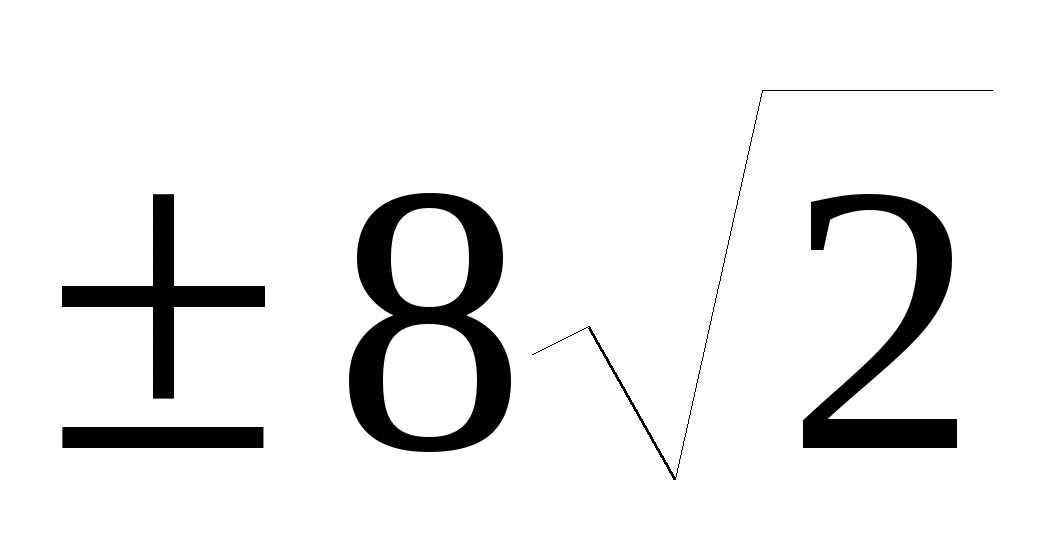
2. cn= -2n-16, cn= -2n+16
3. наименьшее x1=3, наиб. нет
4. x=4 и -1; 5;9;13 или 0; -1; -2
Сумма n первых членов арифметической и геометрической прогрессии
1. Понятие суммы n первых членов последовательности.
Пусть в последовательности (аn) известны первые n ее членов: а1, а2, а3,… аn. Выражение а1+ а2+ а3+…+ аn. Называется суммой n первых ее членов. Обозначается Sn.
Sn= а1+ а2+ а3+…+ аn.
Пример. Сумма пяти первых членов некоторой последовательности – это сумма всех ее членов с первого по пятый, т.е. S5= а1+ а2+ а3+ а4+ а5.
Сумма двадцати первых членов последовательности – это сумма всех ее членов в первого по двадцатый, т.е. S20= а1+ а2+ а3+…+ а19+ а20.
2. Формулы суммы n первых членов арифметической и геометрической прогрессии
Для того, чтобы в некоторой последовательности найти сумму ее первых n членов необязательно знать все эти члены. Можно воспользоваться формулами.
Д ля арифметической прогрессии
ля арифметической прогрессии  или
или 

Для геометрической прогрессии 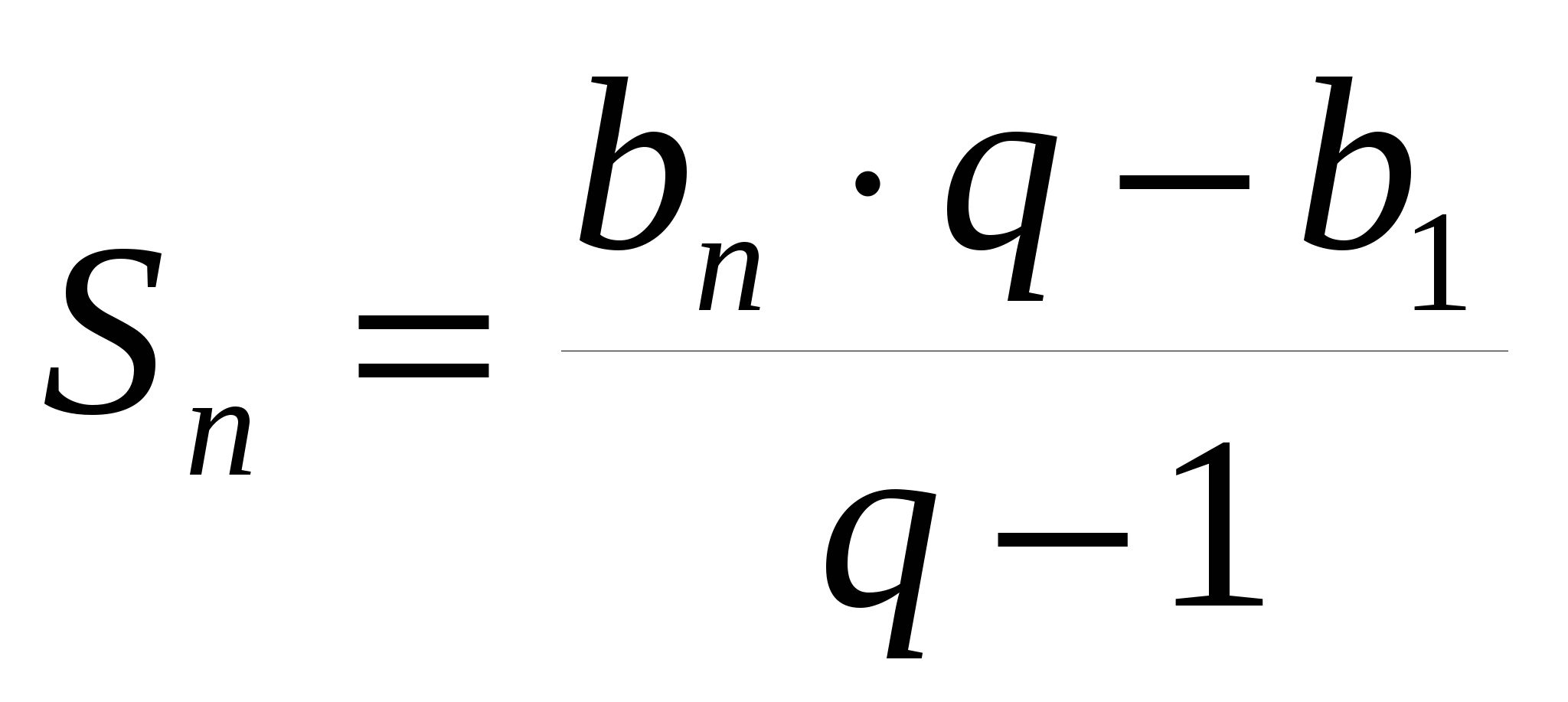 или
или 
В этих формулах: а1 и b1 – первые слагаемые в сумме
an и bn— последние слагаемые в сумме
n- количество слагаемых (совпадает с номером последнего слагаемого)
d и q- соответственно разность и знаменатель прогрессии
(□ Объясните, как из одной формулы получить вторую)
( Разберите вывод формул по учебнику)
Примеры.
Найдем сумму пяти первых членов геометрической прогрессии, в которой с1=3; q=2. Для этого удобнее воспользоваться второй формулой нахождения суммы n первых членов геометрической прогрессии. Т.к. нужно найти сумму пяти первых ее членов, т.е. сумму с первого члена по пятый, то n=5. Значит
 . Проверим! Для этого найдем все члены этой прогрессии с первого по пятый: 3; 6; 12; 24;48. Найдем их сумму 3+ 6+12+24+48=93. Т.е.
. Проверим! Для этого найдем все члены этой прогрессии с первого по пятый: 3; 6; 12; 24;48. Найдем их сумму 3+ 6+12+24+48=93. Т.е.  .
.Найдем сумму всех двухзначных чисел, не превосходящих 50. Выпишем числа – члены некоторой последовательности – сумму которых необходимо найти: 10; 11; 12; 13;…50. Заметим, что эти числа составляют арифметическую прогрессию, в которой а1=10; d=1, значит для нахождения суммы этих чисел можно применить одну из приведенных выше формул. Применим первую формулу
 . Первое слагаемое в искомой сумме а1=10, последнее слагаемое аn=50. необходимо знать количество слагаемых, т.е. n, которое совпадает с номером последнего слагаемого. Т.к. для членов арифметической прогрессии справедливо равенство аn= а1+d(n-1), то применив его, найдем номер члена аn равного 50. 10+1(n-1)=50, откуда n=41. Т.е. в искомой сумме 41 слагаемое, а значит 50 – это а41. Найдем сумму
. Первое слагаемое в искомой сумме а1=10, последнее слагаемое аn=50. необходимо знать количество слагаемых, т.е. n, которое совпадает с номером последнего слагаемого. Т.к. для членов арифметической прогрессии справедливо равенство аn= а1+d(n-1), то применив его, найдем номер члена аn равного 50. 10+1(n-1)=50, откуда n=41. Т.е. в искомой сумме 41 слагаемое, а значит 50 – это а41. Найдем сумму  . Можно применить и вторую формулу
. Можно применить и вторую формулу  .
.
Использовать нужно ту формулу, которая наиболее удобна в зависимости от условия,
3. Сумма бесконечно убывающей геометрической прогрессии
Геометрическая прогрессия, в которой 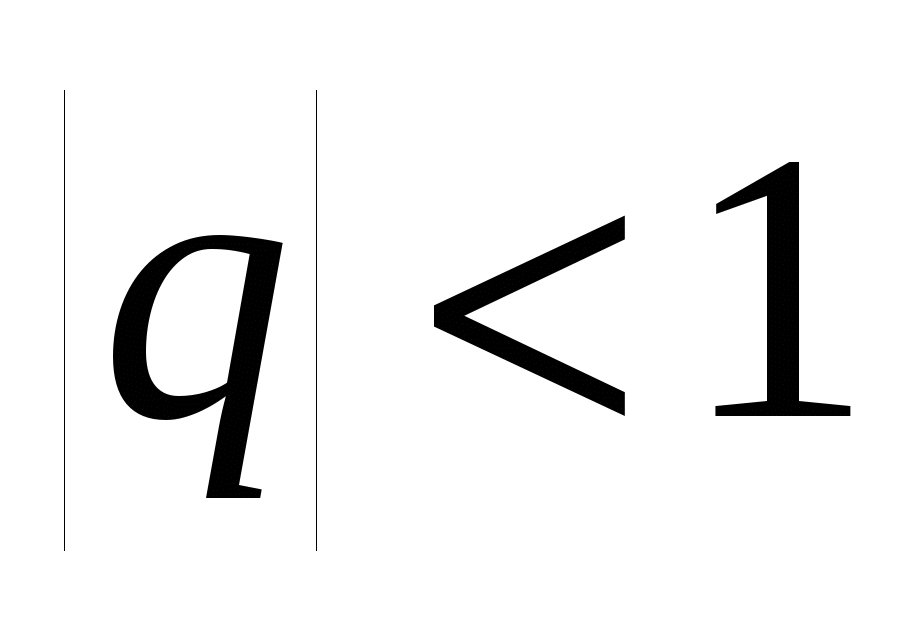 , т.е.-1<q<1, является убывающей.
, т.е.-1<q<1, является убывающей.
Например. Последовательность (аn):2; 1; 0,5; 0,25; 0,125;… является бесконечной убывающей геометрической прогрессией знаменатель которой равен 0,5 (0,5<1). Геометрическая прогрессия (сn):3; -0,3; 0,03; -0,003;… также является убывающей, q=-0.1 (-1<0.1<1).
Ясно, что с увеличением номера члены последовательности уменьшаются, становясь все меньше и меньше отличными от нуля. Говорят, что с возрастанием n члены прогрессии bn стремятся к нулю. Значит, члены прогрессии с большими номерами практически не влияют на сумму n первых ее членов. Поэтому, при больших n сумма  .
.
Д ля бесконечной убывающей геометрической прогрессии сумма бесконечного числа слагаемых находится по формуле
ля бесконечной убывающей геометрической прогрессии сумма бесконечного числа слагаемых находится по формуле 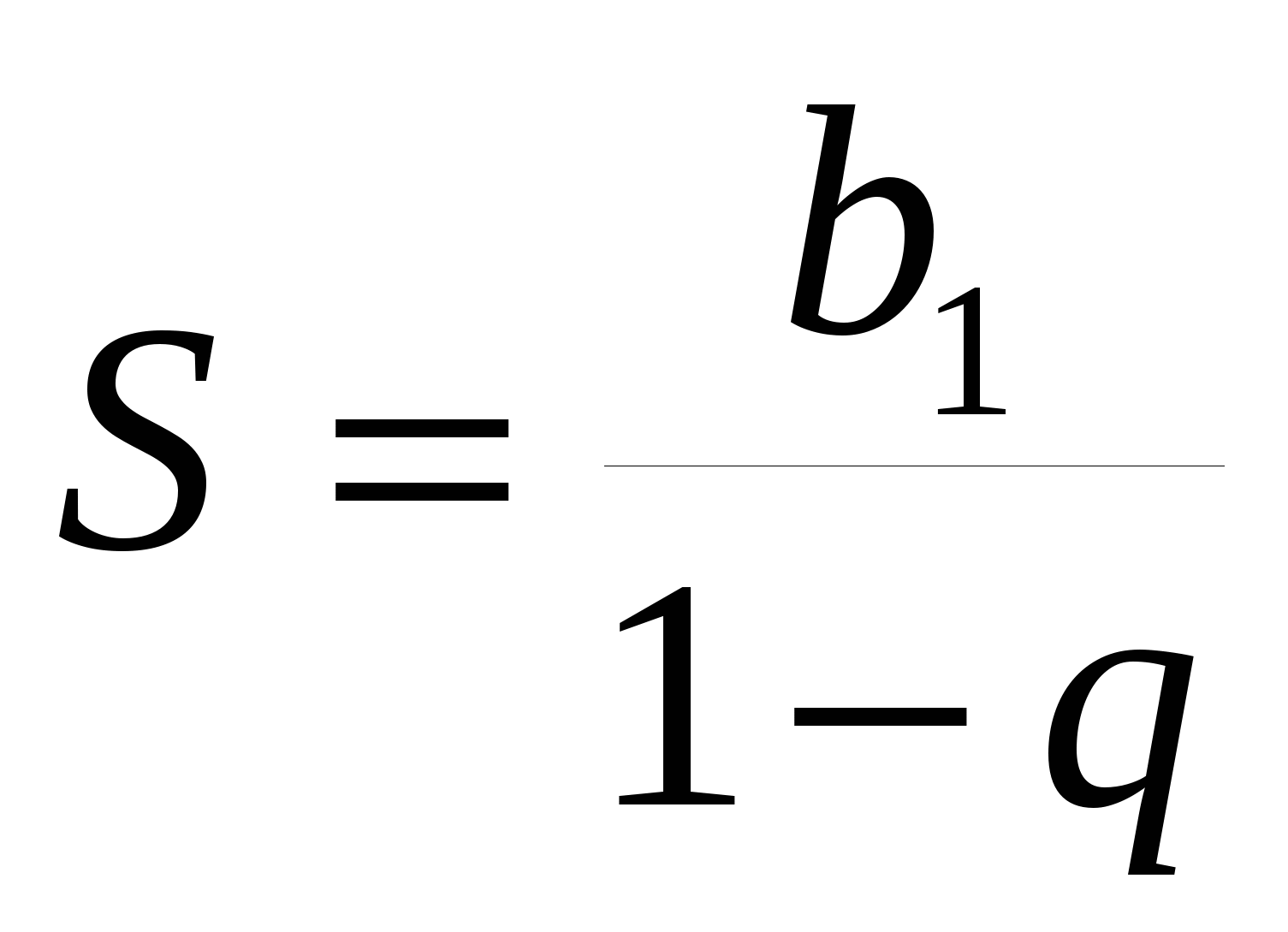
Пример.
Найдем сумму 0,3+0,03+0,003+0,0003+… Заметим, что слагаемые данной суммы являются членами геометрической прогрессии, в которой а1=0.3, q=0.1. q<1, прогрессия убывающая, а значит сумма бесконечного числа слагаемых находится по формуле 
О
!
братите внимание, что 0,3+0,03+0,003+0,0003+…=0,3333…= . Это можно использовать для перевода бесконечной десятичной периодической дроби в обыкновенную.
. Это можно использовать для перевода бесконечной десятичной периодической дроби в обыкновенную.Источник информации: учебник Алгебры, 9 кл., под ред. С.А.Теляковского, п.17,19,20.
Разберите примеры, приводимые в учебнике.
Выполните задания для самостоятельной учебной деятельности
По учебнику △
□
Сумма членов арифметическая и геометрическая прогрессии
Задания для разработки темы
Необходимо знать: понятие суммы n первых членов последовательности
формулы, для нахождения суммы n первых членов арифметической прогрессии
формулы, для нахождения суммы n первых членов геометрической прогрессии
понятие суммы бесконечно убывающей геометрической прогрессии
формулу суммы бесконечно убывающей геометрической прогрессии
Источник информации: учебник Алгебры, 9 кл., под ред. С.А.Теляковского, п.17,19,20.
Обязательный уровень
Запишите сумму первых пяти членов арифметической прогрессии (аn): 2; 7;12;…. Найдите эту сумму непосредственно сложением и по формуле.
Запишите сумму первых пяти членов геометрической прогрессии (хn): 2; 10;50;…. Найдите эту сумму непосредственно сложением и по формуле.
Найдите сумму пятнадцати первых членов арифметической прогрессии,( аn) в которой а1=5; d=3.
Найдите сумму шести первых членов геометрической прогрессии,( хn) в которой х1=5; q=1/2.
Найдите сумму 2+4+6+…+20
3+6+9+…+99
-50+(-45)+(-40)+…+40+45+50.
(Подсказка: найдите номер последнего слагаемого в сумме)
Найдите сумму: всех двухзначных чисел
двухзначных чисел, кратных 5
Найдите сумму двенадцати первых членов арифметической прогрессии, заданной формулой n-го члена хn=12n-3; сумму шести первых членов геометрической прогрессии заданной формулой уn=4n.
Найдите сумму бесконечной геометрической прогрессии, проверив сначала, что ее знаменатель q удовлетворяет условию
 : 10; 2; 0,4;…
: 10; 2; 0,4;…
□
Найдите первый член геометрической прогрессии, в которой q=3, S4=560.
Представьте бесконечную периодическую дробь 0,(8) в виде обыкновенной.
В арифметической прогрессии а1=1, а сумма первых восьми ее членов равна 120. Найдите разность этой прогрессии.
В арифметической прогрессии сумма первых четырех ее членов равна 42, а сумма восьми первых членов в 3 раза больше. Найдите первый член и разность арифметической прогрессии.
Арифметическая прогрессия задана формулой хn=10-7n. Найдите сумму ее членов с десятого по двадцатый.
Сколько надо сложить последовательных натуральных чисел, кратных 7, чтобы их сумма была равна 546?
В геометрической прогрессии разность между шестым и четвертым членами равна 192, а разность между третьим и первым равна 24. Найдите сумму первых восьми членов этой прогрессии.
Решите уравнение, в котором слагаемые составляют арифметическую прогрессию: 4+7+10+…+ъ=116; 26+24+22+…+х=136.
Найдите сумму первых шести членов геометрической прогрессии (хn), если известно, что
 и S3=42.
и S3=42.Является ли арифметической прогрессией последовательность, сумма первых n ее членов которой вычисляется по формуле а) Sn=3n2 ; б) Sn=n2-4n.
Сумма n первых членов арифметической и геометрической прогрессии
Задание для разработки темы
Ключ для самопроверки
Обязательный уровень




а)
 б)
б)  в) 0
в) 0а)
 б)
б) 
а)
 б)
б) 

□

8/9
d=4
a1=6, d=3



а) х=25 б)х=16; х=-14

а) да, d=6 б)нет
infourok.ru
 .
.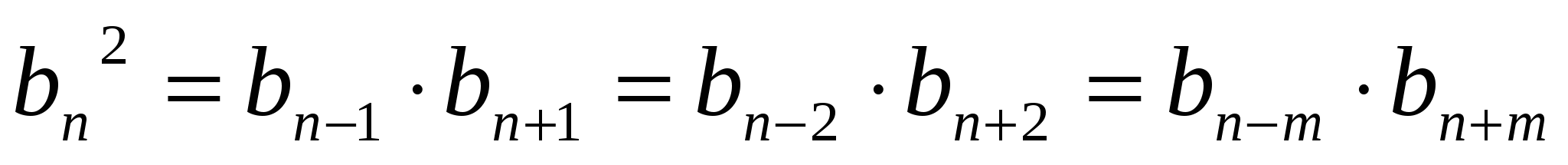 .
.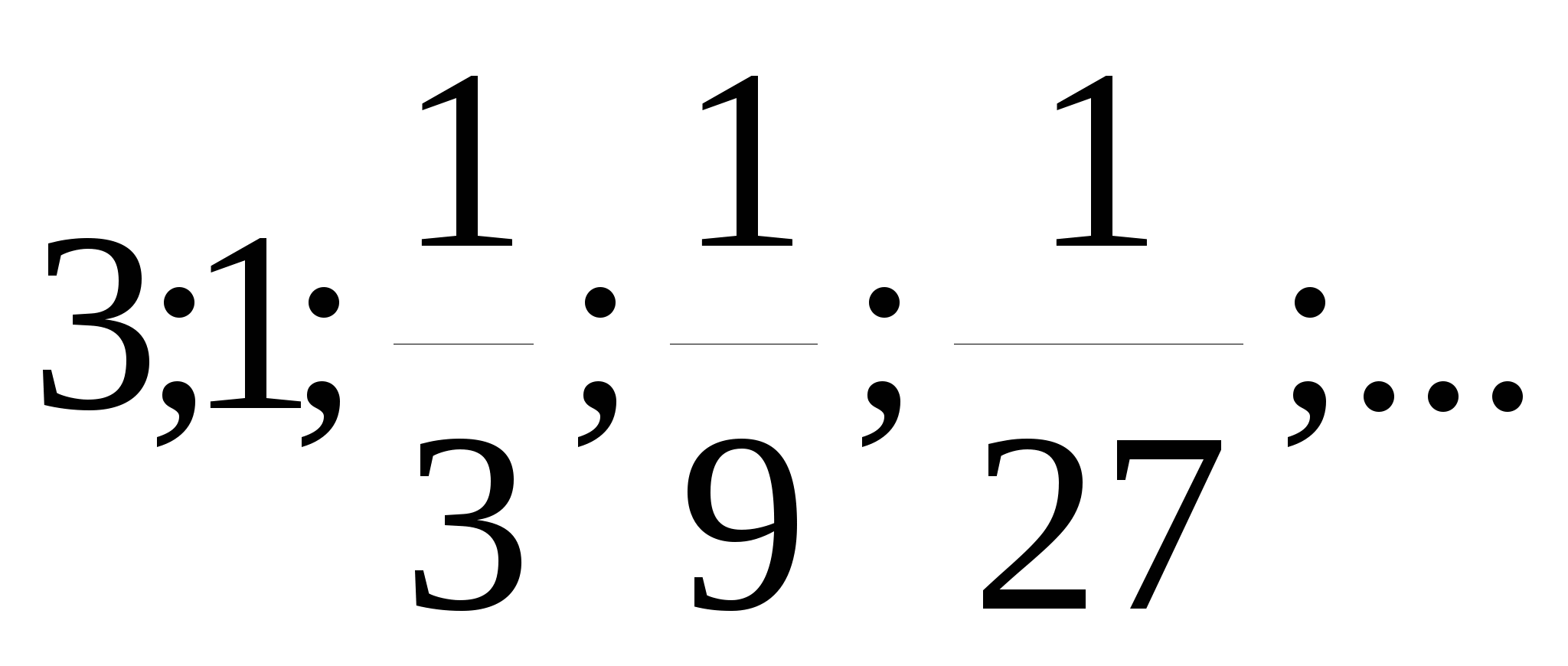
 20; 4; 0,8; 0,16;0,032;… 5; ±2,5; 1,25; ±0,625; 0,3125;…
20; 4; 0,8; 0,16;0,032;… 5; ±2,5; 1,25; ±0,625; 0,3125;… d=
d=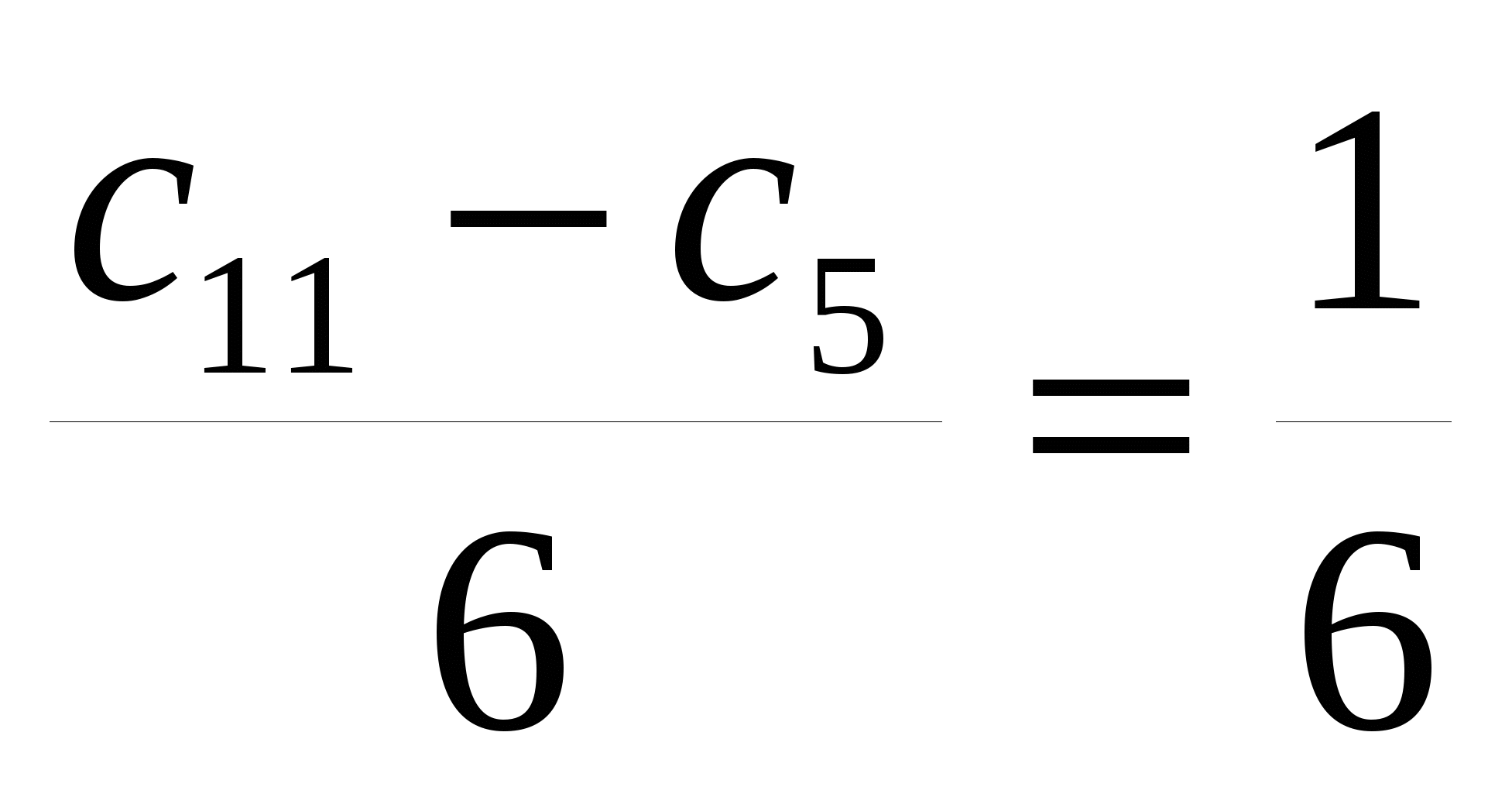 c1=c5-4d=
c1=c5-4d=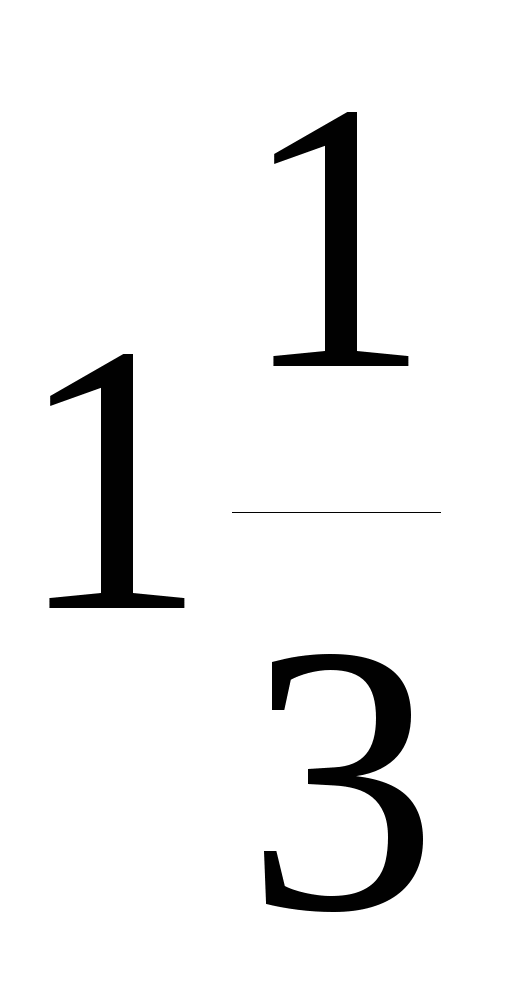
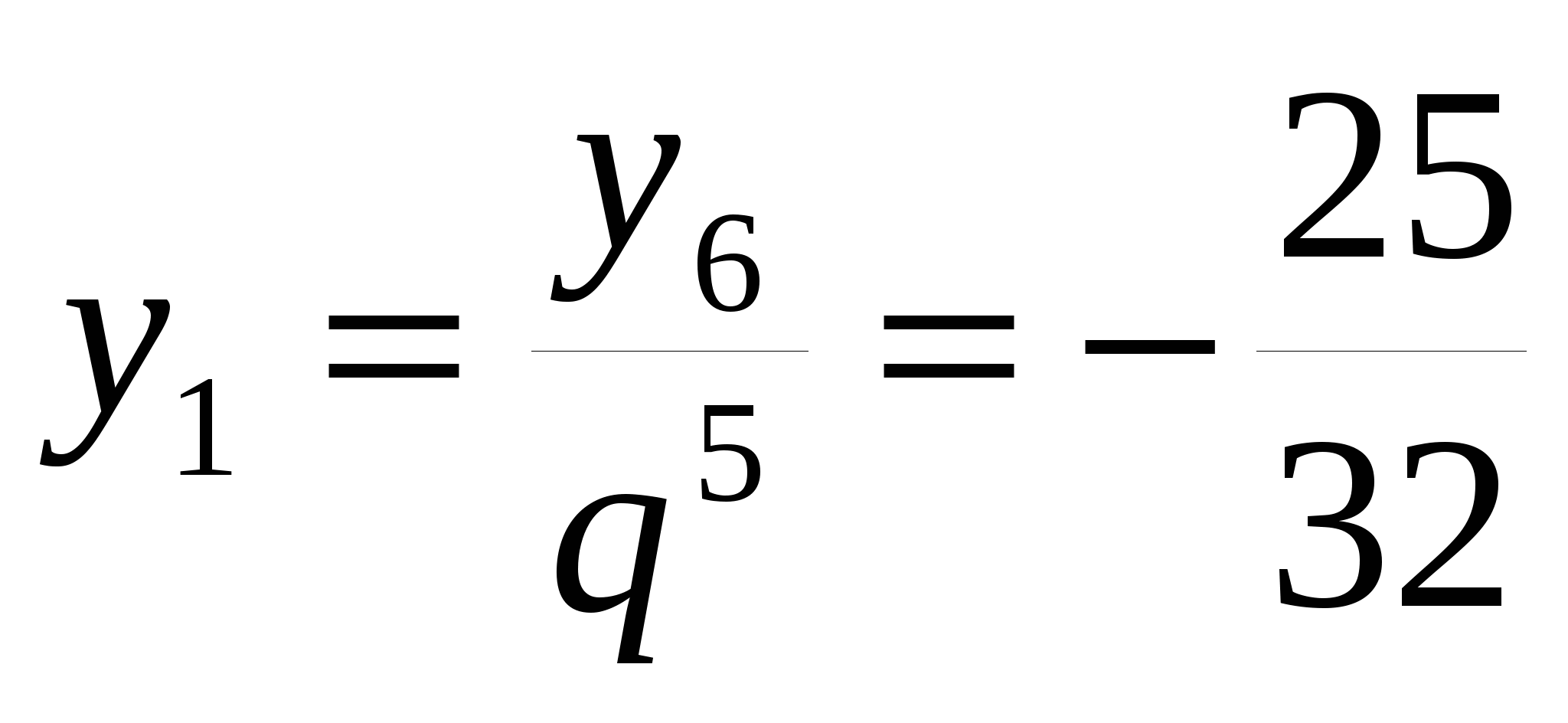

 . Найдите у2 и у6.
. Найдите у2 и у6.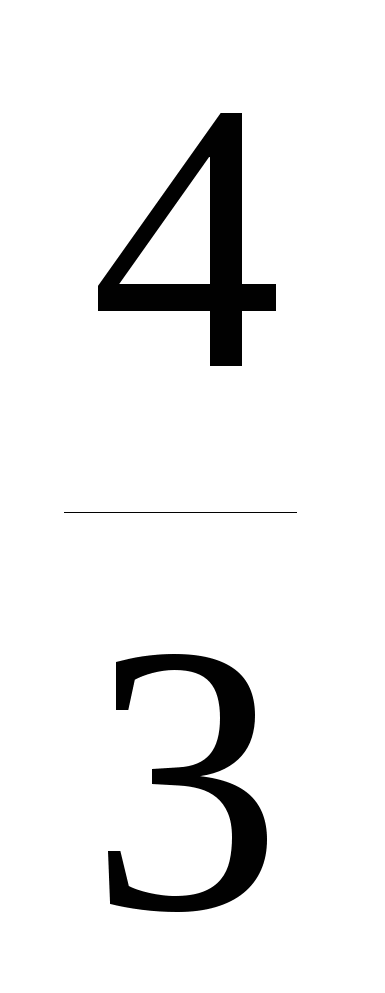 . Найдите у4 и у7.
. Найдите у4 и у7.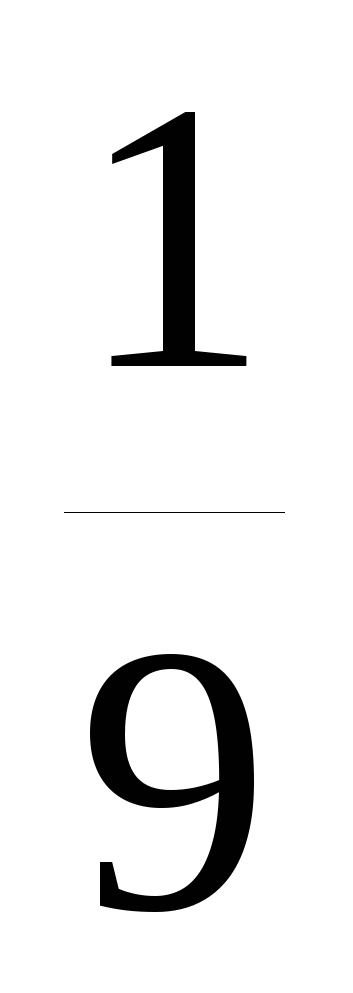 ,q=
,q= .
.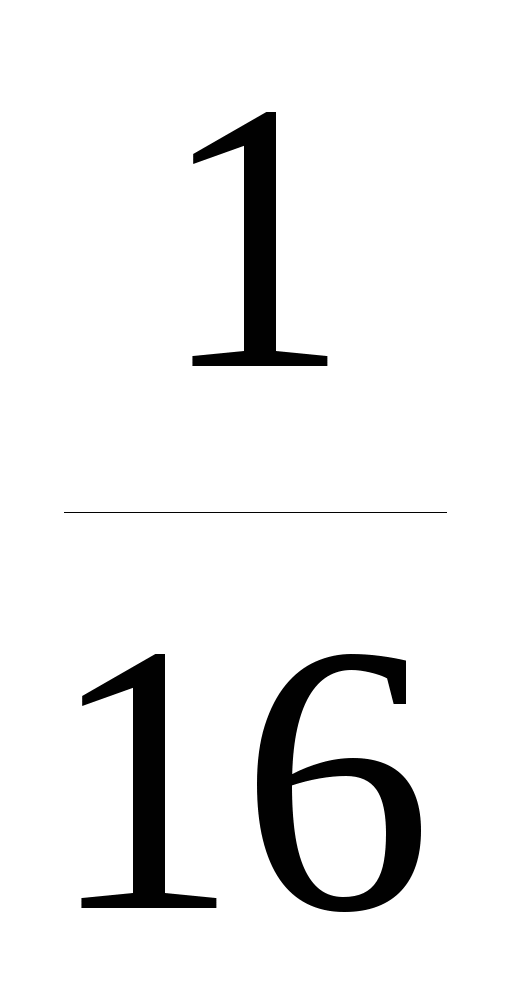 вставьте три таких числа, чтобы вместе с данными они составляли геометрическую прогрессию.
вставьте три таких числа, чтобы вместе с данными они составляли геометрическую прогрессию.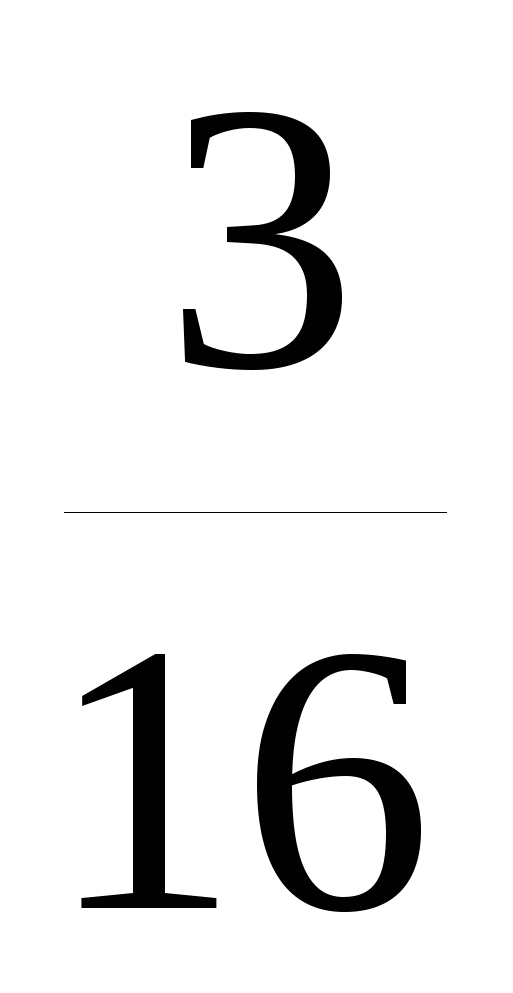 .
.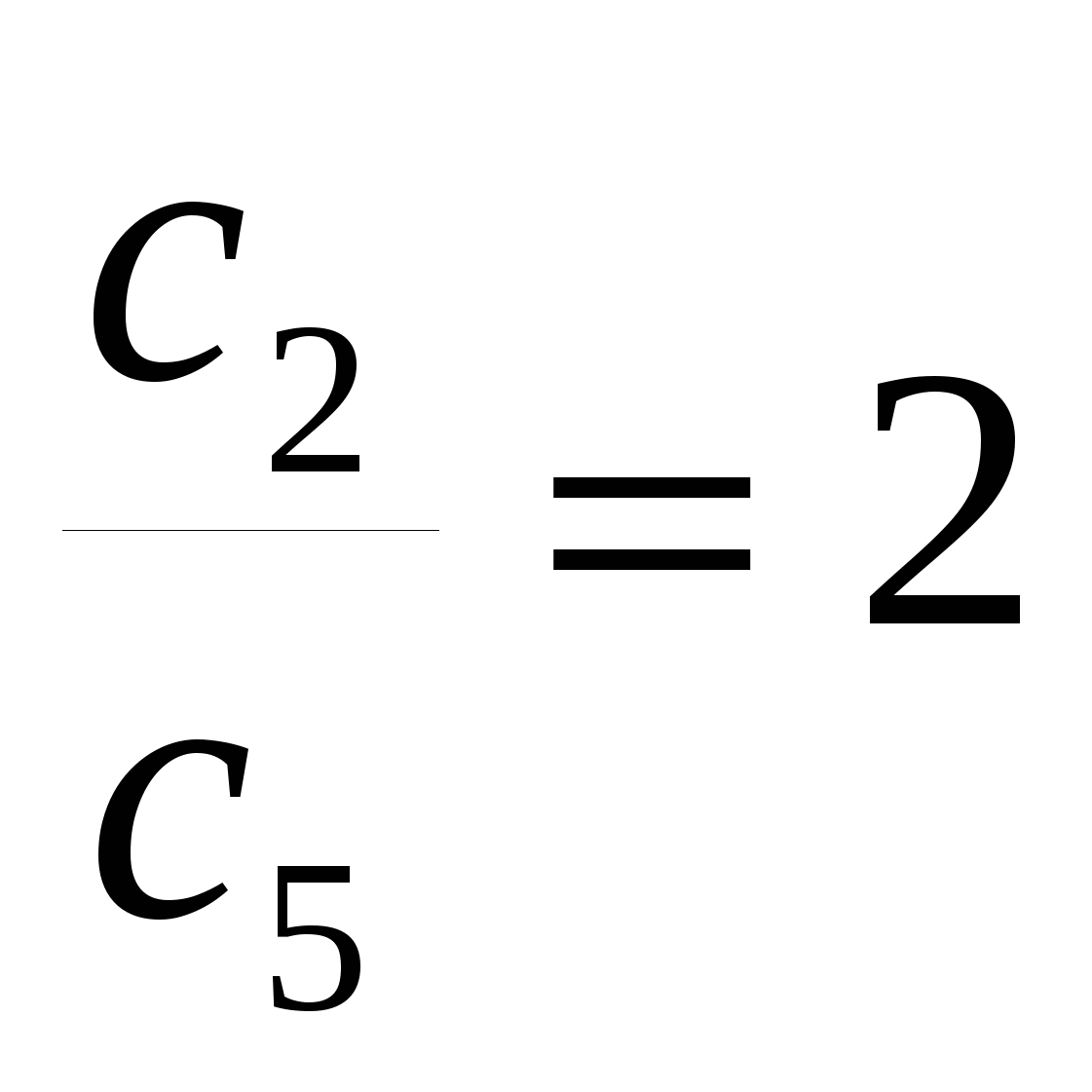 ..
..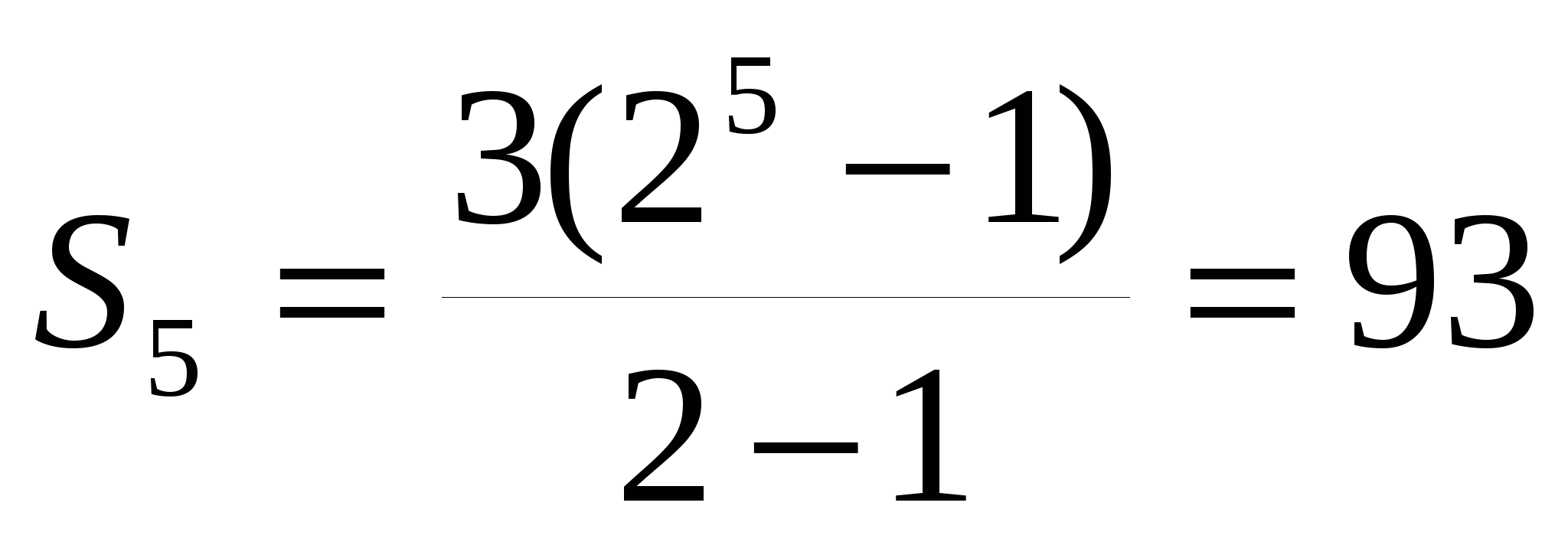 . Проверим! Для этого найдем все члены этой прогрессии с первого по пятый: 3; 6; 12; 24;48. Найдем их сумму 3+ 6+12+24+48=93. Т.е.
. Проверим! Для этого найдем все члены этой прогрессии с первого по пятый: 3; 6; 12; 24;48. Найдем их сумму 3+ 6+12+24+48=93. Т.е.  .
.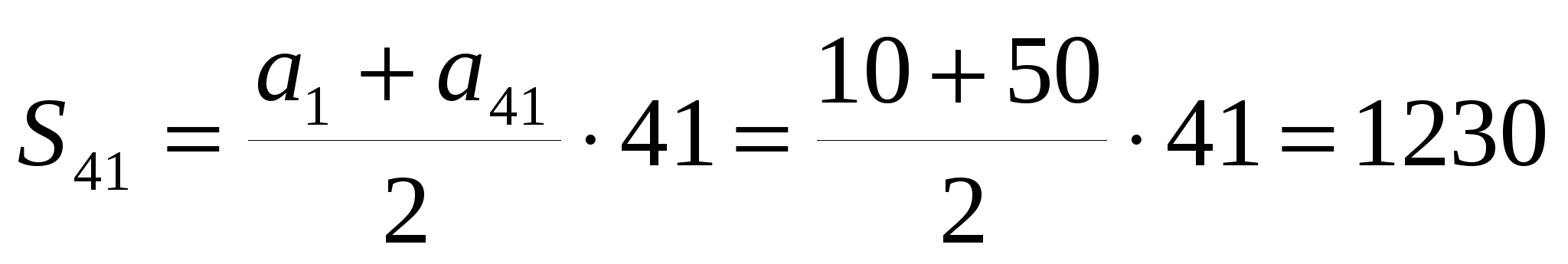 . Можно применить и вторую формулу
. Можно применить и вторую формулу 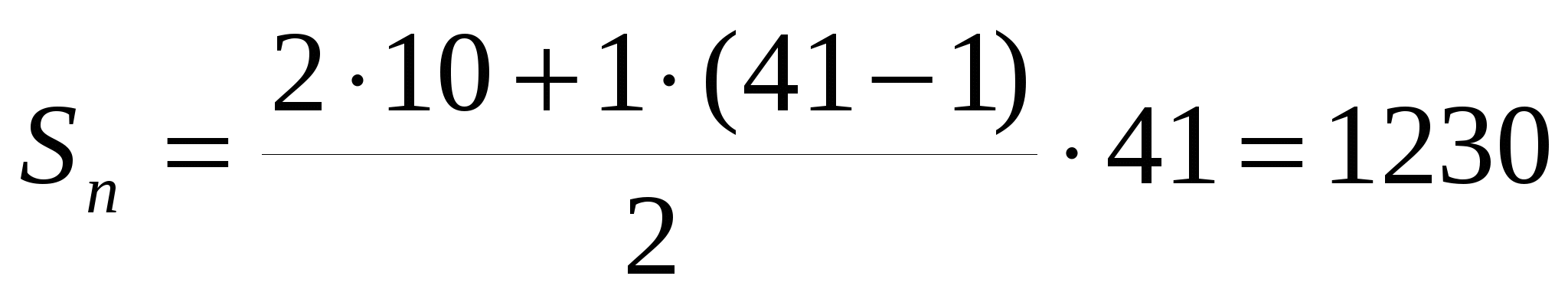 .
. : 10; 2; 0,4;…
: 10; 2; 0,4;… и S3=42.
и S3=42.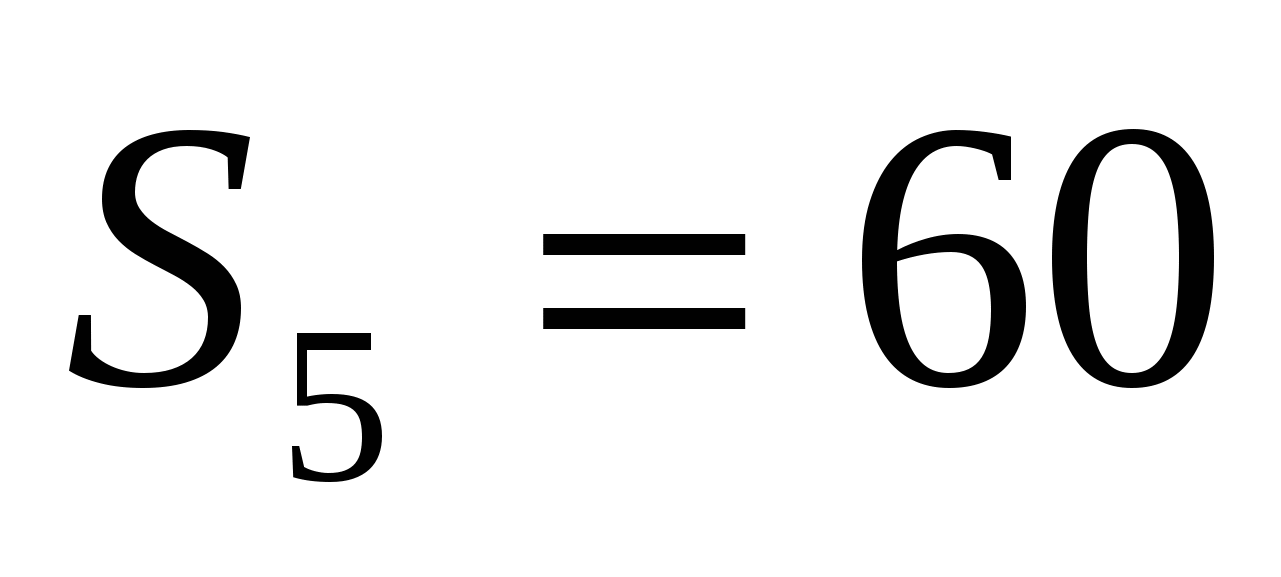
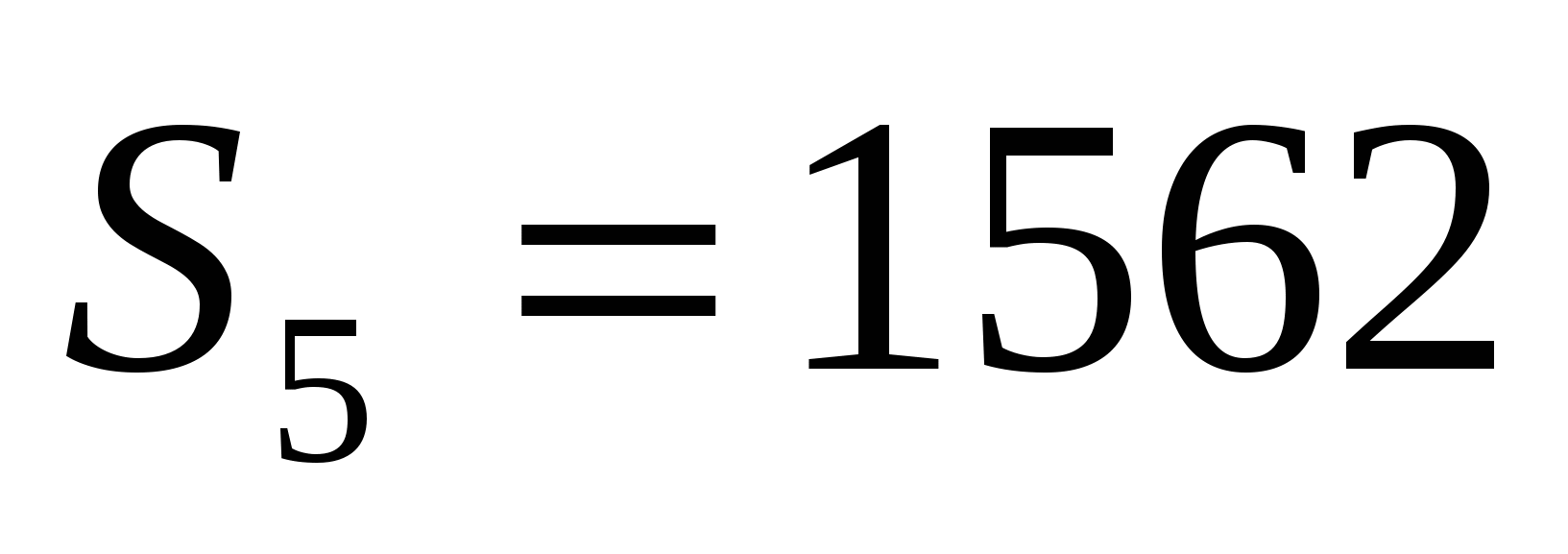


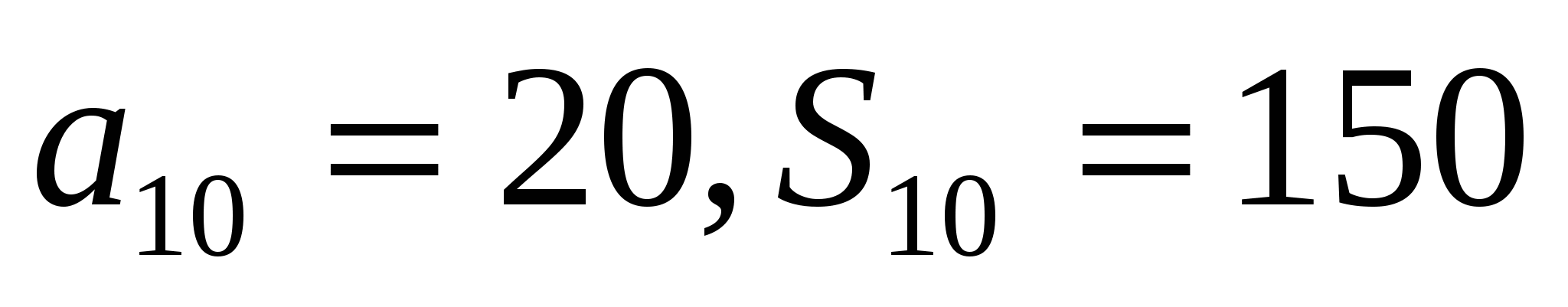 б)
б) 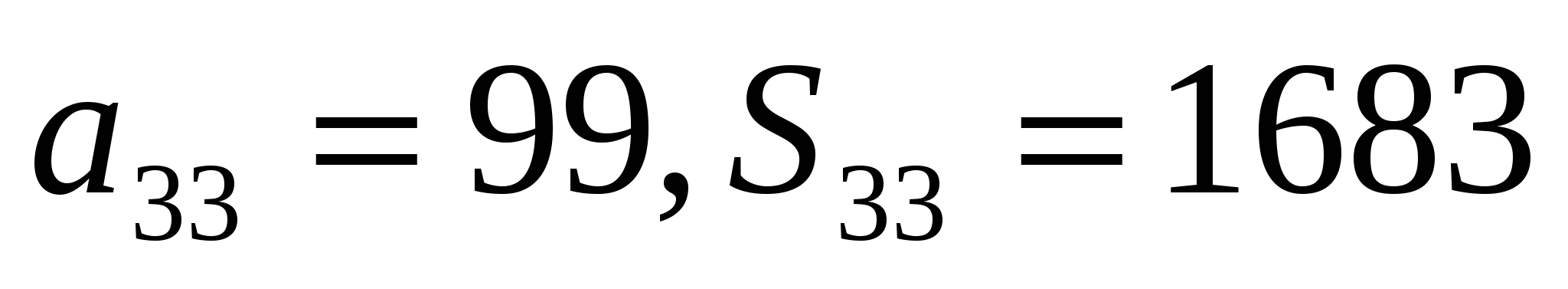 в) 0
в) 0 б)
б) 
 б)
б)