ее график и свойства при k0
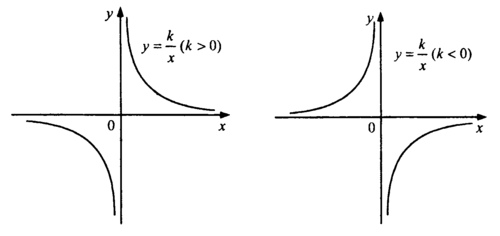
Рассмотрим функцию y=k/y. Графиком этой функции является линия, называемая в математике гиперболой. Общий вид гиперболы, представлен на рисунке ниже. (На графике представлена функция y равно k разделить на x, у которой k равно единице.)
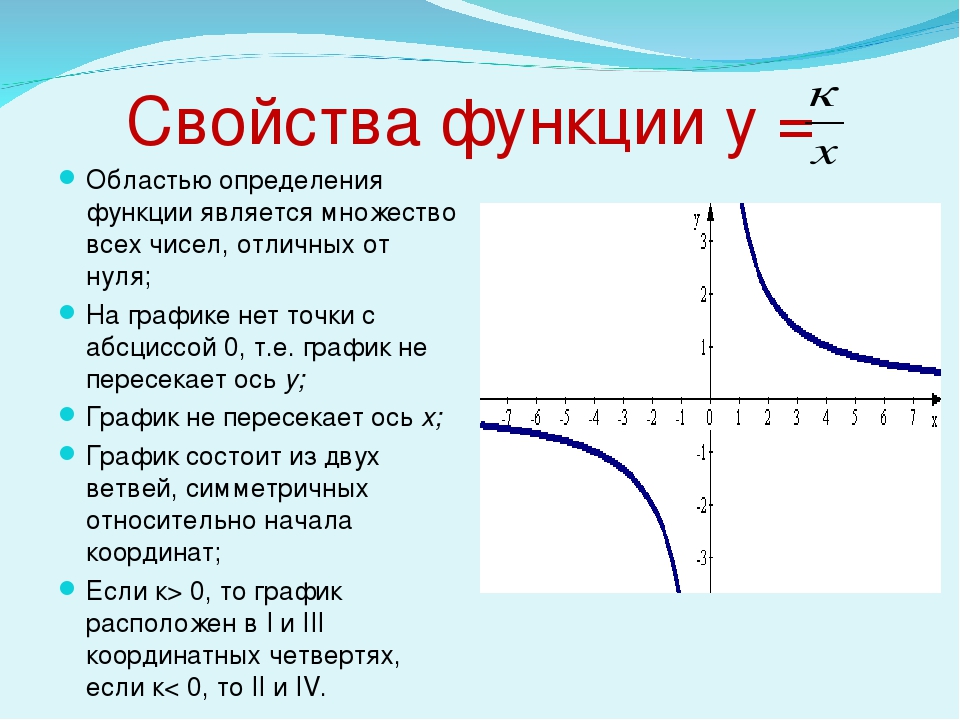
Видно, что график состоит из двух частей. Эти части называют ветвями гиперболы. Стоит отметить также, что каждая ветвь гиперболы подходит в одном из направлений все ближе и ближе к осям координат. Оси координат в таком случае называют асимптотами.
Вообще любые прямые линии, к которым бесконечно приближается график функции, но не достигает их, называются асимптотами. У гиперболы, как и у параболы, есть оси симметрии. Для гиперболы, представленной на рисунке выше, это прямая y=x.
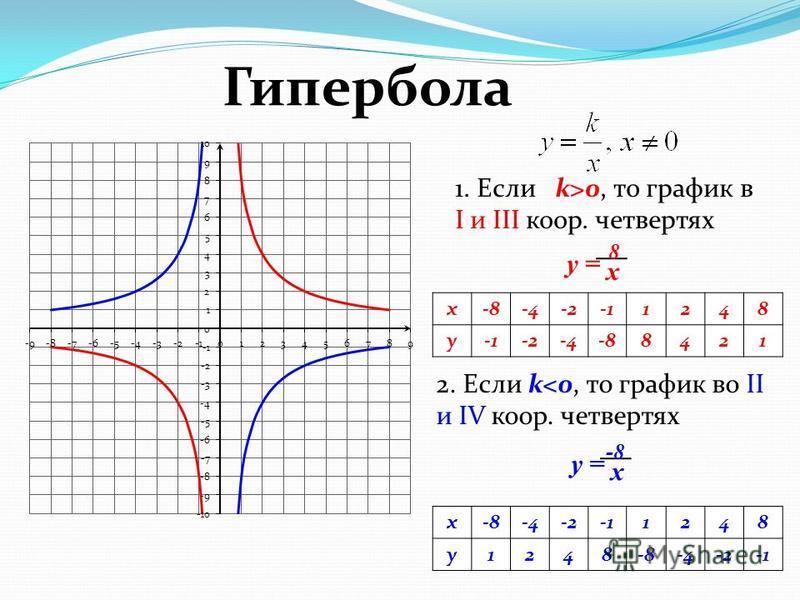
Теперь разберемся с двумя общими случаями гипербол. Графиком функции y = k/x, при k ≠0, будет являться гипербола, ветви которой расположены либо в первом и третьем координатных углах, при k>0, либо во втором и четвертом координатных углах, при k<0.
Основные свойства функции y = k/x, при k>0
График функции y = k/x, при k>0
1. Точка (0;0) центр симметрии гиперболы.
2. Оси координат – асимптоты гиперболы.
3. Прямая y=x ось симметрии гиперболы.
4. Область определения функции все х, кроме х=0.
5. y>0 при x>0; y6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).
7. Функция не ограничена ни снизу, ни сверху.
8. У функции нет ни наибольшего, ни наименьшего значений.
9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).
Основные свойства функции y = k/x, при k<0
График функции y = k/x, при k<0
1. Точка (0;0) центр симметрии гиперболы.
2. Оси координат – асимптоты гиперболы.
3. Прямая y=-x ось симметрии гиперболы.
4. Область определения функции все х, кроме х=0.
5. y>0 при x0.
6. Функция возрастает как на промежутке (-∞;0), так и на промежутке (0;+∞).
7. Функция не ограничена ни снизу, ни сверху.
8. У функции нет ни наибольшего, ни наименьшего значений.
9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).
Нужна помощь в учебе?
Предыдущая тема: Преобразование рациональных выражений: способы преобразований и примеры
Следующая тема:   Рациональные числа: определение, сумма, разность, умножение, деление
Ejercicio de Функция y-k-x -1
Ejercicio de Функция y-k-x -1
¡Terminado!
|
¿Qué quieres hacer ahora?
| ||||
| Cancelar |
Estilo del cuadro de texto:
Fuente: AldrichAmatic SCAnnie Use Your TelescopeArchitects DaughterArialBaloo PaajiBangersBlack Ops OneBoogalooBubblegum SansCherry Cream SodaChewyComic NeueComing SoonCovered By Your GraceCrafty GirlsCreepsterDancing ScriptEscolarExo 2Fontdiner SwankyFreckle FaceFredericka the GreatFredoka OneGloria HallelujahGochi HandGrand HotelGurmukhiHenny PennyIndie FlowerJolly LodgerJust Me Again Down HereKalamKrankyLobsterLobster TwoLove Ya Like A SisterLuckiest GuyMountains of ChristmasNeuchaOpen SansOrbitronOswaldPacificoPatrick HandPernament MarkerPinyon ScriptRanchoReenie BeanieRibeye MarrowRock SaltRusso OneSacramentoSatisfySchoolbellShadows Into Light TwoSpecial EliteUbuntuUnkemptVT323Yanone Kaffeesatz Tamaño: 89101112131416182022242832364050607080px
Color de fuente  Color de fondo  Color del borde
Opacidad del fondo:
0.
Tamaño del borde: 012345678910
Esquinas redondeadas: 02468101216202430
Alineación de texto: CentroIzquierdaDerechaJustificar
Últimos comentarios
Por favor, permite el acceso al micrófono
Mira en la parte alta de tu navegador. Si ves un mensaje pidiendo tu permiso para acceder al micrófono, por favor permítelo.
Cerrar
Функция y=k/x, её график и свойства
1. УРОК АЛГЕБРЫ В 8 КЛАССЕ
Лучший способ изучить что-либо — это открыть самому.(Д. Пойа)
2. Задание для учащихся
Закончите предложения:а) С увеличением цены за единицу товара
количество товара, которое можно закупить на
данную сумму денег …
уменьшится
б) С уменьшением скорости движения на данном
отрезке пути время движения …
увеличится
в) С увеличением производительности труда при
выполнении данного объёма работы
количество рабочих …
уменьшится
1
Пешеход проходит путь S со скоростью v за t часов.

Выразите время пешехода через путь и скорость.
1) Если
S 60 , то
60
t
v
Задачи, приводящие к понятию обратной пропорциональности.
2
Площадь прямоугольника со сторонами
x и y равна S. Выразите у через S и х.
1) Если
S 24 , то
y=24/x
5. ТЕМА УРОКА
Функция y=k/x,её график
и свойства
6. Определение
Обратной пропорциональностью называетсяфункция, заданная формулой
y = k/x, где k≠0,
где х – независимая переменная.
Число k называется коэффициентом обратной
7. Построение графика функции у=к/х
1 варианту = 8/х
2 вариант
у = — 8/х
1 ) Составим таблицу значений для х и у
2 ) Начертим координатную плоскость
3) Проставим точки в координатной плоскости
4) Соединим точки плавной линией
График
функции
1 вариант
у = 8/х
у = к/х
и её свойства
2 вариант
гипербола
у = — 8/х
D ( у ) ; 0 U 0 ; 1.
 Область определения функции D ( у ) ; 0 U 0 ;
Область определения функции D ( у ) ; 0 U 0 ; E ( у ) ; 0 U 0 ; 2.Область значений функции
E ( у ) ; 0 U 0 ;
y 0, х 0 ; y 0, х ;0 3. у>0 , у
4.Наибольшее и наименьшее значение функции
9. Тестовые задания по теме“Обратная пропорциональность”
1) Какая из формул задаёт обратную пропорциональностьх
1)у
3
4)
2)
3
у
х
у 3х
5)
3)
у х 3
у х
3
Тестовые задания по теме“Обратная пропорциональность”
2) Какая из указанных точек принадлежит
графику функции y = -8/x ?
1) A(1;8)
2) B(-1;-8)
3) С(1;-8)
Тестовые задания по теме“Обратная пропорциональность”
3) На чертеже показан график функции
у=к/х.
Укажите формулу, которой
задана функция
1) y=-3/x
2) y=6/x
3) y=-6/x
4) y=3/x
Тестовые задания по теме“Обратная пропорциональность”
4) Укажите среди графиков гиперболу
1
2
3
13. Тест
1. На одном из рисунков изображена гипербола.
Укажите этот рисунок.
1
2
3
4
2 . На одном из рисунков изображена парабола.
Укажите этот рисунок.
1
2
3
4
3 . На одном из рисунков изображен график функции
у = 2/х.
Укажите этот рисунок.
1
3
2
4
4 . Как называется функция у = к/х ?
5 . Как называется график функции у = к/х ?
18. Проверь себя
1) 22) 4
3) 3
4) обратная пропорциональность
5) гипербола
21. Сегодня на уроке
Я научился….Мне понравилось …
Я не понял…
22. Домашнее задание
Выучитьконспект
1
вариант № 18.5, №18.9
2
вариант №18.8, №18.18(а,б)
Творческое домашнее задание
1)Изобразите афоризм «Чем скорее проедешь, тем скорее приедешь»
с помощью графика, установив при этом функциональную зависимость.
2)Проиллюстрируйте графически свою пословицу на выбор.
23. Вопросы для проверки
Приведите пример обратной пропорциональнойзависимости
Дайте определение обратной пропорциональности
Что представляет собой график обратной
пропорциональности
Укажите свойства обратной пропорциональности
Задания: http://mathgia.
 ru:8080/or/gia12/Main
ru:8080/or/gia12/Main1
Первый слайд презентации: Функция y=k/x, её свойства и график
Изображение слайда
2
Слайд 2: Определение
Обратной пропорциональностью называется функция, заданная формулой y = k/x, где k ≠ 0, где х – независимая переменная. Число k называется коэффициентом обратной пропорциональности
3
Слайд 3
В явлениях природы, в человеческой деятельности часто встречаются обратно пропорциональные зависимости между двумя величинами. Как графиком можно представить эту зависимость?
График обратно пропорциональной функции называется ГИПЕРБОЛА
Как графиком можно представить эту зависимость?
График обратно пропорциональной функции называется ГИПЕРБОЛА
Изображение слайда
4
Слайд 4: График функции
12 х _ у = х у -1 -2 -4 -3 -6 -8 -12 -12 -6 -4 -3 -2 -1,5 -1 х у 1 2 3 4 6 8 12 12 6 4 3 2 1,5 1 Построим по точкам график функции
Изображение слайда
5
Слайд 5
Изображение слайда
6
Слайд 6
гипербола
Изображение слайда
7
Слайд 7
1 вариант 2 вариант
Г рафик функции у = к/ х и её свойства
у = к/х,к˂0
у = к/х,к˃0
1.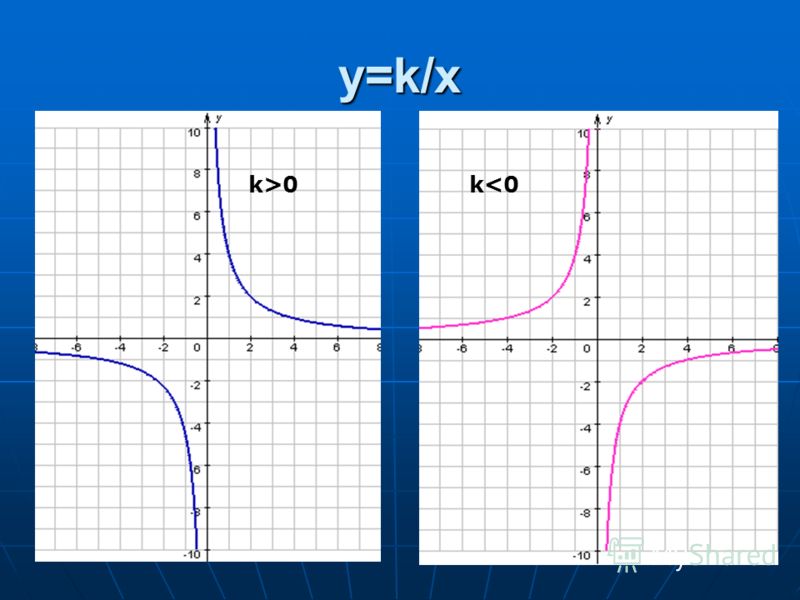 Область определения функции
2. Область значений функции
3. у >0, у <0 при х-?
4. Наибольшее и наименьшее значение функции
гипербола
Область определения функции
2. Область значений функции
3. у >0, у <0 при х-?
4. Наибольшее и наименьшее значение функции
гипербола
Изображение слайда
8
Слайд 8: Тестовые задания по теме “ Обратная пропорциональность ”
1) Какая из формул задаёт обратную пропорциональность 3) 4) 5) 1) 2)
Изображение слайда
9
Слайд 9
2 ) Какая из указанных точек принадлежит графику функции y = -8/x ? 1 ) A(1;8) 2) B(-1;-8) 3) С(1 ; -8) Тестовые задания по теме “ Обратная пропорциональность ”
Изображение слайда
10
Слайд 10
3. На одном из рисунков изображена гипербола. Укажите этот рисунок.
1
3
4
2
На одном из рисунков изображена гипербола. Укажите этот рисунок.
1
3
4
2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
Изображение для работы со слайдом
Изображение для работы со слайдом
11
Слайд 11: Проверьте свои ответы
1) 4 2) 3 3) 2
Изображение слайда
12
Последний слайд презентации: Функция y=k/x, её свойства и график
Что является графиком функции В каких координатных четвертях расположен график функции в зависимости от коэффициента К? Какова область определения функции? Какими свойствами обладает график функции обратной пропорциональной зависимости? Как называется график обратно пропорциональной функции? Из чего состоит гипербола? 12 Итог урока
Изображение слайда
ПРЯМАЯ И ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ
ПРЯМАЯ И ОБРАТНАЯ
ПРОПОРЦИОНАЛЬНОСТЬ.
I. Прямая пропорциональность.
О: Функция вида y = kx + b называется линейной функцией.
k, b — числа (параметры), x — переменная (аргумент)
О: Линейная функция вида y = kx называется прямой пропорциональностью.
Свойства функции y = kx График функции y = kx
1.
|
|
|
|
2. Корни: x = 0
Корни: x = 0
3. При k > 0 Þ y > 0 при x Î (0;+¥)
y < 0 при x Î (-¥; 0)
При k < 0 Þ y > 0 при x Î (-¥; 0)
y < 0 при x Î (0;+¥)
4. При k > 0 Þ функция возрастает
При k > 0 Þ функция возрастает
При k < 0 Þ функция убывает
5. Экстремумов нет.
6.
|
7. Ey = R
8. Нечётная, непериодическая.
График - прямая, строим по двум точкам.
Замечание: График функции y = kx + b получаем перемещением графика функции y = kx по вертикали:
если b > 0 , то вверх на b
если b < 0 , то вниз на b
II. Обратная пропорциональность.
О: Функция
вида y = k / x называется обратной
пропорциональностью.
Свойства функции y = k / x График функции y = k / x
1. Dy = (-¥; 0)È (0; +¥)
2.
|
|
|
|
3. При k > 0 Þ y > 0 при x Î (0;+¥)
При k > 0 Þ y > 0 при x Î (0;+¥)
y < 0 при x Î (-¥; 0)
При k < 0 Þ y > 0 при x Î (-¥; 0)
y < 0 при x Î (0;+¥)
4. При k > 0 Þ функция убывает
При k < 0 Þ функция возрастает
5. Экстремумов нет.
Экстремумов нет.
6.
|
7. Ey = (-¥; 0)È (0; +¥)
8. Нечётная, непериодическая.
График - гипербола, строим заполняя таблицу.
Примеры таких зависимостей:
Тест «График линейной функции», ФГОС
Линейной называется функция вида
1)у=кх+b
2)y=x+kb
3)y=kx:b
4)y=k:x
5)y= k:x+b
2. Графиком линейной функции является
Графиком линейной функции является
1)две точки
2)отрезок
3)прямая
4)окружность
5)луч
3. Областью определения линейной функции является множество
1)натуральных чисел
2)рациональных чисел
3)целых чисел
4)положительных чисел
5)отрицательных чисел
4. Областью значений линейной функции является
1)натуральных чисел
2)рациональных чисел
3)целых чисел
4)положительных чисел
5)отрицательных чисел
5. Линейная функция возрастает, если
1) к>0
2)к<0
3)к=0
4) b=0
5) b <0
6. Линейная функция убывает, если
1) к>0
2)к<0
3)к=0
4) b=0
5) b <0
7. Точка А(1,3) принадлежит графику функции
Точка А(1,3) принадлежит графику функции
1)у=х+3
2) у=2х+3
3) у=х+2
4) у=2х-3
5) у=х-3
8. График функции у=2х-1 не проходит через точку
1)(1,1)
2)(3,5)
3)(0,-1)
4)(0,0)
5)(4,7)
9. График функции у=2х-1 пересекает ось ординат в точке
1)1
2)2
3)3
4)0,5
5)-1
10. График функции у=2х-1 пересекает ось абсцисс в точке
1)1
2)2
3)3
4)0,5
5)-1
11. График линейной функции проходит через 1, 2 и 3 четверти, если
1) к>0, b>0
2)к<0 , b <0
3)к=0, b <0
4) b=0 , к=0
5) b <0, к>0
12. Графики функций у=ах+в и у=сх+д параллельны, если
Графики функций у=ах+в и у=сх+д параллельны, если
1)в=д
2)ас=вд
3)а/с=в/д
4)а=с
5)а=с, в=д
13. найти сумму координат точек пересечения графика функции у=2х+4 с осями координат
1)6
2)4
3)2
4)0
5)-2
14. Какой знак будет иметь произведение координат, не равных нулю, точек пересечения с осями координат возрастающей линейной функции
1)+
2)-
15. Сколько точек необходимо для построения графика линейной функции
1)1
2)2
3)3
4)4
5)5
16. При каком значении аргумента функция у=3х+5 принимает значение равное 23
1)3
2)4
3)5
4)6
5)8
17. Какое значение принимает функция у=5х-4 в точке с абсциссой равной 4
1)20
2)1
3)16
4)0
5)1,6
18.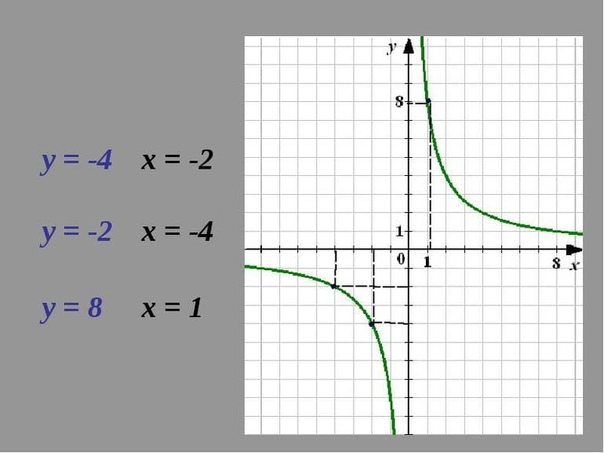 График линейной функции проходит через начало координат при условии
График линейной функции проходит через начало координат при условии
1) к>0
2)к<0
3)к=0
4) b=0
5) b <0
19. Биссектрисой первой и третьей координатный четвертей является график функции
1)у=х+3
2) у=2х+3
3) у=х
4) у=2х-3
5) у=х-3
20. График линейной функции параллелен оси абсцисс при условии
1) к>0
2)к<0
3)к=0
4) b=0
5) b <0
Функция y=k/x и ее график — Математика
На этом уроке мы познакомимся с понятием функция обратной пропорциональности и ее графиком. А также научимся работать с функцией и ее графиком при выполнении заданий.
Нажмите на картинку, чтобы посмотреть видео этого занятия
Задания по теме для самостоятельного решения
Задание 1
(2 балла)Задание 2
(2 балла)Задание 3
(2 балла)В каких четвертях координатной плоскости расположен график, изображенный на рисунке?
Изображение:
\
Выберите несколько из 4 вариантов ответа:
1) II — четверть
2) IV — четверть
3) I — четверть
4) III — четверть
% PDF-1. 6
%
457 0 объект
>
endobj
xref
457 712
0000000016 00000 н.
0000016761 00000 п.
0000016907 00000 п.
0000017997 00000 п.
0000018695 00000 п.
0000018745 00000 п.
0000018796 00000 п.
0000018847 00000 п.
0000022487 00000 п.
0000022595 00000 п.
0000022696 00000 п.
0000023236 00000 п.
0000023485 00000 п.
0000023728 00000 п.
0000024260 00000 п.
0000024311 00000 п.
0000024420 00000 п.
0000025007 00000 п.
0000025660 00000 п.
0000025835 00000 п.
0000026158 00000 п.
0000027480 00000 п.
0000027669 00000 п.
0000028001 00000 п.
0000030573 00000 п.
0000030827 00000 п.
0000031218 00000 п.
0000031269 00000 п.
0000031320 00000 н.
0000031371 00000 п.
0000031422 00000 п.
0000031471 00000 п.
0000032170 00000 п.
0000033306 00000 п.
0000033369 00000 п.
0000033476 00000 п.
0000034141 00000 п.
0000034396 00000 п.
0000034982 00000 п.
0000035219 00000 п.
0000035277 00000 п.
0000038792 00000 п.
0000039125 00000 п.
0000039306 00000 п.
0000039950 00000 н.
0000040193 00000 п.
6
%
457 0 объект
>
endobj
xref
457 712
0000000016 00000 н.
0000016761 00000 п.
0000016907 00000 п.
0000017997 00000 п.
0000018695 00000 п.
0000018745 00000 п.
0000018796 00000 п.
0000018847 00000 п.
0000022487 00000 п.
0000022595 00000 п.
0000022696 00000 п.
0000023236 00000 п.
0000023485 00000 п.
0000023728 00000 п.
0000024260 00000 п.
0000024311 00000 п.
0000024420 00000 п.
0000025007 00000 п.
0000025660 00000 п.
0000025835 00000 п.
0000026158 00000 п.
0000027480 00000 п.
0000027669 00000 п.
0000028001 00000 п.
0000030573 00000 п.
0000030827 00000 п.
0000031218 00000 п.
0000031269 00000 п.
0000031320 00000 н.
0000031371 00000 п.
0000031422 00000 п.
0000031471 00000 п.
0000032170 00000 п.
0000033306 00000 п.
0000033369 00000 п.
0000033476 00000 п.
0000034141 00000 п.
0000034396 00000 п.
0000034982 00000 п.
0000035219 00000 п.
0000035277 00000 п.
0000038792 00000 п.
0000039125 00000 п.
0000039306 00000 п.
0000039950 00000 н.
0000040193 00000 п. 0000040368 00000 п.
0000041442 00000 п.
0000041906 00000 п.
0000042551 00000 п.
0000043091 00000 п.
0000043410 00000 п.
0000043515 00000 п.
0000046471 00000 п.
0000046628 00000 п.
0000046929 00000 п.
0000052948 00000 п.
0000054073 00000 п.
0000054321 00000 п.
0000054519 00000 п.
0000055107 00000 п.
0000055647 00000 п.
0000056053 00000 п.
0000056804 00000 п.
0000057319 00000 п.
0000060718 00000 п.
0000063599 00000 п.
0000063955 00000 п.
0000064188 00000 п.
0000064289 00000 п.
0000064662 00000 п.
0000064891 00000 п.
0000066921 00000 п.
0000067242 00000 п.
0000067506 00000 п.
0000068482 00000 п.
0000069145 00000 п.
0000069687 00000 п.
0000070109 00000 п.
0000070395 00000 п.
0000071397 00000 п.
0000075616 00000 п.
0000075721 00000 п.
0000075984 00000 п.
0000077105 00000 п.
0000077630 00000 п.
0000077995 00000 п.
0000078402 00000 п.
0000078456 00000 п.
0000078816 00000 п.
0000078871 00000 п.
0000079074 00000 п.
0000080605 00000 п.
0000080872 00000 п.
0000040368 00000 п.
0000041442 00000 п.
0000041906 00000 п.
0000042551 00000 п.
0000043091 00000 п.
0000043410 00000 п.
0000043515 00000 п.
0000046471 00000 п.
0000046628 00000 п.
0000046929 00000 п.
0000052948 00000 п.
0000054073 00000 п.
0000054321 00000 п.
0000054519 00000 п.
0000055107 00000 п.
0000055647 00000 п.
0000056053 00000 п.
0000056804 00000 п.
0000057319 00000 п.
0000060718 00000 п.
0000063599 00000 п.
0000063955 00000 п.
0000064188 00000 п.
0000064289 00000 п.
0000064662 00000 п.
0000064891 00000 п.
0000066921 00000 п.
0000067242 00000 п.
0000067506 00000 п.
0000068482 00000 п.
0000069145 00000 п.
0000069687 00000 п.
0000070109 00000 п.
0000070395 00000 п.
0000071397 00000 п.
0000075616 00000 п.
0000075721 00000 п.
0000075984 00000 п.
0000077105 00000 п.
0000077630 00000 п.
0000077995 00000 п.
0000078402 00000 п.
0000078456 00000 п.
0000078816 00000 п.
0000078871 00000 п.
0000079074 00000 п.
0000080605 00000 п.
0000080872 00000 п. 0000080967 00000 п.
0000081866 00000 п.
0000082731 00000 н.
0000083748 00000 п.
0000084330 00000 п.
0000084446 00000 п.
0000084788 00000 п.
0000085028 00000 п.
0000085268 00000 п.
0000085699 00000 п.
0000085939 00000 п.
0000085989 00000 п.
0000086099 00000 п.
0000086655 00000 п.
0000086706 00000 п.
0000087153 00000 п.
0000087207 00000 п.
0000087256 00000 п.
0000087425 00000 п.
0000087766 00000 п.
0000087817 00000 п.
00000
0000080967 00000 п.
0000081866 00000 п.
0000082731 00000 н.
0000083748 00000 п.
0000084330 00000 п.
0000084446 00000 п.
0000084788 00000 п.
0000085028 00000 п.
0000085268 00000 п.
0000085699 00000 п.
0000085939 00000 п.
0000085989 00000 п.
0000086099 00000 п.
0000086655 00000 п.
0000086706 00000 п.
0000087153 00000 п.
0000087207 00000 п.
0000087256 00000 п.
0000087425 00000 п.
0000087766 00000 п.
0000087817 00000 п.
00000
00000 н.
0000296902 00000 н. 0000298411 00000 н.
0000298651 00000 п.
0000298893 00000 н.
0000299135 00000 н.
0000299190 00000 н.
0000299486 00000 н.
0000299547 00000 н.
0000300551 00000 п.
0000300812 00000 н.
0000301100 00000 н.
0000301185 00000 н.
0000301600 00000 н.
0000301966 00000 н.
0000302275 00000 н.
0000302683 00000 п.
0000303051 00000 н.
0000303388 00000 н.
0000303693 00000 н.
0000305582 00000 н.
0000305865 00000 н.
0000306239 00000 п.
0000306393 00000 п.
0000306746 00000 н.
0000308350 00000 н.
0000308628 00000 н.
0000308977 00000 н.
0000309122 00000 н.
0000309497 00000 н.
0000309832 00000 н.
0000310202 00000 н.
0000310507 00000 н.
0000310794 00000 п.
0000311171 00000 н.
0000311549 00000 н.
0000311902 00000 н.
0000312032 00000 н.
0000312105 00000 н.
0000312204 00000 н.
0000312313 00000 н.
0000312429 00000 н.
0000312542 00000 н.
0000312627 00000 н.
0000312684 00000 н.
0000312783 00000 н.
0000312840 00000 н.
0000312928 00000 н.
0000312985 00000 н.
0000313079 00000 н.
0000298411 00000 н.
0000298651 00000 п.
0000298893 00000 н.
0000299135 00000 н.
0000299190 00000 н.
0000299486 00000 н.
0000299547 00000 н.
0000300551 00000 п.
0000300812 00000 н.
0000301100 00000 н.
0000301185 00000 н.
0000301600 00000 н.
0000301966 00000 н.
0000302275 00000 н.
0000302683 00000 п.
0000303051 00000 н.
0000303388 00000 н.
0000303693 00000 н.
0000305582 00000 н.
0000305865 00000 н.
0000306239 00000 п.
0000306393 00000 п.
0000306746 00000 н.
0000308350 00000 н.
0000308628 00000 н.
0000308977 00000 н.
0000309122 00000 н.
0000309497 00000 н.
0000309832 00000 н.
0000310202 00000 н.
0000310507 00000 н.
0000310794 00000 п.
0000311171 00000 н.
0000311549 00000 н.
0000311902 00000 н.
0000312032 00000 н.
0000312105 00000 н.
0000312204 00000 н.
0000312313 00000 н.
0000312429 00000 н.
0000312542 00000 н.
0000312627 00000 н.
0000312684 00000 н.
0000312783 00000 н.
0000312840 00000 н.
0000312928 00000 н.
0000312985 00000 н.
0000313079 00000 н. 0000313136 00000 н.
0000313222 00000 н.
0000313279 00000 н.
0000313370 00000 н.
0000313427 00000 н.
0000313526 00000 н.
0000313583 00000 н.
0000313672 00000 н.
0000313729 00000 н.
0000313857 00000 н.
0000313937 00000 н.
0000313994 00000 н.
0000314129 00000 н.
0000314257 00000 н.
0000314337 00000 н.
0000314394 00000 н.
0000314529 00000 н.
0000314657 00000 н.
0000314737 00000 н.
0000314794 00000 н.
0000314929 00000 н.
0000315058 00000 н.
0000315138 00000 н.
0000315195 00000 н.
0000315330 00000 н.
0000315458 00000 н.
0000315538 00000 н.
0000315595 00000 н.
0000315715 00000 н.
0000315841 00000 н.
0000315919 00000 н.
0000315976 00000 н.
0000316096 00000 н.
0000316193 00000 п.
0000316250 00000 н.
0000316348 00000 п.
0000316405 00000 н.
0000316508 00000 н.
0000316565 00000 н.
0000316660 00000 н.
0000316717 00000 н.
0000316822 00000 н.
0000316943 00000 н.
0000317044 00000 н.
0000317151 00000 н.
0000317243 00000 н.
0000317300 00000 н.
0000317384 00000 н.
0000313136 00000 н.
0000313222 00000 н.
0000313279 00000 н.
0000313370 00000 н.
0000313427 00000 н.
0000313526 00000 н.
0000313583 00000 н.
0000313672 00000 н.
0000313729 00000 н.
0000313857 00000 н.
0000313937 00000 н.
0000313994 00000 н.
0000314129 00000 н.
0000314257 00000 н.
0000314337 00000 н.
0000314394 00000 н.
0000314529 00000 н.
0000314657 00000 н.
0000314737 00000 н.
0000314794 00000 н.
0000314929 00000 н.
0000315058 00000 н.
0000315138 00000 н.
0000315195 00000 н.
0000315330 00000 н.
0000315458 00000 н.
0000315538 00000 н.
0000315595 00000 н.
0000315715 00000 н.
0000315841 00000 н.
0000315919 00000 н.
0000315976 00000 н.
0000316096 00000 н.
0000316193 00000 п.
0000316250 00000 н.
0000316348 00000 п.
0000316405 00000 н.
0000316508 00000 н.
0000316565 00000 н.
0000316660 00000 н.
0000316717 00000 н.
0000316822 00000 н.
0000316943 00000 н.
0000317044 00000 н.
0000317151 00000 н.
0000317243 00000 н.
0000317300 00000 н.
0000317384 00000 н.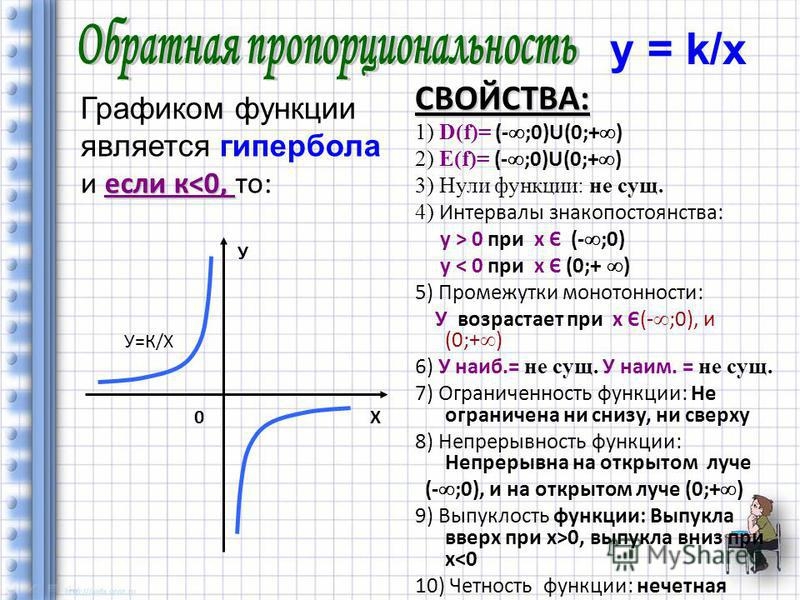 0000317475 00000 н.
0000317532 00000 н.
0000317625 00000 н.
0000317682 00000 н.
0000317775 00000 н.
0000317832 00000 н.
0000317925 00000 н.
0000317982 00000 н.
0000318075 00000 н.
0000318132 00000 н.
0000318225 00000 н.
0000318282 00000 н.
0000318375 00000 н.
0000318432 00000 н.
0000318525 00000 н.
0000318582 00000 н.
0000318699 00000 н.
0000318816 00000 н.
0000318933 00000 н.
0000319050 00000 н.
0000319167 00000 н.
0000319284 00000 н.
0000319401 00000 п.
0000319516 00000 н.
0000319573 00000 н.
0000319665 00000 н.
0000319722 00000 н.
0000319845 00000 н.
0000319968 00000 н.
0000320085 00000 н.
0000320142 00000 н.
0000320259 00000 н.
0000320374 00000 н.
0000320431 00000 н.
0000320548 00000 н.
0000320640 00000 н.
0000320697 00000 н.
0000320781 00000 н.
0000320872 00000 н.
0000320929 00000 н.
0000321020 00000 н.
0000321077 00000 н.
0000321170 00000 н.
0000321227 00000 н.
0000321320 00000 н.
0000321377 00000 н.
0000321470 00000 н.
0000321527 00000 н.
0000317475 00000 н.
0000317532 00000 н.
0000317625 00000 н.
0000317682 00000 н.
0000317775 00000 н.
0000317832 00000 н.
0000317925 00000 н.
0000317982 00000 н.
0000318075 00000 н.
0000318132 00000 н.
0000318225 00000 н.
0000318282 00000 н.
0000318375 00000 н.
0000318432 00000 н.
0000318525 00000 н.
0000318582 00000 н.
0000318699 00000 н.
0000318816 00000 н.
0000318933 00000 н.
0000319050 00000 н.
0000319167 00000 н.
0000319284 00000 н.
0000319401 00000 п.
0000319516 00000 н.
0000319573 00000 н.
0000319665 00000 н.
0000319722 00000 н.
0000319845 00000 н.
0000319968 00000 н.
0000320085 00000 н.
0000320142 00000 н.
0000320259 00000 н.
0000320374 00000 н.
0000320431 00000 н.
0000320548 00000 н.
0000320640 00000 н.
0000320697 00000 н.
0000320781 00000 н.
0000320872 00000 н.
0000320929 00000 н.
0000321020 00000 н.
0000321077 00000 н.
0000321170 00000 н.
0000321227 00000 н.
0000321320 00000 н.
0000321377 00000 н.
0000321470 00000 н.
0000321527 00000 н. 0000321620 00000 н.
0000321677 00000 н.
0000321770 00000 н.
0000321827 00000 н.
0000321920 00000 н.
0000321977 00000 н.
0000322070 00000 н.
0000322127 00000 н.
0000322244 00000 н.
0000322361 00000 н.
0000322478 00000 н.
0000322595 00000 н.
0000322712 00000 н.
0000322829 00000 н.
0000322946 00000 н.
0000323063 00000 н.
0000323178 00000 н.
0000323235 00000 н.
0000323327 00000 н.
0000323384 00000 н.
0000323507 00000 н.
0000323630 00000 н.
0000323747 00000 н.
0000323804 00000 н.
0000323921 00000 н.
0000324036 00000 н.
0000324093 00000 н.
0000324210 00000 н.
0000324324 00000 н.
0000324381 00000 н.
0000324479 00000 н.
0000324578 00000 н.
0000324635 00000 н.
0000324728 00000 н.
0000324785 00000 н.
0000324878 00000 н.
0000324935 00000 н.
0000325028 00000 н.
0000325085 00000 н.
0000325178 00000 н.
0000325235 00000 н.
0000325328 00000 н.
0000325385 00000 н.
0000325478 00000 н.
0000325535 00000 н.
0000325628 00000 н.
0000325685 00000 н.
0000325778 00000 н.
0000321620 00000 н.
0000321677 00000 н.
0000321770 00000 н.
0000321827 00000 н.
0000321920 00000 н.
0000321977 00000 н.
0000322070 00000 н.
0000322127 00000 н.
0000322244 00000 н.
0000322361 00000 н.
0000322478 00000 н.
0000322595 00000 н.
0000322712 00000 н.
0000322829 00000 н.
0000322946 00000 н.
0000323063 00000 н.
0000323178 00000 н.
0000323235 00000 н.
0000323327 00000 н.
0000323384 00000 н.
0000323507 00000 н.
0000323630 00000 н.
0000323747 00000 н.
0000323804 00000 н.
0000323921 00000 н.
0000324036 00000 н.
0000324093 00000 н.
0000324210 00000 н.
0000324324 00000 н.
0000324381 00000 н.
0000324479 00000 н.
0000324578 00000 н.
0000324635 00000 н.
0000324728 00000 н.
0000324785 00000 н.
0000324878 00000 н.
0000324935 00000 н.
0000325028 00000 н.
0000325085 00000 н.
0000325178 00000 н.
0000325235 00000 н.
0000325328 00000 н.
0000325385 00000 н.
0000325478 00000 н.
0000325535 00000 н.
0000325628 00000 н.
0000325685 00000 н.
0000325778 00000 н. 0000325835 00000 н.
0000325952 00000 н.
0000326069 00000 н.
0000326186 00000 н.
0000326303 00000 н.
0000326420 00000 н.
0000326537 00000 н.
0000326654 00000 н.
0000326771 00000 н.
0000326886 00000 н.
0000326943 00000 н.
0000327044 00000 н.
0000327101 00000 н.
0000327224 00000 н.
0000327347 00000 н.
0000327464 00000 н.
0000327521 00000 н.
0000327638 00000 н.
0000327753 00000 н.
0000327810 00000 н.
0000327927 00000 н.
0000328041 00000 н.
0000328098 00000 н.
0000328196 00000 н.
0000328295 00000 н.
0000328352 00000 н.
0000328444 00000 н.
0000328501 00000 н.
0000328594 00000 н.
0000328651 00000 н.
0000328744 00000 н.
0000328801 00000 н.
0000328894 00000 н.
0000328951 00000 н.
0000329044 00000 н.
0000329101 00000 н.
0000329194 00000 н.
0000329251 00000 н.
0000329344 00000 н.
0000329401 00000 н.
0000329494 00000 н.
0000329551 00000 н.
0000329644 00000 н.
0000329701 00000 н.
0000329818 00000 н.
0000329935 00000 н.
0000330052 00000 н.
0000330169 00000 н.
0000325835 00000 н.
0000325952 00000 н.
0000326069 00000 н.
0000326186 00000 н.
0000326303 00000 н.
0000326420 00000 н.
0000326537 00000 н.
0000326654 00000 н.
0000326771 00000 н.
0000326886 00000 н.
0000326943 00000 н.
0000327044 00000 н.
0000327101 00000 н.
0000327224 00000 н.
0000327347 00000 н.
0000327464 00000 н.
0000327521 00000 н.
0000327638 00000 н.
0000327753 00000 н.
0000327810 00000 н.
0000327927 00000 н.
0000328041 00000 н.
0000328098 00000 н.
0000328196 00000 н.
0000328295 00000 н.
0000328352 00000 н.
0000328444 00000 н.
0000328501 00000 н.
0000328594 00000 н.
0000328651 00000 н.
0000328744 00000 н.
0000328801 00000 н.
0000328894 00000 н.
0000328951 00000 н.
0000329044 00000 н.
0000329101 00000 н.
0000329194 00000 н.
0000329251 00000 н.
0000329344 00000 н.
0000329401 00000 н.
0000329494 00000 н.
0000329551 00000 н.
0000329644 00000 н.
0000329701 00000 н.
0000329818 00000 н.
0000329935 00000 н.
0000330052 00000 н.
0000330169 00000 н. 0000330286 00000 н.
0000330403 00000 н.
0000330520 00000 н.
0000330637 00000 п.
0000330756 00000 н.
0000330871 00000 п.
0000330928 00000 н.
0000331029 00000 н.
0000331086 00000 н.
0000331209 00000 н.
0000331332 00000 н.
0000331449 00000 н.
0000331506 00000 н.
0000331623 00000 н.
0000331738 00000 п.
0000331795 00000 н.
0000331912 00000 н.
0000332026 00000 н.
0000332083 00000 н.
0000332181 00000 н.
0000332280 00000 н.
0000332337 00000 н.
0000332430 00000 н.
0000332487 00000 н.
0000332580 00000 н.
0000332637 00000 н.
0000332730 00000 н.
0000332787 00000 н.
0000332880 00000 н.
0000332937 00000 н.
0000333030 00000 н.
0000333087 00000 н.
0000333180 00000 н.
0000333237 00000 н.
0000333330 00000 н.
0000333387 00000 н.
0000333480 00000 н.
0000333537 00000 н.
0000333654 00000 н.
0000333771 00000 н.
0000333888 00000 н.
0000334005 00000 н.
0000334122 00000 п.
0000334239 00000 п.
0000334356 00000 п.
0000334473 00000 п.
0000334588 00000 н.
0000334645 00000 н.
0000330286 00000 н.
0000330403 00000 н.
0000330520 00000 н.
0000330637 00000 п.
0000330756 00000 н.
0000330871 00000 п.
0000330928 00000 н.
0000331029 00000 н.
0000331086 00000 н.
0000331209 00000 н.
0000331332 00000 н.
0000331449 00000 н.
0000331506 00000 н.
0000331623 00000 н.
0000331738 00000 п.
0000331795 00000 н.
0000331912 00000 н.
0000332026 00000 н.
0000332083 00000 н.
0000332181 00000 н.
0000332280 00000 н.
0000332337 00000 н.
0000332430 00000 н.
0000332487 00000 н.
0000332580 00000 н.
0000332637 00000 н.
0000332730 00000 н.
0000332787 00000 н.
0000332880 00000 н.
0000332937 00000 н.
0000333030 00000 н.
0000333087 00000 н.
0000333180 00000 н.
0000333237 00000 н.
0000333330 00000 н.
0000333387 00000 н.
0000333480 00000 н.
0000333537 00000 н.
0000333654 00000 н.
0000333771 00000 н.
0000333888 00000 н.
0000334005 00000 н.
0000334122 00000 п.
0000334239 00000 п.
0000334356 00000 п.
0000334473 00000 п.
0000334588 00000 н.
0000334645 00000 н. 0000334746 00000 н.
0000334803 00000 п.
0000334926 00000 н.
0000335049 00000 н.
0000335166 00000 н.
0000335223 00000 п.
0000335340 00000 н.
0000335455 00000 н.
0000335512 00000 н.
0000335629 00000 н.
0000335743 00000 н.
0000335800 00000 н.
0000335898 00000 н.
0000335997 00000 н.
0000336054 00000 н.
0000336146 00000 н.
0000336203 00000 н.
0000336296 00000 н.
0000336353 00000 п.
0000336446 00000 н.
0000336503 00000 н.
0000336596 00000 н.
0000336653 00000 п.
0000336746 00000 н.
0000336803 00000 п.
0000336896 00000 н.
0000336953 00000 п.
0000337046 00000 н.
0000337103 00000 н.
0000337196 00000 н.
0000337253 00000 н.
0000337346 00000 н.
0000337403 00000 п.
0000337520 00000 н.
0000337637 00000 н.
0000337754 00000 н.
0000337871 00000 н.
0000337988 00000 н.
0000338105 00000 н.
0000338222 00000 п.
0000338339 00000 н.
0000338456 00000 н.
0000338573 00000 н.
0000338630 00000 н.
0000338731 00000 н.
0000338788 00000 н.
0000338911 00000 н.
0000339034 00000 н.
0000334746 00000 н.
0000334803 00000 п.
0000334926 00000 н.
0000335049 00000 н.
0000335166 00000 н.
0000335223 00000 п.
0000335340 00000 н.
0000335455 00000 н.
0000335512 00000 н.
0000335629 00000 н.
0000335743 00000 н.
0000335800 00000 н.
0000335898 00000 н.
0000335997 00000 н.
0000336054 00000 н.
0000336146 00000 н.
0000336203 00000 н.
0000336296 00000 н.
0000336353 00000 п.
0000336446 00000 н.
0000336503 00000 н.
0000336596 00000 н.
0000336653 00000 п.
0000336746 00000 н.
0000336803 00000 п.
0000336896 00000 н.
0000336953 00000 п.
0000337046 00000 н.
0000337103 00000 н.
0000337196 00000 н.
0000337253 00000 н.
0000337346 00000 н.
0000337403 00000 п.
0000337520 00000 н.
0000337637 00000 н.
0000337754 00000 н.
0000337871 00000 н.
0000337988 00000 н.
0000338105 00000 н.
0000338222 00000 п.
0000338339 00000 н.
0000338456 00000 н.
0000338573 00000 н.
0000338630 00000 н.
0000338731 00000 н.
0000338788 00000 н.
0000338911 00000 н.
0000339034 00000 н.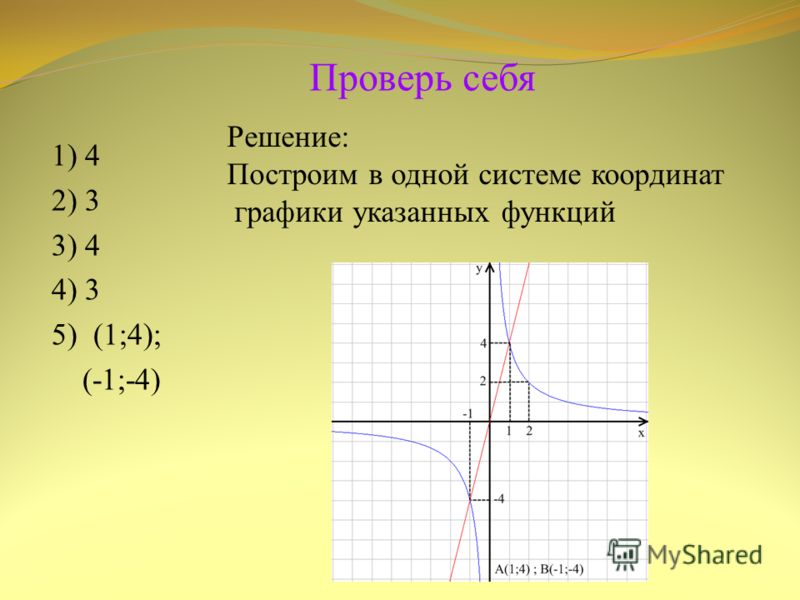 0000339151 00000 п.
0000339208 00000 н.
0000339325 00000 н.
0000339440 00000 н.
0000339497 00000 н.
0000339614 00000 н.
0000339741 00000 н.
0000339876 00000 н.
0000340003 00000 п.
0000340134 00000 н.
0000340263 00000 н.
0000340378 00000 п.
0000340521 00000 н.
0000340606 00000 н.
0000340686 00000 н.
0000340744 00000 н.
0000340829 00000 н.
0000340955 00000 н.
0000341035 00000 н.
0000341093 00000 п.
0000341178 00000 н.
0000341304 00000 н.
0000341384 00000 н.
0000341442 00000 н.
0000341527 00000 н.
0000341653 00000 н.
0000341733 00000 н.
0000341791 00000 н.
0000341875 00000 п.
0000342001 00000 п.
0000342079 00000 н.
0000342136 00000 п.
0000342219 00000 п.
0000342276 00000 н.
0000342365 00000 н.
0000342422 00000 н.
0000342513 00000 н.
0000342570 00000 н.
0000342661 00000 п.
0000342718 00000 н.
0000342809 00000 н.
0000342866 00000 н.
0000342957 00000 н.
0000343014 00000 н.
0000343105 00000 п.
0000343162 00000 п.
0000343253 00000 н.
0000343310 00000 п.
0000339151 00000 п.
0000339208 00000 н.
0000339325 00000 н.
0000339440 00000 н.
0000339497 00000 н.
0000339614 00000 н.
0000339741 00000 н.
0000339876 00000 н.
0000340003 00000 п.
0000340134 00000 н.
0000340263 00000 н.
0000340378 00000 п.
0000340521 00000 н.
0000340606 00000 н.
0000340686 00000 н.
0000340744 00000 н.
0000340829 00000 н.
0000340955 00000 н.
0000341035 00000 н.
0000341093 00000 п.
0000341178 00000 н.
0000341304 00000 н.
0000341384 00000 н.
0000341442 00000 н.
0000341527 00000 н.
0000341653 00000 н.
0000341733 00000 н.
0000341791 00000 н.
0000341875 00000 п.
0000342001 00000 п.
0000342079 00000 н.
0000342136 00000 п.
0000342219 00000 п.
0000342276 00000 н.
0000342365 00000 н.
0000342422 00000 н.
0000342513 00000 н.
0000342570 00000 н.
0000342661 00000 п.
0000342718 00000 н.
0000342809 00000 н.
0000342866 00000 н.
0000342957 00000 н.
0000343014 00000 н.
0000343105 00000 п.
0000343162 00000 п.
0000343253 00000 н.
0000343310 00000 п.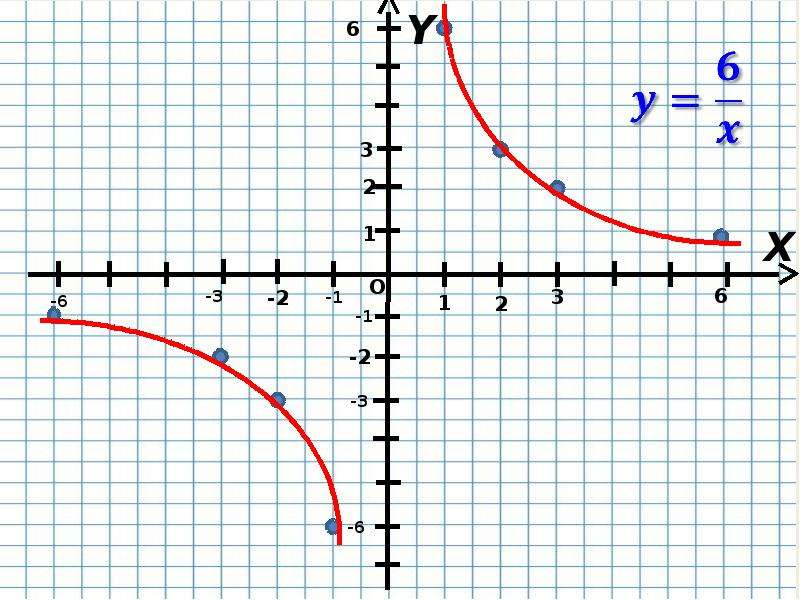 0000343401 00000 п.
0000343458 00000 н.
0000343549 00000 н.
0000343606 00000 п.
0000343763 00000 н.
0000343920 00000 н.
0000344077 00000 н.
0000344234 00000 н.
0000344391 00000 п.
0000344548 00000 н.
0000344705 00000 п.
0000344862 00000 н.
0000345017 00000 н.
0000345174 00000 н.
0000345331 00000 п.
0000345388 00000 п.
0000345545 00000 н.
0000345603 00000 п.
0000345695 00000 п.
0000345754 00000 н.
0000345849 00000 н.
0000345908 00000 н.
0000346003 00000 п.
0000346062 00000 н.
0000346157 00000 н.
0000346216 00000 н.
0000346311 00000 н.
0000346370 00000 п.
0000346465 00000 н.
0000346524 00000 н.
0000346619 00000 п.
0000346678 00000 н.
0000346773 00000 н.
0000346832 00000 н.
0000346926 00000 н.
0000346985 00000 п.
0000347141 00000 п.
0000347297 00000 н.
0000347453 00000 п.
0000347609 00000 н.
0000347765 00000 н.
0000347921 00000 п.
0000348077 00000 н.
0000348233 00000 н.
0000348387 00000 н.
0000348543 00000 н.
0000348699 00000 н.
0000348758 00000 н.
0000343401 00000 п.
0000343458 00000 н.
0000343549 00000 н.
0000343606 00000 п.
0000343763 00000 н.
0000343920 00000 н.
0000344077 00000 н.
0000344234 00000 н.
0000344391 00000 п.
0000344548 00000 н.
0000344705 00000 п.
0000344862 00000 н.
0000345017 00000 н.
0000345174 00000 н.
0000345331 00000 п.
0000345388 00000 п.
0000345545 00000 н.
0000345603 00000 п.
0000345695 00000 п.
0000345754 00000 н.
0000345849 00000 н.
0000345908 00000 н.
0000346003 00000 п.
0000346062 00000 н.
0000346157 00000 н.
0000346216 00000 н.
0000346311 00000 н.
0000346370 00000 п.
0000346465 00000 н.
0000346524 00000 н.
0000346619 00000 п.
0000346678 00000 н.
0000346773 00000 н.
0000346832 00000 н.
0000346926 00000 н.
0000346985 00000 п.
0000347141 00000 п.
0000347297 00000 н.
0000347453 00000 п.
0000347609 00000 н.
0000347765 00000 н.
0000347921 00000 п.
0000348077 00000 н.
0000348233 00000 н.
0000348387 00000 н.
0000348543 00000 н.
0000348699 00000 н.
0000348758 00000 н. 0000348914 00000 н.
0000348973 00000 п.
0000349065 00000 н.
0000349124 00000 н.
0000349220 00000 н.
0000349279 00000 н.
0000349374 00000 п.
0000349433 00000 н.
0000349528 00000 п.
0000349587 00000 н.
0000349682 00000 н.
0000349741 00000 н.
0000349836 00000 н.
0000349895 00000 п.
0000349990 00000 н.
0000350049 00000 н.
0000350144 00000 н.
0000350203 00000 н.
0000350298 00000 н.
0000350357 00000 н.
0000350451 00000 н.
0000350510 00000 н.
0000350666 00000 н.
0000350822 00000 н.
0000350978 00000 н.
0000351134 00000 н.
0000351290 00000 н.
0000351446 00000 н.
0000351602 00000 н.
0000351758 00000 н.
0000351914 00000 н.
0000352068 00000 н.
0000352224 00000 н.
0000352380 00000 н.
0000352439 00000 н.
0000352595 00000 н.
0000352654 00000 н.
0000352746 00000 н.
0000352805 00000 н.
0000352900 00000 н.
0000352959 00000 н.
0000353054 00000 н.
0000353113 00000 п.
0000353208 00000 н.
0000353267 00000 н.
0000353362 00000 н.
0000353421 00000 н.
0000353516 00000 н.
0000348914 00000 н.
0000348973 00000 п.
0000349065 00000 н.
0000349124 00000 н.
0000349220 00000 н.
0000349279 00000 н.
0000349374 00000 п.
0000349433 00000 н.
0000349528 00000 п.
0000349587 00000 н.
0000349682 00000 н.
0000349741 00000 н.
0000349836 00000 н.
0000349895 00000 п.
0000349990 00000 н.
0000350049 00000 н.
0000350144 00000 н.
0000350203 00000 н.
0000350298 00000 н.
0000350357 00000 н.
0000350451 00000 н.
0000350510 00000 н.
0000350666 00000 н.
0000350822 00000 н.
0000350978 00000 н.
0000351134 00000 н.
0000351290 00000 н.
0000351446 00000 н.
0000351602 00000 н.
0000351758 00000 н.
0000351914 00000 н.
0000352068 00000 н.
0000352224 00000 н.
0000352380 00000 н.
0000352439 00000 н.
0000352595 00000 н.
0000352654 00000 н.
0000352746 00000 н.
0000352805 00000 н.
0000352900 00000 н.
0000352959 00000 н.
0000353054 00000 н.
0000353113 00000 п.
0000353208 00000 н.
0000353267 00000 н.
0000353362 00000 н.
0000353421 00000 н.
0000353516 00000 н. 0000353575 00000 н.
0000353670 00000 н.
0000353729 00000 н.
0000353824 00000 н.
0000353883 00000 н.
0000353977 00000 н.
0000354036 00000 н.
0000354192 00000 н.
0000354348 00000 п.
0000354504 00000 н.
0000354660 00000 н.
0000354816 00000 н.
0000354972 00000 н.
0000355128 00000 н.
0000355284 00000 н.
0000355438 00000 п.
0000355594 00000 н.
0000355750 00000 н.
0000355809 00000 н.
0000355965 00000 н.
0000356024 00000 н.
0000356116 00000 п.
0000356175 00000 н.
0000356271 00000 н.
0000356330 00000 н.
0000356425 00000 н.
0000356484 00000 н.
0000356579 00000 п.
0000356638 00000 н.
0000356733 00000 н.
0000356792 00000 н.
0000356887 00000 н.
0000356946 00000 н.
0000357041 00000 н.
0000357100 00000 н.
0000357195 00000 н.
0000357254 00000 н.
0000357349 00000 н.
0000357408 00000 н.
0000357502 00000 н.
0000357561 00000 н.
0000357717 00000 н.
0000357873 00000 н.
0000358029 00000 н.
0000358185 00000 н.
0000358341 00000 п.
0000358497 00000 н.
0000358653 00000 н.
0000353575 00000 н.
0000353670 00000 н.
0000353729 00000 н.
0000353824 00000 н.
0000353883 00000 н.
0000353977 00000 н.
0000354036 00000 н.
0000354192 00000 н.
0000354348 00000 п.
0000354504 00000 н.
0000354660 00000 н.
0000354816 00000 н.
0000354972 00000 н.
0000355128 00000 н.
0000355284 00000 н.
0000355438 00000 п.
0000355594 00000 н.
0000355750 00000 н.
0000355809 00000 н.
0000355965 00000 н.
0000356024 00000 н.
0000356116 00000 п.
0000356175 00000 н.
0000356271 00000 н.
0000356330 00000 н.
0000356425 00000 н.
0000356484 00000 н.
0000356579 00000 п.
0000356638 00000 н.
0000356733 00000 н.
0000356792 00000 н.
0000356887 00000 н.
0000356946 00000 н.
0000357041 00000 н.
0000357100 00000 н.
0000357195 00000 н.
0000357254 00000 н.
0000357349 00000 н.
0000357408 00000 н.
0000357502 00000 н.
0000357561 00000 н.
0000357717 00000 н.
0000357873 00000 н.
0000358029 00000 н.
0000358185 00000 н.
0000358341 00000 п.
0000358497 00000 н.
0000358653 00000 н.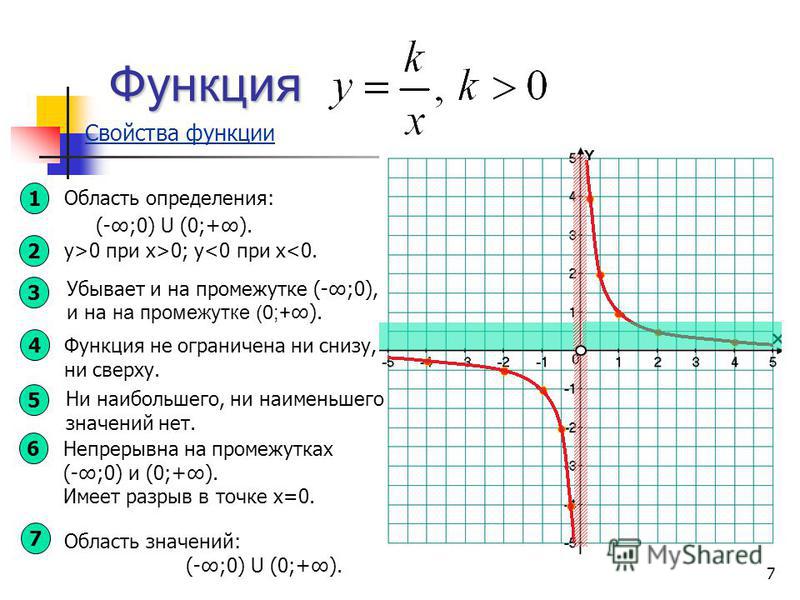 0000358809 00000 н.
0000358965 00000 н.
0000359119 00000 н.
0000359275 00000 н.
0000359431 00000 н.
0000359490 00000 н.
0000359646 00000 н.
0000359727 00000 н.
0000359786 00000 н.
0000359872 00000 н.
0000359931 00000 н.
0000360024 00000 н.
0000360083 00000 н.
0000360178 00000 н.
0000360237 00000 н.
0000360332 00000 н.
0000360391 00000 п.
0000360486 00000 н.
0000360545 00000 н.
0000360640 00000 п.
0000360699 00000 н.
0000360794 00000 н.
0000360853 00000 п.
0000360948 00000 н.
0000361007 00000 н.
0000361102 00000 п.
0000361161 00000 н.
0000361319 00000 н.
0000361477 00000 н.
0000361635 00000 н.
0000361793 00000 н.
0000361951 00000 н.
0000362109 00000 п.
0000362267 00000 н.
0000362423 00000 н.
0000362581 00000 н.
0000362739 00000 н.
0000362798 00000 н.
0000362956 00000 н.
0000363015 00000 н.
0000016586 00000 п.
0000014831 00000 п.
трейлер
] >>
startxref
0
%% EOF
1168 0 объект
> поток
x ڼ V {PSWνy ܐ
0000358809 00000 н.
0000358965 00000 н.
0000359119 00000 н.
0000359275 00000 н.
0000359431 00000 н.
0000359490 00000 н.
0000359646 00000 н.
0000359727 00000 н.
0000359786 00000 н.
0000359872 00000 н.
0000359931 00000 н.
0000360024 00000 н.
0000360083 00000 н.
0000360178 00000 н.
0000360237 00000 н.
0000360332 00000 н.
0000360391 00000 п.
0000360486 00000 н.
0000360545 00000 н.
0000360640 00000 п.
0000360699 00000 н.
0000360794 00000 н.
0000360853 00000 п.
0000360948 00000 н.
0000361007 00000 н.
0000361102 00000 п.
0000361161 00000 н.
0000361319 00000 н.
0000361477 00000 н.
0000361635 00000 н.
0000361793 00000 н.
0000361951 00000 н.
0000362109 00000 п.
0000362267 00000 н.
0000362423 00000 н.
0000362581 00000 н.
0000362739 00000 н.
0000362798 00000 н.
0000362956 00000 н.
0000363015 00000 н.
0000016586 00000 п.
0000014831 00000 п.
трейлер
] >>
startxref
0
%% EOF
1168 0 объект
> поток
x ڼ V {PSWνy ܐ
Прямое изменение
Прямое изменение
описывает простые отношения между двумя
переменные
. Мы говорим
y напрямую меняется с участием Икс
(или так как Икс
, в некоторых учебниках), если:
Мы говорим
y напрямую меняется с участием Икс
(или так как Икс
, в некоторых учебниках), если:
y знак равно k Икс
для некоторых постоянный k , называется постоянная вариации или константа пропорциональности . (Некоторые учебники описывают прямое изменение, говоря » y изменяется прямо как Икс «,» y изменяется пропорционально как Икс «, или » y прямо пропорциональна Икс .»)
Это означает, что как Икс увеличивается, y увеличивается и как Икс уменьшается, y уменьшается — и что соотношение между ними всегда остается неизменным.
График уравнения прямого изменения представляет собой прямую линию, проходящую через начало координат.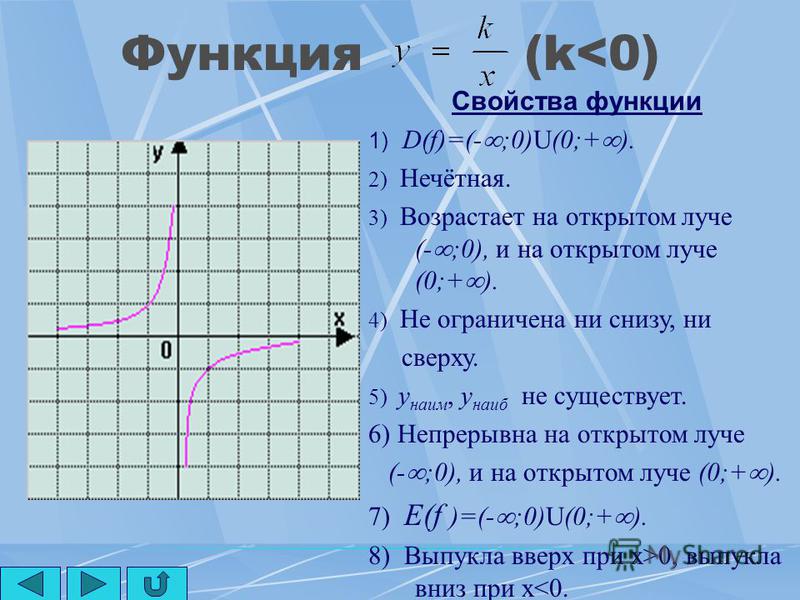
Уравнение прямого изменения для 3 разные значения k |
Пример 1:
При условии y изменяется прямо как Икс , с постоянной вариации k знак равно 1 3 , найти y когда Икс знак равно 12 .
Напишите уравнение прямой вариации.
y знак равно 1 3 Икс
Заменить данный Икс ценность.
y знак равно 1 3 ⋅ 12 y знак равно 4
Пример 2:
При условии
y
изменяется прямо как
Икс
, найти постоянную вариации, если
y
знак равно
24
и
Икс
знак равно
3
.
Напишите уравнение прямой вариации.
y знак равно k Икс
Заменить данный Икс и y значения и решить для k .
24 знак равно k ⋅ 3 k знак равно 8
Пример 3:
Предположим y изменяется прямо как Икс , и y знак равно 30 когда Икс знак равно 6 .В чем ценность y когда Икс знак равно 100 ?
Напишите уравнение прямой вариации.
y знак равно k Икс
Заменить данный
Икс
и
y
значения и решить для
k
.
30 знак равно k ⋅ 6 k знак равно 5
Уравнение y знак равно 5 Икс .Теперь замените Икс знак равно 100 и найти y .
y знак равно 5 ⋅ 100 y знак равно 500
Обратная вариация
В то время как прямое изменение описывает линейную связь между двумя переменные , обратная вариация описывает другой вид отношений.
Для двух величин с обратным изменением, когда одна величина увеличивается, другая величина уменьшается.
Например, когда вы путешествуете в определенное место, по мере увеличения вашей скорости время, необходимое для прибытия в это место, уменьшается. Когда вы уменьшаете скорость, время, необходимое для прибытия в это место, увеличивается. Итак, количества обратно пропорциональны.
Когда вы уменьшаете скорость, время, необходимое для прибытия в это место, увеличивается. Итак, количества обратно пропорциональны.
Обратную вариацию можно представить уравнением Икс y знак равно k или y знак равно k Икс .
Это, y изменяется обратно пропорционально Икс если есть некоторая ненулевая константа k так что, Икс y знак равно k или y знак равно k Икс где Икс ≠ 0 , y ≠ 0 .
Предположим y изменяется обратно пропорционально Икс такой, что Икс y знак равно 3 или y знак равно 3 Икс . Показан график этого уравнения.
поскольку
k
является положительным значением, так как значения
Икс
увеличиваются, значения
y
уменьшение.
Примечание. Для уравнений прямой вариации вы говорите, что y изменяется прямо как Икс .Для уравнений обратной вариации вы говорите, что y изменяется обратно пропорционально Икс .
Правило произведения для обратной вариации
Если ( Икс 1 , y 1 ) и ( Икс 2 , y 2 ) являются решениями обратной вариации, то Икс 1 y 1 знак равно k и Икс 2 y 2 знак равно k .
Замена Икс 1 y 1 для k .
Икс 1 y 1 знак равно Икс 2 y 2 или Икс 1 Икс 2 знак равно y 2 y 1
Уравнение
Икс
1
y
1
знак равно
Икс
2
y
2
называется правилом произведения для обратных вариаций.
Пример:
На заводе, 10 мужчины могут делать работу в 30 дней. Сколько дней потребуется, если 20 мужчины делают ту же работу?
Здесь, когда численность персонала увеличится, им потребуется меньше 30 дней на выполнение той же работы. Итак, это обратная вариация.
Позволять Икс быть числом рабочих, и пусть y быть количеством дней на выполнение работы.
Так, Икс 1 знак равно 10 , Икс 2 знак равно 20 и y 1 знак равно 30 .
По правилу произведения обратной вариации,
( 10 ) ( 30 ) знак равно ( 20 ) ( y 2 ) 300 знак равно 20 y 2
Решить для
y
2
.
y 2 знак равно 300 20 знак равно 15
Следовательно, 20 мужчины могут выполнять ту же работу в 15 дней.
Аппроксимация кривой— гипертекст по физике
Обсуждение
введение
Я украл это у «Triple A-S» (Американской ассоциации содействия развитию науки).Они знают, как это делать правильно, так зачем это менять.
Из-за своей абстрактности математика универсальна в том смысле, что другие области человеческой мысли — нет. Он находит полезные применения в бизнесе, промышленности, музыке, исторической науке, политике, спорте, медицине, сельском хозяйстве, инженерии, а также в социальных и естественных науках. Особенно сильна связь между математикой и другими областями фундаментальной и прикладной науки.
Я вижу одиннадцать различных полей, упомянутых в этом единственном предложении.Я имею дело только с одним из них ежедневно, но я согласен с тем, что все они обязаны математике. Если вы принимаете решения о том, чему вы посвятите свою жизнь (или, по крайней мере, чему будете учиться профессионально), основываясь на каком-то понятии «важности», тогда откажитесь от всего, кроме математики. Это одна из древнейших областей человеческого знания. Единственное, что старше, — это сельское хозяйство… ммм… да… а еще есть инструменты, огонь и… ну, язык очень важен, а математика — прямо там. Ага, математика!
Что это значит для вас сейчас?
Работает обычным образом.Предполагается, что существует некоторая математическая связь между отображаемыми величинами. Данные стремятся к этому математическому идеалу, но из-за ограниченности людей и их инструментов они только приближаются к нему. Точки данных на графике образуют облако вокруг кривой функции. Если бы только у нас было лучшее «зрение». Если бы только наши устройства лучше записывали фактические значения. Если бы мы действительно знали, в чем заключается сущность природы, чтобы мы могли назначить эти устройства для их предполагаемой задачи.Потом. Тогда мы увидим, что каждая точка данных попадает в точную аналитическую кривую. Ах, какой это был бы прекрасный мир. К сожалению, реальные данные никогда не выглядят в точности как идеальные кривые математики.
Если бы только наши устройства лучше записывали фактические значения. Если бы мы действительно знали, в чем заключается сущность природы, чтобы мы могли назначить эти устройства для их предполагаемой задачи.Потом. Тогда мы увидим, что каждая точка данных попадает в точную аналитическую кривую. Ах, какой это был бы прекрасный мир. К сожалению, реальные данные никогда не выглядят в точности как идеальные кривые математики.
| горизонтальная ось ( x ) | вертикальная ось ( y ) |
|---|---|
| независимая переменная | зависимая переменная |
| объясняющая переменная | переменная ответа |
| ∞ | ∝ | α |
| бесконечность | пропорционально | Греческая «альфа» |
Также.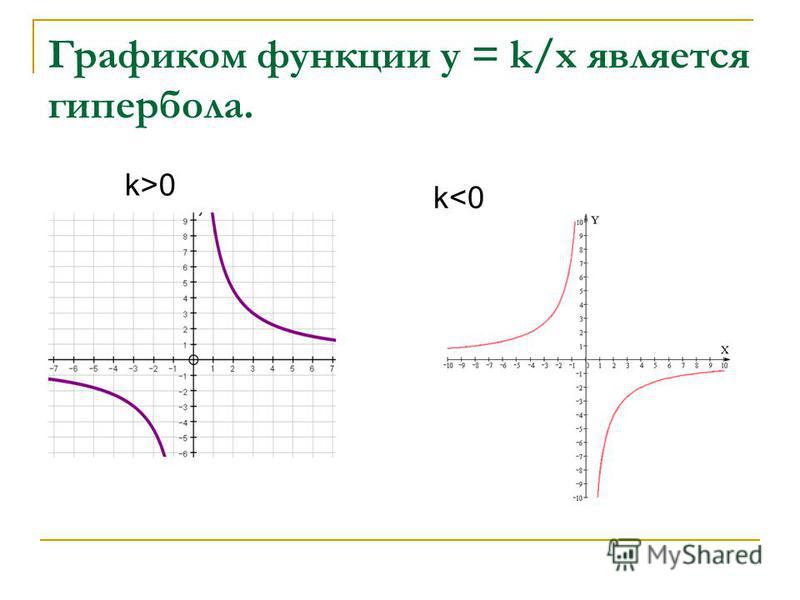
- категориальные переменные — представлены разными символами в одной системе координат
- скрытые переменные или скрытые переменные — источник некоторых экспериментальных ошибок
В поисках отношений.
Ваш друг — символ соразмерности.
независимый
Посмотрите на кривую справа. Независимо от того, какое значение принимает переменная x на кривой, переменная y остается неизменной.Это классический пример отношений под названием независимости . Две величины являются независимыми , если одна не влияет на другую. Кривая представляет собой горизонтальную прямую линию, представленную уравнением общего вида…
и = к
, где k — постоянная.
Подходящим выводом из такой взаимосвязи будет то, что…
- y не зависит от x .
- y не зависит от x .

- y постоянна для всех значений x .
- y не зависит от x .
- y и x независимы.
Например…
- Ускорение свободного падения не зависит от массы. При отсутствии сопротивления воздуха тяжелые предметы падают так же быстро, как и легкие.
- Период простого маятника не зависит от его массы. Простые маятники, которые идентичны во всех отношениях, за исключением веса груза на конце, будут качаться взад и вперед одинаковым образом.
- Скорость света в вакууме c постоянна для всех значений v , скорости системы отсчета. Независимо от того, как я двигаюсь, скорость света в вакууме всегда остается неизменной.
- На силу сухого трения не влияет площадь двух соприкасающихся поверхностей. Перетаскивание прямоугольника за его нижнюю или боковую часть приводит к той же силе трения.
- Масса и расположение не зависят. Если замороженная индейка имеет массу 10 кг в Нью-Йорке, она будет иметь массу 10 кг в Нью-Джерси, в Нью-Дели, на горе Эверест, в самолете, на орбите, на поверхности Луны, в Галактика Андромеды, в…Ну вы поняли.

Независимые отношения могут быть скучными и глубокими. Скучно, когда мы понимаем, что между двумя величинами нет связи. Глубоко, когда мы понимаем, что определили фундаментальный принцип или основополагающую концепцию, имеющую большое значение. Одно из этих утверждений — независимость скорости света и скорости системы отсчета. Скорость света — фундаментальная постоянная, одна из трех или четырех в физике.
прямой
А теперь взгляните на эту кривую.При увеличении переменной x увеличивается и переменная y . Но есть много кривых, которые делают это. Что делает его уникальным? Что отличает его от всех остальных кривых, которые монотонно увеличиваются (как говорят математики) на ? Ключ в форме — прямой негоризонтальной линии, проходящей через начало координат. С этой конкретной формой происходит нечто особенное.
Укажите точку на линии и запишите ее координаты. Удвойте значение переменной x и посмотрите, как отреагирует переменная y . Новое значение и также должно удвоиться. Попробуйте снова. Только на этот раз сократите переменную x пополам. Переменная y должна была отреагировать таким же образом; то есть его тоже нужно разрезать пополам. Что бы ни делал x , y делает то же самое. Это иллюстрирует простейшую, нетривиальную форму пропорциональности — прямая пропорциональность . Две величины равны прямо пропорциональным , если их соотношение является постоянным.
Новое значение и также должно удвоиться. Попробуйте снова. Только на этот раз сократите переменную x пополам. Переменная y должна была отреагировать таким же образом; то есть его тоже нужно разрезать пополам. Что бы ни делал x , y делает то же самое. Это иллюстрирует простейшую, нетривиальную форму пропорциональности — прямая пропорциональность . Две величины равны прямо пропорциональным , если их соотношение является постоянным.
Изменив это определение, мы получим уравнение в общем виде…
y = kx
, где k — постоянная пропорциональности, которую каждый должен распознать как наклон прямой в плоскости xy .
Подходящим выводом из такой взаимосвязи будет то, что…
- y прямо пропорционально x .
- y напрямую зависит от x
- y и x прямо пропорциональны.
- y ∝ x
Например,
- Регулярная заработная плата прямо пропорциональна количеству отработанных часов.
 За сорок часов работы оплачивается в четыре раза больше, чем за десять часов работы.За один час работы оплачивается одна десятая десяти часов работы.
За сорок часов работы оплачивается в четыре раза больше, чем за десять часов работы.За один час работы оплачивается одна десятая десяти часов работы. - Вес напрямую зависит от массы. В три раза больше массы означает в три раза больше веса. Точно так же половина массы означает половину веса.
- Расстояние и время прямо пропорциональны, когда скорость постоянна. Вождение в течение двух часов дает вам вдвое большее расстояние, чем за один час, но только половину до четырех часов.
Внимание! Не думайте, что прямо пропорциональный означает «когда одно увеличивается, другое увеличивается» или «когда одно уменьшается, другое уменьшается».Это более конкретные отношения, чем эти. Приведу противоположный пример. Рабочий, отработавший 60 часов, работает в 1,5 раза больше, чем работник, отработавший 40 часов.
Но рабочие, работающие более 40 часов в неделю в США, должны получать оплату сверхурочной работы, которая обычно в полтора раза превышает их обычную заработную плату. Таким образом, 60-часовой рабочий зарабатывает в 1,75 раза больше, чем 40-часовой рабочий.
Таким образом, 60-часовой рабочий зарабатывает в 1,75 раза больше, чем 40-часовой рабочий.
| 1 × 40 обычных часов | = 1.75 |
| 1 × 40 обычное время |
Так как изменения не те…
1,75 ≠ 1,5
заработная плата в этом примере не прямо пропорциональна отработанному времени. Прямые отношения гораздо более специфичны, чем общее утверждение: «когда одно увеличивается, другое увеличивается». Это больше похоже на «когда один изменяется в определенном соотношении, другой изменяется в таком же отношении».
обратный
Идем дальше.Взгляните на эту кривую. Эта форма называется прямоугольной гиперболой — гиперболой, поскольку она имеет асимптот (линии, к которым кривая приближается, но никогда не пересекает), и прямоугольной, поскольку асимптоты представляют собой оси x и y (которые расположены под прямым углом. для другого).
для другого).
Некоторые говорят, что эта кривая показывает поведение, противоположное предыдущему; то есть, когда переменная x увеличивается, переменная y уменьшается, а при уменьшении переменной x увеличивается переменная y .Но, как и в случае с предыдущей кривой, происходит более конкретное изменение. Убедитесь сами. Выберите удобную точку на кривой. Обратите внимание на значения координат в этой точке. Теперь удвойте координату x и посмотрите, что произойдет с координатой y . Он разрезан пополам. Теперь попробуйте обратное. Укажите точку на кривой и разрежьте ее координату x пополам. Координата y теперь в два раза больше исходного значения. Трижды x , вы получите одну треть от y .Уменьшите x до одной четвертой и посмотрите, как y увеличится на четыре. Однако вы изменяете одну из переменных, а другая изменяется на обратную величину. Это иллюстрирует другой простой вид пропорциональности — обратная пропорциональность .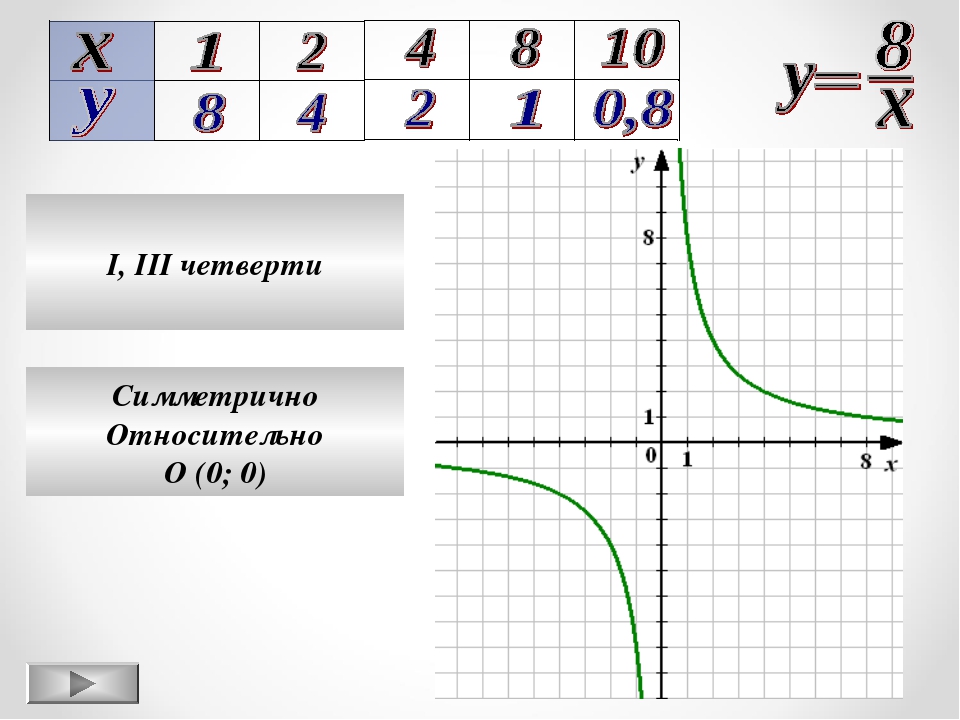 Две величины называются обратно пропорциональными , если их произведение является константой.
Две величины называются обратно пропорциональными , если их произведение является константой.
xy = к
Преобразование этого определения дает нам уравнение общего вида…
, где k — константа пропорциональности.
Подходящим выводом из такой взаимосвязи будет то, что…
- y обратно пропорционально x .
- y изменяется обратно пропорционально x .
- y и x обратно пропорциональны.
- y ∝ 1/ x
- y ∝ x −1
Например…
- Время, необходимое для завершения работы, обратно пропорционально количеству рабочих.Больше рабочих означает меньше времени на выполнение работы. (В два раза больше означает половину времени.) Меньше рабочих означает больше времени. (Если появится только одна треть от нормального числа рабочих, работа займет в три раза больше.)
- Объем массы газа обратно пропорционален действующему на него давлению.
 Поместите баллон в барокамеру и увеличьте давление вдвое — баллон сократится до половины своего первоначального объема. Поместите баллон в вакуумную камеру и уменьшите давление до одной десятой атмосферного — баллон расширится в десять раз в объеме (при условии, что сначала он не сломается).
Поместите баллон в барокамеру и увеличьте давление вдвое — баллон сократится до половины своего первоначального объема. Поместите баллон в вакуумную камеру и уменьшите давление до одной десятой атмосферного — баллон расширится в десять раз в объеме (при условии, что сначала он не сломается).
квадрат
Что у нас здесь? Почему это парабола с вершиной в начале координат. Такая кривая получается, когда одно количество пропорционально квадрату другого. Поскольку эта парабола симметрична относительно оси y , это делает ее вертикальной параболой , и мы знаем, что квадрат получает горизонтальная переменная. Вот уравнение общего вида для такой кривой…
y = kx 2
Подходящим выводом из такой взаимосвязи будет то, что…
- y пропорционально квадрату x .
- y ∝ x 2
Например…
- Расстояние, пройденное объектом, упавшим из состояния покоя, пропорционально квадрату времени.
 Сколько времени нужно, чтобы упасть на один метр? Удвойте это время, и вы упадете на 4 м, утроите его, и вы упадете на 9 м, и так далее.
Сколько времени нужно, чтобы упасть на один метр? Удвойте это время, и вы упадете на 4 м, утроите его, и вы упадете на 9 м, и так далее. - Скорость, с которой электрическая цепь производит тепло, пропорциональна квадрату силы тока. Удвоение силы тока в тостере увеличивает ее тепловыделение в четыре раза.Уменьшите ток в процессоре компьютера до половины его предыдущего значения, и вы уменьшите тепловыделение до четверти от предыдущего значения.
корень квадратный
Вот еще одна парабола с вершиной в начале координат. Эта парабола наклонена на бок и симметрична относительно оси x . Для горизонтальной параболы , подобной этой, квадрат получает вертикальная переменная. Уравнение общего вида для такой кривой…
y = k √ x
Подходящим выводом из такой зависимости было бы то, что…
- y пропорционально квадратному корню из x .
- y ∝ √ x
- y ∝ x ½
Например…
- Скорость пропорциональна квадратному корню из расстояния для свободно падающих объектов.
 Насколько быстро движется объект после падения на один метр? На четырех метрах он будет иметь вдвое большую скорость; на девяти метрах — тройной; шестнадцать, четырехместные; и так далее.
Насколько быстро движется объект после падения на один метр? На четырех метрах он будет иметь вдвое большую скорость; на девяти метрах — тройной; шестнадцать, четырехместные; и так далее.
Что нужно запомнить — квадратный корень не является явной функцией. Это не однозначно.Каждое число имеет два квадратных корня: положительный и отрицательный. Типичное программное обеспечение для построения кривой игнорирует отрицательный корень, поэтому я нарисовал только половину параболы на диаграмме выше. Еще кое-что нужно запомнить — область квадратного корня ограничена неотрицательными значениями. Это причудливый способ сказать, что вы не можете найти квадратный корень из отрицательного числа (то есть не без расширения вашего понятия «число»).
мощность
На данный момент у нас есть пять кривых и пять уравнений общего вида…
| • независимый | y = к |
| • прямой | y = kx |
| • обратный | y = k / x |
| • квадрат | y = kx 2 |
| • корень квадратный | y = k √ x |
У них есть три общих компонента…
| x = | независимая переменная (или независимая переменная) |
| y = | зависимая переменная (или переменная ответа) |
| к = | константа пропорциональности |
и один компонент, который меняется…
| n = | степень независимой переменной |
Мы могли бы переписать эти общие уравнения с двумя переменными, константой пропорциональности и такой степенью…
| • независимый | y = kx 0 |
| • прямой | y = kx 1 |
| • обратный | y = kx −1 |
| • квадрат | y = kx 2 |
| • корень квадратный | y = kx ½ |
Мы могли бы даже пойти дальше и написать уравнение общего вида для всего семейства уравнений…
y = kx n
Говорят, что любые две переменные, которые связаны друг с другом уравнением этой формы, имеют отношение мощности между ними.
| мощность | общая форма | описание | внешний вид |
|---|---|---|---|
| 0 | y = к | независимый | горизонтальный, прямой |
| 1 | y = kx | прямой | Негоризонтальная прямая линия через начало координат |
| 2 | y = kx 2 | квадрат | вертикальная парабола с вершиной в начале координат |
| 3 | y = kx 3 | куб | |
| -1 | y = k / x | обратный | прямоугольная гипербола |
| -2 | y = k / x 2 | обратный квадрат | |
| −3 | y = k / x 3 | обратный куб | |
| ½ | y = k √ x | квадратный корень | горизонтальная парабола с вершиной в начале координат |
| ⅓ | y = k ∛ x | кубический корень |
линейный
Описание: Комбинация постоянного и прямого.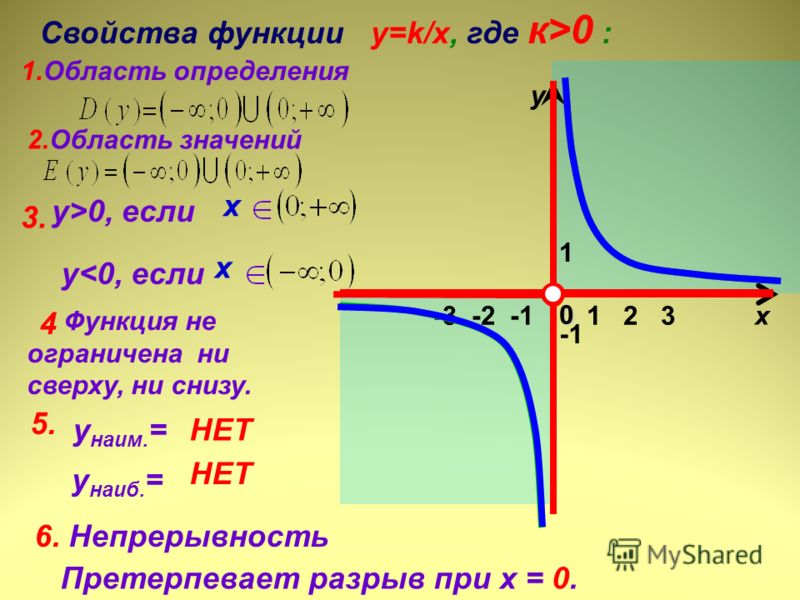 Фиксированная сумма добавляется (или вычитается) через равные промежутки времени.
Фиксированная сумма добавляется (или вычитается) через равные промежутки времени.
Общий вид.
y = ax + b
Подходящим выводом из такой взаимосвязи будет то, что…
- y линейно с x .
- y изменяется линейно с x .
- y является линейной функцией x .
Внешний вид: любая прямая линия, независимо от наклона или точки пересечения оси Y
Пример (ы): счета за коммунальные услуги (всегда есть плата за обслуживание)
квадратичный
Описание: Комбинация квадрата, прямого и постоянного.
Общая форма
y = ax 2 + bx + c
Подходящим выводом из такой связи будет следующее:
- y квадратично с x .
- y изменяется квадратично с x .
- y — квадратичная функция x .
Внешний вид: Вертикальная парабола на графике. Его вершина может быть где угодно.Его также можно было перевернуть вверх дном.
Его вершина может быть где угодно.Его также можно было перевернуть вверх дном.
Пример (ы): расстояние при равномерном ускорении
полином
Описание: Комбинация постоянного, прямого, квадрата, куба,…. Продолжайте идти так далеко, как хотите.
Общий вид.
y = a + bx + cx 2 + dx 3 +…
Подходящим выводом из такой взаимосвязи будет то, что…
- y может быть аппроксимируется полиномом n-го порядка размером x .
- Полином n-го порядка x соответствовал y .
Внешний вид: любая непериодическая функция без асимптот
Пример (ы): Полиномиальные функции могут использоваться для аппроксимации многих непрерывных однозначных кривых
| заказать | общая форма | название |
|---|---|---|
| 0 | и = а | постоянная |
| 1 | y = a + bx | линейный |
| 2 | y = a + bx + cx 2 | квадратный |
| 3 | y = a + bx + cx 2 + dx 3 | куб.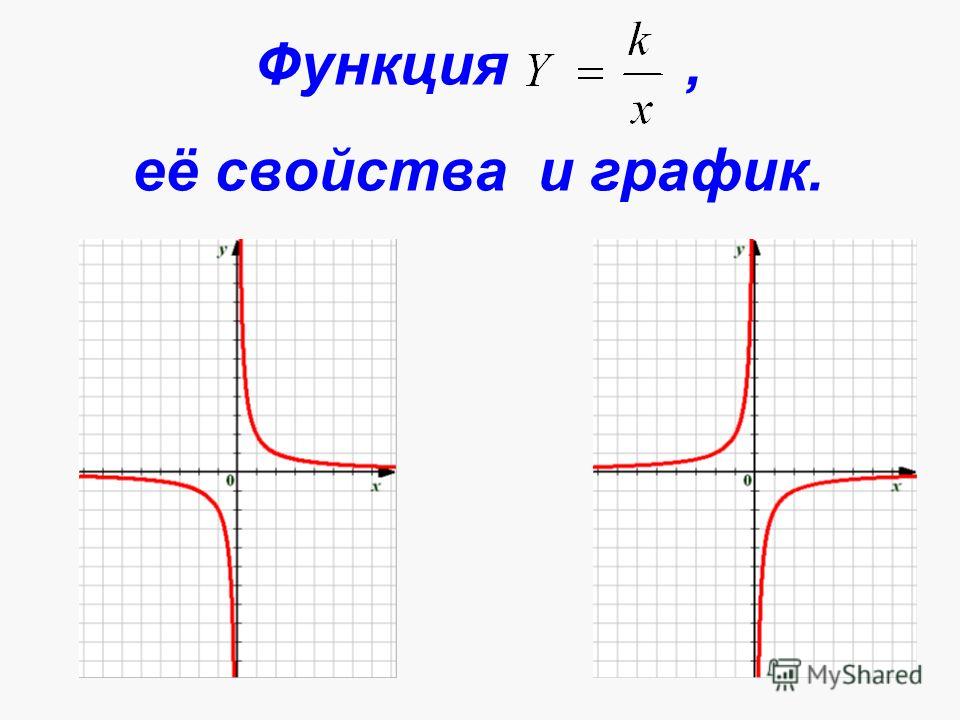 |
| 4 | y = a + bx + cx 2 + dx 3 + ex 4 | квартика |
| 5 | y = a + bx + cx 2 + dx 3 + ex 4 + fx 5 | квинтик |
| ⋮ | ⋮ | ⋮ |
| n | y = a 0 x 0 + a 1 x 1 + a 2 x 970 3 x 3 +… + a n x n | Многочлен n-го порядка |
экспоненциальный рост
Описание:
Общий вид.
y = an bx
Подходящим выводом из такой взаимосвязи будет то, что…
- y возрастает экспоненциально с x .

- y экспоненциально растет с x .
- y ∝ n x
Отношение последовательных итераций является постоянным. Количество умножается на фиксированное количество через равные промежутки времени.
Внешний вид: асимптотика с отрицательной осью x , за которой следует неконтролируемое расширение
Пример (ы): неограниченный рост населения, магия сложных процентов
экспоненциальный спад
Описание:
Общий вид.
y = an — bx
Подходящим выводом из такой зависимости было бы то, что…
- y убывает экспоненциально с x .
- y экспоненциально затухает с x .
- y ∝ n — x
Отношение последовательных итераций постоянно. Количество делится на фиксированное количество через равные промежутки времени.
Внешний вид: большое начальное значение, за которым следует резкий коллапс, асимптотически приближается к положительной оси x
Пример (ы): радиоактивный распад, разрядка конденсатора, обесточивание катушки индуктивности
экспоненциальный подход
Описание:
Общий вид.
y = a (1 — n — bx ) + c
Подходящим выводом из такой связи будет то, что…
- y приближается к окончательному значению экспоненциально .
Внешний вид: асимптотически приближается к горизонтальной прямой
Пример (ы): зарядка конденсатора, включение индуктора, обучение (половина студентов получает это, затем половина оставшихся студентов получает это, затем половина оставшихся студентов получает это, и так далее…)
периодический
Описание:
Общий вид.
y = a sin ( bx + c )
Подходящим выводом из такой связи будет следующее:
- y периодически изменяется в пределах x .
- y периодичен с x .
Внешний вид: Синусоидальная кривая является прототипом, а не единственным примером. Любая повторяющаяся кривая периодична.
Пример (ы): Любое ежедневное (суточное), ежемесячное (лунное), годовое (годовое, сезонное) или другое периодическое изменение.
Асимптоты
Асимптота кривой \ (y = f \ left (x \ right) \), имеющей бесконечную ветвь, называется прямой такой, что расстояние между точкой \ (\ left ({x, f \ left (x \ right)} \ right) \), лежащий на кривой, и прямая стремится к нулю, когда точка движется по ветви на бесконечность.
Асимптоты могут быть вертикальными, наклонными (наклонными) и горизонтальными. Горизонтальную асимптоту часто рассматривают как частный случай наклонной асимптоты.
Вертикальная асимптота
Прямая \ (x = a \) является вертикальной асимптотой графика функции \ (y = f \ left (x \ right) \), если выполняется хотя бы одно из следующих условий:
\ [{\ lim \ limits_ {x \ to a — 0} f \ left (x \ right) = \ pm \ infty, \; \; \;} \ kern-0.3pt {\ lim \ limits_ {x \ to a + 0} f \ left (x \ right) = \ pm \ infty.} \]
Другими словами, хотя бы один из односторонних пределов в точке \ (x = a \) должен быть равен бесконечности.
Вертикальная асимптота встречается в рациональных функциях в точках, когда знаменатель равен нулю, а числитель не равен нулю (т. Е. В точках разрыва второго рода). Например, график функции \ (y = {\ large \ frac {1} {x} \ normalsize} \) имеет вертикальную асимптоту \ (x = 0 \) (рисунок \ (1 \ text {).} \) В этом случае оба односторонних предела (слева и справа) стремятся к бесконечности:
Е. В точках разрыва второго рода). Например, график функции \ (y = {\ large \ frac {1} {x} \ normalsize} \) имеет вертикальную асимптоту \ (x = 0 \) (рисунок \ (1 \ text {).} \) В этом случае оба односторонних предела (слева и справа) стремятся к бесконечности:
\ [{\ lim \ limits_ {x \ to 0 — 0} \ frac {1} {x} = — \ infty, \; \; \;} \ kern-0.3pt {\ lim \ limits_ {x \ to 0 + 0} \ frac {1} {x} = + \ infty.} \]
Рисунок 1.Функция, непрерывная на всем наборе действительных чисел, не имеет вертикальных асимптот.
Косая асимптота
Прямая \ (y = kx + b \) называется наклонной (наклонной) асимптотой графика функции \ (y = f \ left (x \ right) \) при \ (x \ to + \ infty \) (Рисунок \ (2 \)), если
\ [{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — \ left ({kx + b} \ right)} \ right]} = {0.} \]
Рис. 2.Аналогичным образом мы вводим наклонные асимптоты как \ (x \ to — \ infty. \)
Наклонные асимптоты графика функции \ (y = f \ left (x \ right) \) могут быть разными как \ (x \ to + \ infty \) и \ (x \ to — \ infty. \)
\)
Таким образом, при нахождении наклонных (или горизонтальных) асимптот рекомендуется вычислять их отдельно.
Коэффициенты \ (k \) и \ (b \) наклонной асимптоты \ (y = kx + b \) определяются следующей теоремой:
Прямая \ (y = kx + b \) является асимптотой функции \ (y = f \ left (x \ right) \) при \ (x \ to + \ infty \) тогда и только тогда, когда следующие два предела конечны:
\ [
{\ lim \ limits_ {x \ to + \ infty} \ frac {{f \ left (x \ right)}} {x} = k \; \; \ text {and} \; \; \ ;} \ керн-0.3pt
{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — kx} \ right] = b.}
\]
Доказательство.
Необходимость. Пусть прямая \ (y = kx + b \) является асимптотой графика \ (y = f \ left (x \ right) \) при \ (x \ to + \ infty. \). Тогда выполняется следующее условие верно:
\ [\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — \ left ({kx + b} \ right)} \ right] = 0 \]
или, что эквивалентно,
\ [
{е \ влево (х \ вправо) = кх + Ь + \ альфа \ влево (х \ вправо), \; \; \;} \ керн-0. 3pt
3pt
{\ text {where} \; \; \ lim \ limits_ {x \ to + \ infty} \ alpha \ left (x \ right) = 0.}
\]
Разделив обе части уравнения на \ (x, \), получим:
\ [
{\ frac {{f \ left (x \ right)}} {x} = \ frac {{kx + b + \ alpha \ left (x \ right)}} {x}, \; \; } \ Rightarrow
{\ frac {{f \ left (x \ right)}} {x} = k + \ frac {b} {x} + \ frac {{\ alpha \ left (x \ right)}} { x}.}
\]
Следовательно, в пределе \ (x \ to + \ infty, \) имеем
\ [
{\ lim \ limits_ {x \ to + \ infty} \ frac {{f \ left (x \ right)}} {x}}
= {\ lim \ limits_ {x \ to + \ infty} \ left [{k + \ frac {b} {x} + \ frac {{\ alpha \ left (x \ right)}} {x}} \ right]} = {k,}
\]
\ [
{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — kx} \ right]}
= {\ lim \ limits_ {x \ to + \ infty } \ left [{b + \ alpha \ left (x \ right)} \ right]} = {b.}
\]
Достаточность. Предположим, что существуют конечные пределы
\ [
{\ lim \ limits_ {x \ to + \ infty} \ frac {{f \ left (x \ right)}} {x} = k \; \; \; \ text {and} \; \ ; \;} \ kern-0. 3pt
3pt
{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — kx} \ right] = b.}
\]
Второй предел можно записать как
.\ [{\ lim \ limits_ {x \ to + \ infty} \ left [{f \ left (x \ right) — \ left ({kx + b} \ right)} \ right]} = {0,} \]
, удовлетворяющий определению наклонной асимптоты.Таким образом, прямая \ (y = kx + b \) является асимптотой функции \ (y = f \ left (x \ right). \)
Примечание: аналогично мы можем доказать теорему для случая \ (x \ to \ infty. \)
Горизонтальная асимптота
В частности, если \ (k = 0, \), мы получаем горизонтальную асимптоту, которая описывается уравнением \ (y = b. \) Теорема о необходимых и достаточных условиях существования горизонтальной асимптоты формулируется как следует:
Прямая \ (y = b \) является асимптотой функции \ (y = f \ left (x \ right) \) при \ (x \ to + \ infty, \) тогда и только тогда, когда следующий предел конечно:
\ [\ lim \ limits_ {x \ to + \ infty} f \ left (x \ right) = b. \]
\]
Случай \ (x \ to — \ infty \) рассматривается аналогично.
Асимптоты параметрически определенной кривой
Пусть плоская кривая определяется параметрическими уравнениями
\ [{x = \ varphi \ left (t \ right), \; \; \;} \ kern-0.3pt {y = \ psi \ left (t \ right).} \]
Эта кривая имеет вертикальную асимптоту \ (x = a \) при \ (t \ to {t_1} \), если выполняются следующие условия:
\ [
{\ lim \ limits_ {t \ to {t_1}} \ varphi \ left (t \ right) = a \; \; \; \ text {и} \; \; \;} \ kern-0 .3pt
{\ lim \ limits_ {t \ to {t_1}} \ psi \ left (t \ right) = \ pm \ infty.}
\]
Аналогично, параметрически заданная кривая имеет горизонтальную асимптоту \ (y = b \) как \ (t \ to {t_2} \), если
\ [
{\ lim \ limits_ {t \ to {t_2}} \ varphi \ left (t \ right) = \ pm \ infty \; \; \; \ text {and} \; \; \;} \ kern-0.3pt
{\ lim \ limits_ {t \ to {t_2}} \ psi \ left (t \ right) = b.}
\]
Здесь \ (a \) и \ (b \) — конечные величины.
Параметрически заданная кривая имеет наклонную (наклонную) асимптоту \ (y = kx + b \) как \ (t \ to {t_3} \), если при этом значении \ (t, \) оба предела бесконечны:
\ [
{\ lim \ limits_ {t \ to {t_3}} \ varphi \ left (t \ right) = \ pm \ infty, \; \; \;} \ kern-0.3pt
{\ lim \ limits_ {t \ to {t_3}} \ psi \ left (t \ right) = \ pm \ infty,}
\]
, а коэффициенты \ (k \) и \ (b \) имеют конечные значения:
\ [
{k = \ lim \ limits_ {t \ to {t_3}} \ frac {{\ psi \ left (t \ right)}} {{\ varphi \ left (t \ right)}}, \; \; \;} \ kern-0.3pt
{b = \ lim \ limits_ {t \ to {t_3}} \ left [{\ psi \ left (t \ right) — k \ varphi \ left (t \ right) } \ right].}
\]
Асимптота полярной кривой
Рассмотрим кривую, заданную в полярных координатах уравнением
\ [{\ rho = \ rho \ left (\ varphi \ right) \; \; \; \ text {или} \; \; \;} \ kern-0.3pt {F \ left ({\ rho, \ varphi} \ right) = 0.} \]
Его асимптота (если она существует) может быть описана двумя параметрами: расстоянием \ (p \) от центра до асимптоты (отрезок \ (OA \) на рисунке \ (3 \ text {)} \) и угол \ (\ alpha \) наклона асимптоты к полярной оси.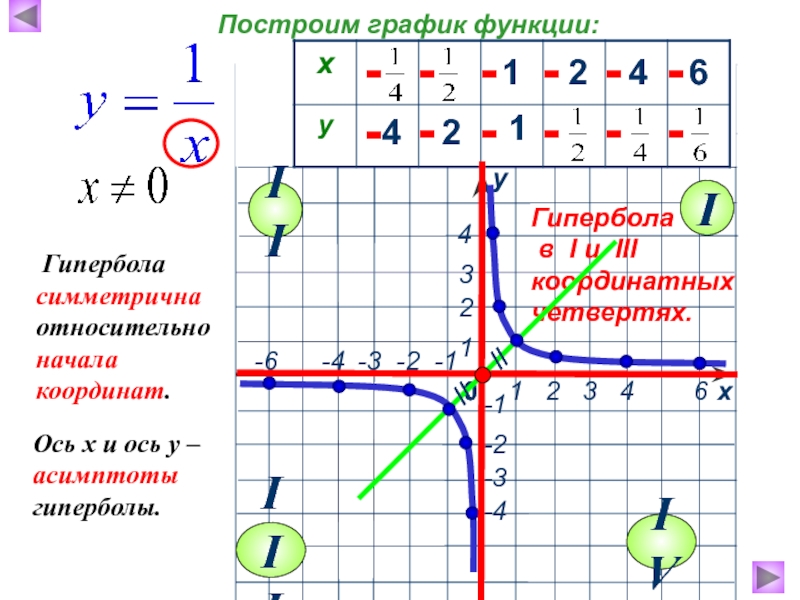
Эти параметры \ (\ alpha \) и \ (p \) определяются формулами
\ [
{\ alpha = \ lim \ limits _ {\ rho \ to \ infty} \ varphi, \; \; \;} \ kern-0.3pt
{p = \ lim \ limits _ {\ rho \ to \ infty } \ left [{\ rho \ sin \ left ({\ alpha — \ varphi} \ right)} \ right].}
\]
Примечания:
- В последней формуле предельный переход \ (\ rho \ to \ infty \) может быть заменен эквивалентным условием \ (\ varphi \ to \ alpha; \)
- Параметр \ (p \) может быть как положительный и отрицательный.
Асимптоты неявной кривой
Неявно заданная алгебраическая кривая описывается уравнением
\ [F \ left ({x, y} \ right) = 0, \]
, где левая часть — многочлен от переменных \ (x \) и \ (y.{n — 1}} + \ ldots} + {{A_ {n — 1}} x + {A_n} = 0,} \]
, где коэффициенты \ ({A_i} \) зависят от параметров асимптоты \ (k \) и \ (b \) (коэффициент \ ({A_0} \) зависит только от \ (k \)). Значения \ (k \) и \ (b \) можно определить из условия:
\ [\ left \ {\ begin {array} {l}
{A_0} \ left (k \ right) = 0 \\
{A_1} \ left ({k, b} \ right) = 0
\ end {array} \ right . {n — 1}} + \ ldots} + {{B_ {n — 1}} y + {B_n} = 0.n} \) в последнем уравнении.
{n — 1}} + \ ldots} + {{B_ {n — 1}} y + {B_n} = 0.n} \) в последнем уравнении.
Значение параметра \ (a \) определяется из условия
\ [{B_1} \ left (a \ right) = 0. \]
Приведенные выше формулы для асимптот неявной кривой действительны, если кривая не имеет особых точек на бесконечности.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Найдите асимптоты функции \ [f \ left (x \ right) = \ frac {x} {{x + 1}}. \]Пример 2
Найдите асимптоты функции \ [f \ left (x \ right) = {\ frac {{2x — 3}} {{x + 1}}}.2} + 1}}} \] асимптотически равны друг другу как \ (x \ to + \ infty. \) Оцените погрешность приближенного равенства \ (f \ left ({100} \ right) \ приблизительно g \ left ({100} \ right). \)Пример 1.
Найдите асимптоты функции \ [f \ left (x \ right) = \ frac {x} {{x + 1}}. \]Решение.
При \ (x = -1, \) функция имеет разрыв второго рода. Действительно:
Действительно:
\ [
{\ lim \ limits_ {x \ to — 1 — 0} f \ left (x \ right)}
= {\ lim \ limits_ {x \ to — 1 — 0} \ frac {x} {{ x + 1}}}
= {\ frac {{- 1}} {{\ left ({- 1 — 0} \ right) + 1}}}
= {\ frac {{- 1}} {{- 0}} = + \ infty,}
\]
\ [
{\ lim \ limits_ {x \ to — 1 + 0} f \ left (x \ right)}
= {\ lim \ limits_ {x \ to — 1 + 0} \ frac {x} {{ x + 1}}}
= {\ frac {{- 1}} {{\ left ({- 1 + 0} \ right) + 1}}}
= {\ frac {{- 1}} {{+ 0}} = — \ infty.}
\]
Следовательно, \ (x = -1 \) — уравнение вертикальной асимптоты.
Найдите горизонтальную асимптоту. Вычислите предел:
\ [{\ lim \ limits_ {x \ to \ pm \ infty} \ frac {x} {{x + 1}}} = {\ lim \ limits_ {x \ to \ pm \ infty} \ frac {1} {{1 + \ frac {1} {x}}}} = {1.} \]
Таким образом, для кривой существует горизонтальная асимптота, и ее уравнение равно \ (y = 1. \)
Функция не имеет наклонных асимптот. В этом можно убедиться, вычислив коэффициенты \ (k \) и \ (b: \)
\ [
{k = \ lim \ limits_ {x \ to \ pm \ infty} \ frac {{y \ left (x \ right)}} {x}}
= {\ lim \ limits_ {x \ to \ pm \ infty} \ frac {x} {{\ left ({x + 1} \ right) x}}}
= {\ lim \ limits_ {x \ to \ pm \ infty} \ frac {x} {{{ x ^ 2} + x}}}
= {\ lim \ limits_ {x \ to \ pm \ infty} \ frac {{\ frac {1} {x}}} {{1 + \ frac {1} {x }}} = 0,}
\]
\ [
{b = \ lim \ limits_ {x \ to \ pm \ infty} \ left [{y \ left (x \ right) — kx} \ right]}
= {\ lim \ limits_ {x \ to \ pm \ infty} \ left ({\ frac {x} {{x + 1}} — 0} \ right)}
= {\ lim \ limits_ {x \ to \ pm \ infty} \ frac {1} { {1 + \ frac {1} {x}}} = 1. }
}
\]
Видно, что фактически мы получили горизонтальную асимптоту, которая уже была определена выше.
Итак, график функции имеет вертикальную асимптоту \ (x = -1 \) и горизонтальную асимптоту \ (y = 1 \) (рисунок \ (4 \)).
Рисунок 4.Пример 2.
Найдите асимптоты функции \ [f \ left (x \ right) = {\ frac {{2x — 3}} {{x + 1}}}. \]Решение.
Функция определена для всех \ (x \ ne -1. \). Вычислить односторонние пределы при \ (x = -1: \)
\ [{\ mathop {\ lim} \ limits_ {x \ to — 1 — 0} f \ left (x \ right)} = {\ mathop {\ lim} \ limits_ {x \ to — 1 — 0} \ frac {{2x — 3}} {{x + 1}}} = {\ frac {{- 5}} {{- 0}}} = {+ \ infty;} \]
\ [{\ mathop {\ lim} \ limits_ {x \ to — 1 + 0} f \ left (x \ right)} = {\ mathop {\ lim} \ limits_ {x \ to — 1 + 0} \ гидроразрыв {{2x — 3}} {{x + 1}}} = {\ frac {{- 5}} {{+ 0}}} = {- \ infty.} \]
Следовательно, \ (x = -1 \) — вертикальная асимптота функции.
Найдите возможные горизонтальные асимптоты в точке \ (x \ to \ pm \ infty: \)
\ [{\ mathop {\ lim} \ limits_ {x \ to \ pm \ infty} f \ left (x \ right)} = {\ mathop {\ lim} \ limits_ {x \ to \ pm \ infty} \ frac {{2x — 3}} {{x + 1}}} = {\ mathop {\ lim} \ limits_ {x \ to \ pm \ infty} \ frac {{2 — \ frac {3} {x}} } {{1 + \ frac {1} {x}}}} = {2.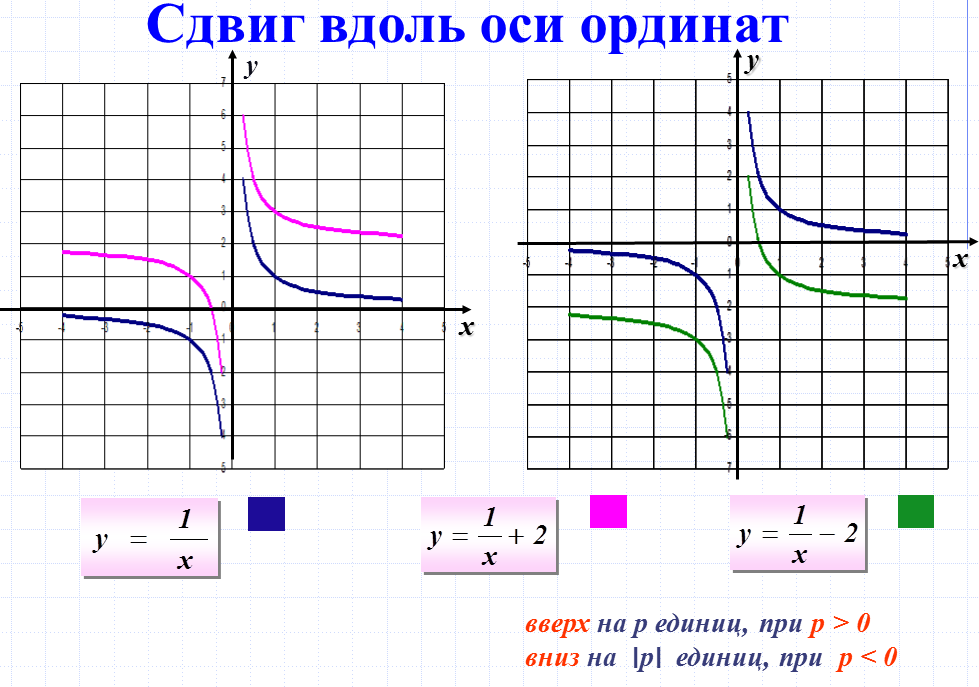 2}}}}} {{1 + \ frac {1} {x}}}} = {\ frac {0} {1}} = {0.2} — 3x + x — 1 + 2}} {{x — 1}}}
2}}}}} {{1 + \ frac {1} {x}}}} = {\ frac {0} {1}} = {0.2} — 3x + x — 1 + 2}} {{x — 1}}}
= {\ frac {{3x \ cancel {\ left ({x — 1} \ right)}}} {\ cancel {x — 1}} + \ frac {\ cancel {x — 1}} {\ cancel {x — 1}} + \ frac {2} {{x — 1}}}
= {3x + 1 + \ frac {2 } {{x — 1}}} = {3x + 1 + \ alpha \ left (x \ right),}
\]
, где \ (\ alpha \ left (x \ right) \ to 0 \) как \ (x \ to \ pm \ infty. \)
Таким образом, функция имеет наклонную асимптоту \ (y = 3x + 1. \)
Обратите внимание, что рациональная функция может иметь наклонную асимптоту, если степень числителя на единицу больше степени знаменателя.2} — x + x — 1 + 1}} {{x — 1}}} = {\ frac {{x \ left ({x — 1} \ right) + \ left ({x — 1} \ right) + 1}} {{x — 1}}} = {\ frac {{x \ cancel {\ left ({x — 1} \ right)}}} {\ cancel {x — 1}} + \ frac {\ cancel {x — 1}} {\ cancel {x — 1}} + \ frac {1} {{x — 1}}} = {x + 1 + \ frac {1} {{x — 1}}.}.} \]
Как \ (\ mathop {\ lim} \ limits_ {x \ to \ pm \ infty} \ large {\ frac {1} {{x — 1}}} \ normalsize = 0, \) уравнение наклонной асимптоты записывается в виде
\ [y = x + 1. \]
\]
Эта наклонная асимптота существует для \ (x \ to \ pm \ infty.\) Следовательно, функция не имеет горизонтальных асимптот.
Рисунок 9.Введение в линейные функции | Безграничная алгебра
Что такое линейная функция?
Линейные функции — это алгебраические уравнения, графики которых представляют собой прямые линии с уникальными значениями наклона и пересечения по оси Y.
Цели обучения
Описание частей и характеристик линейной функции
Основные выводы
Ключевые моменты
- Линейная функция — это алгебраическое уравнение, в котором каждый член является либо константой, либо произведением константы и (первой степени) одной переменной.
- Функция — это отношение со свойством, что каждый вход связан ровно с одним выходом.
- Отношение — это набор упорядоченных пар.
- График линейной функции — это прямая линия, но вертикальная линия не является графиком функции.
- Все линейные функции записываются в виде уравнений и характеризуются своим наклоном и интервалом [латекс] y [/ латекс].

Ключевые термины
- отношение : набор упорядоченных пар.
- переменная : символ, представляющий величину в математическом выражении, используемом во многих науках.
- линейная функция : алгебраическое уравнение, в котором каждый член является либо константой, либо произведением константы и (первой степени) одной переменной.
- функция : отношение между набором входов и набором допустимых выходов со свойством, что каждый вход связан ровно с одним выходом.
Что такое линейная функция?
Линейная функция — это алгебраическое уравнение, в котором каждый член является либо константой, либо произведением константы и (первой степени) одной переменной.Например, обычное уравнение [латекс] y = mx + b [/ latex] (а именно форма пересечения наклона, о которой мы узнаем больше позже) является линейной функцией, потому что оно удовлетворяет обоим критериям с [латекс] x [/ latex] и [latex] y [/ latex] как переменные и [latex] m [/ latex] и [latex] b [/ latex] как константы.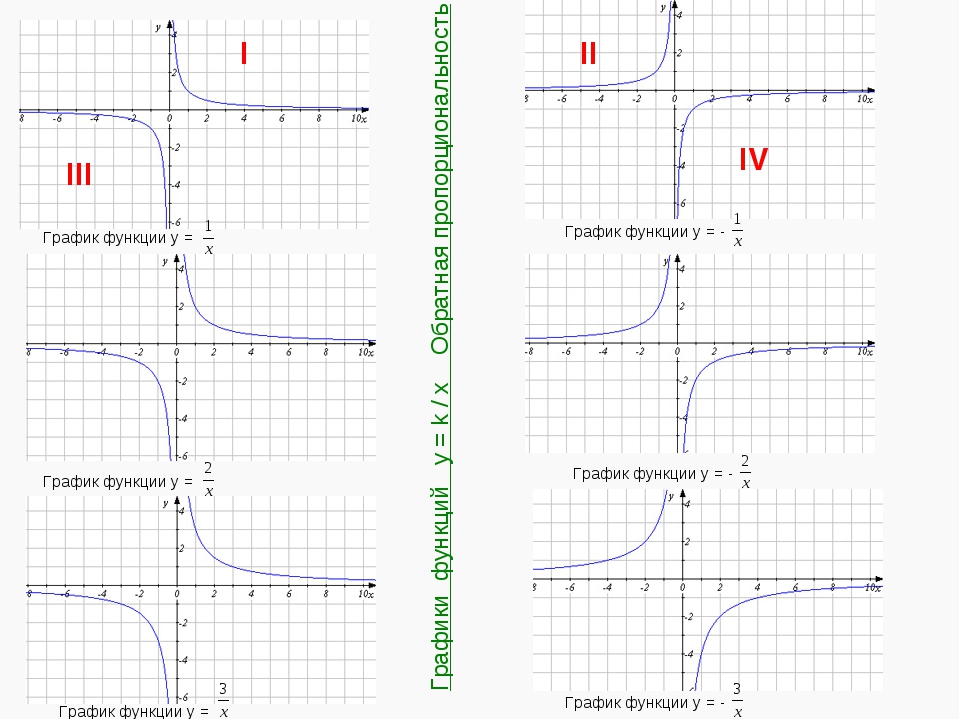 Он линейный: показатель степени члена [latex] x [/ latex] равен единице (первая степень), и он следует определению функции: для каждого входа ([latex] x [/ latex]) существует ровно один выход ([latex] y [/ latex]). Также его график представляет собой прямую линию.
Он линейный: показатель степени члена [latex] x [/ latex] равен единице (первая степень), и он следует определению функции: для каждого входа ([latex] x [/ latex]) существует ровно один выход ([latex] y [/ latex]). Также его график представляет собой прямую линию.
Графики линейных функций
Название «линейный» произошло от того факта, что множество решений такого уравнения образует прямую линию на плоскости. На графиках линейной функции ниже константа [latex] m [/ latex] определяет наклон или градиент этой линии, а постоянный член [latex] b [/ latex] определяет точку, в которой линия пересекает ось [latex] y [/ latex], иначе известная как перехватчик [latex] y [/ latex].
Графики линейных функций: Синяя линия, [latex] y = \ frac {1} {2} x-3 [/ latex] и красная линия, [latex] y = -x + 5 [/ latex] обе являются линейными функциями.Синяя линия имеет положительный наклон [latex] \ frac {1} {2} [/ latex] и [latex] y [/ latex] -пересечение [latex] -3 [/ latex]; красная линия имеет отрицательный наклон [латекс] -1 [/ латекс] и пересечение [латекс] y [/ латекс] [латекс] 5 [/ латекс].
Вертикальные и горизонтальные линии
Вертикальные линии имеют неопределенный наклон и не могут быть представлены в форме [latex] y = mx + b [/ latex], а могут быть представлены в виде уравнения формы [latex] x = c [/ latex] для константы [ latex] c [/ latex], потому что вертикальная линия пересекает значение на оси [latex] x [/ latex], [latex] c [/ latex].Например, график уравнения [latex] x = 4 [/ latex] включает одно и то же входное значение [latex] 4 [/ latex] для всех точек на линии, но будет иметь разные выходные значения, такие как [latex ] (4, -2), (4,0), (4,1), (4,5), [/ latex] и так далее. Однако вертикальные линии НЕ являются функциями, поскольку каждый вход связан с более чем одним выходом.
Горизонтальные линии имеют нулевой наклон и представлены в виде [latex] y = b [/ latex], где [latex] b [/ latex] — пересечение [latex] y [/ latex]. График уравнения [latex] y = 6 [/ latex] включает в себя одно и то же выходное значение 6 для всех входных значений в строке, например [latex] (- 2,6), (0,6), (2 , 6), (6,6) [/ латекс] и так далее. Горизонтальные линии ЯВЛЯЮТСЯ функцией, потому что отношение (набор точек) имеет характеристику, заключающуюся в том, что каждый вход связан ровно с одним выходом.
Горизонтальные линии ЯВЛЯЮТСЯ функцией, потому что отношение (набор точек) имеет характеристику, заключающуюся в том, что каждый вход связан ровно с одним выходом.
Наклон
Наклон описывает направление и крутизну линии и может быть рассчитан по двум точкам на линии.
Цели обучения
Рассчитайте наклон линии с помощью «превышения пробега» и определите роль наклона в линейном уравнении
Основные выводы
Ключевые моменты
- Наклон линии — это число, которое описывает как направление, так и крутизну линии; его знак указывает направление, а величина указывает крутизну.
- Отношение подъема к разбегу — это наклон линии, [латекс] m = \ frac {rise} {run} [/ latex].
- Наклон линии можно рассчитать по формуле [латекс] m = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} [/ latex], где [латекс] (x_1, y_1) [/ latex] и [latex] (x_2, y_2) [/ latex] — это точки на линии.
Ключевые термины
- крутизна : скорость, с которой функция отклоняется от задания.

- направление : увеличение, уменьшение, горизонтальное или вертикальное.
Наклон
В математике наклон линии — это число, которое описывает как направление , так и крутизну линии. Наклон часто обозначают буквой [латекс] м [/ латекс]. Вспомните форму отрезка-пересечения линии, [латекс] y = mx + b [/ latex]. Ввод уравнения линии в эту форму дает вам наклон ([латекс] м [/ латекс]) линии и его [латекс] y [/ латекс] -пересечение ([латекс] b [/ латекс]). Теперь мы обсудим интерпретацию [latex] m [/ latex] и то, как рассчитать [latex] m [/ latex] для данной линии.
Направление линии: возрастающее, убывающее, горизонтальное или вертикальное. Линия увеличивается, если она идет вверх слева направо, что означает, что наклон положительный ([латекс] m> 0 [/ latex]). Линия уменьшается, если она идет вниз слева направо и наклон отрицательный ([латекс] m <0 [/ latex]). Если линия горизонтальна, наклон равен нулю и является постоянной функцией ([latex] y = c [/ latex]).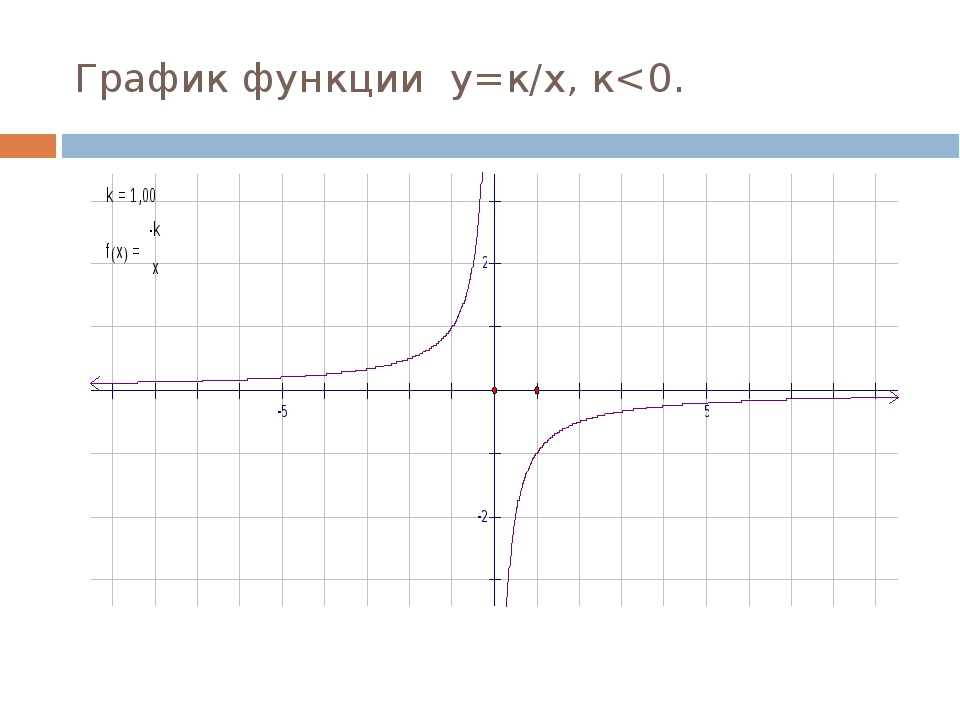 Если линия вертикальная, наклон не определен.
Если линия вертикальная, наклон не определен.
Уклон линий: наклон линии может быть положительным, отрицательным, нулевым или неопределенным.
Крутизна или уклон линии измеряется абсолютной величиной уклона. Уклон с большим абсолютным значением указывает на более крутую линию. Другими словами, линия с наклоном [латекс] -9 [/ латекс] круче, чем линия с наклоном [латекс] 7 [/ латекс].
Расчет уклона
Наклон рассчитывается путем нахождения отношения «вертикального изменения» к «горизонтальному изменению» между любыми двумя отдельными точками на линии. Это отношение представлено частным («подъем за пробегом») и дает одинаковое число для любых двух различных точек на одной линии.Он представлен как [латекс] m = \ frac {rise} {run} [/ latex]. [Latex] [/ latex]
Визуализация наклона: наклон линии рассчитывается как «подъем за пробегом».
Математически уклон м линии составляет:
[латекс] \ displaystyle m = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} [/ latex]
Чтобы найти [латекс] м [/ латекс], необходимы две точки на линии. Учитывая две точки [латекс] (x_1, y_1) [/ latex] и [латекс] (x_2, y_2) [/ latex], взгляните на график ниже и обратите внимание, как «подъем» наклона определяется разницей в значениях [latex] y [/ latex] двух точек, а «пробег» определяется разницей в значениях [latex] x [/ latex].
Учитывая две точки [латекс] (x_1, y_1) [/ latex] и [латекс] (x_2, y_2) [/ latex], взгляните на график ниже и обратите внимание, как «подъем» наклона определяется разницей в значениях [latex] y [/ latex] двух точек, а «пробег» определяется разницей в значениях [latex] x [/ latex].
Наклон, представленный графически: Наклон [латекс] m = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} [/ latex] рассчитывается по двум точкам [латекс ] \ left (x_1, y_1 \ right) [/ latex] и [latex] \ left (x_2, y_2 \ right) [/ latex].
Теперь посмотрим на графики на координатной сетке, чтобы найти их наклоны. Во многих случаях мы можем найти уклон, просто посчитав подъем и разбег. Начнем с определения двух точек на линии. Если возможно, мы стараемся выбирать точки с координатами, которые являются целыми числами, чтобы упростить наши вычисления.
Пример
Найдите наклон линии, показанной на координатной плоскости ниже.
Найдите наклон линии: Обратите внимание, что линия увеличивается, поэтому обязательно ищите положительный наклон.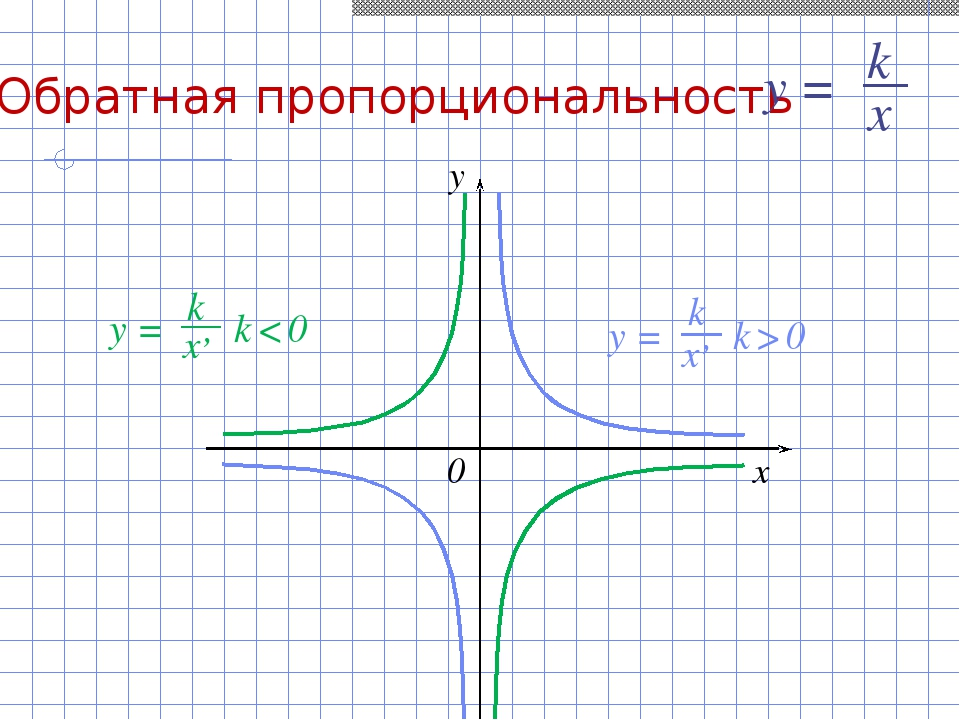
Найдите две точки на графике, выбирая точки, координаты которых являются целыми числами. Мы будем использовать [latex] (0, -3) [/ latex] и [latex] (5, 1) [/ latex]. Начиная с точки слева, [latex] (0, -3) [/ latex], нарисуйте прямоугольный треугольник, идущий от первой точки ко второй точке, [latex] (5, 1) [/ latex].
Определите точки на линии: нарисуйте треугольник, чтобы обозначить подъем и бег.
Посчитайте подъем на вертикальной ножке треугольника: [латекс] 4 [/ латекс] единицы.
Подсчитайте пробег по горизонтальной стороне треугольника: [латекс] 5 [/ латекс] единиц.
Воспользуйтесь формулой наклона, чтобы определить коэффициент подъема за пробег:
[латекс] \ displaystyle \ begin {align} m & = \ frac {rise} {run} \\ & = \ frac {4} {5} \ end {align} [/ latex]
Наклон линии [латекс] \ frac {4} {5} [/ latex].Обратите внимание, что наклон положительный, так как линия наклонена вверх слева направо.
Пример
Найдите наклон линии, показанной на координатной плоскости ниже.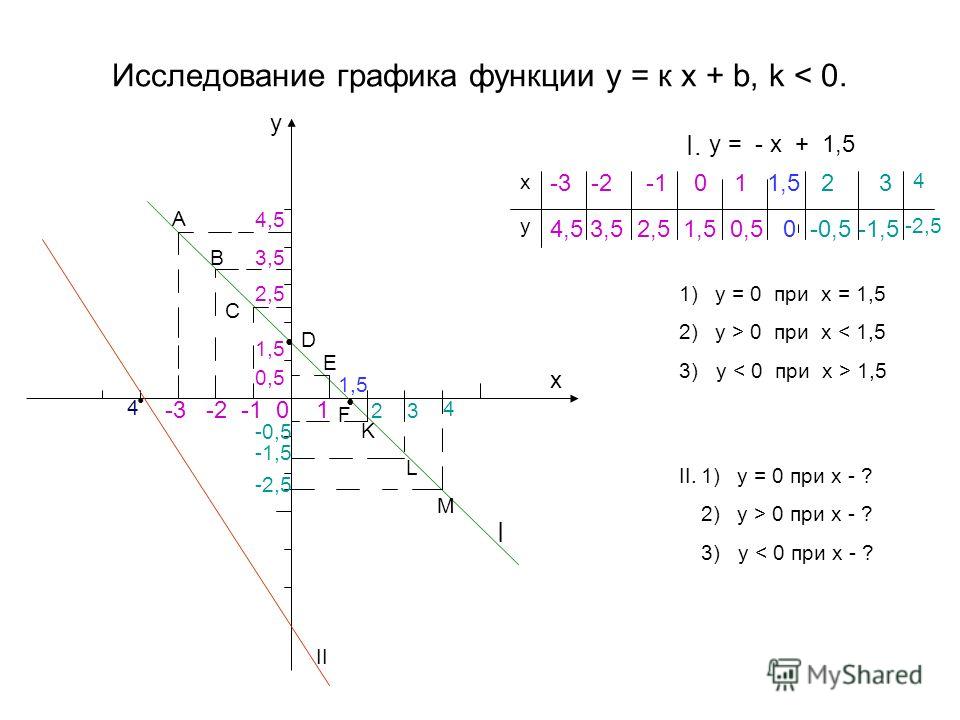
Найдите наклон линии: мы видим, что наклон уменьшается, поэтому обязательно ищите отрицательный наклон.
Найдите две точки на графике. Ищите точки с целыми числами. Мы можем выбрать любые точки, но мы будем использовать [latex] (0, 5) [/ latex] и [latex] (3, 3) [/ latex].
Определите две точки на линии: Точки [латекс] (0, 5) [/ латекс] и [латекс] (3, 3) [/ латекс] находятся на линии.
[латекс] \ displaystyle m = \ frac {y_ {2} — y_ {1}} {x_ {2} — x_ {1}} [/ latex]
Пусть [latex] (x_1, y_1) [/ latex] будет точкой [latex] (0, 5) [/ latex], а [latex] (x_2, y_2) [/ latex] будет точкой [latex] ( 3, 3) [/ латекс].
Подставляя соответствующие значения в формулу наклона, получаем:
[латекс] \ displaystyle \ begin {align} m & = \ frac {3-5} {3-0} \\ & = \ frac {-2} {3} \ end {align} [/ latex]
Наклон линии [латекс] — \ frac {2} {3} [/ latex]. Обратите внимание, что наклон отрицательный, так как линия наклоняется вниз слева направо.
Прямая и обратная вариация
Две переменные в прямой вариации имеют линейную зависимость, а переменные в обратной вариации — нет.
Цели обучения
Узнавайте примеры функций, которые изменяются прямо и обратно
Основные выводы
Ключевые моменты
- Две переменные, которые изменяются пропорционально друг другу, считаются находящимися в прямом изменении.
- Связь между двумя прямо пропорциональными переменными может быть представлена линейным уравнением в форме пересечения наклона и легко моделируется с помощью линейного графика.
- Обратное изменение противоположно прямому изменению; две переменные считаются обратно пропорциональными, когда изменение выполняется для одной переменной, а
— для другой. - Связь между двумя обратно пропорциональными переменными не может быть представлена линейным уравнением, а его графическое представление — не линия, а гипербола.
Ключевые термины
- гипербола : Коническое сечение, образованное пересечением конуса с плоскостью, которая пересекает основание конуса и не касается конуса.

- пропорциональный : с постоянным соотношением. Две величины (числа) называются пропорциональными, если вторая арифметически изменяется в прямой зависимости от первой.
Прямое изменение
Проще говоря, две переменные находятся в прямом изменении, когда то же самое, что происходит с одной переменной, происходит с другой. Если [latex] x [/ latex] и [latex] y [/ latex] находятся в прямой вариации, а [latex] x [/ latex] удваивается, то [latex] y [/ latex] также удваивается.Эти две переменные можно считать прямо пропорциональными.
Например, зубная щетка стоит [латекс] 2 [/ латекс] доллара. Покупка зубных щеток [латекс] 5 [/ латекс] будет стоить [латекс] 10 [/ латекс] долларов, а покупка зубных щеток [латекс] 10 [/ латекс] будет стоить [латекс] 20 [/ латекс] долларов. Таким образом, мы можем сказать, что стоимость напрямую зависит от стоимости зубных щеток.
Прямое изменение представлено линейным уравнением и может быть смоделировано путем построения графика линии. Поскольку мы знаем, что отношения между двумя значениями постоянны, мы можем дать их отношение с:
Поскольку мы знаем, что отношения между двумя значениями постоянны, мы можем дать их отношение с:
[латекс] \ displaystyle \ frac {y} {x} = k [/ latex]
Где [латекс] k [/ латекс] — постоянная величина.
Переписав это уравнение, умножив обе части на [латекс] x [/ латекс], получим:
[латекс] \ displaystyle y = kx [/ latex]
Обратите внимание, что это линейное уравнение в форме пересечения наклона, где [latex] y [/ latex] -intercept [latex] b [/ latex] равно [latex] 0 [/ latex].
Таким образом, любая линия, проходящая через начало координат, представляет собой прямую вариацию между [latex] x [/ latex] и [latex] y [/ latex]:
Прямо пропорциональные переменные: График [latex] y = kx [/ latex] демонстрирует пример прямого изменения между двумя переменными.
Возвращаясь к примеру с зубными щетками и долларами, мы можем определить ось [латекс] x [/ латекс] как количество зубных щеток, а ось [латекс] y [/ латекс] как количество долларов. При этом переменные будут подчиняться соотношению:
При этом переменные будут подчиняться соотношению:
[латекс] \ displaystyle \ frac {y} {x} = 2 [/ latex]
Любое увеличение одной переменной приведет к равному увеличению другой. Например, удвоение [latex] y [/ latex] приведет к удвоению [latex] x [/ latex].
Обратная вариация
Обратное изменение противоположно прямому изменению.В случае обратной вариации увеличение одной переменной приводит к уменьшению другой. Фактически, две переменные считаются обратно пропорциональными, когда операция изменения выполняется для одной переменной, а противоположное — для другой. Например, если [latex] x [/ latex] и [latex] y [/ latex] обратно пропорциональны, если [latex] x [/ latex] удваивается, то [latex] y [/ latex] уменьшается вдвое.
Например, время, затрачиваемое на поездку, обратно пропорционально скорости движения.Если ваш автомобиль движется с большей скоростью, путь к пункту назначения будет короче.
Зная, что связь между двумя переменными постоянна, мы можем показать, что их связь:
[латекс] \ displaystyle yx = k [/ latex]
Где [латекс] k [/ латекс] — это константа, известная как константа пропорциональности. Обратите внимание, что пока [latex] k [/ latex] не равно [latex] 0 [/ latex], ни [latex] x [/ latex], ни [latex] y [/ latex] не могут быть равны [latex] 0 [/ latex] тоже.Мы можем изменить приведенное выше уравнение так, чтобы переменные располагались по разные стороны:
Обратите внимание, что пока [latex] k [/ latex] не равно [latex] 0 [/ latex], ни [latex] x [/ latex], ни [latex] y [/ latex] не могут быть равны [latex] 0 [/ latex] тоже.Мы можем изменить приведенное выше уравнение так, чтобы переменные располагались по разные стороны:
[латекс] \ displaystyle y = \ frac {k} {x} [/ latex]
Обратите внимание, что это не линейное уравнение. Невозможно представить это в виде пересечения склона. Таким образом, обратная зависимость не может быть представлена линией с постоянным наклоном. Обратную вариацию можно проиллюстрировать с помощью графика в форме гиперболы, изображенного ниже.
Обратно пропорциональная функция: Обратно пропорциональная связь между двумя переменными графически представлена гиперболой.
Нули линейных функций
Ноль или перехват [латекс] x [/ latex] — это точка, в которой значение линейной функции будет равно нулю.
Цели обучения
Практика нахождения нулей линейных функций
Основные выводы
Ключевые моменты
- Ноль — это точка, в которой значение функции будет равно нулю.
 Его координаты: [latex] (x, 0) [/ latex], где [latex] x [/ latex] равно нулю графика.
Его координаты: [latex] (x, 0) [/ latex], где [latex] x [/ latex] равно нулю графика. - Нули можно наблюдать графически или решать алгебраически.
- Линейная функция не может иметь нуля, одного или бесконечного числа нулей. Если функция является горизонтальной линией (slope = [latex] 0 [/ latex]), она не будет иметь нулей, если только ее уравнение не будет [latex] y = 0 [/ latex], и в этом случае их будет бесконечно много. Если линия не горизонтальна, у нее будет один ноль.
Ключевые термины
- ноль : также известен как корень; значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна [latex] 0 [/ latex].
- линейная функция : алгебраическое уравнение, в котором каждый член является либо константой, либо произведением константы и (первой степени) одной переменной.
- y-intercept : точка, в которой линия пересекает ось [latex] y [/ latex] декартовой сетки.

График линейной функции представляет собой прямую линию. Графически то место, где линия пересекает ось [latex] x [/ latex], называется нулем или корнем. Алгебраически ноль — это значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна [latex] 0 [/ latex].Линейные функции не могут иметь нуля, одного или бесконечного числа нулей. Если через любую точку оси [latex] y [/ latex] проходит горизонтальная линия, кроме нуля, нулей нет, так как линия никогда не пересечет ось [latex] x [/ latex]. Если горизонтальная линия перекрывает ось [latex] x [/ latex] (проходит через ось [latex] y [/ latex] в нуле), то имеется бесконечно много нулей, поскольку линия пересекает [latex] x [/ latex] — ось несколько раз. Наконец, если линия вертикальная или имеет наклон, то будет только один ноль.
Нахождение нулей линейных функций графическим способом
Нули можно наблюдать графически. [Latex] x [/ latex] -перехват, или ноль, является свойством многих функций. Поскольку точка пересечения [latex] x [/ latex] (ноль) является точкой, в которой функция пересекает ось [latex] x [/ latex], она будет иметь значение [latex] (x, 0) [/ латекс], где [латекс] х [/ латекс] — ноль.
Поскольку точка пересечения [latex] x [/ latex] (ноль) является точкой, в которой функция пересекает ось [latex] x [/ latex], она будет иметь значение [latex] (x, 0) [/ латекс], где [латекс] х [/ латекс] — ноль.
Все линии со значением наклона будут иметь один ноль. Чтобы найти нуль линейной функции, просто найдите точку, в которой линия пересекает ось [latex] x [/ latex].
Нули линейных функций: синяя линия, [latex] y = \ frac {1} {2} x + 2 [/ latex], имеет ноль в [latex] (- 4,0) [/ latex]; красная линия [latex] y = -x + 5 [/ latex] имеет ноль в [latex] (5,0) [/ latex]. Поскольку каждая линия имеет значение для наклона, каждая линия имеет ровно один ноль.
Алгебраическое нахождение нулей линейных функций
Чтобы найти нуль линейной функции алгебраически, установите [latex] y = 0 [/ latex] и решите для [latex] x [/ latex].
Нуль от решения линейной функции выше графически должен соответствовать алгебраическому решению той же функции.
Пример: найти ноль [latex] y = \ frac {1} {2} x + 2 [/ latex] алгебраически
Сначала замените [latex] 0 [/ latex] на [latex] y [/ latex]:
[латекс] \ displaystyle 0 = \ frac {1} {2} x + 2 [/ латекс]
Затем найдите [латекс] x [/ латекс]. Вычтите [латекс] 2 [/ латекс], а затем умножьте на [латекс] 2 [/ латекс], чтобы получить:
Вычтите [латекс] 2 [/ латекс], а затем умножьте на [латекс] 2 [/ латекс], чтобы получить:
[латекс] \ displaystyle \ begin {align} \ frac {1} {2} x & = — 2 \\ x & = — 4 \ end {align} [/ latex]
Ноль — [латекс] (- 4,0) [/ латекс]. Это тот самый ноль, который был найден графическим методом.
Уравнения пересечения наклона
Форма линии с пересечением наклона резюмирует информацию, необходимую для быстрого построения ее графика.
Цели обучения
Преобразуйте линейные уравнения в форму с пересечением наклона и объясните, почему это полезно
Основные выводы
Ключевые моменты
- Угловая форма линии определяется выражением [latex] y = mx + b [/ latex], где [latex] m [/ latex] — наклон линии, а [latex] b [/ latex] — [latex] y [/ latex] -перехват.
- Константа [latex] b [/ latex] известна как перехват [latex] y [/ latex]. Из формы пересечения наклона, когда [латекс] x = 0 [/ latex], [latex] y = b [/ latex], а точка [latex] (0, b) [/ latex] является уникальной точкой на линия также на оси [latex] y [/ latex].

- Чтобы построить линию в форме пересечения наклона, сначала постройте точку пересечения [latex] y [/ latex], а затем используйте значение наклона, чтобы найти вторую точку на линии. Если значение наклона является целым числом, используйте в качестве знаменателя [латекс] 1 [/ латекс].
- Используйте алгебру, чтобы найти [latex] y [/ latex], если уравнение не записано в форме пересечения наклона. Только тогда можно точно определить значение наклона и точки пересечения [латекс] у [/ латекс] из уравнения.
Ключевые термины
- наклон : отношение вертикального и горизонтального расстояний между двумя точками на линии; ноль, если линия горизонтальная, неопределенная, если линия вертикальная.
- y-intercept : точка, в которой линия пересекает ось [latex] y [/ latex] декартовой сетки.
Форма пересечения откоса
Одним из наиболее распространенных представлений линии является форма пересечения наклона.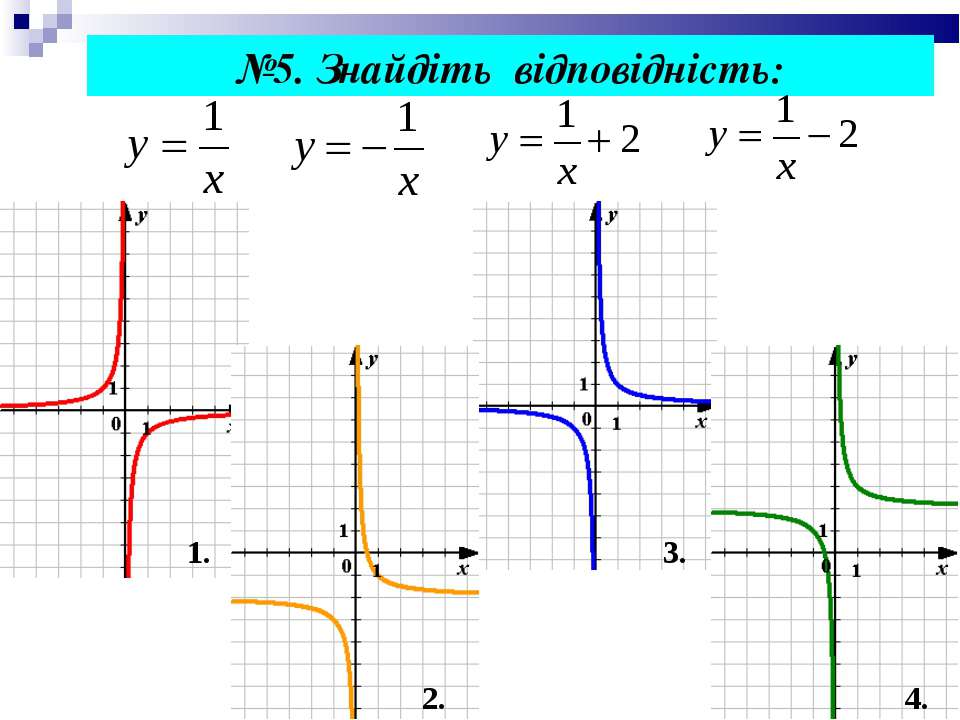 Такое уравнение задается формулой [латекс] y = mx + b [/ latex], где [latex] x [/ latex] и [latex] y [/ latex] — переменные, а [latex] m [/ latex] и [ latex] b [/ latex] — константы. При записи в этой форме константа [latex] m [/ latex] является значением наклона, а [latex] b [/ latex] является перехватом [latex] y [/ latex]. Обратите внимание, что если [latex] m [/ latex] равно [latex] 0 [/ latex], то [latex] y = b [/ latex] представляет собой горизонтальную линию.Обратите внимание, что это уравнение не допускает вертикальных линий, так как для этого потребуется, чтобы [latex] m [/ latex] было бесконечным (неопределенным). Однако вертикальная линия определяется уравнением [латекс] x = c [/ latex] для некоторого постоянного [латекса] c [/ latex].
Такое уравнение задается формулой [латекс] y = mx + b [/ latex], где [latex] x [/ latex] и [latex] y [/ latex] — переменные, а [latex] m [/ latex] и [ latex] b [/ latex] — константы. При записи в этой форме константа [latex] m [/ latex] является значением наклона, а [latex] b [/ latex] является перехватом [latex] y [/ latex]. Обратите внимание, что если [latex] m [/ latex] равно [latex] 0 [/ latex], то [latex] y = b [/ latex] представляет собой горизонтальную линию.Обратите внимание, что это уравнение не допускает вертикальных линий, так как для этого потребуется, чтобы [latex] m [/ latex] было бесконечным (неопределенным). Однако вертикальная линия определяется уравнением [латекс] x = c [/ latex] для некоторого постоянного [латекса] c [/ latex].
Преобразование уравнения в форму пересечения наклона
Написание уравнения в форме пересечения наклона полезно, поскольку по форме легко определить наклон и точку пересечения [латекс] y [/ латекс]. Это помогает находить решения различных проблем, таких как построение графиков, сравнение двух линий, чтобы определить, параллельны они или перпендикулярны, и решение системы уравнений.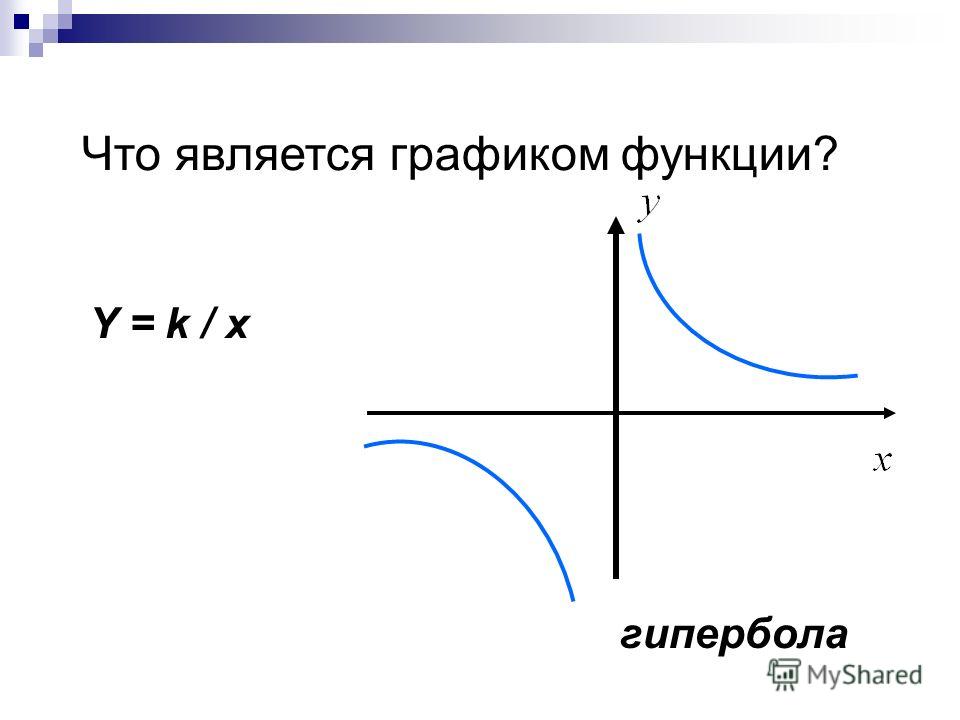
Пример
Напишем уравнение в форме пересечения наклона с [латексом] m = — \ frac {2} {3} [/ latex] и [latex] b = 3 [/ latex]. Просто подставьте значения в форму пересечения наклона, чтобы получить:
[латекс] \ displaystyle y = — \ frac {2} {3} x + 3 [/ latex]
Если уравнение не в форме пересечения наклона, решите для [латекс] y [/ латекс] и перепишите уравнение.
Пример
Давайте запишем уравнение [латекс] 3x + 2y = -4 [/ latex] в форме пересечения наклона и определим наклон и точку пересечения [латекс] y [/ латекс].Чтобы решить уравнение для [latex] y [/ latex], сначала вычтите [latex] 3x [/ latex] из обеих частей уравнения, чтобы получить:
[латекс] \ displaystyle 2y = -3x-4 [/ латекс]
Затем разделите обе части уравнения на [латекс] 2 [/ латекс], чтобы получить:
[латекс] \ displaystyle y = \ frac {1} {2} (- 3x-4) [/ latex]
Что упрощается до [латекс] y = — \ frac {3} {2} x-2 [/ latex]. Теперь, когда уравнение имеет форму пересечения наклона, мы видим, что наклон [латекс] m = — \ frac {3} {2} [/ latex] и [латекс] y [/ latex] -перерез [латекс] б = -2 [/ латекс].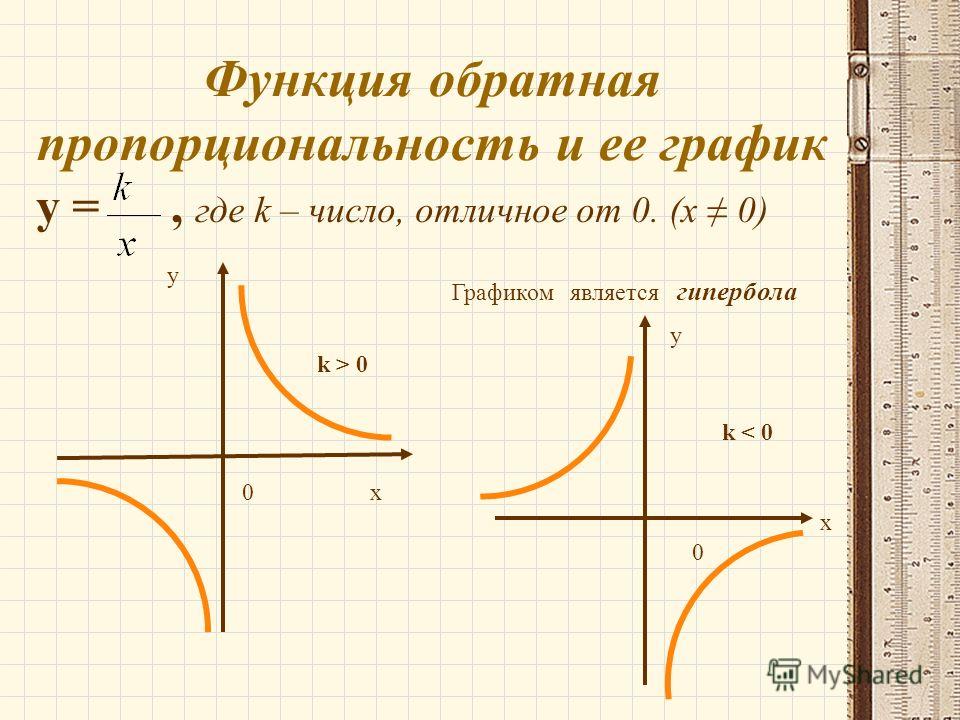
Построение уравнения в форме пересечения наклона
Начнем с построения графика уравнения из предыдущего примера.
Пример
Построим график линии [latex] y = — \ frac {3} {2} x-2 [/ latex], используя метод пересечения наклона. Начнем с построения [latex] y [/ latex] -intercept [latex] b = -2 [/ latex], координаты которого равны [latex] (0, -2) [/ latex]. Величина наклона диктует, где разместить следующую точку.
Так как значение наклона равно [latex] \ frac {-3} {2} [/ latex], подъем составляет [latex] -3 [/ latex], а пробег — [latex] 2 [/ latex].Это означает, что от интервала [latex] y [/ latex], [latex] (0, -2) [/ latex] переместите [latex] 3 [/ latex] единицы вниз и переместите [latex] 2 [/ латекс] единицы правая. Таким образом, мы приходим к точке [латекс] (2, -5) [/ латекс] на линии. Если поставить знак минус вместе со знаменателем, вместо этого наклон будет записан как [latex] \ frac {3} {- 2} [/ latex], вместо этого мы можем переместить [latex] 3 [/ latex] единицы и влево [ latex] 2 [/ latex] единицы из [latex] y [/ latex] -перехвата, чтобы прибыть в точку [latex] (- 2,1) [/ latex], также на линии.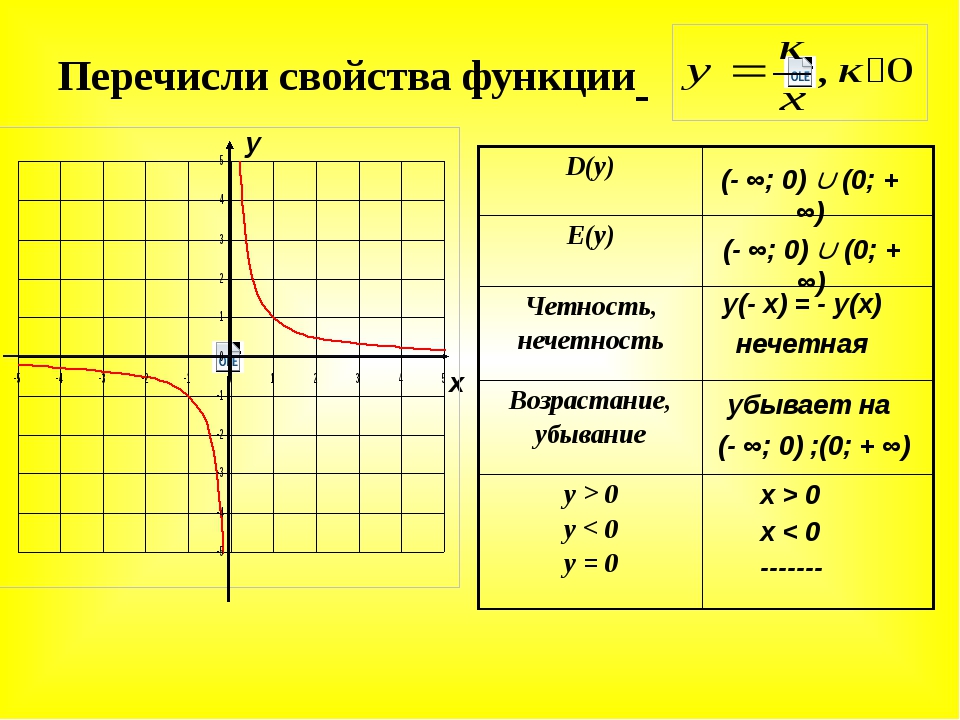
График угла наклона: график линии [латекс] y = — \ frac {3} {2} x-2 [/ latex].
Пример
Изобразим уравнение [латекс] 12x-6y-6 = 0 [/ latex]. Сначала мы решаем уравнение для [латекса] y [/ latex] путем вычитания [latex] 12x [/ latex], чтобы получить:
[латекс] \ displaystyle -6y-6 = -12x [/ латекс]
Далее добавляем [latex] 6 [/ latex] и получаем:
[латекс] \ displaystyle -6y = -12x + 6 [/ латекс]
Наконец, разделите все члены на [latex] -6 [/ latex], чтобы получить форму пересечения наклона:
[латекс] \ displaystyle y = 2x-1 [/ латекс]
Наклон составляет [латекс] 2 [/ latex], а интервал [latex] y [/ latex] — [latex] -1 [/ latex].Используя эту информацию, легко построить графики. Начните с построения [latex] y [/ latex] -intercept [latex] (0, -1) [/ latex], затем используйте значение наклона, [latex] \ frac {2} {1} [/ latex ], чтобы переместить [латекс] на 2 [/ латекс] единицы и вправо [латекс] на 1 [/ латекс] единицу.
График угла наклона: График линии [латекс] y = 2x-1 [/ latex].
Уравнения точечного уклона
Уравнение «точка-наклон» — это еще один способ представления линии; нужен только уклон и одна точка.
Цели обучения
Используйте форму «точка-наклон», чтобы найти уравнение прямой, проходящей через две точки, и убедитесь, что оно эквивалентно форме «наклон-пересечение» уравнения
Основные выводы
Ключевые моменты
- Уравнение точки и наклона задается следующим образом: [латекс] y-y_ {1} = m (x-x_ {1}) [/ latex], где [латекс] (x_ {1}, y_ {1}) [ / latex] — это любая точка на линии, а [latex] m [/ latex] — это наклон линии.
- Уравнение «точка-уклон» требует наличия как минимум одной точки и уклона. Если есть две точки и нет наклона, наклон можно сначала рассчитать по двум точкам, а затем выбрать одну из двух точек для записи уравнения.
- Уравнение точки-наклона и уравнения пересечения наклона эквивалентны.
 Можно показать, что с учетом точки [латекс] (x_ {1}, y_ {1}) [/ latex] и наклона [латекс] m [/ latex], [латекс] y [/ latex] -перехват ([ latex] b [/ latex]) в уравнении угла наклона есть [latex] y_ {1} -mx_ {1} [/ latex].
Можно показать, что с учетом точки [латекс] (x_ {1}, y_ {1}) [/ latex] и наклона [латекс] m [/ latex], [латекс] y [/ latex] -перехват ([ latex] b [/ latex]) в уравнении угла наклона есть [latex] y_ {1} -mx_ {1} [/ latex].
Ключевые термины
- Уравнение угла наклона точки : Уравнение линии с учетом точки [латекс] (x_ {1}, y_ {1}) [/ латекс] и наклона [латекс] м [/ латекс]: [латекс] y-y_ {1} = m (x-x_ {1}) [/ латекс].
Уравнение точки-наклона
Уравнение точки-наклона — это способ описания уравнения прямой. Форма «точка-наклон» идеальна, если вам дан наклон и только одна точка, или если вам даны две точки и вы не знаете, что такое перехват [latex] y [/ latex].Учитывая наклон, [латекс] м [/ латекс] и точку [латекс] (x_ {1}, y_ {1}) [/ latex], уравнение угла наклона точки составляет:
[латекс] \ displaystyle y-y_ {1} = m (x-x_ {1}) [/ latex]
Убедитесь, что форма «точка-уклон» эквивалентна форме для пересечения уклона
Чтобы показать, что эти два уравнения эквивалентны, выберите общую точку [latex] (x_ {1}, y_ {1}) [/ latex].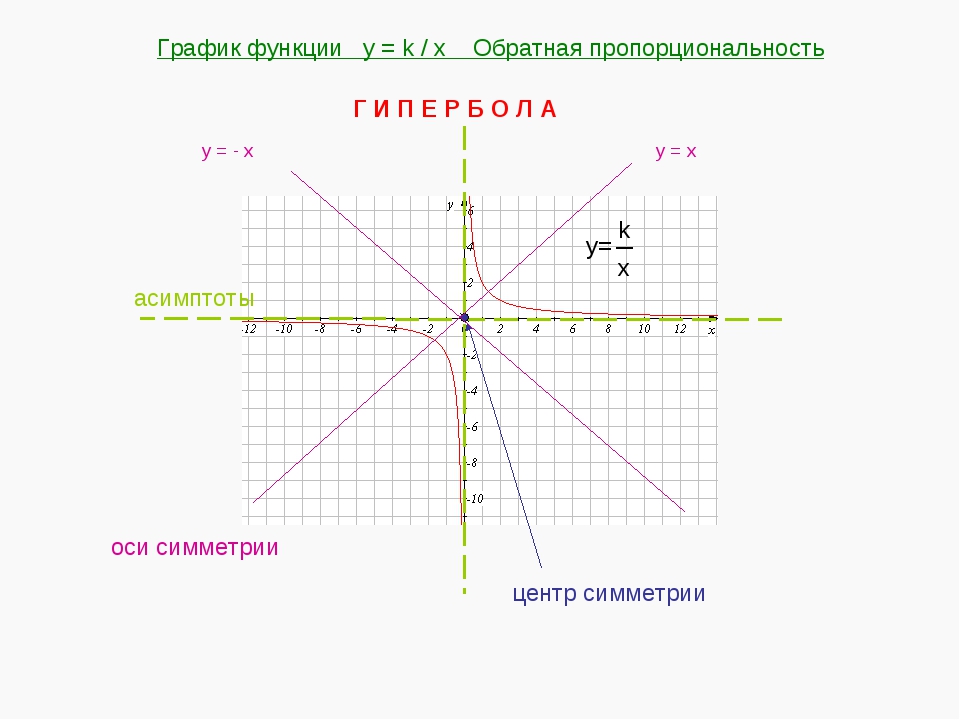 Подставьте общую точку в уравнение [латекс] y = mx + b [/ latex]. Уравнение теперь [латекс] y_ {1} = mx_ {1} + b [/ latex], что дает нам упорядоченную пару, [латекс] (x_ {1}, mx_ {1} + b) [/ latex] .Затем подставьте эту точку в уравнение угла наклона точки и решите для [latex] y [/ latex], чтобы получить:
Подставьте общую точку в уравнение [латекс] y = mx + b [/ latex]. Уравнение теперь [латекс] y_ {1} = mx_ {1} + b [/ latex], что дает нам упорядоченную пару, [латекс] (x_ {1}, mx_ {1} + b) [/ latex] .Затем подставьте эту точку в уравнение угла наклона точки и решите для [latex] y [/ latex], чтобы получить:
[латекс] \ displaystyle y- (mx_ {1} + b) = m (x-x_ {1}) [/ latex]
Распределить знак минус через и распределить от [latex] m [/ latex] до [latex] (x-x_ {1}) [/ latex]:
[латекс] \ displaystyle y-mx_ {1} -b = mx-mx_ {1} [/ latex]
Добавьте [латекс] mx_ {1} [/ latex] с обеих сторон:
[латекс] \ displaystyle y-mx_ {1} + mx_ {1} -b = mx-mx_ {1} + mx_ {1} [/ latex]
Объедините похожие термины:
[латекс] \ displaystyle y-b = mx [/ латекс]
Добавьте [латекс] b [/ латекс] с обеих сторон:
[латекс] \ displaystyle y-b + b = mx + b [/ латекс]
Объедините похожие термины:
[латекс] \ displaystyle y = mx + b [/ латекс]
Следовательно, эти два уравнения эквивалентны, и любое из них может выразить уравнение линии в зависимости от того, какая информация дается в задаче или какой тип уравнения требуется в задаче.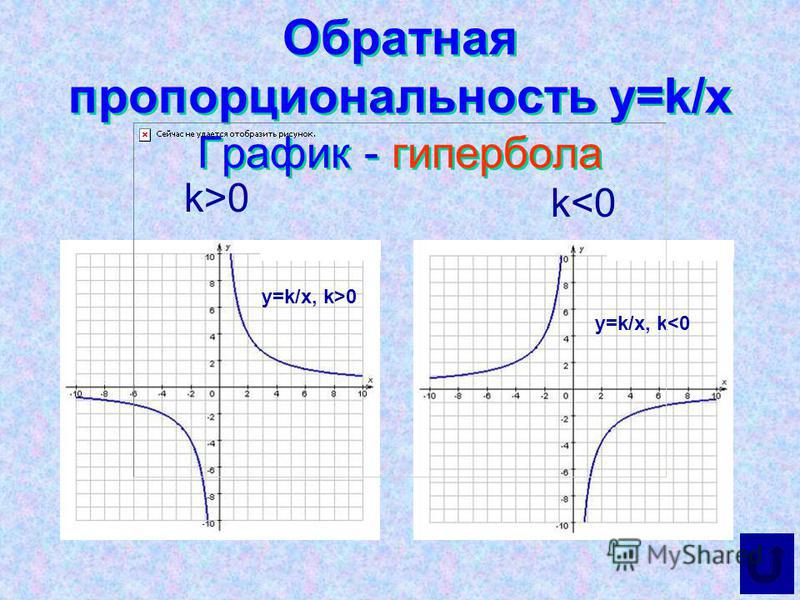
Пример: напишите уравнение линии в форме точки-наклона, учитывая точку [латекс] (2,1) [/ latex] и наклон [латекс] -4 [/ latex], и преобразуйте в форму пересечения наклона
Запишите уравнение прямой в форме точки-наклона:
[латекс] \ displaystyle y-1 = -4 (x-2) [/ latex]
Чтобы преобразовать это уравнение в форму пересечения наклона, решите уравнение для [латекс] y [/ латекс]:
[латекс] \ displaystyle y-1 = -4 (x-2) [/ latex]
Распределить [латекс] -4 [/ латекс]:
[латекс] \ displaystyle y-1 = -4x + 8 [/ латекс]
Добавьте [латекс] 1 [/ латекс] с обеих сторон:
[латекс] \ displaystyle y = -4x + 9 [/ латекс]
Уравнение имеет тот же смысл, в какой бы форме оно ни было, и дает один и тот же график.
Линейный график: График линии [латекс] y-1 = -4 (x-2) [/ latex] через точку [latex] (2,1) [/ latex] с наклоном [латекс] -4 [/ latex], а также наклонно-перехватывающая форма [latex] y = -4x + 9 [/ latex].
Пример: напишите уравнение линии в форме «точка-уклон», учитывая точку [латекс] (- 3,6) [/ latex] и точку [латекс] (1,2) [/ latex], и преобразуйте ее в наклон- форма перехвата
Поскольку у нас есть две точки, но нет наклона, мы должны сначала найти наклон:
[латекс] \ displaystyle m = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} [/ latex]
Подставляем значения баллов:
[латекс] \ displaystyle \ begin {align} m & = \ frac {-2-6} {1 — (- 3)} \\ & = \ frac {-8} {4} \\ & = — 2 \ end {align} [/ латекс]
Теперь выберите любую из двух точек, например [латекс] (- 3,6) [/ латекс].Подставьте эту точку и рассчитанный наклон в уравнение угла наклона точки, чтобы получить:
[латекс] \ displaystyle y-6 = -2 [x — (- 3)] [/ латекс]
Будьте осторожны, если одна из координат отрицательная. Распределяя отрицательный знак через круглые скобки, окончательное уравнение будет:
[латекс] \ displaystyle y-6 = -2 (x + 3) [/ латекс]
Если вы выберете другой пункт, уравнение будет выглядеть следующим образом: [латекс] y + 2 = -2 (x-1) [/ latex], и любой ответ правильный.
Далее раздаем [латекс] -2 [/ латекс]:
[латекс] \ displaystyle y-6 = -2x-6 [/ латекс]
Добавьте [латекс] 6 [/ латекс] с обеих сторон:
[латекс] \ displaystyle y = -2x [/ латекс]
Опять же, две формы уравнений эквивалентны друг другу и дают одну и ту же линию.Единственное отличие — это форма, в которой они написаны.
Линейные уравнения в стандартной форме
Линейное уравнение, записанное в стандартной форме, позволяет легко вычислить нулевое значение или точку пересечения [latex] x [/ latex] уравнения.
Цели обучения
Объясните процесс и полезность преобразования линейных уравнений в стандартную форму
Основные выводы
Ключевые моменты
- Стандартная форма линейного уравнения записывается как: [латекс] Ax + By = C [/ latex].
- Стандартная форма полезна при вычислении нуля уравнения. Для линейного уравнения в стандартной форме, если [latex] A [/ latex] не равно нулю, то перехват [latex] x [/ latex] происходит в [latex] x = \ frac {C} {A} [/ latex ].

Ключевые термины
- ноль : Также известный как корень, ноль — это значение [latex] x [/ latex], при котором функция [latex] x [/ latex] равна 0.
- форма пересечения наклона : Линейное уравнение, записанное в форме [латекс] y = mx + b [/ latex].
- Y-intercept : точка, в которой линия пересекает ось y декартовой сетки.
Стандартная форма
Стандартная форма — это еще один способ составления линейного уравнения. В стандартной форме линейное уравнение записывается как:
[латекс] \ displaystyle Ax + By = C [/ latex]
где [latex] A [/ latex] и [latex] B [/ latex] не равны нулю. Уравнение обычно записывается так, что [latex] A \ geq 0 [/ latex], по соглашению. График уравнения представляет собой прямую линию, и каждая прямая линия может быть представлена уравнением в стандартной форме.
Например, рассмотрим уравнение в форме перехвата наклона: [латекс] y = -12x +5 [/ latex]. Чтобы записать это в стандартной форме, обратите внимание, что мы должны переместить член, содержащий [latex] x [/ latex], в левую часть уравнения. Добавляем [latex] 12x [/ latex] с обеих сторон:
Чтобы записать это в стандартной форме, обратите внимание, что мы должны переместить член, содержащий [latex] x [/ latex], в левую часть уравнения. Добавляем [latex] 12x [/ latex] с обеих сторон:
[латекс] \ displaystyle y + 12x = 5 [/ латекс]
Уравнение теперь в стандартной форме.
Использование стандартной формы для поиска нулей
Напомним, что ноль — это точка, в которой значение функции будет равно нулю ([latex] y = 0 [/ latex]), и это перехват функции [latex] x [/ latex].Мы знаем, что точку пересечения y линейного уравнения можно легко найти, поместив уравнение в форму углового пересечения. Однако, когда линейное уравнение находится в такой форме, нуль уравнения не сразу очевиден. Однако нулевой или [latex] x [/ latex] -перехват линейного уравнения может быть легко найден путем его преобразования в стандартную форму.
Для линейного уравнения в стандартной форме, если [latex] A [/ latex] не равно нулю, то пересечение [latex] x [/ latex] происходит в [latex] x = \ frac {C} {A} [/ латекс].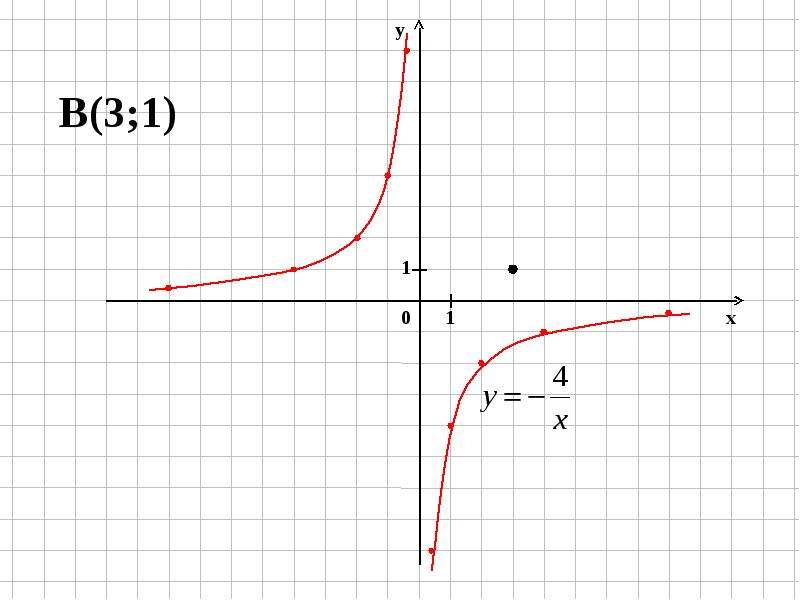
Например, рассмотрим уравнение [латекс] y + 12x = 5 [/ латекс].
В этом уравнении значение [latex] A [/ latex] равно 1, а значение [latex] C [/ latex] равно 5. Следовательно, ноль уравнения встречается при [latex] x = \ frac {5} {1} = 5 [/ латекс]. Ноль — это точка [латекс] (5, 0) [/ латекс].
Обратите внимание, что пересечение и наклон [latex] y [/ latex] также могут быть рассчитаны с использованием коэффициентов и константы уравнения стандартной формы. Если [latex] B [/ latex] не равно нулю, то точка пересечения y , то есть координата y точки, в которой график пересекает ось y (где [latex] x [ / latex] равно нулю), это [latex] \ frac {C} {B} [/ latex], а наклон линии равен [latex] — \ frac {A} {B} [/ latex].
Пример: Найдите ноль уравнения [латекс] 3 (y — 2) = \ frac {1} {4} x +3 [/ latex]
Мы должны записать уравнение в стандартной форме, [latex] Ax + By = C [/ latex], что означает получение членов [latex] x [/ latex] и [latex] y [/ latex] с левой стороны, и константы в правой части уравнения.
Распределите 3 слева:
[латекс] \ displaystyle 3y — 6 = \ frac {1} {4} x +3 [/ латекс]
Добавьте 6 к обеим сторонам:
[латекс] \ displaystyle 3y = \ frac {1} {4} x + 9 [/ латекс]
Вычтите [латекс] \ frac {1} {4} x [/ latex] с обеих сторон:
[латекс] \ displaystyle 3y — \ frac {1} {4} x = 9 [/ latex]
Переставить в [латекс] Ax + By = C [/ latex]:
[латекс] \ displaystyle — \ frac {1} {4} x + 3y = 9 [/ latex]
Уравнение имеет стандартную форму, и мы можем подставить значения для [латекс] A [/ латекс] и [латекс] C [/ латекс] в формулу для нуля:
[латекс] \ displaystyle \ begin {align} x & = \ frac {C} {A} \\ & = \ frac {9} {- \ frac {1} {4}} \\ & = -36 \ end {align} [/ латекс]
Ноль — [латекс] (- 36, 0) [/ латекс].
вариационных уравнений | Purplemath
Purplemath
Проблемы с вариациями не сложны, если вы научитесь говорить на жаргоне. Единственная реальная трудность — выучить несколько специализированный словарный запас и методы этой классификации проблем.
Единственная реальная трудность — выучить несколько специализированный словарный запас и методы этой классификации проблем.
Проблемы вариации включают довольно простые отношения или формулы, в которых одна переменная равна одному члену.Этот термин может быть линейным (что-то с просто « x »), квадратичным (что-то в « x 2 »), более чем одной переменной (например, « r 2 h »). , квадратный корень (что-то вроде «
«) или что-то еще.Но в формуле всегда есть только один член; этот член будет умножен на некоторое число, и, если вы еще не знаете, что это за число, это число обычно обозначается как « k ». Это число k называется «постоянной вариации».
MathHelp.com
Итак, вариационные уравнения могут иметь сложные выражения, но в них всегда будет только один член. В их уравнениях никогда не будет двух или более членов, сложенных вместе. Например, y = 3 x — это уравнение вариации, а y = 3 x + 2 — нет.
В их уравнениях никогда не будет двух или более членов, сложенных вместе. Например, y = 3 x — это уравнение вариации, а y = 3 x + 2 — нет.
Примером вариационного уравнения может служить формула для площади круга:
На языке вариантов:
площадь A прямо пропорциональна квадрату радиуса r
…и постоянная вариации k = π. Эта формула является примером «прямого» изменения. «Прямое изменение» означает, что в одном члене формулы переменная находится «сверху».
(Кстати, если вы видите формулу со знаком «∝» вместо знака «равно», этот символ произносится как «прямо пропорционален» и указывает на то, что они дали вам прямой- уравнение вариации, но не сообщая вам, что такое постоянная вариации.)
С другой стороны, «обратная вариация» означает, что переменная находится внизу, внизу дроби.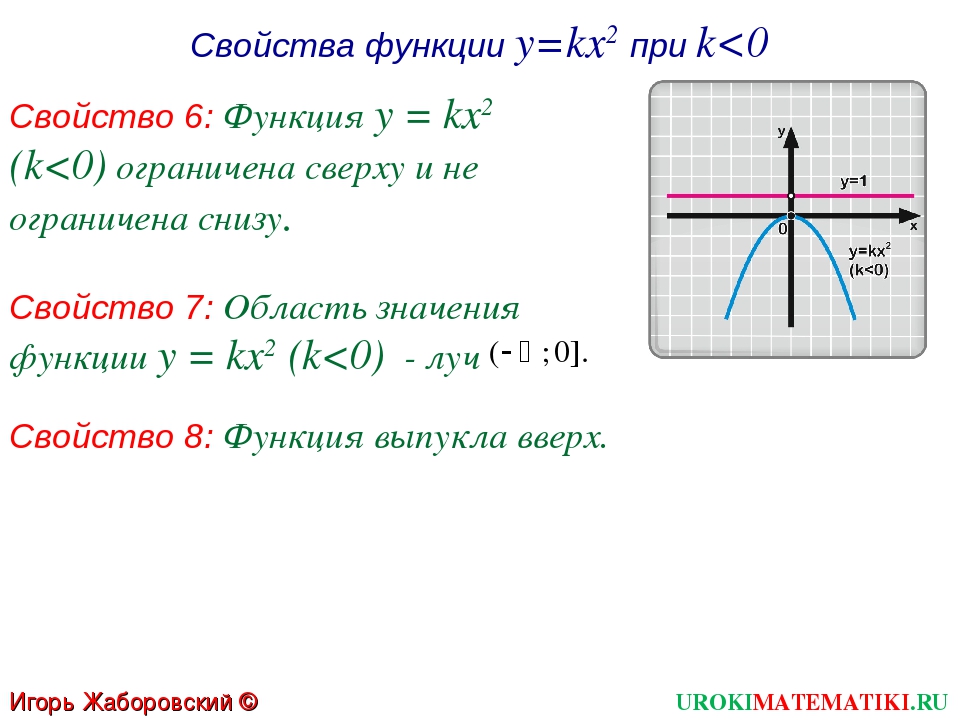 Предположим, например, что вы унаследовали счет денежного рынка, содержащий 100 000 долларов, и задаетесь вопросом, сколько денег ваш богатый дядя изначально вложил восемь лет назад. В зависимости от средней процентной ставки « r » вы можете использовать формулу:
Предположим, например, что вы унаследовали счет денежного рынка, содержащий 100 000 долларов, и задаетесь вопросом, сколько денег ваш богатый дядя изначально вложил восемь лет назад. В зависимости от средней процентной ставки « r » вы можете использовать формулу:
… где P — это основная сумма, которую вложил ваш дядя. (Между прочим, эта формула является вариантом формулы сложных процентов.) На языке вариаций эта формула читается как:
основной P изменяется обратно пропорционально
…с постоянной вариации k = 100000.
Другой вариант вариации — «совместно». «Совместное изменение» означает «напрямую, но с двумя или более переменными». Примером может служить формула для площади треугольника с основанием « b » и высотой « h »:
Прописью:
площадь A варьируется вместе с b и h
Константа вариации для этого уравнения равна
k = 1 / 2 .
На рассмотрение:
- «F изменяется как x » означает F = kx .
- «F изменяется вместе как x и y » означает F = kxy
- «F изменяется как x + y » означает F = k ( x + y )
- «F изменяется обратно пропорционально, так как x » означает
Будьте осторожны с этими двумя средними утверждениями выше.Почти всегда, когда вы переводите словесные задачи с английского на математику, «и» означает «плюс» или «добавлено к». Но в совместном варианте «и» просто означает, что «оба вместе находятся на одной стороне дроби» (обычно сверху), и вы умножаетесь. Если вы должны добавить две переменные, они будут использовать формат, указанный в третьем маркированном примере выше, или скажут «варьируется как сумма x и y ».
(Если они заставляют вас работать с чем-то, что «прямо» меняется с одним и «обратно» с другим, это можно назвать «комбинированным» вариантом.)
Перевод вариационных задач не так уж и плох, как только вы освоитесь. Но затем они хотят, чтобы вы перешли к настройке и решению текстовых задач. Обычно они делятся на две категории: те, где они хотят, чтобы вы нашли значение « k », и те, где они хотят, чтобы вы нашли какое-то другое значение, но только после того, как вы сначала нашли « k ». . Вот несколько примеров:
Если y изменяется прямо как x 2 и y = 8, когда x = 2, найдите y , когда x = 1.
Так как это прямая вариация, формула: « y = kx 2 ». Причина, по которой мне дали точку данных ( x , y ) = (2, 8), заключается в том, что Я должен найти значение « k ».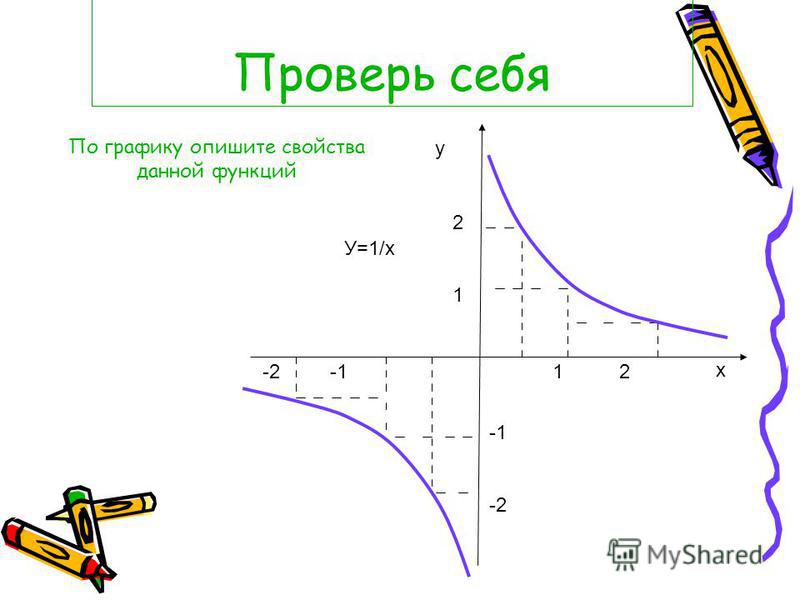 Я вставлю информацию, которую они мне дали, и решу k :
Я вставлю информацию, которую они мне дали, и решу k :
y = k x 2
8 = к (2 2 )
8 = 4 к
2 = к
Теперь, когда у меня есть k , я могу полностью переписать формулу:
Этим я могу ответить на вопрос, который они фактически задали: «Найдите y , когда x = 1.«
y = 2 x 2
y = 2 (1) 2
y = 2 (1)
y = 2
Тогда ответ:
Если y изменяется вместе как x и z , и y = 5, когда x = 3 и z = 4, то найдите y , когда x = 2 и z = 3.

Переводя формулу с английского на математику, получаю:
Вставив точку данных, которую они мне дали, и решив значение k , я получил:
5 = к (3) (4)
5 = 12 к
5 / 12 = к
Теперь, когда у меня есть значение k , я могу вставить новые значения и найти новое значение y :
y = ( 5 / 12 ) xz
y = ( 5 / 12 ) (2) (3)
y = ( 5 / 12 ) (6)
y = 5 / 2
Тогда ответ:
Учитывая, что y изменяется обратно пропорционально квадрату разности w и x , и что y = 6, когда w = 3 и x = 1, найдите уравнение для y .

Это довольно сложно. Я буду работать небольшими частями.
Мне сказали, что y изменяется обратно пропорционально указанному выражению, поэтому я знаю, что форма выражения будет иметь константу вариации поверх рационального выражения (то есть полиномиальную дробь) и переменную выражение в нижней части этого выражения.Но что такое переменное выражение?
«Разница между w и x » означает:
Квадрат этой разницы:
Это выражение будет в нижней части дроби, а постоянная вариации k будет вверху, поэтому мое уравнение на данный момент таково:
Чтобы найти полное уравнение для y , мне нужно найти значение константы.Для этого я вставлю значения, которые они мне дали:
6 = к / (3 — 1) 2
6 = к / (2) 2
6 = к /4
24 = к
Теперь у меня есть все части моего уравнения, и мой ответ:
URL: https: // www.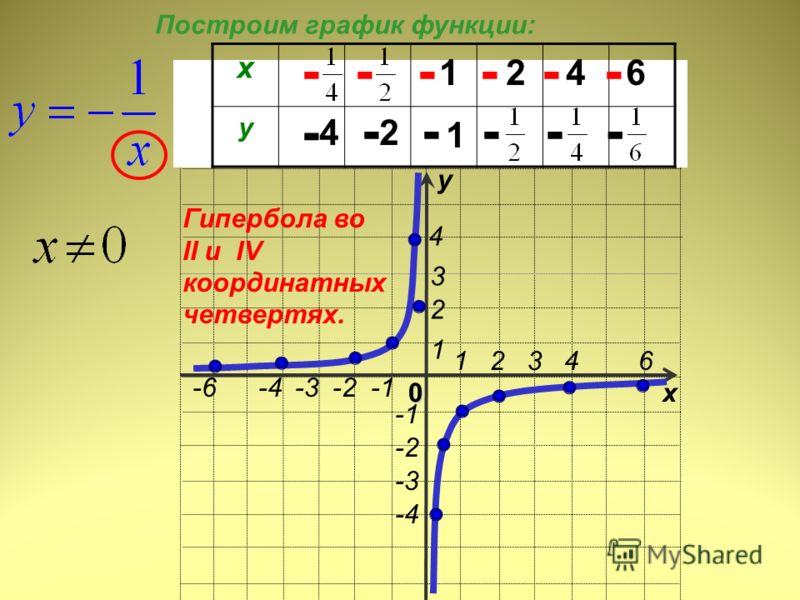

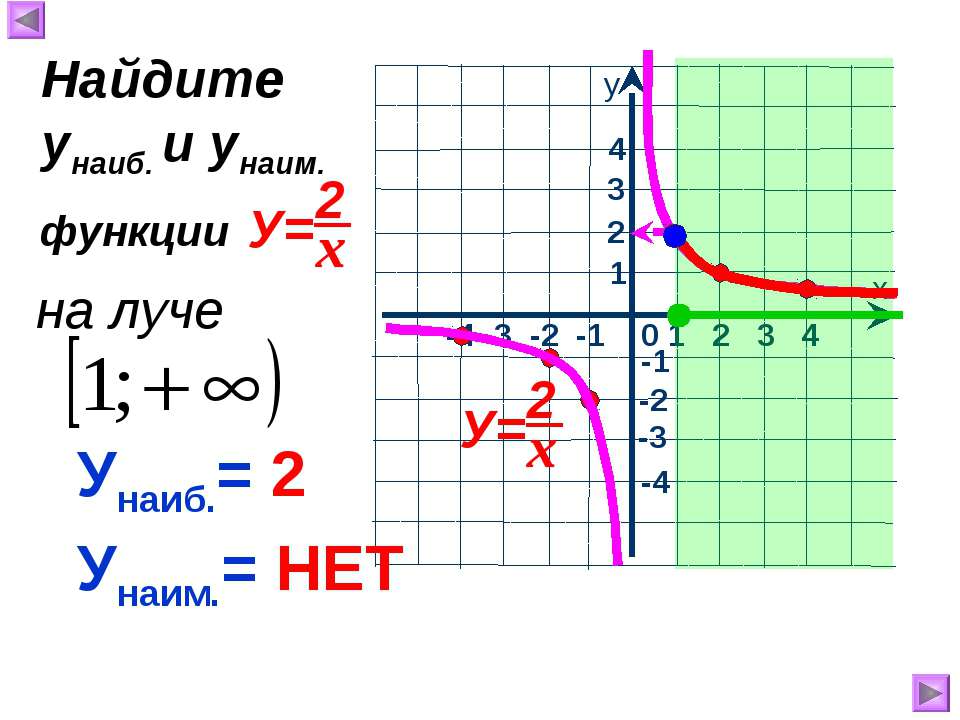

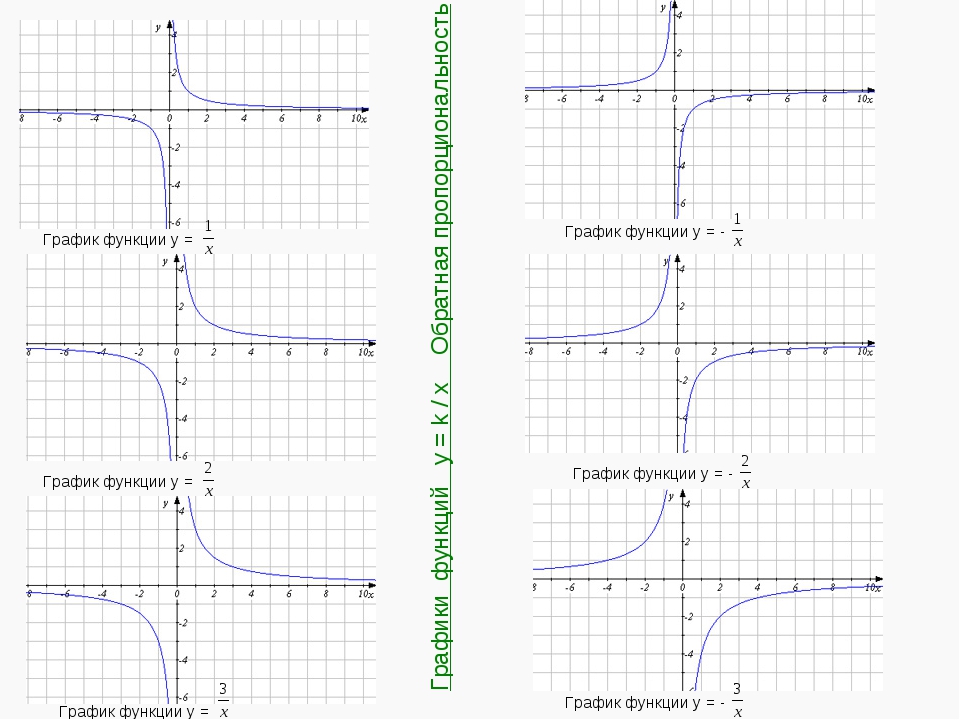 За сорок часов работы оплачивается в четыре раза больше, чем за десять часов работы.За один час работы оплачивается одна десятая десяти часов работы.
За сорок часов работы оплачивается в четыре раза больше, чем за десять часов работы.За один час работы оплачивается одна десятая десяти часов работы.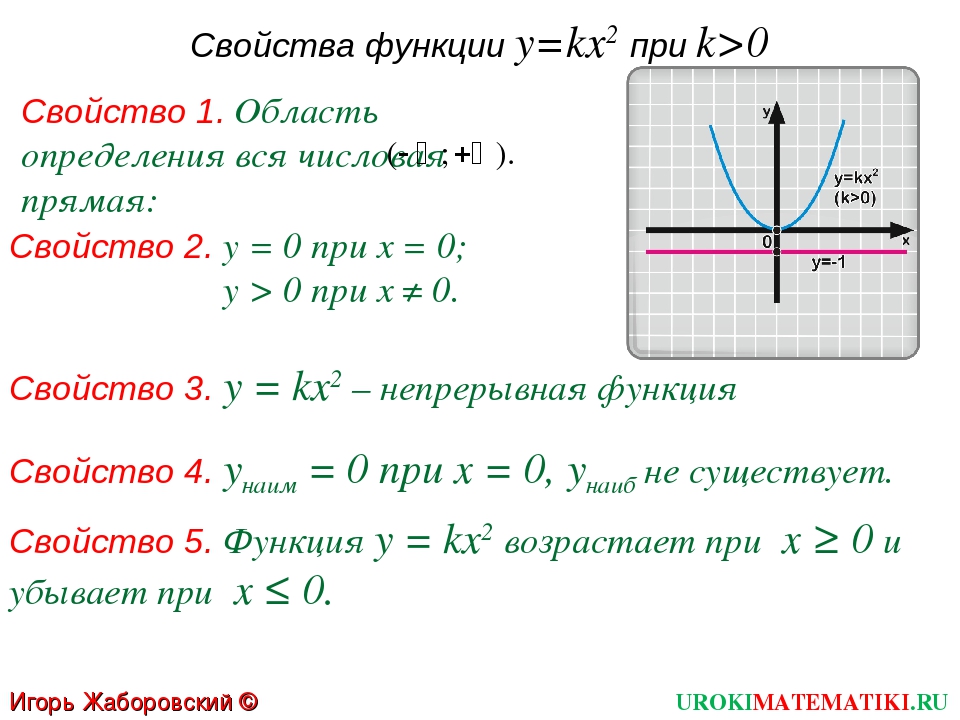 Поместите баллон в барокамеру и увеличьте давление вдвое — баллон сократится до половины своего первоначального объема. Поместите баллон в вакуумную камеру и уменьшите давление до одной десятой атмосферного — баллон расширится в десять раз в объеме (при условии, что сначала он не сломается).
Поместите баллон в барокамеру и увеличьте давление вдвое — баллон сократится до половины своего первоначального объема. Поместите баллон в вакуумную камеру и уменьшите давление до одной десятой атмосферного — баллон расширится в десять раз в объеме (при условии, что сначала он не сломается). Сколько времени нужно, чтобы упасть на один метр? Удвойте это время, и вы упадете на 4 м, утроите его, и вы упадете на 9 м, и так далее.
Сколько времени нужно, чтобы упасть на один метр? Удвойте это время, и вы упадете на 4 м, утроите его, и вы упадете на 9 м, и так далее.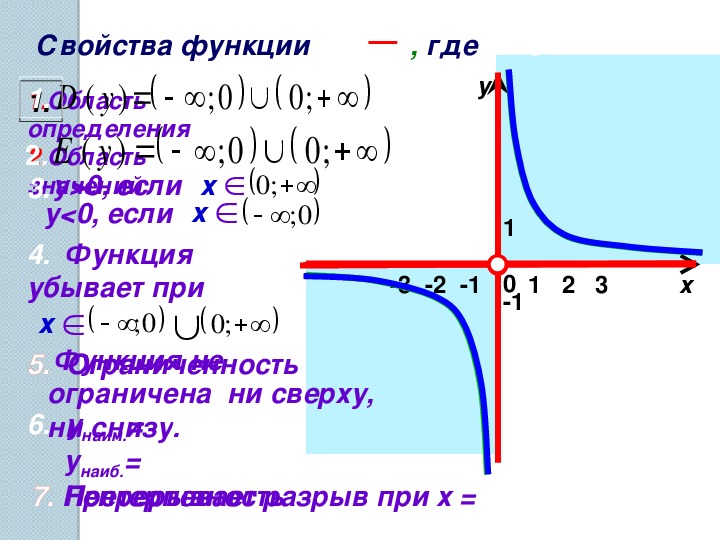 Насколько быстро движется объект после падения на один метр? На четырех метрах он будет иметь вдвое большую скорость; на девяти метрах — тройной; шестнадцать, четырехместные; и так далее.
Насколько быстро движется объект после падения на один метр? На четырех метрах он будет иметь вдвое большую скорость; на девяти метрах — тройной; шестнадцать, четырехместные; и так далее.
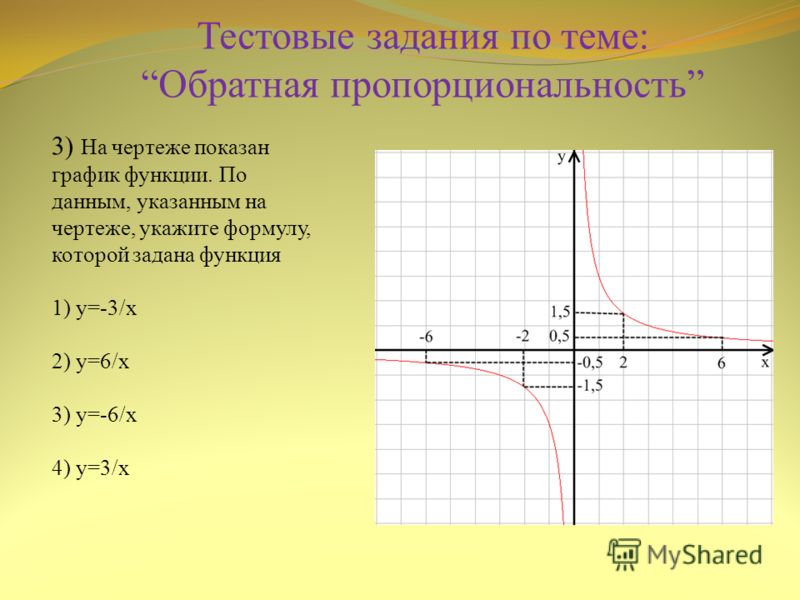
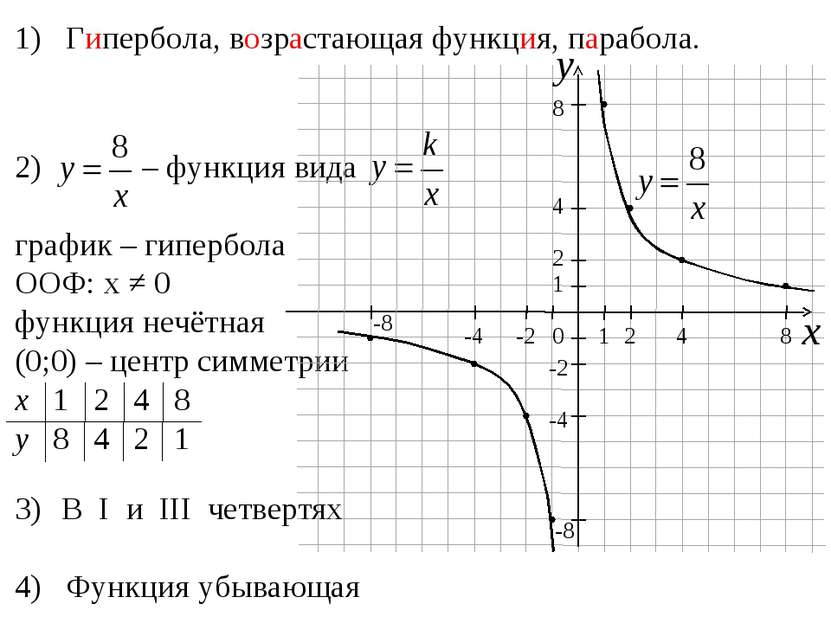

 Его координаты: [latex] (x, 0) [/ latex], где [latex] x [/ latex] равно нулю графика.
Его координаты: [latex] (x, 0) [/ latex], где [latex] x [/ latex] равно нулю графика.

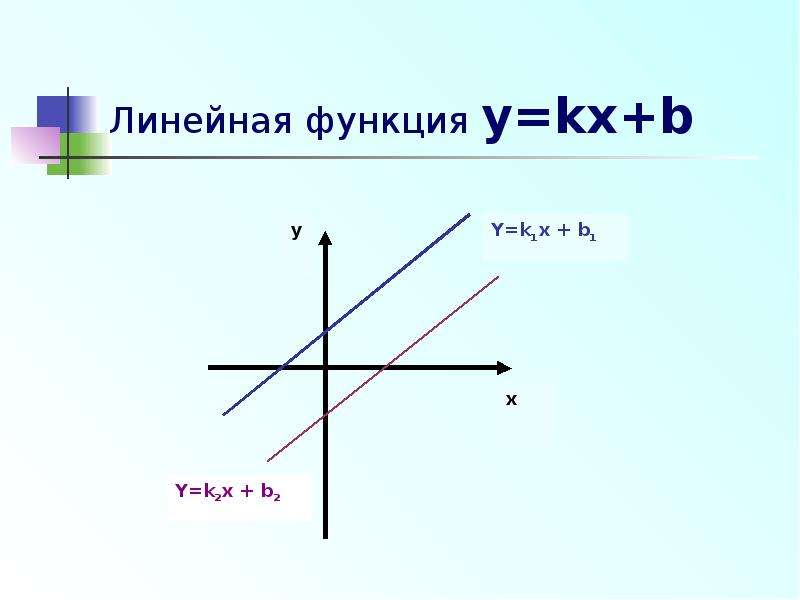 Можно показать, что с учетом точки [латекс] (x_ {1}, y_ {1}) [/ latex] и наклона [латекс] m [/ latex], [латекс] y [/ latex] -перехват ([ latex] b [/ latex]) в уравнении угла наклона есть [latex] y_ {1} -mx_ {1} [/ latex].
Можно показать, что с учетом точки [латекс] (x_ {1}, y_ {1}) [/ latex] и наклона [латекс] m [/ latex], [латекс] y [/ latex] -перехват ([ latex] b [/ latex]) в уравнении угла наклона есть [latex] y_ {1} -mx_ {1} [/ latex].