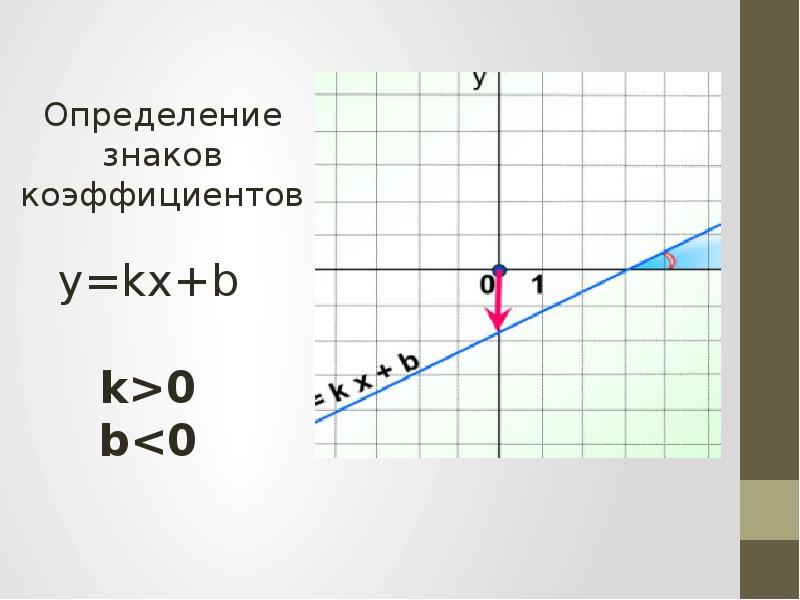
3.Линейная функция вида y = kx + b
Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
В частном случае, если k = 0, получим постоянную функцию y = b, график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b).
Если b = 0, то получим функцию y = kx, которая является прямой пропорциональностью.
Геометрический смысл коэффициента b – длина отрезка, который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
 Если k = 0, то область значений линейной функции состоит из числа b;
Если k = 0, то область значений линейной функции состоит из числа b;3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b.
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k, следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b, следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х. Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞),
y = kx + b – отрицательна при x из (-∞; -b/k).
b) k < 0; kx + b < 0, kx < -b, x < -b/k.
y = kx + b – положительна при x из (-∞; -b/k),
y = kx + b – отрицательна при x из (-b/k; +∞).
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b < 0; y = kx + b
7) Промежутки монотонности линейной функции зависят от коэффициента k.
k > 0, следовательно y = kx + b возрастает на всей области определения,
k < 0, следовательно y = kx + b убывает на всей области определения.
8) Графиком линейной функции является прямая. Для построения прямой
достаточно знать две точки. Положение прямой на координатной плоскости
зависит от значений коэффициентов k и b. Ниже приведена таблица, которая наглядно это иллюстрирует.
Для построения прямой
достаточно знать две точки. Положение прямой на координатной плоскости
зависит от значений коэффициентов k и b. Ниже приведена таблица, которая наглядно это иллюстрирует.Линейная функция y = kx — урок. Алгебра, 7 класс.
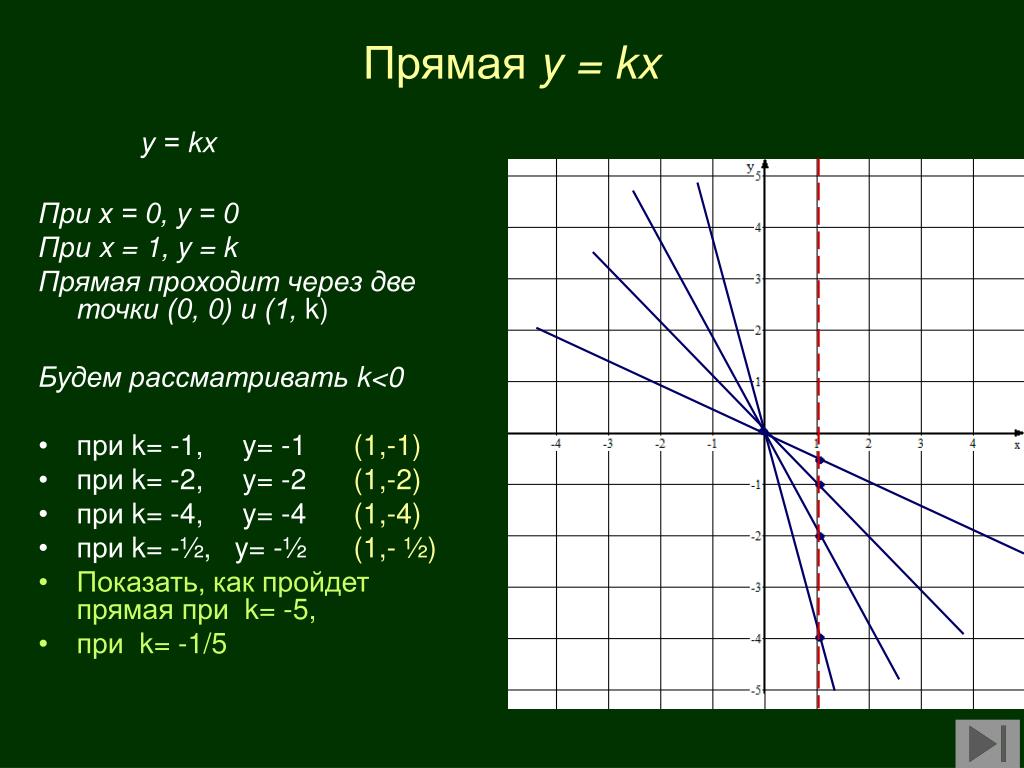
Рассматривая линейную функцию вида \(y=kx + m\), особо выделяют случай, когда \(m=0\).
Тогда линейная функция принимает вид \(y=kx\).
Графиком линейной функции \(y=kx\) является прямая, проходящая через начало координат.
Важно уметь переходить от аналитической модели \(y=kx\) к геометрической и, наоборот, от геометрической к аналитической модели.
Например, рассмотрим прямую, изображённую на рисунке.
Эта прямая является графиком линейной функции \(y=kx\), так как проходит через начало координат. Нужно лишь определить значение коэффициента \(k\).
Из формулы линейной функции \(y=kx\) получим, что k=yx.
Чтобы определить коэффициент \(k\), необходимо выбрать некоторую точку на прямой и вычислить частное ординаты и абсциссы заданной точки.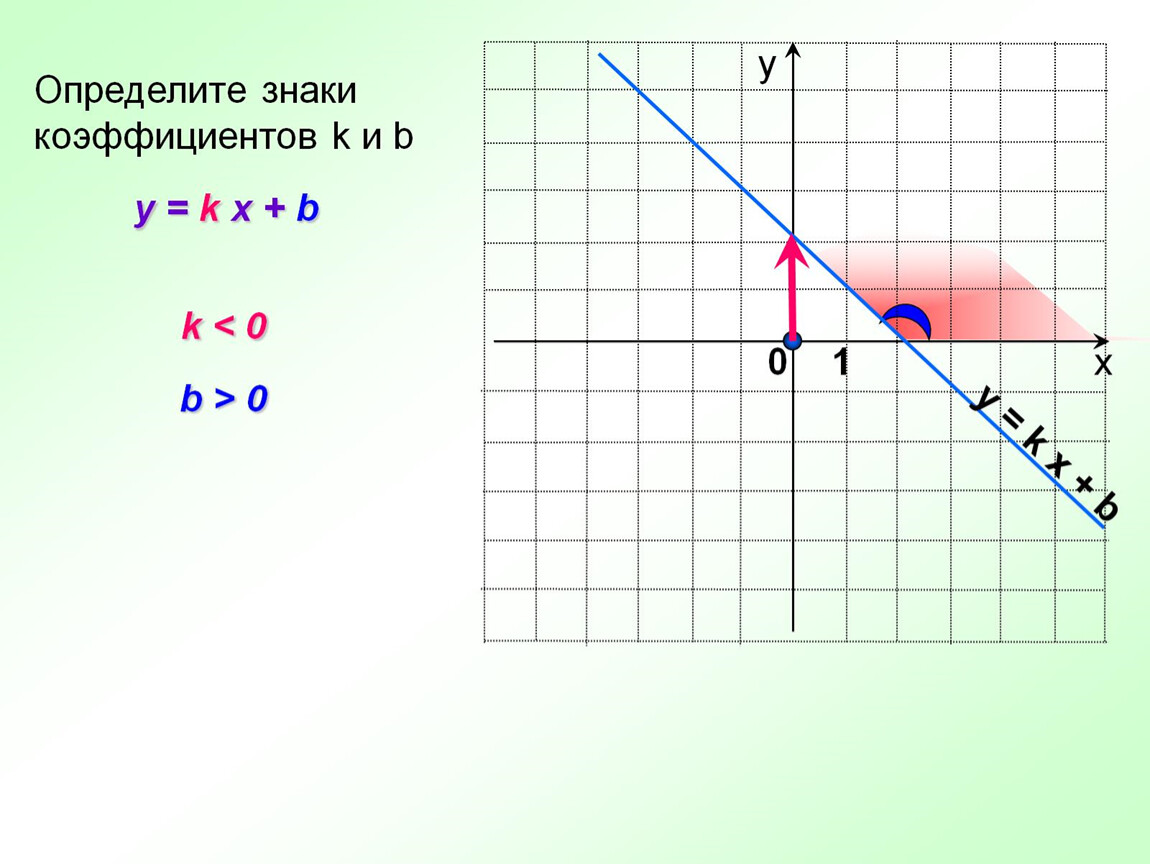
Прямая проходит через точку \(M(4; 2)\), следовательно получим 24=0,5. Значит, \(k=0,5\), и данная прямая является графиком линейной функции \(y=0,5x\).
Если в формуле \(y=kx\) вместо \(x\) подставим \(1\), то получим \(y=k\). Это означает, что прямая \(y=kx\) проходит через точку \((1; k)\). Поэтому график линейной функции можно строить по двум точкам: \((0;0)\) и \((1; k)\).
Иногда вместо точки \((1; k)\) удобнее взять другую точку.
Коэффициент \(k\) определяет угол между прямой и положительным направлением оси \(x\).
Если \(k>0\), то этот угол острый (как на первом рисунке), а
если \(k<0\), то этот угол тупой (как на втором рисунке).
Поэтому коэффициент \(k\) в записи \(y=kx\) называют угловым коэффициентом.
Обобщая сведения о линейных функциях, можно сделать вывод:
прямая, служащая графиком линейной функции \(y=kx + m\), параллельна прямой, служащей графиком линейной функции \(y=kx\).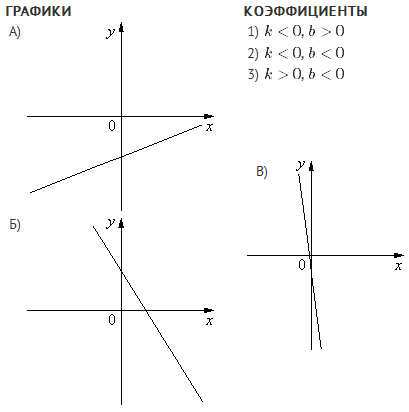
На рисунке показаны параллельные прямые с одним и тем же коэффициентом \(k = 4\).
Поэтому коэффициент \(k\) в записи \(y=kx + m\) также называют угловым коэффициентом, и
если \(k>0\), то прямая \(y=kx + m\) образует с положительным направлением оси \(x\) острый угол;
если \(k<0\), то этот угол тупой.
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов.
| ||||
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Линейная функция
Линейной функцией называют функцию, заданную формулой
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия.
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом.
График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график (прямая линия) имеет вид, изображенный на рис. 1, 2 и 3.
1, 2 и 3.
| k > 0 | ||||||
|
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
| k = 0 | ||||||
|
При k < 0 линейная функция (1) убывает на всей числовой прямой, а её график (прямая линия) имеет вид, изображенный на рис. 7, 8 и 9.
7, 8 и 9.
| k < 0 | ||||||
|
Прямые линии
y = kx + b1 и y = kx + b2 ,
имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны.
Прямые линии
y = k1x + b1 и y = k2x + b2 ,
имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.
Прямые линии
y = kx + b1 и
перпендикулярны при любых значениях свободных членов.
Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
|
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .
При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
Прямые, параллельные оси ординат
Прямые, параллельные оси Oy, задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
13, 14, 15.
|
Замечание 1. Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;
Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
Рассмотрим уравнение
где p, q, r – произвольные числа.
В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию.
Действительно,
что и требовалось.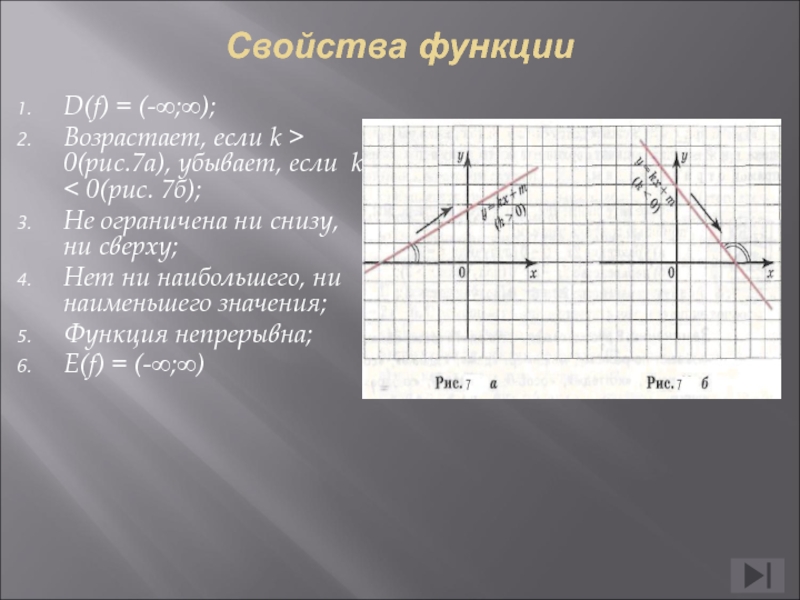
В случае, когда получаем:
откуда вытекает, что уравнение (4) задает прямую линию вида (3).
В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости:
В случае, когда уравнение (5) решений вообще не имеет.
Замечание 2. При любом значении r1, не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4).
Замечание 3. При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4).
Пример. Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
- параллельной к прямой
- перпендикулярной к прямой (8).

Решение.
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, уравнение прямой, параллельной к прямой
4x + 5y = 7,
задаётся уравнением
4x + 5y = – 7 .
В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, прямая, перпендикулярная к прямой
4x + 5y = 7 ,
задаётся уравнением
– 5x + 4y = – 22 .
Прямая y kx b. Линейная функция
Линейной функцией называется функция вида y = kx + b , заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
В частном случае, если k = 0 , получим постоянную функцию y = b , график которой есть прямая, параллельная оси Ox, проходящая через точку с координатами (0; b) .
Если b = 0 , то получим функцию y = kx , которая является прямой пропорциональностью.
b – длина отрезка , который отсекает прямая по оси Oy, считая от начала координат.
Геометрический смысл коэффициента k – угол наклона прямой к положительному направлению оси Ox, считается против часовой стрелки.
Свойства линейной функции:
1) Область определения линейной функции есть вся вещественная ось;
2) Если k ≠ 0 , то область значений линейной функции есть вся вещественная ось. Если k = 0 , то область значений линейной функции состоит из числа b ;
3) Четность и нечетность линейной функции зависят от значений коэффициентов k и b .
a) b ≠ 0, k = 0, следовательно, y = b – четная;
b) b = 0, k ≠ 0, следовательно y = kx – нечетная;
c) b ≠ 0, k ≠ 0, следовательно y = kx + b – функция общего вида;
d) b = 0, k = 0, следовательно y = 0 – как четная, так и нечетная функция.
4) Свойством периодичности линейная функция не обладает;
5) Точки пересечения с осями координат:
Ox: y = kx + b = 0, x = -b/k , следовательно (-b/k; 0) – точка пересечения с осью абсцисс.
Oy: y = 0k + b = b , следовательно (0; b) – точка пересечения с осью ординат.
Замечание.Если b = 0 и k = 0 , то функция y = 0 обращается в ноль при любом значении переменной х . Если b ≠ 0 и k = 0 , то функция y = b не обращается в ноль ни при каких значениях переменной х .
6) Промежутки знакопостоянства зависят от коэффициента k.
a) k > 0; kx + b > 0, kx > -b, x > -b/k.
y = kx + b – положительна при x из (-b/k; +∞) ,
y = kx + b – отрицательна при x из (-∞; -b/k) .
b) k
y = kx + b – положительна при x из (-∞; -b/k) ,
y = kx + b – отрицательна при x из (-b/k; +∞) .
c) k = 0, b > 0; y = kx + b положительна на всей области определения,
k = 0, b отрицательна на всей области определения.
7) Промежутки монотонности линейной функции зависят от коэффициента k .
k > 0 , следовательно y = kx + b возрастает на всей области определения,
k , следовательно y = kx + b убывает на всей области определения.
8) Графиком линейной функции является прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b . Ниже приведена таблица, которая наглядно это иллюстрирует.
Линейной функцией называется
функция, заданная формулой y = kx + b , где k и b — любые действительные числа.
Графиком линейной функции является прямая.
Если k = 0, то функция y = b называется постоянной. Её графиком, является прямая, параллельная оси Ox .
Если b = 0, то формула y = kx задает прямо пропорциональную зависимость. Графиком такой функции является прямая, проходящая через начало координат.
Верно и обратное — любая прямая, не параллельная оси Oy , является графиком некоторой линейной функции.
Число k называется угловым коэффициентом прямой , оно равно тангенсу угла между прямой и положительным направлением оси Ox .
На рисунке — угол α.
Построить график
линейной функции очень легко.
Положение любой прямой однозначно определяется заданием двух её точек. Поэтому линейная функция вполне определяется заданием её значений для двух значений аргумента.
Например,
Если Вы являетесь моим учеником или , то можете поработать с интерактивными версиями этих графиков.
Свойства линейной функции
при k ≠ 0, b ≠ 0.
1) Область определения функции — множество всех действительных чисел: R или (−∞; ∞).
2) Функция y = kx + b ни четна, ни нечетна.
3) При k > 0 функция монотонно возрастает, а при k
Упражнение:
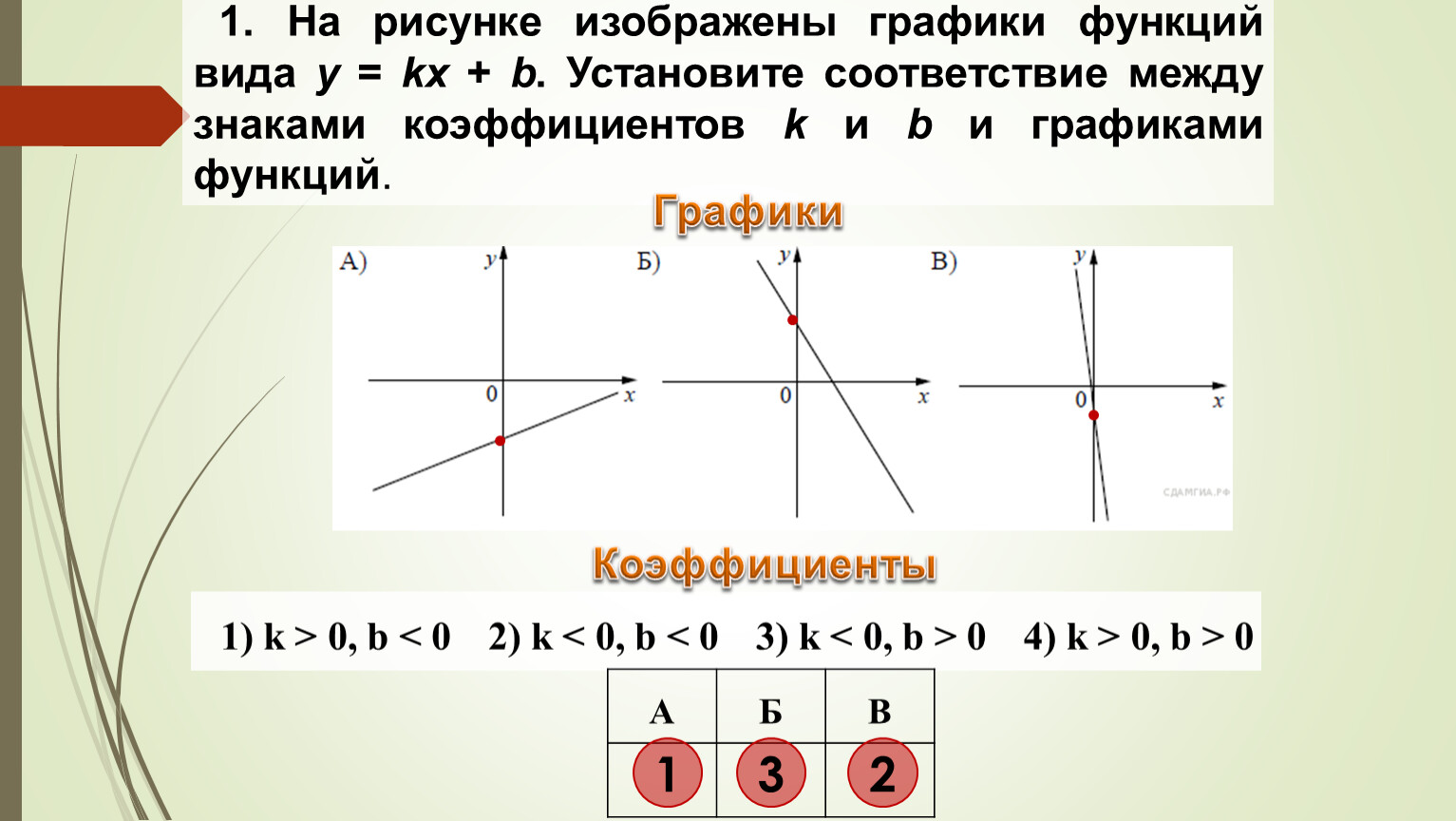
На рисунке представлены 4 прямые линии. Могут ли они являться графиками функций? Если да, то определите каких.
Посмотреть ответ.
Прямые, наклоненные к оси абсцисс под острым или тупым углом — графики линейной функции общего вида: y = kx + b. Параметр b легко определить по точке пересечения линии с осью ординат (Oy ). Параметр k определяется построеним по клеточкам треугольника, содержащего угол α для острых углов или смежный с ним — для тупых. Точные ответы на рисунке.
Прямая, параллельная оси абсцисс (здесь — горизонтальная линия), является графиком частного вида линейной функции y = b , который называют постоянной или константой. Значение этой функции не изменяется, поэтому ординаты точки графика всегда находятся на одной высоте относительно оси Ox .
Следующая прямая линия НЕ является графиком какой-либо функции. Здесь нет однозначности. Если x = 6, то y = ? Любому действительному числу! Т.е., для неё не удовлетворяется определение функции, а именно условие, что каждому значению аргумента x должно соответствовать единственное значение функции y . Но такие линии нам тоже встречаются, например, в качестве вертикальных асимптот. Поэтому нужно знать, что их уравнение x = a , где а — заданное число.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Линейной функцией называется функция вида y=kx+b, где x-независимая переменная, k и b-любые числа.
Графиком линейной функции является прямая.
1. Чтобы постороить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.
Например, чтобы построить график функции y= ⅓
x+2, удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3.
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2:
2. В формуле y=kx+b число k называется коэффицентом пропорциональности:
если k>0, то функция y=kx+b возрастает
если k
Коэффициент b показывает смещение графика функции вдоль оси OY:
если b>0, то график функции y=kx+b получается из графика функцииy=kx сдвигом на b единиц вверх вдоль оси OY
если b
На рисунке ниже изображены графики функций y=2x+3; y= ½
x+3; y=x+3
Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OX.
Во всех функциях b=3 – и мы видим, что все графики пересекают ось OY в точке (0;3)
Теперь рассмотрим графики функций y=-2x+3; y=- ½ x+3; y=-x+3
На этот раз во всех функциях коэффициент k меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Рассмотрим графики функций y=2x+3; y=2x; y=2x-3
Теперь во всех уравнениях функций коэффициенты k равны 2. И мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
График функции y=2x+3 (b=3) пересекает ось OY в точке (0;3)
График функции y=2x (b=0) пересекает ось OY в точке (0;0) — начале координат.
График функции y=2x-3 (b=-3) пересекает ось OY в точке (0;-3)
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k 0
Если k>0 и b>0 , то график функции y=kx+b имеет вид:
Если k>0 и b , то график функции y=kx+b имеет вид:
Если k, то график функции y=kx+b имеет вид:
Если k=0 , то функция y=kx+b превращается в функцию y=b и ее график имеет вид:
Ординаты всех точек графика функции y=b равны b Если b=0 , то график функции y=kx (прямая пропорциональность) проходит через начало координат:
3. Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соотвутствуют разные значения функции, что не соответствует определению функции.
4. Условие параллельности двух прямых:
График функции y=k 1 x+b 1 параллелен графику функции y=k 2 x+b 2 , если k 1 =k 2
5. Условие перепендикулярности двух прямых:
График функции y=k 1 x+b 1 перепендикулярен графику функции y=k 2 x+b 2 , если k 1 *k 2 =-1 или k 1 =-1/k 2
6. Точки пересечения графика функции y=kx+b с осями координат.
С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты (-b/k;0):
Линейная функция — подготовка к ЕГЭ по Математике
Линейная функция — функция вида График линейной функции — прямая.
Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.
Угловой коэффициент прямой
Величина k в формуле линейной функции называется угловым коэффициентом прямой
Если , линейная функция возрастает. Чем больше х, тем больше у, то есть график идет вправо и вверх.
Если , линейная функция убывает. Чем больше х, тем меньше у, то есть график идет вправо и вниз.
Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.
Пусть Чем больше k, тем круче вверх идет график функции.
А что же будет, если ? Мы получим горизонтальную прямую На рисунке показан график функции
Заметим, что прямая (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова. В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества Х соответствует один и только один элемент множества Y.
Для прямой это не выполняется: значению соответствует бесконечно много значений у.
Если прямые параллельны.
При этом, чем больше b, тем выше расположен на координатной плоскости график функции.
Например, прямые и параллельны. Их угловые коэффициенты равны.
Если прямые перпендикулярны. Например, прямые и пересекаются под прямым углом. Произведение их угловых коэффициентов равно — 1.
Построение графика линейной функции
График линейной функции построить легко — достаточно двух точек.
Оказывается, что привычный нам вид уравнения прямой — не единственно возможный.
Уравнение прямой можно записать также в виде
Построим, например, прямую, заданную уравнением
При получаем, что
При получаем, что
Значит, наша прямая проходит через точки и
Выразив у из уравнения , получим уравнение прямой вида
Если вы поступаете в вуз на специальность, связанную с математикой, — уже на первом курсе вы познакомитесь и с другими видами уравнения прямой.
Зачем изучать линейную функцию?
Дело в том, что многие зависимости в природе и технике описываются формулой виде
Например, закон Ома для участка цепи: Напряжение U прямо пропорционально силе тока I.
Формула для равномерного прямолинейного движения: . Пройденное расстояние S прямо пропорционально времени.
Закон теплового расширения , который вам встретится в одной из задач под номером 10 варианта Профильного ЕГЭ по математике — тоже линейная функция. И таких примеров можно привести очень много.
Обратите внимание, что в формулу линейной функции аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент k и прибавляем b.
Если в формулу функции входит аргумент в любой другой степени — например, в квадрате или в кубе, если мы делим на х, если в формуле присутствует или , или показательные или логарифмические выражения, зависящие от х, — график функции уже не будет прямой линией.
Уравнение прямой с угловым коэффициентом
Рассмотрим три случая положения прямой в координатной плоскости.
1) Если прямая параллельна оси Oy.
В этом случае все её точки имеют одинаковые абсциссы. Например, если точка пересечения прямой с осью Ox имеет абсциссу a, то для всех точек прямой верно равенство
Это равенство является уравнением прямой, параллельной оси Oy.
2) Если прямая параллельна оси Ox.
Все точки прямой имеют одинаковые ординаты. Если точка пересечения прямой с осью Oy имеет ординату b, то для всех точек прямой верно равенство
это равенство является уравнением прямой, параллельной оси Ox.
3) Если прямая не параллельна ни одной из осей.
Пусть α — угол, который прямая образует с положительным направлением оси Ox, b — ордината точки пересечения прямой с осью Oy.
Выберем на прямой произвольную точку A(x;y). Проведём через точку A прямые, параллельные осям.
Рассмотрим образованный этими прямыми прямоугольный треугольник ABC.
AC=y-b, BC=x, ∠ABC=α (как соответственные при BC∥Ox и секущей AB).
По определению тангенса
Обозначим tgα=k. Число k называют угловым коэффициентом прямой (эта величина играет очень важную роль). Тогда
откуда
Это уравнение называют уравнением прямой с угловым коэффициентом.
Если A — точка, лежащая не в I четверти, рассуждения усложняются, но в результате приходим к тому же уравнению: y=kx+b.
Если угол α — тупой, в прямоугольном треугольнике находят тангенс угла, смежного с α.
Уравнение y=b можно считать частным случаем уравнения y=kx+b, что согласуется с геометрическим смыслом k, поскольку для прямой, параллельной оси Oy, α=0°, а tg0°=0.
Для прямой, параллельной оси Oy, уравнение x=a не является частным случаем уравнения y=kx+b (что также согласуется с геометрическим смыслом k, так как в этом случае α=90°, а tg 90° не существует).
Таким образом, уравнение прямой с угловым коэффициентом задает все прямые, не параллельные оси Oy:
y=kx+b или y=b.
Прямые, параллельные оси Oy, задаются уравнением x=a другого вида.
Прямая вариация — ChiliMath
Концепция прямого изменения резюмируется приведенным ниже уравнением.
Мы говорим, что y напрямую зависит от x, если y выражается как произведение некоторого постоянного числа k и x.
Случаи прямого изменения
Однако значение k не может равняться нулю , т.е. k \ ne 0.
Случай 1: k> 0 (k положительно)
Если x увеличивается, значение y также увеличивается, или если x уменьшается, значение y также уменьшается.
Случай 2: k
<0 (k отрицательно)Если x увеличивается, значение y уменьшается, или если x уменьшается, значение y увеличивается.
Если мы изолировать k с одной стороны, это показывает, что k — постоянное отношение между y и x. Другими словами, деление y на x всегда дает постоянный результат.
k также известно как постоянная вариации или константа пропорциональности.
Примеры прямого изменения
Пример 1: Укажите, изменяется ли y напрямую с x в таблице ниже.Если да, напишите уравнение, чтобы представить прямую вариацию.
Решение :
Чтобы показать, что y напрямую зависит от x, нам нужно проверить, всегда ли деление y на x дает нам одно и то же значение.
Поскольку при делении y на x мы всегда получали одно и то же значение 2, мы можем утверждать, что y напрямую зависит от x. Фактически, это постоянное число является нашим k = 2.
Чтобы написать уравнение прямой вариации, заменим букву k на цифру 2 в уравнении y = kx.
Когда уравнение, представляющее прямую вариацию, строится на декартовой плоскости, это всегда прямая линия , проходящая через начало координат.
Думайте об этом как о форме пересечения наклона линии, записанной как
y = mx + b , где b = 0
Вот график найденного выше уравнения.
Пример 2: Укажите, изменяется ли y напрямую с x в таблице ниже. Если да, напишите уравнение, чтобы представить прямую вариацию.
Решение :
Разделите каждое значение y на соответствующее значение x.
Частное y и x всегда равно k = — \, 0,25. Это означает, что y напрямую зависит от x. Вот уравнение, представляющее его прямую вариацию.
Вот график. Отрицательное значение k означает, что линия имеет отрицательный наклон. Как видите, линия убывает слева направо.
Кроме того, поскольку k отрицательно , мы видим, что, когда x увеличивается, значение y уменьшается.
Пример 3: Сообщите, изменяется ли y напрямую с x в таблице. Если да, напишите уравнение, показывающее прямое изменение.
Решение :
Найдите отношение y и x и посмотрите, сможем ли мы получить общий ответ, который мы назовем константой k.
Похоже, значение k в третьей строке отличается от остальных. Чтобы это была прямая вариация, все они должны иметь одинаковое значение k.
Таблица не представляет прямого изменения, поэтому мы не можем написать уравнение для прямого изменения.
Пример 4: При условии, что y напрямую зависит от x. Если x = 12, то y = 8.
- Напишите уравнение прямого изменения, которое связывает x и y.
- Каково значение y при x = — \, 9?
a) Напишите уравнение прямого изменения, которое связывает x и y.
Поскольку y напрямую зависит от x, я бы сразу записал формулу, чтобы увидеть, что происходит.
Нам дана информация, что когда x = 12, тогда y = 8.Подставьте значения x и y в формулу и решите k.
Замените «k» в формуле значением, решенным выше, чтобы получить уравнение прямого изменения, которое связывает x и y.
б) Каково значение y при x = — \, 9?
Чтобы найти y, подставьте x = — \, 9 в уравнение, найденное в части a).
Пример 5: Если y напрямую зависит от x, найдите недостающее значение x в
Решение :
Мы будем использовать первую точку, чтобы найти константу пропорциональности k и составить уравнение y = kx.
Подставьте значения x и y, чтобы найти k.
Уравнение прямой пропорциональности, связывающее x и y, равно…
Теперь мы можем найти x в (x, — \, 18), подставив y = — \, 18.
Пример 6: Длина окружности (C) напрямую зависит от ее диаметра. Если круг диаметром 31,4 дюйма имеет радиус 5 дюймов,
- Напишите уравнение прямого изменения, которое связывает длину окружности и диаметр круга.
- Каков диаметр окружности с радиусом 7 дюймов?
a) Напишите уравнение прямого изменения, которое связывает длину окружности и диаметр.
Нам не нужно постоянно использовать формулу y = k \, x. Но мы можем использовать его для создания аналогичной настройки в зависимости от того, что задает проблема.
Задача говорит нам, что длина окружности напрямую зависит от ее диаметра. Вместо этого мы можем написать следующее уравнение прямой пропорциональности.
Диаметр не указан, но радиус есть. Поскольку радиус задан как 5 дюймов, это означает, что мы можем найти диаметр, потому что он равен удвоенной длине радиуса. Это дает нам диаметр 10 дюймов.
Уравнение прямой пропорциональности, которое связывает окружность и диаметр, показано ниже. Обратите внимание, что k заменяется числовым значением 3.14.
б) Каков диаметр окружности с радиусом 7 дюймов?
Поскольку уравнение требует диаметра, а не радиуса, нам нужно сначала преобразовать значение радиуса в диаметр.Помните, что диаметр в два раза больше радиуса, поэтому 7 дюймов радиуса равны 14 дюймам в диаметре.
Теперь мы подставляем d = 14 в формулу, чтобы получить ответ для длины окружности.
Вас также может заинтересовать:
Обратная вариация
Алгебра миссис Гризер вики: WikiGrieser / Прямая вариация
Прямое изменение происходит, когда по мере увеличения одной переменной в таком же множителе увеличивается другая переменная.Прямое изменение иногда называют прямой пропорциональностью, поскольку переменные пропорциональны друг другу. Противоположностью прямого изменения является обратное изменение.
Запишем: y = kx
Мы говорим: y прямо пропорционально x
В уравнении y = kx, k называется постоянной вариации .
Если мы начнем с уравнения y = kx и разделим обе части на x, мы получим y / x = k. Следовательно, в случае прямого изменения частное переменных дает нам константу изменения.
Если вам представлена таблица значений (x, y) и вас спросят, представляет ли таблица значений прямое изменение, то по истине должно быть, что y / x = k для каждого значения в таблице. Проверьте каждое значение, разделив y на x; если вы получите такое же постоянное значение, то у вас есть прямая вариация.
Мы можем сравнить y = kx с формой пересечения наклона прямой y = mx + b.
Мы можем видеть, что y = kx является линейным уравнением с угловым коэффициентом k и точкой пересечения оси y 0.
Это говорит нам, что график прямого изменения — это линия, проходящая через начало координат, точку (0,0). Поэтому, если вас спросят, представляет ли график прямое изменение, ответ будет «нет», если это не прямая линия, проходящая через начало координат.
Примеры прямого изменения
Нахождение постоянной вариации :
Если y изменяется прямо как x, а y = 4, когда x = 2, то найдите константу изменения и напишите уравнение, которое выражает прямое изменение.
Решение : Если y изменяется прямо как x, тогда y = kx (определение прямого изменения). Когда y = 4, тогда x = 2, мы подставляем эти значения в уравнение y = kx. Мы получаем 4 = k * 2. Разделим обе части на 2 и k = 2. Таким образом, наша постоянная вариации равна 2. Поэтому мы подставляем 2 вместо k в нашем уравнении прямого изменения, чтобы получить: y = 2x.
Задача со словом :
Если пройденное расстояние напрямую зависит от количества использованного газа, а автомобиль использует 7 галлонов бензина для проезда 280 миль, сколько газа будет использовано для проезда 450 миль?
Решение : Если пробег напрямую зависит от используемого газа, то мы можем написать m = кг.Мы знаем, что на путешествие в 280 миль было использовано 7 галлонов газа, поэтому мы можем подставить эти значения в уравнение: m = kg => 280 = k * 7. Решая, мы получаем k = 40, поэтому наше уравнение принимает вид m = 40g. Я знаю, что хочу, чтобы мой пробег составлял 450 миль, поэтому я вставляю это в уравнение и решаю для g, количество бензина: 450 = 40 г; разделите обе стороны на 40 и получите g = 11,25 галлона.
Эти заметки для занятий содержат дополнительные пояснения и примеры.
Решение задач с прямой вариацией
Решение задач с прямой вариацией Вот шаги, необходимые для решения проблем прямого изменения:| Шаг 1 : | Напишите правильное уравнение.Прямые вариационные задачи решаются с помощью уравнения y = kx. При работе с текстовыми задачами вам следует подумать об использовании переменных, отличных от x и y, вы должны использовать переменные, которые имеют отношение к решаемой проблеме. Также внимательно прочтите задачу, чтобы определить, есть ли какие-либо другие изменения в уравнении прямого изменения, такие как квадраты, кубы или квадратные корни. |
| Шаг 2 : | Используйте информацию, указанную в задаче, чтобы найти значение k, которое называется постоянной вариации или константой пропорциональности. |
| Шаг 3 : | Перепишите уравнение из шага 1, подставив значение k, найденное на шаге 2. |
| Шаг 4 : | Используйте уравнение, найденное на шаге 3, и оставшуюся информацию, приведенную в задаче, чтобы ответить на заданный вопрос. Решая задачи со словами, не забудьте включить единицы в свой окончательный ответ. |
Пример 1 — Если x изменяется прямо как y, а x = 9, когда y = 6, найдите x, когда y = 15.
| Шаг 1 : Напишите правильное уравнение. Прямые вариационные задачи решаются с помощью уравнения y = kx. | |
| Шаг 2 : Используйте информацию, указанную в задаче, чтобы найти значение k. В этом случае вам нужно найти k, когда x = 9 и y = 6. | |
| Шаг 3 : Перепишите уравнение из шага 1, подставив значение k, найденное на шаге 2. | |
| Шаг 4 : Используйте уравнение, найденное на шаге 3, и оставшуюся информацию, указанную в задаче, чтобы ответить на заданный вопрос. В этом случае вам нужно найти x, когда y = 15. |
Пример 2 –Если p изменяется прямо как квадрат q, а p = 20, когда q = 5, найдите p, когда q = 8.
| Шаг 1 : Напишите правильное уравнение. Прямые вариационные задачи решаются с помощью уравнения y = kx.В этом случае вы должны использовать p и q вместо x и y и заметить, как слово «квадрат» меняет уравнение. | |
| Шаг 2 : Используйте информацию, указанную в задаче, чтобы найти значение k. В этом случае нужно найти k при p = 20 и q = 5. | |
| Шаг 3 : Перепишите уравнение из шага 1, подставив значение k, найденное на шаге 2. | |
| Шаг 4 : Используйте уравнение, найденное на шаге 3, и оставшуюся информацию, указанную в задаче, чтобы ответить на заданный вопрос.В этом случае вам нужно найти p при q = 15. |
Щелкните здесь для практических задач
Пример 3 — Если c изменяется прямо как квадратный корень из d, и c = 6, когда d = 256, найдите c, когда d = 625.
| Шаг 1 : Напишите правильное уравнение. Прямые вариационные задачи решаются с помощью уравнения y = kx. В этом случае вы должны использовать c и d вместо x и y и заметить, как слово «квадратный корень» меняет уравнение. | |
| Шаг 2 : Используйте информацию, указанную в задаче, чтобы найти значение k. В этом случае вам нужно найти k, когда c = 6 и d = 256. | |
| Шаг 3 : Перепишите уравнение из шага 1, подставив значение k, найденное на шаге 2. | |
| Шаг 4 : Используйте уравнение, найденное на шаге 3, и оставшуюся информацию, указанную в задаче, чтобы ответить на заданный вопрос.В этом случае вам нужно найти c, когда d = 625. |
Щелкните здесь для практических задач
Пример 4 — Закон Гука для упругой пружины гласит, что расстояние, на которое растягивается пружина, изменяется прямо пропорционально приложенной силе. Если сила в 160 ньютонов растянет пружину на 5 см, насколько сила в 368 ньютонов растянет ту же пружину?
| Шаг 1 : Напишите правильное уравнение.Прямые вариационные задачи решаются с помощью уравнения y = kx. В этом случае вы должны использовать d для расстояния и f для силы вместо x и y. | |
| Шаг 2 : Используйте информацию, указанную в задаче, чтобы найти значение k. В этом случае нужно найти k при f = 160 и d = 5. | |
| Шаг 3 : Перепишите уравнение из шага 1, подставив значение k, найденное на шаге 2. | |
| Шаг 4 : Используйте уравнение, найденное на шаге 3, и оставшуюся информацию, указанную в задаче, чтобы ответить на заданный вопрос. В этом случае вам нужно найти d при f = 368. |
Щелкните здесь для практических задач
Пример 5 — Расстояние, на которое тело падает из состояния покоя, прямо пропорционально квадрату времени его падения (без учета сопротивления воздуха). Если мяч упадет с высоты 144 футов за три секунды, как далеко упадет мяч за семь секунд?
| Шаг 1 : Напишите правильное уравнение.Прямые вариационные задачи решаются с помощью уравнения y = kx. В этом случае вы должны использовать d для расстояния и t для времени вместо x и y и заметить, как слово «квадрат» меняет уравнение. | |
| Шаг 2 : Используйте информацию, указанную в задаче, чтобы найти значение k. В этом случае нужно найти k при d = 144 и t = 3. | |
| Шаг 3 : Перепишите уравнение из шага 1, подставив значение k, найденное на шаге 2. | |
| Шаг 4 : Используйте уравнение, найденное на шаге 3, и оставшуюся информацию, указанную в задаче, чтобы ответить на заданный вопрос. В этом случае нужно найти d при t = 7. |
Щелкните здесь для практических задач
линейных уравнений | Введение в статистику
Результаты обучения
- Обсудить основные идеи линейной регрессии и корреляции
Линейная регрессия для двух переменных основана на линейном уравнении с одной независимой переменной.Уравнение имеет вид:
, где a и b — постоянные числа.
Переменная x — независимая переменная, а y — зависимая переменная. Обычно вы выбираете значение для замены независимой переменной, а затем решаете зависимую переменную.
Следующие примеры представляют собой линейные уравнения.попробуйте
Следующий пример является линейным уравнением?
y = –0.125 — 3,5 x
График линейного уравнения вида y = a + bx представляет собой прямую линию . Любая линия, которая не является вертикальной, может быть описана этим уравнением.
Изобразите уравнение y = –1 + 2 x .
попробуйте
- Следующий пример является линейным уравнением? Почему или почему нет?
Служба обработки текстов Аарона (AWPS) занимается обработкой текста.Стоимость услуг составляет 32 доллара в час плюс единовременная оплата в размере 31,50 доллара. Общая стоимость для клиента зависит от количества часов, необходимых для выполнения работы.
Найдите уравнение, которое выражает общую стоимость через количество часов , необходимых для выполнения работы.
попробуйте
Emma’s Extreme Sports нанимает инструкторов по дельтапланеризму и платит им гонорар в размере 50 долларов за класс, а также 20 долларов за каждого ученика в классе.Общая стоимость, которую платит Эмма, зависит от количества студентов в классе. Найдите уравнение, которое выражает общую стоимость через количество учеников в классе.
Для линейного уравнения y = a + bx , b = наклон и a = y — перехват. Из алгебры напомним, что наклон — это число, которое описывает крутизну линии, а точка пересечения y — это координата y точки (0, a ), где линия пересекает ось y . .
Три возможных графика y = a + bx . (a) Если b > 0, линия наклоняется вверх вправо. (b) Если b = 0, линия горизонтальная. (c) Если b <0, линия наклоняется вниз вправо. Светлана занимается репетитором, чтобы подзаработать в колледже. За каждую сессию репетиторства она взимает единовременную плату в размере 25 долларов плюс 15 долларов за час репетиторства. Линейное уравнение, которое выражает общую сумму денег, которую Светлана зарабатывает за каждое занятие, которое она проводит, составляет y = 25 + 15 x .Какие бывают независимые и зависимые переменные? Что такое пересечение и и какой угол наклона? Интерпретируйте их, используя полные предложения.
попробуйте
Итан ремонтирует бытовую технику, например посудомоечные машины и холодильники. За каждое посещение он берет 25 долларов плюс 20 долларов за час работы. Линейное уравнение, которое выражает общую сумму денег, которую Итан зарабатывает за посещение, составляет y = 25 + 20 x .
Какие бывают независимые и зависимые переменные? Что такое пересечение и и какой угол наклона? Интерпретируйте их, используя полные предложения.
Данные Центров по контролю и профилактике заболеваний.
Данные Национального центра профилактики ВИЧ, ИППП и ТБ.
Самый простой тип ассоциации — это линейная ассоциация. Этот тип взаимосвязи может быть определен алгебраически с помощью используемых уравнений, численно с фактическими или прогнозируемыми значениями данных или графически по построенной кривой. (Линии классифицируются как прямые кривые.) С алгебраической точки зрения линейное уравнение обычно принимает форму y = mx + b , где m и b — константы, x — независимая переменная, y — зависимая переменная.В статистическом контексте линейное уравнение записывается в виде y = a + bx , где a и b — константы. Эта форма используется, чтобы помочь читателям отличить статистический контекст от алгебраического. В уравнении y = a + bx константа b , которая умножает переменную x ( b называется коэффициентом), называется наклоном .Наклон описывает скорость изменения между независимыми и зависимыми переменными; другими словами, скорость изменения описывает изменение, которое происходит в зависимой переменной при изменении независимой переменной. В уравнении y = a + bx константа a называется перехватом y . Графически точка пересечения y — это координата y точки, где график линии пересекает ось y . На данный момент x = 0.
Наклон линии — это значение, которое описывает скорость изменения между независимыми и зависимыми переменными. Наклон сообщает нам, как зависимая переменная ( y ) изменяется в среднем на каждую единицу увеличения независимой ( x ) переменной. Перехват y используется для описания зависимой переменной, когда независимая переменная равна нулю. Графически наклон представлен тремя типами линий в элементарной статистике.
y = a + bx , где a — пересечение y , а b — наклон. Переменная x является независимой переменной, а y — зависимой переменной.
Основные уравнения прямых и плоскостей
Основные уравнения прямых и плоскостейОсновные уравнения прямых и плоскостей
Уравнение прямой
Важной темой школьной алгебры является «уравнение прямой».» Это означает уравнение относительно x и y, множество решений которого представляет собой линию в (x, y) самолет.
Самая популярная форма в алгебре — это форма «наклон-пересечение»
y = mx + b.
Фактически это использует x как параметр и записывает y как функцию от x: y = f (x) = mx + b. Когда x = 0, y = b и точка (0, b) является пересечением прямой с осью Y.
Думая о линии как о геометрическом объекте, а не о графике функции, имеет смысл относиться к x и y более беспристрастно.Общее уравнение для строка (нормальная форма) —
топор + по = c,
с условием, что хотя бы один из a или b ненулевой. Это может легко преобразовать в форму пересечения наклона путем решения для y:
y = (-a / b) + c / b,
, за исключением особого случая b = 0, когда линия параллельна оси y.
Если коэффициенты в нормальной форме умножить на ненулевую константу, множество решений точно такое же, поэтому, например, все эти уравнения имеют ту же строку, что и решение.
2x + 3 y = 4
4x + 6y = 8
-x — (3/2) y = -2
(1/2) x + (3/4) y = 1
В общем, если k — ненулевая константа, то это уравнений для та же строка , так как у них одинаковые решения.
ax + by = c
(ka) x + (kb) y = kc.
Популярный выбор для k в случае, когда c не равно нулю, это k = (1 / с). Тогда уравнение принимает вид
(в / в) х + (б / в) у = 1.
Еще одна полезная форма уравнения — разделить на | (a, b) |, квадратный корень из 2 + b 2 . Этот выбор будет объяснен в разделе Normal Vector.
Упражнение : Если на линии стоит O, покажите, что уравнение принимает вид ax + by = 0 или y = mx.
Упражнение: Найдите пересечения этой прямой с оси координат.
Упражнение : Каково уравнение прямой, проходящей через (0,0) а точка (h, k)?
Нахождение уравнения прямой через 2 точки на плоскости
Для любых двух точек P и Q существует ровно одна прямая PQ, проходящая через точки.Если координаты точек P и Q известны, то коэффициенты a, b, c Уравнение для линии можно найти, решив систему линейных уравнений.
Пример : Для P = (1, 2), Q = (-2, 5) найдите уравнение ax + by = c линейки PQ.
Поскольку точка P находится на прямой, ее координаты удовлетворяют уравнению: a1 + b2 = c,
или a + 2b = c.
Поскольку Q находится на линии, его координаты удовлетворяют уравнению: a (-2) + b5 = c,
или -2 a + 5b = c.
Умножьте первое уравнение на 2 и сложите, чтобы исключить a из уравнения: 4b + 5b = 9b = 2c + c = 3c, поэтому b = (1/3) c.Затем подставляя в первый уравнение, a = c — 2b = c — (2/3) c = (1/3) c.
Это дает уравнение [(1/3) c] x + [(1/3) c} y = c . Почему не решено? Помните, что существует бесконечное количество уравнений для линии, каждая из которых кратна другой. Мы можем вынести c (или установить c = 1 для того же результата) и получите (1/3) x + (1/3) y = 1 как один из вариантов уравнение для линии. Другой вариант: c = 3: x + y = 3 , что очистил знаменатели.
Этот метод всегда работает для любых различных P и Q. Конечно, существует формула для a, b, c также. Это может быть выражено детерминантами , или крестное произведение .
Упражнения : Найдите уравнения этих прямых. Обратите внимание на особые случаи.
Линия через (3, 4) и (1, -2).
Строка через (3, 4) и (-6, -8).
Строка через (3, 4) и (3, 7).
Связь с параметрической формой линии
Для двух точек P и Q точки прямой PQ можно записать как F (t) = (1-t) P + tQ, если t пробегает все действительные числа.Если и P, и Q удовлетворяют одному и тому же уравнение ax + by = c, то вычисление показывает, что это также верно для (1-t) P + tQ для любого выбора t.
Вот это вычисление. Пусть P = (p 1 , p 2 ), Q = (q 1 , q 2 ). Тогда, поскольку точки находятся на линии, мы знаем, что оба
ap 1 + bp 2 = c
aq 1 + bq 2 = c.
Для точки F (t) мы должны проверить a [(1-t) p 1 + tq 1 ] + b [(1-t) p 2 + tq 2 ] = с.Но левую часть можно переставить как (1-t) (ap 1 + bp 2 ) + t (aq 1 + bq 2 ), и это равно (1-t) c + tc = c. Итак уравнение выполнено. Сравните это явное вычисление с данным вычислением для плоскости, которая использует точечное произведение. Вычисления те же, но одно показывает больше деталей, а один скрывает координаты и показывает более концептуальный картина.
Уравнение плоскости
Самолет в 3-м пространстве имеет уравнение
топор + по + cz = d,
, где хотя бы одно из чисел a, b, c должно быть ненулевым.
Что касается линии, если уравнение умножить на любую ненулевую константу k, чтобы получаем уравнение kax + kby + kcz = kd, плоскость решений такая же.
Если c не равно нулю, часто полезно думать о плоскости как о графике функция z от x и y. Уравнение можно переформулировать так:
z = — (a / c) x + (-b / c) y + d / c
Еще один полезный выбор, когда d не равно нулю, — разделить на d так, чтобы константа термин = 1.
(а / д) х + (б / д) у + (в / д) z = 1.
Еще одна полезная форма уравнения — разделить на | (a, b, c) |, квадрат корень 2 + b 2 + c 2 . Этот выбор будет быть объяснено в разделе Вектор нормалей.
Упражнение: Где плоскость ax + by + cz = d пересекает координату топоры?
Упражнение: В чем особенность уравнения плоскости, проходящей через через 0.
Нахождение уравнения плоскости через 3 точки в космос
Даны точки P, Q, R в пространстве, найти уравнение плоскости через 3 точки.
Пример : P = (1, 1, 1), Q = (1, 2, 0), R = (-1, 2, 1). Ищем коэффициенты уравнения ax + by + cz = d, где P, Q и R удовлетворяют уравнениям, таким образом:
a + b + c = d
a + 2b + 0c = d
-a + 2b + c = d
Вычитая первое уравнение из второго и затем добавляя первое уравнение к третьему, мы исключаем a, чтобы получить
b — c = 0
4b + c = 2d
Сложение уравнений дает 5b = 2d или b = (2/5) d, затем решение для c = b = (2/5) d, а затем a = d — b — c = (1/5) d.
Итак, уравнение (с ненулевой константой, которую можно выбрать): d (1/5) x + d (2/5) y + d (2/5) z = d, поэтому один выбор константы дает
х + 2у + 2z = 5
или другой вариант: (1/5) x + (2/5) y + (2/5) z = 1
Учитывая координаты точек P, Q, R, существует формула для коэффициентов плоскость, в которой используются детерминанты или перекрестное произведение .
Упражнение. Какое уравнение плоскости проходит через точки I, J, K?
Упражнение: Каково уравнение плоскости через (1, 1, 1), (-1, 1, -1) и (1, -1, -1)?
Упражнение: сравните этот метод нахождения уравнения плоскости с перекрестным произведением. метод.
Связь с параметрической формой плоскости
Для 3 точек P, Q, R все точки плоскости могут быть записаны в параметрическом образуют F (s, t) = (1 — s — t) P + sQ + tR, где s и t пробегают все действительные числа.
Вычисление, подобное приведенному выше для уравнения линии, показывает, что если P, Q, R все удовлетворяют одному и тому же уравнению ax + by + cz = d, тогда все точки F (s, t) также удовлетворяют тому же уравнению.
Это ключ к пониманию того, что уравнение ax + by + cz = d на самом деле является уравнением плоскости (когда хотя бы один из a, b, c не равен нулю.
Это вычисление здесь производиться не будет, так как оно может быть выполнено гораздо проще. с использованием скалярного произведения .
Вернуться к индексу векторных координат
Уравнение прямой
Уравнение прямой обычно записывают так:
(или «y = mx + c» в Великобритании см. ниже)
Что это означает?
y = насколько выше
x = расстояние от
м = Наклон или градиент (насколько крутая линия)
b = значение y , когда x = 0
Как найти «м» и «б»?
- b легко: просто посмотрите, где линия пересекает ось Y.
- м (Уклон) требует расчета:
| м = Изменение в Y Изменение в X |
Зная это, мы можем составить уравнение прямой:
Пример 1
м = 2 1 = 2
b = 1 (значение y при x = 0)
Итак: y = 2x + 1
Теперь вы можете воспользоваться этим уравнением…
… выберите любое значение для x и найдите соответствующее значение для y
Например, если x равен 1:
y = 2 × 1 + 1 = 3
Убедитесь сами, что x = 1 и y = 3 действительно на линии.
Или мы могли бы выбрать другое значение для x, например 7:
y = 2 × 7 + 1 = 15
Итак, когда x = 7, у вас будет y = 15
Положительный или отрицательный наклон?
Двигаясь слева направо, велосипедист должен пройти P на выезде P Угол наклона:
Пример 2
м = −3 1 = −3
b = 0
Это дает нам y = −3x + 0
Нам ноль не нужен!
Итак: y = −3x
Пример 3: Вертикальная линия
Какое уравнение представляет собой вертикальная линия?
Наклон undefined … а где он пересекает ось Y?
Фактически, это особый случай , и вы используете другое уравнение, а не « y = …», а вместо этого вы используете « x = …».
Как это:
x = 1,5
Каждая точка на линии имеет координату x 1,5 ,
, поэтому ее уравнение x = 1,5
Взлетай и беги
Иногда используются слова «взлетать» и «бегать».
- Подъем — насколько далеко вверх
- Run — это расстояние до
Итак, уклон «м» равен:
м = подъем пробег
Возможно, вам будет легче запомнить.
Другие формы
Мы смотрели на форму «наклон-пересечение». Уравнение прямой можно записать многими другими способами .
Еще одна популярная форма — это уравнение прямой и наклонной линии.
Сноска
Страна Примечание:
В разных странах учат разным «обозначениям» (прислал мне добрые читатели):
| В США, Австралии, Канаде, Эритрее, Иране, Мексике, Португалии, Филиппинах и Саудовской Аравии используется запись: | у = mx + b |
| В Великобритания, Австралия (также), Багамы, Бангладеш, Бельгия, Бруней, Болгария, Кипр, Египет, Германия, Гана, Индия, Индонезия, Ирландия, Ямайка, Кения, Кувейт, Малайзия, Малави, Мальта, Непал , Новая Зеландия, Нигерия, Оман, Пакистан, Перу, Сингапур, Соломоновы Острова, Южная Африка, Шри-Ланка, Турция, ОАЭ, Замбия и Зимбабве | y = mx + c |
| В Афганистан, Албания, Алжир, Бразилия, Китай, Чешская Республика, Дания, Эфиопия, Франция, Ливан, Нидерланды, Косово, Кыргызстан, Норвегия, Польша, Румыния, Южная Корея, Суринам, Испания, Тунис и Вьетнам Нам: | у = ах + Ь |
| В Азербайджане, Китае, Финляндии, России и Украине : | у = kx + b |
| В Греция : | ψ = αχ + β |
| В Италия : | у = mx + q |
| В Япония : | y = mx + d |
| В Куба и Израиль : | y = mx + n |
| В Румыния : | у = gA + C |
| В Латвии и Швеции : | y = kx + m |
| В Сербия и Словения : | у = кх + п |
| В вашей стране: | дайте нам знать! |
… но все это означает одно и то же, только разные буквы.
Графический обозреватель линейных функций (mx + b)
Графический обозреватель линейных функций (mx + b) — Math Open ReferenceСм. Также Общий обозреватель функций, где можно построить до трех функций в виде графиков. по вашему выбору, одновременно используя ползунки для независимых переменных, как указано выше.
Линейные функции
К линейным функциям относятся функции, в которых независимая переменная x никогда не имеет показателя степени.Так, например, в них не будет такой переменной, как 3x 2 . Линейная функция на этой странице — это общий способ напишите уравнение прямой. Это имеет вид
| у = mx + b | Где:
|
Другая форма
Иногда линейное уравнение записывают y = ax + b, используя a для наклона вместо m. Если вы предпочитаете это, используйте Линейный исследователь (топор + b).
Что попробовать
Самый простой корпус.
Y = постоянная. (у = б)- Щелкните «ноль» под каждым ползунком
Поскольку m и b оба установлены в ноль, это график уравнения у = 0х + 0. Это упрощается до y = 0 и, конечно, равно нулю для всех значений x. Следовательно, его график представляет собой горизонтальную прямую линию, проходящую через начало координат.
- Теперь переместите крайний правый ползунок для b и дайте ему установить, скажем, 5.
Линейное уравнение.
(y = mx + b)- Нажмите «сбросить»
- Щелкните «ноль» под правым ползунком b.
Значение m равно 0,5, а b равно нулю, Итак, это график уравнения y = 0,5x + 0, которое упрощается до y = 0,5x. Это простое линейное уравнение, как и прямая линия с наклоном 0,5. То есть y увеличивается на 0.5 каждый раз, когда x увеличивается на единицу. Поскольку наклон положительный, линия идет вверх и вправо. Поскольку b равно нулю, точка пересечения по оси y равна нулю, и линия проходит через начало координат (0,0). Поиграйте с ползунком и наблюдайте за результатами, включая отрицательные значения.
- Нажмите «сбросить» и переместите ползунок b, скажем, на 8.
Значение m равно 0,5, а b равно 8, так что это график y = 0.5x + 8. Эффект изменения b с нуля на 8 заключается в том, что график переместился вверх и теперь проходит через 8 по оси y.
- Переместите оба ползунка и наблюдайте за общими эффектами этих двух коэффициентов (a и b), работающих вместе.
Попробуйте сами
- Нажмите «сбросить», затем «скрыть детали»
- Регулируйте ползунки, пока не увидите линию, которая вам нравится
- Оцените наклон и точку пересечения оси Y линии и запишите уравнение для линии .
- Нажмите «Показать подробности» и посмотрите, насколько близко вы подошли к
Подсказки
- Точка, где линия пересекает (вертикальную) ось Y, является пересечением оси Y — b
- При каждом увеличении на единицу по (горизонтальной) оси x, насколько линия идет вверх или вниз?
Это м, наклон линии - Если линия идет вниз и вправо, наклон (м) будет отрицательным.
 Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2:
Получим точки А(0;2) и В(3;3). Соединим их и получим график функции y= ⅓
x+2: И мы получили три параллельные прямые.
И мы получили три параллельные прямые. График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
График этого уравнения представляет собой прямую линию, параллельую оси OY все точки которой имеют абсциссу x=a.
 [+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. В таких случаях говорят о графическом задании функции. Образование класса элементарных функций. Степенная функция у=х0,5. Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ.
[+] – сложение, [-] – вычитание, [*] – умножение, [:] – деление. В таких случаях говорят о графическом задании функции. Образование класса элементарных функций. Степенная функция у=х0,5. Иовлева Максима Николаевича, учащегося 9 класса РМОУ Радужская ООШ.



 Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций». На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.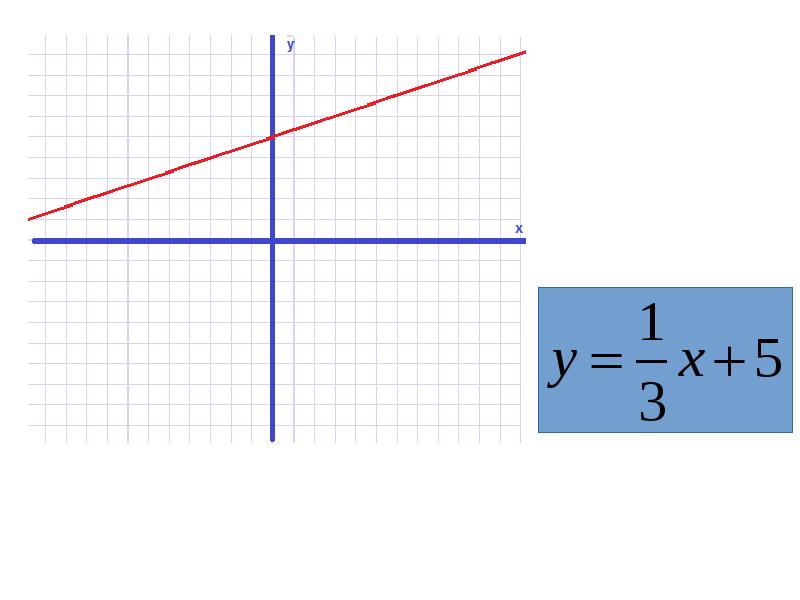 Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций». Здесь пример для y = 2 x (a = 2 > 1).
Здесь пример для y = 2 x (a = 2 > 1).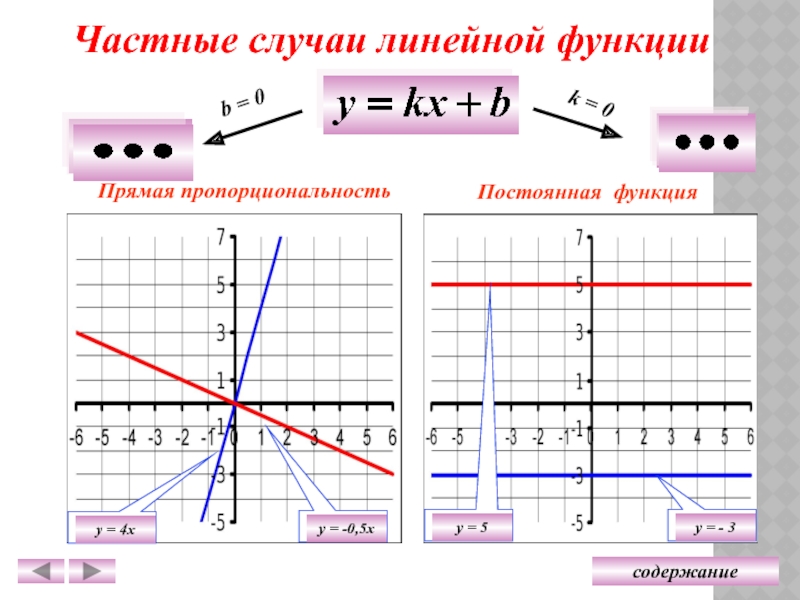 Графики функции существенно зависят от значения параметра a . Здесь пример для y = log 0,5 x (a = 1/2
Графики функции существенно зависят от значения параметра a . Здесь пример для y = log 0,5 x (a = 1/2
