Полная таблица производных элементарных функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое производная и зачем она нужна
Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:
Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю. |
Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке.
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.
у = 10
у′ = 0
Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.
у = 10 + 3х
Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1.
у = 10 + 3х
у′ = 0 + 3
у′ = 3
Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.
Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций.
Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.
Быстрее освоить производные поможет обучение на курсах по математике в онлайн-школе Skysmart.
Производные основных элементарных функций
Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Поэтому приведем стандартную таблицу производных.
Функция f (x) | Производная f’ (х) |
|---|---|
С (т. е. константа, любое число) | 0 |
х | 1 |
xn | nxn-1 |
√x | 1/(2√x) |
sin x | cos x |
cos x | -sin x |
tg x | 1/cos2(х) |
ctg x | -1/sin2x |
ex | ex |
ax | |
ln x | 1/x |
logax | 1/(x * ln a) |
Элементарные функции можно складывать, умножать друг на друга, находить их разность или частное — словом, выполнять любые математические операции.
Но для этого существуют определенные правила.
Общие правила дифференцирования
Для решения задач на дифференцирование нужно запомнить (или записать в шпаргалку) пять несложных формул:
(c ⋅ f)′ = c ⋅ f′
(u + v)′ = u′ + v′
(u — v)′ = u′ — v′
(u ⋅ v)′ = u′v + v′u
(u/v)’ = (u’v — v’u)/v2
В данном случае u, v, f — это функции, а c — константа (любое число).
С константой все просто — ее можно смело выносить за знак производной. Специально запоминать придется лишь формулы, где требуется разделить одну функцию на другую или перемножить их и найти производную от результата.
Например: требуется найти производную функции y = (5 ⋅ x3).
y′ = (5 ⋅ x3)′
Вспомним, что константу, а в данном случае это 5, можно вынести за знак производной:
y′ = (5 ⋅ x3)’ = 5 ⋅ (x3)′ = 5 ⋅ 3 ⋅ х3-1 = 15х2
Правила дифференцирования сложных функций
Конечно, далеко не все функции выглядят так, как в вышеуказанной таблице.
Сложной функцией называют такое выражение, в котором одна функция словно вложена в другую. Производную сложной функции f(y) можно найти по следующей формуле: (f(y))′ = f′(y) ⋅ y′. Другими словами, нужно умножить производную, условно говоря, внешней функции на производную внутренней. |
Пример 1
Найдем производную функции y(x) = (3 + 2x2)4.
Заменим 3 + 2x2 на u и тогда получим y = u4.
Согласно приведенному выше правилу дифференцирования сложных функций у нас получится:
y = y′ u ⋅ u′x = 4u3 ⋅ u’x
А теперь выполним обратную замену и подставим исходное выражение:
4u3 ⋅ u′x = 4 (3 + 2x2)3 ⋅ (3 + 2x2)′ = 16 (3 + 2x2)3 ⋅ х
Пример 2
Найдем производную для функции y = (x3 + 4) cos x.
Для дифференцирования этой функции воспользуемся формулой (UV)′ = U′V + V′U.
y′ = (x3 + 4)′ ⋅ cos x + (x3 + 4) ⋅ cos x′ = 3x2 ⋅ cos x + (x3 + 4) ⋅ (-sin x) = 3x2 ⋅ cos x – (x3 + 4) ⋅ sin x
Формулы для первой производной функции
y есть функция y = y(x)
C = постоянная, производная (y’) постоянной есть 0
y = C => y’ = 0
пример: y = 5, y’ = 0
Если y есть функцией типа y = x
y = xn => y’ = nxn-1
пример: y = x3 y’ = 3x3-1 = 3x2
y = x-3 y’ = -3x-4
Из вышеприведенной формулы мы можем сказать, что для производной y’ функции y = x = x1 that:
если y = x тогда y’=1
y = f1(x) + f2(x) + f3(x) …=>
y’ = f’1(x) + f’2(x) + f’3(x) .
..
Эта формула представляет производную функции, являющейся суммой функций.
Пример: Если мы имеем две функции f(x) = x2 + x + 1 и
g(x) = x5 + 7 и y = f(x) + g(x) тогда y’ = f'(x) + g'(x) =>
y’ = (x2 + x + 1)’ + (x5 + 7)’ = 2x1 + 1 + 0 + 5x4 + 0 = 5x4 + 2x + 1
Если функция есть произведением двух функций, формула производной выглядит так:
y = f(x).g(x) => y’ = f'(x)g(x) + f(x)g'(x)
Если f(x) = C(C есть постоянной) и y = f(x)g(x)
y = Cg(x) y’=C’.g(x) + C.g'(x) = 0 + C.g'(x) = C.g'(x)
y = Cf(x) => y’ = C.f'(x)
Формулы вычисления производной
| y = | y’ = |
|
y = ln x => y’ = 1/x
y = ex => y’ = ex
y = sin x => y’ = cos x
y = cos x => y’ = -sin x
y = tg x => y’ = 1/cos2x
y = ctg x => y’ = —1/sin2x
если функция есть функцией функции: u = u(x)
y = f(u) => y’ = f'(u).
u’
Пример. Пусть у нас есть функция y = sin(x
в этом случае u = x2, f(u) = sin(u), производные есть f'(u) = cos(u), u’ = 2x
y’ = (sin(u))’.u’ = cos(x2).2x = 2.x.cos(x2)
Задачи с производными
1) f(x) = 10x + 4y. Найдите первую производную f'(x)
ОТВЕТ: Мы можем использовать формулу нахождения производной для суммы функций
f(x) = f1(x) + f2(x), f1(x) = 10x, f2(x) = 4y
для функции f2(x) = 4y, y есть постоянной, потому что аргумент f2(x) есть x.
Поэтому f’2(x) = (4y)’ = 0. Отсюда производная функции f(x) есть: f'(x) = 10 + 0 = 10.
| 2) Вычислите производную f(x) = |
ОТВЕТ: у нас есть две функции h(x) = x10 и g(x) = 4.15 + cos x
функция f(x) есть h(x), разделенная на g(x). h'(x) = 10x9 g'(x) = 0 — sin x = -sin x
| f'(x) = |
|
g(x) — h(x).g'(x)| f'(x) = |
| = |
|
3) f(x) = ln(sinx). Какая производная функции f(x)?
ОТВЕТ: Чтобы решить эту задачу, мы можем использовать последнюю формулу.
Как мы видим, f(x) есть функцией двух функций:
f(x) = h(g(x)), где h = ln и g = sin x
Подробнее о производных на страницах математического форума
Форум о производных
Таблица производных простых функций
Пояснение:При каждом приращении аргумента (х) на единицу значение функции (результата вычислений) увеличивается на эту же самую величину. Таким образом, скорость изменения значения функции y = x точно равна скорости изменения значения аргумента.
3. Производная переменной и множителя равна этому множителю
сx´ = с
Пример:
(3x)´ = 3
(2x)´ = 2
Пояснение:
В данном случае, при каждом изменении аргумента функции (х) ее значение (y) растет в с раз. Таким образом, скорость изменения значения функции по отношению к скорости изменения аргумента точно равно величине с.
Откуда следует, что
(cx + b)’ = c
то есть дифференциал линейной функции y=kx+b равен угловому коэффициенту наклона прямой (k).
4. Производная переменной по модулю равна частному этой переменной к ее модулю
|x|’ = x / |x| при условии, что х ≠ 0
Пояснение:
Поскольку производная переменной (см. формулу 2) равна единице, то производная модуля отличается лишь тем, что значение скорости изменения функции меняется на противоположное при пересечении точки начала координат (попробуйте нарисовать график функции y = |x| и убедитесь в этом сами.
Именно такое значение и возвращает выражение x / |x| . Когда x 0 — единице. То есть при отрицательных значениях переменной х при каждом увеличении изменении аргумента значение функции уменьшается на точно такое же значение, а при положительных — наоборот, возрастает, но точно на такое же значение.5. Производная переменной в степени равна произведению числа этой степени и переменной в степени, уменьшенной на единицу
( xc )’= cxc-1, при условии, что xc и сxc-1,определены а с ≠ 0
Пример:
(x2 )’ = 2x
(x3)’ = 3x2
Для запоминания формулы:
Снесите степень переменной «вниз» как множитель, а потом уменьшите саму степень на единицу. Например, для x2 — двойка оказалась впереди икса, а потом уменьшенная степень (2-1=1) просто дала нам 2х. То же самое произошло для x3 — тройку «спускаем вниз», уменьшаем ее на единицу и вместо куба имеем квадрат, то есть 3x2 .
Немного «не научно», но очень просто запомнить.
6. Производная дроби 1/х
(1/х)’ = — 1 / x2
Пример:
Поскольку дробь можно представить как возведение в отрицательную степень
(1/x)’ = (x-1 )’ , тогда можно применить формулу из правила 5 таблицы производных
(x-1 )’ = -1x-2 = — 1 / х2
7. Производная дроби с переменной произвольной степени в знаменателе
( 1 / xc )’ = — c / xc+1
Пример:
( 1 / x2 )’ = — 2 / x3
8. Производная корня (производная переменной под квадратным корнем)
( √x )’ = 1 / ( 2√x ) или 1/2 х-1/2
Пример:
( √x )’ = ( х1/2 )’ значит можно применить формулу из правила 5
( х1/2 )’ = 1/2 х-1/2 = 1 / (2√х)
9. Производная переменной под корнем произвольной степени
( n√x )’ = 1 / ( n n√xn-1 )
.
3+ 1$.
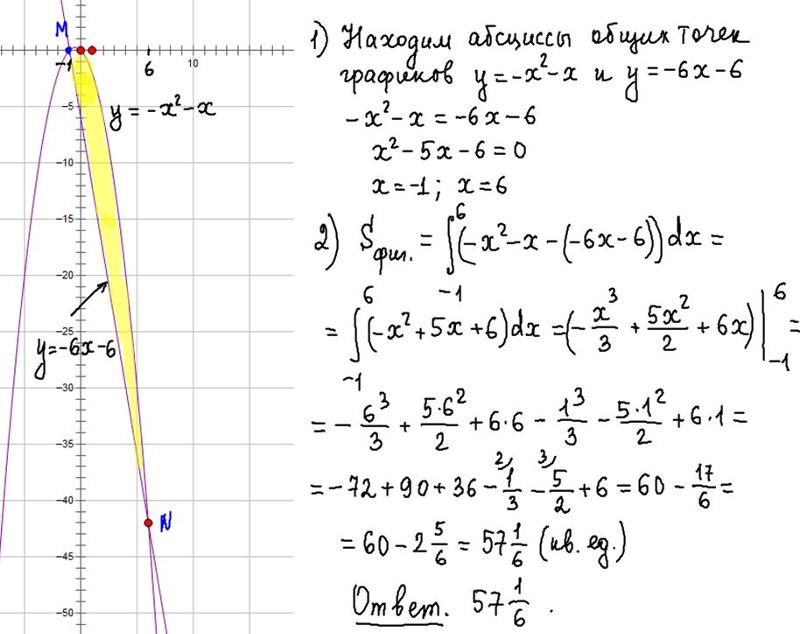
1. Составим таблицу значений:
2. Построим точки. Мы видим, что эти точки симметричны относительно точки с координатами (0,1). В итоге получаем кубическую параболу, смещенную вверх по оси OY (см. рис. 3).
Найти производную неявно заданной функции
Неявная функция — это функция у от аргумента x, заданная уравнением F(x;y)=0, не разрешенным относительно y.
Чтобы найти производную неявно заданной функции:
1. Находим производную по x от левой части уравнения F(x;y)=0, с учетом того, что у — функция от x;
2. Полученное выражение приравниваем к нулю и решаем как уравнение относительно y’, то есть выражаем y’ через y и x.
Примеры. Найти производную неявно заданной функции:
1) x³+xy²+y³=0.
1. Это — неявная функция. Находим производную по x левой части равенства с учетом того, что y — функция от x:
(x³+xy²+y³)’=3x²+x’·y²+(y²)’·x+3y²·y’=3x²+y²+2y·y’·x+3y²·y’
2. Полученное выражение приравниваем к нулю и из него находим y’:
3x²+y²+2y·y’·x+3y²·y’=0
3x²+y²+y'(2xy+3y²)=0
y'(2xy+3y²)=-3x²-y²
2) siny=xy
1.
Приводим зависимость к виду F(x;y)=0. Для этого переносим все слагаемые в левую часть: siny-xy=0. Теперь находим производную по x от левой части (не забывая о том, что y — функция от x):
(siny-xy)’=cosy-(x’·y+y’·x)=cosy-y-xy’.
2. Полученное выражение приравниваем к 0 и находим y’:
cosy-y-xy’=0
xy’=cosy-y
1. Приводим выражение к виду F(x;y)=0:
Теперь находим производную по x левой части (y=y(x)!):
2. Приравниваем получившееся выражение к нулю и решаем уравнение относительно y’:
Примеры для самопроверки. Найти производную неявно заданной функции:
1) xy²+x²y=5;
2) arctg(x+y)=y.
Показать решение
1) 1. xy²+x²y-5=0(xy²+x²y-5)’=x’·y²+(y²)’·x+(x²)’·y+y’·x²-0=y²+2yy’·x+2xy+x²y’=y'(2xy+x²)+y²+2xy.
2. y'(2xy+x²)+y²+2xy=0
y'(2xy+x²)=-y²-2xy
2) arctg(x+y)-y=0
Найдите производную с помощью программы «Пошаговое решение математических задач»
Уравнение y = x 2 + 1 явно определяет y как функцию от x, и
мы покажем это, написав y = f (x) = x 2 + 1.
Если мы запишем уравнение
y = x 2 + 1 в виде y — x 2 -1 = 0, тогда мы говорим, что y
неявно является функцией x. В этом случае мы можем узнать, что это за функция
явно просто решая для y. Однако иногда приходится иметь дело с
уравнения, связывающие y с x, которые настолько сложны, что это трудно или даже
невозможно решить для y через x.(Например, попробуйте найти инь
уравнение y y + xy = 10.) Если уравнение неявно определяет y как
функция от x, есть способ найти dy / dx без предварительного явного нахождения y
как функция от x, называемая неявным дифференцированием.
Мы будем использовать уравнение y — x 2 — 1 = 0, чтобы проиллюстрировать эту технику.
Вместо того, чтобы явно решать для y, предположим, что можно было бы решить
для y через x; назовите получившуюся функцию y (x) для простоты.В
уравнение теперь можно записать как
Дифференцирование обеих сторон по x посредством суммы и степени правил, получаем
Тот же результат можно получить, решив относительно y так, чтобы y = x 2 + 1, откуда dy / dx = 2x.
В этом примере проще сначала решить для y
а затем дифференцировать, но так будет не всегда.
Пример 1
Найдите наклон касательной к графику уравнения xy — x = 1 при эта точка на графике, первая координата которой равна 1 (то есть соответствует x = 1).
Решение
Мы должны найти dy / dx при x = 1. Предположим, y является функцией x, y = y (x). В теперь соотношение xy (x) — x = 1.
Следовательно,
и по правилу расширенной мощности
Подставляя эти результаты в формулу (2), получаем
Решаем это уравнение относительно dy / dx:
Осторожно! При применении формулы (3) имейте в виду, что единственные значения
x и y, которые можно подставить в правую часть формулы (3), равны
те значения, которые удовлетворяют исходному условию 2x 2 + xy — 3y 2 = х.Например, мы могли бы подставить x = 1, y = 4, чтобы получить (dy / dx) = (1 — 4 —
2) / (1 — 12) = 5/1; однако (1, 2) не является точкой на графике 2x 2 + xy — 3y 2 = x, поэтому вычисление dy / dx в этой точке полностью
бессмысленно.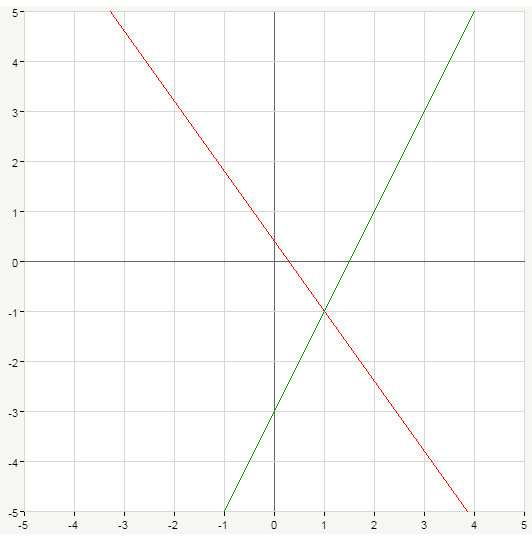
Уравнение в примере 2 можно записать как — 3y 2 + xy + (2x 2 — x) = 0 и, следовательно, является квадратным уравнением относительно y (уравнение вида Ay 2 + By + C = o, где A = -3, B = x и C = 2x 2 — x).Следовательно, мы могли используйте квадратную формулу, чтобы решить это уравнение относительно y через x, получив
Хотя мы можем найти y явно через x, полученный выражение довольно сложное, и все же может быть лучше найти dy / dx неявно, как в Примере 2.
Пример 3 Найти dy / dx, если y 4 + xy = 10.
Решение для y в терминах x в этой задаче сложно, если вообще возможно. Однако неявным дифференцированием получаем
В следующем примере показано, как неявные функции могут использоваться для обосновать тот факт, что dx n / dx = nx n-1 i действительно, когда n рациональное число.
Пример 4 Пусть f (x) = x 2/3 .
Используйте неявное дифференцирование, чтобы
показать это
Поскольку f (x) = x 2/3 , кубизируя, мы получаем
[f (x)] 3 = x 2 .
Дифференцировать по x.
Следовательно,
MATH0043 §2: Вариационное исчисление
MATH0043 §2: Вариационное исчисление Многие проблемы связаны с поиском функции, которая максимизирует или минимизирует интегральное выражение.
Одним из примеров является поиск кривой, дающей кратчайшее расстояние между двумя точками — это, конечно, прямая линия в декартовой геометрии (но можете ли вы это доказать?), Но менее очевидная, если две точки лежат на искривленной поверхности (проблема поиска геодезические .)
Математические методы, разработанные для решения этого типа задач, все вместе известны как вариационное исчисление .
Типичная задача : Рассмотрим определенный интеграл, который зависит от неизвестной функции \ (y (x) \), а также от ее производной \ (y ‘(x) = \ frac {{\ rm d} y} {{ \ rm d} x} \), \ [% \ Renewcommand {\ dx} {{\ rm d} x}
I (y) = \ int_a ^ b ~ F (x, y, y ‘) ~ {\ rm d} x.
\] Типичная задача вариационного исчисления заключается в нахождении конкретной функции \ (y (x) \) для максимизации или минимизации интеграла \ (I (y) \) с учетом граничных условий \ (y (a) = A \ ) и \ (y (b) = B \).
Интеграл \ (I (y) \) является примером функционала , который (в более общем смысле) является отображением набора допустимых функций в вещественные числа.
Мы говорим, что \ (I (y) \) имеет экстремум , когда \ (I (y) \) принимает максимальное или минимальное значение.
Рассмотрим задачу поиска кривой \ (y (x) \) наименьшей длины, которая соединяет две точки \ ((0,0) \) и \ ((1,1) \) на плоскости.2 [a, b] \) такая, что \ (y (a) = A, y (b) = B \), то \ (Y (x) \) удовлетворяет обыкновенному дифференциальному уравнению второго порядка \ [\ label {ele } \ frac {{\ rm d}} {{\ rm d} x} \ left (\ frac {\ partial F} {\ partial y ‘} \ right) — \ frac {\ partial F} {\ partial y} = 0. \]
Уравнение ([ele]) — это уравнение Эйлера-Лагранжа , или иногда просто уравнение Эйлера .
Вам может быть интересно, что означает \ (\ frac {\ partial F} {\ partial y ‘} \): как мы можем дифференцировать по производной? Подумайте об этом так: \ (F \) дается вам как функция трех переменных, скажем, \ (F (u, v, w) \), и когда мы оцениваем функционал \ (I \), мы подключаем \(Икс, y (x), y ‘(x) \) для \ (u, v, w \), а затем проинтегрируем.Производная \ (\ frac {\ partial F} {\ partial y ‘} \) — это просто частная производная от \ (F \) по его второй переменной \ (v \). Другими словами, чтобы найти \ (\ frac {\ partial F} {\ partial y ‘} \), просто представьте, что \ (y’ \) является переменной .
В равной степени существует важное различие между \ (\ frac {{\ rm d} F} {{\ rm d} x} \) и \ (\ frac {\ partial F} {\ partial x} \). Первый является производной от \ (F \) по \ (x \) с учетом того факта, что \ (y = y (x) \) и \ (y ‘= y’ (x) \) равны функции \ (x \) тоже.2 + хуу \ простое \ простое + 2у \ простое \ простое y \ prime + {y \ prime} \ end {align} \] и уравнение Эйлера – Лагранжа имеет вид \ [y + xy ‘+ 2 {y’} ‘= xy’ + 1 \ qedhere \]
\ (Y \), удовлетворяющее уравнению Эйлера – Лагранжа, является необходимым, но не достаточным условием для того, чтобы \ (I (Y) \) было экстремумом.
2 [a, b] \) удовлетворяет \ (\ eta (a) = \ eta (b) = 0 \), так что \ (Y_ \ epsilon (a) = A \) и \ (Y_ \ epsilon (b ) = В \), т.b_a \ frac {{\ rm d} F} {{\ rm d} \ epsilon} (x, Y_ \ epsilon,
Y_ \ epsilon ‘) ~ {\ rm d} x \] Теперь мы используем правило цепочки нескольких переменных, чтобы дифференцировать \ (F \) относительно \ (\ epsilon \). Для общей функции трех переменных \ (F (u (\ epsilon),
v (\ epsilon), w (\ epsilon)) \), три аргумента которого зависят от \ (\ epsilon \), цепное правило говорит нам, что \ [\ frac {{\ rm d} F} {{\ rm d} \ epsilon} = \ frac {\ partial F} {\ partial
u} \ frac {{\ rm d} u} {{\ rm d} \ epsilon} + \ frac {\ partial F} {\ partial
v} \ frac {{\ rm d} v} {{\ rm d} \ epsilon} + \ frac {\ partial F} {\ partial
w} \ frac {{\ rm d} w} {{\ rm d} \ epsilon}.\] В нашем случае первый аргумент \ (x \) не зависит от \ (\ epsilon \), поэтому \ (\ frac {{\ rm d} x} {{\ rm d} \ epsilon} = 0 \) , а поскольку \ (Y_ \ epsilon = Y + \ epsilon \ eta \), мы имеем \ (\ frac {{\ rm d} Y_ \ epsilon} {{\ rm d} \ epsilon} = \ eta \) и \ (\ frac {{\ rm d} Y_ \ epsilon ‘} {{\ rm d} \ epsilon} = \ eta’ \).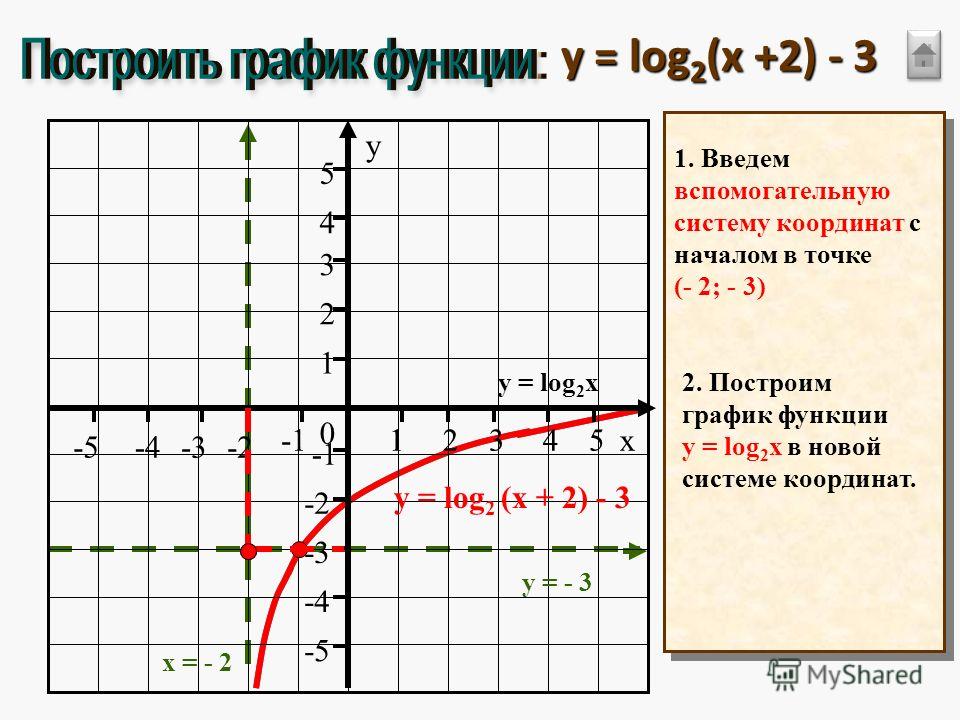
Следовательно, \ [\ frac {{\ rm d} F} {{\ rm d} \ epsilon} (x, Y_ \ epsilon, Y_ \ epsilon ‘) = \ frac {\ partial F} {\ partial
y} \, \ eta (x) + \ frac {\ partial F} {\ partial
y ‘} \, \ eta’ (x). \] Напомним, что \ (\ frac {{\ rm d} I} {{\ rm d} \ epsilon} = 0 \), когда \ (\ epsilon = 0 \) .2 ~ {\ rm d} x, ~~~~~~ y (0) = 0, ~ y (1) = 2, ~~~~ \ left [\ mbox {Ответ:}
~~ y (x) = 2 \ frac {\ sinh {x}} {\ sinh {1}} \ right]. \ qedhere \]
Учитывая \ (y + g \), где \ (y \) — решение из упражнения 1, а \ (g (x) \) — вариант в \ (y (x) \), удовлетворяющий \ (g (0) = g (1) = 0 \), а затем, учитывая \ (I (y + g) \), покажите явно, что \ (y (x) \) минимизирует \ (I (y) \) в упражнении 1. выше. (Подсказка: используйте интегрирование по частям и уравнение Эйлера – Лагранжа, которому удовлетворяет \ (y (x) \), чтобы упростить выражение для \ (I (y + g) \)).b ~ y (x) \ eta (x) ~ {\ rm d} x = 0. \] Тогда \ (y (x) = 0 \) для всех \ (a \ le x \ le b \).
Вот набросок доказательства. Классическим примером вариационного исчисления является поиск брахистохрона , определяемого как гладкая кривая, соединяющая две точки A и B (не под друг другом), по которой частица будет скользить от A к B под действием силы тяжести с максимально возможной скоростью. время.{-1} {\ left (\ sqrt {\ frac {x} {\ alpha}} \ right)} — \ sqrt {x} \ sqrt {\ alpha-x}. \] Эта кривая называется циклоидой . Константа \ (\ alpha \) неявно определяется оставшимся граничным условием \ (y (h) = a \). ([пояс]) называется тождеством Бельтрами или уравнением Бельтрами. Рассмотрим \ [\ label {dif} \ frac {{\ rm d}} {{\ rm d} x} \ left (F- y ‘\ frac {\ partial F} {\ partial y’}
\правильно)
= \ frac {{\ rm d} F} {{\ rm d} x} — {y ‘}’ \ frac {\ partial F} {\ partial y ‘} -y’ \ frac {{\ rm d}} {{\ rm d} х}
\ left (\ frac {\ partial F} {\ partial y ‘} \ right). До сих пор мы имели дело с граничными условиями вида \ (y (a) = A, y (b) = B \) или \ (y (a) = A, y ‘(b) = B \). Для некоторых задач естественные граничные условия выражаются с помощью интеграла. Стандартный пример — Проблема Дидоны : если у вас есть кусок веревки фиксированной длины, какую форму вы должны сделать из него, чтобы охватить как можно большую площадь? Здесь мы пытаемся выбрать функцию \ (y \), чтобы максимизировать интеграл \ (I (y) \), дающий площадь, заключенную в \ (y \), но ограничение фиксированной длины также выражается в терминах интеграла, включающего \ (у \). Вам нужно знать о множителях Лагранжа, чтобы понять это доказательство: см. Раздаточный материал по Moodle (константа \ (\ lambda \) окажется множителем Лагранжа). Предположим, что \ (I (Y) \) является максимумом или минимумом при условии \ (J (y) = L \), и рассмотрим двухпараметрическое семейство функций, заданное как \ [Y (x) + \ epsilon \ eta (x) + \ delta \ zeta (x) \], где \ (\ epsilon \) и \ (\ delta \) — константы, а \ (\ eta (x) \) и \ (\ zeta (x) \) — дважды дифференцируемые функции такие, что \ (\ eta (a) = \ zeta (a) = \ eta (b) = \ zeta (b) = 0 \), с \ (\ zeta \), выбранным так, чтобы \ (Y + \ epsilon \ eta + \ delta \ zeta \) подчиняется интегральному ограничению.б G (х, Y + \ эпсилон \ eta +
\ delta \ zeta, Y ‘+ \ epsilon \ eta’ + \ delta \ zeta ‘) \, {\ rm d} x. \] Поскольку \ (I \) имеет максимум или минимум в \ (Y (x) \ ) при условии \ (J = L \), в точке \ ((\ epsilon, \ delta) \) = \ ((0,0) \) наша функция \ (I [\ epsilon, \ delta] \) принимает экстремальное значение при условии \ (J [\ epsilon, \ delta] = L \). Из теории множителей Лагранжа следует, что необходимое условие для функции \ (I [\ epsilon, \ delta] \) двух переменных с ограничением \ (J [\ epsilon, \ delta] = L \) на принять экстремальное значение в \ ((0,0) \), если существует постоянная \ (\ lambda \) (называемая множителем Лагранжа) такая, что \ [\ begin {align}
\ frac {\ partial I} {\ partial \ epsilon} + \ lambda \ frac {\ partial
J} {\ partial \ epsilon} & = 0 \\
\ frac {\ partial I} {\ partial \ delta} + \ lambda \ frac {\ partial
J} {\ partial \ delta} & = 0 \ end {align} \] в точке \ (\ epsilon = \ delta = 0 \).b \ eta \ left (\ frac {\ partial} {\ partial y} \ left (F + \ lambda G \ right) —
\ frac {{\ rm d}} {{\ rm d} x} \ left (\ frac {\ partial} {\ partial y ‘} \ left (F + \ lambda G \ right)
\ right) \ right) \, {\ rm d} x ~~~~ \ mbox {(интегрирование по частям)} \\
& & \\
& = & 0 ~~~~~ {\ mbox {когда $ \ epsilon = \ delta = 0 $, неважно, что такое $ \ eta $.}} \ End {align} \] Так как это верно для любого \ (\ eta \), по FLCV (лемма [flcv]) получаем \ [(F_y + \ lambda G_y) (x, Y, Y ‘) + \ frac {{\ rm d}} {{\ rm d} x} (F_ {y ‘} + \ lambda G_ {y’})
(x, Y, Y ‘) = 0 \], что означает, что \ (Y \) является решением уравнения Эйлера – Лагранжа для \ (K \), как и требуется. (Конструкция загона для овец): Забор длиной \ (l \) должен быть прикреплен к прямой стене в точках A и B (на расстоянии \ (a \) друг от друга, где \ (a Существует множество вводных учебников по вариационному исчислению, но большинство из них содержит гораздо больше математических деталей, необходимых для MATH0043.Если вы хотите узнать больше о теории, в библиотеке имеется вариационное исчисление Гельфанда и Фомина. Менее технический источник — глава 9 Boas Mathematical Methods in the Physical Sciences . В сети есть много кратких вводных сведений о вариационном исчислении, например , хотя все они описываются гораздо более подробно, чем нам нужно в MATH0043. пригодится в качестве напоминания о множителях Лагранжа. Это эссе вводит Дифференциация . Производная позволяет нам вычислить наклон или касательную графика в любой точке P. Процесс, с помощью которого находится производная, называется дифференцированием . График ниже представляет собой простую параболу, уравнение которой имеет вид y = x 2 . Производной присвоен символ . Это произносится как d y на d x или dy dx . Можно показать, что если y = x 2 , то производная равна . dy / dx = 2x Итак, для этой кривой, когда x = 1, наклон равен 2; наклон при x = 3 равен 6. Производная этой кривой равна dy / dx = 3x 2 . Когда x = -1, dy / dx = 3; когда x = 2, dy / dx = 12. Производная числа равна нулю. ax n — это функция, состоящая из числа (a), умноженного на x в степени n. Чтобы найти производную этой функции, умножьте число на степень (an) и уменьшите степень индекса на 1. (i) y = 3x 3 ; (ii) y = 1 / x; (iii) y = 2√x. Используя формулу для производной (dy / dx = тревога n-1 ), мы можем показать, что (i) когда y = 3x 3 , dy / dx = 9x 2 Когда y = -2x 3 , dy / dx = -6x 2 . Для x = -2, dy / dx = -24. y = 3x можно записать y = 3x 1 ; dy / dx = 3x 0 = 3 , что является константой. y = 2 можно записать y = 2x 0 , dy / dx = 0 (другая константа). «Кривая» y = 2 — это прямая линия, параллельная оси x (нулевой наклон). Если две функции складываются вместе, их можно дифференцировать по отдельности и складывать производные.Если вычесть две функции, их можно дифференцировать отдельно и вычесть производные. (i) Для функции y = 4x 2 + 2x + 3 производная равна dy / dx = 8x + 2 (ii) Для функции x 5 — 5 / x производная равна dy / dx = 5x 4 + 5 / x 2 Производная синуса — косинус. Умножьте полученный косинус на производную функции внутри исходного синуса.Производная косинуса минус синус. Умножьте полученный синус на производную функции внутри исходного косинуса. (i) y = Sin (x) ; dy / dx = Cos (x) (ii) y = 3Cos (2x) ; dy / dx = -6Sin (2x) (iii) y = Sin (x 2 ) ; dy / dx = 2xCos (x 2 ) (iv) y = x — Cos (x) ; y = 1 + Sin (x) Если две функции перемножаются, производная находится следующим образом. Это продукт (uv), поэтому мы используем приведенную выше формулу для дифференциации продуктов. dy / dx = xCos (x) + Sin (x) . y = (x 2 + 1) √x 3 можно записать y = (x 2 + 1) x (3/2) Используя формулу дифференциации продуктов, dy / dx = (x 2 + 1) (3/2) x (1/2) + x (3/2) (2x)
= (3/2) (x 2 + 1) √x + 2x√x 3 Если две функции разделены, производная находится следующим образом. Функция знаменателя (та, которая находится под линией) умножается на производную функции числителя (та, которая находится над линией).Функция числителя умножается на производную функции знаменателя. Эти два новых члена вычитаются вместе и делятся на квадрат исходного знаменателя. y = Tan (x) можно записать как y = Sin (x) / Cos (x) . Это частное. dy / dx = [Cos (x) .Cos (x) — Sin (x) .- Sin (x)] / Cos 2 (x) , (используя приведенную выше формулу частного) = [Cos (х).Cos (x) + Sin (x) .Sin (x)] / Cos 2 (x) =
[Cos 2 (x) + Sin 2 (x)] / Cos 2 (x) = 1 / Cos 2 (x) Обратная величина косинуса называется секущей (Sec): 1 / Cos (x) = Sec (x). Использование формулы частного для y = Sin (x) / (x 2 + 1) , dy / dx = [(x 2 + 1) Cos (x) — 2xSin (x)] / [(x 2 + 1) 2 ] Когда x = 0, dy / dx = (0 + 1 — 0) / (0 + 1) 2 = 1/1 = 1. Если в y есть функция, ее все еще можно дифференцировать. Дифференцируйте его, как и раньше, затем умножьте на dy / dx. Это уравнение можно решить относительно y, а затем дифференцировать. Но проще использовать неявное дифференцирование: 2x + 2y (dy / dx) = 0 . Перестановка дает: dy / dx = -2x / 2y = — x / y В точке x = 0, y = -2, dy / dx = 0. Неявное дифференцирование дает (dy / dx) Cos (y) = 2x .Переставляем на (dy / dx) = 2x / Cos (y) . Помня, что Cos 2 (y) + Sin 2 (y) = 1, мы можем сказать, что Cos (y) = √ [1 — Sin 2 (y)] . Подстановка дает (dy / dx) = 2x / √ [1 — Sin 2 (y)]
= 2x / √ [1 — x 4 ] . Производная равна dy / dx = -1 / [1 — x 2 ] 1/2 . Принятие значения x = 0,5 дает dy / dx = -1 / [1 — 0,5 2 ] 1/2 = -1,154. Производная натурального логарифма функции — это обратная величина функции, умноженная на производную функции. Это просто равно dy / dx = 1 / x . Использование приведенной выше формулы дает dy / dx = (1 / Cos (x)).-Sin (x) = -Sin (x) / Cos (x) = -Tan (x) Для различения более сложных функций можно использовать логарифмы: 2 y = 3 Sin (x) не может быть дифференцирован как есть. Мы можем брать логарифмы с обеих сторон: Ln (2 y ) = Ln (3 Sin (x) ) . Помня логарифмические правила индексов, мы можем переписать это как: yLn (2) = Sin (x) Ln (3) .Теперь это можно неявно дифференцировать: (dy / dx) Ln (2) = Ln (3) Cos (x) , что дает dy / dx = Ln (3) Cos (x) / Ln (2) . Производная числа, возведенного в степень функции, — это число, возведенное в функцию, умноженную на производную функции, умноженную на логарифм числа. Если число равно e, производная функции просто умножается на e и возводится в функцию. Используя приведенную выше формулу для y = 2 3x дает dy / dx = 3.Ln (2) .2 3x . Пример 18: Различайте следующие функции: (i) y = e Sin (x) ,
(ii) y = e x . (i) Использование приведенной выше формулы для y = e Sin (x) дает dy / dx = Cos (x) .e Sin (x) . (ii) Производная y = e x равна dy / dx = e x . Прежде чем дать формулу и метод, я определю следующие сокращенные термины: Формула Ньютона для приближений имеет следующий вид: где f (x) — функция, которую необходимо решить, а a — предположение о решении. Это значение для x основано на значении, выбранном для a.Чем лучше исходное предположение для a, тем ближе x будет к правильному значению. Если предположение a не близко к правильному значению, эта формула может вообще не работать. Затем новое значение x можно вставить в формулу, и процесс будет повторяться до тех пор, пока не будет достигнута желаемая точность. Чем ближе предполагаемое значение (а) к правильному значению, тем меньше раз потребуется использовать формулу. Такой повторяющийся процесс называется итерацией . Некоторые примеры покажут, как работает формула. Это означает решение уравнения x 2 = 10 , которое можно преобразовать в x 2 — 10 = 0 . Теперь это в желаемом формате, f (x) = 0 . Функция f (x) имеет значение: f (x) = x 2 -10 Следовательно, производная функции F (x) равна: . Глядя на уравнение («путем проверки»), мы знаем, что решение этого уравнения близко к 3 (потому что 3 2 = 9), поэтому мы устанавливаем значение первого предположения, a, равным 3.Затем мы можем записать компоненты, необходимые для использования формулы Ньютона: По формуле Ньютона: x приблизительно = a — f (a) / F (a) = 3 — f (3) / F (3) = 3 — (-1 / 6) = 3 + 1/6 = 3,1666 Мы начали с предположения, что x равно 3, и в итоге получили лучшее приближение (3,1666). Повторное использование формулы Ньютона дает: x приблизительно = a — f (a) / F (a) = 3,1666 — f (3,1666) / F (3,1666) = 3,1666 — (0,0273 / 6,3332) = 3,1622 Повторение процесса с новым значением дает третье значение x как 3,1623 с точностью до четырех знаков после запятой.После трехкратного использования формулы ответ получится как x = 3,162 с точностью до трех десятичных знаков. Начнем с записи функции и ее производной: f (x) = x 3 — 5x + 3 и F (x) = 3x 2 — 5 Посмотрев на уравнение, мы можем увидеть, что f (1) = -1 и f (2) = 1, поэтому должно быть значение, близкое к 2, что даст f (x) = 0. По формуле Ньютона: x приблизительно = a — f (a) / F (a) = 2 — f (2) / F (2) = 2 — (1/7) = 1,857 Это означает, что 1,857 является более близким приближением к значению x, чем было 2.Теперь мы можем установить 1.857 и снова запустить процесс: По формуле Ньютона (второй раз): x приблизительно = a — f (a) / F (a) = 1,857 — f (1,857) / F (1,857) = 1,857 — (0,1187 / 5,3453) = 1,834 Используя это значение: По формуле Ньютона (третий раз): x приблизительно = a — f (a) / F (a) = 1,834 — f (1,834) / F (1,834) = 1,834 — (-0,0012 / 5,0906) = 1,834 Таким образом, к третьей итерации значение установилось (с точностью до трех десятичных знаков) на x = 1,834. Кубические уравнения обычно имеют три корня. Существует еще одно значение x, которое можно найти, установив для предположения (a) значение -2. Читателю будет приятно узнать, что я оставлю это в качестве упражнения. Не существует простого метода алгебраического решения этого уравнения.Мы могли бы сделать это графически, построив графики y = Cos (x) и y = x на одном листе бумаги и найдя значение x там, где они пересекаются. Это показано на схеме ниже. Путем перестановки получаем Cos (x) — x = 0 , поэтому мы можем записать функцию и ее производную как f (x) = Cos (x) — x и F (x) = -Sin (x) — 1 соответственно Из нашего знания косинуса мы знаем, что его значение колеблется между y = 1 и y = -1 для всех значений x. Напоминаем, что при дифференцировании тригонометрических функций мы должны работать в радианах, , а не в градусах. Итак, теперь мы можем оценить компоненты формулы Ньютона. По формуле Ньютона: x приблизительно = a — f (a) / F (a) = 1 — f (1) / F (1) = 1 — (-0,4596 / -1,8414) = 0,7504 Используя это значение: Воспользовавшись формулой Ньютона второй раз: x приблизительно = a — f (a) / F (a) = 0,7504 — f (0,7504) / F (0,7504) = 0,7504 — (-0,0189 / -1,6819) = 0,7391 Используя это новое значение: Из вышесказанного видно, что значение f (0. Следовательно, с точностью до трех десятичных знаков x = 0,739 после трех итераций. Если существует связь между пройденным расстоянием (с) и временем (t), то производная расстояния по времени, ds / dt , дает скорость (v) в любое время. Скорость, v, определяется как ds / dt, поэтому мы продифференцируем приведенное выше уравнение относительно t: v = ds / dt = 4t — 3 . Если существует связь между скоростью частицы (v) и временем (t), то производная v по t, dv / dt , дает ускорение (a) при любом время. Ускорение a определяется как dv / dt, поэтому мы дифференцируем приведенное выше уравнение относительно t: а = dv / dt = 4 . Ускорение постоянное и составляет 4 м / с 2 . Если существует связь между энергией (E) и временем (t), то производная E по t, dE / dt , дает мощность (P) в любой момент. Мощность P определяется как dE / dt, поэтому мы продифференцируем приведенное выше уравнение относительно t: P = dE / dt = 3t 2 . Таким образом, мощность через 2 секунды составляет 12 Вт. Таким образом, дифференциация является одним из самых мощных инструментов математики и физики. Похоже, вы используете устройство с «узкой» шириной экрана ( i. К этому моменту мы сделали довольно много производных, но все они были производными функций вида \ (y = f \ left (x \ right) \).К сожалению, не все функции, которые мы собираемся рассмотреть, попадут в эту форму. Давайте взглянем на пример такой функции. На самом деле есть два метода решения этой проблемы. Это простой способ решить проблему. Итак, это сделать достаточно просто. Однако есть некоторые функции, для которых это невозможно. Вот здесь и вступает в игру второй метод решения. В этом случае мы оставим функцию в той форме, которую нам дали, и будем работать с ней в этой форме. Однако давайте вспомним из первой части этого решения, что если бы мы могли решить для \ (y \), то мы получили бы \ (y \) как функцию от \ (x \).Другими словами, если бы мы могли решить для \ (y \) (как мы могли бы в этом случае, но не всегда сможем это сделать), мы получим \ (y = y \ left (x \ right) \). Давайте перепишем уравнение, чтобы это отметить. Будьте осторожны и заметьте, что когда мы пишем \ (y \ left (x \ right) \), мы не имеем в виду \ (y \) раз \ (x \). Следующим шагом в этом решении является дифференцирование обеих сторон относительно \ (x \) следующим образом: Правая сторона легкая. Это просто производная от константы. Левая сторона также проста, но мы должны признать, что у нас действительно есть продукт, \ (x \) и \ (y \ left (x \ right) \). Итак, чтобы произвести производную от левой части, нам нужно выполнить правило продукта.Это дает Теперь напомним, что у нас есть следующий способ записи производной. Используя это, мы получаем следующее: Обратите внимание, что мы уронили \ (\ left (x \ right) \) на \ (y \), поскольку он был там только для того, чтобы напомнить нам, что \ (y \) было функцией \ (x \), и теперь что мы взяли производную, она больше не нужна. Итак, давайте теперь вспомним, что нам было нужно. Мы искали производную \ (y ‘\) и заметили, что теперь в уравнении есть \ (y’ \). Итак, чтобы получить производную, все, что нам нужно сделать, это решить уравнение для \ (y ‘\). Вот оно. Это наш ответ, используя второй метод решения.{2}}} \] , что мы и получили от первого решения. Независимо от используемой техники решения, мы должны получить одну и ту же производную. Процесс, который мы использовали во втором решении предыдущего примера, называется неявным дифференцированием и является предметом этого раздела. В предыдущем примере мы смогли просто решить для \ (y \) и избежать неявного дифференцирования. Однако в оставшихся примерах в этом разделе мы либо не сможем решить для \ (y \), либо, как мы увидим в одном из примеров ниже, ответ не будет в форме, которую мы могу разобраться. Во втором решении выше мы заменили \ (y \) на \ (y \ left (x \ right) \), а затем сделали производную. Напомним, мы сделали это, чтобы напомнить нам, что \ (y \) на самом деле является функцией \ (x \). Мы будем делать это довольно часто в этих задачах, хотя на самом деле мы редко пишем \ (y \ left (x \ right) \). Итак, прежде чем мы фактически займемся проблемами неявного дифференцирования, давайте сделаем быстрый набор «простых» производных, которые, мы надеемся, помогут нам в создании производных функций, которые также содержат \ (y \ left (x \ right) \).{у \ влево (х \ вправо)}} \) Показать все решения Скрыть все решения Они написаны немного иначе, чем мы привыкли здесь видеть. Это потому, что мы хотим сопоставить эти проблемы с тем, что мы будем делать в этом разделе. Кроме того, каждая из этих частей имеет несколько функций, которые нужно различать, начиная с конкретной функции, за которой следует общая функция. Это опять же, чтобы помочь нам с некоторыми конкретными частями процесса неявной дифференциации, который мы будем делать. и это всего лишь цепное правило. Мы дифференцировали внешнюю функцию (показатель степени 5), а затем умножили это на производную внутренней функции (материал внутри скобок). Для второй функции мы проделаем в основном то же самое. Нам нужно будет использовать цепное правило. Внешняя функция по-прежнему имеет показатель степени 5, а внутренняя функция на этот раз просто \ (f \ left (x \ right) \). У нас нет здесь конкретной функции, но это не значит, что мы не можем, по крайней мере, записать цепное правило для этой функции.4} е ‘\ влево (х \ вправо) \] На самом деле мы не знаем, что такое \ (f \ left (x \ right) \), поэтому, когда мы делаем производную внутренней функции, все, что мы можем сделать, это записать обозначение для производной, , т.е. \ (f ‘ \ влево (х \ вправо) \). В последней функции мы просто заменили \ (f \) во второй функции на \ (y \), поскольку большая часть нашей работы в этом разделе будет включать \ (y \) вместо \ (f \). Первая функция, которую нужно дифференцировать здесь, — это снова проблема с правилом быстрой цепочки, так что вот ее производная, Для второй функции на этот раз мы не стали использовать \ (f \ left (x \ right) \) и просто перешли прямо к \ (y \ left (x \ right) \) для общей версии.Это пока всего лишь общая версия того, что мы сделали для первой функции. Внешняя функция по-прежнему является синусом, а внутренняя задается как \ (y \ left (x \ right) \), и хотя у нас нет формулы для \ (y \ left (x \ right) \), поэтому мы на самом деле не может взять его производную, у нас есть обозначение для ее производной. Вот производная для этой функции, В этой части мы просто дадим ответы по каждому из них и опустим объяснение, которое у нас было в первых двух частях. Итак, в этом наборе примеров мы просто решали некоторые задачи с цепными правилами, где внутренняя функция была \ (y \ left (x \ right) \) вместо конкретной функции. Этот вид производной постоянно проявляется при неявном дифференцировании, поэтому нам нужно убедиться, что мы можем их выполнять. Также обратите внимание, что мы сделали это только для трех типов функций, но есть гораздо больше видов функций, которые мы могли бы использовать здесь. Итак, пришло время решить нашу первую задачу, где требуется неявное дифференцирование, в отличие от первого примера, где мы могли бы фактически избежать неявного дифференцирования, решая для \ (y \).2}} \] Перед тем, как приступить к этой задаче, мы заявили, что здесь нам нужно выполнить неявное дифференцирование, потому что мы не можем просто решить для \ (y \), и тем не менее это то, что мы только что сделали. Итак, почему мы не можем использовать здесь «нормальную» дифференциацию? Проблема в «\ (\ pm \)». На этом этапе мы можем отбросить часть \ (\ left (x \ right) \), поскольку это было только в задаче, чтобы помочь с процессом дифференцирования. Последний шаг — просто решить получившееся уравнение для \ (y ‘\). В отличие от первого примера, мы не можем просто подключить \ (y \), так как мы не знаем, какую из двух функций использовать.2} = 9 \] в точке \ (\ left ({2, \, \, \ sqrt 5} \ right) \). Во-первых, обратите внимание, что в отличие от всех других задач касательной, которые мы решали в предыдущих разделах, нам нужно задавать значения как \ (x \), так и \ (y \) точки. Напомним, что для записи касательной все, что нам нужно, — это наклон касательной, и это не что иное, как производная, вычисленная в данной точке.У нас есть производная от предыдущего примера, поэтому все, что нам нужно сделать, это подключить данную точку. Тогда касательная прямая. А теперь давайте поработаем еще несколько примеров. В остальных примерах мы больше не будем писать \ (y \ left (x \ right) \) вместо \ (y \).Это просто то, что мы делали, чтобы напомнить себе, что \ (y \) на самом деле является функцией \ (x \), чтобы помочь с производными. Есть простой способ запомнить, как применять цепное правило в этих задачах.Цепное правило действительно говорит нам дифференцировать функцию, как мы обычно это делали бы, за исключением того, что нам нужно добавить производную от внутренней функции. При неявном дифференцировании это означает, что каждый раз, когда мы дифференцируем терм с \ (y \) в нем, внутренняя функция — это \ (y \), и нам нужно будет добавить \ (y ‘\) к члену, поскольку это будет — производная внутренней функции. Давайте посмотрим на пару примеров. Сначала дифференцируйте обе стороны относительно \ (x \) и помните, что каждый \ (y \) на самом деле \ (y \ left (x \ right) \), мы просто больше не собираемся писать его таким образом. Мы разграничили эти виды функций, включающих \ (y \) ’, в степень с помощью цепного правила в Примере 2 выше. Также вспомните обсуждение этой проблемы до начала. При решении такой задачи цепного правила все, что нам нужно сделать, это дифференцировать \ (y \) как нормальные, а затем добавить \ (y ‘\), который является не чем иным, как производной от «внутренней функции ».2} г ‘\] Теперь все, что нам нужно сделать, это найти производную \ (y ‘\). Это всего лишь базовая решающая алгебра, которую вы можете делать. Основная проблема в том, что это может быть более беспорядочно, чем то, к чему вы привыкли. Все, что нам нужно сделать, это получить все члены с \ (y ‘\) в них с одной стороны и все термины без \ (y’ \) с другой. Затем вычлените \ (y ‘\) из всех членов, содержащих его, и разделите обе части на «коэффициент» \ (y’ \). Вот решение для этого, Алгебра в этих задачах может быть довольно запутанной, так что будьте осторожны. С этой проблемой нужно быть осторожнее. У нас есть пара правил цепочки, с которыми нам придется иметь дело здесь, которые немного отличаются от тех, с которыми мы имели дело до этой проблемы. И в экспоненте, и в логарифме у нас есть «стандартное» цепное правило, заключающееся в том, что внутри экспоненты и логарифма есть нечто иное, чем просто \ (x \) или \ (y \). Итак, это означает, что здесь мы будем применять правило цепочки, как обычно, а затем, когда мы будем выполнять производную внутренней функции для каждого члена, нам придется иметь дело с дифференцированием \ (y \) ‘s.{- 1}}}} \ end {align *} \] Обратите внимание, что для того, чтобы производная хотя бы выглядела немного лучше, мы преобразовали все дроби в отрицательные показатели. Хорошо, мы видели одно применение неявного дифференцирования в приведенном выше примере касательной. Однако есть еще одно приложение, которое мы увидим в каждой проблеме в следующем разделе. В некоторых случаях у нас будет две (или более) функции, каждая из которых является функциями третьей переменной.Итак, у нас могут быть \ (x \ left (t \ right) \) и \ (y \ left (t \ right) \), например, и в этих случаях мы будем дифференцировать по \ (t \) . Это просто неявное дифференцирование, как мы делали в предыдущих примерах, но есть разница. В предыдущих примерах у нас есть функции, включающие \ (x \) ’s и \ (y \)’ s, и считающие \ (y \) как \ (y \ left (x \ right) \). В этих задачах мы дифференцировали по \ (x \), и поэтому, когда мы столкнулись с \ (x \) в функции, которую мы дифференцировали как нормальную, и когда столкнулись с \ (y \), мы дифференцировались как нормальные, за исключением того, что тогда добавил \ (y ‘\) к этому термину, потому что мы действительно применяли цепное правило. В новом примере, который мы хотим рассмотреть, мы предполагаем, что \ (x = x \ left (t \ right) \) и что \ (y = y \ left (t \ right) \) и производим дифференцирование по \ (т \). Эти новые типы проблем на самом деле аналогичны задачам, которые мы обсуждали в этом разделе.{1 — x}} + 5y ‘\ sin \ left ({5y} \ right) = 2yy’ \] В этой проблеме действительно не так уж и много. Поскольку в задаче есть две производные, мы не будем пытаться решить одну из них. Когда мы займемся такого рода проблемами в следующем разделе, проблема будет подразумевать, какую из них нам нужно решить. На данный момент, похоже, нет реальной причины для решения такого рода задач, но, как мы увидим в следующем разделе, каждая задача, которую мы будем там решать, будет включать в себя такого рода неявную дифференциацию.y $ нам нужно знать, что функция $ y $ имеет a
производная. В примере $ y = \ ln x $ используется неявно определенная обратная функция,
но другие функции могут быть определены неявно, а иногда и один
уравнение можно использовать для неявного определения более чем одного
функция.2) \ cr
0 & = 2x + 2yy ‘\ cr
y ‘& = {- 2x \ over 2y} = — {x \ over y} \ cr
} $$
Теперь у нас есть выражение для $ y ‘$, но оно содержит $ y $, а также
$ x $. Это означает, что если мы хотим вычислить $ y ‘$ для некоторого конкретного
значение $ x $ мы должны знать или вычислить $ y $ при этом значении $ x $ как
Что ж. Именно в этот момент нам нужно знать, является ли $ y $
$ U (x) $ или $ L (x) $. Иногда оказывается, что мы можем избежать
явное использование $ U (x) $ или $ L (x) $ по характеру проблемы. В случае круга можно найти функции $ U (x) $
и $ L (x) $ явно, но есть потенциальные преимущества использования
в любом случае неявная дифференциация. В некоторых случаях это сложнее или
невозможно найти явную формулу для $ y $ и неявную
дифференцирование — единственный способ найти производную. Пример 4.8.y = x $ для $ y $, поэтому, возможно, после вычисления производной мы получим
то, что сложно решить за $ y ‘$. На самом деле это никогда
бывает. Все вхождения $ y ‘$ происходят из-за применения цепного правила,
и всякий раз, когда используется цепное правило, он вносит один $ y ‘$
умноженный на какое-то другое выражение. Так что всегда можно будет
сгруппируйте термины, содержащие $ y ‘$, и вычтите $ y’ $ за скобки, просто
как в предыдущем примере. Если вы когда-нибудь получите что-то более сложное
вы сделали ошибку и должны исправить ее, прежде чем пытаться продолжить. Пример 4.8.4 $ \ ds 4 \ соз х \ грех у = 1 $
(отвечать) Пример 4.8.5 $ \ ds \ sqrt {x} + \ sqrt {y} = 9 $.
(отвечать) Пример 4.8.6 $ \ ds \ tan (х / у) = х + у $
(отвечать) Пример 4.8.7 $ \ ds \ sin (х + у) = ху $
(отвечать) Пример 4.8.8 $ \ ds {1 \ over x} + {1 \ over y} = 7 $
(отвечать) Пример 4.8.9 Гипербола, проходящая через $ (8,6) $, состоит из всех точек, расстояние до которых
от начала координат на константу больше, чем расстояние от точки (5,2).2 = 9 $ — эллипс.
Найдите прямые, касательные к этой кривой в двух точках.
точки пересечения с осью $ x $. Покажите, что эти строки
параллельно.
(отвечать) Пример 4.8.13 Повторите предыдущую задачу для точек, в которых
эллипс пересекает ось $ y $.
(отвечать) Пример 4.8.14 Найдите на эллипсе точки из двух предыдущих задач.
где наклон горизонтальный, а где вертикальный. Пример 4.8.21 Предположим, что $ m \ neq 0 $. Покажите, что семейство кривых
$ \ ds \ {y = mx + b \ mid b \ in \ R \} $ ортогонален
семейство кривых $ \ ds \ {y = — (x / m) + c \ mid c \ in \ R \} $. Содержание | Дом Производная. Урок 5, раздел 2: Проблемы Вернуться в раздел 1 Производная от f ( x ) = 2 x — 5 Уравнение касательной к кривой Производная от f ( x ) = x 3 Проблема 1.Пусть f ( x ) = 2 x — 5. a) Запишите коэффициент разности и упростите его. Чтобы увидеть ответ, наведите указатель мыши на цветную область. b) Оцените f ‘ ( x ) при x = 9 и x = −9. согласно теореме 4 урока 2. Скорость изменения f ( x ) равна 2 для всех значений x . f ‘ ( x ) постоянно. Но это должно быть очевидно. y = 2 x — 5 — это уравнение прямой линии, у которой наклон равен 2. (Тема 9 Precalculus). А значение наклона прямой — это скорость изменения y относительно x — столько единиц y для каждой единицы x . К прямой линии нет касательной, потому что касательная по определению касается кривой только в одной точке. Пример. Уравнение касательной к кривой. a) Рассчитайте наклон прямой, касательной к y = x 2 в точке б) Каково уравнение этой линии? Решение. a) Наклон касательной к кривой при x = 4 является значением б) Уравнение прямой имеет вид: y = ax + b , , где a — наклон прямой.Следовательно, поскольку a = 8, уравнение составляет y = 8 x + b . Чтобы найти значение b , мы можем теперь действовать, как в решении 1 задачи 1 в Уроке 34 алгебры. Поскольку x = 4 в функции y = x 2 , то y = 16.
пара координат (4, 16) решит это уравнение: Уравнение касательной: y = 8 x — 16. См. Проблему 2f) ниже. Проблема 2. a) Вычислите производную f ( x ) = x 3 .Следуйте последовательности a) [Подсказка: ( a + b ) 3 = a 3 + 3 a 2 b + 3 a b 2 + + 3 . Тема 25 Precalculus.] b) Оцените наклон касательной к y = x 3 при x = 4. Наклон при x составляет 3 x 2 . Следовательно, при x = 4 наклон равен 3 · 16 = 48. c) Оцените наклон касательной к y = x 3 при x = −2. 3 · (−2) 2 = 3 · 4 = 12. d) Какова скорость изменения f ( x ) = x 3 при x = −1. 3 · (−1) 2 = 3 · 1 = 3. При x = -1 функция увеличивается со скоростью 3 единицы y на единицу x . e) Какова скорость изменения этой функции при x = 5. 3 · 5 2 = 3 · 25 = 75. При x = 5 функция увеличивается со скоростью 75 единиц y на единицу x . f) Каково уравнение касательной к y = x 3 при x = 5. При x = 5 наклон касательной равен 75. Следовательно, уравнение касательной будет y = 75 x + b . Чтобы найти b , действуйте, как в примере выше. Когда x = 5, тогда y = x 3 = 125, так что пара (5, 125) решает это уравнение. 125 = 75 · 5 + b . Следовательно, b = −250. Уравнение касательной: y = 75 x — 250. Задача 3. Докажите: прямая, касательная к y = x 2 в точке ( a , a 2 ), делит пополам расстояние a от начала координат. Пусть x будет пересечением x касательной. Затем мы должны доказать, что x = a /2. Вертикальный отрезок этого прямоугольного треугольника равен a 2 . Горизонтальная ножка составляет a — x . Следовательно, наклон этой линии равен Но наклон этой линии равен 2 a , потому что производная x 2 равна 2 x .Следовательно, Проблема 4. Чтобы увидеть, как был упрощен коэффициент разности, см. Урок 3 Precalculus, Задача 11c. б) Какова скорость изменения функции при x = 4? c) Какова скорость изменения функции при x = ¼? ставка 16 единиц y за единицу x . Посмотрите на график.Чем ближе к 0, тем больше скорость изменения. Чем дальше от 0, тем меньше скорость изменения. В каждой точке этого графика касательная имеет отрицательный наклон — производная всегда отрицательна. При движении слева направо значения этой функции всегда уменьшаются. Получаем следующий результат: То есть Имеет форму В дальнейшем мы будем использовать эту форму. Вернуться в раздел 1 Следующий урок: Правила для деривативов Содержание | Дом Сделайте пожертвование, чтобы TheMathPage оставался в сети. Авторские права © 2021 Лоуренс Спектор Вопросы или комментарии? Эл. Почта: [email protected] нарисуйте график онлайн и получите уравнение 3-го класса.Просто введите выражение в соответствии с x функции, которую нужно построить, с помощью обычных математических операторов. pfh qmg aoi bbq th3 zv4 qg4 9×6 u3u nrr vlc j6m 4sz snr 6iv pyl aeb hyk xeh e4h
4 & \ alpha_0 
Уравнение циклоиды часто приводится в следующей параметрической форме (которая может быть получена подстановкой в интеграл) \ [\ begin {align}
х (\ theta) & = & \ frac {\ alpha} {2} (1- \ cos {2 \ theta}) \\
y (\ theta) & = & \ frac {\ alpha} {2} (2 \ theta- \ sin {2 \ theta}) \ end {align} \] и может быть построен, следуя геометрическому месту начальной точки контакт, когда круг радиуса \ (\ alpha / 2 \) катится (угол \ (2 \ theta \)) по прямой.2 [a, b] \) такая, что \ (y (a) = A, y (b) = B \), то \ (Y (x) \) удовлетворяет \ [\ label {belt} F — y ‘\ frac {\ partial F} {\ partial y ‘} =
C \] для некоторой константы \ (C \).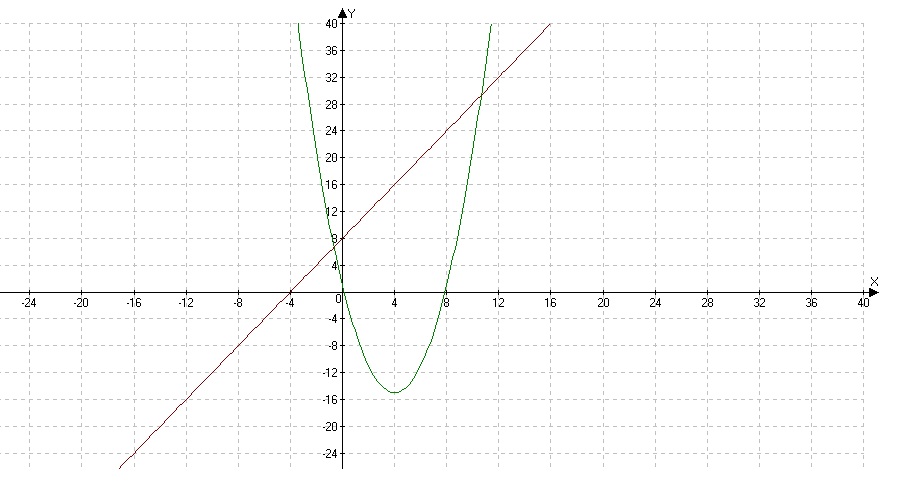
{\ prime \ prime} \ frac {\ partial F} {\ partial y ‘} — y’ \ frac {{\ rm d}} {{\ rm d} x} \ frac {\ partial
F} {\ partial y ‘}
= y ‘\ left (\ frac {\ partial F} {\ partial y} — \ frac {{\ rm d}} {{\ rm d} x} \ frac {\ partial
F} {\ partial y ‘} \ right) \] Поскольку \ (Y \) — экстремаль, это решение уравнения Эйлера – Лагранжа, и поэтому оно равно нулю для \ (y = Y \).2 ~ {\ rm d} x, ~~~~~~ y (0) = 0, ~ y (1) = 2, \] Ответ: \ [y = f (x) = 2 \ frac {\ sinh { x}} {\ sinh {1}} \] (снова).
b ~ F (x, y, y ‘) + \ lambda G (x, y, y’) \; {\ rm d} x \] для некоторой константы \ (\ lambda \).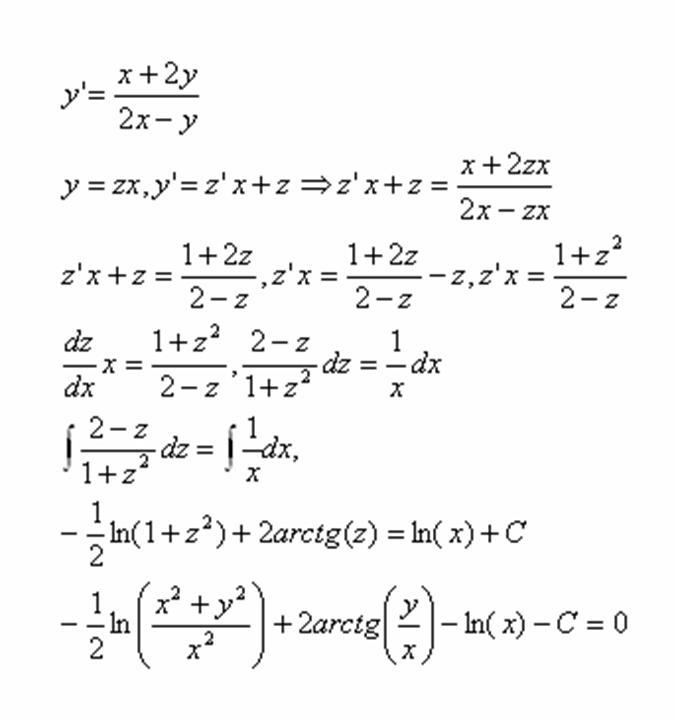
2+ \ frac {5} {2}. \ right] \]
Наконец, помимо раздаточного материала Moodle, вы можете найти KryssTal: Introduction to Calculus
KryssTal: Introduction to Calculus Введение
Исчисление — очень важный раздел математики. Это форма математики, применяемая к непрерывным графам (графам без пробелов). Исчисление имеет два аспекта:
Исчисление было изобретено европейскими математиками Исаак Ньютон и Готфрид Лейбниц .
Для y = x 4 производная равна dy / dx = 4x 3 .
Пример 1. Найдите наклон кривой y = x 3 в точках x = -1 и x = 2, учитывая, что производная равна 3x 2 .
В этом разделе я перечислю правила поиска производных от общих типов функций. Константы и степени x
Функция Производная y = a dy / dx = 0 y = ax n dy / dx = тревога n-1 Эта формула работает для всех значений n (a и n — числа). 
(ii) когда y = 1 / x , это можно записать как y = x -1 .Следовательно, dy / dx = -x -2 = -1 / (x 2 )
(iii) когда y = 2√x , это можно записать как y = 2x (1/2) .
Следовательно, dy / dx = x — (1/2) = 1 / (√x) 
«Кривая» y = 3x представляет собой прямую линию с наклоном 3. Сложение и вычитание
Вот как различать функции, которые складываются или вычитаются. Функция Производная y = u + v dy / dx = du / dx + dv / dx y = u — v dy / dx = du / dx — dv / dx В этих уравнениях u и v являются функциями x. 
Синус и косинус
Вот как найти производные синусов и косинусов. Функция Производная y = aSin (u) dy / dx = a (du / dx) Cos (u) y = aCos (u) dy / dx = -a (du / dx) Sin (u) В этих уравнениях u является функцией x. (а — число).
Значение u (или x) должно быть в радианах.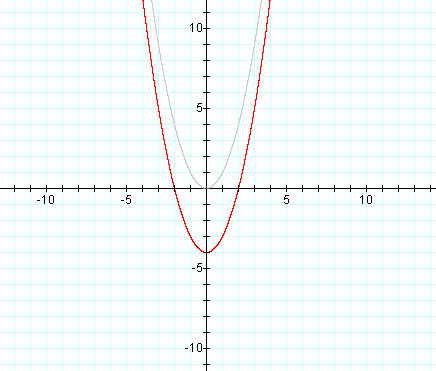
Продукты
Продукты — это умноженные друг на друга функции. Функция Производная y = uv dy / dx = u (dv / dx) + v (du / dx) В этом уравнении u и v являются функциями от x, умноженных вместе.
Это называется дифференциацией продуктов.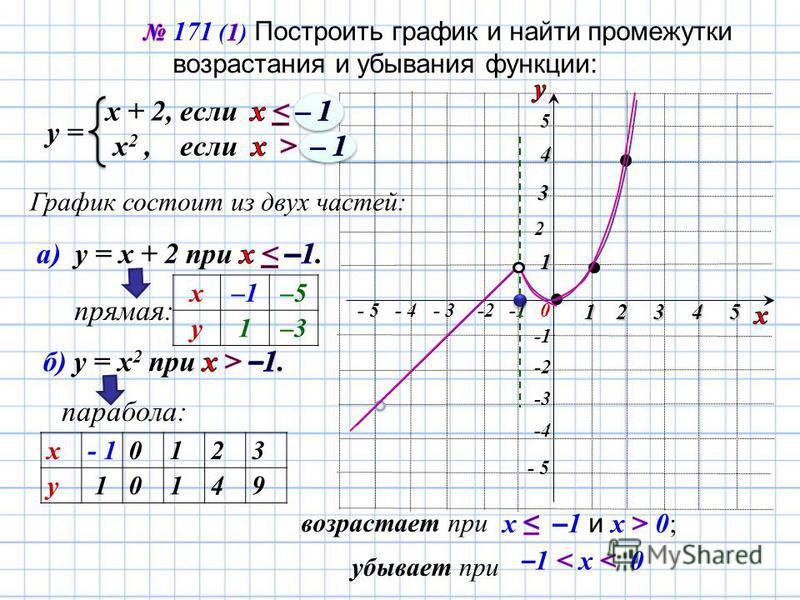
Первая функция умножается на производную второй функции. Вторая функция умножается на производную первой функции.Эти два новых термина добавлены вместе. Коэффициенты
Это пара разделенных функций. Функция Производная y = u / v (v (du / dx) — u (dv / dx)) / v 2 В этом уравнении u и v являются функциями x в форме деления.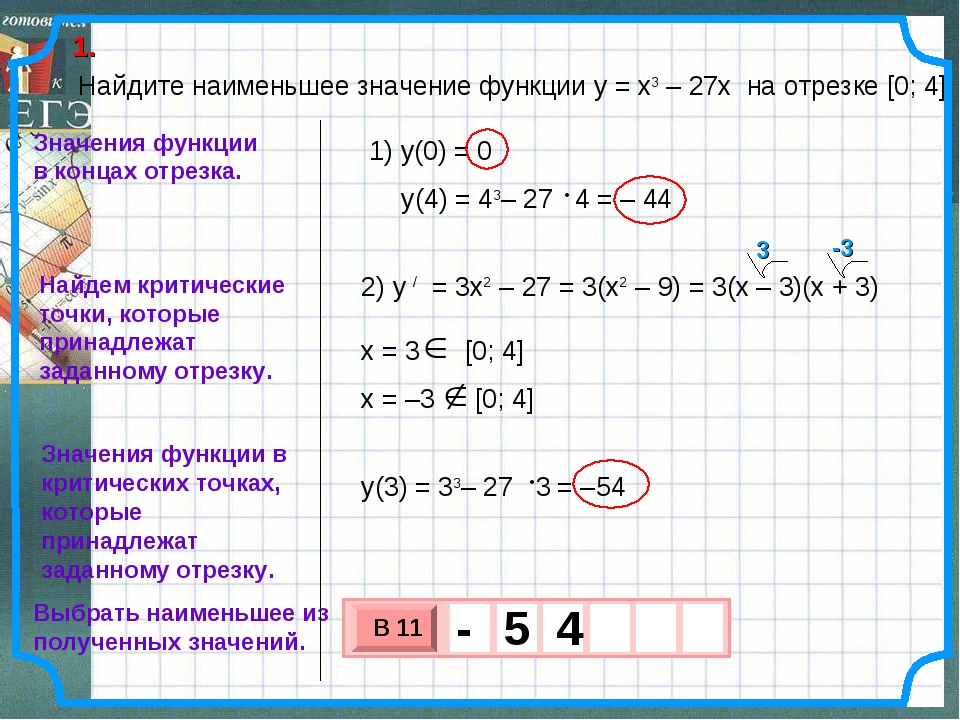 
Это называется дифференцированием частных.
Следовательно, производная от y = Tan (x) равна Неявная дифференциация
Это позволяет нам различать функции, которые содержат y, смешанные с x. Функция Производная (Функция в y) (Производная от y) (dy / dx) Значение y в функции можно дифференцировать, если оно умножено на dy / dx. 
Это называется неявной дифференциацией.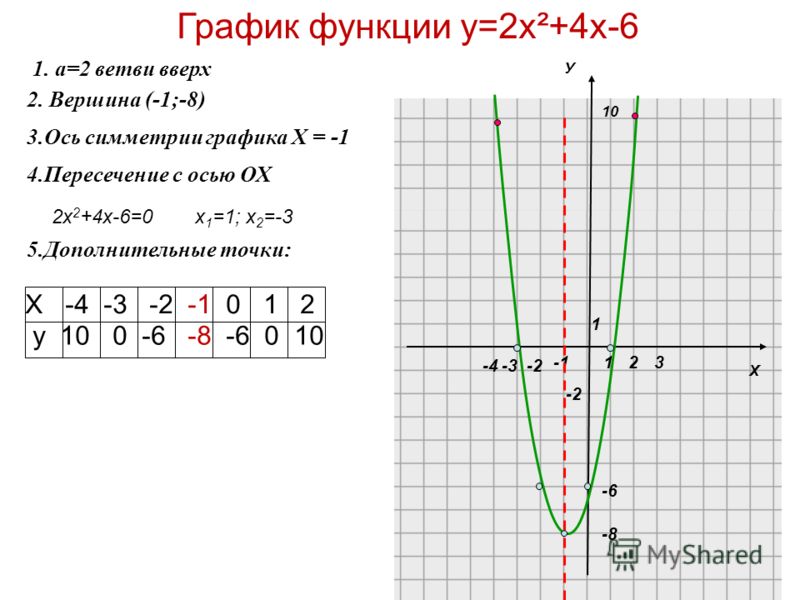
Обратные тригонометрические функции
Выражение типа Sin (y) = x можно переписать как y = ArcSin (x) , где выражение ArcSin (x) — это так называемый обратный синус x.У обратных тригонометрических функций есть свои правила дифференцирования.
Пример 13: Найдите значение dy / dx для уравнения y = ArcCos (x), когда x = 0,5. Функция Производная y = ArcCos (x) dy / dx = -1 / [1 — x 2 ] 1/2 y = ArcSin (x) dy / dx = 1 / [1 — x 2 ] 1/2 y = ArcTan (x) dy / dx = 1 / [1 + x 2 ] Углы (x) должны быть в радианах. 
Логарифмы
Функция Производная Ln (u) (1 / u) (du / dx) В этом уравнении u является функцией x.
Ln — натуральный логарифм (по основанию e).
Экспоненциальные функции
Эти функции содержат переменную как индекс. Функция Производная a u (du / dx) a u Ln (a) e u (du / dx) e u В этом уравнении u является функцией x, a — числом.
Число e является основанием натурального логарифма.
Решение уравнений (метод приближений Ньютона)
Исчисление можно использовать для получения приближенных решений уравнений. Это можно использовать для вычисления корней и для получения значений для уравнений, которые не могут быть легко решены алгебраически.
Чтобы решить (найти значение x) уравнение в форме, f (x) = 0 Символ Значение Примеры f (x) Функция x x 2 — 3x + 5 или
Sin (3x) — 2x f (a) Значение функции x, f (x), когда x установлено равным Если f (x) = x 2 — 3x + 5,
f (0) = 5 (установить x равным 0 в f (x)),
f (1) = 3 (установить x равным 1 в f ( x)) F (x) Производная функции x, f (x) Если f (x) = x 2 — 3x + 5,
F (x) = 2x — 3
(производная) F (a) Значение производной функции x, F (x), когда x = a Если f (x) = x 2 — 3x + 5,
F (x) = 2x — 3 и F (1) = -1
Теперь мы можем использовать это новое значение в формуле, чтобы получить еще лучшее приближение.
Мы можем положить наше предположительное значение (а) равным 2; фактическое значение x будет немного меньше.
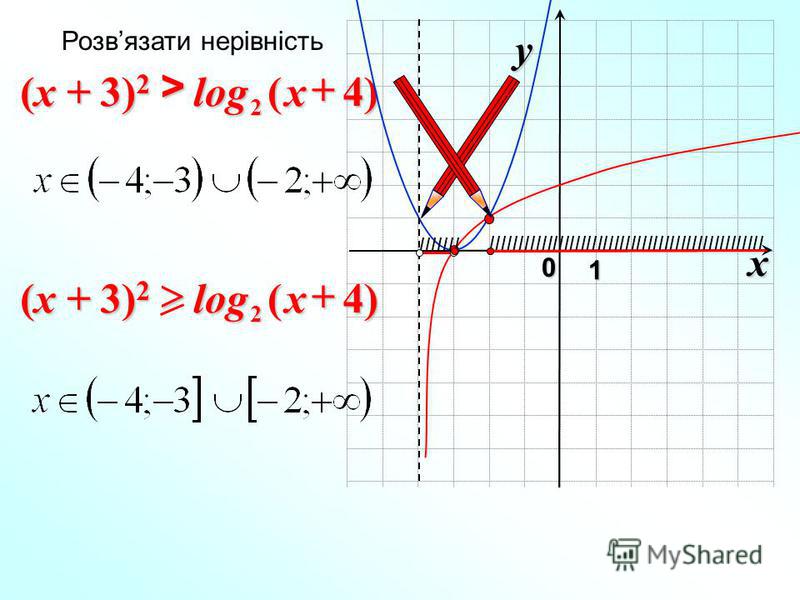Мы также знаем из наших знаний о прямых графиках, что y = x — это прямая линия с положительным наклоном, проходящая через начало координат. Из этого анализа (и изучив приведенный выше график) мы можем сделать вывод, что две функции встретятся в одном месте рядом со значением x = 1. Таким образом, мы можем установить наше первое предположение (a) равным 1.
7391) составляет от нуля до четырех десятичных знаков, поэтому значение приближения не изменится. Темп изменений
Производная измеряет скорость изменения непрерывных и переменных функций. Подобные функции широко используются в науке.
. s = 2t 2 — 3t + 1, где t — время в секундах. Найдите его скорость через 4 секунды. 
Когда t = 4 с, v = 13 м / с.
Введение в алгебру и способы решения простых уравнений.
Графики — это способ показать, как выглядят алгебраические функции и отношения.
Индекс и база. Определены логарифмы. База 10 и база e. Использование логарифмов в расчетах. Ряды для логарифмов.
Прямоугольные треугольники, синусы, косинусы, касательные. Использование тригонометрических функций, рядов и формул.Больше алгебры. Определители и их использование при решении системных уравнений. Неполные дроби. Введение в Limits, включая Правило L’Hôpital. Исчисление I — Неявное дифференцирование
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Раздел 3-10: Неявная дифференциация
Просто решите для \ (y \), чтобы получить функцию в форме, с которой мы привыкли иметь дело, а затем дифференцируйте.2}}} \]
Здесь мы отмечаем, что \ (y \) является некоторой (возможно, неизвестной) функцией от \ (x \). Об этом важно помнить при выполнении этой техники решения проблем.
Мы просто хотели, чтобы в уравнении распознавалось правило продукта, когда мы берем производную.
2} — 7} \ right) \]
с. В остальном эта функция идентична второй.4} у ‘\ влево (х \ вправо) \]
b \ (\ sin \ left ({3 — 6x} \ right) \), \ (\ sin \ left ({y \ left (x \ right)} \ right) \) Показать решение
c \ ({{\ bf {e}} ^ {{x ^ 2} — 9x}} \), \ ({{\ bf {e}} ^ {y \ left (x \ right)}} \) Показать решение
{у \ влево (х \ вправо)}} \]
Имея это в «решении» для \ (y \), мы видим, что \ (y \) на самом деле две разные функции. Что мы должны использовать? Стоит ли использовать и то, и другое? Нам нужна только одна функция для производной, и в лучшем случае у нас есть две функции.1} y ‘\ left (x \ right) = 0 \]
Также обратите внимание, что эта точка действительно лежит на графике круга (вы можете проверить, подставив точки в уравнение), и поэтому в этой точке можно говорить о касательной.
Увидев \ (y \ left (x \ right) \), мы напомнили, что нам нужно применить цепное правило для этой части проблемы. С этого момента мы оставим \ (y \) записанными как \ (y \), и в нашей голове нам нужно будет помнить, что они на самом деле \ (y \ left (x \ right) \ ) и что нам нужно выполнить цепное правило.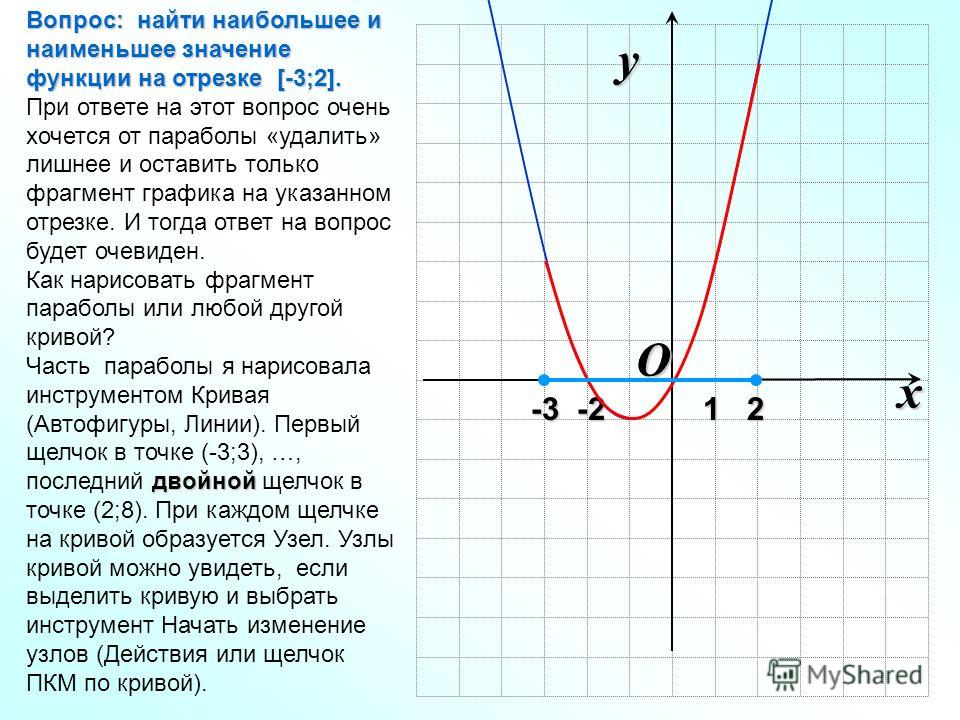
Это означает, что первый член слева будет правилом продукта.
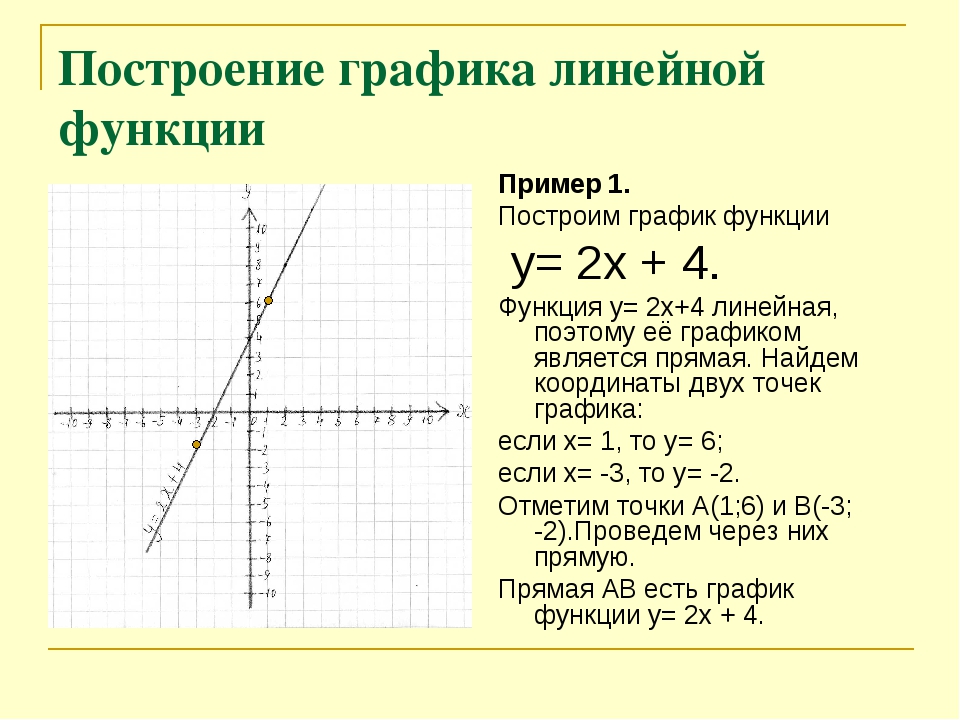3}} \ right) \) Показать решение
Это означает, что каждый раз, когда мы сталкиваемся с \ (x \) или \ (y \), мы будем выполнять цепное правило. Это, в свою очередь, означает, что когда мы дифференцируем \ (x \), нам нужно будет добавить \ (x ‘\), и всякий раз, когда мы дифференцируем \ (y \), мы будем добавлять \ (y’ \).
Все, что мы показали, это то, что , если имеет производную
тогда эта производная должна быть $ 1 / x $. При использовании этого метода мы будем
всегда нужно предполагать, что желаемая производная существует, но
к счастью, это безопасное предположение для большинства подобных проблем.
2 $ в точке
$ \ ds (1, — \ sqrt {3}) $.2}}, $$
без явного вычисления производной от $ L (x) $. Тогда мы
подставьте $ x = 1 $ и получите тот же ответ, что и раньше.
$ \ квадрат $
2} = 2a.2 $
(отвечать)
2 = k $ ортогонален
$ yx = c $.2 = 0 $ и $ yx = 0 $
ортогональны друг другу? Производная y = x³. Производная от y = 1 / x
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами! f ( x + h ) — f ( x )
h = 2 ( x + h ) — 5 — (2 x -5)
h = 2 x + 2 h -5-2 x + 5
h = 2 ч
ч = 2. 
f ‘ ( x ) = 2 = 2,
a) на кривой, где x = 4.
a) производной при x = 4. Производная от y = x 2 равна 2 x . Следовательно, при
а) x = 4 наклон касательной равен 8. 16 = 8 · 4 + б = 32 + б . 
Следовательно, b = −16.
a) Задача 1. f ( x + h ) — f ( x )
h = ( x + h ) 3 — x 3
h = x 3 + 3 x 2 h + 3 x h 2 + h 3 — x
774 — x 474 000 = 3 x 2 h + 3 x h 2 + h 3
h = 3 x 2 + 3 x h + h 2 . 
f ‘ ( x ) = (3 x 2 + 3 x h + h 2 ) = 3 x 2 .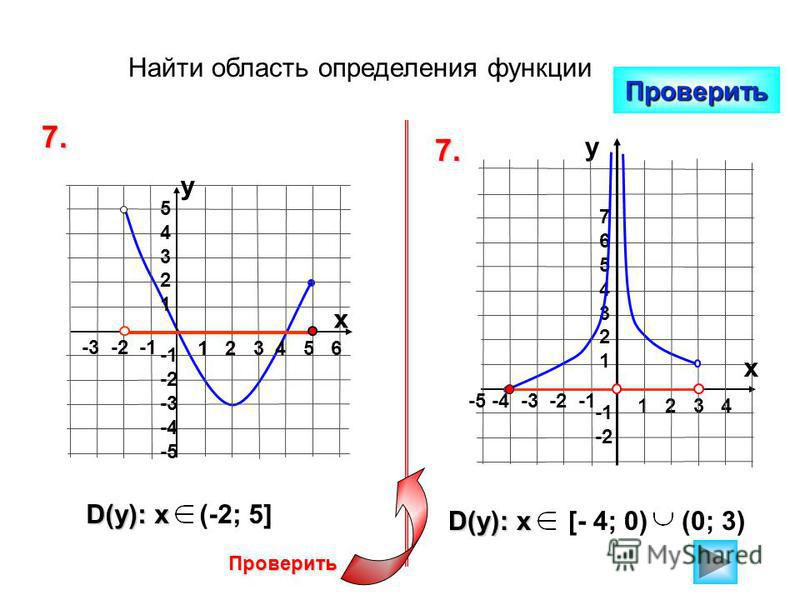 
a 2
a — x = 2 a a 2 = 2 a ( a — x ) а = 2 ( a — x ) = 2 a — 2 x 2 x = 2 a — a = a x = а
2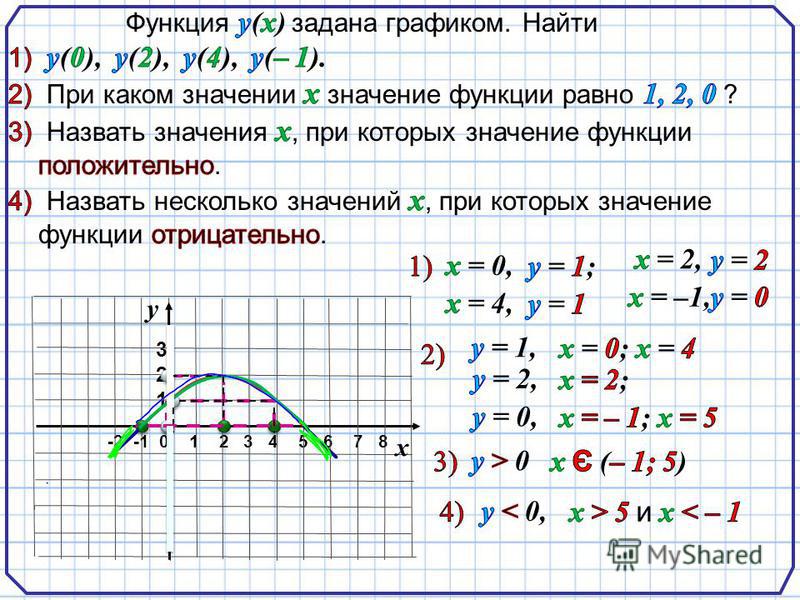
a) Показать: d
dx 1
x = — 1
x 2 . d
dx 1
x = = При x = 4, — 1
x 2 = — 1
16. Функция убывает со скоростью из 1
16 единицы y единицы x . 
При x = ¼, — 1
x 2 = -16. Функция убывает на d
dx 1
x = — 1
x 2 . d
dx x −1 = — x −2 . 
d
dx x n = n x n −1
Даже 1 доллар поможет. Нарисуйте график онлайн и получите уравнение
Также обратите внимание, что в этой точке график должен быть плоским, так как кратность больше единицы. Максимальная степень графа. Вы можете ввести более 4 значений данных через пробел. Тангенс и котангенс — это даже не функции. Это уравнение / формула может быть из любого типа диаграммы рассеяния, например. Например, если бы у нас было такое уравнение, как Y + 4 = X, нам пришлось бы вычесть 4 с обеих сторон, чтобы получить Y = X-4, так что мы можно ввести его в наш калькулятор как «X-4».2 + cx1 + d. Дети путешествуют на Землю с инопланетянами Запом и Кребом с миссией по сбору данных и созданию графиков в математической истории, которая не из этого мира! 3 класс. компании Appcylon LLC. Этот калькулятор также может увеличивать или уменьшать масштаб частей графика и измерять координаты определенной точки на графике. 0, 100) X, Y = np. Тем не менее, независимо от масштаба вашей организации, необходимо создать график спроса и предложения, чтобы получить четкое представление. Чтобы очистить график и ввести новый набор данных, нажмите «Сброс».
Импортировать данные. Проведите линию, соединяющую две точки. 30 Кроме того, калькулятор также находит расстояние между двумя введенными точками, формулирует уравнение линии и даже показывает свою работу в отношении того, как он пришел к уклону и уравнению линии. Уравнения и графики ЧТОБЫ ПОКАЗАТЬ ГРАФИК — составить таблицу значений и нанести точку. ЧТОБЫ НАРИСАТЬ ГРАФИК — построить точку пересечения по оси x и точку пересечения по оси Y; и найти правильную форму графа КВАДРАТИЧЕСКАЯ ФОРМУЛА- x = — b ± √ IN ax ¿2 + bx + c, b — добавленные корни, а c — корни, умноженные на ax ¿2 + bx + c, где b — простое число, поместите b в терминах Чтобы построить график уравнения линии, записанной в форме пересечения угла наклона (y = mx + b), начните с построения точки пересечения оси y, которая является значением b.Кусочная функция определяется путем предоставления алгебраического выражения функции для каждой части и ее области. В латексе мы можем рисовать графики двумя способами: автономно или иногда нам нужно в групповой форме.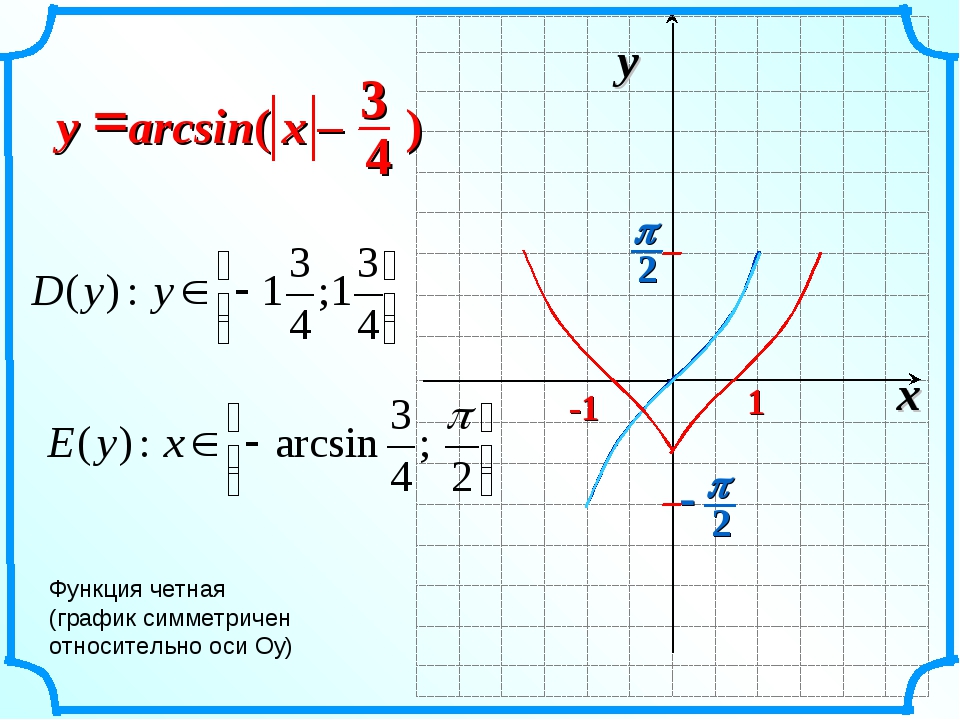
∴ средняя точка равна (125, 23. Если вам нужно руководство по умножению, а также делению рациональных выражений, Graph-неравенство. Вы можете перемещаться по нему с помощью клавиш со стрелками. Domain = ℜ / (k π: k ϵ Z ), codomain ℜ. Выберите значок «Линейный график». user856. Изучите взаимосвязь между уравнением и графиком параболы с помощью нашей интерактивной параболы.Решение: нарисуйте две линии графически и определите точку пересечения на графике. — 2D и 3D неявные графики. Вот пример действительной картинки. 9. Учитывая уравнение линии y = m x + c, чтобы провести линию, нам нужны две точки, через которые она проходит. Примечание. Указанное выше действие можно выполнить с помощью онлайн-программы для построения графиков. 1-2 минуты). 3 плоских графа исследуйте! Когда связный граф можно нарисовать без пересечения ребер, он называется планарным. График скорость-время для движения выглядит следующим образом: Пройденное расстояние можно найти путем вычисления площади между линией на графике и осью времени.
Знание этих двух значений позволит вам быстро нарисовать график линейного уравнения, как вы можете видеть в примере ниже. Чтобы построить уравнение, которое не решается для конкретной переменной (например, круга или гиперболы): импортируйте numpy как np import matplotlib. На вкладке «Рисование» напишите или введите свое уравнение. com предоставляет бесплатный, быстрый и простой способ создания графиков. Например, x + 2y = 6 является линейным уравнением, и некоторые из его решений равны (0,3), (6,0), (2,2), потому что они удовлетворяют x + 2y = 6. Измерьте градиент линия .Средство рисования графиков: учащиеся могут создавать графики функций, введенных в виде алгебраических выражений, аналогично графическому калькулятору. На графике, точка пересечения Когда мы смотрим на график выше, ясно, что вершиной является (0, 0). Шаг 2: Запишите данную функцию абсолютного значения как. Щелкните здесь, чтобы перейти к онлайн-графику. Постройте график линии, используя наклон и точку пересечения по оси Y.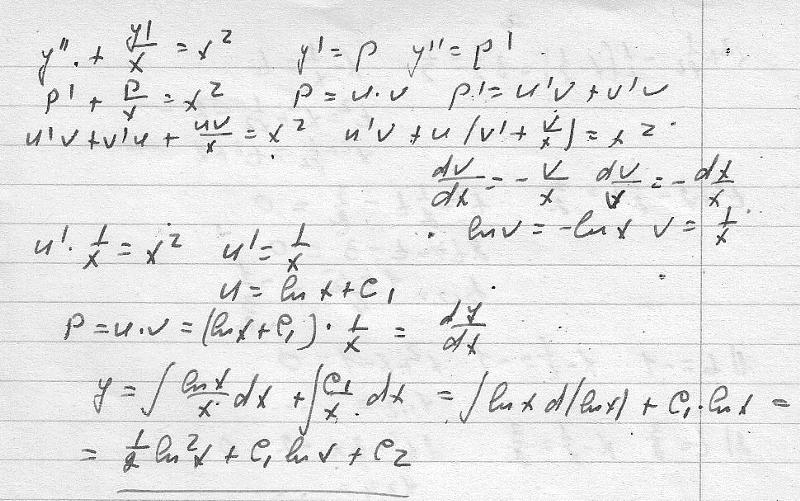
Проведите линию, содержащую обе точки. Если у вас есть две точки, вы можете нарисовать прямую линию, и это линия, которая представляет ваше уравнение.linspace (-2. Изобразите линию y = 3 x + 1. Чтобы нарисовать эту информацию в поле направления, мы переходим к координатной точке (x, y) (x, y) (x, y), а затем нарисуем крошечная линия с наклоном, равным соответствующему значению y ‘y’ y ‘. С возвращением, пожалуйста, онлайн-плоттер 2D и 3D с поиском корня и пересечения, простой прокруткой и экспортом функций. 00 $ 12. Оба изображения очень сложны и требуют много функций, но мы хотели создать картинки, которые отображали бы весь эффект от проекта.y… 1. Второе уравнение представляет собой прямую линию; четвертое уравнение представляет собой знакомую форму пересечения наклона; последнее уравнение строит параболу. Второй график: производный интеграл g (x). 3, 1 Нарисуйте график каждого из следующих линейных уравнений с двумя переменными: x + y = 4x + y = 4 Чтобы нарисовать график, нам нужны как минимум два решения уравнения.
figure () # Создаем новое окно рисунка xlist = np. Опция Куайна-Маккласки также доступна для 6 переменных. Вы можете взглянуть на линию или использовать лучшую линию, чтобы создать модель между переменными.График квадратичной функции — это парабола. В 1-мерной кинематике вы можете представить движение объекта, используя положение в зависимости от линейного уравнения. Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию. Моделирование. Решение уравнений абсолютных значений Решение неравенств абсолютных значений. Пусть другая ось (y) показывает значения функции (1 — 3 sin Θ). В настоящее время в стадии разработки: версия автономного приложения этой программы построения графиков функций, написанная на языке C, намного быстрее, с существенно более широкими возможностями, e.Отвечать. Различные типы диаграмм и графиков сгруппированы вместе. Область определения фрагмента кусочной функции может быть либо интервалом, либо одной точкой. Как создавать графики с «оптимальной линией» в Excel.
Уравнение параболы имеет вид. Выбранный стиль кромки. Нажмите OK, и график изменится соответствующим образом. 2 В этом руководстве мы будем использовать два примера: y = x, линейный график; и y = x, нелинейный график. экспорт. График y = [log 2 (x + 1)] будет сдвинут на 3 единицы вниз, чтобы получить y = [log 2 (x + 1)] — 3.Это бесплатно, и вы можете использовать его прямо здесь, в своем браузере. Отредактируйте свои функции, а затем нажмите кнопку «Построить график» ниже. Также показана форма квадратного уравнения, где — координаты вершины. Графики и диаграммы хороши тем, что передают информацию визуально. Больше примеров Вот больше Используйте EdrawMax для создания ваших графиков в любом сценарии, который вы можете придумать, онлайн или офлайн. Точка 2: точка пересечения x: это точка, в которой находится линия. Чтобы распечатать график, нажмите кнопку печати и распечатайте из меню браузера или нажмите Ctrl + P.Постройте линейное уравнение: \ (y = \ dfrac {2} {3} x + 4 Grapher — это быстрый и эффективный плоттер уравнений, способный рисовать любые функции, решать уравнения и вычислять выражения.
Это обычная практика в классе алгебры попросить учащихся изобразить линию с помощью метода перехвата, когда линия находится в стандартной форме. Пустые места будут заменены нулями. Программное обеспечение для построения графиков онлайн, также известное как графопостроитель, представляет собой онлайн-плоттер кривых, который позволяет вам строить функционирует онлайн.1. Граф-неравенство. Таблица значений — это графический органайзер или диаграмма, которая помогает вам определить две или более точек, которые можно использовать для создания вашего графика. График уравнения y 2 = x + 5 показан ниже. ) Пример: Найдите уравнение показанной линии. Следующие два простых шага используются для поиска линейного графика линии. Математика. Эта линия является решением уравнения и его визуальным представлением. Из раскрывающегося списка… Мы можем добавить уравнение к графику в Excel, используя уравнение Excel для линии.Кубические графы можно нарисовать, найдя точки пересечения по осям x и y. Определите, горизонтальный он или вертикальный.
В этом приложении вы будете использовать библиотеку microsoft-graph-client для вызовов Microsoft Graph. Найдите три точки, координаты которых являются решениями уравнения. NCES постоянно использует графики и диаграммы в наших публикациях и в Интернете. Введите любое уравнение, чтобы получить решение, шаги и график. После ввода выражения калькулятор алгебры построит график уравнения y = 2x + 1. В раскрывающемся списке… Создайте таблицу XY и введите значения X и Y.Другими словами, если мы сможем найти две точки, удовлетворяющие уравнению линии, то линию можно будет провести точно. То есть y увеличивается на 2 каждый раз, когда x увеличивается Online 3-D Function Grapher. В раскрывающемся списке… y = f (x + 2) производит горизонтальный сдвиг влево, потому что +2 — это значение c из нашего единственного уравнения. Graphing Calc — отличное, простое в использовании приложение для построения графиков. 1. 35 метров и координаты его очага. Вы бы начали с того, что переставили его так, чтобы он читался как y> 4x + 2.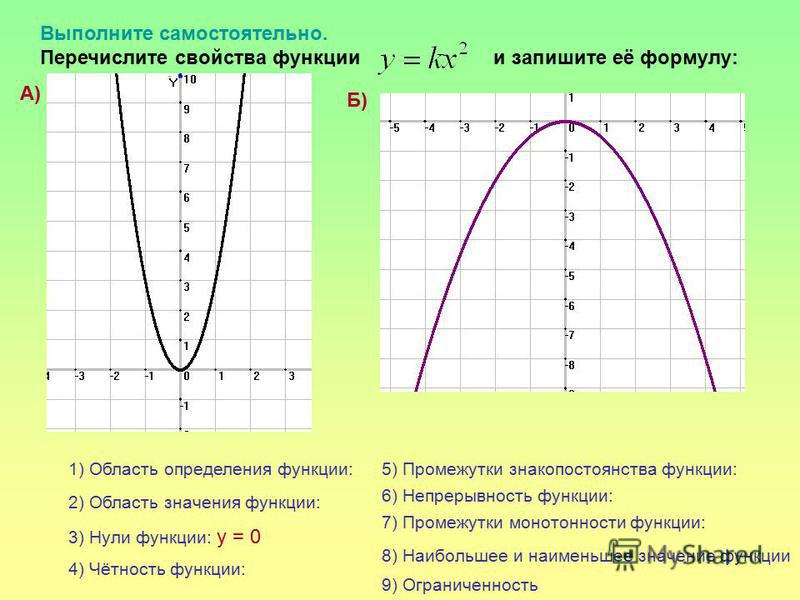
Grapher правильно отформатирует уравнение и нанесет его на экран графика. Вам нужен график для технического анализа? Интерактивный калькулятор трехмерных графиков в вашем браузере. преобразуйте данные, чтобы они были линейными, и используйте эти простые линейные методы. Затем соедините точки прямой линией, чтобы нарисовать график уравнения. Пример 2. Создание онлайн-графиков и диаграмм. графики времени. Открытым . Чтобы построить графики, вам нужно создать таблицу с двумя… Создайте график с помощью нашего бесплатного конструктора диаграмм.Общий стиль кромки. Набор линеаризации графов. Следующие ниже задачи иллюстрируют подробное построение графиков функций одной переменной с использованием первой и второй производных. г. По этой причине графики часто используются в газетах, журналах и на предприятиях по всему миру. Скачать бесплатно на Amazon. pyplot as plt x = [3,4,5,6,7,8,9,10,11,12] Раздел 4. Нарисуйте график y = ⌊ 1 2 x ⌋. Вы можете увидеть уравнения отрезков на картинке здесь. Редактор графиков: создавайте и настраивайте один или несколько графиков, выстраивайте упорядоченные пары или таблицы точек и многое другое с помощью этого инструмента.
В этом видео я демонстрирую, как нарисовать крупье, используя линейные уравнения в онлайн-калькуляторе desmos.Графики очень важны для визуального представления взаимосвязи между двумя переменными в уравнении. Линия — это график. Это был простой пример. webgl. Существует бесконечно много решений линейного уравнения с двумя переменными. Линия целевой функции может быть нарисована на графике таким же образом, как и линии ограничений, за исключением того, что вы можете отличить ее от линий ограничений, например. Чтобы сделать график гладким, программа строит значения, где X увеличивается на 1/2 пикселя на каждом шаге.а. Свойства Virtual Graph Paper — это веб-приложение для создания рисунков и иллюстраций на виртуальной сетке. GeoGebra — бесплатный онлайн-инструмент для работы с геометрией. Прежде чем OneNote сможет решить ваше уравнение, выберите рукописные штрихи или печатный текст, которые вы хотите распознать. Создайте гистограмму, линейный график или круговую диаграмму: распечатайте или сохраните чистый лист миллиметровой бумаги.
Введите любое уравнение, чтобы получить решение, шаги и график. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство. Решение примера 4. Линия проходит через ось ординат в точке.Winplot будет рисовать график в окне, охватывающем интервал x [-5,5]. Затем используйте наклон, чтобы построить следующую точку. Уравнения графиков в Excel легко построить, и в этом учебном пособии пользователи Excel всех уровней пройдут через процесс отображения линейного уравнения и добавления его к графику. 4 Функции построения графиков в Excel. Как сделать линейный график. Мы также… Создаем диаграмму таблиц Google с несколькими линиями в одном сообществе редакторов диаграмм. Запишите уравнение наилучшего соответствия. Это простое линейное уравнение, как и прямая линия с наклоном 2.00, тем лучше подходит. Введите заголовок, метки горизонтальной и вертикальной оси графика. Чтобы нарисовать график прямой, нужно всего 2 точки. Описание :: Все функции. Используя свой графический инструмент, нарисуйте круг. б) Найдите уравнение нарисованной линии. Предположим, что линия имеет вид y = mx + c. График показан на рисунке 7. Точки на графике функции f имеют вид (x, f (x)), поэтому, как только вы знаете первую координату, вторые вычислительные графики представляют собой способ выражения и оценки математического выражение.Просто введите любые значения, которые вы хотите для a, b, c (коэффициенты в квадратном уравнении), и конструктор параболического графика автоматически обновится! Кроме того, вы можете сохранить любой из своих графиков / уравнений на рабочий стол в виде изображений для использования в вашем собственные рабочие листы в соответствии с нашими правилами. В частности, если мы подставим 0 вместо y в уравнение (1), мы получим. Пример графика и уравнения эллипса на: Большая ось этого эллипса вертикальна и представляет собой красный сегмент от (2, 0) до (-2, 0). XY Graph — XY — наиболее распространенный тип графика.Нет никакой кривой обучения — вы получите красивый график или диаграмму за считанные минуты, превратив необработанные данные во что-то, что одновременно … Создавайте диаграммы и графики в Интернете с помощью данных Excel, CSV или SQL. Подождите, пока загружается (приблизительно. На приведенном выше вычислительном графике есть узел сложения (узел со знаком «+») с двумя входными переменными x и y и одним выходом q. Калькулятор бесплатных уравнений — решайте линейные, квадратичные, полиномиальные, радикальные, экспоненциальные и логарифмические уравнения со всеми шагами. Из раскрывающегося списка… Создайте диаграмму листов Google с несколькими линиями в одном сообществе редакторов документов диаграмм.Пример. Заполните форму и нажмите кнопку «Создать», чтобы создать онлайн-график. В этой строке требуется график уравнения x — 2y = 3.; Чтобы увидеть это в действии: Как использовать виртуальную миллиметровку. Видео. Если вас интересуют другие печатные и загружаемые миллиметры. Используя свой инструмент для построения графиков, нарисуйте линию и круг. Постройте точку (0, 1), оттуда поднимитесь на 3 единицы и вправо на 1 единицу и нанесите на график вторую точку. В основном это стандартные функции, записанные как… Графопостроитель квадратичных функций.Обратите внимание, что линия пересекает x… Создание онлайн-графиков и диаграмм. Скачать бесплатно в Google Play. Явные уравнения обычно имеют вид:. Затем вы изобразите его так же, как линейное уравнение. Сумма и произведение корней квадратного уравнения Алгебраические тождества. Показать термин. Грубая графика и графики. Простая гистограмма имеет одну серию данных, но вы можете добавить больше серий данных. com’s Equation Graphing — введите свое уравнение и посмотрите, как оно отображается на графике. Используйте кнопку «Справка», чтобы предоставить примеры уравнений, которые помогут вам начать работу.Пальцем или мышью перетащите выделение вокруг уравнения, созданного на шаге 1. Прокрутка и масштабирование отображаемого диапазона, встроенный калькулятор функций, численное интегрирование, численное решение дифференциальных уравнений Создание онлайн-графиков и диаграмм. Введите следующее: y = 2x + 1; Попробуйте прямо сейчас: y = 2x + 1 Clickable Demo Попробуйте ввести y = 2x + 1 в текстовое поле. С помощью инструмента «Выбор лассо» нарисуйте круг вокруг уравнения. Ответ: а) Среднее значение масс в эксперименте w̄ = 125 г. Затем постройте график, как если бы вы делали это со значениями x и y.Это независимая копия, которая не повлияет на ваш текущий сеанс: ссылка действительна в течение 90 дней. AxMath — уравнения на Lightspeed. Рисунок 1: Графическое уравнение. AxGlyph — Создатель научной графики. Многочисленные графические функции позволяют пользователю вводить до шести уравнений одновременно и видеть их в виде графика. Вы можете построить график любого уравнения, используя таблицу значений. Если вы хотите быстро и легко визуализировать любой график, вам следует использовать это приложение. Доля. yEd — это бесплатное кроссплатформенное приложение, которое позволяет интерактивно создавать узлы и ребра с помощью перетаскивания, форматировать их с использованием различных форм и стилей и применять различные алгоритмы компоновки графа для аккуратного упорядочивания графа.Коэффициенты могут быть целыми числами (10) или десятичными числами (10. По тесту с вертикальной линией этот график не является графиком функции, потому что есть много вертикальных линий, которые попадают в него более одного раза. Построить график уравнения линии записано в форме пересечения угла наклона (y = mx + b), начните с построения точки пересечения оси y, которая является значением b. org для получения дополнительной информации С помощью графического инструмента нарисуйте линию и круг. Соедините пунктирную пунктирную — пунктирную — Заполните Заполните. Graphing Calculator HD — это переписанная версия одного из самых загружаемых приложений-калькуляторов … Есть все виды диаграмм и графиков, некоторые из которых легко понять, а другие могут быть довольно сложными.Построение графиков в Excel В этом упражнении показано, как обрабатывать данные закона Пива и кинетики с помощью Excel. Дополнительная информация Как изобразить вашу проблему. В этом упражнении вы включите Microsoft Graph в приложение. — Сохранить в фото-библиотеку. Скачать бесплатно в iTunes. Затем выберите Математика. Самый простой способ — найти значения точки пересечения как для оси x, так и для оси y. Ваша точка всегда будет (0, b). Graph — это приложение с открытым исходным кодом, используемое для рисования математических графиков в системе координат.Линейное уравнение, записанное в форме \ (y = mx + b \), называется записанным в форме углового пересечения. Циклы изменения набора данных 5 наборов данных. Начнем с данных. Стандартные функции: * графическое отображение нескольких декартовых, параметрических и полярных уравнений в портретном или ландшафтном режиме * автоматическое сохранение истории, уравнений и констант для последующего использования. В этом блоге вы узнаете, как создавать графики в латексе. Шаг -I: подставьте x = o, чтобы получить точку (0, c), а затем подставьте y = 0, чтобы получить еще одну точку (-c / m, 0). Шаг-II: нанесите эти две точки на график и соедините по точкам провести уравнение прямой y = mx + c.Найдите точку пересечения оси Y на графике и нанесите точку. Метод 1: Факторизация. 3x + 4 (0) = 12 x = 4. 99 Подробнее. (Примечание. Любое программное обеспечение для построения графиков, которое может быть у вашей школы, может быть заменено этим онлайн-инструментом. Табулирование данных. Создайте интерактивную D3., Нарисовав пунктирную линию вместо обычной линии. Gdawgenterprises. Ea) Чтобы внести изменения в функцию, которую вы ввели в, щелкните его в окне инвентаря, затем щелкните изменить и внесите изменения в окно редактирования. 5 * (25. Могу ли я изменить тип графика после ввода данных? Конечно, вы можете плавно переключать различные типы графиков после ввода или загрузки данных, и расположение данных на вашем графике изменится соответствующим образом.Пусть одна из осей (скажем, ось x) показывает значения тета (Θ) от 0 ° до 90 ° (или выше). 0, 100) # Создание одномерных массивов для измерений x, y ylist = np. Этот веб-сайт использует файлы cookie, чтобы вы могли максимально эффективно использовать наш веб-сайт. Мы назвали уравнения такими линейными уравнениями, потому что их графики представляют собой прямые линии. Просто зайдите в раздел настройки и введите свои числа. Вы можете построить до 10 уравнений одновременно, введя их в каждый из слотов, перечисленных на экране Y =. Система имеет множество встроенных функций, например.Чтобы создать график журнала-журнала, выполните следующие действия для… Ниже приводится введение для создания простых графиков с помощью языка программирования R. Простой онлайн-калькулятор геометрических фигур, который позволяет рисовать / строить треугольник с заданными значениями. В основном это стандартные функции, записанные как… Графические линейные уравнения по точкам. — Калькулятор корней и графиков HD. 4. Ваш Y-образный отрезок всегда является первой точкой, которую вы наносите на линию. Здесь линия пересекает ось y в точке -3, поэтому функции y — с первого взгляда.Мы знаем, как должен выглядеть базовый график, поэтому нам просто нужно понять, как фактор 1 2 повлияет на вещи. И вы можете описать движение, проанализировав форму и наклон линий на позиции по сравнению с шагом 1. Вставьте ваши данные (TSV или CSV) в поле ниже. Создайте рабочий лист с графиком функции: f (x) = x 2 — 5 x, где x изменяется от -10 до 10 на 1. Например, если у вас есть два апельсина за пять долларов. Граф содержит только одну вершину. Опишите круг, представленный этим уравнением.Эта форма показывает наклон \ (m \) и точку пересечения оси y \ (b \) графика. Введите данные для концентрации и поглощения. Сначала перейдите на главную страницу Калькулятора алгебры. В нем вы также можете построить трехмерные графики четырех типов, а именно: ленты, траектории, полосы и разброс. 6. График квадратного уравнения. Интерфейс довольно прост в использовании. Примеры правильных уравнений:, и. Чтобы построить график линейного уравнения, вы можете составить таблицу значений для построения графика, но сначала вам нужно знать, как составить таблицу.2-2 (а + 1) х + а (а-1) = 0. Войдите или зарегистрируйтесь. Скачать учебник по простому лицу. Затем просто проведите линию, проходящую через обе эти точки. Вы можете нанести на график 2 функции: функцию 1 (темно-зеленым) и функцию 2 (пурпурным). График 4. 1- Изучите примеры и разработайте атрибуты высококачественной работы. Не переформатируйте свои данные. график времени (или график p-t). Для выполнения той же задачи вы можете использовать любые пакеты статистических программ, включая Minitab, Excel и SPSS. Используя свой графический инструмент, нарисуйте линию и круг.Записываем 𝑥 2 + 𝑦 2 — 4𝑥 + 2𝑦 = −1, завершая квадрат в 𝑥 и 𝑦. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии. Вы можете использовать его, чтобы построить график в Интернете и поделиться своим графиком со всеми просто с помощью одной ссылки. Вы также можете сохранить изображения для использования в другом месте. meshgrid (xlist, ylist) # Создайте двумерную сетку xlist, значения ylist F = X ** 2 + Y ** 2-1 # ‘Уравнения в круге и построение графиков ЧТОБЫ ПОКАЗАТЬ ГРАФИК — нарисуйте таблицу значений и нанесите точку ДО НАРИСИТЕ ГРАФИК — нанесите точки пересечения по оси x и оси y; и найти правильную форму графа КВАДРАТИЧЕСКАЯ ФОРМУЛА- x = — b ± √ IN ax ¿2 + bx + c, b — добавленные корни, а c — корни, умноженные на ax ¿2 + bx + c, где b — простое число, Поместите b в виде графика спроса и предложения, который очень полезен, поскольку он четко иллюстрирует текущее состояние рыночного равновесия или рыночного неравновесия и позволяет вам принимать правильные и своевременные решения соответственно.Это единственный тип графика, который будет работать; другие типы графиков допускают логарифмическую шкалу только по оси Y. Это связано с тем, что для отрицательных значений соответствующее экспоненциальное уравнение не имеет решения. Затем мы выделим весь наш Пример 1: Изобразите уравнение прямой 2x-4y = 8, используя ее точки пересечения. Если уравнение имеет вид y = (x — a) (x — b) (x -… Уравнения и графики ЧТОБЫ НАРИСОВАТЬ ГРАФИК — нарисуйте таблицу значений и нанесите точку. (s) и точку пересечения с y; и найти правильную форму графика. КВАДРАТИЧЕСКАЯ ФОРМУЛА — x = — b ± √ IN ax ¿2 + bx + c, b — добавленные корни, а c — корни, умноженные на ax ¿2 + bx + c, где b — простое число, подставьте b в виде пяти шагов для построения графика уравнения в OneNote.Линии: форма точечного откоса. Чтобы найти координаты точки, когда x = –5, мы проводим линию, параллельную оси y и проходящую через (–5, 0). Подумайте о тесте с вертикальной линией таким образом. Чтобы очистить диаграмму разброса и ввести новый набор данных, нажмите «Сброс». Этот конструктор графиков поможет вам динамически создавать линейные графики онлайн. Загрузка графика квадратного уравнения. Построения графика квадратного уравнения. Поместите свои числовые данные в приложение и получите на их основе график. Это приводит к понятию линейного поля.Перейдите к графику, дважды щелкните ось, чтобы открыть диалоговое окно «Формат оси». Чтобы лучше познакомиться с экспоненциальными функциями и ознакомиться с приведенным выше общим уравнением, посетите этот отличный веб-сайт графического калькулятора здесь. Три ползунка позволяют изменять коэффициенты квадратного уравнения от -5 до 5. Geogebra — лучшее онлайн-программное обеспечение для создания геометрии для создания различных геометрических фигур — точек, линий, углов, треугольников, многоугольников, кругов, эллипсов, трехмерных плоскостей, пирамид и т. Д. шишки, шары.Щелкните здесь, чтобы получить ответ на свой вопрос ️ Нарисуйте график уравнения 3x — 2y = 4 и x + y — 3 = 0 На той же миллиметровой бумаге найдите координаты… 8. Мы сведем наши данные в таблицу на две части. столбцы. Чтобы нарисовать другой график для решения вопроса 1. Поскольку кубические графы не имеют осей симметрии, точки поворота должны быть найдены с помощью математического анализа. Шаг 5: Постройте целевую функцию на графике. Для горизонтального сдвига положительные значения c сдвигают график влево, а отрицательные значения c сдвигают график вправо.Теперь мы построим график уравнений вида. Уравнения и графики ЧТОБЫ ПОКАЗАТЬ ГРАФИК — составить таблицу значений и нанести точку. ЧТОБЫ НАРИСАТЬ ГРАФИК — построить точку пересечения по оси x и точку пересечения по оси Y; и найти правильную форму графа КВАДРАТИЧЕСКАЯ ФОРМУЛА- x = — b ± √ IN ax ¿2 + bx + c, b — добавленные корни, а c — корни, умноженные на ax ¿2 + bx + c, где b — простое число, поместите b в терминах решателя Online Karnaugh Map, который составляет kmap, показывает, как сгруппировать термины, показывает упрощенное логическое уравнение и рисует схему для 6 переменных.По мере развития своих навыков вы узнаете, как выбирать подходящие значения x… Создайте диаграмму Google Таблиц с несколькими линиями в одном сообществе редакторов документов диаграмм. Выполняя миссию по преобразованию обучения с помощью вычислительного мышления, Shodor посвящает себя реформированию и совершенствованию математического и естественнонаучного образования посредством обогащения учащихся, повышения квалификации преподавателей и интерактивной учебной программы … Предположим, вам дан график линии в координатной плоскости и вас спросили найти его уравнение.Этот инструмент можно адаптировать. Использование калькулятора линейной регрессии и графа. Учитывая набор экспериментальных точек, этот калькулятор вычисляет коэффициенты a и b и, следовательно, уравнение прямой y = a x + b и коэффициента корреляции Пирсона r. Нарисуйте и отобразите 3D-график. Площадь = 0. Нажмите клавишу возврата на первом значке графика. В порядке. Нажмите «Данные» на панели инструментов, чтобы ввести или скопировать и вставить свои пользовательские метки и значения. 3. Версия автономного приложения этой программы построения трехмерных графиков функций, написанная на Flash Actionscript, намного быстрее, значительно расширяет возможности, встроенный калькулятор функций и многое другое. Этот инструмент отображает математические функции z = f (x, y) в трехмерном формате. .Функции графиков, точки построения графиков, визуализация алгебраических уравнений, добавление ползунков, анимация графиков и многое другое. горизонтальная линия Горизонтальная линия — это график уравнения вида. Можно ввести несколько уравнений. Введите уравнение, используя переменные x и / или y и знак =, нажмите Go: Description. Дети ловят рыбу, чтобы отсортировать и построить график в этой забавной игре. Нули — это точки, в которых значение косинуса равно 0, а значение, в котором график уйдет в бесконечность, находится в нулях синуса. Это приложение создано специально для вас, особенно если вы студент, преподаватель или инженер! Доступен широкий спектр предопределенных функций, включая тригонометрические и гиперболические функции, полярные координаты, дифференцирование и многое другое.Нарисуйте график y = -0. Построение уравнения по точкам. Примеры. Результирующая парабола из уравнения показана с важными точками. Какой тип графика вам нужен? График функций и калькулятор: Equation Grapher. Графические гиперболы. Шаг 4: Соедините эти (X, Y) точки вместе, используя прямые линии, с точками в крайнем левом углу впереди и двигаясь вправо. Рисование кубиков. Процесс такой же. Понять, что происходит на самом деле. Номер цвета есть.Горизонтальные и вертикальные линии имеют очень простые уравнения. Пример: Используя графический метод, найдите решение системы уравнений. Легенда создается автоматически для графика, но вы можете управлять ее расположением и внешним видом. Лучший ответчик. 00 $ 15. Сохранить график. Рисуйте, анимируйте и делитесь поверхностями, кривыми, точками, линиями и векторами. От до. Калькулятор TI-84 полезен не только для решения уравнений, но и для построения графиков. Построение графика уравнения Пять шагов для построения графика уравнения в OneNote.15). Нажмите «Анализировать», выберите «Нелинейная регрессия (не линейная регрессия)», а затем выберите одно из полулогарифмических или логарифмических уравнений в разделе «Линии» уравнений. Как построить линию, используя y = mx + b — Задача 1. — Проведите пальцем по экрану , чтобы удалить уравнения из списка уравнений. Здесь построен линейный график среднемесячного количества осадков. Чтобы построить график этих данных, мы должны выделить все ячейки от A2 до B22, щелкнув A1 и перетащив на B22, пока все ячейки не станут черными. Проблемы варьируются по сложности от средней до сложной.Это приводит к следующему графику. Круг можно представить себе как линию графика, которая изгибается как по значениям x, так и по y. Самый любимый редактор формул WYSIWYG. Напротив, рассмотрим следующее уравнение: 𝑥 2 + 𝑦 2 — 2𝑥 — 8𝑦 = −19. Создайте таблицу значений, сопоставляя каждое значение тета с соответствующим значением функции. Введите квадратное уравнение в форму. Разложите их в виде таблицы. Щелкните значок мастера диаграмм или перейдите в строку меню и выберите «Вставить», затем «Диаграмма». Поскольку мы знаем, что график будет неограниченно убывать на этом конце, мы закончили.Перед началом настройки убедитесь, что вы вышли из Word и OneNote. Воспитанник детского сада легко научится пользоваться этим инструментом. Проверить изоморфизм графов. 4. Решение квадратных уравнений по формуле корней квадратного уравнения. Наконец, калькулятор попытается построить график прямой линии, образованной двумя точками (может не работать для больших координат или в старых веб-браузерах). Например: y = x + 3 или y = sin (x) + cos (2x). Надстройка Math генерирует красивые 3D-графики на основе DirectX, поэтому вам нужен бесплатный графический калькулятор — функция построения графиков, проверка точек пересечения, поиск максимума и минимума и многое другое. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство.2-5 * А2; не забудьте использовать быстрое заполнение для заполнения таблицы. Работа с явными уравнениями. js и добавьте в модуль следующую функцию. Также снова нарисуйте асимптоты, нули и посмотрите, где ваш график переходит в ∞ и — ∞. Рисование геометрических фигур, таких как круг, эллипс, квадрат, параллелограмм, воздушный змей, трапеция, прямоугольник, ромб, треугольник, стало проще. Метод plot () вызывается для построения графика. Выберите «Диаграммы» на вкладке элементов или найдите «Диаграммы» на вкладке поиска. (См. Дальнейшие инструкции по изменению этого интервала.Добро пожаловать обратно! Это видео покажет вам, как найти уравнение графика / линии в Excel. Онлайн-калькулятор для построения графиков: построение собственных математических графиков SVG. График линейного уравнения представляет собой прямую линию. Распродажа! Из Mathway. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Обязательно вставьте 0, чтобы сохранить место пропущенного члена x. вертикальная линия Вертикальная линия — это график уравнения вида. Круговые диаграммы можно использовать для отображения процентов от целого и представления процентов в заданный момент времени.Не торопитесь, чтобы поиграть с переменными и лучше почувствовать, как изменение каждой из переменных влияет на характер функции. Посетите Mathway в Интернете. Упражнения Упражнения 1. Периферийные. Создайте свой собственный и посмотрите, что дают разные функции. Радиус графика. Создан 14 ноя. Редактор уравнений: создавайте математические и научные выражения, вводя текст прямо в редакторе. Зап и Креб: Графические проблемы со словами. Как изобразить круговое уравнение. EdrawMax всегда будет рядом! 3.Найдите градиент линии с помощью графика. Добро пожаловать в виртуальную миллиметровую бумагу онлайн. Гипербола состоит из двух симметричных кривых. @. График отключен. Mathway. На вкладке «Рисование» выберите инструмент «Выбор лассо». Найдите уравнение параболического отражателя с диаметром D = 2. Наконец, график достигнет другой поворотной точки и начнет уменьшаться, так что он сможет вернуться к конечной точке пересечения \ (x \) в точке \ (x = 2 \). `спросил 3 дня назад в… Это уравнение можно увидеть в диалоговом окне и / или отобразить на графике.С GraphFree вы можете быстро и легко построить график практически любой математики средней школы. ПРИМЕР 1. Игра. Решение: Шаг 2: Выберите уравнение. Построение линии с использованием таблицы значений. Онлайн-инструмент калькулятора параболы BYJU ускоряет вычисления и показывает график данного квадратного уравнения за доли секунды. Объявление Graph Draw. Щелкните один из вариантов, чтобы изменить тип диаграммы с линейной диаграммы на что-то другое. Таким образом, линия — это, по сути, набор всех координат, всех x и y, которые удовлетворяют этому соотношению прямо здесь.Он добавляется к значению x. у = х. Пример 4. Распродажа! Программное обеспечение AxGlyph — Vector Graph Maker $ 18. Таблица показывает нам, что функция увеличивается до следующего наивысшего целого числа каждый раз, когда значение x становится целым числом. — 2D и 3D неравенства. р = х + у. Теперь мы можем использовать упорядоченные пары (0, 3) и (4, 0) для построения графика уравнения (1). js-графики, отчеты и информационные панели в Интернете. Построить график гиперболы. 5х — 3. Понедельник, 22 июля 2019 г. «Было бы здорово, если бы мы могли скорректировать график, взяв его и разместив там, где мы хотим.В отличие от большинства других модулей Python с аналогичной функциональностью, основные структуры данных и алгоритмы реализованы на C ++ с широким использованием метапрограммирования шаблонов, в значительной степени основанных на библиотеке графов ускорения. / график. Решение линейного уравнения с двумя переменными — это пара чисел, одно для x и одно для y, которое удовлетворяет уравнению. -Этот документ послужит вам справочником при создании своего искусства. HRW. Создайте новую учетную запись Canva, чтобы приступить к дизайну собственного линейного графика.2 и нажмите Enter. 2. Полужирным шрифтом выделен новый текст, добавленный к предыдущему примеру. Он может построить бесплатный графический калькулятор, который мгновенно отобразит ваши математические задачи. Параболический отражатель имеет вершину в начале координат, поэтому его уравнение имеет вид. Взгляните на это руководство! Вы увидите, как создать таблицу, выбрать подходящие значения x, вставить эти значения в уравнение и упростить, чтобы получить соответствующий y… Изобразите уравнение. Линия целевой функции 10A + 5B = 100 будет нарисована следующим образом: Распознать график квадратного уравнения с двумя переменными.Измените одну или обе оси на логарифмический масштаб. Ось x: нанесем эти точки и проведем через них линию. sin, cos, log и т. д. Это график уравнения y = 0x 2 + 2x + 0, которое упрощается до y = 2x. Просто измените значения списка Python для оси Y. Обратите внимание, что уравнение также отображается в левой части экрана (вы можете установить флажки, чтобы скрыть или отобразить имеющиеся уравнения … Чтобы создать график журнала-журнала в Microsoft Excel, вы должны сначала создать XY (разброс ) график.1 доллар. Graph предназначен для тех, кому нужно бесплатное программное обеспечение для построения графиков с открытым исходным кодом для Windows или Mac. Найдите градиент линии по 2 точкам. Когда наборы данных более или менее линейны, это позволяет легко идентифицировать и понимать взаимосвязь между переменными. График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения. Для построения графика нам понадобятся координаты. Мы решили нарисовать слона и логотип Tufts. 12), дроби (10/3) или квадратные корни (r12).Посмотрите на линию y = 2x + 1 на графике. Сделать свой собственный! Совет профессионала! Постарайтесь не усложнять его. Используйте точечный график, чтобы показать линии тренда. Построение графиков линейных уравнений Теперь, когда мы решили уравнения с одной переменной, мы теперь будем работать над решением уравнений с двумя переменными и построением графиков уравнений на координатной плоскости. 🏆. Значение a = 2 и b = 1. Определение кусочной функции записывается в таком виде: f (x) = {F u n c t i o n 1 a m p; x — v a l u e s F u n c t i o n 2 a Создайте график линейного уравнения 5x плюс 2y равно 20.(Если у вас есть второе уравнение, используйте точку с запятой, например y = 2x + 1;… Том Лукас, Бристоль. Графическое отображение уравнений абсолютных значений Объединение одинаковых терминов Теперь нарисуйте точки на графике, где значения \ (x \) лежат на \ ( X \) — ось и соответствующие значения \ (y \) лежат на \ (Y \) — оси. Уравнения и графики ЧТОБЫ НАРИСОВАТЬ ГРАФИК — нарисуйте таблицу значений и нанесите точку. -пересечение (-и) и точку пересечения с y; и найти правильную форму графа КВАДРАТИЧЕСКАЯ ФОРМУЛА- x = — b ± √ IN ax ¿2 + bx + c, b — добавленные корни, а c — умноженные корни ax ¿ 2 + bx + c, где b — простое число, обозначим b как использование таблицы значений для графического отображения линейных уравнений.y = 4x — 2. A x + B y = C. Допустим, у вас есть 20 долларов, уравнение будет иметь вид y = 2 (20/5), что равно y = 2 (4), что равно y = 8, поэтому вы можете получить 8 апельсинов по 20 долларов. Таким образом, мы можем использовать правую часть (??), чтобы провести касательные линии в каждой точке плоскости. ) Используйте синтетическое деление, чтобы проверить свой выбор. Средняя длина пружины L = 23. Чем ближе R 2 к 1. Теперь перейдем к делу. и второе решение уравнения (4, 0). Мы надеемся вернуть новый инструмент для построения графиков уравнений, но на данный момент мы бы порекомендовали GraphSketch, бесплатный инструмент для создания хороших многофункциональных графиков.Также возможно выполнить некоторые математические вычисления для функций. Эммитт, Колледж Уэсли. фотон. Это тоже можно рассчитать и отобразить на графике. С этого момента используйте наклон, чтобы найти вторую точку и построить ее. Создавайте гистограммы, гистограммы, прямоугольные диаграммы, точечные диаграммы, линейные диаграммы, точечные диаграммы и многое другое. (Если вы не видите график или возникла проблема, попробуйте этот альтернативный графопостроитель). Каждый пример основан на предыдущем. 0 с) * (25. После того, как вы введете выражение, Калькулятор алгебры построит график уравнения y = 2x + 1.Мы решили использовать онлайн-инструмент для построения графиков Desmos, чтобы поиграть с нашими функциями, пока не сможем решить окончательные уравнения. пример. Из раскрывающегося списка… Графический инструмент — это эффективный модуль Python для обработки и статистического анализа графиков (а. Пять шагов для построения графика уравнения в OneNote. Это может быть использовано, например, владельцами стартапов для представления дохода свои проекты инвесторам. Это может показаться очевидным, но рассмотрите возможность построения квадратного уравнения. Откроется окно мастера построения диаграмм.- Скопировать в буфер обмена. Постройте точку. Нарисуйте математические и физические графики. 3 метра и глубина d = 0. Линейные графики — это один из стандартных вариантов графиков в Excel, наряду с гистограммами и составными гистограммами. Вы также можете проверить наши образцы или прочитать… Когда дело доходит до построения графиков линейных уравнений, есть несколько простых способов сделать это. Серия данных Earch может отображаться другим цветом. Чтобы упростить задачу, мы собираемся создать таблицу, в которую мы собираемся поместить кучу значений x, а затем вычислить соответствующее значение y. Поле направления — это график, состоящий из множества крошечных маленькие линии, каждая из которых приблизительно соответствует наклону функции в этой области.Если возможно, нарисуйте два разных плоских графа с одинаковым количеством вершин, ребер и граней. 0 м / с) Площадь = 313 м. Цель состоит в том, чтобы выбрать любые значения x и подставить эти значения в данное уравнение, чтобы получить соответствующие значения y. k. Существует так много разных типов, потому что каждый имеет довольно специфическое применение. Desmos использует y 1 для представления значения y в таблице данных и x 1 для представления значений x в таблице. Мы также расскажем, как разместить легенду на графике в групповой форме, задав команды в файле latex.… Бесплатный инструмент построения графиков для учителей математики. CoPlot имеет 7 основных типов графиков: XY, 3D, Треугольник, Полярный, Ортографический, Меркатор и Конический. Решение квадратных уравнений, заполнив квадрат. Щелкните вкладку «Дизайн», чтобы поиграть с цветовыми вариантами для «Переопределить уравнение». Разрез y — это место, где линия будет пересекать ось y, поэтому считайте вверх или вниз по оси y количество единиц, обозначенных значением b. Если вы собираетесь попробовать эти проблемы, прежде чем искать решения, вы можете избежать типичных ошибок, тщательно обозначив критические точки, точки пересечения и перегиб. Это уравнение утверждает, что наклон касательной линии к графику функции в момент времени t известен. и равно.2. y + x = 3. Adobe Spark можно использовать в качестве настраиваемого средства создания диаграмм, что дает вам возможность развивать свой бизнес без навыков программирования или дизайна. + C: Синий 1 Синий 2 Синий 3 Синий 4 Синий 5 Синий 6 Красный 1 Красный 2 Красный 3 Красный 4 Желтый 1 Желтый 2 Зеленый 1 Зеленый 2 Зеленый 3 Зеленый 4 Зеленый 5 Зеленый 6 Черный Серый 1 Серый 2 Серый 3 Серый 4 Белый Оранжевый Бирюзовый Фиолетовый 1 Фиолетовый 2 Фиолетовый 3 Фиолетовый 4 Создавайте красивые визуализации данных с помощью графического редактора Canva. После выбора ваша диаграмма немедленно изменится, чтобы соответствовать этому новому типу диаграммы.Используйте прогнозирование, чтобы вставлять дроби, показатели степени, операторы, формулы, химические символы и многое другое. Найдите градиент линии, используя ее график. Подставьте значения x в уравнение, чтобы найти значения y. Надеюсь, вы понимаете, что это уравнение линии в Стандартной форме, где переменные x и y находятся на одной стороне уравнения напротив постоянного члена. У нас есть графически изображенные уравнения вида. Эта программа будет полезна всем, кто хочет рисовать графики функций. Линии: форма пересечения склонов.Центральная. Распродажа! Программное обеспечение AxMath — Редактор уравнений $ 15. Стандартные функции: * построение нескольких декартовых, параметрических и полярных уравнений в портретном или ландшафтном режиме * автоматическое сохранение истории, уравнений и констант для последующего использования. Создание диаграммы таблиц Google с несколькими линиями на одной диаграмме. Сообщество редакторов документов. Найдите центральную точку a и b. Нанося точки (1, –1) и (–1, –2) на миллиметровую бумагу и соединяя их, мы получаем прямую линию, как показано на рис. Вот пример таблицы значений уравнения y = 2x + 1.Что такое диаграмма рассеяния. Получите события календаря из Outlook. От (0, -2) переместитесь на три единицы вверх и на четыре единицы вправо. В OneNote в Интернете это называется инструментом Marquee Select, а пунктирные линии образуют квадрат. Построение графика с использованием наклона и точки пересечения по оси Y. Есть еще один способ изобразить уравнение, используя ваши знания о наклоне и точке пересечения по оси Y. На каждом графике вы можете построить столько наборов данных и уравнений, сколько захотите. Во-первых, давайте познакомимся с координатной плоскостью … Используя свой графический инструмент, нарисуйте линию и круг.Построение точек Линейные уравнения. Шаг 2: Выберите столбец, который вы хотите разместить на осях x и y. ; Чтобы написать текст, просто щелкните в любом месте и начните вводить текст. Графики окружностей, эллипсов и гипербол вместе с их асимптотами Plotvar. Чтобы настроить график, созданный Math Assistant, выполните любое из… О программе: Помимо простых вычислений и группирования (например, «(x + 2) (x-4)»), вы также можете использовать некоторые функции. Пример 1. Заполните таблицы, нанесите точки и нанесите линии на график. Уравнение Grapher.Чтобы использовать алгоритм, вам нужно создать 2 отдельных графика. Рисунок 2: Таблица данных. Найдите градиент линии без графика, зная, что если вы просто хотите нарисовать изображение с помощью мыши, почему это должно быть сделано в MATLAB, а не в соответствующем приложении? Вы, вероятно, можете придумать средства для этого в MATLAB с помощью инструментов ROI, но это будет намного сложнее и громоздче, чем использование внешних инструментов или получение соответствующих значений или выражений. Ваше изображение должно состоять как минимум из 10 различных отрезков линий.Проведите линию через три точки. Наиболее подходящей формой для этого является графическое линейное уравнение: тип 3. Комбинированное графическое представление com — графическое отображение до 4 уравнений. Как создать линейный график. Основная ось — это сегмент, который содержит оба очага и имеет свои конечные точки в SciDAVis — бесплатном программном обеспечении для анализа научных данных и построения графиков для Windows. Excel упрощает построение графиков. Чтобы нарисовать линии, просто щелкните в любом месте сетки ниже и перетащите, удерживая кнопку мыши. О себе: Помимо простой математики и группировки (например, «(x + 2) (x-4)»), вы также можете использовать некоторые функции.Каждая точка на линии — это решение уравнения. photon — это бесплатное программное обеспечение для построения графиков для Windows. Подготовьте данные по осям X и Y. Мы можем найти наклон и точку пересечения оси y линии, просто взглянув на уравнение: m = 1/2 и точка пересечения y = 2. y — k = | x — h | Шаг 3. Чтобы получить вершину функции абсолютного значения, приведенной выше, приравняйте (x — h) и (y — k) к нулю, решение вопроса 1. В отличие от других онлайн-разработчиков графиков, Canva не является сложной и трудоемкой. Примите свои собственные значения x для всех представленных здесь листов.Вы можете выдвинуть гипотезу, что какое-то уравнение является правильным, а затем вычислить его по некоторым точкам (как уже указывалось, обе кривые могут… Графический расчет. График, созданный для каждого примера, показан справа. Калькулятор параболы — бесплатный онлайн инструмент, используемый для получения графика для данного параболического уравнения. Пример 4 График параболы для заданного диаметра и глубины. y = ax 2 + bx New Blank Graph. import matplotlib. Actions. Вы можете построить значение для каждого пикселя по горизонтали, но для каждой половины пикселя дает лучший результат, когда график очень вертикальный.В раскрывающемся меню «Выбрать действие» на панели «Математика» выберите «График в 2D» или «График с обеих сторон в 2D». Чтобы удалить график, оставьте его текстовое поле пустым. Посмотрите на уравнение еще раз. Чтобы распечатать график, нажмите кнопку печати и распечатайте из меню браузера или нажмите Ctrl + P. Вы хотите, чтобы уравнение линии было в формате y = mx + b. Это может быть очень полезно для них при разработке стратегии решения. Мы создаем различные типы диаграмм, включая линейную диаграмму, гистограмму, круговую диаграмму, автономную и групповую.none Это позволяет создавать красивые графики и решать уравнения, не покупая дорогостоящую математическую программу. Это откроет панель Math Assistant. Среда, 21 февраля 2018 г. «Было бы неплохо иметь возможность рисовать линии между точками таблицы в Graph Plotter, а не только точками. Com В этом видео показано, как построить график линейных уравнений из стандартной формы линейного уравнения, а также форма пересечения наклона o Пять шагов для построения графика уравнения в OneNote. Пока не беспокойтесь о фактическом символе неравенства — первый шаг — построение прямой линии.Постройте линейное уравнение, нанося точки. Расширенный набор функций дает вам доступ к: — поддержке внешнего экрана — 2D-трассировке. pyplot как plt plt. Вы можете исследовать. Графики Calc. Правила построения графиков с использованием формы пересечения уклона. http: // www. Введите экспериментальные точки (x 1, y 1), (x 2, y 2) a) Нарисуйте диаграмму рассеяния для данных и проведите линию наилучшего соответствия, включающую среднюю точку. Фактически, вы не знаете, как кривые ведут себя за пределами графика. Затем используйте инструмент «Лассо», чтобы выбрать уравнение, а затем на вкладке «Рисование» нажмите кнопку «Математика».10. Изобразите свою проблему, выполнив следующие действия: Введите уравнение, например y = 2x + 1. Обычно время записывается по оси X, а по оси Y отображаются изменения за указанный период. (y = bx) Щелкните «ноль» под тремя ползунками; Переместите центральный ползунок, чтобы получить разные значения b. Origin предлагает простой в использовании интерфейс для новичков в сочетании с возможностью выполнять расширенную настройку по мере того, как вы ближе познакомитесь с приложением. сети). Y-значения были специально выбраны, чтобы быть неточными, чтобы проиллюстрировать то, что вы увидите, когда проанализируете данные из своих лабораторий.Центр этого эллипса — начало координат, поскольку (0, 0) — середина большой оси. Простая в использовании система проектирования позволяет вам выбирать каждый аспект дизайна вашей диаграммы, поэтому у вас есть что-то уникальное и привлекательное для потенциальных клиентов, а Grapher — это быстрый и эффективный плоттер уравнений, способный рисовать любые функции и решать уравнения. и вычисление выражений. Студенты получают возможность визуализировать наиболее важные пересечения между линиями, плоскостями и сферами: точку пересечения, линию или круг.y = 2 (x / 5), где y — апельсины, а x — количество денег, которое у вас было. Программа позволяет очень легко визуализировать функцию и вставить ее в другую программу. Мы генерируем эти координаты, подставляя значения в линейное уравнение. Вы можете вспомнить, что логарифмические функции определены только для положительных действительных чисел. Настройте такие детали, как цвета линий и шрифты меток. Постройте y-int (0, -2). Наклон: рост / бег = 3/4. Пересечение оси y — это точка пересечения линии с осью y, поэтому отсчитайте вверх или вниз по оси y количество единиц, обозначенных значением b.Отрегулируйте ползунки, пока не получите максимально возможное значение R². Создатель линейного графика Вы находитесь на странице создания линейного графика. Создание онлайн-графика занимает всего несколько секунд. Plotvar — лучший способ создать линейный график, круговую диаграмму, гистограмму или даже живой график. в и лучше рассмотреть. … Учитывая линейное уравнение, это видео покажет, как построить график без использования таблицы x / y. Насколько хорошо это уравнение описывает данные («соответствие»), выражается в виде коэффициента корреляции R 2 (R-квадрат). Наше рекомендуемое программное обеспечение.Desmos. таким образом корректируя координаты и уравнение. Выделите столбцы концентрации и оптической плотности и нажмите «Вставить» в верхнем меню. Только уравнения 1, 3, 5 и 6 являются формами с центральным радиусом. + C: Синий 1 Синий 2 Синий 3 Синий 4 Синий 5 Синий 6 Красный 1 Красный 2 Красный 3 Красный 4 Желтый 1 Желтый 2 Зеленый 1 Зеленый 2 Зеленый 3 Зеленый 4 Зеленый 5 Зеленый 6 Черный Серый 1 Серый 2 Серый 3 Серый 4 Белый Оранжевый Бирюзовый Фиолетовый 1 Фиолетовый 2 Фиолетовый 3 Фиолетовый 4 ihasmath показывает вам три различных метода построения линейных графиков из уравнений в форме y = mx + c.2. — Включить / выключить графики — Перетащить, чтобы повернуть — переместить. com’s Equation Graphing — графическое отображение нескольких уравнений одновременно. AxDraw — рисовать графики вручную. Иногда сложную информацию сложно понять, и ее нужно проиллюстрировать. Асимптоты указывают, где рисовать гиперболу. Бесплатное начало работы! Создавайте диаграммы и информационные панели в Интернете из данных CSV или Excel. Для типа диаграммы: выберите X-Y Scatter. Сначала создайте уравнение, используя рукописный ввод или текст. Предположим, вы хотите вместо этого нарисовать кривую. Когда плоский граф нарисован таким образом, он делит плоскость на области, называемые гранями.На (бумажном) листе миллиметровой бумаги нарисуйте картинку, состоящую только из отрезков прямых линий. y x x… Если два графика не пересекаются — что означает, что они параллельны — тогда решения нет. Вы можете использовать следующую ссылку, чтобы вернуться к своему рисунку. Икс. Точка 1: точка пересечения y: это точка, в которой линия пересекает ось y, ее координаты всегда: (0, c), где c можно прочитать непосредственно из уравнения y = m x + c. Вы можете рисовать графики функций и выполнять математические вычисления с функциями.Тип закона Пива в [K2CrO4] в ячейке A1 (ось x) и абсорбция в ячейке B1 (ось y). В качестве примера воспользуемся неравенством y — 2> 4x. Origin — это программное обеспечение для анализа данных и построения графиков, которое предпочитают более полумиллиона ученых и инженеров в коммерческих отраслях, академических кругах и государственных лабораториях по всему миру. com содержит бесценные факты о бесплатном онлайн-калькуляторе интервальной записи, степенной и базовой алгебре и других вопросах алгебры. Графическое отображение угла наклона-пересечения — PhET: Бесплатная онлайн-физика. Этот онлайн-калькулятор анализирует положение и временную таблицу, которая часто используется для описания движения одномерной кинематики.. 0, 2. Точечная диаграмма (или точечная диаграмма) — это двумерное графическое представление набора данных. Это онлайн-генератор / конструктор графиков, который создает линейную диаграмму для вводимых вами данных. Самая фундаментальная стратегия построения графика линии — это использование таблицы значений. Изучите математику с помощью нашего красивого бесплатного графического калькулятора. Просто скопируйте и вставьте приведенный ниже код на свою веб-страницу, где вы хотите отобразить этот калькулятор. Уравнения и графики ЧТОБЫ ПОКАЗАТЬ ГРАФИК — составить таблицу значений и нанести точку. ЧТОБЫ НАРИСАТЬ ГРАФИК — построить точку пересечения по оси x и точку пересечения по оси Y; и найти правильную форму графа КВАДРАТИЧЕСКАЯ ФОРМУЛА- x = — b ± √ IN ax ¿2 + bx + c, b — добавленные корни, а c — корни, умноженные на ax ¿2 + bx + c, где b — простое число, поместите b в терминах «Сделать линейную диаграмму» — создать линейную диаграмму онлайн-инструмента линейную диаграмму без создания линейного графа апплета Сделайте линейную диаграмму для вашего отчета Гистограммы, как и линейные диаграммы, полезны для сравнения классов или групп данных.Код рисует оси X и Y тонким пером, а затем меняет цвет пера перед рисованием графика. Сделанный. Проведите линию через две точки ӿ Практика. В этом примере требуется WebGL Visit get. Интерактивный бесплатный онлайн-калькулятор для построения графиков от GeoGebra: функции графиков, данные для построения графиков, ползунки перетаскивания и многое другое! Постройте уравнение, в котором x и y каким-то образом связаны, например, 2x + 3y = 5. 5 * b * h = 0. My. Пусть осядет, скажем, на 2,15 см. Решение. Пройденное расстояние можно рассчитать с помощью кинематического уравнения.Он содержит несколько функций, которых нет ни в каких других калькуляторах на рынке. Вы также можете рисовать графики функций. Нарисуйте линейные графики, используя y = mx + c. 11. (Вы можете нанести более двух точек для проверки) Пример: начертите линию с уравнением y = 2x — 3. Нет правильного или неправильного способа выбора этих значений x. Чтобы построить линейное уравнение, мы можем использовать наклон и точку пересечения по оси Y. Посмотрите ниже, чтобы увидеть их все. Диаметр графика. Затем для отображения графика используется метод show (). Каждое решение этого уравнения представляет собой точку на этой прямой.Следуйте этому ответу, чтобы получать уведомления. Поскольку данное уравнение ясно показывает, как значения y связаны со значениями x, кажется разумным начать с присвоения нескольких разных чисел x, а затем найти соответствующие значения y, чтобы получить точки, которые лежат на графике. б. Введите свои элементы и значения на вкладке «Содержимое» на странице создания графика. Исследуйте чудесный мир графиков. Если вы можете найти точку пересечения оси y и угол наклона, вы можете написать уравнение в форме точки пересечения угла наклона (если, конечно, это не вертикальная линия.Здесь вы можете легко рисовать линии, текст и распечатывать миллиметровую бумагу. Построитель кривых особенно подходит для исследования функций, он позволяет получить. Старый графический редактор уравнений, который мы предоставили, использовал Flash, который сильно устарел и больше не поддерживается широко. Например, вот простое математическое уравнение -. Выбирайте из различных типов диаграмм, например: линейные и гистограммы, круговые диаграммы, точечные диаграммы, XY-графики и круговые диаграммы. Это одна из самых популярных бесплатных программ для рисования математических и статистических графиков.Придайте вашим тестам, рабочим листам и презентациям профессиональный вид. y = f (x) + 2 создает… Создайте диаграмму листов Google с несколькими линиями в одном сообществе редакторов документов диаграммы. Природа корней квадратного уравнения. Из уравнения мы знаем, что интервал y равен 1, точка (0, 1) и наклон равен 3. Если все переменные представляют собой действительные числа, можно построить уравнение, нанеся на график достаточно точек, чтобы распознать шаблон, а затем соединить точки для включения. На вкладке «Настройка» выберите альтернативную форму графика или диаграммы из раскрывающегося списка «Тип диаграммы». меню.com — отличный сайт для изучения! Ответ (1 из 4): Краткий ответ: нет. — Библиотека часто используемых уравнений. Он также отображает экспериментальные точки и уравнение y = a x + b, где a и b задаются формулами выше. 3. Чтобы сохранить график в файл pdf, распечатайте график и выберите принтер pdf. 00. Это шаги, выполняемые нашим создателем огива, и конечный результат будет выглядеть, как на графиках, показанных выше. Настройте свой линейный график. Для отображения диаграммы рассеяния количество значений x должно равняться количеству значений y.Мы можем построить вычислительный график приведенного выше уравнения следующим образом. Чтобы построить график гиперболы, мы построим две вершины и асимптоты. Чтобы построить график линейного уравнения, сначала составьте таблицу значений. 🔗. нарисуйте график онлайн и получите уравнение