Как решать типовые задачи по физике
Обучаясь в школе, каждый сталкивается с решением задач по физике. Не всем дисциплина дается легко.
Бытует мнение, что для успешного решения задач по этому предмету, нужно досконально разбираться в физических процессах. Это не совсем так. Мы считаем, что достаточно использовать определенный алгоритм, чтобы добиться значительных успехов. Спешим поделиться с вами ценной информацией!
Как решать задачи по физике
Итак, чтобы задачи по физике давались легко, предлагаем придерживаться следующей системы:
- Внимательно прочитайте условия задачи, при необходимости, несколько раз; вникнете в то, о чем говорится в тексте.
- Запишите условия. Все известные в задаче данные нужно записать в столбик под названием «Дано».

- С столбце «СИ» приведите все данные в задаче к международным единицам измерения. Так как в международной системе основными единицами измерения массы считаются килограммы (кг), массу из приведенной выше задачи необходимо привести в нужное значение: 1 000 тонн = 1 000 000 кг.
- Нарисуйте схематичный рисунок. Он нужен не для всех задач. Но в тех, где упоминаются действующие на тело силы и векторы скоростей, изображение может существенно облегчить понимание процесса и натолкнуть на правильное решение.
- Определите неизвестную величину, ту, что необходимо узнать, решив задание. Написав в столбике все, что известно в задаче, проведите черту под известными данными и пропишите ту величину, которую будете искать.

- Подберите формулы. Это самый важный пункт в нашем алгоритме! Решение задачи после выбора формулы будет заключаться в математических вычислениях, которые имеют к физике лишь опосредованное отношение. На черновике выпишите те формулы, которые могут подойти для конкретной задачи и выберите ту, которая будет способствовать решению.
- Математические вычисления. Остальное решение задачи сводится к математике. Нужно сделать необходимые преобразования и сокращения, если они нужны. Затем составить уравнение или систему уравнений. Остается только их решить и найти все неизвестные, а в конце искомую величину. Ответ обведите в прямоугольник.
Примеры решения типовых задач по разделам
Рассмотрим подробнее решение задач из разных разделов физики по предложенному алгоритму. И дадим все необходимые объяснения к каждой из них.
Система абсолютно универсальна и подходит для решения заданий по динамике, кинематике, статике и другим разделам физики.
Кинематика
Источник: znanio.ruКинематика — это раздел механики, который изучает математическое описание движения тел.
Данный раздел охватывает следующие темы:
- равномерное и равноускоренное движение тел;
- движение тела по окружности;
- относительность движения;
- свободное падение тел.
Рассмотрим типовые задачи на каждую из этих тем.
Равномерное и равноускоренное движение тел
Для решения задач по этой теме нужно знать уравнение движения тела, понимать, что такое средняя, постоянная скорости и ускорение, уметь выяснять их векторное направление в конкретной задаче.
Как правило, в задачах на равномерное и равноускоренное движение необходимо найти или пройденный путь (S), или скорость движения (V), или время (t).
Задача:
Поезд длиной 240 метров, двигаясь равномерно, прошел мост за 2 минуты. Какова была скорость поезда, если длина моста равна 360 метрам?
Какова была скорость поезда, если длина моста равна 360 метрам?
Решение:
- Записываем известные нам данные:\( l_1=240\) м., \(l_2=360\) м., \(t=2\) мин., \(V\)=?
- Проводим необходимые преобразования времени до принятых в мире единиц измерения — секунд: 2 минуты = 120 секунд.
- Мы знаем, что скорость равномерного движения определяется по формуле: \(V=\frac st\)
- Время нам известно, для того, чтобы найти скорость, нужно сначала определить путь пройденный поездом. Если мы схематично изобразим перемещение поезда по мосту, то увидим, что путь, пройденный поездом, равен длине самого поезда плюс длине самого моста, т.е. \(s=l_1+l_2\).
- Переходим к математическим вычислениям: \(s=240+360=600\) метров.
- \(V=600/120= 5\) м/с.
Задача:
При равноускоренном движении с начальной скоростью 5 м/с тело за 3 секунды прошло 20 метров. С каким ускорением двигалось тело? Какова его скорость в конце третьей секунды?
Решение:
- Фиксируем данные известных нам величин: \(V_1=5 \) м/с, \(t=3\) с, s=20 м.
 2.\)
2.\) - Нам известна формула для определения скорости при равноускоренном движении: \(V_2=V_1+a\times t\)
- Все данные у нас для вычисления скорости есть, подставляем их в формулу и получаем скорость, равную \(8,3\) м/с.
Движение тела по окружности
Чтобы успешно решать задачи по этой теме, необходимо знать формулы, характеризующие движение тел по окружности. В задачах на движение тела по окружности обычно необходимо вычислить скорость, центростремительное ускорение, радиус или длину окружности.Задача:
Каково центростремительное ускорение поезда, который движется по закругленной железной дороге радиусом 800 метров со скоростью 72 км/ч?
Решение:
- Записываем вводные данные: \(R=800 м\), \(V=72\) км/ч, \(a\)=?
- Переводим скорость из км/ч в м/с, получаем 20 м/с.
- Мы знаем формулу, по которой можно определить центростремительное ускорение: \(a=\frac{V^2}R\)
- Все данные нам известны, подставляем числовые значения в формулу и получаем искомую нами величину, равную \(0,5 м/с^2\)
Свободное падение тел
Для решения задач по этой теме нужно знать закон движения при свободном падении и закономерность изменения скорости тела со временем, а также помнить про постоянную величину — коэффициент силы тяжести.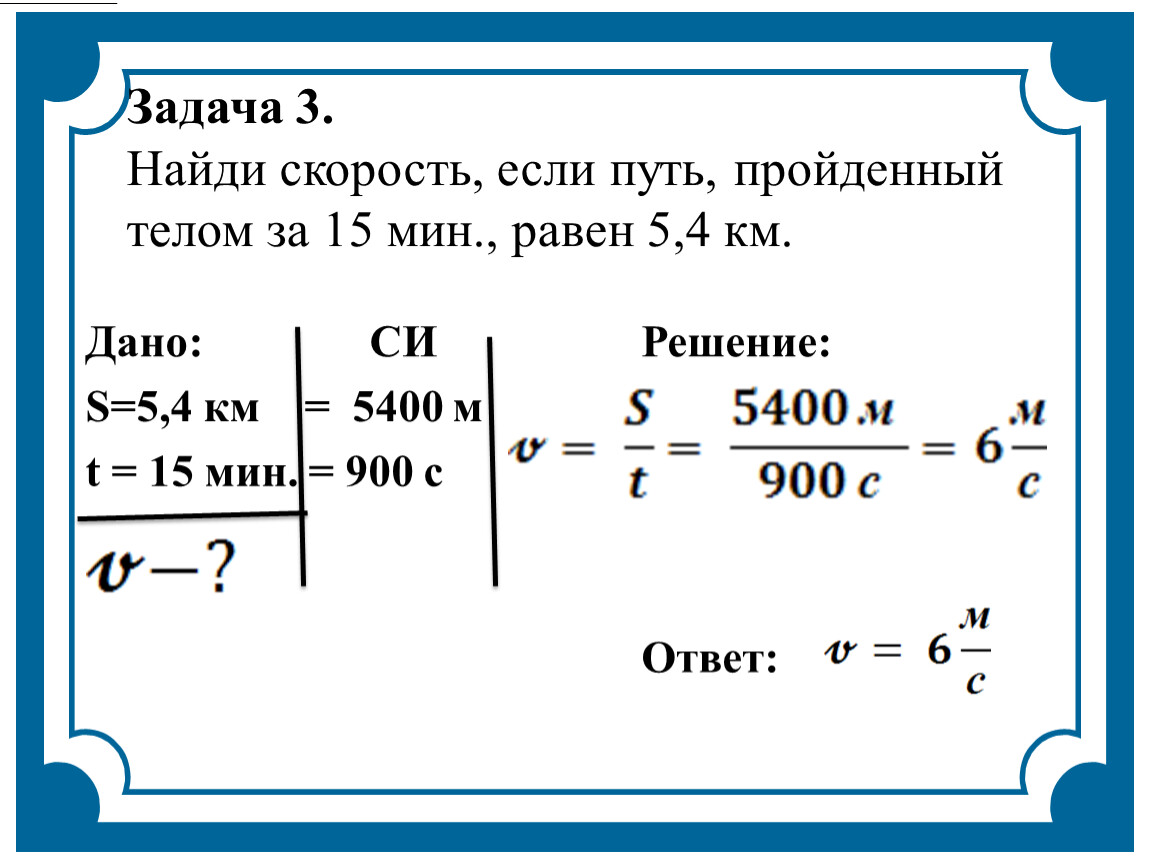
В задачах на свободное падение тел может быть предложено найти скорость движения тела, высоту, с которой оно падало или время его движения.
Задача:
Камень брошен вниз с высоты \(85\) метров. Он летит со скоростью \(8\) м/с. С какой скоростью он ударяется о землю?
Решение:
- Определяем известные и неизвестные нам данные: \(h=85\) метров, \(V_1=8\) м/с., \(V_2=?\) Мы помним, что на любое падающее тело воздействует коэффициент силы тяжести, равный \(9,8\) Н/кг.
- У нас есть все вводные для определения конечной скорости по формуле: \(V_2=V_1+g\times t\)
- Подставляем числовые значения в уравнение и получаем скорость тела в момент удара о землю, равную \(41,3\) м/с.
Относительность движения
Задачи на относительность движения всегда требует выбрать неподвижную систему координат, относительно которой и будут производиться все расчеты. В таких заданиях ученикам обычно предлагают найти относительную скорость объекта, минимальное время, продолжительность пути или длину объекта.
Задача:
Два поезда движутся навстречу друг другу по параллельным ж/д путям. Один — со скоростью 72 км/ч, другой — со скоростью 54 км/ч. Пассажир первого поезда отмечает, что второй проходит мимо него в течение 10 секунд. Определите длину второго поезда.
Решение:
- Записываем известные нам данные: \(V_1=72\) км/ч, \(V_2=54\) км/ч, \(t=10\) с, \(l_2=?\)
- Переводим км/ч в м/с: \(V_1= 20\) м/с, \(V_2=15\) м/с.
- Определяем систему координат, от которой будем отталкиваться при вычислении искомой величины. Логично будет, если такой системой станет линейная система координат, связанная с первым поездом и направленная по ходу его движения. Получается, что второй поезд двигается со скоростью \(V_2=15\) м/с в направлении со скоростью \(V_1=20\) м/с.
- Находим общую скорость движения по формуле: \(V=V_1+V_2\)
- Она равна \(35\) м/с.
- Определяем длину поезда по формуле: \(l_2=V\times t\)
- Получаем длину поезда, равную \(350\) метрам.
 2}\) вычисляем силу притяжения между книгами.
2}\) вычисляем силу притяжения между книгами. - Произведя математические вычисления получаем ответ: книги притягиваются друг к другу с силой приблизительно равной \(2,4\) Н.
Сила упругости
Задача:
К покоящейся на горизонтальной поверхности системе, которая состоит из куба массой 1 кг и 2-х пружин, приложена постоянная горизонтальная сила величиной 25 Ньютонов. Между кубом и поверхностью трения нет. Жесткость первой пружины составляет \(450 Н/м\), жесткость второй пружины \(550 Н/м\). Определите удлинение пружин.
Решение:
- Записываем в столбце «Дано» данные, которые нам известны: \(m=1\) кг,\( F=25\) Н, \(k_1=450\) Н/м, \(k_2=550\) Н/м, \(\Delta l_1=?\), \(\Delta l_2=? \)
- Согласно 3-му закону Ньютона \(F=F_упр\)
- По закону Гука \(F_упр=F=k\times\Delta l\) отсюда выводим формулы для нахождения удлинения пружин: \(\Delta l_1=\frac F{k_1}\) и \(\Delta l_2=\frac F{k_2}\)
- Подставляем известные нам числовые значения в формулы и получаем ответ: \(6 см\) — удлинение первой пружины, \(5 см\) — удлинение второй пружины.
 2.\)
2.\) - Переводим минуты в часы: \(1\) минута=\(60\) секунд.
- Найти работу можно по формуле: \(A=F\times S\)
- В данных условиях \(S=h\), а \(F=g\times m\)
- В условиях задачи нет значения массы тела, но мы помним, что массу можно найти по формуле: \(m=p\times V\)
- Формула нахождения работы приобретает следующий вид: \(A=p\times V\times g\times h\)
- Подставляем известные числовые значения в формулу и получаем ответ: работа = 3 528 000 000 Дж = 3 528 МДж.
Закон сохранения энергии и импульса
Задача:
Тепловоз массой 130 тонн приближается со скоростью 2 м/с к неподвижному составу массой 1170 тонн. С какой скоростью будет двигаться состав после сцепления с тепловозом?
Решение:
- Записываем известные нам данные: \(m_1=130\) тонн, \(V_1=2\) м/с, \(m_2=1170\) тонн, \(V_2=0\) м/с, V=?
- Согласно закону сохранения импульса \(m_1\times V_1+m_2\times V_2=m_3\times V_3\)
- Из этой формулы получаем уравнение для нахождения скорости состава после сцепления: \(V_3=\frac{m_1\times V_1}{m_1+m_2}\)
- Подставляем известные нам значения в формулу и получаем искомую скорость, равную \(0,2\) м/с.

Статика
Источник: infourok.ruСтатика — третий раздел механики, который изучает механические системы в условиях равновесия и действие приложенных к ним сил.
Для решения задач по статике необходимо обязательно рисовать схемы, иллюстрирующие заданные процессы, определять модули и направления сил, пользоваться законами сопротивления материалов.
Статика включает в себя следующие разделы:
- равновесие тел;
- давление в жидкостях и газе;
- закон Архимеда.
Равновесие тел
Источник: infourok.ruДавление в жидкостях и газе
Задача:
Водолаз в жестком скафандре может погружаться на глубину 250 метров, искусный ныряльщик — на 20 метров. Определите давление воды в море на этих глубинах.
Решение:
- Записываем известные нам данные из условия задачи: \(h_1\)=250 м, \(h_2\) =20 м, \(p=1030 кг/м^3\), \(g=9,8\) Н/кг, \(p_1=?,\) \(p_2=?\)
- По формуле \(P_1=p\times g\times h_1\) определяем давление воды для водолаза, оно будет равно примерно 2524 кПа.
 3.\)
3.\)
Молекулярная физика
Молекулярная физика — это один из разделов физики, описывающий физические свойства объектов путем изучения их молекулярного строения.
В основе всех задач по молекулярной физике лежит уравнение молекулярно-кинетической теории: \(P=\frac13\times m_0\times n\times V_2\)
Источник: znakka4estva.ruТермодинамика
Источник: present5.comТермодинамика — физический раздел, который изучает общие свойства макроскопических систем, способы передачи и превращения энергии в них.
В раздел термодинамики входят следующие темы:
- теплота сгорания топлива;
- изменение внутренней энергии тела при совершении работы;
- внутренняя энергия идеального газа;
- первый закон термодинамики;
- КПД теплового двигателя.
Теплота сгорания топлива
При решении задач на сгорание топлива, важно помнить про удельную теплоту сгорания каждого вида топлива. 7\) Дж/кг, \(Q=?\)
7\) Дж/кг, \(Q=?\)
Изменение внутренней энергии тела при совершении работы
Задача:
Вычислите внутреннюю энергию 1 килограмма воды при ее нагревании на 2 Кельвина.
Решение:
- Записываем известные и неизвестные величины из условий задачи: \(m=1\) кг, \(T=2\)К, \(U=?\), не забываем про удельную теплоемкость воды \(c=4200\) Дж/кгхК.
- Количество теплоты, которое получит вода, будет затрачено на изменение ее внутренней энергии, т.е. \(U=Q\).
- \(Q=c\times m\times T\) следовательно, \(U=c\times m\times T\)
- Подставляем числовые значения в формулу и получаем ответ: 8400 Дж.
Внутренняя энергия идеального газа, первый закон термодинамики
При решении таких задач важно помнить про молярную массу вещества и универсальную газовую постоянную.
Задача:
Чему будет равна внутренняя энергия гелия массой 200 грамм при условии, что температура будет увеличена на 20 Кельвинов?
Решение:
- Фиксируем известные величины: \(m=200\) г, \(\Delta T= 20\) К.
 3\).
3\). - Коэффициент полезного действия определяется по формуле: \(\eta=\frac{A_п}{A_з}\)
- \(A_п\) равна количеству теплоты (\(Q\)), которое необходимо для изменения температуры воды. \(A_п=Q=c\times m\times T.\) Массу воды найдем по формуле: \(m_1=p_1\times V_1\)
- \(A_з\) равна количеству теплоты, выделенному при сгорании керосина массой 80 грамм, следовательно, \(A_з=q\times m_2\)
- Подставив все известные величины в формулу, получаем ответ: КПД = 0,33.
Электростатика
Источник: infourok.ruЭлектростатика — это раздел физики об электричестве, который изучает взаимодействие электрических зарядов, находящихся в неподвижности.
К задачам по электростатике относятся задачи на :
- закон Кулона;
- напряженность и работу электростатического поля;
- электроемкость.
Закон Кулона
Задача:
Определите силу взаимодействия двух одинаковых точечных зарядов по 1 микро кулону, которые находятся на расстоянии 30 сантиметров друг от друга. 2/м\).
2/м\).
Задача на работу и мощность тока:
Определите мощность и работу электродвигателя вентилятора за 10 минут, если при напряжении 220 Вольт сила тока в электродвигателе составила 1 Ампер.
Решение:
- Записываем условия: \(t=10\) мин, \(U= 220\) В, \(I=1 А\), \(P=?\) \(A=?\)
- Переводим минуты в секунды, получаем 600 секунд.
- По формуле \(P=I\times U\) определяем мощность тока. Она равна 220 Вт.
- По формуле \(A=P\times t\) находим работу, получаем 132000 Дж или 132 кДж.
Магнитное поле
К задачам раздела «Магнитное поле» относятся задания на:
- силу Ампера;
- силу Лоренца;
- магнитный момент, индукцию и самоиндукцию, энергию магнитного поля.
 -15 Н\).
-15 Н\). - механические гармонические колебания математических маятников;
- пружинный маятник;
- энергия механических колебаний;
- механические волны;
- колебательный контур;
- электромагнитные волны.
- Подробности
- Просмотров: 1936
- Учебная группа Забавные задачки
- ключевое слово по вашему выбору
- Вопросы о физических явлениях, зависящие от реальных данных.
- Вопросы, требующие теории и математики. Задания на конец главы в учебнике обычно такого рода. Иногда это идеализированные предположения.
- Вопросы, требующие скрытного, хитрого, умного или проницательного подхода. Их правильнее называть «головоломками».
- Определите это! Головоломки, требующие использования тщательных и точных определений или формулируемые с неоднозначными определениями.
- Самореферентный. Головоломки с простыми или концептуальными ответами возможны только из-за того, что головоломка поставлена особым образом.
- Головоломки. Головоломки, описывающие особые ситуации, которые являются (а) нефизическими или (б) имеют особые условия, которые позволяют просто решить запутанную и сложную ситуацию.
- Концептуальные путаницы. Головоломки, в которых используются распространенные заблуждения о природе, физике или математике.
- Парадоксы (кажущиеся). Головоломки, предназначенные для описания явно противоречивых или парадоксальных ситуаций или объяснений.
- Визуальные обманы. Головоломки, в которых прилагаемая диаграмма вводит в заблуждение или обманывает. (Картинки могут лгать.)
- Разве это не предел? Головоломки, требующие большой осторожности при достижении пределов от нуля до бесконечности.
 Многие классические доказательства математических парадоксов (иногда называемые «пуфами») зависят от такого рода обмана, такого как скрытое деление на ноль. Например, доказательство того, что 2 + 2 = 5. (Ну, оно действительно для достаточно больших значений 2.)
Многие классические доказательства математических парадоксов (иногда называемые «пуфами») зависят от такого рода обмана, такого как скрытое деление на ноль. Например, доказательство того, что 2 + 2 = 5. (Ну, оно действительно для достаточно больших значений 2.) - Движение по центростремительным кругам. Две одинаковые массы (черные) соединены шнурами Т 1 и Т 2 одинаковой длины и качаются вокруг «неподвижной» оси. Если дано T 1 , что такое T 2 ? Объясните свой ответ, не используя слово «центробежный». Сначала сделайте быстрое предположение. Тогда решите правильно.
Придирчивые могут заметить, что из-за гравитации это движение не будет лежать в одной плоскости, потому что мячи будут вращаться ниже, чем рука свингера.
 Не обращайте внимания на это отвлечение.
Не обращайте внимания на это отвлечение. - Водный мост. В Европе есть несколько необычных мостов. Обычно мосты (с улицей или железной дорогой наверху) пересекают реку. Но есть исключения. Иногда канал проводят через мост, перекинутый через шоссе или даже через реку. Это так называемые водные мосты.
Магдебургский водный мост. Фото Сандры Сандрок Дуглас. Проектировщики мостов учитывают максимальный вес трафика, который мост может выдержать.Как это относится к водным мостам? Предположим, что уровень воды на таком мосту остается почти постоянным, когда его пересекают корабли, равно как и масса воды над мостом — она может составлять 10 000 тонн. Корабль, идущий по каналу, имеет вес 1000 тонн. Какова дополнительная нагрузка на мост, когда судно стоит посреди моста?
Магдебургский водный мост — судоходный акведук в Германии, который соединяет канал Эльба-Хафель с каналом Миттельланд, позволяя судам пересекать реку Эльба.
 918 метров — это самый длинный судоходный акведук в мире.
918 метров — это самый длинный судоходный акведук в мире.Водные мосты редкость в США. Стантон де Риэль сообщил мне об одном.
Канал D&R (Делавэр и Раритан) имеет то, что вы могли бы назвать водным мостом через приток реки Миллстоун, к северу от Принстона, штат Нью-Джерси. Канал судоходен, хотя в настоящее время только на каноэ (коммерческое судоходство некоторое время назад прекратилось; шлюзы больше не обслуживаются).
Головоломка, представленная Хансом-Петером Граматке.
- Могучий Мускус. Скорый поезд движется со скоростью 100 миль в час. Муха на встречном курсе движется со скоростью 5 миль в час точно против поезда. Муха ударяется в оконное стекло локомотива, застревает (RIP) и продолжает двигаться вместе с поездом — конечно, со скоростью поезда 100 миль в час. Когда муха изменила направление своего движения, должна была быть точка, в которой ее скорость была равна нулю, хотя бы на мгновение. Если бы муха имела нулевую скорость, то в этот момент и скорость поезда должна была быть равна нулю.
 Объясните, как эта сильная муха смогла остановить (даже на короткое время) поезд, движущийся со скоростью 100 миль в час.
Объясните, как эта сильная муха смогла остановить (даже на короткое время) поезд, движущийся со скоростью 100 миль в час.Головоломка, представленная Хансом-Петером Граматке.
- Драг-рейсинг. Дик и Джейн проводят лабораторный эксперимент, измеряя трение, определяя время скольжения деревянных блоков по наклонной плоскости с постоянной скоростью. Блоки размером 3 х 4 х 5 дюймов. Дик предлагает гонку и предсказывает, что если блок скользит по своей грани 3×4, у него будет меньшая площадь контакта и меньшее трение, чем если бы блок скользил по своей грани 4×5 дюймов, поэтому с меньшим сопротивлением трения он выиграет гонку, когда оба скатиться вниз по самолету.Джейн не соглашается, утверждая, что они по-прежнему весят одинаково, поэтому гонка закончится ничьей. Кто прав и почему?
Скатывание по склону. - Отправляйтесь на гонки. Стандартная физическая задача (и демонстрация) заключается в том, что цилиндры катятся по наклонной плоскости.
 Цилиндры сконструированы так, чтобы иметь одинаковую массу и одинаковый внешний радиус, но один из них сделан из цельного дерева, а другой представляет собой металлический обруч. Обруч, имея больший момент инерции, меньше разгоняется под действием силы тяжести и проигрывает гонку.
Цилиндры сконструированы так, чтобы иметь одинаковую массу и одинаковый внешний радиус, но один из них сделан из цельного дерева, а другой представляет собой металлический обруч. Обруч, имея больший момент инерции, меньше разгоняется под действием силы тяжести и проигрывает гонку.Но что, если мы форсируем эту гонку по-другому? Изготовьте два цельных цилиндра одинаковой длины и радиуса, но из материалов очень разной плотности. У них будут очень неравные массы. Кто из них победит и почему?
Теперь гоняйте два сферических шара одинакового радиуса, но разных масс, скажем, один из стали, другой из дерева. Что победит?
Как обычно в этих головоломках, вы можете предположить идеальные материалы, пренебрежимо малое трение и качение без проскальзывания (несмотря на отсутствие трения!).Эти головоломки могут быть решены без явного использования математики. Галилей мог бы их решить. Возможно, Архимед мог бы.
Запутанная снасть. 
- Запутанная снасть. . Время от времени изобретательные мастера пытаются улучшить Архимеда. Вот умный вариант стандартной системы шкивов. Вычислите его механическое преимущество, предполагая отсутствие трения, невесомые шкивы и совершенно гибкий канат незначительной массы.
- Мыльница Дерби. Ребёнок строит безмоторный гоночный автомобиль. У него есть блестящая идея использовать вместо четырех колес только три колеса, чтобы уменьшить трение автомобиля. Повысит ли эта модификация характеристики автомобиля в скоростном спуске? Почему?
- Очень честная гонка . Несколько лет назад кому-то пришла в голову блестящая идея провести гонку на воздушной подушке. Судно на воздушной подушке поддерживается над землей большим вентилятором, который нагнетает воздух вниз.Корабль движется так, как если бы он находился на поверхности с очень низким коэффициентом трения. Эти транспортные средства также имеют еще один вентилятор для движения.
 Это довольно большие автомобили, поэтому организаторы гонки разработали круговую трассу с наклоном, чтобы автомобили, находящиеся внутри трассы, не имели преимущества. Судя по всему, ипподром так и не был построен, и такие гонки никогда не проводились. Почему?
Это довольно большие автомобили, поэтому организаторы гонки разработали круговую трассу с наклоном, чтобы автомобили, находящиеся внутри трассы, не имели преимущества. Судя по всему, ипподром так и не был построен, и такие гонки никогда не проводились. Почему?Тянет йо-йо. - Йо-йо. Игрушка йо-йо лежит на краю ровного стола.
- Если струна выйдет над осью, что произойдет, если вы потянете струну параллельно столу? Будет ли он катиться влево или вправо?
- Если струна выйдет ниже оси, что произойдет, если вы потянете струну параллельно столу?
- Если нить натянуть прямо вверх, в какую сторону она покатится?
- Под каким углом можно потянуть за веревку, чтобы она скользила по столу, не перекатываясь? Коэффициент трения скольжения на границе со столом равен 0.5.
Подтвердите свои ответы анализом лесов.
- Воздействие.
 Две одинаковые круглые шайбы лежат на горизонтальном столе без трения. Одна шайба продвигается к неподвижной шайбе. Они сталкиваются, и столкновение абсолютно упругое. Шайба Нитера вращается до или после столкновения. Докажите, что после столкновения скорости двух шайб равны друг другу, независимо от того, как произошло столкновение.
Две одинаковые круглые шайбы лежат на горизонтальном столе без трения. Одна шайба продвигается к неподвижной шайбе. Они сталкиваются, и столкновение абсолютно упругое. Шайба Нитера вращается до или после столкновения. Докажите, что после столкновения скорости двух шайб равны друг другу, независимо от того, как произошло столкновение. - Левитация. Почему этого не происходит?
Утренняя левитация. - Горящая свеча с обоих концов.
Harpo Marx зажигает свечу с обоих концов.
Лошадиные перья (1932).Свеча обрезается снизу так, чтобы торчали оба конца фитиля. Гвоздь или длинная игла втыкается в середину свечи и опирается на края двух стаканов. Затем свеча зажигается с обоих концов.Обычно свеча будет колебаться вокруг оси.
 Является ли результирующее движение простым гармоническим движением или просто периодическим? Является ли его период постоянным?
Является ли результирующее движение простым гармоническим движением или просто периодическим? Является ли его период постоянным? Парадокс давления. Старомодная бутылка негомогенизированного молока остается нетронутой. Сливки в молоке поднимаются и занимают узкое горлышко в более узкой верхней части бутылки. Давление молока на дно бутылочки теперь такое же, больше или меньше, чем раньше?
Вы знаете, что эта загадка старая, потому что эти молочные бутылки сегодня редко увидишь.Также не распространено негомогенизированное молоко. Однако многие продукты питания поставляются в похожих бутылках с узким горлышком. Для современной версии представьте себе взболтанную бутылку масляно-уксусной заправки для салата. Затем масло медленно отделяется и поднимается к узкому горлышку бутылки. Примечание. Многие материалы при смешивании занимают объем, отличный от их общего объема в отдельности.
 Обычно это небольшой эффект. В этой задаче эта разница в объеме будет проигнорирована. На самом деле, это имело бы незначительный вклад в рассматриваемые здесь изменения давления.
Обычно это небольшой эффект. В этой задаче эта разница в объеме будет проигнорирована. На самом деле, это имело бы незначительный вклад в рассматриваемые здесь изменения давления.- У маятника есть ковш для боба. Он наполовину заполнен водой. Вода замерзает. Что происходит с периодом маятника?
- Тепловое давление. Твердый куб лежит на ровной поверхности. Куб сильно нагревается. Увеличивается ли давление куба на поверхность
- ?
- остаются прежними?
- уменьшить?
Не обращайте внимания на релятивистские эффекты и придерживайтесь классической физики.Объясните свои рассуждения.
- У большого корабля, пришвартованного в доке, веревочная лестница свисает с борта до самого конца воды. Его ступени находятся на расстоянии 30 см друг от друга, а 20 ступенек находятся над водой. Прилив идет со скоростью 15 см/час. Через 6 часов сколько шагов над водой?
- Упрямый мяч.
Гладкий шар лежит на стыке пола и наклонной стены.
 При соприкосновении тел на границе раздела действует сила, направленная по нормали к поверхности контакта.Мы показываем силу наклонной стены (зеленый цвет) в точке B и силу пола (синий цвет) в точке A. Синий вектор не имеет горизонтальной составляющей, поэтому мяч не катится. Но у зеленого вектора есть горизонтальная составляющая. Почему эта сила не заставляет мяч откатиться от стены?
При соприкосновении тел на границе раздела действует сила, направленная по нормали к поверхности контакта.Мы показываем силу наклонной стены (зеленый цвет) в точке B и силу пола (синий цвет) в точке A. Синий вектор не имеет горизонтальной составляющей, поэтому мяч не катится. Но у зеленого вектора есть горизонтальная составляющая. Почему эта сила не заставляет мяч откатиться от стены? - Простой маятник имеет небольшую массу (B), прикрепленную к нити незначительной массы, подвешенной к неподвижной опоре (F). Натяжение струны во время качания непостоянно.Для маятника с длиной нити L = 30 см , качающегося по дуге θ = 10° по обе стороны от вертикали, какую работу совершает сила натяжения нити, действующая на массу за один период маятника?
- Жесткие кузова. Говорят, что законы Ньютона универсальны, то есть применимы везде и во все времена, по крайней мере, для макроскопических (крупномасштабных) явлений. Почти в каждом учебнике по механике есть глава, посвященная твердым телам .
 Это тела, сохраняющие свою физическую форму именно во время взаимодействия. Покажите, что совершенно твердых тел не может быть, потому что они нарушили бы законы Ньютона.
Это тела, сохраняющие свою физическую форму именно во время взаимодействия. Покажите, что совершенно твердых тел не может быть, потому что они нарушили бы законы Ньютона. - Важные вопросы. Учебники часто определяют вес тела как силу, с которой гравитация действует на тело на поверхности земли. Но далее говорят о случаях, когда тело полностью или частично погружено в жидкость, и говорят о «потере веса» тела, погруженного в жидкость. Тогда при обсуждении орбитальных пилотируемых спутников Земли говорят о «невесомых космонавтах».Говорят, что физика — «точная» наука, но кажется, что язык, используемый в учебниках, далеко не точен. Решите эту дилемму.
- Болван Леонардо 1. В записных книжках Леонардо да Винчи есть ряд ошибок.
Источник: Леонардо да Винчи, Кодекс Арундела, лист 1030, рисунок №. 68: Лондон, Британский музей На этом рисунке показан его военный танк, приводимый в движение, как показано слева, шестернями и кривошипами.
 Два человека внутри крутили рукоятки, приводившие в движение колеса. Зубчатая передача — это обычная «фонарная шестерня» того времени. Не обращая внимания на тривиальное наблюдение, что для этого потребуется два очень сильных человека, почему это не сработает? Нет никаких записей о том, что он когда-либо строился и использовался.
Два человека внутри крутили рукоятки, приводившие в движение колеса. Зубчатая передача — это обычная «фонарная шестерня» того времени. Не обращая внимания на тривиальное наблюдение, что для этого потребуется два очень сильных человека, почему это не сработает? Нет никаких записей о том, что он когда-либо строился и использовался. Лох Ленардо 2. В записных книжках Ленардо да Винчи есть ряд ошибок. Вот один из них, показывающий потоки воды из отверстий на разной высоте в резервуаре для воды.
Что не так с этой схемой. Как это должно выглядеть?
Воздушный винт Леонардо. Атлантический кодекс. - Болван Леонардо 3. Леонардо да Винчи предложил несколько идей летательных аппаратов с приводом от человека. Один, называемый «воздушным винтом», имел вращающийся аэродинамический профиль в форме винта, который приводили в движение два человека на платформе внизу, вращающие рукоятки.
 Помимо тривиального наблюдения, что даже два человека не обеспечат достаточной мощности, у этой идеи есть серьезный недостаток физики, который не позволяет ей оставаться в воздухе.Что это? Очевидно, эта идея не взлетела.
Помимо тривиального наблюдения, что даже два человека не обеспечат достаточной мощности, у этой идеи есть серьезный недостаток физики, который не позволяет ей оставаться в воздухе.Что это? Очевидно, эта идея не взлетела. - В учебниках часто говорится, что когда предмет находится в фокальной плоскости собирающей линзы, свет от него, проходя через линзу, образует реальное изображение «на бесконечности». Однако с таким же успехом можно сказать, что он также формирует мнимое изображение «минус бесконечность», которое легко увидеть, глядя через линзу на источник света. Таким образом, один объектив дает два изображения. Как это может быть?
Мы играем быстро и свободно со словом «бесконечность» здесь? На некоторых курсах математики учителя говорили, что «параллельные прямые пересекаются в бесконечности».Более небрежный язык, кажется. Разрешите эту путаницу.
Это поднимает другой вопрос. Любая линза может создавать реальные изображения или мнимые изображения, в зависимости от местоположения объекта и определяется уравнением линзы 1/p + 1/q = 1/f .
 Но это все? Производит ли линза какие-либо другие изображения?
Но это все? Производит ли линза какие-либо другие изображения? - Изображение, которое вы видите, когда смотрите в зеркало, перевернуто влево/вправо, но не вверх/вниз. Если вы правша, ваше зеркальное отражение — левша.Если вы коснетесь своего правого уха, ваше изображение коснется его левого уха. Но твой образ не стоит с ног на голову. На первый взгляд это кажется парадоксальным, поскольку зеркало симметрично относительно своей нормали. Вы можете вращать зеркало вокруг своей нормальной оси, и изображение не вращается. Так почему же изображение также не симметрично этой нормали? Разрешите эту путаницу с помощью простого аргумента. Вы должны быть осторожны и точны в использовании языка.
- Вращение виртуального изображения. Призма Дова обладает интересным свойством: когда вы смотрите через нее и поворачиваете ее, изображение поворачивается на угол, вдвое больший угла поворота призмы. Объяснять.
Если у вас нет такой призмы, используйте равностороннюю призму, глядя сквозь нее, как показано на рисунке, чтобы свет имел внутреннее отражение с одной стороны призмы.

- Верхний перископ. Подводные лодки проекта сыграли важную роль во Второй мировой войне. Вы видели те фильмы, где капитан ищет вражеские корабли через перископ, длинную узкую трубку, уходящую вверх прямо над поверхностью воды.Это было за несколько дней до появления телевидения и оптоволокна, поэтому в перископе использовались только линзы и отражающие призмы. Вы знаете, что, глядя через длинную узкую трубу, вы не можете увидеть больше, чем очень узкое поле зрения, тогда как перископы могут видеть гораздо большее поле. Эти перископы могли иметь длину 30 футов и диаметр шесть дюймов. Глядя в такую трубку, вы увидите поле всего в один градус. Тем не менее, перисокпы обычно имели поля 9° и более. Как это можно сделать, используя только оптическую систему со стеклянными линзами?
- Физика падения. В каждом вводном учебнике по физике сказано, что при отсутствии сопротивления воздуха два тела разной массы падают с одинаковым ускорением, то есть они будут падать на одинаковые расстояния за одинаковое время.
 В этом контексте обычно упоминается Галилей, хотя до него этот опыт ставили другие, и он, вероятно, никогда не ставил эксперимент со свободно падающими телами (уж точно не на Пизанской башне). Но у Галилея был простой логический аргумент, чтобы заключить, что масса падающего тела не имеет значения.Помните, что во времена Галилея алгебра еще не была изобретена, а исчисление появилось еще позже. Понятие гравитации и закон Ньютона F = м a тоже появились позже. Так как же Галилей пришел к этому важному выводу, используя только простой логический аргумент?
В этом контексте обычно упоминается Галилей, хотя до него этот опыт ставили другие, и он, вероятно, никогда не ставил эксперимент со свободно падающими телами (уж точно не на Пизанской башне). Но у Галилея был простой логический аргумент, чтобы заключить, что масса падающего тела не имеет значения.Помните, что во времена Галилея алгебра еще не была изобретена, а исчисление появилось еще позже. Понятие гравитации и закон Ньютона F = м a тоже появились позже. Так как же Галилей пришел к этому важному выводу, используя только простой логический аргумент?Взвешивание подвижной системы
. - Снижение веса? Нам часто говорят, что если мы будем продолжать двигаться, то похудеем.Но зависит ли вес движущегося объекта от его движения? Классический физический лабораторный эксперимент — это машина Этвуда: две неравные массы на конце струны, проходящей через шкив.
 Систему можно заставить разгоняться достаточно медленно, чтобы легко измерить ее ускорение и, применив немного математики, определить значение ускорения под действием силы тяжести. Показанная машина Этвуда подвешена на пружинных балансах. Масса одной подвески M , массы другой (M+m) . Предположим, что более тяжелая сторона (правая
сбоку) подвеска крепится к крючку пружинных весов дополнительной нитью, препятствующей перемещению масс.Шкала показывает (2M+m) .
Систему можно заставить разгоняться достаточно медленно, чтобы легко измерить ее ускорение и, применив немного математики, определить значение ускорения под действием силы тяжести. Показанная машина Этвуда подвешена на пружинных балансах. Масса одной подвески M , массы другой (M+m) . Предположим, что более тяжелая сторона (правая
сбоку) подвеска крепится к крючку пружинных весов дополнительной нитью, препятствующей перемещению масс.Шкала показывает (2M+m) .Удерживающая нить сжигается или обрезается, и система приводится в движение, левая сторона поднимается, а более тяжелая правая сторона опускается. Пока массы находятся в движении, пружинные весы показывают
- то же, что и раньше.
- больше, чем раньше.
- меньше, чем раньше.
- ноль.
Объяснить, почему.
- При обсуждении кинетической теории в учебниках идеальный газ часто моделируется как ящик с бесконечно массивными стенками, содержащими мельчайшие частицы, отскакивающие от стенок.
 Часть аргумента рассматривает одну такую частицу, отскакивающую от стены. Нам говорят, что столкновение абсолютно упругое и частица отскакивает от стенки с той же скоростью, с какой она имела перед ударом о стену. Это говорит нам о том, что мяч отскакивает с неизменной кинетической энергией, что все студенты готовы некритически принять. Мы разумно заключаем, что энергия не терялась стенкой. Но как насчет импульса? Частица имела импульс mv до столкновения и импульс − mv после, поскольку импульс является вектором.Таким образом, импульс частицы изменился на -2mv , а по закону сохранения импульса должно было произойти изменение импульса стенки на + 2mv .
Часть аргумента рассматривает одну такую частицу, отскакивающую от стены. Нам говорят, что столкновение абсолютно упругое и частица отскакивает от стенки с той же скоростью, с какой она имела перед ударом о стену. Это говорит нам о том, что мяч отскакивает с неизменной кинетической энергией, что все студенты готовы некритически принять. Мы разумно заключаем, что энергия не терялась стенкой. Но как насчет импульса? Частица имела импульс mv до столкновения и импульс − mv после, поскольку импульс является вектором.Таким образом, импульс частицы изменился на -2mv , а по закону сохранения импульса должно было произойти изменение импульса стенки на + 2mv .Так как же стена может набирать скорость, не приобретая никакой энергии? Учебники снова нас обманывают? Решите это с помощью расчета энергии и импульса.
- Эластичные определения. Учебники говорят нам, что абсолютно упругое тело — это такое тело, которое при деформации возвращается к своей первоначальной форме без потери энергии.
 Они также говорят нам, что при абсолютно упругом столкновении участвующие тела сохраняют как кинетическую энергию, так и импульс.
Они также говорят нам, что при абсолютно упругом столкновении участвующие тела сохраняют как кинетическую энергию, так и импульс.Но рассмотрите колокол, сделанный из латуни с латунным звонком. Колокола и их колотушки сделаны из почти эластичных металлов, и оба сохраняют свою форму после многих столкновений. Совершенно упругое столкновение — это столкновение, при котором механическая энергия сохраняется без потерь на диссипативные процессы. Столкновение хлопушки и колокольчика не является абсолютно упругим столкновением, поскольку значительная часть энергии теряется в виде звука, излучаемого от колокола.Также качающийся колокольчик и хлопушка вскоре останавливаются, так что вы знаете, что их энергия каким-то образом рассеялась. Так как же упругие тела могут подвергаться неупругим столкновениям? Разрешите это кажущееся противоречие.
Праздный вопрос: будут ли издавать звук колокольчик и хлопушка, сделанные из совершенно эластичных материалов?
- Эквивалентность? Учебники теории относительности иногда иллюстрируют «принцип эквивалентности» на примере человека в лифте.
 Трос лифта рвется, и несчастный пассажир падает вместе с лифтом, оказываясь в состоянии «невесомости», в котором он свободно парит в своей системе отсчета лифта, как будто на него не действуют внешние силы. В учебниках часто говорится, что человек внутри не сможет ни одним экспериментом определить, что в его лифте есть гравитационное поле. Этот пример, конечно, ошибочен, так как с помощью чувствительных приборов человек в лифте мог обнаружить гравитационное поле.Как?
Трос лифта рвется, и несчастный пассажир падает вместе с лифтом, оказываясь в состоянии «невесомости», в котором он свободно парит в своей системе отсчета лифта, как будто на него не действуют внешние силы. В учебниках часто говорится, что человек внутри не сможет ни одним экспериментом определить, что в его лифте есть гравитационное поле. Этот пример, конечно, ошибочен, так как с помощью чувствительных приборов человек в лифте мог обнаружить гравитационное поле.Как? - Эллипс или парабола? Учебники по физике много места уделяют обсуждению траекторий снарядов в гравитационном поле Земли. Они подчиняются закону d = v o t + ½ г т 2 , что является уравнением параболы. Но Ньютон говорит нам, что траектория пушечного ядра (в отсутствие сопротивления воздуха) — это часть эллипса с центром Земли в одном из фокусов.Знаменитая картина «Гора Ньютона» иллюстрирует это.
Итак, если бы вас спросили: «Какова траектория полета снаряда, эллипса или параболы?», какой ответ вы бы дали? Разрешите это кажущееся противоречие.

- Третий закон Ньютона гласит: если тело А воздействует на тело В, то тело В действует на А с равной и противоположно направленной силой. Другие законы Ньютона были бы бесполезны без этого важного закона. Говорят, что законы Ньютона универсальны и применимы везде и всегда.Но третий закон Ньютона не может быть правильным во всех случаях, даже в классической физике. Покажите почему на простом примере.
- Закон всемирного тяготения Ньютона , F = GMm/R 2 безоговорочно принимается первокурсником. Но небольшое размышление показывает, что это не может быть правдой во всех случаях. Когда R = 0, сила становится бесконечной, что является нефизическим результатом. Приведите аргумент, почему это не является серьезной проблемой.
- Парящая идея. Стакан с водой стоит на весах, используемых для измерения ее веса. Мяч, менее плотный, чем вода, обычно плавает на воде. Но он привязан, полностью погружен в воду, на веревке, прикрепленной ко дну стакана.
 Шар окружен водой и не касается стенок стакана. Веревка, очевидно, оказывает направленное вверх усилие на дно стакана. Струна рвется, и шарик всплывает на поверхность, плавая там. Веревка больше не оказывает восходящей силы на стакан.Теперь шкала больше, меньше или такая же, как раньше? Подтвердите свои рассуждения свободной диаграммой тела.
Шар окружен водой и не касается стенок стакана. Веревка, очевидно, оказывает направленное вверх усилие на дно стакана. Струна рвется, и шарик всплывает на поверхность, плавая там. Веревка больше не оказывает восходящей силы на стакан.Теперь шкала больше, меньше или такая же, как раньше? Подтвердите свои рассуждения свободной диаграммой тела. - Дырявая физика. Физические задачи часто обрамляются сильно идеализированными ситуациями. Вот классическая проблема такого рода. Если бы в земле просверлили прямое отверстие прямо через центр земли, и камень упал бы в отверстие, сколько времени потребуется, чтобы вернуться?
Для простоты игнорируйте тот факт, что дыру нельзя просверлить в горячем материале земли, а если бы и удалось, то она сразу же заполнилась бы магмой.Кроме того, есть надоедливое усложнение вращения Земли, поэтому мы должны остановить это, потому что камень столкнется со стенкой дыры. Какая стена, кстати? Одним из способов избежать этой проблемы было бы бурение скважины вдоль оси вращения Земли с севера на юг.

Чтобы завершить идеализацию, предположим, что плотность Земли однородна.
А чтобы расширить задачу, после того, как вы нашли предыдущий ответ, предположим, что был прорыт прямой туннель из Нью-Йорка в Сан-Франциско.Теперь установите железнодорожный путь через туннель. Сколько времени займет поездка в вагоне без двигателя, если его не толкать, не учитывать трение и т. д.?
Как обычно, мы ищем самое простое решение, желательно даже не требующее вычислений.
- Навсегда — это долго. Может ли совершенный цилиндр при первоначальном толчке катиться вечно на бесконечной плоскости без трения?
- Трение мешает. Студенты иногда полагают, что трение всегда препятствует движению тела, стремясь уменьшить его скорость.Но есть много повседневных примеров, показывающих, что трение может быть необходимо, чтобы инициировать и поддерживать движение. Приведите несколько примеров. Дайте определение трения так, чтобы его нельзя было неправильно истолковать.

- Гоночные фотоны. Рассмотрим свет, проходящий через собирающую линзу от точечного источника к точечному изображению. Лучи света, проходящие через линзу вблизи ее края, должны проходить большее расстояние от источника до изображения, чем лучи, проходящие через центр линзы.Не приведет ли это к тому, что лучи придут в разное время и, возможно, вызовут деструктивную интерференцию изображения? Объяснять.
- Расплетение спектра. Сэр Исаак Ньютон (1642-1727) известен своими экспериментами со светом и призмами. Он показал, что свет, проходящий через призму, разделяется (рассеивается) на цветной веер (спектр). Он также показал, что если этот цветной свет затем пропустить через другую правильно расположенную призму, он может быть рекомбинирован в белый свет.Таким образом, утверждал он, на самом деле 90 323 цвета представляют собой 90 324 белого света, а не 90 323, созданные 90 324 призмой.
 Вот галерея примеров из Интернета, которые должны иллюстрировать этот эксперимент.
Вот галерея примеров из Интернета, которые должны иллюстрировать этот эксперимент.Учебники и веб-страницы часто иллюстрируют этот эксперимент такими красивыми картинками — и это ужасно неправильно! Призма Google рекомбинирует белый свет и просматривает изображения. Большинство изображений будут ошибочными по одному или нескольким серьезным причинам. Это наглядный пример того, почему сеть называют «магистралью дезинформации», поскольку она опасно скомпрометирована выбоинами.Если вы попытаетесь воспроизвести этот эксперимент в лаборатории, следуя этим примерам, вы наверняка потерпите неудачу. Найдите ошибки в каждом из них. Как правильно разложить белый свет на цвета, а затем снова скомбинировать его в белый свет? Есть несколько способов.
Однажды у меня был студент, который хотел получить проект за дополнительные баллы, чтобы поднять свой невыразительный средний балл. Я предложил ему пойти в лабораторию и повторить этот эксперимент. Он копировал иллюстрации из учебников и каждый раз терпел неудачу.
 Он был расстроен. В конце концов я предложил ему выяснить, где находится библиотека колледжа, а затем найти «Оптикс» Ньютона. Там он нашел один способ сделать это успешно.
Он был расстроен. В конце концов я предложил ему выяснить, где находится библиотека колледжа, а затем найти «Оптикс» Ньютона. Там он нашел один способ сделать это успешно. - Банка газировки. Вот головоломка из коллекции Мартина Гарднера. Это старая проблема, но метод по-прежнему поучителен.
Предположим, что у полной цилиндрической банки газировки центр тяжести находится в ее геометрическом центре, на полпути вверх и прямо посередине банки.По мере потребления газировки центр тяжести сначала понижается. Однако, когда банка пуста, центр тяжести возвращается в центр банки. Следовательно, должна быть точка, в которой центр тяжести находится ниже всего.
Зная вес пустой банки и ее вес в наполненном состоянии, как можно определить, какой уровень газировки в вертикальной банке сместит центр тяжести в самую низкую возможную точку?
Чтобы разработать точную задачу, предположим, что пустая банка весит 1.5 унций. Это идеальный цилиндр, и любая асимметрия, вызванная пробивкой отверстий в верхней части, не принимается во внимание.
 Банка вмещает 12 унций (42 грамма) содовой, поэтому ее общий вес при наполнении составляет 13,5 унций (382 грамма).
Банка вмещает 12 унций (42 грамма) содовой, поэтому ее общий вес при наполнении составляет 13,5 унций (382 грамма). - Обратный осмос. Корреспондент из Новой Зеландии посылает нам эту гениальную идею, которую он увидел в колонке журнала Scientific American Amateur Scientist за декабрь 1971 года. Мы позволим ему описать это:
Осмос – это процесс, при котором вода течет через полупроницаемую мембрану из менее концентрированного раствора в более концентрированный.При обратном осмосе вода течет через мембрану из сильного раствора в слабый. Конечно, у вас должно быть давление за мембраной, чтобы она текла «неправильным» путем. Чтобы заставить пресную воду течь из морской через мембрану, требуется давление около 20 атмосфер. На этом основаны опреснительные устройства, применяемые на крупных кораблях.
На рисунке показана труба в океане, ее верхний конец изогнут, чтобы направить воду к маленькому водяному колесу W. Вам должны понравиться предложения о вечном двигателе, которые настолько просты, без движущихся частей и обещают решить нашу мировую энергию. проблемы, а также наши проблемы с ресурсами пресной воды. То есть, если только мы сможем получить достаточное количество этих машин, работающих одновременно.В любом случае, вам нужно взять очень длинную трубу с полупроницаемой заглушкой на конце, наполнить ее пресной водой и опустить через борт лодки так, чтобы один конец был на несколько метров выше поверхности, а другой — на пробка находится на дне самой глубокой океанской впадины, которую вы можете найти, скажем, на 12 км ниже или на любой другой глубине океана.
 Теперь на этой глубине напор соленой воды в океане вокруг конца трубы составляет более 20 атмосфер, скажем, 21 атмосферу, поэтому пресная вода вытекает из соленой воды океана в трубу пресной воды. Пресная вода будет подниматься примерно на 10 м (21 — 20 = 1 атмосфера) над поверхностью, что-то вроде артезианской скважины. Возможно, вам придется немного отрегулировать глубину в зависимости от плотности морской воды, но принцип кажется правдоподобным.
Теперь на этой глубине напор соленой воды в океане вокруг конца трубы составляет более 20 атмосфер, скажем, 21 атмосферу, поэтому пресная вода вытекает из соленой воды океана в трубу пресной воды. Пресная вода будет подниматься примерно на 10 м (21 — 20 = 1 атмосфера) над поверхностью, что-то вроде артезианской скважины. Возможно, вам придется немного отрегулировать глубину в зависимости от плотности морской воды, но принцип кажется правдоподобным.Это устройство не только даст бесконечный поток пресной воды, но и может использоваться для запуска небольшого генератора.

Давление в океане линейно меняется с глубиной, увеличиваясь примерно на 1 атмосферу на каждые 10 метров глубины.Так, давление в океане на глубине около 200 метров (700 футов) на 20 атмосфер выше атмосферного. Этот факт может быть полезным, а может и не быть.
Кажется, это отличная идея. Но это не сработает. Почему нет? Ответ дан в апреле. 1972 г., журнал Scientific American, но это немного косвенно. См. также июньский номер 1971 года.
- Какое яйцо вареное? Это очень старая проблема. Два яйца на столе, одно свежее и одно сваренное вкрутую.Как можно определить, какие из них сварились, не разбив их скорлупы?
- Какой полый? Две сферы имеют одинаковый диаметр, одинаковый вес и окрашены в один цвет. Один прочный, из легкого материала. Другой представляет собой полую оболочку из более плотного материала. Не повредив их, как вы можете определить, какой из них полый?
- Интересная головоломка. Эту головоломку часто критикуют за кажущуюся двусмысленность.
 Вот версия, в которой устранена большая часть двусмысленности.
Вот версия, в которой устранена большая часть двусмысленности.Вам даны два железных бруска, идентичных за исключением того, что один брусок намагничен, а другой не намагничен. Используя только два стержня и свои руки, как вы можете определить, что является магнитом? Мы позволим гравитации действовать как обычно на вас и на решетку.»
Небрежно сформулированные версии этой задачи приводят к таким ответам:
- Подвесьте один из них на нитке, привязанной к его центру, и посмотрите, направлена ли она на север.
- Очень сильно нагрейте один из батончиков и дайте ему остыть. Если стержни больше не притягиваются так сильно, значит, то, что вы нагрели, было магнитом.
- Несколько раз уроните одну на пол. Если притяжение между стержнями уменьшилось, то тот, что вы уронили, был магнитом.
 Вы даже не можете использовать магнитное поле Земли.Так как же проще всего идентифицировать намагниченный стержень?
Вы даже не можете использовать магнитное поле Земли.Так как же проще всего идентифицировать намагниченный стержень?Одним из хорошо известных ответов является Т-тест. Поместите стержни, соприкасаясь в Т-образной конфигурации, с концом одного в центре другого. Если они притягиваются, то та, которая является вертикалью буквы Т, является магнитом, ибо другая имеет полюса на обоих концах и не имеет полюсов в центре.
Но магниты из материалов с высокой магнитной проницаемостью могут быть изготовлены со многими полюсами, например, с расположением [N SS N].Такой магнит , а не будет склонен указывать на север, когда он подвешен, и может не пройти Т-тест. Как проще всего определить магнит, независимо от того, как расположены полюса этого магнита?
- Что длиннее? Подготовьте две металлические трубки. Мои вырезаны из алюминиевой трубы диаметром 1 дюйм из хозяйственного магазина. Одна трубка имеет длину 11 дюймов. Другой на 1/4 дюйма короче. Старайтесь, чтобы на трубках не было царапин и дефектов, по которым можно было бы отличить одну трубку от другой.

Подержите их по одному в каждой руке и спросите, видит ли кто-нибудь визуально, что один короче другого. Конечно никто не может. Держите их рядом, соприкасаясь, и разница очевидна. Попросите кого-нибудь взять их, затем повернитесь, чтобы скрыть их от глаз, выберите один и верните его вам. Вы делаете вид, что оцениваете ее длину между руками, касаясь трубочки за ее концы, только кончиками пальцев. Отложите его и попросите другого, делая то же самое, затем объявите: «Это (короче/длиннее, в зависимости от обстоятельств).»
Вы могли бы сделать это с завязанными глазами, но это, вероятно, слишком много для демонстрации физики. В чем твой секрет?
- Роллинг парадокс. Учебники по физике определяют силу трения как силу, касающуюся двух поверхностей в точке их соприкосновения. Рассмотрим шар или цилиндр, катящийся без скольжения по идеально плоской и ровной поверхности. Мы ожидаем, что он замедлится. Мы наивно предполагаем, что трение является причиной замедления и, в конце концов, остановки.
 Конечно, трение противоположно скорости мяча и, следовательно, замедляет движение мяча по второму закону Ньютона. Но эта сила из-за трения имеет крутящий момент, и этот вектор крутящего момента вокруг центра масс мяча имеет то же направление, что и вектор угловой скорости мяча. Это увеличит угловую скорость мяча, заставляя его катиться все быстрее и быстрее. Разрешите это кажущееся противоречие.
Конечно, трение противоположно скорости мяча и, следовательно, замедляет движение мяча по второму закону Ньютона. Но эта сила из-за трения имеет крутящий момент, и этот вектор крутящего момента вокруг центра масс мяча имеет то же направление, что и вектор угловой скорости мяча. Это увеличит угловую скорость мяча, заставляя его катиться все быстрее и быстрее. Разрешите это кажущееся противоречие.Когда изобретатели впервые предложили железнодорожный транспорт с использованием стальных колес на стальных рельсах, некоторые скептики сказали: «Колеса будут просто вращаться на месте, и это хитроумное изобретение никуда не денется.» Может, этот парадокс был у них в голове.
- Принцип начальной загрузки. Небылицы о бароне Мюнхгаузене включают в себя рассказ о том, как ему чудом удалось вырваться из щекотливой ситуации, когда он увяз в болоте. Находчивый барон наклонился и поднялся, потянув за ремни ботинок. Мы знаем, что это невозможно, но может ли человек, используя физику и систему шкивов, поднять себя, используя только свою силу?
Рассмотрим показанную систему.
 Используется легкий стул с верхним шкивом. Может ли это работать? Есть ли ограничения в этой системе? Показать векторный анализ с бесплатными диаграммами тела.
Используется легкий стул с верхним шкивом. Может ли это работать? Есть ли ограничения в этой системе? Показать векторный анализ с бесплатными диаграммами тела. - В покое . Редкая книга по физике не говорит что-то вроде «Сила, действующая на покоящееся тело, равна нулю» в главах по статике.
И это также говорит, что если результирующая сила равна нулю, ускорение тела равно нулю.
Затем в главах о динамике мы можем увидеть: «Тело, брошенное прямо вверх, на мгновение покоится в высшей точке своей траектории».Затем ученик логически заключает, что в этой точке результирующая сила, действующая на тело, равна нулю (по крайней мере, на мгновение), и, следовательно, его ускорение в этой точке равно нулю. Это заблуждение «в состоянии покоя → нулевая результирующая сила → равновесие → нулевое ускорение». Можем ли мы обвинять студентов в том, что они верят учебникам на слово?
Сможете ли вы разрешить это кажущееся противоречие?
- Потеря энергии?
Парадокс конденсатора. 
Этот парадокс конденсатора обсуждался в Интернете и в опубликованных статьях, но люди до сих пор спорят об этом.
Возьмите два одинаковых конденсатора. Зарядите один из них. Затем соедините их вместе, чтобы заряд распределялся поровну между ними. Простой расчет показывает, что энергия двух заряженных конденсаторов после этой операции составляет лишь половину энергии одного первоначально заряженного конденсатора. Что случилось с потерянной энергией?
Конечно, сразу возникает подозрение, что энергия теряется при нагреве соединительных проводов.Поэтому мы идеализируем проблему и используем безрезистивные соединительные провода. Тем не менее, мы должны учитывать энергию, излучаемую ускоряющими зарядами при начальном процессе замыкания переключателей и при последующем ускорении электронов при перераспределении заряда. Тем не менее опубликованные работы спорят о деталях этих процессов.
Так что же происходит? Является ли теория цепей и классическая электромагнитная теория ошибочными? Вы можете решить это просто?
- Соломинки для захвата.

1. Мы все сделали эту демонстрацию, используя питьевую соломинку и стакан воды. Поместите соломинку в воду (A), закройте верхушку соломинки пальцем, затем поднимите соломинку, оставив верхнюю часть закрытой. Это поднимает столб воды внутри соломинки (B), несмотря на открытый конец. Какая физика демонстрируется?
2. Обычно мы не рассматриваем детали этой простой демонстрации, но как насчет нижнего конца соломинки? Там есть поверхность воды, открытая воздуху.Какова его форма?
- Он выпирает вниз.
- Выпирает вверх.
- Он почти плоский.
3. Теперь давайте сделаем его более интересным. Сделайте отверстие в соломинке для питья примерно в двух дюймах от дна. Сделайте отверстие таким же большим, как торцевые отверстия соломинки. Теперь погрузите соломинку в стакан с водой. Боковое отверстие должно быть ниже уровня воды. Теперь закройте верхний конец соломинки пальцем.
 Поднимите соломинку, пока она полностью не выйдет из воды (С). Что, по вашему прогнозу, произойдет? Подтвердите свой ответ аргументом, основанным на физических законах. В частности, обсудите, что происходит в боковой дыре. Теперь попробуйте.
Поднимите соломинку, пока она полностью не выйдет из воды (С). Что, по вашему прогнозу, произойдет? Подтвердите свой ответ аргументом, основанным на физических законах. В частности, обсудите, что происходит в боковой дыре. Теперь попробуйте. - Скользкий путь. Если вы спускаетесь по скользкому склону на автомобиле, сохраните ли вы лучшую управляемость, если ваши передние или задние колеса заблокируются?
- Мощные магниты? Часто можно услышать, как сильные магниты называют «мощными».Но являются ли они источником силы? Я часто слышу, как люди утверждают, что магниты должны быть неисчерпаемым источником энергии. Они цитируют скромный магнит холодильника, говоря: «Он удерживает собственный вес на стенке холодильника навсегда или, по крайней мере, в течение многих лет. Таким образом, магниты должны быть источником значительной энергии». Я часто слышу это от людей, которые думают, что могут изобрести вечный двигатель, расположив магниты во вращающемся механизме для извлечения накопленной энергии.

Что не так с их аргументом?
- Улучшение гравитации. Генри Кавендиш (1731–1810) измерил силу гравитационного притяжения между двумя свинцовыми шариками в лабораторных условиях. Он использовал чувствительную торсионную подвеску для измерения такой небольшой силы. Предположим, у нас есть жидкость в U-образной трубке, находящаяся в равновесии, а затем поместим тяжелый свинцовый шар (красный) прямо под левую сторону трубки. Как это повлияет на уровень жидкости в трубке?
- Отрицательная реакция? Обычно, когда мы что-то тянем, оно движется к нам в направлении приложенной силы (если только оно не приколочено).Можете ли вы придумать или разработать простую систему, которая отдаляет 90 149 от вас на 90 150, когда вы пытаетесь притянуть ее к себе?
- Маятник Фуко.
Маятник Фуко в Пантоне в Париже. 
Леон Фуко (1819–1868) установил большой маятник в 1851 году в Пантеоне в Париже, чтобы продемонстрировать, что Земля вращается. Это было 220 футов в длину с 62-фунтовым бобом. Когда он раскачивался, он медленно прецессировал, потому что сохранял свою первоначальную плоскость качания, в то время как земля вращалась под ним.Это было легко наблюдать в течение дня, когда его плоскость качания менялась по отношению к полу под ним. Такие маятники есть в музеях науки по всему миру, а также в некоторых университетских физических корпусах.
Но почему маятник сохраняет свое движение в исходной плоскости? Ведь его подвесная проволока прикреплена вверху, и вращение здания обязательно будет оказывать на проволоку крутящий момент. Не приведет ли это к тому, что маятник будет следовать движению здания, в котором он находится? Требуется некоторое объяснение.
Тогда есть вопрос о начальных условиях. Когда утром маятник оттягивают назад и отпускают, этот процесс происходит в уже вращающейся системе отсчета — самом здании.
 Не должно ли это начальное движение смещать маятник, чтобы он сохранял это движение до конца дня, чтобы его плоскость движения совсем не менялась по отношению к зданию? Следовательно, никакой явной прецессии не наблюдалось бы.
Не должно ли это начальное движение смещать маятник, чтобы он сохранял это движение до конца дня, чтобы его плоскость движения совсем не менялась по отношению к зданию? Следовательно, никакой явной прецессии не наблюдалось бы.Когда я был студентом университета, мне однажды дали хороший совет по физике.— Вы понимаете все, что знаете об этом? Эти простые вопросы, заданные маятником Фуко, не давали мне покоя за много лет до того, как я нашел ответы. Учебники и преподаватели избегают этого, редко поднимая подобные вопросы.
- Ходить по кругу. Человечество, иногда называемое «ползающей болезнью по лицу земли», влияет на землю разными способами. Но редко упоминается один эффект человеческой деятельности. В большинстве стран автомобили движутся по правой стороне дороги.Круговые движения проходятся против часовой стрелки. Большинство легковых и грузовых автомобилей после поездки возвращаются домой, поэтому их движение направлено против часовой стрелки. В США карнавальные карусели (карусели) также вращаются против часовой стрелки, а скачки, человеческие, конные, собачьи и автомобильные, проводятся против часовой стрелки.
 Единственным исключением является Великобритания (и несколько других стран), где все они идут по часовой стрелке, включая автомобильное движение и кольцевые развязки.
Единственным исключением является Великобритания (и несколько других стран), где все они идут по часовой стрелке, включая автомобильное движение и кольцевые развязки.Изменяет ли это вращательное движение на земной поверхности скорость вращения Земли, хотя бы чуть-чуть? Может ли это ускорить или замедлить вращение Земли? Должны ли мы быть обеспокоены? И каков эффект всех тех спутников Земли, которые мы вывели на орбиту, большинство из которых направлено на восток?
Иллюстрация центростремительной силы. - Круговой аргумент. Мяч на конце веревки. Удерживая другой конец веревки, вы вращаете мяч по большому кругу. Учебники часто представляют это как задачу, требуя, чтобы вы связали угловую скорость мяча с натяжением струны, используя известную формулу для центростремительной силы F = mω 2 R . Но действительно ли натяжение равно центростремительной силе?
Из-за сопротивления воздуха мяч будет замедляться.
 Чтобы он продолжал работать, что-то еще должно поставлять энергию в форме работы. Но если струна радиальна, а мяч движется по касательной к своей круговой траектории, сила и перемещение перпендикулярны друг другу. Так как же струна может воздействовать на мяч, чтобы поддерживать его движение?
Чтобы он продолжал работать, что-то еще должно поставлять энергию в форме работы. Но если струна радиальна, а мяч движется по касательной к своей круговой траектории, сила и перемещение перпендикулярны друг другу. Так как же струна может воздействовать на мяч, чтобы поддерживать его движение? - Недоумение маятника. Каждый учебник по физике говорит нам, что период простого маятника не зависит от массы груза. Но в этих книгах редко затрагивается вопрос: «Почему период не зависит от массы?» Если вы проследите за выводом формулы периода, вы увидите, что масса выпадает из расчета.Но есть простой и наглядный способ доказать это, даже не занимаясь математикой. Не могли бы вы?
- Наклонный шар. Однородный шар массой м и радиусом r висит на веревке у гладкой вертикальной стены, линия нити проходит через центр шара. Нить прикреплена на высоте h = √(3r) над точкой касания мячом стены. Чему равно T натяжение нити и сила F , действующая на стену со стороны мяча? Если мяч шероховатый, с коэффициентом трения покоя μ с , как увеличиваются или уменьшаются эти силы?
- Действие и противодействие.
 Учебники часто говорят нам, что закон Ньютона звучит примерно так: «Каждому действию есть равное и противоположное противодействие». Конечно, это небрежно сформулировано. Как могут две вещи быть равными и противоположными? Следует сказать: «На всякое действие есть равная по величине и противоположно направленная реакция».
Учебники часто говорят нам, что закон Ньютона звучит примерно так: «Каждому действию есть равное и противоположное противодействие». Конечно, это небрежно сформулировано. Как могут две вещи быть равными и противоположными? Следует сказать: «На всякое действие есть равная по величине и противоположно направленная реакция».Но каково определение «действия»? Можно возразить, что «реакция» — это негативное «действие». Если это так, исходное утверждение может быть правильным, но оно все еще сбивает с толку. Серьезно, когда у вас есть пара действие/противодействие, как вы можете определить, где действие, а где реакция?
- Ставить телегу впереди лошади. Лошадь запряжена в телегу. Лошадь действует на телегу с силой 90 323 F 90 324, а телега действует на лошадь с такой же силой в соответствии с третьим законом Ньютона. Так что лошадь и телега никуда не поедут.
В чем недостаток этого аргумента?
- Лунный аттракцион. Стоя на земле, вы ближе к солнцу в полдень во время новолуния или в полдень через полмесяца во время полнолуния? Почему?
- Ходить по кругу .
 Птолемеевская модель Солнечной системы была геоцентрической (в центре Земли) и полностью основывалась на кругах (которые считались идеальной фигурой). Чтобы согласиться с наблюдениями за положением планет, он стал чрезвычайно геометрически сложным, с кругами (циклами) и меньшими кругами (эпицилами), деферентами и эквантами и другими уловками, чтобы согласовать его с наблюдениями.
Птолемеевская модель Солнечной системы была геоцентрической (в центре Земли) и полностью основывалась на кругах (которые считались идеальной фигурой). Чтобы согласиться с наблюдениями за положением планет, он стал чрезвычайно геометрически сложным, с кругами (циклами) и меньшими кругами (эпицилами), деферентами и эквантами и другими уловками, чтобы согласовать его с наблюдениями.Система Птолемея, упрощенная. Не в масштабе.
Адаптировано из Ван Аллена, Джеймса А. 924 Элементарные задачи
и ответы в астрономии Солнечной системы. U. of Iowa Press, 1993.Коперник попытался упростить это, используя гелиоцентрическую (солнцецентрированную) модель. Но он по-прежнему настаивал на геометрии, основанной на кругах. Его система по-прежнему нуждалась в эпициклах, но, как он утверждал, их было меньше. Менее важным, чем количество эпициклов, является свойство конкретных эпициклов, которые его система устранила.
 Шесть заброшенных циклов и эпициклов имели в системе Птолемея одну важную общую черту.Что это было?
Шесть заброшенных циклов и эпициклов имели в системе Птолемея одну важную общую черту.Что это было? - Постоянная ошибка. Бесконечно растягивающаяся резинка соединяет дерево с задним бампером автомобиля. По мере того, как автомобиль удаляется с постоянной скоростью, лента растягивается. Жук на полосе медленно ползет к авто. Сможет ли жук добраться до автомобиля, если будет достаточно времени?
- Дырявая сфера.
Дырявая сфера. Д = 6″.
Из мира математики.wolfram.com.Просматривая книги Мартина Гарднера, я наткнулся на эту дьявольскую загадку. Гарднер называет это «невероятной проблемой». Он также прослеживает это до Сэмюэля И. Джонса, Mathematical Nuts , 1932, с. 86.
Встречается в Сети в различных формах, часто двусмысленных в формулировках, наряду с бесконечными дискуссиями, часто ни к чему не приводящими.
 Я попытался переформулировать его, чтобы устранить двусмысленность (что непросто).
Я попытался переформулировать его, чтобы устранить двусмысленность (что непросто).Отверстие просверливается полностью через сферу, прямо через центр сферы и центрируется на ней.Отверстие в сфере представляет собой цилиндр длиной 6 дюймов. Каков объем остатка сферы (не считая высверленного материала).
Можно подумать, что информации недостаточно. Но есть. Решение не требует вычислений. Гарднер дает проницательное решение, которое требует всего двух предложений, включая всего одно уравнение.
- Сплюснутая земля . Из-за своего вращения Земля не имеет сферической формы. Это сплюснутый сфероид, выпуклый на экваторе.Его радиус кривизны больше на экваторе или на полюсах?
- Резисторная цепь.
Резисторная цепь. Каждый резистор в этой цепочке имеет сопротивление 1 Ом. К клеммам А и В подключается источник питания. Ток в крайних двух резисторах равен 1 ампер.
 Какова разность потенциалов на входах А и В этой цепи? Чему равно сопротивление всей цепи, измеренное в точках А и В? Какой ток подает источник питания в эту цепь?
Какова разность потенциалов на входах А и В этой цепи? Чему равно сопротивление всей цепи, измеренное в точках А и В? Какой ток подает источник питания в эту цепь?Эта задача проста, хотя и утомительна, поскольку в цепи всего четыре «звена».Он не достоин ярлыка «головоломка». Но что, если в цепочке 500 звеньев? Дальнейшее удлинение цепочки не имеет практического смысла, но решение ее для бесконечного числа звеньев представляет собой интересную головоломку, поскольку по мере ее решения возникает удивительная закономерность.
Подсказка 1: иногда помогает решить головоломку, если подойти к ней с другого конца.
Подсказка 2: Иногда это не так.
Подсказка 3. Как это может быть связано с Фибоначчи? - Обшивка контактной сети. Силовой кабель натянут между двумя опорами. Конечно, он провисает в форме кривой, называемой контактной сетью. На каждом
конец, где он прикреплен к столбу, образует угол 10° с горизонтом. Вес этого отрезка троса равен W.
 Чему равно натяжение троса в его нижней точке? Чему равно его напряжение на каждом из полюсов?
Чему равно натяжение троса в его нижней точке? Чему равно его напряжение на каждом из полюсов? - Поиск центра.
Рис. 1. Найдите центр масс
.На рис. 1 показан L-образный плоский лист металла одинаковой толщины и состава. Сможете ли вы найти его центр масс, используя только линейку без опознавательных знаков?
- Падающий Слинки. Подвесьте пружину Slinky™ с одного конца. Если вы отпустите этот конец, как падет весна?
- Вся пружина падает, сохраняя свою растянутую длину до тех пор, пока нижний конец не коснется пола, затем падает остальная часть пружины, сжимаясь при движении.
- Вся пружина падает, сжимаясь при движении.
- Нижний конец поднимается, чтобы встретиться с верхним концом, затем пружина опускается в сжатом состоянии.
- Нижний конец сохраняет свое положение до тех пор, пока остальная часть пружины не сожмется, после чего пружина опускается в сжатом состоянии.

Дополнительный вопрос: каково начальное ускорение верхнего конца пружины при падении?
- Ускорение свободного падения, g
- Ускорение свыше g .
- Ускорение менее g .
И еще вопрос: если бы к нижней части подвесного обтекателя был прикреплен груз, как бы это повлияло на наши предыдущие ответы?
О, еще один момент: если бы жесткость пружины или скорость импульса сжатия в пружине были другими, мог ли бы нижний конец ненадолго подняться сразу после отпускания верхнего конца пружины?
Как всегда, объясните свои ответы.
- Щелчок! .
Все мы умеем «щелкать» пальцами, что проще сделать, чем описать словами. Сильно сожмите большой и средний пальцы вместе, позволяя пальцу внезапно соскользнуть с большого, и вы услышите щелчок. Не делая этого, объясните, откуда именно исходит звук.
Перетягивание каната. 
- Перетягивание каната. Два одинаковых груза W расположены, как показано на рисунке. Старомодные пружинные весы подсоединены к середине горизонтального шнура и поддерживаются так, чтобы шнуры не провисали.(Возможно, используйте невесомые пружинные весы.) Каковы приблизительные показания пружинных весов?
- 3 Вт
- 2 Вт
- Вт
- Ноль
- Вт/2
- 15 магических квадратов-пазлов.
Деревянная головоломка 15. Классическая «головоломка на 15» до сих пор встречается в магазинах игрушек. Он состоит из квадратных плиток, пронумерованных от 1 до 15, в корпусе размером 4×4 плитки.При заполнении остается одно пустое место, позволяющее перетасовывать плитки в разном порядке. Обычно плитки пытаются расположить в числовом порядке влево-вправо, сдвигая их, никогда не вынимая из коробки.

Мастер головоломок Сэм Лойд утверждал, что изобрел эту игрушку в 1891 году, но идея пришла не ему первой. Нойес Чепмен подал заявку на патент на него в марте 1880 года. Лойд описал шутку, которую можно сыграть с ним: просто поменяйте местами две плитки, чтобы их нельзя было решить в числовом порядке слева направо.Он назвал это головоломкой 14-15, потому что он поменял местами эти две плитки, но замена любых двух плиток дала бы тот же результат. Загадку все еще можно было решить окольными методами.
1 5 9 13 2 6 10 14 3 7 11 15 4 8 12
Или переверните головоломку боком:4 8 12 3 7 11 15 2 6 10 14 1 5 9 13
Но возможностей для головоломок больше. Можете ли вы перетасовать плитки стандартной головоломки из 15, чтобы составить «магический квадрат», в котором сумма плиток в каждой строке, столбце и диагонали равна 30? - Быстрое затмение. Если смотреть с северного полюса Земли, Земля вращается вокруг Солнца против часовой стрелки.
 Луна вращается вокруг Земли против часовой стрелки. Земля вращается вокруг своей оси против часовой стрелки. Тогда почему область полного солнечного затмения перемещается по земле с запада на восток? Например, во время солнечного затмения в США в 2017 году полная область прибыла на западное побережье в штате Орегон примерно через 1,5 часа и была замечена на восточном побережье в Чарльстоне, Южная Каролина. Проверьте свой ответ, рассчитав время, которое потребовалось полной области, чтобы пересечь У.S.A.
Луна вращается вокруг Земли против часовой стрелки. Земля вращается вокруг своей оси против часовой стрелки. Тогда почему область полного солнечного затмения перемещается по земле с запада на восток? Например, во время солнечного затмения в США в 2017 году полная область прибыла на западное побережье в штате Орегон примерно через 1,5 часа и была замечена на восточном побережье в Чарльстоне, Южная Каролина. Проверьте свой ответ, рассчитав время, которое потребовалось полной области, чтобы пересечь У.S.A.Скольжение или скольжение? - Скольжение или скольжение? Представьте, что новый процесс позволяет производить твердые материалы без трения. Сплошной цилиндр помещен наверху наклонной плоскости, оба сделаны из этого материала. Цилиндр освобождают, стараясь не толкать его и не вращать. Будет ли цилиндр катиться по плоскости без скольжения или он будет скользить по плоскости без вращения? Или он будет и скользить, и скользить?
- Сезонная головоломка.
 В Северном полушарии лето теплее зимы. Почему? Обычный поверхностный ответ таков: «Потому что земная ось имеет фиксированное направление в пространстве, и летом она наклоняется к солнцу, а зимой отклоняется от солнца». Это правда, но это не полный ответ. Не упомянуты два важных процесса. Можете ли вы объяснить, почему наклон влияет на сезонные температуры?
В Северном полушарии лето теплее зимы. Почему? Обычный поверхностный ответ таков: «Потому что земная ось имеет фиксированное направление в пространстве, и летом она наклоняется к солнцу, а зимой отклоняется от солнца». Это правда, но это не полный ответ. Не упомянуты два важных процесса. Можете ли вы объяснить, почему наклон влияет на сезонные температуры? - Любопытный аттракцион. Эти визитные карточки с магнитной обратной стороной представляют собой интересную головоломку.Их черные спины имеют чередующиеся полосы магнитных полюсов N и S, отстоящих друг от друга на 1 мм. Вы можете проверить это с двумя одинаковыми картами. Положите их лицевой стороной вверх, стопкой, двигайте их по длине, и они будут плавно двигаться. Переместите их перпендикулярно их длине, и движение «прыгает», когда вы переходите от N к S намагниченных полос. Поверните их так, чтобы их черные стороны соприкасались, будут видны аналогичные результаты. Но… Поверните одну относительно другой (черные поверхности все еще соприкасаются) и под углами от 10° до 90° движение будет плавным и продолжает оставаться привлекательным даже с картами, повернутыми на 90°.
 Почему это должно быть так, если при 90° должно быть столько же притяжения, сколько и отталкивания, и вы ожидаете, что карты не будут притягиваться?
Почему это должно быть так, если при 90° должно быть столько же притяжения, сколько и отталкивания, и вы ожидаете, что карты не будут притягиваться?Эти магниты называются магнитами на молнии. Магнитные элементы в них находятся в массиве Хальбаха. Вот некоторые веб-ссылки, которые могут помочь вам визуализировать их поведение, но они не дают ответа на эту загадку.
Центр физики. Магниты на молнии.
EngineerDog.com. Почему магниты на холодильник прилипают только с одной стороны?
Ответа пока никто не дал.
- Армагедон. Если мы обнаружим (достаточно скоро) большой космический камень, направляющийся на курс столкновения с Землей, и захотим предотвратить его, что будет лучшей стратегией?
- Поднимите большую ракету, чтобы толкнуть камень против его скорости и замедлить его.
- Отправьте большую ракету с ядерной боеголовкой, чтобы она приземлилась на скалу и разнесла ее вдребезги.
- Запустите большую ракету с ядерной боеголовкой, чтобы она приземлилась на скалу и взорвалась, чтобы сбить ее с курса.

- Запустите большую ракету, чтобы толкнуть камень вбок (под прямым углом к скорости камня), чтобы изменить его курс.
Почему это сработает? Как шансы на успех будут зависеть от массы и относительной скорости камня?
- Мрачная тайна. Мы все видели облака многих видов, тонкие облака, туманные облака и пушистые кучевые облака. Кумулятивные образования принимают различные формы, но сохраняют свою индивидуальность, когда вы наблюдаете за ними с момента их образования до момента их исчезновения.Почему они сохраняются так долго? Они состоят из капель воды, которые тяжелее воздуха. Почему бы им просто не растечься в однородную дымку, покрывающую все небо? Что так долго удерживает облака водяного пара в определенной (хотя и медленно меняющейся) форме? Как они вообще образуются «из воздуха»? Какая у него физика?
Вы можете сравнить клубы пара из чайника или старомодный паровоз, пока ищете ответ. Или дым из дымовой трубы.
- Горячий воздух.
 Где-то в своем ответе на предыдущую задачу вы, возможно, утверждали, что «горячий воздух поднимается вверх». Это поднимает фундаментальный вопрос: «Почему горячий воздух поднимается вверх?» Упрощенные объяснения из учебников утверждают, что воздух рядом с пламенем расширяется и, следовательно, становится менее плотным, а более легкие предметы поднимаются в более плотных жидкостях. Это действительно объясняет процесс? Почему нагретый воздух ведет себя как объем меньшей плотности, чем окружающий воздух?
Где-то в своем ответе на предыдущую задачу вы, возможно, утверждали, что «горячий воздух поднимается вверх». Это поднимает фундаментальный вопрос: «Почему горячий воздух поднимается вверх?» Упрощенные объяснения из учебников утверждают, что воздух рядом с пламенем расширяется и, следовательно, становится менее плотным, а более легкие предметы поднимаются в более плотных жидкостях. Это действительно объясняет процесс? Почему нагретый воздух ведет себя как объем меньшей плотности, чем окружающий воздух?Представьте себе горячий предмет, например зажженную спичку или свечу.От него тут же поднимается дым. Но почему бы молекулам воздуха, нагретым вблизи пламени, просто не разлететься во все стороны вверх, вниз и в стороны одинаково? Что заставляет молекулы двигаться преимущественно вверх?
Конечно, нагретые молекулы в среднем движутся быстрее и вскоре взаимодействуют с другими молекулами, обмениваясь энергией и импульсом. Что в этом процессе побуждает их двигаться вверх? Любое объяснение на молекулярном уровне должно включать гравитацию.

- 2 I 1 , y I 2 , и Y I 3 выбраны из другого набора логических переменных: x 1 , …, x N , x 1 , …, x N .
- 3, E W I ) является полным графом для каждого W I (IE, делает каждый набор цветных вершин образует клику?). Известно, что эта задача является NP-полной [18].
- 2 90 . Минимум E найдет минимальное остовное дерево с учетом ограничения степени.
- 3 > 903, когда i 903 > 903Мы также определяем переменные y uv , y vu , которые мы принимаем равными 1, когда конечный узел «направленного» ребра находится в наборе вершин обратной связи.
 Теперь мы можем записать очень похожую энергию для минимального остовного дерева:
Теперь мы можем записать очень похожую энергию для минимального остовного дерева: - 2 UV UV на каждом краю, что составляет 1, если UV ∉ F , и define x УФ , I , чтобы быть 1, если оба uv = 1 и высота узла u равна i .Мы также добавляем бинарную переменную x v , i , как для набора вершин обратной связи. Затем наша энергия ограничения должна обеспечить следующее: каждая вершина и включенное ребро имеют четко определенную высоту, и что каждое ребро указывает от более низкой высоты к более высокой высоте:.
 HA=A∑v(1−∑ixv,i)2+A∑uv∈E(yuv−∑ixuv,i)2 +A∑uv∑ixuv,i(2−xu,i−∑j>ixv,j ). (68)
HA=A∑v(1−∑ixv,i)2+A∑uv∈E(yuv−∑ixuv,i)2 +A∑uv∑ixuv,i(2−xu,i−∑j>ixv,j ). (68)Затем мы используем
HB=B∑uv∈E(1−yuv) (69)для подсчета количества ребер в F — минимизируется, когда это число наименьшее.Как и прежде, нужно B < A , чтобы закодировать правильную задачу. Необходимое количество спинов | Е | + | В |(| В | + | Е |).
9. Изоморфизмы графов
Графы G 1 и G 2 , имеющие N вершин в каждом, изоморфны, если существует нумерация вершин 1, …, N в каждом графе смежности такая, что идентичен.Более внимательно: любой граф G = ( V, E ), с вершинами, помеченными как 1, …, N , имеет N × N матрицу смежности A с
Aij={1(ij)∈E,0(ij)∉E., (70), который содержит всю информацию о наборе ребер E . Пусть A 1,2 — матрицы смежности графов G 1,2 .
 Если существует такая матрица перестановок P, что A 2 = P T A 1 P, то мы говорим, что G 1,2 изоморфны.
Если существует такая матрица перестановок P, что A 2 = P T A 1 P, то мы говорим, что G 1,2 изоморфны.Вопрос о ли два графика г 1 1 = ( V 1 , E 1 ) и г 2 = ( V 2 , E 2 ) изоморфен, считается трудным, но его отнесение к классу сложности до сих пор остается загадкой [55]. Поскольку это (на практике) трудная задача, давайте, тем не менее, опишем для нее формулировку Изинга. Изоморфизм возможен, только если | В 1 | = | В 2 | ≡ N , поэтому ограничимся этим случаем и без ограничения общности обозначим вершины G 1 через 1, …, N .
Запишем это как модель Изинга следующим образом. Давайте описываем предложенный изоморфизм через двоичные переменные x . Энергия
HA=A∑v(1−∑ixv,i)2+A∑i(1−∑vxv,i)2 (71)гарантирует, что эта карта биективна.
HB=B∑ij∉E1∑uv∈E2xu,ixv,j+B∑ij∈E1∑uv∉E2xu,ixv,j (72) Затем мы используем энергию
Затем мы используем энергиюдля наказания за плохое сопоставление: i.то есть ребро, не входящее в G 1 , находится в G 2 или ребро, входящее в G 1 , не входящее в G 3 90. Как обычно, предположим, что A, B > 0. Если основное состояние этого гамильтониана имеет H = 0, то имеет место изоморфизм. N Требуется 2 оборотов.
Приближенный алгоритм, использующий квантовый отжиг для различения неизоморфных графов с помощью спектров зависимых от графов гамильтонианов, был представлен Хеном и Янгом [56].
10. Заключение
Основное внимание в исследованиях AQO уделялось NP-полным/сложным задачам, поскольку модель Изинга является NP-сложной, а также потому, что ученые-компьютерщики изо всех сил пытались найти эффективные способы решения этих проблем. В этой статье мы представили стратегии для сопоставления широкого спектра NP-задач со спиновыми стеклами Изинга на примере демонстрации стакана для каждой из 21 NP-полной задачи Карпа.
 Остается открытым вопрос, в какой степени AQO поможет найти эффективные решения этих проблем, будут ли эти решения точными или приблизительными.
Остается открытым вопрос, в какой степени AQO поможет найти эффективные решения этих проблем, будут ли эти решения точными или приблизительными.Однако физики заинтересованы в создании универсального квантового компьютера, способного решать гораздо больше, чем просто модели Изинга. Например, универсальный квантовый компьютер также сократит время поиска в несортированном списке из N элементов с O( N ) до O(N) [57]. Это было бы невероятно полезно для многих практических приложений, несмотря на то, что поиск — это простой алгоритм линейного времени. Аналогичным образом может случиться так, что существует семейство «простых» задач, которые AQO может решить за полиномиальное время, но более эффективно, чем классический алгоритм с полиномиальным временем.Это утверждение может быть верным даже для оборудования AQO, реализующего Ising, хотя если это так, то это не очевидно.
Безусловно, устройство, реализующее AQO, можно использовать для решения простых задач.
H=A (1−∑ixi)2−B∑inixi (73) Рассмотрим простую задачу поиска наибольшего целого числа в списке n 1 , …, n N (это алгоритм поиска, который может эффективно выполнять универсальный квантовый компьютер). Введение бинарных переменных x i for i = 1, …, N , модель Изинга
Рассмотрим простую задачу поиска наибольшего целого числа в списке n 1 , …, n N (это алгоритм поиска, который может эффективно выполнять универсальный квантовый компьютер). Введение бинарных переменных x i for i = 1, …, N , модель Изингадля A > B max( n i ) решает эту проблему.На самом деле эта задача чем-то похожа на пример модели Изинга со случайным полем на полном графе, и все же она имеет очень простой классический алгоритм O( N ). Конечно, программирование этого алгоритма в квантовом устройстве заняло бы больше времени, чем решение самой проблемы.
Приведенный выше пример демонстрирует, что иногда «сложность» проблемы может быть обманчивой — можно сформулировать что-то легкое таким образом, что оно покажется сложным. Стоит более подробно обсудить сложность NP-задач, поскольку оказывается, что иногда NP-задачи могут быть проще, чем кажутся на первый взгляд.
 Чтобы быть NP-полной, но не P (если P ≠ NP), нужно только небольшое семейство экземпляров задачи, которая не может быть решена за полиномиальное время с помощью детерминированного алгоритма. Тем не менее, типичные экземпляры могут быть не такими сложными. Многие популярные задачи NP почти наверняка могут быть решены точно за полиномиальное время на больших случайных экземплярах [58, 59], и существуют рандомизированные алгоритмы для некоторых задач NP, которые могут быть сколь угодно близки к решению с произвольно низкой вероятностью отказа за полиномиальное время [60]. , 61] (хотя мультипликативные коэффициенты или полиномиальные показатели должны расходиться, поскольку вероятность отказа и/или ошибка при определении основного состояния стремится к нулю, если P ≠ NP).Кроме того, популярные алгоритмы в P, такие как декомпозиция матриц, могут служить узкими местами практических вычислений, и их не следует считать «простыми». Типичные случаи приближаются к асимптотическим границам для наихудшего времени выполнения, в отличие от случая для некоторых проблем NP; многие недавние разработки сосредоточены на рандомизированных алгоритмах [62–64].
Чтобы быть NP-полной, но не P (если P ≠ NP), нужно только небольшое семейство экземпляров задачи, которая не может быть решена за полиномиальное время с помощью детерминированного алгоритма. Тем не менее, типичные экземпляры могут быть не такими сложными. Многие популярные задачи NP почти наверняка могут быть решены точно за полиномиальное время на больших случайных экземплярах [58, 59], и существуют рандомизированные алгоритмы для некоторых задач NP, которые могут быть сколь угодно близки к решению с произвольно низкой вероятностью отказа за полиномиальное время [60]. , 61] (хотя мультипликативные коэффициенты или полиномиальные показатели должны расходиться, поскольку вероятность отказа и/или ошибка при определении основного состояния стремится к нулю, если P ≠ NP).Кроме того, популярные алгоритмы в P, такие как декомпозиция матриц, могут служить узкими местами практических вычислений, и их не следует считать «простыми». Типичные случаи приближаются к асимптотическим границам для наихудшего времени выполнения, в отличие от случая для некоторых проблем NP; многие недавние разработки сосредоточены на рандомизированных алгоритмах [62–64].Гамильтонианы в этой статье могут быть обманчиво «жесткими» — это может означать, что они включают слишком много спинов. Другая возможность состоит в том, что эти гамильтонианы имеют небольшие спектральные лакуны, а альтернативные варианты имеют гораздо большие спектральные лакуны — это вопрос, который мы вообще не затрагивали в этой статье.Изучение того, как упростить квантовые алгоритмы и, что более важно, увеличить энергетические щели (и, таким образом, уменьшить T ), даже на постоянные множители, является весьма необходимой задачей.
Заявление о конфликте интересов
Автор заявляет, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Эндрю Лукас получает поддержку от стипендии семьи Смитов в области науки и техники в Гарварде.Он хотел бы поблагодарить Роберта Лукаса за указание на отсутствие сборника способов сопоставления известных проблем NP с очками Изинга, Джейкоба Биамонте за поощрение публикации, а также Вики Чой, Джейкоба Сандерса, Федерико Спедальери, Джона Трана и особенно рецензентов. за множество полезных комментариев по AQO и информатике.
Материалы и методы
В этой статье обсуждаются теоретические результаты; материалы не нужны. Используемая методология обсуждалась на протяжении всей статьи.
Сноски
Каталожные номера
1. Фархи Э., Голдстоун Дж., Гутманн С., Лапан Дж., Лундгрен А., Преда Д. Алгоритм квантовой адиабатической эволюции, примененный к случайным случаям NP-полной задачи. Наука (2001) 292 :472. doi: 10.1126/science.1057726
Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки
2. Дас А., Чакрабарти Б.К. Коллоквиум: квантовый отжиг и аналоговые квантовые вычисления. Rev Mod Phy .(2008) 80 :1061. doi: 10.1103/RevModPhys.80.1061
Полнотекстовая перекрестная ссылка
5. Бапст В., Фойни Л., Крзакала Ф., Семерджян Г., Зампони Ф. Применение квантового адиабатического алгоритма к задачам случайной оптимизации: перспектива квантового спинового стекла. Физический представитель . (2013) 523 :127. doi: 10.1016/j.physrep.2012.10.002
Полнотекстовая перекрестная ссылка
6. Фархи Э., Голдстоун Дж., Госсет Д., Гутманн С., Шор П. Неструктурированная случайность, небольшие пробелы и локализация. Квантовые вычисления Информ . (2011) 11 :840. Доступно в Интернете по адресу: http://arxiv.org/abs/1010.0009
.7. Фархи Э., Госсет Д., Хен И., Сандвик А.В., Шор П., Янг А.П. и др. Производительность квантового адиабатического алгоритма на случайных экземплярах двух задач оптимизации на обычных гиперграфах. Физическая версия . (2012) A86 :052334. doi: 10.1103/PhysRevA.86.052334
Полнотекстовая перекрестная ссылка
9. Йорг Т., Крзакала Ф., Семерджян Г., Дзампони Ф.Переходы первого порядка и производительность квантовых алгоритмов в задачах случайной оптимизации. Phys Rev Letter . (2010) 104 :207206. doi: 10.1103/PhysRevLett.104.207206
Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки
12. Boixo S, Rønnow TF, Isakov SV, Wang Z, Wecker D, Lidar DA, et al. Квантовый отжиг с более чем сотней кубитов (2013 г.). Доступно в Интернете по адресу: http://arxiv.org/abs/1304.4595
.14. Уитфилд Дж.Д., Фаччин М., Биамонте Дж.Д.Логика вращения основного состояния. Еврофиз Летт . (2012) 99 :57004. дои: 10.1209/0295-5075/99/57004
Полнотекстовая перекрестная ссылка
15. Биамонте Д.Д., Лав П.Дж. Реализуемые гамильтонианы для универсальных адиабатических квантовых компьютеров. Физическая версия . (2008) A78 :012352. doi: 10.1103/PhysRevA.78.012352
Полнотекстовая перекрестная ссылка
16. Брави С., Ди Винченцо Д.П., Оливейра Р.И., Терхал Б.М. Сложность стоквастических локальных гамильтоновых задач. Quantum Inform Comput . (2008) 8 :0361. Доступно в Интернете по адресу: http://arxiv.org/abs/quant-ph/0606140
.17. Барахона Ф. О вычислительной сложности моделей спинового стекла Изинга. Дж Физ . (1982) A15 :3241.
18. Карп Р.М. Сводимость среди комбинаторных задач. В: Миллер Р.Е., Тэтчер Дж.В. и Болингер Дж.Д., редакторы. Сложность компьютерных вычислений . Нью-Йорк, штат Нью-Йорк: Plenum Press (1972), с. 85. doi: 10.1007/978-1-4684-2001-2_9
Полнотекстовая перекрестная ссылка
19.Гэри М.Р., Джонсон Д.С. Компьютеры и неразрешимость: руководство по теории NP-полноты . Сан-Франциско, Калифорния: WH Фриман (1979).
20. Фу Ю., Андерсон П.В. Применение статистической механики к NP-полным задачам комбинаторной оптимизации. Дж Физ . (1986) A19 :1605.
21. Мезар М., Паризи Г., Вирасоро М. Теория спинового стекла и не только . Сингапур: World Scientific (1987).
22. Хартманн А.К., Вейгт М. Фазовые переходы в задачах комбинаторной оптимизации: основы, алгоритмы и статистическая механика . Вайнхайм: Wiley-VCH (2006).
24. Мезар М., Монтанари А. Информация, физика и вычисления . Оксфорд: Издательство Оксфордского университета (2009). doi: 10.1093/acprof:oso/9780198570837.001.0001
Полнотекстовая перекрестная ссылка
28. Бушо Ж.П. Кризисы и коллективные социально-экономические явления: простые модели и вызовы. J Стат Физ .(2013) 151 :567. doi: 10.1007/s10955-012-0687-3
Полнотекстовая перекрестная ссылка
30. Xu N, Zhu J, Lu D, Zhou X, Peng X, Du J. Квантовая факторизация числа 143 в системе ядерного магнитного резонанса с дипольной связью. Phys Rev Letter . (2012) 108 :130501 [ Erratum (2012) 109 :269902E]. doi: 10.1103/PhysRevLett.108.130501
Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки
32. Пердомо-Ортиз А., Диксон Н., Дрю-Брук М., Роуз Г., Аспуру-Гузик А.Нахождение низкоэнергетических конформаций моделей решетчатых белков с помощью квантового отжига. Научный представитель . (2012) 2 :571. дои: 10.1038/srep00571
Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки
33. Баббуш Р., Пердомо-Ортиз А., О’Горман Б., Макреди В., Аспуру-Гузик А. Построение энергетических функций для моделей решетчатых гетерополимеров: тематическое исследование программирования удовлетворения ограничений и адиабатической квантовой оптимизации (2013). Доступно в Интернете по адресу: http://arxiv.орг/абс/1211.3422
34. Невен Х., Роуз Г., Макриди В.Г. Распознавание изображений с помощью адиабатического квантового компьютера I. Преобразование в квадратичную неограниченную бинарную оптимизацию (2008). Доступно в Интернете по адресу: http://arxiv.org/abs/0804.4457
.35. Денчев В., Дин Н., Вишванатан С.В.Н., Невен Х. «Надежная классификация с адиабатической квантовой оптимизацией». Материалы 29-й Международной конференции по машинному обучению . (Эдинбург), с. 863 (2012).
36. Борос Э., Хаммер П.Л.Задача о максимальном разрезе и квадратичная оптимизация 0-1; полиэдральные аспекты, релаксации и оценки. Аннал Опер Рес . (1991) 33 :151. дои: 10.1007/BF02115753
Полнотекстовая перекрестная ссылка
37. Борос Э., Хаммер П.Л. Псевдобулевая оптимизация. Дискретная прикладная математика . (2002) 123 :155. doi: 10.1016/S0166-218X(01)00341-9
Полнотекстовая перекрестная ссылка
38. Борос Э., Хаммер П.Л., Таварес Г. Предварительная обработка квадратичной бинарной оптимизации без ограничений. Исследовательский отчет РУТКОР 10-2006 (2006).
39. Billionnet A, Jaumard B. Метод декомпозиции для минимизации квадратичных псевдобулевых функций. Оперативный бюллетень . (1989) 8 :161. дои: 10.1016/0167-6377(89)
-6Полнотекстовая перекрестная ссылка
40. Биамонте Д.Д. Непертурбативные гамильтонианы преобразования k тел в двухтеловые коммутирующие и вложение примеров задачи в изинговские спины. Физическая версия . (2008) A77 :052331.doi: 10.1103/PhysRevA.77.052331
Полнотекстовая перекрестная ссылка
41. Баббуш Р., О’Горман Б., Аспуру-Гузик А. Ресурсоэффективные гаджеты для решения задач адиабатической квантовой оптимизации. Аннал. Физ . (2013) 525 :877. doi: 10.1002/andp.201300120
Полнотекстовая перекрестная ссылка
42. Peng X, Liao Z, Xu N, Qin G, Zhou X, Suter D, et al. Квантовый адиабатический алгоритм факторизации и его экспериментальная реализация. Phys Rev Letter .(2008) 101 :220405. doi: 10.1103/PhysRevLett.101.220405
Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки
43. Чой В. Минорное вложение в адиабатических квантовых вычислениях: I проблема настройки параметров. Процесс Quantum Inform . (2008) 7 :193. doi: 10.1007/s11128-008-0082-9
Полнотекстовая перекрестная ссылка
44. Чой В. Минорное вложение в адиабатических квантовых вычислениях: II Минорно-универсальный дизайн графа. Процесс Quantum Inform .(2011) 10 :343. doi: 10.1007/s11128-010-0200-3
Полнотекстовая перекрестная ссылка
45. Климко С., Салливан Б.Д., Хамбл Т.С. Адиабатическое квантовое программирование: незначительное встраивание с серьезными ошибками. Процесс Quantum Inform . Доступно в Интернете по адресу: http://arxiv.org/abs/1210.8395
.46. Алон Н., Кривелевич М., Судаков Б. Нахождение большой скрытой клики в случайном графе. Алгоритм случайных структур . (1998) 13 :457. doi: 10.1002/(SICI)1098-2418(199810/12)13:3/4<457::AID-RSA14>3.3.СО;2-К
Полнотекстовая перекрестная ссылка
47. Чайлдс А.М., Фархи Э., Голдстоун Дж., Гутманн С. Поиск клик с помощью квантовой адиабатической эволюции. Quantum Inform Comput . (2002) 2 :181. Доступно в Интернете по адресу: http://arxiv.org/abs/quant-ph/0012104
.48. Шривер А. Теория целочисленного и линейного программирования . Чичестер, Нью-Йорк: Wiley (1998).
49. Чой В. Адиабатические квантовые алгоритмы для NP-полного независимого множества максимального веса, точного покрытия и задач 3SAT (2010).Доступно в Интернете по адресу: http://arxiv.org/abs/1004.2226
.50. Келлерер Х., Пферши У. Задачи о рюкзаке . Берлин: Спрингер (2004). дои: 10.1007/978-3-540-24777-7
Полнотекстовая перекрестная ссылка
51. Ву Ф.Ю. Модель Поттса. Rev Mod Phys . (1982) 54 :1. doi: 10.1103/RevModPhys.54.235
Полнотекстовая перекрестная ссылка
52. Аппель К., Хакен В. Каждая плоская карта представляет собой четыре раскраски I: разрядка. Иллинойс J Math . (1977) 21 :429.
53. Аппель К., Хакен В., Кох Дж. Каждая плоская карта является четырехцветной. II Сводимость. Иллинойс J Math . (1977) 21 :491.
54. Чжоу Х.Дж. Подход спинового стекла к проблеме множества вершин с обратной связью. Eur Phys J (2013) B86 :455. doi: 10.1140/epjb/e2013-40690-1
Полнотекстовая перекрестная ссылка
55. Джонсон Д.С. Столбец NP-полноты. Трансалгоритм ACM . (2005) 1 :160. дои: 10.1145/1077464.1077476
Полнотекстовая перекрестная ссылка
56. Курица I, Молодой А.П. Решение проблемы изоморфизма графов с помощью квантового отжига. Физическая версия . (2012) A86 :042310. doi: 10.1103/PhysRevA.86.042310
Полнотекстовая перекрестная ссылка
57. Нильсен М.А., Чуанг И.А. Квантовые вычисления и квантовая информация . Кембридж: Издательство Кембриджского университета (2000).
58. Бейер Р., Фёкинг Б. «Случайный рюкзак за ожидаемое полиномиальное время». Материалы 35-го ежегодного симпозиума ACM по теории вычислений (Сан-Диего, Калифорния), с.232 (2004).
59. Кривелевич М., Виленчик Д. «Решение случайных выполнимых формул 3CNF за ожидаемое полиномиальное время». Материалы 17-го ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (Майами, Флорида), с. 454 (2006). дои: 10.1145/1109557.1109608
Полнотекстовая перекрестная ссылка
60. Дайер М., Фриз А., Каннан Р. Алгоритм случайного полиномиального времени для аппроксимации объема выпуклых тел. Дж АСМ . (1991) 38 :1. дои: 10.1145/102782.102783
Полнотекстовая перекрестная ссылка
61. Вазирани В.В. Алгоритмы аппроксимации . Берлин: Спрингер (2003). дои: 10.1007/978-3-662-04565-7
Полнотекстовая перекрестная ссылка
62. Либерти Э., Вульф Ф., Мартинссон П.Г., Рохлин В., Тайгерт М. Рандомизированные алгоритмы аппроксимации матриц низкого ранга. Proc Natl Acad Sci USA . (2007) 104 :20167. doi: 10.1073/pnas.0709640104
Опубликовано Резюме | Опубликован полный текст | Полный текст перекрестной ссылки
63.Халко Н., Мартинссон П., Тропп Дж.А. Нахождение структуры со случайностью: вероятностные алгоритмы построения приближенных матричных разложений. СИАМ Ред. . (2011) 53 :217. дои: 10.1137/0
806
Полнотекстовая перекрестная ссылка
64. Лукас А., Сталцер М., Фео Дж. Параллельная реализация быстрого рандомизированного алгоритма разложения матриц низкого ранга. Письмо о параллельном процессе . (принятый). Доступно в Интернете по адресу: http://arxiv.org/abs/1205.3830
. .
Задача на магнитный поток и ЭДС индукции:
Источник: kopilkaurokov.ruИсточник: kopilkaurokov.ruКолебания и волны
Источник: prezentacii.orgВ разделе физики «Колебания и волны» изучают следующие темы:
Задача на колебания математического маятника:
Источник: videouroki.netЗадача на пружинный маятник:
Источник: znanio.ruЗадача на колебательный контур:
Источник: mypresentation.ruДля того, чтобы задания по физике решались совсем легко, предмет нужно полюбить. Если это не про вас, не переживайте! Посвящайте свое время любимым дисциплинам и хобби, а физику оставьте для профессионалов Феникс. Хелп.
Хелп.
Задачи по физике для поступающих в вузы (Бендриков Г.А. и др.)
Содержит задачи в рамках вступительных экзаменов по физике из числа предлагавшихся в течение ряда лет на различных факультетах Московского Государственного университета. К каждой теме даны краткие указания, касающиеся общей методики решения задач, и основные формулы, используемые при решении.
Подробные решения приведены для методически наиболее важных задач.
Для слушателей подготовительных отделений вузов, учащихся средних
общеобразовательных и профессиональных школ, а также лиц, занимающихся
самообразованием.
| Автор | Бендриков Григорий Авксентьевич, Буховцев Борис Борисович, Керженцев Василий Васильевич, Мякишев Геннадий Яковлевич |
| Издательство | ООО «Физматлит» |
| Дата издания | 2018 |
| Кол-во страниц | 344 |
| ISBN | 978-5-9221-1497-4 |
| Тематика |
Физика. Химия. Биология (егэ,вуз) Химия. Биология (егэ,вуз)
|
| Вес книги | 363 г |
| № в каталоге | 1648 |
Категории: Для подготовки к ЕГЭ и поступлению в ВУЗ
Решение задач по 📝 физике быстро и качественно без посредников
Как известно, физики отличаются от лириков не только способом мышления, но и необходимостью решать задачи. Это не минует ни одного студента, поступившего в технический вуз. На какой бы специальности вы не учились, какой бы раздел не проходили, будь то общая физика или механика, термодинамика, оптика или электродинамика – все равно придется их выполнять.
Это не минует ни одного студента, поступившего в технический вуз. На какой бы специальности вы не учились, какой бы раздел не проходили, будь то общая физика или механика, термодинамика, оптика или электродинамика – все равно придется их выполнять.
Выполнение заданий по данному предмету
Существует безотказно работающий способ, облегчающий суровую студенческую жизнь, сдать домашнюю работу, контрольную, решение задач или зачет. Оказывается, чтобы получить хорошую оценку по предмету, совсем необязательно заучивать километры формул. Нужно всего лишь заказать работу и очень скоро подробно расписанный пример окажется у вас на экране телефона или компьютера.
Работы, решенные грамотным специалистом, обеспечат вам хорошую успеваемость в течение всего семестра, своевременную сдачу домашних и проверочных работ. Вы сможете занять почетное место среди лучших студентов курса и заслужить благосклонность преподавателя, которая обязательно пригодится вам на экзамене или защите курсовой работы.
К слову, мы можем оказать вам виртуальную помощь, выполнив все задания за максимально короткое время и отправив готовое задание вам на телефон прямо во время экзамена. А если вы проходите аттестацию в форме компьютерного тестирования, мы будем рады предложить вам помощь в сдаче тестов.
Где заказать необходимую работу?
Вам не нужно набирать в поисковой строке браузера необходимые термины. Вам не придется заходить на сомнительные сайты и разбираться в сложных системах оформления заказов.
Чтобы сделать любой заказ, нужно всего лишь зайти на сайт vsesdal.com и опубликовать там проект. Вы можете сразу указать в проекте раздел или тему. Кинематика, статика, динамика – все эти разделы физики хорошо знакомы нашим специалистам. Даже если вам нужен такой раздел, как техническая механика, решение по этому предмету также сможет выполнить кто-либо из исполнителей.
Когда ваш проект появится на сайте, вам начнут поступать предложения от исполнителей, готовых взяться за решение ваших задач. Вам останется только выбрать из них того, кто вызовет у вас наибольшее доверие. Чтобы больше узнать об исполнителе, можно посмотреть его профиль, узнать, выполнял ли он, к примеру, ядерный вариант, (если вам нужен именно этот раздел), почитать отзывы, оставленные предыдущими заказчиками.
Вам останется только выбрать из них того, кто вызовет у вас наибольшее доверие. Чтобы больше узнать об исполнителе, можно посмотреть его профиль, узнать, выполнял ли он, к примеру, ядерный вариант, (если вам нужен именно этот раздел), почитать отзывы, оставленные предыдущими заказчиками.
Детали сотрудничества, такие, как цена или стоимость онлайн решения задач, время выполнения, и другие аспекты, касающиеся содержания работы, вы можете обсудить лично с исполнителем. Вы всегда можете высказать свои пожелания к выполнению и оформлению работы. Например, если вариант по молекулярной тематике нужно выполнить строго определенным способом, чтобы преподаватель в университете ничего не заподозрил, следует договориться с исполнителем об этом заранее.
Срочно выполнить работу
Если время поджимает, и решение задач по физике нужно сдать как можно скорее, мы поможем вам предотвратить учебную катастрофу и сделаем за вас все задания за минимальное время. Срочно выполнить то, что нужно может любой специалист, которого вы выберете на нашем сайте. Договариваясь с исполнителем о выполнении задания и сроках, всегда можно сделать так, чтобы выполнение по любому предмету было сделано и прислано вам как можно скорее. Выполнение нужным вам способом на заказ будут у вас, как только исполнитель справится с этой работой.
Договариваясь с исполнителем о выполнении задания и сроках, всегда можно сделать так, чтобы выполнение по любому предмету было сделано и прислано вам как можно скорее. Выполнение нужным вам способом на заказ будут у вас, как только исполнитель справится с этой работой.
Заказать решение задач по физике, избавившись от необходимости самому сидеть над учебниками и конспектами, – этот способ сдачи университетских работ отлично подходит современным, живущим активной жизнью молодым людям. Причины того, чтобы не делать решение задач самостоятельно, могут быть совершенно разные. Кто-то предпочитает наслаждаться молодостью, а кто-то уже с первого курса устроился на работу и старательно совершает подъем по крутой карьерной лестнице. Но эти группы людей объединены одним: у них нет свободного времени по материаловедению и прочим предметам, которые вряд ли пригодятся в дальнейшей жизни. Поэтому намного проще заказать рещшение задач на сайте vsesdal.com – и не отвлекаться от своих основных жизненных занятий.
Примеры решения задач по физике для 7 класса — смешные и серьезные
Примеры решения задач по физике для 7 класса — смешные и серьезные
Задачи по физике — это просто!
Серьезные задачи по физике для 7 класса
Средняя скорость. Решение задач ………. смотреть
Плотность. Решение задач. 7 класс ………. смотреть
Механическое движение. Решение задач. 7 класс ………. смотреть
Сила тяжести, вес тела, сила упругости. Решение задач. 7 класс ………. смотреть
Смешные задачи для юных физиков Григория Остера
Как решить задачу по физике? ………. смотреть
Воздухоплавание ………. смотреть
Что изучает физика? ………. смотреть
Наблюдения, опыты, физические величины ………. смотреть
Строение вещества . ……… смотреть
……… смотреть
Диффузия. Агрегатные состояния ………. смотреть
Взаимодействие тел. Движение ………. смотреть
Взаимодействие тел ………. смотреть
Масса. Плотность ………. смотреть
Сила. Вес тела ………. смотреть
Силы в физике ………. смотреть
Трение ………. смотреть
Давление ………. смотреть
Сила тяжести ………. смотреть
Давление в жидкости и газе ………. смотреть
Давление. Барометр. Манометр. Насос ………. смотреть
Выталкивающая сила. Плавание тел ………. смотреть
Механическая работа ………. смотреть
Механическая мощность ………. смотреть
Простые механизмы ………. смотреть
Энергия ………. смотреть
Лабораторные работы ………. смотреть
Знаете ли вы?
Физиологи установили
… что работа дыхательных органов человека в течение суток достигает 20 тыс. килограммометров. 1 ватт-час соответствует 367 килограммометрам. Следовательно, суточной работы легких достаточно для накаливания 10-вт электрической лампы в течение 5,5 часа.
килограммометров. 1 ватт-час соответствует 367 килограммометрам. Следовательно, суточной работы легких достаточно для накаливания 10-вт электрической лампы в течение 5,5 часа.
За сутки человек выдыхает в среднем 1—2 кг углекислого газа, а в год примерно полтонны. Таким образом, все человечество выдыхает ежегодно в атмосферу Земли около миллиарда тонн углекислого газа.
Возможно ли это?
Два человека рассуждали о том, какое светило, солнце или луна, заслуживает преимущества.
Один, не колеблясь, назвал солнце, но другой глубокомысленно заметил: а я так думаю, что луне принадлежит эта честь; что за важность светить, когда солнце, днем, когда и без того светло, а ведь месяц светит ночью, когда темно.
Скажи, могла бы светить луна, если бы не было солнца?
Некто утверждает, что в полдень 22 июня видел радугу на небе.
Возможно ли это?
Оказывается, радуга видна лишь тогда, когда высота солнца над горизонтом не превышает 42 градусов.
22 июня в полдень солнце стоит на небе выше, и нет возможности увидеть радугу.
Интересно, что с земли радуга выглядит обычно как часть окружности, а с самолета она может представлять собой и целую окружность!
Школьный сайт — Физика_профиль
для 10 класса:
ДЛЯ ТЕХ КТО СДАЁТ ЕГЭ ПО ФИЗИКЕ скачать ЗАДАЧИ С РЕШЕНИЕМ
10 КЛАСС (ПРОФИЛЬ-ФИЗИКА) СКАЧАТЬ КНИГУ-УЧИМСЯ РЕШАТЬ ЗАДАЧИ ПО МЕХАНИКЕ и её просмотреть.
ЗАГЛЯНИТЕ СЮДА
ДЛЯ ТЕХ КТО СДАЁТ ФИЗИКУ » ВЛАЖНОСТЬ» СМОТРЕТЬ
ЗДЕСЬ ВЫ НАЙДЕТЕ ВИРТУАЛЬНЫЕ ОПЫТЫ ПО ФИЗИКЕ
ПОЛОЖЕНИЕ
о текущем контроле и промежуточной аттестации обучающихся
Требования к оформлению рефератов
Как получить максимальный балл на ЕГЭ. Физика. Решение заданий повышенного и высокого уровня сложности. Ханнанов Н.К.
РЕШЕНИЕ ЗАДАЧ ПО ФИЗИКЕ ПОДГОТОВКА К ЕГЭ
электростатика
для тех кто хочет сдать физику
ЗАДАЧИ части «С» С РЕШЕНИЕМ
Учимся решать задачи по физике скачать книгу здесь
для учеников 10(ПРОФИЛЬ) классов сборник задач Рымкевич скачать
КАК НАУЧИТЬСЯ РЕШАТЬ ЗАДАЧИ ПО ФИЗИКЕ
примеры задач части с
ЗАДАЧИ С РЕШЕНИЕМ ЧАСТИ С1
Содержание страницы:
Пособие по физике
Я написал электронную книгу, содержащую весь курс школьной физики. В ней имеется вся теория, необходимая для подготовки к ЕГЭ.
В ней имеется вся теория, необходимая для подготовки к ЕГЭ.
Книгу лучше читать не в браузере, а с помощью программы просмотра PDF (например, Adobe Reader). Тогда сбоку в закладках (bookmarks) будет отображена вся структура книги в виде ссылок на соответствующие разделы. То есть наряду с оглавлением (пункты которого являются ссылками) вы получаете ещё одно меню навигации по книге.
Разумеется, чтения пособия недостаточно; самое главное — уметь решать физические задачи. Этому мы и учимся на наших занятиях.
Главы пособия
При желании вы можете скачать каждую главу в отдельности (если, например, хотите освоить лишь механику или электродинамику).
Параграфы пособия: «Физика в листках»
Если вам необходимо ознакомиться с отдельными вопросами, то перед вами — содержание пособия в виде листков. Именно с этой «Физики в листках», собственно, пособие и начиналось 🙂
Необходимая математика
Механика
Электродинамика
Молекулярная физика и термодинамика
Теория относительности
Оптика
Квантовая физика
Статьи о подготовке к ЕГЭ по физике
1. Научная «Оксфордская видеоэнциклопедия для детей»
Научная «Оксфордская видеоэнциклопедия для детей»
Великобритания, 1996 год — Часть1.
Скачать: Яндекс
Содержание всех частей:
Часть 1: антибиотики, атмосфер, атомная энергия, атомы, бактерии и вирусы, вакуум, вода, воздух, время, газы, голограмма.
Часть 2: давление, дыхание, животные, живые существа, жидкости, загрязнение среды, звук, кислород, кислоты, клетки, кристаллы, линзы.
Часть 3: магниты, металлы, механизмы, мощность, нефть, огонь, озон, органы чувств, парниковый эффект, плавучесть, пластмассы, полет.
Часть 4: радар, радиация, радио, растения, рентгеновские лучи, рост, свет, сила тяжести, соли, температура, тепло, топливо, трение.
Часть 5: углерод, химические вещества, цвет, цепи питания, эволюция, экология, электричество, электроника, элементы, энергия.
Общая длительность всех частей фильма — 183 мин.
Физика-класс!
… электронная библиотека
Советую посмотреть видео ролики здесь
Сборник составлен к классическому курсу физики для 10— 11 классов авторов Г. Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского.
Я. Мякишева, Б. Б. Буховцева, Н. Н. Сотского.
В первой части пособия приведены задачи по всем темам, включенным в названный курс физики с указанием соответствующих параграфов учебника.
Вторая часть содержит задачи на темы, не включенные в классический курс физики. Умение решать такие задачи необходимо при поступлении в технические вузы.
для учеников 10-11 классов сборник задач Рымкевич скачать
Программа для просмотра файла
Здесь приведены справочные данные
КАК РЕШАТЬ ЗАДАЧИ ПО КИНЕМАТИКЕ
КАК РЕШАТЬ ЗАДАЧИ НА ЗАКОНЫ НЬЮТОНА
1. Научно-популярные лекции по физике для школьников с демонстрацией физических экспериментов
Лекция 1 Величие и простота законов Ньютона
— знакомит с маятником Фуко, инерцией, законами Ньютона, примерами применения законов динамики. Слушателелям демонстрируются знаменитые опыты, подтверждающие правоту основных законов механики.
Лекция 2. Мир бесконечного движения (основные положения МКТ, явления переноса)
— излагаются основные положения молекулярно-кинетической теории (МКТ), приводятся их экспериментальные обоснования. Рассказывается о различии механического и статистического подхода к описанию физических систем. Демонстрируются эксперименты, подтверждающие основные положения МКТ, в том числе эксперименты, связанные с явлениями диффузии, теплопроводности и вязкости.
Лекция 3. Красота вращающегося мира (гироскопы и волчки)
— рассматриваются эффекты, связанные с вращательным движением тел. Демонстрируется действие центробежной силы и силы Кориолиса. Обсуждается закон сохранения количества движения и связанные с ним эффекты. Демонстрируются гироскопы, устойчивость ориентации вращающихся тел. Демонстрируются необычные движения кельтских камней.
Лекция 4. Размышления о силе пламени (тепловые машины)
— посвящена тепловым машинам. Рассматриваются общие принципы перевода тепла в работу и работы в тепло. Демонстрируются тепловые машины, действующие на различных физических принципах, оценивается эффективность их работы.
Рассматриваются общие принципы перевода тепла в работу и работы в тепло. Демонстрируются тепловые машины, действующие на различных физических принципах, оценивается эффективность их работы.
Лекция 5. Отчего люди не летают? (гидродинамика и аэродинамика)
— посвящена эффектам гидростатики, аэростатики, гидродинамики и аэродинамики. Обсуждаются вопросы, связанные с движением тел в вязкой среде, разбирается причины появления подъемной силы у самолетного крыла. Демонстрируются движение тел в жидкостях и газах, особенности обтекания тел потоком воздуха, подъемная сила.
Лекция 6. Загадочные превращения (испарение и кипение, поверхностные явления, плавление и кристаллизация)
— рассматриваются явления испарения, кипения, плавления и отвердевания. Демонстрируются неравновесные состояния: перегретая жидкость, переохлажденная жидкость и переохлажденный пар. В лекции также рассматриваются явления на поверхности жидкости. Демонстрируются эффекты на поверхности мыльных пленок, воды, и др. жидкостей.
жидкостей.
Лекция 7. Физика и музыка (колебания и волны, акустика)
— посвящена волновым явлениям, в том числе распространению звуковых волн. Демонстрируются соотношение длины звуковых волн и высоты музыкального тона. Демонстрируется явления звукового резонанса. Демонстрируются необычные «музыкальные» инструменты.
Лекция 8. Мир искривленных лучей (геометрическая оптика)
— посвящена известным и малоизвестным явлениям, связанным с распространением световых лучей в линзах, световодах, жидкостях и газа.
Лекция 9. Все цвета радуги (явления интерференции и дифракции)
— рассказывается о разложении белого света в спектр от красного до фиолетового цвета (явление дисперсии), а также о радужных пятнах в лужах с бензином, на мыльных пленках, лазерных дисках и др.
Лекция 10. Мир лазеров и поляризованного света
— рассказывается о явлении поляризации света и его многочисленных проявлениях в окружающей природе и технике, а также об устройстве лазеров и особенностях их использования.
2. Научно-популярные лекции по физике для школьников И. Иванова
Лекция 1. (часть 1) Удивительный мир внутри атомного ядра
Лекция 1. (часть 2) Удивительный мир внутри атомного ядра
Лекция 1. (часть 3) Удивительный мир внутри атомного ядра
Лекция 2. Как расщепляют мгновение
Лекция 3. Вещество в экстремальных состояниях, или Рассказ о том, что произойдет с кирпичом, если его очень сильно сжать и нагреть
Лекция 4. Школьные задачи про современную физику
3. Научно-популярные лекции
Лекция К. Богданова «Физика внутри нас»
Лекция А. Селиверстова «Оптика в старших классах»
Лекция А. Варламова «Физика на кухне»
Лекция Л. Стрельниковой «Нанотехнологии: невидимая революция?»
Лекция В. Шевченко «Физика элементарных частиц для школьников: материя, силы, симметрии»
Лекция В. Баранова «Где границы Солнечной системы?»
Баранова «Где границы Солнечной системы?»
Лекция В. Баранова «Эволюция наших представлений об окружающем Солнечную систему космическом пространстве»
Лекция А. Зильбермана «Электростатика для умных школьников»
Лекция А. Зильбермана «Чему, как и зачем нужно будущих физиков обучать на уроках физики»
Лекция А. Зильбермана «Олимпиады по физике. Практический аспект. Часть 1»
Лекция А. Зильбермана «Олимпиады по физике. Практический аспект. Часть 2»
063. Оптическая система глаза. — 66,9 мв
Скачать: Яндекс
062. Собирающая линза. — 32,1 МВ
Скачать: Яндекс
060. Фокальная плоскость, побочная ось, побочный фокус. -64 МВ
Скачать: Яндекс
059. Фокус и фокусное расстояние. — 72,5 МВ
Скачать: Яндекс
057. Полное отражение в трехгранной призме. -62,4МВ
Скачать: Яндекс
055. Полное внутреннее отражение. — 60,6МВ
— 60,6МВ
Скачать: Яндекс
054. Явление обратимости светового луча. — 8,29 МВ
Скачать: Яндекс
053. Закон преломления света. — 25,6МВ
Скачать: Яндекс
052. Закон отражения света. — 40МВ
Скачать: Яндекс
051. Тень и полутень. -35,3МВ
Скачать: Яндекс
050. Влияние значения индуктивности и емкости на частоту колебаний контура. — 85,4МВ
Скачать: Яндекс
049. Электрические колебания в колебательном контуре. — 74,5МВ
Скачать: Яндекс
048. Резонанс в цепи переменного тока. — 48МВ
Скачать: Яндекс
045. Индуктивность в цепи переменного и постоянного тока. — 38,4МВ
Скачать: Яндекс
044. Емкость в цепи переменного и постоянного тока. — 11,7МВ
Скачать: Яндекс
042. Явление самоиндукции. — 67,4МВ
Скачать: Яндекс
041. Спидометр. — 32,5МВ
Скачать: Яндекс
040. Применение токов Фуко. — 70МВ
Скачать: Яндекс
039. Электросварка. -29,5МВ
Электросварка. -29,5МВ
Скачать: Яндекс
038. Применение индукционного тока. — 37,6МВ
Скачать: Яндекс
037. Индукционный ток в кольце. — 25,4МВ
Скачать: Яндекс
036. Причина возникновения индукционного тока. — 62,5МВ
Скачать: Яндекс
035. Явление электромагнитной индукции. — 24,3МВ
Скачать: Яндекс
034. Термоэлектронная эмиссия. — 59,7МВ
Скачать: Яндекс
033. Термоэлектронная эмиссия. -27,4МВ
Скачать: Яндекс
032. Реле на фоторезисторе. — 33МВ
Скачать: Яндекс
4-е изд., перераб. и доп. 1983. — 434с.
Настоящая книга представляет собой пособие по решению задач повышенной трудности по курсу элементарной физики. Создавая пособие, автор стремился разработать единые методы решения задач по курсу элементарной физики, показать, как нужно использовать эти методы при решении конкретных задач.
Построение книги не является стандартным для задачника. В начале каждой главы даны краткие теоретические сведения, позволяющие вспомнить основные понятия и законы курса физики, приведены формулы, которые используются при решении задач. Далее следуют методические указания по решению задач и примеры их решения. Каждая глава заканчивается задачами для самостоятельного решения. Большинство задач, приведенных в пособии, предлагалось на физических олимпиадах и вступительных экзаменах по физике в ведущих вузах страны. Многие задачи составлены автором. В конце книги помещены ответы к задачам, а также решения некоторых задач.
В начале каждой главы даны краткие теоретические сведения, позволяющие вспомнить основные понятия и законы курса физики, приведены формулы, которые используются при решении задач. Далее следуют методические указания по решению задач и примеры их решения. Каждая глава заканчивается задачами для самостоятельного решения. Большинство задач, приведенных в пособии, предлагалось на физических олимпиадах и вступительных экзаменах по физике в ведущих вузах страны. Многие задачи составлены автором. В конце книги помещены ответы к задачам, а также решения некоторых задач.
Четвертое издание пособия было переработано с учетом усовершенствованной программы по физике для средней школы и переработанных изданий учебников.
Саратов: Научная книга, 2006. — 60 с.
Сборник содержит 50 оригинальных задач физических олимпиад, которые будут полезны будущим исследователям. Ко всем задачам даны подробные решения.
Сборник будет полезен учащимся, заинтересованным в глубоком изучении физики, и их учителям.
Формат: pdf / zip
Размер: 1,2 Мб
Скачать / Download файл
Книги, посвященные как олимпиадным задачам, так и «неформальной» физике (оценки, метод размерностей, компьютерное моделирование, исследовательская работа школьников и т.д.).
В электронном варианте эти книги можно найти в сети Internet по адресам:
http://www.sgtnd.narod.ru/publ/rus/main.htm#other
http://www.sgtnd.narod.ru/wts/rus/olimprobl.htm
http://www.sgtnd.narod.ru/wts/rus/krdf.htm
Извиняюсь если ссылки на сторонние сайты запрещены,но хотелось бы поделиться лекциями:
http://4ege.ru/fizika/215-video-konsult … ast-1.html
http://4ege. ru/fizika/216-video-konsult … oraja.html
ru/fizika/216-video-konsult … oraja.html
http://4ege.ru/fizika/217-video-konsult … ast-3.html
http://4ege.ru/fizika/218-video-konsult … ast-4.html
http://4ege.ru/fizika/219-video-konsult … ast-5.html
Решение типовых задач по физике :: Класс!ная физика
Здесь приводятся решения задач из сборника задач Бендрикова Г.А. для школьников 9-11 классов и студентов:
Механика. Прямолинейное равномерное и равнопеременное движение
Механика. Криволинейное движение (бросок под углом к горизонту, движение по окружности)
Механика. Динамика прямолинейного движения
Механика. Закон сохранения импульса
Механика. Статика
Механика. Закон сохранения энергии
Механика. Динамика вращательного движения
Колебания и волны
Оптика
Молекулярная физика и термодинамика
Гидро- и аэродинамика
Успехов в разборе «полетов»!
Так как же решить задачу по физике?
Задача: Как, не понимая ни бельмеса в физике, все-таки научиться вычислять действующую на тебя силу тяжести?
Ответ: не снимая ботинок и не вынимая из карманов гайки и гвозди, встань на весы.
Посмотри, сколько килограммов весы показывают — это твоя масса. Не вес, а масса.
Запомни, не ВЕС, а МАССА!
Запомнил?
Теперь быстро умножай свою массу на девять и восемь десятых.
Только не спрашивай, зачем.
Так надо!
Умножил?
Теперь припиши к тому что получилось буковку «н» и можешь хвастаться, что на тебя действует сила тяжести в столько-то ньютонов.
С солнечным приветом от Григория Остера
Задача
Что заметил передовой Галилей, когда от него сначала отстала инквизиция, а потом все остальные тела?
Ответ: инквизиция, конечно, не тело, но передовой Галилей верно заметил, что если к нему никто не пристает, то он либо находится в покое, либо равномерно и прямолинейно движется сам не зная куда. По инерции.
Задача
Почему мороженое, которое уронил Вовочка, катаясь на карусели, перестало весело кружиться вместе с лошадками и летит прямо в милиционера, присматривающего за порядком?
Ответ: когда Вовочка отпустил недоеденное эскимо, на эскимо перестала действовать карусель, кружившая его вместе с Вовочкой. Однако, скорость свою эскимо, по законам инерции, сохранило. И помчалось прямолинейно и равномерно. Когда б ему ничто не мешало — вечно бы летело эскимо мимо звезд и
туманностей. Но на пути мороженого встал милиционер.
Однако, скорость свою эскимо, по законам инерции, сохранило. И помчалось прямолинейно и равномерно. Когда б ему ничто не мешало — вечно бы летело эскимо мимо звезд и
туманностей. Но на пути мороженого встал милиционер.
Задача
Коля и Толя нашли сжатую пружину в пакетике, перевязанном веревочками, и стали эти веревочки развязывать. Тут-то пружина и распрямилась. В результате взаимодействия Толя с хорошей скоростью улетел в одну сторону, а Коля с вдвое большей в прямо противоположную. Укажите, как отличается Толина масса
от Колиной?
Ответ: поскольку пружина послала Толю хоть и с хорошей, но вдвое меньшей скоростью чем Колю, Толина масса в два раза больше Колиной, тоже хорошей.
Задача
Лютый враг нежно прижался щекой к прикладу и нажал курок. Пуля массой 10 г выскочила из винтовки и понеслась искать невинную жертву со скоростью 800 м/с. А винтовка в результате отдачи со скоростью 2 м/с послала врага в нокаут. Вычисли массу, сбившую с ног врага.
Вычисли массу, сбившую с ног врага.
Ответ: врага нокаутировало его собственное оружие массой в 4 кг. Кто к нам с чем придет — от того и упадет.
Задача
После того как трое мышей на дне рождения мышки Мушки угостились одним крупным куском хозяйственного мыла, их общая масса увеличилась на 540 г. Мыло до того, как мыши его съели, имело размеры 10см, 12см, 3см. Определите плотность уже не существующего мыла.
Ответ: 1,5 г/куб.См — вот она плотность бывшего мыла.
Задача
Масса листика, сорвавшегося с березы, — 0,1 г, а масса кота Яшки, размечтавшегося о птичках и сорвавшегося с той же самой березы, 10 кг. Во сколько раз сила тяжести, действующая на планирующий листик, меньше силы тяжести, действующей на планирующего кота?
Ответ: в 10000 раз. Во столько же раз, во сколько масса листика меньше массы кота. Птички считают, что это
справедливо.
Задача
Если с интеллигентного, скромного и тактичного физика требуют деньги за два килограмма колбасы, а он видит, что весы с колбасой показывают всего один килограмм, то закричит ли физик на весь магазин: «нет уж, простите, вес вашей поганой колбасы не два — только один килограмм!»?
Ответ: не закричит. Вежливый физик не станет так грубо выражаться, потому что помнит: в килограммах выражается лишь одна физическая величина — масса. Вес выражается совсем в других величинах — в ньютонах.
Вежливый физик не станет так грубо выражаться, потому что помнит: в килограммах выражается лишь одна физическая величина — масса. Вес выражается совсем в других величинах — в ньютонах.
Задача
Массы голубого большого воздушного шарика и мелкого ржавого железного гвоздика, который мечтает этот шарик когда-нибудь проткнуть, одинаковы. Как отличаются силы тяжести, действующие на шарик и гвоздик?
Ответ: никак не отличаются. Один голубой и воздушный, другой мелкий и ржавый. Ну и что? Массы у них одинаковы? Одинаковы! Значит одинаковы и действующие на обоих силы тяжести.
Решение задач по физике — Как проверить решение задачи?
«Кто никогда не совершал
ошибок, тот никогда не
пробовал что-то новое».
Альберт Эйнштейн
Конечно, можно посмотреть в ответ, но это если есть учебник или сборник задач, из которого дана задача. Но очень часто приходится решать задачи, к которым нет ответа по той причине, что на экзамен, на контрольную работу, на зачёт даются только тексты задач. Без сборника или методички с ответами.
Без сборника или методички с ответами.
Главной проблемой является решение данной задачи, что не всегда просто.
Но, допустим, Вы справились с её решением, но определить, является ли решение правильным или нет, не знаете как. Но самостоятельно проверить правильность решения задачи не так сложно.
Если из уравнения, которое Вы получили в процессе решения задачи, находите неизвестную величину, т.е. получаете конечную формулу, то следующим шагом должна быть проверка размерности этой величины, т.е. её единицы измерения.
Подставьте в полученную формулу единицы измерения тех величин, которые входят в полученную формулу. В этом случае необходимо знать все единицы измерения. Но при условии, что Вы всё-таки дошли до последней формулы, то знания теории есть, а единицы измерения – это самое простое, что надо помнить.
Теперь произведите все действия по формуле с единицами измерения так же, как делаете действия с числами: одинаковые единицы измерения в числителе и знаменателе сократите, действия со степенями выполняете согласно свойствам степеней с одинаковыми основаниями. В результате сокращения, деления и умножения получаете конечную единицу измерения нужной величины. Если Вы находите, например, массу и получили конечную единицу измерения в кг (килограммах), или находите напряжение и получилась единица измерения В (вольт) и т.п., то полученная Вами формула скорее всего правильная. Если находите силу тока, которая измеряется в А (амперах), а получилась единица измерения м (метр), ищите ошибку или в решении, или в преобразованиях формул, т.е. в решении уравнения. Дальше можете не решать, пока не найдёте ошибку. Последнее выполненное Вами действие называется проверкой размерности. Если размерность совпадает с правильной, теперь осталось подставить численные значения и произвести вычисления.
В результате сокращения, деления и умножения получаете конечную единицу измерения нужной величины. Если Вы находите, например, массу и получили конечную единицу измерения в кг (килограммах), или находите напряжение и получилась единица измерения В (вольт) и т.п., то полученная Вами формула скорее всего правильная. Если находите силу тока, которая измеряется в А (амперах), а получилась единица измерения м (метр), ищите ошибку или в решении, или в преобразованиях формул, т.е. в решении уравнения. Дальше можете не решать, пока не найдёте ошибку. Последнее выполненное Вами действие называется проверкой размерности. Если размерность совпадает с правильной, теперь осталось подставить численные значения и произвести вычисления.
По полученным численным значениям также можно определить правильность решения задачи. В этом случае понимаем, что задачи по физике составляются таким образом, чтобы все данные в условии задачи значения в результате решения приводили к реальному результату. Ведь всем изучающим физику известно, что физика – наука об окружающем нас мире, поэтому результаты в любой, правильно решённой задаче должны подтверждать правильность законов физики, т. 0. Если полученный ответ входит в эти пределы, задача решена верно, даже не сомневайтесь. Неправильное решение, как правило, приводит к абсурдному ответу.
0. Если полученный ответ входит в эти пределы, задача решена верно, даже не сомневайтесь. Неправильное решение, как правило, приводит к абсурдному ответу.
Ещё много примеров подобных можно привести для проверки правильности ответа: масса автомобиля не может равняться 5 кг, если он не игрушечный, скорость пули не может равняться скорости тележки; мощность лампочки, в зависимости от того, для чего она используется: если осветительная, то может быть равна 25Вт или 50 Вт, 100 Вт и больше, если для карманного фонаря, то до 10 Вт.
Решайте, не бойтесь ошибиться, ошибки можно исправить, намного хуже ничего не делать…
7 самых больших оставшихся без ответа вопросов в физике
Загадки на этом не заканчиваются. Известно, что атомы электрически нейтральны — положительный заряд протонов уравновешивается отрицательным зарядом электронов — но почему это так, Линкольн говорит: «Никто не знает».
2. Почему гравитация такая странная?
Нет силы более привычной, чем гравитация — ведь именно она удерживает наши ноги на земле. А общая теория относительности Эйнштейна дает математическую формулировку гравитации, описывая ее как «искривление» пространства.Но гравитация в триллион триллионов триллионов раз слабее трех других известных взаимодействий (электромагнетизма и двух видов ядерных сил, действующих на крошечных расстояниях).
А общая теория относительности Эйнштейна дает математическую формулировку гравитации, описывая ее как «искривление» пространства.Но гравитация в триллион триллионов триллионов раз слабее трех других известных взаимодействий (электромагнетизма и двух видов ядерных сил, действующих на крошечных расстояниях).
Одна возможность — на данный момент спекулятивная — заключается в том, что в дополнение к трем измерениям пространства, которые мы замечаем каждый день, существуют скрытые дополнительные измерения, возможно, «свернутые» таким образом, что их невозможно обнаружить. Если эти дополнительные измерения существуют — и если гравитация способна «просачиваться» в них — это может объяснить, почему гравитация кажется нам такой слабой.
«Возможно, гравитация так же сильна, как и эти другие силы, но она быстро разбавляется, выплескиваясь в другие невидимые измерения», — говорит Уайтсон. Некоторые физики надеялись, что эксперименты на БАК дадут намек на эти дополнительные измерения, но пока безрезультатно.
3. Почему кажется, что время течет только в одном направлении?
Со времен Эйнштейна физики рассматривали пространство и время как образующие четырехмерную структуру, известную как «пространство-время». Но пространство отличается от времени в некоторых очень фундаментальных аспектах.В космосе мы вольны двигаться как хотим. Когда дело доходит до времени, мы застряли. Мы взрослеем, а не моложе. И мы помним прошлое, но не будущее. Время, в отличие от пространства, кажется, имеет предпочтительное направление — физики называют его «стрелой времени».
Некоторые физики подозревают, что второй закон термодинамики дает ключ к разгадке. В нем говорится, что энтропия физической системы (грубо говоря, степень беспорядка) со временем увеличивается, и физики считают, что это увеличение определяет направление времени.(Например, разбитая чашка имеет большую энтропию, чем целая, и, конечно же, разбитые чашки всегда появляются после целых, а не раньше.)
Энтропия может расти сейчас, потому что раньше она была ниже, но почему это низко для начала? Была ли энтропия Вселенной необычно низкой 14 миллиардов лет назад, когда она возникла в результате Большого взрыва?
Для некоторых физиков, включая Шона Кэрролла из Калифорнийского технологического института, это недостающая часть головоломки. «Если вы можете сказать мне, почему в ранней Вселенной была низкая энтропия, тогда я смогу объяснить все остальное», — говорит он.По мнению Уайтсона, энтропия — это еще не все. «Для меня, — говорит он, — самая глубокая часть вопроса заключается в том, почему время так отличается от пространства?» (Недавние компьютерные симуляции, кажется, показывают, как асимметрия времени может возникнуть из-за фундаментальных законов физики, но эта работа противоречива, и окончательная природа времени продолжает вызывать бурные споры.)
«Если вы можете сказать мне, почему в ранней Вселенной была низкая энтропия, тогда я смогу объяснить все остальное», — говорит он.По мнению Уайтсона, энтропия — это еще не все. «Для меня, — говорит он, — самая глубокая часть вопроса заключается в том, почему время так отличается от пространства?» (Недавние компьютерные симуляции, кажется, показывают, как асимметрия времени может возникнуть из-за фундаментальных законов физики, но эта работа противоречива, и окончательная природа времени продолжает вызывать бурные споры.)
Связанные
4. Откуда все антивещество уходит?
Антиматерия может быть более известна в художественной литературе, чем в реальной жизни.В оригинальном «Звездном пути» антивещество вступает в реакцию с обычным веществом, приводя в действие варп-двигатель, который приводит в движение США. Предприятие на сверхсветовых скоростях. В то время как варп-двигатель — чистая выдумка, антиматерия вполне реальна. Мы знаем, что для каждой частицы обычного вещества может быть идентичная частица с противоположным электрическим зарядом. Например, антипротон похож на протон, но с отрицательным зарядом. Между тем античастица, соответствующая отрицательно заряженному электрону, — это положительно заряженный позитрон.
Например, антипротон похож на протон, но с отрицательным зарядом. Между тем античастица, соответствующая отрицательно заряженному электрону, — это положительно заряженный позитрон.
Физики создали антивещество в лаборатории. Но когда они это делают, они создают равное количество материи. Это говорит о том, что Большой взрыв должен был создать материю и антиматерию в равных количествах. Однако почти все, что мы видим вокруг себя, от земли под нашими ногами до самых отдаленных галактик, состоит из обычного вещества.
Что происходит? Почему материи больше, чем антиматерии? Наше лучшее предположение состоит в том, что Большой взрыв каким-то образом произвел чуть больше материи, чем антиматерии.«То, что должно было произойти в начале истории Вселенной — в самые моменты после Большого взрыва — это то, что на каждые 10 миллиардов частиц антиматерии приходилось 10 миллиардов и одна частица материи», — говорит Линкольн. «И материя и антиматерия уничтожили 10 миллиардов, оставив один. И этот маленький «один» — это масса, из которой мы состоим».
И этот маленький «один» — это масса, из которой мы состоим».
Но почему в первую очередь небольшой избыток материи над антиматерией? «Мы действительно этого не понимаем, — говорит Линкольн. «Это странно.«Если бы начальные количества материи и антиматерии были равны, они бы полностью уничтожили друг друга в результате выброса энергии. В этом случае, говорит Линкольн, «нас бы не существовало».
Эта новая гипотеза претендует на решение 5 самых больших проблем в физике
Физики придумали новую модель, которая, по их словам, решает пять самых больших оставшихся без ответа вопросов в современной физике, одновременно объясняя странность темной материи, нейтринные осцилляции, бариогенез, космическую инфляцию и сильную проблему СР.
Новая модель под названием SMASH предполагает, что нам нужно всего шесть новых частиц, чтобы устранить все эти пробелы в стандартной модели физики, и команда, стоящая за ней, говорит, что ее не так уж сложно проверить.
Модель была разработана группой французских и немецких физиков, и они говорят, что она не требует каких-либо серьезных изменений в стандартной модели — только несколько новых дополнений.
Это еще только начало, но это довольно крутое предложение, потому что другие модели, предназначенные для объяснения тайн квантовой механики, такие как суперсимметрия, требуют добавления сотен новых частиц, следов которых мы никогда не видели.
SMASH, с другой стороны, требует всего шесть: три нейтрино, фермион и поле, включающее две частицы. (В физике поле — это физическая или математическая сущность, имеющая значение для каждой точки пространства и времени. Частица — это возбужденное состояние поля.)
Чтобы дать вам представление об этих пяти фундаментальных проблемах, мы рассмотрим их все, начиная с темной материи.
1. Темная материя
В настоящее время имеются неопровержимые доказательства того, что 26-27 процентов Вселенной состоит из материи неизвестного типа.Хотя мы можем обнаружить его гравитационную силу, эта неизвестная материя, по-видимому, не излучает какую-либо форму света или излучения, которые мы можем наблюдать.
Несмотря на годы поисков, мы до сих пор не знаем, из чего на самом деле состоит темная материя, но мы знаем, что ее присутствие имеет решающее значение для стабильности Вселенной.
2. Осцилляции нейтрино
В прошлом году Нобелевская премия по физике была присуждена двум физикам, которые доказали, что нейтрино могут колебаться между «ароматами».
Нейтринные осцилляции — это квантово-механическое явление, при котором нейтрино, созданное с определенным лептонным ароматом (например, электрон, мюон или тау), позже может иметь другой аромат.
Поскольку только частицы с массой могут менять вкус или колебаться, нейтрино должны иметь массу, и это представляет проблему для стандартной модели, потому что никто не знает, откуда на самом деле берется масса нейтрино.
Он может исходить от бозона Хиггса, но также может исходить от совершенно новой частицы, которую нам еще предстоит открыть.
3. Бариогенез
Эту главную нерешенную проблему физики можно сформулировать очень просто: почему в наблюдаемой Вселенной больше материи, чем антиматерии?
Согласно стандартной модели, Большой взрыв должен был произвести равное количество материи и антиматерии, и, поскольку они аннигилируют друг друга при контакте, это должно было привести к Вселенной без частиц — только радиация.
Очевидно, тот факт, что во Вселенной много частиц, означает, что с этим сценарием что-то не так, потому что как во Вселенной сейчас может быть так много материи, но почти нет антиматерии?
4.Космическая инфляция
Считается, что в течение доли секунды после Большого взрыва Вселенная претерпела период ускоренного расширения, называемого инфляцией.
В то время как большинство физиков признают реальность космической инфляции, никто не смог выяснить точный механизм, ответственный за то, что Вселенная расширяется быстрее скорости света, почти мгновенно изменяясь от субатомного размера до размера мяча для гольфа.
В качестве основной причины инфляции было предложено гипотетическое поле, называемое инфлатоном, но мы еще не обнаружили его на самом деле.
5. Сильная проблема СР
Описанная как «серьезный недостаток стандартной модели», сильная проблема СР помогает объяснить, почему во Вселенной больше материи, чем антиматерии, но несет с собой свои нерешенные загадки. .
.
Это особенно длинная история, но в двух словах сильная проблема CP описывает, как CP-нарушение — нарушение фундаментальной симметрии Вселенной — не происходит в квантовой хромодинамике (КХД), которая относится к взаимодействиям между кварками. и глюонов.И никто не мог понять, почему.
До сих пор, возможно, если новая модель окажется правильной.
Решение?
Модель SMASH основана на модели, предложенной физиком Михаилом Шапошниковым из Швейцарского федерального технологического института в Лозанне еще в 2005 году, которая называется нейтринной минимальной стандартной моделью (или νMSM).
Тогда предполагалось, что расширение Стандартной модели тремя правыми нейтрино с определенными массами может одновременно объяснить темную материю и барионную асимметрию Вселенной, а также согласуется с экспериментами по нейтринным осцилляциям.
Теперь команда под руководством французского физика Гильермо Бальестероса из Университета Париж-Сакле говорит, что мы можем добавить эти три правых нейтрино к трем существующим нейтрино в стандартной модели, а также субатомную частицу, называемую цветовым тройным фермионом, чтобы решить первые четыре проблемы, перечисленные выше.
Добавление нового неопознанного поля, по-видимому, решает пятую проблему, как объясняет Шеннон Холл для New Scientist :
«SMASH добавляет новое поле, чтобы немного по-другому объяснить некоторые из этих проблем.Это поле включает в себя две частицы: аксион, темную лошадку, кандидата в темную материю, и инфлатон, частицу, стоящую за инфляцией.
И, наконец, SMASH использует поле, чтобы представить решение пятой головоломки: сильной проблемы CP.»
Команда говорит, что тот факт, что их гипотеза может быть проверена с использованием следующего поколения ускорителей частиц, означает, что она не выходит за рамки возможного, и это делает ее более убедительной, чем другие решения этих проблем, которые были предложены в прошлом.
«Самое лучшее в этой теории то, что ее можно протестировать или проверить в течение следующих 10 лет или около того», — сказал Холлу один из членов команды, Андреас Рингвальд из Немецкого электронного синхротрона.
«Всегда можно изобрести новые теории, но если их можно будет проверить только через 100 лет или никогда, то это не настоящая наука, а метанаука.»
Следует отметить, что модель SMASH еще не была опубликована в рецензируемом журнале, поэтому она все еще должна пройти тщательную проверку в мире физики элементарных частиц, но теперь она размещена на веб-сайте предварительной печати arXiv.org, поэтому у независимых физиков есть шанс сделать именно это.
Это, вероятно, не станет окончательным решением «пяти больших вопросов» — физика никогда не бывает такой четкой — но может стать началом чего-то потрясающего.
Как говорит Рингуолд: «Битва открыта».
PhysicsLAB Забавные задачи по физике
Эта группа сложных юмористических задач была впервые опубликована в 1985 г. Дж.Уэстон Уолч из Портленда, штат Орегон. Они были созданы Дугласом С. Дженкинсом и проиллюстрировано Тимом Харрисом.
Разрешение было дано издателем J. Weston Walch для публикации их в PhysicsLAB как студенческий ресурс. Прежде чем вы начнете просматривать проблемы, найдите минутку и познакомьтесь с актерским составом вокруг кого вращаются эти эпизоды. Учителя, вы также можете прочитать Дугласа Записка Дженкинса «Учителю» и изучите следующий список их приключений.
Студенты, чтобы получить наибольшую пользу от этих проблем, вы должны сначала изучить каждую ситуацию и самостоятельно проработать свое решение. После проверки вашего ответ, вы можете нажать на решение, чтобы прочитать шаг за шагом Дженкинса решение. Все эти проблемы умно представлены и основаны на физике твердого тела. концепции.
Для поиска в этой коллекции используйте нашу поисковую систему.
Пример поиска
Вы можете найти эти материалы с помощью нашей поисковой системы, выбрав:
Попробуй!
4 трюка для решения любой физической задачи
Физика может быть пугающей — все эти шкивы, протоны и движение снарядов.Однако, если вы подходите к этому с правильным настроем, даже самые сложные проблемы обычно легче, чем вы думаете. Когда вы сталкиваетесь с трудным вопросом, не паникуйте. Вместо этого начните с этих коротких и простых приемов, которые помогут вам справиться с проблемой.
Когда вы сталкиваетесь с трудным вопросом, не паникуйте. Вместо этого начните с этих коротких и простых приемов, которые помогут вам справиться с проблемой.
4 приема для решения любой задачи по физике:
1. Что такое предмет?
Почти каждый вопрос по физике проверяет определенные знания. Когда вы читаете вопрос, задайте себе вопрос: исследуете ли вы электричество? Крутящий момент? Параболическое движение? Каждая тема связана с определенными уравнениями и подходами, поэтому знание предмета направит ваши усилия в правильном направлении.Ищите ключевые слова и фразы, раскрывающие тему.
2. Что вы пытаетесь найти?
Этот простой шаг может сэкономить много времени. Прежде чем приступить к решению задачи, подумайте, как будет выглядеть ответ. Какие единицы; окончательный ответ будет в килограммах или литрах? Также подумайте, какие другие физические величины могут иметь отношение к вашему ответу. Если вы пытаетесь найти скорость, может быть полезно найти ускорение, а затем решить его для скорости. Раннее определение ограничений на ответ также гарантирует, что вы ответите на конкретный вопрос; распространенной ошибкой в физике является решение не той вещи.
Раннее определение ограничений на ответ также гарантирует, что вы ответите на конкретный вопрос; распространенной ошибкой в физике является решение не той вещи.
3. Что ты знаешь?
Подумайте, какие детали упоминаются в задаче. Если вопрос действительно плохой, они, вероятно, дали вам именно ту информацию, которая вам нужна для решения проблемы. Не удивляйтесь, если иногда эта информация закодирована в языке; задача, в которой упоминается пружина с «массой, удаленной с конца», говорит вам что-то важное о величине силы. Запишите каждую величину, которую вы знаете из задачи, затем переходите к…
.4.Какие уравнения можно использовать?
Какие уравнения включают в себя величины, которые вы знаете, а также ту, которую вы ищете? Если у вас есть масса объекта и сила, и вы пытаетесь найти ускорение, начните с F=ma (второй закон Ньютона). Если вы пытаетесь найти электрическое поле, но у вас есть заряд и расстояние, попробуйте E=q/(4πε*r 2 ).
Если вам трудно понять, какое уравнение использовать, вернитесь к нашему первому трюку. Какие уравнения связаны с этой темой? Можете ли вы манипулировать количеством, которое у вас есть, чтобы поместиться в любой из них?
Какие уравнения связаны с этой темой? Можете ли вы манипулировать количеством, которое у вас есть, чтобы поместиться в любой из них?
Этот трюк не всегда работает, но он может дать толчок вашему мозгу.Во-первых, определите единицы количества, которое вы пытаетесь найти, и количество, которое у вас есть. Используйте только базовые единицы (метры, килограммы, секунды, заряд), а не составные единицы (сила измеряется в ньютонах, то есть просто кг*м/с 2 ). Умножайте и делите количества до тех пор, пока единицы не совпадут с единицами ответного количества. Например, если вы пытаетесь найти Потенциальную энергию (кг*м 2 /с 2 ) и у вас есть высота (м), масса (кг) и ускорение свободного падения (м/с 2 ) , вы можете сопоставить единицы, умножив три величины (м*кг*м/с 2 = кг*м 2 /с 2 ).
Примечание: в отличие от других, этот трюк не всегда срабатывает. Остерегайтесь безразмерных констант. Например, кинетическая энергия равна ½*масса*скорость 2 , а не просто масса*скорость 2 , как предполагают единицы измерения. Несмотря на то, что этот трюк не идеален, тем не менее, он может быть отличным началом.
Остерегайтесь безразмерных констант. Например, кинетическая энергия равна ½*масса*скорость 2 , а не просто масса*скорость 2 , как предполагают единицы измерения. Несмотря на то, что этот трюк не идеален, тем не менее, он может быть отличным началом.
Вопросы по физике делятся на несколько категорий. Они попадают в учебники и служат кажущимися недостижимыми моделями для учащихся. Острые ощущения от игры пропали. Они попадают в учебники и служат кажущимися недостижимыми моделями для учащихся. Острые ощущения от игры пропали.Так было не всегда. Книги и опубликованные статьи пионеров науки 17-го и 18-го веков часто подробно описывали творческий процесс со всеми его фальстартами, тупиками и неудачными гипотезами.Сейчас это не считается правильным стилем. Есть задачи по физике и головоломки по физике. Мне нравятся головоломки. Этот сборник побуждает искать простые, умные и проницательные методы для получения ответа. Мне особенно нравятся те, которые поддаются только элементарной математике. Некоторые также могут быть решены с помощью утомительного формального математического анализа, но только в крайнем случае. Некоторые из этих головоломок довольно старые, с неясными источниками. Некоторые из них являются моим собственным изобретением.Я старался не включать загадки, правильные ответы на которые можно легко найти в Интернете. Темы.Несколько категорий головоломок. Головоломки.© 2017, 2019, Дональд Э.Симанек. Вернитесь на главную страницу Дональда Симанека с полным меню, |
(PDF) 10 крупнейших нерешенных задач физики
будут получены из (будущей) универсальной теории перехода между
линейным и нелинейным, т.е. квантовые и классические.
Сложность возникает в системах с нелинейной «обратной связью».И те же
вполне могут применяться для масс частиц [14].
Темная энергия может не понадобиться для объяснения космологических данных. Материя
во Вселенной в действительности распределена неравномерно, в отличие от основного предположения стандартной космологической модели (идеализированная Вселенная;
совершенно однородная и изотропная), предназначенной для того, чтобы сделать строго
нелинейные уравнения Эйнштейна более значительными. проще и аналитически разрешима. Существует
проще и аналитически разрешима. Существует
агрегатов материи (галактики и т.), которые нарушают этот идеализированный образ, также
разница между пустотами и комками автоматически растет по мере расширения вселенной, т.е. нелинейность увеличивается со временем. Эти комочки в
реальной Вселенной создают эффект, имитирующий ускорение в полностью
равномерно размытой, идеализированной Вселенной [15].
Пока нет фундаментального объяснения трения, опять же потому, что отсутствует фундаментальное понимание перехода линейный → нелинейный.
Аналогично с загадкой турбулентности — по мере увеличения потока ламинарное (почти
линейное) поведение превращается в резко турбулентное (сильно нелинейное).
Есть даже шанс связать все с, пожалуй, самой большой загадкой
из всех — проблемой квантовых измерений; как, когда и почему призрачный
и неопределенный квантовый мир порождает наш конкретный, определенный макроскопический мир
, т. е. как на самом деле возникает то, что мы называем реальностью [16].Когда определенный тип
е. как на самом деле возникает то, что мы называем реальностью [16].Когда определенный тип
гелия охлаждается почти до абсолютного нуля, он становится сверхтекучим и течет совершенно без трения; поднимите немного температуру
и она будет вести себя как обычная (нелинейная) жидкость. Было бы круто, в
буквальном смысле, если бы в этом переходе можно было изучить и разгадать тайны трения, турбулентности, стрелы времени, сложности и квантовой
проблемы измерения… сразу несколько жирных зайцев? Принцип
линейный → нелинейный, и я говорю, как Вольфганг Паули, который в письме Георгию
Гамов писал: «Не хватает только технических деталей…» на пустой странице
.
Однако мы должны помнить и предостерегающие слова Фримена Дайсона:
«Люди часто спрашивают меня, что будет дальше в науке, что
важно, и, конечно, все дело в том, что если это важно, то это что-
то, чего мы не ожидали. Все действительно важные вещи становятся большим сюрпризом.
Все, что я упомяну, не будет сюрпризом.
8
Границы | Формулировки Изинга многих задач NP
1.Введение
1.1. Квантовая адиабатическая оптимизация
В последнее время большой интерес вызывает возможность использования адиабатической квантовой оптимизации (АКО) для решения NP-полных и NP-трудных задач [1, 2]. Это связано со следующим трюком: предположим, у нас есть квантовый гамильтониан H P , основное состояние которого кодирует решение интересующей нас задачи, и другой гамильтониан H 0 , основное состояние которого является (как найти, так и приготовить в экспериментальной установке).Тогда, если мы подготовим квантовую систему к нахождению в основном состоянии H 0 , а затем адиабатически изменим гамильтониан на время T согласно
H(t)=(1−tT) H0+tTHP, (1), то если T достаточно велико, а H 0 и H P не коммутируют, квантовая система будет оставаться в основном состоянии все время, согласно адиабатической теореме квантовой механики. . В момент времени T измерение квантового состояния вернет решение нашей проблемы.
. В момент времени T измерение квантового состояния вернет решение нашей проблемы.
Были споры о том, будут ли эти алгоритмы на самом деле полезными, т. е. будет ли адиабатический квантовый оптимизатор работать быстрее, чем классические алгоритмы [3-9], из-за того, что если задача имеет размер N , обычно находят
T=O [exp (αNβ)], (2), чтобы система оставалась в основном состоянии, при положительных коэффициентах α и β, как N → ∞. Это является следствием требования, чтобы экспоненциально малые энергетические щели между основным состоянием H ( t ) и первым возбужденным состоянием в какой-то промежуточный момент времени не приводили к переходам Ландау–Зинера в возбужденные состояния [5].Хотя маловероятно, что NP-полные задачи могут быть решены с помощью AQO за полиномиальное время, коэффициенты α,β могут быть меньше, чем у известных классических алгоритмов, поэтому все еще существует вероятность того, что алгоритм AQO может быть более эффективным, чем классические алгоритмы, на некоторые классы задач.
Был достигнут существенный экспериментальный прогресс в создании устройства, способного запускать такие алгоритмы [11–13], когда гамильтониан H P может быть записан как квантовая версия изинговского спинового стекла.Классическая модель Изинга может быть записана как квадратичная функция набора N спинов с i = ±1:
H (s1,…,sN)=−∑iГде σ Z Z I I I — матрица Pauli (матрица 2 × 2, чья двоюродный брат (1 + Σ Z I ) / 2 имеет собственные вещества | 0, 1> с собственными значениями 0, 1), действующими на i -й кубит в гильбертовом пространстве из N кубитов {|+〉, |−〉} ⊗ N , и J 3 3 3 h i — действительные числа.Затем мы выбираем H 0 состоящим из поперечных магнитных полей [11]:
H0=−h0∑i=1Nσix, (5), так что основное состояние H 0 равной суперпозиции всех возможных состояний в собственном базисе H P [эквивалентно собственному базису множества операторов σ z i ( i = 1, …, N )]. Это означает, что никаких железнодорожных переездов не ожидается.Дополнительные сведения о выборе H см. в Whitfield et al. [14]. Также отметим, что этот класс гамильтонианов считается недостаточным для построения универсального адиабатического квантового компьютера [15] — во все времена H ( t ) принадлежали к особому классу гамильтонианов, называемых стоквастическими гамильтонианами [15]. 16].
Это означает, что никаких железнодорожных переездов не ожидается.Дополнительные сведения о выборе H см. в Whitfield et al. [14]. Также отметим, что этот класс гамильтонианов считается недостаточным для построения универсального адиабатического квантового компьютера [15] — во все времена H ( t ) принадлежали к особому классу гамильтонианов, называемых стоквастическими гамильтонианами [15]. 16].
1.2. Очки Ising Spin
Известно, что спиновых стекол Изинга являются NP-трудными задачами для классических компьютеров [17], поэтому естественно подозревать тесную связь со всеми другими NP-задачами.Для целей данной статьи NP-полная задача — это всегда проблема решения с ответом «да» или «нет» (имеет ли основное состояние H энергия ≤0?), тогда как NP-сложная задача — это задача оптимизации ( какова энергия основного состояния H ?). Класс NP-полных задач включает в себя множество заведомо трудных задач и, таким образом, вызывает большой интерес в течение последних 40 лет [18, 19]. Математически, поскольку форма решения модели Изинга является NP-полной, существует полиномиальное отображение времени на любую другую NP-полную задачу.
Математически, поскольку форма решения модели Изинга является NP-полной, существует полиномиальное отображение времени на любую другую NP-полную задачу.
Аналогии между статистической физикой изинговских спиновых стекол и задачами NP часто изучались в прошлом [20–22] и использовались для построения алгоритмов имитации отжига [23], которые оказались весьма плодотворными в приближенных алгоритмах для задач на классические компьютеры. Эти связи предложили физическое понимание возникновения жесткости в этих проблемах через сложный энергетический ландшафт со многими локальными минимумами [24]. И наоборот, вычислительная сложность решения стеклянных задач влияет на сложность решения важных научных задач, начиная от сворачивания полимеров [25, 26] и заканчивая памятью [27] и коллективным принятием решений в экономике и социальных науках [28, 29].Задачи, представляющие практический научный интерес, уже кодировались и решались (в простых случаях) на экспериментальных устройствах с использованием гамильтонианов Изинга [30–35].
Наконец, отметим, что очки Изинга часто носят название QUBO (квадратичная неограниченная бинарная оптимизация) в более математической литературе [36, 37]. Были разработаны полезные приемы для немедленной фиксации значений некоторых спинов [38] и разложения больших задач QUBO на более мелкие [39].
1.3. Цель этой статьи
Математически тот факт, что проблема является NP-полной, означает, что мы можем найти отображение в форму решения модели Изинга с полиномиальным числом шагов.Это отображение можно интерпретировать как задачу псевдобулевой оптимизации [37]. Поскольку конструкции этих псевдобулевых задач оптимизации (или « p -спиновые очки») часто приводят к трехчастичным или более высоким взаимодействиям в H (например, термы вида s 1 s 2 s 3 ), мы заключаем, используя «приспособления», чтобы свести задачу к спиновому стеклу Изинга, вводя полиномиальное число вспомогательных спинов, которые помогают усилить трехчастичное взаимодействие за счет многократного двух- взаимодействия тел ( с 1 с 2 ) [40, 41]. Таким образом, мы можем перейти от любой NP-полной задачи к гамильтониану изинговского спинового стекла, проблема решения которого (имеет ли основное состояние энергию ≤0?) решает интересующую NP-полную проблему. Классические гаджеты полезны для решения многих задач в физике, поскольку физическая энергия (гамильтониан) содержит взаимодействия трех тел, но они также полезны для записи многих алгоритмов в других областях (например, целочисленная факторизация [42]).
Таким образом, мы можем перейти от любой NP-полной задачи к гамильтониану изинговского спинового стекла, проблема решения которого (имеет ли основное состояние энергию ≤0?) решает интересующую NP-полную проблему. Классические гаджеты полезны для решения многих задач в физике, поскольку физическая энергия (гамильтониан) содержит взаимодействия трех тел, но они также полезны для записи многих алгоритмов в других областях (например, целочисленная факторизация [42]).
Однако для общих задач это очень неэффективная процедура, так как мощность полинома может расти довольно быстро.Таким образом, типичную NP-полную задачу (размером 90 323 N 90 324 ), изучаемую в контексте очков Изинга, очень просто записать в виде стакана с 90 323 N 90 324 спинами (такими как разбиение чисел или выполнимость). Основная цель этой статьи состоит в том, чтобы представить конструкции гамильтонианов Изинга для задач, в которых выбор гамильтониана является довольно тонким делом; в педагогических целях мы также предоставим обзор некоторых простых отображений от разбиения и выполнимости до спинового стекла Изинга. В частности, мы опишем, как «все знаменитые NP-проблемы» Карпа [18], Гэри и Джонсона [19] могут быть записаны как модели Изинга с полиномиальным числом спинов, которые масштабируются не быстрее, чем N 3 . На протяжении большей части этой статьи мы не обнаружим, что решить NP-сложную задачу оптимизации не сложнее, чем задачу NP-полного решения, и поэтому мы обычно сосредотачиваемся на задачах оптимизации. Методы, используемые в этой статье, которые редко встречаются в литературе по квантовым вычислениям, в основном относятся к нескольким разновидностям, которые примерно соответствуют решению следующих задач: задачи минимаксной оптимизации, задачи с неравенствами в качестве ограничений (например, n ≥ 1, в отличие от n = 1), и задач, которые задают глобальные вопросы о графах.Методы, которые мы используем, чтобы сформулировать эти проблемы как очки Изинга, очень естественно обобщают.
В частности, мы опишем, как «все знаменитые NP-проблемы» Карпа [18], Гэри и Джонсона [19] могут быть записаны как модели Изинга с полиномиальным числом спинов, которые масштабируются не быстрее, чем N 3 . На протяжении большей части этой статьи мы не обнаружим, что решить NP-сложную задачу оптимизации не сложнее, чем задачу NP-полного решения, и поэтому мы обычно сосредотачиваемся на задачах оптимизации. Методы, используемые в этой статье, которые редко встречаются в литературе по квантовым вычислениям, в основном относятся к нескольким разновидностям, которые примерно соответствуют решению следующих задач: задачи минимаксной оптимизации, задачи с неравенствами в качестве ограничений (например, n ≥ 1, в отличие от n = 1), и задач, которые задают глобальные вопросы о графах.Методы, которые мы используем, чтобы сформулировать эти проблемы как очки Изинга, очень естественно обобщают.
1.4. Какие проблемы легко (встроить) в экспериментальные устройства AQO?
Мы надеемся, что после прочтения этой статьи читатель вдохновится на размышления о решении некоторых из этих классических вычислительных задач или подобных им на экспериментальных устройствах, реализующих AQO. С этой целью читатель должен обратить внимание на три вещи в реализациях, описанных в этой статье. Во-первых, это количество спинов, необходимых для кодирования проблемы.В некоторых случаях требуются только «логические вращения/биты» (вращения, необходимые для кодирования решения задачи); но в целом нам могут потребоваться вспомогательные «вспомогательные спины/биты», которые необходимы для обеспечения соблюдения ограничений в задаче. Иногда требуемое количество вспомогательных битов может быть довольно большим и может составлять доминирующую долю спинов в гамильтониане. Еще одна вещь, на которую следует обратить внимание, — это возможность того, что требуются большие разделения шкал энергии: e.г., отношение связей J 12 / J 23 в некотором стекле Изинга пропорционально N , размеру изучаемой задачи. Последнее, что следует отметить, это должен ли граф быть высокосвязным: типичная степень вершин на графе вложений Изинга (не на графе, связанном с проблемой NP) масштабируется линейно с N ?
С этой целью читатель должен обратить внимание на три вещи в реализациях, описанных в этой статье. Во-первых, это количество спинов, необходимых для кодирования проблемы.В некоторых случаях требуются только «логические вращения/биты» (вращения, необходимые для кодирования решения задачи); но в целом нам могут потребоваться вспомогательные «вспомогательные спины/биты», которые необходимы для обеспечения соблюдения ограничений в задаче. Иногда требуемое количество вспомогательных битов может быть довольно большим и может составлять доминирующую долю спинов в гамильтониане. Еще одна вещь, на которую следует обратить внимание, — это возможность того, что требуются большие разделения шкал энергии: e.г., отношение связей J 12 / J 23 в некотором стекле Изинга пропорционально N , размеру изучаемой задачи. Последнее, что следует отметить, это должен ли граф быть высокосвязным: типичная степень вершин на графе вложений Изинга (не на графе, связанном с проблемой NP) масштабируется линейно с N ?
Вероятно, очевидно, почему нам не нужно слишком много вспомогательных битов — это просто означает, что мы можем кодировать только более мелкие задачи на аппаратном обеспечении того же размера. Немного сложнее понять, почему полные графики или разделение энергетических шкал проблематичны. Вполне вероятно, что успешные экспериментальные реализации AQO с наибольшим количеством кубитов находятся на устройствах, созданных DWave Systems [11–13]. Таким образом, мы теперь обсудим легкость, с которой эти гамильтонианы могут быть закодированы на таком устройстве. Эти устройства могут кодировать проблемы только с помощью «химерного» графа. Основная проблема с гамильтонианами на полном графе состоит в том, что неэффективно [43, 44] вкладывать полные графы в граф-химеру.Первичную трудность демонстрирует следующий простой случай: узел v в полном графе должен быть поставлен в соответствие двум парам узлов u и w на графе-химере со связью J uw больше по сравнению с другими масштабами в задаче, чтобы гарантировать, что s u = s w (таким образом, эти узлы фактически действуют как один спин).
Немного сложнее понять, почему полные графики или разделение энергетических шкал проблематичны. Вполне вероятно, что успешные экспериментальные реализации AQO с наибольшим количеством кубитов находятся на устройствах, созданных DWave Systems [11–13]. Таким образом, мы теперь обсудим легкость, с которой эти гамильтонианы могут быть закодированы на таком устройстве. Эти устройства могут кодировать проблемы только с помощью «химерного» графа. Основная проблема с гамильтонианами на полном графе состоит в том, что неэффективно [43, 44] вкладывать полные графы в граф-химеру.Первичную трудность демонстрирует следующий простой случай: узел v в полном графе должен быть поставлен в соответствие двум парам узлов u и w на графе-химере со связью J uw больше по сравнению с другими масштабами в задаче, чтобы гарантировать, что s u = s w (таким образом, эти узлы фактически действуют как один спин). Вторая проблема заключается в том, что некоторые гамильтонианы требуют разделения шкал энергии.Однако на практике эти устройства могут кодировать только константы связи 1, …, 16 из-за экспериментальных неопределенностей [11–13]. Это означает, что маловероятно, что для очень связных графов можно успешно закодировать любой H с разделением шкал энергии. Последняя проблема заключается в том, что иногда связи или кубиты нарушаются — на этой ранней стадии разработки оборудования оптимальные алгоритмы имеют вложения, которые нечувствительны к этой возможности [45].
Вторая проблема заключается в том, что некоторые гамильтонианы требуют разделения шкал энергии.Однако на практике эти устройства могут кодировать только константы связи 1, …, 16 из-за экспериментальных неопределенностей [11–13]. Это означает, что маловероятно, что для очень связных графов можно успешно закодировать любой H с разделением шкал энергии. Последняя проблема заключается в том, что иногда связи или кубиты нарушаются — на этой ранней стадии разработки оборудования оптимальные алгоритмы имеют вложения, которые нечувствительны к этой возможности [45].
2. Проблемы с разделами
Первый класс задач, которые мы будем изучать, — это задачи о разбиении, которые (как следует из названия) представляют собой задачи о разделении множества на два подмножества.Эти карты получили признание в сообществе спиновых стекол [24], поскольку они помогли физикам осознать возможность использования технологии спиновых стекол для понимания вычислительной сложности в случайных ансамблях вычислительных задач. Для полноты обзора мы рассматриваем эти отображения здесь и представляем новое, основанное на аналогичных идеях (проблема клики).
Для полноты обзора мы рассматриваем эти отображения здесь и представляем новое, основанное на аналогичных идеях (проблема клики).
2.1. Разделение номера
Разбиение чисел спрашивает следующее: учитывая набор из N положительных чисел S = { n 1 , …, n N }, существует ли разделение этого набора чисел на два непересекающихся подмножества R и S − R такие, что сумма элементов в обоих множествах одинакова? Например, можно ли разделить набор активов со значениями n 1 , …, n N между двумя людьми? Известно, что эта задача является NP-полной [18].Это можно тривиально сформулировать как модель Изинга следующим образом. Пусть n i ( i = 1, …, N = | S |) описывают числа в множестве S , и пусть
H=A (∑i=1Nnisi)2 (6) — функция энергии, где s i = ±1 — изинговская спиновая переменная. Здесь A > 0 — некоторая положительная константа. Обычно в литературе такие константы масштабируются до 1, но для простоты мы сохраним их, поскольку во многих формулировках окажется полезным разделение шкал энергии, а сохранение каждой шкалы может облегчить концептуальное следование.Классические исследования этой проблемы несколько облегчаются, если квадрат выше заменить абсолютным значением [24].
Здесь A > 0 — некоторая положительная константа. Обычно в литературе такие константы масштабируются до 1, но для простоты мы сохраним их, поскольку во многих формулировках окажется полезным разделение шкал энергии, а сохранение каждой шкалы может облегчить концептуальное следование.Классические исследования этой проблемы несколько облегчаются, если квадрат выше заменить абсолютным значением [24].
Ясно, что если существует решение модели Изинга с H = 0, то существует конфигурация спинов, где сумма n i для +1 спинов одинакова для сумма n i для спинов -1. Таким образом, если энергия основного состояния H = 0, существует решение проблемы разделения чисел.
Это стекло Изинга имеет вырождения , т. е. всегда есть по крайней мере два различных решения задачи. Это можно увидеть, заметив, что если s * i обозначает решение задачи, то − s * i также является решением. Физически это соответствует тому факту, что нам все равно, какое множество помечено как ±. В литературе по спиновому стеклу изменение s i → − s i , которое не меняет формы H , часто (довольно условно) называют преобразованием 42 калибровки .Существование калибровочного преобразования, оставляющего связи неизменными (поскольку нет линейных членов), означает, что все энергетические уровни H вырождены. Возможно, что имеется 2 m основных состояний (при m > 1). Это означает, что существует m физически различных решений вычислительной задачи. Нам нужно только найти один из них, чтобы наш адиабатический квантовый алгоритм был доволен. Мы можем снять это двойное вырождение, зафиксировав s 1 = 1.Это также позволяет нам убрать один спин: теперь на график включены только с 2 , …, с N , а с 1 служит эффективным магнитным полем.
Физически это соответствует тому факту, что нам все равно, какое множество помечено как ±. В литературе по спиновому стеклу изменение s i → − s i , которое не меняет формы H , часто (довольно условно) называют преобразованием 42 калибровки .Существование калибровочного преобразования, оставляющего связи неизменными (поскольку нет линейных членов), означает, что все энергетические уровни H вырождены. Возможно, что имеется 2 m основных состояний (при m > 1). Это означает, что существует m физически различных решений вычислительной задачи. Нам нужно только найти один из них, чтобы наш адиабатический квантовый алгоритм был доволен. Мы можем снять это двойное вырождение, зафиксировав s 1 = 1.Это также позволяет нам убрать один спин: теперь на график включены только с 2 , …, с N , а с 1 служит эффективным магнитным полем. Таким образом, в общем случае нам требуется N − 1 спинов, которые живут на полном графе, чтобы закодировать эту задачу.
Таким образом, в общем случае нам требуется N − 1 спинов, которые живут на полном графе, чтобы закодировать эту задачу.
Если основное состояние имеет H > 0, мы знаем, что нет решений проблемы разбиения, но основное состояние, которое мы находим, является (одним из) наилучших возможных решений в том смысле, что оно минимизирует несоответствие.Минимизация этого несоответствия — NP-сложная задача, и мы видим, что для решения задачи оптимизации не требуется никаких дополнительных усилий — тот же самый гамильтониан делает свое дело.
2.2. Разделение графа
Разбиение графа — это оригинальный [20] пример отображения между физикой спиновых стекол Изинга и NP-полными задачами. Рассмотрим неориентированный граф G = ( V, E ). с четным числом N = | В | вершин. Спросим: как можно разбить множество V на два подмножества одинакового размера N /2 так, чтобы количество ребер, соединяющих два подмножества, было минимальным? У этой проблемы много приложений: нахождение этих разделов может позволить нам запустить некоторые графовые алгоритмы параллельно на двух разделах, а затем внести некоторые изменения из-за нескольких соединяющих ребер в конце [39]. Известно, что разбиение графа является NP-сложной задачей; соответствующая проблема решения (менее k ребер, соединяющих два множества?) является NP-полной [18]. Мы поместим спин Изинга s v = ±1 на каждую вершину v ∈ V на графе, и мы обозначим через +1 и −1 вершину, принадлежащую либо множеству +, либо — набор. Решим это с помощью функционала энергии, состоящего из двух компонент:
Известно, что разбиение графа является NP-сложной задачей; соответствующая проблема решения (менее k ребер, соединяющих два множества?) является NP-полной [18]. Мы поместим спин Изинга s v = ±1 на каждую вершину v ∈ V на графе, и мы обозначим через +1 и −1 вершину, принадлежащую либо множеству +, либо — набор. Решим это с помощью функционала энергии, состоящего из двух компонент:
где
HA=A (∑n=1Nsi)2 (8)— это энергия, которая дает штраф, если количество элементов в наборе + не равно количеству элементов в наборе —, а
HB=B∑(uv) ∈ E1−susv2 (9) — это термин, который обеспечивает штраф за энергию B каждый раз, когда ребро соединяет вершины из разных подмножеств.Если B > 0, то мы хотим минимизировать количество ребер между двумя подмножествами; если B < 0, мы выберем максимизацию этого числа. Если мы выберем B < 0, мы должны убедиться, что B достаточно мало, чтобы никогда не было выгодно нарушать ограничение H A для минимизации энергии. Чтобы определить довольно простую нижнюю границу для A , зададимся вопросом: каково минимальное значение Δ H B — изменения энергии, вносимой B -членом, — если мы нарушаем ограничение A один раз.Легко видеть, что штраф за нарушение ограничения A равен Δ H A ≥ 4 A . Наилучший выигрыш, который мы можем получить, перевернув спин, — это получить энергию 90 323 B 90 324 мин(Δ, 90 323 N 90 324 /2), где Δ — максимальная степень 90 323 G 90 324 . Делаем вывод
Чтобы определить довольно простую нижнюю границу для A , зададимся вопросом: каково минимальное значение Δ H B — изменения энергии, вносимой B -членом, — если мы нарушаем ограничение A один раз.Легко видеть, что штраф за нарушение ограничения A равен Δ H A ≥ 4 A . Наилучший выигрыш, который мы можем получить, перевернув спин, — это получить энергию 90 323 B 90 324 мин(Δ, 90 323 N 90 324 /2), где Δ — максимальная степень 90 323 G 90 324 . Делаем вывод
N спинов на полном графе требуется для кодирования этой задачи.
Этот гамильтониан инвариантен относительно того же калибровочного преобразования s i → − s i .Мы заключаем, что мы всегда можем удалить один спин, зафиксировав одну вершину в наборе +.
Мы записали H в несколько иной форме, чем в исходной [20], где использовалось ограничение на пространство решений задачи, что
Мы не хотим, чтобы ни одна из наших формулировок этого не делала (т. е. мы хотим решить задачу неограниченной оптимизации), поскольку экспериментальное оборудование, создаваемое для квантовой оптимизации, может решать только неограниченные задачи.Вместо этого мы кодируем уравнения ограничений, создавая штрафные гамильтонианы, которые повышают энергию состояния, которое их нарушает.
е. мы хотим решить задачу неограниченной оптимизации), поскольку экспериментальное оборудование, создаваемое для квантовой оптимизации, может решать только неограниченные задачи.Вместо этого мы кодируем уравнения ограничений, создавая штрафные гамильтонианы, которые повышают энергию состояния, которое их нарушает.
2.3. Клики
Клика размера K в неориентированном графе G = ( V, E ) является подмножеством W ⊆ V вершин размера | Вт | = K , так что подграф ( W , E W ) (где E W ограничен ребрами между узлами s) полный граф — т.е.т. е. все возможные K ( K − 1)/2 ребер в графе присутствуют, потому что каждая вершина в клике имеет ребро к любой другой вершине в клике. Клики в социальных сетях могут быть полезны, поскольку они являются «сообществами друзей»; обнаружение аномально больших клик также является ключевым признаком того, что в графе есть структура, которая в противном случае может казаться случайной [46]. NP-полная проблема принятия решения о том, существует или нет клика размера K [18], может быть записана в виде модели, подобной Изингу, следующим образом.Поместим спиновую переменную s v = ±1 на каждую вершину v ∈ V графа. В общем, в этой статье для спиновой переменной s α мы определим двоичную битовую переменную
NP-полная проблема принятия решения о том, существует или нет клика размера K [18], может быть записана в виде модели, подобной Изингу, следующим образом.Поместим спиновую переменную s v = ±1 на каждую вершину v ∈ V графа. В общем, в этой статье для спиновой переменной s α мы определим двоичную битовую переменную
Как правило, будет удобнее сформулировать энергии в терминах этой переменной x α , как это будет для этой задачи. Обратите внимание, что любой функционал энергии, который был квадратичным в s v , останется квадратичным в x v , и наоборот, поэтому мы можем использовать любую переменную.Затем мы выбираем
H=A (K−∑vxv)2+B [K(K−1)2−∑(uv) ∈ Exuxv] (13), где A, B > 0 — положительные константы. Мы хотим, чтобы основное состояние этого гамильтониана было 90 323 H 90 324 = 0 тогда и только тогда, когда существует клика размером 90 323 K 90 324. Легко видеть, что H = 0, если существует клика размера K . Однако теперь мы хотим показать, что H ≠ 0 для любого другого решения. Легко видеть, что если есть n x v s , равные 1, то минимально возможное значение H равно
Легко видеть, что H = 0, если существует клика размера K . Однако теперь мы хотим показать, что H ≠ 0 для любого другого решения. Легко видеть, что если есть n x v s , равные 1, то минимально возможное значение H равно
Самое «опасное» возможное значение n = 1 + K . Легко видеть, что пока A > КБ, H min ( K + 1) > 0. Наконец, отметим, что, учитывая решение в основном состоянии, конечно, легко считывается из x v , из которых K узлов образуют клику. Для решения этой задачи требуется N спинов на полном графе.
Квантовый алгоритм для этой NP-полной задачи можно сделать несколько более эффективным, если можно тщательно подготовить начальное состояние [47].
NP-сложная версия задачи о кликах требует от нас найти (одну из) самых больших клик в графе. Мы можем изменить приведенный выше гамильтониан, чтобы учесть это, добавив дополнительную переменную y i ( i = 2, …, Δ), которая равна 1, если самая большая клика имеет размер i , и 0 иначе. Пусть H = H A + H B + H 3 C 4 9 , где
HA=A (1−∑i=2Nyi)2+A (∑i=2nnyn−∑vxv)2 (15)
Мы можем изменить приведенный выше гамильтониан, чтобы учесть это, добавив дополнительную переменную y i ( i = 2, …, Δ), которая равна 1, если самая большая клика имеет размер i , и 0 иначе. Пусть H = H A + H B + H 3 C 4 9 , где
HA=A (1−∑i=2Nyi)2+A (∑i=2nnyn−∑vxv)2 (15)
и
HB=B [12(∑i=2Nnyn) (−1+∑i=2Nnyn) −∑(uv) ∈ Exuxv].(16) Мы хотим, чтобы клики удовлетворяли H A = H B = 0 и были единственными основными состояниями. Приведенный выше гамильтониан удовлетворяет этому, если A / B достаточно велико, поэтому ограничения H A = 0 всегда выполняются — мы можем увидеть это, отметив, что первый член H заставляет нас выбрать только одно значение y i = n , а второй член заставляет нас выбрать n вершин. Тогда H B = 0 гарантирует, что у нас есть клика. Аналогично обсуждению выше, мы видим, что отсутствие состояний с отрицательной энергией требует A > NB . Если максимальная степень графа равна Δ, это можно упростить до A > Δ B . Теперь, когда мы знаем, что все основные состояния являются кликами, нам нужно найти состояние с наименьшим значением y n . Это можно получить, выбрав
Тогда H B = 0 гарантирует, что у нас есть клика. Аналогично обсуждению выше, мы видим, что отсутствие состояний с отрицательной энергией требует A > NB . Если максимальная степень графа равна Δ, это можно упростить до A > Δ B . Теперь, когда мы знаем, что все основные состояния являются кликами, нам нужно найти состояние с наименьшим значением y n . Это можно получить, выбрав
, где C > 0 — некоторая константа.Если C достаточно мало, то энергия основного состояния равна H = − CK , где K — размер наибольшей клики в графе. Чтобы определить верхнюю границу для C , чтобы решить проблему клик (в отличие от какой-либо другой проблемы), мы должны убедиться, что никогда не выгодно красить дополнительную вершину за счет небольшого нарушения H A ограничение. Штраф за окраску одной дополнительной вершины при заданных y i = n составляет как минимум A − nB − C . Делаем вывод, что надо выбрать
Делаем вывод, что надо выбрать
Так, например, мы могли бы взять A = (Δ + 2) B и B = C .
2.4. Преобразование
N в журнал N Spins in Some ConstraintsСуществует прием, который можно использовать для резкого уменьшения количества дополнительных y i спинов, которые необходимо добавить в NP-сложной версии задачи о кликах, описанной выше [48]. В общем, этот трюк можно использовать на протяжении всей этой статьи, поскольку мы увидим неоднократное появление подобных конструкций вспомогательных битов и .
Мы знаем, что хотим закодировать переменную, которая может принимать значения 2, …, N (или Δ, если мы знаем максимальную степень графа — аргумент в любом случае идентичен). Для простоты предположим, что мы хотим закодировать значения 1, …, N (это незначительная разница в большом пределе N ). Определите целое число M так, чтобы
Альтернативно, M = ⌊log N ⌋ — в этой статье основание 2 подразумевается в логарифме. В этом случае нам нужно только м + 1 двоичные переменные: y 0 , …, y м , вместо N Двоичные переменные, y 1 , …, y N , чтобы закодировать переменную, которая может принимать N значений. Легко проверить, что замена
В этом случае нам нужно только м + 1 двоичные переменные: y 0 , …, y м , вместо N Двоичные переменные, y 1 , …, y N , чтобы закодировать переменную, которая может принимать N значений. Легко проверить, что замена
решает ту же проблему клики без потери общности. (Вообще это верно для всех наших NP-задач.) Если N ≠ 2 M + 1 — 1, основное состояние может быть вырожденным, поскольку сумма y с до заданного целого числа не всегда уникальна. При кодировании этих задач для вычислительных целей, конечно, следует использовать этот трюк, но для педагогики и простоты мы не будем описывать его в явном виде до конца статьи.
Используя этот прием, заметим, что для решения NP-сложной версии задачи о кликах требуется N + 1 + ⌊log ⌋ спинов.
3. Двоичное целочисленное линейное программирование
Пусть x 1 , …, x N будут N бинарными переменными, которые мы упорядочим в вектор x . Задача бинарного целочисленного линейного программирования (ILP) спрашивает: каково наибольшее значение c · x для некоторого вектора c при заданном ограничении
Задача бинарного целочисленного линейного программирования (ILP) спрашивает: каково наибольшее значение c · x для некоторого вектора c при заданном ограничении
с матрицей S m × N и b вектором с m компонентами.Это NP-сложная [18] с соответствующей NP-полной проблемой решения. Многие проблемы могут быть поставлены как ILP: например, поставщик, который хочет максимизировать прибыль, учитывая нормативные ограничения [48].
Гамильтониан Изинга, соответствующий этой задаче, можно построить следующим образом. Пусть Н = Н А + Н В где
HA=A∑j=1m[bj−∑i=1NSjixi]2 (22)и A > 0 является константой. Основные состояния H A = 0 обеспечивают (конечно, если такое основное состояние существует!) ограничение S x = b .Затем мы устанавливаем
HB=−B∑i=1Ncixi. (23)
(23)с B ≪ A другая положительная константа.
Чтобы найти ограничения на требуемое отношение A / B , действуем аналогично предыдущему. Для простоты предположим, что уравнение ограничения (21) может удовлетворяться для некоторого выбора x . При таком выборе наибольшее возможное значение −Δ H B составляет, в принципе, B , где
Наименьшее возможное значение Δ H A связано со свойствами матрицы S и будет иметь место, если мы нарушим только одно ограничение и нарушим это ограничение на наименьшую возможную величину, заданную
Эту оценку можно было бы улучшить, если бы мы знали более конкретные свойства S и/или b .Делаем вывод
Если коэффициенты C I I и и S IJ IJ являются o (1) целые числа, у нас есть ≤ N MAX ( C I ), а ≥ 1, поэтому мы заключаем A / B ≳ N .
4. Проблемы с покрытием и упаковкой
В этом разделе мы обсудим еще один простой класс отображений NP-задач в модели Изинга: задачи «покрытия» и «упаковки».Эти проблемы часто можно рассматривать как вопрос: как я могу выбрать элементы из набора (например, вершины из набора вершин графа), чтобы они «покрывали» граф каким-то простым способом (например, их удаление делает ребро установить пустым). В этом классе задач существуют ограничения, которые должны точно выполняться. Многие из проблем, описанных ниже, часто обсуждаются в литературе, но мы снова рассмотрим их здесь для полноты. Мы завершаем раздел задачей о минимальном максимальном паросочетании, которая представляет собой несколько более сложную задачу, ранее не обсуждавшуюся в литературе по AQO.
Это, безусловно, самый популярный класс проблем, обсуждаемых в литературе AQO. Как мы упоминали во введении, это связано с тем, что это единственный класс задач NP (обсуждаемых в этой статье), для которых легко встроить задачу с помощью графа, который не является полным (или почти полным).
4.1. Точная крышка
Задача о точном покрытии выглядит следующим образом: рассмотрим множество U = {1, …, n } и подмножества V i ⊆ U ( i
Вопрос: существует ли подмножество множества множеств { V i }, называемое R , такое, что элементы R являются непересекающимися множествами, а объединение элементов R это U ? Эта проблема была описана в Choi [49], но для простоты мы повторим ее здесь.Эта проблема решения является NP-полной [18]. Используемый нами гамильтониан равен
. HA=A∑α=1n(1−∑i:α∈Vixi)2. (28) В приведенном выше гамильтониане α обозначает элементы U , а i обозначает подмножества V i . H A = 0 именно тогда, когда каждый элемент включен ровно один раз, что означает, что объединения не пересекаются. Существование основного состояния с энергией H = 0 соответствует существованию решения задачи о точном покрытии. Если это основное состояние является вырожденным, существует несколько решений. Требуется N вращений.
Если это основное состояние является вырожденным, существует несколько решений. Требуется N вращений.
Это также легко расширить и найти наименьшее точное покрытие (это делает задачу NP-сложной). Это делается просто добавлением вторым масштабом энергии: H = H = H = H A + H B , с H A Приведены выше, а
Основное состояние этой модели будет мБ , где м — наименьшее количество требуемых подмножеств.Чтобы найти отношение A / B , необходимое для кодирования правильной задачи, заметим, что в худшем случае существует очень небольшое количество подмножеств с одним общим элементом, объединение которых равно U . Чтобы этого не произошло, можно установить A > nB .
4.2. Комплект упаковки
Давайте рассмотрим ту же схему, что и в предыдущей задаче, но теперь зададим другой вопрос: каково наибольшее число подмножеств V i , которые все не пересекаются? Это называется проблемой упаковки множества; эта задача оптимизации является NP-трудной [18]. Для этого используем H = H A + H B :
Для этого используем H = H A + H B :
, который минимизируется только тогда, когда все подмножества не пересекаются. Затем мы используем
HB=−B∑ixi (31), который просто подсчитывает количество включенных наборов. Выбор B < A гарантирует, что нарушение ограничения H A никогда не будет благоприятным (поскольку всегда будет штраф в размере не менее A за дополнительный включенный набор) [4].
Заметим, что изоморфная формулировка этой задачи в контексте теории графов выглядит следующим образом: рассмотрим множества, которые нужно закодировать в неориентированном графе G = ( V, E ), где каждое множество V i отображается в вершину i ∈ V . Ребро ij ∈ E существует, когда V i ∩ V j непусто. Легко видеть, что если мы заменим
Легко видеть, что если мы заменим
, вопрос о том, какое максимальное число вершин можно «раскрасить» ( x i = 1), чтобы никакие две окрашенные вершины не соединялись ребром, в точности эквивалентен задаче упаковки множества описано выше.Эта версия называется задачей максимального независимого множества (MIS).
4.3. Крышка вершины
Для данного неориентированного графа G = ( V, E ), каково наименьшее количество вершин, которые можно «раскрасить» так, чтобы каждое ребро инцидентно окрашенной вершине? Это NP-сложно; форма решения является NP-полной [18]. Пусть x v будет бинарной переменной для каждой вершины, которая равна 1, если она окрашена, и 0, если она не окрашена. Наш гамильтониан будет H = H A + H B .Ограничение, заключающееся в том, что каждое ребро имеет хотя бы цветную вершину, закодировано в H A :
. HA=A∑uv∈E(1−xu)(1−xv). (33)
HA=A∑uv∈E(1−xu)(1−xv). (33)Затем мы хотим минимизировать количество окрашенных вершин с помощью H B :
Выберите B < A , так как если мы обесцветим любую вершину, которая испортит решение, по крайней мере одно ребро больше не будет соединяться с окрашенной вершиной. Необходимое количество спинов | V |, размер набора вершин.
4.4. Выполнимость
Выполнимость — одна из самых известных NP-полных задач [18]. Каждая проблема выполнимости может быть записана как так называемая задача 3SAT в конъюнктивной нормальной форме (и этот алгоритм требует только полиномиальных шагов/времени), поэтому для простоты мы сосредоточимся на этом случае. В этом случае мы спрашиваем, является ли
Ψ=C1∧C2⋯∧Cm (35) может принимать значение true, т. е. каждое C i for 1 ≤ i ≤ m истинно, где форма each C i 9
Ci=yi1∨yi2∨yi3 (36) Вот Y I Существует хорошо известная редукция 3SAT к MIS [49], которую мы воспроизводим здесь для полноты картины. Рассмотрим решение задачи упаковки множеств на графе G с 3 m узлами, который мы построим следующим образом. Для каждого предложения C i мы добавляем в граф 3 узла и соединяем каждый узел с 3 другими.После этого шага, если существуют y 1 и y 2 такие, что y 1 = y 2 , то мы также добавляем ребро между этими двумя узлами. Решение MIS на этом графе и вопрос, имеет ли решение ровно m узлов, эквивалентно решению задачи 3SAT. Это можно увидеть следующим образом: если решение проблемы 3SAT существует, только один элемент каждого пункта должен быть истинным — если истинных больше, это также приемлемо, но мы должны иметь, чтобы этот элемент был истинным, поэтому давайте выберем раскрасить вершину, соответствующую той переменной, которая истинна. Обратите внимание, что мы можем решить NP-сложную версию этой задачи (если нам придется нарушить некоторые пункты, какое будет наименьшее число?), решив оптимизационную версию задачи MIS. Задача минимального максимального (минимаксного) паросочетания на графе определяется следующим образом: пусть G = ( V, E ) обозначает неориентированный граф, а C ⊆ E — предлагаемая «раскраска». Ограничения на C следующие: для каждого ребра в C раскрасим две вершины, которые оно соединяет: т. Обратите внимание, что с этого момента в этой статье мы не нашли ни одной из формулировок Изинга этой статьи в литературе. Мы будем использовать спины на графике, чтобы смоделировать, окрашено ли ребро.Давайте используем двоичную переменную x e , чтобы указать, окрашено ли ребро; таким образом, количество спинов | Е | = O(Δ N ), размер набора ребер; как и прежде, Δ представляет собой максимальную степень. Первый и самый большой член, H A , будет накладывать ограничение, что никакая вершина не имеет двух цветных ребер. Это можно сделать, установив Здесь A > 0 — положительная энергия, а ∂ v соответствует подмножеству E ребер, которые соединяются с v . Таким образом, основные состояния состоят из H A = 0; если H A > 0, то это потому, что есть вершина, два ребра которой окрашены. Мы также можем определить для состояний с H A = 0, переменную Подчеркнем, что это определение справедливо только для состояний с H A = 0, так как в этих состояниях каждая вершина имеет либо 0, либо 1 окрашенное ребро. Обратите внимание, что, поскольку 1 − y v может быть отрицательным, мы должны выбрать B > 0, чтобы оно было достаточно маленьким. Чтобы связать b , отметим, что единственная проблема (отрицательный срок в ч b ) приходит когда y U = 0, Y V > 1, и ( uv ) ∈ E .Предположим, что м соседей м имеют y y u u = 0. A  Это очень краткое описание выполнимости; физикам, незнакомым с этой проблемой, следует прочитать соответствующие главы Мезара и Монтанари [24].
Это очень краткое описание выполнимости; физикам, незнакомым с этой проблемой, следует прочитать соответствующие главы Мезара и Монтанари [24].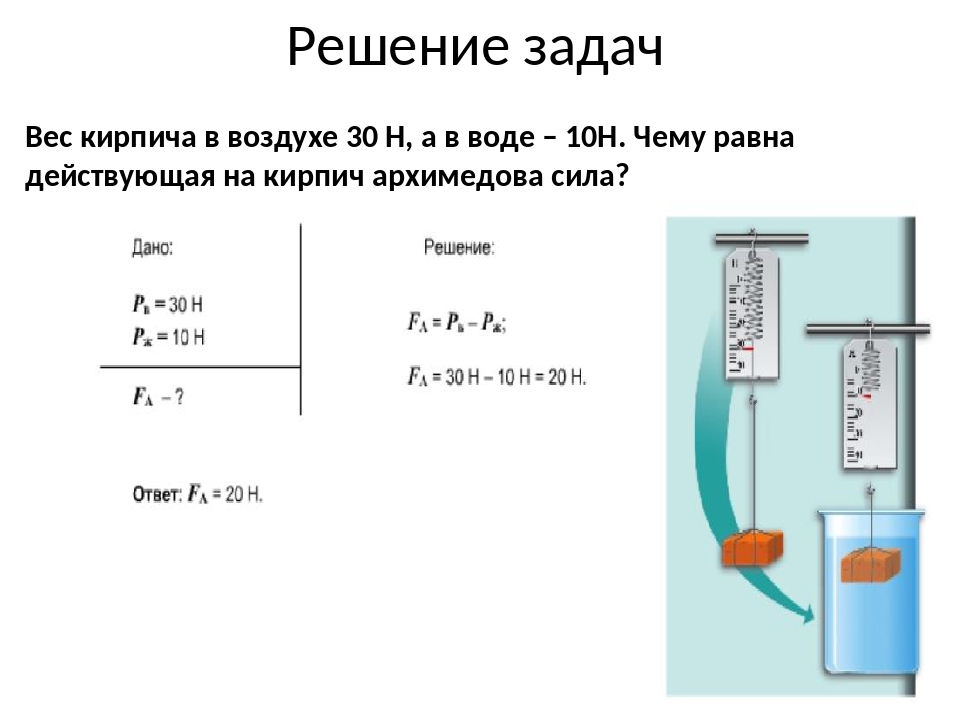 Однако мы также можем не выбрать, чтобы x 1 были истинными, а x 1 были истинными, поэтому нам необходимо соединить все такие точки ребром. Поскольку граф состоит из 90 323 m 90 324 связанных треугольников, единственный способ раскрасить 90 323 m 90 324 вершин, если каждая вершина находится в отдельном треугольнике, поэтому должен быть элемент каждого предложения C i , который истинный.
Однако мы также можем не выбрать, чтобы x 1 были истинными, а x 1 были истинными, поэтому нам необходимо соединить все такие точки ребром. Поскольку граф состоит из 90 323 m 90 324 связанных треугольников, единственный способ раскрасить 90 323 m 90 324 вершин, если каждая вершина находится в отдельном треугольнике, поэтому должен быть элемент каждого предложения C i , который истинный. 4.5. Минимальное максимальное соответствие
 е. пусть D = ∪ e ∈ C ∂ e . Затем мы будем требовать: нет двух краев в C Поделиться вершиной (если E 1 , E 2 ∈ C , ∂ E 1 ∩ ∂ E 2 = ∅) и что если u, v ∈ D , то ( uv ) ∉ E .Это NP-сложно; проблема решения является NP-полной [19]. Это минимально в том смысле, что мы не можем добавить больше ребер к C (окрашивая любые подходящие вершины) без нарушения первого ограничения, и максимально в том смысле, что решение тривиального пустого множества не разрешено — мы должны включить все ребра между неокрашенными вершинами. .
е. пусть D = ∪ e ∈ C ∂ e . Затем мы будем требовать: нет двух краев в C Поделиться вершиной (если E 1 , E 2 ∈ C , ∂ E 1 ∩ ∂ E 2 = ∅) и что если u, v ∈ D , то ( uv ) ∉ E .Это NP-сложно; проблема решения является NP-полной [19]. Это минимально в том смысле, что мы не можем добавить больше ребер к C (окрашивая любые подходящие вершины) без нарушения первого ограничения, и максимально в том смысле, что решение тривиального пустого множества не разрешено — мы должны включить все ребра между неокрашенными вершинами. . Чтобы закодировать эту проблему, мы используем серию из трех гамильтонианов:
Чтобы закодировать эту проблему, мы используем серию из трех гамильтонианов: Затем мы определяем энергию H B так, чтобы решения минимаксной задачи раскраски также имели H B = 0. H B поднять энергию всех решений, где существует возможное ребро, которое можно раскрасить, но при этом не нарушать условие окрашивания, из основного состояния.Для этого мы можем просуммировать по всем ребрам в графе и проверить, соединяет ли ребро две вершины, ни одна из которых не окрашена:
Затем мы определяем энергию H B так, чтобы решения минимаксной задачи раскраски также имели H B = 0. H B поднять энергию всех решений, где существует возможное ребро, которое можно раскрасить, но при этом не нарушать условие окрашивания, из основного состояния.Для этого мы можем просуммировать по всем ребрам в графе и проверить, соединяет ли ребро две вершины, ни одна из которых не окрашена: Тогда, вклад в H
Тогда, вклад в H
Обратите внимание, что m + y u ≤ k , если k степень узла v . Собрав все это вместе, мы заключаем, что если Δ является максимальной степенью в графе, потому что наихудший сценарий y v = 2, m = Δ − 2, если мы выберем
, то никогда не выгодно иметь y v > 1.Это гарантирует, что наземное состояние ч + ч 3 + ч 3 + ч 3 + ч b будет иметь H A = H B = 0: IE государства которые не нарушают минимаксных ограничений.
Теперь, учитывая штаты, где H a 3 = ч 3 = ч 3 = ч b = 0, мы сейчас хотим основное состояние h A + H B + H C — состояние, в котором окрашено наименьшее количество ребер. Для этого мы просто даем
Для этого мы просто даем
подсчитайте количество цветных ребер. Здесь C — шкала энергий, выбранная достаточно малой, чтобы никогда не было энергетически выгодно нарушать ограничения, налагаемые условиями H A или H B : требуется C < B , так как существует потеря энергии B , связанная с каждым ребром, которое может быть окрашено, но не окрашено. Член с наименьшим H C имеет наименьшее количество ребер и, очевидно, является решением минимаксной задачи.Каждое основное состояние этой спиновой модели эквивалентно решению минимаксной задачи.
5. Задачи с неравенствами
Теперь мы обратимся к задачам NP, формулировки которых в виде моделей Изинга более тонкие, поскольку ограничения включают неравенства, а не равенства. Эти ограничения можно переписать как ограничения, включающие только равенство, путем расширения числа спинов.
Как и в случае с проблемами разбиения, мы обнаружим, что эти гамильтонианы требуют встраивания высокосвязных графов в квантовое устройство. Это может ограничить их использование на текущем оборудовании.
Это может ограничить их использование на текущем оборудовании.
5.1. Комплект крышки
Рассмотрим набор U = {1, …, n }, с наборами V i ⊆ U ( i ) = 1, 3 9032 , что 9 4 N 9032 U=∪i=1NVα. (44)
Задача покрытия множества состоит в том, чтобы найти наименьшее возможное количество V i s такое, что их объединение равно U . Это обобщение задачи точного покрытия, где нас не волнует, встречается ли некоторый α ∈ U в кратных множествах V i ; найти наименьшее число множеств, «покрывающих» U , NP-трудно [18].
Обозначим x i как двоичную переменную, которая равна 1, если набор i включен, и 0, если набор i не включен. Затем обозначим x α, m как двоичную переменную, которая равна 1, если число V i s, включающих элемент α, равно m ≥ 1, и 0 в противном случае. Набор H = H A + H B .Наша первая энергия накладывает ограничения, согласно которым ровно одно x α, m должно быть равно 1, поскольку каждый элемент U должен включаться фиксированное число раз, и что количество раз, которое мы утверждали, α равно на самом деле равно числу V i , которое мы включили с α в качестве элемента:
Набор H = H A + H B .Наша первая энергия накладывает ограничения, согласно которым ровно одно x α, m должно быть равно 1, поскольку каждый элемент U должен включаться фиксированное число раз, и что количество раз, которое мы утверждали, α равно на самом деле равно числу V i , которое мы включили с α в качестве элемента:
Наконец, мы минимизируем по количеству V α включенных:
HB=B∑i=1Nxi, (46)с 0 < B < A требуется, чтобы никогда не нарушались ограничения H A (в худшем случае один набор должен быть включен для получения одного элемента U ; изменение в H , если мы включим этот последний элемент, будет B − A , что должно быть отрицательным).
Пусть M ≤ N будет максимальным числом наборов, содержащих любой заданный элемент U ; тогда требуется N x i с и n ⌊1 + log M ⌋ вращений (используя описанный выше прием) для x α вращений м; поэтому общее число равно N + n ⌊1 + log M ⌋ спинов.
5.2. Рюкзак с целыми весами
Задача о рюкзаке — это следующая задача: у нас есть список из N предметов, помеченных индексами α, где вес каждого предмета определяется как w α , а его значение определяется как c α , и у нас есть рюкзак, который может выдержать только вес W .Если x α является бинарной переменной, обозначающей, содержится ли (1) или нет (0) объект α в рюкзаке, то общий вес в рюкзаке равен
.и общая стоимость
NP-трудная [18] задача о рюкзаке требует от нас максимизации при условии, что ≤ W . Он имеет огромное разнообразие приложений, особенно в экономике и финансах [50].
Пусть y n для 1 ≤ n ≤ W обозначает двоичную переменную, которая равна 1, если конечный вес рюкзака равен n , и 0 в противном случае.Наше решение состоит в том, чтобы H = H A + H B , где
HA=A (1−∑n=1Wyn)2+A (∑n=1Wnyn-∑αwαxα)2 (49), который гарантирует, что вес может принимать только одно значение и что вес предметов в рюкзаке равен значению, которое мы утверждали, и, наконец,
. HB=−B∑αcαxα. (50)
HB=−B∑αcαxα. (50)Так как мы требуем невозможности найти решение, при котором H A слабо нарушается за счет H B становится более отрицательным, мы требуем, чтобы 0 < B( max c α ) < A (не допускается добавление в рюкзак одного предмета, делающего его слишком тяжелым).Требуемое количество вращений (используя трюк с логарифмом) N + ⌊1 + log W ⌋.
6. Раскраски
Теперь перейдем к задачам раскраски. Наивно, задачи раскраски часто лучше всего формулировать как модели Поттса [51], где спины могут принимать более двух значений, но эти классические модели Поттса можно преобразовать в классические модели Изинга с расширением числа спинов. Этот простой прием лежит в основе наших решений этого класса проблем.
6.1. Раскраска графа
Для заданного неориентированного графа G = ( V, E ) и набора из n цветов можно ли раскрасить каждую вершину графа в определенный цвет так, чтобы ни одно ребро не соединяло две вершины такого же цвета? Это одна из наиболее известных NP-полных [18] задач, поскольку ее можно рассматривать как обобщение задачи о том, сколько цветов необходимо для раскрашивания карты, чтобы никакие две страны, имеющие общую границу, не имели одинаковых границ. цвет. Конечно, в этом частном случае можно доказать, что всегда существует раскраска для n ≥ 4 [52, 53].Эта проблема называется проблемой раскраски графа.
цвет. Конечно, в этом частном случае можно доказать, что всегда существует раскраска для n ≥ 4 [52, 53].Эта проблема называется проблемой раскраски графа.
Наше решение состоит из следующего: мы обозначаем x v , i как двоичную переменную, которая равна 1, если вершина v окрашена в цвет i , и 0 в противном случае. Энергия
H=A∑v (1−∑i=1nxv,i)2+A∑(uv)∈E∑i=1nxu,ixv,i. (51) Первое слагаемое накладывает ограничение на то, что каждая вершина имеет ровно один цвет, и дает штраф за энергию каждый раз, когда это нарушается, а второе слагаемое дает штраф за энергию каждый раз, когда ребро соединяет две вершины одного цвета.Если существует основное состояние этой модели с H = 0, то существует решение задачи раскраски на этом графе с n цветами. Мы также можем прочитать цвет каждого узла (в одной из таких схем раскраски), посмотрев, какие x равны 1. Обратите внимание, что количество спинов можно немного уменьшить, поскольку среди раскрасок существует симметрия перестановок, выбрав например, конкретный узел в графе имеет цвет 1, а один из его соседей — цвет 2. Таким образом, общее число требуемых спинов составляет нН .
Таким образом, общее число требуемых спинов составляет нН .
6.2. Крышка клика
Задача о покрытии клики для неориентированного графа G = ( V, E ) заключается в следующем: при наличии n цветов мы назначаем разные цвета каждой вершине графа. Пусть W W 1 , …, W N Быть подмножениями V , соответствующие каждому цвету, и E W 1 , …, E W n набор ребер, ограниченный ребрами между вершинами в наборах W i .Проблема Cliack Cover задает ли или нет ( W I , E
Наше решение очень похоже на задачу раскраски графа. Опять же, мы используем те же бинарные переменные, что и для раскраски графа, и используем гамильтониан, очень похожий на проблему клик:
Опять же, мы используем те же бинарные переменные, что и для раскраски графа, и используем гамильтониан, очень похожий на проблему клик:
Первое слагаемое обеспечивает ограничение, согласно которому каждая вершина имеет ровно один цвет, давая штраф за энергию каждый раз, когда это ограничение нарушается. Во втором члене, поскольку сумма по v x v , i подсчитывает количество узлов с цветом i , первая сумма подсчитывает максимально возможное количество ребер, которые могут существовать с цветом и . Затем второй член проверяет, действительно ли существует это количество ребер.Таким образом, H = 0 тогда и только тогда, когда задача о кликовом покрытии решается заданной раскраской. Если существует основное состояние с H = 0, существует решение проблемы кликового покрытия. Обсуждение требуемого отношения A / B для кодирования правильного решения аналогично обсуждению проблемы клик. Общее количество требуемых спинов составляет nN .
Общее количество требуемых спинов составляет nN .
6.3. Последовательность заданий с целыми длинами
Задача упорядочивания заданий выглядит следующим образом: нам дан список из N заданий для m компьютерных кластеров.Каждое задание i имеет длину L i . Как каждое задание может быть назначено компьютеру в кластере таким образом, что если набор заданий в кластере α равен V α , то длина этого кластера, определенная как
Mα≡∑i∈VαLi, (53)выбраны таким образом, чтобы max( M α ) было минимальным? По сути, это означает, что если мы запустим все задания одновременно, все задания будут завершены за кратчайшее время.Это NP-трудно [18], и существует версия решения [is max( M α ) ≤ M 0 ?], которая является NP-полной. Предположим, что L i ∈ ℕ.
Для этого начнем с требования, чтобы без ограничения общности M 1 ≥ M α для любого α. Введем переменные x i ,α , которые равны 1, если задание i добавляется в компьютер α, и 0 в противном случае, и переменные y n ,1α 3 и для α n ≥ 0, что равно 1, если разность M 1 − M α = n .Тогда гамильтониан
Введем переменные x i ,α , которые равны 1, если задание i добавляется в компьютер α, и 0 в противном случае, и переменные y n ,1α 3 и для α n ≥ 0, что равно 1, если разность M 1 − M α = n .Тогда гамильтониан
кодирует, что каждое задание может быть поручено только одному компьютеру, и что ни один компьютер не может иметь общую длину больше, чем компьютер 1. Число должно быть выбрано пользователем и связано с количеством вспомогательных вращений, необходимых для адекватного наложения ограничения длины, что M 1 ≥ M α : в худшем случае это дается как N max( L i ). Чтобы найти минимальную максимальную длину M 1 , мы просто используем
HB=B∑iLixi,1.(55) Аналогично нахождению границ A / B для задачи о рюкзаке, чтобы этот гамильтониан кодировал решение задачи, нам требуется (в худшем случае) 0 < B max( L i ) < А . Используя трюк с логарифмом, необходимое количество вращений здесь составляет мН + ( м — 1)⌊1 + log⌋.
Используя трюк с логарифмом, необходимое количество вращений здесь составляет мН + ( м — 1)⌊1 + log⌋.
7. Гамильтоновы циклы
В этом разделе мы опишем решение (ненаправленной или направленной) проблемы гамильтоновых циклов, а затем и задачи коммивояжера, которая для формулировки спинового стекла Изинга является тривиальным расширением.
7.1. Гамильтоновы циклы и пути
Пусть G = ( V, E ), и N = | В |. Граф может быть направленным или неориентированным; наш метод решения не изменится. Проблема гамильтонова пути выглядит следующим образом: начиная с некоторого узла в графе, можно ли двигаться по ребру, посещая другие узлы в графе, так, чтобы можно было достичь каждого отдельного узла в графе, никогда не возвращаясь к одному и тому же узлу дважды? Проблема гамильтоновых циклов требует, чтобы, кроме того, путешественник мог вернуться в исходную точку из последнего посещенного им узла.Гамильтоновы циклы являются обобщением известной проблемы Кенигсбергского моста [24] и являются NP-полными [18].
Не ограничивая общности, обозначим вершины 1, …, N , а множество ребер ( uv ) возьмем направленным, т. е. порядок uv имеет значение. Тривиально расширить до неориентированных графов, просто рассматривая ориентированный граф с добавлением ( vu ) к набору ребер всякий раз, когда ( uv ) добавляется к набору ребер. Наше решение будет использовать N 2 бит x v , i , где v представляет вершину, а i представляет ее порядок в предполагаемом цикле.Наша энергия будет состоять из трех компонентов. Первые две вещи, которые нам потребуются, это то, что каждая вершина может появиться только один раз в цикле, и что для каждого j в цикле должно быть j узлов. Наконец, для узлов в нашем предполагаемом порядке, если x u , j и x v , j + 1 , ( ув ) ∉ E . Обратите внимание, что N + 1 следует читать как 1 в приведенных ниже выражениях, если мы решаем проблему циклов. Они закодированы в гамильтониане:
Они закодированы в гамильтониане:
A > 0 является константой. Ясно, что основное состояние этой системы имеет H = 0, только если мы имеем порядок вершин, при котором каждая вершина входит только один раз, а соседние вершины в цикле имеют ребра на графе, т. е. мы имеем гамильтониан цикл.
Чтобы вместо этого решить гамильтонову задачу о пути, ограничьте последнюю сумму по j выше от 1 до N − 1; нас не волнует, связаны ли также первый и последний узлы. N 2 вращений требуется для решения этой задачи.
Несложно немного уменьшить размер пространства состояний для задачи гамильтоновых циклов следующим образом: ясно, что узел 1 всегда должен входить в гамильтонов цикл, и без ограничения общности можно положить x 1, i = δ 1, i : это просто означает, что общий порядок цикла выбран так, что узел 1 идет первым. Это уменьшает количество вращений до ( N − 1) 2 .
Это уменьшает количество вращений до ( N − 1) 2 .
7.2. Коммивояжер
Задача коммивояжера для графа G = ( V, E ), где каждое связанное с ним ребро uv имеет вес W uv , состоит в нахождении гамильтонова цикла так что сумма весов каждого ребра в цикле минимальна. Обычно задача коммивояжера предполагает наличие полного графа, но у нас есть технология, позволяющая решать ее на более произвольном графе.Проблема решения (существует ли путь полного веса ≤ W ?) является NP-полной [18].
Чтобы решить эту проблему, мы используем H = H = H = H A + H 93 + H B , с H A A A Hamiltonian дано для направленного (или неопределенного) гамильтона проблема циклов. Затем мы просто добавляем
HB=B∑(uv)∈EWuv∑j=1Nxu,jxv,j+1. (57) с B достаточно маленьким, чтобы никогда не было выгодно нарушать ограничения H A ; Одним из таких ограничений составляет 0 < B MAX ( W UV ) < A (мы предполагаем, что в полной общности W UV ≥ 0 для каждого ( UV ) ∈ E ). Если коммивояжеру не нужно возвращаться в исходное положение, мы можем ограничить сумму по j от 1 до N − 1, как и раньше. Как и в случае с гамильтоновыми циклами, требуется ( N − 1) 2 спинов, поскольку мы можем зафиксировать узел 1 так, чтобы он появлялся первым в цикле.
Если коммивояжеру не нужно возвращаться в исходное положение, мы можем ограничить сумму по j от 1 до N − 1, как и раньше. Как и в случае с гамильтоновыми циклами, требуется ( N − 1) 2 спинов, поскольку мы можем зафиксировать узел 1 так, чтобы он появлялся первым в цикле.
8. Проблемы с деревьями
Наиболее тонкие проблемы NP, которые нужно решить с помощью моделей Изинга, — это проблемы, требующие нахождения связных подграфов дерева больших графов. Поскольку для определения того, является ли подграф деревом, требуется глобальная информация о связности графа, мы будем полагаться на приемы, аналогичные тем, которые мы использовали для записи гамильтоновых циклов в виде модели Изинга.
8.1. Минимальное остовное дерево с максимальным ограничением степени
Задача минимального остовного дерева состоит в следующем: задан неориентированный граф G = ( V, E ), где каждое ребро ( uv ) ∈ E связано со стоимостью c uv , какое дерево T ⊆ G , содержащее все вершины, такое, что стоимость T , определенная как
c(T)≡∑(uv)∈ETcuv, (58) свернут (если такое дерево существует)? Без ограничения общности возьмем в этом подразделе c uv > 0 (к каждому c uv всегда можно добавить положительную константу c , чтобы наименьшее значение является строго положительным, без изменения деревьев T , которые решают задачу). Мы также добавим ограничение степени, чтобы каждая степень в T была ≤ Δ. Это делает задачу NP-трудной с соответствующей NP-полной проблемой решения [18].
Мы также добавим ограничение степени, чтобы каждая степень в T была ≤ Δ. Это делает задачу NP-трудной с соответствующей NP-полной проблемой решения [18].
Чтобы решить эту проблему, мы помещаем двоичную переменную y e на каждое ребро, чтобы определить, включено ли это ребро в T :
ye≡{1e∈ET0иначе. (59) Мы также размещаем большое количество двоичных переменных x V , I на каждой вершине, и x , UV , I , x Vu , I на ребре ( uv ) (это разные спины): число i = 0, 1, …, N /2 будет использоваться для отслеживания глубины узла в дереве, и если x uv = 1, значит u ближе к корню, чем v , а если x vu = 1, то корень 9 ближе к = 1 .Наконец, мы используем другую переменную z v , i ( i = 1, … Δ) для подсчета количества степеней каждого узла. Теперь мы используем энергию H = H = H = H A + H 93 + H B , где термины в ч A A используются для навязывания ограничений, которые: есть ровно один корня дерева, каждая вершина имеет глубину, каждая связь имеет глубину, и две ее вершины должны быть на разной высоте, дерево связно (т.т. е. ровно одно ребро к некорневой вершине исходит из вершины с меньшей глубиной), каждый узел может иметь не более Δ ребер, и каждое ребро на глубине i указывает между узлом на глубине i − 1 и я , соответственно:
Теперь мы используем энергию H = H = H = H A + H 93 + H B , где термины в ч A A используются для навязывания ограничений, которые: есть ровно один корня дерева, каждая вершина имеет глубину, каждая связь имеет глубину, и две ее вершины должны быть на разной высоте, дерево связно (т.т. е. ровно одно ребро к некорневой вершине исходит из вершины с меньшей глубиной), каждый узел может иметь не более Δ ребер, и каждое ребро на глубине i указывает между узлом на глубине i − 1 и я , соответственно:
Основные состояния с H A = 0 являются деревьями, которые включают каждую вершину. В последнем члене суммы помните, что x uv , i и x vu , i являются вращениями каждого ребра, которые включены для каждого ребра; обозначения в суммировании призваны напомнить нам об этом. Затем мы добавляем
В последнем члене суммы помните, что x uv , i и x vu , i являются вращениями каждого ребра, которые включены для каждого ребра; обозначения в суммировании призваны напомнить нам об этом. Затем мы добавляем
Чтобы решить правильную задачу, нам нужно убедиться, что мы никогда не удаляем x uv , i из H B для того, чтобы иметь более отрицательное значение H 9023 9023 .Поскольку каждое ограничение в H A вносит вклад в энергию ≥ A , если оно нарушается, мы заключаем, что установка 0 < B max( c uv 3 4 A
Необходимое количество спинов | В |(⌊| В | + 1⌋ + 2)/2 + | E |(| V | + 1) + | В | ⌊1 + лог Δ⌋. Максимально возможное количество ребер на любом графе равно | Е | = O(| V | 2 ), поэтому эта формулировка Изинга может потребовать кубического числа спинов в размере множества вершин.
Максимально возможное количество ребер на любом графе равно | Е | = O(| V | 2 ), поэтому эта формулировка Изинга может потребовать кубического числа спинов в размере множества вершин.
8.2. Деревья Штайнера
NP-трудная [18] задача дерева Штейнера чем-то похожа на задачу выше: при наших затратах c uv мы хотим найти минимальное остовное дерево для подмножества U ⊂ V вершины (т.е., такое дерево, что сумма c uv s по всем включенным ребрам минимальна). Мы больше не накладываем ограничения по степени; проблема уже оказывается «сложной», так как теперь мы допускаем возможность не включать узлы, которых нет в U .
Чтобы решить эту проблему, найдя основное состояние модели Изинга, мы используем тот же гамильтониан, что и для минимального остовного дерева, за исключением того, что мы добавляем бинарные переменные или узел v не включен в дерево. Мы используем гамильтониан h = h = h A + h 3 + h b b , где h A Обеспечение ограничений Ограничения аналогично в предыдущем случае:
Мы используем гамильтониан h = h = h A + h 3 + h b b , где h A Обеспечение ограничений Ограничения аналогично в предыдущем случае:
Затем мы используем H B из предыдущей модели для определения дерева минимального веса; применяются те же ограничения, что и для A / B .Количество спинов | В | (⌊| V | + 1⌋ + 4 + 2| E |)/2 + | Е |.
8.3. Набор вершин направленной обратной связи
Множество вершин обратной связи для ориентированного графа G = ( V, E ) есть подмножество F ⊂ V такое, что подграф ( V − F , ∂( F )) ацикличен (не имеет циклов). Мы будем ссылаться на F как на набор обратной связи. Решение проблемы принятия решения о том, существует ли набор обратной связи для | Ф | ≤ k является NP-полным [18].Сначала мы решаем оптимизационную задачу поиска наименьшего размера набора обратной связи для ориентированного графа — расширение до неориентированного графа будет немного сложнее.
Мы будем ссылаться на F как на набор обратной связи. Решение проблемы принятия решения о том, существует ли набор обратной связи для | Ф | ≤ k является NP-полным [18].Сначала мы решаем оптимизационную задачу поиска наименьшего размера набора обратной связи для ориентированного графа — расширение до неориентированного графа будет немного сложнее.
Перед решением этой задачи поможет доказать две леммы. Первая лемма довольно проста: в ориентированном ациклическом графе существует узел, не являющийся концом ни одного ребра. Предположим, что для каждой вершины существует ребро, которое заканчивается в этой вершине. Затем выберите произвольную вершину, выберите любое ребро, заканчивающееся в этой вершине, и следуйте этому ребру в обратном направлении к начальной вершине.Повторите этот процесс более 90 323 N 90 324 раз, и простой аргумент подсчета подразумевает, что мы должны были посетить один и тот же узел более одного раза, по крайней мере, один раз. Таким образом, мы прошли цикл в обратном порядке, что противоречит нашему предположению.
Вторая лемма такова: ориентированный граф G = ( V, E ) ацикличен тогда и только тогда, когда существует функция высоты h : V → ℕ такая, что если uv ∈ E, h ( u ) < h ( v ): i.т. е. каждое ребро указывает от узла с меньшей высотой к узлу с большей высотой. То, что существование функции высоты подразумевает ацикличность, проще всего доказать с помощью противопоставления: предположим, что граф является циклическим. Тогда в цикле ребер у нас есть
0<∑[h(ui+1)−h(ui)]=h(u1)−h(un)+h(un) −h(un−1)+⋯−h(u1)=0 (63) — противоречие. Чтобы доказать, что ациклический граф имеет функцию высоты, мы построим ее рекурсивно. Используя нашу первую лемму, мы знаем, что существует вершина u только с исходящими ребрами, поэтому назовем h ( u ) = 1.Для любой другой вершины мы будем называть высоту этой вершины h ( v ) = 1 + h ′( v ), где h ′( v ) находится путем повторения этого процесса. на графе с удаленными узлами и (которые также должны быть ациклическими). Ясно, что этот процесс завершится и назначит ровно одну высоту узла i для каждого целого числа 1 ≤ i ≤ | В |.
на графе с удаленными узлами и (которые также должны быть ациклическими). Ясно, что этот процесс завершится и назначит ровно одну высоту узла i для каждого целого числа 1 ≤ i ≤ | В |.
Теперь мы можем использовать эту лемму, чтобы записать изинговскую формулировку этой проблемы.Мы помещаем двоичную переменную y v в каждую вершину, которая равна 0, если v является частью набора обратной связи, и 1 в противном случае. Затем мы помещаем двоичную переменную x v , i в каждую вершину, которая равна 1, если вершина v находится на высоте i . Пока высоты i произвольны, и требование справедливости функции высоты будет наложено энергией. Функционал энергии, который мы используем, равен H = H A + H B , где
HA=A∑v(yv−∑ixv,i)2+A∑uv∈E∑i≥jxu,ixv,j.(64) Первый член гарантирует, что если вершина не является частью набора обратной связи, она имеет четко определенную высоту; второй член гарантирует, что ребро соединяет только узел с меньшей высотой с узлом с большей высотой. Затем мы находим наименьший возможный набор обратной связи, добавляя
Затем мы находим наименьший возможный набор обратной связи, добавляя
Чтобы решить правильную задачу, мы не можем добавить слишком мало узлов в набор обратной связи. Если мы установим y v = 1 для узла, который должен быть частью набора обратной связи, мы получим потерю энергии A от H A и выигрыш B из H B .Мы заключаем, что B < A достаточно, чтобы убедиться, что мы решаем правильную задачу. Мы видим, что | В |(| В | + 1) требуется спин.
8.4. Набор вершин ненаправленной обратной связи
Расширение для неориентированных графов требует немного больше внимания. В этом случае мы должны быть осторожны, потому что нет априорного различия в том, меньше или больше высота одного конца ребра, чем другой — это, на первый взгляд, делает проблему гораздо более сложной.Кроме того, неверно, что ориентированный ациклический граф является ациклическим, если не учитывать ориентацию ребер. Однако для неориентированного графа мы также знаем, что набор вершин обратной связи должен сводить граф к деревьям, хотя больше не требуется, чтобы эти деревья были связаны (это называется лесом). Имея это в виду, мы обнаруживаем, что проблема на самом деле очень похожа на минимальное остовное дерево, но без ограничений степени или ограничений связности. Однако новая тонкость заключается в том, что мы не можем удалять ребра.
Однако для неориентированного графа мы также знаем, что набор вершин обратной связи должен сводить граф к деревьям, хотя больше не требуется, чтобы эти деревья были связаны (это называется лесом). Имея это в виду, мы обнаруживаем, что проблема на самом деле очень похожа на минимальное остовное дерево, но без ограничений степени или ограничений связности. Однако новая тонкость заключается в том, что мы не можем удалять ребра.
Для решения этой задачи делаем следующее: вводим бинарную переменную x v , i , которая равна 1, если v является вершиной в любом дереве (в любом месте леса) на глубине i и 0 в противном случае. Однако, чтобы учесть тот факт, что мы можем удалить вершины, мы допустим, что y v = 1, если v является частью набора вершин обратной связи, и 0 в противном случае. Проделываем то же самое с ребрами: считаем, что x uv , i , x vu , i
Изменения заключаются в следующем: мы больше не ограничиваем только 1 узел корнем или ограничиваем степень вершины — однако мы должны добавить новый термин, чтобы гарантировать, что ребра игнорируются в ограничении дерева только в том случае, если они указывают к узлу в наборе обратной связи.Затем мы добавляем
с B < A требуется, чтобы ограничения A никогда не нарушались. Это подсчитывает количество узлов в наборе обратной связи, поэтому H минимизируется, когда H B наименьшее, т. Е. Мы должны удалить наименьшее количество узлов. Требуемое количество вращений (| E | + | V |)⌈(| V | + 3)/2⌉ .
В недавней статье [54] есть более эффективная реализация отображения для использования в понимании случайных ансамблей этой задачи методом реплик. К сожалению, этот метод не эффективен для AQO; гамильтониан содержит N -частичных членов.
К сожалению, этот метод не эффективен для AQO; гамильтониан содержит N -частичных членов.
8.5. Набор фронтов обратной связи
Для ориентированного графа задача набора ребер с обратной связью состоит в том, чтобы найти наименьшее множество ребер F ⊂ E такое, что ( V , E − F ) является ориентированным ациклическим графом. Известно, что он NP-труден [18]. Наше решение будет чем-то похоже на набор вершин направленной обратной связи. Мы размещаем двоичную переменную y


 2.\)
2.\) 2}\) вычисляем силу притяжения между книгами.
2}\) вычисляем силу притяжения между книгами. 2.\)
2.\)
 3.\)
3.\) 3\).
3\). -15 Н\).
-15 Н\). Разрешение было дано издателем J. Weston Walch для публикации их в PhysicsLAB как
студенческий ресурс. Прежде чем вы начнете просматривать проблемы, найдите минутку
и познакомьтесь с актерским составом
вокруг кого вращаются эти эпизоды. Учителя, вы также можете прочитать Дугласа
Записка Дженкинса «Учителю»
и изучите следующий список их приключений.
Разрешение было дано издателем J. Weston Walch для публикации их в PhysicsLAB как
студенческий ресурс. Прежде чем вы начнете просматривать проблемы, найдите минутку
и познакомьтесь с актерским составом
вокруг кого вращаются эти эпизоды. Учителя, вы также можете прочитать Дугласа
Записка Дженкинса «Учителю»
и изучите следующий список их приключений.
 Многие классические доказательства математических парадоксов (иногда называемые «пуфами») зависят от такого рода обмана, такого как скрытое деление на ноль. Например, доказательство того, что 2 + 2 = 5. (Ну, оно действительно для достаточно больших значений 2.)
Многие классические доказательства математических парадоксов (иногда называемые «пуфами») зависят от такого рода обмана, такого как скрытое деление на ноль. Например, доказательство того, что 2 + 2 = 5. (Ну, оно действительно для достаточно больших значений 2.)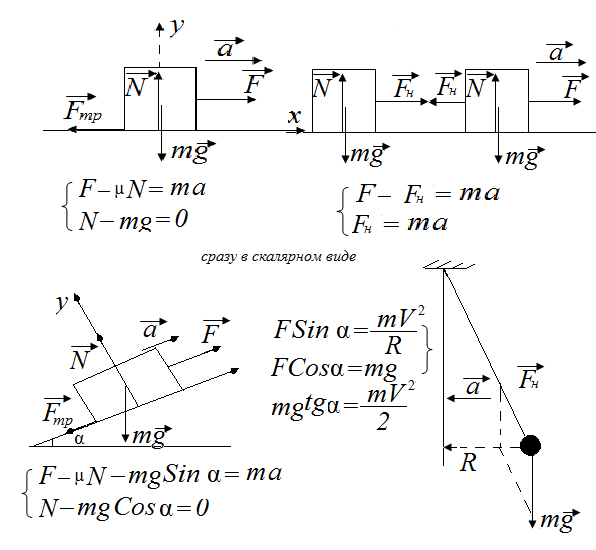 Не обращайте внимания на это отвлечение.
Не обращайте внимания на это отвлечение. 918 метров — это самый длинный судоходный акведук в мире.
918 метров — это самый длинный судоходный акведук в мире. Объясните, как эта сильная муха смогла остановить (даже на короткое время) поезд, движущийся со скоростью 100 миль в час.
Объясните, как эта сильная муха смогла остановить (даже на короткое время) поезд, движущийся со скоростью 100 миль в час. Цилиндры сконструированы так, чтобы иметь одинаковую массу и одинаковый внешний радиус, но один из них сделан из цельного дерева, а другой представляет собой металлический обруч. Обруч, имея больший момент инерции, меньше разгоняется под действием силы тяжести и проигрывает гонку.
Цилиндры сконструированы так, чтобы иметь одинаковую массу и одинаковый внешний радиус, но один из них сделан из цельного дерева, а другой представляет собой металлический обруч. Обруч, имея больший момент инерции, меньше разгоняется под действием силы тяжести и проигрывает гонку.
 Это довольно большие автомобили, поэтому организаторы гонки разработали круговую трассу с наклоном, чтобы автомобили, находящиеся внутри трассы, не имели преимущества. Судя по всему, ипподром так и не был построен, и такие гонки никогда не проводились. Почему?
Это довольно большие автомобили, поэтому организаторы гонки разработали круговую трассу с наклоном, чтобы автомобили, находящиеся внутри трассы, не имели преимущества. Судя по всему, ипподром так и не был построен, и такие гонки никогда не проводились. Почему? Две одинаковые круглые шайбы лежат на горизонтальном столе без трения. Одна шайба продвигается к неподвижной шайбе. Они сталкиваются, и столкновение абсолютно упругое. Шайба Нитера вращается до или после столкновения. Докажите, что после столкновения скорости двух шайб равны друг другу, независимо от того, как произошло столкновение.
Две одинаковые круглые шайбы лежат на горизонтальном столе без трения. Одна шайба продвигается к неподвижной шайбе. Они сталкиваются, и столкновение абсолютно упругое. Шайба Нитера вращается до или после столкновения. Докажите, что после столкновения скорости двух шайб равны друг другу, независимо от того, как произошло столкновение. Является ли результирующее движение простым гармоническим движением или просто периодическим? Является ли его период постоянным?
Является ли результирующее движение простым гармоническим движением или просто периодическим? Является ли его период постоянным? Обычно это небольшой эффект. В этой задаче эта разница в объеме будет проигнорирована. На самом деле, это имело бы незначительный вклад в рассматриваемые здесь изменения давления.
Обычно это небольшой эффект. В этой задаче эта разница в объеме будет проигнорирована. На самом деле, это имело бы незначительный вклад в рассматриваемые здесь изменения давления. При соприкосновении тел на границе раздела действует сила, направленная по нормали к поверхности контакта.Мы показываем силу наклонной стены (зеленый цвет) в точке B и силу пола (синий цвет) в точке A. Синий вектор не имеет горизонтальной составляющей, поэтому мяч не катится. Но у зеленого вектора есть горизонтальная составляющая. Почему эта сила не заставляет мяч откатиться от стены?
При соприкосновении тел на границе раздела действует сила, направленная по нормали к поверхности контакта.Мы показываем силу наклонной стены (зеленый цвет) в точке B и силу пола (синий цвет) в точке A. Синий вектор не имеет горизонтальной составляющей, поэтому мяч не катится. Но у зеленого вектора есть горизонтальная составляющая. Почему эта сила не заставляет мяч откатиться от стены? Это тела, сохраняющие свою физическую форму именно во время взаимодействия. Покажите, что совершенно твердых тел не может быть, потому что они нарушили бы законы Ньютона.
Это тела, сохраняющие свою физическую форму именно во время взаимодействия. Покажите, что совершенно твердых тел не может быть, потому что они нарушили бы законы Ньютона. Два человека внутри крутили рукоятки, приводившие в движение колеса. Зубчатая передача — это обычная «фонарная шестерня» того времени. Не обращая внимания на тривиальное наблюдение, что для этого потребуется два очень сильных человека, почему это не сработает? Нет никаких записей о том, что он когда-либо строился и использовался.
Два человека внутри крутили рукоятки, приводившие в движение колеса. Зубчатая передача — это обычная «фонарная шестерня» того времени. Не обращая внимания на тривиальное наблюдение, что для этого потребуется два очень сильных человека, почему это не сработает? Нет никаких записей о том, что он когда-либо строился и использовался. Помимо тривиального наблюдения, что даже два человека не обеспечат достаточной мощности, у этой идеи есть серьезный недостаток физики, который не позволяет ей оставаться в воздухе.Что это? Очевидно, эта идея не взлетела.
Помимо тривиального наблюдения, что даже два человека не обеспечат достаточной мощности, у этой идеи есть серьезный недостаток физики, который не позволяет ей оставаться в воздухе.Что это? Очевидно, эта идея не взлетела. Но это все? Производит ли линза какие-либо другие изображения?
Но это все? Производит ли линза какие-либо другие изображения?
 В этом контексте обычно упоминается Галилей, хотя до него этот опыт ставили другие, и он, вероятно, никогда не ставил эксперимент со свободно падающими телами (уж точно не на Пизанской башне). Но у Галилея был простой логический аргумент, чтобы заключить, что масса падающего тела не имеет значения.Помните, что во времена Галилея алгебра еще не была изобретена, а исчисление появилось еще позже. Понятие гравитации и закон Ньютона F = м a тоже появились позже. Так как же Галилей пришел к этому важному выводу, используя только простой логический аргумент?
В этом контексте обычно упоминается Галилей, хотя до него этот опыт ставили другие, и он, вероятно, никогда не ставил эксперимент со свободно падающими телами (уж точно не на Пизанской башне). Но у Галилея был простой логический аргумент, чтобы заключить, что масса падающего тела не имеет значения.Помните, что во времена Галилея алгебра еще не была изобретена, а исчисление появилось еще позже. Понятие гравитации и закон Ньютона F = м a тоже появились позже. Так как же Галилей пришел к этому важному выводу, используя только простой логический аргумент? Систему можно заставить разгоняться достаточно медленно, чтобы легко измерить ее ускорение и, применив немного математики, определить значение ускорения под действием силы тяжести. Показанная машина Этвуда подвешена на пружинных балансах. Масса одной подвески M , массы другой (M+m) . Предположим, что более тяжелая сторона (правая
сбоку) подвеска крепится к крючку пружинных весов дополнительной нитью, препятствующей перемещению масс.Шкала показывает (2M+m) .
Систему можно заставить разгоняться достаточно медленно, чтобы легко измерить ее ускорение и, применив немного математики, определить значение ускорения под действием силы тяжести. Показанная машина Этвуда подвешена на пружинных балансах. Масса одной подвески M , массы другой (M+m) . Предположим, что более тяжелая сторона (правая
сбоку) подвеска крепится к крючку пружинных весов дополнительной нитью, препятствующей перемещению масс.Шкала показывает (2M+m) . Часть аргумента рассматривает одну такую частицу, отскакивающую от стены. Нам говорят, что столкновение абсолютно упругое и частица отскакивает от стенки с той же скоростью, с какой она имела перед ударом о стену. Это говорит нам о том, что мяч отскакивает с неизменной кинетической энергией, что все студенты готовы некритически принять. Мы разумно заключаем, что энергия не терялась стенкой. Но как насчет импульса? Частица имела импульс mv до столкновения и импульс − mv после, поскольку импульс является вектором.Таким образом, импульс частицы изменился на -2mv , а по закону сохранения импульса должно было произойти изменение импульса стенки на + 2mv .
Часть аргумента рассматривает одну такую частицу, отскакивающую от стены. Нам говорят, что столкновение абсолютно упругое и частица отскакивает от стенки с той же скоростью, с какой она имела перед ударом о стену. Это говорит нам о том, что мяч отскакивает с неизменной кинетической энергией, что все студенты готовы некритически принять. Мы разумно заключаем, что энергия не терялась стенкой. Но как насчет импульса? Частица имела импульс mv до столкновения и импульс − mv после, поскольку импульс является вектором.Таким образом, импульс частицы изменился на -2mv , а по закону сохранения импульса должно было произойти изменение импульса стенки на + 2mv . Они также говорят нам, что при абсолютно упругом столкновении участвующие тела сохраняют как кинетическую энергию, так и импульс.
Они также говорят нам, что при абсолютно упругом столкновении участвующие тела сохраняют как кинетическую энергию, так и импульс. Трос лифта рвется, и несчастный пассажир падает вместе с лифтом, оказываясь в состоянии «невесомости», в котором он свободно парит в своей системе отсчета лифта, как будто на него не действуют внешние силы. В учебниках часто говорится, что человек внутри не сможет ни одним экспериментом определить, что в его лифте есть гравитационное поле. Этот пример, конечно, ошибочен, так как с помощью чувствительных приборов человек в лифте мог обнаружить гравитационное поле.Как?
Трос лифта рвется, и несчастный пассажир падает вместе с лифтом, оказываясь в состоянии «невесомости», в котором он свободно парит в своей системе отсчета лифта, как будто на него не действуют внешние силы. В учебниках часто говорится, что человек внутри не сможет ни одним экспериментом определить, что в его лифте есть гравитационное поле. Этот пример, конечно, ошибочен, так как с помощью чувствительных приборов человек в лифте мог обнаружить гравитационное поле.Как?
 Шар окружен водой и не касается стенок стакана. Веревка, очевидно, оказывает направленное вверх усилие на дно стакана. Струна рвется, и шарик всплывает на поверхность, плавая там. Веревка больше не оказывает восходящей силы на стакан.Теперь шкала больше, меньше или такая же, как раньше? Подтвердите свои рассуждения свободной диаграммой тела.
Шар окружен водой и не касается стенок стакана. Веревка, очевидно, оказывает направленное вверх усилие на дно стакана. Струна рвется, и шарик всплывает на поверхность, плавая там. Веревка больше не оказывает восходящей силы на стакан.Теперь шкала больше, меньше или такая же, как раньше? Подтвердите свои рассуждения свободной диаграммой тела.

 Вот галерея примеров из Интернета, которые должны иллюстрировать этот эксперимент.
Вот галерея примеров из Интернета, которые должны иллюстрировать этот эксперимент. Он был расстроен. В конце концов я предложил ему выяснить, где находится библиотека колледжа, а затем найти «Оптикс» Ньютона. Там он нашел один способ сделать это успешно.
Он был расстроен. В конце концов я предложил ему выяснить, где находится библиотека колледжа, а затем найти «Оптикс» Ньютона. Там он нашел один способ сделать это успешно. Банка вмещает 12 унций (42 грамма) содовой, поэтому ее общий вес при наполнении составляет 13,5 унций (382 грамма).
Банка вмещает 12 унций (42 грамма) содовой, поэтому ее общий вес при наполнении составляет 13,5 унций (382 грамма). Теперь на этой глубине напор соленой воды в океане вокруг конца трубы составляет более 20 атмосфер, скажем, 21 атмосферу, поэтому пресная вода вытекает из соленой воды океана в трубу пресной воды. Пресная вода будет подниматься примерно на 10 м (21 — 20 = 1 атмосфера) над поверхностью, что-то вроде артезианской скважины. Возможно, вам придется немного отрегулировать глубину в зависимости от плотности морской воды, но принцип кажется правдоподобным.
Теперь на этой глубине напор соленой воды в океане вокруг конца трубы составляет более 20 атмосфер, скажем, 21 атмосферу, поэтому пресная вода вытекает из соленой воды океана в трубу пресной воды. Пресная вода будет подниматься примерно на 10 м (21 — 20 = 1 атмосфера) над поверхностью, что-то вроде артезианской скважины. Возможно, вам придется немного отрегулировать глубину в зависимости от плотности морской воды, но принцип кажется правдоподобным.
 Вот версия, в которой устранена большая часть двусмысленности.
Вот версия, в которой устранена большая часть двусмысленности. Вы даже не можете использовать магнитное поле Земли.Так как же проще всего идентифицировать намагниченный стержень?
Вы даже не можете использовать магнитное поле Земли.Так как же проще всего идентифицировать намагниченный стержень?
 Конечно, трение противоположно скорости мяча и, следовательно, замедляет движение мяча по второму закону Ньютона. Но эта сила из-за трения имеет крутящий момент, и этот вектор крутящего момента вокруг центра масс мяча имеет то же направление, что и вектор угловой скорости мяча. Это увеличит угловую скорость мяча, заставляя его катиться все быстрее и быстрее. Разрешите это кажущееся противоречие.
Конечно, трение противоположно скорости мяча и, следовательно, замедляет движение мяча по второму закону Ньютона. Но эта сила из-за трения имеет крутящий момент, и этот вектор крутящего момента вокруг центра масс мяча имеет то же направление, что и вектор угловой скорости мяча. Это увеличит угловую скорость мяча, заставляя его катиться все быстрее и быстрее. Разрешите это кажущееся противоречие. Используется легкий стул с верхним шкивом. Может ли это работать? Есть ли ограничения в этой системе? Показать векторный анализ с бесплатными диаграммами тела.
Используется легкий стул с верхним шкивом. Может ли это работать? Есть ли ограничения в этой системе? Показать векторный анализ с бесплатными диаграммами тела.

 Поднимите соломинку, пока она полностью не выйдет из воды (С). Что, по вашему прогнозу, произойдет? Подтвердите свой ответ аргументом, основанным на физических законах. В частности, обсудите, что происходит в боковой дыре. Теперь попробуйте.
Поднимите соломинку, пока она полностью не выйдет из воды (С). Что, по вашему прогнозу, произойдет? Подтвердите свой ответ аргументом, основанным на физических законах. В частности, обсудите, что происходит в боковой дыре. Теперь попробуйте.

 Не должно ли это начальное движение смещать маятник, чтобы он сохранял это движение до конца дня, чтобы его плоскость движения совсем не менялась по отношению к зданию? Следовательно, никакой явной прецессии не наблюдалось бы.
Не должно ли это начальное движение смещать маятник, чтобы он сохранял это движение до конца дня, чтобы его плоскость движения совсем не менялась по отношению к зданию? Следовательно, никакой явной прецессии не наблюдалось бы. Единственным исключением является Великобритания (и несколько других стран), где все они идут по часовой стрелке, включая автомобильное движение и кольцевые развязки.
Единственным исключением является Великобритания (и несколько других стран), где все они идут по часовой стрелке, включая автомобильное движение и кольцевые развязки. Чтобы он продолжал работать, что-то еще должно поставлять энергию в форме работы. Но если струна радиальна, а мяч движется по касательной к своей круговой траектории, сила и перемещение перпендикулярны друг другу. Так как же струна может воздействовать на мяч, чтобы поддерживать его движение?
Чтобы он продолжал работать, что-то еще должно поставлять энергию в форме работы. Но если струна радиальна, а мяч движется по касательной к своей круговой траектории, сила и перемещение перпендикулярны друг другу. Так как же струна может воздействовать на мяч, чтобы поддерживать его движение? Учебники часто говорят нам, что закон Ньютона звучит примерно так: «Каждому действию есть равное и противоположное противодействие». Конечно, это небрежно сформулировано. Как могут две вещи быть равными и противоположными? Следует сказать: «На всякое действие есть равная по величине и противоположно направленная реакция».
Учебники часто говорят нам, что закон Ньютона звучит примерно так: «Каждому действию есть равное и противоположное противодействие». Конечно, это небрежно сформулировано. Как могут две вещи быть равными и противоположными? Следует сказать: «На всякое действие есть равная по величине и противоположно направленная реакция». Птолемеевская модель Солнечной системы была геоцентрической (в центре Земли) и полностью основывалась на кругах (которые считались идеальной фигурой). Чтобы согласиться с наблюдениями за положением планет, он стал чрезвычайно геометрически сложным, с кругами (циклами) и меньшими кругами (эпицилами), деферентами и эквантами и другими уловками, чтобы согласовать его с наблюдениями.
Птолемеевская модель Солнечной системы была геоцентрической (в центре Земли) и полностью основывалась на кругах (которые считались идеальной фигурой). Чтобы согласиться с наблюдениями за положением планет, он стал чрезвычайно геометрически сложным, с кругами (циклами) и меньшими кругами (эпицилами), деферентами и эквантами и другими уловками, чтобы согласовать его с наблюдениями. Шесть заброшенных циклов и эпициклов имели в системе Птолемея одну важную общую черту.Что это было?
Шесть заброшенных циклов и эпициклов имели в системе Птолемея одну важную общую черту.Что это было? Я попытался переформулировать его, чтобы устранить двусмысленность (что непросто).
Я попытался переформулировать его, чтобы устранить двусмысленность (что непросто). Какова разность потенциалов на входах А и В этой цепи? Чему равно сопротивление всей цепи, измеренное в точках А и В? Какой ток подает источник питания в эту цепь?
Какова разность потенциалов на входах А и В этой цепи? Чему равно сопротивление всей цепи, измеренное в точках А и В? Какой ток подает источник питания в эту цепь? Чему равно натяжение троса в его нижней точке? Чему равно его напряжение на каждом из полюсов?
Чему равно натяжение троса в его нижней точке? Чему равно его напряжение на каждом из полюсов?


 Луна вращается вокруг Земли против часовой стрелки. Земля вращается вокруг своей оси против часовой стрелки. Тогда почему область полного солнечного затмения перемещается по земле с запада на восток? Например, во время солнечного затмения в США в 2017 году полная область прибыла на западное побережье в штате Орегон примерно через 1,5 часа и была замечена на восточном побережье в Чарльстоне, Южная Каролина. Проверьте свой ответ, рассчитав время, которое потребовалось полной области, чтобы пересечь У.S.A.
Луна вращается вокруг Земли против часовой стрелки. Земля вращается вокруг своей оси против часовой стрелки. Тогда почему область полного солнечного затмения перемещается по земле с запада на восток? Например, во время солнечного затмения в США в 2017 году полная область прибыла на западное побережье в штате Орегон примерно через 1,5 часа и была замечена на восточном побережье в Чарльстоне, Южная Каролина. Проверьте свой ответ, рассчитав время, которое потребовалось полной области, чтобы пересечь У.S.A. В Северном полушарии лето теплее зимы. Почему? Обычный поверхностный ответ таков: «Потому что земная ось имеет фиксированное направление в пространстве, и летом она наклоняется к солнцу, а зимой отклоняется от солнца». Это правда, но это не полный ответ. Не упомянуты два важных процесса. Можете ли вы объяснить, почему наклон влияет на сезонные температуры?
В Северном полушарии лето теплее зимы. Почему? Обычный поверхностный ответ таков: «Потому что земная ось имеет фиксированное направление в пространстве, и летом она наклоняется к солнцу, а зимой отклоняется от солнца». Это правда, но это не полный ответ. Не упомянуты два важных процесса. Можете ли вы объяснить, почему наклон влияет на сезонные температуры? Почему это должно быть так, если при 90° должно быть столько же притяжения, сколько и отталкивания, и вы ожидаете, что карты не будут притягиваться?
Почему это должно быть так, если при 90° должно быть столько же притяжения, сколько и отталкивания, и вы ожидаете, что карты не будут притягиваться?
 Где-то в своем ответе на предыдущую задачу вы, возможно, утверждали, что «горячий воздух поднимается вверх». Это поднимает фундаментальный вопрос: «Почему горячий воздух поднимается вверх?» Упрощенные объяснения из учебников утверждают, что воздух рядом с пламенем расширяется и, следовательно, становится менее плотным, а более легкие предметы поднимаются в более плотных жидкостях. Это действительно объясняет процесс? Почему нагретый воздух ведет себя как объем меньшей плотности, чем окружающий воздух?
Где-то в своем ответе на предыдущую задачу вы, возможно, утверждали, что «горячий воздух поднимается вверх». Это поднимает фундаментальный вопрос: «Почему горячий воздух поднимается вверх?» Упрощенные объяснения из учебников утверждают, что воздух рядом с пламенем расширяется и, следовательно, становится менее плотным, а более легкие предметы поднимаются в более плотных жидкостях. Это действительно объясняет процесс? Почему нагретый воздух ведет себя как объем меньшей плотности, чем окружающий воздух?
 Теперь мы можем записать очень похожую энергию для минимального остовного дерева:
Теперь мы можем записать очень похожую энергию для минимального остовного дерева: HA=A∑v(1−∑ixv,i)2+A∑uv∈E(yuv−∑ixuv,i)2 +A∑uv∑ixuv,i(2−xu,i−∑j>ixv,j ). (68)
HA=A∑v(1−∑ixv,i)2+A∑uv∈E(yuv−∑ixuv,i)2 +A∑uv∑ixuv,i(2−xu,i−∑j>ixv,j ). (68) Если существует такая матрица перестановок P, что A 2 = P T A 1 P, то мы говорим, что G 1,2 изоморфны.
Если существует такая матрица перестановок P, что A 2 = P T A 1 P, то мы говорим, что G 1,2 изоморфны. Затем мы используем энергию
Затем мы используем энергию Остается открытым вопрос, в какой степени AQO поможет найти эффективные решения этих проблем, будут ли эти решения точными или приблизительными.
Остается открытым вопрос, в какой степени AQO поможет найти эффективные решения этих проблем, будут ли эти решения точными или приблизительными. Рассмотрим простую задачу поиска наибольшего целого числа в списке n 1 , …, n N (это алгоритм поиска, который может эффективно выполнять универсальный квантовый компьютер). Введение бинарных переменных x i for i = 1, …, N , модель Изинга
Рассмотрим простую задачу поиска наибольшего целого числа в списке n 1 , …, n N (это алгоритм поиска, который может эффективно выполнять универсальный квантовый компьютер). Введение бинарных переменных x i for i = 1, …, N , модель Изинга Чтобы быть NP-полной, но не P (если P ≠ NP), нужно только небольшое семейство экземпляров задачи, которая не может быть решена за полиномиальное время с помощью детерминированного алгоритма. Тем не менее, типичные экземпляры могут быть не такими сложными. Многие популярные задачи NP почти наверняка могут быть решены точно за полиномиальное время на больших случайных экземплярах [58, 59], и существуют рандомизированные алгоритмы для некоторых задач NP, которые могут быть сколь угодно близки к решению с произвольно низкой вероятностью отказа за полиномиальное время [60]. , 61] (хотя мультипликативные коэффициенты или полиномиальные показатели должны расходиться, поскольку вероятность отказа и/или ошибка при определении основного состояния стремится к нулю, если P ≠ NP).Кроме того, популярные алгоритмы в P, такие как декомпозиция матриц, могут служить узкими местами практических вычислений, и их не следует считать «простыми». Типичные случаи приближаются к асимптотическим границам для наихудшего времени выполнения, в отличие от случая для некоторых проблем NP; многие недавние разработки сосредоточены на рандомизированных алгоритмах [62–64].
Чтобы быть NP-полной, но не P (если P ≠ NP), нужно только небольшое семейство экземпляров задачи, которая не может быть решена за полиномиальное время с помощью детерминированного алгоритма. Тем не менее, типичные экземпляры могут быть не такими сложными. Многие популярные задачи NP почти наверняка могут быть решены точно за полиномиальное время на больших случайных экземплярах [58, 59], и существуют рандомизированные алгоритмы для некоторых задач NP, которые могут быть сколь угодно близки к решению с произвольно низкой вероятностью отказа за полиномиальное время [60]. , 61] (хотя мультипликативные коэффициенты или полиномиальные показатели должны расходиться, поскольку вероятность отказа и/или ошибка при определении основного состояния стремится к нулю, если P ≠ NP).Кроме того, популярные алгоритмы в P, такие как декомпозиция матриц, могут служить узкими местами практических вычислений, и их не следует считать «простыми». Типичные случаи приближаются к асимптотическим границам для наихудшего времени выполнения, в отличие от случая для некоторых проблем NP; многие недавние разработки сосредоточены на рандомизированных алгоритмах [62–64].