Задачи на растворы и концентрацию

Для того, чтобы решать задачи на растворы и концентрацию, необходимо чётко понимать, что называется концентрацией раствора.

Концентрация раствора — это часть, которую составляет масса растворённого вещества от массы всего раствора.

• 9%-я концентрация раствора соли — это 9 грамм соли в 100 граммах раствора.

Килограмм соли растворили в 9 л воды. Чему равна концентрация полученного раствора? (Масса 1 л воды составляет 1 кг)

Используя определение концентрации данное выше, решим задачу следующим образом.

• 1 кг — масса растворённого вещества (соли)

• 9 кг — масса воды в растворе (не путать с общей массой раствора)

• 9 + 1 = 10 кг — общая масса раствора.

Ответ: 10% — концентрация раствора.

Сколько соли получится при выпаривании 375 граммов 12%-го раствора?

Чтобы найти массу выпаренной соли из раствора, умножим общую массу раствора на процент концентрации. Не забудем предварительно перевести процент в десятичную дробь.

Ответ: 45 г соли.

Сложная задача на растворы

В растворе 40% соли. Если добавить 120 г соли, то процентное содержание соли станет равным 70. Сколько грамм соли было первоначально в растворе?

Для составления пропорции обозначим за «x» первоначальную массу соли в растворе, а за «y» массу воды в растворе. Так как концентрация соли в исходном растворе 40%, то соответственно вода составляет 

100% — 40%= 60% 

Изобразим графически условия задачи.

Составим пропорцию, связывающую эти величины до добавления соли.

Для решения задачи нам надо определить какая из неизвестных (x или y) остаётся неизменной после добавления соли.

Этой величиной является масса воды в растворе (y).

Выразим её, учитывая изменения в растворе после добавления соли.

• (x + 120) г — масса соли в новом растворе

• 100% — 70% = 30% — процентное содержание воды в новом растворе.

Составим пропорцию аналогично предыдущей, но с учётом изменений произошедших после добавления соли.

Так как масса воды осталось неизменной после добавления соли, приравняем её значения до и после добавления соли и решим уравнение.

Ответ: 48 г — масса соли в первоначальном растворе.

Задачи по вкладам

Естественно, люди кладут деньги в банк (открывают вклад), не по доброте душевной. Вклады открываются с целью получения прибыли. Банк предлагает следующее: вы кладёте в банк определённую сумму на определённый срок. Например, на год. В течение года вы не сможете воспользоваться своими деньгами (ими будет пользоваться банк), но за это банк вам заплатит, вернув через год не только вложенную вами сумму, но и небольшое вознаграждение.

Какова будет сумма вознаграждения? Для её нахождения банк устанавливает процент годовых. Если вы умножите сумму вашего вклада на процент годовых, вы найдёте, какое вознаграждение добавит банк к вашему вкладу.

.

Вкладчик внес в банк 1200 р. В какую сумму вклад превратится через год, если банк начисляет доход в размере 4 % годовых?

Решение:

Найдем какое вознаграждение банк доложит вкладчику. Для этого умножим 1200 р. на процент годовых 4%.

4% = 0,04

1200 • 0, 04 = 48 р. — такое вознаграждение доложит банк вкладчику через год.

Теперь найдем общую сумму, которую заберет вкладчик через год.

1200 + 48 = 1248 р. — в такую сумму превратится вклад через год.

Ответ: 1248 р. — в такую сумму превратится вклад через год.

Задачи на скидку (уценку)

Скидка — это понижение цены товара или услуги. Чаще всего скидку указывают в процентах. Поэтому, чтобы найти на сколько в рублях понизилась цена товара, нужно цену товара умножить на процент скидки.

Задача из ГИА 9 класс

Цена изделия составляет 5000 р. На изделие предложена скидка 10%. Найти цену товара с учетом скидки.

Решение:

Найдем скидку в рублях.

10% = 0,1

5000 • 0,1 = 500 р. — скидка в рублях.

Теперь найдем цену товара с учетом скидки.

5000 — 500 = 4500 р. — цена товара с учетом скидки.

Ответ: 4500 р. — цена товара с учетом скидки.

Процент — это одна сотая часть от числа.

Процент записывается с помощью знака %.

• Чтобы перевести проценты в дробь, нужно убрать знак % и разделить число на 100.

• Чтобы перевести десятичную дробь в проценты, нужно дробь умножить на 100 и добавить знак %.

• Чтобы перевести обыкновенную дробь в проценты, нужно сначала превратить её в десятичную дробь.

Перевод дробей в проценты

Как вы поняли, проценты тесно связаны с обыкновенными и десятичными дробями. Поэтому стоит запомнить несколько простых равенств. В повседневной жизни нужно знать о числовой связи дробей и процентов. Так, половина — 50%, четверть — 25%, три четверти — 75%, одна пятая — 20%, а три пятых — 60%.

Знание наизусть соотношений из таблицы внизу облегчит вам решение многих задач.

1 = 100%

Дробь	1/2		1/4	3/4	1/5	2/5	3/5	1/10	1/20		1/50
Десятичная дробь	0,5		0,25	0,75	0,2	0,4	0,6	0,1	0,05		0,02
Проценты	50%		25%	75%	20%	40%	60%	10%	5%		2%

Проценты можно складывать и вычитать только с самими процентами.

Сложение и вычитание процентов

Проценты складываются и вычитаются друг с другом как обычные числа.

Примеры:

• 1% + 37% — 25% = 38% — 25% = 13%

• 70% — (42% + 3%) = 70% — 45% = 25%

В повседневной жизни полезно знать разные формы выражения одного и того же изменения величин, сформулированных без процентов и с помощью процентов.

Например, увеличить в 2 раза, значит увеличить на 100%. Разберёмся, почему это так.

Пусть x — это 100%.

Тогда, увеличив «x» в 2 раза, получим «2x».

Сравним полученные результаты.

Получилось, что общее количество процентов равно 200%. Увеличить в 2 раза означает увеличить на 100% и наоборот.

Рассуждая, таким же образом, докажем, что увеличить на 50%, значит увеличить в 1,5 раза .

Уменьшение числа также может быть выражено в процентах.

Пусть x — 100%.

Известно, что «x» уменьшилось на 80%. Найдём, во сколько раз уменьшилось «x».

Вначале найдём, сколько процентов от «x» осталось.

100% — 80% = 20% 

20% осталось от «x». Обозначим остаток «x» за «y».

Составим пропорцию. По числовому коэффициенту определяем, во сколько раз уменьшился «x».

Таким образом, мы установили, что уменьшить на 80%, значит уменьшить в 5 раз.

Поняв связь между процентами и «разами», вы без труда сможете понимать о чём так часто говорят в новостях и в газетах, приводя различные статические данные.

Некоторые, наиболее употребимые фразы, желательно просто запомнить, чтобы всегда точно понимать о чём идёт речь. Список таких фраз представлен ниже.

Значение фраз «увеличить и уменьшить на … процентов»

Увеличить на 50%, значит увеличить в 1,5 раза

• на 100% → в 2 раза

• на 150% → в 2,5 раза

• на 200% → в 3 раза

• на 300% → в 4 раза

Уменьшить на 80%, значит уменьшить в 5 раз

• на 75% → в 4 раза

• на 50% → в 2 раза

• на 25% → в ≈ 1,33 раза

• на 20% → в 1,25 раза

Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Предприятие изготовило за квартал 500 насосов, из которых 60 % имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?

Решение:

Найдем 60 % от 500 (общее количество насосов).

60 % = 0,6

500 • 0,6 = 300 насосов высшей категории качества.

Ответ: 300 насосов высшей категории качества.

Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать текст. Если вам встречаются слова «который», «что составляет» и «который составляет», скорее всего перед вами задача «число по его проценту«.

Ученик прочитал 138 страниц, что составляет 23 % числа всех страниц в книге. Сколько страниц в книге?

Решение:

Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую прочитал ученик (138 страниц) составляет 23 % от общего количества страниц в книге. Так как 138 стр. — это всего лишь часть, само количество страниц, естественно, будет больше 138. Это поможет нам при проверке.

Проверка: 600 138 (это означает, что 138 является частью 600).

Ответ: 600 (стр.) — общее количество страниц в книге.

Сколько процентов одно число составляет от другого

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100 %.

Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелый арбузы?

Решение:

О чем спрашивают? О незрелых арбузах. Значит, 16 делим на общее количество арбузов и умножаем на 100 %.

Ответ: 8 % — составляют незрелые арбузы от всех арбузов.

Урок алгебры в 9-м классе по теме «Решение задач на концентрацию»

Цель урока: развивать у учащихся навыки решения и оформления задач на концентрацию; сформировать общие подходы к решению задач на концентрацию.

Задачи, которые мы будем решать, относятся к традиционным задачам математики. Они охватывают большой круг ситуаций: жидкостей с различным содержанием соли, кислот разной концентрации, сплавление металлов с различным содержанием некоторого металла. Когда-то они имели исключительно практическое значение. В настоящее время эти задачи часто встречаются в тестах на выпускных экзаменах и на вступительных экзаменах в вузы.

Мы рассмотрим задачи на смешение, которые можно решить алгебраическим способом.

Для успешной работы нам понадобится повторить основные понятия этой темы.

Ход урока

Приложение

I. Фронтальная работа с классом.

1.

Сформулируйте определение концентрации.

(Концентрация вещества в смеси – это часть, которую составляет масса вещества в смеси от массы смеси) Нахождение части от целого. В химии вы называли эту величину массовой долей вещества.

Концентрация вещества может быть указана и числом и %.

2

. Объясните значение высказываний:

а)

Концентрация раствора 23 %;

(В 100 г раствора содержится 23 г вещества).

б)

Молоко имеет 1,8 % жирности;

(В100 г молока содержится 1,8 г жира).

в) Сколько сахара содержится в 200 г 10%– го сахарного сиропа?

Теперь давайте попробуем решить устно несколько задач.

3.

К одной части сахара прибавили 4 части воды. Какова концентрация полученного раствора?

(1: 5 ·100 = 20 %)

4.

Килограмм соли растворили в 9 л воды. Какова концентрация раствора?

(1 : 10 ·100 = 10%)

II. Решение задач

Конечно, вы понимаете, что не все задачи можно решить устно. Следующие задачи мы решим с вами с помощью уравнения.

Рассмотрим решения задач с применением таблицы.

№ 199 Сколько граммов воды надо добавить к 80 % раствора, содержащего 15 % соли, чтобы получить 12 % раствор?

Наименование веществ, смесей	Масса раствора, г	% содержание (доля) вещества	Масса соли, г
I раствор	80	15% = 0, 15	0, 15*80 = 12
вода	х	0%	0
Новый раствор	(80 + х)	12% = 0,12	0,12*(80 + х)

0,12*(80 + х) = 12

(80 + х) = 100

Х = 100 – 80

Х = 20 (г) Ответ: надо добавить 20 г воды.

№ 200 Сколько граммов воды надо добавить к 180 г сиропа, концентрация сахара в котором 25%, чтобы получить сироп с концентрацией сахара 20 %?

Наименование веществ, смесей	Масса раствора, г	% содержание (доля) вещества	Масса сахара, г
I сироп	180	25% = 0, 25	0, 25*180 = 45
вода	х	0%	0
Новый сироп	(180 + х)	20% = 0,2	0,2*(180 + х)

Составим уравнение, используя данные четвертого столбца

0,2*(180 + х) = 45

36 + 0,2х = 45

0,2х = 45 – 36

0,2х = 9

Х = 9:0,2

Х = 45 (г) Ответ: надо добавить 45 г воды.

№ 204 Сколько граммов 30 %-ного раствора надо добавить к 80 г 12 %-ного раствора этой же соли, чтобы получить 20 %-ный раствор соли?

Наименование веществ, смесей	Масса раствора, г	% содержание (доля) вещества	Масса соли, г
I раствор	х	30% = 0, 3	0,3х
I I раствор	80	12% = 0,12	0,12*80 = 9,6
Новый раствор	(80 + х)	20% = 0,2	0,2*(80 + х)

Составим уравнение, используя данные четвертого столбца

0,3х + 9,6 = 0,2*(80 + х)

0,3х + 9,6 = 16 + 0,2х

0,3х – 0,2х =16 – 9,6

0,1х = 6,4

Х = 64(г) Ответ: надо добавить 64 г 30 %-ного раствора соли.

№ 205 Два слитка, один из которых содержит 35% серебра, а другой – 65 %, сплавляют и получают слиток массой 20 г, содержащий 47 % серебра. Чему равна масса каждого из этих слитков?

Наименование веществ, сплава	Масса раствора, г	% содержание (доля) вещества	Масса серебра, г
I слиток	х	35% = 0, 35	0,35х
I I слиток	(20 – х)	65% = 0,65	0,65(20 – х)
Новый сплав	20	47% = 0,47	0,47*20 = 9,4

Анализируя таблицу, составляем уравнение

0,35х + 0,65(20 – х) = 9,4

0,35х + 13 – 0,65х = 9,4

– 0,3х = 9,4 –13

– 0,3х = – 3,6

Х = – 3,6 : (– 0,3)

Х = 12 (г) 35 %-ного раствора

20 – 12 = 8 (г) 65 %-ного раствора.

Ответ: 12 (г) 35 %-ного раствора; 8 (г) 65 %-ного раствора.

Подведем итог урока. Сегодня мы познакомились с алгебраическим способом решения задач на смешение. Конечно, не все задачи можно решить этим способом, но я думаю, что вам интересно было познакомиться с ним. Дома еще раз осмыслить способ решения и я думаю, что на уроках в 9 классе при подготовке к итоговой аттестации вы успешно примените этот способ.

Задачи на концентрацию смесей и сплавов

Пусть M – масса смеси, которая содержит некоторое вещество массой m. Тогда концентрацией данного вещества в смеси называют величину C = m/M, а процентным содержанием называют величину C · 100%.

Задачи на смеси и сплавы разделяют на два вида:

а) даны две смеси с массами m₁ и m₂ с концентрацией в них вещества C₁ и C₂. Смеси сливают. Требуется определить массу этого вещества в новой смеси и его новую концентрацию.

C₁m₁ + C₂m₂ – масса данного вещества в новой смеси.

C = (C₁m₁ + C₂m₂) / (m₁ + m₂) – концентрация вещества в новой смеси. Заметим, что при решении такого рода задач главное не заучивание данных формул, а понимание математической сути решения.

б) изменение объема смесей с помощью долива или отлива. В таких задачах необходимо установить контроль за количеством данного вещества и его концентрацией.

Решим несколько задач.

Задача 1.

Имеются два раствора соли. Чтобы получить 10 %-ый  раствор, их смешивают. Причем первого раствора берут вдвое больше, чем второго. Через некоторое время из каждого раствора испарилось по 200 грамм воды на 1 килограмм смеси. Теперь на приготовление такой же смеси первого раствора требуется уже вчетверо больше, чем второго. Какова была концентрация растворов первоначально?

Решение.

1-й способ. Довольно путаное условие. Какие величины надо ввести, чтобы решить задачу? Во-первых, искомые p и q – начальные концентрации, s₁ и s₂ кг – массы соли, m₁ и m₂ – массы растворов. Тогда p₁ = s₁/m₁, p₂ = s₂/m₂ – начальные концентрации.

До испарения:

Возьмем 2x первого раствора и x – второго. Всего получим 3x раствора, в котором будет (2s₁ + s₂) соли. Концентрация соли составляет (2s₁ + s₂)/3x и равна 10%, т.е. (2s₁ + s₂)/3x = 0,1. Откуда 2s₁ + s₂ = 0,3x.

После испарения:

Что изменилось? Соль осталась, а общая масса раствора уменьшилась. Теперь та же доза весит 0,8x, т.к. от каждого килограмма осталось 800 грамм. Четыре дозы первого раствора и одна второго теперь весят
4 · 0,8x + 0,8x = 4x, а соли в них будет 4s₁ + s₂ = 0,4x.

Таким образом, мы получили четыре уравнения и пять неизвестных. Ясно, что из условия задачи массу раствора найти нельзя, ее можно исключить из уравнений. Для решения системы необходимо уменьшить число неизвестных. Для этого выразим их через искомые величины:

{2p₁x + p₂x = 0,3x,
{4p₁x + p₂x = 0,4x.

Разделив на x каждое уравнение системы, легко найти искомые величины.

2-й способ. После подробного разбора посмотрим, где можно сократить решение и какие величины можно не вводить. Так как масса дозы не влияет на ответ, ее можно взять за 1. Величины s₁ и s₂ так же не участвуют в решении.

Окончательное и рациональное решение выглядит так: Обозначим концентрацию соли в первом и втором растворе p и q. Это значит, что в одном килограмме первого раствора до испарения содержалось p кг соли, а во втором q кг. Возьмем 2 кг первого и 1 кг второго раствора. В этой смеси будет (2p + q) кг соли, что составляет 0,4 кг.

Получили систему

{2p + q = 0,3,
{4p + q = 0,4.

Решая систему, найдем p = 0,05 = 5 %, q = 0,2 = 20 %.

Ответ: 5 % и 20 %.

Как видим, в окончательном решении нам понадобилось всего две переменные. Однако это не означает, что все промежуточные переменные мы вводили зря: они помогли нам лучше разобраться в ситуации и экономно составить уравнения.

Заметим, что в каждом конкретном случае необходимо найти компромисс между красотой решения и усилиями, затраченными на его поиск. Например, на экзамене важно время, особенно если он проводится в тестовой форме, когда учитывается только ответ. А вот на олимпиаде жюри учитывает качество решения не меньше, чем его правильность.

Задача 2.

Первый раствор содержит 0,8 кг, а второй 0,6 кг серной кислоты, при этом процентное содержание кислоты в первом растворе на 10 % больше, чем во втором. Какова масса каждого из растворов, если их общая масса равна 10 кг?

Решение.

Если x кг – масса первого раствора, то (10 – x) кг – масса второго. Процентное содержание серной кислоты в растворах выражается формулами:

(0,8 · 100 %) / x и (0,6 · 100 %) / (10 – x) · 80/x – 60 / (10 – x) = 10 %. Упростив уравнение, получим x² – 24x + 80 = 0 и найдем x = 4.

Ответ: 4 кг и 6 кг.

Задача 3. Сплав состоит из олова, меди и цинка. Если от этого сплава отделить 20 г и сплавить их с 2 г олова, то в новом сплаве масса меди равна массе олова. Если же отделить от первоначального сплава 30 г и прибавить 9 г цинка, то в новом сплаве масса олова будет равна массе цинка. Определить в процентах состав первоначального сплава.

Решение.

Пусть x, y, z – концентрация меди, олова и цинка (можно брать и процентное содержание).

По условию 20x = 20y + 2 и 30y = 30z + 9.

Имеем систему:

{10x = 10y + 1,
{10y = 10z + 3,
{x + y + z = 1.

Решая систему, получим: x = 0,5; y = 0,4; z = 0,1.

Ответ: 50 %, 40 %, 10 %.

Задачи на смеси и сплавы включены в материалы ГИА и ЕГЭ, часто встречаются на олимпиадах. Кроме того, эти задачи являются хорошим средством развития мышления, а так же имеют  большое практическое значение.

 Остались вопросы? Не знаете, как решать задачи на концентрацию?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Отношение (концентрация). 6-й класс

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель: создать условия для формирования умений решать задачи на растворы на основе знаний процентов, отношений и умений работы с дробями.

Задачи:

Образовательные

• повторить понятия проценты, отношения;
• закрепить знания, умения и навыки решения задач на нахождение числа по его дроби и нахождение дроби от числа, работы с дробями;
• показать практическую значимость математических знаний для решения задач на концентрацию.

Воспитательные

• показать практическую значимость математических знаний для решения задач на концентрацию из повседневной жизни;
• воспитание у учащихся интереса к предмету.

Развивающие

• развивать наблюдательность, логическое мышление учащихся;
• развивать жизненную смекалку и интуицию.

Необходимое оборудование и материалы: доска, мел, карточка с задачами, презентация.

План урока:

1. Мотивационный момент (1 минута).
2. Подготовка учащихся к сознательному усвоению нового материала (5 минут).
3. Изучение нового материала (12 минут).
4. Решение задач на отработку формул (3 мин).
5. Физминутка (1 минута).
6. Первичное закрепление нового материала (15минут).
7. Рефлексия (1 минута).
8. Подведение итогов. Домашнее задание (2 минуты).

Ход урока

I. Мотивационный момент.

Ребята, мы с вами решали задачи, содержащие проценты. Мы также знаем, что отношения существуют и между людьми, и между числами, и между величинами. Они часто встречаются в задачах. А могут быть отношения и проценты в задачах на смеси и растворы? Ответ на этот вопрос найдем на уроке.

II. Подготовка к сознательному усвоению нового материала.

(Слайд 2)

1. Выразить десятичной дробью, а потом обыкновенной: 25%, 10%, 50%, 75%, 125%.
2. Указать в виде процентов: 0,7; 0,04; 1,3.
3. Найти 15% от числа 60.
4. Найти число, 15% которого равны 30.
5. Из 25 семян взошло 24 семени. Найдите процент всхожести.
6. Итак, известные нам отношения: (Слайд 3)

Всхожесть = ; .

Значения данных отношений мы представляли в виде процентов.

III. Изучение нового материала.

Человеку часто приходится смешивать различные жидкости, порошки, вещества или разбавлять что-нибудь водой. При этом используют слово «концентрация». Как вы понимаете это слово?

В большом энциклопедическом словаре «концентрация (от новолат. concentratio) – сосредоточение, скапливание, собирание кого-либо, чего-либо в к.-л. месте» [1].

Концентрация в химии – величина, выражающая относительное количество данного компонента (независимой составной части) в физико-химической системе (смеси, растворе, сплаве) [2].

Сейчас разберемся с этим понятием с точки зрения математики. (Слайд 4)

Нальем в стакан 150 г воды и растворим в ней 50 г сахара. Какой станет масса раствора?[3]

50+150=200 (г) – масса общая. (Слайд 5)

Раствор тщательно перемешиваем.

Найдите процентное содержание сахара в растворе.

50 : 200=1: 4 = 0,25;

0,25=25%

25% – процентное содержание сахара в данном растворе.

Число 0,25 называют концентрацией сахара в растворе. (Слайд 6)

Итак, в математике, концентрацию можно представить как отношение чистого вещества к раствору (сплаву, смеси).

Концентрация = , т.е. К=.

Как по этой формуле найти М_ч.в? М_общ?

М_ч.в. = М_общ · К

М_общ = Мч.в: К

(Слайд 7)

IV. Решение задач на отработку формул:

(Слайд 8)

1. В 500 г раствора содержится 100 г соли. Найдите концентрацию соли в данном растворе. Процентное содержание соли в растворе?
2. 200 г раствора содержит 80% соли. Найдите массу соли в этом растворе.
3. Какова масса раствора, в котором 150 г сахара составляют 25%.

Во многих текстовых задачах понятие «концентрация» может быть заменено на:[3] (Слайд 9-10)

Рис.1.

Подумайте, отношение каких величин используется в понятиях «жирность, соленость, проба».

Встречая эти слова в текстах задач, вы должны понимать, что речь идет о «концентрации» того или другого чистого вещества в растворах или сплавах или смесях.

V. Физминутка.

(Слайд 11)

Следите глазами за движениями черепашек.

VI. Первичное закрепление нового материала.

Решим несколько задач на «концентрацию».

(Задачи 1-4 заранее распечатаны на листочке. (Приложение 1) Данные условий задач вносим в таблицу, обсуждаем ход решения. Отвечаем на вопросы к действиям.

Задача 1. В одну банку мама налила 480 г воды и насыпала 120 г сахара, в другую – 840 г воды и 160 г сахара. В какой банке вода слаще? [4] (Слайд 12-13)

Чтобы ответить на вопрос задачи, необходимо найти концентрации сахара в растворах каждой банки и сравнить их.

Решение:

1. Какова масса раствора в первой банке?
   480+120 = 600 (г)

2. Какова концентрация сахара в растворе первой банки?
   120:600 = 0,2; 0,2=20%

3. Какова масса раствора во второй банке?
   840+160 = 1000(г)

4. Какова концентрация сахара в растворе второй банки?
   160:1000 = 0,16; 0,16=16%

5. В какой банке вода слаще?
   20% > 16%

Ответ: в первой банке вода слаще.

Задача 2. Смешивают 200 г 80%-го раствора соли и 700 г 20%-го раствора той же соли. Сколько соли в полученном растворе? (Слайд 14-15)

Решение:

80% – это процентное содержание соли в 200г раствора (концентрация 0,8)

1. Сколько г соли в этом растворе?
   0,8 ·200=160(г)

20% – это содержание соли в 700 г раствора (концентрация соли 0,2)

2. Сколько г соли во втором растворе?
   0,2·700=140 (г)
3. Сколько г соли в полученном растворе?
   160+140=300 (г)

Ответ: 300 г.

Задача 3. Какой раствор получится при смешивании 200 г 50% раствора соли и раствора, в котором 150 г соли составляют 25%? (Слайд 16-17)

Решение:

50% – процентное содержание соли в 200 г растворе (концентрация 0,5).

1. Сколько г соли в этом растворе?
   0,5·200=100 (г)
   Что мы знаем про второй раствор? – Знаем количество соли (150г) и его процентное содержание25% (значит, концентрация соли 0,25)

2. Какова масса второго раствора?
   150:0,25= 600 (г)
   Чтобы найти концентрацию соли в новом растворе, что надо знать? – Массу соли и массу всего раствора.

3. Какова масса соли в двух растворах?
   100+150=250 (г)

4. Какова масса нового раствора?
   200+600 =800 (г)

5. Какова концентрация соли в новом растворе?
   250:800=0,3125; 0,3125 = 31,25%

Ответ: 31,25%.

Задача для самостоятельного решения (дома).

Задача 4. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%?[5]

Решение:

1. Сколько кг соли в морской воде?
   0,05·30=1,5 (кг)
   Пресная вода содержит соль? – Нет. – Значит, масса соли и в новом растворе будет 1,5 кг, но ее концентрация составит уже 0,015.

2. Какова масса нового раствора (с добавлением пресной воды)?
   1,5: 0,015= 100 (кг)

3. Сколько пресной воды нужно добавить?
   100 – 30 = 70 (кг)

Ответ: 70 кг.

VII. Этап рефлексии.

(Слайд 18)

Ответ на листочке:

• Сегодня я узнал….
• У меня получилось…
• Было трудно….
• Было интересно….
• Теперь я умею…

VIII. Итог урока. Домашнее задание.

(Слайд 19)

№754, 755, подготовить библиографическую справку о Магницком Л.Ф.; о его схеме решения задач на смеси, растворы.

Используемая литература:

1. Большой энциклопедический словарь. -2-е изд., перераб.и доп. – М.:Большая Российская энциклопедия, 1998. — 1456 с.: ил.
2. slovari. yandex.ru
3. festival.1september.ru/articles/520040
4. Математика: учеб. для 6 кл. общеобразоват. учреждений/ [Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева, И.Ф. Шарыгина. – 8-е изд.-М.: Просвещение, 2006. – 302 с. :ил.
5. Сборник задач по математике для поступающих во втузы (с решениями). В 2-х кн. Кн. 1. Алгебра: Учеб. пособие / В.К. Егерев, В.В. Зайцев, Б.А. Кордемский и др.; под ред. М.И. Сканави. – 7-е изд., перераб. и доп. – М.: Высш.шк., 1994. — 528 с.: ил.

Урок по математике»Задачи на концентрацию и сплавы»

Работа на тему: «Решение задач на концентрацию, смеси и сплавы».

Задачи на концентрацию, смеси, сплавы.

Задачи на концентрацию традиционно являются слабым звеном в подготовке школьников и абитуриентов, кажутся многим из них довольно сложными. Обучение решению этих задач начинается с 6 класса и продолжается на продолжении всей основной школы. Однако, в 11 классе эти задачи у большинства вызывают затруднения. При повторении можно начинать с решения самых простых задач, взятых из учебника математики для 6 класса. В таких задачах речь обычно идет о растворах некоторого вещества в другом веществе и об изменении концентрации этого вещества после каких-либо манипуляций. При этом водные растворы, смеси, сплавы играют сходные роли и позволяют лишь несколько разнообразить сюжеты задач без изменения математического содержания. Ключевой при решении таких задач является идея отслеживания изменений, происходящих с «чистым» веществом.

В качестве модельной задачи рассмотрим следующую.

Смешали х литров п- процентного водного раствора некоторого вещества с у литрами к- процентного водного раствора этого же вещества. Требуется найти концентрацию получившейся смеси.

Воспользуемся ключевой идеей: проследим за изменениями, происходящими с чистым веществом. В первом растворе его было 0,01хп литров, во втором растворе 0,01ук литров. Значит количество чистого вещества в полученной смеси будет равно 0,01хп + 0,01ук литров, а всего смеси получится х + у литров. Теперь найти искомую концентрацию легко.

( 0,01хп + 0,01ук): (х + у) ×100= (хп + ук):(х + у). Заметим, что растворы в этой задаче можно было бы заменить двумя сплавами разной массы и с разным содержанием чистого вещества. Решение при этом практически не изменится, поменяются лишь единицы измерения и названия веществ.

Тема : Задачи на проценты и концентрацию.

Цель: формировать умение решать задачи на концентрацию, смеси и сплавы.

1.Устная работа.

Найдите:

а) 50% от 80; б) 10% от 300 в) 1% от 30 г) 20% от 25 д)25% от 400

е) 5% от 200; ж) 50% от 17 з) 40% от 10 и) 70% от 30 к) 9% от 500.

2.Формирование умений и навыков.

Задача. Имеются 3 раствора морской соли в воде: первый раствор содержит 10% соли, второй содержит 15 % соли и третий – 20% соли. Смешали 130 мл первого раствора, 200 мл второго раствора и 170 мл третьего раствора.

Определите, сколько процентов составляет морская соль в полученном растворе

Решение:

1. В 130 мл первого раствора содержится 130 × 0,1 = 13 (г) морской соли. В 200 мл второго раствора содержится 200 × 0,15 = 30 (г) морской соли. В 170 мл третьего раствора содержится 170 × 0,2 = 34 (г) морской соли.

2. После того, как эти растворы смешали, получили 130 + 200 + 170 = 500 (мл) нового раствора, который содержит 13 + 30 + 34 = 77 (г) морской соли.

3. Найдем, сколько процентов составляют 77 (г) морской соли от 500 мл раствор

_.

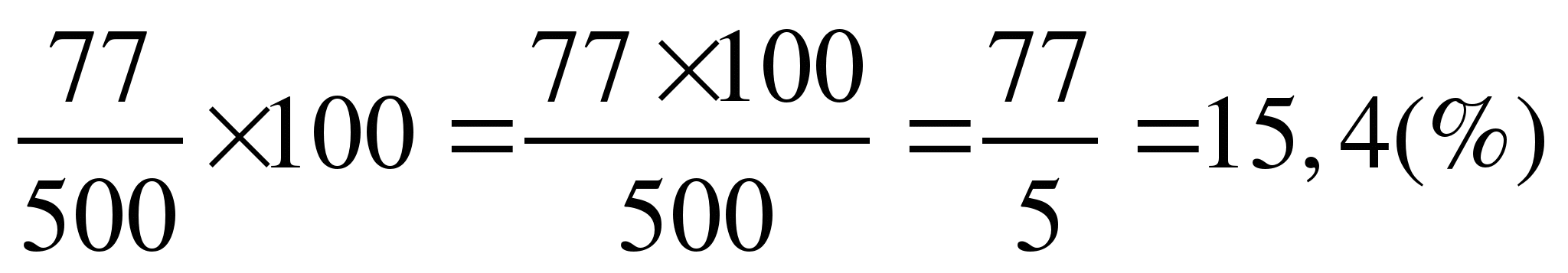_{Задача. Сколько граммов воды надо добавить к 50 г раствора, содержащего 8 % соли, чтобы получить 5 % — ный раствор?}

_{Заметим, что задачи на концентрацию вызывают наибольшие затруднения у учащихся. Поэтому следует подробнее остановиться на решении данной задачи, начав не с составления уравнения, а с вопросов, которые помогут учащимся уяснить условие и осознанно подойти к её решению.}

_{Вопросы учащимся:}

_{1) Сколько граммов соли содержится в имеющемся растворе?}

_{(50×0,08 = 4 г).}

_{2) Если к имеющемуся раствору добавить воды, изменится ли массовая составляющая соли? (Нет.)}

_{3) При добавлении воды изменится ли процентное содержание соли в растворе? (Да.)}

_{4) Если к имеющемуся раствору добавить х г воды, какова станет масса всего раствора? (50 + х). Сколько граммов соли в нем будет? (4г).}

_{5) Каково процентное содержание соли в новом растворе? (5%.)}

_{6) Какую пропорцию, согласно полученным результатам, можно составить?}

_{4 г соли – 5%}

_{(50 + х) г раствора – 100%.}

_{Имеем уравнение:}

_{5(50 + х) = 400, откуда х = 30.}

_{Ответ: 30г.}

_{Алгоритм.}

_{Поскольку при добавлении к раствору какого-либо вещества масса другого вещества не изменяется, а меняется его процентное содержание, то сначала необходимо найти массу изменяющегося вещества.}

_{Затем за х обозначить массу добавляемого вещества и составить пропорцию, в которой масса неизмененного вещества будет составлять новое количество процентов, а масса всего раствора 100%.}

_{Задание учащимся.}

_{Решите следующие две задачи по составленному выше алгоритму.}

_{Задача №1.}

_{Сколько граммов воды надо добавить к 180 г сиропа, содержащего 25% сахара, чтобы получить 20%-ый сироп?}

_{Решение.}

_{Веществом, которое не меняет своей массы в новом растворе, является сахар. Поэтому найдем его массу.}

_{180×0,25 = 45 г.}

_{После добавления воды 45 г сахара в новом растворе будут составлять 20 % от всей массы. Пусть х г воды надо добавить, тогда масса нового раствора составляет (180 + х) г.}

_{Имеем пропорцию:}

_{45 г сахара – 20%;}

_{(180 + х) г сиропа – 100%.}

_{Из пропорции составим уравнение:}

_{20(180 + х)= 4500, откуда х = 45.}

_{Ответ: 45г.}

_{Задача №2.}

_{Сколько граммов воды надо выпарить из 80 г 6%-ого раствора соли, чтобы получить 10%-й раствор?}

_{Решение.}

_{Масса соли в имеющемся растворе равна 80 × 0,06 = 4,8 г. В новом растворе соль будет составлять 10%.}

_{Пусть х граммов воды нужно выпарить, тогда масса нового раствора будет равна (80 — х) г.}

_{Составим пропорцию:}

_{4,8 г соли – 10%;}

_{(80 — х) г раствора – 100%.}

_{Получаем уравнение:}

_{10(80 – х) = 4,8×100, откуда х = 32.}

_{Ответ: 32 г.}

_{Задача №3.}

_{Имеются два сплава. Первый сплав содержит 10% никеля, второй 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25 % никеля. Насколько кг масса первого сплава меньше массы второго?}

_{Решение.}

_{Пусть масса первого сплава х кг, а масса второго у кг. Масса третьего сплава х + у и по условию задачи х + у = 200. Первый сплав содержит 0,1х кг чистого вещества, а второй 0,3у кг. Третий сплав содержит 0,25×200=50 кг. Значит, 0,1х + 0,3у =50. Получили систему из двух линейных уравнений. Решением системы является пара чисел х=50 и у=150. Итак, масса первого сплава на 150 – 50 =100 кг меньше.}

_{Ответ: 100.}

_{Задача №4.}

_{Первый сплав содержит 10% меди, второй – 40 % меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.}

_{Решение.}

_{Пусть масса первого сплава х кг, тогда масса второго сплава ( х + 3 )кг. Масса третьего сплава х + х + 3 = 2х +3 кг. Масса чистого вещества в первом сплаве 0,1х кг, во втором – 0,4×( х+3), значит всего чистого вещества 0,1х + 0,4(х+3). Так как третий сплав содержит 30% меди, т.е. 0,3( 2х +3), то имеем уравнение 0,3( 2х +3)= 0,1 + 0,4( х+3), откуда х = 3. Масса третьего сплава равна 2×3 +3 = 9 кг.}

_{Ответ: 9.}

_{Задача №5.}

_{Виноград содержит 91% влаги, а изюм – 7%. Сколько килограммов винограда требуется для получения 21 килограмма изюма?}

_{Решение.}

_{Используем ключевую идею: будем следить за массой «чистого», т.е. в данном случае «сухого» вещества в винограде и изюме. Виноград содержит чистого вещества 100% — 91% = 9%, а изюм содержит чистого вещества 100% — 7% = 93%. Пусть для получения 21 килограмма изюма требуется х кг винограда. Из условия следует, что масса «сухого» вещества в х кг винограда равна 0,09х кг. Поскольку эта масса равна массе «сухого»вещества в 21 килограмме изюма, то по условию задачи можно составить уравнение}

_{0,09х=0,93×21,}

_откуда

_{9х = 93×21,}

_{т.е. х = 217 кг.}

_{Ответ: 217 кг.}

_{Задача для самостоятельного решения.}

_{Виноград содержит 90% влаги, а изюм – 5%. Сколько килограммов винограда требуется для получения 20 килограмма изюма?}

_{Ответ:190кг.}

_{Задача №6.}

_{В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?}

_{Решение.}

_{В 5 литрах раствора содержится 0,12×5 = 0,6 л чистого вещества. Масса нового раствора 12 литров, а чистого вещества в нем по прежнему 0,6 л. Значит концентрация нового раствора равна 0,6 : 12×100% =5%.}

_{Ответ: 5.}

_{Задача №7.}

_{Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19- процентного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?}

_{Решение.}

_{Пусть масса первого раствора х г, он содержит 0,15х г чистого вещества. Масса второго раствора тоже х г, он содержит 0,19х г чистого вещества. Масса нового раствора равна х + х = 2х г и он содержит 0,15х + 0,19х = 0,34х г чистого вещества. Тогда концентрация нового раствора равна ( 0,34х) : (2х)×100% = 17%.}

_{Ответ: 17.}

_{Задача для самостоятельного решения.}

_{Смешали 4 литра 15-процентного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?}

_{Ответ: 21.}

_{Итоги урока.}

_{Вопросы учащимся:}

_{— Как найти процент от величины?}

_{— Как найти величину по ее проценту?}

_{— Как найти, сколько процентов одна величина составляет от другой величины?}

_{— Каков алгоритм решения задач на концентрацию, в которых к имеющемуся раствору добавляют одно из составляющих его веществ?}

_{— По какому плану решаются задачи на смешивание нескольких растворов?}

_{ЛИТЕРАТУРА}

_{1.Математика. 6 класс: поурочные планы по учебнику Г.В.Дорофеева, С.Б.Суворовой, И.Ф.Шарыгина. Часть 1/авт.-сост. Т.Ю.Дюмина. – Волгоград: Учитель,2007.}

_{2.Алгебра. 7 класс: поурочные планы по учебнику под редакцией Г.В.Дорофеева / авт.-сост. М.Ф. Калинина. – Волгоград: Учитель,2008.}

_{3.Алгебра. 8 класс: поурочные планы по учебнику под редакцией Г. .В. Дорофеева / авт. – сост. Т. Ю. Дюмина. – Волгоград: Учитель,2008.}

_{4.Шестаков С.А., Гущин Д.Д. ЕГЭ 2011. Математика. Задача В12. Задачи на составление уравнений. Рабочая тетрадь / Под ред. А.Л.Семенова и И.В.Ященко. – М.: МЦНМО, 2011.}

Решение текстовых задач на смешение растворов и процентное содержание вещества в растворе и сплаве при подготовке к ГИА.

Решение текстовых задач на смешение растворов и процентное содержание вещества в растворе и сплаве при подготовке к ГИА.

«Нахождение способа решения задачи подобно изобретению,

а изобретение требует воображения, догадки, фантазии.

Поэтому развивайте у себя эти качества»

 (А.И. Маркушевич).

При подготовке учащихся к сдаче экзаменов ЕГЭ и ГИА по математике постоянно наталкиваешься на «боязнь» учащихся текстовых задач и неумение их решать, хотя у них за плечами все темы школьного курса математики 5-9 классов: «Решение линейных уравнений», «Решение текстовых задач с помощью линейных уравнений», «Решение квадратных уравнений», «Системы уравнений с двумя неизвестными», «Решение задач с помощью квадратных уравнений и систем уравнений с двумя неизвестными».

Основные затруднения:

а) выделение неизвестной величины, ее связи с другими величинами задачи;

б) составление уравнений, систем уравнений;

в) выбор ответа.

После занятия выпускники должны уяснить, что существует последовательная система работы с задачей, которая приводит к положительному результату.

Существует много способов решения задач .

Стандартные способы решения задач:

1. Арифметический способ;

2. С помощью уравнений или систем уравнений;

Нестандартные способы решения задач:

1. Переформулировка задач;

2. «Лишние» неизвестные;

3. Использование делимости;

4. Решение задач в общем виде;

5. Метод подобия.

Ученикам нужно обосновывать необходимость структурного подхода к решению текстовых задач. Научить их строить наглядную схему процесса решения задач и параллельный пошаговый план работы при решении текстовой задачи.

Процесс решения задачи

Схема решения задачи

• Анализ условия задачи

• Составление плана решения

• Построение математической модели

• Решение задачи в различных моделях

• Поиск других решений

• Описание решения задачи и выделение общей схемы

• Составление обратных задач и их решение

• Установление границ применения способа решения задачи для задач с другим содержанием

• Составление обобщений задачи, ее решения и исследования.

. На первом шаге рассматриваются приемы анализа условия задач.

Приемы анализа текста задачи: «Чтобы узнать, надо знать».

1. Переформулировка вопроса задачи, замена поставленного вопроса.

2. Постановка вопроса к данному условию задачи.

3. Нахождение необходимых для ответа на поставленный вопрос.

4. Исследование задач с недостающими, лишними , противоречивыми данными

5. Сравнение условий нескольких задач.

При разборе математических моделей большее внимание уделяется решению текстовых задач с помощью уравнений.

Решение задач с помощью уравнения

Чтобы составить уравнение по задаче, нужно ответить на вопросы, постепенно оформляя на черновике краткое условие задачи.

1. О каком процессе в задаче идет речь? Какими величинами характеризуется этот процесс?

2. Сколько процессов в задаче?

3. Какие величины известны и что нужно найти?

4. Как связаны величины в задаче?

5. Какую величину удобно обозначить, например, буквой Х.

6. Какое условие нужно использовать для составления уравнения?

7. Легко ли решить полученное уравнение?

После окончания разбора каждого пункта плана решения задач на примере конкретной задачи разбираются различные способы ее решения. Учащимся нужно продемонстрировать необходимость сознательно-творческого подхода к задаче, а также то, что каждый из них может решить задачу правильно, но различными способами.

«Решение задач на смешение растворов и процентное содержание вещества в растворе и сплаве»

Что интереснее всего: решать задачи про то, чего не можешь представить или представлять то, чего не можешь решить? Что интереснее в математике: решать задачи про движение или же про смеси растворов? Искать количество или процентное содержание? На самом деле, интерес к данным тематикам может быть вполне равным, но сегодня я хочу поговорить о втором типе задач, наиболее редко встречающемся, но крайне полезным в жизни. Вы спросите: «Где же в жизни нам могут понадобится задачи на сплавы и растворы? Разве не находят они применение только в химии или же бытовых экспериментах?» Я же могу сказать, что задачи на процентное содержание вещества в сплавах и растворах поджидают человека всегда: решаете ли вы сколько сахара положить в чай в соответствии с пропорцией обычной чашки или же пытаетесь определить стоимость кольца, содержание золота в котором менее 50%. Такие задачи, как выяснилось, не самые простые не только для понимания школьниками, но и для решения даже взрослыми, именно поэтому я хотела бы сегодня о них рассказать. Примечательно также, что такие задачи встречаются в ГИА и ЕГЭ, поэтому их решение очень полезно для учащихся. Как и у множества задач, применимых к жизни, данный тип имеет несколько нестандартных видов решения, которые я бы с удовольствием продемонстрировала на наглядных примерах, поэтому в этой работе я ставлю для себя следующие цели:

1. Изложение теории задач на процентное содержание в растворах

2. Представление различных способов решения задач с примерами

3. Выбор наиболее простого на мой взгляд решения

Надеюсь, моя работа покажется Вам интересной и во многом поможет в дальнейшем, поэтому, давайте приступим!

Теория задач на процентное содержание.

Прежде того, как изучать, непосредственно, саму теорию, я считаю нужным, пояснить, что же такое, собственно, задачи на процентное содержание вещества в растворе или сплаве.

Задачи на процентное содержание – задачи, в которых требуется выяснить содержание того или иного элемента. В такой задаче может быть задан вопрос, например, о концентрации какого-то вещества, после переливания жидкости или смешения еще одного металла в сплаве. Чаще всего, в такого типа задачах, речь идет о смещение именно двух металлов или же смешении воды и какого-то вещества, однако встречаются также и задачи на смешение трех и более элементов, но, спешу заверить, они встречаются гораздо реже, так как рассчитаны на достаточно высокий уровень знаний.

Также, хочу сказать, что эти задачи можно рассматривать с двух сторон: математической стороны и стороны химии. Мы будем рассматривать со стороны математической, однако даже в их решение принимаются допущения из химии.

Как и у многих математических задач, задачи на смешение растворов и сплавов имеют несколько способ решения. Но для начала, давайте вспомним теорию.

Составными частями данного типа задач являются:

1. Масса/массовая доля растворенного вещества

2. Масса/массовая доля раствора

3. масса получившейся смеси

Концентрация вещества — отношение количества растворённого вещества или его массы к объёму раствора (моль/л, г/л), то есть это отношение неоднородных величин. Концентрация – отношение объема чистого вещества к объему всего раствора.

Если раствор m и состоит из веществ A, B, C, массы которых соответственно mA, mB, mC, то величину mA/m( а также mB/m и mC/m) и называют концентрацией вещества в растворе.

Процентное содержание – величина, показывающая в процентах долю вещества. Похожа на концентрацию, только уже в процентах.

mA/m * 100% — процентное содержание вещества. (а также mB/m*100% и mC/m*100%).

Поскольку доли в растворе всегда должны быть равны единому веществу, то для любой задачи справедливо данное выражение:

(mA/m)+(mB/m)+(mC/m)=1

В таких задачах используют следующие допущения:

1. все полученные растворы(сплавы или смеси) – однородны

2. смешивание растворов происходит мгновенно

3. объем полученного раствора или сплава всегда равен сумме его составляющих

4. объем растворов и массы сплавов не могут быть отрицательными

5. не делается различия между литром, как мерой вместимости сосуда и литром как мерой жидкости (или газа)

6. потери некоторого количества вещества(массы), которые возможны в силу протекания соответствующей хим. реакции (или физических процессов) считаются незначительными, если происходят во время хим. реакции.

Сегодня мы рассмотрим с вами более простой ( для учащихся )

«метод стаканчиков » решения задач на смеси и сплавы.

Одним из интереснейших и наиболее наглядных и простых методов решения задач на сплавы и растворы является так называемый «Метод стаканчиков».

Метод стаканчиков, по сути, является новым методом, поскольку был введен тогда, когда задачи по смешиванию растворов стали входить в обязательный курс математики, потому что когда эти задачи решались в химии, то использовались чаще методы Креста и таблицы, о которых я расскажу чуть позже.

Суть данного метода заключается в том, что условие задачи вписывается в три нарисованных стакана(первый и второй – смешиваемые вещества, третий – желаемое) , где сверху приписывается масса, данная в условии, чуть ниже – процентное содержание вещества, а внизу – общая масса, то есть произведение массы вещества и ее процентного содержания.

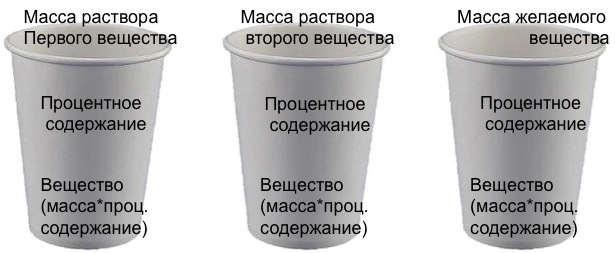
Теперь давайте попробуем решить задачи данной схемой.

Задача1

В сосуд, содержащий 7 литров 14-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

1способ

Решение:

Пусть в сосуде изначально было  х л некоторого вещества.

Составляем пропорцию:7л-100%, х л-14%,то х=7*14/100

Откуда  х=0,98л.

После того, как в сосуд долили 7 литров воды, воды стало 14 л, а некоторого вещества по-прежнему 0,98л.

Составим очередную пропорцию:14л-100%, 0,98л-?,то 0,98*100/14=7%

Откуда  процент некоторого вещества в сосуде есть 7%.

Ответ: 7.

2способ. Решим задачу методом «стаканчиков»

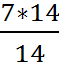
Ответ: 7

Задача 2.
Даны два куска с различным содержанием олова. Первый, массой 300г, содержит 20% олова. Второй, массой 200г, содержит 40% олова. Сколько процентов олова будет содержать сплав, полученный из этих кусков?

Решение.

1. 300 •20 : 100 = 60 (г) — олова в первом сплаве,

2. 200 • 40 : 100 = 80 (г) — олова во втором сплаве ;

3. 60 + 80 = 140 (г) — олова в двух сплавах вместе;

4. 200 + 300 = 500 (г) – масса куска после сплавления;

5. 140 : 500 • 100 = 28% -содержится олова после сплавления.

2способ . Решим задачу методом «стаканчиков»

Тогда 300*20 +200*40 = 500*х , то х = 28%

Ответ: 28

Задача 3.

Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Тогда 10*15 +10*19 = 20*х , то х =17%

Ответ: 17

Задача4.

Какие массы 25% и 5% раствора серной кислоты потребуется для приготовления 40г 20% раствора этой кислоты? В ответе укажите массу меньшего раствора.

Решение.

Тогда 25*х +(40-х)*5 = 800*х , то х = 30%

40-х= 40 — 30 = 10

Ответ: 10

Задача5.

В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5% железа, содержание железа в оставшейся руде повысилось на 20%. Определите, сколько процентов железа в оставшейся руде.

Решение.

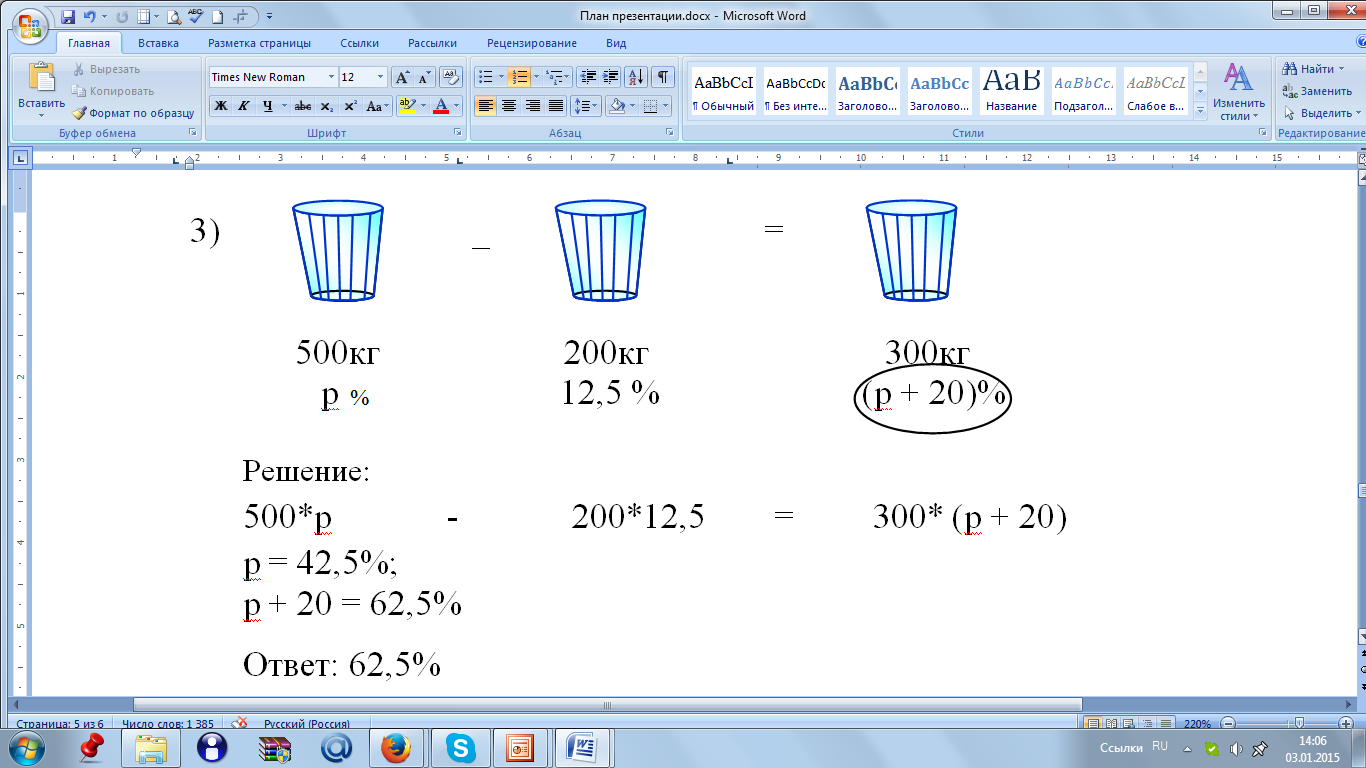
Выбирая удобный способ решения, предлагаю рассмотреть следующие задачи.

• №1. Смешали некоторое количество 11%-ного раствора некоторого вещества с таким же количеством 19%-ного раствора этого же вещества. Найдите концентрацию получившегося раствора. Ответ: 15%

• №2. Сколько килограммов 20%-ного раствора соли нужно добавить к 1 кг 10%-ного раствора, чтобы получить 12%-ный раствор соли? Ответ: 0,25 кг

• №3. Сколько граммов 75%-ного раствора кислоты надо добавить к 30 г 15%-ного раствора кислоты, чтобы получить 50%-ный раствор кислоты? Ответ: 42 г

• №4. Сколько воды нужно добавить к 0,5 л раствора спирта в воде, чтобы объемное содержание спирта в растворе уменьшилось с 60% до 40%? Ответ: 0,25 л

• №5. Слиток сплава меди и цинка массой 36 кг содержал 45% меди. Какую массу меди надо добавить к этому куску, чтобы полученный сплав содержал 60% меди? Ответ: 13,5 кг

• №6. Сколько граммов сахарного сиропа, концентрация которого 25%, надо добавить к 200 г воды, чтобы в полученном растворе содержание сахара составляло 5%? Ответ:50 г

• №7. Имеются 2 слитка. Масса 2 слитка на 3 кг. больше, чем масса 1 слитка. Процентное содержание меди в первом слитке – 10%; во втором – 40%. После сплавления этих двух слитков получился слиток, процентное содержание меди в котором – 30%. Определить массу полученного слитка. Ответ: 9 кг

• №8. В сосуд, содержащий 13 литров 18%-ного водного раствора некоторого вещества, добавили 5 литров воды. Найти концентрацию получившегося раствора. Ответ: 13%

• №9. В одном бидоне смешали 0,5 л молока 2,6%-ой жирности с 1 л молока 3,2%-ой жирности. Какова стала жирность в бидоне? Ответ: 3%

• №10. При смешивании первого раствора кислоты, концентрация которого 20%, и второго раствора этой же кислоты, концентрация которого 50%, получили раствор, содержащий 30% кислоты. В каком отношении были взяты первый и второй растворы? Ответ: 0,5.

• №11. Сколько граммов воды можно выпарить из 80 г 6%-ой соли, чтобы получить раствор, содержащий 10% соли. Ответ: 32 г

• №12. Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получиться сухих грибов из 22 кг свежих? Ответ: 2,5 кг

• №13. Виноград содержит 90% влаги, а изюм — 5%. Сколько килограммов винограда требуется для получения 82 кг изюма? Ответ: 779 кг

• №14. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. Ответ: 15 кг

• №15. Имеется два сосуда. Первый содержит 100 кг, а второй — 60 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 41% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 50% кислоты. Сколько килограммов кислоты содержится в первом сосуде? Ответ: 41 кг

Вывод: любая задача проверяет не только владение определенным набором математических умений, но и умение анализировать ситуацию, рассуждать, делать выводы, проверять правильность полученного результата, применять знания в нестандартной ситуации. Я очень надеюсь, что моя работа не только ознакомила вас с методом решения задач, казавшихся до сих пор сложными, но и значительно упростила для вас понятие о задачах в целом и, что когда-то, возможно, вам пригодится решение таких задач и вы вспомните как это делать благодаря данной работе. Благодарю вас за внимание!

Литература

1. Р. Г. Зияитдинов «Решение текстовых задач»

2. Л. М. Фридман «Как научиться решать задачи»

3. М.К.Кузин «Задачи как цель и средство обучения математике», Ж-л. «Математика в школе», №4, 1980г.

4. В.П.Рудченко «Текстовые задачи и развитие продуктивного мышления учащихся», Ж-л. «Математика в школе», №4, 1993г.

5. А.В.Шевкин «Текстовые задачи в школьном курсе математики» (5-9 классы)

6. П.Сапунов «Решение задач методом составления уравнения с одним неизвестным»

7. А. Горский «К вопросу методики решения задач на составление уравнений»

Электронные ресурсы:

1. «Решение задач на смеси и сплавы с помощью схем и таблиц» учителя химии школы № 1954(Москвы) Т.Н. Епифановой.

2. «Решение задач на сплавы и смеси» учителя математики МБОУ СОШ №3 Стромынского района Краснодарского края Соколян Татьяны Вячеславовны

3. http://ext.spb.ru/index.php/2011-03-29-09-03-14/104-integrated-lessons/823—lr-.html

4. http://egemaximum.ru/v14-zadachi-na-smesi-i-splavy/

Консультация по алгебре (11 класс) по теме: Основные приемы решения задач на концентрацию, растворы, сплавы и смеси

Основные приемы решения задач на концентрацию, растворы, сплавы и  смеси

Выступление

на городском МО учителей математики

учителя математики

 МКОУ СОШ № 10

Х. Перевальный

Асановой Аминат Аргуновны

                                  Ноябрь 2013 г.

Тема:   «Основные приемы решения задач на концентрацию, растворы, сплавы и  смеси»

Рассмотрим задачи, решение которых связано с понятиями «концентрация», «процентное содержание». В условиях таких задач речь идет, чаще всего, о сплавлении каких-либо металлов, растворении друг в друге различных веществ или переливании жидкостей, состоящих из нескольких компонентов. У многих учащихся эти задачи вызывают затруднения. Вероятно, это связано с тем, что таким задачам в школьном курсе математики уделяется совсем мало времени. Вместе с тем эти задачи встречаются в  диагностических и тренировочных работах СТАТГРАД  МИОО и  на ЕГЭ.  Говоря о смесях, растворах и сплавах будем употреблять термин «смесь» не зависимо от её вида (твердая, жидкая, сыпучая, газообразная). Смесь состоит из основного вещества и примеси. Что такое основное вещество, в каждой задаче определяем отдельно.

Формула для нахождения концентрации

              СА=  · 100, где

А  – вещество в сплаве

          М  – масса сплава

МА  – масса вещества А в сплаве

СА – концентрация вещества А в сплаве (в %)

В большинстве случаев задачи на смеси и сплавы становятся нагляднее если при их решении использовать схемы, рисунки, таблицы.

Задача №1

В колбе было 140г 10%-го раствора марганцовки (перманганат калия). В нее долили 60г 30 %-го раствора марганцовки. Определить процентное содержание марганцовки  в полученном растворе.

Решение.

Заполним таблицу по условию задачи:

	СА	М	МА
1-й раствор	10% или 0,1	140	0,1·140
2-й раствор	30% или 0,3	60	0,3·60
3-й раствор		200	0,1·140 +0,3·60

Концентрация раствора равна :  СА=  ·100 = 16 (%)

Ответ: 16%

Задача №2

I способ

Сколько нужно взять 10%-го и 30%-го раствора марганцовки, чтобы получить 200г  16%-го раствора марганцовки?

Решение.

Заполним таблицу по условию задачи:

	СА	М	МА
1-й раствор	10% или 0,1	х	0,1х
2-й раствор	30% или 0,3	у	0,3у
3-й раствор	16% или 0,16	200	0,16· 200

Составим и решим систему уравнений:

   

Ответ: 140г 10%-го раствора и 60г 30%-го раствора.

Намного проще, на мой взгляд, решить задачу по правилу «прямоугольника» или «креста», применяемому  химиками:

Смешали два раствора: первый — массой m1 г и концентрацией с1 и второй – массой m2г и концентрацией с2, получили раствор  массой (m1 + m2)г и концентрацией с3, причем с1 с3с2.

Найдем зависимость масс исходных растворов от их концентраций.

Масса основного вещества в первом растворе равна с1 m1 г, во втором растворе —  с2 m2, а в смеси с3(m1 + m2)г.

Составим равенство с1 m1 + с2 m2= с3(m1 + m2), откуда следует пропорция

  =  

с1                            с2-  с3                  с3 с2                             с3 –с1

II способ

10        14         16 30        6

х

200- х 

х= 140(г)- 10% р-р

200 -140 = 60(г) 30% р-р

Ответ: 140г 10%-го раствора и 60г 30%-го раствора.

Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

15        19-х         х 19        х- 15

1ч

1ч

Пусть концентрация раствора равна х%.

 = 1; х= 17

Ответ: 17%.

Задача №3  (Д.Гушин. Решу ЕГЭ)

Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Какова концентрация  кислоты  в первом сосуде?

Решение.

Пусть концентрация первого раствора кислоты – с1,а концентрация второго – с2 .

	СА	М	МА
1-й раствор	с1	30	30с1
2-й раствор	с2	20	20с2
3-й раствор	0,68	50	50· 0,68= 34
4-й раствор	70% или 0,7	mс1+mс2	2m·0,7

Решим полученную систему уравнений:

Поэтому  m1= 0,6·30=18

Ответ: 18%

Задача №4 (Д.Гушин. Решу ЕГЭ)

Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение.

Пусть масса первого сплава  х кг, а масса второго –  (х+3)кг

10        10         30 40        20

х кг

(х+3)

 = ; х= 3(кг)- масса первого сплава

3+(3+3)= 9(кг) масса второго сплава

 Ответ: 9кг.

Задача №5 (Д.Гушин. Решу ЕГЭ)

Имеется два сплава. Первый сплав содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Решение аналогично решению задачи № 4

10        5         25 30        15

х кг

(200-х)

 

 = ;   х= 50(кг)- масса первого сплава

200- 50= 150(кг)- масса второго сплава

150-50 = 100(кг)

Ответ: 100кг.

Задача №6  (Тренировочная работа № 1 от 22 ноября 2012г)

Смешав 14-процентный и 50-процентный растворы кислоты, и добавив 10 кг чистой воды, получили 22-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 32 -процентный раствор кислоты. Сколько килограммов 14-процентного раствора использовали для получения смеси?

Решение.

Пусть масса 14-процентного раствора кислоты –  х кг, а масса 50-процентного – у кг . Если смешать 14-процентный и 50-процентный растворы кислоты и добавить  кг чистой воды, получится 22-процентный раствор кислоты:0,14х+0,5у= 0,22(х + у +10). Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 32% раствор кислоты:0,14х+0,5у+0,5·10=0,32(х +у+10) . Решим полученную

систему уравнений:

Ответ: 25кг.

Задача №6  (Диагностическая работа №3 от 13 марта 2013г)

 Имеется два сосуда. Первый содержит 100кг, а второй- 20кг растворов кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 72% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 78 % кислоты.  Каково процентное содержание кислоты в первом сосуде?

Решение.

Пусть концентрация первого раствора х%, а второго у%.

1)

х        у- 72         72 у        72-х

100 кг

20 кг

         =5;

2)

х        у- 78         78 у        78-х

1ч

1ч

         =1;

3) решим систему уравнений

     

Ответ: 69%.

Задача №7

Сплав из золота и серебра весом 13кг 410г при полном погружении в воду стал весить 12 кг 510г. определите массы золота и серебра в сплаве, если плотность золота 19.3 г/см3,а серебра 10,5 г/см3.

Решение.

По закону Архимеда, сплав при погружении в воду теряет в весе столько, сколько весит вытесненная им вода, то есть 13.41- 12,51= 0,9(кг).

Плотность воды равна 1г/см3, поэтому объем сплава равен 900 см3, а его плотность равна

 = 14.9 (г/см3).

Составим схему, где в левой колонке и в центре стоят массы 1см3 серебра, золота и сплава:

10,5                     4,4             14,9 19,3                    4,4

Рассматривая правую колонку, видим, что золота и серебра в сплаве одинаковое число частей. Значит, массы золота и серебра в сплаве равны.

13, 41 :2 = 6, 705 (кг)

Ответ: по 6.705 кг

Задача №8

Концентрация спирта в трех растворах образует геометрическую прогрессию. Если смещать первый, второй и третий растворы в отношении 2:3:4, то получится раствор, содержащий 32% спирта. Если смешать эти растворы в отношении3:2:1, то получится раствор, содержащий 22% спирта. Какова доля спирта в каждом растворе?

Решение:

Пусть первый раствор содержит х%, второй –у%, а третий z% спирта. При первом перемешивании смешали 2ч первого раствора, 3ч второго раствора и 4ч третьего и получили раствор, содержащий 32% спирта. Получим  первое уравнение: 0,02х + 0,03у +0,04z =0,32·9,

2х +3у+ 4z =  288.

При повторном перемешивании смешали 3ч первого раствора, 2 ч второго и 1ч третьего и получили раствор, содержащий 22% спирта. Получим второе уравнение: 0,03х + 0,02у+ 0,01 z = 0,22·6,

3х+ 2у+ z =132.

Учитывая, что концентрация спирта в трех растворах образует геометрическую прогрессию: х, у, z, получим третье уравнение: у2= хz.

Составим и решим систему уравнений:

Из первых двух уравнений выразим у и z через х.

у = 48- 2х, z = х+36, подставляя в третье уравнение получим:

(48-2х)2 = х(х+ 36)

482 – 192х +4х2 =х2 + 36х

3х2- 228х+ 2304= 0

х2- 76х+ 768= 0

х1=12

х2= 64 не является решением так как если х= 64, у

Ответ: в первом 12%, во втором 24%, в третьем 48%.

Задачи на переливание

При решении этих задач еще раз следует напомнить учащимся, что выполняются следующие допущения: «закон сохранения масс» и «закон сохранения объемов», как для всей смеси, так и для каждого из ее компонентов. При этом следует считать, что плотности растворов изменяются незначительно и примерно равны плотности воды, то есть растворы сильно разбавлены, или наоборот, мы имеем дело с сильно концентрированными растворами и разбавляем их незначительно, но тогда плотность раствора близка к плотности основного вещества.

Задача № 9

В первой кастрюле был 1л кофе, а во второй- 1л молока.  Из второй кастрюли в первую перелили 0,13л молока и хорошо размешали. После этого из первой кастрюли во вторую перелили 0,13л смеси. Чего больше: молока в кофе или кофе в молоке?

Решение.

1. В первой кастрюле стало 1,13л смеси, в которой молоко составило

 = , а кофе – 1-  = .

2. Во второй кастрюле осталось0,87л молока и добавили 0,13л смеси, в которой кофе было 0,13 ·  = .

Ответ: одинаково.

Задача №9

Баллон емкостью 8л наполнен кислородно-азотной смесью, причем кислород составляет 16% смеси. Из баллона выпускают некоторый объем смеси, после чего дополняют баллон азотом и вновь выпускают такой же объем смеси, после чего опять дополняют сосуд азотом. В результате в баллоне остается 9% кислорода. Сколько литров смеси выпустили из баллона в первый раз?

Решение.

Предположим, что в первый раз выпустили х литров смеси и дополнили баллон х литрами азота. После первого выпуска смеси  в баллоне осталось  (8-х) · 0,16 л кислорода, а его концентрация стала равна  = (8 – х)· 0,02. После  второго выпуска х л смеси в баллоне осталось (8 – х) л смеси с концентрацией кислорода, равной (8 – х)· 0,02. Концентрация кислорода на этом этапе равна  = 0,09, откуда (8 – х)2 = 36, то есть х1 = 2, х2 = 14.

х2 не удовлетворяет условию задачи, так как х

Ответ: 2 л.