Решение логических задач с помощью кругов эйлера
Муниципальное общеобразовательное учреждение
лицей № 8 «Олимпия»
Дзержинского района г. Волгограда
Телефоны (8442) 58-80-83, 51-81-31 адрес электронной почты lyceum8@mail.ru
Решение логических задач с помощью кругов Эйлера
Выполнил:
Назаретян Сюзана Горовна,
ученица 5 Б класса
Учитель:
Кокиева Лилия Диляверовна, учитель
математики высшей категории
Волгоград, 2011
Оглавление | С. |
Введение. | 3 — 4 |
Глава I. Логические задачи и круги Эйлера ……………..…….…… | 5 — 9 |
1.1. Трудно решать логические задачи? …..……………………. | 5 — 6 |
1.2. Немного о множествах ………..…………………………… | 6 — 8 |
1.3. Из истории кругов Эйлера …….……..……………………. | 8 — 9 |
Глава II. Решение логических задач с помощью кругов Эйлера….. | 7 — 14 |
2. | 9 —12 |
2.2. Задачи на пересечение и объединение трёх множеств …… | 12 — 14 |
Заключение……………………………………………………………………………….. | 15 |
Список источников и литературы………………………………………………. | 16 |
Приложения ……………………………………………………………………………… | 17—20 |
Введение.
Сколько гостей Вам встречать,
если собираются друзья с 15 угощениями
и 20 украшениями? Может ли хватить всем
места за столом, вмещающем 22 человека?
Первое, что приходит на ум, это 35 человек. А причём здесь 22 человека? Есть подвох?
Конечно! Ведь надо рассмотреть несколько
вариантов.
А причём здесь 22 человека? Есть подвох?
Конечно! Ведь надо рассмотреть несколько
вариантов.
Как узнать количество учащихся класса, посещающих одновременно две или три секции, если известны количества участников каждой секции отдельно? Можно ли научиться решать такие задачи, планируя результат? Хочется ответить положительно.
А как решить такую задачу: «Министерство послало в один из лицеев инспектора для проверки, как в нём ведётся преподавание иностранных языков. Сотрудник министерства в отчёте записал, что в лицее учатся 100 детей. Каждый изучает по крайней мере один из трёх языков: французский, немецкий и испанский. Причём все три языка изучают 5 человек; немецкий и испанский 10;французский и испанский 8; немецкий и французский 20; испанский 30, немецкий 23, французский 50. Инспектор, представивший отчёт, был уволен. Почему?»? Такое длинное условие: пока дочитали до конца – забыли начало. Что делать?
Оказывается, такие задачи решаются
с помощью кругов Эйлера. Изображение условий задачи в виде кругов
Эйлера, как правило, упрощает и облегчает
путь к её решению.
Изображение условий задачи в виде кругов
Эйлера, как правило, упрощает и облегчает
путь к её решению.
Актуальность нашей работы заключается в том, чтобы такие задачи не ставили нас «в тупик» и мы могли их решать.
С учетом этого и была выбрана тема исследования: «Решение логических задач с помощью кругов Эйлера».
Объект исследования — логические задачи.
Предмет исследования —использование кругов Эйлера для решения логических задач .
Гипотеза исследования. Можно решать логические задачи определённого вида специальными способами и в 5 – 6 классах.
Целью нашего исследования является исследование механизма решения определённых логических задач при помощи кругов Эйлера.
Для достижения цели исследования и обоснования гипотезы нам необходимо решить ряд задач:
Найти необходимые сведения о пересечении и объединении множеств, о кругах Эйлера.

Рассмотреть способы решения логических задач на пересечение и объединение двух и трёх множеств.
Вывести в общем виде способ решения логических задач определённого вида с помощью кругов Эйлера.
Научиться решать конкретные логические задачи с помощью кругов Эйлера.
Создать модели «Круги Эйлера» для решения задач с двумя и тремя множествами в помощь учащимся.
Методы исследования:
1. Поиск, анализ и синтез различных источников информации.
2. Интервьюирование, беседы.
Практическая значимость заключается в расширении аппарата для
решения логических задач. Данный
материал можно будет использовать на
некоторых уроках, для проведения кружков,
факультативных занятий по математике.
Применение кругов
Эйлера придает задачам наглядность и
простоту.
Теоретическая значимость заключается в разработке способа действий при решении логических задач с помощью кругов Эйлера в общем виде.
Здесь будет выводиться история переписки.
Глава I. Логические задачи и круги Эйлера
1.1. Трудно решать логические задачи?
Логика – это искусство рассуждать, умение делать правильные выводы. Это не всегда легко, потому что очень часто необходимая информация «замаскирована», представлена неявно, и надо уметь её извлечь.
Решение логических задач – одно из важнейших средств развития мыслительных способностей.
Логические задачи обладают рядом
достоинств, позволяющих использовать
их для развития соображения и улучшения
логического мышления детей, начиная с
детского сада и заканчивая старшими
классами средней школы. Логические
задачи допускают изложение в занимательной,
игровой форме.
Вдоль овражка
Шла фуражка,
Две
косынки,
Три корзинки
И от них не
отставала
Белоснежная панама.
Посчитай
поскорей
Сколько было детей?
Задача предполагает несколько
решений. Потому что мы точно не знаем,
носил ли кто — нибудь и головной убор, и
корзинку.
1 Решение. Предполагается,
что каждый ребёнок носил 1 предмет.
Значит, детей было 7.
2 Решение.
Предполагается, что 1 из детей нёс
корзинку и головной убор. Следовательно,
детей было 6.
3 Решение. Предполагается,
что 2 из детей носили и корзинку, и
головной убор. Следовательно, детей
было 5 .
4 Решение. Предполагается, что
3 из детей носили и корзинку, и головной
убор. Следовательно, детей было 4.
1.2. Немного о множествах
Множество – одно из основных
понятий математики. Его смысл выражается
словами: совокупность, собрание, класс,
набор, команда и т.
Множества обозначаются прописными буквами латинского алфавита А, В, С, …
О предметах, составляющих множество, говорят, что они принадлежат этому множеству или являются его элементами. Множества, элементами которых являются числа, называются числовыми множествами.
Множество может быть задано перечислением всех его элементов в произвольном порядке. Такое множество называют конечным. Мы будем рассматривать только конечные множества.
Множество, в котором нуль элементов, называют пустым.
Над множествами, как
и над числами, производят операции.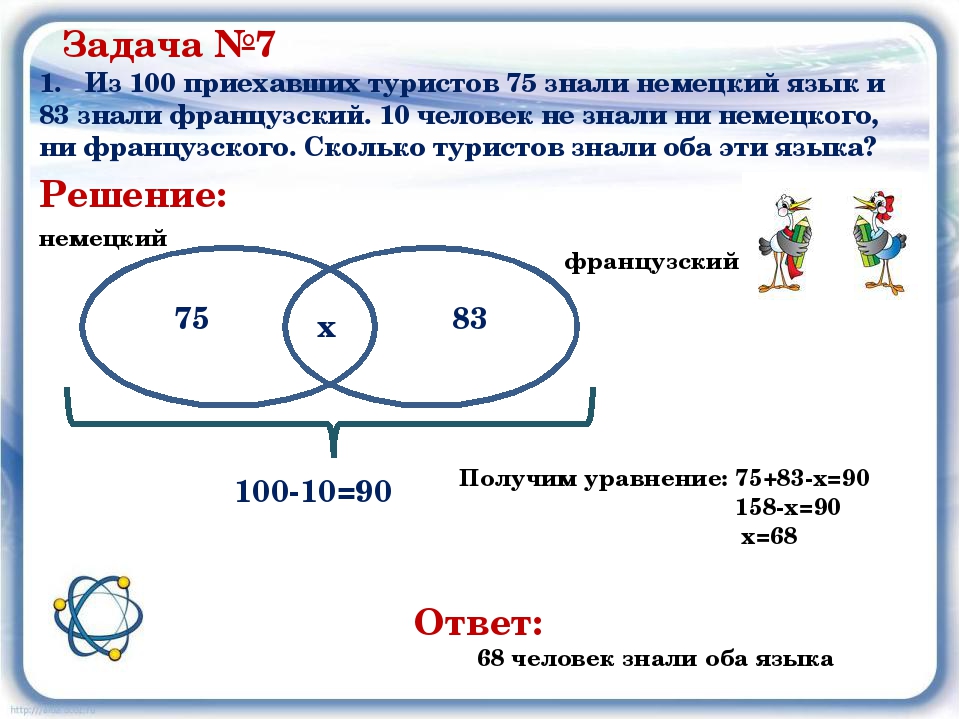 Рассмотрим некоторые из них: пересечение,
объединение и
разность.
Рассмотрим некоторые из них: пересечение,
объединение и
разность.
Пересечение множеств
Возьмем множество X, состоящее из букв а, б, в, г, д, и множество Y, состоящее из букв г, д, е, ж:
X = {а, б, в, г, д}, Y= {г, д, е, ж}.
Эти множества имеют общие элементы гид. Множества X и Y называются пересекающимися множествами. Множество общих элементов X и Y называют пересечением множеств X и Y и обозначают с помощью знака :Х Y={г, д} (рис. 1).
Пусть множество А = {1, 3, 5}. Множества А и X не имеют ни одного общего элемента. В таком случае множества А и X называются непересекающимися множествами. Пересечением множеств А и X является пустое множество: А Х= (рис. 2).
Пересечением множеств называется
новое множество, состоящее
из элементов,
принадлежащих одновременно нескольким
множествам
Рис. 1
1
Рис. 2
Объединение множеств
Если из элементов множеств X и Y составить новое множество, состоящее из всех элементов этих множеств и не содержащее других элементов, то получится объединение множеств Х и Y, которое обозначают с помощью знака :
X и Y= {а, б, в, г, д, е, ж) (рис. 4).
Объединение множеств А и X не является пустым:
А X = {1, 3, 5, а, б, в, г, д) (рис. 5).
Объединением
множеств называется новое множество,
состоящее
из элементов, принадлежащих
хотя бы одному из множеств.
Рис. 3
Рис. 4
Рис. 4Разность
Разность множеств
X
и Y
— это множество всех элементов
из X,
не являющихся элементами из Y. Разность
обозначают Х\Y
= {а, б, в}
(рис. 5).
Разность
обозначают Х\Y
= {а, б, в}
(рис. 5).
Рис. 5
1.3. Из истории кругов Эйлера
Часто множество изображают кругами, эти круги обычно называют «кругами Эйлера» по имени величайшего математика Леонарда Эйлера.
Леонард Эйлер (Euler) (1707 – 1783 г.г.) – математик, механик, физик и астроном. По происхождению швейцарец, а работал в основном в Росси и в Германии. В 1726 году был приглашен в Петербургскую АН и в 1727 году переехал в Россию. В 1741 – 1766 годах работал в Берлине, член Берлинской АН. Эйлер – ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки.
Одним из первых, кто разрабатывал
метод решения задач с помощью кругов
Эйлера, был выдающийся немецкий математик
и философ Готфрид Вильгельм Лейбниц
(1646 – 1716). В его черновых набросках были
обнаружены рисунки с такими кругами.
Затем этот метод довольно основательно
развил швейцарский математик Леонард
Эйлер (1707 – 1783). Он долгие годы работал
в Петербургской Академии наук. К этому
времени относятся его знаменитые «Письма
к немецкой принцессе», написанные в
период с 1761 по 1768 год. В некоторых из
этих «Писем…» Эйлер как раз и рассказывает
о кругах, которые «очень подходят для
того, чтобы облегчить наши размышления».
После Эйлера этот же метод разрабатывал
чешский математик Бернард Больцано
(1781 – 1848).
В его черновых набросках были
обнаружены рисунки с такими кругами.
Затем этот метод довольно основательно
развил швейцарский математик Леонард
Эйлер (1707 – 1783). Он долгие годы работал
в Петербургской Академии наук. К этому
времени относятся его знаменитые «Письма
к немецкой принцессе», написанные в
период с 1761 по 1768 год. В некоторых из
этих «Писем…» Эйлер как раз и рассказывает
о кругах, которые «очень подходят для
того, чтобы облегчить наши размышления».
После Эйлера этот же метод разрабатывал
чешский математик Бернард Больцано
(1781 – 1848).
Только в отличие от Эйлера он
рисовал не круговые, а прямоугольные
схемы. Методом кругов пользовался и
немецкий математик Эрнест Шредер (1841 –
1902). Этот метод широко используется в
книге «Алгебра логики». Но наибольшего
расцвета графические методы достигли
в сочинениях английского логика Джона
Венна (1843 – 1923). С наибольшей полнотой
этот метод изложен им в книге «Символическая
логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера
соответствующие рисунки называют иногда
диаграммами Венна; в некоторых книгах
их называют также диаграммами (или
кругами) Эйлера – Венна.
В честь Венна вместо кругов Эйлера
соответствующие рисунки называют иногда
диаграммами Венна; в некоторых книгах
их называют также диаграммами (или
кругами) Эйлера – Венна.
Глава II. Решение логических задач с помощью кругов Эйлера
2.1. Задачи на пересечение и объединение двух множеств
К Лене на День Рождения пришли
гости с подарками. Получилось так, что
подарили только букеты цветов и воздушные
шарики. Шесть гостей подарили букеты
цветов, четыре — воздушные шарики. Сколько
было гостей?
Задача
предполагает несколько решений. Потому
что мы точно не знаем, брал ли кто — нибудь
из гостей два подарка.
1 Решение. Предполагается, что каждый гость с одним подарком. Следовательно, гостей 10.
2 Решение. Предполагается, что 1 из гостей пришел и с шариком, и с букетом цветов. Следовательно, 6 + 3 = 9 гостей.
3 Решение. Предполагается, что 2
из гостей пришли с двумя подарками.
Следовательно, гостей 8.
Предполагается, что 2
из гостей пришли с двумя подарками.
Следовательно, гостей 8.
4 Решение. Предполагается, что 3 из гостей пришли и с шариком, и с букетом цветов. Следовательно, 6 + 1 = 7.
5 Решение. Предполагается, 4 из гостей пришли с 2 подарками. Следовательно, 4 + 2 = 6 гостей.
1
Ц
) 2)Ш
Ш
4
5
1
3
Ш
Ц
Ш
Ц
) 4)4
2
2
3
3
Ш
Ц
5)2
В одном множестве 40 элементов, а в другом 30. Сколько элементов может быть в их:
а) пересечении; б) объединении?
Ответ: а) от 0 до 30; б) от 40 до 70.
«Ёлки» и «Неудержимый»:
Некоторые ребята из нашего класса любят
ходить в кино. Известно, что 12 ребят
смотрели фильм «Ёлки», 9 человек – фильм
«Неудержимый», из них 6 смотрели и «Ёлки»,
и «Неудержимый». Сколько человек смотрели
только фильм «Неудержимый»?
Сначала заполняем пересечение. Это
будет число 6. Потом заполняем множество
ребят, смотревших фильм «Ёлки». Это
будет число 6. Так как 6 из двенадцати к
тому же ещё смотрели фильм «Неудержимый».
После заполняем множество ребят,
смотревших фильм «Неудержимый». Это
будет число 3. Так как 6 из 9 к тому же ещё
смотрели фильм «Ёлки».
Ответ: 3 человека
смотрели только фильм «Неудержимый».
20 человек знают английский и 10 — немецкий, из них 5 знают и английский, и немецкий. Сколько человек всего?
Способ 1. С помощью модели «Круги Эйлера» (Приложение 1).
10+20 – 5=25 человек.
Способ 2.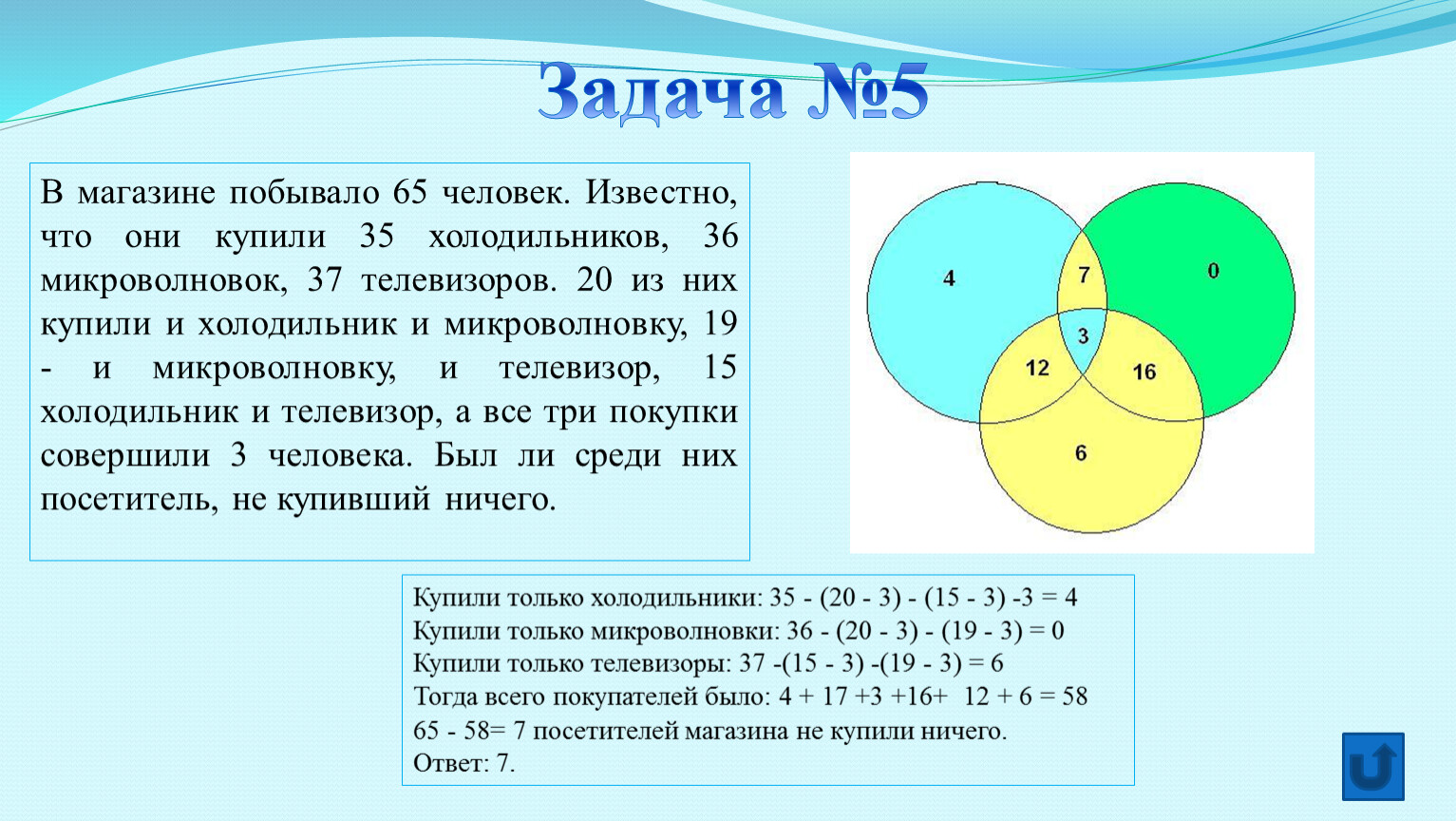
1) 20 – 5 = 15(чел.) – знают только английский язык;
2) 10 – 5 = 5 (чел.) – знают только немецкий язык;
3) 15+5+5 = 25 (чел.) – всего.
15
5
10
А
Можно решать и короче:
20 – 5 = 15(чел.) – знают только английский язык;
10+15 = 25 (чел.) — знают немецкий и только английский
2.2. Задачи на пересечение и объединение трёх множеств
В классе всего 36 человек. Учащиеся
посещают математический, физический и
химический кружки, причем, математический
кружок посещают 18 человек, физический
— 14 человек, химический — 10 человек. Кроме
того, известно, что все три кружка
посещают 2 человека, математический и
физический -8,математический и химический
— 5, физический и химический — 3.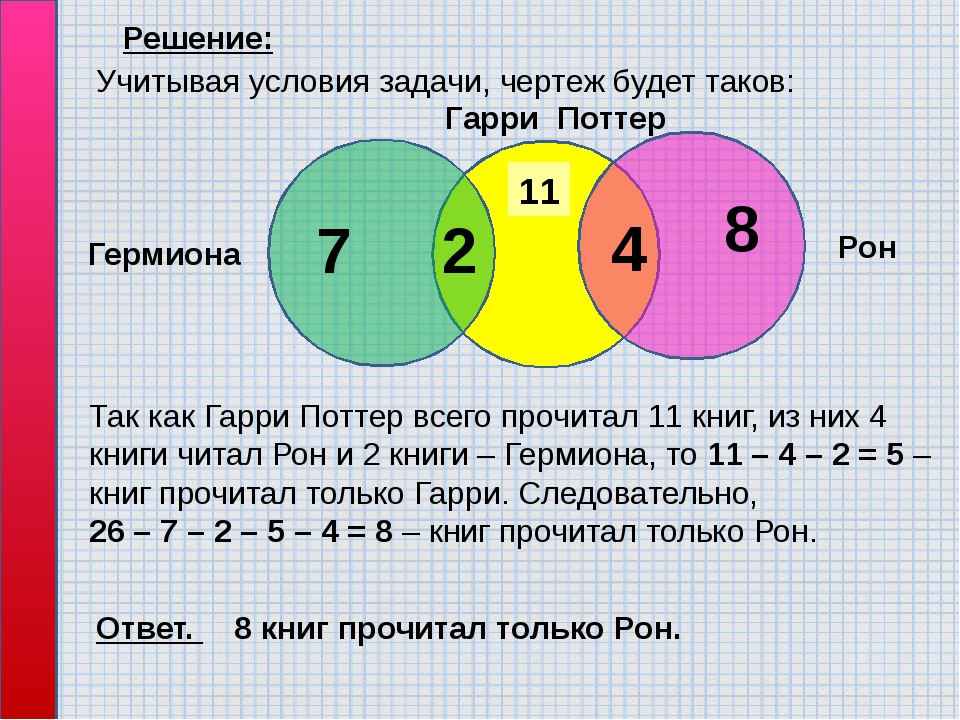
Сколько учеников класса не посещают никаких кружков?
Способ 1. На рисунке большой круг изображает множество всех учеников класса. Внутри этого круга расположены три пересекающихся круга меньшего диаметра: эти круги изображают соответственно множества членов математического, физического и химического кружков. Эти круги обозначены буквами М, Ф, Х.
Общей части всех трех кругов соответствует множество ребят, посещающих все три кружка, поэтому она обозначена МФХ.
Через обозначено множество ребят, посещающих математический и физический кружки, но не посещающих химический кружок. Аналогичным образом обозначены и все остальные области. Здесь для удобства обозначений мы будем отсутствие отмечать чертой над символом.
Теперь обратимся к числовым данным (см. Приложение 2).
В область МФХ впишем число 2, т.к.
все три кружка посещают 2 ученика. Далее
известно, что ребят, посещающих
математический и физический кружки,
было 8. Значит, в область МФ надо вписать
число 8. Но область МФ состоит из двух
частей: и МФХ, причем в МФХ входят 2 человека.
Значит, на долю остается 6 человек.
Далее
известно, что ребят, посещающих
математический и физический кружки,
было 8. Значит, в область МФ надо вписать
число 8. Но область МФ состоит из двух
частей: и МФХ, причем в МФХ входят 2 человека.
Значит, на долю остается 6 человек.
Теперь рассмотрим множество МХ, на которое приходится 5 человек. Эта область также состоит из двух частей. На МФХ приходится 2 человека, значит, на приходится 3.
Рассмотрим теперь множество М, в которое входят 18 учеников. Оно состоит из 4 частей. Количественный состав трех подмножеств мы уже нашли: это 2, 6 и 3. Значит, в четвертое подмножество входит 18 – (2+3+6) = 7 человек.
Рассмотрим множество ФХ, на которое приходится 3 человека. Эта область также состоит из двух частей. На МФХ приходится 2 человека, значит, на приходится 1.
Рассмотрим множество Ф, в которое
входят 14 учеников. Оно состоит из 4
частей. Количественный состав трех
подмножеств мы уже нашли: это 2, 6 и 1. Значит, в четвертое подмножество входит 14 – (2+1+6) = 5 человек.
Значит, в четвертое подмножество входит 14 – (2+1+6) = 5 человек.
36 – (10+7+6+5) = 8 человек. Таким образом, в классе 8 ребят, не посещающих никаких кружков.
М
6
5
7
2
3
1
4
? 8
Способ 2. С помощью модели «Круги Эйлера» (Приложение 1).
Представим множества учащихся,
посещающих математический, физический
и химический кружки, в виде кругов,
вырезанных из плотной бумаги. Будем
считать, что площадь каждого из этих
кругов равна числу учащихся, посещающих
соответствующий кружок. Наложим
круги друг на друга так, чтобы было
понятно, что есть учащиеся, посещающие
один, два или три кружка. Вычислим площадь
получившейся фигуры:
Вычислим площадь
получившейся фигуры:
14 + 18 + 10 – ((8 + 5 + 3) 2) – 2 = 8 (чел.)— не посещают кружки.
Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.
Аналогично получаем, что только английским и немецким владеют 8-3=5 человек, а немецким и французским 5-3=2 туриста.
Немецкий знают 30 человек, но
5+3+2=10 из них владеют и другими языками,
следовательно, только немецкий знают
20 человек.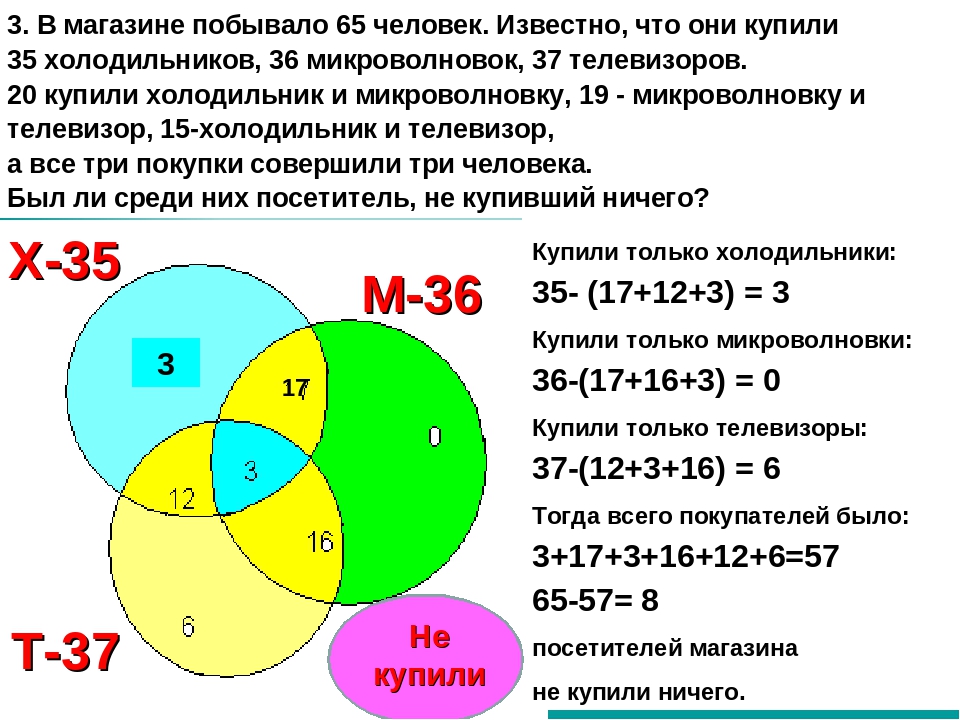 Аналогично получаем, что
одним английским владеют 13 человек,а
одним французским — 30.
Аналогично получаем, что
одним английским владеют 13 человек,а
одним французским — 30.
Всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.
Заключение
Существует множество приемов, которые используются при решении текстовых логических задач (Приложение 3). Очень часто решение задачи помогает найти рисунок, он делает решение простым и наглядным. Задачи, решаемые с помощью кругов Эйлера, предлагаются на математических олимпиадах, но в школьной программе не отводятся часы на изучение данной темы. Ценность использования кругов Эйлера состоит в том, что решения задач с громоздкими условиями и со многими данными становятся проще.
Подобные задачи часто имеют
практический характер, что немаловажно
в современной жизни. Они заставляют
задумываться, подходить к решению
какой-либо проблемы с разных сторон,
уметь выбирать из множества способов
решения наиболее простой, легкий путь.
Нами созданы модели «Круги Эйлера» для решения логических задач на пересечение двух и трёх множеств, которыми можно пользоваться как на месте (за партой), так и у доски (Приложение 4).
Поиск готовых способов решения выделенных логических задач, самостоятельное описание способа действий при использовании кругов Эйлера для их решения, а также попытки рассмотрения другой формы представления данных условия позволили нам решить поставленные задачи.
Цель была достигнута. С результатами работы были ознакомлены наши одноклассники, что позволило решать логические задачи этого вида не только нам.
Теперь наши одноклассники решают такие задачи, используя не только модели, но и памятку со способом действий, написанных нами.
Теперь мы точно будем знать, сколько друзей нам надо встречать в гости. От 20 до 35! А значит, и за стол всех всё же можно будет посадить.
Данная тема, безусловно,
расширяет математический кругозор
учащихся, обогащает арсенал средств,
используемых в решении разнообразных
задач.
Литература
Задачи для внеклассной работы по математике в V – VI классах: Пособие для учителей Текст/ Сост. В.Ю. Сафонова. Под ред. Д.Б. Фукса, А. Л. Гавронского. М.: МИРОС, 1993. с. 42. – ISBN 5-7084-0023-4
Занимательная математика. 5 – 11 классы. Текст: (Как сделать уроки нескучными) / Авт. – сост. Т.Д. Гаврилова. Волгоград: Учитель, 2005. с.32-38. – 10000 экз. –5-7057-0482-8
Депман,И.Я., Виленкин, Н.Я. За страницами учебника математики Пособие для учащихся 5 – 6 кл. Текст/ И.Я Депман. М.: Просвещение, 1999. с. 189 – 191, 231. – 10000 экз. – ISBN 5-09-007107-1
Смыкалова, Е.В. Дополнительные главы по математике для учащихся 5 класса. Текст: СПб: СМИО Пресс, 2009. с.14-20. – 2000 экз. – ISBN 5-7704-0055-2
Фарков, А.В. Математические олимпиады в школе.5–11 классы.Текст / А.
 В. Фарков. М.: Айрис–пресс, 2007. с. 27,
34, 61. – 7000 экз. – ISBN
978-5-8112-2394-7
В. Фарков. М.: Айрис–пресс, 2007. с. 27,
34, 61. – 7000 экз. – ISBN
978-5-8112-2394-7Энциклопедия для детей. Т. 11. Математика Текст/ Глав.ред. М.Д. Аксёнова. М.: Аванта +,2001. с. 537 — 542. – 20000экз. – ISBN 5-8483-0015-1
Иванищев, Д. М. Поляна загадок – математика царица.
/
Дистанционная обучающая олимпиада по математике (ДООМ)
/
Сопова, С. С. Диаграмма Эйлера-Вена и «дерево». Взаимодополнение.
/
Приложение 1
Модель «Круги Эйлера» на пересечение двух множеств
На листе бумаги нарисовать два круга.
Разрезать по пунктирным линиям и получить детали.
На бумаге цвета 1 обвести и вырезать детали № 1 () (), № 2 ().

На бумаге цвета 2 обвести и вырезать детали № 2, № 3 () ().
— окошко для названия множества, — окошко для числа
Модель «Круги Эйлера» на пересечение трёх множеств
На листе бумаги нарисовать три круга.
Разрезать по пунктирным линиям и получить детали.
На бумаге цвета 1 обвести и вырезать детали № 5 () (), № 2, № 1, № 4.
На бумаге цвета 2 обвести и вырезать детали № 6 (), (), № 2, № 1, № 3.
На бумаге цвета 3 обвести и вырезать детали № 7 (), (), № 4 (), № 1 (),
№ 3 ().
Приложение 2.
Способ действий при решении задач
на пересечение и объединение трёх множеств с помощью кругов Эйлера
Начертить три пересекающихся круга.
 Обозначить множества: A, B, C.
Обозначить множества: A, B, C.Начертить большой круг, в котором окажутся три маленьких. Это общее количество объектов – множество Е.
Начертить отдельное множество D – подмножество множества E Это те, кто не является элементом множеств А, В и С.
Найти часть круга, являющуюся общей для всех трёх множеств (№1) и записать данные.
Найти часть круга, являющуюся общей для двух множеств (№1 и №2) и записать данные в №2.
Найти часть круга, являющуюся общей для двух множеств (№1 и №3) и записать данные в №3.
Найти часть круга, являющуюся общей для двух множеств (№1 и №4) и записать данные в №4.
Найти часть круга, отвечающую за каждое множество в отдельности:
5 = А – (1 +
2 +
4), 6 = В – (1
+ 2
+
3), 7 = С – (1
+ 3
+
4).
Должно выполняться: 1 + 2 + 3 + 4 + 5 + 6 + 7 + D = E/
Записываем ответ на вопрос задачи.
Приложение 3.
Задача (/). а) На 3 курсе факультета обучается 81 студент. Многие из них выбрали одинаковые дисциплины, посещают одни и те же лекции и хорошо знают друг друга. б) 43 студента посещают лекции по философии, в)32 — по логике и г)41 — по естествознанию. д) Философию и логику выбрали 11 человек. е) Философию и естествознание посещает 21 студент, ж)а логику и естествознание — 16. з) 4 человека выбрали только философию и логику.
Сколько студентов посещают лекции:
1) по всем трём предметам,
2)только по философии и естествознанию,
3)только по логике и естествознанию,
4)только по философии,
5)только по естествознанию,
6)только по логике,
7)не выбрали ни одну из этих
дисциплин.
Каждое высказывание из условия записать в виде логического выражения, строго подписывая друг под другом элементы. Решать систему будем с тех уравнений, где меньше всего неизвестных, попарно вычитая уравнения. При решении стремимся убрать как можно больше неизвестных.
1) Возможные варианты перебираем с учетом
а) + + + + + + + = 81
б) + 0 + 0 + + + 0 + + 0 = 43
в) 0 + + 0 + + 0 + + + 0 = 32
г) 0 + 0 + + 0 + + + + 0 = 41
д) 0 + 0 + 0 + + 0 + 0 + + 0 = 11
е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21
ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16
з) 0 + 0 + 0 + + 0 + 0 + 0 + 0 = 4
2) Четко видно, что = 4. Подписываем под чертой вычисленные
значения и убираем использованные
уравнения. Ниже приведен подробный ход
решения.
а) + + + + + + + = 81
б) + 0 + 0 + + + 0 + + 0 = 43
в) 0 + + 0 + + 0 + + + 0 = 32
г) 0 + 0 + + 0 + + + + 0 = 41
д) 0 + 0 + 0 + + 0 + 0 + + 0 = 11
е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21
ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16
и) 4
а) + + + + + + + = 81
б) + 0 + 0 + + + 0 + + 0 = 43
в) 0 + + 0 + + 0 + + + 0 = 32
г) 0 + 0 + + 0 + + + + 0 = 41
е) 0 + 0 + 0 + 0 + + 0 + + 0 = 21
ж) 0 + 0 + 0 + 0 + 0 + + + 0 = 16
и) 4 7
а) + + + + + + + = 81
б) + 0 + 0 + + + 0 + + 0 = 43
в) 0 + + 0 + + 0 + + + 0 = 32
г) 0 + 0 + + 0 + + + + 0 = 41
и) 4 14 9 7
а) + + + + + + + = 81
и) 18 12 11 4 14 9 7
0) + + ++ + + + = 81
и) 18 12 11 4 14 9 7 6
Ответ:1) по всем трём предметам, , 7
2)только по философии и естествознанию, , 14
3)только по логике и естествознанию, , 9
4)только по философии, , 18
5)только по естествознанию, , 11
6)только по логике, , 12
7)не выбрали ни одну из этих дисциплин, , 6
Приложение 4
Отчёт о проделанной работе перед коллегами
Круги Эйлера.
 Решение задач — презентация онлайн Муниципальное общеобразовательное учреждение
Решение задач — презентация онлайн Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №1 г.Суздаля»
и
г
у
р
К
а
р
е
л
й
Э
Задача №1:
Из 100 туристов, отправляющихся в заграничное
путешествие, немецким языком владеют 30 человек,
английским – 28, французским – 42. Английским и немецким
одновременно владеют 8 человек, английским и
французским 10 , немецким и французским – 5, всеми тремя
языками – 3.
Сколько туристов не владеют ни одним языком?
Решение:
Выразим условие задачи графически. Обозначим кругом тех, кто
знает английский, другим кругом – тех, кто знает французский, и
третьим кругом – тех, кто знают немецкий.
французский
немецкий
английский
Всеми тремя языками владеют три туриста, значит, в
общей части кругов вписываем число 3.
французский
немецкий
5
3
7
английский
Английским и французским
языками владеют 10 человек, а 3
из них владеют ещё и немецким.
Значит, английским и
французским владеют 103=7
человек.
В общую часть английского и
французского кругов вписываем
цифру 7.
Английским и немецким языками владеют 8 человек, а 3 из
них владеют ещё и французским. Значит, английским и
немецким владеют 83=5 человек.
В общую часть английского и немецкого кругов
вписываем число 5.
французский
немецкий
20
5
2
3
7
30
13
английский
Немецким и французским
языками владеют 5 человек, а
3 из них владеют ещё и
английским. Значит,
немецким и французским
владеют 53=2 человека.
В общую часть немецкого и
французского кругов вписываем
цифру 2.
Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из
них владеют и другими языками, значит, только немецкий знают
20 человек.
Английский язык знают 28 человек, но 5+3+7=15 человек владеют и
другими языками, значит, только английский знают 13 человек.

Французский язык знают 42 человека, но 2+3+7=12 человек владеют
и другими языками, значит, только французский знают 30 человек.
По условию задачи всего 100 туристов. 20+30+13
+5+2+3+7=80 туристов знают хотя бы один язык,
следовательно, 20 человек не владеют ни одним языком.
Ответ:
20 человек.
Рисунки, подобные тем, что мы
рисовали при решении этой задачи,
называются «кругами Эйлера». Один из
величайших математиков Петербургской
академии Леонард Эйлер написал более
850 научных работ. В одной из них и
появились эти круги. Эйлер писал тогда,
что «они очень подходят для того, чтобы
облегчить наши размышления». Наряду с
кругами в подобных задачах применяют
прямоугольники и другие фигуры.
Задача №2:
В ясельной группе 11 деток любят манную кашу, 13 –
гречневую и 7 малышей – перловую. Четверо любят и
манную, и гречневую, 3 – манную и перловую, 6 гречневую и
перловую, а двое с удовольствием «уплетают» все три вида
каши.
 Сколько детей в этой группе, если в ней нет ни одного
Сколько детей в этой группе, если в ней нет ни одного ребёнка, вовсе не любящего кашу?
Решение:
манная
перловая
11 6
0
31
4 2
2
13
7
64
5
гречнева
я
Ответ:
6+1+2+2+0+4+5=20 ребят
Задача №3:
В одной семье было много детей. 7 из них любили капусту,
6 – морковь, 5 – горох, 4 – капусту и морковь, 3 – капусту и
горох, 2 – морковь и горох, 1 – и капусту, и морковь, и горох.
Сколько детей было в семье?
Решение:
капуста
7
морковь
1
43
32
1
5 1
горох
21
6
1
Ответ: 10 человек.
Задача №4:
В группе 29 студентов. Среди них 14 любителей
классической музыки, 15джаза, 14 – народной музыки.
Классическую музыку и джаз слушают 6 студентов,
народную музыку и джаз – 7, классику и народную – 9.
Пятеро студентов слушают всякую музыку, а остальные не
любят никакой музыки. Сколько их?
Решение:
джаз
15 7
6 1
7 2
5
14
4
классическая
музыка
9 4
14 3
народная
музыка
Ответ:
297215344=3(человека)
– не любят никакую музыку.

Задача №5:
Учащиеся 5 и 6 классов отправились на экскурсию.
Мальчиков было 16, учащихся 6 класса – 24, пятиклассниц
столько, сколько мальчиков из 6 класса. Сколько всего детей
побывали на экскурсии?
Решение:
16
мальчики
5 класс
мальчики
6 класс
девочки
5 класс
девочки
6 класс
24
Ответ: 40 человек.
Задача №6:
На полу комнаты площадью 24 м² лежат три ковра. Площадь
одного из них 10 м², другого – 8 м², третьего – 6 м². Каждые
два ковра перекрываются по площади 3 м², а площадь
участка пола, покрытого всеми тремя коврами, составляет 1
м². Найдите площадь участка пола:
а)покрытого первым и вторым коврами, но не покрытого
третьим ковром;
б)покрытого только первым ковром;
в)не покрытого коврами.
Решение:
Ответ:
а) 10м²;
б)5 м²;
в) 241051=8 м²
1
2
10
5
32
32
3
1
6
8
3 2
1
3
Задача №7
1.
 Из 100 приехавших туристов 75 знали немецкий язык и
Из 100 приехавших туристов 75 знали немецкий язык и 83 знали французский. 10 человек не знали ни немецкого,
ни французского. Сколько туристов знали оба эти языка?
Решение:
немецкий
французский
75
х
10010=90
83
Получим уравнение: 75+83х=90
158х=90
х=68
Ответ:
68 человек знали оба языка
Задача для самостоятельного решения:
1. Из 40 опрошенных человек 32
любят молоко, 21 – лимонад, а 15 – и
молоко, и лимонад. Сколько человек
не любят ни молоко, ни лимонад?
Ответ: 2 человека
Задача для самостоятельного решения:
2. В воскресенье 19 учеников нашего
класса побывали в планетарии, 10 – в
цирке и 6 – в музее. Планетарий и цирк
посетили 5 учеников; планетарий и музей –
трое, в цирке и музее был один человек.
Сколько учеников в нашем классе, если
никто не успел посетить все три места, а
трое вообще никуда не ходили?
Ответ: 20 человек
Задача для самостоятельного решения:
3.
 В детском лагере отдыхало 70 ребят. Из
В детском лагере отдыхало 70 ребят. Из них 20 занимаются в драмкружке, 32 поют
в хоре, 22 увлекаются спортом. В
драмкружке 10 ребят из хора, в хоре 6
спортсменов, в драмкружке 8
спортсменов, а 3 спортсмена посещают и
драмкружок, и хор. Сколько ребят не
поют в хоре, не увлекаются спортом и не
занимаются в драмкружке? Сколько
ребят заняты спортом?
Ответ: 10 ребят, 11 спортсменов.
Задача для самостоятельного решения:
4.Из сотрудников фирмы 16
побывали во Франции, 10 – в
Италии, 6 – в Англии. В Англии и
Италии – пятеро, в Англии и
Франции – 6, во всех трёх странах
– 5 сотрудников. Сколько человек
посетили и Италию, и Францию,
если всего в фирме работает 19
человек, и каждый их них
побывал хотя бы в одной из
названных стран?
Ответ: 7 сотрудников
с
ч
е
р
т
с
в
и
х
м
ы
ы
в
н
о
ь
н
л
о
е
т
Д
а
м
и
и
м
н
а
а
ч
з
а
д
за
Решение задач с помощью кругов Эйлера
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
Решение задачи №1
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б,В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача №2
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросу Выпечка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.Решение задачи №2
Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б,В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти сектор В, для этого из общего множества (Пироженое │ Выпечка ) отнимем множествоПироженое.
Сектор В равен 4500, следовательно Выпечка = Б + В = 4300+5100 = 9400
Задача №3
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры | овчарки |
Решение задачи №3
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача №4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | барокко | классицизм | ампир |
| 2 | барокко | классицизм & ампир |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение задачи №4
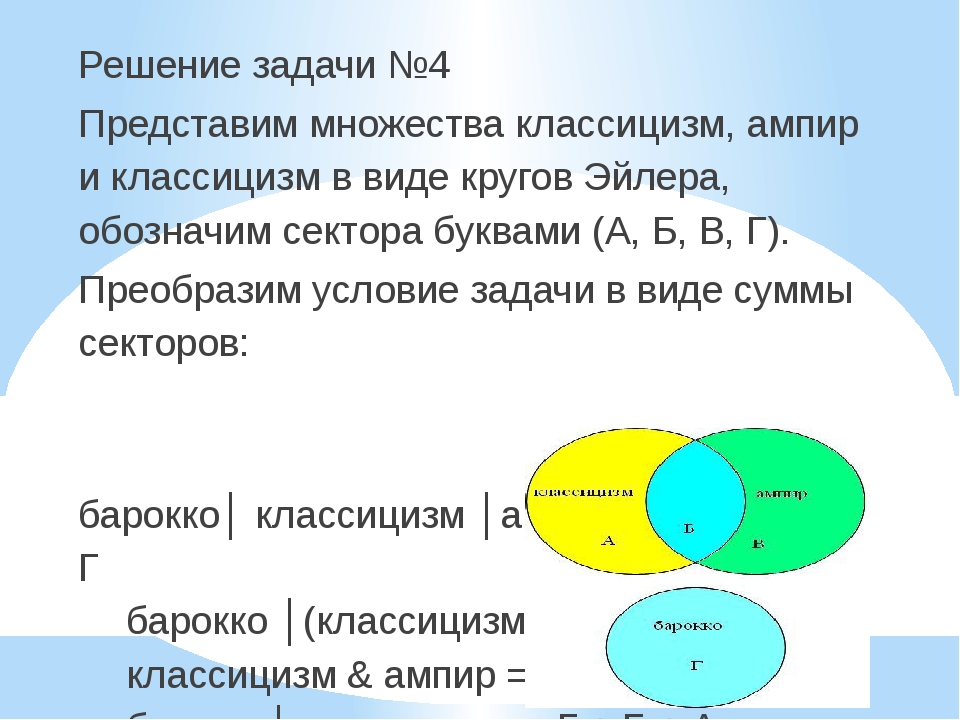
Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Гбарокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача №5В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | канарейки | терьеры | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение задачи №5
Для решения задачи представим запросы в виде кругов Эйлера.
K — канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задачи для самостоятельного решения
Задача №6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача №7
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
Решение задач с помощью кругов Эйлера
При
решении задач с использованием кругов Эйлера очень важно правильно нарисовать
картинку, отображающую найденные запросы. В таблице на страницах 2-3
представлены наиболее часто встречаемые случаи.
В таблице на страницах 2-3
представлены наиболее часто встречаемые случаи.
Отметив области, которые надо найти по условию, поняв, что требуется найти, решить задачу визуально становится довольно просто.
Самые простые задачи – на два круга, немного сложнее – на три. Достаточно трудно изобразить четыре круга. К счастью, такие задачи предоставляют возможность сделать сокращения и свести решение задачи к трём кругам. Например, даны такие запросы.
Запрос | Найдено страниц (в тысячах) |
Леннон & Маккартни & Старр | 1100 |
Леннон & Маккартни & Харрисон | 1300 |
Леннон & Маккартни & Старр & Харрисон | 1000 |
Какое количество
страниц (в тыс. ) будет найдено по запросу
) будет найдено по запросу
(Леннон & Маккартни & Старр) | (Леннон & Маккартни & Харрисон)?
При решении этой задачи можно сократить в исходных запросах и в тех, что надо найти запрос «Леннон», так как он выступает здесь как общий множитель. В итоге, задача сведётся к трём кругам.
Иногда надо круги рисовать не «ромашкой», а в ряд. Это бывает в задачах, в которых представлены запросы, в двух из которых нет пересечения. Например, в этой таблице запросов явно указано, что нет пересечения между Напряжённость и Пшеница
Запрос | Найдено страниц (в сотнях тысяч) |
Поле | 54 |
Пшеница | 40 |
Напряжённость | 44 |
Поле & Пшеница | 30 |
Напряжённость & Поле | 14 |
Напряжённость & Пшеница | 0 |
Картинка будет выглядеть так ->
Сложнее рисовать картинку в таком виде,
когда пересечение равное 0 не задано и
надо догадаться, что у двух запросов нет
пересечения. Как правило,
в центре располагается запрос, представляющий собой слово-омоним. Справа и
слева от него значения запросов даны, а также дано бывает их объединение (ИЛИ).
Например, если Пшеница – 40, Напряжённость – 44, а Напряжённость|Пшеница – 84, то складывая 40 и 44, понимаем, что пересечения нет, так как сумма
и запрос ИЛИ дают одно и то же число 84.
Как правило,
в центре располагается запрос, представляющий собой слово-омоним. Справа и
слева от него значения запросов даны, а также дано бывает их объединение (ИЛИ).
Например, если Пшеница – 40, Напряжённость – 44, а Напряжённость|Пшеница – 84, то складывая 40 и 44, понимаем, что пересечения нет, так как сумма
и запрос ИЛИ дают одно и то же число 84.
Ученикам, которые впервые решают задачи на круги Эйлера, бывает сразу не очень понятно, почему если есть значение двух запросов, то их объединение не равно их сумме. Понять это легко можно на следующем примере. Допустим, есть запросы Пушкин и Лермонтов. Изобразим, что всего было найдено 5 страниц. На каких то страницах речь шла только о Пушкине, на других только о Лермонтове, а где то писали о них обоих.
По
картинке видно, что запрос Пушкин выдал 4 страницы, Лермонтов –
3, Пушкин&Лермонтов – 2, а Пушкин|Лермонтов – 5. Запрос ИЛИ
не выдаст 7, так как из условия физически не существует столько страниц. Их
всего 5.
Запрос ИЛИ
не выдаст 7, так как из условия физически не существует столько страниц. Их
всего 5.
Пушкин Лермонтов
«2» входит и в круг «Пушкин» и в круг «Лермонтов», поэтому
Пушкин ИЛИ Лермонтов = 4 + 3 — 2 = 5
Презентация к уроку «Решение задач ЕГЭ с помощью кругов Эйлера-Венна»
библиотека
материалов
Содержание слайдов
Номер слайда 1
http://anisimovaiv.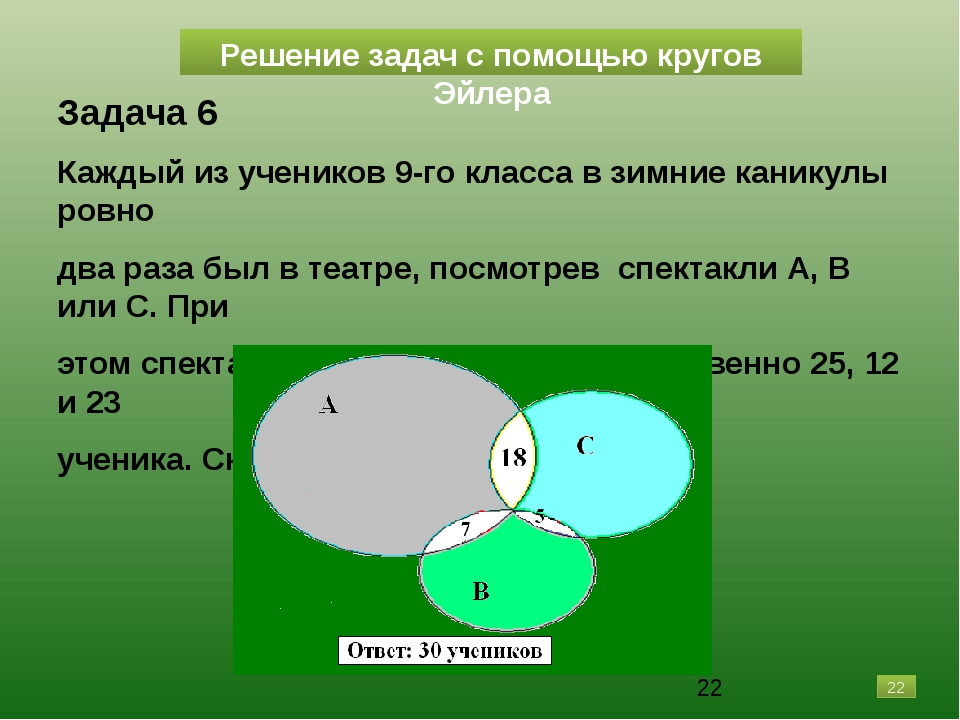 edusite.ru/p32aa1.html
edusite.ru/p32aa1.html
Номер слайда 2
Номер слайда 3
Тема: Решение задач с помощью кругов Эйлера-Венна Цель: Научиться использовать круги Эйлера-Венна при решении задач
Номер слайда 4
Учить всему надо легко, доступно и наглядно. Леонард Эйлер
Леонард Эйлер
Номер слайда 5
Задача №17(ЕГЭ). Запросы для поисковых систем с использованием логических выражений Два поля Три поля с пустым пересечением Три поля Более трёх полей
Номер слайда 6
Экзамен Репетитор 1 2 3 формула включений и исключений NA & B = NA + NB – NA | B Решение: 2=500+370-750=120 Два поля
Номер слайда 7
формула включений и исключений NA & B = NA + NB – NA | B NA = NA & B + NA | B – NB Торты=6500+12000-7700=10800
Номер слайда 8
Вопрос: Как понять пересекаются поля или нет? Три поля с пустым пересечением
Номер слайда 9
Три поля с пустым пересечением Демоверсия ЕГЭ-2020
Номер слайда 10
ПШЕНИЦА ПОЛЕ НАПРЯЖЕННОСТЬ Дано: N1+N2=40 (1) N2+N3+N4=54 (2) N4+N5=44 (3) N2=30 N4=14 N1+N2+N3+N4+N5=? Решение: из (2) N3=54-30-14=10 Напряженность | Поле | Пшеница = N1+N2+N3+N4+N5=40+10+44=94 1 2 3 4 5
Номер слайда 11
Вопрос: Как понять что поля не пересекаются? Ответ: Если в результате конъюнкции двух полей получается 0, эти поля не пересекаются Три поля с пустым пересечением
Номер слайда 12
Три поля с пустым пересечением Открытый банк заданий ЕГЭ-2019 (fipi. ru)
ru)
Номер слайда 13
ГОРЛО НОС КОРАБЛЬ Дано: N1+N2=35 (1) N4+N5=30 (2) N2+N3+N4=40 (3) N1+N2+N3+N4+N5=70 (4) N2=10 (5) N4=? Решение: N1+N2+N3+N4+N5=70 N3=70-35-30=5 Из (3) находим N4=40-10-5=25 n 4 2 1 3 5
Номер слайда 14
Номер слайда 15
Варианты логических выражений (три поля с пересечением)
Номер слайда 16
Три поля с пересечением Дано: N5=50 (1) N2+N5=150 (2) N4+N5=130 (3) N2+N3+N4+N5+N6+N7=660 (4) N1+N2+N3+N4+N5+N6+N7=900 (5) N1+N2+N4+N5=? Решение: N1=900-660=240 N2=150-50=100 N4=130-50=80 Ночь=N1+N2+N4+N5=240+100+80+50=470
Номер слайда 17
1 1 1 2 3 4 5 6 7 Дано: N5+N6=165 N4+N5=125 N5=80 N4+N5+N6=? Решение: N4=125-80=45 N6=165-80=85 N4+N5+N6=45+80+85=210 Фотон Протон Бозон
Номер слайда 18
Стр. 184 № 5, 6, 7
184 № 5, 6, 7
Решение задач с помощью кругов Эйлера
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
Задача №1
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| Запрос | Найдено страниц (в тысячах) |
| Торты | Пироги | 12000 |
| Торты & Пироги | 6500 |
| Пироги | 7700 |
Какое количество страниц (в тысячах) будет найдено по запросу Торты?Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение задачи №1
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача №2
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросу Выпечка?
Считается,
что все запросы выполнялись практически одновременно, так что набор
страниц, содержащих все искомые слова, не изменялся за время выполнения
запросов.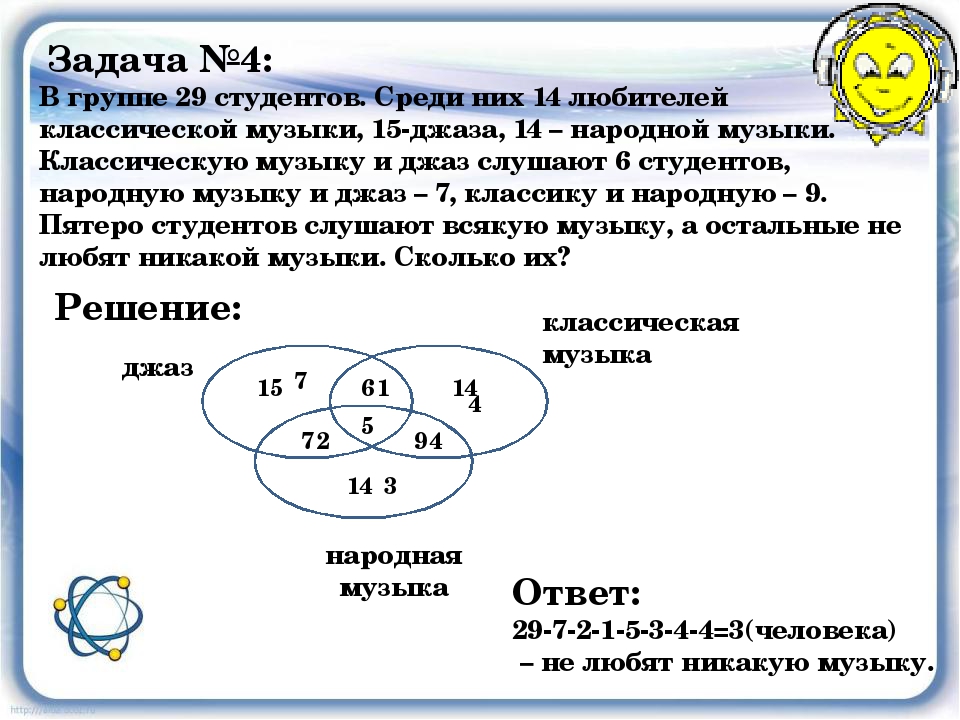 Решение задачи №2
Решение задачи №2
Для решения задачи отобразим множества Пироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти сектор В, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое.
Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500Сектор В равен 4500, следовательно Выпечка = Б + В = 4300+5100 = 9400
Задача №3
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры | овчарки |
Решение задачи №3
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача №4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | барокко | классицизм | ампир |
| 2 | барокко | классицизм & ампир |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение задачи №4
Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Гбарокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача №5В таблице приведены запросы к поисковому серверу.
 Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | канарейки | терьеры | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение задачи №5
Для решения задачи представим запросы в виде кругов Эйлера.
K — канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
| канарейки | терьеры | содержание | канарейки & содержание | канарейки & щеглы & содержание | разведение & содержание & канарейки & щеглы |
Самая большая область закрашенных секторов у первого
запроса, затем у второго, затем у третьего, а у четвертого запроса самый
маленький.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задачи для самостоятельного решения
Задача №6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача №7
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
Использованные материалы >>>
Решение подобных задач по информатике >>>
Ответы к задачам для самостоятельного решения
| Номер задачи | Ответ |
| 6 | ГБВА |
| 7 | БВАГ |
Как построить круги эйлера в презентации.
 Презентация — решение задач с помощью кругов эйлера. Презентация
Презентация — решение задач с помощью кругов эйлера. ПрезентацияЭйлеровы круги (круги Эйлера).
Цель урока: Познакомить обучающихся с решением простейших логических задач методом кругов Задачи урока Образовательная: дать обучающимся представление о методе кругов Эйлера; Развивающая: развитие логического и аналитического мышления; Воспитательная: воспитание умения выслушивать мнение других обучающихся и отстаивать свою точку зрения.
Эйлеровы круги (круги Эйлера) — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов, предложенный знаменитым математиком Л. Эйлером (1707–1783). Обозначение отношений между объемами понятий посредством кругов было применено еще представителем афинской неоплатоновской школы — Филопоном (VI в.), написавшим комментарии на «Первую Аналитику» Аристотеля.
1.Условно принято, что круг наглядно изображает объем одного какого-нибудь понятия. Объем же понятия отображает совокупность предметов того или иного класса предметов. Поэтому каждый предмет класса предметов можно изобразить посредством точки, помещенной внутри круга:
Поэтому каждый предмет класса предметов можно изобразить посредством точки, помещенной внутри круга:
2. Группа предметов, составляющая вид данного класса предметов, изображается в виде меньшего круга, нарисованного внутри большего круга. Такое именно отношение существует между объемами понятий «небесное тело» (А) и «комета» (B). Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело».
3 . Когда же ни один предмет, отображенный в объеме понятия A, не может одновременно отображаться в объеме понятия B, то в таком случае отношение между объемами понятий изображается посредством двух кругов, нарисованных один вне другого. Ни одна точка, лежащая на поверхности одного круга, не может оказаться на поверхности другого круга. Такое именно отношение существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник». В объеме понятия «тупоугольный треугольник» не отображается ни один остроугольный треугольник, а в объеме понятия «остроугольный треугольник» не отображается ни один тупоугольный треугольник.
В объеме понятия «тупоугольный треугольник» не отображается ни один остроугольный треугольник, а в объеме понятия «остроугольный треугольник» не отображается ни один тупоугольный треугольник.
4 . Иначе выглядит схема отношения между объемами субъекта и предиката в общеутвердительном суждении, не являющемся определением понятия. В таком суждении объем предиката больше объема субъекта, объем субъекта целиком входит в объем предиката. Поэтому отношение между ними изображается посредством большого и малого кругов, как показано на рисунке:
5.Отношения между равнозначащими понятиями, объемы которых совпадают, отображаются наглядно посредством одного круга, на поверхности которого написаны две буквы, обозначающие два понятия, имеющие один и тот же объем: Такое отношение существует, например, между понятиями «родоначальник английского материализма» и «автор „Нового Органона“». Объемы этих понятий одинаковы, в них отобразилось одно и то же историческое лицо — английский философ Ф. Бэкон.
6 . Нередко бывает и так: одному понятию (родовому) подчиняется сразу несколько видовых понятий, которые в таком случае называются соподчиненными. Отношение между такими понятиями изображается наглядно посредством одного большого круга и нескольких кругов меньшего размера, которые нарисованы на поверхности большего круга: Такое именно отношение существует между понятиями «скрипка», «флейта», «пианино», «рояль», «барабан». Эти понятия в равной мере подчинены одному общему родовому понятию «музыкальные инструменты».
7. В тех случаях, когда между понятиями имеется отношение противоположности, отношение между объемами таких понятий отображается посредством одного круга, обозначающего общее для обоих противоположных понятий родовое понятие, а отношение между противоположными понятиями обозначается так: А — родовое понятие, B и C — противоположные понятия. Противоположные понятия исключают друг друга, но входят в один и тот же род, что можно выразить такой схемой: При этом видно, что между противоположными понятиями возможно третье, среднее, так как они не исчерпывают полностью объема родового понятия. Такое именно отношение существует между понятиями «легкий» и «тяжелый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и легкий, и тяжелый. Но между данными понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но также и среднего веса.
Такое именно отношение существует между понятиями «легкий» и «тяжелый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и легкий, и тяжелый. Но между данными понятиями есть среднее, третье: предметы бывают не только легкого и тяжелого веса, но также и среднего веса.
8.Когда же между понятиями существует противоречащее отношение, тогда отношение между объемами понятий изображается иначе: круг делится на две части так: А — родовое понятие, B и не-B (обозначается как B) — противоречащие понятия. Противоречащие понятия, исключают друг друга и входят в один и тот же род, что можно выразить такой схем ой: При этом видно, что между противоречащими понятиями третье, среднее, невозможно, так как они полностью исчерпывают объем родового понятия. Такое отношение существует, например, между понятиями «белый» и «небелый». Они исключают друг друга. Нельзя об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении, сказать, что он и белый и небе лый.
9.Посредством Эйлеровых кругов изображаются также отношения между объемами субъекта и предиката в суждениях. Так, в общеутвердительном суждении, выражающем определение какого-либо понятия, объемы субъекта и предиката, как известно, равны. Наглядно такое отношение между объемами субъекта и предиката изображается посредством одного круга, подобно изображению отношений между объемами равнозначащих понятий. Разница только в том, что в данном случае всегда на поверхности круга надписываются две определенные буквы: S (субъект) и P (предикат), как это показано на рисунке:
Задача 1. Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро — собак. И только у двоих есть и те и другте. Угадайте, сколько у меня подруг? Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом — собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части «кошачьего» круга ставим цифру 4 (6 — 2 = 4). В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части «кошачьего» круга ставим цифру 4 (6 — 2 = 4). В свободной части «собачьего» круга ставим цифру 3 (5 — 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
Ответ. 9 подруг.
Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 — в районной. Сколько учеников не являются читателями школьной библиотеки? Решение: Пусть круг Ш изображает читателей только школьной библиотеки, круг Р — только районной. Тогда ШР — изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно: (не Ш) = Р — ШР. Всего 30 учеников, Ш = 20 человек, Р = 15 человек. Тогда значение ШР может быть найдено так (см. рисунок): ШР = (Ш + Р) — 30 = (20 + 15) — 30 = = 5, т.е. 5 учеников являются читателями школьной и районной библиотек одновременно. Тогда (не Ш) = = Р — ШР= 15 — 5= 10.
Тогда (не Ш) = = Р — ШР= 15 — 5= 10.
Ответ: 10 учеников не являются читателями школьной библиотеки.
Задача 3. Любимые мультфильмы. Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», » Винни Пух», «Микки Маус». Всего в классе 28 человек. «Белоснежку и семь гномов» выбрали 16 учеников, среди которых трое назвали еще «Микки Маус», шестеро — » Винни Пух», а один написал все три мультфильма. Мультфильм «Микки Маус» назвали 9 ребят, среди которых пятеро выбрали по два мультфильма. Сколько человек выбрали мультфильм » Винни Пух»? Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только «Белоснежку» выбрали 16-6-3-1=6 человек. Только «Микки-Маус» выбрали 9-3-2-1=3 человека. Только » Винни-Пух » выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что » Винни-Пух » выбрали 7+6+1+2=16 человек.
Задача 7. Спорт для всех. В классе 38 человек. Из них 16 играют в баскетбол, 17 — в хоккей, 18 — в футбол. Увлекаются двумя видами спорта — баскетболом и хоккеем — четверо, баскетболом и футболом — трое, футболом и хоккеем — пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом. Сколько ребят увлекаются одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта? Решение. Воспользуемся кругами Эйлера. Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта — баскетболом занимаются 16 — (4 + z + 3) = 9 — z ; одним лишь хоккеем 17 — (4 + z + 5) = 8 — z ; одним лишь футболом
18 — (3 + z + 5) = 10 — z . Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам: 3 + (9 — z) + (8 — z) + (10 — z) + 4 + 3 + 5 + z = 38,z = 2. Таким образом, двое ребят увлекаются всеми тремя видами спорта. Складывая числа 9 — z , 8 — z и 10 — z , где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек. Ответ: Двое ребят увлекаются всеми тремя видами спорта человека. Увлекающихся лишь одним видом спорта: 21 человек.
Таким образом, двое ребят увлекаются всеми тремя видами спорта. Складывая числа 9 — z , 8 — z и 10 — z , где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек. Ответ: Двое ребят увлекаются всеми тремя видами спорта человека. Увлекающихся лишь одним видом спорта: 21 человек.
Задача Спортивный класс. В классе 35 учеников. 24 из них играют в футбол, 18 — в волейбол, 12 — в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 — в футбол и баскетбол, а 5 — в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно? Домашнее задание
1 слайд
2 слайд
3 слайд
Один из величайших математиков петербургский академик, за свою долгую жизнь он написал более 850 научных работ. В одной из них появились эти круги. Эйлер писал, что «они очень подходят для того, чтобы облегчит наши размышления». Леонардо Эйлер 1707-1783
4 слайд
Задача №1 В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?
Из них 20 занимаются в математическом кружке, 11 – в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?
5 слайд
Решение (По рисунку) в левом кругу (М) помещены все математики, а в правом – все биологи, те ребята, которые не ходят на кружки и помещены они в самый большой круг. Теперь посчитаем: Внутри большого круга 35 ребят. Внутри 2-х меньших 35-10=25 ребят. Внутри М находятся 20 ребят. Внутри Б находятся 25-20=5 биологов (не посещающих математический кружок) Внутри МБ находятся 11-5=6 биологов увлекающиеся математикой. М Б МБ
6 слайд
Задача №2 В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 10 спортсменов; 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
7 слайд
Решение (По рисунку) Д – драмкружок, Х – хор, С – спортсмены. 2. А В С 5-1-0,5-1=2,5 4-1-0,5-1=1,5 3-1-0,5-1=0,5 1 1 АВС 0,5
2. А В С 5-1-0,5-1=2,5 4-1-0,5-1=1,5 3-1-0,5-1=0,5 1 1 АВС 0,5
10 слайд
Задача №4 В классе 38 человек. Из них 16 играют в баскетбол, 17 – в хоккей, 18 – в волейбол. Увлекаются двумя видами спорта — баскетболом и хоккеем – четверо, баскетболом и волейболом – трое, волейболом и хоккеем – пятеро. Трое не увлекаются ни баскетболом, ни волейболом, ни хоккеем. Сколько ребят увлекается одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?
Слайд 2
Круги Эйлера
Слайд 3
Один из величайших математиков петербургский академик, за свою долгую жизнь он написал более 850 научных работ. В одной из них появились эти круги. Эйлер писал, что «они очень подходят для того, чтобы облегчит наши размышления». Леонардо Эйлер 1707-1783
Слайд 4
Задача №1
В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?
Слайд 5
Решение
(По рисунку) в левом кругу (М) помещены все математики, а в правом – все биологи, те ребята, которые не ходят на кружки и помещены они в самый большой круг.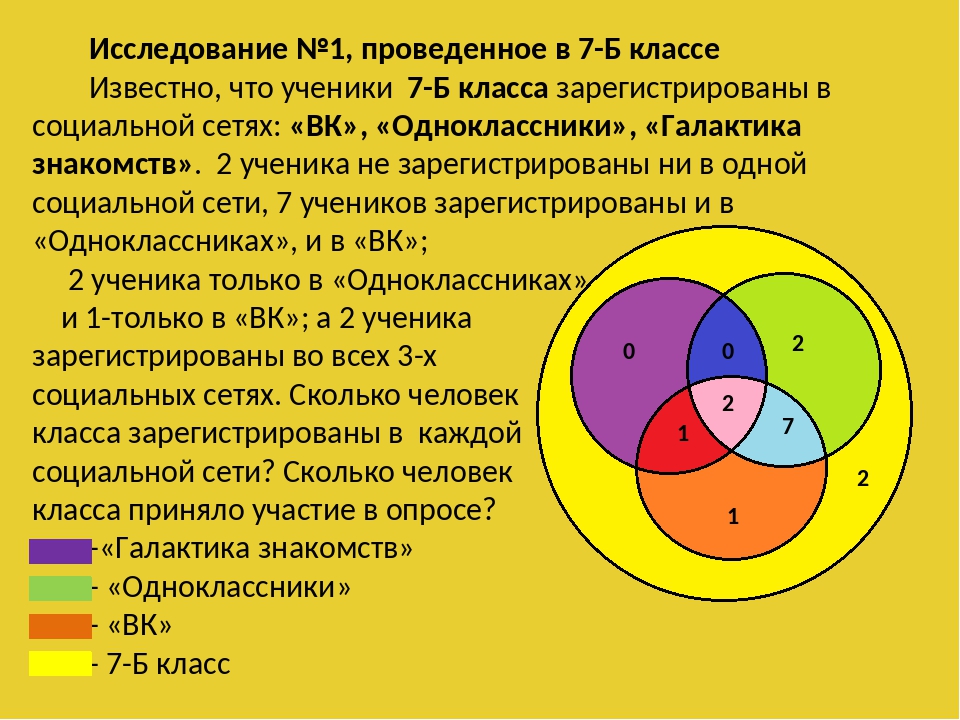 Теперь посчитаем:
Внутри большого круга 35 ребят.
Внутри 2-х меньших 35-10=25 ребят.
Внутри М находятся 20 ребят.
Внутри Б находятся 25-20=5 биологов (не посещающих математический кружок)
Внутри МБ находятся 11-5=6 биологовувлекающиеся математикой.
М
Б
МБ
Теперь посчитаем:
Внутри большого круга 35 ребят.
Внутри 2-х меньших 35-10=25 ребят.
Внутри М находятся 20 ребят.
Внутри Б находятся 25-20=5 биологов (не посещающих математический кружок)
Внутри МБ находятся 11-5=6 биологовувлекающиеся математикой.
М
Б
МБ
Слайд 6
Задача №2
В пионерском лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 10 спортсменов; 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Слайд 7
Решение
(По рисунку) Д – драмкружок, Х – хор, С – спортсмены. 5+3+3=11спортсменов посещают хор и драмкружок тогда 22-11=11 увлекаются только спортом 70-12-7-19-5-3-3-11=10 ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке. Х С Д ДХС 12 19 10-3=7 3 8-3=5 6-3=3 22-5-3-3=11
Слайд 8
Задача №3
Пол комнаты площадью 12 м^2 покрыт тремя коврами: площадь одного ковра 5 м^2, другого – 4м^2 и третьего – 3 м^2. 2.
А
В
С
5-1-0,5-1=2,5
4-1-0,5-1=1,5
3-1-0,5-1=0,5
1
1
АВС
0,5
2.
А
В
С
5-1-0,5-1=2,5
4-1-0,5-1=1,5
3-1-0,5-1=0,5
1
1
АВС
0,5
Слайд 10
Задача №4
В классе 38 человек. Из них 16 играют в баскетбол, 17 – в хоккей, 18 – в волейбол. Увлекаются двумя видами спорта — баскетболом и хоккеем – четверо, баскетболом и волейболом – трое, волейболом и хоккеем – пятеро. Трое не увлекаются ни баскетболом, ни волейболом, ни хоккеем. Сколько ребят увлекается одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?
Слайд 11
Решение
Большой круг изображает всех учащихся класса, а три меньших круга Б, Х и В изображают соответственно баскетболистов, хоккеистов и волейболистов. Фигура БХВ обозначает ребят, увлекающихся всеми тремя видами спорта – z. Одним баскетболом занимаются 16-(4+z+3)=9-z, хоккеем 8-z, волейболом 10-z. Составляем уравнение: 38=3+(9-z)+(8-z)+(10-z)+4+3+5+z, откуда z=2 3 Б Х В 9-Z 8-Z 4 Z 3 5 10-Z
Слайд 12
П.А.Вакульчик «Нестандартные и олимпиадные задачи по математике»
В. А.Гусев. А.Н.Орлов. А П. Розенталь «Внеклассная работа
по математике»
И.Л. Бабинская «Задачи математических олимпиад»
А.В.Фарков «Готовимся к олимпиадам по математике»
И.С.Петраков «Математические кружки»
Литература:
http://poznayko.at.ua/photo/16-2-0-0-2
http://www.math-on-line.com.forum-tur
http://images.yandex.ru/yandsearch?text
А.Гусев. А.Н.Орлов. А П. Розенталь «Внеклассная работа
по математике»
И.Л. Бабинская «Задачи математических олимпиад»
А.В.Фарков «Готовимся к олимпиадам по математике»
И.С.Петраков «Математические кружки»
Литература:
http://poznayko.at.ua/photo/16-2-0-0-2
http://www.math-on-line.com.forum-tur
http://images.yandex.ru/yandsearch?text
Посмотреть все слайды
Вычислите значение выражения. Ничего не сказала рыбка, лишь хвостом по воде плеснула и ушла в глубокое море. Сказка о мертвой царевне и семи богатырях. Из какой сказки этот отрывок. Сказка о золотом петушке. Сказка о царе Салтане. К 213–летию со дня рождения А.С.Пушкина. Выполните действия, результаты найдите в таблице и отгадайте зашифрованные слова. Найдите значение выражения. Устная работа. Ответы уравнений в конкурсе «Рыбалка».
«Координаты точек на координатной плоскости» — Карл Гаусс. Тренажер. Выбери нужную ячейку таблицы. Абсцисса точки. Учебники. Координатная плоскость. Координаты точки. Николай Иванович Лобачевский. Объяснение нового материала. Цвет. Леонард Эйлер. Исаак Ньютон. Четверть. Готфрид Лейбниц. Координата. Курсор. Координатная четверть. Точка лежит на оси Х. Великие математики. Тест. Технические рекомендации. Отметьте точку. Рене Декарт. Блез Паскаль.
Объяснение нового материала. Цвет. Леонард Эйлер. Исаак Ньютон. Четверть. Готфрид Лейбниц. Координата. Курсор. Координатная четверть. Точка лежит на оси Х. Великие математики. Тест. Технические рекомендации. Отметьте точку. Рене Декарт. Блез Паскаль.
«Приемы устного умножения» — Умножение и деление на 25 и 75. Значимость устных приёмов умножения. Умножение чисел, оканчивающихся на 1. Устные приёмы умножения двузначных натуральных чисел. Умножение чисел, близких к 100. Умножение двузначных чисел, у которых цифры десятков одинаковые. Умножение на 11. Умножение двузначных чисел, у которых сумма цифр десятков равна. Умножение чисел, оканчивающихся на 5. Умножение на число, оканчивающиеся на 5.
«Дни недели» — Воскресенье — день Солнца (старое название – неделя). Понедельник. Воскресенье -день Солнца. У славян неделя называлась седмица. Суббота – день Сатурна. Гипотеза. Среда. Названия дней недели в русском и английском языках. Загадка. Библия говорит, что семидневная неделя создана Богом. Как появились 7 дней недели. Среда день Меркурия (среда – середина). Неделя днями красна. Конёк – Горбунок. Четверг – день Юпитера (четвёртый).
Как появились 7 дней недели. Среда день Меркурия (среда – середина). Неделя днями красна. Конёк – Горбунок. Четверг – день Юпитера (четвёртый).
«Путешествие в мир математики» — Остров « Умейка». Решить с помощью координатной прямой. Измерим температуру за бортом корабля. Прибавить к числу А число В — значит изменить число А на число В. Сумма двух противоположных чисел равна нулю. Остров « Повторика». Найдём сумму чисел. Результаты двух последовательных изменений находят с помощью сложения. Найдём сумму чисел. Показания приборов на корабле. Любое число от прибавления положительного числа увеличивается.
«Десятичная система и двоичная» — Перевод целых десятичных чисел в двоичную систему счисления. Перевод целых чисел из двоичной системы счисления в десятичную. Ей было 1100 лет, она в 101 класс ходила. Калькулятор. Какую цель перед собой мы ставили в начале первого урока. Переведите числа из двоичной системы счисления в десятичную. «Рождение» цветка. Необычное стихотворение. Закрасьте клеточки. Разделить целое десятичное число на 2.
Разделить целое десятичное число на 2.
«Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе…», где появились впервые «круги Эйлера» «Письма о разных физических и философических материях, написанные к некоторой немецкой принцессе…», где появились впервые «круги Эйлера»
Решение задач с помощью кругов Эйлера. Часть жителей нашего города умеет говорить только по-русски, часть – только по- башкирски и часть умеет говорить на обоих языках. По- башкирски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?
Спортивная задача В футбольной команде «Баймак» 30 игроков: 18 нападающих. 11 полузащитников, 17 защитников Вратари 3 могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Баймак» вратарей?
Сколько в команде «Баймак» вратарей?
Решение =28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит вратарей будет 30-28=2. Ответ: 2 вратаря.
«Озеро Графское» Из 100 отдыхающих на турбазе «Графское», 30 детей — отличники учебы, 28 — участники олимпиад, 42 — спортсмены. 8 учащихся одновременно участники олимпиад и спортсмены, 10 – участники олимпиад и отличники, 5 – спортсмены и отличники учебы, 3 – и отличники, и участники олимпиад, и спортсмены. Сколько отдыхающих не относятся ни к одной из групп?
Выводы Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными. Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.
Эйлеровы пути и схемы
Расследуй!35
Путь Эйлера в графе или мультиграфе — это обход графа, в котором каждое ребро используется ровно один раз. Цепь Эйлера — это путь Эйлера, который начинается и заканчивается в одной и той же вершине. Наша цель — найти быстрый способ проверить, имеет ли граф (или мультиграф) эйлеров путь или цепь.
Цепь Эйлера — это путь Эйлера, который начинается и заканчивается в одной и той же вершине. Наша цель — найти быстрый способ проверить, имеет ли граф (или мультиграф) эйлеров путь или цепь.
Какие из приведенных ниже графов имеют пути Эйлера? Какие имеют схемы Эйлера?
Перечислите степени каждой вершины приведенных выше графов.Есть ли связь между степенями и существованием эйлеровых путей и контуров?
Может ли граф с вершиной степени 1 иметь эйлерову цепь? Если да, нарисуйте один. Если нет, объясните почему. Как насчет пути Эйлера?
Что, если каждая вершина графа имеет степень 2. Существует ли путь Эйлера? Цепь Эйлера? Нарисуйте несколько графиков.
Ниже часть графика. Даже если вы можете видеть только некоторые вершины, можете ли вы сделать вывод, будет ли граф иметь эйлеров путь или цепь?
Если мы начнем с вершины и проследим вдоль ребер, чтобы добраться до других вершин, мы создадим обход по графу. Точнее, обход в графе — это последовательность вершин, такая, что каждая вершина в последовательности смежна с вершинами до и после нее в последовательности. Если блуждание проходит по каждому ребру ровно один раз, то блуждание называется эйлеровым путем (или эйлеровым обходом ). Если, кроме того, начальная и конечная вершины совпадают (таким образом, вы проходите по каждому ребру ровно один раз и заканчиваете там, где начали), то обход называется -й эйлеровой схемой (или -й эйлеровой схемой ).Конечно, если граф несвязен, нет никакой надежды найти такой путь или цепь. В оставшейся части этого раздела предположим, что все обсуждаемые графы связаны.
Точнее, обход в графе — это последовательность вершин, такая, что каждая вершина в последовательности смежна с вершинами до и после нее в последовательности. Если блуждание проходит по каждому ребру ровно один раз, то блуждание называется эйлеровым путем (или эйлеровым обходом ). Если, кроме того, начальная и конечная вершины совпадают (таким образом, вы проходите по каждому ребру ровно один раз и заканчиваете там, где начали), то обход называется -й эйлеровой схемой (или -й эйлеровой схемой ).Конечно, если граф несвязен, нет никакой надежды найти такой путь или цепь. В оставшейся части этого раздела предположим, что все обсуждаемые графы связаны.
Задача о мостах Кёнигсберга на самом деле является вопросом о существовании эйлеровых путей. Будет маршрут, который пересекает каждый мост ровно один раз, если и только если граф ниже имеет путь Эйлера:
Этот граф достаточно мал, чтобы мы могли проверить все возможные обходы, не использующие повторно ребра, и при этом убедиться, что эйлерова пути не существует (не говоря уже об эйлеровом цикле). На небольших графах, у которых есть путь Эйлера, найти его обычно нетрудно. Наша цель — найти быстрый способ проверить, есть ли в графе эйлерова путь или цепь, даже если граф довольно большой.
На небольших графах, у которых есть путь Эйлера, найти его обычно нетрудно. Наша цель — найти быстрый способ проверить, есть ли в графе эйлерова путь или цепь, даже если граф довольно большой.
Один из способов гарантировать, что граф , а не имеет эйлерову схему, состоит в том, чтобы включить «шип», вершину степени 1.
Вершина \(a\) имеет степень 1, и если вы попытаетесь построить эйлеров цикл, вы увидите, что застрянете в вершине. Это тупик. То есть, если вы не начнете там.Но тогда уже нет возможности вернуться, поэтому нет надежды найти эйлерову схему. Однако существует путь Эйлера. Он начинается в вершине \(a\text{,}\) и зацикливается вокруг треугольника. Вы закончите в вершине степени 3.
Вы сталкиваетесь с похожей проблемой всякий раз, когда у вас есть вершина любой нечетной степени. Если вы начнете с такой вершины, вы не сможете там закончить (после прохождения каждого ребра ровно один раз). После использования одного ребра для выхода из начальной вершины у вас останется четное количество ребер, исходящих из вершины. Половину из них можно использовать для возврата в вершину, а другую половину — для выхода. Итак, вы возвращаетесь, а затем уходите. Вернитесь, затем уходите. Единственный способ израсходовать все ребра — использовать последнее, оставив вершину. С другой стороны, если у вас есть вершина с нечетной степенью, в которой вы не начинаете путь, то в конечном итоге вы застрянете в этой вершине. Путь будет использовать пары ребер, инцидентных вершине, чтобы войти и выйти снова. В конце концов, все эти ребра, кроме одного, будут израсходованы, останется только ребро, по которому можно добраться, и больше не останется ни одного ребра, по которому можно было бы уйти.
Половину из них можно использовать для возврата в вершину, а другую половину — для выхода. Итак, вы возвращаетесь, а затем уходите. Вернитесь, затем уходите. Единственный способ израсходовать все ребра — использовать последнее, оставив вершину. С другой стороны, если у вас есть вершина с нечетной степенью, в которой вы не начинаете путь, то в конечном итоге вы застрянете в этой вершине. Путь будет использовать пары ребер, инцидентных вершине, чтобы войти и выйти снова. В конце концов, все эти ребра, кроме одного, будут израсходованы, останется только ребро, по которому можно добраться, и больше не останется ни одного ребра, по которому можно было бы уйти.
Все это говорит о том, что если в графе есть путь Эйлера и две вершины с нечетной степенью, то путь Эйлера должен начинаться в одной из вершин нечетной степени и заканчиваться в другой. В такой ситуации каждая другая вершина должна иметь четную степень, поскольку нам нужно равное количество ребер, чтобы попасть в эти вершины и выйти из них. Как у нас может быть схема Эйлера? В графе не может быть вершины с нечетной степенью, поскольку путь Эйлера должен был бы начинаться там или заканчиваться там, но не и то, и другое.Таким образом, чтобы граф имел эйлеров цикл, все вершины должны иметь четную степень.
Как у нас может быть схема Эйлера? В графе не может быть вершины с нечетной степенью, поскольку путь Эйлера должен был бы начинаться там или заканчиваться там, но не и то, и другое.Таким образом, чтобы граф имел эйлеров цикл, все вершины должны иметь четную степень.
Верно и обратное: если все вершины графа имеют четную степень, то в графе есть эйлерова цепь, а если ровно две вершины с нечетной степенью, то граф имеет эйлеров путь. Доказать это немного сложно, но основная идея состоит в том, что вы никогда не застрянете, потому что для каждого «входящего» ребра в каждой вершине есть «исходящее» ребро. Если вы попытаетесь создать путь Эйлера и пропустите несколько ребер, вы всегда сможете «склеить» схему, используя ребра, которые вы ранее пропустили.
Эйлеровы пути и схемы
Поскольку мосты Кенигсбергского графа имеют все четыре вершины с нечетной степенью, эйлерова пути через граф не существует. Таким образом, горожане не могут пересечь каждый мост ровно по одному разу.
ПодразделГамильтон Пути
¶Предположим, вы хотите совершить поездку по Кёнигсбергу таким образом, чтобы вы посетили каждую часть суши (два острова и оба берега) ровно один раз. Это можно сделать. В терминах теории графов мы спрашиваем, существует ли путь, который посещает каждую вершину ровно один раз.Такой путь называется гамильтоновым путем (или гамильтоновым путем ). Мы могли бы также рассмотреть циклов Гамильтона , которые представляют собой пути Хэмлитона, которые начинаются и заканчиваются в одной и той же вершине.
Пример 4.4.1
Определите, есть ли на приведенных ниже графах путь Гамильтона.
РешениеГраф слева имеет путь Гамильтона (на самом деле много разных), как показано здесь:
Граф справа не имеет пути Гамильтона. Вам нужно будет посетить каждую из «внешних» вершин, но как только вы посетите одну из них, вы застрянете.Обратите внимание, что этот граф не имеет пути Эйлера, хотя есть графы с путями Эйлера, но нет путей Гамильтона.
Кажется, что нахождение путей Гамильтона будет проще, потому что графы часто имеют больше ребер, чем вершин, поэтому необходимо выполнить меньше требований. Однако никто не знает, правда ли это. Не существует известного простого теста на наличие в графе пути Гамильтона. Для небольших графов это не проблема, но по мере роста размера графа становится все труднее и труднее проверять, существует ли путь Гамильтона.На самом деле, это пример вопроса, который, насколько нам известно, слишком сложен для решения компьютеров; это пример NP-полной задачи.
ПодразделУпражнения
¶1
Вы и ваши друзья хотите совершить путешествие по юго-западу на машине. Вы посетите девять штатов ниже, со следующим довольно странным правилом: вы должны пересечь каждую границу между соседними штатами ровно один раз (так, например, вы должны пересечь границу Колорадо-Юта ровно один раз). Ты можешь сделать это? Если да, имеет ли значение, где вы начнете свое путешествие? Какой факт из теории графов решает эту проблему?
Решение Это вопрос о нахождении путей Эйлера. Нарисуйте граф с вершиной в каждом состоянии и соедините вершины, если их состояния имеют общую границу. Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих штатов, а закончить его в другом.
Нарисуйте граф с вершиной в каждом состоянии и соедините вершины, если их состояния имеют общую границу. Ровно две вершины будут иметь нечетную степень: вершины для Невады и Юты. Таким образом, вы должны начать свое путешествие в одном из этих штатов, а закончить его в другом.
2
Какой из следующих графов содержит путь Эйлера? Какие из них содержат схему Эйлера?
- \(К_4\)
- \(К_5\текст{.}\)
- \(К_{5,7}\)
- \(К_{2,7}\)
- \(С_7\)
- \(P_7\)
- \(K_4\) не имеет эйлерова пути или цепи.
- \(K_5\) имеет эйлерову схему (а значит, и эйлеров путь).
- \(K_{5,7}\) не имеет эйлерова пути или схемы.
- \(K_{2,7}\) имеет эйлеров путь, но не эйлерову схему.
- \(C_7\) имеет схему Эйлера (это граф цепи!)
- \(P_7\) имеет путь Эйлера, но не имеет схемы Эйлера.
3
Эдвард А. Маус только что закончил свой новый дом. План этажа показан ниже:
Эдвард хочет провести экскурсию по своей новой квартире подружке-мышке.
 Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начинать и заканчивать экскурсию? Объяснять.
Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начинать и заканчивать экскурсию? Объяснять.Можно ли обойти дом, зайдя в каждую комнату ровно один раз (не обязательно через каждый дверной проем)? Объяснять.
Через несколько мышиных лет Эдвард решает перестроиться. Он хотел бы добавить несколько новых дверей между комнатами, которые у него есть. Конечно, он не может добавить двери снаружи дома. Может ли в каждой комнате быть нечетное количество дверей? Объяснять.
4
Для каких \(n\) граф \(K_n\) содержит эйлерову схему? Объяснять.
Решение. Когда \(n\) нечетно, \(K_n\) содержит схему Эйлера. Это связано с тем, что каждая вершина имеет степень \(n-1\text{,}\), поэтому нечетное \(n\) приводит к тому, что все степени четные.
5
Для каких \(m\) и \(n\) граф \(K_{m,n}\) содержит путь Эйлера? Цепь Эйлера? Объяснять.
Решение. Если оба числа \(m\) и \(n\) четны, то \(K_{m,n}\) имеет эйлерову схему. Когда оба нечетны, пути или цепи Эйлера не существует. Если одно равно 2, а другое нечетно, то существует эйлерова путь, но не эйлерова схема.
Когда оба нечетны, пути или цепи Эйлера не существует. Если одно равно 2, а другое нечетно, то существует эйлерова путь, но не эйлерова схема.
6
Для каких \(n\) \(K_n\) содержит путь Гамильтона? Цикл Гамильтона? Объяснять.
РешениеВсе значения \(n\text{.}\) В частности, \(K_n\) содержит \(C_n\) в качестве подгруппы, которая представляет собой цикл, включающий каждую вершину.
7
Для каких \(m\) и \(n\) граф \(K_{m,n}\) содержит путь Гамильтона? Цикл Гамильтона? Объяснять.
РешениеПока \(|m-n| \le 1\text{,}\) граф \(K_{m,n}\) будет иметь путь Гамильтона. Чтобы иметь цикл Гамильтона, мы должны иметь \(m=n\text{.}\)
8
В Кенигсберг приехал строитель мостов и хочет добавить мосты так, чтобы можно было пройти по каждому мосту ровно один раз. Сколько мостов нужно построить?
Решение. Если мы построим один мост, у нас может быть путь Эйлера. Для схемы Эйлера необходимо построить два моста.
9
Ниже приведен граф, изображающий дружбу между группой студентов (каждая вершина — студент, а каждое ребро — дружба). Возможно ли, чтобы ученики сидели за круглым столом так, чтобы каждый ученик сидел между двумя друзьями? Какое отношение этот вопрос имеет к путям?
Возможно ли, чтобы ученики сидели за круглым столом так, чтобы каждый ученик сидел между двумя друзьями? Какое отношение этот вопрос имеет к путям?
. Мы ищем гамильтонов цикл, и в этом графе он есть:
.10
Предположим, что граф имеет путь Гамильтона. Какое максимальное количество вершин степени один может иметь граф? Объясните, почему ваш ответ правильный.
Найдите граф, в котором нет пути Гамильтона, даже если ни одна вершина не имеет степени один.Объясните, почему ваш пример работает.
11
Рассмотрим следующий график:
- Найдите путь Гамильтона. Можно ли расширить ваш путь до цикла Гамильтона?
- Является ли граф двудольным? Если да, то сколько вершин в каждой «части»?
- Используйте свой ответ на пункт (b), чтобы доказать, что в графе нет цикла Гамильтона.
- Предположим, у вас есть двудольный граф \(G\), в одной части которого как минимум на две вершины больше, чем в другой.
 Докажите, что \(G\) не имеет пути Гамильтона.
Докажите, что \(G\) не имеет пути Гамильтона.
Циклы Эйлера: почему они так уникальны и важны ли они для нас в 21 веке? | by Jaival Patel
Эйлеровы циклы и пути, безусловно, являются одной из самых влиятельных концепций в теории графов. Однако что на самом деле представляют собой эйлеровы циклы и пути и какое значение имеет путь 18-го века для футуристического 21-го века?
Эйлеровы циклы и пути на сегодняшний день являются одними из самых влиятельных концепций теории графов в мире математики и инновационных технологий.Эти цепи и пути были впервые обнаружены Эйлером в 1736 году, поэтому они получили название «Эйлеровы циклы» и «Эйлеровы пути». Когда дело доходит до теории графов, понимание графов и их создание немного сложнее, чем кажется. Есть много переменных, которые нужно учитывать, что делает их больше похожими на загадку, чем на реальную проблему. Однако когда мы говорим об эйлеровых циклах и путях, относительно легко понять, что происходит.
Пример цикла Эйлера | Изображение автора Эйлеров путь — это путь в графе, в котором каждое ребро посещается ровно один раз. Путь Эйлера может иметь любую начальную точку с любой конечной точкой; однако наиболее распространенные пути Эйлера ведут обратно в начальную вершину. Мы можем легко обнаружить эйлеров путь в графе, если сам граф удовлетворяет двум условиям: все вершины с ребрами ненулевой степени связаны, и если ноль или две вершины имеют нечетные степени, а все остальные вершины имеют четные степени. Обратите внимание, что в неориентированном графе невозможна только одна вершина с нечетной степенью (Эйлеровы пути обычно встречаются в неориентированных графах), поскольку сумма всех степеней всегда четна в неориентированном графе.Но вы можете спросить: «Как мы узнаем, имеет ли вершина нечетную или четную степень?». Для тех, кто не знает о градусах в графах, нахождение степеней вершин отличается от нахождения степеней типичных углов. Если общее количество ребер вершины нечетно, говорят, что вершина имеет нечетную степень. Однако, если общее количество ребер вершины четное число, говорят, что вершина имеет четную степень.
Путь Эйлера может иметь любую начальную точку с любой конечной точкой; однако наиболее распространенные пути Эйлера ведут обратно в начальную вершину. Мы можем легко обнаружить эйлеров путь в графе, если сам граф удовлетворяет двум условиям: все вершины с ребрами ненулевой степени связаны, и если ноль или две вершины имеют нечетные степени, а все остальные вершины имеют четные степени. Обратите внимание, что в неориентированном графе невозможна только одна вершина с нечетной степенью (Эйлеровы пути обычно встречаются в неориентированных графах), поскольку сумма всех степеней всегда четна в неориентированном графе.Но вы можете спросить: «Как мы узнаем, имеет ли вершина нечетную или четную степень?». Для тех, кто не знает о градусах в графах, нахождение степеней вершин отличается от нахождения степеней типичных углов. Если общее количество ребер вершины нечетно, говорят, что вершина имеет нечетную степень. Однако, если общее количество ребер вершины четное число, говорят, что вершина имеет четную степень. Это нечетно-четное условие вершины позволяет нам понять, является ли данный граф эйлеровым или нет.
Это нечетно-четное условие вершины позволяет нам понять, является ли данный граф эйлеровым или нет.
Чтобы узнать, является ли граф эйлеровым, или, другими словами, чтобы узнать, имеет ли граф эйлеров цикл, мы должны понимать, что вершины графа должны располагаться там, где каждое ребро посещается один раз, и что последнее ребро ведет назад в начальную вершину. Эйлеровский цикл — это, по сути, просто расширенное определение Эйлерова пути. Если это кажется запутанным, то изобразите это так: «Можно ли нарисовать график, не отрывая карандаша или ручки (одним росчерком)?». Циклы Эйлера обычно не так распространены, и это из-за одного из его условий относительно его вершин.Помните четные и нечетные степени вершины? Да, чтобы граф был эйлеровым, все вершины должны иметь четную степень, поскольку не существует «конкретной» вершины, представляющей середину графа. Более того, наличие четного числа ребер для каждой вершины позволяет нам пройти по графу и вернуться обратно к начальной вершине, независимо от того, какую вершину мы выбрали в качестве начальной точки, что по определению является нашей основной целью.
Если вы его не получили, не волнуйтесь; давайте посмотрим на небольшую визуализацию и на то, как мы можем пройти и найти эйлеров путь и эйлеров цикл с модифицированным алгоритмом обхода в глубину.Мы будем проходить тот же граф, что и на диаграмме выше, используя обход в глубину, поскольку мы хотим проходить пути по глубине, а не в поперечном направлении, потому что это было бы неэффективно.
В Эйлеровом пути каждый раз, когда мы посещаем вершину, мы проходим через два непосещенных ребра с конечной точкой. По определению все средние вершины Эйлерова пути должны иметь четную степень. Однако вместо предположения, что все средние вершины имеют четное число ребер, мы предположили, что абсолютная средняя вершина — это вершина с наибольшим количеством ребер.Более того, на всякий случай, если две вершины имеют одинаковое количество вершин, которые являются наибольшими из графа, мы можем выбрать любую из них, потому что это не повлияет на обход. Вершина с наибольшим количеством ребер означает, что вершина является серединой большинства вершин, создавая пути к большинству вершин графа. Таким образом, мы поняли, что вершину с наибольшим количеством ребер нужно пройти как минимум более одного раза по разным ребрам, чтобы пройти весь граф.
Таким образом, мы поняли, что вершину с наибольшим количеством ребер нужно пройти как минимум более одного раза по разным ребрам, чтобы пройти весь граф.
С помощью алгоритма обхода в глубину мы проходим каждый путь по глубине, начиная с каждой вершины.Помните, что каждую вершину можно посетить только один раз; однако вершину с наибольшим количеством ребер можно посетить несколько раз, чтобы обеспечить полный обход графа, поскольку некоторые вершины могут не вести к другим вершинам на противоположной стороне графа. Алгоритм увидит, не посещалась ли вершина (или соседи текущей вершины), и добавит ее в путь. В противном случае, используя возврат (отслеживание предыдущей вершины и ее ребер), алгоритм гарантирует, что если текущая вершина совпадает с самой большой вершиной, мы можем добавить ее к пути; в противном случае мы можем покинуть вершину и продолжить обход ее ребер, если текущая вершина уже была посещена.Этот процесс повторяется для каждой вершины и ее соседей в графе, чтобы создать все возможные потенциальные эйлеровы пути.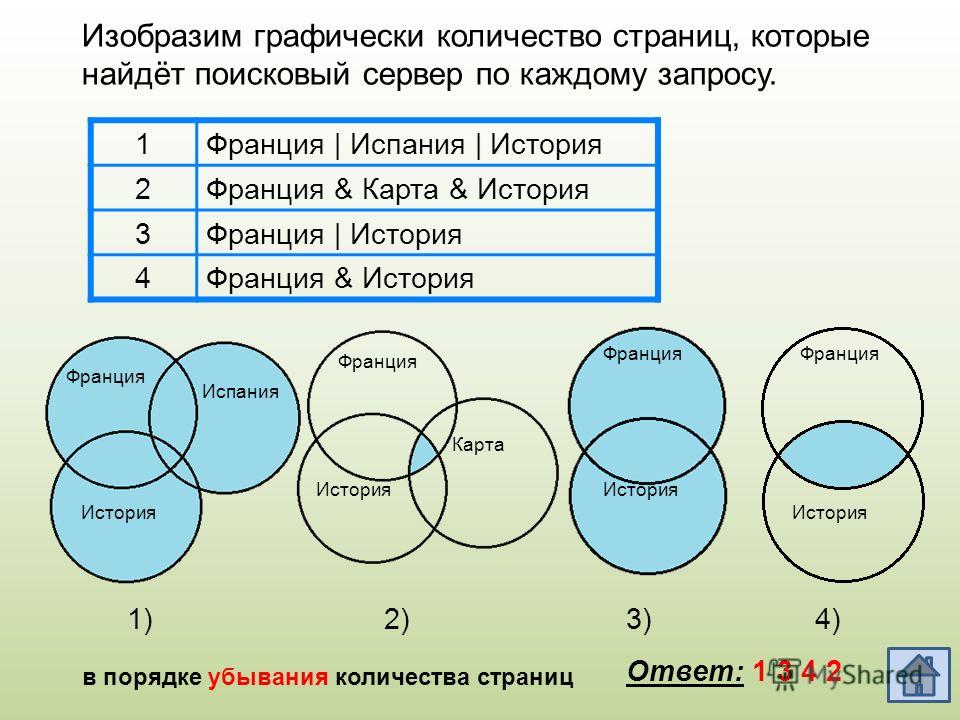 Конечно, у алгоритма есть погрешность; при нахождении эйлеровых путей алгоритм может перейти к другим вершинам, которые не могут быть частью соседей текущей вершины. По этой причине, в конце концов, мы заставляем алгоритм оценивать каждый путь и проверять, является ли самая большая вершина корневой вершиной пути, поскольку самая большая вершина имеет ребра, ведущие к нескольким вершинам.Если это так, мы можем заключить, что путь является эйлеровым путем.
Конечно, у алгоритма есть погрешность; при нахождении эйлеровых путей алгоритм может перейти к другим вершинам, которые не могут быть частью соседей текущей вершины. По этой причине, в конце концов, мы заставляем алгоритм оценивать каждый путь и проверять, является ли самая большая вершина корневой вершиной пути, поскольку самая большая вершина имеет ребра, ведущие к нескольким вершинам.Если это так, мы можем заключить, что путь является эйлеровым путем.
Для Эйлерова цикла помните, что любая вершина может быть средней вершиной. Следовательно, все вершины по определению должны иметь четную степень. Но помните, что эйлеров цикл — это просто расширенное определение эйлерова пути: последняя вершина должна вести к непосещенному ребру, которое ведет обратно к начальной вершине. При естественном поведении обхода в глубину последняя вершина всегда будет иметь непосещенные ребра, пока сама вершина не будет пройдена.Мы знаем это, потому что алгоритм DFS отслеживает посещенные вершины. Если последняя вершина является единственной непосещенной вершиной в графе, то ее ребра следует считать единственными непосещенными, оставшимися в графе. Однако, если осталось несколько ребер, это означает, что либо граф не является эйлеровым (последняя вершина имеет нечетное число ребер), либо есть еще одна непосещенная вершина. Таким образом, чтобы подвести итог, только одно ребро ведет к начальной вершине. Обходя каждое ребро одно за другим по глубине и получая наши эйлеровы пути (поскольку граф с эйлеровыми путями считается полуэйлеровым) , мы можем сравнить, имеет ли последняя вершина эйлерова пути ребро, которое ведет к вершина с которой мы начали.Если это так, то граф считается эйлеровым. Но вы можете спросить: «А что, если в графе нет эйлеровых путей?». Хороший вопрос! В графе всегда есть эйлеровы пути. Все дело в реорганизации графа таким образом, чтобы можно было создать путь, в котором каждое ребро пересекается только один раз. Вы можете думать об этом как о решении головоломки!
Если последняя вершина является единственной непосещенной вершиной в графе, то ее ребра следует считать единственными непосещенными, оставшимися в графе. Однако, если осталось несколько ребер, это означает, что либо граф не является эйлеровым (последняя вершина имеет нечетное число ребер), либо есть еще одна непосещенная вершина. Таким образом, чтобы подвести итог, только одно ребро ведет к начальной вершине. Обходя каждое ребро одно за другим по глубине и получая наши эйлеровы пути (поскольку граф с эйлеровыми путями считается полуэйлеровым) , мы можем сравнить, имеет ли последняя вершина эйлерова пути ребро, которое ведет к вершина с которой мы начали.Если это так, то граф считается эйлеровым. Но вы можете спросить: «А что, если в графе нет эйлеровых путей?». Хороший вопрос! В графе всегда есть эйлеровы пути. Все дело в реорганизации графа таким образом, чтобы можно было создать путь, в котором каждое ребро пересекается только один раз. Вы можете думать об этом как о решении головоломки!
Вот ссылка на мое моделирование эйлеровых циклов и путей: https://github. com/GEEGABYTE1/Eulerian
com/GEEGABYTE1/Eulerian
Но почему эйлеровы циклы и пути так важны? Что такого важного в том, чтобы пройти каждое ребро ровно один раз и закончить там, где мы начали? Эйлеровы схемы и пути имеют множество практических применений.В математике графы можно использовать для решения многих сложных задач, таких как задача Кенигсбергского моста. Более того, почтальоны могут использовать эйлеровы пути, чтобы иметь маршрут, по которому им не нужно повторять предыдущие шаги. В более широком смысле эйлеровы циклы и пути полезны художникам, сборщикам мусора, пилотам самолетов, разработчикам GPS (например, разработчикам Google Maps), маркетологам, распространяющим рекламу; по сути любой или что-либо, что использует пути.
Давайте рассмотрим распространенную графовую задачу, называемую Коммивояжер, , чтобы посмотреть, какое значение Эйлеровы пути и циклы имеют для продавцов и продавщиц.Проблема в том, что у вас есть граф городов с определенными расстояниями (весами ребер) между ними. Цель состоит в том, чтобы найти кратчайший путь, который позволит вам посетить каждый город один раз, оставив вас в городе, где вы начали свое путешествие.
Цель состоит в том, чтобы найти кратчайший путь, который позволит вам посетить каждый город один раз, оставив вас в городе, где вы начали свое путешествие.
Чтобы решить эту проблему и дать вам представление о том, какую роль Эйлеровы пути и циклы играют в реальных приложениях, я разработал жадный алгоритм, который выводит наиболее экономичный путь для посещения всех городов.
Предположим, что продавец должен отправиться в города [a,b,c,d] с определенными затратами на проезд по пути (например, путешествие из пункта a в пункт d стоит значение 5) алгоритм оценивает веса каждого соседа города (текущей вершины).Начнем с того, что установим все места как unvisited , потому что на самом деле мы их еще не прошли. На данный момент мы получаем текущую вершину (нашу начальную точку) случайным образом, поскольку мы хотим, чтобы наш алгоритм вычислял все возможные варианты и пути, которые в данном случае будут равны 4! (так как у нас 4 входа). Чтобы сравнить ребра и их веса, мы берем ребро с самым незначительным весом (при условии, что оно самое дешевое) и устанавливаем его в качестве текущей вершины после добавления его в окончательный путь, который будет возвращен в конце.Подобно отслеживанию ребер и вершин, чтобы увидеть, есть ли в графе эйлеров путь или цикл, алгоритм отслеживает все посещенные вершины каждый раз, когда текущая вершина обновляется (переходит к следующему городу), постоянно обновляя словарь, который хранит трек непосещенных и посещенных вершин. Мы делаем это, потому что не хотим, чтобы продавец возвращался к уже пройденному пути, точно так же, как мы не хотели, чтобы наш алгоритм обхода пересекал ребро, которое уже было пройдено при поиске эйлерова пути.
Чтобы сравнить ребра и их веса, мы берем ребро с самым незначительным весом (при условии, что оно самое дешевое) и устанавливаем его в качестве текущей вершины после добавления его в окончательный путь, который будет возвращен в конце.Подобно отслеживанию ребер и вершин, чтобы увидеть, есть ли в графе эйлеров путь или цикл, алгоритм отслеживает все посещенные вершины каждый раз, когда текущая вершина обновляется (переходит к следующему городу), постоянно обновляя словарь, который хранит трек непосещенных и посещенных вершин. Мы делаем это, потому что не хотим, чтобы продавец возвращался к уже пройденному пути, точно так же, как мы не хотели, чтобы наш алгоритм обхода пересекал ребро, которое уже было пройдено при поиске эйлерова пути.
Ознакомьтесь с моим полным решением задачи о коммивояжёре: https://github.com/GEEGABYTE1/TravelingSalesMan
Предположим, мне нужно обобщить два предыдущих абзаца о значимости эйлеровых циклов и путей. В этом случае они необходимы, потому что они являются основой оптимального поиска пути или поиска пути в целом. За прошедшие годы поиск пути значительно расширился благодаря внедрению новых алгоритмов, но что в них такого важного? Хотите верьте, хотите нет, но большинство известных нам алгоритмов — это алгоритмы поиска пути.Одними из самых популярных алгоритмов, использующих концепции поиска пути и пути Эйлера, являются Карты Google и их эффективные алгоритмы поиска маршрута, алгоритм поиска водителей и путешественников Uber (когда мы заказываем Uber и видим, где находится водитель, это их алгоритм поиска пути в действии! ), функция Tesla, благодаря которой их автомобиль может самостоятельно подъезжать к владельцу, маршрутизировать пакеты через Интернет и многое другое! Видите ли вы что-нибудь общее в этих алгоритмах, которые я только что перечислил? Эти алгоритмы сокращают дополнительную работу по преодолению ненужных путей и расстояний, чтобы добраться до нужного места.Благодаря эйлеровым путям и циклам эти алгоритмы поиска пути подняли эффективность перемещения на совершенно новый уровень (помните, что алгоритмы поиска пути и эйлеровы пути имеют одно и то же базовое поведение).
За прошедшие годы поиск пути значительно расширился благодаря внедрению новых алгоритмов, но что в них такого важного? Хотите верьте, хотите нет, но большинство известных нам алгоритмов — это алгоритмы поиска пути.Одними из самых популярных алгоритмов, использующих концепции поиска пути и пути Эйлера, являются Карты Google и их эффективные алгоритмы поиска маршрута, алгоритм поиска водителей и путешественников Uber (когда мы заказываем Uber и видим, где находится водитель, это их алгоритм поиска пути в действии! ), функция Tesla, благодаря которой их автомобиль может самостоятельно подъезжать к владельцу, маршрутизировать пакеты через Интернет и многое другое! Видите ли вы что-нибудь общее в этих алгоритмах, которые я только что перечислил? Эти алгоритмы сокращают дополнительную работу по преодолению ненужных путей и расстояний, чтобы добраться до нужного места.Благодаря эйлеровым путям и циклам эти алгоритмы поиска пути подняли эффективность перемещения на совершенно новый уровень (помните, что алгоритмы поиска пути и эйлеровы пути имеют одно и то же базовое поведение).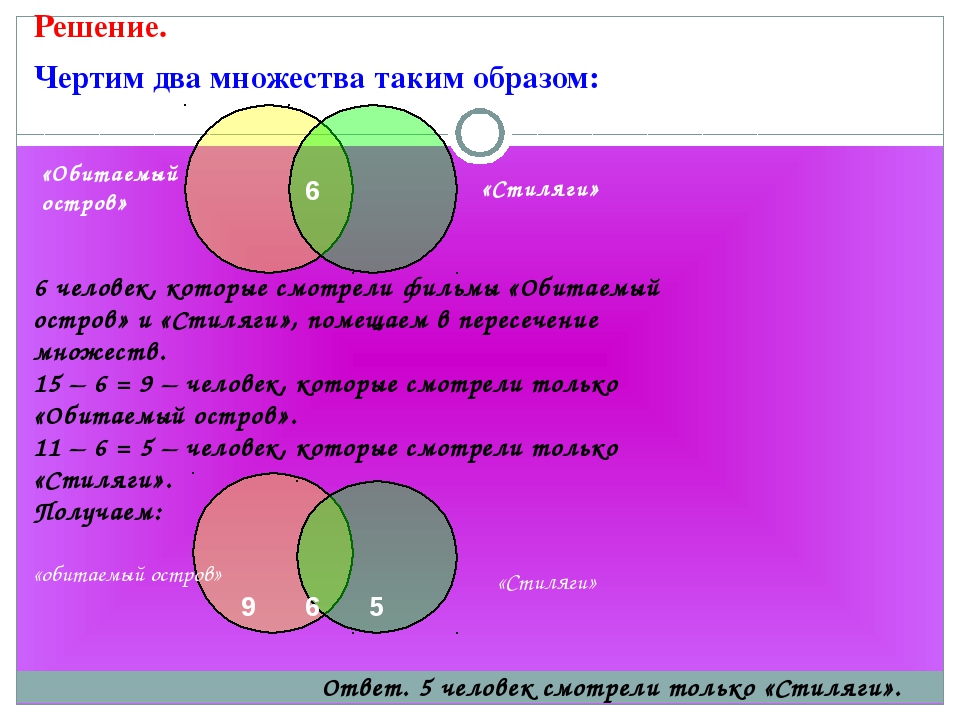 Они будут продолжать делать это с еще большей скоростью, поскольку развитие технологий и алгоритмов продолжает расти. Еще раз вернитесь к задаче о коммивояжере. Вместо того, чтобы заставлять продавца путешествовать по случайным путям со случайной стоимостью в каждый дом, пока он не выполнит свою задачу, эйлеровы пути позволили продавцу путешествовать более эффективно за счет сокращения энергии, необходимой для поездки, и потенциальных общих затрат продавца.
Они будут продолжать делать это с еще большей скоростью, поскольку развитие технологий и алгоритмов продолжает расти. Еще раз вернитесь к задаче о коммивояжере. Вместо того, чтобы заставлять продавца путешествовать по случайным путям со случайной стоимостью в каждый дом, пока он не выполнит свою задачу, эйлеровы пути позволили продавцу путешествовать более эффективно за счет сокращения энергии, необходимой для поездки, и потенциальных общих затрат продавца.
Эйлеровы циклы и пути полезны в различных областях. Математика и поиск путей оказались одними из многих выдающихся и актуальных примеров, которые мы имеем сегодня. Эти циклы и пути — одна из многих небольших математических моделей, которые привнесли прорыв в нашу повседневную жизнь. Итак, представьте себе, сколько других математических выражений, моделей и парадоксов создали в нашей жизни прорывы, на которые мы даже не обращаем внимания! Не волнуйтесь, хотя; как человек, увлеченный математикой и информатикой, я буду продолжать писать о том, как различные математические концепции известных математиков и современные постоянно развивающиеся инновационные технологии соотносятся и работают вместе, чтобы помочь нам жить более «эффективно»!
Искусство решения проблем
Треугольник ABC с окружностью из девяти точек светло-оранжевого цветаОкружность с девятью точками (также известная как окружность Эйлера или окружность Фейербаха ) данного треугольника представляет собой окружность, которая проходит через 9 «значащих» точек:
«Окружность с девятью точками касается вписанной окружности, имеет радиус, равный половине радиуса описанной окружности, а ее центр является серединой отрезка, соединяющего ортоцентр и центр описанной окружности. »
-hankinjg
»
-hankinjg
То, что такая окружность существует, является нетривиальной теоремой евклидовой геометрии.
Центр девятиконечной окружности является девятиконечным центром и обычно обозначается .
Окружность с девятью точками касается вписанной окружности, имеет радиус, равный половине радиуса описанной окружности, и ее центр является серединой отрезка, соединяющего ортоцентр и центр описанной окружности, на который также падает центр тяжести.
Также обозначается как Kimberling center.
Первое доказательство существования
Поскольку является серединой и является серединой , параллельно .Используя аналогичную логику, мы видим, что это также параллельно . Поскольку это середина и середина , параллельна , которая перпендикулярна . Подобная логика дает нам и то, что перпендикулярно. Следовательно, это прямоугольник, который является циклической фигурой. Диагонали и являются диагоналями описанной окружности. Логика, аналогичная приведенной выше, дает нам прямоугольник с общей диагональю . Поэтому описанные окружности двух прямоугольников идентичны. Мы также можем получить, что прямоугольник также находится на круге.
Поэтому описанные окружности двух прямоугольников идентичны. Мы также можем получить, что прямоугольник также находится на круге.
Теперь у нас есть круг с точками , , , , , а на нем диаметры , , и . Мы сейчас это отмечаем. Поэтому , , и также лежат на окружности. Теперь у нас есть круг с серединами сторон на нем, три середины отрезков, соединяющих вершины треугольника с его ортоцентром на нем, и три основания высот треугольника на нем. Следовательно, девять точек находятся на окружности, а девятиконечная окружность существует.
Второе доказательство существования
Мы знаем, что отражение ортоцентра относительно сторон и середин сторон треугольника лежит на описанной окружности.Таким образом, рассмотрим гомотетию с центром в точке отношения . Он отображает описанную окружность в окружность из девяти точек, а вершины треугольника — в его точки Эйлера. Значит доказано.
См. также
Эта статья незавершенная. Помогите нам, расширив его.
6.
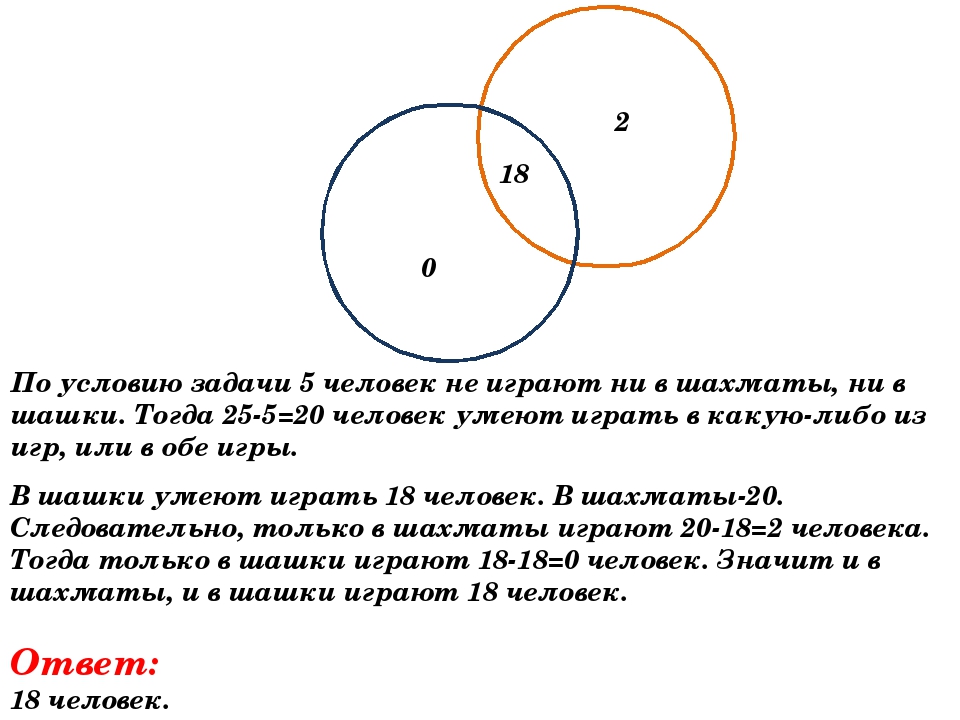 3: Цепи Эйлера — Математика LibreTexts
3: Цепи Эйлера — Математика LibreTexts- Последнее обновление
- Сохранить как PDF
- Определение: Путь Эйлера
- Пример \(\PageIndex{1}\): Путь Эйлера
- Определение: Цепь Эйлера
- Пример \(\PageIndex{2}\): Цепь Эйлера
- Теорема Эйлера \(\ PageIndex{1}\): Если в графе есть вершины нечетной степени, то он не может иметь эйлеровой схемы.
- Теорема Эйлера \(\PageIndex{2}\): если граф имеет более двух вершин нечетной степени, то он не может иметь эйлерова пути.
- Теорема Эйлера \(\PageIndex{3}\): сумма степеней всех вершин графа равна удвоенному количеству ребер (и, следовательно, должно быть четным числом).
- Поиск схем Эйлера
- Пример \(\PageIndex{3}\): Поиск эйлеровой схемы
Леонард Эйлер впервые обсудил и использовал пути и схемы Эйлера в 1736 году. Вместо поиска минимального остовного дерева, которое посещает каждую вершину графа, можно использовать путь Эйлера или схему, чтобы найти способ посетить каждое ребро графа один и только один раз. Это было бы полезно для проверки счетчиков парковки на улицах города, патрулирования улиц города или доставки почты.
Вместо поиска минимального остовного дерева, которое посещает каждую вершину графа, можно использовать путь Эйлера или схему, чтобы найти способ посетить каждое ребро графа один и только один раз. Это было бы полезно для проверки счетчиков парковки на улицах города, патрулирования улиц города или доставки почты.
Определение: Путь Эйлера
Путь, который проходит через каждое ребро связного графа один и только один раз и начинается и заканчивается в разных вершинах
Пример \(\PageIndex{1}\): Путь Эйлера
Рисунок \(\PageIndex{1}\): Пример пути ЭйлераОдним из путей Эйлера для приведенного выше графа является F, A, B, C, F, E, C, D, E, как показано ниже.
Рисунок \(\PageIndex{2}\): Путь Эйлера Этот путь Эйлера проходит каждое ребро один и только один раз и начинается и заканчивается в разных вершинах. Этот граф не может иметь эйлеровой цепи, поскольку ни один эйлеров путь не может начинаться и заканчиваться в одной и той же вершине, не пересекая хотя бы одно ребро более одного раза.
Определение: схема Эйлера
Путь Эйлера, который начинается и заканчивается в одной и той же вершине
Пример \(\PageIndex{2}\): схема Эйлера
Рисунок \(\PageIndex{3}\): Пример схемы Эйлера. Одна схема Эйлера для приведенного выше графика — это E, A, B, F, E, F, D, C, E, как показано ниже.
Рисунок \(\PageIndex{4}\): Схема ЭйлераЭтот путь Эйлера проходит каждое ребро один и только один раз и начинается и заканчивается в одной и той же вершине. Следовательно, это также схема Эйлера.
Теорема Эйлера \(\PageIndex{1}\): если в графе есть вершины нечетной степени, то он не может иметь эйлеровой схемы.
Если граф связен и каждая вершина имеет четную степень, то он имеет хотя бы один эйлеров цикл (обычно больше).
Теорема Эйлера \(\PageIndex{2}\): если граф имеет более двух вершин нечетной степени, то в нем не может быть эйлерова пути.
Если граф связен и имеет ровно две вершины нечетной степени, то он имеет хотя бы один эйлеров путь (обычно больше). Любой такой путь должен начинаться в одной из вершин нечетной степени и заканчиваться в другой.
Любой такой путь должен начинаться в одной из вершин нечетной степени и заканчиваться в другой.
Теорема Эйлера \(\PageIndex{3}\): сумма степеней всех вершин графа равна удвоенному количеству ребер (и, следовательно, должна быть четным числом).
Следовательно, количество вершин нечетной степени должно быть четным.
Нахождение схем Эйлера
- Убедитесь, что все вершины в сети имеют четную степень.
- Начать цикл Эйлера в любой вершине сети.
- При выборе ребер никогда не используйте ребро, которое является единственным подключением к той части сети, которую вы еще не посещали.
- Обозначьте ребра в том порядке, в котором вы их проходили, и продолжайте это делать, пока не пройдете по каждому ребру ровно один раз и не окажетесь в начальной вершине.
Пример \(\PageIndex{3}\): поиск схемы Эйлера
Рисунок \(\PageIndex{5}\): Граф для нахождения эйлеровой цепи Граф, показанный выше, имеет эйлерову цепь, поскольку каждая вершина во всем графе имеет четную степень. Таким образом, начните с одной четной вершины, пройдите через каждую вершину один и только один раз и закончите в начальной точке. Одним из примеров схемы Эйлера для этого графа является A, E, A, B, C, B, E, C, D, E, F, D, F, A. Это схема, которая проходит по каждому ребру только один раз. один раз и начинается и заканчивается в одном и том же месте. Существуют и другие схемы Эйлера для этого графа. Это только один пример.
Таким образом, начните с одной четной вершины, пройдите через каждую вершину один и только один раз и закончите в начальной точке. Одним из примеров схемы Эйлера для этого графа является A, E, A, B, C, B, E, C, D, E, F, D, F, A. Это схема, которая проходит по каждому ребру только один раз. один раз и начинается и заканчивается в одном и том же месте. Существуют и другие схемы Эйлера для этого графа. Это только один пример.
Степень каждой вершины отмечена красным. Порядок ребер цепи отмечен синим цветом, а направление цепи показано синими стрелками.
Решение Леонардом Эйлером проблемы Кенигсбергского моста
Примечание редактора
Следующий студенческий исследовательский отчет был подготовлен для класса 255 профессора Юдит Кардос по математике в Колледже Нью-Джерси. Это был 3-кредитный вводный курс по истории математики. Этот отчет был засчитан в 30% итоговой оценки. Это пример того, какие исторические исследования студенты могут проводить с использованием вторичных источников.
Решение Леонарда Эйлера проблемы Кенигсбергского моста
Кенигсберг
Наша история начинается в 18 веке в причудливом городке Кёнигсберг, Пруссия, на берегу реки Прегель.В 1254 году тевтонские рыцари основали город Кенигсберг под предводительством чешского короля Оттокера II после своего второго крестового похода против пруссаков. В средние века Кенигсберг стал очень важным городом и торговым центром благодаря своему расположению на берегу реки. Произведения искусства восемнадцатого века изображают Кенигсберг как процветающий город, где флотилии кораблей заполняют Прегель, а их торговля обеспечивает комфортный образ жизни как для местных купцов, так и для их семей. Здоровая экономика позволила горожанам построить семь мостов через реку, большинство из которых соединялись с островом Кнайпхоф; их расположение можно увидеть на прилагаемой картинке [источник: MacTutor History of Mathematics Archive].
Поскольку река текла вокруг Кнайпхофа, что буквально означает паб, и другого острова, она разделяла город на четыре отдельных района. Семь мостов назывались Мост Кузнеца, Соединительный мост, Зеленый мост, Купеческий мост, Деревянный мост, Высокий мост и Медовый мост. Согласно преданиям, жители Кенигсберга проводили воскресные дни, гуляя по своему прекрасному городу. Во время прогулки жители города решили создать для себя игру, цель которой состояла в том, чтобы придумать способ, которым они могли бы ходить по городу, пересекая каждый из семи мостов только один раз.Хотя никто из жителей Кенигсберга не мог придумать маршрут, который позволил бы им пересечь каждый из мостов только один раз, но они не могли доказать, что это невозможно. К счастью для них, Кенигсберг находился недалеко от Санкт-Петербурга, где жил знаменитый математик Леонард Эйлер.
Семь мостов назывались Мост Кузнеца, Соединительный мост, Зеленый мост, Купеческий мост, Деревянный мост, Высокий мост и Медовый мост. Согласно преданиям, жители Кенигсберга проводили воскресные дни, гуляя по своему прекрасному городу. Во время прогулки жители города решили создать для себя игру, цель которой состояла в том, чтобы придумать способ, которым они могли бы ходить по городу, пересекая каждый из семи мостов только один раз.Хотя никто из жителей Кенигсберга не мог придумать маршрут, который позволил бы им пересечь каждый из мостов только один раз, но они не могли доказать, что это невозможно. К счастью для них, Кенигсберг находился недалеко от Санкт-Петербурга, где жил знаменитый математик Леонард Эйлер.
Эйлер и проблема моста
Зачем Эйлеру заниматься проблемой, столь не связанной с областью математики? Зачем такому выдающемуся математику тратить много времени на решение тривиальной задачи вроде проблемы Кенигсбергского моста? Эйлер, очевидно, был занятым человеком, опубликовавшим за свою жизнь более 500 книг и статей. Только в 1775 году он писал в среднем одну математическую статью в неделю, а в течение своей жизни он писал на множество тем, помимо математики, включая механику, оптику, астрономию, навигацию и гидродинамику. Неудивительно, что Эйлер считал эту проблему тривиальной, заявляя в письме 1736 года Карлу Леонхарду Готлибу Элеру, мэру Данцига, который просил его решить проблему [цитируется по Hopkins, 2]:
Только в 1775 году он писал в среднем одну математическую статью в неделю, а в течение своей жизни он писал на множество тем, помимо математики, включая механику, оптику, астрономию, навигацию и гидродинамику. Неудивительно, что Эйлер считал эту проблему тривиальной, заявляя в письме 1736 года Карлу Леонхарду Готлибу Элеру, мэру Данцига, который просил его решить проблему [цитируется по Hopkins, 2]:
. . . Таким образом, вы видите, благороднейший сэр, как этот тип решения имеет мало отношения к математике, и я не понимаю, почему вы ожидаете, что его даст математик, а не кто-либо другой, ибо решение основано только на разуме, и его открытие не зависит ни от какого математического принципа.Из-за этого я не знаю, почему даже вопросы, имеющие столь малое отношение к математике, математики решают быстрее, чем другие.
Несмотря на то, что Эйлер нашел проблему тривиальной, он все равно был заинтригован ею. В письме, написанном в том же году Джованни Маринони, итальянскому математику и инженеру, Эйлер сказал [цитируется по Хопкинсу, 2],
Вопрос этот так банален, но показался мне достойным внимания тем, что [ни] геометрии, ни алгебры, ни даже искусства счета не было достаточно для его решения.
Эйлер полагал, что эта проблема связана с темой, которую Готфрид Вильгельм Лейбниц когда-то обсуждал и с которой очень хотел поработать. Эта так называемая геометрия положения — это то, что теперь называется теорией графов, которую Эйлер вводит и использует при решении этой знаменитой проблемы.
Доказательство Эйлера
26 августа 1735 года Эйлер представил статью, содержащую решение проблемы Кенигсбергского моста.Он обращается как к этой конкретной проблеме, так и к общему решению с любым количеством участков суши и любым количеством мостов. Эта статья под названием «Solutio Problematis ad geometriam situs pertinentis» была позже опубликована в 1741 г. [Hopkins, 2]. Статья Эйлера разделена на двадцать один пронумерованный абзац, и далее будет представлена упрощенная версия абзацев Эйлера.
В первых двух абзацах доказательства Эйлера он вводит проблему Кенигсбергского моста. В параграфе 1 Эйлер заявляет, что, по его мнению, эта проблема касается геометрии, но не той геометрии, которая хорошо известна его современникам и включает в себя измерения и расчеты, а нового вида геометрии, которую Лейбниц называл геометрией положения. Затем в параграфе 2 Эйлер объясняет своей аудитории, как работает проблема Кенигсберга. Эйлер представил набросок проблемы (см. Рисунок Эйлера 1 ) и назвал семь различных мостов: a, b, c, d, e, f и g. В этом абзаце он формулирует общий вопрос задачи: «Можно ли узнать, можно ли пересечь каждый мост ровно один раз?»
Затем в параграфе 2 Эйлер объясняет своей аудитории, как работает проблема Кенигсберга. Эйлер представил набросок проблемы (см. Рисунок Эйлера 1 ) и назвал семь различных мостов: a, b, c, d, e, f и g. В этом абзаце он формулирует общий вопрос задачи: «Можно ли узнать, можно ли пересечь каждый мост ровно один раз?»
Рисунок Эйлера 1 из «Solutio problematis ad geometriam situs pertinentis», Eneström 53 [источник: Архив Эйлера MAA]
Сформулировав общий вопрос, который он пытается решить, Эйлер начинает исследовать различные методы поиска решения.В параграфе 3 Эйлер сообщает читателю, что для решения этой конкретной проблемы он мог бы записать все возможные пути, но этот метод занял бы много времени и не работал бы для более крупных конфигураций с большим количеством мостов и участков суши. Из-за этих проблем Эйлер решил выбрать другой метод решения этой проблемы.
В параграфе 4 он начинает упростить задачу, изобретая удобную систему для представления пересечения моста. Эйлер решает, что вместо того, чтобы использовать строчные буквы для обозначения пересечения моста, он будет писать заглавными буквами, обозначающими массивы суши.Например, ссылаясь на свой рисунок 1 , AB будет означать путешествие, которое началось на суше A и закончилось на B. Более того, если после путешествия с суши A на B кто-то решит переместиться на сушу D, это будет просто обозначено , АБД. В параграфе 5 Эйлер продолжает свое обсуждение этого процесса, объясняя, что в ABDC, хотя есть четыре заглавных буквы, было пересечено только три моста. Эйлер объясняет, что сколько бы ни было мостов, будет еще одна буква для обозначения необходимого перехода.Из-за этого вся проблема Кенигсбергского моста требовала пересечения семи мостов и, следовательно, восьми заглавных букв.
Эйлер решает, что вместо того, чтобы использовать строчные буквы для обозначения пересечения моста, он будет писать заглавными буквами, обозначающими массивы суши.Например, ссылаясь на свой рисунок 1 , AB будет означать путешествие, которое началось на суше A и закончилось на B. Более того, если после путешествия с суши A на B кто-то решит переместиться на сушу D, это будет просто обозначено , АБД. В параграфе 5 Эйлер продолжает свое обсуждение этого процесса, объясняя, что в ABDC, хотя есть четыре заглавных буквы, было пересечено только три моста. Эйлер объясняет, что сколько бы ни было мостов, будет еще одна буква для обозначения необходимого перехода.Из-за этого вся проблема Кенигсбергского моста требовала пересечения семи мостов и, следовательно, восьми заглавных букв.
В параграфе 6 Эйлер продолжает объяснять детали своего метода. Он говорит читателю, что если есть более одного моста, который можно пересечь при переходе с одного участка суши на другой, не имеет значения, какой мост используется. Например, даже если есть два моста, a и b, которые могут привести путешественника из A в B, в системе обозначений Эйлера не имеет значения, какой мост будет взят.В этом абзаце Эйлер также обсуждает конкретную проблему, с которой он имеет дело. Он объясняет, используя свой исходный рисунок, что в задаче Кёнигсберга требуется ровно восемь букв, где пары (A, B) и (A, C) должны стоять рядом друг с другом ровно два раза, независимо от того, какая буква появляется первой. Кроме того, пары (A,D), (B,D) и (C,D) должны встречаться вместе ровно один раз, чтобы путь, пересекающий каждый мост один и только один раз, существовал.
Например, даже если есть два моста, a и b, которые могут привести путешественника из A в B, в системе обозначений Эйлера не имеет значения, какой мост будет взят.В этом абзаце Эйлер также обсуждает конкретную проблему, с которой он имеет дело. Он объясняет, используя свой исходный рисунок, что в задаче Кёнигсберга требуется ровно восемь букв, где пары (A, B) и (A, C) должны стоять рядом друг с другом ровно два раза, независимо от того, какая буква появляется первой. Кроме того, пары (A,D), (B,D) и (C,D) должны встречаться вместе ровно один раз, чтобы путь, пересекающий каждый мост один и только один раз, существовал.
Рисунки Эйлера 2 и 3 из «Solutio Problematis ad geometriam situs pertinentis», Eneström 53 [источник: Архив Эйлера MAA]
В параграфе 7 Эйлер сообщает читателю, что либо ему нужно найти восьмибуквенную последовательность, удовлетворяющую задаче, либо нужно доказать, что такой последовательности не существует.Прежде чем сделать это для проблемы Кенигсбергского моста, он решает найти правило, чтобы выяснить, существует ли путь для более общей задачи. Он делает это в параграфе 8, рассматривая гораздо более простой пример массивов суши и мостов. Эйлер рисует рис. 2 и начинает оценивать ситуации, в которых проходит область А. Эйлер утверждает, что если мост а пройден один раз, то путь А либо начинался, либо заканчивался, и поэтому использовался только один раз. Если все мосты a, b и c пройдены один раз, A используется ровно дважды, независимо от того, является ли он начальным или конечным местом.Точно так же, если пять мостов ведут к А, участок суши А будет встречаться на пути ровно три раза. Эйлер утверждает, что «в общем случае, если количество мостов равно любому нечетному числу и если его увеличить на единицу, то количество вхождений A составляет половину результата». Другими словами, если существует нечетное количество мостов, соединяющих A с другими массивами суши, добавьте один к количеству мостов и разделите его на два, чтобы узнать, сколько всего раз A должно быть использовано на пути, где каждый мост используется один и только один раз (т.
Он делает это в параграфе 8, рассматривая гораздо более простой пример массивов суши и мостов. Эйлер рисует рис. 2 и начинает оценивать ситуации, в которых проходит область А. Эйлер утверждает, что если мост а пройден один раз, то путь А либо начинался, либо заканчивался, и поэтому использовался только один раз. Если все мосты a, b и c пройдены один раз, A используется ровно дважды, независимо от того, является ли он начальным или конечным местом.Точно так же, если пять мостов ведут к А, участок суши А будет встречаться на пути ровно три раза. Эйлер утверждает, что «в общем случае, если количество мостов равно любому нечетному числу и если его увеличить на единицу, то количество вхождений A составляет половину результата». Другими словами, если существует нечетное количество мостов, соединяющих A с другими массивами суши, добавьте один к количеству мостов и разделите его на два, чтобы узнать, сколько всего раз A должно быть использовано на пути, где каждый мост используется один и только один раз (т. е. Общее количество вхождений A, где A имеет нечетное количество мостов = (количество мостов — 1) / 2 ).
е. Общее количество вхождений A, где A имеет нечетное количество мостов = (количество мостов — 1) / 2 ).
Используя этот факт, Эйлер решает проблему Кенигсбергского моста в параграфе 9. В этом случае, поскольку есть пять мостов, ведущих к A, это должно произойти три раза (см. его рис. 1 выше). Точно так же B, C и D должны появиться дважды, так как все они имеют три моста, ведущих к ним. Следовательно, 3 (для A) + 2 (для B) + 2 (для C) + 2 (для D) = 9, но Эйлер уже заявил, что для семи мостов должно быть только восемь вхождений.Это противоречие! Поэтому по мостам в городе Кёнигсберг нельзя проехать один и только один раз. Конец или нет? В то время как жители Кенигсберга могут быть довольны этим решением, великий математик Леонард Эйлер не был удовлетворен. Эйлер продолжает свое доказательство, чтобы иметь дело с более общими ситуациями.
Обобщение Эйлера
В параграфе 10 Эйлер продолжает свое обсуждение, отмечая, что если ситуация включает все массивы суши с нечетным числом мостов, то можно сказать, можно ли совершить путешествие по каждому мосту только один раз. Эйлер утверждает, что если сумма количества раз, которое должна появиться каждая буква, на единицу больше, чем общее количество мостов, путешествие можно совершить. Однако, если количество вхождений более чем на один больше, чем количество мостов, путешествие невозможно, как в задаче о Кенигсбергском мосту. Это потому, что правило, которое Эйлер дает для нечетного числа мостов, используя свой рисунок 2, верно для общей ситуации, есть ли только один другой массив суши или более одного.
Эйлер утверждает, что если сумма количества раз, которое должна появиться каждая буква, на единицу больше, чем общее количество мостов, путешествие можно совершить. Однако, если количество вхождений более чем на один больше, чем количество мостов, путешествие невозможно, как в задаче о Кенигсбергском мосту. Это потому, что правило, которое Эйлер дает для нечетного числа мостов, используя свой рисунок 2, верно для общей ситуации, есть ли только один другой массив суши или более одного.
В абзацах 11 и 12 Эйлер рассматривает ситуацию, когда к области примыкает четное число мостов.Эта ситуация не возникает в кенигсбергской задаче и поэтому до сих пор игнорировалась. В ситуации с массивом суши X с четным числом мостов могут возникнуть два случая. Первый случай, когда X является отправной точкой путешествия. В этом случае X появится дважды, один раз как начальная точка и еще раз как конечная точка. В другом случае X не является отправной точкой. Если бы это произошло, X появился бы только один раз, так как путешествие должно было бы начинаться через один мост и немедленно выходить через единственный другой доступный мост. Точно так же, если к X подключено четыре моста, количество вхождений X зависит от того, является ли он начальной точкой. Если путешествие начинается в X, оно должно появиться три раза, но если оно не начинается в X, оно появится только дважды. Таким образом, в общем, если X имеет четное количество подключенных мостов, то, если путешествие не начинается в X, X появляется в половине случаев как мосты (т.е. Вхождения X, где X четное, а не начальная точка = (# мостов) / 2). Если путешествие действительно начинается в X, то X появляется в половине случаев как мосты плюс один раз (т.е. Вхождения X, где X четно и начальная точка = ((количество мостов) / 2) + 1).
Точно так же, если к X подключено четыре моста, количество вхождений X зависит от того, является ли он начальной точкой. Если путешествие начинается в X, оно должно появиться три раза, но если оно не начинается в X, оно появится только дважды. Таким образом, в общем, если X имеет четное количество подключенных мостов, то, если путешествие не начинается в X, X появляется в половине случаев как мосты (т.е. Вхождения X, где X четное, а не начальная точка = (# мостов) / 2). Если путешествие действительно начинается в X, то X появляется в половине случаев как мосты плюс один раз (т.е. Вхождения X, где X четно и начальная точка = ((количество мостов) / 2) + 1).
В абзацах с 13 по 15 Эйлер объясняет, как выяснить, существует ли путь, использующий каждый мост один и только один раз, и представляет свой собственный пример, чтобы показать, как это работает. Эйлер сначала объясняет свой простой шестишаговый метод решения любой общей ситуации с массивами суши, разделенными реками и соединенными мостами. Первый Эйлер обозначает каждый массив суши с заглавной буквы. Во-вторых, он берет общее количество мостов, добавляет один и записывает это над таблицей, которую собирается составить.Далее он берет заглавные буквы, ставит их в столбик, а рядом пишет количество мостов. В-четвертых, он указывает звездочками участки суши, на которых имеется четное число мостов. Затем рядом с каждым четным числом он пишет ½ числа, а рядом с каждым нечетным числом ставит ½ числа плюс один. Наконец, Эйлер складывает числа, записанные в крайнем правом столбце, и если сумма на единицу меньше или равна количеству мостов плюс один, то требуемое путешествие возможно. Однако важно отметить, что если сумма на один меньше, чем количество мостов плюс один, то путешествие должно начинаться с одного из участков суши, отмеченных звездочкой.Если сумма равна количеству мостов плюс один, путешествие должно начинаться в регионе, не отмеченном звездочкой.
Первый Эйлер обозначает каждый массив суши с заглавной буквы. Во-вторых, он берет общее количество мостов, добавляет один и записывает это над таблицей, которую собирается составить.Далее он берет заглавные буквы, ставит их в столбик, а рядом пишет количество мостов. В-четвертых, он указывает звездочками участки суши, на которых имеется четное число мостов. Затем рядом с каждым четным числом он пишет ½ числа, а рядом с каждым нечетным числом ставит ½ числа плюс один. Наконец, Эйлер складывает числа, записанные в крайнем правом столбце, и если сумма на единицу меньше или равна количеству мостов плюс один, то требуемое путешествие возможно. Однако важно отметить, что если сумма на один меньше, чем количество мостов плюс один, то путешествие должно начинаться с одного из участков суши, отмеченных звездочкой.Если сумма равна количеству мостов плюс один, путешествие должно начинаться в регионе, не отмеченном звездочкой.
Примеры
Используя задачу Кенигсберга в качестве своего первого примера, Эйлер показывает следующее:
Количество перемычек = 7, количество перемычек плюс один = 8
Регион Мосты Время Регион должен отображаться
A 5 3
B 3 2
C 3 2
D 3 2
Однако 3 + 2 + 2 + 2 = 9, что больше 8, поэтому путешествие невозможно.
Поскольку этот пример довольно простой, Эйлер решает создать собственную ситуацию с двумя островами, четырьмя реками и пятнадцатью мостами. Ситуацию, созданную Эйлером, можно увидеть на его рис. 3 выше. Теперь Эйлер пытается выяснить, существует ли путь, позволяющий пройти по каждому мосту один и только один раз. Эйлер выполняет те же шаги, что и выше, называя пять различных областей заглавными буквами и создает таблицу, чтобы проверить это, если это возможно, например:
Количество перемычек = 15, количество перемычек плюс один = 16
Регион Мосты Время Регион Должен появиться
A* 8 4
B* 4 2
C* 4 2
D 3 2
E 5 3
F* 6 3
Кроме того, 4 + 2 + 2 + 2 + 3 + 3 = 16, что равно количеству мостов, плюс один, что означает, что путешествие действительно возможно. Поскольку сумма равна количеству мостов плюс один, путешествие должно начинаться либо в D, либо в E. Теперь, когда Эйлер знает, что путешествие возможно, все, что ему нужно сделать, это указать, каким будет путь. Эйлер выбирает путь EaFbBcFdAeFfCgAhCiDkAmenApBoElD, где он указывает, какие мосты пересекаются между буквами, представляющими массивы суши. Хотя эта информация является лишней, поскольку точный мост не имеет значения для понимания того, что путешествие возможно, она полезна при выборе пути.Это хороший пример, показывающий метод, которым воспользовался бы Эйлер при решении любой задачи такого рода.
Поскольку сумма равна количеству мостов плюс один, путешествие должно начинаться либо в D, либо в E. Теперь, когда Эйлер знает, что путешествие возможно, все, что ему нужно сделать, это указать, каким будет путь. Эйлер выбирает путь EaFbBcFdAeFfCgAhCiDkAmenApBoElD, где он указывает, какие мосты пересекаются между буквами, представляющими массивы суши. Хотя эта информация является лишней, поскольку точный мост не имеет значения для понимания того, что путешествие возможно, она полезна при выборе пути.Это хороший пример, показывающий метод, которым воспользовался бы Эйлер при решении любой задачи такого рода.
Выводы Эйлера
В следующих нескольких абзацах Эйлер предлагает еще один способ выяснить, можно ли совершить путешествие по любому набору участков суши, мостов и рек. В параграфе 16 Эйлер указывает, что сумма чисел, перечисленных непосредственно справа от суши, в сумме в два раза превышает общее количество мостов. Позже этот факт станет известен как лемма о рукопожатии. По сути, лемма о рукопожатии утверждает, что каждый мост считается дважды, по одному разу для каждого участка суши, к которому он прикреплен. В параграфе 17 Эйлер продолжает утверждать, что сумма всех мостов, ведущих в каждую область, четна, поскольку половина этого числа равна общему количеству мостов. Однако это невозможно, если есть нечетное количество участков суши с нечетным количеством мостов. Таким образом, Эйлер доказывает, что если есть нечетные числа, связанные с массивами суши, то должно быть четное количество этих массивов суши.
По сути, лемма о рукопожатии утверждает, что каждый мост считается дважды, по одному разу для каждого участка суши, к которому он прикреплен. В параграфе 17 Эйлер продолжает утверждать, что сумма всех мостов, ведущих в каждую область, четна, поскольку половина этого числа равна общему количеству мостов. Однако это невозможно, если есть нечетное количество участков суши с нечетным количеством мостов. Таким образом, Эйлер доказывает, что если есть нечетные числа, связанные с массивами суши, то должно быть четное количество этих массивов суши.
Однако этого недостаточно, чтобы доказать, когда существует путь, на котором каждый мост используется один и только один раз, поскольку в задаче о Кенигсбергском мосту есть четное количество массивов суши с нечетным количеством мостов, ведущих к ним. Из-за этого Эйлер добавляет дополнительные ограничения в параграфах 18 и 19. Эйлер объясняет, что, поскольку общее количество мостов, прикрепленных к каждому массиву суши, равно удвоенному количеству мостов (как видно из леммы о рукопожатии), поэтому, если вы добавьте два к этой сумме, а затем разделите на два, вы получите общее количество мостов плюс один. Этот номер такой же, как тот, который использовался ранее, и используется, чтобы сказать, возможен ли путь. Если все числа четные, то сумма в третьем столбце таблицы будет на единицу меньше, чем общее количество мостов плюс один.
Этот номер такой же, как тот, который использовался ранее, и используется, чтобы сказать, возможен ли путь. Если все числа четные, то сумма в третьем столбце таблицы будет на единицу меньше, чем общее количество мостов плюс один.
Затем Эйлер объясняет, что очевидно, что если есть два массива суши с нечетным числом мостов, то путешествие всегда будет возможно, если путешествие начинается в одном из регионов с нечетным числом мостов. Это потому, что если четные числа разделить пополам, а каждое из нечетных увеличить на единицу и разделить пополам, то сумма этих половинок будет на единицу больше, чем общее количество мостов.Однако если имеется четыре или более массивов суши с нечетным числом мостов, то пути быть не может. Это потому, что сумма половин нечетных чисел плюс один вместе с суммой всех половинок четных чисел сделает сумму третьего столбца больше, чем общее количество мостов плюс один. Следовательно, Эйлер только что доказал, что может быть не более двух участков суши с нечетным числом мостов.
После этого Эйлер может сделать выводы относительно более общих форм проблемы Кенигсбергского моста.В параграфе 20 Эйлер дает три рекомендации, которые можно использовать, чтобы выяснить, существует ли путь, использующий каждый мост один и только один раз. Во-первых, он утверждал, что если существует более двух участков суши с нечетным числом мостов, то такое путешествие невозможно. Во-вторых, если количество мостов нечетно ровно для двух участков суши, то путешествие возможно, если оно начинается на одном из двух участков суши с нечетными номерами. Наконец, Эйлер утверждает, что если нет регионов с нечетным количеством суши, то путешествие можно совершить, начав с любого региона.Установив эти три факта, Эйлер завершает свое доказательство параграфом 21, в котором просто говорится, что после того, как кто-то выяснил, что путь существует, он все равно должен приложить усилия, чтобы написать работающий путь. Эйлер считал, что метод достижения этого тривиален, и не хотел тратить на него много времени. Однако Эйлер действительно предлагал сконцентрироваться на том, как добраться с одного массива суши на другой, вместо того, чтобы сначала концентрироваться на конкретных мостах.
Однако Эйлер действительно предлагал сконцентрироваться на том, как добраться с одного массива суши на другой, вместо того, чтобы сначала концентрироваться на конкретных мостах.
Доказательство Эйлера и теория графов
При чтении оригинального доказательства Эйлера открывается относительно простая и понятная математическая работа; однако не фактическое доказательство, а промежуточные шаги делают эту проблему известной.Великое нововведение Эйлера заключалось в том, что он рассматривал проблему Кенигсбергского моста абстрактно, используя линии и буквы для представления более крупной ситуации с массивами суши и мостами. Он использовал заглавные буквы для обозначения массивов суши и строчные буквы для обозначения мостов. Это был совершенно новый тип мышления для того времени, и в своей статье Эйлер случайно запустил новую область математики, названную теорией графов, где граф — это просто набор вершин и ребер. Сегодня путь в графе, который содержит каждое ребро графа один и только один раз, называется эйлеровым путем из-за этой проблемы. С тех пор, как Эйлер решил эту проблему, и до сегодняшнего дня теория графов стала важным разделом математики, лежащим в основе наших представлений о сетях.
С тех пор, как Эйлер решил эту проблему, и до сегодняшнего дня теория графов стала важным разделом математики, лежащим в основе наших представлений о сетях.
Проблема Кенигсбергского моста — вот почему Биггс заявляет [Biggs, 1],
Истоки теории графов скромны, даже легкомысленны… Проблемы, которые привели к развитию теории графов, часто были не более чем головоломками, предназначенными для проверки изобретательности, а не для стимулирования воображения. Но, несмотря на кажущуюся тривиальность таких головоломок, они привлекли внимание математиков, в результате чего теория графов стала предметом, богатым теоретическими результатами удивительного разнообразия и глубины.
Как следует из утверждения Биггса, эта проблема настолько важна, что упоминается в первой главе каждой книги по теории графов, которую просматривали в библиотеке.
После открытия Эйлера (или изобретения, в зависимости от того, как на это смотрит читатель) теория графов пережила бум благодаря крупным вкладам, внесенным такими великими математиками, как Огюстен Коши, Уильям Гамильтон, Артур Кэли, Густав Кирхгоф и Джордж Полиа.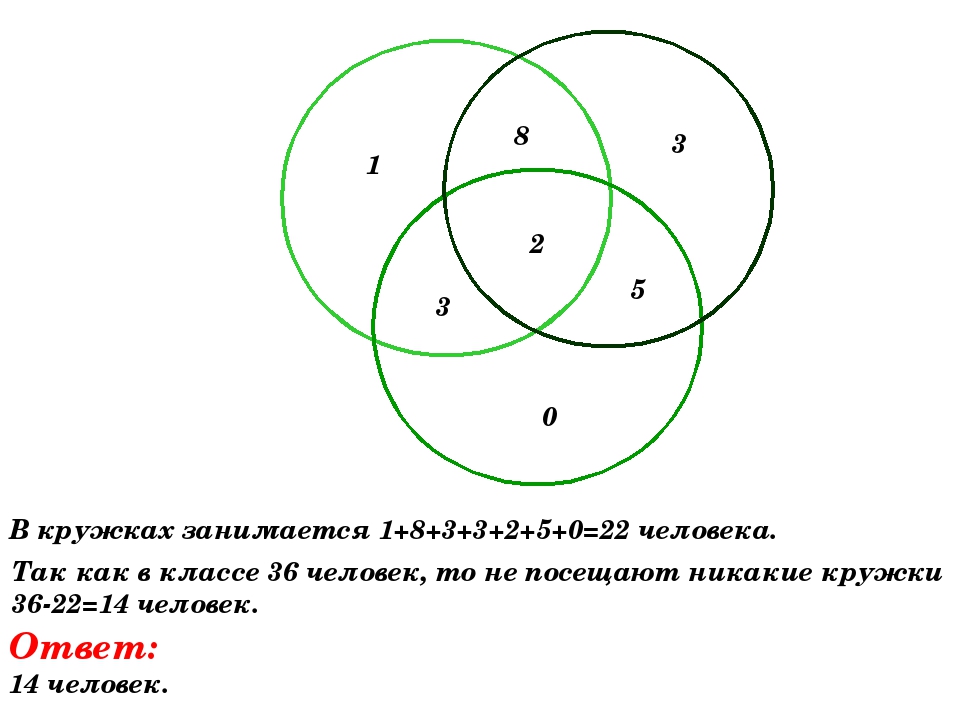 Все эти люди внесли свой вклад в раскрытие «практически всего, что известно о больших, но упорядоченных графах, таких как решетка, образованная атомами в кристалле, или гексагональная решетка, созданная пчелами в улье [ ScienceWeek, 2].К другим известным задачам теории графов относятся поиск способа выхода из лабиринта или лабиринта или определение порядка ходов коня на шахматной доске, при котором каждое поле попадает только один раз, а конь возвращается на клетку, на которой он находится. началось [ ScienceWeek, 2]. Некоторые другие проблемы теории графов оставались нерешенными на протяжении столетий [ ScienceWeek, 2].
Все эти люди внесли свой вклад в раскрытие «практически всего, что известно о больших, но упорядоченных графах, таких как решетка, образованная атомами в кристалле, или гексагональная решетка, созданная пчелами в улье [ ScienceWeek, 2].К другим известным задачам теории графов относятся поиск способа выхода из лабиринта или лабиринта или определение порядка ходов коня на шахматной доске, при котором каждое поле попадает только один раз, а конь возвращается на клетку, на которой он находится. началось [ ScienceWeek, 2]. Некоторые другие проблемы теории графов оставались нерешенными на протяжении столетий [ ScienceWeek, 2].
Судьба Кенигсберга
В то время как теория графов процветала после того, как Эйлер решил проблему Кенигсбергского моста, у города Кенигсберга была совсем другая судьба.В 1875 году жители Кенигсберга решили построить новый мост между узлами B и C, увеличив количество соединений этих двух массивов суши до четырех. Это означало, что только два массива суши имели нечетное количество связей, что давало довольно простое решение проблемы. Создание дополнительного моста могло быть или не быть подсознательно вызвано желанием найти путь, чтобы решить известную проблему города.
Создание дополнительного моста могло быть или не быть подсознательно вызвано желанием найти путь, чтобы решить известную проблему города.
Однако новый мост не решил всех будущих проблем Кенигсберга, так как город не ожидал еще в девятнадцатом веке «печальной и истерзанной войной участи, которая ожидала его как место проведения одного из самых жестоких сражений Второй мировой войны.В течение четырех дней августа 1944 года британские бомбардировщики уничтожили как старый город, так и северные части Кенигсберга. В январе и феврале 1945 года район Кенигсберга окружен русскими войсками. Немецкое гражданское население начинает эвакуацию из города, но слишком поздно. Тысячи людей гибнут, пытаясь бежать на лодках и пешком по ледяным водам Куршского залива. В апреле 1945 года Красная Армия захватывает Кенигсберг, и около девяноста процентов старого города лежат в руинах.
Текущая карта улиц Кенигсберга приведена ниже [источник: MacTutor History of Mathematics Archive]. Эта карта показывает, насколько сильно изменился город. Многие мосты были разрушены во время бомбардировок, и город больше не может задавать тот же интригующий вопрос, что и в восемнадцатом веке. Наряду с принципиально иной планировкой город Кенигсберг носит новое название Калининград, а река Прегель переименована в Преголю [Гопкинс, 6]. В то время как судьба Кенигсберга ужасна, старая кофейная проблема горожан пройти каждый из своих старых семи мостов ровно по одному разу привела к формированию совершенно нового раздела математики, теории графов.
Многие мосты были разрушены во время бомбардировок, и город больше не может задавать тот же интригующий вопрос, что и в восемнадцатом веке. Наряду с принципиально иной планировкой город Кенигсберг носит новое название Калининград, а река Прегель переименована в Преголю [Гопкинс, 6]. В то время как судьба Кенигсберга ужасна, старая кофейная проблема горожан пройти каждый из своих старых семи мостов ровно по одному разу привела к формированию совершенно нового раздела математики, теории графов.
Ссылки
Биггс, Норман Л., Э. К. Ллойд и Робин Дж. Уилсон. Теория графов: 1736-1936 . Оксфорд: Кларендон Пресс, 1976.
.Данэм, Уильям. Эйлер: Повелитель всех нас . Вашингтон: Математическая ассоциация Америки, 1999.
.Эйлер, Леонхард, «Solutio problematis ad geometriam situs pertinentis» (1741), Eneström 53, MAA Euler Archive.
«История математики: О Леонарде Эйлере (1707-1783). ScienceWeek (2003). 6 ноября 2005 г.
Хопкинс, Брайан и Робин Уилсон. «Правда о Кенигсберге». College Mathematics Journal (2004), 35, 198-207.
«Кенигсбергские мосты». Архив истории математики MacTutor:
http://www-history.mcs.st-and.ac.uk/history/Miscellaneous/other_links/Konigsberg.html
Примечание редактора: Эта статья была первоначально опубликована в Convergence, Volume 3 (2006).
Диаграммы Венна и диаграммы Эйлера с объяснением на примерах
Диаграммы Венна и диаграммы Эйлера выглядят очень похоже, поэтому понятно, что многим людям трудно понять разницу. Хотя оба типа диаграмм основаны на теории множеств, существуют некоторые тонкие различия, которые делают их уникальными. Надеюсь, эта статья рассеет ваши сомнения по поводу диаграмм Венна и диаграмм Эйлера, и я приведу несколько примеров, чтобы было понятнее.
Венн против Эйлера: определение
Как я упоминал ранее, оба набора диаграмм основаны на теории множеств. Диаграмма Венна показывает все возможные логические отношения между наборами множеств. Но диаграмма Эйлера показывает только те отношения, которые существуют в реальном мире.
Диаграммы Венна и
Диаграммы Эйлера ПримерыДавайте начнем с очень простого примера. Давайте рассмотрим надмножество Animals с млекопитающими и птицами в качестве подмножеств. Диаграмма Венна показывает пересечение двух множеств, хотя в реальном мире такой возможности не существует.Диаграмма Эйлера, с другой стороны, не показывает пересечения.
Диаграммы Венна показывают все возможные комбинации, даже если они не существуют в реальном сценарии.Теперь рассмотрим более сложный пример с колодой карт. Опять же важно помнить о разнице между двумя типами диаграмм, всеми возможными комбинациями и реальными комбинациями . Возьмем карты как надмножество, а черные карты, красные карты и бубны — как подмножества.
Как одни и те же данные представляются по-разному с использованием диаграмм Венна и диаграмм ЭйлераКак видно из приведенного выше примера, на диаграммах Венна показаны четыре пересечения, для которых нет данных, поскольку они должны отображать все возможные комбинации.
Существуют различные методы преобразования диаграммы Венна в диаграмму Эйлера и наоборот. Посмотрите эту замечательную вики-статью о диаграммах Эйлера, в которой объясняются некоторые методы, которые вы можете использовать для преобразования диаграмм Венна в диаграммы Эйлера.Я надеюсь, что приведенные выше примеры помогли вам развеять ваши сомнения относительно диаграмм Венна и диаграмм Эйлера. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в разделе комментариев.
Независимо от того, рисуете ли вы диаграммы Венна или диаграммы Эйлера, Creately предоставляет вам все необходимые инструменты. Вы можете быстро приступить к работе, используя шаблоны диаграмм Венна, доступные нашим пользователям, или начать с нуля в области рисования. Если вы хотите добавить значки и изображения на диаграмму Венна, это можно легко сделать с помощью встроенного поиска изображений Google, доступного на левой боковой панели.С таким количеством супер крутых функций вы не ошибетесь с Creately.
Присоединяйтесь к более чем тысячам организаций, которые используют Creately для мозгового штурма, планирования, анализа и успешного выполнения своих проектов.
Начните здесьЧто такое круги Эйлера | Наука 2022
Схемы и диаграммы призваны помочь вам решать проблемы и принимать простые жизненные решения. Люди пользуются ими десятилетиями, не подозревая, что в их основе лежит научно обоснованное представление математика Эйлера о пересечении взаимодополняющих и взаимоисключающих факторов, которые схематично изображаются в виде окружностей.
Что такое круги ЭйлераЕсли вы думаете, что ничего не знаете о таком понятии, как круги Эйлера, то глубоко ошибаетесь. Еще из начальной школы известны схематические изображения, или круги, позволяющие наглядно осмыслить взаимосвязь между понятиями и элементами системы.
Метод, изобретенный Леонардом Эйлером, применялся ученым для решения сложных математических задач. Он изобразил множества в кругах и положил эту схему в основу такого понятия, как символическая логика.Методика призвана максимально упростить рассуждения, направленные на решение той или иной задачи, именно поэтому методика активно используется как в начальной школе, так и в академической среде. Интересно, что подобный подход ранее применялся немецким философом Лейбницем, а позже был подхвачен и применен в различных модификациях известными умами в области математики. Например, прямоугольные диаграммы чешских математиков Больцано, Шредера, Венна, известных созданием популярной диаграммы на основе этого простого, но удивительно эффективного метода.
Круги лежат в основе так называемых «визуальных интернет-мемов», в основе которых лежит сходство признаков отдельных наборов. Забавно, наглядно, а главное понятно.
Круги мысли
Кружки позволяют наглядно описать условия задачи и моментально принять правильное решение, либо обозначить направление движения в сторону правильного ответа. Как правило, круги Эйлера используются для решения логических и математических задач, связанных с множествами, их объединениями или частичными наложениями.В пересечение окружностей попадают предметы, обладающие свойствами каждого из множеств, изображенных кружком. Предметы, не входящие в набор, находятся вне того или иного круга. Если понятия абсолютно эквивалентны, их обозначают одним кругом, представляющим собой объединение двух множеств, имеющих одинаковые свойства и объемы.
Логика отношений
С помощью кругов Эйлера можно решить ряд бытовых задач и даже определиться с выбором будущей профессии, стоит только проанализировать свои возможности и желания и выбрать их максимальное пересечение.
Теперь становится ясно, что круги Эйлера вовсе не являются абстрактным математико-философским понятием из разряда теоретических знаний, они имеют весьма прикладное и практическое значение, позволяя заниматься не только простейшими математическими задачами, но и решать важные жизненные дилеммы в ясной и понятной для всех форме.

 1. Задачи
на пересечение и объединение двух
множеств…….
1. Задачи
на пересечение и объединение двух
множеств…….
 В. Фарков. М.: Айрис–пресс, 2007. с. 27,
34, 61. – 7000 экз. – ISBN
978-5-8112-2394-7
В. Фарков. М.: Айрис–пресс, 2007. с. 27,
34, 61. – 7000 экз. – ISBN
978-5-8112-2394-7
 Обозначить множества: A, B, C.
Обозначить множества: A, B, C. Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начинать и заканчивать экскурсию? Объяснять.
Могут ли они пройти через каждый дверной проем ровно один раз? Если да, то в каких комнатах они должны начинать и заканчивать экскурсию? Объяснять. Докажите, что \(G\) не имеет пути Гамильтона.
Докажите, что \(G\) не имеет пути Гамильтона.