Задачи на совместную работу: примеры и решение
Рассмотрим задачи, в которых речь идёт о совместном выполнении некоторой работы. При этом всё равно, какую работу выполняют и чем эту работу измеряют – числом деталей, количеством вспаханных гектаров и т. п. Если, например, некоторая работа выполняется за 10 часов, то за 1 ч, очевидно, выполняется 
всей работы, а вся работа составляет десять таких частей 
. Поэтому обычно в таких задачах всю работу принято считать равной единице, объём выполненной работы выражают как часть этой единицы.
Задача 1. Первая бригада может выполнить задание за 36 ч, а вторая бригада может выполнить то же задание за 18 ч. За сколько часов это задание выполнят две бригады при совместной работе?
Решение: примем всю работу за единицу, тогда за 1 ч первая бригада выполняет 
всей работы. При совместной работе за 1 ч две бригады выполняют 
всей работы, поэтому всю работу они выполнят за 
Ответ: при совместной работе бригады выполнят задание за 12 часов.
Под совместной работой можно понимать и одновременную работу двух труб при наполнении бассейна, и прохождение некоторого пути при движении навстречу друг другу и т. п. Метод решения остаётся тем же.
Задача 2. Расстояние между двумя сёлами пешеход проходит за 60 мин, а велосипедист проезжает за 20 мин. Через сколько минут они встретятся, если отправятся одновременно навстречу друг другу из этих сёл?
Решение: примем расстояние между сёлами за единицу.
– проходит пешеход за 1 мин.
– проезжает велосипедист за 1 мин.
– такую часть расстояния они проходят за 1 мин при движении навстречу друг другу
– время движения до встречи
Ответ: они встретятся через 15 минут.
Задача 3. Два печника сложили печь за 16 ч. Известно, что первый из них, работая один, сложил бы печь за 24 ч. За сколько часов второй печник, работая один, сложил бы ту же печь?
Решение: примем объём всей работы за 1.
– выполняют два печника за 1 час, работая вместе
– выполняет первый печник за 1 час, работая один
– выполняет второй печник за 1 час, работая один
– за столько времени сложил бы печь второй печник
Ответ: второй печник, работая один, сложил бы печь за 48 часов.
Задача 4. Из пунктов A и B одновременно вышли два пешехода. Они встретились через 40 минут после своего выхода, а через 32 мин после встречи первый пришёл в B. Через сколько минут после своего выхода из B второй пришёл в A?
Решение: примем расстояние между пунктами A и B за единицу.
– такую часть расстояния проходят два пешехода за 1 мин при движении навстречу друг другу
2) 40 + 32 = 72 (мин) – время первого пешехода за весь путь
– проходит первый пешеход за 1 мин
– проходит второй пешеход за 1 мин
– время второго пешехода за весь путь
Ответ: через 90 минут после своего выхода из B второй пешеход пришёл в A.
naobumium.info
Решение задач на совместную работу
Типичные задачи на совместную работу в 6 классе
1) Двое рабочих, работая вместе, выполняют некоторую работу за 6 часов. Один из них, работая самостоятельно, может выполнить эту работу за 15 часов. За сколько часов может выполнить эту работу другой рабочий?
В отличие от всех других типов задач, задачи на совместную работу начинаются с того, что всю работу (все задание, весь бассейн, все поле — то, о чем идет речь в задаче) принимаем за единицу. То есть объем работы в этом случае равен единице. Чтобы найти объем работы, надо производительность труда умножить на время работы. Соответственно, чтобы найти производительность труда (часть работы, выполненную за определенную единицу времени), надо объем работы разделить на время работы: Решение задач на совместную работу упрощается, если условие оформить в виде таблицы.
Перейдем с решению нашей задачи.
Решение.
Примем всю работу за 1.
Чтобы найти производительность труда второго рабочего, из производительности труда совместной работы вычтем производительность труда первого рабочего:
Такую часть работы в 1 час выполняет второй рабочий.
Зная производительность труда второго рабочего и объем работы, можем найти время, за которое он может выполнить работу самостоятельно. Чтобы найти время работы, надо объем работы разделить на производительность труда:
Значит, второй рабочий, работая отдельно, может выполнить работу за 10 часов.
Ответ: за 10 часов.
2) Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?
Решение.
Примем весь бассейн за 1.
Сначала найдем производительность труда совместной работы обеих труб за один час. Поскольку одна труба бассейн наполняет, а другая — опустошает, производительность совместной работы равна разности производительности первой и второй труб:
Теперь найдем время, за которое бассейн будет наполнен при открытии обеих труб одновременно. Чтобы найти время работы, надо объем работы разделить на производительность труда:
Таким образом, за 56 часов совместной работы обеих труб бассейн будет наполнен.
Ответ: за 56 часов.
www.for6cl.uznateshe.ru
Задачи на совместную работу
Научить решать опорные задачи, которые помогут
“открыть” решение составных задач на
совместную работу.
Расширить представления учащихся о практике
решения задач различными способами
Дети учатся находить сначала указанную часть
величины, а потом, увеличивая или уменьшая эту
величину на найденную часть, построение
схематического рисунка к условию задачи его
использование при решении задачи,
устанавливается соответствие между задачами на
работу и аналогичными задачами на движение.
Особенно сложен переход от дроби к числу, которое
указывает на число часов работы, нахождения в
пути и т. д. Необходимо больше уделять внимания
опорным задачам, выстроить определенную цепочку
рассуждений, научить связывать порознь
усвоенные приемы решения, комбинировать их при
поиске решений новых задач.
Цели урока:
- Воспитательные:
- вырабатывать умение преодолевать трудности,
- стимулировать мотивацию и интерес к изучению математики,
- приучать к эстетическому оформлению записи в тетради,
- формировать умение выслушивать других.
- Развивающие:
- развивать логическое мышление сообразительность, познавательный интерес;
- развивать умение контролировать свои действия;
- обучение действию по аналогии;
- развивать культуру математической речи;
- вырабатывать умение общения.
- Образовательные:
- проверить, с помощью самостоятельной работы, навыки сложения и вычитания обыкновенных дробей с разными знаменателями;
- познакомить с методом решения задач на совместную работу;
- расширять кругозор учащихся;
- научить использовать арифметический способ для решения задач на «совместную работу»;
- стимулировать учащихся к овладению этим методом для решения других текстовых задач.
ХОД УРОКА
1. Организационный момент
2. Постановка целей и задач урока
Сегодня на уроке мы продолжим отрабатывать навыки решения текстовых задач арифметическим способом; решение исторических задач и старинных способов их решения расширит представление о практике решения задач в старые времена.
3. Устная работа
1. Бассейн наполняется за 3 ч. Какая часть бассейна наполняется за 1 ч?
Решение:
1: 3 = 1/3 часть бассейна наполнится за 1 час.
Ответ: 1/3
2. Работу выполнили за 5 часов. Какую часть работы выполняли в каждый час?
Решение:
1 : 5 = 1/5 часть работы выполняли каждый час.
Ответ: 1/5
3. В каждый час труба наполняет 1/12часть бассейна. За сколько часов она наполнит бассейн?
Решение:
1: 1/12 = 12 часов – время для наполнения бассейна.
Ответ: 12 часов.
4. Путник проходит в час 1/6 часть пути. За сколько часов он пройдет весь путь?
Решение:
1 : 1/6 = 6 часов затратит путник на весь путь.
Ответ: 6 ч.
5. В каждый час первая труба наполняет 1/4 бассейна, а вторая – 1/3 бассейна. Какую часть бассейна наполняют обе трубы за 1 час совместной работы.
Решение:
1/4 + 1/3 = (3 + 4)/12 = 7/12 (часть бассейна) – наполняют обе трубы за 1 час
Ответ: 7/12
6. Два путника одновременно вышли навстречу друг другу и встретились через 3 часа. На какую часть первоначального расстояния они сближались в каждый час?
Решение:
1 : 3 = 1/3 часть расстояния соответствует сближению путников за час.
Ответ: 1/3.
4. Проверка домашнего задания
Учащиеся должны были придумать сами или
подобрать из различных источников
опорные задачи на совместную работу
5. «Открытие» детьми нового знания. Способы действия в новой ситуации
Учитель: Хорошо. Все успешно
справились с предложенным заданием, а теперь
прошу все внимание на доску. Мы начинаем изучать
новую тему, которая называется «Задачи на
совместную работу».
Сегодня на уроке мы научимся решать новые задачи
на совместную работу, опираясь на усвоенные
методы решения опорных задач
Хочу напомнить, что всю работу принято
считать равной единице и при этом всё равно,
какую работу выполняют и в чём её измеряют.
Решение старинной задачи всем классом.
На экране вы видите текст одной из задач
«Арифметики Магницкого», попробуйте ее решить.
Какие будут варианты? (Дети высказывают свои
варианты решения).
Лошадь съедает воз сена за два месяца, овца – за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?
Решение:
1) Известно, что лошадь съедает воз сена за
месяц.
2) 1 : 2 = 1/2 (воза) съедает за месяц коза.
3) 1 : 3 = 1/3 (воза) съедает за месяц овца.
4) 1 + 1/2 + 1/3 = (6 + 3 + 2)/6 = 11/6 (воза) съедает за месяц
лошадь, коза и овца.
5) 1 : 11/6 = 1 · 6/11 = 6/11 (месяца) съедят воз сена лошадь,
коза и овца.
Ответ: 6/11 (месяца).
А теперь посмотрите, как решалась эта задача в 17 веке.
Пусть лошадь, коза и овца едят сено 6 месяцев. Тогда лошадь съедает 6 возов, коза – 3, а овца – 2. Всего 11 возов, значит, в месяц они съедают 11/6 воза, а один воз съедят за 1 : 11/6 = 6/11 (месяца)
Приведенный способ решения задачи указывает на то, что авторы решения применяли такое рассуждение, видимо, потому, что не умели действовать с дробями.
Учитель: Продолжим изучение методов решения задач на совместную работу.
Задача 1.
В городе есть искусственный водоем. Одна из труб может заполнить его за 4 часа, вторая – за 8часов, а третья – за 24 часа. За сколько времени наполнится водоем, если открыть сразу три трубы?
Решение:
- 1 : 4 = 1/4 (водоема) – наполнится через первую трубу за час.
- 1 : 8 = 1/8 (водоема) – наполнится через вторую трубу за час.
- 1 : 24 = 1/24 (водоема) – наполнится через третью трубу за час.
- 1/4 + 1/8 + 1/24 = (6 + 3 + 1)/24 = 10/24 (водоема) – наполнится через три трубы за час.
- 1: 10/24 = 1· 24/10 = 12/5 = 2(ч)
Ответ: через три трубы, работающие
одновременно, водоем наполнится за 2ч.
Таким образом, при решении задач на совместную
работу складывается не время работы, а часть
работы, которую делают ее участники.
Итак, алгоритм.
При решении задач на совместную работу вся
выполненная работа принимается за единицу.
а) Находим часть работы выполненной одним
объектом за единицу времени (производительность
Р1). (Р = 1/Т)
б) Находим часть работы выполненной другим
объектом за единицу времени (производительность
Р2).
в) Находим часть работы выполненной двумя и более
объектами за единицу времени
(производительность Р = Р1 + Р2).
г) Находим время, затраченное на выполнение всей
работы всеми участвующими объектами (Т = 1 : Р).
6. Первичное закрепление изученного материала
Устная работа
Задача. Маша принесла своим друзьям медведям торт. Известно, что старший медведь может съесть торт за два дня, средний медведь за три дня, а младший за шесть дней. За сколько дней три медведя вместе съедят торт?
Решение:
1 : 2 = 1/2 (часть торта) – съест старший медведь за 1
день
1 : 3 = 1/3 (часть торта) – съест средний медведь за 1
день
1 : 6 = 1/6 (часть торта) – съест младший медведь за 1
день
1/2 + 1/3 + 1/6 = (3 + 2 + 1)/6 = 1 (то есть один торт) – вместе
три медведя съедят торт за 1 день
Ответ: за 1 день.
Кто быстрее всех решит верно, следующую задачу:
За пять недель пират Ерёма способен выпить
бочку рома.
А у пирата у Емели ушло б на это две недели.
За сколько дней прикончат ром пираты, действуя
вдвоём?
Учитель: Давайте теперь решим задачу следующего содержания
Задача 2.
Два пешехода вышли одновременно из двух
поселков навстречу друг другу. Один пешеход
может пройти весь путь за три часа, а другой – за 4ч.
Через сколько времени они встретятся?
Решение:
Это тоже задача на «совместную работу», хотя,
строго говоря, никто не работает. Но можно
считать, что «работа» пешеходов – это
прохождение пути. Поэтому весь путь принимаем за
«единицу» и вычисляем часть пути, пройденную
каждым пешеходом.
- 1:3 = 1/3 (расстояния) – проходит первый пешеход за один час.
- 1 : 4 = 1 : = 1 · = (расстояния) – проходит второй пешеход за один час.
- + = = (расстояния) – сближаются оба пешехода за час.
- 1 : = 1 · = = 1(ч).
Ответ: пешеходы встретятся через 1ч.
5. Самостоятельное решение подобных задач по рядам с самопроверкой
Задача 3. Один ученик может убрать класс за 20 мин, а второй за 30 мин. За сколько минут они могут убрать класс, работая вместе?
Решение:
Примем всю работу за единицу.
1 : 20 = 1/20 (часть всей работы) – выполнит первый
ученик за 1 мин
1 : 30 = 1/30 ( часть всей работы) – выполнит второй
ученик за 1 мин;
1/20 + 1/30 = 5/60 = 1/12 (часть всей работы) – выполнят при
совместной работе два ученика за 1 мин
1 : 1/12 = 12 (мин) – выполнят всю работу два ученика
Ответ: 12 мин
Задача 4. Через первую трубу водоем можно наполнить за 5ч, а через вторую – за 6 ч. За сколько часов наполнится водоем при совместной работе этих труб?
Задача 5. Грузовая машина проезжает расстояние между двумя городами за 3 ч, а легковая – за 2 ч. Машины одновременно выехали из этих городов навстречу друг другу. Через сколько часов они встретятся?
6. Работа с учебником по дифференцированным заданиям
№ 612, №613(1)
для сильных учащихся № 614(1) и № 615(2).
7. Рефлексия деятельности
С помощью беседы обсудить с учащимися вопросы:
– Задачи, какого типа научились решать?
– Что нового на уроке узнали?
– Что научились делать?
– Что находим первоначально при решении задач на
совместную работу?
– Где испытывали затруднения?
8. Домашнее задание.
№ 613(2),611Выучить алгоритм решения задач на
совместную работу, повторить правила сложения и
вычитания обыкновенных дробей
Учащиеся должны придумать сами или подобрать из
различных источников задачи на нахождение
времени при совместной работе.
Сообщить, что на следующем уроке будем решать
задачи с более сложной формулировкой.
Назвать оценки, которые получили учащиеся
Используемая литература
- Учебник Г.В.Дорофеев, Л.Г. Петерсон и др. «Математика 5».
- Методические рекомендации к учебнику «Математика5» Г.В.Дорофеев, Л.Г. Петерсон и др
urok.1sept.ru
Задачи на совместную работу
Задачи на работу содержат сведения о выполнении несколькими объектами некоторой работы с указанием объема или без указания объема работ. Зачастую, когда величина и объем работ не конкретизируется и не интересуют нас, то объем принимают за единицу. В задачах данного типа важную роль играет понятие производительность (P) – объем работы, выполненной за единицу времени.
P = A / t.
Рассмотрим несколько задач.
Задача 1.
Две машинистки должны отпечатать рукописи с одинаковым числом страниц. Первая приступила к работе на 3 часа раньше второй и отпечатала к определенному моменту времени больше, чем вторая, на 5/18 страниц рукописи. Проработав после этого момента еще 5 часов, обе машинистки одновременно закончили свою работу. За сколько времени каждая отпечатала свою рукопись?
Решение.
Некоторые задачи на работу аналогичны задачам на движение. Попробуем применить в решении этой задачи графический метод. Всю работу принимаем за 1 и делаем соответствующий рисунок (рис. 1).
Ответ: 9 часов и 6 часов.
К задачам на работу относятся так же задачи на планирование, в которых объем работы, который необходимо выполнить либо известен, либо его необходимо определить (в отличие от задач на совместную работу). При этом работа, которая должна быть выполнена по плану, сравнивается с работой, которую выполнили в действительности, т.е. фактически. Основными элементами задач на планирование, так же, как и в задачах на совместную работу, являются:
а) работа, выполненная в действительности и запланированная;
б) фактическое время выполнения работы и запланированное;
в) реальная производительность труда и запланированная.
Замечание. В некоторых задачах на совместную работу вместо времени выполнения некоторой работы дается количество рабочих, участвующих в ее выполнении.
Задача 2.
Планом было предусмотрено, что предприятие на протяжении нескольких месяцев сделает 1000 насосов. В результате реконструкции оборудования предприятие стало изготавливать ежемесячно на 20 насосов больше, чем планировалось, и на 1 месяц раньше срока перевыполнило задание на 8 %. Сколько насосов в месяц стало выпускать предприятие?
Решение.
Пусть по плану предприятие должно было выпускать x насосов в месяц, а выпускало (x + 20) насосов. Тогда 1000/x месяцев – это срок выполнения плана. Предприятие выпустило 1000 + 0,08 · 1000 = 1080 насосов за 1080 / (x + 20) месяцев. По условию задачи известно, что
1000/x – 1080 / (x + 20) = 1.
Решим полученное уравнение.
1000/x – 1080 / (x + 20) – 1 = 0;
(1000(x + 20) – 1080x – x(x + 20)) / (x(x + 20)) = 0.
Раскроем скобки в числителе дроби, получим:
(1000x + 20000 – 1080x – x2 + 20x) / (x(x + 20)) = 0;
(-x2 – 100x + 20000) / (x(x + 20)) = 0. Домножим дробь на (-1), получим:
(x2 + 100x – 20000) / (x(x + 20)) = 0.
Полученная дробь будет равна нулю, если будут выполняется следующие условия (запишем их в виде системы):
{x2 + 100x – 20000 = 0,
{x(x + 20) ≠ 0.
Таким образом, из первого уравнения имеем, что x = -200 или x = 200, а из второго: x ≠ 0, x ≠ -20.
Следовательно, предприятие стало выпускать 100 + 20 = 120 насосов.
Ответ: 120 насосов.
Задача 3.
Бригада рыбаков должна была выловить в определенный срок 1800 
центнеров рыбы. Третью часть этого срока был шторм, именно поэтому плановое задание ежедневно недовыполнялось, причем на 20 центнеров. Однако в остальные дни бригаде удавалось вылавливать рыбы больше, чем было запланировано первоначально, причем, на 20 центнеров. В итоге задание по отлову рыбы было выполнено на 1 день раньше срока. Сколько центнеров рыбы ежедневно планировала вылавливать бригада рыбаков изначально?
Решение.
Пусть x дней – планируемый срок для отлова рыбы, а y центнеров – план по отлову рыбы в день. Составим первое уравнение: xy = 1800.
Так как третью часть планируемого срока работы был шторм, то за это время бригада смогла выловить (y – 20) · 1x/3 (центнеров рыбы). В оставшееся время бригада выловила (y – 20) · (2x/3 – 1) (центнеров рыбы). Составим второе уравнение:
(y – 20) · x/3 + (y + 20) · (2x/3 – 1) = 1800. Решим полученную систему уравнений:
{(y – 20) · x/3 + (y + 20)(2x/3 – 1) = 1800,
{xy = 1800.
В результате решения системы получим, что y = 100.
Ответ: 100 центнеров.
Рассмотрим метод решения задачи, где число неизвестных превышает число уравнений.
Задача 4.
В соревновании принимают участие три бригады лесорубов. Первая и 
третья бригады обработали древесины в 2 раза больше, чем вторая, а вторая и третья – в 3 раза больше, чем первая. Какая бригада победила в этом соревновании?
Решение:
Пусть a, b и c – количество древесины, которое обработали первая, вторая и третья бригады соответственно. По условию задачи можно составить систему:
{a + c = 2b,
{b + c = 3a.
Отнимем из первого уравнения системы второе, получим:
4a = 3b. Таким образом, b = 4a/3 и это больше либо равно a. Подставим полученное значение для b в первое уравнение системы. Будем иметь:
a + b = 8a / 3 или c = 5a/3. Сравнив b и c, получим, что c > b. Делаем вывод.
Ответ: победила третья бригада.
Задачи на совместную работу очень часто имеют сложный и запутанный сюжет, именно поэтому его не всегда легко перевести на математический язык, так называемый, язык чисел. Если вы хотите научиться решать подобные задачи, то обязательно попрактиковаться в решении текстовых задач, то можете провести бесплатное 25-минутное занятие с онлайн репетитором после регистрации. Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам тарифный план.
Остались вопросы? Не знаете, как решать задачи на совместную работу?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Решение задач на совместную работу. Задание В13
Решение задач на совместную работу. Задание 11
Задачи на работу делятся на два типа:
- задачи, в которых выполняется раздельная работа — эти задачи решаются аналогично задачам на движение.
- задачи на совместную работу.
Если в задаче встречаются слова «выполнили работу вместе» или слова «совместная работа», значит это задача на совместную работу.
В этой статье я подробно остановлюсь на алгоритме решения задач на совместную работу.
1. В задачах на совместную работу мы имеем дело с теми же тремя параметрами, что и в задачах на раздельную работу:
- объем работы,
- время,
- производительность,
которые связаны между собой формулой:
объем работы=производительность 
время.
2. Объем работы, если он не указан отдельно, принимаем равным 1.
3. Вводим два неизвестных:
х — время выполнения всей работы кем-то (или чем-то) первым
y — время выполнения всей работы кем-то (или чем-то) вторым.
(В некоторых задачах «выгоднее» принять за неизвестные производительность)
Тогда
— производительность кого-то (или чего-то) первого
— производительность кого-то (или чего-то) первого
И в этом месте появляется параметр, которого не было в задачах на раздельную работу, а именно — совместная производительность
совместная производительность равна 
Рассмотрим примеры решения задач из Открытого банка заданий для подготовки к ЕГЭ по математике:
1. Задание 11 (№ 99617)
Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
Про Машу нам все известно: время её работы равно 20, следовательно, её производительность равна 
.
Пусть Даша пропалывает грядку за х минут, тогда её производительность равна .
Тогда совместная производительность равна 
Объем работы примем равным 1.
Время совместной работы равно 12 минут, отсюда получаем уравнение:
Решим его:
Ответ: 30
2. Классическая задача на совместную работу:
Задание 11 (№ 99619)
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
1. Введем неизвестные:
Пусть
х — время заполнения резервуара первой трубой
y — время заполнения резервуара второй трубой
— производительность первой трубы
— производительность второй трубы
— совместная производительность
2. Примем объем резервуара равным 1.
3. У нас 2 неизвестных, поэтому будем составлять систему из двух уравнений.
По условию задачи, первая труба наполняет резервуар на 6 минут дольше, чем вторая, следовательно время работы первой трубы на 6 минут больше, чем второй:
Обе трубы наполняют этот же резервуар за 4 минуты, следовательно, время совместной работы равно 4 минуты. Получаем второе уравнение системы:
Получили систему уравнений:
, 
— не подходит по смыслу задачи.
Ответ: 6
3. Предлагаю вам посмотреть ВИДЕОУРОК, в котором я показываю решение такой задачи:
Задание 11 (№ 99616)
Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь — за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?
4. И, наконец, видеорешение такой задачи:
Три экскаватора разной производительности роют котлован. Работа будет выполнена, если каждый проработает 12 часов. Она также будет выполнена, если первый проработает 8 часов, второй 16, а третий 10. Сколько часов должен проработать второй экскаватор, чтобы завершить работу, если до него первый проработал 10 часов, а третий — 11?
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Методика решения задач на совместную работу
Задачи на совместную работу
1. Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
Решение.
Пусть первый оператор может выполнить данную работу за 
часов, а второй за 
часов. За один час первый оператор выполняет 
часть всей работы, а второй 
. Составим систему уравнений:
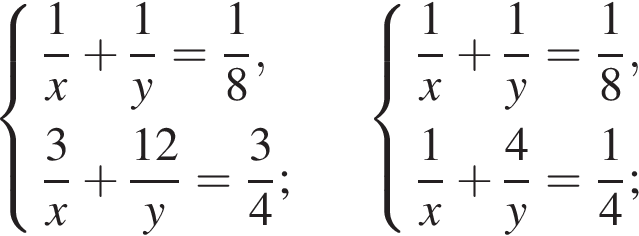
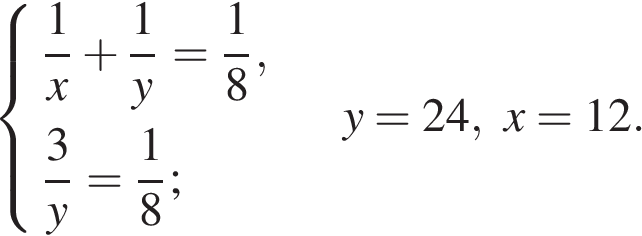
Ответ: первый оператор за 12 ч, второй оператор за 24 ч.
2. На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
Решение.
Предположим, что ученик делает 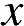деталей в час, 
. Тогда мастер делает 
детали в час.
Составим таблицу по данным задачи:
Производительность
(дет/ч)
Время (ч)
Объём работ (дет)
Ученик
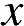
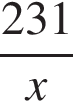
231
Мастер
462
Так как ученик потратил на работу на 11 часов больше, можно составить уравнение:
.
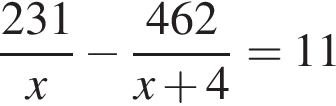Решим уравнение:
.
Корни полученного квадратного уравнения: −28 и 3. Отбрасывая отрицательный корень, находим, что ученик делает в час 3 детали.
Ответ: 3.
3. Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
Решение.
Пусть за минуту в бак накачивается 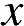литров воды, . Тогда за минуту выкачивается 
л воды.
Составим таблицу по данным задачи:
Производительность
(л/мин)
Время (мин)
Объём работ (л)
Накачивается
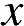
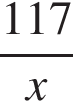
117
Выкачивается
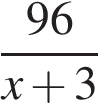
96
Так как на накачивание было затрачено на 5 мин. больше времени, составим уравнение:
,
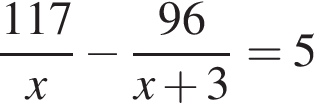откуда:
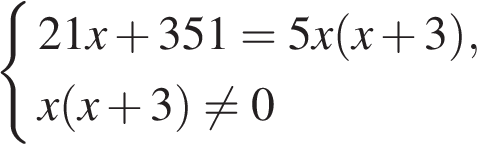
Получаем квадратное уравнение:
,
имеющее корни: 
и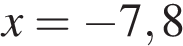 
.
Отбрасывая отрицательный корень, находим, что за минуту в бак накачивается 9 л воды.
Ответ: 9.
4. Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
Решение.
Пусть x — количество вопросов теста. Тогда получаем:
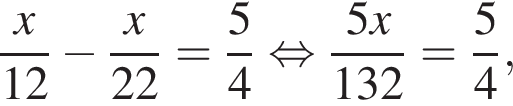
откуда находим x = 33 .
Ответ: 33
5. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 час. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По условию первая труба за одну минуту наполняет 
часть бассейна, а две трубы вместе за одну минуту наполняют 
часть бассейна. Таким образом, одна вторая труба за минуту наполняет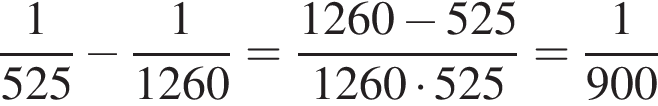 
часть бассейна, то есть она наполнит весь бассейн за 15 часов.
Ответ: 15.
6. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объёмом 136 литров?
Решение.
Пусть вторая труба пропускает 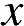литров воды в минуту, 
, тогда первая труба пропускает 
литра в минуту.
Составим таблицу по данным задачи:
Производительность
(л/мин)
Время (мин)
Объём работ (л)
Первая труба
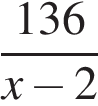
136
Вторая труба
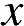
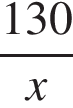
130
Так как первая труба заполнила резервуар на 4 мин. быстрее, получаем уравнение:
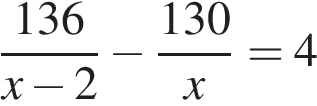
Решим уравнение:
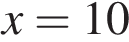или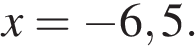 
Отбрасывая постороннее решение −6,5, получаем, что вторая труба пропускает 10 литров в минуту.
Ответ: 10.
7. Две трубы наполняют бассейн за 6 часов 18 минут, а одна первая труба наполняет бассейн за 9 часов. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По условию первая труба за одну минуту наполняет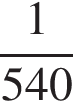 
часть бассейна, а две трубы вместе за одну минуту наполняют 
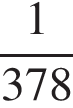часть бассейна. Таким образом, одна вторая труба за минуту наполняет 
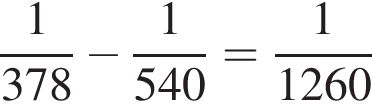часть бассейна, то есть она наполняет весь бассейн за 21 час.
Ответ: 21.
8. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Решение.
Пусть 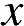— число деталей, изготавливаемых первым рабочим за час, 
, тогда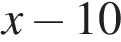 
— число деталей, изготавливаемых вторым рабочим за час.
Составим таблицу по данным задачи:
Производительность
(дет/ч)
Время (ч)
Объём работ (дет)
Первый рабочий
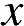
60
Второй рабочий
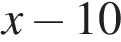
60
Так как первый рабочий справляется с работой на 3 часа быстрее, составим уравнение:
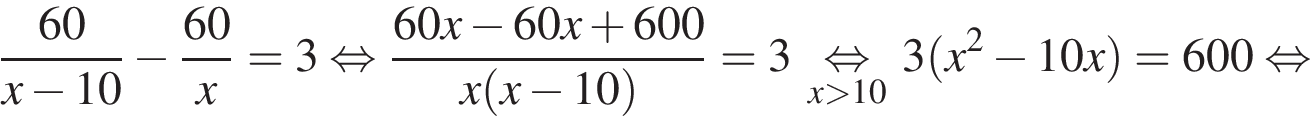
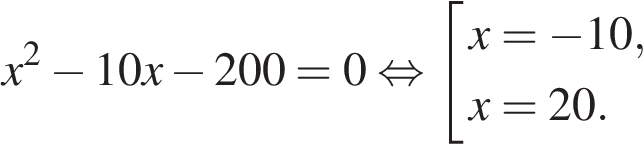
Корень −10 не подходит по условию задачи, следовательно, первый рабочий изготавливает 20 деталей в час. Значит, второй рабочий изготавливает 10 деталей в час.
Ответ: 10.
9. Три бригады изготовили вместе 266 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
Решение.
Пусть 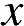— число деталей, изготовленных второй бригадой, тогда первая бригада изготовила 
деталей, а третья — 
деталей. Вместе три бригад изготовили 266 деталей, составим уравнение:
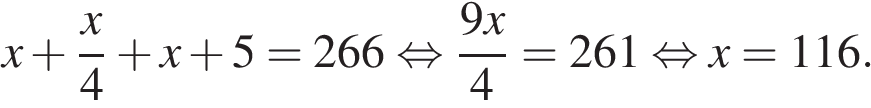
Вторая бригада изготовила 116 деталей, следовательно, первая бригада изготовила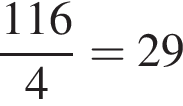 
деталей, а третья — 121 деталь. Таким образом, третья бригада изготовила на 121 − 29 = 92 детали больше.
Ответ: 92.
10. Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь — за 30 часов. За сколько часов мальчики покрасят забор, работая втроём?
Решение.
Обозначим выполняемую мальчиками работу по покраске забора за 1. Пусть за 
, 
, 
часов Игорь, Паша и Володя, соответственно, покрасят забор, работая самостоятельно. Игорь и Паша красят забор за 20 часов:
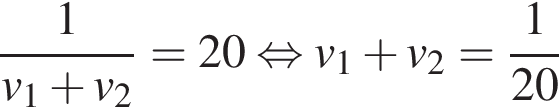
Паша и Володя красят этот же забор за 24 часа:
,
а Володя и Игорь — за 30 часов:
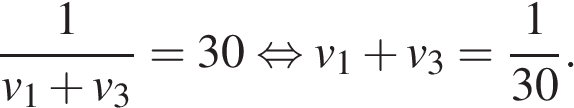
Получаем систему уравнений:
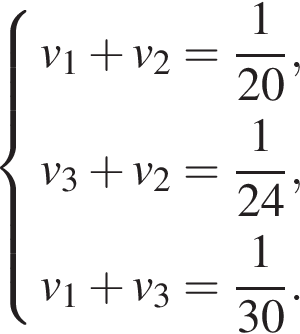
Просуммируем левые и правые части данных трех уравнений, получим:
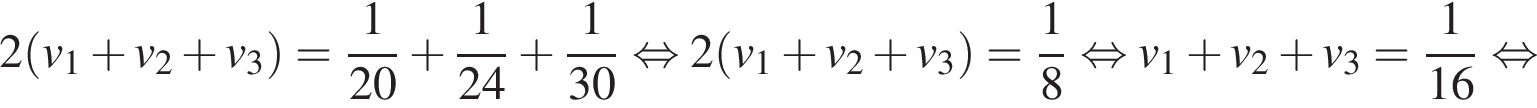
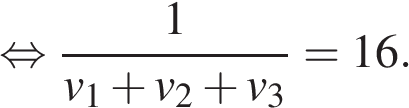
Ответ: 16.
Приведём другое решение.
За один час Игорь и Паша красят 1/20 забора, Паша и Володя красят 1/24 забора, а Володя и Игорь — за 1/30 забора. Работая вместе, за один час два Игоря, Паши и Володи покрасили бы:
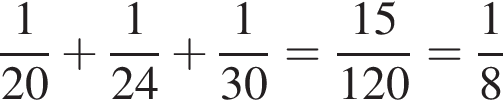забора.
Тем самым, они могли бы покрасить один забор за 8 часов. Поскольку каждый из мальчиков был учтен два раза, в реальности Игорь, Паша и Володя могут покрасить забор за 16 часов.
Примечание Дмитрия Гущина.
Заметим, что за 120 часов Игорь и Паша могут покрасить 6 заборов, Паша и Володя — 5 заборов, а Володя и Игорь — 4 забора. Работая вместе, за 120 часов они могли бы покрасить 15 заборов. Следовательно, один забор два Игоря, два Паши и два Володи могут покрасить за 8 часов. Поэтому, работая втроем, Игорь, Паша и Володя покрасят забор за 16 часов.
11. Три бригады вместе изготовили 114 карданных валов. Известно, что вторая бригада изготовила карданных валов в 3 раза больше, чем первая, и на 16 карданных валов меньше, чем третья. На сколько карданных валов больше изготовила третья бригада, чем первая?
Решение.
Пусть первая бригада изготовила x карданных валов. Тогда вторая бригада изготовила 3x карданных валов, а третья 3x +16 карданных валов. Из уравнения 7x +16 =114 находим, что первая бригада изготовила 14 карданных валов, а третья 58 карданных валов. Таким образом, третья бригада изготовила на 44 карданных вала больше, чем первая.
Ответ: 44.
12. Три бригады изготовили вместе 114 деталей. Известно, что вторая бригада изготовила деталей в 3 раза больше, чем первая, и на 16 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
Решение.
Пусть первая бригада изготовила x деталей. Тогда вторая бригада изготовила 3x деталей, а третья 3x +16 деталей. Значит, вместе они изготовили 7x +16 деталей. Из уравнения 7x +16 =114 находим, что первая бригада изготовила 14 деталей, а третья 58 деталей. Таким образом, третья бригада изготовила на 44 детали больше, чем первая.
Ответ: 44.
13. Три бригады вместе изготовили 114 синхронизаторов передач. Известно, что вторая бригада изготовила синхронизаторов в 3 раза больше, чем первая, и на 16 синхронизаторов меньше, чем третья. На сколько синхронизаторов передач больше изготовила третья бригада, чем первая.
Решение.
Пусть первая бригада изготовила x синхронизаторов. Тогда вторая бригада изготовила 3xсинхронизаторов, а третья 3x +16 синхронизаторов. Из уравнения 7x +16 =114 находим, что первая бригада изготовила 14 синхронизаторов, а третья 58 синхронизаторов. Таким образом, третья бригада изготовила на 44 синхронизатора больше, чем первая.
Ответ: 44.
14. Игорь и Паша красят забор за 18 часов. Паша и Володя красят этот же забор за 20 часов, а Володя и Игорь — за 30 часов. За сколько минут мальчики покрасят забор, работая втроём?
Решение.
За один час Игорь и Паша красят 1/18 забора, Паша и Володя красят 1/20 забора, а Володя и Игорь — за 1/30 забора. Работая вместе, за один час два Игоря, Паши и Володи покрасили бы:
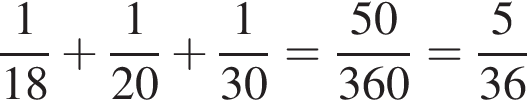забора.
Тем самым, они могли бы покрасить один забор за 7,2 часа. Поскольку каждый из мальчиков был учтен два раза, в реальности Игорь, Паша и Володя могут покрасить забор за 14,4 часа=864 минуты.
Ответ: 864.
15. Три бригады изготовили вместе 248 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая.
Решение.
Пусть 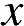— число деталей, изготовленных второй бригадой, тогда первая бригада изготовила деталей, а третья — деталей. Вместе три бригад изготовили 248 деталей, составим уравнение:
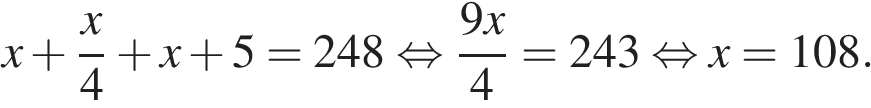
Вторая бригада изготовила 108 деталей, следовательно, первая бригада изготовила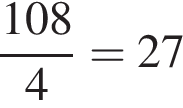 
деталей, а третья — 113 деталь. Таким образом, третья бригада изготовила на 113 − 27 = 86 деталей больше.
Ответ: 86.
16. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Решение.
Пусть 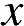— число деталей, изготавливаемых первым рабочим за час, 
, тогда 
— число деталей, изготавливаемых вторым рабочим за час.
Составим таблицу по данным задачи:
Производительность
(дет/ч)
Время (ч)
Объём работ (дет)
Первый рабочий
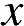
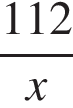
112
Второй рабочий
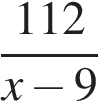
112
Заказ, состоящий из 112 деталей, первый рабочий выполняет на 4 часа быстрее, чем второй, составим уравнение:
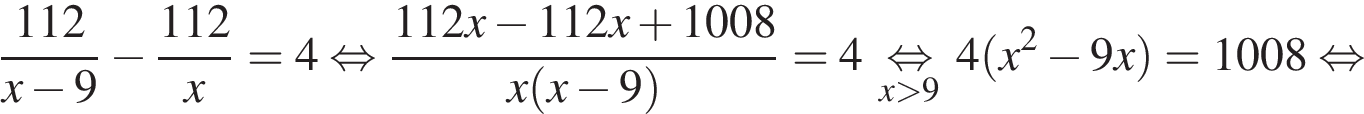
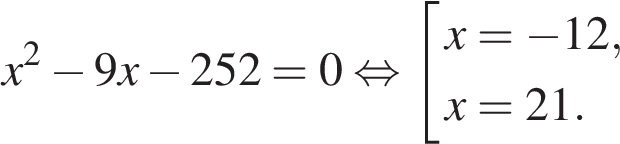
Корень −12 не подходит по условию задачи, следовательно, первый рабочий изготавливает 21 деталь в час. Значит, второй рабочий изготавливает 12 деталей в час.
Ответ: 12.
infourok.ru
Задачи на совместную работу
Рассмотрим типичные задачи на совместную работу из курса алгебры 8-9 классов. Решение таких задач начинается с того, что принимаем всю работу за единицу.
Большинство задач на совместную работу можно решить с помощью дробного рационального уравнения. Для решения более сложных задач составляют систему уравнений.
Как и другие задачи на работу, задачи на совместную работу связывают время работы, производительность труда и время работы соотношением:
Чаще всего за x принимают время работы, а производительность труда выражают через x.
1) Двое рабочих, работая вместе, могут выполнить производственное задание за 20 дней. За сколько дней может выполнить задание каждый из них, работая самостоятельно, если одному из них для этого надо на 9 дней больше, чем другому?
Решение:
Примем все задание за единицу. Пусть II рабочий, работая самостоятельно, может выполнить все задание за x дней, тогда I — за x+9 дней.
Время работы | Производительность труда | Объем работы | |
I рабочий | x+9 | 1 | |
II рабочий | x |
| 1 |
Вместе за 1 день рабочие выполняют
задания. За 20 дней вместе они выполнят все задание. Составим уравнение:
Второй корень не подходит по смыслу задачи (так как время не может быть отрицательным числом). Значит, II рабочий, работая самостоятельно, может выполнить всю работу за 36 дней, а I — за 36+9=45 дней.
Ответ: за 45 дней и 36 дней.
И еще одна задача на совместную работу.
2) Один насос может наполнить бассейн на 24 часа быстрее, чем другой. Через 8 часов после того, как был включен второй насос, включили первый, и через 20 часов совместной работы оказалось, что заполнено 2/3 бассейна. За сколько часов может наполнить бассейн каждый насос, работая самостоятельно?
Решение:
Примем весь бассейн за 1. Пусть I насос, работая самостоятельно, может наполнить весь бассейн за x часов, тогда II — за x+24 часа.
Время работы | Производительность труда | Объем работы | |
I насос | x | 1 | |
II насос | x+24 |
| 1 |
Известно, что II насос был включен 8+20=28 часов, а I — 20 часов, и за это время они наполнили 2/3 бассейна. Составим и решим уравнение:
Обе части уравнения делим почленно на 2 и переносим все слагаемые в левую часть:
Второй корень — посторонний. Значит, I насос может наполнить бассейн самостоятельно за 60 часов, а II — за 60+24=84 часа.
Ответ: за 60 часов и 84 часа.
www.uznateshe.ru