Задачи на Закон сохранения импульса с решениями
Задачи на Закон сохранения импульса с решениями
Формулы, используемые на уроках «Задачи на импульс тела. Задачи на Закон сохранения импульса».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Определите массу автомобиля, имеющего импульс 2,5•104 кг•м/с и движущегося со скоростью 90 км/ч.
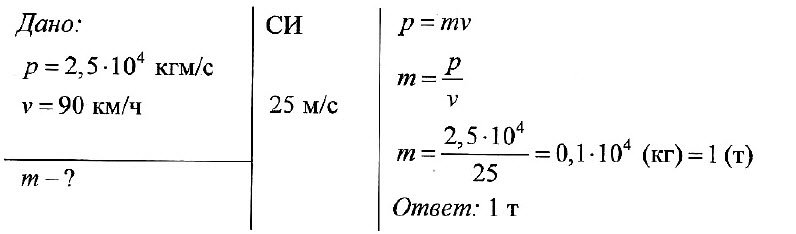
Задача № 2. Тележка массой 40 кг движется со скоростью 4 м/с навстречу тележке массой 60 кг, движущейся со скоростью 2 м/с. После неупругого соударения тележки движутся вместе. В каком направлении и с какой скоростью будут двигаться тележки ?
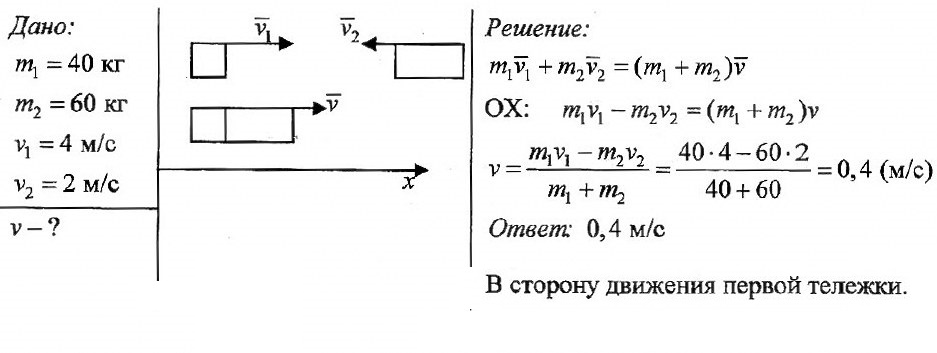
Задача № 3. Снаряд, выпущенный вертикально вверх, разорвался в верхней точке траектории. Первый осколок массой 1 кг приобрел скорость 400 м/с, направленную горизонтально. Второй осколок массой 1,5 кг полетел вверх со скоростью 200 м/с. Какова скорость третьего осколка, если его масса равна 2 кг?
Решение. Взрывающийся снаряд можно считать замкнутой системой, потому, что сила тяжести намного меньше, чем сила давления пороховых газов, разрывающих снаряд на осколки. Значит, можно использовать закон сохранения импульса. Поскольку разрыв снаряда произошел в верхней точке траектории, векторная сумма импульсов всех осколков должна быть равна нулю. Следовательно, векторы импульсов осколков образуют треугольник; этот треугольник прямоугольный, а искомый вектор — его гипотенуза.
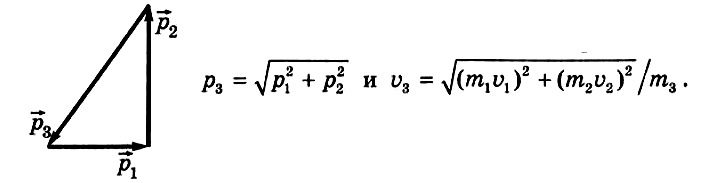
Ответ: 250 м/с.
Задача № 4. К стене прикреплен шланг с насадкой, изогнутой под прямым углом (см. рисунок). Из шланга вытекает вода со скоростью
v = 10 м/с. Найдите горизонтальную составляющую силы, с которой шланг давит на стену. Площадь сечения шланга S = 10 см2.
Ответ: 100 Н.
Задача № 5. Какую силу тяги развивает реактивный двигатель, выбрасывающий каждую секунду 10 кг продуктов сгорания топлива со скоростью 3 км/с относительно ракеты?

Ответ: 30 кН.
Задача № 6. Повышенной сложности Конькобежец массой М = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью v = 8 м/с относительно льда. Найдите, на какое расстояние S откатится при этом конькобежец, если μ = 0,02.

Ответ: 0,3 м.
Задача № 7. Повышенной сложности Деревянный брусок, движущейся вертикально, падает со скоростью v = 3 м/с на горизонтальную ленту транспортера, движущегося со скоростью u = 1 м/с. Брусок после удара не подскакивает. При каком коэффициенте трения брусок не будет проскальзывать по транспортеру?

Ответ: μ ≥ 0.33
Задача № 8. ОГЭ Конькобежец массой M = 70 кг, стоя на льду, бросает в горизонтальном направлении шайбу массой m = 0,3 кг со скоростью v = 40 м/с. На какое расстояние s откатится конькобежец, если коэффициент трения коньков о лёд μ = 0,02?

Задача № 9. ЕГЭ Вагон массой m = 4•104 кг, движущийся со скоростью v = 2 м/с, в конце запасного пути ударяется о пружинный амортизатор. На сколько он сожмёт пружину амортизатора, жёсткость которой k = 2,25•106 Н/м?

Краткая теория для решения задачи на Закон сохранения импульса.

Алгоритм решения задач на закон сохранения импульса:
1. Записать «дано».
2. Сделать чертеж, на котором изобразить направления импульсов (или скоростей) каждого тела до взаимодействия и после взаимодействия.
4. Выбрать координатную ось (оси), найти проекции векторов на эту ось (оси).
5. Записать закон сохранения импульса в скалярной форме.
6. Решить получившееся уравнение относительно неизвестной величины.
7. Оценить ответ на реальность.
Рассмотрим взаимодействия тел, при котором они движутся вдоль одной прямой в одном направлении или навстречу друг другу. При столкновении тела испытывают соударение. Соударение может быть двух типов: упругий удар и неупругий удар.
Упругий удар — тела после взаимодействия приобретают скорости, направленные в разные стороны.
Неупругий удар — тела после взаимодействия будут двигаться вместе, как одно целое.
Материал взят с сайта:
http://class-fizika.ru/sd018.html
Задачи на тему Закон сохранения импульса
Задачи на тему «Закон сохранения импульса» из учебника авторов
для 10 класса, 19-е издание.
39.1 Точка движется равномерно по окружности. Изменяется ли ее импульсРЕШЕНИЕ
39.2 Как определяется импульс тела
РЕШЕНИЕ
39.3 Автомобиль трогается с места. Куда направлен вектор изменения импульса
РЕШЕНИЕ
39.4 Хоккейная шайба скользит прямолинейно и замедленно. Куда направлен вектор изменения импульса
РЕШЕНИЕ
40.1 Сформулируйте закон сохранения импульса
РЕШЕНИЕ
40.2 В каких случаях можно применять закон сохранения импульса
РЕШЕНИЕ
40.3 В лежащий на гладком столе брусок попадает пуля, летящая горизонтально. Почему для нахождения скорости бруска с пулей можно применять закон сохранения импульса, хотя на брусок и пулю действуют внешние силы: сила тяжести, нормальная сила реакции стола
РЕШЕНИЕ
42.1 Может ли парусная лодка приводиться в движение с помощью компрессора, установленного на ней, если струя воздуха направлена на паруса! Что произойдет, если поток воздуха будет направлен мимо парусов
РЕШЕНИЕ
42.2 Может ли ракета двигаться в пустоте
РЕШЕНИЕ
42.3 Как возникает реактивная сила
РЕШЕНИЕ
42.4 Осьминоги и каракатицы перемещаются со скоростью до 60 км/ч, периодически выбрасывая вбираемую в себя воду. По какому принципу перемещаются эти животные
РЕШЕНИЕ
1 Два шара, массы которых m1=0,5 кг и m2=0,2 кг, движутся по гладкой горизонтальной поверхности навстречу друг другу со скоростями v1 = 1 м/с и v2=4 м/с. Определите их скорость v после центрального абсолютно неупругого удара. Абсолютно неупругим ударом называется взаимодействие тел, после которого тела движутся с одинаковыми скоростями.
РЕШЕНИЕ
2 Два пластилиновых шарика, отношение масс которых m2/m1 = 4, после соударения слиплись и стали двигаться по гладкой горизонтальной поверхности со скоростью u (рис. 5.8, вид сверху). Определите скорость легкого шарика до соударения, если он двигался в 3 раза быстрее тяжелого (v1 = 3v2), а направления движения шариков были взаимно перпендикулярны. Трением пренебречь.
РЕШЕНИЕ
8.1 Неподвижный вагон массой 2*10^4 кг сцепляется с платформой массой 3*10^4 кг. До сцепки платформа имела скорость 1 м/с. Чему равна скорость вагона и платформы после их сцепки
РЕШЕНИЕ
8.2 На плот массой 100 кг, имеющий скорость 1 м/с, направленную вдоль берега, прыгает человек массой 50 кг со скоростью 1,5 м/с перпендикулярно берегу. Какой будет общая скорость плота и человека
РЕШЕНИЕ
8.3 Будет ли увеличиваться скорость ракеты, если скорость истечения газов относительно ракеты меньше скорости самой ракеты и вытекающие из сопла газы летят вслед за ракетой
РЕШЕНИЕ
8.4 Охотник стреляет с легкой надувной лодки. Какую скорость приобретет лодка в момент выстрела, если масса охотника 70 кг, масса дроби 35 г и средняя начальная скорость дробинок равна 320 м/с? Ствол ружья во время выстрела образует с горизонтом угол 60
РЕШЕНИЕ
Задачи на столкновения и законы сохранения импульса и энергии — Викиучебник
- Автор исходного текста — В. И. Плис, к. ф.-м. н., доцент кафедры общей физики МФТИ, Соровский учитель. Журнал Потенциал
В статье на основе законов сохранения импульса и энергии рассматриваются неупругие и упругие столкновения макроскопических тел и объектов в микромире. Анализированы энергетические превращения при неупругих столкновениях. Показана техника исследования упругих столкновений в системе центра масс. Рассматриваются упругие и неупругие процессы в микромире; как в рамках классической физики, так и с привлечением элементарных сведений по квантовой физике и специальной теории относительности.
В физике под столкновениями понимают процессы взаимодействия между телами (частицами) в широком смысле слова, а не только в буквальном – как соприкосновение тел. Сталкивающиеся тела на большом расстоянии свободны. Проходя друг мимо друга, тела взаимодействуют, причём могут происходить различные процессы: соединение в одно тело (абсолютно неупругий удар), возникновение новых тел и, наконец, может иметь место упругое столкновение, при котором тела после некоторого сближения вновь расходятся без изменения своего внутреннего состояния. Столкновения, сопровождающиеся изменением внутреннего состояния тел, называются неупругими.

Тела (частицы), участвующие в столкновении, характеризуются (до и после столкновения) импульсами, энергиями. Процесс столкновения сводится к изменению этих величин в результате взаимодействия. Законы сохранения энергии и импульса позволяют достаточно просто устанавливать соотношения между различными физическими величинами при столкновении тел. Особенно ценно здесь то обстоятельство, что зачастую законы сохранения могут быть использованы даже в тех случаях, когда действующие силы неизвестны. Так обстоит дело, например, в физике элементарных частиц.
Происходящие в обычных условиях столкновения макроскопических тел почти всегда бывают в той или иной степени неупругими – уже хотя бы потому, что сопровождаются нагреванием тел, т. е. переходом части их кинетической энергии в тепло. Но понятие об упругих столкновениях играет важную роль в физике, поскольку со столкновениями часто приходится иметь дело в физическом эксперименте в области атомных явлений, да и обычные столкновения можно часто с достаточной степенью точности считать упругими.
Сохранение импульса тел (частиц) при столкновении обусловлено тем, что совокупность тел, участвующих в столкновении, составляет либо изолированную систему, когда на входящие в систему тела не действуют внешние силы, либо систему замкнутую: внешние силы отличны от нуля, а сумма внешних сил равна нулю. Несколько сложнее обстоит дело с применением закона сохранения энергии при столкновениях. В классической физике следует учитывать кинетическую и потенциальную энергии. В релятивистском случае надо применять выражение для энергии (как иногда, например, пишут «учитывать энергию покоя»). Обращение к сохранению энергии требует порой учёта различных форм внутренней энергии.
Действие законов сохранения импульса и энергии в процессах столкновения подтверждено всевозможными опытами.
Переходя к характерным примерам, напомним, что в физике при решении задач должна быть указана система отсчёта (тело отсчёта, оси координат и часы), в которой рассматривается динамика процесса. Исследование столкновений традиционно проводится как в лабораторной системе отсчёта (ЛСO), то есть в инерциальной системе отсчёта, связанной с лабораторией, где проводится опыт, так и в системе центра масс, которая будет введена в статье. Напомним также, что центральным ударом шаров (шайб) называют удар, при котором скорости шаров (шайб) направлены вдоль прямой, проходящей через их центры.
Неупругие столкновения[править]
Задача № 1[править]
Частица массой m{\displaystyle m\,\!} с кинетической энергией K{\displaystyle K\,\!} сталкивается с неподвижной частицей массой M{\displaystyle M\,\!}. Найдите приращение Q{\displaystyle Q\,\!} внутренней энергии системы частиц в результате абсолютно неупругого столкновения.
Решение.
Рассмотрим абсолютно неупругий удар двух тел в ЛСО. Налетающая частица движется до столкновения в положительном направлении оси OX со скоростью V→{\displaystyle {\vec {V}}\,\!}, кинетическая энергия частицы K=mV22{\displaystyle K={{mV^{2}} \over 2}\,\!}. В результате абсолютно неупругого удара (слипания) частицы движутся с одинаковой скоростью u→{\displaystyle {\vec {u}}\,\!}. По закону сохранения импульса mV=(m+M)u{\displaystyle mV=(m+M)u\,\!},по закону сохранения энергии mV22=(m+M)u22+Q{\displaystyle {{mV^{2}} \over 2}={{(m+M)u^{2}} \over 2}+Q\,\!}. Из приведённых соотношений находим Q=Mm+MK{\displaystyle Q={M \over {m+M}}K\,\!}.
Отметим, что в предельных случаях Q=K,m<<M;Q=MmK<<K,m>>M{\displaystyle Q=K,m<<M;Q={M \over m}K<<K,m>>M\,\!}.
Как видим, при неупругом столкновении лёгкой частицы с массивной, например, электрона с атомом, происходит полная передача её кинетической энергии атому: атом возбуждается, а затем испускает фотон.
При равенстве масс (m=M){\displaystyle (m=M)\,\!} Q=K2{\displaystyle Q={K \over 2}\,\!}.
Отсюда следует, например, что при столкновении двух одинаковых автомобилей, один из которых неподвижен, а другой движется по направлению к нему, половина кинетической энергии идёт на разрушение.
Задача № 2[править]
Найдите минимальную относительную скорость двух одинаковых метеоритов, необходимую для их нагрева и полного испарения в результате абсолютно неупругого соударения. Удельная теплота нагревания и испарения вещества метеоритов q=106{\displaystyle q=10^{6}\,\!} Дж/кг.
Решение.
Рассмотрим в ЛСО абсолютно неупругий удар двух тел. Введём обозначения: m1{\displaystyle m_{1}\,\!} и m2{\displaystyle m_{2}\,\!} – массы тел, V→1{\displaystyle {\vec {V}}_{1}\,\!} и V→2{\displaystyle {\vec {V}}_{2}\,\!} – их скорости до столкновения, V→′{\displaystyle {\vec {V}}’\,\!} – скорость составного тела после столкновения. Считая, что в процессе столкновения импульс системы тел сохраняется (внешние силы отсутствуют), m1V→1+m2V→2=(m1+m2)V→′{\displaystyle m_{1}{\vec {V}}_{1}+m_{2}{\vec {V}}_{2}=(m_{1}+m_{2}){\vec {V}}’\,\!}, находим скорость составного тела V→′=m1V→1+m2V→2m1+m2{\displaystyle {\vec {V}}’={{m_{1}{\vec {V}}_{1}+m_{2}{\vec {V}}_{2}} \over {m_{1}+m_{2}}}\,\!}.
Кинетические энергии системы тел до взаимодействия и после равны соответственно Kbefore=m1V122+m2V222{\displaystyle K_{before}={m_{1}V_{1}^{2} \over 2}+{m_{2}V_{2}^{2} \over 2}\,\!} , Kafter=(m1+m2)(V′)22{\displaystyle K_{after}={(m_{1}+m_{2})(V’)^{2} \over 2}\,\!}.
Тогда убыль кинетической энергии системы после несложных преобразований принимает вид Kbefore−Kafter=12m1m2m1+m2(V→2−V→1)2=12μ(V→rel)2{\displaystyle K_{before}-K_{after}={1 \over 2}{m_{1}m_{2} \over m_{1}+m_{2}}({\vec {V}}_{2}-{\vec {V}}_{1})^{2}={1 \over 2}\mu ({\vec {V}}_{rel})^{2}\,\!}, где μ=m1m2m1+m2{\displaystyle \mu ={{m_{1}m_{2}} \over {m_{1}+m_{2}}}\,\!} – приведённая масса системы тел, V→rel=V→2−V→1{\displaystyle {\vec {V}}_{rel}={\vec {V}}_{2}-{\vec {V}}_{1}\,\!} относительная скорость. Таким образом, при абсолютно неупругом ударе в другие формы энергии переходит кинетическая энергия макроскопического движения, равная половине произведения приведённой массы на квадрат относительной скорости.
Вернёмся к задаче о минимальной относительной скорости метеоритов. Будем считать, что вся убыль кинетической энергии переходит в тепло, которое идёт на нагревание и испарение метеоритов, тогда 12μ(V→rel)2=2mq{\displaystyle {1 \over 2}\mu ({\vec {V}}_{rel})^{2}=2mq\,\!}. С учётом равенства масс сталкивающихся метеоритов μ=m2{\displaystyle \mu ={m \over 2}\,\!}. Это приводит к оценке минимальной скорости Vrel=22q≈2,8⋅103{\displaystyle V_{rel}=2{\sqrt {2q}}\approx 2,8\cdot 10^{3}\,\!}м/с.
Задача № 3[править]
На гладком горизонтальном столе лежит твёрдая шайба. На неё налетает мягкая, довольно упругая шайба такой же массы и между ними происходит центральный удар. Скорость мягкой шайбы после удара уменьшилась в 5 раз. Какая часть максимальной энергии деформации перешла в тепло при этом ударе? Считайте, что тепло выделяется в мягкой шайбе в процессе деформации.
Решение.
Задачу рассмотрим в ЛСО, ось OX которой направим по линии центров шайб в момент соударения. В процессе взаимодействия на систему шайб действуют только вертикальные внешние силы: это силы тяжести и силы нормальной реакции опоры. Их сумма равна нулю, отсюда следует, что импульс системы шайб в результате соударения не изменяется MV=MV5+MVX{\displaystyle MV=M{V \over 5}+MV_{X}\,\!}.
Скорость твёрдой шайбы после удара VX=0,8⋅V{\displaystyle V_{X}=0,8\cdot V\,\!} (если предположить, что налетающая шайба после соударения движется в отрицательном направлении оси OX со скоростью V5{\displaystyle {V \over 5}\,\!}, то скорость твёрдой шайбы после соударения VX=1,2⋅V{\displaystyle V_{X}=1,2\cdot V\,\!} и её кинетическая энергия больше кинетической энергии налетающей шайбы). Найдём по закону сохранения энергии количество Q{\displaystyle Q\,\!} теплоты, которое выделится в мягкой шайбе за всё время удара,MV22=M(0,2⋅V)22+M(0,8⋅V)22+Q{\displaystyle {{MV^{2}} \over 2}={{M\left({0,2\cdot V}\right)^{2}} \over 2}+{{M\left({0,8\cdot V}\right)^{2}} \over 2}+Q\,\!}, отсюда Q=0,32⋅MV22{\displaystyle Q=0,32\cdot {{MV^{2}} \over 2}\,\!}.
Вычислим максимальную энергию Edef{\displaystyle E_{def}\,\!} деформации мягкой шайбы. Для этого заметим, что при максимальной деформации шайбы друг относительно друга не движутся. Тогда по закону сохранения импульса MV=(M+M)V∗{\displaystyle MV=(M+M)V_{*}\,\!}, шайбы в момент максимальной деформации движутся в ЛСО со скоро-стьюV∗=V/2{\displaystyle V_{*}=V/2\,\!}. Естественно предположить, что теплота в равных количествах выделяется как при сжатии шайбы, так и при растяжении. Тогда по закону сохранения энергии в момент максимальной деформации MV22=M(0,5⋅V)22+M(0,5⋅V)22+Q2+Edef{\displaystyle {\frac {MV^{2}}{2}}={\frac {M\left({0,5\cdot V}\right)^{2}}{2}}+{\frac {M\left({0,5\cdot V}\right)^{2}}{2}}+{\frac {Q}{2}}+E_{def}\,\!}. Отсюда Edef=0,34⋅MV22{\displaystyle E_{def}=0,34\cdot {\frac {MV^{2}}{2}}\,\!}.
Искомое отношение QEdef=1617{\displaystyle {\frac {Q}{E_{def}}}={\frac {16}{17}}\,\!}.
Упругие столкновения[править]
Задача № 4[править]
Решение.
Задачу рассмотрим в ЛСО, ось OX которой направим по линии центров шаров в момент соударения. Внешние силы, действующие на шары в процессе соударения, — это силы тяжести и силы нормальной реакции опоры. Их сумма равна нулю. Следовательно импульс системы шаров в процессе взаимодействия не изменяется. По закону сохранения импульса mV→=mV→1+MV→2{\displaystyle m{\vec {V}}=m{\vec {V}}_{1}+M{\vec {V}}_{2}\,\!}. Переходя к проекциям на ось OX, получаем mV=mV1X+MV2{\displaystyle mV=mV_{1X}+MV_{2}\,\!}, здесь учтено, что направление скорости V→1{\displaystyle {\vec {V}}_{1}\,\!} налетающего шара после соударения неизвестно. По закону сохранения энергии mV22=mV1X22+MV222{\displaystyle {\frac {mV^{2}}{2}}={\frac {mV_{1X}^{2}}{2}}+{\frac {MV_{2}^{2}}{2}}\,\!}. Полученные соотношения перепишем в виде m(V−V1X)=MV2{\displaystyle m(V-V_{1X})=MV_{2}\,\!}, m(V2−V1X2)=MV22{\displaystyle m(V^{2}-V_{1X}^{2})=MV_{2}^{2}\,\!}. Разделив второе равенство на первое, приходим к линейной системе V2=V+V1X{\displaystyle V_{2}=V+V_{1X}\,\!}, m(V−V1X)=MV2{\displaystyle m(V-V_{1X})=MV_{2}\,\!}, решение которой имеет вид V1X=m−Mm+MV{\displaystyle V_{1X}={\frac {m-M}{m+M}}V\,\!}, V2=2mm+MV{\displaystyle V_{2}={\frac {2m}{m+M}}V\,\!}. Налетающий шар будет двигаться после соударения в прежнем направлении (V1X>0{\displaystyle V_{1X}>0\,\!}) при m>M{\displaystyle m>M\,\!}, т.е. если его масса больше массы покоящегося шара.
Задача № 5[править]
Две гладкие упругие круглые шайбы движутся по гладкой горизонтальной поверхности со скоростями V→1{\displaystyle {\vec {V}}_{1}\,\!} и V→2{\displaystyle {\vec {V}}_{2}\,\!}. Найдите скорости шайб после абсолютно упругого нецентрального соударения. Массы шайб m1{\displaystyle m_{1}\,\!} и m2{\displaystyle m_{2}\,\!}.
Решение.
Задачу рассмотрим в ЛСО, оси координат OX и OY которой лежат в горизонтальной плоскости, при этом ось OX направлена по линии центров шайб в момент соударения (рис.1). В течение времени соударения на систему шайб действуют только вертикальные внешние силы: это силы тяжести и силы нормальной реакции опоры. Их сумма равна нулю. Тогда импульс системы шайб в процессе взаимодействия сохраняется p→1+p→2=p→1′+p→2′{\displaystyle {\vec {p}}_{1}+{\vec {p}}_{2}={\vec {p}}’_{1}+{\vec {p}}’_{2}\,\!}, здесь и – импульсы шайб до и после соударения.
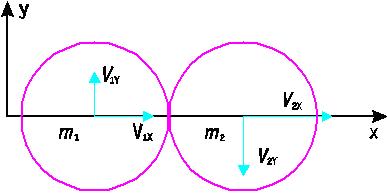
Рис.1.
Так как шайбы идеально гладкие, то в процессе соударения внутренние силы – силы упругого взаимодействия шайб – направлены только по оси OX . Эти силы не изменяют Y-составляющие импульсов шайб. Тогда из p1Y=p1Y′{\displaystyle p_{1Y}=p’_{1Y}\,\!}, p2Y=p2Y′{\displaystyle p_{2Y}=p’_{2Y}\,\!} находим Y-составляющие скоростей шайб после соударения V1Y′=V1Y{\displaystyle V’_{1Y}=V_{1Y}\,\!}, V2Y′=V2Y{\displaystyle V’_{2Y}=V_{2Y}\,\!}, т.е. в проекции на ось OY скорости шайб в результате соударения не изменились.
Найдём X-составляющие скоростей шайб после абсолютно упругого соударения. При таком соударении сохраняется кинетическая энергия m1(V1X2+V1Y2)2+m2(V2X2+V2Y2)2={\displaystyle {\frac {m_{1}\left({V_{1X}^{2}+V_{1Y}^{2}}\right)}{2}}+{\frac {m_{2}\left({V_{2X}^{2}+V_{2Y}^{2}}\right)}{2}}=\,\!} =m1((V1X′)2+(V1Y′)2)2+m2((V2X′)2+(V2Y′)2)2.{\displaystyle ={\frac {m_{1}\left({\left({V’_{1X}}\right)^{2}+\left({V’_{1Y}}\right)^{2}}\right)}{2}}+{\frac {m_{2}\left({\left({V’_{2X}}\right)^{2}+\left({V’_{2Y}}\right)^{2}}\right)}{2}}.\,\!}
С учётом равенства Y-составляющих скоростей шайб до и после соударения последнее равенство принимает вид m1V1X22+m2V2X22=m1(V1X′)22+m2(V2X′)22{\displaystyle {\frac {m_{1}V_{1X}^{2}}{2}}+{\frac {m_{2}V_{2X}^{2}}{2}}={\frac {m_{1}\left({V’_{1X}}\right)^{2}}{2}}+{\frac {m_{2}\left({V’_{2X}}\right)^{2}}{2}}\,\!}.
Обратимся к закону сохранения импульса и перейдём к проекциям импульсов шайб на ось OX m1V1X+m2V2X=m1V1X′+m2V2X′{\displaystyle m_{1}V_{1X}+m_{2}V_{2X}=m_{1}V’_{1X}+m_{2}V’_{2X}\,\!}.
Таким образом, исходная задача сведена к задаче об абсолютно упругом центральном ударе: именно такой вид приняли бы законы сохранения энергии и импульса, если бы скорости шайб были направлены по линии центров. Полученную нелинейную систему уравнений можно свести к линейной. Для этого следует (как и в предыдущей задаче) в обоих уравнениях по одну сторону знака равенства объединить слагаемые, относящиеся к первой шайбе, а по другую – ко второй, и разделить полученные соотношения друг на друга. Это приводит к линейному уравнению вида V1x+V1X′
Закон сохранения импульса
«Я принимаю, что во Вселенной…
есть известное количество движения,
которое никогда не увеличивается,
не уменьшается, и, таким образом,
если одно тело приводит в движение
другое, то теряет столько своего
движения, сколько его сообщает»
Рене Декарт
Данная тема посвящена изучению методов решения задач на закон сохранения импульса.
Задача 1. Железнодорожная платформа движется со скоростью 2,5 м/с. Из орудия, закрепленного на платформе, производится выстрел. Масса снаряда 25 кг, его скорость 700 м/с, а масса платформы с орудием 20000 кг. Определите скорость платформы после выстрела, если выстрел произведен: а) в направлении движения платформы; б) в противоположном направлении; в) ствол орудия во время выстрела составляет угол 60о с направлением движения. Считать, что силы сопротивления движению пренебрежимо малы.
|
ДАНО:
|
РЕШЕНИЕ:
Запишем закон сохранения импульса:
Импульсы тел до взаимодействия:
Импульсы тел после взаимодействия:
а) Запишем закон сохранения импульса в проекциях на ось Ох:
Преобразуем данное уравнение
Тогда искомая скорость платформы
б) Рассмотрим случай, когда выстрел произведён в противоположном направлении. Запишем закон сохранения импульса в проекциях на ось Ох:
Преобразуем данное уравнение
Тогда
в) Рассмотрим случай, когда ствол орудия во время выстрела составляет угол 60о с направ-лением движения. Запишем закон сохранения импульса в проекциях на ось Ох:
Преобразуем последнюю формулу
Тогда искомая скорость
|
Задача 2. Зенитный снаряд, выпущенный вертикально вверх, разорвался в верхней точке траектории на три осколка. Первый осколок массой 9 кг имел скорость 60 м/с, направленную вертикально вверх, скорость второго равна 40 м/с и направлена горизонтально, а его масса 18 кг. Масса третьего осколка 4,5 кг. Найдите величину и направление вектора скорости меньшего осколка.
|
ДАНО:
|
РЕШЕНИЕ:
Если длительность процесса взаимодействия настолько мала, что импульс внешних сил за это время можно считать равным нулю (как в случае удара, взрыва и тому подобное), то к такой системе тел можно применять закон сохранения импульса. Разрыв снаряда произошел в результате действия внутренних сил. Поэтому вектор полного импульса системы после взрыва остался неизменным и равным нулю, так как импульс снаряда в начальный момент взрыва равен нулю
Чтобы указанная векторная сумма импульсов осколков была равна нулю, графически найдем направление полета третьего осколка. И так, импульс третьего осколка должен находиться в одной плоскости с импульсами первого и второго осколков, быть равным их суммарному вектору и противоположно ему направлен. Закон сохранения импульса в проекциях на ось Ох:
Закон сохранения импульса в проекциях на ось Оу:
И разделим почленно второе уравнение на первое, помня о том, что отношение синуса на косинус, есть тангенс данного угла
Тогда угол a равен
Скорость меньшего осколка (1 способ): Для того чтобы определить скорость меньшего осколка, можно воспользоваться законом сохранения импульса в проекциях на какую-либо ось координат
Скорость меньшего осколка (2 способ): Возведём почленно в квадрат левые и правые части уравнений в проекциях на оси Ох и Оу и сложим их
|
Ответ: α = 36,9о; υ3 = 200 м/с.
Задача 3. Длина лодки 6 м. Человек, масса которого вдвое меньше массы лодки, переходит с носа лодки на корму. На какое расстояние относительно воды переместится лодка, если сопротивлением воды при движении лодки можно пренебречь.
|
|
РЕШЕНИЕ:
Запишем закон сохранения импульса:
Закон сохранения импульса в проекциях на ось Ох:
Запишем закон сложения скоростей
Закон сложения скоростей в проекциях на ось Ох:
Тогда
Так как движение лодки и человека равномерное, то:
Следовательно
|
|
|
Ответ: 2 м.
Задача 4. Человек, сидящий в лодке, бросает камень вдоль нее под углом 60о к горизонту. Масса камня составляет 1 кг, масса человека и лодки — 150 кг, начальная скорость камня относительно берега равна 10 м/с. Определите расстояние между точкой падения камня и лодкой в момент, когда камень коснется воды.
|
ДАНО:
|
РЕШЕНИЕ:
Расстояние между точкой падения камня и лодкой:
Дальность полета камня:
Расстояние, пройденное лодкой:
где время полёта камня
Закон сохранения импульса:
Запишем закон сохранения импульса в проекциях на ось Ох:
Тогда искомое расстояние
|
|
|
Ответ: 8,8 м.
Методическая разработка по физике (10 класс): Задачи на закон сохранения импульса.
Задачи на законы сохранения
- Пуля вылетает из винтовки в горизонтальном направлении со скоростью 800м/с. Какова скорость винтовки при отдаче, если ее масса в 400 раз больше массы пули?
- Мальчик стоит неподвижно на льду рядом с санками. Масса мальчика М, масса санок m. Мальчик толкает санки и сообщает им скорость V, а сам движется в противоположном направлении. Какую работу совершил мальчик?
- Пуля массой m=10 г, летящая со скоростью V=800м/с, попадает в дерево и углубляется на S=10 см. Найти силу F сопротивления дерева и время t движения пули в дереве, считая это движение равнозамедленным.
- Электровоз при движении со скоростью V=72 км/ч потребляет мощность 600 кВт. Определить силу тяги электровоза, если его коэффициент полезного действия КПД равен 80%.
- Взрыв разрывает камень на три части. Два куска летят под прямым углом друг к другу: кусок массой m1=1кг со скоростью V1=12м/с и m2=2 кг со скоростью V2= 8м/с. Третий кусок отлетает со скоростью V2= 40 м/с. Какова масса третьего осколка и в каком направлении он летит?
- Какую работу совершает сила F=30Н, подняв по наклонной плоскости груз массой m=2кг на высоту h=2,5 м с ускорением a=5 м/с2. Сила действует параллельно наклонной плоскости. Трением о плоскость пренебречь.
- Груз начинает скользить с начальной скоростью V вверх по наклонной плоскости, имеющей длину L высоту h. Коэффициент трения равен µ. Какой путь S пройдет груз до остановки?
- Санки съезжают с горы высотой Н и углом наклона α и движутся дальше по горизонтальному участку. Коэффициент трения на всем пути санок одинаков и равен µ. Определить расстояние S, которое пройдут санки по горизонтальному участку до полной остановки.
- Тело массой m1 ударяется неупруго о тело массой m2. Найти долю k потерянной при этом кинетической энергии, если тело m2 до удара было в покое. (k= К1 – К2 / К1)
- Груз массой m1 соскальзывает без трения с наклонной доски на неподвижную платформу. С какой скоростью начнет двигаться платформа, когда груз упадет на нее. Масса платформы m2, высота начального положения груза над уровнем платформы h, угол наклона доски к горизонту α. Трение отсутствует.
- В покоящийся шар массой М=1кг, подвешенный на легком несжимаемом стержне, закрепленном в подвесе на шарнире, попадает пуля массой m = 0,01 кг. Угол между направлением пули и линией стержня α=45ᵒ. После удара пуля застревает в шаре и шар вместе с пулей, откачнувшись, поднимается на высоту h=0,2м относительно первоначального положения. Найти скорость пули.
Урок 9 класс «решение задач на закон сохранения импульса»
















 Муниципальное казенное общеобразовательное учреждение
Муниципальное казенное общеобразовательное учреждение
«Михайловская средняя общеобразовательная школа» имени историка-краеведа,
основателя школьного музея Вячеслава Александровича Казанского
301950 Тульская область, Куркинский район,
п. Михайловский, ул. Центральная, д.1,
тел.(848743)33-2-26, Е-mail:mik—shkola@yndex.ru
Районный предметный семинар по физике
Конспект урока по физике
в 9 классе на тему:
«Решение задач на закон сохранения импульса»
Подготовила: учитель физики
Гуськова Наталья Ивановна
п. Михайловский
2015 год
Тема урока: Решение задач на закон сохранения импульса.
Урок обобщения и систематизации знаний в 9 классе.
Цели урока:
Образовательная
научить применять имеющиеся знания к различным теоретическим и практическим заданиям;
повторить основные законы, определения, понятия и формулы в ходе урока;
совершенствовать навыки решения качественных и расчетных задач;
Воспитательная
формирование навыков коллективной работы;
формирование сознательной дисциплины;
воспитание уважительного отношения друг к другу, к точке зрения товарищей;
повышение познавательной деятельности и активности учащихся;
воспитание умения достойно проигрывать, анализировать пробелы и промахи
выработка системы подготовки к ГИА.
Развивающая
развитие интереса к физике;
развитие речи учащихся,
развитие коммуникативных способностей;
развитие культуры общения;
В ходе урока планируется формирование у школьников ключевых компетенций:
1. в познавательной деятельности:
использование для познания окружающего мира естественнонаучных методов наблюдения, измерения, эксперимента;
формирование умений применять законы Ньютона
овладение адекватными способами решения теоретических и экспериментальных задач;
2. в информационно-коммуникативной деятельности:
3. в рефлексивной деятельности:
4. здоровье сбережения:
знание и соблюдение правил техники безопасности; четкая смена видов деятельности, опора на эмоциональный подъём и интерес при решении задач.
Оборудование и материалы : проектор, ПК, тестовые задания, раздаточный материал, карточки – задания.
ХОД УРОКА.
Организационный момент(2 мин.).
Учитель: Здравствуйте, ребята! Я очень рада вас видеть.
Желаю вам хорошего настроения на весь урок. Надеюсь, что урок пройдет интересно и увлекательно.
(слайд1).Эпиграфом сегодняшнего урока я взяла слова Луция Анне Сенека, который жил 4 до н.э. — 65 гг., Это древнеримский философ, поэт и государственный деятель.
Через тернии к звёздам.
Луций Анне Сенек.
Учитель: Как вы думаете, почему я выбрала именно эти слова?
(практическая направленность темы урока).
Итак тема сегодняшнего урока «решение задач на закон сохранения импульса» (слайд2)
Наша задача повторить изученный материал по теме: «Импульс тела. Закон сохранения импульса»; обобщить, закрепить и применить полученные знания, подготовиться к контрольной работе. Мы продолжим решать задачи на закон сохранения импульса. (слайд3) На уроке мы с вами будем использовать материалы портала сдачи общего государственного экзамена.
Фронтальный опрос по вопросам кроссворда и дополнительным вопросам по теме «Законы динамики». (10 мин)
Учитель: На общем государственном экзамене мы обязательно встретимся с заданиями такого типа(слайд 4):

Учитель: Чтобы ответить на вопросы такого задания, мы должны повторить понятия данной темы. Сделаем мы это, решив кроссворд. У вас на парте кроме ваших обычных принадлежностей лежит раздаточный материал. Кроссворд содержит ключевое слово, которое получится после разгадывания кроссворда (приложение1). (слайд 5)
4.
1.
6.
2.
3.
7.
(слайд6) Что является причиной ускоренного движения тел? (сила)
Дополнительные вопросы: Какие виды движения вам знакомы, назовите их отличия?
(слай7) Вставьте пропущенное слово «Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению ——?—- этих тел и обратно пропорциональной квадрату расстояния между ними». (масса)
Дополнительные вопросы: О каком законе идет речь? Чему равна гравитационная постоянная?
(слайд8) Открытие этой планеты,18 февраля 1930 г., сделано исключительно с помощью расчетов, основанных на законах физики. (Плутон)
(сообщение учащегося о Плутоне)
Дополнительные вопросы: Какой скоростью должна обладать ракета, чтобы, преодолев притяжение Земли, полететь на Плутон? Чему равна 1 космическая скорость? Куда направлено ускорение тела при его движении по окружности с постоянной по модулю скоростью? Как называется это ускорение? Как рассчитать это ускорение?
(слайд9) Вставьте пропущенное слово «В —-?—- системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой». (замкнутой) Дополнительные вопросы: О каком законе идет речь? Что означает утверждение о том, что несколько тел образуют замкнутую систему?
(слайд10) Какой советский учёный, конструктор реализовал идею использования ракет для космических полетов. (С.П.Королёв).
(слайд11) Английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда «Математические начала натуральной философии», в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. ( Исаак Ньютон)
Дополнительные вопросы: Сформулируйте законы Исаака Ньютона.
(слайд12) От чего зависит наибольшая высота подъема брошенного вверх тела в том случае, когда сопротивлением воздуха можно пренебречь?(скорость)
Дополнительные вопросы: Что называется свободным падением тела? Скорость величина векторная или скалярная, в чем их различие.
Учитель: (слайд13) Кроссворд разгадан и ключевое слово «импульс», что же называют импульсом тела? Какой закон связан с импульсом тела? (ответы детей).
(Разбор задания огэ, предложенного выше) (слайд14)
Проверка домашнего задания.
С законом сохранения импульса была связана задача домашней работы. (разбор учеником домашнего задания, сделанного в виде презентации (приложение2)).
Решение задач
Учитель: Мы продолжаем работать с заданиями общего государственного экзамена. И теперь по решаем задачи на закон сохранения импульса. Вы отлично знаете, что у каждого раздела физики свои, характерные теме, формулы и задачи. Если, читая задачу, мы будем чётко понимать из какого раздела физики она, то нам будет гораздо легче её понять и решить. В раздаточном материале (приложение 3) вам даны задачи не только нашей темы и ваша задача, найти и решить задания, характерные именно нашей теме. ( один из учеников находит и решает задачу, на закон сохранения импульса онлайн на сайте http://sdamgia.ru/)
(слайд15) Задача №1: Кубик массой m движется по гладкому столу со скоростью  и налетает на покоящийся кубик такой же массы (рис1). После удара кубики движутся как единое целое, при этом скорость кубиков равна:
и налетает на покоящийся кубик такой же массы (рис1). После удара кубики движутся как единое целое, при этом скорость кубиков равна:
1) 0 (рисунок 1)
2) /2
/2
3)
4)2
(слайд16) Задача №2: Вдоль оси Ох движется тело массой m=1 кг со скоростью V0= 2 м/с. Вдоль направления движения действует сила F = 4 Н в течение некоторого времени t = 2 с. Определите скорость тела после окончания действия этой силы.
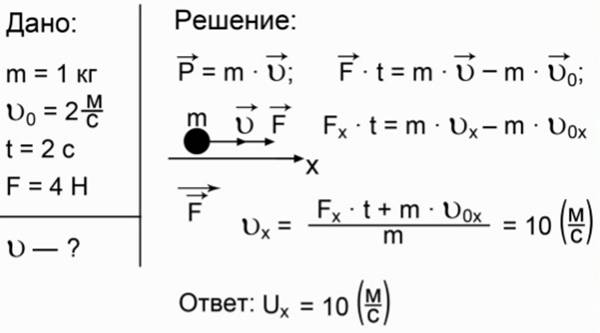
(слайд17) Задача №.3
Человек массой 80 кг переходит с носа на корму покоящейся лодки, длиной s = 5 м. Какова масса лодки, если она за время этого перехода переместилась в стоячей воде на L = 2 м? Сопротивление воды не учитывать.
Дано:
mч=80кг
S=5м
L = 2 м
Найти:
mл ?
Решение:
P= 0
P’= mч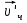 + (mч+ mл)
+ (mч+ mл) 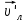
Так как движение в замкнутой системе, то  =
= , отсюда
, отсюда
— mч +(mч+ mл)
+(mч+ mл)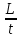 mл= mчS/L — mч
mл= mчS/L — mч
mл = 80кг*5м/2м – 80кг = 120кг Ответ: 120 кг.
Самостоятельная работа.
(слайд18) Задача №3. Какую скорость приобретёт, лежащее на льду, чугунное ядро, если пуля, летящая горизонтально со скоростью 500 м/с, отскочит от него и будет двигаться в противоположном направлении со скоростью 400 м/с? Масса пули 10 г, масса ядра 25 кг
.
Дано:
 =500м/с
=500м/с  =400 м/с
=400 м/сmп =10г
mя=25кг
Решение:

0
 = mп
= mп  + 0
+ 0

 = mп
= mп + mя
+ mя 
 =
=  mп
mп  + 0 = mп
+ 0 = mп + mя
+ mя 
Проекция на ось ох:
mп
 = — mп
= — mп + mя
+ mя  , отсюда
, отсюда  =
= 

 = 0,36 м/с
= 0,36 м/сОтвет: 0,36м/с
(разбор задачи (слайд29) )
Найти:

Подведение итогов. Оценивание.
Учитель подводит итоги урока.
Домашнее задание. (слайд20)
п.21-23(повторить)
Рефлексия.
Учащимся необходимо выбрать три слова из 14, которые наиболее точно передают их состояние на уроке (слова прописаны на доске):
Раздражение
Интерес
Страх
Удовлетворение
Равнодушие
Неуверенность
Самостоятельность
Скука
Тревога
Чувство успеха
Чувство новизны
Спад настроения
Уверенность
Решение задач по теме «Закон сохранения импульса» (разработка урока)
Тема урока: Решение задач по теме «Закон сохранения импульса»
Цели: в ходе урока обучить ребят поэтапному решению задач по теме «Закон сохранения импульса» с использованием плана и отработать умение пользоваться им при решении задач различного уровня сложности, в том числе и нестандартных.
Развивать умение мыслить логически, выражать неизвестную физическую величину из полученной формулы, совершенствовать счетные навыки ребят.
Оборудование:авторская презентация «Решение задач по теме «Закон сохранения импульса», сборник задач (автор Л. А. Кирик)
Ход урока:
- Оргмомент.
- Фронтальный опрос, проверка усвоения основных понятий предыдущего урока:
— Дайте определение импульса тела, укажите, как он обозначается;
— Назовите единицу импульса в СИ;
— Из двух шаров различной массы, имеющих одинаковые скорости, больший импульс будет у шара ……

— Из двух шаров равной массы, движущихся с различными скоростями, больший импульс имеет…

— Укажите, проекция какого из шаров будет положительной, отрицательной и равной нулю. Поясните свой ответ;

— Дайте определение замкнутой системы тел;
— Сформулируйте закон сохранения импульса, запишите формулу;
— Рыбак сидит в лодке, покоящейся на поверхности воды. Что произойдёт с лодкой, если он начнёт переходить с носа лодки на корму?
— Две тележки равной массы движутся навстречу друг другу с равными по модулю скоростями. Чему равен импульс системы тел?
3. Сообщение темы урока. Изложение нового материала.
Ребята, сегодня на уроке мы познакомимся с особенностями решения расчетных задач по теме «Закон сохранения импульса», но, самое главное, научимся преодолевать сложности, которые могут возникнуть у вас в процессе работы над задачей. Как показывает многолетняя практика, основная проблема возникает из-за того, что отсутствует универсальная формула, которая будто «по мановению волшебной палочки» сразу могла бы вас привести к правильному решению задачи! В каждом конкретном случае формулы будут различными, и именно для того, чтобы вам было проще, я хочу предложить воспользоваться планом.
Поверьте, с его использованием решение задач превращается в настоящее удовольствие! Это совсем не сложно, ведь его НЕ нужно заучивать, им просто нужно руководствоваться (учащиеся записывают план в тетрадь).
План решения задач на закон сохранения импульса
1) Сделать рисунок, на котором обозначить направления: оси координат, векторов скорости тел до и после взаимодействия;
2) Глядя на рисунок, записать в векторном виде закон сохранения импульса;
3) Записать закон сохранения импульса в проекции на ось координат;
4) Из полученного уравнения выразить неизвестную величину и найти её значение.
Особенно хочу обратить ваше внимание на важность рисунка!
Именно рисунок— ваш основной помощник для того, чтобы правильно записать формулу закона сохранения импульса для конкретной задачи, которую вы решаете в данный момент, он же поможет вам правильно расставить знаки проекций импульсов тел на ось координат, допустив минимум ошибок!
4.Знакомство с решением задачи по плану (работа с презентацией):
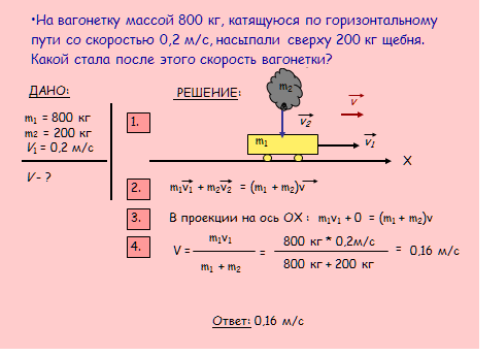
5. Решение обучающимися задач у доски с подробными комментариями.
Дети выходят по очереди к доске и с опорой на предложенный план, записанный у каждого в тетради, решают предложенные учителем задачи.
−Вагон массой 20 т, движущийся со скоростью 0,3 м/с, нагоняет вагон массой 30 т, движущийся со скоростью 0,2 м/с. Какова скорость вагонов после того, как сработает сцепка?
−Какую скорость приобретёт лежащее на льду чугунное ядро, если пуля, летящая горизонтально со скоростью 500 м/с, отскочит от него и будет двигаться в противоположном направлении со скоростью 400 м/с? Масса пули 10 г, масса ядра 25 кг.
−Человек, массой 80 кг переходит с носа на корму в покоящейся лодке длиной s = 5 м. Какова масса лодки, если она за время этого перехода переместилась в стоячей воде на L = 2 м? Сопротивление воды не учитывать.
(В случае возникновения каких-либо сложностей при решении задачи, можно в любой момент обратиться к нужному слайду презентации, и, без сомнения, настроенная анимация позволит акцентировать внимание обучающихся именно на тех местах, которые чаще всего вызывают затруднения у учеников).
6. Самостоятельное решение задачи в тетради с последующей проверкой.
−Два человека массой 60 кг и 90 кг стоят на носу и на корме в лодке, покоящейся на поверхности озера. Они решают поменяться местами. На какое расстояние сместится при этом лодка, если ее длина 5м, а масса 150 кг?

7. Домашнее задание.
1. Начинающий ковбой, накинув лассо на бегущего быка, от рывка полетел вперёд со скоростью 5 м/с, а скорость быка уменьшилась с 9 м/с до 8 м/с. Какова масса быка, если масса ковбоя 70 кг?
8. Подведение итогов урока.
Литература:
- Л. А. Кирик Самостоятельные и контрольные работы по физике 9 класс. Москва, Илекса, 2005.
- Презентация «Решение задач по теме «Закон сохранения импульса»» [Электронный ресурс]: Персональный сайт учителя физики Бахтиной Ирины Владимировны. URL:https://bakhtinairina.ucoz.ru/load/prezentacii_9_klass/reshenie_zadach_po_teme_quot_zakon_sokhranenija_impulsa_quot/13–1–0–12 (дата обращения: 29.11.2019).
Основные термины (генерируются автоматически): сохранение импульса, решение задач, ось координат, больший импульс, равная масса, решение задачи, вагон массой, скорость.





































































 =500м/с
=500м/с  =400 м/с
=400 м/с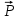 = mп
= mп 
 = mп
= mп + mя
+ mя  = — mп
= — mп + mя
+ mя  , отсюда
, отсюда 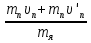
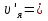
 = 0,36 м/с
= 0,36 м/с