Решение задач на сложение скоростей — КИНЕМАТИКА — Уроки физики в 10 классе — конспекты уроков — План урока — Конспект урока — Планы уроков — разработки уроков по физике

КИНЕМАТИКА

 

Урок № 5

Тема. Решение задач на сложение скоростей

 

Цель: вырабатывать умения и навыки учащихся с использование правила сложения скоростей; развивать умение выбирать наиболее удобную систему отсчета при решении задач, логическое мышление; воспитывать самостоятельность, настойчивость, грамотность в оформлении задач.

Тип урока: совершенствование знаний и формирование умений решать задачи.

Ожидаемые результаты. После урока ученики:

— будут уметь решать задачи с использование правила сложения скоростей.

ХОД УРОКА

I. Проверка домашнего задания

• Обзорная проверка тетрадей с целью выяснения наличия решения учащимися задач, которые были заданы домой.

• Физический диктант с взаимопроверкой.

 

II. Решение задач

Сообщение темы и цели урока, ожидаемых результатов.

Решение качественных задач

1. При каком условии летчик реактивного истребителя может рассмотреть артиллерийский снаряд, пролетающий недалеко от него?

2. Пассажир скорого поезда смотрит в окно на вагоны встречного поезда. В тот момент, когда последний вагон встречного поезда проехал мимо его окна, пассажир ощутил, что его движение резко замедлилось. Почему?

3. Почему дождевые капли безветренной погоды оставляют наклонные полосы на стекле автомобиля, который равномерно движется?

4. Двое пловцов, переплывающих реку. Один плывет перпендикулярно течению, второй — кратчайшим путем. Который из них переправиться на другой берег реки за наименьшее время, если модули их скоростей относительно воды одинаковы?

5. Мешает или помогает течение переплыть реку за кратчайшее время? кратчайшим путем? Считайте, что ширина реки и скорость течения есть везде одинаковыми.

Решения. Если держать курс под прямым углом к берегу (то есть если скорость пловца относительно воды направлена перпендикулярно к берегу), то пловца будет сносить вниз по течению. Поскольку течение не приближает плавника до противоположного берега и не отдаляет от него, кратчайшее время переправы не зависит от скорости течения. А вот для переправы кратчайшим путем следует держать курс вверх по течению, чтобы скорость относительно берега была перпендикулярной к берегу. Поскольку < пл (см. рисунок), течение мешает переплыть реку кратчайшим путем. Если пл < т, то такая переправа невозможна.

 

 

Решение расчетных задач

1. Пассажир поезда заметил, что две встречные электрички промчались мимо него с интервалом t1 = 6 мин. С каким интервалом времени t2 проехали эти электрички мимо станции, если поезд, на котором находится пассажир, двигался со скоростью 1 = 100 км/ч, а скорость каждой из электричек 2 = 60 км/ч?

Решения. Найдем расстояние между электричками в двух системах отсчета — в системе отсчета «поезд», связанной с пассажиром, и в системе отсчета, связанной со станцией. В системе отсчета «поезд» электрички движутся со скоростью . Поскольку они проходят мимо пассажира с интервалом времени t1, расстояние между электричками составляет . В системе же отсчета, связанной со станцией, . Приравнивая два выражения для s, получаем: . Подставляя числовые данные, находим t2 = 16 мин.

2. Эскалатор поднимает человека, стоящего на нем, за t1 = 1 мин, а если человек идет вверх остановившимся эскалатором, на поднятие тратится t2 = 3 мин. Сколько времени понадобится на поднятие, если человек будет идти вверх по эскалатору, который движется вверх?

 

III. Выполнение самостоятельной работы «Сложение перемещений и скоростей, переход в другие системы отсчета»

Начальный уровень

1. С полки вагона равномерно движется, падает яблоко. Которой является траектория движения яблока относительно наблюдателя, стоящего на перроне? Изобразите траекторию на рисунке.

2. Корабль подходит к пристани. Относительно каких тел пассажиры, стоящие на палубе этого корабля, находятся в движении: а) реки; б) палубы корабля; в) берега?

Средний уровень

1. Два поезда движутся в одном направлении со скоростями 70 и 50 км/час. относительно земли. Определите: а) модуль скорости первого поезда относительно второго б) модуль скорости второго поезда относительно первого.

2. Скорость первого автомобиля относительно второго 30 км/ч, а относительно земли 120 км/час. Определите модуль скорости второго автомобиля относительно земли, если автомобили движутся в одном направлении.

 

IV. Домашнее задание

1. Повторить соответствующий параграф учебника.

2. Решить задачи.

• Встречные поезда одинаковой длины проходят друг мимо друга. Пассажир первого поезда заметил, что второй поезд прошел мимо за 20 сек. За какое время мимо пассажира второго поезда прошел первый, если скорости поездов 40 и 60 км/ч?

• Катер пересекает реку шириной 1 км. Скорость катера относительно воды направлена перпендикулярно к берегу, ее модуль 4 м/сек. На какое расстояние течение снесет катер за время переправы, если скорость течения равна 1 м/с? Какой путь пройдет катер?

Самостоятельная работа Средняя скорость. Сложение скоростей 10 класс

Самостоятельная работа Средняя скорость. Сложение скоростей 10 класс с ответами. Самостоятельная работа представлена в пяти вариантах, в каждом варианте по 2 задания.

Вариант 1

1. Автомобиль первую половину пути двигался со скоростью 36 км/ч, другую половину пути — со скоростью 15 м/с. Определите среднюю скорость движения автомобиля.

2. Два автомобиля движутся вдоль одной прямой навстречу друг другу. Скорость первого автомобиля 72 км/ч, скорость второго 10 м/с. Определите модуль скорости сближения.

Вариант 2

1. Автомобиль проехал треть пути со скоростью 18 км/ч, а оставшуюся часть пути со скоростью 54 км/ч. Определите среднюю скорость движения автомобиля.

2. Два автомобиля движутся навстречу друг другу. Первый автомобиль — со скоростью 15 м/с в направлении оси ОХ, второй — со скоростью 10 м/с. С какой скоростью второй автомобиль движется относительно первого?

Вариант 3

1. Автомобиль треть времени ехал со скоростью 12 м/с, а остальное время — со скоростью 15 м/с. Определите среднюю скорость движения.

2. Моторная лодка движется по течению реки со скоростью 4 м/с, а по пруду со скоростью 3 м/с. Определите скорость течения реки.

Вариант 4

1. Первую треть пути трамвай двигался со скоростью 18 км/ч. Определите скорость трамвая на оставшемся участке, если средняя скорость движения на всём пути составила 7,5 м/с.

2. Человек бежит со скоростью 5 м/с в вагоне поезда против движения состава. Скорость поезда равна 18 км/ч относительно рельсов. Определите скорость человека относительно земли.

Вариант 5

1. Велосипедист на треке двигался первые 10 кругов со скоростью 20 м/с, следующие 20 кругов со скоростью 10 м/с. Определите его среднюю скорость.

2. Два автомобиля движутся по взаимно перпендикулярным траекториям. Скорость первого автомобиля 6 м/с, скорость второго — 8 м/с. С какой скоростью первый автомобиль удаляется от второго?

Ответы на самостоятельную работу Средняя скорость. Сложение скоростей 10 класс
Вариант 1
1. 12 м/с
2. 30 м/с
Вариант 2
1. 9 м/с
2. -25 м/с
Вариант 3
1. 14 м/с
2. 1 м/с
Вариант 4
1. 10 м/с
2. 0
Вариант 5
1. 12 м/с
2. 10 м/с

Относительность движения. Сложение скоростей

Просмотр содержимого документа
«Относительность движения. Сложение скоростей»

10 класс Урок ____ Дата ________

ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ. СЛОЖЕНИЕ СКОРОСТЕЙ

Цели урока 

Дидактические:

• расширить и углубить понятие относительности движения,

• сформировать навыки сложения скоростей и перемещений, перехода из одной системы отсчета к другой;

Развивающие:

• продолжить формировать научное мировоззрение с помощью основных методов познания: наблюдения, сравнения и сопоставления изучаемых явлений,

• продолжить развивать воображение, логическое мышление, зрительную память,

• продолжить развивать ИКТ-компетенции;

Воспитательные

:

• воспитывать познавательный интерес, любознательность, активность, аккуратность при выполнении заданий и интерес к изучаемому предмету,

• воспитывать коммуникативные способности учащихся при работе в группах

Тип урока: изучение нового материала

Оборудование: компьютеры

ХОД УРОКА

1. Мотивация обучения. Формулирование цели урока

– Может ли тело одновременно двигаться и находиться в покое? Приведите примеры.

– Какова тема сегодняшнего урока? Что мы сегодня узнаем? Чему научимся?

1. Актуализация опорных знаний

Учащиеся работают с компьютерной моделью, которая последовательно демонстрирует движения тел в системах отсчета, связанных с различными телами, дает представление о сложении векторов скоростей:

http://eornp.ru/sites/default/files/eor/8d/9c/ae/15/1e/1f/ab/12/30/f7/e6/02/8c/e3/25/34/html/index.html

Вопросы:

1. В чем заключается относительность покоя и движения?

2. В чем заключается относительность формы траектории? Приведите примеры.

3. В чем заключается относительность перемещения и скорости? Приведите примеры.

4. В чем заключается сложение скоростей?

1. Решение задач

1. Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместился на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором.	Дано: ________ t-?	Решение: Ответ: 20 с
2. Два поезда движутся навстречу друг другу со скоростями 72 км/ч и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда?	Дано: v1 = 72 км/ч =20 м/с v2 = 54 км/ч =15 м/с t = 14 с	Решение: Ответ: 490 м

1. Закрепление изученного материала

Работа в группах. Решение задач с последующей проверкой с помощью компьютерной модели «Относительность движения».

1. Катер, переправляясь через реку, движется перпендикулярно течению реки со скоростью 5 м/с в системе отсчета связанной с водой. Скорость течения реки 4,3 м/с. С какой скоростью лодка движется относительно берега?	Дано: υ′ = 5 м/c υт = 4,3 м/c υ – ?	Решение: Ответ: 6,6 м/с
2. По условию предыдущей задачи определите, на сколько метров будет снесен катер течением, если ширина реки 150 м?	Дано: υ′ = 5 м/c υт = 4,3 м/c y = 150 м x – ?	Решение: Ответ: 129 м
3. Используя данные из предыдущих задач, определите, какой курс должен держать капитан катера, чтобы пришвартоваться на другом берегу напротив пристани, от которой он отплыл? («курс» определяет угол между вектором скорости течения реки и скорости катера в системе отсчета связанной с водой).	Дано: υ′ = 5 м/c υт = 4,3 м/c υ = 6,6 м/с αк – ?	Решение: Ответ: 1500

После того как учащиеся произвели все вычисления, ученики садятся за компьютеры и проверяют свои результаты с помощью компьютерной модели, выставив необходимые параметры:

http://files.school-collection.edu.ru/dlrstore/b4190a68-3485-600a-dc9c-5e8479245660/00144675394211897/00144675394211897.htm

Если результаты не совпадают, то учащиеся корректируют свои вычисления.

1. Домашнее задание

• Изучить § 6 , ответить на вопросы,

• зад. ЕГЭ (стр. 28) – выполнить,

Дополнительно:

• § 7 – разобрать задачи,

• зад. 2 (стр. 30) – решить

1. Рефлексия

1. Сегодня я научился …

2. Мне понравилось …

3. Эти знания мне пригодятся …

4. Теперь я могу …

5. Я понял, что …

6. У меня получилось …

7. Было трудно …

8. Мне захотелось …

Закон сложения скоростей — Физика

Сложение скоростей

Ещё в младших классах вы сталкивались с тем, что иногда необходимо складывать скорости. Например, если две машины едут навстречу друг другу, то скорость их сближения — это сумма скоростей первой и второй машины.

Если же они двигаются в одном направлении, то скорость их сближения (или удаления) будет определяться разностью скоростей. Как мы уже говорили, решающее значение имеет выбор системы отсчёта.

Закон сложения скоростей: если тело двигается со скоростью в системе отсчёта а система отсчёта двигается со скоростью в системе отсчёта , то скорость движения тела, относительно системы равна:

Напомним, что скорость — это векторная величина, поэтому, скорости складываются геометрически.

Пример решения задач.

Лодка двигается по реке с собственной скоростью 8 м/с, так, как показано на рисунке. Скорость течения реки составляет 1 м/с. Определите скорость лодки относительно берега.

Расположим оси координат так, чтобы направление оси х совпадало с направлением течения реки. Тогда проекция скорости на ось х будет равна , т.к. на рисунке нам указан угол между направлением течения и скоростью лодки. Обратите внимание, что эта проекция будет отрицательной. В этом можно убедиться при построении проекции, да и чисто логически ясно, что лодка плывет против течения, а значит, одну из скоростей нужно обозначить за отрицательную. Проекция скорости течения на ось х, конечно же, будет равна 1 м/с, поскольку направление течение совпадает с направлением оси х. Тогда скорость движения лодки по оси х относительно берега равна:

 Проекция вектора скорости лодки на ось у равна

Разумеется, проекция скорости течения на ось у будет равна нулю, потому что вектор скорости течения перпендикулярен этой оси. С помощью геометрической суммы проекций мы можем найти модуль скорости лодки, относительно берега:

Давайте рассмотрим теперь пример, который научит вас складывать какие угодно скорости.

Найдём скорость машины, относительно самолёта в заданной системе координат. Сначала найдем проекции скорости машины на оси х и у. Точно так же, как и в предыдущем примере, проекция на ось х равна: , а проекция на ось у равна . Точно так же находим проекции скорости самолёта на координатные оси:

Напомним, что проекции являются скалярными величинами, поэтому их мы складываем алгебраически:

Теперь, когда мы нашли проекции скорости машины относительно самолёта на оси х и у, мы можем найти модуль скорости с помощью геометрической суммы:

Таким образом, мы получили расчётную формулу для вычисления модуля скорости одного движущегося тела, относительно другого движущегося тела. Эта формула справедлива для тех случаев, когда оба тела двигаются в одной плоскости.

Заметим, что закон сложения скоростей справедлив и для неравномерного движения. В этом случае нужно складывать мгновенные скорости.

Пример решения задачи.

Задача. Мяч катится с постоянной скоростью 10 м/с. Ему наперерез бежит футболист со скоростью 7 м/с, так, как показано на рисунке. Через какое время футболист поймает мяч, если изначально между футболистом и мячом было 40 метров?

Начнём с того, что когда футболист поймает мяч, они будут находиться в одной точке. Расположим систему координат так, чтобы направление движения футболиста совпадало с направлением оси х. Тогда, скорость мяча будет направлена под углом 45^о градусов к оси х. Сделаем проекции скорости мяча на оси х и у.

Презентация по физике на тему «Мгновенная скорость. Сложение скоростей»

Инфоурок › Физика ›Презентации›Презентация по физике на тему «Мгновенная скорость. Сложение скоростей»

Описание презентации по отдельным слайдам:

1 слайд Описание слайда:

Мгновенная скорость. Сложение скоростей Урок №7 10 класс

2 слайд Описание слайда:

Вспомни! Что такое РПД? Скорость РПД? Уравнение РПД?

3 слайд Описание слайда: 4 слайд Описание слайда:

Неравномерное движение — движение при котором расстояния, пройденные за одинаковые промежутки времени, не равны.

5 слайд Описание слайда:

Мгновенная скорость

6 слайд Описание слайда:

Мгновенная скорость — скорость в данный момент времени

7 слайд Описание слайда:

Мгновенная скорость — это величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

8 слайд Описание слайда: 9 слайд Описание слайда:

Средняя путевая скорость Определяется отношением пройденного пути к промежутку времени, за который этот путь пройден.

10 слайд Описание слайда:

Сложение скоростей

11 слайд Описание слайда:

Закон сложения скоростей Закон сложения скоростей: если тело двигается со скоростью v1 в системе отсчёта K1 а система отсчёта  K1 двигается со скоростью  v2 в системе отсчёта  K2, то скорость движения тела, относительно системы  равна:

12 слайд Описание слайда:

Пример решения задач. Лодка двигается по реке с собственной скоростью 8 м/с, так, как показано на рисунке. Скорость течения реки составляет 1 м/с. Определите скорость лодки относительно берега.

13 слайд Описание слайда: 14 слайд Описание слайда:

Задача. Мяч катится с постоянной скоростью 10 м/с. Ему наперерез бежит футболист со скоростью 7 м/с, так, как показано на рисунке. Через какое время футболист поймает мяч, если изначально между футболистом и мячом было 40 метров?

15 слайд Описание слайда:

Домашнее задание §9, 10

Курс профессиональной переподготовки

Учитель физики

Курс повышения квалификации

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Проверен экспертом

Общая информация

Номер материала: ДБ-219944

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Следствие из постулатов теории относительности. Видеоурок. Физика 11 Класс

Перед тем как начать урок, вспомним постулаты СТО.

1. Все процессы в природе протекают одинаково во всех инерциальных системах отсчета (принцип относительности).

2. Скорость света в вакууме одинакова во всех инерциальных системах отсчета, она не зависит ни от скорости источника, ни от скорости приемника светового сигнала.

Оказывается, что расстояние не является абсолютной величиной, а зависит от скорости движения объекта относительно выбранной системы отсчета (Рис. 1.).

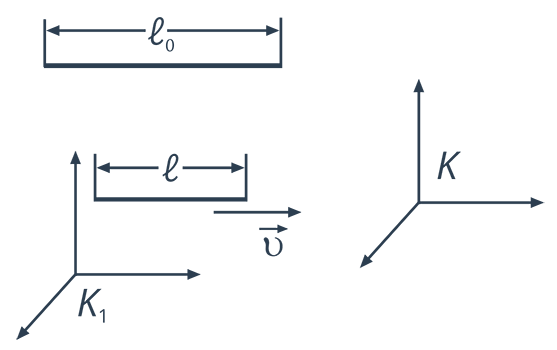
Рис. 1. Следствие 1

Пусть у нас есть стержень длиной 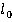 в системе отсчета 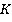, относительно которой этот стержень покоится. Тогда длина 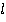, этого стержня в системе отсчета 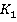, относительно которой стержень движется со скоростью 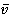, определяется формулой:

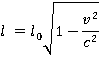
Получается, что длина стержня 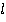 будет меньше ее первоначальной длины, если эта ручка будет двигаться со скоростью 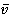. В этом и состоит релятивистское сокращение длины.

В повседневной жизни мы сталкиваемся с относительно небольшими скоростями и поэтому наблюдать релятивистское сокращение длины не можем.

Оказывается, в зависимости от выбора системы отсчета и от того, с какой скоростью одна система отсчета движется относительно другой, будет зависеть и тот промежуток времени, который будет фиксироваться в той или иной системе.

Пусть интервал времени между двумя событиями, происходящими в одной и той же точке инерциальной системы 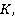 равен 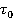 (Рис. 2.).

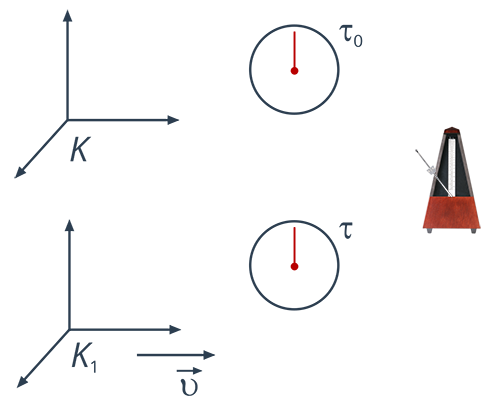
Рис. 2. Следствие 2

Например, этими событиями могут быть два удара метронома, отсчитывающего секунды, тогда интервал 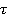 между этими событиями в системе отсчета 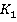, которая движется относительно системы 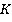, со скоростью 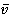, выражается формулой:

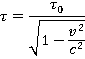
Очевидно, что 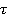 будет больше чем 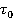, в этом и состоит релятивистское замедление времени в движущейся системе отсчета.

Для начала вспомним, каким был закон сложения скоростей в классической механике. Если, например, едет автомобиль со скоростью 20 км/час, а в этом авто летит муха со скоростью 5 км/час, то для наблюдателя на земле скорость мухи будет казаться 25 км/час.

Теперь рассмотрим сложение скоростей с точки зрения теории относительности.

Парадокс близнецов

Рассмотрим интересное следствие из релятивистского замедления времени (парадокс близнецов):

Представьте, что есть два брата-близнеца, Петр и Иван. Ваня – космонавт и отправляется в путешествие на ракете со скоростью, близкой к скорости света. Его нет приблизительно один год (по своему субъективному времени).

И, вернувшись на Землю, он встречается с братом, который, к его удивлению, выглядит намного старше него.

Рассмотрим это следствие на частном примере (Рис. 3.).

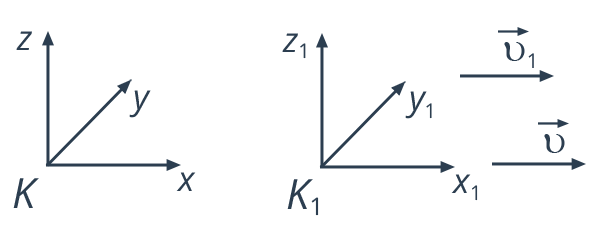
Рис. 3. Следствие 3

Пусть тело движется вдоль оси 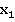системы отсчета 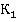, которая, в свою очередь, движется со скоростью  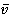относительно системы отсчета 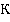. Причем в процессе движения координатные ос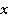и  и 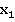все время совпадают, а координатные ос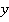и 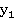 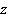и , и 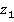 остаются параллельными.

Обозначим скорость тела относительно 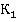через скорость 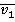, а скорость этого же тела относительно  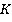через 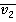. Тогда релятивистский закон сложения скоростей будет иметь следующий вид:

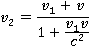
Попробуем соотнести этот закон с эквивалентным ему в классической механике. Рассмотрим предельные случаи, когда скорости очень малы в сравнении со скоростью света.

Если скорость 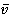 значительно меньше скорости света и скорость  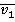тоже значительно меньше скорости света, то частью знаменателя в формуле 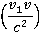, можно пренебречь, и в таком случае мы получим классический закон сложения скоростей:

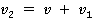
Рассмотрим еще один предельный случай. Представьте, что вы едете на поезде и включаете фонарик, для тех, кто стоит на земле, скорость света от фонарика останется 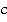, а не  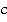плюс скорость поезда, как могло показаться (случай, когда одна из скоростей равна скорости света).

Тогда выходит, что 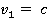, подставим это значение в формулу, тогда:

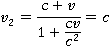
Выходит, что и скорость 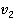тоже будет равняться 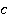, как этого требует второй постулат теории относительности.

Релятивистский закон сложения скоростей справедлив, хотя и не совсем нагляден. Представьте себе наблюдателя на земле, он смотрит на большую ракету, которая движется относительно Земли со скоростью, близкой к скорости света. И от этой большой ракеты отделяется маленькая ракета, которая тоже начинает двигаться относительно большой со скоростью .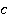

Из релятивистского закона сложения скоростей следует, что для наблюдателя на Земле и первая, и вторая ракеты будут двигаться со скоростями, близкими к скорости света 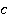. Выходит, что фактически отличие в скоростях отсутствует. Хотя мы понимаем, что малая ракета движется с огромной скоростью относительно большой.

На этом уроке мы ознакомились со следствиями постулатов теории относительности и сравнили некоторые из них с эквивалентными следствиями и законами из классической механики.

 

Список литературы

1.  Жилко В.В., Маркович Я.Г. Физика. 11 класс. – 2011.

2. Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика. 11 класс. Учебник.

3. Касьянов В.А. Физика, 11 класс. – 2004.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Сайт объединения учителей физики Санкт-Петербурга (Источник)

2. Интернет-сайт serg.fedosin.ru (Источник)

 

Домашнее задание

1. Задача № 1. Посчитать, на сколько мы сможем замедлить время, если будем мчаться на космическом корабле со скоростью 0,8 с? Сколько будет длиться урок, если на Земле он идет 40 минут?

2. Задача № 2. Найдите полную энергию космического корабля с массой покоя 10 т, движущегося со скоростью  Какую скорость должно иметь тело, чтобы его продольные размеры уменьшились для наблюдателя в 3 раза?