Олимпиадные задачи на четность и нечетность. Занимательная математика 4 — 5 класс
Предлагаю будущим Перельманам их родителям странички дидактической коллекции олимпиадного репетитора. Если Вас интересует нестандартная математика для поступления в хорошую школу (в 5 — 7 классе), то Ваш репетитор по математике непременно должен рассмотреть на занятиях задачи на четность и нечетность. Это классика олимпиадной математики 5 — го класса и любимая тема у составителей необычных задач.
1) На бильярдном столе лежит три шара. За один ход можно ударить по одному из них так, чтобы он пролетел между двумя другими. Удастся ли за 555 ударов вернуть шары в исходное положение? Можно ли это сделать за 556 ударов?
2) На столе лежат 5 монет в ряд. Первая – орлом вверх, вторая – решкой вверх, третья – орлом вверх, четвертая – решкой вверх, пятая – орлом вверх. За один ход разрешается перевернуть любые две соседние монеты. Можно ли
а) все монеты расположить орлами вверх?
б) можно ли их положить решками вверх?
3) Решите предыдущую задачу, если разрешается перевернуть любые 3 рядом расположенные монеты?
4) На волшебном дереве растут персики и дыни. Если сорвать какой-то один фрукт, то вырастет точно такой же. Если сорвать два разных фрукта, то вырастет персик, а если сорвать два одинаковых, то вырастет дыня.
а) Можно ли так сорвать фрукты, чтобы на дереве ни одного из них не осталось?
б) Можно ли сорвать их так, чтобы на дереве остался только 1 персик?
в) Можно ли сделать так, чтобы осталась только одна дыня?
5) Имеются 101 гирька весом 1г, 2г, 3г, … 100г и 101г. Случайно гирька в 20г потерялась. Можно на чашечные весы положить остальные гирьки так, чтобы весы эти весы оказались в положении равновесия?
6) По кругу расставили 18 блюдец и разложили по ним 59 монет. Могло ли так получиться, что количество монет на любых двух соседних блюдцах отличается друг от друга на 1?
7) Имеется 13 зубчатых колес, сцепленных по порядку: первое со вторым, второе с третьим, третье с четвертым и так далее. Тринадцатое сцеплено с первым. Может ли эта система вращаться?
8) Из книги вырвали 99 листов. Может ли сумма номеров на их страницах оказаться равной 990?
9) Имеется 7 больших листочков бумаги. Некоторые из них разорвали на 5 частей, а некоторые на 9 частей. Затем некоторые из получившихся снова разорвали на 5 или на 9 частей. И так далее. Могло ли получиться в итоге 1100 листочков?
Репетитор о комплекте задач: Решения головоломок с применением четности и нечетности чисел всегда отличались необычайной логической красотой и абсолютной прозрачностью выводов. Они основываются на простейших свойствах арифметических операций (обычно на сложении или вычитании). Как правило, свойства четности и нечетности репетитор по математике сокращает до записей:
Олимпиадные задачи по математике на четность и нечетность часто требуют опровержений тех факты, о которых спрашивается, и имеют сходную логику с методом доказательства от противного. При самом распространенном ответе «не может» требуется объяснить репетитору, почему именно этого не может быть. Если ребенок говорит: «Может», то достаточно привести пример такого расклада, распределения или комбинации. Помимо прямых задач на четноть и нечетность олимпиадный урок репетитора по математике может включать в себя разбор близких по замыслу задач (на две противоположности), решаемых при помощи анализа отнесения объекта (или варианта) в ту или иную группу. К ним относятся номера про шары и колеса.
Составляйте и присылайте интересные задачки, я с удовольствием включу их в комплект.
Ваш олимпиадный консультант — репетитор по математике А.Н. Колпаков.
ankolpakov.ru
Олимпиадные задачи на четность и нечетность.
c Трушин Б.В., г. Троицк, 2 декабря 2006 г.
 Тема I. Четность Задача 1. Квадратная таблица 25 25 раскрашена в 25 цветов так, что в каждой строке и в каждом столбце представлены все цвета. Докажите, что если расположение цветов симметрично относительно
Тема I. Четность Задача 1. Квадратная таблица 25 25 раскрашена в 25 цветов так, что в каждой строке и в каждом столбце представлены все цвета. Докажите, что если расположение цветов симметрично относительно
Математическая индукция
 Математическая индукция Задача 1 Из квадрата клетчатой бумаги размером 16х16 вырезали одну клетку. Докажите, что полученную фигуру можно разрезать на «уголки» из трёх клеток. Первое соображение 16. 16
Математическая индукция Задача 1 Из квадрата клетчатой бумаги размером 16х16 вырезали одну клетку. Докажите, что полученную фигуру можно разрезать на «уголки» из трёх клеток. Первое соображение 16. 16
ЕГЭ. 19 задание 2018 года
 Квант-10. Математика ГРЦФМО, Лицей 40. г. Нижний Новгород 7 октября 2018 г. Контактные данные Группа в Телеграм https://t.me/joinchat/f-8ewhb8v6j2nkdmgmlnza Это группа для вопросов и общения. Так же здесь
Квант-10. Математика ГРЦФМО, Лицей 40. г. Нижний Новгород 7 октября 2018 г. Контактные данные Группа в Телеграм https://t.me/joinchat/f-8ewhb8v6j2nkdmgmlnza Это группа для вопросов и общения. Так же здесь
ЛОМАНЫЕ И МНОГОУГОЛЬНИКИ
 ЛОМАНЫЕ И МНОГОУГОЛЬНИКИ Фигура на плоскости, образованная конечным набором отрезков, расположенными так, что конец первого является началом второго, конец второго — началом третьего и т.д. называется
ЛОМАНЫЕ И МНОГОУГОЛЬНИКИ Фигура на плоскости, образованная конечным набором отрезков, расположенными так, что конец первого является началом второго, конец второго — началом третьего и т.д. называется
Трушин Б.В., 26 июня 2011 г.
 Тема 1. Четность 1. На столе лежат 13 шестеренок, соединенных в замкнутую цепочку. Могут ли все шестеренки вращаться одновременно? 2. Может ли прямая, не содержащая вершин замкнутой 13 звенной ломаной,
Тема 1. Четность 1. На столе лежат 13 шестеренок, соединенных в замкнутую цепочку. Могут ли все шестеренки вращаться одновременно? 2. Может ли прямая, не содержащая вершин замкнутой 13 звенной ломаной,
Устная олимпиада по комбинаторике
 VIII Командно-личный турнир «Математическое многоборье» 2 7 ноября 2015 года, Москва Устная олимпиада по комбинаторике Старшая лига 1. Можно ли расставить по кругу числа от 1 до 2016 так, чтобы все суммы
VIII Командно-личный турнир «Математическое многоборье» 2 7 ноября 2015 года, Москва Устная олимпиада по комбинаторике Старшая лига 1. Можно ли расставить по кругу числа от 1 до 2016 так, чтобы все суммы
Ошибка! Источник ссылки не найден. 1
 Ошибка! Источник ссылки не найден. 1 2 Электронная школа Знаника Разбор задач третьей части заданий 1 4 5 класс Задача 1. 20 спичек разложили в 13 коробков и на каждом написали количество спичек в этом
Ошибка! Источник ссылки не найден. 1 2 Электронная школа Знаника Разбор задач третьей части заданий 1 4 5 класс Задача 1. 20 спичек разложили в 13 коробков и на каждом написали количество спичек в этом
Геометрия (решения) Младшая лига

РЕШЕНИЯ ЗАДАЧ 4 КЛАССА
 РЕШЕНИЯ ЗАДАЧ 4 КЛАССА Задача 1. Нотки До, Ре, Ми, Фа и Ля организовали концерт. При этом двое играли на барабанах, а трое на гитарах. До и Ре играли на одинаковых инструментах, До и Фа на разных, как
РЕШЕНИЯ ЗАДАЧ 4 КЛАССА Задача 1. Нотки До, Ре, Ми, Фа и Ля организовали концерт. При этом двое играли на барабанах, а трое на гитарах. До и Ре играли на одинаковых инструментах, До и Фа на разных, как
Примеры и конструкции

Найдите все такие значения x.
 Числа и их свойства 1. Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100. а) Может ли частное этого числа и суммы его цифр быть равным 90? б) Может ли частное этого
Числа и их свойства 1. Дано трёхзначное натуральное число (число не может начинаться с нуля), не кратное 100. а) Может ли частное этого числа и суммы его цифр быть равным 90? б) Может ли частное этого
Решения для 4 5 класса
 1 1. Первая часть Задача 1: Решения для 4 5 класса Сколькими способами можно поставить двух королей одного цвета на доске 3х3 так, чтобы они не били друг друга? А. 4 Б. 8 В. 12 Г. 16 В центре доски король
1 1. Первая часть Задача 1: Решения для 4 5 класса Сколькими способами можно поставить двух королей одного цвета на доске 3х3 так, чтобы они не били друг друга? А. 4 Б. 8 В. 12 Г. 16 В центре доски король
Блок 6. Площади и периметры
 Блок 6. Площади и периметры Задания интернет-карусели 1. Второклассник Виктор в качестве домашнего задания по математике должен был нарисовать прямоугольник. Ему нужно найти число A его периметр (в сантиметрах).
Блок 6. Площади и периметры Задания интернет-карусели 1. Второклассник Виктор в качестве домашнего задания по математике должен был нарисовать прямоугольник. Ему нужно найти число A его периметр (в сантиметрах).
Межшкольная олимпиада. 4 класс
 Межшкольная олимпиада 30.01.16 4 класс 1. Соедините пять звеньев цепи в одну цепь при помощи только шести операций (операции состоят из расковывания и заковывания колец) 2. Скорый поезд вышел из Москвы
Межшкольная олимпиада 30.01.16 4 класс 1. Соедините пять звеньев цепи в одну цепь при помощи только шести операций (операции состоят из расковывания и заковывания колец) 2. Скорый поезд вышел из Москвы
LXIII Олимпиада Эстонии по математике
 LXIII Олимпиада Эстонии по математике 30 января 2016 г. Региональный тур 7 класс I часть. Время, отводимое для решения: 40 минут. На этом листке написать только ответы, для решения можно использовать дополнительную
LXIII Олимпиада Эстонии по математике 30 января 2016 г. Региональный тур 7 класс I часть. Время, отводимое для решения: 40 минут. На этом листке написать только ответы, для решения можно использовать дополнительную
ПЕРВЫЕ ШАГИ НА ПУТИ К ОЛИМПУ
 УДК 51 ПЕРВЫЕ ШАГИ НА ПУТИ К ОЛИМПУ Соколова В.В., Мандров Г. научные руководители учитель математики старших классов Новикова О.В., учитель информатика старших классов Мясникова И.С. Муниципальное общеобразовательное
УДК 51 ПЕРВЫЕ ШАГИ НА ПУТИ К ОЛИМПУ Соколова В.В., Мандров Г. научные руководители учитель математики старших классов Новикова О.В., учитель информатика старших классов Мясникова И.С. Муниципальное общеобразовательное
Error! Reference source not found. 1
 Error! Reference source not found. 1 2 Электронная физико-техническая школа Решебник для 4-5 класса 1 Первая часть задания Задача 1 Кот в Сапогах поймал четырех щук и еще половину улова. Сколько щук поймал
Error! Reference source not found. 1 2 Электронная физико-техническая школа Решебник для 4-5 класса 1 Первая часть задания Задача 1 Кот в Сапогах поймал четырех щук и еще половину улова. Сколько щук поймал
Как работать с пособием
 Как работать с пособием Уважаемые взрослые! Предлагаемое пособие рассчитано на совместную работу воспитателей, педагогов и родителей с дошкольниками, готовящимися к школьному обучению. Первоначальной задачей
Как работать с пособием Уважаемые взрослые! Предлагаемое пособие рассчитано на совместную работу воспитателей, педагогов и родителей с дошкольниками, готовящимися к школьному обучению. Первоначальной задачей
Решение задач 3 тура 2010/2011 года. (3 балла)
 Приносим свои извинения за то, что в решении последней задачи предыдущего тура была допущена ошибка, решение исправлено, баллы полученные участниками подкорректированы. В соответствующих файлах были внесены
Приносим свои извинения за то, что в решении последней задачи предыдущего тура была допущена ошибка, решение исправлено, баллы полученные участниками подкорректированы. В соответствующих файлах были внесены
Пояснительная записка
 Пояснительная записка Все задания предполагают творческое применение программных знаний, умений и навыков по данным предметам. Материалы данной работы могут быть использованы учителем при подготовке к
Пояснительная записка Все задания предполагают творческое применение программных знаний, умений и навыков по данным предметам. Материалы данной работы могут быть использованы учителем при подготовке к
7+8=15. Получим группы D={1,2,3}, E={4,5,6}, F={7,8}, C={11,12,13}, а монеты 9 и 10 уже определились. Третье взвешивание: 32= d 1.
 XI Всероссийская смена «Юный математик». ВДЦ «Орлёнок» X Южный математический турнир. Старт-лига. 4 тур. 1 октября 015 года. Высшая лига. Полуфиналы. Решения. 1. Есть 13 внешне одинаковых монет. Суд знает,
XI Всероссийская смена «Юный математик». ВДЦ «Орлёнок» X Южный математический турнир. Старт-лига. 4 тур. 1 октября 015 года. Высшая лига. Полуфиналы. Решения. 1. Есть 13 внешне одинаковых монет. Суд знает,
Error! Reference source not found. 1
 Error! Reference source not found. 1 2 Электронная физико-техническая школа 1 Введение Конкурс Волшебный сундучок это заочный конкурс по математике для школьников, который проводится совместно с Московским
Error! Reference source not found. 1 2 Электронная физико-техническая школа 1 Введение Конкурс Волшебный сундучок это заочный конкурс по математике для школьников, который проводится совместно с Московским
Ошибка! Источник ссылки не найден. 1
 Ошибка! Источник ссылки не найден. 1 2 Электронная школа Знаника Разбор задач второй части заданий 4 5 класс 6 7 8 9 10 Б А В Б Г Задача 6 На дне рождения у Саши каждый мальчик (и Саша тоже!) съел по 4
Ошибка! Источник ссылки не найден. 1 2 Электронная школа Знаника Разбор задач второй части заданий 4 5 класс 6 7 8 9 10 Б А В Б Г Задача 6 На дне рождения у Саши каждый мальчик (и Саша тоже!) съел по 4
Ориентированные графы. 10 класс
 С.Л. Бабичев, [email protected], math.babichev.org Ориентированные графы. 10 класс Определение: Вершины u и v графа называются сильно связанными, если существует путь по рёбрам от u до v и от v до u
С.Л. Бабичев, [email protected], math.babichev.org Ориентированные графы. 10 класс Определение: Вершины u и v графа называются сильно связанными, если существует путь по рёбрам от u до v и от v до u
Ошибка! Источник ссылки не найден. 1
 Ошибка! Источник ссылки не найден. 1 2 Электронная школа Знаника Решебник для 6 7 класса Первая часть Задача 1 Если Семён стоит на столе, а Гриша на полу, то Семён на 80 см выше Гриши. А если Гриша стоит
Ошибка! Источник ссылки не найден. 1 2 Электронная школа Знаника Решебник для 6 7 класса Первая часть Задача 1 Если Семён стоит на столе, а Гриша на полу, то Семён на 80 см выше Гриши. А если Гриша стоит
Домашняя работа по алгебре за 7 класс
 Домашняя работа по алгебре за 7 класс к задачнику «Алгебра. 7 класс: Задачник для общеобразоват. учреждений. 3-е изд., доработ.» А.Г. Мордкович и др. М.: «Мнемозина», 2000 г. Часть II учебно-практическое
Домашняя работа по алгебре за 7 класс к задачнику «Алгебра. 7 класс: Задачник для общеобразоват. учреждений. 3-е изд., доработ.» А.Г. Мордкович и др. М.: «Мнемозина», 2000 г. Часть II учебно-практическое
4 класс, первая лига, 3 тур, 6 ноября
 X Ижевский омандный Турнир Математиков, 4-6 ноября 2017 4 класс, первая лига, 3 тур, 6 ноября 1. В семье есть Андрей, Богдан, Василий, Анна, Дарья и Жанна. Сколькими способами их можно посадить на диван
X Ижевский омандный Турнир Математиков, 4-6 ноября 2017 4 класс, первая лига, 3 тур, 6 ноября 1. В семье есть Андрей, Богдан, Василий, Анна, Дарья и Жанна. Сколькими способами их можно посадить на диван
Экспресс проверка знаний по математике.
 ГБОУ школа 583 Приморского района Санкт-Петербурга Экспресс проверка знаний по математике. Таблица умножения и деления. Учитель: Смирнова Елена МИхайловна. Отметь верные ответы(). 1. 2 х 5 = 10 2. Произведение
ГБОУ школа 583 Приморского района Санкт-Петербурга Экспресс проверка знаний по математике. Таблица умножения и деления. Учитель: Смирнова Елена МИхайловна. Отметь верные ответы(). 1. 2 х 5 = 10 2. Произведение
ДОРОГИЕ ШЕСТИКЛАССНИКИ!
 ДОРОГИЕ ШЕСТИКЛАССНИКИ! Рабочая тетрадь «Делимость чисел. Рациональные числа» включает в себя три раздела. В первый раздел вошли задания тренировочного характера по таким темам: признаки делимости целых
ДОРОГИЕ ШЕСТИКЛАССНИКИ! Рабочая тетрадь «Делимость чисел. Рациональные числа» включает в себя три раздела. В первый раздел вошли задания тренировочного характера по таким темам: признаки делимости целых
docplayer.ru
Чётность и нечётность функций
Привет всем посетителям! Сегодня рассматриваем вопрос четности и нечетности функций.
Правило:
Если  , то функция четная.
, то функция четная.
Если  , то функция нечетная.
, то функция нечетная.
При этом важно, чтобы область определения функции была бы симметричной относительно оси ординат, а при наличии в ней выколотых точек или интервалов они также должны располагаться симметрично.
Алгоритм исследования:
Установить, симметрична ли область определения функции. Если это так, то найти  и сравнить с
и сравнить с 
Если  то функция — четная.
то функция — четная.
Если  , то функция нечетная.
, то функция нечетная.
Функция совсем не обязана быть четной или нечетной, она может быть «никакой», несмотря на то, что область определения симметрична.
Примеры:
1. Определить, является ли четной функция:  .
.
Область определения этой функции – все действительные числа, то есть она симметрична. Теперь подставим вместо x – (-x) и посмотрим, что получится:

 – функция четна.
– функция четна.
Надо отметить, что график четной функции симметричен относительно оси ординат, она для него словно зеркало. Поэтому графики таких функций можно строить в правой полуплоскости, а в левую просто отражать.
Верно и следующее: если функция задана графиком, который симметричен относительно оси ординат, то она четная.
2. Определить, является ли четной функция:  .
.
Область определения этой функции может быть найдена из системы неравенств:
Оба неравенства всегда соблюдаются, так как дискриминант обоих трехчленов всегда меньше 0, и ветви парабол направлены вверх – таким образом, мы установили, что область определения симметрична – это вся числовая ось.
Теперь подставим вместо x – (-x):  – данная функция нечетна.
– данная функция нечетна.

График нечетной функции симметричен относительно начала координат, то есть каждой его точке соответствует точка, получить которую можно поворотом на 180 градусов относительно начала координат. Поэтому графики таких функций можно строить в правой полуплоскости, а изображение в левой полуплоскости получить, повернув картинку на 180 градусов.
Верно и следующее: если функция задана графиком, который симметричен относительно начала координат, то она нечетная.
3. Определить, является ли четной функция:  .
.
Область определения может быть найдена из системы неравенств:
Таким образом, область определения симметрична, и не содержит выколотые точки (1) и (-1).
Подставляем (-х) вместо х:
 – исходную функцию не получили, а получили совсем другую – значит, исходная функция не является ни четной, ни нечетной (что и подтверждает график). Мы убедились, что симметрия области определения еще не означает, что функция четная или же нечетная.
– исходную функцию не получили, а получили совсем другую – значит, исходная функция не является ни четной, ни нечетной (что и подтверждает график). Мы убедились, что симметрия области определения еще не означает, что функция четная или же нечетная.

4. Определить, является ли четной функция:  .
.

Область определения – вся числовая ось, кроме 0 – симметричная.
Подставляем (-х) вместо х:
 – функция нечетна.
– функция нечетна.
5. Определить, является ли четной функция:  .
.
Область определения – вся числовая ось, кроме точек 3 и (-3) – симметричная.
Подставляем (-х) вместо х:
 – функция четная.
– функция четная.

6. Определить, является ли четной функция:  .
.

Область определения – вся числовая ось – симметричная.
Подставляем (-х) вместо х:
 – функция четная.
– функция четная.
7. Определить, является ли четной функция:  .
.
Область определения – вся числовая ось, кроме 0 – симметричная.
Подставляем (-х) вместо х:
 – функция нечетная.
– функция нечетная.
Кроме того, здесь мы имеем дело с суммой двух функций.
Правило:
Сумма двух нечётных функций – нечётна.
Сумма двух чётных функций – чётна.
А вот сумма двух функций разной четности – как правило, ни четна, ни нечетна.
Определим четность этих функций по отдельности.
 – функция нечетная.
– функция нечетная.
 – функция нечетная.
– функция нечетная.

8. Исследуем теперь такую функцию:

Одна из них нечётна – это мы только что показали, а вторая?
Область определения функции  симметрична, функция нечётна, так как
симметрична, функция нечётна, так как  . Тогда по правилу сложение двух нечетных функций даст функцию нечетную.
. Тогда по правилу сложение двух нечетных функций даст функцию нечетную.

9. Наконец, последняя:
 – имеем произведение двух функций.
– имеем произведение двух функций.
Правило:
Произведение или частное двух нечётных функций чётно.
Произведение или частное двух чётных функций чётно.
Произведение или частное нечётной и чётной функций нечётно.
Так как обе функции являются чётными, то и их произведение чётно.

Проверим?
Область определения – вся числовая ось. Производим подстановку:
 – функция четная.
– функция четная.
easy-physic.ru
Четность и нечетность функции ☑️ как определить, примеры решения задач на исследование функции на определение четности и нечетности, условие

Общие сведения
Исследование функции на четность и нечетность — базовый элемент, показывающий ее поведение, которое зависит от значения аргумента. Последний является независимой переменной, соответствующей определенным допустимым значениям. Множество чисел, которое может принимать неизвестная независимого типа, называется областью определения. Областью значений функции вида y = f (x) являются все значения зависимой переменной «y».
Теперь следует сформулировать список базовых знаний, которые необходимы для анализа выражений на четность. Если нужно выполнить другие процедуры исследования, то его следует расширить. Например, для нахождения максимума следует ознакомиться с производной. Необходимый минимум знаний о функциях следующий:
- Область определения — D (f).
- Виды.
- Правила.
- Свойства для четных и нечетных.
- Классификация.
Первый элемент необходим для выявления аргумента, при котором можно узнать его недопустимые значения, а также определить симметричность. От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.
Область определения

Первый элемент, который нужен для анализа, следует рассмотреть подробнее. Область определения функции z = g (y) специалисты рекомендуют обозначать литерой «D». Полная запись выглядит таким образом: D (z). Кроме того, следует выяснить симметричность множества. Под последним понимается некоторый интервал, который нужно найти.
D (z) записывается в виде множества. Например, D (z) = [1;8]. Запись значит ограниченность аргумента, принимающего значения от 1 включительно до 8 включительно, то есть следующие цифры: 1, 2, 3, 4, 5, 6, 7 и 8. Если указана запись в виде (1;4), то ее нужно трактовать таким образом: от 1 не включительно до 4 не включительно, то есть в интервал входят только числа 2 и 3.
Для определения величины D (z) необходимо решить неравенство, корнем которого являются все значения аргумента. Для этих целей можно использовать и специализированное программное обеспечение. Математики рекомендуют свести пользование решебниками и программами к минимуму, поскольку не всегда предоставится возможность воспользоваться ими на экзаменах или контрольных.
Основные виды
Исследование функции зависит от ее вида, который нужно правильно определять. Для начала следует обозначить сложность, поскольку от этого параметра зависят дальнейшие действия и свойства, которыми придется руководствоваться. Математики производят разделение таким образом:
- Простые: алгебраические, трансцендентные и тригонометрические.
- Составные или сложные.
Алгебраические делятся на рациональные (без корня) и иррациональные (наличие радикала). Первые состоят из целых и дробных. D (z) для этих типов — все множество действительных чисел. Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.

Все функции, содержащие sin, cos, tg и ctg, являются тригонометрическими. Кроме того, arcsin, arccos, arctg и arcctg — обратные тригонометрические. Трансцендентные можно разделить на такие три группы: показательные, степенные и логарифмические.
Второе отличается от первого формулой. Другой тип классификации основан на периодичности. В зависимость от этого параметра все функции делятся на периодические и непериодические. Параметр периодичности означает повторение ее поведения через определенный период Т.
Существует еще один критерий. Он называется монотонностью. В зависимости от него, функции бывают монотонными и немонотонными. Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.
Правила для выявления

Для того чтобы исследовать на четность, существует два правила или теоремы, которые записываются в виде двух формул. Четная — функция вида w (x), для которой справедливо такое равенство: w (-x) = w (x). Для нечетной соотношение немного другое: w (-x) = w (x). Однако бывают выражения, к которым не применимы эти тождества. Они принадлежат общему виду.
Для оптимизации решения специалисты рекомендуют использовать некоторую последовательность действий или специальный алгоритм. Он позволяет определить четность за минимальный промежуток времени и без ошибок. Необходимо обратить внимание на пункты или шаги, по которым выполняется подробная оценка:
- Разложить при необходимости на простые элементы.
- Определить D (z). Если ее график симметричный, то нужно переходить к следующему шагу. В противном случае результатом является функция общего вида.
- Проверить, подставив в выражение отрицательное значение аргумента w (-x).
- Выполнить сравнение: w (-x) = w (x).
- Сделать соответствующий вывод.
Если w (-x) = w (x), то это свидетельствует о четности. При выполнении тождества w (-x) = -w (x) функция является нечетной. Важно обратить внимание на D, поскольку в некоторых точках равенства и условия могут не выполняться. Это свидетельствует о том, что искомая функция принадлежит к общему виду, то есть не является четной и нечетной.
Одним интересным способом является графический метод (принцип). Для его реализации нужно выполнить построение графика. Если он будет симметричным относительно оси ординат ОУ, то равенство w (-x) = w (x) будет выполняться. В случае симметричности относительно начала системы координат (точка пересечения осей абсцисс и ординат), будет справедливым равенство w (-x) = -w (x).
Следствия из утверждений
Свойства или следствия из утверждений расчетов позволяют оптимизировать процесс решения, поскольку нет необходимости выполнять какие-либо действия. Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут. Математики выделяют следующие свойства для таких функций:

- Симметричность графика: четная — относительно ОУ, а нечетная — относительно начала координат.
- Функция эквивалентна сумме четной и нечетной.
- Результат комбинации четных эквивалентен четной, а нечетных — нечетной.
- Результирующее произведение: 2 четных — четное, 2 нечетных — четная, а 2 разной четности — нечетной.
- Композиция: 2 нечетных — нечетна, четная и нечетная — четна, любая с четной — четна (не наоборот).
- При взятии производной от четной результирующая является нечетной, а от нечетной — четной.
- Определенный интеграл вида ∫(g (x))dx с границами от -А до А равен двойным интегралам ∫(g (x))dx с границей от -А до 0 и от 0 до А: ∫(g (x))dx |(-A;A) = 2∫(g (x))dx |(-A;0) = 2∫(g (x))dx |(0;A).
- Определенный интеграл нечетной функции с границами -А и А равен 0.
- Ряд Маклорена: четные степени соответствуют четной и наоборот.
- Ряд Фурье: четная содержит только выражения с cos, а нечетная — sin.
Второе свойство можно записать математически таким образом: z (x) = y (x) + w (x). Выражение y (x) можно выразить следующим образом: y (x) = [z (x) — z (-x)] /2. Тождество w (x) выражается через z (x) формулой: w (x) = [z (x) + z (-x)] /2.
Классификация по четности
Специалисты давно уже исследовали некоторые функции. Примеры четных и нечетных можно классифицировать по признаку четности. Эти данные значительно ускоряют процесс анализа любого выражения. К нечетным функциям относятся следующие (следует учитывать, что аргумент «x» принадлежит множеству действительных чисел Z):

- Возведение в степень, показатель которой является целым и нечетным.
- Сигнум (sgn) — кусочно-постоянный тип, который задан несколькими формулами, объединенными в систему.
- Радикал положительной нечетной степени.
- Тригонометрические: sin (x), tg (x), ctg (x) и cosec (x).
- Обратные тригонометрические: arcsin (x), arcctg (x), arcsec (x) и arccosec (x).
- Гиперболические и их обратные выражения: гиперболические синус и косинус, а также ареасинус, ареатангенс и ареакотангенс.
- Гудермана и обратная ей: gd (x) = arctg (sh (x)) и arcgd (x) = arch (sec (x)).
- Интегральный синус: Si (x).
- Матье: se (x).
Кроме того, существуют еще составные выражения, элементами которых являются простые функции. Для анализа необходимо руководствоваться свойствами. Следующий класс, который объединяет все четные выражения, состоит из следующего перечня:
- Возведение в четную и целую степень.
- Модуль аргумента.
- Константа.
- Тригонометрические: cos (x) и sec (x).
- Гиперболические: косинус и секанс.
- Дельта-функция Дирака: z (x) = δ(x).
- Гаусса: z (x) = a * exp[(-(x — b)^2) / 2c 2 ].
- Кардинальный синус: sinc (x).

Остальные составляют класс общего вида, который не принадлежит к четным и нечетным. При решении задач необходимо иметь таблицу всех функций, которая должна быть составлена перед обучением. Следует учитывать, что на экзаменах и контрольных функции, используемые для описания каких-либо процессов, практически не исследуются. Зная алгоритм, не составит особого труда проверить выражение на четность. Следующим этапом, который поможет закрепить теоретические знания, считается практика.
Пример решения
Задачи исследования функции на четность встречаются редко, поскольку этот элемент входит в полный анализ ее поведения. Пусть дано тождество z (y) = (y 2 — y — 2) / (y 2 — 1). В этом случае следует действовать по алгоритму:
- Состоит из двух элементов: g (y) = y 2 — y — 2 и h (y) = y 2 — 1.
- Область значений: D (y 2 — y — 2) = (-бесконечность; +бесконечность) и D (y 2 — 1) = (-бесконечность; -1) U (-1;1) U (1; +бесконечность).
- График функции является симметричным, поскольку задан параболой.
- Выполнить анализ по формулам: g (-y) = (-y)^2 + y — 2 = y 2 + y — 2 и h (-y) = (-y)^2 — 1 = y 2 — 1.
- В двух случаях функции являются нечетными: в первом — изменение знака, а во втором — от четной отнимается 1. Следовательно, искомое выражение является нечетной функцией.

Задачу можно решить вторым способом — проанализировать составляющие элементы. Например, знаменатель всегда будет нечетным, поскольку от четного y 2 отнимается нечетное число (6 — 1 = 5). Этот способ используется в некоторых языках программирования, для написания подпрограмм и процедур, позволяющих проверить или отобрать все нечетные значения. Числитель также является нечетным, поскольку он содержит нечетный элемент «y». Если построить график, используя любой из веб-ресурсов, то он окажется симметричным относительно начала координат.
Первое свойство свидетельствует о том, что функция является нечетной. Некоторые новички делают распространенную ошибку, считая, что отношение нечетных есть величина четная. Однако такое утверждение не применимо в этом случае. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.
Таким образом, для исследования функции на предмет ее четности или нечетности нужно воспользоваться специальным алгоритмом, который рекомендуют математики. Он позволит выполнить операцию без ошибок и за короткий промежуток времени.
nauka.club
Определения и свойства четных и нечетных функций. Видеоурок. Алгебра 9 Класс
В этом уроке будут даны строгие определения четных и нечетных функций, рассмотрены их свойства, решены некоторые задачи.
Определение 1: Функция  называется четной, если для любого значения x из множества X выполняется равенство:
называется четной, если для любого значения x из множества X выполняется равенство: 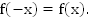
Определение 2: Функция  называется нечетной, если для любого значения x из множества X выполняется равенство:
называется нечетной, если для любого значения x из множества X выполняется равенство: 
Примеры:
1. 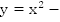 четная, т.к.
четная, т.к. 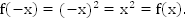
2. 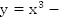 нечетная, т.к.
нечетная, т.к. 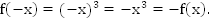
3. 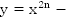 четная,
четная, 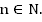
4. 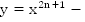 нечетная,
нечетная, 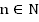 .
.
Дадим развернутое определение четной функции.
Определение 3: Функцию  называют четной, если выполнены два условия для всех
называют четной, если выполнены два условия для всех 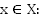
1. Область определения симметрична относительно нуля, т.е.
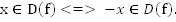
2. 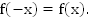
Из определения вытекает важное свойство четной функции:
График четной функции симметричен относительно оси y (Рис. 1).
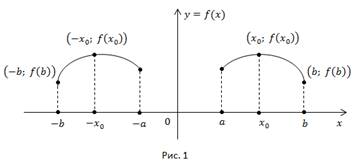
Дадим развернутое определение нечетной функции.
Определение 4: Функцию  называют нечетной, если выполнены два условия для всех
называют нечетной, если выполнены два условия для всех 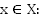
1. Область определения симметрична относительно нуля, т.е. 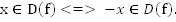
2. 
Из определения нечетной функции вытекает свойство: График нечетной функции симметричен относительно т. (0; 0) (Рис. 2).
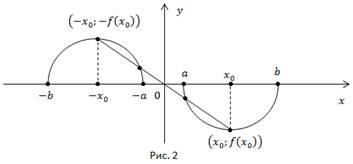
Если функция 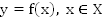 не является ни четной, ни нечетной, то ее называют функцией общего вида.
не является ни четной, ни нечетной, то ее называют функцией общего вида.
Примеры:
Пример 1. Определите вид функции 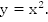

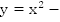 четная функция, ее график симметричен относительно оси y.
четная функция, ее график симметричен относительно оси y.
Пример 2. Определите вид функции 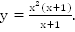
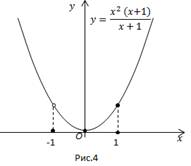
В точке 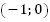 функция не существует, а в точке
функция не существует, а в точке 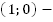 существует. Область определения несимметрична относительно нуля, значит
существует. Область определения несимметрична относительно нуля, значит 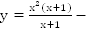 функция общего вида.
функция общего вида.
Пример 3.Определите вид функции 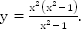

Обе точки выколотые, график и область определения симметричны относительно начала координат, функция четная.
Пример 4. Определите вид функции 

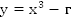 рафик и область определения симметричны относительно начала координат, функция нечетная.
рафик и область определения симметричны относительно начала координат, функция нечетная.
Пример 5. Определите вид функции 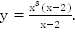

В точке с абсциссой 2 функция не существует, в точке с абсциссой -2 существует. Область определения несимметрична относительно нуля, это функция общего вида.
Пример 6. Определите вид функции 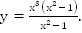

Область определения симметрична относительно нуля, функция нечетная.
Рассмотрим примеры на свойства четных и нечетных функций.
Пример 7: Исследовать на четность функцию 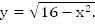
Решение:
Первый способ:

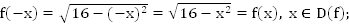
 ,функция четная.
,функция четная.
Второй способ:
Возведем в квадрат обе части равенства. Тогда вместо уравнения получим систему:
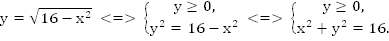
Второе уравнение полученной системы – уравнение окружности с центром в т.(0; 0) радиусом 4. Но т.к.  , графиком уравнения
, графиком уравнения  является верхняя полуокружность (Рис. 9).
является верхняя полуокружность (Рис. 9).
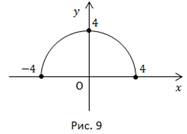
График симметричен относительно оси y, поэтому функция четная.
Ответ: Функция четная.
Пример 8. Известно, что функция  четная и убывает при
четная и убывает при 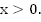 Определите характер монотонности функции при
Определите характер монотонности функции при 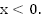
Решение:
Нам известно, что функция убывает на луче 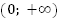 . Раз она определена на луче
. Раз она определена на луче 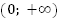 и является четной, то она определена и на луче
и является четной, то она определена и на луче 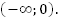
График четной функции симметричен относительно оси y, т.е. функция возрастает на луче 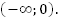
В качестве примера изобразим график функции 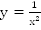 (Рис. 10).
(Рис. 10).
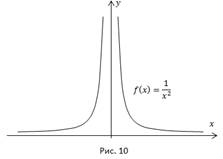
Ответ: Функция возрастает при 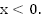
Пример 9. Дана функция  , где
, где 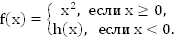
Задайте  так, чтобы функция
так, чтобы функция  являлась
являлась
а. четной
б. нечетной.
Решение:
Если функция четная, ее график симметричен относительно оси y, т.е. 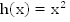 (Рис. 11).
(Рис. 11).
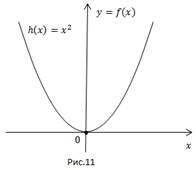
Если функция нечетная, ее график симметричен относительно т. (0; 0), т.е. 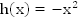 (Рис. 12).
(Рис. 12).

Мы рассмотрели определения и свойства четных и нечетных функций, решили некоторые типовые задачи На следующем уроке мы продолжим изучение свойств четных и нечетных функций.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 275 – 278.
interneturok.ru
Четные и нечетные числа от 1 до 20
В этом материале дети узнают, что такое четные и нечетные числа от 1 до 20 и научатся различать их, выполняя различные задания в картинках. Дети дошкольного возраста еще не умеют делить числа, поэтому основное правило четных чисел (т.е. четное — это число, которое делится на 2) им будет очень сложно понять. Чтобы решить эту проблему, воспользуйтесь нашими рекомендациями и заданиями, которые предназначены для первого ознакомления с этим математическим понятием.
Четные и нечетные числа от 1 до 20 для дошкольников
Прежде чем выполнять задания, ребенок должен понять, что такое четные и нечетные числа от 1 до 20. Для этого можете распечатать и показать ему самое первое правило, которое он должен запомнить (можно прикрепить его к стене на время обучения). Объясните ребенку, что все числа, заканчивающиеся на 0, 2, 4, 6 и 8 — четные. Руководствуясь этим правилом, пусть ребенок ответит, на какие цифры должны заканчиваться нечетные числа (т.е. на 1, 3, 5, 7, 9).

Затем объясните ребенку, что все четные числа делятся на 2, а нечетные — не делятся на 2. Распечатайте второе правило:

Распечатайте Лист задания №1 и предложите ребенку обвести все четные числа, затем все нечетные числа.
Лист задание №1

Можете пояснить ребенку, что деление числа на 2 означает, что число делится пополам. Попросите его поделить пополам некоторые числа. Если ребенок затрудняется с ответами, то делить поровну нужно не числа, а предметы. Разложите перед ним несколько конфет, карандашей или других мелких предметов. Попросите его, например, поделить поровну 6 карандашей. Когда ребенок разделит карандаши, скажите ему, что он только что разделил число 6 на 2. Значит, 6 — это четное число. Попросите поделить поровну 5 карандашей. Когда ребенок поймет, что 5 невозможно поделить на одинаковое количество — скажите, что это и есть НЕчетное число, его невозможно разделить на 2.
Соедини числа по правилу — четное, нечетное
После того, как ребенок разобрался с понятием четных и нечетных чисел, предложите ему выполнить наши веселые задания в картинках. В первом задании обаятельного волка из всеми известного мультика «Ну погоди!» нужно привести к зайцу . Волк в этом задании настроен очень дружелюбно и совершенно не хочет конфликтовать с зайцем, поэтому идет к нему с цветами. Чтобы волк смог дойти, ему нужно проложить путь с помощью кружочков с числами. Но соединять эти числа между собой нужно определенным образом. Пусть ребенок возьмет цветной карандаш и, начиная с самой маленькой цифры, начнет проводить путь только через кружки с четными числами, и самое главное — по порядку счета! Второе задание выполняется аналогично — только теперь путь прокладывается через кружки с нечетными числами.
Скачать задание «Соедини четные и нечетные числа» вы можете внизу страницы.

Посчитай и найди четные или нечетные числа
Еще одна проверка знаний четных и нечетных чисел для детей представлена в следующем упражнении. В первом задании ребенок должен сказать, какие продукты зайчики поделили поровну между собой. Чтобы узнать это, ребенку необходимо посчитать количество продуктов в каждой группе и сказать, четное оно или нечетное. Если четное — продукты поделятся поровну, если нечетное — то нет. Во втором задании нужно посчитать, сколько на картинке: солнечных лучиков, тучек, яблок, грибов, птичек, зверят, деревьев, цветов. А затем ответить, чего или кого получилось четное количество?
Скачать задания по нахождению четных и нечетных чисел вы можете во вложениях внизу страницы.

Вам могут быть полезны и другие материалы по обучению счету для распечатки:
 Состав числа до 20 — Распечатать числовую таблицу
Состав числа до 20 — Распечатать числовую таблицу
Здесь вы можете состав числа до 20 распечатать в виде числовой таблицы и дать ребенку для заполнения. Такое занятие прекрасно тренирует навыки счета дошкольников, а также приучает решать примеры до 20.
 Учимся считать до 20 с героями мультфильмов
Учимся считать до 20 с героями мультфильмов
В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.
 Считаем до 20 — Карточки с числами и предметами
Считаем до 20 — Карточки с числами и предметами
Здесь мы считаем до 20, используя карточки с числами. На каждом листе-карточке расположено число от 1 до 20 и различные предметы, количество которых равняется данному числу.
 Устный счет в пределах 10 — Картинки с заданиями
Устный счет в пределах 10 — Картинки с заданиями
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках.
 Раскраски с заданиями на счет в пределах 10
Раскраски с заданиями на счет в пределах 10
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями.
 Прописи-цифры от 1 до 10 для распечатки — Скачай и обводи
Прописи-цифры от 1 до 10 для распечатки — Скачай и обводи
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
А также потренируйтесь в математических играх от лисенка Бибуши:
 Игра «Счет от 1 до 10 — Посчитай картинки и выбери число»
Игра «Счет от 1 до 10 — Посчитай картинки и выбери число»
В этой игре малыш должен посчитать количество предметов на игровом экране и нажать на соответствующее число. После этого он увидит и услышит порядковый счет до данного числа.
 Игра «Найди числа на картинке» для малышей от 4 лет
Игра «Найди числа на картинке» для малышей от 4 лет
Здесь ребенку нужно быть внимательным, чтобы найти все спрятанные числа на картинке. В игре также используется порядковый счет.
 Математическая игра «Найди наибольшее и наименьшее число»
Математическая игра «Найди наибольшее и наименьшее число»
В этой игре ребенку необходимо выбрать среди предложенных чисел самое большое или самое маленькое.
 Игра «Сложение и вычитание до 10» — Задачки в картинках
Игра «Сложение и вычитание до 10» — Задачки в картинках
Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши
 Задачи-примеры для малышей в картинках
Задачи-примеры для малышей в картинках
Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10.
bibusha.ru
2. Исследование функции на четность и нечетность.
Функция 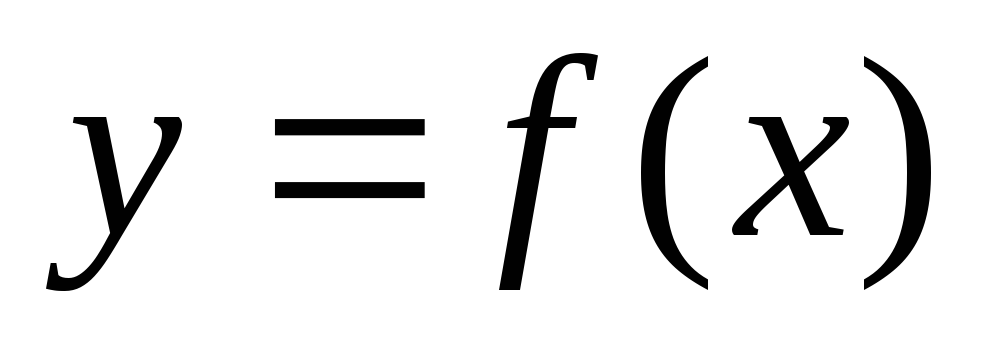 называется четной (нечетной), если для
любого
называется четной (нечетной), если для
любого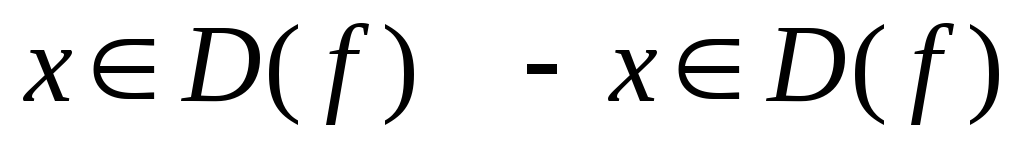 и выполняется равенство
и выполняется равенство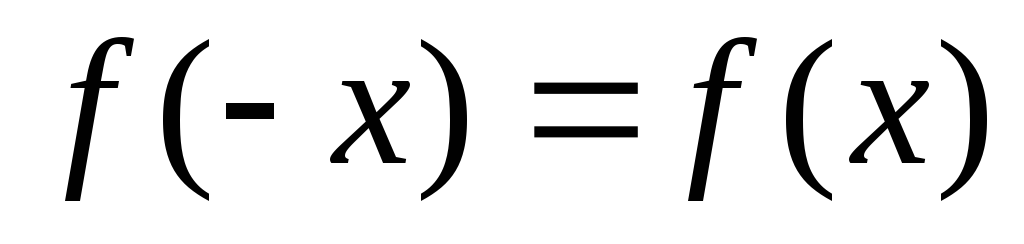
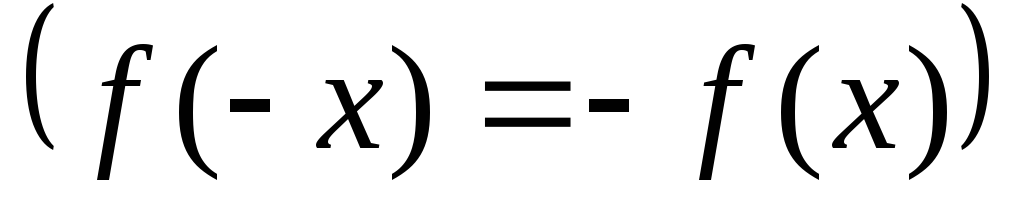 .
.
График четной
функции симметричен относительно оси  .
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1) 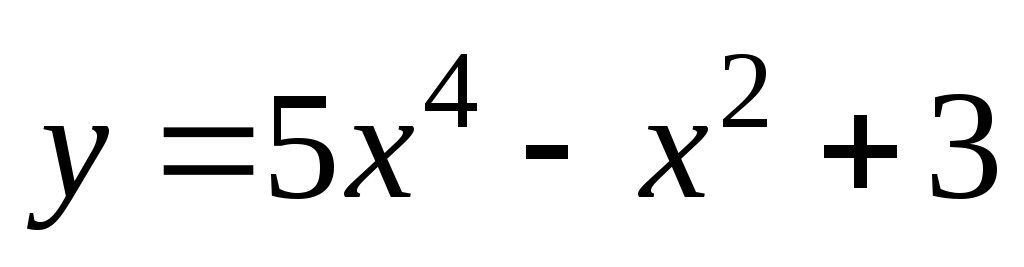 ;
2)
;
2) ;
3)
;
3)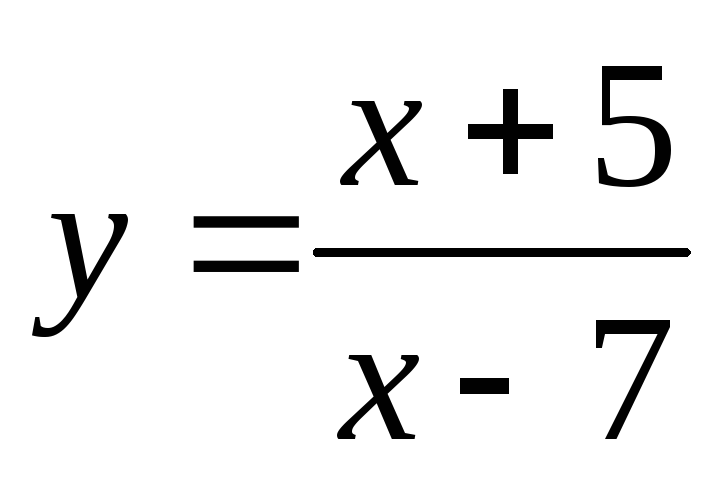 .
.
Решение.
1) Функция определена
при  .
Найдем
.
Найдем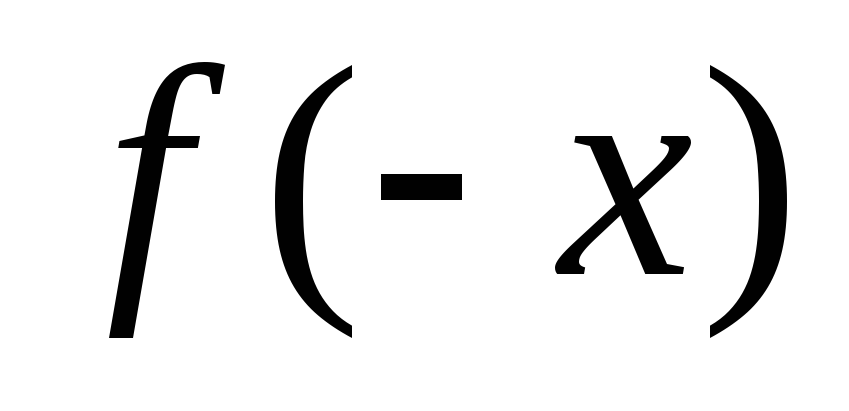 .
.
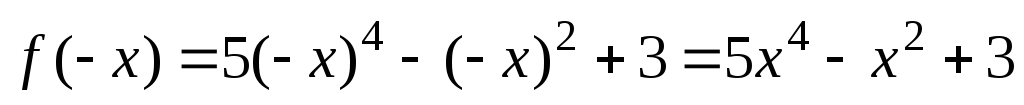 ,
т.е.
,
т.е. 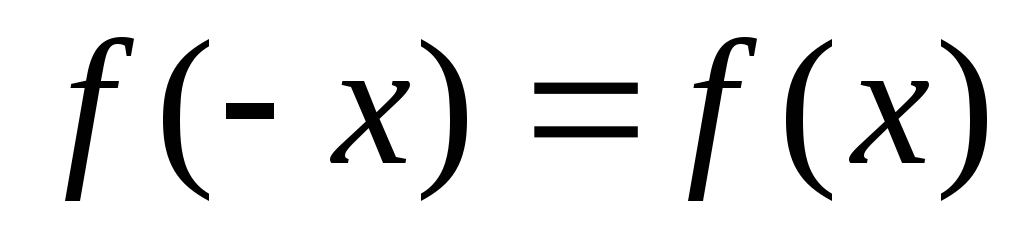 .
Значит, данная функция является четной.
.
Значит, данная функция является четной.
2) Функция определена
при 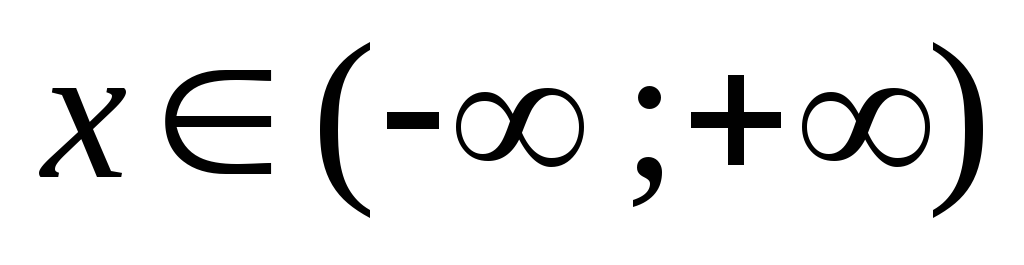
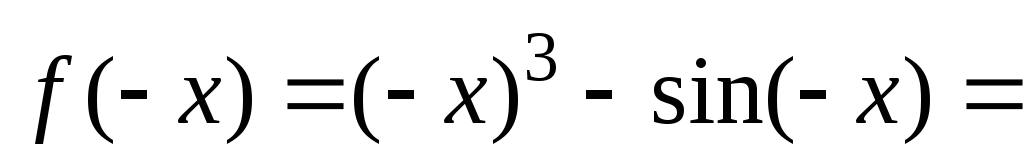
 ,
т.е.
,
т.е. 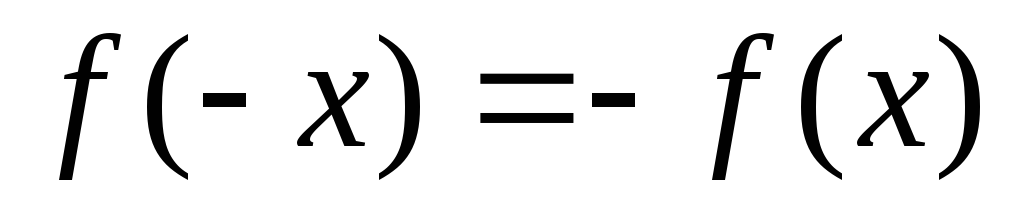 .
Таким образом, данная функция нечетная.
.
Таким образом, данная функция нечетная.
3) функция определена
для 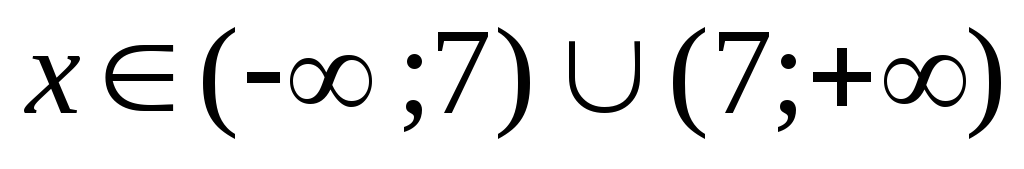 ,
т.е. для
,
т.е. для
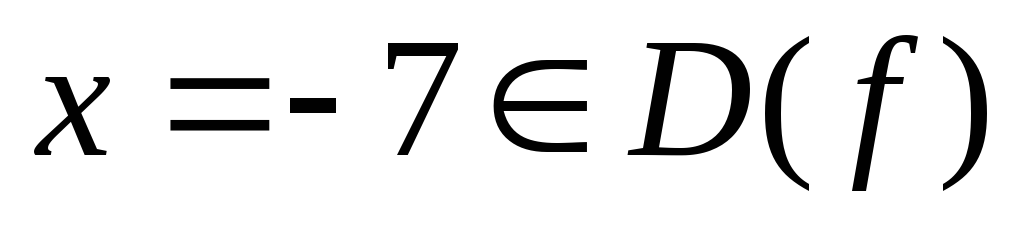 ,
,  .
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция 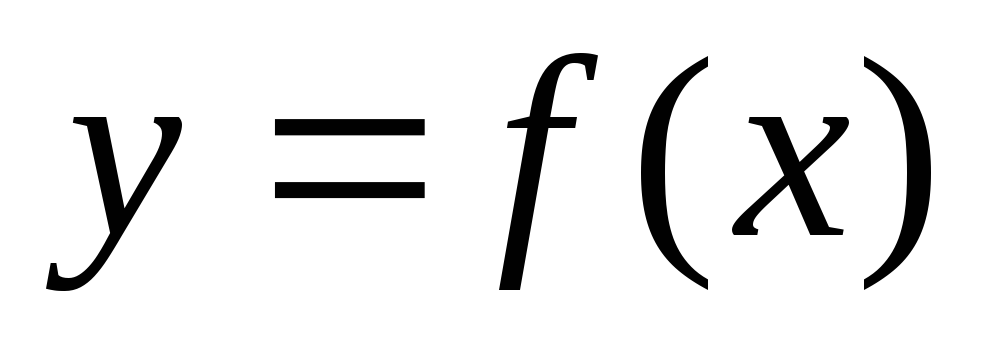 называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие (убывающие) на некотором интервале называются монотонными.
Если функция 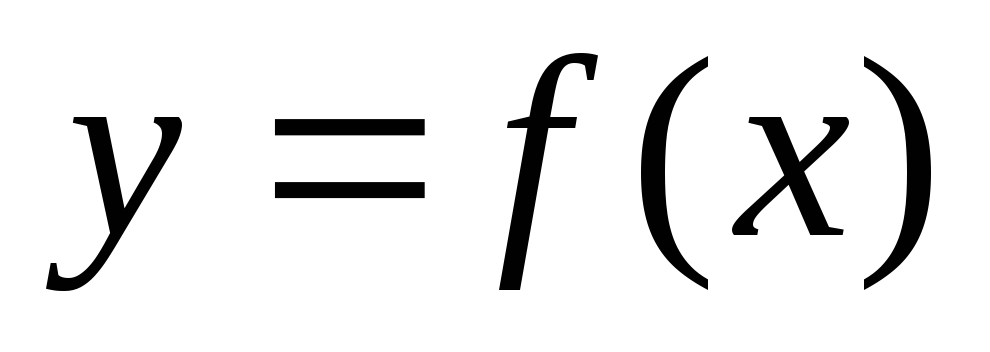 дифференцируема на интервале
дифференцируема на интервале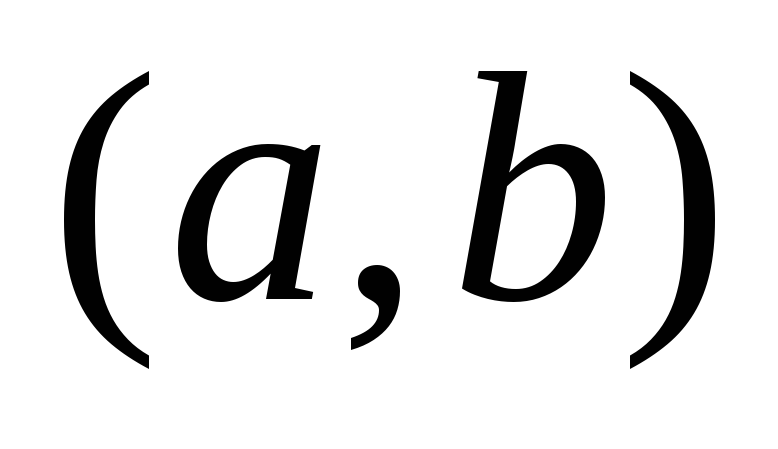 и имеет положительную (отрицательную)
производную
и имеет положительную (отрицательную)
производную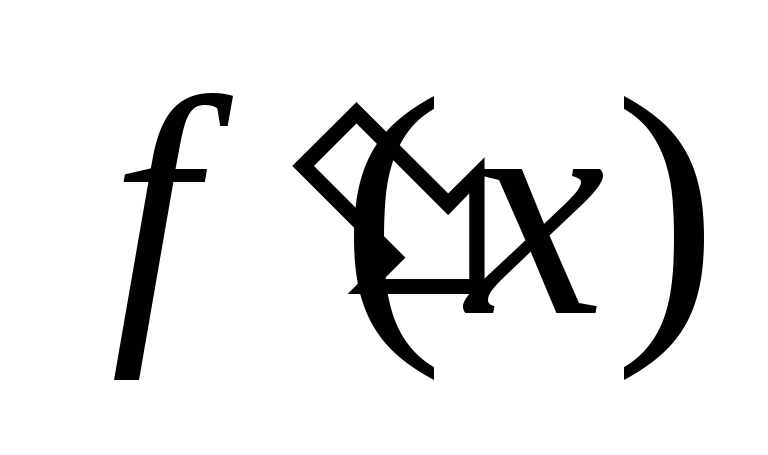 ,
то функция
,
то функция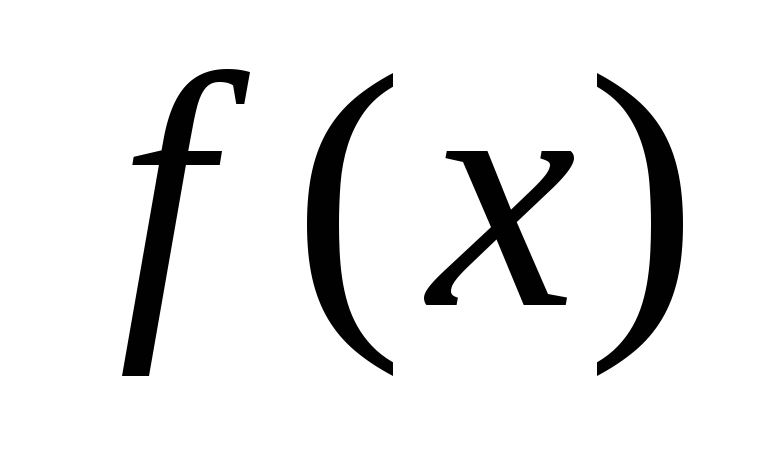 возрастает (убывает) на этом интервале.
возрастает (убывает) на этом интервале.
Пример 6.3. Найти интервалы монотонности функций
1) 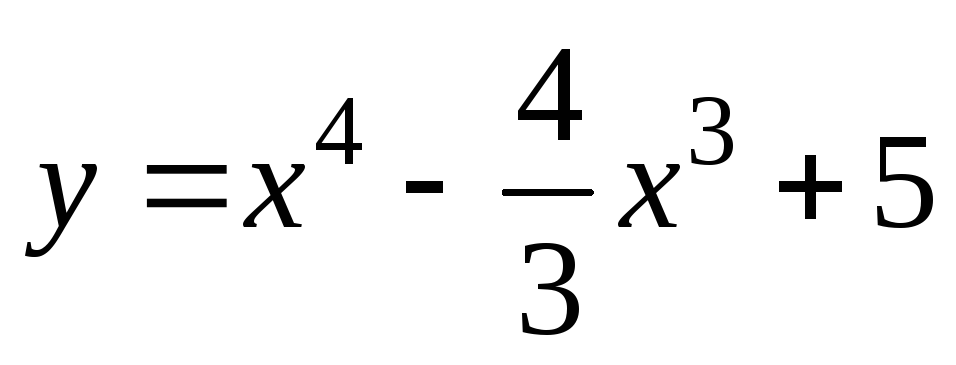 ;
3)
;
3)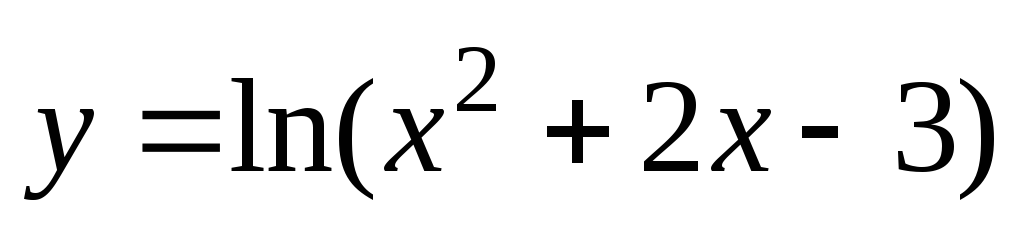 .
.
Решение.
1) Данная функция
определена на всей числовой оси. Найдем
производную  .
.
Производная равна
нулю, если 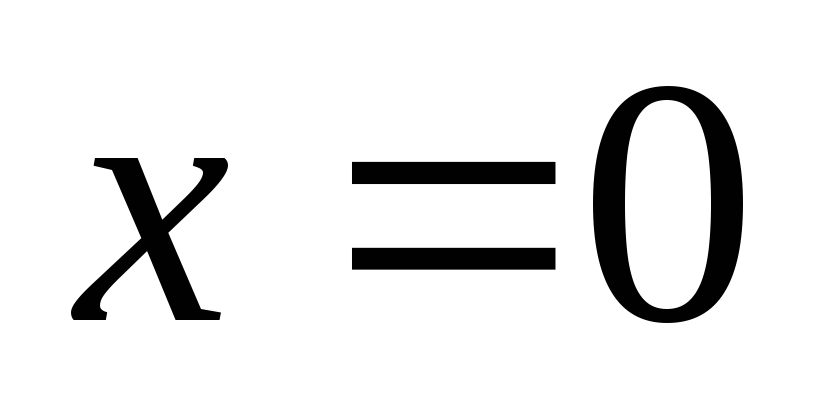 и
и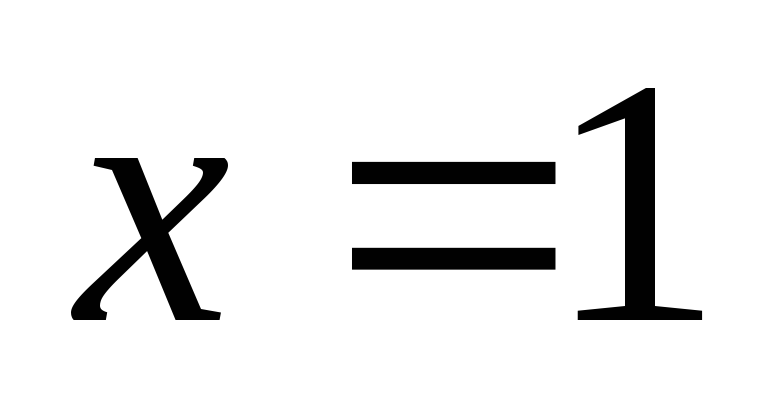 .
Область определения – числовая ось,
разбивается точками
.
Область определения – числовая ось,
разбивается точками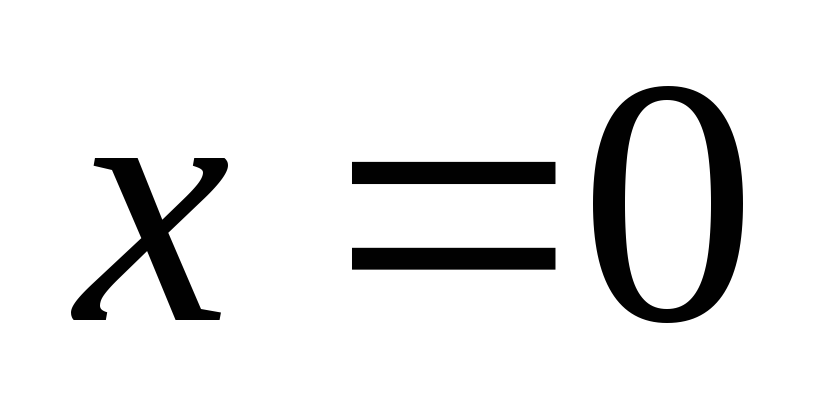 ,
,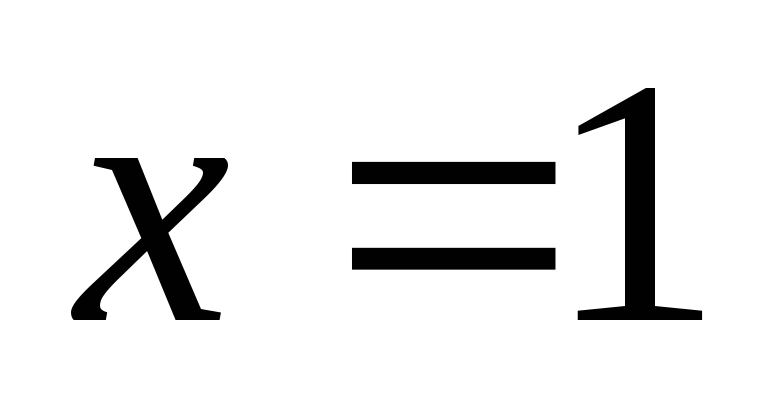 на интервалы. Определим знак производной
в каждом интервале.
на интервалы. Определим знак производной
в каждом интервале.
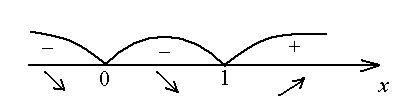
В интервале 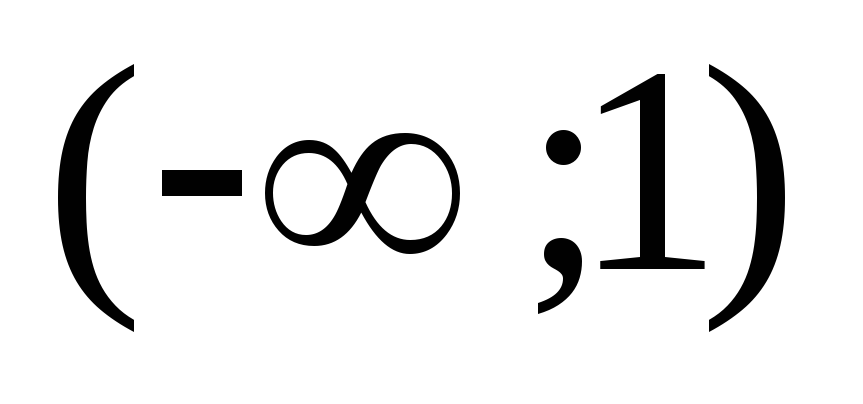 производная отрицательна, функция на
этом интервале убывает.
производная отрицательна, функция на
этом интервале убывает.
В интервале 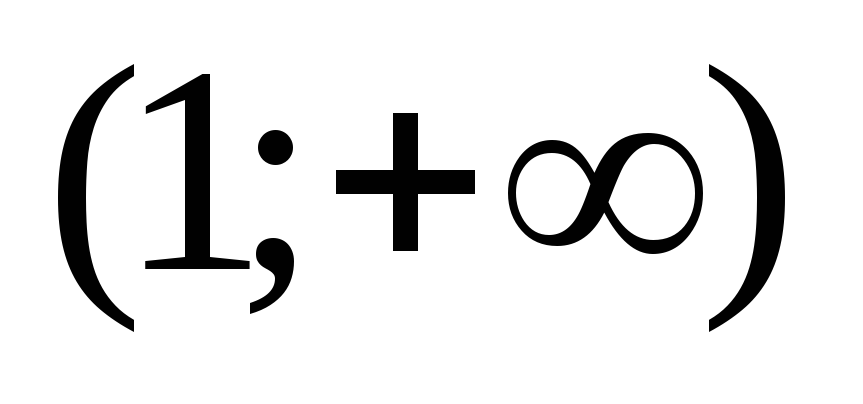 производная положительна, следовательно,
функция на этом интервале возрастает.
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если 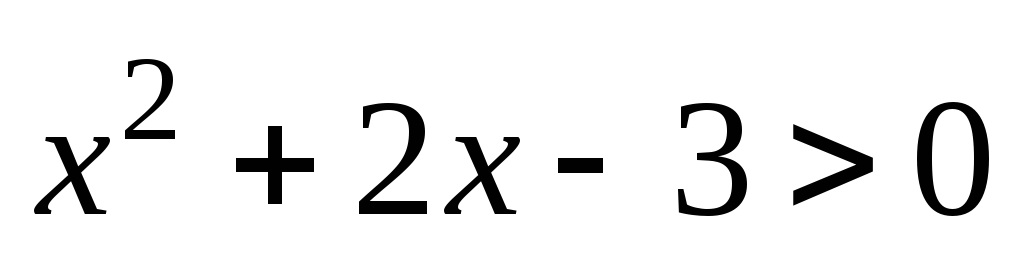 или
или
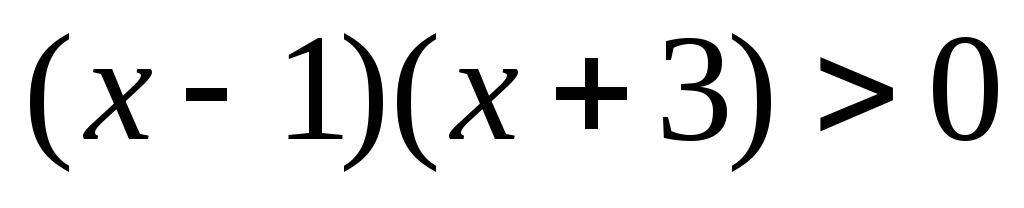 .
.
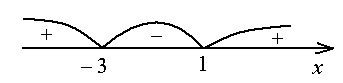
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
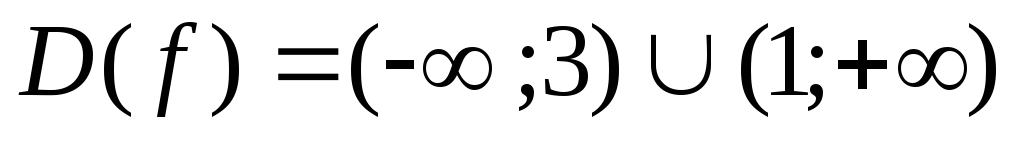 .
.
Найдем производную 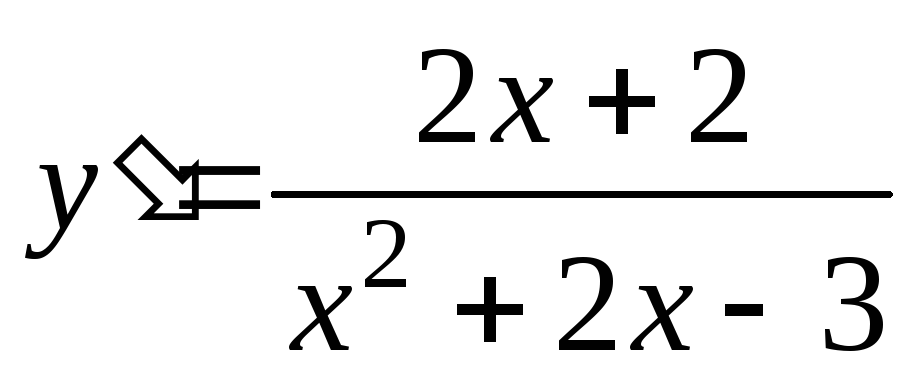 ,
,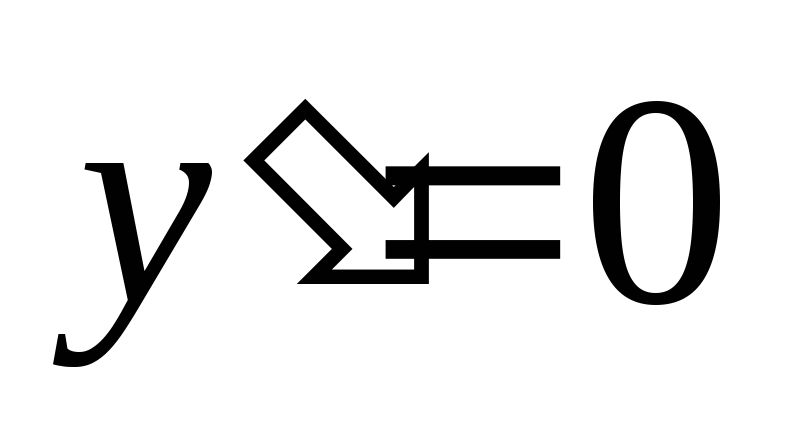 ,
если
,
если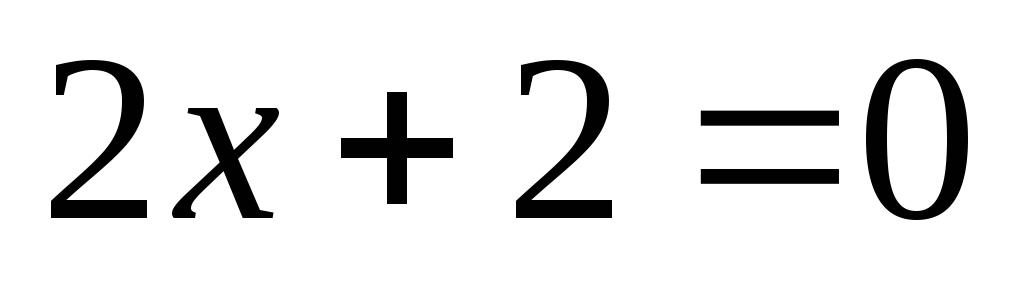 ,
т.е.
,
т.е.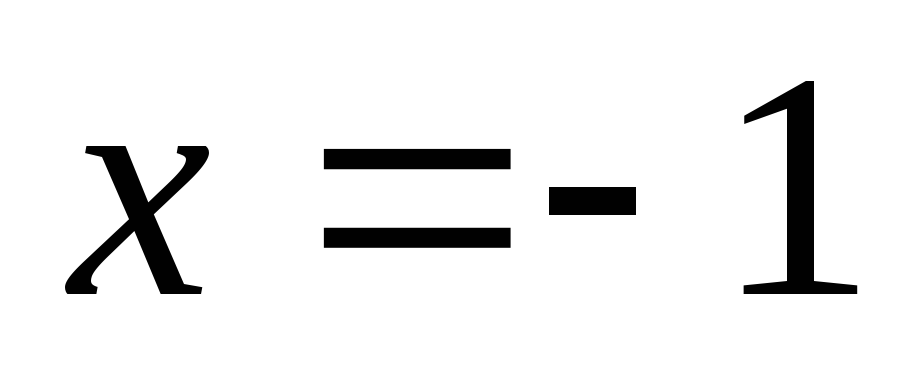 ,
но
,
но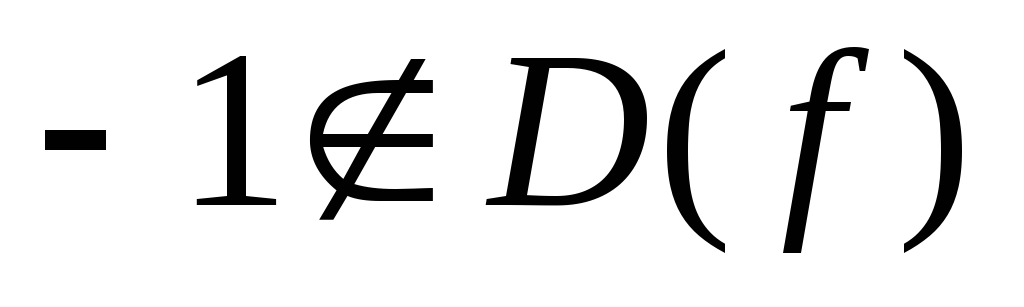 .
Определим знак производной в интервалах
.
Определим знак производной в интервалах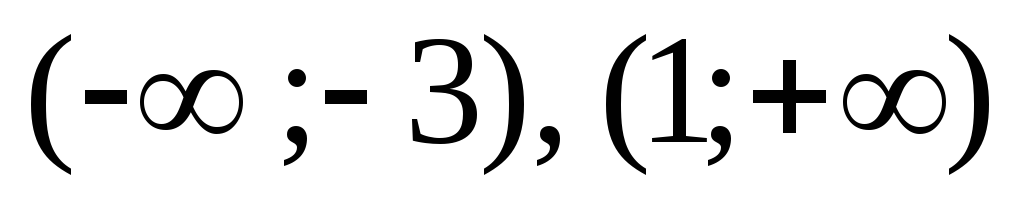 .
.
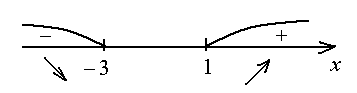
В интервале 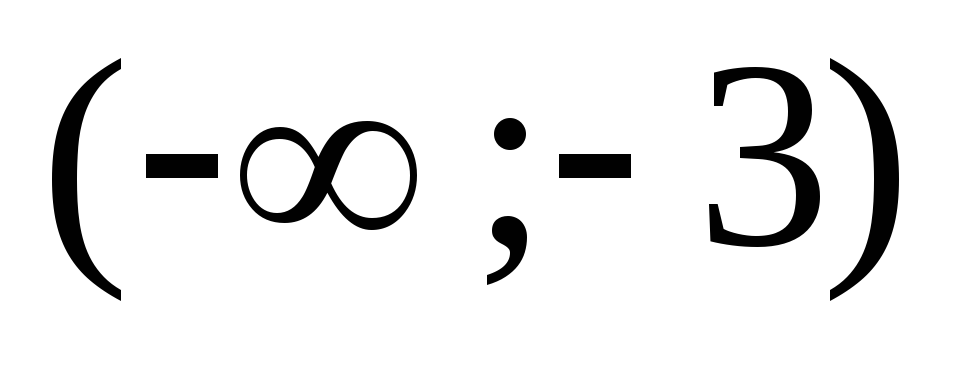 производная отрицательна, следовательно,
функция убывает на интервале.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале.
В интервале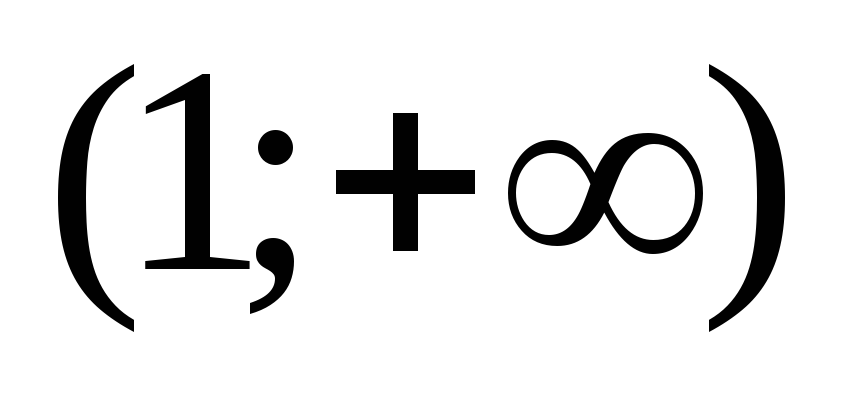 производная положительна, функция
возрастает на интервале
производная положительна, функция
возрастает на интервале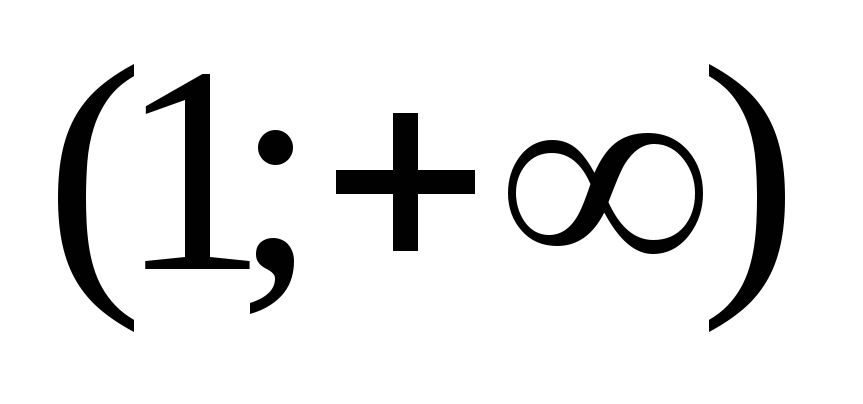 .
.
4. Исследование функции на экстремум.
Точка 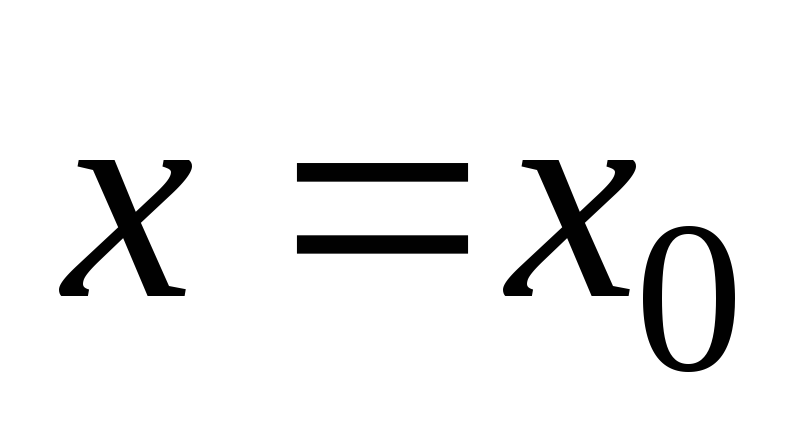 называется точкой максимума (минимума)
функции
называется точкой максимума (минимума)
функции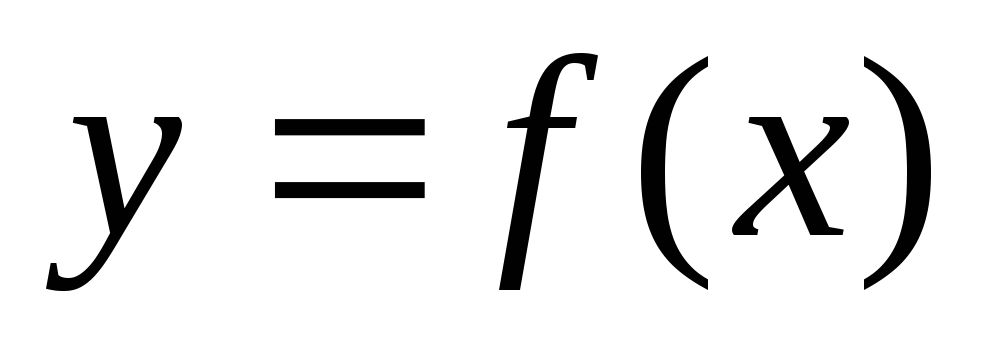 ,
если существует такая окрестность точки
,
если существует такая окрестность точки ,
что для всех
,
что для всех из этой окрестности выполняется
неравенство
из этой окрестности выполняется
неравенство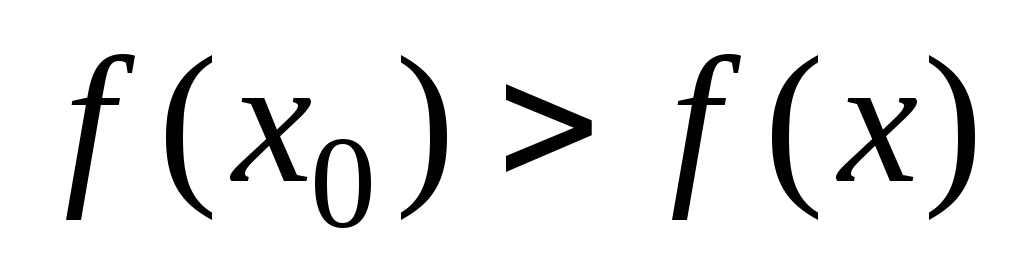
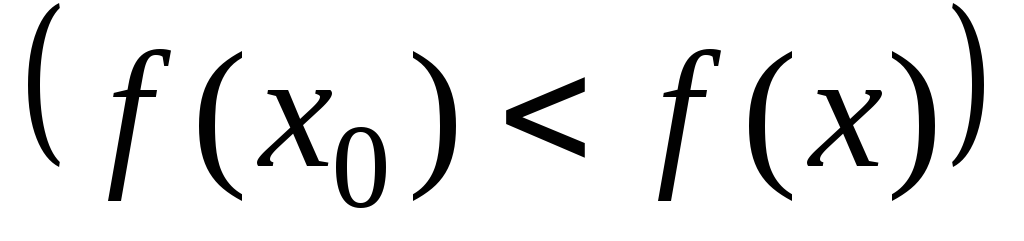 .
.
Точки максимума и минимума функции называются точками экстремума.
Если функция 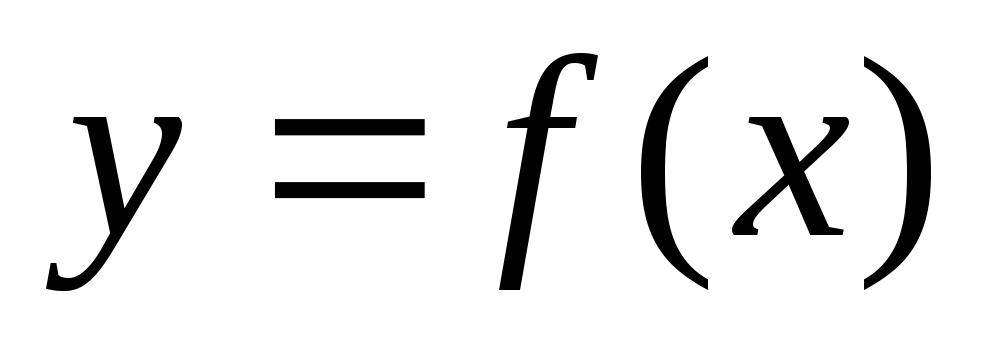 в точке
в точке имеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
имеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых производная равна нулю или не существует называются критическими.
5. Достаточные условия существования экстремума.
Правило 1.
Если при переходе (слева направо) через
критическую точку  производная
производная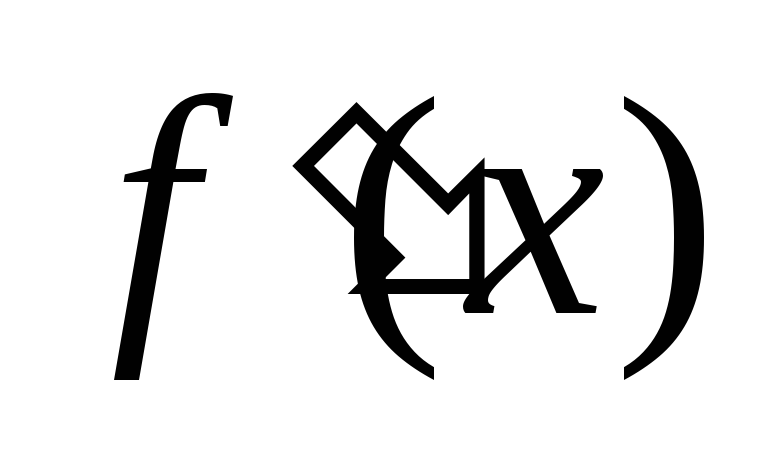 меняет знак с «+» на «–», то в точке
меняет знак с «+» на «–», то в точке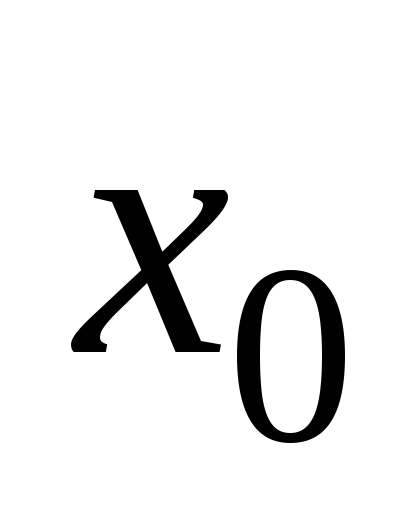 функция
функция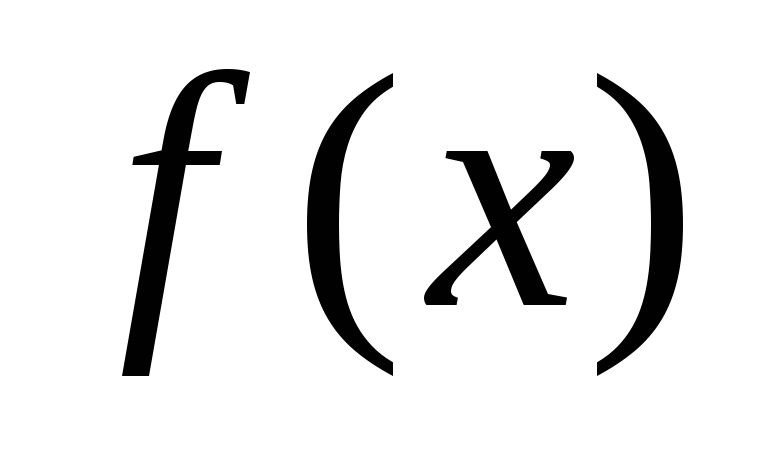 имеет максимум; если с «–» на «+», то
минимум; если
имеет максимум; если с «–» на «+», то
минимум; если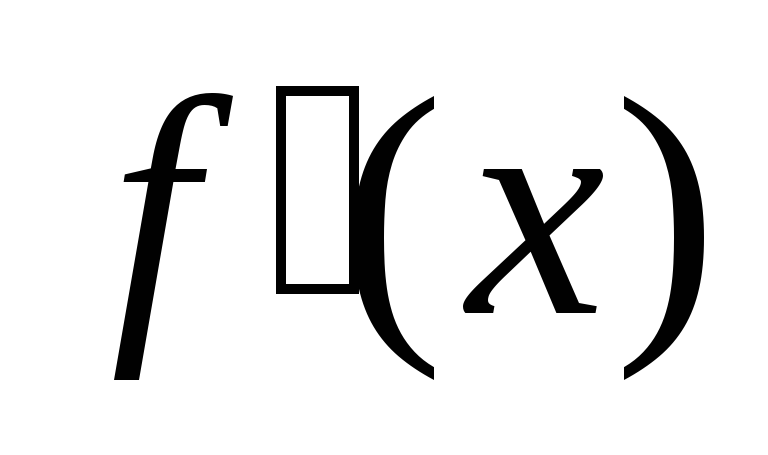 не меняет знак, то экстремума нет.
не меняет знак, то экстремума нет.
Правило 2.
Пусть в точке  первая производная функции
первая производная функции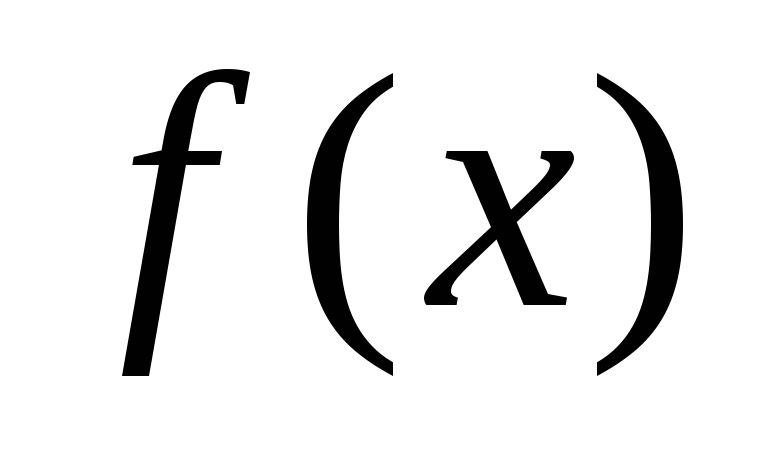 равна нулю
равна нулю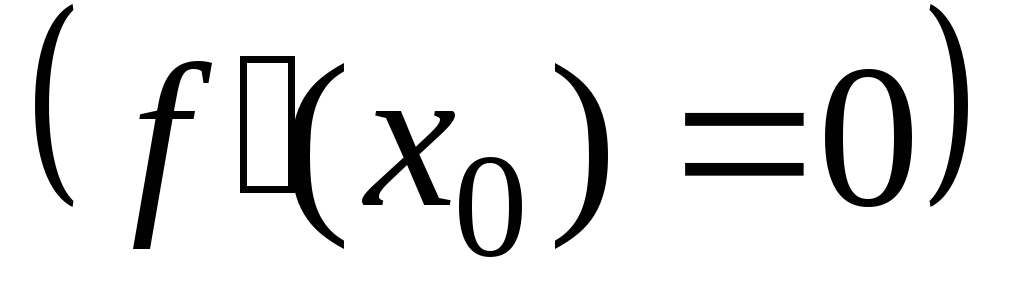 ,
а вторая производная существует и
отлична от нуля. Если
,
а вторая производная существует и
отлична от нуля. Если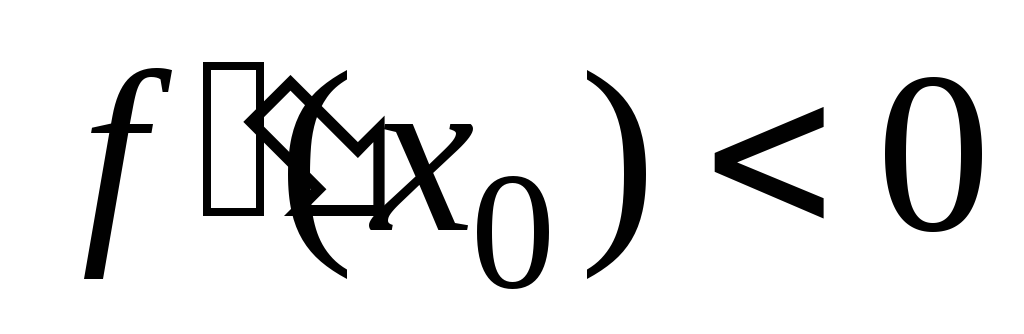 ,
то
,
то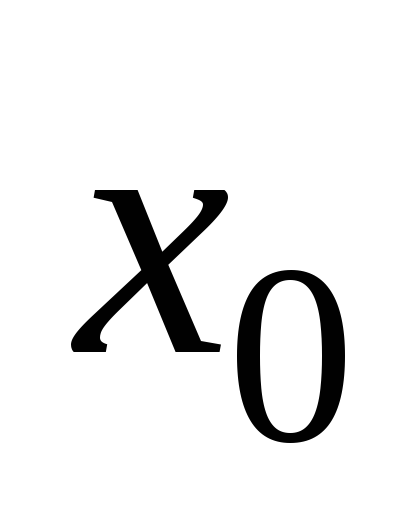 – точка максимума, если
– точка максимума, если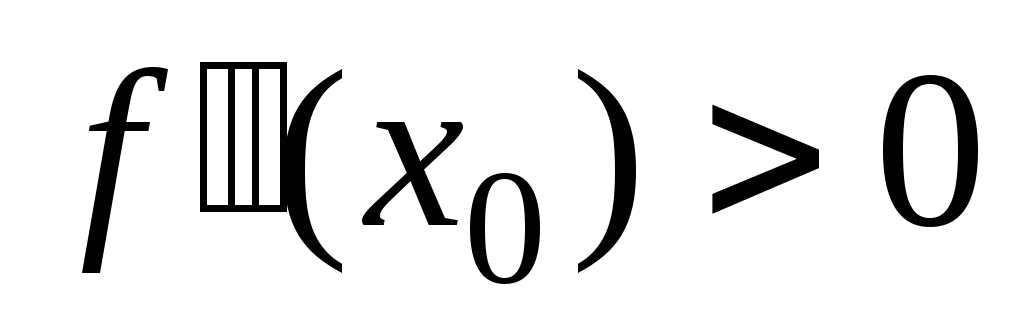 ,
то
,
то – точка минимума функции.
– точка минимума функции.
Пример 6.4. Исследовать на максимум и минимум функции:
1) 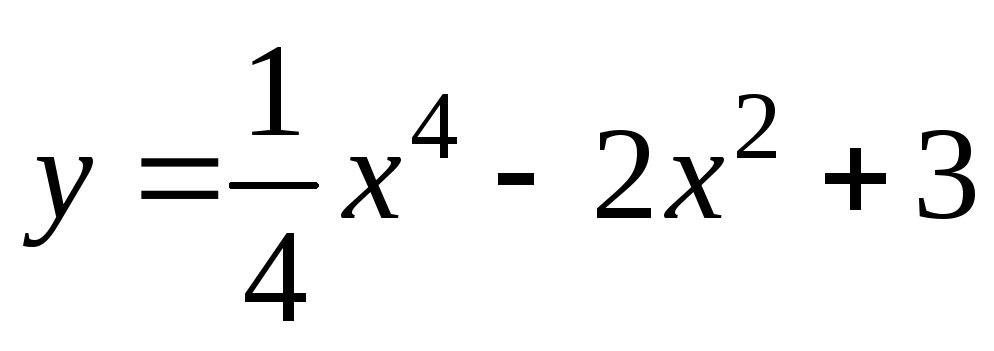 ;
2)
;
2)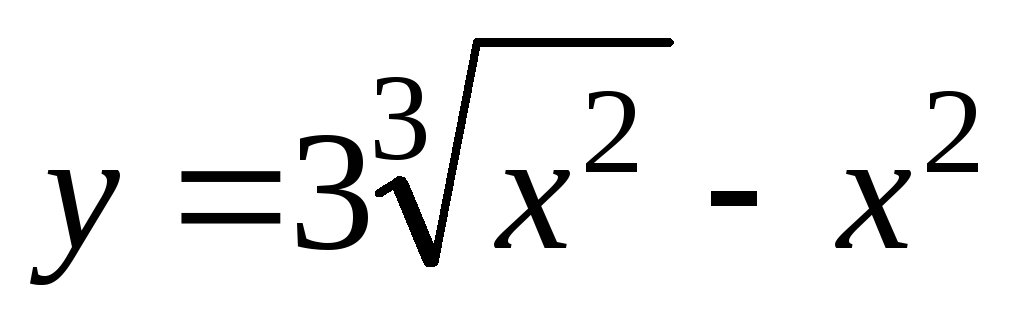 ;
3)
;
3) ;
;
4)  .
.
Решение.
1) Функция определена
и непрерывна на интервале 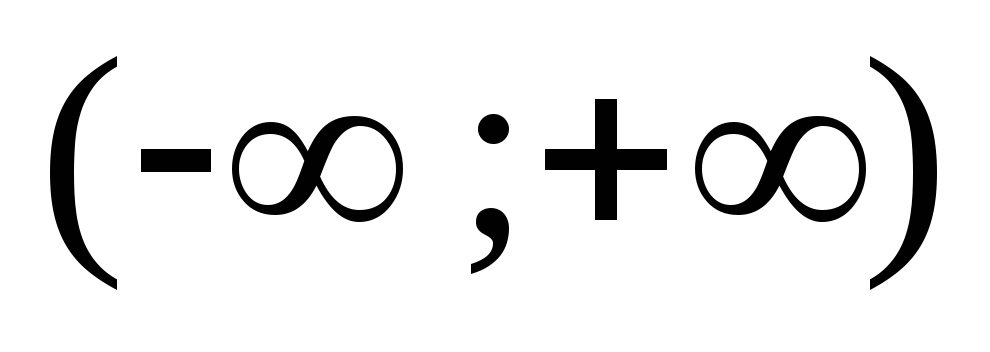 .
.
Найдем производную 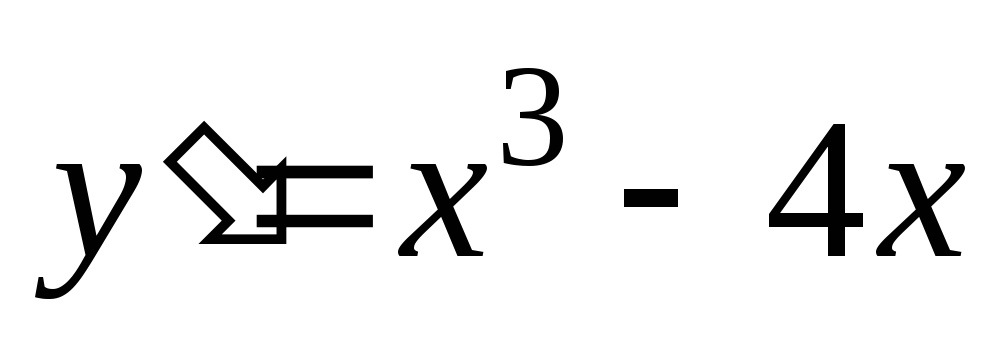 и решим уравнение
и решим уравнение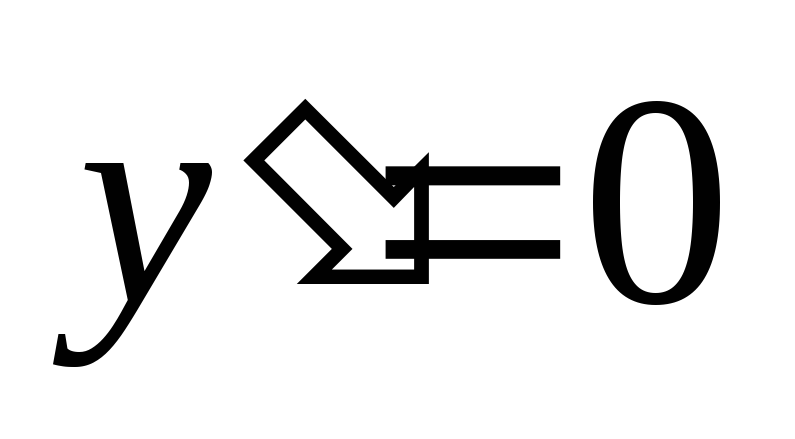 ,
т.е.
,
т.е. .Отсюда
.Отсюда – критические точки.
– критические точки.
Определим знак
производной в интервалах  ,
,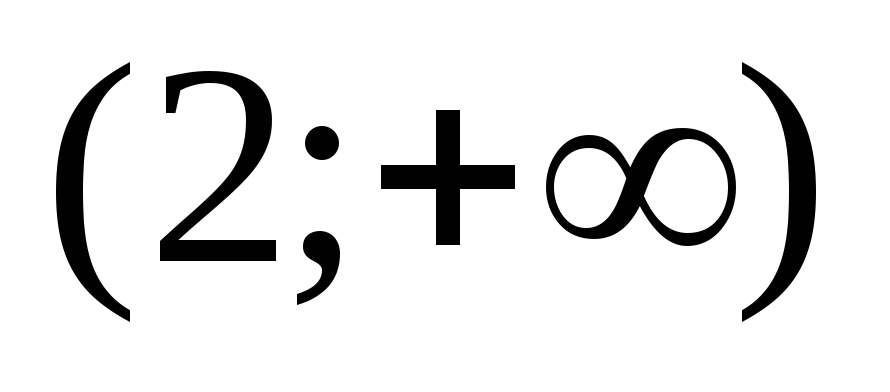 .
.
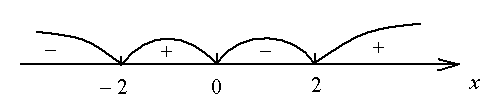
При переходе через
точки
и производная меняет знак с «–» на «+»,
поэтому по правилу 1
производная меняет знак с «–» на «+»,
поэтому по правилу 1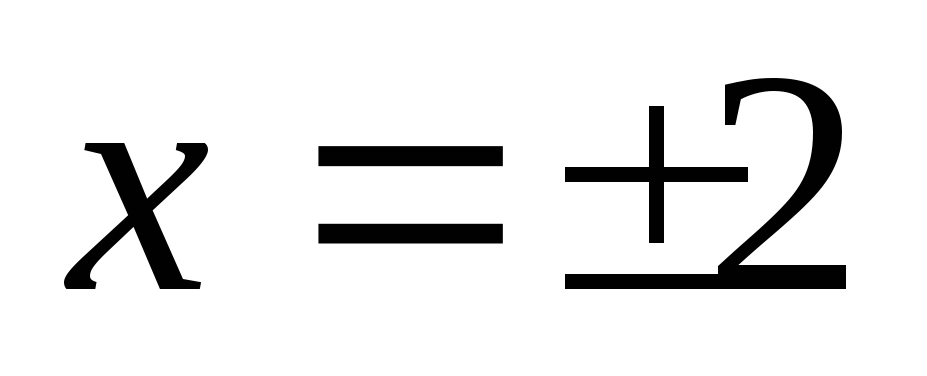 – точки минимума.
– точки минимума.
При переходе через
точку 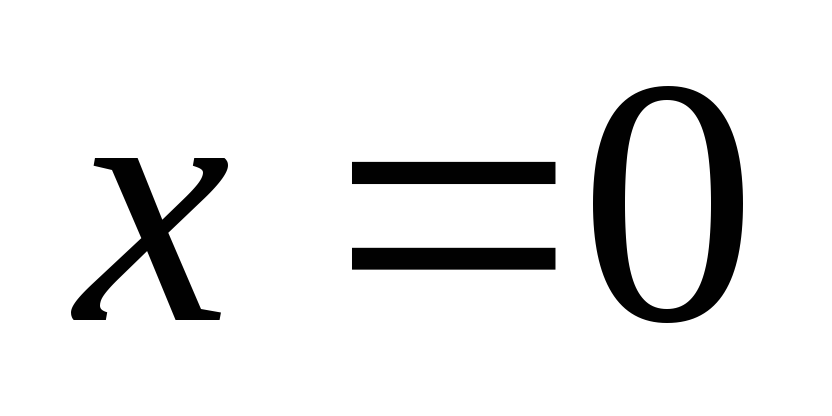 производная меняет знак с «+» на «–»,
поэтому
производная меняет знак с «+» на «–»,
поэтому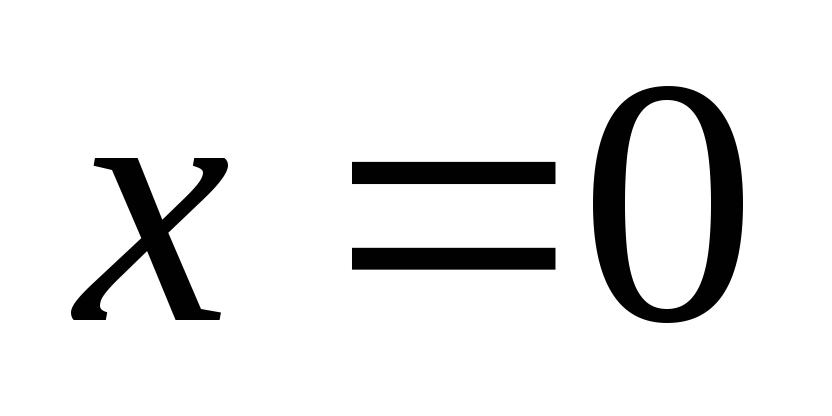 – точка максимума.
– точка максимума.
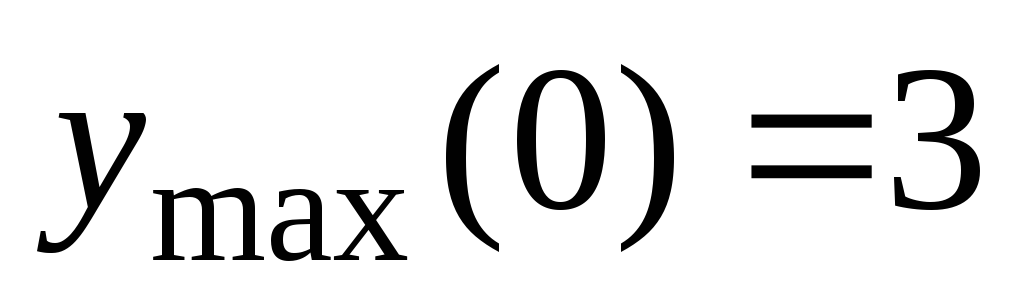 ,
,  .
.
2) Функция определена
и непрерывна в интервале 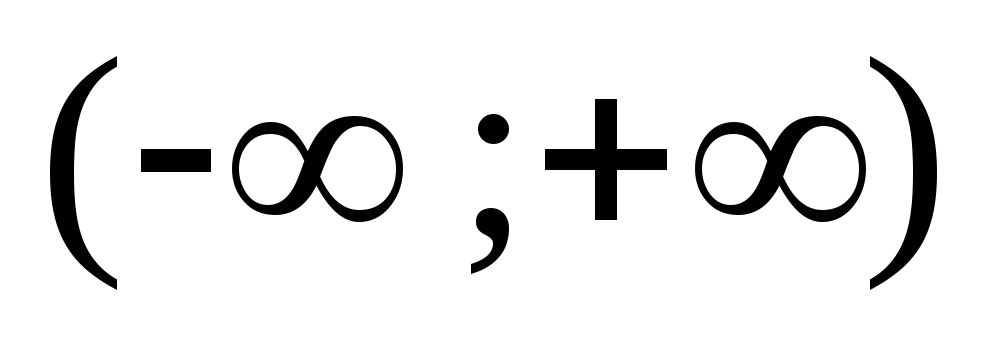 .
Найдем производную
.
Найдем производную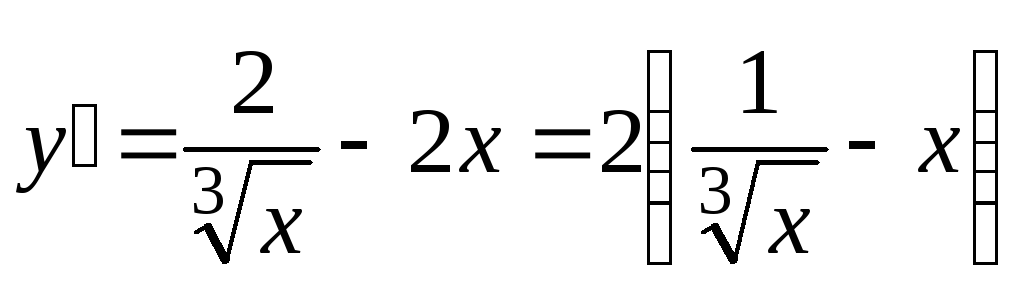 .
.
Решив уравнение 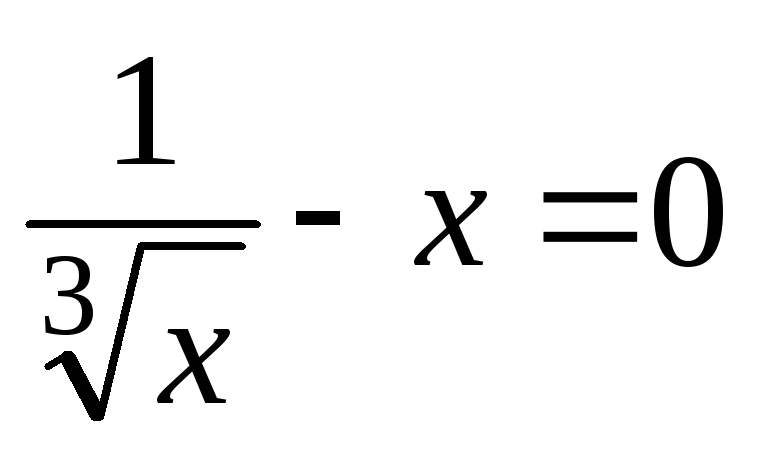 ,
найдем
,
найдем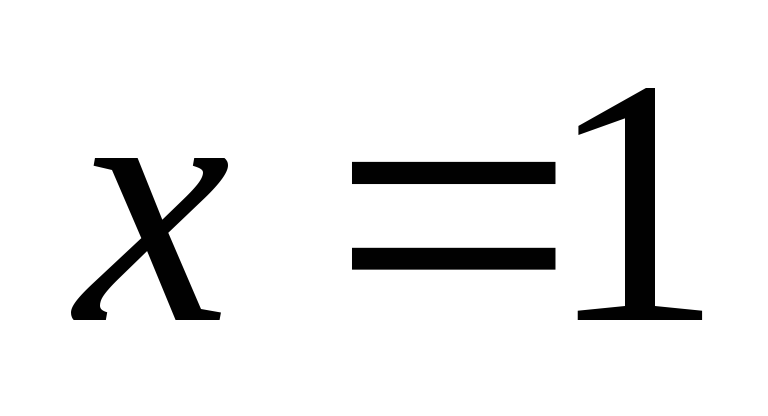 и
и – критические точки. Если знаменатель
– критические точки. Если знаменатель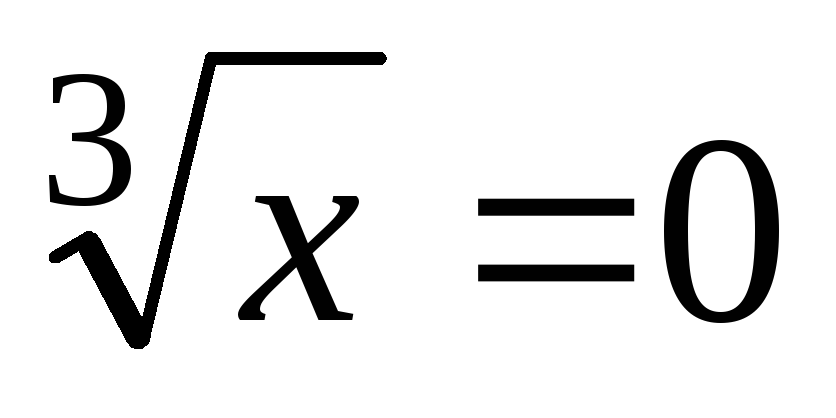 ,
т.е.
,
т.е.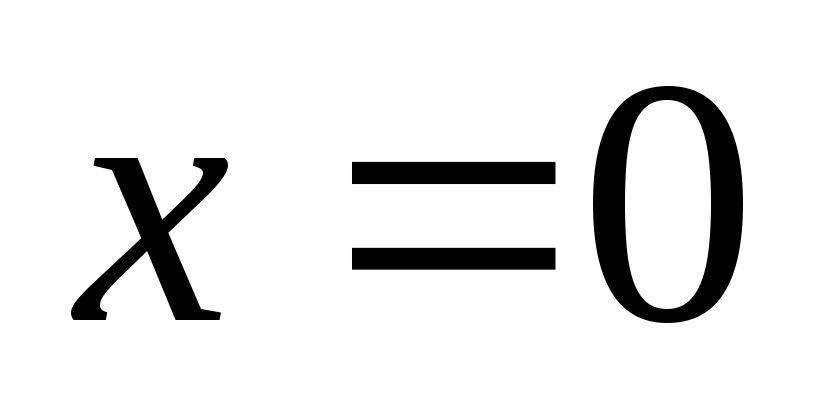 ,
то производная не существует. Итак,
,
то производная не существует. Итак,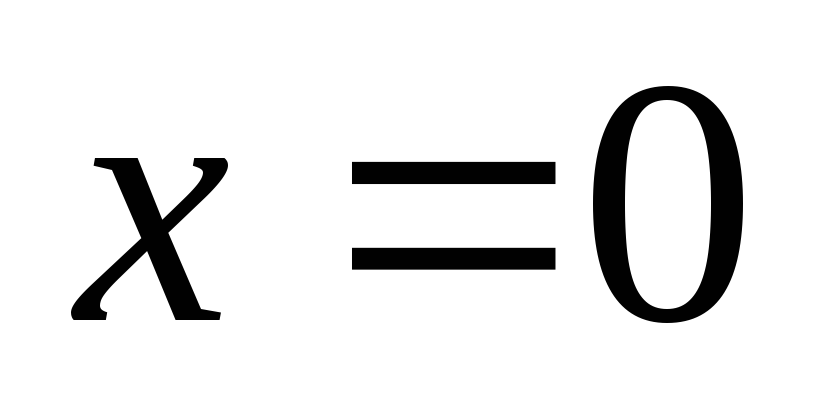 – третья критическая точка. Определим
знак производной в интервалах
– третья критическая точка. Определим
знак производной в интервалах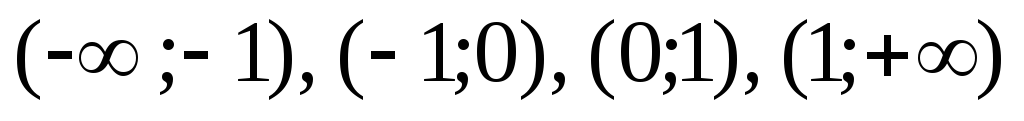 .
.
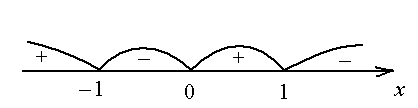
Следовательно,
функция имеет минимум в точке  ,
максимум в точках
,
максимум в точках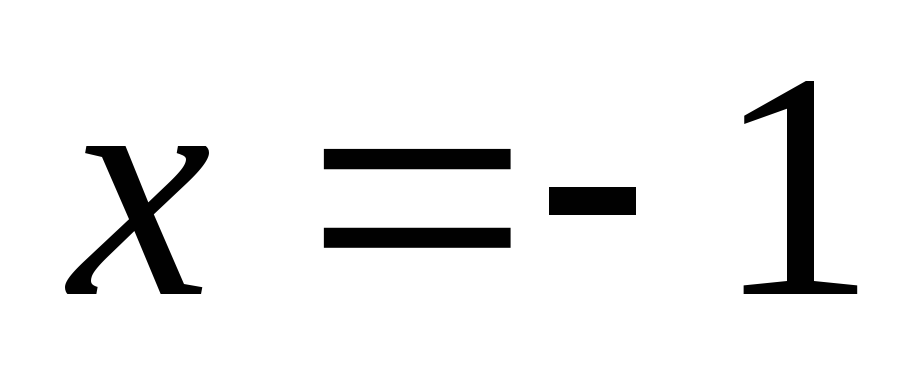 и
и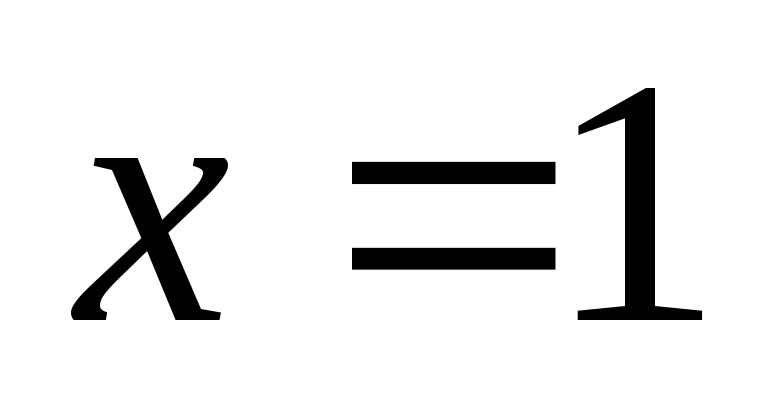 .
.
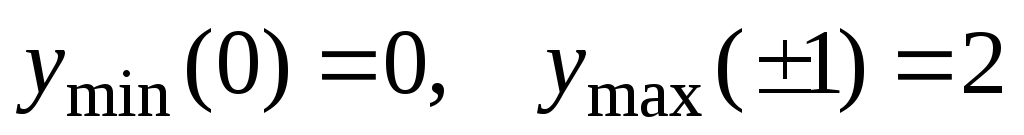 .
.
3) Функция определена
и непрерывна, если 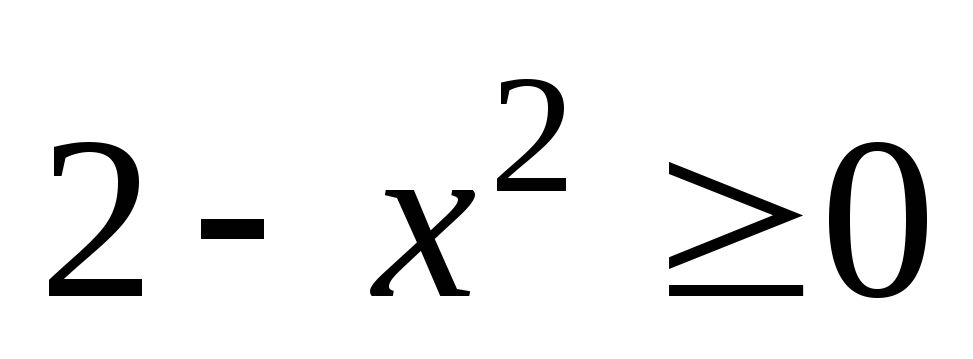 ,
т.е. при
,
т.е. при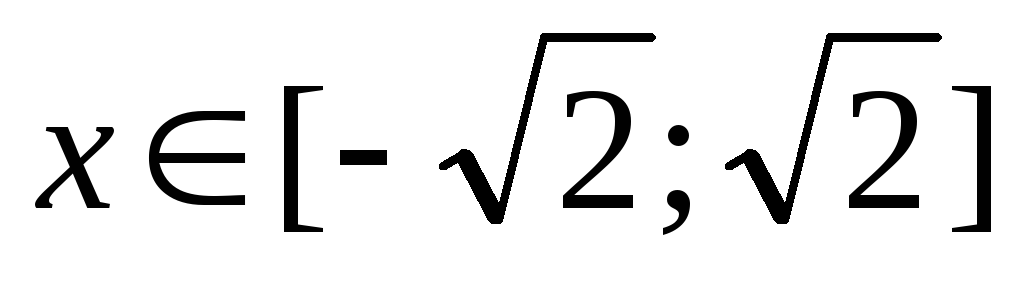 .
.
Найдем производную 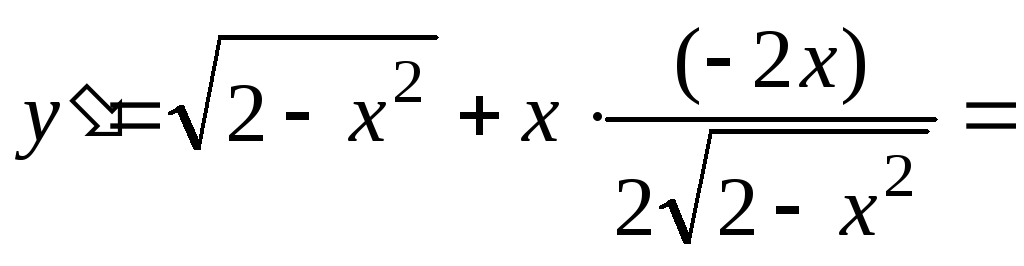
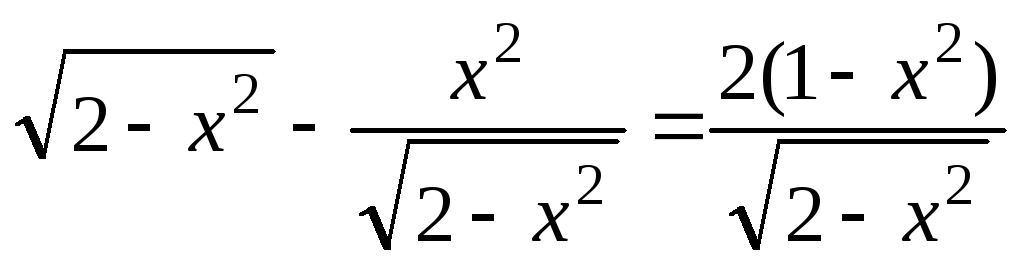 .
.
Найдем критические
точки: 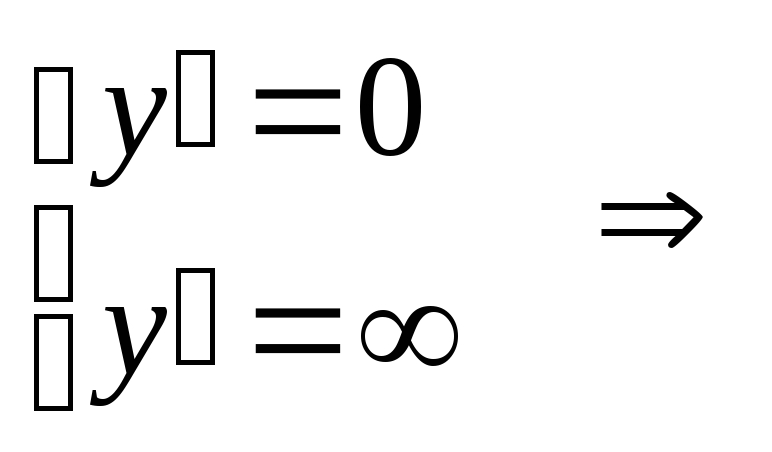
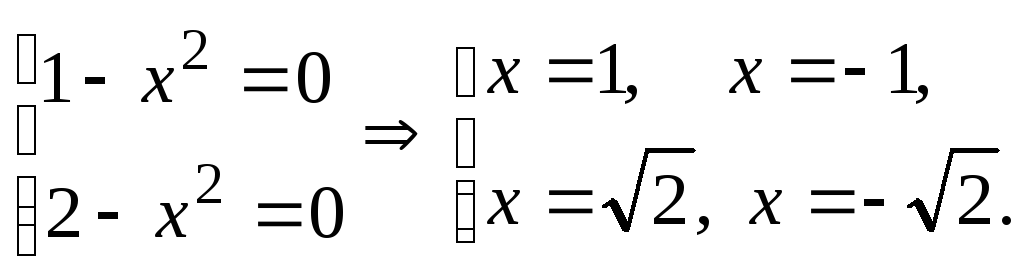
Окрестности точек 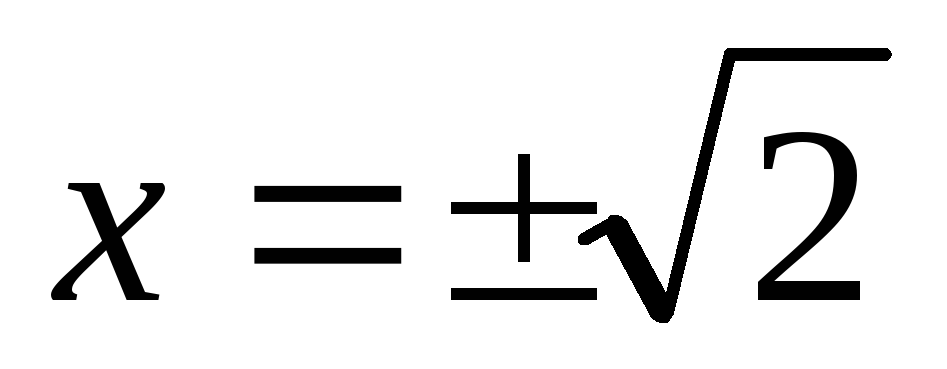 не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки
не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки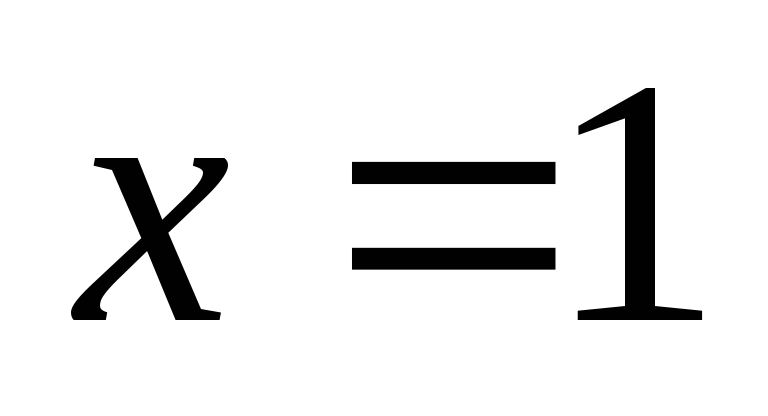 и
и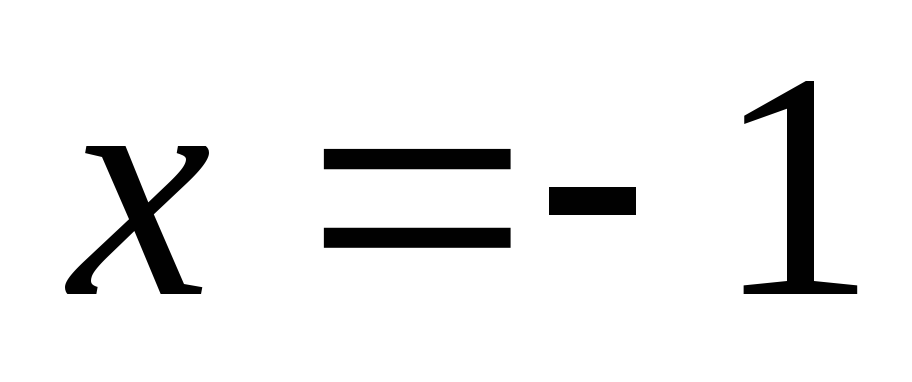 .
.

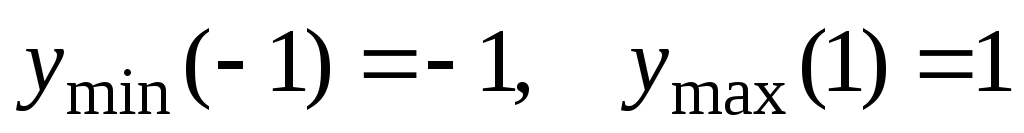 .
.
4) Функция определена
и непрерывна на интервале 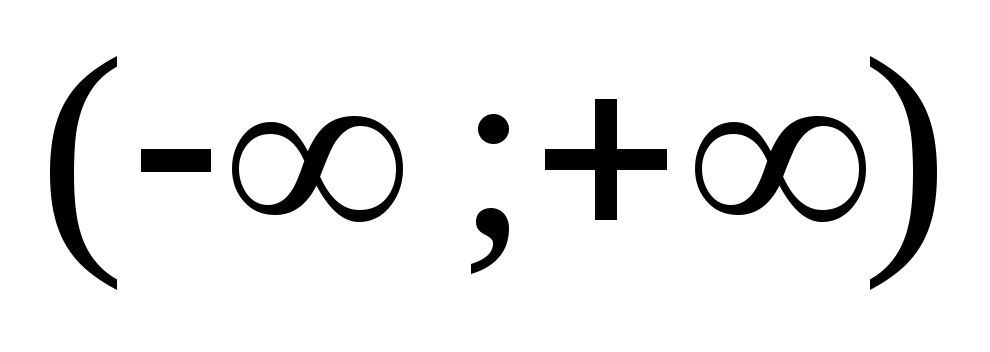 .
Используем правило 2. Найдем производную
.
Используем правило 2. Найдем производную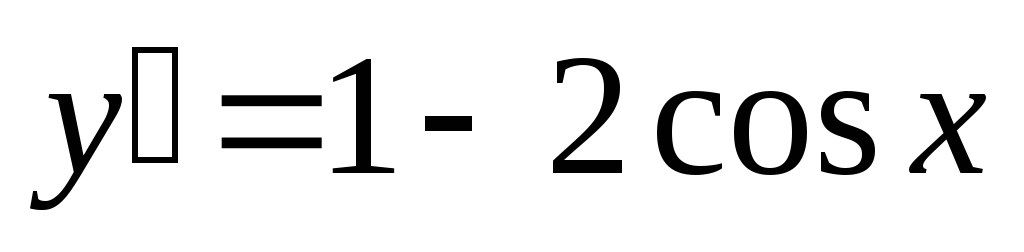 .
.
Найдем критические точки:

Найдем вторую
производную 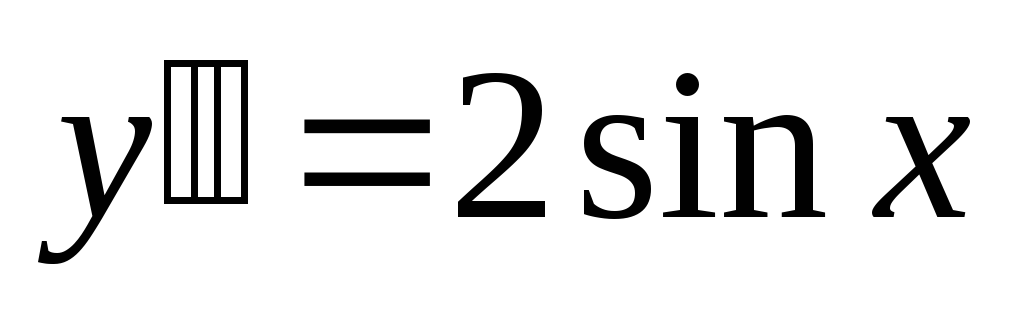 и определим ее знак в точках
и определим ее знак в точках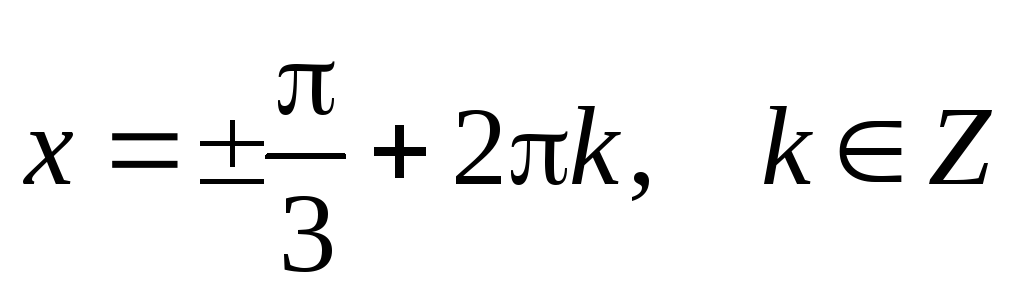
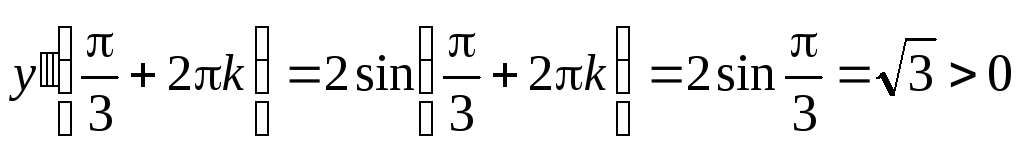 .
.
В точках  функция имеет минимум.
функция имеет минимум.
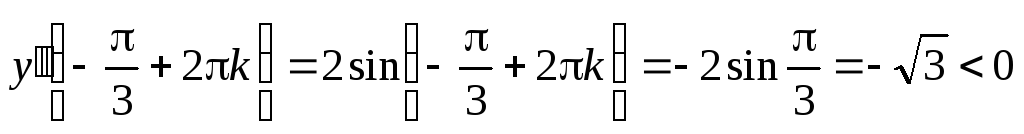 .
.
В точках 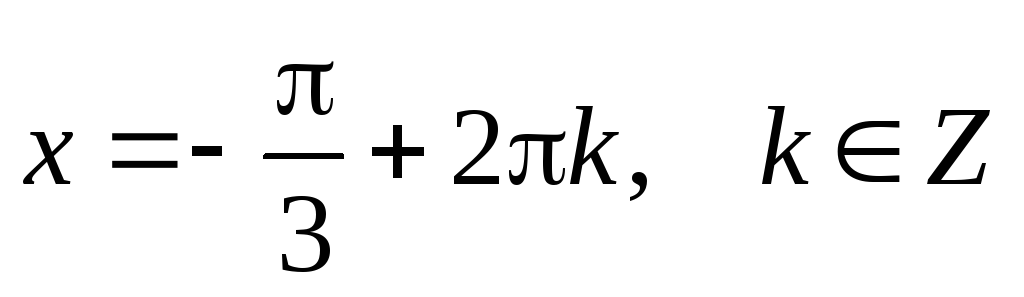 функция имеет максимум.
функция имеет максимум.
studfile.net