Как найти Время, Скорость и Расстояние
Расстояние
Мы постоянно ходим пешком и ездим на транспорте из одной точки в другую. Давайте узнаем, как можно посчитать это пройденное расстояние.
Расстояние — это длина от одного пункта до другого.
- Например: расстояние от дома до школы 3 км, от Москвы до Петербурга 705 км.
Расстояние обозначается латинской буквой S.
Единицы расстояния чаще всего выражаются в метрах (м), километрах (км).
Формула пути Чтобы найти расстояние, нужно умножить скорость на время движения: S = V * T |
Скорость
Двигаться со скоростью черепахи — значит медленно, а со скоростью света — значит очень быстро. Сейчас узнаем, как пишется скорость в математике и как ее найти по формуле.
Скорость определяет путь, который преодолеет объект за единицу времени.
Проще говоря, скоростью называют расстояние, пройденное телом за единицу времени.
Впервые формулу скорости проходят на математике в 5 классе. Сейчас мы ее сформулируем и покажем, как ее использовать.
Формула скорости Чтобы найти скорость, нужно разделить путь на время: V = S/T |
Показатели скорости чаще всего выражаются в м/сек; км/час.
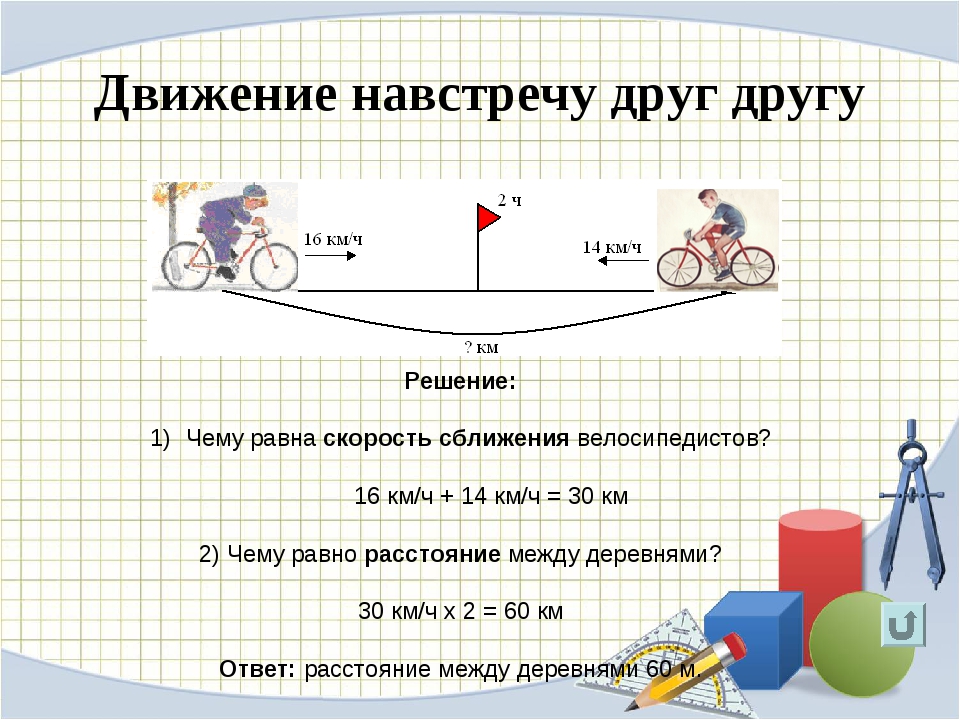
Скорость сближения — это расстояние, которое прошли два объекта навстречу друг другу за единицу времени. Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, которые движутся в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.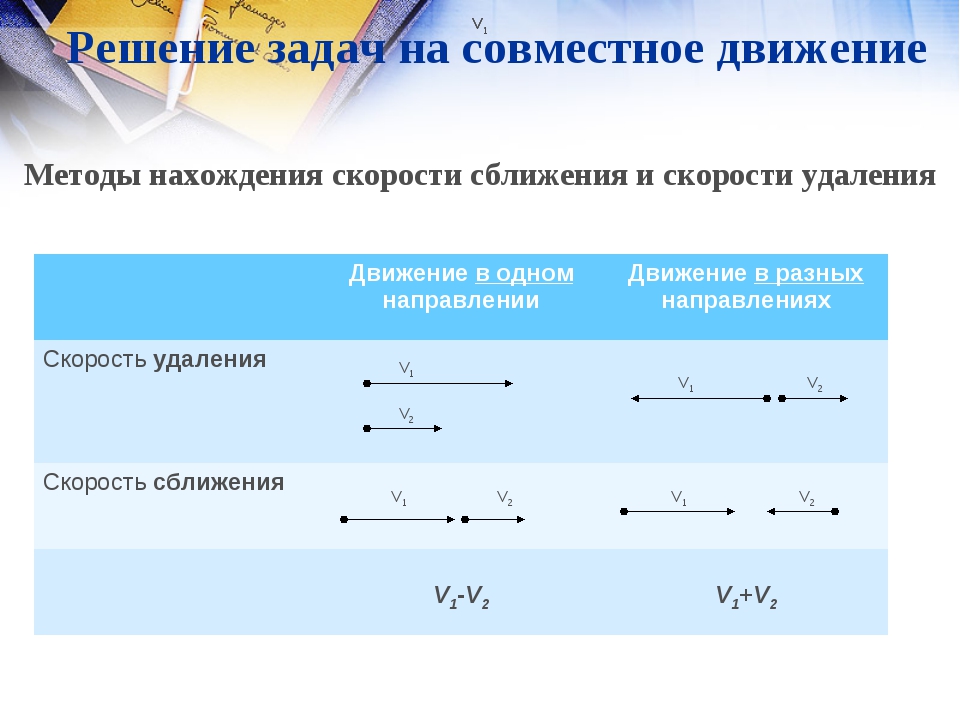
Время
Время — самое дорогое, что у нас есть. Но кроме философии, у времени есть важная роль и в математике.
Время — это продолжительность каких-то действий, событий.
- Например: от метро до дома — 10 минут, от дома до дачи — 2 часа.
Время движения обозначается латинской буквой t.
Единицами времени могут быть секунды, минуты, часы.
Формула времени Чтобы найти время, нужно разделить расстояние на скорость: T = S/V |
Эта формула пригодится, если нужно узнать за какое время тело преодолеет то или иное расстояние.
Взаимосвязь скорости, времени, расстояния
Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.
Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?
Как рассуждаем:
Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:
v = 50 (м/мин)
t = 15 минут
s = v × t = 50 × 15 = 750
Ответ: мы прошли 750 метров.
Если известно время и расстояние, то можно найти скорость: v = s : t.
Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?
Как рассуждаем:
Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.
В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.
Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:
100 : 25 = 4
Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).
100 м : 25 с = 4 м/с
Так мы узнали, что скорость движения первого школьника 4 метра в секунду.
Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:
100 : 50 = 2
Значит скорость движения второго школьника составляет 2 метра в секунду.
Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.
Ответ: первый школьник добежал быстрее.
Если известна скорость и расстояние, то можно найти время: t = s : v.
Задачка 3.
От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?Как рассуждаем:
Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?
Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:
s = 500 метров
v = 100 (м/мин)
t = s : v = 500 : 100 = 5
Ответ: от школы до стадиона мы дойдем за 5 минут.
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.
Задачи на движение (математические формулы) | Учебно-методическое пособие по математике (4 класс) на тему:
t- время
S
V сближения = V1 + V2
S=(V1 + V2) • t
t = S: ( V1 + V2)
d
t- время t- время
S
V удаления = V1 + V2
S= V удаления • t + d
t- время t- время
S
V удаления = V1 + V2
S= V удаления • t
V1 > V2
d t- встречи
V сближения = V1 — V2
S= (V1 — V2) • t встречное — d t встречное = S: V сближения
V1 = S: t + V2
V1
t- время
d s
V удаления = V1 — V2
S= (V1 — V2) • t + d
t= S: (V1 — V2) d-расстояние между точками
1. Задачи на встречное движение
Задачи на встречное движение
2. Движение в противоположных
направлениях
3. Движение в противоположных
направлениях
4. Движение вдогонку
5. Движение с остановками
Эта книжка – помощница будет полезна учащимся 4 класса, учителям, родителям, желающим помочь своим детям научиться решать задачи «на движение».
В книжке представлены математические модели и формулы по решению задач на разные виды движения. Это основная группа задач, которые считаются трудными для учеников начальных классов.
Научиться преодолевать трудности в решении задач на движение – это значит научиться определять зависимость между величинами: скорость, время, расстояние.
Урок математики «Движение с отставанием»
Цели:
- Вывести формулы зависимости расстояния, скорости и времени движения при движении с отставанием;
- Развивать математическую речь, мышление, внимание, память, умение обобщать и делать выводы, самостоятельность;
- Воспитывать уважение к товарищам, аккуратность.

Оборудование: формулы движения, компьютер, проектор, экран.
Ход урока
I. Организационный момент.II. Актуализация знаний:– Над задачами какого типа мы работали с вами на предыдущих уроках? (на движение)
Работа по схемам и формулам.
– Посмотрите на схему задачи. Как называется этот вид движения? (движение в противоположных направлениях)
– Определите, какая формула подходит. (2)
На экране:
(слайд 1)
– Как называется этот вид движения? (встречное движение)
– Определите, какая формула подходит. (3)
На экране:
(слайд 2)
– Как называется этот вид движения? (движение вдогонку)
– Определите, какая формула подходит. (1)
На экране:
(слайд 3)
 Фиксация затруднения в деятельности и постановка проблемы:
Фиксация затруднения в деятельности и постановка проблемы:1) Сравните задачи:
а) «Из пунктов А и В одновременно в одном направлении выехали два поезда. Скорость первого поезда 80 км/ч, расстояние между пунктами 120 км. Найдите скорость второго поезда, если встреча произойдёт через 4 часа».
На экране:
(слайд 4)
– Какое это движение? (вдогонку)
– Скорость второго поезда будет больше или меньше скорости первого поезда? (больше)
– Какую формулу будем использовать? (S= Uсбл.∙t)
– Как решим?
Решают на доске и в тетради:
- 120:4=30(км/ч) – скорость сближения.
- 80+30=110(км/ч) – скорость второго поезда.
Ответ: 110 км/ч скорость второго поезда.
б) «Миша начал догонять Борю, когда расстояние между ними было 100 м. Миша идёт со скоростью 80 м/мин. Найдите скорость Бори, если мальчики встретились через 5 минут».
На экране:
(слайд 5)
– Это, какое движение? (вдогонку)
– У какого мальчика скорость больше? (у Миши)
– Как решить эту задачу?
Решают на доске и в тетради:
- 100:5=20(м/мин.) – скорость сближения.
- 80-20=60 (м/мин.) – скорость Бори.
Ответ: 60 м/мин. скорость Бори.
2) Почему в первой задаче скорость находится сложением, а во второй – вычитанием? (В первой задаче надо найти скорость догоняющего поезда – она больше, поэтому находим сложением. Во второй задаче мы находим скорость мальчика, которого догоняют. Она меньше, поэтому надо вычитать.)
3) Поменяйте данные скоростей в последней задаче. Что получается? (новая задача – движение с отставанием)
Меняются данные на схеме к задаче.
На экране:
(слайд 5)
– Подойдёт ли наше решение к новой задаче? (нет, т. к. встречи не будет)
к. встречи не будет)
– Сумеем ли мы решить новую задачу? Что необходимо вывести для её решения? (формулу зависимости между расстоянием, скоростью и временем движения)
IV. Определение темы и цели урока:– Так какова тема нашего урока? (задачи на движение с отставанием)
– Наша цель на уроке: вывести формулу зависимости расстояния от скорости и времени при движении с отставанием.
V. Построение проекта выхода из затруднения:1) №1 (с. 101) решают письменно в тетрадях.
Учащиеся изображают движение по числовому лучу и находят расстояние между ними через 4 часа.
– Чему равно расстояние между ними через 4 часа? (16 км)
– Как найти это расстояние с помощью вычислений, не выполняя построения?
Решение: (6-2)∙4=16
– Вычитая 2 из 6, что мы находим? (скорость удаления)
2) №2 (с. 101) работа в учебнике и на доске.
Учитель читает задачу до вопросов, учащиеся рассматривают схему.
– Как изменяется расстояние между ними за 1 час? (увеличивается на 3 ед./ч)
– Чему оно будет равно через 1 час? (8 ед.), 2часа? (11 ед.), 3 часа? (14 ед.)
– Сможет ли вертолёт догнать самолёт? Почему?
– Продолжите построение на луче, и заполним таблицу:
На доске: Uуд.=4-1=3(ед./ч)
| t, час | d, ед. |
| 0 | 5 |
| 1 | 5+(4-1)∙1=8 |
| 2 | 5+(4-1)∙2=11 |
| 3 | 5+(4-1)∙3=14 |
| t | 5+(4-1) t |
– О какой скорости мы говорим в этой задаче? (удаления) Как её найти? (4-1)
Заполняется таблица:
– Что обозначает 0 часов? (начало пути)
– Какое между ними было расстояние? (5км)
– Как найти, какое стало через 1 час? 2 часа? 3 часа? t часов?
– А теперь, используя таблицу, выведем формулу зависимости расстояния d между вертолётом и самолётом от времени движения t.
– Что такое 5 ед.? (do)
– Что такое 4-1? (U1-U2=Uуд.)
– Что такое t? (время)
– Кто запишет получившуюся формулу? (d=do+( U1-U2)∙t)
– Как её ещё можно записать? (d=do+ Uуд.∙t)
– Знакома ли нам эта формула? При каком движении? (при противоположном направлении)
3) На основе полученных формул найдите:
На доске:
VI. Первичное закрепление:do=d-Uуд.∙t
t=(d-do):Uуд.
Uуд.=(d-do):t
№3 (с. 101) 1 ученик чертит схему на доске и объясняет:
Решение:
(32-25)∙6=42
Ответ: 42 км будет между ними через 6 часов.
VII. Физминутка.VIII. Закрепление пройденного:№ 6 (с.102): устно составляют задачи, самостоятельно решают.
– Охарактеризуйте данную задачу. (на одновременное движение с отставанием)
– Какую формулу будете использовать? (d=do+ Uуд.∙t)
– Что может двигаться со скоростью 30 км/ч? 60 км/ч?
Первую задачу решают коллективно, остальные по рядам самостоятельно. Дети, решившие первыми, проверяют у учащихся своего ряда.
– Составьте задачи.
Примеры задач:
а) Из двух городов, расстояние между которыми 100 км, одновременно в одном направлении выехали две лодки. Скорость первой 60 км/ч, второй – 30 км/ч. Какое расстояние между ними будет через 3 часа?
100+(60-30)∙3=190
Ответ: 190 км.
б) Из двух городов, расстояние между которыми 100 км, одновременно в одном направлении выехали две лодки. Скорость первой 60 км/ч, второй – 30 км/ч.
Через какое время расстояние между ними будет 190 км?
(190-100):(60-30)=3
Ответ: через 3 часа.
в) Из двух городов, расстояние между которыми 100 км, одновременно в одном направлении выехали две лодки. Скорость первой 60 км/ч. Через 3 часа расстояние между ними было 190 км. С какой скоростью движется вторая лодка?
60-(190-100):3=30
Ответ: 30 км/ч.
г) Из двух городов, расстояние между которыми 100 км, одновременно в одном направлении выехали две лодки. Скорость первой 60 км/ч, второй – 30 км/ч. Через 3 часа расстояние между ними было 190 км. Какое расстояние между ними было в начале пути?
190-(60-30)∙3=100
Ответ: 100км.
IX. Итог:На экране:
(слайд 6)
– Произойдёт ли встреча? (нет)
– Как называется этот вид движения? (движение с отставанием)
– По какой формуле будете решать такие задачи? (d=do+ Uуд. ∙t)
∙t)
- №4 (с. 102) – решение задачи,
- №9 (с.103) 1р.-а), 2р.-б), 3р.-в) – решение уравнений.
Приложение.
наши формулы — математика лучшая наука
Математика в 4 классе запомнилась мне последним уроком, на котором произошло расставание с начальной школой.
В 4 классе мы решали задачи, в которых нужно было знать простейшие формулы, например, нахождение расстояния по времени и скорости при равномерном движении. Большинство задач решались с составлением пропорций. Мы очень много решали примеров столбиком: складывали, отнимали, умножали, делили. Также решали уравнения вида: X×X×X=8, где нужно найти X.
Математика в 4 классе почему-то для многих моих одноклассников далась тяжело. Я старался помагать многим из них, некоторые даже после моей помощи хорошо писали контрольные.
На данной странице Вы можете посмотреть или бесплатно скачать самые востребованные математические формулы, таблицы, а также справочные материалы по высшей математике. Все математические таблицы составлены лично мной и снабжены дополнительными комментариями. Сделано это в целях преодоления трудностей, с которыми часто сталкиваются студенты-заочники в ходе решения задач. Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.
Все математические таблицы составлены лично мной и снабжены дополнительными комментариями. Сделано это в целях преодоления трудностей, с которыми часто сталкиваются студенты-заочники в ходе решения задач. Я не претендую на всеобъемлющую полноту материалов, но то, что ОЧЕНЬ ЧАСТО встречается, Вы найдете.
Рассмотрим, например, таблицу тригонометрических формул. Тригонометрических формул достаточно много, они давно известны, и нет никакого смысла переписывать справочники. А вот те формулы, которые очень часто используются для решения задач курса высшей математики, собраны воедино, и могут быть очень полезны при выполнении практических заданий. При этом в комментариях я указываю, в каком разделе высшей математики (пределы, производные, интегралы, и т.д.) практически всегда фигурирует та или формула.
Итак, прямо сейчас у Вас есть бесплатный доступ к ценным справочным материалам, возможен, как онлайн-просмотр, так и скачивание. Удобнее всего сразу распечатать математические таблицы и справочные материалы, которые Вас заинтересуют.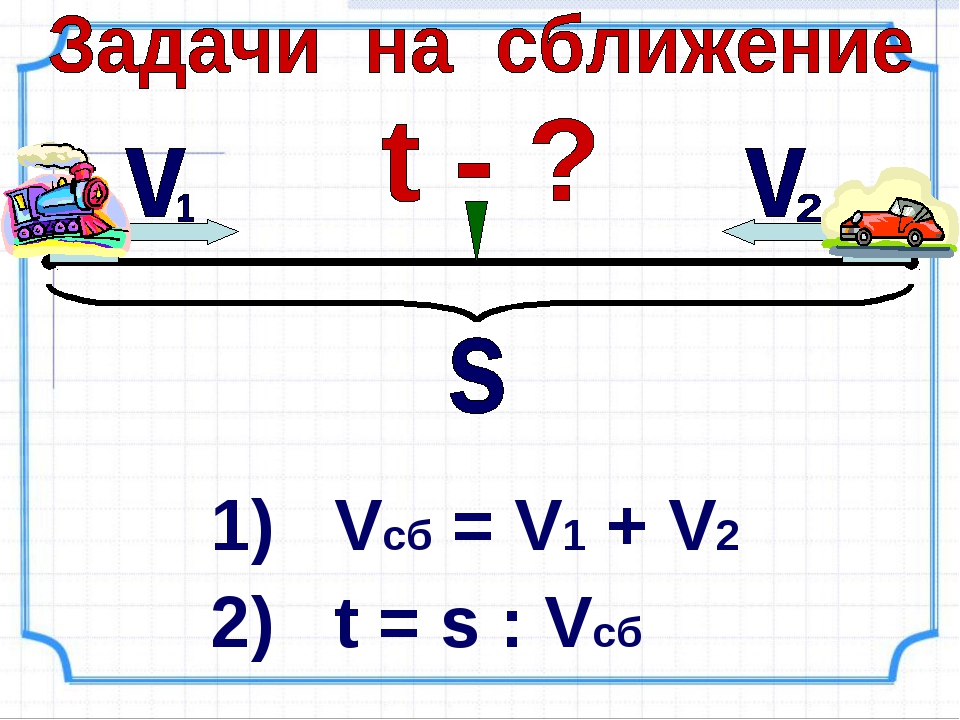 Как показывает практика, информация на экране монитора усваивается хуже, чем на бумаге, да и читать с монитора труднее.
Как показывает практика, информация на экране монитора усваивается хуже, чем на бумаге, да и читать с монитора труднее.
Почти все файлы размещены прямо на сайте, а значит, могут быть получены в максимально короткие срок, ограниченный только скоростью Вашего Интернет-подключения.
Горячие формулы школьного курса математики
Рекомендую просмотреть всем. Данные формулы встречаются в ходе решения задач по высшей математике буквально на каждом шагу. Без знания этих формул – никуда. С чего начать изучение высшей математики? С повторения этого. Независимо от уровня Вашей математической подготовки на данный момент, крайне желательно СРАЗУ ВИДЕТЬ возможность выполнения элементарных действий, применения простейших формул в ходе решения пределов, интегралов, дифференциальных уравнений и т.д.
В справочнике есть краткая информация о модуле, формулы сокращенного умножения, алгоритм решения квадратного уравнения, правила упрощения многоэтажных дробей, а также важнейшие свойства степеней и логарифмов.
Калькулятор для автоматических расчетов
Универсальный калькулятор реализован в рабочей книге MS Excel и на данный момент содержит три листа. Программа может заменить обычный калькулятор с множеством функций. Любые степени, корни, логарифмы, тригонометрические функции, арки – без проблем! Кроме того, калькулятор в автоматическом режиме выполняет основные действия с матрицами, считает определители (до определителя 5 на 5 включительно), мгновенно находит миноры и алгебраические дополнения матриц. За считанные секунды можно решить систему линейных уравнений с помощью обратной матрицы и по формулам Крамера, посмотреть основные этапы решения. Всё это очень удобно для самопроверки. Просто введите свои числа и получите готовый результат!
Тригонометрические формулы
Приведены самые «ходовые» тригонометрические формулы, которые применяются в ходе решения задач по высшей математике. На самом деле таких формул НЕМНОГО, и, собирать десятки других по различным математическим справочникам – пустая трата времени. Всё (или почти всё), что может потребоваться – здесь.
Всё (или почти всё), что может потребоваться – здесь.
Тригонометрические таблицы
При выполнении заданий по математике нередко возникает необходимость заглянуть в тригонометрические таблицы. В данном справочном материале представлена таблица значений тригонометрических функций (синуса, косинуса, тангенса и котангенса) при значениях аргумента от нуля до 360 градусов. Держать в памяти данную информацию нет никакого смысла, но некоторые значения тригонометрических функций хорошо бы знать. Также представлены формулы приведения для вышеуказанных тригонометрических функций,иногда (чаще всего при решении пределов) требуются. По просьбам посетителей сайта в pdf-файл добавлена таблица значений обратных тригонометрических функций и две формулы: формула перевода градусов в радианы, формула перевода радианов в градусы.
Графики и свойства элементарных функций
Методический материал представляет собой обзор графиков основных элементарных функций и их свойств. Будет полезен при изучении практически всех разделов высшей математики, более того, справочное пособие поможет вам намного лучше и качественнееразобраться в некоторых темах. Также вы сможете узнать, какие значения функций следуетзнать наизусть, чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб-страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».
Будет полезен при изучении практически всех разделов высшей математики, более того, справочное пособие поможет вам намного лучше и качественнееразобраться в некоторых темах. Также вы сможете узнать, какие значения функций следуетзнать наизусть, чтобы не получить «два автоматом» при ответе на простейший вопрос экзаменатора. Справка выполнена в форме веб-страницы и содержит много графиков функций, которые также желательно помнить. По мере развития проекта методичка стала играть роль вводного урока по теме «Функции и графики».
Замечательные пределы
На практике у студентов-заочников практически всегда возникает необходимость использовать первый и второй замечательные пределы, о которых и идет речь в данной справке. Также рассмотрены еще три замечательных предела, которые встречаются значительно реже. Все замечательные пределы снабжены дополнительными важными комментариями. Кроме того, файл дополнен информацией о замечательных эквивалентностях.
Таблица производных
В справке приведены правила дифференцирования и таблица производных от основных элементарных функций. Таблица снабжена очень важными примечаниями.
Таблица снабжена очень важными примечаниями.
Схема полного исследования функции
Ваш гид по разделу «Функции и графики». В pdf-ке систематизирована и законспектирована информация об основных этапах исследования функции одной переменной. Руководство сопровождается ссылками, а значит, экономит массу времени. Мануал полезен как чайнику, так и подготовленному читателю.
Таблица интегралов
В общем-то, почти то же самое, что в дифференциальном исчислении. Правила интегрирования и таблица интегралов с моими комментариями.
Таблица разложений некоторых функций в степенные ряды
Справочный материал незаменим при изучении степенных рядов. В таблице представлены разложения в степенной ряд следующих функций: экспоненты, синуса, косинуса, логарифма, арктангенса и арксинуса. Также приведено биномиальное разложение и наиболее распространенные частные случаи биномиального разложения. Разложение функции в ряд является самостоятельным заданием, используется для приближенных вычислений, приближенных вычислений определенного интеграла и в некоторых других задачах.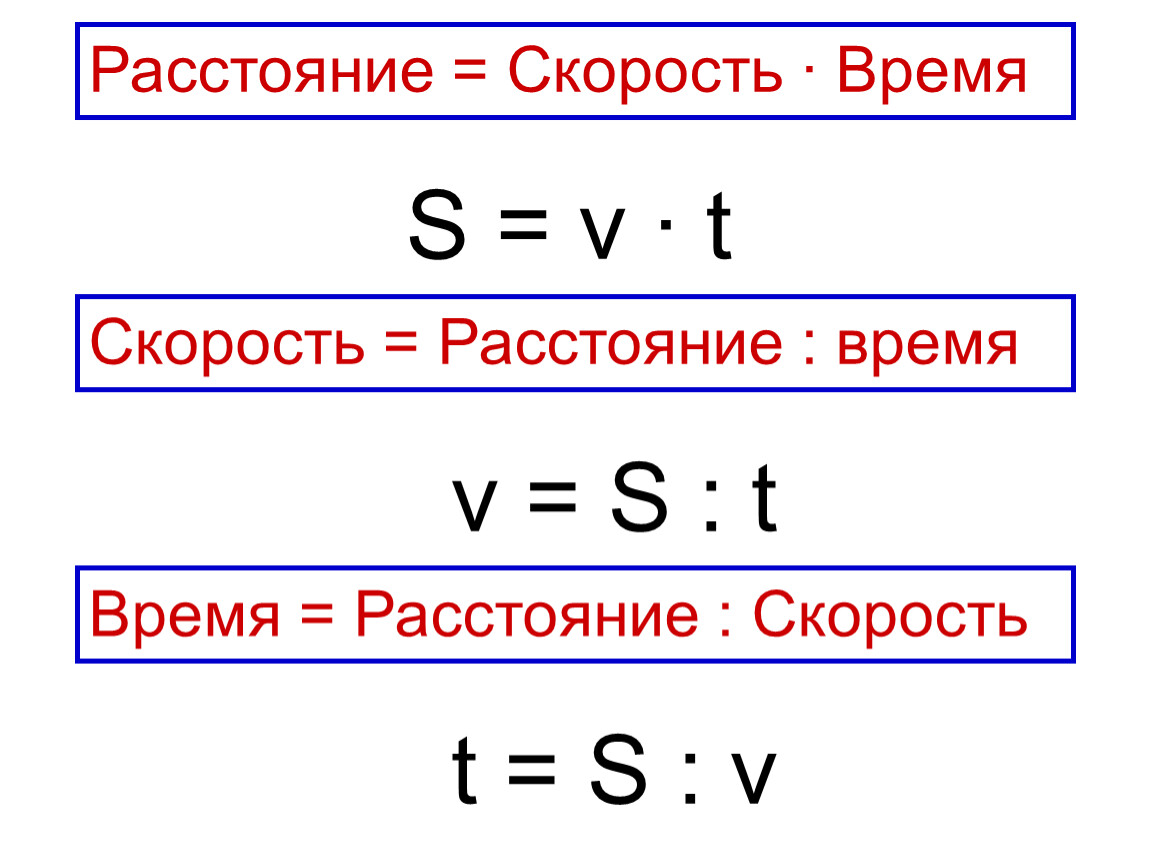
Таблица подбора частного решения неоднородного дифференциального уравнения
Основной трудностью при решении неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами является правильный подбор частного решения по виду правой части. Данная методичка, относится, прежде всего, к уроку Как решить неоднородное уравнение второго порядка? и поможет вам легко разобраться в подборе частного решения. Справка не претендует на основательную научную полноту, она написана простым и понятным языком, однако в 99,99% случаев в ней найдется именно тот случай, который вы ищете.
Таблица оригиналов и изображений (преобразование Лапласа)
Справка незаменима в ходе решения прикладных задач комплексного анализа – нахождения частного решения ДУ операционным методом и нахождения частного решения системы ДУ этим же способом. Таблица отличается от аналогов тем, что «заточена» именно под вышеуказанные задания, данная особенность позволяет легко освоить алгоритмы решения. Приведено как прямое, так и обратное преобразование Лапласа для наиболее распространенных функций. В случае если информации окажется недостаточно, рекомендую обратиться к солидному математическому справочнику – полная версия содержит более сотни пунктов.
Приведено как прямое, так и обратное преобразование Лапласа для наиболее распространенных функций. В случае если информации окажется недостаточно, рекомендую обратиться к солидному математическому справочнику – полная версия содержит более сотни пунктов.
Специальные расчётные программы:
В данном разделе вы можете найти вспомогательные программы для решения узколокальных математических задач. Они помогут вам быстро выполнить расчёты и оформить решение.
Калькулятор формулы трапеций и формулы Симпсона
Данная полуавтоматическая программа относится к уроку Формула трапеций, формула Симпсона и помогает рассчитать приближенное значение определенного интеграла на 2, 4, 8, 10 и 20-ти отрезках разбиения. Прилагается видеоурок по работе с калькулятором. Вычислите ваш определенный интеграл в считанные минуты, и даже секунды!
На данный момент пока всё.
Данный раздел постепенно будет пополняться дополнительными справочными материалами. Каждое справочное пособие постоянно улучшается, в том числе, с учетом Ваших пожеланий и замечаний! Если Вы считаете, что упущено что-то важное, нашли какие-либо неточности, а может быть что-то разъяснено недостаточно понятно, обязательно пишите! Связаться со мной можно единственным способом – через форму обратной связи.
Каждое справочное пособие постоянно улучшается, в том числе, с учетом Ваших пожеланий и замечаний! Если Вы считаете, что упущено что-то важное, нашли какие-либо неточности, а может быть что-то разъяснено недостаточно понятно, обязательно пишите! Связаться со мной можно единственным способом – через форму обратной связи.
Автор: Колян Сафонов
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?формулы для задач на движение, сближение, отдаление
S — расстояние v — скорость t — время
………………………………………………………………………………………………………………….
ГЛАВНАЯ ФОРМУЛА: S = v * t
расстояние = скорость * время
………………………………………………………………………………………….. ……………………..
……………………..
v = S : t — скорость = расстояние : время
………………………………………………………………………………………………………………….
t = S : v — время = расстояние : скорость
………………………………………………………………………………………………………………….
S = t * v сб.
расстояние = время * скорость сближение
………………………………………………………………………………………………………………….
ВСТРЕЧНОЕ ДВИЖЕНИЕ:
v сб. = v₁ + v₂ ( скорость сближения = сумме скоростей)
……………………………………………………………………………………………………………………
ДВИЖЕНИЕ ВДОГОНКУ:
v сб = v₁ — v₂ ( скорость сближения = разности скоростей)
…. …………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………
S = t * v уд.
расстояние = время * скорость удаления
………………………………………………………………………………………………………………………..
ДВИЖЕНИЕ В ПРОТИВОПОЛОЖНЫХ НАПРАВЛЕНИЯХ:
v уд. = v₁ + v₂ ( скорость удаления = сумме скоростей)
……………………………………………………………………………………………………………………
ДВИЖЕНИЕ С ОТСТАВАНИЕМ:
v уд. = v₁ — v₂ ( скорость удаление = разности скоростей)
Движение вдогонку (формула расчета). Решение задач на движение вдогонку
Движение является способом существования всего, что человек видит вокруг себя. Поэтому задачи на перемещение разных объектов в пространстве являются типичными проблемами, которые предлагается разрешить школьникам. В данной статье подробно рассмотрим движение вдогонку и формулы, которые необходимо знать, чтобы уметь решать задачи такого типа.
В данной статье подробно рассмотрим движение вдогонку и формулы, которые необходимо знать, чтобы уметь решать задачи такого типа.
Перед тем, как переходить к рассмотрению формул движения вдогонку, необходимо разобраться с этим понятием подробнее.
Под движением подразумевают изменение пространственных координат объекта за определенный промежуток времени. Например, автомобиль, который движется по дороге, самолет, который летит в небесах, или кошка, бегущая по траве, — все это примеры движения.
Важно отметить, что рассматриваемый движущийся объект (автомобиль, самолет, кошка) считают безмерным, то есть его размеры не имеют совершенно никакого значения для решения проблемы, поэтому ими пренебрегают. Это своего рода математическая идеализация, или модель. Для подобного объекта существует название: материальная точка.
Движение вдогонку и его особенности
Теперь перейдем к рассмотрению популярных школьных задач на движение вдогонку и формул для него. Под этим видом движения понимают перемещение двух или более объектов в одном направлении, которые отправляются в свой путь из разных пунктов (материальные точки имеют разные начальные координаты) или/и в разное время, но из одного и того же пункта. То есть создается ситуация, при которой одна материальная точка пытается догнать другую (другие), поэтому эти задачи получили такое название.
Согласно определению, особенностями движения вдогонку являются следующие:
- Наличие двух и более движущихся объектов. Если двигаться будет только одна материальная точка, то ей «некого» будет догонять.
- Прямолинейное перемещение в одном направлении. То есть объекты осуществляют движение вдоль одной и той же траектории и в одном направлении. Движение навстречу друг другу не входит в число рассматриваемых задач.
- Пункт отправления играет важную роль. Идея заключается в том, чтобы в момент начала движения объекты были разделены в пространстве. Такое разделение будет иметь место, если они стартуют в одинаковое время, но из разных пунктов или же из одного пункта, но в разное время. Старт двух материальных точек из одного пункта и в одинаковое время к задачам вдогонку не относится, поскольку в этом случае один объект будет постоянно удаляться от другого.
Формулы движения вдогонку
В 4 классе общеобразовательной школы обычно рассматриваются подобные задачи. Это означает, что формулы, которые необходимы для решения, должны быть максимально простыми. Такому случаю удовлетворяет равномерное прямолинейное движение, в котором фигурируют три физических величины: скорость, пройденный путь и время движения:
- Скорость — величина, показывающая расстояние, которое проходит тело за единицу времени, то есть она характеризует быстроту изменения координат материальной точки. Обозначается скорость латинской буквой V и измеряется, как правило, в метрах в секунду (м/с) или в километрах в час (км/ч).
- Путь — это расстояние, которое проходит тело за время своего движения. Он обозначается буквой S (D) и выражается обычно в метрах или километрах.
- Время — период движения материальной точки, который обозначается буквой T и приводится в секундах, минутах или часах.
Описав основные величины, приведем формулы движения вдогонку:
- s = v*t;
- v = s/t;
- t = s/v.
Решение любой задачи рассматриваемого типа базируется на применении этих трех выражений, которые необходимо запомнить каждому школьнику.
Пример решения задачи №1
Приведем пример задачи движения вдогонку и решения (формулы, необходимые для него, приведены выше). Проблема формулируется следующим образом: «Грузовик и легковой автомобиль одновременно выезжают из пунктов A и B со скоростями 60 км/ч и 80 км/ч соответственно. Оба транспортных средства движутся в одном направлении так, что автомобиль приближается к пункту A, а грузовик удаляется от обоих пунктов. Через какое время автомобиль догонит грузовик, если расстояние между A и B составляет 40 км?».
Перед тем как решать задачу, необходимо научить ребят определять суть проблемы. В данном случае она заключается в неизвестном времени, которое проведут оба транспортных средства в пути. Предположим, что это время равно t часам. То есть через время t автомобиль догонит грузовик. Найдем это время.
Рассчитаем расстояние, которое пройдет каждый из движущихся объектов за время t, имеем: s1 = v1*t и s2 = v2*t, здесь s1, v1 = 60 км/ч и s2, v2 = 80 км/ч — пройденные пути и скорости движения грузовика и автомобиля до того момента, когда второй догонит первого. Поскольку расстояние между пунктами A и B равно 40 км, то автомобиль, догнав грузовик, пройдет путь на 40 км больше, то есть s2 — s1 = 40. Подставляя в последнее выражение формулы для путей s1 и s2, получим: v2*t — v1*t = 40 или 80*t — 60*t = 40, откуда t = 40/20 = 2 ч.
Отметим, что данный ответ можно получить, если использовать понятие скорости сближения между движущимися объектами. В задаче она равна 20 км/ч (80-60). То есть при этом подходе возникает ситуация, когда один объект движется (автомобиль), а второй относительно него стоит на месте (грузовик). Поэтому достаточно поделить расстояние между пунктами A и B на скорость сближения, чтобы решить задачу.
Пример решения задачи №2
Приведем еще один пример задач на движение вдогонку (формулы для решения используются те же): «Из одного пункта выезжает велосипедист, а через 3 часа в ту же сторону выезжает автомобиль. Через какое время после начала своего движения автомобиль догонит велосипедиста, если известно, что он движется в 4 раза быстрее?».
Решать эту задачу следует так же, как и предыдущую, то есть необходимо определить, какой путь пройдет каждый участник движения до момента, когда один догонит другого. Предположим, что автомобиль догнал велосипедиста через время t, тогда получаем следующие пройденные пути: s1 = v1*(t+3) и s2 = v2*t, здесь s1, v1 и s2, v2 — пути и скорости велосипедиста и автомобиля соответственно. Заметим, что до того, как автомобиль догнал велосипедиста, последний находился в пути t + 3 часа, так как он выехал на 3 часа раньше.
Зная, что оба участника отправились из одного пункта, и пройденные ими пути будут равны, получаем: s2 = s1 или v1*(t+3) = v2*t. Скорости v1 и v2 нам не известны, однако в условии задачи сказано, что v2 = v1. Подставляя это выражение в формулу для равенства путей, получим: v1*(t+3) = v1*t или t+3 = t. Решая последнее, приходим к ответу: t = 3/3 = 1 ч.
Некоторые советы
Формулы движения вдогонку являются простыми, тем не менее школьников в 4 классе важно научить мыслить логически, понимать значение величин, с которыми они имеют дело, и осознавать проблему, которая перед ними стоит. Ребят рекомендуется призывать к рассуждениям вслух, а также к командной работе. Кроме того, для наглядности задач можно использовать компьютер и проектор. Все это способствует развитию у них абстрактного мышления, коммуникативных навыков, а также математических способностей.
Задачи на движение | Фізика – легко!
Для начала вспомним формулы, которые используют при решении подобных задач: S = υ·t, υ = S : t, t = S : υ
где S – расстояние, υ – скорость движения, t – время движения.
Когда два объекта движутся равномерно с разными скоростями, то расстояние между ними за каждую единицу времени или увеличивается, или уменьшается.
Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.
Скорость удаления – это расстояние, на которое удаляются объекты за единицу времени.
Движение на сближение можно разделить на два вида: встречное движение и движение вдогонку. Движение на удаление можно разделить на два вида: движение в противоположных направлениях и движение с отставанием.
Трудность для некоторых учеников заключается в том, чтобы правильно поставить «+» или «–» между скоростями при нахождении скорости сближения объектов или скорости удаления.
Рассмотрим таблицу.
Из неё видно, что при движении объектов в противоположные стороны их скорости складываются. При движении в одну сторону – вычитаются.
Примеры решения задач.
Задача №1. Две автомашины движутся навстречу друг другу со скоростями 60км/ч и 80 км/ч. Определите скорость сближения машин.
υ1 = 60 км/ч
υ2 = 80 км/ч
Найти υсб
Решение.
υсб = υ1 + υ2 – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υсб = 60 + 80 = 140 (км/ч)
Ответ: скорость сближения 140 км/ч.
Задача №2. Из одного пункта в противоположных направлениях выехали две автомашины со скоростями 60 км/ч и 80 км/ч. Определите скорость удаления машин.
υ1 = 60 км/ч
υ2 = 80 км/ч
Найти υуд
Решение.
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υуд = 80 + 60 = 140 (км/ч)
Ответ: скорость удаления 140 км/ч.
Задача №3. Из одного пункта в одном направлении выехали сначала автомобиль со скоростью 60 км/ч, а затем мотоцикл со скоростью 80 км/ч. Определите скорость сближения машин.
(Видим, что здесь случай движения вдогонку, поэтому находим скорость сближения)
υав = 60 км/ч
υмот = 80 км/ч
Найти υсб
Решение.
υсб = υ1 – υ2– скорость сближения (знак «–» так как из условия понятно, что машины движутся в одном направлении)
υсб = 80 – 60 = 20 (км/ч)
Ответ: скорость сближения 20 км/ч.
То есть название скорости – сближения или удаления – не влияют на знак между скоростями. Имеет значение только направление движения.
Рассмотрим другие задачи.
Задача № 4. Из одного пункта в противоположных направлениях вышли два пешехода. Скорость одного из них 5 км/ч, другого – 4 км/ч. Какое расстояние будет между ними через 3 ч?
υ1 = 5 км/ч
υ2 = 4 км/ч
t = 3 ч
Найти S
Решение.
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υуд = 5 + 4 = 9 (км/ч)
(Пройденное расстояние находим по формуле)
S = υуд·t
S = 9·3 = 27 (км)
Ответ: через 3 ч расстояние будет 27 км.
Задача № 5. Два велосипедиста одновременно выехали навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10 км/ч, второго 8 км/ч. Через сколько часов они встретятся?
S = 36 км
υ1 = 10 км/ч
υ2 = 8 км/ч
Найти t
Решение.
υсб = υ1 + υ2 – скорость сближения (знак «+» так как из условия понятно, что машины движутся в разных направлениях)
υсб = 10 + 8 = 18 (км/ч)
(время встречи можно рассчитать по формуле)
t = S : υсб
t = 36 : 18 = 2 (ч)
Ответ: встретятся через 2 ч.
Задача №6. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 60 км/ч и 70км/ч. Через сколько часов расстояние между ними будет 260 км?
υ1 = 60 км/ч
υ2 = 70 км/ч
S = 260 км
Найти t
Решение.
1 способ
υуд = υ1 + υ2 – скорость удаления (знак «+» так как из условия понятно, что пешеходы движутся в разных направлениях)
υуд = 60 + 70 = 130 (км/ч)
(Пройденное расстояние находим по формуле)
S = υуд·t ⇒ t = S : υуд
t = 260 : 130 = 2 (ч)
Ответ: через 2 ч расстояние между ними будет 260 км.
2 способ
Сделаем пояснительный рисунок:
Из рисунка видно, что
1) через заданное время расстояние между поездами будет равно сумме расстояний, которые прошли каждый из поездов:
S = S1 + S2;
2) каждый из поездов ехал одинаковое время (из условия задачи), значит,
S1 =υ1· t – расстояние которое проехал 1 поезд
S2 =υ2· t – расстояние которое проехал 2 поезд
Тогда,
S = S1 + S2 = υ1· t + υ2· t = t · (υ1 + υ2) = t · υуд
t = S : (υ1 + υ2) – время за которое оба поезда проедут 260 км
t = 260 : (70 + 60) = 2 (ч)
Ответ: расстояние между поездами будет 260 км через 2 ч .
1. Два пешехода одновременно вышли навстречу друг другу из двух пунктов, расстояние между которыми 18 км. Скорость одного из них 5 км/ч, другого – 4 км/ч. Через сколько часов они встретятся? (2 ч)
2. Два поезда отошли от одной станции в противоположных направлениях. Их скорости 10 км/ч и 20 км/ч. Через сколько часов расстояние между ними будет 60 км? (2 ч)
3. Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Скорость первого 4 км/ч, скорость второго 5 км/ч. На сколько километров за час пешеходы сближаются друг с другом? Какое расстояние будет между ними через 3 часа? (9 км, 27 км)
4. Расстояние между двумя городами 900 км. Два поезда вышли из этих городов навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга были поезда за 1 час до встречи? Есть ли в задаче лишнее условие? (140 км, есть)
5. Велосипедист и мотоциклист выехали одновременно из одного пункта в одном направлении. Скорость мотоциклиста 40 км/ч, а велосипедиста 12 км/ч. Какова скорость их удаления друг от друга? Через сколько часов расстояние между ними будет 56 км? (28 км/ч, 2 ч)
6. Из двух пунктов, удаленных друг от друга на 30 км, выехали одновременно в одном направлении два мотоциклиста. Скорость первого 40 км/ч, второго 50 км/ч. Через сколько часов второй догонит первого?
7. Расстояние между городами А и В 720 км. Из А в В вышел скорый поезд со скоростью 80 км/ч. Через 2 часа навстречу ему из В в А вышел пассажирский поезд со скоростью 60 км/ч. Через сколько часов они встретятся?
8. Из села вышел пешеход со скоростью 4 км/ч. Через 3 часа вслед за ним выехал велосипедист со скоростью 10 км/ч. За сколько часов велосипедист догонит пешехода?
9. Расстояние от города до села 45 км. Из села в город вышел пешеход со скоростью 5 км/ч. Через час навстречу ему из города в село выехал велосипедист со скоростью 15 км/ч. Кто из них в момент встречи будет ближе к селу?
10. Старинная задача. Некий юноша пошел из Москвы к Вологде. Он проходил в день 40 верст. Через день вслед за ним был послан другой юноша, проходивший в день 45 верст. Через сколько дней второй догонит первого?
11. Старинная задача. Собака усмотрела в 150 саженях зайца, который пробегает в 2 минуты по 500 сажен, а собака за 5 минут – 1300 сажен. Спрашивается, в какое время собака догонит зайца?
12. Старинная задача. Из Москвы в Тверь вышли одновременно 2 поезда. Первый проходил в час 39 верст и прибыл в Тверь двумя часами раньше второго, который проходил в час 26 верст. Сколько верст от Москвы до Твери?
Кинематические уравнения и решение проблем
Четыре кинематических уравнения, которые описывают математическую связь между параметрами, описывающими движение объекта, были введены в предыдущей части Урока 6. Четыре кинематических уравнения:
В приведенных выше уравнениях символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался. Символ a обозначает ускорение объекта.А символ v обозначает мгновенную скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v f ) указывает, что значение скорости является окончательным значением скорости.
Стратегия решения проблем
В этой части Урока 6 мы исследуем процесс использования уравнений для определения неизвестной информации о движении объекта.Процесс включает использование стратегии решения проблем, которая будет использоваться на протяжении всего курса. Стратегия предполагает следующие шаги:
- Постройте информативную диаграмму физической ситуации.
- Определите и перечислите данную информацию в переменной форме.
- Определите и перечислите неизвестную информацию в переменной форме.
- Укажите и перечислите уравнение, которое будет использоваться для определения неизвестной информации из известной информации.
- Подставьте известные значения в уравнение и используйте соответствующие алгебраические шаги, чтобы найти неизвестную информацию.
- Проверьте свой ответ, чтобы убедиться, что он разумный и математически правильный.
Использование этой стратегии решения проблем при решении следующей проблемы смоделировано в примерах A и B ниже.
Пример задачи A
Има Харрин приближается к светофору, движущемуся со скоростью +30.0 м / с. Загорается желтый свет, и Има тормозит и останавливается. Если ускорение Имы составляет -8,00 м / с 2 , то определите смещение автомобиля во время заноса. (Обратите внимание, что направление векторов скорости и ускорения обозначено знаками «+» и «-».)
Решение этой проблемы начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг включает идентификацию и перечисление известной информации в переменной форме.Обратите внимание, что значение v f может быть принято равным 0 м / с, поскольку машина Имы останавливается. Начальная скорость (v i ) кабины +30,0 м / с, так как это скорость в начале движения (заносное движение). А ускорение (а) автомобиля задано как — 8,00 м / с 2 . (Всегда обращайте особое внимание на знаки + и — для данных количеств.) Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме.В этом случае проблема запрашивает информацию о перемещении автомобиля. Итак, d — неизвестная величина. Результаты первых трех шагов показаны в таблице ниже.
| Схема: | Дано: | Находка: |
|---|---|---|
| v i = +30,0 м / с v f = 0 м / с a = — 8,00 м / с 2 | d = ?? |
Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину.На выбор предлагается четыре кинематических уравнения. В общем, вы всегда будете выбирать уравнение, которое содержит три известные и одну неизвестную переменные. В этом конкретном случае три известные переменные и одна неизвестная переменная: v f , v i , a и d. Таким образом, вы будете искать уравнение, в котором перечислены эти четыре переменные. Анализ четырех приведенных выше уравнений показывает, что уравнение в правом верхнем углу содержит все четыре переменные.
v f 2 = v i 2 + 2 • a • d
После того, как уравнение идентифицировано и записано, следующий шаг стратегии включает в себя замену известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации.Этот шаг показан ниже.
(0 м / с) 2 = (30,0 м / с) 2 + 2 • (-8,00 м / с 2 ) • d
0 м 2 / с 2 = 900 м 2 / с 2 + (-16,0 м / с 2 ) • d
(16,0 м / с 2 ) • d = 900 м 2 / с 2 — 0 м 2 / с 2
(16,0 м / с 2 ) * d = 900 м 2 / с 2
d = (900 м 2 / с 2 ) / (16.0 м / с 2 )
d = (900 м 2 / с 2 ) / (16,0 м / с 2 )
d = 56,3 м
Решение, приведенное выше, показывает, что автомобиль заносит расстояние 56,3 метра. (Обратите внимание, что это значение округлено до третьей цифры.)
Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является одновременно разумным и точным. Стоимость кажется достаточно разумной. Машине требуется значительное расстояние, чтобы занести из 30.0 м / с (примерно 65 миль / ч) до остановки. Расчетное расстояние составляет примерно половину футбольного поля, что делает его очень разумным расстоянием для заноса. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения. В самом деле!
Пример задачи B
Бен Рушин ждет на светофоре.Когда он наконец стал зеленым, Бен ускорился из состояния покоя со скоростью 6,00 м / с 2 за время 4,10 секунды. Определите перемещение машины Бена за этот период времени.
И снова решение этой проблемы начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг стратегии включает идентификацию и перечисление известной информации в переменной форме. Обратите внимание, что значение v i можно вывести как 0 м / с, поскольку машина Бена изначально находится в состоянии покоя.Ускорение (а) автомобиля составляет 6,00 м / с 2 . Время (t) равно 4,10 с. Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае проблема запрашивает информацию о перемещении автомобиля. Итак, d — неизвестная информация. Результаты первых трех шагов показаны в таблице ниже.
| Схема: | Дано: | Находка: |
|---|---|---|
| v i = 0 м / с т = 4.10 с a = 6,00 м / с 2 | d = ?? |
Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину. На выбор предлагается четыре кинематических уравнения. Опять же, вы всегда будете искать уравнение, которое содержит три известные переменные и одну неизвестную переменную. В этом конкретном случае три известные переменные и одна неизвестная переменная — это t, v i , a и d.Анализ четырех приведенных выше уравнений показывает, что уравнение в левом верхнем углу содержит все четыре переменные.
d = v i • t + ½ • a • t 2
После того, как уравнение идентифицировано и записано, следующий шаг стратегии включает в себя замену известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.
d = (0 м / с) • (4.1 с) + ½ • (6,00 м / с 2 ) • (4,10 с) 2
d = (0 м) + ½ • (6,00 м / с 2 ) • (16,81 с 2 )
d = 0 м + 50,43 м
d = 50,4 м
Решение, приведенное выше, показывает, что автомобиль преодолеет расстояние 50,4 метра. (Обратите внимание, что это значение округлено до третьей цифры.)
Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является одновременно разумным и точным.Стоимость кажется достаточно разумной. Автомобиль с ускорением 6,00 м / с / с достигнет скорости примерно 24 м / с (примерно 50 миль / ч) за 4,10 с. Расстояние, на которое такая машина будет перемещена в течение этого периода времени, будет примерно половиной футбольного поля, что делает это расстояние очень разумным. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения.В самом деле!
Два приведенных выше примера задач иллюстрируют, как кинематические уравнения могут быть объединены с простой стратегией решения проблем для прогнозирования неизвестных параметров движения для движущегося объекта. Если известны три параметра движения, можно определить любое из оставшихся значений. В следующей части Урока 6 мы увидим, как эту стратегию можно применить к ситуациям свободного падения. Или, если интересно, вы можете попробовать несколько практических задач и сравнить свой ответ с данными решениями.
Уравнения движения — Практика — Физика Гипертекст
Ограничение скорости на определенном участке автострады составляет 25 м / с. Правая полоса движения соединяется с съездом с короткой вспомогательной полосой движения. Автомобили имели бы комфортное замедление -2,0 м / с 2 за 3,0 с на вспомогательной полосе, если бы они ехали на предельной скорости.- Какая скорость будет у автомобилей, когда они прекратят замедление таким образом? (Это также ограничение скорости съезда.)
- Какой минимальной длины должна быть вспомогательная полоса, чтобы обеспечить такое замедление?
Водители не всегда ездят на предельной скорости, и дорожные инженеры это учитывают.
- Предположим, что автомобиль может замедлиться со скоростью, в четыре раза превышающей «комфортную», без потери управления. На какой максимальной скорости автомобиль может выехать на вспомогательную полосу, длина которой рассчитана в части b.и по-прежнему выходить с заданной скоростью?
- Предположим, водитель ехал по автостраде со скоростью, которую вы рассчитали в части c. Какое расстояние необходимо для того, чтобы этот автомобиль замедлился до предельной скорости съезда на «комфортном» темпе?
- 30 миль / ч
- 20 миль / ч
- 10 миль / ч
Первый способ.
Трудный способ решить эту проблему — сделать это так, как думают многие ученики, — «набери, ответь» или «подключи и пей». Этот метод кажется простым, поскольку не требует особых размышлений, но оказывается довольно сложным.
Сначала конвертируем в единицы СИ.
| 60 миль | 1609 кв.м | 1 час | = 26.8 м / с | ||
| 1 час | 1 миля | 3600 с | |||
| 30 миль | 1609 кв.м | 1 час | = 13,4 м / с | ||
| 1 час | 1 миля | 3600 с | |||
| 20 миль | 1609 кв.м | 1 час | = 8,94 м / с | ||
| 1 час | 1 миля | 3600 с | |||
| 10 миль | 1609 кв.м | 1 час | = 4.47 м / с | ||
| 1 час | 1 миля | 3600 с | |||
| 144 футов | 1 миля | 1609 кв.м | = 43,9 м | ||
| 1 | 5280 футов | 1 миля | |||
Затем рассчитайте замедление от 60 миль в час.
| v 0 = | 26.8 м / с |
| v = | 0 м / с |
| ∆ с = | 43,9 м |
| а = | ? |
| в 2 = | v 0 2 + 2 a ∆ s | |
| а = | ||
| а = | — (26.8 м / с) 2 | |
| 2 (43,9 м) | ||
| a = −8,18 м / с 2 | ||
Затем используйте это число для расчета расстояний для других скоростей.
v 2 = v 0 2 + 2 a ∆ s
Удалите нулевой член и найдите смещение.
Цифры входят. Ответы выходят.
| ∆ с = | — (13,4 м / с) 2 | = 11,0 м |
| 2 (−8,18 м / с 2 ) | ||
| ∆ с = | — (8,94 м / с) 2 | = 4,89 м |
| 2 (−8,18 м / с 2 ) | ||
| ∆ с = | — (4,47 м / с) 2 | = 1.22 м |
| 2 (−8,18 м / с 2 ) |
И, наконец, конвертируем обратно в английские единицы.
| 11,0 м | 1 миля | 5280 футов | = 36 футов | ||
| 1 | 1609 кв.м | 1 миля | |||
| 4,89 м | 1 миля | 5280 футов | = 16 футов | ||
| 1 | 1609 кв.м | 1 миля | |||
| 1.22 м | 1 миля | 5280 футов | = 04 фута | ||
| 1 | 1609 кв.м | 1 миля |
Второй способ.
Стандартные методы решения проблем работают, но для решения этой проблемы они — огромная трата времени. Любая небольшая ошибка уничтожит ответы и приведет к потере личной умственной энергии, чего мы все хотели бы избежать. Простой способ решить эту проблему не требует никаких обманов.Это требует, чтобы вы определили и поняли ключевые концепции, необходимые для решения проблемы. В середине массы уравнений было сделано важное предположение. Предполагалось, что тормозное ускорение автомобиля останется постоянным для всех начальных скоростей. Эта проблема состоит в том, чтобы определить взаимосвязь между смещением и скоростью. Уравнение, которое делает это, выглядит так:
v 2 = v 0 2 + 2 a ∆ s
, который показывает, что смещение пропорционально квадрату скорости (когда ускорение постоянное и либо начальная, либо конечная скорость равна нулю).
∆ с ∝ v 2
В этой задаче мы сравниваем тормозной путь на скорости 30, 20 и 10 миль в час с тормозным путем на скорости 60 миль в час. Квадрат отношения новой скорости к исходной скорости будет отношением нового тормозного пути к исходному тормозному пути.
| в 2 | ∝ | ∆ с | ||||||||||||||
| ⎜ ⎝ | 30 миль / ч | ⎞ 2 ⎟ ⎠ | = | ⎛ ⎜ ⎝ | 1 | 2 ⎟ ⎠ | = | 1 | = | 36 футов | ||||||
| 60 миль / ч | 2 | 4 | 144 футов | |||||||||||||
| ⎛ ⎜ ⎝ | 20 миль / ч | ⎞ 2 ⎟ ⎠ | = | ⎛ ⎜ ⎝ | 1 | 2 ⎟ ⎠ | = | 1 | = | 16 футов | ||||||
| 60 миль / ч | 3 | 9 | 144 футов | |||||||||||||
| ⎜ ⎝ | 10 миль / ч | 2 ⎟ ⎠ | = | ⎛ ⎜ ⎝ | 1 | ⎞ 2 ⎟ ⎠ | = | 1 | = | 04 фута | ||||||
| 60 миль / ч | 6 | 36 | 144 футов | |||||||||||||
Это те же ответы, которые мы получили, используя метод «подключи и глотай».
Поезд метро на 10 вагонов сидит на станции. Крейсерская скорость достигается после разгона 0,75 м / с 2 на расстояние, эквивалентное длине станции (184 м). Затем он с постоянной скоростью движется к следующей станции в 18 кварталах (1425 м).- Определите крейсерскую скорость поезда.
- Определите время, за которое поезд разгоняется до крейсерской скорости.
- Сколько времени нужно поезду, чтобы проехать 18 кварталов до следующей станции?
- Какое замедление поезда на второй станции?
4 уловки для решения любой физической проблемы
Физика может быть устрашающей, все эти шкивы, протоны и движение снарядов. Однако, если вы подойдете к этому с правильным мышлением, даже самые сложные проблемы, как правило, будут проще, чем вы думаете. Когда вы сталкиваетесь с трудным вопросом, не паникуйте. Вместо этого начните с этих коротких простых приемов, которые помогут вам справиться с проблемой.
1.Какая тема?
Практически каждый физический вопрос проверяет конкретные знания. Когда вы читаете вопрос, спросите себя, исследует ли это электричество? Крутящий момент? Параболическое движение? Каждая тема связана с определенными уравнениями и подходами, поэтому распознавание предмета направит ваши усилия в правильном направлении. Ищите ключевые слова и фразы, раскрывающие тему.
2. Что вы пытаетесь найти?
Этот простой шаг может сэкономить много времени. Прежде чем приступить к решению проблемы, подумайте, как будет выглядеть ответ.Какие бывают единицы; окончательный ответ будет в килограммах или литрах? Также подумайте, какие другие физические величины могут иметь отношение к вашему ответу. Если вы пытаетесь найти скорость, может быть полезно найти ускорение, а затем решить его для скорости. Раннее определение ограничений для ответа также гарантирует, что вы ответите на конкретный вопрос; распространенная ошибка в физике — решение неправильного.
3. Что ты знаешь?
Подумайте, какие детали упоминаются в проблеме. Если вопрос действительно плохой, они, вероятно, предоставили вам именно ту информацию, которая вам нужна для решения проблемы.Не удивляйтесь, если иногда эта информация закодирована на языке; проблема, в которой упоминается пружина с «снятой с конца массой», говорит вам кое-что важное о количестве силы. Запишите каждое количество, известное вам из проблемы, затем переходите к…
4. Какие уравнения вы можете использовать?
Какие уравнения включают величины, которые вам известны, а также те, которые вы ищете? Если у вас есть масса объекта и сила, и вы пытаетесь найти ускорение, начните с F = ma (второй закон Ньютона).Если вы пытаетесь найти электрическое поле, но у вас есть заряд и расстояние, попробуйте E = q / (4πε * r 2 ).
Если вы не можете решить, какое уравнение использовать, вернитесь к нашему первому трюку. Какие уравнения связаны с темой? Можете ли вы манипулировать количествами, которые у вас есть, чтобы уместить любое из них?
Бонусный трюк: «взломать» юнитыЭтот трюк не всегда работает, но он может дать толчок вашему мозгу. Сначала определите единицы количества, которое вы пытаетесь найти, и количество, которое у вас есть.Используйте только базовые единицы (метры, килограммы, секунды, заряд), а не составные единицы (сила измеряется в ньютонах, а это всего лишь кг * м / с 2 ). Умножайте и делите количества до тех пор, пока единицы не совпадут с единицами количества в ответе. Например, если вы пытаетесь найти потенциальную энергию (кг * м 2 / с 2 ) и у вас есть высота (м), масса (кг) и ускорение свободного падения (м / с 2 ), вы можете сопоставить единицы, умножив три величины (м * кг * м / с 2 = кг * м 2 / с 2 ).
Примечание: в отличие от других, этот трюк не всегда работает. Остерегайтесь безразмерных констант. Например, кинетическая энергия равна ½ * масса * скорость 2 , а не просто масса * скорость 2 , как предполагают единицы измерения. Несмотря на то, что этот трюк не идеален, он все же может быть отличным местом для начала.
Квадратичный Проблемы со словами: Движение снаряда (стр. 1 из 3) Ячейки: Снаряд движение, Общие проблемы со словами, Макс. / мин. проблемы Для наших целей «снаряд» — это любой объект, который бросают, стреляют или роняют.Обычно объект двигаясь прямо вверх или прямо вниз.
Какая высота (вверху уровень земли), когда объект врезается в землю? Ну, очевидно, ноль. Вот и ищу момент когда высота с = 0.Ставлю с равным нулю, и решаем: Затем т = 6 или т = 2. Второе решение за две секунды до запуска, что не имеет смысла в данном контекст. (На графике это имеет смысл, потому что линия пересекает x — ось в 2, но отрицательное время не сработает в этой проблеме со словом.) Итак, « t = 2 «является посторонним решение, и я проигнорирую его. Обратите внимание на строительство уравнение высоты в задаче выше. Начальная высота пуска составляла 58,8 метров, а постоянный член составил «58,8». Начальная скорость (стартовая скорость) 19,6 м / с. м / с, а коэффициент при линейном члене составил «19,6». Это всегда верно для этих проблем с движением снаряда вверх / вниз. (Если у вас есть упражнение с боковыми движениями, уравнение будет иметь другое форма, но они всегда дают вы это уравнение.) Начальная скорость — это коэффициент для среднего члена, а начальная скорость высота — постоянный член. А коэффициент главный член происходит от силы тяжести. Этот коэффициент отрицательно, так как сила тяжести тянет вниз, и значение будет либо «4,9» (если ваши единицы измерения «метры») или «16» (если ваши единицы — «футы»). В общем, формат: с ( т ) = gt 2 + в 0 т + час 0 …где « г » вот «4.9» или «16» выводится из значения силы тяжести (технически это половина силы тяжести, но вам, вероятно, не нужно знать это правильно сейчас), « v 0 » («vee-naught» или «vee-sub-zero») — начальная скорость, и « h 0 » («aitch-naught» или «aitch-sub-zero») — начальная высота. Запомните это уравнение (или, по крайней мере, его значение), потому что вам может потребоваться это знать на тесте.
Хм … Не дали мне уравнение на этот раз.Но это нормально, потому что я могу создать уравнение из информации, что они сделали дай мне. Начальная высота 80 футов над землей и начальная скорость 64 фут / с. Поскольку мои единицы измерения — футы, то число гравитации будет 16, и мое уравнение: Они хотят, чтобы я нашел максимальная высота. Для такой отрицательной квадратичной функции максимум будет быть в вершине перевернутой параболы.Так что они действительно хотят меня найти вершину. Из графика Я знаю, как найти вершину; в этом случае вершина находится в точке (2, 144): Но что это за вершина скажи-ка? Согласно моему уравнению, я вставляю значения времени и извлекаю значения высоты, поэтому ввод «2» должно быть время и на выходе «144» должен быть рост. Авторские права Элизабет Стапель 2004-2011 Все права защищены
Мои единицы на этот раз «метров», поэтому гравитационное число будет «4,9». Поскольку объект стартовал на уровне земли, начальная высота была равна 0. Тогда мое уравнение: Поскольку это отрицательный квадратичный, график представляет собой перевернутую параболу.Я могу найти двоих раз, когда объект ровно 34,3 метров, и я знаю, что объект будет выше 34,3 метров все время между ними. Почему «два раза» и как знаю ли я, что промежуток времени находится между этими двумя временами? Поскольку первый раз будет, когда объект пройдет высоту 34,3 метров на пути к максимальной высоте, и второй раз, когда быть, когда он пройдет 34,3 метров, когда он снова падает на землю.Итак, я должен решить следующее: Тогда объект находится на 34,3 метра через одну секунду после запуска (поднимается) и снова через семь секунд после запуск (возвращаясь вниз). Вычитая, чтобы найти разницу, я нахожу что: Не удивляйтесь, если многие ваших упражнений выполняются так же «аккуратно», как и в приведенных выше примерах. имеют. Многие учебники по-прежнему тщательно разрабатывают упражнения, так что вы можете решить с помощью факторизации (то есть, быстро выполнив алгебру).Тем не мение, сильная зависимость от калькуляторов приводит к тому, что все больше текстов создают «интересные» (то есть излишне сложные) упражнения, поэтому некоторые (или все) ваши упражнения могут включать в себя гораздо больше беспорядочных вычислений, чем было показано здесь. Если да, внимательно изучите эти «аккуратные» примеры, пока не получите совершенно уверены, что вы следуете рассуждениям.
Наша начальная высота запуска будет то же самое: мы оба стартуем со 160 футов над землей.И число силы тяжести, поскольку мы работаем в ногах, будет быть 16. Моя начальная скорость равна нулю, так как я только что уронил книгу, но мой приятель Скорость Германа — минус 48, негатив проистекает из того факта, что он выбросил свою книгу на а не вверх. Итак, наши уравнения «высоты»: В каждом случае мне нужно найти время, чтобы книги достигли нулевой высоты («ноль» «на уровне земли»), поэтому: шахта: 0
= 16 т 2 + 160, т 2 10 = 0,
так т = кв. (10) Я проигнорирую негатив значения времени.Его книга попадает в воду через две секунды, а моя попадает в после sqrt (10) секунд, или примерно через 3,16 секунд. То есть: Время от времени они станьте умнее и поместите проблему «снаряда» в другую среду. Уравнение останется прежним по структуре, но вам, возможно, придется учитывать для другого значения силы тяжести.
Чтобы составить моё уравнение для В этом упражнении нужно иметь в виду, что значение коэффициента « г » из уравнения «движения снаряда» выше составляет половину значения силы тяжести. В физике есть — «универсальная гравитационная постоянная» G ; тогда каждый объект проявляет свою собственную гравитационную силу, которая связана с к собственной массе и универсальной постоянной G .В формуле «движение снаряда» « г » составляет половину значения гравитационной силы для этого конкретного тело. Например, гравитационная сила на Земле направлена вниз 32. фут / с 2 , но мы использовали «16» в уравнении. Так « г » для моего уравнения на этот раз будет 98 2 = 49. Тогда: Затем т = 0 или т = 3.Первое решение представляет, когда мяч был запущен, поэтому второе решение — это один я хочу. Примечание: на Земле это было бы требуется чуть больше девяти секунд, чтобы мяч упал на землю. Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
|
Алгебра: Задачи с дистанционным словом
Урок 10: Задачи с дистанционным словом
/ ru / algebra-themes / Introduction-to-word-tasks / content /
Что такое проблемы с дистанционным словом?
Задачи с дистанционным словом — это распространенный тип задач по алгебре.Они включают сценарий, в котором вам нужно выяснить, насколько быстро , насколько далеко или как длинный перемещался один или несколько объектов. Их часто называют проблемами поездов , потому что один из самых известных типов задач расстояния включает в себя определение того, когда два поезда, идущие навстречу друг другу, пересекаются.
В этом уроке вы узнаете, как решать задачи с поездами и несколько других распространенных типов задач на расстояние. Но сначала давайте рассмотрим некоторые основные принципы, которые применимы к любой задаче о расстоянии .
Основы дистанционных задач
Существует три основных аспекта движения и перемещения: расстояние , скорость и время . Чтобы понять разницу между ними, вспомните, когда вы в последний раз куда-то ездили.
Расстояние — это расстояние , которое вы прошли. Скорость — это то, насколько быстро вы проехали. Время , — это время , , которое длилось путешествие.
Связь между этими вещами можно описать следующей формулой:
расстояние = скорость x время
d = rt
Другими словами, расстояние , которое вы проехали, равно скорости , с которой вы проехали, умноженному на раз, когда вы проехали .Для примера того, как это будет работать в реальной жизни, представьте, что ваша последняя поездка была такой:
- Вы проехали 25 миль — это расстояние .
- Вы ехали в среднем со скоростью 50 миль в час — это показатель .
- Поездка заняла 30 минут или 0,5 часа — это время .
Согласно формуле, если мы умножим коэффициент на и на , произведение должно быть нашим расстоянием.
И это так! Мы проехали 50 миль в час за 0.5 часов — и 50 ⋅ 0,5 равно 25, что соответствует нашему расстоянию.
Что, если бы мы проехали 60 миль в час вместо 50? Как далеко мы сможем проехать за 30 минут? Мы могли бы использовать ту же формулу, чтобы выяснить это.
60 ⋅ 0,5 равно 30, поэтому наше расстояние будет 30 миль.
Решение задач с расстоянием
Когда вы решаете любую задачу о расстоянии, вам нужно будет сделать то, что мы только что сделали — использовать формулу, чтобы найти расстояние , скорость или время .Попробуем еще одну простую задачу.
В свой выходной Ли отправился в зоопарк. Он ехал со средней скоростью 65 миль в час, и ему потребовалось два с половиной часа, чтобы добраться от дома до зоопарка. Как далеко зоопарк от его дома?
Во-первых, мы должны идентифицировать информацию, которую мы знаем. Помните, мы ищем любую информацию о расстоянии, скорости или времени. По задаче:
- Скорость составляет 65 миль в час.
- Время составляет два с половиной часа, или 2.5 часов.
- Расстояние неизвестно — это то, что мы пытаемся найти.
Вы можете представить поездку Ли на такой диаграмме:
Эта диаграмма — начало понимания этой проблемы, но нам все еще нужно выяснить, что делать с числами для расстояния , скорости и времени . Чтобы отслеживать информацию в задаче, мы создадим таблицу. (Сейчас это может показаться чрезмерным, но это хорошая привычка даже для простых задач и может значительно упростить решение сложных проблем.) Вот как выглядит наша таблица:
Мы можем поместить эту информацию в нашу формулу: расстояние = скорость ⋅ время .
Мы можем использовать формулу расстояние = скорость ⋅ время , чтобы найти расстояние, пройденное Ли.
d = rt
Формула d = rt выглядит так, когда мы подставляем числа из задачи. Неизвестное расстояние представлено переменной d .
d = 65 ⋅ 2,5
Чтобы найти d , все, что нам нужно сделать, это умножить 65 на 2.5. 65 ⋅ 2,5 равно 162,5.
d = 162,5
У нас есть ответ на нашу задачу: d = 162,5. Другими словами, расстояние, которое Ли проехал от своего дома до зоопарка, составляет 162,5 мили.
Будьте осторожны, используйте те же единицы измерения , для скорости и времени. Можно умножить 65 миль на часов на 2,5 часов , потому что они используют одну и ту же единицу: часов . Однако что, если бы время было записано в другой единице, например, минут ? В этом случае вам нужно будет преобразовать время в часы, чтобы использовать ту же единицу, что и скорость.
Решение для скорости и времени
В только что решенной задаче мы вычислили расстояние , но вы можете использовать формулу d = rt , чтобы решить и для скорости и времени . Например, взгляните на эту проблему:
После работы Джанаэ полчаса гуляла по своему району. Всего она прошла полторы мили. Какая у нее была средняя скорость в милях в час?
Мы можем представить себе прогулку Джанэ примерно так:
И мы можем настроить информацию из известной нам проблемы так:
Таблица повторяет факты, которые мы уже знаем из задачи.Джанаэ прошла полторы мили или 1,5 мили за полчаса, или 0,5 часа.
Как всегда, мы начинаем с нашей формулы. Далее мы заполним формулу информацией из нашей таблицы.
d = rt
Скорость представлена как r , потому что мы еще не знаем, насколько быстро шла Джанаэ. Так как мы решаем для r , нам придется получить его в одиночку с одной стороны уравнения.
1,5 = r ⋅ 0,5
Наше уравнение требует r умножить на 0.5, поэтому мы можем получить r только на одной стороне уравнения, если разделить с обеих сторон на 0,5:
1,5 / 0,5 = 3.
3 = г
r = 3, поэтому 3 — это ответ на нашу проблему. Джанаэ прошла 3 миль в час.
В задачах на этой странице мы решили для расстояния и для расстояния пути, но вы также можете использовать уравнение перемещения для решения для времени . Вы даже можете использовать его для решения определенных задач, когда вы пытаетесь определить расстояние, скорость или время двух или более движущихся объектов.Мы рассмотрим подобные проблемы на следующих нескольких страницах.
Двухчастные задачи и задачи туда и обратно
Вы знаете, как решить эту проблему?
Билл поехал навестить друга. Его друг живет в 225 милях от города. Он ехал по городу со средней скоростью 30 миль в час, затем он ехал по автомагистрали со скоростью в среднем 70 миль в час. Поездка заняла в общей сложности три с половиной часа. Как далеко Билл проехал по шоссе?
Это классическая задача , состоящая из двух частей, , потому что она просит вас найти информацию об одной части двухэтапной поездки.Эта проблема может показаться сложной, но не пугайтесь!
Вы можете решить эту проблему, используя те же инструменты, которые мы использовали для решения более простых задач на первой странице:
- Уравнение перемещения d = rt
- Таблица для отслеживания важной информации
Начнем с таблицы . Взгляните еще раз на проблему. На этот раз информация, относящаяся к расстоянию , скорости и времени , была подчеркнута.
Билл поехал навестить друга. Его друг живет в 225 милях от нас. Он проехал по городу со средней скоростью 30 миль в час , затем он проехал по автомагистрали со средней скоростью 70 миль в час . Поездка заняла три с половиной часа, всего часов. Как далеко Билл проехал по шоссе?
Если вы попытались заполнить таблицу так, как мы это делали на предыдущей странице, вы могли заметить проблему: слишком много информации . Например, проблема содержит две скорости — 30 миль / час и 70 миль / час .Чтобы включить всю эту информацию, давайте создадим таблицу с дополнительной строкой. Верхний ряд чисел и переменных будет обозначен как в городе , а нижний ряд будет обозначен как между штатами .
| расстояние | тариф | время | |
|---|---|---|---|
| в городе | 30 | ||
| межгосударственный | 70 |
Мы заполнили ставки, но как насчет расстояния и время ? Если вы посмотрите на проблему, то увидите, что это всего цифр , то есть они включают время в городе и на межштатной автомагистрали.Таким образом, общее расстояние равно 225. Это означает, что это правда:
Межгосударственное расстояние + расстояние до города = Общее расстояние
Вместе, расстояние между штатами и расстояние между городами равны общему расстоянию . Видеть?
В любом случае, мы пытаемся выяснить, как далеко проехал Билл на межгосударственной автомагистрали , поэтому представим это число как d . Если расстояние между штатами составляет d , это означает, что расстояние между городом — это число, равное итоговому значению 225, когда прибавило к d .Другими словами, это 225 — d .
Мы можем заполнить нашу диаграмму так:
| расстояние | скорость | время | |
|---|---|---|---|
| в городе | 225 — d | 30 | |
| межгосударственный | d | 70 |
Мы можем использовать ту же технику для заполнения столбца время . Общее время 3,5 часов . Если мы говорим, что время на межштатной автомагистрали t , то оставшееся время в городе равно 3.5 — т . Мы можем заполнить остальную часть нашей диаграммы.
| расстояние | тариф | время | |
|---|---|---|---|
| в городе | 225 — d | 30 | 3,5 — t |
| межгосударственный | d | 70 | t |
Теперь мы можем работать над решением проблемы. Основное различие между задачами на первой странице и этой задачей состоит в том, что эта задача включает двух уравнений.Вот модель для поездок по городу :
225 — d = 30 ⋅ (3,5 — т)
А вот и для межгосударственного проезда :
d = 70 т
Если вы попытались решить любую из этих задач самостоятельно, вы могли бы найти это невозможным: поскольку каждое уравнение содержит две неизвестные переменные, они не могут быть решены сами по себе. Попробуйте сами. Если вы работаете с любым уравнением отдельно, вы не сможете найти числовое значение для d . Чтобы найти значение d , нам также необходимо знать значение t .
Мы можем найти значение t в обеих задачах, объединив их. Давайте еще раз посмотрим на наше уравнение путешествия между штатами.
Хотя нам неизвестно числовое значение d , это уравнение говорит нам, что d равно 70 t .
d = 70 т
Поскольку 70 t и d равны , мы можем заменить d на 70 t .Подстановка 70 t на d в нашем уравнении для межгосударственного путешествия не поможет нам найти значение t — все это говорит нам о том, что 70 t равно самому себе, что мы уже знали.
70т = 70т
А как насчет нашего другого уравнения, уравнения для путешествий по городу?
225 — d = 30 ⋅ (3,5 — т)
Когда мы заменяем d в этом уравнении на 70 t , уравнение внезапно становится намного проще решать.
225 — 70 т = 30 ⋅ (3,5 — т)
Наше новое уравнение может показаться более сложным, но на самом деле мы можем его решить. Это потому, что у него только одна переменная: t . Найдя t , мы можем использовать его для вычисления значения d — и найти ответ на нашу проблему.
Чтобы упростить это уравнение и найти значение t , нам нужно получить только t по одну сторону от знака равенства. Нам также необходимо максимально упростить правую сторону .
225 — 70 т = 30 ⋅ (3,5 — т)
Начнем с правой стороны: 30 умножить на (3,5 — т ) это 105 — 30 т .
225 — 70 т = 105 — 30 т
Затем давайте исключим 225 рядом с 70 t . Для этого вычтем 225 с обеих сторон. Справа это означает вычитание 225 из 105. 105 — 225 равно -120.
— 70 т = -120 — 30 т
Наш следующий шаг — объединить в группу подобных терминов — помните, наша конечная цель — иметь t слева от знака равенства и число справа .Мы сократим -30 t с правой стороны на , добавив 30 t к обеим сторонам. С правой стороны добавим -70 t . -70 т + 30 т составляет -40 т .
— 40 т = -120
Наконец, чтобы получить t отдельно, разделим каждую сторону на ее коэффициент: -40. -120 / — 40 составляет 3.
т = 3
Итак, t равно 3. Другими словами, время , которое Билл проехал по межгосударственной магистрали, равно 3 часам .Помните, мы в конечном итоге пытаемся найти distanc e , которые Билл путешествовал по межштатной автомагистрали. Давайте снова посмотрим на строку между штатами нашего графика и посмотрим, достаточно ли у нас информации, чтобы выяснить это.
| расстояние | скорость | время | |
|---|---|---|---|
| межгосударственный | d | 70 | 3 |
Похоже, что мы. Теперь, когда нам не хватает только одной переменной, мы сможем довольно быстро найти ее значение.
Чтобы найти расстояние, воспользуемся формулой перемещения расстояние = скорость ⋅ время .
d = rt
Теперь мы знаем, что Билл ехал по межгосударственной автомагистрали 3 часа на скорости 70 миль в час , поэтому мы можем заполнить эту информацию.
d = 3 ⋅ 70
Наконец, мы закончили упрощать правую часть уравнения. 3 ⋅ 70 это 210.
д = 210
Итак, d = 210. У нас есть ответ на нашу проблему! Расстояние 210.Другими словами, Билл проехал 210 миль по шоссе.
Решение задачи туда и обратно
Может показаться, что решение первой проблемы заняло много времени. Чем больше вы будете практиковаться в решении этих задач, тем быстрее они решатся. Попробуем аналогичную задачу. Эта задача называется задачей «туда и обратно» , потому что она описывает поездку туда и обратно — поездку, которая включает в себя обратный путь. Несмотря на то, что поездка, описанная в этой задаче, немного отличается от поездки в нашей первой задаче, вы сможете решить ее таким же образом.Давайте посмотрим:
Ева ехала на работу со средней скоростью 36 миль в час. По дороге домой она попала в пробку и проехала в среднем 27 миль в час. Ее общее время в машине составило 1 час 45 минут, или 1,75 часа. Как далеко Ева живет от работы?
Если у вас возникли проблемы с пониманием этой проблемы, вы можете представить себе дорогу Евы на работу следующим образом:
Как всегда, начнем с заполнения таблицы с важной информацией. Сделаем ряд с информацией о ее поездке на работу и с работы .
1,75 — т для описания поездки с работы. (Помните, что общее время в пути составляет 1,75 часа , поэтому время с до работы и от работы должно равняться 1,75.)
Из нашей таблицы мы можем написать два уравнения:
- Поездку на работу можно представить как d = 36 t .
- Поездку с работы можно представить как d = 27 (1.75 — т ).
В обоих уравнениях d представляет собой общее расстояние. Из диаграммы вы можете видеть, что эти два уравнения равны друг другу — в конце концов, Ева проезжает на одинаковое расстояние до и от работы .
Как и в случае с последней решенной задачей, мы можем решить эту, объединив два уравнения.
Начнем с нашего уравнения для поездки из работы .
d = 27 (1.75 — т)
Затем мы подставим значение d из нашего в уравнение , d = 36 t . Поскольку значение d равно 36 t , мы можем заменить любое вхождение d на 36 t .
36т = 27 (1,75 — т)
Теперь давайте упростим правую часть. 27 ⋅ (1,75 — т ) составляет 47,25.
36 т = 47,25 — 27 т
Затем мы сократим -27 t на , добавив 27 t к обеим сторонам уравнения. 36 т + 27 т это 63 т .
63т = 47,25
Наконец, мы можем получить t отдельно, разделив обе части на его коэффициент: 63. 47,25 / 63 равно 0,75.
т = 0,75
т равно 0,75. Другими словами, время, , которое потребовалось Еве, чтобы ехать на работу, составляет ,75 часа . Теперь, когда мы знаем значение t , мы сможем найти расстояние до работы Евы.
Если вы догадались, что мы снова будем использовать уравнение перемещения , вы были правы. Теперь мы знаем значение двух из трех переменных, что означает, что мы знаем достаточно, чтобы решить нашу проблему.
d = rt
Во-первых, давайте введем известные нам значения. Будем работать с номерами на рейс на работу . Мы уже знали коэффициент : 36. И мы только что узнали время : 0,75.
d = 36 ⋅ 0,75
Теперь все, что нам нужно сделать, это упростить уравнение: 36 ⋅.75 = 27,
д = 27
d равно 27. Другими словами, расстояние до работы Евы составляет 27 миль . Наша проблема решена.
Проблемы с пересекающимися расстояниями
Проблема с расстоянием пересечения — это проблема, при которой два объекта движутся навстречу друг другу. Вот типичная проблема:
Пауни и Спрингфилд находятся в 420 милях друг от друга. Поезд отправляется из Пауни в Спрингфилд, в то время как поезд уходит из Спрингфилда в сторону Пауни.Один поезд движется со скоростью 45 миль в час, а другой — 60 миль в час. Как долго они будут путешествовать до встречи?
Эта задача просит вас рассчитать, сколько времени потребуется этим двум поездам, движущимся навстречу друг другу, чтобы пересечь пути. Поначалу это может показаться запутанным. Несмотря на то, что это реальная ситуация, может быть сложно абстрактно представить расстояние и движение. Эта диаграмма может помочь вам понять, как выглядит эта ситуация:
Если вы все еще не уверены, не волнуйтесь! Вы можете решить эту проблему так же, как вы решили две задачи на предыдущей странице.Вам просто понадобится диаграмма и формула перемещения .
Пауни и Спрингфилд находятся на расстоянии 420 миль друг от друга . Поезд покидает Пауни, направляясь в Спрингфилд, в то время как поезд покидает Спрингфилд, направляясь в Пауни. Один поезд движется со скоростью 45 миль в час , а другой движется со скоростью 60 миль в час . Как долго они будут путешествовать до встречи?
Начнем с заполнения нашей диаграммы. Это снова проблема, на этот раз с подчеркнутой важной информацией.Начнем с заполнения самой очевидной информации: рейтинг . Проблема дает нам скорость каждого поезда. Мы обозначим их , быстрый поезд и медленный поезд , . Скоростной поезд идет со скоростью 60 миль / ч и км / ч. Медленный поезд идет всего 45 миль в час .
Мы также можем поместить эту информацию в таблицу:
| расстояние | скорость | время | |
|---|---|---|---|
| быстрый поезд | 60 | ||
| медленный поезд | 45 |
Мы не знаем расстояние, на которое едет каждый поезд встретить другого еще — мы просто знаем общее расстояние .Чтобы встретиться, поезда преодолеют суммарное расстояние , равное общему расстоянию. Как вы можете видеть на этой диаграмме, это верно независимо от того, как далеко едет каждый поезд.
Это означает, что, как и в прошлый раз, мы представим расстояние одного как d , а расстояние до другого — как общее минус d. Таким образом, расстояние для быстрого поезда будет d , а для медленного поезда — 420 — d .
| расстояние | скорость | время | |
|---|---|---|---|
| быстрый поезд | d | 60 | |
| медленный поезд | 420 — d | 45 |
Потому что мы ищем для времени и оба поезда едут до встречи, время будет одинаковым для обоих поездов. Мы можем представить это с t .
| расстояние | скорость | время | |
|---|---|---|---|
| быстрый поезд | d | 60 | t |
| медленный поезд | 420 — d | 45 | t |
Таблица дает нам два уравнения : d = 60 t и 420 — d = 45 t .Так же, как мы сделали с двумя задачами , мы можем объединить эти два уравнения.
Уравнение для быстрого поезда само по себе не решается, но оно говорит нам, что d равно 60 t .
d = 60 т
Другое уравнение, описывающее медленный поезд , тоже не может быть решено в одиночку. Однако мы можем заменить d его значением из первого уравнения.
420 — d = 45 т
Поскольку мы знаем, что d равно 60 t , мы можем заменить d в этом уравнении на 60 t .Теперь у нас есть уравнение, которое мы можем решить.
420 — 60 т = 45 т
Чтобы решить это уравнение, нам нужно получить t и его коэффициенты с одной стороны от знака равенства и любые другие числа с другой. Мы можем начать с отмены -60 t слева на , добавив 60 t к обеим сторонам. 45 т + 60 т — 105 т .
420 = 105 т
Теперь нам просто нужно избавиться от коэффициента рядом с t .Мы можем сделать это, разделив обе стороны на 105. 420/105 равно 4.
4 = т
t = 4. Другими словами, время , необходимое поездам для встречи, равно 4 часам . Наша проблема решена!
Если вы хотите быть уверены в своем ответе, вы можете проверить его , используя уравнение расстояния с t равным 4. Для нашего скоростного поезда уравнение будет иметь вид d = 60 ⋅ 4. 60 ⋅ 4 равно 240, поэтому расстояние, которое проехал наш быстрый поезд , составит 240 миль. Для нашего медленного поезда уравнение будет: d = 45 ⋅ 4. 45 ⋅ 4 равно 180, поэтому расстояние, пройденное медленным поездом , составляет 180 миль .
Помните, как мы сказали, что расстояние, на которое едет медленный поезд и быстрый поезд, должно равняться общему расстоянию ? 240 миль + 180 миль равно 420 миль, что является полным расстоянием от нашей задачи. Наш ответ правильный.
Практическая задача 1
Вот еще одна проблема с расстоянием пересечения.Он похож на тот, который мы только что решили. Посмотрим, сможете ли вы решить эту проблему самостоятельно. Когда вы закончите, прокрутите вниз, чтобы увидеть ответ и объяснение.
Джон и Дэни живут в 270 милях друг от друга. Однажды они решили ехать навстречу друг другу и тусоваться везде, где встречались. Джон ехал в среднем 65 миль в час, а Дэни ехал в среднем 70 миль в час. Как долго они ехали, прежде чем встретились?
Задача 1 ответ
Вот практическая задача 1:
Джон и Дэни живут в 270 милях друг от друга.Однажды они решили ехать навстречу друг другу и тусоваться везде, где встречались. Джон проехал в среднем 65 миль в час, а Дэни — 70 миль в час. Как долго они ехали, прежде чем встретились?
Ответ: 2 часа .
Давайте решим эту задачу так же, как и другие. Сначала попробуйте составить диаграмму. Должно получиться так:
| расстояние | скорость | время | |
|---|---|---|---|
| Jon | d | 65 | t |
| Dani | 270 — d | 70 | t |
Вот как мы заполнено в графике:
- Расстояние: Вместе, Дэни и Джон преодолеют общее расстояние между собой к тому времени, когда они встретятся.Это 270. Расстояние Джона представлено как d , поэтому расстояние Дэни составляет 270 — d .
- Оценить: Проблема сообщает нам скорости Дэни и Джона. Дани проезжает 65 миль в час , а Джон — 70 миль в час .
- Время: Поскольку Джон и Дэни проезжают одинаковое количество времени до встречи, их время в пути равно t .
Теперь у нас есть два уравнения. Уравнение перемещения Джона: d = 65 t .Уравнение путешествия Дэни: 270 — d = 70 t . Чтобы решить эту проблему, нам нужно объединить их.
Уравнение для Джона говорит нам, что d равно 65 t . Это означает, что мы можем объединить два уравнения, заменив d в уравнении Дэни на 65 t .
270 — 65 т = 70 т
Давайте получим t с одной стороны уравнения и число с другой. Первый шаг к этому — избавиться от -65 t с левой стороны.Отменим его на , добавив 65 t к обеим сторонам: 70 t + 65 t равно 135 t .
270 = 135 т
Все, что осталось сделать, это избавиться от 135 рядом с t . Мы можем сделать это, разделив обе стороны на 135: 270/135 равно 2.
2 = т
Вот и все. t равно 2. У нас есть ответ на нашу проблему: Дэни и Джон проехали 2 часа до встречи.
Проблемы с дистанцией обгона
Последний тип задачи о расстоянии, которую мы обсудим в этом уроке, — это задача, в которой один движущийся объект обгоняет — или проходит — другой. Вот типичная проблема при обгоне:
Семья Хилл и семья Платтеров отправляются в путешествие. Холмы уехали за 3 часа до Platters, но Platters едут в среднем на 15 миль в час быстрее. Если семье Платтер требуется 13 часов, чтобы догнать семью Хилл, насколько быстро едут Хиллз?
Вы можете представить себе момент, когда семья Платтеров отправилась в путешествие, примерно так:
Задача говорит нам, что семья Платтеров догонит семью Хилл через 13 часов, и просит нас использовать эту информацию, чтобы найти для семьи Хилл рейтинг .Как и в случае с некоторыми другими проблемами, которые мы решили в этом уроке, может показаться, что у нас недостаточно информации для решения этой проблемы, но у нас есть. Приступим к составлению нашей диаграммы. Расстояние может быть d как для Холмов, так и для Платтеров — когда Платтеры догонят Холмы, обе семьи пройдут одинаковое расстояние.
| расстояние | скорость | время | |
|---|---|---|---|
| холмы | d | ||
| пластины | d |
Заполнение ставки и время будет требуется еще немного подумать.Мы не знаем ставки для каждой семьи — помните, это то, что мы пытаемся выяснить. Однако мы знаем, что Platters проехали на миль в час быстрее , чем Hills. Это означает, что если ставка семьи Хилл составляет руб. , то ставка семьи Платтер будет руб. + 15.
| расстояние | скорость | время | |
|---|---|---|---|
| холмы | d | r | |
| пластины | d | r + 15 |
Теперь все, что осталось, — время.Мы знаем, что Platters потребовалось 13 часов , чтобы догнать Холмы. Однако помните, что Хиллс выехал из на 3 часа раньше, чем Платтерс — это означает, что когда Платтерс догнал, они проехали на 3 часа больше, чем Плэттерс. 13 + 3 равно 16, так что мы знаем, что Хиллз ехали 16 часов к тому времени, когда Платтерс их догнали.
| расстояние | скорость | время | |
|---|---|---|---|
| холмы | d | r | 16 |
| пластины | d | r + 15 | 13 |
Наши диаграмма дает нам два уравнения.Путешествие семьи Хилл можно описать следующим образом: d = r ⋅ 16. Уравнение путешествия семьи Платтеров: d = ( r + 15) ⋅ 13. Как и в случае с другими задачами, мы можем объедините этих уравнений, заменив переменную в одном из них.
Уравнение семейства Хиллов уже имеет значение d , равное r ⋅ 16. Поэтому мы заменим d в уравнении Платтера на r ⋅ 16 .Таким образом, это будет уравнение, которое мы сможем решить.
р 16 = (г + 15) ⋅ 13
Во-первых, давайте упростим правую часть: r ⋅ 16 равно 16 r .
16r = (r + 15) ⋅ 13
Далее упростим правую часть и умножим ( r + 15) на 13.
16р = 13р + 195
Мы можем получить r и их коэффициенты слева, вычитая 13 r из 16 r : 16 r — 13 r равно 3 r .
3р = 195
Теперь все, что осталось сделать, это избавиться от 3 рядом с r . Для этого разделим обе стороны на 3: 195/3 равно 65.
г = 65
Итак, вот наш ответ: r = 65. Семья Хилл проехала в среднем 65 миль в час .
Вы можете решить любую проблему обгона так же, как мы. Просто не забудьте уделить особое внимание настройке диаграммы. Так же, как семья Хилл решила эту проблему, человек или транспортное средство, начавшее движение первым , всегда будет иметь большее время в пути .
Практическая задача 2
Попробуйте решить эту проблему. Это похоже на проблему, которую мы только что решили. Когда вы закончите, прокрутите вниз, чтобы увидеть ответ и объяснение.
Поезд, движущийся со скоростью 60 миль в час, отправляется со станции в полдень. Час спустя поезд, движущийся со скоростью 80 миль в час, уезжает в том же направлении по параллельному пути. Во сколько второй поезд догоняет первый?
Ответ на задачу 2
Вот практическая задача 2:
Поезд, движущийся со скоростью 60 миль в час, отправляется со станции в полдень.Час спустя поезд, движущийся со скоростью 80 миль в час, уезжает в том же направлении по параллельному пути. Во сколько второй поезд догоняет первый?
Ответ: 16:00
Чтобы решить эту проблему, начните с построения диаграммы. Вот как это должно выглядеть:
| расстояние | скорость | время | |
|---|---|---|---|
| быстрый поезд | d | 80 | t |
| медленный поезд | d | 60 | t + 1 |
Вот пояснение к диаграмме:
- Расстояние: Оба поезда пройдут одинаковое расстояние к тому времени, когда быстрый поезд догонит медленный, поэтому расстояние для обоих составляет d .
- Оценить: Задача сообщает нам, насколько быстро ехал каждый поезд. У быстрого поезда скорость 80 миль в час , а у медленного поезда — 60 миль в час .
- Время: Мы будем использовать t , чтобы представить время в пути скоростного поезда до того, как он догонит его. Поскольку медленный поезд отправился на час раньше, чем быстрый, он должен будет ехать на час больше, когда его догонит быстрый поезд. Это t + 1.
Теперь у нас есть два уравнения.Уравнение для скоростного поезда: d = 80 t . Уравнение для медленного поезда: d = 60 ( t + 1). Чтобы решить эту проблему, нам нужно объединить уравнений.
Уравнение для скоростного поезда говорит, что d равно 80 t . Это означает, что мы можем объединить два уравнения, заменив d в уравнении медленного поезда на 80 t .
80т = 60 (т + 1)
Во-первых, давайте упростим правую часть уравнения: 60 ⋅ ( t + 1) равно 60 t + 60.
80т = 60т + 60
Чтобы решить уравнение, нам нужно получить t с одной стороны от знака равенства и число с другой. Мы можем избавиться от 60 t справа, вычитая 60 t с обеих сторон: 80 t -60 t равно 20 t .
20т = 60
Наконец, мы можем избавиться от 20 рядом с t , разделив обе стороны на 20. 60 разделить на 20 равно 3.
т = 3
Итак, т равно 3. Скорый поезд прошел 3 часа . Однако это не ответ на нашу проблему. Давайте снова посмотрим на исходную проблему. Обратите внимание на последнее предложение — вопрос, на который мы пытаемся ответить.
Поезд, движущийся со скоростью 60 миль в час, отправляется со станции в полдень. Час спустя поезд, движущийся со скоростью 80 миль в час, уезжает в том же направлении по параллельному пути. Во сколько второй поезд догоняет первый?
Наша проблема не спрашивает, сколько длин проехал любой из поездов.Он спрашивает , в какое время второй поезд догонит первый.
Задача говорит нам, что медленный поезд ушел в полдень, а быстрый — на час позже. Это означает, что скорый поезд ушел в , 13:00 и . Из наших уравнений мы знаем, что скоростной поезд проехал 3 часов . 1 + 3 равно 4, поэтому быстрый поезд догнал медленный в 16:00 . Ответ на задачу — 16:00.
Использование весенних уравнений — Физика средней школы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Дифференциальные уравнения — моделирование с помощью DE
первого порядкаИтак, это в основном та же ситуация, что и в предыдущем примере. 2} \).Кроме того, мы просто собираемся найти скорость в любой момент времени \ (t \) для этой проблемы, потому что решение будет действительно неприятным, и определение скорости, когда масса ударяется о землю, — это просто больше работы, чем мы хотим поставить задачу, чтобы проиллюстрировать тот факт, что нам нужно отдельное дифференциальное уравнение для движения массы вверх и вниз.
Как и в предыдущем примере, мы будем использовать соглашение, что все вниз положительно.2} \\ & v \ left ({{t_0}} \ right) = 0 \ end {выровнено} \ end {array} \]
Это явно разные дифференциальные уравнения, поэтому, в отличие от предыдущего примера, мы не можем просто использовать первое для полной задачи.
Кроме того, их решение будет немного сложнее, чем в предыдущем примере, поскольку ни одно из дифференциальных уравнений не является линейным. Однако оба они являются отделимыми дифференциальными уравнениями.
Итак, приступим к процессу решения.{- 1}} \ left ({\ frac {v} {{\ sqrt {98}}}} \ right) & = t + c \ end {align *} \]
Обратите внимание, что мы немного переписали подынтегральную функцию, чтобы упростить процесс на втором этапе.
Теперь у нас есть два варианта продолжения. Либо мы можем решить для скорости сейчас, что нам нужно будет сделать в конечном итоге, либо мы можем применить начальное условие на этом этапе. Хотя мы всегда решали функцию перед применением начального условия, мы могли бы так же легко применить его здесь, если бы захотели, и в этом случае, вероятно, будет немного проще.{- 1}} \ left ({\ frac {{- 10}} {{\ sqrt {98}}}} \ right)} \ right) \ end {align *} \]
Теперь нам нужно определить, когда объект достигнет вершины своей траектории. Для этого все, что нам нужно сделать, это установить его равным нулю, учитывая, что объект на вершине будет иметь нулевую скорость прямо перед тем, как он начнет движение вниз. Мы предоставим вам проверить, что скорость равна нулю при следующих значениях \ (t \). {- 1}} \ left ({\ frac {{10}} {{\ sqrt {98}}}} \ right) + \ pi n} \ right] \ hspace {0.25 дюймов} n = 0, \ pm 1, \ pm 2, \ pm 3, \ ldots \]
Мы явно не хотим всего этого. Нам нужно первое положительное значение \ (t \), которое даст нулевую скорость. Нет смысла принимать отрицательное значение \ (t \), учитывая, что мы начинаем процесс в точке \ (t = 0 \), и как только он достигает вершины (, т.е. , первое положительное значение \ (t \) для при которой скорость равна нулю) решение больше не действует, поскольку объект начнет двигаться вниз, и это решение предназначено только для движения вверх.2} = \ left ({\ sqrt {98} — v} \ right) \ left ({\ sqrt {98} + v} \ right) \). Вы, вероятно, не привыкли к таким вещам, но работа с частичными дробями позволяет нам избежать подстановки триггеров, и она работает точно так же, как когда все является целым числом, поэтому мы сделаем это для этого интеграла.
Мы оставим вам детали частичного дробления. После частичного дробления интеграл принимает вид
.\ [\ begin {align *} 10 \ left ({\ frac {1} {{2 \ sqrt {98}}}} \ right) \ int {{\ frac {1} {{\ sqrt {98} + v}} + \ frac {1} {{\ sqrt {98} — v}} \, dv}} & = \ int {{dt}} \\ \ frac {5} {{\ sqrt {98}}} \ left [{\ ln \ left | {\ sqrt {98} + v} \ right | — \ ln \ left | {\ sqrt {98} — v} \ right |} \ right] & = t + c \\ \ frac {5} {{\ sqrt {98}}} \ ln \ left | {\ frac {{\ sqrt {98} + v}} {{\ sqrt {98} — v}}} \ right | & = t + c \ end {выровнять *} \]
Опять же, на этом этапе мы применим начальное условие, чтобы немного облегчить нашу жизнь.Это дает
\ [\ begin {align *} \ frac {5} {{\ sqrt {98}}} \ ln \ left | {\ frac {{\ sqrt {98} + v \ left ({0.79847} \ right)}} {{\ sqrt {98} — v (0.79847}}} \ right | & = 0.79847 + c \\ \ frac { 5} {{\ sqrt {98}}} \ ln \ left | {\ frac {{\ sqrt {98} + 0}} {{\ sqrt {98} — 0}}} \ right | & = 0,79847 + c \\ \ frac {5} {{\ sqrt {98}}} \ ln \ left | 1 \ right | & = 0,79847 + c \\ c & = — 0,79847 \ end {align *} \]
Решения, как мы уже писали, тогда
\ [\ frac {5} {{\ sqrt {98}}} \ ln \ left | {\ frac {{\ sqrt {98} + v}} {{\ sqrt {98} — v}}} \ right | = т — 0.79847 \]
Хорошо, теперь нам нужно решить для \ (v \), и для этого нам действительно нужно убрать столбцы абсолютных значений, и мы не можем просто отбросить их, чтобы облегчить нашу жизнь. Нам нужно знать, что их можно отбросить без какого-либо влияния на окончательное решение.
Для этого давайте сделаем быстрое поле направления или, что более уместно, несколько набросков решений из поля направления. Вот тот набросок,
Обратите внимание, что \ (\ sqrt {98} = 9.89949 \) и поэтому немного выше / ниже линий -10 и 10, показанных на эскизе. Здесь важно обратить внимание на среднюю область. Если скорость начинается где-нибудь в этой области, как у нас, учитывая, что \ (v \ left ({0.79847} \ right) = 0 \), то скорость всегда должна быть меньше \ (\ sqrt {98} \).
Для нас это означает, что и \ (\ sqrt {98} + v \), и \ (\ sqrt {98} — v \) должны быть положительными, и поэтому количество в столбцах абсолютного значения также должно быть положительным.