Система заданий по математике к теме «Обыкновенные дроби»




 КГАОУДПО(ПК)С «Красноярский краевой институт повышения квалификации и профессиональной переподготовки работников образования»
КГАОУДПО(ПК)С «Красноярский краевой институт повышения квалификации и профессиональной переподготовки работников образования»
Аттестационная работа
по программе «Развитие у учащихся познавательных универсальных учебных действий средствами
Способа диалектического обучения»
Система заданий по математике к теме «Обыкновенные дроби»
Выполнил(а)
Учитель математики
Новоозёрновской ООШ
Скибина Наталья Ивановна
Проверил:
__________________________________
«____» ____________________ 2014 г.
Тема: «Обыкновенные дроби»:
Класс: 5
Учебник: Зубарева И.И., Мордкович А.Г. Математика, 5 кл.: учебник для общеобразовательных учреждений .- М.: Мнемозина, 2002. – 293 с.
№Система заданий
Ответы учащихся
Предметные умения
ПУУД
1.
Сформулируйте проблемные вопросы к теме урока, которые будут отражать цель урока.
— Что называется обыкновенной дробью?
— Каким образом обыкновенная дробь отличаются от других дробных чисел?
— Каковы свойства и виды обыкновенных дробей?
Отличать обыкновенную дробь от других дробных чисел;
Указывать существенные признаки обыкновенных дробей.
Анализ объектов с целью выделения признаков (сущ.и несущ.) (ЛогУУД)
Осознанное и произвольное построение речевого высказывания в устной и письменной форме (ОУ)
Сформулируйте такие проблемные вопросы по карточке №1, ответы на которые позволят достичь цель усвоения темы «Обыкновенные дроби»
Карточка № 1 (вопрос-понятие)
Что называется обыкновенной дробью?
Что считается дробным числом?
Что понимается под числителем обыкновенной дроби?
Что представляет собой знаменатель обыкновенной дробь?
Что выражает основное свойство дроби?
Что является приведением обыкновенных дробей к общему знаменателю?
Что такое — перевод из неправильной дроби в смешанную дробь?
Каковы свойства и виды обыкновенных дробей?
В чем заключается сущность сравнения дробей?
Отличать обыкновенную дробь от других дробных чисел;
Указывать существенные признаки обыкновенных дробей.
структурирование знаний;
Осознанное и произвольное построение речевого высказывания в устной и письменной форме
4
Установить вид правильного определения понятия «Обыкновенная дробь»:
Каждый может за версту
Видеть дробную черту.
Над чертой – числитель, знайте,
Под чертою –знаменатель.
Дробь такую, непременно,
Надо звать обыкновенной.
Обыкновенная дробь — это целое число (числитель), деленное на другое целое число (знаменатель).
Обыкновенная дробь – это дробное число (дробь), представленное как частное от деления натуральных чисел m и n, записанная в виде 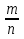
Обыкновенная дробь – это дробное число (дробь), представленное как частное от деления натуральных чисел m и n, запи-
санная в виде 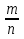 Задание не выполнено: надо было установить вид правильного определения, желательно, с обоснованием
Задание не выполнено: надо было установить вид правильного определения, желательно, с обоснованием
Устанавливать истинность признаков принадлежащих понятию «Обыкновенная дробь», определить существенные признаки
понятия «Обыкновенная дробь»
анализ объектов с целью выделения признаков (существенных, несущественных)
•синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты; •подведение под понятия, выведение следствий;
построение логической цепи рассуждений,
•доказательство; •осознанное и произвольное построение речевого высказывания в устной форме;
В определении понятий подчеркнуть одной чертой родовой признак и двойной чертой видовые признаки:
Правильной дробью называется дробь, которая меньше единицы и у которой числитель меньше знаменателя.
Обыкновенная дробь – это дробное число (дробь), представленное как частное от деления натуральных чисел m и n, запи-
санная в виде 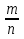
Правильной дробью называется дробь, которая меньше единицы и у которой числитель меньше знаменателя.
Обыкновенная дробь – это дробное число (дробь), представленное как частное от деления натуральных чисел m и n, запи-
санная в виде 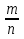
Распознавать и определять истинность существенных признаков понятия «Обыкновенная дробь»
анализ объектов с целью выделения признаков (существенных, несущественных);
построение логической цепи рассуждений,
подведение под понятия
6
Восстановить пропущенные элементы в определении понятия:
«Обыкновенная дробь – это______________, представленное как __________от _________натуральных чисел m и n, запи-
санная в виде 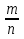
(дробное число, натуральное число, дробь, произведение,
частное, деление, разность)
Обыкновенная дробь – это дробное число (дробь), представленное как частное от деления натуральных чисел m и n, запи-
санная в виде 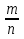
Выделять существенные признаки понятия «Обыкновенная дробь»;
Формулировать определение понятия «обыкновенная дробь»
•синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты;
•подведение под понятия
7
указать каждому понятию ближайший родовой признак:
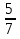 ; 2,3; неправильная дробь; натуральное число; у-23=46.
; 2,3; неправильная дробь; натуральное число; у-23=46.
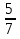 — Обыкновенная дробь
— Обыкновенная дробь
2,3- десятичная дробь
неправильная дробь -дробь
уравнение — равенство
у-23=46 — уравнение
Распознавать и определять истинность существенных признаков понятия
«Обыкновенная дробь»
•подведение под понятия
анализ объектов с целью выделения признаков (существенных, несущественных)
8
Как доказать, что определение «Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби» истинным определением понятия «смешанная дробь»?
Определение «Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби» является истинным определением понятия «смешанная дробь», т.к. содержит родовой признак – дробь и видовые — записанная в виде целого числа и правильной дроби, понимается как сумма этого числа и дроби.
Распознавать и определять истинность существенных признаков понятия
«Обыкновенная дробь»
анализ объектов с целью выделения признаков (существенных, несущественных)
•подведение под понятия, выведение следствий;
построение логической цепи рассуждений,
•доказательство; •осознанное и произвольное построение речевого высказывания в устной форме;
9
Найти основание деления понятий:
Правильная и неправильные дроби.
Критерии деления-
По соотношению с единицей.
Находить основания для логического деления понятий по теме «Обыкновенная дробь»
•выбор оснований и критериев для сравнения, сериации, классификации объектов;
•анализ объектов с целью выделения признаков (существенных, несущественных)
10
Найти лишнее понятие, указав основание деления:
Делитель, числитель, делимое, деление, знаменатель.
Лишнее понятие – деление, означает действие, остальные – это компоненты деления.
Находить основания для логического деления понятий по теме «Обыкновенная дробь»
•выбор оснований и критериев для сравнения, сериации, классификации объектов;
•анализ объектов с целью выделения признаков (существенных, несущественных)
11
Выстроить ряд понятий по следующему признаку – порядок действий по переводу смешанного числа в неправильную дробь
Знаменатель дробной части смешанного числа умножить на целую часть и прибавить числитель; ответ записать числителем неправильной дроби, знаменатель записать тот же.
Устанавливать алгоритм выполняемых действий по признаку – порядок действий по переводу смешанного числа в неправильную дробь
осознанное и произвольное построение речевого высказывания в устной и письменной форме
•анализ объектов с целью выделения признаков (существенных, несущественных)
Самостоятельное создание алгоритмов деятельности при решении задач творческого и поискового характера
12
Прочитав текст, установить соблюдение\нарушение логических правил деления понятия «Дробь» Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. По способу записи дроби делятся на 2 группы: обыкновенные вида 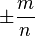 и десятичные.
и десятичные.
В тексте соблюдены логические правила деления понятия «Дробь», т.к. указано основание деления – «По способу записи»
устанавливать соблюдение\нарушение логических правил деления понятия «Дробь»
•анализ объектов с целью выделения признаков (существенных, несущественных)
•выбор оснований и критериев для сравнения, сериации, классификации объектов;
осознанное и произвольное построение речевого высказывания в устной и письменной форме
•поиск и выделение необходимой информации;
Смысловое чтение
13
Составить карточку, №3 сравнив правильные и неправильные дроби.
Карточка №3 «Сравнение правильных и неправильных дробей»
1. По сравнению с правильной дробью, которая меньше 1, неправильная дробь равна или больше 1.
2. Так же, как и правильная дробь, и неправильная дробь относится к обыкновенным дробям.
З. Как правильная дробь, так и неправильная дробь имеют способ записи через дробную черту.
4. Сравнивая правильную и неправильную дробь, можно сказать, что все это дробные числа.
5. Кроме правильной дроби 4/5, еще и неправильная дробь 7/5 имеет одинаковый знаменатель.
6. Помимо правильной дроби, неправильная дробь также представляет собой частное от деления натуральных чисел m и n, записанная в виде 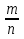 .
.
7. Неправильная дробь всегда больше, чем правильная дробь.
8. Не только правильная дробь, а и неправильная дробь имеют одинаковый алгоритм выполнения действий умножения и деления..
9. Наряду с правильными дробями, а и неправильные дроби при сравнении приводят к общему знаменателю.
10. Если правильную дробь можно представить в виде ответа, то неправильную дробь обязательно нужно преобразовать.
11. В отличие от неправильной дроби, которую можно записать в виде целого числа и правильной дроби, правильная дробь не обладает таким свойством.
12.Так же как и правильная дробь, неправильная дробь может быть сократимой (несократимой).
13. Кроме правильной обыкновенной дроби, еще неправильная обыкновенная дробь имеет знаменатель всегда не равный нулю.
14. Не только для правильной, а и для неправильной обыкновенных дробях можно найти дополнительный множитель.
15. Наряду с правильной обыкновенной дробью, для неправильной обыкновенной дроби можно применить основное свойство дроби.
16. В отличие от правильной обыкновенной дроби, неправильная обыкновенная дробь на координатном луче расположена правее.
Называть общие и отличительные существенные признаки правильных и неправильных дробей, их свойства
14
Система заданий:
Из предложенного перечня понятий «правильная дробь, десятичная дробь, неправильная дробь, сократимая дробь, обыкновенная дробь, несократимая дробь» (выпишите пары противоположных понятий.
Обобщите каждую пару противоположных понятий до ближайшего рода.
Ответьте на вопрос – каким образом одна противоположность отличается от другой?
Назовите основание деления.
1.«правильная дробь, неправильная дробь»,
«десятичная дробь, обыкновенная дробь»,
«сократимая дробь, несократимая дробь».
2.обыкновенная дробь,
десятичная дробь – это дроби.
3. По сравнению с правильной дробью, которая меньше 1, неправильная дробь равна или больше 1.
В отличие от обыкновеннмой дроби, которая записывается через дробную черту десятичная дробь записывается с помощью запятой, которая отделяет целую и дробную части.
Сравнивая сократимую и несократимую дробь, можно сказать, что в сократимой дроби числитель и знаменатель делят на один и тот же делитель, а несократимая дробь не обладает таким свойством.
осознанное и произвольное построение речевого высказывания в устной и письменной форме;
•анализ объектов с целью выделения признаков (существенных, несущественных)
•синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты;
•выбор оснований и критериев для сравнения, сериации, классификации объектов;
•построение логической цепи рассуждений,
•доказательство;
установление причинно-следственных связей
15
Определите правильность или ложность сравнения и доказать свой ответ:
«Сократимую правильную дробь надо обязательно сокращать, так и неправильную дробь надо обязательно сокращать», «Правильная дробь меньше 1, а неправильная дробь равна или больше 1».
Ложное суждение, т.к. не все неправильные дроби имеют свойство сокращаться.
Правильное сравнение, т.к. в правильной дроби числитель меньше знаменателя и частное будет меньше единицы, а в неправильной дроби все наоборот.
Определять свойства правильных дробей
16
Отразить содержание параграфа «Обыкновенные дроби» посредством составленных умозаключений, определив их вид.
К дроби 3/6 применяют основное свойство дроби.
К дроби 15/5 применяют основное свойство дроби.
К дроби 12/18 применяют основное свойство дроби.
3/6, 15/5, 12/18 – сократимые обыкновенные дроби.
Следовательно, ко всем сократимым обыкновенным дробям применяют основное свойство дроби.
— неполная индукция.
Смешанное число относится к обыкновенным дробям и состоит из числителя, знаменателя, дробной черты и целой части.
Неправильная дробь относится к обыкновенным дробям и состоит из числителя, знаменателя, дробной черты.
Вероятно, неправильная дробь также имеет целую часть. – аналогия.
Если числитель обыкновенной дроби меньше знаменателя, то дробь правильная, то В дробях 16/5 и 7/7 числитель не меньше знаменателя. Следовательно, дроби 16/5 и 7/7 – неправильные.- дедукция.
Все обыкновенные дроби имеют способ записи через дробную черту; 4,7 имеет способ записи не через дробную черту, следовательно, 4,7 не относится к обыкновенным дробям (дедукция)
Если в дроби числитель меньше знаменателя, то дробь правильная. В дроби 4/7 числитель меньше знаменателя (4<7). Следовательно, дробь 4/7 – правильная. .- дедукция
2\3 – дробь меньшая 1.
4\5 – дробь меньше 1.
1\7 – дробь меньше 1.
3\10 – дробь меньше 1.
2\3, 4\5, 1\7, 3\10 – правильные дроби.
Следовательно, правильные дроби меньше 1. (индукция)
Дробь, у которой числитель и знаменатель имеют общий делитель, отличный от 1 называется сократимой дробью.
В дроби 5\7 числитель и знаменатель не имеет общий делитель отличный от 1.
Следовательно, дробь 5\7 не является сократимой (дедукция)
Если 10\15 сократимая дробь.
То 11\15 несократимая дробь. (аналогия)
выбор оснований и критериев для сравнения, сериации, классификации объектов;
построение логической цепи рассуждений
•анализ объектов с целью выделения признаков (существенных, несущественных)
•синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты;
•подведение под понятия, выведение следствий;
•установление причинно-следственных связей,
•построение логической цепи рассуждений,
•доказательство;
•выдвижение гипотез и их обоснование.
17
Определить вид умозаключения:
Если 10\15 сократимая дробь.
То 11\15 несократимая дробь.
Если 10\15 сократимая дробь.
То 11\15 несократимая дробь.
Данное умозаключение является умозаключением по аналогии отношений.
знает виды обыкновенных дробей и их определения
•структурирование знаний;
•осознанное и произвольное построение речевого высказывания в устной и письменной форме;
•анализ объектов с целью выделения признаков (существенных, несущественных)
•синтез как составление целого из частей, в том числе самостоятельно достраивая, восполняя недостающие компоненты;
•подведение под понятия, выведение следствий;
•установление причинно-следственных связей,
•построение логической цепи рассуждений,
•доказательство;
•выдвижение гипотез и их обоснование.
18
Проверить правильность формулировки умозаключения:
2\3 – правильная дробь меньшая 1.
4\5 – правильная дробь меньше 1.
1\7 – правильная дробь меньше 1.
3\10 – правильная дробь меньше 1.
Следовательно, все правильные дроби меньше 1.
формулировка умозаключения неправильная, т.к. отсутствует обобщающая посылка
Понимать мировоззренческое значение обыкновенных дробей
19
Сформулировать дедуктивные умозаключения, используя понятия данных групп:
— дробь 4/7, дробь правильная, в дроби числитель меньше знаменателя.
Если в дроби числитель меньше знаменателя, то дробь правильная. В дроби 4/7 числитель меньше знаменателя (4<7). Следовательно, дробь 4/7 – правильная. .- дедукция
овладение базовым понятийным аппаратом по теме «Обыкновенная дробь»,
распознавания правильные и неправильные дроби
20
Приложение.
Обыкнов. дробь
По способу записи по наличию НОД и с по соотнош с единицей
пособности делить на него
Десят. Простая смеш число сокр. несократимая прав. неправильная
Решение задач на сложение и вычитание обыкновенных дробей
Класс: 5 «Б» Предмет: Математика Урок № 97 Дата: 09.01.2015
Тема: Решение задач на сложение и вычитание обыкновенных дробей
Цель: Повторение умений и навыков решения задач на сложение и вычитание обыкновенных дробей и смешанных чисел
Задачи: — повторить с учащимися умения и навыки решения задач на сложение и вычитание обыкновенных дробей и смешанных чисел;
— развивать у учащихся вычислительные навыки самостоятельного выполнения заданий на решение задач на сложение и вычитание обыкновенных дробей и смешанных чисел;
— воспитывать у учащихся осознанное отношение к правильному решению заданий.
Тип: Урок повторения.
Метод: Практическое решение заданий по карточкам.
Ход урока
Организационный момент
Проверка подготовленности учащихся к уроку.
Приветствие учителя и учащихся.
Фиксация отсутствующих учащихся.
Постановка цели и задач урока.
Актуализация опорных знаний
Алгоритм выполнения сложения и вычитания обыкновенных дробей.
Алгоритм выполнения сложения и вычитания смешанных чисел.
Основная часть
Вычислите:
1) 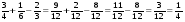 ;
;
2) 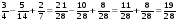 ;
;
3) 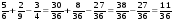 ;
;
4) 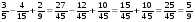
В первый день вспахали
 часть всего поля, во второй день – на
часть всего поля, во второй день – на  часть больше, чем в первый день. Сколько всего земли вспахали за два дня?
часть больше, чем в первый день. Сколько всего земли вспахали за два дня?
Решение
 – во второй день
– во второй день
 – за два дня
– за два дня
Ответ: за два дня вспахали 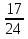 часть всего поля.
часть всего поля.
Первое число
 , второе число меньше на
, второе число меньше на  м. Найдите сумму данных двух чисел.
м. Найдите сумму данных двух чисел.
Решение
 – второе число
– второе число
 – за два дня
– за два дня
Ответ: 1.
На первой машине было
 т груза. Когда с нее сняли
т груза. Когда с нее сняли  т груза, груз первой машины продолжал превышать груз второй машины на
т груза, груз первой машины продолжал превышать груз второй машины на  т. Сколько тонн груза было во второй машине?
т. Сколько тонн груза было во второй машине?
Решение
 – т груза в первой машине после снятия
– т груза в первой машине после снятия
 – т груза во второй машине
– т груза во второй машине
Ответ: во второй машине 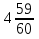 т груза.
т груза.
Дополнительно:
Подведение итогов урока
Обсуждение успешности достижения цели и задач урока.
Аргументированное выставление оценок за урок.
Разъяснение домашнего задания – № 722 (2) стр. 184
Вычислите:
1) 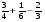 ; 2)
; 2) 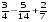 ; 3)
; 3) 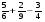 ; 4)
; 4) 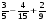
В первый день вспахали
 часть всего поля, во второй день – на
часть всего поля, во второй день – на  часть больше, чем в первый день. Сколько всего земли вспахали за два дня?
часть больше, чем в первый день. Сколько всего земли вспахали за два дня?
Первое число
 , второе число меньше на
, второе число меньше на  м. Найдите сумму данных двух чисел.
м. Найдите сумму данных двух чисел.
На первой машине было
 т груза. Когда с нее сняли
т груза. Когда с нее сняли  т груза, груз первой машины продолжал превышать груз второй машины на
т груза, груз первой машины продолжал превышать груз второй машины на  т. Сколько тонн груза было во второй машине?
т. Сколько тонн груза было во второй машине?
Дополнительно:
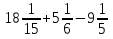
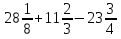
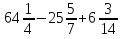

Вычислите:
1) 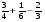 ; 2)
; 2) 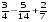 ; 3)
; 3) 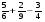 ; 4)
; 4) 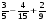
В первый день вспахали
 часть всего поля, во второй день – на
часть всего поля, во второй день – на  часть больше, чем в первый день. Сколько всего земли вспахали за два дня?
часть больше, чем в первый день. Сколько всего земли вспахали за два дня?
Первое число
 , второе число меньше на
, второе число меньше на  м. Найдите сумму данных двух чисел.
м. Найдите сумму данных двух чисел.
На первой машине было
 т груза. Когда с нее сняли
т груза. Когда с нее сняли  т груза, груз первой машины продолжал превышать груз второй машины на
т груза, груз первой машины продолжал превышать груз второй машины на  т. Сколько тонн груза было во второй машине?
т. Сколько тонн груза было во второй машине?
Дополнительно:
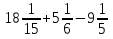
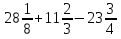
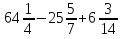

Конспект урока по математике » Решение задач на все действия с обыкновенными дробями»
Тема Решение задач на все действия с обыкновенными дробями.
Цель обучения закрепление навыков выполнения действий над обыкновенными дробями
Задачи
закрепление изученного материала;
развитие сообразительности, умения ориентироваться в нестандартных ситуациях;
3.расширение и углубление знаний школьников о главном Законе страны — Конституции Украины
Добрый день, ребята!
Как вы думаете, зачем надо изучать математику? Ответ на этот вопрос вы найдёте, если узнаете, что означает в переводе с греческого слово “математика”. “Математика” — знание, наука. Именно поэтому, если человек был сведущ в математике, то это всегда означало высшую степень учёности. А умение правильно видеть и слышать – первый шаг к мудрости. Хочется, чтобы сегодня на уроке все ученики в классе показали, насколько они мудры и насколько сведущие люди в математике 6 класса.
Откройте, пожалуйста, тетради. Запишите сегодняшнее число. Классная работа.
Тема урока “ Решение задач на все действия с обыкновенными дробями ”.
А сейчас все дружно встали. Проведем мозговой штурм.
1. Как называется деление числителя и знаменателя на одно и то же число.
2. Как называется элемент дроби, стоящий над чертой, под чертой.
3. Каким действием можно заменить дробную черту.
4. Для того чтобы сравнить дроби с разными знаменателями нужно…
5. Для нахождения общего знаменателя нужно найти НОК или НОД.
6. Какие числа называются взаимно обратными.
7. Как найти дробь от числа.
8. Как называется сотая часть числа.
9. Какая дробь называется правильной.
10. Как называется умножение числителя и знаменателя на одно и тоже число?
11.Сформулировать правило умножения обыкновенных дробей.
12.Как умножить дробь на натуральное число?
13.Как поделить обыкновенные дроби?
14.Какие числа называются взаимно-обратными?
15.Какая дробь называется неправильной?
16.Как найти число по данной дроби?
17.Как умножить смешанные числа?
18. Какие числа называются взаимно простыми?
19. Как разделить смешанные числа?
20. НОД каких чисел равен 1?
21. Как называется число,на которое надо умножить числитель и знаменатель, чтобы привести дробь к новому знаменателю?
22. На какое число нельзя делить?
23.Она бывает охотничья, барабанная и математическая. Что это?
24.Как возвести дробь в степень?
Вы готовы поработать? (Да!)
Вы готовы отвечать? (Да!)
Вы готовы, если надо,
Что-то вспомнить и узнать? (Да!)
Ну а главное – готовы
Вы сегодня рассуждать? (Да!)
Сегодня наш урок посвящен теме, которая касается всех нас вместе и каждого в отдельности. Для этого нам потребуются знания, полученные по теме «Все действия с обыкновенными дробями».
А о чём же пойдёт речь? Об этом вы узнаете, выполнив задания устного счета.
Устный счет.
Решить цепочку примеров и записав ответы в порядке возрастания, прочитать слово
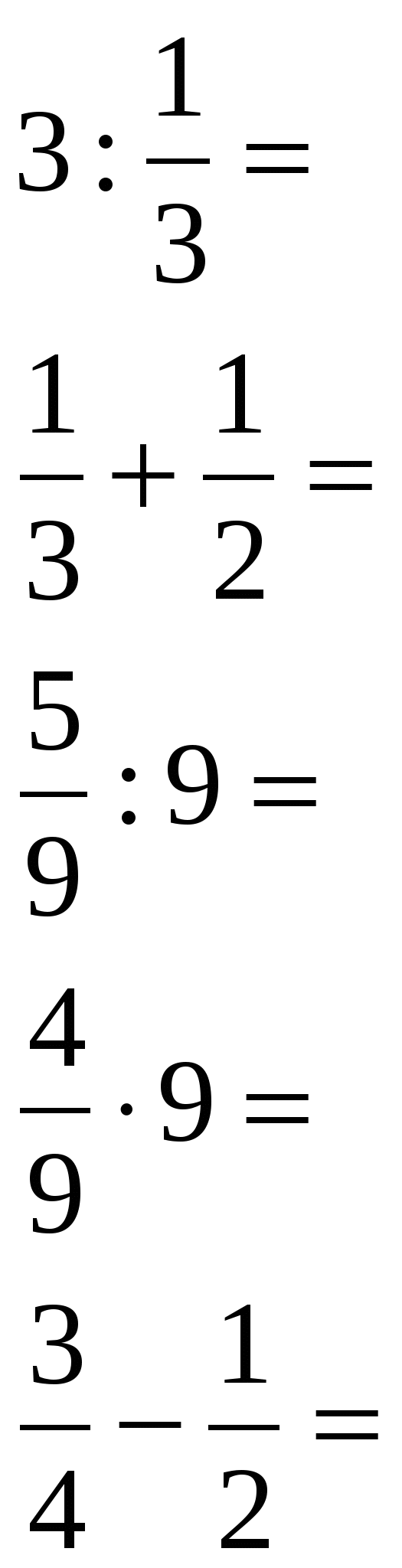
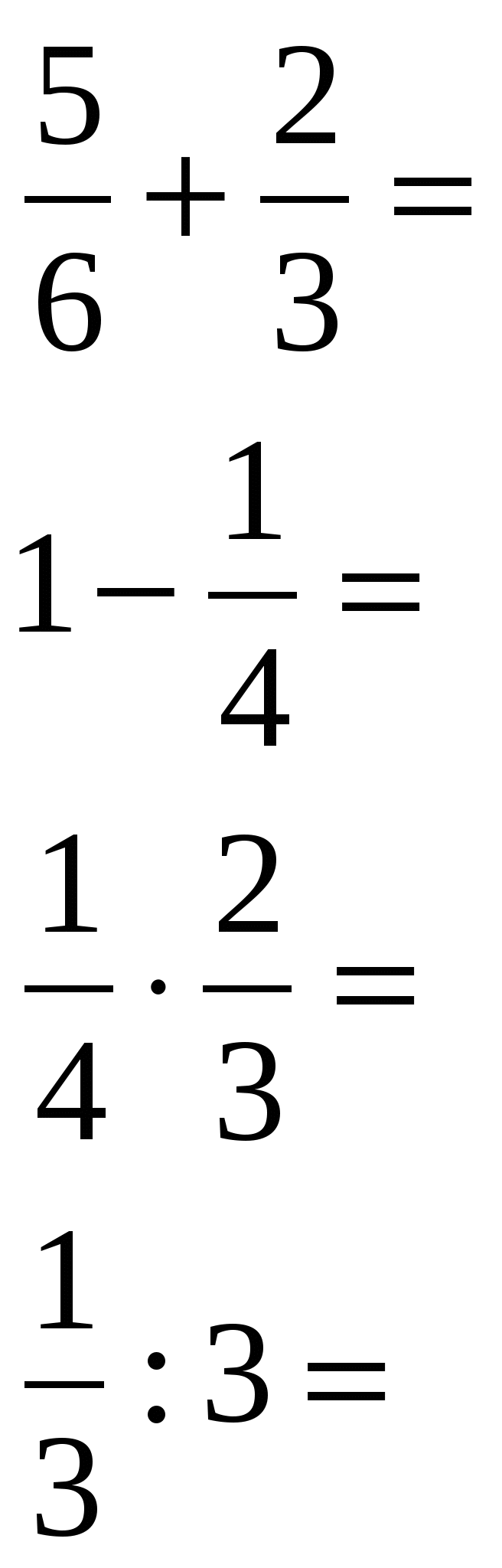
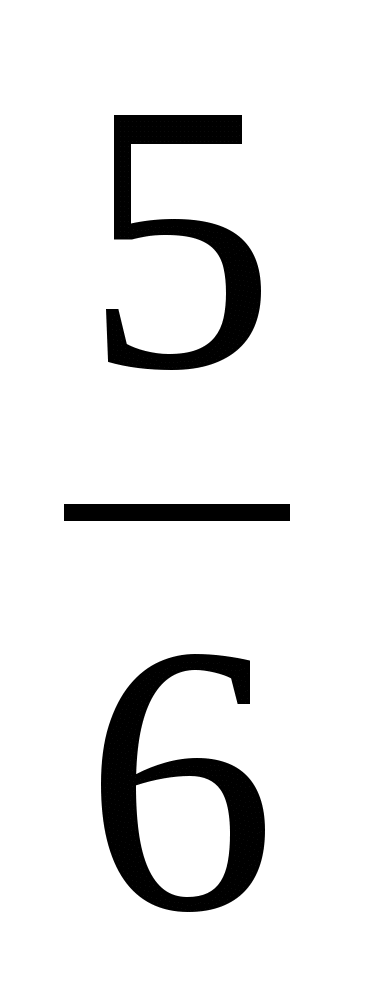
4
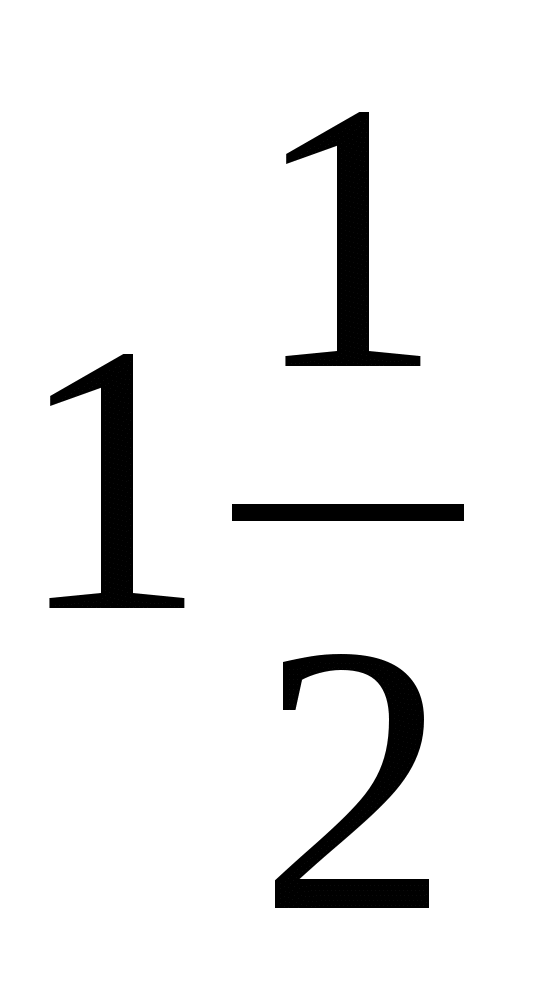
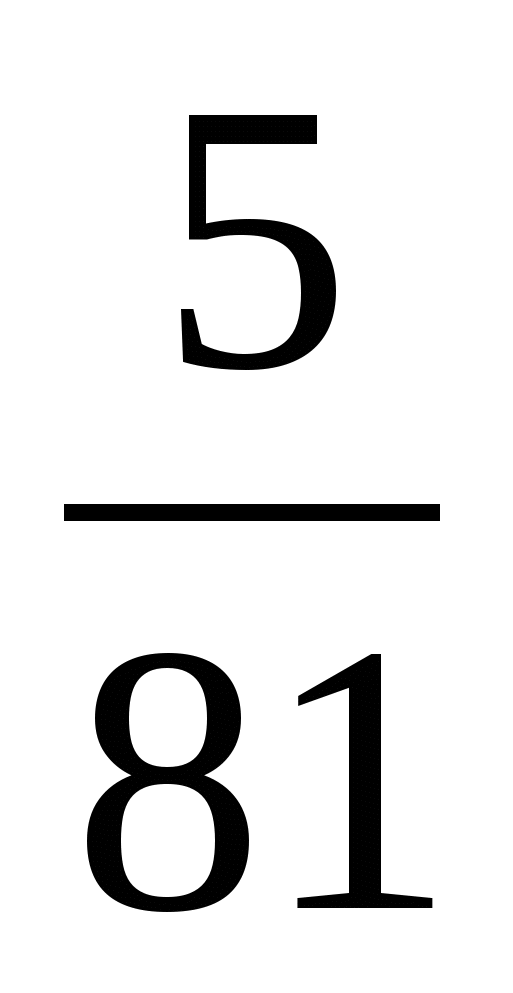
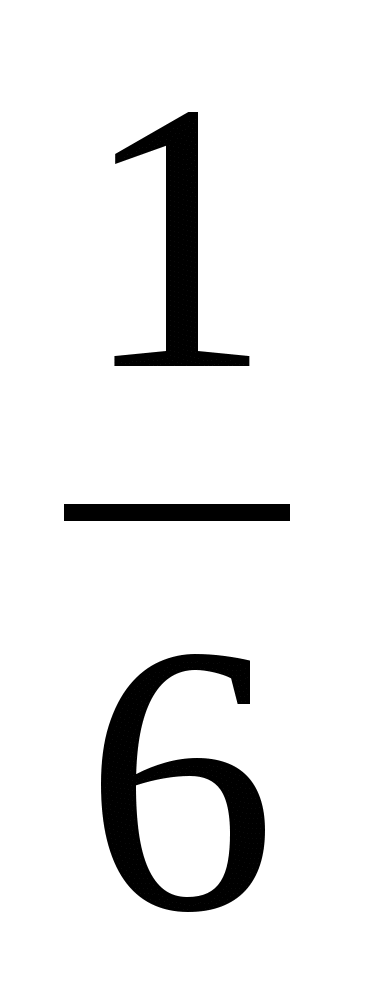
9
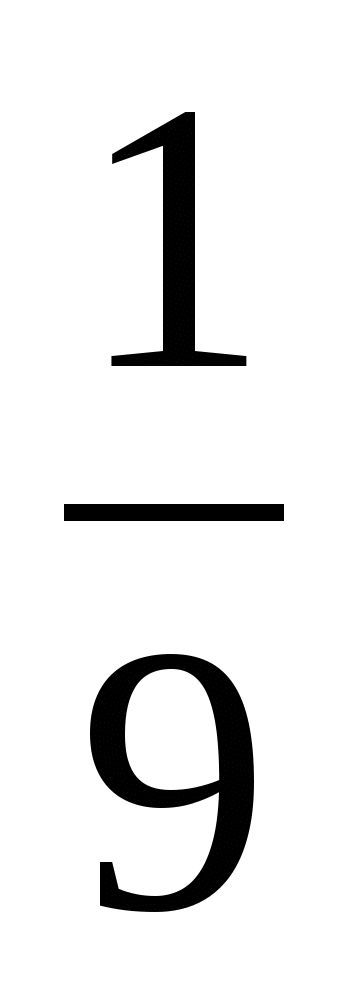
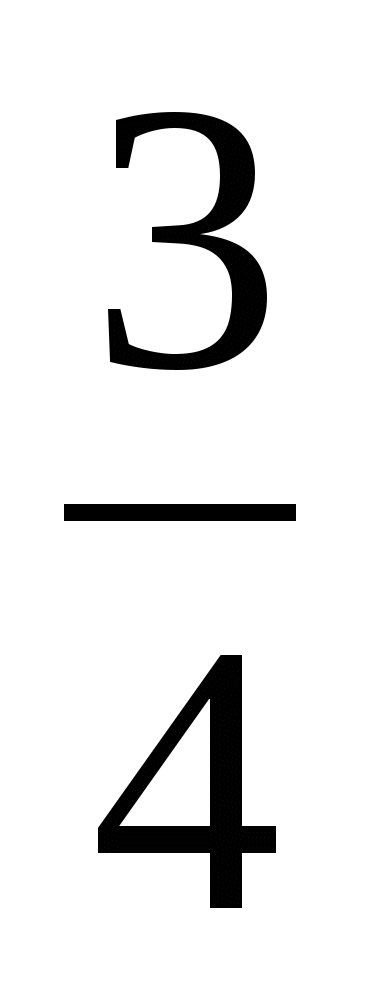
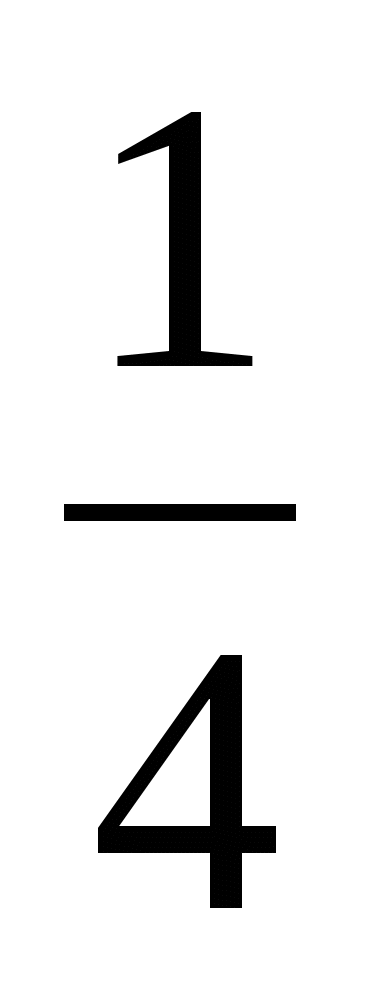
а
е
а
у
р
с
к
н
и
Какое слово мы получили? (Украина европейская страна)
Ответы детей.
А что вы знаете про Украину? Презентация
Работа в парах.
Решим кроссворд (в выделенных ячейках учащиеся должны получить слово).
с
о
к
р
а
щ
е
н
и
е
н
е
с
о
к
р
а
т
и
м
а
я
е
д
и
н
и
ц
е
ч
и
с
л
и
т
е
л
ь
з
н
а
м
е
н
а
т
е
л
ь
п
р
а
в
и
л
ь
н
а
я
о
б
р
а
т
н
о
е
н
у
л
ь
ц
е
л
а
я
д
е
л
е
н
и
е
о
б
ы
к
н
о
в
е
н
н
а
я
Вопросы:
Деление числителя и знаменателя на их общий делитель.
Дробь, у которой числитель и знаменатель взаимно простые числа.
Чему равно произведение взаимно-обратных чисел?
Как называется элемент дроби, стоящий над чертой.
Как называется элемент дроби, стоящий под чертой.
Дробь, у которой числитель меньше знаменателя.
Чтобы разделить одну дробь на другую, надо делимое умножить на число … делителю.
На какое число делить нельзя.
Как называется 5 в числе
 ?
?Действие, обозначенное чертой в дробном выражении.
Дробь, которая записывается с помощью черты.
В итоге выполнения задания появляется слово «КОНСТИТУЦИЯ».
Что означает полученное слово?
КОНСТИТУЦИЯ (от лат. constitutio — установление) — особый юридический документ, основной закон государства, обладающий высшей юридической силой.
В нашей стране много законов, но главным законом нашего государства, основные правила по которым мы живём, записаны в Конституции. Конституция гарантирует права и свободы человека.
Когда принята действующая Конституция? (28 июня 1996 года). Сколько лет действующей Конституции? (19 лет).
Работа в группах.
Конституция определяет основы государственного и общественного строя; систему органов власти, порядок их образования и деятельности; права и обязанности граждан.
А сколько разделов и статей в Конституции? Чтобы ответить на этот вопрос выполним задание.
Найдите значение выражения и определите количество разделов и статей в Конституции.
I группа(вариант)
Количество разделов.
II группа(вариант)
Количество статей.
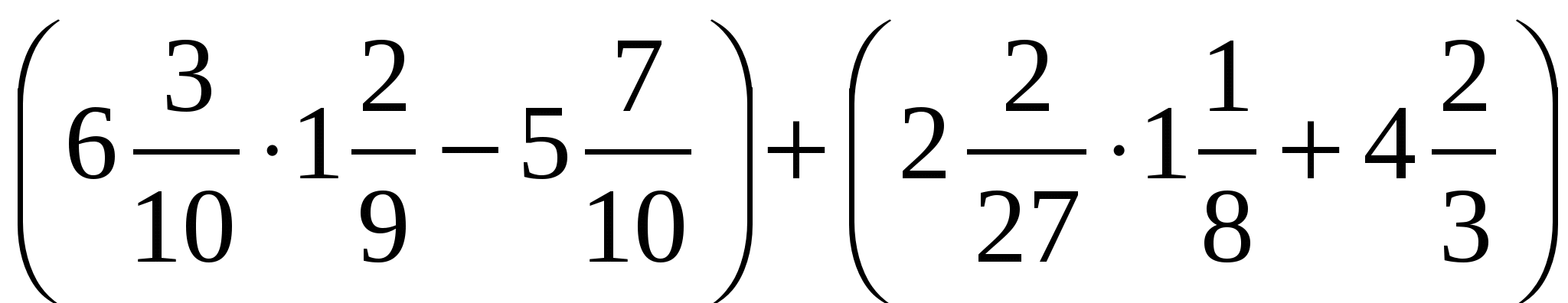 +
+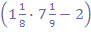
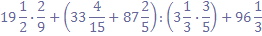
Украина состоит из областей и районов. Как вы думаете сколько входит в Украину областей и районов?
(задачу решает весь класс, 1 ученик работает у доски)
Задача. В составе Украины 24 области. Районов в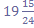 , а городов в
, а городов в 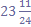 раза больше. Сколько районов и городов в Украине?
раза больше. Сколько районов и городов в Украине?
Кто является главой государства?
Президент Украины является главой государства, его высшим должностным лицом, определяющим основные направления внутренней и внешней политики государства и представляющим Украину внутри страны и в международных отношениях.
В Конституции правам и свободам человека отведена целая глава, включающая в себя 30 статей, причём права даются в совокупности со свободами. Статья 27 гласит, что каждый имеет право на охрану здоровья, а как мы можем сохранить свое здоровье на уроке? (физкультминутка)
Дружно встали, улыбнулись!
Руки вверх и… Потянулись!
Потянулись, потянулись.
Друг на дружку оглянулись!
Мы, конечно, лучше всех!
Нам сопутствует УСПЕХ!
Самостоятельная работа.
Выполните задания и выберете букву, соответствующую правильному ответу.
I вариант
II вариант
III вариант
Найдите число, обратное числу 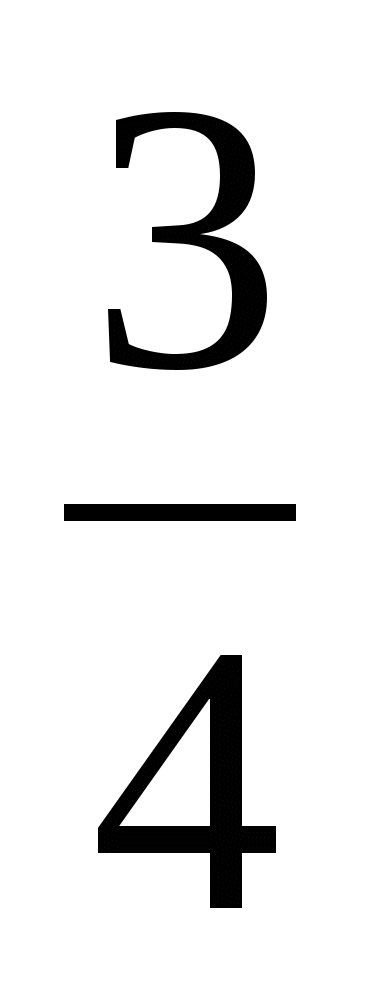
г) 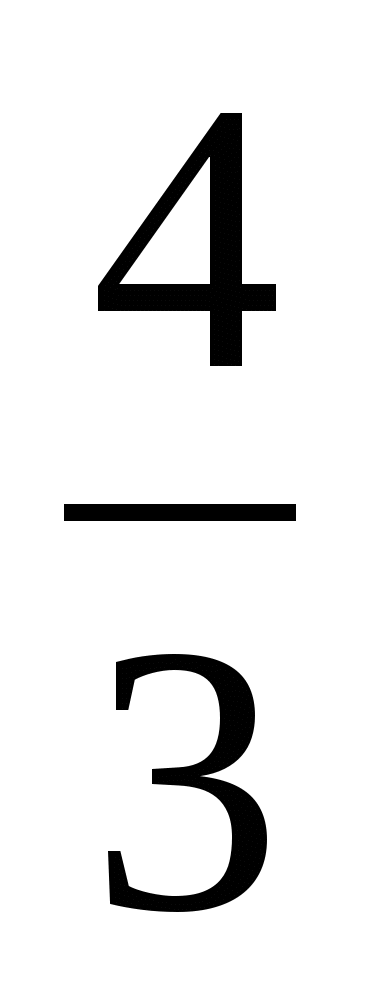 ; о) 4; ф)
; о) 4; ф) 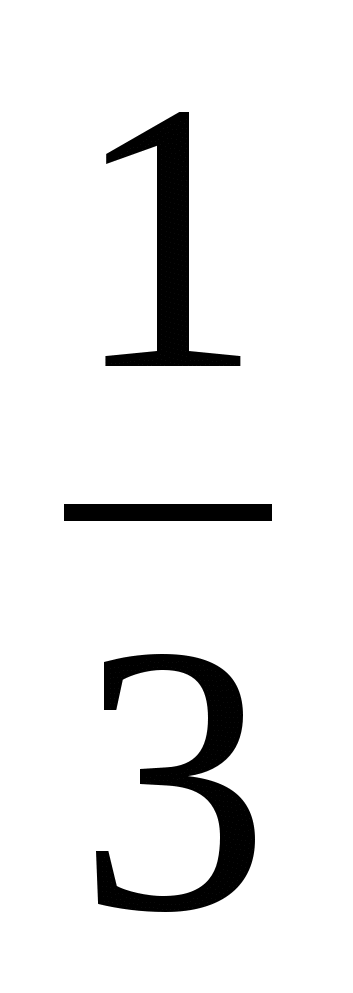 .
.
Найдите число, обратное числу 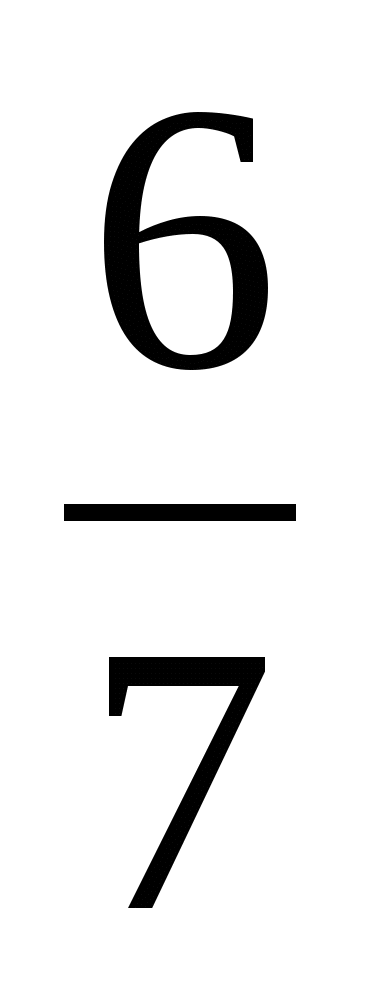
п) 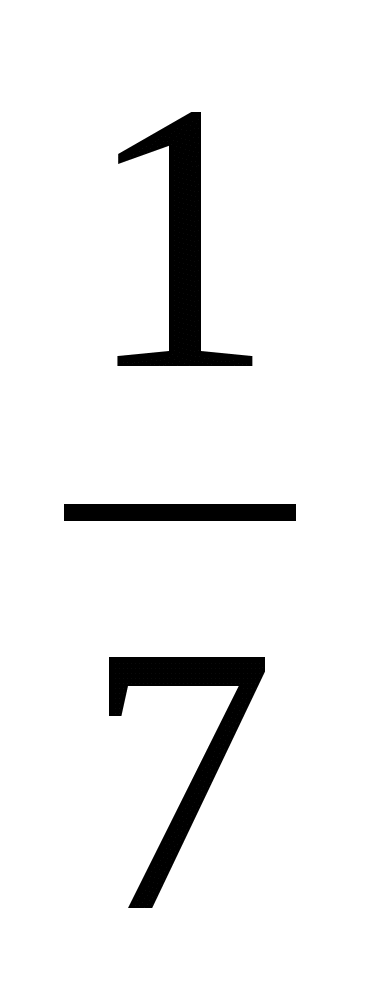 ; о) 7; ф)
; о) 7; ф) 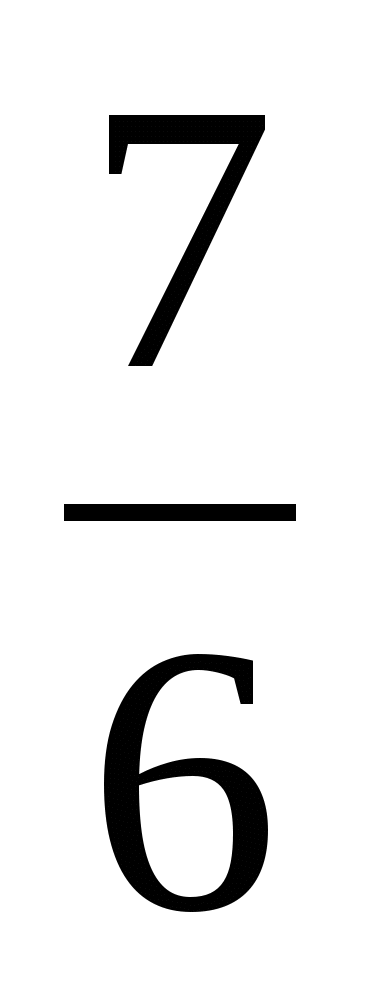 .
.
Найдите число, обратное числу 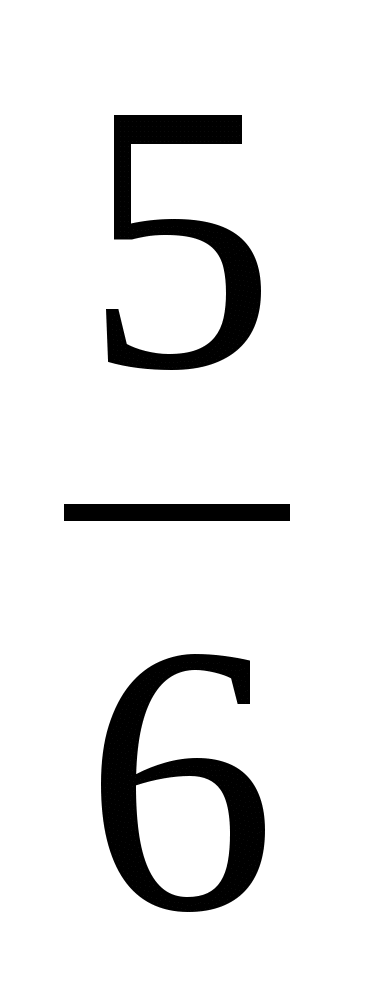
л) 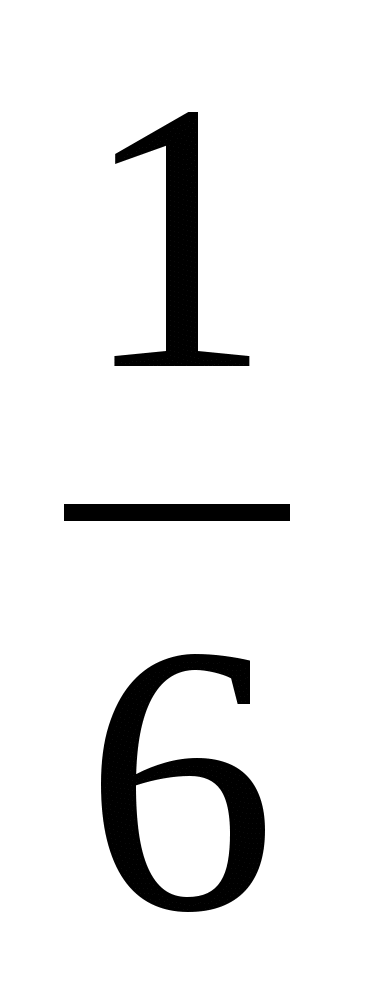 ; ш) 6; г)
; ш) 6; г) 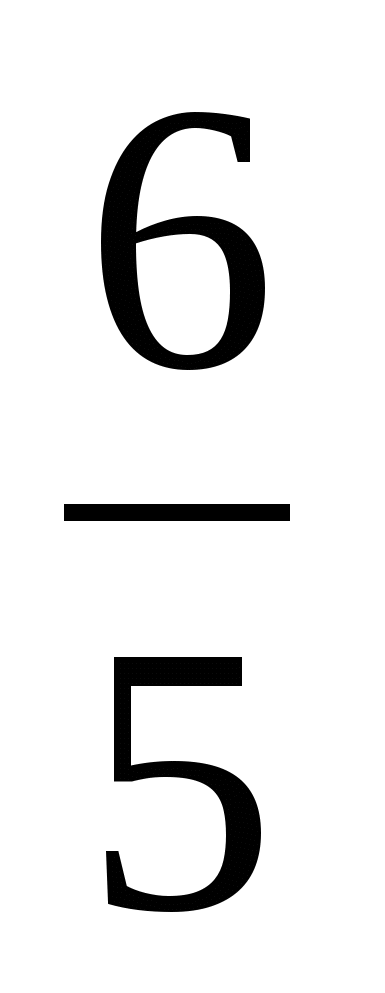 .
.
Выделите целую часть дроби 
с) 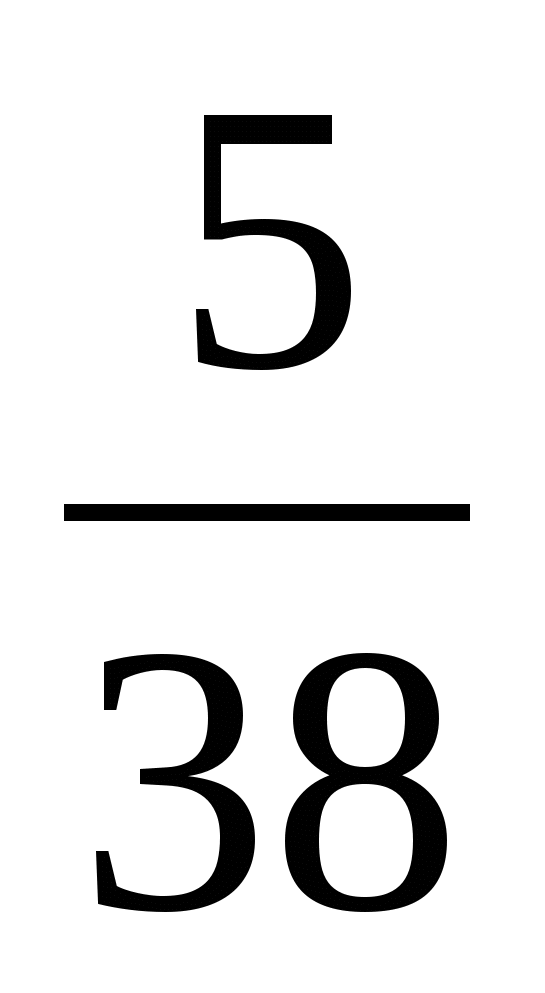 ; к)
; к)  ; е)
; е) 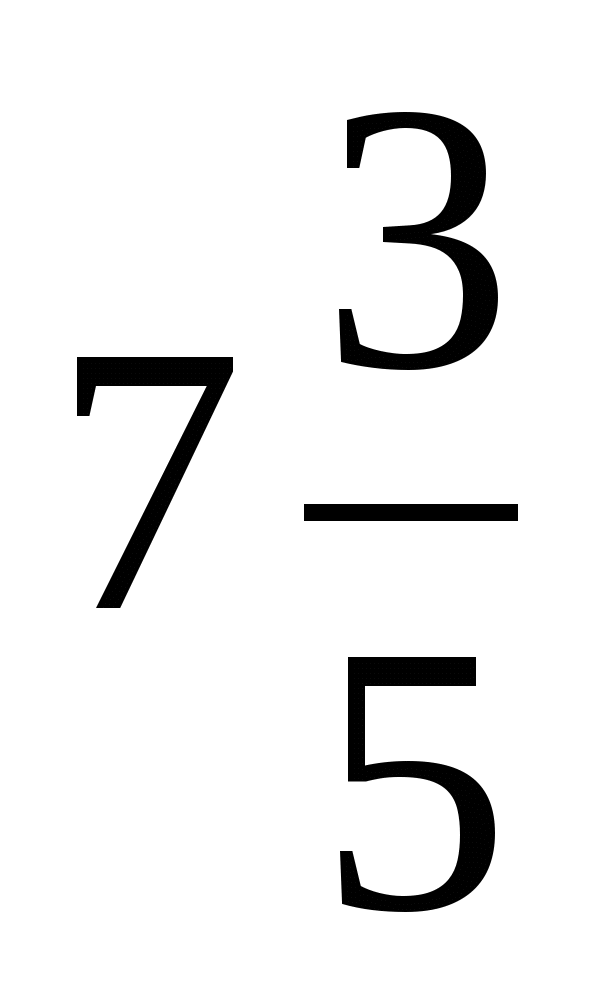 .
.
Выделите целую часть дроби 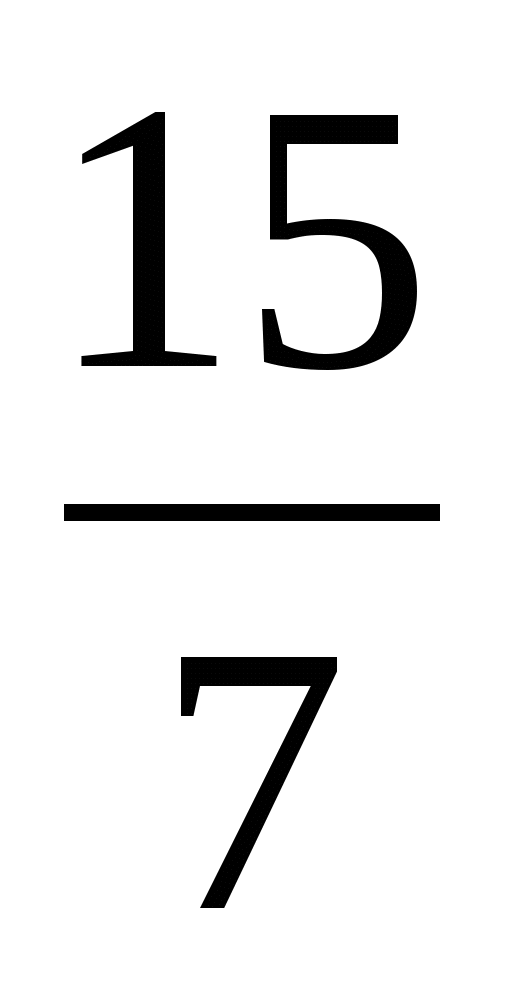
л) 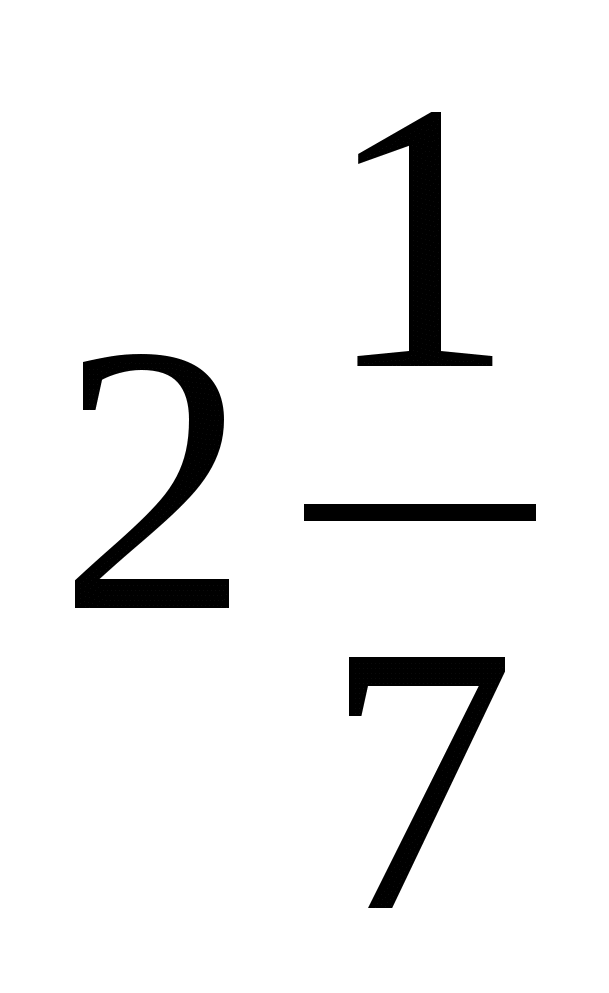 ; д)
; д) 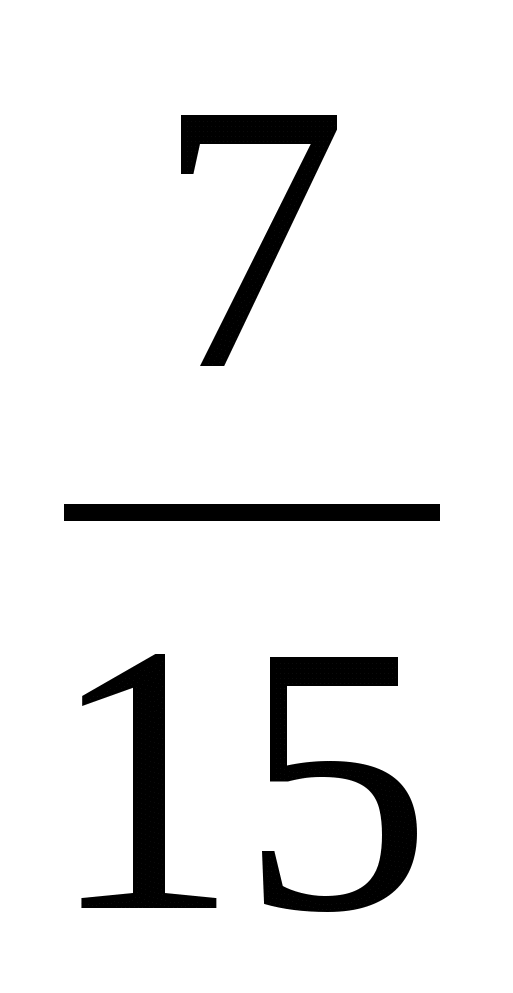 ; р)
; р) 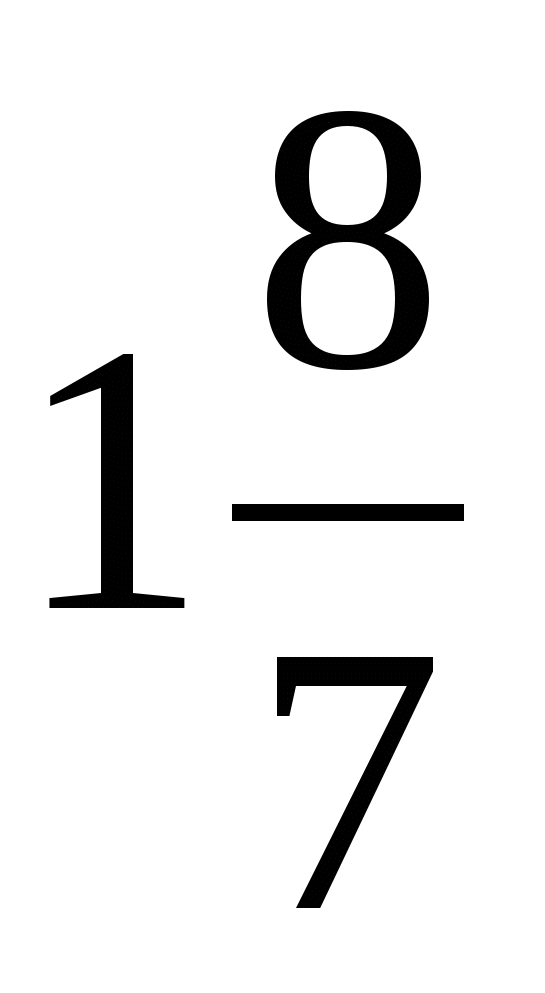 .
.
Выделите целую часть дроби 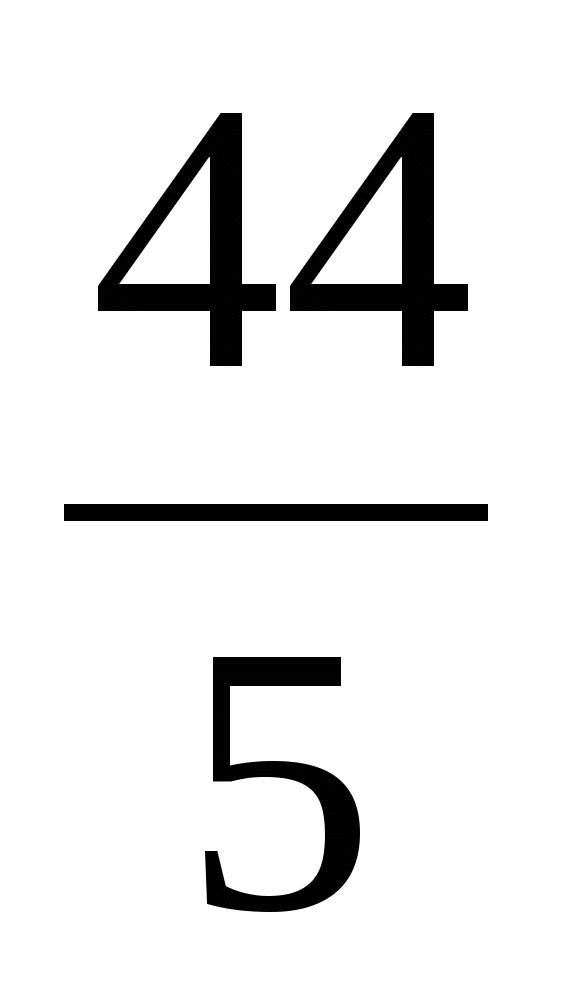
б)  ; и)
; и) 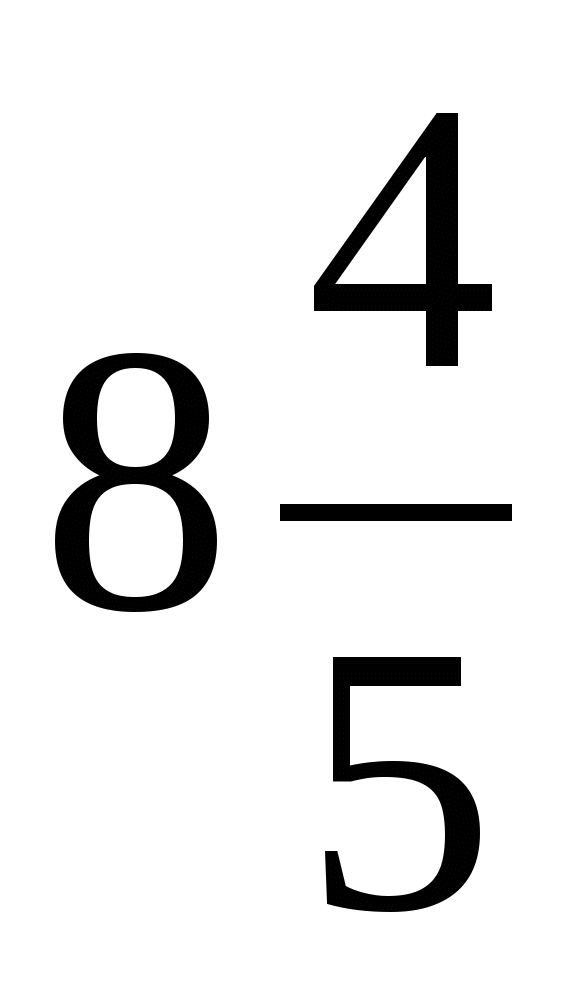 ; е)
; е)  .
.
Выполните деление 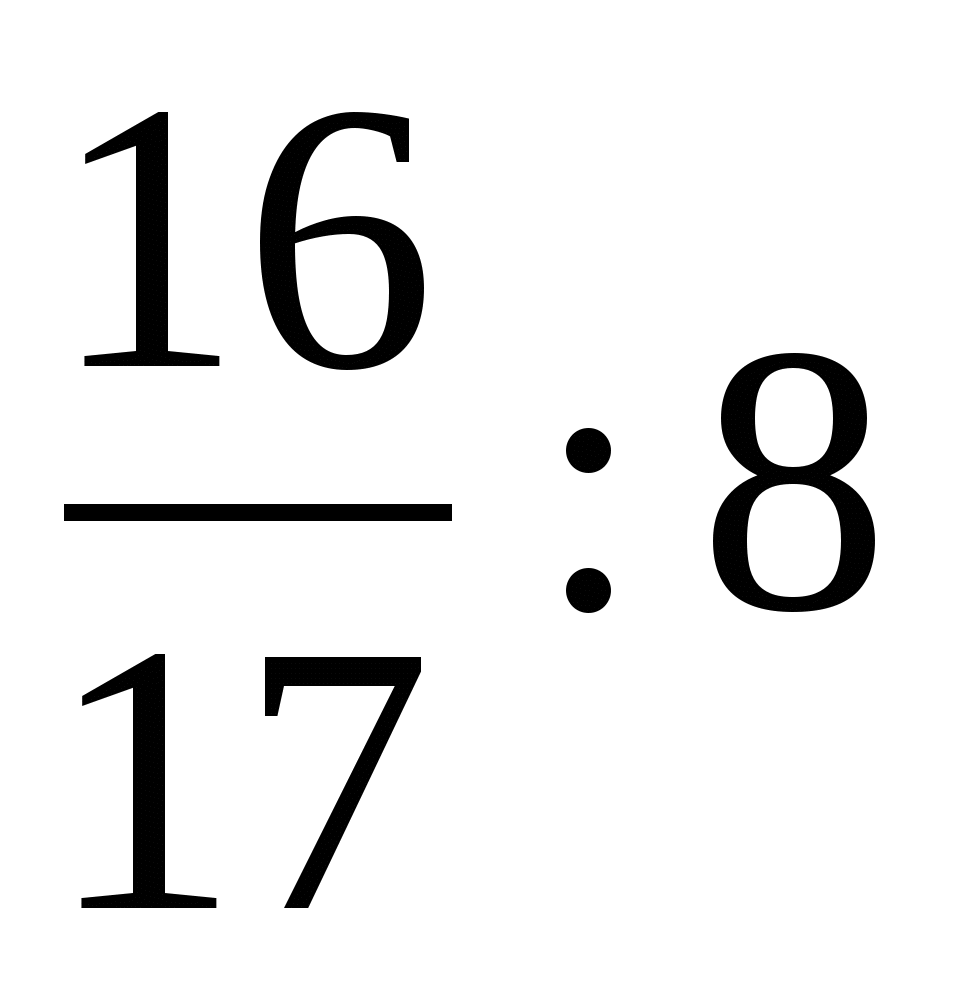
л) 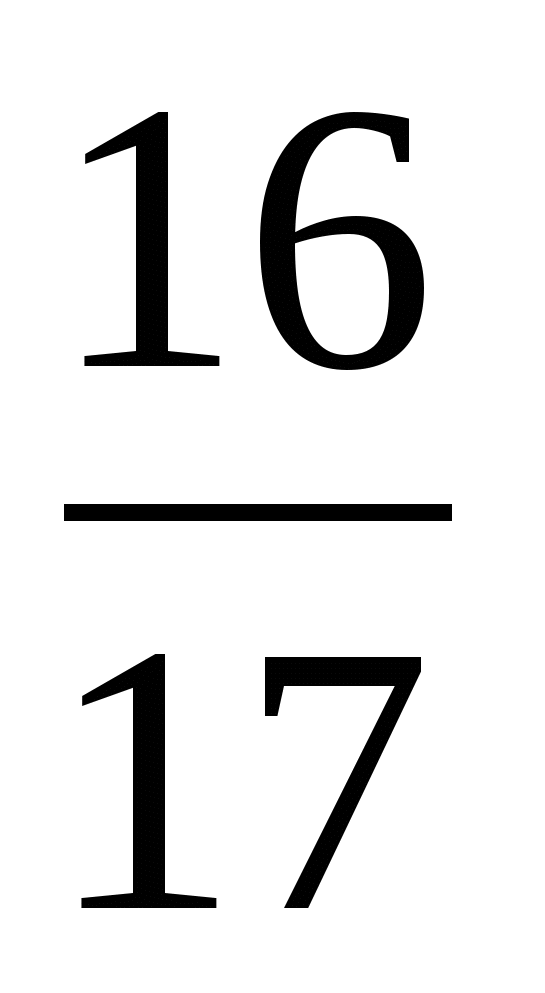 ; р)
; р) 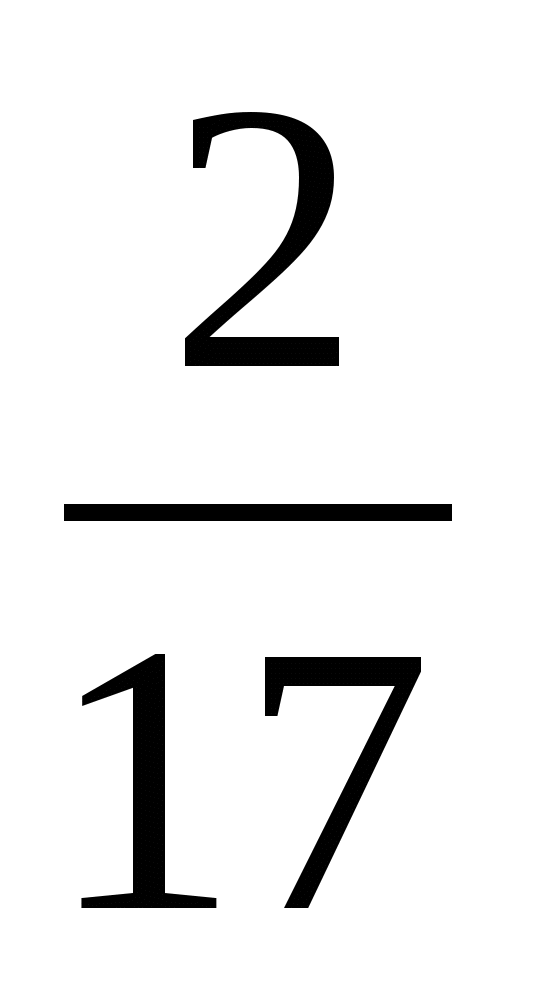 ; д)
; д) 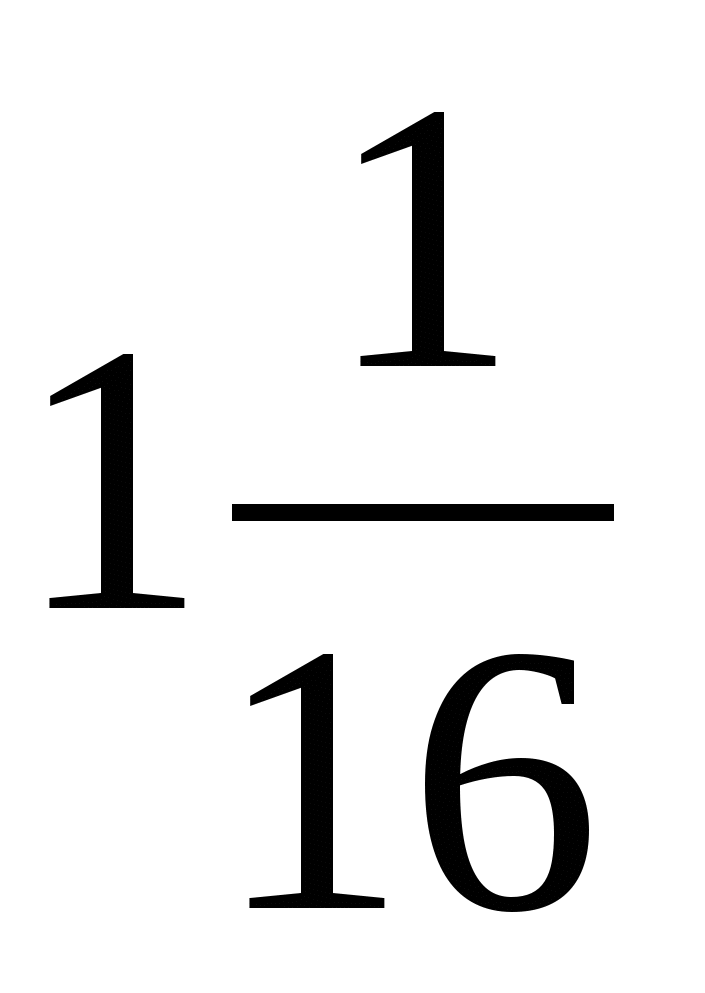 .
.
Выполните деление 
з) 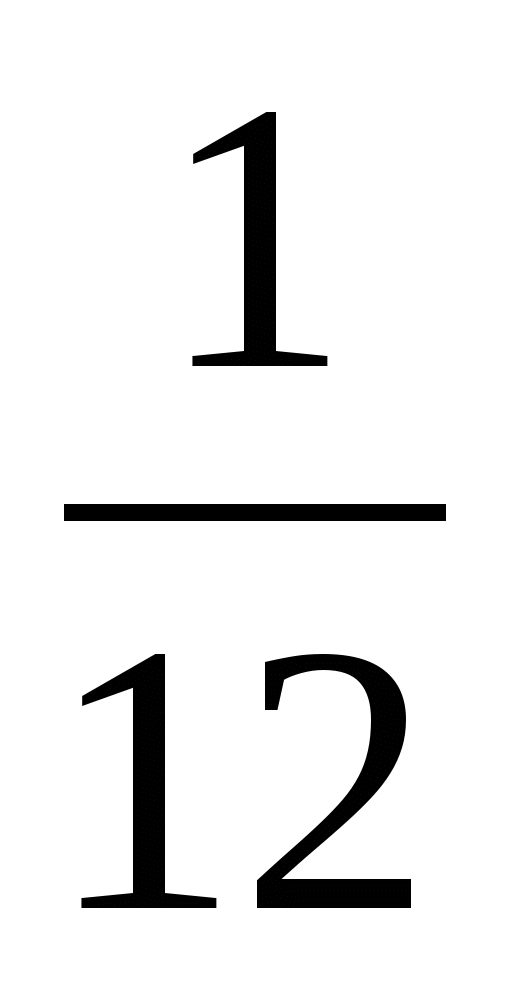 ; н)
; н) 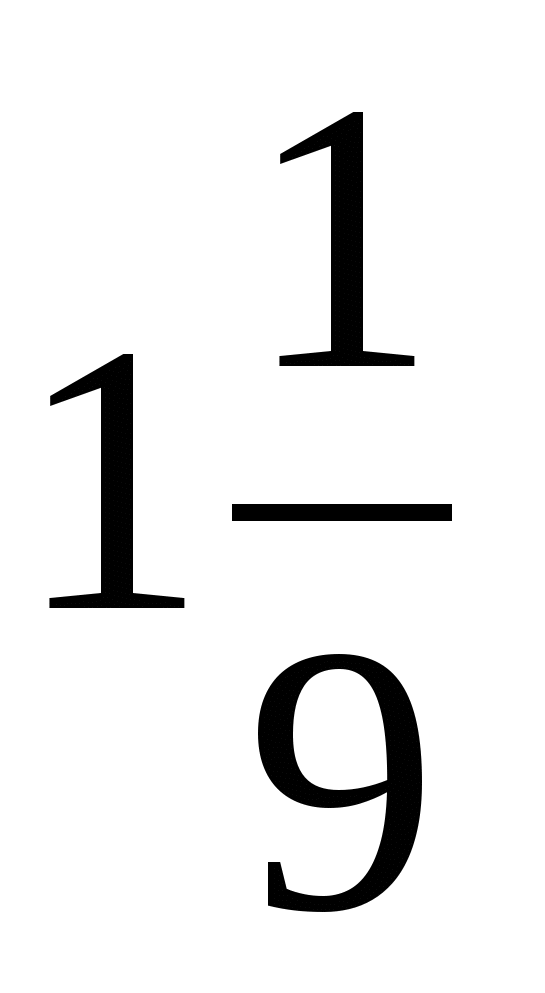 ; а)
; а) 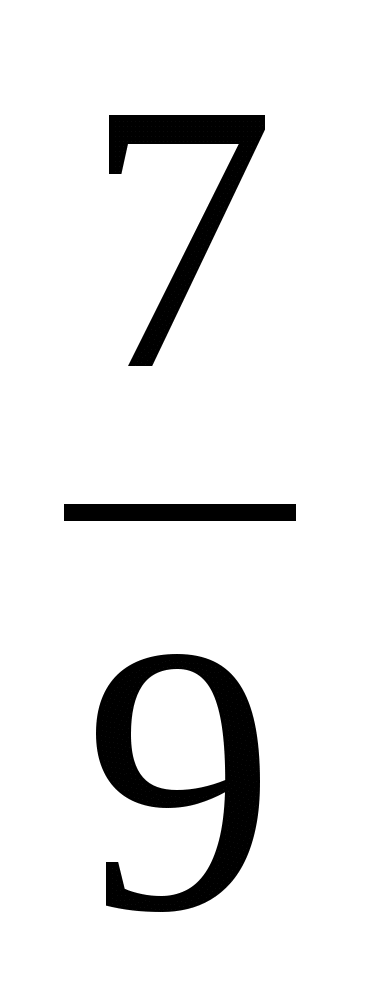 .
.
Выполните деление 
м) 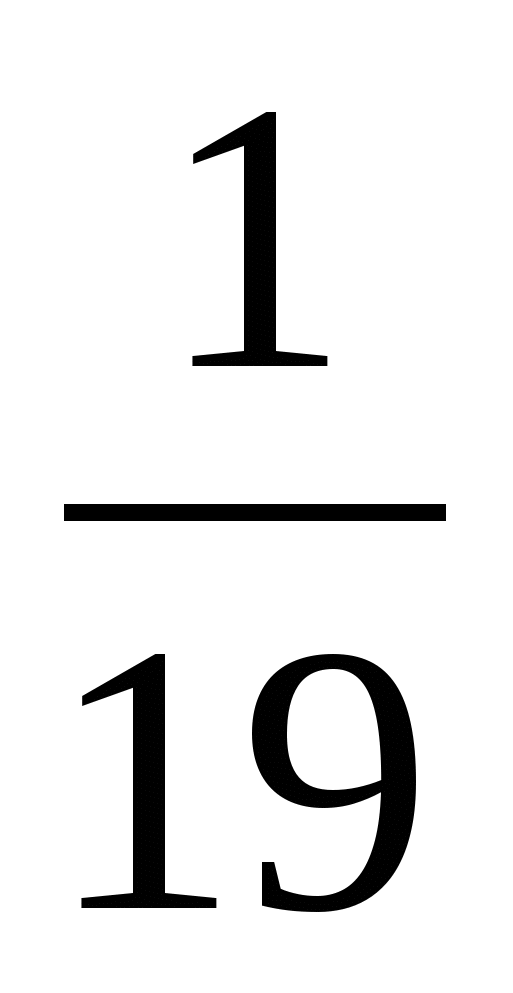 ; щ)
; щ) 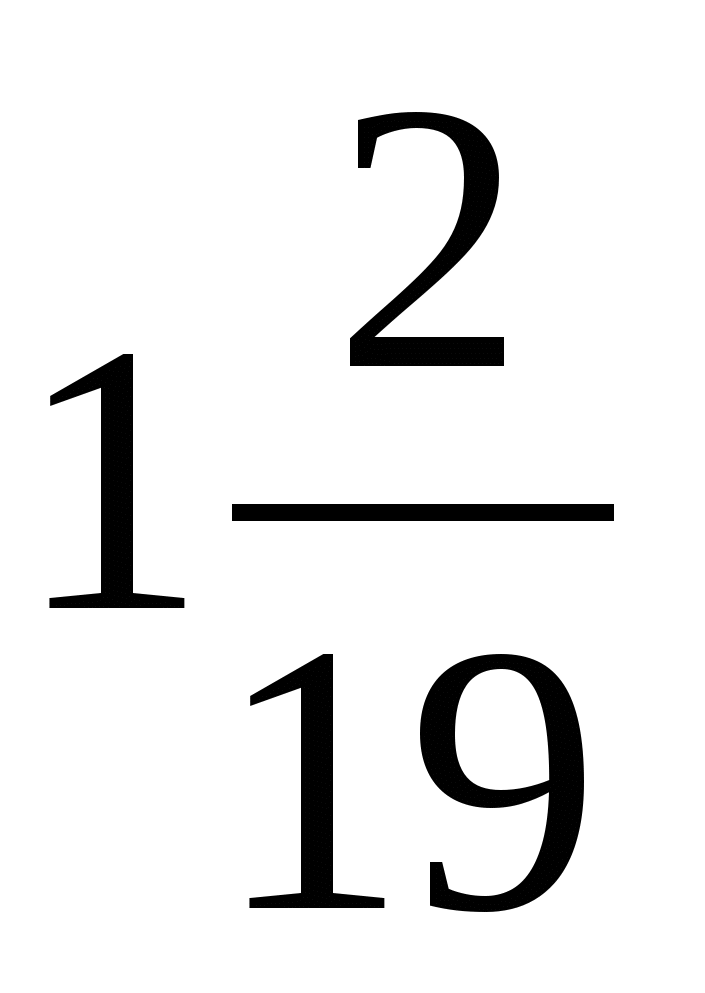 ; а)
; а)  .
.
Выполните умножение  · 35
· 35
б) 40; и) 4; ж) 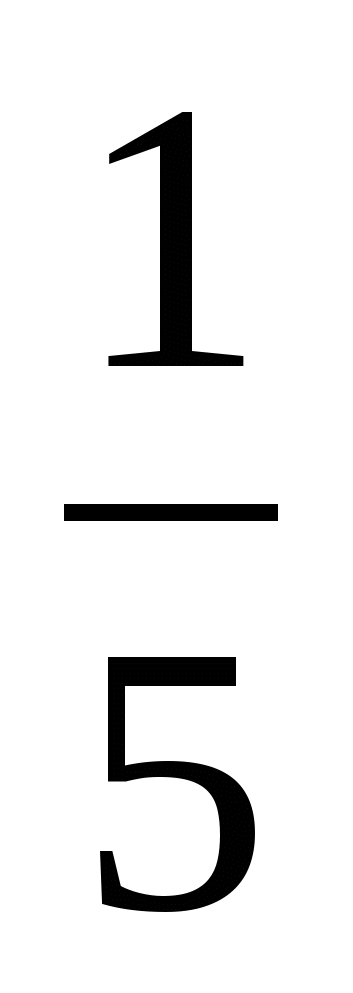 .
.
Выполните умножение 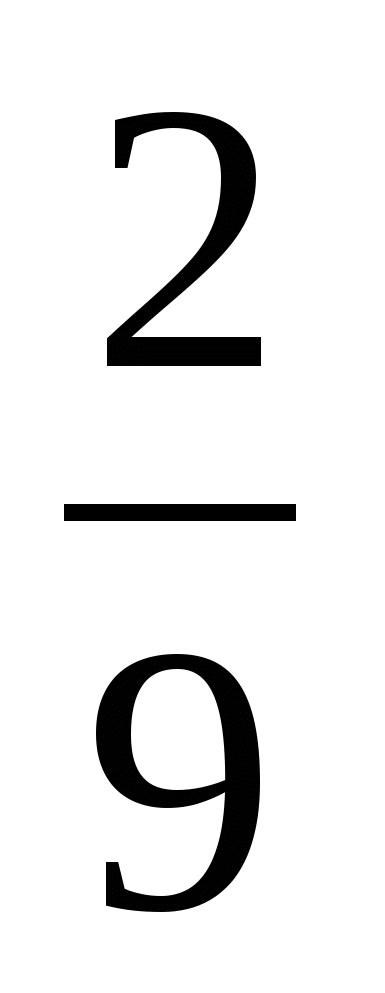 · 45
· 45
х) 1; г) 10; у) 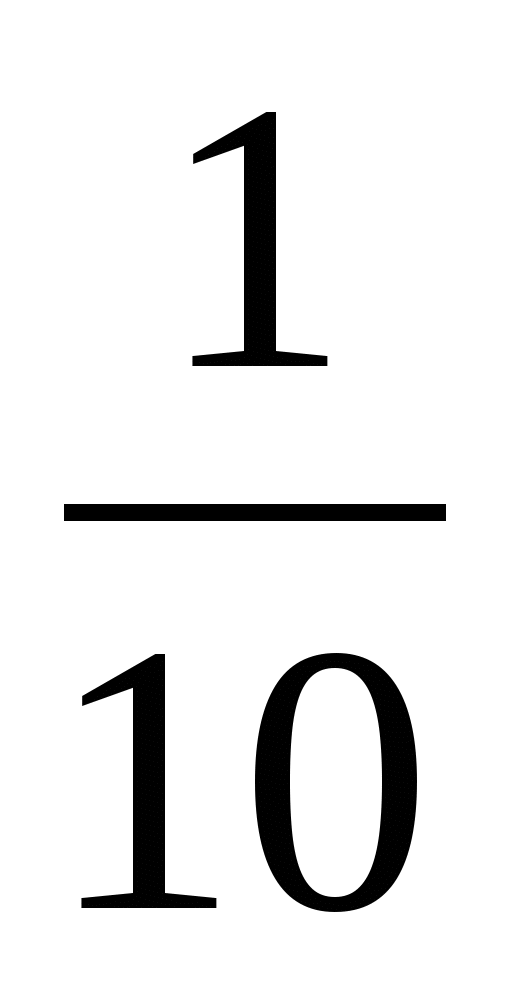 .
.
Выполните умножение 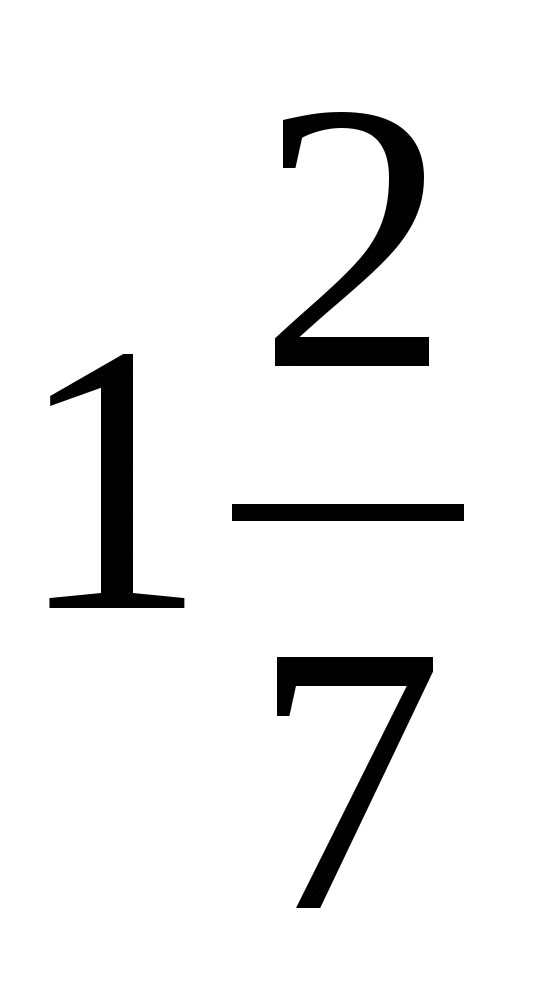 · 63
· 63
б) 18; н) 81; ж) 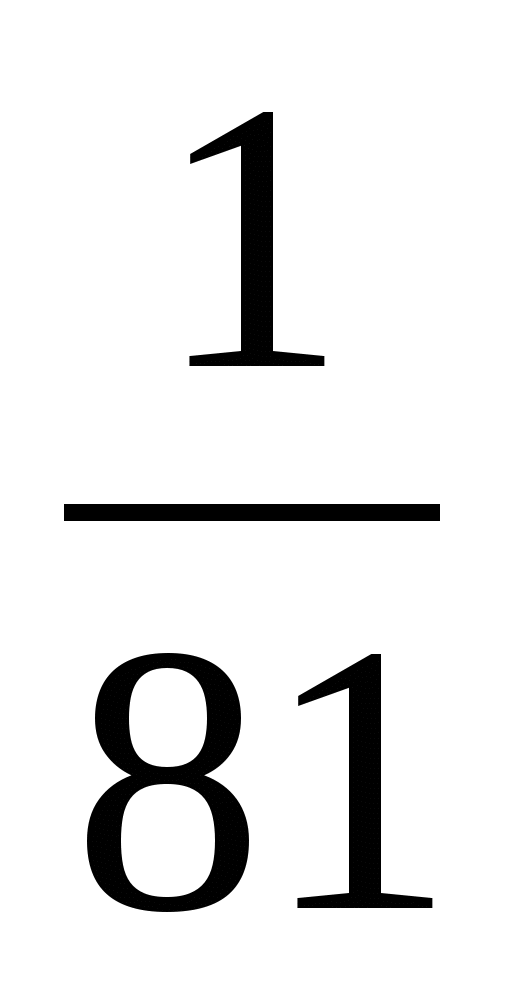 .
.
герб
флаг
гимн
Выполнив задания, вы получили — государственные символы Украины. Что вы знаете о них?
Поработаем в парах.
Вычислите:
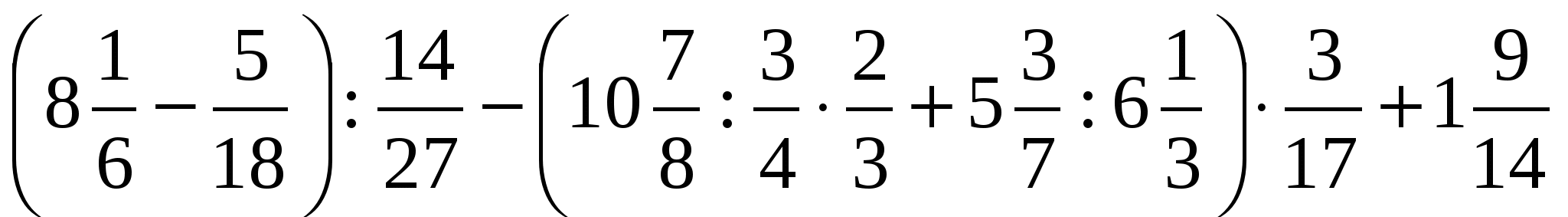

Какой мы получили ответ? Вспомним ещё раз, с чем связано это число? Молодцы!
Рефлексия
Прием «Телеграмма»: Каждому ученику предлагаю заполнить бланк телеграммы, выдаю при этом следующую инструкцию: «Что вы думаете о прошедшем уроке? Что было для вас важным? Что вам понравилось? Что осталось неясным? В каком направлении нам стоит продвигаться дальше? Напишите мне, пожалуйста, об этом короткое послание – телеграмму из 11 слов. Я хочу узнать ваше мнение для того, чтобы учитывать
Домашнее задание:. Творческое задание: придумать задачу с дробями про Украину.
Обобщающий урок по теме «Обыкновенные дроби» (5 класс)
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №276»
«Учебно-дидактические игры как средство развития познавательной активности»
Конспект урока по теме:
«Обыкновенные дроби».
( 5 класс)
Учитель математики
Куканова Ирина Анатольевна
Мурманская область
ЗАТО Александровск
г. Гаджиево
Урок «Обыкновенные дроби» — урок на повторение и закрепление пройденного материала. У этого урока нет сюжетной линии, но все задания подобраны таким образом, чтобы максимально заинтересовать учеников. Работа снова происходит в групповой форме. Это дает положительный результат, потому что у детей не сильных в математике имеется возможность несколько раз услышать и посмотреть, как выполняется то или иное задание. Кроме заданий для общего решения, есть задания для индивидуального решения. В них проявляется самостоятельность детей. Занимательно сформулированная проблема позволяет учащимся высказывать идеи, соответствующие их уровню развития.
Цели урока:
Предметные: обобщить и систематизировать знания учащихся об обыкновенных дробях, закрепить умение решать примеры и задачи на обыкновенные дроби, проверить умение работать с координатным лучом.
Личностные: развивать познавательный интерес к математике, быструю работу мысли, внимательность и смекалку; воспитывать дружеские отношения в классе и чувство сопереживания друг к другу.
Метапредметные: формировать умение самостоятельно определять учебные цели и задачи, развивать понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом, формировать умение выдвигать гипотезы при решении задач.
Планируемые результаты:
Учащийся обобщит и систематизирует знания об обыкновенных дробях, научится пошагово контролировать правильность и полноту выполнения алгоритма по повторяемой теме, закрепит навыки действий с обыкновенными дробями, научится применять приобретенные знания, умения, навыки в конкретной деятельности, самостоятельно выбирать способ решения задачи.
Материалы и оборудование урока:
Раздаточный материал (карточки с задачами, карточки тесты)
Рисунки и фотографии к заданиям
Плакат с изображением координатного луча
Набор магнитных рыбок
Плакат с высказыванием «Математика – царица наук»
Организационная структура урока:
1.Организационный этап.
Приветствие. Проверка готовности класса к уроку.
2.Актуализация опорных знаний.
Фронтальная беседа с учащимися:
Прежде чем сформулировать тему урока, учитель предлагает учащимся отгадать загадку.
Загадка: «Она бывает охотничья, барабанная и математическая». (дробь)
Учитель: «Мы заканчиваем изучение темы «Обыкновенные дроби», эта тема в курсе математики занимает одно из первых мест. Почему?».
Ученики: «Так как на протяжении всей своей жизни мы постоянно сталкиваемся с дробями. Ведь человеку нужно не только считать предметы, но и измерять величины: длины, площади, объемы, массы и т д. А величины не всегда удается измерить целыми числами».
Учитель: «А какие бы вы поставили цели и задачи нашего урока?».
Ученики: «Мы должны вспомнить и закрепить все, что знаем про обыкновенные дроби. повторить правила сложения и вычитания дробей с одинаковыми знаменателями, закрепить навыки решения задач по данному правилу».
Учитель: Чтобы наша работа не была скучной, мы будем решать какие-то задания устно, а какие-то письменно, какие-то задания будут групповыми, а какие-то индивидуальными. В конце урока вы выполните самостоятельную работу по теме «Обыкновенные дроби».
Устные упражнения.
Учитель: Начнем с устной работы. Вспомните понятие обыкновенной дроби. Я буду диктовать вам предложения, а вы должны назвать дробь, которая соответствует ответу.
Торт разрезан на 10 кусков, Оля съела 3 из них. Какую часть торта съела Оля?
В вазе лежит 13 фруктов, из них 5 бананов, 4 апельсина. Какую часть составляют бананы от всех фруктов?
Золушке высыпали 200 зерен пшена и 99 горошин. Какую часть от всех зерен составляют горошины?
У бабушки было 3 собаки и 5 попугаев. Еще ей принесли 2 котят. Какую часть составляют кошки и собаки от всех домашних животных?
К каждому заданию – рисунок.
Учитель: Теперь обратное задание. Придумайте объяснение для дроби 5/7.
Дети придумывают свои условия на заданное число.
Учитель: «Вспомним определение правильных и неправильных дробей. Поиграем в игру «Хлопушка». Я читаю дробь, вы хлопаете в ладоши, если дробь правильная: 15/17; 5/9; 20/19; 50/51; 100/200; 4/9; 75/57; 6/15; 53/23; 7/54; 3/2».
3. Основной этап
1)Решение примеров.
Учитель: Следующее задание – письменное.
Составить все правильные дроби со знаменателем 17;
Составить все неправильные дроби с числителем 15.
На выполнение задания дается 2 минуты. Двое учеников записывают дроби на доске, остальные – в тетрадях. При проверке у ребят появляется возможность добавить дроби или исправить их.
Учитель: «Итак, мы с вами вспомнили, что означает дробь, какие дроби бывают. А сейчас мы вспомним правила перевода неправильных дробей в смешанные числа и наоборот, смешанных чисел в неправильные дроби».
На каждую парту дается карточка, на которой есть неправильные дроби и смешанные числа. На выполнение данного задания дается максимально 3 минуты.
Учитель: «Когда все будут готовы, мы будем создавать кораблики. Лодки для корабликов со знаменателем на борту уже есть на карточках. Ваша задача – правильно подобрать паруса. К знаменателю подбирается числитель из получившихся дробей. А у смешанных чисел целую часть показывает флажок на палочке».
Если кораблик составлен неверно, то его исправляют участники из других групп. На карточке записать три неправильные дроби и три смешанных числа: 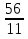 ;
; 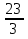 ;
; 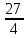 ; 2
; 2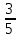 ; 5
; 5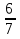 ;
;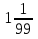 .
.
7
41
11
1
5
13
5



99
100
3
2
7
4
3
6



Класс делится на 4-5 команд.
Учитель: Следующее задание займет очень мало времени, но будет показательным. Оно покажет, умеете ли вы складывать и вычитать дроби, и то, как от одной ошибки зависит результат всего класса. На доске зашифрована фраза, вам ее нужно отгадать. На доске записаны примеры для каждого ряда. Вы по очереди решаете задания из своего столбика, а затем возвращаетесь назад, отдав мел следующему члену своей команды. Затем все вместе по таблице с алфавитом мы расшифруем предложение. Вывешивается плакат. Должно получится: « Математика – царица наук».
 +
+ 
5)  —
— 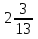
9)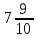 —
— 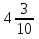
13)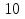 —
— 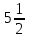
17)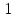 +
+ 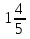
 +
+ 
6)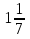 +
+ 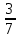
10)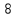 —
— 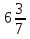
14)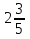 +
+ 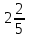
18)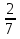 +
+ 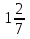
 —
— 
7)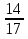 —
— 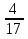
11)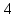 —
— 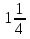
15)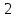 +
+ 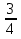
19)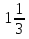 +
+ 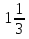
 +
+ 
8) 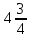 +
+ 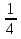
13)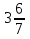 —
— 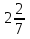
16)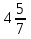 —
— 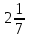
20)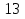 —
— 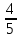
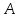 —
— 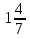
Е — 10
Л — 3
Р — 4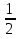
Х — 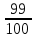
Ь, Ъ — 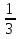
Б — 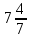
Ж — 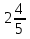
М — 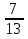
С — 11
Ц — 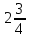
Ы — 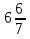
В — 
З — 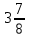
Н — 2 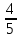
Т — 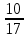
Ч — 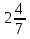
Э — 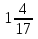
Г- 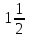
И, Й — 5
О -3 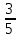
У — 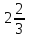
Ш — 1
Ю — 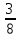
Д — 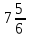
К+ 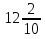
П — 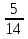
Ф — 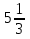
Щ — 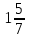
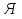 — 9
— 9 
2)Решение задач.
Учитель: А сейчас мы приступим к решению задач. Раздаются карточки, и после 4 минут решения начинается обсуждение. Чтобы успеть обсудить и записать все задачи, нужно экономить время. Для этого пока один ученик объясняет решение, кто-то другой готовит запись на доске. При раздаче карточек нужно обратить внимание, что с 1 по 4 задания задачи усложняются.
Расстояние от села до города 15 км. Путник прошел
 этого расстояния. Сколько километров осталось ему пройти?
этого расстояния. Сколько километров осталось ему пройти?
В коробке находилось 24 мяча. Красные мячи составляли
 мячей, а зеленые –
мячей, а зеленые –  оставшихся мячей. Сколько было зеленых мячей?
оставшихся мячей. Сколько было зеленых мячей?
Отремонтировали 80 тракторов, что составляет
 всех тракторов. Сколько всего было тракторов?
всех тракторов. Сколько всего было тракторов?
В бензобаке автомашины был бензин. Перед поездкой в него налили еще 10 литров бензина. За время поездки была истрачена
 часть находившегося в баке бензина. Сколько бензина было в бензобаке первоначально, если во время поездки было истрачено 12 литров?
часть находившегося в баке бензина. Сколько бензина было в бензобаке первоначально, если во время поездки было истрачено 12 литров?
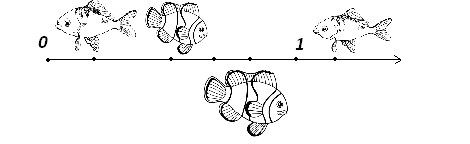
3) Работа на числовом луче. «Математическая рыбалка».
Учитель: Теперь мы перейдем к работе на координатном луче. Это задание в некотором смысле творческое и потребует от вас не только знаний, но и сообразительности. На нашем плакате четыре рыбки, нужно назвать точную координату каждой рыбки как можно большим количеством способов. Для этого даются длина единичного отрезка – 30 см и расстояние до каждой рыбки. На обсуждение – 4 минуты. Если три координаты являются верными, то рыбка считается пойманной. Дети должны сообразить, что единичный отрезок можно изначально разделить на число, а уже затем составлять дробь. Например, для 6 см единичный отрезок можно разделить на 30 см; на 6см; на 3см, и получатся дроби: 6/30; 1/5; 2/10.
4) Тесты по вариантам ( 8-10 минут).
Вариант 1
№1. Выберите из данных дробей те, которые обозначают половину: 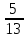 ,
, 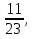
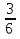 ,
, 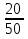 ,
, 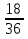 .
.
№2. Сравните дроби: а) 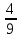
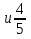 ; б)
; б)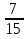
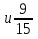 ;
;
в) 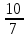
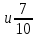 .
.
№3. При каких натуральных значениях х дробь 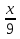 правильная?
правильная?
№4. Решите уравнение: 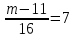 .
.
№5*. На вопрос “Который час?” ответили, что оставшаяся часть суток равна 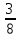 целых суток. Который был час?
целых суток. Который был час?
Вариант 2
№1. Выберите из данных дробей те, которые обозначают половину: 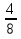 ,
, 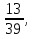
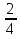 ,
, 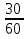 ,
, 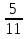 .
.
№2. Сравните дроби: а) 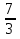
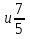 ; б)
; б)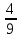
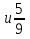 ;
;
в) 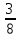
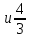 .
.
№3. При каких натуральных значениях х дробь 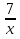 неправильная?
неправильная?
№4. Решите уравнение: 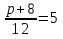 .
.
№5*. Стеклянная бутылка с водой весит 550 г. Когда из бутылки вылили 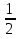 всей воды, ее масса составляла 300 г. Сколько грамм воды было в бутылке сначала?
всей воды, ее масса составляла 300 г. Сколько грамм воды было в бутылке сначала?
4.Рефлексия.
Учащиеся оценивают свою работу, выбирая карточку самооценки, и показывают её:
— Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно (красная карточка)
— Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно (зелёная карточка).
— У меня не было желания работать. Сегодня не мой день ( синяя карточка).
5. Информация о домашнем задании.
Учитель дает пояснения по дифференцированному домашнему заданию:
1 уровень: составить задания для соседа по парте на различные действия с обыкновенными дробями (сложение и вычитание) по 4 примера.
2 уровень: найти в справочном материале историческую справку по теме.
3 уровень: написать сочинение на тему: «Обыкновенные дроби».
6. Подведение итогов.
Учитель благодарит ребят за интересную работу, хорошие отметки, прекрасное настроение и отличные знания.
Список используемых источников и литературы:
1. Конструирование современного урока математики / Манвелов С. Г. –М.: Просвещение 2005 г.
2. Математика: 5 класс: дидактические материалы: сборник задач и контрольных работ / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013.
3. Математика: 5 класс: рабочая тетрадь №1, №2 / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013.
4. Математика: 5 класс: методическое пособие / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013.
5. Математика. Предметное портфолио пятиклассника. Самооценка. Самоанализ. Самоконтроль / Т.Ю. Дюмина, А.А.Махонина – Волгоград: Учитель,2013.
6. Математика 5 класс. Тетрадь 1,2 .Задания для обучения и развития учащихся./ Беленкова Е.Ю., Лебединцева Е.А. – М: Интеллект- Центр, 2013
7. Сборник практических задач по математике: 5 класс / Л.П. Попова . – М.: ВАКО, 2012. .
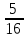 часть всего поля, во второй день – на
часть всего поля, во второй день – на 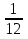 часть больше, чем в первый день. Сколько всего земли вспахали за два дня?
часть больше, чем в первый день. Сколько всего земли вспахали за два дня?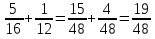 – во второй день
– во второй день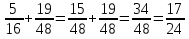 – за два дня
– за два дня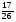 , второе число меньше на
, второе число меньше на 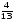 м. Найдите сумму данных двух чисел.
м. Найдите сумму данных двух чисел.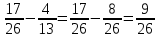 – второе число
– второе число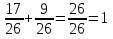 – за два дня
– за два дня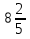 т груза. Когда с нее сняли
т груза. Когда с нее сняли  т груза, груз первой машины продолжал превышать груз второй машины на
т груза, груз первой машины продолжал превышать груз второй машины на 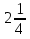 т. Сколько тонн груза было во второй машине?
т. Сколько тонн груза было во второй машине?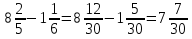 – т груза в первой машине после снятия
– т груза в первой машине после снятия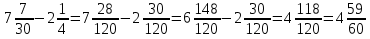 – т груза во второй машине
– т груза во второй машине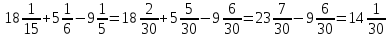
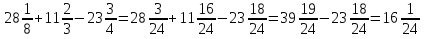
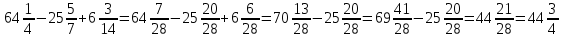
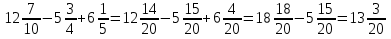
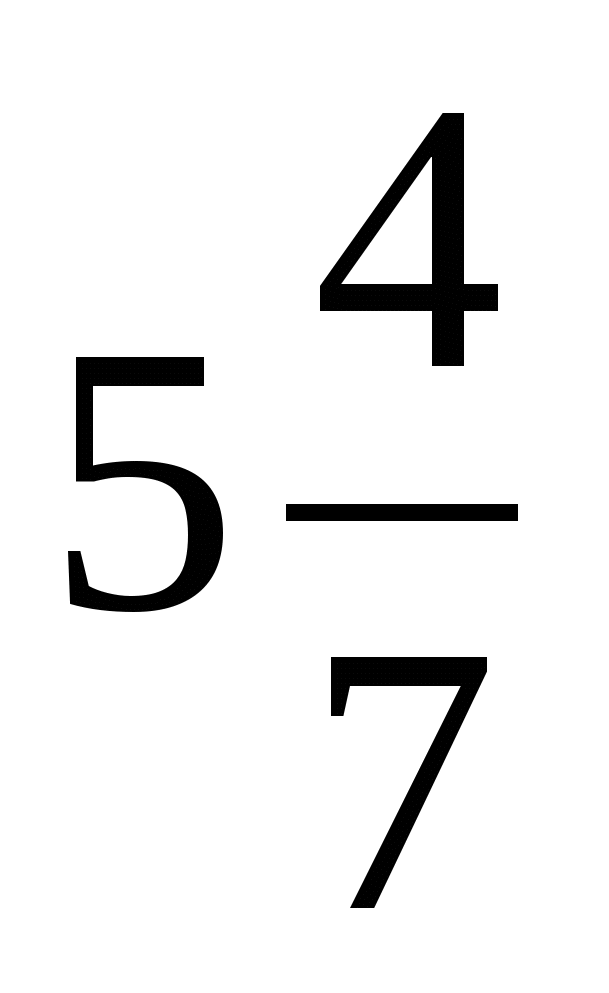 ?
?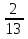 +
+ 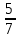 +
+ 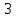 —
— 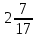
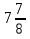 +
+ 
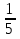 этого расстояния. Сколько километров осталось ему пройти?
этого расстояния. Сколько километров осталось ему пройти?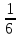 мячей, а зеленые –
мячей, а зеленые – 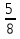 всех тракторов. Сколько всего было тракторов?
всех тракторов. Сколько всего было тракторов?