Текстовые задачи на среднюю скорость
Средняя скорость – есть отношение всего пройденного пути ко всему затраченному времени.
Задача 1. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью км/ч, а вторую половину времени – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение: + показать Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Пусть t часов – полное время движения автомобиля, тогда средняя скорость равна: км/ч. Ответ: 70.
Задача 2. Первые два часа автомобиль ехал со скоростью км/ч, следующий час – со скоростью км/ч, а затем два часа – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение: + показать
Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Тогда
км/ч.
Ответ:
Задача 3. Первую треть трассы автомобиль ехал со скоростью км/ч, вторую треть – со скоростью км/ч, а последнюю – со скоростью км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение: + показать Чтобы найти среднюю скорость на всем пути, нужно весь путь разделить на все время движения. Пусть км – весь путь автомобиля, тогда средняя скорость равна: км/ч. Ответ:
Задача 4. Путешественник переплыл море на яхте со средней скоростью км/ч. Обратно он летел на спортивном самолете со скоростью км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ ч.
Решение: + показать Пусть путь, что проделал путешественник – Время, затраченное на путь в один конец, – ч, время, затраченное на путь в другой конец, – ч. Тогда км/ч. Ответ:
Вы можете пройти тест по теме «Задачи на среднюю скорость»
Как определить среднюю скорость автомобиля формула.
 Задачи
ЗадачиПомните, что скорость задается как численным значением, так и направлением. Скорость описывает быстроту изменения положения тела, а также направление, в котором движется это тело. Например, 100 м/с (на юг).
Найдите общее перемещение, то есть расстояние и направление между начальной и конечной точками пути. В качестве примера рассмотрим тело, движущееся с постоянной скоростью в одном направлении.
- Например, ракета была запущена в северном направлении и двигалась в течение 5 минут с постоянной скоростью 120 метров в минуту. Чтобы вычислить общее перемещение, воспользуйтесь формулой s = vt: (5 минут) (120 м/мин) = 600 м (на север) .
- Если в задаче дано постоянное ускорение, воспользуйтесь формулой s = vt + ½at 2 (в следующем разделе описывается упрощенный способ работы с постоянным ускорением).
Найдите общее время в пути. В нашем примере ракета перемещается в течение 5 минут. Среднюю скорость можно выразить в любых единицах измерения, но в международной системе единиц скорость измеряется в метрах в секунду (м/с). Конвертируйте минуты в секунды: (5 минут) х (60 секунд/минута) = 300 секунд .
Среднюю скорость можно выразить в любых единицах измерения, но в международной системе единиц скорость измеряется в метрах в секунду (м/с). Конвертируйте минуты в секунды: (5 минут) х (60 секунд/минута) = 300 секунд .
- Если даже в научной задаче время дано в часах или других единицах измерения, лучше сначала вычислить скорость, а затем преобразовать ее в м/с.
Вычислите среднюю скорость. Если вы знаете значение перемещения и общее время в пути, вычислить среднюю скорость можно по формуле v ср = Δs/Δt. В нашем примере средняя скорость ракеты равна 600 м (на север) / (300 секунд) = 2 м/с (на север) .
- Не забудьте указать направление движения (например, «вперед» или «на север»).
- В формуле v ср = Δs/Δt символ «дельта» (Δ) означает «изменение величины», то есть Δs/Δt означает «изменение положения к изменению времени».
- Средняя скорость может быть записана как v ср или как v с горизонтальной чертой сверху.

Решение более сложных задач, например, если тело вращается или ускорение не является постоянным. В этих случаях средняя скорость по-прежнему вычисляется как отношение общего перемещения к общему времени. Не имеет значения, что происходит с телом между начальной и конечной точками пути. Вот несколько примеров задач с одинаковым общим перемещением и общим временем (а, следовательно, и одинаковой средней скоростью).
- Анна идет на запад со скоростью 1 м/с в течение 2 секунд, затем мгновенно ускоряется до 3 м/с и продолжает идти на запад в течение 2 секунд. Ее общее перемещение составляет (1 м/с)(2 с) + (3 м/с)(2 с) = 8 м (на запад). Общее время в пути: 2 с + 2 с = 4 с. Ее средняя скорость: 8 м / 4 с =
- Борис идет на запад со скоростью 5 м/с в течение 3 секунд, затем разворачивается и идет на восток со скоростью 7 м/с в течение 1 секунды. Мы можем рассматривать движение на восток как «отрицательное движение» на запад, поэтому общее перемещение равно (5 м/с)(3 с) + (-7 м/с)(1 с) = 8 метров.
 Общее время равно 4 с. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .
Общее время равно 4 с. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) . - Юля проходит 1 метр на север, затем проходит 8 метров на запад, а затем проходит 1 метр на юг. Общее время в пути составляет 4 секунды. Нарисуйте схему этого движения на бумаге, и вы увидите, что оно заканчивается в 8 метрах к западу от начальной точки, то есть общее перемещение равно 8 м. Общее время в пути составило 4 секунды. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .
Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:
- S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
- V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)
Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:
- V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час
Ответ: средняя скорость V ср = 13,3 км/час.
Как найти среднюю скорость движения с ускорением
Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.
Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².
Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:
где V0 — начальная скорость движения, a — ускорение, t — время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.
Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:
Находим среднюю скорость: задача
Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек.
Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно
- а = (V — V0)/ t = (0 — 5)/ 5 = — 1 м/сек².
Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.
В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:
Научимся ее находить на примере следующей задачи:
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.
Частные случаи нахождения средней скорости
1. Два одинаковых участка пути.
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
| Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения. |
Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Сергей Валерьевич
Очень просто! Нужно весь путь разделить на время, которое объект движения находился в пути. Выражаясь иначе, можно определить среднюю скорость как среднее арифметическое всех скоростей движения объекта. Но существуют некоторые нюансы при решении задач данного направления.
Например, для вычисления средней скорости даётся такой вариант задачи: путник сначала шёл со скоростью 4 км в час в течение часа. Затем попутная машина «подобрала» его, и остаток пути он проехал за 15 минут. Причём автомобиль шёл со скоростью 60 км в час. Как определить среднюю скорость перемещения путника?
Затем попутная машина «подобрала» его, и остаток пути он проехал за 15 минут. Причём автомобиль шёл со скоростью 60 км в час. Как определить среднюю скорость перемещения путника?
Не следует просто складывать 4 км и 60 и делить их пополам, это будет неверный ход решения! Ведь пройденные пути пешком и на автомашине нам неизвестны. Значит, сначала нужно вычислить весь путь.
Первую часть пути найти легко: 4 км в час Х 1 час = 4 км
Со второй частью пути небольшие проблемы: скорость выражена в часах, а время движения — в минутах. Этот нюанс частенько мешает найти правильный ответ, когда поставлены вопросы, как найти среднюю скорость, путь или время.
Выразим 15 минут в часах. Для этого 15 мин: 60 мин = 0,25 часа. Теперь рассчитаем, какой же путь путник проделал на попутке?
60 км/ ч Х 0,25ч = 15 км
Теперь найти весь преодолённый путником путь не составит особого труда: 15 км + 4 км = 19 км.
Время движения также довольно легко вычислить. Это 1 час + 0,25 часа = 1,25 часа.
И теперь уже понятно, как найти среднюю скорость: нужно весь путь поделить на время, которое путник затратил на его преодоление. То есть, 19 км: 1,25 часа = 15,2 км/час.
Есть такой анекдот в тему. Мужчина, торопящийся на спрашивает владельца поля: «Можно ли мне пройти к вокзалу через ваш участок? Я немного опаздываю и хотел бы сократить свой путь, пройдя напрямую. Тогда я определённо успею к электричке, которая отходит в 16 часов 45 минут!» — «Конечно, вы можете сократить свой путь, пройдя через мой луг! И если вас там заметит мой бык, то вы успеете даже на ту электричку, которая отходит в 16 часов 15 минут».
Эта комичная ситуация, между тем, имеет самое прямое отношение к такому математическому понятию, как средняя скорость движения. Ведь потенциальный пассажир пытается сократить свой путь по той простой причине, что он знает среднюю скорость своего движения, например, 5 км в час. И пешеход, зная, что обходной путь по асфальтированной дороге равняется 7,5 км, произведя мысленно простые вычисления, понимает, что ему потребуется на эту дорогу полтора часа (7,5 км: 5 км/час = 1,5 час).
Он же, выйдя из дома слишком поздно, ограничен во времени, поэтому и решает сократить свой путь.
И вот тут мы сталкиваемся с первым правилом, которое диктует нам, как найти среднюю скорость движения: учитывая прямое расстояние между крайними точками пути или именно просчитывая Из вышесказанного всем ясно: следует вести расчёт, принимая во внимание именно траекторию пути.
Сократив путь, но не изменяя свою среднюю скорость, объект в лице пешехода получает выигрыш во времени. Фермер же, предполагая среднюю скорость убегающего от разъярённого быка «спринтера», также делает простые расчёты и выдаёт свой результат.
Автомобилисты часто используют второе, немаловажное, правило вычисления средней скорости, которое касается времени нахождения в пути. Это касается того вопроса, как найти среднюю скорость в случае, если объект имеет во время пути остановки.
В этом варианте обычно, если нет дополнительных уточнений, для расчёта берут полное время, включая остановки. Поэтому водитель авто может сказать, что его средняя скорость движения утром по свободной дороге намного выше, чем средняя скорость движения в час-пик, хотя спидометр показывает одну и ту же цифру в обоих вариантах.
Поэтому водитель авто может сказать, что его средняя скорость движения утром по свободной дороге намного выше, чем средняя скорость движения в час-пик, хотя спидометр показывает одну и ту же цифру в обоих вариантах.
Зная эти цифры, опытный шофёр никогда и никуда не опоздает, заранее предположив, какова будет его средняя скорость передвижения в городе в разное время суток.
Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи » » и » » . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.
Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:
Если участков пути было два, тогда
Если три, то соответственно:
*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.
Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:
Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:
Вторую треть пути автомобиль ехал:
Последнюю треть пути автомобиль ехал:
Таким образом
Решите самостоятельно:
Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В условии сказано о трёх участках пути. СК будем искать по формуле:
СК будем искать по формуле:
Участки пути нам не даны, но мы можем без труда их вычислить:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
Вычисляем скорость:
Решите самостоятельно:
Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Сказано о трёх участках пути. Формула:
Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:
Решите самостоятельно:
Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.
Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
1 | Какой путь проходит автобус за 4 ч, если его средняя скорость 50 км/ч? | Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. | Половину времени при переезде из одного пункта в другой автомобиль двигался с постоянной скоростью 60 км/ч. С какой постоянной скоростью он должен двигаться оставшееся время, если средняя скорость движения равна 65 км/ч? | 2 | Первый участок длиной 120 м лыжник прошел за 2 мин, а второй длиной 27 м он прошел за 1,5 мин. Найдите среднюю скорость движения лыжника на всем пути. Ответ дайте в м/с. | Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. | Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч. | 3 | Двигаясь по шоссе, велосипедист проехал 20 км за 40 мин, затем проселочную дорогу длиной 600 м он преодолел за 2 мин, а оставшиеся 39 км 400 м по шоссе он проехал за 78 мин. | Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. | Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. |
Задача про среднюю скорость. Почему в ответах нет опечатки. | ОГЭ математика
Добрый день, уважаемые читатели. Сегодня решим с вами задачу, про которую я очень часто слышу: «там в ответах в сборнике опечатка».
ЗАДАНИЕ 21
Первую половину пути автомобиль проехал со скоростью 90 км/ч, а вторую — со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
С каким решением чаще всего приходится сталкиваться? Как только ученик видит слово «средняя», первое, что приходит на ум — «найти среднюю арифметическую значений скорости». Далее находит (90+110):2=100 (км/ч) и считает, что задача решена верно. НО ЭТО НЕ ТАК!
Разберемся с вами, что же такое средняя скорость.
Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело.
Т.е. при равномерном движении (без ускорения), про которое идет речь в задаче, средняя скорость вычисляется по формуле:
Где S — все расстояние, которое складывается из расстояний пройденных n отрезков , t — время всего пути, которое является суммой времен, затраченных на прохождение каждого отрезка пути.
По условию задачи путь S состоит из двух отрезков равных половине пути (S/2).
Для наглядности условия запишу его в виде таблицы(где I и II отрезки пути):
Выразим время движения на каждом отрезке, учитывая t=S/V
Найдем общее время движения как сумму времён движения на отрезках пути:
Т. к. весь путь равен S, то вычислим среднюю скорость как:
к. весь путь равен S, то вычислим среднюю скорость как:
ОТВЕТ: 99 км/ч
Если вы знаете того, кто готовится к ОГЭ, поделитесь с ним этой информацией. Всегда пригодится.
Не забудь нажать на пальчик вверх после прочтения и подписаться. За это отдельная благодарность
(✿◠‿◠)
Средняя скорость с остановками. Перемещение, путь, средняя скорость примеры решения задач
Задачи на среднюю скорость (далее СК). Мы уже рассматривали задания на прямолинейное движение. Рекомендую посмотреть статьи » » и » » . Типовые задания на среднюю скорость это группа задач на движение, они включены в ЕГЭ по математике и такая задача вполне вероятно может оказаться перед вами в момент самого экзамена. Задачки простые, решаются быстро.
Смысл таков: представьте объект передвижения, например автомобиль. Он проходит определённые участки пути с разной скоростью. На весь путь затрачивается какое-то определённое время. Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:
Так вот: средняя скорость это такая постоянная скорость с которой автомобиль преодолел бы данный весть путь за это же время То есть формула средней скорости такова:
Если участков пути было два, тогда
Если три, то соответственно:
*В знаменателе суммируем время, а в числителе расстояния пройденные за соответствующие им отрезки времени.
Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть – со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Как уже сказано необходимо весь путь разделить на всё время движения. В условии сказано о трёх участках пути. Формула:
Обозначим весь пусть S. Тогда первую треть пути автомобиль ехал:
Вторую треть пути автомобиль ехал:
Последнюю треть пути автомобиль ехал:
Таким образом
Решите самостоятельно:
Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
В условии сказано о трёх участках пути. СК будем искать по формуле:
Участки пути нам не даны, но мы можем без труда их вычислить:
Первый участок пути составил 1∙100 = 100 километров.
Второй участок пути составил 2∙90 = 180 километров.
Третий участок пути составил 2∙80 = 160 километров.
Вычисляем скорость:
Решите самостоятельно:
Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Сказано о трёх участках пути. Формула:
Протяжённость участков дана. Определим время, которое автомобиль затратил на каждый участок: на первый затрачено 120/60 часов, на второй участок 120/80 часов, на третий 150/100 часов. Вычисляем скорость:
Решите самостоятельно:
Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите СК автомобиля на протяжении всего пути. Ответ дайте в км/ч.
*Есть задача про путешественника, который пересёк море. С решением у ребят возникают проблемы. Если вы не видите его, то пройдите регистрацию на сайте! Кнопка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После регистрации войдите на сайт и обновите данную страницу.
Путешественник переплыл море на яхте со средней скоростью 17 км/ч. Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Понятие скорости − одно из главных понятий в кинематике.
Многим наверняка известно, что скорость − это физическая величина, показывающая насколько быстро (или насколько медленно) перемещается в пространстве движущееся тело. Разумеется, речь идет о перемещении в выбранной системе отсчета. Известно ли, однако, Вам, что используются не одно, а три понятия скорости? Есть скорость в данный момент времени, называемая мгновенной скоростью, и есть два понятия средней скорости за данный промежуток времени − средняя путевая скорость (по английски speed) и средняя скорость по перемещению (по-английски velocity).
Будем рассматривать материальную точку в системе координат x , y , z (рис. а).
а).
Положение A точки в момент времени t характеризуем координатами x(t) , y(t) , z(t) , представляющими три составляющих радиуса-вектора (t ). Точка движется, ее положение в выбранной системе координат с течением времени изменяется − конец радиуса-вектора (t ) описывает кривую, называемую траекторией движущейся точки.
Траектория, описанная за промежуток времени от t до t + Δt , показана на рисунке б.
Через B обозначено положение точки в момент t + Δt (его фиксирует радиус-вектор (t + Δt )). Пусть Δs − длина рассматриваемой криволинейной траектории, т. е. путь, пройденный точкой за время от t до t + Δt .
Среднюю путевую скорость точки за данный промежуток времени определяют соотношением
Очевидно, что v п − скалярная величина; она характеризуется только числовым значением.
Показанный на рисунке б вектор
называют перемещением материальной точки за время от t до t + Δt .
Среднюю скорость по перемещению за данный промежуток времени определяют соотношением
Очевидно, что v ср − векторная величина. Направление вектора v ср совпадает с направлением перемещения Δr .
Заметим, что в случае прямолинейного движения средняя путевая скорость движущейся точки совпадает с модулем средней скорости по перемещению.
Движение точки по прямолинейной либо криволинейной траектории называют равномерным, если в соотношении (1) величина vп не зависит от Δt . Если, например, уменьшить Δt в 2 раза, то и длина пройденного точкой пути Δs уменьшится в 2 раза. При равномерном движении точка проходит за равные промежутки времени пути равной длины.
Вопрос :
Можно ли считать, что при равномерном движении точки от Δt не зависит также вектор ср средней скорости по перемещению?
Ответ :
Так можно считать только в случае прямолинейного движения (при этом, напомним, модуль средней скорости по перемещению равен средней путевой скорости). Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения Δt будут изменяться как модуль, так и направление вектора средней скорости по перемещению. При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы v ср ).
Если же равномерное движение совершается по криволинейной траектории, то с изменением промежутка усреднения Δt будут изменяться как модуль, так и направление вектора средней скорости по перемещению. При равномерном криволинейном движении равным промежуткам времени Δt будут соответствовать разные векторы перемещения Δr (а значит, и разные векторы v ср ).
Правда, в случае равномерного движения по окружности равным промежуткам времени будут соответствовать равные значения модуля перемещения |r| (а значит, и равные |v ср | ). Но направления перемещений (а значит, и векторов v ср ) и в данном случае будут различными для одинаковых Δt . Это видно на рисунке,
Где равномерно движущаяся по окружности точка описывает за равные промежутки времени равные дуги AB , BC , CD . Хотя векторы перемещений 1 , 2 , 3 имеют одинаковые модули, однако направления у них различны, так что о равенстве этих векторов говорить не приходится.
Примечание
Из двух средних скоростей в задачах обычно рассматривают среднюю путевую скорость, а среднюю скорость по перемещению используют довольно редко. Однако она заслуживает внимания, так как позволяет ввести понятие мгновенной скорости.
Средней скоростью называется скорость, которая получается, если весь путь поделить на время, за которое объект преодолел этот путь. Формула средней скорости:
- S = S1 + S2 + S3 = v1*t1 + v2*t2 + v3*t3
- V ср = S/t = (v1*t1 + v2*t2 + v3*t3) / (t1 + t2 + t3)
Чтобы не путаться с часами и минутами, переводим все минуты в часы: 15 мин. = 0,4 час, 36 мин. = 0,6 час. Подставляем числовые значения в последнюю формулу:
- V ср = (20*0,4 + 0,5*6 + 0,6*15) / (0,4 + 0,5 + 0,6) = (8 + 3 + 9) / (0,4 + 0,5 + 0,6) = 20 / 1,5 = 13,3 км/час
Ответ: средняя скорость V ср = 13,3 км/час.
Как найти среднюю скорость движения с ускорением
Если скорость в начале движения отличается от скорости в его конце, такое движение называют ускоренным. Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.
Причём далеко не всегда тело действительно двигается всё быстрее и быстрее. Если движение замедляется, всё равно говорят, что оно движется с ускорением, только ускорение будет уже отрицательным.
Иными словами, если автомобиль, трогаясь с места, через секунду разогнался до скорости 10 м/сек, то его ускорение а равно 10 м в секунду за секунду а = 10 м/сек². Если в следующую секунду автомобиль остановился, то его ускорение тоже равно 10 м/сек², только уже со знаком минус: а = -10 м/сек².
Скорость движения с ускорением в конце временного отрезка вычисляется по формуле:
где V0 — начальная скорость движения, a — ускорение, t — время, за которое наблюдалось данное ускорение. Плюс или минус в формуле ставится в зависимости от того, увеличивалась скорость или уменьшалась.
Средняя скорость за отрезок времени t вычисляется как среднее арифметическое начальной и конечной скорости:
Находим среднюю скорость: задача
Шарик толкнули по ровной плоскости с начальной скоростью V0 = 5 м/сек. Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?
Через 5 сек. шарик остановился. Чему равны ускорение и средняя скорость?
Конечная скорость шарика V = 0 м/сек. Ускорение из первой формулы равно
- а = (V — V0)/ t = (0 — 5)/ 5 = — 1 м/сек².
Средняя скорость V ср = (V0 + V) / 2= 5 /2 = 2,5 м/сек.
Неравномерным считается движение с изменяющейся скоростью. Скорость может изменяться по направлению. Можно заключить, что любое движение НЕ по прямой траектории является неравномерным. Например, движение тела по окружности, движение тела брошенного вдаль и др.
Скорость может изменяться по численному значению. Такое движение тоже будет неравномерным. Особенный случай такого движения — равноускоренное движение.
Иногда встречается неравномерное движение, которое состоит из чередования различного вида движений, например, сначала автобус разгоняется (движение равноускоренное), потом какое-то время движется равномерно, а потом останавливается.
Мгновенная скорость
Охарактеризовать неравномерное движение можно лишь скоростью. Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!
Но скорость всегда изменяется! Поэтому можно говорить лишь о скорости в данное мгновение времени. Путешествуя на машине спидометр ежесекундно демонстрирует вам мгновенную скорость движения. Но время при этом надо уменьшить не до секунды, а рассматривать гораздо меньший промежуток времени!
Средняя скорость
Что же такое средняя скорость? Неверно думать, что необходимо сложить все мгновенные скорости и разделить на их количество. Это самое распространенное заблуждение о средней скорости! Средняя скорость — это весь путь разделить на затраченное время . И никакими другими способами она не определяется. Если рассмотреть движение автомобиля, можно оценить его средние скорости на первой половине пути, на второй, на всем пути. Средние скорости могут быть одинаковыми, а могут быть различными на этих участках.
У средних величин рисуют сверху горизонтальную черту.
Средняя скорость перемещения. Средняя путевая скорость
Если движение тела не является прямолинейным, то пройденный телом путь будет больше, чем его перемещение. В этом случае средняя скорость перемещения отличается от средней путевой скорости. Путевая скорость — скаляр .
В этом случае средняя скорость перемещения отличается от средней путевой скорости. Путевая скорость — скаляр .
Главное запомнить
1) Определение и виды неравномерного движения;
2) Различие средней и мгновенной скоростей;
3) Правило нахождения средней скорости движения
Часто требуется решить задачу, где весь путь разбит на равные участки, даны средние скорости на каждом участке, требуется найти среднюю скорость движения на всем пути. Неверное решение будет, если сложить средние скорости и разделить на их количество. Ниже выводится формула, которую можно использовать при решении подобных задач.
Мгновенную скорость можно определить с помощью графика движения. Мгновенная скорость тела в любой точке на графике определяется наклоном касательной к кривой в соответствующей точке. Мгновенная скорость — тангенс угла наклона касательной к графику функции.
Упражнения
Во время езды на автомобиле через каждую минуту снимались показания спидометра. Можно ли по этим данным определить среднюю скорость движения автомобиля?
Можно ли по этим данным определить среднюю скорость движения автомобиля?
Нельзя, так как в общем случае величина средней скорости не равна среднему арифметическому значению величин мгновенных скоростей. А путь и время не даны.
Какую скорость переменного движения показывает спидометр автомобиля?
Близкую к мгновенной. Близкую, так как промежуток времени должен быть бесконечно мал, а при снятии показаний со спидометра так о времени судить нельзя.
В каком случае мгновенная и средняя скорости равны между собой? Почему?
При равномерном движении. Потому что скорость не изменяется.
Скорость движения молотка при ударе равна 8м/с. Какая это скорость: средняя или мгновенная?
В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения тела называется отношение пути , пройденного телом, ко времени , в течение которого двигалось тело:
Научимся ее находить на примере следующей задачи:
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей и , которое равно:
м/с.
Частные случаи нахождения средней скорости
1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.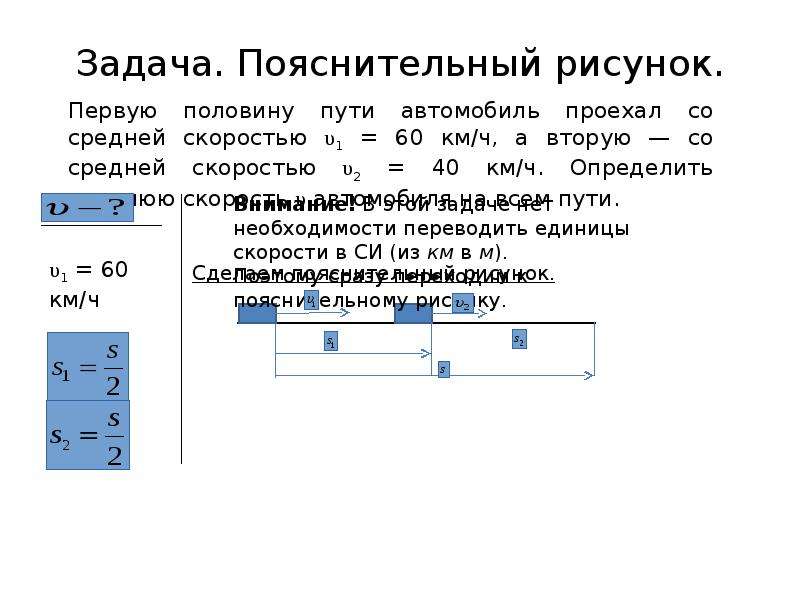 |
Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила:
м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Сергей Валерьевич
Тесты и задания | Лекториум
11 декабря, 2015 — 05:36
#102Trizart
Не в сети
Здравствуйте. Не могу понять, почету в 4 задании 4-ого проверочного теста средняя скорость на всем участке отличается от u в 0.60 раз. У меня получается в 2/3 или 0.67
Не могу понять, почету в 4 задании 4-ого проверочного теста средняя скорость на всем участке отличается от u в 0.60 раз. У меня получается в 2/3 или 0.67
11 декабря, 2015 — 09:53
#103alch
Преподаватель
Не в сети
Доброе утро!
«Не могу понять, почету в 4 задании 4-ого проверочного теста средняя скорость на всем участке отличается от u в 0.60 раз. У меня получается в 2/3 или 0.67».
У Вас пока получается не правильно. 0.67 — это было в тесте после модуля,а теперь тест другой! Как Вы рассуждали, получая 0,67?
12 декабря, 2015 — 23:35
#108Lunnaya
Не в сети
А можно задавать вопросы здесь, уточняющие условия задачи в тесте?)
17 декабря, 2015 — 12:50
#110Бегемот
Не в сети
Вопрос к итоговому тесту главы 5. Вопрос 4: что-то там не так. Там точно радианы, а не градусы? Какой формат подразумевается: 3,14*… (коеффициент при Пи)? Уже и так и эдак. Простейший вроде вопрос, но не принимает ответ с углом настильной траектории. У кого-то получился зачет???
Вопрос 4: что-то там не так. Там точно радианы, а не градусы? Какой формат подразумевается: 3,14*… (коеффициент при Пи)? Уже и так и эдак. Простейший вроде вопрос, но не принимает ответ с углом настильной траектории. У кого-то получился зачет???
17 декабря, 2015 — 13:52
#113alch
Преподаватель
Не в сети
Дорогой Бегемот, а какой Вы пытаетесь ввести ответ (не цифрой, а рассуждением)?
17 декабря, 2015 — 14:51
#114Бегемот
Не в сети
я пытался ввести число, округленное до сотых. Не приняло. А у вас получилось зеленую галочку получить?
Не приняло. А у вас получилось зеленую галочку получить?
17 декабря, 2015 — 17:03
#115Nicolaj
Не в сети
Да, зелёную галочку получил. Но число округлил до тысячных. Попробуйте так.
19 декабря, 2015 — 19:35
#117Trizart
Не в сети
Здравствуйте. Не могу справиться с проверочным тестов 6.1, задание 5.
Не могу справиться с проверочным тестов 6.1, задание 5.
Точечное тело за время 6.37 мин сделало 7 полных оборотов, двигаясь по окружности радиусом в 13.333 м. Найдите величину средней скорости тела за указанный временной промежуток.
ВНИМАНИЕ: ответ следует представить в системе единиц СИ!
Решал так: посчитал пройденный путь (умножил длину окружности на количество оборотов — 2*pi*r*7) и раздел на время в секундах (6.37*60). Получил скорость 1,534 м/с.
19 декабря, 2015 — 20:11
#120alch
Преподаватель
Не в сети
Уважаемый Trizart, вспомните ОПРЕДЕЛЕНИЕ средней скорости и все получится. 2
2
Получился угол поворота 125 рад. Чтобы посчитать количество оборотов — разделил на 2*pi. Итого полных оборотов получилось 19
23 декабря, 2015 — 21:25
#129Trizart
Не в сети
Кстати, ко второму вопросу в тесте к теме 6.4 дана неверная подсказка. Там написано, что количество правильных утверждений равно 2, а на самом деле их там 3
27 декабря, 2015 — 07:28
#136Nicolaj
Не в сети
У меня вопрос по поводу вопроса №3 итогового теста: это так задумано, что y-проекция изменяется по закону x-проекции: rx=Rcos(ωt)?
28 декабря, 2015 — 15:04
#140Nicolaj
Не в сети
Кстати, с апелляциями тоже намудрили: написали до четверга 29 декабря(вторник), а на самом деле c четверга 13 января! 🙁
10 января, 2016 — 06:49
#142Бегемот
Не в сети
Караул! Уважаемые Николай, Trizart, Александр Сергеевич и другие активные участники форума! Помогите!
С момента решения пятого задания темы 6. 5, где я каким-то уверенным способом умудрился получить ответ 1.7 к моменту преступления к решению задачи после корпоративной попойки что-то напрочь отшибло в понимании скорости в сложном мире проекций крутящихся/под углом подкинутых и прочих неподвижных СО. Смотрю пояснение к решению задачи, возвращаюсь в главе 5 к заданию 4 проверочного теста 5.2 и смотрю на него, как баран на новые ворота. Подскажите, друзья, вы ничего не находили подозрительного в том задании? (Тело брошено под углом α к горизонту с малой начальной скоростью v0 с поверхности не имеющей атмосферы, но покрытой океаном из неиспаряющейся жидкости планеты. В какие моменты времени горизонтальная составляющая скорости тела будет иметь значение v0 Cos α?) Как бы при любом значении vx(t) = v0 Cos α, при этом второй вариант, где t = v0 Sin α / g соответствует тому моменту. когда у меня возник провал в памяти (в точке максимальной высоты подъема тела).
5, где я каким-то уверенным способом умудрился получить ответ 1.7 к моменту преступления к решению задачи после корпоративной попойки что-то напрочь отшибло в понимании скорости в сложном мире проекций крутящихся/под углом подкинутых и прочих неподвижных СО. Смотрю пояснение к решению задачи, возвращаюсь в главе 5 к заданию 4 проверочного теста 5.2 и смотрю на него, как баран на новые ворота. Подскажите, друзья, вы ничего не находили подозрительного в том задании? (Тело брошено под углом α к горизонту с малой начальной скоростью v0 с поверхности не имеющей атмосферы, но покрытой океаном из неиспаряющейся жидкости планеты. В какие моменты времени горизонтальная составляющая скорости тела будет иметь значение v0 Cos α?) Как бы при любом значении vx(t) = v0 Cos α, при этом второй вариант, где t = v0 Sin α / g соответствует тому моменту. когда у меня возник провал в памяти (в точке максимальной высоты подъема тела). Помогите восстановить память и разобраться с этим заданием, не имеющем правильного ответа и с этим моментом в частности: что там происходит с горизонтальными проекциями и для чего они нужны?!..
Помогите восстановить память и разобраться с этим заданием, не имеющем правильного ответа и с этим моментом в частности: что там происходит с горизонтальными проекциями и для чего они нужны?!..
10 января, 2016 — 06:54
#144Бегемот
Не в сети
Ах, да! С возвращением всех, дорогие мои! Со святками, со всеми рождественско-новогодними праздниками и новыми сюрпризами и впечатлениям в новом году!! 🙂
12 января, 2016 — 19:05
#145Nicolaj
Не в сети
Уважаемый, Бегемот, вас также с праздниками. А в задании 4 проверочного теста 5.2 нет ни какой ошибки, просто нужно не забывать, что тело если его скорость не более первой и более космических скоростей должно упасть в океан и … о дальнейшем её движении говорить очень сложно 🙂
А в задании 4 проверочного теста 5.2 нет ни какой ошибки, просто нужно не забывать, что тело если его скорость не более первой и более космических скоростей должно упасть в океан и … о дальнейшем её движении говорить очень сложно 🙂
P.S. косинус угла не может быть больше единицы (дополнение на всякий случай)
Разбор задач тренировочных заданий по кинематике
В большинстве компьютерных вариантов заданий для каждого участника генерируются свои наборы данных
Задание 1 «С какой скоростью движется вторая машина относительно первой (4 балла)».
Две машины приближаются к перекрестку, двигаясь под прямым углом друг к другу со скоростями 54 км/ч и 72 км/ч. С какой скоростью движется вторая машина относительно первой?
|
Дано: |
Перевод единиц: |
|
v1 = 54 км/ч |
15 м/с |
|
v2 = 72 км/ч |
20 м/с |
|
= ? |
|
Решение. Скорости, заданные в условии,
измерены относительно системы отсчета, связанной с землей. Уточним обозначение
этих скоростей:
Скорости, заданные в условии,
измерены относительно системы отсчета, связанной с землей. Уточним обозначение
этих скоростей:
, .
Скорость второй машины относительно первой — это скорость второй машины измеренная в системе отсчета, связанной с первой машиной (например, водителем первой машины). Если первая машина двигается относительно земли со скоростью , то в системе отсчета первой машины земля двигается с такой же по величине скоростью, но в обратном направлении:
.
Для водителя первой машины скорость второй машины будет складываться из ее скорости относительно земли и скорости земли в системе отсчета первой машины:
.
Величина относительной
скорости второй машины v21
равна гипотенузе прямоугольного треугольника, образованного скоростями машин
относительно земли. По теореме Пифагора находим:
По теореме Пифагора находим:
.
Заметим, если относительная скорость окажется направленной по линии, соединяющей машины, то продолжая двигаться с такими скоростями, они неминуемо столкнутся!
Ответ: 25 м/с.
Задание 2 «Вычислите среднюю скорость движения человека (8 баллов)»
Вычислите среднюю скорость движения человека, если первую треть пути он шел со скоростью 1,5 м/с, а оставшуюся часть пути со скоростью 1,0 м/с.
|
Дано: |
|
v1 = 1,5 м/с |
|
v2 = 1,0 м/с |
|
= ? |
Решение. Согласно общему определению средней скорости:
,
где S — весь пройденный путь, а t —
все время движения.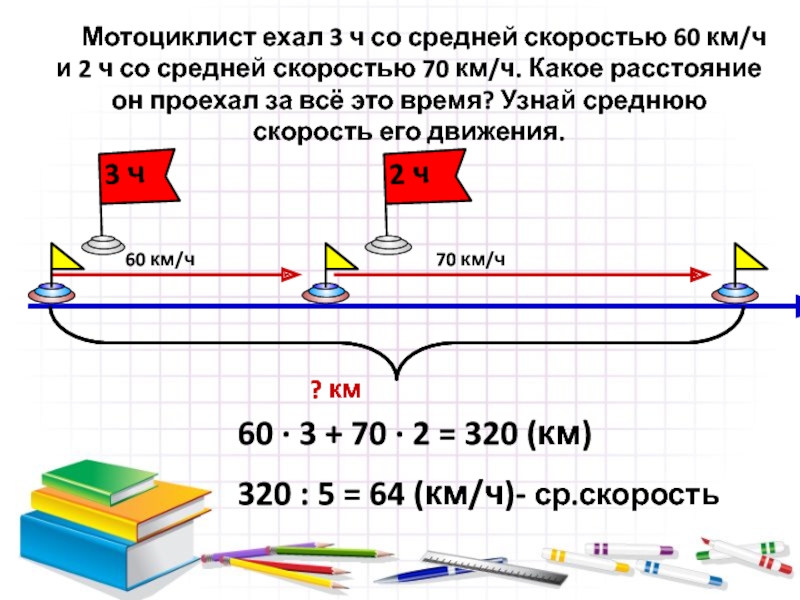
Времена t1 и t2 прохождения первой трети пути и остальных двух третей равны, соответственно
, .
Учитывая, что t = t1 + t2 находим
.
Ответ: 1,125 м/с.
Задание 3 «Найдите ускорение и путь автомобиля (8 баллов)»
Автомобиль, движущийся со скоростью 36 км/ч, разгоняется в течение десяти секунд до 108 км/ч и затем за полминуты сбрасывает скорость до нуля. Считая движение при разгоне и торможении равнопеременным, найдите ускорение и путь для каждого из промежутков времени.
|
Дано: |
Перевод единиц: |
|
v1 = 36 км/ч |
10 м/с |
|
t1 = 10 c |
|
|
v2 = 108 км/ч |
30 м/с |
|
t2 = 0,5 мин |
30 c |
|
a1, S1, a2, S2 = ? |
|
Решение. Применяя формулу скорости для равноускоренного движения в течение
времени t1,
получим
Применяя формулу скорости для равноускоренного движения в течение
времени t1,
получим
,
откуда
.
Находим путь, пройденный на участке разгона:
.
Скорость при торможении машины меняется по формуле
v = v2 – a2t, (1)
убывая за время t2 до v = 0. Подставляя нуль в правую часть уравнения (1), и выражая величину ускорения, получаем
.
Отметим, что в данном случае проекция ускорения на ось OX отрицательна: a2x = —a2 = –1 м/с2.
Соответствующий путь составляет
.
Ответ: a1 = 2 м/с2, S1 = 200 м, a2 = 1 м/с2 (a2x = –1 м/с2), S2 = 450 м.
Задание 4 «Вычислите максимальную высоту подъема тела, брошенного под углом к горизонту (8 баллов)»
Вычислите максимальную высоту подъема тела, брошенного под углом 30 к горизонту со скоростью 20 м/с. Сопротивлением воздуха пренебрегите.
|
Дано: |
|
= 30 |
|
v0 = 20 м/с |
|
hmax = ? |
Решение. Проанализируем, как изменяется со временем
проекция скорости на ось OY. Cуществует такой момент
времени t1 = v0y/g, при котором проекция vy
обращается в нуль. До этого момента времени vy
положительна, то есть тело движется вверх. После момента времени проекция vy
становится отрицательной, то есть тело движется вниз.
Очевидно, что в этот момент времени достигается максимальная высота hmax.:
.
Используя численные данные, находим:
.
Ответ: 5 м.
Задание 5 «Модель: Измерьте скорость тележки (8 баллов)»
Задание: Измерьте с помощью оптических
датчиков скорость тележки. Занесите результаты в отчёт (меню в верхней части
программы) и отошлите отчёт на сервер.
Стойки с датчиками расположите так, чтобы они фиксировали моменты прохождения
тележки. Позицию датчиков можно менять мышью или с помощью пункта ввода.
Конечный результат округляйте до сотых. Пример округления: 0,605 можно
округлять до 0,60 или до 0,61.
Рис.1 Начальное состояние системы
Для измерения скорости
следует установить стойки с датчиками, например, на позиции с координатами x1=0.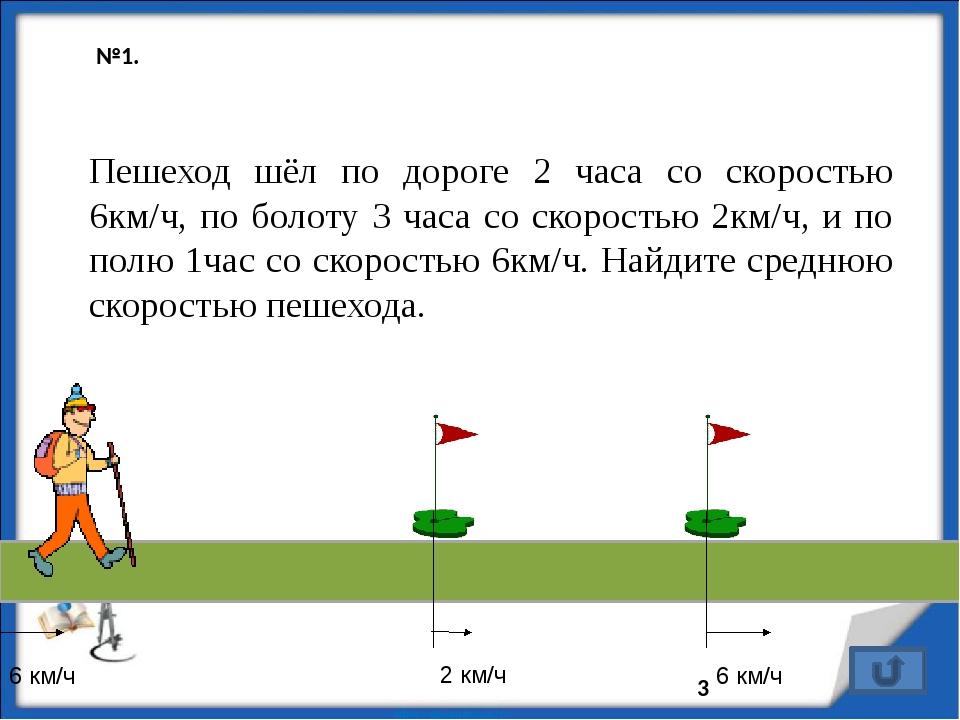 2 м и x2=0.8 м и
нажать кнопку “Пуск”. Тележка доедет до противоположной стенки и остановится, а
на датчиках появятся показания (рис.2).
2 м и x2=0.8 м и
нажать кнопку “Пуск”. Тележка доедет до противоположной стенки и остановится, а
на датчиках появятся показания (рис.2).
Рис.2 Конечное состояние системы
Скорость находим как отношение пути между x2 и x1 к затраченному времени t2-t1:
v=(x2-x1)/(t2-t1)
При этом пусть мы сначала ошибемся и напишем v= (0.8-0.2)/(2.5-0.278) м/с = 0.6/2.222 м/с = 0.270027 … м/с
(вместо x2=0.9 м написали x2=0.8 м). Округляем до сотых: v=0.27 м/с
Открываем пункт меню “Отчёт…” в верхней части программы, и в появившемся окне вводим это значение (рис.3):
Рис.3 Отсылка отчёта
Нажимаем кнопку “Отправить результаты на сервер” и получаем отзыв с сервера с информацией о неправильном решении:
Рис.4 Результат проверки со стороны сервера
При нажатии кнопки “Закрыть”
любая информация в окне отчета сохраняется и показывается вновь при открытии
отчета. При нажатии кнопки “Очистить” восстанавливается первоначальное
состояние окна отчета с пустыми пунктами ввода.
При нажатии кнопки “Очистить” восстанавливается первоначальное
состояние окна отчета с пустыми пунктами ввода.
Мы можем нажать кнопку “Очистить”, затем кнопку “Закрыть”, проверить правильность наших действий и вычислений.
Например, заново проделать измерения при тех же или других расстояниях между датчиками. Обнаруживаем ошибку и исправляем ее:
v=(x2-x1)/(t2-t1) = (0.9-0.2)/(2.5-0.278) м/с = 0.7/2.222 м/с = 0.360036 … м/с
Округляем до сотых: v=0.36 м/с.
Открываем отчет, вводим ответ, отсылаем отчет на сервер и получаем:
Рис.5 Результат проверки нового результата
Итоговый балл за выполнение задания получился 7 из 8 возможных, так как имелась одна дополнительная попытка отсылки результатов на сервер.
Задание 6 «Тест: Кинематика (16 вопросов, 25 баллов)»
Тест будет разбираться в отдельном документе.
Задание 7 «Модель: Измерьте среднюю и мгновенную скорость тележки (12 баллов)»
Задание: По наклонному рельсу из точки с
координатой х=0 из состояния покоя начинает равноускоренно двигаться тележка. Определите время движения тележки до её удара о стенку, а также её среднюю и
конечную скорость на отрезке от x=0 до x=0.5
Определите время движения тележки до её удара о стенку, а также её среднюю и
конечную скорость на отрезке от x=0 до x=0.5
Время определите с точностью до тысячных, а остальные величины до сотых, и отошлите результаты на сервер. В промежуточных вычислениях сохраняйте не менее 4 значащих цифр.
Оптические датчики срабатывают при пересечении светового луча датчика флажком тележки. Положение ворот с оптическими датчиками можно изменять при помощи мыши или задавая значения их координат х1 и х2 при помощи клавиатуры.
На рис.6 показано начальное состояние системы.
Рис.6 Начальное состояние системы
Первую стойку передвигаем в
позицию x1=0.5 м, вторую (с помощью пункта ввода для x2) — в позицию x2=0.99999 м (если x2=1 м тележка не пересекает луч, поэтому ставим стойку
очень близко к x=1 м). Нажимаем кнопку “Пуск” и
получаем, например, t1=1. 443 с, t2=2.041 с (рис.7).
443 с, t2=2.041 с (рис.7).
Рис.7 Конечное состояние системы
Полное время движения равно t2. Средняя скорость vср движения на отрезке от x=0 м до x=0.5 м равна x1/t1. Конечная скорость v1 движения на этом отрезке в два раза больше, так как при равноускоренном движении vср=(v0+v1)/2, а v0=0. То есть v1 проще вычислить чем измерить с достаточной точностью.
Как повысить среднюю скорость выполнения задач?
Я люблю то, чем занимаюсь, и не воспринимаю это как должное. Я знаю так много людей, которые не чувствуют то же самое. В то же время бывают дни, когда я хочу сделать как можно больше и как можно быстрее. Вот как увеличить среднюю скорость выполнения задач.
Иногда это происходит из-за того, что у меня есть другие планы, например, отпуск или новое хобби. В других случаях это просто потому, что я вложил слишком много и просто переутомился. Независимо от точной причины, я просто хочу ускорить процесс, чтобы выполнить свою работу и продолжить свой день. Но как я могу достичь этой цели, не жертвуя качеством?
Независимо от точной причины, я просто хочу ускорить процесс, чтобы выполнить свою работу и продолжить свой день. Но как я могу достичь этой цели, не жертвуя качеством?
Вы слышали о законе Паркисона? Это изречение, приписываемое британскому военно-морскому историку К. Норткоту Паркинсону, гласит: «Работа расширяется, чтобы заполнить время, отведенное для ее завершения». Но вы пришли сюда не на урок истории. Вы хотите знать, как это применимо к тому, как вы можете работать быстрее.
Допустим, вы выделили два часа для работы над конкретной задачей. Или, что еще хуже, вы уходите, а также не выделяете конкретный период времени. Вам потребуется больше времени, чем требуется для выполнения этой задачи. И вас действительно нельзя за это винить. Я имею в виду, когда кажется, что у вас есть все время в слове, чтобы что-то сделать, конечно, вы будете его доить.
Самый простой способ борьбы с законом Паркинсона — выделить подходящее время для выполнения задачи.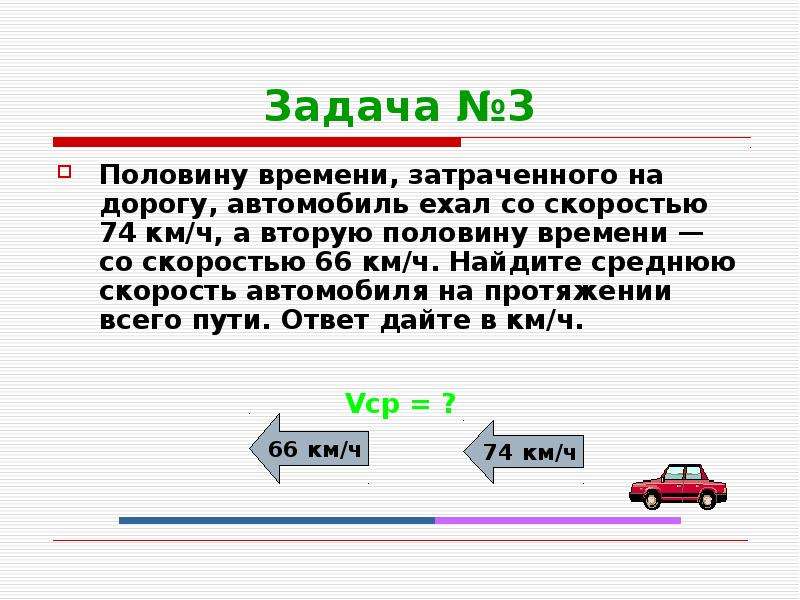 Итак, если на написание отчета у вас уходит три часа, то выделите три часа в своем календаре исключительно для этой ответственности.Я бы посоветовал вам сначала отслеживать свое время на пару недель раньше. Это даст вам более точное представление о том, как вы проводите свое время, чтобы вы могли реально блокировать время.
Итак, если на написание отчета у вас уходит три часа, то выделите три часа в своем календаре исключительно для этой ответственности.Я бы посоветовал вам сначала отслеживать свое время на пару недель раньше. Это даст вам более точное представление о том, как вы проводите свое время, чтобы вы могли реально блокировать время.
Это почти как игра. Если вы знаете, что на написание отчета обычно уходит три часа, дайте себе более короткий срок, например, 2 часа. Такой вызов самому себе побудит вас работать быстрее.И, как отмечает Саймон Рейнольдс в Forbes , вы также будете чаще испытывать Поток.
Еще один трюк, который вы можете попробовать, — это притвориться, что ваш день заканчивается рано, например, около 11 часов утра. «Если бы вы знали, что вам нужно идти домой в этот момент, но все же хотели бы получить какую-то достойную работу, что бы вы сделали?» — спрашивает Рейнольдс. «Создайте небольшой список, а затем сразу приступайте к этим важным задачам». Использование этой «техники работает блестяще, потому что заставляет вас действовать быстро в том, что имеет значение.
«Создайте небольшой список, а затем сразу приступайте к этим важным задачам». Использование этой «техники работает блестяще, потому что заставляет вас действовать быстро в том, что имеет значение.
Похожим хаком будет внедрение 4-х дневной рабочей недели. «Тот факт, что вы работаете меньше часов при 4-дневной рабочей неделе, не означает, что вы должны быть менее эффективными», — объясняет Чонсе Мэддокс в предыдущей статье «Календарь». «Поскольку вы знаете, что сокращение рабочего графика сократит время, которое вы можете потратить на работу, посмотрите, сможете ли вы сосредоточиться на более эффективной работе».
Найки на ноги.
Мы не бессовестно подключаем сюда продукт. Однако мы отстаиваем культовый слоган бренда: «Просто сделай это.
Я знаю. Это звучит слишком просто. Но это практичный способ дать отпор двум самым мощным силам, которые мешают вам работать быстрее; прокрастинация и перфекционизм.
Честно говоря, на это есть множество причин. Как объясняет Макс Палмер в статье «Начало работы должно быть главной стратегией в вашем списке», это может быть связано с недостатком уверенности или «слишком большими мечтами». Иногда из-за того, что вы себя накручиваете. Мы все смотрели в список дел или календарь и видели задачу, которую мы не ждем с нетерпением.Не осознавая этого, мы, возможно, даже выпалили: «Это будет отстой».
Иногда из-за того, что вы себя накручиваете. Мы все смотрели в список дел или календарь и видели задачу, которую мы не ждем с нетерпением.Не осознавая этого, мы, возможно, даже выпалили: «Это будет отстой».
Независимо от точной причины, начать можно с чего угодно. Просто нужно заранее немного спланировать.
- Разработайте план, который подтолкнет вас к началу работы. Если вам нужно было написать этот отчет, убедитесь, что у вас есть все инструменты и ресурсы, необходимые для выполнения этой задачи.
- Внесите свои самые важные обязанности в календарь.
- Будьте в центре внимания, избавляясь от отвлекающих факторов и работая в лучшее время.
- Разбивайте большие задачи на более управляемые части.
- Установить ограничения по времени.
- Практикуйте самосострадание.
- Перестаньте быть идеальным — его не существует.
Если ничего не помогло, попробуйте правило пяти минут. Это простой метод когнитивно-поведенческой терапии прокрастинации, когда вы обязуетесь работать над чем-то, чего избегаете. Если вы все еще чувствуете себя ужасно из-за пяти минут, перейдите к чему-нибудь другому. Однако вы должны заметить, что это создает импульс, и вы будете продолжать, пока задача не будет выполнена.
Если вы все еще чувствуете себя ужасно из-за пяти минут, перейдите к чему-нибудь другому. Однако вы должны заметить, что это создает импульс, и вы будете продолжать, пока задача не будет выполнена.
Я всегда окружаю себя музыкой. Это одна из моих самых больших любви в жизни. Хотя это может показаться смелым заявлением, музыка по-прежнему со мной, независимо от того, что я чувствую. Если у меня стресс, я катаюсь и включаю хард-рок. Если я хочу получить мотивацию для тренировок, нет ничего лучше «саундтрека Рокки». Ладно, признаюсь — иногда я включаю «Отчаяние Диснея», если у меня проблемы с работой.
Кроме того, музыка — проверенный способ попасть в зону.Как указано в Quartz, это потому, что музыка способна:
- Улучшить ваше настроение.
- Повышение физической работоспособности.
- Сделайте повторяющиеся задачи более приятными.
- Способствует сосредоточению и концентрации.
 Это также может заставить вас работать усерднее, лучше, быстрее, сильнее.
Это также может заставить вас работать усерднее, лучше, быстрее, сильнее. Еще одно преимущество прослушивания музыки? Он также может блокировать фоновый шум, который может вас отвлекать.Вместо того, чтобы вовлекаться в разговор, который ведут ваши коллеги, вы можете сосредоточиться на своей работе, слушая свои любимые мелодии.
И, говоря о отвлекающих факторах, определите наиболее значимых виновников, чтобы можно было их устранить. Например, если вам постоянно мешают эти надоедливые уведомления со смартфона, выключите телефон, заблокируйте приложения в определенное время или оставьте его в другой комнате.
Заткните утечки энергии.
Если вы не знали, у нас ограниченный запас умственной и физической энергии.Таким образом, вы не должны быть небрежными с этим драгоценным ресурсом. Если это так, вы просто не будете на пике производительности.
Чтобы решить эту проблему, заткните эти утечки энергии, чтобы избежать дефицита энергии, например:
- Многозадачность.
 Если вы не говорите о чем-то легком, например, о том, как сложить белье во время разговора по телефону, это миф. Мозг просто не способен к многозадачности. Кроме того, переключение между задачами дорого и вредно. Сохраняйте свое время и энергию, сосредотачиваясь на одном деле за раз.Вы также можете попробовать пакетную обработку задач.
Если вы не говорите о чем-то легком, например, о том, как сложить белье во время разговора по телефону, это миф. Мозг просто не способен к многозадачности. Кроме того, переключение между задачами дорого и вредно. Сохраняйте свое время и энергию, сосредотачиваясь на одном деле за раз.Вы также можете попробовать пакетную обработку задач. - Закрыть открытые петли. Это те незавершенные действия, которые вытягивают «из вас энергию, занимая место в вашем подсознании». Аманда Буччи предлагает в статье Fast Company «уделить час, день или неделю, чтобы замкнуть цикл и сделать это».
- Установить границы. Если вы уже работаете на полную мощность или у вас плотный график, скажите «нет» просьбам о дополнительном времени.
- Снижение усталости от принятия решений. Перестаньте тратить время на менее важные решения, чтобы вы могли сохранить свою энергию для более важных целей.Например, каждое воскресенье планируйте свое питание и одежду на неделю, чтобы вам не приходилось делать этот выбор в течение всей недели.

- Позаботьтесь о своем благополучии. Как минимум, это включает в себя заботу о себе и более разумное использование времени простоя. Например, отключиться на выходные и заняться любимым делом, например, отправиться в поход, посетить спа-центр или посетить концерт.
Многочисленные исследования показывают, что беспорядок вызывает стресс и отвлекает.Это также может замедлить вас и помешать вам эффективно обрабатывать новую информацию. Итак, давай, избавься от этого беспорядка раз и навсегда.
Это кажется слишком широким. Итак, начните с создания контрольного списка, чтобы у вас было наглядное представление о том, что вы можете уменьшить. Например, какие пункты в вашем списке дел можно делегировать или удалить? После определения этих пунктов у вас должен остаться скудный и средний список, которым гораздо легче управлять.
Вам также следует организовать свое рабочее место, упростить свои цели и пересмотреть свой распорядок дня.
«Машины в хорошем состоянии не устают и не имеют выходных», — пишет Джеймс Маллинсон в Productive! Журнал. И, «хотя мы, люди, не можем поддерживать 100% уровень энергии все время, есть меры, которые мы можем предпринять, чтобы оставаться как можно более бдительными и энергичными и не пытаться работать в высоком темпе, когда наши уровни энергии низки (вы бы не Не могли бы вы попробовать водить машину с почти пустым топливным баком?)».
Самое очевидное — высыпаться, заниматься спортом и есть здоровые закуски.Я имею в виду, как быстро, по-вашему, вы будете работать, если вы поспали всего четыре часа, съели на обед гамбургер и едва можете подняться по лестнице?
Я не пытаюсь быть покровительственным. Это просто факт. Если вы хотите иметь больше энергии и концентрации, вам нужно больше походить на хорошо обслуживаемую машину.
Я бы также добавил, что вы должны работать над своими самыми важными задачами в свое лучшее биологическое время. Поскольку это варьируется от человека к человеку, вы можете узнать это, проснувшись без будильника и записывая уровень своей энергии по часам.После того, как вы будете делать это в течение трех недель, вы должны узнать, когда ваша энергия вспыхивает, а когда падает.
Поскольку это варьируется от человека к человеку, вы можете узнать это, проснувшись без будильника и записывая уровень своей энергии по часам.После того, как вы будете делать это в течение трех недель, вы должны узнать, когда ваша энергия вспыхивает, а когда падает.
Зная это, вы сможете планировать свои дни по уровню энергии, чтобы успевать больше за меньшее время.
Скорость — Методы обучения | IOPSpark
Силы и движение
Занятия в классе на 11-14
Что такое деятельность для
Обсуждение самого быстрого и самого короткого времени.
Цель этого упражнения состоит в том, чтобы учащиеся узнали, что скорости можно ранжировать путем сравнения времени при условии, что пройденное расстояние одинаково. В этом случае учащиеся должны понимать тот факт, что кратчайшее время означает наибольшую среднюю скорость.
Что приготовить
- простая беговая дорожка – карниз или пространство между двухметровыми линейками
- шарики (или шарики для настольного тенниса или полистирола) и соломинки
- правила счетчика и секундомеры
- выберите материалы, чтобы ученики не засекали нереально короткие события
Что происходит во время этого действия
Ученики пускают шарики по гоночной трассе как можно быстрее. Учащиеся соревнуются в группах по четыре человека. Один ученик должен выдуть шарик, а остальные зафиксировать время, затраченное на прохождение 200-сантиметрового маршрута. Победитель из каждой группы выходит в финальные этапы конкурса.
Учащиеся соревнуются в группах по четыре человека. Один ученик должен выдуть шарик, а остальные зафиксировать время, затраченное на прохождение 200-сантиметрового маршрута. Победитель из каждой группы выходит в финальные этапы конкурса.
Указание по технике безопасности: Имейте в виду, что у учеников есть астма или проблемы с дыханием.
Проведение и использование измерений
В этом упражнении не предполагается, что участники соревнуются друг с другом в одно и то же время. Ученики видят необходимость договориться о надежных измерениях, чтобы найти победителя.Побеждает шарик с наибольшей средней скоростью. Конечно, вам не нужно знать скорость. Побеждает самое короткое время. В нашем контексте важно расширить задачу до вычисления средней скорости мрамора. Таким образом, каждая группа должна вести учет своих результатов. В зависимости от возраста и способностей учеников вы можете предоставить структурированную таблицу результатов или предложить ученикам составить свою собственную.
Некоторым учащимся будет сложно использовать уравнение скорости. Им может не хватать уверенности в математике.Возможно, вы захотите попробовать подход, основанный на простых пропорциях.
Например:
Учитель: Шарик прошел 200 сантиметров за 5 секунд – сколько сантиметров он прошел за 10 секунд? Сколько сантиметров в 1 секунде?
Как только учащиеся познакомятся с идеей, что скорость равна расстоянию, пройденному за 1 секунду
, решение задач на пропорции часто может стать более простым.
Учитель: Если я проеду 60 метров за 10 секунд, какое расстояние я проеду за 1 секунду?
Майк: 60 метров разделить на 10 секунд, поэтому вы проходите 6 метров за 1 секунду.
Учитель: Какова моя скорость?
Jaz: 6 метров в секунду, что составляет 6 метров в секунду.
В задачах этого типа учащиеся не пользуются непосредственно уравнением скорости, а вычисляют скорость по пропорции, зная ее единицы.
Часть решения также состоит в том, чтобы выполнить множество примеров с использованием уравнения – сначала на доске, когда весь класс предлагает следующий шаг, затем в небольших группах, работающих над задачами, и, наконец, на индивидуальном уровне. Некоторым учащимся может быть трудно вспомнить уравнение для расчета скорости. Написав уравнение крупным шрифтом и повесив его на стену, вы устраните это препятствие. На данном этапе нет необходимости заниматься перестановкой уравнения для расчета расстояний. Это придет позже.
Некоторым учащимся может быть трудно вспомнить уравнение для расчета скорости. Написав уравнение крупным шрифтом и повесив его на стену, вы устраните это препятствие. На данном этапе нет необходимости заниматься перестановкой уравнения для расчета расстояний. Это придет позже.
Скорость обработки — обзор
Индекс скорости обработки (PSI)
PSI измеряет скорость умственной обработки с использованием визуальных стимулов и графомоторных навыков и имеет важное значение для эффективного использования других когнитивных способностей.Слабость в простом визуальном сканировании и отслеживании может оставить пациенту меньше времени и умственной энергии для сложной задачи понимания нового материала.
PSI состоит из подтестов кодирования (CD), поиска символов (SS) и отмены (CA). В этих задачах используется, по-видимому, простой формат визуального сканирования и отслеживания. Прямой тест на скорость и точность, подтест CD оценивает способность пациента быстро и правильно сканировать и упорядочивать простую визуальную информацию. На выполнение этого субтеста также могут влиять кратковременная зрительная память, внимание или зрительно-моторная координация.Таким образом, несмотря на то, что низкий балл действительно поднимает вопрос о скорости обработки, на него также могут влиять графомоторные проблемы, поэтому практикующие врачи должны быть готовы к альтернативным причинам низких баллов. Пациенты могут выполнить меньше заданий в этом задании, если у них возникают проблемы с мелкой моторикой из-за инсульта, хронического алкоголизма, побочных эффектов лекарств и т. д., но это не обязательно означает проблемы со скоростью обработки. Обсессивно-компульсивный пациент также может получить более низкие баллы по CD, опять же не из-за дефицита скорости обработки, а скорее из-за личностных особенностей.
Прямой тест на скорость и точность, подтест CD оценивает способность пациента быстро и правильно сканировать и упорядочивать простую визуальную информацию. На выполнение этого субтеста также могут влиять кратковременная зрительная память, внимание или зрительно-моторная координация.Таким образом, несмотря на то, что низкий балл действительно поднимает вопрос о скорости обработки, на него также могут влиять графомоторные проблемы, поэтому практикующие врачи должны быть готовы к альтернативным причинам низких баллов. Пациенты могут выполнить меньше заданий в этом задании, если у них возникают проблемы с мелкой моторикой из-за инсульта, хронического алкоголизма, побочных эффектов лекарств и т. д., но это не обязательно означает проблемы со скоростью обработки. Обсессивно-компульсивный пациент также может получить более низкие баллы по CD, опять же не из-за дефицита скорости обработки, а скорее из-за личностных особенностей.
Подтест SS требует, чтобы пациент проверил несколько наборов символов и указал, появились ли специальные целевые символы в каждом наборе. Это также прямой тест на скорость и точность, оценивающий скорость сканирования и последовательное отслеживание простой визуальной информации. На выполнение этого подтеста могут влиять зрительная дискриминация и зрительно-моторная координация. Здесь мы снова призываем психологов использовать свои навыки наблюдения, а также обеспечиваем, чтобы результаты WAIS-IV подтверждались или подтверждались другими «клинически значимыми» данными.Например, маниакальный пациент, который торопится выполнить это задание, скорее всего, совершит достаточно ошибок, что снизит оценку SS. Опять же, это не обязательно связано с основным дефицитом скорости обработки, а скорее может быть поведенческим коррелятом (то есть импульсивностью) психического расстройства.
Это также прямой тест на скорость и точность, оценивающий скорость сканирования и последовательное отслеживание простой визуальной информации. На выполнение этого подтеста могут влиять зрительная дискриминация и зрительно-моторная координация. Здесь мы снова призываем психологов использовать свои навыки наблюдения, а также обеспечиваем, чтобы результаты WAIS-IV подтверждались или подтверждались другими «клинически значимыми» данными.Например, маниакальный пациент, который торопится выполнить это задание, скорее всего, совершит достаточно ошибок, что снизит оценку SS. Опять же, это не обязательно связано с основным дефицитом скорости обработки, а скорее может быть поведенческим коррелятом (то есть импульсивностью) психического расстройства.
Отмена — это дополнительный субтест скорости обработки информации только для лиц в возрасте от 16 до 69 лет. Это задание впервые появилось в WISC-IV, и для включения в WAIS-IV был разработан вариант этого задания для взрослых. Работая в течение определенного периода времени, испытуемый сканирует структурированное расположение фигур и отмечает целевые фигуры. Это похоже на ранее разработанные задачи отмены, предназначенные для измерения скорости обработки информации, зрительного избирательного внимания, бдительности, скорости восприятия и зрительно-моторных способностей (Гельдмахер, Фрич и Ридель, 2000; Бейт, Матиас и Кроуфорд, 2001; Войчулик, Хусейн). , Clarke & Driver, 2001; Sattler, 2008a, 2008b). Задания на отмену широко использовались в нейропсихологических исследованиях в качестве меры зрительного пренебрежения, подавления реакции и персеверации моторики (Adair, Na, Schwartz, & Heilman, 1998; Na, Adair, Kang, Chung, Lee, & Heilman, 1999; Geldmacher ). и другие., 2000; Лезак, Хоуисон и Лоринг, 2004 г.). По сравнению с версией CA WISC-IV, компонент принятия решений субтеста CA WAIS-IV был разработан, чтобы предъявлять более сложные когнитивные требования к пациентам: компонент принятия решений требует, чтобы пациенты одновременно различали цвет и форму стимулы и подавляют реакцию, когда присутствует только один из этих двух признаков.
Это похоже на ранее разработанные задачи отмены, предназначенные для измерения скорости обработки информации, зрительного избирательного внимания, бдительности, скорости восприятия и зрительно-моторных способностей (Гельдмахер, Фрич и Ридель, 2000; Бейт, Матиас и Кроуфорд, 2001; Войчулик, Хусейн). , Clarke & Driver, 2001; Sattler, 2008a, 2008b). Задания на отмену широко использовались в нейропсихологических исследованиях в качестве меры зрительного пренебрежения, подавления реакции и персеверации моторики (Adair, Na, Schwartz, & Heilman, 1998; Na, Adair, Kang, Chung, Lee, & Heilman, 1999; Geldmacher ). и другие., 2000; Лезак, Хоуисон и Лоринг, 2004 г.). По сравнению с версией CA WISC-IV, компонент принятия решений субтеста CA WAIS-IV был разработан, чтобы предъявлять более сложные когнитивные требования к пациентам: компонент принятия решений требует, чтобы пациенты одновременно различали цвет и форму стимулы и подавляют реакцию, когда присутствует только один из этих двух признаков.
С точки зрения развития нервной системы существуют большие и очевидные возрастные тенденции в скорости обработки информации, которые сопровождаются возрастными изменениями количества временных связей с центральной нервной системой и усилением миелинизации.Несколько исследователей обнаружили, что показатели скорости обработки информации младенцами предсказывают более поздние показатели IQ (см., например, Dougherty and Haith, 1997), а показатели PSI WISC-IV потенциально чувствительны к неврологическим расстройствам, таким как эпилепсия (Wechsler, 1991).
Таким образом, скорость умственной обработки — это больше, чем просто выполнение задачи в более быстром или более медленном темпе, но сама по себе она является ключевой переменной когнитивных и индивидуальных различий. Имеются убедительные доказательства того, что время простой реакции и время реакции выбора коррелируют около 0.20 или чуть выше с результатами тестов интеллекта, в то время как время проверки (которое некоторые предполагают как меру скорости обработки информации) коррелирует примерно на 0,40 с результатами тестов интеллекта (см. Deary, 2001; Deary & Stough, 1996). Значительная роль умственной скорости была вовлечена в исследования познания и старения. Солтхаус (1996a, 1996b, 2000a, 2000b) утверждал, что снижение общих умственных способностей, наблюдаемое с возрастом, в основном связано с замедлением скорости мыслительной обработки.На самом деле, удаление влияния скорости мышления на результаты тестов интеллекта также устраняет самые большие эффекты, которые были связаны с возрастом.
Deary, 2001; Deary & Stough, 1996). Значительная роль умственной скорости была вовлечена в исследования познания и старения. Солтхаус (1996a, 1996b, 2000a, 2000b) утверждал, что снижение общих умственных способностей, наблюдаемое с возрастом, в основном связано с замедлением скорости мыслительной обработки.На самом деле, удаление влияния скорости мышления на результаты тестов интеллекта также устраняет самые большие эффекты, которые были связаны с возрастом.
В отличие от измерения времени реакции субтесты PSI, включенные в такие тесты, как WAIS-IV, представляют собой относительно простые задачи визуального сканирования для большинства пациентов. Однако было бы ошибкой думать о PSI как о мере простых канцелярских функций, которые не имеют отношения к интеллектуальному функционированию или не связаны с ним. Хотя PSI указывается последним в представлениях факторных структур Векслера по соглашению, он часто занимает третье место в большинстве факторных анализов и объясняет большую дисперсию интеллекта, чем фактор рабочей памяти. В сопоставимых контролируемых клинических групповых исследованиях с WAIS-IV наблюдалось, что PSI имеет самые большие размеры эффекта среди четырех индексов в группах с черепно-мозговой травмой, болезнью Альцгеймера, аутизмом, синдромом Аспергера, СДВГ и депрессией, хотя величина эффекта для группа депрессии была небольшой. В большинстве случаев один или несколько других индексов занимали второе место с точки зрения величины эффекта: PRI имел следующую по величине величину эффекта для группы с ЧМТ, VCI имел следующую по величине величину эффекта для группы с аутизмом, а WMI имел следующую по величине величину эффекта для группы с аутизмом. следующий по величине размер эффекта для группы СДВГ.Хотя эти исследования поучительны в отношении возможного взаимодействия между когнитивными функциями при конкретных расстройствах, мы еще раз не рекомендуем практикующим врачам рассматривать эти профили в качестве диагностических маркеров и призываем к полной клинической оценке, основанной на результатах тестов в сочетании с анамнезом и фоновыми факторами.
В сопоставимых контролируемых клинических групповых исследованиях с WAIS-IV наблюдалось, что PSI имеет самые большие размеры эффекта среди четырех индексов в группах с черепно-мозговой травмой, болезнью Альцгеймера, аутизмом, синдромом Аспергера, СДВГ и депрессией, хотя величина эффекта для группа депрессии была небольшой. В большинстве случаев один или несколько других индексов занимали второе место с точки зрения величины эффекта: PRI имел следующую по величине величину эффекта для группы с ЧМТ, VCI имел следующую по величине величину эффекта для группы с аутизмом, а WMI имел следующую по величине величину эффекта для группы с аутизмом. следующий по величине размер эффекта для группы СДВГ.Хотя эти исследования поучительны в отношении возможного взаимодействия между когнитивными функциями при конкретных расстройствах, мы еще раз не рекомендуем практикующим врачам рассматривать эти профили в качестве диагностических маркеров и призываем к полной клинической оценке, основанной на результатах тестов в сочетании с анамнезом и фоновыми факторами.
Согласно операциональному определению WASI-IV, PSI показывает скорость, с которой пациент обрабатывает простую или рутинную информацию, не совершая ошибок в виде пропусков или совершения ошибок.Многие новые учебные задачи включают в себя обработку информации, которая является как рутинной (например, чтение служебной записки на работе), так и сложной (например, определение влияния служебной записки на служебную функцию). Когда скорость обработки информации находится, по крайней мере, в среднем диапазоне или относительной силе для пациента, это может облегчить как рассуждение, так и получение новой информации. Низкая скорость обработки рутинной информации может сделать задачу понимания и интеграции новой информации более трудоемкой и, следовательно, более сложной.Можно предположить, что работающие взрослые с дефицитом скорости обработки информации усваивают меньше материала за то же время или дольше усваивают тот же объем материала по сравнению с коллегами без дефицита скорости обработки. Эти люди легче умственно устают на работе из-за дополнительных когнитивных усилий, необходимых для выполнения рутинных задач за столом, что может привести к более частым ошибкам в оформлении документов, стрессу на работе, плохой оценке работы и возможным неудачам на работе. С годами эти люди, вероятно, будут тратить меньше времени на умственные задачи, связанные с новым обучением, что со временем приведет к уменьшению запасов кристаллизованных знаний по сравнению с коллегами и, возможно, к остановке или срыву карьерного пути.Как описано, медленный PS нагружает всю когнитивную сеть и оказывает широкомасштабное влияние на другие когнитивные процессы, наблюдаемые за пределами испытательной комнаты, что имеет важные последствия в жизни таких людей. Таким образом, скорость обработки критически важным образом взаимодействует с другими когнитивными функциями более высокого порядка и может влиять на общее когнитивное функционирование, новое обучение и повседневную производительность (Weiss, Saklofske, & Prifitera, 2005).
Эти люди легче умственно устают на работе из-за дополнительных когнитивных усилий, необходимых для выполнения рутинных задач за столом, что может привести к более частым ошибкам в оформлении документов, стрессу на работе, плохой оценке работы и возможным неудачам на работе. С годами эти люди, вероятно, будут тратить меньше времени на умственные задачи, связанные с новым обучением, что со временем приведет к уменьшению запасов кристаллизованных знаний по сравнению с коллегами и, возможно, к остановке или срыву карьерного пути.Как описано, медленный PS нагружает всю когнитивную сеть и оказывает широкомасштабное влияние на другие когнитивные процессы, наблюдаемые за пределами испытательной комнаты, что имеет важные последствия в жизни таких людей. Таким образом, скорость обработки критически важным образом взаимодействует с другими когнитивными функциями более высокого порядка и может влиять на общее когнитивное функционирование, новое обучение и повседневную производительность (Weiss, Saklofske, & Prifitera, 2005).
Рабочие листы скорости, времени и расстояния
You are here: Home → Рабочие листы → Скорость, время и расстояниеСоздавайте настраиваемые рабочие листы с постоянной (или средней) скоростью, временем и расстоянием для курсов pre-алгебра и алгебра 1 (6-9 классы).Доступны форматы PDF и html. Вы можете выбрать типы текстовых задач на листе, количество задач, метрические или обычные единицы, способ выражения времени (часы/минуты, дробные часы или десятичные часы) и объем рабочего пространства для каждой задачи.
Есть СЕМЬ различных типов текстовых задач на выбор, от простых до сложных, так что вы можете создавать самые разнообразные рабочие листы. Семь типов проблем подробно объясняются в фактическом генераторе ниже.
Все рабочие листы содержат ключ ответа на 2-й странице файла.
Воспользуйтесь приведенными ниже быстрыми ссылками для создания некоторых распространенных типов рабочих листов.
Упрощенный рабочий лист скорости, времени и расстояния 1: Как далеко можно проехать или сколько времени займет поездка — за пол часа или полчаса
Упрощенный рабочий лист скорости, времени и расстояния 2: Как далеко он может проехать, сколько времени занимает поездка или какова средняя скорость — за полные или полчаса
Рабочий лист скорости, времени и расстояния 3: Как далеко он может проехать, сколько времени занимает поездка или какова средняя скорость — с использованием четверти часа
Рабочий лист скорости, времени и расстояния 4: Как далеко он может пройти, сколько времени занимает поездка или какова средняя скорость — время до 5-минутных интервалов
Таблица 5 скорости, времени и расстояния: задачи на перевод минут в часы.
Найдите среднюю скорость: время дается с точностью до четверти часа.
Найдите среднюю скорость: время дано с точностью до двенадцатой доли часа.
Найдите среднюю скорость: задачи на преобразование единицы времени
Скорость, время и расстояние: более сложные задачи 1
Скорость, время и расстояние: более сложные задачи 2
Алгебра реального мира Эдварда Заккаро
Алгебра часто преподается абстрактно, практически без акцента на том, что такое алгебра или как ее можно использовать для решения реальных задач.Подобно тому, как английский можно перевести на другие языки, текстовые задачи можно «перевести» на математический язык алгебры и легко решить. Real World Algebra объясняет этот процесс в простом для понимания формате с помощью мультфильмов и рисунков. Это облегчает самообучение как ученику, так и любому учителю, который никогда не понимал алгебру в полной мере. Включает главы по алгебре и деньгам, алгебре и геометрии, алгебре и физике, алгебре и рычагам и многим другим. Предназначено для детей 4-9 классов с более высокими математическими способностями и интересом, но может быть использовано также учащимися старшего возраста и взрослыми.Содержит 22 главы с инструкциями и задачами на трех уровнях сложности.
Предназначено для детей 4-9 классов с более высокими математическими способностями и интересом, но может быть использовано также учащимися старшего возраста и взрослыми.Содержит 22 главы с инструкциями и задачами на трех уровнях сложности.
=> Узнать больше
Скорочтение — эффективное обучение с MindTools.com
Гас достигает информационной перегрузки. Он должен представить отчет о трех крупных исследованиях рынка своему менеджеру завтра в полдень. У него куча информации, которую нужно прочитать, а часы тикают.
Невозможно просить о продлении срока. Но ему нужно убедиться, что он «покрыл все основы», иначе он будет выглядеть небрежным.Паника начинается.
Гас хочет быстро просмотреть материал и при этом сохранить достаточно информации для составления хорошего резюме. Ему нужно уметь быстро читать.
В этой статье мы рассмотрим навык скорочтения и рассмотрим техники, которые можно использовать, чтобы читать лучше и быстрее. Мы также рассмотрим плюсы и минусы скорочтения — когда его целесообразно использовать и какое влияние оно может оказать на понимание.
Нажмите здесь чтобы просмотреть расшифровку этого видео.
Что такое скорочтение?
Скорочтение — это процесс быстрого распознавания и усвоения фраз или предложений на странице одновременно, а не определения отдельных слов.
Количество информации, которую мы обрабатываем, растет с каждым днем, будь то электронные письма, отчеты и веб-сайты на работе или социальные сети, книги и журналы дома. Мы, вероятно, чувствуем давление, чтобы получить эту информацию быстрее, чтобы мы могли «оставаться в курсе». и принимать обоснованные решения.
Большинство людей читают со средней скоростью 250 слов в минуту (слов в минуту), хотя некоторые, естественно, быстрее других. Но способность к быстрому чтению может означать, что вы удваиваете эту скорость.
Теперь мы рассмотрим некоторые навыки, которые вы можете использовать для ускорения чтения.
Как быстро читать
У всех методов скорочтения есть одна общая черта: вы избегаете произносить и «слышать» каждое слово в своей голове, когда читаете его, процесс, известный как «суб-вокализация».Вместо этого вы «просматриваете» строки или группы слов, так как понимаете слова быстрее, чем произносите их.
Один из способов удержать себя от субвокализации — сосредоточиться на блоках слов, а не на отдельных словах. Сделайте это, расслабив лицо и «смягчив» или расширив взгляд на странице, чтобы вы перестали видеть слова как отдельные отдельные единицы. По мере того, как вы будете это практиковать, ваши глаза будут быстрее перескакивать по странице.
Затем, когда вы подходите к концу строки, позвольте своему периферическому зрению обратить внимание на последний набор слов.Это поможет устранить паузы в чтении (часто на полных точках), а это означает, что вы быстрее просматриваете и опускаете следующую строку.
Теперь давайте рассмотрим три способа повысить скорость чтения:
1.
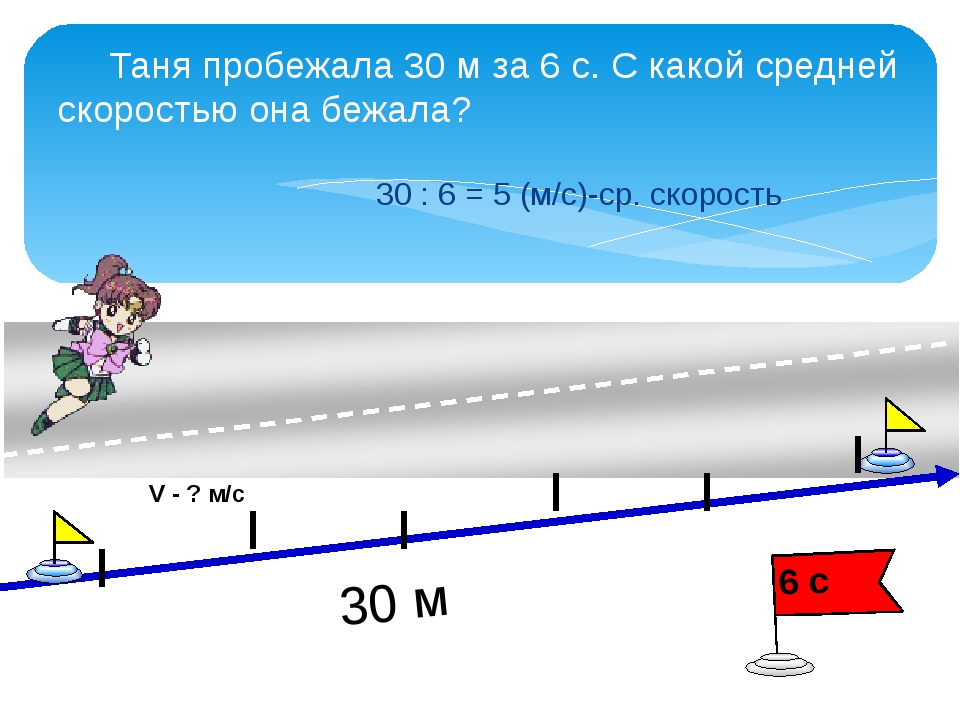 Метод указателя
Метод указателяУчительница школы из Юты Эвелин Нильсен Вуд была одной из пионеров скорочтения. В 1950-х годах она утверждала, что может читать со скоростью до 2700 слов в минуту, если во время чтения проводит пальцем по строке.
Этот метод стал известен как метод указателя, а также его иногда называют «ручным шагомированием» или «мета-наведением».» Держите карточку под каждой строкой и рисуйте ее вниз по странице, когда читаете, работает так же хорошо.
2. Метод отслеживания и кардиостимуляции
Это вариант метода указки, при котором вы держите ручку с надетым колпачком и подчеркиваете или отслеживаете каждую строку по мере ее чтения, не сводя глаз с кончика ручки. Это поможет увеличить скорость, с которой вы читаете каждую строчку, и улучшите ваше внимание к словам. Будете ли вы на самом деле подчеркивать слова, это ваш выбор.
Старайтесь тратить на каждую строку не более одной секунды, а затем увеличивайте скорость с каждой последующей страницей. Вы, вероятно, обнаружите, что поначалу запоминаете очень мало информации, но по мере того, как вы тренируете свой мозг и осваиваете технику, ваше понимание должно улучшаться.
Вы, вероятно, обнаружите, что поначалу запоминаете очень мало информации, но по мере того, как вы тренируете свой мозг и осваиваете технику, ваше понимание должно улучшаться.
Примечание:
Преимущество методов Pointer и Tracker-and-Pacer заключается в том, что они уменьшают потребность в пролистывании и перечитывании предложений — препятствие для скорочтения, известное как «регрессия».
3. Метод сканирования (или предварительного просмотра)
«Сканирование» включает в себя быстрое перемещение взгляда вниз по странице — часто вниз по центру — и определение определенных слов и фраз по мере продвижения.Это могут быть ключевые предложения (часто первое предложение каждого абзаца), имена, числа или триггерные слова и идеи. В этом может помочь расширение вашего периферийного зрения.
Вы не будете читать каждое слово, но ваш взгляд будет останавливаться на самом важном, что позволит вам уловить основную идею. Может быть полезно использовать интеллект-карту® систематизировать информацию, которую вы получаете.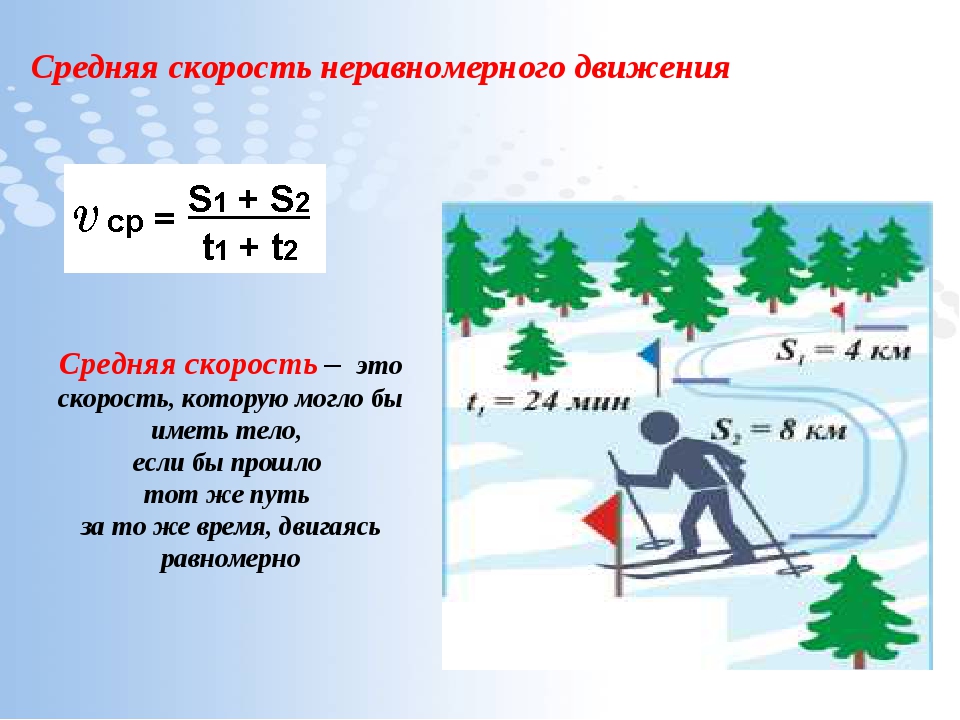
Совет:
Приложения, такие как Spritz и Spreeder, используют такие методы, как «Быстрая последовательная визуальная презентация», чтобы научить вас быстрее обрабатывать информацию.
Когда нужно быстро читать
Все эти методы могут помочь вам читать быстрее, но подходят ли они для того, чего вы пытаетесь достичь?
Эффективное скорочтение — это баланс между темпом и пониманием. Исследования показали, что чем быстрее вы читаете, тем меньше информации вы усваиваете, особенно когда речь идет о запоминании деталей.
Таким образом, скорочтение явно не является решением, если вы читаете сложный юридический или технический документ, даже если вы ограничены во времени.Точно так же было бы разумно замедлить темп, если материал, который вы читаете, новый или незнакомый, или если вам нужно научить этому кого-то еще.
Однако, когда вам нужно понять только основные аргументы или выводы, можно использовать технику скорочтения.
Это может быть особенно актуально, если вы собираетесь вернуться и перечитать что-то медленнее, когда вы менее заняты. На самом деле, одно исследование показало, что беглый просмотр текста может улучшить ваше понимание во второй раз.
На самом деле, одно исследование показало, что беглый просмотр текста может улучшить ваше понимание во второй раз.
Вообще говоря, если вы хотите что-то запомнить, вам нужно читать медленно, со скоростью менее 100 слов в минуту. Нормальная скорость обучения составляет 100–200 слов в минуту, а понимания — 200–400 слов в минуту.
Скорость чтения обычно составляет около 400-700 слов в минуту. Все, что выше 500-600 слов в минуту, означает жертвование пониманием, хотя это варьируется от человека к человеку.
Как улучшить скорость чтения
Знание «как» и «когда» скорочтения — это только первый шаг к успеху.Вот еще несколько советов, которые помогут вам:
- Не отвлекайтесь. Создайте среду, в которой будет как можно меньше отвлекающих факторов, чтобы вы могли сосредоточиться полностью на слова перед вами.
- Полегче. Прочтите несложный роман или простую статью в Интернете, чтобы понять, какая техника лучше всего подходит для вас.
 Оцените, сколько вы запомнили или поняли, и установите таймер, чтобы увидеть, насколько быстрее вы теперь читаете.
Оцените, сколько вы запомнили или поняли, и установите таймер, чтобы увидеть, насколько быстрее вы теперь читаете. - Сопроводительные слова, которые вы уже читали. Это поможет вам перестать возвращаться к более ранним словам и замедлить чтение.
- Знайте, что вы хотите от текста. Это может быть полезно, если вы используете метод беглого просмотра, так как он побуждает вас обращать внимание, когда вы видите релевантные слова, предложения или фразы. Затем вы можете замедлиться в этих точках или обвести их кружком, чтобы выделить их, но в остальном быстро перемещаться по странице.
- Сравните свой прогресс. Так вы сможете узнать, окупается ли ваша практика. В Интернете есть множество бесплатных тестов на скорость чтения, например, на ReadingSoft.com.
- Практика, практика, практика. Чтобы научиться быстрому чтению, вам нужно потренироваться. Чем больше вы тренируетесь, тем естественнее это будет ощущаться.

Существуют различные методы, которые можно использовать для повышения скорости чтения. Все они включают беглый просмотр страницы, а не «подзвучку» каждого слова, как вас, вероятно, учили в школе.
Превосходное скорочтение требует практики и переподготовки, а также умения больше сосредотачиваться на том, что находится перед вами, и избегать отвлекающих факторов.
Но важно соблюдать правильный баланс между скоростью и пониманием: иногда скорочтение нецелесообразно или нецелесообразно.
Скорость обработки — Когнитивные навыки
Что такое скорость обработки?
Скорость обработки данных является одним из основных элементов когнитивного процесса, поэтому она является одним из наиболее важных навыков в обучении, успеваемости, интеллектуальном развитии, рассуждениях и опыте.
Скорость обработки — это когнитивная способность, которую можно определить как время, необходимое человеку для выполнения умственной задачи . Это связано с скоростью, с которой человек может понимать и реагировать на информацию, которую он получает , будь то визуальная (буквы и цифры), слуховая (язык) или движение. Другими словами, скорость обработки — это время между получением стимула и реакцией на него.
Это связано с скоростью, с которой человек может понимать и реагировать на информацию, которую он получает , будь то визуальная (буквы и цифры), слуховая (язык) или движение. Другими словами, скорость обработки — это время между получением стимула и реакцией на него.
Низкая или плохая скорость обработки не связана с интеллектом, а это означает, что одно не обязательно предсказывает другое.Низкая скорость обработки означает, что некоторые определенные задачи будут сложнее, чем другие, например чтение, выполнение математических операций, прослушивание и ведение заметок или поддержание беседы. Это также может мешать исполнительным функциям, так как человеку с медленной скоростью обработки будет труднее планировать, ставить цели, принимать решения, начинать задачи, концентрировать внимание и т. д.
Скорость обработки подразумевает большую способность легко выполнять простые или ранее -выученные задачи. Это относится к способности автоматически обрабатывать информацию, что означает быструю и неосознанную обработку информации. Чем выше скорость обработки, тем эффективнее вы можете думать и учиться .
Чем выше скорость обработки, тем эффективнее вы можете думать и учиться .
Скорость обработки — это время, прошедшее с момента получения вами информации до момента, когда вы ее понимаете и начинаете реагировать.
Примеры скорости когнитивной обработки
Скорость обработки можно использовать в упражнениях на распознавание простых визуальных образов, задачи визуального исследования, выполнение тестов, требующих простого принятия решений, выполнение основных математических расчетов, манипулирование числами или выполнение задачи на рассуждение под давлением.
Некоторые примеры, которые могут быть идентифицированы с низкой скоростью обработки: Вам требуется час, чтобы выполнить задание, на которое у других уходит всего 30 минут? Вам трудно следовать инструкциям или планировать определенное действие, особенно если у вас не так много времени, чтобы закончить его? Вы плохо сдаете экзамены, даже зная материал?
Нарушения и патологии, связанные с низкой скоростью обработки информации
Низкая скорость обработки информации структурно не является проблемой обучения или внимания, а также не связана с интеллектом, хотя она влияет на каждый этап обучения . Когда мы говорим о низкой скорости обработки информации, мы должны помнить, что она может способствовать некоторым расстройствам обучения, таким как СДВГ, дислексия, дискалькулия или нарушение слуховой обработки.
Когда мы говорим о низкой скорости обработки информации, мы должны помнить, что она может способствовать некоторым расстройствам обучения, таким как СДВГ, дислексия, дискалькулия или нарушение слуховой обработки.
Это может повлиять на такие задачи, как планирование целей, решение проблем и настойчивость в достижении личных целей.
Скорость обработки также связана с расстройствами аутистического спектра, а другие патологии, такие как деменция или шизофрения, также могут вызывать низкую скорость обработки.
Как определить дефицит скорости когнитивной обработки?
CogniFit («КогниФит») способен точно измерить общий когнитивный уровень пользователя с помощью нашей специализированной батареи когнитивных тестов (CAB)™, состоящей из серии когнитивных тестов, разработанных для оценки скорости обработки информации .
Чтобы оценить скорость обработки, мы используем тест для измерения скорости обработки , который основан на классическом тесте Коннера (CPT) и тесте прямых и косвенных цифр из шкалы памяти Вешлера (WMS) .
Тест скорости обработки предназначен для автоматической оценки скорости обработки. Предполагается, что чем выше скорость обработки, тем эффективнее они усваивают новую информацию. Этот процесс состоит из получения информации, ее понимания и выработки ответа.Если результаты неудовлетворительны в этой области, это значительно повлияет на способность принимать решения, исполнительные функции и выполнение инструкций .
Помимо скорости обработки, этот тест также измеряет рабочую память, фонологическую кратковременную память, кратковременную память и время отклика.
Можно ли повысить скорость когнитивной обработки?
Определенно. Как и в случае с любой другой когнитивной способностью, вы можете тренировать, изучать и повышать скорость обработки, и CogniFit («КогниФит») может вам помочь. . В основе повышения скорости обработки информации лежит разработка метакогнитивных стратегий.
Ключом к повышению скорости обработки данных является создание более прочных связей в мозгу, что позволяет сигналам быстрее передаваться друг другу. Хотя большинство этих типов связей создаются в детстве, с некоторой практикой и тренировкой вы можете сохранить и даже улучшить скорость обработки вашего мозга.
Хотя большинство этих типов связей создаются в детстве, с некоторой практикой и тренировкой вы можете сохранить и даже улучшить скорость обработки вашего мозга.
Благодаря пластичности мозга мозг способен изменять свою структуру и функции.Пластичность мозга позволяет нам создавать новые мозговые связи и увеличивать количество нейронных цепей, улучшая функциональность.
Если нейробиология и изучение пластичности мозга что-то нам и показали, так это то, что чем больше нейронных цепей мы используем, тем сильнее они станут , что применимо к скорости обработки.
CogniFit («КогниФит») поможет вам провести полную нейрокогнитивную оценку, в ходе которой мы оценим скорость вашей обработки информации и на основе ваших результатов предоставим вам полный набор персонализированных когнитивных упражнений для улучшения скорости вашей когнитивной обработки
Когнитивная нейропсихологическая оценка и Программа стимуляции CogniFit («КогниФит») разработана командой неврологов и когнитивных психологов, изучающих процессы синаптической пластичности и нейрогенеза. Вам нужно всего 15 минут в день, 2-3 раза в неделю, чтобы стимулировать свои когнитивные способности и когнитивные процессы .
Вам нужно всего 15 минут в день, 2-3 раза в неделю, чтобы стимулировать свои когнитивные способности и когнитивные процессы .
Эта программа доступна онлайн. Различные интерактивные упражнения представлены в виде забавных игр для мозга, которые вы можете практиковать на своем компьютере или планшете. После каждого занятия CogniFit («КогниФит») будет отображать подробный график вашего прогресса.
Доказано, что онлайн-упражнения CogniFit («КогниФит») помогают в создании новых синапсов и нейронных цепей, которые позволяют реорганизовать и восстановить функции наиболее нарушенных когнитивных областей.
Лаборатория 2 Средняя скорость — Задание для Основ Физического Мира — Лаборатория 2 Изучение Средней Скорости
Лаборатория 2
Исследование Средней Скорости
Лаборатория 2 ссылка на видео: https://youtu.be/Ldlfs-aQwBA
Предыстория знание.
Скорость движущегося объекта является мерой скорости, с которой преодолевается расстояние x.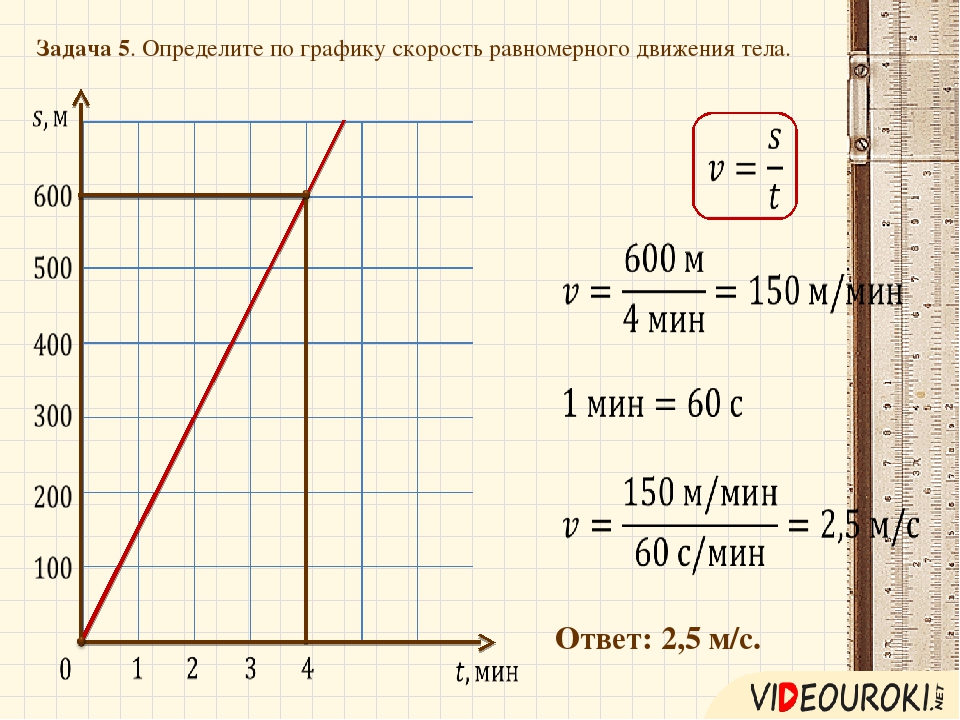 Если
Если
расстояние x м преодолевается движущимся объектом за интервал времени t с, то скорость, с которой
преодолевается расстояние, равна v =
, и это мера средней скорости
движущегося объекта.Средняя скорость измеряется в м/с. Если v — средняя скорость, то расстояние x
, пройденное за время t s, равно x = v t. Если построить график зависимости x от t, то это будет прямая линия
, а наклон графика будет мерой средней скорости v объекта. Скорость
, с которой изменяется положение движущегося объекта, называется его средней скоростью. Обратите внимание, что
положение всегда меняется в определенном направлении. Скорость имеет направление, тогда как скорость
не имеет направления.Не забудьте использовать единицы измерения для всех измеряемых и вычисляемых величин.
Помните, что наклон графика имеет единицу измерения, и это единица измерения по оси Y, деленная на
единицу измерения по оси X.
1. Определить среднюю скорость движущегося объекта.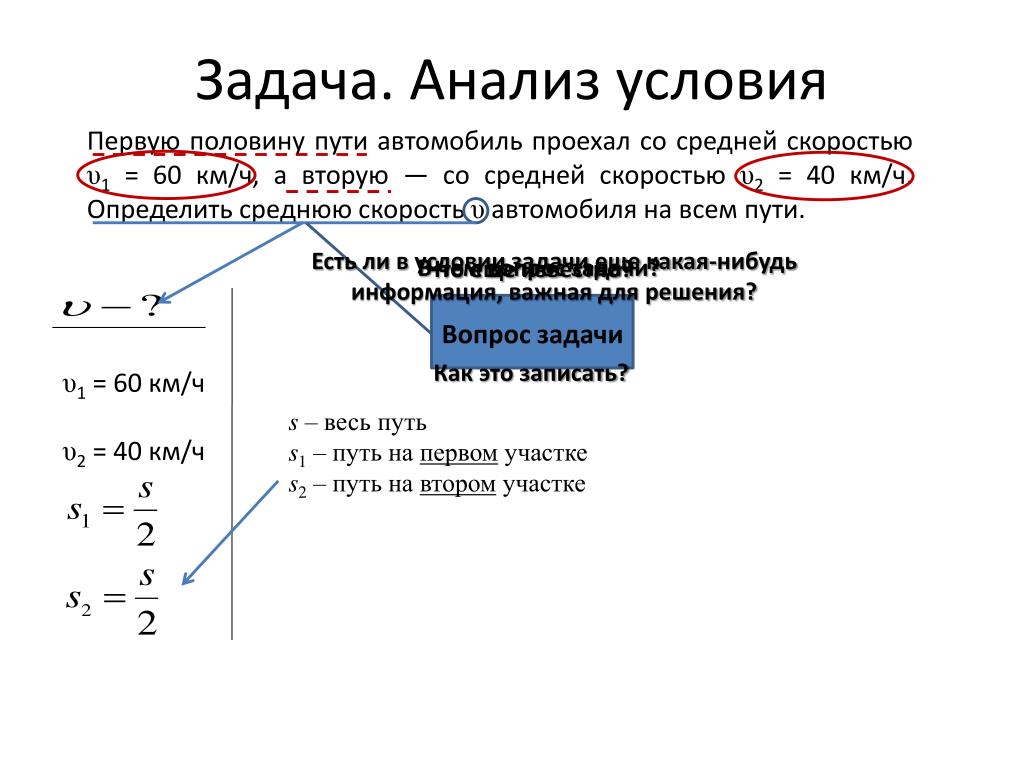 В чем разница между скоростью
В чем разница между скоростью
и скоростью?
Средняя скорость — это скорость, с которой преодолевается расстояние. Средняя скорость — это
скорость, с которой изменяется положение движущегося объекта, включая его направление.
Скорость не включает направление.
2. Тележка движется с постоянной скоростью v за время t и проезжает расстояние x. Запишите
отношение, соединяющее x, v и t.
x=vt
3. Если рассматриваемое отношение 2 равно x = v t, какой формы будет график, нарисованный
с x на вертикальной оси и t на горизонтальной оси?
Прямая линия.
4. Каков будет наклон графика, который вы описали в вопросе 3?
с.
5. Если изменение положения тележки составляет x = 4,8 м за промежуток времени t = 5 с, какова
средняя скорость тележки?
4,8 м = v5s = 0,96 м/с
6. Лабораторная работа:
Анимационный видеоролик показывает автомобиль, движущийся вправо с постоянной скоростью.

 Общее время равно 4 с. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) .
Общее время равно 4 с. Средняя скорость равна 8 м (на запад) / 4 с = 2 м/с (на запад) . Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. Чему равна средняя скорость на всем пути? Ответ в м/с.
Чему равна средняя скорость на всем пути? Ответ в м/с.
 Если вы не говорите о чем-то легком, например, о том, как сложить белье во время разговора по телефону, это миф. Мозг просто не способен к многозадачности. Кроме того, переключение между задачами дорого и вредно. Сохраняйте свое время и энергию, сосредотачиваясь на одном деле за раз.Вы также можете попробовать пакетную обработку задач.
Если вы не говорите о чем-то легком, например, о том, как сложить белье во время разговора по телефону, это миф. Мозг просто не способен к многозадачности. Кроме того, переключение между задачами дорого и вредно. Сохраняйте свое время и энергию, сосредотачиваясь на одном деле за раз.Вы также можете попробовать пакетную обработку задач.
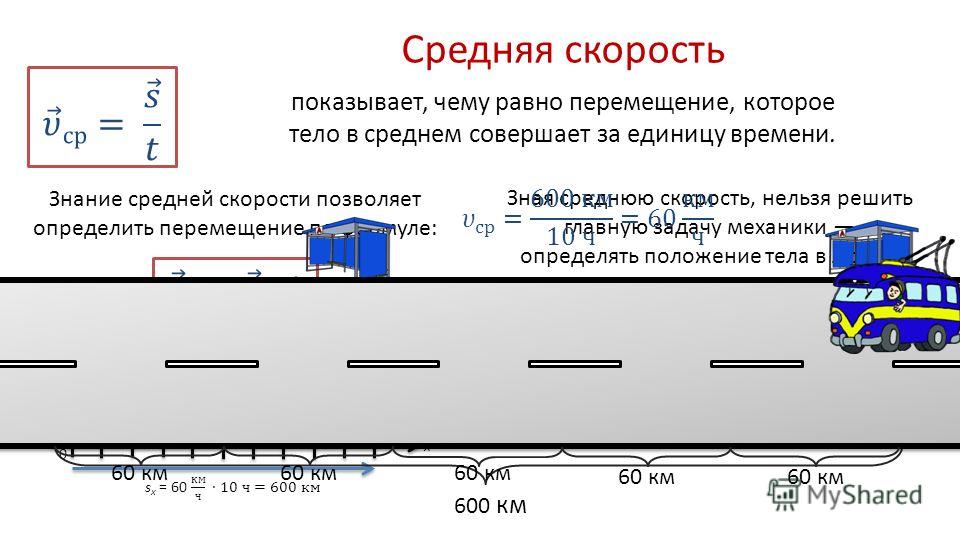 Оцените, сколько вы запомнили или поняли, и установите таймер, чтобы увидеть, насколько быстрее вы теперь читаете.
Оцените, сколько вы запомнили или поняли, и установите таймер, чтобы увидеть, насколько быстрее вы теперь читаете.