Задачи на пропорции 7 класс с решением – Определение процента. Решение трёх видов задач на проценты. Составление и решение пропорций, применяя их свойства. Расчёт процентной концентрации растворов. — Детская игровая комната «Волшебный лес»

Posted on 02.12.202012.01.2020 by alexxlab

Содержание

Дорофеев Г. В. Алгебра. 7 класс

Глава 2. Прямая и обратная
пропорциональность

…………………………………………………………..
(8 уроков)

Примерное поурочное планирование
учебного материала

Пункт учебника	Число уроков
2.1. Зависимости и формулы	2
2.2. Прямая пропорциональность. Обратная пропорциональность	2
2.3. Пропорции. Решение задач с помощью пропорций	2
2.4. Пропорциональное деление	1
Зачет № 2	1

Основные цели: сформулировать представление о прямой и обратной пропорциональностях как специальных видах зависимостей между двумя величинами; ввести понятие пропорции и показать возможность решения задач с помощью пропорций; разъяснить смысл понятия «пропорциональное деление» и продемонстрировать его применение в реальных ситуациях.
Обзор главы. В содержательном отношении данная глава может рассматриваться как вводный фрагмент в функциональную линию курса алгебры. Начинается она с рассмотрения примеров зависимостей между величинами и описания их формулами. Далее рассматривается центральный вопрос темы — прямо пропорциональная и обратно пропорциональная зависимости. Учащиеся должны понимать, что этими словами обозначены два широко распространенных вида зависимостей, с которыми они постоянно имеют дело и в жизни, и при изучении школьных предметов. Даются определения прямой и обратной пропорциональностей, обсуждаются их характеристические свойства, а также общий вид формул, которыми они описываются.

Далее вводится понятие пропорции, и тем самым расширяется «технический арсенал» школьников: они учатся решать уже знакомые задачи с помощью пропорций.
Завершается глава вопросом о пропорциональном делении, который может рассматриваться как обобщение знакомого учащимся из курса 6 класса приема деления величины в заданном отношении.

2.1. Зависимости и формулы

Методический комментарий

Этот пункт является своего рода преамбулой к изучению центрального вопроса главы — прямой и обратной пропорциональностей. Здесь учащиеся рассматривают примеры зависимостей между величинами, на основе которых будут вводиться указанные понятия, и выполняют разнообразную работу с формулами, описывающими эти зависимости. По содержанию этот пункт продолжает практическую деятельность с формулами, начатую в 6 классе.

      В объяснительном тексте вводится новое понятие — переменная. Естественно, никакого определения этому понятию не дается, просто разъясняется, что так мы теперь будем называть буквы, обозначающие изменяющиеся величины. Слово «переменная» должно войти в активный словарный запас школьников. Одновременно в качестве антонима вводится термин «постоянная» (или «константа»).
      Система упражнений к пункту достаточно богата и разнообразна с точки зрения предъявляемых сюжетов и видов формул, с которыми учащимся придется иметь дело. Через нее реализуется одна из основных идей курса — прикладная и практическая ориентация обучения математике, связь с жизнью, с другими учебными предметами (геометрией, физикой).
      Упражнения из раздела А направлены в основном на формирование умений вычислять по формулам, причем проводимые вычисления не абстрактны, а всегда являются средством для ответа на поставленный вопрос. Кроме того, в упражнениях
150—152 продолжается формирование умений выражать переменные из формул (оно основано на знании зависимостей между компонентами арифметических действий), а также составлять формулы, описывающие несложные ситуации (упражнения 144 и 145).
      Упражнения из раздела Б более трудные и в содержательном, и в техническом отношении. Здесь акцент, в частности, сделан на переход от одних единиц измерения к другим, что обычно является для учащихся делом нелегким. Рекомендуем для выработки соответствующего умения предлагать учащимся упражнения такого типа:
      1. Выразите скорость, равную 80 м/мин, в километрах в час.
      2. Выразите скорость, равную 4,5 км/ч, в метрах в минуту.
      Важен последовательный осознанный переход от одних единиц к другим. Можно практиковать такую запись:

80ммин=801000кммин=80⋅601000кмч=50кмч,
4,5кмч=4,5⋅1000мч=4,5⋅100060ммин=75ммин.
Для выполнения трудоемких вычислений следует использовать калькулятор (например, при решении упражнений 157—160).
В классах с невысоким уровнем подготовки рекомендуем прежде всего выполнить упражнения 144—147, 149 (а), 150—152. Из раздела Б при наличии времени можно рассмотреть упражнения 153, 155, 158, 159.

Комментарий к упражнениям

148. Выразим нормальную температуру тела человека, принятую в России, в градусах Фаренгейта: 1,8 · 36,6 + 32 = 97, 88, т. е. имеем 97,88 °F. Так как 97,88 < 98,8, то более высокой в качестве нормальной принята температура там, где она измеряется по шкале Фаренгейта.
Дополнительный вопрос:

какая температура по шкале Цельсия соответствует нормальной температуре по шкале Фаренгейта? Ответ: 37,1 °С.
      149. В условии задано расстояние; оно равно 1 км.
      а) t=180 ч=60⋅6080 c=45 c;
      б) 1 мин 12 с=1,2 мин=1,260 ч=150 ч; υ=1 км150ч=50кмч.
      Замечание. Предварительно нужно проверить знание соотношения между единицами длины и единицами времени.
      151—152. Переменные выражаем на основе зависимости между компонентами действия.
      153. Полезно подсчитать устно по формуле несколько значений S, подставляя в формулу, например, такие значения переменной z: 10 с, 3 с.
      154. В формулу υ=lnt подставим значения переменных и выразим результат в километрах в час:
      60⋅7005сммин=60⋅70⋅605⋅100 000кмч=504100кмч≈5кмч.
      155. 1-й этаж — 5 ступенек,
              2-й этаж — (5 + 16) ступенек,

              3-й этаж — (5 + 16 · 2) ступенек,
              4-й этаж — (5 + 16 · 3) ступенек,
              …………
      Отсюда понятно, что формула имеет вид

N=5+16⋅(n−1)
      и переменные могут принимать только натуральные значения.
      156. Так как 1 км электропоезд проходит за 1,5 мин, то его скорость равна 11,5кммин=1⋅601,5кмч=40кмч. Чтобы сократить время на полминуты, электропоезд должен проходить 1 км за 1 мин. Тогда его скорость будет равна 60 км/ч, т. е. нужно увеличить скорость на 20 км/ч.
      157. На первом участке бегун развил скорость, равную 25050мс=5⋅60⋅601000кмч=18кмч, на втором — равную 18,9 км/ч, на третьем — равную 19,3 км/ч. Он бежал с нарастающей скоростью.
      158. Ответ: на 5,6%.
      159. Выразим 30 см и 35 см в дюймах; получим соответственно 12 дюймов и 14 дюймов. Подставив их в соответствующие формулы, получим следующие размеры: 14 и 16.

      160. В России: P = 180 − 100 = 80 (кг).
      Чтобы воспользоваться второй формулой, нужно 180 см выразить в дюймах. Ответ будет получен в фунтах; его надо выразить в килограммах:
      180 см=1802,54 дюйма,
      W=(112⋅1802,54−220) фунтов,
      W=(112⋅1802,54−220)⋅0,454 кг=77 кг.
      Мы записали числовое выражение, которое на калькуляторе можно вычислять непрерывной цепочкой, без фиксации промежуточных результатов. Возможно, что учащимся будет понятнее, если решать задачу по действиям, доводя каждый раз результат до числа.

2.2. Прямая пропорциональность.
Обратная пропорциональность

Методический комментарий

Изучение прямой и обратной пропорциональностей строится по одному и тому же плану: рассматривается вводный пример, дается определение и показывается использование нового термина в речи; затем рассматривается алгебраический способ описания зависимости — с помощью формулы определенного вида; наконец, формулируется свойство зависимости данного вида.

Важно, чтобы учащиеся осознали, что, хотя прямая и обратная пропорциональности очень часто встречаются в жизни, вовсе не все зависимости относятся к одному из этих видов. В результате изучения пункта они должны распознавать прямую и обратную пропорциональности и приводить примеры, а также называть зависимости, не относящиеся ни к одному из указанных видов. Учащиеся должны понимать смысл оборотов речи типа: «при постоянной скорости путь пропорционален времени движения»; «при постоянном объеме работы время обратно пропорционально производительности».
Выработке соответствующих умений способствуют упражнения к пункту. Заметим, что разбор очередной задачи не следует начинать с вопроса: «Какая здесь зависимость?» Ученики могут вначале рассуждать, опираясь на здравый смысл, а уж потом делать вывод о наличии той или иной зависимости.

Упражнения раздела Б достаточно трудные, особенно упражнения 178 и 179. Поэтому в классах с невысоким уровнем подготовки следует ограничиться заданиями раздела А. Для работы в классе из раздела А рекомендуем упражнения 161, 163—167, 169, 171 (а), 173—175.

Комментарий к упражнениям

      163. Удобно записать на доске краткое условие:
              7 с — 20 л
              ? с — 200 л
      Ученик рассуждает следующим образом: «Так как объем бака увеличился в 10 раз, а скорость наполнения бака водой осталась прежней, то и время должно увеличиться в 10 раз. Значит, на наполнение 200 л потребуется 70 с, т. е. 1 мин 10 с».

      Дополнительный вопрос: какой зависимостью связаны объем бака и время его наполнения при постоянной скорости работы электромотора?
      164. а) Формула C = 5t имеет вид y = kx, где x и y — переменные, k — число. Следовательно, это прямая пропорциональность. Коэффициент пропорциональности равен Сt=5 (р./мин) — это стоимость в рублях одной минуты разговора.
      Можно рассуждать и так. При увеличении времени разговора в несколько раз его стоимость увеличивается во столько же раз. Значит, эта зависимость — прямая пропорциональность.
      б) Данная формула не имеет вид y = kx. Следовательно, эта зависимость не является прямой пропорциональностью. В случае затруднений в этом можно убедиться следующим образом: если n = 2, то N = 80; если n = 4, то N = 140; т. е. при увеличении n в 2 раза N не увеличивается в 2 раза.
      168. 2 кролика — 120 дней
             10 кроликов — ? дней
      Кроликов стало в 5 раз больше, значит, они в 5 раз быстрее съедали весь корм, т. е. дней уйдет в 5 раз меньше; таким образом, корма хватит на 24 дня. Зависимость между количеством кроликов и числом дней, на которые хватит данного запаса корма, — обратная пропорциональность.
      171. Развешиваемая масса чая постоянна. Чем больше масса упаковки, тем меньшее количество упаковок потребуется, и наоборот. Зависимость между массой упаковки и количеством упаковок, необходимым для развеса одной и той же массы чая, обратная пропорциональность.
      а) Для заполнения таблицы рассуждаем так:
      240 г больше 60 г в 4 раза, следовательно, потребуется 80 : 4 = 20 упаковок,
      30 г меньше 60 г в 2 раза, следовательно, потребуется 80 · 2 = 160 упаковок,
      300 г больше 30 в 10 раз, следовательно, потребуется 160 : 10 = 16 упаковок.
      176. Запишем кратко условие:
              4 машинистки — 3 дня — 222 страницы
              2 машинистки — 12 дней — ? страниц
      Четыре машинистки за 3 дня напечатали 222 страницы; две машинистки за 3 дня напечатали в 2 раза меньше, т. е. 2222=111 страниц. Две машинистки за 12 дней напечатают в 4 раза больше, т. е. 444 страницы.
      177. а) Производительность труда увеличилась на 20%, т. е. в 1,2 раза. Тогда время выполнения этой же работы должно уменьшиться в 1,2 раза, т. е. на облицовку подъезда потребуется 181,2=15 (дней).
      178. Приведем разные решения.
      Способ 1. Количество новых кустов составляет 68=34 от количества старых. Значит, урожайность увеличилась в 43=113 раза. Так как 113≈1,33, то урожайность нового куста составляет 133% от урожайности старого, т. е. она увеличилась на 33%.
      Способ 2. С одного куста собирали 18 часть урожая, а стали собирать 16 часть урожая, т. е. на 16−18=124 часть урожая больше. Найдем, какой процент составляет 124 от 18. Имеем 124:18=13≈0,33, а это примерно 33%.
      179. Масса пряников в упаковке была 100% и стала 125%, т. е. увеличилась в 54 раза, а стоимость упаковки осталась прежней, следовательно, цена пряников во столько же раз уменьшилась. Примем прежнюю цену за 1, тогда новая цена стала 1:54=45, т. е. меньше прежней на 15, иначе — на 20%.
      180. а) Расходы столовой сначала увеличились в 1,2 раза и затем, в связи с подорожанием муки, увеличились еще в 1,5 раза, следовательно, всего они увеличились в 1,2 · 1,5 = 1,8 раза.

2.3. Пропорции. Решение задач с помощью пропорций

Методический комментарий

      Прежде всего нужно убедиться, что учащиеся помнят, что называют отношением (с этим понятием они познакомились в 6 классе). Для этого можно предложить такие вопросы:
      1. Вычислите отношение: а) 4 : 12; б) 100 : 75; в) 1,5 : 3,5.
      2. Запишите несколько отношений, равных: а) 3; б) 12.
      3. После контрольной работы учитель проверил 10 тетрадей учеников, и ему осталось проверить еще 20. Что показывает отношение: а) 10 : 30; б) 20 : 30; в) 20 : 10?
      После этого можно ввести понятие пропорции. Заметим, что часто пропорцией называют равенство двух отношений. Эта формулировка в силу ее двусмысленности не очень удачна. В самом деле, отношения 23 и 46 равны, но пропорции здесь нет.
      Для проверки осознанности усвоения нового понятия полезны такие устные упражнения:
      1. Используя какие-либо из отношений 23, 49, 1218, составьте пропорцию.
      2. Составьте какую-нибудь пропорцию, в которой каждое из отношений равно: а) 14; б) 5; в) 0,2.
      Важно, чтобы учащиеся понимали смысл требования: «Выясните, является ли данное равенство пропорцией» — и умели решать эту задачу разными способами (по определению, проверяя, равны ли отношения, или на основе уже известного им перекрестного правила, проверяя, равны ли соответствующие произведения).
      Знание основного свойства пропорции полезно для решения часто встречающейся задачи на нахождение неизвестного члена пропорции. Подчеркнем, что мы не считаем необходимым для всех учащихся владение «свернутым» алгоритмом нахождения неизвестного члена пропорции (например: неизвестный крайний член пропорции равен произведению средних ее членов, деленному на известный крайний). Такая задача естественно решается в два этапа (см. пример 1 в объяснительном тексте), что позволяет не перегружать память учащихся необязательными правилами. В то же время в качестве упражнения и обобщения свернутый алгоритм также может быть рассмотрен (см. упражнение 184).
      В этом же пункте рассматривается решение задач на прямую и обратную пропорциональности новым способом — с помощью пропорций. Полезно, чтобы учащиеся по условию одной и той же задачи составляли разные пропорции, объясняя смысл записанных отношений (см. пример 2).
      В классах с невысоким уровнем подготовки, кроме задач раздела А, рекомендуем выполнить практическую работу, составляющую содержание упражнения 195, а также упражнение 196, которое можно расценивать как содержательную подготовку к изучению темы «Подобие» в курсе геометрии. При работе с сильными учащимися рекомендуем обратить внимание на группу задач, в которых рассматриваются некоторые дополнительные теоретические аспекты данного вопроса (см. упражнения 192, 193, а также задачу-исследование 202).

Комментарий к упражнениям

      187. а) По условию расстояние на картерасстояние в действительности=15 000 000. Пусть x — расстояние в действительности (в см). Тогда 9x=15 000 000, x = 45 000 000 (см). Ответ: расстояние между Москвой и Курском равно 450 км.
      б) Для вычисления расстояния между Москвой и Ригой на той же карте можно также составить пропорцию. Но можно рассуждать иначе, опираясь на результат предыдущего задания: 900 км больше 450 км в 2 раза, поэтому и искомое расстояние на карте также будет больше расстояния, соответствующего 450 км, в 2 раза, т. е. оно равно 9 · 2 = 18 см.
      190. а) Обозначим через x часть стакана, которая заполнится, если в него насыпать 11 столовых ложек сахара, и кратко запишем условие задачи:
      8 ст. л. — 23 стакана
      11 ст. л. — x
      Количество столовых ложек прямо пропорционально заполненной части стакана: во сколько раз увеличится количество ложек, во столько же раз увеличится заполненная часть. Имеем пропорцию 811=23x. Из пропорции находим, что x=1112.
      Итак, если в стакан насыпать 11 столовых ложек сахара, то заполнится 1112 стакана. Ответ: не хватит.
      192. а) 4 · 8 = 2 · 16. Значит, 4 и 8 могут быть одновременно либо средними членами пропорции, либо крайними.
      Пусть 4 и 8 — средние члены, тогда возможно четыре варианта:

24=816, 28=416, 164=82, 168=42.
Пусть 4 и 8 — крайние члены. Получим еще четыре варианта:

42=168, 82=164, 416=28, 816=24.
      Однако эти четыре пропорции могут быть получены из предыдущей четверки перестановкой левой и правой частей. Поэтому всего имеем четыре различные пропорции.
      193. а) Обозначим искомое число через x. Возможны три случая:
      20 · 5 = 7 · x, 20 · 7 = 5 · x, 20 · x = 5 · 7.
      Таким образом, таких чисел три: 1427, 28 и 1,75. Полезно в каждом случае записать какую-нибудь пропорцию.
      197. 50 км/ч — 12 мин
              x км/ч — 10 мин
      Здесь x км/ч — новая скорость электропоезда. Имеем пропорцию 50x=1012, откуда x = 60. Ответ: на 10 км/ч.
      Обсудить вопрос: почему время, данное в минутах, мы не стали выражать в часах, хотя скорость дана в километрах в час?
      198. Указание: количество шерсти прямо пропорционально площади шарфа.
      199. Четверть расстояния (25%) останется проехать после того, как автомобиль уже проехал 75% пути. Краткое условие выглядит так:
      2,4 ч — 40% пути
       x ч — 75% пути
      Во сколько раз больше пройденное расстояние, во столько раз больше времени потребуется автомобилю на его преодоление. Получаем пропорцию 2,4x=4075. Отсюда x=2,4⋅7540=4,5.
      Разница во времени составляет 4,5 − 2,4 = 2,1 (ч).
      201. б) Если расстояние постоянно, то скорости пешеходов обратно пропорциональны времени, которое они тратят на его прохождение, т. е. скорость первого относится к скорости второго как 3 : 2. Обозначим через x расстояние, которое прошел второй пешеход, вышедший из пункта B, до встречи. Так как время движения пешеходов до встречи одно и то же, то расстояния, пройденные ими, пропорциональны их скоростям. Имеем пропорцию 3,6x=32, x = 2,4. Расстояние между пунктами A и B равно 3,6 + 2,4 = 6 (км).
      202. б) Так как равенство ab=cd — пропорция, то ad = bc.
      Меняем местами крайние члены: db=ca. Так как ad = bc, то по перекрестному правилу отношения db и ca равны и это равенство — пропорция и т. д. Таким образом, если в пропорции поменять местами крайние или средние члены или заменить каждое отношение обратным, то опять получится пропорция.
      в) Поменяем местами в пропорции a : 1,2 = b : 1,5 средние члены. Получим пропорцию a : b = 1,2 : 1,5. Отсюда ab=45.

2.4. Пропорциональное деление

Методический комментарий

      Учащиеся имеют хорошую базу для изучения материала этого пункта. Во-первых, начиная с 5 класса они решают задачи на части, а именно к подобной задаче сводится решение задачи на пропорциональное деление. Во-вторых, в курсе 6 класса в связи с введением понятия отношения рассматривался вопрос о делении величины в данном отношении. Теперь, по сути, мы возвращаемся к этому же вопросу, но в более широкой его постановке.
      В качестве вводного примера в пункте рассматривается задача о делении пропорционально вложенным средствам прибыли, полученной фирмами. В связи с этим можно сообщить учащимся, что пропорциональное деление с древних времен использовалось для распределения денег — когда надо было делить завещанный капитал между наследниками, когда вставал вопрос о дележе заработка и т. д. Но и сейчас пропорциональное деление используется в самых разных ситуациях; с некоторыми из них учащиеся познакомятся, решая задачи.
      Обращаем внимание на задачу 206 (б), содержащую буквенные данные. Здесь предлагается, решив задачу на пропорциональное деление в общем виде, записать общее правило решения таких задач, а делается это по аналогии с решением задачи 206 (а). Такая работа полезна с точки зрения формирования умения выполнять обобщения.
      В классах с невысоким уровнем подготовки можно ограничиться разбором примеров в объяснительном тексте и решением задач из раздела А. В них отражены все существенные моменты данного вопроса. Все задачи из раздела Б довольно трудные.

Комментарий к упражнениям

      210. Ответ: а) 30 собак; б) 45 собак; в) 60 собак.
      211. Ответ: а) 3x; б) 2y.
      212. Если массу семян в первом пакете принять за 1 часть, то масса семян во втором пакете составит 2 части, в третьем — 4 части. Следовательно, 350 г семян распределены в отношении 1 : 2 : 4.
      1) 1 + 2 + 4 = 7 (частей) — приходятся на 350 г;
      2) 350 : 7 = 50 (г) — столько семян приходится на 1 часть;
      3) 50 · 2 = 100 (г) — столько семян во втором пакете;
      4) 50 · 4 = 200 (г) — столько семян в третьем пакете.
      Ответ: 50 г, 100 г, 200 г.
      213. Заметим, что достоинства купюр определяют отношение стоимости газонокосилок следующим образом: 1000 : 500 : 100, а поэтому, сократив это отношение, имеем 10 : 5 : 1.
      214. Прежде всего надо найти число акций, которыми владеют фирмы A, B и C. Из условия ясно, что 25% всех акций предприятия составляют 350 000 акций, тогда 75% — в 3 раза больше, т. е. фирмам принадлежит 1 050 000 акций. Распределив 1 050 000 акций в отношении 4 : 12 : 9, получим соответственно 168 000, 504 000, 378 000 акций.
      215—216. В каждой из этих задач даны два отношения, и их нужно преобразовать так, чтобы можно было записать одно отношение. При этом пользуемся следующим свойством отношения: отношение не изменится, если оба его члена умножить или разделить на одно и то же число.
      215. Имеем отношения 3 : 5 и 2 : 3. Так как наименьшее общее кратное чисел 5 и 2 равно 10, то заменяем их такими: 3 : 5 = 6: 10 и 2 : 3 = 10 : 15. Значит, AB : BC : AC = 6 : 10 : 15.
      216. По условию имеем: отношение первой суммы ко второй равно 1:23, или, иначе, 3 : 2; отношение второй суммы к первой равно 113:45, или, иначе, 20 : 12. Заменим отношение 3 : 2 равным ему отношением 30 : 20. Тогда призы на сумму 12 400 р. разделены в отношении 30 : 20 : 12, или, иначе, 15 : 10 : 6.

2.5. Задачи на «сложные» пропорции
(Для тех, кому интересно)

Методический комментарий

Все предлагаемые задачи — на пропорциональную зависимость величин. Их можно решать по действиям, каждый раз получая конкретный числовой результат. Но учащимся предлагается более удобный и эффективный прием, суть которого состоит в том, что «выражение — ответ» конструируется в процессе цепочки логических рассуждений. Задачи несложные, и предлагаемый прием решения интересен школьникам. При наличии времени две-три задачи можно разобрать со всем классом.

Комментарий к упражнениям

      217. 5 лошадей — 30 дней — 1000 кг
             10 лошадей — x дней — 200 кг
             1000 кг овса 5 лошадей съедят за 30 дней,
             200 кг овса 5 лошадей съедят в 5 раз быстрее, т. е. за 6 дней,
             200 кг овса 10 лошадей съедят в 2 раза быстрее, т. е. за 3 дня.
      218. Запишем кратко условие задачи:
      3 строителя — 8 ч — 4 м — производительность 100%
      4 строителя — x ч — 10 м — производительность 120%
      3 строителя выложили 4 м за 8 ч,
      3 строителя будут выкладывать 10 м в 104 раза дольше, т. е. за 8⋅104 ч,
      4 строителя при той же производительности выложат 10 м быстрее в 43 раза, т. е. за 8⋅10⋅34⋅4 ч.
      Теперь учтем, что производительность труда бригады увеличилась в 120100 раз. Поэтому время необходимо уменьшить во столько же раз: 8⋅10⋅3⋅1004⋅4⋅120=12,5 (ч).
      219. а) 15 чел. — 20 дней — 300 бут.
                  20 чел. — 30 дней — x бут.
      Кратко решение можно записать так:
      15 чел. — 20 дней — 300 бут.
      15 чел. — 30 дней — 300⋅3020 бут.
      20 чел. — 30 дней — 300⋅30⋅2020⋅15=600 бут.
      600 − 300 = 300 (бут.).
      Ответ: на 300 бутылок воды.
      220. 3 оператора — 6 ч в день — 4 дня — 700 с
              x операторов — 2 ч в день — 2 дня — 350 с
      Возможна такая запись решения:
      6 ч в день — 4 дня — 700 с — 3 оператора
      6 ч в день — 4 дня — 350 с — 3⋅350700 операторов
      6 ч в день — 2 дня — 350 с — 3⋅350⋅4700⋅2 операторов
      2 ч в день — 2 дня — 350 с — 3⋅350⋅4⋅6700⋅2⋅2 операторов
      Итак, понадобится 9 операторов; 9 − 3 = 6 (человек) — на столько необходимо увеличить команду операторов.

Дополнительные задания к главе 2

Указания и решения

229. Обозначим через x (ч) время заполнения бассейна водой при одновременном включении 6 кранов. Зная, что время обратно пропорционально числу кранов, составим пропорцию:

34:x=6:4.
      Получим x = 0,5. Ответ: 30 мин.
      230. Обозначив расстояние через x (км), запишем кратко условие:
      80 км — 5,6 л
      x км — 40 л
      Так как речь идет о прямо пропорциональных величинах, то имеем пропорцию 80 : x = 5,6 : 40. Решив ее, получим x = 571,42… . Округлим ответ до десятков: 570 км.
      234. Все тетради надо распределить в отношении 6 : 8 : 7. Всего имеется 21 часть, и на каждую часть приходится 588 : 21 = 28 тетрадей. Поэтому 1А класс получит 28 · 6 = 168, 1Б класс получит 28 · 8 = 224, 1В — 28 · 7 = 196 тетрадей.
      235. Всего имеется 3 + 5 + 4 + 2 = 14 равных частей, а поэтому на каждую часть приходится 0,5 см. Длина отрезка AP больше длины отрезка KB на одну такую часть, т. е. на 0,5 см.

Контрольная работа по математике по теме «Пропорции. Решение задач»

Контрольная работа №8 Вариант № 1	Контрольная работа №8 Вариант № 2
Для изготовления 42 кг земляной смеси использовали песок и чернозем в отношении 2 : 5. Определите массу песка и массу чернозема в этой смеси. Расход бензина на 760 км составил 49,4 л. Сколько бензина потребуется на 1140 км? 18 самосвалов одинаковой грузоподъемности могут вывезти грунт за 200 поездок. Сколько самосвалов потребуется, чтобы вывезти этот грунт за 150 поездок? В городе N живет 200 000 жителей. Среди них 15% детей и подростков. Среди взрослых жителей 45% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает? Вычислите: + .	Для изготовления начинки для пирога смешали курагу с черносливом в отношении 4 : 1. Определите массу каждого компонента в 37 кг начинки. Для изготовления 15 платьев требуется 48 м ткани. Сколько ткани потребуется на изготовление 22 таких же платьев? Двигаясь со скоростью 75 км/ч, поезд прибыл в пункт назначения через 4,2 ч. С какой скоростью должен двигаться поезд, чтобы сократить время в пути до 3 ч? В школе 800 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается? Вычислите: + .
Контрольная работа №8 Вариант № 3	Контрольная работа №8 Вариант № 4
Для изготовления смеси взяли чай двух сортов в отношении 3 : 1. Найдите массу чая каждого сорта в 54 кг смеси. Для окрашивания 72 м² поверхности требуется 10,8 л краски. Сколько краски потребуется для окрашивания 126 м² поверхности? Для расфасовки крупы понадобилось 50 пакетов вместимостью 0,9 кг. Сколько потребуется пакетов вместимостью 0,5 кг для расфасовки того же количества муки? Среди 40000 жителей города 60% не интересуются футболом. Среди жителей, интересующихся футболом, 80% смотрели по телевизору финал Лиги чемпионов. Сколько жителей города смотрело этот матч по телевизору? Вычислите: + .	Для изготовления сплава взяли золото и серебро в отношении 2 : 3. Определите, сколько килограммов каждого металла в слитке этого сплава массой 7,5 кг. Для изготовления 12 деталей требуется 0,48 кг металла. Сколько деталей можно изготовить из 0,8 кг металла? Двигаясь со скоростью 64 км/ч, автобус прибыл в пункт назначения через 3,5 ч. Сколько времени ему потребовалось бы на этот путь, если бы он двигался со скоростью 89,6 км/ч? В городе 180 000 жителей, причем 30% из них ― пенсионеры. Среди остальных жителей 35% не работает (дети, подростки, студенты, домохозяйки и т.п.). Сколько жителей работает? Вычислите: + .
Контрольная работа №8 Вариант № 1	Контрольная работа №8 Вариант № 2
Для изготовления 42 кг земляной смеси использовали песок и чернозем в отношении 2 : 5. Определите массу песка и массу чернозема в этой смеси. Расход бензина на 760 км составил 49,4 л. Сколько бензина потребуется на 1140 км? 18 самосвалов одинаковой грузоподъемности могут вывезти грунт за 200 поездок. Сколько самосвалов потребуется, чтобы вывезти этот грунт за 150 поездок? В городе N живет 200 000 жителей. Среди них 15% детей и подростков. Среди взрослых жителей 45% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает? Вычислите: + .	Для изготовления начинки для пирога смешали курагу с черносливом в отношении 4 : 1. Определите массу каждого компонента в 37 кг начинки. Для изготовления 15 платьев требуется 48 м ткани. Сколько ткани потребуется на изготовление 22 таких же платьев? Двигаясь со скоростью 75 км/ч, поезд прибыл в пункт назначения через 4,2 ч. С какой скоростью должен двигаться поезд, чтобы сократить время в пути до 3 ч? В школе 800 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается? Вычислите: + .
Контрольная работа №8 Вариант № 3	Контрольная работа №8 Вариант № 4
Для изготовления смеси взяли чай двух сортов в отношении 3 : 1. Найдите массу чая каждого сорта в 54 кг смеси. Для окрашивания 72 м² поверхности требуется 10,8 л краски. Сколько краски потребуется для окрашивания 126 м² поверхности? Для расфасовки крупы понадобилось 50 пакетов вместимостью 0,9 кг. Сколько потребуется пакетов вместимостью 0,5 кг для расфасовки того же количества муки? Среди 40000 жителей города 60% не интересуются футболом. Среди жителей, интересующихся футболом, 80% смотрели по телевизору финал Лиги чемпионов. Сколько жителей города смотрело этот матч по телевизору? Вычислите: + .	Для изготовления сплава взяли золото и серебро в отношении 2 : 3. Определите, сколько килограммов каждого металла в слитке этого сплава массой 7,5 кг. Для изготовления 12 деталей требуется 0,48 кг металла. Сколько деталей можно изготовить из 0,8 кг металла? Двигаясь со скоростью 64 км/ч, автобус прибыл в пункт назначения через 3,5 ч. Сколько времени ему потребовалось бы на этот путь, если бы он двигался со скоростью 89,6 км/ч? В городе 180 000 жителей, причем 30% из них ― пенсионеры. Среди остальных жителей 35% не работает (дети, подростки, студенты, домохозяйки и т.п.). Сколько жителей работает? Вычислите: + .
Контрольная работа №8 Вариант № 1	Контрольная работа №8 Вариант № 2
Для изготовления 42 кг земляной смеси использовали песок и чернозем в отношении 2 : 5. Определите массу песка и массу чернозема в этой смеси. Расход бензина на 760 км составил 49,4 л. Сколько бензина потребуется на 1140 км? 18 самосвалов одинаковой грузоподъемности могут вывезти грунт за 200 поездок. Сколько самосвалов потребуется, чтобы вывезти этот грунт за 150 поездок? В городе N живет 200 000 жителей. Среди них 15% детей и подростков. Среди взрослых жителей 45% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает? Вычислите: + .	Для изготовления начинки для пирога смешали курагу с черносливом в отношении 4 : 1. Определите массу каждого компонента в 37 кг начинки. Для изготовления 15 платьев требуется 48 м ткани. Сколько ткани потребуется на изготовление 22 таких же платьев? Двигаясь со скоростью 75 км/ч, поезд прибыл в пункт назначения через 4,2 ч. С какой скоростью должен двигаться поезд, чтобы сократить время в пути до 3 ч? В школе 800 учеников, из них 30% — ученики начальной школы. Среди учеников средней и старшей школы 20% изучают немецкий язык. Сколько учеников в школе изучают немецкий язык, если в начальной школе немецкий язык не изучается? Вычислите: + .
Контрольная работа №8 Вариант № 3	Контрольная работа №8 Вариант № 4
Для изготовления смеси взяли чай двух сортов в отношении 3 : 1. Найдите массу чая каждого сорта в 54 кг смеси. Для окрашивания 72 м² поверхности требуется 10,8 л краски. Сколько краски потребуется для окрашивания 126 м² поверхности? Для расфасовки крупы понадобилось 50 пакетов вместимостью 0,9 кг. Сколько потребуется пакетов вместимостью 0,5 кг для расфасовки того же количества муки? Среди 40000 жителей города 60% не интересуются футболом. Среди жителей, интересующихся футболом, 80% смотрели по телевизору финал Лиги чемпионов. Сколько жителей города смотрело этот матч по телевизору? Вычислите: + .	Для изготовления сплава взяли золото и серебро в отношении 2 : 3. Определите, сколько килограммов каждого металла в слитке этого сплава массой 7,5 кг. Для изготовления 12 деталей требуется 0,48 кг металла. Сколько деталей можно изготовить из 0,8 кг металла? Двигаясь со скоростью 64 км/ч, автобус прибыл в пункт назначения через 3,5 ч. Сколько времени ему потребовалось бы на этот путь, если бы он двигался со скоростью 89,6 км/ч? В городе 180 000 жителей, причем 30% из них ― пенсионеры. Среди остальных жителей 35% не работает (дети, подростки, студенты, домохозяйки и т.п.). Сколько жителей работает? Вычислите: + .

План урока по теме «Решение задач с помощью пропорций»

Тема 4. Решение задач с помощью пропорций.

Тема урока 4.3. Решение задач.

Цель урока. Уметь решать задачи на соотношения и с помощью пропорций, используя правила прямо пропорциональной, обратно пропорциональной величины.

Развитие логического мышления, вычислительных навыков.

Воспитание трудолюбия, усердия на уроках математики, взаимодействию друг с другом.

Формы работы: групповая, фронтальная.

Этапы урока.

1. Орг.момент.

2. Устный счет (Распечатано- вывесить на доске).

3. Проверка домашенего задания.

4. Решение задач.

1) Работа в группах.

Задание. Определить в каких задачах используется правила прямо пропорциональной величины, а в какой обратно пропорциональной величины.

Пр.пр.вел

Обр.пр.вел

Пр.пр.вел

Обр.пр.вел

Пр.пр.вел

2) Оценивание работы по принципу «Карусель», ученики отмечают мини-стикерами задачи, в которых правила, как они считают, определены не правильно.

3)Обсуждение задач, ученики высказывают свое мнение по работе своих одноклассников.

4)Решение задач. (Каждая группа работает самостоятельно).

№ 673

Ткань время

0,6м————2,16 мин

х—————-1,44 мин х=0,6*1,44/2,16=0,4 м

№ 674

Длина кол-во

6 м—————240

8 м—————х х=6*240/8=180

№ 675

Кол-во масса

5—————1,75

12————-х х=12*1,75/5=4,2

№ 676

Человек время

3 ————4

2 ————х х=3*4/2=6

№ 679

Расстояние время

900——————0,6

Х——————-3,4 х=900*3,4/0,6=5100 м

№ 681

Кол-во масса

7—————33,6

10—————х х=10*33,6/7=48

5) Проверка выполненных заданий. Взаимопроверка работы групп.

5. Самооценивание работы в группе. (Ученики заполняют таблицу взамооценки)

6. Подведение итогов урока.

1) Какие затруднения возникают у вас при выполнении задач?

2) Помогла ли работа в группах вам лучше понять принцип решения задач?

3) Подумайте вместе и решите, как сработала ваша группа в течение урока и при выполнении основного задания и при оценивании своих товарищей, и поставьте себе общую оценку.

7. Домашнее задание № 677, №678

Самоанализ урока.

( по Куриленко Т.М.)

Класс- 6 Б. Учащиеся данного класса имеют высокую учебную мотивацию, но знания и практические навыки учащихся слабые.

Присутствовали на уроке все ученики класса.

Была ли достигнута цель урока? Я считаю, что цель урока была достигнута. Ученики успешно справились с работой, сделали, в большинстве, правильные выводы, что помогло им справится с решением задач. При взаимооценивании своих знаний и знаний своих товарищей, ребята, по большей части, адекватно оценили свои знания и знания своих товарищей по данной теме.
Как были использованы воспитательные возможности учебного материала в целях всестороннего развития личности учащегося?

Реализации воспитательных целей способствовала групповая работа- ребята старались не повести своих товарищей, работали с отдачей, активно защищали свои работы при общем обсуждении работ.

Все ли учащиеся работали на уроке и как они работали? Планирование урока способствовало занятости всех учеников на уроке, более сильные ученики помогали разобраться с решением задач слабым ученикам, в течение урока ребятам оказывалась учительская поддержка.
Как использовалось время на урока? Время было использовано рационально. Имели ли место потери времени на уроке и что было их причиной? Особое внимание требовалось сохранить темп урока , так как групповая работа занимает больше времени, чем фронтальная. В случае затягивания времени при решении задач, я работала с данной группой вместе пока темп работы не возвращался в свое русло.
Какие знания усвоили учащиеся, какие умения закрепили? Закрепили умения решать задачи с помощью пропорций.
Какие были недостатки в ходе урока и почему? В связи с тем, что класс является слабым, необходим постоянный контроль за группами, чтобы не потерять темп работы групп. Необходимо лучше обдумывать состав групп, с целью повышения эффективности работы учеников на уроке.
Какие изменения в структуру и содержание урока внес бы учитель, если бы его пришлось повторить? Изменила бы состав групп.

Тема 4.

«Решение задач с помощью пропорций»

Класс 6

Учитель математики: Ахметова Л.А.

КГУ «Средняя школа № 1 им. М.В.Инюшина г.Серебрянск»

Разработка урока по теме «Решение задач с помощью пропорций»

Ф.И.О. учителя: _Анфилофьева Галина Борисовна____________________________________________________________
Предмет:_Математика___________________________________________________________________________
Класс: _6___________________________________________________________________________________________

Тема урока: _ «Решение задач с помощью пропорций»___________________________________________________

Тип урока:_ урок обобщения и систематизации предметных навыков ЗУНов _________________________________

Место урока в системе уроков :_Урок 5 в теме «Решение задач с помощью пропорций»

Цель:	систематизация и обобщение знаний по теме » Решение задач с помощью пропорций ”
Задачи:	— развивать логическое мышление, умение обобщать и систематизировать материал; — способствовать развитию коммуникабельности; — формировать способность к сотрудничеству при работе в паре, группе.
УУД: Предметные УУД: Регулятивные УУД: Коммуникативные УУД: Познавательные УУД: Личностные УУД:	Предметные: применять определение понятий: отношения, пропорции, прямая и обратная пропорциональная зависимость на практике находить неизвестную величину в задаче с помощью обобщенного алгоритма решения задачи в соответствии с ее типом. Регулятивные • осуществлять регулятивные действия самонаблюдения, самоконтроля, самооценки в процессе коммуникативной деятельности на уроке. • соотносить свои знания с той учебной информацией, которую нужно усвоить. Коммуникативные распределять обязанности в группе, осуществлять взаимоконтроль слушать, выступать, рецензировать ответы сверстников в соответствии с поставленной коммуникативной задачей; Познавательные анализировать , сравнивать виды пропорциональностей; составлять краткую запись задачи в виде таблицы; выявлять и решать проблемы при составлении задач по схеме; Личностные • формировать готовность к саморазвитию, самообразованию и самооценке; •формировать коммуникативную компетентностъ в общении и сотрудничестве со сверстниками. • формировать устойчивую учебно-познавательную мотивацию и интерес к учению.
Планируемые результаты:	Предметные результаты: знать и понимать смысл понятий :отношения, пропорция, крайний и средний член пропорции, прямая и обратная пропорциональная зависимость, уметь находить неизвестный член пропорции, анализировать условие задачи и выявлять тип задач, применять полученные знания на других уроках. Метапредметные результаты: Познавательные: способность понимать учебную задачу урока, выделять и формулировать познавательные цели, строить логическую цепочку рассуждений, устанавливать причинно-следственные связи. Регулятивные: контролировать и оценивать собственную деятельность и деятельность партнеров, планировать и корректировать свою деятельность; Коммуникативные: уметь достаточно полно и чётко выражать свои мысли, слушать собеседника и вести диалог. Личностные: определять границы собственного знания и незнания по теме; иметь мотивацию к учебной деятельности, принимать и осваивать социальную роль обучающегося, использовать приобретенные знания учебного сотрудничества со взрослыми и сверстниками в разных ситуациях; знать, как важны в учебной деятельности мышление, внимание, любознательность, аккуратность, личная ответственность.
Основные понятия:	Отношения, пропорция, крайние и средние члены пропорции, прямая пропорциональность, обратная пропорциональность.
Межпредметные связи:	Архитектура, технология, кулинария, в быту.
Ресурсы:	-Учебник, книга для учителя, презентация с заданиями по теме урока, смайлики для определения настроения, стикеры для самооценки.
Формы работы:	Фронтальная беседа Индивидуальная работа Парная работа Групповая работа
Этапы урока	Деятельность учителя	Деятельность учеников
1.Организационный этап (1 мин.)	Учитель приветствует учащихся, проверяет их готовность к уроку.	Учащиеся слушают учителя.
2.Мотивация учебной деятельности (2 мин.)	Ребята, сегодняшний урок я хочу начать с такого эпиграфа: Кто воздвигнет тебя к небесам? Только сам. Кто низвергнет тебя с высоты? Только ты. Где куются ключи к твоей горькой судьбе? Лишь в тебе. Чем расплатишься ты за проигранный бой? Лишь собой. (Данный эпиграф позволит не только настроить учеников на самостоятельную работу, но и показать им, что очень многое зависит от них самих.) — В чем смысл этого эпиграфа? Правильно ребята многое зависит от вас самих! — Вот и мы с вами будем тренировать свои умения и навыки, чтобы достичь успехов в дальнейшем обучении. Я желаю вам успехов, у вас всё получится!	Ученики отвечают на вопросы учителя
3. Этап целепологания и постановки задач урока. (2мин)	Сегодня у нас последний урок по теме «Решение задач с помощью пропорции». Скажите мне какие цели вы ставите перед собой на этом уроке? Хорошо, а я ещё хочу добавить цель: показать практическое применение данных задач в различных сферах деятельности. Сегодня на уроке вы будете работать самостоятельно, в парах, в группах. У каждого из вас есть лист оценивания, куда вы будете выставлять оценки за каждый вид работы. Оценивать вы будете себя сами. В конце урока вы выведите свою итоговую оценку, которую я выставлю в журнал.	Ученики называют цели урока Изучают лист самооценки
4. Актуализация и систематизация знаний Этап повторения теоретического материала (3 мин.)	А теперь давайте вспомним основные понятия, которые касаются пропорции(фронтальный опрос): — Что называется отношением? -Как записывается отношение? -Что показывает отношение? -Что такое пропорция? -Записать и прочитать пропорцию. -Как проверить верна ли пропорция? -Основное свойство пропорции. -Как можно из 1 пропорции получить ещё несколько верных? -Как найти неизвестный крайний(средний) член пропорции? -Какие величины называются прямопропорциональными? Обратно пропорциональными? -Алгоритм решения задач с помощью пропорций.	Ученики отвечают на вопросы учителя
5. Обобщение и систематизация знаний(подготовка учащихся к обобщенной деятельности) (5мин) 1.Устная работа 2.Проверка творческого домашнего задания(пословицы на прямую и обратную пр.зависимости)	Устная работа(по слайдам): 1.Создание проблемной ситуации Шестиклассник решил найти отношение массы мышки к массе слона. Мышка весит 50г, слон – 5т. “Составив отношение: 50/5, — сказал Невнимательный ученик. – Мышка в 10 раз тяжелее слона!” В чем он ошибся? Что важное он неучёл? Найдите, во сколько раз масса слона больше массы мышки. 2. Проверка творческого домашнего задания Вам на дом были даны 12 пословиц, ваша задача была разбить их на пословицы отражающие прямую зависимость и обратную. Проверим как вы справились.	1. Решение проблемы: Отношение величин находят, если они выражены в одних единицах измерения! 5т = 5000 кг = 5000000 г 50:5000000 = Ответ: мышка легче слона в 100000 раз. Ученики отвечают: 39 10 24 3 21 13 Ученики заполняют лист самооценки за устную работу. Ученики зачитывают ответы: Пословицы, отражающие прямую зависимость: Чем дальше в лес, тем больше дров. Как аукнется, так и откликнется. Много снега, много хлеба. Как потопаешь, так и полопаешь. Выучишь правило, выполнишь верно задание. Кто много читает, тот много знает. Пословицы, отражающие обратную зависимость: Тише едешь, дальше будешь. Мир строит, а война разрушает. Меньше народа, больше кислорода. Лето собирает, зима съедает. Было густо, стало пусто. Меньше слов – больше дела. Ученики заполняют лист самооценки за домашнюю работу.
6. Обобщение и систематизация знаний(подготовка учащихся к обобщенной деятельности) (2мин) Графический диктант	Сейчас ребята вы будите работать в парах.	Ученики заполняют лист самооценки за работу в паре.
	Слайд	Учащиеся сменили вид деятельности и готовы продолжить работу.
8. Применение имеющихся знаний на практике	Математика применяется практически во всех сферах жизни человека. И в повседневной жизни мы используем математические навыки, в том числе и пропорцию. Сейчас вы будите работать в группах. Каждой группе даётся 2 задачи из определённой сферы деятельности. Вы их должны решить и оформить на плакатах лежащих на парте, а затем выбрать кто выйдет защищать своё решение. 1группа «Архитектура» 1. На строительство двух домов идет 4 тыс. штук кирпича. Сколько тысяч штук кирпича необходимо для строительства 15 таких же домов. 2. Для перевозки песка при строительстве потребовалось 14 автомашин грузоподъемностью 4,5 т. Сколько потребуется автомашин грузоподъемностью 7 т для перевозки этого же песка? 2группа «Кулинария» 1. Для приготовления варенья из 2 кг крыжовника необходимо 3 кг сахара. Сколько кг сахара необходимо для приготовления варенья из 4,4 кг крыжовника. 2. Мама с дочкой тратят на засолку капусты 4,5 часа, за какое время они засолят это же количество капусты, если им будет помогать папа? 3группа «Технология» 1. К Рождеству для детей четверо сотрудниц фабрики игрушек выполнили заказ за 10 дней. За сколько дней выполнят тот же заказ пятеро сотрудниц? 2. Длина деревянной указки 18см, а масса 75 г. Найдите длину указки, сделанной из того же материала, если ее масса – 125 г. 4группа «В быту» 1. Для отопления здания школы заготовлено угля на 180 дней при норме расхода 0,6т угля в день. На сколько дней хватит этого запаса, если его расходовать ежедневно по 0,5т? 2. Со 100 яблонь собрали 500 ящиков яблок. Сколько яблок соберут с 276 яблонь, если количество яблок на каждой яблоне одинаково?	Работают в группах, защита работы: Указать какая пропорциональность в задаче и объяснить почему, сказать ответ и ответить на вопрос с какой сферой деятельности связаны задачи. Ученики заполняют лист самооценки за работу в группе.
9. Применение знаний и умений в решении задач ОГЭ (5 минут)	Самостоятельная работа по 2 вариантам с последующей взаимопроверкой. 1 вариант Средний вес мальчиков того же возраста, что и Гоша, равен 57 кг. Вес Гоши составляет 150 % среднего веса. Сколько килограммов весит Гоша? 2 вариант Свежие фрукты содержат 75% воды, а высушенные – 25%. Сколько требуется свежих фруктов для приготовления 45 кг высушенных фруктов?	Выполняют работу, осуществляют взаимопроверку. 1 вариант 57 кг – 100 % х кг – 150 %, получим х = 57 • 150 / 100 = 85,5 (кг) Ответ: 85,5 кг. 2 вариант х кг – 75 % 45 кг – 25 %, получим х= 135(кг) Ученики заполняют лист самооценки за самостоятельную работу.
	Ребята наш урок подходит к концу. Теперь вспомните те цели, которые вы ставили перед собой в начале урока и скажите вы их достигли? А какую цель я вам подсказала? (практическое применение задач) Скажите мы с вами показали применение данных задач в различных сферах деятельности? Проставьте баллы в лист самооценки. Посчитайте общее количество баллов и выставьте себе оценку за урок. Удовлетворены ли вы результатом своей работы? Нарисуйте у себя в тетради того человечка, который соответствует вашему восприятию урока. Молодцы! Вы хорошо поработали на уроке.	Ученики осуществляют самооценку собственной учебной деятельности, анализируют достигнутый результат с затруднением и поставленной целью, определяют степень их соответствия.
	Творческое. Придумать и решить задачу на спортивную тематику. Девочки на прямую пропорциональность, а мальчики на обратную пропорциональность.	Дети записывают задания в дневнике.
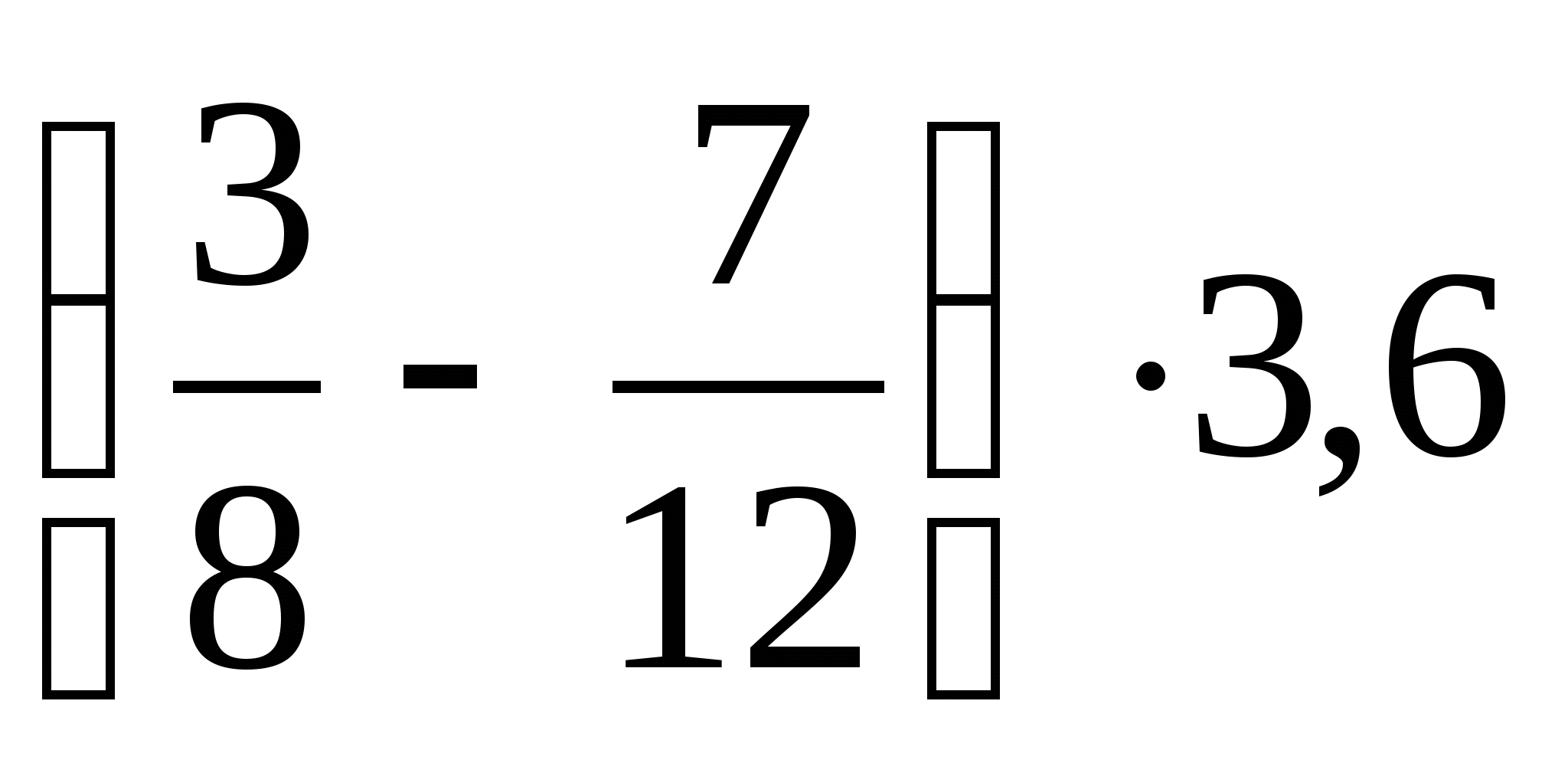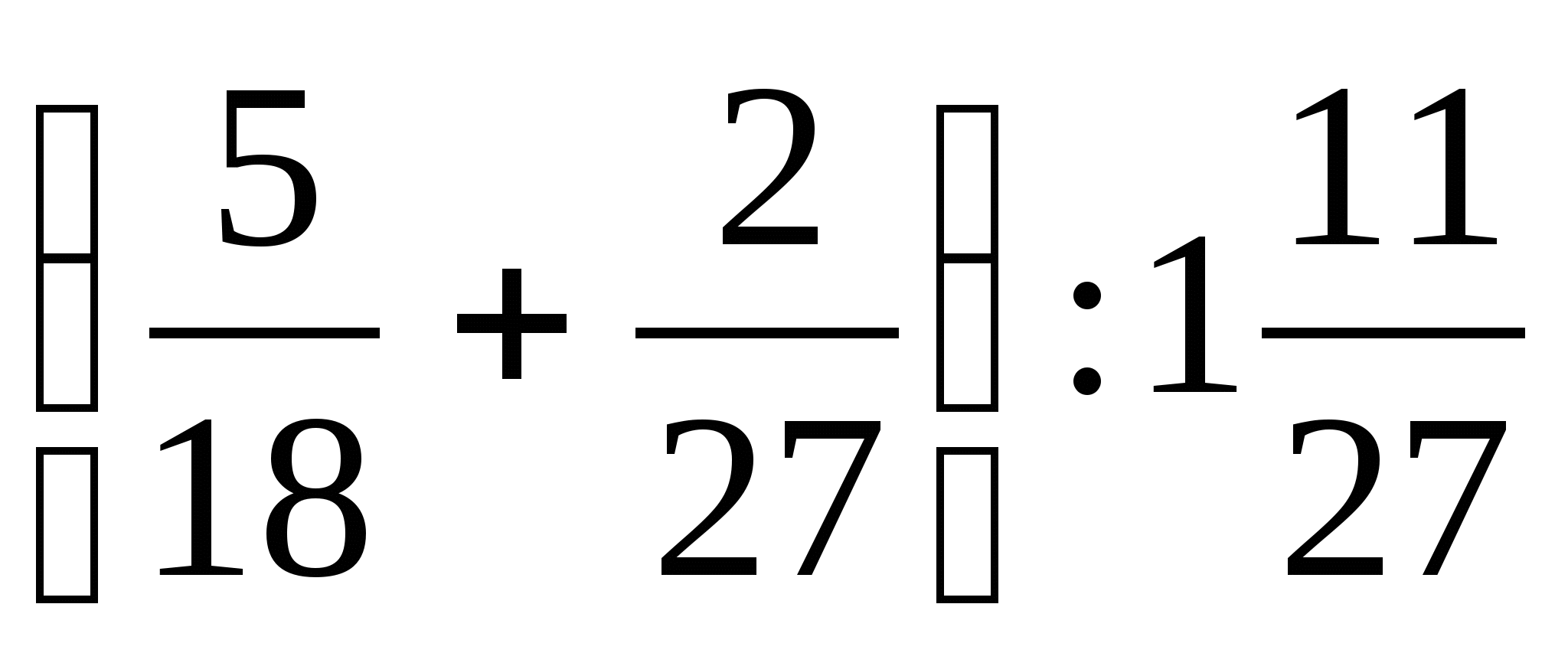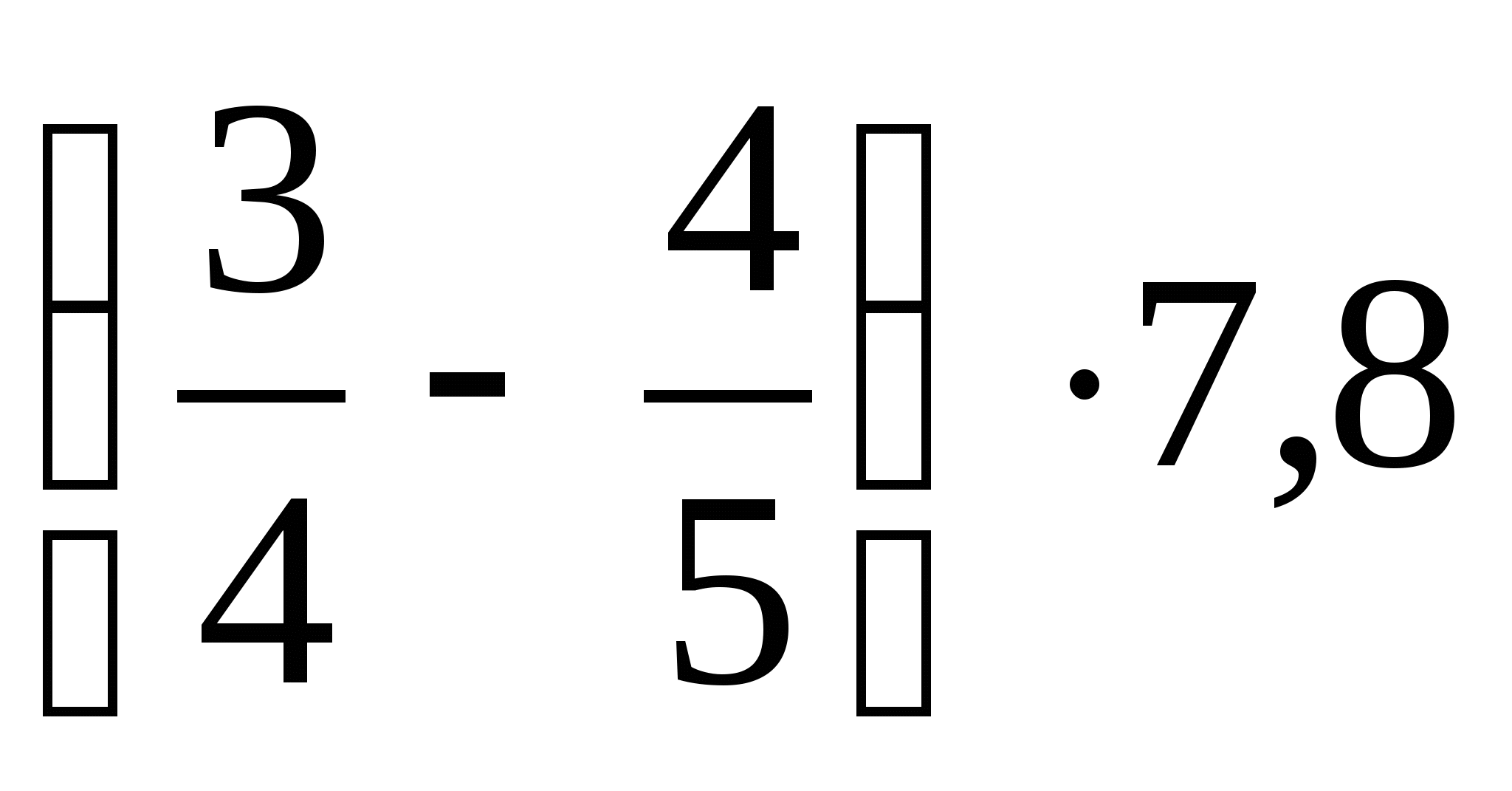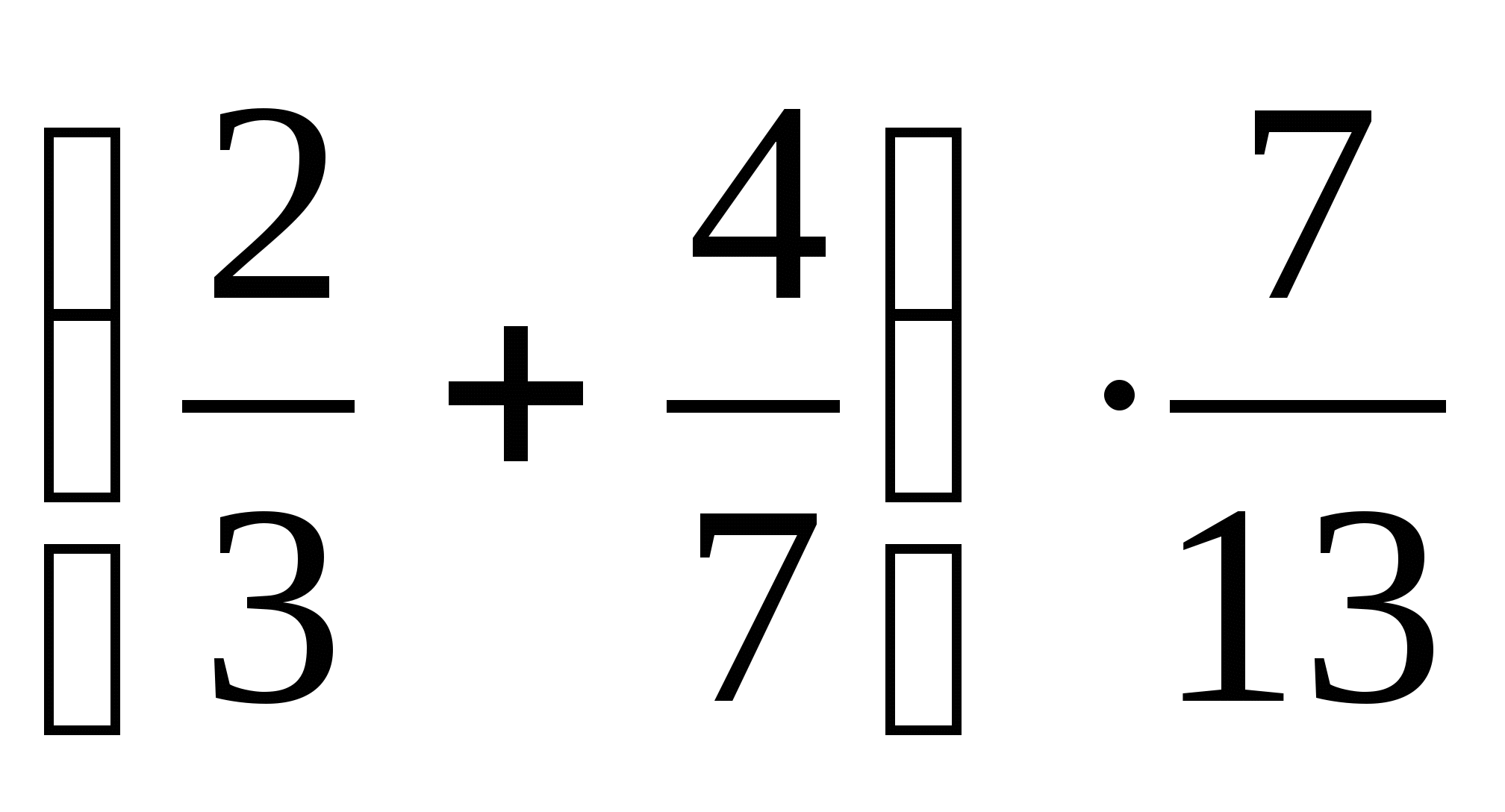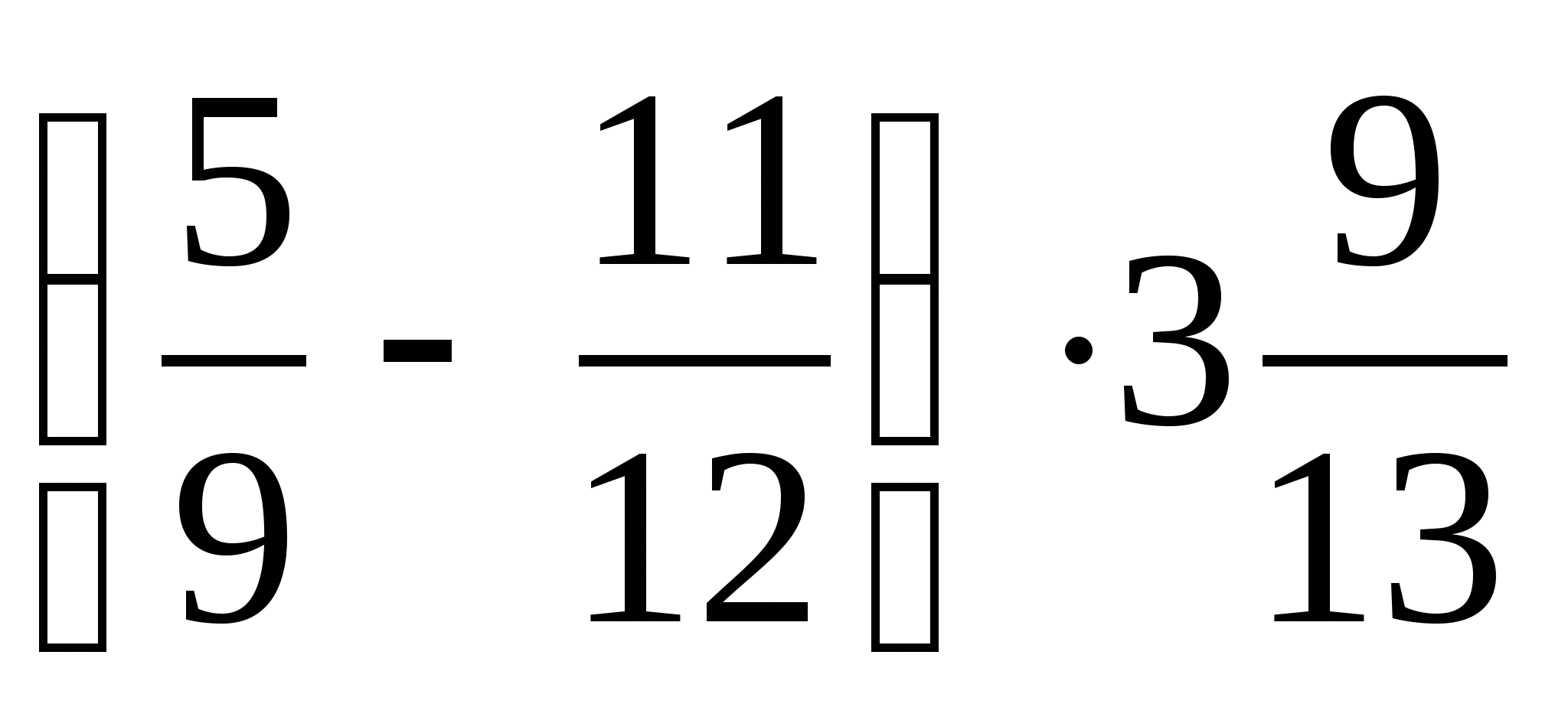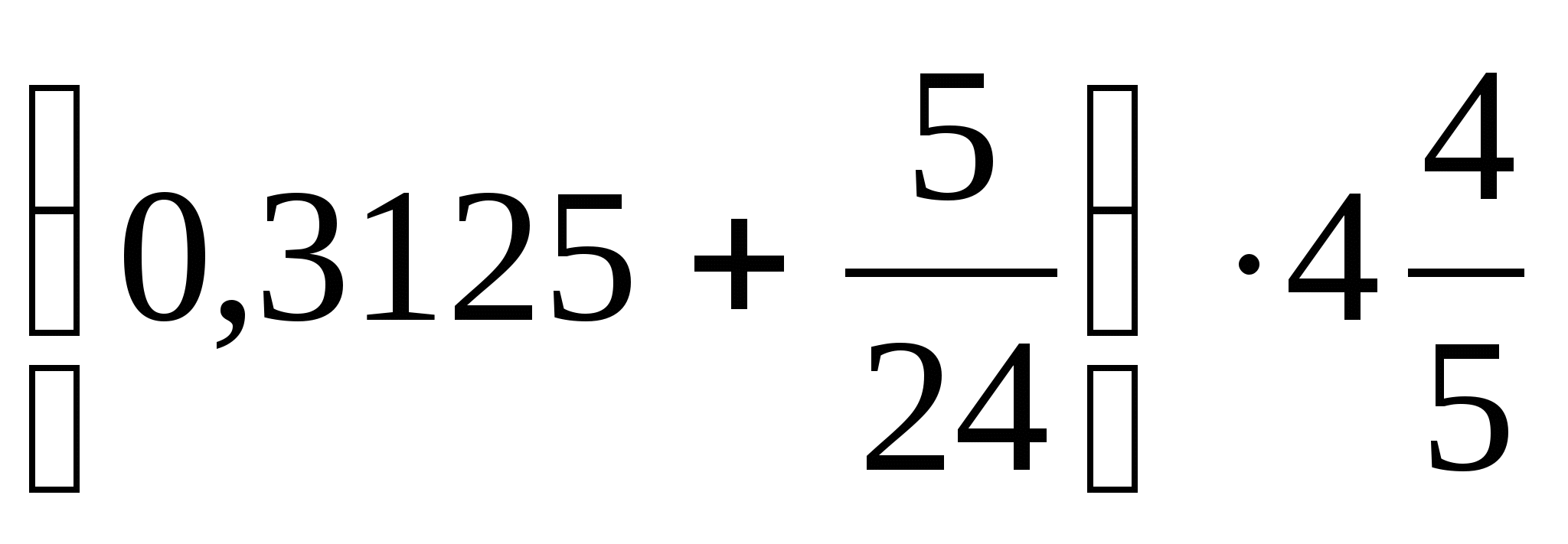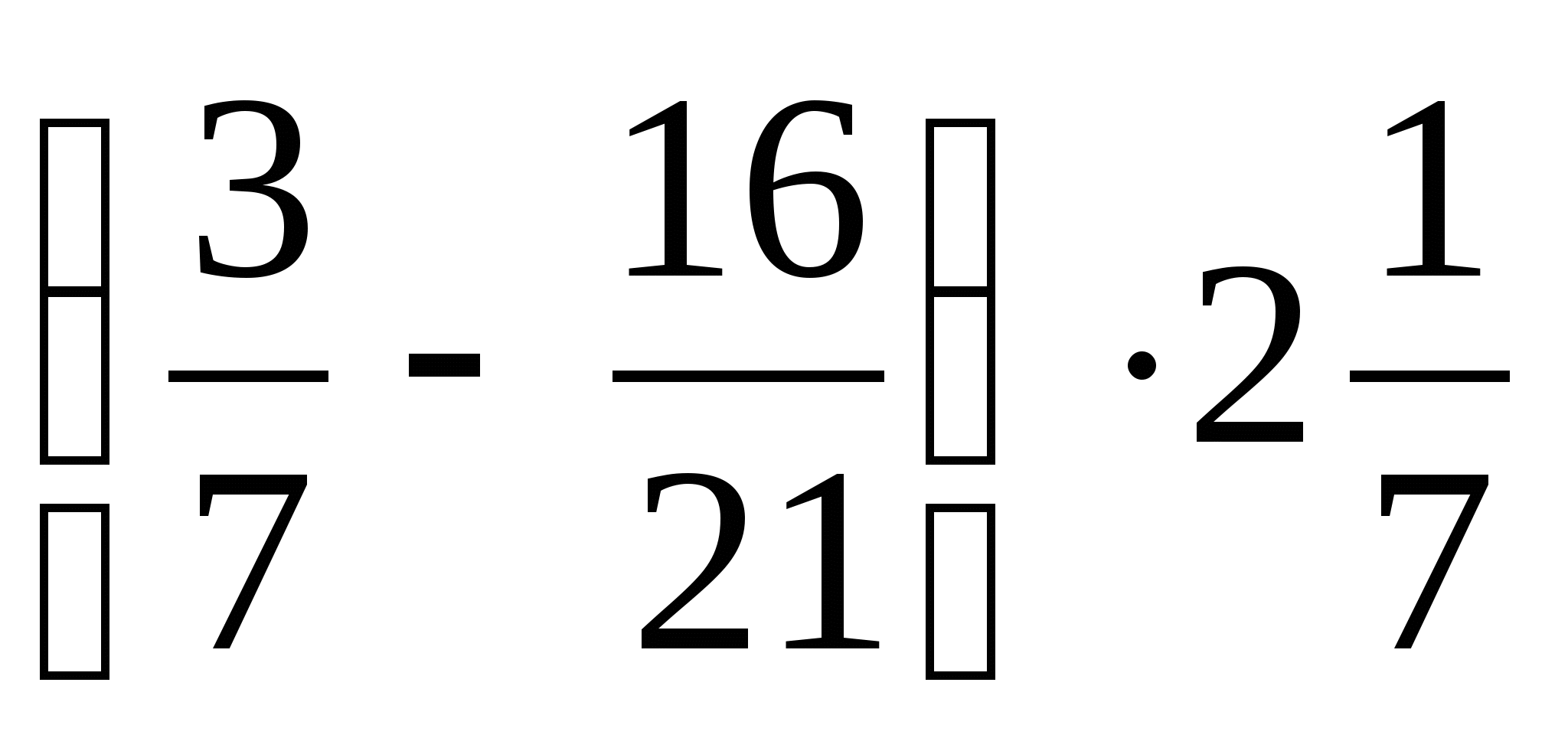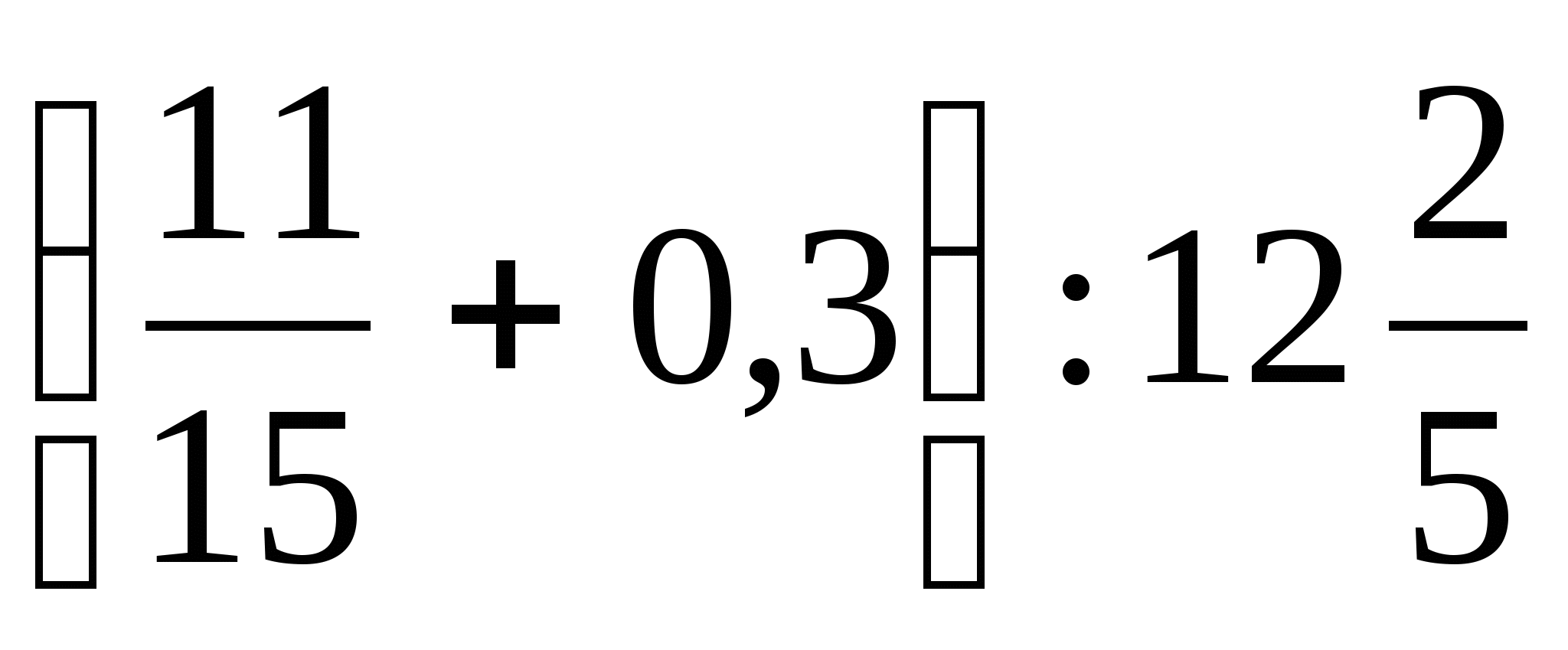