Задачи на пропорции 6 класс
Задача 1.
400 листов бумаги для печати на принтере имеют толщину 4,4 см. Вычислить толщину пачки, в которой 500 листов бумаги для принтера.
Решение.
Обозначим через х см толщину пачки бумаги из 500 листов.
Согласно условию составим соотношение:
400 листов — 4,4 см
500 листов — х см
Запишем пропорцию:
Найдем неизвестное число:
Ответ. Толщина пачки бумаги из 500 листов 5,5 см.
Задача 2.
Сколько килограмм воды содержится в 7 кг арбуза, если воды в арбузе 98\%?
Решение.
Согласно условию составим соотношение:
7 кг — 100\%
х кг — 98\%
Запишем пропорцию:
Найдем неизвестное число:
(кг).
Ответ. В 7 кг содержится 6,86 кг воды.
Задача 3.
Масса 42 литров нефти составляет 33,6 кг. Найдем массу 28 литров нефти?
Решение.
Обозначим массу 28 литров нефти через х кг.
Составим соотношение согласно условию:
42 литра — 33,6 кг
28 литров — х кг
Запишем пропорцию и найдем из нее неизвестное число:
(кг).
Ответ. Массу 28 литров нефти составляет 22,4 кг.
Задача 4.
Вспахали 74\% поля, после чего осталось вспахать всего 13 га. Найти общую площадь поля.
Решение.
Обозначим площадь всего поля через х га.
Согласно условию составим соотношение:
х га — 100\%
13 га — (100—74)\%.
Запишем пропорцию:
Найдем неизвестное число:
(га).
Ответ. Общая площадь поля 50 га.
ru.solverbook.com
Задачи по теме «Отношения и пропорции» 6 класс
Математика
6 класс
1. Задачи на отношения.
1. Отрезок АВ разделён точкой С на отрезки АС и ВС в отношении 2:7. Найти длину отрезка АВ, если длина отрезка АС на 5,5 см меньше длины отрезка ВС.
2. С двух участков собрали урожай. Каков урожай на каждом участке, если их отношение равно 11:14, а урожай, собранный со второго участка, на 18 тонн больше, чем с первого?
3. Сплав состоит из меди и цинка. Отношение массы меди к массе цинка равно 7:2. Найдите массу сплава, если масса меди на 4кг больше массы цинка в сплаве.
4. Найти массу сплава цинка и меди, если отношение массы меди к массе цинка в сплаве равно 3:5 и меди на 2,4г меньше, чем цинка.
2. Задачи на прямо пропорциональные величины.
1. Из 90 цветов, посаженных в цветнике, принялись 72. На сколько процентов меньше не принявшихся цветов, чем принявшихся?
3. 4 м3 зерна ржи весят 2,8 т. На сколько тонн больше весит 6,5 m3 зерна ржи?
4. Поезд за 4,5 часа проехал 360 км. За какое время, двигаясь с тон же скоростью, поезд проедет расстояние, увеличенное на 80 км?
3. Задачи на обратно пропорциональные величины.
1. Все члены бригады работают в одинаковом темпе. Четверо, рабочих успевают выполнить работу за 32ч. Сколько времени понадобится для выполнения этой же работы трем рабочим?
2. Чтобы вывезти товар потребуется 21 автомашина грузоподъёмностью 2,5 т. Сколько потребовалось бы для выполнения этой работы автомашин грузоподъёмностью 3,5 т?
3. 15 рабочих закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы эту работу 18 рабочих?
4. Пешеход затратил на путь 2,5 ч, двигаясь со скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь, если его скорость будет 4,5 км/ч?
4. Задачи на масштаб.
1. Комната имеет прямоугольную форму. Размеры пола этой комнаты на плане 4см и 6см. В действительности меньшая сторона пола 5 м. Найдите площадь комнаты н масштаб плана.
2. 125 м на местности соответствуют 2,5 см на плане. Найти масштаб плана и расстояние между двумя точками на местности, если на плане оно 4,2 см.
3. План земельного участка квадратной формы выполнен в масштабе 1:500. Сторона участка на плане 16см. Вычисли площадь участка.
4. На карте расстояние между годами А и В равно 2,6см. а расстояние между городами В и С – 3,7см, На местности расстояние между- городами В и С равно 296км. Найдите расстояние на местности между годами А и В и масштаб карты.
Урок по математике «Пропорции. Решение задач на пропорции»(6 класс)
Ош № 93 г.Донецка Учитель математики: Крыль Т. Н.
6 класс
Урок – путешествие
Тема: Пропорция. Решение задач с помощью пропорции
Цели: обобщить и систематизировать знания учащихся по теме «Пропорция» проверить умение и навыки находить неизвестный член пропорции; совершенствовать умения решать задачи с помощью пропорции;
развитие мыслительной деятельности, логического мышления;
привитие интереса к предмету,к разным профессиям
Оборудование урока: карточки для дополнительной самостоятельной работы; карта путешествие по некоторым уголкам города Донецка; плакаты с заданиями; карточки с задачами; карточки для индивидуальной работы.
Ход урока
1.Организационный момент.
2.Мотивация учебной деятельности.
Постановка целей и задач урока.
Учитель:
Пройдет еще пять лет, и вы закончите школу. Перед вами станет вопрос: какую профессию выбрать? Профессий много, как же тут разобраться? Вы уже знакомы с профессией своих родственников, с профессией учителя. Но ведь существует еще много интересных профессий. Чтобы узнать как можно больше о них, на наших уроках мы иногда можем путешествовать, встречаясь с людьми разных профессий, с различных предприятий, знакомиться с продукцией этих предприятий. А как мы будем это делать – вы сегодня увидите. Это не совсем обычный урок. Мы с вами отправимся в путешествие по интересным местам нашего города Донецка. Путешествуя, выясним, как вы усвоили тему «Пропорции». Ведь данная тема служит основой для решения многих задач практического характера. С задачами, решение которых сводится к составлению пропорций, встречаются люди любой профессии. Итак, в путь!
3.Совершенствование умений и навыков учащихся
Станция «Технический университет»
Учитель:
Внимание. На нашем пути студенческий городок. Заглянем в одну из аудиторий университета. Здесь идет конференция по истории математики.
Историческая справка (сообщение делает ученик).
Ученые Древней Греции не признавали дробных чисел и из-за этого у них возникали затруднения с измерением величин. Пришлось греческим ученым придумать способ, как обходиться в науке без того, чтобы выражать длины, площади и объемы числами. Так было создано учение об отношениях величин, о равенстве таких отношений.
Равенство двух отношений стали, потом называться латинским словом «пропорция». С пропорциями имели дело строители уже в древнем мире. Правильное соотношение размеров возводимых ими дворцов и храмов придавало этим зданиям ту необыкновенную красоту, которая и сегодня восхищает нас.
А в другой аудитории идет практическое занятие. Давайте примем в нем участие.
Работа по карточкам. Два человека работают на откидных досках, двое отвечают с места.
КАРТОЧКА 1
Найдите неизвестный член пропорции

КАРТОЧКА 2
Найдите неизвестный член пропорции
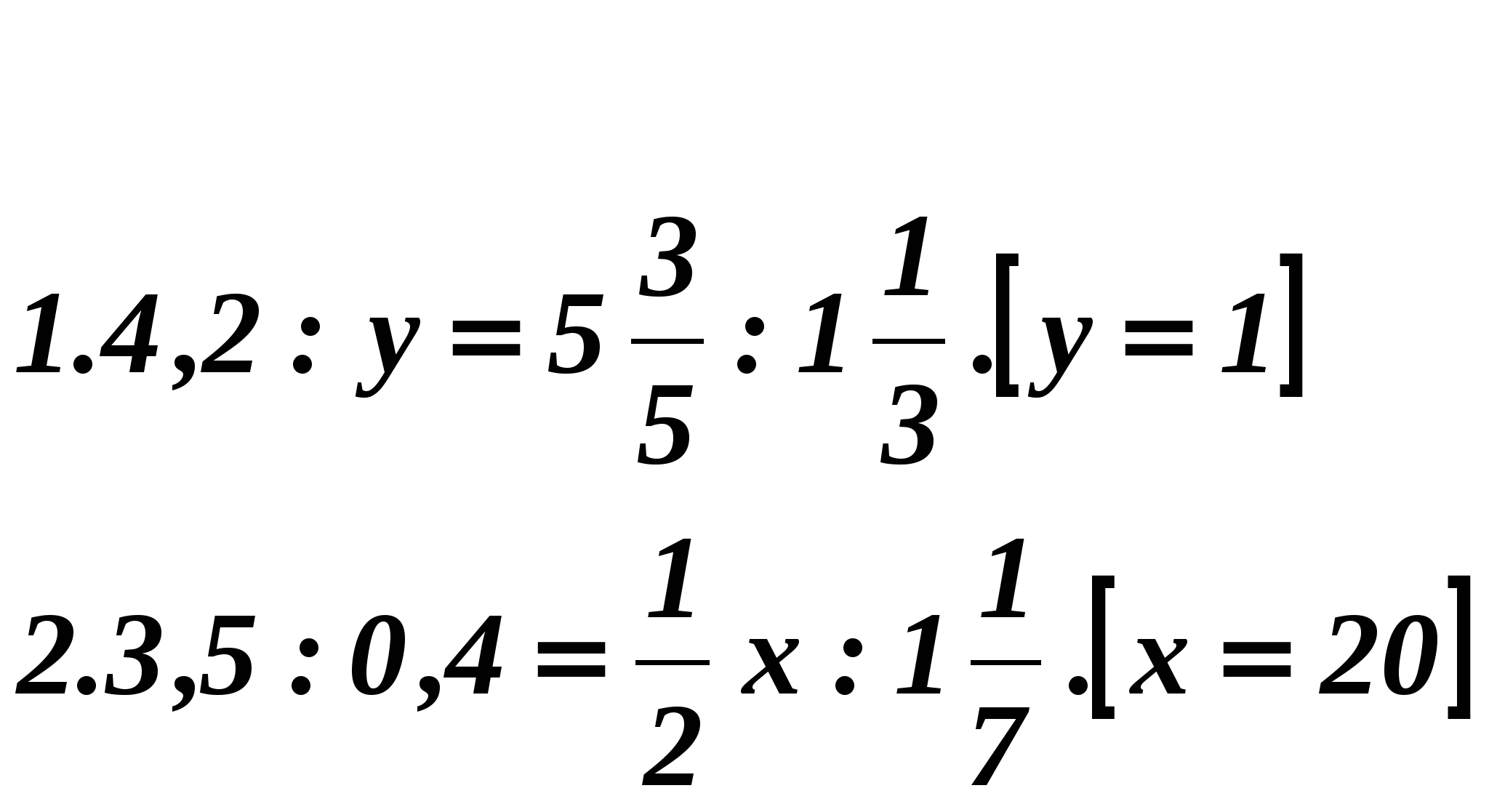
Устная работа
Учитель:
-Какие из данных равенств являются пропорциями? Почему?
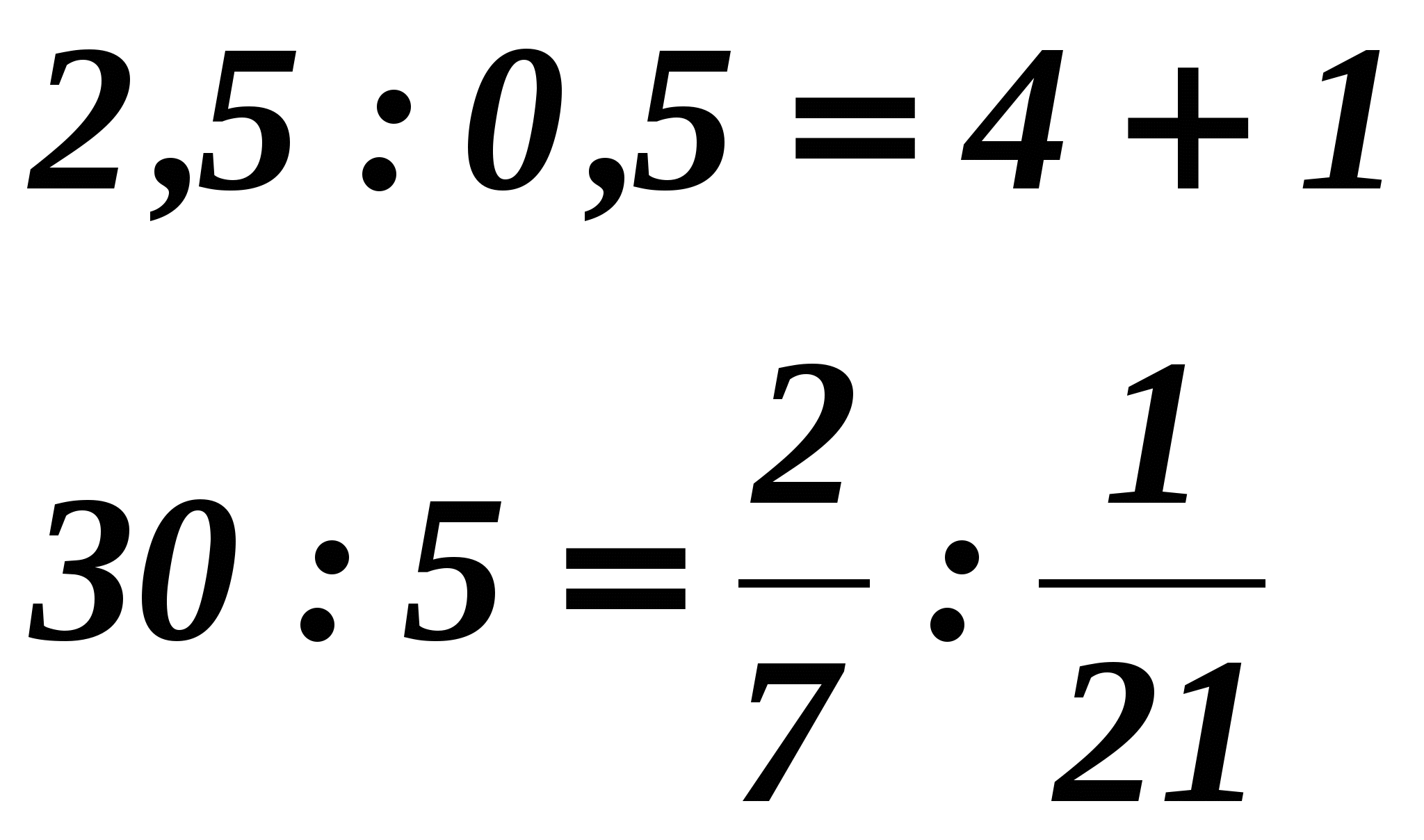
-Назовите недостающие члены пропорции
а) 104: =160:20
б) 10:5 = :
1) Какие из этих заданий имеют конечное множество решений? Бесконечное? Почему?
2) Проверьте составленную пропорцию в пункте б) двумя способами.
3)Прочитайте пропорцию в пункте а) тремя способами.
4) Назовите крайние и средние члены пропорции в пункте а).
— Из чисел 4,2,5,10 составьте пропорцию. Как из данной пропорции получить верную пропорцию?
— Проверьте, правильно ли найден неизвестный член пропорции
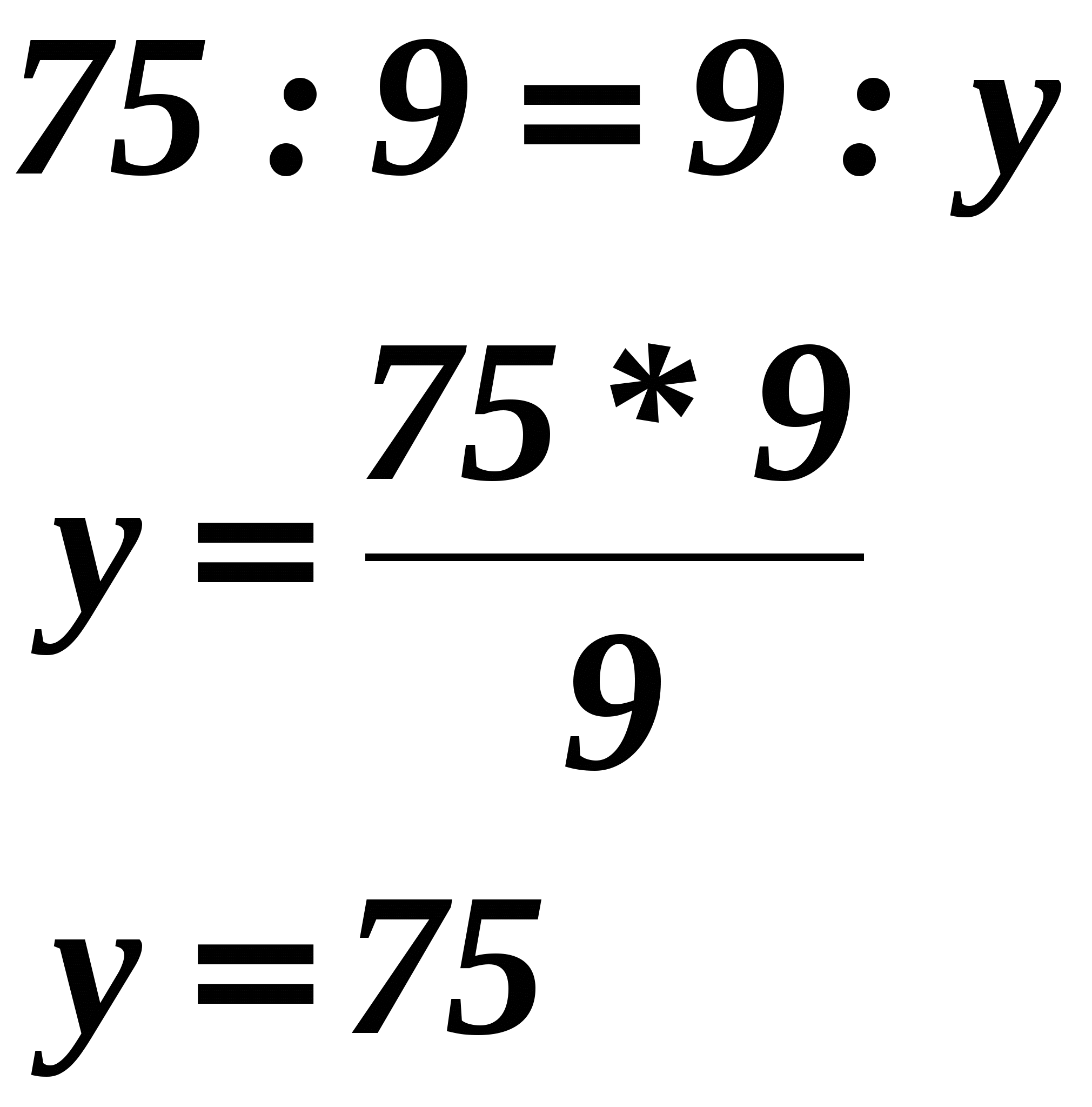
-Как найти неизвестный средний член пропорции?
-Как найти неизвестный крайний член пропорции?
Учитель:
Так как следующие станции, связанные с решением задач практического характера, давайте ответим на следующие вопросы:
-Какие величины называются прямо пропорциональными?
-Какие величины называются обратно пропорциональными?
-Приведите примеры прямо пропорциональных величин.
-Приведите примеры обратно пропорциональных величин.
-Приведите примеры величин, не являющиеся пропорциональными.
Станция «Хлебозавод»
Один ученик решает у доски с объяснением.
Задача. При выпечке хлеба из килограмма ржаной муки пекарь получает 1,4 кг хлеба. Сколько килограммов муки расходуется на выпечку 21ц хлеба?
Решение. Пусть х муки расходуется на выпечку 21 ц хлеба.
1 кг – 1,4 кг
х кг – 2100 кг


Учитель:
Итак. Где мы сегодня побывали? О какой профессии мы узнали из этой задачи?
Станция «Строительная»
Два ученика решают на откидных досках, остальные самостоятельно с последующей проверкой.
Задача. Пять каменщиков могут закончить работу за 9 дней. Инженер попросил ускорить работу и для этого добавил еще 10 каменщиков. За какое время они закончат работу, считая, что все каменщики будут работать с одинаковой производительностью?
Решение. Пусть х дн. Каменщики закончат работу.
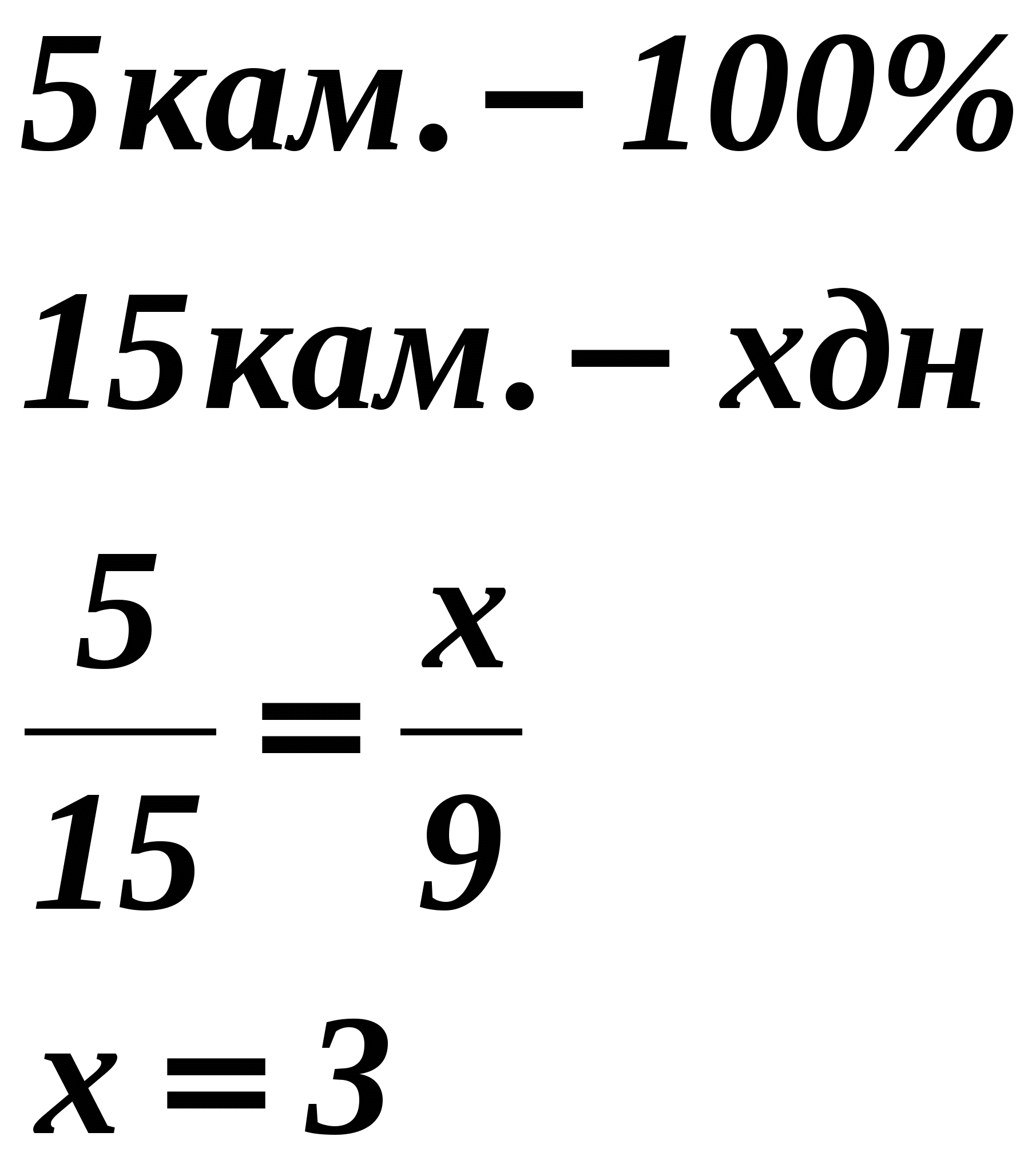
Ответ: 3 дня
Учитель:
— Каким свойством пользовались при решении задач? Сформулируйте.
— В какой организации мы с вами побывали? Чем занимается эта организация? С какими профессиями мы с вами познакомились?
Станция «Сахарный завод»
Один ученик решает у доски с объяснением.
Задача. В сахарной свекле содержится 18,5% сахара. Сколько сахара содержится в 50 т сахарной свеклы?
Решение. Пусть х т сахара содержится в 50т сахарной свеклы.
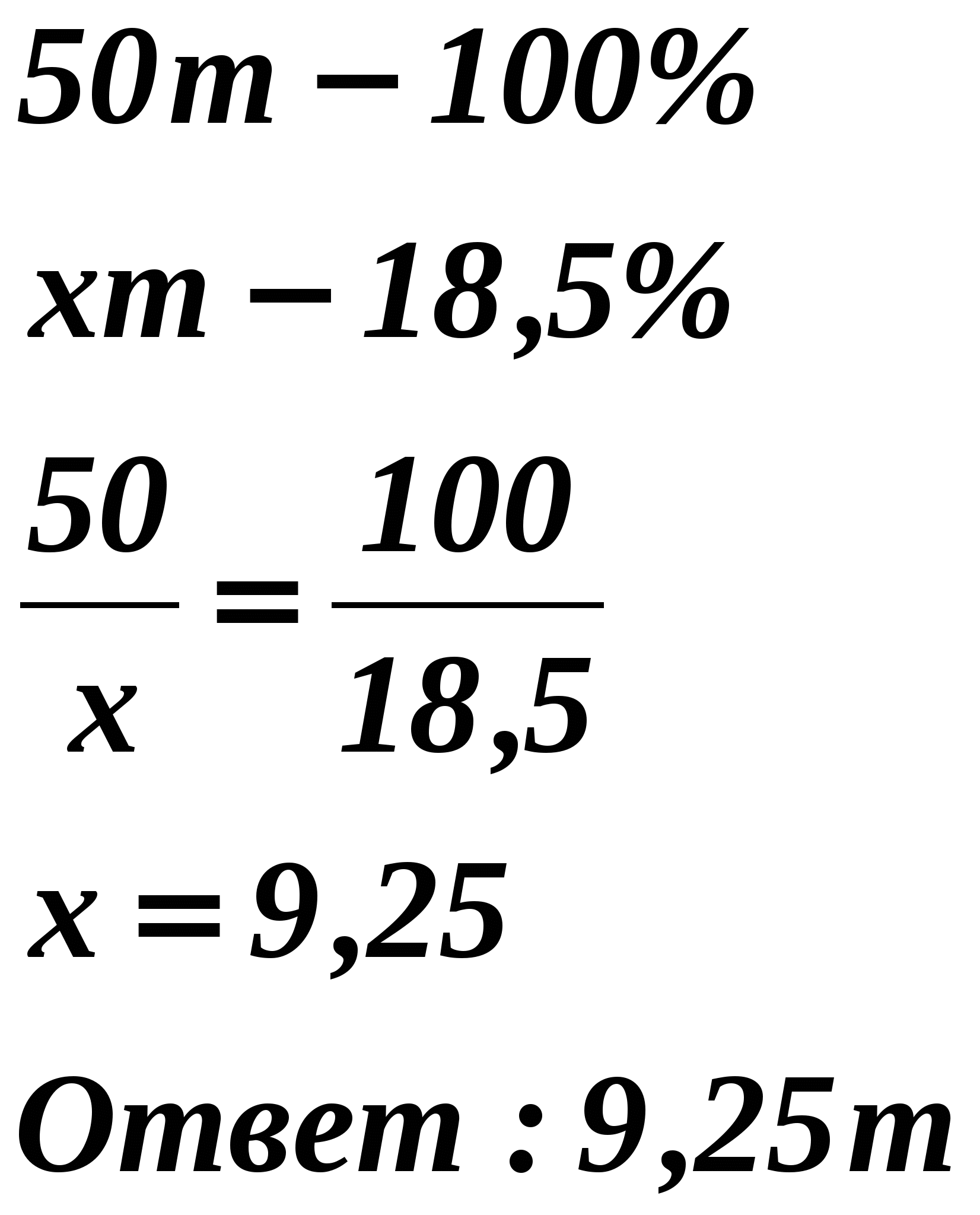
Плакат
50 т — 100% х t — 100%
х т — 18,5% 9,25т — 18,5%
Учитель: -Что вы видите на доске?
(Краткая запись задачи и краткая запись обратной задачи.)
-По краткой записи обратной задачи сформулируйте условие.
(Условие. В сахарной свекле содержится 18,5% сахара. Сколько надо взять сахарной свеклы, чтобы в ней содержалось 9,25 т сахара?)
-Где мы с вами побывали? Какой продукт там производится? Из чего получается сахар?
Самостоятельная работа
По итогам путешествия проводится самостоятельная работа.
Вариант 1
Найдите неизвестный член пропорции

2.Найдите неизвестный член пропорции
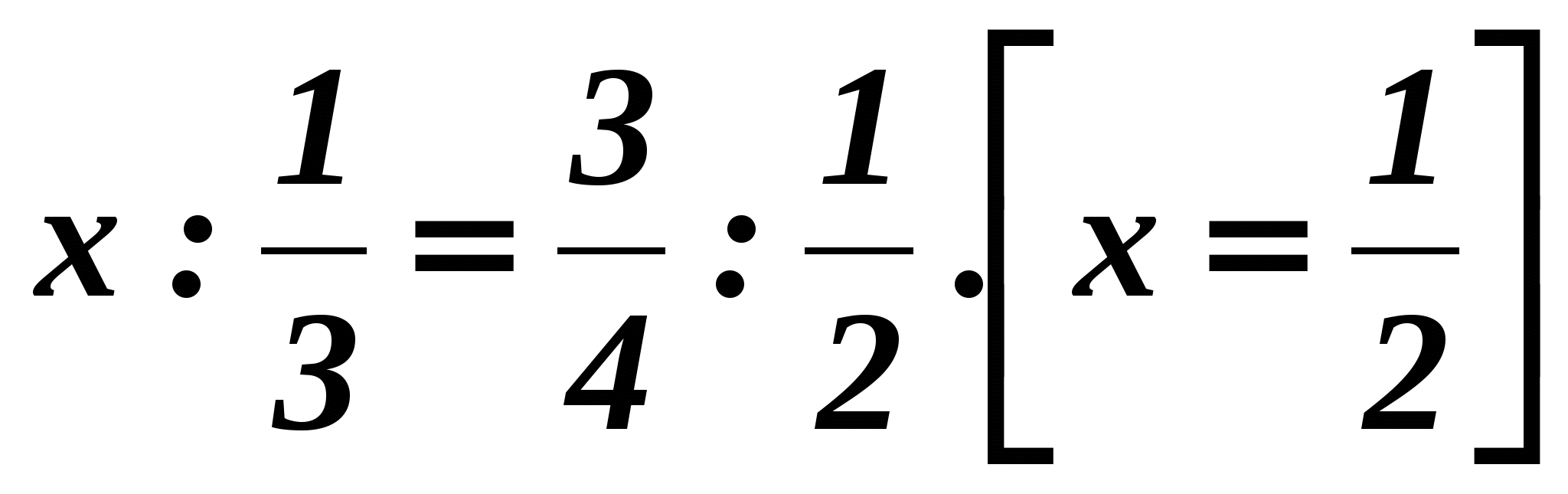
3. Реши задачу.
 На 20 км пути автомашина расходует
На 20 км пути автомашина расходует 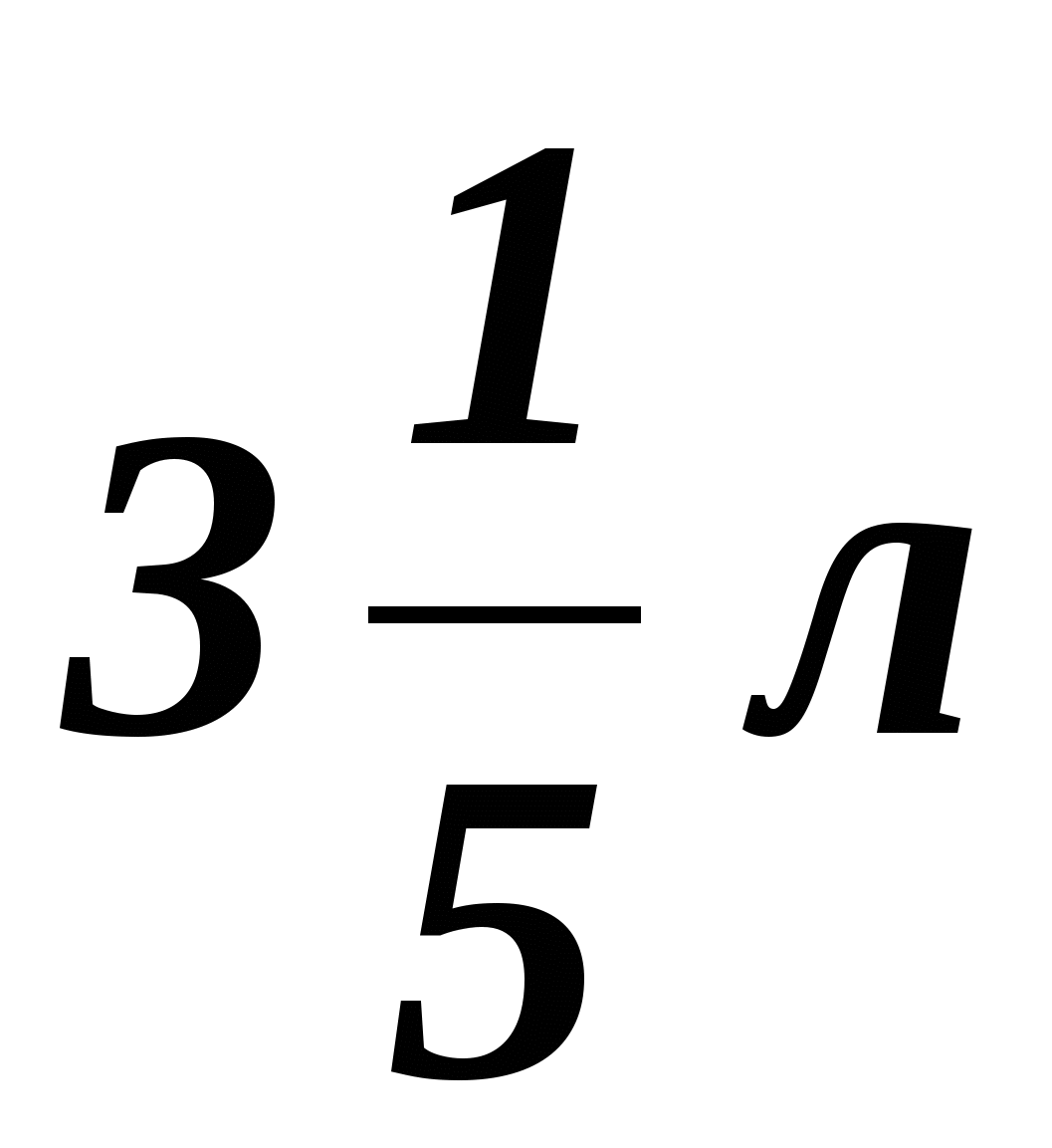 горючего. Сколько горючего автомашина израсходует на 50км пути?
горючего. Сколько горючего автомашина израсходует на 50км пути? 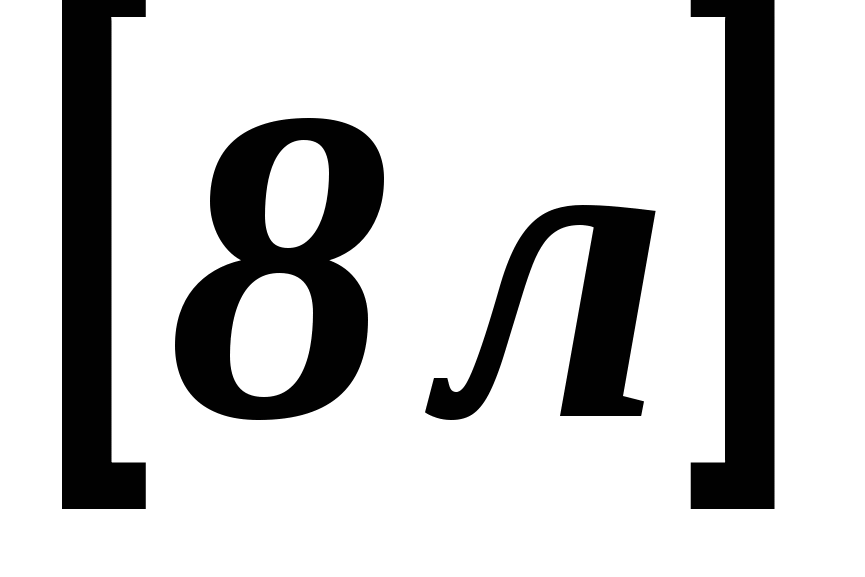
Вариант 2
Найдите неизвестный член пропорции.
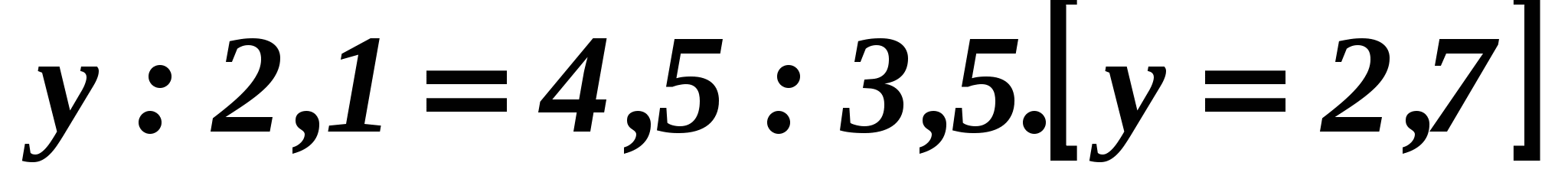
найдите неизвестный член пропорции
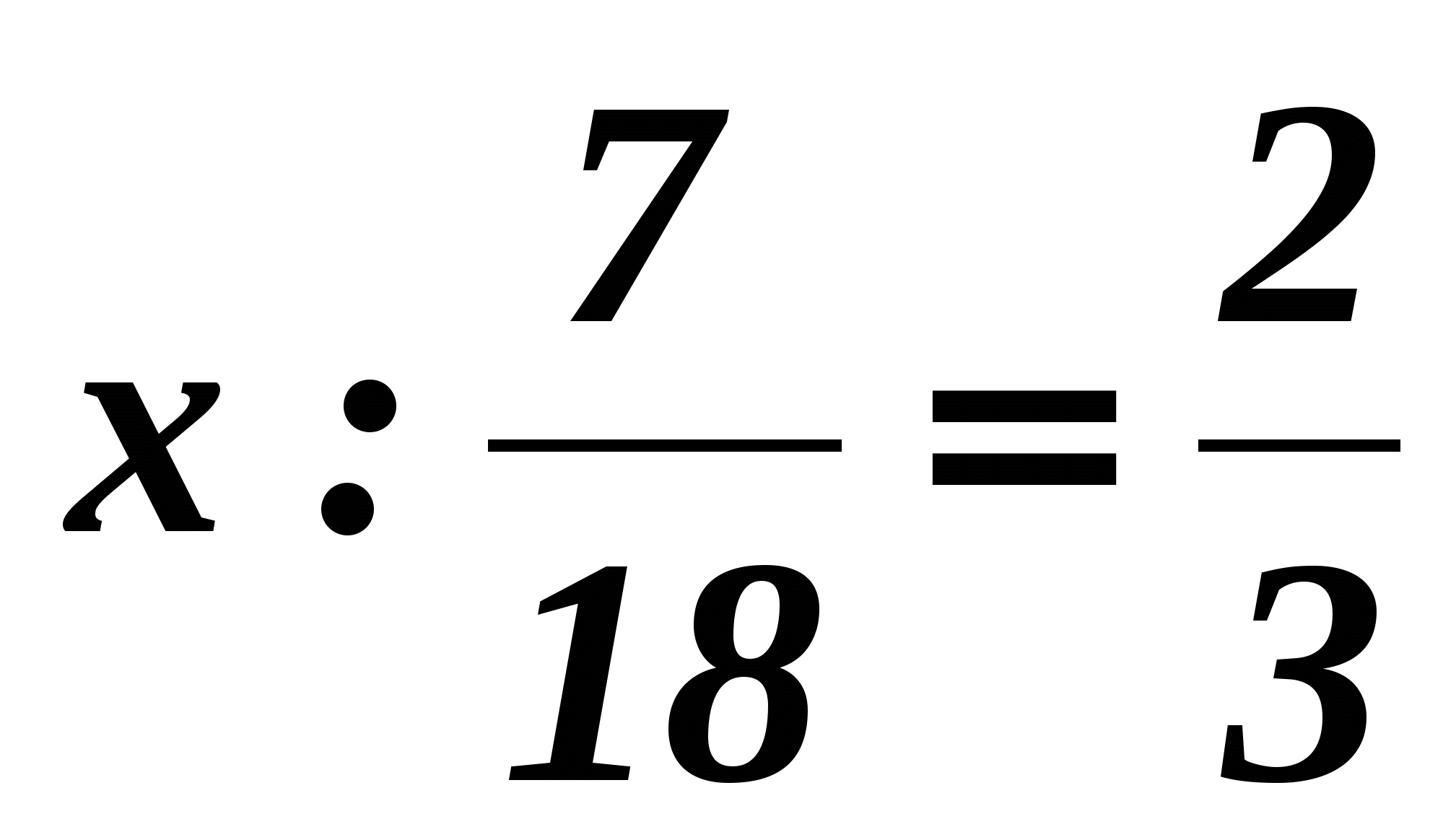 :
: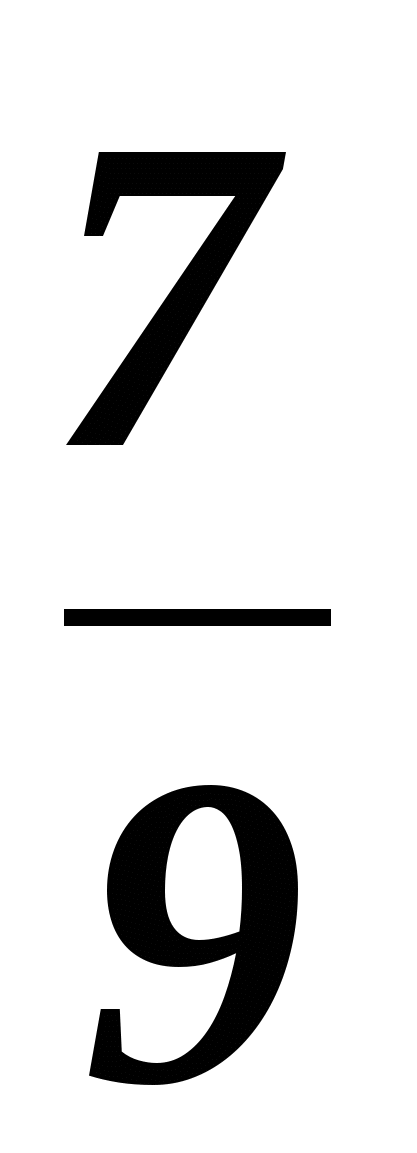
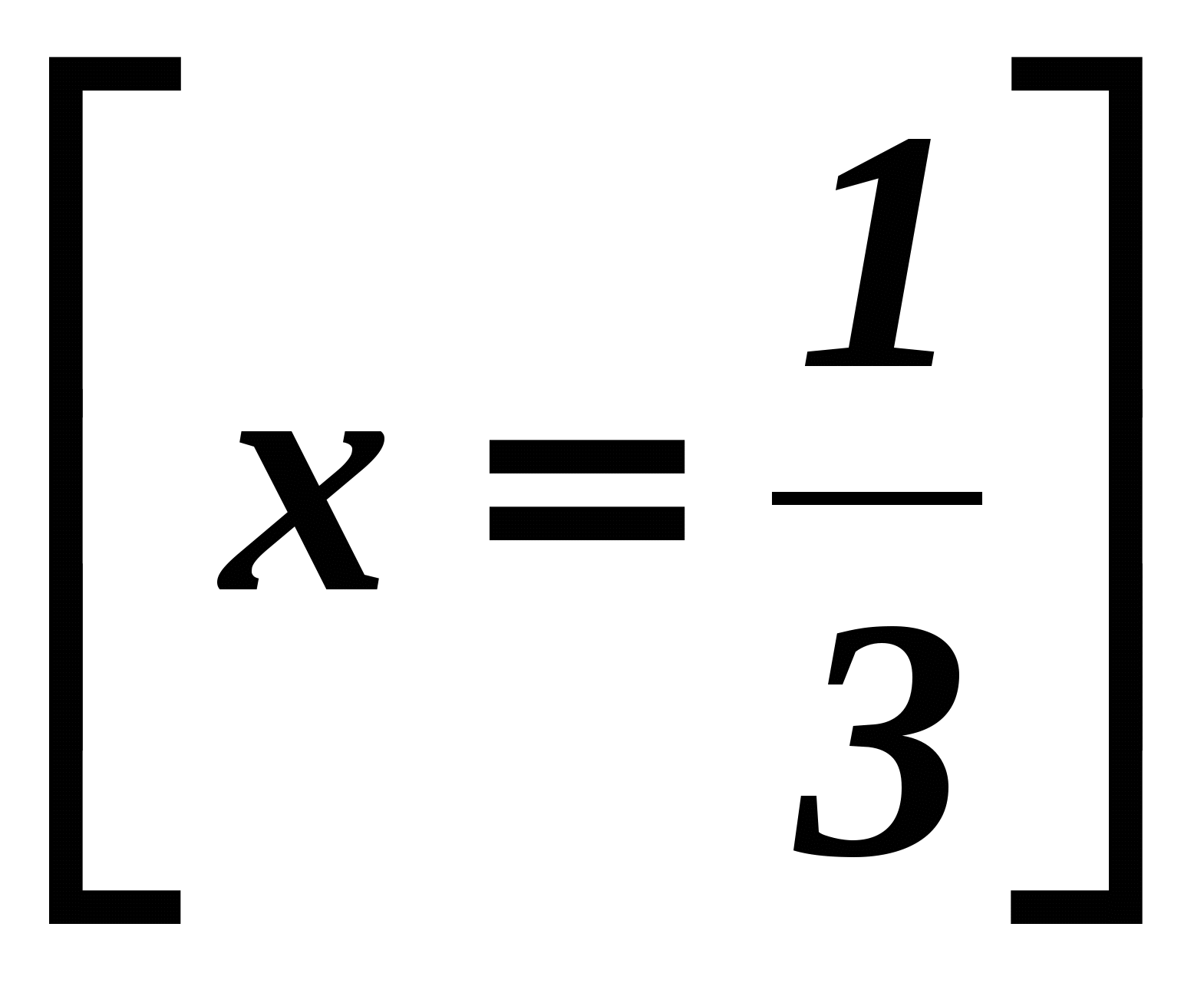
3.Решить задачу. Участок клубники 24 человека пропололи за 6 дней. За сколько дней выполнят ту же работу 36 человек, если будут работать с той же производительностью?( )
)
4.Подведение итогов урока.
5. Комментирование оценок
6.Задание на дом. Придумайте две новые станции, две задачи и решите их.
infourok.ru
«Решение задач с помощью пропорций» (6 класс)
Конспект открытого урока
Технологическая карта изучения новой темы: «Решение задач с помощью пропорций»
— развивать логическое мышление, умение обобщать и систематизировать материал;— способствовать развитию коммуникабельности;
— формировать способность к сотрудничеству при работе в паре, группе.
Тип урока
Изучение нового материала
Планируемые результаты
Предметные результаты: знать и понимать смысл понятий: отношения, пропорция, крайний и средний член пропорции, прямая и обратная пропорциональная зависимость, уметь находить неизвестный член пропорции, анализировать условие задачи и выявлять тип задач, применять полученные знания на других уроках.
Метапредметные результаты:
Познавательные: способность понимать учебную задачу урока, выделять и формулировать познавательные цели, строить логическую цепочку рассуждений, устанавливать причинно-следственные связи.
Регулятивные: контролировать и оценивать собственную деятельность и деятельность партнеров, планировать и корректировать свою деятельность;
Коммуникативные: уметь достаточно полно и чётко выражать свои мысли, слушать собеседника и вести диалог.
Личностные: определять границы собственного знания и незнания по теме; иметь мотивацию к учебной деятельности, принимать и осваивать социальную роль обучающегося, использовать приобретенные знания учебного сотрудничества со взрослыми и сверстниками в разных ситуациях; знать, как важны в учебной деятельности мышление, внимание, любознательность, аккуратность, личная ответственность.
Ресурсы:
-основные
— дополнительные
Учебник: Математика 6 класс Зубарева И.И., Мордкович А.Г.,
Презентация к уроку; листы с заданием для работы в парах, в группах; таблица с алгоритмом
«Решение задач с помощью пропорций».
Организация
Работа фронтальная, самостоятельная, индивидуальная, работа в парах, в группах.
Аннотация
Данный урок проведён во 6 классе. Тип урока — изучение новой темы. Урок с презентацией. Содержит интересный и познавательный материал по теме. В ходе урока используются различные методы и приёмы для формирования УУД.
Используемые технологии: проблемного обучения, критического мышления, ИКТ.
Используемые методы:
-По источникам знаний: словесные, наглядные.
-По степени взаимодействия: учитель-ученик, ученик-ученик, эвристическая беседа.
-Относительно дидактических задач: подготовка к восприятию.
-Относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
Используемые формы организации познавательной деятельности: беседа, фронтальная работа, самостоятельная работа, работа в парах, работа в группах.
Сведения о публикации
Конспект урока опубликован на сайте https://infourok.ru/ Инфоурок
Деятельностьучителя
Деятельность учеников
Обучающие и развивающие задания каждого этапа
Формирующие
УУД
1 этап.
Эмоциональный настрой
Цель: настроить на работу
Приветствует обучающихся, создаёт эмоциональный настрой на урок.
Приветствуют учителя, гостей.
— Сегодня у нас ответственный урок. К нам пришли гости. И, как гостеприимные хозяева, подарим свои добрые улыбки и порадуем всех активной работой.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
2 этап.
Организационный момент
Цель:
-Проверка готовности обучающихся
Проверяет готовность к уроку, организует внимание детей, обращает внимание на девиз урока «Помогая другим, учимся сами!» (слайд 2) предлагает правила работы на уроке
Принимают девиз урока.
Уточняют, принимают правила работы на уроке.
Распределяют роли в группах.
Коммуникативные: распределение обязанностей в группе;
Регулятивные:
планирование учебного сотрудничества с учителем и сверстниками.
Личностные:
нравственно-этическая ориентация.
3 этап.
Актуализация опорных знаний
Работают фронтально. Отвечают на вопросы.
— Проговаривают правило нахождения неизвестного члена пропорции, определяют вид пропорциональной зависимости, обосновывая выбор.
Устные упражнения. Слайд №3
(Приложение 1)
Особое внимание обратить на задание (4-6)
(В задачах 4-6 речь идет не о пропорциях)
Коммуникативные: планирование учебного сотрудничества с учителем, сверстниками.
Познавательные: определение основной и второстепенной информации, анализ объектов с целью выделения признаков.
4 этап.
Целеполагание и мотивация
Предлагает решить задачу любым известным способом.
Работают фронтально. Отвечают на вопросы.
Подводит детей к формулировке темы урока
— Предлагают традиционный способ решения.
— Различные варианты ответов. Предполагаемые ответы.
— Да. В задаче присутствует прямо пропорциональная зависимость: во сколько раз увеличится число юбок, во столько же раз увеличится и количество метров. Т.е. юбок увеличить в …
— Через х, или любой другой буквой.
4 юбки — 7,2 м
6 юбок — ?
4/6=7,2/х
х=6*7,2/4=10,8 (м.)
— Решение задач с помощью пропорций (записали в тетрадях).
— Научиться решать задачи с помощью пропорций.
Задача Слайд 4
(Приложение 2)
1) 7,2/4=1,8м – на 1 юбку
2) 1,8*6=10,8м – на 6 шт.
Ответ: 10,8 м.
— Можно ли решить эту задачу другим способом?
— Что можно заметить?
— Можно ли составить отношение?
1) 6/4=1,5 раза, значит
2) 7,2/1,5=10,8 м.
-Как лучше обозначить неизвестную величину?
— Какое получим соотношение?
— Решаем уравнение
-Какова тема нашего урока? (Учитель записывает на доске)
-Какова цель урока?
Слайд №5
Регулятивные: целеполагание
Познавательные: выбор наиболее эффективных способов решения задач, самостоятельное выделение —
формулирование цели Коммуникативные: взаимодействие с учителем и учащимися во время фронтальной беседы
5 этап.
Усвоение новых знаний
Работа в группах по 4 человека на рабочих листах
(по 1 из группы зачитывают)
Выявляют проблему, выдвигают предположения, формулируют алгоритм решения задач с помощью пропорций
Выполняют в тетради
— Пробуют решать, у многих возникает проблема.
-Нет алгоритма решения задач.
— Алгоритм решения.
— Составление алгоритма
решения задач с помощью пропорций.
— Обсуждение предложенных алгоритмов и выбор оптимального алгоритма.
-Решение задачи, предложенной выше.
— Задача: Слайд №6 (решаем самостоятельно)
(Приложение 2)
— В чем возникла сложность?
— Что нужно знать, чтобы быстро решать такие задачи?
— Какова задача нашего урока. Слайд №7
— Составляем алгоритм
Слайд № 8.
Коммуникативные: постановка вопросов, поиск и оценка альтернативных способов решения.
Познавательные: самостоятельное выделение -формулирование познавательной цели.
Логические: формулирование проблемы, построения логической цепи рассуждения.
6 этап.
Динамическая пауза
Меняет деятельность, обеспечивает эмоциональную разгрузку учащихся
Выполняют предложенные упражнения, тем самым меняют вид деятельности и восстанавливают силы.
Физкультминутка
— Быстро встали, улыбнулись,
Выше- выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
А теперь, друзья, садитесь!
Коммуникативные: дружное выполнение зарядки
Регулятивные: самоконтроль своих действий.
7 этап.
Первичное закрепление
Выполняют письменное задание в тетради и у доски по составленному алгоритму
— С места, комментируя решения по пунктам.
— У доски ученик.
Слайд № 9.
— Решаем задачу по алгоритму
№ 1056
48 кг -12%
х кг – 100%
х=48*100/12=400
Ответ: 400 кг.
Познавательные: выбор наиболее эффективных способов решения задачи, умение структурировать знания.
8 этап.
Организация первичного контроля
Самостоятельная работа (2 варианта) с самопроверкой по эталону.
Организует работу по парам.
Слайд № 10, 11.
(Приложение 3)
Самостоятельное решение в тетради. Самопроверка.
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения.
Личностные: самоопределение.
9 этап.
Подведение итогов
Цель:
— подвести итог проделанной работе на уроке
Отвечают на вопросы учителя.
— Решение задач с помощью пропорций.
— Формулировка алгоритма.
-Что мы изучали сегодня на уроке?
— Сформулируйте алгоритм решения задач на пропорции.
-Оценить отдельных учащихся
Регулятивные: оценка-осознание уровня и качества усвоения.
10 этап.
Рефлексия
Цель:
-организовать рефлексию и самооценку учениками собственной учебной деятельности
Организует рефлексию. Организует самооценку учебной деятельности. Акцентирует внимание на результатах учебной деятельности учащихся на уроке. Слайд № 12
(Приложение 4)
Выбирают фразу подходящего смысла, как конечный результат своей работы на уроке.
Закончите фразу:
Сегодня я узнал …
Было интересно …
Было трудно …
Теперь я могу…
Я приобрёл…
Я научился …
У меня получилось…
Я смог…
Я попробую…
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли.
Познавательные: рефлексия.
11 этап.
Домашнее задание
Даёт комментарий к домашнему заданию.
Записывают домашнее задание в дневниках.
№ 1058, 1060
Итог
— Наш урок закончился, вы молодцы, хорошо потрудились, открыли новое знание, которое, я надеюсь, вам поможет правильно и быстро решать задачи. Спасибо за урок.
Слайд №2
Помогая другим,
учимся сами!
Слайд №3

Слайд №4
Чтобы сшить 4 юбки, необходимо 7,2м ткани. Сколько метров ткани потребуется для 6 юбок?
Слайд №5
Тема урока:
«Решение задач с помощью пропорций».
Цель урока: Научиться решать задачи с помощью пропорций.
Слайд №6
Работница расфасовала 1,4 кг конфет за 4,2 мин. За сколько минут она расфасует 7 кг конфет?
Слайд №7
Задача урока:
Составить удобный алгоритм решения задач.
Слайд №8
Алгоритм решения задач с помощью пропорций
Записать схематично условие задачи, обозначив неизвестную величину через x.
Определить вид пропорциональной зависимости.
Составить соответствующую пропорцию.
Найти неизвестный член пропорции.
Ответить на поставленный в задаче вопрос
Слайд №9
Масса сушеных яблок составляет 12% массы свежих. Сколько нужно взять свежих яблок, чтобы получилось 48 кг сушеных?
Слайд №10
Самостоятельная работа
Слайд №11
Самостоятельная работа. Ответы:
Слайд №12
Рефлексия
Закончите фразу:
Сегодня я узнал …
Было интересно …
Было трудно …
Теперь я могу…
Я приобрёл…
Я научился …
У меня получилось…
Я смог…
Я попробую…
infourok.ru
Конспекты уроков по математике на тему «Пропорции» (6 класс)
6 класс
УРОК № 11. Глава 1. Отношения, пропорции, проценты (26 часов)
Тема. Пропорции.
Цель. Продолжить формировать навыки в использовании определения и основного свойства пропорции, решения пропорции.
Ход урока.
Организационный момент.
Проверка домашнего задания.
Устное решение задач.
1. Из одного и того же пункта одновременно в противоположных направлениях вышли Гена и Чарли. Через 3 часа расстояние между ними стало 21 км. Найдите скорость Чарли, если скорость Гены 4 км/ч. Ответ: 3 км/ч.
2. На автомобильной стоянке стоят 24 автомобиля, причем легковых автомобилей в три раза больше, чем грузовых. Сколько грузовых автомобилей на стоянке? Ответ: 6 автомобилей.
3. Мультимедийная доска. Фронтально. Тестовые задания. (Электронное приложение. Каталог. Интерактивные модели. Увеличение и уменьшение (5 заданий)).
1) Масштаб карты 1 : 10 000. Определите расстояние на местности, если на карте оно равно 10 см. (Ответ: 1 км)
2) Длина комнаты прямоугольной формы на плане равна 50 мм. Определите истинную длину комнаты, если численный масштаб плана 1 : 200. (Ответ: 10 м)
3) Длина реки 80 м. Чему равна длина её изображения на карте с масштабом 1 : 1 000. (Ответ: 8 см)
4) Длина крыла бабочки 15 мм. Чему равна длина изображения крыла в масштабе 4 : 1. (Ответ: 6 см)
5) Бабочка изображена в масштабе плана 2 : 1. Найдите истинную длину переднего крыла бабочки, если длина его изображения равна 5 см. (Ответ: 25 мм)
Решение упражнений. (Задания по карточке).
1. Упростите отношение:
1) 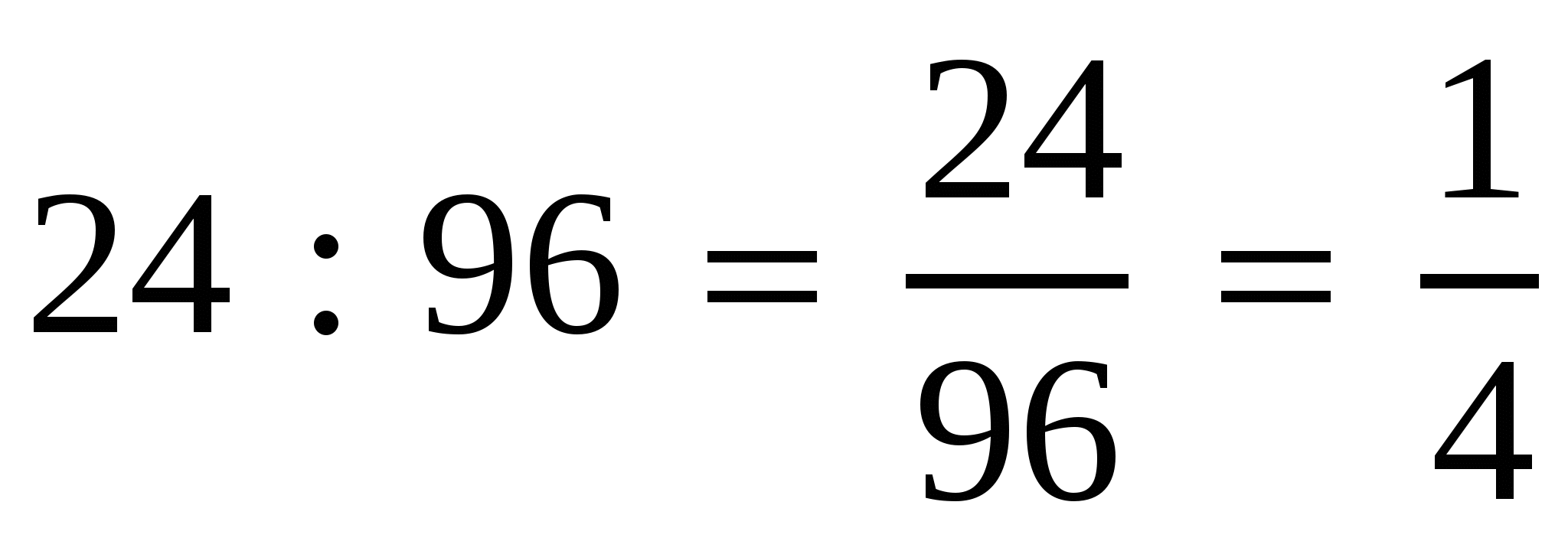 ;
;
2) 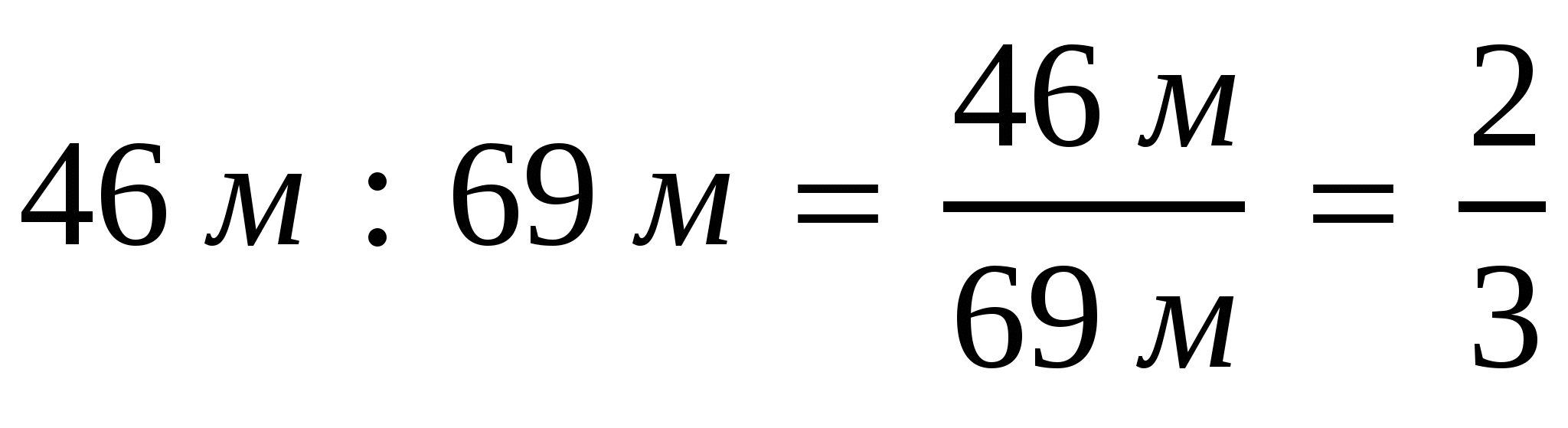 ;
;
3) 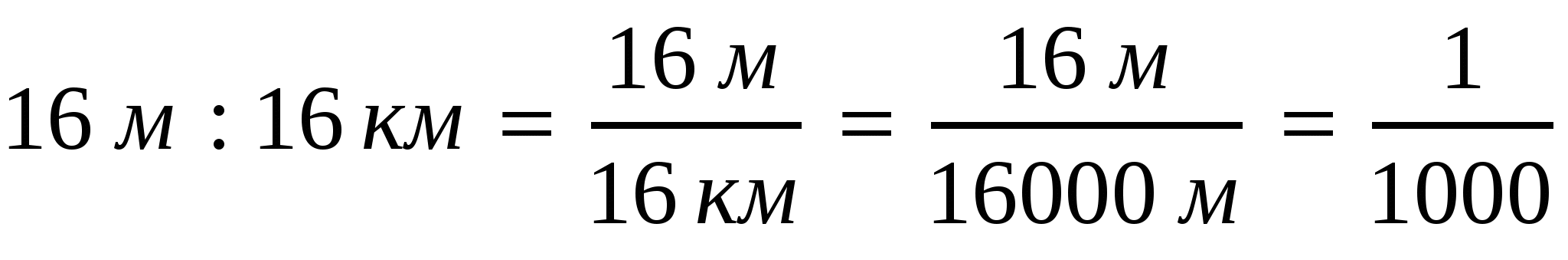 ;
;
4) 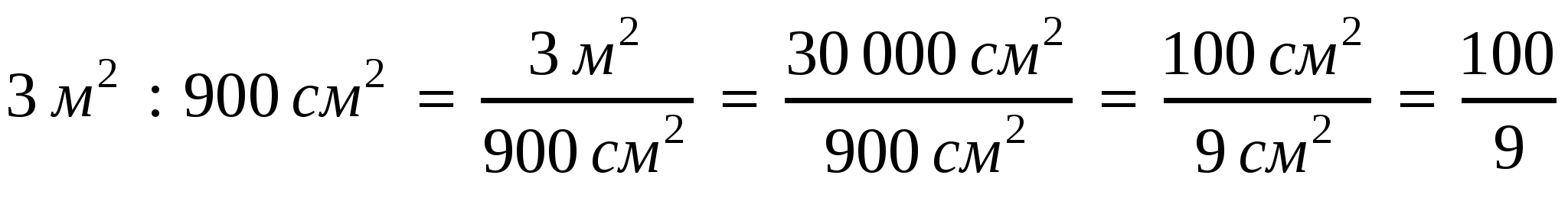 .
.
2. Используя числа 56; 15; 8; 105, составьте пропорцию: 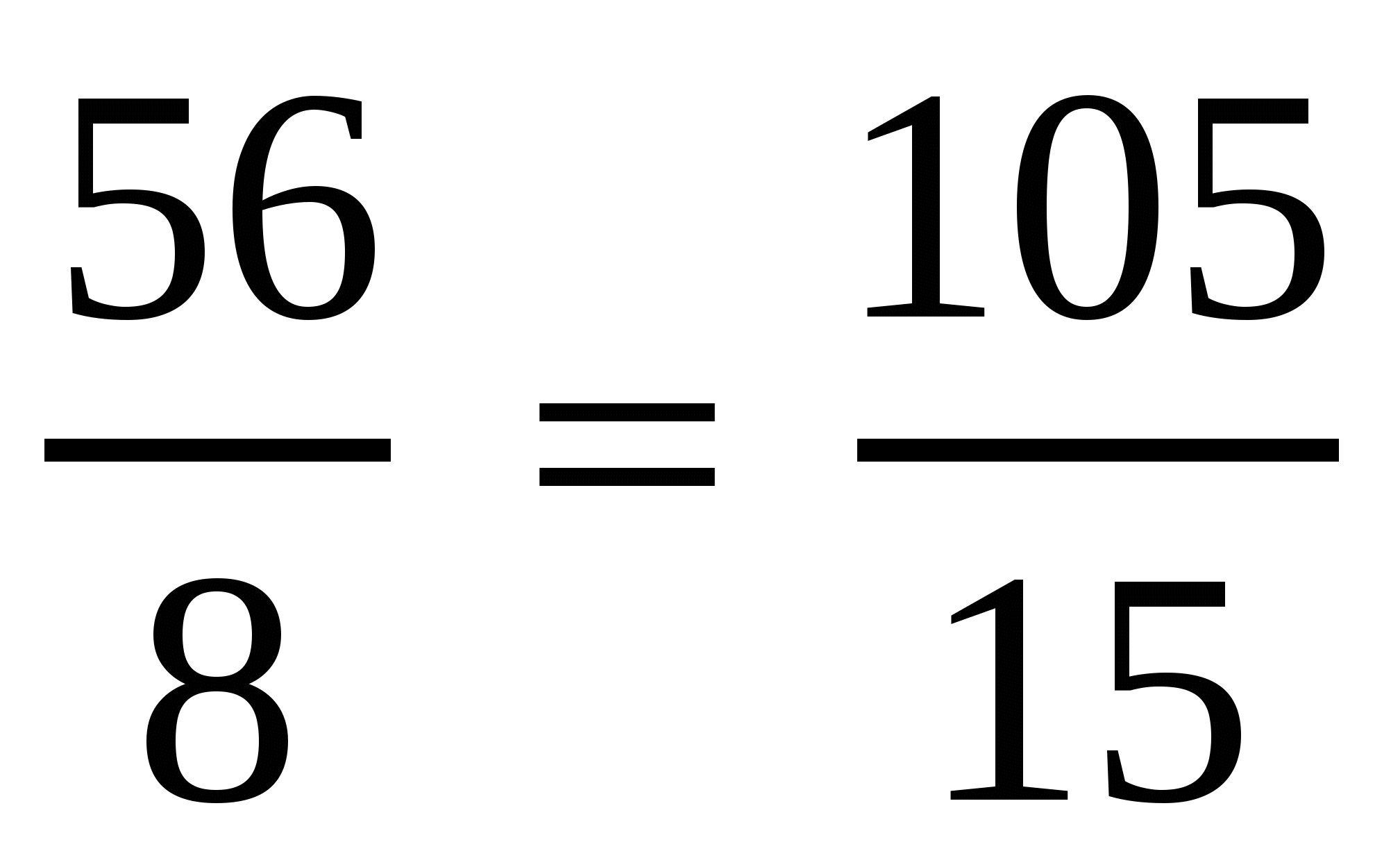 .
.
3. Вычислив данные отношения, установите, можно ли из них составить пропорцию:
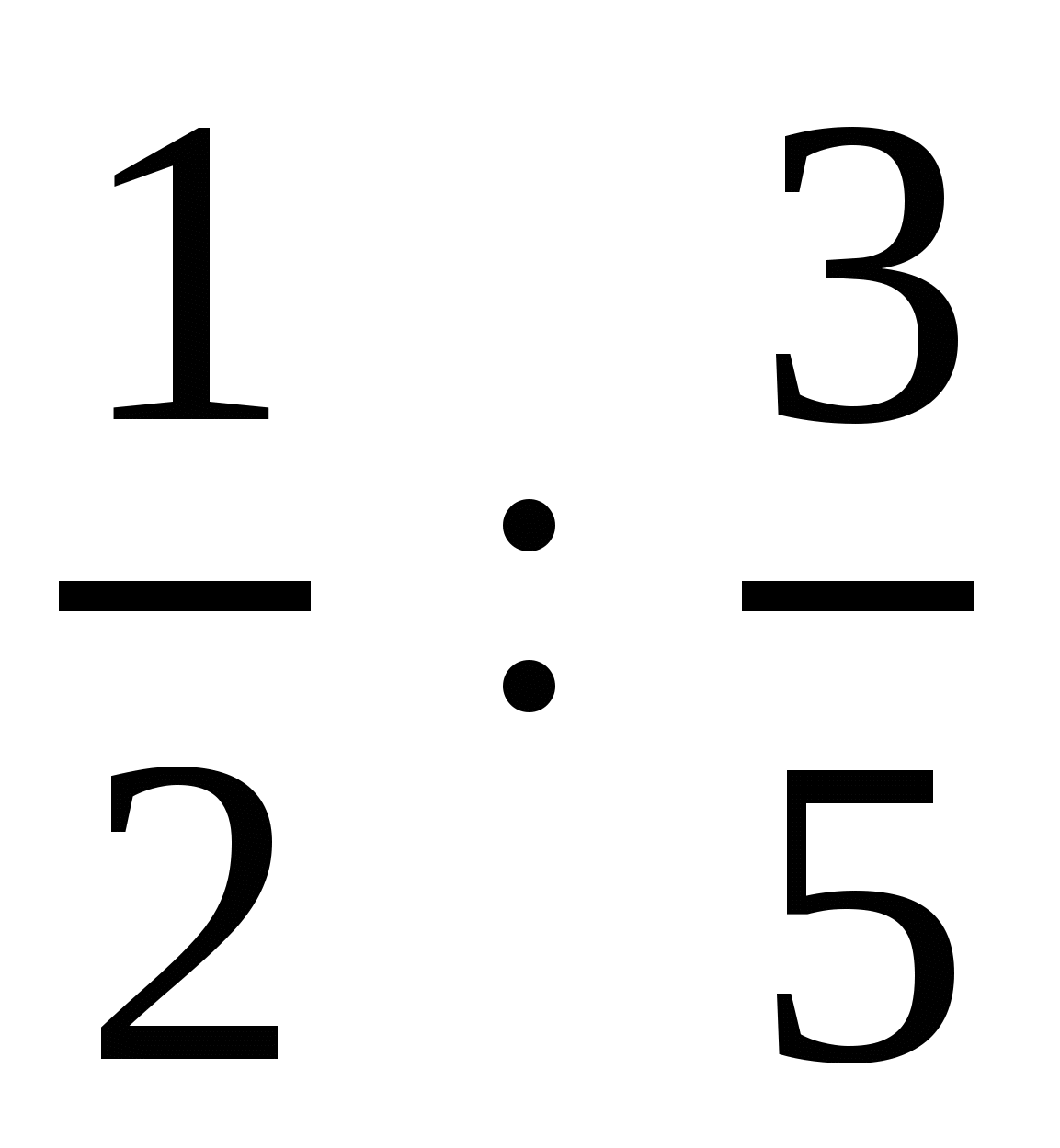 и
и 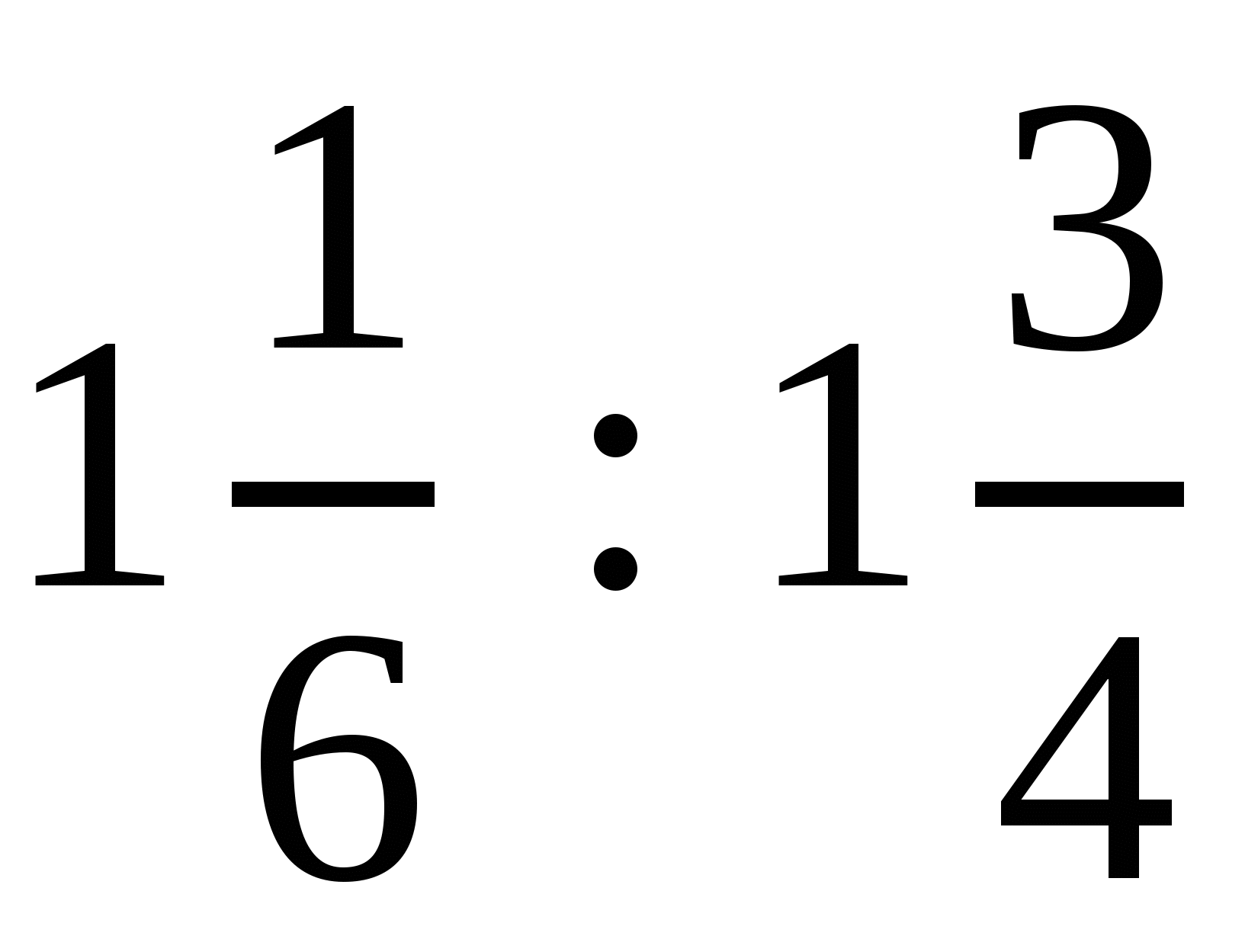 ,
,
 ,
,
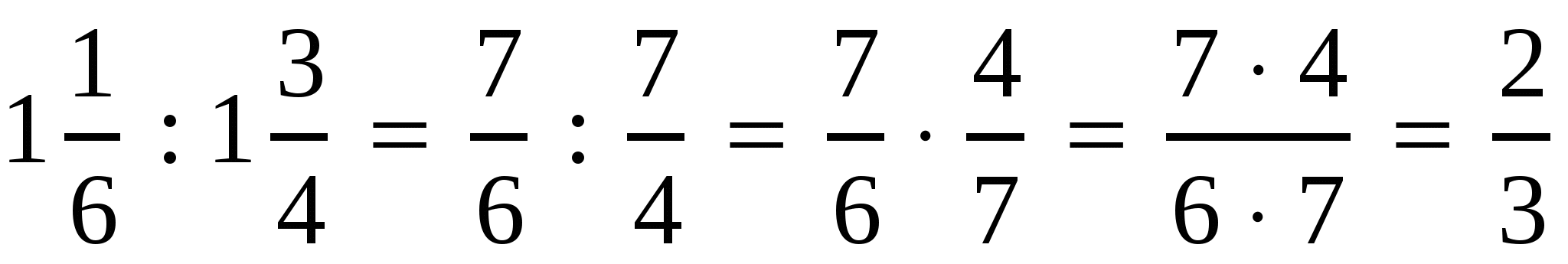 ,
,
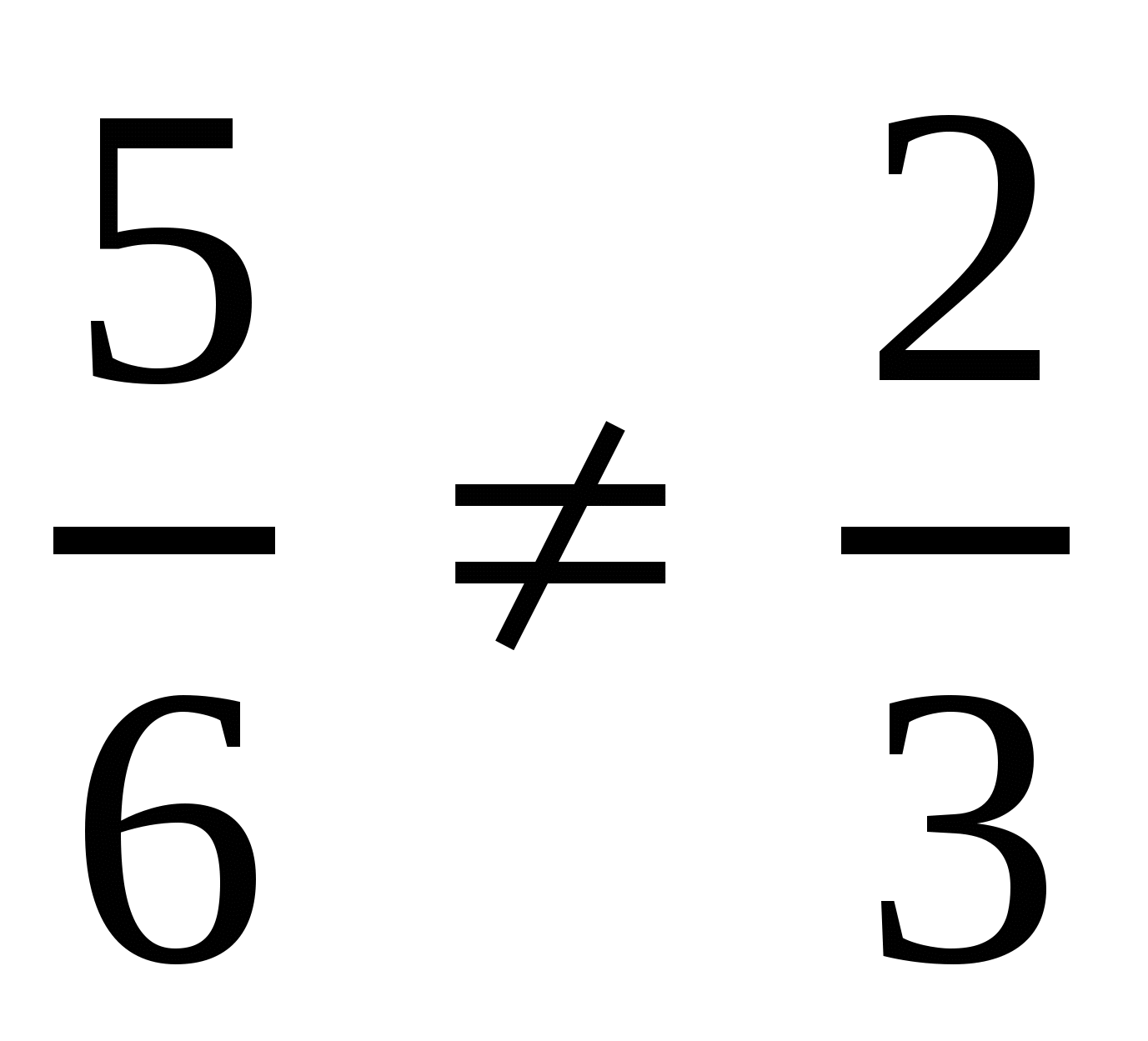 , то составить пропорцию нельзя (по определению пропорции).
, то составить пропорцию нельзя (по определению пропорции).
4. Решить пропорцию:
1) 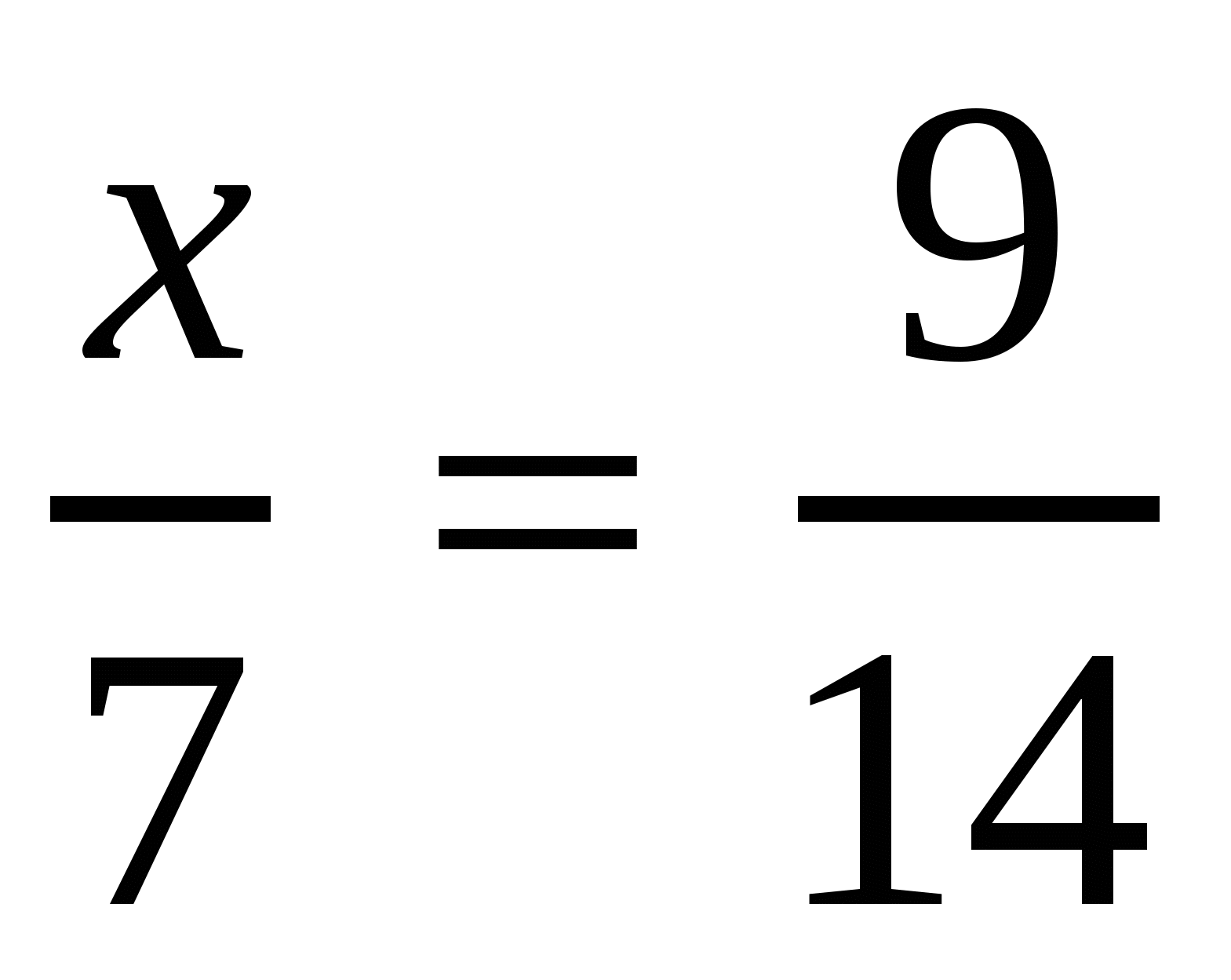 , 2)
, 2) 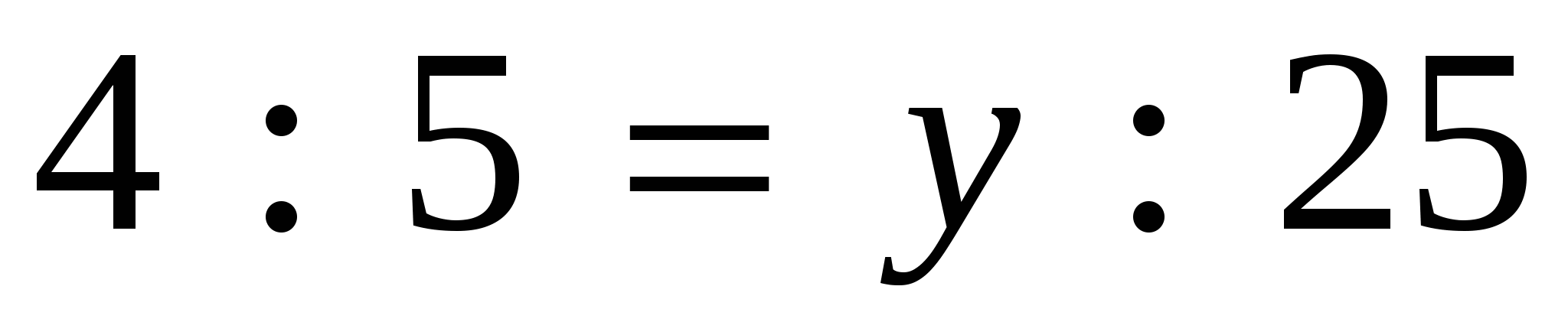 ,
,
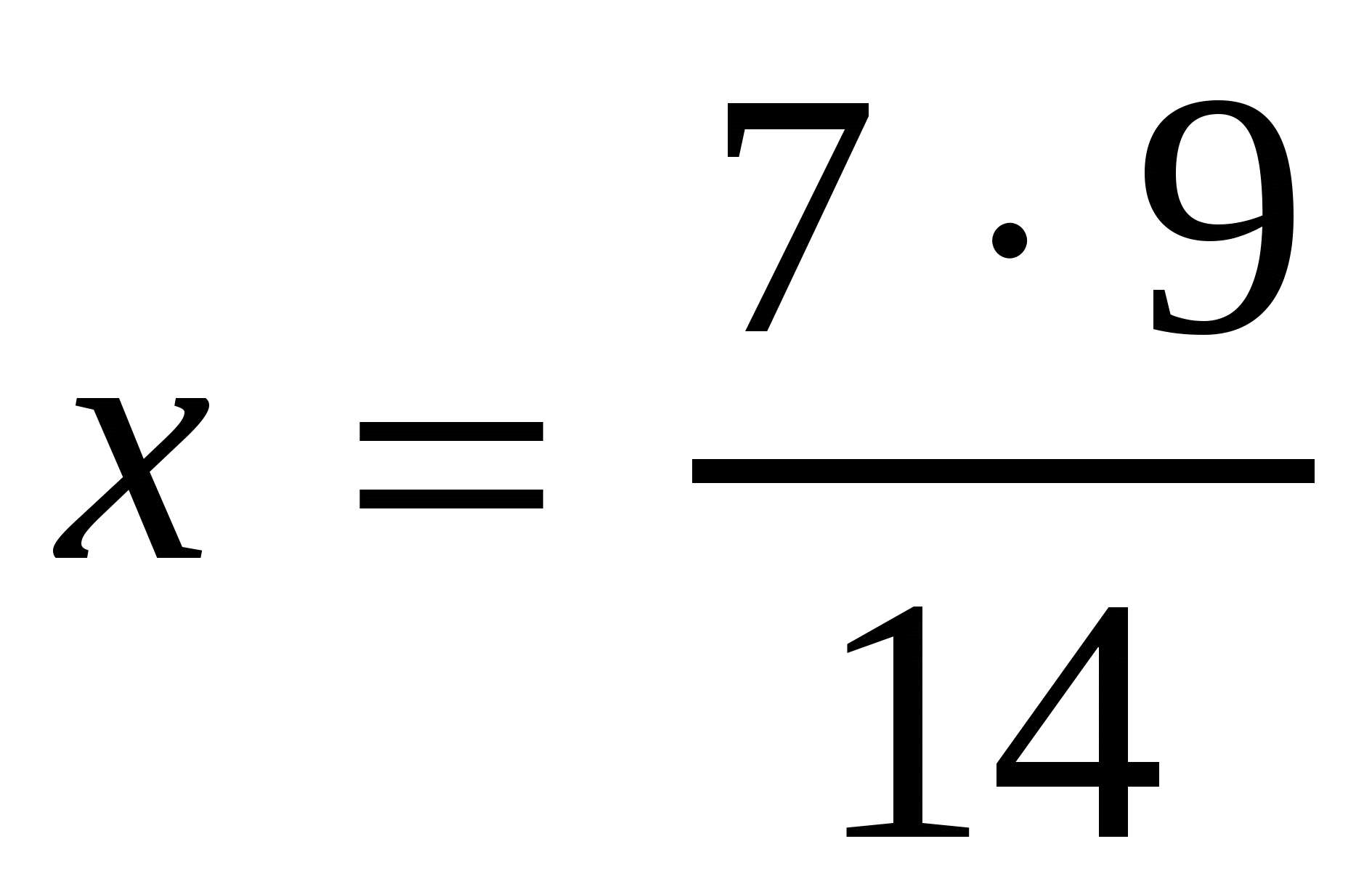 ,
, 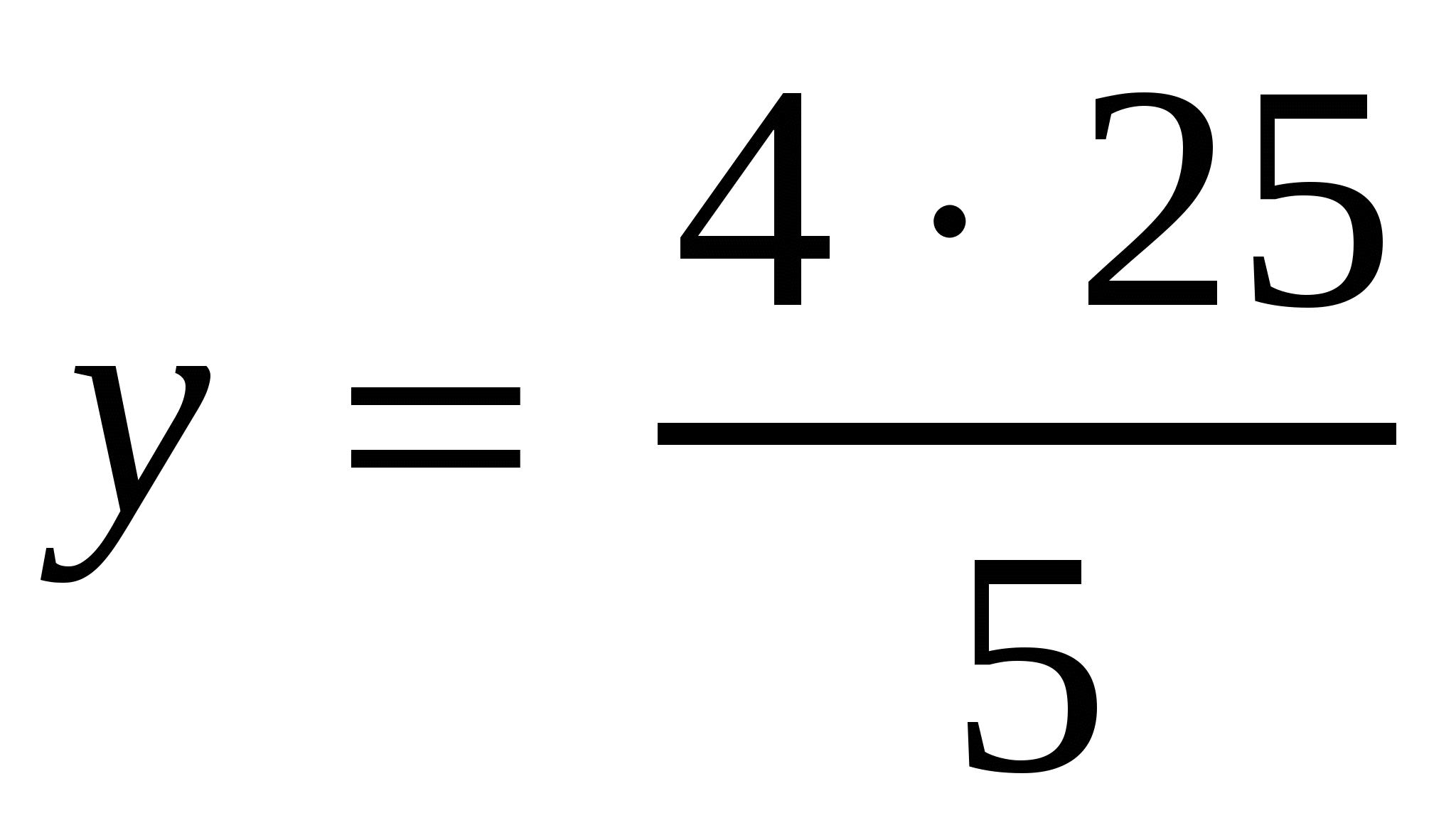 ,
,
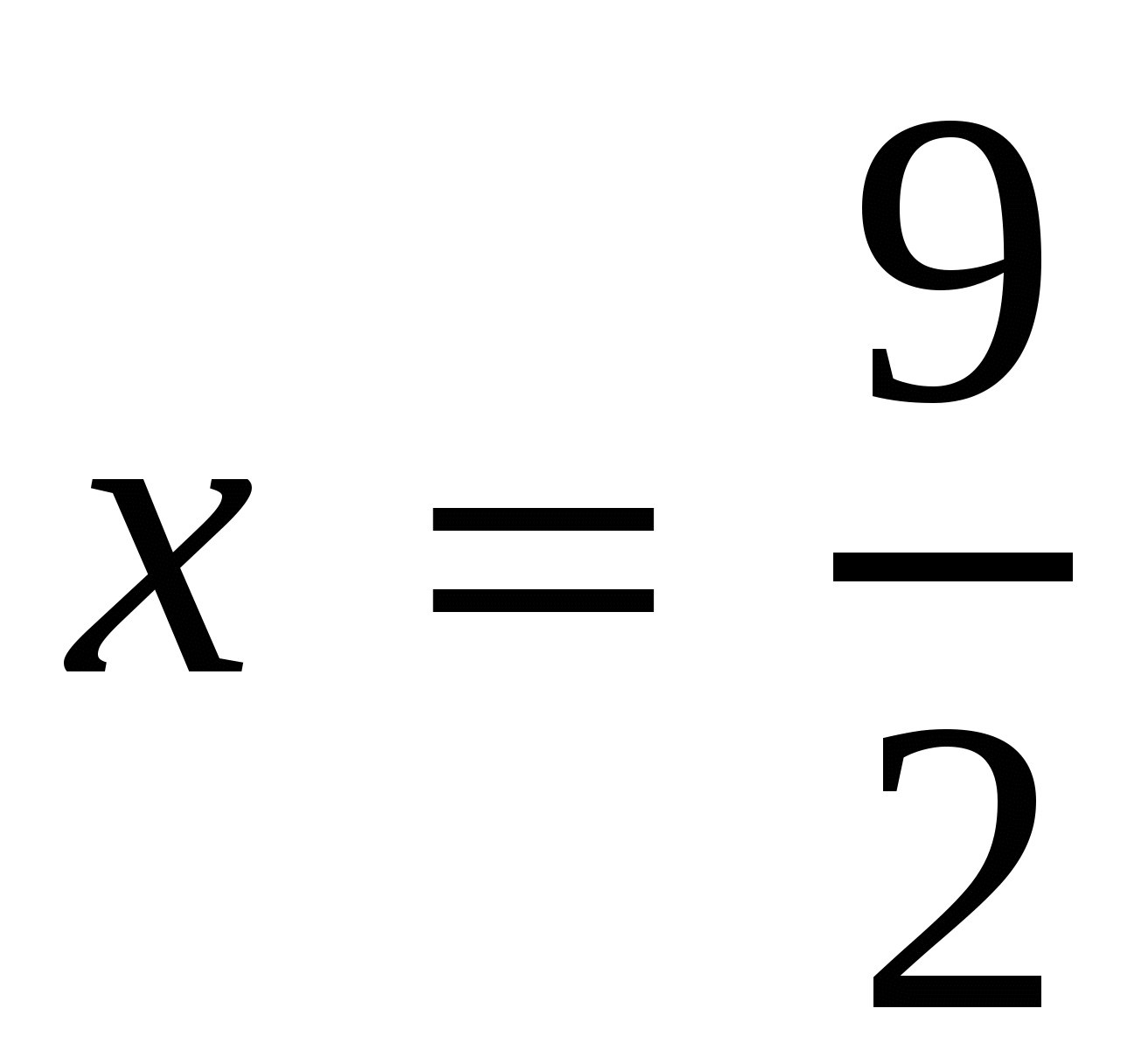 ,
, 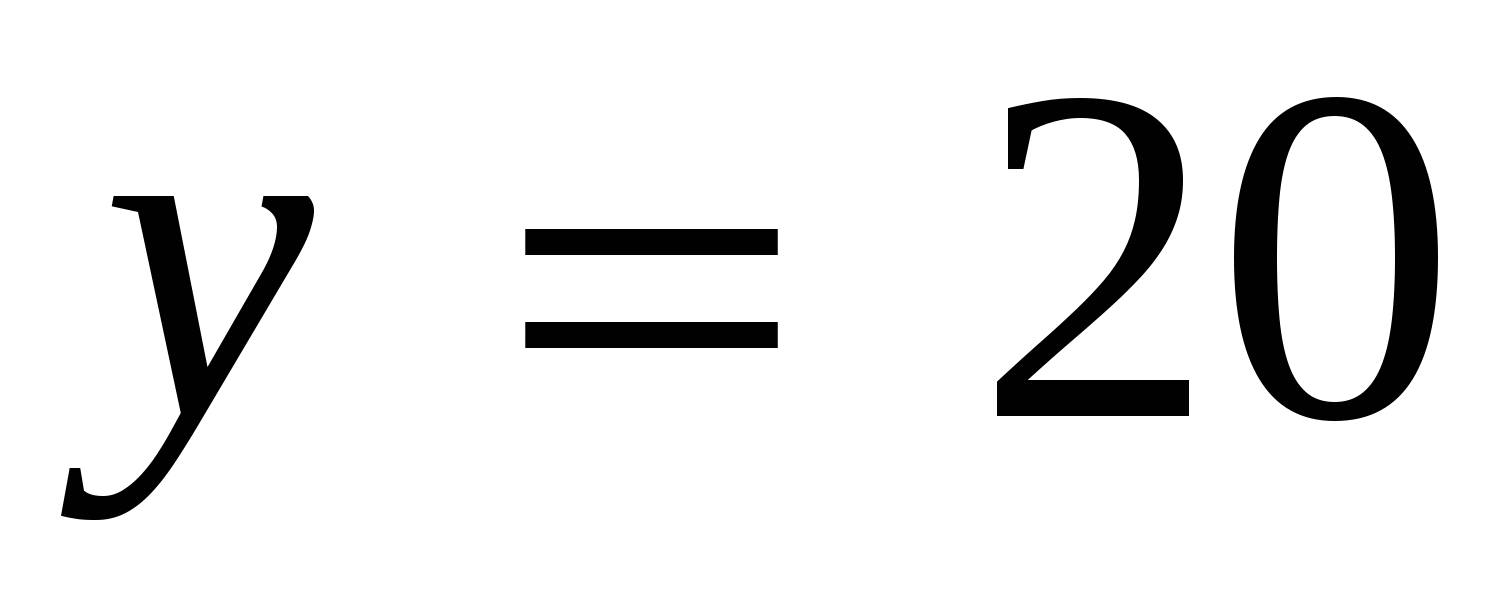 .
.
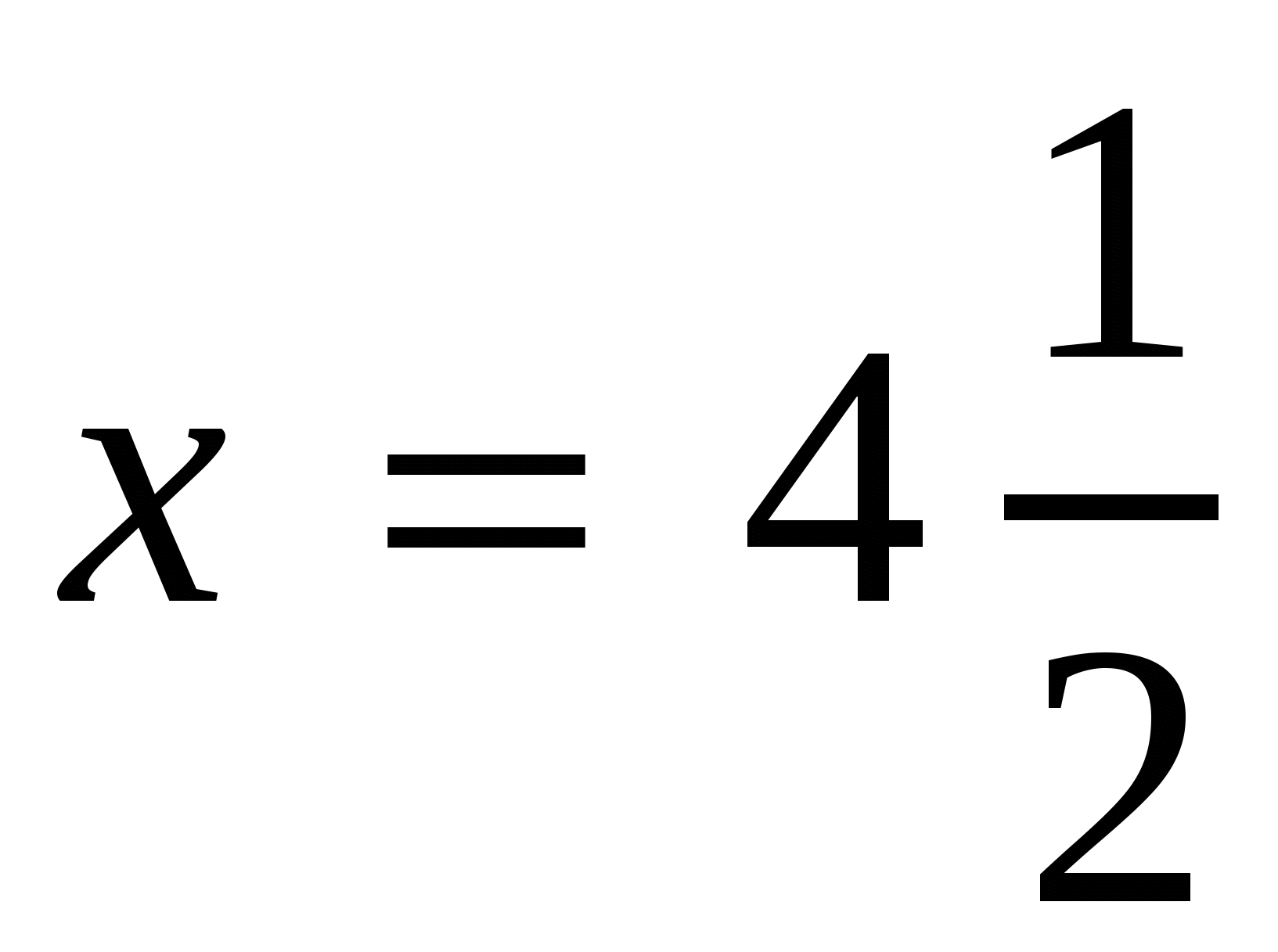 . Ответ:
. Ответ: 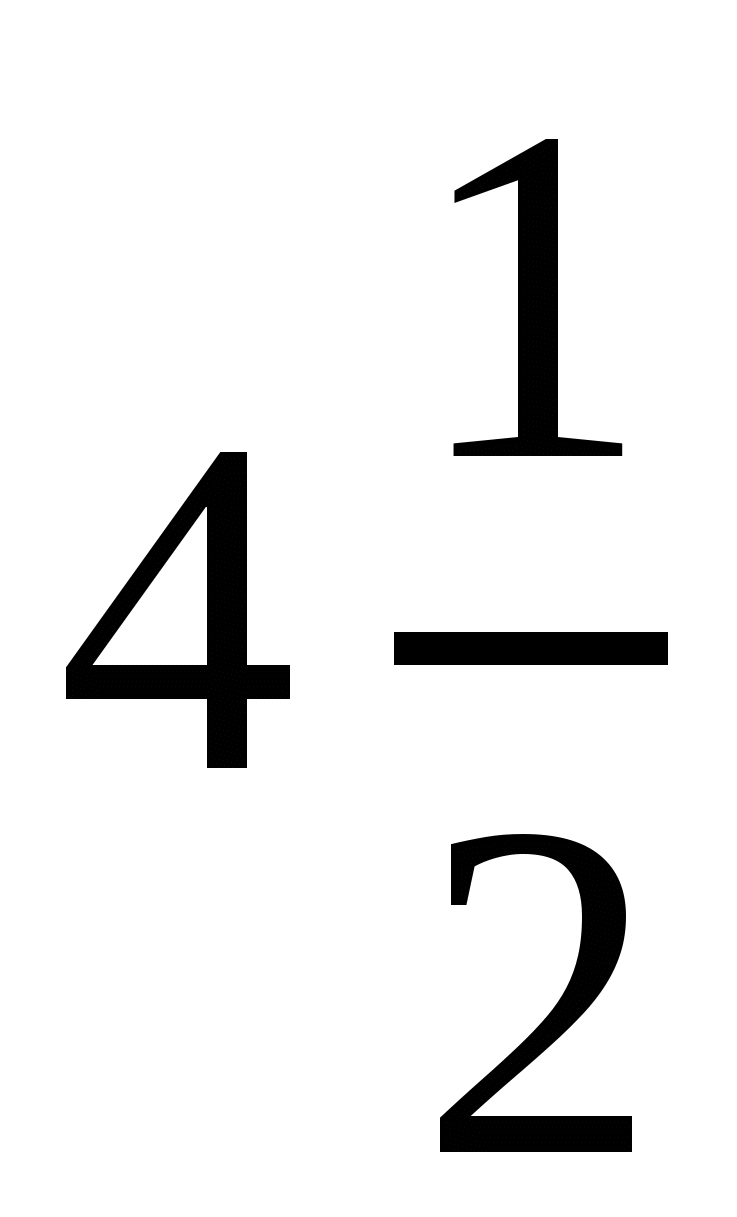 . Ответ:
. Ответ: 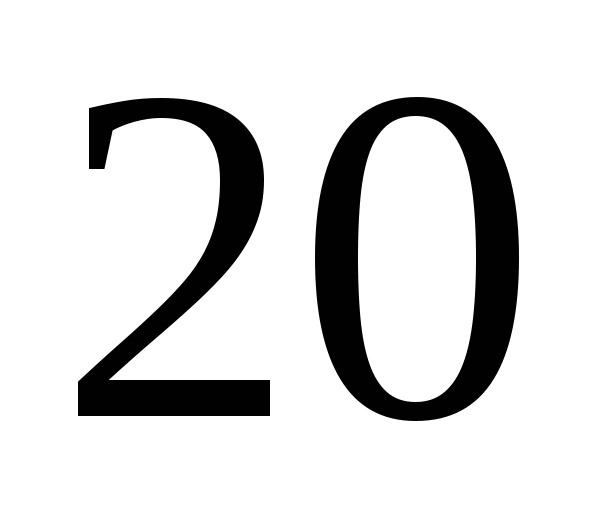 .
.
Уч.с.17 № 60(а,в). Решить пропорцию:
а)  , в)
, в) 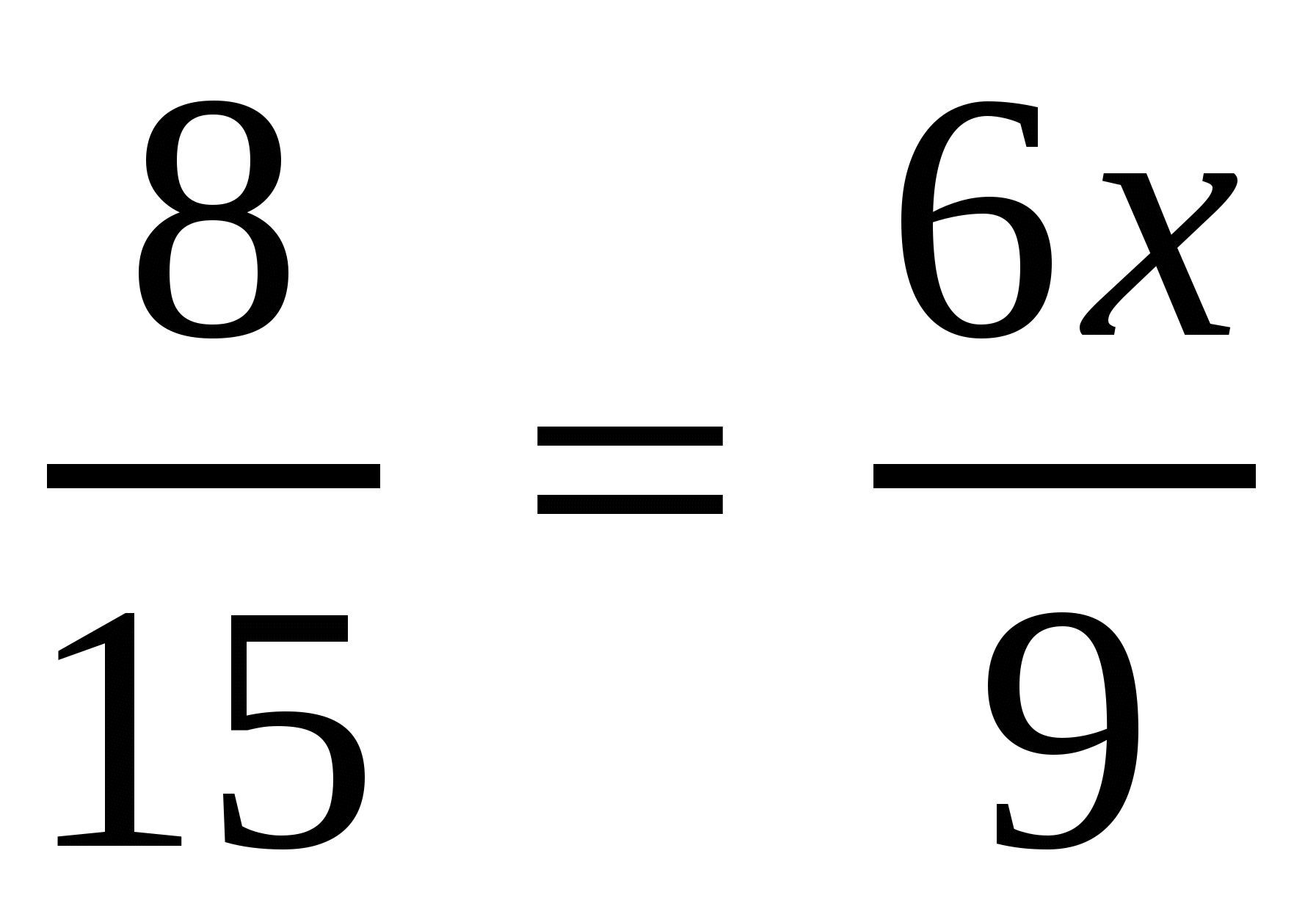 ,
,
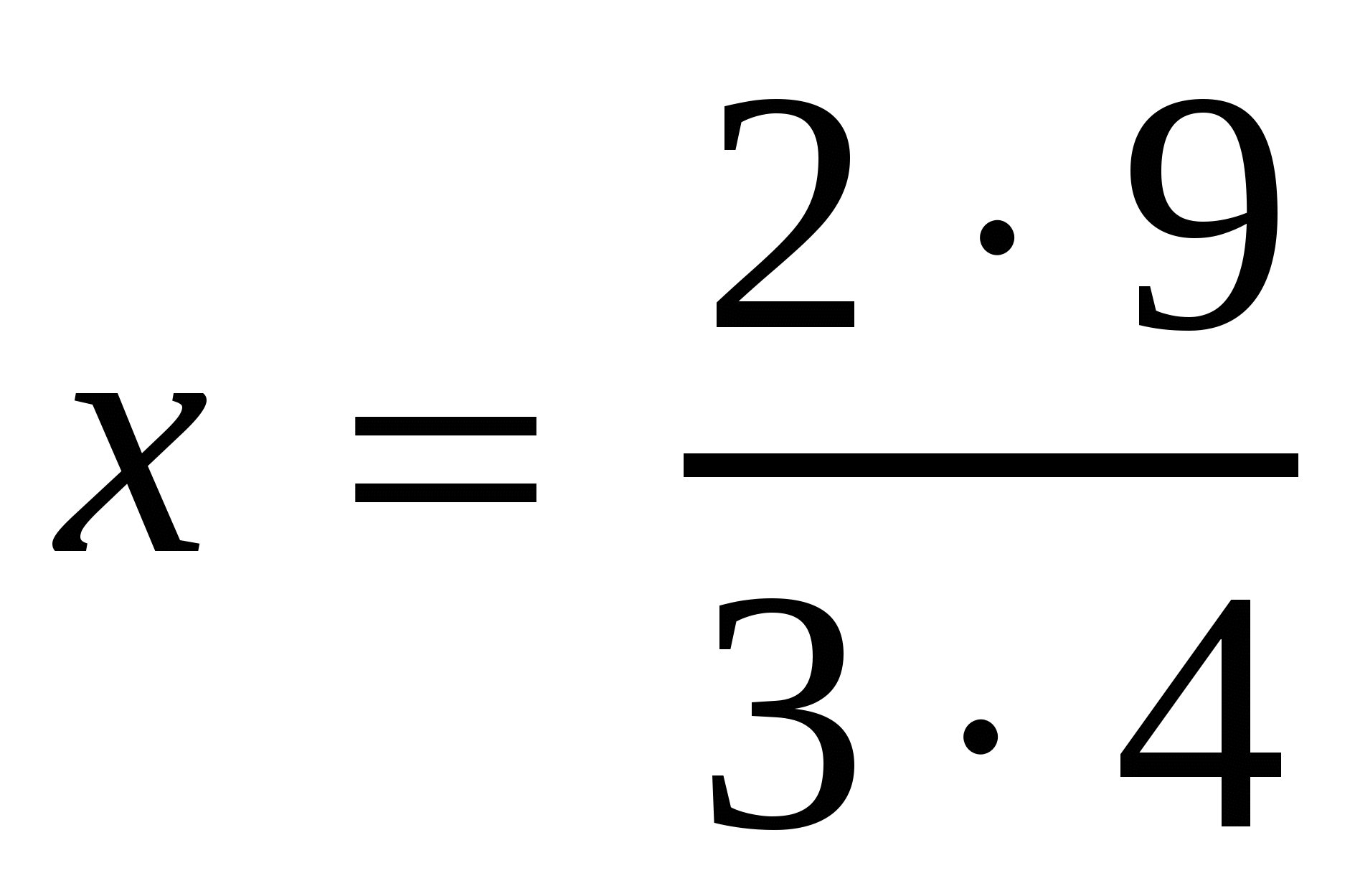 ,
,  ,
,
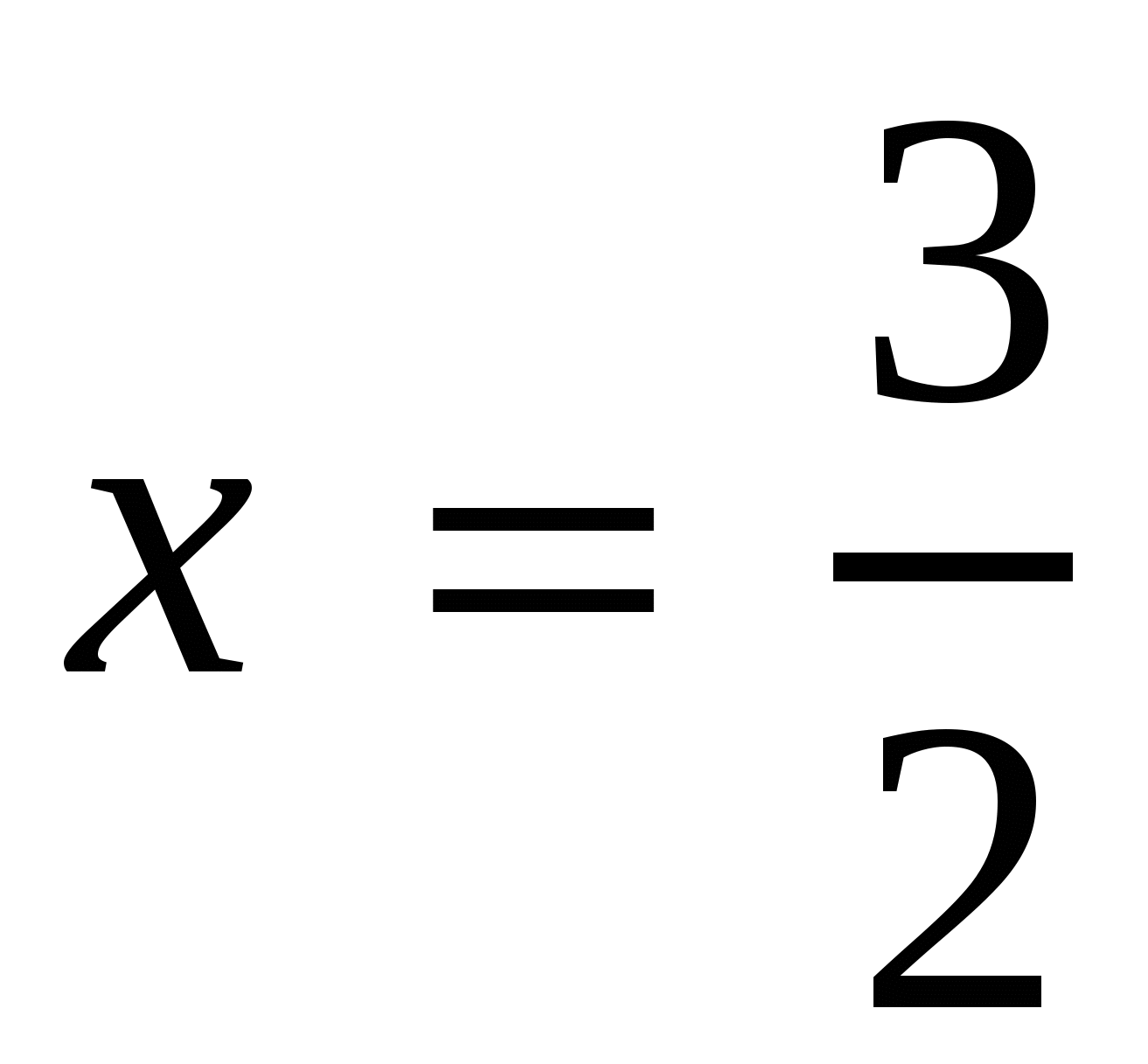 ,
, 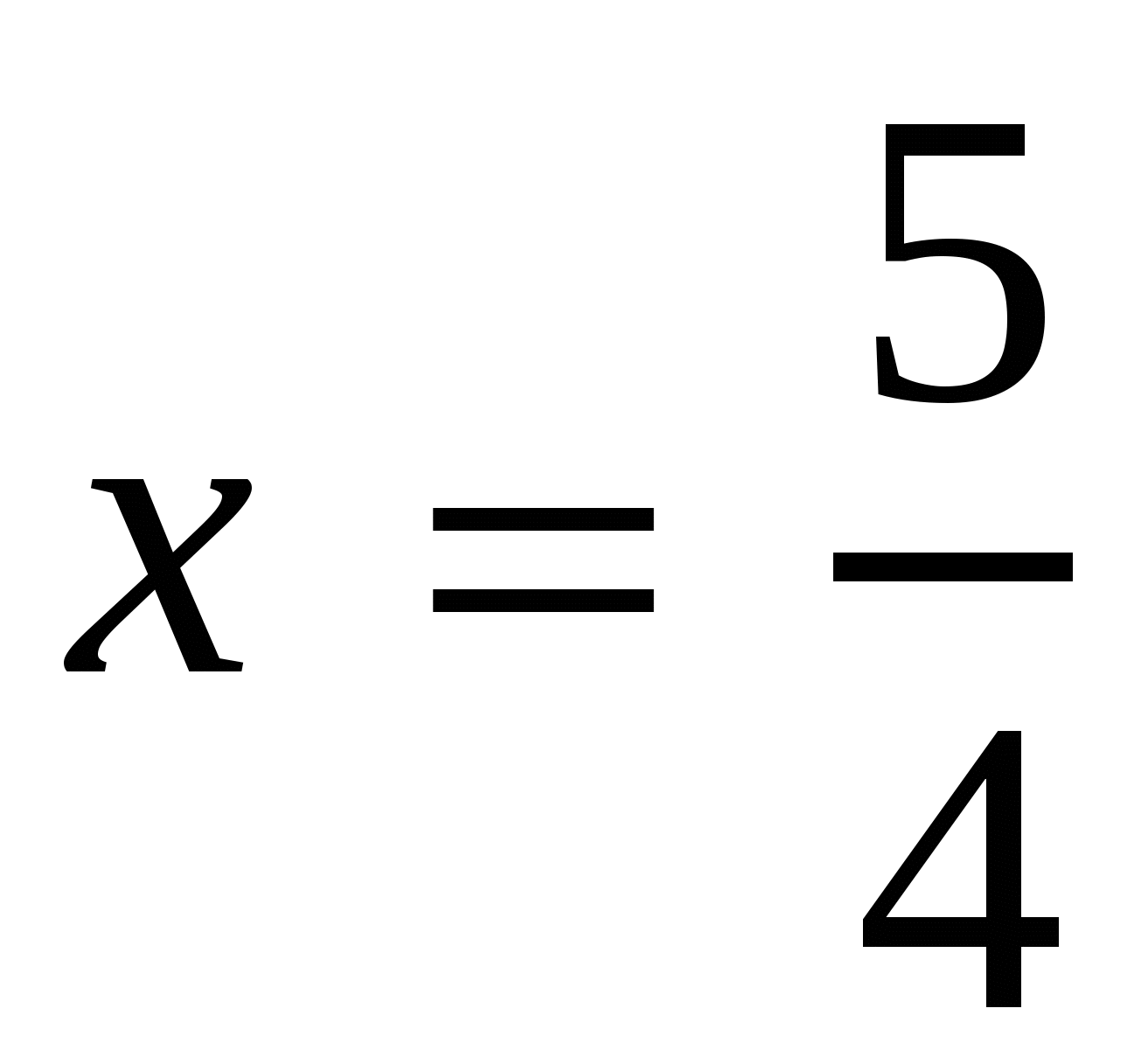 ,
,
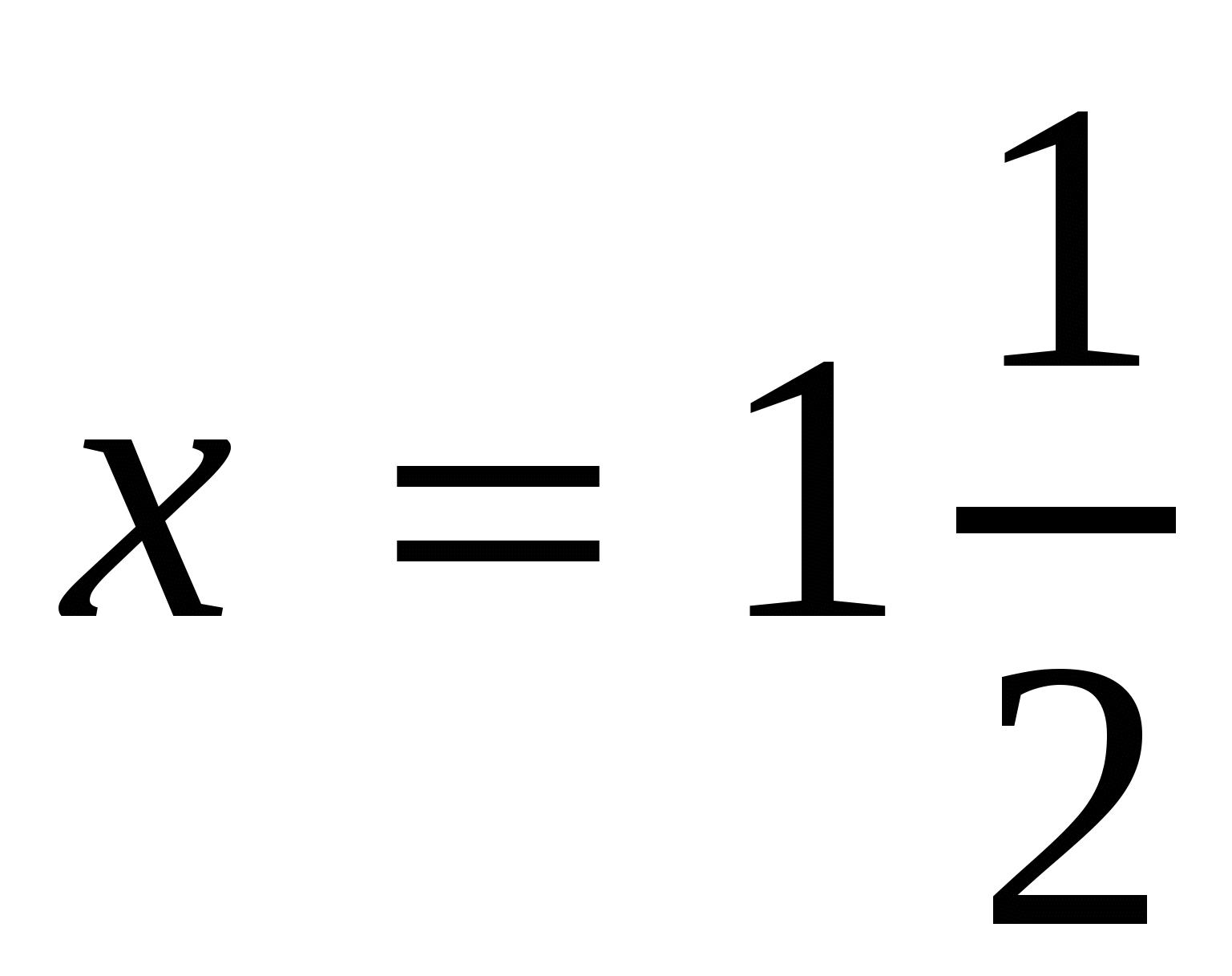 . Ответ:
. Ответ: 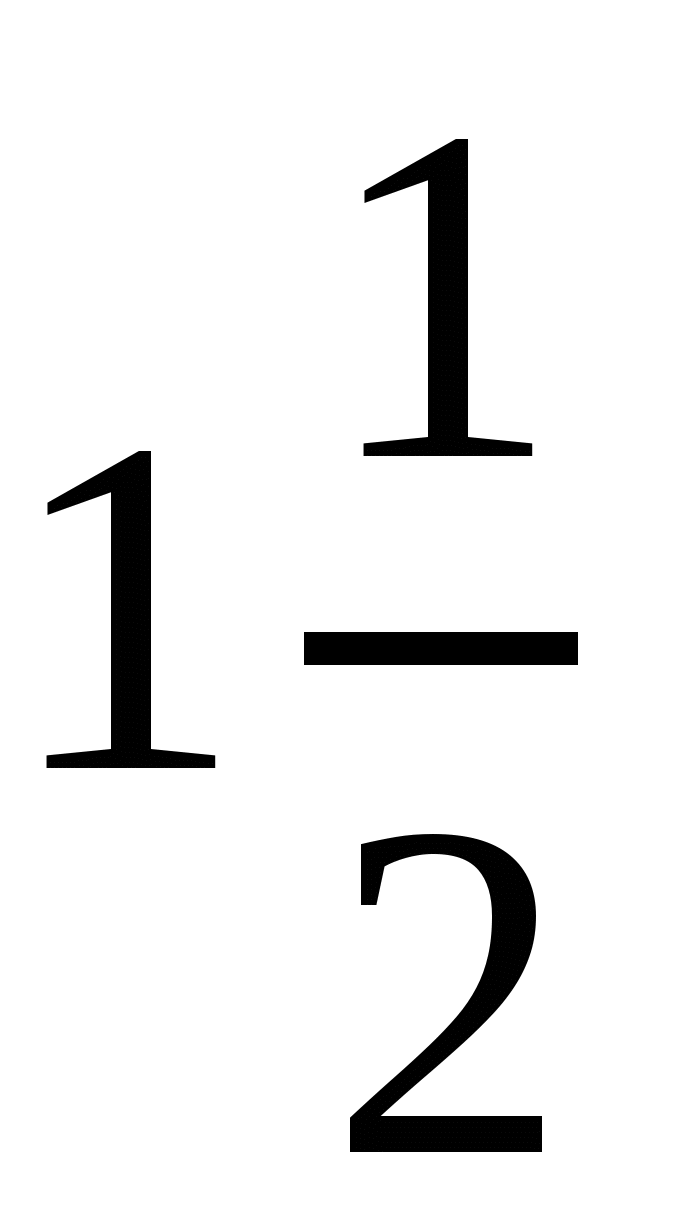 .
. 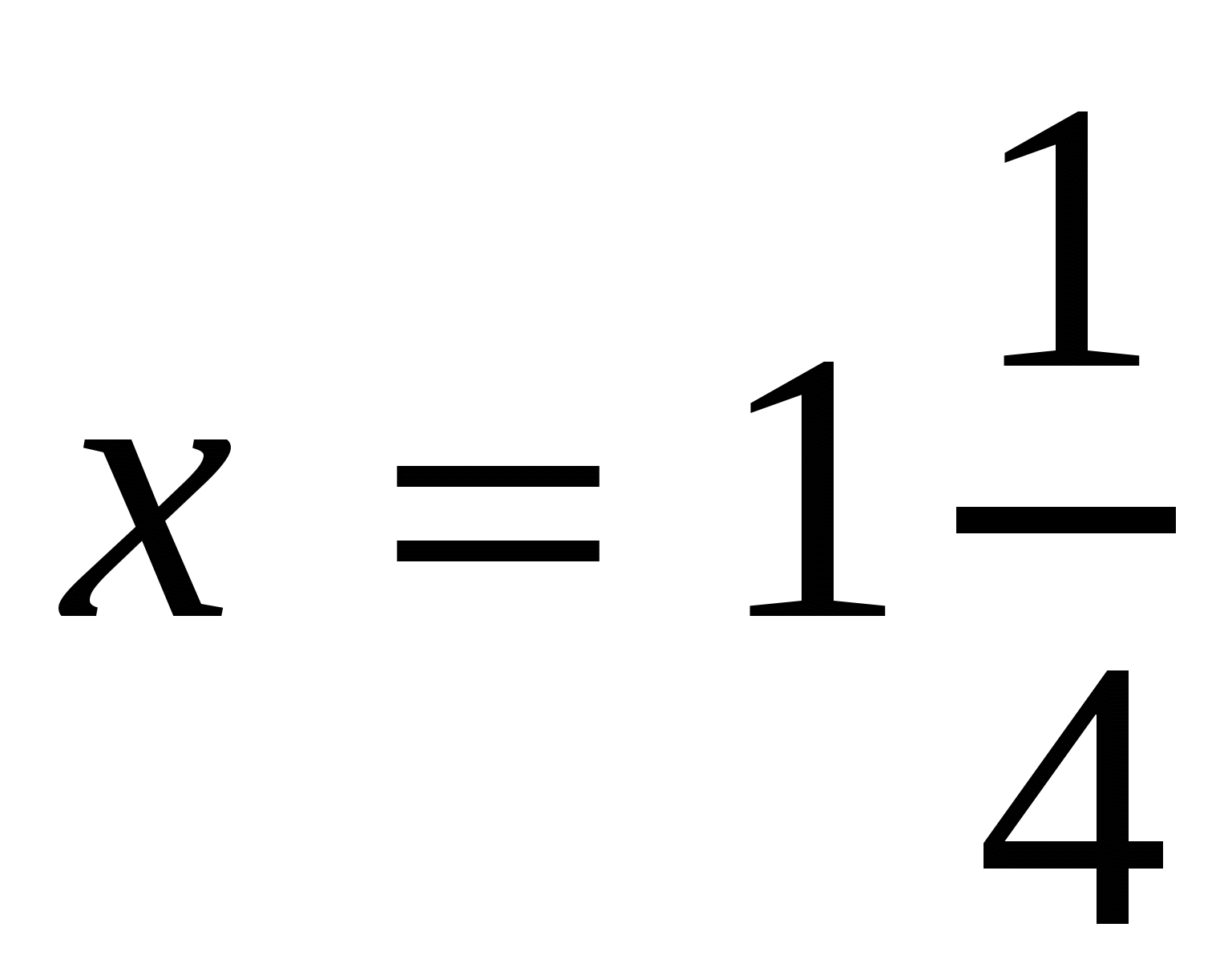 . Ответ:
. Ответ: 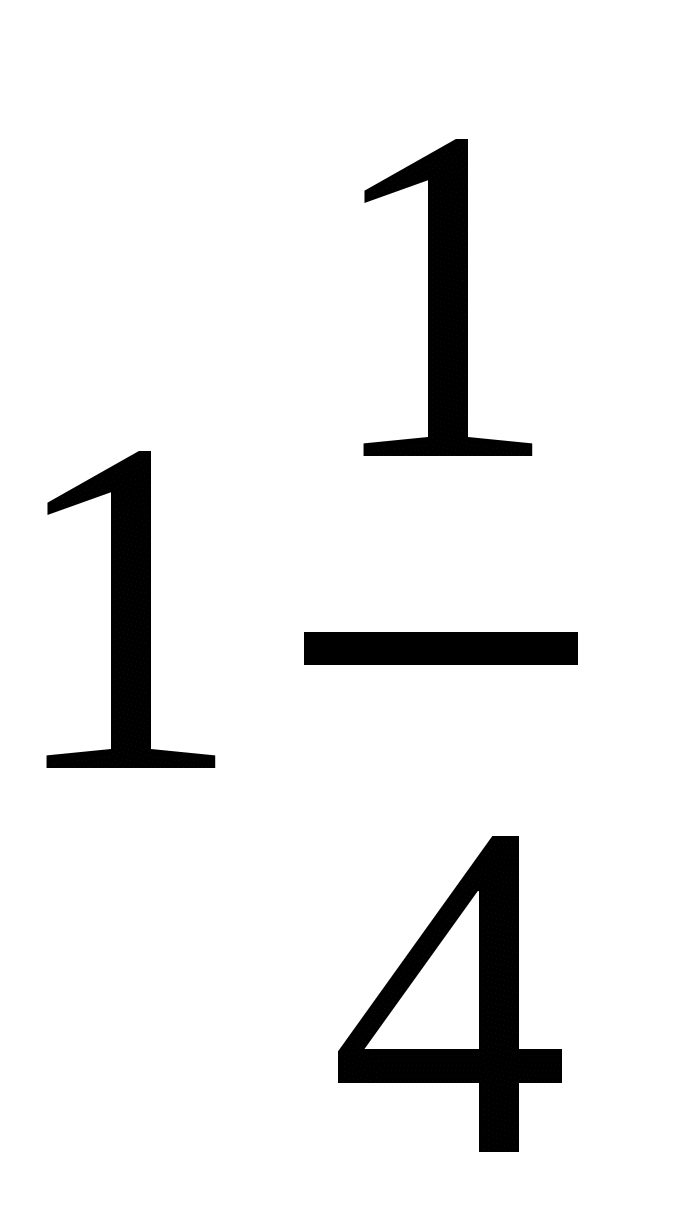 .
.
Уч.с.17 № 61(а,в). Решить пропорцию:
а) 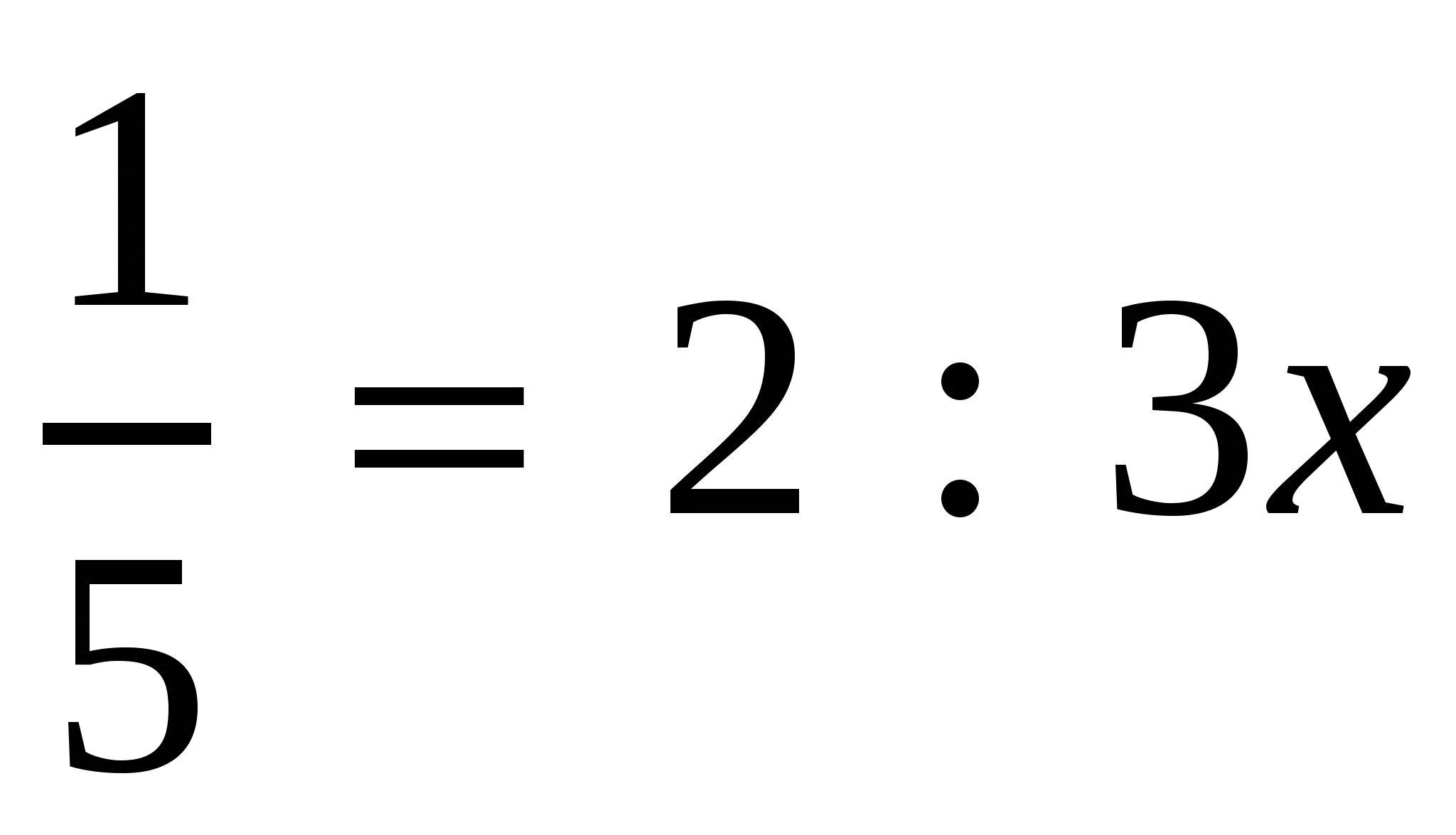 , в)
, в) 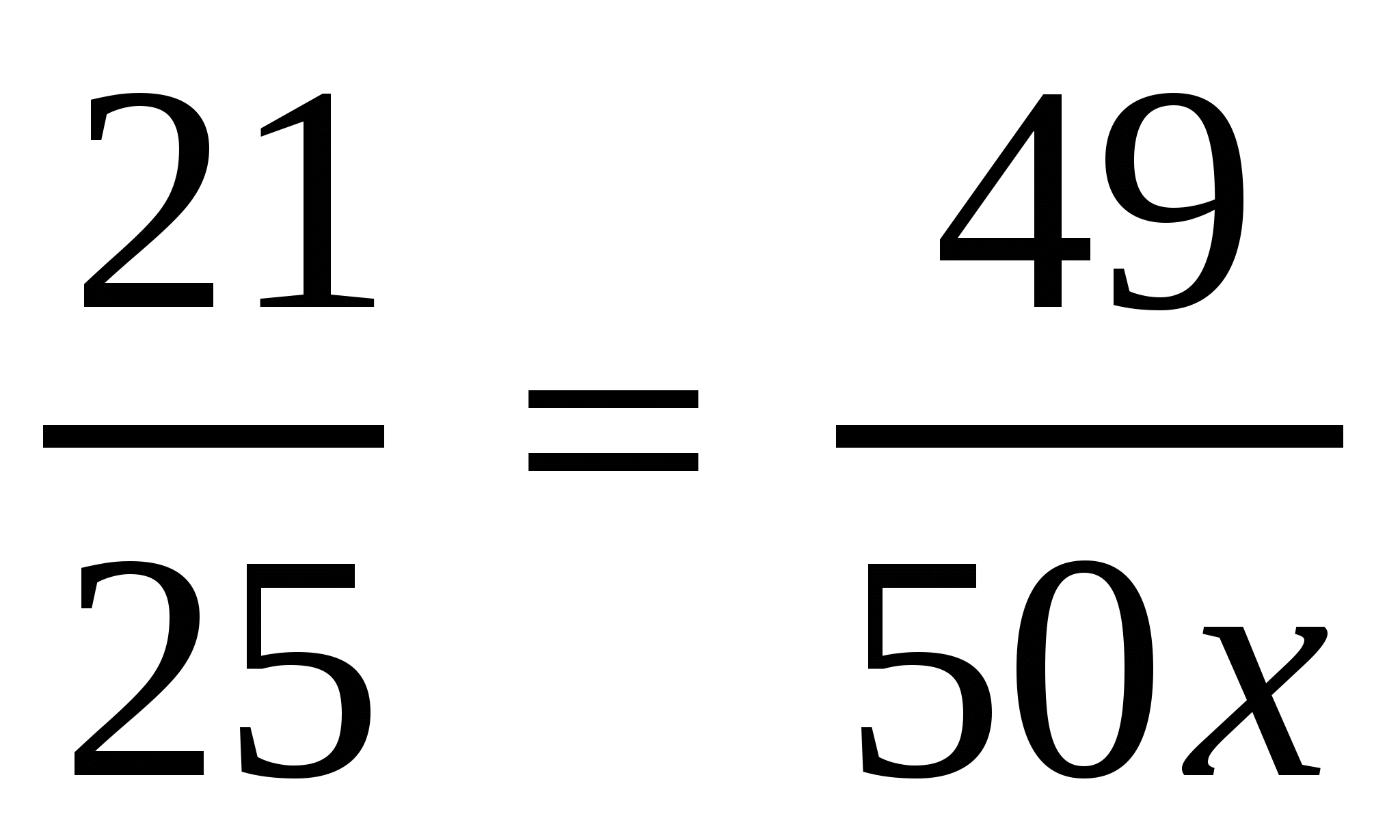 ,
,
 ,
, 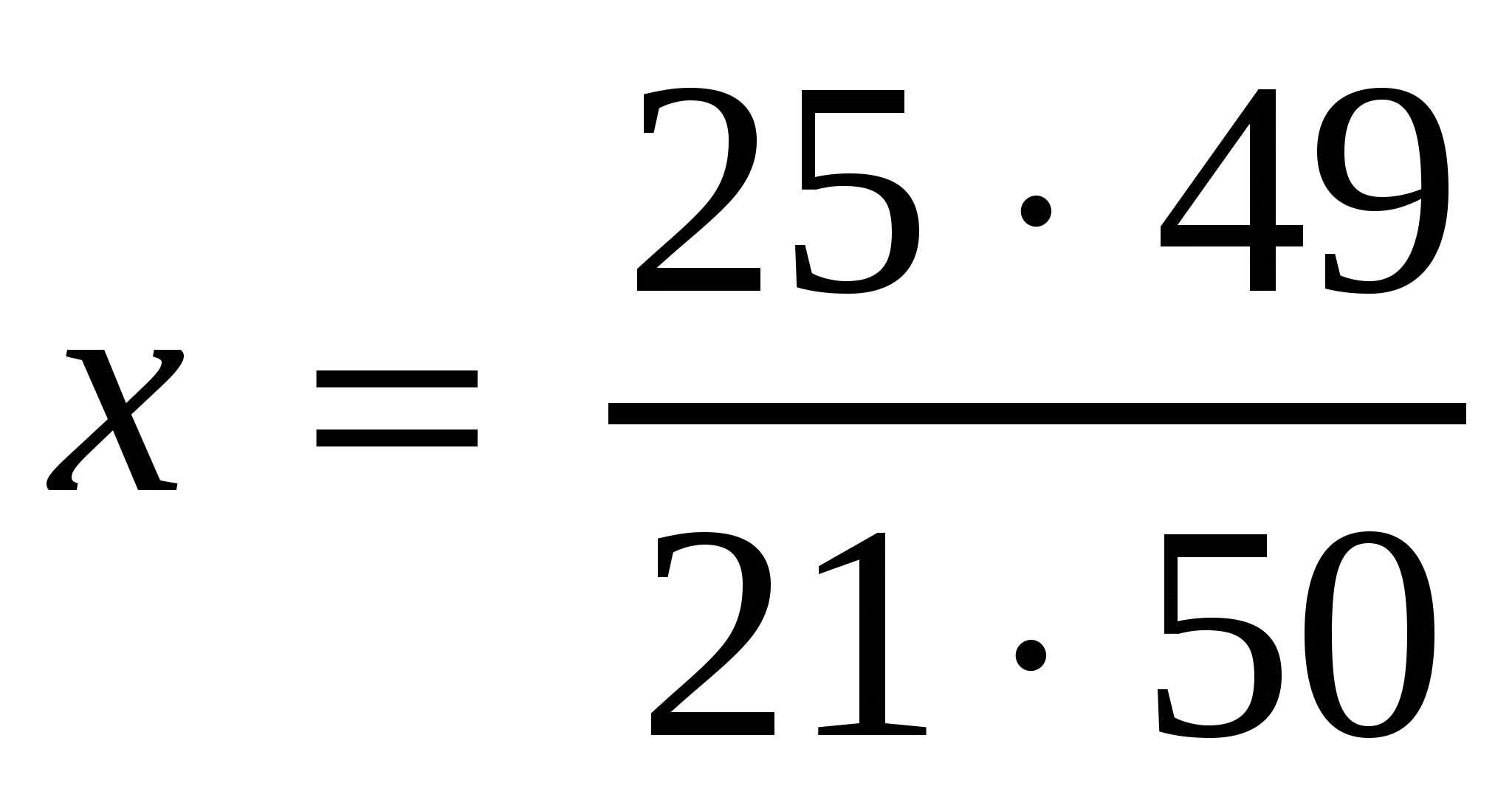
 ,
, 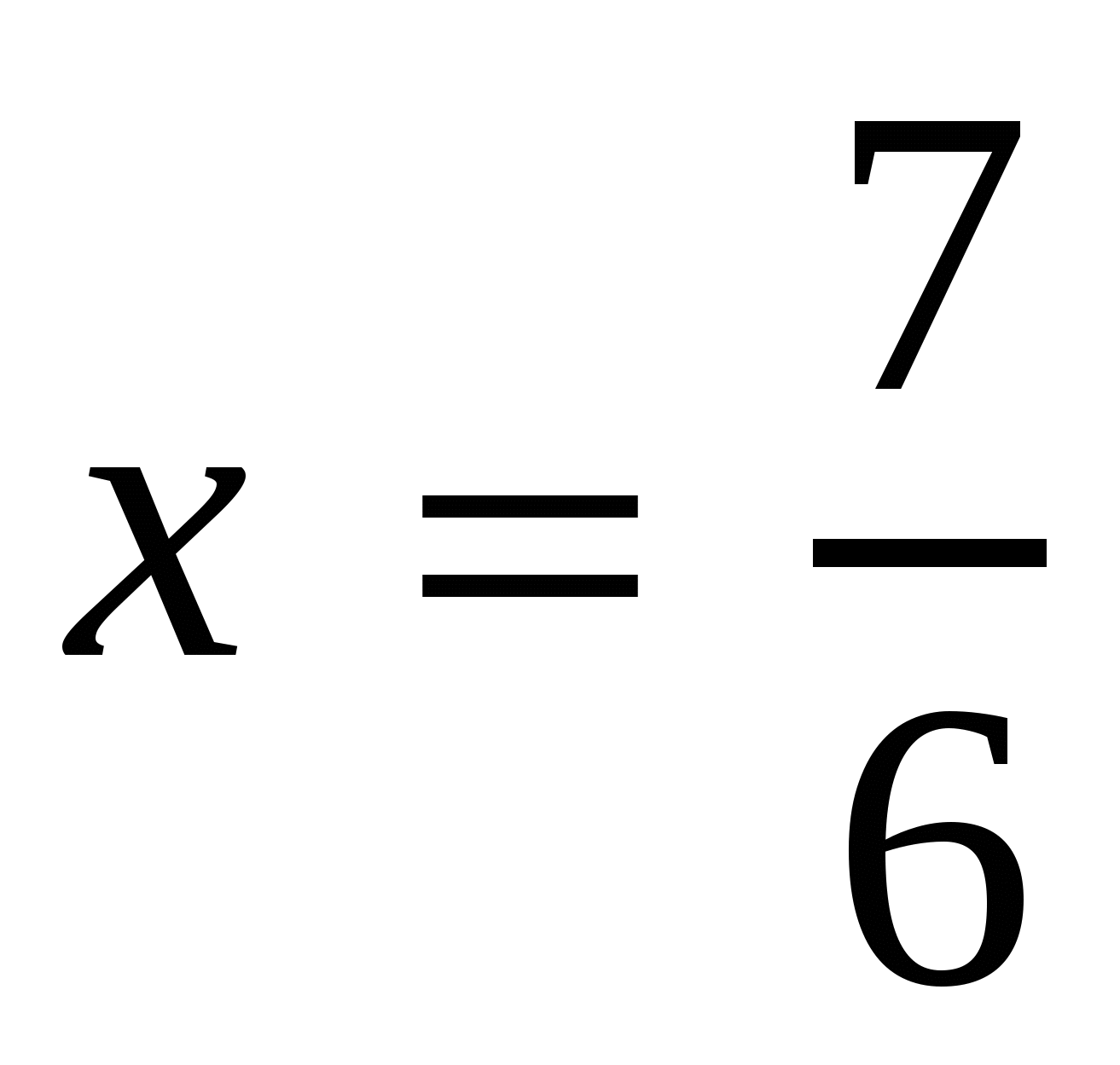
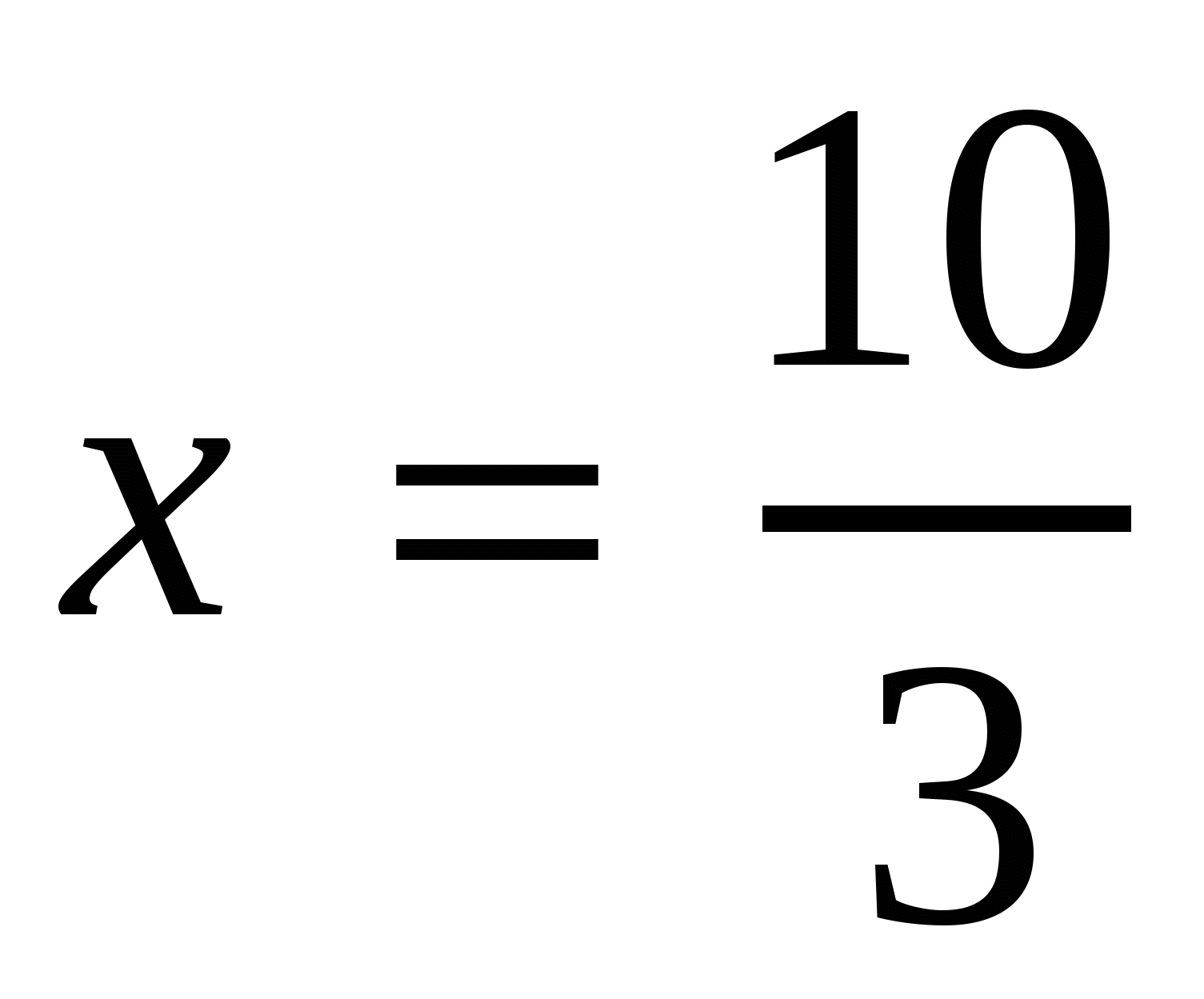 ,
, 
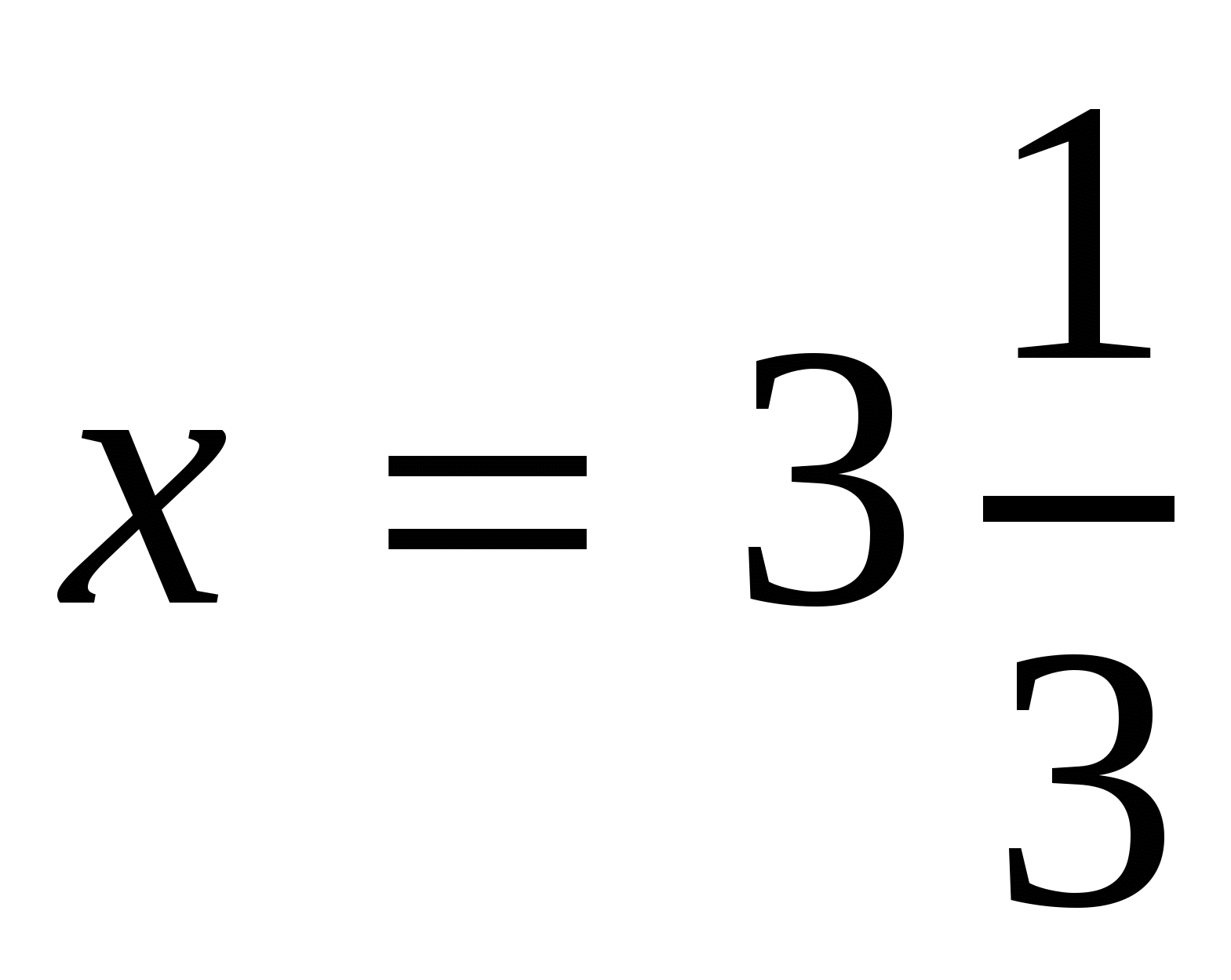 . Ответ:
. Ответ: 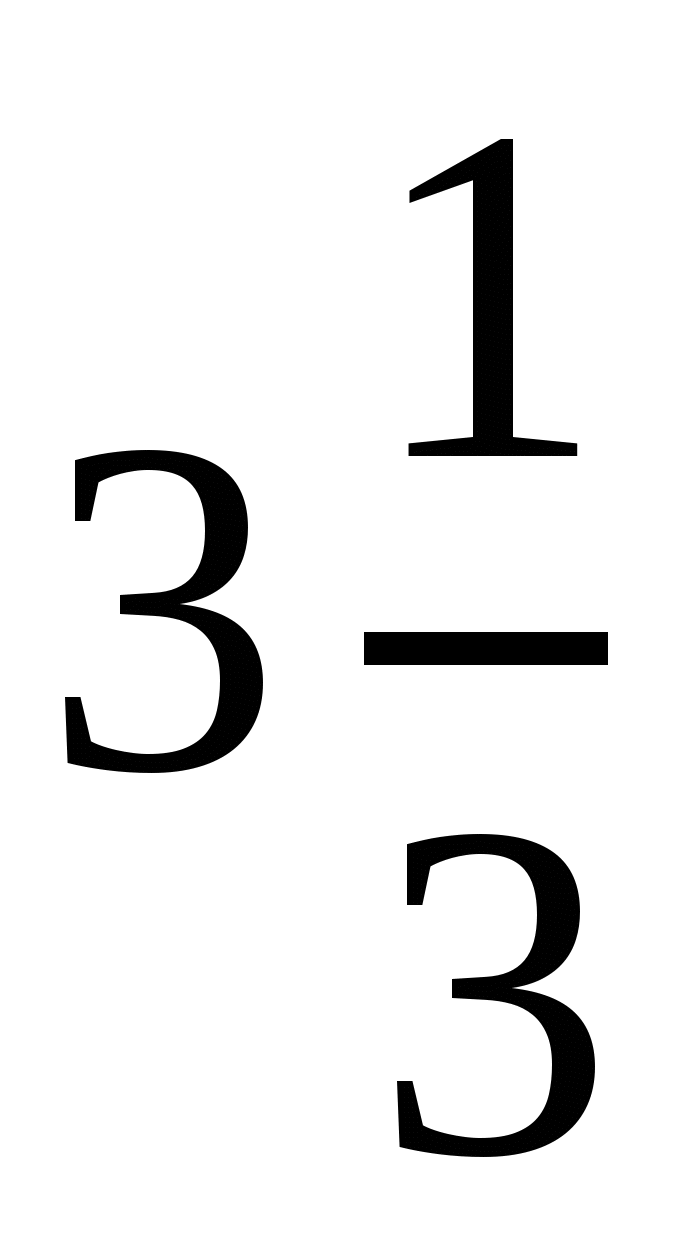 . Ответ:
. Ответ: 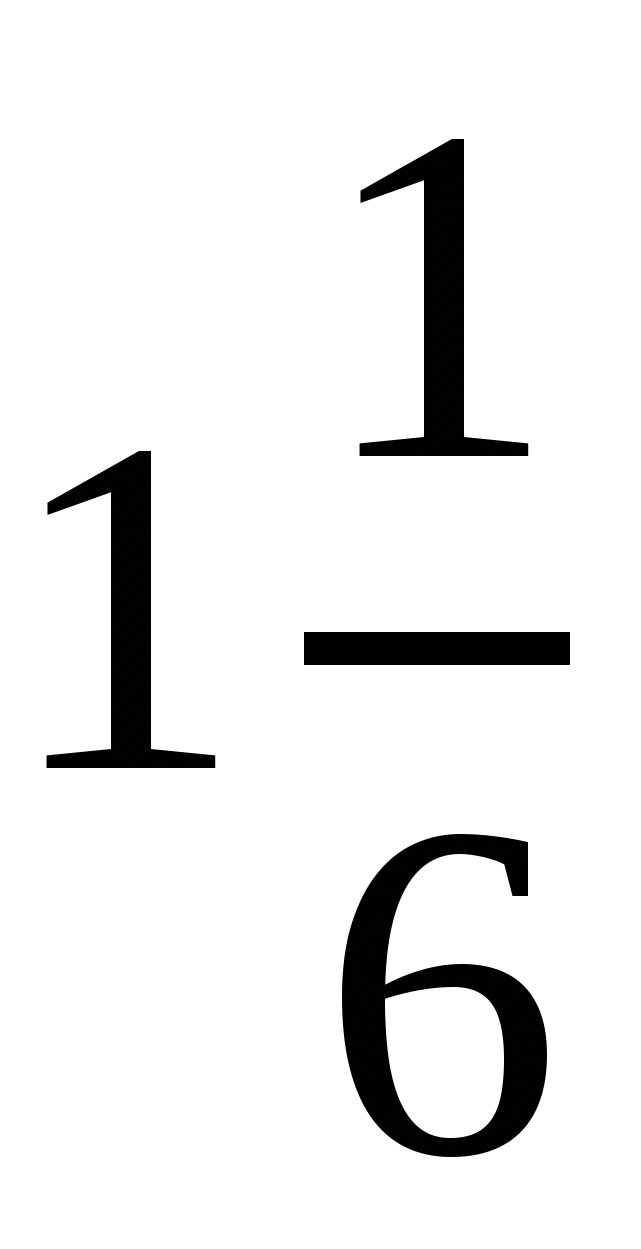 .
.
Подведение итогов урока.
Домашнее задание. § 1.4 (повторить теорию). № 53(г), 60(б,г), 61(б,г), 28(а) (прокомментировать Мультимедийная доска. Электронное приложение. Каталог. Анимация. Решение задачи 28(а) (32 секунды)).
(На следующем уроке с/р по теме «Пропорции»)
Урок 11. Пропорции.
1. Упростите отношение:
1) 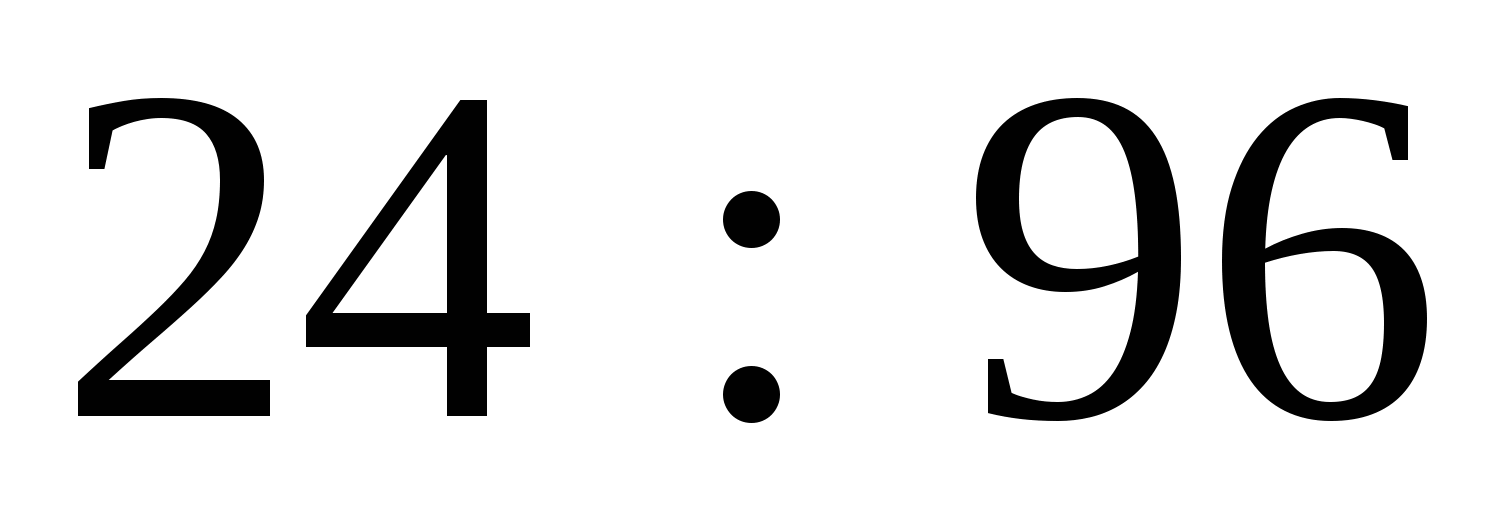 ; 3)
; 3) 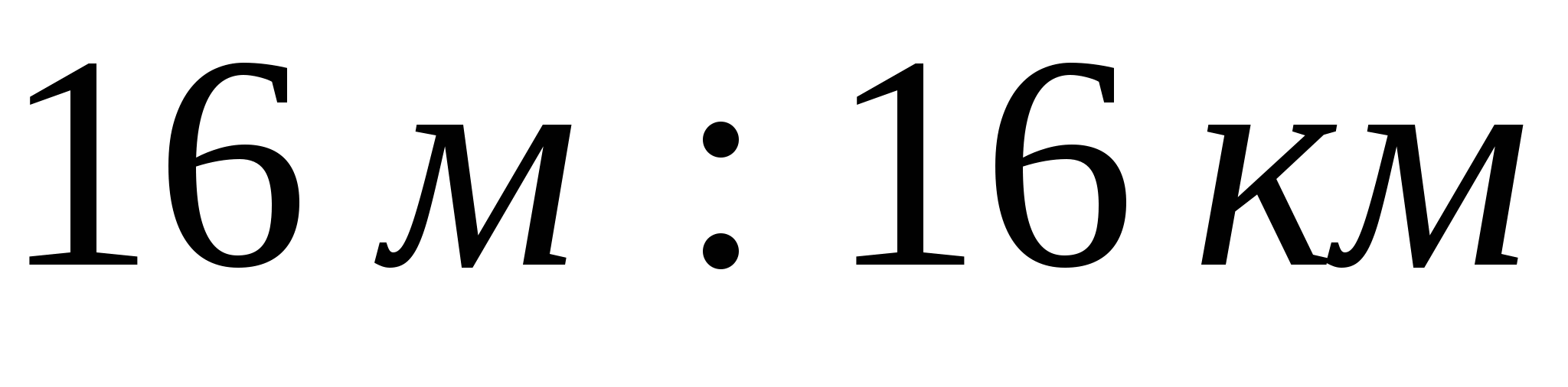 ;
;
2) 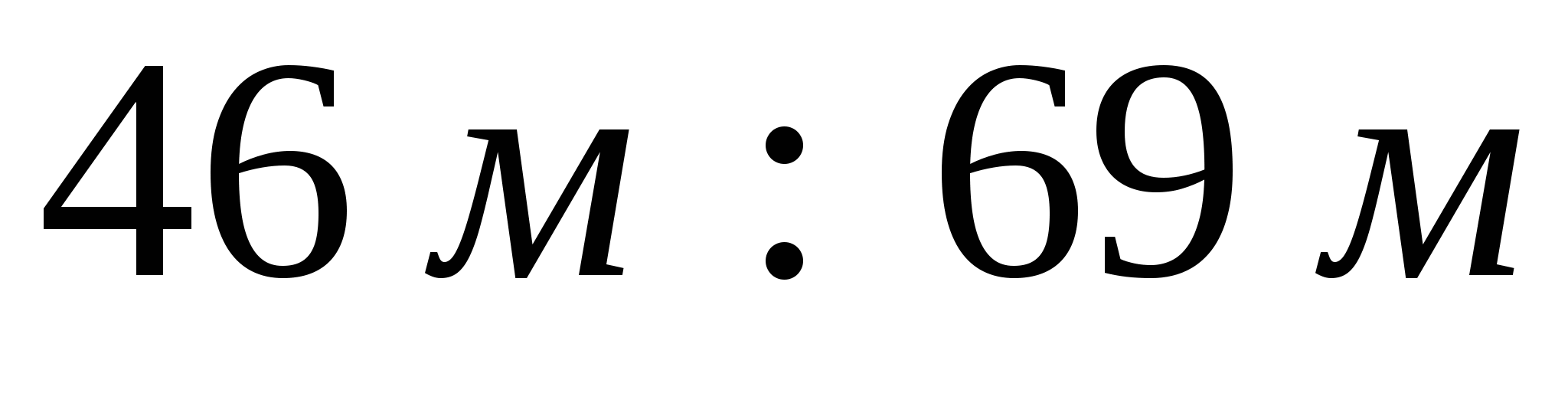 ; 4)
; 4)  .
.
2. Используя числа 56; 15; 8; 105, составьте пропорцию.
3. Вычислив данные отношения, установите, можно ли из них составить пропорцию: 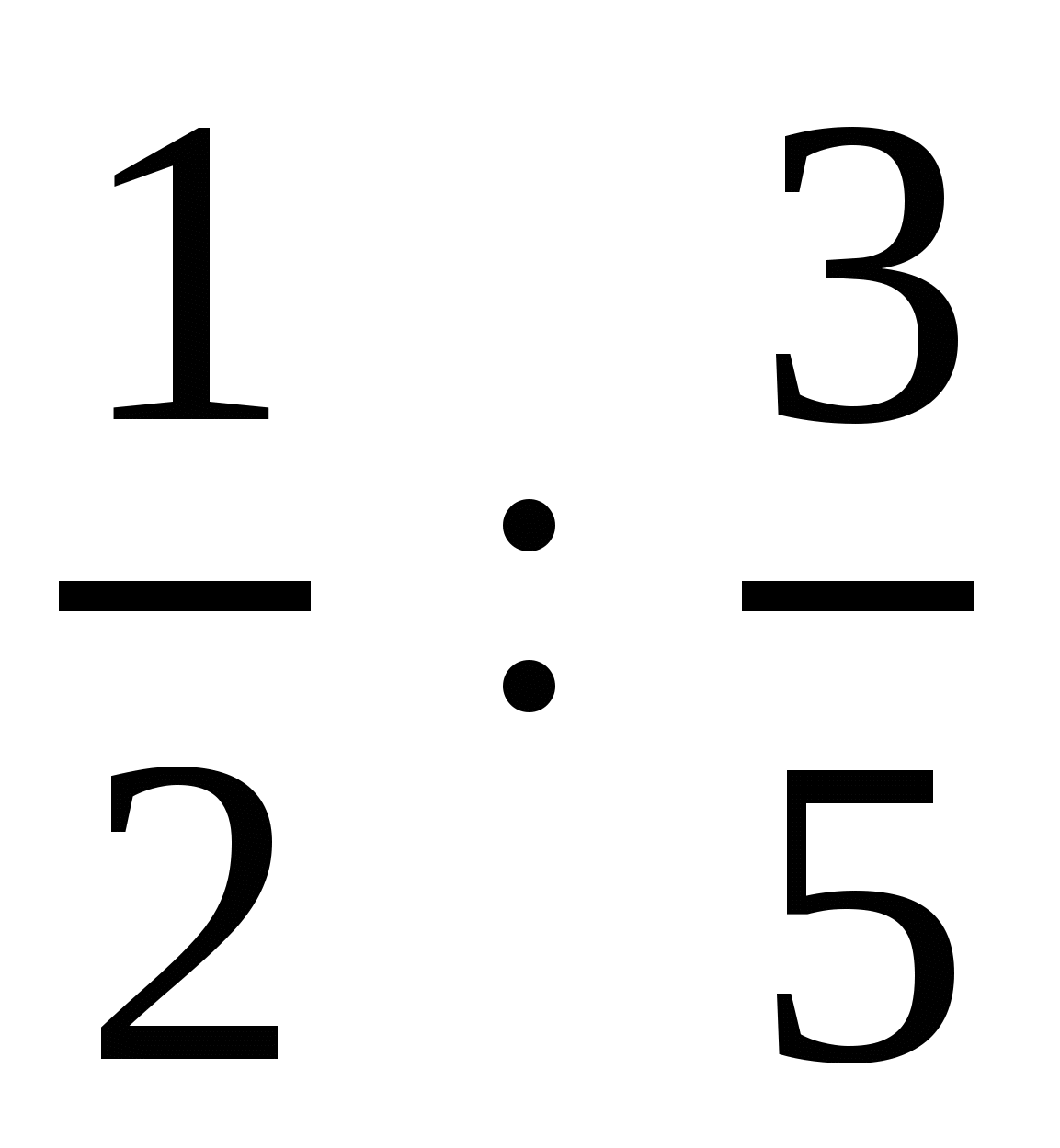 и
и 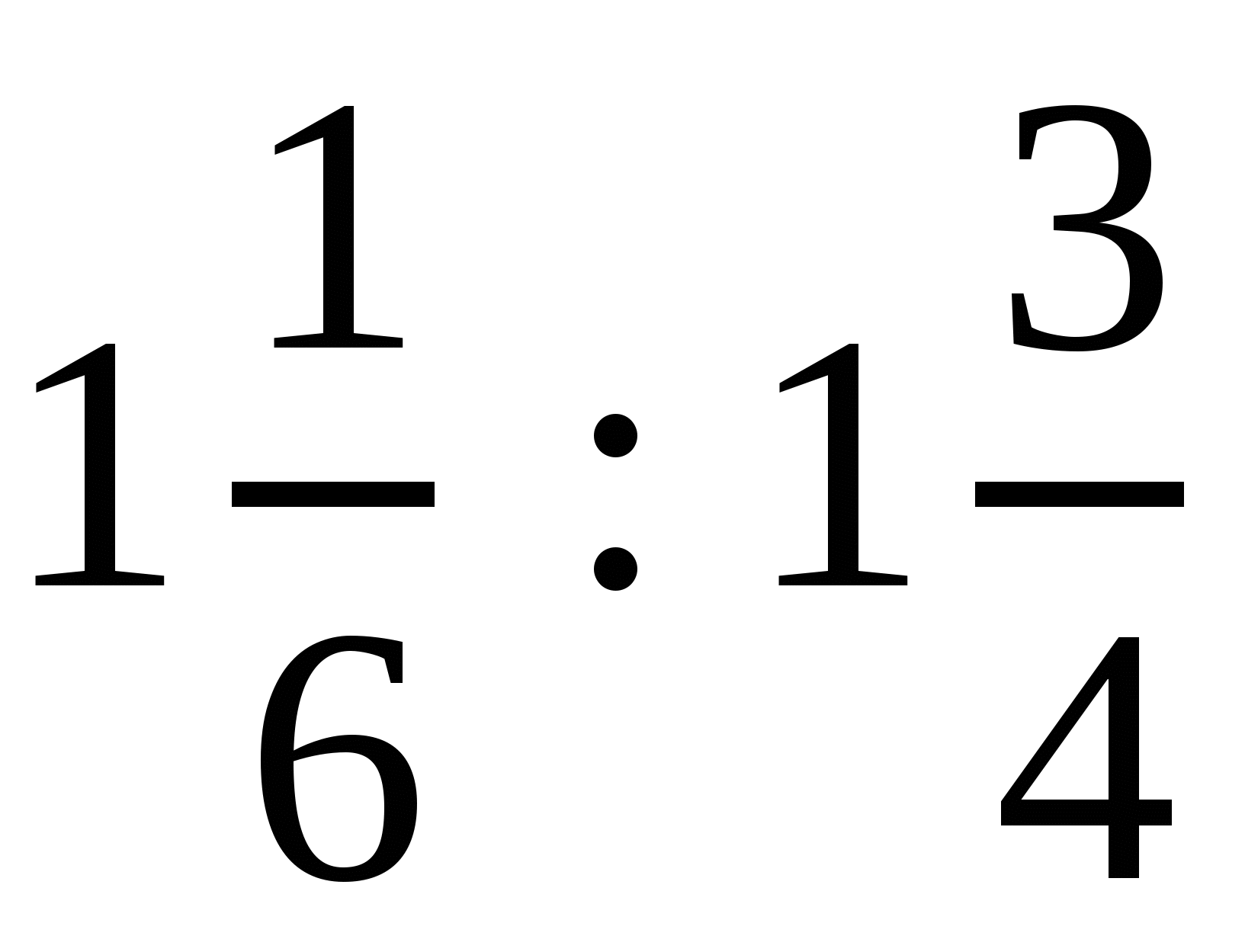 .
.
4. Решить пропорцию:
1) 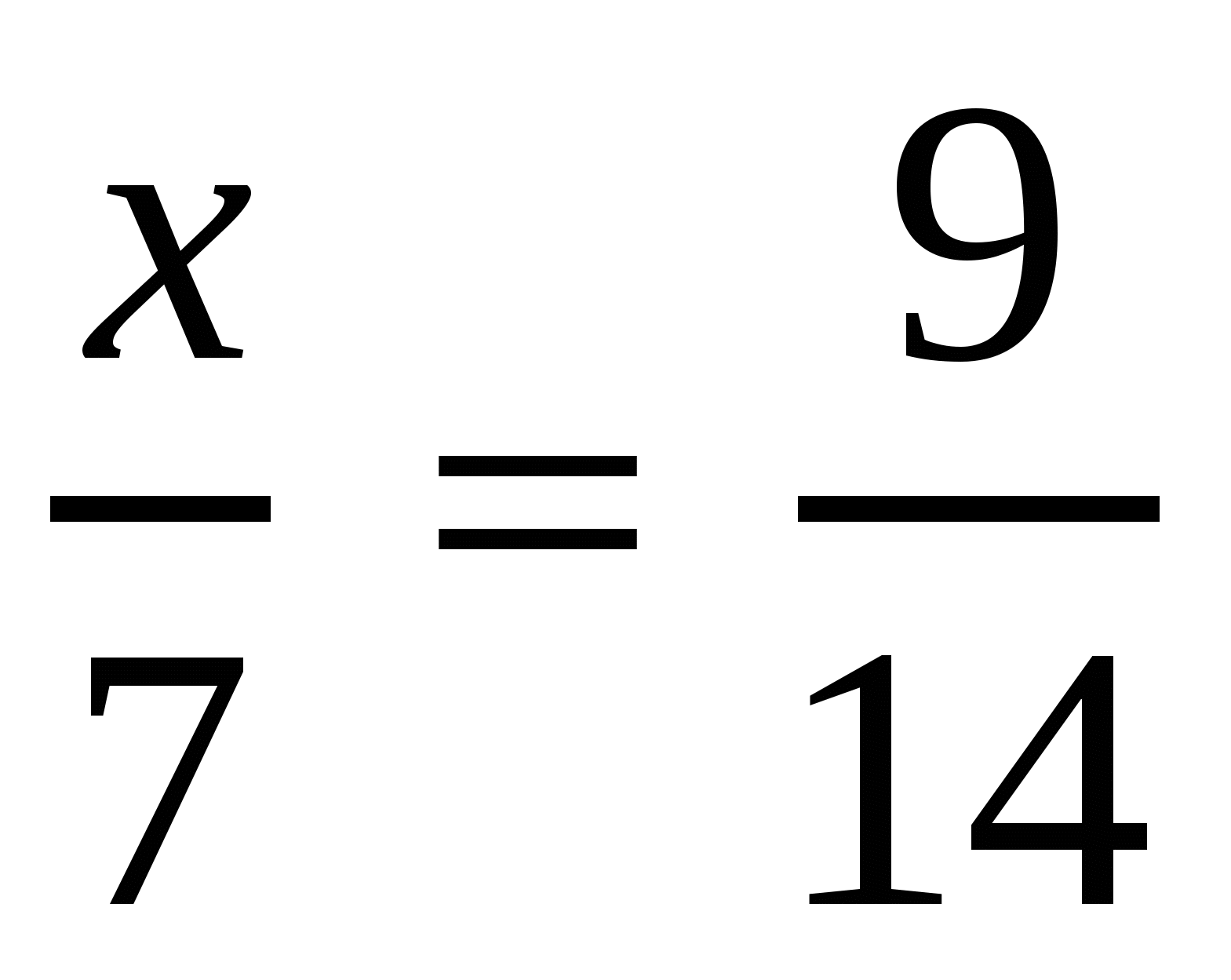 ; 2)
; 2) 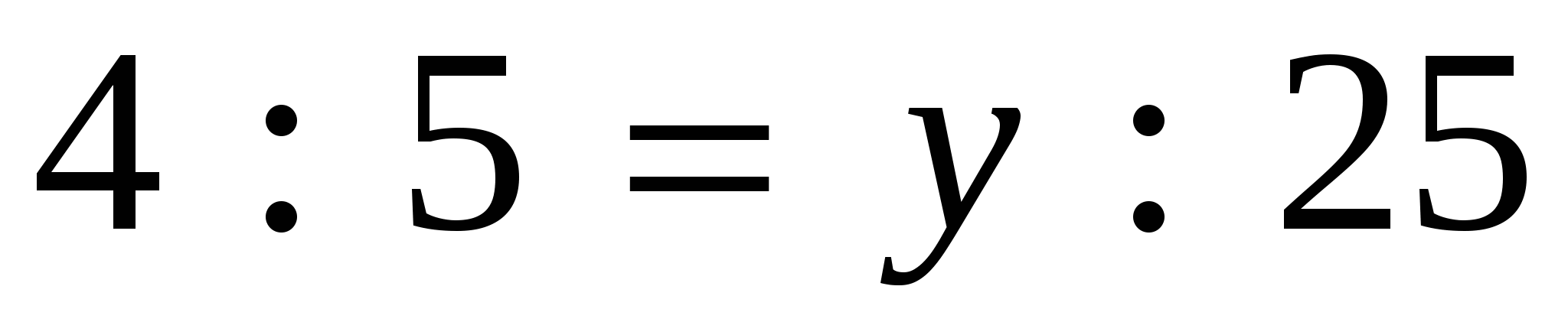 .
.
Урок 11. Пропорции.
1. Упростите отношение:
1) 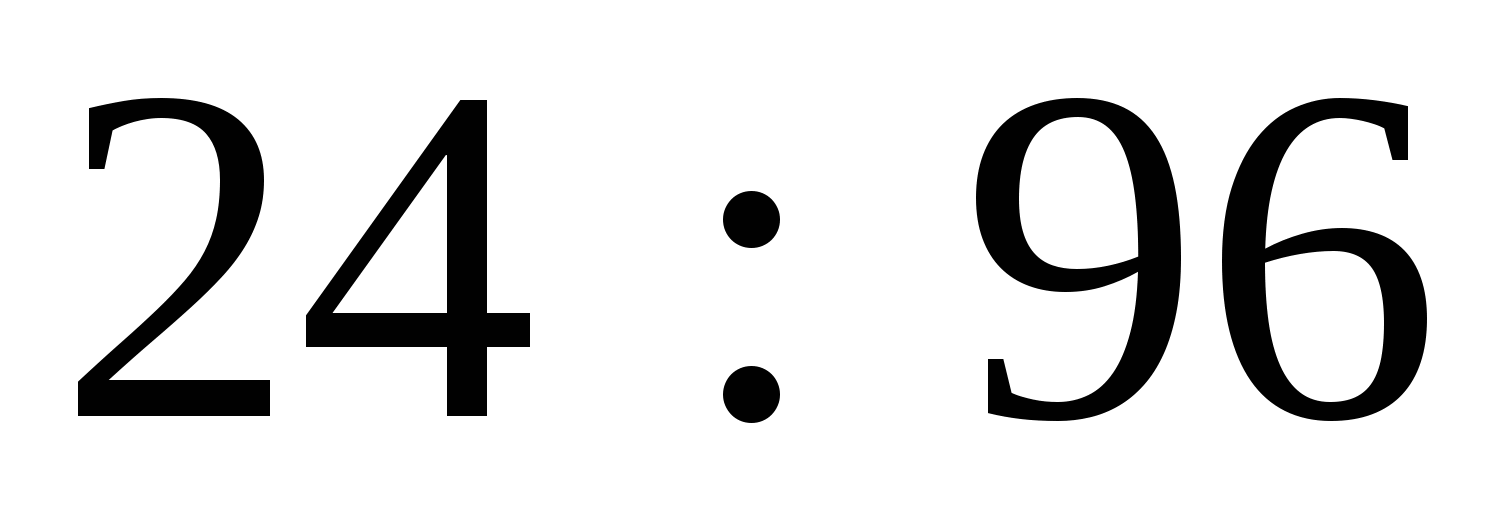 ; 3)
; 3) 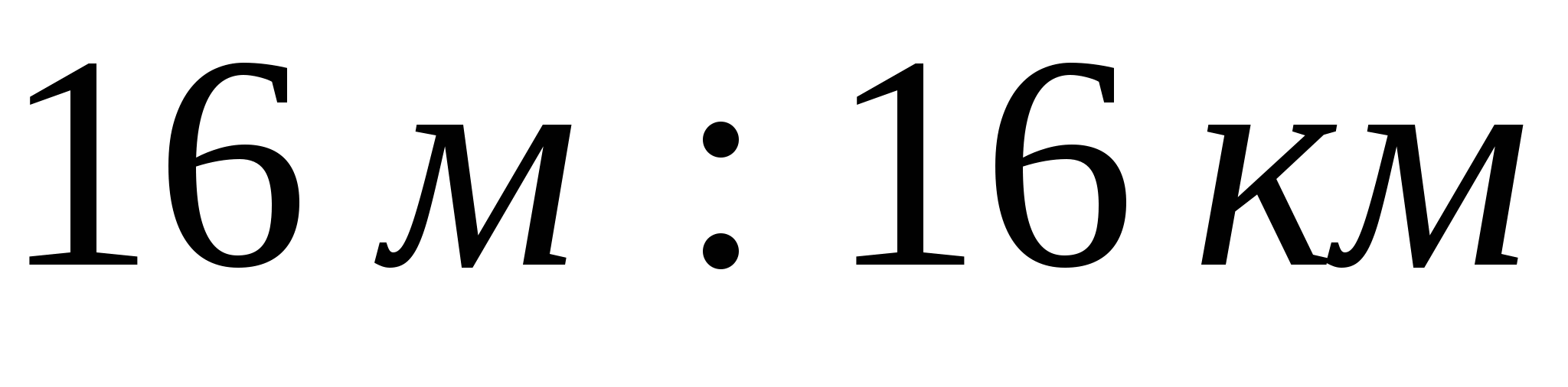 ;
;
2) 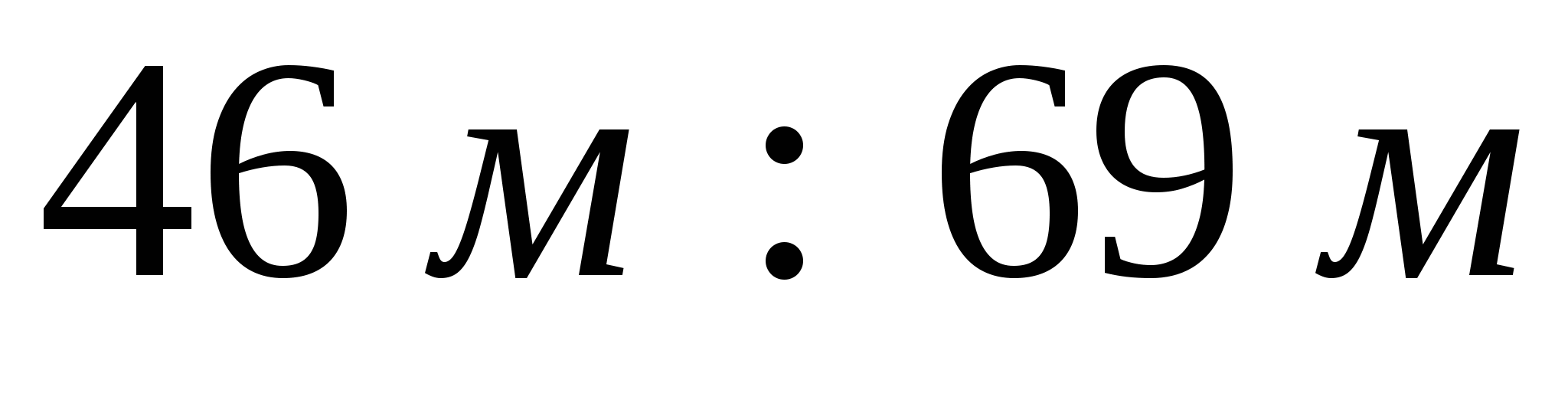 ; 4)
; 4)  .
.
2. Используя числа 56; 15; 8; 105, составьте пропорцию.
3. Вычислив данные отношения, установите, можно ли из них составить пропорцию: 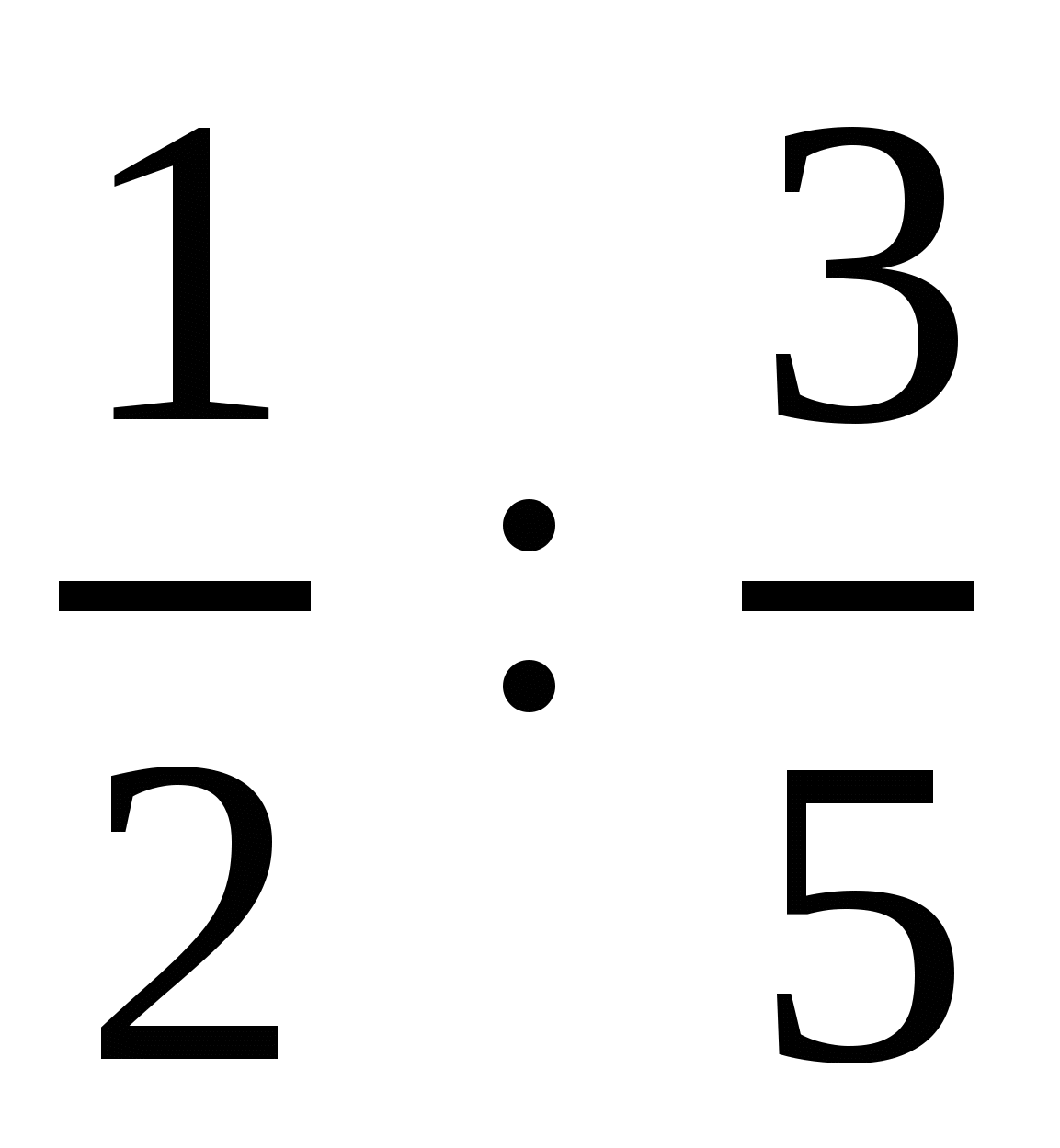 и
и 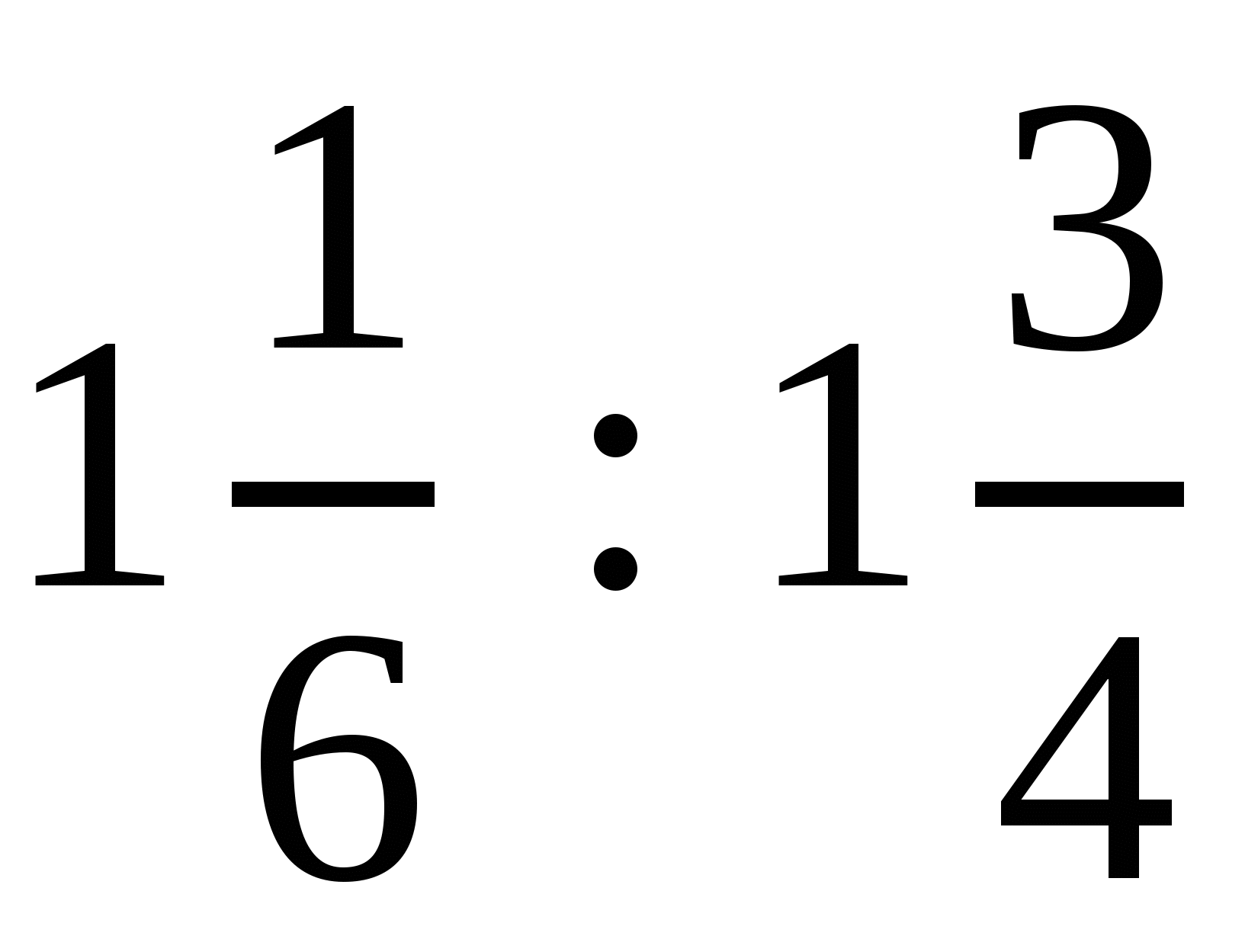 .
.
4. Решить пропорцию:
1) 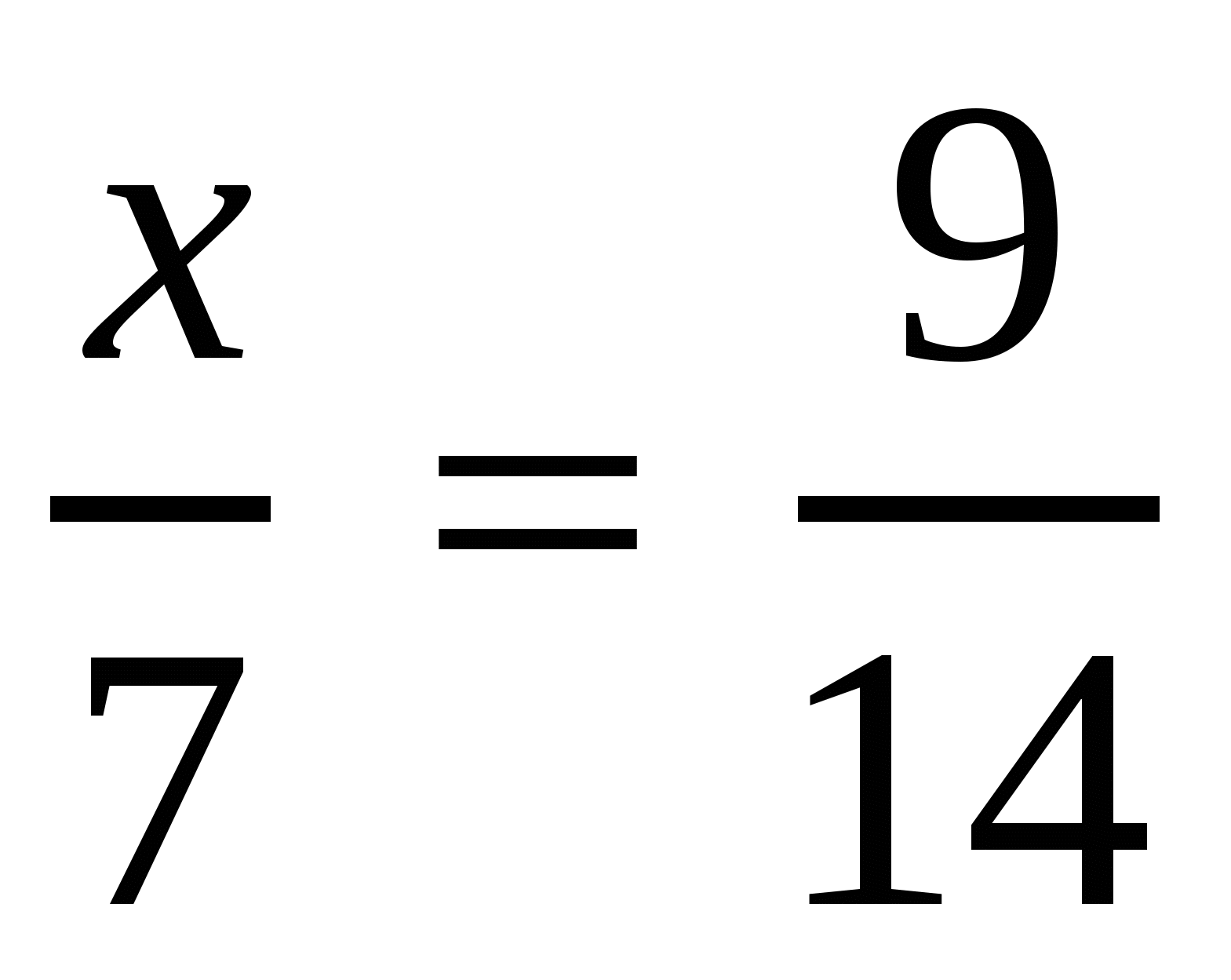 ; 2)
; 2) 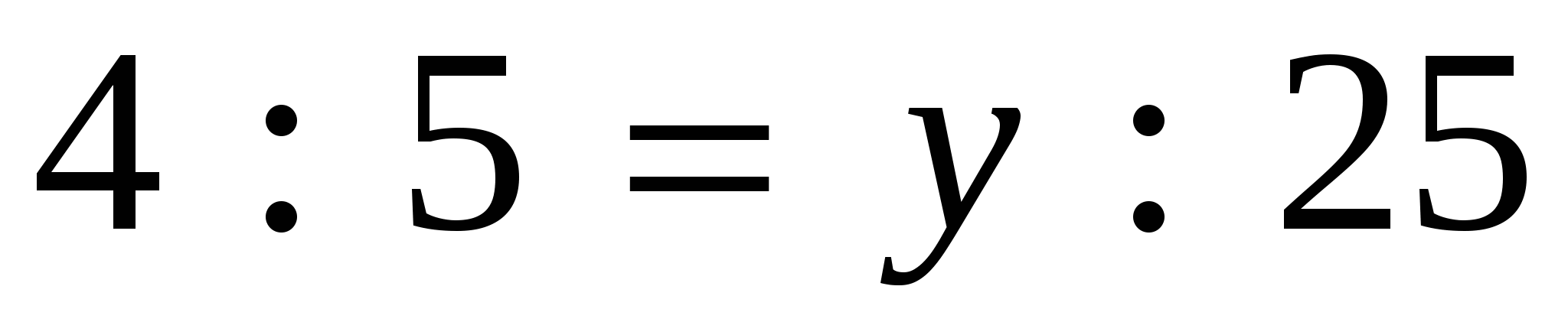 .
.
Урок 11. Пропорции.
1. Упростите отношение:
1) 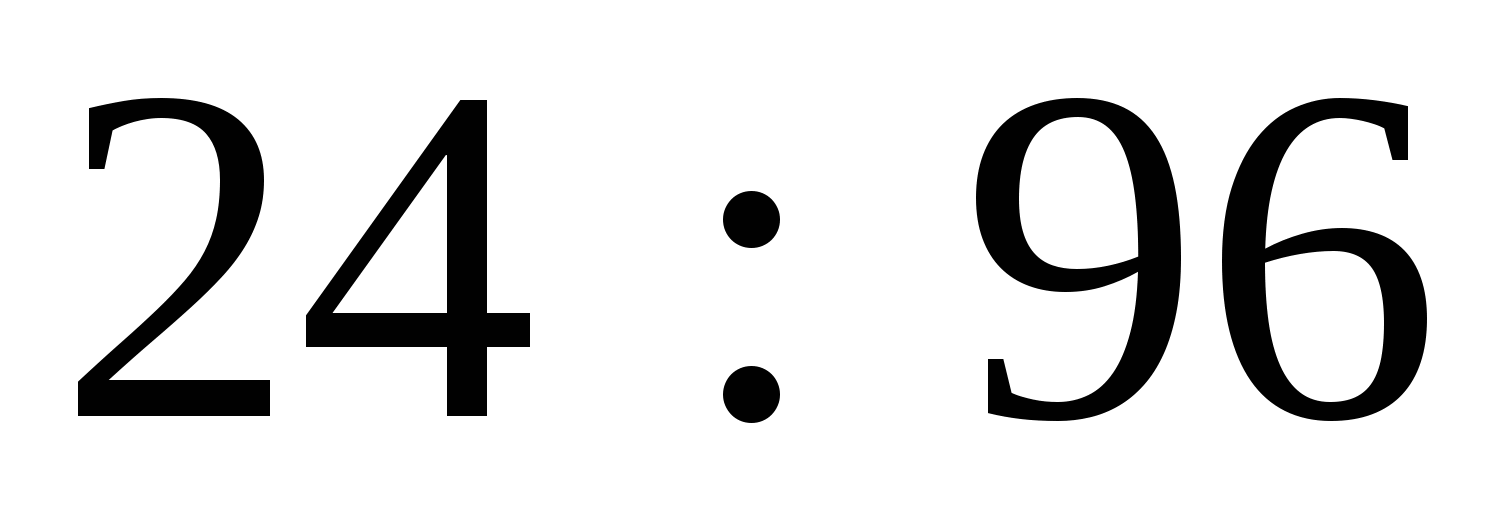 ; 3)
; 3) 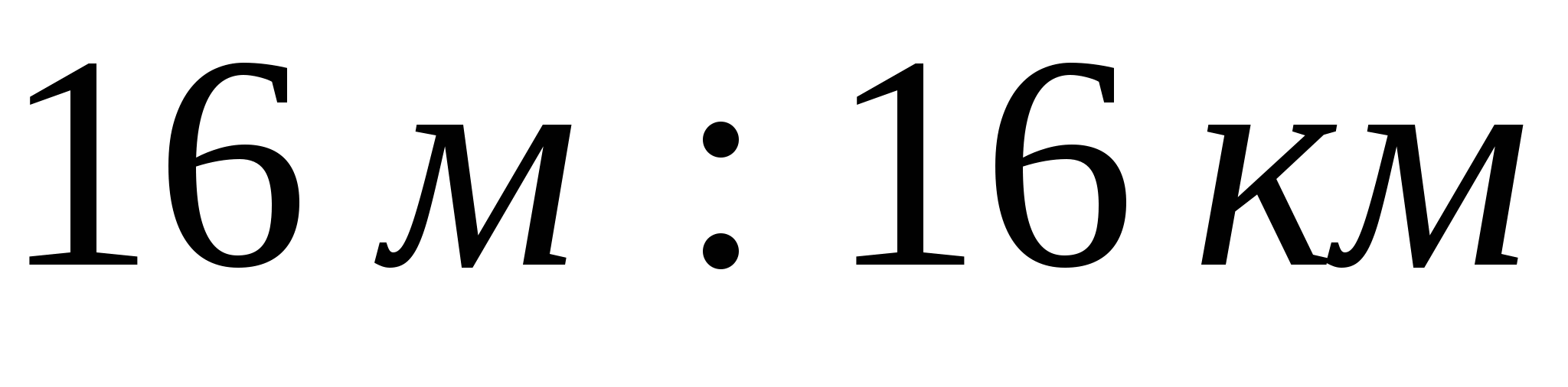 ;
;
2) 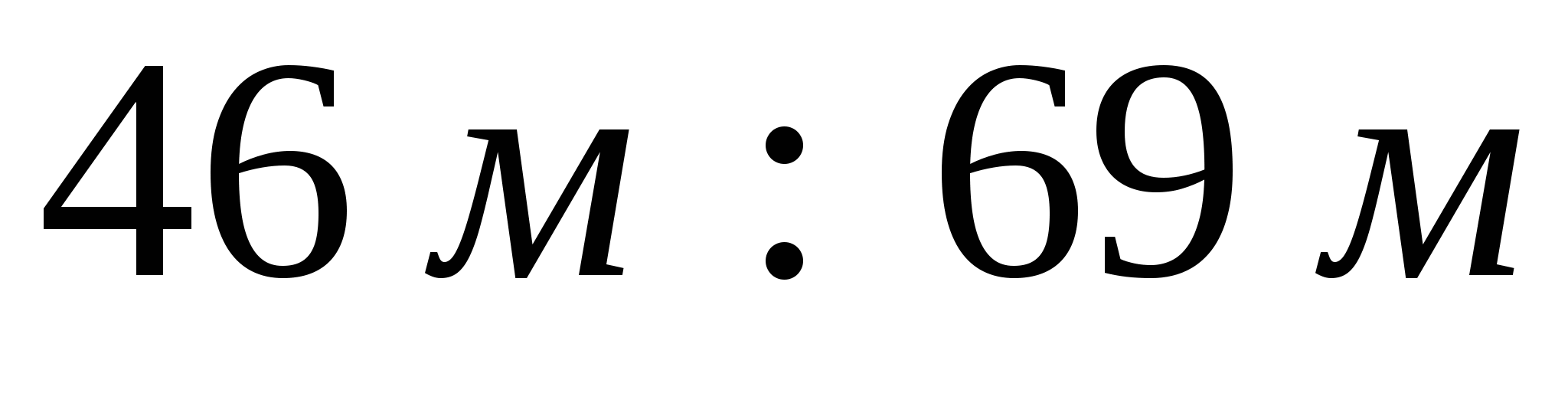 ; 4)
; 4)  .
.
2. Используя числа 56; 15; 8; 105, составьте пропорцию.
3. Вычислив данные отношения, установите, можно ли из них составить пропорцию: 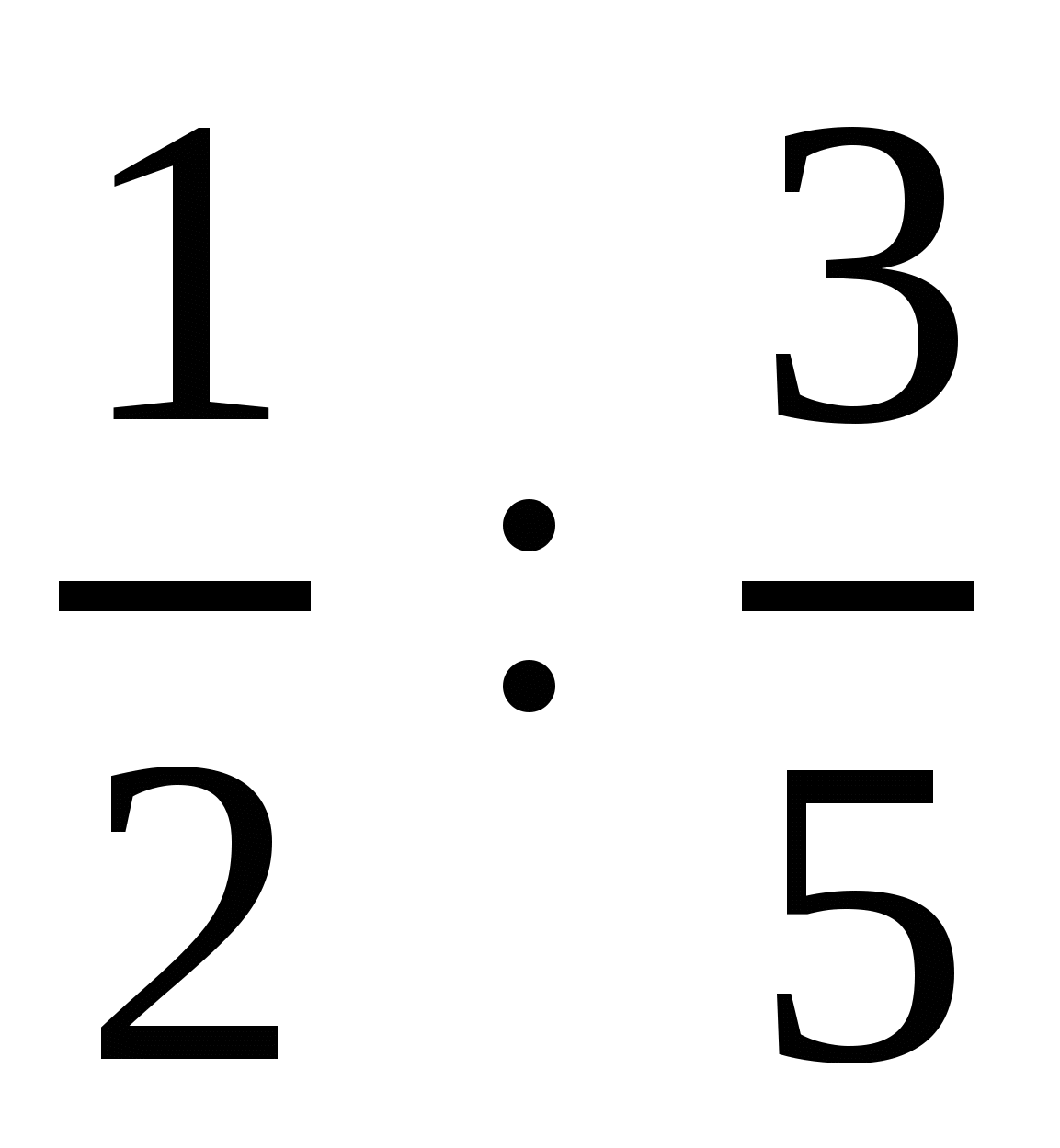 и
и 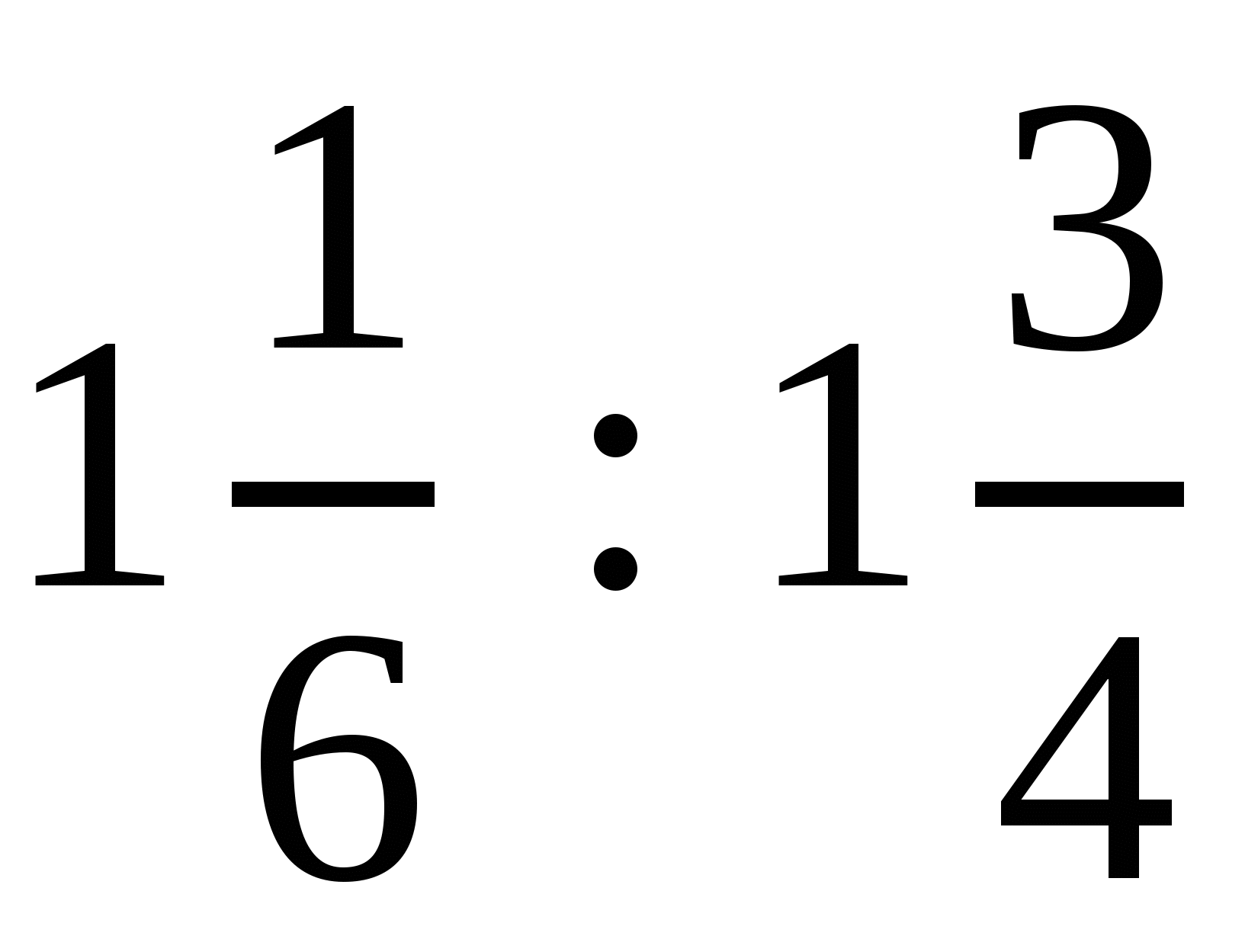 .
.
4. Решить пропорцию:
1) 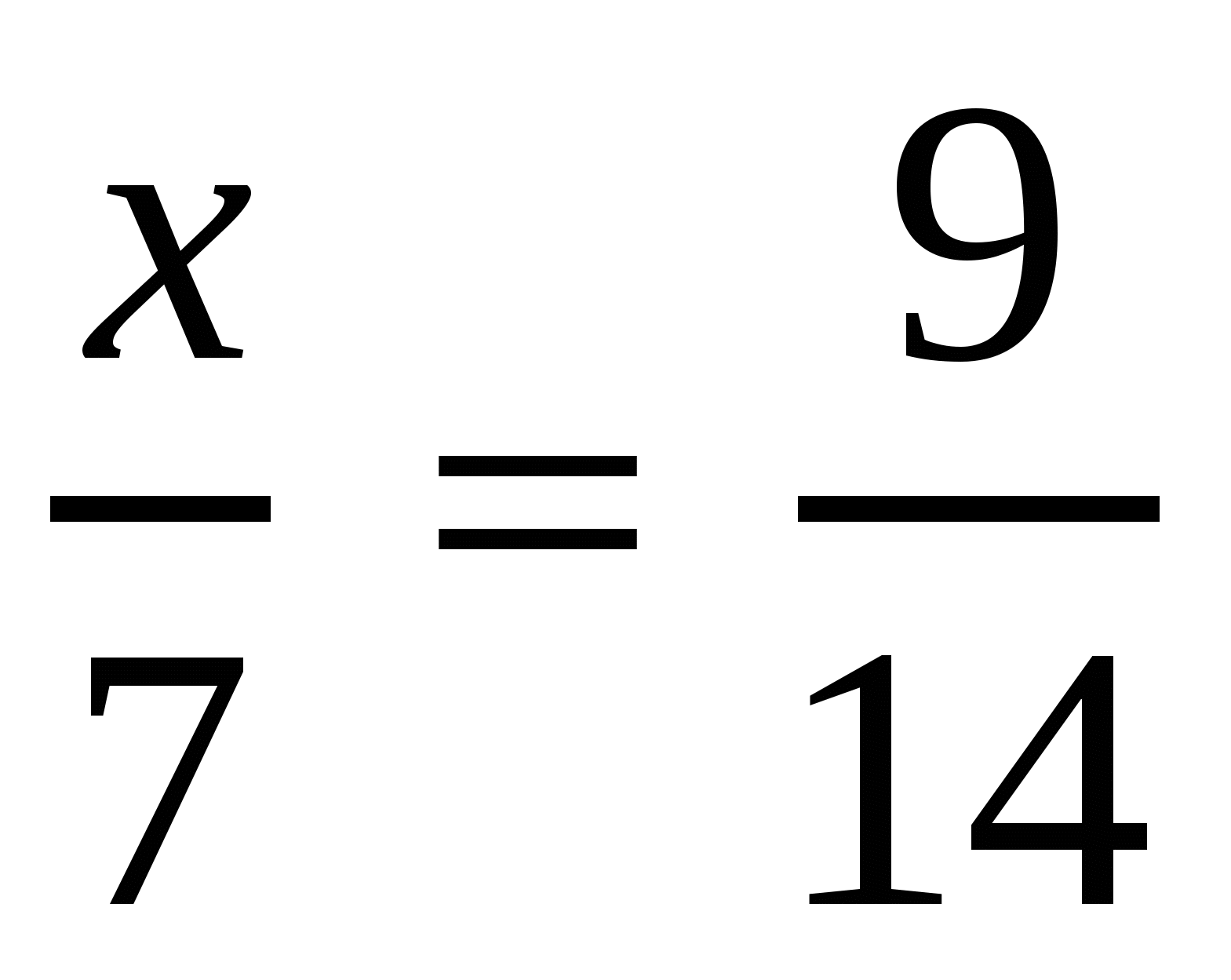 ; 2)
; 2) 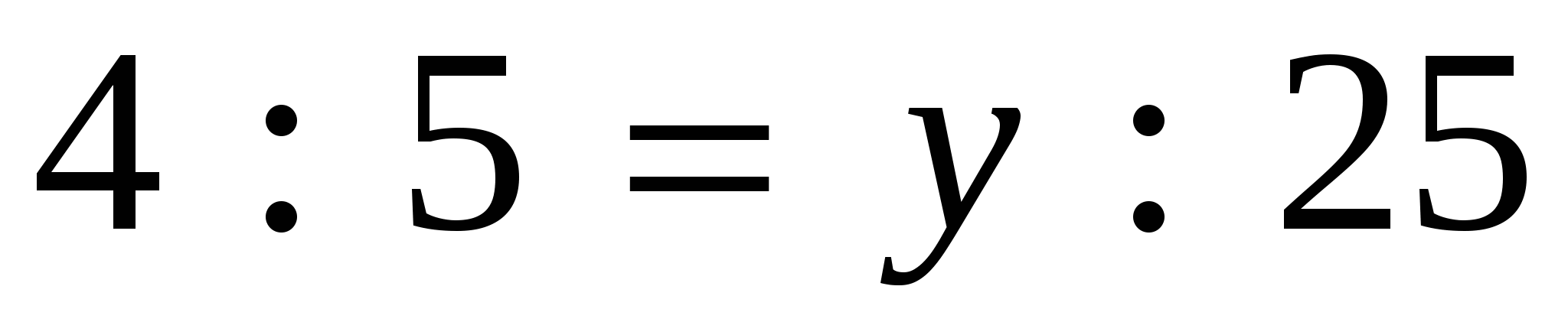 .
.
infourok.ru
Методическая разработка по алгебре (6 класс) на тему: Пропорции.Решение задач с помощью пропорций.
КАРТАЛИНСКИЙ РАЙОННЫЙ ОТДЕЛ ОБРАЗОВАНИЯ
МОУ ЕЛЕНИНСКАЯ СОШ
для учащихся 6 класса
Подготовила:
учитель математики
ЯРКЕЕВА Л.М.
ЕЛЕНИНКА 2015 год
Тема: Пропорция. Решение задач с помощью пропорции.
Тип урока: урок-путешествие
Цель урока: проверить умение находить неизвестный член пропорции; решать задачи с помощью пропорции.
Ход урока.
Учитель: Пройдет еще немного времени и перед вами встанет вопрос: какую профессию выбрать? Профессий много, как же тут разобраться? Вы уже знакомы с профессиями своих родственников, с профессией учителя. Но ведь существует еще много интересных. Чтобы узнать как можно больше о них, на наших уроках мы иногда можем путешествовать, встречаясь с людьми разных профессий с различных предприятий, знакомиться с продукцией этих предприятий. А как мы это будем делать — вы сегодня увидите. Это не совсем обычный урок. Мы с вами отправляемся в поездку по некоторым местам нашего города. Путешествуя, выясним, как вы усвоили тему: «Пропорция». Ведь данная тема служит основой для решения многих задач практического характера. С задачами, решение которых сводится к составлению пропорции, встречаются люди разных профессий. Итак, в путь!
КАРТА ПУТЕШЕСТВИЯ
УНИВЕРСИТЕТ
ШКОЛА ХЛЕБОЗАВОД
САХАРНЫЙ ЗАВОД ДОМСТРОЙ
1.Станция «УНИВЕРСИТЕТ».
Учитель: Внимание. На нашем пути студенческий городок. Заглянем в одну из аудиторий университета. Здесь идет конференция по истории математики.
1.1 Историческая справка (сообщение делает ученик). Ученые в Древней Греции не признавали дробных чисел и из-за этого у них возникали затруднения с измерением величин. Пришлось греческим ученым придумать способ, как обходиться в науке без того, чтобы выражать длины, площади и объемы числами. Так было создано учение об отношениях величин, о равенстве таких отношений. Равенство двух отношений стало потом называться латинским словом «пропорция». С пропорциями имели дело строители уже в Древнем мире.
Правильное соотношение размеров возводимых ими дворцов и храмов придавало этим зданиям ту необыкновенную красоту, которая и сегодня восхищает нас.
Учитель: А в другой аудитории идет практическое занятие. Давайте примем в нем участие.
1.2.Устная работа:
— Какие из данных равенств являются пропорциями? Почему?
а) 2,5 : 0,5 = 4 + 1,
2 1
б) 30 : 5 = 7 : 21.
-Допишите недостающие члены пропорции:
а) 104 : … = 160 : 20,
б) 10 : 5 = … : …
Сколько решений имеет пропорция?
Проверьте составленную пропорцию двумя способами. Назовите крайние и средние члены пропорции.
— Проверьте, правильно ли найден неизвестный член пропорции:
75 : 9 = 9 : у
75 * у = 9 * 9
75 * 9
у = 9
у = 75
-Из чисел 4, 2, 5, 10 составьте пропорцию. Как из данной пропорции получить верную пропорцию?
Учитель: Так как следующие станции связаны с решением задач практического характера, давайте ответим на следующие вопросы:
— Какие величины называются прямо пропорциональными?
— Какие величины называются обратно пропорциональными?
— Приведите примеры прямо пропорциональных величин.
— Приведите примеры обратно пропорциональных величин.
2.Станция «ХЛЕБОЗАВОД»
Один ученик решает у доски с объяснением.
Задача: При выпечке хлеба из килограмма ржаной муки пекарь получит 1,4 кг хлеба. Сколько килограммов муки расходуется на выпечку 21 ц хлеба?
1 кг — 1,4 кг
х кг — 2100 кг
Прямая пропорциональность.
1 1, 4
х = 2100
х = 1500 кг
Ответ: 15 центнеров.
Учитель: Итак, где мы сейчас побывали? О какой профессии узнали из этой задачи?
3. Станция «ДОМСТРОЙ».
Один ученик решает около доски с объяснением.
Задача: Пять каменщиков могут закончить работу за 9 дней. Инженер попросил ускорить работу и для этого добавил еще 10 каменщиков. За какое время они закончат работу, считая, что все каменщики будут работать с одинаковой производительностью?
Решение: Пусть за х дней каменщики закончат работу.
5 каменщ. — 9 дней
15 каменщ. — х дней
Обратная пропорциональность.
5 х
15 = 9
х = 3
Ответ: 3 дня.
Вопрос классу: Каким свойством пользовались при решении задачи? Сформулируйте.
Учитель: В какой организации мы побывали? Чем занимается эта организация? С какими профессиями мы познакомились?
4. Станция «САХАРНЫЙ ЗАВОД»
Один ученик решает у доски с объяснением.
Задача: В сахарной свекле содержится 18,5% сахара. Сколько сахара содержится в 50 т сахарной свеклы?
Решение: Пусть х т сахара содержится в 50 т сахарной свеклы.
50т — 100%
х т — 18,5%
Обратная пропорциональность.
50 100
х = 18,5
х = 9,25
Ответ: 9,25 т
Работа с плакатом.
50 т — 100% х т — 100%
х т — 18,5% 9, 25 т — 18,5%
Вопросы к классу:
1. Что вы видите на доске?
(Краткая запись задачи и краткая запись обратной задачи).
2. По краткой записи обратной задачи сформулируйте условие.
(Условие: В сахарной свекле содержится 18,5% сахара. Сколько надо взять сахарной свеклы, чтобы в ней содержалось 9, 25 т сахара?)
Учитель: Где мы с вами побывали? Какой продукт там изготавливали? Из чего получается сахар?
5. Физкультминутка
Дружно встал 6 «а» класс — это «раз».
Повернулась голова — это «два».
Влево, вправо посмотри — это «три».
Свои плечи развернули на «четыре».
Пальцы надо нам размять — это «пять».
Всем ребятам надо сесть — это «шесть».
6. Станция «ШКОЛА».
Самостоятельная работа.
1 вариант:
1. Найдите неизвестный член пропорции 2,8 : 3,2 = 2,1 : х.
Ответ: х = 2,4.
2. Решите задачу:
На 20 км пути автомашина расходует 3,2 л горючего. Сколько горючего автомашина израсходует на 50 км пути?
Ответ: 8л.
2 вариант:
1. Найдите неизвестный член пропорции у : 2,1 = 4,5 : 3,5.
Ответ: у = 2,7.
2. Решите задачу:
Участок клубники 24 человека пропололи за 6 дней. За сколько дней выполнят ту же работу 36 человек, если будут работать с такой же производительностью?
Ответ: 4 дня.
7. Подведение итогов урока, рефлексия.
8. Домашнее задание: Придумайте две новые станции, две задачи и решите их.
nsportal.ru
Урок на тему: «Виды задач на пропорции» 6 класс
Тема: «Виды задач на пропорции»
Цели:
- Продолжить формирование навыков решения задач на пропорции
- Развитие логического мышления
- Воспитание самостоятельности
Оборудование: раздаточный материал (карточки с набором задач)
Ход урока:
- Организационный момент и проверка домашнего задания.
- Актуализация теоретических знаний:
(выполняется на листке, один правильный ответ – 1 балл, проверяется учителем в течение урока)
- Две величины прямо пропорциональны, если… при возрастании (убывании) одной величины возрастает (убывает) вторая.
- Две величины обратно пропорциональны, если… при возрастании (убывании) одной величины убывает (возрастает) вторая.
- Все ли величины прямо или обратно пропорциональны? Нет, есть величины не пропорциональные вообще.
- Сформулировать основное свойство пропорции.Произведение крайних членов пропорции = произведению средних.
- Привести пример прямо пропорциональной зависимости.
- Фронтальное решение задач.
№ 749
№ 799
№ 803
- Самостоятельная работа: решение задач на карточках (прилагаются)
- Подведение итогов урока.
- Домашнее задание: п. 21-22 повторить, № 811, № 819 решить.
Просмотр содержимого документа
«урок на тему: «Виды задач на пропорции» 6 класс »
Тема: «Виды задач на пропорции»
Цели:
Продолжить формирование навыков решения задач на пропорции
Развитие логического мышления
Воспитание самостоятельности
Оборудование: раздаточный материал (карточки с набором задач)
Ход урока:
Организационный момент и проверка домашнего задания.
Актуализация теоретических знаний:
(выполняется на листке, один правильный ответ – 1 балл, проверяется учителем в течение урока)
Две величины прямо пропорциональны, если… при возрастании (убывании) одной величины возрастает (убывает) вторая.
Две величины обратно пропорциональны, если… при возрастании (убывании) одной величины убывает (возрастает) вторая.
Все ли величины прямо или обратно пропорциональны? Нет, есть величины не пропорциональные вообще.
Сформулировать основное свойство пропорции. Произведение крайних членов пропорции = произведению средних.
Привести пример прямо пропорциональной зависимости.
Фронтальное решение задач.
№ 749
№ 799
№ 803
Самостоятельная работа: решение задач на карточках (прилагаются)
Подведение итогов урока.
Домашнее задание: п. 21-22 повторить, № 811, № 819 решить.
Приложение
Задачи на пропорцию
1.При изготовлении 9 одинаковых приборов потребовалось 300г серебра. Сколько серебра потребуется для изготовления 6 таких приборов?
2.Для изготовления 18 одинаковых приборов потребовалось 27г платины. Сколько платины потребуется для изготовления 28 таких приборов?
3.Трое маляров могут закончить работу за 5дней. Для ускорения работы добавили еще двух маляров. За какое время они закончат работу, если все маляры работают с одинаковой производительностью?
4.Для строительства стадиона 5 бульдозеров расчистили площадку за 210 мин. За какое время 7 бульдозеров расчистили бы эту площадку?
5.Для приготовления борща на каждые 100г мяса надо взять 60г свёклы. Сколько свёклы надо взять на 650 г мяса?
6.Для перевозки груза потребовалось 24 машины грузоподъемностью 7,5т. Сколько нужно машин грузоподъемностью 4,5т, чтобы перевезти тот же груз?
7. В 80 кг картофеля содержится 14кг крахмала. Найдите процентное содержание крахмала в таком картофеле.
8.Из 20кг яблок получается 16 кг яблочного пюре. Сколько яблочного пюре получится из 45 кг яблок?
9.На изготовления 12 костюмов требуется 49,8 м ткани. Сколько таких же костюмов можно сшить из 74,7м той же ткани?
10.Для погрузки нефти нужно 35 цистерн емкостью 60м3 каждая. Однако на железной дороге оказалось только цистерны емкостью 70м3. Сколько таких цистерн потребуется для погрузки того же количества нефти?
11.На изготовления 3,5 кг ржаного хлеба требуется 2,5 кг муки. Сколько хлеба можно испечь из 17,5 т ржаного хлеба?
12. Из 79 л молока получается 3,2кг сливочного масла. Сколько нужно взять молока, чтобы получить 16 кг масла?
13.12 тракторов одинаковой мощности могут вспахать поле за 88ч. Сколько нужно таких же тракторов, чтобы вспахать это поле за 33ч?
14.Из 0,3 т свежих яблок получилось 57 кг сушеных. Сколько получится сушеных яблок из 2,1т свежих?
15. 16 солдат могут отрыть окоп полного профиля за 21ч. Сколько солдат нужно поставить на эту работу, чтобы окоп был готов через 14ч?
kopilkaurokov.ru