04:15

Подборка задач ОГЭ по теме «Площадь» для 8 класса

Квадрат

1. Сторона квадрата равна 10. Найдите его площадь.

2. Периметр квадрата равен 40. Найдите площадь квадрата.

4. Периметр квадрата равен 160. Найдите площадь квадрата.

5. Найдите площадь квадрата, если его диагональ равна 1.

6. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

Прямоугольник

1.  В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сторона равна 12. Най­ди­те площадь прямоугольника.

2.  В пря­мо­уголь­ни­ке диагональ равна 10, а угол между ней и одной из сто­рон равен 30°. Най­ди­те площадь прямоугольника, делённую на  .

3. В пря­мо­уголь­ни­ке диагональ равна 10, угол между ней и одной из сто­рон равен 30°, длина этой сто­ро­ны  . Най­ди­те площадь прямоугольника, деленную на 

4.  Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 44 и одна сто­ро­на на 2 боль­ше другой.

5. Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 60, а от­но­ше­ние со­сед­них сто­рон равно 4:11.

6.  Найдите пло­щадь прямоугольника, если его пе­ри­метр равен 58 и одна сто­ро­на на 5 боль­ше другой.

7.  В пря­мо­уголь­ни­ке одна сто­ро­на равна 96, а диа­го­наль равна 100. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

8.  На сто­ро­не BC пря­мо­уголь­ни­ка ABCD, у ко­то­ро­го AB = 12 и AD = 17, от­ме­че­на точка E так, что ∠EAB = 45°. Най­ди­те ED.

Треугольник

1. В пря­мо­уголь­ном треугольнике один из ка­те­тов равен 10, а угол, ле­жа­щий напротив него, равен 45°. Най­ди­те площадь треугольника.

2. Най­ди­те пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 28 и 100.

3. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 4, а ост­рый угол, при­ле­жа­щий к нему, равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

4. В пря­мо­уголь­ном тре­уголь­ни­ке ги­по­те­ну­за равна 70, а один из ост­рых углов равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

5. Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.

6. Два катета прямоугольного треугольника равны 4 и 9. Найдите площадь этого треугольника.

7. Сторона рав­но­сто­рон­не­го треугольника равна 10. Най­ди­те его площадь, делённую на  .

8. Периметр рав­но­сто­рон­не­го треугольника равен 30. Най­ди­те его площадь, делённую на  .

9. Высота рав­но­сто­рон­не­го треугольника равна 10. Най­ди­те его площадь, делённую на 

10. В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, а угол, ле­жа­щий напротив основания, равен 120°. Най­ди­те площадь треугольника, делённую на 

11. Периметр рав­но­бед­рен­но­го треугольника равен 16, а бо­ко­вая сторона — 5. Най­ди­те площадь треугольника.

12. В рав­но­бед­рен­ном треугольнике бо­ко­вая сторона равна 10, основание —  , а угол, ле­жа­щий напротив основания, равен 30°. Най­ди­те площадь треугольника.

13. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 34, а ос­но­ва­ние равно 60. Най­ди­те пло­щадь этого тре­уголь­ни­ка.

14. Пе­ри­метр рав­но­бед­рен­но­го тре­уголь­ни­ка равен 216, а бо­ко­вая сто­ро­на — 78. Най­ди­те пло­щадь тре­уголь­ни­ка.  

15. В тре­уголь­ни­ке одна из сто­рон равна 10, а опу­щен­ная на нее высота — 5. Най­ди­те площадь треугольника.

16. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна  , а угол между ними равен 60°. Най­ди­те площадь треугольника.

17. Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ражённого на ри­сун­ке.

1. В тре­уголь­ни­ке ABC от­ре­зок DE — сред­няя линия. Пло­щадь тре­уголь­ни­ка CDE равна 97. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

2. Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.

Трапеция

1.  Най­ди­те площадь трапеции, изображённой на рисунке.

2. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна  , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те площадь трапеции.

3. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а синус угла между ней и одним из ос­но­ва­ний равен  . Най­ди­те площадь трапеции.

4. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен  . Най­ди­те площадь трапеции.

5. Основания тра­пе­ции равны 18 и 12, одна из бо­ко­вых сторон равна 6, а тан­генс угла между ней и одним из ос­но­ва­ний равен  . Най­ди­те площадь трапеции.

6. Средняя линия тра­пе­ции равна 11, а мень­ше основание равно 5. Най­ди­те большее ос­но­ва­ние трапеции.

7. Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

8. В рав­но­бед­рен­ной тра­пе­ции ос­но­ва­ния равны 3 и 9, а один из углов между бо­ко­вой сто­ро­ной и ос­но­ва­ни­ем равен 45°. Най­ди­те пло­щадь тра­пе­ции.

9. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 5 и 17, а ее бо­ко­вые сто­ро­ны равны 10. Най­ди­те пло­щадь тра­пе­ции.

10. Ос­но­ва­ния тра­пе­ции равны 7 и 49, одна из бо­ко­вых сто­рон равна 18 , а ко­си­нус угла между ней и одним из ос­но­ва­ний равен   Най­ди­те пло­щадь тра­пе­ции.

11.Основания тра­пе­ции равны 1 и 13, одна из бо­ко­вых сто­рон равна  , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те пло­щадь трапеции.

12. В тра­пе­ции ABCD AD = 5, BC = 2, а её пло­щадь равна 28. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

13. В тра­пе­ции ABCD AD = 3, BC = 1, а её пло­щадь равна 12. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

14. Тангенс остро­го угла пря­мо­уголь­ной тра­пе­ции равен   Най­ди­те её боль­шее основание, если мень­шее ос­но­ва­ние равно вы­со­те и равно 58.

15. Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен  . Найдите площадь трапеции.

16.В тра­пе­ции ABCD известно, что AD = 6, BC = 2, а её пло­щадь равна 32. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

17. В тра­пе­ции ABCD известно, что AD = 5, BC = 1, а её пло­щадь равна 51. Най­ди­те пло­щадь тра­пе­ции BCNM, где MN – сред­няя линия тра­пе­ции ABCD.

18. Основания тра­пе­ции равны 6 и 24, одна из бо­ко­вых сторон равна 11, а синус угла между ней и одним из ос­но­ва­ний равен  . Най­ди­те площадь трапеции.

19. Основания тра­пе­ции равны 7 и 63, одна из бо­ко­вых сторон равна 18, а ко­си­нус угла между ней и одним из ос­но­ва­ний равен  . Най­ди­те площадь трапеции.

Параллелограмм, ромб

1. Найдите пло­щадь параллелограмма, изображённого на рисунке.

2.  Сторона ромба равна 5, а диа­го­наль равна 6. Най­ди­те площадь ромба.

3.  Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

4. Периметр ромба равен 24, а синус од­но­го из углов равен  . Най­ди­те площадь ромба.

5.  Одна из сто­рон параллелограмма равна 12, а опу­щен­ная на нее вы­со­та равна 10. Най­ди­те площадь параллелограмма.

6.  Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а один из углов — 45°. Най­ди­те площадь параллелограмма, делённую на  .

7. Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а синус од­но­го из углов равен  . Най­ди­те площадь параллелограмма.

8.  Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а ко­си­нус одного из углов равен  . Най­ди­те площадь параллелограмма.

9.  Одна из сто­рон параллелограмма равна 12, дру­гая равна 5, а тан­генс одного из углов равен  . Най­ди­те площадь параллелограмма.

10.  Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

11.  В ромбе сто­ро­на равна 10, одна из диагоналей —  , а угол, ле­жа­щий напротив этой диагонали, равен 30°. Най­ди­те площадь ромба.

12. Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 56. Точка E — се­ре­ди­на сто­ро­ны CD. Най­ди­те пло­щадь тра­пе­ции AECB.

13. Сто­ро­на ромба равна 9, а рас­сто­я­ние от цен­тра ромба до неё равно 1. Най­ди­те пло­щадь ромба.

14.  Пе­ри­метр ромба равен 116, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

15.  Сто­ро­на ромба равна 50, а диа­го­наль равна 80. Най­ди­те пло­щадь ромба.

17.  Высота BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH = 1 и HD = 28. Диа­го­наль параллелограмма BD равна 53. Най­ди­те площадь параллелограмма.

Фигуры на квадратной решётке

1. На клетчатой бумаге с размером клетки 1см × 1см найти площадь фигуры

Тренажёр по геометрии (8 класс): Задачи по теме: Площади фигур.

Задачи по теме: « Площади фигур» 8 класс

1.Найдите площадь квадрата, сторона которого равна 1,3дм.

2. Найдите площадь параллелограмма, если сторона его равна 6 см, а высота, проведенная к этой стороне равна 12см.

3.Большая из сторон параллелограмма равна 14 см, а его высоты равны 5см и 7 см. Найдите меньшую сторону параллелограмма.

Найдите площадь параллелограмма, если две стороны его равны 23 см и 11 см, а угол между ними равен 30.

4. Найдите площадь треугольника, если одна из его сторон равна 18 дм, а высота, проведенная к ней равна 12 дм.

5. Площадь треугольника равна 96  , а две стороны этого треугольника равны 16 см и 8 см. Высота, проведенная к большей стороне равна 12см. Найдите высоту, проведенную к меньшей стороне.

6. Найдите площадь ромба, если его диагонали равны 9 см и 12 см.

7. Площадь ромба равна 48 см, а одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ.

8. Найдите площадь трапеции, если основания равны 6см и 9 см, а высота трапеции равна 5 см.

9. Основания трапеции равны 4 см и 14 см, а боковая сторона равная 22 см, образует  с одним из оснований трапеции угол равный 30.

Найдите площадь трапеции.

10. Найдите площадь прямоугольного треугольника, если один из катетов равен 12 см, а гипотенуза равна 13 см.

1.Найдите площадь ромба, если его диагонали равны 14 и 6.

2.Периметр ромба равен 96, а один из углов равен 30. Найдите площадь ромба.

3.Сторона ромба равна10, а расстояние от центра ромба до нее равно 3. Найдите площадь ромба.

4.Найдите площадь трапеции, основания которой равны 13 см и 7 см, а высота равна 8 см.

5. В равнобедренной трапеции, угол при основании равен 45 , а основания равны 2см и 6 см. Найдите площадь трапеции.

Разработка урока по геометрии 8 класс «Ромб»

МОУ ГИМНАЗИЯ № 55 Учитель: Ященко Ирина Владимировна

Разработка урока геометрии 8 класс.

(Урок изучения нового материала к учебнику Л.С. Атанасяна Геометрия 7 — 9)

Тема: Ромб.

Цели и задачи урока:

• Ввести определения и свойства ромба на основе, ранее изученного материала и научить учащихся применять изученный материал в процессе решения задач.

• Формировать умения применять свойства в стандартных и нестандартных ситуациях.

• Развивать внимательность и смекалку у учащихся.

• Воспитывать такие качества, как честность ответственность и аккуратность.

Оборудование урока: учебник, чертёжные принадлежности, мультимедийный проектор, интерактивная доска, фигуры из бумаги параллелограмма и ромба, ножницы, бумага.

Ребята рассаживаются по группам.

Ход урока:

1.Проверка домашнего задания. Если есть вопросы, разобрать вместе с детьми.

2. Сегодня на уроке мы продолжим знакомство с четырехугольниками. Давай те вспомним какие фигуры нам уже знакомы (параллелограмм, трапеция, прямоугольник). Каждая группа выбирает фигуру и защищает её. Дает определение. Какими свойствами она обладает, называет признаки, где применяется.

Хорошо, а теперь мы решим следующие задачи. Задачи выдаются группе и высвечиваются на интерактивной доске. Дается время для обсуждения в группе. 1.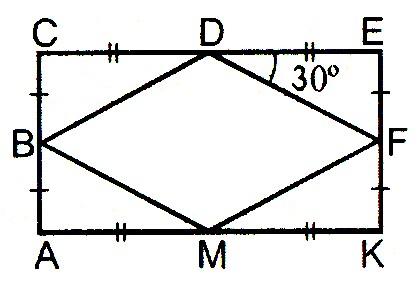АСЕК – прямоугольник, ВС= 5 см. Найдите P_BDFM.
2.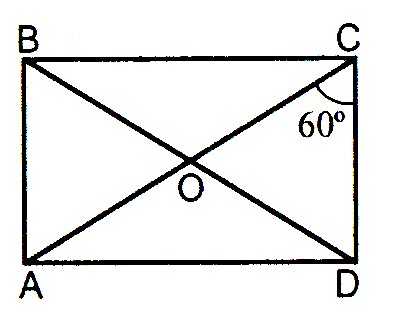ABCD – прямоугольник. Найти: АОВ, ВОС.

3.

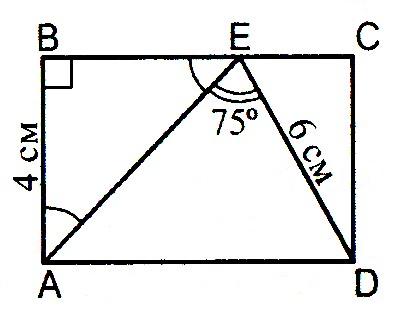ABCD – прямоугольник. Найти: AD.

Решая первую задачу мы увидели, что в прямоугольник вписана фигура. А что это за фигура, кто знает? (ромб)

Назовите тогда тему нашего урока. Дети формулируют тему урока.

Какие цели и задачи мы должны перед собой поставить изучая эту тему. Ребята формулируют тему и задачи урока.

Цели: познакомится с фигурой, рассмотреть основные свойства и признаки, показать применение в процессе решения задач.

У вас на столе лежат фигуры, вы наверное их уже узнали. Определите какая фигура ромб…почему? Что объединяет эти фигуры, чем они отличаются, как проверить что вы выбрали именно ромб?

Попробуйте дать определение…. дети высказывают свои предположения.

Ромб — параллелограмм, у которого все все стороны равны.

Какими свойствами будет обладать ромб? Попробуйте доказать.

Если ромб является параллелограммом то и все свойства параллелограмма будут присуще ромбу.

Решим задачи:

1.Если периметр ромба равен 60 см, то чему равна сторона ромба?

2. Если один угол ромба равен 40, то остальные углы равны ?

3. Если проведем диагональ, будет ли треугольник равнобедренным…, а может ли он быть равносторонним … а тогда чему будут равны углы нашего ромба…

4. Может ли диагональ быть в два раза больше его стороны? (нет)

А теперь я попрошу вас на листе бумаги нарисовать ромб,

Или вырезать…

Возьмите ромб и проведите в нем диагонали, что заметили… правильно ли вы нарисовали…

Характеристическое свойство ромба

Диагонали ромба взаимно перпендикулярны, и делят его углы пополам.

…попробуйте доказать самостоятельно.

Сформулируйте признак ромба…и запишите основные моменты в тетрадь.

А теперь я попрошу еще раз нарисовать ромб, и вырезать ромб. Кто может сделать это быстрее, дети догадались что можно только одним разрезом вырезать ромб.

Из данного ромба «сложите конверт» без припусков. Докажите, что можно из ромба получить конверт.

— А если в четырехугольнике диагонали перпендикулярны, это ромб?

Где применяется ромб (выступление одного из ребят)

— изображая на писанках (расписанных пасхальных яйцах) ромб, разделенный на четыре части, художники имели в виду вспаханное и засеянное поле;

— Первый кроссворд в его современном виде сложил и опубликован в 1913 году американский журналист А.Уинн. Составленный им вордкросс , позже ставший кроссвордом, был ромбовидной формы. В нем не было пустых черных клеток, а слова читались как по вертикали, так и по горизонтали. Успех новинки был ошеломляющим.

— На флаге Бразилии изображен желтый ромб с вписанным в него кругом.

— В начале Великой Отечественной войны офицерские звания ещё различались не по звездочкам на погонах, а по ромбикам в петлицах.

— Игра в бейсбол проходит на поле в форме ромба. В его центре находится игрок, подающий мяч.

— Скай-дайверы со всего мира поставили рекорд по купольной парашютной акробатике в классе больших формаций. Спортсмены прыгнули сразу с пяти самолетов, летящих на высоте шести с половиной тысяч метров над землей Флориды, и выстроили в воздухе под открытыми куполами огромный ромб из 100 парашютистов.

— пример стиха – ромба:

Мы-

Среди тьмы.

Глаз отдыхает.

Сумрак ночи живой.

Сердце жадно вздыхает.

Шепот звезд долетает порой,

И лазурные чувства в блеске росистом.

Поцелуем душистым

Поскорее блесни!

Снова шепни,

Как тогда:

«Да!»

Э. Маратов

Решим такую задачу: (используем интерактивную доску)

На доске нарисовали ромб АВСД, провели диагональ АС, и отметили некоторую точку М на стороне ВС. Затем часть рисунка стерли, оставив сторону АВ и точку М. Можно ли восстановить рисунок.

Если можно сделайте это.

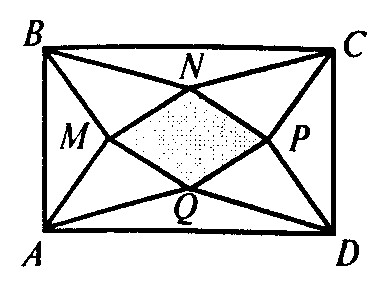
На рисунке изображен прямоугольник АВСD, на сторонах которого внутри него построены равные равнобедренные треугольники: АВМ = CDP, BCN = ADG. Докажите, что четырехугольник MNPG – ромб.

Подводим итоги. Обсуждаем все ли задачи которые ставили дети решены. Проводим рефлексию.

Домашняя работа. П.46., № 408, 407.

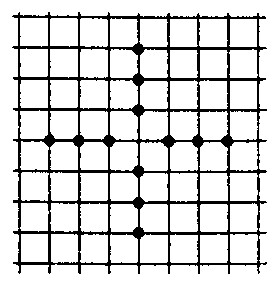
Сколько всего ромбов с вершинами в данных точках можно построить?

Конспект «ЗАДАЧИ по теме Прямоугольники»

«ЗАДАЧИ по теме Прямоугольники»

Прямоугольник — это параллелограмм, у которого все углы прямые.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

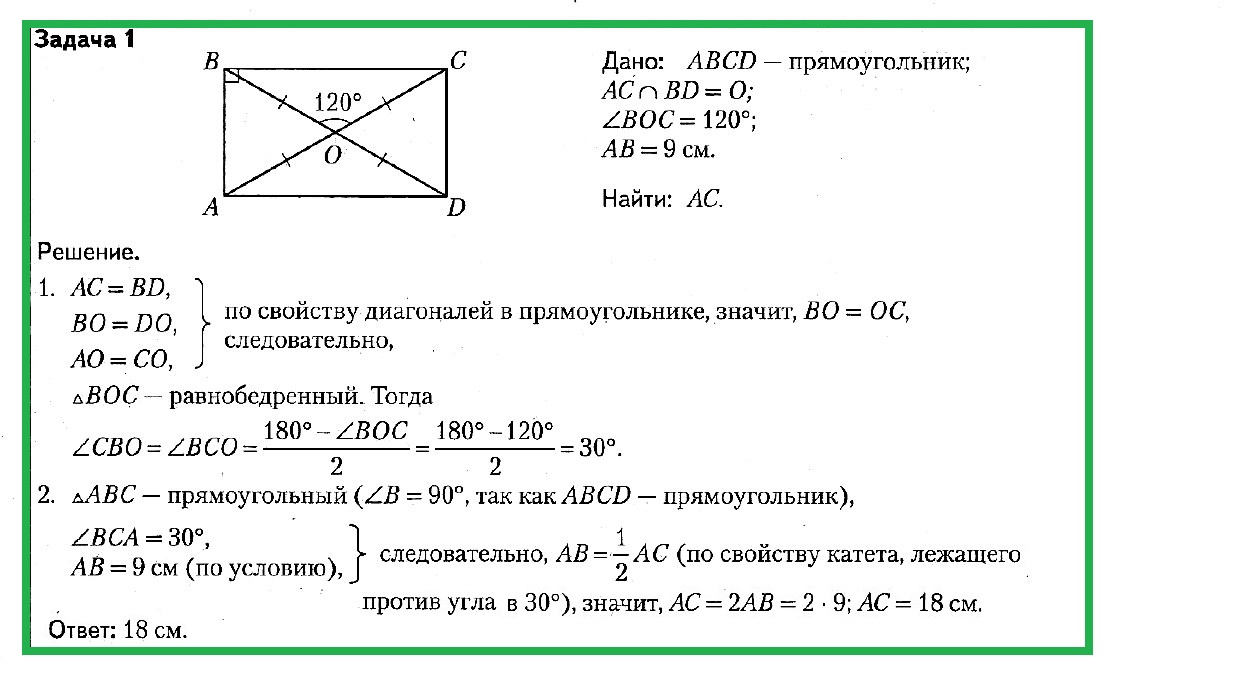
Задача № 1. Дано: ABCD — прямоугольник; AC ∩ BD = 0; ∠BOC = 120°; AB = 9 см. Найти: AC.

Задача № 2. Дано: ABCD — прямоугольник; AC ∩ BD = 0; ∠CAD = 30°; AC = 12 см. Найти: P_AOB.

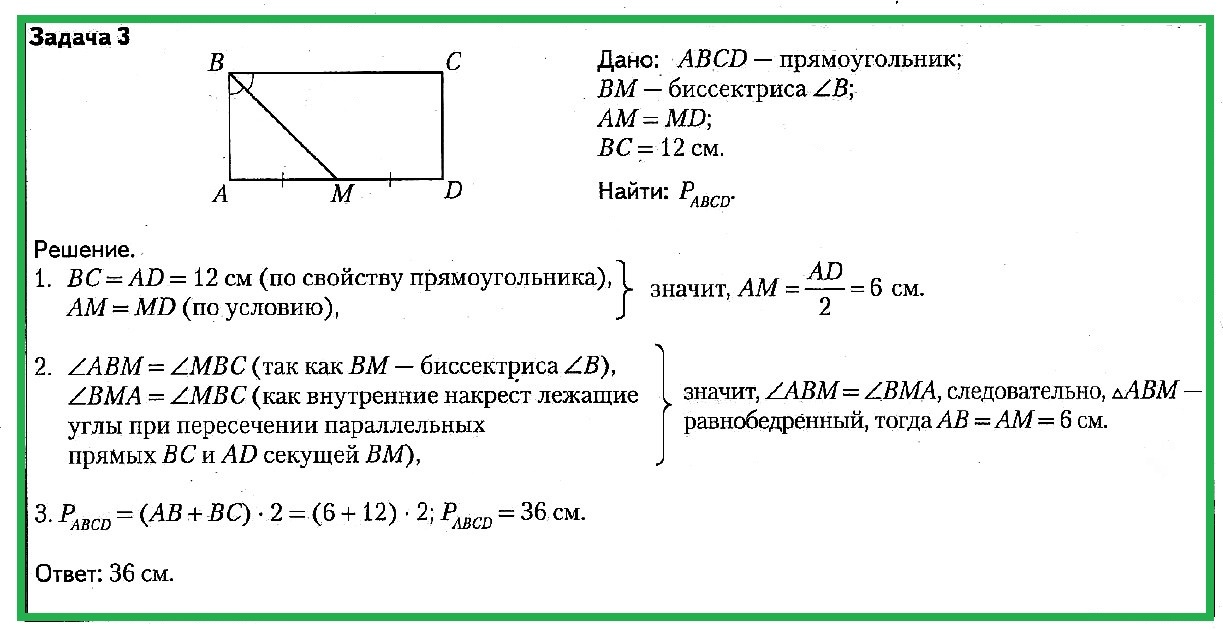
Задача № 3. Дано: ABCD — прямоугольник; BM — биссектриса угла B; AM = MD; BC = 12 см. Найти: P_ABCD.

Задача № 4. Дано: ABCD — прямоугольник; BK — биссектриса ∠DBC; BD — биссектриса ∠ABK; DL ∥  BK; KC = 3 см. Найти: P_DLBK.

Задача № 5.  Дано:  ABCD — прямоугольник; AC ∩ BD = 0; расстояние от точки О до АВ на 4 см больше расстояния от точки О до AD; P_ABCD = 56 см. Найти: AB; BC; CD; AD.

Это конспект по теме «ЗАДАЧИ по теме Прямоугольники». Выберите дальнейшие действия: