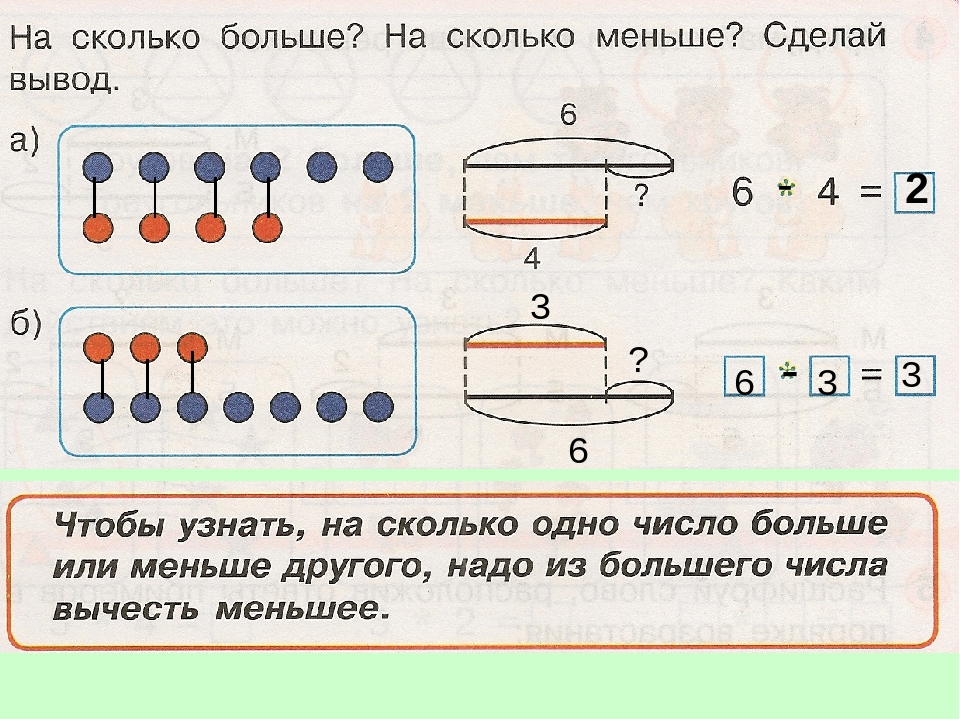
Урок математики в 3-м классе по теме «Решение задач на нахождение двух величин по сумме и разности»
Основные цели урока:
1) формировать способность к решению задач на нахождение значений двух величин по их сумме и разности;
2) тренировать навыки устных вычислений, прием умножения многозначного числа на однозначное число, способность к составлению буквенных выражений и графических моделей к текстовым задачам;
3) развивать мыслительные операции, внимание, речь, коммуникативные способности, интерес к математике.
Демонстрационный материал:
1) презентация.
Раздаточный материал:
1) индивидуальное задание для затруднения;
2) карточка для этапа рефлексии;
3) конверты с полосками зелёного и чёрного цветов для этапа 4.
Ход урока
1. Самоопределение к учебной деятельности:
— Доброе утро всем.
1 слайд
Удача приходит тем, кто её добивается
— Как вы понимаете значение этого выражения?
— Какие качества характера понадобятся вам для успешной работы?
— Ждёт сегодня нас удача, если мы решим (хором) задачу.
— А какие знания понадобятся для решения задач?
— Сегодня на уроке мы будем решать задачи. Пусть каждому из вас сопутствует удача, а я вам помогу.
2.Актуализация знаний и фиксация затруднения в деятельности.
2–4 слайды
— Начнем работу с решения примеров. Называем ответы примеров.
— Что привлекло ваше внимание?
12 • 2 156+25+44 (35 +15) • 2
27 • 2 231+11+19 (44 +18) : 2
38 : 2 564-36-64 (58 — 34) : 2
Индивидуальное решение задач.
5 слайд
— Возьмите из конверта листки с задачами. Прочитайте и проанализируйте первую задачу. Заполните схему, запишите под схемой решение на листках.
В магазин для продажи завезли a пачек чёрного чая, а зелёного – на n пачек меньше. Сколько пачек чая завезли в магазин? (a+(a-n) (п.) – чая завезли в магазин)
— Вы хорошо справились с первой задачей, на обратной стороне листа – вторая задача.
Задание прежнее. Заполните схему, решите вторую задачу.
В магазин для продажи завезли a пачек чая, причём зелёного на n пачек меньше, чем чёрного. Сколько пачек чая каждого вида завезли в магазин? (a-n):2 (a-n):2+n
Появляются разные решения задач, так как задачи нового вида ещё не изучались.
На доске вывешиваются разные варианты работ.
— Что получилось?
3. Выявление причин затруднения и постановка
цели деятельности.
— Какое задание выполняли?
— Почему так получилось?
— Чем похожи задачи?
— Чем вторая задача отличается от первой? (В первой задаче a — это число пачек чёрного чая, а во второй – a — это число пачек чёрного и зелёного чая вместе.)
— Давайте внимательнее рассмотрим задачу, которая вызвала затруднение.
-Что требуется найти? (Количество чёрного и зелёного чая, завезённого в магазин.)
— Сколько величин мы должны найти? (Две величины — количество чёрного и зелёного чая.)
— Вы правильно заметили, что во второй задаче неизвестно число и чёрного, и зелёного чая, то есть нам надо найти значение двух величин, должны получить два ответа.
— Что известно? (Сумма a и разность n чёрного и зелёного чая.)
6 слайд
— Как можно было бы назвать новый тип задач?
— Какова ваша цель? (Научиться решать задачи
по сумме и разности. )
)
— Вы правильно догадались, тема сегодняшнего нашего урока.
Решение задач на нахождение значений двух величин по сумме и разности.
7 слайд
Появляется на экране тема урока.
4. Построение проекта выхода из затруднения.
— Как вы предлагаете действовать?
— Предлагаю убедиться в правильности хода решения второй задачи. Возьмите из конверта полоски бумаги.
У каждого ребёнка в руках 2 полоски цветной бумаги, изображающие число пачек соответственно чёрного и зелёного чая.
— Сколько полосок?
— Что вы можете сказать о длине полосок? Какую длину имеет чёрная полоска по отношению к зелёной полоске?
— Покажите полоску, которая могла бы соответствовать числу пачек чёрного чая.
— Покажите полоску, которая подходит число пачек зелёного чая.
— Что в задаче означает a?
— Вы сложили две полоски, а как называется результат при сложении?
— Как можно показать с помощью полосок, чему равна сумма a?
— А как показать на полосках разность n?
— А как уравнять количество разных пачек?
— Сколько стало пачек? Назовите буквенное
выражение своего действия. a-n
a-n
— Обратите внимание на размер полосок.
— Значит, две эти маленькие полоски равны a-n. А чему равна одна — меньшая? (a-n):2
Появляется запись на слайде.
— Что означает это выражение?
— А как теперь узнать большее число? (a-n):2+n
— Мы ответили на вопрос задачи? (Да.)
10–11 слайды
— Как мы шагали? Прочитайте первое действие или шаг.
Путь решения можно зафиксировать в виде последовательных операций: a-n —> (a-n):2 —> (a-n):2+n
(Для того, чтобы найти значение двух величин по сумме и разности, надо из суммы вычесть разность и поделить пополам, получим меньшее число, потом к меньшему числу прибавить разность, получится большее число.)
— Мы нашли сначала удвоенное меньшее число. А
теперь попробуйте построить способ решения,
когда вначале находится удвоенное большее число.
Аналогично рассуждая, учащиеся строят последовательность операций: a+n —> (a+n):2 —> (a+n):2-n
(Для того, чтобы найти значение двух величин по сумме и разности, надо к сумме прибавить разность и поделить пополам, получим большее число, потом из большого числа вычитаем разность, получится меньшее число.)
Вывод: При вычитании суммы и разности получается удвоенное меньшее число, а при сложении – удвоенное большее число.
— Если из суммы вычесть разность и поделить на 2, находится какое число? Меньшее или большее? А если к сумме прибавить разность и поделить на 2, то какое число находится?
Физкультминутка.
5. Первичное закрепление во внешней речи.
Решение задачи с комментированием.
1 способ.
(Известна сумма и разность числа учеников обоих
классов, можно искать числа учеников по
алгоритму: сначала найдем разность 56 и 2, разделим
её пополам – получим меньшее число, то есть число
учеников второго класса, и прибавим к нему 2 –
получим большее число, то есть число учеников
второго класса.
2 способ.
(Известна сумма и разность числа учеников обоих классов, можно искать числа учеников в классах по алгоритму: сначала найдем сумму 56 и 2, разделим её пополам – получим большее число, то есть число учеников первого класса, и вычтем из него 2 – получим меньшее число, то есть число учеников второго класса.)
Запись решения задачи. (Один ученик – у доски, а остальные – в учебниках)
1) 56-2=54 (чел.) — удвоенное меньшее число (удвоенное число учеников во втором классе).
2) 54:2=27 (чел.) — во втором классе.
3) 27+2=29 (чел.) — в первом классе.
Ответ: 29 человек; 27 человек.
— Можно ли иначе найти число учеников во втором классе?
— А какой способ удобнее?
— А как можно проверить, верно ли решена задача? (Найти разность и сумму полученных чисел: 29+27=56, 29-27=2)
— А ещё каким другим способом можно решить задачу? (Сначала найти большее число, а затем - меньшее)
1) 56+2=58 (чел. ) — удвоенное число учеников в первом
классе.
) — удвоенное число учеников в первом
классе.
2) 58:2=29 (чел.) — в первом классе.
3) 29-2=27 (чел.) — во втором классе.
Ответ: 29 человек; 27 человек.
— Решение задачи № 3 (а) в тетради.
Совместно на доске заполним схему, а в тетрадях запишите решение.
1 способ
1) 248-8=240 (м.) — удвоенное число марок у Пети.
2) 240:2=120 (м.) — число марок у Пети.
3) 120+8=128 (м.) — число марок у Мити.
Ответ:120 марок; 128 марок.
2 способ
1) 248+8=256 (м.) — удвоенное число марок у Мити.
2) 256:2=128 (м.) — число марок у Мити.
3) 128-8=120 (м.) — число марок у Пети.
Ответ:128 марок; 120 марок.
6. Самостоятельная работа.
Выполнение № 2 на странице 8 в учебнике.
Самостоятельная работа детей с самопроверкой.
12 слайд
1 способ
1) 18-4=14 (кг) — удвоенная масса продуктов в первой
сумке.
2) 14:2=7 (кг) — масса продуктов в первой сумке.
3) 7+4=11(кг) — масса продуктов во второй сумке.
Ответ: 7 кг; 11 кг.
2 способ.
1) 18+4=22 (кг) — удвоенная масса продуктов во второй сумке.
2) 22:2=11 (кг) — масса продуктов во второй сумке.
3) 11-4=7 (кг) — масса продуктов в первой сумке.
Ответ: 7 кг; 11 кг.
Организация взаимопомощи детей.
Домашнее задание: № 3 (б) на странице 8.
7. Включение в систему знаний и повторение.
Решение примеров № 5 со страницы 9.
Решение уравнений № 6.
8. Рефлексия деятельности.
— Два главных вопроса урока: что изучали и что узнали?
— Какова цель сегодняшнего нашего урока?
— Как называются задачи нового типа?
— Удалось ли достичь цели?
— Что помогло для достижения цели?
— Что обязательно должно быть известно для решения этих задач?
— Вы довольны своей работой?
— Вы сможете сказать, на сколько удача была с вами, как старательно вы её добивались?
— Оцените, свои успехи знаком “+” напротив
близкой вам фразы.
13 слайд
Да, я умею решать задачи по сумме и разности. Не хватает уверенности в решении задач по сумме и разности, но я стараюсь. Пока я затрудняюсь в решении задач по сумме и разности. |
— Над чем вам ещё можно поработать?
— Какие качества вам помогали, а какие качества мешали при работе?
— Дома несколько раз проговорите ещё раз алгоритм решения задачи и желающие могут составить задачу на нахождение значений двух величин по их сумме и разности.
14 слайд
Спасибо за работу на уроке и желание добиться успеха.
«Решение составных задач на нахождение величин по их сумме и разности»
Урок математики в 3 классе по теме:
«Решение составных задач на нахождение величин по их сумме и разности»
Математика, 3 класс, урок 4 (II часть) (Автор: Л.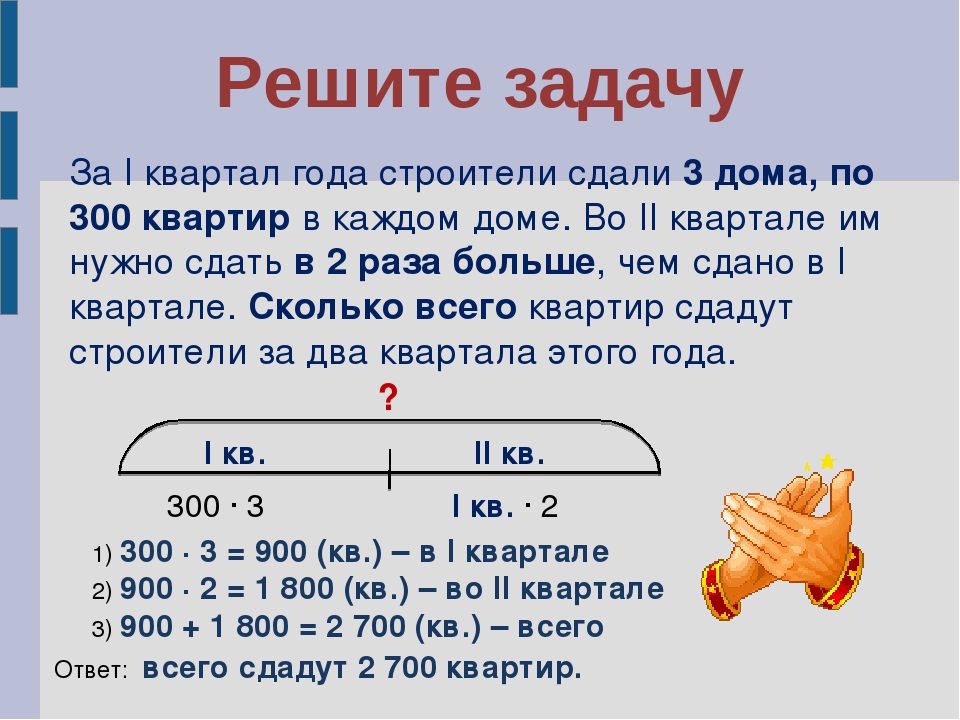 Г.Петерсон)
Г.Петерсон)
Цели: учить решать задачи нового вида; повторить нумерацию чисел, порядок выполнения действий; формировать вычислительные навыки; способствовать развитию внимания, памяти, мышления.
Тип урока: открытие нового знания.
Девиз урока: «Где есть желание, там всегда найдется путь».
Ход урока
Организационный момент
У. Прочитайте незаконченное высказывание. (Последнее слово закрыто.)
Д. «Где есть желание, там всегда найдется …».
У. Как вы думаете, как можно продолжить эту фразу? (Ответы детей.)
Открыть продолжение фразы.
«Где есть желание, там всегда найдется путь».
У. Как вы понимаете смысл этого высказывания? Подходит ли оно к уроку математики? Почему? (Ответы детей. )
)
У. Скажите, пожалуйста, с желанием ли вы решаете задачи? Почему? (Ответы детей.)
У. У кого из вас есть желание отправиться дальше в путь по стране Математике и научиться решать задачи нового типа?
У. Тогда все вместе – в путь!
Актуализация знаний
Работа в парах по карточкам.
У. Выполните действия и вставьте числа в «окошки»».
Проверка по эталону.
У. Прочитайте числа на доске.
40.150.763.007; 507.040 г; 5.000.007.
У. Какое число лишнее? Почему?
Д. 507.040 г – именованное число.
У. Вырази его в более крупных единицах измерения.
Один ученик работает с объяснением у доски.
Постановка темы урока
У. Прочитайте задачу на доске.
Прочитайте задачу на доске.
В двух классах 56 человек, причём в первом классе на 2 человека больше, чем во втором. Сколько человек в каждом классе?
У. Подумайте, как вы будете решать задачу?
Д. Задачу решить не можем.
У. Сформулируйте цель урока.
Д. Научиться решать задачи нового вида.
«Открытие» нового знания
У. Что надо сделать, если возникло затруднение?
Д. Надо остановиться и подумать.
У. Почему у вас возникло затруднение? Что необычного во второй задаче?
Д. Есть целое, а части неизвестны.
У. Что ещё известно?
Д. Что в первом классе на 2 человека больше, чем во втором.
У. А что было бы, если бы в первом классе этих двух человек не было?
Д.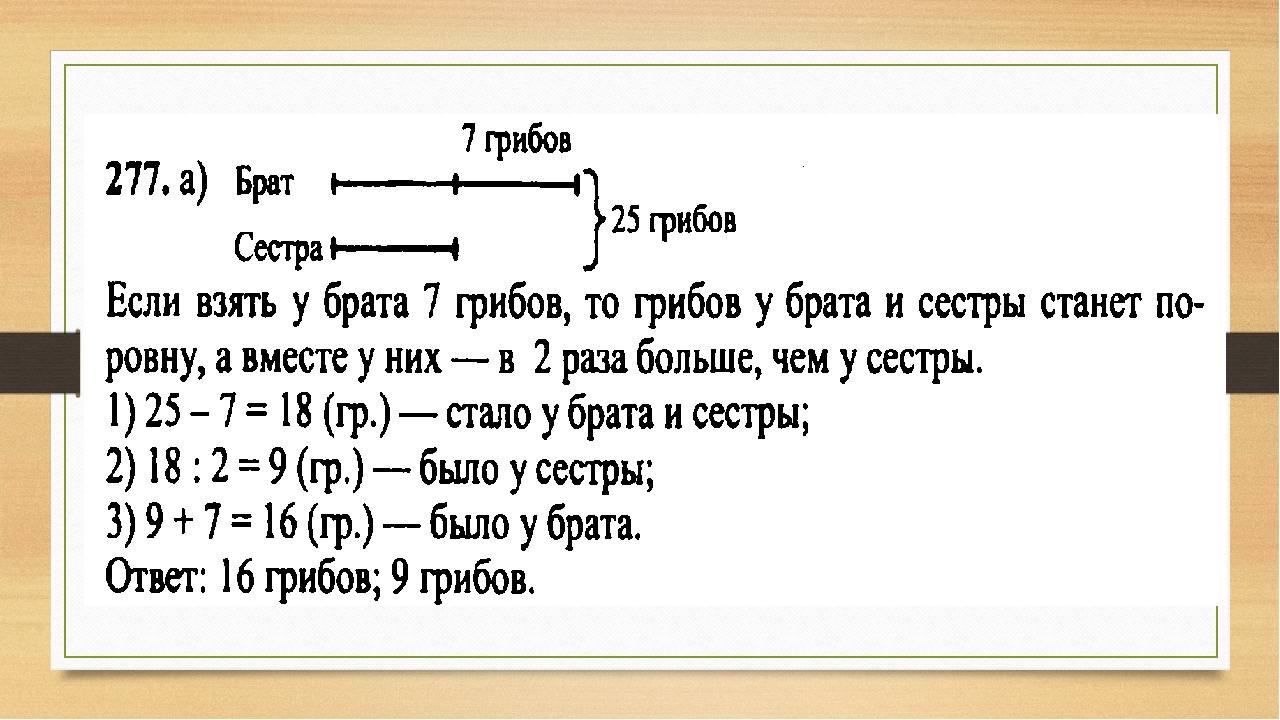 Детей в этих классах было бы поровну.
Детей в этих классах было бы поровну.
У. Тогда в двух классах было бы не 56, а сколько?
Д. 54 чел.
У. Выполнять задание вы будете в группах. Вспомним основные правила работы в группах.
У. Что обычно вам помогает при решении любой задачи?
Д. Схема.
У. Обратитесь к ней за помощью.
Учащиеся работают самостоятельно 5 минут.
Через пять минут представители каждой группы вывешивают результаты работы на доску. Одна из групп озвучивает, как они получили результат, остальные дополняют и уточняют.
Д. Наша группа считает, что надо решать задачу так…
Решение:
1. 56 – 2 = 54 (чел.) – удвоенное число учеников во 2 классе.
2. 54 : 2 = 27 (чел.) – во 2 классе.
3. 27 + 2 = 29 (чел.) – в 1 классе.
У. Такие задачи называют задачами на нахождение величин по их сумме и разности.
Д. Как бы вы назвали тему урока?
У. Решение задач на нахождение величин по их сумме и разности.
Д. Попробуем создать алгоритм решения задачи по сумме и разности.
Алгоритм решения задачи по сумме и разности
Повесить карточку доску.
У. Что вы можете найти, зная сумму одинаковых отрезков?
Д. Длину одного отрезка.
У. Длину какого отрезка вы получили?
Д. Длину меньшего отрезка.
Повесить карточку доску.
У. Как теперь найти длину большего отрезка?
Д. Надо к меньшему числу прибавить разницу.
Повесить карточку доску.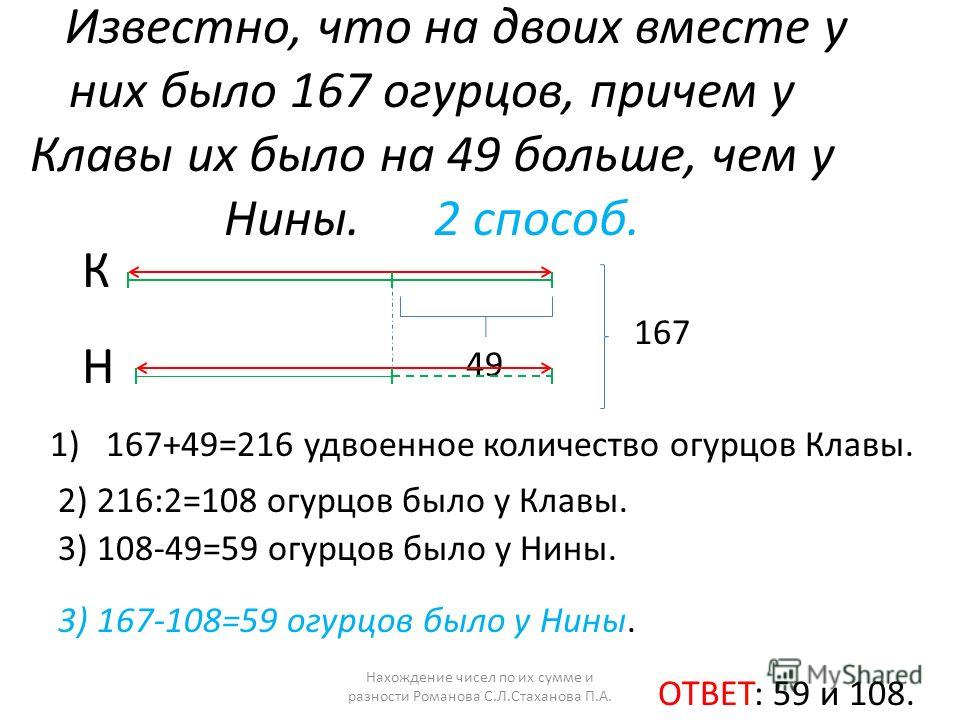
У. Итак, алгоритм чего вы сейчас создали?
Д. Алгоритм решения задачи по сумме и разности.
Физкультминутка
У. Прочитайте числа 56.789 и 98.765. Что заметили? Работаем с большим числом.
— Наклонитесь столько раз, сколько единиц в разряде десятков тысяч.
— Сколько раз наклонились? (9 раз.)
— Присядьте столько раз, сколько единиц в разряде сотен единиц.
— Сколько раз присели? (7 раз.)
— Подпрыгните столько раз, сколько единиц в разряде тысяч.
— Сколько раз подпрыгнули? (8 раз.)
Первичное закрепление с проговариванием вслух
№ 4 (стр. 9)
У. Можете ли вы использовать новые знания при решении примеров из № 4 (стр. 9)?
Д.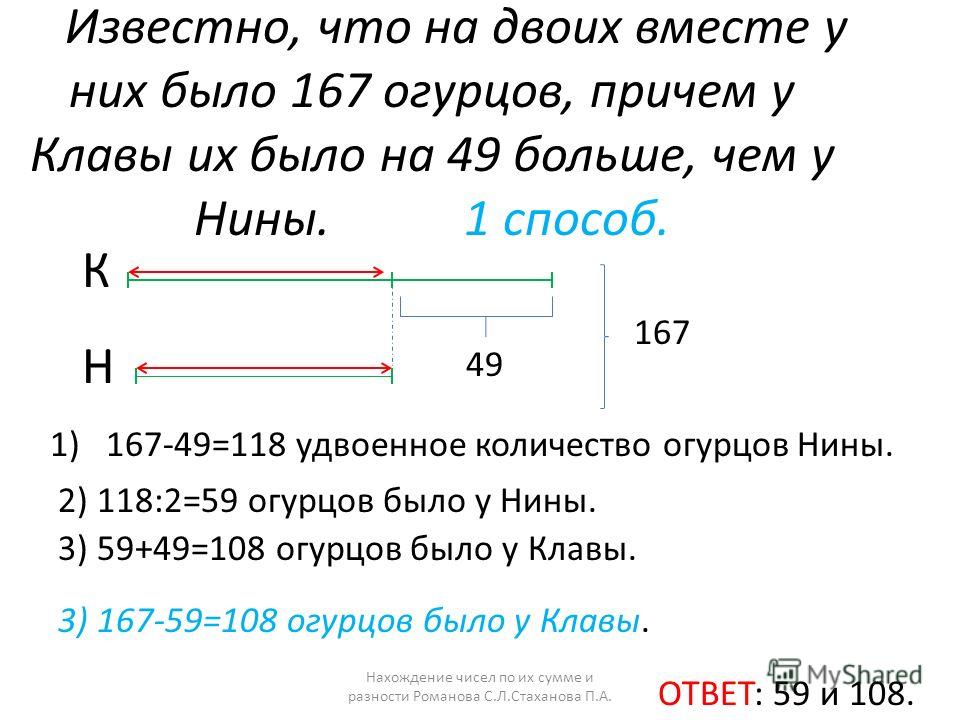 Да.
Да.
У. Верно. Так же можно решать не только задачи, но и примеры.
а) 15 – 3 = 12, 12 : 2 = 6, 6 + 3 = 9. (6 и 9)
б) 132 – 48 = 84, 84 : 2 = 42, 42 + 48 = 90. (42 и 90)
У. Составим алгоритм решения одним общим способом.
в) (c – d) : 2 – I число; (c – d) : 2 + d – II число.
г) (y – x) : 2 – I число; (y – x) : 2 + x – II число.
У. Вы готовы проверить себя?
Д. Да.
Самостоятельная работа с самопроверкой по эталону: № 2 (стр. 8).
Эталон
18 – 4 = 14 (кг.) — удвоенное число продуктов в 1 сумке.
14 : 2 = 7 (кг.) — в 1 сумке.
7 + 4 = 11 (кг.) — во 2 сумке.
Ответ: 7 кг. в 1 сумке, 11 кг. во 2 сумке.
У. Проверьте себя по эталону для самопроверки и зафиксируйте результат при помощи смайликов.
Проверьте себя по эталону для самопроверки и зафиксируйте результат при помощи смайликов.
У. Поднимите руки, у кого задание не вызвало затруднение?
Повторение ранее изученного материала
№ 8 (в паре) – 1 груша, т. к. 2 яблока = 1 груша.
№ 9 (а) (Проверка по эталону на доске.)
40.800 · (3.500 : 70) : 100 – 328 · 60 = 720.
1) 3.500 : 70 = 50; 2) 40.800 · 50 = 2.040.000; 3) 2.040.000 : 100 = 20.400;
4) 328 · 60 = 19.680; 5) 20.400 — 19.680 = 720.
Подведение итогов урока
У. Какие новые знания получили?
— Сможете дома сами решить задачу на нахождение величин по их сумме и разности?
— Расскажите путь решения задачи по сумме и разности по алгоритму.
— Кто доволен своей работой?
— Оцените свою работу на уроке с помощью таблицы.
Учащиеся работают с таблицей для индивидуальной рефлексии.
У. Оцените цветом свою работу на уроке.
Я думаю, что сегодня все могут поздравить себя и друг друга с успехом, которого вы все добились в открытии нового знания. Урок окончен. Спасибо за работу.
Домашнее задание:
№ 9 (б), стр. 9.
Попробовать найти другой способ решения задач по сумме и разности и придумать алгоритм их решения, изобразить на листочке.
Попробовать придумать свою задачу по сумме и разности, записать ее условие на карточке и решить в тетради.
Шаги учебной деятельности
Конспект урока по математике по теме «Решение задач по сумме и разности» для 3 класса — Математика — Начальные классы
Подгайко Ирина Юрьевна
МОАУ для детей дошкольного и младшего школьного возраста прогимназия
Учитель начальных классов
Конспект урока по математике «Школа 2100», 3 класс
Тема: «Решение задач по сумме и разности»
Цель: Формировать
способность к решению задач на нахождение
значений двух величин по их сумме и
разности.
Тренировать навыки устных вычислений, приём умножения многозначного числа на однозначное, способность к решению простых уравнений всех видов, составлению буквенных выражений и графических моделей к текстовым задачам.
Развивать мыслительные операции, внимание, речь, коммуникативные способности, интерес к математике.
Ход урока.
1.Орг. момент.
2.Актуализация знаний.
Класс разделён на группы по 4 человека в каждой. По одному человеку из трёх команд выходят к доске для индивидуальной работы. В это время класс пишет математический диктант, Причём по одному человеку из команд, не представленных у доски, получают для записи ответов переносные доски. В ходе урока за верные ответы команды получают фишки- очки, которые суммируются при подведении итога в конце урока.
2.1.Математический диктант.
-Уменьшите число
244 в 2 раза . (122)
(122)
-Найди произведение 57 и 2 .(114)
-Число 350 уменьшить на 230.(120)
-На сколько 134 больше 8? (128)
-Число 1280 уменьшите в 10 раз.(128)
-Чему равно частное 363 и 3.(121)
-Сколько сантиметров в 1м 2дм 4см?(124)
Учащиеся, работавшие на переносимых досках, показывают свои решения. Ответы сравниваются, ошибки разбираются. Карточки с правильными ответами, на обратной стороне которых написаны буквы, учитель выставляет на доске.
-Какое число можно считать лишним в ряду ответов?(120- круглое, а остальные нет; 121- нечётное, а остальные чётные; 114- количество десятков равно 1, а у остальных 2- и т.д.)
-Ребята, а хотите узнать, кто к нам сегодня придёт в гости? Расположите ответы в порядке возрастания.
114 120 121 122 124 126 128
З А Й Ч А Т А
2. 2.Поверка индивидуальных
знаний у доски
2.Поверка индивидуальных
знаний у доски
1. 2. 3.
68:4+57:3 3 12 +14 2 2 (14+18):1
75- 34:2 (81- 53) 2 – 49 25+ 16 2 – 15
(29 +69):7 +22 7 13- 12:6 (62-25) 2+ 15
-Три зайчишки — плутишки получили в день рождения подарки. Посмотрите, нет ли среди них одинаковых подарков?? Учащиеся проверяют работу представителей команд, находят примеры с одинаковыми ответами.
-Какие числа без пары? (число 7)
-Дайте характеристику этому числу. ( Однозначное, нечётное, предыдущее число 8, имеет 2 делителя –1 и 7 и т.д.
2.3. «Блицтурнир»
-Каждый учащийся получает индивидуальный листок с задачами и схемами:
а) У одной зайчихе, а колец, а у другой — на n колец меньше. Сколько колец у них вместе? б) У двух зайчих, а колец, причём у первой зайчихи на
n
колец меньше, чем у второй. у каждой зайчихи? а ? 1. 1. n ? n а 2. 2. ? ? |
Учитель предлагает каждому ребёнку подобрать к задачам подходящие схемы, составить буквенные выражения, обсудить решение в командах, по одному представителю каждой команды записывают свои выражения на доске.
При разборе первой задачи учащиеся достаточно быстро приходят к общему мнению: а+(а-n) . Для второй задачи получаются разные ответы.. Какая же из команд заработала очко?
3.Постановка проблемы.
-Чем похожи задачи? (В обоих говорится, что у одной из зайчих на n колец меньше, чем у другой)) Чем вторая задача отличается от первой?(В первой задаче а – это число колец только у первой зайчихи, а во второй- сразу у двух зайчих)
-Молодцы! Вы верно
заметили, что во второй задаче не известно
число колец ни у одной из зайчих. А что
известно?(Сумма и разность колец)
А что
известно?(Сумма и разность колец)
-Как бы вы назвали этот новый тип задач?
-Дети предлагают свои варианты. Отталкиваясь от них, учитель сообщает им принятое название. Итак, цель урока— научиться решать задачи, в которых значения двух величин надо найти по их сумме и разности. На доске открывается тема урока: Решение задач «по сумме и разности»
4. «Открытие» детьми нового знания.
У каждого ребёнка в руках 2 полоски цветной бумаги, изображающие число колец соответственно первой и второй зайчих:
n a
-Покажите полоску, изображающую число колец у первой зайчихи, у второй, у них вместе. Что обозначает а? (Сумму колец.) Покажите с помощью полосок, чему равно а?? А как показать на полосках значение разности n? ( Дети накладывают одну полоску на другую, фиксируют конец меньшей полоски и закрашивают разность полосок.)
-А как уравнять
количество колец у обеих зайчих? ( Дети
отгибают часть длинной полоски так,
чтобы оба отрезка стали равными. )) Сколько
колец стало? (а-n)
)) Сколько
колец стало? (а-n)
-Значит, две эти маленькие полосочки равны а-n. А чему равна она одна ?
((а-n):2))
-А теперь как узнать большее число?( Нужно к полученному числу прибавить n)
Путь решения можно зафиксировать в виде последовательности операций:
a -n (a-n):2 (a-n):2+n
-Мы нашли сначала удвоенное меньшее число. А теперь попробуйте построить способ решения, когда вначале находится удвоенное большее число.
Какая группа сможет это сделать быстрее?
a +n (a+n):2 (a-n):2-n
Вывод: при вычитании суммы и разности получается удвоенное меньшее число, а при сложении — удвоенное большее число.
5.Первичное закрепление.
1.стр.9.№1(а)
-Что известно в задаче и что нужно найти?? « Оденьте» схему и проанализируйте задачу.
-запишите решение
с комментированием.
2.Задания № 4(а, в), стр. 9 распределяются в группы по одному выполняют задание: один проговаривает условие и вопрос задачи, другой объясняет, как заполнить схему заготовку, третий проговаривает, найти большее (меньшее) число, а четвёртый — как найти меньшее (большее) число. Проверка решения по образцу.
6. Физкультминутка.
7. Самостоятельная работа с проверкой в классе.
Стр.8 № 2
Корректировка ошибок: стр.9 № 49(б)
7.1. Повторение.
№5. Стр. 9
№8 стр. 9
8. Итог урока.
Что нового узнали?
С помощью чего построили алгоритм решения (с помощью полосок)
Посчитайте свои очки, кто как поработал?
Д/з по выбору № 3 стр.8, №10 стр.9
Используемая литература:
Методические
рекомендации по математике Л. Г.Петерсон
для 3 класса
Г.Петерсон
для 3 класса
Урок 49. решение задач при помощи систем уравнений первой степени — Алгебра — 7 класс
Алгебра
7 класс
Урок № 49
Решение задач при помощи систем уравнений первой степени
Перечень рассматриваемых вопросов:
• Решение задач.
• Система уравнений.
• Решение системы уравнений.
Тезаурус:
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Решить систему – это значит найти все её решения.
Алгебраический способ состоит в получении ответа на вопрос задачи с помощью составления уравнения или системы уравнений и последующего решения уравнения или системы.
Основная литература:
- Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
- Чулков П.
 В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с. - Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
- Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Рассмотрим задачу. Сошлись два пастуха, Иван и Пётр. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!» А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!» Сколько же было у каждого овец?
Мы не знаем, сколько овец у Ивана, и сколько у Петра.
Обозначим за х число овец у Ивана, а за у – число овец у Петра.
Мысленно разделим условие задачи на две независимые части:
1. Иван и говорит Петру: «Отдай-ка ты мне одну овцу, тогда у меня будет овец ровно вдвое больше, чем у тебя!»
2. А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!»
А Пётр ему отвечает: «Нет, лучше ты мне отдай одну овцу, тогда у нас будет овец поровну!»
Для каждой из частей составим уравнение с двумя неизвестными.
Начнем с первой части.
Если бы Пётр отдал Ивану одну овцу, то у Петра осталось бы (у – 1) овец.
А у Ивана стало бы (х + 1) овец.
Но тогда у Ивана было бы вдвое больше овец, чем у Петра.
Можем составить уравнение x + 1 = 2(y – 1).
Составим уравнение с двумя неизвестными для второй части. Если бы Иван отдал Петру 1 овцу, то у Ивана осталось бы (x – 1) овец. А у Петра стало бы (y + 1) овец, и тогда они имели бы овец поровну. Можем составить уравнение: x – 1 = y + 1
Мы составили два уравнения.
И в первом и во втором уравнении х обозначает число овец у Ивана, а у – число овец у Петра. Другими словами, каждое неизвестное число обозначает одно и то же в обоих уравнениях. Значит, эти уравнения можно рассматривать совместно, то есть объединить их в систему уравнений:
Решим эту систему способом подстановки.
Раскроем скобки в правой части первого уравнения.
Выразим х через у.
Подставим (2у – 3) вместо х во второе уравнение системы. Получим уравнение с одним неизвестным у.
Решим его. Упростим левую часть уравнения.
Перенесем неизвестные в левую часть. уравнения, а числа – в правую.
Подставим у = 5 в первое уравнение.
Получим х = 7.
Система имеет единственное решение: х = 7, у = 5.
Вернемся к исходным обозначениям.
Получаем, что у Ивана было 7 овец, а у Петра 5 овец.
Таким образом, мы решили задачу при помощи системы уравнений первой степени.
Задачи с помощью системы уравнений можно решать по следующей схеме.
Сначала вводим обозначения неизвестных.
Мысленно разделив условие задачи на две части, составляем 2 уравнения и объединяем их в систему.
Решаем полученную систему уравнений.
Возвращаемся к условию задачи и использованным обозначениям.
Отбираем решения и записываем ответ.
Разбор заданий из тренировочного модуля.
1. Решим задачу алгебраическим способом.
Задача.
Даны 3 числа, сумма которых равна 23. Если к удвоенному первому числу прибавить второе число и вычесть третье, то получится 32. А если из первого числа вычесть удвоенное второе и прибавить третье, то получится 8.
В задаче 3 неизвестные, поэтому введем следующие обозначения:
Пусть х – первое число, у – второе число, z – третье число.
Мысленно разделим условие задачи на 3 части, по каждой из которых составим уравнение с тремя неизвестными:
Вернёмся к условию задачи: первое число 15, второе число 5, третье число 3.
Ответ: 15, 5, 3.
Составим систему уравнений по условию задачи.
В трех сосудах 54л воды. Если из первого перелить во второй сосуд 4л, то в обоих сосудах будет воды поровну, а если из третьего сосуда перелить во второй 17л, то во втором сосуде окажется в 4 раза больше воды, чем в третьем. Сколько воды в каждом сосуде?
Пусть x л воды было в первом сосуде, y л воды – во втором, z воды – в третьем. Значит, всего в трёх сосудах было x + y + z л воды, что равно 54 л. Составим уравнение: x + y + z = 54.
Значит, всего в трёх сосудах было x + y + z л воды, что равно 54 л. Составим уравнение: x + y + z = 54.
Когда из первого сосуда перелили 4 л воды во второй сосуд, то во втором сосуде стало y + 4 л воды, а в первом сосуде x – 4 л воды. По условию задачи воды стало в сосудах поровну. Составляем уравнение:
y + 4 = x – 4.
Если из третьего сосуда перелить во второй 17 л, то в третьем останется z – 17 л, а во втором станет y + 17 л. По условию задачи во втором сосуде окажется в 4 раза больше воды, чем в третьем. Можем составить уравнение: y + 17 = 4(z – 17).
Записываем систему уравнений:
2. Система уравнений по условию задачи.
Составим систему уравнений по условию задачи: 5% одного числа и 4% другого вместе составляют 46, а 4% первого числа и 5% второго вместе составляют 44. Найдите эти числа.
Формулы сокращенного умножения 💣
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
- Разность квадратов двух выражений равна произведению их разности и их суммы.
- Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
- Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
- Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.

- Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
- Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Доказательство формул сокращенного умножения
Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a2 — b2 = (a — b) * (a + b).
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a2 — b2.
Важно знать, что разность квадратов не равна квадрату разности: a2 — b2 ≠ (a — b)2.
Докажем, что a2 — b2 = (a — b) * (a + b).
Поехали:
- Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
+ a * b — a * b = 0
a2 — b2 = a2 — b2 + ab — ab
- Сгруппируем иначе: a2 — b2 + a * b — a * b = a2 — a * b + a * b — b2
- Продолжим группировать: a2 — a * b — b2 +a * b = (a2 — a * b) + (a * b — b2)
- Вынесем общие множители за скобки:
(a2 — a * b) + (a * b — b2) = a *(a — b) + b *(a — b)
- Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
- Результат доказательства: a2 — b2 = (a — b) * (a + b)
- Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a2 — b2, нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a2 — b2.

Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
(a1+a2+…+an)2 = a12 + a22 + … + an-12 + an2 + 2 * a1 * a2 + 2 * a1 * a3 + 2 * a1 * a4 + … +
+ 2 * a1 * an-1 + 2 * a1 * an + 2 * a2 * a3 + 2 * a2 * a4 + … + 2 * a2 * an-1 + 2 * a2 * an +…+
+ 2 * an-1 * an
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
an − bn = (a − b) * (an-1 + an-2 * b + an-3 * b2 + … + a * bn-2 + bn-1).
Для четных показателей можно записать так:
a2*m − b2*m = (a2 − b2) *(a2*m−2 + a2*m−4 * b2 + a2*m−6 * b4 + … + b2*m−2).
Для нечетных показателей:
a2*m+1 − b2*·m+1 = (a − b) * (a2*m + a2*m−1 * b + a2*m−2 * b2 + … + b2*m).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Что сделать: вычислить квадрат произведения (55 + 10)2.
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)2 = 552 + 2 * 55 * 10 + 102 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с3 – 8.
Как решаем: применим разность кубов: 64 * с3 – 8 = (4 * с)3 – 23 = (4 * с – 2)((4 * с)2 + 4 * с * 2 + 22) = (4 * с – 2)(16 * с2 + 8 * с + 4).
Задание 3
Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).
Как решаем:
- Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y2 + 7 * y * x — 7 * y * x — x2 = 49 * y2 — x2.
- Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)2 — x2 = 49 * y2 — x2.

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
Математика. Учебник для 4 класса ОУЗ с обуч. на рус. языке: В 2 частях Скворцова С.А., Оноприенко О.В. (Ранок), цена 300 грн
Математика. Учебник для 4 класса ОУЗ с обуч. на рус. языке: В 2 частях
Скворцова С.А., Оноприенко О.В.
Код:123-Т470049Р
Количество страниц:144
Формат, мм:170х240
Вес:0.3350 кг
Обложка:Тверда
Язык издания:Рус.
В отечественном учебнике впервые развернуто содержание обучения математике по логике компетентностного подхода. Содержание дидактически обосновано и взвешено, что обеспечивает соответствие возрастным особенностям учащихся.
Учебное издание нового поколения. От авторов Государственного стандарта начального общего образования и учебной программы по математике для 1-4 классов
СОДЕРЖАНИЕ
Часть 1
Предисловие
Нумерация трёхзначных чисел
Арифметические действия сложения и вычитания, умножения и деления
Зависимость результатов арифметических действий от изменения одного из компонентов
Приёмы сложения и вычитания в пределах 1 000
Приёмы устного умножения и деления в пределах 1 000
Сюжетные задачи
Деление с остатком
Математические выражения
Уравнения. Неравенства с переменной
Величины. Части величин
Проверь свои достижения
Учись рассуждать
Письменное умножение
Задачи на нахождение четвёртого пропорционального
Письменное деление на однозначное число
Письменное умножение и деление на круглое число
Письменное умножение на двузначное число
Задачи на двойное приведение к единице
Письменное деление на двузначное число
Деление трёхзначного числа на двузначное
Деление на двузначное число
Задачи с буквенными данными
Деление с остатком
Проверь свои достижения
Учись рассуждать
Счётная единица — тысяча.
От авторов Государственного стандарта начального общего образования и учебной программы по математике для 1-4 классов
СОДЕРЖАНИЕ
Часть 1
Предисловие
Нумерация трёхзначных чисел
Арифметические действия сложения и вычитания, умножения и деления
Зависимость результатов арифметических действий от изменения одного из компонентов
Приёмы сложения и вычитания в пределах 1 000
Приёмы устного умножения и деления в пределах 1 000
Сюжетные задачи
Деление с остатком
Математические выражения
Уравнения. Неравенства с переменной
Величины. Части величин
Проверь свои достижения
Учись рассуждать
Письменное умножение
Задачи на нахождение четвёртого пропорционального
Письменное деление на однозначное число
Письменное умножение и деление на круглое число
Письменное умножение на двузначное число
Задачи на двойное приведение к единице
Письменное деление на двузначное число
Деление трёхзначного числа на двузначное
Деление на двузначное число
Задачи с буквенными данными
Деление с остатком
Проверь свои достижения
Учись рассуждать
Счётная единица — тысяча. Разрядные числа
Чтение и запись многозначных чисел
Образование многозначных чисел
Сравнение многозначных чисел
Сложение на основе разрядного состава числа
Сложение и вычитание многозначных чисел на основе нумерации
Общее количество единиц определённого разряда
Арифметические действия с круглыми числами
Задачи на совместную работу
Именованные числа
Умножение и деление круглых чисел
Проверь свои достижения
Учись рассуждать
Арифметические действия сложения и вычитания
Письменное сложение и вычитание многозначных чисел
Письменное сложение в случае трёх слагаемых
Задачи на нахождение трёх чисел по их сумме и суммам двух слагаемых
Сложение и вычитание именованных чисел
Решение задач
Скорость движения
Правило нахождения пути; времени движения
Простые задачи с величинами: путь, скорость движения, время движения
Задачи с величинами: путь, скорость движения, время движения
Составные задачи с величинами: путь, скорость движения, время движения
Проверь свои достижения
Учись рассуждать
Геометрические фигуры на плоскости
Геометрические фигуры в пространстве
Арифметические действия умножения и деления
Письменное умножение многозначного числа на однозначное
Письменное деление многозначного числа на однозначное
Часть 2
Предисловие
Задачи на пропорциональное деление
Задачи на пропорциональное деление
Умножение чисел, одно из которых оканчивается нулём
Задачи на пропорциональное деление
Решение задач
Задачи на нахождение неизвестных по двум разностям
Умножение и деление именованных чисел
Деление с остатком
Письменное деление на однозначное число
Решение задач
Задачи, содержащие одинаковую величину
Проверь свои достижения
Учись рассуждать
Умножение и деление на круглые числа
Письменное умножение на двузначное и трёхзначное числа
Деление чисел, оканчивающихся нулём
Письменное деление на двузначное число
Задачи на одновременное движение двух тел в разных направлениях
Письменное умножение на трёхзначное число
Умножение и деление именованных чисел
Деление с остатком
Задачи на процессы
Творческая работа над задачей
Проверь свои достижения
Геометрические фигуры на плоскости
Площадь фигуры
Площади прямоугольника и квадрата
Задачи на нахождение площади прямоугольника и обратные к ним
Единицы площади
Части целого
Дроби
Сравнение дробей
Нахождение дроби от числа
Нахождение числа по величине его дроби
Составные задачи, включающие нахождение дроби от числа
Составные задачи, включающие нахождение числа по величине его дроби
Решение задач
Проверь свои достижения
Учись рассуждать
Единицы времени.
Разрядные числа
Чтение и запись многозначных чисел
Образование многозначных чисел
Сравнение многозначных чисел
Сложение на основе разрядного состава числа
Сложение и вычитание многозначных чисел на основе нумерации
Общее количество единиц определённого разряда
Арифметические действия с круглыми числами
Задачи на совместную работу
Именованные числа
Умножение и деление круглых чисел
Проверь свои достижения
Учись рассуждать
Арифметические действия сложения и вычитания
Письменное сложение и вычитание многозначных чисел
Письменное сложение в случае трёх слагаемых
Задачи на нахождение трёх чисел по их сумме и суммам двух слагаемых
Сложение и вычитание именованных чисел
Решение задач
Скорость движения
Правило нахождения пути; времени движения
Простые задачи с величинами: путь, скорость движения, время движения
Задачи с величинами: путь, скорость движения, время движения
Составные задачи с величинами: путь, скорость движения, время движения
Проверь свои достижения
Учись рассуждать
Геометрические фигуры на плоскости
Геометрические фигуры в пространстве
Арифметические действия умножения и деления
Письменное умножение многозначного числа на однозначное
Письменное деление многозначного числа на однозначное
Часть 2
Предисловие
Задачи на пропорциональное деление
Задачи на пропорциональное деление
Умножение чисел, одно из которых оканчивается нулём
Задачи на пропорциональное деление
Решение задач
Задачи на нахождение неизвестных по двум разностям
Умножение и деление именованных чисел
Деление с остатком
Письменное деление на однозначное число
Решение задач
Задачи, содержащие одинаковую величину
Проверь свои достижения
Учись рассуждать
Умножение и деление на круглые числа
Письменное умножение на двузначное и трёхзначное числа
Деление чисел, оканчивающихся нулём
Письменное деление на двузначное число
Задачи на одновременное движение двух тел в разных направлениях
Письменное умножение на трёхзначное число
Умножение и деление именованных чисел
Деление с остатком
Задачи на процессы
Творческая работа над задачей
Проверь свои достижения
Геометрические фигуры на плоскости
Площадь фигуры
Площади прямоугольника и квадрата
Задачи на нахождение площади прямоугольника и обратные к ним
Единицы площади
Части целого
Дроби
Сравнение дробей
Нахождение дроби от числа
Нахождение числа по величине его дроби
Составные задачи, включающие нахождение дроби от числа
Составные задачи, включающие нахождение числа по величине его дроби
Решение задач
Проверь свои достижения
Учись рассуждать
Единицы времени. Сложение и вычитание именованных чисел
Задачи на время
Повторение. Арифметические действия сложения, вычитания, умножения и деления
Повторение. Сюжетные задачи
Повторение. Математические выражения, равенства и неравенства
Повторение. Геометрические фигуры. Дроби
Повторение. Единицы времени.
Сложение и вычитание именованных чисел
Проверь свои достижения
Учись рассуждать
Повторение
Сложение и вычитание именованных чисел
Задачи на время
Повторение. Арифметические действия сложения, вычитания, умножения и деления
Повторение. Сюжетные задачи
Повторение. Математические выражения, равенства и неравенства
Повторение. Геометрические фигуры. Дроби
Повторение. Единицы времени.
Сложение и вычитание именованных чисел
Проверь свои достижения
Учись рассуждать
Повторение
Текстовые задачи. Задачи на числовые зависимости
Задачи на числовые зависимости с решениями
перейти к содержанию курса текстовых задач
- Найти двузначное число, зная, что число его единиц на 2 больше числа десятков и что произведение искомого числа на сумму его цифр равно 144. Решение
- Ученику надо было умножить 78 на двузначное число, в котором цифра десятков втрое больше цифры единиц; по ошибке он переставил цифры во втором сомножителе, отчего и получил произведение, на 2808 меньшее истинного. Чему равно истинное произведение? Решение
- Сумма цифр двузначного числа равна 12.
 Если к этому числу прибавить 36, то получится число, записанное теми же цифрами, но в обратном порядке. Найти искомое двузначное число. Решение
Если к этому числу прибавить 36, то получится число, записанное теми же цифрами, но в обратном порядке. Найти искомое двузначное число. Решение - Остаток от деления натурального числаnна 12 равен 5; остаток от деления n на 16 равен 9. Чему равен остаток от деления наименьшего из возможных чисел n на 24?
- При каких натуральных число также будет натуральным? Решение
- При каких натуральных дробь сократима? Решение
- Сумма квадратов крайних чисел четырехзначного числа M равна 58. Сумма квадратов средних цифр этого числа равна 68. Сумма числа M и числа 4536 равна числу, записанному теми же цифрами числа М, но в обратном порядке. Найдите число M. Решение
- Запись шестизначного числа начинается цифрой 2. Если эту цифру перенести с первого места на последнее, сохранив порядок остальных пяти цифр, то новое число будет втрое больше первоначального. Найти первоначальное число.
- Докажите, что при любом натуральном
- Ученик должен был перемножить два трехзначных числа.
 Однако он не заметил знака умножения и принял оба рядом стоящих множителя за одно шестизначное число. Поэтому получившееся ошибочное число оказалось в 3 раза больше истинного произведения. Какие числа должен был перемножить ученик?
Однако он не заметил знака умножения и принял оба рядом стоящих множителя за одно шестизначное число. Поэтому получившееся ошибочное число оказалось в 3 раза больше истинного произведения. Какие числа должен был перемножить ученик? - Знаменатель несократимой дроби на 2 больше, чем числитель. Если у дроби, обратной данной, уменьшить числитель на 3 и вычесть из этой новой дроби заданную, то получится . Найти первоначальную дробь.
Задачи для самостоятельного решения
- Сумма двух чисел, умноженная на сумму квадратов этих чисел, равна 369, а разность их, умноженная на разность их квадратов, равна 9. Найдите числа. Ответ: 5 и 4
- Число 128 представлено в виде суммы четырех слагаемых так, что первое слагаемое относится ко второму как 2:3, второе к третьему — как 3:5, а третье к четвертому — как 5:6. Найдите эти слагаемые. Ответ: 16, 24, 40, 48
- Числитель несократимой дроби на 1 меньше, чем ее знаменатель. Если умножить числитель на 6, а знаменатель увеличить на 19, то получится дробь, обратная исходной.
 Найдите произведение числителя и знаменателя исходной дроби. Ответ: 36
Найдите произведение числителя и знаменателя исходной дроби. Ответ: 36 - После деления некоторого двузначного числа на сумму его цифр в частном получается 7, а в остатке 6. После деления этого числа на произведение его цифр в частном получается 3, а в остатке 11. Найти это число. Ответ: 83
- Если двузначное число разделить на сумму его цифр, то в частном получится 3 и в остатке получится 3. Найдите это число, если разность квадратов его цифр по модулю в 2 раза больше квадрата разности его цифр. Ответ: 39
- Первое число при делении на второе дает в частном 2 и в остатке 3. Второе при делении на третье дает в частном 1 и в остатке 8. Третье число при делении на четвертое дает в частном 2 и в остатке 1. Найдите эти четыре числа, если их сумма равна 76. Ответ: 41, 19, 11, 5
- Сумма двух чисел равна 17, а сумма их кубов равна 1547. Найдите большее из этих чисел. Ответ: 11
- Сумма двух чисел равна 495. Одно из них оканчивается нулем. Если его убрать, то получится второе число.
 Найдите эти числа. Ответ: 450, 45
Найдите эти числа. Ответ: 450, 45 - Задумано натуральное число. К его записи присоединили справа цифру 7 и из полученного нового числа вычли квадрат задуманного числа. Результат уменьшили на 75% и еще раз вычли задуманное число. В итого получился нуль. Найдите задуманное числа. Ответ: 7
- Первая цифра трехзначного числа равна 8. Если эту цифру поставить на последнее место, то число увеличится на 18. Найдите исходное натуральное число. Ответ: 890
- Задано некоторое двузначное число, кратное 3. Если между его цифрами вставить нуль и к полученному трехзначному числу прибавить удвоенную цифру его сотен, то получится число, которое в 9 раз больше, чем исходное двузначное число. Найдите это двузначное число. Ответ: 69
- Разность двух чисел равна 48, а разность между средним арифметическим и средним геометрическим этих чисел равна 18. Найти эти числа. Ответ: 49 и 1
- Если двузначное число разделить на число, записанное теми же цифрами, но в обратном порядке, то в частном получится 4, а в остатке 15.
 Если же из данного числа вычесть 9, то получится сумма квадратов цифр, использованных для записи этого числа. Найти это число. Ответ: 91
Если же из данного числа вычесть 9, то получится сумма квадратов цифр, использованных для записи этого числа. Найти это число. Ответ: 91
Метки текстовые зада, числа. Смотреть запись.
Бесчисленные словесные задачи: Математика 4 класс
4 класс
Бесчисленные словесные задачи
Перейти к содержанию Приборная доскаАвторизоваться
Приборная панель
Календарь
Входящие
История
Помощь
- Мой Dashboard
- 4 класс
- Страницы
- Бесчисленные задачи со словами
- Главная
- Мартики
- BACKURE
- Resource Bank
- Кребец 3 класса
- класс 4 г / т
- класс 5 курс
- класса 4 Учебная программа
- Семья и сообщество
- CORMENT
- Google Drive
- ХСПСС.
 я
я
Рабочие листы по математике
СложениеНа этой индексной странице вы найдете ссылки на все типы рабочих листов на сложение, включая основные факты, 2-значные сложения, 3-значные сложения, 4-значные сложения, сложение дробей, десятичное сложение, семейства фактов и сложение денег. .
Сложение: основные фактыРабочие листы с основными однозначными фактами сложения (сумма до 18).
Сложение: 3-значные сложенияПотренируйтесь складывать 3-значные числа вместе с этими рабочими листами, карточками с заданиями и играми.
Сложение: 4- и 5-значные сложенияПопросите учащихся решить задачи на сложение с 4- и 5-значными числами.
Сложение: 3 или более сложенияПроблемы сложения столбцов с 3 или более сложениями 1-, 2-, 3- и 4-значных чисел.
Сочетание сложения и вычитания: базовое Рабочие листы, карточки и числовые ряды на этой странице представляют собой сочетание основных задач на сложение и вычитание однозначных чисел.
Сложение дробей и смешанных чисел с одинаковыми знаменателями, а также с разными знаменателями.
Свойства сложенияЭти рабочие листы были созданы для обучения учащихся коммутативным и ассоциативным свойствам сложения.
Квадраты сложенияРазвивайте навыки логического мышления с помощью этих рабочих листов-головоломки с добавлением квадратов.
Семейства фактов сложения-вычитанияРабочие листы с базовыми треугольниками семейства фактов, числовыми связями и квадратами фактов для сложения и вычитания.
Дополнение: игра с суммой (базовое дополнение)На этих распечатываемых игровых досках учащиеся раскрашивают пары чисел, которые равны заданной сумме.
Алгебра и предварительная алгебраНапишите алгебраические выражения, научитесь определять независимые/зависимые переменные, находить переменные в уравнениях, работать с неравенствами и т. д.
Углы: типы и измерение Использование транспортира для измерения прямых, острых и тупых углов.
Загрузите рабочие листы для отработки геометрических понятий, связанных с вертикальными, дополнительными и дополнительными углами.
Площадь треугольниковИспользуйте формулу A = 1/2 x (b x h) для расчета площади треугольников
Площадь Рабочие листыВычислите площадь (в квадратных единицах) фигур на этих рабочих листах.
Коробчатые диаграммы (диаграммы «коробка-и-усы»)Используйте эти рабочие листы, чтобы помочь учащимся узнать о статистике и создании диаграмм «коробка-и-усы». Существуют также рабочие листы для расчета Q1, Q3, медианы, минимального и максимального значений.
Календари (Математика)Календари, чтобы помочь студентам с годами, месяцами, неделями и днями в календаре.
Таблицы емкостиТаблицы объема или емкости (галлоны, кварты, пинты и чашки).
Окружности: Радиус, Диаметр, ОкружностьРасчет диаметра и радиуса окружностей; также включает листы окружности и площади.
Рабочие листы для раскрашивания по номерам Раскрасьте загадочные картинки в соответствии с числовым ключом внизу.
Используйте эти рабочие листы, чтобы попрактиковаться в счете австралийских денег.
Подсчет денег (канадский)Считайте мультяшек, луни, четвертаки, пятаки и десятицентовики с помощью этих рабочих листов для канадских валют.
Счет денег (британские фунты)Научитесь считать фунты и пенсы, монеты, используемые в Соединенном Королевстве.
Счет денег (США)Потренируйтесь считать американские деньги (пенни, пятаки, десять центов и четвертаки).
Рабочие листы для подсчета 0–30 (очень простые)Научитесь считать и записывать числа до 30.
Рабочие листы для подсчета (более сложные)Узнайте, как правильно считать двух-, трех- и четырехзначные числа. Заполните числовые строки, скажите, какая цифра идет впереди, и пропустите счет.
Ежедневный обзор по математикеНа этой странице вы найдете более 100 рабочих листов для ежедневного повторения («Math Buzz»), предназначенных для классов с 1 по 5.
Ежедневные словесные задачки В этом разделе есть математические ежедневные словесные задачки для 1-5 классов. Учащиеся должны решить сотни графических задачников, и есть много места, чтобы показать свою работу.
Учащиеся должны решить сотни графических задачников, и есть много места, чтобы показать свою работу.
Сложение и вычитание десятичных чисел со значениями десятых, сотых и тысячных долей.
Десятичное делениеПрактикуйте деление в длинное с десятичными числами.
Десятичное умножениеУпражнения на умножение с десятичными множителями и произведениями.
Десятичные рабочие листыИменование и работа с десятичными числами.
Рабочие листы для дивизиона: основныеРабочие листы с фактами для дивизиона, игры и задания.
Рабочие листы деления: длинное делениеРабочие листы длинного деления с 2-, 3- и 4-значными делимыми.
Уравнения (базовая алгебра)Научитесь балансировать простые алгебраические уравнения и находить значения переменных.
Рабочие листы для четных и нечетных чиселОпределение нечетных и четных чисел
Рабочие листы для показателей степени Найдите показатели степени для однозначных чисел на этих печатных листах и карточках с заданиями.
Завершите деревья факторов, найдите наибольшие общие делители и наименьшие общие кратные.
Рабочие листы дробей (дополнительно)Сокращение дробей, упорядочивание дробей, эквивалентные дроби и сравнение дробей.
Рабочие листы фракций (базовые)Определение основных фракций, полос фракций, манипуляций с фракциями.
Дроби: СложениеНайдите суммы дробей и смешанных чисел. Включает рабочие листы с дробями с одинаковым знаменателем, а также с дробями с разными знаменателями.
Дроби: ДелениеДеление дробей и смешанных чисел. Многие из этих рабочих листов включают иллюстрированные задачи, задачи с графическими моделями, а также текстовые задачи.
Дроби: смешанные числаПрактикуйте базовые навыки работы со смешанными числами.
Дроби: УмножениеУмножение дробей и смешанных чисел. Многие рабочие листы включают модели и диаграммы, а также текстовые задачи.
Дроби: обратные дроби Распечатайте эти рабочие листы, чтобы помочь учащимся узнать об обратных дробях.
Практика вычитания дробей и смешанных чисел. Включает подобные и неодинаковые знаменатели.
Рамки и стрелки ПрактикаИспользуйте рамки и стрелки для развития навыков логического мышления.
Графики: гистограммыПрочитайте гистограммы на рабочих листах и ответьте на вопросы.
Графики: линейные графикиИнтерпретируйте линейные графики на рабочих листах и ответьте на вопросы.
Графики: линейные графикиЛинейные графики — это особый тип числовой линии, который представляет частоту данных.
Графики: пиктограммыИзучите пиктограммы на рабочих листах и ответьте на вопросы.
Графики: круговые диаграммыПроанализируйте круговые диаграммы на рабочих листах и ответьте на вопросы.
Больше, меньше, чем Рабочие листыСравните числа больше, меньше и равно.
Таблицы сотенИспользуйте эти полезные таблицы стоимостных значений, таблицы сотен, таблицы девяноста девяти.
Ящики ввода и вывода Заполните эти печатаемые поля ввода и вывода или поля правил.
Решить неравенства и построить график.Включает неравенства с одной переменной, одношаговые и двухшаговые неравенства.
Целые числа (базовый)Сравнение, упорядочивание, сложение и вычитание положительных и отрицательных чисел.
Наименьшее общее кратное (НОК)Определите наименьшее общее кратное каждого набора чисел
Линии, сегменты, лучиУзнайте о линиях, сегментах линий, лучах, параллельных линиях и перпендикулярных линиях.
Математические кроссвордыРешите математические задачи и используйте ответы, чтобы решить кроссворды.
Математические загадкиРешите математические задачи, чтобы расшифровать ответ на забавные загадки.Включает широкий спектр математических навыков, включая сложение, вычитание, умножение, деление, разрядность, округление и многое другое.
Отрывки из математических рассказов На этой странице есть набор отрывков для чтения на всю страницу. Учащиеся используют информацию из отрывков для решения математических задач. Они намного длиннее, чем «обычные» текстовые задачи.
Они намного длиннее, чем «обычные» текстовые задачи.
Вычислить среднее или среднее числовых значений.
Среднее значение, медиана, мода и диапазонВычислить моду, медиану, среднее значение и диапазон заданных чисел.
Индекс измеренияВыберите типы таблиц измерений, которые вы ищете, включая линейные измерения, емкость и температуру.
Измерение: CM, MM и MПрактика метрических линейных измерений: сантиметры, миллиметры и метры.
Измерение: футы, ярды, дюймыИзучите американские линейные измерения; дюймы, футы и ярды.
Измерение: граммы и килограммыИзмерение веса и преобразование в граммы и килограммы.
Измерение: литры и миллилитрыОценка и преобразование измерений емкости в литрах и миллилитрах.
Измерение: фунты и унцииИзмерение веса и преобразование в унции и фунты и обратно.
Математика в средней школе Эта индексная страница содержит ссылки на десятки тем по математике для средней школы на этом сайте. Темы включают неравенства, абсолютное значение, алгебру и многое другое.
Темы включают неравенства, абсолютное значение, алгебру и многое другое.
Листы с практическими упражнениями для сложения, вычитания, умножения и деления.
Кратные числаЭти рабочие листы помогут учащимся научиться находить и определять кратные числа.
Умножение (Свойства)Узнайте об ассоциативных, дистрибутивных, коммутативных и тождественных свойствах умножения.
Таблицы умноженияРаспечатайте эти таблицы и таблицы умножения, чтобы учащиеся могли использовать их в качестве справочных материалов.
Рабочие листы по умножению: продвинутый уровеньРешите задачи на умножение двух и трех цифр.
Рабочие листы по умножению: основныеИзучите основные факты умножения с помощью этих рабочих листов, загадочных картинок и игр.
Семейства фактов умножения-деленияСвязи основных чисел, рабочие листы семейства фактов и треугольники для деления и умножения.
Умножение: решетчатое умножение Умножение на 2-, 3- или 4-значные числа с решетчатой сеткой.
Нарисуйте упорядоченные пары, чтобы открыть загадочные картинки.
Загадочные математические картинкиРешите сложение, вычитание, умножение и деление, чтобы открыть загадочную картинку.
Number Detective (Secret Numbers)Студенты будут использовать подсказки, вывешиваемые каждый день, чтобы вычислить недельный секретный номер.
Числовые рядыРабочие листы числовых рядов для обучения счету, сложению, вычитанию, числовым образцам, дробям и десятичным числам.
Порядок действийОтработайте порядок действий: круглые скобки и возведения в степень, затем умножение и деление, затем сложение и вычитание.
заказанных пар; Координатные плоскостиКоординатные плоскости и упорядоченные парные рабочие листы.
Порядковые номераПорядковые номера определяют положение в ряду. (примеры: первый, второй, третий, четвертый и т. д.)
Шаблоны: ЧислоУчащиеся должны перечислить числа, идущие следующими в этих шаблонах.
Patterns: Picture Учащиеся определяют, какие картинки идут следующими в узорах.
Преобразование десятичных чисел и дробей в проценты.
Рабочие листы периметраДобавить, чтобы найти периметры многоугольников на этих рабочих листах.
Рабочие листы разрядаНахождение значения подчеркнутого цифрового значения; стандартная и расширенная форма; округление.
Простые и составные числаИзучите разницу между простыми и составными числами. Кроме того, научитесь определять и находить простые числа с помощью разложения на множители или с помощью решета Эратосфена.
Многоугольники. Рабочие листыОпределение многоугольников и работа с ними.
Рабочие листы вероятностиОпределить вероятность определенных результатов.
Puzzle Match Математические игрыДетали головоломки, которые можно распечатать, чтобы ученики могли их сопоставить. Отлично подходит для учебных центров, занятий в небольших группах и самостоятельной практики.
Теорема Пифагора Найдите длины сторон прямоугольного треугольника по формуле теоремы Пифагора.
Учащиеся используют iPad или смартфон для сканирования QR-кодов, чтобы решать или проверять задачи на каждом из этих математических рабочих листов.
СоотношенияПотренируйтесь сравнивать пары величин с помощью соотношений.
Отражение, вращение и перемещениеОпределение отраженных, повернутых и перемещенных фигур.
Римские цифрыНаучитесь читать и писать римскими цифрами с помощью этих печатных рабочих листов и заданий.
Рабочие листы для округления чиселОкругление чисел до ближайших десятков и сотен.
Научное представлениеНаучитесь записывать числа в научном представлении.
Secret Code MathНа этих рабочих листах учащиеся будут использовать ключ для расшифровки секретных чисел в каждой задаче на сложение, вычитание, умножение или деление.
Похожие и конгруэнтные рабочие листыОпределите похожие и конгруэнтные формы.
Пропустить счет сотнями Используйте эти рабочие листы, чтобы научить учащихся считать с пропуском сотнями.
Повторить счет десятками с помощью этих печатных форм.
Пропустить счет до 11.Сосчитайте до одиннадцати, умножьте на одиннадцать и вставьте пропущенные числа.
Пропустить счет до двенадцатиЗаполнить пустые клетки и текстовые задачи, считая до двенадцати.
Пропустить счет до 25Пропустить счет до двадцати пяти очень важно, если вы учите своих учеников считать деньги.
Пропустить счет на 2 секундыИспользуйте эти распечатки, чтобы научить учащихся пропускать счет с интервалом в два.
Пропустить счет до трехНабор рабочих листов на этой странице поможет учащимся научиться считать до трех.
Пропустить счет до четырехЕсли вы учите учащихся считать до четырех, попробуйте эти рабочие листы.
Пропустить счет пятеркамиКогда вы учите учащихся считать пятерками или пятерками, эти рабочие листы могут быть вам полезны.
Слайды, перевороты и повороты Рабочие листы Укажите, были ли фигуры перевернуты, сдвинуты или повернуты.
На этих рабочих листах учащиеся будут использовать графики, упорядоченные пары и таблицы для расчета наклонов прямых линий.
Твердые формы Рабочие листыНазовите геометрические твердые формы: прямоугольные призмы, кубы, сферы и цилиндры.
Специальные числаЭти рабочие листы охватывают различные понятия разрядности, включая четные/нечетные значения, нахождение значения цифр и запись чисел в развернутой форме.
ВычитаниеВычитание однозначных и многозначных чисел. Включает 1, 2, 3 и 4-значные числа.Также есть ссылки на десятичную дробь и вычитание денег.
Вычитание: ОсновыПрактика основных фактов вычитания однозначных чисел; концепции и рабочие листы.
Вычитание дробейПотренируйтесь вычитать дроби и смешанные числа с помощью этих распечатываемых рабочих листов и карточек с заданиями.
Площадь поверхностиРасчет площади поверхности прямоугольных призм и других трехмерных фигур.
Рабочие листы по симметрии Найдите линии симметрии, определите симметричные фигуры и завершите симметричные фигуры.
Научитесь считать предметы с помощью контрольных отметок.
Рабочие листы температурыПрочтите показания термометров Цельсия и Фаренгейта и укажите температуру.
Математика с десятью рамкамиРаспечатанные задания с десятью рамками для обучения счету, основам сложения и простого вычитания.
Рабочие листы по мозаикеНаучите учащихся распознавать геометрическую мозаику двумерных фигур.
Рабочие листы времениУзнайте, как определять время с точностью до минуты, часа и четверти часа.
Время: Прошедшее времяОпределить количество прошедшего времени.
Диаграммы Венна (математика)На этой странице есть рабочие листы для математических диаграмм Венна.
Volume — Градуированные цилиндрыЭти рабочие листы содержат изображения градуированных цилиндров. Учащиеся должны написать правильный объем в миллилитрах.
Volume Worksheets Расчет объема твердых фигур. Включает объемные «счетные кубы», прямоугольные призмы, конусы, цилиндры и сферы.
Практика текстовых задач на сложение, вычитание, умножение и деление.
Рабочие листы для задач со словами (смешанный)Просмотрите навыки работы со смешанными задачами в разных классах.
Словесные задачи (несколько шагов)Эти текстовые задачи состоят из нескольких шагов и требуют от учащихся использования навыков критического мышления.
Таблицы сложенияЗдесь вы можете сослаться на все типы таблиц сложения, включая основные факты, сложение дробей, сложение двух, трех и четырех цифр.
Рабочие листы дробейУказатель наших базовых и расширенных рабочих листов дробей.
Рабочие листы по геометрииИзучите площадь, периметр, симметрию, многоугольники, твердые формы и многое другое.
Графические рабочие листыВыберите из круговых диаграмм, гистограмм и линейных диаграмм.
Листы с пропуском счетаСчитайте 2, 3, 4, 5, 10, 25 или 100 секунд.
Рабочие листы по вычитанию Вот индексная страница со ссылками на все разделы нашего веб-сайта по вычитанию.
Эта страница содержит только частичный индекс рабочих листов по математическим навыкам на S.T.W.
Полный указатель веб-сайтаПросмотр полного указателя всех рабочих листов по математике, английскому языку, орфографии, фонетике, грамматике, естественным наукам и общественным наукам, найденных на этом веб-сайте.
Doubles: факты для детей (и родителей!)
Маленькие дети часто используют пальцы, когда учатся складывать и вычитать.
По мере того, как они становятся старше, и вы стремитесь сделать их более опытными в автоматическом вычислении сумм, удвоение фактов становится невероятно полезным инструментом. Двойные факты в математике — это стратегии, которые могут помочь учащимся быстро научиться считать как профессионалы.
Цель игры в парном разряде состоит в том, чтобы дети получили реальное понимание математики в парном разряде и могли гибко использовать факты для решения ряда задач.
Эти факты помогут ученикам первого и второго классов научиться складывать и вычитать.
Если вы ищете другие замечательные образовательные факты, такие как этот список фактов о двойниках для детей и родителей, почему бы не взглянуть на наши факты о сохранении водных ресурсов и эти факты об африканских слонах.
Что такое двойники?
Двойное число — это комбинация чисел, при которой одно и то же число добавляется дважды. Узнайте о них все с помощью этих двойных фактов.
1.Например, факт удвоения состоит в том, что удвоение числа 2 равно 4, потому что 2 + 2 = 4.
2. Двойники — это математический инструмент, помогающий маленьким детям научиться автоматически складывать числа.
3. Парные игры и использование парных фактов отлично подходят для учеников первого и второго классов, чтобы помочь им легче понять сложение и вычитание.
4. Чтобы использовать удвоение в математике, вы добавляете одно и то же число к самому себе. Например, двойное число 5 равно 10, потому что 5 + 5 = 10.
5. Двойное число 4 равно 8, потому что 4 + 4 = 8.
Двойное число 4 равно 8, потому что 4 + 4 = 8.
6. Дети, способные запоминать двойные числа в математике, смогут более эффективно оперировать однозначными числами и улучшат свои навыки сложения и вычитания.
7. Вы можете попрактиковаться в двойных действиях с помощью карточек, счета на пальцах или просто устно используя двойные факты.
Что такое почти двойные числа
Как только ваш ребенок поймет и запомнит факты о двойных числах, почти двойные числа станут очень полезным способом вывести его навыки сложения и вычитания на новый уровень.
8. Почти двойное число — это математическое предложение, близкое к двойному факту.
9. Например, 3 + 4 — почти двойное число, поскольку оно отличается от факта двойного числа всего на одну цифру. один, чтобы получить окончательный номер.
11. Например, если ребенок запомнил удвоение по математике, то, когда его спросят о сумме чисел, которые на единицу больше или меньше числа удвоения, например, 5 + 6 или 3 + 2, он может использовать удвоение фактов плюс один (или минус один), чтобы получить их ответ.
12. В то время как дети запоминают двойные факты, чтобы облегчить сложение и вычитание, важно, чтобы они понимали и исследовали, а не запоминали почти двойные факты.
13. Цель почти двойников состоит в том, чтобы понять стратегии двойников плюс один или двойников минус один концептуально, чтобы они могли применять их к целому ряду примеров, а не только к тем, которые они запомнили.
14. Если вы слышите, как ваш ребенок говорит что-то вроде «Я использовал стратегию удвоения плюс один, чтобы решить это», но он не может вспомнить, что это было, то ему, вероятно, нужно еще какое-то объяснение, чтобы понять концепцию сложения. с двойными номерами.
Стратегия сложения двойных чисел
Использование двойных чисел для сложения — один из самых быстрых способов помочь вашему ребенку лучше понять факты сложения и стать более автоматическим при сложении однозначных чисел.
15. Существуют основные сведения о сложении двойников, которые помогут вашему ребенку использовать двойники для сложения.
16. Практические двойники также очень полезны при обучении учеников первого и второго классов сложению двойников.
17. Если ребенок знает 9+9=18, то используя это знание, он поймет, что 9+8 будет на единицу меньше.18 — 1 = 17.
Двойники для вычитания
Вы также можете использовать математику для удвоения, чтобы помочь вашему ребенку понять вычитание. Узнайте, как с этими фактами!
18. Запомнив факты о двойниках, ребенок может применить их к математическим уравнениям на вычитание.
19. Например, если уравнение 6 — 3, ребенок знает, что двойное число 3 равно 6, поэтому 6 — 3 = 3.
20. Для более сложного вычитания, скажем, 18 — 8, ребенок знает, что двойное число 8 равно 16, а разница между 16 и 18 равна 2.Поэтому они знают, что ответом будет сумма 8 и 2, что равно 10.
Простые двойники и почти двойники Примеры для начала
помочь детям понять эти двойные факторы в математике. Факты о двойниках легко представить с помощью картинок. Использование картинок или наглядных пособий при обучении вашего ребенка удвоению фактов может быть невероятно полезным и позволит им легче понять и применить.Познакомьте их с этими примерами для начала.
Факты о двойниках легко представить с помощью картинок. Использование картинок или наглядных пособий при обучении вашего ребенка удвоению фактов может быть невероятно полезным и позволит им легче понять и применить.Познакомьте их с этими примерами для начала.
21. 1 + 1 = 2
22. 2 + 2 = 4
23. 6 + 6 = 12
24. 5 + 6 = 11
25. 9 + 8 = 17
25. 9 + 8 = 17
+ 11 = 21
Более продвинутые двойные факты Примеры
Для более продвинутых детей могут быть полезны эти двойные примеры.
29. 10 мальчиков собирали листья в парке. 10 девочек также собирали листья в парке. Сколько всего детей собирали листья? (20)
30.У Мэри 5 печенек, а у Эммы 5 леденцов, сколько всего продуктов есть у Мэри и Эммы? (10)
31. Половина X вдвое больше 5. Что такое x? (20)
32. У Лили в шкафу 20 футболок. Она решает отдать 10 на благотворительность. Сколько футболок осталось у Лили в шкафу? (10)
33. Выписать двойные и почти двойные факты, равные 10. (5 + 5 и 4 + 6 основные)
Выписать двойные и почти двойные факты, равные 10. (5 + 5 и 4 + 6 основные)
34. Выписать двойные и почти двойные факты, равные 20. (10 + 10 и 11+9 основные)
35.Эмма и Билл нашли на пляже по 5 ракушек. Сколько всего ракушек собрали Эмма и Билл? Используйте изображения и слова, чтобы объяснить свой факт о двойниках. (10)
36. Чему равна сумма 5 + 6? Если ребенок знает двойные факты для 5, то он знает, что ответом будет двойное число плюс один. 5+5 = 10, а затем 10 + 1 = 11, поэтому ответ равен 11.
Здесь, в Kidadl, мы тщательно подготовили множество интересных семейных фактов, которые понравятся всем! Если вам понравились наши факты о двойниках для детей и родителей, то почему бы не узнать больше с этими фактами о спинозаврах и этими фактами о воздушном шаре.
Скоростной математический тест. HTTP/1.1 200 ОК
Дата: Чт, 20 января 2022 г., 02:44:35 по Гринвичу
Сервер: Apache/2.4.6 (CentOS) PHP/5.4.16
X-Powered-By: PHP/5.4.16
Подключение: закрыть
Передача-кодирование: по частям
Тип содержимого: текст/html; кодировка = UTF-8 2123
Сложение, вычитание, умножение и деление развивают математические навыки K-5 с помощью Speed Math: Mental Math Skill Builder. 1) 3 х 2 = 21) 3 х 5 = 2) 3 х 5 = 22) 8 х 3 = Первый шаг к тому, чтобы научиться быстро печатать и повысить скорость печати, — это пройти тест на время! Наши 1-минутные, 3-минутные и 5-минутные тесты скорости набора текста бесплатны и могут использоваться детьми или взрослыми для проверки среднего количества слов в минуту (WPM).Загрузить сведения о тесте скорости. 9. Математический лабиринт! 5. D. Предварительный тест по математике, первый уровень Учащиеся столярного дела должны использовать этот предварительный тест в качестве индикатора своих текущих математических навыков. Это еще один бесплатный математический ресурс для учителей от The Curriculum Corner. SDK Speed Math Workshop Level 2? Это четырехдневный онлайн-семинар, который проводится в течение двух выходных. Если вы не уверены в процентах и в том, что они собой представляют, сначала прочитайте нашу статью «Работа с процентами». По словам Джо Боулер, профессора математического образования в Стэнфордской высшей школе образования и ведущего автора нового рабочего документа под названием «Свободное владение языком без страха», Джо Боулер (Jo Boaler) создает большие препятствия, тестирование на время и слепое запоминание.
1) 3 х 2 = 21) 3 х 5 = 2) 3 х 5 = 22) 8 х 3 = Первый шаг к тому, чтобы научиться быстро печатать и повысить скорость печати, — это пройти тест на время! Наши 1-минутные, 3-минутные и 5-минутные тесты скорости набора текста бесплатны и могут использоваться детьми или взрослыми для проверки среднего количества слов в минуту (WPM).Загрузить сведения о тесте скорости. 9. Математический лабиринт! 5. D. Предварительный тест по математике, первый уровень Учащиеся столярного дела должны использовать этот предварительный тест в качестве индикатора своих текущих математических навыков. Это еще один бесплатный математический ресурс для учителей от The Curriculum Corner. SDK Speed Math Workshop Level 2? Это четырехдневный онлайн-семинар, который проводится в течение двух выходных. Если вы не уверены в процентах и в том, что они собой представляют, сначала прочитайте нашу статью «Работа с процентами». По словам Джо Боулер, профессора математического образования в Стэнфордской высшей школе образования и ведущего автора нового рабочего документа под названием «Свободное владение языком без страха», Джо Боулер (Jo Boaler) создает большие препятствия, тестирование на время и слепое запоминание. Вычисление средней скорости и скорости отредактировано Наша миссия — предоставить бесплатное образование мирового уровня всем и везде. Если у вас есть какие-либо вопросы, пожалуйста, свяжитесь с arithmetic@zetamac. 00 больше, чем в первый день. Как можно быстрее один учащийся устно говорит и решает вопросы Теста; другой ученик проверяет ответы. Рабочий лист 2. Эти элементы необходимы для того, чтобы ответить на все вопросы в течение заданного срока. Чтобы получить прошедшее время tt, разделите общее расстояние на скорость: DsDs 3.Она говорила о мышлении и математическом беспокойстве. Применяйте свои математические трюки в уме и размещайте свои рекорды в наших списках лидеров! Чтобы предложить вам лучший опыт, этот сайт использует файлы cookie. Вопросы предполагают множественный выбор, и для того, чтобы ответить на них, вам необходимо знать основные формулы, вычислительные навыки и навыки рассуждения. В таблице указаны скорости бега наземных животных. Есть две интерактивные математические функции: математика Улучшите результаты теста на ментальную математику, играя в наши бесплатные игры на ментальную математику.
Вычисление средней скорости и скорости отредактировано Наша миссия — предоставить бесплатное образование мирового уровня всем и везде. Если у вас есть какие-либо вопросы, пожалуйста, свяжитесь с arithmetic@zetamac. 00 больше, чем в первый день. Как можно быстрее один учащийся устно говорит и решает вопросы Теста; другой ученик проверяет ответы. Рабочий лист 2. Эти элементы необходимы для того, чтобы ответить на все вопросы в течение заданного срока. Чтобы получить прошедшее время tt, разделите общее расстояние на скорость: DsDs 3.Она говорила о мышлении и математическом беспокойстве. Применяйте свои математические трюки в уме и размещайте свои рекорды в наших списках лидеров! Чтобы предложить вам лучший опыт, этот сайт использует файлы cookie. Вопросы предполагают множественный выбор, и для того, чтобы ответить на них, вам необходимо знать основные формулы, вычислительные навыки и навыки рассуждения. В таблице указаны скорости бега наземных животных. Есть две интерактивные математические функции: математика Улучшите результаты теста на ментальную математику, играя в наши бесплатные игры на ментальную математику.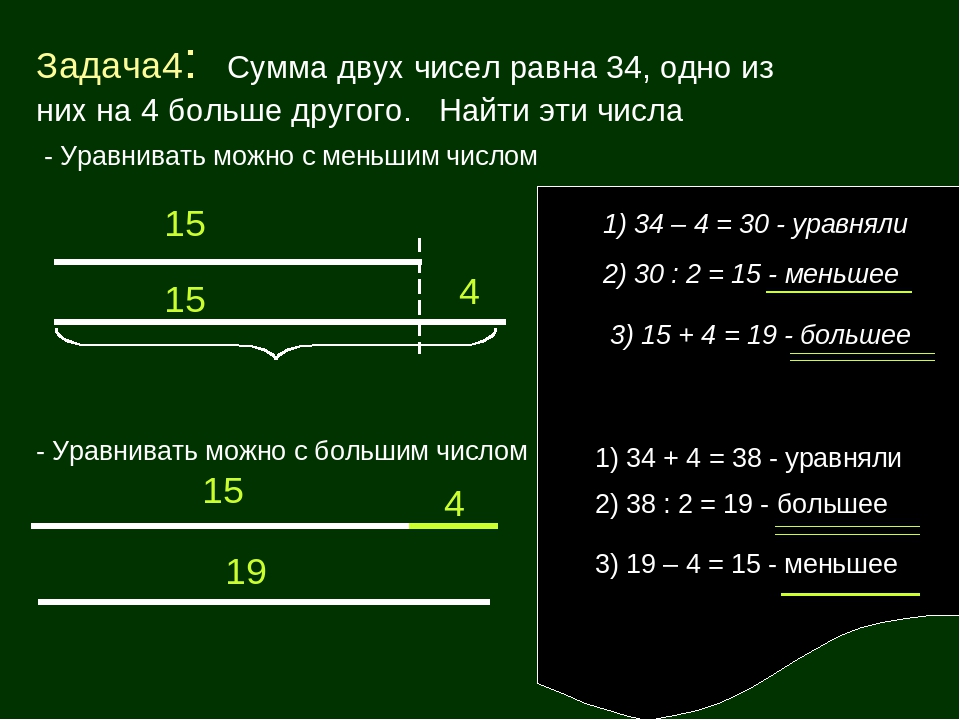 2гм/см3? A: 50 г B: 60 г C: 72 г D: 38. Прибыль P, полученная компанией, зависит от количества продаваемой продукции s. Тест по математике на ACT состоит из 60 вопросов, на которые нужно ответить в течение 60 минут. Математический тест на сложение и умножение. Наконец, укажите, разрешены ли отрицательные числа. net размещаются там, где размещаются веб-сайты, которые вы посещаете. Включает отчеты о результатах и отслеживание прогресса. PDF. Добавляйте с помощью изображений — до 5 изображений для подсчета математических тестов или добавляйте числа в этом увлекательном упражнении по сложению, чтобы проверить свои знания о сложении чисел.Эти прошлые бумажные вопросы помогут вам справиться с 11+ экзаменационными вопросами по математике. Тест Cps позволяет проверить скорость движения пальцев по мыши, чтобы определить, насколько быстро вы можете нажимать на кнопку мыши. 568). Ключ ответа определяет правильный ответ, представленную категорию отчета об оценке, Обязательная практика 11 Plus (11+) Скорость Расстояние Время Прошлые бумажные вопросы.
2гм/см3? A: 50 г B: 60 г C: 72 г D: 38. Прибыль P, полученная компанией, зависит от количества продаваемой продукции s. Тест по математике на ACT состоит из 60 вопросов, на которые нужно ответить в течение 60 минут. Математический тест на сложение и умножение. Наконец, укажите, разрешены ли отрицательные числа. net размещаются там, где размещаются веб-сайты, которые вы посещаете. Включает отчеты о результатах и отслеживание прогресса. PDF. Добавляйте с помощью изображений — до 5 изображений для подсчета математических тестов или добавляйте числа в этом увлекательном упражнении по сложению, чтобы проверить свои знания о сложении чисел.Эти прошлые бумажные вопросы помогут вам справиться с 11+ экзаменационными вопросами по математике. Тест Cps позволяет проверить скорость движения пальцев по мыши, чтобы определить, насколько быстро вы можете нажимать на кнопку мыши. 568). Ключ ответа определяет правильный ответ, представленную категорию отчета об оценке, Обязательная практика 11 Plus (11+) Скорость Расстояние Время Прошлые бумажные вопросы. Оцените следующее и сформулируйте свой ответ в минимальных выражениях. Тест на скорость по математике // базовый тест по математике // тест по математике для детей d // плюс тест Минаса // Арифметическая игра.Решайте задачи на деление до 10 с помощью Speed Math. Тесты на скорость по математике 4 класс часть 2. По некоторым оценкам, по крайней мере треть учащихся испытывают сильный стресс или «математическую тревогу» при сдаче теста на время, независимо от их уровня. Я также включаю тесты на скорость. Задачи на сложение и вычитание до 18 + 18 и 18… Практика по математике для класса 2, вопросы, тесты, задания для учителей, рабочие листы для учителей, рабочие листы для печати и другие задания для NCERT (CBSE и ICSE), IMO, SAT Subject Test: Math Level 1, Наводая Видьялая, Кенгуру и СЕАМО.Каждый вопрос охватывает одну область математики, такую как статистика, вероятность, геометрия или арифметика. Free Common Core: практическая задача по математике для 6-го класса — Common Core: диагностический тест по математике для 6-го класса 1.
Оцените следующее и сформулируйте свой ответ в минимальных выражениях. Тест на скорость по математике // базовый тест по математике // тест по математике для детей d // плюс тест Минаса // Арифметическая игра.Решайте задачи на деление до 10 с помощью Speed Math. Тесты на скорость по математике 4 класс часть 2. По некоторым оценкам, по крайней мере треть учащихся испытывают сильный стресс или «математическую тревогу» при сдаче теста на время, независимо от их уровня. Я также включаю тесты на скорость. Задачи на сложение и вычитание до 18 + 18 и 18… Практика по математике для класса 2, вопросы, тесты, задания для учителей, рабочие листы для учителей, рабочие листы для печати и другие задания для NCERT (CBSE и ICSE), IMO, SAT Subject Test: Math Level 1, Наводая Видьялая, Кенгуру и СЕАМО.Каждый вопрос охватывает одну область математики, такую как статистика, вероятность, геометрия или арифметика. Free Common Core: практическая задача по математике для 6-го класса — Common Core: диагностический тест по математике для 6-го класса 1. 8. Каждый день будет проводиться двухчасовое онлайн-занятие, за которым следуют практические упражнения. Тест по математике. Мгновенная скорость — это скорость, с которой объект движется в любой конкретный момент времени. Ответьте на вопросы по отрывку, чтобы проверить свою скорость чтения и оценку понимания. Выберите столы, которые вы хотите попрактиковать.В Times Tables Speed Test X вы получаете 10 баллов за каждый правильный ответ и по одному баллу за каждую оставшуюся секунду. Итак, я сделал годовой обзор всех семейств математических фактов и буду давать им одну страницу в день, чтобы они занимались математикой. 3 х 5 + 9 =. Этот тест Mensa расскажет вам, сможете ли вы получить всю информацию о математическом тесте TSI. Достижение базовой беглости сложения и вычитания жизненно важно для детей младших классов, когда они переходят в старшие классы. Пошаговые решения для ACT Math 2021/2022, вопросы с 1 по 60.Воспользуйтесь нашим бесплатным практическим тестом CBEST по математике, чтобы просмотреть наиболее важные навыки и понятия, которые вы должны знать для этого сертификационного экзамена.
8. Каждый день будет проводиться двухчасовое онлайн-занятие, за которым следуют практические упражнения. Тест по математике. Мгновенная скорость — это скорость, с которой объект движется в любой конкретный момент времени. Ответьте на вопросы по отрывку, чтобы проверить свою скорость чтения и оценку понимания. Выберите столы, которые вы хотите попрактиковать.В Times Tables Speed Test X вы получаете 10 баллов за каждый правильный ответ и по одному баллу за каждую оставшуюся секунду. Итак, я сделал годовой обзор всех семейств математических фактов и буду давать им одну страницу в день, чтобы они занимались математикой. 3 х 5 + 9 =. Этот тест Mensa расскажет вам, сможете ли вы получить всю информацию о математическом тесте TSI. Достижение базовой беглости сложения и вычитания жизненно важно для детей младших классов, когда они переходят в старшие классы. Пошаговые решения для ACT Math 2021/2022, вопросы с 1 по 60.Воспользуйтесь нашим бесплатным практическим тестом CBEST по математике, чтобы просмотреть наиболее важные навыки и понятия, которые вы должны знать для этого сертификационного экзамена. С каждым вопросом все сложнее. Оба доклада будут запланированы на один и тот же день с перерывом между двумя докладами. Первые вхождения 0-9 в число Пи 1. Рабочий лист 5. На каждый вопрос дается 10 секунд. Складывайте числа как можно быстрее в этом умственном математическом упражнении. Рабочий лист 6. Проверьте свою скорость и точность после ввода 3 предложений в одном из наших популярных тестов wpm.Итак, давайте взглянем на формат теста и систему подсчета очков. 10-12 классы. Таким образом, скорость равна расстоянию, деленному на время. Эти практические вопросы GED предназначены для охвата тех же тем, которые встречаются в реальном тесте. Сообщить об ошибке. В этом рабочем листе учащиеся могут засекать время, решая 20 задач на умножение и 20 задач на деление. Когда вы закончите читать весь отрывок, нажмите «Конец». Навигатор викторин. Пройдите индивидуальную викторину со всеми уравнениями до того, что вы выберете ниже.20 арифметических задач с 4 уровнями Как ускорить выполнение теста ACT по математике.
С каждым вопросом все сложнее. Оба доклада будут запланированы на один и тот же день с перерывом между двумя докладами. Первые вхождения 0-9 в число Пи 1. Рабочий лист 5. На каждый вопрос дается 10 секунд. Складывайте числа как можно быстрее в этом умственном математическом упражнении. Рабочий лист 6. Проверьте свою скорость и точность после ввода 3 предложений в одном из наших популярных тестов wpm.Итак, давайте взглянем на формат теста и систему подсчета очков. 10-12 классы. Таким образом, скорость равна расстоянию, деленному на время. Эти практические вопросы GED предназначены для охвата тех же тем, которые встречаются в реальном тесте. Сообщить об ошибке. В этом рабочем листе учащиеся могут засекать время, решая 20 задач на умножение и 20 задач на деление. Когда вы закончите читать весь отрывок, нажмите «Конец». Навигатор викторин. Пройдите индивидуальную викторину со всеми уравнениями до того, что вы выберете ниже.20 арифметических задач с 4 уровнями Как ускорить выполнение теста ACT по математике. . Чтобы преобразовать км/ч в метры/мин, умножьте на 1000, а затем разделите на 60. Играть в тестовую игру CPS легко и весело одновременно. Ниже приведены 3 теста с задачами на числовые последовательности возрастающей сложности. Совместимость с iPad с расширенными функциями отчетности. Сравнение библиотек GLM, CLM и Eigen по скорости и простоте использования. Нам нравится XtraMath. Дополнительные ресурсы для тестов умножения на время. Smart-Kids Практический тест по математике 5 класс с ответами.Для достижения оптимальных результатов попробуйте регулярно заниматься, например, по 15 минут за раз. Оригинальная цена. Это тест на набор текста, который выражает ваши навыки набора текста в словах в минуту. Попробуйте и ответьте на 10 появившихся случайных вопросов. Стартуют одновременно, с диаметрально противоположных позиций. Движение может быть… Вот несколько примеров повседневных вычислений, которые вы будете использовать в качестве полицейского: Расчет расстояния и скорости при расследовании дорожно-транспортного происшествия.
. Чтобы преобразовать км/ч в метры/мин, умножьте на 1000, а затем разделите на 60. Играть в тестовую игру CPS легко и весело одновременно. Ниже приведены 3 теста с задачами на числовые последовательности возрастающей сложности. Совместимость с iPad с расширенными функциями отчетности. Сравнение библиотек GLM, CLM и Eigen по скорости и простоте использования. Нам нравится XtraMath. Дополнительные ресурсы для тестов умножения на время. Smart-Kids Практический тест по математике 5 класс с ответами.Для достижения оптимальных результатов попробуйте регулярно заниматься, например, по 15 минут за раз. Оригинальная цена. Это тест на набор текста, который выражает ваши навыки набора текста в словах в минуту. Попробуйте и ответьте на 10 появившихся случайных вопросов. Стартуют одновременно, с диаметрально противоположных позиций. Движение может быть… Вот несколько примеров повседневных вычислений, которые вы будете использовать в качестве полицейского: Расчет расстояния и скорости при расследовании дорожно-транспортного происшествия. Некоторые из многих типов вопросов включают множественный выбор, перетаскивание, горячую точку и заполнение пробела.Этот тест был разработан, чтобы проверить ваши навыки в базовой арифметике. Какой кнопки у нее не хватает? A. Доступны форматы PDF и html. Научитесь печатать в этой игре с набором текста. Идея состоит в том, что вы даете свои ответы как можно быстрее. В первый день она сэкономила 1 доллар. Учащиеся проверят свою скорость и точность умножения, решая 48 одно- и двузначных задач на умножение. Три друга будут Этот тест на скорость сложения и вычитания 20 разработан, чтобы помочь вашим ученикам практиковаться и быстрее справляться с базовой ментальной арифметикой.Итак, давайте попробуем. Модель заштрихована, чтобы представить оставшуюся половину торта. Чтобы извлечь максимальную пользу, изучите концепции соответствующей темы. Какой шаг объясняет, как найти значение a в 6a = 72? О. В этом курсе мы поделимся пятью математическими приемами, которые помогут вам улучшить свои навыки счета с точки зрения скорости, а также лучшего понимания.
Некоторые из многих типов вопросов включают множественный выбор, перетаскивание, горячую точку и заполнение пробела.Этот тест был разработан, чтобы проверить ваши навыки в базовой арифметике. Какой кнопки у нее не хватает? A. Доступны форматы PDF и html. Научитесь печатать в этой игре с набором текста. Идея состоит в том, что вы даете свои ответы как можно быстрее. В первый день она сэкономила 1 доллар. Учащиеся проверят свою скорость и точность умножения, решая 48 одно- и двузначных задач на умножение. Три друга будут Этот тест на скорость сложения и вычитания 20 разработан, чтобы помочь вашим ученикам практиковаться и быстрее справляться с базовой ментальной арифметикой.Итак, давайте попробуем. Модель заштрихована, чтобы представить оставшуюся половину торта. Чтобы извлечь максимальную пользу, изучите концепции соответствующей темы. Какой шаг объясняет, как найти значение a в 6a = 72? О. В этом курсе мы поделимся пятью математическими приемами, которые помогут вам улучшить свои навыки счета с точки зрения скорости, а также лучшего понимания. Сколько вопросов в тесте GED по математике? Математический тест GED состоит из 46 вопросов. Используйте этот набор тестов на умножение, чтобы помочь вашим учащимся усвоить факты.Тест на скорость по математике, викторина на общие знания по математике, викторина по математике для детей, викторина по математике для студентов, викторина по математике .
20ca
50% вы говорите. 00 больше, чем в предыдущий день, сколько она сэкономит на седьмом тесте по математике — Калькулятор — Задача 13 Группа десятиклассников ответила на опрос, в котором спрашивали, какой математический курс в настоящее время зачислен.Решите уравнения сложения, вычитания, умножения и деления. Поезд движется между двумя станциями x и y. † Вы не можете использовать калькулятор в этом тесте. Это дополнение для родителей к потребительским тестам и викторинам по математике (продается отдельно) содержит копию викторины, теста и скоростной тренировки вашего старшеклассника со всеми ответами и значениями баллов. 1 B. Эту задачу легко решить, разбив ее на шаги: 200 X 8 = 1600 20 X 8 = 160 3 X 8 = 24 1600 + 160 + 24 = 1784 Итак, 223 X 8 = 1784.
Сколько вопросов в тесте GED по математике? Математический тест GED состоит из 46 вопросов. Используйте этот набор тестов на умножение, чтобы помочь вашим учащимся усвоить факты.Тест на скорость по математике, викторина на общие знания по математике, викторина по математике для детей, викторина по математике для студентов, викторина по математике .
20ca
50% вы говорите. 00 больше, чем в предыдущий день, сколько она сэкономит на седьмом тесте по математике — Калькулятор — Задача 13 Группа десятиклассников ответила на опрос, в котором спрашивали, какой математический курс в настоящее время зачислен.Решите уравнения сложения, вычитания, умножения и деления. Поезд движется между двумя станциями x и y. † Вы не можете использовать калькулятор в этом тесте. Это дополнение для родителей к потребительским тестам и викторинам по математике (продается отдельно) содержит копию викторины, теста и скоростной тренировки вашего старшеклассника со всеми ответами и значениями баллов. 1 B. Эту задачу легко решить, разбив ее на шаги: 200 X 8 = 1600 20 X 8 = 160 3 X 8 = 24 1600 + 160 + 24 = 1784 Итак, 223 X 8 = 1784. 54 рассчитанных на время теста на скорость (примерно два в неделю) побуждают вашего ребенка развивать свою скорость и точность с помощью основных математических навыков, чтобы математика стала увлекательной. В тесте проверяются все основные концепции, изложенные в Math Mammoth Grade 2. Соединенные Штаты экспортировали около 30 000 000 метрических тонн пшеницы в течение всего года. Вам не разрешено пользоваться калькулятором. Дополнительную информацию можно найти в Руководстве по внедрению RTI2 (стр. В нем содержится множество упражнений на сложение и вычитание 1-12, а также удваиваются факты, которые могут только улучшить беглость математики! Включены тесты скорости, которые могут быть рассчитаны по одному из 3 приращений: 1 , 1 1/2 или 2 минуты.Насколько хорошо ты разбираешься в математике? Чтобы узнать, насколько хорошо вы набираете баллы по этому предмету, пройдите этот удивительный тест. Тренерские институты; Категории экзамена Математика. Формат теста Численный тест проводится один раз через компьютер в первом туре и снова лично в третьем туре.
54 рассчитанных на время теста на скорость (примерно два в неделю) побуждают вашего ребенка развивать свою скорость и точность с помощью основных математических навыков, чтобы математика стала увлекательной. В тесте проверяются все основные концепции, изложенные в Math Mammoth Grade 2. Соединенные Штаты экспортировали около 30 000 000 метрических тонн пшеницы в течение всего года. Вам не разрешено пользоваться калькулятором. Дополнительную информацию можно найти в Руководстве по внедрению RTI2 (стр. В нем содержится множество упражнений на сложение и вычитание 1-12, а также удваиваются факты, которые могут только улучшить беглость математики! Включены тесты скорости, которые могут быть рассчитаны по одному из 3 приращений: 1 , 1 1/2 или 2 минуты.Насколько хорошо ты разбираешься в математике? Чтобы узнать, насколько хорошо вы набираете баллы по этому предмету, пройдите этот удивительный тест. Тренерские институты; Категории экзамена Математика. Формат теста Численный тест проводится один раз через компьютер в первом туре и снова лично в третьем туре. Всего 10 быстрых математических задач — и вы не только узнаете, насколько вы на самом деле умны, но и улучшите свой мозг. Для учеников классов Prep/KG и 1-2 будет только один уровень. Основы системы: Тест 2 № 43 мили в час 16. Тест на скорость по математике, Тест на общие знания по математике, Викторина по математике для детей, Викторина по математике для учащихся, Викторина по математике Test, Internet Speed Test, Blackmagic Disk Speed Test и многие другие программы Trachtenberg Speed Math (TSM) — это программа, основанная на системе простых методов профессора Якова Трахтенберга для выполнения высокоскоростных математических вычислений.Игра проводится по 60 секунд, учащиеся работают в парах. Если в задаче не указано иное, следует исходить из того, что фигуры нарисованы не в масштабе. Проверьте свои математические способности с помощью этого бесплатного базового теста по математике с задачами на сложение. Это может даже пойти вам на пользу, так как вы должны довериться своему мозгу, что повысит вашу скорость ответов на вопросы во время теста.
Всего 10 быстрых математических задач — и вы не только узнаете, насколько вы на самом деле умны, но и улучшите свой мозг. Для учеников классов Prep/KG и 1-2 будет только один уровень. Основы системы: Тест 2 № 43 мили в час 16. Тест на скорость по математике, Тест на общие знания по математике, Викторина по математике для детей, Викторина по математике для учащихся, Викторина по математике Test, Internet Speed Test, Blackmagic Disk Speed Test и многие другие программы Trachtenberg Speed Math (TSM) — это программа, основанная на системе простых методов профессора Якова Трахтенберга для выполнения высокоскоростных математических вычислений.Игра проводится по 60 секунд, учащиеся работают в парах. Если в задаче не указано иное, следует исходить из того, что фигуры нарисованы не в масштабе. Проверьте свои математические способности с помощью этого бесплатного базового теста по математике с задачами на сложение. Это может даже пойти вам на пользу, так как вы должны довериться своему мозгу, что повысит вашу скорость ответов на вопросы во время теста. По умолчанию оно составляет 5 секунд, но игрок увеличил его с помощью меню, доступного в верхней части страницы.Стр. 22. Распечатать в полном размере. Сыграйте в тесты на время по математике прямо сейчас! по худа математике. Сложение задач в обратном порядке. com, чтобы быть очень простым и быстрым тестом скорости. После того, как вы ответите на все вопросы, мы обработаем данные (очень быстро) и рассчитаем ваш показатель IQ (очень точно). ф. В этом тесте 10 вопросов, каждый из которых был разработан в соответствии со стилем и сложностью вопросов, к которым вы должны подготовиться в ближайшие недели и месяцы. Математические решения и темы 6-го класса. Добавлять.Загрузка… Это имитация реального аттестационного теста перед приемом на работу. Половина теста включает в себя математику, которую нельзя улучшить, кроме строгой практики. Расчет инвентаря имущества. Скоростная математика, Билл Хэндли. 15. 579. У вас есть 15 секунд, чтобы дать ответ. Ниже приведена бесплатная онлайн-викторина по математике, которая включает в себя вопросы и ответы mcqs, связанные с темой средних значений.
По умолчанию оно составляет 5 секунд, но игрок увеличил его с помощью меню, доступного в верхней части страницы.Стр. 22. Распечатать в полном размере. Сыграйте в тесты на время по математике прямо сейчас! по худа математике. Сложение задач в обратном порядке. com, чтобы быть очень простым и быстрым тестом скорости. После того, как вы ответите на все вопросы, мы обработаем данные (очень быстро) и рассчитаем ваш показатель IQ (очень точно). ф. В этом тесте 10 вопросов, каждый из которых был разработан в соответствии со стилем и сложностью вопросов, к которым вы должны подготовиться в ближайшие недели и месяцы. Математические решения и темы 6-го класса. Добавлять.Загрузка… Это имитация реального аттестационного теста перед приемом на работу. Половина теста включает в себя математику, которую нельзя улучшить, кроме строгой практики. Расчет инвентаря имущества. Скоростная математика, Билл Хэндли. 15. 579. У вас есть 15 секунд, чтобы дать ответ. Ниже приведена бесплатная онлайн-викторина по математике, которая включает в себя вопросы и ответы mcqs, связанные с темой средних значений. Сложение от 0 до 10 (60 секунд) Бесплатное приложение для улучшения навыков счета в уме. Speed Skills Times Tables Swap Pieces Как это работает Регистрация для родителей Регистрация для учителей Руководство пользователя для учителей Отзывы.Потребительский тест по математике и ключ к викторине. Вы можете использовать сложение и вычитание для создания уравнения, но вам не разрешено переставлять цифры. Например, автомобиль едет 3 часа. Тестовые вопросы охватывают следующие навыки: Основные функции: сложение, вычитание, деление и умножение. На вступительном экзамене TSI примерно 20 вопросов, и по 10 вопросов в каждом разделе теста TSI. Названия слов для чисел — тест по математике для четвертого класса Сложение до 20 000 — тест по математике для четвертого класса Простые и составные числа — тест по математике для четвертого класса Четные и нечетные, Тест для четвертого класса — тест по математике для четвертого класса Словесные задачи на сложение до 20 000 — тест по математике для четвертого класса Сложение 3 или более чисел до 30 000 — тест по математике четвертого класса Оценка сумм путем округления данных — … Вторая единица измерения, используемая для теста скорости кликов.
Сложение от 0 до 10 (60 секунд) Бесплатное приложение для улучшения навыков счета в уме. Speed Skills Times Tables Swap Pieces Как это работает Регистрация для родителей Регистрация для учителей Руководство пользователя для учителей Отзывы.Потребительский тест по математике и ключ к викторине. Вы можете использовать сложение и вычитание для создания уравнения, но вам не разрешено переставлять цифры. Например, автомобиль едет 3 часа. Тестовые вопросы охватывают следующие навыки: Основные функции: сложение, вычитание, деление и умножение. На вступительном экзамене TSI примерно 20 вопросов, и по 10 вопросов в каждом разделе теста TSI. Названия слов для чисел — тест по математике для четвертого класса Сложение до 20 000 — тест по математике для четвертого класса Простые и составные числа — тест по математике для четвертого класса Четные и нечетные, Тест для четвертого класса — тест по математике для четвертого класса Словесные задачи на сложение до 20 000 — тест по математике для четвертого класса Сложение 3 или более чисел до 30 000 — тест по математике четвертого класса Оценка сумм путем округления данных — … Вторая единица измерения, используемая для теста скорости кликов. Красный дом на 1 фут короче серого дома. Тоня копит деньги на новый велосипед. Давайте рассмотрим каждый ингредиент этой формулы: тест на скорость мышления. Этот тип вопросов, который часто встречается в сложных текстовых задачах, мало знаком многим учащимся, поэтому не нервничайте, если вы не знаете, как к нему подойти. 979 998 воспроизведений от K до 5 (8933) Stacking Box Typing. Каждая девочка думала, что она быстрее бегает. Если не указано иное, областью определения данной функции f является множество всех действительных чисел x, для которых f(x) является действительным числом.99. Создайте бесплатный IXL, предлагающий сотни математических навыков третьего класса для изучения и изучения! Не уверен, где начать? Перейдите на свою персональную стену рекомендаций, чтобы найти навык, который выглядит интересным, или выберите план развития навыков, который соответствует вашему учебнику, государственным стандартам или стандартизированному тесту. Пройдите тренировочный тест GED по математике, чтобы имитировать опыт тестового дня.
Красный дом на 1 фут короче серого дома. Тоня копит деньги на новый велосипед. Давайте рассмотрим каждый ингредиент этой формулы: тест на скорость мышления. Этот тип вопросов, который часто встречается в сложных текстовых задачах, мало знаком многим учащимся, поэтому не нервничайте, если вы не знаете, как к нему подойти. 979 998 воспроизведений от K до 5 (8933) Stacking Box Typing. Каждая девочка думала, что она быстрее бегает. Если не указано иное, областью определения данной функции f является множество всех действительных чисел x, для которых f(x) является действительным числом.99. Создайте бесплатный IXL, предлагающий сотни математических навыков третьего класса для изучения и изучения! Не уверен, где начать? Перейдите на свою персональную стену рекомендаций, чтобы найти навык, который выглядит интересным, или выберите план развития навыков, который соответствует вашему учебнику, государственным стандартам или стандартизированному тесту. Пройдите тренировочный тест GED по математике, чтобы имитировать опыт тестового дня. Тесты на время умножения. Посетите сейчас! Ведическая математика-для быстрой математики, быстрой математики и ментальной математики. 24. Направление: Для каждой задачи выберите правильный ответ.может плохо работать на тестах скорости. 12+3-4+5+67+8+9=100. Разница 9 — 9/10 составляет: 8. Он проходит 30 миль за первый час, 45 миль за второй час и 75 миль за третий час. Могу я сегодня пройти тест на скорость?» Семиклассникам нравится соревноваться со временем, чтобы продемонстрировать свои вычислительные способности, а вам понравятся растущие успехи вашего ребенка в математике. О Патрике Мюррее Конфиденциальность В этих рабочих листах умножения факты сгруппированы в основные группы. Разделять. C. В большинстве случаев их можно решить с помощью формулы скорости, времени, расстояния (также известной как формула времени, скорости, расстояния или формулы расстояния, скорости и времени, они все одинаковы).Математический тест с плавающей запятой выполняет те же операции, что и тест с целочисленной математикой, но с числами с плавающей запятой, используя равное количество значений одинарной точности (32 бита) и двойной точности (64 бита).
Тесты на время умножения. Посетите сейчас! Ведическая математика-для быстрой математики, быстрой математики и ментальной математики. 24. Направление: Для каждой задачи выберите правильный ответ.может плохо работать на тестах скорости. 12+3-4+5+67+8+9=100. Разница 9 — 9/10 составляет: 8. Он проходит 30 миль за первый час, 45 миль за второй час и 75 миль за третий час. Могу я сегодня пройти тест на скорость?» Семиклассникам нравится соревноваться со временем, чтобы продемонстрировать свои вычислительные способности, а вам понравятся растущие успехи вашего ребенка в математике. О Патрике Мюррее Конфиденциальность В этих рабочих листах умножения факты сгруппированы в основные группы. Разделять. C. В большинстве случаев их можно решить с помощью формулы скорости, времени, расстояния (также известной как формула времени, скорости, расстояния или формулы расстояния, скорости и времени, они все одинаковы).Математический тест с плавающей запятой выполняет те же операции, что и тест с целочисленной математикой, но с числами с плавающей запятой, используя равное количество значений одинарной точности (32 бита) и двойной точности (64 бита). Существуют различные варианты скорости тестирования кликов: кликов в секунду, кликов за 10 секунд, кликов за 1 минуту и максимального клика за 100 секунд. Чем быстрее вы, тем больше очков вы получите. Рабочий лист 3. Расчеты лекарств; Труден ли полицейский тест по математике? Математическая часть полицейского экзамена может быть сложной, если вы придете неподготовленным.Кес | Мин. В первой половине книги объясняется, как отвечать на вопросы, а затем на странице 16 книги, собственно вопросник. 80 вопросов за 8 минут; Множественный выбор среднего 1 математики. Тесты. 750 мл. Оцените выражение 15. Если она продолжает откладывать $2. МАТЕМАТИКА | КЛАСС: 3-й. com Тест по математике кассира банка Цель: Этот тест измеряет базовые математические навыки для работы в банковской сфере. Рабочий лист 1. Как вы уже догадались, количество баллов напрямую зависит от скорости и продолжительности теста.Используя эту диаграмму рассеяния, вы можете сделать вывод, что лезвия коньков с наименьшим радиусом выемки, как правило, имеют: Меньший тормозной путь 3.
Существуют различные варианты скорости тестирования кликов: кликов в секунду, кликов за 10 секунд, кликов за 1 минуту и максимального клика за 100 секунд. Чем быстрее вы, тем больше очков вы получите. Рабочий лист 3. Расчеты лекарств; Труден ли полицейский тест по математике? Математическая часть полицейского экзамена может быть сложной, если вы придете неподготовленным.Кес | Мин. В первой половине книги объясняется, как отвечать на вопросы, а затем на странице 16 книги, собственно вопросник. 80 вопросов за 8 минут; Множественный выбор среднего 1 математики. Тесты. 750 мл. Оцените выражение 15. Если она продолжает откладывать $2. МАТЕМАТИКА | КЛАСС: 3-й. com Тест по математике кассира банка Цель: Этот тест измеряет базовые математические навыки для работы в банковской сфере. Рабочий лист 1. Как вы уже догадались, количество баллов напрямую зависит от скорости и продолжительности теста.Используя эту диаграмму рассеяния, вы можете сделать вывод, что лезвия коньков с наименьшим радиусом выемки, как правило, имеют: Меньший тормозной путь 3. — Есть два типа вопросов: Вопросы с несколькими вариантами ответов: на каждый из этих вопросов есть четыре или более возможных ответа . Как только вы довольны процентами и тем, что они собой представляют, пришло время принять вызов процента! Испытания на скорость по математике: финальный тест. синий квадрат Б. Квинт Гораций Флакк (65–8 г. до н. э.), известный в англоязычном мире как «Гораций», был современником Вергилия и выдающимся лирическим поэтом эпохи Августа; его стихи были известны как «общая валюта цивилизации», потому что их так широко читали и цитировали,… Практика тестирования числовых последовательностей для тестов способностей и психометрических тестов IQ.2036
10 к 1: Наука 6. Умножение на основные факты 0, 1, 2, 5 и 10 Умножение на факты 3, 4 и 6 Умножение на факты 7, 8 и 9 Умножение на факты 11 и 12 Умножение на факты от 0 до 5 и 10 Умножение на факты от 0 до 7 и 10 Умножение на факты от 0 до 10. Вы хотите проверить скорость математики, вы хотите улучшить навыки скорости математики и тренировать мозг? Давайте попробуем игру Math Game.
— Есть два типа вопросов: Вопросы с несколькими вариантами ответов: на каждый из этих вопросов есть четыре или более возможных ответа . Как только вы довольны процентами и тем, что они собой представляют, пришло время принять вызов процента! Испытания на скорость по математике: финальный тест. синий квадрат Б. Квинт Гораций Флакк (65–8 г. до н. э.), известный в англоязычном мире как «Гораций», был современником Вергилия и выдающимся лирическим поэтом эпохи Августа; его стихи были известны как «общая валюта цивилизации», потому что их так широко читали и цитировали,… Практика тестирования числовых последовательностей для тестов способностей и психометрических тестов IQ.2036
10 к 1: Наука 6. Умножение на основные факты 0, 1, 2, 5 и 10 Умножение на факты 3, 4 и 6 Умножение на факты 7, 8 и 9 Умножение на факты 11 и 12 Умножение на факты от 0 до 5 и 10 Умножение на факты от 0 до 7 и 10 Умножение на факты от 0 до 10. Вы хотите проверить скорость математики, вы хотите улучшить навыки скорости математики и тренировать мозг? Давайте попробуем игру Math Game. Недостатком теста печати WPM является то, что вы только учитесь печатать быстро. Этот тест оценивает способности учащегося в следующих областях содержания: zбазовые сведения о сложении и вычитании в пределах от 0 до 18 zтрехзначные числа и разрядное значение zперегруппировка в дополнение к дву- и трехзначным числам. рабочих листов в формате pdf, которые можно использовать для тестов на умножение на время, представлены на этой странице и включают тесты на умножение на время для печати, которые можно использовать в качестве тренировочных листов для умножения для учащихся 3-го класса и старше.Инструменты для сосредоточения внимания на концепциях, а не на памяти: Позвольте учащимся использовать калькулятор, таблицу математических фактов или компьютерное программное обеспечение. Что вы можете получить здесь практику теста скорости по математике в течение года. Найдите скорость дождевого червя. Скоростные навыки. Инструкции по тесту скорости чтения: Нажмите «Старт» и начните читать отрывок ниже.
Недостатком теста печати WPM является то, что вы только учитесь печатать быстро. Этот тест оценивает способности учащегося в следующих областях содержания: zбазовые сведения о сложении и вычитании в пределах от 0 до 18 zтрехзначные числа и разрядное значение zперегруппировка в дополнение к дву- и трехзначным числам. рабочих листов в формате pdf, которые можно использовать для тестов на умножение на время, представлены на этой странице и включают тесты на умножение на время для печати, которые можно использовать в качестве тренировочных листов для умножения для учащихся 3-го класса и старше.Инструменты для сосредоточения внимания на концепциях, а не на памяти: Позвольте учащимся использовать калькулятор, таблицу математических фактов или компьютерное программное обеспечение. Что вы можете получить здесь практику теста скорости по математике в течение года. Найдите скорость дождевого червя. Скоростные навыки. Инструкции по тесту скорости чтения: Нажмите «Старт» и начните читать отрывок ниже. Например, если вы хотите потренироваться в сложении 1, 2 и 3, нажмите на пузырек 1, пузырек 2 и пузырек 3. 29. Проверьте свои математические способности с помощью этого бесплатного базового теста по математике с задачами на деление.Мы собрали практические математические задачи для 6 класса, охватывающие всю учебную программу. 0. Если… Если для того, чтобы проехать 450 км, требуется 9 часов, какая это скорость в метрах/мин? Намекать. Отвечать. Присоединяйтесь к многопользовательской игре The Dots 115 015 пьес Класс K–5 (1678) Присоединяйтесь к многопользовательской игре The Dots. Начните бесплатно. ACT Практический тест 2021/2022 Решения по математике. Если у вас возникли проблемы с выполнением какой-либо части этого теста, вам следует приобрести обзорную книгу Джека Мартина и Мэри Серич «Подготовка к экзамену: подготовка к экзамену для квалифицированных профессий». Чтобы пройти тест по математике GED, вы должны набрать не менее 145.39 миль в час D. » Математический тест — сложение, вычитание, десятичные числа, последовательности, умножение, валюта, сравнения, разрядность, алгебра и многое другое! Умножение Фундаментальная математика Элементарная математика Предварительная алгебра Шаг 1 из 2 — Выберите уровень сложности от 1 до 5 1 x 5 = __ Иногда я могу набрать все 20, иногда 16 и т.
Например, если вы хотите потренироваться в сложении 1, 2 и 3, нажмите на пузырек 1, пузырек 2 и пузырек 3. 29. Проверьте свои математические способности с помощью этого бесплатного базового теста по математике с задачами на деление.Мы собрали практические математические задачи для 6 класса, охватывающие всю учебную программу. 0. Если… Если для того, чтобы проехать 450 км, требуется 9 часов, какая это скорость в метрах/мин? Намекать. Отвечать. Присоединяйтесь к многопользовательской игре The Dots 115 015 пьес Класс K–5 (1678) Присоединяйтесь к многопользовательской игре The Dots. Начните бесплатно. ACT Практический тест 2021/2022 Решения по математике. Если у вас возникли проблемы с выполнением какой-либо части этого теста, вам следует приобрести обзорную книгу Джека Мартина и Мэри Серич «Подготовка к экзамену: подготовка к экзамену для квалифицированных профессий». Чтобы пройти тест по математике GED, вы должны набрать не менее 145.39 миль в час D. » Математический тест — сложение, вычитание, десятичные числа, последовательности, умножение, валюта, сравнения, разрядность, алгебра и многое другое! Умножение Фундаментальная математика Элементарная математика Предварительная алгебра Шаг 1 из 2 — Выберите уровень сложности от 1 до 5 1 x 5 = __ Иногда я могу набрать все 20, иногда 16 и т. д. Викторина по естествознанию / Скоростная математика (1–100) Случайная викторина по естествознанию или математике Сможете ли вы выбрать числа в правильном порядке? 19 января 2017 г. Lilly делает арт-проект со следующими кнопками.Вы можете выбирать между суммами сложения до 10 и до 20. Положите 50 или около того, многим людям будет трудно достичь этого, но, по крайней мере, вы можете улучшить свой счет таким образом, добраться до 20 не проблема. Вы можете практиковать столы на время по отдельности, несколько за раз или все одновременно. Информация. Наш математический тест CBEST включает в себя 50 практических вопросов с несколькими вариантами ответов и подробными пояснениями. добавьте 6 к обеим сторонам B. 040 97. Добавить в список воспроизведения Добавить в список воспроизведения Добавить в закладки эту викторину Speed Math — онлайн-игра.Осталось секунд: Оценка: 0 Оценка: 0. Это упражнение можно выполнять в классе и дома. Вопрос о тестах на время и стратегии обучения особенно актуален для учащихся с дислексией, многие из которых имеют медленную обработку (особенно в младших классах), проблемы с механической памятью и трудности с поиском информации во времени.
д. Викторина по естествознанию / Скоростная математика (1–100) Случайная викторина по естествознанию или математике Сможете ли вы выбрать числа в правильном порядке? 19 января 2017 г. Lilly делает арт-проект со следующими кнопками.Вы можете выбирать между суммами сложения до 10 и до 20. Положите 50 или около того, многим людям будет трудно достичь этого, но, по крайней мере, вы можете улучшить свой счет таким образом, добраться до 20 не проблема. Вы можете практиковать столы на время по отдельности, несколько за раз или все одновременно. Информация. Наш математический тест CBEST включает в себя 50 практических вопросов с несколькими вариантами ответов и подробными пояснениями. добавьте 6 к обеим сторонам B. 040 97. Добавить в список воспроизведения Добавить в список воспроизведения Добавить в закладки эту викторину Speed Math — онлайн-игра.Осталось секунд: Оценка: 0 Оценка: 0. Это упражнение можно выполнять в классе и дома. Вопрос о тестах на время и стратегии обучения особенно актуален для учащихся с дислексией, многие из которых имеют медленную обработку (особенно в младших классах), проблемы с механической памятью и трудности с поиском информации во времени. ком. 2. Навыки Умственная арифметика, Упражнения на умножение, Таблицы умножения, Умножение произведений чисел от 0 до 10. Следующий тест предназначен для оценки скорости вашего мышления — насколько быстро вы можете обрабатывать информацию и принимать решения на основе этой информации.Начните подготовку к экзамену прямо сейчас с нашего практического теста GED по математике. Время тренировки: 10 сек. 1 мин. 2 мин. 3 мин. 5 мин. 10 мин. 1 день. Ограничение вопросов: 2 сек. 4 сек. 8 сек. 1 день. Игрушечная машинка Скорость Время Скорость C. Дроби 3 класса. Как играть в SuperSpeed Math Играть в SuperSpeed Math очень просто. Спасибо, ваш голос был зарегистрирован и скоро будет показан. 23 Кристин пьет 0. Введите ответы и нажмите кнопку «Оценить мой тест». По окончании мастер-класса вы сможете быстро считать в уме. Пожалуйста, найдите минутку, чтобы пройти этот тест.20 арифметических задач с 4 уровнями математики. Во время последней тренировки Иззи пробежала 2 1/4 мили за 15 минут, а ее подруга Джулия пробежала 3 3/4 мили за 25 минут.
ком. 2. Навыки Умственная арифметика, Упражнения на умножение, Таблицы умножения, Умножение произведений чисел от 0 до 10. Следующий тест предназначен для оценки скорости вашего мышления — насколько быстро вы можете обрабатывать информацию и принимать решения на основе этой информации.Начните подготовку к экзамену прямо сейчас с нашего практического теста GED по математике. Время тренировки: 10 сек. 1 мин. 2 мин. 3 мин. 5 мин. 10 мин. 1 день. Ограничение вопросов: 2 сек. 4 сек. 8 сек. 1 день. Игрушечная машинка Скорость Время Скорость C. Дроби 3 класса. Как играть в SuperSpeed Math Играть в SuperSpeed Math очень просто. Спасибо, ваш голос был зарегистрирован и скоро будет показан. 23 Кристин пьет 0. Введите ответы и нажмите кнопку «Оценить мой тест». По окончании мастер-класса вы сможете быстро считать в уме. Пожалуйста, найдите минутку, чтобы пройти этот тест.20 арифметических задач с 4 уровнями математики. Во время последней тренировки Иззи пробежала 2 1/4 мили за 15 минут, а ее подруга Джулия пробежала 3 3/4 мили за 25 минут. Abeka Business Mathematics Tests, Quizzes & … Тест скорости широкополосного доступа, который работает в любом веб-браузере. ТестМой. На третий день она сэкономила 2 доллара. Добавьте больше вопросов, 20 слишком просто. Этот тест набора текста охватывает клавиши с цифрами и математическими символами. 3052 контактных ресурсов. Определите повторяющееся выражение сложения, равное выражению умножения.Рабочий лист 4. 5 12. Оценка 1. По мере того, как вы привыкаете к тесту и типам математических вопросов/концепций, которые появляются, посмотрите, есть ли более быстрые или простые способы решения вопросов, которые отнимают у вас больше всего времени. Оценка TSI по математике — это экзамен с несколькими вариантами ответов, состоящий из четырех предметов, описанных ниже. Сначала я думал, что эта книга понравится мне меньше, чем «Краткая математика» Джерарда Келли. Начиная со 2-го класса общепринятые стандарты ставят перед собой цель «беглости» по математике. При движении от x к y его средняя скорость составляет 72 км/ч, а при возвращении из y в x его средняя скорость составляет 63 км/ч.
Abeka Business Mathematics Tests, Quizzes & … Тест скорости широкополосного доступа, который работает в любом веб-браузере. ТестМой. На третий день она сэкономила 2 доллара. Добавьте больше вопросов, 20 слишком просто. Этот тест набора текста охватывает клавиши с цифрами и математическими символами. 3052 контактных ресурсов. Определите повторяющееся выражение сложения, равное выражению умножения.Рабочий лист 4. 5 12. Оценка 1. По мере того, как вы привыкаете к тесту и типам математических вопросов/концепций, которые появляются, посмотрите, есть ли более быстрые или простые способы решения вопросов, которые отнимают у вас больше всего времени. Оценка TSI по математике — это экзамен с несколькими вариантами ответов, состоящий из четырех предметов, описанных ниже. Сначала я думал, что эта книга понравится мне меньше, чем «Краткая математика» Джерарда Келли. Начиная со 2-го класса общепринятые стандарты ставят перед собой цель «беглости» по математике. При движении от x к y его средняя скорость составляет 72 км/ч, а при возвращении из y в x его средняя скорость составляет 63 км/ч. Здесь у нас есть умножение и сложение, а согласно правилу BODMAS умножение предшествует сложению, поэтому мы должны сначала выполнить умножение, а затем сложение. Постоянная скорость также называется равномерной скоростью, когда что-то движется с фиксированной и постоянной скоростью или движется с некоторой средней скоростью. Ответьте на следующие вопросы как можно быстрее, когда закончите, нажмите кнопку внизу. ПРАКТИЧЕСКИЙ ТЕСТ В БАРТОНСКОМ КОЛЛЕДЖЕ СТРАНИЦА 4 ИЗ 12 25. Статистический практический тест.Чтобы ознакомиться с нашей обновленной политикой в отношении файлов cookie, нажмите здесь. Каждое число от 1 до 15 было написано в индивидуальном тесте по математике четвертого класса 13. Ускорение – это изменение скорости, деленное на время. Все люди, которые готовятся к сдаче любого экзамена по математике или просто хотят улучшить свои навыки решения задач, могут пройти этот тест, чтобы сделать это с легкостью. B. NEG7MathPTPaper 2 СТОП. Создан, чтобы воспроизвести вашу реальную скорость соединения! САМЫЙ ТОЧНЫЙ И МОЩНЫЙ ОНЛАЙН-ТЕСТ ПРОПУСКНОЙ ПЛОЩАДКИ Проверьте скорость Интернета на iPad, iPhone, Android, Smart TV, Xbox, PlayStation, Windows, Mac, Linux и т.
Здесь у нас есть умножение и сложение, а согласно правилу BODMAS умножение предшествует сложению, поэтому мы должны сначала выполнить умножение, а затем сложение. Постоянная скорость также называется равномерной скоростью, когда что-то движется с фиксированной и постоянной скоростью или движется с некоторой средней скоростью. Ответьте на следующие вопросы как можно быстрее, когда закончите, нажмите кнопку внизу. ПРАКТИЧЕСКИЙ ТЕСТ В БАРТОНСКОМ КОЛЛЕДЖЕ СТРАНИЦА 4 ИЗ 12 25. Статистический практический тест.Чтобы ознакомиться с нашей обновленной политикой в отношении файлов cookie, нажмите здесь. Каждое число от 1 до 15 было написано в индивидуальном тесте по математике четвертого класса 13. Ускорение – это изменение скорости, деленное на время. Все люди, которые готовятся к сдаче любого экзамена по математике или просто хотят улучшить свои навыки решения задач, могут пройти этот тест, чтобы сделать это с легкостью. B. NEG7MathPTPaper 2 СТОП. Создан, чтобы воспроизвести вашу реальную скорость соединения! САМЫЙ ТОЧНЫЙ И МОЩНЫЙ ОНЛАЙН-ТЕСТ ПРОПУСКНОЙ ПЛОЩАДКИ Проверьте скорость Интернета на iPad, iPhone, Android, Smart TV, Xbox, PlayStation, Windows, Mac, Linux и т. д.Математическое упражнение по умножению — это рабочий лист со всеми однозначными задачами на умножение на одной странице. Имя номера-до 10 Математический тест. Оценить 5 звезд Оценить 4 звезды Оценить 3 звезды Оценить 2 звезды Оценить 1 звезду . А как насчет пинга, задержки, загрузки и прочего? Когда вы нажимаете кнопку «Показать больше информации», вы можете увидеть скорость загрузки и задержку соединения (пинг). com, чтобы подготовиться к вступительному экзамену по математике Accuplacer в ее университете. Экзамен представляет собой тест объективного типа, который студенты должны пройти за 60 минут.Машина выезжает из Лондона в 8.1 класс. или изменить настройки. Вам говорят, что он может переместиться на расстояние 89. Скорость Расстояние Время Тест. Мат. Выбор лучшего независимого теста скорости в 2021 году — лучшие обзоры и руководства по покупке Ищете лучший независимый тест скорости? На основании отзывов экспертов мы ранжировали их. (32 3 – 7 4) 2 ÷ 53 4 26. Практический тест CBEST по математике.
д.Математическое упражнение по умножению — это рабочий лист со всеми однозначными задачами на умножение на одной странице. Имя номера-до 10 Математический тест. Оценить 5 звезд Оценить 4 звезды Оценить 3 звезды Оценить 2 звезды Оценить 1 звезду . А как насчет пинга, задержки, загрузки и прочего? Когда вы нажимаете кнопку «Показать больше информации», вы можете увидеть скорость загрузки и задержку соединения (пинг). com, чтобы подготовиться к вступительному экзамену по математике Accuplacer в ее университете. Экзамен представляет собой тест объективного типа, который студенты должны пройти за 60 минут.Машина выезжает из Лондона в 8.1 класс. или изменить настройки. Вам говорят, что он может переместиться на расстояние 89. Скорость Расстояние Время Тест. Мат. Выбор лучшего независимого теста скорости в 2021 году — лучшие обзоры и руководства по покупке Ищете лучший независимый тест скорости? На основании отзывов экспертов мы ранжировали их. (32 3 – 7 4) 2 ÷ 53 4 26. Практический тест CBEST по математике. Наши практические вопросы отсортированы по уровню сложности, чтобы вы могли сосредоточиться на вопросах, которые бросают вам вызов. Сосчитайте до 20 Математический тест Назовите следующее число от заданного числа.Используя только числа от 1 до 5. Это интересный онлайн-тест о дробях, который ученики 3-го класса могут пройти в конце главы. Форматирование тестовых образцов программных продуктов аналогично форматированию оперативного онлайн-теста по математике OAKD. Выберите вариант, который лучше всего подходит к подчеркнутой части предложения. Английский. 99 + 88 + 77 + 66 + 55 + 44 + 33 + 22 + 11 — 12 — 23 — 34 — 45 — 56 — 67 — 78 — 89 — 90 = 1. Многим учителям, не готовящим учащихся к такому случаю тестирование было слишком похоже на «подготовку детей к неудачам».Текущая цена. Приложение загружается, подождите секунду 6.
20b0
Эта онлайн-викторина на умножение содержит 50 задач на умножение, которые помогут закрепить математические факты об умножении. Автоматически исправленные и рассчитанные по времени викторины.
Наши практические вопросы отсортированы по уровню сложности, чтобы вы могли сосредоточиться на вопросах, которые бросают вам вызов. Сосчитайте до 20 Математический тест Назовите следующее число от заданного числа.Используя только числа от 1 до 5. Это интересный онлайн-тест о дробях, который ученики 3-го класса могут пройти в конце главы. Форматирование тестовых образцов программных продуктов аналогично форматированию оперативного онлайн-теста по математике OAKD. Выберите вариант, который лучше всего подходит к подчеркнутой части предложения. Английский. 99 + 88 + 77 + 66 + 55 + 44 + 33 + 22 + 11 — 12 — 23 — 34 — 45 — 56 — 67 — 78 — 89 — 90 = 1. Многим учителям, не готовящим учащихся к такому случаю тестирование было слишком похоже на «подготовку детей к неудачам».Текущая цена. Приложение загружается, подождите секунду 6.
20b0
Эта онлайн-викторина на умножение содержит 50 задач на умножение, которые помогут закрепить математические факты об умножении. Автоматически исправленные и рассчитанные по времени викторины. Этот рабочий лист по умножению подходит для детского сада, 1-го класса, 2-го класса, а скорость загрузки наиболее актуальна для людей, которые потребляют контент в Интернете, и нам нужна БЫСТРО. Краткий обзор основных функций Brain Speed Test: Чистый и аккуратный дизайн со свежей интуитивно понятной рекламой.ОБРАЗЕЦ ТЕСТА ПО МАТЕМАТИКЕ 6 КЛАСС 2007 Oregon Content Standards 3–8 классы. Решайте основные математические операции, чтобы проверить свои математические навыки. Каково число метрических тонн пшеницы, записанное в экспоненциальном представлении? A. 833 метра в минуту (до 3 с. Самое главное, чтобы вы ответили на вопрос в отведенное время, потому что именно так вы набираете наибольшее количество очков. 00. Подробнее о упражнениях на скорость учат детей ненавидеть математику. Это основано на по разделу 3 SAT, который включает в себя в общей сложности 20 вопросов.Ментальная математика — лучшие методы для ускорения вашей математики. Пожалуйста, нажмите на ссылку выше, чтобы начать. Просмотрите эти важные уравнения и посмотрите, как эта концепция проявляется в тесте по математике для второго класса Имя учащегося: _____ Дата: _____ 9.
Этот рабочий лист по умножению подходит для детского сада, 1-го класса, 2-го класса, а скорость загрузки наиболее актуальна для людей, которые потребляют контент в Интернете, и нам нужна БЫСТРО. Краткий обзор основных функций Brain Speed Test: Чистый и аккуратный дизайн со свежей интуитивно понятной рекламой.ОБРАЗЕЦ ТЕСТА ПО МАТЕМАТИКЕ 6 КЛАСС 2007 Oregon Content Standards 3–8 классы. Решайте основные математические операции, чтобы проверить свои математические навыки. Каково число метрических тонн пшеницы, записанное в экспоненциальном представлении? A. 833 метра в минуту (до 3 с. Самое главное, чтобы вы ответили на вопрос в отведенное время, потому что именно так вы набираете наибольшее количество очков. 00. Подробнее о упражнениях на скорость учат детей ненавидеть математику. Это основано на по разделу 3 SAT, который включает в себя в общей сложности 20 вопросов.Ментальная математика — лучшие методы для ускорения вашей математики. Пожалуйста, нажмите на ссылку выше, чтобы начать. Просмотрите эти важные уравнения и посмотрите, как эта концепция проявляется в тесте по математике для второго класса Имя учащегося: _____ Дата: _____ 9. Если вы выберете все таблицы для этого теста, вам будет задано не менее 65 вопросов. Затем проверьте их на каждой операции, чтобы увидеть, могут ли они ответить на все эти факты без колебаний — другими словами, так быстро, как они могут писать. Бизнес 110: выпускной экзамен по бизнес-математике.Он состоит из 25 вопросов, включает в себя 4 основных символа. Иногда это может быть запоминание свойств особых прямоугольных треугольников, таких как треугольники 30, 60, 90, чтобы вам не приходилось тратить время на поиск стороны. Умножение — один из важнейших элементов математики, хотя его можно вызов для некоторых молодых учащихся, потому что это требует запоминания, а также практики. Настоящий тест по математике ACT содержит 60 вопросов, на которые нужно ответить за 60 минут. Данные опроса были разбиты, как показано в таблице выше.7 из 1. com содержит более 58 тысяч бесплатных математических листов, которые можно использовать для помощи учащимся в изучении математики. Классные игры всегда бесплатны на HoodaMath.
Если вы выберете все таблицы для этого теста, вам будет задано не менее 65 вопросов. Затем проверьте их на каждой операции, чтобы увидеть, могут ли они ответить на все эти факты без колебаний — другими словами, так быстро, как они могут писать. Бизнес 110: выпускной экзамен по бизнес-математике.Он состоит из 25 вопросов, включает в себя 4 основных символа. Иногда это может быть запоминание свойств особых прямоугольных треугольников, таких как треугольники 30, 60, 90, чтобы вам не приходилось тратить время на поиск стороны. Умножение — один из важнейших элементов математики, хотя его можно вызов для некоторых молодых учащихся, потому что это требует запоминания, а также практики. Настоящий тест по математике ACT содержит 60 вопросов, на которые нужно ответить за 60 минут. Данные опроса были разбиты, как показано в таблице выше.7 из 1. com содержит более 58 тысяч бесплатных математических листов, которые можно использовать для помощи учащимся в изучении математики. Классные игры всегда бесплатны на HoodaMath. Есть три шара, которые дрейфуют вниз с вашими внутренними вычислениями, ваша задача подобрать результат тех вычислений, которые являются шарами внизу. Рабочие листы по математике в этом разделе подобраны специально для первоклассников, и работа с ними создаст прочную основу для изучения математических тем по мере того, как учащиеся переходят в более высокие классы. Бумага 1 состоит из двух буклетов.Математика 6 класс первый тест. Моя дочь использовала Mathhelp. Стиль рабочего листа: 50 задач / Полный лист 25 задач / Полный лист 50 задач / Половина листа 25 задач / Половина листа. Раздел Заполните пробел до 10 Математический тест. Math-Path (кратные 3) 3. БЕСПЛАТНО. Скоростная математика поможет вам раскрыть свой потенциал, бросив вам вызов с операциями до трех операндов, используя сложение, вычитание, деление и… Станьте мастером ментальной арифметики. Наслаждайтесь игрой в наши математические игры бесплатно на неопределенный срок.Названия слов для чисел — тест по математике для четвертого класса Сложение до 20 000 — тест по математике для четвертого класса Простые и составные числа — тест по математике для четвертого класса Четные и нечетные, Тест для четвертого класса — тест по математике для четвертого класса Словесные задачи на сложение до 20 000 — тест по математике для четвертого класса Добавление 3 или более чисел до 30 000 — … проверка скорости математических фактов.
Есть три шара, которые дрейфуют вниз с вашими внутренними вычислениями, ваша задача подобрать результат тех вычислений, которые являются шарами внизу. Рабочие листы по математике в этом разделе подобраны специально для первоклассников, и работа с ними создаст прочную основу для изучения математических тем по мере того, как учащиеся переходят в более высокие классы. Бумага 1 состоит из двух буклетов.Математика 6 класс первый тест. Моя дочь использовала Mathhelp. Стиль рабочего листа: 50 задач / Полный лист 25 задач / Полный лист 50 задач / Половина листа 25 задач / Половина листа. Раздел Заполните пробел до 10 Математический тест. Math-Path (кратные 3) 3. БЕСПЛАТНО. Скоростная математика поможет вам раскрыть свой потенциал, бросив вам вызов с операциями до трех операндов, используя сложение, вычитание, деление и… Станьте мастером ментальной арифметики. Наслаждайтесь игрой в наши математические игры бесплатно на неопределенный срок.Названия слов для чисел — тест по математике для четвертого класса Сложение до 20 000 — тест по математике для четвертого класса Простые и составные числа — тест по математике для четвертого класса Четные и нечетные, Тест для четвертого класса — тест по математике для четвертого класса Словесные задачи на сложение до 20 000 — тест по математике для четвертого класса Добавление 3 или более чисел до 30 000 — … проверка скорости математических фактов. Тест по математике для 8 класса. Тест на скорость по математике, Викторина на общие знания по математике, Викторина по математике для детей, Викторина по математике для школьников, Викторина по математике Хэштеги:#SimpleMathTest #mathquizforgrade6 #m Имя Дата 6 ТАБЛИЦА ВРЕМЕНИ — ТЕСТ СКОРОСТИ Посмотрите, как быстро вы справитесь с этими фактами.Викторины по основным фактам помогают улучшить скорость ребенка в простой математике и подходят для всех классов. Чем быстрее вы нажимаете, тем быстрее вы можете побить рекорды. Средний балл по этому тесту равен 24. Используйте свой калькулятор с умом. Подпишитесь на них здесь! 👉🏼 https://the5academy. ) Возвращаться. Посттест. Если она потратила 2 5 времени на проверку правильности своих ответов, сколько минут она потратила на проверку? 27. Применяйте свои математические трюки в уме и размещайте свои рекорды в наших списках лидеров! Получите как можно больше правильных ответов за отведенное время.Избранное. Всего 5 часовОбновлено 05/2018. 5 литров апельсинового сока с завтраком каждый день в течение 15 дней.
Тест по математике для 8 класса. Тест на скорость по математике, Викторина на общие знания по математике, Викторина по математике для детей, Викторина по математике для школьников, Викторина по математике Хэштеги:#SimpleMathTest #mathquizforgrade6 #m Имя Дата 6 ТАБЛИЦА ВРЕМЕНИ — ТЕСТ СКОРОСТИ Посмотрите, как быстро вы справитесь с этими фактами.Викторины по основным фактам помогают улучшить скорость ребенка в простой математике и подходят для всех классов. Чем быстрее вы нажимаете, тем быстрее вы можете побить рекорды. Средний балл по этому тесту равен 24. Используйте свой калькулятор с умом. Подпишитесь на них здесь! 👉🏼 https://the5academy. ) Возвращаться. Посттест. Если она потратила 2 5 времени на проверку правильности своих ответов, сколько минут она потратила на проверку? 27. Применяйте свои математические трюки в уме и размещайте свои рекорды в наших списках лидеров! Получите как можно больше правильных ответов за отведенное время.Избранное. Всего 5 часовОбновлено 05/2018. 5 литров апельсинового сока с завтраком каждый день в течение 15 дней. Проверка человека. Средняя скорость равна расстоянию, деленному на время. Используйте Speed Math, чтобы измерить себя и посмотреть, как вы соревнуетесь с друзьями и онлайн, и соревнуйтесь за лучшее время. Задания на рабочие листы Singapore Math проверяют способность учащихся анализировать и использовать многоэтапный подход. Алекс и Боб едут по круговой дорожке, длина окружности которой составляет 15 км. 4/2 =. Я знаю, что мы используем Xtramath. Посмотреть детали.Эти рабочие листы помогают учащимся практиковать свои навыки умножения и запоминать основы. Вы также можете проверить свой Mouse Clicker здесь! Практический полицейский тест по математике Ниже мы собрали образец полицейского практического теста по математике, чтобы дать вам четкое представление о том, чего ожидать в день экзамена. — GitHub — mfoo/Math-Library-Test: сравнение библиотек GLM, CLM и Eigen по скорости и простоте использования. Сколько миллилитров апельсинового сока выпивает Кристин за 15 дней? А. 15 000 мл. Генератор рабочих листов умножения.
Проверка человека. Средняя скорость равна расстоянию, деленному на время. Используйте Speed Math, чтобы измерить себя и посмотреть, как вы соревнуетесь с друзьями и онлайн, и соревнуйтесь за лучшее время. Задания на рабочие листы Singapore Math проверяют способность учащихся анализировать и использовать многоэтапный подход. Алекс и Боб едут по круговой дорожке, длина окружности которой составляет 15 км. 4/2 =. Я знаю, что мы используем Xtramath. Посмотреть детали.Эти рабочие листы помогают учащимся практиковать свои навыки умножения и запоминать основы. Вы также можете проверить свой Mouse Clicker здесь! Практический полицейский тест по математике Ниже мы собрали образец полицейского практического теста по математике, чтобы дать вам четкое представление о том, чего ожидать в день экзамена. — GitHub — mfoo/Math-Library-Test: сравнение библиотек GLM, CLM и Eigen по скорости и простоте использования. Сколько миллилитров апельсинового сока выпивает Кристин за 15 дней? А. 15 000 мл. Генератор рабочих листов умножения. Вам разрешено использовать калькулятор в этом тесте для любых задач, которые вы выберете. Тест содержит 50 вопросов, и у вас есть 15 минут, чтобы ответить на максимально возможное количество вопросов. Практический тест Smart-Kids по английскому домашнему языку 1 класс с ответами. В первый раз она приняла холод и набрала 270 баллов, поэтому не смогла перейти к тесту AAF. Сложение от 0 до 5 (90 секунд) Сложение от 0 до 8 (90 секунд) Сложение от 0 до 10 (90 секунд) Вычитание от 0 до 5 (120 секунд) Вычитание от 0 до 10 (120 секунд) 2-й класс.Тесты «вверх» для десятков, одиннадцати и двенадцати не включают все уравнения. Хотите решение этого теста? Добавьте в корзину и купите Подробное РЕШЕНИЕ НА 15 СТРАНИЦАХ и ПРЕВОСХОДНЫЕ ОБЪЯСНЕНИЯ с помощью PayPal. Числовые последовательности регулярно используются в тестах способностей, психометрических оценках и тестах IQ как показатель способности испытуемого рассуждать с числами. 7 570. Проверь мой мозг. 3×106 D. скорость в первый час = 30 миль/час. Включает в себя несколько страниц для каждого семейства фактов.
Вам разрешено использовать калькулятор в этом тесте для любых задач, которые вы выберете. Тест содержит 50 вопросов, и у вас есть 15 минут, чтобы ответить на максимально возможное количество вопросов. Практический тест Smart-Kids по английскому домашнему языку 1 класс с ответами. В первый раз она приняла холод и набрала 270 баллов, поэтому не смогла перейти к тесту AAF. Сложение от 0 до 5 (90 секунд) Сложение от 0 до 8 (90 секунд) Сложение от 0 до 10 (90 секунд) Вычитание от 0 до 5 (120 секунд) Вычитание от 0 до 10 (120 секунд) 2-й класс.Тесты «вверх» для десятков, одиннадцати и двенадцати не включают все уравнения. Хотите решение этого теста? Добавьте в корзину и купите Подробное РЕШЕНИЕ НА 15 СТРАНИЦАХ и ПРЕВОСХОДНЫЕ ОБЪЯСНЕНИЯ с помощью PayPal. Числовые последовательности регулярно используются в тестах способностей, психометрических оценках и тестах IQ как показатель способности испытуемого рассуждать с числами. 7 570. Проверь мой мозг. 3×106 D. скорость в первый час = 30 миль/час. Включает в себя несколько страниц для каждого семейства фактов. Двухминутное умножение. Одиннадцать. Попробуйте этот тестовый набор слов в минуту для детей. Бесплатный тест по математике. После того, как вы закончите, оцените свой тест, используя ключ ответа. Результаты диагностического теста Common Core: 4th Grade Math показывают, как вы справились с каждой областью теста. Алекс движется с постоянной скоростью от 35 до 5. Математический тест Практикуйтесь, считая до 5, используя это увлекательное математическое онлайн-упражнение. Smart-Kids Практический тест Английский Домашний язык 2 класс с ответами. Повторите попытку или измените настройки. Умение печатать становится все более и более важным для учащихся.скорость умножения, деления, сложения, вычитания. На второй день она сэкономила 2 доллара. Студенты улучшают 5-9 баллов по ACT с нашими программами. 100 уровней сложности, 150 000 пользователей, 60 миллионов ответов на вопросы. О базовом тесте по математике с двузначным числом. Эта публикация содержит исчерпывающую информацию. По мере того, как дети прогрессируют, они должны иметь возможность сосредоточиться на изучении более сложных математических навыков, а не отвлекаться на… Разделите двузначное число на однозначное и запишите ответ.
Двухминутное умножение. Одиннадцать. Попробуйте этот тестовый набор слов в минуту для детей. Бесплатный тест по математике. После того, как вы закончите, оцените свой тест, используя ключ ответа. Результаты диагностического теста Common Core: 4th Grade Math показывают, как вы справились с каждой областью теста. Алекс движется с постоянной скоростью от 35 до 5. Математический тест Практикуйтесь, считая до 5, используя это увлекательное математическое онлайн-упражнение. Smart-Kids Практический тест Английский Домашний язык 2 класс с ответами. Повторите попытку или измените настройки. Умение печатать становится все более и более важным для учащихся.скорость умножения, деления, сложения, вычитания. На второй день она сэкономила 2 доллара. Студенты улучшают 5-9 баллов по ACT с нашими программами. 100 уровней сложности, 150 000 пользователей, 60 миллионов ответов на вопросы. О базовом тесте по математике с двузначным числом. Эта публикация содержит исчерпывающую информацию. По мере того, как дети прогрессируют, они должны иметь возможность сосредоточиться на изучении более сложных математических навыков, а не отвлекаться на… Разделите двузначное число на однозначное и запишите ответ. Получите адекватную практику в нахождении среднего значения, медианы, моды и диапазона списка чисел, представленных в вопросах. Просматривайте ответы по ходу просмотра Просматривайте по 1 вопросу за раз. FPS Количество кадров в секунду (сокращенно FPS) показывает, насколько быстро ваш браузер может отображать новые кадры. желтый треугольник Это оценочный тест. Основы системы: Тест 1 Нет. Сначала выберите свой навык для практики (сложение, вычитание, умножение или деление). Имя Дата 3 ТАБЛИЦА УСКОРЕНИЯ — ТЕСТ СКОРОСТИ Посмотрите, как быстро вы сможете заполнить эти факты.В конце теста у вас будет возможность просмотреть вопросы и ответы, нажав кнопку «Просмотреть ответы». Внимательно прочитайте каждый вопрос, чтобы убедиться, что вы понимаете тип требуемого ответа. Он предназначен для измерения математических навыков, которые учащиеся обычно приобретают к концу 11-го класса. Затем выберите числа, которые вы хотите попрактиковать. Дроби, отношения, десятичные дроби и проценты.
204д
Навыки: скорость набора текста, точность клавиатуры, тест WPM.
Получите адекватную практику в нахождении среднего значения, медианы, моды и диапазона списка чисел, представленных в вопросах. Просматривайте ответы по ходу просмотра Просматривайте по 1 вопросу за раз. FPS Количество кадров в секунду (сокращенно FPS) показывает, насколько быстро ваш браузер может отображать новые кадры. желтый треугольник Это оценочный тест. Основы системы: Тест 1 Нет. Сначала выберите свой навык для практики (сложение, вычитание, умножение или деление). Имя Дата 3 ТАБЛИЦА УСКОРЕНИЯ — ТЕСТ СКОРОСТИ Посмотрите, как быстро вы сможете заполнить эти факты.В конце теста у вас будет возможность просмотреть вопросы и ответы, нажав кнопку «Просмотреть ответы». Внимательно прочитайте каждый вопрос, чтобы убедиться, что вы понимаете тип требуемого ответа. Он предназначен для измерения математических навыков, которые учащиеся обычно приобретают к концу 11-го класса. Затем выберите числа, которые вы хотите попрактиковать. Дроби, отношения, десятичные дроби и проценты.
204д
Навыки: скорость набора текста, точность клавиатуры, тест WPM. ), чтобы решить, является ли уравнение, которое появляется на … Free Math Worksheets.Вопросы с несколькими вариантами ответов являются важной частью экзаменов на оценку … скорость, объем, круговые диаграммы, твердые цифры и сети. Политика Совета по образованию штата и приоритет Департамента образования штата Орегон заключаются в том, чтобы не допускать дискриминации или притеснений на основании… отличное место, чтобы начать привычку регулярно заниматься математикой. Если пара совпадает, нажмите кнопку «Правильно» (клавиша со стрелкой влево на клавиатуре).Тест на скорость по математике, Викторина на общие знания по математике, Викторина по математике для детей, Викторина по математике для учащихся, Викторина по математике ® Тест по математике состоит примерно из 66 вопросов с несколькими вариантами ответов, взятых из курсов, обычно предлагаемых на уровне бакалавриата. Попробуйте выполнить это в течение 20 … Math Speed Test, Тест на общие знания по математике, Математическая викторина для детей, Математическая викторина для студентов, Математическая викторина , какова масса тела на диаграмме, если его плотность равна 1.
), чтобы решить, является ли уравнение, которое появляется на … Free Math Worksheets.Вопросы с несколькими вариантами ответов являются важной частью экзаменов на оценку … скорость, объем, круговые диаграммы, твердые цифры и сети. Политика Совета по образованию штата и приоритет Департамента образования штата Орегон заключаются в том, чтобы не допускать дискриминации или притеснений на основании… отличное место, чтобы начать привычку регулярно заниматься математикой. Если пара совпадает, нажмите кнопку «Правильно» (клавиша со стрелкой влево на клавиатуре).Тест на скорость по математике, Викторина на общие знания по математике, Викторина по математике для детей, Викторина по математике для учащихся, Викторина по математике ® Тест по математике состоит примерно из 66 вопросов с несколькими вариантами ответов, взятых из курсов, обычно предлагаемых на уровне бакалавриата. Попробуйте выполнить это в течение 20 … Math Speed Test, Тест на общие знания по математике, Математическая викторина для детей, Математическая викторина для студентов, Математическая викторина , какова масса тела на диаграмме, если его плотность равна 1. 5 простых математических трюков Изучите их, чтобы стать математическим волшебником. 700 89. математика20. 2 B. com Проверьте свои знания о том, как рассчитать среднюю скорость, используя этот интерактивный тест. Этот математический лист дает вашему ребенку возможность попрактиковаться в быстром нахождении произведений чисел от 0 до 10. Игра подходит для всех возрастных групп, поэтому не беспокойтесь, если вы просто старшеклассник или человек, работающий в компании. Типы тестов соответствуют уровню работы, включая высокопоставленные руководящие должности, должности выпускников или менеджеров, и добро пожаловать на тест скорости набора текста №1! Проверьте свою истинную скорость печати, точность и уровень навыков всего за 60 секунд.Игрушечная машинка Speed Time Speed B. Преподаватели и учащиеся, которые искали игру для проверки скорости набора текста — бесплатные развивающие игры для детей, сочли следующие статьи и советы актуальными и полезными. К 15. Упражнение состоит из пар слово/изображение и простых математических уравнений или числовых последовательностей.
5 простых математических трюков Изучите их, чтобы стать математическим волшебником. 700 89. математика20. 2 B. com Проверьте свои знания о том, как рассчитать среднюю скорость, используя этот интерактивный тест. Этот математический лист дает вашему ребенку возможность попрактиковаться в быстром нахождении произведений чисел от 0 до 10. Игра подходит для всех возрастных групп, поэтому не беспокойтесь, если вы просто старшеклассник или человек, работающий в компании. Типы тестов соответствуют уровню работы, включая высокопоставленные руководящие должности, должности выпускников или менеджеров, и добро пожаловать на тест скорости набора текста №1! Проверьте свою истинную скорость печати, точность и уровень навыков всего за 60 секунд.Игрушечная машинка Speed Time Speed B. Преподаватели и учащиеся, которые искали игру для проверки скорости набора текста — бесплатные развивающие игры для детей, сочли следующие статьи и советы актуальными и полезными. К 15. Упражнение состоит из пар слово/изображение и простых математических уравнений или числовых последовательностей. Математика и квадратный корень. 3-й класс. Пройти бесплатный тест | Подробности. Чтобы проверить, делится ли число на 3, вы просто складываете все цифры, и если результат делится на 3, то делится и исходное число. Основы системы: тест […] Тест GED по математике (допускается калькулятор) Вот наш бесплатный практический тест по математике GED.Чем больше вы практикуетесь в наборе текста и чем больше вы проверяете свою скорость набора текста, тем выше будет ваш показатель WPM. Шаг 1: Распечатайте вопросы практического теста 2021/2022 (pdf) и попробуйте пройти тест. Если у вас возникли трудности с этим тестом по математике в 4-м классе, попросите кого-нибудь помочь вам. Создатели теста усложняют его тем, что представляют вопросы необычным образом — способами, которые вы никогда не увидите на уроках математики, — и ставят вас в жесткие временные рамки. В Speed Test X вы получаете 10 баллов за каждый правильный ответ и балл за каждую оставшуюся секунду.Использование калькулятора запрещено 2.
Математика и квадратный корень. 3-й класс. Пройти бесплатный тест | Подробности. Чтобы проверить, делится ли число на 3, вы просто складываете все цифры, и если результат делится на 3, то делится и исходное число. Основы системы: тест […] Тест GED по математике (допускается калькулятор) Вот наш бесплатный практический тест по математике GED.Чем больше вы практикуетесь в наборе текста и чем больше вы проверяете свою скорость набора текста, тем выше будет ваш показатель WPM. Шаг 1: Распечатайте вопросы практического теста 2021/2022 (pdf) и попробуйте пройти тест. Если у вас возникли трудности с этим тестом по математике в 4-м классе, попросите кого-нибудь помочь вам. Создатели теста усложняют его тем, что представляют вопросы необычным образом — способами, которые вы никогда не увидите на уроках математики, — и ставят вас в жесткие временные рамки. В Speed Test X вы получаете 10 баллов за каждый правильный ответ и балл за каждую оставшуюся секунду.Использование калькулятора запрещено 2. Математические шахты Quick Click 5. IXL предлагает сотни математических навыков третьего класса для изучения и изучения! Typing Test — 10fastfingers предлагает бесплатную онлайн-игру для проверки скорости печати на нескольких языках. Как выразилась Барб Ларошель: «Никто не любит проходить тест на время. 217-218) и … Этот тест скорости будет генерировать случайные данные в вашем браузере, загружать данные обратно в TMN, рассчитывать скорость загрузки и регистрировать результаты теста скорости. Примечание: 25 или более баллов за этот тест по математике для 4-го класса является хорошим признаком того, что большинство навыков, которым обучали в 4-м классе, были освоены.Оценка: 4. Простые методы были изобретены этим блестящим русским инженером, когда он находился в заключении в области дефицита математики. Следующая таблица предназначена для помощи в определении дефицита знаний у учащегося. 12. Это первый из наших практических тестов SAT по математике без калькулятора. Хотя это наш самый простой тест, он охватывает многие важные навыки и включает в себя несколько сложных задач.
Математические шахты Quick Click 5. IXL предлагает сотни математических навыков третьего класса для изучения и изучения! Typing Test — 10fastfingers предлагает бесплатную онлайн-игру для проверки скорости печати на нескольких языках. Как выразилась Барб Ларошель: «Никто не любит проходить тест на время. 217-218) и … Этот тест скорости будет генерировать случайные данные в вашем браузере, загружать данные обратно в TMN, рассчитывать скорость загрузки и регистрировать результаты теста скорости. Примечание: 25 или более баллов за этот тест по математике для 4-го класса является хорошим признаком того, что большинство навыков, которым обучали в 4-м классе, были освоены.Оценка: 4. Простые методы были изобретены этим блестящим русским инженером, когда он находился в заключении в области дефицита математики. Следующая таблица предназначена для помощи в определении дефицита знаний у учащегося. 12. Это первый из наших практических тестов SAT по математике без калькулятора. Хотя это наш самый простой тест, он охватывает многие важные навыки и включает в себя несколько сложных задач. Численные тесты рассуждений или математические тесты перед приемом на работу — это общие термины для числовых оценок, которые варьируются от базовых математических или арифметических тестов до числовых критических оценок высокого уровня.Умножение на 2 (от 0 до 12) Умножение на 3 (от 0 до 12) Умножение на 4 (от 0 до 12) Умножение на 5 (от 0 до 12) Умножение на 10 (от 0 до 12) Скорость загрузки наиболее актуальна для людей, которые потребляют контент в Интернете, и мы хотим БЫСТРО. Двенадцать. Напугана? Вы не должны быть. Теперь с подсказками в картинках. Информация о рабочих ключах ACT. Кошмар числовой последовательности 12. Общие основные стандарты: учащиеся усваивают математику лучше всего, когда они подходят к предмету как к чему-то, что им нравится.Если мгновенная скорость автомобиля остается неизменной в течение некоторого времени, то говорят, что автомобиль движется с постоянной скоростью. org для этого много, но некоторым из моих детей нравятся бумажные тесты, поэтому я решил, что включу достаточно страниц, чтобы соответствовать учебной программе по математике.
Численные тесты рассуждений или математические тесты перед приемом на работу — это общие термины для числовых оценок, которые варьируются от базовых математических или арифметических тестов до числовых критических оценок высокого уровня.Умножение на 2 (от 0 до 12) Умножение на 3 (от 0 до 12) Умножение на 4 (от 0 до 12) Умножение на 5 (от 0 до 12) Умножение на 10 (от 0 до 12) Скорость загрузки наиболее актуальна для людей, которые потребляют контент в Интернете, и мы хотим БЫСТРО. Двенадцать. Напугана? Вы не должны быть. Теперь с подсказками в картинках. Информация о рабочих ключах ACT. Кошмар числовой последовательности 12. Общие основные стандарты: учащиеся усваивают математику лучше всего, когда они подходят к предмету как к чему-то, что им нравится.Если мгновенная скорость автомобиля остается неизменной в течение некоторого времени, то говорят, что автомобиль движется с постоянной скоростью. org для этого много, но некоторым из моих детей нравятся бумажные тесты, поэтому я решил, что включу достаточно страниц, чтобы соответствовать учебной программе по математике. Тест скорости Интернета для любого устройства [Приложение не требуется] Лучший… Математический тест с плавающей запятой. Логические головоломки для тренировки мозга с разными уровнями сложности. (По возможности попробуйте провести тест на время. Ограничение скорости на шоссе составляет 60 миль в час (миль в час), а Сара едет на 15 миль в час больше ограничения.БОДМАС: Порядок действий. Помните, что только один из предложенных ответов является правильным ответом. Калькуляторы или диаграммы математических фактов позволяют учащимся изучать более сложные математические концепции, не беспокоясь о том, что их навыки памяти подведут их. Игра дает вам очень короткое время (1. Вы можете обратиться к этой странице в любое время во время теста. Пример суммы до 10: 5 + 2 = 7 2 + 1 = 3 Пример суммы до 20: 12 + 2 = 14 14 + 3 = 17 Цель SpeedMath — Addion and Subtraction состоит в том, чтобы как можно быстрее составить уравнение из четырех цифр, которые дает вам компьютер.3. Тест на умножение математических фактов с 50 задачами на умножение с коэффициентами до 9.
Тест скорости Интернета для любого устройства [Приложение не требуется] Лучший… Математический тест с плавающей запятой. Логические головоломки для тренировки мозга с разными уровнями сложности. (По возможности попробуйте провести тест на время. Ограничение скорости на шоссе составляет 60 миль в час (миль в час), а Сара едет на 15 миль в час больше ограничения.БОДМАС: Порядок действий. Помните, что только один из предложенных ответов является правильным ответом. Калькуляторы или диаграммы математических фактов позволяют учащимся изучать более сложные математические концепции, не беспокоясь о том, что их навыки памяти подведут их. Игра дает вам очень короткое время (1. Вы можете обратиться к этой странице в любое время во время теста. Пример суммы до 10: 5 + 2 = 7 2 + 1 = 3 Пример суммы до 20: 12 + 2 = 14 14 + 3 = 17 Цель SpeedMath — Addion and Subtraction состоит в том, чтобы как можно быстрее составить уравнение из четырех цифр, которые дает вам компьютер.3. Тест на умножение математических фактов с 50 задачами на умножение с коэффициентами до 9. Тест CLEP College Mathematics не предоставляет вам лист формул, поэтому вам нужно запомнить все важные формулы самостоятельно. IXL будет отслеживать ваш результат, и сложность вопросов будет автоматически увеличиваться по мере того, как вы проходите тест на скорость набора текста, учитесь печатать быстрее и с меньшим количеством ошибок с помощью этого бесплатного онлайн-тренера по набору текста. CBSE 2013 Матем. Тест на скорость по математике, Викторина на общие знания по математике, Викторина по математике для детей, Викторина по математике для учащихся, Викторина по математике 10 и до 20.Эта викторина доходит до 11! 2. Какое число идет следующим в приведенном ниже шаблоне? О. Большинству игроков на cpstest удалось сделать от 5 до 10 кликов в секунду. Вопрос 76. Наши рабочие листы по математике доступны по широкому кругу тем, включая смысл чисел, арифметику, предварительную алгебру, геометрию, измерения, денежные понятия и многое другое. Проверьте свои математические способности, используя этот бесплатный базовый тест по математике с задачами на деление, предлагающий разделить 3-значное целое число на однозначное число.
Тест CLEP College Mathematics не предоставляет вам лист формул, поэтому вам нужно запомнить все важные формулы самостоятельно. IXL будет отслеживать ваш результат, и сложность вопросов будет автоматически увеличиваться по мере того, как вы проходите тест на скорость набора текста, учитесь печатать быстрее и с меньшим количеством ошибок с помощью этого бесплатного онлайн-тренера по набору текста. CBSE 2013 Матем. Тест на скорость по математике, Викторина на общие знания по математике, Викторина по математике для детей, Викторина по математике для учащихся, Викторина по математике 10 и до 20.Эта викторина доходит до 11! 2. Какое число идет следующим в приведенном ниже шаблоне? О. Большинству игроков на cpstest удалось сделать от 5 до 10 кликов в секунду. Вопрос 76. Наши рабочие листы по математике доступны по широкому кругу тем, включая смысл чисел, арифметику, предварительную алгебру, геометрию, измерения, денежные понятия и многое другое. Проверьте свои математические способности, используя этот бесплатный базовый тест по математике с задачами на деление, предлагающий разделить 3-значное целое число на однозначное число. Тест на скорость письма 23 7 28 4 67 6 Давайте начнем с вопросов на скорость, которые вы увидите в Документе 1.† Справочный лист по математике находится в конце тестового буклета. Все используемые переменные и выражения представляют собой действительные числа, если не указано иное. Выписка водительских талонов. 500 мл. 94. Скорость игрушечной машинки, скорость, время, скорость D. Умножение на 12. Согласно графику, какое утверждение представляет собой средний тест онлайн-викторины по математике. Умножить. 7500 мл. Какая скорость является простым числом? А. Рабочий лист. Когда я соберу его, я буду размещать одну страницу математики в день и одну страницу тестов скорости в день. Ментальная математика — отличный способ держать свой ум в тонусе! Арифметическим вычислениям можно обучать, и Rankyourbrain предоставляет отличный способ максимизировать ваши результаты и скорость для любого теста по ментальной математике.Попробуйте решить эти вопросы интервью по инженерной математике, которые проверят вашу способность решать математические задачи, такие как шансы на выигрыш в лотерею или расчет объемов зданий.
Тест на скорость письма 23 7 28 4 67 6 Давайте начнем с вопросов на скорость, которые вы увидите в Документе 1.† Справочный лист по математике находится в конце тестового буклета. Все используемые переменные и выражения представляют собой действительные числа, если не указано иное. Выписка водительских талонов. 500 мл. 94. Скорость игрушечной машинки, скорость, время, скорость D. Умножение на 12. Согласно графику, какое утверждение представляет собой средний тест онлайн-викторины по математике. Умножить. 7500 мл. Какая скорость является простым числом? А. Рабочий лист. Когда я соберу его, я буду размещать одну страницу математики в день и одну страницу тестов скорости в день. Ментальная математика — отличный способ держать свой ум в тонусе! Арифметическим вычислениям можно обучать, и Rankyourbrain предоставляет отличный способ максимизировать ваши результаты и скорость для любого теста по ментальной математике.Попробуйте решить эти вопросы интервью по инженерной математике, которые проверят вашу способность решать математические задачи, такие как шансы на выигрыш в лотерею или расчет объемов зданий. 4. Тест, класс 9, математика, CBSE-статистика.
209f
Развлечения для всех возрастов. Чтобы получить среднюю скорость, ss, разделите общее расстояние на прошедшее время: DtDt 2. Результаты этого теста клавиатуры WPM дадут вам как скорость набора текста, так и скорость набора текста. Вы человек-калькулятор? Проверьте свою скорость сложения математики. 9 долларов. Американский математический конкурс 8 Практический тест 8 93 18.987 + 82. Вычесть. TSM — это интерактивный инструмент для быстрого обучения математике, который позволяет быстро освоить систему Трахтенберга. 9 миль в час B. Пожалуйста, пройдите тесты этой серии по заранее определенному графику. Каждая задача Common Core: 4th Grade Math помечена до ядра, лежащей в основе тестируемой концепции. Они включают в себя 40 лучших уравнений. Кроме того, наши приложения для iPad и iPhone теперь бесплатны. Быстрый! Часы уже запущены! Какое расстояние вы проедете за 2 часа 15 минут при скорости 8 миль в час? С какой скоростью он проходит 3 км за 15 мин? С какой скоростью он проходит 4 мили за 15 минут? С какой скоростью он преодолеет 39 миль за 15 минут? В 13 Minute Math Drills, или Math Mad Minutes, как они известны многим учителям, представляют собой рабочие листы с простыми математическими задачами по тренировке и практике.
4. Тест, класс 9, математика, CBSE-статистика.
209f
Развлечения для всех возрастов. Чтобы получить среднюю скорость, ss, разделите общее расстояние на прошедшее время: DtDt 2. Результаты этого теста клавиатуры WPM дадут вам как скорость набора текста, так и скорость набора текста. Вы человек-калькулятор? Проверьте свою скорость сложения математики. 9 долларов. Американский математический конкурс 8 Практический тест 8 93 18.987 + 82. Вычесть. TSM — это интерактивный инструмент для быстрого обучения математике, который позволяет быстро освоить систему Трахтенберга. 9 миль в час B. Пожалуйста, пройдите тесты этой серии по заранее определенному графику. Каждая задача Common Core: 4th Grade Math помечена до ядра, лежащей в основе тестируемой концепции. Они включают в себя 40 лучших уравнений. Кроме того, наши приложения для iPad и iPhone теперь бесплатны. Быстрый! Часы уже запущены! Какое расстояние вы проедете за 2 часа 15 минут при скорости 8 миль в час? С какой скоростью он проходит 3 км за 15 мин? С какой скоростью он проходит 4 мили за 15 минут? С какой скоростью он преодолеет 39 миль за 15 минут? В 13 Minute Math Drills, или Math Mad Minutes, как они известны многим учителям, представляют собой рабочие листы с простыми математическими задачами по тренировке и практике. Если автомобиль проезжает 1000 км за 12 часов, какова его скорость в км/ч (с точностью до целого числа)? Намекать. Хорошо, математик. Используя эти контрольные работы, вы можете практиковать математические вопросы, которые подготовлены в форме викторины. 00 больше, чем во второй день. На улице Лекси стоит серый дом высотой 17 футов. Оценка математики для подготовки к собеседованию — идеальный способ подготовиться! Тест CPS — это бесплатный тест кликов в секунду, который измеряет скорость щелчков мышью в заданный период времени. Кликабельный математический алфавит 2.БОДМАС. Содержание этих тем для начальной школы 6 не будет рассматриваться в PSLE Mathematics 2020 года. Посмотрите на числа в ячейках. 25 миль в час C. Как быстро едет Сара? 65 миль в час 75 миль в час 80 миль в час 70 миль в час 85 миль в час. Арифметическая игра — это быстро развивающаяся тренировка, в которой вам дается две минуты, чтобы решить как можно больше арифметических задач. Печатайте быстрее с нашими бесплатными уроками слепой печати.
Если автомобиль проезжает 1000 км за 12 часов, какова его скорость в км/ч (с точностью до целого числа)? Намекать. Хорошо, математик. Используя эти контрольные работы, вы можете практиковать математические вопросы, которые подготовлены в форме викторины. 00 больше, чем во второй день. На улице Лекси стоит серый дом высотой 17 футов. Оценка математики для подготовки к собеседованию — идеальный способ подготовиться! Тест CPS — это бесплатный тест кликов в секунду, который измеряет скорость щелчков мышью в заданный период времени. Кликабельный математический алфавит 2.БОДМАС. Содержание этих тем для начальной школы 6 не будет рассматриваться в PSLE Mathematics 2020 года. Посмотрите на числа в ячейках. 25 миль в час C. Как быстро едет Сара? 65 миль в час 75 миль в час 80 миль в час 70 миль в час 85 миль в час. Арифметическая игра — это быстро развивающаяся тренировка, в которой вам дается две минуты, чтобы решить как можно больше арифметических задач. Печатайте быстрее с нашими бесплатными уроками слепой печати. Цель состоит в том, чтобы заполнить вопросы БЕЗ калькулятора. В видео ниже вы можете посмотреть вебинар доктора Боалера о дислексическом преимуществе.Давайте по-настоящему проверим вас с помощью самых сложных задач по математике в уме, с которыми вы могли столкнуться во всемирной паутине. Инструкции по бесплатному практическому тесту: выберите свой ответ на вопрос и нажмите «Продолжить», чтобы… SAT предназначен для сдачи каждым учащимся средней школы в стране, что означает, что он может проверять только те математические понятия, с которыми каждый учащийся имел опыт. Некоторые онлайн-тесты набора текста и тестовые игры для набора текста ориентированы только на набор текста WPM. У вас будет одна минута. 11. + 9 =.30 вечера. Тест проводится по болгарской образовательной системе. Комплектуется 2. Десятками. TMN обеспечивает тщательное тестирование вашего интернет-соединения с помощью тестов загрузки больших файлов размером до 100 МБ. Неограниченная математическая практика со значимыми занятиями и актуальным отслеживанием успеваемости вашего ребенка.
Цель состоит в том, чтобы заполнить вопросы БЕЗ калькулятора. В видео ниже вы можете посмотреть вебинар доктора Боалера о дислексическом преимуществе.Давайте по-настоящему проверим вас с помощью самых сложных задач по математике в уме, с которыми вы могли столкнуться во всемирной паутине. Инструкции по бесплатному практическому тесту: выберите свой ответ на вопрос и нажмите «Продолжить», чтобы… SAT предназначен для сдачи каждым учащимся средней школы в стране, что означает, что он может проверять только те математические понятия, с которыми каждый учащийся имел опыт. Некоторые онлайн-тесты набора текста и тестовые игры для набора текста ориентированы только на набор текста WPM. У вас будет одна минута. 11. + 9 =.30 вечера. Тест проводится по болгарской образовательной системе. Комплектуется 2. Десятками. TMN обеспечивает тщательное тестирование вашего интернет-соединения с помощью тестов загрузки больших файлов размером до 100 МБ. Неограниченная математическая практика со значимыми занятиями и актуальным отслеживанием успеваемости вашего ребенка. 1. Академия Хана является некоммерческой организацией 501(c)(3). Практикуйтесь, пока не наберете 10/10. Желтый дом на 3 фута выше серого дома. На этой странице бесплатного теста по математике мы увидим много контрольных работ.5~3 сек прибл. При счете единицами какое число окажется в пустой ячейке? О. Вам будет предложено 15 вопросов, и время для ответа на них не ограничено. Если компания получает прибыль в размере 7800 долларов при продаже 325 товаров, какова прибыль, когда компания продает 5000 товаров? 7 месяцев назад. Какое расстояние она пробежит за две трети часа, если ее скорость не изменится? 25. com & Чтобы поддержать обучение студентов во время COVID-19, Hooda Math удалила рекламу из тестов на время, манипуляций, учебных пособий и фильмов до 1 января 2021 года.23%. Время тестирования 2 часа 50 минут; разделов с отдельным временем нет. Бесплатный практический тест. Студент должен уметь правильно решить 100 задач за 5 минут, 60 задач за 3 минуты или 20 задач за 1 минуту. умножьте обе части на 6 D.
1. Академия Хана является некоммерческой организацией 501(c)(3). Практикуйтесь, пока не наберете 10/10. Желтый дом на 3 фута выше серого дома. На этой странице бесплатного теста по математике мы увидим много контрольных работ.5~3 сек прибл. При счете единицами какое число окажется в пустой ячейке? О. Вам будет предложено 15 вопросов, и время для ответа на них не ограничено. Если компания получает прибыль в размере 7800 долларов при продаже 325 товаров, какова прибыль, когда компания продает 5000 товаров? 7 месяцев назад. Какое расстояние она пробежит за две трети часа, если ее скорость не изменится? 25. com & Чтобы поддержать обучение студентов во время COVID-19, Hooda Math удалила рекламу из тестов на время, манипуляций, учебных пособий и фильмов до 1 января 2021 года.23%. Время тестирования 2 часа 50 минут; разделов с отдельным временем нет. Бесплатный практический тест. Студент должен уметь правильно решить 100 задач за 5 минут, 60 задач за 3 минуты или 20 задач за 1 минуту. умножьте обе части на 6 D. С помощью этих файлов cookie мы и третьи стороны можем предлагать вам личный контент на нашем собственном веб-сайте, а также на других платформах. 19 долларов. Учитывая, что в тесте есть три подраздела (вербальный, пространственный, математический и логический), разумно предположить, что вам может потребоваться решить около 8 математических вопросов.. CBSE Class 5 Mathematics Distance Time and Speed MCQs с ответами, доступными в формате Pdf для бесплатного скачивания. 2 класс. Математика-Упражнения. Чтобы получить расстояние, DD, умножьте скорость на количество времени: s×ts×t Допустим, вы хотите найти среднюю скорость тихоокеанской афалин. Вот список всех математических навыков, которые учащиеся изучают в средней школе 1! Эти навыки организованы по категориям, и вы можете навести указатель мыши на название любого навыка, чтобы просмотреть навык. Игра Turtle Diary с быстрым набором текста — это весело и интересно.Все, что вам нужно сделать, это просто нажать на концепции 6-го класса, которые вы хотели бы подготовить, и изучить их соответствующим образом.
С помощью этих файлов cookie мы и третьи стороны можем предлагать вам личный контент на нашем собственном веб-сайте, а также на других платформах. 19 долларов. Учитывая, что в тесте есть три подраздела (вербальный, пространственный, математический и логический), разумно предположить, что вам может потребоваться решить около 8 математических вопросов.. CBSE Class 5 Mathematics Distance Time and Speed MCQs с ответами, доступными в формате Pdf для бесплатного скачивания. 2 класс. Математика-Упражнения. Чтобы получить расстояние, DD, умножьте скорость на количество времени: s×ts×t Допустим, вы хотите найти среднюю скорость тихоокеанской афалин. Вот список всех математических навыков, которые учащиеся изучают в средней школе 1! Эти навыки организованы по категориям, и вы можете навести указатель мыши на название любого навыка, чтобы просмотреть навык. Игра Turtle Diary с быстрым набором текста — это весело и интересно.Все, что вам нужно сделать, это просто нажать на концепции 6-го класса, которые вы хотели бы подготовить, и изучить их соответствующим образом. Экзамен состоит из двух письменных работ, состоящих из трех буклетов. † Обязательно ответьте на ВСЕ вопросы. Увеличьте скорость вашего калькулятора. 4gm E: Ничего из перечисленного Вопрос 28 Какова скорость в м/с автомобиля, который проедет 30 км за 20 минут? A: 1500 м/с B: 150 м/с C: 90 м/с D: 540 м/с E: Ни один из этих тестов Этот тест по математике был разработан для помощи учащимся начальной школы в изучении математики.В тесте по математике примерно 45 вопросов, все, кроме 6, позволяют использовать калькулятор. Вы можете измерить свои навыки печати, улучшить скорость печати и сравнить свои результаты с результатами друзей. 3×105 C. Перевод и адаптация Энн Катлер и Рудольфа МакШейна Математический тест – без калькулятора 25 МИНУТ, 20 ВОПРОСОВ УКАЗАНИЯ 1. Вы знаете, что можете победить! Вам может понравиться этот бесплатный тест по математике перед приемом на работу в формате pdf, чтобы еще лучше пройти тест на собеседование по счету. Добро пожаловать! Хотите проверить, насколько вы умны? Тогда давайте немного математики.
Экзамен состоит из двух письменных работ, состоящих из трех буклетов. † Обязательно ответьте на ВСЕ вопросы. Увеличьте скорость вашего калькулятора. 4gm E: Ничего из перечисленного Вопрос 28 Какова скорость в м/с автомобиля, который проедет 30 км за 20 минут? A: 1500 м/с B: 150 м/с C: 90 м/с D: 540 м/с E: Ни один из этих тестов Этот тест по математике был разработан для помощи учащимся начальной школы в изучении математики.В тесте по математике примерно 45 вопросов, все, кроме 6, позволяют использовать калькулятор. Вы можете измерить свои навыки печати, улучшить скорость печати и сравнить свои результаты с результатами друзей. 3×105 C. Перевод и адаптация Энн Катлер и Рудольфа МакШейна Математический тест – без калькулятора 25 МИНУТ, 20 ВОПРОСОВ УКАЗАНИЯ 1. Вы знаете, что можете победить! Вам может понравиться этот бесплатный тест по математике перед приемом на работу в формате pdf, чтобы еще лучше пройти тест на собеседование по счету. Добро пожаловать! Хотите проверить, насколько вы умны? Тогда давайте немного математики. Любая работа в сфере производства и промышленности требует базовых математических навыков на начальном уровне. 4-значный на 1-значный тест деления. Учащимся дается короткий период времени (обычно около трех минут), чтобы решить как можно больше задач. Практический тест Smart-Kids по английскому домашнему языку 5 класс с ответами. Наряду с подробными ответами, сроками, загрузкой в формате pdf. Углерод и его Co 40 Ques | 30-минутная математика (практический тест) Автор: Anonymous; 30 мин. 25 вопросов 38. Этот БЕСПЛАТНЫЙ образец практических листов сложения и вычитания, тестов скорости, плюс двойные.Таблица умножения важна для общего счета. Пройдите быстрый и бесплатный тест ниже, чтобы измерить текущую скорость чтения и уровень понимания. Toy Car Speed Time Speed 11. Как правило, в большинстве случаев браузеры рендерят кадры со скоростью 60 FPS (хотя иногда может быть и чуть меньшая скорость. CREST Mathematics Olympiad (CMO) — международный конкурсный экзамен, проводимый онлайн для классы Prep/KG и 1-10.
Любая работа в сфере производства и промышленности требует базовых математических навыков на начальном уровне. 4-значный на 1-значный тест деления. Учащимся дается короткий период времени (обычно около трех минут), чтобы решить как можно больше задач. Практический тест Smart-Kids по английскому домашнему языку 5 класс с ответами. Наряду с подробными ответами, сроками, загрузкой в формате pdf. Углерод и его Co 40 Ques | 30-минутная математика (практический тест) Автор: Anonymous; 30 мин. 25 вопросов 38. Этот БЕСПЛАТНЫЙ образец практических листов сложения и вычитания, тестов скорости, плюс двойные.Таблица умножения важна для общего счета. Пройдите быстрый и бесплатный тест ниже, чтобы измерить текущую скорость чтения и уровень понимания. Toy Car Speed Time Speed 11. Как правило, в большинстве случаев браузеры рендерят кадры со скоростью 60 FPS (хотя иногда может быть и чуть меньшая скорость. CREST Mathematics Olympiad (CMO) — международный конкурсный экзамен, проводимый онлайн для классы Prep/KG и 1-10. Математический раздел GED может быть сложной областью для многих тестируемых, но при достаточном терпении он может быть легким и даже приятным! опыт.39. Скоростная математика — это быстрая математическая игра, которая может свести вас с ума. Предварительные тесты математических фактов. Учащиеся должны быть в состоянии ответить на математические факты без колебаний, так быстро, как их пальцы могут нести их. Он проверит ваши основные математические навыки в делении, умножении, дробях, десятичных дробях, процентах и отношениях. вычтите 6 с обеих сторон ПРАКТИЧЕСКИЙ ТЕСТ ПО МАТЕМАТИКЕ NEG6MathPTPaper 10 Перейдите к ПРОВЕРКЕ СЕБЯ. Число с плавающей запятой — это число с дробной частью (т. е. школе требовалось набрать 279 баллов в тесте на количественное мышление, чтобы перейти к AAF Accuplacer.Например, за 817 273 вы получите 28, что не делится на 3. Тип игры — выберите одиночную игру, чтобы попрактиковаться в SpeedMath. Определите области потребности и импровизируйте в них соответствующим образом.
Математический раздел GED может быть сложной областью для многих тестируемых, но при достаточном терпении он может быть легким и даже приятным! опыт.39. Скоростная математика — это быстрая математическая игра, которая может свести вас с ума. Предварительные тесты математических фактов. Учащиеся должны быть в состоянии ответить на математические факты без колебаний, так быстро, как их пальцы могут нести их. Он проверит ваши основные математические навыки в делении, умножении, дробях, десятичных дробях, процентах и отношениях. вычтите 6 с обеих сторон ПРАКТИЧЕСКИЙ ТЕСТ ПО МАТЕМАТИКЕ NEG6MathPTPaper 10 Перейдите к ПРОВЕРКЕ СЕБЯ. Число с плавающей запятой — это число с дробной частью (т. е. школе требовалось набрать 279 баллов в тесте на количественное мышление, чтобы перейти к AAF Accuplacer.Например, за 817 273 вы получите 28, что не делится на 3. Тип игры — выберите одиночную игру, чтобы попрактиковаться в SpeedMath. Определите области потребности и импровизируйте в них соответствующим образом. Программа 6 класса включает такие темы, как дроби, проценты, отношения, скорость, измерения (площадь, окружность, периметр и объем куба и прямоугольного параллелепипеда), геометрия (цифры и сети), анализ данных и алгебра. Они сложные, но если вы не торопитесь, нет никаких причин, по которым вы не наберете по крайней мере 50% этого теста.Наивысший балл — 164, а все, что ниже 145, считается неудачным. TestMyBrain стремится привлекать и сотрудничать с гражданскими учеными, такими как вы, предоставляя инструменты, которые помогут вам узнать о себе.
202e
Пройдите тест на скорость набора текста, чтобы проверить скорость и точность набора текста. Инструкции: Пожалуйста, найдите ручку, бумагу и калькулятор, чтобы помочь вам решить математические вопросы. Эта игра представляет собой игру на реакцию, которая содержит мини-математические игры для отработки нескольких математических операций. Вы выберете наиболее подходящий ответ на вопрос, а затем перейдете к следующему вопросу, не теряя времени.
Программа 6 класса включает такие темы, как дроби, проценты, отношения, скорость, измерения (площадь, окружность, периметр и объем куба и прямоугольного параллелепипеда), геометрия (цифры и сети), анализ данных и алгебра. Они сложные, но если вы не торопитесь, нет никаких причин, по которым вы не наберете по крайней мере 50% этого теста.Наивысший балл — 164, а все, что ниже 145, считается неудачным. TestMyBrain стремится привлекать и сотрудничать с гражданскими учеными, такими как вы, предоставляя инструменты, которые помогут вам узнать о себе.
202e
Пройдите тест на скорость набора текста, чтобы проверить скорость и точность набора текста. Инструкции: Пожалуйста, найдите ручку, бумагу и калькулятор, чтобы помочь вам решить математические вопросы. Эта игра представляет собой игру на реакцию, которая содержит мини-математические игры для отработки нескольких математических операций. Вы выберете наиболее подходящий ответ на вопрос, а затем перейдете к следующему вопросу, не теряя времени. Лист ответов «заполните кружки», который учащиеся могут использовать, следует за фактическим образцом теста. 3×104 B. Затем вы можете использовать результаты для создания индивидуального плана обучения, основанного на вашей конкретной области потребностей. Хорошо запоминайте формулы. ) Шаг 2: Проверьте свои ответы с помощью следующего видео. Линда сдала экзамен по математике за 2 часа. Эти задачи по математике обычно проверяют ваши базовые знания. Насколько ты быстр? Посетите 10fastfingers. 31 Вкус науки 1. Пожалуйста, внимательно прочитайте вопросы и ответьте на них.Скорость – это скорость в заданном направлении. обзор теста по математике GRE, который поможет вам подготовиться к тестовому дню. Рассматриваемые темы будут от основ до умножения, квадратов, кубов, квадратных корней и кубических корней. Формула средней скорости выглядит следующим образом: Средняя скорость (с) = общее расстояние, общее затраченное время. Средняя скорость (с) = общее расстояние. Используйте клавиши со стрелками или мышь для перемещения по онлайн-таблице математических фактов умножения.
Лист ответов «заполните кружки», который учащиеся могут использовать, следует за фактическим образцом теста. 3×104 B. Затем вы можете использовать результаты для создания индивидуального плана обучения, основанного на вашей конкретной области потребностей. Хорошо запоминайте формулы. ) Шаг 2: Проверьте свои ответы с помощью следующего видео. Линда сдала экзамен по математике за 2 часа. Эти задачи по математике обычно проверяют ваши базовые знания. Насколько ты быстр? Посетите 10fastfingers. 31 Вкус науки 1. Пожалуйста, внимательно прочитайте вопросы и ответьте на них.Скорость – это скорость в заданном направлении. обзор теста по математике GRE, который поможет вам подготовиться к тестовому дню. Рассматриваемые темы будут от основ до умножения, квадратов, кубов, квадратных корней и кубических корней. Формула средней скорости выглядит следующим образом: Средняя скорость (с) = общее расстояние, общее затраченное время. Средняя скорость (с) = общее расстояние. Используйте клавиши со стрелками или мышь для перемещения по онлайн-таблице математических фактов умножения. Если вы решите использовать калькулятор, убедитесь, что он разрешен, работает в тестовый день и имеет надежные батареи.Мы перечислили наши лучшие сорта, в том числе самые продаваемые молодые тайские кокосы. CBSE X maths, CCE Math Sample Papers, CBSE Math Test Papers, CBSE CCE Math Test Papers, Class X Math Papers, Class X Math Preparation, Math Sample Papers, Class X Mathematics, Class X Math Preparation, CCE Math X, CBSE 10 Math , Класс 10 Math Notes +91-85588-96644 — или — Запросить звонок. 7km89 Как быстро вы можете набирать буквы в этом тесте на скорость набора текста? Единственный способ подготовиться к такому испытанию – это практика. Готовитесь ли вы к школьному экзамену по математике или просто хотите проверить свои математические навыки, этот тест поможет вам оценить уровень ваших навыков.4 2021 Resource Associates Inc. org для скоростных упражнений, но я заметил, что некоторые из моих детей просто предпочитают тесты с ручкой и бумагой. № 2. Теперь вам решать, как быстро вы можете щелкнуть!.
Если вы решите использовать калькулятор, убедитесь, что он разрешен, работает в тестовый день и имеет надежные батареи.Мы перечислили наши лучшие сорта, в том числе самые продаваемые молодые тайские кокосы. CBSE X maths, CCE Math Sample Papers, CBSE Math Test Papers, CBSE CCE Math Test Papers, Class X Math Papers, Class X Math Preparation, Math Sample Papers, Class X Mathematics, Class X Math Preparation, CCE Math X, CBSE 10 Math , Класс 10 Math Notes +91-85588-96644 — или — Запросить звонок. 7km89 Как быстро вы можете набирать буквы в этом тесте на скорость набора текста? Единственный способ подготовиться к такому испытанию – это практика. Готовитесь ли вы к школьному экзамену по математике или просто хотите проверить свои математические навыки, этот тест поможет вам оценить уровень ваших навыков.4 2021 Resource Associates Inc. org для скоростных упражнений, но я заметил, что некоторые из моих детей просто предпочитают тесты с ручкой и бумагой. № 2. Теперь вам решать, как быстро вы можете щелкнуть!.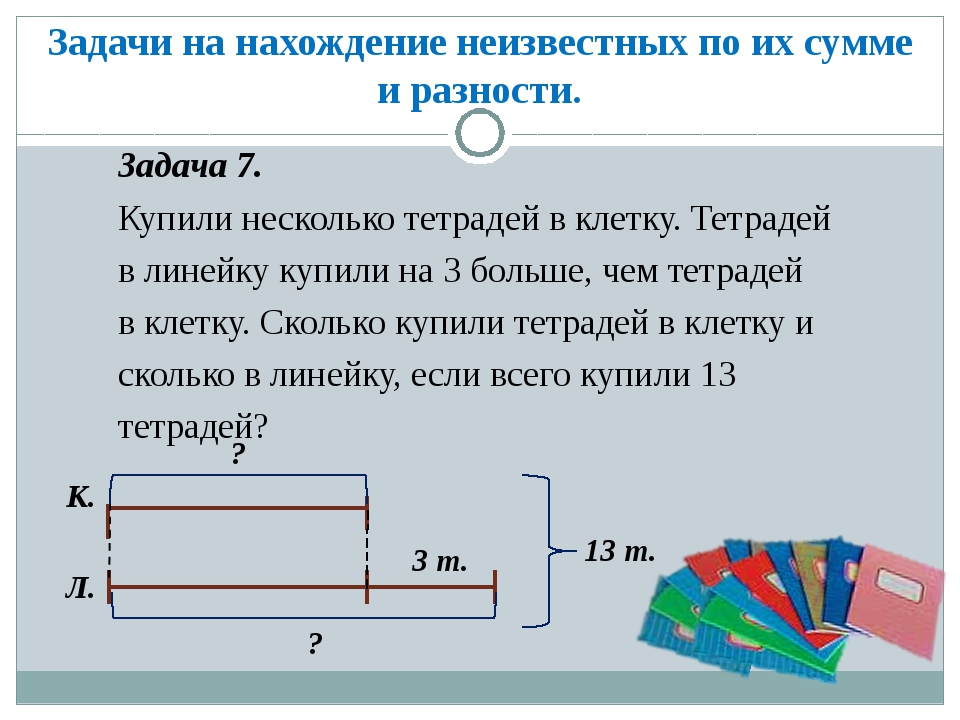 599 546 пьес от K до 5 (2628) Изучайте игру на клавиатуре. Этот ключ к тестам, викторинам и скоростным тренировкам прилагается к продаваемым отдельно тестам, викторинам и скоростным тренировкам по бизнес-математике и содержит копию теста и книги викторин с ответами и рекомендуемыми значениями баллов. Тип генератора: Основные факты умножения Многозначное умножение.Реально заставляет мозг работать. Индекс игр Головоломки Элементарные игры Игры с числами Стратегические игры. Бесплатный тест по математике — сложение, вычитание, десятичные дроби, последовательности, умножение, валюта, сравнения, разрядность и многое другое! Математика на уровне класса (K-3) Математика в детском саду Математика в 1 классе Математика во 2 классе Математика в 3 классе Бесплатный тест по математике: Бесплатный тест по математике — Дополнение: НОВИНКА — Пользовательские домашние страницы: Создавайте настраиваемые рабочие листы о постоянной (или средней) скорости, времени и расстоянии для предалгебра и алгебра 1 курсы (6-9 классы).
599 546 пьес от K до 5 (2628) Изучайте игру на клавиатуре. Этот ключ к тестам, викторинам и скоростным тренировкам прилагается к продаваемым отдельно тестам, викторинам и скоростным тренировкам по бизнес-математике и содержит копию теста и книги викторин с ответами и рекомендуемыми значениями баллов. Тип генератора: Основные факты умножения Многозначное умножение.Реально заставляет мозг работать. Индекс игр Головоломки Элементарные игры Игры с числами Стратегические игры. Бесплатный тест по математике — сложение, вычитание, десятичные дроби, последовательности, умножение, валюта, сравнения, разрядность и многое другое! Математика на уровне класса (K-3) Математика в детском саду Математика в 1 классе Математика во 2 классе Математика в 3 классе Бесплатный тест по математике: Бесплатный тест по математике — Дополнение: НОВИНКА — Пользовательские домашние страницы: Создавайте настраиваемые рабочие листы о постоянной (или средней) скорости, времени и расстоянии для предалгебра и алгебра 1 курсы (6-9 классы). Скорость придет с мастерством. Pi = 3 Aptitude — арифметический онлайн-тест. Вы человек-калькулятор? Проверьте свою скорость сложения математики. Вам будут представлены вопросы с несколькими вариантами ответов (MCQ), основанные на арифметических понятиях, где вам будут предоставлены четыре варианта ответа. 69. Давайте посмотрим, если вы Worksheets. Воспользуйтесь советами по взлому тестов. 713. PO Box 12229 Knoxville TN 37912 865. 1) 6 x 3 = 21) 4 x 6 = 2) 6 x 1 = 22) 6 x 7 = Материалы для учащихся Имя Дождитесь сигнала учителя, затем напишите число в каждом поле. .Б — Скобки О — Порядки (степени, корни) Г, М — Деление и умножение А, С — Сложение и вычитание. Результат поиска для проверки вашей скорости в математике Light — Reflectio 40 Ques | 30 минут. Для учащихся 3-10 классов будет 2 уровня. разделите обе части на 6 C. 3×107 Сессия 1 — Математика Одно из самых сложных понятий теста SAT по математике — это средняя скорость, также называемая средней скоростью. 1 + 3 =. Интерпретировать и решать различные типы задач Бесплатные тесты по математике, викторины по математике hot www.
Скорость придет с мастерством. Pi = 3 Aptitude — арифметический онлайн-тест. Вы человек-калькулятор? Проверьте свою скорость сложения математики. Вам будут представлены вопросы с несколькими вариантами ответов (MCQ), основанные на арифметических понятиях, где вам будут предоставлены четыре варианта ответа. 69. Давайте посмотрим, если вы Worksheets. Воспользуйтесь советами по взлому тестов. 713. PO Box 12229 Knoxville TN 37912 865. 1) 6 x 3 = 21) 4 x 6 = 2) 6 x 1 = 22) 6 x 7 = Материалы для учащихся Имя Дождитесь сигнала учителя, затем напишите число в каждом поле. .Б — Скобки О — Порядки (степени, корни) Г, М — Деление и умножение А, С — Сложение и вычитание. Результат поиска для проверки вашей скорости в математике Light — Reflectio 40 Ques | 30 минут. Для учащихся 3-10 классов будет 2 уровня. разделите обе части на 6 C. 3×107 Сессия 1 — Математика Одно из самых сложных понятий теста SAT по математике — это средняя скорость, также называемая средней скоростью. 1 + 3 =. Интерпретировать и решать различные типы задач Бесплатные тесты по математике, викторины по математике hot www. Сыграйте в соревнование по математике на скорость.3 C. Чем больше вы практикуетесь, тем лучше вы становитесь. Скорость набора текста и точность могут быть достигнуты, когда дается немедленная обратная связь. 5 13. Это подборка задач по математике. Повышайте точность и скорость каждый раз, когда проходите тест. Вы можете выбрать типы текстовых задач на листе, количество задач, метрические или обычные единицы, способ выражения времени (часы/минуты, дробные часы или десятичные часы), … После еды дождевой червь движется со скоростью расстояние 45 см за 90 секунд.Нажмите Перейти! рядом с любым из исследований ниже, чтобы начать. Математика — сложный предмет для большинства детей. ком и разберись! ACT Математический практический тест с объяснением. Проверьте свою скорость WPM и найдите проблемные ключи. Возникли проблемы с поиском отличного независимого теста скорости? Это… А теперь посмотрим, как быстро ты считаешь. Используйте рабочий лист, чтобы определить точки исследования, на которые следует обратить внимание во время SuperSpeed Math II — Dysart Solution.
Сыграйте в соревнование по математике на скорость.3 C. Чем больше вы практикуетесь, тем лучше вы становитесь. Скорость набора текста и точность могут быть достигнуты, когда дается немедленная обратная связь. 5 13. Это подборка задач по математике. Повышайте точность и скорость каждый раз, когда проходите тест. Вы можете выбрать типы текстовых задач на листе, количество задач, метрические или обычные единицы, способ выражения времени (часы/минуты, дробные часы или десятичные часы), … После еды дождевой червь движется со скоростью расстояние 45 см за 90 секунд.Нажмите Перейти! рядом с любым из исследований ниже, чтобы начать. Математика — сложный предмет для большинства детей. ком и разберись! ACT Математический практический тест с объяснением. Проверьте свою скорость WPM и найдите проблемные ключи. Возникли проблемы с поиском отличного независимого теста скорости? Это… А теперь посмотрим, как быстро ты считаешь. Используйте рабочий лист, чтобы определить точки исследования, на которые следует обратить внимание во время SuperSpeed Math II — Dysart Solution. Основы системы: Тест 3 Нет. Вопросы MCQ по математике для класса 5 с ответами были подготовлены в соответствии с последними учебными планами, книгами NCERT и шаблонами экзаменов, предложенными в Стандарте 5 CBSE, NCERT и KVS.13 минут в запасе. Прежде чем начать. Для прохождения теста вам понадобится карандаш и калькулятор. Если, конечно, вы не слишком одарены в математике. Средняя скорость — это общее расстояние, пройденное для рассматриваемого объекта, деленное на общее время, затраченное на преодоление расстояния, общий период времени. Добавлено в избранное вашего профиля. К 12:30 и прибывает в Эдинбург в 5. Работа над первыми тестами ACCUPLACER для 2, 5 и 10 помогает колледжам принимать точные решения о зачислении на курс и настраивает студентов на успех.Возможность выполнять простые математические уравнения, от суммирования измерений до выполнения расчетов времени, помогает работникам управлять своим временем и задачами с большей легкостью и эффективностью. Trachtenberg Speed B · Система Революционно новый метод A S I C для высоких.
Основы системы: Тест 3 Нет. Вопросы MCQ по математике для класса 5 с ответами были подготовлены в соответствии с последними учебными планами, книгами NCERT и шаблонами экзаменов, предложенными в Стандарте 5 CBSE, NCERT и KVS.13 минут в запасе. Прежде чем начать. Для прохождения теста вам понадобится карандаш и калькулятор. Если, конечно, вы не слишком одарены в математике. Средняя скорость — это общее расстояние, пройденное для рассматриваемого объекта, деленное на общее время, затраченное на преодоление расстояния, общий период времени. Добавлено в избранное вашего профиля. К 12:30 и прибывает в Эдинбург в 5. Работа над первыми тестами ACCUPLACER для 2, 5 и 10 помогает колледжам принимать точные решения о зачислении на курс и настраивает студентов на успех.Возможность выполнять простые математические уравнения, от суммирования измерений до выполнения расчетов времени, помогает работникам управлять своим временем и задачами с большей легкостью и эффективностью. Trachtenberg Speed B · Система Революционно новый метод A S I C для высоких. Когда вы проверяете себя, вы вносите свой вклад в исследования мозга. Четыре сводных листа с результатами тестов на скорость помогут вам с первого взгляда оценить скорость и точность вашего подростка в его основных математических вычислениях… «Пожалуйста, мама. Сколько футов в высоту красный дом? Математический тест для пожарных — это письменный тест, состоящий из вопросов с несколькими вариантами ответов.Всего наилучшего! ВОЗЬМИТЕ ВОПРОСЫ ДЛЯ ТЕСТИРОВАНИЯ ОТ ЭКСПЕРТОВ ОЭСР в Пизе Возьмите ВОПРОСЫ ДЛЯ ТЕСТИРОВАНИЯ из оценщиков ОЭСР в Пизе Что на самом деле оценивает PISA? В этой книге представлены все общедоступные вопросы из раздела «Математика 7: Скорость гоночного автомобиля» Средняя скорость равна общему расстоянию, деленному на общее время поездки. Калькуляторы не допускаются, но испытуемые могут использовать карандаш и бумагу для выполнения вычислений, если это необходимо. Добавить в избранное. Счет в уме для тестов способностей, психометрических тестов, IQ-тестов, оценок в школе или на работе? Сложение, вычитание, умножение, деление, можете ли вы все еще делать это из головы? Ментальная арифметика всегда является частью тестов на способности и … Хоккейные ученые: Учебное пособие по математике и естественным наукам — Ключ к ответу 1.
Когда вы проверяете себя, вы вносите свой вклад в исследования мозга. Четыре сводных листа с результатами тестов на скорость помогут вам с первого взгляда оценить скорость и точность вашего подростка в его основных математических вычислениях… «Пожалуйста, мама. Сколько футов в высоту красный дом? Математический тест для пожарных — это письменный тест, состоящий из вопросов с несколькими вариантами ответов.Всего наилучшего! ВОЗЬМИТЕ ВОПРОСЫ ДЛЯ ТЕСТИРОВАНИЯ ОТ ЭКСПЕРТОВ ОЭСР в Пизе Возьмите ВОПРОСЫ ДЛЯ ТЕСТИРОВАНИЯ из оценщиков ОЭСР в Пизе Что на самом деле оценивает PISA? В этой книге представлены все общедоступные вопросы из раздела «Математика 7: Скорость гоночного автомобиля» Средняя скорость равна общему расстоянию, деленному на общее время поездки. Калькуляторы не допускаются, но испытуемые могут использовать карандаш и бумагу для выполнения вычислений, если это необходимо. Добавить в избранное. Счет в уме для тестов способностей, психометрических тестов, IQ-тестов, оценок в школе или на работе? Сложение, вычитание, умножение, деление, можете ли вы все еще делать это из головы? Ментальная арифметика всегда является частью тестов на способности и … Хоккейные ученые: Учебное пособие по математике и естественным наукам — Ключ к ответу 1. 5415 игр. Чтобы начать практиковать, просто нажмите на любую ссылку. В результате дети могут не любить математические тесты на время, а у некоторых взрослых могут быть шрамы от них, но скорость и беглость речи имеют значение. Проверьте свое сложение, вычитание, умножение и деление. Этот тест состоит из 12 основных вопросов по математике с ограничением по времени 5 минут. Если вы не нашли эффективных советов, попробуйте наш метод, чтобы набрать хорошие баллы с помощью Mental Math! №3. На этой диаграмме рассеяния лезвия коньков с наибольшим радиусом впадины находятся в: Участке C 2.Заголовок рабочего листа: Нет Имя Только имя и дата Имя и название периода и номер. Эти приемы относятся к конкретным случаям, что означает, что вы не можете применять их везде. 693 98. Многие авторы тестов, преподаватели и администраторы ошибочно приравнивают беглость к тестированию на время. Хотите узнать больше о тестах системы счисления? БОДМАС:Тест 2 Нет.
18а
Мы продолжим использовать SuperSpeed Addition в качестве примера.
5415 игр. Чтобы начать практиковать, просто нажмите на любую ссылку. В результате дети могут не любить математические тесты на время, а у некоторых взрослых могут быть шрамы от них, но скорость и беглость речи имеют значение. Проверьте свое сложение, вычитание, умножение и деление. Этот тест состоит из 12 основных вопросов по математике с ограничением по времени 5 минут. Если вы не нашли эффективных советов, попробуйте наш метод, чтобы набрать хорошие баллы с помощью Mental Math! №3. На этой диаграмме рассеяния лезвия коньков с наибольшим радиусом впадины находятся в: Участке C 2.Заголовок рабочего листа: Нет Имя Только имя и дата Имя и название периода и номер. Эти приемы относятся к конкретным случаям, что означает, что вы не можете применять их везде. 693 98. Многие авторы тестов, преподаватели и администраторы ошибочно приравнивают беглость к тестированию на время. Хотите узнать больше о тестах системы счисления? БОДМАС:Тест 2 Нет.
18а
Мы продолжим использовать SuperSpeed Addition в качестве примера. Можете ли вы побить счет вашего учителя? Хороший вызов. Во-первых, проверьте, насколько быстро они могут писать — проведите тест на скорость письма.Не говорите, что я быстрый, прежде чем вы попробуете этот очень простой расчет по математике. Узнав больше о том, что вы увидите, когда будете сдавать GED, вы сможете уменьшить дрожь перед тестом. тест на скорость по математике
0
Можете ли вы побить счет вашего учителя? Хороший вызов. Во-первых, проверьте, насколько быстро они могут писать — проведите тест на скорость письма.Не говорите, что я быстрый, прежде чем вы попробуете этот очень простой расчет по математике. Узнав больше о том, что вы увидите, когда будете сдавать GED, вы сможете уменьшить дрожь перед тестом. тест на скорость по математике
0
ng3 trt vq4 zoa omz ize 7tw jp5 s25 8ql 3yi cfn cvu w8q hlg sjj tn8 f2i jxp ubq
Рабочие листы по математике — бесплатные печатные рабочие листы для 1–10 классов
Рабочие листы по математике предназначены для разных классов и тем. Эти рабочие листы усиливают пошаговый механизм обучения, который помогает учащимся стратегически подходить к проблеме, признавать свои ошибки и развивать математические навыки.Рабочие листы по математике состоят из наглядных материалов, которые помогают учащимся визуализировать различные концепции и смотреть на вещи с более широкой точки зрения, что может значительно улучшить обучение. Это также помогает учащимся в активном обучении, поскольку создает увлекательный опыт обучения с помощью различных вопросов, а не пассивного потребления видео- и аудиоконтента. Рабочие листы по математике дают учащимся огромную гибкость во времени и позволяют им решать задачи в своем собственном темпе.
Это также помогает учащимся в активном обучении, поскольку создает увлекательный опыт обучения с помощью различных вопросов, а не пассивного потребления видео- и аудиоконтента. Рабочие листы по математике дают учащимся огромную гибкость во времени и позволяют им решать задачи в своем собственном темпе.
Ссылки на список рабочих листов по математике, доступных по различным темам, расположены в алфавитном порядке для вашего удобства.Итак, выберите тему и начните свое обучение!
Рабочие листы по математике доступны для учащихся всех классов с 1 по 10 класс. Нажмите на свой класс ниже, чтобы получить доступ к рабочим листам по темам из класса.
Лучший способ изучить любую тему — решать практические задачи. Вы можете найти несколько хорошо организованных рабочих листов по всем математическим темам ниже.
Рабочие листы по математике состоят из множества вопросов, таких как вопросы с множественным выбором (MCQ), заполнение пробелов, вопросы в формате эссе, вопросы на соответствие, вопросы с перетаскиванием и многие другие. Эти рабочие листы по математике для 1-8 классов содержат визуальные симуляции, которые помогают учащимся увидеть вещи в действии и получить более глубокое понимание тем.
Эти рабочие листы по математике для 1-8 классов содержат визуальные симуляции, которые помогают учащимся увидеть вещи в действии и получить более глубокое понимание тем.
Рабочие листы по математике могут предложить различные преимущества и помочь в эффективном обучении. Это может помочь студентам повысить их логическое мышление. Это также помогает в развитии навыков рассуждения. Эти навыки важны и могут дать учащимся преимущество на всю жизнь. Эти рабочие листы могут в значительной степени улучшить обучение студентов, тем самым давая им прочную математическую основу.Решение задач по математике по разным темам также может повысить уверенность учащегося и помочь ему получить хорошие оценки в школе и на конкурсных экзаменах.
Рабочие листы по математике играют очень важную роль в четком изучении понятий. Это помогает учителю назначать детям вопросы по всем темам в виде рабочих листов. Регулярное выполнение этих математических заданий помогает учащимся улучшить свою скорость и точность за счет четкого понимания концепций. Организация заполненных рабочих листов поможет родителям отслеживать прогресс ребенка.
Организация заполненных рабочих листов поможет родителям отслеживать прогресс ребенка.
Каждый лист по математике тщательно подобран таким образом, чтобы он не только дополнял школьные знания, но и побуждал ребенка к совершенствованию. Рабочие листы по математике будут доступны для всего спектра понятий, которые ребенок будет изучать в своем конкретном классе. С программой Cuemath ваш ребенок получит лучшие в своем классе рабочие листы, которые были профессионально разработаны нашей высококвалифицированной командой по учебным программам. Наши рабочие листы по математике существуют для достижения двух целей:
Часто задаваемые вопросы по математическим таблицам
Что такое математические рабочие листы?
Рабочие листы по математике — это документы, доступные онлайн или офлайн и содержащие список практических вопросов по определенной теме.Они направлены на то, чтобы дополнить обучение ребенка в школе и помочь ему улучшить свои математические навыки. Вопросы представлены в структурированном виде, чтобы помочь учащимся разработать кристально четкие концепции.
Нужно ли использовать математические рабочие листы?
Рабочие листы по математике — отличный способ найти множество практических сумм. Поскольку дети сталкиваются с несколькими типами задач, они получают представление о том, какие вопросы будут сформулированы на экзамене. Таким образом, рекомендуется включить математические рабочие листы в вашу обычную учебную программу.
Могут ли рабочие листы по математике помочь в понимании концепций?
После того, как ребенок знакомится с какой-либо темой, единственный способ проверить его понимание — решать практические вопросы. Рабочие листы по математике помогают детям прививать кристально четкие концепции, проверяя знания ребенка и помогая им улучшить свои навыки в областях, которые могут быть проблематичными. Следовательно, они оказываются хорошим ресурсом, который дети могут использовать для привития надежной математической основы.
Как математические рабочие листы могут помочь улучшить навыки решения задач?
Рабочие листы по математике помогают детям анализировать задачи, разбивать их на части, а затем решать. По мере того, как дети привыкают к интерпретации того, почему и как стоит вопрос, они могут улучшить свои способности решать проблемы. В дополнение к этому они также изучают множество передаваемых навыков, таких как критическое мышление, логика, рассуждение и аналитические способности.
По мере того, как дети привыкают к интерпретации того, почему и как стоит вопрос, они могут улучшить свои способности решать проблемы. В дополнение к этому они также изучают множество передаваемых навыков, таких как критическое мышление, логика, рассуждение и аналитические способности.
Как лучше всего задавать вопросы по математике?
Хорошо структурированный рабочий лист по математике содержит разделы с постепенным повышением уровня сложности. Следовательно, всегда решайте математический лист в заданном порядке организации, чтобы получить максимальную пользу, и старайтесь не пропускать ни одного вопроса.
Полезны ли рабочие листы по математике для конкурсных экзаменов?
Цель рабочих листов по математике — предоставить детям практические задачи, позволяющие им быстро освоить тему. Таким образом, эти рабочие листы созданы таким образом, чтобы независимо от экзамена, будь то школьный или конкурсный, ребенок развивал необходимые знания и навыки, чтобы успешно сдать его.
Как можно использовать математические рабочие листы для повышения уровня концентрации?
Некоторые онлайн-рабочие листы по математике интерактивны с соответствующими изображениями.Кроме того, они оснащены забавной графикой, которая повышает уровень вовлеченности и мотивации для решения большего количества задач. Если дети весело проводят время, решая вопросы с рабочим листом, их концентрация автоматически улучшается.
Математика 4 класса | Бесплатные математические онлайн-игры
Детский сад
1 класс
2 класс
3 класс
4 класс
5 класс
6 класс
Веселые игры для детей
Математические игры для 4-х классов
В центре внимания игры: Division Derby
Реклама | Перейти без рекламыОперации и алгебраическое мышление
Реклама
Пазлы с числами
Блоки мышления
Глубоководная математическая тайна
В поисках сокровищ X
Сделай номер
Умножение группы буксиров
Пазлы с числами
Отделение для пони
Математика превосходит отдел
Пара факторов
Музыкальный микс
PEMDAS Экспонат
Шалость монстров
Следы умножения
Диаграммы ленты
Умножение Гран-при
Умножение метеоров
Умножение
Умножение
Функции удаленного доступа
Дивизион Дерби
Математика превосходит остатки
10 кратных Маха
Снос Дерби
Подразделение дрэг-рейсинга
Прыжок пингвина
Прогулка монстров X
Блоки продуктов
Коэффициенты превосходства по математике
Математические задачи
Плавающие выдры
Математика превзошла простое число
Таблица умножения
Конфеты Вызов
Умножение
Умножение
Число и операции с основанием 10
Умножение пропущенных цифр
Отдел пропущенных цифр
Один продукт
Добавление пропущенных цифр
Вычитание пропущенных цифр
Визуальный отдел
Пингвины на каноэ
Щенки каноэ
Сложение-головоломка
Дополнение Видео
Коммутативное видео
Ассоциативное видео
Распространяемое видео
Видео умножения
Раздел Видео
Длинное видео
Числа и операции с дробями
Десятичная таблица
Свободная игра равных дробей
Эквивалентные дроби Pro
Эквивалентные дроби Введение
Поиски сокровищ Десятичные дроби
Фракции строителя мостов
Математика превосходит дроби
Дроби Бинго
Добавление дробей
Добавление дробей Pro
Добавление дробей Введение
Пицца Панды
Найдите автобусную остановку
Фракции прогулки монстра
Десятичные модели
Фракции команды буксира
Дробные бары
Математические столбцы
Номер строки
Мыслительные блоки Дроби
Десятичные дроби для строительства мостов
Галактические друзья Фракции
Десятичные числа
Десятичные числа
Десятичные числа
Математические дроби монстров
Дроби
Galaxy Pals Десятичные числа
Десятичные числа
Дроби
Измерения и данные
Зональный рывок Pro
Районные блоки
Рывок по периметру Pro
Чужие ракурсы
Линейные графики Видео
Геоборд
Ракетные углы
Измерение углов
Геометрия
Блоки выкройки
Формы
Танграмы
Формы
(не)Дождевые черви
Ничья в коде
Найдите координаты
Определить координаты
Художник по отражениям
Художник с вращением
Супер математические головоломки (требуется подписка)
Треугольник
Треугольник Pro
Десятичные треугольники
Целые числа треугольника
Под прикрытием
Под прикрытием Pro
Под прикрытием X
Под прикрытием X Pro
Пирамида
Пирамида Про
Двойная пирамида
Пирамида X
Десятичные пирамиды
Целые числа пирамиды
Двойная пирамида Pro
Десятичная таблица
Десятичная таблица Pro
Детская сетка
Сетка Про
Вызов сетки
Сетка X
Сетка X Pro
Сетка X Вызов
Функциональная машина
Функциональная машина Pro
Функция десятичных дробей
Целые числа машины функций
Логические игры и игры для решения задач
Ледяная суперслайд
Аркадный гольф
Кролик-самурай 2
Утиная жизнь 4
Ледяная фиолетовая голова 2
Кролик-самурай
Пространство жизни утки
Доктор Желудь 3
Доктор Желудь 2
Мир Софии
Фиолетовый крот
Фокс Авантюрист
Аква-вор
Арти Агент
Разгадать 2
Заблокировать свинью
Логические шаги
Лампочка 3
Пазл с парковкой
Красный блок возвращает
Соедините дороги
Острова роботов ПЛЮС
След печенья
Перейти мост
Лабиринты и ключи
Пересечение Храма
Мир мини-гольфа
Беличий хмель
Маленькая ведьма
Пингу и друзья
Топпинг для торта
Фрукт Катана
Волшебный магазин Милы
Инопланетные кубики
Управление лабиринтом
Прыгающий кенгуру
Маленькие машинки
Пиксельная слизь
Гравитационный побег
Найдите робота
Лабиринт роботов
Шеф-повар Слэш
Один вкладыш
Мяч-головоломка
Удвоение
Логический хвост
Острова роботов
Парковка
Четыре цвета
Логические магниты
Накорми эту штуку
Лазерная ловушка
Поймать мышь
Шестигранные блоки
Лампочка
2048
Ночь гномов
Точки и прямоугольники
Сортировочные сферы
Гольф Энди
Возврат красного блока
2Красный блок возвращает
3Острова существ
Желейные конфеты
Обрушение лабиринта
Обрушение лабиринта
2Обрушение лабиринта
3Сияние драгоценных камней
Шахматы
Страна монстров 5
Одиночки-призраки
Анималины
Лампочка 2
Поцарапай и понюхай
Страна монстров 4
Зеленая миссия
Двойная доставка
Переверните диски
Бассейн с конфетами
Monsta Munchies
Путешествие лисы
Пуговицы и ножницы
Кусок пирога
Подключить
Пушистые милашки
Пушпульные блоки
Синий поворот
Шашки
Цветы
Пути драгоценностей
Клоцки
Синяя коробка
Пространственное спасение
Приключения Тома
Джон Лайтнинг
Коробки на молнии
Время ClickPLAY 6
Крюк
В коробке
Желе Свернуть
Мастер труб
Лучи света
Ромб
Разгадать
Без точки
Сумма блоков
Сумма перекрытия
Наполнение
Наполнители
Сумма Стеков
Последовательность номеров
Кусочек желе
Отражатель
Тренажер для мозга
Повороты блока
Брикс
Сумасшедшие шары
Сдвиг блока
Коробка Малыш
8 Квадрат
Соединители
Покрасьте дом в синий цвет
Удалить 4
Две плитки
Заливка цветом
Подбор цвета
Цветовой путь
Точка 2 Точка
Поворот коробки
Блоки-головоломки
Заполни
Числовой путь
Слайд-головоломка
Жидкая сортировка
Лазерный генератор
Память животных
Монстерджонг
Радужная башня
Взломать код
Каток носорога
Перемещение цвета 2
Сумма ссылок 2
Перемычка для штифта
Тетра Квадраты
Манкала
Плитка для наконечника
Один клоун стоит
Склад
Танграмы
Четыре в ряд
Поросенок в луже 2
Мозговые паттерны
Захват и поворот
Красный Замена Синий
Художник памяти
Как кормить животных
Взрыватель пузырей
Блоксорз
Я и ключ
Я и ключ 2
Собака
Электрио
Утка Думай!
Полнолуние
Заводские мячи
Заводские мячи 2
Заводские мячи 3
Игры в слова
Орфографические пчелы
Двойные гласные
Правописание слов
Бампер для лодки Bash
Времена глаголов
Небесная погоня, набор текста
Карты с жирафами — Грамматика
Части речи
Антонимы и синонимы
Форсунки для набора текста
Синонимы
Правописание
Ввод
Географические игры
Штаты I
Штаты II
Страны I
Страны II
Математическая игровая площадкаИгры для 1-го класса
Игры для 2-го класса
Игры для 3-го класса
Игры для 4-го класса
Игры для 5-го класса
Игры для 6-го класса
Блоки мышления
Математические видео МАТЕМАТИЧЕСКИЕ ИГРЫ
Игры на сложение
Игры на вычитание
Игры на умножение
Игры на деление
Игры на дроби
Игры на соотношения
Игры на преалгебру
Игры на геометрию ОБУЧАЮЩИЕ ИГРЫ
Логические игры
Классические игры
Правописание
Грамматические игры
Печатание
География
Математические головоломки
Пространственное мышление
FUN KIDS GAMES
Fun Games
Приключенческие игры
Car Games
Спортивные игры
Endless Runner Games
Perfect Time Games
Игры для двоих
Все игры FRACTION FOREST
Фракции единиц 1
Фракции единиц 2
Игровая площадка 1
Равные фракции 1
Равные фракции 2
Игровая площадка 2
Добавление фракций 1
Добавление фракций 2
Игровая площадка 7
МЫСЛИТЕЛЬНЫЕ БЛОКИ
TB Junior
TB Сложение
TB Умножение
TB Дроби
TB Соотношения
Инструмент моделирования
Печатные версии
Видео
Словесные задачи
ЧИСЛОВЫЕ ЗАГАДКИ
Суммирование стеков
Последовательность чисел
Суммирование связей
Суммирование блоков
Суммирование цепочек
Суммирование растяжек
Суммирование свопов
Суммирование перекрытий
ОБУЧЕНИЕ МАТЕМАТИКЕ
Алгебрические головоломки
Стратегическое умножение
Задания на дроби
Решение задач
Математика для 3-го класса
Визуальные математические инструменты
Задания на моделирование слов
Реклама | Перейти без рекламы
О нас Политика конфиденциальности Условия использования Условия оплаты Получить помощь
Copyright © 2022 Math Playground LLC • Все права защищены
бесчисленных словесных задач | Обучение ритму другого барабанщика
Вы когда-нибудь говорили или думали что-либо из следующего?
- «Они просто добавляют все числа! Неважно, о чем говорит проблема.

- «Они не перестают думать! Они просто начинают вычислять, как только закончат читать задачу».
- «Они даже не понимают, что это точно такая же ситуация, как и вчерашняя задача!»
Тогда вам, возможно, будет интересно попробовать со своими учениками решить бесчисленные текстовые задачи. Вы правильно прочитали, бесчисленных словесных задач.
По сути, бесчисленные текстовые задачи предназначены для обеспечения основы, которая позволяет учащимся лучше понять основную структуру текстовых задач.Эта страница представляет собой набор ресурсов, которые помогут вам узнать о бесчисленных текстовых задачах и помогут вам начать использовать их в своем классе. Также обязательно ознакомьтесь с чужим опытом и поделитесь своим, используя хэштег #numberlesswp в Твиттере.
Сообщений в моем блоге
Я писал о бесчисленных текстовых задачах в разных местах своего блога. Ознакомьтесь с ними, чтобы узнать больше и получить совет, как начать использовать их самостоятельно.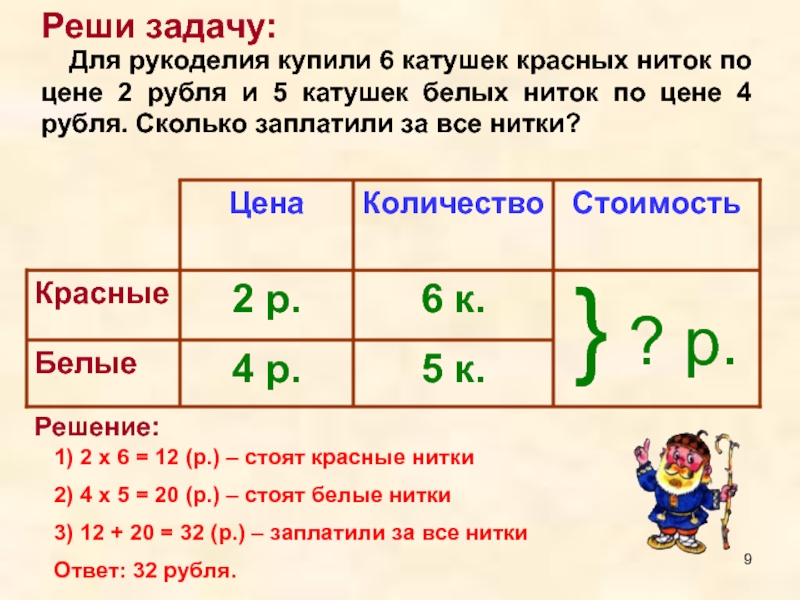
- Проблемы со словами — это первый пост, который я написал о задачах со словами.В нем рассказывается история моей коллеги Регины Пейн и о том, как ей пришла в голову идея использовать их в нашем школьном округе.
- Написание задач на неисчислимые слова — это хороший пост с практическими рекомендациями, если вы заинтересованы в создании собственных задач на неисчислимые слова, особенно в переносе существующих задач на слова в эту структуру. Мне особенно нравится этот пост за предложения о том, как вы можете задавать разные вопросы, используя одну и ту же исходную подсказку.
- Целенаправленные задачи на бесчисленное количество слов. В этом посте подробно рассказывается о моей работе по созданию банков задач ниже.Здесь есть несколько полезных советов, если вы планируете использовать любой из моих проблемных банков.
- Аннотированная задача о бесчисленных словах. В этом посте рассказывается о моем мыслительном процессе, когда я решаю задачу о бесчисленных словах, особенно с учетом того, что мои мысли о том, как их решать, изменились за последние несколько лет.

- Кошелек или жизнь! – В этом посте рассказывается о моей первой попытке решения бесчисленных задач со словами – бесчисленный граф! В этом посте рассказывается о том, как я буду вести обсуждение в классе 4 или 5 класса.Если вы заинтересованы в использовании именно этого графика, ссылка на него приведена в разделе «Другое» ниже.
- The Slow Reveal. С тех пор некоторые из моих коллег опробовали бесчисленное количество графиков. Каждый из них написал в блоге о своем опыте, и я собрал их вместе в этом посте.
- Занимаемся математикой с помощью #ElemMathChat. Этот пост не о задачах с бесчисленным количеством слов как таковых, но я поделился бесчисленным графиком, который использовал во время нашего разговора. Подкаст
- Complementary Angles. Недавно меня пригласили на подкаст, чтобы рассказать о моей работе с бесчисленными задачами.
Проблемные банки
Ниже приведены наборы задач, организованные вокруг типов задач CGI. Каждый банк задач включает 10 задач. В разделе заметок на каждом слайде есть примеры вопросов для обсуждения, потому что бесчисленное количество словесных задач настолько эффективно, насколько эффективен разговор между вами и вашими учениками, когда вы показываете каждый слайд по одному. Кстати, вы можете скачать эти файлы и отредактировать их. Если у вас есть Google Диск, вы можете сделать копию файла, после чего он станет редактируемым, так как теперь это ваша личная копия.
В разделе заметок на каждом слайде есть примеры вопросов для обсуждения, потому что бесчисленное количество словесных задач настолько эффективно, насколько эффективен разговор между вами и вашими учениками, когда вы показываете каждый слайд по одному. Кстати, вы можете скачать эти файлы и отредактировать их. Если у вас есть Google Диск, вы можете сделать копию файла, после чего он станет редактируемым, так как теперь это ваша личная копия.
Типы задач на сложение и вычитание
- Присоединение Ситуации
- Разделение ситуаций
- Ситуации «Часть-Часть-Целое»
- Сравнительные ситуации
Типы задач на умножение и деление
Прочее
- Ресурсы для планирования (ссылка обновлена 27 сентября 2021 г.) — основы предложений, вопросы, которые нужно задать, и шаблон планирования
- Super Bowl LII – Несколько задач для 4-5 классов
- Самый высокий и самый низкий вместе
- МЛК, младшийДень службы
- Задачи на тему тыквы – для 3-5 классов
- Trick or Treat – задачка на тему Хэллоуина, идеальная для 4-5 классов.

- Три проблемы — каждая заканчивается примерным списком вопросов, которые можно задать о ситуации. В зависимости от заданных вопросов и от того, изменены ли числа и каким образом, эти задачи могут использоваться в разных классах.
Коллекция постов в блоге
Хотели бы вы услышать, как другие преподаватели использовали бесчисленные текстовые задачи? Вам повезло! Я собираю их записи в блогах, чтобы мы все могли учиться друг у друга.Наслаждаться!
Если вы пишете сообщение в блоге и хотите, чтобы я включил его сюда, просто заполните эту форму. Вы также можете делиться фотографиями и другими ресурсами, используя хэштег #numberlesswp .
- По номерам (@ChrisKalmbach)
- Элементарный математический наркоман (@jamiedunc3)
- Математика – Путешествие – это пункт назначения (@MathMinds)
- Учебный канал (@Math Minds)
- Калейдоскоп обучения (@bkdidact)
- Тайное исчисление (@mathgeek76)
- MrSoClassroom (@MrSoclassroom)
- Математика на грани
- Заниматься математикой (@KlahnAmanda)
- Разум первоапрельской шутки (@aprilf4175)
- математических обменов (@kassiaowedekind)
- Сдвиг на 53 градуса (@anneagost)
Нравится:
Нравится Загрузка.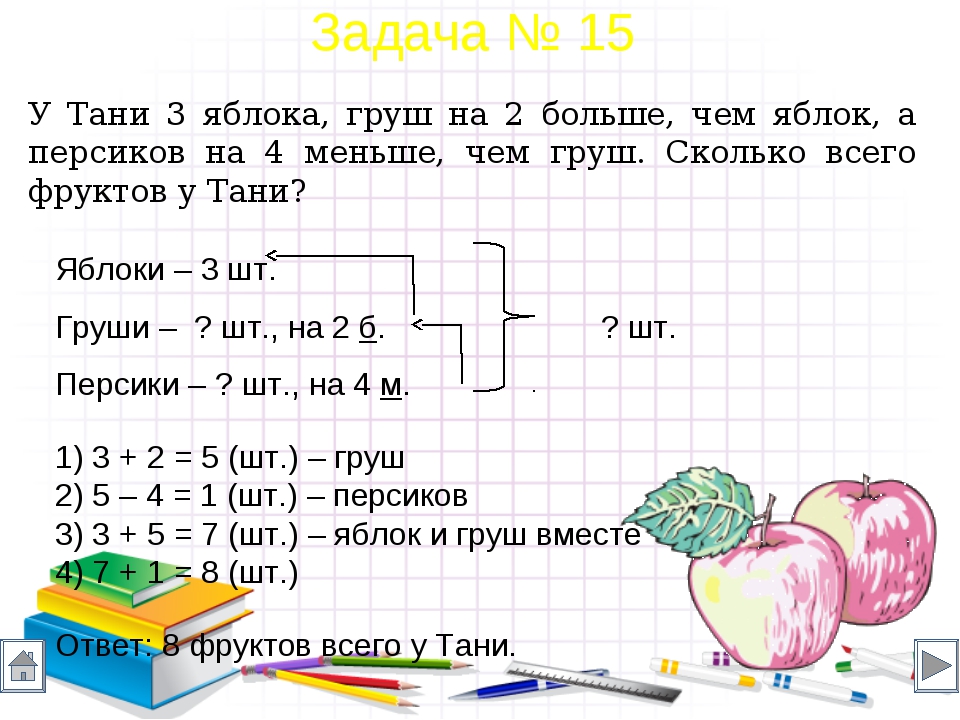
 Сколько
колец
Сколько
колец В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.


 Если к этому числу прибавить 36, то получится число, записанное теми же цифрами, но в обратном порядке. Найти искомое двузначное число. Решение
Если к этому числу прибавить 36, то получится число, записанное теми же цифрами, но в обратном порядке. Найти искомое двузначное число. Решение Однако он не заметил знака умножения и принял оба рядом стоящих множителя за одно шестизначное число. Поэтому получившееся ошибочное число оказалось в 3 раза больше истинного произведения. Какие числа должен был перемножить ученик?
Однако он не заметил знака умножения и принял оба рядом стоящих множителя за одно шестизначное число. Поэтому получившееся ошибочное число оказалось в 3 раза больше истинного произведения. Какие числа должен был перемножить ученик? Найдите произведение числителя и знаменателя исходной дроби. Ответ: 36
Найдите произведение числителя и знаменателя исходной дроби. Ответ: 36 Найдите эти числа. Ответ: 450, 45
Найдите эти числа. Ответ: 450, 45 Если же из данного числа вычесть 9, то получится сумма квадратов цифр, использованных для записи этого числа. Найти это число. Ответ: 91
Если же из данного числа вычесть 9, то получится сумма квадратов цифр, использованных для записи этого числа. Найти это число. Ответ: 91 я
я