Задачи по геометрии 8 класс
Задачи по геометрии для 8 класса для подготовки к итоговой контрольной работе
1. В прямоугольном треугольнике найдите гипотенузу с, если его катеты равны: а=5 см, b=12 см.
2. В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите: а)высоту треугольника, проведенную к основанию треугольника; б) площадь треугольника.
3. В прямоугольном треугольнике гипотенуза с=25 см, один из его катетов: а=24 см. Найдите другой катет b.
4. В равнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. Найдите: а)высоту этого треугольника, проведенную к основанию треугольника; б) площадь треугольника.
5. Высота равнобедренного треугольника, проведенная к основанию, равна 8 см, основание равно 12 см. Найдите боковую сторону.
6. Найдите площадь равнобедренной трапеции, если ее основания равны 4 и 10 см, а боковая сторона — 5 см.
7. Найдите сторону ромба, если его диагонали равны 24 и 32 см.
8. Найдите площадь равнобедренной трапеции, если одно из оснований равно 6 см, боковая сторона — 15 см, высота — 9 см.
9. Найдите длину основания АD, изображенной на рисунке трапеции ABCD, если BC=7, BO=3, OD=6.
4. В равнобедренном треугольнике, основание равно 14, угол между боковыми сторонами равен 60°. Найдите длину высоты, проведенной к основанию.
10. Найдите длину основания BC, изображенной на рисунке трапеции ABCD, если AD=15, BO=2, OD=6.
11. В равнобедренном треугольнике, основание равно 16, угол между основанием и боковой стороной 60°. Найдите длину высоты, проведенной к основанию.
Запишите ответ к заданиям 4 и 5.
12. В окружности с центром в точке О и радиусом равным 3 см, проведена касательная ВС (В — точка касания). Найдите длину отрезка ВС, если ОС=5.

14. Используя данные рисунка, найдите площадь равнобедренной трапеции.

15. Найдите боковую сторону равнобедренного треугольника, если его высота равна 8, а угол при основании равен 30°.
16. В окружности с центром в точке О и радиусом равным 8 см, проведена касательная ВС (В — точка касания). Найдите длину отрезка OС, если BС=15.
17. На рисунке Р и Н середины сторон, ВК – высота треугольника. Найдите площадь треугольника, если РН=18см, ВК=17см.
18. В квадрате ABCD диагональ АС пересекает отрезок ВM (МϵAD) в точке Р. Найдите длины отрезков ВР и РМ, если сторона квадрата равна 12 см, а отрезок АМ=5см.
Задачи по геометрии тема » Площадь» 8 класс.

Площадь треугольника
Теорема 1. Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.
Теорема 2. Площадь треугольника равна половине произведение двух его сторон на синус угла между ними.
Теорема 3. Площадь треугольника выражается формулой (формула Герона): где a , b , c – стороны треугольника, p – его полупериметр.
В режиме слайдов ответы появляются после кликанья мышкой

Площадь многоугольника
Теорема 1 . Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне .
Теорема 2 . Площадь трапеции равна произведению полусуммы оснований на высоту.
Теорема 3 . Площадь многоугольника, описанного около окружности радиуса r , выражается формулой S = pr , где p – полупериметр многоугольника.
В режиме слайдов ответы появляются после кликанья мышкой

Площадь круга
Теорема 1 . Площадь круга равна половине произведения длины его окружности на радиус.
Теорема 2 . Отношение площадей подобных фигур равно квадрату коэффициента подобия.
В режиме слайдов ответы появляются после кликанья мышкой

Упражнение 1
Найдите периметр прямоугольника, если его площадь равна 72, а отношение соседних сторон равно 1 : 2.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 36.

Упражнение 2
Периметр прямоугольника равен 74, а площадь 300. Найдите большую сторону прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 25.

Упражнение 3
Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 8 и 18.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12.

Упражнение 4
Сторона прямоугольника относится к его диагонали, как 3:5, а другая сторона равна 8. Найдите площадь прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 48.

Упражнение 5
Даны два квадрата, диагонали которых равны 5 и 3. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4.

Упражнение 6
Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2.

Упражнение 7
Стороны параллелограмма равны 15 и 9. Высота, опущенная на первую сторону, равна 6. Найдите высоту, опущенную на вторую сторону параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.

Упражнение 8
Площадь параллелограмма равна 40, стороны — 5 и 10. Найдите меньшую высоту этого параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4.

Упражнение 9
Найдите площадь параллелограмма, если его стороны равны 4 и 5, а угол между ними равен 30°.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.

Упражнение 10
Найдите площадь ромба, если его стороны равны 10, а один из углов равен 150°.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 50.

Упражнение 11
Найдите площадь прямоугольного треугольника, если его катеты равны 4 и 7.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 14.

Упражнение 12
Найдите площадь треугольника, две стороны которого равны 4 и 6, а угол между ними равен 30°.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 6.

Упражнение 13
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 100.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 20.

Упражнение 14
Периметр треугольника равен 12, а радиус вписанной окружности – 1. Найдите площадь этого треугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 6.

Упражнение 15
Основания трапеции равны 10 и 35, площадь равна 225. Найдите ее высоту.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.

Упражнение 16
Основания трапеции равны 36 и 12, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 84.

Упражнение 17
Основание трапеции равно 26, высота 10, а площадь 200. Найдите второе основание трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 14.

Упражнение 18
Высота трапеции равна 20, площадь — 400. Найдите среднюю линию трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 20.

Упражнение 19
Найдите площадь прямоугольной трапеции, основания которой равны 3 и 1, большая боковая сторона составляет с основанием угол 45 о .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4.

Упражнение 20
Найдите площадь треугольника с вершинами в узлах сетки, состоящей из единичных квадратов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 6.

Упражнение 21
Периметр прямоугольника равен 14, а площадь 12. Найдите диагональ этого прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 5.

Упражнение 22
Прямоугольник со сторонами 4 и 17 разделен отрезком на два подобных прямоугольника. Найдите площадь большего из них.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 64.

Упражнение 23
Периметры двух подобных многоугольников относятся как 3:5. Площадь большего многоугольника равна 50. Найдите площадь меньшего многоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 18.

Упражнение 24
Стороны прямоугольника 3 и 1. Найдите площадь четырехугольника, ограниченного биссектрисами углов этого прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2.

Упражнение 25
Острый угол параллелограмма равен 30°, а высоты, проведенные из вершины тупого угла, равны 2 и 3. Найдите площадь параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12.

Упражнение 26
Диагонали параллелограмма равны 4 и , а угол между ними равен 45 о . Найдите площадь параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 4.

Упражнение 27
Найдите площадь ромба, если его высота равна 12, а меньшая диагональ 15.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 150.

Упражнение 28
Середины сторон параллелограмма последовательно соединены между собой. Найдите площадь образовавшегося четырехугольника, если площадь данного параллелограмма равна 16?
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8.

Упражнение 29
Площадь параллелограмма равна 36, а расстояния от точки пересечения диагоналей до сторон параллелограмма соответственно равны 2 и 3. Найдите периметр параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 30.

Упражнение 30
Стороны треугольника равны 13, 14, 15. Найдите его площадь.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 84.

Упражнение 31
Сумма двух сторон треугольника равна 15, а высоты, опущенные на эти стороны, равны 4 и 6. Найдите площадь треугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 18.

Упражнение 32
Найдите площадь равнобедренного треугольника, основание которого равно 30, а высота, опущенная на боковую сторону, равна 24.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 300.

Упражнение 33
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 30.

Упражнение 34
Средняя линия трапеции, равная 2, делит площадь трапеции в отношении 3:5. Найдите большее основание трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3.

Упражнение 35
Диагонали четырехугольника перпендикулярны и равны 4 и 5. Найдите площадь этого четырехугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.

Упражнение 36
Около окружности описан четырехугольник. Найдите площадь этого четырехугольника, если две его противоположные стороны равны 2 и 3, а радиус окружности равен 1.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 5.

Упражнение 37
Около окружности, радиуса 2, описан многоугольник, периметр которого равен 18. Найдите его площадь.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 18.

Упражнение 38
Найдите площадь правильного двенадцатиугольника, вписанного в единичную окружность.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 3.

Упражнение 39
Найдите площадь четырехугольника с вершинами в узлах сетки, состоящей из единичных квадратов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 10.

Упражнение 40
Найдите площадь круга, длина окружности которого равна .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 25.

Упражнение 41
Найдите площадь прямоугольника, если его периметр равен 36, а отношение соседних сторон равно 1 : 2.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 72.

Упражнение 42
Периметр прямоугольника равен 74, а площадь 300. Найдите меньшую сторону прямоугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 12.

Упражнение 43
Площадь параллелограмма равна 40, стороны — 5 и 10. Найдите большую высоту этого параллелограмма.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8.

Упражнение 44
Найдите площадь параллелограмма, если его стороны равны 8 и 10, а угол между ними равен 30°.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 40.

Упражнение 45
Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 24.

Упражнение 46
Обозначим S площадь треугольника, стороны которого равны 5, 6, 7. Найдите .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 36.

Упражнение 47
Основания равнобедренной трапеции равны 7 и 13, а ее периметр равен 30. Найдите площадь трапеции.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 40.

Упражнение 48
Около окружности, радиуса 2, описан многоугольник, площадь которого равна 18. Найдите его периметр.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 18.

Упражнение 49
Площадь круга равна . Найдите длину его окружности.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 8.

Упражнение 50
Найдите площадь четырехугольника с вершинами в узлах сетки, состоящей из единичных квадратов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 14.
Тренажёр по геометрии (8 класс) на тему: Задачи на площадь четырехугольников на три уровня
Задачи 1 уровня
1.Найдите площадь прямоугольника, если его длина 2 дм, а ширина 4 см.
2.Найдите площадь параллелограмма, если одна из его сторон равна 6 см, а высота, проведенная к этой стороне, равна 9 см.
3.Катеты прямоугольного треугольника 12 и 8см. Найдите площадь треугольника.
4.Найдите площадь прямоугольника, если его длина 110 см, а ширина 10 м.
5.Найдите площадь прямоугольной трапеции, если основания равны 8 см и 10 см, а боковая сторона, перпендикулярная нижнему основанию равно 5 см.
6.Найдите площадь прямоугольника, если его длина 15 дм, а ширина 20 м.
7.Основания трапеции 6см и 8 см, высота 2 см. Найдите площадь трапеции.
8.Основания трапеции 9 см и 1 см, высота 4 см. Найдите площадь трапеции.
9.Основание треугольника 16, а высота, проведенная к основанию 5. Найдите площадь треугольника.
10.Основание параллелограмма равно 20, а высота, проведенная к основанию равна 7. Найдите площадь параллелограмма.
_______________________________________________________________________________________
Задачи 2 уровня.
1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
2.Найдите площадь ромба с диагоналями 5см и 8 см.
3.Стороны параллелограмма равны 10 см и 18 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
4.Периметр квадрата 40 см. Найдите его площадь.
5.Площадь квадрата 81 кв. см. Найдите его периметр.
6.Найдите площадь прямоугольного треугольника, если его катеты 8 см и 15 см.
7.Основание равнобедренного треугольника 16 см, а медиана, проведенная к основанию, равна 6 см. Найдите площадь треугольника.
8.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
_____________________________________________________________________________________
Задачи 3 уровня.
1.Стороны параллелограмма равны 6 см и 10 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
2.Высоты параллелограмма равны 3 см и 4 см, острый угол между сторонами равен 30 градусов. Найдите площадь параллелограмма.
3.Найдите площадь трапеции со сторонами 6 см, 6 см, 10см и 14 см, если угол между боковой стороной и нижнем основанием 30 градусов.
4.Стороны параллелограмма равны 8 см и 15 см и угол между ними 150 градусов. Найдите площадь параллелограмма.
5.Найдите высоту прямоугольного треугольника, проведённую к гипотенузе, если его катеты 8 см и 6 см., а гипотенуза равна 10 см
Геометрия 8 класс. Контрольная работа № 2 с ответами
Контрольная работа № 2 по геометрии в 8 классе «Площадь» с ответами и решениями (3 уровня сложности по 2 варианта). УМК Атанасян и др. (Просвещение). Поурочное планирование по геометрии для 8 класса. Урок 30. Геометрия 8 класс. Контрольная работа по теме «Площадь».
Смотреть Список всех контрольных по геометрии в 8 классе по УМК Атанасян.
Контрольная работа № 2
«Площадь» (8 класс)
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
ХОД УРОКА
1. Организационный момент
Мотивация к учебной деятельности. Учитель сообщает тему урока, формулирует цели урока.
2. Выполнение контрольной работы
Контрольная работа по геометрии.
I уровень сложности
- Сторона треугольника равна 5 см, а высота, проведенная к ней, в два раза больше стороны. Найдите площадь треугольника.
- Катеты прямоугольного треугольника равны 6 см и 8 см. Найдите гипотенузу и площадь треугольника.
- Найдите площадь и периметр ромба, если его диагонали равны 8 см и 10 см.
- * В прямоугольной трапеции АВСК большая боковая сторона равна З√2 см, угол К равен 45°, а высота СН делит основание АК пополам. Найдите площадь трапеции.
Вариант 2
- Сторона треугольника равна 12 см, а высота, проведенная к ней, в три раза меньше высоты. Найдите площадь треугольника.
- Один из катетов прямоугольного треугольника равен 12 см, а гипотенуза 13 см. Найдите второй катет и площадь треугольника.
- Диагонали ромба равны 10 см и 12 см. Найдите его площадь и периметр.
- * В прямоугольной трапеции ABCD большая боковая сторона равна 8 см, угол А равен 60°, а высота ВН делит основание AD пополам. Найдите площадь трапеции.
Контрольная работа по геометрии.
II уровень сложности
Вариант 1
- Смежные стороны параллелограмма равны 52 см и 30 см, а острый угол равен 30°. Найдите площадь параллелограмма.
- Вычислите площадь трапеции ABCD с основаниями AD и ВС, если AD = 24 см, ВС = 16 см, ∠A = 45°, ∠D = 90°.
- Дан треугольник АВС. На стороне АС отмечена точка С так, что АК = 6 см, КС = 9 см. Найдите площади треугольников АВК и СВК, если АВ = 13 см, ВС = 14 см.
- * Высота равностороннего треугольника равна 6 см. Найдите сумму расстояний от произвольной точки, взятой внутри этого треугольника, до его сторон.
Вариант 2
- Высота ВК, проведенная к стороне AD параллелограмма ABCD, делит эту сторону на два отрезка АК = 7 см, KD = 15 см. Найдите площадь параллелограмма, если ∠A = 45°.
- Вычислите площадь трапеции ABCD с основаниями AD и ВС, если ВС = 13 см, AD = 27 см, CD = 10 см, ∠D = 30°.
- Дан треугольник МКР. На стороне МК отмечена точка Т так, что МТ = 5 см, КТ = 10 см. Найдите площади треугольников МРТ и КРТ, если МР = 12 см, КР = 9 см.
- * В равностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
Контрольная работа по геометрии.
III уровень сложности
Вариант 1
- На стороне AD параллелограмма ABCD взята точка Е так, что АЕ — 4 см, ED = 5 см, BE = 12 см, BD = 13 см. Найдите площадь параллелограмма.
- В остроугольном треугольнике АВС проведены высоты АК и СЕ, СЕ = 12 см, BE = 9 см, АК = 10 см. Найдите АС.
- В равнобедренной трапеции ABCD AD||ВС, ∠A = 30°, высота ВК = 1 см, ВС = 2√3 см. Найдите площадь треугольника KMD, если М — середина отрезка BD.
- * В выпуклом четырехугольнике ABCD проведены диагонали. Известно, что площади треугольников ABD, ACD, BCD равны. Докажите, что данный четырехугольник является параллелограммом.
Вариант 2
- В трапеции ABCD AD — большее основание, СК — высота, АВ = 5 см. На отрезке АК взята точка Е так, что АЕ = 3 см, ЕК = 6 см, KD = 1 см, BE = 4 см. Найдите площадь трапеции.
- В треугольнике АВС угол А тупой, ВК и CD — высоты, ВК = 12 см, АК = 9 см, CD = 10 см. Найдите AD.
- В параллелограмме ABCD ∠A = 60°, диагональ BD перпендикулярна к стороне АВ. Прямая, проходящая через середину отрезка BD — точку М — параллельно AD, пересекает сторону АВ в точке К, МК = 4 см. Найдите площадь треугольника AMD.
- * В выпуклом четырехугольнике ABCD проведены диагонали. Известно, что площади треугольников ABD и ACD равны, а площади треугольников ACD и BCD не равны. Докажите, что данный четырехугольник является трапецией.
3. Рефлексия учебной деятельности
В конце урока учитель раздает на каждую парту краткую запись решения задач контрольной работы.
Домашнее задание: решить задачи, с которыми ученик не справился.
Решения и ответы на контрольную работу
I уровня сложности


Решения и ответы на контрольную работу
II уровня сложности
Решения и ответы на контрольную работу
III уровня сложности
Критерии оценивания результатов контрольной работы
- оценка «5» — правильно решены три задачи;
- оценка «4» — правильно решены две задачи или правильно решена одна задача, а при решении двух других задач допущены ошибки;
- оценка «3» — правильно решена одна задача;
- оценка «2» — все задачи решены неправильно.
За правильно решенную дополнительную задачу (№ 5) ставится дополнительная оценка.
Вы смотрели: Геометрия 8 класс. Контрольная работа № 2. Поурочное планирование по геометрии для 8 класса. УМК Атанасян (Просвещение). Урок 30. Контрольная работа № 2 по теме «Площадь» + ОТВЕТЫ и РЕШЕНИЯ.
Смотреть Список всех контрольных по геометрии в 8 классе по УМК Атанасян.
Вернуться к Списку уроков Тематического планирования в 8 классе.
Методическая разработка урока геометрии в 8 классе «Определение подобных треугольников»
Муниципальное бюджетное общеобразовательное учреждение «Гульцовская основная общеобразовательная школа»
Методическая разработка урока геометрии по технологии АМО
ПО ТЕМЕ
«Определение подобных треугольников», 8 класс
Черняева Леся Васильевна, учитель математики
КОНСПЕКТ АМО-УРОКА
Тема урока /занятия/мероприятияОпределение подобных треугольников
Автор учебника или УМК, по которому ведётся обучение (если имеется)
Л.С Атанасян «Геометрия 7-9».
Классификация урока/занятия/мероприятия в системе образовательных мероприятий (тип, взаимосвязь с предыдущим и последующим уроками/занятиями/мероприятиями)
Урок ознакомления с новым материалом, первый урок темы «Подобные треугольники».
Психолого – педагогическая характеристика особенностей класса /коллектива/группы
В классе обучаются 2 ученика. Одна ученица высокого уровня обученности, а второй ученик на удовлетворительном уровне. У учащейся Черняевой А. высокий познавательный интерес к предмету физики, она активна и целеустремленна, чего не скажешь о стремлениях Носорова Н. он пассивен и не проявляет интереса к предмету.
В этом возрасте проявляется «чувство взрослости», которое проявляется в стремлении сделать что-то значимое, социально поощряемое, в отстаивании собственной точки зрения, соблюдении принципов справедливости. Поэтому в данный возрастной период удачным будет применение групповых форм работы, что позволит создать условия для формирования широкого спектра способностей, выделению круга устойчивых интересов, развитию навыков личностного общения в группе сверстников и способов их взаимопонимания. Ориентируясь на средние статистические данные можно предположить, что в классе дети делятся по типу восприятия учебного материала: 50% обладают смешанным типом восприятия, а 50%-визуалы. Поэтому в данный урок были включены различные формы подачи учебного материала: иллюстративные, аудиальные (диалог, проговаривание выводов, эмоциональное «живое» слово учителя и др.), игровые ситуации. В данном классе есть одна мотивированная учащаяся. Она проявляет желание изучать физику на продвинутом уровне. При организации работы на уроке с этой учащейся учтен тот факт, что она отличается высоким уровнем самостоятельности, обладает аналитическими способностями и логическим мышлением, умеет сопоставлять и сравнивать. Вовлечение обучающихся в деятельностный процесс, создание комфортной психологической обстановки, обеспечение благоприятных эмоциногенных условий (ситуации даже маленького успеха) будет способствовать повышению мотивации к изучению математики.
Цели урока/ занятия/ мероприятия
Познакомить с новым понятием «пропорциональные отрезки», «подобны треугольники», Формировать умения использовать полученные знания при решении задач.
Задачи урока/ занятия/ мероприятия
Образовательные: создание организационных и содержательных условий для успешного усвоения учащимися понятия «пропорциональные отрезки, подобные треугольники», формирования знаний о понятии подобных треугольников и их основных свойств.
форование универсальных учебных действий, обеспечивающих обучающимися умения учиться, способность к саморазвитию и самосовершенствованию;
Развивающие:
Формирование целеполагания. Развитие продуктивного чтения.
РАЗВИТИЕ МЫШЛЕНИЯ — умения выделять существенные признаки и свойства, устанавливать единые, общие признаки и свойства целого, составлять план изучаемого материала, умения квалифицировать информацию по теме , выделять общие и существенные признаки, отличать несущественные признаки и отвлекаться от них, развитие умений применять знания на практике.
РАЗВИТИЕ ПОЗНАВАТЕЛЬНЫХ УМЕНИЙ — выделять главное, составлять план, делать выводы.
РАЗВИТИЕ ОБЩЕТРУДОВЫХ И ПОЛИТЕХНИЧЕСКИХ УМЕНИЙ — нешаблонно, творчески подходить к решению самых разнообразных задач, умение планировать, оценивать результаты выполненных действий.
РАЗВИТИЕ УМЕНИЯ УЧЕБНОГО ТРУДА — развитие умения работать в должном темпе, читать, писать, вычислять.
РАЗВИТИЕ ВОЛИ И САМОСТОЯТЕЛЬНОСТИ — развитие инициативы, уверенности в своих силах, развитие настойчивости, умение преодолевать трудности для достижения цели, развитие умения самостоятельно добывать информацию в ходе исследовательской деятельности.
Воспитательные – воспитывать умения слушать сверстников, уважать чужое мнение, способствовать воспитанию ответственности учащихся за свою деятельность на уроке, умению самостоятельно добывать знания, овладению способами и критериями самоконтроля и самооценки.
Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят/др. ученики/коллектив в ходе урока / занятия/ мероприятия
Предметные:
Знать: понятие «пропорциональные отрезки, подобные треугольники», свойство отношения площадей и периметров подобных треугольников.
Уметь: распознавать пропорциональные отрезки и подобные треугольники.
Личностные УУД: создавать позитивно-эмоциональное отношение учеников к уроку и предмету; четко выражать и объяснять (излагать) свои мысли (способы решения), умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблемы, ответственность и аккуратность. Формировать умения по самоопределению, смыслообразованию.
Регулятивные УУД: формировать умение контролировать и корректировать свою деятельность, в том числе умение давать адекватную оценку своей деятельности, воспитывать адекватное восприятие оценки со стороны, умение взаимодействовать со сверстниками в учебной деятельности, планировать свою деятельность.
Коммуникативные УУД: формирование коммуникативной компетентности учащихся (работа в паре), планирование учебного сотрудничества.
Познавательные УУД: анализ, синтез, аналогия, классификация, подведение под понятие, выполнение действий по алгоритму, контроль и оценка процесса и результатов деятельности.
Учебный материал, подлежащий усвоению, актуализации, закреплению
Актуализация:
Понятие пропорция, отношение величин, основное свойство пропорции,
Усвоение нового материала: пропорциональные отрезки, подобные треугольники, площадь и периметр подобных треугольников, коэффициент подобия.
Закрепление:
Знать определение «пропорциональных отрезков, подобных треугольников,
уметь доказывать подобие треугольников, пользуясь определением подобных треугольников, уметь пользоваться формулами: 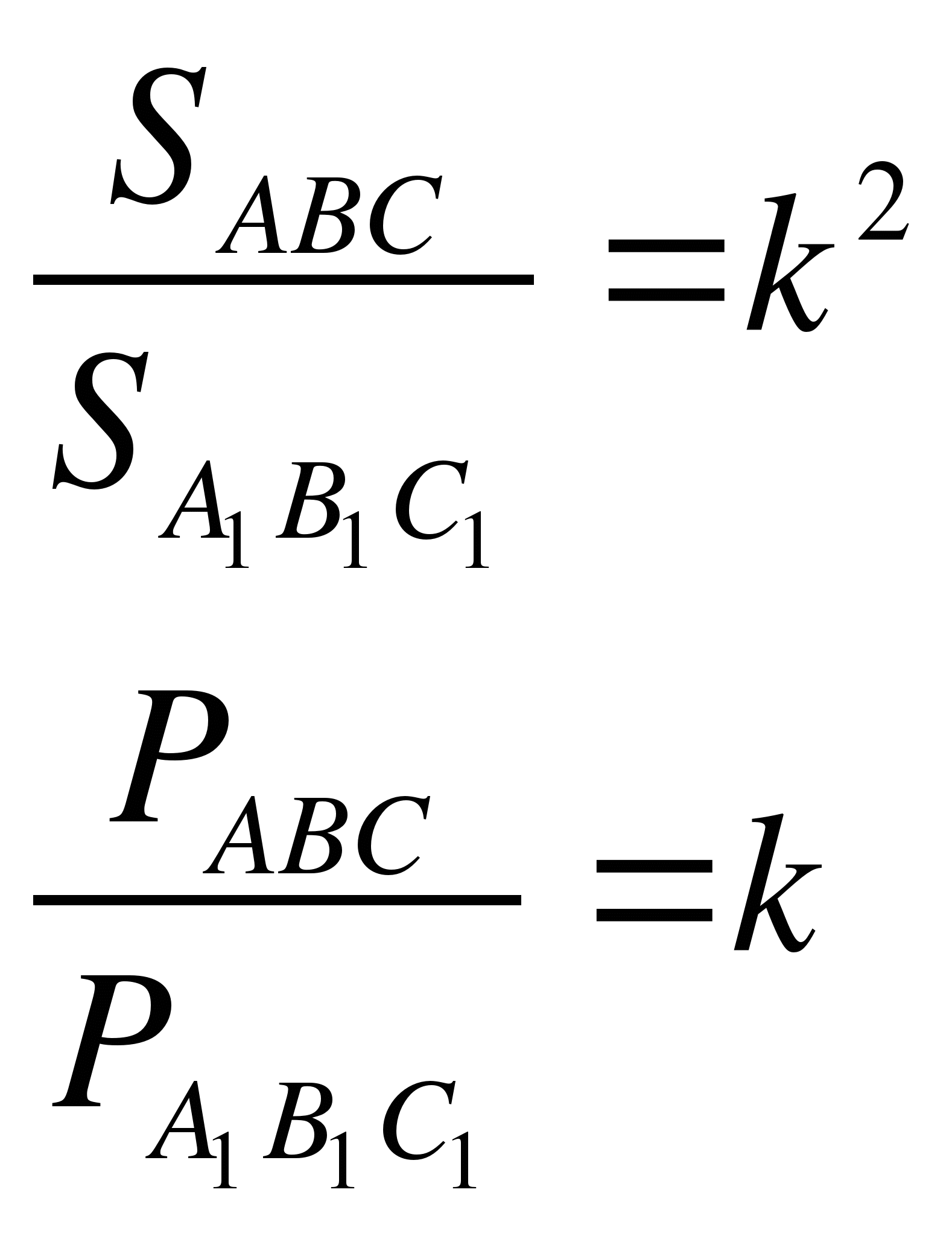 .
.
ГРАФИЧЕСКИЙ КОНСПЕКТ АМО-УРОКА
Класс: 8
Предмет: геометрия
Тема: Определение подобных треугольников.
Цель: Познакомить с новым понятием «пропорциональные отрезки, подобные треугольники» , с формулами 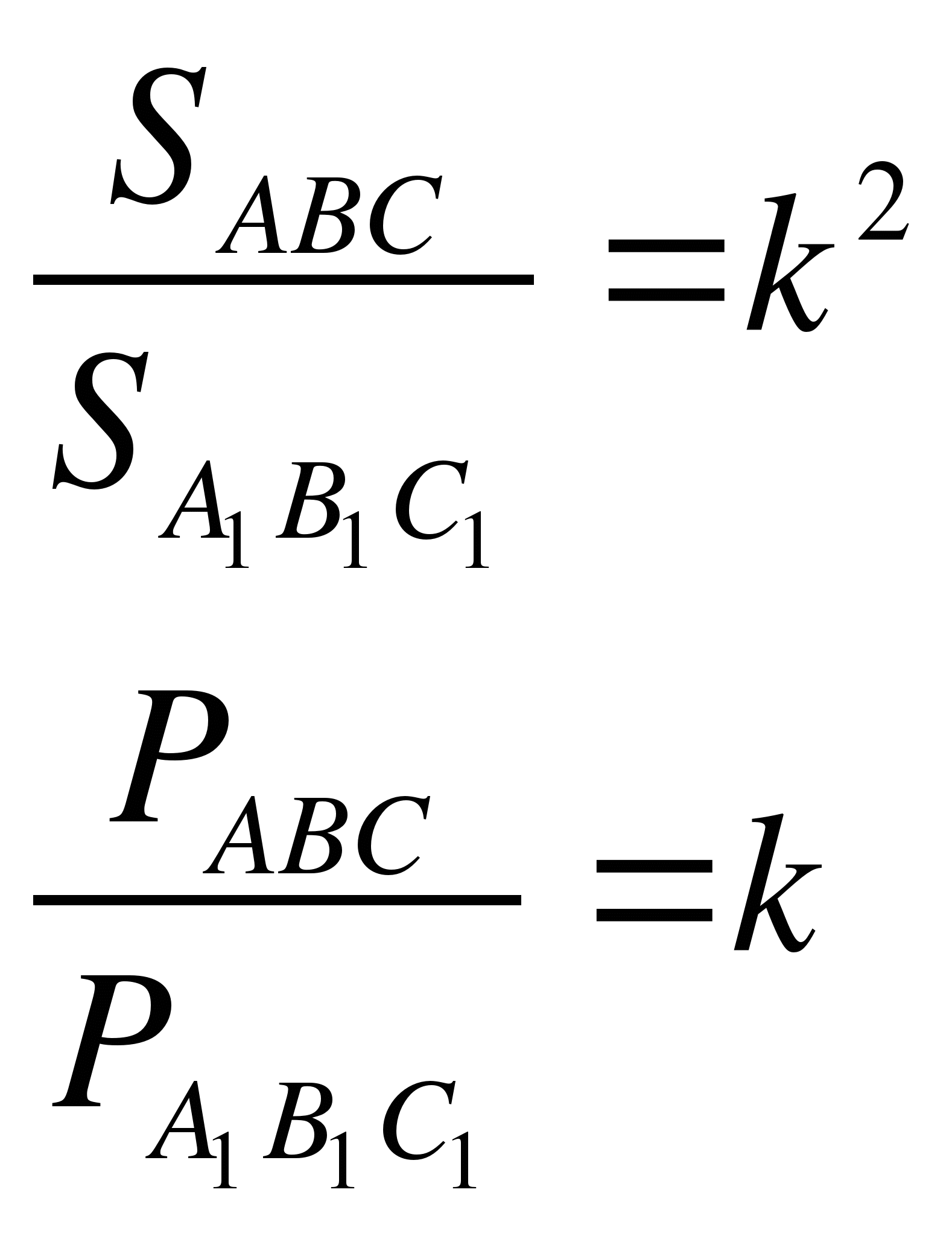 .
.
Формировать умения применять полученные знания для решения задач.
Тип урока: Урок ознакомления с новым материалом
Содержание:
основные понятия: пропорциональные отрезки, подобные треугольники.
ЗУН или УУД: знать определения пропорциональных отрезков и подобных треугольников. Уметь применять полученные знания при решении задач.
Структура урока по технологии АМО:
I фаза ОМII фаза ОМ
III фаза ОМ
1 этап
2 этап
3 этап
4этап
5этап
6 этап
7 этап
8 этап
Приветствие/ знакомство
Вхождение в тему урока (определение целей урока)
Определение ожиданий и опасений учащихся
Закрепление изученного, обсуждение домашнего задания.
Инпут (интерактивная лекция)
Проработка содержания темы
Эмоциональная разрядка
Рефлексия
АМО «Приветствие по- японски»
«Фиксирование у учащихся мотивов предыдущих достижений» «Дыши всегда!»
«Импровизированные цели»
«Восстанови запись»
«Клуб знатоков»
«Исследовательская лаборатория»
«Земля, воздух, огонь, вода»
«Что я почти забыл?»
Длительность
2 мин
5
5
6
10
10
2
5
ОПИСАНИЕ АКТИВНЫХ МЕТОДОВ ОБУЧЕНИЯ, ВКЛЮЧЕННЫХ В КОНСПЕКТ
Этап.
Название метода
Приветствие по-японски
Количество участников
2 человека
Цели задачи использования метода
Поприветствовать друг друга, создать атмосферу дружеского сотрудничества
Продолжительность проведения
2 мин
Необходимые материалы (канцелярские товары и др.), которые понадобятся для успешного проведения метода
Не требуется
Предварительная подготовка (если требуется)
Ознакомиться с обычаями приветствия в восточных странах, выявить особенности приветствия японцами.
Подробная технология проведения
Учитель просит учащихся представить себе, что они прибыли с важным визитом в страну Восходящего Солнца. В какую страну мы прибыли? (Японию). Нам необходимо расположить наших партнеров с японской стороны к нашему проекту. Как известно дружба начинается с улыбки, а деловые отношения с приветствия. Как нужно поприветствовать, чтобы переговоры прошли успешно? Поприветствуйте друг друга по-японски.
2 Этап.
Название метода
«Фиксирование у учащихся мотивов предыдущих достижений», «Дыши всегда!»
Количество участников
2 человека
Цели задачи использования метода
Обеспечение мотивации и обучения и осмысленности процесса обучения, определение цели урока, сообщение того, с чем предстоит познакомиться
Продолжительность проведения
5 мин
Необходимые материалы (канцелярские товары и др.), которые понадобятся для успешного проведения метода
________.
Предварительная подготовка (если требуется)
Не требуется.
Подробная технология проведения
Цели: Обеспечение мотивации и обучения и осмысленности процесса обучения, определение цели урока, сообщение того, с чем предстоит познакомиться.
Подготовить материал по теме. Технология проведения: Учитель предлагает учащимся не дышать. Кто дольше сможет не дышать.
Вызвать мотивы относительной неудовлетворенности.
Далее сформулировать тему урока, цели урока.
3 Этап.
Название метода
«Импровизированные цели»
Количество участников
25 человек
Цели задачи использования метода
Цель: Концентрация внимания, обеспечение ответственности за результат.
Задачи: Формулирование задач, необходимых для достижения целей урока через выяснение ожиданий и опасений учащихся
Продолжительность проведения
5 мин
Необходимые материалы (канцелярские товары и др.), которые понадобятся для успешного проведения метода
Лист бумаги формата А2 с записанной целью урока: «Изучить понятие пропорциональных отрезков и подобных треугольников»
Предварительная подготовка (если требуется)
На доску вывешивается лист А2, в середине которого в кругу записана цель урока (записывается после её озвучивания). Вокруг неё, изображены пустые круги или овалы.
Подробная технология проведения
Учащимся предлагают подумать и обсудить в группах задания, над которыми будет проведена работа на уроке. Среди них могут быть такие: «повторить понятия пропорция, основное свойство пропорции. «учиться работать в группе» и т.д. Затем представители каждой группы выходят к доске и записывают сформулированные задачи в чистых кружках. в овалах записывают свои опасения по данному заданию.
4 Этап.
Название метода
«Восстанови запись»
Количество участников
2 человека
Цели задачи использования метода
Закрепление ранее изученного материала
Продолжительность проведения
6 мин
Необходимые материалы (канцелярские товары и др.), которые понадобятся для успешного проведения метода
Задания с пропусками по пройденным темам.
Предварительная подготовка (если требуется)
Подготовить задания на тему «Отношение отрезков», содержащих пропуски.
Подробная технология проведения
Участникам предлагается представить решения задачи домашнего задания на доске и в тетради. В отдельных фрагментах необходимо восстановить по смыслу содержание, далее соединить фрагменты задания в нужном порядке (склеить листы бумаги), так чтобы получилась связанная запись. Далее восстановленная запись зачитывается и обсуждается. (Могут возникнуть моменты, когда группы допускают ошибки, обсудить возникшие ошибки, внести исправления).
5 этап
Название метода
«Клуб знатоков»
Количество участников
2 человека
Цели задачи использования метода
Получение новых знаний по теме.
Продолжительность проведения
10 мин
Необходимые материалы (канцелярские товары и др.), которые понадобятся для успешного проведения метода
Карточки с примерами и заданиями для самостоятельной работы.
и опорные конспекты для каждого учащегося.
Предварительная подготовка (если требуется)
Подготовка и распечатка вопросов заданий для составления опорного конспекта.
Подробная технология проведения
Учащиеся работают в группе. В каждой группе обсуждаются вопросы:
Что показывает отношение отрезков?
Что такое подобные треугольники?
Что такое коэффициент подобия? Чему он равен?
Чему равно отношение площадей и периметров подобных треугольников?
Учащиеся фиксируют свои ответы на опорном конспекте.
6 этап
Название метода
«Исследовательская лаборатория»
Количество участников
2 человека
Цели задачи использования метода
Получение новых знаний по теме.
Продолжительность проведения
10 мин
Необходимые материалы (канцелярские товары и др.), которые понадобятся для успешного проведения метода
Карточки с примерами и заданиями для самостоятельной работы.
и опорные конспекты для каждого учащегося.
Предварительная подготовка (если требуется)
Подготовка и распечатка вопросов заданий для составления опорного конспекта.
Подробная технология проведения
Учащиеся работают в группе. В каждой группе обсуждаются вопросы:
Что показывает отношение отрезков?
Что такое подобные треугольники?
Что такое коэффициент подобия? Чему он равен?
Чему равно отношение площадей и периметров подобных треугольников?
Учащиеся фиксируют свои ответы на опорном конспекте.
7 Этап.
Название метода
«Земля, воздух, огонь, вода»
Количество участников
2 человека
Цели задачи использования метода
Повысить уровень энергии в классе
Продолжительность проведения
2 мин
Необходимые материалы (канцелярские товары и др.), которые понадобятся для успешного проведения метода
Не требуется
Предварительная подготовка (если требуется)
Не требуется
Подробная технология проведения
Учитель просит обучающихся по его команде изобразить одно из состояний – воздух, землю, огонь и воду.
Воздух. Ученики начинают дышать глубже, чем обычно. Они встают и делают глубокий вдох, а затем выдох. Каждый представляет, что его тело, словно большая губка, жадно впитывает кислород из воздуха. Все стараются услышать, как воздух входит в нос, почувствовать, как он наполняет грудь и плечи, руки до самых кончиков пальцев; как воздух струится в области головы, в лицо; воздух заполняет живот, область таза, бедра, колени и стремится дальше – к лодыжкам, ступням и кончикам пальцев. Ученики делают несколько глубоких вдохов и выдохов. Можно предложить всем пару раз зевнуть. Зевота – естественный способ компенсировать недостаток кислорода.
Земля. Теперь ученики должны установить контакт с землей, «заземлиться» и почувствовать уверенность. Учитель вместе с обучающимися начинает сильно давить на пол, стоя на одном месте, можно топать ногами и даже пару раз подпрыгнуть верх. Можно потереть ногами пол, покрутиться на месте. Цель – по-новому ощутить свои ноги, которые находятся дальше всего от центра сознания, и благодаря этому телесному ощущению почувствовать большую стабильность и уверенность.
Огонь. Ученики активно двигают руками, ногами, телом, изображая языки пламени. Учитель предлагает всем ощутить энергию и тепло в своем теле, когда они двигаются подобным образом.
Вода. Эта часть упражнения составляет контраст с предыдущей. Ученики просто представляют себе, что комната превращается в бассейн, и делают мягкие, свободные движения в «воде», следя за тем, чтобы двигались суставы – кисти рук, локти, плечи, бедра, колени.
Можно дать дополнительные 2 минуты времени, чтобы каждый мог создать свою индивидуальную комбинацию элементов.
8 Этап.
Название метода
«Что я почти забыл?»
Количество участников
2 человека.
Цели задачи использования метода
Получение эмоциональной и содержательной оценки процесса и результатов обучения
Продолжительность проведения
5 мин
Необходимые материалы (канцелярские товары и др.), которые понадобятся для успешного проведения метода
Карточки, листы бумаги.
Предварительная подготовка (если требуется)
Лучше подготовить не полный перечень опорных слов, которые бы поэтапно характеризовали урок.
Подробная технология проведения
Учащимся предлагается обсудить то с чем они столкнулись во время урока. Составить список дел за урок. Далее каждый по очереди говорит: «Я почти забыл, что на уроке (произошло, изучалось, повторялось) ….
Презентация к уроку по геометрии (8 класс) на тему: Решение задач на применение признаков подобия треугольников.
Слайд 1
Решение задач на применение признаков подобия треугольников. Учитель математики ГБОУ школы № 655, Кулешовой Галины Михайловны .Слайд 2
Цели урока. Дидактическая цель : создание условий для осознания и осмысления нового учебного материала о признаках подобия треугольников , об использовании признаков при решении задач, постановки и конструктивного решения учебных проблем, развития внутренней мотивации учения школьников. Обучающая : Познакомить детей с признаками подобия треугольников, научить выяснять, являются ли треугольники подобными, научить доказывать теоремы – признаки подобия треугольников. Развивающая : Развивать познавательный интерес к предмету, умение доказывать теоремы, а также умение рассуждать, делать выводы, опираясь на ранее полученные знания. Воспитательная : Воспитывать чувство коллективизма, показать значимость каждого из учеников в единой работе класса через совместное выполнение познавательных заданий; способствовать развитию познавательного интереса к предмету при организации проблемных ситуаций на уроке. Методы обучения: репродуктивный, объяснительно-иллюстративный и частично-поисковый.
Слайд 3
Ход урока. I . Организационный момент. II . Повторение теоретического материала. III . Решение задач на готовых чертежах. IV . Работа с учебником. V . Самостоятельная работа ( двух уровней). VI .Домашнее задание.
Слайд 4
: Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональны сходственным сторонам другого. А 1 В 1 С 1 А В С А 1 = А, В 1 = В, С 1 = С , А 1 В 1 В 1 С 1 А 1 С 1 АВ ВС АС k. A 1 B 1 C 1 ABC , K – коэффициент подобия . ~ Сходственными сторонами в подобных треугольниках называются стороны, лежащие против равных углов .
Слайд 6
Задачи на готовых чертежах. 1 2
Слайд 12
Самостоятельная работа .
Презентация к уроку по геометрии (8 класс) по теме: Прямоугольный треугольник.Решение задач
Слайд 2
Если один из углов треугольника прямой, то треугольник называется прямоугольным. А В С Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой , гипотенуза катет а две другие – катетами . Треугольник – это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки. катет
Слайд 3
С A B α β α + β = 90 0
Слайд 4
30 0 C A B
Слайд 5
A B C M r CM = AM = BM = r Медиана отсекает равнобедренные треугольники
Слайд 6
1.Если катеты одного прямоугольного треугольника равны катетам другого, то эти треугольники равны. A B C E D F
Слайд 7
2.Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого , то эти треугольники равны. A B C D F E
Слайд 8
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то эти треугольники равны. A B C E F D
Слайд 9
4.Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то эти треугольники равны A B C D E F
Слайд 11
Квадрат гипотенузы равен сумме квадратов катетов . a b c
Слайд 12
1. Синусом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе. A B C
Слайд 13
2 . Косинусом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе A B C
Слайд 14
3 . Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему A B C
Слайд 15
4 . Котангенсом острого угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему. A B C
Слайд 16
0 0 30 0 45 0 60 0 90 0 sin 0 1 cos 1 0 tg 0 1 — ctg — 1 0
Слайд 17
Задачи по готовым чертежам А С В D ? В А С 37 0 ? ? А В С 70 0 ? А В С 30 0 16 см ? 120 0 4 см D С А В ? 4,2 см 8,4 см Ответ:53 Ответ:50 Ответ:8 Ответ:30;60 Ответ:8
Слайд 18
1. В прямоугольном треугольнике АВС, угол С равен 90 0 ,АВ=55, cos B=0.8. Найдите АС. А В С Решение Ответ:33 ( по т.Пифагора)
Слайд 19
2. Катеты прямоугольного треугольника равны 40 см. и 42 см.Найдите радиусы описанной и вписанной окружностей . Решение (по т.Пифагора) Ответ:29;12 A B C 40 42
Слайд 20
3.В прямоугольном треугольнике ABC, угол А= 90 0 , АВ=20 см, высота AD=12 см. Найти АС и cosC? Решение Ответ:15; 0,6 A B C D 20 12