Конспект урока по физике Решение задач по теме «Статика. Условие равновесия тел» (10 кл)
Урок Решение задач «Статика. Условие равновесия тел» 10 кл
Учитель Смирнова С.Г.
МОУ «Луховский лицей»
Тип урока: Урок-практикум.
Цель урока: Привить умение применять законы Ньютона и правило моментов при решении расчетных задач
Задачи урока:
Образовательные: повторить условие равновесия тела, второй закон Ньютона
Развивающие: развивать внимание и речь, совершенствовать навыки самостоятельной работы, привить умения применять второй закон Ньютона и условие равновесия тел при решении расчетных задач
Воспитательные формировать целостное представление обучающихся о мире (природе, обществе и самом себе), о роли и месте физики в системе наук.
Оборудование: компьютер учителя, мультимедийный проектор, Физика 7-11 Библиотека электронных наглядных пособий. “Кирилл и Мефодий”.
Ход урока
1. Орг.момент
2. Организация внимания учащихся
Тема нашего урока: Решение задач «Статика. Условие равновесия тел»
3. Актуализация опорных знаний
Прежде чем перейти к решению задач, предлагаю проверить как вы к этому готовы.
Фронтальный опрос:
При каком условии тело находится в равновесии?
Покажите на рисунке силы, действующие на тело, равномерно движущееся по горизонтали
Покажите на рисунке силы, действующие на тело при его движении равномерно вверх по наклонной плоскости
Выберите систему координат, определите проекции этих сил на координатные оси
Изучение нового материала (решение задач)
Задача 1. Груз висит на двух тросах (рис. на слайде). Угол АСВ равен 120°. Сила тяжести, действующая на груз, равна 600 Н. Определите силы натяжения тросов АС и СВ.
Решение. Силы натяжения тросов обозначим через 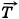 1и
1и 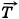 2. Эти силы направлены вдоль тросов от точки С (рис. 7.5, б). Кроме этих сил, на точку С действует сила тяжести m
2. Эти силы направлены вдоль тросов от точки С (рис. 7.5, б). Кроме этих сил, на точку С действует сила тяжести m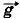 . Точка С находится в равновесии. Следовательно, сумма сил, действующих на неё, равна нулю:
. Точка С находится в равновесии. Следовательно, сумма сил, действующих на неё, равна нулю:
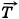 1 +
1 + 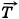 2 + m
2 + m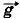 = 0.
= 0.
Оси координат выберем так, как показано на рисунке (7.5, в). При равновесии сумма проекций всех сил на оси координат равна нулю:
T1x + T2х + mgх = 0, Т1у + Т2у + mgy = 0,или
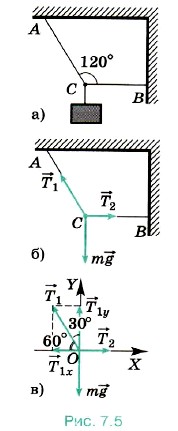
T1 — T1cos60° = 0, T1cos30° — mg = 0. Отсюда
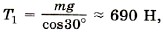 Т2 = T1cos60° ≈ 345 Н.
Т2 = T1cos60° ≈ 345 Н.
Задача 2. Дверь люка АО, которая может поворачиваться в шарнире О без трения, удерживается в горизонтальном положении верёвкой (рис. на слайде). Определите натяжение верёвки и силу реакции шарнира, если верёвка образует с дверью угол α = 60°. Дверь однородна и на неё действует сила тяжести 300 Н.
Решение. На дверь люка действуют три силы (рис. на слайде). сила тяжести m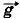 , приложенная к середине двери в точке D, сила натяжения
, приложенная к середине двери в точке D, сила натяжения 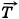 со стороны верёвки и сила реакции
со стороны верёвки и сила реакции 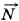 со стороны шарнира.
со стороны шарнира.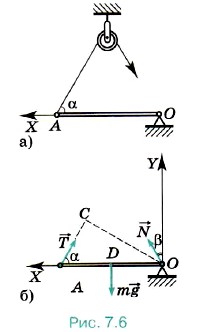
Выберем оси координат так, как показано на рисунке (рис. на слайде). Поскольку дверь находится в равновесии, то сумма моментов всех сил относительно, например, шарнира равна нулю: М1 + М + М2 = 0.
Здесь M1, М, М2 — моменты сил 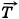 , m
, m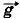 и
и 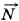 . Найдём плечи этих сил, обозначив |АО| = l. Тогда OD = l/2 — плечо силы m
. Найдём плечи этих сил, обозначив |АО| = l. Тогда OD = l/2 — плечо силы m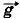 , СО = AOsinα = lsinα — плечо силы
, СО = AOsinα = lsinα — плечо силы 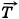 . Плечо силы
. Плечо силы 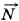 равно нулю, так как она приложена в шарнире.
равно нулю, так как она приложена в шарнире.
Значит, М1 = -Tlsinα, 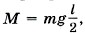 М2 = 0.
М2 = 0.
Теперь запишем правило моментов сил, учитывая знаки этих моментов: 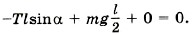
Отсюда находим силу натяжения верёвки:
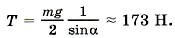
Для нахождения силы реакции шарнира воспользуемся первым условием равновесия:
m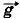 +
+ 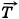 +
+ 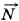 =0.
=0.
Запишем это векторное уравнение в проекциях на координатные оси:
—Тх + Nx = 0, Ту + Ny — mg = 0,
или Nх = Тcosα, 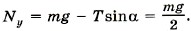
Отсюда Nх = 86,5 H; Nхy = 150 H.
Модуль силы N равен 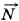
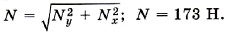
Угол, который образует сила 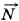 с координатной осью OY:
с координатной осью OY: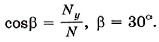
Задача 3. Лестница прислонена к стене. При каком минимальном угле наклона к полу она не будет падать? Коэффициенты трения между лестницей и стеной и между лестницей и полом соответственно равны μ1 и μ2.
Решение. На лестницу действуют следующие силы (рис. на слайде). тяжести m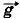 , нормальной реакции со стороны стены
, нормальной реакции со стороны стены 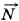 1 и пола
1 и пола 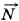 2, трения
2, трения 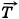 тр1 и
тр1 и 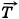 тр2.
тр2.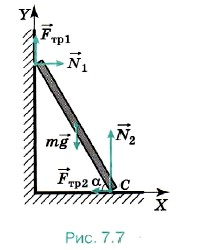
Первое условие равновесия для лестницы имеет вид
m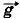 +
+ 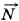 1 +
1 + 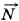 2 +
2 + 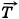 тр1 +
тр1 + 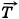 тр2 = 0. (1)
тр2 = 0. (1)
Для записи правила моментов выберем ось вращения, проходящую через точку С, и запишем:
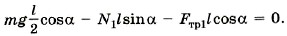
Из последнего уравнения следует: 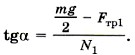
Выразим силы N1 и Fтp1 через силу тяжести. Для этого запишем уравнение (1) в проекциях на оси координат:
на ось X: N1 — F.rp2 = О,
на ось Y: Fтp1 + N2 — mg = 0.
По условию задачи требуется найти минимальное значение угла amin, поэтому берём максимальные значения сил трения, т. е. Fтp1 = μ1N1, и Fтp2 = μ2N2. Тогда 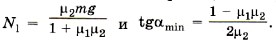
На дом: решить задачу
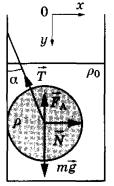
Свинцовый шар подвешен на нити и полностью погружён в воду (см. рисунок). Нить образует с вертикалью угол a =30°. Модуль силы, с которой нить действует на шар, Т = 30 Н. Плотность свинца p =11300 кг/м3. Чему равна масса шара? Трением шара о стенку пренебречь. Сделайте схематический рисунок с указанием сил, действующих на шар.
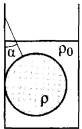
Решение (на следующем уроке разобрать)
Систему отсчёта, связанную с Землей, считаем инерциальной. Запишем второй закон Ньютона: 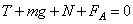 . Поскольку трение шара о стенку отсутствует, линия действия силы натяжения нити будет проходить через центр шара. В проекциях на оси Ох и Оу второй закон Ньютона запишем в виде:
. Поскольку трение шара о стенку отсутствует, линия действия силы натяжения нити будет проходить через центр шара. В проекциях на оси Ох и Оу второй закон Ньютона запишем в виде:
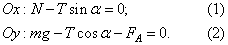
 Объём шара
Объём шара 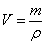 .
.
Величина выталкивающей силы 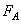 определяется по закону Архимеда: где
определяется по закону Архимеда: где 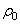 — плотность воды. Выполняя математические преобразования с формулами (2) и (3), получим:
— плотность воды. Выполняя математические преобразования с формулами (2) и (3), получим:
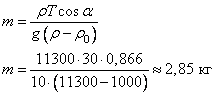
infourok.ru
Статика. Часть 3. Решение задач.
В этой статье продолжим разбирать решение задач по теме «Статика».
Задача1.
На тело массой 2 кг, лежащее на столе действует горизонтальная сила 10 Н. На сколько необходимо увеличить массу тела, чтобы тело оставалось в покое, если коэффициент трения между телом и столом µ = 0,4, g = 10 м/с2?
Решение.
Если увеличить массу тела на m2, то его масса станет m1 + m2. На чертеже обозначим все силы, действующие на тело: со стороны Земли – сила тяжести (m1 + m2)g, со стороны стола – сила реакции опоры N, горизонтальная сила F и сила трения Fтр.
Запишем II закон Ньютона для этого случая: (m1 + m2)g-> + N-> + F->
+ Fтр-> = 0.Запишем это уравнение в проекциях на оси, с учётом знаков:
ОХ: -F + Fтр = 0 (1)
ОУ: -(m1 + m2)g + N = 0 (2)
Из уравнения (1) => F = Fтр (3).
С учётом того, что Fтр = µN получаем F = µN, откуда N = F/µ (4)
Из уравнения (2) и (4) => (m1 + m2)g = N = F/µ
m1 + m2 = F/µg
m2 = F/µg – m1
В полученную конечную формулу подставляем числовые значения:
m2 = 10 Н / 0,4 · 10 м/с2 – 2 кг = 0,5 кг
Ответ: m2 = 0,5 кг.
Задача 2.
Труба лежит на земле. Рассчитайте массу трубы, если известно, что для того, чтобы приподнять её за один конец, необходимо приложить силу F = 20 Н, g = 10 м/с

Если в этой задаче слово «приподнять» заменить словом «оторвать», то довольно легко заметить из чертежа, что мы получаем рычаг с осью вращения в точке О.
Считая угол отрыва очень малым, запишем правило моментов для этого условия:
Mmg – MF = 0
mg0,5L – FL = 0
mg0,5 = F
m = F/0,5g
m = 20 Н / 0,5 · 10 м/с2 = 4 кг
Ответ: m = 4 кг.
Задача 3.
Рассчитайте минимальную горизонтальную силу необходимую для поворота через нижнее ребро покоящегося на горизонтальной плоскости куба массой m и длиной ребра а.
Решение.
Точку О на нижней грани выберем как ось поворота, тогда:

Запишем правило моментов для этой задачи, с учётом знаков:
MF – Mmg = 0
Fа – mg0,5а = 0
F = 0,5mg
Ответ: F = 0,5mg
Остались вопросы? Не знаете, как решить задачу по статике?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Решение задач по теме «Статика»
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- Повторить условия равновесия тел;
- Углубить знания учащихся по данной теме;
- Продемонстрировать возможности поэтапного решения задач по теме “Статика” с использованием предложенного плана и отработать умение пользоваться им при решении задач различного уровня сложности;
- Развивать умение мыслить логически, выражать неизвестную величину из полученной формулы, совершенствовать счетные навыки ребят
Оборудование: презентация.
Ход урока
1. Оргмомент. Вводное слово учителя.
2. Повторение изученного материала:
(Слайды № 2- 6)
- На столе лежат три книги (рис.1). Значения сил тяжести, действующих на каждую книгу, указаны на рисунке. Какова величина суммарной силы, действующей на книгу №2?
1) 0. 2) 12 Н. 3) 5 Н. 4) 9 Н.
- Однородный куб опирается одним ребром на пол, другим – на вертикальную
Стену (рис 2). Плечо силы упругости N
1) 0 2) О2О1 3) О1О 4)О2О
- Труба массой М = 1 т лежит на земле. Какую силу (в кН) надо приложить, чтобы приподнять краном трубу за один из ее концов?
1) 10 кН 2) 5 кН 3) 15 кН 4) 20 кН
- На рисунке (рис.3) схематически изображена
металлическая труба, прислонённая к гладкой
стене. Каков момент силы трения F
1) 0 2) FТР·OD 3) FТР·AB 4) FТР·AM
- Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно точки В, если АВ=0,5 м и угол =450 (рис.4)
1) 10 Н·м. 2)5 Н·м. 3) 0 Н·м. 4) 200 Н·м.
(Опрос ведется в достаточно быстром темпе, все ответы даются с объяснением)
3. Сообщение темы урока. Изложение нового материала.
Ребята! Сегодня мы продолжим решать расчетные задачи по теме “Статика”.
Повторим алгоритм решения задач по данной теме.
(слайд № 7)
При решении задач на равновесие тел:
1. Сделать рисунок, показать все силы, действующие на тело (или тела системы), находящиеся в положении равновесия, выбрать систему координат и определить направление координатных осей.
2. Для тела, не имеющего оси вращения, записать первое условие равновесия в векторной форме F = 0, затем записать это условие равновесия в проекциях на оси координат и получить уравнение в скалярной форме.
3. Для тела, с закрепленной осью вращения, следует определить плечи всех сил относительно этой оси и использовать второе условие равновесия (правило моментов): М = 0. Если из условия задачи следует, что ось вращения тела не закреплена, то необходимо использовать оба условия равновесия. При этом положение оси вращения следует выбирать так, чтобы через нее проходило наибольшее число линий действия неизвестных сил.
4. Решить полученную систему уравнений и определить искомые величины.
Задачи без рисунка, даже решенные правильно, я не рассматриваю!
Итак, начнем с поэтапного решения первой задачи
(слайд №8)
(Рассматривается ход решения предложенной задачи с пошаговой опорой на анимированный слайд. Причем, делается акцент на каждом шаге на умение правильно использовать ранее изученный (и проработанный вначале урока) материал в процессе решения задачи. При решении задачи применяется и первое, и второе условия равновесия. Выбор оси вращения в центре шара устраняет момент неизвестной силы тяжести.)
4. Решение задач у доски (слайды №№ 9–15).
Учащиеся выходят по очереди к доске и с опорой на предложенный план решают остальные задачи и сравнивают с предложенным решением
Задача №1. К гвоздю, вбитому в стенку, привязана нить, намотанная на катушку. Катушка висит, касаясь стенки, как показано на рисунке. Радиус оси катушки r = 0,5 см, радиус ее щечек R = 10 см. Коэффициент трения между стенкой и катушкой = 0,1. При каком угле между нитью и стенкой катушка висит неподвижно? (рис.5)
Задача №2. Цилиндр массой m = 150 кг удерживается на наклонной плоскости с помощью ленты, с одной стороны закрепленной на наклонной плоскости, а с другой направленной параллельно плоскости. Найти силу натяжения ленты. Угол наклона плоскости = 30°. (рис.6)
(Задачу можно решить, применяя либо только первое условие равновесия, либо только второе)
Задача №3. Однородный шар радиуса R
подвешен на нити длиной
(При решении задачи применяются и первое, и второе условия равновесия)
Задача №4. Какой минимальной горизонтальной силой можно опрокинуть через ребро куб, лежащий на горизонтальной плоскости?
Дополнительно для сильных учеников задача №5. Тонкостенная полусфера массой M и радиусом R покоится на горизонтальном столе. На какую высоту опустится край полусферы, если на него сядет муха массой m? Центр тяжести полусферы расположен на расстоянии a = 1/2R от ее центра. (Рис.8) (слайд № 16-17)
5. Подведение итогов урока.
Домашнее задание (слайд № 18)по сборнику Л.А.Кирик. Физика. Разноуровневые самостоятельные и контрольные работы по физике 9 класс. Москва, Илекса,2006.
Решение задач
urok.1sept.ru
Примеры решения задач по теме «Равновесие твёрдых тел»
Примеры решения задач по теме «Равновесие твёрдых тел»
«Физика — 10 класс»
При решении задач статики надо использовать условия равновесия (7.9). Причём от векторного уравнения для суммы сил следует перейти к проекциям сил на координатные оси. Иногда удобнее решать задачу, используя геометрическое правило сложения векторов. При равновесии многоугольник сил должен быть замкнутым, так как сумма сил равна нулю (подобный пример будет рассмотрен ниже).
При записи для правила моментов сил надо подумать, как выбрать ось, чтобы плечи сил определялись наиболее просто и в сумме моментов сил содержалось меньше слагаемых.
В задачах часто рассматриваются стержни, которые скрепляются шарнирно. При этом имеется в виду, что трение в шарнире отсутствует.
Задача 1.
Груз висит на двух тросах (рис. 7.5, а). Угол АСВ равен 120°. Сила тяжести, действующая на груз, равна 600 Н. Определите силы натяжения тросов АС и СВ.
Р е ш е н и е.
Силы натяжения тросов обозначим через 1 и 2. Эти силы направлены вдоль тросов от точки С (рис. 7.5, б). Кроме этих сил, на точку С действует сила тяжести m. Точка С находится в равновесии. Следовательно, сумма сил, действующих на неё, равна нулю:
1 + 2 + m = 0.
Оси координат выберем так, как показано на рисунке (7.5, в). При равновесии сумма проекций всех сил на оси координат равна нулю:
T1x + T2х + mgх = 0, Т1у + Т2у + mgy = 0,
или
T1 — T1cos60° = 0, T1cos30° — mg = 0.
Отсюда
Т2 = T1cos60° ≈ 345 Н.
Задача 2.
Дверь люка АО, которая может поворачиваться в шарнире О без трения, удерживается в горизонтальном положении верёвкой (рис. 7.6, а). Определите натяжение верёвки и силу реакции шарнира, если верёвка образует с дверью угол α = 60°. Дверь однородна и на неё действует сила тяжести 300 Н.
>Р е ш е н и е.
На дверь люка действуют три силы (рис. 7.6, б): сила тяжести m, приложенная к середине двери в точке D, сила натяжения со стороны верёвки и сила реакции со стороны шарнира.
Выберем оси координат так, как показано на рисунке (7.6, б). Поскольку дверь находится в равновесии, то сумма моментов всех сил относительно, например, шарнира равна нулю: М1 + М + М2 = 0.
Здесь M1, М, М2 — моменты сил , m и . Найдём плечи этих сил, обозначив |АО| = l. Тогда OD = l/2 — плечо силы m, СО = AOsinα = lsinα — плечо силы . Плечо силы равно нулю, так как она приложена в шарнире.
Значит, М1 = -Tlsinα, М2 = 0.
Теперь запишем правило моментов сил, учитывая знаки этих моментов:
Отсюда находим силу натяжения верёвки:
Для нахождения силы реакции шарнира воспользуемся первым условием равновесия:
m + + =0.
Запишем это векторное уравнение в проекциях на координатные оси:
—Тх + Nx = 0, Ту + Ny — mg = 0,
или Nх = Тcosα,
Отсюда Nх = 86,5 H; Nхy = 150 H.
Модуль силы N равен
Угол, который образует сила с координатной осью OY:
Задача 3.
Лестница прислонена к стене. При каком минимальном угле наклона к полу она не будет падать? Коэффициенты трения между лестницей и стеной и между лестницей и полом соответственно равны μ1 и μ2.
Р е ш е н и е.
На лестницу действуют следующие силы (рис. 7.7): тяжести m, нормальной реакции со стороны стены 1 и пола 2, трения тр1 и тр2.
Первое условие равновесия для лестницы имеет вид
m + 1 + 2 + тр1 + тр2 = 0. (1)
Для записи правила моментов выберем ось вращения, проходящую через точку С, и запишем:
Из последнего уравнения следует:
Выразим силы N1 и Fтp1 через силу тяжести. Для этого запишем уравнение (1) в проекциях на оси координат:
на ось X: N1 — F.rp2 = О,
на ось Y: Fтp1 + N2 — mg = 0.
По условию задачи требуется найти минимальное значение угла amin, поэтому берём максимальные значения сил трения, т. е. Fтp1 = μ1N1, и Fтp2 = μ2N2
Тогда
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Статика — Физика, учебник для 10 класса — Класс!ная физика
Равновесие тел — Примеры решения задач по теме «Равновесие твёрдых тел»
class-fizika.ru
Статика: задачи ненулевого уровня
В этой статье собраны задачи из задачника Русакова и др. Задачи «крепкие» – тянут на подготовку к городскому этапу олимпиады. Вполне доступны для решения школьниками от 8 класса, знакомыми с азами тригонометрии – геометрическими определениями основных функций.
Задача 1. Грузы  и
и  висят на нити, перекинутой через блок. Система находится в равновесии. Найти массу груза
висят на нити, перекинутой через блок. Система находится в равновесии. Найти массу груза  , если известны углы
, если известны углы  ,
,  и масса
и масса  .
.

Рисунок 1
Запишем условие равновесия груза  :
:
![Rendered by QuickLaTeX.com \[m_2g=T_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-23ad4a5204aea17494e68880f5cb9365_l3.png)
И условие равновесия груза  :
:
![Rendered by QuickLaTeX.com \[T_1\sin{\beta}+T_2\sin{\alpha}=m_1g~~~~~~~~~~~~~~(1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-69b12a1ee42d547dff3498734030e30d_l3.png)
Очевидно также, что
![Rendered by QuickLaTeX.com \[T_1\cos{\beta}=T_2\cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ad4f25b59c32aa25630f5148e5fba5c3_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[T_2=\frac{ T_1\cos{\beta}}{\cos{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c7fc20c5da5f7c0f2c157963f336a2e4_l3.png)
Подставим в (1):
![Rendered by QuickLaTeX.com \[T_1\sin{\beta}+\frac{ T_1\cos{\beta}}{\cos{\alpha}}\sin{\alpha}= m_1g\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ecbece323b379d2e3b70d9f411098828_l3.png)
Или
![Rendered by QuickLaTeX.com \[m_2\sin{\beta}+m_2\cos{\beta}}\operatorname{tg}{\alpha}= m_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5265f9c16679762bfe54c6d704bf0599_l3.png)
Ответ:  .
.
Задача 2. Два мальчика – маленький  и большой
и большой  , качаются на уравновешенной доске, сидя на ее концах. Известно, что точка опоры находится на расстоянии, равном
, качаются на уравновешенной доске, сидя на ее концах. Известно, что точка опоры находится на расстоянии, равном  длины доски от маленького мальчика. Найти массу доски.
длины доски от маленького мальчика. Найти массу доски.

Рисунок 2
Условие равновесия доски:
![Rendered by QuickLaTeX.com \[m_1g\cdot \frac{3L}{4}+Mg\cdot\frac{L}{4}=m_2g\frac{L}{4}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1e2a9ee53c2592ef0768e19105092586_l3.png)
Или
![Rendered by QuickLaTeX.com \[M=m_2-3m_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4b1023d762e4ea0b9f6afebb64528cc9_l3.png)
Ответ: 
Задача 3. Квадрат со стороной  составлен из четырех тонких стержней, плотность материала которых
составлен из четырех тонких стержней, плотность материала которых  и
и  . С квадратом связана система координат. Найти координаты центра масс системы.
. С квадратом связана система координат. Найти координаты центра масс системы.

Рисунок 3
Определим координату центра тяжести по оси  :
:
![Rendered by QuickLaTeX.com \[x=\frac{1}{M}\sum m_i x_i=\frac{1}{aS\rho+ 2aS\rho+ 3aS\rho+4aS\rho}\left(\frac{a^2}{2}S(2\rho+4\rho)+0\cdot aS\rho+a^2S\cdot 3\rho\right)= \frac{6a^2S}{10aS}=0,6a\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-40ddd46afe5b1241d57dd7a7b19ab30d_l3.png)
Аналогично по оси  :
:
![Rendered by QuickLaTeX.com \[y=\frac{1}{M}\sum m_i y_i=\frac{1}{aS\rho+ 2aS\rho+ 3aS\rho+4aS\rho}\left(\frac{a^2}{2}S(\rho+3\rho)+0\cdot 4aS\rho+a^2S\cdot 2\rho\right)= \frac{4a^2S}{10aS}=0,4a\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a675c87ea5a932e1358ab0c8aa089bc1_l3.png)
Ответ:  .
.
Задача 4. Тонкий однородный стержень укреплен шарнирно в точке  и удерживается в равновесии горизонтальной нитью. Нить и стержень образуют угол
и удерживается в равновесии горизонтальной нитью. Нить и стержень образуют угол  . Масса стержня
. Масса стержня  . Найти: а) силу натяжения нити; б) модуль силы реакции шарнира при
. Найти: а) силу натяжения нити; б) модуль силы реакции шарнира при  .
.

Рисунок 4
По теореме о трех непараллельных силах линии действия таких сил обязаны пересекаться в одной точке, что и показано на рисунке. То есть сила реакции  не обязательно направлена вдоль стержня, а может образовывать угол
не обязательно направлена вдоль стержня, а может образовывать угол  с вертикалью.
с вертикалью.
Условия равновесия:
![Rendered by QuickLaTeX.com \[N_x=T\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8377207a3c86accfea1f76b6a397cf48_l3.png)
![Rendered by QuickLaTeX.com \[N_y=mg\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bb4a3eb68bddc4b70aff9304b42cbec7_l3.png)
Тогда реакция в шарнире
![Rendered by QuickLaTeX.com \[N=\sqrt{N_x^2+N_y^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5c80b4c290691f01d8dec24431286e73_l3.png)
Условие равенства моментов сил относительно шарнира:
![Rendered by QuickLaTeX.com \[Tl\sin{\alpha}-mg\frac{l}{2}\cos{\alpha}=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-33a1069082b2bb0a2b1e8ea0e7f8e709_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[T=\frac{mg}{2}\operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-273af27a673d0b2daa8c460dc19e780c_l3.png)
Следовательно,
![Rendered by QuickLaTeX.com \[N=\sqrt{\frac{m^2g^2}{4}\operatorname{ctg^2}{\alpha}+m^2g^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-18a0b06ec4b3862b5c8d8734ebb2d093_l3.png)
При  :
:
![Rendered by QuickLaTeX.com \[N=mg\sqrt{\frac{1}{4}\operatorname{ctg^2}{\alpha}+1}= mg\sqrt{\frac{1}{4}+1}=\frac{mg\sqrt{5}}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a63d6602ff9abec91c39abf3d9db4059_l3.png)
![Rendered by QuickLaTeX.com \[\beta=\operatorname{arctg}{\frac{N_x}{N_y}}=\operatorname{arctg}{\frac{\operatorname{ctg}{\alpha}}{2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f485bbd04a3d950c5196e95926738842_l3.png)
Ответ:  ,
,  ,
,  .
.
Задача 5. Два однородных шара массами 10 и 12 кг с радиусами 4 и 6 см соединены посредством однородного стержня массой 2 кг и длиной 10 см. Центры шаров лежат на продолжении оси стержня. Найти расстояние в см от центра тяжести этой системы до оси, проходящей через середину стержня.

Рисунок 5
Относительно центра тяжести запишем уравнение моментов этой системы:
![Rendered by QuickLaTeX.com \[M_1g\cdot(x+\frac{L}{2}+r_1)+mg\cdot x=M_2g\cdot(\frac{L}{2}-x+r_2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7bfeea6a44de8904fd8b60755953cbbc_l3.png)
![Rendered by QuickLaTeX.com \[x(mg+M_2g+M_1g)= -M_1g\cdot(\frac{L}{2}+r_1)+M_2g(\frac{L}{2}+r_2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8b10c8ae7e8a92834f0906f525a54e7c_l3.png)
![Rendered by QuickLaTeX.com \[x=\frac{ M_2(\frac{L}{2}+r_2) -M_1\cdot(\frac{L}{2}+r_1)}{ m+M_2+M_1}=\frac{ 12(5+6) -10\cdot(5+4)}{ 10+12+2}=\frac{42}{24}=\frac{7}{4}=1,75\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-74936c20c4583ff300cb9fe563169cb3_l3.png)
Ответ: 1,75 см.
easy-physic.ru
Статика. Подготовка к олимпиадам, 10 класс.
Задачи этой статьи уже появлялись (в статье, ориентированной на 8 класс, подготовка к олимпиадам ). Но не все. Вообще тем, кто готовится, очень советую не пренебрегать статьями для 8 класса – там очень хорошие задачи, многие из которых лучше этих.
Задача 1. Тонкий однородный стержень длиной  м, сделанный из материала с плотностью
м, сделанный из материала с плотностью  г/см
г/см шарнирно прикреплен к стенке бассейна и опирается на дно так, что составляет угол
шарнирно прикреплен к стенке бассейна и опирается на дно так, что составляет угол  с вертикалью. В бассейн начинают наливать воду. При какой высоте уровня воды стержень перестанет давить на дно? Ускорение свободного падения
с вертикалью. В бассейн начинают наливать воду. При какой высоте уровня воды стержень перестанет давить на дно? Ускорение свободного падения  м/с
м/с Плотность воды
Плотность воды  кг/м
кг/м Ответ дать в сантиметрах, округлив до целых.
Ответ дать в сантиметрах, округлив до целых.

К задаче 1
Решение.
Расставим силы на стержень. Сила Архимеда приложена к центру тяжести вытесненной воды, сила тяжести – к центру масс стержня. Запишем уравнение моментов относительно шарнира.
![Rendered by QuickLaTeX.com \[\rho\cdot l\cdot S\cdot g\cdot\frac{l}{2}\cdot\sin\alpha=S\cdot\rho_{_B}\cdot g\cdot\frac{h}{\cos\alpha}\cdot\sin\alpha\left(l-\frac{h}{2\cos\alpha}\right).\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-cddce31f0f6524138a6df238ec827335_l3.png)
Упрощая и решая квадратное уравнение, получаем, что
![Rendered by QuickLaTeX.com \[h=l\cdot\cos\alpha\left(1-\sqrt{1-\frac{\rho}{\rho_{_B}}}\right)=70.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f4ee55a9702f3d2fc4dfa1e1206ac3c2_l3.png)
Здесь выбран меньший из корней квадратного уравнения, иначе уровень жидкости превысил бы высоту шарнира.
Ответ: 70 см.
Задача 2. В цилиндрический сосуд массой  кг и площадью дна
кг и площадью дна  см
см налита вода до уровня
налита вода до уровня  м. Вода сверху закрыта поршнем, в котором имеется крючок. Каким будет давление под поршнем, если сосуд приподнять за этот крючок? Атмосферное давление равно
м. Вода сверху закрыта поршнем, в котором имеется крючок. Каким будет давление под поршнем, если сосуд приподнять за этот крючок? Атмосферное давление равно  кПа. Ускорение свободного падения
кПа. Ускорение свободного падения  м/с
м/с Ответ дать в кПа, округлив до целых. Плотность воды
Ответ дать в кПа, округлив до целых. Плотность воды  кг/м
кг/м

К задаче 2
Решение.
На цилиндр, кроме силы тяжести, действуют еще силы давления со стороны атмосферы (вверх) и со стороны воды с давлением у дна (вниз). Запишем условие равновесия цилиндра:
![Rendered by QuickLaTeX.com \[M\cdot g+(p+\rho\cdot g\cdot h)\cdot S=p_{_A}\cdot S,\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0af4b8a3fe5170b905416eddcb9414c7_l3.png)
откуда
![Rendered by QuickLaTeX.com \[p= p_{_A}-\rho\cdot g\cdot h-\frac{M\cdot g}{S}=80.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2215d9af8e95216cd68784020df17be0_l3.png)
Ответ: 80 кПа.
Задача 3. Тележка приводится в движение пружиной. В начальном состоянии тележка удерживается нитью, а пружина растянута силой  Н. Точка крепления пружины к колесу находится на расстоянии
Н. Точка крепления пружины к колесу находится на расстоянии  см над центром колеса. Радиус колеса тележки равен
см над центром колеса. Радиус колеса тележки равен  см, а масса тележки
см, а масса тележки  кг. С каким ускорением начнет двигаться тележка, если перерезать нить? Массой колес пренебречь. Считать, что колеса не проскальзывают. Ответ дать в м/с
кг. С каким ускорением начнет двигаться тележка, если перерезать нить? Массой колес пренебречь. Считать, что колеса не проскальзывают. Ответ дать в м/с округлив до целых.
округлив до целых.

К задаче 3
Решение.
Сила, приводящая систему в движение, есть сила упругости, действующая со стороны пружины на колесо. Важно понять, какую силу она сообщает посредством жесткого колеса массивной тележке, которая начинает двигаться. Тележка движется за счет силы трения покоя, возникающей в точке касания колеса с поверхностью. Сила  создает вращательный момент
создает вращательный момент  относительно центра колеса. Этот момент и передается силе трения. Тогда можно записать равенство моментов сил относительно центра колеса:
относительно центра колеса. Этот момент и передается силе трения. Тогда можно записать равенство моментов сил относительно центра колеса:
![Rendered by QuickLaTeX.com \[FL=F_{mp}R\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b231b515bd217f6ccd5b1017fb7f8ceb_l3.png)
Тогда  Согласно второму закону Ньютона, именно эта сила двигает массивную тележку вперед и ее ускорение будет равно
Согласно второму закону Ньютона, именно эта сила двигает массивную тележку вперед и ее ускорение будет равно
![Rendered by QuickLaTeX.com \[a=\frac{F_{mp}}{m}=\frac{FL}{mR}=1.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-42d14485455b3a4c29ab9d1c2e93a667_l3.png)
Ответ: 1 м/с .
.
Задача 4. Четыре одинаковых ледяных бруска длиной  см сложены так, как показано на рисунке. Каким может быть максимальное расстояние
см сложены так, как показано на рисунке. Каким может быть максимальное расстояние  при условии, что все бруски расположены горизонтально? Считайте, что все бруски гладкие, и что сила тяжести приложена к центру соответствующего бруска. Ответ дать в см, округлив до целых.
при условии, что все бруски расположены горизонтально? Считайте, что все бруски гладкие, и что сила тяжести приложена к центру соответствующего бруска. Ответ дать в см, округлив до целых.

Решение.
Система, состоящая из четырех брусков, будет находиться в равновесии, при условии, что сумма моментов сил, действующих на бруски 1 и 2, равна нулю. Запишем уравнение моментов для бруска 1 относительно точки  Сила тяжести приложена к центру бруска. Поскольку он сдвинут на
Сила тяжести приложена к центру бруска. Поскольку он сдвинут на  то и плечо силы тяжести
то и плечо силы тяжести  Сила реакции от верхнего бруска
Сила реакции от верхнего бруска  делится поровну и равна
делится поровну и равна  Тогда
Тогда
![Rendered by QuickLaTeX.com \[\frac{mgd}{2}=\frac{mg}{2}\cdot\left(\frac{L}{2}-\frac{d}{2}\right),\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-20fd521853378a755339e504c4a064af_l3.png)
откуда  см.
см.
Ответ: 8 см.
Задача 5. Легкий рычаг изогнут так, что стороны его  образуют друг с другом прямые углы. Ось рычага находится в точке
образуют друг с другом прямые углы. Ось рычага находится в точке  Перпендикулярно плечу рычага
Перпендикулярно плечу рычага  в точке
в точке  приложена сила
приложена сила  Н. Определить минимальное значение силы, которую нужно приложить в точке
Н. Определить минимальное значение силы, которую нужно приложить в точке  чтобы рычаг остался в равновесии. Ответ дать в Н, округлив до целых.
чтобы рычаг остался в равновесии. Ответ дать в Н, округлив до целых.

Решение.
Из уравнения моментов относительно точки  следует, что уравновешивающая сила, приложенная к точке
следует, что уравновешивающая сила, приложенная к точке  будет минимальна, если максимально ее плечо. Из геометрии рычага, максимальное плечо равно длине отрезка
будет минимальна, если максимально ее плечо. Из геометрии рычага, максимальное плечо равно длине отрезка  Тогда минимальная сила
Тогда минимальная сила  Н.
Н.
Ответ: 28 Н.
easy-physic.ru
Технологическая карта урока «Решение задач по теме «Статика». 10 класс.
Технологическая карта урока «Решение задач по теме «Статика». 10 класс.
урок комплексного применения знаний и умений.Цель
создать условия для усвоения знаний и способов деятельности обучающихся в системе, для формирования умений применять эти знания при решении стандартных и творческих задач.
Задачи
Образовательные:
1. углубить теоретические и практические знания, полученные при изучении темы «Статика».
2.продолжить формирование умений решать компетентностно — ориентированные задачи.
3. организовать деятельность обучающихся по применению полученных знаний на практике.
Воспитания:
1. в ходе проведения урока вовлекать обучающихся в активную практическую деятельность;
2.содействовать формированию положительной «Я — компетенции».
Развития:
1. в ходе проведения урока пробудить у обучающихся любознательность и инициативу, способствовать развитию устойчивого познавательного интереса к предмету;
2. развивать интеллект, культуру речи, память, волю, умение преодолевать трудности при решении задач;
3. совершенствовать навыки анализа, систематизации, обобщения, а так же умений выступать и защищать свою точку зрения.
Планируемый результат. Учащиеся приобретают навыки решения экспериментальных, компетентностно — ориентированных и расчетных задач по теме.
УУД
Личностные. Формируются ответственное отношение к учению, готовность и способность к саморазвитию и самообразованию на основе мотивации к обучению и познанию; коммуникативная компетентность в общении и сотрудничестве со сверстниками в процессе образовательной деятельности.
Познавательные. Выделяют и формулируют познавательную цель. Производят анализ и преобразование информации.
Регулятивные. Учатся определять цель своей деятельности, на основе соотнесения того, что уже усвоено, и того, что еще неизвестно, самостоятельно двигаться по заданному плану, оценивать и корректировать полученный результат.
Коммуникативные. Формируются речевые умения: учатся высказывать суждения с использованием физических терминов и понятий, формулировать вопросы и ответы в ходе выполнения задания.
Основные понятия темы
Момент силы, плечо силы, центр тяжести, равновесие.
Организация пространства
Основные виды учебной деятельности обучающихся
Основные технологии
Основные методы
Формы работы
Ресурсы Оборудование
1.Слушание учителя.
2.Самостоятельная работа с оборудованием.
3.Работа с раздаточным материалом.
4.Решение задач.
Технология: проблемное обучение.
1.словесные;
2.наглядные;
3.практические.
Индивидуальная, общеклассная, в парах постоянного состава.
Оборудование:
1) мел, доска; 2)оборудование; 3)мультимедийный проектор,4) презентация.
Структура урока.
Деятельностьучителя
Деятельность
ученика
УУД
Время
Мотивационно – ориентировочный компонент
1.
Организационный этап
Психологическая подготовка к общению
Обеспечивает благоприятный настрой.
Настраиваются на работу.
Личностные
1 мин.
2.
Этап мотивации. Создание положительного эмоционального настроения учеников.
Обеспечить деятельность по актуализации знаний и определению целей урока.
Фронтальная беседа.
Слушают. Отвечают.
Личностные, познавательные, регулятивные
10 мин.
Операционно – исполнительный компонент
3.
Закрепление изученного материала. Поддержание делового настроя учащихся.
Способствовать деятельности обучающихся по самостоятельному решению задач.
Предлагает организовать деятельность согласно предложенным заданиям.
Выполняют. Работают индивидуально, в парах. Общеклассная работа. Выступают.
Личностные, познавательные, регулятивные
20 мин.
Рефлексивно – оценочный компонент
4.
Контроль и самопроверка знаний.
Выявить качество усвоения материала.
Предлагает решить компетентностно — ориентированное задание.
Решают. Обсуждают.
Личностные, познавательные, регулятивные
10 мин.
5.
Домашнее задание.
Закрепление изученного материала.
Информация о домашнем задании, инструктаж по его выполнению
Решают. Обсуждают. Записывают.
Личностные, познавательные
2 мин.
6.
Рефлексия.
Подведение итогов занятия.
Учитель организует беседу о достижении поставленных целей урока по вопросам.
Отвечают.
Личностные, познавательные
2 мин.
Фронтальная беседа по вопросам.
1.Что называют плечом силы?
2.Что называют моментом силы?
3. Какая формула выражает смысл понятия момент силы?
4.Какова основная единица измерения момента силы?
5.Какие простые механизмы вы знаете?
6.Чему равен момент силы, проходящий через ось вращения?
7.Что называют центром тяжести?
8.Сформулируйте и запишите условие равновесия тела с закрепленной осью вращения?
9. Назовите общие условия равновесия любого твердого тела?
10.Перечислите способы определения центра тяжести?
Решение задач.
Класс делится на три группы, и каждая группа получает свое задание.
1. Инженеры: решите задачу упражнение №10 (2).
Инструкция. Примеры решения задач на странице 141-142.
2.Экспериментаторы: определить центр тяжести плоской фигуры, используя нить, груз, иголочку.
Инструкция. Если плоскую пластину подвесить в какой-либо точке, она расположится так, что вертикальная прямая, проведенная через точку подвеса, пройдет через центр тяжести пластины. Подвешивая пластину в разных точках, находят точку пересечения вертикальных прямых – центр тяжести пластины. Можно также уравновесить пластину на острие булавки. Пластина будет находиться в равновесии, если точка опоры совпадает с центром тяжести.
3.Теоретики: решить задачу «Лежачий камень».
После самостоятельной работы каждая группа отчитывается по проделанной работе.
Компетентностно — ориентированное задание.
Лежачий камень.

Задача. Корчуя садовый участок, мы обнаружили большущий камень. Как и следовало ожидать, он лежал как раз там, где не следовало. Естественно, его нужно было убрать, и мы приступили. Камень был далеко не круглым, поэтому кантовать его было трудно, хотя путь по которому мы его катили, был достаточно ровным. Мы дружно кричали «раз – два, взяли!» — и камень, поднявшись на попа, затем шлепался вперед.
— Стой, ребята, не так! – закричал Гена Иванов, наш сосед.
Вопросы.
1. Как вы думаете, что предложил Гена Иванов?
2. Всякому ли камню можно приготовить ровную дорогу? Почему неровная дорога в определенных случаях лучше ровной?
3. Каковы принципы конструирования наилучшей дороги для камней разного сечения?
Подсказки.
1. Наш сосед Гена Иванов быстро набросал впереди камня горку обрезков досок и вместе с нами налег на камень. Тот легко перевалил через доски. Приказав нам держать его вертикально, Гена перенес горку обрезков опять вперед камня и последний опять сам, почти без нашей помощи форсировал это препятствие. Это было как в сказке: по ровной дороге камень катиться не желал, а по ухабам – с удовольствием!
2. Для камня шарообразной формы наилучшая дорога — ровная, гладкая и горизонтальная. А если она к тому же твердая, то шар массой в тонну можно катить по ней одним пальчиком. В силу шаровой симметрии его центр масс движется равномерно и прямолинейно, параллельно дороге и следовательно горизонтально и поэтому в принципе никаких затрат энергии не требует. На практике энергия нужна для преодоления силы трения и – в начале – для придания камню поступательного и вращательного движения, а в конце – для остановки (если не поручить это трению). То же верно и для цилиндрического камня с круглым сечением.
3.Камень любого другого сечения требует дополнительной работы по поднятию его центра масс при переходе из «лежачего» в «стоячее» состояние. Поэтому сделав подставку определенной высоты, изменение центра масс при переходе камня из вертикального положения в горизонтальное будет минимальным. Для эллиптического камня высота равна разности длин его большой и малой полуоси сечения. Тогда в обоих положения центр масс будет на одной высоте, то есть качение по «ухабам» эквивалентно качению камня по ровной дороге.
4. Рельеф дороги должен соответствовать определенным требования. В каждой точке дороги равновесие камня должно быть безразличным. Это требование геометрии и статики. Требование кинематики: катящийся камень должен иметь равномерно поступательное и вращательное движение.
Рефлексия.
Учитель организует беседу по вопросам:
Сегодня я узнал…
Я почувствовал, что…
Мне представляется интересным то, что…
Я бы хотел (а) еще раз услышать…
Работа над заданием помогла мне…
Меня удивило…
У меня появилось желание…
Литература.
1. П.В. Маковецкий «Смотри в корень!»: сборник любопытных задач и вопросов. – М.: Наука. 1984.-288с.
2. festival.1september.ru/articles/579867/
infourok.ru