Задачи с переменной – Решение задач с помощью уравнений

Posted on by alexxlab

Выражение с переменной. Видеоурок. Математика 3 Класс

Рассмотрим предложенные записи.

12 — 3

12 — 1

х + 5

5 + 3 = 8

12 — 4

4 — y

12 — 6

 

 

Какая запись является «лишней»?

Правильный ответ: запись 5 + 3 = 8 – «лишняя», потому что она называется «равенство», а остальные записи – «выражения».

Рассмотрим выражения.

12 — 3

12 — 1

х + 5

12 — 4

12 — 6

 

4 — y

На какие группы можно разделить эти выражения?

Правильный ответ: эти выражения можно разделить на две группы: разности и буквенные выражения.

 

Х + 5

12 — 3

4 — y

12 — 6

 

12 — 1

 

12 — 4

Найдем значение выражения х+5, если х=0, х=3, х=16, х=35

Рассуждаем так:

если х=0, то значение суммы равняется 5, так как 0+5=5

если х=3, то значение суммы равняется 8, так как 3+5=8

если х=16, то значение суммы равняется 21, так как 16+5=21

если х=35, то значение суммы равняется 40, так как 35+5=40

Какие еще значения может принимать х?

Х может быть равен 43 или 68. Вообще можно сказать, что х может принимать любые значения.

Как бы вы назвали букву, которая может принимать любые значения?

Можно назвать ее по-разному: изменчивая, переменчивая.

Правильный ответ: в математике ее называют переменной.

Обратите внимание: в математике переменная позволяет записывать несколько выражений одним.

Рассмотрим выражения. Что можно сказать о них?

12 — 1

12 — 3

12 — 4

12 — 6

Правильный ответ: уменьшаемые одинаковые, а вычитаемые меняются. Значит, можно записать так:

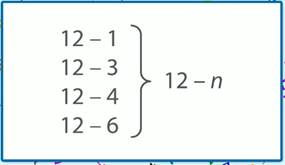
Рассмотрим выражения с переменной.

2+х 2*y 2-z

Что общего? Чем отличаются?

Правильный ответ: во всех выражениях одно действие, во всех выражениях имеется число 2. Отличия: разные действия, разные буквы обозначают переменную.

Какие значения может принимать переменная в этих выражениях?

В выражении 2+х, х может быть любым числом.

В выражении 2*y, у может быть любым числом.

В выражении 2-z, z может принимать только несколько значений: z=2, z=1, z=0.

Сегодня на уроке мы повторили отличия простой и составной задачи, вспомнили, как складывать и вычитать двузначные числа столбиком.

Найдем значение этих выражений, если х=5, у=3, z=2.

Рассуждаем так: подставим данные числа в выражения.

Если х=5, то 2+х=2+5=7

Если у=3, то 2*y=2*3=6

Если z=2, то 2-z=2-2=0

Прочитаем и сравним задачи.

1. У Тани 3 розы и 6 пионов. Сколько цветков у Тани?

2. У Тани 3 розы и 4 пиона. Сколько цветков у Тани?

3. У Тани 3 розы и 2 пиона. Сколько цветков у Тани?

Обратим внимание на то, что в задаче меняется количество цветков пионов. Заменим все три задачи одной задачей с переменной. Тогда задача будет звучать так: у Тани 3 розы и k пионов. Сколько цветков у Тани?

Чтобы узнать, сколько цветков у Тани, надо к 3 прибавить k.

Подставим значения в буквенное выражение.

3+k

если k=6 3+6=9 (цв.)

если k=4 3+4=7 (цв.)

если k=2 3+2=5 (цв.)

[00:06.53/5. Выражения с двумя переменнымию]

Важно отметить, что иногда в выражении бывают две переменные.

Тогда выражения могут выглядеть так:

18+b=a

n-4 = m

c+7= d

k-t =5

Определим, какая переменная больше и на сколько.

Правильный ответ:

в первом равенстве сравниваем переменные b и а, а – результат сложения, поэтому a>b на 18;

во втором равенстве сравниваем переменные n и m, n – уменьшаемое, значит n>m на 4;

в третьем равенстве сравниваем переменные c и d, c – это слагаемое, d – значение суммы, значит d>c на 7;

в четвертом равенстве k-t =5 сравниваем уменьшаемое и вычитаемое, уменьшаемое больше, поэтому k>t на 5.

Сегодня на уроке мы учились составлять выражения с переменной, находили значения выражений при данном значении переменной.

  

Список литературы

  1. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
  2. М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
  3. М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
  4. Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
  5. «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
  6. С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
  7. В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. Nsportal.ru (Источник).
  2. Prosv.ru (Источник).
  3. Do.gendocs.ru (Источник).

 

Домашнее задание

1. Найди значение выражения 36 — а, если а = 15, а = 16, а = 20, а = 35.

2. Найди значение выражения 12 + х, если х = 10, х = 34, х = 48, х = 59

3. Сравни выражения с переменной и поставь знак сравнения. 36 + к …37 + к

4. Замени данные выражения одним общим с переменной.

24 — 2; 24 — 3; 24 — 5;

interneturok.ru

Введение переменных и составление уравнений в задачах

Цели и задачи урока:

  • Систематизировать способы введения переменной в текстовых задачах через повторение вариантов составления уравнений и закрепление навыков составления краткой записи.
  • Развивать логическое мышление учащихся, учить сравнивать, анализировать, выбирать наиболее рациональное решение, формировать правильную математическую речь.
  • Развивать навыки самостоятельности, самообучения.

Форма урока: урок обобщения навыков, исследовательская работа.

Оборудование урока:

  • Магнитная доска.
  • Индивидуальные доски учащихся, фломастеры.
  • Таблички для обобщения, формулировки выводов.
  • Кружки разного размера для работы на доске.
  • Раздаточный материал для учащихся с текстом задач /приложение 1/.

Структура урока:

1. Организационный этап. (2 мин)

2. Пропедевтический этап. Актуализация опорных знаний и умений учащихся (3 мин).

3. Постановка цели и задач урока (1 мин).

4. Выбор переменной в задачах (10 мин).

5. Способы составления уравнений (15 мин).

6. Итог урока (3 мин)

7. Комментирование домашнего задания (1 мин).

8. Самостоятельная работа (10 мин)

На доске:

  • Тема урока, число (центральная доска слева).
  • Примеры для устного счета (дополнительная доска слева).
  • Домашнее задание (дополнительная доска справа)
  • Тексты задач 1д, 1е из раздаточного материала (доп.доска справа внутри, т.е. не видна в начале урока)

1. Организационный этап (2 мин).

Перед началом урока (до звонка) учитель собирает тетради с домашней работой.

Учитель: Здравствуйте, ребята! Садитесь.

Откройте тетради, запишите число. В дневник запишите домашнее задание (показывает на доске):

№1373в, задача №3 в приложении.

Закройте дневники, подготовьте доски, поиграем в «молчанку».

2. Актуализация опорных знаний и умений учащихся. (3 мин).

Учитель раскрывает дополнительную доску, учащиеся пишут ответы на индивидуальных досках:

  • Привести подобные слагаемые:
  • Записать в виде десятичной дроби: 40%; 20%; 185%; 7%.
  • Выразить значение десятичной дроби в процентах: 0,35; 02; 0,03; 1,25.
  • Найти 2/3 oт     x; 5/7 от     a.
  • Найти число, если 3/4 его составляют r. Найти число, если 5/7 его составляют n;
  • Выделить целую часть 5/3; 3/2; 8/3.

Учащиеся по просьбе учителя записывают ответ на индивидуальной доске, показывают учителю ответ. При затруднении кто – либо из учащихся комментирует решение. При значительном затруднении решение записывается в тетрадь. Но к данному уроку эти задания должны быть достаточно отработаны и только повторяются.

3. Постановка цели и задач урока (1 мин).

Учитель: Мы говорили ранее, что умение решать задачи является основным. Задачи можно решать по-разному. Одним из способов является решение с помощью составления уравнения. Этим способом мы с вами только начинаем овладевать. Важным моментом для умения решения задачи с помощью уравнений является выбор переменной. Ведь это самое начало решения! А как начнешь дело, так и его закончишь.

Сегодня на уроке мы повторим некоторые возможные способы выбора переменной, рассмотрим достоинства и недостатки этих способов.

А в конце урока мы должны будем определиться в ответе на вопрос: как же вводить переменную и составить уравнение, чтобы задача легче решалась? Запишите тему урока.

4. Выбор переменной в задачах (10 мин).

Предлагаем отработанный блок вопросов для работы с условием текстовой задачи:

Учитель: Посмотрите на задачу 1а (см. Приложение 1). Прочитайте условие задачи.

  • О чем говориться в задаче? (Предполагаемый ответ: в задаче говорится о поле)
  • На какие части можно условно разделить поле в задаче? (I участок, II участок)
  • Какая величина характеризует поле? (Площадь поля)
  • В чем она измеряется? (Гектарах)
  • Какова площадь поля? (2,4 га)
  • Какова площадь первого участка? (Неизвестна)
  • Какова площадь второго участка? (Неизвестна)
  • Какова зависимость между неизвестными величинами? (s1>s2 на 0,8 га)
    В процессе беседы по типовым вопросам на доске и в тетрадях учащихся появляется краткая запись условия задачи

  • Какую смысловую нагрузку несет значение величины s=2,4га? (Если к площади первого участка прибавить площадь второго участка, то получим значение площади всего поля или 2,4 га по условию задачи).

Если в задаче неизвестны значения каких-либо величин, но известна зависимость между ними, то задачу можно решать с помощью составления уравнения. Для этого необходимо ввести переменную и составить уравнение.

  • Значение какой величины можно обозначить через переменную? (Площадь второго поля обозначим через х, т.к. она меньшая)
  • Как выразить другую величину? ((х+0,8)га)
  • Можно ли обозначить буквой значение другой величины? (Да: площадь первого поля обозначим через у)

В результате этой части беседы краткая запись дополняется кружками, обозначающими зависимость между величинами:

  • Каким из этих способов предпочтительнее вводить переменную? (Первым, но незначительно. Способы практически равнозначны)

Разберем в парах введение переменной в задаче 1б (см. Приложение 1)

Учащиеся работают в парах с соседом по парте. Один ученик задает вопросы, другой отвечает. Считаем необходимым отметить, что одним из навыков решения задачи является умение задавать вопросы самому себе. К данному уроку работа над умением задавать вопросы велась неоднократно. Две пары учеников выполняют работу на доске. После пары проверяют записи на доске друг у друга вместе с классом. Лучшую запись оставляют на доске. Ответы учащихся оцениваются друг другом. Учитель комментирует сам или требует комментариев от учащихся по вопросу выставления оценок. В результате на доске остается запись:

  • Какой способ введения переменной рациональнее? (Первый)
  • Можно ли вводить переменную вторым способом? (Да, если выполнить преобразования: y : 3 = y * 1/3 = 1/3 y)

Аналогично организовать работу над задачами 1в, 1г.

Получить на доске краткие записи работы:

В соответствии с уровнем подготовки школьников следует уделять внимание логическим пояснениям и математическим преобразованиям в каждом случае. Обязательно подвести учащихся к выводу, что любой способ введения переменной является правильным, но не любой – самым легким для последующего решения.

Учитель: Какие зависимости между неизвестными величинами мы уже рассмотрели? (Больше – меньше, одна величина является частью от другой, в том числе процентной) Рассмотрим другие случаи зависимости: (тексты дублировать на дополнительной доске, краткая запись – в результате беседы)

Необходимо отметить, что мы уделяем особое внимание символическим обозначениям. Мы вводим свои условные знаки, которые являются как бы мостиком при переводе информации с русского на математический язык. Так, зависимость между величинами мы обозначаем кружками, которые позволяют легче усвоить смысл уравнивания величин с помощью весов, а разность обозначаем в виде гири, которая к этому времени трансформировалась в прямоугольник. Поэтому наиболее тяжелая для учащихся зависимость «разность чисел» легко переформулируется в «больше — меньше».

Учитель: Подведем итог нашей работы.

Нужно, чтобы учащиеся самостоятельно сделали ряд выводов:

  • Существуют различные зависимости между величинами (больше – меньше, часть – целое, сумма, разность)
  • Выбор переменной может быть любым.
  • От выбора переменной зависит дальнейшее решение задачи.

5. Способы составления уравнений (15 мин).

Учитель: Мы уже отметили, что умение ввести переменную для решения задачи очень важно. Но в тексте задачи обычно несколько условий, характеризующих зависимость между величинами. Причем никогда не сообщается, при помощи какого условия надо вводить переменную. Кроме того, решение не ограничивается введением переменной. Давайте вспомним, как расчленять условие задачи на отдельные части.

Прочитайте задачу №2 (см.Приложение)

  1. О чем говорится в задаче? (В задаче говорится о возрасте)
  2. На какие части можно условно разделить возраст? (Возраст отца и возраст сына)
  3. Знаем ли мы возраст отца? (Нет)
  4. Знаем ли мы возраст сына? (Нет)
  5. Прочитайте условие, которое связывает возраст отца и возраст сына. (Их два: сын младше отца в 4 раза; отец старше сына на 27 лет)
  6. Переформулирем эти условия так, чтобы использовалась уже известная зависимость. (Возраст сына в 4 раза меньше, чем возраст отца; возраст отца на 27 лет больше возраста сына)
  7. Переформулируем условия так, чтобы сравнивался возраст отца с возрастом сына. (Возраст отца больше возраста сына в 4 раза, возраст отца больше возраста сына на 27 лет)
  8. Переформулируем условия так, чтобы сравнивался возраст сына с возрастом отца. (Возраст сына меньше возраста отца на 27 лет. Возраст сына меньше возраста отца в 4 раза.).

В результате на доске и в тетрадях учащихся появляется основная краткая запись (учащиеся в тетради её не делают, но на доске эта запись будет в работе в течение всего решения):

  1. В задаче выделились два условия и вопрос. (Вопрос: сколько лет отцу?)
  2. Каким способом можно решать задачу? (Задачу можно решать с помощью уравнения, так как значения обеих величин неизвестны, а известна зависимость между ними)
  3. С помощью какого условия можно ввести переменную? (Возраст сына на 27 лет меньше, чем возраст отца).
  4. Для чего тогда можно использовать второе условие? (Второе условие можно использовать для составления уравнения.) На доске прикрепляются таблички:

    Для введения
    переменной

    		  

    Для составления
    уравнения
  5. Составьте в тетради и на доске краткую запись:

  6. Составьте схемы уравнений и сами уравнения по второму условию. Учащиеся составляют в тетради и на доске схемы и уравнения по ним:

  7. Какой вариант кажется вам рациональнее? (Обычно учащиеся выбирают третье уравнение. Остальные решать пока не умеем. Обводим его в рамку.) Желательно учителю выписывать выбранные уравнения на отдельной доске для того, чтобы учащиеся сделали общий вывод.

  8. Возможно ли обозначить переменной значение другой величины? Введите переменную по-другому, составьте схемы уравнений, сами уравнения, сделайте вывод.

Дети составляют краткую запись, схемы уравнений, уравнения самостоятельно в тетрадях. На дополнительных досках работают два ученика. Вместе выбираем уравнение, которое наиболее удобно для решения. Сравниваем его с первоначальным, делаем выводы: схемы для составления уравнений одинаковые, т.к. условие для составления уравнения не изменилось. Схемы можно было не составлять. Уравнения отличаются незначительно.

  1. Можно ли было использовать первое условие для составления уравнения, а второе – для введения переменной. (Да) Меняем таблички с надписями «для составления уравнения», «для введения переменной» местами в основной краткой записи.

    2. Учащиеся самостоятельно составляют схемы уравнений, уравнения. На доске записываем только то, которое они считают рациональным.

  2. Можно ли ввести переменную по-другому, используя условия для тех же целей? (Да)

      Составляем краткую запись, схемы уравнений, уравнения самостоятельно в тетрадях. Вместе выбираем уравнение, которое наиболее удобно для решения, записываем его на доске.

6. Итог урока (3 мин).

При подведении итога урока учащиеся просматривают вторую часть классной работы, подсчитывают количество возможных вариантов составления уравнения в зависимости от введения переменной в задачу (пишут: I способ, II способ…). Повторяют вывод, уже сделанный для каждого способа. Учителю при самостоятельной работе учащихся необходимо следить за тем, чтобы наиболее рациональные варианты стояли на различных местах по порядку, иначе учащиеся могут сделать неправильный вывод.

7. Комментирование домашнего задания (1 мин).

Учитель: Дома вы будете решать пример (№1373в) и задачу № 3 из приложения. Каким способом будете вводить переменную? Верно, каждый своим способом. Решение задачи полностью записать в тетради.

  • Так какой же способ самый правильный? (Никакой, правильные все)
  • Какой саамы рациональный и легкий для решения? (Учащиеся могут назвать разные варианты) Запишите решение тем способом, который кажется вам рациональнее.

8. Самостоятельная работа (10 мин).

Учащиеся записывают решение уравнения и сдают тетради на проверку. Из опыта работы можем утверждать, что учитель успевает проверить работу учащихся и выставить отметки за урок за время выполнения всем классом самостоятельной работы. Учащиеся выполняют следующую домашнюю работу в этих же тетрадях.

Использование данной методики работы над текстовой задачей дает хорошие результаты.

Учебник: Н.Я. Виленкин и др., Математика, 6 класс.

urok.1sept.ru

Решение задач с помощью уравнений в курсе алгебры 7 класса.

 

Учебник для учащихся 7 класса общеобразовательных учреждений Ю. Н. Макарычев,  Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского.  Алгебра.  7 класс -М.: Просвещение, 2017г.

  1.  Тема: Решение задач с помощью уравнений.
  2. Классифицировать все текстовые и логические задачи.
  3. Проанализировать особенности решения каждой задачи.

Классификация задач

Содержание

Основные виды учебной  деятельности

обучающихся

Простые и определённые по известным формулам

Алгоритм решения задач с помощью составления уравнений.

Запоминают алгоритм решения задач с помощью составления уравнений.

Составные и с перестановкой в  условии

Свойства урав­нений, приме­няемые при ре­шении.

Учатся ре­шать задачи с помощью ли­нейных урав­нений с одной переменной.

Движение объекта  (по формуле нахождения расстояния)

Задачи на движение .

Учатся решать задачи с помощью уравнений на движение согласно S=Vt.

4)Использовать  способы применения ИКТ: Презентации  илюстрирующая задачу.

Комплект задач для  стартовой диагностики.

1. Составьте равенство, используя условие, и найдите значение переменной:

     а) Одна деталь весит х кг, а другая 4х кг. Вместе эти детали весят 55 кг.

     б) Длина прямоугольника равна 2х см, ширина х см, а периметр равен     156 см.

2. Отцу и сыну вместе 60 лет. Сколько лет каждому, если отец в 3 раза  старше сына.

3. В первый день продали на 4 телевизора меньше, чем во второй. Сколько телевизоров продали в каждый день, если известно, что всего продали 18 телевизоров.

Комплект задач для  промежуточной диагностики.

  1. За два дня на элеватор отправили  574 т зерна, причем в первый день в 1,8 раза меньше, чем во второй. Сколько тонн зерна было отправлено в первый день и сколько во второй?
  2. За три дня было продано 830 кг апельсинов. Во второй день продали на 30 кг меньше, чем в первый, а в третий – в 3 раза больше, чем во второй. Сколько килограммов апельсинов было продано в первый день
  3. Яблонь в саду на 12 деревьев меньше, чем груш, и в 2 раза меньше, чем вишен. Сколько посажено яблонь, сколько груш и сколько вишен, если всего в саду 100 деревьев
  4. На нижней полке было в 4 раза книг меньше, чем на верхней. После того как на нижнюю полку переставили с верхней  27 книг, на полках книг оказалось поровну. Сколько книг было на каждой полке первоначально

 

Комплект задач для  итоговой  диагностики.

 

  1. На нижней полке было в 3 раза книг болььше, чем на верхней. После того как на верхнюю полку переставили с нижней  15 книг, на полках книг оказалось поровну. Сколько книг было на каждой полке первоначально?
  2.  На первом катере было в 2 раза больше людей, чем на втором. Когда на ближайшей пристани с первого катера сошли 98 человек, а со второго 16 человек, то на обоих катерах людей стало поровну. Сколько человек было на каждом катере первоначально?
  3. Турист шел от турбазы до станции со скоростью 6 км/ч. Если бы он шел  со скоростью 4 км/ч, то затратил бы на дорогу на 1 час больше. Чему равно расстояние от турбазы до станции?
  4. Из поселка в город едет автомобиль. Если он увеличит скорость на 8  км/ч, то приедет в город через 6 часов. Если же автомобиль уменьшит  скорость на 12 км/ч, то приедет в город через 8 часов. С какой скоростью движется автомобиль?

Ресурс: http://videouroki.net

 

 

mega-talant.com

Линейное уравнение с двумя переменными и его график (более сложные случаи)

На данном уроке мы научимся решать более сложные задачи, в которых речь идет о линейных уравнениях с двумя неизвестными. Мы закрепим технику решения данных уравнений и построения графиков, вспомним теоретические основы и добавим к ним некоторые факты.

Напомним, что линейным уравнением с двумя переменными называется уравнение вида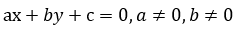

Мы научились строить графики подобных уравнений и узнали, что они имеют бесчисленное множество решений – пар чисел х и у, которые на графике отображаются в виде точек.

В предыдущих задачах нам было задано уравнение, но как и все другие – линейное уравнение с двумя переменными это математическая модель некоторой реальной ситуации. Теперь рассмотрим такие задачи, в которых нужно для простейшей задачи составить уравнение – математическую модель, а затем его решить.

Пример 1:

Сумма двух чисел равна четырем. Построить математическую модель, то есть соответствующее линейное уравнение, и его график.

Пусть искомые числа это х и у, сумма их равна четырем:

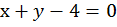 – линейное уравнение с двумя переменными. Построим график, для этого составим таблицу, для контроля возьмем три точки, а не две:

Решение задачи сведено в таблицу:

Словесная модель

Сумма двух чисел равна четырем

Алгебраическая модель

,

Геометрическая модель

 

Следующая группа задач связана с тем, что в одной задаче могут участвовать два линейных уравнения.

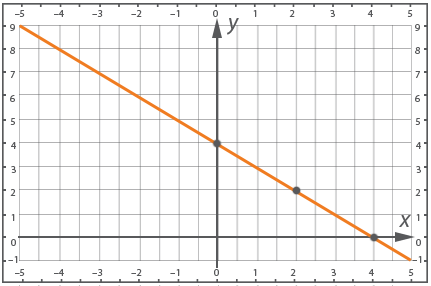
Пример 2:

Графически найти точку пересечения прямых 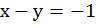 и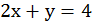

Обе прямые являются графиками соответствующих уравнений, построим их. Для этого составим таблицы. Для удобства представим уравнение в следующем виде:

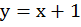
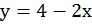
Графически найдена точка пересечения А(1; 2)

Чтобы проверить, что точка А(1; 2) удовлетворяет обоим уравнениям, нужно подставить ее координаты в уравнения:

;

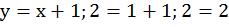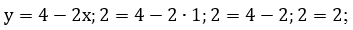
точка А удовлетворяет обоим уравнениям, значит, точка пересечения прямых найдена верно.

Следующий тип задач – это задачи с параметрами.

Пример 3:

Найдите значение коэффициента 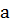 в уравнении 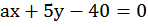, если известно, что решением уравнения является пара чисел (3; 2)

Ранее у нас было задано или мы сами составляли линейное уравнение с известными коэффициентами, в данном случае один из коэффициентов неизвестен, но дано одно из решений уравнения, то есть пара значений х и у, удовлетворяющих уравнению. Чтобы найти параметр 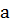 подставим данные значения в уравнение:

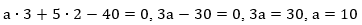
итак, исходное уравнение имеет вид:

Итак, мы рассмотрели линейное уравнение с двумя неизвестными:

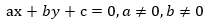
Отметим, что в случае, если , мы получаем частный случай данного уравнения – уравнение с одной переменной:

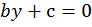
Аналогично если 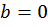 мы получим линейное уравнение с одной переменной:

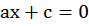
Вывод: в данном уроке мы рассмотрели более сложные задачи на линейные уравнения с двумя переменными, в частности текстовые задачи, уравнения с параметрами, задачи на два уравнения. Кроме того мы закрепили знание понятий и терминов.

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ 

3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет

1. Интернет-портал Nado5.ru (Источник).

2. Портал для семейного просмотра (Источник).

3. Интернет-портал Nado5.ru (Источник).

 

Рекомендованное домашнее задание

Задание 1: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 980, ст.212;

Задание 2: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 981, ст.212;

Задание 3: Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7, № 986, ст.212;

interneturok.ru

Урок по математике «Выражение с переменной»

Урок математики во втором классе с использованием проблемно-диалогического метода обучения по программе «Начальная школа ХХI века».

Бартавова Г..Р

Тема: «Выражение с переменной»

Цели урока: учащиеся должны познакомиться с понятием «переменная»; уметь читать выражения с переменной; уметь выделять из множества выражений выражения с переменной; уметь формулировать учебную задачу урока, задавать вопросы по новой теме урока, отвечать на поставленные вопросы; уметь сотрудничать друг с другом.

Оборудование: схема-опора (x+7), карточки с дополнительным заданием для работы в парах, карточка с названием «ВЫРАЖЕНИЯ».

Ход урока.

Организационный момент

-Настройтесь на активную работу. Закройте глаза и скажите про себя: «У меня всё сегодня получится. Я буду активен на уроке!».

-Откройте тетради и запишите число, классная работа. А начнём урок с проверки домашнего задания. Что было задано на дом?

-Что было трудным при выполнении домашнего задания? Что получилось?

-Какие знания помогли при выполнении данного задания?

-А мы уже всё знаем о переменных?

-Что ещё нужно сделать?

II. Актуализация опорных знаний.

(На доске: 5*3, 7*4, 8+6, 30-25, 48/6, 3+9, 4+7, x+3)

-Что записано на доске?

(На доске появляется карточка с названием «ВЫРАЖЕНИЯ»).

-Давайте найдём значения этих выражений! (Учащиеся испытывают затруднения в нахождении значения последнего выражения х+3)

III. Постановка учебной задачи (проблемы).

-Выполнили задание?

-Почему?

-Какой возникает вопрос?

-Значит, какова тема нашего урока?

IV. Поиск решения учебной задачи.

-Какие будут предположения?

-Где можно проверить наши предположения?

-Откройте учебники на странице 128. прочитайте правило самостоятельно.

-Правы ли мы в своих догадках?

V. Первичное закрепление.

-Задайте друг другу вопросы по новой теме.

-Может ли вам помочь схема-опора (х+7)? Как?

-А теперь я предлагаю вам поработать в парах: подумайте и ответьте на вопрос. Может ли выражение с переменной не иметь ни одного значения? Если да, то приведите примеры.

VI. Самостоятельная работа с самопроверкой по эталону.

-А теперь № 436 в учебниках выполните самостоятельно.

-Сравните свою работу с эталоном.

-Оцените себя при помощи шкалы.

-Какие испытывали затруднения? Что получилось?

-Что ещё нужно сделать?

VII. Выполнение упражнений на закрепление.

— А теперь давайте найдём значения выражения с переменной, рассуждая точно по алгоритму: х+11, при х=6, 9, 89. Все в тетрадях, а … у доски.

-Я предлагаю вам снова поработать в парах. У вас на партах лежит карточка с заданиями. Задания двух уровней: уровень «А» легче, уровень «В» немного сложнее и объёмнее. Вы можете выбрать, какой уровень вы будете выполнять. Можно решить задания и двух уровней.

-Проверьте свою работу по эталону.

— Оцените себя при помощи шкалы.

VIII. Итог урока.

-Над какой темой работали?

-Где могут пригодиться полученные знания?

-Оцените свою работу на этом уроке?

-Оцените работу класса на данном уроке при помощи игры «Дистанция».

Домашнее задание.

Учебник с.130 №438 или №439 (задание по выбору учащихся).

-Выполнить № 425 в учебнике.

-всё было понятно

-помогли знания о переменной.

-нет

-Надо ещё работать над темой «Выражения».

-Выражения

(К доске выходят 2 ученика, остальные ребята работают у себя в тетрадях).

-Нет.

— Не смогли решить последнее выражение. Не умеем находить значение таких выражений.

-Как найти значение выражения с переменной?

-Выражение с переменной

-Для того, чтобы найти значение выражения с переменной, надо вместо переменной подставить какое-либо число, то есть значения данной переменной.

В учебнике.

(Читают).

-Да.

-Как найти значение выражения с переменной? Сколько значений может иметь выражение с переменной?

-Нужно вместо переменной х подставлять её значения: 3, 9, 5 (3+7, 9+7, 5+7).

(Работают в парах)

-Да. Например, х-3, если х=1, 2, 0.

х/5, если х=1, 2, 3, 4.

(Работают самостоятельно)

(Оценивают себя на полях тетради).

-Надо ещё работать по данной теме.

Х+11–это выражение с переменной.Х- переменная, которая принимает значения 6, 9, 89.Нужно подставить вместо переменной х её значения. Если х=6, то 6+11=17. Если х=9, то 9+11=20. Если х=89, то 89+11=100.

(Работают в парах).

(Проверяют свою работу).

(Оценивают себя при помощи шкалы).

-Выражение с переменной.

-В средней школе, в других учебных заведениях…

Дети встают возле своих мест и оценивают работу класса на уроке и сам урок. Чем успешнее прошёл урок, чем активнее были дети (по их мнению), тем ближе каждый ребёнок подходит к доске.

infourok.ru

«Решение задач с помощью систем уравнений»

Класс: 7

Предмет: Алгебра.

Тема урока: Решение задач с помощью систем уравнений.

Цели урока:

Обучающие:

  • изучить способ решения задач с помощью составления систем уравнений;

  • формировать умение составлять системы уравнений по условию задачи и решать их.

Развивающие:

  • развивать умение обобщать, конкретизировать; развивать логическое мышление и вычислительные навыки, творческую активность, инициативу.

Воспитательные:

  • расширение кругозора и развитие интереса к предмету, используя присущую математике красоту и увлекательность; приобретение знаний и навыков, применяемых в повседневной жизни.

УУД:

Личностные:

  • формирование смысла учебной деятельности на основе развития познавательного интереса и учебных мотивов.

  • положительное отношение к урокам математики, ответственное отношение к учению, совершенствование имеющихся знаний и умений.

  • умение ясно, точно излагать свои мысли в письменной и устной речи, активность при решении задач

Познавательные:

  • воспроизводить по памяти информацию, необходимую для решения учебной задачи.

  • уметь осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от конкретных условий

  • формулирование познавательной цели, поиск и выделение информации.

Регулятивные:

  • составление плана последовательности действий, адекватное реагирование на трудности, не бояться сделать ошибку.

Коммуникативные:

  • определять цели и функции участников, способы взаимодействия;

  • планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений;

  • умение точно выражать свои мысли вслух.

Тип урока: урок усвоения новых знаний

Оборудование: учебник, мультимедийный комплекс, презентация.

Ход урока:

  1. Организационный момент

Проверка готовности.

Психологический настрой.

Проверь-ка, дружок,

Ты готов начать урок?

Все ль на месте,

Все в порядке,

Ручка, книжка и тетрадка?

Все ли правильно сидят?

Все ль внимательно глядят?

  1. Мотивация учебной деятельности учащихся. Сообщения темы, цели, задач урока и мотивация учебной деятельности школьников.

Чем больше я знаю, 
Тем больше умею.
Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает. (Роман Сеф).

Учитель: Посмотрите на слайд. Как вы понимаете эти слова? Как мы можем отнести их к сегодняшнему уроку?

  1. Воспроизведение и коррекция опорных знаний учащихся.

Учитель: Сегодня вам самим предстоит открыть новые знания. Прежде, чем совершать открытие, давайте проверим себя, готовы ли мы совершить его, всё ли было усвоено на уроках, имеются ли слабые места.

1. Дайте определение линейного уравнения с двумя переменными. (Линейным уравнением с двумя переменными называется уравнение вида ах + ву = с, где х и у — переменные а, в, с — некоторые числа)

2. Что называется решением уравнения с двумя переменными? (Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство)

3. Дайте определение системы линейных уравнений с двумя переменными. 

4. Что называется решением системы уравнений с двумя переменными? (Решением уравнения с двумя переменными называется пара значений переменных, обращающая эти уравнения в верные равенства).

5. Алгоритм решения системы линейных уравнений с двумя переменными способом подстановки.

6. Алгоритм решения системы линейных уравнений с двумя переменными способом сложения.

7. Устная работа.

1. Являются ли следующие системы уравнений равносильными:

а) hello_html_m3e5d5008.gif и hello_html_m34d2f2b7.gif

б) hello_html_40575dcf.gif и hello_html_129d6f8.gif

2. Какое из уравнений нужно записать в систему hello_html_m4496dc4d.gif чтобы она имела единственное решение? не имела решений? имела бесконечное множество решений?

а) y + 3x = 7; в) y – 2x = 3;

б) 4x – 2y = 2; г) hello_html_768e6a91.gifx = 5.

  1. Восприятие и первичное осознание нового материала.

Сначала следует вспомнить, в чём заключается способ решения задач с помощью составления уравнения, а затем показать, что задачи могут решаться и с помощью составления системы уравнений.

Алгоритм

решения задач с помощью уравнения

1. Одну из неизвестных величин обозначить переменной.

2. Выразить через переменную значение других неизвестных величин.

3. Составить уравнение.

4. Решить уравнение.

5. Соотнести корень уравнения с вопросом задачи.

6. Записать ответ к задаче.

Сначала необходимо дать учащимся несколько заданий на составление системы уравнений по условию задачи, а затем уже переходить непосредственно к решению задач.

1. Запишите с помощью системы уравнений следующую ситуацию:

а) Сумма двух чисел равна 17. Одно из них на 7 меньше другого.

б) Периметр прямоугольника равен 400 м. Его длина в 3 раза больше ширины.

в) Четыре боксёра тяжёлого веса и пять боксёров лёгкого веса вместе весят 730 кг. Спортсмен тяжелого веса весит на 70 кг больше спортсмена лёгкого веса.

г) Таня заплатила за 3 тетради и 2 карандаша 58 р., а Лена за 3 такие же тетради и 1 карандаш – 78 р.

Вывести на доске алгоритм:

Алгоритм

решения задач с помощью систем уравнений с двумя переменными

1. Ввести две переменные.

2. По условию задачи составить 2 уравнения с двумя переменными.

3. Составить систему уравнений с двумя переменными.

4. Решить систему уравнений.

5. Соотнести решение системы с условием задачи.

6. Записать ответ к задаче.

  1. Первичная проверка понимания усвоенного, первичное закрепление усвоенного.

1. Рассмотреть задачи в учебнике на странице 219-220

2. № 1099, № 1101.

№ 1099 (составить математическую модель к задаче, 1 ученик у доски).

В фермерском хозяйстве под гречиху и просо отведено 19 га, причем гречиха занимает на 5 га больше, чем просо. Сколько гектаров отведено под каждую из культур?

S, га

Сумма площадей

Разность площадей

Гречиха

x

xЛевая фигурная скобка 8+y

xЛевая фигурная скобка 10-y

Просо

y

199

5

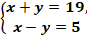
hello_html_m60fb44ec.gif

3. № 1103.

VI. Итоги урока. Рефлексия.

  • Что называется решением системы уравнений с двумя переменными?

  • Какие вы знаете способы решения систем уравнений?

  • Сформулируйте алгоритм решения задач с помощью систем уравнений.

  • Сколько решений может иметь система линейных уравнений?

VII. Домашнее задание: Прочитать п.45.

infourok.ru

«Решение текстовых задач с одной переменной» 6 класс

Школа: КГУ «Средняя школа № 14 имени Д.М. Карбышева»

Дата

Учитель

Класс

25.01.2019

Утемисова Ш.А.

6 «Б»

Тема

«Решение текстовых задач с одной переменной»

Цель обучения

6.5.1.6 решать текстовые задачи с помощью составления линейных уравнений

Уровни навыков мышления

Знание, применение, анализ

Цель урока

— Развитие умений решать задачи с помощью уравнений;

— Применять правила решения линейных уравнений, находить ответ (корни уравнения)

— Анализировать условие задачи с ее решением

Тип урок

Урок применения знаний и умений

Критерии оценивания

  • Знает, как решать линейные уравнения

  • Понимает, как составлять уравнение по условию задачи

  • Применяет правила решения линейных уравнений, находит ответ (корни уравнения)

  • Анализирует решение, проверяет корни уравнения в соответствии условия задачи, записывает ответ

Языковые цели

Развитие математического языка, навыки устной и письменной речи, навыки логического мышления и вычислений

Приобщение к ценностям

Взаимопомощь, ответственность, трудолюбие, интерес к предмету.

Межпредметная связь

Связь с жизнью через практические задачи

Предыдущие знания по теме

6.2.2.1- знать определение линейного уравнения с одной переменной, равносильных уравнений

6.2.2.2- решать линейные уравнения с одной переменной

Ход урока

Начало урока

2 мин

3 мин

2 мин

Середина урока

5 мин

5 мин

Приветствие учителя и учеников.

I.Организационный момент.

-Здравствуйте ребята,

Добрый день и добрый час!

Я очень рада видеть вас

Подтянулись, подравнялись

Друг на друга посмотрели

И тихонько дружно сели.

II. Мотивация урока.

Кто-то сегодня будет доволен, что сумел решить сам или с помощью одноклассников смешную или трудную задачу; кто-то тем, что он узнал что-то новое. Повернитесь друг другу и пожелайте удачи на сегодняшнем уроке.

Деление группы по карточкам. Для того, чтобы узнать тему урока разгадайте ребус.

— Правильно тема урока – решение задач на уравнения

— Чему же мы должны научиться на этом уроке?

Учитель раздает учащимся:

1) оценочный лист.

2) критерии оценивания по заданиям на каждом этапе урока.

В течение урока учащиеся заполняют соответствующие столбцы по заданиям. В конце урока подсчитают баллы.

-А начнем мы наш урок с повторение основных понятий.

Фронтальный опрос «мозговой штурм» РАЗМИНКА

(активный метод дискуссия).

-Что называют уравнением?

(это равенство, содержащее переменную, значение которой надо найти)

-Что значит решить уравнение?

(найти его корни или доказать, что их нет).

-Что такое корни уравнения?

(значение переменной, при котором уравнение превращается в верное числовое равенство)

-Что значит решить задачу при помощи уравнения?

(обозначить неизвестный элемент через переменную, составить уравнение по условию, выполнить вычисления, сделать проверку, записать ответ.)

-Какие ситуации могут возникнуть, когда будут найдены корни уравнения?

(не все корни могут удовлетворять решению)

—А теперь узнаем, что мы знаем и умеем решать.

Устный счет

hello_html_21697438.jpg

Кроме этих знаний для того чтобы решить любую задачу с неизвестным нужно уметь решать, что?

— Конечно же уравнения.

Учитель раздает учащимся:

1) оценочный лист.

2) критерии оценивания по заданиям на каждом этапе урока.

В течение урока учащиеся заполняют соответствующие столбцы по заданиям. В конце урока подсчитают баллы.

  1. Индивидуальная работа

Карточки с QR – кодом

Данный этап урока предлагается провести, используя приложение. QR – код

Каждому ученику предлагается на листочке решить уравнение, на которых установлен QR – код. Учащиеся на специальных листочках с номерами, записывают свою фамилию, имя. Рядом с каждой цифрой записывают ответ. После некоторого времени, учащимся предлагается обменяться карточками группе и сделать взаимопроверку. А помогают им это сделать приложение QR – код. Учащимся нужно запустить приложение QR – код, навести на код, который при наведении выдает верный ответ, и проверить верно ли решили уравнения. У кого нет телефона сверяются с доской. При этом оказывается помощь соседу при решениях уравнений.

1 задание. С помощью рисунка составить уравнение к задачеhello_html_m41d9cad4.jpg

Критерии оценивания

Дескриптор

Балл

Анализирует решение, проверяет корни уравнения в соответствии условия задачи, записывает ответ

-знает метрическую систему мер (переводит килограммы в граммы)

-составляет уравнение

-решает уравнение

-находит ответ к задаче

1

1

1

1

Группы меняются своими листами, и командиры групп комментирует по критериям работу другой группы. Дают две звезды одно пожелание.

Слайд 2,3,4

На доске

Слайд 5

QR — код, карточки с QR – кодом.

7 мин

2 мин

10 мин

2. Метод «Диалоговое обучение» (работа в парах). (идет взаимообучение, побуждается мотивация к учебной деятельности)

Решить задачу.

В первом ряду кустов смородины в 2,5раза больше чем во втором. Если с первого ряда пересадить 12 кустов на второй, то количество кустов смородины в каждом ряду станет одинаковым. Сколько кустов смородины было во втором ряду первоначально?

Критерий оценивания

Дескрипторы

балл

Понимает, как составлять уравнение по условию задачи

Составляет краткую запись, или делает схему

1

Задает параметр к задаче (обозначает неизвестный элемент)

1

Составляет уравнение по условию задачи

1

Решает уравнение, находит корень уравнения

1

Проверяет ответ по условию, записывает

1

Краткая запись

1ряд

2,5Х кустов

2,5х-12

2 ряд

Х кустов

Х+12

2,5х-12= Х+12

Решение

2,5Х-12= Х+12

2,5х-х=12+12

1,5х=24

Х=24/1,5

Х=16 кустов было во втором ряду

Ответ:16 кустов

Физминутка. «Танцующий ежик»

  1. Групповая работа Метод «карусель»

Учащимся раздается карточка с задачами. Вам необходимо прочитать задачу, сделать краткую запись, составить уравнение и решить задачу.

Задача 1 группы: В одном элеваторе было зерна в 3 раза больше, чем в другом. Из первого элеватора вывезли 960 т зерна, а во второй привезли 240 т, после чего обоих элеваторах зерна стало поровну. Сколько тонн зерна было в каждом элеваторе первоначально?

Задача 2 группы: В первом бидоне в три раза больше молока, чем во втором бидоне. Когда из первого перелили во второй двадцать литров, то количество молока в двух бидонах стало поровну. Сколько стало молока в каждом бидоне?

Задача 3 группы: с учебника задача № 792

Задача 4 группы: с учебника задача №791

Задача 5 группы: На одной полке было в 3 раза больше книг, чем на другой. Когда с одной полки сняли 8 книг, а на другую поставили 32 книги, то на полках стало книг поровну. Сколько книг было на каждой полке первоначально?

Вначале группа обсуждает задачу в паре, потом в группе. Каждая группа после решения представить из каждой группы меняется и объясняет решение своей задачи другой группе.

Формативное оценивание «Две звезды и одно пожелание»

Слайд

с ответом

Слайд с решением

Оформление на постере

Карточки, учебник

Конец урока

5 минут

Рефлексия

-Над какой темой мы сегодня трудились? (решали задачи)

-Что сегодня повторили?

-Что было легко?

-С чем справился?

-Что было трудно?

-Над чем надо поработать?

-Материал урока мне был:

понятен / не понятен

полезен / бесполезен,

интересен / скучен

Формативное Оценивание

-подсчитать результаты.

-заполнить лист достижений.

Учитель проводит обратную связь достижений ученика с пояснениями.

0-6 надо стараться, внимательно читай задачу ,….

7-10 направление верное, но нужно правильно составлять уравнение.

11-13 ты идешь в нужном направлении, но есть погрешности в вычислении

14-16 все хорошо, но не останавливайся на достигнутом

Домашнее задание

Уровень А: №797

Уровень В: составить уравнения

Уровень С: составить задачу. Можно выполнить задачку в картинках.

Приложение1.

1 задание

Находит корень уравнения

Записывает ответ

1

1

2 задание

Понимает, как составлять уравнение по условию задачи

Составляет краткую запись, или делает схему

1

Задает параметр к задаче (обозначает неизвестный элемент)

1

Составляет уравнение по условию задачи

1

Решает уравнение, находит корень уравнения

1

Проверяет ответ по условию, записывает

1

3 задание

Применяет правила решения линейных уравнений, находит ответ (корни уравнения)

-составить рисунок к задаче

— знает формулу расстояния

-составить уравнение

-решить уравнение

-найти ответ к задаче

1

1

1

1

1

4 задание

Анализирует решение, проверяет корни уравнения в соответствии условия задачи, записывает ответ

-знает метрическую систему мер (переводит килограммы в граммы

-составляет уравнение

-решает уравнение

-находит ответ к задаче

1

1

1

1

Лист самооценивания _______________________________(Фамилия Имя)

0-6 надо стараться, внимательно читай задачу ,….

7-10 направление верное, но нужно правильно составлять уравнение.

11-13 ты идешь в нужном направлении, но есть погрешности в вычислении

14-16 все хорошо, но не останавливайся на достигнутом результате.

infourok.ru

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *