Статика. Силы и моменты
В задачах, связанных с равновесием тел, нужно, как правило, найти две силы (или больше) которые стремятся это тело повернуть по и против часовой стрелки. Если моменты этих сил равны, тело будет находиться в равновесии. А чтобы рассчитать момент, нужно также правильно определить плечо силы: это расстояние от оси вращения до линии действия силы.
Задача 1. Однородный куб весит 100 Н. Какую горизонтальную силу нужно приложить к верхней точке куба, чтобы его опрокинуть?
Куб будет поворачиваться вокруг точки правой нижней точки основания. Мешать опрокидыванию будет сила тяжести. Плечо силы, с которой будем толкать – длина ребра куба. А плечо силы тяжести – половина ребра, так как она приложена в центре куба.

К задаче 1
Тогда правило моментов:
![Rendered by QuickLaTeX.com \[Fl=mg \frac{l}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-55f00c96529f6f5306237d4742e2152c_l3.png)
Отсюда
![Rendered by QuickLaTeX.com \[F= \frac {mg}{2}=\frac{100}{2}=50\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-393c8eaade0115813842af5f990e60e3_l3.png)
Ответ: 50 Н.
Задача 2. Лестница составляет с землей угол  и опирается о вертикальную стену, трение о которую пренебрежимо мало. Найдите силы, действующие на лестницу со стороны земли и стены, если человек массой 70 кг поднялся по лестнице на две трети ее длины.
и опирается о вертикальную стену, трение о которую пренебрежимо мало. Найдите силы, действующие на лестницу со стороны земли и стены, если человек массой 70 кг поднялся по лестнице на две трети ее длины.
Сделаем чертеж. Запишем уравнения по осям, а также уравнение моментов относительно точки основания лестницы.

К задаче 2
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ N_1d_2=N_2 d_1}\\{ N_1=F_{tr}\\{N_2=mg }\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b5be54e000c2fb50d547839519638d28_l3.png)
Плечо силы  равно
равно  , плечо силы
, плечо силы  – расстояние от основания лестницы до линии действия силы –
– расстояние от основания лестницы до линии действия силы –  .
.
Тогда:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ N_1 l \sin{\alpha}=N_2 \frac{2}{3}l \cos{\alpha}}\\{ N_1=F_{tr}\\{N_2=mg }\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4083d176f36f9f06c24655af545c5f8b_l3.png)
![Rendered by QuickLaTeX.com \[N_1=\frac{2mg}{3}\operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f9adf5305b1965f66d2a879684c6a0f9_l3.png)
Подставим численные данные:
![Rendered by QuickLaTeX.com \[N_2=70 \cdot 9,8=686\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a950d50bc1eb55e9515f55713c0c1713_l3.png)
![Rendered by QuickLaTeX.com \[N_1=\frac{2\cdot686}{3}\operatorname{ctg}{70^{\circ}}=169\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d319a477ed2f621ddfd309bff95f058a_l3.png)
Ответ: со стороны стены 169 Н, со стороны земли 686 Н.
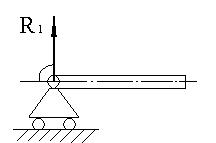
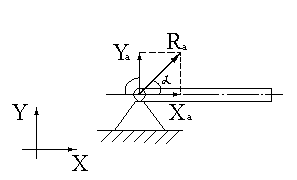
Задача 3. Рабочий удерживает за один конец доску массой 40 кг так, что доска образует угол  с горизонтальным направлением. Какую силу прикладывает рабочий в случае, когда эта сила направлена перпендикулярно доске? Найдите силу реакции опоры по модулю и направлению.
с горизонтальным направлением. Какую силу прикладывает рабочий в случае, когда эта сила направлена перпендикулярно доске? Найдите силу реакции опоры по модулю и направлению.

К задаче 3
Составим уравнение моментов относительно точки опоры доски:
![Rendered by QuickLaTeX.com \[N \cdot0-mg \cos{\alpha}\cdot \frac{l}{2}+Fl=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9d359b213bf81dfcba9dd59fb2fe8415_l3.png)
Откуда находим:
![Rendered by QuickLaTeX.com \[F= mg \cos{\alpha}\cdot \frac{1}{2}=400 \cdot \frac{\sqrt{3}}{4}=100\sqrt{3}=173\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-474154cb3d0a95c2fef649343e414b32_l3.png)
Определим теперь силу трения:
![Rendered by QuickLaTeX.com \[F_{tr}=F \sin{\alpha}=173 \frac{1}{2}=86,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-eacb699230f8ece46dbf966670fd2ff2_l3.png)
Найдем вертикальную составляющую силы реакции опоры:
![Rendered by QuickLaTeX.com \[N_v+ F \cos{\alpha}-mg=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fad0521dd0a69e2c5b41368e8ef3c698_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[N_v=mg- F \cos{\alpha}=400-173\cdot \frac{\sqrt{3}}{2}=250\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-64cb233acd0ca8af83f648ba59dc1bc6_l3.png)
Тогда сила реакции опоры равна по модулю:
![Rendered by QuickLaTeX.com \[N=\sqrt{ N_v ^2+ F_{tr}^2}=\sqrt{250^2+86,5^2}=264\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d72950d2b3197ef9749892b53c36b2f7_l3.png)
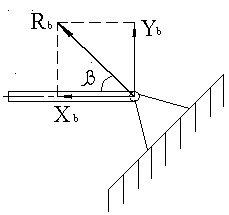
И направлена она под углом  к горизонту, а этот угол можно найти как арктангенс отношения вертикальной составляющей силы реакции опоры к силе трения:
к горизонту, а этот угол можно найти как арктангенс отношения вертикальной составляющей силы реакции опоры к силе трения:
![Rendered by QuickLaTeX.com \[\beta=\operatorname{arctg}{\frac{ N_v }{ F_{tr}}=\operatorname{arctg}{2,9}=71^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8e047a7fa1b0ab65e08830adc5554991_l3.png)
Ответ:  Н,
Н,  Н,
Н,  .
.
Задача 4. Однородная балка массой  и длиной
и длиной  подвешена за концы на двух пружинах. Обе пружины в ненагруженном состоянии имеют одинаковую длину, но при действии одинаковой нагрузки удлинение правой пружины в
подвешена за концы на двух пружинах. Обе пружины в ненагруженном состоянии имеют одинаковую длину, но при действии одинаковой нагрузки удлинение правой пружины в  раз больше, чем удлинение левой. На каком расстоянии от левого конца балки надо положить груз массой
раз больше, чем удлинение левой. На каком расстоянии от левого конца балки надо положить груз массой  , чтобы балка приняла горизонтальное положение?
, чтобы балка приняла горизонтальное положение?

К задаче 4
Рассмотрим рисунок и составим систему уравнений: одно относительно точки  прикрепления левой пружины, второе – относительно точки
прикрепления левой пружины, второе – относительно точки  прикрепления правой.
прикрепления правой.
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ F_1\cdot0-mgx-Mg\frac{l}{2}+F_2 l =0}\\{F_2\cdot0+mg (l-x)+Mg\frac{l}{2}-F_1l=0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-520ca26077b91e6f76f440eeae5db22d_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{ F_2 l =mgx+Mg\frac{l}{2}}\\{ F_1l=mg (l-x)+Mg\frac{l}{2}}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c2be8c387ee447c174932070a0f5ab96_l3.png)
Из условия, что «при действии одинаковой нагрузки удлинение правой пружины в  раз больше, чем удлинение левой» заключаем, что
раз больше, чем удлинение левой» заключаем, что  . На правой части рисунка видно, что
. На правой части рисунка видно, что  , следовательно, можно записать
, следовательно, можно записать
![Rendered by QuickLaTeX.com \[F_1=k_1\Delta x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-11581ddd2494817371a4b5a12c95df37_l3.png)
![Rendered by QuickLaTeX.com \[F_2=k_2\Delta x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e9558a83440811b4c9a6d319b106d458_l3.png)
Разделим теперь первое уравнение системы на второе:
![Rendered by QuickLaTeX.com \[\frac{F_2}{F_1}=\frac{k_2}{k_1}=\frac{1}{n}=\frac{ mgx+Mg\frac{l}{2}}{ mg (l-x)+Mg\frac{l}{2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c420d5a1c551d82b0a7b9d75702c09e0_l3.png)
Разделим теперь еще на  :
:
![Rendered by QuickLaTeX.com \[\frac{1}{n}=\frac{ 2mg\frac{x }{ l }+Mg}{ 2mg -2mg\frac{x }{ l }+Mg}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5787a7038ffbcbb8822ada6f282d8d00_l3.png)
![Rendered by QuickLaTeX.com \[2mg\frac{x }{ l }+Mg=\frac{1}{n}\left(2mg -2mg\frac{x }{ l }+Mg \right)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e695e0cfda43de33c92f0164a9d19850_l3.png)
![Rendered by QuickLaTeX.com \[\left(2mg\frac{x }{ l }+Mg\right)n= 2mg -2mg\frac{x }{ l }+Mg\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7eae27355efddedb6d1bf0fc89c497b5_l3.png)
![Rendered by QuickLaTeX.com \[2m\frac{x }{ l }(n+1)= 2m+M(1- n)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1eaae771aed13f9a004105eb684bc681_l3.png)
![Rendered by QuickLaTeX.com \[x=\frac{2m+M(1- n)}{ 2m(n+1) }l\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fa2ca60e2a2fadc89d369d42ec496533_l3.png)
Ответ: 
easy-physic.ru
3. Решение задач статики (краткая методика).
Решаемые методами статики задачи могут быть одного из двух следующих типов:
1) задачи, в которых известны (полностью или частично) действующие на тело силы и требуется найти, в каком положении или при каких соотношениях между действующими силами тело будет в равновесии;
2) задачи, в которых известно, что тело заведомо находится в равновесии, и требуется найти, чему равны при этом все или некоторые из действующих на тело сил.
Реакции связей являются величинами, наперед неизвестными во всех задачах статики.При инженерных расчетах в результате решения задач статики определяются условия равновесия конструкции (если она не закреплена наложенными связями жестко), а также давления на опоры или усилия в тех или иных частях конструкции при ее равновесии. Так как рассматриваемая конструкция, как правило, представляет собой совокупность ряда связанных друг с другом тел, то, приступая к решению конкретной задачи надо, прежде всего, установить, равновесие какого именно тела следует рассмотреть, чтобы найти искомые величины.
Весь процесс решения задач сводится к следующим операциям:
1. Выбор тела, равновесие которого должно быть рассмотрено. Для решения задачи надо рассмотреть равновесие тела, к которому приложены заданные и искомые силы. Если заданные силы приложены к одному телу, а искомые к другому, может оказаться необходимым рассмотреть последовательно равновесие каждого тела в отдельности, а иногда и равновесие промежуточных тел.
2. Установление связей, т.е. выявление всех тел, предметов, частей конструкции, которые препятствуют перемещению в плоскости или в пространстве рассматриваемого тела.
3. Освобождение рассматриваемого тела от связей и изображение действующих на него заданных сил и реакций связей. Тело, освобожденное от связей, желательно изображать на отдельном рисунке. Также, на этом этапе следует выбрать систему координат. Если действующие на тело заданные силы и силы реакций лежат в одной плоскости, выбираем плоскую систему отсчета. Если действующие на тело силы имеют пространственную ориентацию, то следует выбрать пространственную систему координат.
4. Составление уравнений равновесия. Вид уравнений равновесия зависит от того, какая система сил (сходящаяся, плоская или пространственная) действует на рассматриваемое тело.
При решении задач “плоской” статики рекомендуется для получения более простых уравнений равновесия:
а) составляя уравнение проекций, выбирать координатную ось перпендикулярно какой-нибудь неизвестной силе;
б) составляя уравнение моментов, выбрать центр (точку) моментов в точке, где пересекается большее количество неизвестных сил.
При решении задач “пространственной” статики в случаях, когда из общего чертежа трудно усмотреть, чему равен момент данной силы относительно какой-нибудь оси, рекомендуется изобразить на вспомогательном рисунке проекцию рассматриваемого тела вместе с действующими нагрузками на плоскость, перпендикулярную к этой оси. В тех случаях, когда при вычислении момента возникают затруднения в определении проекции силы на соответствующую плоскость или в вычислении плеча этой проекции, рекомендуется разложить силу на две взаимно перпендикулярные составляющие (из которых одна параллельна какой-нибудь координатной оси), а затем воспользоваться теоремой Вариньона.
studfile.net
Лекция №1 статика
Статика – это раздел теоретической механики, в котором изучают условия равновесия системы сил, приложенных к твердому телу, а также приведение сложной системы сил к простейшему виду.
Основные понятия.
В теоретической механике реальные объекты заменяются моделями так, чтобы в этих моделях нашли отражения основные, существенные факторы, которые будут определять главные черты рассматриваемого явления.
Материальная точка – точка, имеющая массу. Если размерами реального тела можно пренебречь, то оно рассматривается как материальная точка.
Абсолютно твердое тело – тело, в котором расстояние между двумя любыми точками остается неизменным.
Механическая система – совокупность материальных точек или тел, в которой положение и движение каждой точки (тела) зависит от положения и движения всех остальных.
Сила – мера механического взаимодействия материальных тел. Сила является векторной величиной. Характеризуется точкой приложения, модулем (абсолютным числовым значением), направлением. Прямая, вдоль которой направлена сила, называется линией действия силы (рис.1).
Основной
единицей измерения модуля силы в
Международной системе единиц (СИ)
является 1 ньютон (1 Н).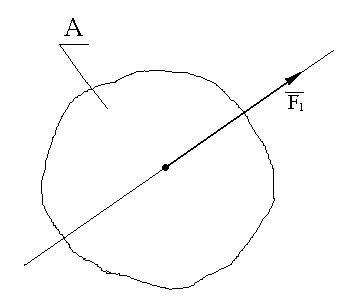
Рис. 1
Система сил – совокупность сил, действующих на данное тело или систему тел. (),гдеn-число сил в системе.
Эквивалентные системы сил – системы сил, действие которых на одно и то же тело одинаково при прочих равных условиях (рис.2).
( )(
)(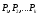 )
)
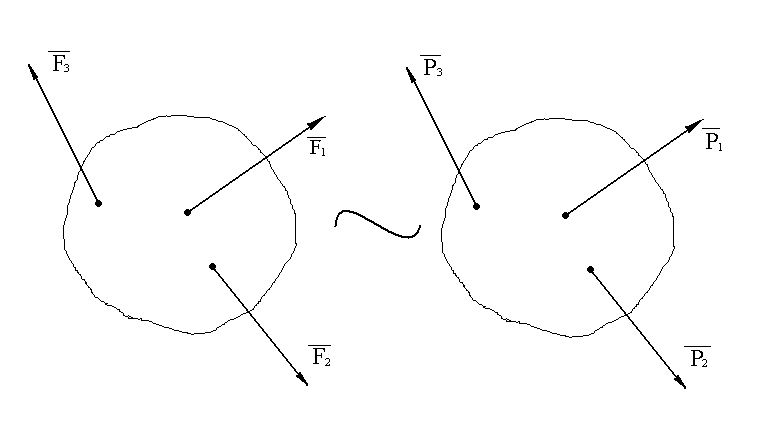
Рис. 2
Равнодействующая сила – сила, действие которой на тело или материальную точку эквивалентно действию данной системе сил (рис.3).
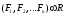

Рис. 3
Уравновешенная система сил (эквивалентная 0) –система сил, под действием которой свободное тело находится в покое.
(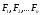 )0
)0
Уравновешенная система сил не имеет равнодействующей.
Сосредоточенная сила – сила, приложенная к какой-либо точке твердого тела.
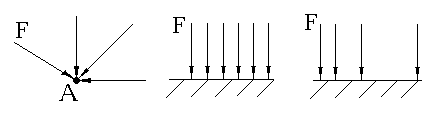
Рис. 4а Рис.4б Рис 4в
Распределенные силы – силы, действующие на все точки данного объема или данной части поверхности, или линии. Распределенные силы характеризуются интенсивностьюq, т.е. силой, приходящейся на единицу объема, поверхности или длины линии. Распределенные силы обычно заменяют сосредоточенными. На рис.4 приведены примеры сосредоточенных сил (рис.4 а) и распределенных сил: равномерно распределенные силы (рис.4б) и распределенные силы, изменяющиеся по линейному закону (рис.4в).
Внутренние силы – силы взаимодействия между телами, входящими в механическую систему.
Внешние силы – силы, с которыми действуют тела не входящие в рассматриваемую механическую систему.
Задачи статики
Преобразование систем сил, действующих на твердое тело, в эквивалентные или системы сил простейшего вида.
Определение условий равновесия систем сил, действующих на твердое тело.
Все теоремы и методы, с помощью которых решаются эти задачи, основываются на аксиомах, справедливость которых проверена многовековой практической деятельностью человечества.
Аксиомы статики
Аксиома 1 .
Если свободное тело находится в равновесии под действием 2-х сил, то эти силы равны по величине и направлены в противоположные стороны по прямой, проходящей через точки приложения этих сил.
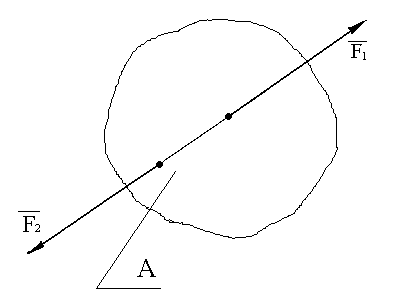
Рис. 5
Аксиома 2.
Действие системы сил на тело не изменится, если к телу приложить или отнять от него уравновешенную систему сил.
(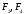 )0; (
)0; (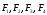 )(
)(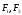 )
)

Рис. 6
Следствие:действие силы на абсолютно твердое тело не изменится перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
Рис. 7
Аксиома 3.
Равнодействующая 2-х сил, приложенных в одной точке абсолютно твердого тела равна по величине и направлению диагонали параллелограмма, построенного на этих силах как на сторонах.
Справедливо и обратное утверждение, т.е. одну силу, приняв за равнодействующую, можно разложить на две составляющие силы.
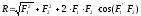 ;
;
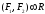 ;
;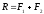
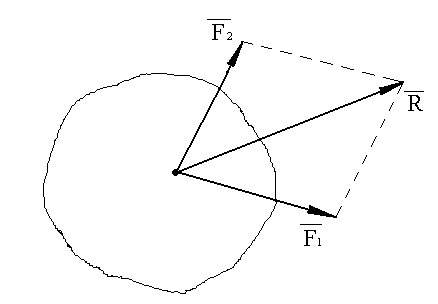
Рис. 8
Аксиома 4 .
Силы, с которыми взаимодействуют 2 тела, равны по величине и направлены по одной прямой в противоположные стороны (третий закон Ньютона).

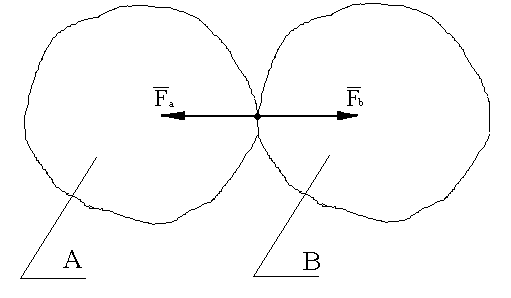
Рис.9
Аксиома 5.
Если деформируемое тело находится в равновесии, то равновесие этого тела не нарушится, если, не изменяя формы, размеров, положения в пространстве, оно превратится в абсолютно твердое тело, т.е. затвердеет.
Например, если под действием сил резиновое тело находится в равновесии, то равновесие сохранится, когда это тело станет абсолютно твердым.
Аксиома 6.
Всякое несвободное тело можно рассматривать как свободное, если отбросить связи, заменив их действие на тело реакциями связи.
Свободное тело – тело, перемещения которого ничем не ограничиваются.
Несвободное тело – тело, перемещения которого в пространстве ограничены другими телами.
Связью – называются тела, которые препятствуют перемещению данного тела.
Реакции связи – силы, с которыми связи воздействуют на данное тело.
Связи и реакции связи
Абсолютно гладкая (без трения) поверхность, (рис.10).

Рис.10
Реакция
связи 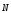 направлена по нормали к общей касательной
соприкасающихся поверхностей.
направлена по нормали к общей касательной
соприкасающихся поверхностей.
Гибкая нерастяжимая связь (нить, трос) (рис. 11).

Рис.11
Реакция связи направлена вдоль нити.
Невесомый стержень с двумя шарнирами (рис.12)

Рис.12
Цилиндрическая шарнирно-подвижная опора (рис.13)


Рис.13
Реакция
связи ( )
перпендикулярна опорной поверхности.
)
перпендикулярна опорной поверхности.
Цилиндрическая шарнирно-неподвижная опора (рис.14а, 14б)


Рис.14
Направление реакции неизвестно, но по 3 аксиоме статики реакцию можно разложить на две составляющие по двум осям координат.
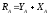 ;
;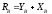 ;
;
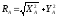 ;
;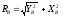 ;
;
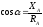 ;
;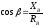 .
.
Жесткая заделка.
Связь
запрещает любое перемещение тела,
поэтому возникает сила реакции связи 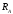 ,
направление которой неизвестно. По 3
аксиоме статики реакцию можно разложить
на две составляющие по осям координат
(
,
направление которой неизвестно. По 3
аксиоме статики реакцию можно разложить
на две составляющие по осям координат
(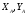 ).
Жесткая заделка запрещает поворот
вокруг любой оси, проходящей через точку
А, поэтому возникает пара сил реакции,
момент которой
).
Жесткая заделка запрещает поворот
вокруг любой оси, проходящей через точку
А, поэтому возникает пара сил реакции,
момент которой не
известен ни по величине, ни по направлению
(рис. 15).
не
известен ни по величине, ни по направлению
(рис. 15).

Рис.15
studfile.net
Методы решения физических задач по статике
«Равновесие получается в результате
уничтожения нескольких сил, которые
борются и взаимно сводят на нет действие,
производимое ими друг на друга; статика
имеет своей целью дать законы, согласно
которым происходит это уничтожение».
Ж.Л. Лагранж
В данной теме разговор пойдёт об элементах статики, вспомним основные формулы, связанные с данным разделом физики, а также дадим некоторые рекомендации по решению задач на данную тему.
Статика — это раздел физики, который изучает равновесия материальной точки и абсолютно твердого тела.
Абсолютно твердое тело — это тело, размеры и форму которого можно считать неизменными.
Условия равновесия — это условия, при которых тело при наличии внешних воздействия может находиться в покое относительно инерциальной системы отсчета; двигаться поступательно, равномерно и прямолинейно; равномерно вращаться относительно оси, проходящей через центр масс.
Основные физические величины, используемые в статике, — это сила и момент силы.
Сила — это векторная физическая величина, описывающая и измеряющая воздействие одного тела на другое, в результате которого тела приобретают ускорение или деформируются. Она характеризуется: модулем, направлением в пространстве и точкой приложения.
При осуществлении различных операций над силами необходимо всегда помнить, что точку приложения силы можно переносить только вдоль прямой, вдоль которой эта сила действует.
Важным понятием является и понятие равнодействующей силы, то есть силы, которая производит на тело такое же действие, как и несколько одновременно действующих на него сил. Она равна геометрической сумме этих сил. Иными словами, сложить силы — это значит найти их равнодействующую.
Рассмотрим некоторые правила сложения сил. Начнем со сложения параллельных сил. Представим, что имеется некое твердое тело, которое изобразим в виде прямоугольника, на концы которого действую две силы, направленные в одну и ту же сторону параллельно друг другу. Для того, чтобы найти равнодействующую этих двух сил, необходимо параллельным переносом совместить конец одного вектора с началом второго.

Из рисунка хорошо видно, что равнодействующая двух параллельных одинаково направленных сил равна по модулю сумме их модулей, параллельна им и направлена в ту же сторону. Помимо этого, линия действия равнодействующей силы делит отрезок, соединяющий точки приложения слагаемых сил, на участки, обратно пропорциональные силам.
Теперь вспомним, как найти равнодействующую двух антипараллельных сил, то есть сил, которые параллельны друг другу, но направлены в противоположные стороны. Как и в предыдущем случае, нам необходимо параллельным переносом совместить конец одного вектора силы с началом вектора другой силы. Из рисунка видно, что равнодействующая двух антипараллельных сил равна по модулю разности их модулей, параллельна им и направлена в сторону большей силы. При этом точка приложения равнодействующей лежит на продолжении линии, соединяющей точки приложения слагаемых сил на расстояниях от них, обратно пропорциональных силам.
Теперь вспомним, как найти равнодействующую не параллельных сил. Пусть к некоторому телу приложено две силы в одной точке, направленные под некоторым углом альфа друг к другу. Тогда их равнодействующую находят по правилу параллелограмма.

Если же непараллельные силы приложены в разных точках тела, то для нахождения их равнодействующей поступают следующим образом: сначала проводят прямые, вдоль которых действуют эти силы, до их пересечения в некоторой точке. Затем, действующие силы переносят в точку пересечения прямых, вдоль которых они действуют. А затем производят их векторное сложение по правилу параллелограмма. При этом точкой приложения равнодействующей силы может быть любая точка прямой, вдоль которой эта сила действует.
Модуль равнодействующей двух непараллельных сил можно определить по теореме косинусов. А если угол между векторами сил равен девяносто градусов, то по теореме Пифагора.
Теперь поговорим об условиях равновесия. Начнем с равновесия тела, которое не имеет оси вращения. Если под действием приложенных к телу сил оно движется поступательно, то все его точки движутся одинаково и достаточно рассмотреть движение одной точки. Условие равновесия такого тела, как и условие равновесия материальной точки, вытекает из основного уравнения динамики: чтобы не вращающееся тело находилось в равновесии, необходимо, чтобы геометрическая сумма сил, действующих на тело, была равна нулю (или алгебраическая сумма проекций этих сил на оси координат была равна нулю).

Если же тело, под действием приложенных к нему сил поступательно не движется, а поворачивается вокруг некоторой закрепленной оси, то для его равновесия необходимо выполнения следующего условия: алгебраическая сумма моментов сил, приложенных к телу, относительно оси вращения, должна равняться нулю.


Момент силы — это произведение модуля силы на ее плечо, то есть на кратчайшее расстояние от оси вращения до линии действия силы. Обратите внимание: не до точки приложения силы, а именно до линии, вдоль которой действует сила. При этом принято считать момент силы положительным, если сила вращает тело относительно данной оси по ходу часовой стрелки, и отрицательным, если сила вращает тело против хода часовой стрелки.
В общем случае, если тело под действием приложенных к нему сил может и поворачиваться, и двигаться поступательно, то для того, чтобы оно находилось в равновесии, необходимо выполнение данных двух условий одновременно.
Для того чтобы судить о поведении тела в реальных условиях, мало знать, что оно находится в равновесии. Надо еще оценить это равновесие. Поэтому различают три вида равновесия: устойчивое равновесие, неустойчивое равновесие и безразличное равновесие.

Равновесие тела называют устойчивым, если при отклонении от него возникают силы, возвращающие тело в положение равновесия.
Неустойчивым называют такое равновесие тела, при котором даже самое незначительное отклонение от положения равновесия, равнодействующая действующих на тело сил вызывает дальнейшее отклонение тела.
А вот равновесие, при котором смещение тела в любом направлении не вызывает изменений действующих на него сил и равновесие тела сохраняется, называют безразличным.
Объяснение видов равновесия может быть дано и на основании определения центра тяжести (или центра масс) тела. Центр тяжести — это такая точка приложения равнодействующей сил тяжести, действующих на все части тела, которая не изменяет своего положения при любых поворотах тела.
Таким образом, в устойчивом равновесии центр тяжести тела занимает наинизшее из всех возможных положений и связан с минимум потенциальной энергии по отношению ко всем близким соседним положениям тела.
При неустойчивом равновесии высота центра тяжести максимальна, как максимальна и потенциальная энергия по отношению к другим близким положениям тела.
Безразличное равновесие связано с неизменной потенциальной энергией всех близких состояний, и высота центра тяжести одинакова во всех достаточно близких положениях.
Сведем в таблицу основные формулы элементов статики.
|
Формула |
Описание формулы |
|
|
Равнодействующая нескольких сил |
|
|
Момент силы, где l – плечо силы. |
|
|
Условия
равновесия твердого тела, где |
Методические рекомендации по решению задач, относящихся к равновесию тел
1) Проанализировав условие задачи, сделать чертеж с указанием на нем всех сил, действующих на тело, находящееся в положении равновесия.
Задача. Однородный деревянный кубик массой т находится на наклонной плоскости. Определите действующую на него силу трения покоя.

Во-первых, рисуем рисунок, на котором указываем наклонную плоскость и кубик на ней,а затем указываем действующие на кубик силы: силу тяжести, силу нормальной реакции плоскости и силу трения покоя. Исходя из рисунка, делаем вывод о том, что данная задача является задачей на условие равновесия тела, не имеющего оси вращения.
2) Для тела, не имеющего оси вращения, достаточно использовать первое условие равновесия, которое говорит нам о том, что геометрическая сумма приложенных к телу сил должна равняться нулю.

3) Выбрать оси координат и записать это уравнение в проекциях.



4) Для тела с закрепленной осью вращения достаточно использовать правило моментов, согласно которому, тело с закрепленной осью вращения будет находиться в равновесии, если алгебраическая сумма моментов всех сил, действующих на тело, будет равна нулю.

Для этого надо найти плечи всех сил относительно данной закрепленной оси. А затем составить алгебраическую сумму моментов этих сил с учетом знаков и приравнять ее к нулю.
5) Если ось вращения тела не закреплена, то необходимо использовать оба условия равновесия. Для конкретного примера, используем то, что алгебраическая сумма проекций сил на оси координат должна равняться нулю.
6) Для записи правила моментов необходимо выбрать ось вращения. Лучше ее выбирать так, чтобы через нее проходило наибольшее число линий действия неизвестных сил. Тогда моменты этих сил, относительно выбранной точки, будут равны нулю.
7) Необходимо решить полученную систему уравнений относительно искомой величины.
videouroki.net
Алгоритм решения задач статики
Выбирают систему отсчёта.
Выбирают тело, к которому приложена система уравновешивающихся сил.
Показывают все действующие на тело активные нагрузки.
Согласно аксиоме связей действие связей на тело заменяют соответствующими реакциями связей.
К полученной системе сил применяют уравнения равновесия, соответствующие этой системе сил.
Из уравнений равновесия определяют неизвестные величины.
1.8. Пример решения задачи на плоскую сходящуюся систему сил
Два стержня АС и ВС соединены шарнирно в узле С, к которому через блок D подвешен груз 1 весом 12 Н (рис. 1.33).
Определить реакции стержней АС, ВС, если угол = 60о.

Рис. 1.33
Решение. Решаем задачу по изложенному алгоритму.
Выбираем правую систему отсчёта OYZ.
Вырезаем узел С и рассмотрим его равновесие.Активных сил к узлу С не приложено. Следовательно, Σ FiE = 0.
От узла С отбрасываем невесомые стержни АС и ВС и показываем реакции RA и RB. Эти реакции направлены вдоль стержней. Условимся рассматривать их растянутыми. Отбрасываем нить и показываем на рисунке реакцию Т нити. Нить растянута. Модуль Т реакции Т равен весу G груза 1.
На узел С действует плоская система сходящихся реакций связей. Поскольку Σ FiE = 0, то геометрическое условие равновесия приобретает вид Σ RiE = RA + RB + T = 0. Аналитические условия равновесия выражаются двумя уравнениями:
Σ = 0 =
– RA·sin()
+ RB·cos()
+ T = 0; (1)
= 0 =
– RA·sin()
+ RB·cos()
+ T = 0; (1)
Σ = 0 = RA·cos()
+ RB·sin()
= 0. (2)
= 0 = RA·cos()
+ RB·sin()
= 0. (2)
Из уравнения (2) определим RA = – RB·
 =
– RB·tg().
При подстановке RA в уравнение (1) имеем
=
– RB·tg().
При подстановке RA в уравнение (1) имеем
RB·tg()·sin() + RB·cos() + T = 0.
Откуда
RB = – 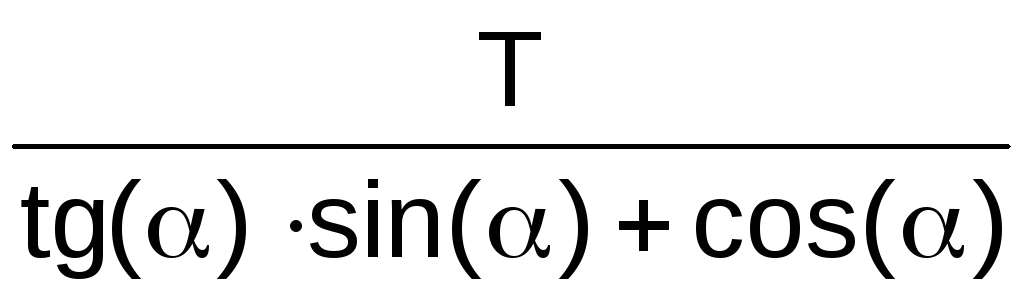 =
=
=
– 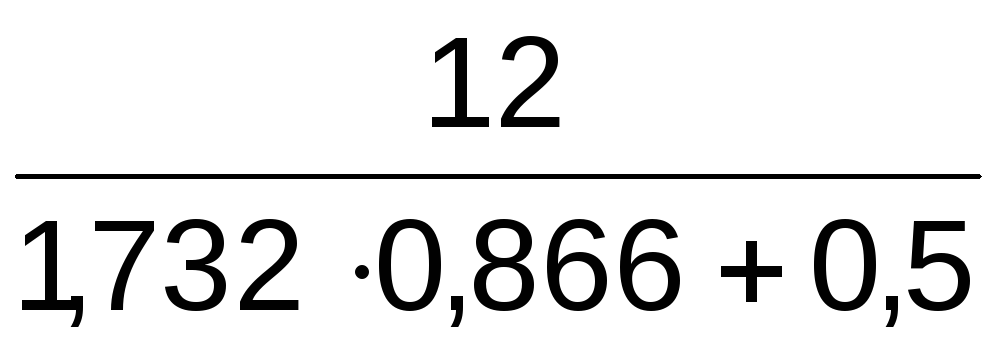 = – 6 Н.
= – 6 Н.
Так как RB 0, то стержень ВС сжат.
RA = – RB·tg() = – (– 6)·1,732 = 10, 392 Н.
Так как RA > 0, то стержень АС растянут.
Вопросы и задания для самоконтроля
Сформулировать определение термина «проекция силы на ось».
Записать формулы для определения проекций силы F на координатные оси декартовой системы отсчёта OXYZ.
Записать формулу для определения силы F через компоненты этой силы в декартовой системе отсчёта OXYZ.
Записать формулы для определения направляющих косинусов силы в декартовой системе отсчёта OXYZ.
Записать формулы для определения проекций равнодействующей системы сходящихся сил в декартовой системе отсчёта OXYZ.
Записать формулу, выражающую геометрическое условие равновесия сходящейся системы сил.
Записать уравнения равновесия для пространственной системы сходящихся сил в декартовой системе отсчёта OXYZ.
Записать уравнения равновесия для плоской системы сходящихся сил в декартовой системе отсчёта OXYZ.
1.9. Пара сил
Пару сил в механике рассматривают как одно из основных понятий, наряду с понятием силы.
Пара сил – система двух параллельных, противоположно направленных и равных по модулю сил, не лежащих на одной прямой.
Плоскость действия пары сил – плоскость, в которой находятся линии действия сил.
Плечо пары сил – кратчайшее расстояние (длина перпендикуляра) между линиями действия сил, составляющих пару сил.
На рис. 1.34 изображена пара сил, плоскость действия которой лежит в плоскости OXY системы отсчёта OXY.
Силы F1, F2 образуют пару сил. F1 = F2; F1 = – F2. Однако силы пары не уравновешиваются, так как они направлены не по одной прямой. Пара сил стремится произвести вращение тела, к которому она приложена. Действие пары сил на тело характеризуется её моментом.
Д

Рис. 1.34
ля количественной характеристики действия пары сил на тело и указания направления, в котором пара сил стремится вращать тело, вводится понятиеалгебраического момента пары сил.Алгебраический момент пары сил – величина, равная взятому с соответствующим знаком произведению модуля одной из сил на её плечо.
M = ± F1·h = ± F2·h.
Алгебраический момент пары сил считают положительным, если пара сил стремится повернуть тело против вращения часовой стрелки, и отрицательным, если в сторону вращения часовой стрелки. В системе СИ момент пары сил измеряется в Н·м.
Н
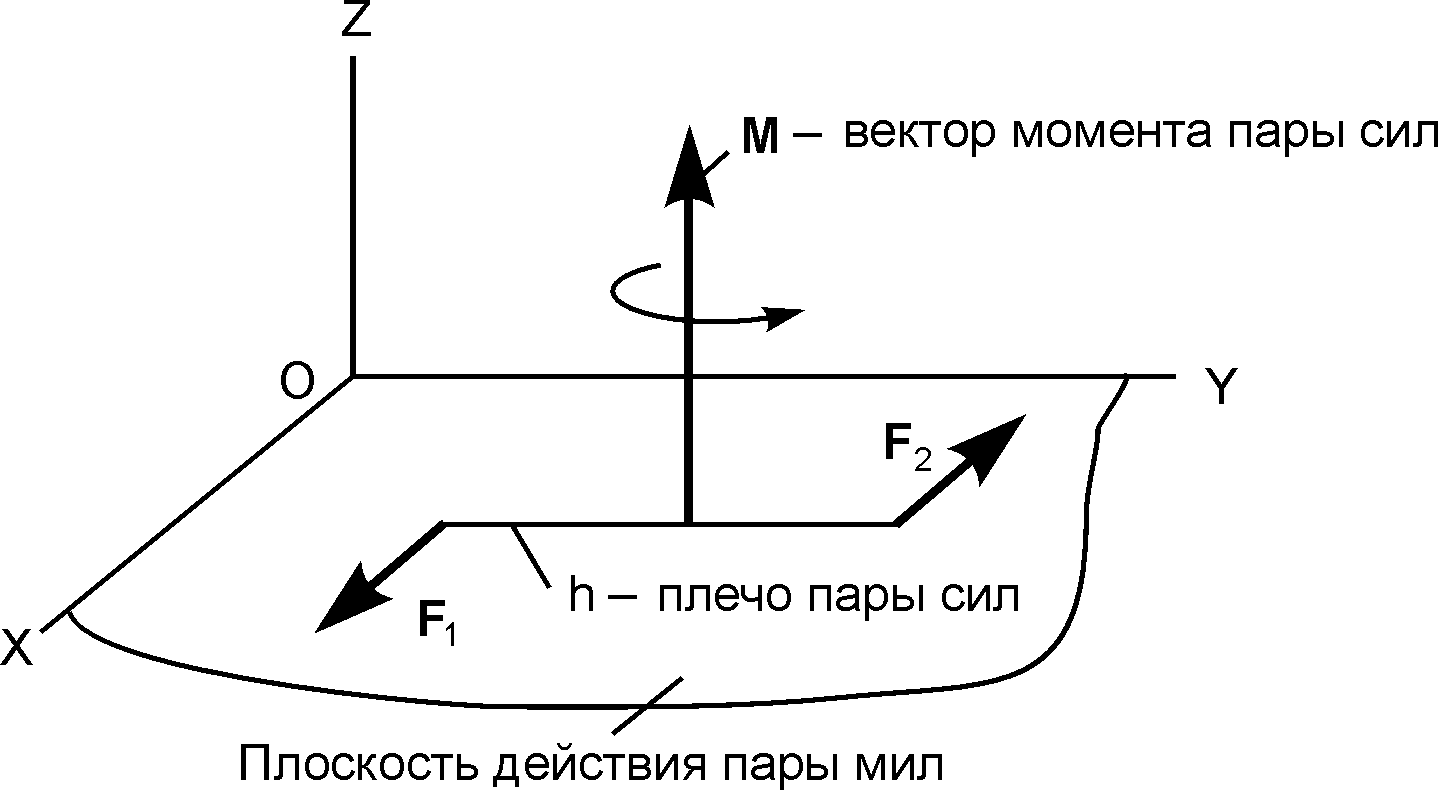
Рис. 1.35
а рис. 1. 35 изображена пара сил (F1, F2), линии действия которых лежат в плоскости OXY.Момент пары сил – векторная мера механического действия пары сил, равная моменту одной из сил пары относительно точки приложения другой силы.
Момент пары сил изображается вектором М. Вектор момента М пары сил (F1, F2) направлен перпендикулярно к плоскости действия пары сил в сторону, откуда видно пару сил, стремящуюся вращать плоскость её действия в сторону, противоположную вращению часовой стрелки. Согласно определению (см. рис. 1.35), M j, M i, M = F1h = F2·h. Таким образом, пара сил полностью характеризуется её моментом M.
Теорема. Пары сил, лежащие в одной плоскости, эквивалентны, если их алгебраические моменты численно равны и одинаковы по знаку.
Доказательство этой теоремы несложно и здесь оно не приводится.
studfile.net
Сборник задач на тему «статика, статическое равновесие». Общие принципы решения. План решения задач
Задачи на статику узнать достаточно просто. Тела в таких задачах обязательно покоятся. Тогда, соотношения, позволяющие решать задачу:
(1)Т.е. при равновесии тела сумма сил, действующих на тело равна нулю.
(2)Т.е. при равновесии тела сумма моментов сил, действующих на тело равна нулю.
Тогда общее решение таких задач достаточно линейно:
- находим проекции второго закона Ньютона на две оси в декартовой системе координат согласно плану.
- если полученных уравнений не хватает, то ищем значения моментов всех сил, действующих на тело
- пользуемся соотношением моментов (2) и получаем ещё одно уравнение.
Важно: в задачах на статику необходимо начинать с анализа уравнения (1), т.к. поиск моментов долгий, а соотношения (1) часто хватает.
Задачи, в которых достаточно соотношения (1):
- Под действием двух чугунных кубиков, объёмом…
Задачи в которых необходимо уравнение моментов (2):
- На концах лёгкого стержня длиной…
Метровая линейка, находящаяся на опоре, удерживается в равновесии…
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
www.abitur.by
Статика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Основы статики
К оглавлению…
Статикой называется раздел механики, изучающий условия равновесия тел. Равновесием называют такое состояние тела или системы тел, в котором оно не движется в данной системе отсчета. Различают три вида равновесия:
- Устойчивое равновесие. Если систему вывести из состояния устойчивого равновесия, то она самопроизвольно в него вернется, то есть при выведении из положения равновесия возникает сила, возвращающая систему к равновесию. Для этого необходимо, чтобы потенциальная энергия системы в состоянии устойчивого равновесия имела минимальное значение. Любая физическая система стремится к состоянию устойчивого равновесия. Это значит, что любой самопроизвольный процесс всегда проходит с уменьшением потенциальной энергии.
- Неустойчивое равновесие. В данном случае при выведении из состояния равновесия возникают силы, уводящие систему от равновесия, и система самопроизвольно не может в него вернуться. В состоянии неустойчивого равновесия потенциальная энергия системы имеет максимальное значение.
- Безразличное равновесие. При выведении из состояния равновесия в системе не возникает ни возвращающих, ни уводящих в сторону сил.
Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к невращающемуся телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение (действительно, ведь ускорение тела при этом равно нулю). В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей силы все силы, действующие на тело, можно прикладывать к центру масс. Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело.
Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю. Иными словами, векторная сумма всех сил, приложенных к телу должна быть равна нолю:

Момент силы. Правило моментов
К оглавлению…
Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.
Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие — момент силы. Произведение модуля силы F на плечо d и называется моментом силы M. Таким образом момент силы в статике вычисляется по формуле:

Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет. Поэтому, важно запомнить, что моменты сил, вращающих тело в различных направлениях относительно часовой стрелки, берутся с различными знаками.
Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата.
Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м).
Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов.
Алгоритм решения задач на правило моментов (задач по статике):
- Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы.
- Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем.
- Записать правило моментов относительно данной оси, на забывая про правило знаков.
- При необходимости записать также условие согласно которому равнодействующая сила равна нолю.
- Выразить искомую силу.
Рычаги и блоки
К оглавлению…
Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот). Это значит, что при увеличении силы за счет некоторого механизма неизбежно будет уменьшено и перемещение. Рассмотрим основные типы простых механизмов изучаемых в школьной физике:
- Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр.
- Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку.
- Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить. Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении.
- Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение.
- Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.
Центр тяжести тела
К оглавлению…
Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее).
Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике:
1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии.
2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел:

где: l1 – расстояние от центра масс до тела с массой m1, а l2 – до тела с массой m2.
3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле:
Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно).
4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ.
5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему:
Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:
educon.by
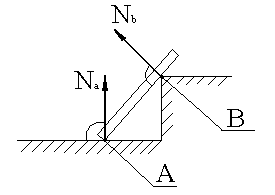






 –
силы действующие на тело, Mi —
моменты этих сил.
–
силы действующие на тело, Mi —
моменты этих сил.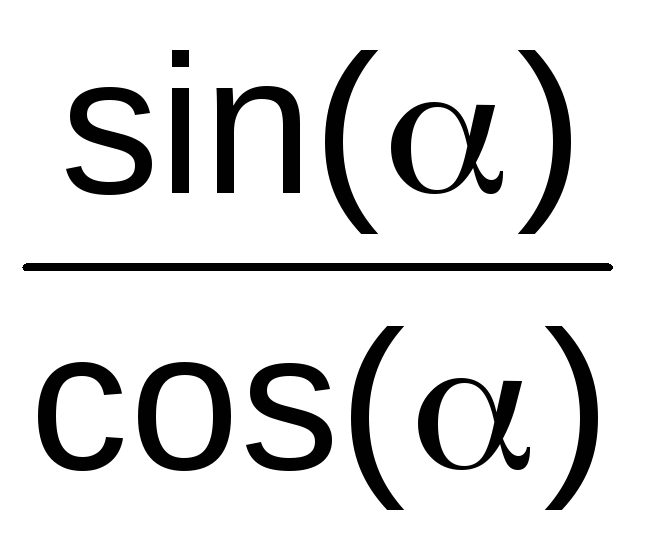 =
– RB·tg().
При подстановке RA в уравнение (1) имеем
=
– RB·tg().
При подстановке RA в уравнение (1) имеем