Теорема Виета. Решение задач. Видеоурок. Алгебра 8 Класс

Теорему Виета мы доказали на прошлом уроке. Она связывает корни квадратного уравнения и коэффициенты этого уравнения. Напомним ее:

Числа 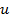,  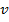являются корнями уравнения 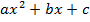,  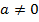тогда и только тогда, когда пара  является решением системы:

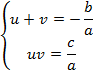
Cфера применения теоремы Виета весьма обширна. Здесь мы рассмотрим основные типы задач, в которых она применяется.

Прежде всего, теорема Виета дает еще один способ нахождения корней уравнения и их проверки.

Найти и проверить корни уравнения .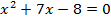

Решение

Во-первых, корни мы можем найти через дискриминант:

a)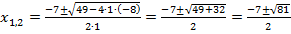 

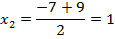
Итак, корни найдены, их надо проверить.

Первый способ проверки – подстановка в исходное уравнение. Второй способ – подставить корни в теорему Виета. Используем второй способ:

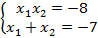
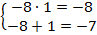 – верно

Корни найдены правильно.

Ответ: ; .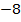

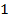b) Кроме того, теорема Виета дает новый способ нахождения корней:

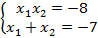
Если разложить  и зная, что сумма корней равна -7, можно легко подобрать корни уравнения.

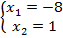
Получили тот же самый ответ.

Ответ:; .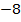

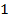Итак, на примере данного несложного примера мы показали, что теорема Виета позволяет проверить корни и найти эти корни методом подбора.

Найти корни уравнения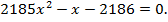

Это уравнение можно решить через дискриминант, но это очень неудобно.

Взглянув на это уравнение можно заметить, что 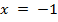 является корнем уравнения.

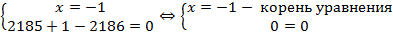
Один корень мы подобрали, как найти второй? Воспользуемся теоремой Виета, согласно ей произведение корней уравнения:

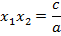
Подставим в равенство найденный корень:

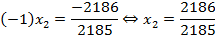
Итак, нам нужно было решить уравнение. Первый корень мы подобрали, второй нашли по теореме Виета.

Ответ:

; .

Теорема Виета позволяет легко найти сумму и произведение корней, не зная самих корней. Это является ключом к решению многих задач, в которых не требуется найти корни, но требуется найти выражения, которые зависят от суммы и произведения корней. В общем виде – найти функцию 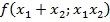, которая зависит от суммы корней и от их произведения.

Рассмотрим конкретную задачу.

Для уравнения , найти:

a)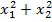 

;

b) ;

c) .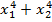

Решение

Заметим, что дискриминант 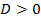. Значит, у уравнения существуют два корня, .

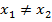Эту задачу можно решить, найдя его корни через дискриминант и произведя над корнями все действия, но можно поступить более изящно, используя теорему Виета.

a)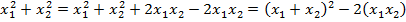 

Здесь мы выделили полный квадрат суммы, теперь составим систему по теореме Виета:

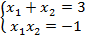
Подставим в наш пример:

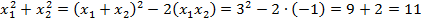
b) Приведем к общему знаменателю:

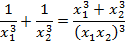
Значение выражения в знаменателе уже можно найти. В числителе наша цель – выразить сумму кубов через сумму и произведение корней:

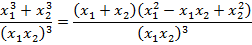
Можно подставлять значения:

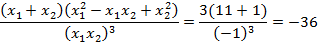
c)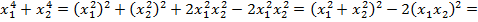 

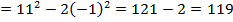
Ответ: 11, -36, 119.

Теорема Виета используется в так называемых задачах «с параметрами». Рассмотрим одну из таких задач.

Найти все 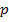, при каждом из которых отношение корней уравнения  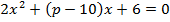равно 12.

Решение

Есть параметр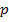

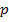. При некоторых значениях  у уравнения может вообще не быть корней, при других значениях корни будут 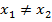, но нужно подыскать такие значения параметра, при которых корни отличаются в 12 раз.

Сформируем систему, из которой мы найдем :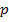

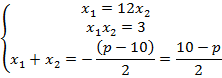
Мы получили систему трех уравнений относительно трех неизвестных: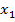

, , .

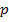Решим систему. Заметим, что первые два уравнения зависят только от 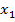 и , если мы их решим, то подставим в третье уравнение и найдем .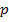

Подставим значение 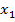 из первого уравнения во второе:

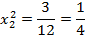
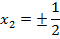
Рассмотрим оба варианта :

a)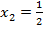 

Подставляем в третье уравнение:

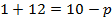
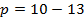
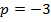
Первый ответ получен.

b)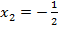 

Подставляем в третье уравнение:

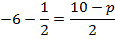
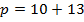
Ответ:; .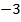

Задача решена.

Сделаем следующие примечания: при найденных 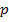 система

имеет решение, значит, и само квадратное уравнение 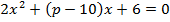 имеет решение и проверять дискриминант не нужно. Дискриминант будет больше нуля, поскольку система и квадратное уравнение равносильны в силу теоремы Виета.

Мы рассмотрели теорему Виета, применили ее для решения основных типовых задач.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение. 2004.

2.Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «ЯКласс» (Источник)

2. Интернет-сайт dist-tutor.info (Источник)

3. Интернет-сайт mathematics-repetition.com (Источник)

 

Домашнее задание

1. Используя теорему Виета, найти корни уравнения .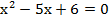

2. При каких значениях параметра 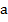 сумма квадратов корней уравнения  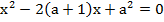равна 4?

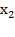3.  и  – корни уравнения 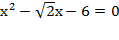. Найдите значение выражений:

А)

Б)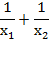 

Теорема Виета

Тип урока: урок изучения и первичного закрепления новых знаний и способов деятельности.

Цель урока: организовать деятельность учащихся по изучению т.Виета; по применению полученных знаний; создать: а) условия для развития умений учащихся самостоятельно применять полученные знания; б) условия для развития информационных умений; для развития монологической и диалогической речи.

Оборудование: мультимедийный проектор, интерактивная доска портрет Виета, карточки, таблицы, сообщение учащегося, звёздочки.

Логика урока: мотивация – восприятие – осмысление и первичное запоминание – первичная проверка понимания изученного материала – анализ изученного содержания – рефлексия.

Ход урока

I. Организационный этап.

Вводное слово учителя.

На доске написано высказывание: «Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе». М.И. Калинин.

Вот и сегодня на нашем уроке у каждого из вас есть такая возможность.

II. Подготовка к изучению нового материала.

1. проверочный диктант.

1. Запишите, пожалуйста, общий вид квадратного уравнения.
2. Запишите общий вид приведённого квадратного уравнения.
3. Неполное квадратное уравнение, если в = 0; с = 0; В и С равно 0.
4. Запишите формулу вычисления дискриминанта.
5. Запишите слово дискриминант.
6. Чему равно X₁ и X₂.

Диктант проверяется с использованием презентации.

У доски по карточкам учащиеся решают уравнения, используя дифференцированный подход в обучении.

Столько же учащихся по карточкам решают в тетради.

Карточка 1. Решите уравнение: х² – 8х + 15 = 0.

Карточка 2. Решите уравнение: х² + 12х + 20 = 0.

Карточка 3. Решите уравнение: х² – 5х -6=0.

Карточка 4. Решите уравнение: х² – 8х – 9 = 0.

Карточка 5. Решите уравнение: 2х² – 9х + 10 = 0.

Карточка 6. Решите уравнение: 5х² + 3х – 8 = 0.

Карточка 7. Решите уравнение: х² – 7х + 10 = 0.

Карточка 8. Решите уравнение: х² + вх + с = 0.

Найдите сумму и произведение корней этого уравнения:

х₁ + x₂ =
х₁ * x₂ =

Проверку задания осуществляем с использованием интерактивной доски слайдов. Полученные ответы учащиеся вписывают в таблицу.

x1+x2= 8 x1*x2= 15	Я		x1+x2= 9/2 x1*x2= 10/2	В
x1+x2= -12 x1*x2= 20	желаю		x1+x2= -3/5 x1*x2= -8/5	изучении
x1+x2= 5 x1*x2= -6	Вам		x1+x2= 7 x1*x2= 10	важной
x1+x2= 8 x1*x2= -9	успехов		x1+x2= -в x1*x2= с	темы

Когда учащиеся работают по карточкам, в это время устно поработаем со слабыми учащимися.

Учитель задаёт вопросы ученикам:

– К какому виду относится данное уравнение? 2х² – 9х + 10 =0.

– Назовите чему равно а – ?; в – ?; с – ?;

– Определите, к какому виду уравнений относится данное уравнение х² + 5х – 6 = 0;

– Вычислите его дискриминант;

– В уравнении x²+ 2х + 1 выделите квадрат двучлена;

– Выясните сколько корней имеет данное уравнение 2х² + х + 2 = 0.

III. ОЗНАКОМЛЕНИЕ С НОВЫМ МАТЕРИАЛОМ

– Обратите внимание на числа В и С и на числа, которые являются суммой корней и произведением корней.

– Кто из вас увидел какую-нибудь зависимость.

– Оказывается корни квадратного уравнения можно вычислить и без вычисления дискриминанта.

Для приведённого квадратного уравнения зависимость:

x₁ + x₂ = – в;
x₁ * x₂ = с

для неприведённого квадратного уравнения зависимость

x₁ + x₂ = –
x₁*x₂ =

Я желаю вам успехов в изучении важной темы.

На интерактивной доске записаны только две формулы:

x1 + x2 = – в x1 * x2 = с

x1 + x2 = – x1 * x2 = –

Эту связь заметил первым французский математик Франсуа Виет (портрет учёного прикрепляется к доске). Как вы уже смогли заметить, тема нашего урока: «Теорема Виета».

Выполняя задания по карточкам вы самостоятельно доказали теорему Виета.

Виет – «отец алгебры» родился в г. Фонтан ле Конт. В трудах Виета алгебра становится общей наукой об алгебраических уравнениях, основанной на символических обозначениях. Виет первый обозначил буквами не только неизвестные, но и данные величины, т.е. коэффициенты соответствующих уравнений. Благодаря этому стало впервые возможным выражение свойств уравнений и их корней общими формулами, и сами алгебраические выражения превратились в объекты, над которыми можно производить действия. Он разработал единообразный приём решения уравнений 2-й, 3-й, 4-й степени и новый метод решения кубических уравнений.

Сообщение учащегося «О теореме Виета»

Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 году следующим образом: «Если В + Д, умноженное на минус А минус А2 , равно ВД, то А равно В и равно Д. Чтобы понять Виета, следует вспомнить, что А, как и всякая гласная буква, означала у него неизвестное (наше X), гласные же В, Д – коэффициенты при неизвестном. На языке современной алгебры вышеприведённая формулировка Виета означает: если имеет место:

(А + В)Х – X² = АВ
т.е. х² – (А + В)х+АВ=0, то x₁ = А; x₂ = В.

Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приёмах решения уравнений. Однако символика Виета ещё далека от современного вида. Он не признавал отрицательных чисел и поэтому при решении уравнений рассматривал лишь случаи, когда все корни положительны.

***

Для коэффициентов и корней квадратного уравнения выполняются соотношения:

x₁+x₂=-
x₁*x₂ =

Эти соотношения называют теоремой Виета по имени французского математика Ф.Виета (1540-1603). Особенно удобна эта теорема для приведённого квадратного уравнения:

x₁ + x₂ = – р ;
x₁*x₂ =g

Давайте мысленно представим, что Виет не только смотрит на нас, но и слушает нас.

– Кто из вас попытается сформулировать теорему Виета.

– Откройте учебник на странице 121.

Прочитайте формулировку теоремы и её доказательство.

Ученик, выполняя задание на карточке № 8 самостоятельно выполнил доказательство теоремы.

IV. Первичное осмысление и заучивание теорем.

Как вы успели заметить, теорему Виета можно применять к уравнению вида Ах²+ Вх+ С = 0.

Однако сам Виет признавал только положительные корни. Лишь в 17 веке благодаря трудам Декарта и Ньютона и других учёных способ решения квадратных уравнений принимает современный вид.

задание № 573 а, в, д, ж выполняем устно, б, г, з, е выполняем самостоятельно, с проверкой у доски. (стр.124 учебника).

№ 576. Найдите подбором корни уравнения.

Задание выполняется самостоятельно. Корни записываются на интерактивной доске.

x1+x2= x1*x2=		5 4
x1+x2= x1*x2=		-12 1
x1+x2= x1*x2=		-8 7
x1+x2= x1*x2=		11 8

Как вы считаете, можно ли, зная корни квадратного уравнения составить само уравнение. Такую закономерность заметил Виет, и существует теорема, обратная теореме Виета.

– Кто из вас попробует её сформулировать. Посмотрите в учебнике на странице 125 и прочитайте эту теорему.

Предлагаю поиграть.

Игра «Кто быстрее составит квадратное уравнение».

Условие игры: Какой ряд быстрее и правильно выполнит задание.

Через слайд предлагается задание. От каждого ряда ученик решает и записывает получившийся ответ, только одного задания.

x1+x2= 4 x1*x2= 3	х2 +4х +3 =0	спасибо
x1+x2= -3 x1*x2=-10	х2+3х -10 =0	за
x1+x2=9/2 x1*x2=10/2	2х2 – 9х +10 =0	чудесный
x1+x2= – 3/5 x1*x2=-8/5.	5х2 +3х – 8 =0	урок

Добрый старый наш Виет видит – вас трудолюбивей нет.

V. Подведение итогов урока и оценка ответов учащихся.

Вот и пришла пора прощаться с добрым Виетом и его прекрасной теоремой.

Я думаю, что Франсуа Виет хотел бы увидеть лучших в работе на уроке.

Возьмите все свои звёздочки в руки и поднимите их вверх.

У кого из Вас только красные звёздочки или большее количество их, тот получает оценку «5» за работу на уроке; если жёлтые звёздочки, то оценка «4», если зелёные звёздочки, то оценка «3».

VI. Постановка домашнего задания.

Изучить пункт 23 учебника, выучить наизусть формулировки т. Виета

решите 575, 577.

Пусть долго помнится известный всем Виет, открывший формулу для уравнений.

Ученик читает стихотворение.

По праву достойна в стихах быть воспета
О свойстве корней теорема Виета.
Что лучше, скажи, постоянства такого.
Умножишь ты корни и дробь уж готова
В числителе С, в – знаменателе А,
А сумма корней тоже дроби равна
Хоть с минусом дробь эта, что за беда
В числителе В, в знаменателе А.

Литература:

1. Учебник алгебры 8 класс.
2. А.И. Бородин, А.С. Бугой. Выдающиеся математики. Киев. 1987, стр. 108.
3. Г.И. Глейзер. История математики в школе. М., Просвещение, 1982, стр. 24-25.
4. Энциклопедический словарь юного математика. М., Просвещение, 1989, стр.133, 203, 288.
5. «За гранью урока», стр. 50.

Теорема виета в задачах с параметрами

Г ОРОДСКОЙ МЕТОДИЧЕСКИЙ ЦЕНТР УПРАВЛЕНИЯ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ ГОРОДА КОСТРОМЫ

Теорема Виета в задачах с параметрами.

КОСТРОМА

2006

Теорема Виета в задачах с параметрами: В помощь учителю / Составитель С. А. Сорокина. – Кострома, 2006. – 8 с.

Составитель пособия «Теорема Виета в задачах с параметрами» — Почётный работник Российской Федерации, учитель математики высшей квалификационной категории МОУ лицея №17 города Костромы Сорокина Светлана Анатольевна. Светлана Анатольевна работает в классах углублённого изучения математики. Её учащиеся – призёры и победители математических олимпиад различных уровней.

В пособии представлен практикум «Теорема Виета в задачах с параметрами» и один из способов решения заданий практикума.

Задания расположены в порядке возрастания сложности и носят обучающий характер.

Рецензент:

Л. К. Борткевич – методист ГМЦ

Ó С.А. Сорокина

Ó Оформление и вёрстка Л. К. Борткевич

Теорема Виета в задачах с параметрами.

Теорема.Если квадратное уравнение ax²+bx+c=0 имеет корни x₁ и x₂ ,то для них справедливы соотношения — , .

Задачи.

1. При каких значениях k произведение корней квадратного уравнения равно нулю?

2. При каких значениях k сумма корней квадратного уравнения равна нулю?

3. В уравнении сумма квадратов корней равна 16.Найдите а.

4. Найдите все значения а, при которых сумма квадратов корней уравнения равна 10.

5. В уравнении квадрат разности корней равен 16.Найдите а.

6. Найдите все значения а, для которых разность корней уравнения равна 1.

7. При каких значениях а сумма корней уравнения равна сумме квадратов его корней?

8. При каком значении параметра m сумма квадратов корней уравнения наименьшая?

9. При каком значении параметра m сумма квадратов корней уравнения наибольшая?

10. При каких значениях коэффициента b сумма квадратов корней уравнения принимает наименьшее значение?

11. Найдите сумму квадратов всех корней уравнения .

12. При каких значениях p и q корни уравнения равны и ?

13. Не решая уравнения найти, при каком значении а один из корней в 2 раза больше другого.

14. В уравнении определить а так, чтобы отношение корней равнялось 2.

15. При каких значениях параметра а разность корней уравнения равна их произведению?

16. Известно, что корни уравнения на 1 меньше корней уравнения . Найдите а и корни каждого из этих уравнений.

17. Известно, что корни уравнения равны соответственно квадратам корней уравнения . Найдитеa и b и корни каждого из уравнений.

18. При каких значениях коэффициента с один из корней уравнения равен квадрату другого корня?

19. При каких значениях параметра а уравнение имеет ровно три корня?

20. При каком а уравнение имеет два отрицательных корня?

Решения и ответы.

1. При каких значениях k произведение корней квадратного уравнения равно нулю?

Решение.

По теореме Виета имеем = и по условию =0. Корнями уравнения =0 являются числа 3 и 4. При k=3 и k=4 получим уравнение , произведение корней которого равно 0.

Ответ:3;4.

2. При каких значениях k сумма корней квадратного уравнения равна нулю?

Решение.

По условию =0, по теореме Виета имеем =.

Корнями уравнения являются числа 1 ,-5. При k=1 получим уравнение , сумма корней которого равна 0. При k= -5 получим уравнение , которое не имеет корней.

Ответ:1.

3. В уравнении сумма квадратов корней равна 16.Найдите а.

Решение.

По теореме Виета имеем =4, = а. По условию =16.

4²-2а=16, а=0

При а = 0 уравнение имеет корни, сумма квадратов которых равна 16.

Ответ: 0.

4. Найдите все значения а, при которых сумма квадратов корней уравнения равна 10.

Решение.

Для того, чтобы сумма квадратов корней уравнения равнялась какой-либо величине, эти корни должны существовать. Значит, дискриминант нашего уравнения должен быть неотрицательным, т.е. а²-4(а+7). При таких а у исходного уравнения найдутся (возможно, совпадающие) корни x₁ и x₂. Запишем для них теорему Виета: = а, = а+7 . Теперь, не вычисляя корней, можно найти сумму их квадратов через а:

== а²-2(а+7) Согласно условию, эта сумма квадратов равна 10, откуда получаем квадратное уравнение а²-2(а+7)=10, корнями которого являются числа 6 и -4. При а = 6 дискриминант исходного уравнения отрицательный, а при а = -4 положительный.

Ответ:а = -4.

5. В уравнении квадрат разности корней равен 16.Найдите а.

Решение.

По теореме Виета имеем =2, = а. Чтобы корни существовали, дискриминант нашего уравнения должен быть неотрицательным, 4-4а, т.е. а. По условию

4-4а=16

а = -3, -3.

Ответ:а = -3.

6. Найдите все значения а, для которых разность корней уравнения равна 1.

Решение.

По теореме Виета =; =. Следовательно, =.

По условию =1. Значит, а₁=9, а₂=-3. При данных значениях параметра а дискриминант исходного уравнения больше нуля.

Ответ: 9, -3.

7. При каких значениях а, сумма корней уравнения равна сумме квадратов его корней?

Решение.

По теореме Виета =2а, =2а-1. По условию =.

=

2а=(2а)²-2(2а-1),

а=1, а =.

При а =1 уравнение имеет корень 1 , при а = уравнение имеет корни 1 и 0.

Ответ: 1 , .

8. При каком значении параметра m сумма квадратов корней уравнения наименьшая?

Решение.

По теореме Виета имеем = m-2, = —m-3

==(2-m)²-2(-m-3)=m²-2m +10=(m-1)²+9.

Сумма квадратов корней наименьшая при m =1. При m=1 уравнение имеет два корня.

Ответ: 1.

9. При каком значении параметра m сумма квадратов корней уравнения наибольшая?

Решение.

По теореме Виета имеем = —m+1, = m²-1,5.

==(-m+1)²-2(m²-1,5)= —m²-2m+4= -(m+1)²+5

При m= -1 выражение -(m+1)²+5 принимает наибольшее значение. При m = -1 уравнение имеет корни.

Ответ: -1.

10. При каких значениях коэффициента b сумма квадратов корней уравнения принимает наименьшее значение?

Решение.

Выразим сумму квадратов корней данного уравнения через его коэффициенты при помощи теоремы Виета следующим образом:

==b²-2.

Выражение b²-2 принимает наименьшее значение при b=0. При этом значении b сумма квадратов корней отрицательна. Надо обязательно добавить условие неотрицательности дискриминанта b²-4. Теперь уже нетрудно заключить, что сумма квадратов корней уравнения принимает наименьшее значение приb=

Ответ:

11. Найдите сумму квадратов всех корней уравнения .

Решение.

Пусть = t. Рассмотрим уравнение . >0, по теореме Виета t₁+t₂=3, =1.

Уравнение имеет два положительных корня, следовательно, исходное уравнение имеет 4 корня. Причем t₁=, t₂=

+==2(=2((t₁+t₂)²-2t₁t₂)=2(9-2)=14

Ответ: 14.

12. При каких значениях p и q корни уравнения равны и ?

Решение.

Пусть . По теореме Виета имеем = —p, =q, =p²-4q, следовательно, ;

q= -6p

q.

Если q=0, тоp=0, =0, если p=1, то q= -6, >0. Уравнение имеет корни.

Ответ:p=q=0 илиp=1, q= -6.

13. Не решая уравнения найти, при каком а один из корней в 2 раза больше другого.

Решение.

По условию . По теореме Виета имеем .

Значит, При а = 4 уравнение имеет корни 6 и 3.

Ответ: 4.

14. В уравнении определить а так, чтобы отношение корней равнялось 2.

Решение.

Пусть х — корень уравнения. Тогда второй корень 2х.

При a= получим уравнение , корни которого -3 и -6.

Ответ:

15. При каких значениях параметра а разность корней уравнения равна их произведению?

Решение.

Имеем ;

По условию

При а=1 уравнение имеет корни 1 и ,

при а = уравнение имеет корни и , разность которых равна их произведению.

Ответ: 1, .

16. Известно, что корни уравнения на 1 меньше корней уравнения . Найдите а и корни каждого из этих уравнений.

Решение.

Пусть и — корни уравнения .

По условию +1 и +1 корни уравнения .

По теореме Виета имеем

Отсюдаa+5+1=3a-6, a=6.

При а = 6 уравнение имеет корни 2 и 3, а уравнение имеет корни 3 и 4.

Ответ:а = 6, 2 и 3 — корни первого уравнения, 3 и 4 — корни второго уравнения.

17. Известно, что корни уравнения равны соответственно квадратам корней уравнения . Найдитеa и b и корни каждого из уравнений.

Решение.

По условию и теореме Виета имеем

Отсюда b=36, ==

При b= 36 уравнение имеет корни 9 и 4.

При а = 5 уравнение имеет корни -2 и -3.

При а = -5 уравнение имеет корни 2 и 3.

Ответ: при а = -5, b=36 корни первого уравнения 2 и 3,

корни второго уравнения 4 и 9

при а =5 , b=36 корни первого уравнения -2 и -3,

корни второго уравнения 4 и 9

18. При каких значениях коэффициента с корень уравнения равен квадрату другого корня?

Решение.

Пусть числа и являются корнями этого уравнения.

Тогда по теореме Виета должны выполнятся равенства и .

Поскольку корень должен быть равен квадрату корня , то подставим выражение =² в эти два уравнения.

Получим систему .

Первое уравнение этой системы является квадратным и имеет два корня и .

Подставляя эти значения во второе уравнение системы, получаем два уравнения

и . Решая эти уравнения, получим с =1 и с = -27.

При этих значениях с дискриминант больше 0.

Ответ:— 27,1.

19. При каких значениях параметра а уравнение имеет ровно три корня?

Решение.

Чтобы заданное уравнение имело три корня, необходимо, чтобы корни одного из сомножителей заданного уравнения совпадали.

Итак, имеем , если дискриминант равен нулю.

Значит а = -3. Но если а = -3, то при любом x, второй сомножитель отрицателен, что невозможно.

Рассмотрим равенство нулю второго сомножителя: Его корни совпадают, если а+1=0 , т.е. а = -1.

При а = -1 первый сомножитель имеет два корня .

Ответ: -1.

20. При каком а уравнение имеет два отрицательных корня?

Решение.

=(2а-3)² -4(а+5)(а-10)=8а+209>0

Корни будут иметь одинаковые знаки, если

Оба корня будут отрицательны, если при этом

Таким образом, задача свелась к решению системы неравенств 8а+209>0

Ответ:

Теорема Виета. Алгебра, 8 класс: уроки, тесты, задания.

1.	Теорема Виета Сложность: лёгкое	2
2.	Теорема Виета, составление уравнения Сложность: лёгкое	2
3.	Разложение на множители Сложность: лёгкое	1
4.	Корни квадратного уравнения Сложность: среднее	2
5.	Составление квадратного уравнения Сложность: среднее	2
6.	Разложение на множители квадратного трёхчлена Сложность: среднее	2
7.	Сокращение дроби Сложность: сложное	3
8.	Значение выражения Сложность: сложное	3
9.	Разность, сумма, произведение корней квадратного уравнения Сложность: сложное	3

Урок по теме «Применение теоремы Виета при решении квадратных уравнений»

Тип урока: урок обобщения, систематизации и углубления знаний.

Цели урока:

• Систематизация, обобщение и контроль знаний полученных при изучении темы “Теорема Виета”
• Обратить внимание учащихся на решение квадратных уравнений ах²+bх+с=0, в которых а+b+с=0
• Способствовать выработке у школьников умения обобщать изучаемые факты.

Оборудование: кадоскоп, таблицы с уравнениями и ответами к ним из домашней работы, карточки – тесты с закодированными ответами, листы самоконтроля, выставка творческих проектов учащихся (домашнее задание предыдущего урока – придумать рекламу теоремы Виета).

Листок самоконтроля учащегося __________________________________

Домашняя работа	Творческий проект	Тест	Классная работа	Самостоятельная работа	Оценка за урок

Ход урока

1. Организационный момент. Слово учителя.

Ребята, сегодня вы узнаете новый способ решения некоторых квадратных уравнений (уравнения из домашней работы записаны на доске):

x²+x-2=0,
x²+2x-3=0,
x²-3x+2=0,
x²-x-2=0,
x²-2x-3=0,
x²-3x-4=0.

Конечно, вы можете их решить, но как это сделать быстро, рационально вы узнаете на уроке. Сначала необходимо повторить теорему Виета и теорему ей обратную. (Спросить несколько человек, одного пригласить к доске для краткой записи теоремы Виета).

2. Актуализация знаний учащихся. За рекламу учитель выставляет оценку в листок самоконтроля до урока, когда готовится выставка.

(Рисунок 1)

А теперь реклама! Учащиеся показывают один из творческих проектов.

По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни — дробь уж готова!
В числителе с, в знаменателе а.
А сумма корней тоже дроби ровна.
Хоть с минусом дробь, что за беда!
В числителе b, в знаменателе а.

— Ребята, Посмотрите, Ведь реклама сделана не для приведённого квадратного уравнения, а для полного. Как вы считаете, нас не обманывают? Почему?

Пригласить к доске 3 учеников, выполнить следующие задания:

• Один из корней уравнения х²+bх-12=0 равен 2. Найдите второй корень и коэффициент b. {X₂=6; b=8}
• Найти корни квадратного уравнения 6х²-8х+2=0 через дискриминант. {X₁=1/3; X₂=1}
• Найти корни квадратного уравнения 4х²+6х+2=0 через дискриминант. {X₁=-1; X₂=-1,5}

Пока учащиеся решают, с остальным классом работаем устно.

1. Найти подбором корни уравнений:

а) х²-5х+6=0 {2;3}
б) х²+3х+2=0 {-2;-1}
в) х²-7х+10=0 {2;5}
г) х²-9х+20=0 {4;5}

2. Составьте приведённое квадратное уравнение корнями которого являются числа:

а) 3 и 5 {х²-8х+15=0}
б) 3 и -5 {х²+2х-15=0}
в) -3 и 5 {х²-2х-15=0}
г) -3 и -5 {х²+8х+15=0}

Проверить работу учащихся у доски.

3. А теперь давайте посмотрим как вы усвоили и научились применять теорему Виета.

Тест. Ответы на обратной стороне доски. После взаимопроверки оценку учащиеся выставляют в листок самоконтроля. Критерии: 2 задания –“3”, 3 задания – “4”, 4 задания –“5”.

Тест по теме “Теорема Виета”

I вариант

а) х² — 4х + 3 = 0;  Т – {1;3}, Е – {-4;3}, А – {-3;-1};
б) х² — 12х + 11 = 0;  А – {-11;-1}, Е – {1;11}, М – {-3;8};
в) х² + 5х + 4 = 0;  А – {1;4}, М – {-4;-1}, Т – {9;20};
г) При каком значении p один из корней уравнения х² - рх + 9 = 0 равен 1. Найти второй корень. Е – {р=1; х₂=4}, Т – {р=10; х₂=-9}, А – {р=10; х₂=9}.

II вариант

а) х² — 8х + 7 = 0 ; И – {-1;7}, В – {1;7}, Т – {-8;-1};
б) х² + 3х + 2 = 0; И – {-2;-1}, Е – {2;3}, B – {-1;2};
в) х² — 16х + 15+ = 0; Т – {5;10}, Е – {1;15}, B – {-5;20};
г) При каком значении p один из корней уравнения х² — рх + 6 = 0 равен 1. Найти второй корень. В – {р=-2; х₂=4}, Е – {р=1; х₂=10}, Т – {р=7; х₂=6}.

3. Исторические сведения.

А теперь давайте немного передохнём и послушаем вторую часть вашего творческого отчета. (Один ученик сообщает исторические сведения).

 

Француа Виет (рисунок 2)

Франсуа Виет родился в 1540 году на юге Франции в небольшом городке Фантене-ле-Конт.

Отец Виета был прокурором. Сын выбрал профессию отца и стал юристом, окончив университет в Пуату. В 1560 году двадцатилетний адвокат начал свою карьеру в родном городе, но через три года перешел на службу в знатную гугенотскую семью де Партене. Он стал секретарем хозяина дома и учителем его дочери двенадцатилетней Екатерины. Именно преподавание пробудило в молодом юристе интерес к математике.

Когда ученица выросла и вышла замуж, Виет не расстался с ее семьей и переехал с нею в Париж, где ему было легче узнать о достижениях ведущих математиков Европы. Он общался с видным профессором Сорбонны Рамусом, с крупнейшим математиком Италии Рафаэлем Бомбелли вел дружескую переписку.

В 1671 году Виет перешел на государственную службу, став советником парламента, а затем советником короля Франции Генриха III.

В 1580 году Генрих III назначил Виета на важный государственный пост рекетмейстера, который давал право контролировать выполнение распоряжений в стране и приостанавливать приказы крупных феодалов.

В 1584 году по настоянию Гизов Виета отстранили от должности и выслали из Парижа. Обретя покой и отдых, ученый поставил своей целью создание всеобъемлющей математики, позволяющей решать любые задачи.

Виет изложил программу своих исследований и перечислил трактаты, объединенные общим замыслом и написанные на математическом языке новой буквенной алгебры, в изданном в 1591 году знаменитом «Введение в аналитическое искусство». Основу своего подхода Виет называл видовой логистикой, он четко разграничивал числа, величины и отношения, собрав их в некую систему «видов». В эту систему входили, например, переменные, их корни, квадраты, кубы, квадрато-квадраты и т. д. Для этих видов Виет дал специальную символику, обозначив их прописными буквами латинского алфавита. Для неизвестных величин применялись гласные буквы, для переменных — согласные.

Виет показал, что, оперируя с символами, можно получить результат, который применим к любым соответствующим величинам, т. е. решить задачу в общем виде. Это положило начало коренному перелому в развитии алгебры: стало возможным буквенное исчисление.

Знаменитая теорема, устанавливающая связь коэффициентов многочлена с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета, а сам автор формулировал ее так: «Если В+D, умноженное на А, минус А в квадрате равно ВD, то А равно В и равно D».

В трактате «Дополнения к геометрии» он стремился создать некую геометрическую алгебру, используя геометрические методы для решения уравнений третьей и четвертой степеней. Любое уравнение третьей и четвертой степени, утверждал Виет, можно решить геометрическим методом трисекции угла или построением двух средних пропорциональных.

Математиков столетиями интересовал вопрос решения треугольников, так как он диктовался нуждами астрономии, архитектуры, геодезии. Виет первым явно сформулировал в словесной форме теорему косинусов, хотя положения, эквивалентные ей, эпизодически применялись с первого века до нашей эры. Известный ранее своей трудностью случай решения треугольника по двум данным сторонам и одному из противолежащих им углов получил у Виета исчерпывающий разбор. Глубокое знание алгебры давало Виету большие преимущества. Причем интерес его к алгебре первоначально был вызван приложениями к тригонометрии и астрономии. Не только каждое новое применение алгебры давало импульс новым исследованиям по тригонометрии, но и полученные тригонометрические результаты являлись источником важных успехов алгебры. Виету, в частности, принадлежит вывод выражений для синусов (или хорд) и косинусов кратных дуг.

В мемуарах некоторых придворных Франции есть указание, что Виет был женат, что у него была дочь, единственная наследница имения, по которому Виет звался сеньор де ла Биготье. В придворных новостях маркиз Летуаль писал: «…14 февраля 1603 г. господин Виет, рекетмейстер, человек большого ума и рассуждения и один из самых ученых математиков века умер… в Париже. Ему было более шестидесяти лет».

4. Проверка домашнего задания.

Мы ещё не проверили домашней работы. Проверяем с помощью кадоскопа.

• I вариант: x²+x-2=0 (-2;1), x²+2x-3=0 (-3;1), x²-3x+2=0 (1;2).
• II вариант x²-x-2=0 (-1;2), x²-2x-3=0 (-1;3), x²-3x-4=0 (-1;4).

(После проверки оценку в листок самоконтроля: 1 задание –“3”, 2 задания – “4”, 3 задания –“5”).

5. “Открытие” нового знания учащимися.

Давайте обратим внимание на уравнения I варианта.

• Какое число является корнем каждого из них?
• Какова сумма коэффициентов в этих уравнениях?

Записать на доске: 1+1-2=0; 1+2-3=0; 1-3+2=0.

• Какую закономерность вы увидели?

Обратить внимание на уравнение №3 на доске.

• Прийти к заключению, что если в уравнении ах²+bх+с=0, а+b+с=0, то один из его корней равен 1, а другой с/а.
• Отметить, что верно и обратное утверждение: если один из корней квадратного уравнения ах²+bх+с=0, в которых а+b+с=0 ах²+bх+с=0, равен 1 (с/а), то а+b+с=0 и второй корень равен с/а (1).

Решение уравнений для закрепления:

а) 3х²-4х+1=0 {1/3;1} (решает учитель)
б) х²+8х-9=0 {-9;1} (решает ученик на доске)
в) 2х²-6х+4=0 {1;2} (самостоятельно в тетрадях)

Свойство (2). Обратите внимание на уравнения II варианта. Заметили, что один из корней во всех уравнениях -1. Рассмотрим зависимость между коэффициентами:

1-(-1)-2=0,
1-(-2)-3=0,
1-(-3)-4=0.

Рассмотреть уравнение №4 на доске.

Вывод: если в уравнении ах²+bх+с=0, а-b+с=0, то один из его корней равен -1, а другой -с/а.

Решение уравнений для закрепления:

а) 2х²+3х+1=0 {-1;-1/2} (решает ученик на доске)
б) 5х²-4х-9=0 {-1,8;-1} (самостоятельно в тетрадях)
в) 7х²+2х-5=0 {-1;5/7} (самостоятельно в тетрадях)

6. Домашняя работа:

• а) х² — 18х + 17 = 0;
  б) 2х² + 46х – 48 = 0;
  в) 200х² — 194х – 394 = 0;
  г) х² — 12х – 13 = 0.  (на  “3”)
• д) (2х+1)² – 3(2х + 1) – 4 = 0 (на “4”).
• Самостоятельно доказать любое свойство (на  “5”).

— Свойство можно доказывать выразив из условия а+b+с=о коэффициент b, подставить в полное квадратное уравнение записанное в общем виде и решить это уравнение.

7. Рассмотрим уравнение повышенной сложности которое тоже можно решить применяя рассмотренные свойства:

(5х+1)² + 6(5х+1) — 7 = 0,
Введем замену: 5х+1=у,
у² + 6у — 7 = 0,
Так как 1+6-7=0, то 5х+1=1 и х=0 или 5х+1=-7 и х=-8/5.
Ответ: -1,6; 0.

8. Итог урока.

• Что нового узнали сегодня на уроке?
• Повторить свойства.
• Вывести общую оценку за урок, листы самоконтроля сдать учителю.

Решение олимпиадных задач с помощью теоремы Виета

Рассмотрим  некоторые олимпиадные  задания, где используется теорема Виета.

1. Доказать, что для корней  х₁ , х₂  многочлена х² + рх – 1/(2р²), где р Є R и p ≠ 0, выполняется неравенство х₁⁴ + х₂⁴ ≥ 2 + 2^1/2

Решение.

Возведем в четвертую степень выражение х₁ + х₂, получим

(х₁ + х₂)⁴ = С₄⁰ х₁⁴ + С₄¹ х₁³х₂ + С₄² х₁²х₂² + С₄³х₁х₂³ + С₄⁴х₂⁴ =

= х₁⁴+ 4х₁³х₂ + 6х₁²х₂² + 4х₁х₂³ + х₂⁴, поэтому

х₁⁴ + х₂⁴ = (х₁ + х₂)⁴ – 4х₁³х₂ – 6х₁²х₂² – 4х₁х₂³ =

= (х₁ + х₂)⁴ – 2х₁х₂ · (2х₁² + 3х₁х₂ + 2х₂²) =

= (х₁ + х₂)⁴ — 2х₁х₂ · (2 · (х₁² + 2х₁х₂ + х₂²) – х₁х₂) =

= (х₁ + х₂)⁴ – 2х₁х₂ · (2 · (х₁ + х₂)² – х₁х₂).

Имеем х₁⁴ + х₂⁴ = (х₁ + х₂)⁴ – 2х₁х₂ · (2 · (х₁ + х₂)² – х₁х₂).

Используя теорему Виета для многочлена х² + рх – 1/(2р²) имеем

х₁ + х₂ = -р и х₁ · х₂ = -1/(2р²).

Подставим данные значения в х₁⁴ + х₂⁴, получим

х₁⁴ + х₂⁴ = р⁴ + 1/р² · (2р² + 1/(2р²) = р⁴ + 2 + 1/(2р⁴).

Как известно, среднее арифметическое не менше среднего геометрического, то есть (а + b)/2 ≥ (ab)^1/2 , поэтому

х₁⁴ + х₂⁴ = 2 + р⁴ + 1/(2р⁴) ≥ 2 + 2(р⁴/(2р⁴))^1/2 = 2 + 2^1/2.

2. Доказать, что если корнями многочлена х² + рх + 1 являются числа α и β, а корнями многочлена х² + qх + 1 – числа γ и δ, то справедливо равенство (α – γ)(β – γ)(α + δ)(β + δ) = q² – p².

Решение.

Так как числа α и β являются корнями многочлена х² + рх + 1, то по теореме Виета α + β = -р и α · β = 1.

Числа γ и δ являются корнями многочлена х² + qх + 1, поэтому по теореме Виета γ + δ = -q и γ · δ = 1.

(α – γ)(β – γ)(α + δ)(β + δ) = (αβ – βγ – αγ + γ²)(αβ + δβ + αδ + δ²) =

= (αβ – γ(α + β) + γ²)(αβ + δ(β + α) + δ²) = (1 + pγ + γ²)(1 – δp + δ²) =

= 1 + pγ + γ² – δp – p²γδ – pγ²δ + δ² + pγδ² + γ²δ² =

= 1 + pγ + γ² – δp – p² – pγ + δ² + pδ + 1 = 2 + γ² – p² + δ², очевидно, что

γ² + δ² = (γ + δ)² – 2γδ = q² – 2, тогда

(α – γ)(β – γ)(α + δ)(β + δ) = 2 – p² + q² – 2 = -p² + q².

3. Доказать, что для любых ненулевых значений α и β корни х1, х2 и х3 многочлена αх³ – αх² + βх + β удовлетворяют равенству (х₁ + х₂ + х₃)(1/х₁ + 1/х₂ + 1/х₃) = -1.

Решение.

αх³ – αх² + βх + β = α(х³ – х² + βх/α + β/α).

Рассмотрим многочлен  х³ – х² + βх/α + β/α.

Согласно теореме Виета

х₁ + х₂ + х₃ = 1;

х₁х₂ + х₁х₃ + х₂х₃ = β/α;

х₁х₂х₃ = -β/α.

(х₁ + х₂ + х₃)(1/х₁ + 1/х₂ + 1/х₃) = (х₁х₂ + х₁х₃ + х₂х₃ ) / (х₁х₂х₃) = (β/α) : (-β/α) = -1.

4. Найти все значения а, при которых корни х₁, х₂, х₃  многочлена х³ – 6х² + ах + а удовлетворяют равенству (х₁ – 3)³+ (х₂ – 3)³ + (х₃ – 3)³ = 0.

Решение.

Сделаем замену  у = х – 3, т.е. х = у + 3.

у₁ = х₁ – 3,  у₂ = х₂ – 3, у₃ = х₃ – 3, тогда у₁³ + у₂³ +  у₃³ = 0.

(у + 3)³ – 6(у + 3)² + а(у + 3) + а = у³ + 9у² + 27у + 27 – 6у² –36у – 54 + ау +3а +а = 0;

у³ + 3у² + у(а – 9) + 4а – 27 =0.

Согласно теореме Виета для кубического уравнения:

у₁ + у₂ + у₃ = -3;

у₁у₂ + у₁у₃ + у₂у₃ = а – 9;

у₁у₂у₃ = 27 – 4а.

Возведем  в куб выражение у₁ + у₂ + у₃ и выразим

у₁³ + у₂³ + у₃³, получим     

у₁³ + у₂³ + у₃³ = (у₁ + у₂ + у₃)³ – 3(у₁у₂ + у₁у₃ + у₂у₃)(у₁ + у₂ + у₃) + 3у₁у₂у₃ = 0.

у₁³ + у₂³ +  у₃³ = -27 + 3(а – 9) · 3 + 3(-4а + 27 ) = 0.

а = -9 .

Существует много задач повышенной сложности, для решения которых можно использовать теорему Виета, но для успешного их решение необходимо понимание материала, а также систематические занятия по математике.

 Остались вопросы? Не знаете, как решать олимпиадные задачи по математике?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

План-конспект урока по алгебре (8 класс) на тему: Решение задач по теме «Теорема Виета»

Тема: Решение задач по теме «Теорема Виета».

8 класс.
Учитель Лукина И.В.

На уроке используется технология проблемного обучения.

Цели урока:

а) Образовательные:
— обеспечение прочности приобретенных знаний, умений и навыков по теме «Теорема Виета»;

— исследование различных подходов к решению нестандартных задач.

б) Развивающие:
— развитие самостоятельности, ответственности;
— развитие критичности мышления, нестандартного мышления;
— развитие творческих способностей учащихся.

в) Воспитательные:

— воспитание творческой личности;

— воспитание коммуникативных качеств ученика.

Задача: изучить новые способы решения полных квадратных уравнений. Для этого  организовать на уроке проблемные ситуации, оказать учащимся помощь в решении этих проблем, проверить решения.

Ход урока.
Учащиеся работают в четырех разноуровневых группах.

1. Вводная часть

Ученик читает стихотворение, подготовленное заранее:
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни – и дробь уж готова?
В числителе с, в знаменателе а.
А сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда!
В числителе b, в знаменателе а.

2. Проверка творческого домашнего задания.
    На дом было задано сочинить стихотворение, небольшой рассказ или сказку по теме «Теорема Виета». Это задание было задано на неделю. Работы были собраны заранее. Трое учащихся, чьи работы признаны лучшими, выступают перед классом.
3. Объявляется тема урока. 
   Ставится задача: изучить новые нестандартные способы решения полных квадратных уравнений.
4. Постановка 1проблемы.
   Теорема Виета не зря воспета в стихах. Она очень облегчает решение приведенных квадратных уравнений, но мы никогда не использовали ее при решении неприведенных квадратных уравнений. А возможно ли это в принципе?
   Проведем эксперимент. Для этого рассмотрим уравнение 3х2 – 8х + 5 = 0. Его можно решить по формуле, которая применяется для решения полных квадратных уравнений.

                Х1 = 1; Х2 = 5/3

Рассмотрим теперь приведенное квадратное уравнение, которое можно получить из  данного неприведенного, для этого мы свободный член умножим на старший коэффициент.

                         
                         Х2 – 8Х + 5·3 = 0

                          Х2 – 8Х + 15 = 0
Это уравнение легко решается по теореме, обратной теореме Виета.
Обозначим эти корни Х3 и Х4

                Х3 = 3; Х4 = 5.
Сравнивая корни уравнений, получаем, что корни второго уравнения в три раза больше корней первого, т.е. Х1 = Х3/3 и Х2 = Х4/3
Возникает проблема: всегда ли корни неприведенного квадратного уравнения
ax2 + bx + c = 0 и корни приведенного квадратного уравнения x2 + bx + c·a = 0, полученного из первого умножением старшего коэффициента на свободный член, cвязаны равенством   Х1 = Х3/а и Х2 = Х4/а, где Х1 и Х2 – корни неприведенного уравнения, а Х3 и Х4 – корни приведенного уравнения. Было бы здорово решить эту проблему сегодня на уроке. А вы как думаете, это случайное совпадение или нет?
          5. Поиск решения проблемы и признание решения учащимися. 

Учащимся дается возможность высказаться, посовещавшись с членами группы и доказать или опровергнуть выдвинутую гипотезу. Если дети затрудняются, то учитель предлагает подсказки по очереди, давая после каждой подсказки время для обдумывания дальнейшего хода решения и высказывания каждой группе. Подсказки предлагаются на слайдах презентации:
1 подсказка. 
Проверьте еще раз зависимость между корнями уравнений 7Х2 – 6Х — 1 = 0 и
Х2 – 6Х —  1·7 = 0

Двое учащихся работают на досках, а остальные – в тетрадях.

1)7Х2 – 6Х — 1 = 0

          6 ± √62 — 4·7·1

Х1,2 =

Х1 = 1; Х2 = — 1/7

2)Х2 – 6Х —  1·7 = 0

Х2 – 6Х —  7 = 0 – по теореме, обратной теореме Виета находим корни этого уравнения:

Х3 = 7; Х4 = — 1.

Класс делает вывод:  Х1 = Х3/7 и Х2 = Х4/7.
Таким образом, Х1 = Х3/а и Х2 = Х4/а.

2 подсказка. 
Попробуйте записать оба уравнения: неприведенное и полученное из него приведенное квадратные уравнения в общем виде и применить к каждому из них формулу для решения полных квадратных уравнений.
Учащиеся работают в группах, и если они затрудняются, то учитель им помогает.
Представители от групп выходят к доске и объясняют решение. На доске появляются записи:

1) а Х2 + bХ +  c = 0

 

          — b ± √b2 — 4·a·c

Х1,2 =

2) Х2 + bХ +  c·a = 0

 

          — b ± √b2 — 4·a·c

Х3,4 =

3 подсказка. 
Сравните правые части равенств (1) и (2).
Учащиеся снова работают в группах. А затем представители от групп выходят к доске и объясняют решение.
Из формул видно, что если правую часть равенства (2) разделить на а, то получится правая часть равенства (1).
Разделим обе части равенства (2) на а (напоминаю, что на а делить можем т.к. а ≠ 0 по определению квадратного уравнения).

Запись на доске:

         

 

              — b ± √b2 — 4·a·c

Х3,4 =  

Сравнивая полученное равенство с равенством (1) получаем, что правые части этих равенств равны, следовательно, равны и левые. Таким образом
Х1 = Х3/а и Х2 = Х4/а.
Доказательство учащиеся, по мере обсуждения, записывают в тетради.

5. Обобщение и выводы.
   Мы доказали, что неприведенные квадратные уравнения можно решать не только по общей формуле, а так же по теореме, обратной теореме Виета.

Алгоритм решения:
1) составить приведенное квадратное уравнение из данного неприведенного, умножив свободный член на старший коэффициент.
2) решить полученное уравнение по теореме, обратной теореме Виета.
3) получить корни заданного уравнения, разделив корни полученного  приведенного квадратного уравнения на старший коэффициент.

Алгоритм записывается учащимися в тетради.

6. Упражнения.

Каждой группе дается задание на карточке:
1) решить данное учителем уравнение по записанному алгоритму
2) составить и решить свое уравнение для другой группы (творческое задание).
1)Уравнения, данные учителем для групп:
1 группе: 2Х2 – 5Х — 3 = 0;
Запись в тетрадях: Х2 – 5Х — 3·2 = 0;
                                Х2 – 5Х — 6 = 0;
                                Х3 = — 1; Х4 = 6;

                                 Х1 = — 1/2; Х2 = 3.

2 группе: 2Х2 –Х — 6 = 0;
Запись в тетрадях: Х2 – Х — 6·2 = 0;
                                Х2 – Х — 12 = 0;
                                Х3 = — 3; Х4 = 4;

                                 Х1 = — 1.5; Х2 = 2.

3 группе: 6Х2 –Х — 1 = 0;
Запись в тетрадях: Х2 – Х — 6·1 = 0;
                                Х2 – Х — 6 = 0;
                                Х3 = — 2; Х4 = 3;

                                 Х1 = — 1/3; Х2 = 1/2.

4 группе: 5Х2 + 2Х — 3 = 0;
Запись в тетрадях: Х2 + 2Х — 3·5 = 0;
                                Х2 + Х — 15 = 0;
                                Х3 = — 5; Х4 = 3;

                                 Х1 = — 1; Х2 = 3/5.

Учащиеся в группе обсуждают решение, записывают его по алгоритму, и представители от каждой группы выходят к доске и объясняют решение. Остальные слушают.
2) Для составления квадратных уравнений необходимо рассуждать точно в обратном порядке, а именно: сначала по корням, используя теорему Виета составить приведенное квадратное уравнение, а далее, разложив на множители свободный член, получить неприведенное уравнение.  
Далее каждая группа решает уравнение, предложенное другой группой: 1 группа составляет уравнение для 2 группы, 2 группа – для 3 группы, 3 группа – для 4 группы, 4 группа – для 1 группы. Решения оформляются на листах и передаются в группу, которая это уравнение составила, для проверки и выставления оценки за правильность решения и оформление. После чего листы с решением и отметками сдаются учителю.

7. Постановка 2 проблемы.

Дано квадратное уравнение с большими коэффициентами:
1978Х2 – 1984Х + 6 = 0. Решить его по общей формуле не просто, слишком большие коэффициенты. Теорема Виета то же не решит проблему т.к. подобрать корни в уравнении с такими большими коэффициентами очень долговременно. И вообще, имеет ли это уравнение корни, и если – да, то как их найти рациональным способом?

8. Поиск решения проблемы и признание решения учащимися.

Учащимся дается возможность высказаться, посовещавшись с членами группы, и попытаться решить поставленную проблему. Если дети затрудняются, то учитель снова дает подсказки по очереди, давая после каждой подсказки время для обдумывания дальнейшего хода решения и высказывания, используя слайды презентации:

1 подсказка.
 Найдите сумму коэффициентов уравнения.
Сумма коэффициентов равна нулю (1978 – 1984 + 6 = 0).
2 подсказка.
 Исходя из того, что сумма коэффициентов равна нулю, подбором найдите один корень уравнения.

Х1 = 1.

3 подсказка.
 Получите изданного уравнения приведенное, разделив обе части его на старший коэффициент 1978.

1978Х2 – 1984Х + 6 = 0
Х2 – 1984/1978Х + 6/1978 = 0.

4 подсказка. 
По теореме, обратной теореме Виета, найдите второй корень уравнения.

Х1·Х2 = 6/1978
Х1 = 1, следовательно 1·Х2 = 6/1978, значит Х2 = 6/1978 или Х2 = 3/989
Ответ: 1; 3/989.
Решение учащиеся записывают в тетради.

9. Выводы.
   Этот урок можно назвать творческим т.к. на нем были заслушаны лучшие детские сочинения и решались квадратные уравнения нестандартными способоми. Для этого вы пытались самостоятельно выявить связи между уравнениями, учились переносить «старые» знания на новые ситуации и задачи, приучались к самоконтролю, самопроверке и взаимопроверке.
10. Итоги урока.
    Благодарность всем учащимся за работу.
    Каждый ученик получит оценку за урок, которая будет складываться из оценки за решение проблем (активное обсуждение и выступление), за работу на доске, за решение уравнений, предложенных учителем в группе и оценки на листах, выставленной учащимися. Оценки будут объявлены на следующем уроке после суммирования.
11. Домашнее задание (творческое).
    1) придумать 5 уравнений с большими коэффициентами и решить их;
    2) № 434 – решить уравнения по изученному на уроке алгоритму, используя теорему, обратную теореме Виета;
    3) для уравнения 3х2 – 8х + 5 = 0 найти х12 + х22, не решая уравнение.