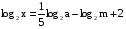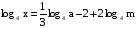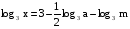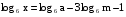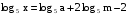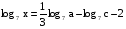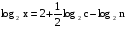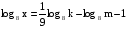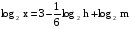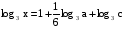Практический материал по теме: » Логарифмы».

МБОУ Алексеево-Лозовская СОШ
Практический материал
по математике
в 10 классе по теме:
«Логарифмы».
ПОДГОТОВИЛА:
учитель математики
высшей категории
МБОУ Ал.-Лозовская СОШ
Чертковского района
Ростовской области
Шконда Ирина Андреевна
2015 год
Содержание.
Задания для устной работы.
Задания для самостоятельной работы (обязательный уровень).
Вопросы теории. Примеры-алгоритмы.
Контрольная работа по теме: « Логарифмы». ( 4 варианта).
Задания для устной работы.
1
1
2
3
1
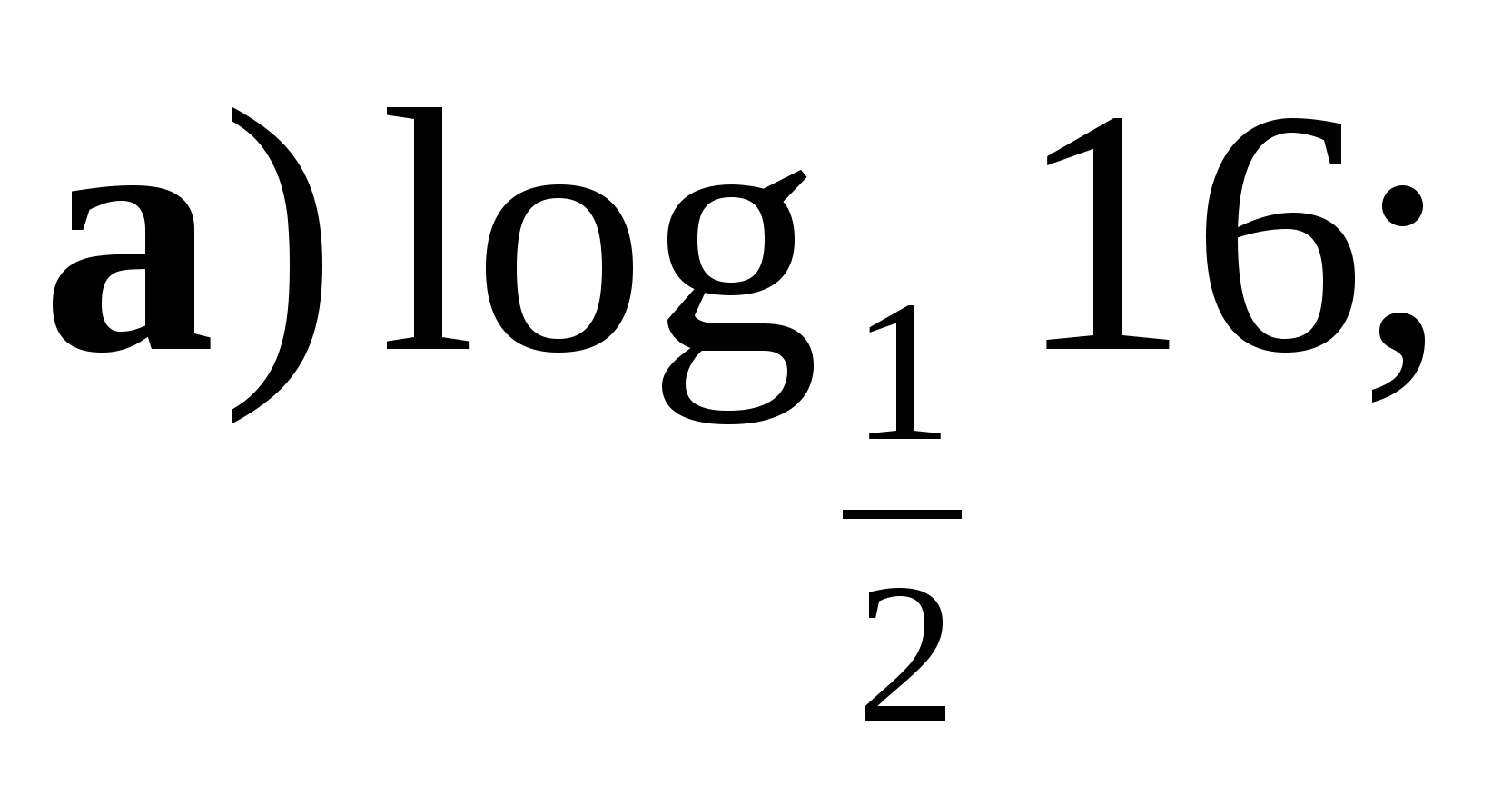
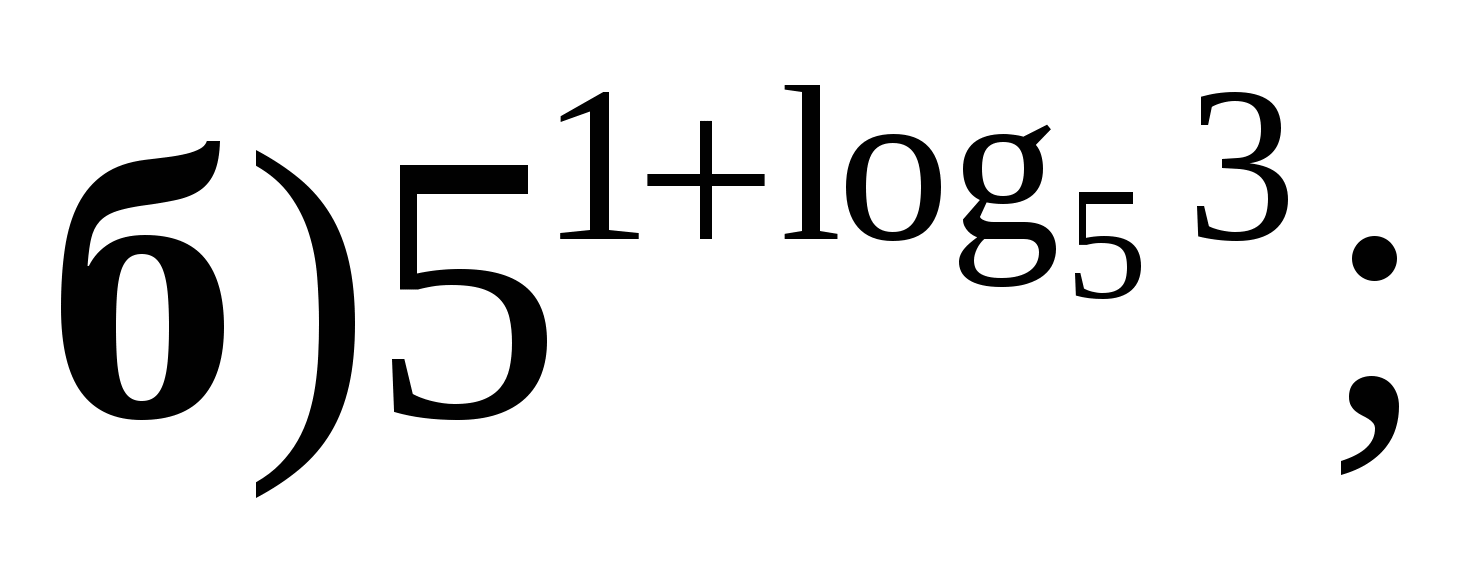
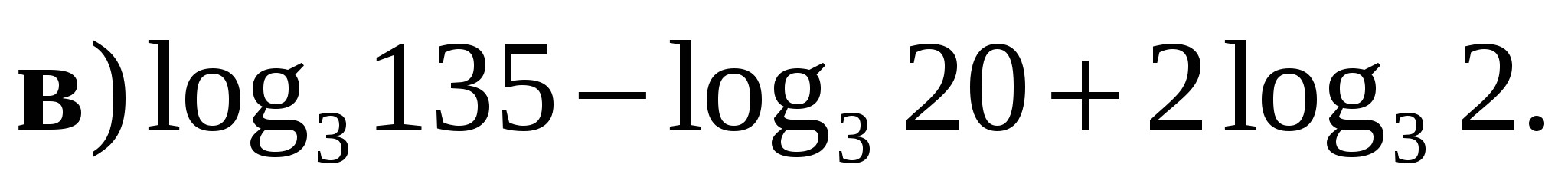
2
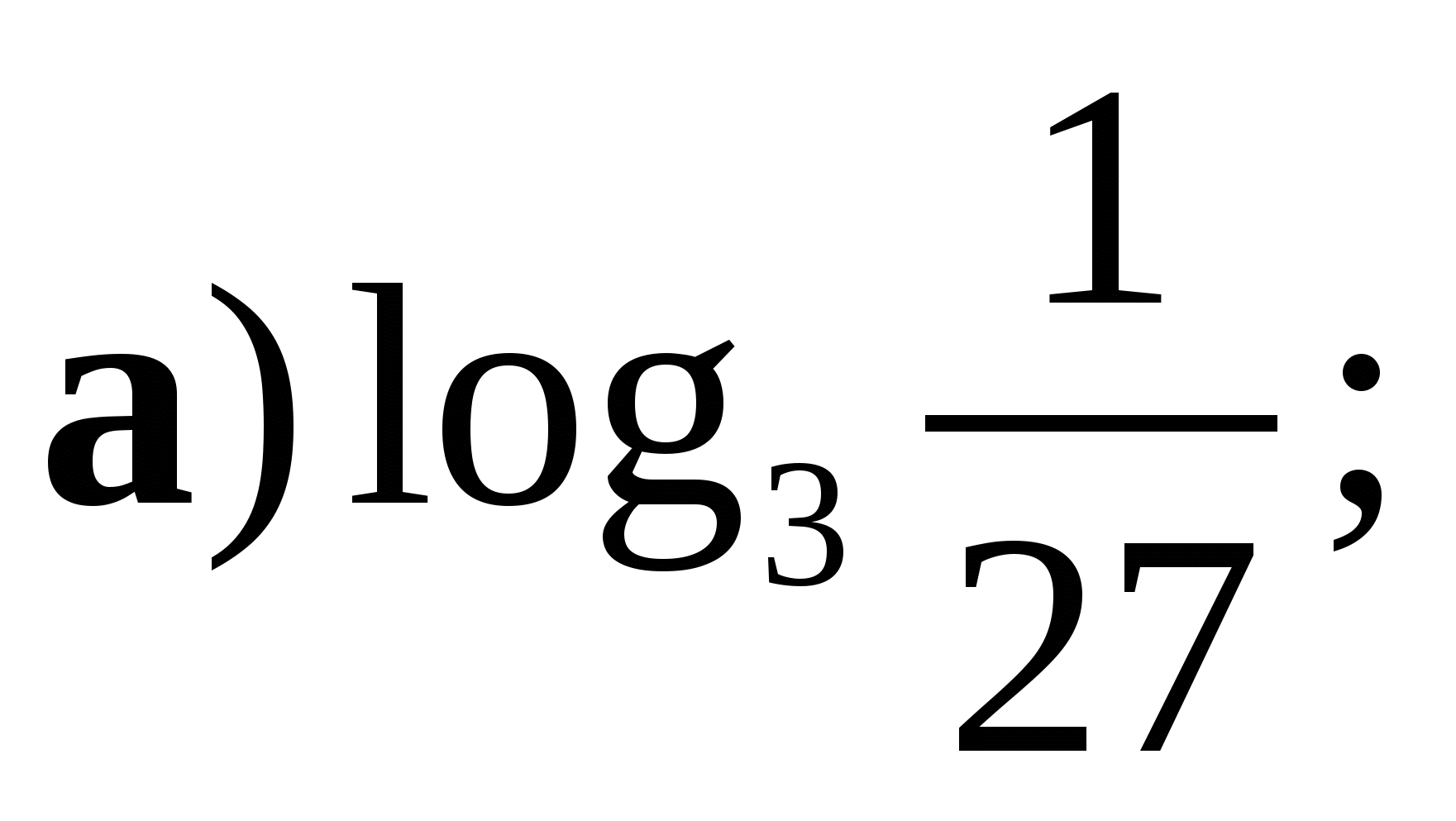
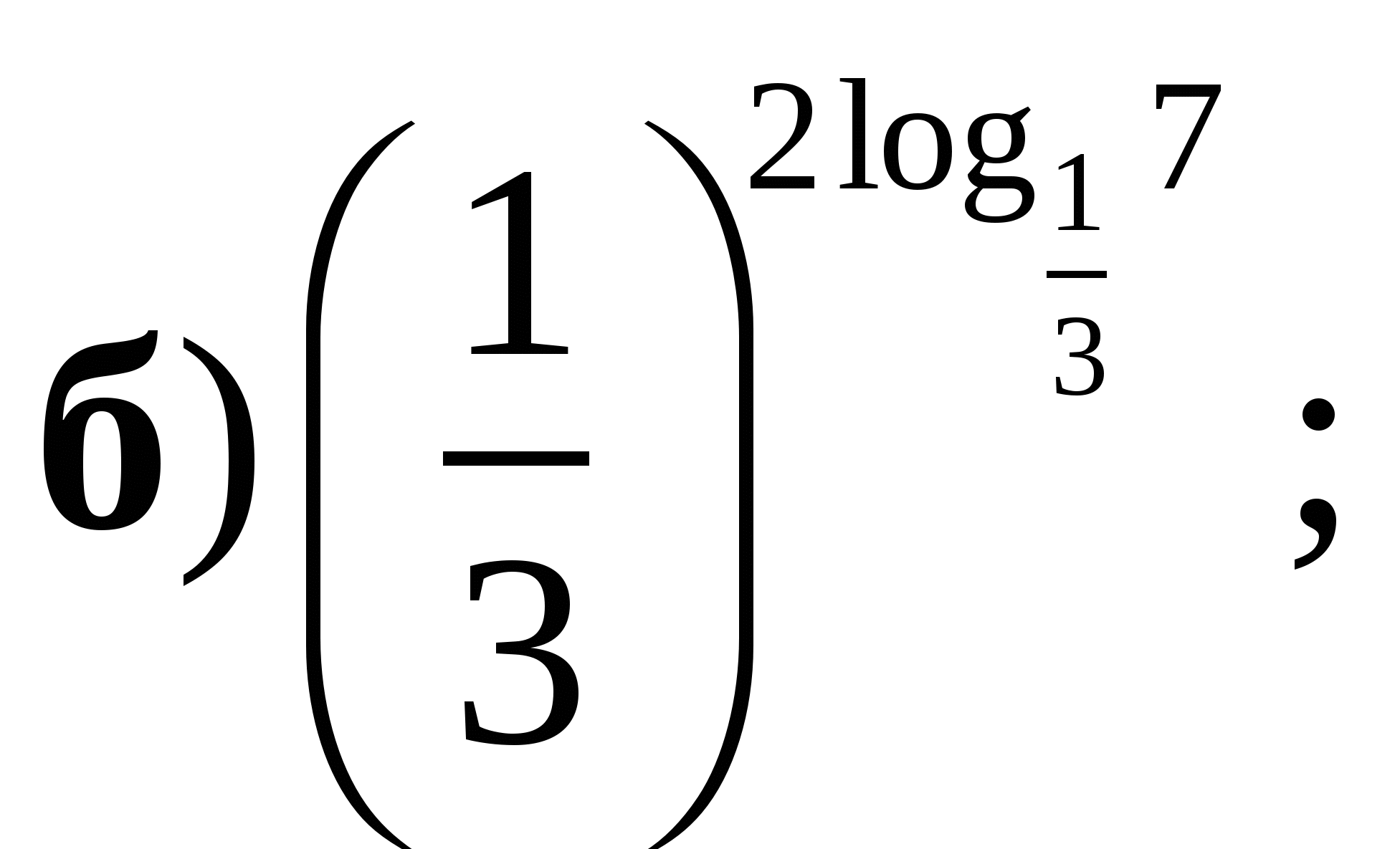
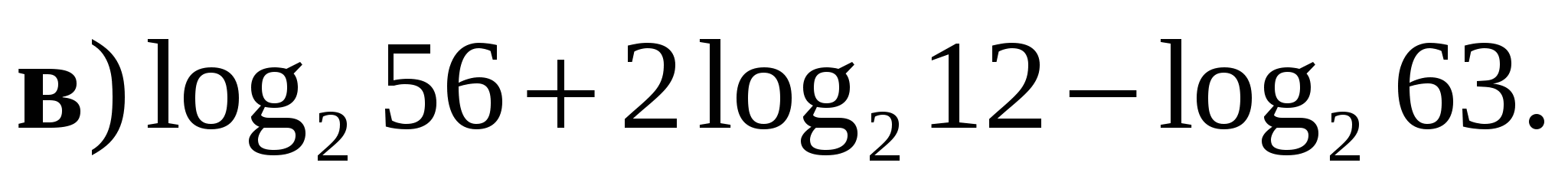
3
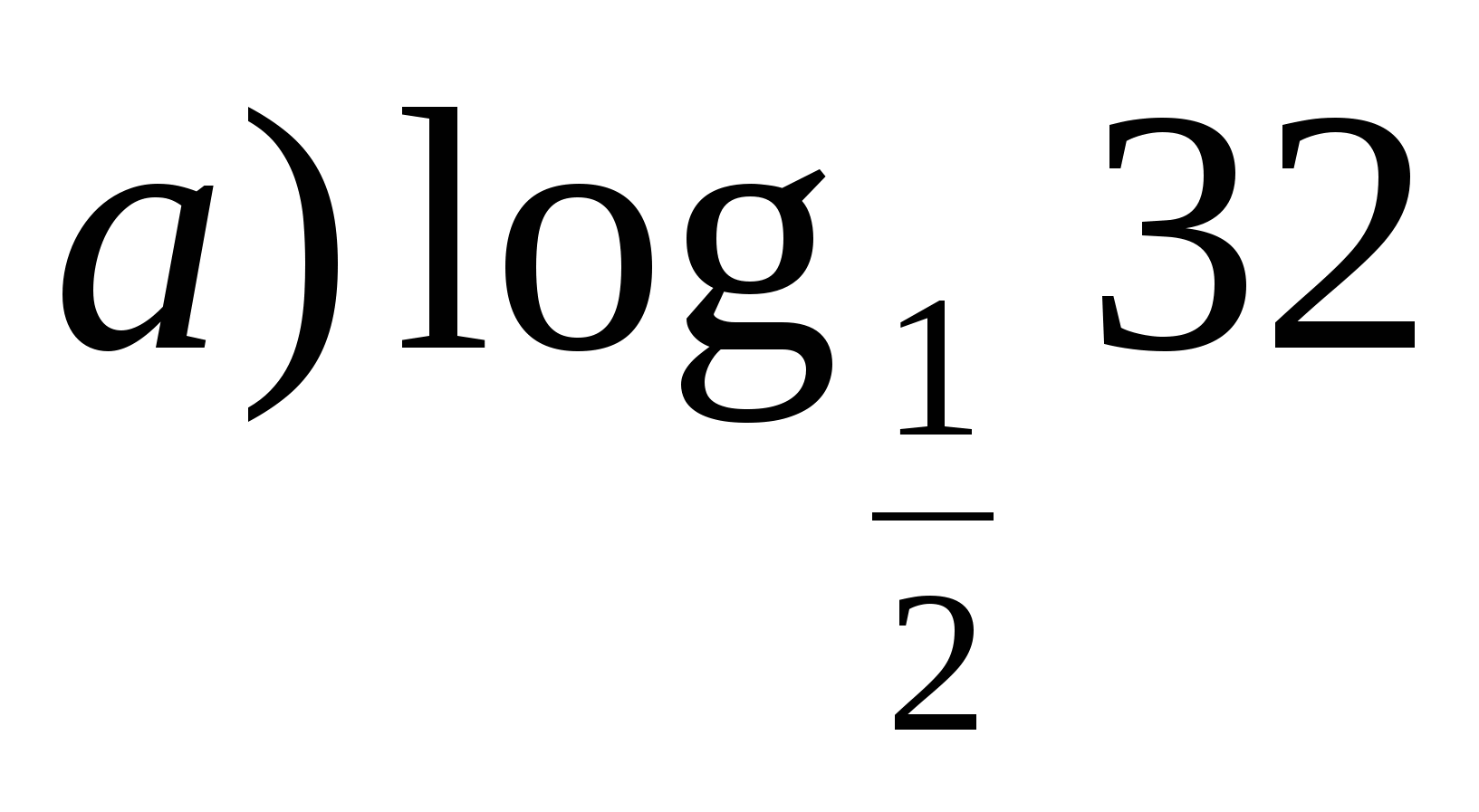
б)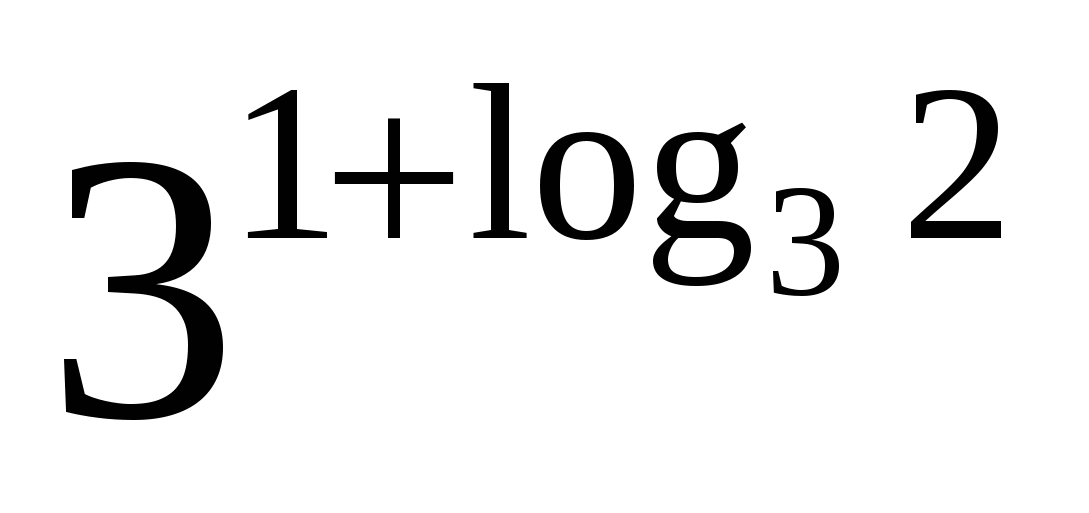
в)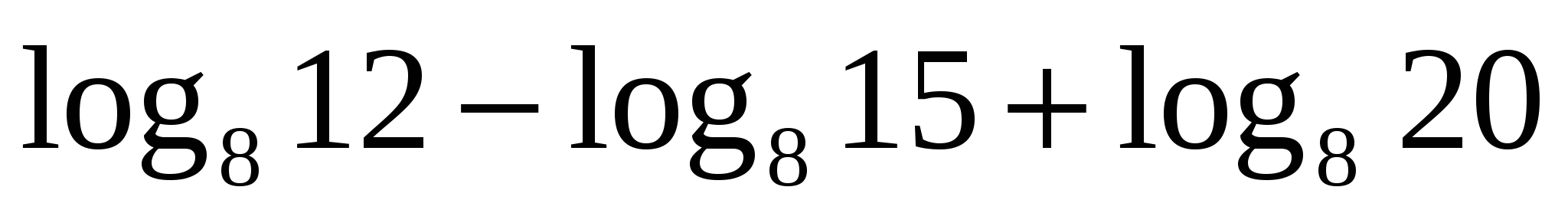
4
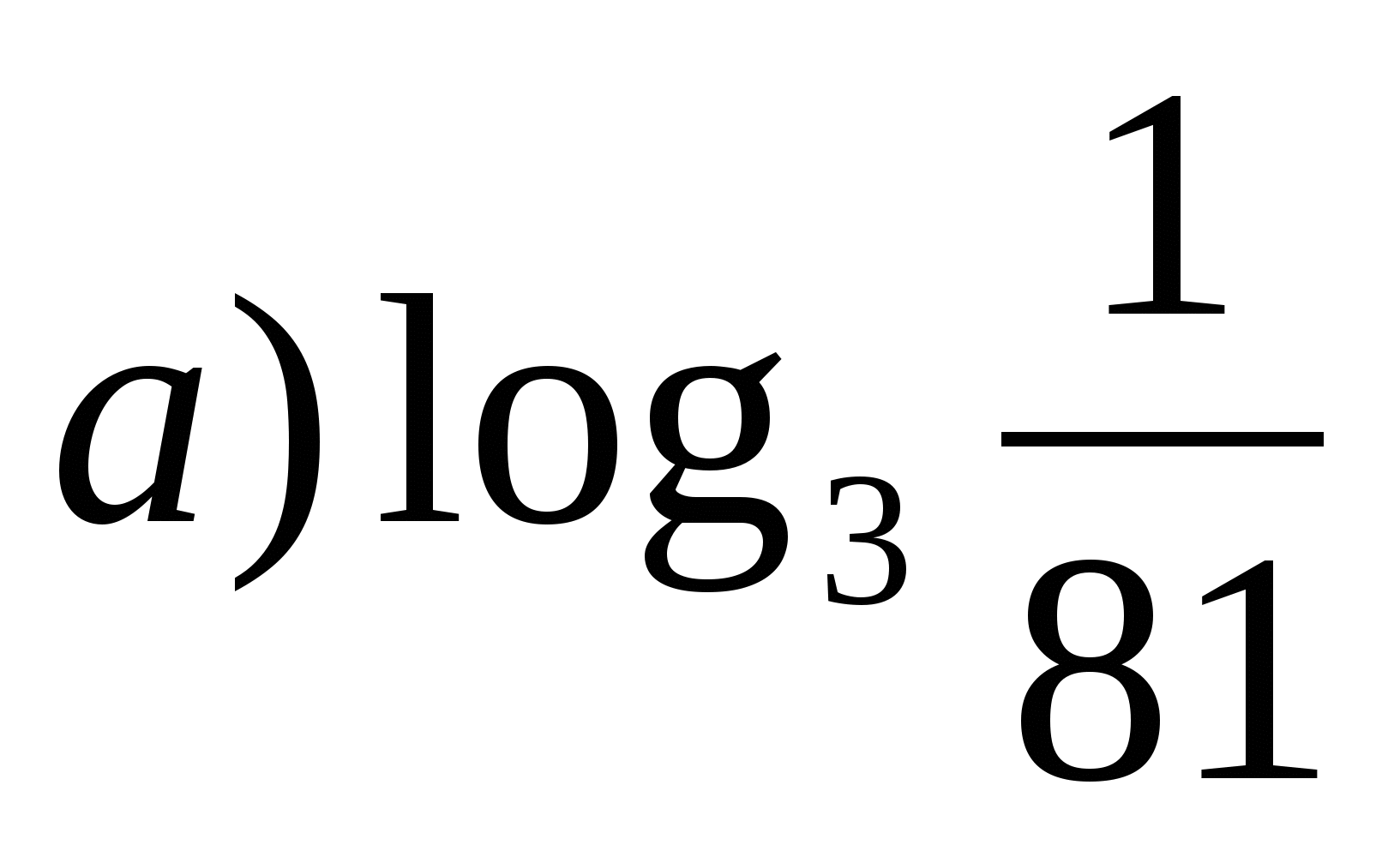
б)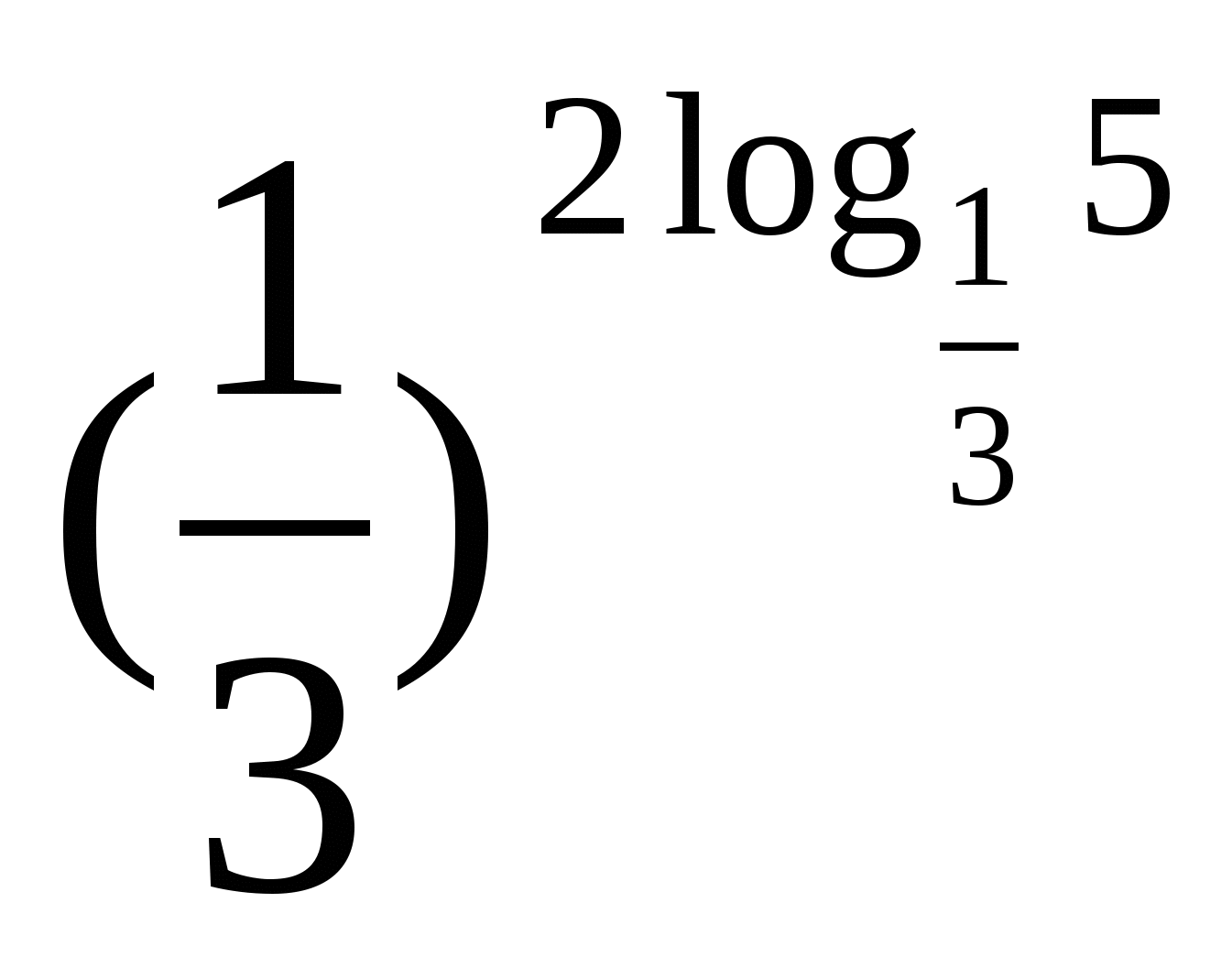
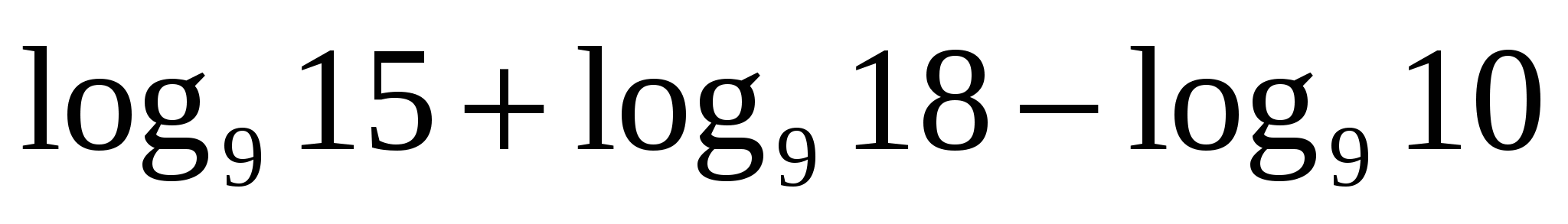
5
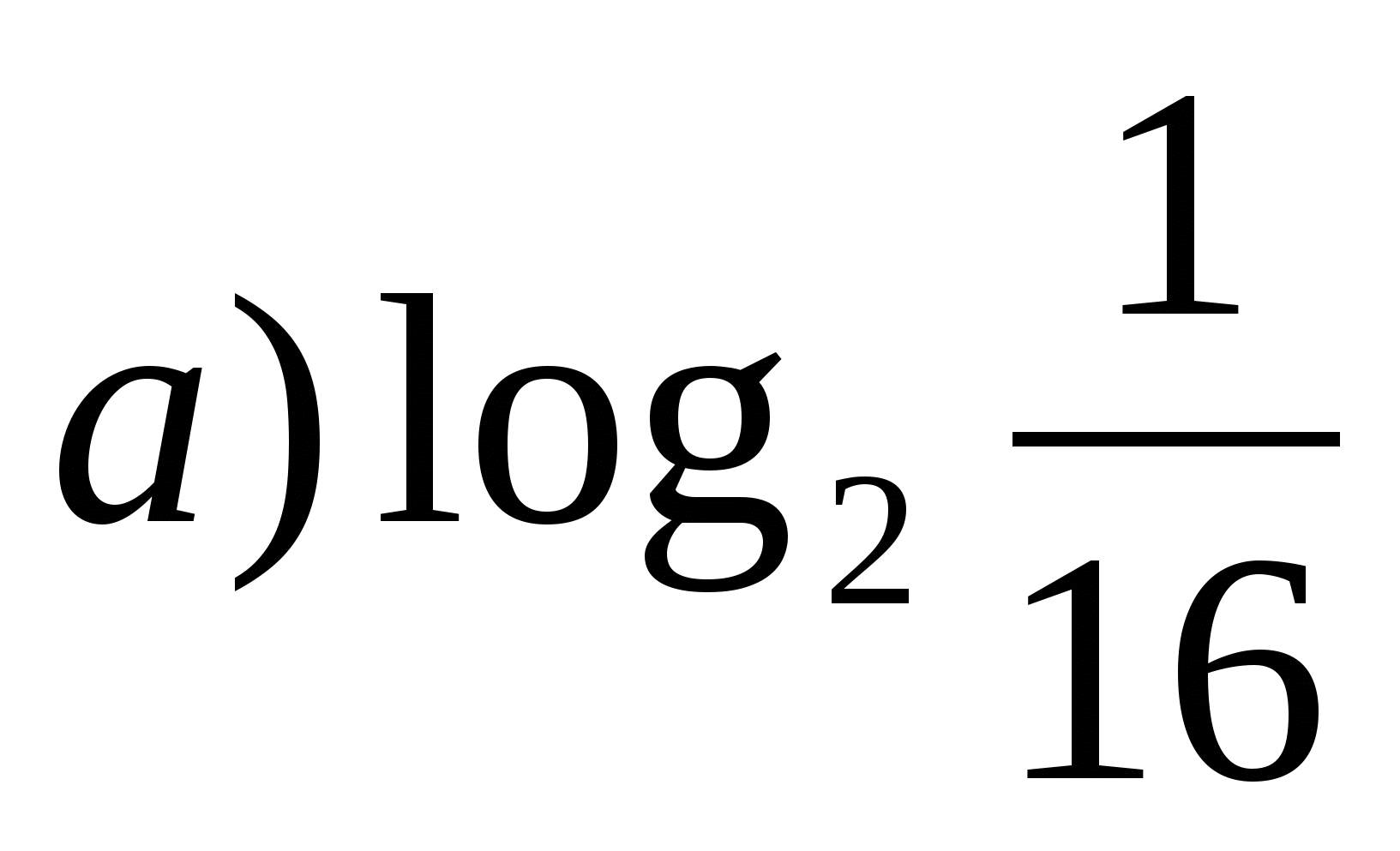
б)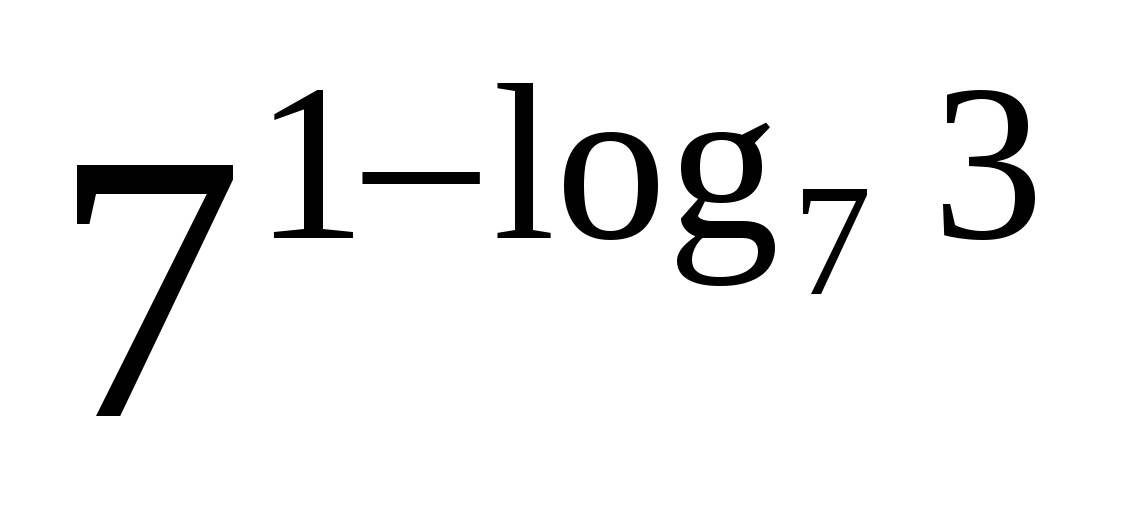
в)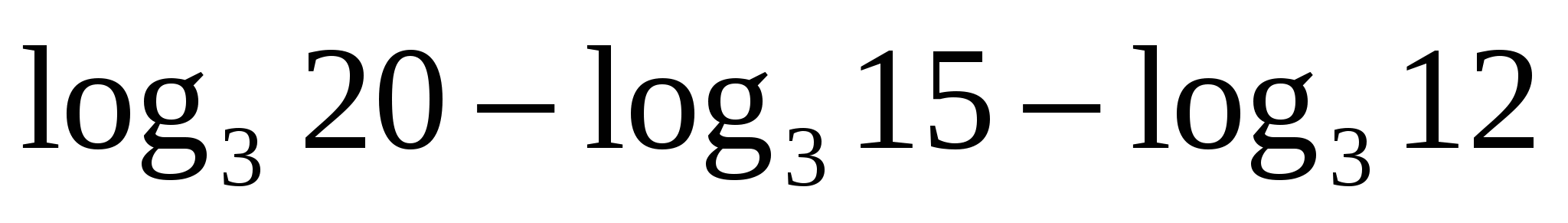
6
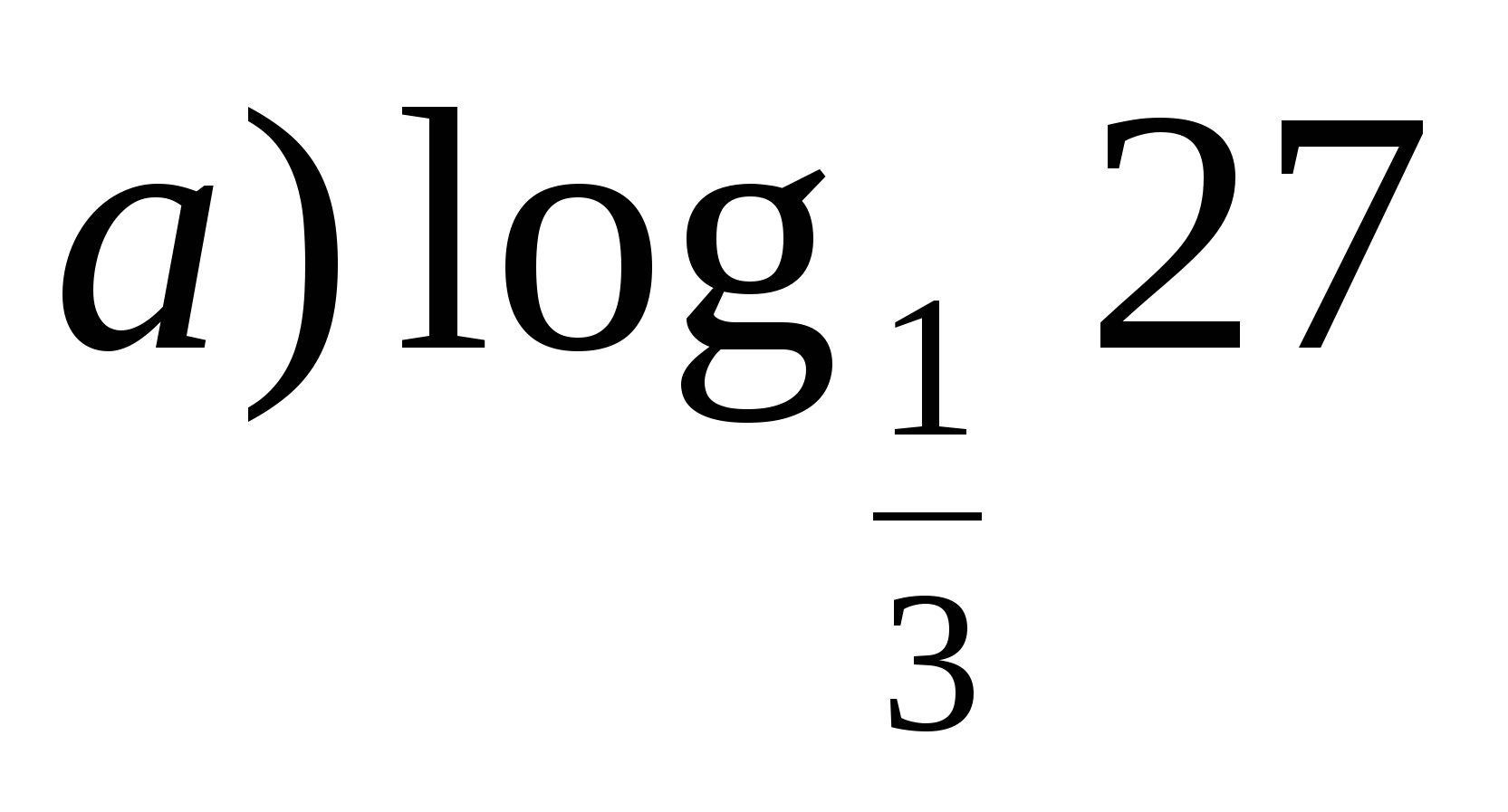
б)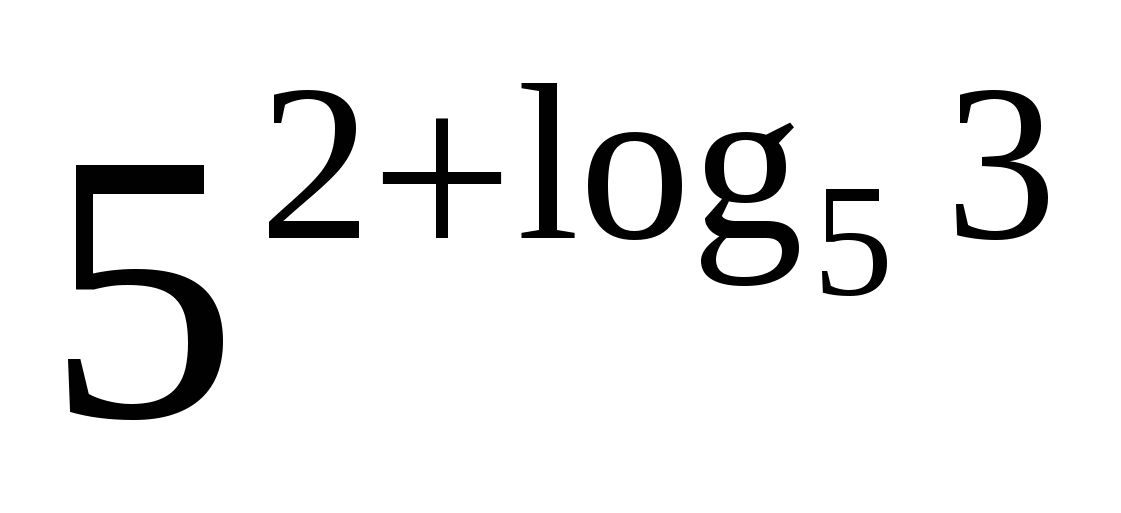
в)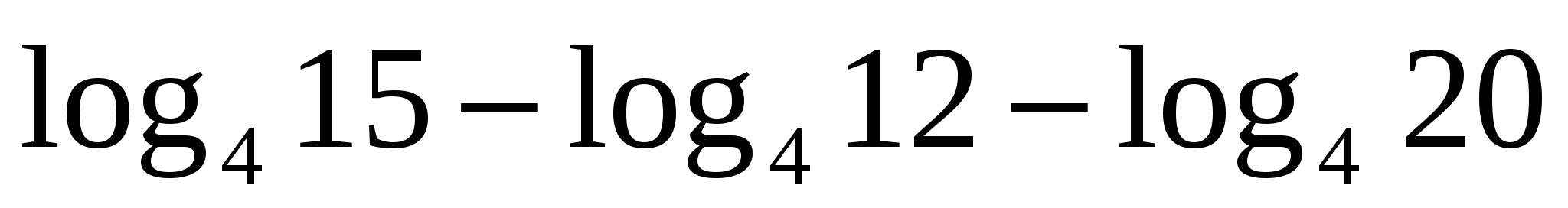
№ варианта
Ответы
1
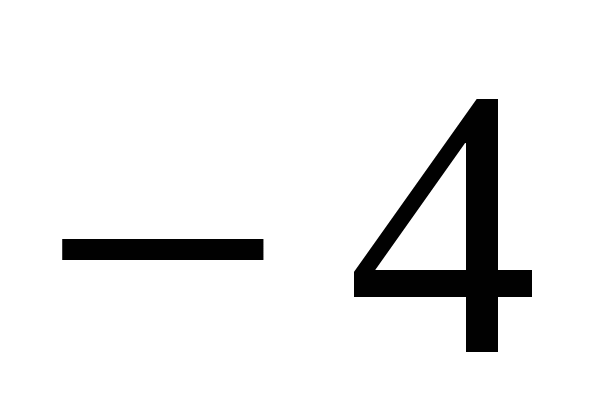

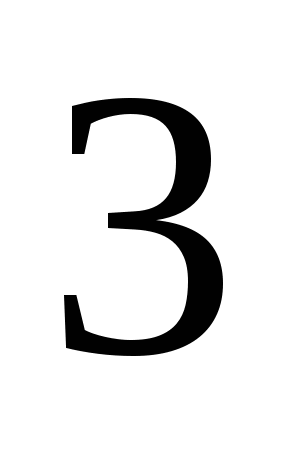
2
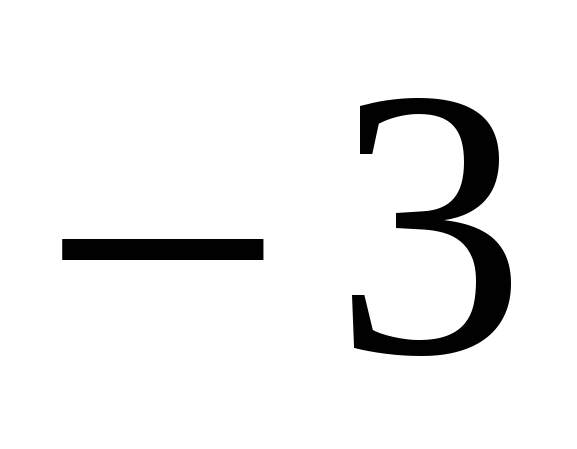


3
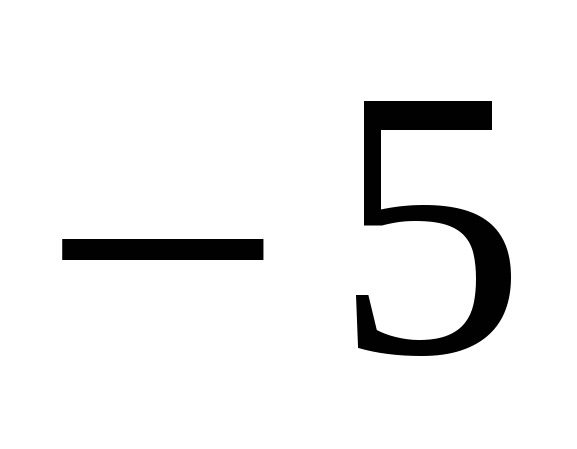
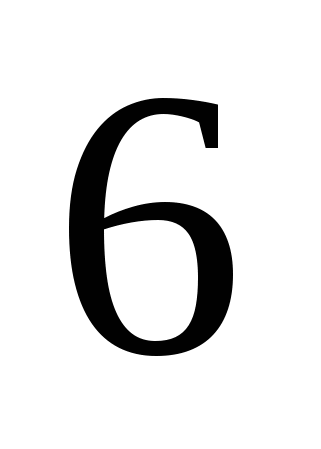
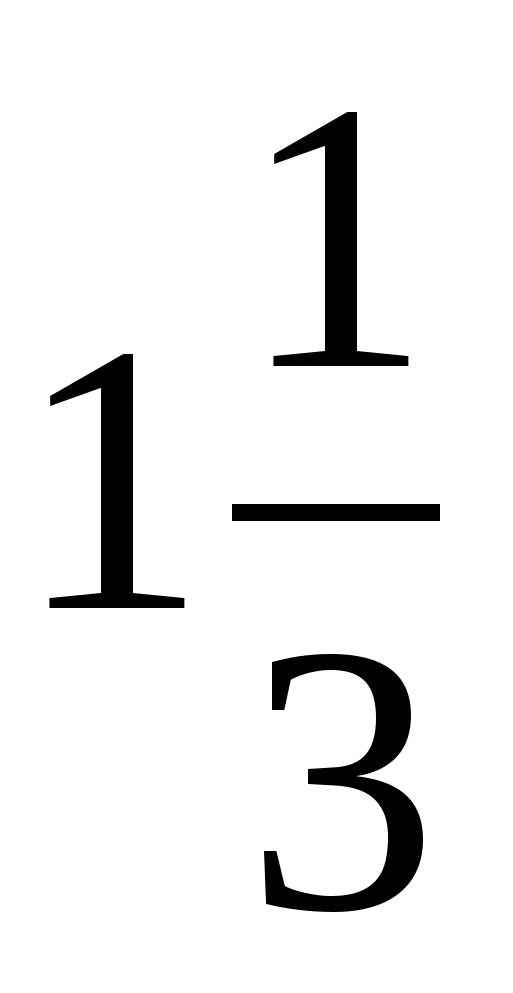
4
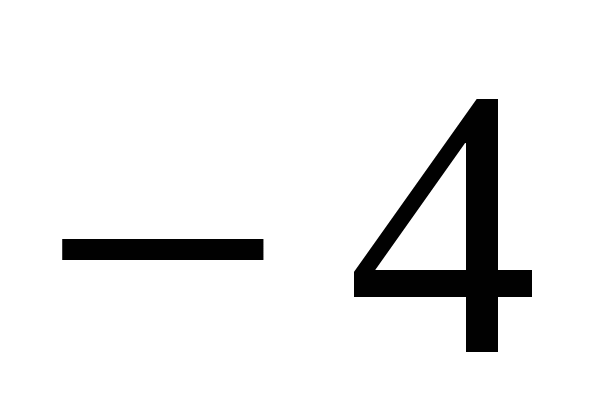
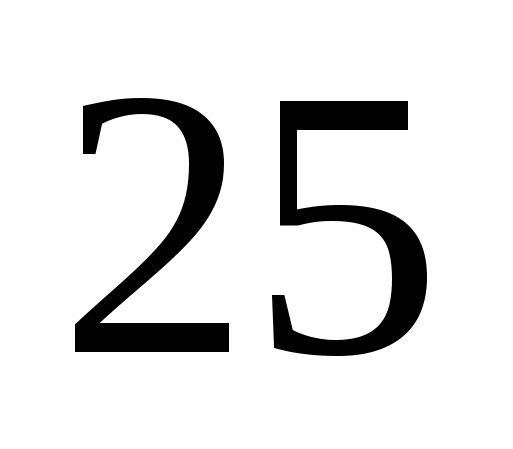
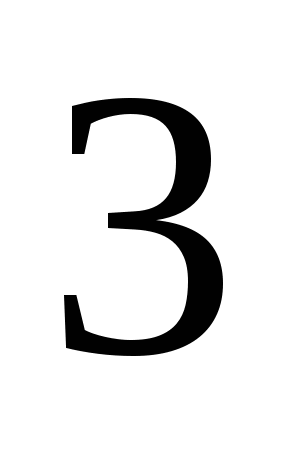
5
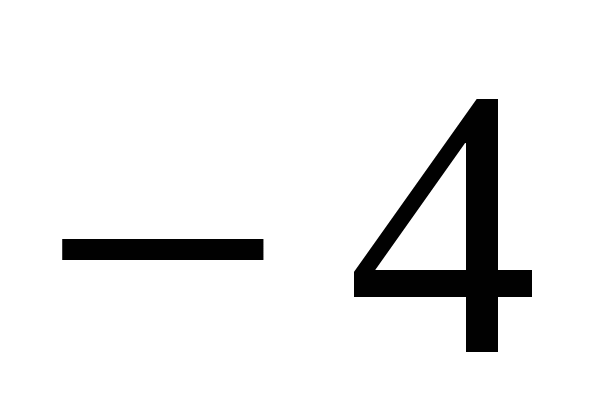
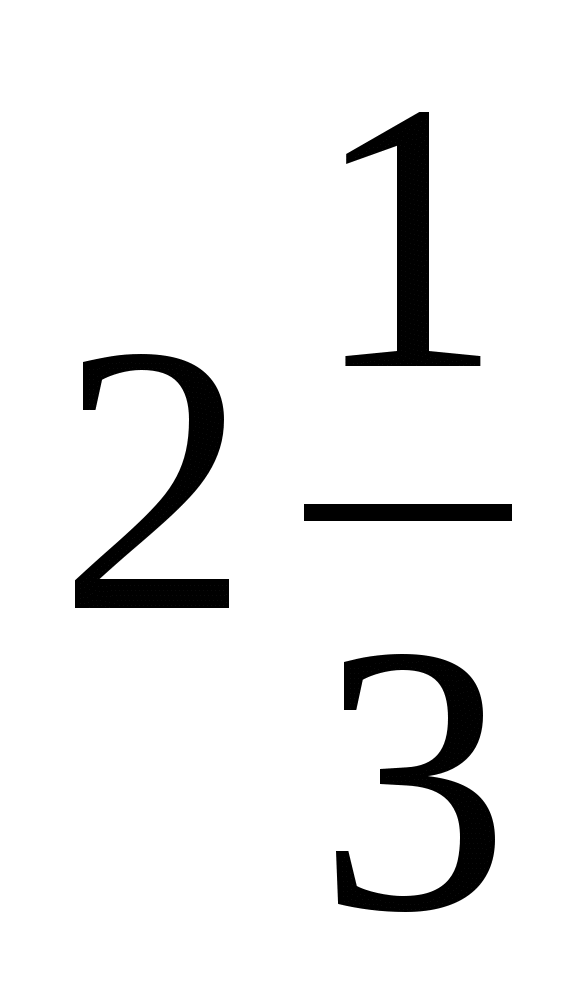
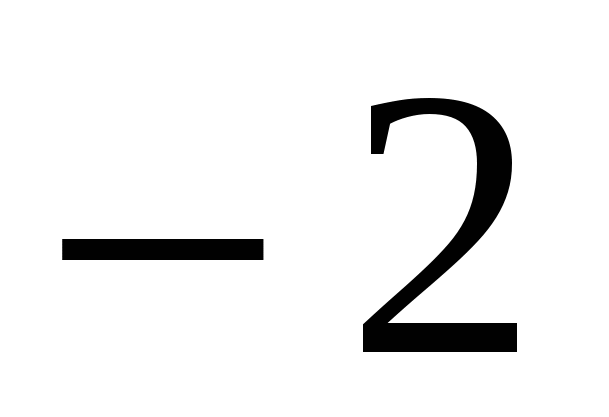
6
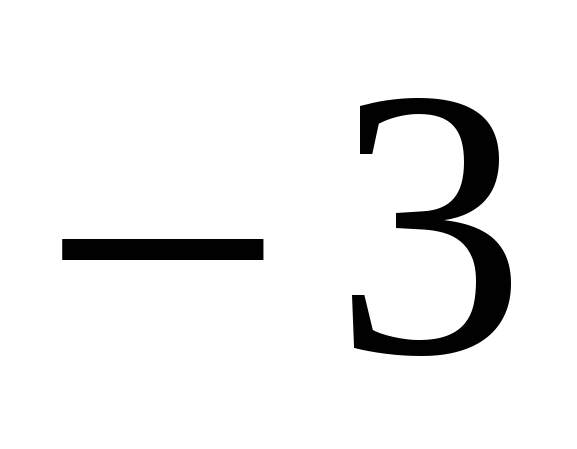

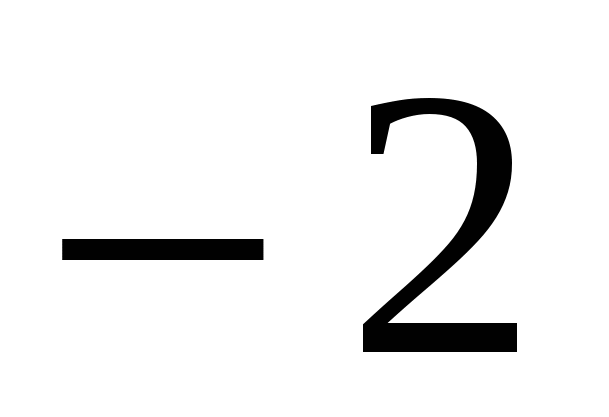
Вычислить:
Вычислить:
Сравнить.
Решить уравнение
Решить неравенство
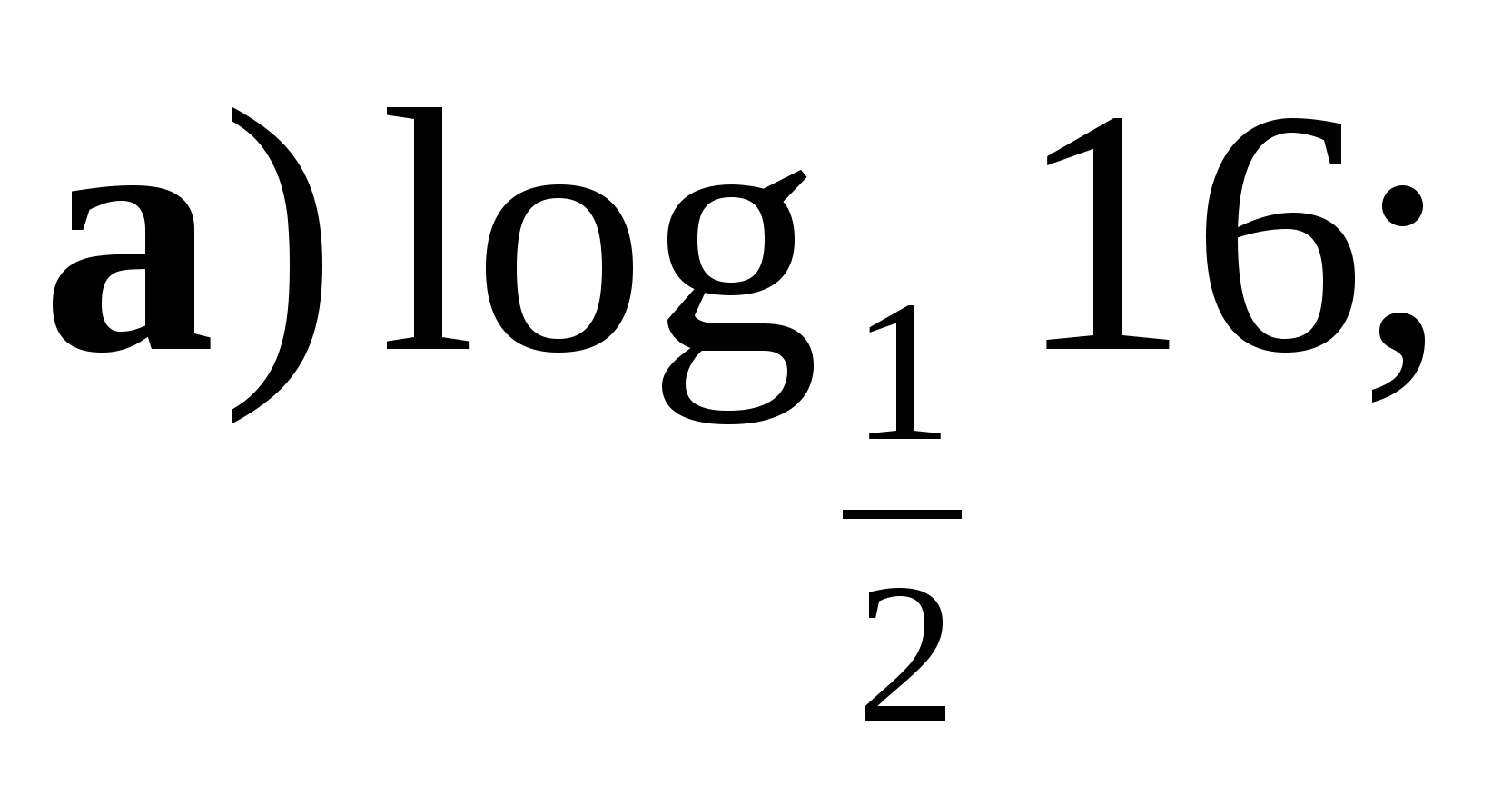
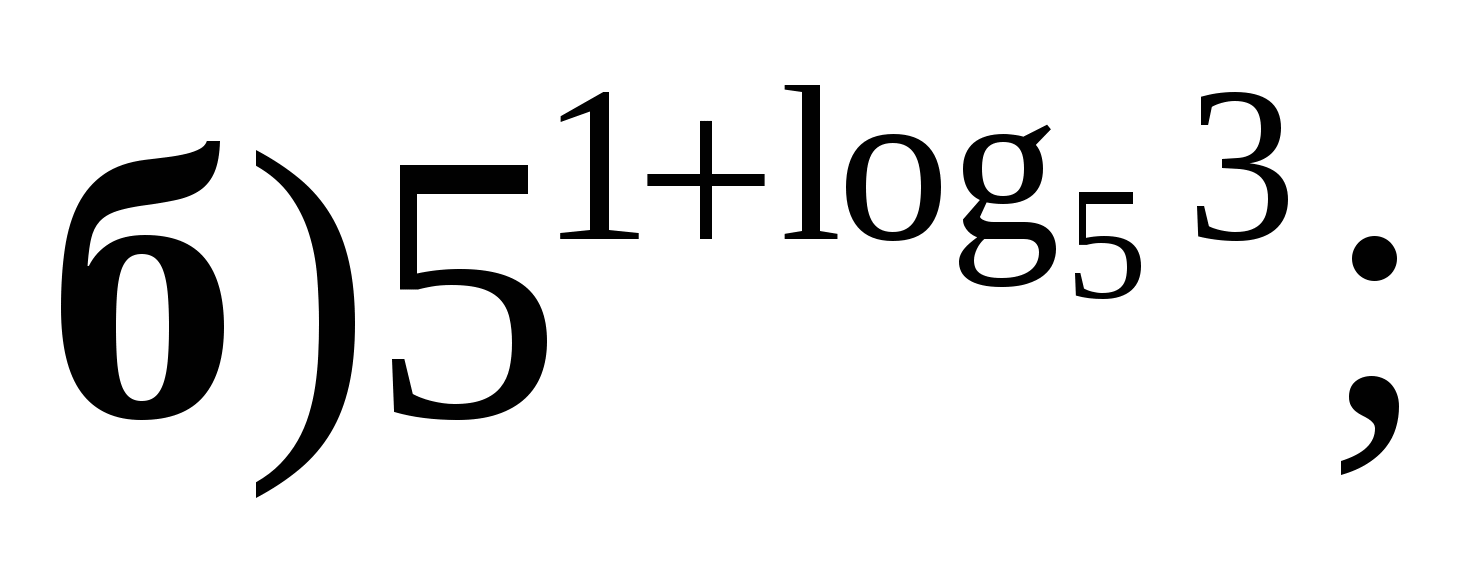
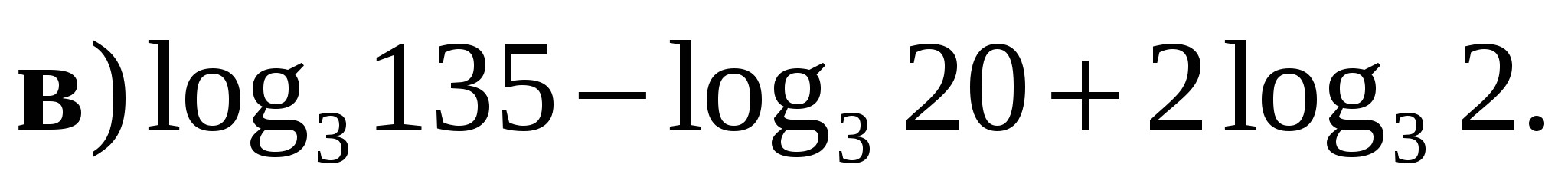
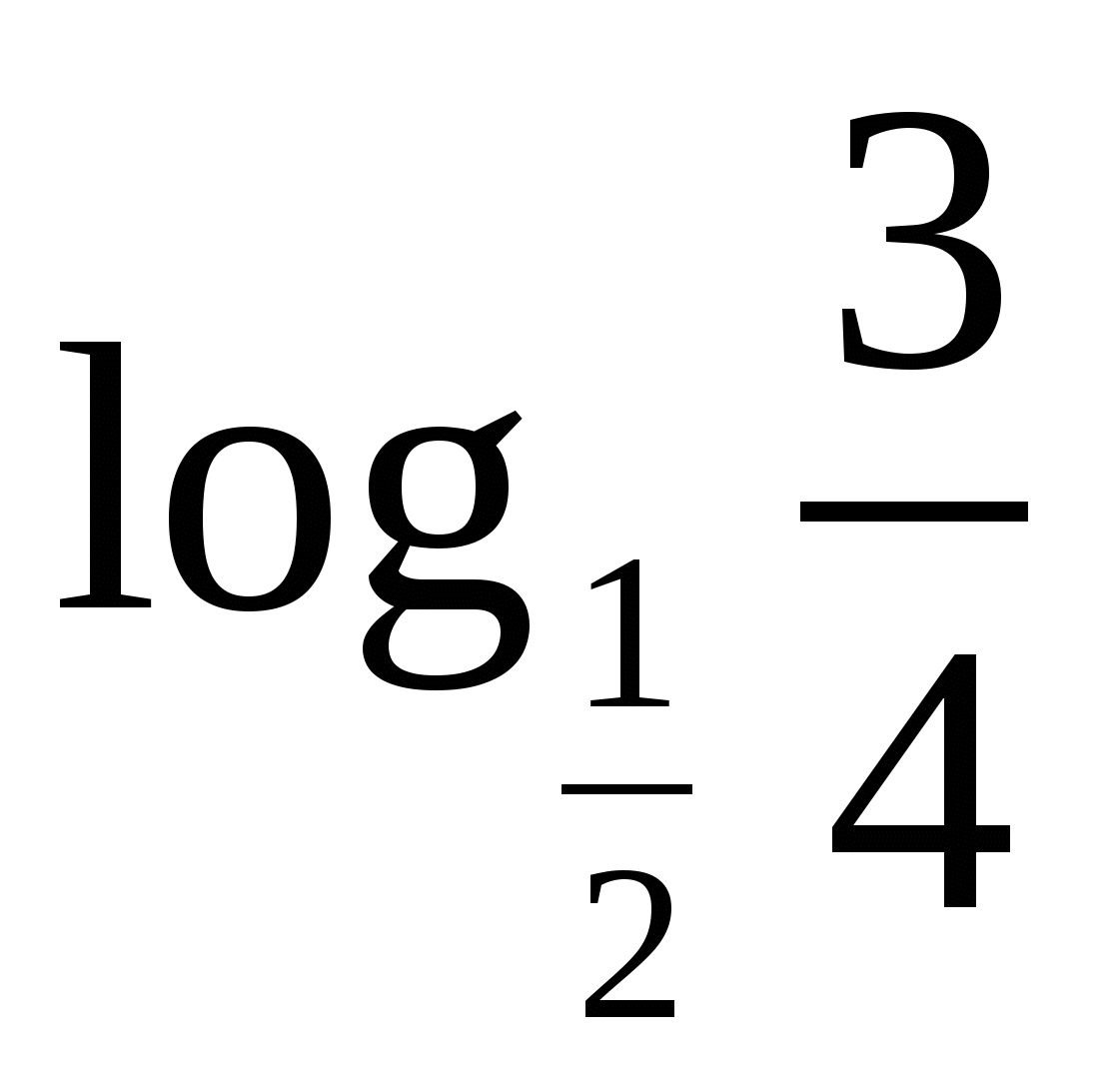 и
и 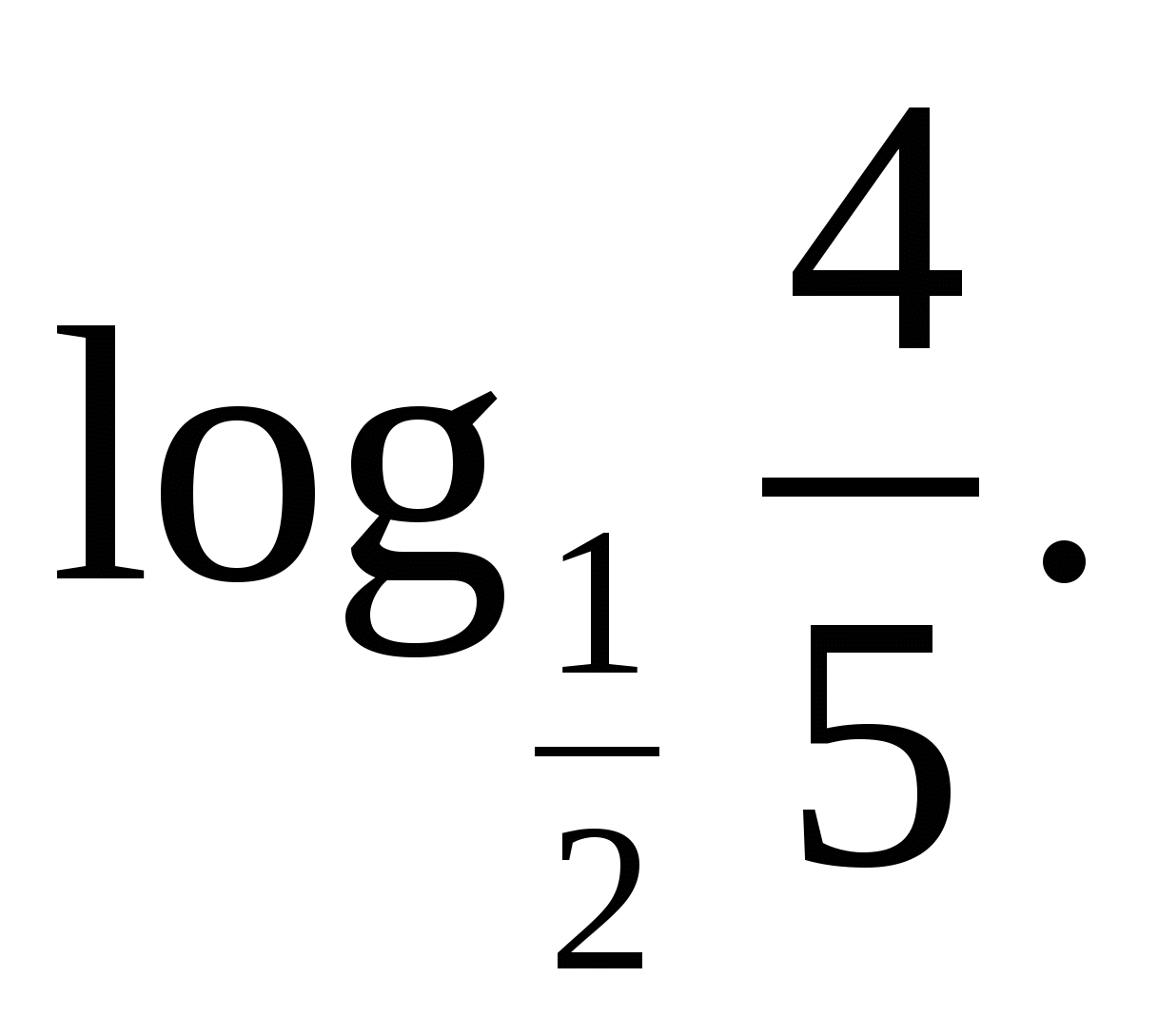
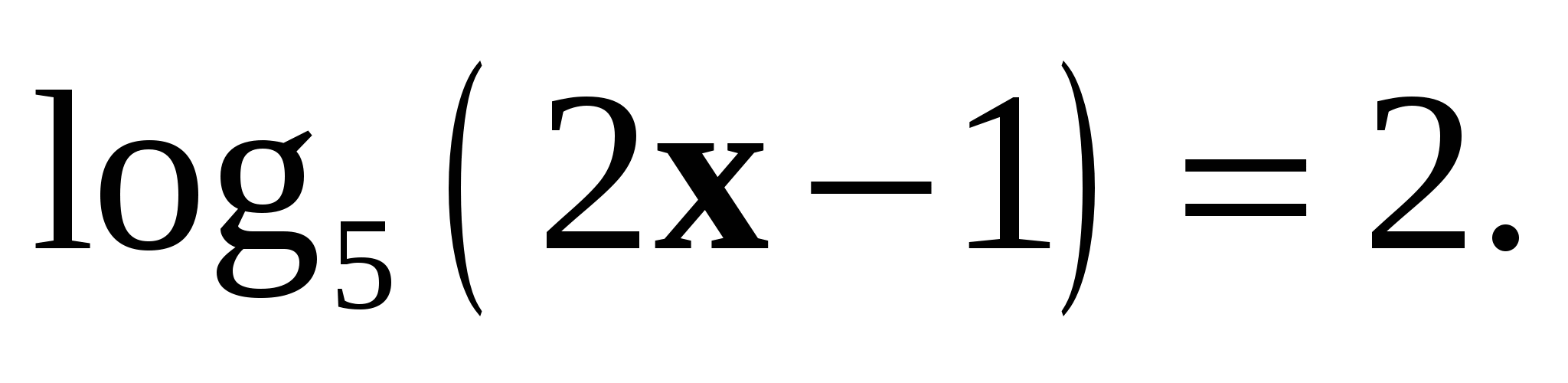
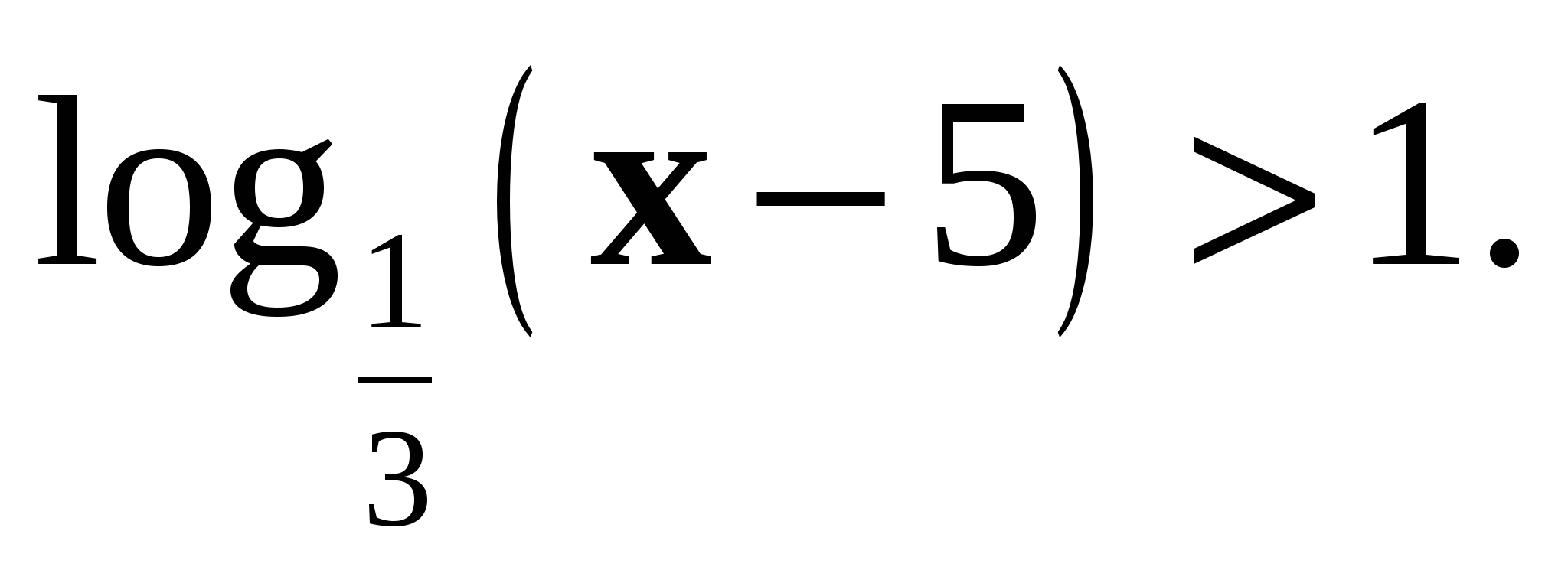
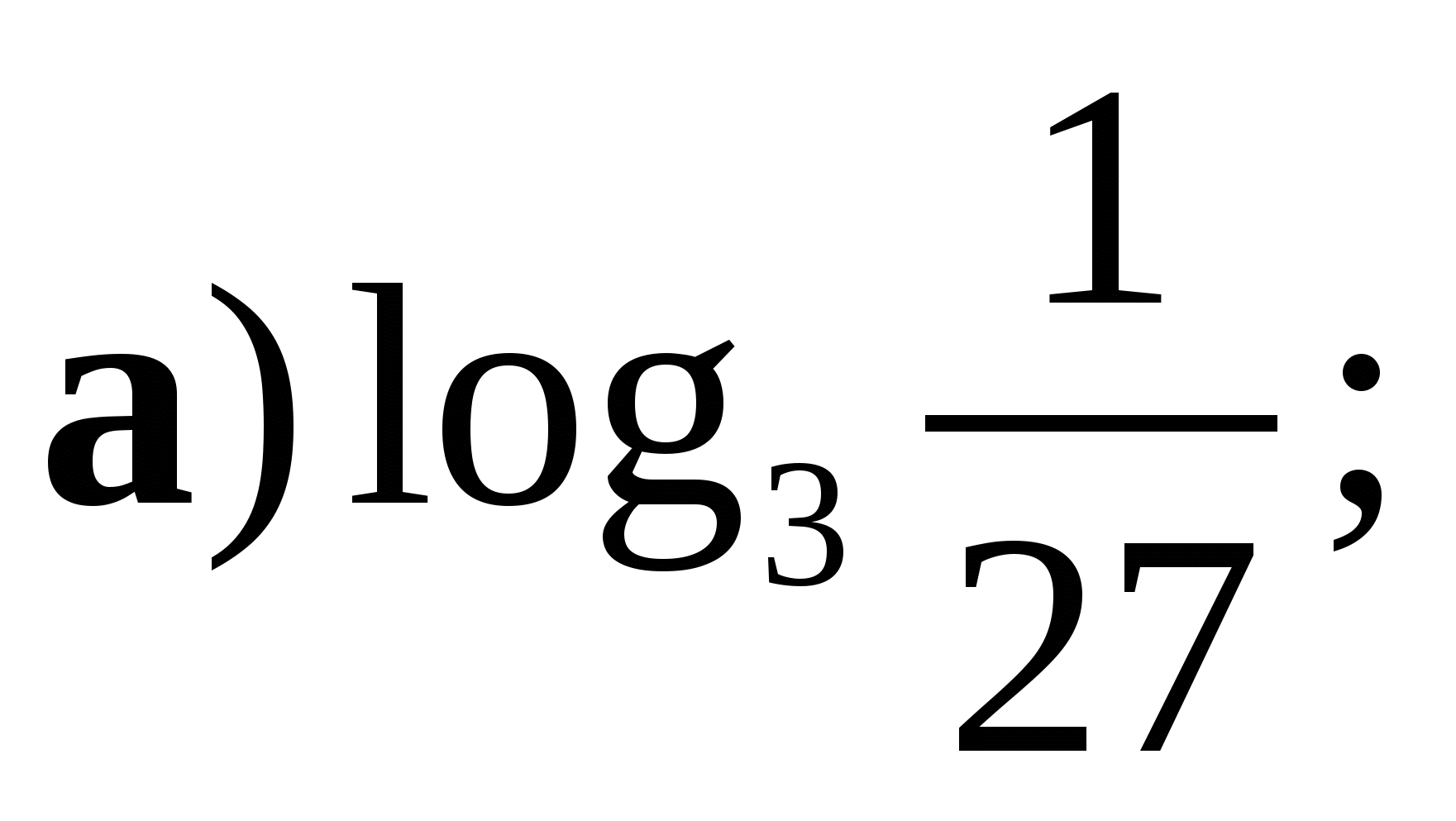
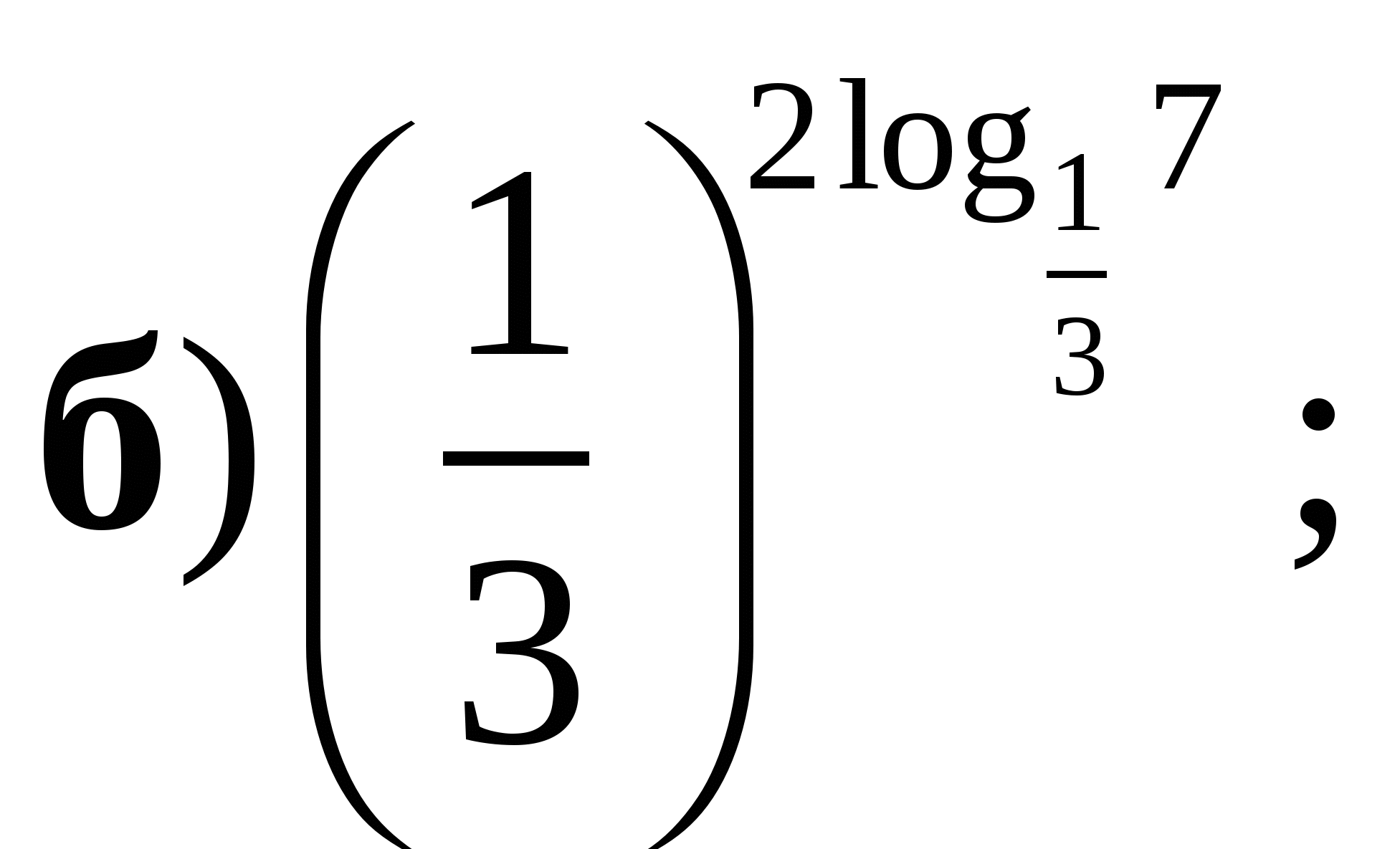
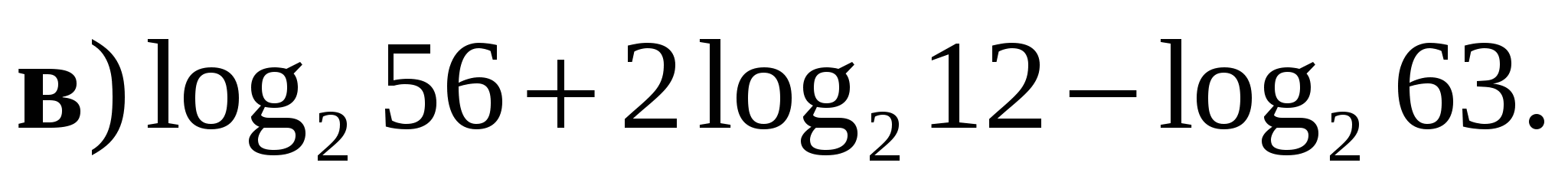
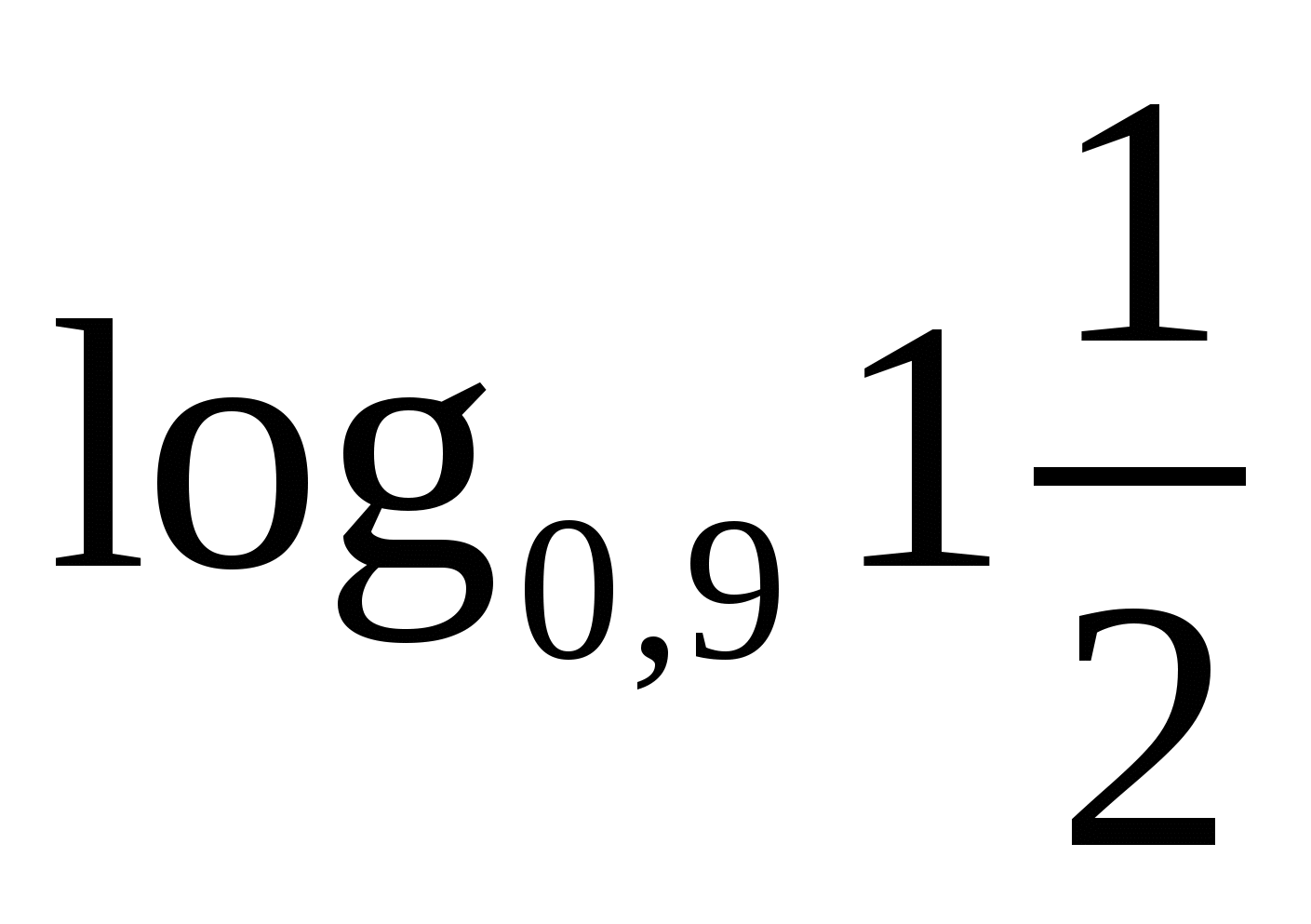
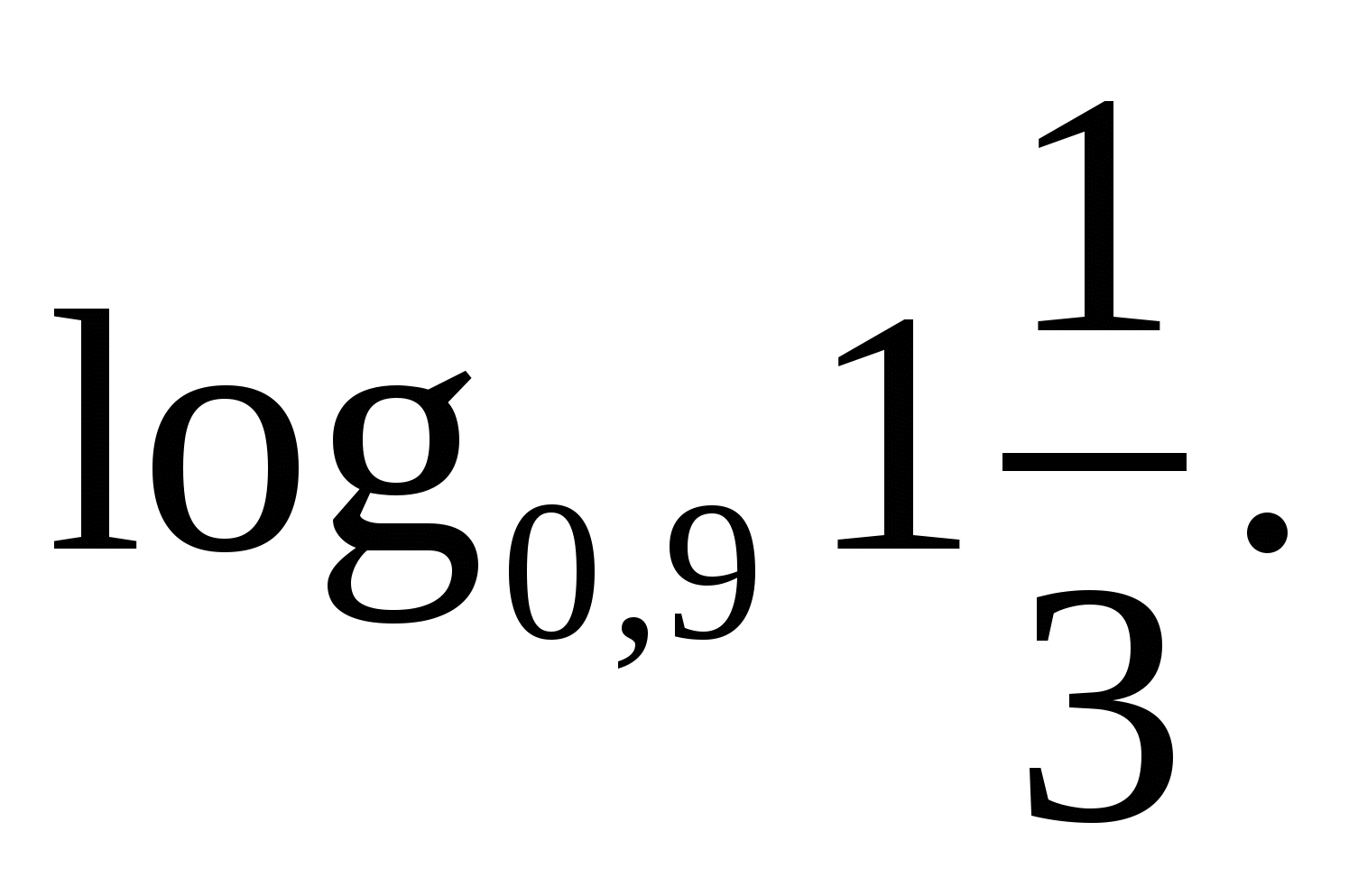
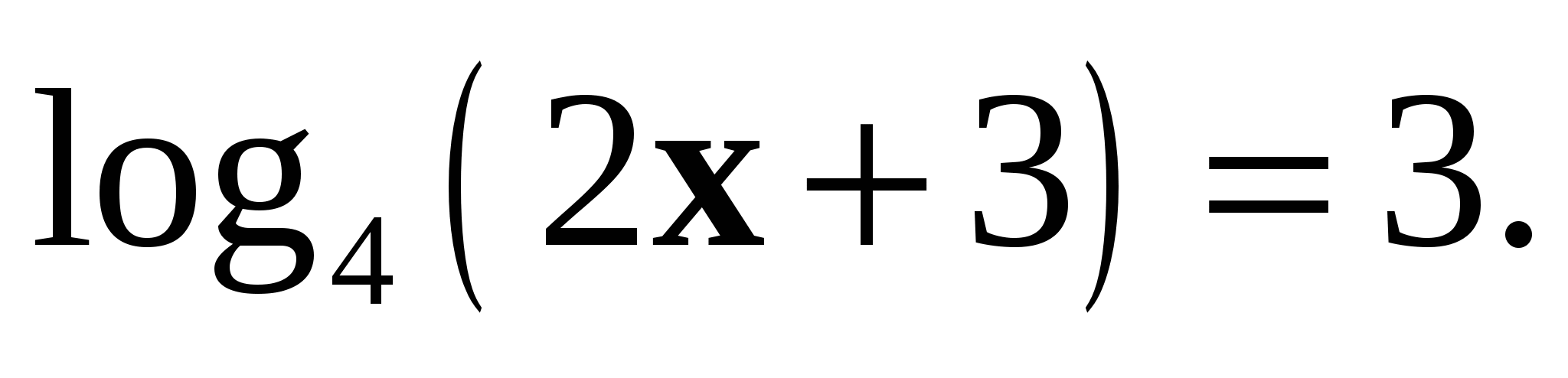

а)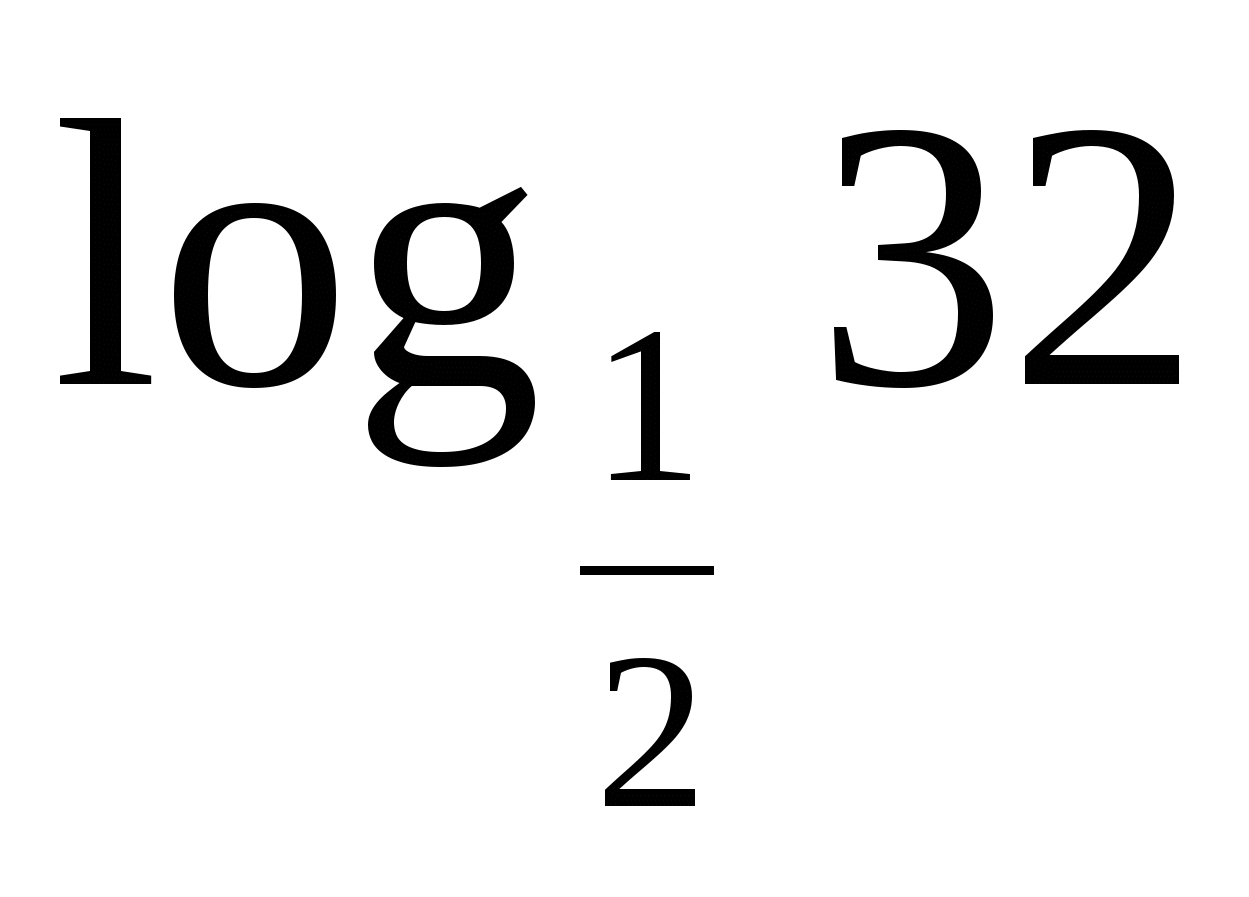
б)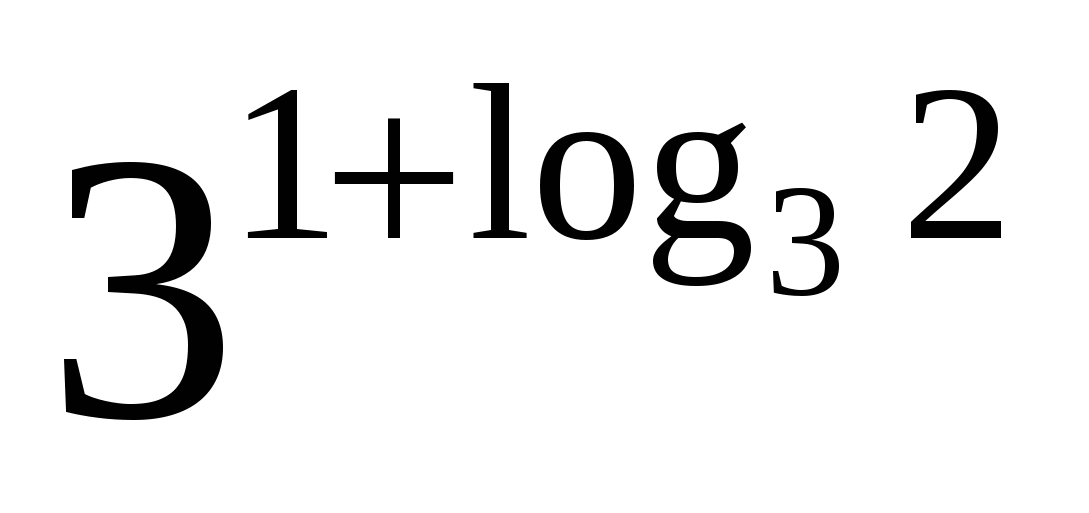
в) 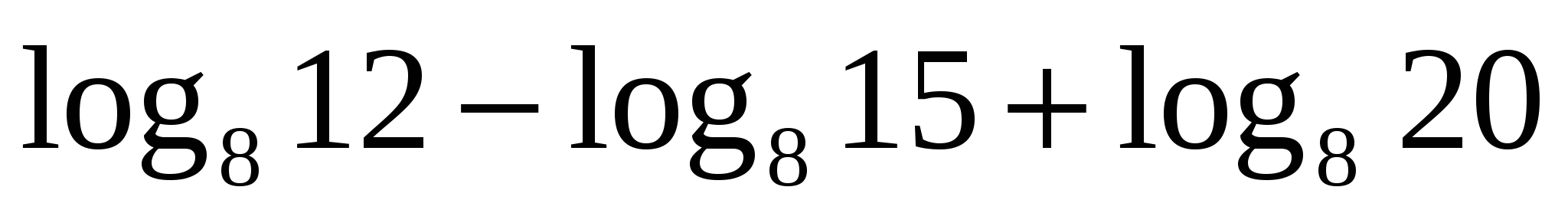
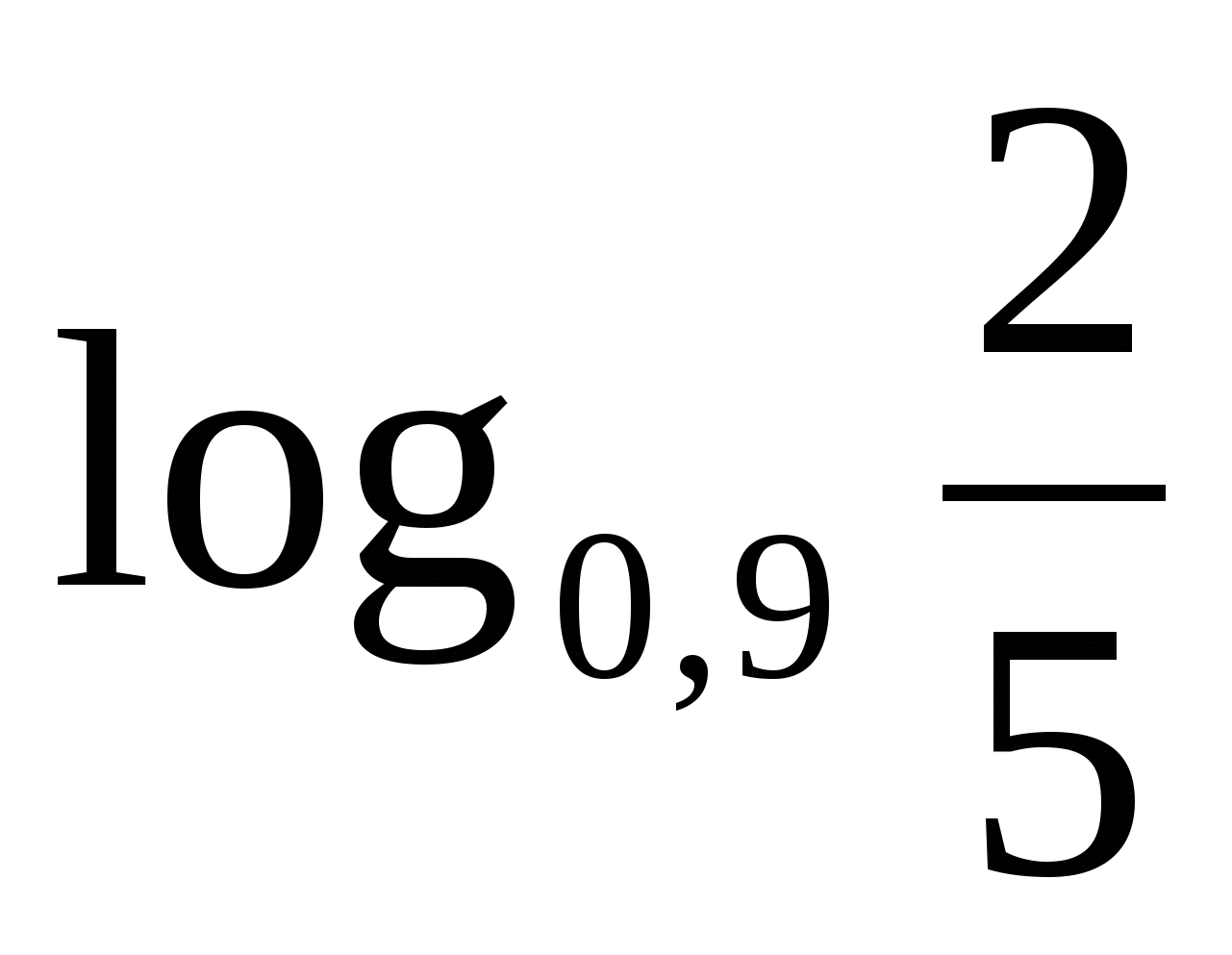
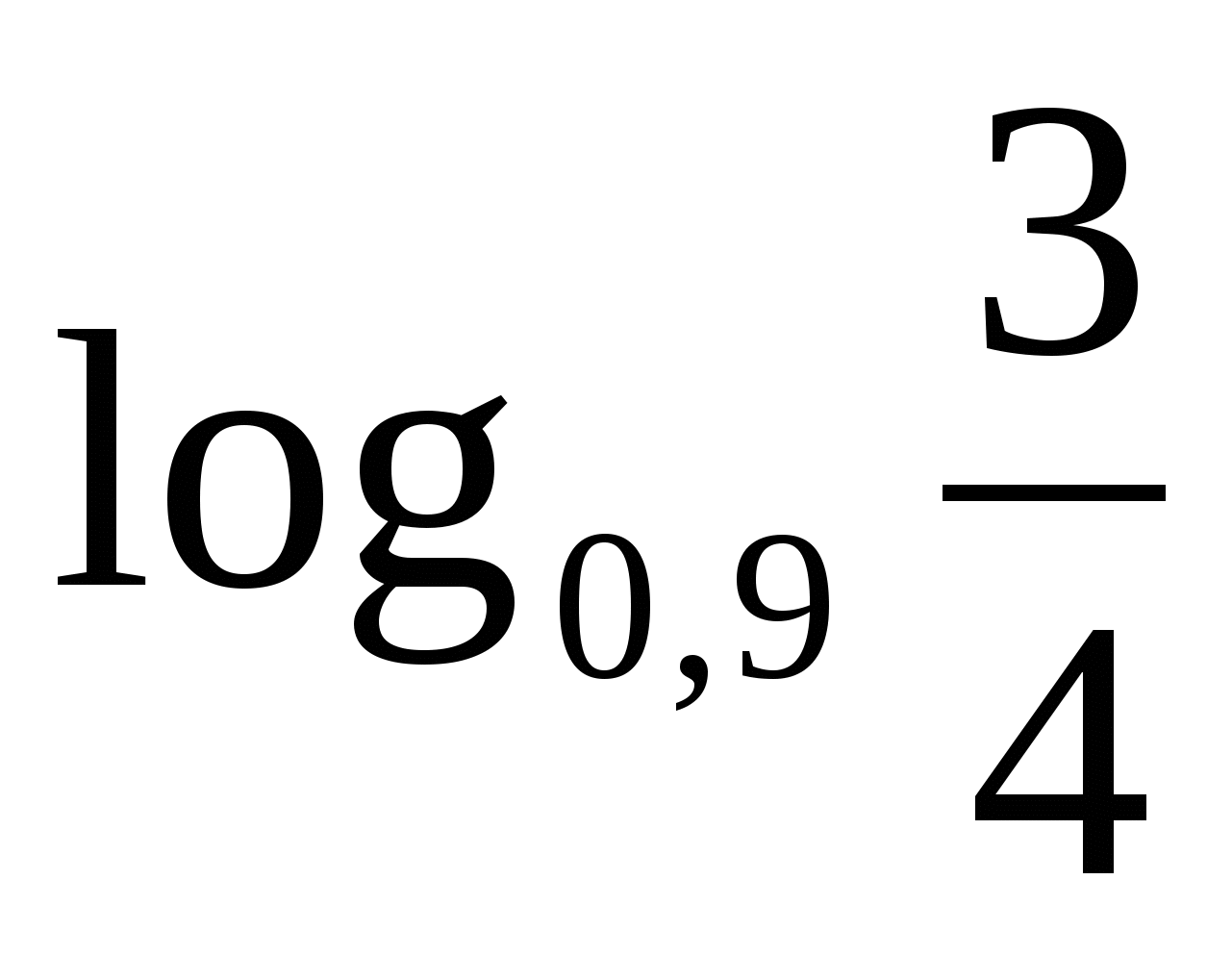
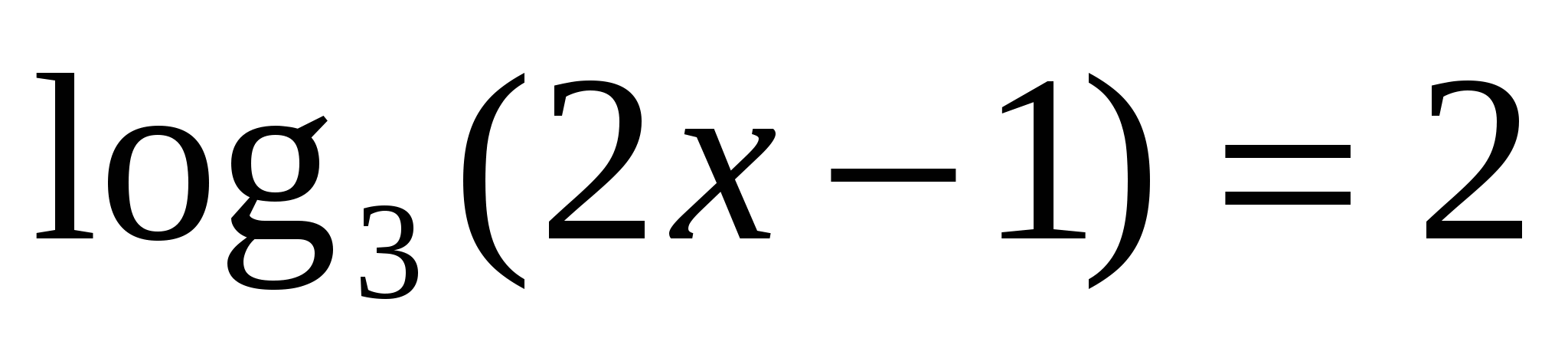
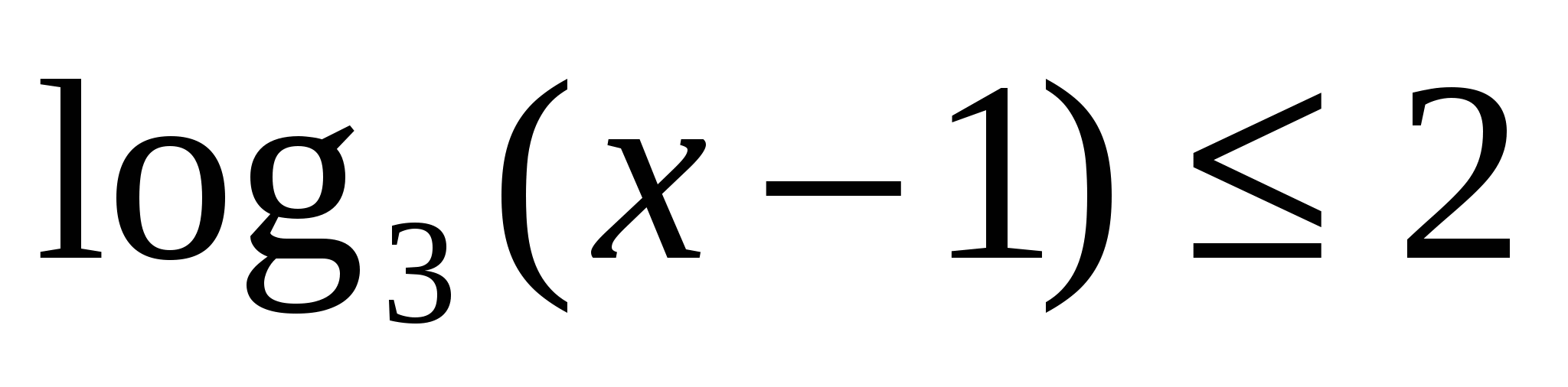
а)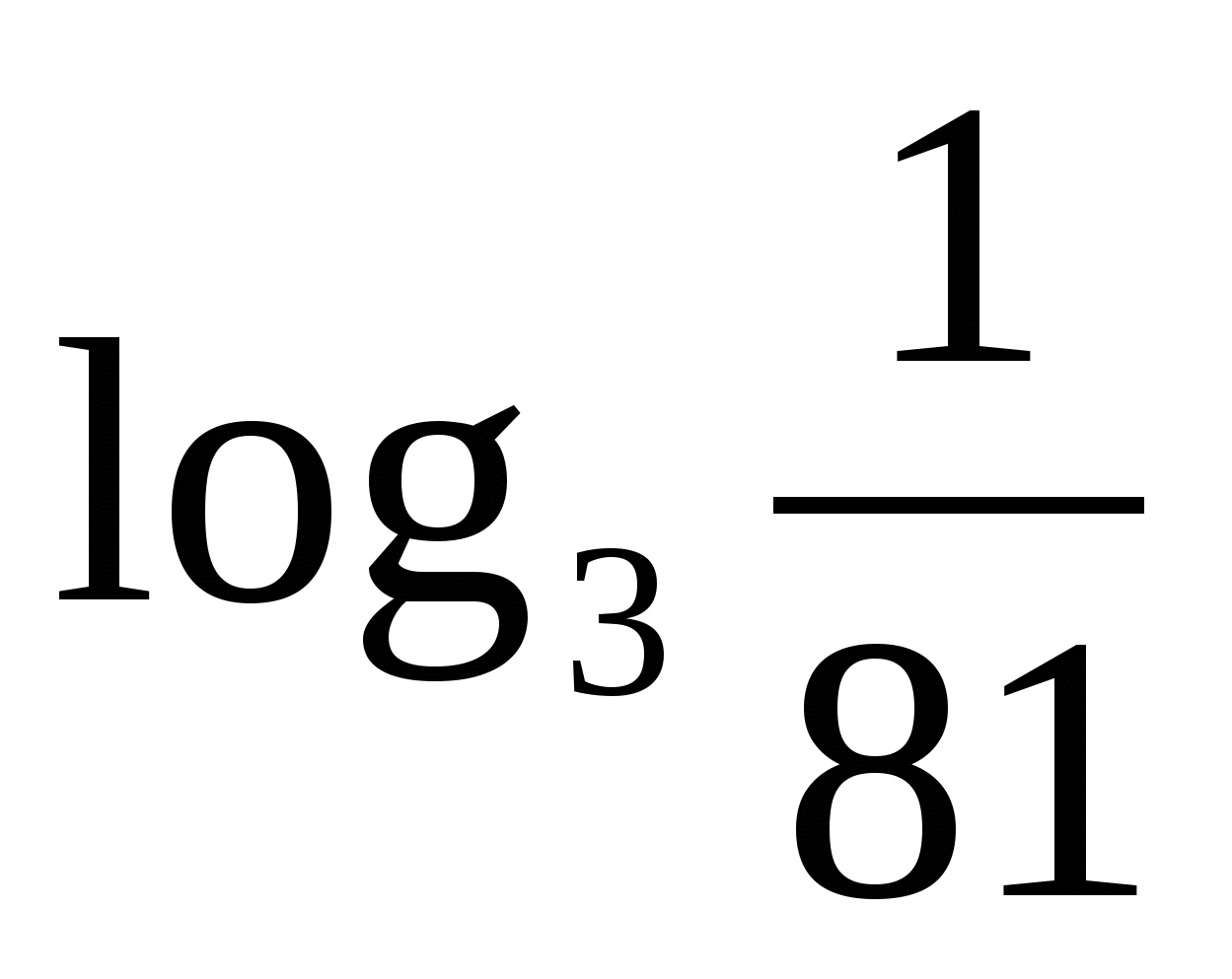
б)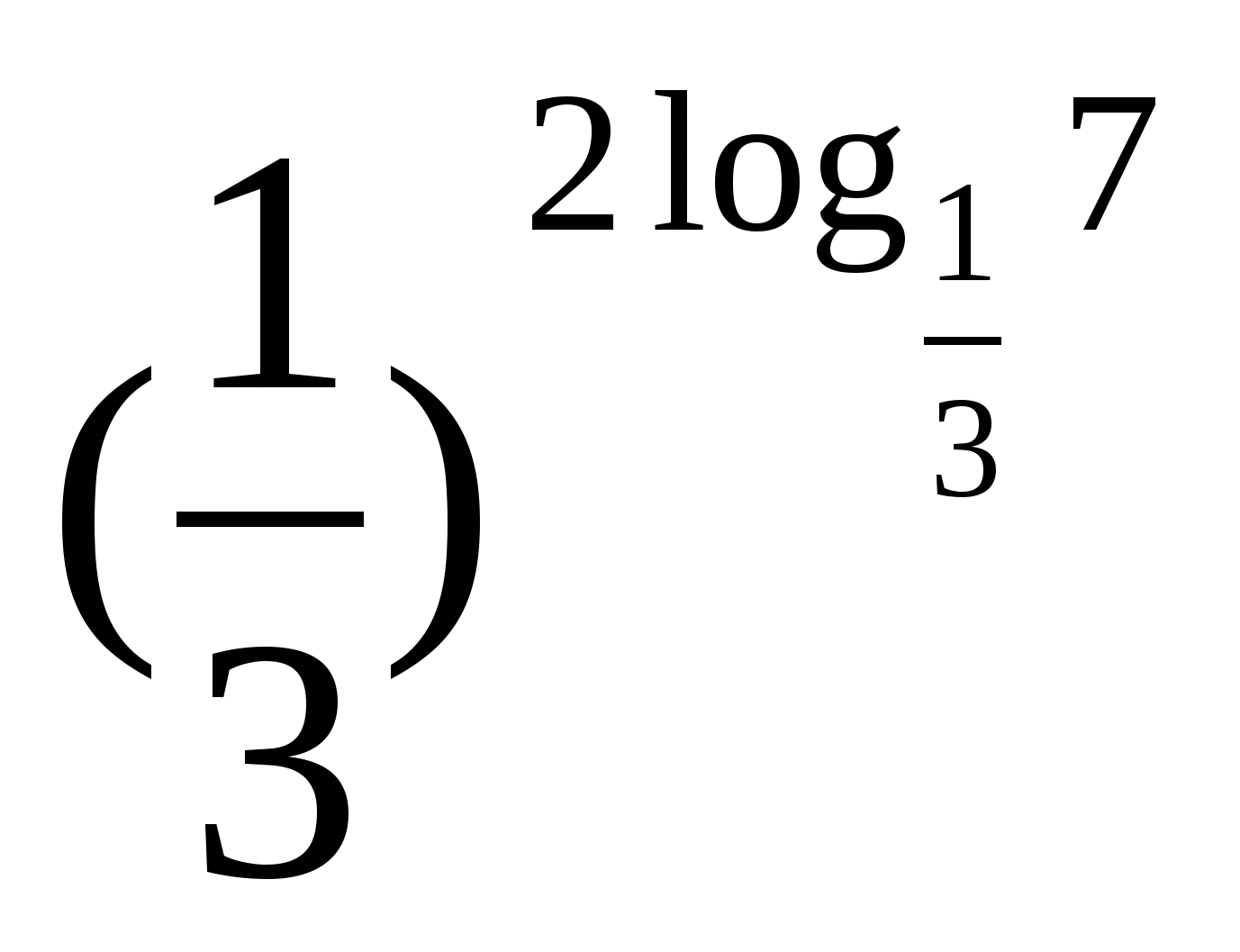
в)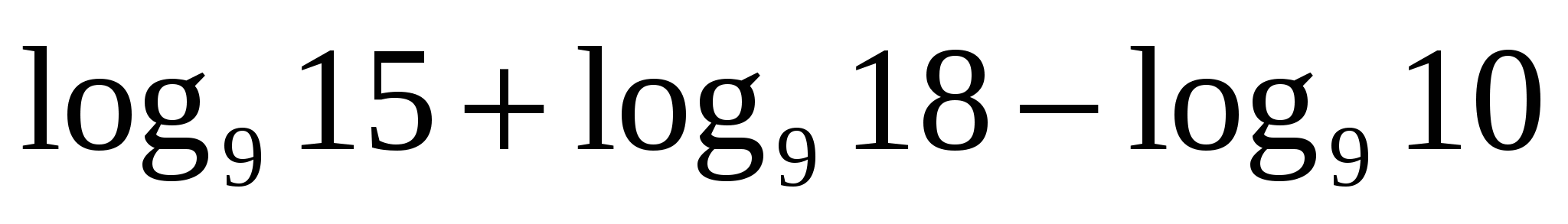
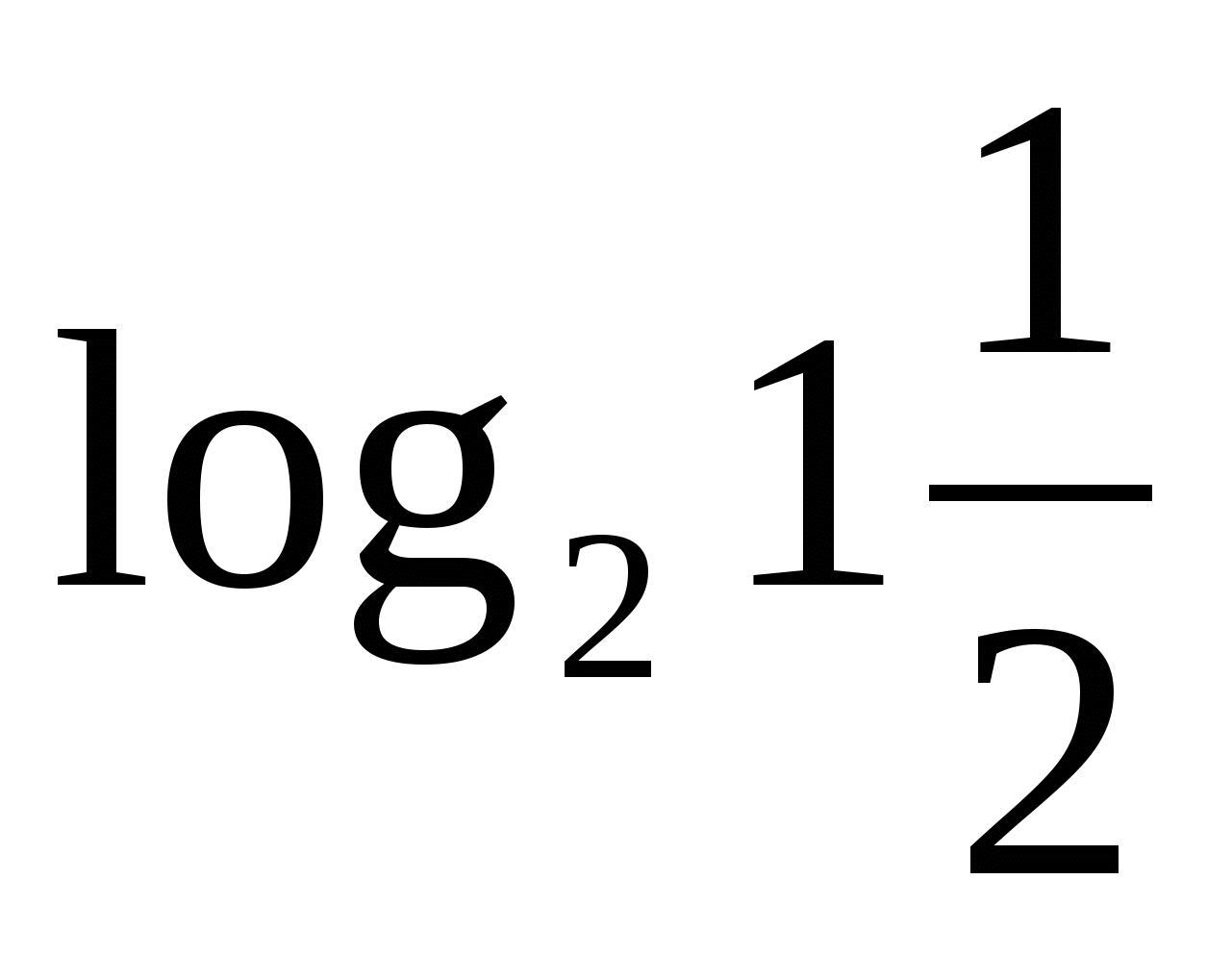
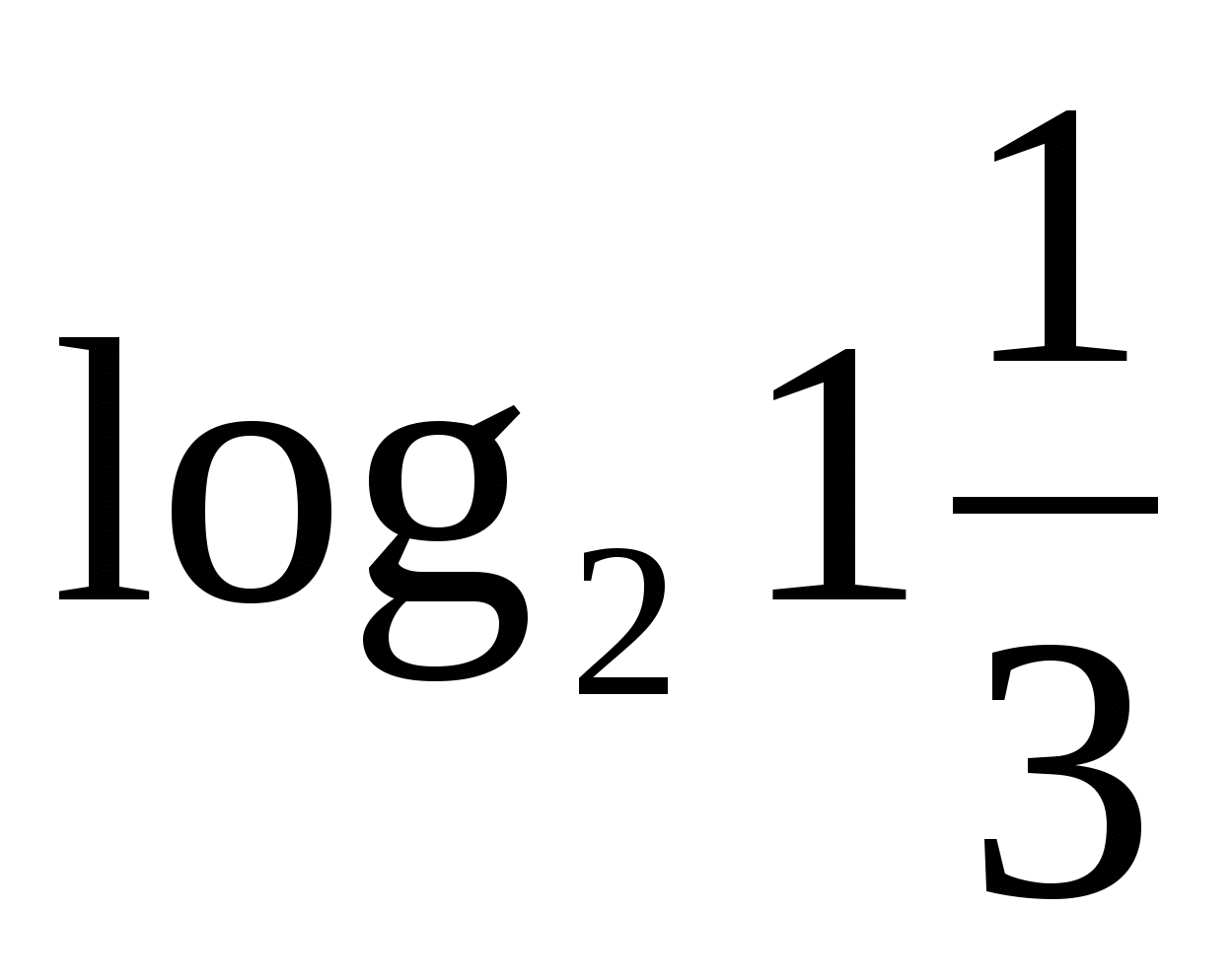
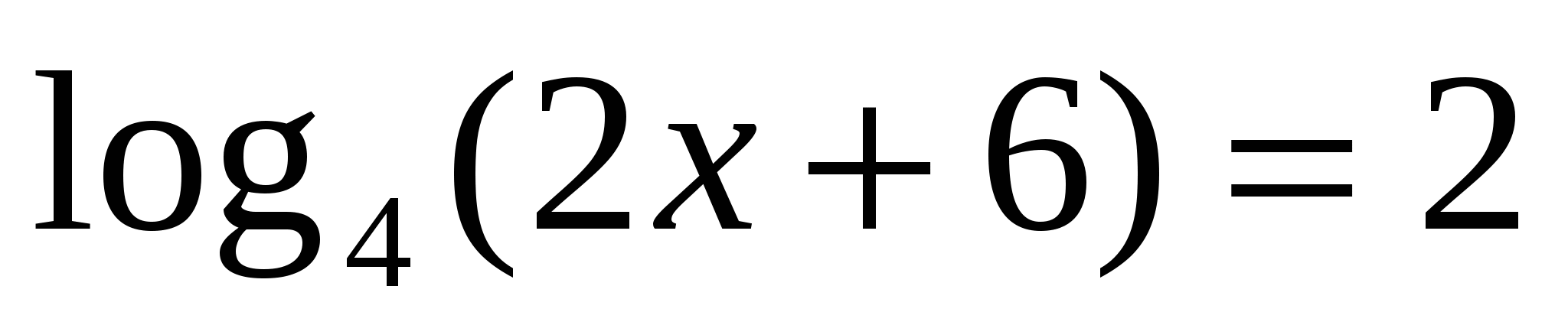
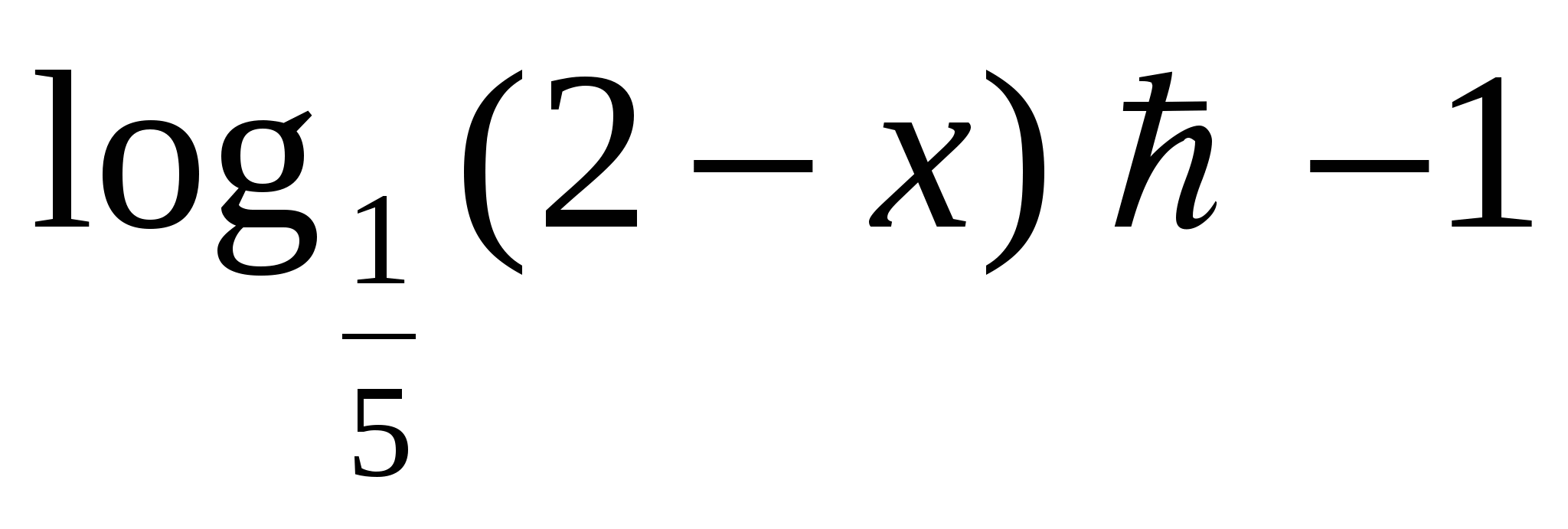
а)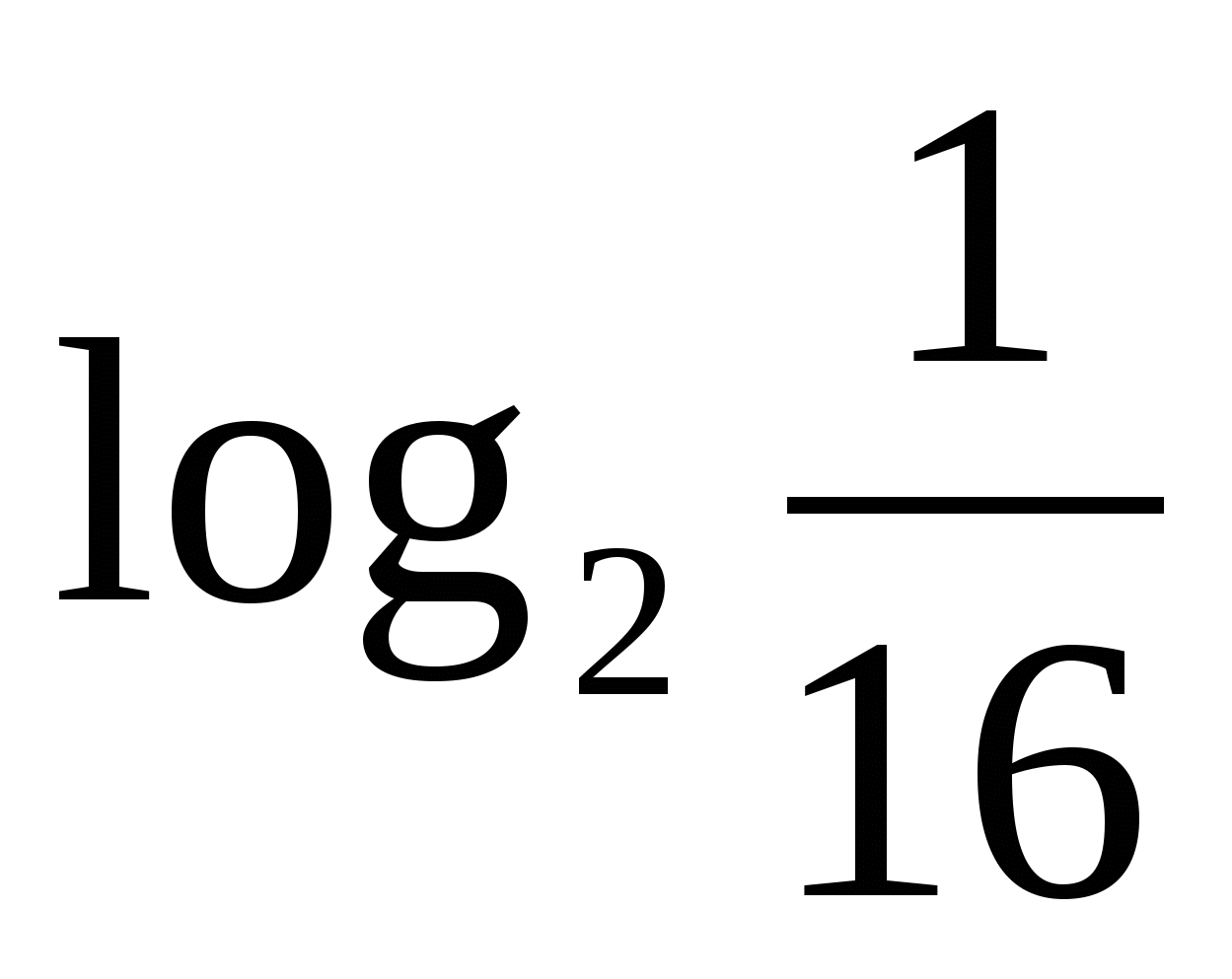
б)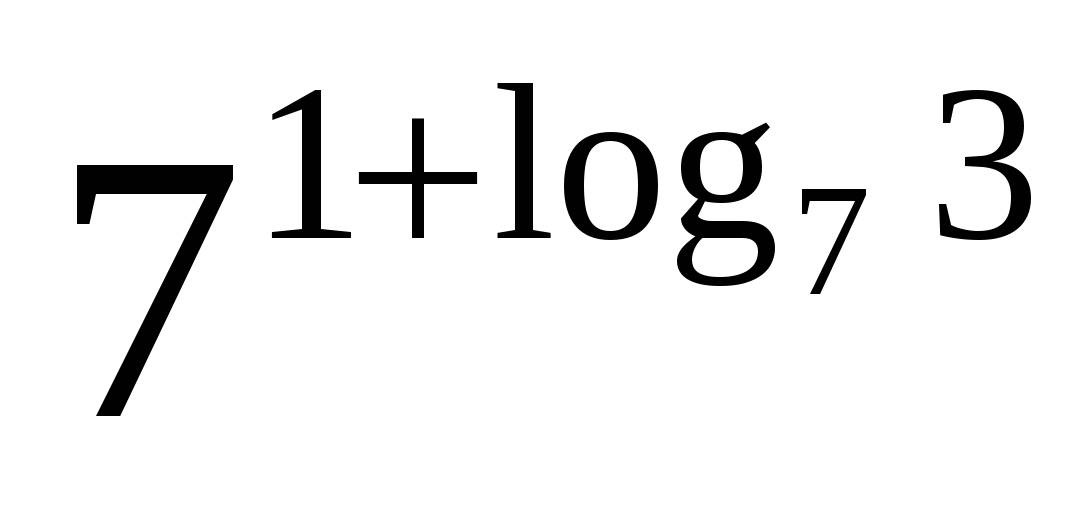
в)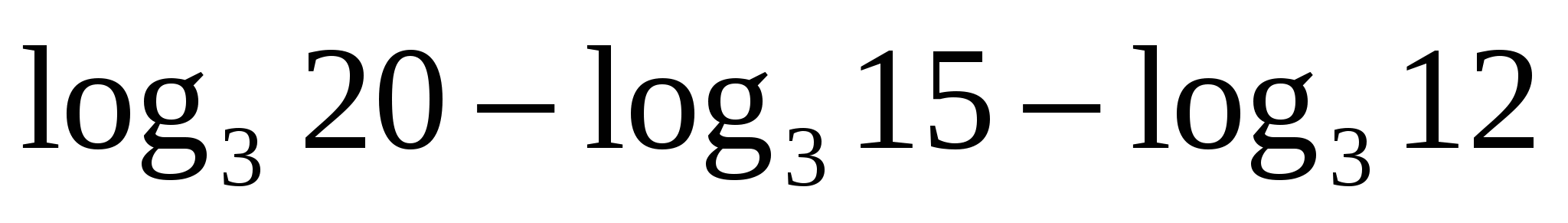
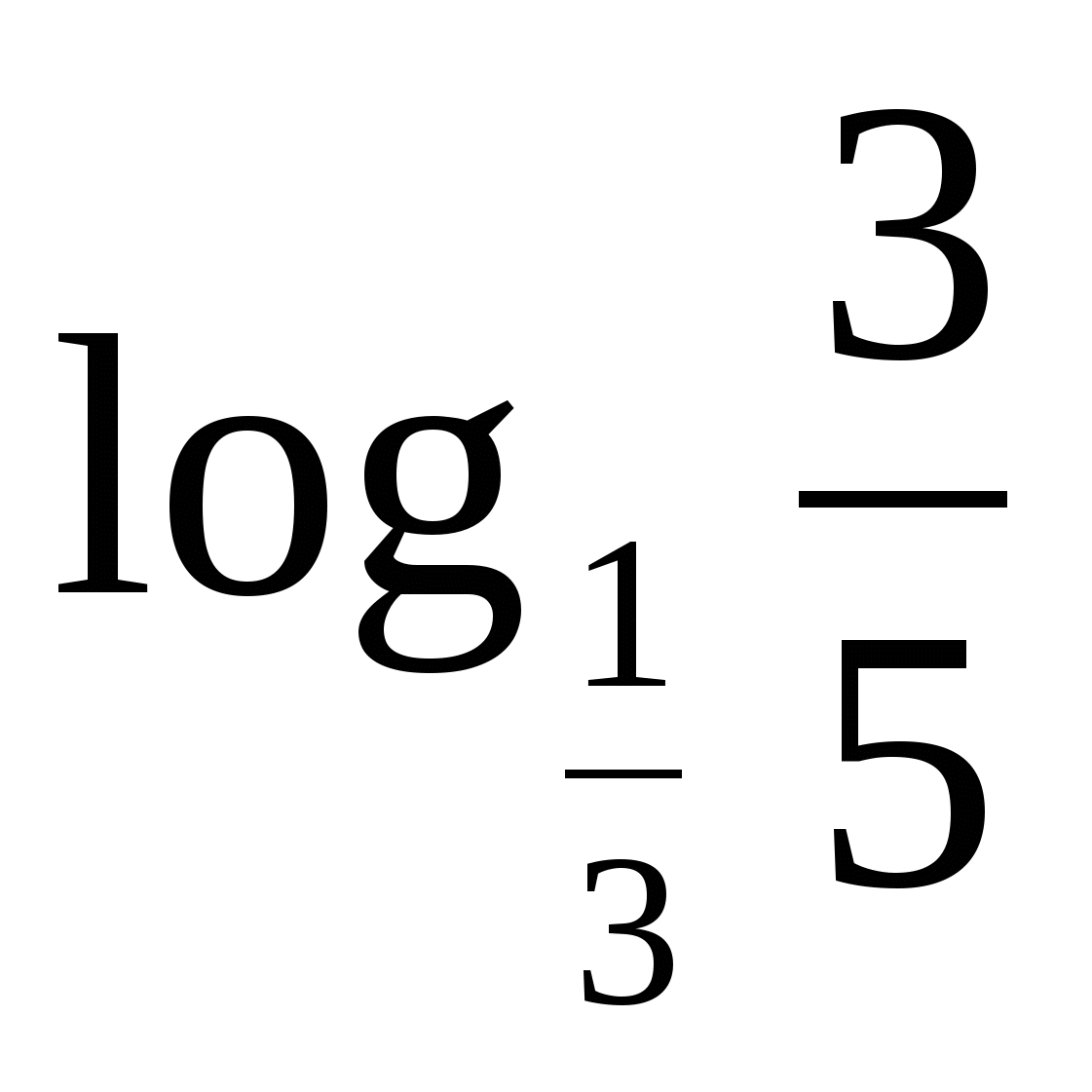
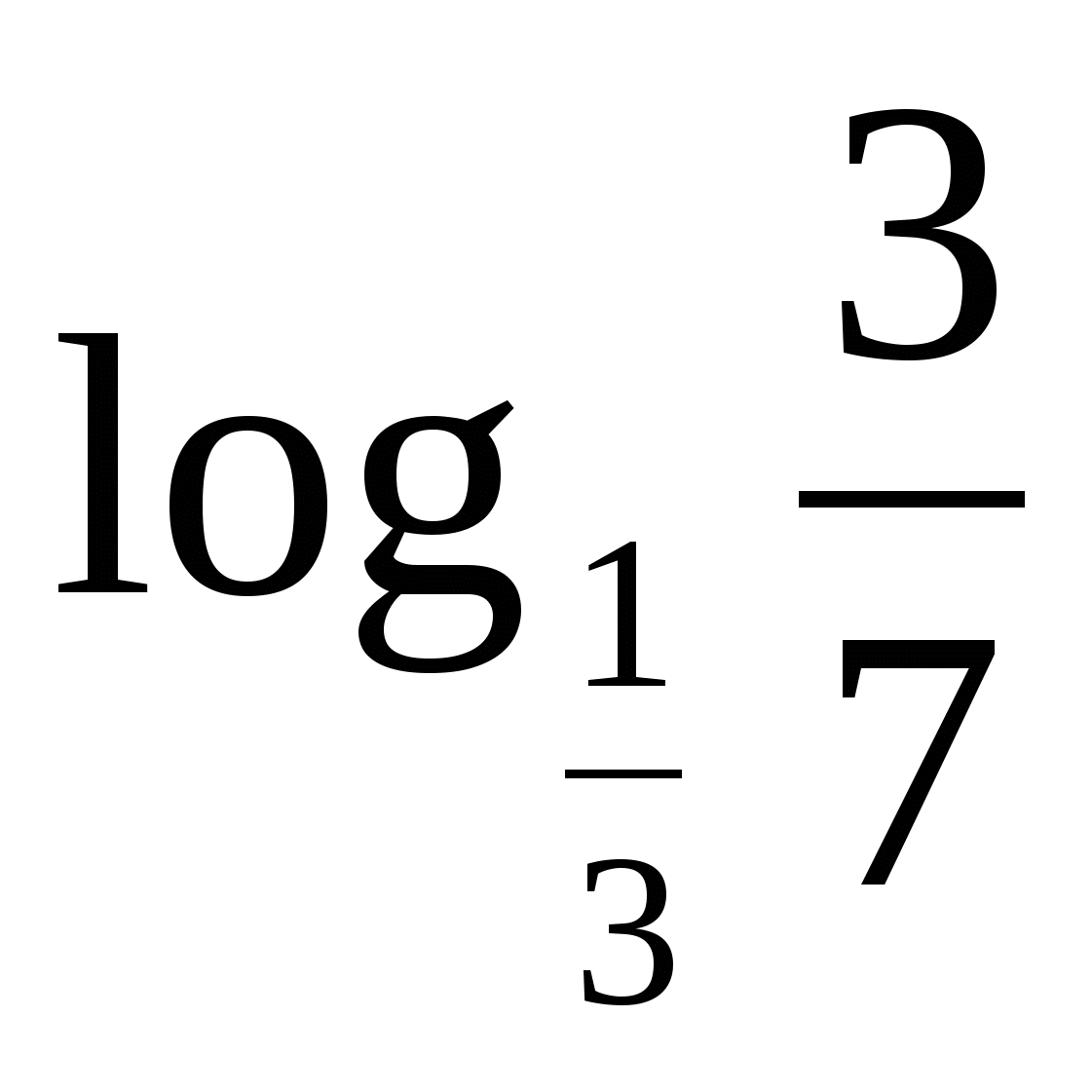
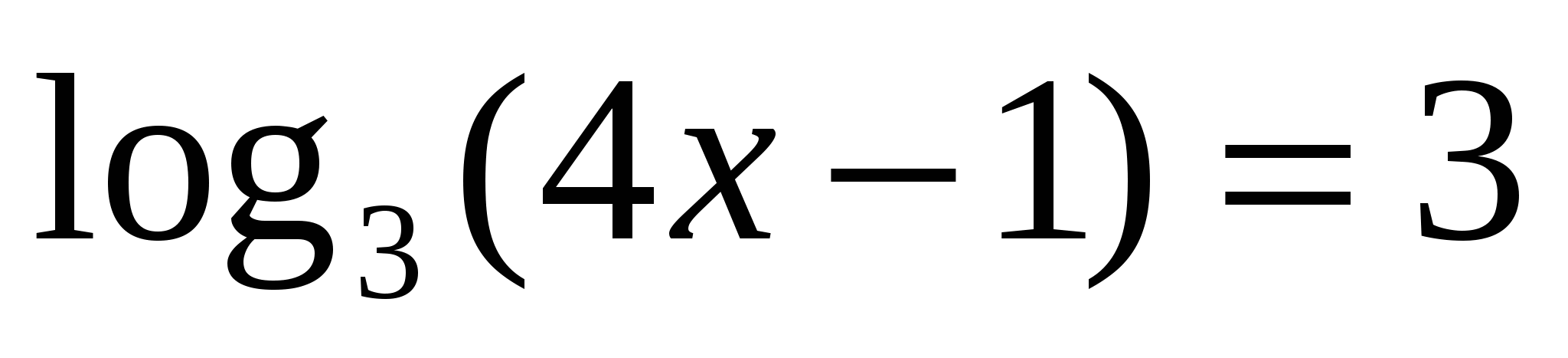
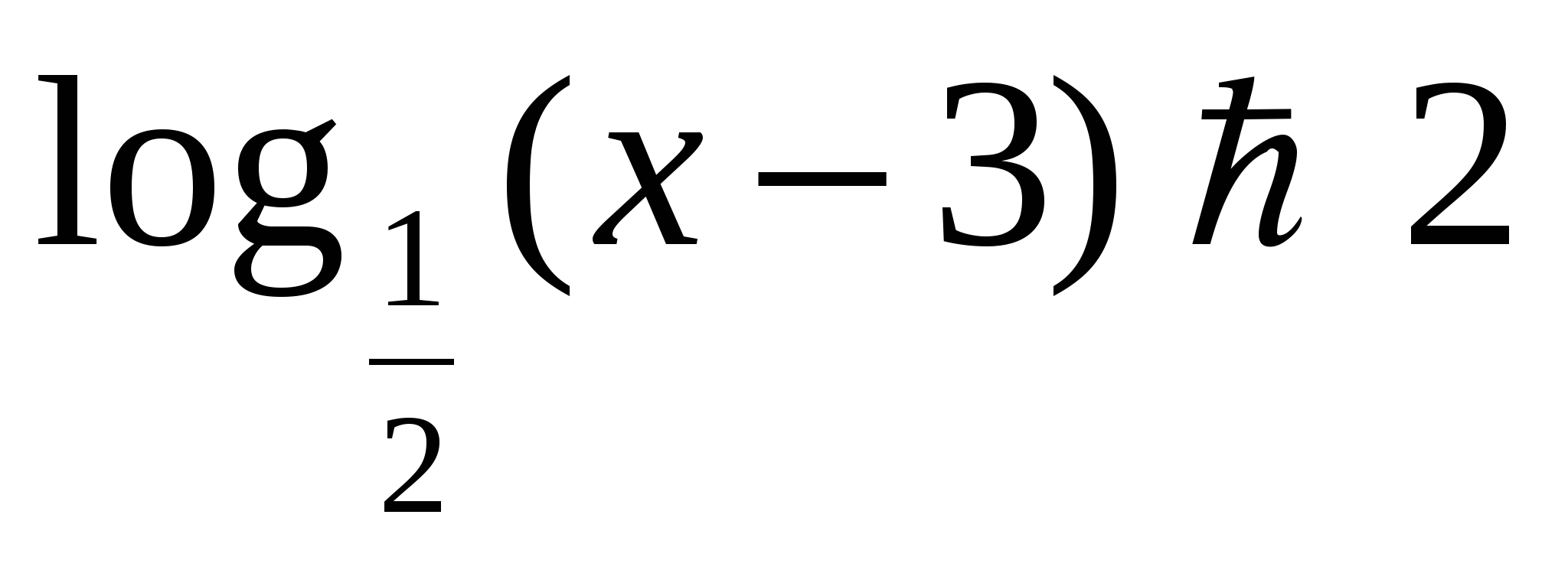
а)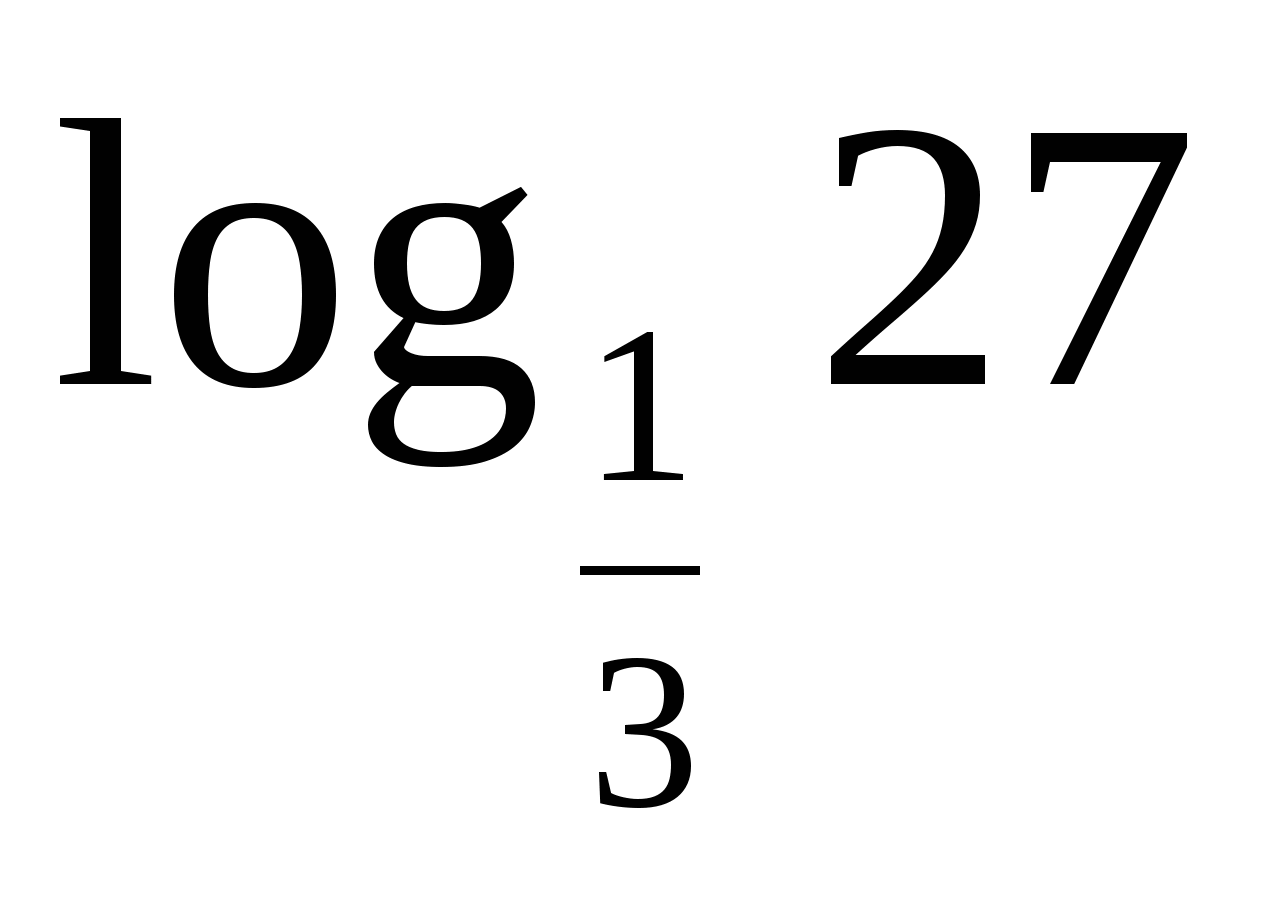
б)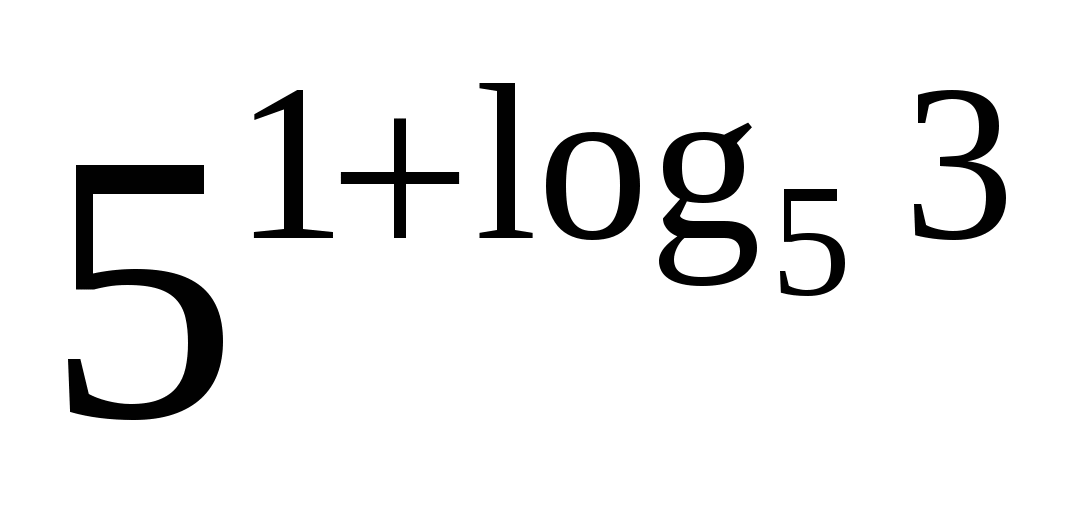
в)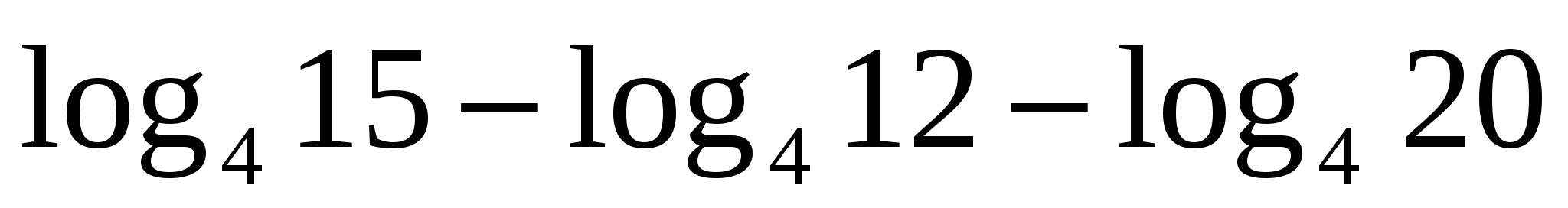
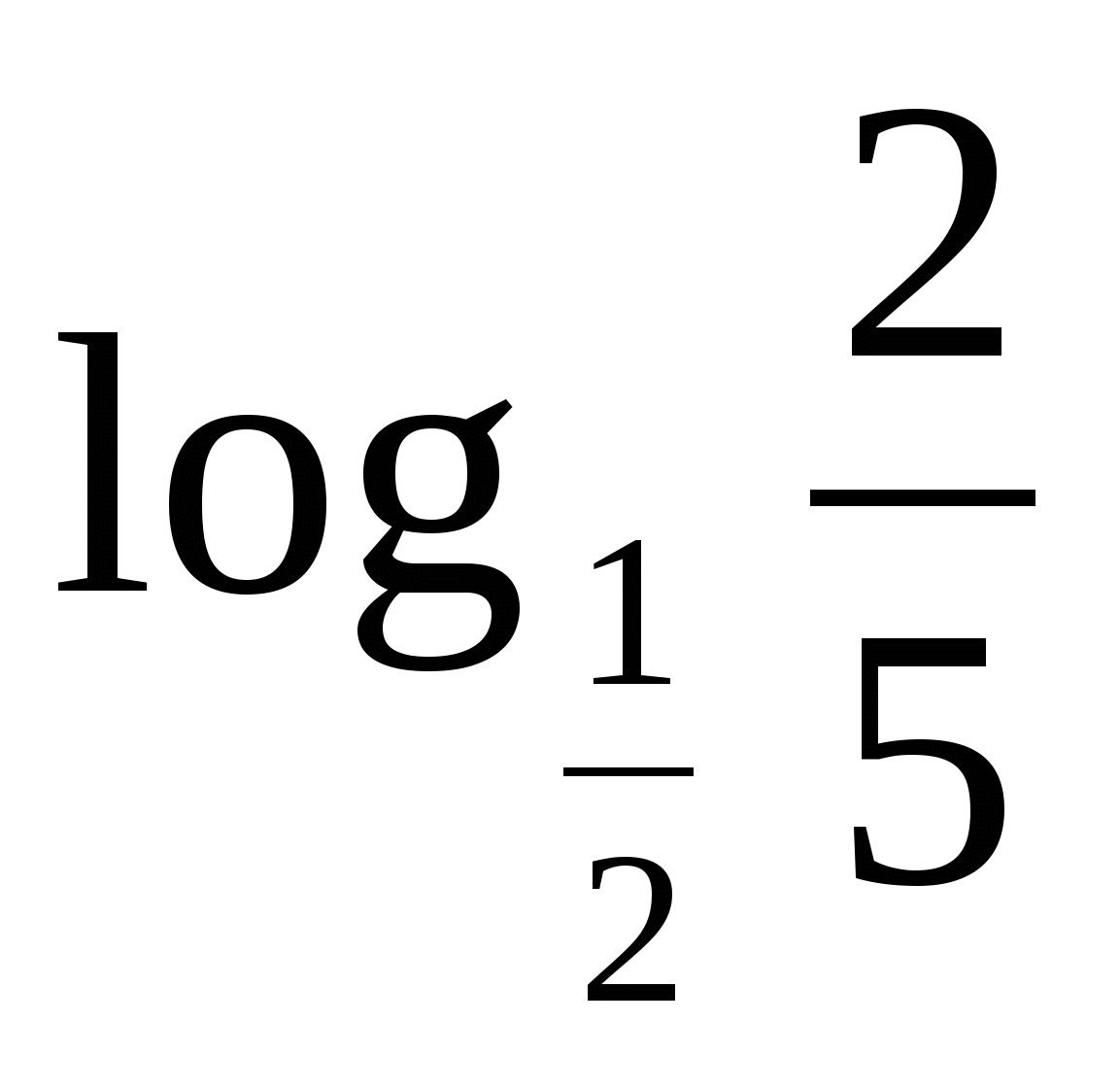
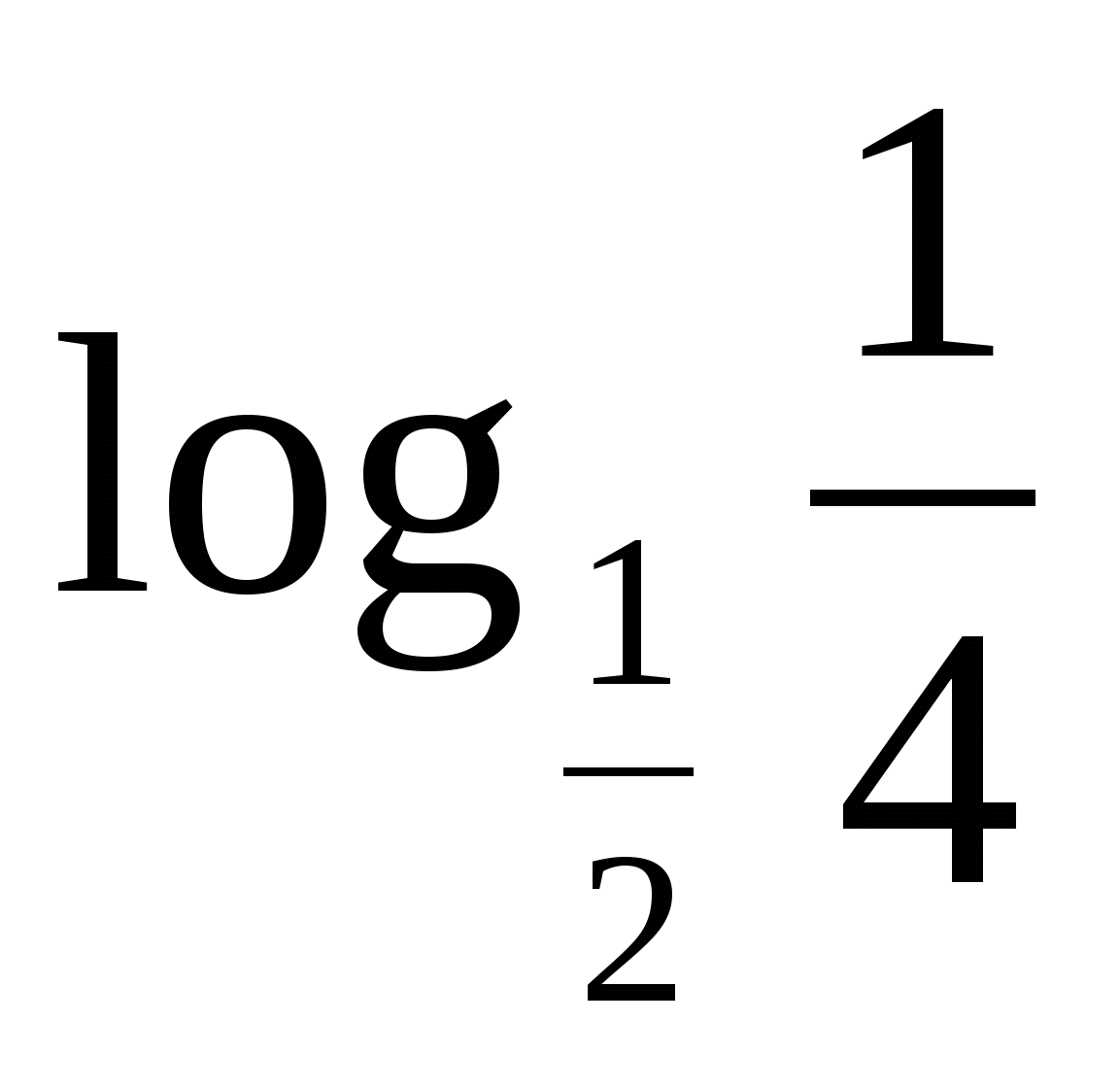
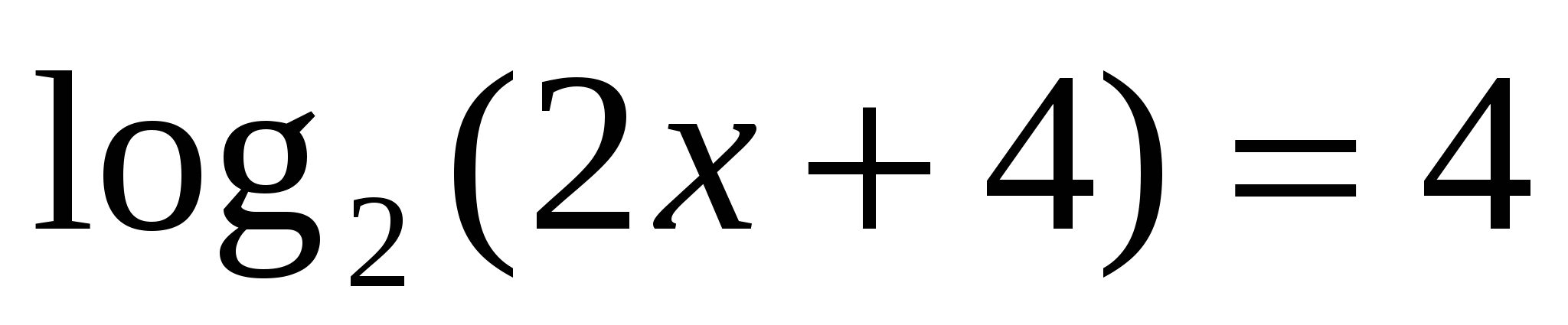
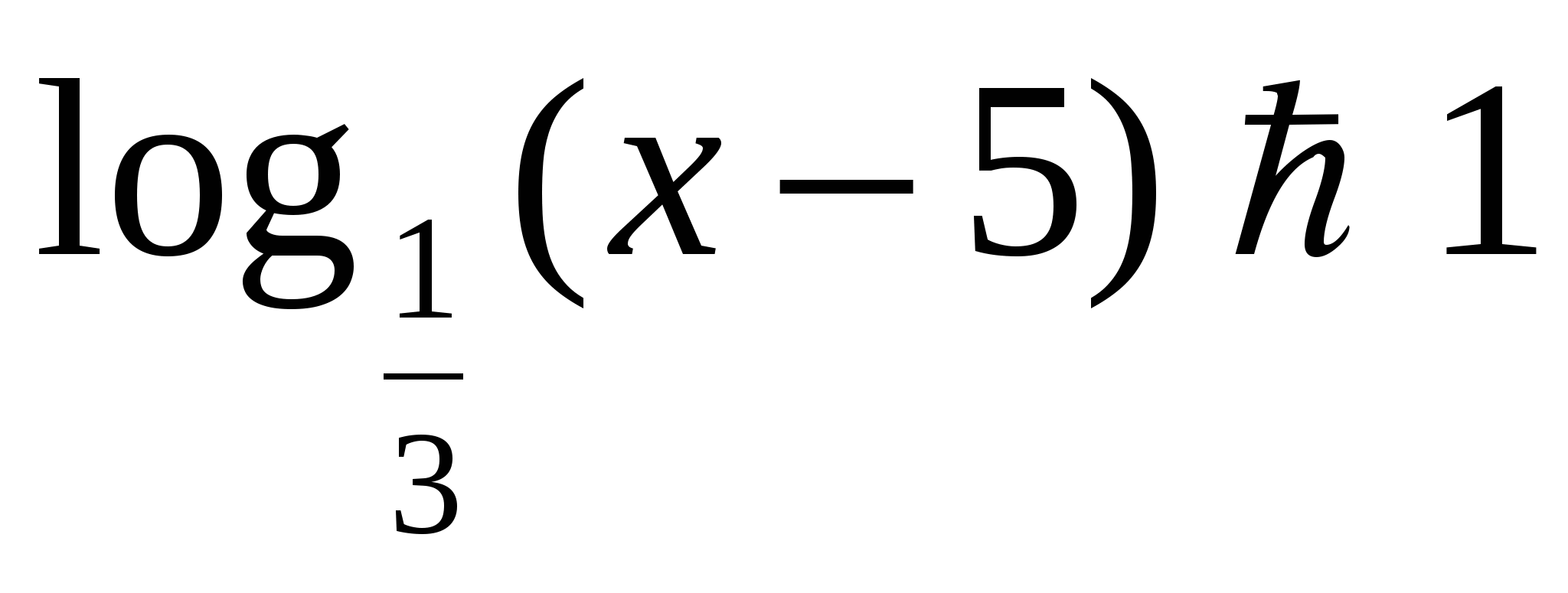
Вопросы теории. Примеры-алгоритмы.
№ п/п
Алгоритмы
1
Логарифмом числа 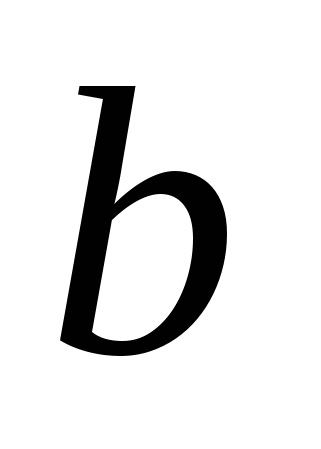 по основанию
по основанию  , где
, где 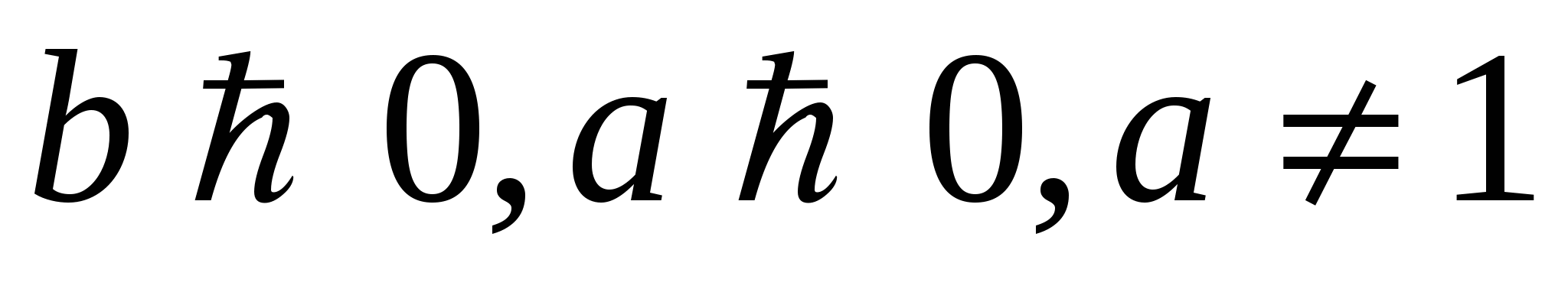 называется показатель степени, в которую нужно возвести число
называется показатель степени, в которую нужно возвести число  , чтобы получить число
, чтобы получить число 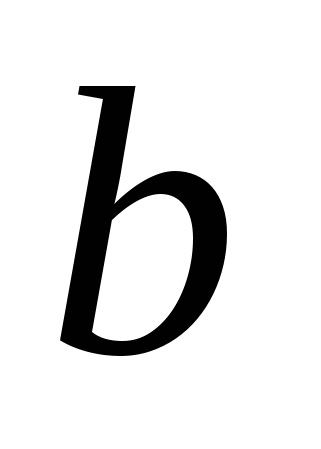 , то есть
, то есть 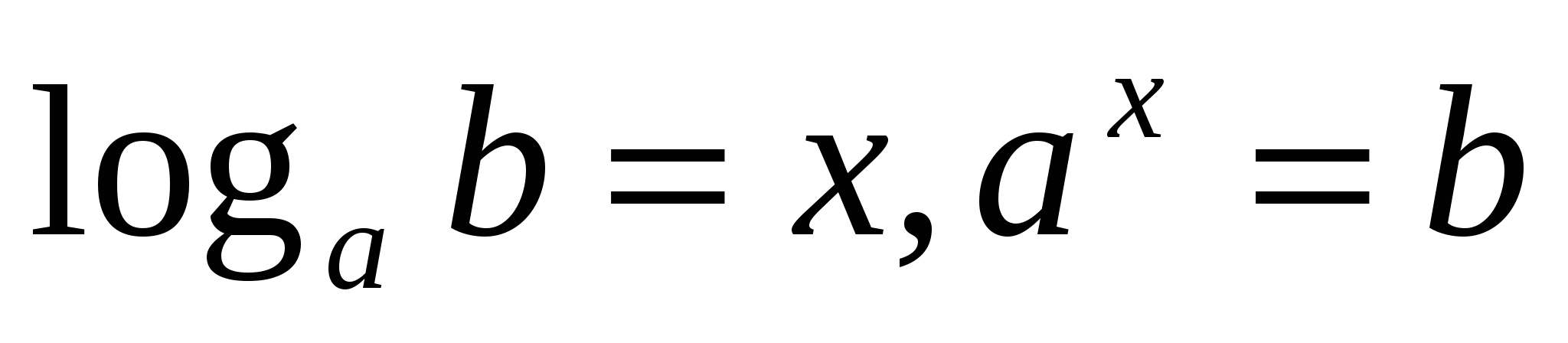
2
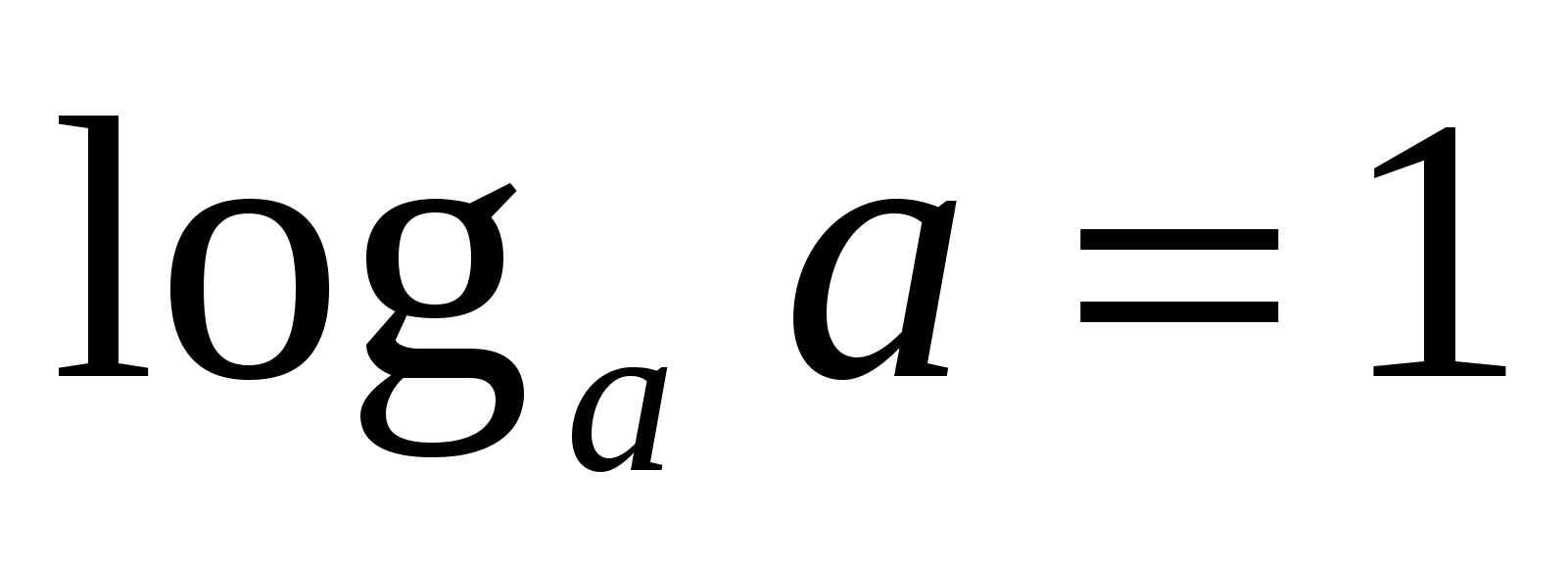 ;
; 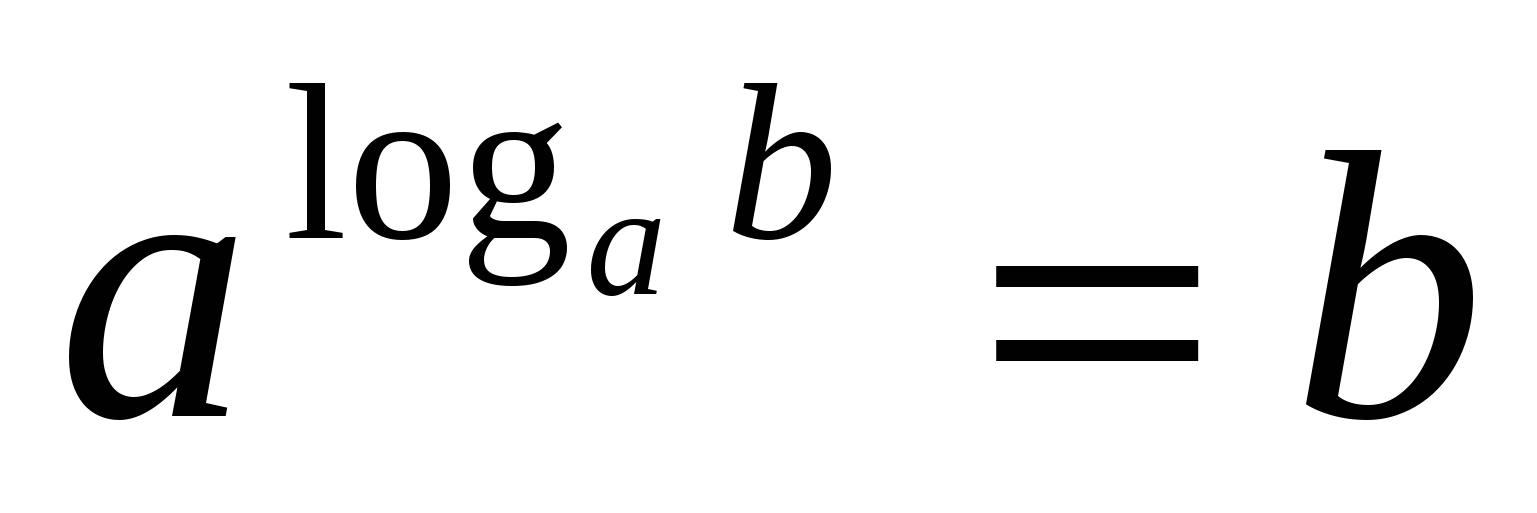 ;
; 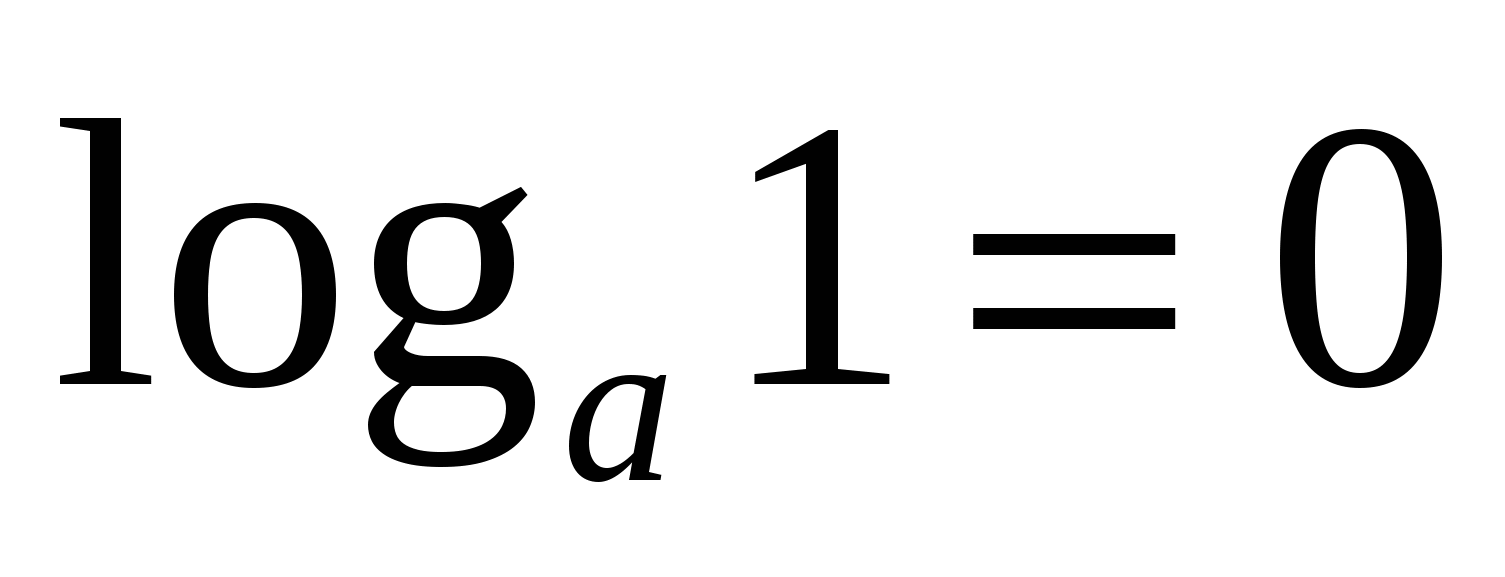
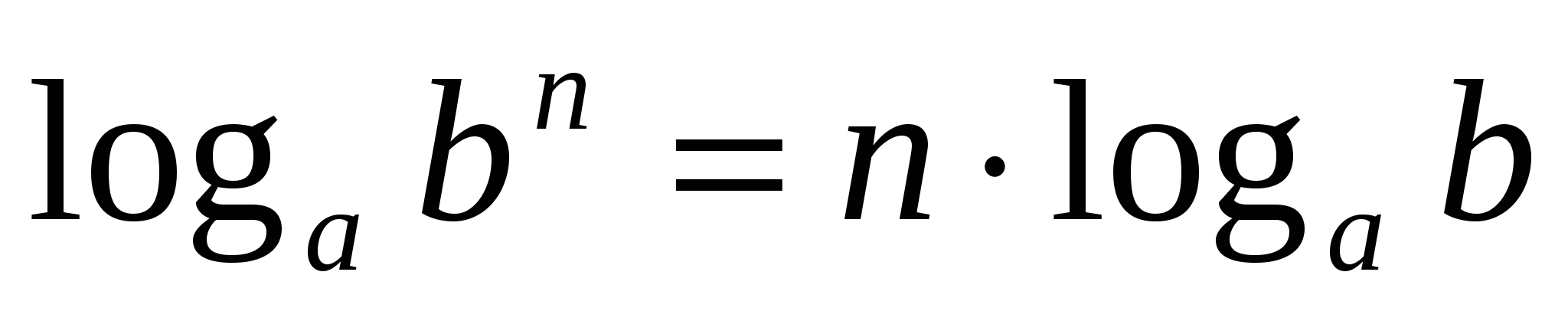 ;
; 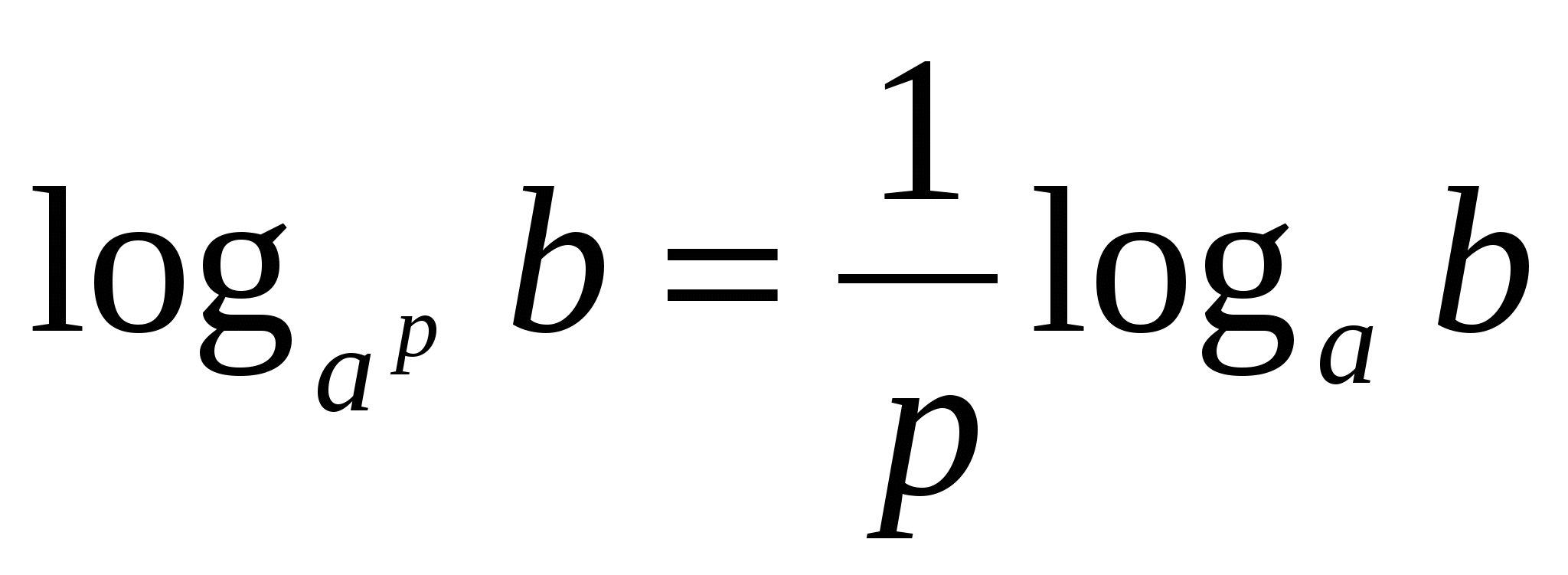
3
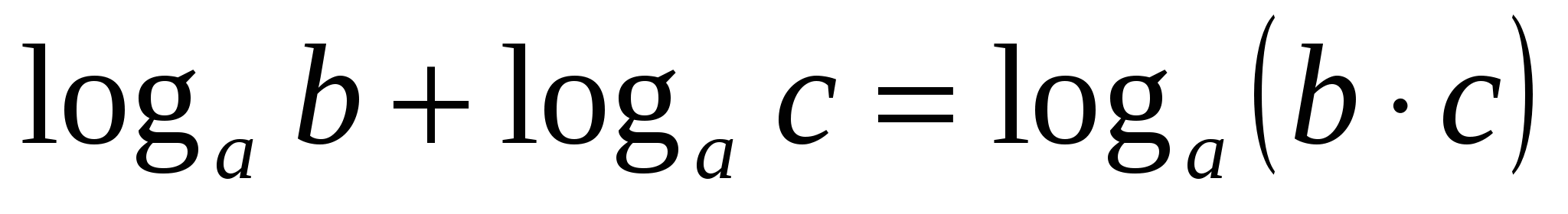
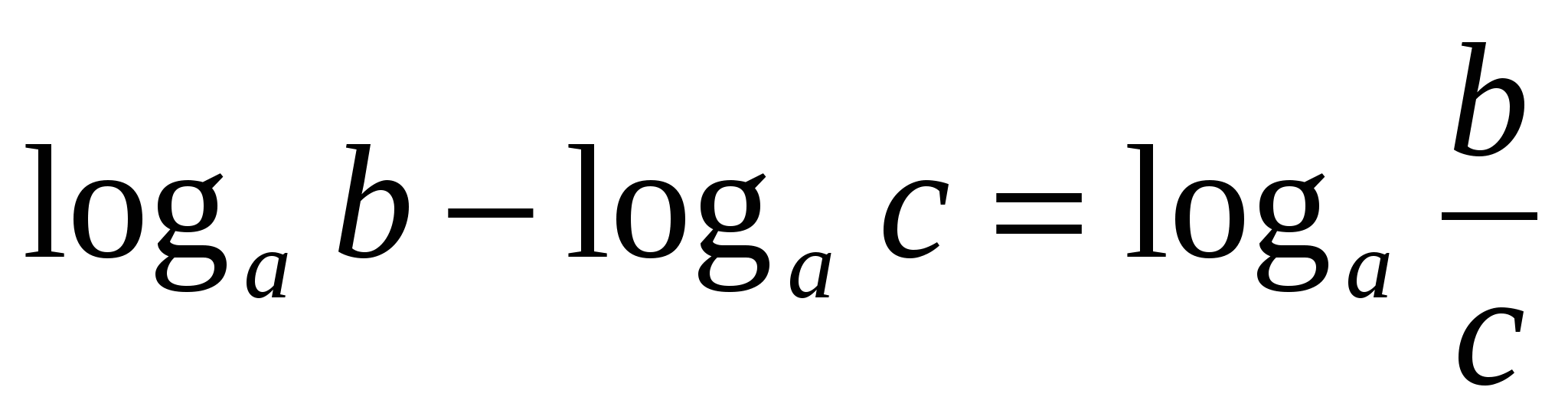
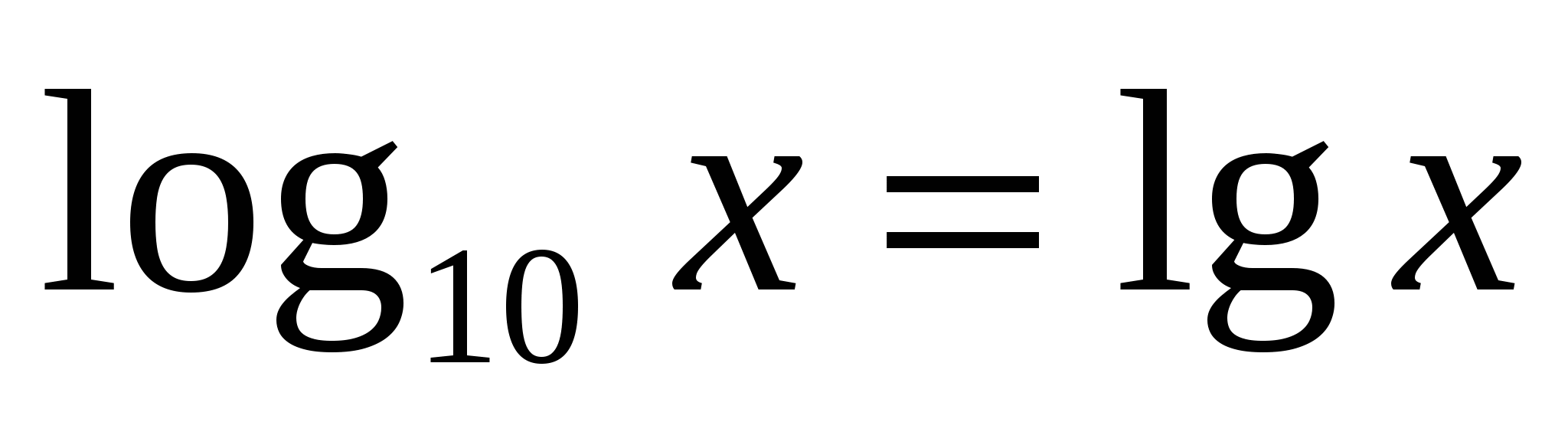 ;
; 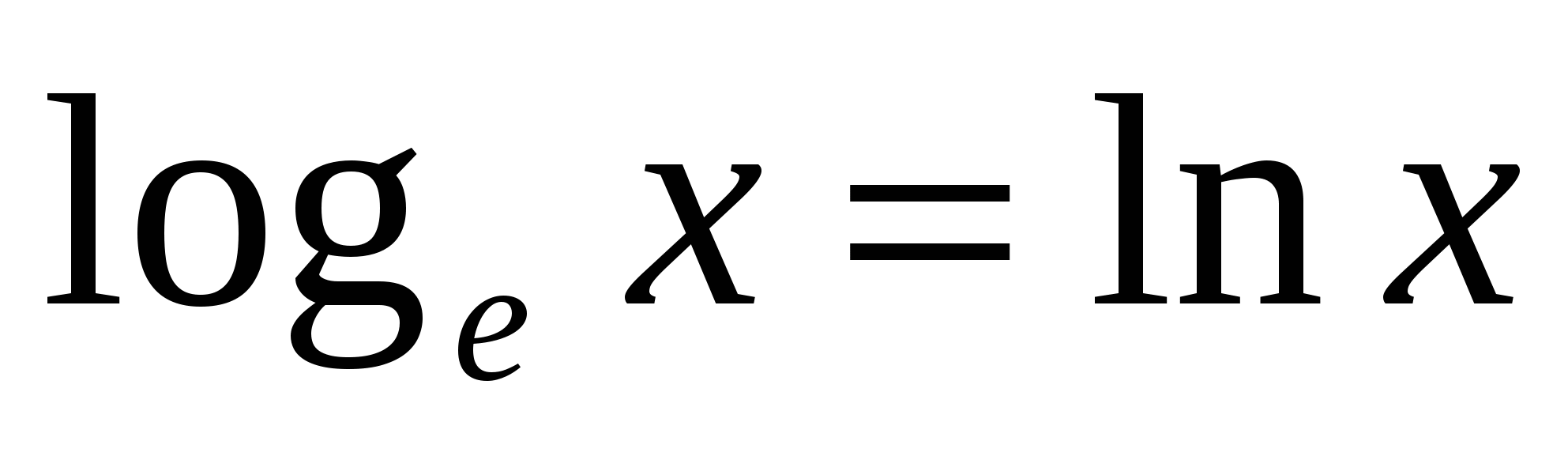
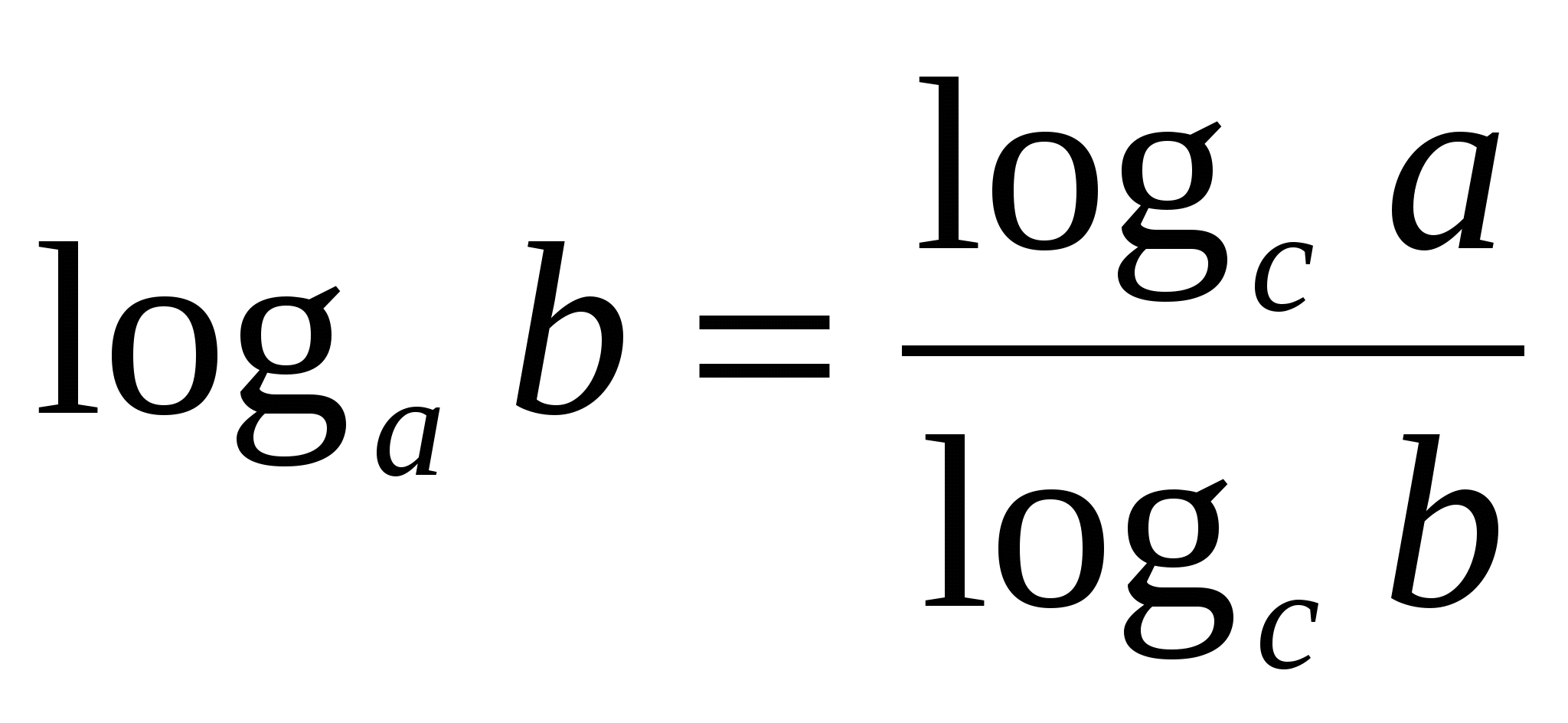 ;
; 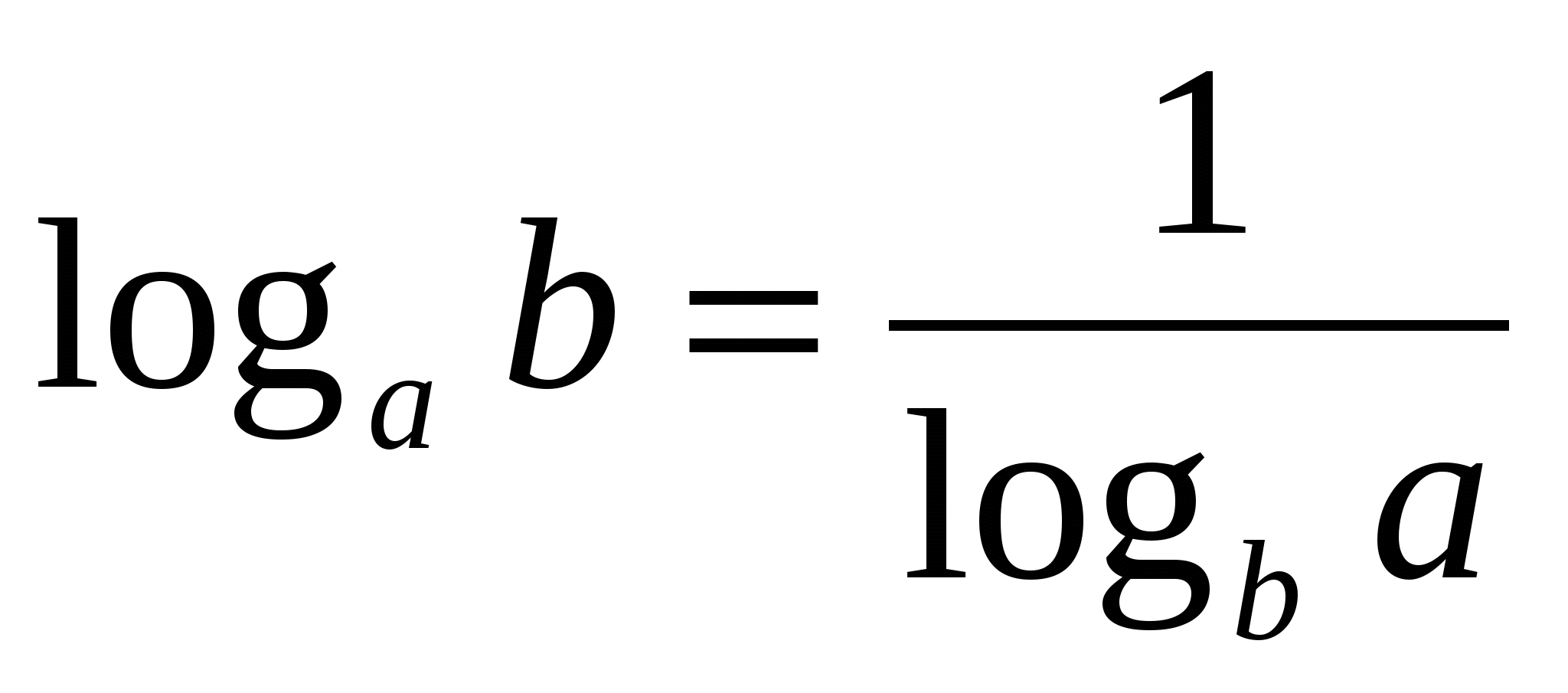
4
5
6
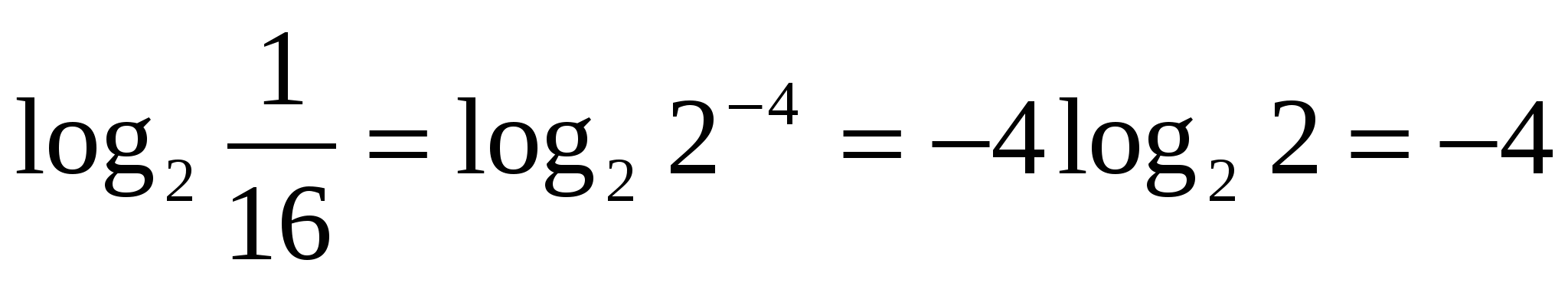
7
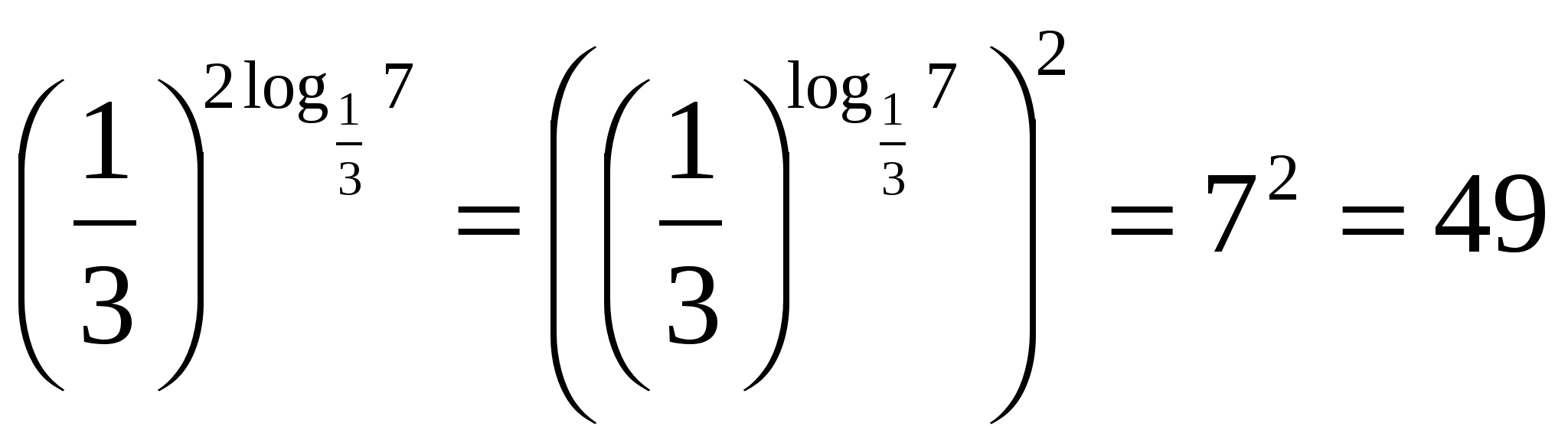
8,9
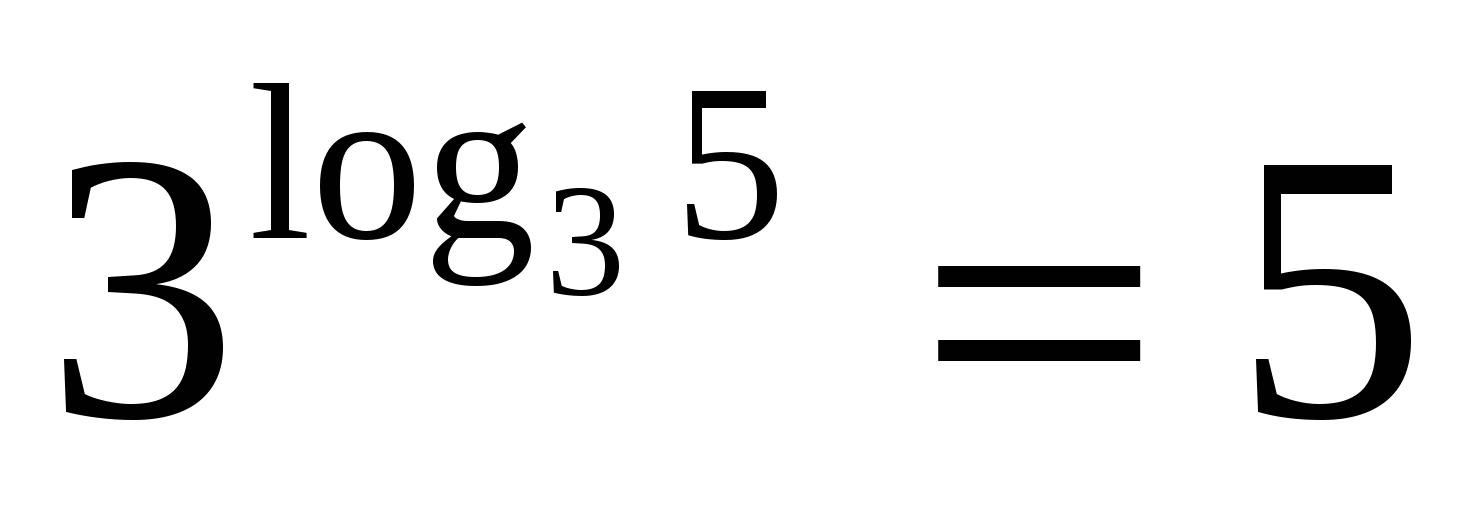 ;
; 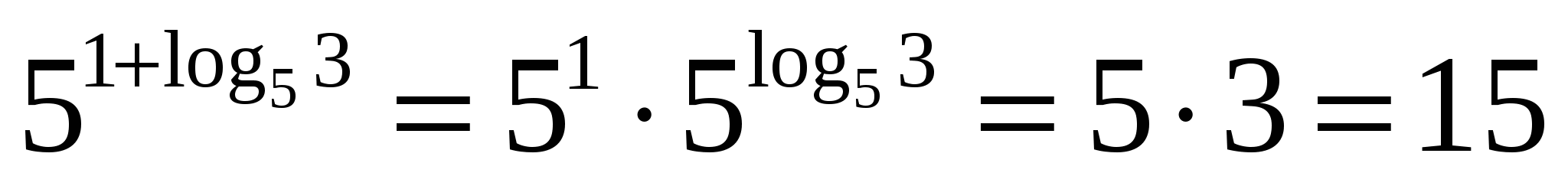
10
11
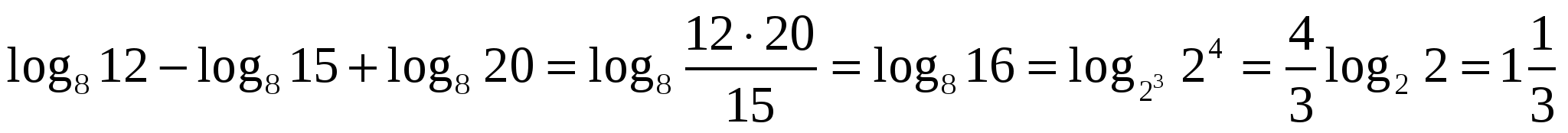
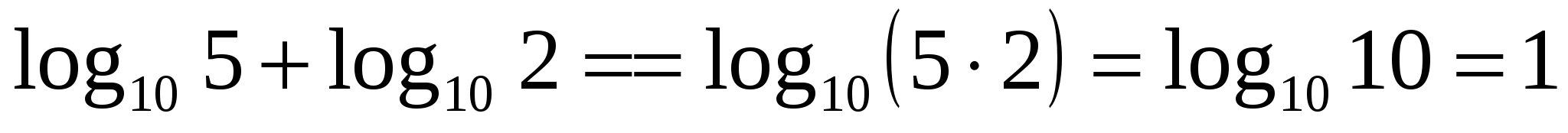
Контрольная работа по теме: « Логарифмы».
Вариант 3
Вариант 4
Вычислить:1)
 ;2)
;2) ;3)
;3)
Сравнить числа:
 и
и  . .
. .Решить уравнение:
 .
.Решите неравенство:
 .
.Решить уравнение:
 .
.Решить неравенство:
 .
.(Дополнительно) Решить неравенство:
 .
.
Вычислить:1)
 ;2)
;2) ;3)
;3)  .
.Сравнить числа:
 и
и  .
.Решить уравнение:
 .
.Решите неравенство:
 .
.Решить уравнение:
 .
.Решить неравенство:
 .
.(Дополнительно) Решить неравенство:
 .
.
Самостоятельная работа 10 класс по теме «Логарифмы»
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 1
1. Вычислите логарифм:
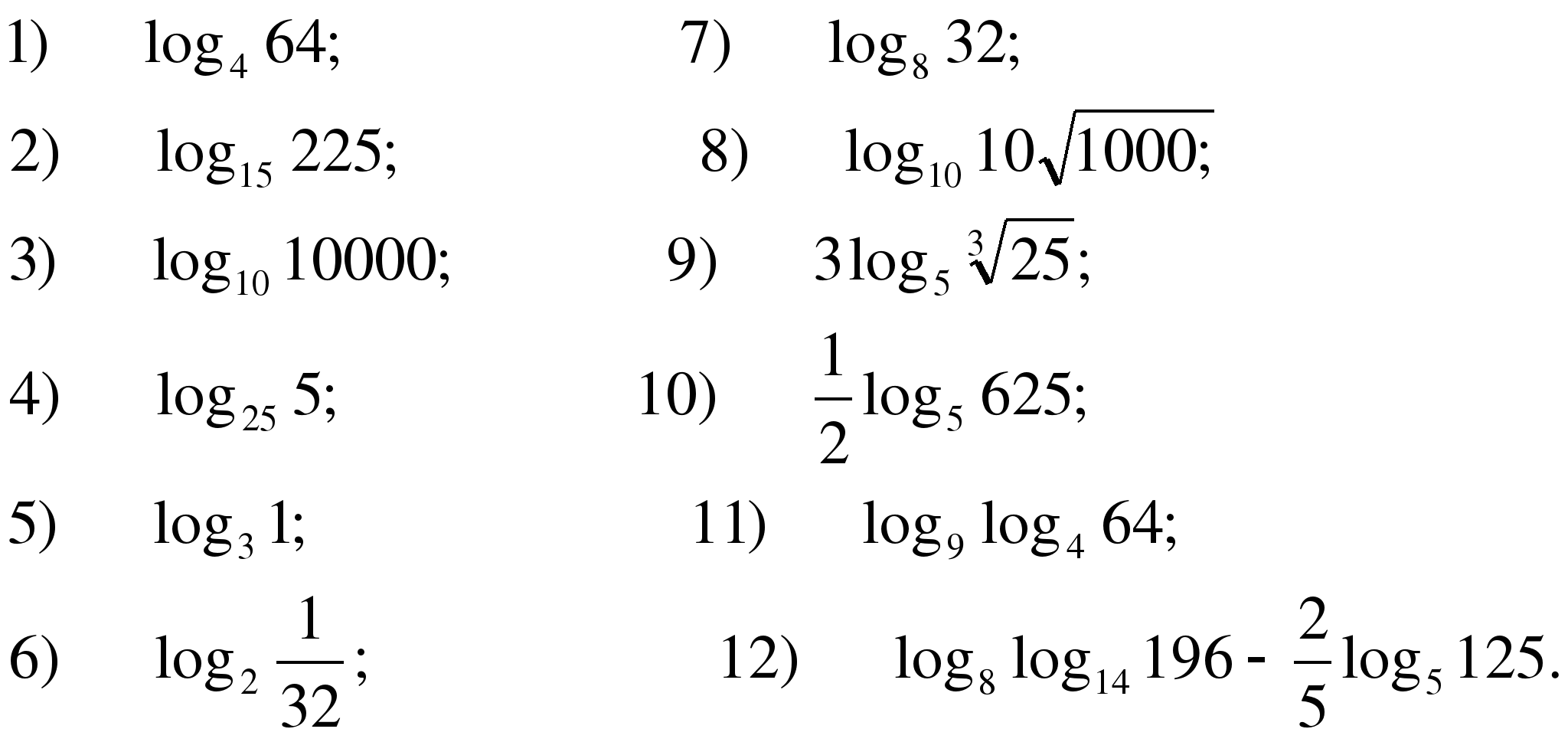
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 2
1. Вычислите логарифм:
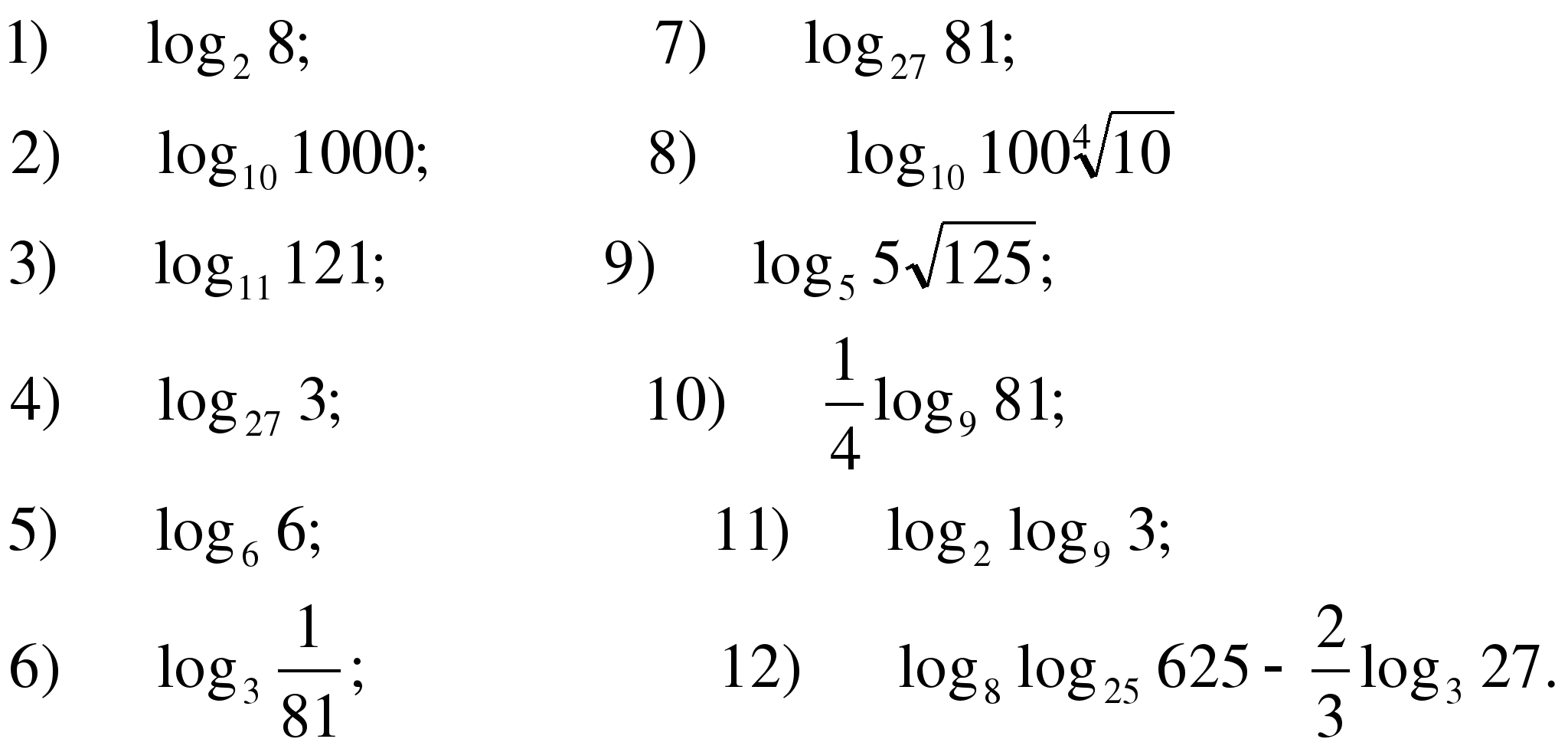
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 3
1. Вычислите логарифм:
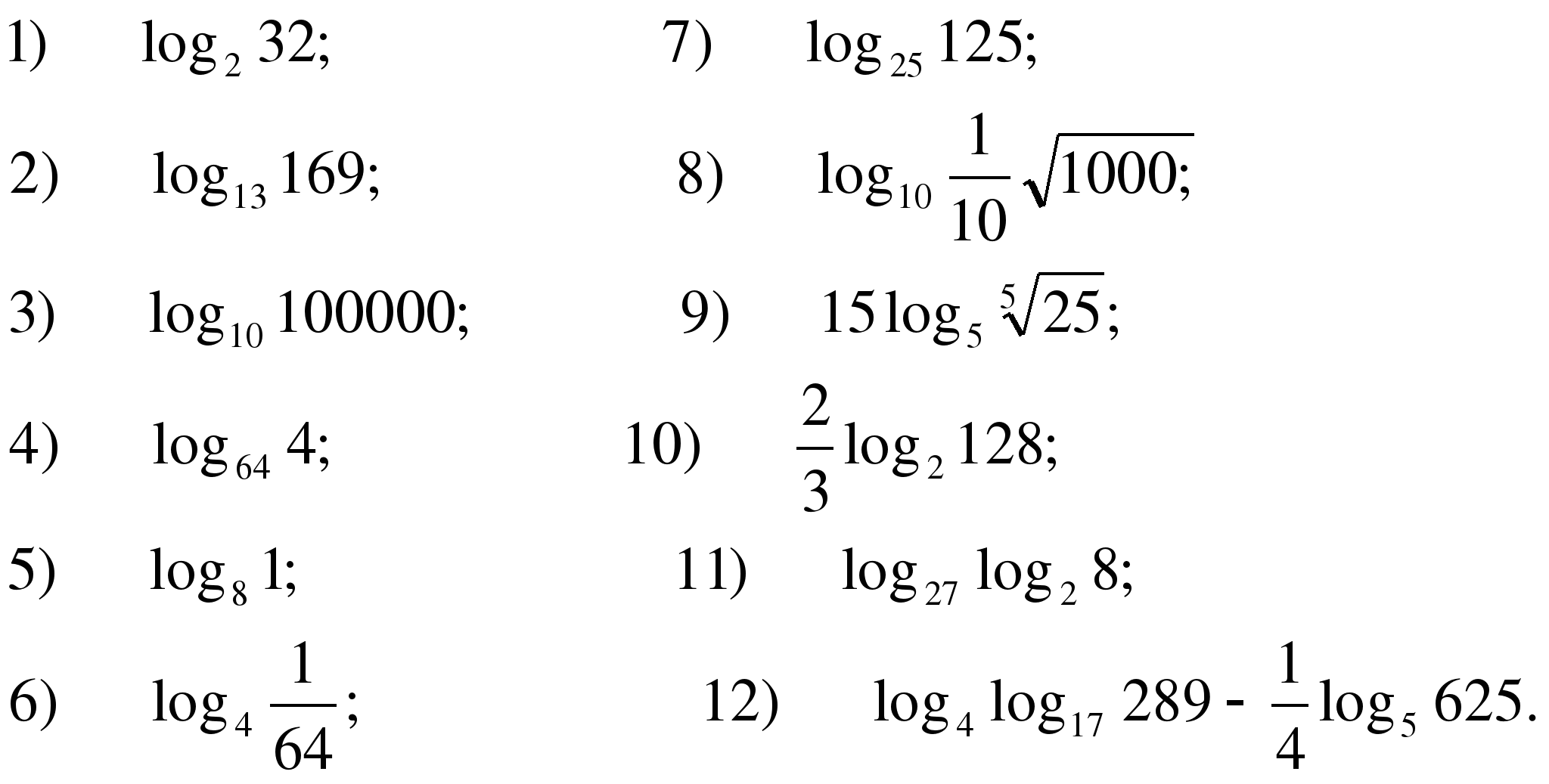
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 4
1. Вычислите логарифм:
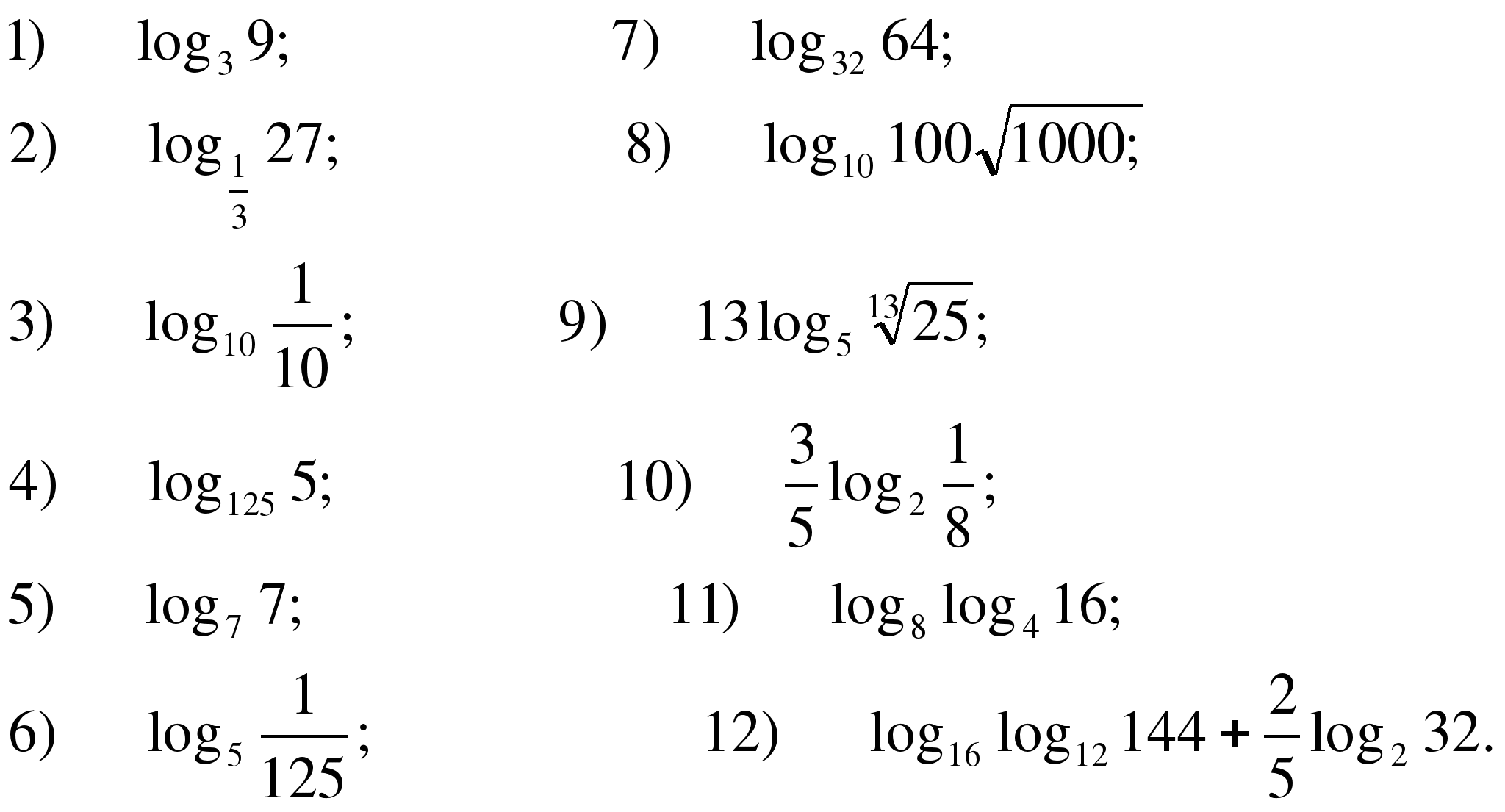
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 5
1. Вычислите логарифм:
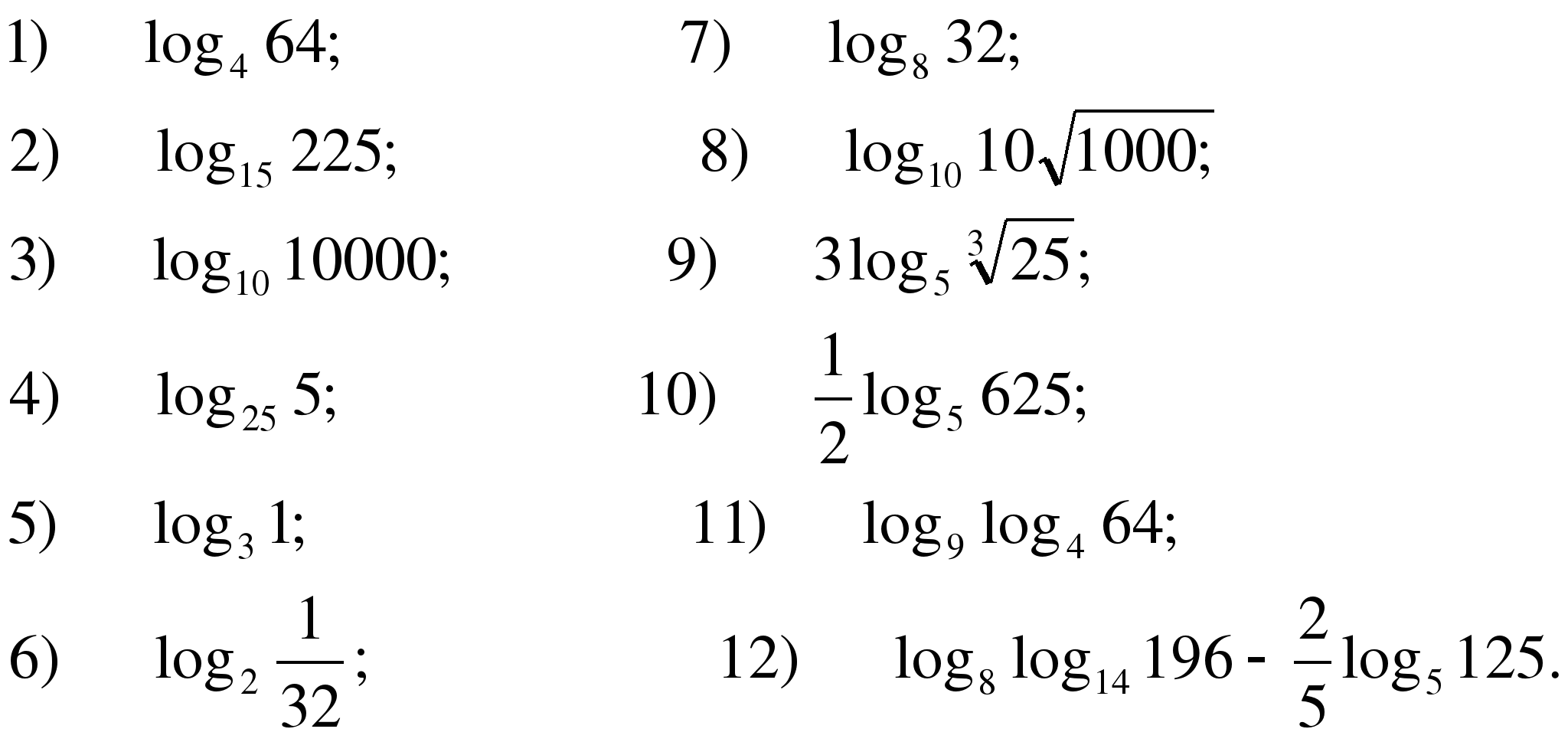
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 6
1. Вычислите логарифм:
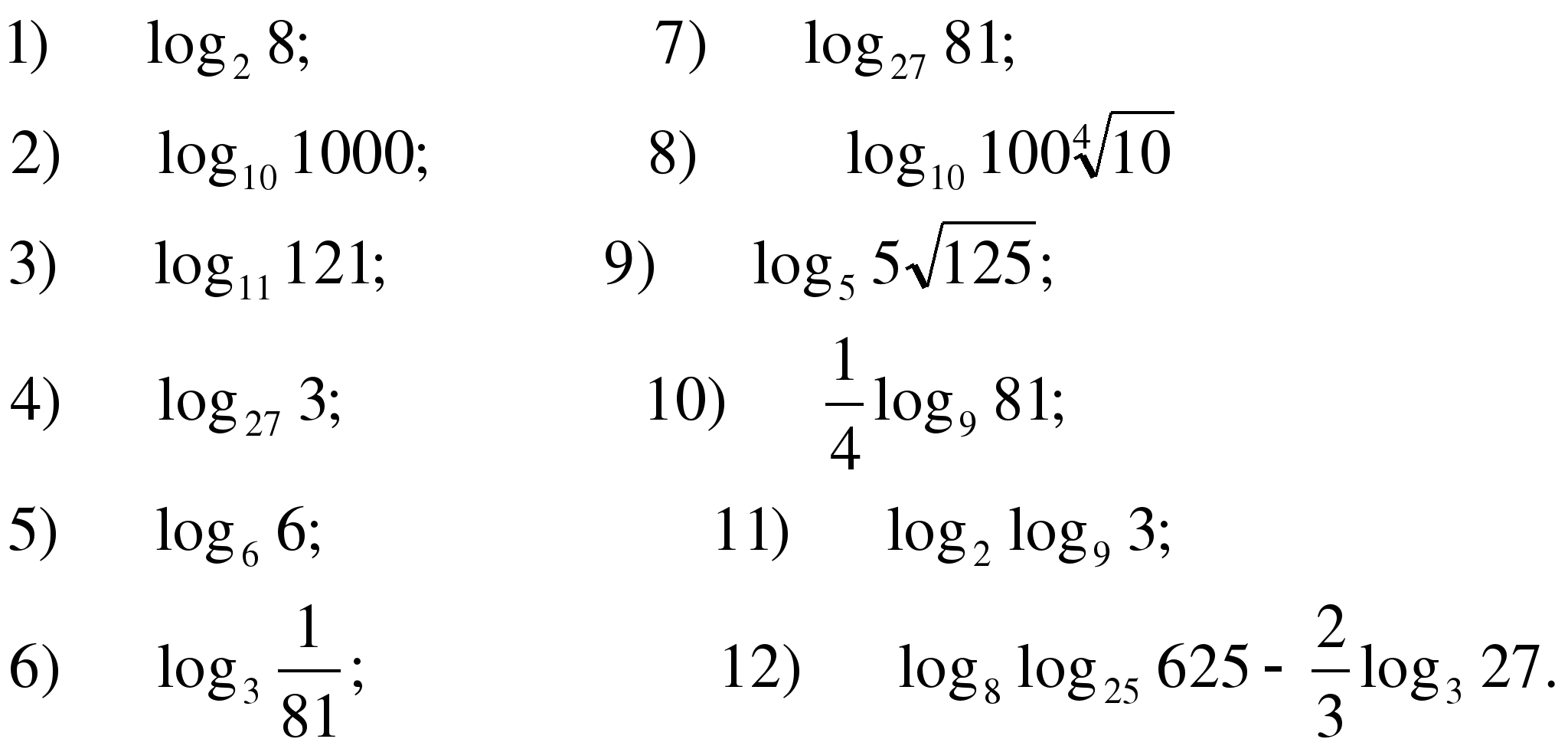
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 7
1. Вычислите логарифм:
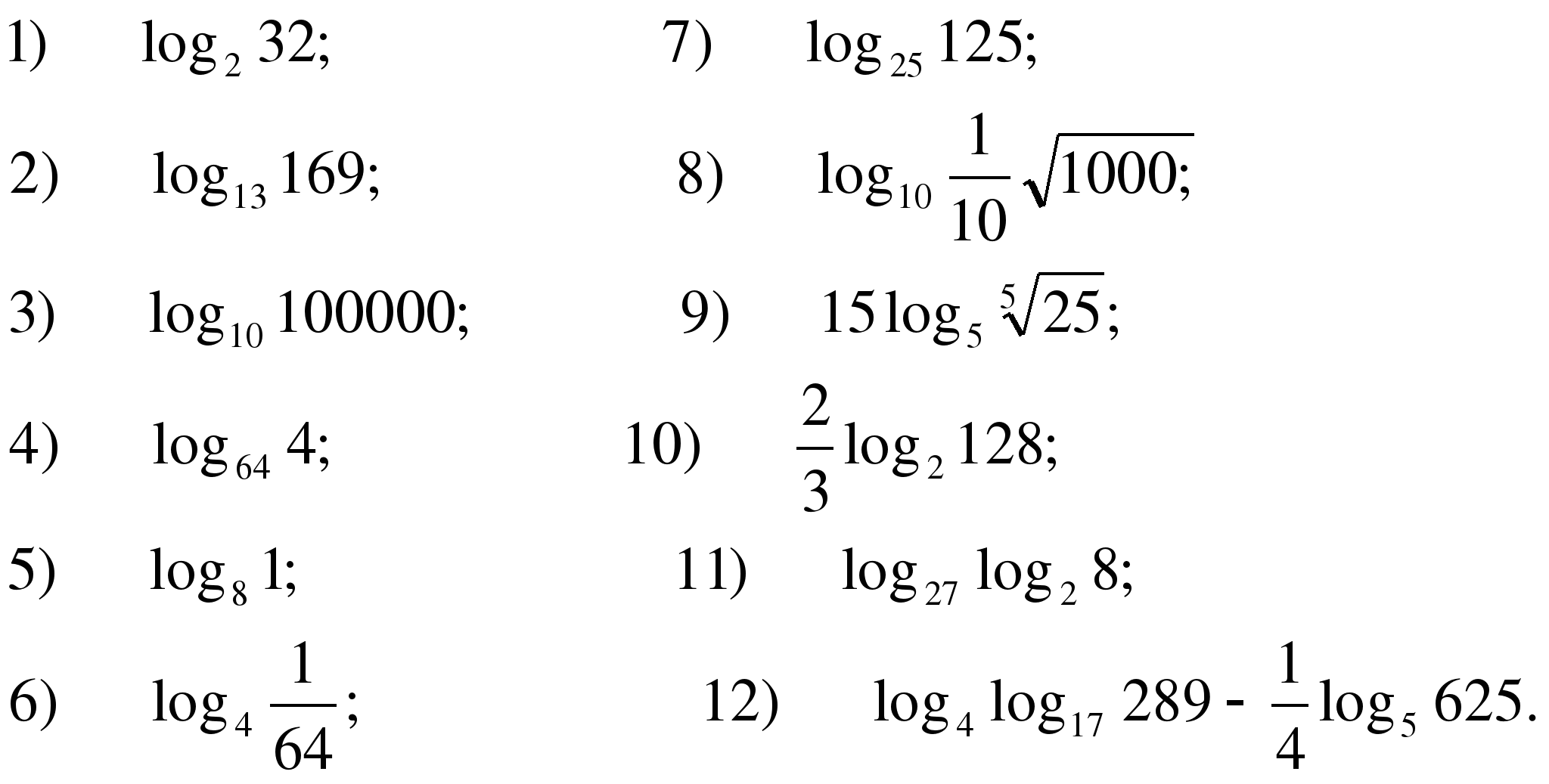
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 8
1. Вычислите логарифм:
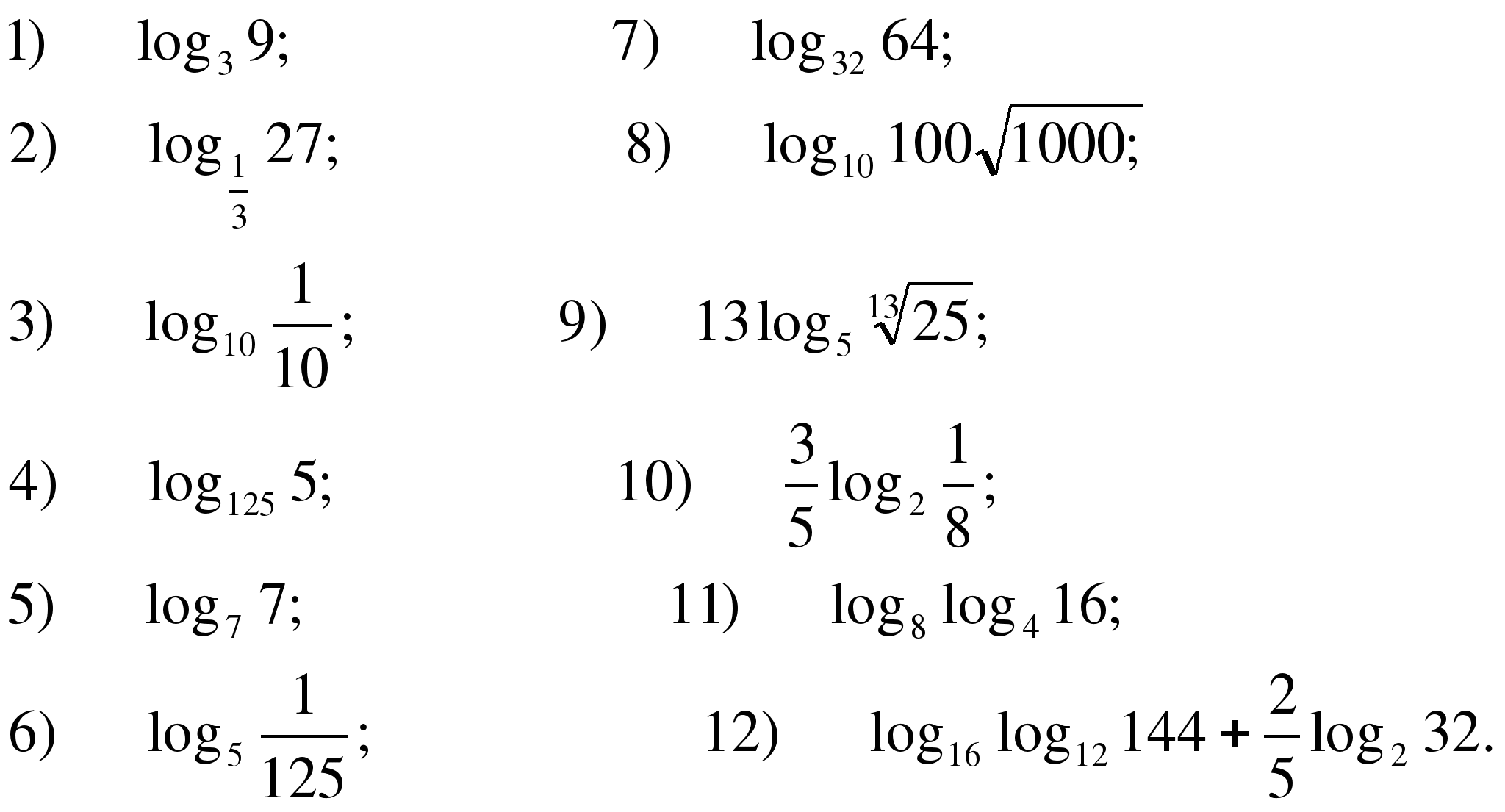
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 9
1. Вычислите логарифм:
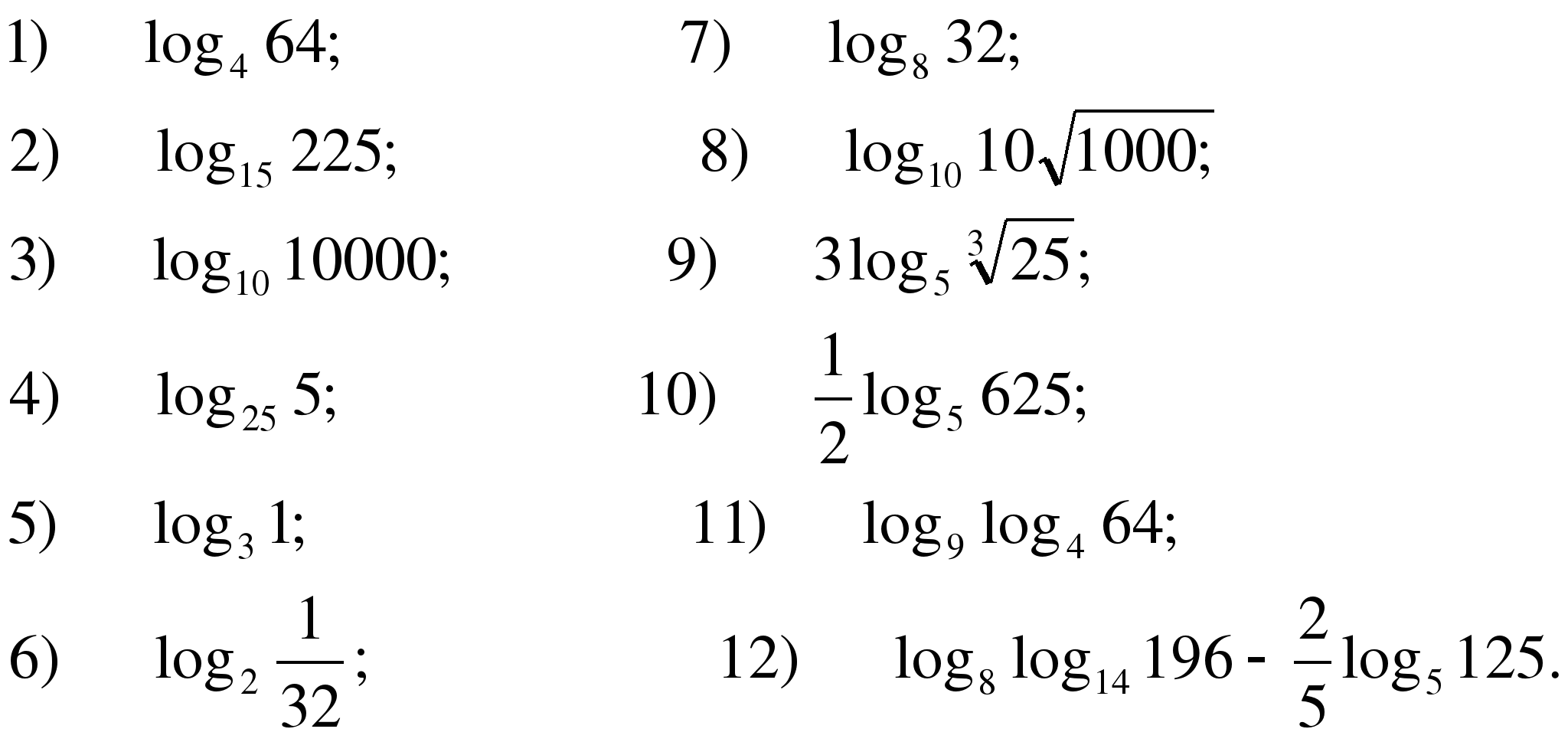
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 10
1. Вычислите логарифм:
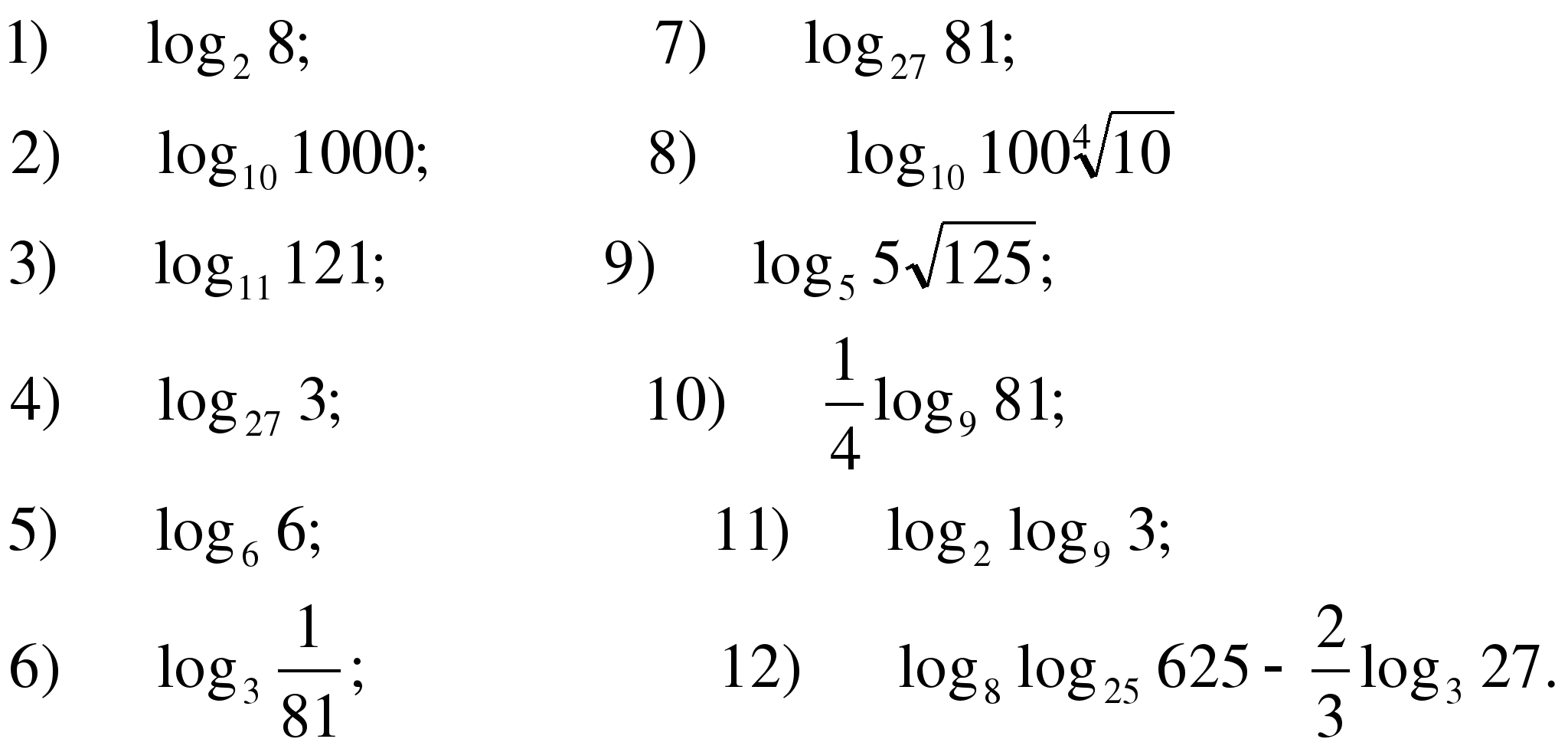
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 11
1. Вычислите логарифм:
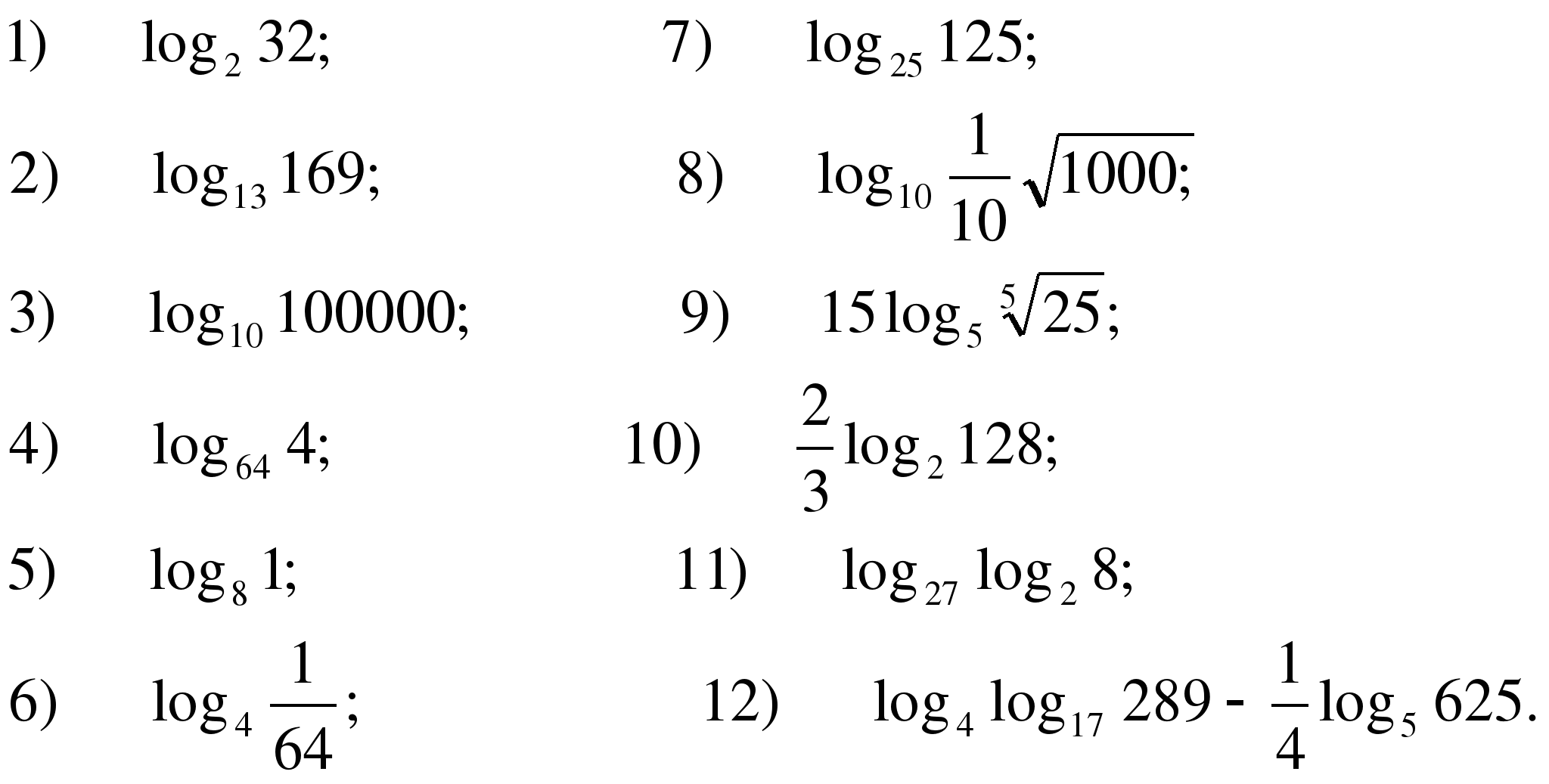
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 12
1. Вычислите логарифм:
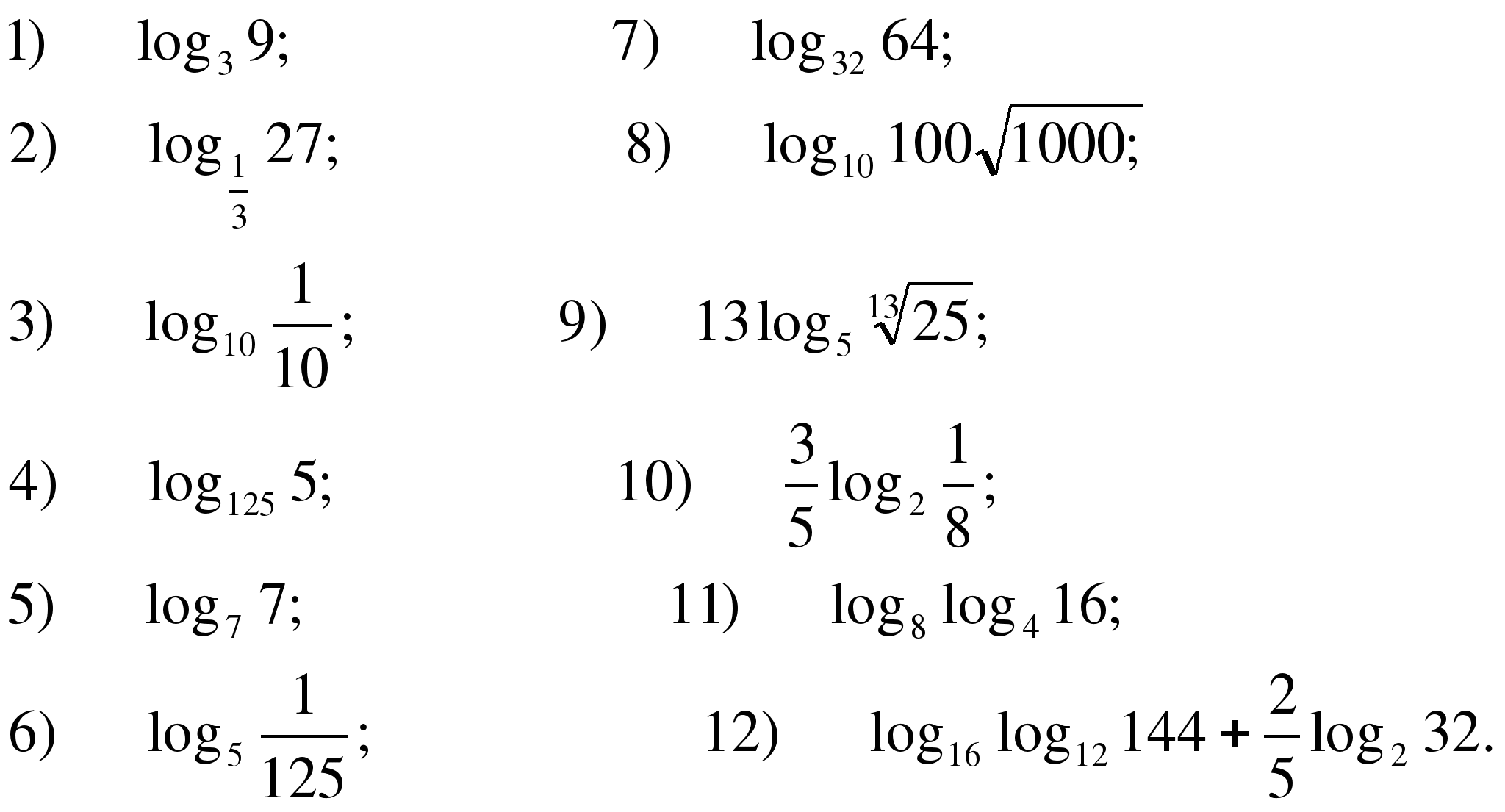
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 13
1. Вычислите логарифм:
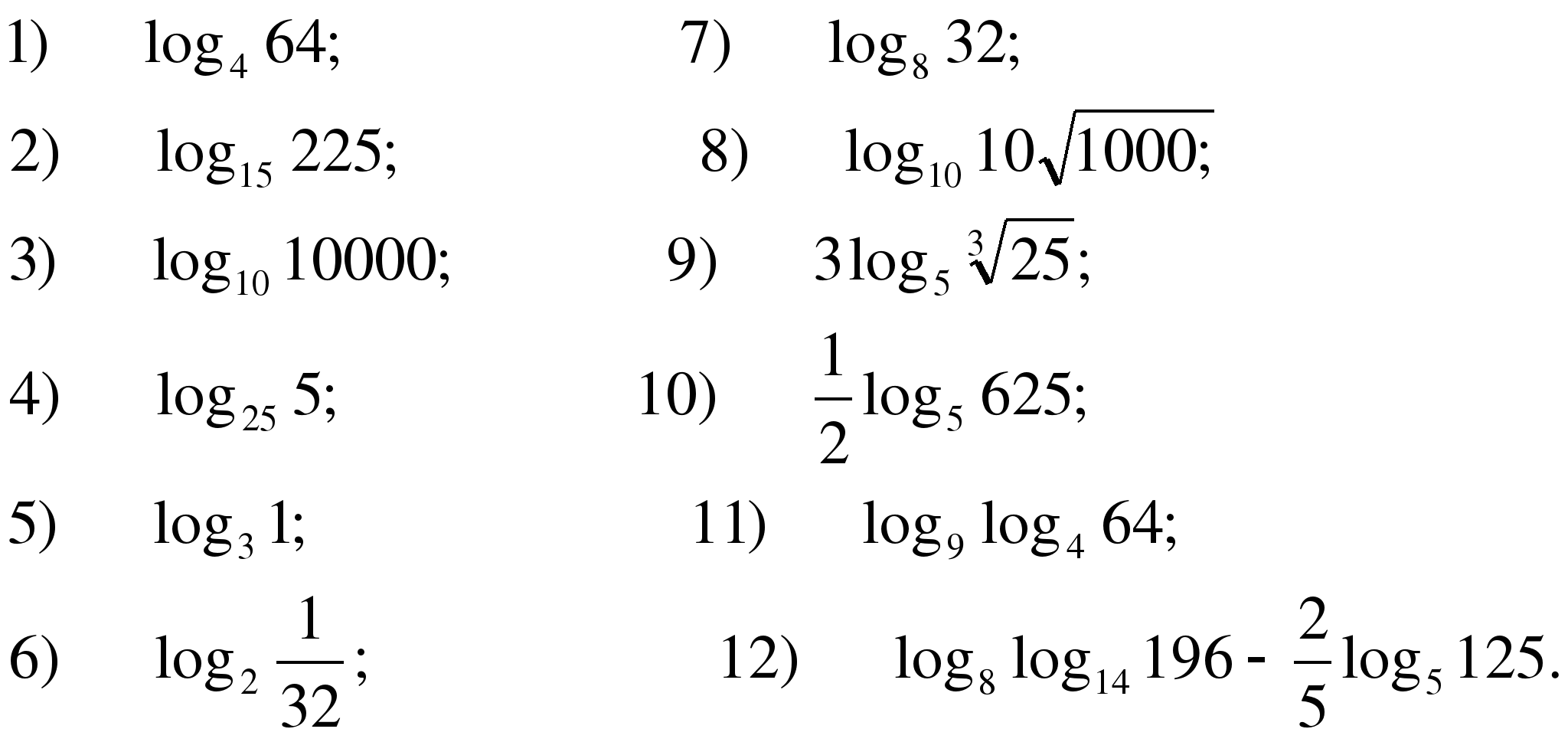
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 14
1. Вычислите логарифм:
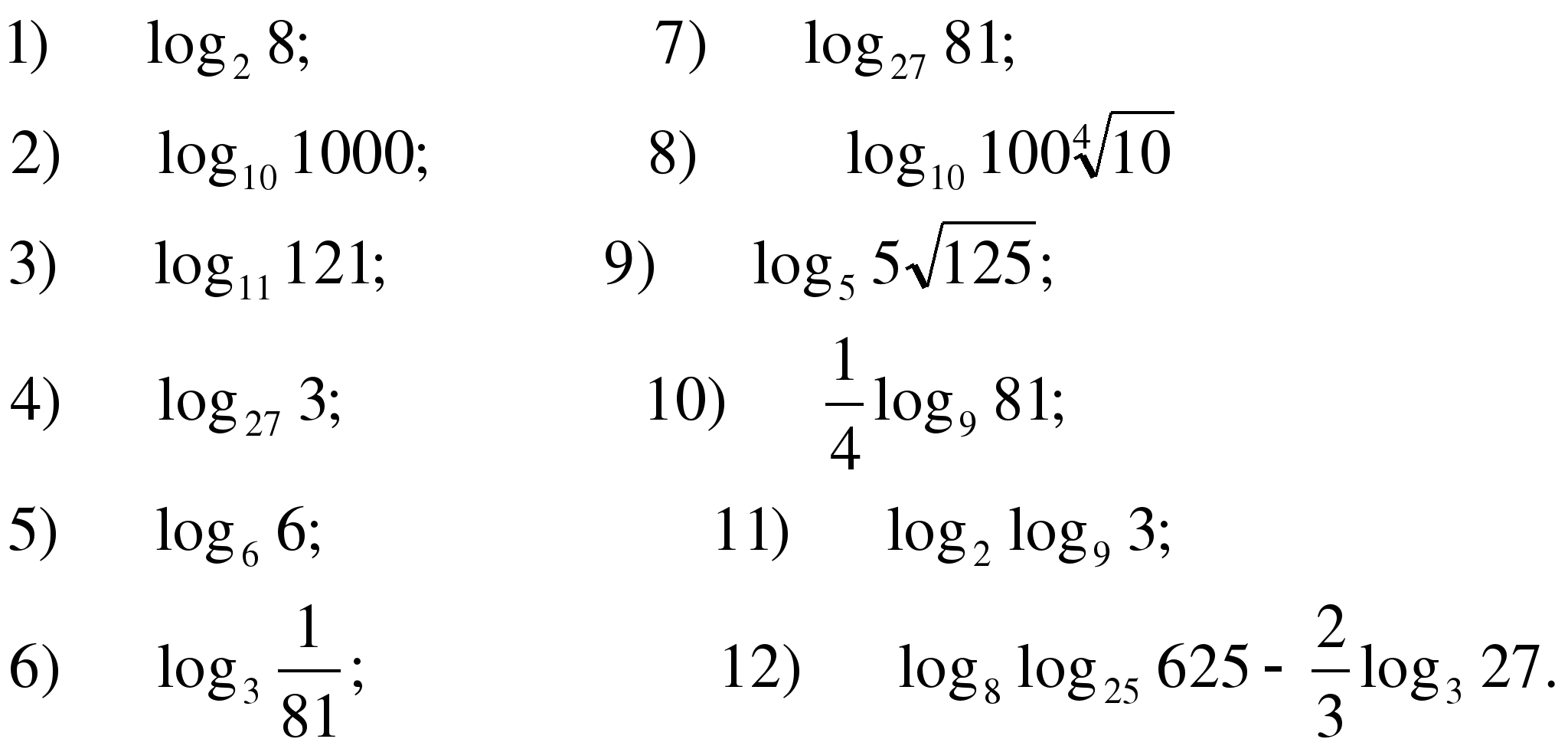
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 15
1. Вычислите логарифм:
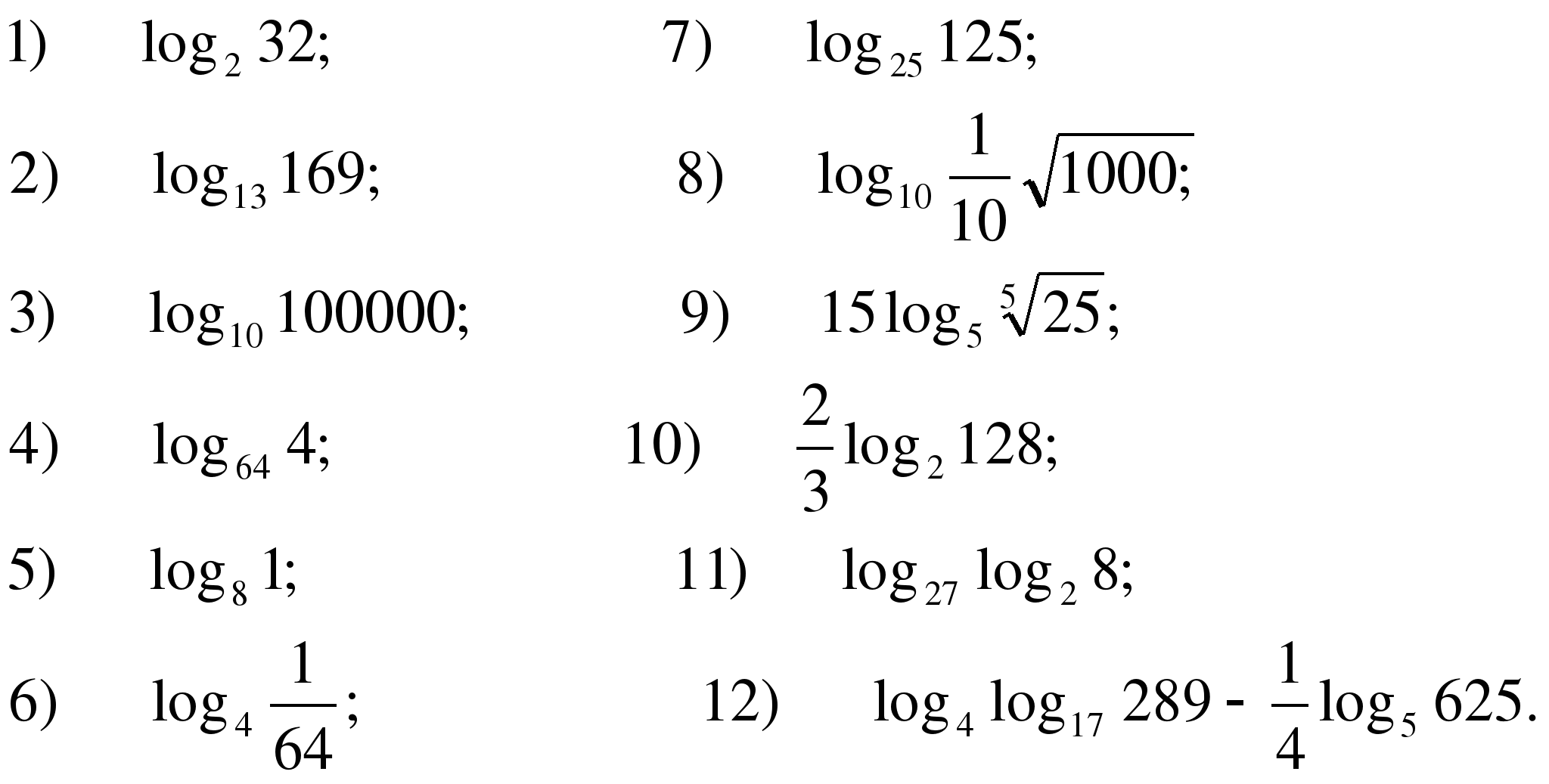
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 16
1. Вычислите логарифм:
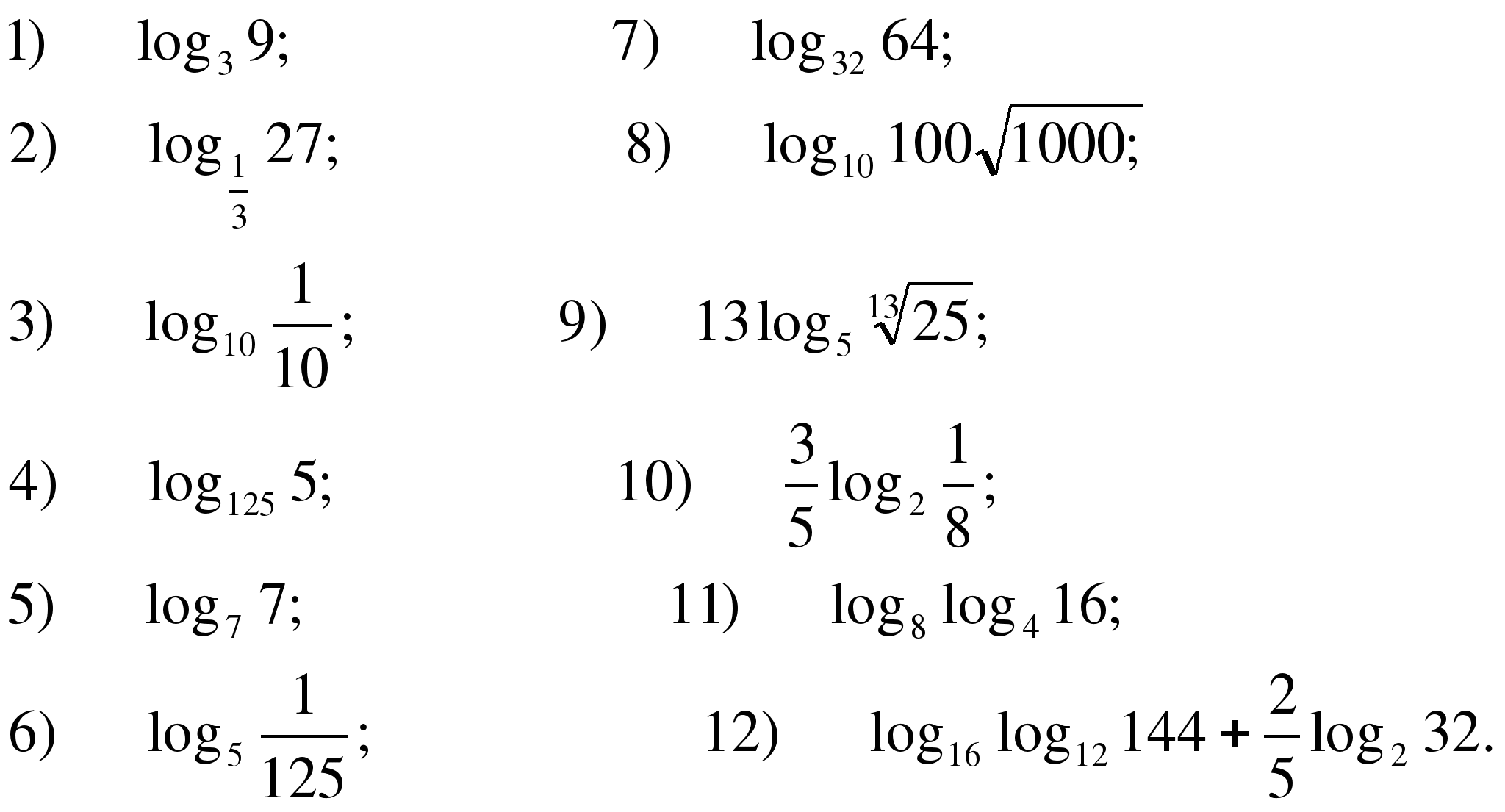
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 17
1. Вычислите логарифм:
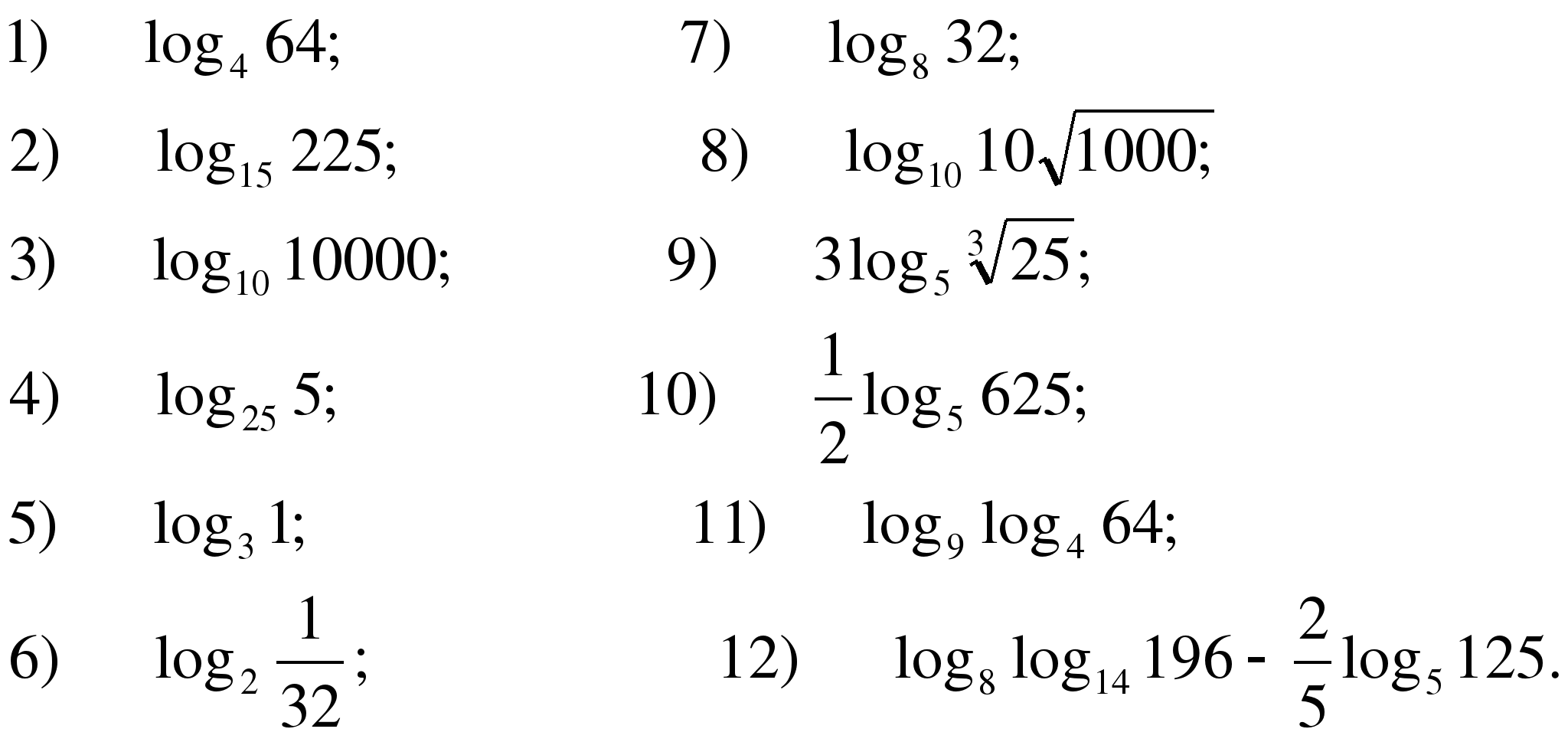
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 18
1. Вычислите логарифм:
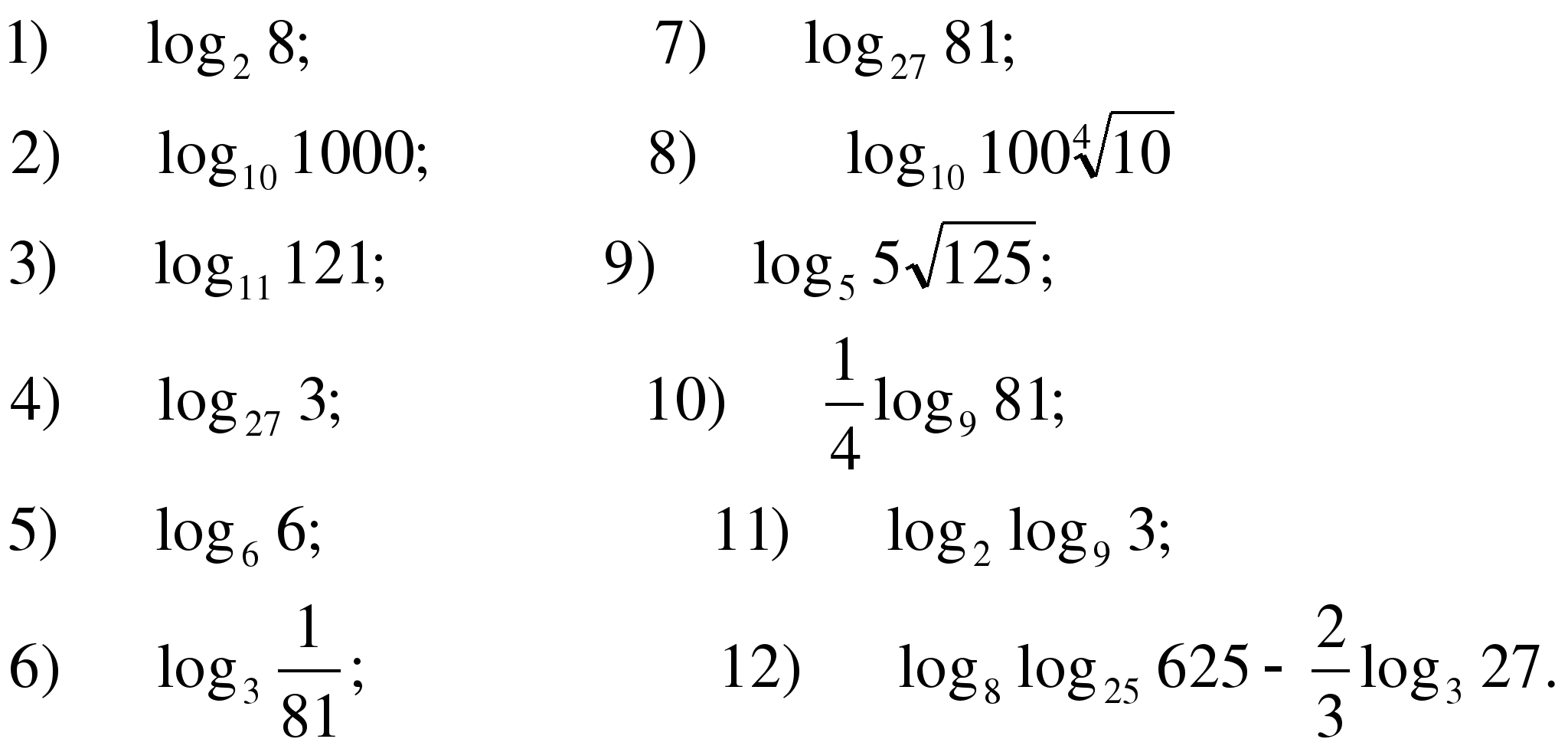
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 19
1. Вычислите логарифм:
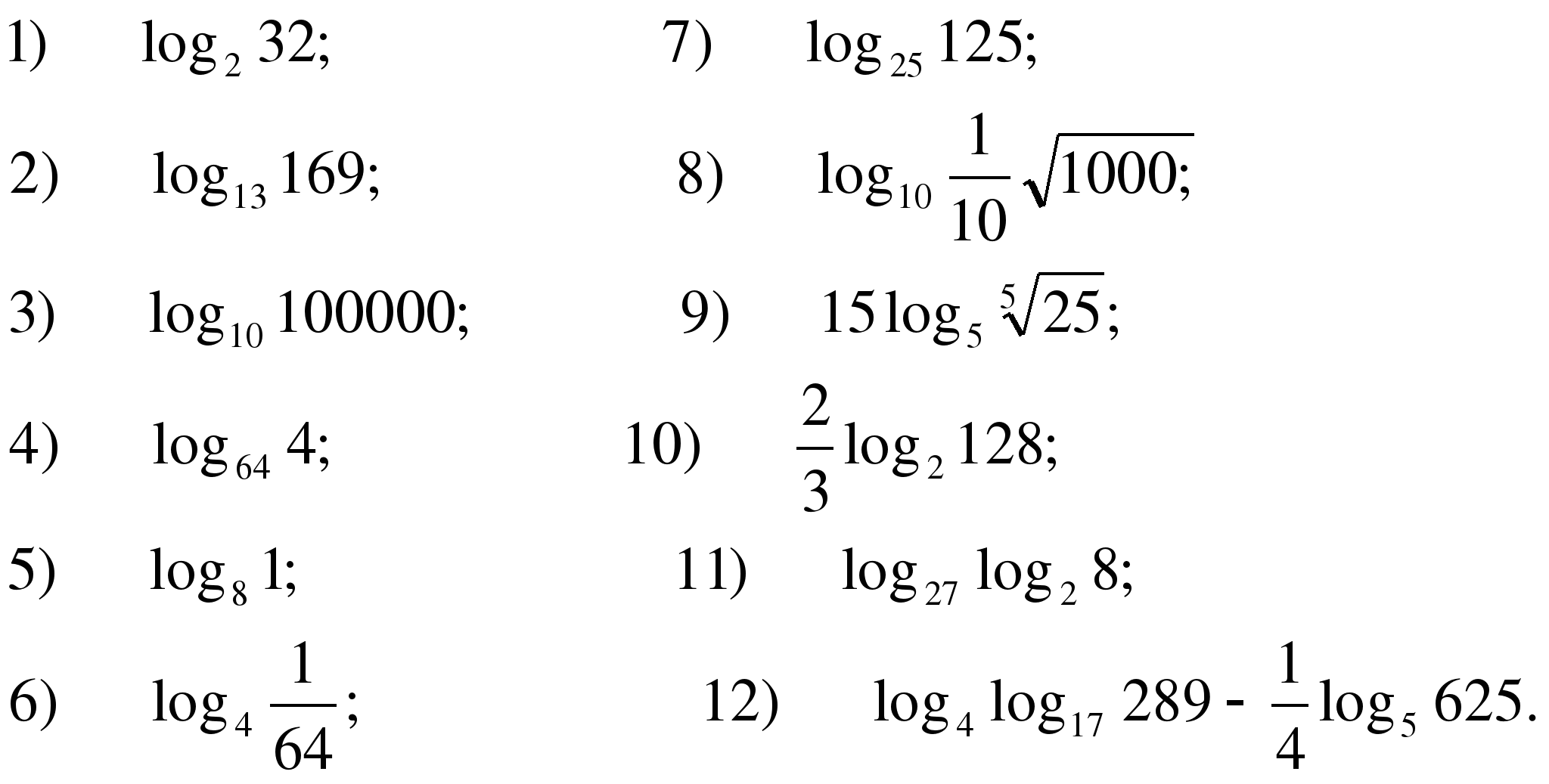
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 20
1. Вычислите логарифм:
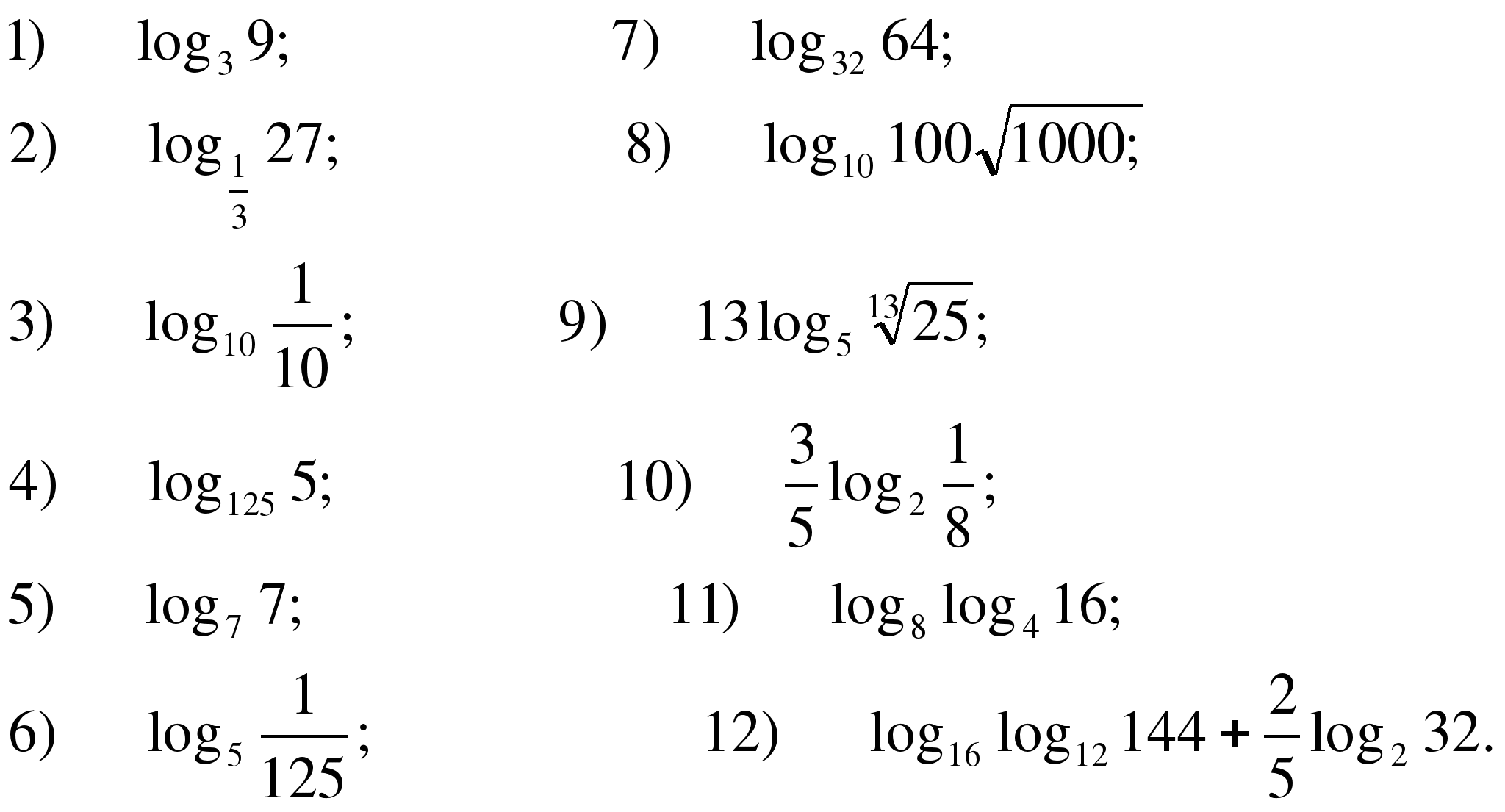
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 21
1. Вычислите логарифм:
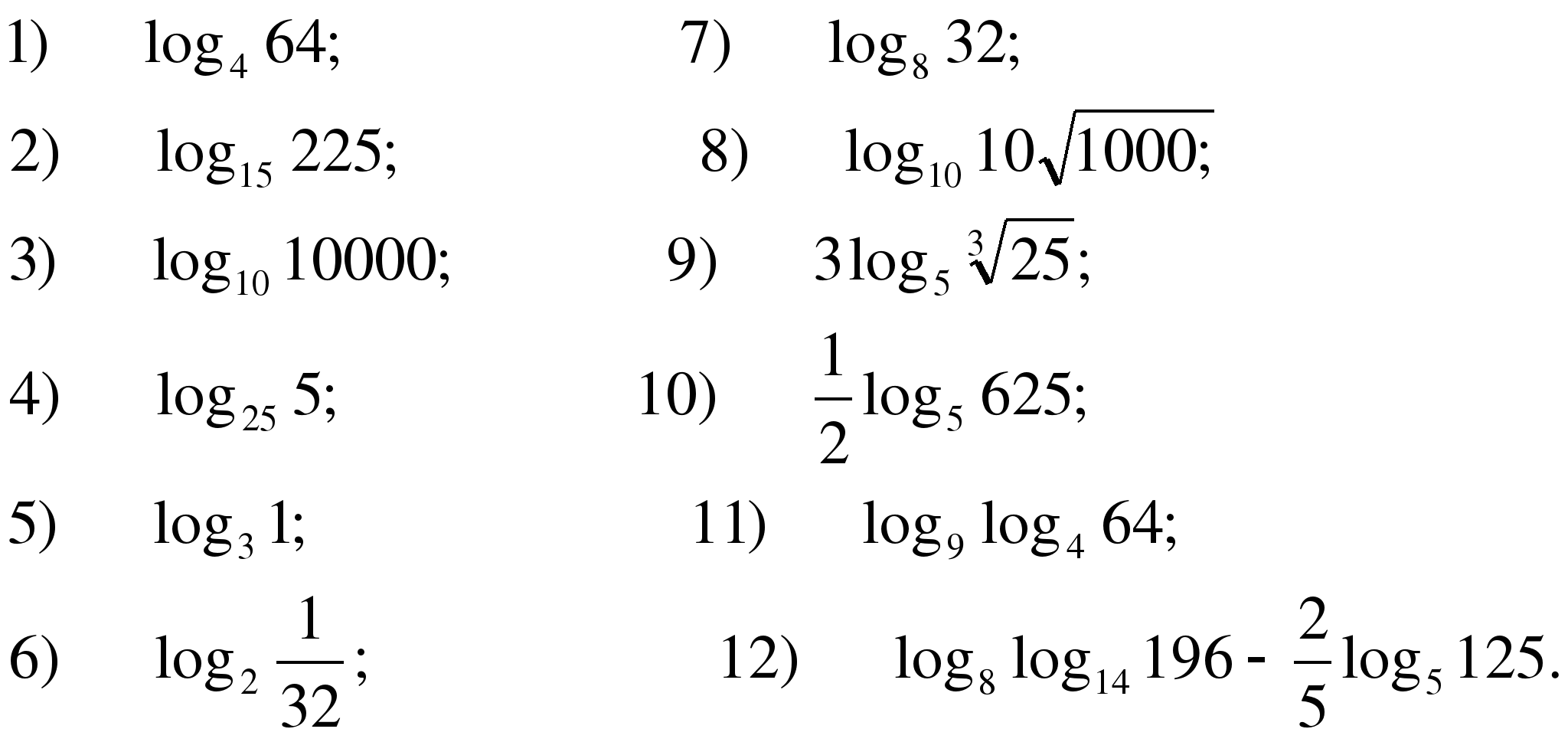
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 22
1. Вычислите логарифм:
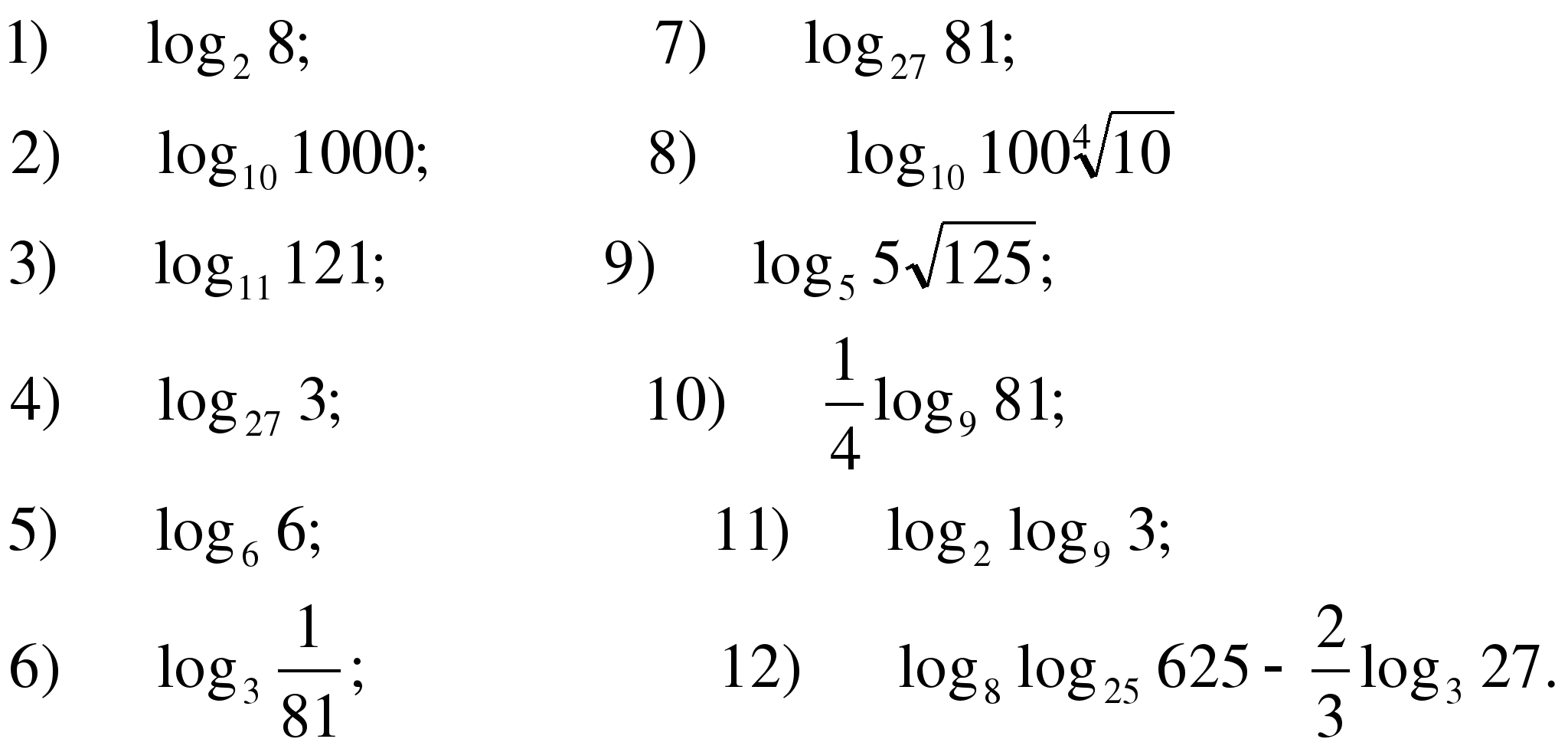
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 23
1. Вычислите логарифм:
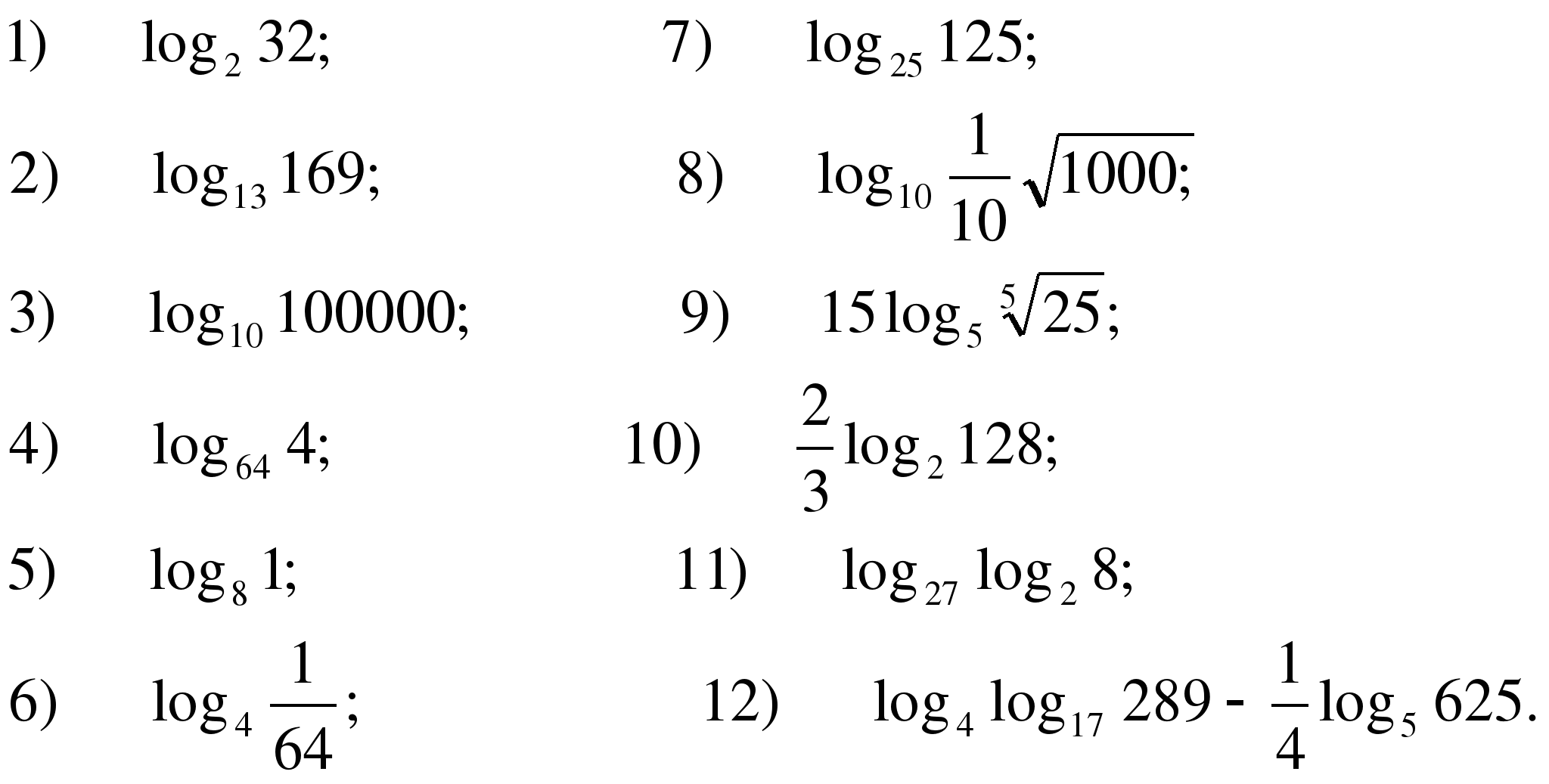
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 24
1. Вычислите логарифм:
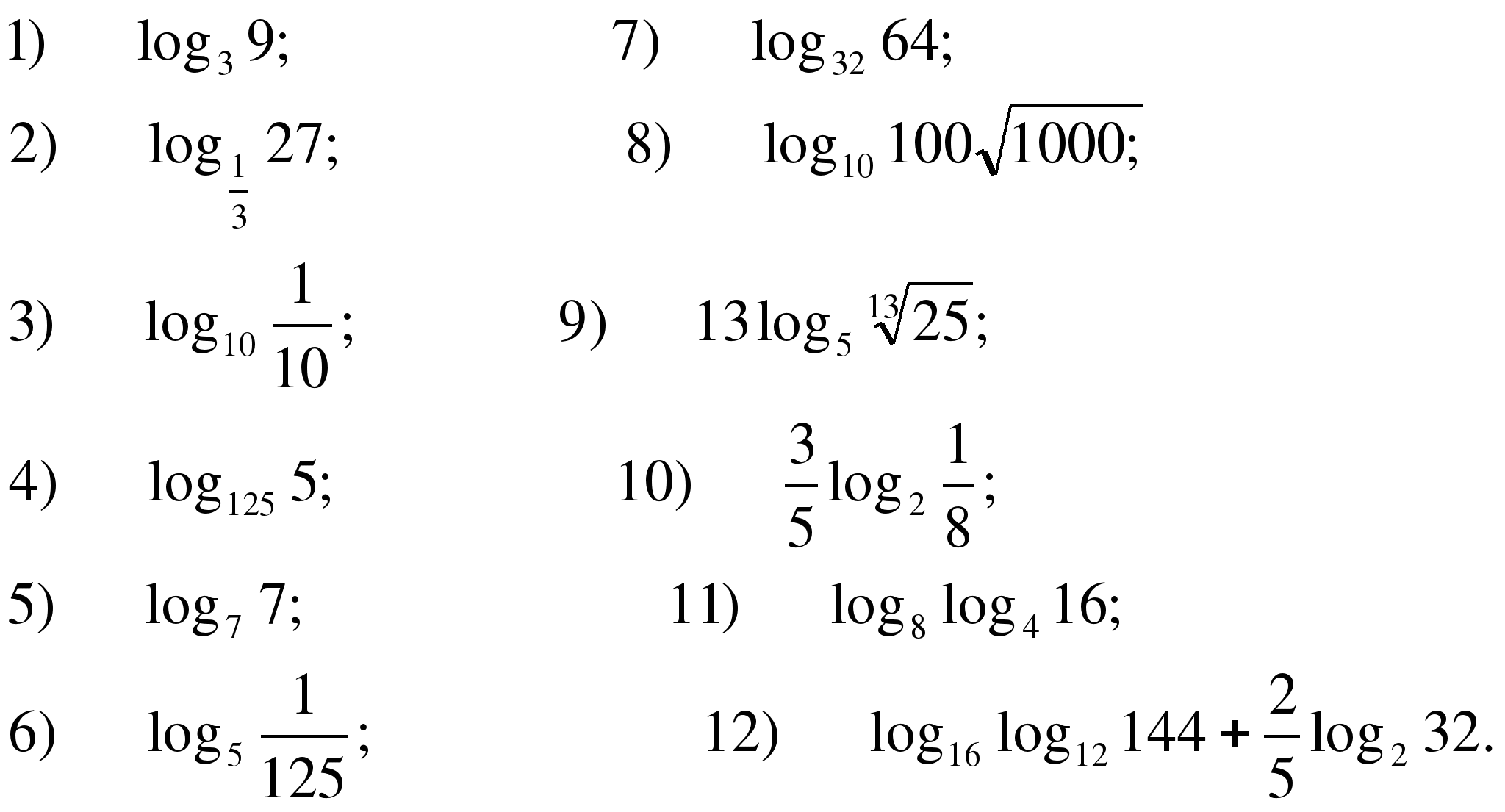
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 25
1. Вычислите логарифм:
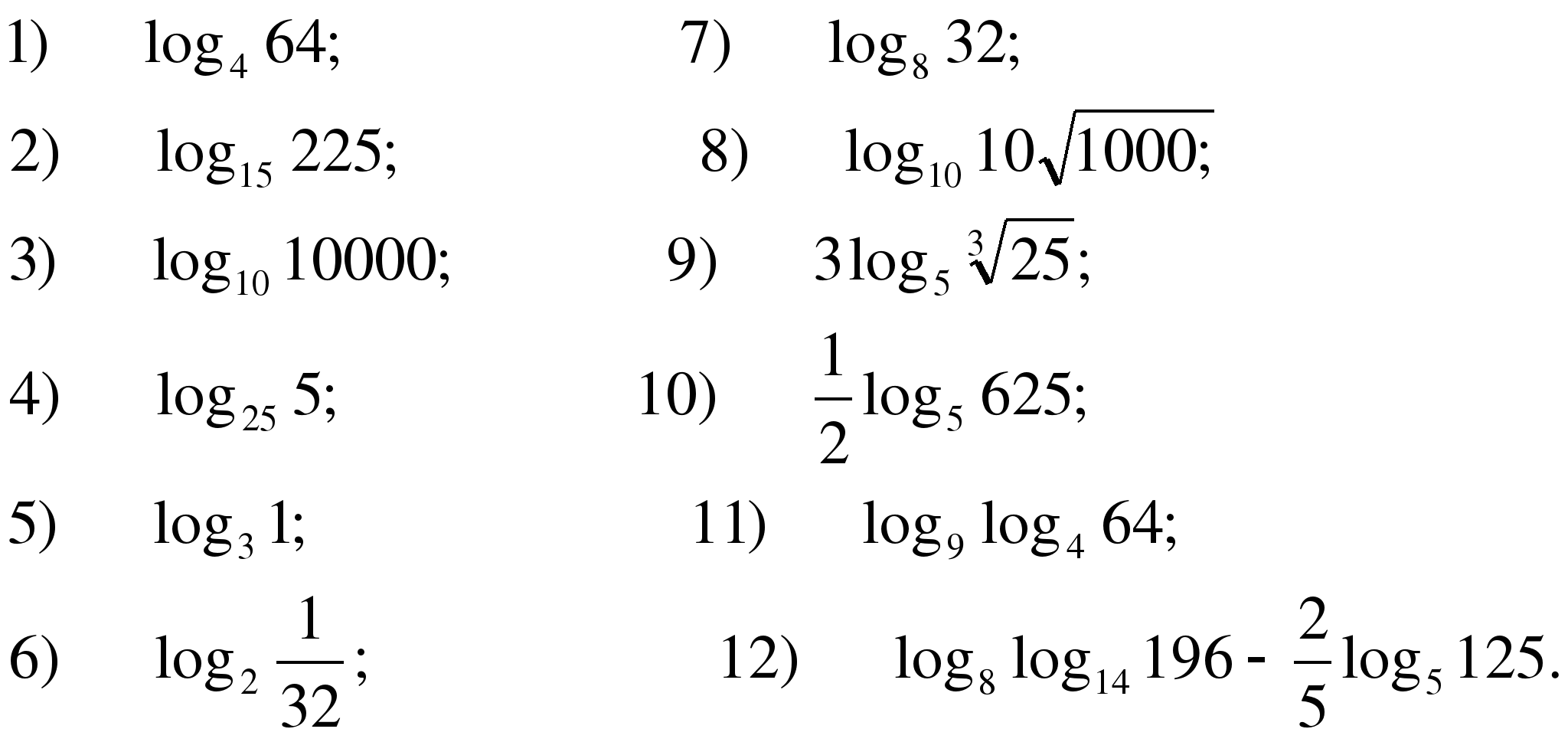
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 26
1. Вычислите логарифм:
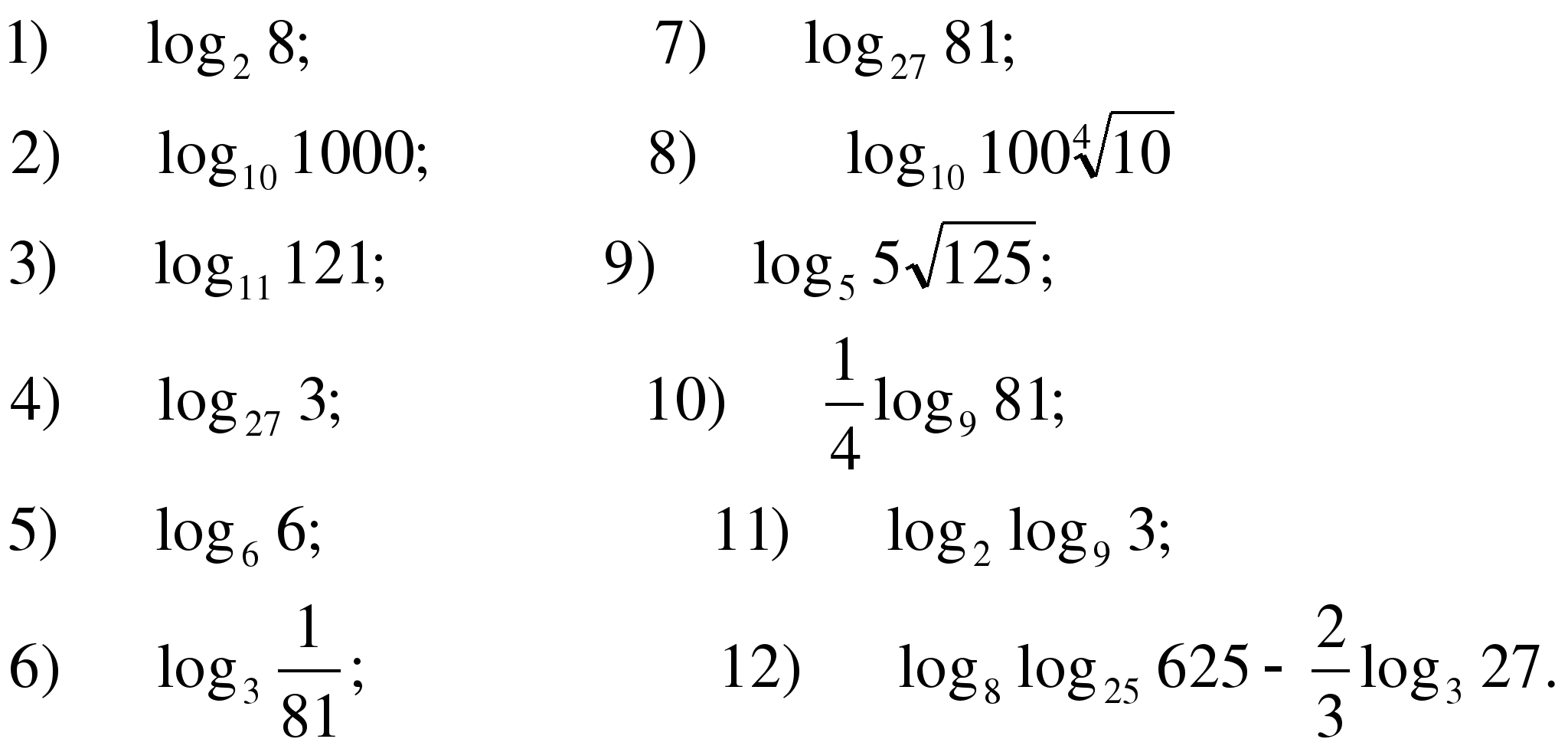
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 27
1. Вычислите логарифм:
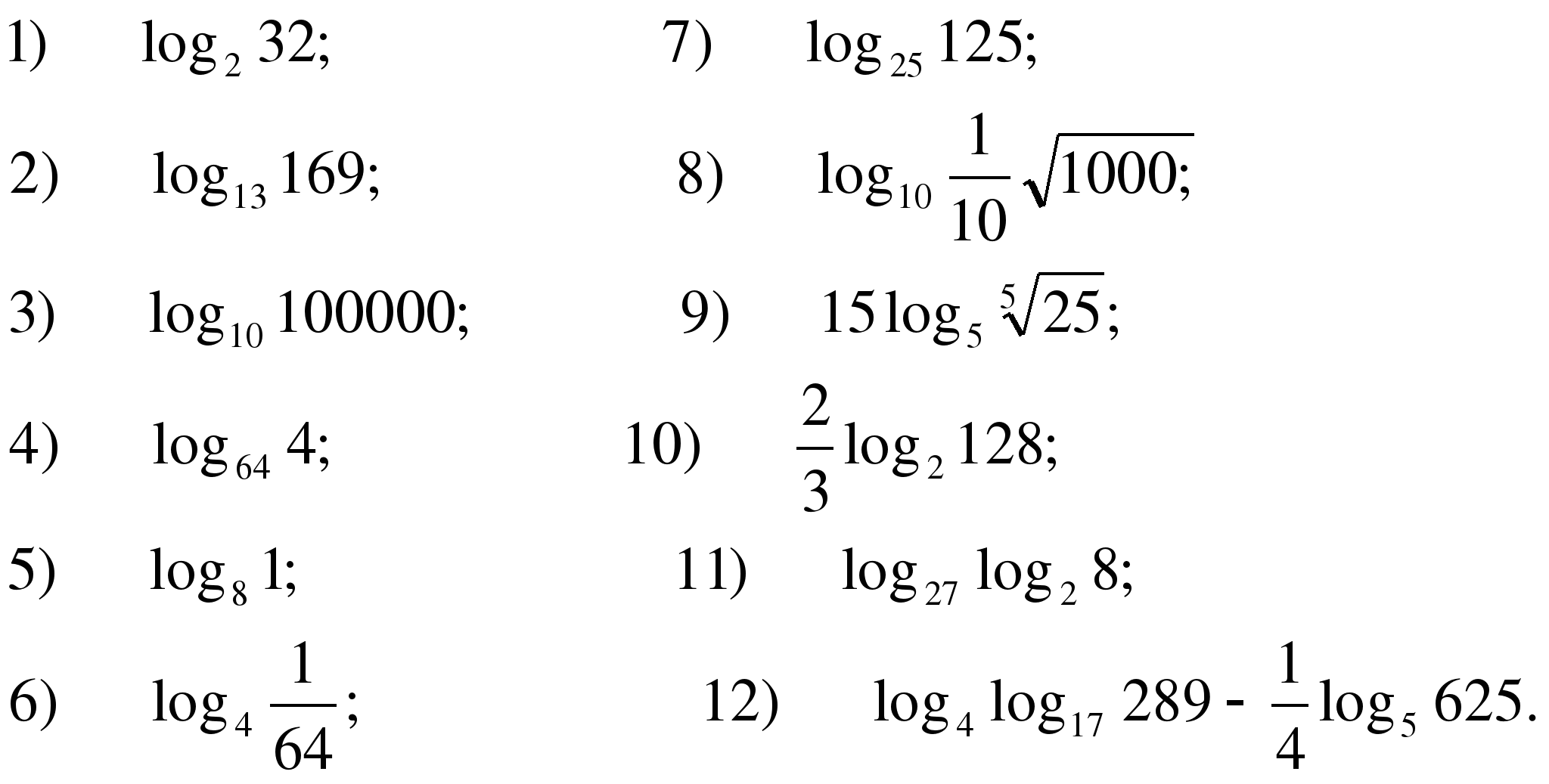
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 28
1. Вычислите логарифм:
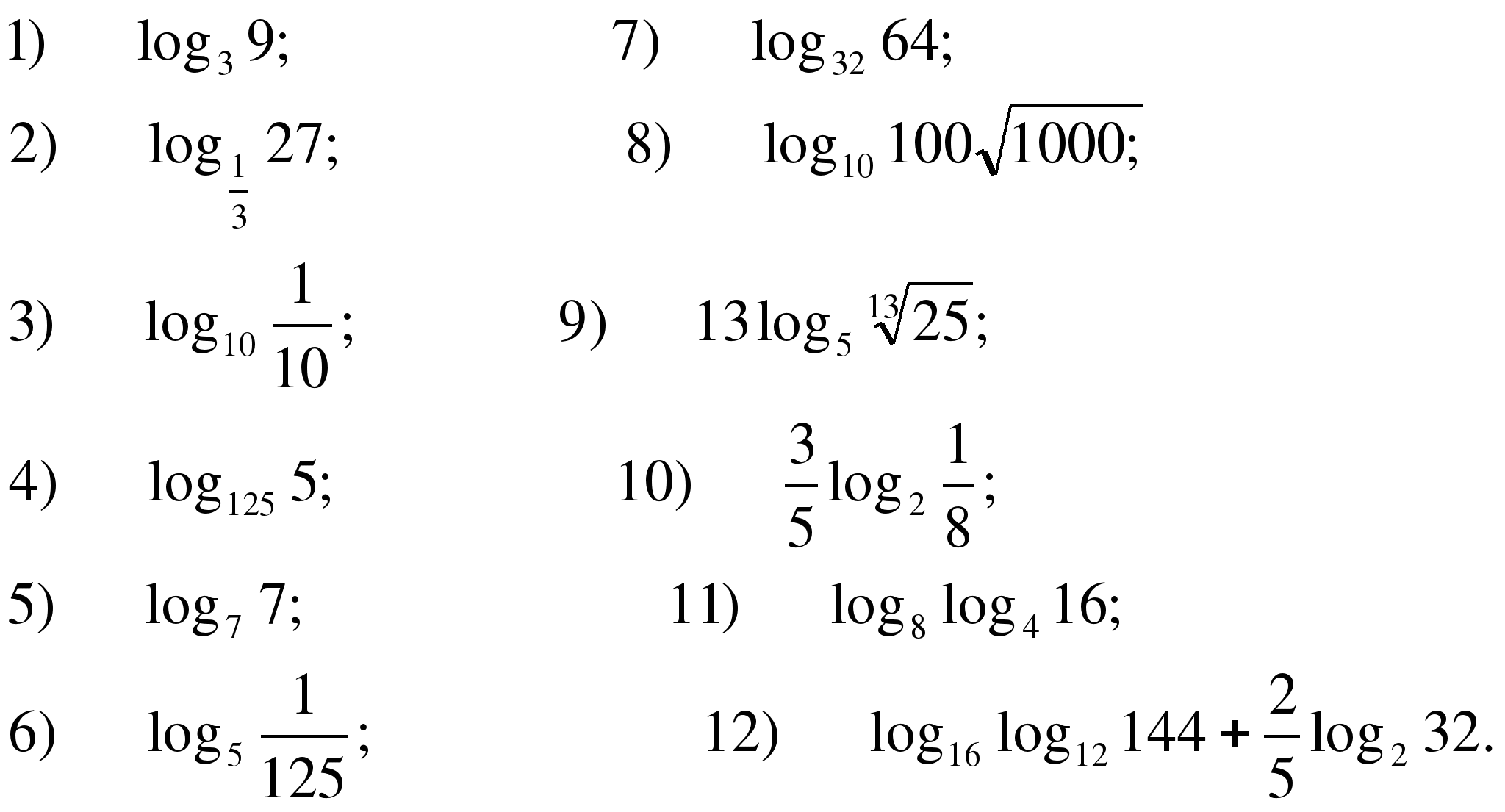
Логарифмы. Методические указания к решению упражнений
Государственное бюджетное образовательное учреждение
БРАТСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ
ЛОГАРИФМЫ
Методические указания к решению упражнений
при изучении темы «Свойства логарифмов»
г. Братск, 2012г.
Логарифмы: Методические указания / Сост. Лапина Н.Л. – Братск: БрПК, 2012– 13с.
Данные методические указания содержат необходимые теоретические сведения по теме «Логарифмы» дисциплины математика, примеры решения упражнений, набор упражнений для самостоятельного решения с ответами к некоторым из них, десять вариантов для выполнения контрольной работы. Вариант заданий определяется по последней цифре номера зачетной книжки.
Содержание
Введение…………………………………………………………………………………………………………..4
Определение логарифма ……………………………………………………………………5
Примеры для самостоятельного решения………………..…………….7
Преобразование логарифмических выражений………………..…………….7
Примеры для самостоятельного решения…………………………………..9
Контрольная работа по теме: «Свойства логарифмов»………………….10
Список литературы ………………………………………………………………….…………13
Введение
Настоящие методические указания предназначены в помощь студентам всех форм обучения при изучении темы «Свойства логарифмов». Разделы указаний содержат необходимые теоретические сведения (определения, формулы без доказательства) и подробно разобранные упражнения. В конце каждого раздела предлагаются задания для самостоятельного решения с ответами для самопроверки.
Теоретические сведения и примеры для самостоятельного решения дают возможность использовать данные методические указания на практических занятиях по математике, а также для самостоятельного изучения темы «Свойства логарифмов».
В конце указаний приведены десять вариантов заданий для выполнения контрольной работы. Вариант определяется последней цифрой номера зачетной книжки студента. Работа выполняется письменно в отдельной тетради.
Определение логарифма
Понятие логарифма числа вводится при решении показательных уравнений, например, решим уравнение 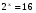 , в котором необходимо найти показатель х, представим правую часть уравнения в виде двух в четвертой степени
, в котором необходимо найти показатель х, представим правую часть уравнения в виде двух в четвертой степени 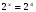 . В этом уравнении удалось левую и правую части представить в виде степени с одинаковым основанием 2. Ответ такого уравнения
. В этом уравнении удалось левую и правую части представить в виде степени с одинаковым основанием 2. Ответ такого уравнения 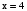 . Но уравнение
. Но уравнение  таким способом решить не удается. А корень все-таки есть. Этот корень называют логарифмом числа b по основанию а и обозначают logаb. Например, корнем уравнения
таким способом решить не удается. А корень все-таки есть. Этот корень называют логарифмом числа b по основанию а и обозначают logаb. Например, корнем уравнения 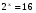 является число 4, т.е log216=4.
является число 4, т.е log216=4.
Из определения следует, что записи logаb=х. и ах=b равносильны.
Например, log28=3, потому что при возведении основания 2 в степень 3 получается 8: 23=8, действительно 2 2
2 2=23=8. Значит в результате вычисления логарифма 8 по основанию 2 получается показатель степени двойки, при возведении в которую получаем восемь.
2=23=8. Значит в результате вычисления логарифма 8 по основанию 2 получается показатель степени двойки, при возведении в которую получаем восемь.
Определение логарифма можно кратко записать так: 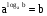 . Это равенство справедливо при b>0, a>0, а
. Это равенство справедливо при b>0, a>0, а 1. Его обычно называют основным логарифмическим тождеством.
1. Его обычно называют основным логарифмическим тождеством.
Для вычислений значений логарифмов полезно использовать значения степени следующих чисел:
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
210 = 1024
31 = 3
32 = 9
33 = 27
34 = 81
35 = 243
41 = 4
42 = 16
43 = 64
44 = 256
45 = 1024
51 = 5
52 = 25
53 = 125
54 = 625
61 = 6
62 = 36
63 = 216
71 = 7
72 = 49
73 = 343
81 = 8
82 = 64
83 = 512
91 = 9
92 = 81
93 = 729
101 = 10
102 = 100
103 = 1000 и т.д.
Также необходимо помнить правила возведения чисел в степень с отрицательным, дробным и нулевым показателем: а0=1; 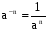 ;
; 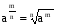
Пример 1. 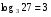 , т.к. 33=27
, т.к. 33=27
Пример 2. 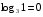 , т.к. 30=1
, т.к. 30=1
Пример 3. 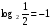 , т.к. 2-1=
, т.к. 2-1=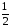
Пример 4. Вычислить 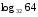
Пусть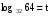 . По определению логарифма 32t=64. Это простейшее показательное уравнение. 32=25, 64=26, поэтому (25)t=26; 25t=26 ; 5t=6, t=
. По определению логарифма 32t=64. Это простейшее показательное уравнение. 32=25, 64=26, поэтому (25)t=26; 25t=26 ; 5t=6, t=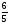
Ответ: 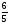
Пример 5. Вычислить 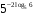
Используя свойства степени и основное логарифмическое тождество, находим 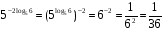
Пример 6. 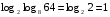
Для некоторых логарифмов имеются специальные обозначения: десятичный log10х=lgx, натуральный logех=lnx.
Пример 7. lg1000=3 , т.к. 103=3
Пример 8. lg0,01=-2 , т.к. 10-2=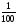 =0,01
=0,01
Примеры для самостоятельного решения:
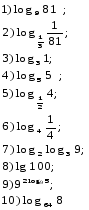
Ответы:
№ задания
1
2
3
4
5
6
7
8
9
10
ответ
2
4
0
1
-2
-1
1
2
25
0,5
Преобразование логарифмических выражений
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а>0, а 1, b>0, с>0, p – любое действительное число. Тогда справедливы формулы
1, b>0, с>0, p – любое действительное число. Тогда справедливы формулы
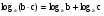 (1)
(1)
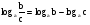 (2)
(2)
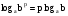 (3)
(3)
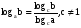 (4)
(4)
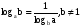 (5)
(5)
Формулы (1) и (2) можно применять к выражениям, содержащим логарифмы с одинаковыми основаниями.
Формулы (4) и (5) позволяют переходить от одного основания логарифмов к другому.
Пример 1. Вычислить: 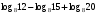
На основе формул (1) и (2) преобразуем 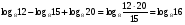
Теперь можно применить формулу (4), т. е. перейти к новому основанию, в данном примере логарифмы чисел 16 и 8 легко вычислить при основании 2, тогда 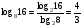
Пример 2. Вычислить 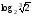
Применим формулу (3), для этого вспомним определение степени с рациональным показателем (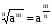 ), тогда
), тогда 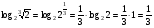
Пример 3. Зная, что 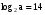 , найти
, найти 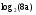
Применяем формулу (1) 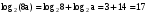
Пример 4. Прологарифмировать выражение 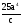 по основанию 5.
по основанию 5.
Запишем данное выражение в виде 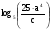
Теперь применим формулы (1), (2) и (3) 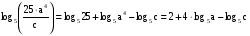
Пример5. Найти х по данному его логарифму (а>0,b>0): 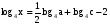
В этом примере необходимо правую часть представить в виде одного логарифма по основанию 4: 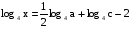
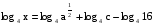 (2 представили в виде log416)
(2 представили в виде log416)
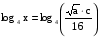 (применили формулы (1), (2) и (3))
(применили формулы (1), (2) и (3))
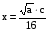
Примеры для самостоятельного решения:







Зная, что
 , найти
, найти 
Прологарифмировать выражение
 по основанию 10.
по основанию 10.Найти х по данному его логарифму (а>0,b>0):

Ответы:
№ задания
1
2
3
4
5
6
7
8
9
10
ответ
9
1
1,5
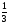
1
2
1,5
0,6
-1+2lga-lgn
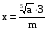
Контрольная работа по теме: «Свойства логарифмов»
Вычислить:
3. 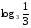
5. 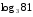
7. 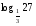
9. 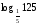
2. 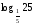
4. 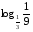
6. 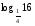
8. 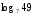
10. 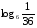
Вычислить:
3.

5.

7.

9.

4.

6.

8.

10.

Вычислить:
3.

5.

7.

9.

4.

6.

8.

10.

Вычислить:
3.

5.

7.

2.

4.

6.

8.

9.

10.

Вычислить:
Вычислить:
1.

3.

5.

7.

9.

2.

4.

6.

8.

10.

Доказать тождество:
Найти значение выражения:
 , если
, если
6.
 , если
, если
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
Прологарифмировать выражение:
1.
 по основанию 2
по основанию 26.
 по основанию 4
по основанию 42.
 по основанию 3
по основанию 37.
 по основанию 2
по основанию 23.
 по основанию 5
по основанию 58.
 по основанию 8
по основанию 84.
 по основанию 3
по основанию 39.
 по основанию 9
по основанию 95.
 по основанию 6
по основанию 610.
 по основанию 10
по основанию 10
Найти х по данному его логарифму (а>0,m>0,c>0,h>0,n>0,k>0):
1.

6.

2.

7.

3.

8.

4.

9.

5.

10.

СПИСОК ЛИТЕРАТУРЫ
Алимов Ш.А. Алгебра и начала анализа – учебник для 10-11 кл. общеобразоват. Учреждений – М.: Просвещение, 2006.- 384с.
Креславская О.А. ЕГЭ-2009. Математика: Сдаем без проблем! – М.: Эксмо, 2008.-192с.
Самостоятельная работа по теме»Свойства логарифмов» 10 класс
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 1
1. Вычислите логарифм:
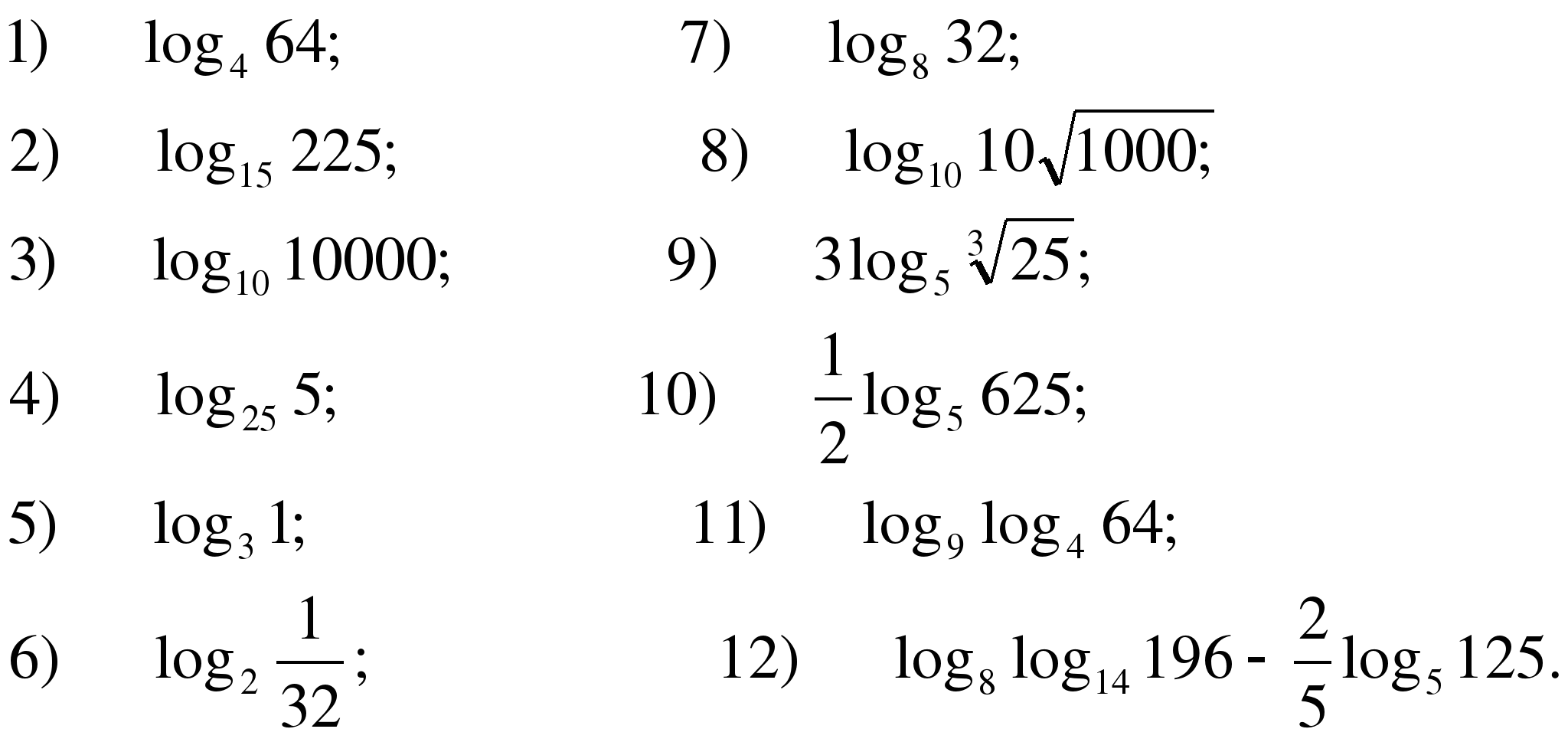
13) log2 96 –log2 3 + log21
14) log3 4√ 2 15) 32 log34
7
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 2
1. Вычислите логарифм:

13)log3 54 –log3 2 + log749 14)log11 3√ 121 15) 32 log35
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 3
1. Вычислите логарифм:
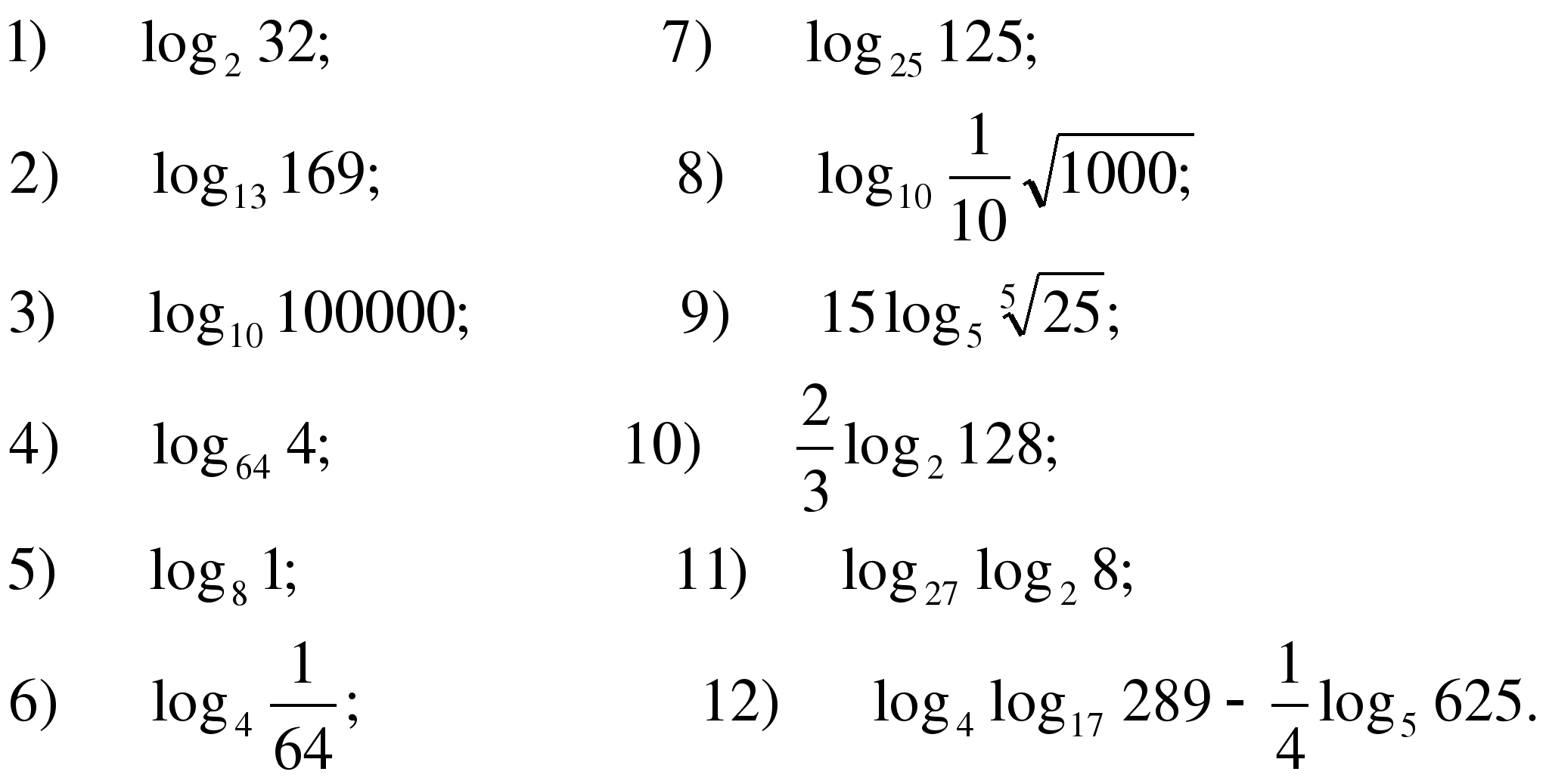
13) log6 144 –log6 4 + log3 81
14)log11 5√ 11 15)2 2 log24
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 4
1. Вычислите логарифм:
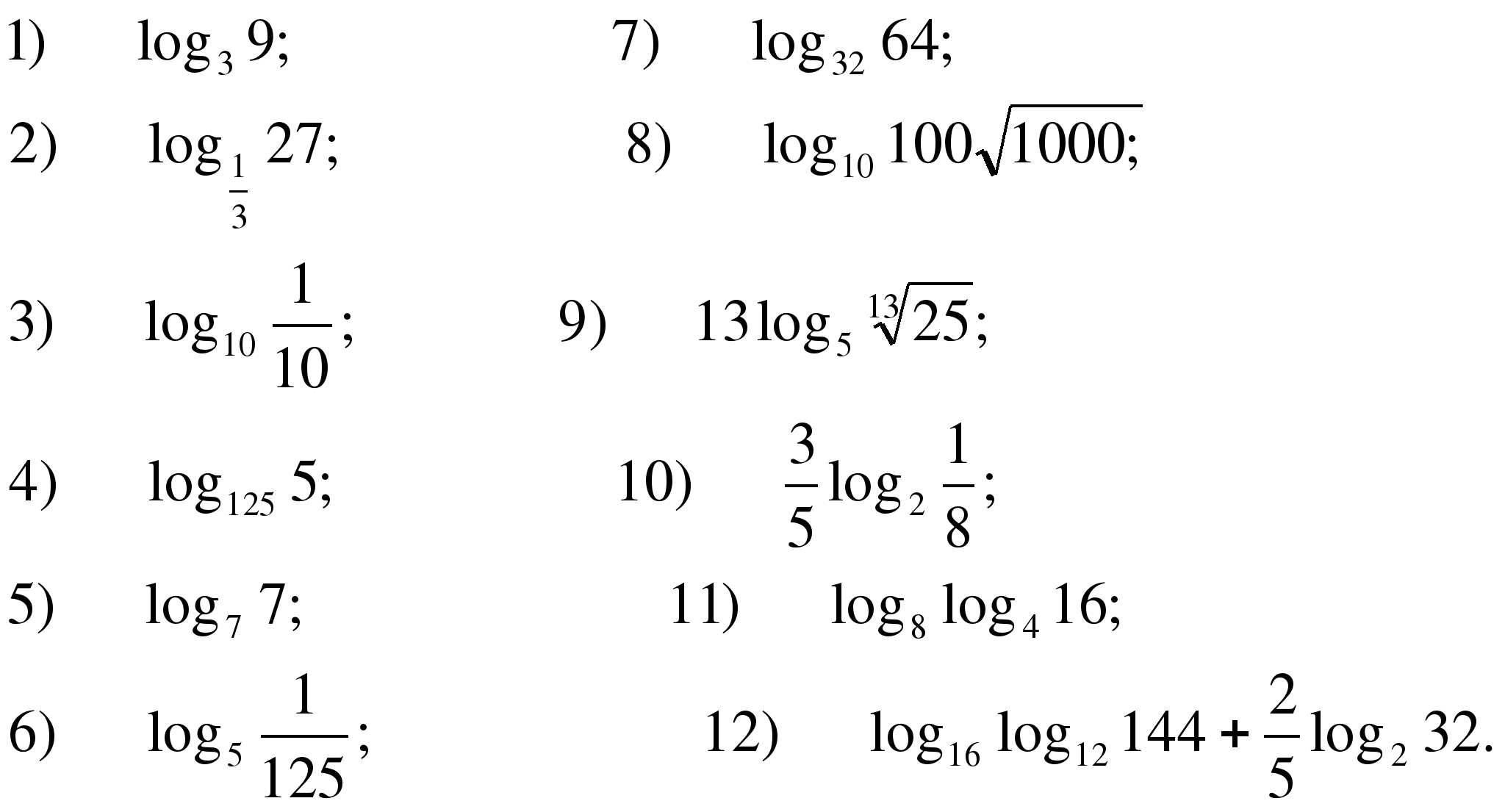
13)log2 80 – log2 5 + log4 4
14)log133√ 13
15) 2 2 log25
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 5
1. Вычислите логарифм:
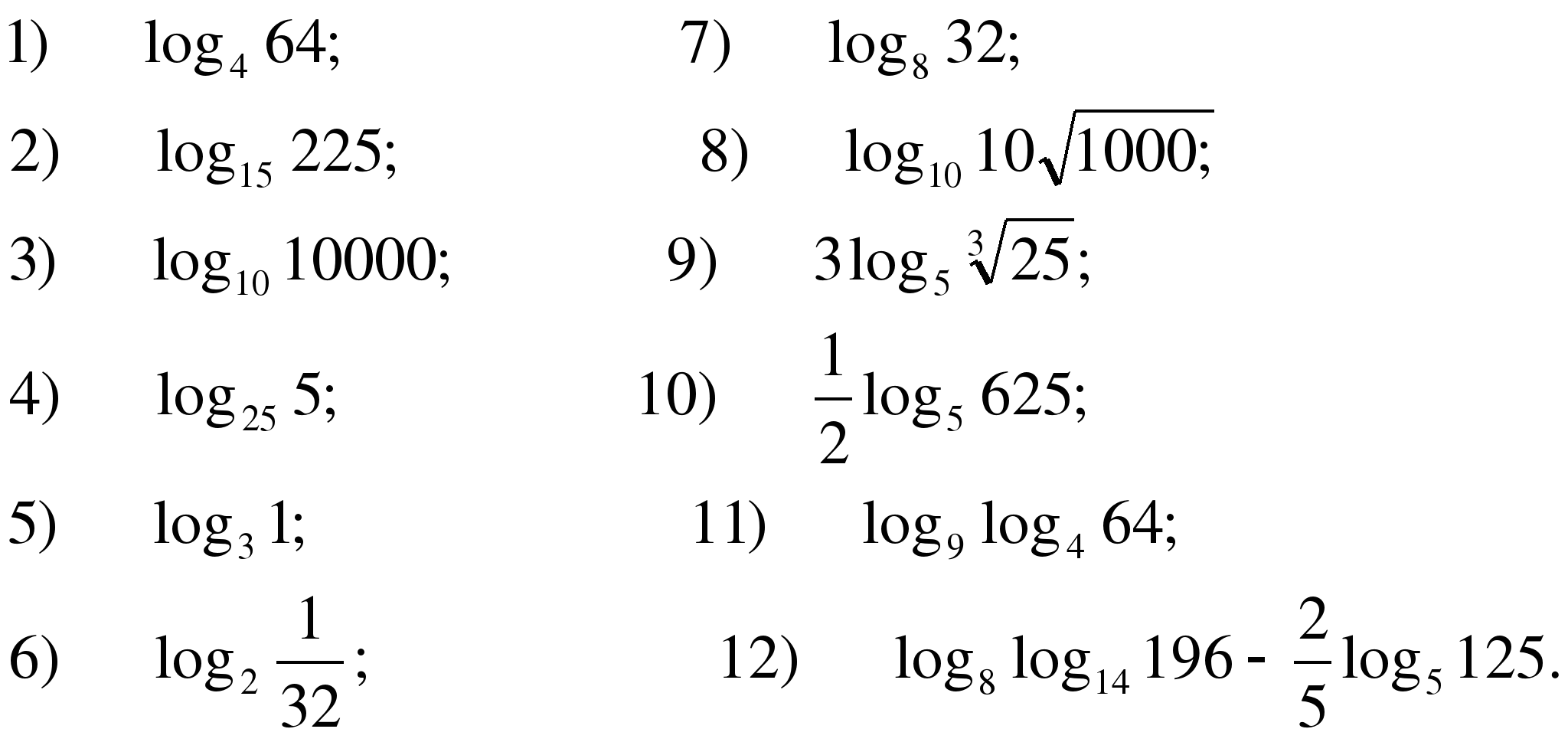
13)log5 1 + log3 45 – log3 5
14)log4 4√ 64
15) 4 3 log42
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 6
1. Вычислите логарифм:

13)log3 6 +log3 15 – log3 10
14) log54 √ 125
15) 2 1+ log23
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 7
1. Вычислите логарифм:
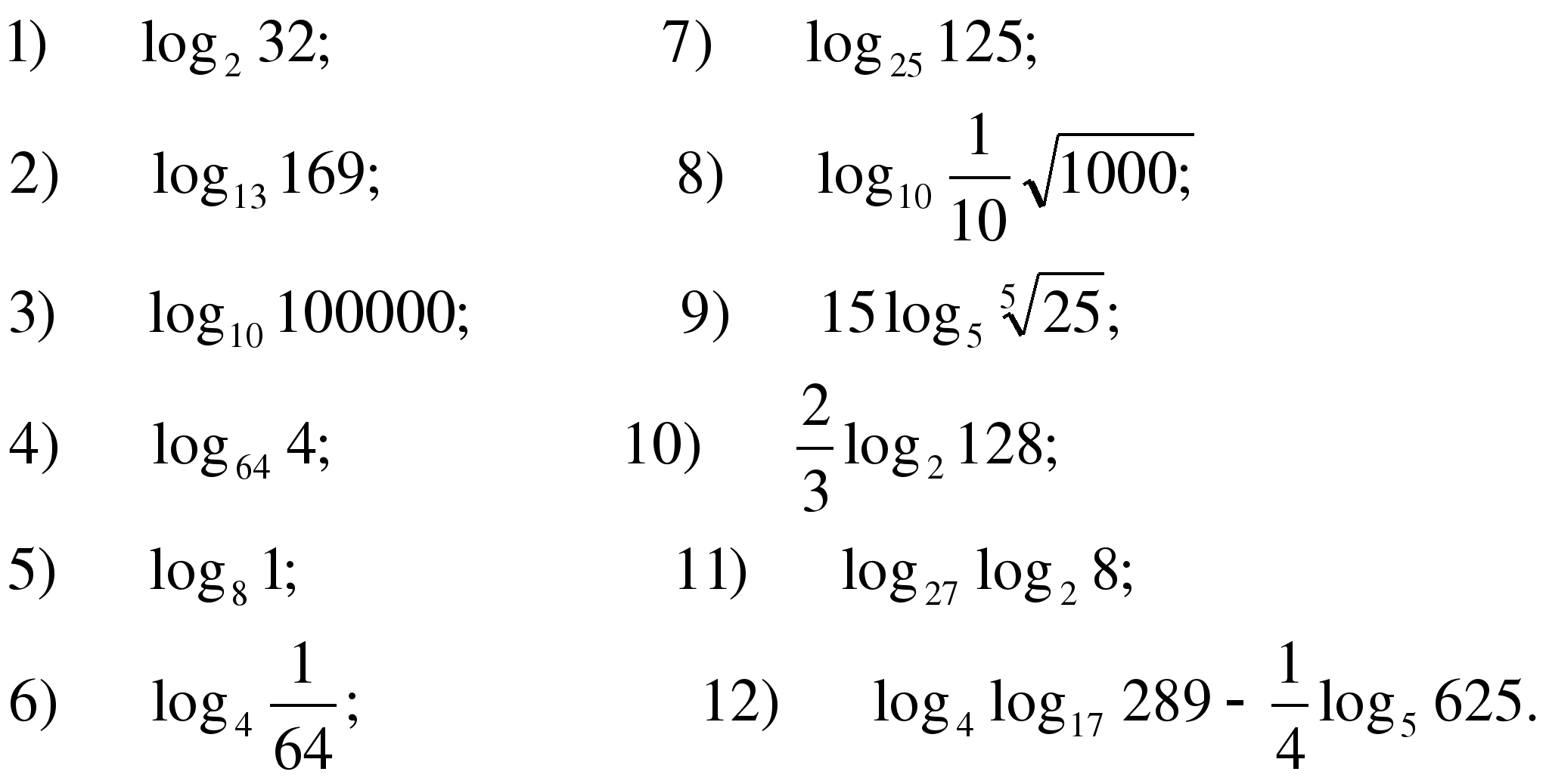
13)log2 6+ log2 10 – log2 15
14)log2 7√ 64
15)2 2+ log25
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 8
1. Вычислите логарифм:
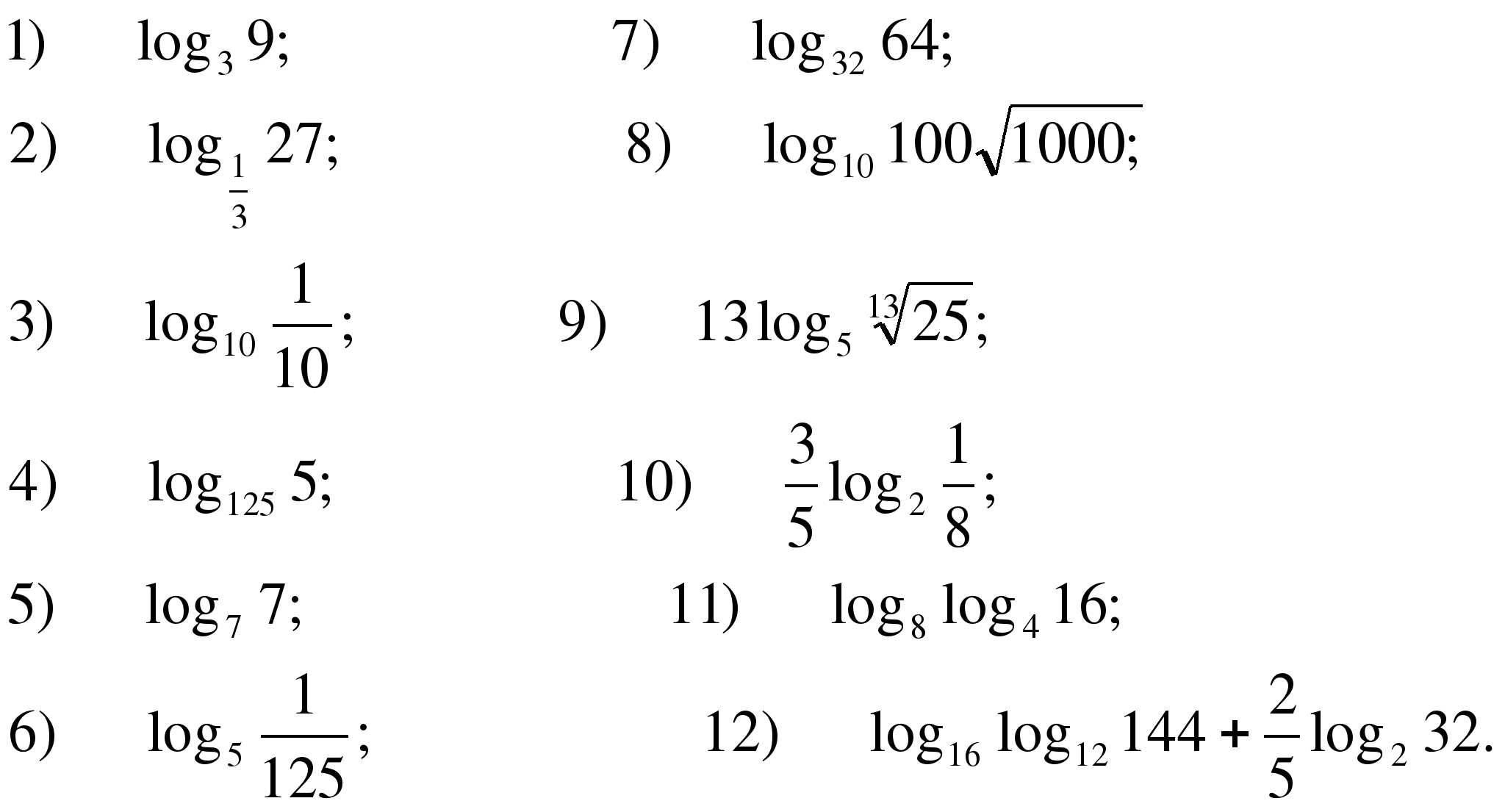
13)log2 12+log2 5 – log2 15 14)log15 5√ 225 15)3 1+log32
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 9
1. Вычислите логарифм:
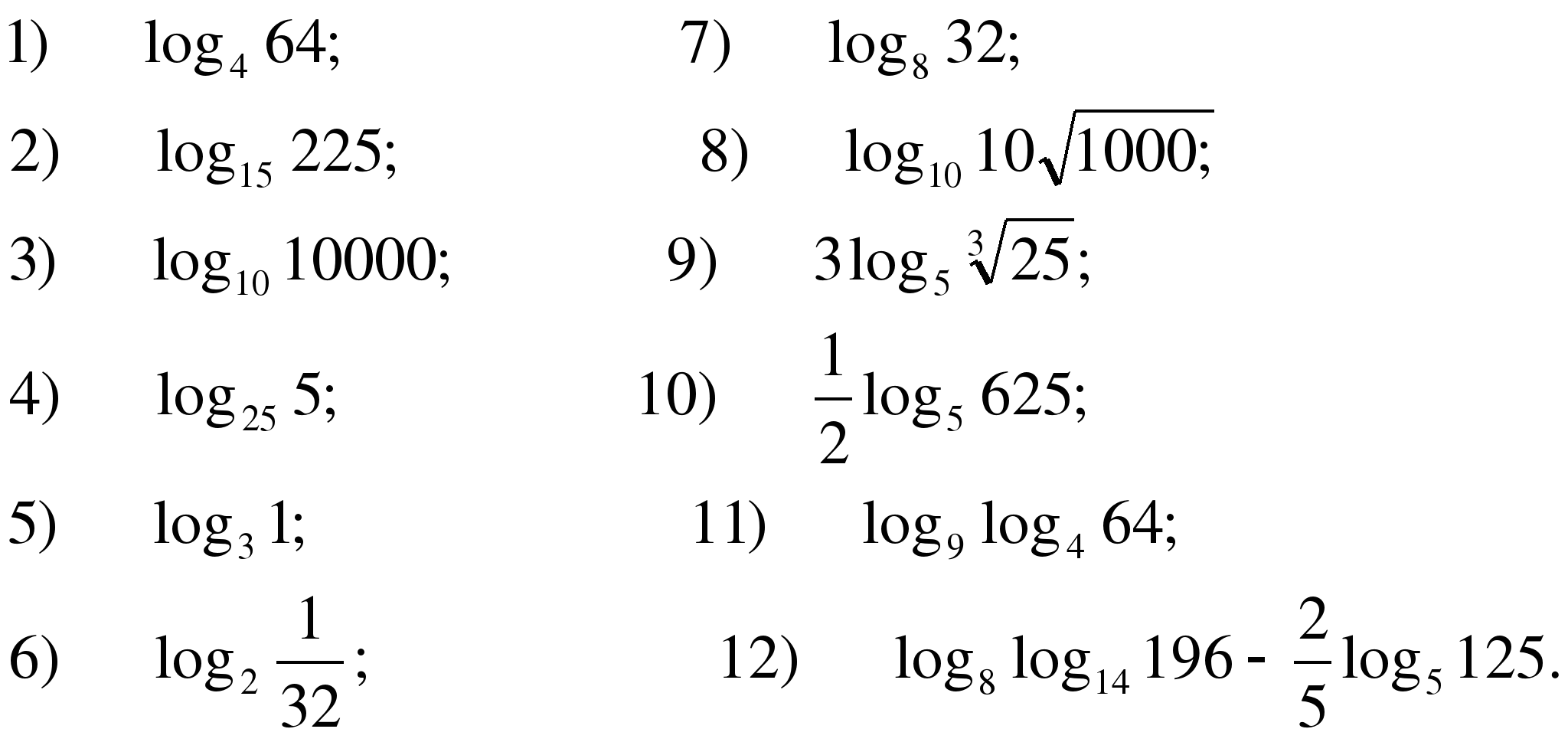
13)log2 48 – log2 3 + log3 1
14)log5 4√ 5
15)3 2 + log35
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 10
1. Вычислите логарифм:

13)log2 20 – log2 15 + log2 24
14)log14 3√ 196
15)4 1 + log43
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 11
1. Вычислите логарифм:
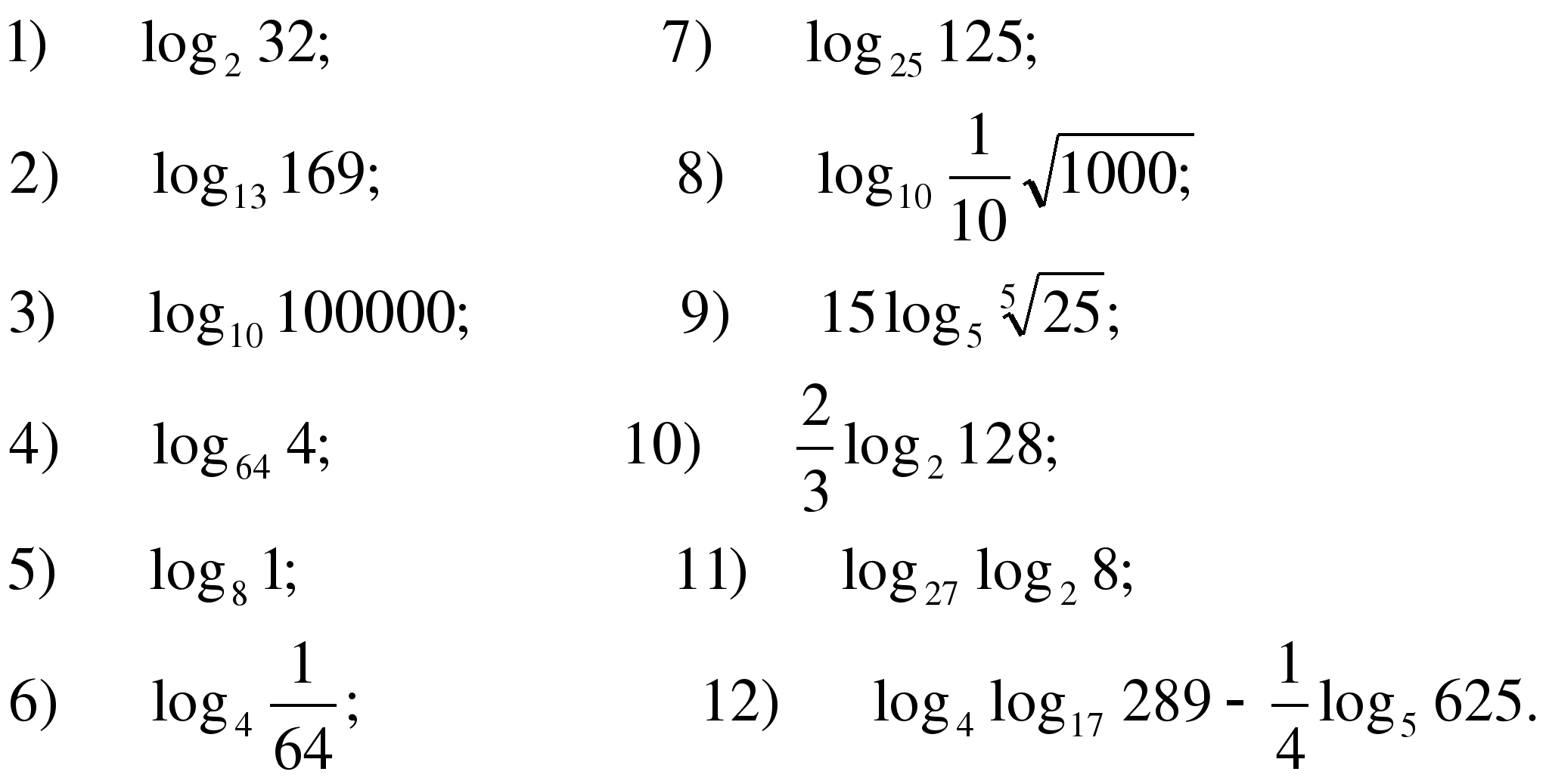
13) log3 18 + log3 12 – log3 8
14) log7 3√ 49
15) 5 1 + log52
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 12
1. Вычислите логарифм:
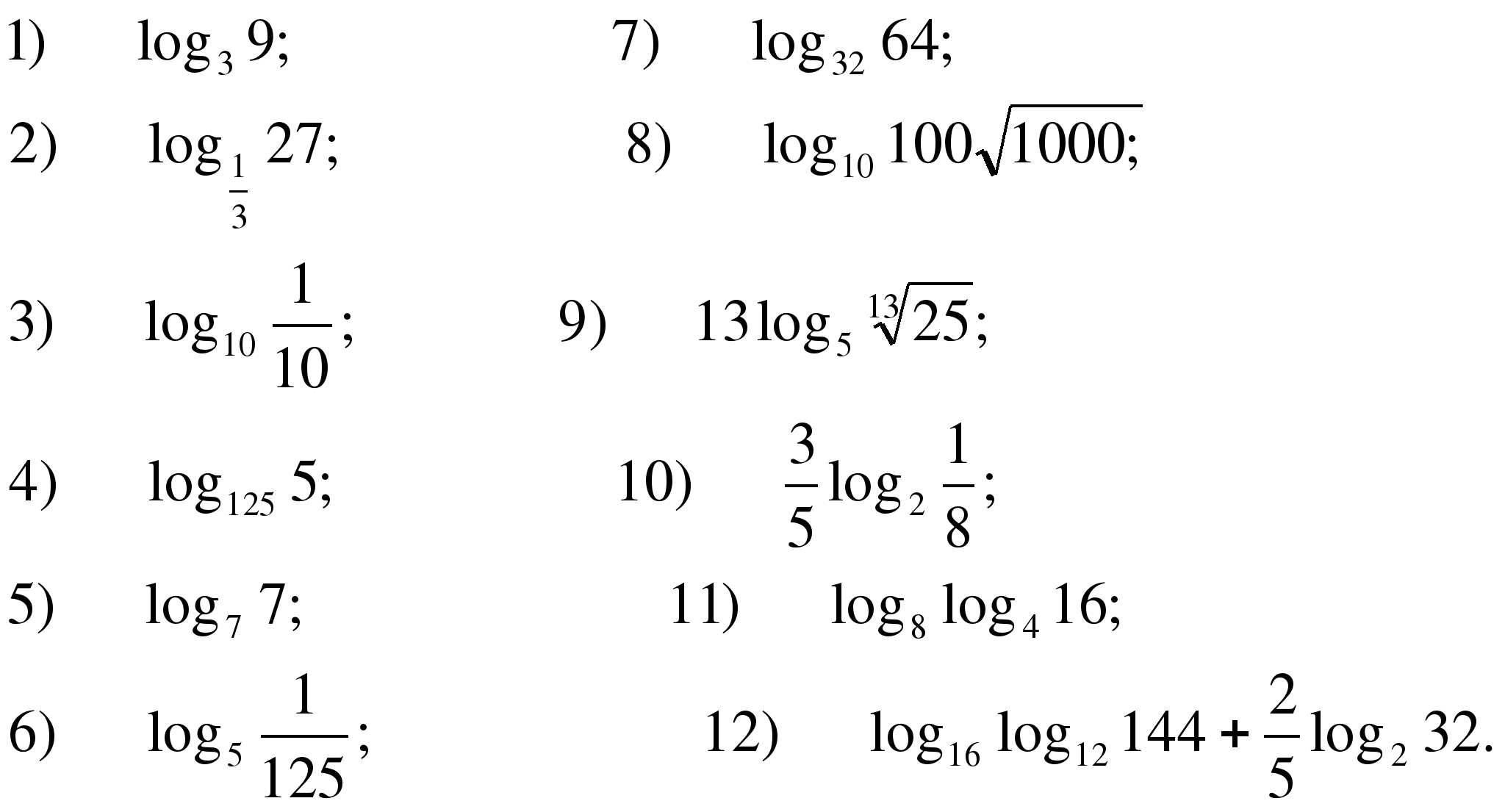
13) log4 12 – log4 15+ log4 20
14) log6 2√ 216
15) 5 2 + log52
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 13
1. Вычислите логарифм:
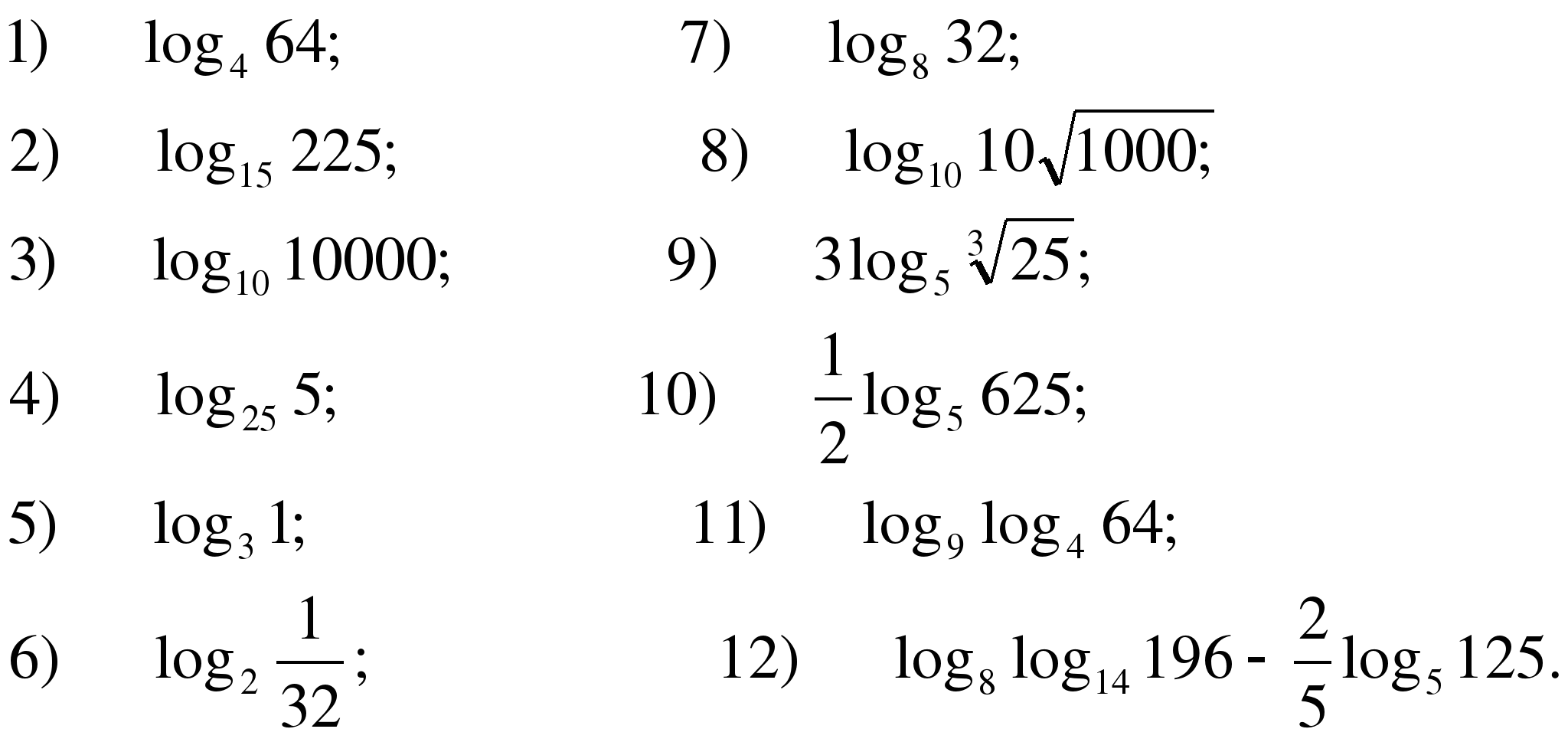
13) log5 10 – log5 6+ log5 15
14) log8 3√ 64
15) 2 3 + log23
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 14
1. Вычислите логарифм:

13) log4 28 – log4 21+ log4 12
14) log16 3√ 256
15) 2 log29 – 1
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 15
1. Вычислите логарифм:
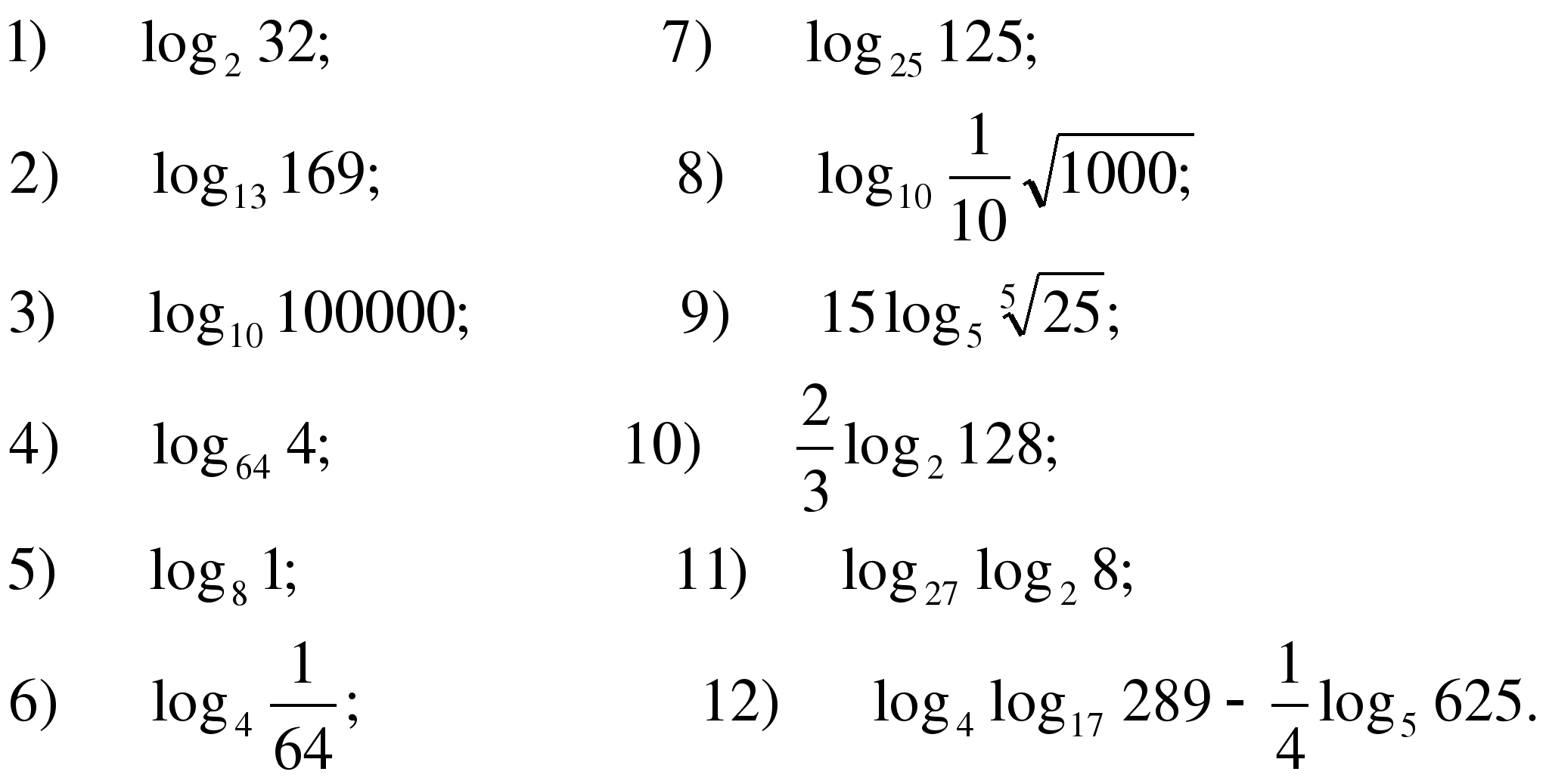
13) log2 28 + log2 12 – log2 21
14) log3 4√ 9
15)2 log211 – 1
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 16
1. Вычислите логарифм:
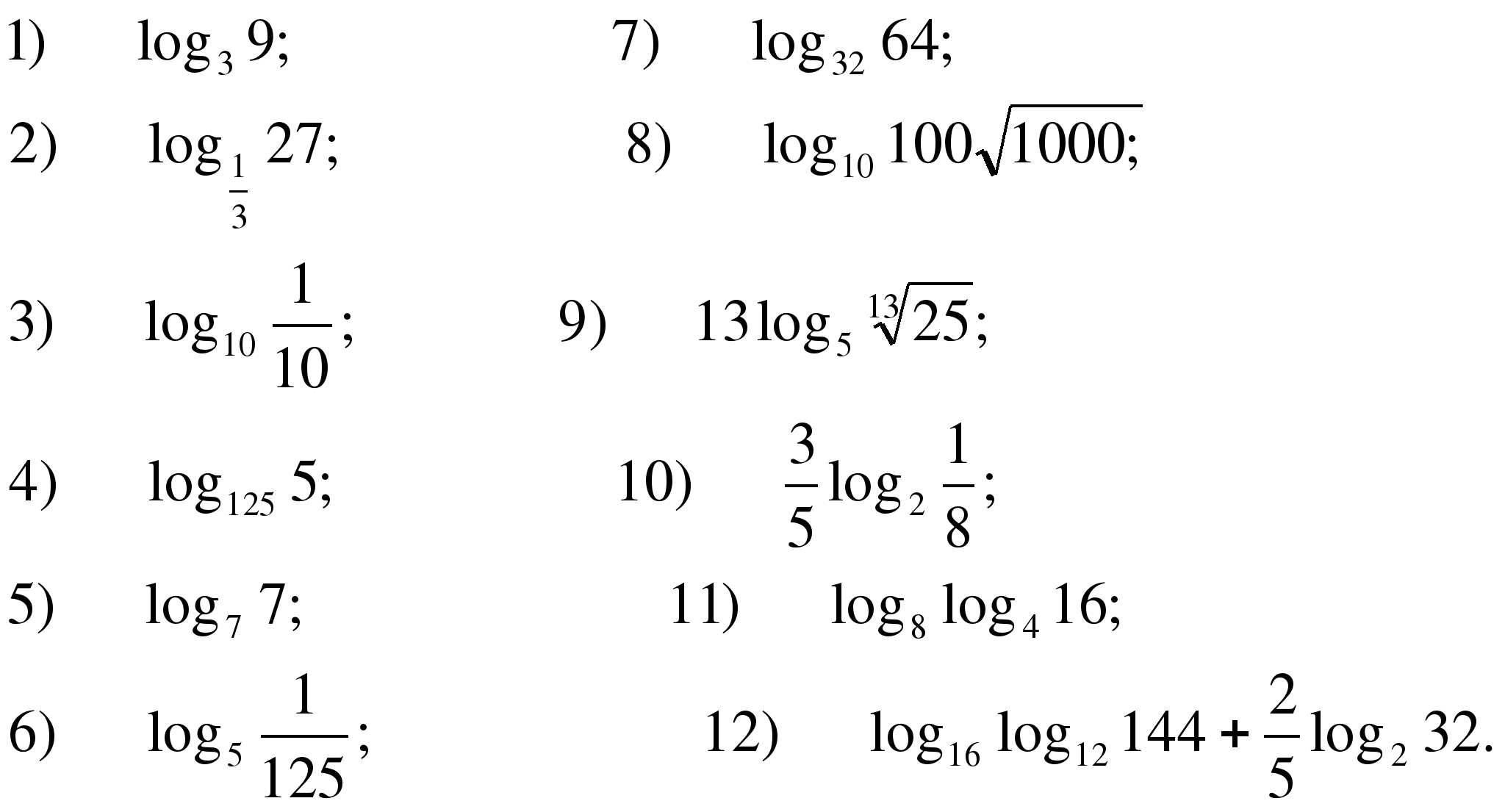
13)log3 21 + log3 15 – log3 35
14)log3 3√ 9
15) 3 log34 – 2
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 17
1. Вычислите логарифм:
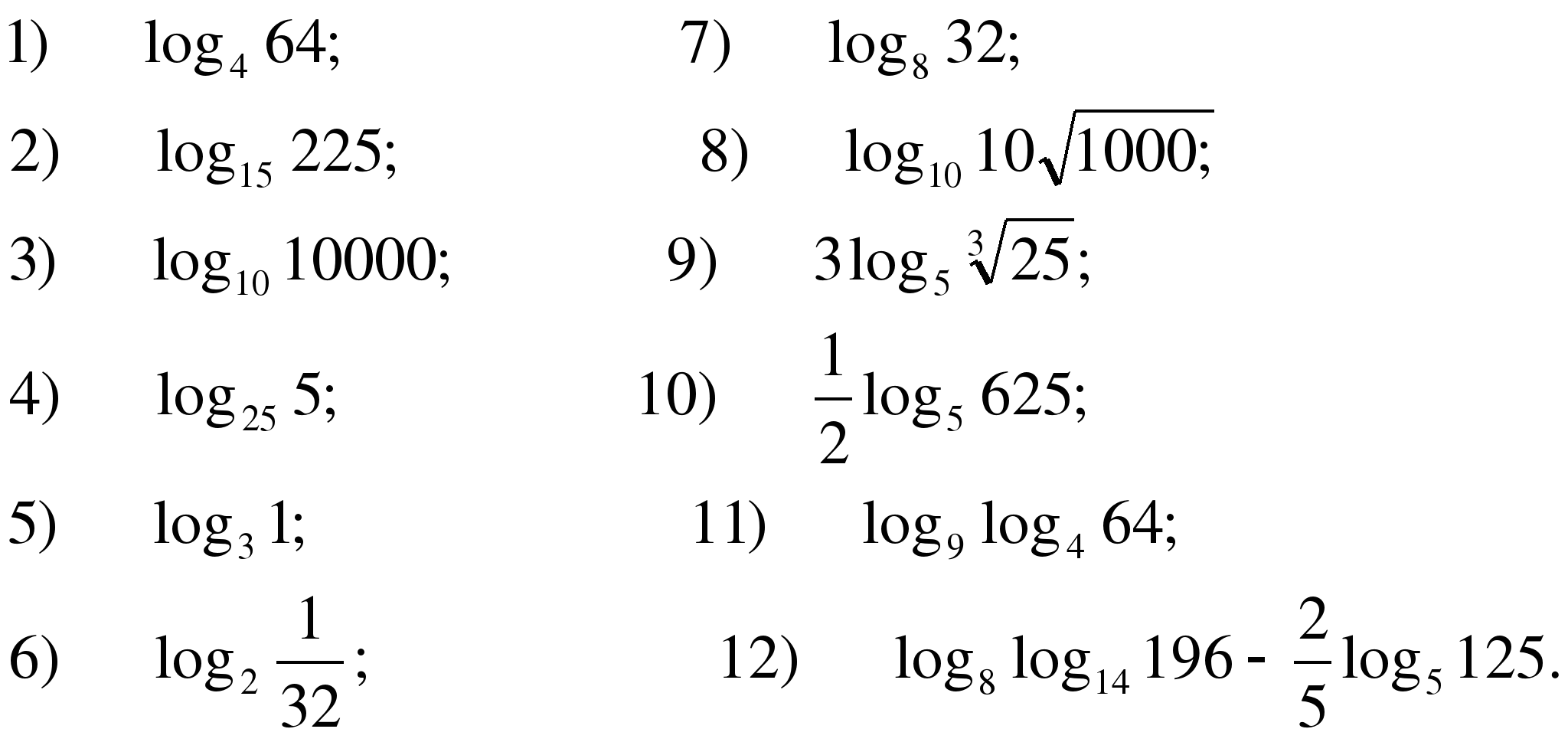
13) log3 15 – log3 20 + log3 12
14)log2 5√ 16
15) 2 3 log23
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 18
1. Вычислите логарифм:

13) log3 36 + log315– log3 20
14) log11 5√ 121
15) 2 3 log25
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 19
1. Вычислите логарифм:
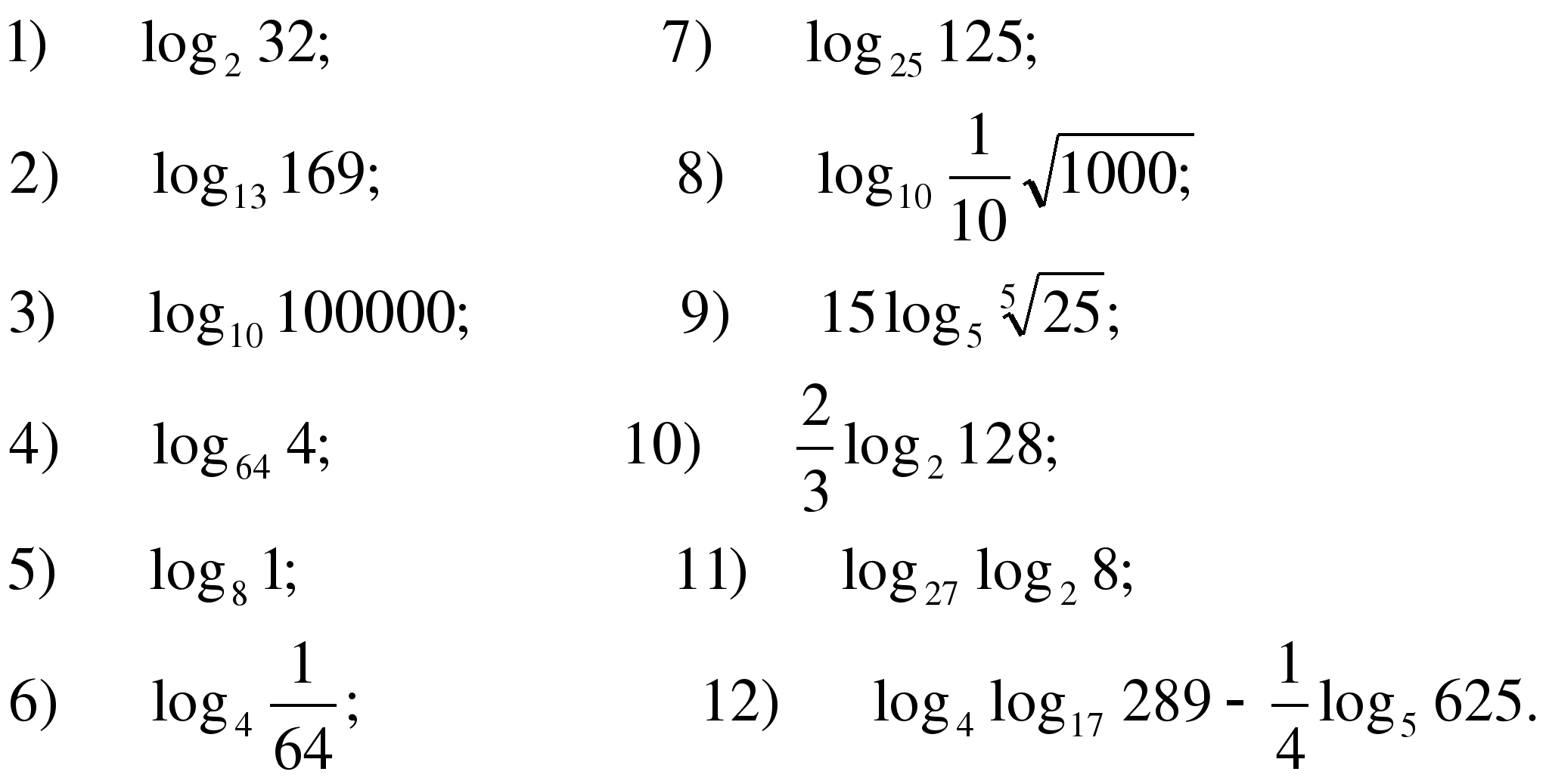
13) log2 24 + log2 14 – log2 21
14) log4 √ 64
15) 3 2 log32
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 20
1. Вычислите логарифм:
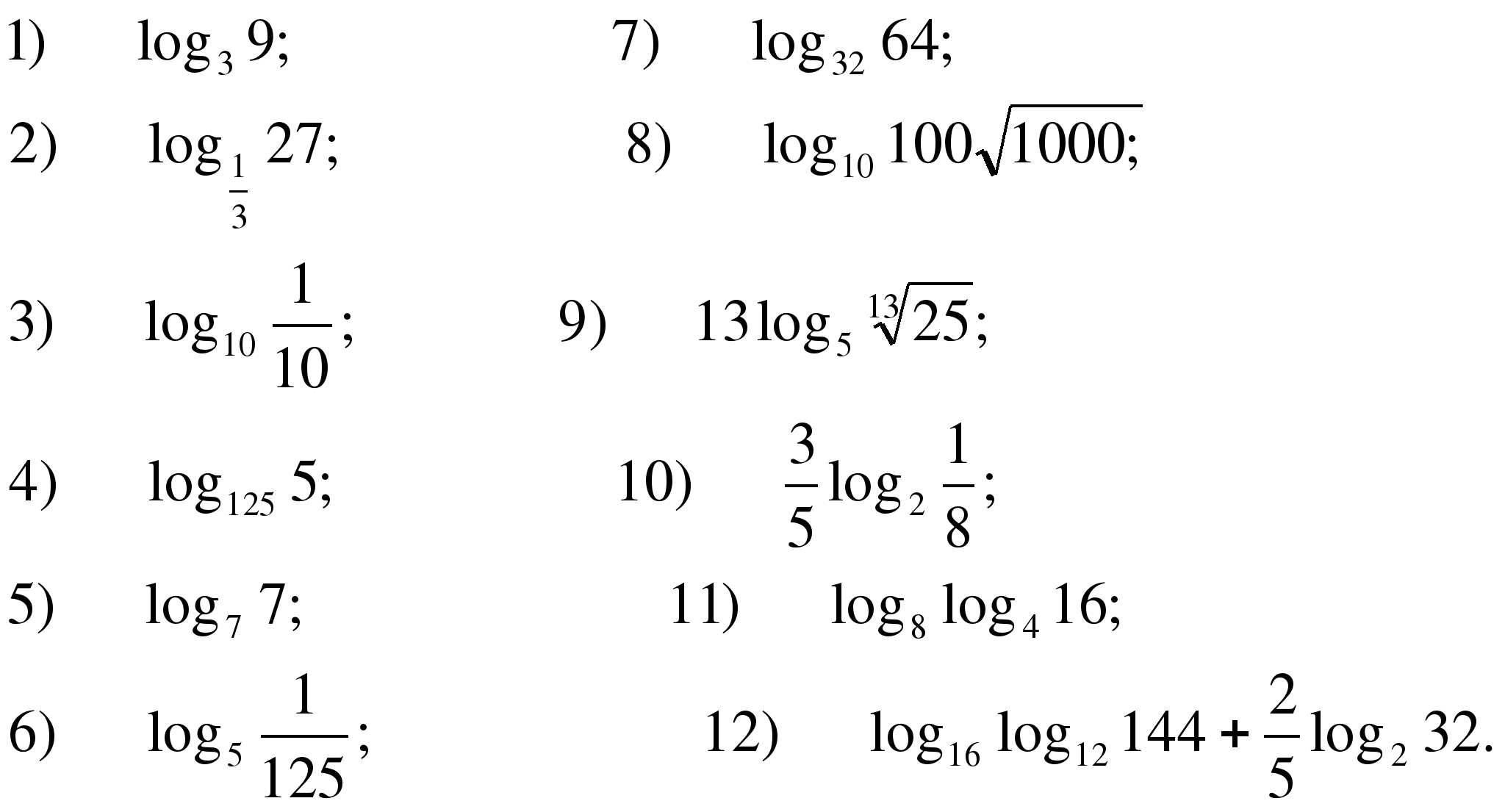
13log256 + log2 6 – log2 21
14) log15 3√ 225 15)7 2 log72
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 21
1. Вычислите логарифм:
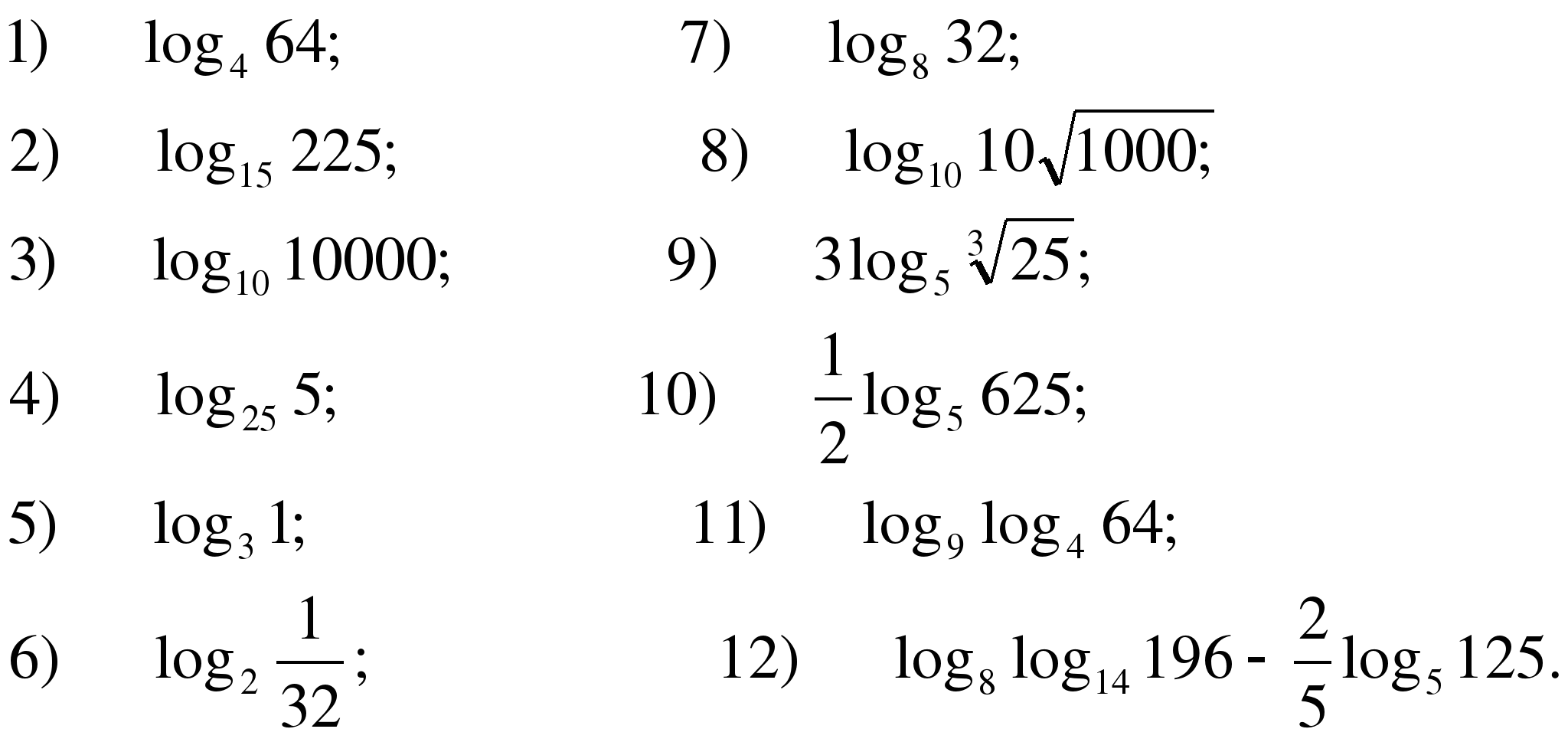
13) log9 18 – log9 14 + log9 63
14) log5 3√ 25
15) 7 1 + log72
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 22
1. Вычислите логарифм:

13) log3 18+ log3 63 – log3 14
14) log15 3√ 15
15) 7 1 + log73
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 23
1. Вычислите логарифм:
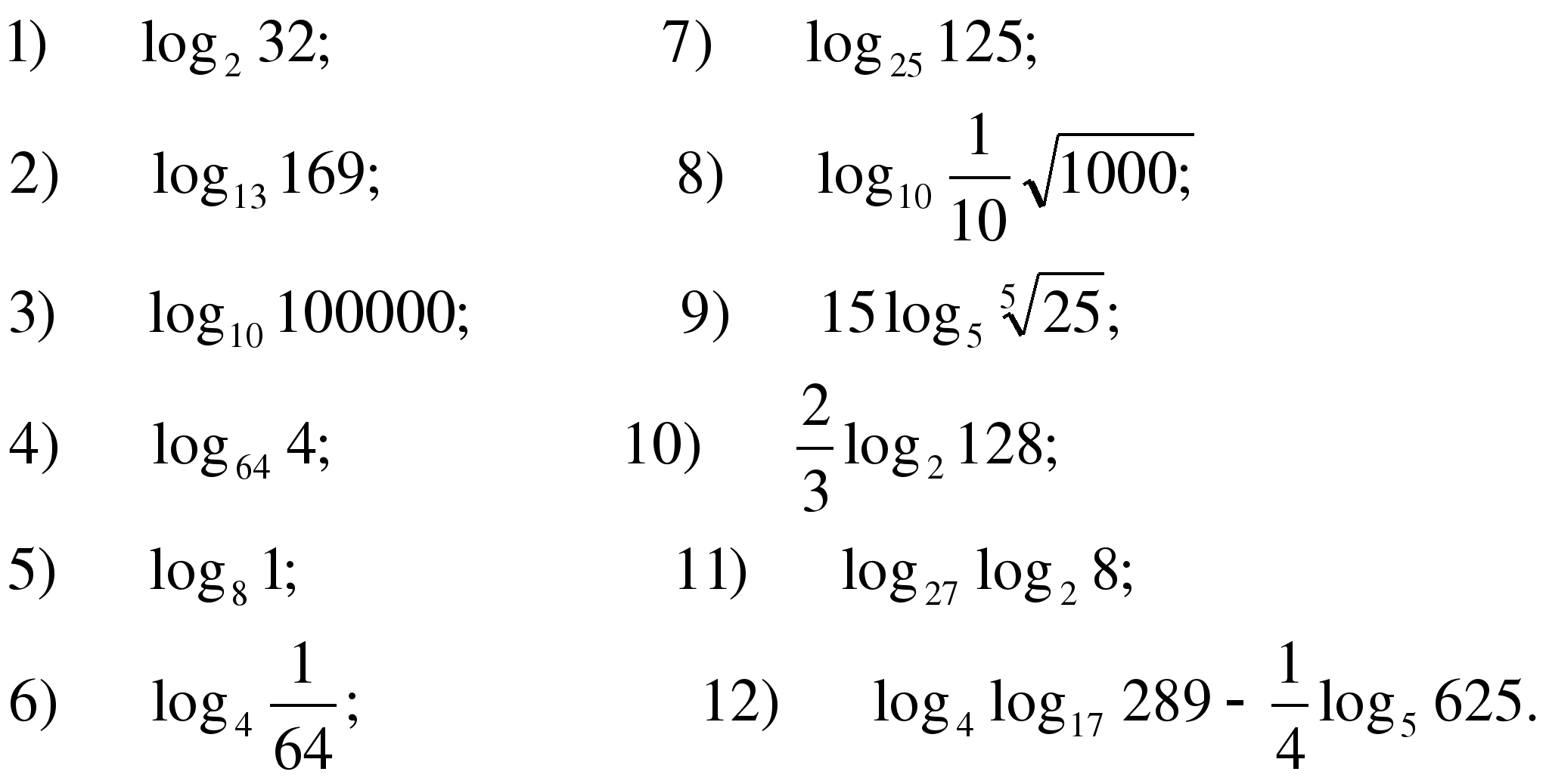
13) log3 75 – log3 25+ log7 7
14) log17 4√ 17
15) 6 1 + log65
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 24
1. Вычислите логарифм:
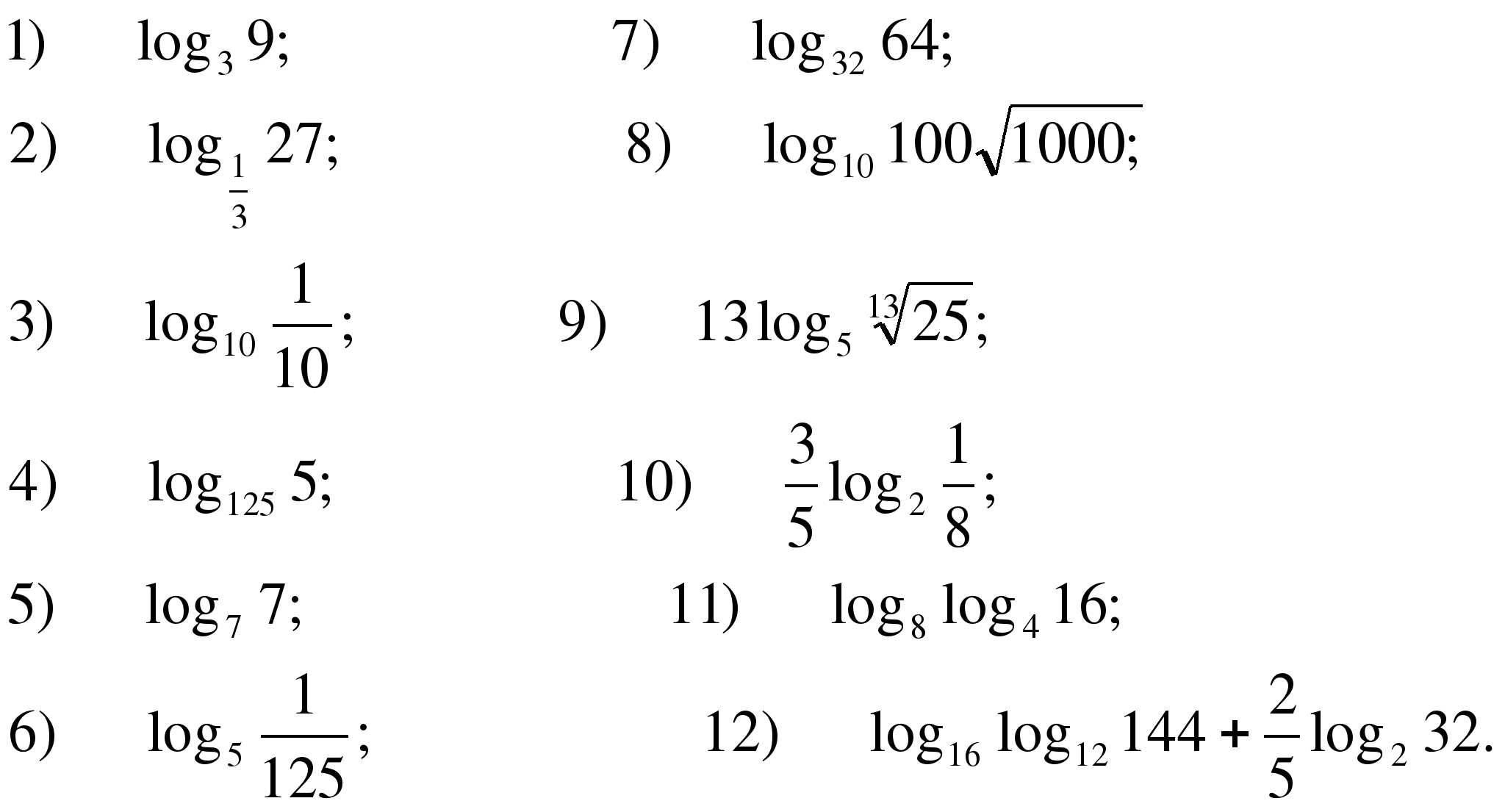
13) log2 8 + log5 75 – log5 3
14) log93√ 81
15) 6 1 + log62
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 25
1. Вычислите логарифм:
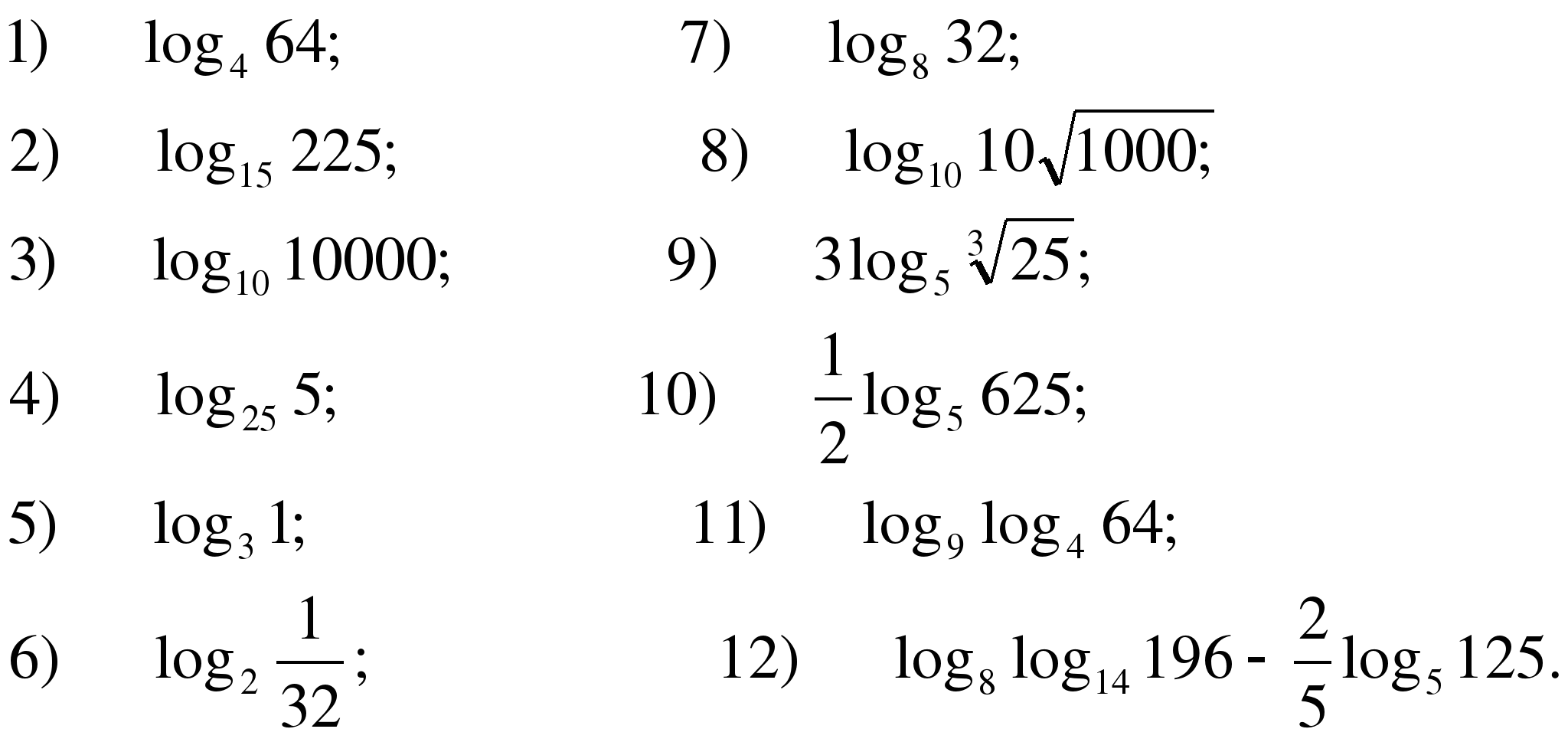
13) log3 9 + log5 100 – log5 4
14)log9 3√ 9
15) 6 1 + log63
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 26
1. Вычислите логарифм:

13) log5 5/6 + log5 2 + log5 15
14) log2√ 32
15) 5 2 log53
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 27
1. Вычислите логарифм:
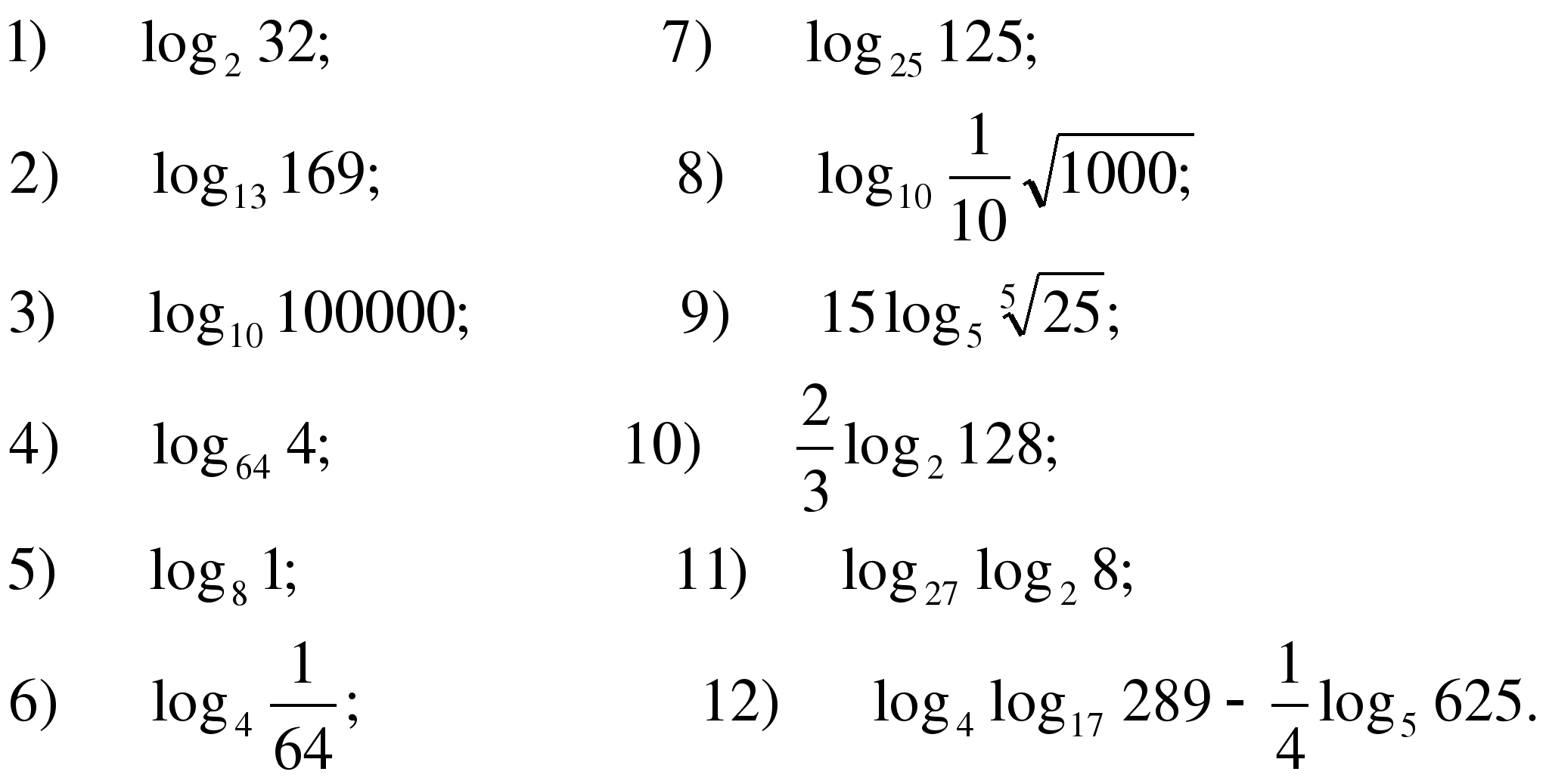
13) log5 50 + log5 15 – log5 6
14) log6 3√ 36
15) 7 3 log72
Самостоятельная работа по теме: «Вычисление логарифмов»
№ 28
1. Вычислите логарифм:
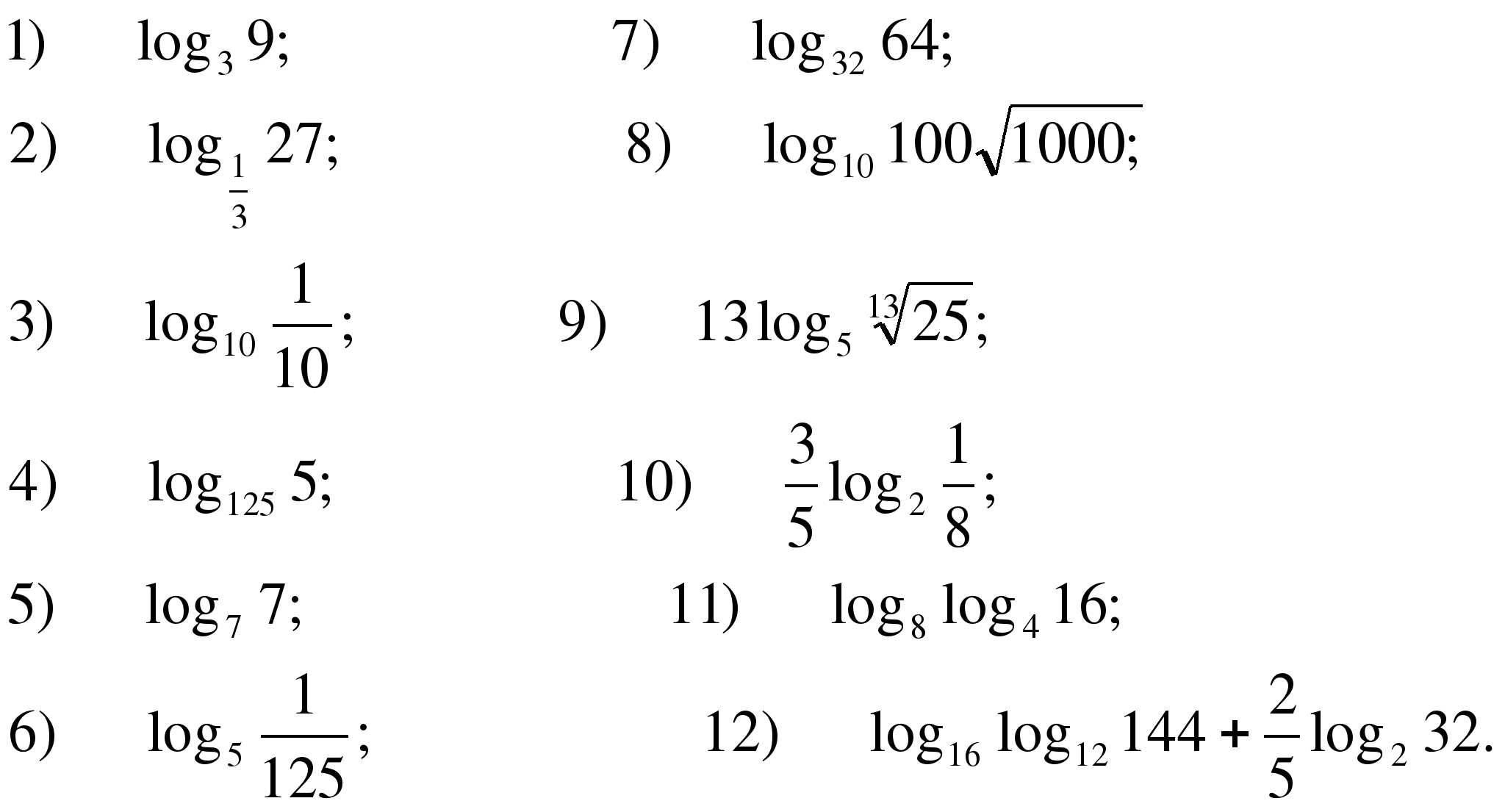
13) log9 18 – log9 14 + log9 63
14) log5 3√ 25
15) 7 1 + log72
Конспект открытого урока и презентация по теме «Логарифмы. Подготовка к ЕГЭ»
Урок математики в 11 классе
Тема урока: Логарифмы. Свойства логарифмов. Решение заданий ЕГЭ. (Слайд 1)
Тип урока: закрепление полученных знаний.
Цели урока:
Образовательные:
обобщить имеющиеся у учащихся знания о логарифмах, их свойствах;
продолжить формирование умения использовать свойства логарифмов для
преобразования логарифмических выражений, решения уравнений;
логарифмическое тождество и свойства логарифмов;
приемами решения простейших логарифмических уравнений.
Развивающие:
способствовать развитию внимания, логического, аналитического мышления,
памяти;
Воспитательные:
формировать навыки общения, умения работать в коллективе, внимательно
выслушивать мнение других;
Оборудование:
персональный компьютер учителя;
мультимедийный проектор, экран;
презентация к уроку;
компьютеры для учащихся;
раздаточный материал: сопроводительный лист с заданиями и оценочной таблицей, справочный материал.
Учебно-методический комплект:
Учебник: А.Г. Мордкович. Алгебра и начала математического анализа, 11 класс, М., «Мнемозина», 2014 г., 2-е издание
Задачник: А.Г. Мордкович. Алгебра и начала математического анализа, 11 класс, М., «Мнемозина», 2014 г., 2-е издание
Основные этапы урока:
Организационный момент.
Актуализация знаний.
Формулирование темы урока, постановка целей и задач урока.
Закрепление знаний.
Блиц – опрос.
Рефлексия.
Подведение итогов урока.
Инструктаж по домашнему заданию.
Ход урока:
Организационный момент
— Здравствуйте, ребята, садитесь. Наш урок я хочу начать словами канадско-американского математика Айвена Нивена:
“Нельзя изучать математику, наблюдая за тем, как это делает другой”
(слайд 2)
Поэтому сегодня каждый из вас будет самостоятельно оценивать свою работу на уроке. Для этого на парте у вас лежат сопроводительные листы, в которых представлена оценочная таблица
(слайд 3)
Этапы урокаТеоретическая
разминка
Работа
в группах
Работа
в парах
Инд. работа
Блиц-опрос
Общее количество баллов за урок
Определение
и свойства логарифмов
Буквенные выражения
Уравнения
Вычислить логарифм, решить уравнение
3 балла
Хорошо знаю определение и свойства
Мне понятен ход решения
Решено верно 2 уравнения, каждое своим способом
Смог(ла) найти приём решения и применить его
5 правил.
ответов
2 балла
Знаю определение, но путаюсь в свойствах
Мне помогли (подсказали) в группе
Решено верно 1 уравнение
Смог(ла) найти подобное уравнение, но не могу применить приём
3-4 правил.
ответов
1 балл
Плохо знаю теорию
Я наблюдаю как решают остальные
Нет верно решенных
Не смог(ла) найти подобное уравнение
0-2 правил.
ответов
Баллы
по этапам урока
После каждого этапа урока вам необходимо оценить свою учебную деятельность и проставить определенное количество баллов. В конце урока вы сможете определить, на каком уровне изучения темы вы находитесь и получить рекомендации к дальнейшему ее изучению.
Актуализация знаний (теоретическая разминка) (Слайд 4)
— Повторим свойства логарифмов, которые мы с вами изучили на предыдущих уроках (слайд 5):

Вопросы:
(Слайд 6) Что называется логарифмом?
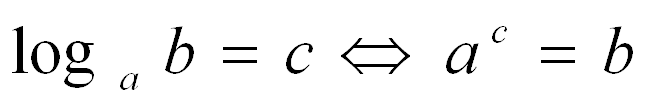 a>0, a≠1, b>0
a>0, a≠1, b>0
(Слайд 7) Какой логарифм называется десятичным?
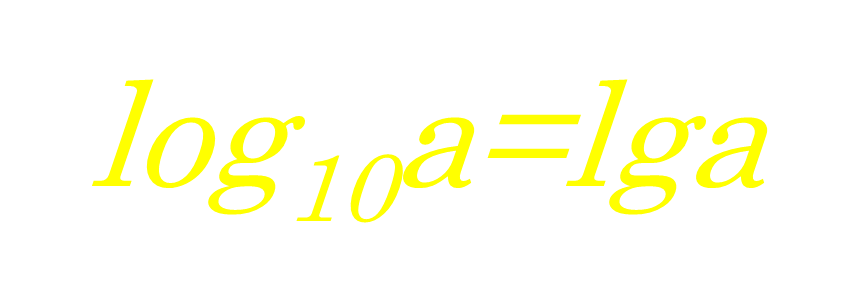
(Слайд 8) Что называется логарифмированием?
(Операцию нахождения логарифма числа называют логарифмированием)
(Слайд 9) Найдите ошибки в записях свойств логарифмов:
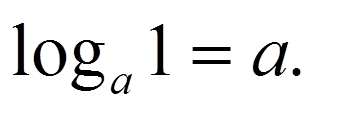
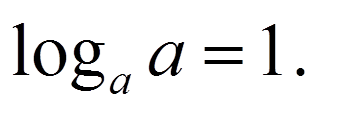

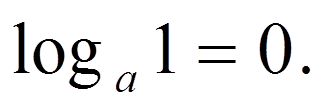
(Слайд 10)
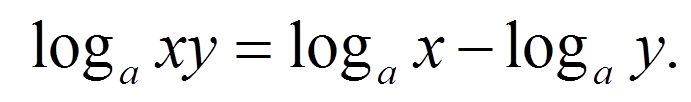
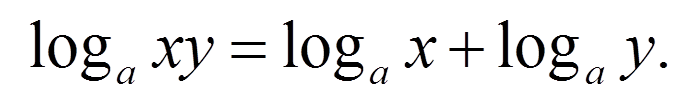
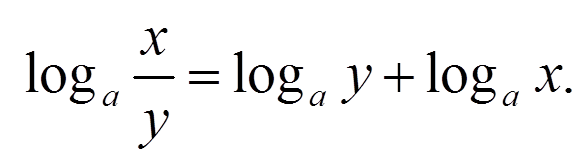
log х / у = log х – log у
(Слайд 11)
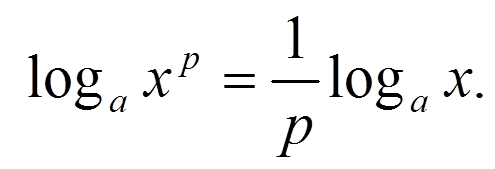
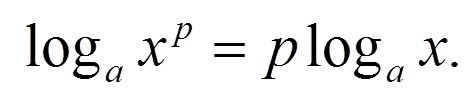
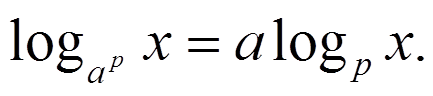
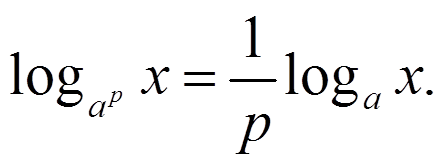
(Слайд 12)
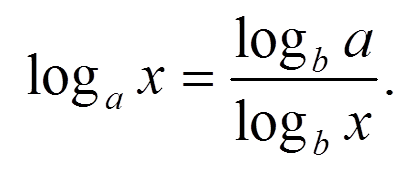
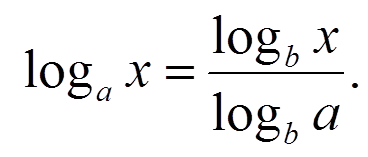
Итак, мы повторили необходимый материал. Оцените свою работу на данном этапе урока, проставьте баллы в оценочной таблице. (Слайд 13)
На что вы опирались при выполнении заданий? (Ответ: На свойства логарифмов).
Формулирование темы урока, постановка целей и задач урока
(Слайд 14) Задания такого типа представлены в Едином Государственном Экзамене. Кроме этого в задании 6 – простейшие логарифмические уравнения.
В КИМах экзамена есть задания повышенной трудности – решение логарифмических уравнений с опорой на свойства логарифмов.
Какова тема урока?
(Ответ: Свойства логарифмов. Подготовка в ЕГЭ) (Слайд 15)
Какова цель урока?
(Ответ: Подготовиться к ЕГЭ) (слайд 16)
Какие задачи для этого нам нужно выполнить?
(Ответ: 1. Вспомнить свойства логарифмов, свойства степеней;
2. Научиться решать простейших логарифмические уравнения;
3. Развивать внимание, мышление, память.
4. Воспитывать познавательный интерес к математике. (слайд 16)
Закрепление знаний.
(Слайд 17) Рассмотрим преобразование буквенного логарифмического выражения.

Работа в группах: задания на (Слайд 18)

Известно, что:
Логарифм в по основанию а равен 5
Логарифм в по основанию а равен 3
Логарифм в по основанию а равен 7
Результат на (слайде 19).

И вновь оцените свою деятельность на этапе работы в группах, проставьте баллы в оценочную таблицу (Слайд 20)
Рассмотрим два способа решения простейшего логарифмического уравнения. (Слайд 21)

Работа в парах: задание на (слайде 22)
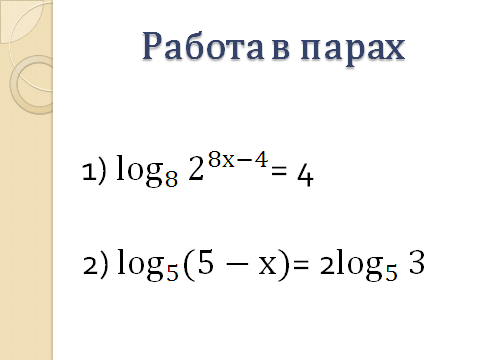
Результат на (слайде 23)

Проставьте баллы в таблицу (Слайд 24)
Индивидуальная работа (Слайд 25) Ответы (Слайд 26)
Выставляем оценку за индивидуальную работу в таблицу (Слайд 27)
Блиц-опрос (Слайд 28)
И напоследок еще раз проверим себя, насколько каждый владеет определением и свойствами логарифмов. В сопроводительных листах необходимо ответить только «да» или «нет». (Слайд 29)
- Подлогарифмическое выражение всегда должно быть больше нуля
да
Основание логарифма всегда строго больше нуля
нет
Логарифм частного равен разности логарифмов
да
Логарифм произведения равен произведению логарифмов
нет
Если подлогарифмическое выражение записано в виде степени, то показатель можно вынести вперед и умножить на логарифм основания
да
Не забудьте оценить свою работу в оценочной таблице (Слайд 30)
Этапы урокаТеоретическая
разминка
Работа в группах
Работа в парах
Инд. работа
Блиц-опрос
Общее количество баллов за урок
Определение
и свойства логарифмов
Буквенные выражения
Уравнения
Уравнение повышенной сложности
3 балла
Хорошо знаю определение и свойства
Мне понятен ход решения
Решено верно 2 уравнения, каждое своим способом
Смог(ла) найти приём решения и применить его
5 правил.
ответов
2 балла
Знаю определение, но путаюсь в свойствах
Мне помогли (подсказали) в группе
Решено верно 1 уравнение
Смог(ла) найти подобное уравнение, но не могу применить приём
3-4 правил.
ответов
1 балл
Плохо знаю теорию
Я наблюдаю как решают остальные
Нет верно решенных
Не смог(ла) найти подобное уравнение
0-2 правил.
ответов
Баллы
по этапам урока
Рефлексия. Посчитайте количество баллов за урок. (Слайд 31)
Согласно полученным баллам прочитайте, на каком уровне вы находитесь и рекомендации к дальнейшему изучению темы.
БаллыУровень
Рекомендации
Оценка
13-15 баллов
Я хорошо ориентируюсь в этой теме: знаю все определения и свойства; могу свободно применять полученные знания при решении заданий ЕГЭ; знаю, где можно найти приёмы решения сложных заданий.
В дальнейшем мне можно рассматривать решение заданий повышенной трудности.
5
10-12 баллов
Я ориентируюсь в свойствах, но не всегда могу применить их на практике при решении заданий ЕГЭ; знаю, где можно найти решение сложных заданий, но не всегда понятны приёмы, используемые в процессе решения.
Мне нужно отрабатывать решение заданий базовой части ЕГЭ и рассматривать решение заданий повышенной трудности.
4
7-9 баллов
Я слабо ориентируюсь в свойствах и не могу применить их на практике самостоятельно; решение многих заданий мне понятно только после обсуждения/объяснения
Мне необходимо учить определение логарифма числа и свойства логарифмов; нужно отрабатывать решение заданий базовой части ЕГЭ.
3
5-6 баллов
Мне сложно ориентироваться в заданиях, непонятно какие свойства нужно применять для решения заданий базового уровня.
Мне нужно начать учить свойства и отрабатывать решение простейших заданий.
2
Какую оценку вы поставите себе за урок? (слайд 31)
Подведение итогов урока.
Пожалуйста, подведите итог урока. Реализовали ли мы поставленные задачи? Каким образом?
(Ответ: 1. Вспомнили свойства логарифмов,
решали задания на преобразования логарифмичских выражений,
решали простейшие логарифмические уравнения
Можно ли сделать вывод, что мы справились с поставленной целью?
(Ответ: мы готовились к ЕГЭ по теме «Логарифмы»)
Инструктаж по домашнему заданию (Слайд 32)
Основное: повторить свойства логарифмов, № 17.19, № 17.23.
Дополнительное: С помощью Интернет-ресурсов найдите уравнения и неравенства повышенной трудности, принцип решения которых вам непонятен.
СПАСИБО ЗА УРОК ! (Слайд 33)
Методическая разработка по теме «Логарифмы»
Министерство образования Московской области
Государственное бюджетное образовательное учреждение среднего профессионального образования
«Российский художественно – технический колледж игрушки»»
ЛОГАРИФМЫ
Методические указания к решению упражнений
при изучении темы «Свойства логарифмов»
рассмотрены и одобрены на заседании предметной (цикловой) комиссии общеобразовательного и социально-экономического циклов
Протокол № _______ от «____» __________20____ г.
Председатель ПЦК ___________ М.В. Рыбалкина
2012 г.
Логарифмы: Методические указания / Сост. Рыбалкина М.В. – Сергиев — Посад: ,
2012– 13с.
Данные методические указания содержат необходимые теоретические сведения по теме «Логарифмы» дисциплины математика, примеры решения упражнений, набор упражнений для самостоятельного решения с ответами к некоторым из них, десять вариантов для выполнения контрольной работы.
Содержание
Введение…………………………………………………………………………………………………………..4
Определение логарифма ……………………………………………………………………5
Примеры для самостоятельного решения………………..…………….7
Преобразование логарифмических выражений………………..…………….7
Примеры для самостоятельного решения…………………………………..9
Контрольная работа по теме: «Свойства логарифмов»………………….11
Список литературы ………………………………………………………………….…………14
Введение
Настоящие методические указания предназначены в помощь учащимся всех форм обучения при изучении темы «Свойства логарифмов». Разделы указаний содержат необходимые теоретические сведения (определения, формулы без доказательства) и подробно разобранные упражнения. В конце каждого раздела предлагаются задания для самостоятельного решения с ответами для самопроверки.
Теоретические сведения и примеры для самостоятельного решения дают возможность использовать данные методические указания на практических занятиях по математике, а также для самостоятельного изучения темы «Свойства логарифмов».
В конце указаний приведены десять вариантов заданий для выполнения контрольной работы.
Определение логарифма
Понятие логарифма числа вводится при решении показательных уравнений, например, решим уравнение 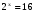 , в котором необходимо найти показатель х, представим правую часть уравнения в виде двух в четвертой степени
, в котором необходимо найти показатель х, представим правую часть уравнения в виде двух в четвертой степени 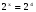 . В этом уравнении удалось левую и правую части представить в виде степени с одинаковым основанием 2. Ответ такого уравнения
. В этом уравнении удалось левую и правую части представить в виде степени с одинаковым основанием 2. Ответ такого уравнения 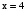 . Но уравнение
. Но уравнение 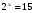 таким способом решить не удается. А корень все-таки есть. Этот корень называют логарифмом числа b по основанию а и обозначают logаb. Например, корнем уравнения
таким способом решить не удается. А корень все-таки есть. Этот корень называют логарифмом числа b по основанию а и обозначают logаb. Например, корнем уравнения 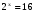 является число 4, т.е log216=4.
является число 4, т.е log216=4.
Из определения следует, что записи logаb=х. и ах=b равносильны.
Например, log28=3, потому что при возведении основания 2 в степень 3 получается 8: 23=8, действительно 2 2
2 2=23=8. Значит в результате вычисления логарифма 8 по основанию 2 получается показатель степени двойки, при возведении в которую получаем восемь.
2=23=8. Значит в результате вычисления логарифма 8 по основанию 2 получается показатель степени двойки, при возведении в которую получаем восемь.
Определение логарифма можно кратко записать так: 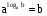 . Это равенство справедливо при b>0, a>0, а
. Это равенство справедливо при b>0, a>0, а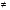 1. Его обычно называют основным логарифмическим тождеством.
1. Его обычно называют основным логарифмическим тождеством.
Для вычислений значений логарифмов полезно использовать значения степени следующих чисел:
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
210 = 1024
31 = 3
32 = 9
33 = 27
34 = 81
35 = 243
41 = 4
42 = 16
43 = 64
44 = 256
45 = 1024
51 = 5
52 = 25
53 = 125
54 = 625
61 = 6
62 = 36
63 = 216
71 = 7
72 = 49
73 = 343
81 = 8
82 = 64
83 = 512
91 = 9
92 = 81
93 = 729
101 = 10
102 = 100
103 = 1000 и т.д.
Также необходимо помнить правила возведения чисел в степень с отрицательным, дробным и нулевым показателем: а0=1; 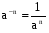 ;
; 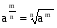
Пример 1. 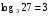 , т.к. 33=27
, т.к. 33=27
Пример 2. 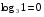 , т.к. 30=1
, т.к. 30=1
Пример 3. 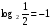 , т.к. 2-1=
, т.к. 2-1=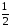
Пример 4. Вычислить 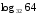
Пусть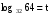 . По определению логарифма 32t=64. Это простейшее показательное уравнение. 32=25, 64=26, поэтому (25)t=26; 25t=26 ; 5t=6, t=
. По определению логарифма 32t=64. Это простейшее показательное уравнение. 32=25, 64=26, поэтому (25)t=26; 25t=26 ; 5t=6, t=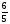
Ответ: 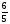
Пример 5. Вычислить 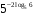
Используя свойства степени и основное логарифмическое тождество, находим 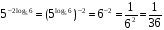
Пример 6. 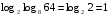
Для некоторых логарифмов имеются специальные обозначения: десятичный log10х=lgx, натуральный logех=lnx.
Пример 7. lg1000=3 , т.к. 103=3
Пример 8. lg0,01=-2 , т.к. 10-2=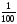 =0,01
=0,01
Примеры для самостоятельного решения:
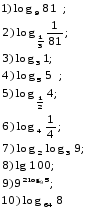
Ответы:
№ задания
1
2
3
4
5
6
7
8
9
10
ответ
2
4
0
1
-2
-1
1
2
25
0,5
Преобразование логарифмических выражений
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются различные свойства логарифмов. Рассмотрим основные из них.
Пусть а>0, а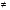 1, b>0, с>0, p – любое действительное число. Тогда справедливы формулы
1, b>0, с>0, p – любое действительное число. Тогда справедливы формулы
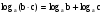 (1)
(1)
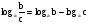 (2)
(2)
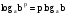 (3)
(3)
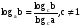 (4)
(4)
 (5)
(5)
Формулы (1) и (2) можно применять к выражениям, содержащим логарифмы с одинаковыми основаниями.
Формулы (4) и (5) позволяют переходить от одного основания логарифмов к другому.
Пример 1. Вычислить: 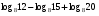
На основе формул (1) и (2) преобразуем 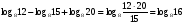
Теперь можно применить формулу (4), т. е. перейти к новому основанию, в данном примере логарифмы чисел 16 и 8 легко вычислить при основании 2, тогда 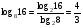
Пример 2. Вычислить 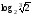
Применим формулу (3), для этого вспомним определение степени с рациональным показателем (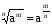 ), тогда
), тогда 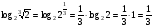
Пример 3. Зная, что 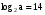 , найти
, найти 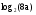
Применяем формулу (1) 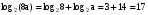
Пример 4. Прологарифмировать выражение 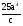 по основанию 5.
по основанию 5.
Запишем данное выражение в виде 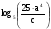
Теперь применим формулы (1), (2) и (3) 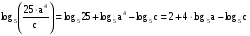
Пример5. Найти х по данному его логарифму (а>0,b>0): 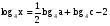
В этом примере необходимо правую часть представить в виде одного логарифма по основанию 4: 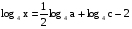
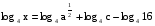 (2 представили в виде log416)
(2 представили в виде log416)
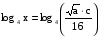 (применили формулы (1), (2) и (3))
(применили формулы (1), (2) и (3))
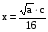
Примеры для самостоятельного решения:







Зная, что
 , найти
, найти 
Прологарифмировать выражение
 по основанию 10.
по основанию 10.Найти х по данному его логарифму (а>0,b>0):

Ответы:
№ задания
1
2
3
4
5
6
7
8
9
10
ответ
9
1
1,5
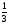
1
2
1,5
0,6
-1+2lga-lgn
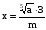
Контрольная работа по теме: «Свойства логарифмов»
Вычислить:
3. 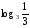
5. 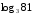
7. 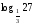
9. 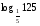
2. 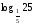
4. 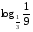
6. 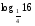
8. 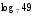
10. 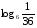
Вычислить:
3.

5.

7.

9.

4.

6.

8.

10.

Вычислить:
3.

5.

7.

9.

4.

6.

8.

10.

Вычислить:
3.

5.

7.

2.

4.

6.

8.

9.

10.

Вычислить:
Вычислить:
1.

3.

5.

7.

9.

2.

4.

6.

8.

10.

Доказать тождество:
Найти значение выражения:
 , если
, если
6.
 , если
, если
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
 , если
, если 
Прологарифмировать выражение:
1.
 по основанию 2
по основанию 26.
 по основанию 4
по основанию 42.
 по основанию 3
по основанию 37.
 по основанию 2
по основанию 23.
 по основанию 5
по основанию 58.
 по основанию 8
по основанию 84.
 по основанию 3
по основанию 39.
 по основанию 9
по основанию 95.
 по основанию 6
по основанию 610.
 по основанию 10
по основанию 10
Найти х по данному его логарифму (а>0,m>0,c>0,h>0,n>0,k>0):
1.

6.

2.

7.

3.

8.

4.

9.

5.

10.

СПИСОК ЛИТЕРАТУРЫ
Алимов Ш.А. Алгебра и начала анализа – учебник для 10-11 кл. общеобразоват. Учреждений – М.: Просвещение, 2006.- 384с.
Креславская О.А. ЕГЭ-2009. Математика: Сдаем без проблем! – М.: Эксмо, 2008.-192с.
вычисления логарифмов — Колпаков Александр Николаевич
Комплект простейших заданий уровня А на вычисление логарифмов, который репетитор по математике регулярно использует на своих занятиях с большинством учеников. Материал предназначен для учащихся 10-11 классов и преподавателей в помощь при подготовке к ЕГЭ, а также для текущей школьной работы, направленной на отработку вычислительных навыков.
Вычислите:
1) 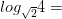
2) 
3) ![log_{0,5} \sqrt[3]{2} = log_{0,5} \sqrt[3]{2} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_111b563416e9e44bcf3fc0369d141eca.png)
4) ![log_{0,25} \sqrt[6]{4} = log_{0,25} \sqrt[6]{4} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_f283291caf0dc2dac91c52020f08e56c.png)
5) 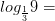
6) 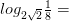
7) 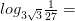
8) ![log_{\frac{1}{\sqrt[5]{2}}} \dfrac{1}{4} = log_{\frac{1}{\sqrt[5]{2}}} \dfrac{1}{4} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_8e111354fea184ccae4ce74b4099f90e.png)
9) ![log_{\frac{3}{\sqrt[4]{3}}} \dfrac{1}{9} = log_{\frac{3}{\sqrt[4]{3}}} \dfrac{1}{9} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_6b69db4efde7be4992d5d2be8a1c55c4.png)
10) 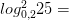
11) 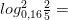
12) ![log_{3\frac{1}{3}} \sqrt[3]{0,09} = log_{3\frac{1}{3}} \sqrt[3]{0,09} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_27b523f7de0e2648c9da90aed03a771b.png)
13) ![log_{\frac{1}{\sqrt[3]{2}}} \sqrt[3]{0,25} = log_{\frac{1}{\sqrt[3]{2}}} \sqrt[3]{0,25} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_b0c434549f6bc5368f7275c5f751fc3c.png)
14) 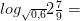
15) ![log_{\sqrt[3]{0,4}} 2,5 = log_{\sqrt[3]{0,4}} 2,5 =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_823059f1529ba0dc8178e9df9bb5503d.png)
16) ![log_{\sqrt{1 \frac{9}{16}}} \sqrt[3]{0,8} = log_{\sqrt{1 \frac{9}{16}}} \sqrt[3]{0,8} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_2b9f50399995cca1860d0ae55a17e7b9.png)
17) ![lg \sqrt[7]{10} lg \sqrt[7]{10}](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_e9c17919eb513b43bda953ac69d45977.png)
18) 
19) 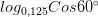
20) 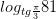
Напутствие репетитора по математике:
Вычисляя логарифмы, применяйте следующие формулы: и
и 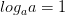
Для решения каждого задания представьте основание логарифма и число под его знаком в виде степени с одним и тем же основанием и вынесите полученные показатели из-под логарифма в его коэффициент. Логарифм с оставшимися равными числами будет равен единице.
Надо сказать, что в 80% задачниках по математике (школьных учебниках и пособиях по подготовке к ЕГЭ) крайне мало вычислительных упражнений на логарифмы, связанных со свойствами степеней. Если репетитор по математике использует стандартные пособия, то в его распоряжении оказывается обычно не более 5 — 6 примеров на логарифмы по каждому алгоритму их вычисления. Я уже давно не пользуюсь никакими задачниками и предлагаю ученикам свои материалы. В заданиях перемешиваю различные виды чисел: десятичные, обыкновенные, корни, дроби, степени с отрицательными показателями.
Вычислите логарифмы с использованием следующих формул: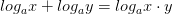 и
и 
1) 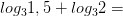
2) 
3) 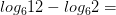
4) 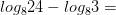
5) 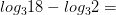
6) 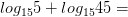
7) 
8) 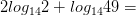
9) 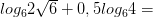
10) 
11) 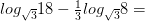
12) ![log_{\sqrt[3]{2}} \sqrt[3]{6} + log_{\frac{1}{8}} 3 = log_{\sqrt[3]{2}} \sqrt[3]{6} + log_{\frac{1}{8}} 3 =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_5419d39de5dadc716df836a2691a3417.png)
13) 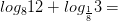
Задачи на основное логарифмическое тождество: 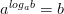
1) 
2) 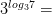
3) 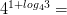
4) 
5) 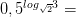
6) 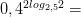
7) ![\sqrt[3]{2}^{log_{4}3}= \sqrt[3]{2}^{log_{4}3}=](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_cb8ed19fa883e0e0092905415a60ac02.png)
8) 
9) 
10) ![4^{0,5-2 log_{\sqrt{2}} \sqrt[8]{3}}= 4^{0,5-2 log_{\sqrt{2}} \sqrt[8]{3}}=](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_1a93d2ec6ee0079d835d6ab8b283fb2f.png)
11) 
12) 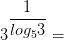
13) 
14) 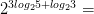
15) 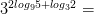
16) 
17) 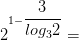
Задачи на формулу перехода к новому основанию
1) 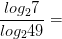
2) 
3) 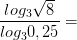
4) ![\dfrac{log_{11} \sqrt[7]{3}}{log_{11} \dfrac{1}{3}} = \dfrac{log_{11} \sqrt[7]{3}}{log_{11} \dfrac{1}{3}} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_bf7ec8f692c2fc0f112dedd9c74f8efb.png)
5) ![\dfrac{log_{2} \sqrt[3]{5}}{log_{4} \frac{1}{25}} = \dfrac{log_{2} \sqrt[3]{5}}{log_{4} \frac{1}{25}} =](/800/600/https/ankolpakov.ru/wp-content/plugins/easy-latex2/cache/tex_2ac5e45d27d02ec6be0fb7a07a701f27.png)
6) 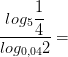
7) 
8) 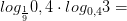
9) 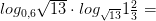
Комментарий репетитора по математике относительно состава задач. Задания на логарифмы составлены по классическим законам методики и дидактики и имеют достаточное количеством однотипных упражнений. На первый взгляд может показаться, что все номера, взятые из одного раздела, как две капли воды похожи друг на друга. Отличие наблюдается только в числах. Но любой опытный репетитор по математике Вам скажет, что достаточно в одном из таких однотипных примеров поменять какое-нибудь целое число, например, на иррациональное или на дробное и перед ученик мгновенно растеряется. Поэтому я постарался обыграть все возможные числовые ситуации разнообразить номера десятичными и обыкновенными дробями, корнями разных степеней, комбинациями действий и коэффициентов, окружающих логарифмы.
В реальности я подаю задания ученику на отдельном листочке А4 с максимально плотным расположением примеров. Все на одном листе! Один из таких планов с представлен ниже:
Ученикам:
Задания можно использовать для самостоятельной подготовки к ЕГЭ по математике с целью научиться решать простейшие задачи на логарифмы из части В. Регулярно повторяйте с репетитором формулы, ибо без их уверенного запоминания Вам будет нелегко соориентироваться в вычислениях, в которых применяются сразу две или даже три формулы сразу.
Преподавателям:
Напишите свое мнение о качестве материалов. Понравилась ли Вам подборка упражнений? Насколько велика потребность в таких задачах у репетитора по математике? Помогли ли мои упражнения в практической работе? Пишите, комментируйте! Присылайте интересные логарифмические задания на вычисления, которые встретились Вам в тот или иной период подготовки к ЕГЭ.
Колпаков А.Н. Репетитор по математике — автор комплекта.
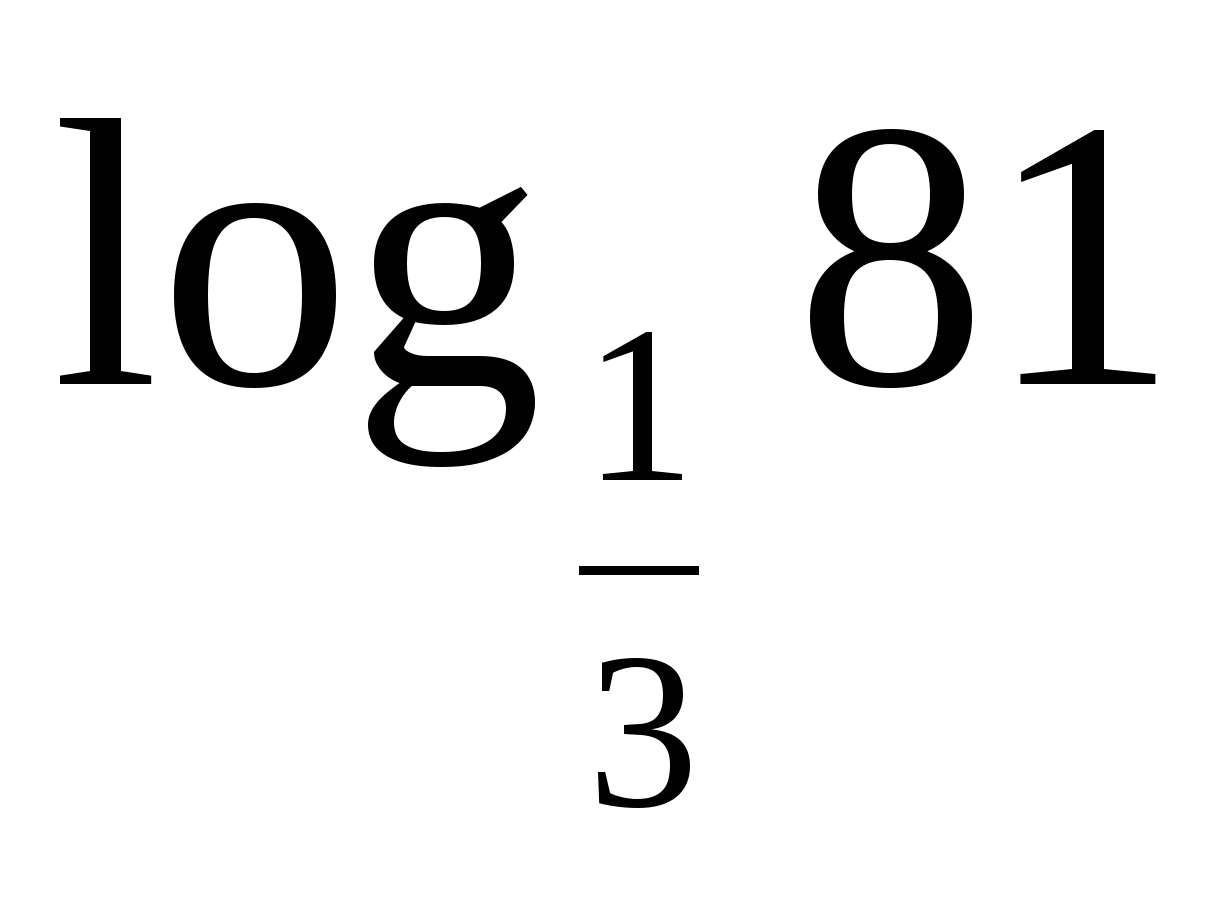 ;2)
;2)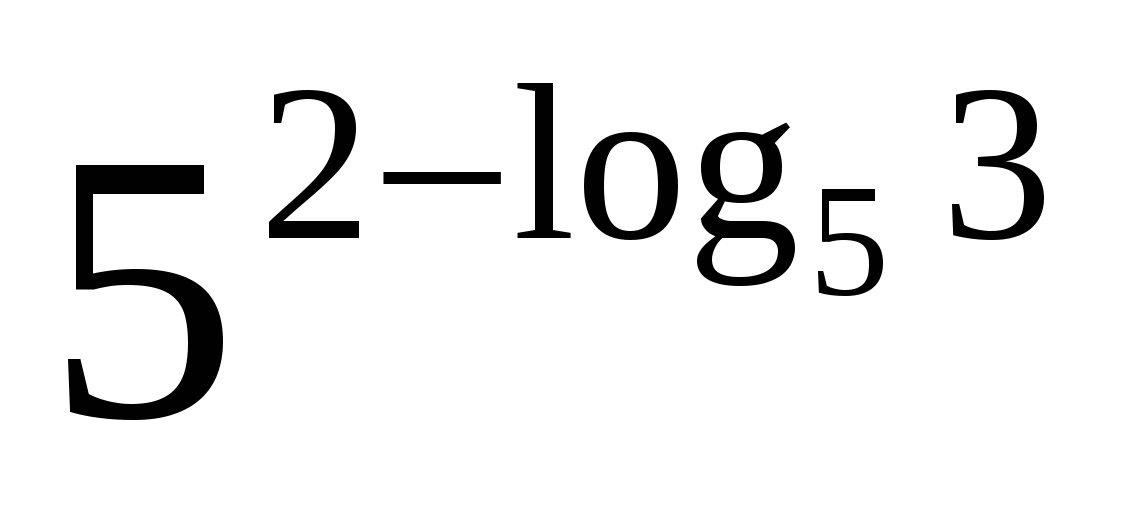 ;3)
;3)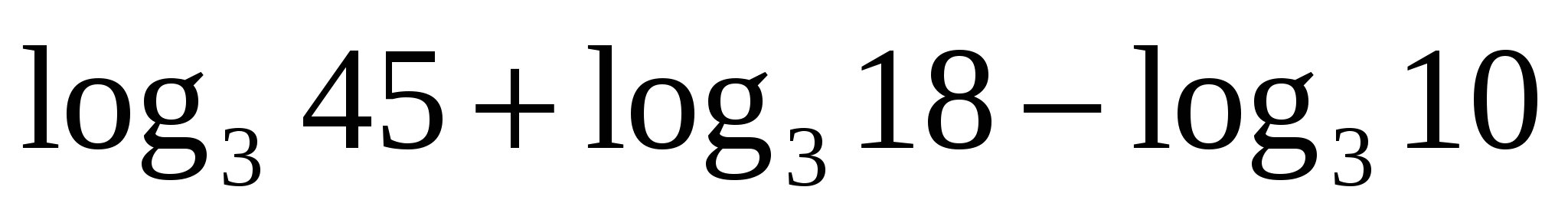
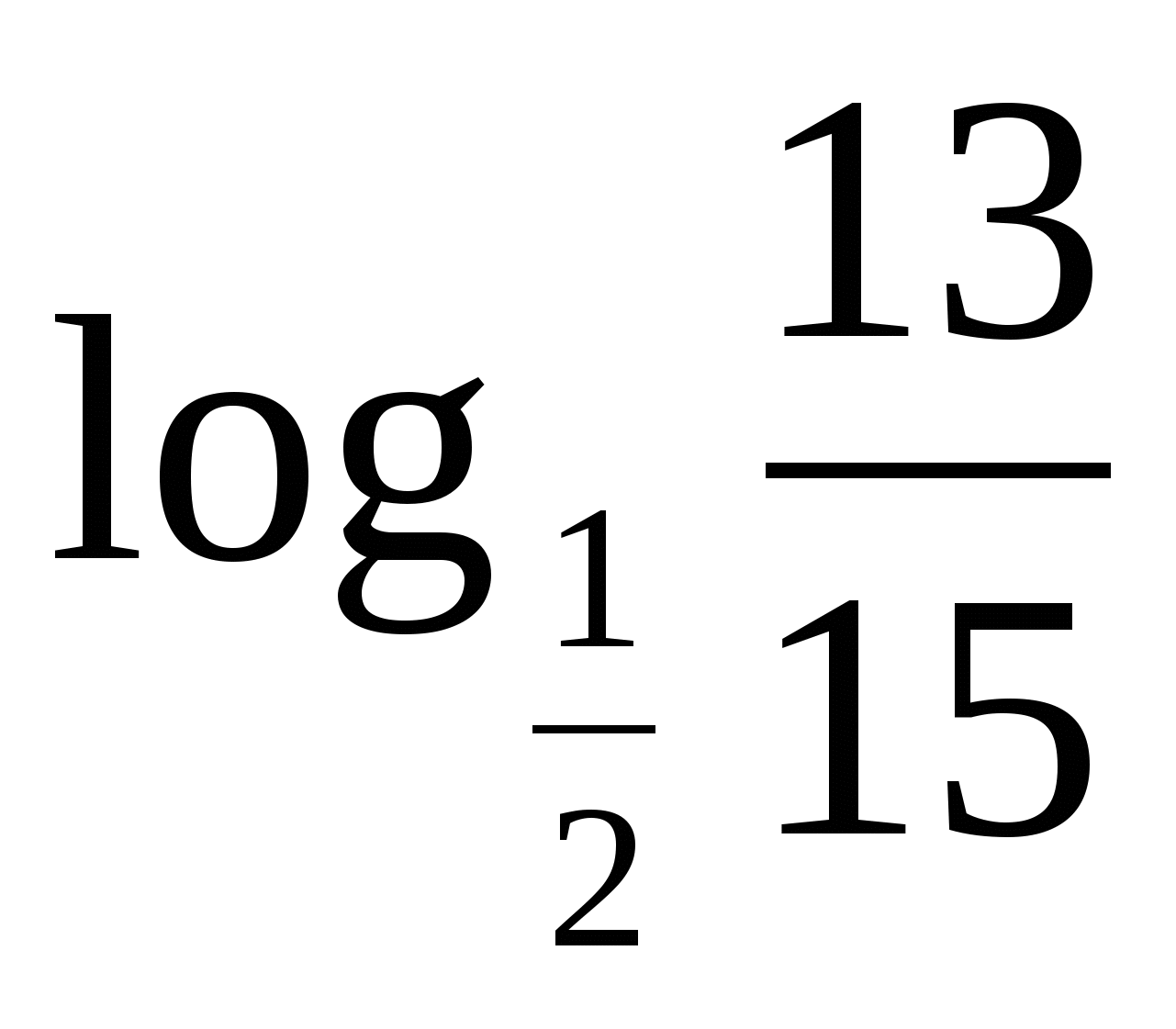 и
и 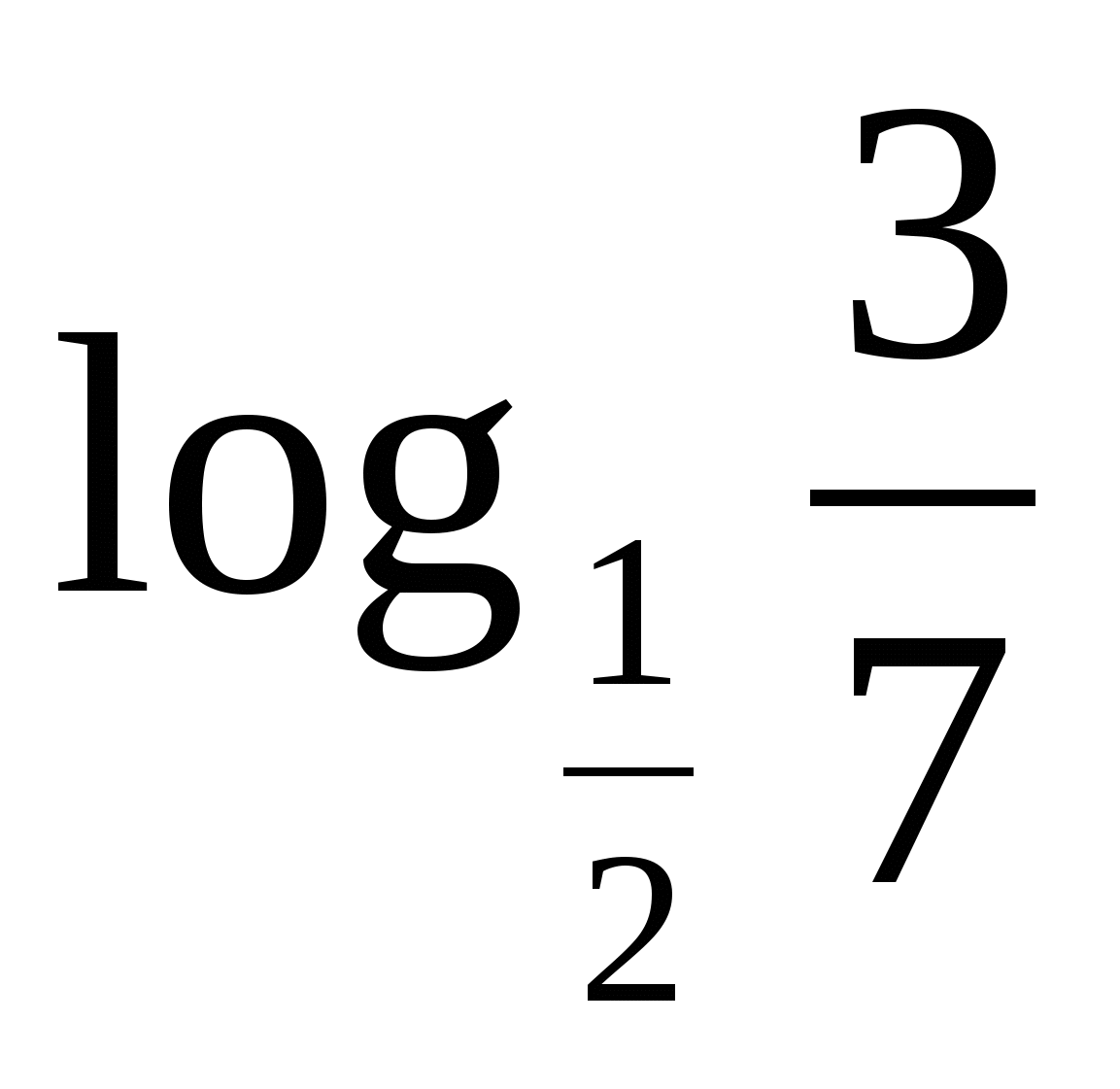 . .
. .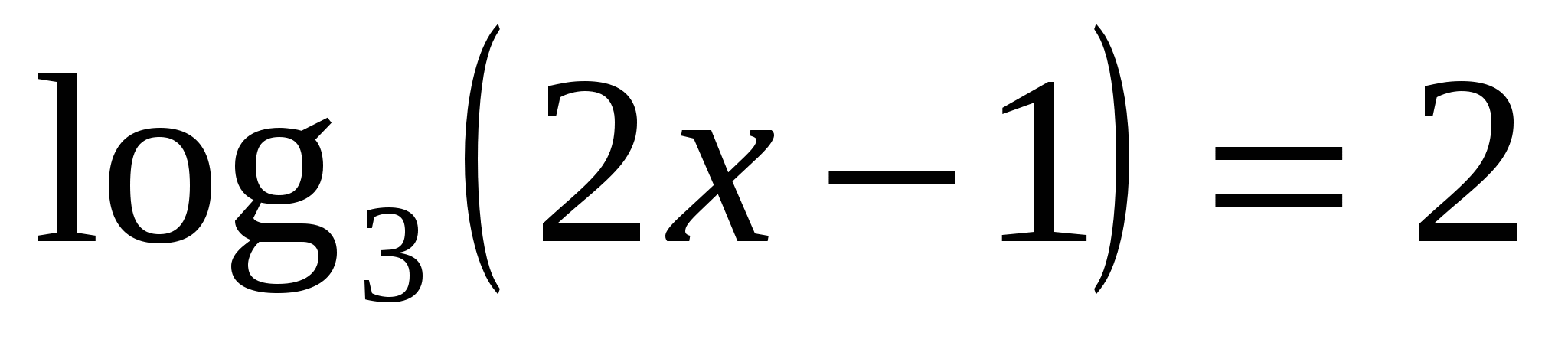 .
.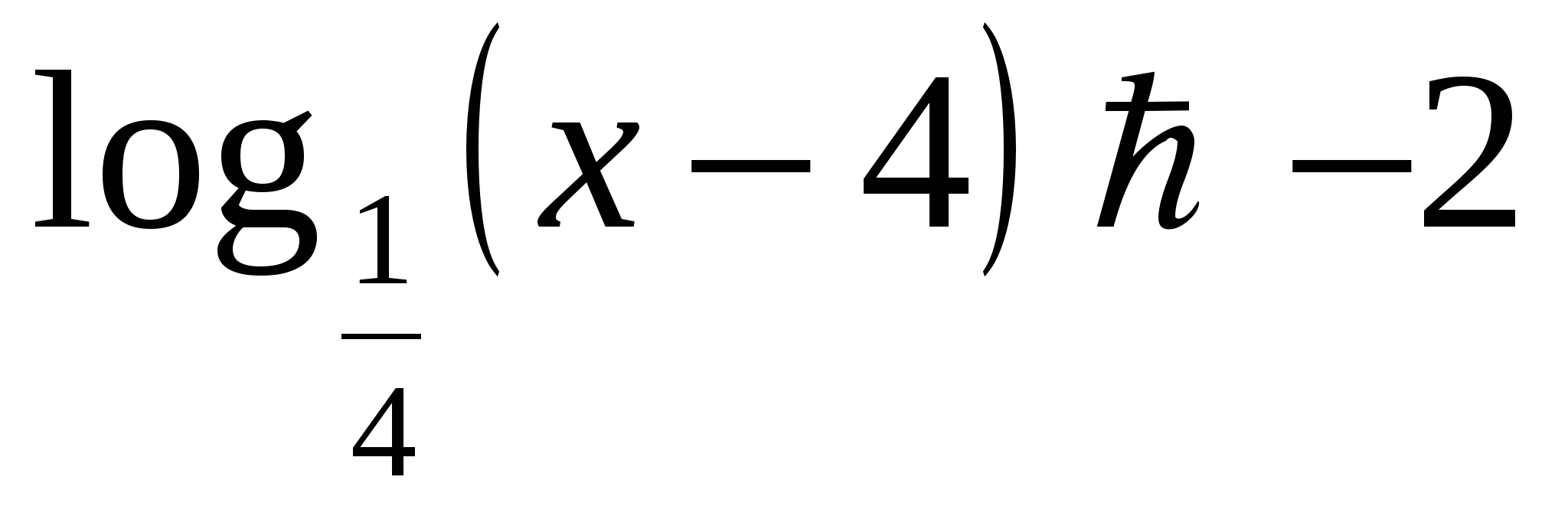 .
.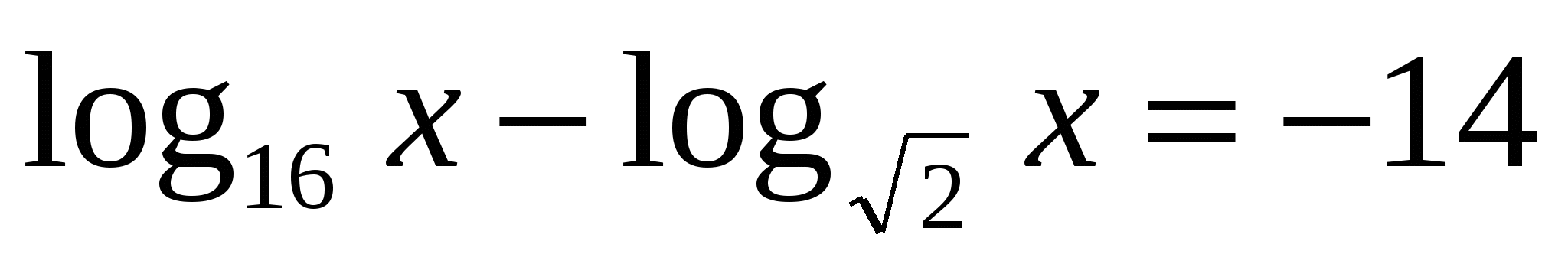 .
.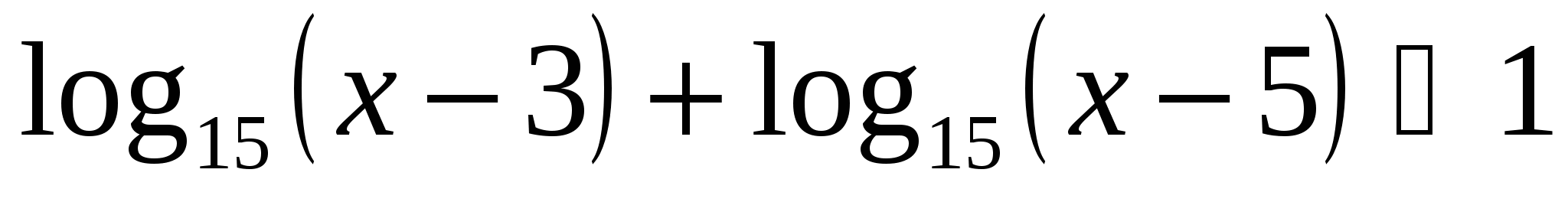 .
.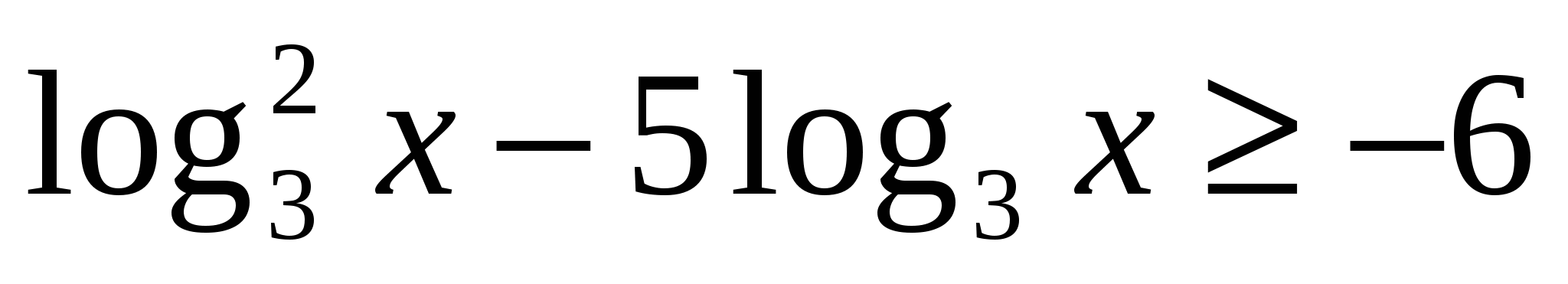 .
.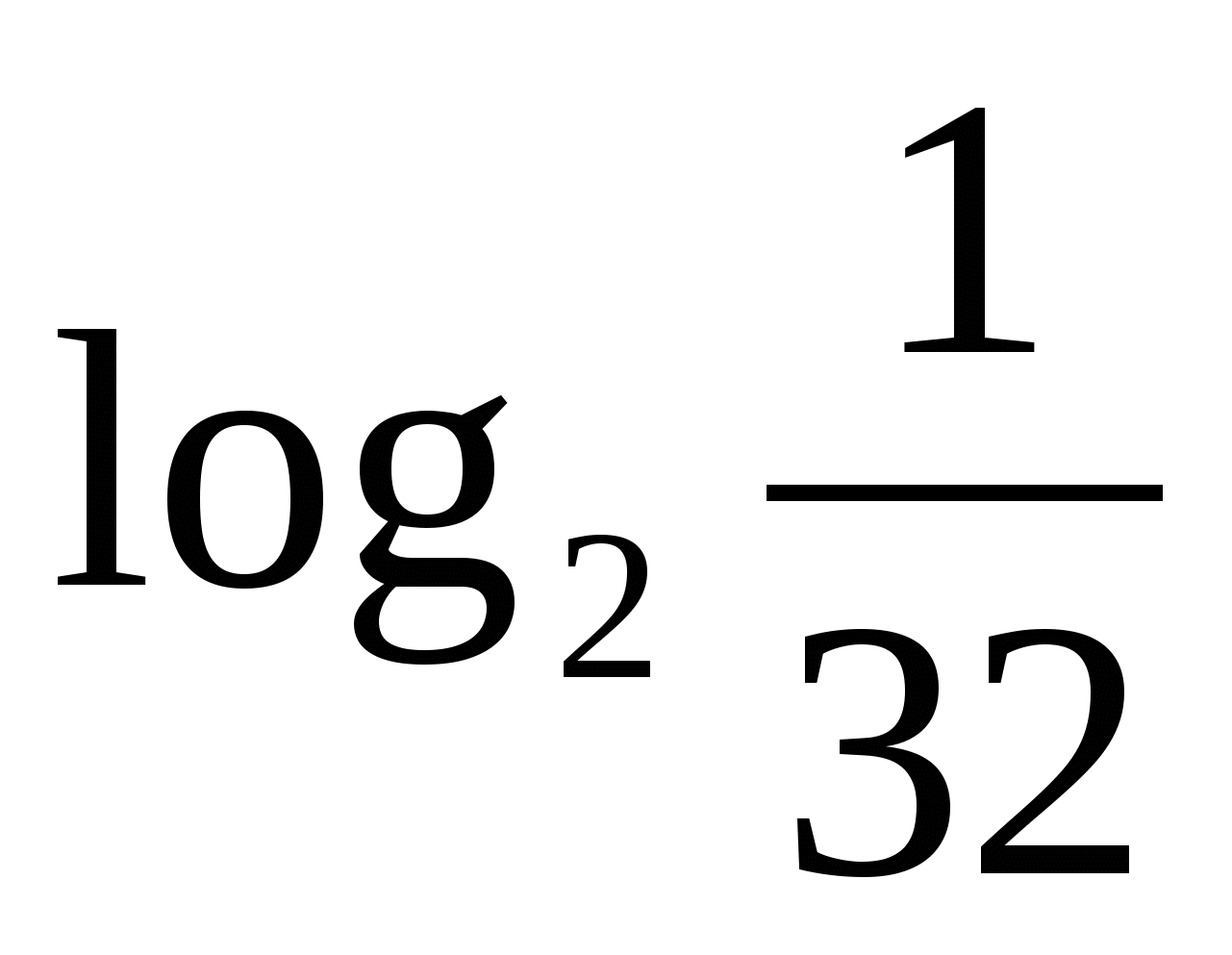 ;2)
;2)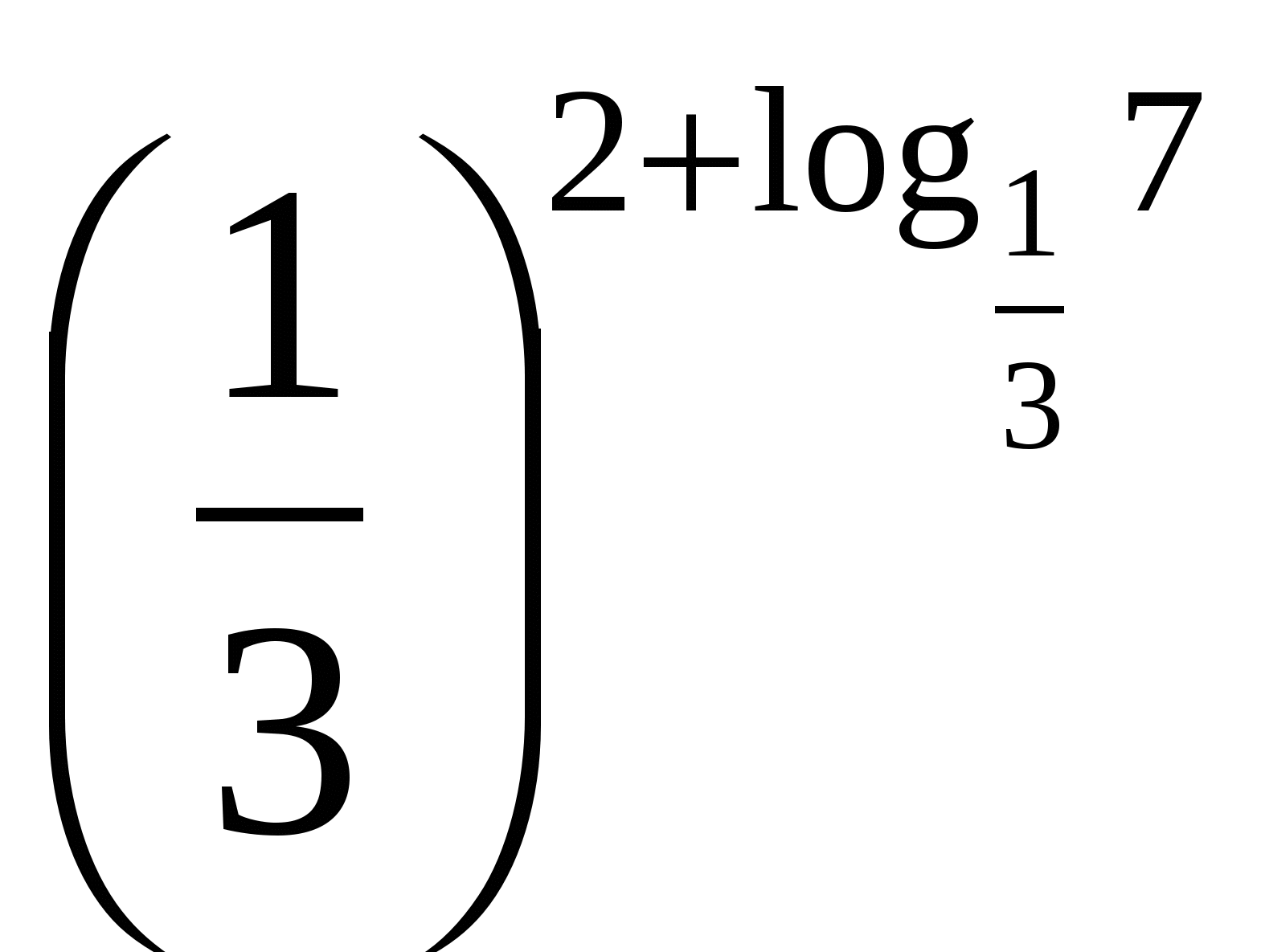 ;3)
;3) 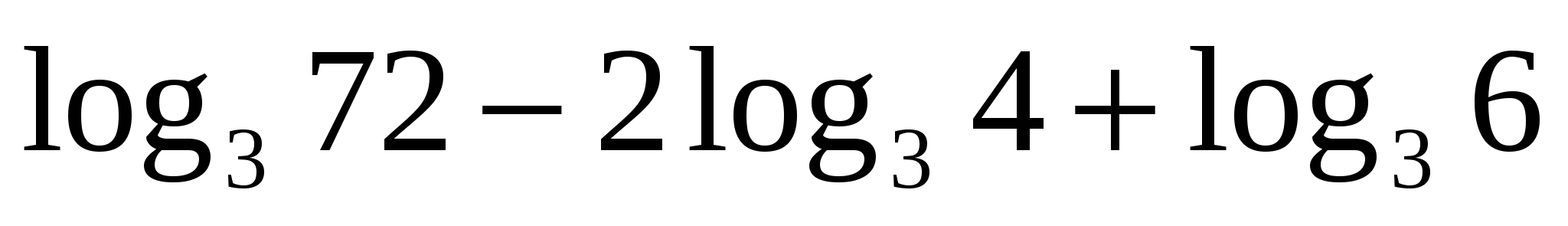 .
.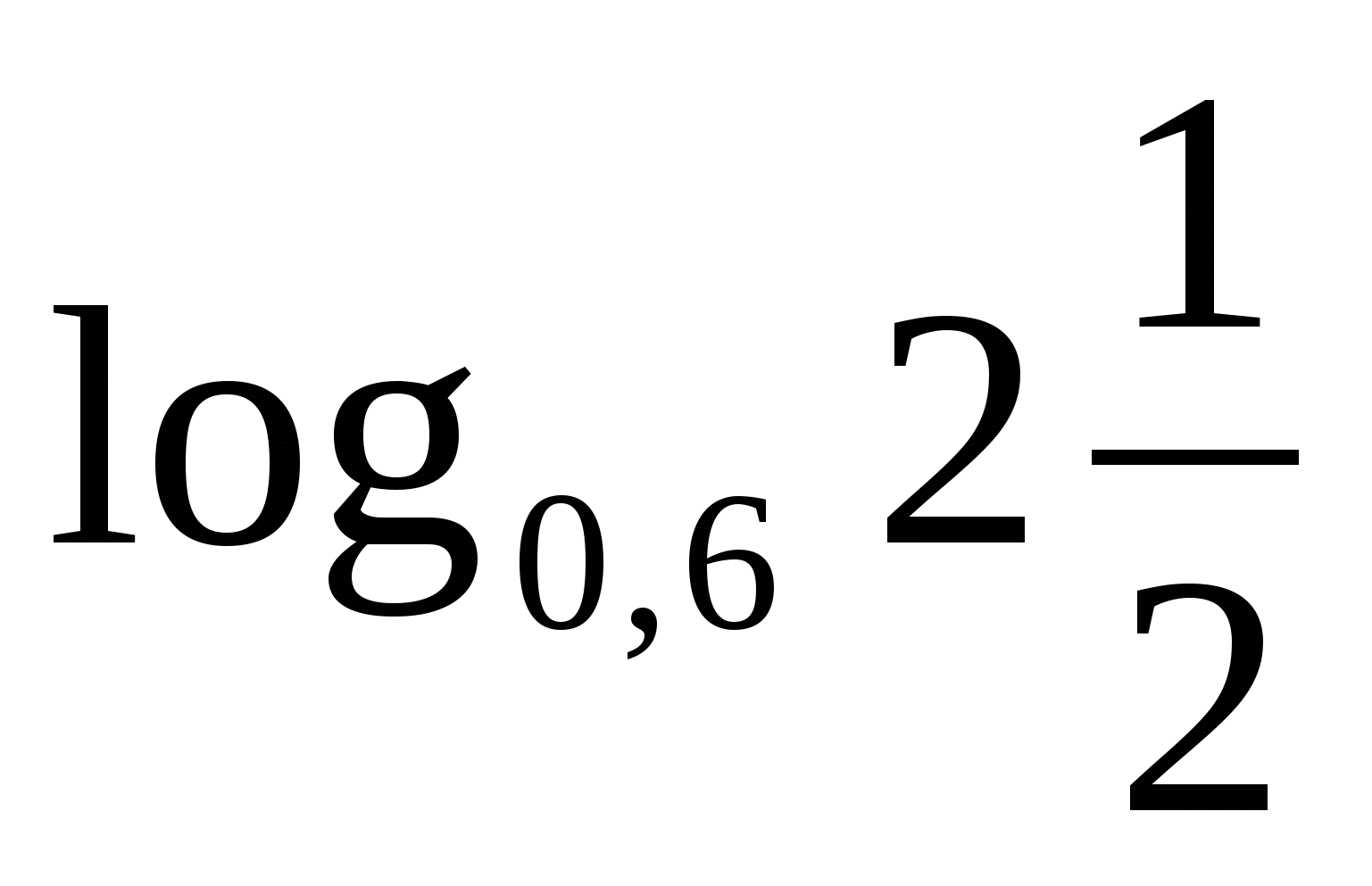 и
и  .
.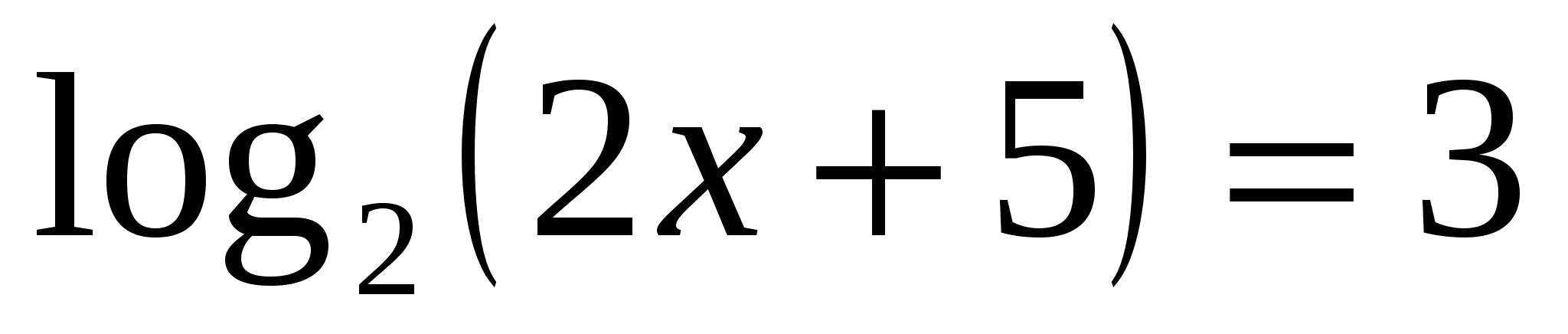 .
.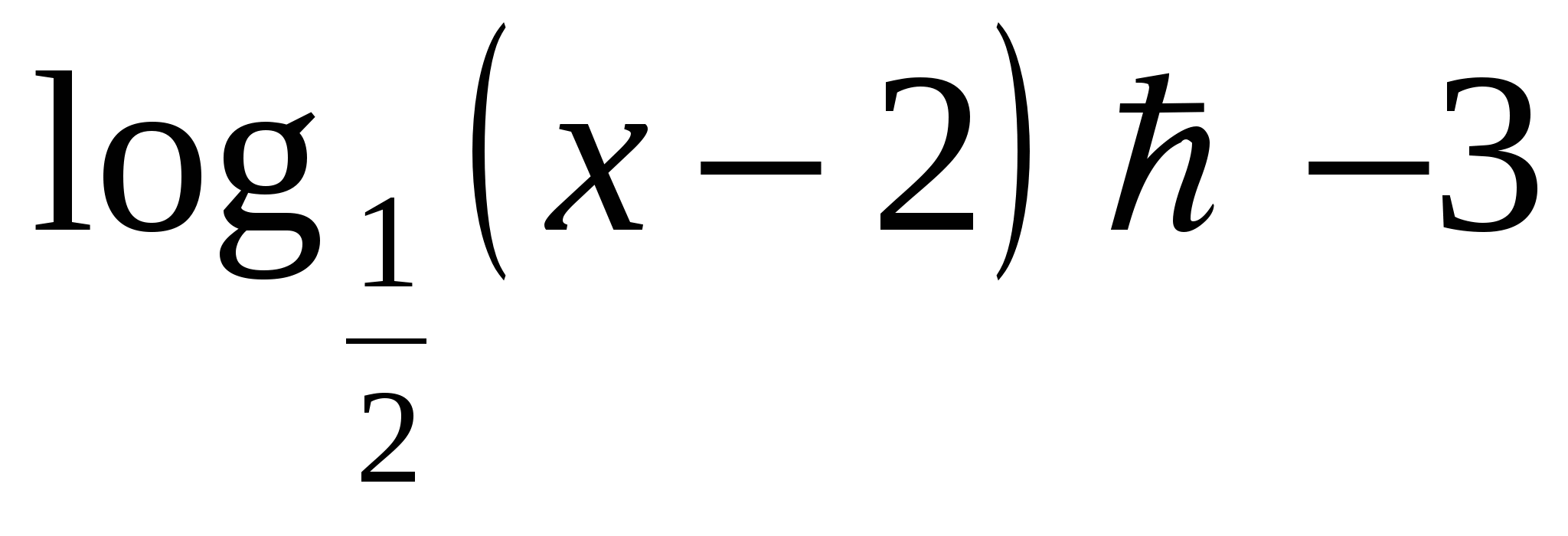 .
.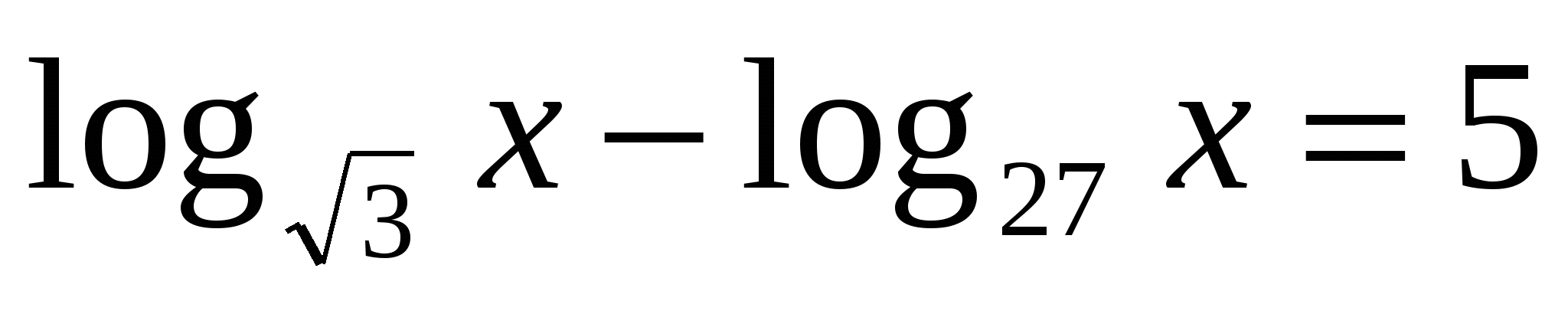 .
.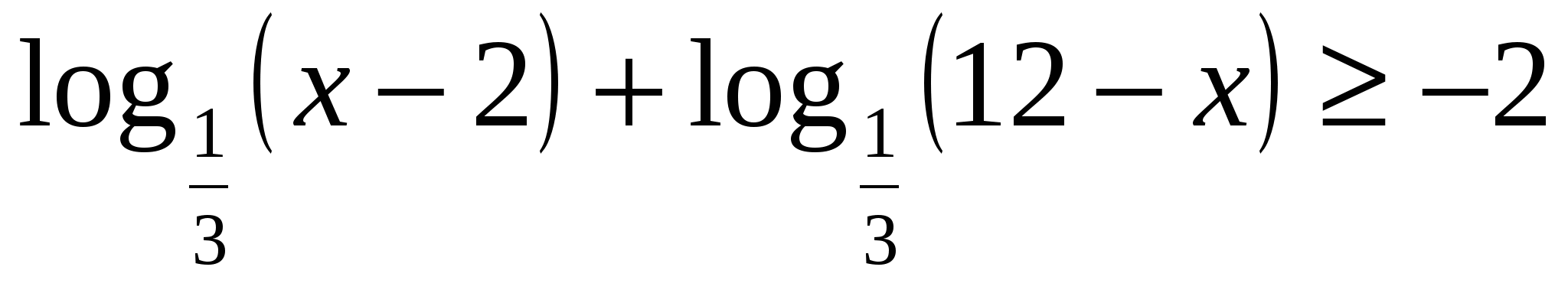 .
.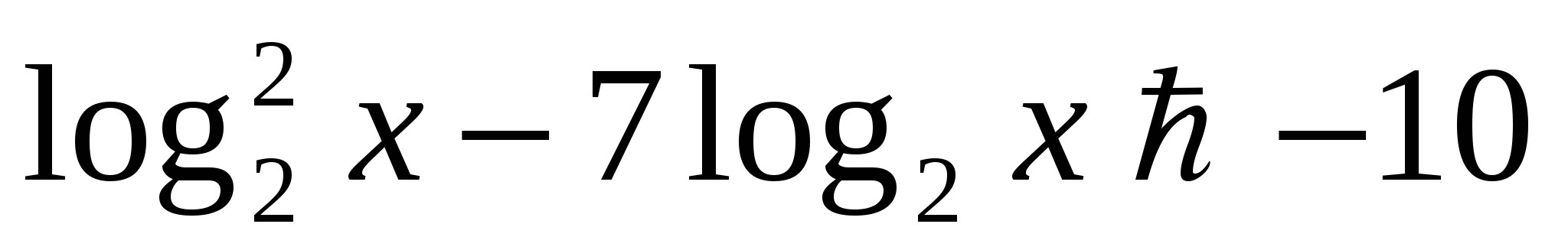 .
.
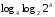
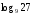
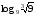
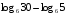
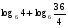
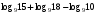
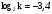 , найти
, найти 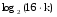
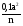 по основанию 10.
по основанию 10.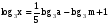

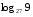
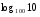
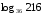
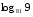
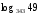
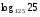
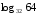
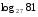
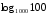

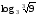
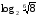

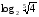
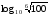
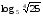
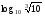
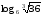
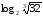
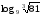
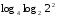
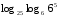
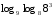
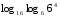
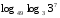
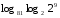
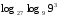
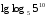
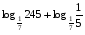
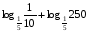
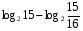
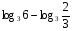
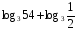

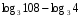
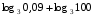
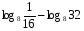

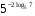


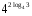
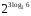
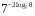

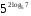
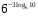
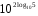
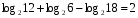
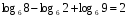
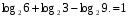
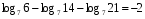

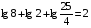
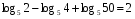
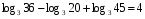
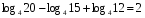
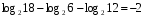
 , если
, если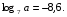
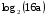 , если
, если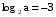
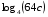 , если
, если 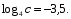
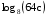 , если
, если 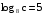
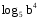 , если
, если 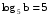
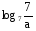 , если
, если 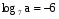
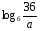 , если
, если 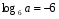
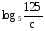 , если
, если 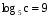
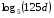 , если
, если 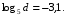
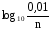 , если
, если 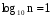
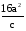 по основанию 2
по основанию 2 по основанию 4
по основанию 4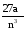 по основанию 3
по основанию 3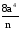 по основанию 2
по основанию 2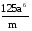 по основанию 5
по основанию 5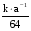 по основанию 8
по основанию 8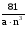 по основанию 3
по основанию 3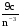 по основанию 9
по основанию 9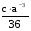 по основанию 6
по основанию 6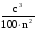 по основанию 10
по основанию 10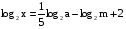
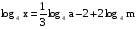
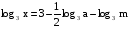
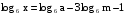
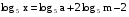
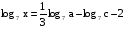
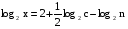
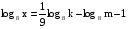
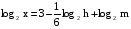
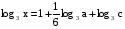
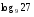
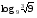
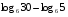
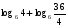
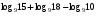
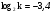 , найти
, найти 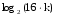
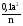 по основанию 10.
по основанию 10.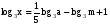
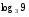
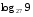

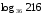

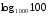
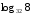
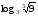
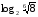

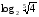
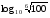
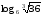
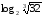

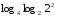
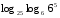
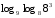
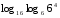
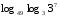
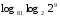
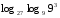
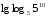
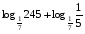
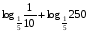
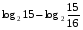
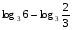
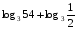

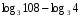
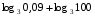
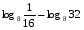
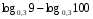
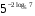
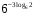
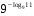
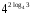
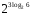
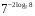


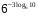
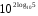
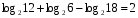
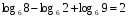

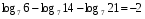
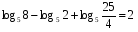
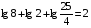

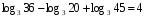
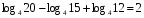
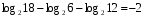
 , если
, если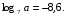
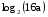 , если
, если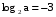
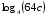 , если
, если 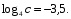
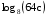 , если
, если 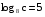
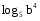 , если
, если 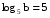
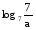 , если
, если 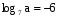
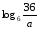 , если
, если 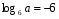
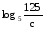 , если
, если 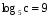
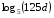 , если
, если 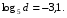
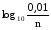 , если
, если 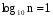
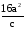 по основанию 2
по основанию 2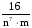 по основанию 4
по основанию 4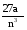 по основанию 3
по основанию 3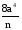 по основанию 2
по основанию 2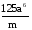 по основанию 5
по основанию 5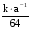 по основанию 8
по основанию 8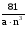 по основанию 3
по основанию 3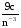 по основанию 9
по основанию 9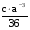 по основанию 6
по основанию 6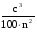 по основанию 10
по основанию 10