Закон Ампера — Википедия

Зако́н Ампе́ра  — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы dF→{\displaystyle d{\vec {F}}}, с которой магнитное поле действует на элемент объёма dV{\displaystyle dV} проводника с током плотности j→{\displaystyle {\vec {j}}}, находящегося в магнитном поле с индукцией B→{\displaystyle {\vec {B}}}, в Международной системе единиц (СИ) имеет вид:

dF→=j→×B→dV{\displaystyle d{\vec {F}}={\vec {j}}\times {\vec {B}}dV}.

Если ток течёт по тонкому проводнику, то j→dV=Idl→{\displaystyle {\vec {j}}dV=Id{\vec {l}}}, где dl→{\displaystyle d{\vec {l}}} — «элемент длины» проводника — вектор, по модулю равный dl{\displaystyle dl} и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Направление силы dF→{\displaystyle d{\vec {F}}} определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

dF=IBdlsin⁡α,{\displaystyle dF=IBdl\sin \alpha ,}

где α{\displaystyle \alpha } — угол между вектором магнитной индукции и направлением, вдоль которого течёт ток.

Сила dF{\displaystyle dF} максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (α=90∘,sin⁡α=1{\displaystyle \alpha =90^{\circ },\sin \alpha =1}):

dFmax=IBdl.{\displaystyle dF_{max}=IBdl.}

Два параллельных проводника

Два бесконечных параллельных проводника в вакууме

Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии r{\displaystyle r} друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}. Требуется найти силу, действующую на единицу длины проводника.

В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током I1{\displaystyle I_{1}} в точке на расстоянии r{\displaystyle r} создаёт магнитное поле с индукцией

B1(r)=μ04π2I1r,{\displaystyle B_{1}(r)={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}}{r}},}

где μ0{\displaystyle \mu _{0}} — магнитная постоянная.

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

dF→1−2=I2dl→×B→1(r).{\displaystyle d{\vec {F}}_{1-2}=I_{2}d{\vec {l}}\times {\vec {B}}_{1}(r).}

По правилу буравчика, dF→1−2{\displaystyle d{\vec {F}}_{1-2}} направлена в сторону первого проводника (аналогично и для dF→2−1{\displaystyle d{\vec {F}}_{2-1}}, а значит, проводники притягиваются).

Модуль данной силы (r{\displaystyle r} — расстояние между проводниками):

dF1−2=μ04π2I1I2rdl.{\displaystyle dF_{1-2}={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}dl.}

Интегрируем, учитывая только проводник единичной длины (пределы l{\displaystyle l} от 0 до 1):

F1−2=μ04π2I1I2r.{\displaystyle F_{1-2}={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}.}

Полученная формула используется в СИ для установления численного значения магнитной постоянной μ0{\displaystyle \mu _{0}}. Действительно, ампер, являющийся одной из основных единиц СИ, определяется в ней как «сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10

−7ньютона»^[1].

Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная μ0{\displaystyle \mu _{0}} равна 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Н/А² или, что то же самое, 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Гн/ м точно.

Проявления

• Электродинамическая деформация шин (токопроводов) трёхфазного переменного тока на подстанциях при воздействии токов короткого замыкания.
• Раздвигание токопроводов рельсотронов при выстреле.

Применение

• Любые узлы в электротехнике, где под действием электромагнитного поля происходит движение каких-либо элементов, используют закон Ампера. Самый широко распространённый и используемый чуть ли не во всех технических конструкциях агрегат, в основе своей работы использующий закон Ампера — это электродвигатель, либо, что конструктивно почти то же самое, генератор.

Именно под действием силы Ампера происходит вращение ротора, поскольку на его обмотку влияет магнитное поле статора, приводя в движение. Любые транспортные средства на электротяге для приведения во вращение валов, на которых находятся колёса, используют силу Ампера (трамваи, электрокары, электропоезда и др). Также магнитное поле приводит в движение механизмы электрозапоров (электродвери, раздвигающиеся ворота, двери лифта). Другими словами, любые устройства, которые работают на электричестве и имеют движущиеся узлы, основаны на эксплуатации закона Ампера.

• Также он находит применение во многих других видах электротехники, например, в громкоговорителе. В громкоговорителе или динамике для возбуждения мембраны, которая формирует звуковые колебания используется постоянный магнит. На него под действием электромагнитного поля, создаваемого расположенным рядом проводником с током, действует сила Ампера, которая изменяется в соответствии с нужной звуковой частотой.
• Принцип работы электромеханических машин (движение части обмотки ротора относительно части обмотки статора).
• Электродинамическое сжатие плазмы, например, в токамаках, установках Z-пинч.
• Электродинамический метод прессования.

История

В 1820 году Ханс Кристиан Эрстед открыл, что провод, по которому идёт ток, создает магнитное поле и заставляет отклоняться стрелку компаса. Он заметил, что магнитное поле перпендикулярно току, а не параллельно ему, как можно было бы ожидать. Ампер, вдохновлённый демонстрацией опыта Эрстеда, обнаружил, что два параллельных проводника, по которым течёт ток, притягиваются или отталкиваются в зависимости от того, в одну ли или разные стороны по ним идёт ток. Таким образом ток не только производит магнитное поле, но магнитное поле действует на ток. Уже через неделю после объявления Эрстедом о своём опыте, Ампер предложил объяснение: проводник действует на магнит, потому что в магните течёт ток по множеству маленьких замкнутых траекторий^[2][3].

Сила Ампера и третий закон Ньютона

Пусть есть два тонких проводника с токами I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}} , заданные кривыми C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}}. Сами кривые могут быть заданы радиус-векторами r1{\displaystyle \mathbf {r} _{1}} и r2{\displaystyle \mathbf {r} _{2}}. Найдем силу, действующую непосредственно на токовый элемент одного провода со стороны токового элемента другого провода. По закону Био — Савара — Лапласа токовый элемент I1dr1{\displaystyle I_{1}\mathrm {d} \mathbf {r} _{1}}, находящийся в точке r1{\displaystyle \mathbf {r} _{1}}, создает в точке r2{\displaystyle \mathbf {r} _{2}} элементарное магнитное поле dB1(r2)=μ04πI1[dr1,r2−r1]|r2−r1|3{\displaystyle \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0} \over 4\pi }{\frac {I_{1}[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}. По закону Ампера сила, действующая со стороны поля dB1(r2){\displaystyle \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})} на токовый элемент I2dr2{\displaystyle I_{2}\mathrm {d} \mathbf {r} _{2}}, находящийся в точке r2{\displaystyle \mathbf {r} _{2}}, равна d2F12=I2dr2×dB1(r2)=μ0I1I24π[dr2,[dr1,r2−r1]]|r2−r1|3{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}=I_{2}\mathrm {d} \mathbf {r} _{2}\times \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0}I_{1}I_{2} \over 4\pi }{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Токовый элемент I2dr2{\displaystyle I_{2}\mathrm {d} \mathbf {r} _{2}}, находящийся в точке r2{\displaystyle \mathbf {r} _{2}}, создает в точке r1{\displaystyle \mathbf {r} _{1}} элементарное магнитное поле dB2(r1)=μ04πI2[dr2,r1−r2]|r2−r1|3{\displaystyle \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})={\mu _{0} \over 4\pi }{\frac {I_{2}[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}. Сила Ампера, действующая со стороны поля dB2(r1){\displaystyle \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})} на токовый элемент I1dr1{\displaystyle I_{1}\mathrm {d} \mathbf {r} _{1}}, находящийся в точке r1{\displaystyle \mathbf {r} _{1}}, равна d2F21=I1dr1×dB2(r1)=μ0I1I24π[dr1,[dr2,r1−r2]]|r2−r1|3{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{21}=I_{1}\mathrm {d} \mathbf {r} _{1}\times \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})={\mu _{0}I_{1}I_{2} \over 4\pi }{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

В общем случае для произвольных r1{\displaystyle \mathbf {r} _{1}} и r2{\displaystyle \mathbf {r} _{2}} силы d2F12{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}} и d2F21{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{21}} даже не коллинеарны, а значит, не подчиняются третьему закону Ньютона: d2F12+d2F21≠0{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}+\mathrm {d} ^{2}\mathbf {F} _{21}\neq 0}. Однако ничего страшного в этом нет. Физиками доказано, что постоянный ток может течь только по замкнутому контуру. Поэтому третий закон Ньютона должен действовать только для сил, с которыми взаимодействуют два замкнутых проводника с током. Убедимся, что для двух таких проводников третий закон Ньютона выполняется.

Пусть кривые C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}} являются замкнутыми. Тогда ток I1{\displaystyle I_{1}} создает в точке r2{\displaystyle \mathbf {r} _{2}} магнитное поле B1(r2)=μ0I14π∮C1⁡[dr1,r2−r1]|r2−r1|3{\displaystyle \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0}I_{1} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}, где интегрирование по C1{\displaystyle C_{1}} производится в направлении течения тока I1{\displaystyle I_{1}}. Сила Ампера, действующая со стороны поля B1(r2){\displaystyle \mathbf {B} _{1}(\mathbf {r} _{2})} на контур C2{\displaystyle C_{2}} с током I2{\displaystyle I_{2}}, равна F12=∮C2⁡(I2dr2×B1(r2))=∮C2⁡(I2dr2×μ0I14π∮C1⁡[dr1,r2−r1]|r2−r1|3)=μ0I1I24π∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3{\displaystyle \mathbf {F} _{12}=\oint \limits _{\mathbb {C} _{2}}(I_{2}\mathrm {d} \mathbf {r} _{2}\times \mathbf {B} _{1}(\mathbf {r} _{2}))=\oint \limits _{\mathbb {C} _{2}}(I_{2}\mathrm {d} \mathbf {r} _{2}\times {\mu _{0}I_{1} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}})={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}, где интегрирование по C2{\displaystyle C_{2}} производится в направлении течения тока I2{\displaystyle I_{2}}. Что характерно, порядок интегрирования значения не имеет.

Аналогично сила Ампера, действующая со стороны поля B2(r1){\displaystyle \mathbf {B} _{2}(\mathbf {r} _{1})}, создаваемого током I2{\displaystyle I_{2}}, на контур C1{\displaystyle C_{1}} с током I1{\displaystyle I_{1}}, равна F21=∮C1⁡(I1dr1×B2(r1))=μ0I1I24π∮C1⁡∮C2⁡[dr1,[dr2,r1−r2]]|r2−r1|3=∮C1⁡∮C2⁡d2F21{\displaystyle \mathbf {F} _{21}=\oint \limits _{\mathbb {C} _{1}}(I_{1}\mathrm {d} \mathbf {r} _{1}\times \mathbf {B} _{2}(\mathbf {r} _{1}))={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}\mathrm {d} ^{2}\mathbf {F} _{21}}.

Равенство F12+F21=0{\displaystyle \mathbf {F} _{12}+\mathbf {F} _{21}=0} эквивалентно равенству ∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3=∮C1⁡∮C2⁡[dr1,[dr2,r2−r1]]|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Чтобы доказать это последнее равенство, заметим, что выражение для силы Ампера очень похоже на выражение для циркуляции магнитного поля по замкнутому контуру, в котором внешнее скалярное произведение заменили векторным произведением. Тогда понятно, в каком направлении нужно двигаться.

Пользуясь тождеством Лагранжа, двойное векторное произведение в левой части доказываемого равенства можно записать так: [dr2,[dr1,r2−r1]]=dr1(dr2,r2−r1)−(r2−r1)(dr2,dr1){\displaystyle [\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]=\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})-(\mathbf {r} _{2}-\mathbf {r} _{1})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1})}.

Тогда левая часть доказываемого равенства примет вид:

∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3=∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3−∮C1⁡∮C2⁡(r2−r1)(dr2,dr1)|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}-\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Рассмотрим отдельно интеграл ∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}, который можно переписать в следующем виде:

∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3=∮C1⁡dr1∮C2⁡(r2−r1,d(r2−r1))|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\mathrm {d} \mathbf {r} _{1}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1},\mathrm {d} (\mathbf {r} _{2}-\mathbf {r} _{1}))}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Сделав замену переменной во внутреннем интеграле на r=r2−r1{\displaystyle \mathbf {r} =\mathbf {r} _{2}-\mathbf {r} _{1}}, где вектор r{\displaystyle \mathbf {r} } изменяется по замкнутому контуру C2′{\displaystyle C_{2}’}, обнаружим, что внутренний интеграл является циркуляцией градиентного поля по замкнутому контуру. А значит, он равен нулю:

∮C2⁡(r2−r1,d(r2−r1))|r2−r1|3=∮C2′⁡(r,dr)|r|3=−∮C2′⁡(grad(1|r|),dr)=0{\displaystyle \oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1},\mathrm {d} (\mathbf {r} _{2}-\mathbf {r} _{1}))}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{2}’}{\frac {(\mathbf {r} ,\mathrm {d} \mathbf {r} )}{|\mathbf {r} |^{3}}}=-\oint \limits _{\mathbb {C} _{2}’}(\mathrm {grad} ({\frac {1}{|\mathbf {r} |}}),\mathrm {d} \mathbf {r} )=0}

Значит, и весь двойной криволинейный интеграл равен нулю. В таком случае для силы F12{\displaystyle \mathbf {F} _{12}} можно записать:

F12=μ0I1I24π∮C1⁡∮C2⁡(r1−r2)(dr2,dr1)|r2−r1|3{\displaystyle \mathbf {F} _{12}={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{1}-\mathbf {r} _{2})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}

Выражение для силы F21{\displaystyle \mathbf {F} _{21}} можно получить из выражения для силы F12{\displaystyle \mathbf {F} _{12}}, просто исходя из соображений симметрии. Для этого произведем замену индексов: 2 меняем на 1, а 1 — на 2. В таком случае для силы

Закон Ампера — Википедия. Что такое Закон Ампера

Зако́н Ампе́ра  — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы dF→{\displaystyle d{\vec {F}}}, с которой магнитное поле действует на элемент объёма dV{\displaystyle dV} проводника с током плотности j→{\displaystyle {\vec {j}}}, находящегося в магнитном поле с индукцией B→{\displaystyle {\vec {B}}}, в Международной системе единиц (СИ) имеет вид:

dF→=j→×B→dV{\displaystyle d{\vec {F}}={\vec {j}}\times {\vec {B}}dV}.

Если ток течёт по тонкому проводнику, то j→dV=Idl→{\displaystyle {\vec {j}}dV=Id{\vec {l}}}, где dl→{\displaystyle d{\vec {l}}} — «элемент длины» проводника — вектор, по модулю равный dl{\displaystyle dl} и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Направление силы dF→{\displaystyle d{\vec {F}}} определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки.

Модуль силы Ампера можно найти по формуле:

dF=IBdlsin⁡α,{\displaystyle dF=IBdl\sin \alpha ,}

где α{\displaystyle \alpha } — угол между вектором магнитной индукции и направлением, вдоль которого течёт ток.

Сила dF{\displaystyle dF} максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (α=90∘,sin⁡α=1{\displaystyle \alpha =90^{\circ },\sin \alpha =1}):

dFmax=IBdl.{\displaystyle dF_{max}=IBdl.}

Два параллельных проводника

Два бесконечных параллельных проводника в вакууме

Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии r{\displaystyle r} друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}. Требуется найти силу, действующую на единицу длины проводника.

В соответствии с законом Био — Савара — Лапласа бесконечный проводник с током I1{\displaystyle I_{1}} в точке на расстоянии r{\displaystyle r} создаёт магнитное поле с индукцией

B1(r)=μ04π2I1r,{\displaystyle B_{1}(r)={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}}{r}},}

где μ0{\displaystyle \mu _{0}} — магнитная постоянная.

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

dF→1−2=I2dl→×B→1(r).{\displaystyle d{\vec {F}}_{1-2}=I_{2}d{\vec {l}}\times {\vec {B}}_{1}(r).}

По правилу буравчика, dF→1−2{\displaystyle d{\vec {F}}_{1-2}} направлена в сторону первого проводника (аналогично и для dF→2−1{\displaystyle d{\vec {F}}_{2-1}}, а значит, проводники притягиваются).

Модуль данной силы (r{\displaystyle r} — расстояние между проводниками):

dF1−2=μ04π2I1I2rdl.{\displaystyle dF_{1-2}={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}dl.}

Интегрируем, учитывая только проводник единичной длины (пределы l{\displaystyle l} от 0 до 1):

F1−2=μ04π2I1I2r.{\displaystyle F_{1-2}={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{r}}.}

Полученная формула используется в СИ для установления численного значения магнитной постоянной μ0{\displaystyle \mu _{0}}. Действительно, ампер, являющийся одной из основных единиц СИ, определяется в ней как «сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10⁻⁷ньютона»^[1].

Таким образом, из полученной формулы и определения ампера следует, что магнитная постоянная μ0{\displaystyle \mu _{0}} равна 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Н/А² или, что то же самое, 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Гн/ м точно.

Проявления

• Электродинамическая деформация шин (токопроводов) трёхфазного переменного тока на подстанциях при воздействии токов короткого замыкания.
• Раздвигание токопроводов рельсотронов при выстреле.

Применение

• Любые узлы в электротехнике, где под действием электромагнитного поля происходит движение каких-либо элементов, используют закон Ампера. Самый широко распространённый и используемый чуть ли не во всех технических конструкциях агрегат, в основе своей работы использующий закон Ампера — это электродвигатель, либо, что конструктивно почти то же самое, генератор.

Именно под действием силы Ампера происходит вращение ротора, поскольку на его обмотку влияет магнитное поле статора, приводя в движение. Любые транспортные средства на электротяге для приведения во вращение валов, на которых находятся колёса, используют силу Ампера (трамваи, электрокары, электропоезда и др). Также магнитное поле приводит в движение механизмы электрозапоров (электродвери, раздвигающиеся ворота, двери лифта). Другими словами, любые устройства, которые работают на электричестве и имеют движущиеся узлы, основаны на эксплуатации закона Ампера.

• Также он находит применение во многих других видах электротехники, например, в громкоговорителе. В громкоговорителе или динамике для возбуждения мембраны, которая формирует звуковые колебания используется постоянный магнит. На него под действием электромагнитного поля, создаваемого расположенным рядом проводником с током, действует сила Ампера, которая изменяется в соответствии с нужной звуковой частотой.
• Принцип работы электромеханических машин (движение части обмотки ротора относительно части обмотки статора).
• Электродинамическое сжатие плазмы, например, в токамаках, установках Z-пинч.
• Электродинамический метод прессования.

История

В 1820 году Ханс Кристиан Эрстед открыл, что провод, по которому идёт ток, создает магнитное поле и заставляет отклоняться стрелку компаса. Он заметил, что магнитное поле перпендикулярно току, а не параллельно ему, как можно было бы ожидать. Ампер, вдохновлённый демонстрацией опыта Эрстеда, обнаружил, что два параллельных проводника, по которым течёт ток, притягиваются или отталкиваются в зависимости от того, в одну ли или разные стороны по ним идёт ток. Таким образом ток не только производит магнитное поле, но магнитное поле действует на ток. Уже через неделю после объявления Эрстедом о своём опыте, Ампер предложил объяснение: проводник действует на магнит, потому что в магните течёт ток по множеству маленьких замкнутых траекторий^[2][3].

Сила Ампера и третий закон Ньютона

Пусть есть два тонких проводника с токами I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}} , заданные кривыми C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}}. Сами кривые могут быть заданы радиус-векторами r1{\displaystyle \mathbf {r} _{1}} и r2{\displaystyle \mathbf {r} _{2}}. Найдем силу, действующую непосредственно на токовый элемент одного провода со стороны токового элемента другого провода. По закону Био — Савара — Лапласа токовый элемент I1dr1{\displaystyle I_{1}\mathrm {d} \mathbf {r} _{1}}, находящийся в точке r1{\displaystyle \mathbf {r} _{1}}, создает в точке r2{\displaystyle \mathbf {r} _{2}} элементарное магнитное поле dB1(r2)=μ04πI1[dr1,r2−r1]|r2−r1|3{\displaystyle \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0} \over 4\pi }{\frac {I_{1}[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}. По закону Ампера сила, действующая со стороны поля dB1(r2){\displaystyle \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})} на токовый элемент I2dr2{\displaystyle I_{2}\mathrm {d} \mathbf {r} _{2}}, находящийся в точке r2{\displaystyle \mathbf {r} _{2}}, равна d2F12=I2dr2×dB1(r2)=μ0I1I24π[dr2,[dr1,r2−r1]]|r2−r1|3{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}=I_{2}\mathrm {d} \mathbf {r} _{2}\times \mathrm {d} \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0}I_{1}I_{2} \over 4\pi }{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Токовый элемент I2dr2{\displaystyle I_{2}\mathrm {d} \mathbf {r} _{2}}, находящийся в точке r2{\displaystyle \mathbf {r} _{2}}, создает в точке r1{\displaystyle \mathbf {r} _{1}} элементарное магнитное поле dB2(r1)=μ04πI2[dr2,r1−r2]|r2−r1|3{\displaystyle \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})={\mu _{0} \over 4\pi }{\frac {I_{2}[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}. Сила Ампера, действующая со стороны поля dB2(r1){\displaystyle \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})} на токовый элемент I1dr1{\displaystyle I_{1}\mathrm {d} \mathbf {r} _{1}}, находящийся в точке r1{\displaystyle \mathbf {r} _{1}}, равна d2F21=I1dr1×dB2(r1)=μ0I1I24π[dr1,[dr2,r1−r2]]|r2−r1|3{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{21}=I_{1}\mathrm {d} \mathbf {r} _{1}\times \mathrm {d} \mathbf {B} _{2}(\mathbf {r} _{1})={\mu _{0}I_{1}I_{2} \over 4\pi }{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

В общем случае для произвольных r1{\displaystyle \mathbf {r} _{1}} и r2{\displaystyle \mathbf {r} _{2}} силы d2F12{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}} и d2F21{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{21}} даже не коллинеарны, а значит, не подчиняются третьему закону Ньютона: d2F12+d2F21≠0{\displaystyle \mathrm {d} ^{2}\mathbf {F} _{12}+\mathrm {d} ^{2}\mathbf {F} _{21}\neq 0}. Однако ничего страшного в этом нет. Физиками доказано, что постоянный ток может течь только по замкнутому контуру. Поэтому третий закон Ньютона должен действовать только для сил, с которыми взаимодействуют два замкнутых проводника с током. Убедимся, что для двух таких проводников третий закон Ньютона выполняется.

Пусть кривые C1{\displaystyle C_{1}} и C2{\displaystyle C_{2}} являются замкнутыми. Тогда ток I1{\displaystyle I_{1}} создает в точке r2{\displaystyle \mathbf {r} _{2}} магнитное поле B1(r2)=μ0I14π∮C1⁡[dr1,r2−r1]|r2−r1|3{\displaystyle \mathbf {B} _{1}(\mathbf {r} _{2})={\mu _{0}I_{1} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}, где интегрирование по C1{\displaystyle C_{1}} производится в направлении течения тока I1{\displaystyle I_{1}}. Сила Ампера, действующая со стороны поля B1(r2){\displaystyle \mathbf {B} _{1}(\mathbf {r} _{2})} на контур C2{\displaystyle C_{2}} с током I2{\displaystyle I_{2}}, равна F12=∮C2⁡(I2dr2×B1(r2))=∮C2⁡(I2dr2×μ0I14π∮C1⁡[dr1,r2−r1]|r2−r1|3)=μ0I1I24π∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3{\displaystyle \mathbf {F} _{12}=\oint \limits _{\mathbb {C} _{2}}(I_{2}\mathrm {d} \mathbf {r} _{2}\times \mathbf {B} _{1}(\mathbf {r} _{2}))=\oint \limits _{\mathbb {C} _{2}}(I_{2}\mathrm {d} \mathbf {r} _{2}\times {\mu _{0}I_{1} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}})={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}, где интегрирование по C2{\displaystyle C_{2}} производится в направлении течения тока I2{\displaystyle I_{2}}. Что характерно, порядок интегрирования значения не имеет.

Аналогично сила Ампера, действующая со стороны поля B2(r1){\displaystyle \mathbf {B} _{2}(\mathbf {r} _{1})}, создаваемого током I2{\displaystyle I_{2}}, на контур C1{\displaystyle C_{1}} с током I1{\displaystyle I_{1}}, равна F21=∮C1⁡(I1dr1×B2(r1))=μ0I1I24π∮C1⁡∮C2⁡[dr1,[dr2,r1−r2]]|r2−r1|3=∮C1⁡∮C2⁡d2F21{\displaystyle \mathbf {F} _{21}=\oint \limits _{\mathbb {C} _{1}}(I_{1}\mathrm {d} \mathbf {r} _{1}\times \mathbf {B} _{2}(\mathbf {r} _{1}))={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{1}-\mathbf {r} _{2}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}\mathrm {d} ^{2}\mathbf {F} _{21}}.

Равенство F12+F21=0{\displaystyle \mathbf {F} _{12}+\mathbf {F} _{21}=0} эквивалентно равенству ∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3=∮C1⁡∮C2⁡[dr1,[dr2,r2−r1]]|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {[\mathrm {d} \mathbf {r} _{1},[\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Чтобы доказать это последнее равенство, заметим, что выражение для силы Ампера очень похоже на выражение для циркуляции магнитного поля по замкнутому контуру, в котором внешнее скалярное произведение заменили векторным произведением. Тогда понятно, в каком направлении нужно двигаться.

Пользуясь тождеством Лагранжа, двойное векторное произведение в левой части доказываемого равенства можно записать так: [dr2,[dr1,r2−r1]]=dr1(dr2,r2−r1)−(r2−r1)(dr2,dr1){\displaystyle [\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]=\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})-(\mathbf {r} _{2}-\mathbf {r} _{1})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1})}.

Тогда левая часть доказываемого равенства примет вид:

∮C2⁡∮C1⁡[dr2,[dr1,r2−r1]]|r2−r1|3=∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3−∮C1⁡∮C2⁡(r2−r1)(dr2,dr1)|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{2}}\oint \limits _{\mathbb {C} _{1}}{\frac {[\mathrm {d} \mathbf {r} _{2},[\mathrm {d} \mathbf {r} _{1},\mathbf {r} _{2}-\mathbf {r} _{1}]]}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}-\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Рассмотрим отдельно интеграл ∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}, который можно переписать в следующем виде:

∮C1⁡∮C2⁡dr1(dr2,r2−r1)|r2−r1|3=∮C1⁡dr1∮C2⁡(r2−r1,d(r2−r1))|r2−r1|3{\displaystyle \oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {\mathrm {d} \mathbf {r} _{1}(\mathrm {d} \mathbf {r} _{2},\mathbf {r} _{2}-\mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{1}}\mathrm {d} \mathbf {r} _{1}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1},\mathrm {d} (\mathbf {r} _{2}-\mathbf {r} _{1}))}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}.

Сделав замену переменной во внутреннем интеграле на r=r2−r1{\displaystyle \mathbf {r} =\mathbf {r} _{2}-\mathbf {r} _{1}}, где вектор r{\displaystyle \mathbf {r} } изменяется по замкнутому контуру C2′{\displaystyle C_{2}’}, обнаружим, что внутренний интеграл является циркуляцией градиентного поля по замкнутому контуру. А значит, он равен нулю:

∮C2⁡(r2−r1,d(r2−r1))|r2−r1|3=∮C2′⁡(r,dr)|r|3=−∮C2′⁡(grad(1|r|),dr)=0{\displaystyle \oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{2}-\mathbf {r} _{1},\mathrm {d} (\mathbf {r} _{2}-\mathbf {r} _{1}))}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}=\oint \limits _{\mathbb {C} _{2}’}{\frac {(\mathbf {r} ,\mathrm {d} \mathbf {r} )}{|\mathbf {r} |^{3}}}=-\oint \limits _{\mathbb {C} _{2}’}(\mathrm {grad} ({\frac {1}{|\mathbf {r} |}}),\mathrm {d} \mathbf {r} )=0}

Значит, и весь двойной криволинейный интеграл равен нулю. В таком случае для силы F12{\displaystyle \mathbf {F} _{12}} можно записать:

F12=μ0I1I24π∮C1⁡∮C2⁡(r1−r2)(dr2,dr1)|r2−r1|3{\displaystyle \mathbf {F} _{12}={\mu _{0}I_{1}I_{2} \over 4\pi }\oint \limits _{\mathbb {C} _{1}}\oint \limits _{\mathbb {C} _{2}}{\frac {(\mathbf {r} _{1}-\mathbf {r} _{2})(\mathrm {d} \mathbf {r} _{2},\mathrm {d} \mathbf {r} _{1})}{|\mathbf {r} _{2}-\mathbf {r} _{1}|^{3}}}}

Выражение для силы F

19. Магнитное поле. Магнитная индукция. Закон Ампера.

Магнитное поле:

Неоднородное и однородное магнитное поле. Сила, с которой поле полосового магнита действует на помещенную в это поле магнитную стрелку, в разных точках поля может быть различной как по модулю, так и по направлению. Такое поле называют неоднородным. Линии неоднородного магнитного поля искривлены, их густота меняется от точки к точке. В некоторой ограниченной области пространства можно создать однородное магнитное поле, т.е. поле, в любой точке которого сила действия на магнитную стрелку одинакова по модулю и направлению. Для изображения магнитного поля пользуются следующим приемом. Если линии однородного магнитного поля расположены перпендикулярно к плоскости чертежа и наплавлены от нас за чертеж, то их изображают крестиками, а если из-за чертежа к нам – то точками.

Магни́тное по́ле— силовоеполе, действующее на движущиесяэлектрические зарядыи на тела, обладающиемагнитным моментом, независимо от состояния ихдвижения; магнитная составляющаяэлектромагнитного поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции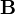

Магнитное поле макротоков описывается вектором напряжённости Н. (B=₀H).

Магнитная индукция:

Магни́тная инду́кция 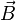—векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 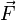магнитное поле действует назаряд 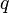, движущийся со скоростью.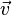

Единицы измерения: Тл.

Модуль вектора магнитной индукции B равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока в проводнике I и длине проводника l.

B=F / (I*l)

Магнитная индукция не зависит ни от силы тока, ни от длины проводника, она зависит только от магнитного поля. То есть, если мы, например, уменьшим силу тока в проводнике, не меняя больше ничего, то уменьшится не индукция, с которой сила тока связана прямо пропорционально, а сила воздействия магнитного поля на проводник. Величина же индукции останется постоянной. В связи с этим индукцию можно считать количественной характеристикой магнитного поля.

Магнитная индукция имеет направление. Графически ее можно зарисовывать в виде линий. Линии индукции магнитного поля это и есть то, что мы до сих пор в более ранних темах называли магнитными линиями или линиями магнитного поля. Так как мы выше вывели определение магнитной индукции, то мы можем дать определение и линиям магнитной индукции.

Линии магнитной индукции это линии, касательные к которым в каждой точке поля совпадают с направлением вектора магнитной индукции.

В однородном магнитном поле линии магнитной индукции параллельны, и вектор магнитной индукции будет направлен так же во всех точках.

В случае неоднородного магнитного поля, вектор магнитной индукции будет меняться в каждой точке пространства вокруг проводника, а касательные к этому вектору создадут концентрические окружности вокруг проводника.

Направление линий магнитной индукции определяется по правилу буравчика.

Закон Ампера:

Закон Ампера показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.

  Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником. 

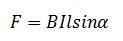
  Если размер проводника произволен, а поле неоднородно, то формула выглядит следующим образом: 

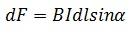
  Направление силы Ампера определяется по правилу левой руки.

  Правило левой руки : если расположить левую руку так, чтобы перпендикулярная составляющая вектора магнитной индукции входила в ладонь, а четыре пальца были вытянуты по направлению тока в проводнике, то отставленный на 90

° большой палец, укажет направление силы Ампера.

ЗАКОН АМПЕРА Применение закона ЗАКОН АМПЕРА

ЗАКОН АМПЕРА Применение закона

ЗАКОН АМПЕРА — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :

Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию : где α — угол между векторами магнитной индукции и тока.

ПРИМЕНЕНИЕ ЗАКОНА Громкоговоритель служит для возбуждения звуковых волн под действием переменного электрического тока, меняющегося со звуковой частотой. В электродинамическом громкоговорителе (динамике) используется действие магнитного поля постоянного магнита на переменный ток в подвижной катушке.

Схема устройства громкоговорителя показана на рисунке 1. 22, а. Звуковая катушка ЗК располагается в зазоре кольцевого магнита М. С катушкой жестко связан бумажный конус — диафрагма D. Диафрагма укреплена на упругих подвесах, позволяющих ей совершать вынужденные колебания вместе с подвижной катушкой. По катушке проходит переменный электрический ток с частотой, paвной звуковой частоте сигнала с микрофона или с выхода радиоприемника, проигрывателя, магнитофона. Под действием силы Ампера катушка колеблется вдоль оси громкоговорителя ОО 1 (см. рис. 1. 22, а) в такт с колебаниями токa. Эти колебания передаются диафрагме, и поверхность диафрагмы излучает звуковые волны. Первоклассные громкоговорители воспроизводят без значительных искажений звуковые колебания в диапазоне 40— 15 000 Гц. Но такие устройства очень сложны. Поэтому обычно применяют системы из нескольких громкоговорителей, каждый из которых воспроизводит звук в определенном небольшом интервале частот. Общим недостатком всех громкоговорителей является их малый КПД. Они излучают лишь 1 3% проводимой энергии.

Звук в радиоприемнике, проигрывателе и магнитофоне возникает в результате движения катушки с током в поле постоянного магнита. Наряду с электромеханическими громкоговорителями в настоящее время широкое применение получили громкоговорители, основаннью на пьезоэлектрическом эффекте. Этот эффект проявляется в виде деформации некоторых типов кристаллов в электростатическом поле. Две пьезопластинки склеивают. Пластинки подбирают так, что одна из них увеличивается но длине под действием поля, а другая уменьшается (см. рис. 1. 22, б). В результате получают элемент, который сильно изгибается под действием поля и при переменном электрическом поле создает акустическую волну. Пьезогромкоговорители очень удобны в изготовлении и могут быть совсем маленькими. Вследствие этого они нашли широкое применение в радиотелефонах, мобильных телефонах, ноутбуках и микрокомпьютерах. Взаимодействие токов и пьезоэлектрический эффект положены в основу принципа работы современных громкоговорителей.

ЭЛЕКТРОДИНАМОМЕТР ВЕБЕРА Закон Ампера взаимодействия токов, или, что то же самое, магнитных полей, порождаемых этими токами, используют для устройства весьма распространенного типа электроизмерительных приборов магнитоэлектрических приборов. Они имеют легкую рамку с проволокой, укрепленную на упругом подвесе той или иной конструкции, способную поворачиваться в магнитном поле. Родоначальником всех магнитоэлектрических приборов является электродинамометр Вебера (рис. 4).

Именно этот прибор позволил провести классические исследования закона Ампера. Внутри неподвижной катушки У висит на бифилярном подвесе поддерживаемая вилкой llў подвижная катушка C, ось которой перпендикулярна оси неподвижной катушки. При последовательном прохождении тока по катушкам, подвижная катушка стремится стать параллельно неподвижной и поворачивается, закручивая бифилярный подвес. Углы поворота отсчитываются при помощи прикрепленного к раме llў зеркала f.

формулировка и применение :: SYL.ru

Закон Ампера, формулировка которого известна любому физику, является одним из четырех уравнений Максвелла, которые в своей совокупности образуют фундамент всей теории классической электродинамики.

Уравнения Максвелла

Часть закона Ампера о том, как электрические токи, источники магнитного поля, относятся к самому полю. Другими словами, это (в совокупности с законом Гаусса для магнетизма) точно описывает картину, в которой электрические токи порождают магнитные поля. Поправочная часть Максвелла является значимой, поскольку она говорит, что магнитные поля появляются, когда электрические поля изменяются во времени. Это также важно, поскольку уравнения Максвелла не согласуются без него. С коррекцией термина можно вывести формулы сохранения электрического заряда и предсказать существование электромагнитных волн, которые перемещаются со скоростью.

В доходчивой форме закон Ампера принимает участие соответственно линейности уравнений Максвелла и, следовательно, всей теории классической электродинамики. Если взять два токовых распределителя и их совместить, тогда магнитное поле будет представлять собой сумму магнитных полей, производимых каждой конфигурацией.

Регулировочный элемент Максвелла является еще линейным, и, следовательно, электромагнитные волны являются линейными тоже. Они мешают друг другу согласно принципу суперпозиции и проходят прямо сквозь друг друга без рассеяния.

Как объяснить закон Ампера простым языком?

Простейшим объяснением является то, что провод переносит ток. Если игнорировать магнитное поле Земли, можно представить, что вертикальный провод с электрическим током идет вверх.

Люди склонны говорить об электромагнетизме, но электричество отдельно от магнетизма, поскольку установлено, что электричество и магнетизм влияют друг на друга и могут быть объединены в систему уравнений. В частности, в случае токоведущих проводов электрический ток производит магнитное поле. Ориентация этих полей не очень понятна, но это заметно. Магнитные компасы могут быть размещены вокруг токоведущих проводов, а направления поля можно увидеть в направлениях игловых точек.

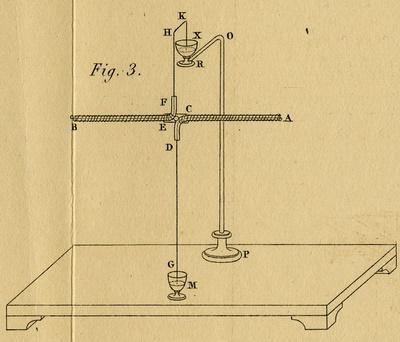
Есть возможность рассмотреть это из-за простой симметрии. Ток в проводе производит магнитное поле, но что должно произойти с узором в этих полях, если провод остается вертикальным и поворачивается на некоторый угол около этой вертикальной оси? Дело в том, что ток не меняется в любом случае на такой поворот. Он по-прежнему идет прямо. Следовательно, это вращение не может изменить картину магнитного поля, которое производится.

Структуры

Есть только две возможные структуры, которые работали бы от этого. Либо поля направлены радиально в сторону или подальше от провода, или вокруг провода. Первая возможность — это то, что люди получают от электрически заряженного провода электрическое поле. Вторая возможность — это то, что можно получить магнитное поле, создаваемое током, через провода.

Для одиночного проводника формы поля имеют круговые структуры по центру провода, и сила поля убывает с расстоянием. Как шаблон, это очень похоже на рябь, которая образуется при падении камня в воду. Существует два основных различия между прудом и картиной магнитного поля. Первый – это то, что магнитное поле остается неизменным на заданном расстоянии. Оно не будет расти, а будет уменьшаться в заданной точке. Второй заключается в том, что магнитное поле имеет направление к каждой точке касания окружности.

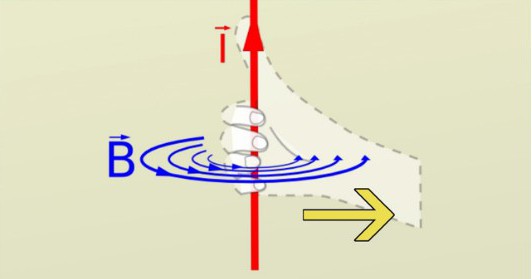
Сила тока и расстояние

Следующая часть закона Ампера гласит, что сила магнитного поля зависит от силы тока и расстояния от провода. В результате получается, что, если умножить силу магнитного поля на окружность круга, этот продукт будет пропорционален силе электрического тока. То есть, если удвоить расстояние от провода, линия окружности удваивается, а величина магнитного поля падает в 2 раза.

Но закон Ампера позволяет разобраться с токами, которые производятся в системах более сложных, чем одиночный провод. Но все эти случаи эквивалентны. Это означает, что идея магнитной напряженности поля, умноженной на длину пути, остается полезной и по-прежнему зависит от суммы всех токов внутри контура, который образует путь.

Как можно понять закон в практическом смысле?

Это влечет за собой некоторые векторные исчисления, которые можно объяснить интуитивно понятным способом:

• Магнитные поля создаются электрическими токами.
• Магнитные поля «накручены» на ток, который их производит в заданном направлении.
• Чем больше ток, тем сильнее создается магнитное поле. Напряженность магнитного поля пропорциональна току.

Закон Ампера связывает вместе эти понятия в одной из двух математических формул. Поле становится более интенсивным по мере приближения к проводу.

Пропорциональность суммарному току

В интегральной форме закона Ампера используется понятие линейного интеграла. В принципе, можно выбрать определенный цикл (т. е. замкнутый путь через космос) и пройтись вдоль петли, сложить составляющие магнитного поля. Это покажет, насколько магнитное поле вьется вокруг поверхности, ограниченной петлей. Утверждение, что эта величина пропорциональна суммарному току, который ограничен петлей, верно.

Чтобы понять это, нужно рассмотреть контур, ограничивающий провод. Если выполнить петлю вокруг провода, магнитное поле всегда идет к точке в том же направлении, что означает, что общая сумма криволинейного интеграла будет положительной. Это говорит, что можно пройти вокруг тока! Кроме того, можно определить направление тока, используя правило правой руки. Если поток тока пошел в другом направлении, значение криволинейного интеграла переворачивается.

Теперь можно предположить, что взят цикл, в котором не подкладывают проволоку, но делают круг против часовой стрелки над проводом. Если пройтись вокруг нижней части петли, в большинстве случаев направление будет идти против течения, поэтому вклад в интеграл будет отрицательным. Но когда направление проходит вокруг верхней части петли, в большинстве случаев оно будет такое же, что и ток, так что вклад будет положительным. Это говорит, что нет ничего внутри цикла (либо нет тока вообще, или течения токов в противоположных направлениях компенсируют друг друга).

Дифференциал

В дифференциальной форме применение закона Ампера происходит в концепции завитков векторной области. Локон — это количественное измерение, векторное поле — это «керлинг» вокруг данной точки. Если брать все меньшие и меньшие циклы вокруг точки и вычислить криволинейный интеграл, результат должен стать примерно пропорциональным площади петли. Коэффициентом пропорциональности является завиток.

Если взять цикл, который не содержат провода, криволинейный интеграл всегда будет равен нулю. Если петли все дальше и дальше, он всегда будет равен нулю. Коэффициент пропорциональности будет равен нулю, и ротор будет равен нолю (если быть точным, то нулевой вектор). Но если находиться внутри провода, то, независимо от того, какие петли, он будет получать ток, протекающий через него. Идея заключается в том, что для бесконечно малого контура только плотность тока в этот момент будет «внутри» него, а так только плотность тока в этой точке будет определять значение криволинейного интеграла. Поэтому ротор должен быть пропорционален плотности тока в данной точке, так как он соотносится по значению криволинейного интеграла по бесконечно малой петле.

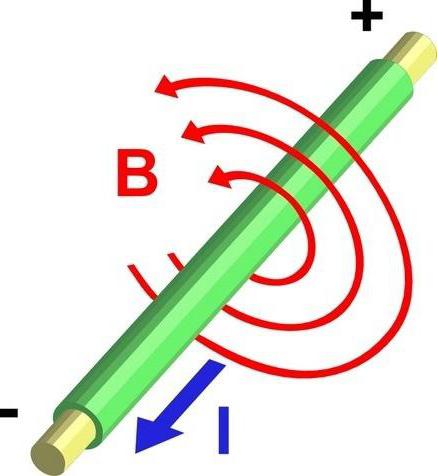
Заключение

В дифференциальной и интегральной формах закон Ампера эквивалентен, он может быть показан путем применения теоремы Стокса. По существу, дифференциальная форма является бесконечно малой версией второго уравнения в «интегральной форме». Но теорема Стокса — это тема другого исследования.

Что такое сила Ампера? :: SYL.ru

Знания о том, что такое сила Ампера, как она относится и чем может быть полезна для людей, необходимы для тех, кто работает с током. Как для собственной безопасности, так и для работы с различной радиоэлектроникой (при конструировании рельсетронов, что довольно популярно). Но хватит ходить вокруг, приступим к выяснению того, что такое сила Ампера, особенности этой силы и где она используется. Также можно будет прочитать потенциал использования в будущем и пользу от использования сейчас.

Закон Ампера

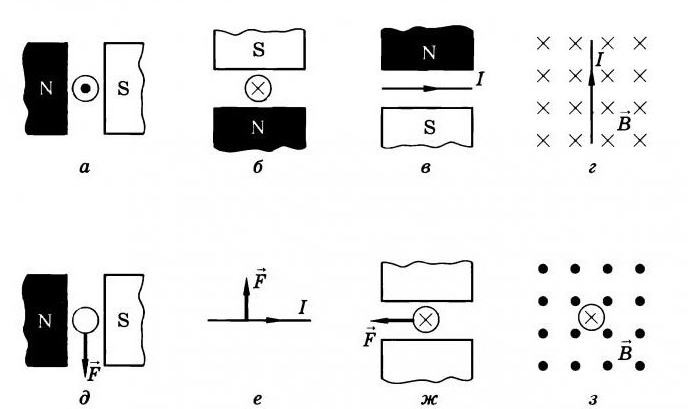Сила Ампера является главной составляющей закона Ампера — закона о взаимодействии электрических токов. В нём говорится, что в параллельных проводниках, в которых электрические токи текут в одном направлении, возникает сила притягивания. А в тех проводниках, в которых электрические токи текут в противоположных направлениях, возникает сила отталкивания.

Также законом Ампера называют закон, который определяет силу действия магнитного поля не небольшую часть проводника, по которой протекает ток. В данном случае она определяется как результат умножения плотности тока, который идёт по проводнику, на индукцию магнитного поля, в котором проводник находится.

Из самого закона Ампера сделаны выводы, что сила Ампера равняется нулю, если величина угла, расположенного между током и линией магнитной индукции, тоже будет равняться нулю. Другими словами, проводник для достижения нулевого значения должен быть расположен вдоль линии магнитной индукции.

А что же такое сила Ампера?

Это сила, с которой магнитное поле влияет на часть проводника, по которому течёт ток. Сам проводник находится в магнитном поле. Сила Ампера прямо зависит от силы тока в проводнике и векторного произведения длины части проводника, множимого на магнитную индукцию.

В формульном виде всё будет выглядеть так: са=ст*дчп*ми. Здесь:

• са – сила Ампера,
• ст – сила тока,
• дчп – длина части проводника,
• ми – магнитная индукция.

История открытия

Впервые его сформулировал Андре Ампер, который применил закон к постоянному току. Открыт он был в 1820 году. Этот закон в будущем имел далеко идущие последствия, ведь без него представить работу целого ряда электрических приборов просто невозможно.

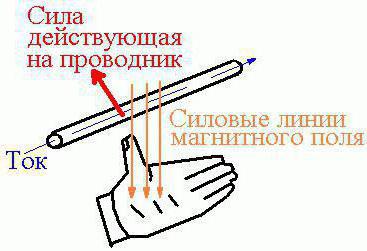
Правило левой руки

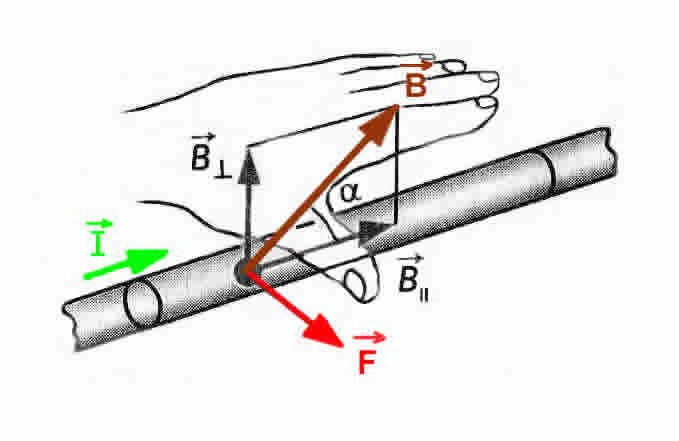Это правило помогает запомнить направление силы Ампера. Само правило звучит так: если рука занимает такое положение, что линии самой магнитной индукции внешнего поля заходят в ладонь, а пальцы с мизинца по указательный указывают направление в сторону движения тока в проводнике, то отторгнутый по углом в 90 градусов большой палец ладони и будет указывать, куда направлена сила Ампера, действующая на элемент проводника. Могут возникнуть некоторые затруднения при использовании этого правила, но только если угол между током и индукцией поля слишком маленький. Для простоты применения этого правила ладонь часто располагают так, чтобы в неё входил не вектор, а модуль магнитной индукции (как изображено на картинке).

Сила Ампера (при использовании двух параллельных проводников)

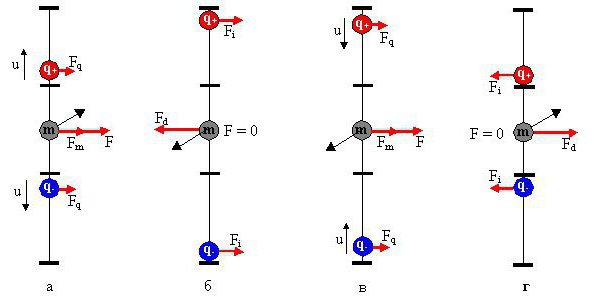
Представьте два бесконечных проводника, которые расположены на определённом расстоянии. По ним протекают токи. Если токи текут в одном направлении, то проводники притягиваются. В противоположном случае они будут отталкиваться один от одного. Поля, которые создают параллельные проводники, направлены встречно друг другу. И чтобы понять, почему они реагируют именно так, вам достаточно вспомнить о том, что одноименные полюса магнитов или одноименные заряды всегда отталкиваются. Для определения стороны направления поля, созданного проводником, следует использовать правило правого винта.

Применение знаний о силе Ампера

Встретиться с областью применения знания о силе Ампера можно практически на каждом шагу цивилизации. Применение силы Ампера настолько обширно, что среднестатистическому гражданину даже сложно представить себе, что можно делать, зная закон Ампера и особенности применения силы. Так, под действием силы Ампера вращается ротор, на обмотку которого оказывает влияние магнитное поле статора, и ротор приходит в движение. Любое транспортное средство, которое использует электротягу для вращения валов (которые соединяют колеса транспорта), использует силу Ампера (это можно увидеть на трамваях, электровозах, электрических машинах и многих других интересных видах транспорта). Также именно магнитное поле влияет на механизмы, которые являются электрическими приборами, что должны открывать/закрывать что-то (двери лифта, открывающиеся ворота, электрические двери и много других). Другими словами, все устройства, что не могут работать без электричества и имеют движимые узлы, работают благодаря знанию о законе Ампера. Для примера:

1. Любые узлы в электротехнике. Самый популярный – элементарный электродвигатель.
2. Различные виды электротехники, которая формирует различные звуковые колебания с использованием постоянного магнита. Механизм действия таков, что на магнит действует электромагнитное поле, что создает расположенный рядом проводник с током, и изменение напряжения приводит к смене звуковой частоты.
3. На силе Ампера построена работа электромеханических машин, в которых движение обмотки ротора происходит относительно обмотки статора.
4. С помощью силы Ампера происходит электродинамический процесс сжатия плазмы, что нашло применение в токамаках и потенциально открывает огромные пути развития термоядерной энергии.
5. Также с помощью электродинамического сжатия применяется электродинамический метод прессования.

Потенциал

Несмотря на уже сейчас существующее практическое применение, потенциал использования силы Ампера настолько огромен, что с трудом поддаётся описанию. Она может использоваться в сложных механизмах, которые призваны облегчить существование человека, автоматизировать его деятельность, а также усовершенствовать природные жизненные процессы.

Эксперимент

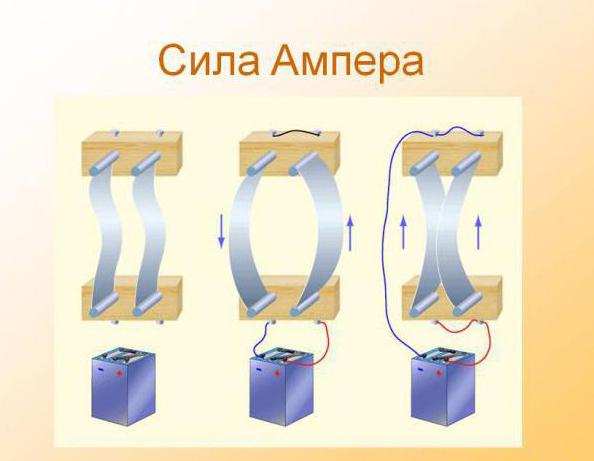
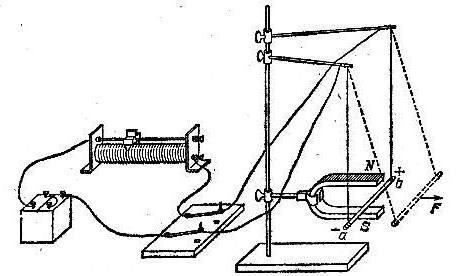Для того чтобы иметь возможность своими глазами увидеть действие силы Ампера, можно провести дома небольшой эксперимент. Для начала необходимо взять магнит-подкову, в котором между полюсами поместить проводник. Всё желательно воспроизвести так, как на картинке. Если замкнуть ключ, то можно увидеть, что проводник начнёт двигаться, смещаясь от начальной точки равновесия. Можно поэкспериментировать с направлениями пропускания тока и увидеть, что зависимо от направления движения меняется направление отклонения проводника. Из самого эксперимента можно вынести несколько наблюдений, которые подтверждают вышесказанное:

• Магнитное поле действует исключительно на проводник с током.
• На проводник с током в магнитном поле действует сила, которая является следствием их взаимодействия. Именно под воздействием этой силы проводник движется в пространстве в границах магнитного поля.
• Характер взаимодействия прямо зависит от напряжения электрического тока и силовых линий магнитного поля.
• Поле не действует на проводник с током, если ток в проводнике течёт параллельно направлению линий поля.

Безопасность при работе с током

При работе с электрическим током необходимо придерживаться нескольких простых правил техники безопасности, которые позволят вам избежать негативных последствий:

• Работать с источниками питания не больше 12 Вольт.
• Не работать на воспламеняемых материалах.
• Не работать с мокрыми руками.
• Не браться за части прибора, которые находятся под напряжением.

Точная формулировка закона Ампера. заранее спасибо

Сила, с которой магнитное поле действует на проводник с током ( сила Ампера) равна произведению магнитной индукции на силу тока, длину участка проводника и на синус угла между вектором магнитной индукции и проводником . Fа= В* I* L*sin a .

параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются.

Закон Ампера — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током.