Закон Архимеда. Плавание тел | Физика

Вы уже знаете, что внутри жидкости в любой точке существует гидростатическое давление. Поэтому если внутрь жидкости в сосуде поместить тело (например, шар), то на все точки его поверхности будут действовать силы гидростатического давления (рис. 165, а). Определим сумму этих сил.

Для этого рассмотрим второй такой же сосуд, заполненный, как и первый, такой же жидкостью (рис. 165, б). Выделим мысленно во втором сосуде объем жидкости, границы которого совпадают с границами тела в первом сосуде. Поскольку этот объем жидкости покоятся относительно Земли, то сумма всех действующих на него сил равна нулю. Иначе говоря, сумма сил гидростатического давления, действующих на выделенный объем жидкости, уравновешивает действующую на него силу тяжести. Следовательно, сумма сил гидростатического давления равна по модулю силе тяжести выделенного объема жидкости. Эта сумма сил направлена вертикально вверх (рис. 165, в). Поэтому ее называют выталкивающей силой.

Сумма сил гидростатического давления, действующих на выделенный объем покоящейся жидкости в сосуде, равна по модулю весу выделенного объема жидкости и направлена вертикально вверх.

Понятно, что на тело в первом сосуде со стороны окружающей жидкости действует такая же выталкивающая сила. Впервые на существование этой силы указал древнегреческий ученый Архимед. Поэтому выталкивающую силу F_A обычно называют силой Архимеда.

Сумму сил гидростатического давления, действующих на тело, покоящееся внутри жидкости, называют силой Архимеда.

Поскольку масса m выделенного объема жидкости равна произведению ее плотности ρ_ж и объема V, то модуль силы Архимеда F_A = ρ_ж · g · V. Другими словами, сила Архимеда по модулю равна весу вытесненной телом жидкости.

Если тело поместить в газ, то на это покоящееся тело будут действовать силы давления со стороны окружающего газа. Поэтому на такое тело также будет действовать выталкивающая сила, равная по модулю F

A = ρ_г · g · V, где ρ_г – плотность газа, в котором находится тело, V – объем тела.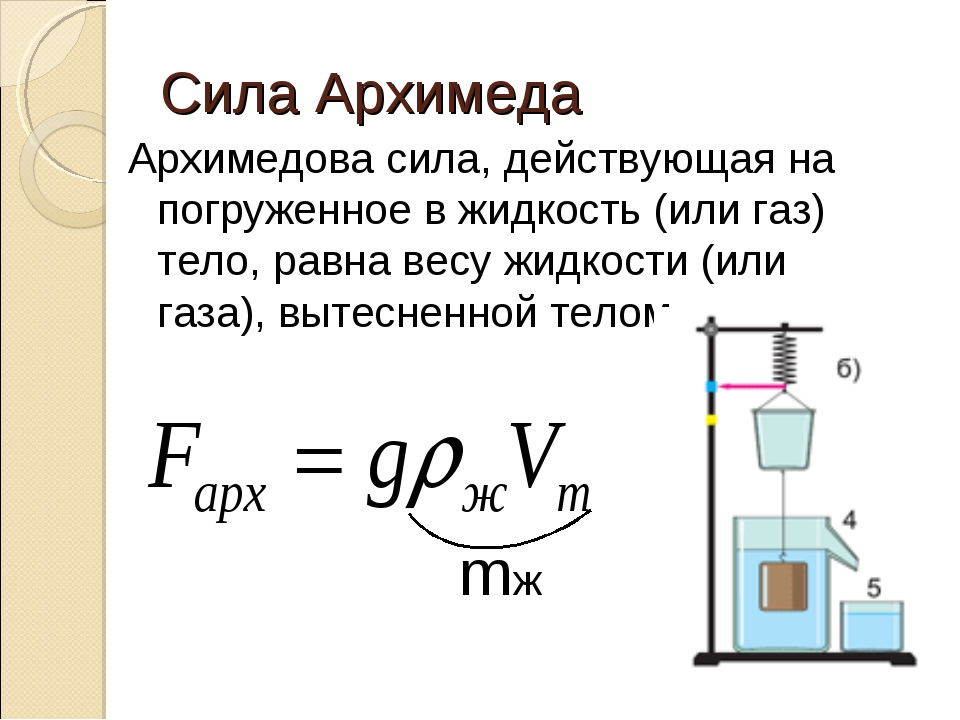 Таким образом,

на погруженное в жидкость (или газ) тело действует выталкивающая и направленная вертикально вверх сила, равная по модулю весу вытесненной этим телом жидкости (или газа).

Это утверждение называют законом Архимеда.

Рассмотрим тело массой M, целиком погруженное в покоящуюся относительно Земли жидкость. Помимо суммы сил гидростатического давления – силы Архимеда F_A – на это тело действует сила тяжести Mg. Если сила тяжести по модулю превышает силу Архимеда, то это тело будет все глубже погружаться в жидкость, т. е. будет тонуть (рис. 166, а). Так как модуль силы тяжести Mg равен (ρ

т · V) · g, где ρ_т – средняя плотность теаа, то тело будет тонуть, если (ρ_т · V) · g > ρ_ж · g · V, т. е. если средняя плотность тела будет больше плотности жидкости: ρ_т > ρ_ж.

Если же модули сил тяжести и Архимеда равны (при этом ρ_т = ρ_ж), то тело будет оставаться в покое (рис. 166, б).

Наконец, если сила тяжести по модулю окажется меньше силы Архимеда (когда ρ_тж), то тело будет всплывать (рис. 166, в). После того как тело своей верхней границей достигнет поверхности жидкости и будет продолжать подниматься, все более выступая над поверхностью, объем погруженной в жидкости части тела будет уменьшаться. Поэтому выталкивающая сила со стороны жидкости также начнет уменьшаться, пока не станет равной по модулю силе тяжести:

F_в = Mg

Для плавания тела на поверхности жидкости необходимо, чтобы сила тяжести уравновешивалась выталкивающей силой.

Это равенство является условием плавания тела на поверхности жидкости. Модуль выталкивающей силы F_в = ρ_ж · g · V_ж, где V_ж – объем вытесненной телом жидкости. Поэтому условие плавания тела на поверхности жидкости F_т = F_в можно представить в виде:

ρ_т · V_т = ρ_ж · V_ж

Рассмотрим примеры применения закона Архимеда для решения практических задач.

Задача 1. Определение подъемной силы воздушного шара

Воздушные шары используют в воздухоплавании для подъема грузов (людей, приборов и т. п.). Для того чтобы шар с грузом мог взлететь, его наполняют газом, плотность которого меньше плотности окружающего воздуха. Таким газом может быть, например, гелий. Однако в последнее время чаще используют нагретый воздух, так как плотность воздуха уменьшается при нагревании. Для нагревания воздуха внутри воздушного шара снизу в нем делают отверстие, под которым располагают горелку. Нагревание воздуха внутри шара и уменьшение его плотности приводит к появлению подъемной силы.

Подъемной силой шара называют силу, равную по модулю весу груза, г которым шар может подниматься равномерно: F_под = P. Определите эту силу.

Решение. На рис. 167 изображены воздушный шар и действующие на него силы: сила тяжести mg, сила Архимеда F_A и P – вес груза. Если шар поднимается равномерно, то его ускорение равно нулю. Поэтому по второму закону Ньютона:

F_A — m · g — P = m · a = m · 0 = 0.

Следовательно,

P = F_A — m · g.

Поэтому

F_под = P = F_A — m · g.

Подъемная сила воздушного шара равна разности модулей действующих на этот шар силы Архимеда и силы тяжести.

Задача 2. Определение водоизмещения и грузоподъемности судна

Пусть судно массой M стоит у причала под погрузкой (рис. 168). На судно помещен груз массой m и судно находится в равновесии. Определите объем той части судна, которая находится ниже уровня воды.

Решение. По второму закону Ньютона сумма сил, действующих на судно, равна нулю (условие плавания):

F_A — (m + M) · g = 0

Вместе с тем модуль силы Архимеда F_A = ρ_в · g · V_п. Здесь ρ_в – плотность воды, а V_п – объем той части судна, которая находится ниже уровня воды. Подставляя выражение для FA в условие плавания, получаем:

ρ_в · g · V_п — (m + M) · g = 0

Следовательно,

V_п = (m + M) / ρ_в

Из последнего выражения видно, что чем больше масса m груза, тем большая часть судна V

п погружается под воду. С увеличением массы груза увеличивается осадка судна – глубина, на которую судно погружается в воду. Максимально допускаемую при загрузке осадку отмечают на корпусе судна линией. Ее называют ватерлинией.

Модуль веса воды, вытесняемой судном при погружении до ватерлинии, называют водоизмещением судна.

Обозначим объем той части судна, которая находится ниже ватерлинии, V_max. Тогда водоизмещение судна равно ρ_в · g · V_max.

Подставляя это выражение в условие плавания, легко найти модуль силы тяжести, действующей на груз максимально допустимой массы:

ρ_в · g · V_max — (m_max + M) · g = 0,
m_max · g = ρ_в · g · V_max — M · g.

Полученную величину называют грузоподъемностью судна. Видно, что грузоподъемность судна равна разности его водоизмещения и модуля силы тяжести судна без груза.

Итоги

Сумму сил гидростатического давления, действующих на тело, покоящееся внутри жидкости, называют силой Архимеда.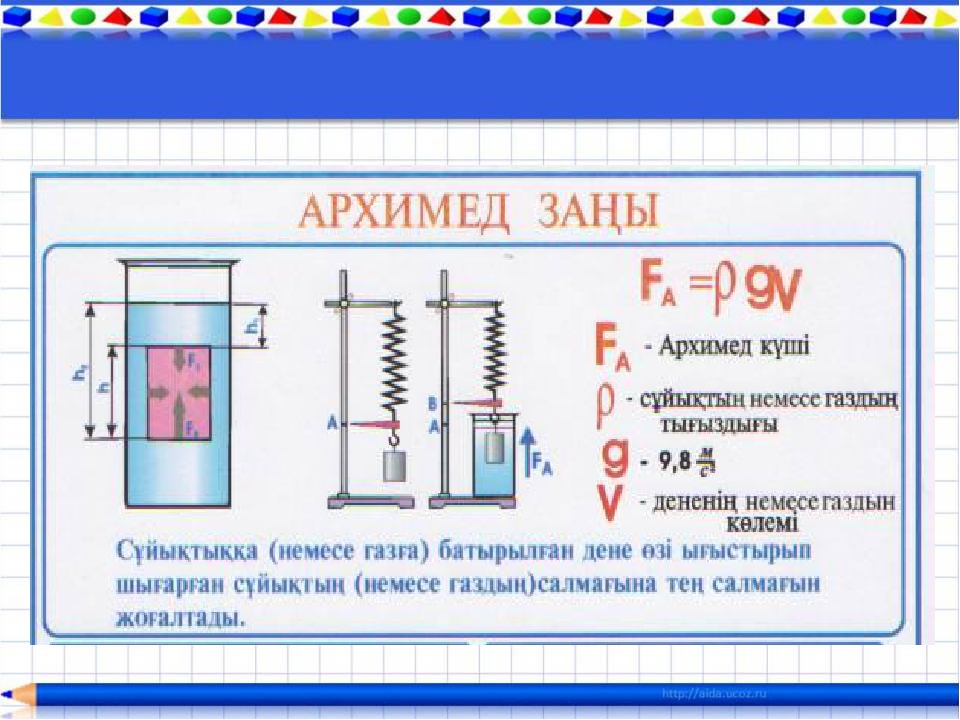

Закон Архимеда. На погруженное в жидкость (или газ) тело действует выталкивающая и направленная вертикально вверх сила, равная по модулю весу вытесненной этим телом жидкости (или газа).

F_A = ρ_ж · g · V

Тело тонет, если ρ_т > ρ_ж; тело всплывает, если ρ_тж.

Условие плавания тела на поверхности жидкости:
для плавания тела на поверхности жидкости необходимо, чтобы сила тяжести уравновешивалась выталкивающей силой:

F_в = M · g

Условие плавания тела на поверхности жидкости можно представить в виде

ρ_т · V_т = ρ_ж · V_ж

Вопросы

1. Какие силы действуют на любое тело, находящееся внутри жидкости или газа?
2. Сформулируйте закон Архимеда.
3. В каком случае тело тонет в жидкости, а в каком всплывает?
4. Почему, находясь под водой, человек может поднять предмет, который он, находясь на суше, не может даже сдвинуть с места?
5. Почему гусиное яйцо тонет в пресной воде, а в соленой плавает?
6. Как зависит глубина погружения плавающего на поверхности жидкости тела от его плотности?
7. Куда направлена сумма сил гидростатического давления, действующих на кубик, который прилип к горизонтальному дну озера своей нижней гранью?
8. К чашкам равноплечих весов подвешены два шарика одинаковой массы. Нарушится ли равновесие весов при погружении шариков в воду, если: а) оба шарика медные; б) один шарик железный, а другой – медный?
9. К чашкам равноплечих весов подвешены два одинаковых стальных шарика. Нарушится ли равновесие весов при погружении шариков в разные жидкости, плотности которых: а) равны; б) различаются в два раза?

Упражнения

1. Пользуясь таблицей плотностей, укажите, шарики из каких металлов будут плавать в ртути, а из каких – тонуть.
2. Пользуясь таблицей плотностей, рассчитайте, какая часть однородной льдины выступает над поверхностью воды в озере.
3. Пользуясь таблицей плотностей, рассчитайте, какая часть однородного березового куба, плавающего на поверхности воды, будет погружена в воду.
4. Определите подъемную силу детского воздушного шарика, заполненного гелием. Объем шарика V = 5 дм³. Масса его оболочки m = 5 г. Плотность гелия считайте равной ρ_г = 0,19 кг/м³, а плотность воздуха атмосферы ρв = 1,3 кг/м³.
5. После разгрузки баржа поднялась из воды на 1 м. Определите вес снятого с баржи груза, считая площадь сечения баржи на уровне воды постоянной и равной 350 м ².
6. После погрузки на паром длиной 40 м и шириной 10 м двух одинаковых комбайнов он погрузился в воду на 10 см. Найдите массу комбайна.

Закон Архимеда

                                     

1. Описание

Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.

Если тело плавает см. плавание тел или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.

Например, воздушный шарик объёмом V {\displaystyle V}, наполненный гелием, летит вверх из-за того, что плотность гелия ρ H {\displaystyle \rho _{H}} меньше плотности воздуха ρ O {\displaystyle \rho _{O}}:

F A > F p ; {\displaystyle F_{A}> F_{p};} ρ O g V > ρ H g V. {\displaystyle \rho _{O}gV> \rho _{H}gV.}

Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление P A {\displaystyle P_{A}} и сила давления F A {\displaystyle F_{A}}, действующие на верхнюю грань тела, равны:

P A = ρ g h A ; {\displaystyle P_{A}=\rho gh_{A};} F A = ρ g h A S, {\displaystyle F_{A}=\rho gh_{A}S,}

где:

• S {\displaystyle S} — площадь горизонтального поперечного сечения тела, м 2.
• ρ {\displaystyle \rho } — плотность жидкости или газа, кг/м 3 ;
• P A {\displaystyle P_{A}} — давление, оказываемое жидкостью или газом на верхнюю грань тела, Па;
• h A {\displaystyle h_{A}} — расстояние между поверхностью жидкости или газа и верхней гранью тела, м;
• F A {\displaystyle F_{A}} — сила давления, действующая на верхнюю грань тела и направленная вниз, Н;

Давление P B {\displaystyle P_{B}} и сила давления F B {\displaystyle F_{B}}, действующие на нижнюю грань тела, равны:

P B = ρ g h B ; {\displaystyle P_{B}=\rho gh_{B};} F B = ρ g h B S, {\displaystyle F_{B}=\rho gh_{B}S,}

где:

• P B {\displaystyle P_{B}} — давление, оказываемое жидкостью или газом на нижнюю грань тела, Па;
• F B {\displaystyle F_{B}} — сила давления, действующая на нижнюю грань тела и направленная вверх, Н;
• h B {\displaystyle h_{B}} — расстояние между поверхностью жидкости или газа и нижней гранью тела, м.

Сила давления жидкости или газа на тело определяется разностью сил F B {\displaystyle F_{B}} и F A {\displaystyle F_{A}}:

F B − F A = ρ g h B S − ρ g h A S = ρ g h B − h A S = ρ g h S = ρ g V, {\displaystyle F_{B}-F_{A}=\rho gh_{B}S-\rho gh_{A}S=\rho g\lefth_{B}-h_{A}\rightS=\rho ghS=\rho gV,}

где:

• h = h B − h A {\displaystyle h=h_{B}-h_{A}} — расстояние между верхней и нижней гранями тела в случае частичного погружения высота части тела, погружённой в жидкость или газ, м;
• V {\displaystyle V} — объём тела, погружённого в жидкость или газ в случае частичного погружения объём части тела, погружённой в жидкость или газ, м 3.

Разница давлений:

P B − P A = ρ g h B − ρ g h A = ρ g h. {\displaystyle P_{B}-P_{A}=\rho gh_{B}-\rho gh_{A}=\rho gh.}

В отсутствие гравитационного поля, то есть, в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление естественной конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов необходимо производить принудительно вентиляторами.

Изучение закона Архимеда — физика, уроки

Повторение предыдущей темы.

в

Работа в парах. Проверка знаний в форме теста , с последующей проверкой (ответы выводятся на доску) взаимопроверка

ТЕСТ по теме «Архимедова сила, плавание тел»

Вариант 1

1. В каких единицах измеряется выталкивающая сила в СИ?
а) Н                        б) кг                             с) Па                            д) Н/кг

2. Если плотность тела равна плотности жидкости, то тело…
а) плавает                          б) тонет                         с) всплывает             

3. Найдите верную формулу архимедовой силы:
а) F_a = ρ_т V_т g                б) F_a = ρ_ж V_т g              с) F_a = ρ_ж V_ж g                    д) F_a = ρ_т V_ж g 

4. Переведи в СИ  1,9 кН
а) 190 Н                          б) 1900 Н                    с) 19 000 Н                        д) 0,19 Н

5. В сосуд налиты три жидкости: вода, керосин, ртуть. Как они будут расположены, считая от дна сосуда?

(Плотность воды 1000 кг/м³, керосина 800 кг/м³, ртути 13600 кг/м³)
а) ртуть, керосин, вода               б) керосин, вода, ртуть                     с) ртуть, вода, керосин

д) вода, керосин, ртуть

6. Чему равна архимедова сила, действующая на  стеклянное тело объемом 125 см³ при полном его погружении в воду? Плотность воды 1000 кг/м³, стекла 2500 кг/м³

а) 1250 Н                          б) 125 Н                           с) 12,5 Н                              д) 1,25 Н

7. Три одинаковых по размеру шарика, 1,2,3, погружены в жидкость. На какой из шариков действует наибольшая выталкивающая сила?

                                               а) На 1-й.

б) На 2-й.

с) На 3-й.

д) На все шары действует одинаковая выталкивающая сила

 

 

 

 

8. Два одинаковых кубика погружены в сосуды с жидкостями. В каком сосуде, 1 или 2, плотность жидкости меньше?

а) В обоих сосудах плотности жидкости одинаковые.

б) В первом.

с) Во втором.

 

 

             1        2

9. На весах уравновешены два тела, 1 и 2. Нарушится ли равновесие, если их опустить в сосуд с керосином?

а) Тело 1 перевесит тело 2.

б) Тело 2 перевесит 1.

с)  Равновесие не нарушится.

 

 

 

 

 

 

   

ТЕСТ по теме «Архимедова сила, плавание тел»

Вариант 2

1. В каких единицах измеряется подъемная сила в СИ?
а) Н                        б) кг                             с) Па                            д) Н/кг

2. Если вес тела больше архимедовой силы, то тело …
а) всплывает                             б) тонет                              с) плавает

3. Найдите верную формулу (Р – вес тела в вакууме, Р₁ – вес тела в жидкости)

а) Р₁ = Р + F_а                   б) F_а = Р + Р₁               с) Р₁ = Р – F_a                    д) Р₁ = F_а — Р

4. Переведи в СИ 3,5 кН

а) 350 Н                          б) 3500 Н                    с) 35 000 Н                        д) 0,35 Н

5. Какие из металлов: золото, серебро, медь не потонут в ртути? (Плотность ртути
13600 кг/м³ , золота 19300 кг/м³, серебра 10500 кг/м³, меди 8900 кг/м³

а) все металлы                           б) ни один из перечисленных
с) золото                                     д) серебро, медь

6. Чему равен объем тела, если при полном погружении в воду на него действует выталкивающая сила 16 Н
а) 0,0016 м³                   б) 0,016 м³                    с)  1,6 м³                      д) 16000 м³

7. Три шарика, 1,2,3, погружены в жидкость. На какой из шариков действует наибольшая выталкивающая сила?

а) На 1-й.

б) На 2-й.

с) На 3-й.

д) На все шары действует одинаковая вытал­кивающая сила.

 

 

 

 

8. Два одинаковых кубика погружены в сосуды с жидкостями. В каком сосуде, 1 или 2, на кубик действует наибольшая выталкивающая сила?

                                             а) В обоих сосудах действует одинаковая выталкивающая сила.

б) В первом.

с) Во втором

 

 

1  2

9. На весах уравновешены два тела, 1 и 2. Нарушится ли равновесие, если тело 1 опустить в воду, а тело 2 — в машинное масло?

а) Тело 1 перевесит тело 2.

б) Тело 2 перевесит 1.

с) Равновесие не нарушится.

    

Выполнение лабораторной работы , используя электронный учебник.

Ученики В парах выполняют работу , делают выводы , о способах измерения Архимедовой силы.

 

Сообщение учителя: ребята,  мы с вами сейчас поработали в виртуальной лаборатории, а теперь я предлагаю вам самим провести небольшой эксперимент , чтобы проверить наши гипотезы (Работа в парах)

1 Опыт с яйцом , чтобы выявить зависимость Архимедовой силы от плотности жидкости. (оборудование: чаши с водой , соль, яйцо, ложка)

2.Опыт  с монетой и прбкой , равных масс , чтобы выявить зависимость силы Архимеда от объёма тела.

 

 

 Каждая пара делает выводы по проделанной  работе.

И сможите ли вы предсказать результат опыта,

Приборы и материалы: школьные весы (без чашек),два груза, масса и объем которых одинаковы, сосуды с водой и любой жидкостью, кроме воды.

Ход работы:

1.установите грузы на плечах весов и уравновесьте весы.

2.Нарушиться ли равновесие весов, если одно из тел погрузить в сосуд с водой, а другое- в сосуд с другой жидкостью? Ответьте на вопрос.

3.Проверьте ответ на опыте.

 

 

Решение расчетных задач. Работа на доске.

1.Вес кирпича в воздухе 30 Н, а в воде – 10Н. Чему равна действующая на кирпич архимедова сила?

2.На погруженный в воду кирпич действует выталкивающая сила, равная 20Н. Чему равен объем этого кирпича ?

Демонстрация опыта : какова грузоподъёмность пробки . (мотивация к изучению новой темы  «Условия плавания тела»)

Академия занимательных наук.

Физика — Архимедова сила. Закон Архимеда. Видеоуроки физики

Архимедова сила. Закон Архимеда. Видеоуроки физики

Выпуск 8

В видеоуроке физики от Академии занимательных наук профессор Даниил Эдисонович расскажет о древнегреческом учёном Архимеде и некоторых из его удивительных открытий. Как узнать, является ли золото чистым? Каким образом многотонные корабли умудряются плавать по океанским волнам? Наша жизнь полна загадочных явлений и хитрых головоломок. Физика способна подобрать ключи к некоторым из них. Посмотрев восьмой видеоурок физики вы познакомитесь с законом Архимеда и Архимедовой силой, а также историей их открытия.

Закон Архимеда

Почему в воде предметы весят меньше, чем на суше? Для человека пребывание в воде сравнимо с пребыванием в состоянии невесомости. Это используют в своих тренировках космонавты. Но из-за чего же так происходит? Дело в том, что на тела, погружённые в воду действует выталкивающая сила, открытая древнегреческим философом Архимедом. Закон Архимеда звучит так — погружённое в жидкость тело теряет в весе столько, сколько весит объём вытесненной им воды. Выталкивающую силу назвали Архимедовой, в честь первооткрывателя. Архимед, был одним из величайших ученых Древней Греции. Этот гениальный математик и механик, жил в Сиракузах в III веке до н. э. Вэто время в Сиракузах правил царь Гиерон. Однажды Гиерон, получив от мастеров заказанную им золотую корону, усомнился в их честности. Ему показалось, что они утаили часть золота, выданного на ее изготовление, и заменили его серебром. Но как уличить ювелиров в подделке? Гиерон поручил Архимеду определить, есть ли в золотой короне примесь серебра. Архимед искал решение задачи постоянно, не переставая думать об этом, когда занимался другими делами. А решение нашлось…  в бане. Архимед, намылился золой и полез в ванну.И произошло то, что бывает всякий раз, когда любой человек, даже не ученый, садится в любую, даже не мраморную ванну — вода в ней поднимается. Но то, на что обычно Архимед не обращал никакого внимания, вдруг заинтересовало его. Он привстал – уровень воды опустился, он снова сел — вода поднялась; причем поднималась она по мере погружения тела. И вот в этот миг Архимеда осенило. Он усмотрел в десятке раз проведенном опыте намек на то, как объем тела связан с его весом. И понял, что задача царя Гиерона разрешима. И так обрадовался своей случайной находке, что как был – голый, с остатками золы на теле – побежал домой через город, оглашая улицу криками: «Эврика! Эврика!». Вот так Архимед, если верить легенде, нашел решение задачи Гиерона. Архимед попросил у царя два слитка — серебряный и золотой. Вес каждого слитка был равен весу короны. Положив в сосуд до краёв наполненный водой сначала серебряный, а затем золотой слиток, учёный измерил объём вытесненной каждым из слитков воды. Золото вытеснило меньше воды, чем серебро. А всё потому, что объём куска золота был меньше куска серебра такого же веса. Ведь золото тяжелее серебра. Затем Архимед погрузил в сосуд корону и измерил объём вытесненной ею воды. Корона вытеснила меньше воды, чем слиток серебра. но больше чем слиток золота. Так мошенничество ювелира было разоблачено. Благодаря Архимедовой силе способны плавать гигантские корабли, весящие сотни тысяч тонн. Это происходит благодаря тому, что они обладают большим водоизмещением. То есть, их объём таков, что вытесняет огромное количество воды. А как вы помните, чем больше объём тела, тем сильнее действует на него Архимедова сила.

Закон архимеда на тело погруженное в жидкость. Закон Архимеда: определение и формула

Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа) . Сила называется силой Архимеда :

где — плотностьжидкости (газа), — ускорение свободного падения, а — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена кцентру тяжестиэтого объёма.

Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.

Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.

Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

Закон Архимеда можно объяснить при помощи разности гидростатических давленийна примере прямоугольного тела.

где P A , P B — давления в точках A и B , ρ — плотность жидкости, h — разница уровней между точками A и B , S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.

18. Равновесие тела в покоящейся жидкости

Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела. P выт = ρ ж gV погр

Для однородного тела плавающего на поверхности справедливо соотношение

где: V — объем плавающего тела; ρ m — плотность тела.

Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.

Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется остойчивостью . Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением , а точку приложения равнодействующей давления (т.е. центр давления) — центром водоизмещения . При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O»-O» , представляющей ось симметрии судна и называемой осью плавания (рис.2.5).

Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K»L»M» , наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d» . Приложим к точке d» подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O»-O» . Полученная точка m называется метацентром , а отрезок mC = h называется метацентрической высотой . Будем считать h положительным, если точка m лежит выше точки C , и отрицательным — в противном случае.

Рис. 2.5. Поперечный профиль судна

Теперь рассмотрим условия равновесия судна:

1)если h > 0, то судно возвращается в первоначальное положение; 2)если h = 0, то это случай безразличного равновесия; 3) если h

Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.

Архимед – греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед обучался в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.

Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.

По легенде, Архимеду принадлежит множество удивительных технических изобретений, которые завоевали ему славу среди современников. Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.

Архимеду также приписывают изобретение катапульты, военной метательной машины, конструирование планетария, в котором планеты двигались. Учёный создал винт для подъёма воды (Архимедов винт), который до сих пор используется и представляет собой водоподъемную машину, вал с винтовой поверхностью, находящийся в наклонной трубе, погруженной в воду. Во время вращения винтовая поверхность вала перемещает воду по трубе на разные высоты.

Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.

Свой знаменитый закон Архимед открыл при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не подмешивали ли ювелиры серебро к золоту, когда изготавливали корону. Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.

Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!

Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую его поместили.

Закон Архимеда гласит: на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам — и разобраться в деталях этого закона, которые могли позабыться.

О чем говорит закон Архимеда?

Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу — и испытал озарение, мгновенно сформулировав суть открытия.

Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:

• погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
• итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
• при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.

Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.

Та же самая закономерность действует и для газов — только здесь объем тела необходимо соотносить с плотностью газа.

Можно сформулировать физический закон и немного проще — сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.

Закон записывается в виде следующей формулы:

Какое значение имеет закон Архимеда?

Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.

Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него — они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства — они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.

Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.

История вопроса

«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.

Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.

Закон Архимеда и молекулярно-кинетическая теория

В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.

Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.

Формулировка и пояснения

Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.

Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.

Формула

Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,

где ρж – плотность жидкости,

g – ускорение свободного падения,

Vпт – объем погруженной в жидкость части тела.

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:

1) Fт > FA – тело тонет;

2) Fт = FA – тело плавает в жидкости или газе;

3) Fт

Продолжим изучение архимедовой силы. Проделаем опыты. К коромыслу весов подвесим два одинаковых шара. Их вес одинаков, поэтому коромысло находится в равновесии (рис. «а»). Подставим под правый шар пустой стакан. От этого вес шаров не изменится, поэтому равновесие сохранится (рис. «б»).

Второй опыт. Подвесим к динамометру большую картофелину. Вы видите, что её вес равен 3,5 Н. Погрузим картофелину в воду. Мы обнаружим, что её вес уменьшился и стал равен 0,5 Н.

Вычислим изменение веса картофеля:

DW = 3,5 Н – 0,5 Н = 3 Н

Почему же вес картофеля уменьшился именно на 3 Н? Очевидно потому, что в воде на картофель подействовала выталкивающая сила такой же величины. Другими словами, сила Архимеда равна изменению веса т ела:

Эта формула выражает способ измерения архимедовой силы: нужно дважды измерить вес тела и вычислить его изменение. Полученное значение равно силе Архимеда.

Для вывода следующей формулы проделаем опыт с прибором «ведёрко Архимеда». Основные его части следующие: пружина со стрелкой 1, ведёрко 2, тело 3, отливной сосуд 4, стаканчик 5.

Сначала пружину, ведёрко и тело подвешивают к штативу (рис. «а») и отмечают положение стрелки жёлтой меткой. Затем тело помещают в отливной сосуд. По мере погружения тело вытесняет некоторый объём воды , который сливается в стаканчик (рис. «б»). Вес тела становится меньше, пружина сжимается, и стрелка поднимается выше жёлтой метки.

Перельём воду, вытесненную телом, из стаканчика в ведёрко (рис. «в»). Самое удивительное в том, что когда вода будет перелита (рис «г»), стрелка не просто опустится вниз, а укажет точно на жёлтую метку! Значит, вес влитой в ведёрко воды уравновесил архимедову силу . В виде формулы этот вывод запишется так:

Обобщая результаты двух опытов, получим закон Архимеда : выталкивающая сила, действующая на тело в жидкости (или газе), равна весу жидкости (газа), взятой в объёме этого тела и направлена противоположно вектору веса.

В § 3-б мы указали, что сила Архимеда обычно направлена вверх. Поскольку она противонаправлена вектору веса, а он не всегда направлен вниз, архимедова сила также не всегда действует вверх. Например, во вращающейся центрифуге в стакане с водой пузырьки воздуха будут всплывать не вверх, а отклоняясь к оси вращения.

история открытия и суть явления для чайников Закон архимеда объем вытесненной жидкости равен объему

Закон Архимеда – закон статики жидкостей и газов, согласно которому на погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости в объеме тела.

История вопроса

«Эврика!» («Нашел!») – именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало – нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото. Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну – и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.

Однако, что правда – то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.

Закон Архимеда и молекулярно-кинетическая теория

В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.

Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, – и корабль плывет.

Формулировка и пояснения

Тот факт, что на погруженное в воду тело действует некая сила, всем хорошо известен: тяжелые тела как бы становятся более легкими – например, наше собственное тело при погружении в ванну. Купаясь в речке или в море, можно легко поднимать и передвигать по дну очень тяжелые камни – такие, которые не удается поднять на суше. В то же время легкие тела сопротивляются погружению в воду: чтобы утопить мяч размером с небольшой арбуз требуется и сила, и ловкость; погрузить мяч диаметром полметра скорее всего не удастся. Интуитивно ясно, что ответ на вопрос – почему тело плавает (а другое – тонет), тесно связан с действием жидкости на погруженное в нее тело; нельзя удовлетвориться ответом, что легкие тела плавают, а тяжелые – тонут: стальная пластинка, конечно, утонет в воде, но если из нее сделать коробочку, то она может плавать; при этом ее вес не изменился.

Существование гидростатического давления приводит к тому, что на любое тело, находящееся в жидкости или газе, действует выталкивающая сила. Впервые значение этой силы в жидкостях определил на опыте Архимед. Закон Архимеда формулируется так: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу того количества жидкости или газа, которое вытеснено погруженной частью тела.

Формула

Сила Архимеда, действующая на погруженное в жидкость тело, может быть рассчитана по формуле: F А = ρ ж gV пт,

где ρж – плотность жидкости,

g – ускорение свободного падения,

Vпт – объем погруженной в жидкость части тела.

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести Fт и архимедовой силы FA, которые действуют на это тело. Возможны следующие три случая:

1) Fт > FA – тело тонет;

2) Fт = FA – тело плавает в жидкости или газе;

3) Fт

F A = ρ g V , {\displaystyle F_{A}=\rho gV,}

Дополнения

Выталкивающая или подъёмная сила по направлению противоположна силе тяжести , прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.

Обобщения

Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы

Гидростатическое давление p {\displaystyle p} на глубине h {\displaystyle h} , оказываемое жидкостью плотностью ρ {\displaystyle \rho } на тело, есть p = ρ g h {\displaystyle p=\rho gh} . Пусть плотность жидкости ( ρ {\displaystyle \rho } ) и напряжённость гравитационного поля ( g {\displaystyle g} ) — постоянные величины, а h {\displaystyle h} — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат O x y z {\displaystyle Oxyz} , причём выберем направление оси z совпадающим с направлением вектора g → {\displaystyle {\vec {g}}} . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку d S {\displaystyle dS} . На неё будет действовать сила давления жидкости направленная внутрь тела, d F → A = − p d S → {\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}} . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

F → A = − ∫ S p d S → = − ∫ S ρ g h d S → = − ρ g ∫ S h d S → = ∗ − ρ g ∫ V g r a d (h) d V = ∗ ∗ − ρ g ∫ V e → z d V = − ρ g e → z ∫ V d V = (ρ g V) (− e → z) .{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z}).}

При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой

Архимед – греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед обучался в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.

Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.

По легенде, Архимеду принадлежит множество удивительных технических изобретений, которые завоевали ему славу среди современников. Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.

Архимеду также приписывают изобретение катапульты, военной метательной машины, конструирование планетария, в котором планеты двигались. Учёный создал винт для подъёма воды (Архимедов винт), который до сих пор используется и представляет собой водоподъемную машину, вал с винтовой поверхностью, находящийся в наклонной трубе, погруженной в воду. Во время вращения винтовая поверхность вала перемещает воду по трубе на разные высоты.

Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.

Свой знаменитый закон Архимед открыл при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не подмешивали ли ювелиры серебро к золоту, когда изготавливали корону. Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.

Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!

Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую его поместили.

Закон Архимеда гласит: на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите

На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной этим телом жидкости или газа.

В интегральной форме

Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.

Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой ) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

Что касается тел, которые находятся в газе, например в воздухе, то для нахождения подъёмной силы (Силы Архимеда) нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.

В отсутствие гравитационного поля (Сила тяготения), то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление конвекции (естественное перемещение воздуха в пространстве), поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами

В формуле мы использовали.

Часто научные открытия становятся следствием простой случайности. Но только люди с подготовленным умом могут оценить важность простого совпадения и сделать из него далеко идущие выводы. Именно благодаря цепи случайных событий в физике появился закон Архимеда, объясняющий поведение тел в воде.

Предание

В Сиракузах об Архимеде слагали легенды. Однажды правитель этого славного города усомнился в честности своего ювелира. В короне, изготовленной для правителя, должно было содержаться определенное количество золота. Проверить этот факт поручили Архимеду.

Архимед установил, что в воздухе и в воде тела имеют разный вес, причем разность прямо пропорциональна плотности измеряемого тела. Измерив вес короны в воздухе и в воде, и проведя аналогичный опыт с целым куском золота, Архимед доказал, что в изготовленной короне существовала примесь более легкого металла.

По преданию, Архимед сделал это открытие в ванне, наблюдая за выплеснувшейся водой. Что стало дальше с нечестным ювелиром, история умалчивает, но умозаключение сиракузского ученого легло в основу одного из важнейших законов физики, который известен нам, как закон Архимеда.

Формулировка

Результаты своих опытов Архимед изложил в труде «О плавающих телах», который, к сожалению, дошел до наших дней лишь в виде отрывков. Современная физика закон Архимеда описывает, как совокупную силу, действующую на тело, погруженное в жидкость. Выталкивающая сила тела в жидкости направлена вверх; ее абсолютная величина равна весу вытесненной жидкости.

Действие жидкостей и газов на погруженное тело

Любой предмет, погруженный в жидкость, испытывает на себе силы давления. В каждой точке поверхности тела данные силы направлены перпендикулярно поверхности тела. Если бы эти они были одинаковы, тело испытывало бы только сжатие. Но силы давления увеличиваются пропорционально глубине, поэтому нижняя поверхность тела испытывает больше сжатие, чем верхняя. Можно рассмотреть и сложить все силы, действующие на тело в воде. Итоговый вектор их направления будет устремлен вверх, происходит выталкивание тела из жидкости. Величину этих сил определяет закон Архимеда. Плавание тел всецело основывается на этом законе и на различных следствиях из него. Архимедовы силы действуют и в газах. Именно благодаря этим силам выталкивания в небе летают дирижабли и воздушные шары: благодаря воздухоизмещению они становятся легче воздуха.

Физическая формула

Наглядно силу Архимеда можно продемонстрировать простым взвешиванием. Взвешивая учебную гирю в вакууме, в воздухе и в воде можно видеть, что вес ее существенно меняется. В вакууме вес гири один, в воздухе — чуть ниже, а в воде — еще ниже.

Если принять вес тела в вакууме за Р о, то его вес в воздушной среде может быть описан такой формулой: Р в =Р о — F а;

здесь Р о — вес в вакууме;

Как видно из рисунка, любые действия со взвешиванием в воде значительно облегчают тело, поэтому в таких случаях сила Архимеда обязательно должна учитываться.

Для воздуха эта разность ничтожна, поэтому обычно вес тела, погруженного в воздушную среду, описывается стандартной формулой.

Плотность среды и сила Архимеда

Анализируя простейшие опыты с весом тела в различных средах, можно прийти к выводу, что вес тела в различных средах зависит от массы объекта и плотности среды погружения. Причем чем плотнее среда, тем больше сила Архимеда. Закон Архимеда увязал эту зависимость и плотность жидкости или газа отражается в его итоговой формуле. Что же еще влияет на данную силу? Другими словами, от каких характеристик зависит закон Архимеда?

Формула

Архимедову силу и силы, которые на нее влияют, можно определить при помощи простых логических умозаключений. Предположим, что тело определенного объема, погруженное в жидкость, состоит из тоже же самой жидкости, в которую оно погружено. Это предположение не противоречит никаким другим предпосылкам. Ведь силы, действующие на тело, никоим образом не зависят от плотности этого тела. В этом случае тело, скорее всего, будет находиться в равновесии, а сила выталкивания будет компенсироваться силой тяжести.

Таким образом, равновесие тела в воде будет описываться так.

Но сила тяжести, из условия, равна весу жидкости, которую она вытесняет: масса жидкости равна произведению плотности на объём. Подставляя известные величины, можно узнать вес тела в жидкости. Этот параметр описывается в виде ρV * g.

Подставляя известные значения, получаем:

Это и есть закон Архимеда.

Формула, выведенная нами, описывает плотность, как плотность исследуемого тела. Но в начальных условиях было указано, что плотность тела идентична плотности окружающей его жидкости. Таким образом, в данную формулу можно смело подставлять значение плотности жидкости. Визуальное наблюдение, согласно которому в более плотной среде сила выталкивания больше, получило теоретическое обоснование.

Применение закона Архимеда

Первые опыты, демонстрирующие закон Архимеда, известны еще со школьной скамьи. Металлическая пластинка тонет в воде, но, сложенная в виде коробочки, может не только удерживаться на плаву, но и нести на себе определенный груз. Это правило — важнейший вывод из правила Архимеда, оно определяет возможность построения речных и морских судов с учетом их максимальной вместимости (водоизмещения). Ведь плотность морской и пресной воды различна и суда, и подводные лодки должны учитывать перепады этого параметра при вхождении в устья рек. Неправильный расчет может привести к катастрофе — судно сядет на мель, и для его подъема потребуются значительные усилия.

Закон Архимеда необходим и подводникам. Дело в том, что плотность морской воды меняет свое значение в зависимости от глубины погружения. Правильный расчет плотности позволит подводникам правильно рассчитать давление воздуха внутри скафандра, что повлияет на маневренность водолаза и обеспечит его безопасное погружение и всплытие. Закон Архимеда должен учитываться также и при глубоководном бурении, огромные буровые вышки теряют до 50% своего веса, что делает их транспортировку и эксплуатацию менее затратным мероприятием.

Как был открыт закон Архимеда?

☰

Знаменитая легенда о том, как нагой Архимед бежал по улице и кричал «Эврика!» («нашел!»), как раз повествует об открытии им того, что выталкивающая сила воды равна по модулю весу вытесненной им воды, объем которой равен объему погруженного в нее тела. Это открытие названо законом Архимеда.

В III веке до нашей эры царь древнегреческого города Сиракузы попросил проверить ученого Архимеда, из чистого ли золота сделал мастер ему корону. Проблема здесь вот в чем. Когда царь заказывал корону, он дал мастеру определенную массу золота. Когда мастер вернул золото в виде короны, то оно весило столько, сколько и масса данного золота. Но ведь мастер мог схитрить.

Если взять из общей массы золота немного золота и положить туда равную взятой массе золота массу серебра (которое дешевле), то никто и не заметит. Ведь на глаз не отличишь, а масса такая, какая и должна быть.

Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: m = ρV. Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. Просто при равной массе отличались бы объемы кусков. Но как определить объем короны? По-сути именно эта задача стояла перед Архимедом.

И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Если объемы окажутся равными, то значит ювелирный мастер честно выполнил свою работу. Архимед выскочил из ванной и побежал проверять свое открытие.

Архимед погрузил в воду корону и измерил, как увеличился объем воды. (Хотя на самом деле Архимед мог измерять потерю веса при погружении тела в воду. Потеря веса равна весу вытесненной воды. А вес воды зависит от вытесненного объема. В свою очередь вытесненный объем воды равен объему погруженного в воду тела.) Также он погрузил в воду кусок золота, у которого масса была такая же как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Архимед был рад своему открытию, а вот ювелир не очень.

Принцип Архимеда: определение, формула и примеры — видео и стенограмма урока

Более внимательный взгляд

Давайте подробнее рассмотрим это определение. Во-первых, нам нужно понять «смещение».

Как гласит история, однажды Архимед вылился в теплую ванну и, войдя в нее, понял, что уровень воды поднялся. Затем он определил, что чем большую часть своего тела он погружает в ванну, тем выше становится уровень воды.

Это означает, что объем его тела, который он поместил в воду, должен был перемещать или вытеснять воду, чтобы он мог поместиться в ванне.Следовательно, смещение в этом контексте — это когда объект перемещает текучую среду, чтобы он мог занять объем, который изначально занимала текучая среда.

Пример — линкор

Давайте возьмем в качестве примера линкор. Линкор сделан из стали. Прямо сейчас вы можете сказать: «Но сталь не плавает!» Так как же линкор может плавать?

Посмотрите на изображение линкора. А теперь представьте, что рисуете линию, где вода выходит на корпус корабля. Затем залейте корпус корабля водой до этой отметки.Как вы думаете, сколько будет весить вода? Если вы сказали «много», вы правы. Фактически он весил бы столько же, сколько весь корабль!

Плавучий линкор

Вес воды, заполняющей корпус корабля, такой же, как и вес самого корабля, поэтому вода создает на корабле выталкивающую силу с такой силой. Поэтому корабль из стали плывет!

Пример — Ice Cube

Рассмотрим другой пример.Если вы поместите кубик льда в стакан с водой, кубик будет плавать, потому что лед менее плотный, чем вода. Итак, лед под водой вытесняет этот объем воды.

Чтобы упростить задачу, мы скажем, что кубик льда — это идеальный куб, каждая сторона которого имеет длину 1 см. Предположим также, что кубик льда плавает на глубине 0,8 см под водой. Сколько весит кубик льда? Чтобы определить это, давайте проведем некоторые вычисления.

Расчет смещения

Помните, что принцип Архимеда гласит, что вес вытесняемой жидкости является выталкивающей силой.Следовательно, нам нужно знать, сколько воды вытесняется.

Если 0,8 см находится под водой, то мы можем найти объем этой формы, умножив три стороны вместе. В этом случае нам нужен только объем куба, который находится под водой, поэтому мы умножаем длину и ширину на величину высоты, которая находится под водой.

V = 1 см * 1 см * 0,8 см

Умножение 1 * 1 * 0,8 = 0,8

Умножение единиц дает нам кубические сантиметры.3

Поскольку 1 кубический сантиметр равен 1 мл, мы можем напрямую преобразовать объем в миллилитры.

V = 0,8 мл

Плотность воды составляет 1 г / мл (один грамм на миллилитр), поэтому масса этого количества воды составляет 0,8 грамма.

м = 0,8 г

Мы еще не закончили. Масса — это количество вещества в чем-то, а вес — это сила, которая толкает вещество на Землю. Чтобы найти вес из массы, нам нужно перевести массу в килограммы.2 = 0,00784 Н

Резюме урока

Принцип Архимеда состоит в том, что любой объект, окруженный жидкостью, поднимается этой жидкостью. Этот подъем представляет собой выталкивающую силу, которая равна весу жидкости, которую перемещает объект. Следовательно, чем больше смещение, тем больше выталкивающая сила, и чем тяжелее жидкость, тем больше выталкивающая сила.

Основные термины Архимеда

• Принцип Архимеда : гласит, что объект, окруженный жидкостью, поднимается вверх
• Выталкивающая сила : эта сила равна весу жидкости, которую она вытесняет
• Смещение : когда объект перемещает жидкость так, чтобы он мог занять объем, который изначально занимал жидкость

Результаты обучения

По окончании урока ученики должны уметь:

• Проиллюстрировать, как работает принцип Архимеда
• Определите смещение и подъемную силу
• Модель математического определения смещения

Определение принципа Архимеда в физике.

Примеры принципа Архимеда в следующих темах:

• Плавучесть и принцип Архимеда

  • Выталкивающая сила, действующая на объект, может быть рассчитана с использованием принципа Архимеда .
  • Более простой метод следует из принципа Архимеда , который гласит, что выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.
  • Обоснование принципа Архимеда состоит в том, что выталкивающая сила, действующая на объект, зависит от давления, оказываемого жидкостью на его погруженную поверхность.
  • Принцип Архимеда Принцип применим для любой жидкости — не только для жидкостей (например, воды), но и для газов (например, воздуха).
  • Мы используем принцип Архимеда ‘ , чтобы определить количество пингвинов, которое может выдержать ледяной плавучий объект.

• Полное погружение

  • Принцип Архимеда Принцип проще всего понять и применить в случае полностью погруженных объектов.
  • Это непосредственно следует из принципа Архимеда ‘ и того факта, что объект полностью погружен (и поэтому объем вытесненной жидкости — это просто объем объекта).
  • Теперь мы вычислим эту силу, используя принцип Архимеда ‘ .

• Флотация

  • Но принцип Архимеда утверждает, что выталкивающая сила — это вес вытесняемой жидкости.
  • Это часто называют «принципом плавучести », когда плавучий объект вытесняет жидкость, равную его собственному весу.
  • Плотность играет решающую роль в Архимед ‘ принцип .

• Принцип Гюйгенса

  • На рисунке 1 показан простой пример принципа Гюйгенса дифракции.
  • Принцип можно показать с помощью следующего уравнения:
  • Этот принцип работает для всех типов волн, а не только для световых.
  • Принцип Гюйгенса применяется к прямому волновому фронту, падающему на зеркало.
  • Принцип Гюйгенса применяется к прямому волновому фронту.

• Принцип Паскаля

  • Принцип Паскаля гласит, что давление передается и не уменьшается в замкнутой статической жидкости.
  • Принцип Паскаля (или Закон Паскаля) применяется к статическим жидкостям и использует зависимость давления от высоты в статических жидкостях.
  • С качественной точки зрения, принцип Паскаля утверждает, что давление передается без уменьшения в замкнутой статической жидкости.
  • Как указано в Принципе Паскаля , давление, прикладываемое к статической жидкости в закрытом контейнере, передается по всей жидкости.
  • По принципу Паскаля , P1 = P2, что дает силу, создаваемую статической жидкостью F2, где F2> F1.

• Принцип неопределенности Гейзенберга

  • Неопределенность Принцип устанавливает базовый предел точности, с которой некоторые физические свойства частицы могут быть известны одновременно.
  • Принцип неопределенности присущ свойствам всех волновых систем и возникает в квантовой механике просто из-за волновой природы материи всех квантовых объектов.
  • Таким образом, принцип неопределенности фактически утверждает фундаментальное свойство квантовых систем, а не является утверждением об успехе современных технологий с точки зрения наблюдений.
  • Принцип довольно нелогичен, поэтому первых исследователей квантовой теории нужно было заверить, что наивные измерения, нарушающие его, всегда были неработоспособны.
  • Свяжите принцип неопределенности Гейзенберга с волновой природой материи всех квантовых объектов

• Постулаты Эйнштейна

  • Специальная теория относительности основана на двух постулатах Эйнштейна: Принципе относительности и Принципе инвариантной скорости света.
  • Принцип Принцип относительности : Законы физики одинаковы и могут быть изложены в их простейшей форме во всех инерциальных системах отсчета.
  • Принцип инвариантной скорости света: Скорость света c — постоянная величина, не зависящая от относительного движения источника и наблюдателя.

• Суперпозиция сил

  • Принцип суперпозиции (свойство суперпозиции) утверждает, что для всех линейных сил общая сила является векторной суммой отдельных сил.
  • Принцип суперпозиции (также известный как свойство суперпозиции) гласит, что: для всех линейных систем суммарный ответ в данном месте и времени, вызванный двумя или более стимулами, представляет собой сумму ответов, которые были бы вызваны каждым стимулом. индивидуально.
  • Следовательно, принцип предполагает, что общая сила — это векторная сумма отдельных сил.
  • Принцип линейной суперпозиции позволяет расширить закон Кулона, чтобы включить любое количество точечных зарядов, чтобы получить силу, действующую на любой точечный заряд, путем векторного сложения этих отдельных сил, действующих только на этот точечный заряд.
  • Примените принцип суперпозиции , чтобы определить общий ответ, вызванный двумя или более стимулами

• Наложение полей

  • Как векторные поля, электрические поля подчиняются принципу суперпозиции .
  • Этот принцип гласит, что для всех линейных систем чистый ответ на множественные стимулы в заданном месте и в определенное время равен сумме ответов, которые были бы вызваны каждым стимулом индивидуально.
  • Следует отметить, что принцип суперпозиции применим к любой линейной системе, включая алгебраические уравнения, линейные дифференциальные уравнения и системы уравнений вышеупомянутых форм.

• Сферические и плоские волны

  • Принцип Гюйгена-Френеля показывает, что, когда волны взаимодействуют друг с другом, они интерферируют конструктивно или деструктивно.
  • Принцип Гюйгена-Френеля использует закон преломления.

Формула плавучести и принципа Архимеда с примерами

Принцип Архимеда гласит, что когда объект полностью или частично погружен в жидкость, на него действует ударная нагрузка, равная весу вытесняемой им жидкости. Лодки и корабли, плавающие на поверхности воды, являются примерами принципа Архимеда. Корабли работают по принципу плавучести.
Воздушный шар, наполненный воздухом, сразу же выстреливает на поверхность при выпуске под водой. То же самое произойдет, если под воду выпустить кусок дерева. Мы могли заметить, что кружка, наполненная водой, кажется легкой под водой, но становится тяжелой, как только мы вынимаем ее из воды.
Более двух тысяч лет назад греческий ученый Архимед заметил, что на объект, находящийся внутри жидкости, действует восходящая сила. В результате в объекте наблюдается явная потеря веса, называемая подъемом жидкости.
См. Также : Закон Паскаля

Формула принципа Архимеда

Рассмотрим сплошной цилиндр площадью поперечного сечения A и высотой h , погруженный в жидкость. Пусть h ₁ и h ₂ — глубины верхней и нижней граней цилиндра соответственно от поверхности жидкости.
Тогда h ₂ — h ₂ = h
Если P ₁ и P ₂ — давление жидкости на глубинах h ₁ и h ₂ соответственно, а ρ — плотность, то согласно уравнению (2):

P ₁ = ρ г в ₁

P ₂ = ρ г в ₂

Тогда сила F ₁ действует в верхней части цилиндра со стороны жидкости из-за давления P ₁ , а сила F ₂ действует в нижней части цилиндра со стороны жидкости из-за P ₂ .

F ₁ = P ₁ A = ρ g h ₁ A

и F ₂ = P ₂ A = ρ g h ₂ A

F ₁ и F ₂ действуют на противоположные стороны цилиндра. Следовательно, чистая сила F составит F ₂ — F ₁ в направлении F ₂ . Эта результирующая сила F, действующая на цилиндр, называется напором жидкости.

F ₂ — F ₁ = ρ g h ₂ A — ρ g h ₁ A

= ρ gA (ч ₂ — ч ₁ )

Подъем жидкости = ρ gAh

или = ρ гВ

Здесь Ah — объем V цилиндра, равный объему жидкости, вытесняемой цилиндром.Следовательно, ρ g V — это вес вытесняемой жидкости. В уравнении говорится, что на тело, погруженное в жидкость, действует подъемный удар, равный весу вытесненной жидкости, что соответствует закону Архимеда.

Плотность объекта по закону Архимеда

Закон Архимеда также полезен для определения плотности объекта. Соотношение масс тела с равным объемом жидкости такое же, как и их плотности.
Пусть Плотность объекта = D
Плотность жидкости = ρ
Вес объекта = w ₁
Вес равного объема жидкости = w = w ₁ — w ₂
Здесь w ₂ — это вес твердых частиц в жидкости.Согласно закону Архимеда, w ₂ меньше его фактического веса w ₁ на величину w.

Таким образом, найдя вес твердого тела в воздухе w и его вес в воде w _2, , мы можем вычислить плотность твердого тела по приведенному выше уравнению.

смотрите также видео

Принцип плавания

Плавающий объект вытесняет жидкость, вес которой равен весу объекта.
Объект тонет, если его вес превышает действующий на него подъемный удар.Объект плавает, если его вес равен или меньше подъема. Когда объект плавает в жидкости, сила подъема, действующего на него, равна весу объекта. В случае плавающего объекта объект может быть частично погружен. Вытягивание вверх всегда равно весу жидкости, вытесняемой объектом. Это принцип плавучести.

Определение принципа Архимеда в физике.

Примеры принципа Архимеда в следующих темах:

• Плавучесть и принцип Архимеда

  • Выталкивающая сила, действующая на объект, может быть рассчитана с использованием принципа Архимеда .
  • Более простой метод следует из принципа Архимеда , который гласит, что выталкивающая сила, действующая на тело, погруженное в жидкость, равна весу жидкости, которую тело вытесняет.
  • Обоснование принципа Архимеда состоит в том, что выталкивающая сила, действующая на объект, зависит от давления, оказываемого жидкостью на его погруженную поверхность.
  • Принцип Архимеда Принцип применим для любой жидкости — не только для жидкостей (например, воды), но и для газов (например, воздуха).
  • Мы используем принцип Архимеда ‘ , чтобы определить количество пингвинов, которое может выдержать ледяной плавучий объект.

• Полное погружение

  • Принцип Архимеда Принцип проще всего понять и применить в случае полностью погруженных объектов.
  • Это непосредственно следует из принципа Архимеда ‘ и того факта, что объект полностью погружен (и поэтому объем вытесненной жидкости — это просто объем объекта).
  • Теперь мы вычислим эту силу, используя принцип Архимеда ‘ .

• Флотация

  • Но принцип Архимеда утверждает, что выталкивающая сила — это вес вытесняемой жидкости.
  • Это часто называют «принципом плавучести », когда плавучий объект вытесняет жидкость, равную его собственному весу.
  • Плотность играет решающую роль в Архимед ‘ принцип .

• Принцип Гюйгенса

  • На рисунке 1 показан простой пример принципа Гюйгенса дифракции.
  • Принцип можно показать с помощью следующего уравнения:
  • Этот принцип работает для всех типов волн, а не только для световых.
  • Принцип Гюйгенса применяется к прямому волновому фронту, падающему на зеркало.
  • Принцип Гюйгенса применяется к прямому волновому фронту.

• Принцип Паскаля

  • Принцип Паскаля гласит, что давление передается и не уменьшается в замкнутой статической жидкости.
  • Принцип Паскаля (или Закон Паскаля) применяется к статическим жидкостям и использует зависимость давления от высоты в статических жидкостях.
  • С качественной точки зрения, принцип Паскаля утверждает, что давление передается без уменьшения в замкнутой статической жидкости.
  • Как указано в Принципе Паскаля , давление, прикладываемое к статической жидкости в закрытом контейнере, передается по всей жидкости.
  • По принципу Паскаля , P1 = P2, что дает силу, создаваемую статической жидкостью F2, где F2> F1.

• Принцип неопределенности Гейзенберга

  • Неопределенность Принцип устанавливает базовый предел точности, с которой некоторые физические свойства частицы могут быть известны одновременно.
  • Принцип неопределенности присущ свойствам всех волновых систем и возникает в квантовой механике просто из-за волновой природы материи всех квантовых объектов.
  • Таким образом, принцип неопределенности фактически утверждает фундаментальное свойство квантовых систем, а не является утверждением об успехе современных технологий с точки зрения наблюдений.
  • Принцип довольно нелогичен, поэтому первых исследователей квантовой теории нужно было заверить, что наивные измерения, нарушающие его, всегда были неработоспособны.
  • Свяжите принцип неопределенности Гейзенберга с волновой природой материи всех квантовых объектов

• Постулаты Эйнштейна

  • Специальная теория относительности основана на двух постулатах Эйнштейна: Принципе относительности и Принципе инвариантной скорости света.
  • Принцип Принцип относительности : Законы физики одинаковы и могут быть изложены в их простейшей форме во всех инерциальных системах отсчета.
  • Принцип инвариантной скорости света: Скорость света c — постоянная величина, не зависящая от относительного движения источника и наблюдателя.

• Суперпозиция сил

  • Принцип суперпозиции (свойство суперпозиции) утверждает, что для всех линейных сил общая сила является векторной суммой отдельных сил.
  • Принцип суперпозиции (также известный как свойство суперпозиции) гласит, что: для всех линейных систем суммарный ответ в данном месте и времени, вызванный двумя или более стимулами, представляет собой сумму ответов, которые были бы вызваны каждым стимулом. индивидуально.
  • Следовательно, принцип предполагает, что общая сила — это векторная сумма отдельных сил.
  • Принцип линейной суперпозиции позволяет расширить закон Кулона, чтобы включить любое количество точечных зарядов, чтобы получить силу, действующую на любой точечный заряд, путем векторного сложения этих отдельных сил, действующих только на этот точечный заряд.
  • Примените принцип суперпозиции , чтобы определить общий ответ, вызванный двумя или более стимулами

• Наложение полей

  • Как векторные поля, электрические поля подчиняются принципу суперпозиции .
  • Этот принцип гласит, что для всех линейных систем чистый ответ на множественные стимулы в заданном месте и в определенное время равен сумме ответов, которые были бы вызваны каждым стимулом индивидуально.
  • Следует отметить, что принцип суперпозиции применим к любой линейной системе, включая алгебраические уравнения, линейные дифференциальные уравнения и системы уравнений вышеупомянутых форм.

• Сферические и плоские волны

  • Принцип Гюйгена-Френеля показывает, что, когда волны взаимодействуют друг с другом, они интерферируют конструктивно или деструктивно.
  • Принцип Гюйгена-Френеля использует закон преломления.

Принцип Архимеда: определение, теория и применение

Определение: что такое принцип Архимеда?

Принцип Архимеда — это физический закон, фундаментальный для гидродинамики. В нем говорится, что восходящая выталкивающая сила, прилагаемая к телу, погруженному в жидкость, полностью или частично погруженному в воду, равна весу жидкости, которую тело вытесняет. Если вес вытесненной жидкости меньше веса объекта, объект утонет.Объект будет плавать, если вес вытесненной жидкости равен весу объекта. Эта восходящая сила известна как тяга или подъемная сила. Это следствие разницы в давлении жидкости на разной высоте. Давление жидкости распространяется во всех направлениях (принцип Паскаля) и увеличивается с глубиной. На дно погруженного объекта действует несбалансированная направленная вверх сила.

Принцип Архимеда

История принципа Архимеда

История этого принципа восходит к 3 ^{году до} века до нашей эры, когда он был открыт Архимедом Сиракузским, греческим математиком, физиком, инженером, изобретателем и астрономом.Это открытие часто ассоциируется с термином «момент эврики».

Согласно популярной легенде, Архимеду было поручено выяснить, была ли корона, сделанная для короля, из чистого золота или поддельного золота. Однажды он принимал ванну и заметил, как поднимался уровень воды, когда он погружал свое тело. Понимая, что если золотую корону уронить в ванну, она вытеснит весь объем воды за борт. Эта идея, по сути, дала ему простой способ измерить объем короны.Взвесив корону, он мог затем эффективно вычислить ее плотность (массу, деленную на объем) и сравнить ее с плотностью золота. Если плотность была ниже, чем у золота, корона была подделкой.

Видео: объяснение принципа Архимеда

Примеры принципа Архимеда

Принцип Архимеда — обычное явление в реальной жизни. Вот несколько ярких примеров.

Пример принципа Архимеда

Изображение предоставлено: Сатьям Бхуян

• Корабль или лодка могут плавать по воде, потому что вес вытесненной воды равен весу корабля или лодки.
• Подводная лодка может нырять в воду или плавать на ней. Подводная лодка состоит из балластных цистерн, наполненных воздухом или водой. Резервуары весят меньше, чем равный объем воды, и заставляют субмарину плавать на поверхности. Если резервуары частично заполнены воздухом, можно заставить подводную лодку плавать на некоторой глубине воды, не поднимаясь и не опускаясь.
• Воздушные шары поднимаются в воздух, потому что более теплый воздух внутри воздушного шара менее плотный, чем более холодный воздух снаружи.Основной принцип воздушного шара — использование горячего воздуха для создания плавучести, которая создает подъемную силу.
• Водомер может плавать по воде, так как его ноги выталкивают воду, а вес выталкиваемой воды равен силе плавания.

Теория принципа Архимеда

Тяга, создаваемая жидкостью, противодействует весу под действием силы тяжести. Объект внутри жидкости ощущает только общую силу, действующую на него, которая называется кажущейся массой.Поскольку тяга жидкости уменьшает действительную гравитационную силу, объект чувствует, как будто его вес уменьшился. Кажущийся вес определяется по формуле:

.

Кажущийся вес = Вес объекта в воздухе — Тяга или выталкивающая сила

Главное уравнение Архимеда

Принцип Архимеда говорит нам, что эта потеря веса равна массе жидкости, полностью или частично вытесненной объектом. Соответствующее уравнение имеет вид,

F _b = ρ X g X V

Где,

F _b — подъемная сила (или тяга)

ρ — плотность жидкости, в которую погружен объект

V — объем объекта, погруженного в жидкость

g — ускорение свободного падения

Вывод формулы принципа Архимеда: закон плавучести

Масса вытесненной жидкости

Масса = Плотность X Объем

M = ρ X V

Масса вытесняемой жидкости

Вес = Масса X Гравитация

W = M X g

Или, W = ρ X V X г

Согласно принципу Архимеда,

Кажущаяся потеря веса = Вес вытесненной жидкости

Эта кажущаяся потеря веса представляет собой тягу или выталкивающую силу ( F _b ).Следовательно,

F _b = ρ X g X V

Именно эта сила отвечает за плавание объектов. Таким образом, это уравнение еще называют законом плавучести.

Главное уравнение Архимеда

Использование и применение принципа Архимеда

Принцип Архимеда применим к следующей ситуации.

• Существенным применением принципа Архимеда является измерение объема и плотности объектов неправильной формы.
• В ареометре твердое тело подвешено в жидкости и поддерживается силой, равной весу жидкости, вытесняемой погруженной частью.
• Он используется в большом количестве научных исследований, включая медицину, инженерию, энтомологию, инженерию и геологию. Например, его используют для определения плотности костей и зубов.

Последний раз статья была пересмотрена 7 июля 2020 г.

Физика: жидкости | Медицинская онлайн-библиотека Lecturio

---

Изображение: «Капля воды» Тима Гирса из Нидерландов — https: // www.flickr.com/photos/timypenburg/4649617096/. Лицензия: CC BY-SA 2.0

.

---

Давление

Определение

Давление определяется как непрерывная физическая сила, которая действует на объект или против него чем-то, что соприкасается с ним. Его можно описать как силу на единицу площади. Это понятие важно в медицине, особенно когда речь идет о кровотоке (сердечно-сосудистая система) и воздушном потоке (дыхательная система).

Пояснение

Представьте себе пляжный мяч, наполненный воздухом.Воздух внутри держит мяч в накачанном состоянии. Внутри мяча происходят столкновения со стенкой мяча, которые прикладывают силу. Только те столкновения, которые перпендикулярны стене, имеют влияние. Молекулы воздуха, движущиеся по боковым стенкам, не повлияют на то, чтобы баллон оставался надутым.

Формула

Формула давления представлена ​​как P = F ₁ / A, где P — давление, F ₁ — сила, а A — задействованная площадь. Глядя на единицы, получаем:

(P) = кг / м-с ² = Н / м ² = Паскали (Па)

Давление измеряется в единицах Паскаля.

Атмосферное

Давление

Когда вы стоите на Земле, на вас оказывается давление, но вы этого не чувствуете. Это давление называется атмосферным давлением или F _air (сила, которую воздух оказывает на человека). Причина, по которой вы не чувствуете атмосферное давление, заключается в том, что давление воды и воздуха внутри вас толкает наружу. Баланс давления не позволяет человеку почувствовать силу воздуха сверху. Атмосферное давление может быть измерено в атмосферах или паскалях:

1 атм = 100000 Па = 100 кПа

Гидростатическое давление

«Гидростатическое давление» Изображение создано Lecturio

Когда вы погружаетесь под воду, сверху на вас действуют два груза: атмосферное давление и давление воды.Давление воды называется гидростатическим давлением или манометрическим давлением. Он обозначается как P = ρ g h , где ρ — плотность жидкой среды, g — сила тяжести, а h — высота воды над человеком. Итак, полное давление, оказываемое на человека под водой, составляет:

P _всего = ρ г в + P _атм

Принцип Архимеда и плавучесть

Определение

Знаменитый греческий математик Архимед утверждал, что на любого человека, полностью или частично погруженного в покоящуюся жидкость, действует восходящая (плавучая) сила.Эта сила равна весу жидкости, которую вытесняет тело. Плавучесть возникает из-за того, что давление воды внизу больше, чем давление воды выше. При измерении вытесненной воды расчет основан на объеме погруженного объекта. Давление, действующее вверх, равно F _B = выталкивающая сила, а давление, действующее вниз, F _g = гравитационная сила.

«Принцип Архимеда» Изображение создано Lecturio

Правила плавания

Объект будет плавать, если:

F _B > F _г

м _вода г> м _объект г

ρ _вода В> ρ _объект В

ρ _вода > ρ _объект

Таким образом, плавучесть F _B = м _{Вытесненная вода} г

Какая часть объекта выйдет из воды?

Если объект плывет, он будет появляться из воды до:

F _B = F _г

м _{вытесненная вода} = м _объект

ρ _вода V _{погруженный} = ρ _объект V _объект

Следовательно, для плавучих объектов: V _{погруженный} / V _объект = ρ _объект / ρ _вода

Закон Паскаля

Определение

Французский ученый Блез Паскаль открыл интересное явление, которое мы теперь знаем как закон Паскаля или принцип Паскаля.В нем говорится, что давление равномерно распределяется по жидкости. В жидкости, покоящейся в закрытом контейнере, изменение давления в одной части передается без потерь на каждую часть жидкости и на стенки контейнера.

Формула

Чтобы определить давления и силы, связанные с законом Паскаля, необходимо соблюдать следующее:

Поскольку давление равномерно распределено по жидкости, P ₁ = P ₂ .

Поскольку давление связано с силой и площадью, то возникает следующая зависимость:

F ₁ / A ₁ = F ₂ / A ₂ , таким образом, на единицу площади приходится равная сила.

«Закон Паскаля» Изображение создано Lecturio

Гидравлика

Закон Паскаля полезен в машинах, использующих гидравлику (наука о механических свойствах и использовании жидкостей). В этих сценариях можно получить механическое преимущество, увеличив одну площадь над другой, например:

F ₂ = F ₁ (A ₂ / A ₁ )

Идеальная гидродинамика

Определение

Гидродинамика — это отрасль науки, изучающая силы, действующие на жидкости или оказываемые ими, а также силы, действующие на твердые тела, погруженные в воду и движущиеся.Гидродинамика состоит из шести различных частей: идеальный поток, скорость потока, непрерывность, принцип Бернулли, эффект Вентури и трубка Пито.

Идеальный поток

Идеальный поток имеет дело с идеальной жидкостью — несжимаемой, не вязкой и ламинарной без турбулентности. Жидкости не сжимаются, в отличие от газов. Течение в жидкостях происходит из-за отсутствия вязкости. Идеальный поток должен быть ламинарным и упорядоченным, без турбулентности или хаоса. Обычно ламинарный поток возникает при более низких скоростях и является плавным, а не грубым.

Расход

Скорость потока — это количество жидкости, которая течет в данный момент времени. Рассчитывается следующим образом:

Расход = Объем в секунду

Q = Объем / Время = (Площадь x Расстояние) / Время

Таким образом, расход Q = Площадь x Скорость (Q = A v), поскольку скорость = расстояние / время

Непрерывность

Когда жидкость находится в движении, она должна двигаться таким образом, чтобы сохранить массу. Если скорость потока слишком низкая, возникнет вакуум.Если скорость потока слишком высока, произойдет перекрытие.

Q ₁ = Q ₂ и A ₁ v ₁ = A ₂ v ₂

Принцип Бернулли

Даниэль Бернулли объяснил важный принцип гидродинамики. Его принцип гласил, что увеличение скорости жидкости происходит одновременно с уменьшением давления или уменьшением потенциальной энергии жидкости. Энергия сохраняется на любом участке трубы.

P ₁ + ½ ρ v ₁ ² + ρ g h ₁ = P ₂ + ½ ρ v ₂ ² + ρ g h ₂

Эффект Вентури

Эффект Вентури — это снижение давления жидкости, которое возникает, когда жидкость протекает через суженный участок трубы. Суженная область будет иметь более высокую скорость, но более низкое давление в данной системе. В гидродинамике скорость жидкости должна увеличиваться, когда она проходит через сужающийся или суженный участок трубы (в соответствии с принципом непрерывности массы).

Однако статическое давление жидкости должно уменьшаться в соответствии с принципом сохранения механической энергии (принцип Бернулли, изложенный выше). Таким образом, в суженном участке трубы жидкость будет иметь более высокую скорость и более низкое давление; а в более широком сечении трубы жидкость будет иметь более высокое давление и более низкую скорость.

Трубка Пито

Трубка Пито — это прибор для измерения давления, используемый для измерения скорости потока жидкости. Базовая установка состоит из трубки, направленной прямо в поток жидкости.Поскольку в этой трубке находится жидкость, можно измерить давление. Движущаяся жидкость останавливается (застаивается), поскольку нет выхода для продолжения потока. Это давление является давлением торможения или общим давлением жидкости.

Используя принцип Бернулли, мы знаем, что давление застоя = статическое давление + динамическое давление.

P _всего = P _{статическое} + ½ ρ v ²

Решение для скорости, v = √ ((2 (P _всего — P _{статическое} )) / ρ)

Что такое плавучесть — Принцип Архимеда

ЧТО ТАКОЕ ПЛАВУЧИЕ?

Плавучесть — это сила, создаваемая жидкостью или газ, противодействующий весу объекта.Плавучесть также может быть заявлен как вес вытесненной жидкости. Давление в жидкости увеличивается с глубиной в результате веса вышележащих жидкость (см. гидростатический давление). Таким образом, объект, погруженный в жидкость, испытывает большее давление внизу жидкости, чем вверху. Эта разница в давлении приводит к чистой силе, которая стремится для ускорения объекта вверх.Величина этой силы пропорциональна разнице давлений между верх и низ столбца, а также эквивалентны к весу жидкости, которая в противном случае занимала бы столбец, т.е. вытесненная жидкость. По этой причине объект, плотность которого больше, чем у жидкости то, что он погружен в воду, утонет. Принцип Архимеда позволяет для экспериментального определения плотности путем обеспечения простой и точный метод определения объема объект неправильной формы.См. Также: Масса, Объемная плотность..для интерактивных занятий.

Принцип Архимеда назван в честь Архимеда из Сиракуз, который первым открыл этот закон в 212 г. до н. э. Архимед’ принцип можно выразить таким образом в силе:

Любой объект, полностью или частично погруженный в воду. в жидкости, поддерживается силой, равной весу жидкость, вытесняемая объектом.

— Архимед Сиракузский

ОБ АРХИМЕДЕ — Архимед был сыном астронома. Он путешествовал в Александрию, Египет, место великой учебы, где он изучал работы некоторых других математиков, например Евклид и Конон. Архимед помог своему другу королю Hiero II, создав машины для королевской армии.В шкив был одним из этих изобретений, но Архимед думал изучение математики было самым важным делом он мог сделать. Архимед написал несколько книг по математике, в том числе «О плавучих телах». Архимед умер во время осады Сиракуз, когда он был убит Римский солдат, несмотря на приказ о том, что ему нельзя причинять вреда

Для объектов, плавающих и затонувших, а также в газы, а также жидкости, принцип Архимеда может быть сформулирован в силе:

Любой объект, полностью или частично погруженный в воду. в жидкости поддерживается силой, равной весу жидкости, вытесненной объектом.с разъяснениями что для затонувшего объекта объем вытесненной жидкости равен объем объекта, а для плавающего объекта на жидкости, вес вытесненной жидкости — это вес объекта.

Принцип Архимеда указывает что восходящая выталкивающая сила, действующая на тело, полностью или частично погруженное в жидкость погружен, равен весу жидкости, которая тело смещается. Обратите внимание, что действующие силы увеличиваются с глубиной жидкости. равнодействующая всех сил вверх называется плавучестью и равна весу вытесненная жидкость.

Принцип Архимеда допускает плавучесть объекта, частично или полностью погруженного в жидкость, подлежащую рассчитано.Сила, направленная вниз на объект, — это просто его масса. Восходящая или плавучая сила, действующая на объект, такова, что утверждается принципом Архимеда, приведенным выше. Таким образом, чистая вверх сила на объекте — это разница между плавучестью сила и ее вес. Если эта результирующая сила положительна, объект плавает; если отрицательный, объект тонет; и если ноль, объект имеет нейтральную плавучесть, то есть остается на месте без либо поднимается, либо опускается.Простыми словами принцип Архимеда утверждает, что когда тело частично или полностью погружено в жидкости он испытывает очевидную потерю веса, которая равна массе жидкости, вытесненной погруженным часть тела.

Примечание: принцип Архимеда не учитывать поверхностное натяжение (капиллярность), действующее на тело но эта дополнительная сила изменяет только количество жидкости смещен, поэтому принцип Плавучесть = вес вытесненная жидкость остается в силе.

Рассмотрим куб, погруженный в жидкость, с его стороны параллельны направлению силы тяжести .. Только силы на верхней и нижней гранях куба будут способствовать к плавучести. Разница давлений между днищем и верхняя грань прямо пропорциональна высоте (разница глубоко). Умножение разницы давлений на площадь грани дает чистую силу на куб — плавучесть , или вес вытесняемой жидкости.

ФОРМУЛЫ Для полностью погруженного объект, принцип Архимеда можно сформулировать как следует: кажущаяся полная масса = вес объекта — вес вытесненной жидкости плотность объекта / плотность жидкости = вес / (вес вытесненной жидкости) плотность объекта / плотность жидкости = вес / (вес — кажущийся погруженный вес) __________________________ «Плавучесть» сила »на погруженном в воду корпусе направлена в направлении, противоположном силе тяжести, и равно по величине до: (плотность жидкости) (Объем вытесняемой жидкости) (ускорение)

Когда объект всплывет или воздушный шар подъем?

Объект будет плавать в жидкости, если плотность этого объекта меньше плотности жидкости.

Пример: Если вы уроните дрова в воду, плавучесть будет держать его на плаву. Древесина менее плотная, чем вода.

Воздушные шары поднимаются в воздух, потому что плотность воздуха (более теплый воздух) внутри воздушного шара составляет менее плотный, чем воздух за пределами воздушного шара (более прохладный воздух). Баллон и корзина вытесняют более тяжелую жидкость. чем воздушный шар и корзина, поэтому он обладает выталкивающей силой действуя на систему.Воздушные шары, как правило, лучше летают по утрам, когда окружающий воздух прохладный.

ОБРАЗЕЦ ПРОБЛЕМА

Блок стальной плотностью 7800 кг / м3 подвешивается на веревке в стакане с водой
так, чтобы блок был полностью погружен, но не оставался в покое на дне. Блок представляет собой куб
со сторонами 3 см (0,03 м).

Подъемная сила = вес вытесненной воды
= масса воды * ускорение свободного падения
= плотность воды * объем куба * г
= 1×10 ³ кг / м ³ * 27 * 10-6 м3 9.8 м / с2 = 2,65 * 10-1 Н = 0,265 Н

вес блока = масса г
W = мг = 2,106 x 10-1 кг x 9,8 м / с2 = 2,106×9,8 x 10-1 кг * м / с2 = 20,64 x 10-1 Н
= 2,064 Н кг * м / с2 = Н (Ньютон)

Проверьте свой Понимание:

.