Закон сохранения и превращения энергии Википедия
Зако́н сохране́ния эне́ргии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда закономерность, его можно именовать не законом, а принципом сохранения энергии.
С фундаментальной точки зрения, согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимости законов физики от момента времени, в который рассматривается система. В этом смысле закон сохранения энергии является универсальным, то есть присущим системам самой разной физической природы. При этом выполнение этого закона сохранения в каждой конкретно взятой системе обосновывается подчинением этой системы своим специфическим законам динамики, вообще говоря, различающимся для разных систем.
В различных разделах физики по историческим причинам закон сохранения энергии формулировался независимо, в связи с чем были введены различные виды энергии. Возможен переход энергии из одного вида в другой, но полная энергия системы, равная сумме отдельных видов энергий, сохраняется. Однако, из-за условности деления энергии на различные виды, такое деление не всегда может быть произведено однозначно.
Для каждого вида энергии закон сохранения может иметь свою, отличающуюся от универсальной, формулировку. Например, в классической механике был сформулирован закон сохранения механической энергии, в термодинамике — первое начало термодинамики, а в электродинамике — теорема Пойнтинга.
С математической точки зрения, закон сохранения энергии эквивалентен утверждению, что система дифференциальных уравнений, описывающая динамику данной физической системы, обладает первым интегралом движения, связанным с симметричностью уравнений относительно сдвига во времени.
ru-wiki.ru
Закон сохранения и превращения энергии :
«Энергия не исчезает и не возникает вновь, она лишь переходит из одного вида в другой в различных физических и химических процессах».
Т.е. для любой изолированной системы (такой термодинамической системы, которая не обменивается с окружающей средой ни теплом, ни работой, ни веществом) количество энергии, заключённое в этой системе, сохраняется неизменным.
Формулировка и уравнение первого закона термодинамики
Первый закон термодинамикиустанавливает эквивалентность при взаимных
превращениях механической и тепловой энергии и математически может быть выражен следующим образом: Q = L, (9)
где Q — количество теплоты, превращенной в работу;
L — работа, полученная за счет теплоты Q.
Количества теплоты Q и работы L измерены в данном случае в соответствии с системой единиц СИ — в одних и тех же единицах — в джоулях.
В результате подвода теплоты к телу температура тела повышается, объем тела увеличивается и производится внешняя работа. При этом «подведенная к телу теплота расходуется на увеличение внутренней энергии тела U и на совершение работы L»:
Q1-2= ∆ U1-2+ L1-2 , (10)
где Q1-2– теплота, сообщенная телу при нагревании от состояния 1 до состояния 2;
∆ U1-2– изменение внутренней энергии тела; ∆ U1-2= U2 — U1
L1-2 — работа, совершаемая телом в процессе 1-2.
Аналитическое выражение первого закона термодинамики или основное уравнение теплоты в дифференциальной форме для любого тела
dQ = dU + dL, (11)
где dQ — количество теплоты, сообщенное извне рабочему телу массой М кг;
dU — изменение внутренней энергии рабочего тела; dL — работа, совершенная рабочим телом по преодолению внешнего давления, «внешняя работа» расширения.
Каждый из трех членов этого уравнения может быть в зависимости от характера изменения состояния положительным, или отрицательным, или равным нулю.
Теплота, подводимая к системе – положительная, отводимая от системы – отрицательная.
Работа, производимая системой – положительная (работа расширения Lрасш ), работа, совершаемая над системой – отрицательная (работа сжатия Lсж).
Так как за единицу работы принят Дж, то единицей мощности будет являться Дж/с. Эта единица носит название ватт (Вт). В технике применяют более крупные единицы энергии (работы) и мощности: килоджоуль (кДж), мегаджоуль (МДж), киловатт (кВт), мегаватт (МВт), киловатт-час (кВт•ч).
В промышленности до последнего времени за единицу тепловой энергии принимали калорию (кал), за единицу механической работы килограмм-силу-метр, или килограммометр (кгС’М), а за единицу мощности — килограммометр в секунду (кгс•м/с). Так как эти единицы слишком малы, то в качестве практических единиц были приняты килокалория (ккал), мегакалория (Мкал), лошадиная сила (л. с.) и киловатт (кВт). Соответствующими единицами работы (энергии) были приняты киловатт-час (кВт•ч), лошадиная сила-час (л. с. ч.), а мощности — килограммометр в секунду (кгс ·м/с).
Соотношения между различными единицами энергии и мощности даны соответственно в таблицах 6.1 и 6.2.
Таблица 6.1- Соотношения между единицами энергии
Единицы измерения | Дж | кгс· м | Кал |
Джоуль | 1 | 0,102 | 0,239 |
9,8067 | 1 | 2,343 | |
Калория | 4,1868 | 0,42686 | 1 |
Килокалория | 4,1868·103 | 4,2686·102 | 103 |
Киловатт-час | 3,6·106 | 3,67·105 | 8,6·105 |
Фут-фунт-сила | 1,356 | 0,138 | 0,325 |
Единицы измерения | ккал | кВт·ч | ft·lbf |
Джоуль | 2,39·10-4 | 2,78·10-7 | 0,7376 |
Килограмм-сила-метр | 2,343·10-3 | 2,72·10-6 | 7,233 |
Калория | 10-3 | 1,16·10-6 | 3,088 |
Килокалория | 1 | 1,16·10-3 | 3,088·103 |
Киловатт-час | 8,6·102 | 1 | 2,653·106 |
Фут-фунт-сила | 3,25·10-4 | 3.76·10-7 | 1 |
Таблица 6.2 — Соотношения между единицами мощности
Единицы измерения | Вт | кгс·м/с | Кал/с | ft·lbf/ s | л.с. |
Ватт | 1 | 0,102 | 0,239 | 0,7376 | 1,36·10-3 |
Килограмм-сила-метр в секунду | 9,8067 | 1 | 2,343 | 7,233 | 1,33·10-2 |
Калория в секунду | 4,1868 | 0,427 | 1 | 3,088 | 5,69·10-3 |
Фут-фунт-сила в секунду | 1,3558 | 0,138 | 0,3246 | 1 | 1,84·10-3 |
Лошадиная сила | 736 | 75 | 175,5 | 542,5 | 1 |
Пользуясь
первым законом термодинамики, можно
определить коэффициент
полезного действия (к.
п. д.) теплосиловых установок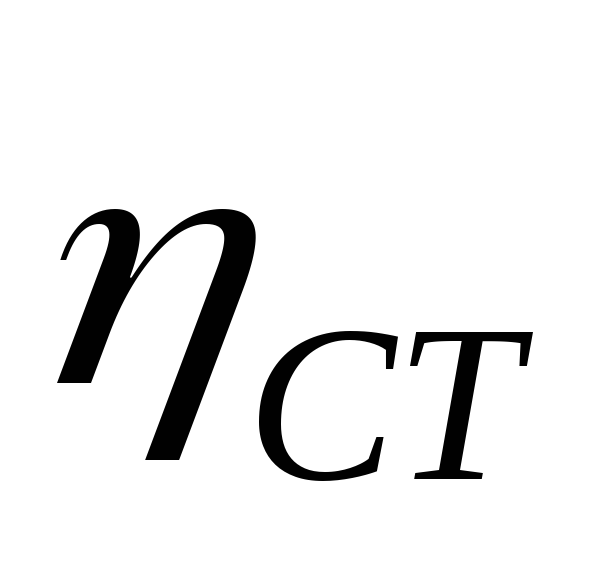 
,
характеризующий степень совершенства
превращения ими теплоты в работу.
К. п. д. может быть вычислен, если известны расход топлива на 1 кВт-ч и теплота сгорания топлива, т.е. то количество теплоты, которое выделяется при полном сгорании массовой или объемной единицы топлива.
Если расход топлива на 1 кВт-ч (удельный расход топлива) b выражен в кг/(кВт •ч), а теплота сгорания топлива Qрн — в кДж/кг, то к. п. д. теплосиловой установки
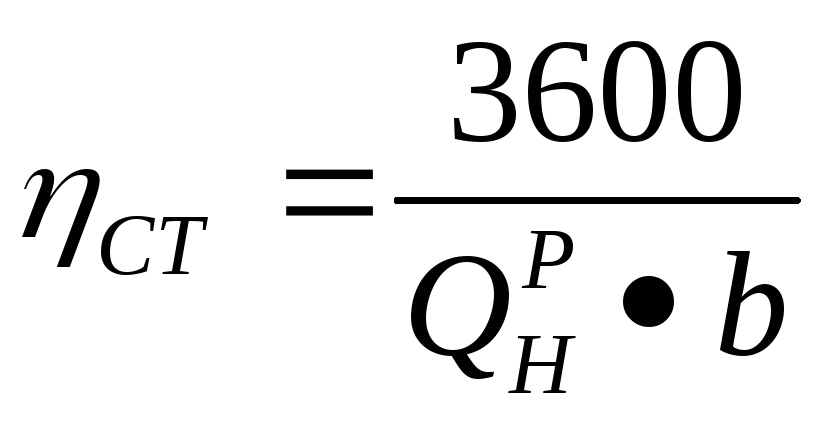(12)
studfile.net
3.5. Закон сохранения механической энергии. Закон сохранения и превращения энергии как проявление неуничтожимости материи и ее движения
Рассмотрим систему,
состоящую из nчастиц с
массамиm1,m2,…mn.Пусть частицы взаимодействуют друг с
другом с силамиFik,
модули которых зависят только от
расстояния между частицами. Такие силы
являются консервативными. Это означает,
что работа, совершаемая этими силами
над частицами, определяется начальной
и конечной конфигурациями системы.
Предположим, что кроме внутренних сил
наi–частицу действует
внешняя консервативная силаfiи внешняя неконсервативная сила
.
Тогда уравнение движенияi–частицы
будет иметь вид
,
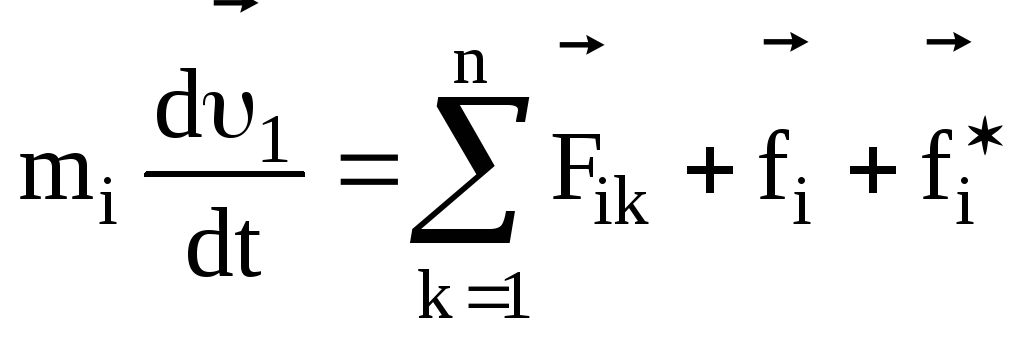(3.25)
причем (ik), и принимает значенияi=1,2…n.
Умножив уравнение
(3.25) на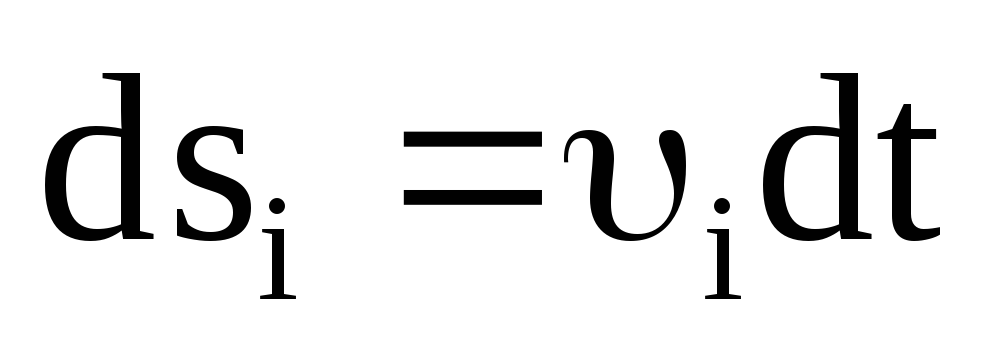 
и, сложив вместе всеnуравнений, получим
.
(3.26)
Левая часть уравнения (3.26) есть приращение кинетической энергии системы:
.
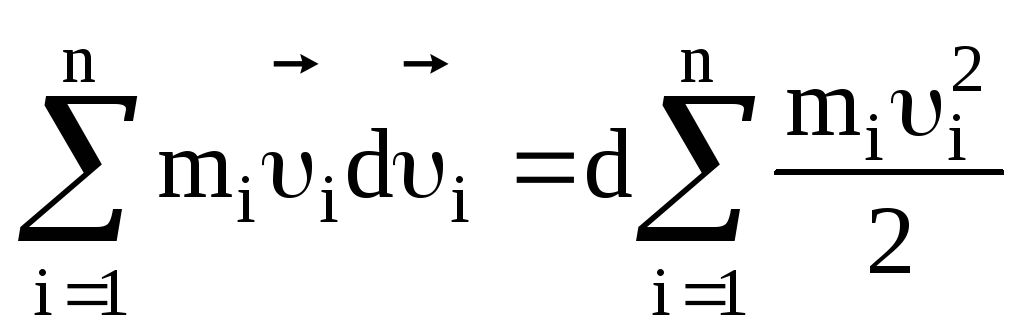Первый член правой
части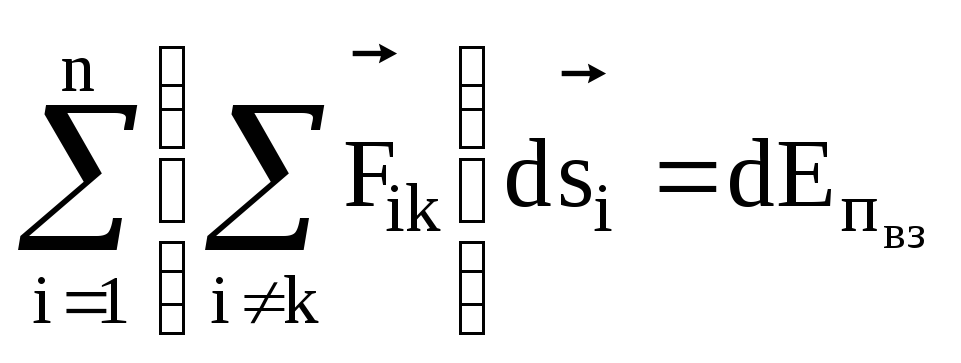 
равен убыли потенциальной энергии
взаимодействия частиц. Второй член
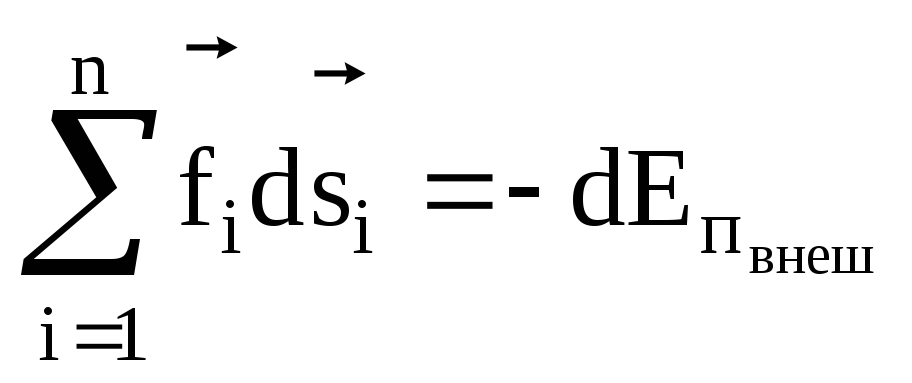равен убыли потенциальной энергии
системы во внешнем поле консервативных
сил. Последний член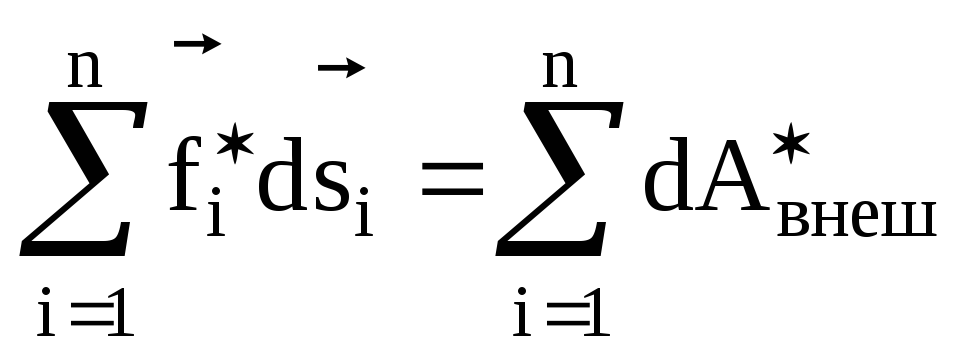
представляет собой работу
неконсер-вативных внешних сил.
Таким образом, равенство (3.26) можно записать в виде
.
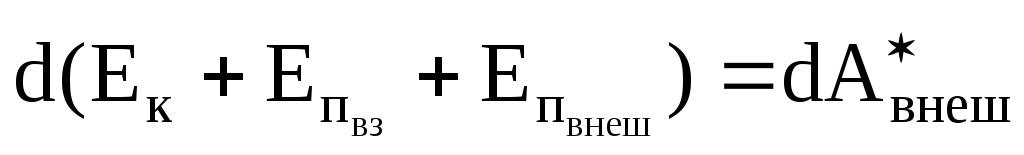(3.27)
Величина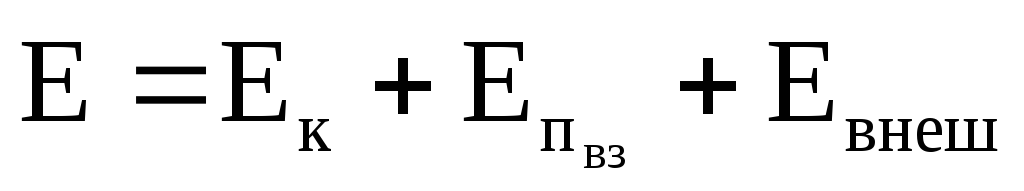 
— есть полная механическая энергия
системы. Если внешние неконсервативные
силы отсутствуют, правая часть уравнения
(3.27) будет равна нулю, и полная энергия
системы остается постоянной:
.
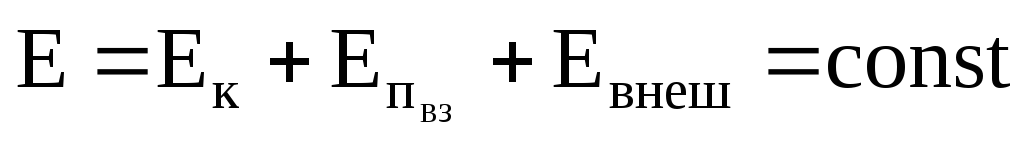Таким образом, полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остается постоянной (закон сохранения механической энергии).
Для замкнутой
системы, т.е. системы, на тела которой
не действуют никакие внешние силы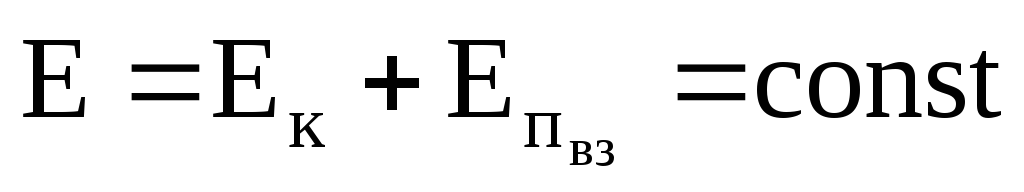 
,
т.е. полная механическая энергия замкнутой
системы тел, между которыми действуют
только консервативные силы, остается
постоянной.
Если в замкнутой системе, кроме консервативных сил, действуют также неконсервативные силы (силы трения), то полная механическая энергия системы не сохраняется:
.
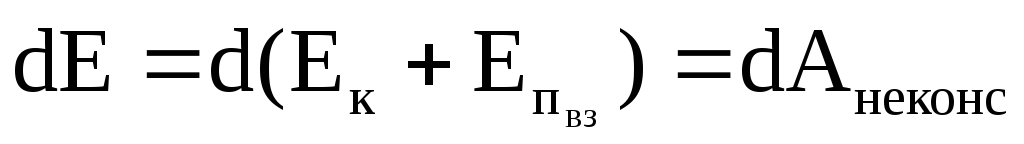Проинтегрировав это выражение, получим, что работа неконсервативных сил равна изменению полной механической энергии системы:
.
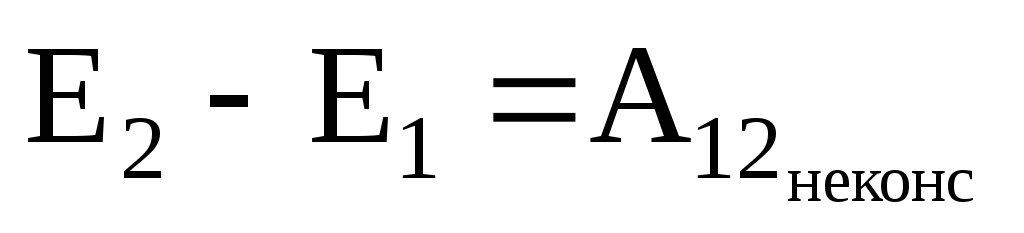Силы трения, как правило, совершают отрицательную работу. Поэтому наличие сил трения в замкнутой системе приводит к уменьшению ее полной механической энергии со временем. Действие сил трения приводит к превращению механической энергии в другие, немеханические виды энергии. Всякий раз, когда «исчезает» энергия одного вида появляется эквивалентное количество энергии другого вида. Энергия никогда не исчезает и не появляется снова, она лишь превращается из одного вида в другой. В этом и заключается закон сохранения энергии в его общем физическом смысле.
3.6. Удар абсолютно упругих и неупругих тел
При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации или в так называемую внутреннюю энергию тел. Увеличение внутренней энергии тел сопровождается повышением температуры. Существуют два предельных вида удара: абсолютно упругий и абсолютно неупругий. Абсолютно упругим ударом называется такой удар, при котором механическая энергия тел не переходит в другие немеханические виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. Потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и тела разлетаются со скоростями, величина и направление которых определяются сохранением полной энергии и сохранением полного импульса системы.
Абсолютно неупругий удар характеризуется тем, что потенциальная энергия деформации не возникает, кинетическая энергия тел полностью или частично превращается во внутреннюю энергию. После удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся.
При абсолютно неупругом ударе выполняется лишь закон сохранения импульса. Закон сохранения механической энергии не соблюдается – имеет место закон сохранения суммарной энергии различных видов – механической и внутренней.
Рассмотрим абсолютно неупругий удар двух частиц, образующих замкнутую систему, движущихся вдоль оси x(рис.3.5)
Пусть m1иm2— массы частиц,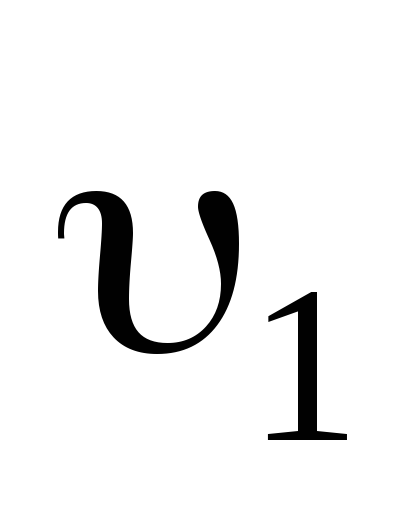
и
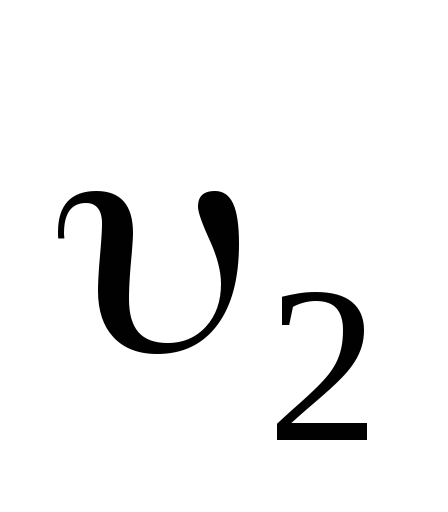— скорости частиц до удара,
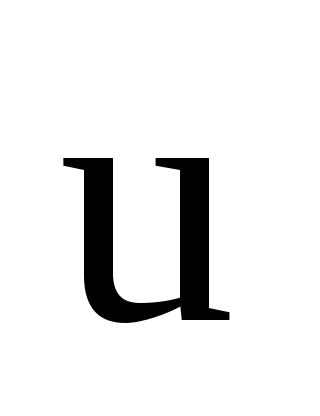— скорость частиц после удара.
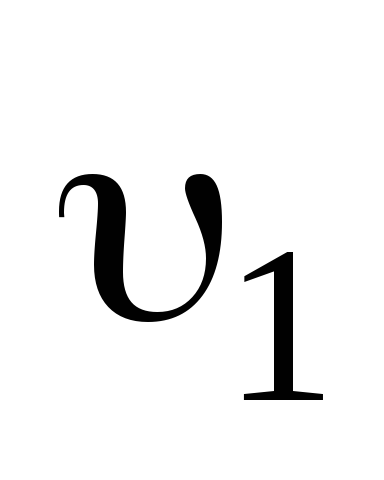
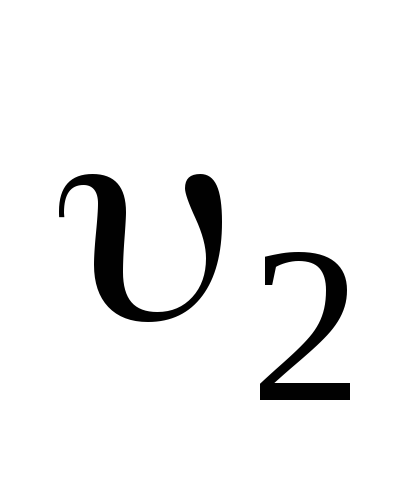
x
m1m2
а)
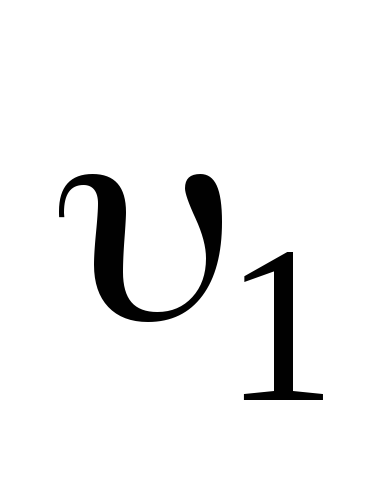
x
m1m2
б)
Рис.3.5
Запишем закон сохранения импульса:
;
.
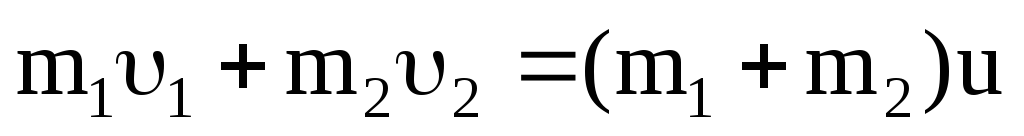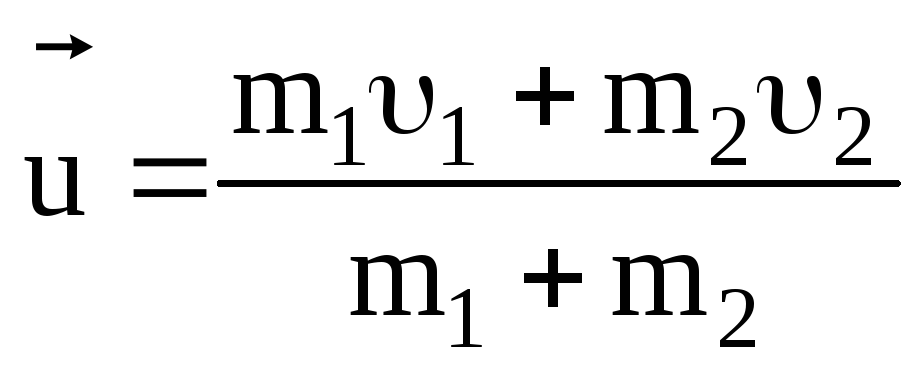(3.28)
Модуль скорости частиц после удара для рис. 3.5,аравен
,
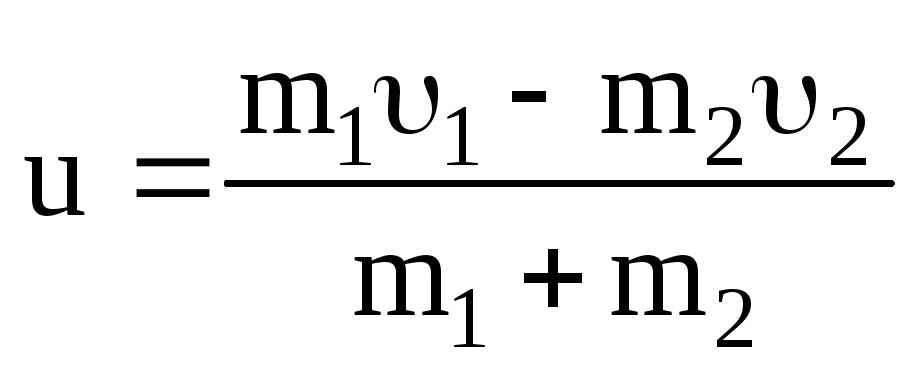для рис. 3.5,б
.
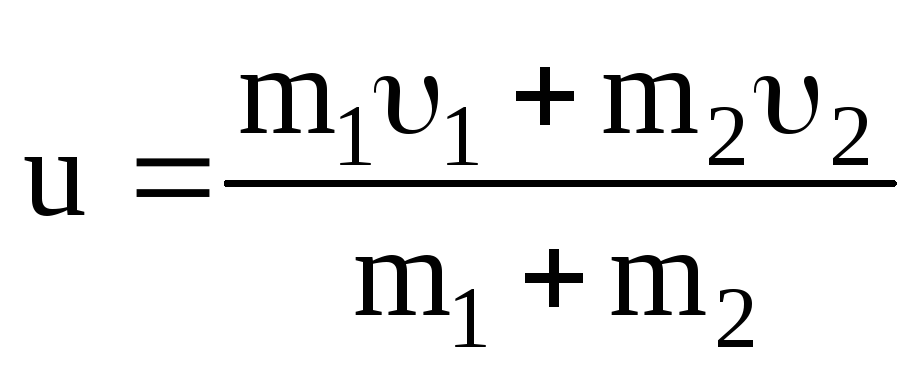Выясним, как изменится полная энергия шаров при абсолютно неупругом ударе. Кинетическая энергия до удара:
,
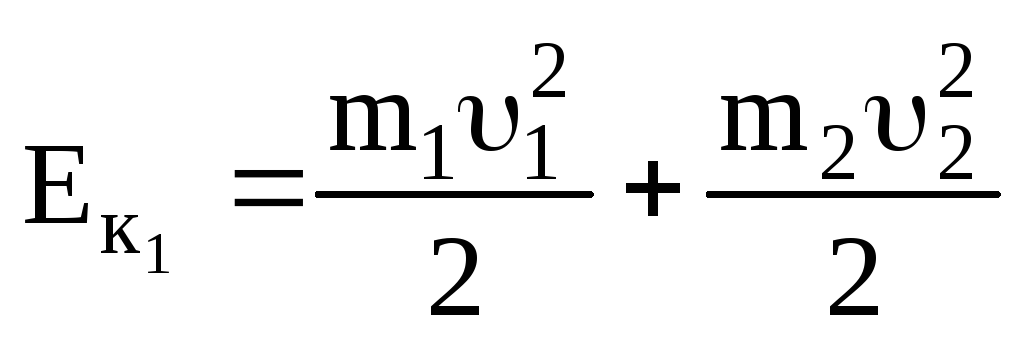после удара:
.
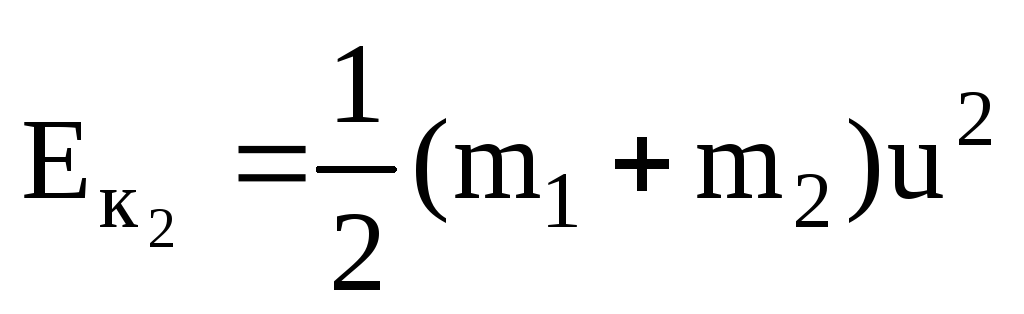Подставим в это выражение общую скорость движения частиц (3.28) для случая, изображенного на рис. 3.5,б
.
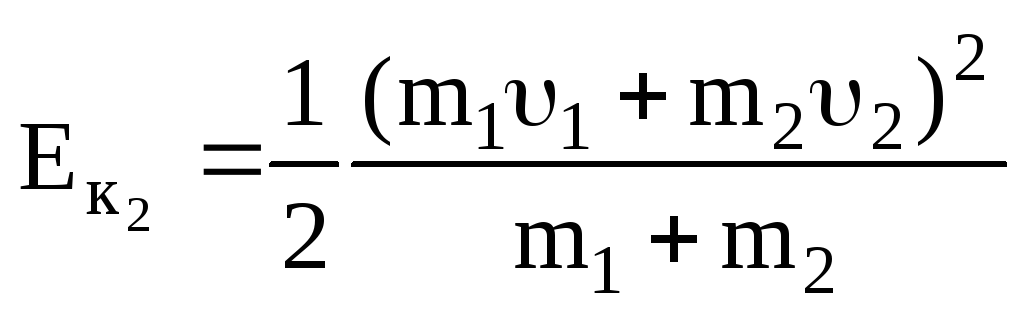Найдем изменение кинетической энергии:
;
.
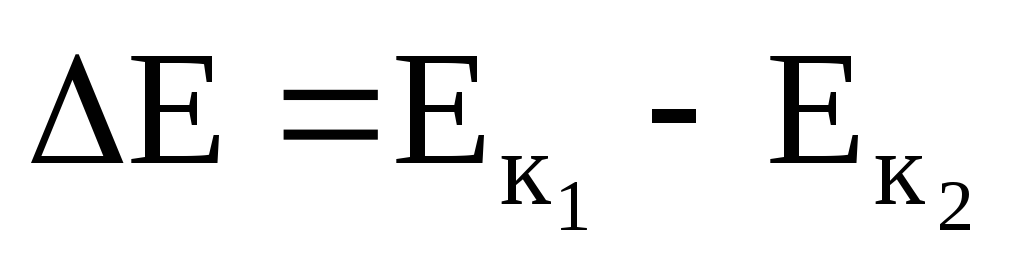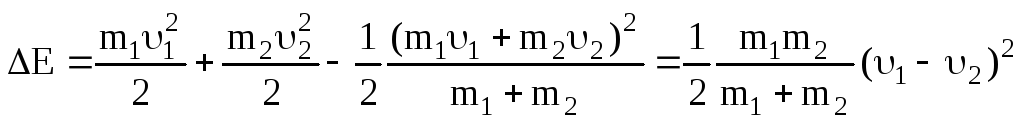(3.29)
Уменьшение кинетической энергии при неупругом ударе означает, что механическая энергия системы при этом ударе не остается постоянной, она частично или полностью превращается в тепловую энергию движущихся молекул.
Рассмотрим абсолютно упругий центральный удар двух однородных шаров (рис.3.6). Удар называется центральным, если шары до удара движутся вдоль прямой, проходящей через их центр. Предполагается, что шары образуют замкнутую систему тел, что внешние силы, приложенные к шарам, уравновешивают друг друга. Кроме того, вращение шаров отсутствует.
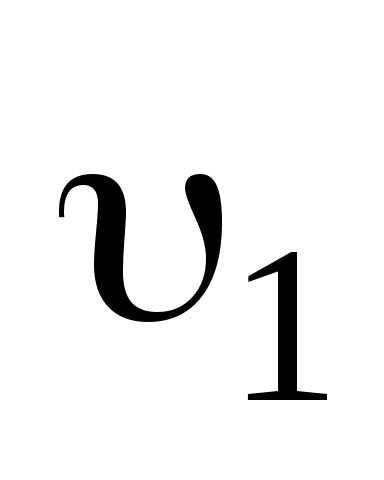
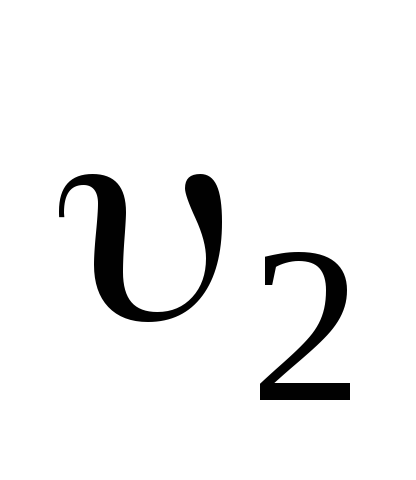
x
m1 m2
Рис.3.6
Обозначим m1 и m2 — массы шаров,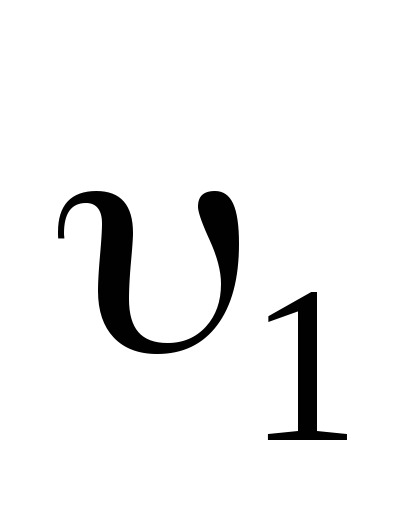 
и 
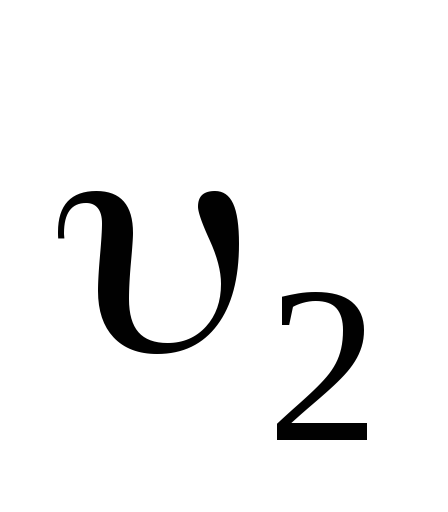— скорости шаров до удара, 
и 
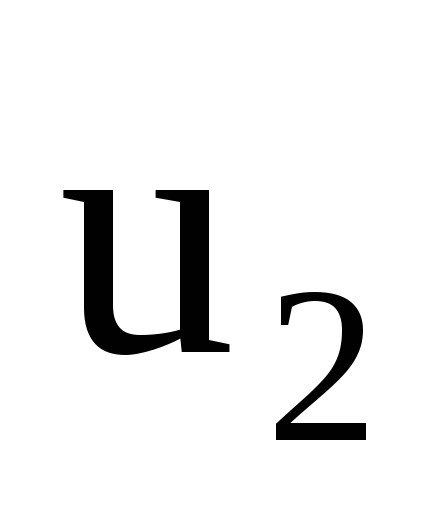— скорости шаров после удара. Положим,
что скорости шаров как до удара, так и
после удара направлены вдоль положительного
направления оси x.
Запишем уравнение закона сохранения импульса и энергии:
;
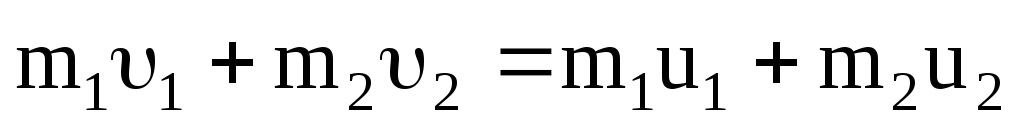(3.30)
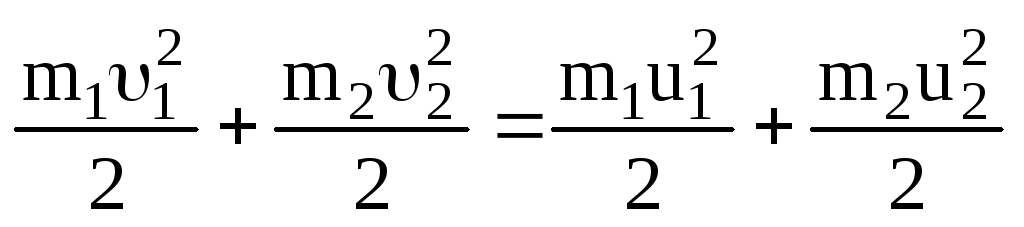. (3.31)
Спроектируем уравнение закона сохранения импульса (3.30) на ось x:
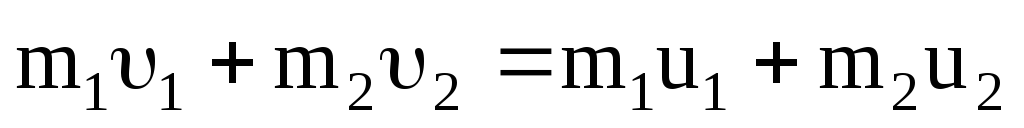
и преобразуем его к виду
. (3.32)
Из закона сохранения энергии (3.31) следует:
.
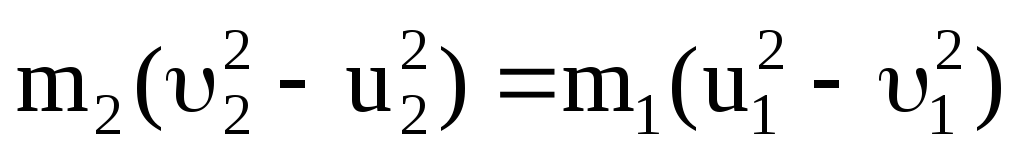(3.33)
Разделим уравнение (3.33) на (3.32), получим
.
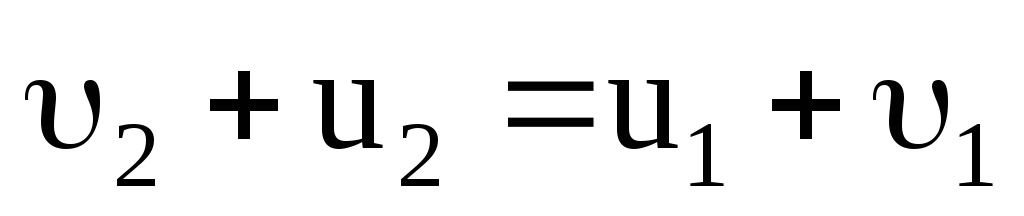(3.34)
Для нахождения скорости u1 умножим (3.34) на m2 и полученное соотношение сложим с уравнением (3.32):
,
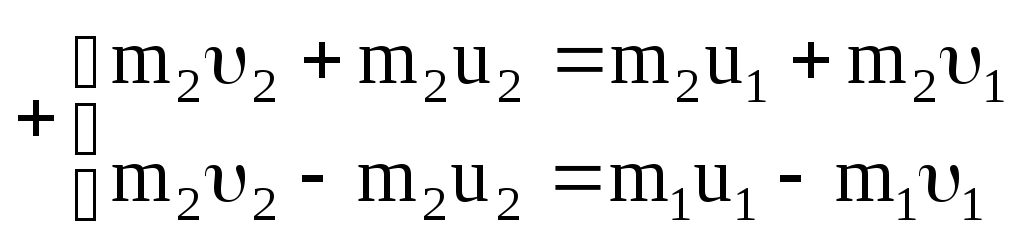получим
,
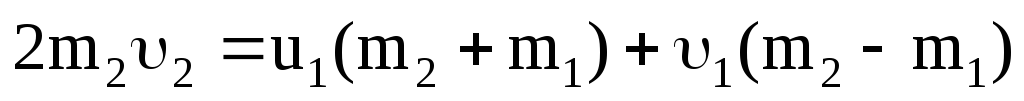откуда
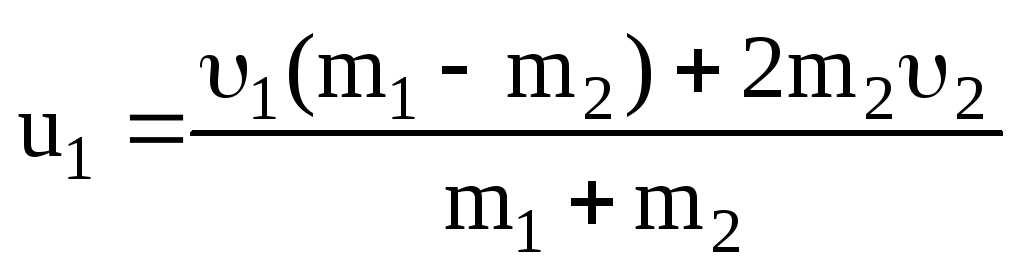. (3.35)
Для определения скорости u2 умножим (3.34) на m1 и полученное соотношение вычтем из уравнения (3.32):
,
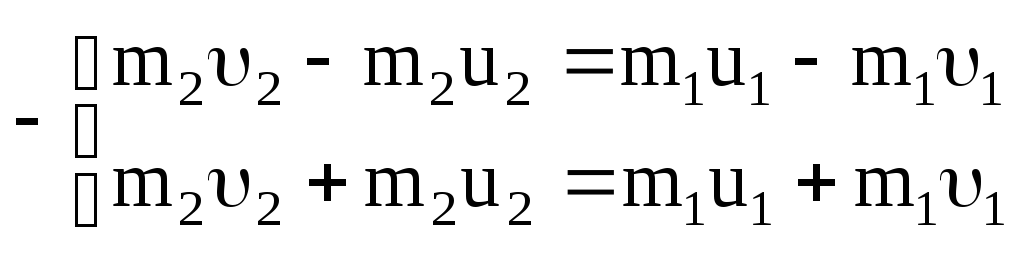получим
,
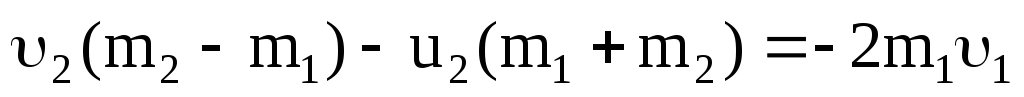откуда
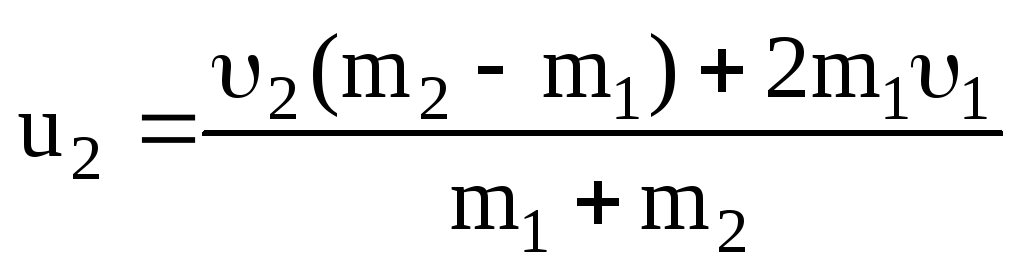. (3.36)
При m1=m2 из (3.35) и (3.36) следует, что u1=2, а u2=1.
studfile.net
Закон сохранения и превращения энергии
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Законы сохранения в механике
1. Энергия, работа, мощность
2. Кинетическая энергия
3. Потенциальная энергия
4. Закон сохранения и превращения энергии
5. Закон сохранения импульса
Энергия, работа, мощность
Изменение механического движения тела вызывается силами, которые действуют на него со стороны других тел.
С целью количественно описать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы.
Если тело движется прямолинейно и на него действует постоянная сила F, составляющая некоторый угол α с направлением перемещения, то работа этой силы равна:
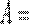
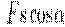
Если взять участок траектории от точки 1 до точки 2, то работа на нем равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути.
Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м.
Работу считают положительной, если вектор силы совпадает с направлением движения, и отрицательной при векторе силы, направленном в противоположную движению сторону. Примером отрицательной работы может быть действие тормозящей силы.
Мощность –это работа, совершенная за единицу времени
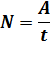
Единица мощности – ватт (Вт).
С работой и мощностью связано понятие о механической энергии.
Механическая энергия — это особая физическая величина, характеризующая способность тел совершать работу. Эквивалентность работы и энергии дает основание измерять эти величины в одинаковых единицах
Энергия — универсальная мера различных форм движения и взаимодействия. В механике различают два вида энергии: кинетическую и потенциальную.
Кинетическая энергия
Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась от v1 до v2, то силы совершили определенную работу A.
Пусть тело движется вдоль прямой линии под действием постоянной силы , при этом тело переместилось на
 |
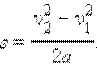Отсюда, с учетом 2 закона Ньютона, следует, что
 |
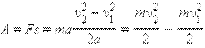Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).
Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:
Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии.
Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.
Кинетическая энергия – это энергия движения, поэтому она всегда положительна и зависит от выбора системы отсчета
Единица кинетической энергии та же, что и единица работы- джоуль (Дж).
Потенциальная энергия
Потенциальная энергия —энергия взаимодействия тел.
Потенциальная энергия определяется взаимным положением тел (например, положением тела относительно поверхности Земли). Понятие потенциальной энергии можно ввести только для сил, работа которых не зависит от траектории движения и определяется только начальным и конечным положениями тела. Такие силы называются консервативными.
Работа консервативных сил на замкнутой траектории равна нулю.
Свойством консервативности обладают сила тяжести и сила упругости. Для этих сил можно ввести понятие потенциальной энергии.
Физическая величина называется потенциальной энергией тела в поле силы тяжести
Eр = mgh.
Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.
Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком
A = –(Eр2 – Eр1).
Потенциальная энергия Eр зависит от выбора нулевого уровня. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔEр = Eр2 – Eр1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.
Понятие потенциальной энергии можно ввести и для силы упругости. Эта сила также обладает свойством консервативности. Растягивая (или сжимая) пружину, мы можем делать это различными способами.
Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину
Ер= (kx2)/2
Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.
Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой посредством сил упругости.
Закон сохранения и превращения энергии
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком, эта же работа определяется и по теореме о кинетической энергии, следовательно:
Ek1 + Ep1 = Ek2 + Ep2.
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему консервативных сил, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.
Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами.
Сила трения не является консервативной. Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.
Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии.
Закон сохранения импульса
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.
В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.
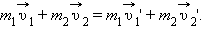
Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился.
Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.
Механические колебания
1. Гармонические колебания.
2. Маятники.
Гармонические колебания
Колебанияминазываются процессы, в той или иной степени, повторяющиеся во времени.
Изменение координаты точки при колебании можно описать уравнением
X(t) = A cos(wt+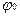 
).
Движение, при котором координата точки изменяется по закону косинуса (или синуса) называетсягармоническим колебанием.
Гармоническое колебание точки определяется тремя параметрами: А, w и φ0.
Параметр A называется амплитудой колебаний, он равен максимальному отклонению точки от центрального положения (положения равновесия). Эта величина имеет ту же размерность, что и координата x, то есть размерность длины. Изменяющаяся величина называется фазой колебания, а величина φ0 — начальной фазой.
Параметр ω называется круговой(циклической) частотой колебаний. Время одного колебания T называется периодом колебаний.
Круговая частота связана с периодом колебания соотношением
.
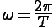Если период – это время одного колебания, то величина обратная периоду равна числу колебаний в единицу времени, то есть частоте колебаний
.
Связь круговой (циклической) и обычной частоты колебаний
.
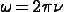Маятники
Маятник — тело, совершающее под действием переменной силы колебания.
1. Пружинный маятник — это груз массой m, который подвешен на пружине и совершает гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины.
Пружинный маятник совершает гармонические колебания по закону
х = А соs (ω0t+φ)
с циклической частотой
и периодом
2. Физический маятник — это твердое тело, которое совершает колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, которая проходит через точку О, не совпадающую с центром масс С тела.
Циклическая частота
,
При малых колебаниях физический маятник совершает гармонические колебания с циклической частотой ω0 и периодом
,
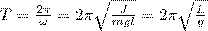где введена величина L=J/(ml) — приведенная длина физического маятника.
3. Математический маятник — это идеализированная система, состоящая из материальной точки массой m, которая подвешена на нерастяжимой невесомой нити, и которая колеблется под действием силы тяжести. Хорошее приближение математического маятника есть небольшой тяжелый шарик, который подвешен на длинной тонкой нити.
Поскольку математический маятник есть частный случай физического маятника, если предположить, что вся его масса сосредоточена в одной точке — центре масс, то найдем выражение для периода малых колебаний математического маятника
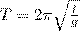
megapredmet.ru
Закон сохранения и превращения энергии
Развитие познания совершается по спирали.
Наступает время, когда наука возвращается
к идеям, однажды уже высказанным.
Но это возвращение совершается на новом,
более высоком уровне, которому предшествовал
длительный исторический опыт познания.
В. И. Ленин
Ранее говорилось о таком понятии, как механическая энергия. Механическая энергия – это физическая величина, являющаяся функцией состояния системы и характеризующая способность системы совершать работу. В свою очередь, механическая энергия делится на два вида — кинетическую и потенциальную.
Кинетическая энергия — это энергия, которой обладает тело вследствие своего движения. А ее изменение равно работе равнодействующей всех сил действующей на тело.
Потенциальная энергия — это энергия, определяемая взаимным расположением тел или частей тела друг относительно друга и характером сил взаимодействия между ними.
Потенциальная энергия делится на два вида: потенциальную энергию тела в поле тяготения — это энергия, обусловленная взаимодействием тела с Землей; и потенциальную энергию упруго деформированного тела — это энергия, обусловленная взаимодействием частей тела между собой.
А могут ли тела обладать одновременно и кинетической и потенциальной энергией?
В курсе физики 7 класса говорилось о том, что сумма кинетической и потенциальной энергии есть полная механическая энергия тела или системы тел.
Рассмотрим замкнутую систему тел «тело — Земля», между которыми действует только сила тяжести.
Под действием этой силы изменяется и кинетическая, и потенциальная энергии тела. Причем работа силы тяжести будет равна как изменению кинетической энергии тела, так и его потенциальной энергии, но взятой с обратным знаком. Т. е. увеличение кинетической энергии системы будет осуществляться за счет убыли ее потенциальной энергии.
Из этих уравнений получаем, что сумма кинетической и потенциальной энергии тела остается неизменной.
Т.о. полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения, остается постоянной, при любых взаимодействиях в системе. Это утверждение носит название закона сохранения энергии в механике.
Это закон справедлив и для замкнутой системы, взаимодействующей силами упругости.
А что, если в системе тел, например, будут действовать силы трения, или же в системе тел будут происходит неупругие деформации? В этих случаях механическая энергия системы будет убывать. Но это не означает, что механическая энергия исчезает бесследно. Она превращается в другой вид энергии, в частности во внутреннюю энергию.
Т.о. для любой замкнутой системы тел всегда выполняется закон сохранения и превращения энергии, который является фундаментальным законом природы: величина полной энергии замкнутой системы остается постоянной. При этом, будучи не созидаемой и неуничтожимой, энергия может превращаться из одного вида энергии в другой.
Обратимся к истории открытия закона сохранения энергии. Ученые и практики всех времен обращались к исследованиям различных энергетических процессов и предпринимали попытки обобщений в которых содержались элементы формулировки закона сохранения и превращения энергии.
Еще мыслители древности Демокрит и Эпикур утверждали вечность и неуничтожимость материи и движения. Повседневная практическая деятельность требовала познаний законов движения, прежде всего, единственно известного — механического. И поэтому не случайно, что закон сохранения энергии начинал вырисовываться в рамках механики. В 1633 г. «Трактате о свете» идея сохранения движения была сформулирована Декартом следующим образом: «Когда одно тело сталкивается с другим, оно может сообщить ему лишь столько движения, сколько само одновременно теряет, а отнять от него лишь столько, на сколько увеличит собственное движение». В таком виде совершенно четко отмечается количественное постоянство движенья, причем никакое другое движение, кроме механического Декарт не рассматривал. Эта идея получила дальнейшее развитие у Лейбница в его законе сохранения живых сил.
Принцип сохранения живой силы гласит: если любое число подвижных материальных точек движется только под влиянием таких сил, которые зависят от взаимодействий точек друг на друга, или которые направлены к неподвижным центрам, то сумма живых сил всех взятых вместе точек останется одна и та же во все моменты времени, в которые все точки получают те же самые относительные положения друг по отношению к другу и по отношению к существующим неподвижным центрам, каковы бы ни были их траектории и скорости в промежутках между соответствующими моментами.
После классических работ И. Ньютона и Г.В. Лейбница принцип сохранения движения получил четкую формулировку в трудах М.В. Ломоносова, который решился объединить два принципа сохранения: движения и материи. Именно М.В. Ломоносову принадлежит открытие закона сохранения вещества, повторенное затем совершенно независимо от него Антуаном Лораном Лавуазье. В 1744 г. М.В. Ломоносов написал ставшие знаменитыми слова «Все перемены в натуре случающиеся, такого суть состояния, что сколько чего у одного тела отнимается, столько присовокупится к другому, так ежели где убудет несколько материи, то умножится в другом месте… сей всеобщий естественный закон простирается и в самые правила движения, ибо тело, движущее своею силою другое, столько же оной у себя теряет, сколько сообщает другому, которое от него движение получает».
Так в середине XVIII столетия М.В. Ломоносовым был четко сформулирован закон сохранения массы и движения как всеобщий закон природы.
Более того, первая часть его выражения («все перемены в натуре случающиеся…») сформулирована так широко, что если бы эти слова были написаны сто лет спустя, когда стали известны другие «перемены в натуре» — многочисленные взаимные преобразования энергии (электрической, тепловой, химической, механической), то другие формулировки закона сохранения к превращения энергии и сохранения материи были бы излишни. Но, к сожалению, и эпоха была еще не та, и научные труды Ломоносова почти полтора столетия оставались неизвестными.
Решающую роль в установлении закона сохранения и превращения энергии история отводит Роберту Майеру, Джеймсу Джоулю и Герману Гельмгольцу.
Роберт Майер был судовым врачом на голландском корабле, когда в 1840 г. «внезапно» ему пришла в голову мысль о законе сохранения и превращения энергии. Слово «внезапно» взято в кавычки недаром: о внезапном озарении писал впоследствии Майер, но может ли быть внезапным открытие, предпосылки которого были хорошо известны выпускнику Тюбингенского университета? Внезапным был для Майера исходный толчок: он обратил внимание на то, что было хорошо известно врачам, работающим постоянно в тропических широтах. Во время стоянки корабля на Яве заболел матрос, и Майер, как тогда было принято, «пустил ему кровь», вскрыв вену. Каково же было его удивление, когда он увидел, что венозная кровь была не стать темной, как в умеренных широтах. Майер понял, что при высокой средней температуре воздуха для поддержания жизнедеятельности и необходимой температуры организма требуется меньше питательных веществ и меньшее «сгорание» последних. Сопоставление многочисленных научных фактов из области химии, физики и биологии привело его к тому, что мысли, согласно выражению Майера, пронзившие его, подоено молнии, навели на вывод о существовании всеобщего закона природы.
Идеи Майера носили столь общий и универсальный характер, что они сначала не были восприняты современниками.
Широкое, философское понимание закона сохранения энергии Майером, обобщение им закона на явления жизни и космос смущали физиков и рассматривались ими как метафизические размышления. Но проводимые одновременно и независимо от Майера эксперименты Джоуля подвели под обобщения Майера прочную экспериментальную основу.
Джеймс Прескотт Джоуль приходит к более общему выводу: «Могучие силы природы… неразрушимы,и… во всех случаях, когда затрачивается механическая сила, получается точное эквивалентное количество теплоты». Он утверждает, что животная теплота возникает в результате химических превращений в организме и что сами химические превращения являются результатом действия химических сил, возникающих из «падения атомов».
Наконец, немецкий ученый Герман Гельмгольц в 1847 г. в работе «О сохранении силы» дал в наиболее общем виде закон сохранения, показав, что сумма потенциальной и кинетической энергий остается постоянной. Большое значение имело приведенное в этой же работе доказательство того, что процессы в живых организмах тоже подчиняются закону сохранения энергии. Здесь же впервые дана математическая трактовка закона.
Завершением длительного пути, пройденного наукой до точной формулировки закона сохранения энергии, можно считать доклад Уильяма Томсона (впоследствии лорда Кельвина) «О динамической теории тепла», где Томсон ввел в науку термин «энергия» в современном его смысле.
Основные выводы:
– Закон сохранения в механике: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или упругости, остается постоянной, при любых взаимодействиях в системе.
– Закон сохранения и превращения энергии: величина полной энергии замкнутой системы остается постоянной. При этом, будучи не созидаемой и неуничтожимой, энергия может превращаться из одного вида энергии в другой
videouroki.net
4. 4. 2. Закон сохранения и превращения энергии – фундаментальный закон природы.
В диссипативных системах механическая энергия постепенно уменьшается за счет преобразования в другие механические формы энергии. Этот процесс получил название диссипации (рассеивания) энергии. Строго говоря, все системы в природе диссипативны. В консервативных системах закон сохранения механической энергии не просто закон сохранения в количественном смысле, а закон сохранения и превращения энергии, выражающий качественную сторону взаимного превращения различных форм движения друг в друга.
Закон сохранения энергии – это результат обобщения многих экспериментальных данных. Идея этого закона принадлежит Ломоносову, изложившему закон сохранения материи и движения, а полная формулировка в количественной форме дана немецким врачом Майером и ученым Гельмгольцем.
Закон сохранения и превращения энергии – фундаментальный закон природы.Он справедлив как для систем макроскопических тел, так и для систем микро тел. В системе, где действуют также неконсервативные силы, полная механическая энергия не сохраняется, однако, при исчезновении механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом,энергия никогда не исчезает и не появляется вновь.
Физическая сущность закона сохранения и превращения энергии — неуничтожимость материи и ее движения.
4. 4. 3. Механическая энергия замкнутой системы.
Механическая
энергия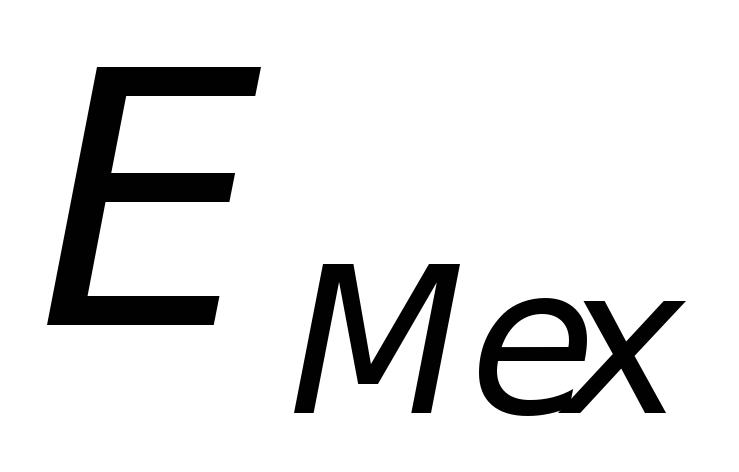 
замкнутой неконсервативной системы
изменяется за счёт работы, совершаемой
всеми силами. Согласно
(4.45):
| (4.47) |
Действие диссипативных сил, например, сил трения, приводит к постепенному уменьшению механической энергии замкнутой системы. Этот процесс называется диссипацией (рассеиванием) энергии.
При диссипации энергии происходит преобразование механической энергии в другие виды энергии, например, в энергию беспорядочного движения молекул вещества.
Преобразование механической энергии в другие виды энергии происходит в полном соответствии со всеобщим законом природы — Законом сохранения энергии.
4. 4. 5. Механическое равновесие системы.
Состоянием механического равновесия системы называается такое её состояние, из которого она может быть выведена только в результате внешнего силового воздействия. В этом состоянии все материальные точки системы находятся в покое, так что кинетическая энергия системы равна нулю.
Состояние механического равновесия системы называется устойчивым, если малое внешнее воздействие на систему вызывает малое изменение её состояния.
Состояние механического равновесия называется неустойчивым, если система при сколь угодно малом внешнем воздействии выходит из этого состояния и больше не возвращается в него. При этом возникают силы, вызывающие дальнейшее отклонение системы от состояния равновесия.
Закон сохранения механической энергии позволяет сформулировать условия устойчивости и неустойчивости консервативных систем: в состоянии устойчивого равновесия потенциальная энерги имеет минимум, а в состоянии неустойчивости равновесия — максимум.
59
studfile.net
ЭНЕРГИИ СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ ЗАКОН — общий закон природы: энергия любой замкнутой системы при всех процесс- сах, происходящих в системе, остается пос- тоянной (сохраняется). Энергия может толь- ко превращаться из одной формы в другую и перераспределяться между частями системы. Для незамкнутой системы увеличение(умень- шение) ее энергии равно убыли (возраста- нию) энергии взаимодействующих с ней тел и физических полей. 1. МЕХАНИКА АРХИМЕДА ЗАКОН-закон гидро- и аэростати- ки: на тело, погруженное в жидкость или газ, действует выталкивающая сила, направлен- ная вертикально вверх, числено равная весу жидкости или газа, вытесненного телом, и приложенная в центре тяжести погруженной части тела. FA= gV, где r — плотность жидкости или газа, V — объем погруженной части тела. Иначе можно сформулировать так: тело, по- груженное в жидкость или газ, теряет в своем весе столько, сколько весит вытесненная им жидкость (или газ). Тогда P= mg — FA Открыт др. гр. ученым Архимедом в 212г. до н.э. Является основой теории плавания тел. ВСЕМИРНОГО
ТЯГОТЕНИЯ ЗАКОН — закон тяготения Ньютона: все тела
притягиваются друг к другу с силой
прямо пропорциональ- ной произведению
масс этих тел и обратно пропорциональной
квадрату расстояния меж- ду ними: ГАЛИЛЕЯ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ, механический принцип относительности — принцип классической механики: в любых инерциальных системах отсчета все механи- ческие явления протекают одинаково при одних и тех же условиях. Ср. относительности принцип. ГУКА ЗАКОН — закон, согласно которому упру- гие деформации прямо пропорциональны вызывающим их внешним воздействиям. ИМПУЛЬСА СОХРАНЕНИЯ ЗАКОН — закон механики: импульс любой замкнутой систе- мы при всех процессах, происходящих в систе ме, остается постоянным (сохраняется) и мо- жет только перераспределяться между частя- ми системы в результате их взаимодействия. НЬЮТОНА ЗАКОНЫ — три закона, лежащие в основе ньютоновской классической механи- ки. 1-й закон (закон инерции): материальная точка находится в состоянии прямолинейно- го и равномерного движения или покоя, если на нее не действуют другие тела или дейст- вие этих тел скомпенсировано. 2-й закон (основной закон динамики): ускорение, полу- ченное телом, прямо пропорционально равно действующей всех сил, действующих на тело, и обратно пропорционально массе тела ( ОТНОСИТЕЛЬНОСТИ ПРИНЦИП — один из постулатов относительности теории, утверждающий, что в любых инерциальных системах отсчета все физические (механические, электромагнитные и др.) явления при одних и тех же условиях протекают одинаково. Является обобщением Галилея принципа относительности на все физические явления (кроме тяготения). ФАРАДЕЯ
ЗАКОНЫ — основные законы электролиза. Первый
Фарадея закон: масса вещества,
выделившегося на электроде при
прохождении электрического тока,
прямо пропорциональна количеству
электричества (заряду), прошедшему
через электролит (m=kq=kIt). Второй Ф.з.:
отношение масс различных веществ,
претерпевающих химии- ческие превращения
на электродах при прохождении одинаковых
электрических зарядов через электролит
равно отношению химических эквивалентов.
Установлены в 1833-34 г. М. Фарадеем.
Обобщенный закон электролиза имеет
вид: ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ ЗАКОН — закон, описывающий явление возникновения электрического поля при изменении магнит- ного (явление электромагнитной индукции): электродвижущая сила индукции прямо пропорциональна скорости изменения магнитного потока. Коэффициент пропорциональности определяется системой единиц, знак — Ленца правилом. Формула в СИ: , где Ф — изменение магнитного потока, а t — промежуток времени, в течение которого это изменение произошло. Открыт М. Фарадеем. 4. ОПТИКА ГЮЙГЕНСА ПРИНЦИП — метод, позволяющий определить положение фронта волны в любой момент времени. Согласно г.п. все точки, через которые проходит фронт волны в момент времени t, являются источниками вторичных сферических волн, а искомое положение фронта волны в момент времени t t совпадает с поверхностью, огибающей все вторичные волны. Позволяет объяснить законы отражения и преломления света. ГЮЙГЕНСА — ФРЕНЕЛЯ — ПРИНЦИП — приближенный метод решения задач о распространении волн. Г.-Ф. п. гласит: в любой точке, находящейся вне произвольной замкнутой поверхности, охватывающей точечный источник света, световая волна, возбуждаемая этим источником, может быть представлена как результат интерференции вторичных волн, излучаемых всеми точками указанной замкнутой поверхности. Позволяет решать простейшие задачи дифракции света. ОТРАЖЕНИЯ ВОЛН ЗАКОН — луч падающий, луч отраженный и перпендикуляр, восстано- вленный в точку падения луча, лежат в одной плоскости, причем угол падения равен углу преломления. Закон справедлив для зеркального отражения. ПРЕЛОМЛЕНИЕ СВЕТА — изменение направления распространения света (электромагнитной волны) при переходе из одной среды в другую, отличающуюся от первой показателем преломления. Для преломления выполняется закон: луч падающий, луч преломленный и перпенди- куляр, восставленный в точку падения луча, лежат в одной плоскости, причем для данных двух сред отношение синуса угла падения к синусу угла преломления есть величина постоянная, называемая относительным показателем преломления второй среды относительно первой. | 2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА АВОГАДРО ЗАКОН — один из основных законов идеальных газов: в равных объемах различных газов при одинаковой температу- ре и давлении содержится одинаковое число молекул. Открыт в 1811 году итал. физиком А.Авогадро(1776-1856). БОЙЛЯ-МАРИОТТА ЗАКОН — один из законов идеального газа: для данной массы данного газа при постоянной температуре произведе- ние давления на объем есть величина постоянная. Формула: pV=const. Описывает изотермический процесс. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ — один из основных законов термодинамики, согласно которому невозможен периодичес- кий процесс единственным результатом которого является совершение работы, экви- валентной количеству теплоты, полученному от нагревателя. Другая формулировка: нево- зможен процесс, единственным результатом которого является передача энергии в форме теплоты от менее нагретого тела к более нагретому. В.з.т. выражает стремление систе- мы, состоящей из большого количества хаоти чески движущихся частиц, к самопроизволь- ному переходу из состояний менее вероятных в состояния более вероятные. Запрещает создание вечного двигателя второго рода. ГЕЙ-ЛЮССАКА
ЗАКОН — газовый закон: для данной массы
данного газа при постоянном давлении
отношение объема к абсолютной
температуре есть величина постоянная ДАЛЬТОНА ЗАКОН — один из основных газо- вых законов: давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений этих газов. ПАСКАЛЯ ЗАКОН — основной закон гидроста- тики: давление, производимое внешними силами на поверхность жидкости или газа, передается одинаково по всем направлениям. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ — один из основных законов термодинамики, явля- ющийся законом сохранения энергии для термодинамической системы: количество теплоты Q, сообщенное системе, расходуется на изменение внутренней энергии системы U и совершение системой работы A против внешних сил. Формула: Q= U+A. Лежит в осно- ве работы тепловых машин. ШАРЛЯ
ЗАКОН — один из основных газовых законов:
давление данной массы идеального газа
при постоянном объеме прямо пропор-
ционально температуре: 3. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ АМПЕРА ЗАКОН — закон взаимодействия двух проводников с токами; параллельные про- водники с токами одного направления притя- гиваются, а с токами противоположного нап- равления — отталкиваются. А.з. называют так- же закон, определяющий силу, действующую в магнитном поле на малый отрезок провод ника с током. Открыт в 1820г.А.М. Ампером. ДЖОУЛЯ-ЛЕНЦА ЗАКОН — закон, описыва- ющий тепловое действие электрического тока. Согласно Д. — Л.з. количество теплоты, выделяющееся в проводнике при прохожде- нии по нему постоянного тока, прямо пропор- ционально квадрату силы тока, сопротивле- нию проводника и времени прохождения. ПРЯМОЛИНЕЙНОГО РАСПРОСТРАНЕНИЯ СВЕТА ЗАКОН — закон геометрической оптики, заключающийся в том, что в однородной среде свет распространяется прямолинейно. Объясняет, напр., образование тени и полутени. 6. АТОМНАЯ И ЯДЕРНАЯ ФИЗИКА. БОРА ПОСТУЛАТЫ — основные допущения, введенные без доказательства Н.Бором, и положенные в основу БОРА ТЕОРИИ: 1) Атомная система устойчива только в стационарных состояниях, которые соответствуют дискретной последовательности значений энергии атома. Каждое изменение этой энергии связано с полным переходом атома из одного стационарного состояния в другое. 2) Поглощение и излучение энергии атомом происходит по закону, согласно которому связанное с переходом излучение является монохроматическим и обладает частотой : h =Ei-Ek, где h -Планка постоянная, а Ei и Ek — энергии атома в стационарных состояниях. | ЗАРЯДА СОХРАНЕНИЯ ЗАКОН — один из фундаментальных законов природы: алгеб- раическая сумма электрических зарядов лю- бой электрически изолированной системы остается неизменной. В электрически изоли- рованной системе З.с.з. допускает появление новых заряженных частиц(напр.,при электро- литической диссоциации, ионизации газов, рождении пар частица — античастица и др), но суммарный электрический заряд появивших- ся частиц всегда должен быть равен нулю. КУЛОНА
ЗАКОН — основной закон электроста тики,
выражающий зависимость силы взаимо
действия двух неподвижных точечных
заря- дов от расстояния между ними:
два неподвиж ных точечных заряда
взаимодействуют с си- лой прямо
пропорциональной произведению величин
этих зарядов и обратно пропорци-
ональной квадрату расстояния между
ними и диэлектрической проницаемости
среды, в которой находятся заряды. В
СИ имеет вид: ЛЕВОЙ РУКИ ПРАВИЛО — правило, определя- ющее направление силы, которая действует на находящийся в магнитном поле проводник с током (или движущуюся заряженную части- цу). Оно гласит: если левую руку расположить так, чтобы вытянутые пальцы показывали направление тока (скорости частицы), а сило- вые линии магнитного поля (линии магнит- ной индукции) входили в ладонь, то отстав- ленный большой палец укажет направление силы, действующей на проводник (положи- тельную частицу; в случае отрицательной ча- стицы направление силы противоположно). ЛЕНЦА ПРАВИЛО —правило, определяющее направление индукционных токов, возника- ющих при электромагнитной индукции. Сог- ласно Л.п. индукционный ток всегда имеет такое направление, что его собственный маг- нитный поток компенсирует изменения внеш него магнитного потока, вызвавшие этот ток. Л.п.-следствие закона сохранения энергии. ОМА ЗАКОН -один из основных законов элек- трического тока: сила постоянного электри- ческого тока на участке цепи прямо пропор- циональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. Справедлив для металличес- ких проводников и электролитов, температу- ра которых поддерживается постоянной. В случае полной цепи формулируется следую- щим образом: сила постоянного электричес- кого тока в цепи прямо пропорциональна эдс источника тока и обратно пропорциональна полному сопротивлению электрической цепи. ПРАВОЙ РУКИ ПРАВИЛО — правило, опреде- ляющее 1) направление индукционного тока в проводнике, движущемся в магнитном поле: если ладонь правой руки расположить так, чтобы в нее входили линии магнитной индукции, а отогнутый большой палец напра- вить по движению проводника, то четыре вы- тянутых пальца покажут направление индук- ционного тока; 2)направление линий магнит- ной индукции прямолинейного проводника с током: если большой палец правой руки рас- положить по направлению тока, то направле- ние обхвата проводника четырьмя пальцами покажет направление линий магнитной индукции. |
,
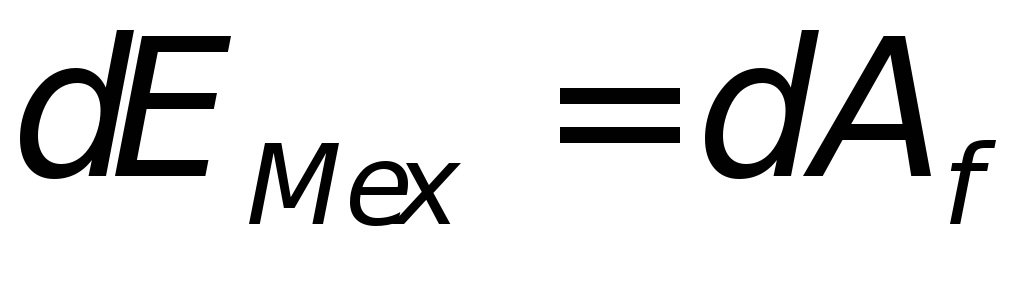
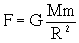где M и m — массы взаимо- действующих
тел, R — расстояние между эти- ми телами,
G — гравитационная постоянная (в СИ
G=6,67.10-11 Н.м2/кг2.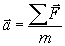
).
3-й закон: две материальные точки
взаимодействуют друг с другом силами
одной природы равными по величине и
про- тивоположными по направлению
вдоль пря- мой, соединяющей эти точки
(
).
,
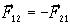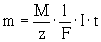где M — молярная (атомная) масса, z —
валентность, F — Фарадея постоянная .
Ф.п. равна произведе- нию элементарного
электрического заряда на постоянную
Авогадро. F=e*NA.
Определяет заряд, прохождение которого
через электро- лит приводит к выделению
на электроде 1 моля одновалентного
вещества. F=(96484,56 0,27) Кл./моль. Названа
в честь М.Фарадея.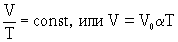
,где =1/273 К-1 — температурный коэффициент объемного
расширения.
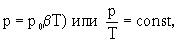где
p0 — давление при 00С, =1/273,15 К-1 — температурный
коэффициент давления.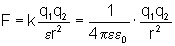
. Величина 
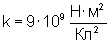числено
равна силе, действую- щей между двумя
точечными неподвижными зарядами по
1 Кл каждый, находящимися в вакууме на
расстоянии 1 м друг от друга. К.з.
является одним из экспериментальных
обоснований электродинамики.studfile.net