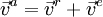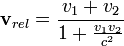Закон сложения скоростей

Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени.

В этом определении ключевой является фраза «относительно других тел». Каждый из нас относительно какой-либо поверхности неподвижен, но относительно Солнца мы совершаем вместе со всей Землей орбитальное движение со скоростью 30 км/с, то есть движение зависит от системы отсчета.

Система отсчета – совокупность системы координат и часов, связанных с телом, относительно которого изучается движение.

Например, описывая движения пассажиров в салоне автомобиля, систему отсчета можно связать с придорожным кафе, а можно с салоном автомобиля или с движущимся встречным автомобилем, если мы оцениваем время обгона

Закон сложения скоростей

Закон сложения скоростей является следствием преобразований координат и времени.

Пусть частица в момент времени t’ находится в точке (x’, y’, z’)

, а через малое время Δt’ в точке (x’ + Δx’, y’ + Δy’, z’ + Δz’) системы отсчета K’. Это два события в истории дви­жущейся частицы. Имеем:

Δx’ = v_x’Δt’,

где
v_x’ — x-я компонента скорости частицы в системе K’.

Аналогичные соотношения имеют место для остальных компонент.

Разности координат и промежутки времени (Δx, Δy, Δz, Δt) преобразуются так же, как координаты:

Δx = Δx’ + VΔt’,

Δy = Δу’,

Δz = Δz’,

Δt = Δt’.

Отсюда следует, что скорость той же частицы в системе K будет иметь компоненты:

v_x = Δx / Δt = (Δx’ + VΔt’) / Δt = v_x’ + V,

v_y = v_y’,

v_z = v_z’.

Это закон сложения скоростей. Его можно выразить в векторной форме:

v̅ = v̅’ + V

(координатные оси в системах K и K’ параллельны).

Закон сложения скоростей

Если тело движется относительно системы отсчета К₁ со скоростью V₁, а сама система отсчета К₁ движется относительно другой системы отсчета К₂ со скоростью V, то скорость тела (V₂) относительно второй системы отсчета К₂ равна геометрической сумме векторов V₁ и V.

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.

\( \vec{V_2} = \vec{V_1} + \vec{V} \)

где всегда

К₂ — неподвижная система отсчета
V₂ — скорость тела относительно неподвижной системы отсчета (К₂)

К₁ — подвижная система отсчета
V₁ — скорость тела относительно подвижной системы отсчета (К₁)

V — скорость подвижной системы отсчета (К₁) относительно неподвижной системы отсчета (К₂)

Закон сложения скоростей

При поступательном движении тела относительно подвижной системы отсчёта и подвижной системы отсчёта относительно неподвижной, вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\ {\overrightarrow{a}}_{АБС}$ (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета ${\overrightarrow{a}}_r=\frac{d{\overrightarrow{v}}_r}{dt}={\overrightarrow{a}}_{ОТН}$ (относительного ускорения) и вектора ускорения подвижной системы отсчёта относительно неподвижной ${\overrightarrow{a}}_е=\frac{d{\overrightarrow{v}}_е}{dt}={\overrightarrow{a}}_{ПЕР}$ (переносного ускорения):

\[{\overrightarrow{a}}_{АБС}={\overrightarrow{a}}_{ОТН}+{\overrightarrow{a}}_{ПЕР}\]

В общем случае, когда движение материальной точки (тела) является криволинейным, его в каждый момент времени можно представить как комбинацию поступательного движения материальной точки (тела) относительно подвижной системы отсчёта со скоростью \( {\overrightarrow{v}}_r \), и вращательного движения подвижной системы отсчёта относительно неподвижной с угловой скоростью \( {\overrightarrow{\omega }}_e \). В этом случае, при сложении ускорений, наряду с относительным и переносным ускорением необходимо учитывать и ускорение Кориолиса \( a_c=2{\overrightarrow{\omega }}_e\times {\overrightarrow{v}}_r \), которое характеризует изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением.

Закон сложения скоростей

Вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта \( \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\ {\overrightarrow{a}}_{АБС} \) (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета \( {\overrightarrow{a}}_r=\frac{d{\overrightarrow{v}}_r}{dt}={\overrightarrow{a}}_{ОТН} \) (относительного ускорения), вектора ускорения подвижной системы отсчёта относительно неподвижной \( {\overrightarrow{a}}_е=\frac{d{\overrightarrow{v}}_е}{dt}={\overrightarrow{a}}_{ПЕР} \) (переносного ускорения), и кориолисова ускорения \( a_c=2{\overrightarrow{{\mathbf \omega }}}_e\times {\overrightarrow{v}}_r={\overrightarrow{a}}_{КОР} \):

\[{\overrightarrow{a}}_{АБС}={\overrightarrow{a}}_{ОТН}+{\overrightarrow{a}}_{ПЕР}+{\overrightarrow{a}}_{КОР}\]

 

Абсолютное перемещение равно сумме относительного и переносного перемещений.

Перемещение тела в неподвижной системе отсчета равно сумме перемещений: тела в подвижной системе отсчета и самой подвижной системы отсчета относительно неподвижной.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

calcsbox.com

Закон сложения скоростей и решение задачи. Кинематика — 10 класс

Закон сложения скоростей и решение задачи. Кинематика — 10 класс

Закон сложения скоростей

Кинематика — это просто!

Формулировка закона:

Как в учебнике Буховцева для 10 класса:

Если тело движется относительно системы отсчета К₁ со скоростью V₁,
а сама система отсчета К₁ движется относительно другой системы отсчета К₂ со скоростью V,
то скорость тела (V₂) относительно второй системы отсчета

К₂
равна геометрической сумме векторов V₁ и V.

Упрощаем форммулировку, не меняя смысла:

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.

Вторая формулировка запоминается проще, какой ползоваться решайте сами!

где всегда
К₂ — неподвижная система отсчета
V₂ — скорость тела относительно неподвижной системы отсчета (К₂)

К₁ — подвижная система отсчета
V₁ — скорость тела относительно подвижной системы отсчета (К₁)

V — скорость подвижной системы отсчета (

К₁) относительно неподвижной системы отсчета (К₂)

Алгоритм решения задачи на закон сложения скоростей

Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!

1. Определить тело — обычно это тело, о скорости которого спрашивается в задаче.
2. Выбрать неподвижную систему отсчета (дорога, берег) и подвижную систему отсчета (обычно это второе движущееся тело).

P.S. В условиях задачи скорости тел заданы обычно относительно неподвижной системы отсчета (например, дороги или берега)

3. Ввести обозначения скоростей (V₁, V₂, V).
4. Сделать чертеж, на котором показать координатную ось ОХ и векторы скорости.
Лучше, если ОХ будет совпадать по направлению с вектором скорости выбранного тела.
5. Записать формулу закона сложения скоростей в векторном виде.

6. Выразить из формулы искомую скорость в векторном виде.
7. Выразить искомую скорость в проекциях.
8. Определить по чертежу знаки проекций.
9. Расчет в проекциях.
10. В ответе не забыть перейти от проекции к модулю.

Пример решения простейшей задачи на закон сложения скоростей

Задача

Два автомобиля движутся равномерно по шоссе навстречу друг другу. Модули их скоростей равны 10 м/с и 20 м/с.
Определить скорость первого автомобиля относительно второго.

Решение:

Еще раз! Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!

1. В задаче спрашивается о скорости первого автомобиля — значит тело — первый автомобиль.
2. По условию задачи выбираем:
K₁ — подвижная система отсчета сязана со вторым автомобилем
К₂ — неподвижная система отсчета связана с дорогой

3. Вводим обозначения скоростей:
V₁ — скорость тела (первого авто) относительно подвижной системы отсчета (второго авто) — найти!
V₂ — скорость тела (первого авто) относительно неподвижной систеы отсчета (дороги) — дано 10м/с
V — скоростьь подвижной системы отсчета (второго авто) относительно неподвижной системы отсчета (дороги) — дано 20двух уравнений:м/с

Теперь понятно, что в задаче надо определить V₁.
4. Делаем чертеж, выписываем формулу:

5. далее по алгоритму …..

Всё, все отдыхают!)))

P.S. Если движение происходит не по пряммой, а на плоскости, то при переводе формулы векторного вида в проекции добавляется еще одно уравнение в прекциях относительно оси OY, далее решаем систему двух уравнений:
V_2x = V

1x + V_x
V_2y = V_1y + V_y

Кинематика — Класс!ная физика

Прямолинейное равномерное движение и решение задач — Закон сложения скоростей и решение задач — Движение с постоянным ускорением и решение задач — Свободное падение — Движение тела, брошенного под углом к горизонту — Решение задач. Тело, брошенное под углом к горизонту — Криволинейное движение

class-fizika.ru

Относительность движения. Закон сложения скоростей Галилея.

Относительное движение — это движение тела, при котором его кинематические характеристики отсчитываются относительно другого движущегося или покоящегося тела.

Приведём пример проблемы: пусть наблюдатель стоит около дороги, по которой движется автомобиль А со скоростью 

км/ч и велосипедист В со скоростью  км/ч. Пусть оба движущихся тела едут в одном направлении. Тогда при равномерном движении мы можем найти путь, пройденный каждым из тел. Проблема возникает тогда, когда наблюдателем является велосипедист: относительно него автомобилист движется со скорость  км/ч. При этой скорости, относительно велосипедиста, автомобилист движется с другой скоростью и преодолевает другой путь. Что странно. Таким образом, нам надо уметь переходить от движения одного тела к другому (из одной системы координат в другую).

Рис. 1. Относительное движение

Для этого введём эти системы координат. Пусть система 

— неподвижная система координат,  — подвижная система координат, A — движущееся тело (рис. 1). Пусть  — радиус-вектор, соединяющий начало координат неподвижной системы отсчёта  и точку А. Пусть  — радиус-вектор, соединяющий начало координат подвижной системы координат  и точку А. Пусть  — радиус-вектор, соединяющий начало координат неподвижной системы  и начало координат подвижной системы .

По правилу сложения векторов получим:

(1)

Поделим левую и правую часть (1) на время (

):

(2)

Зная, что скорость равномерного движения можно найти как 

, то получим:

(3)

Выражение (3) представляет собой закон сложения скоростей Галилея. Текстово: скорость тела относительно неподвижной системы отсчёта равна скорости тела относительно подвижной системы отсчёта плюс скорость подвижной системы отсчёта относительно неподвижной.

Вывод: использование закона сложения скоростей Галилея (или просто закона сложения скоростей) удобно в задачах, где движутся два или более тел. Лучше переходить (мысленно останавливать) тело, относительно которого в дано присутствуют какие-либо расстояния.

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

www.abitur.by

Правило сложения скоростей — это… Что такое Правило сложения скоростей?

При рассмотрении сложного движения (то есть когда точка или тело движутся в одной системе отсчёта, а она движется относительно другой) возникает вопрос о связи скоростей в 2 системах отсчёта.

Классическая механика

В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:

Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.

Примеры

1. Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, с которой её переносит пластинка за счёт своего вращения.
2. Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
3. Если волны движутся относительно берега со скоростью 30 километров в час, а корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть они становятся неподвижными.

Релятивистская механика

В XIX веке классическая механика столкнулась с проблемой распространение этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики, перенесёнными в новую область электромагнитных процессов.

Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).

Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе осчёта — всегда равно их расстоянию в другой инерциальной системе.

Вторая идея — принцип относительности. Находясь на корабле, движущимся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое электродинамическими эффектами? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразованиям. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.

Теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Правило сложение скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:

Можно заметить, что в случае, когда 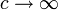, преобразования Лоренца переходят в преобразования Галилея. То же самое происходит в случае, когда 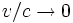. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона либо в мире с бесконечной скоростью света, либо при скоростях, малых по сравнению со скоростью света. Последнее объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.

См. также

Литература

• Б. Г. Кузнецов Эйнштейн. Жизнь, смерть, бессмертие. — М.: Наука, 1972.
• Четаев Н. Г. Теоретическая механика. — М.: Наука, 1987.

Wikimedia Foundation. 2010.

dic.academic.ru

Закон сложения скоростей в классической механике

Классическая механика использует понятие абсолютной скорости точки. Она определяется как сумма векторов относительной и переносной скоростей этой точки. Подобное равенство содержит утверждение теоремы о сложении скоростей. Принято представлять, что скорость движения определенного тела в неподвижной системе отсчета является равной векторной сумме скорости такого же физического тела относительно подвижной системе отсчета. В этих координатах находится непосредственно тело.

сложения скоростей. Автор24 — интернет-биржа студенческих работ»>

Рисунок 1. Классический закон сложения скоростей. Автор24 — интернет-биржа студенческих работ

Примеры закона сложения скоростей в классической механике

Рисунок 2. Пример сложения скоростей. Автор24 — интернет-биржа студенческих работ

Существует несколько основных примеров сложения скоростей, согласно установленным правилам, взятым за основу в механической физике. В качестве простейших объектов при рассмотрении физических законов может быть взят человек и любое движущееся тело в пространстве, с которым происходит прямое или косвенное взаимодействие.

Пример 1

Например, человек, который движется по коридору пассажирского поезда со скоростью пять километров в час, при этом состав двигается со скоростью 100 километров в час, то он относительно окружающего пространства двигается со скоростью 105 километров в час. При этом направление движения человека и транспортного средства должны совпадать. Такой же принцип действует и при движении в обратном направлении. В этом случае человек будет перемещаться относительно земной поверхности со скоростью 95 километров в час.

Если значения скорости двух объектов относительно друг друга будут совпадать, то они станут неподвижными с точки зрения движущихся объектов. При вращении скорость изучаемого объекта равна сумме скоростей движения объекта относительно движущейся поверхности другого объекта.

Принцип относительности Галилея

Ученые смогли сформулировать основные формулы для ускорений объектов. Из нее следует, что движущаяся система отсчета удаляется относительно другой без видимого ускорения. Это закономерно в тех случаях, когда ускорение тел происходит одинаково в разных системах отсчета.

Подобные рассуждения берут начало еще во времена Галилея, когда сформировался принцип относительности. Известно, что по второму закону Ньютона ускорение тел имеет принципиальное значение. От этого процесса зависит относительное положение двух тел в пространстве, скорость физических тел. Тогда все уравнения можно записать одинаковым образом в любой инерциальной системе отсчета. Это говорит о том, что классические законы механики не будут иметь зависимость от положения в инерциальной системе отсчета, как принято действовать при осуществлении исследования.

Наблюдаемое явление также не имеет зависимость от конкретного выбора системы отсчета. Подобные рамки в настоящее время рассматриваются как принцип относительности Галилея. Он вступает в некоторые противоречия с иными догмами физиков-теоретиков. В частности, теория относительности Альберта Эйнштейна предполагает иные условия действия.

Принцип относительности Галилея базируется на нескольких основных понятиях:

• в двух замкнутых пространствах, которые движутся прямолинейно и равномерно относительно друг друга, результат внешнего воздействия всегда будет иметь одинаковое значение;
• подобный результат будет действителен только для любого механического действия.

В историческом контексте изучения основ классической механики, подобная трактовка физических явлений сформировалась во многом, как результат интуитивного мышления Галилея, что подтвердилось в научных трудах Ньютона, когда тот представил свою концепцию классической механики. Однако подобные требования по Галилею могут накладывать на структуру механики некоторые ограничения. Это влияет на ее возможные формулировки, оформление и развитие.

Закон движения центра масс и закон сохранения импульса

Рисунок 3. Закон сохранения импульса. Автор24 — интернет-биржа студенческих работ

Одной из общих теорем в динамике стала теорема центра инерции. Ее также называют теоремой о движении центра масс системы. Подобный закон можно вывести из общих законов Ньютона. Согласно ему, ускорение центра масс в динамической системе не является прямым следствием внутренних сил, которые действуют на тела всей системы. Оно способно связать процесс ускорения с внешними силами, которые действуют на такую систему.

Рисунок 4. Закон движения центра масс. Автор24 — интернет-биржа студенческих работ

В качестве объектов, о которых идет речь в теореме, выступают:

• импульс материальной точки;
• система тел.

Эти объекты можно описать как физическую векторную величину. Она является необходимой мерой воздействия силы, при этом полностью зависит от времени действия силы.

При рассмотрении закона сохранения количества движения утверждается, что векторная сумма импульсов всех тел система полностью представляется как постоянная величина. При этом векторная сумма внешних сил, которые действуют на всю систему, должна быть равна нулю.

При определении скорости в классической механике также используют динамику вращательного движения твердого тела и момент импульса. Момент импульса имеет все характерные признаки количества вращательного движения. Исследователи используют это понятие как величину, которая зависит от количества вращающейся массы, а также как она распределена по поверхности относительно оси вращения. При этом имеет значение скорости вращения.

Вращение также можно понимать не только с точки зрения классического представления вращения тела вокруг оси. При прямолинейном движении тела мимо некой неизвестной воображаемой точки, которая не лежит на линии движения, тело также может обладать моментом импульса. При описании вращательного движения момента импульса играет самую существенную роль. Это очень важно при постановке и решении разнообразных задач, связанных с механикой в классическом понимании.

В классической механике закон сохранения импульса является следствием ньютоновской механики. Он наглядно показывает, что при движении в пустом пространстве импульс сохраняется во времени. Если существует взаимодействие, то скорость его изменения определяется суммой приложенных сил.

spravochnick.ru

Сложение скоростей — Класс!ная физика

Сложение скоростей

«Физика — 10 класс»

Изменится ли движение, если мы будем его описывать в разных системах координат?
В любой ли системе координат удобно описывать движение?

Пусть по реке плывёт моторная лодка и нам известна её скорость ₁ относительно воды, точнее, относительно системы координат K₁, движущейся вместе с водой (рис. 1.19).

Такую систему координат можно связать, например, с мячом, выпавшим из лодки и плывущим по течению. Если известна ещё и скорость течения реки относительно системы координат К₂, связанной с берегом, т. е. скорость системы координат Кх относительно системы координат К₂, то можно определить скорость лодки ₂ относительно берега.

За промежуток времени Δt перемещения лодки и мяча относительно берега равны Δ₂ и Δ (рис. 1.20), а перемещение лодки относительно мяча равно Δ₁. Из рисунка 1.20 видно, что

Δ₂ = Δ₁ + Δ.         (1.7)

Разделив левую и правую части уравнения (1.7) на Δt, получим

Учтём также, что отношения перемещений к интервалу времени равны скоростям. Поэтому

₂ = ₁ + .

Скорости складываются геометрически, как и все другие векторы. Уравнение (1.8) называют законом сложения скоростей.

Закон сложения скоростей

Если тело движется относительно некоторой системы координат К₁ со скоростью и сама система К₁ движется относительно другой системы координат К₂ со скоростью ₁, то скорость тела относительно второй системы равна геометрической сумме скоростей ₁ и .

Как запишется классический закон сложения скоростей, если (1.9) неподвижной считать систему, связанную с мячом, а подвижной — с берегом?

Как и любое векторное уравнение, уравнение (1.8) представляет собой компактную запись скалярных уравнений, в данном случае — для сложения проекций скоростей движения на плоскости:

υ_2x = υ_1x + υ_x,
υ_2y = υ_1y + υ_y.         (1.9)

Проекции скоростей складываются алгебраически.

Закон сложения скоростей позволяет определять скорость тела относительно разных систем отсчёта, движущихся относительно друг друга.

Классический закон сложения скоростей справедлив для тел, движущихся со скоростями, много меньшими скорости света.

Часто скорость тела относительно неподвижной системы координат называют абсолютной скоростью, относительно подвижной системы координат — относительной, а скорость тела отсчёта, связанного с подвижной системой, относительно неподвижной — переносной скоростью.

Тогда закон сложения скоростей имеет вид _a = _отн + _пер.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика — Физика, учебник для 10 класса — Класс!ная физика

Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»

class-fizika.ru

Закон сложения скоростей Википедия

При рассмотрении сложного движения (когда точка или тело движется в одной системе отсчёта, а эта система отсчёта в свою очередь движется относительно другой системы) возникает вопрос о связи скоростей в двух системах отсчёта.

Классическая механика[ | ]

В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:

v→a=v→r+v→e.{\displaystyle {\vec {v}}_{a}={\vec {v}}_{r}+{\vec {v}}_{e}.}

Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей^[1].

Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.

Примеры[ | ]

1. Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).
2. Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
3. Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.

Релятивистская механика[ | ]

В XIX веке физика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики (первая — Пространство-время теории Ньютона, вторая — принцип относительности), перенесёнными в новую область — теорию электромагнитных процессов.

Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).

Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе отсчёта — всегда равно их расстоянию в другой инерциальной системе.

Вторая идея — принцип относительности. Находясь на корабле, движущемся равномерно и прямолинейно, нельзя обнаружить

ru-wiki.ru