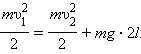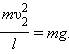Закон сохранения энергии в механических процессах
Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.
Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано. Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:
A=−(Ep2−Ep
По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:
A=Ek2−Ek1 . (18)
Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:
Ek2−Ek1=−(Ep2−Ep1) или Ek1+Ep1=Ek2+Ep2 . (19)
Закон сохранения энергии в механических процессах:
сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.
Сумма кинетической и потенциальной энергии тел называется полной механической энергией.
Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергии тел в равной количественной мере при взаимодействии тел.
Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υнач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Еp = m∙g∙h). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.
В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Еk = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.
Закон сохранения энергии раскрывает физический смысл понятия работы:
работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.
Закон об изменении механической энергии
Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:
Avn=ΔE=E−E0 . (20)
где Е и Е0 – полные механические энергии системы в конечном и начальном состояниях соответственно.
Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения Ftr и элементарным перемещением Δr тела составляет π радиан, работа силы трения отрицательна и равна
Atr=−Ftr⋅s12 ,
где s12 – путь тела между точками 1 и 2.
Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.
Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.
Закон сохранения механической энергии
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна приращению потенциальной энергии тел, взятому с противоположным знаком:
A = –(Ep2 – Ep1). |
По теореме о кинетической энергии эта работа равна приращению кинетической энергии тел:
Следовательно
Ek2 – Ek1 = –(Ep2 – Ep1) или |
|
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
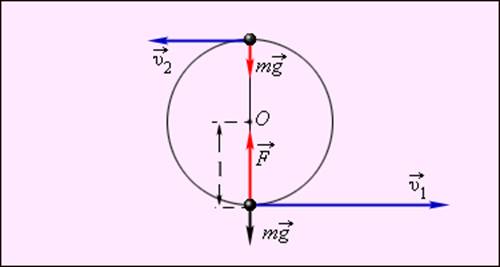
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Х. Гюйгенса). Рис. 1.1.16 поясняет решение этой задачи.
1 |
Рисунок 1.1.16. К задаче
Христиана Гюйгенса. |
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:
|
Обратим внимание на
то, что сила  натяжения
нити всегда перпендикулярна скорости
тела; поэтому она не совершает работы.
натяжения
нити всегда перпендикулярна скорости
тела; поэтому она не совершает работы.
При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:
|
Из этих соотношений следует:
|
Центростремительное
ускорение в нижней точке создается
силами 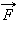
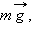 направленными
в противоположные стороны:
направленными
в противоположные стороны:
|
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
Прочность нити должна, очевидно, превышать это значение.
Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.
Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
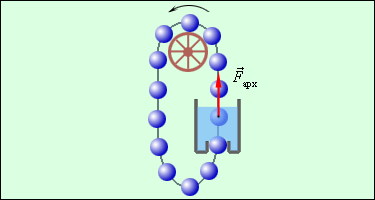
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 1.1.17).
2 |
Рисунок 1.1.17. Один из проектов «вечного двигателя». Почему эта машина не будет работать? |
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
Внимательно рассмотрите окно опыта. Найдите все регуляторы и другие основные элементы. Зарисуйте в свой конспект схему опыта.
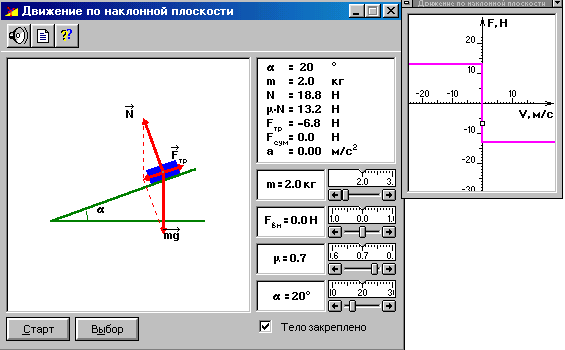
После нажатия мышью кнопки «Выбор» установите с помощью движков регуляторов значения массы тела m, угла наклона плоскости , внешней силы Fвн, коэффициента трения и ускорения а, указанных в табл.1 для вашей бригады.
Потренируйтесь в синхронном включении секундомера и снятия метки «тело закреплено» одиночным щелчком курсора мыши на кнопке в правом нижнем углу окна опыта
Одновременно включите секундомер и снимите метку «тело закреплено». Выключите секундомер в момент остановки тела в конце наклонной плоскости.
Проделайте этот опыт 10 раз и результаты измерения времени соскальзывания тела с наклонной плоскости запишите в табл. 2.
ТАБЛИЦА 1. Исходные параметры опыта
№ бриг. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
m, кг | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 2,9 | 2,7 |
| 0,10 | 0,14 | 0,18 | 0,22 | 0,26 | 0,30 | 0,34 | 0,38 |
,град | 20 | 24 | 26 | 30 | 34 | 38 | 42 | 46 |
Fвн, Н | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 |
а,м/с2 |
ТАБЛИЦА 2. Результаты измерений и расчётов
№ изм. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Сред. знач. | |
t, с | ||||||||||||
v, м/с | ||||||||||||
S, м | ||||||||||||
Wк, Дж | ||||||||||||
Wп , Дж | ||||||||||||
Aтр, Дж | ||||||||||||
Aвн , Дж | ||||||||||||
Wполн, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:
Вычислите по формулам:
а) 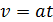 —
скорость тела в конце наклонной плоскости;
—
скорость тела в конце наклонной плоскости;
б) 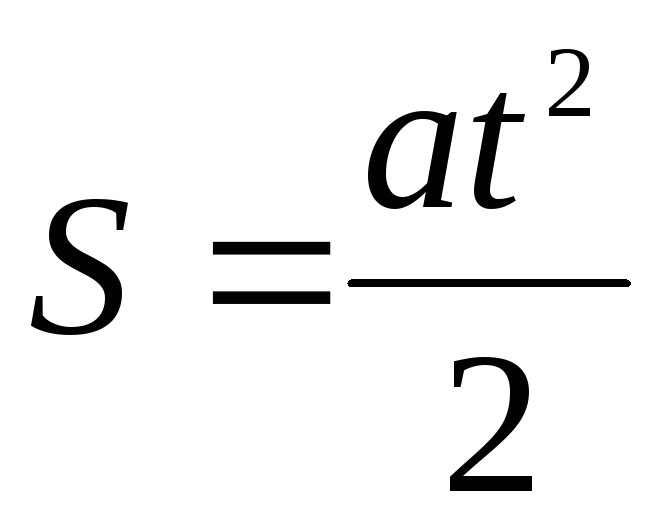 —
длину наклонной плоскости;
—
длину наклонной плоскости;
в) 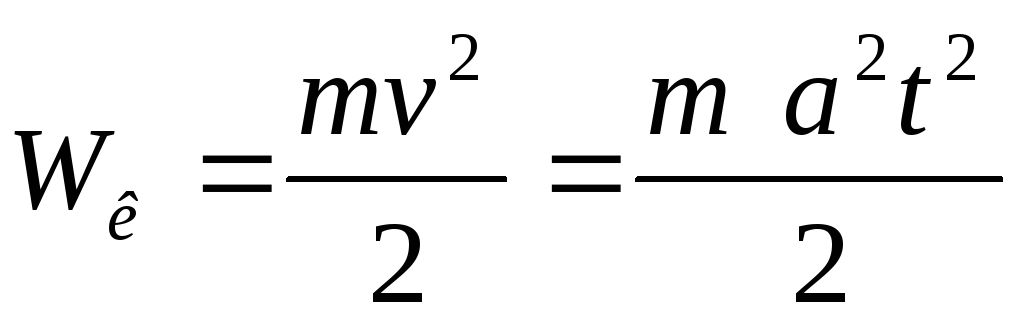 — кинетическую энергию тела, в конце
наклонной плоскости;
— кинетическую энергию тела, в конце
наклонной плоскости;
г) 
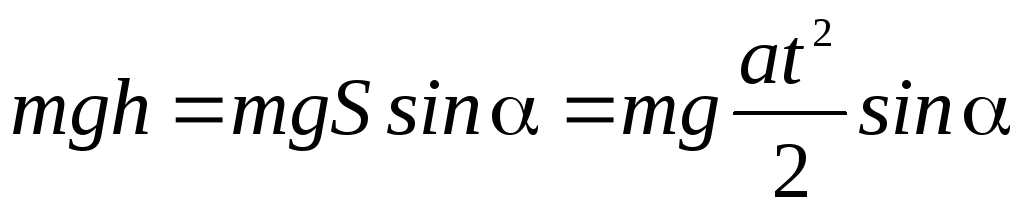 —
потенциальную энергию тела в верхней
точке наклонной плоскости;
—
потенциальную энергию тела в верхней
точке наклонной плоскости;
д) 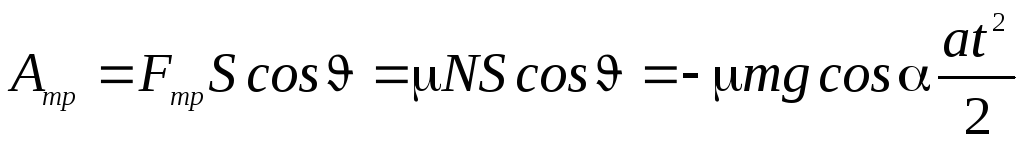 — работу силы трения на участке спуска;
— работу силы трения на участке спуска;
е) 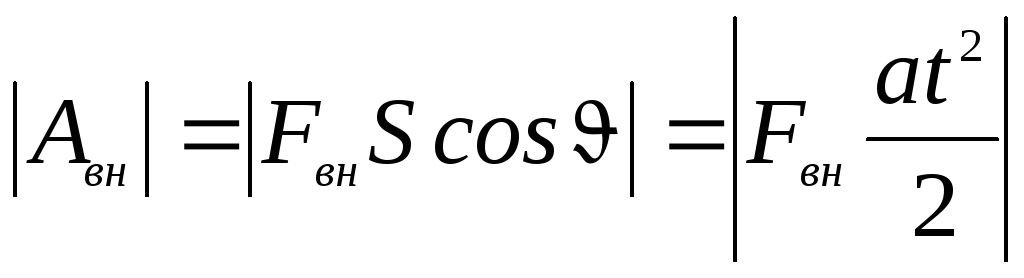 — работу внешней силы на участке спуска (определите знак работы исходя из
условий эксперимента)
— работу внешней силы на участке спуска (определите знак работы исходя из
условий эксперимента)
и запишите эти значения в соответствующие строки табл. 2.
Вычислите средние значения этих параметров и запишите их в столбец «средние значения» табл.2.
По формуле Емех1 = Емех2 проверьте выполнение закона сохранения механической энергии при движении тела по наклонной плоскости, рассчитайте погрешности и сделайте выводы по результатам проведённых опытов.
Вопросы и задания для самоконтроля
В чём заключается закон сохранения механической энергии?
Для каких систем выполняется закон сохранения механической энергии?
В чём состоит различие между понятиями энергии и работы?
Чем обусловлено изменение потенциальной энергии?
Чем обусловлено изменение кинетической энергии?
Необходимо ли выполнение условия замкнутости механической системы тел для выполнения закона сохранения механической энергии?
Какие силы называются консервативными?
Какие силы называются диссипативными?
Тело медленно втаскивают в гору. Зависят ли от формы профиля горы: а) работа силы тяжести; б) работа силы трения? Начальная и конечная точки перемещения тела фиксированы.
Тело соскальзывает с вершины наклонной плоскости без начальной скорости. Зависит ли работа силы трения на всём пути движения тела до остановки на горизонтальном участке: а) от угла наклона плоскости; б) от коэффициента трения?
По наклонной плоскости с одной и той же высоты соскальзывают два тела: одно массой m, другое массой 2m. Какое из тел пройдёт до остановки по горизонтальному участку путь больший и во сколько раз? Коэффициенты трения для обоих тел одинаковы.
Санки массой m скатились с горы высотой Н и остановились на горизонтальном участке. Какую работу необходимо совершить для того, чтобы поднять их на гору по линии скатывания.
С одинаковой начальной скоростью тело проходит: а) впадину; б) горку, имеющие одинаковые дуги траекторий и одинаковые коэффициенты трения. Сравните скорости тела в конце пути в обоих случаях.
ЛАБОРАТОРНАЯ РАБОТА № 1_2
Закон сохранения механической энергии
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
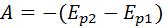
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел (см 1.19):
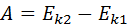
Следовательно:
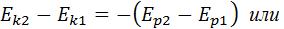
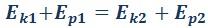
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E = Ek + Ep называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.
Пример применения закона сохранения энергии – нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости (задача Гюйгенса). Рис. 1.20.1 поясняет решение этой задачи.
|
Рисунок 1.20.1. К задаче Христиана Гюйгенса. |
Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде: 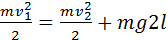
Обратим внимание на то, что сила 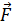 натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.
натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.
При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:

Из этих соотношений следует:
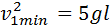
Центростремительное ускорение в нижней точке создается силами  и
и 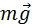 направленными в противоположные стороны:
направленными в противоположные стороны:
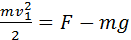
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно
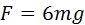
Прочность нити должна, очевидно, превышать это значение.
Очень важно отметить, что закон сохранения механической энергии позволил получить связь между координатами и скоростями тела в двух разных точках траектории без анализа закона движения тела во всех промежуточных точках. Применение закона сохранения механической энергии может в значительной степени упростить решение многих задач.
В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.
Сила трения не является консервативной. Работа силы трения зависит от длины пути.
Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую.
Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Одним из следствий закона сохранения и превращения энергии является утверждение о невозможности создания «вечного двигателя» (perpetuum mobile) – машины, которая могла бы неопределенно долго совершать работу, не расходуя при этом энергии (рис. 1.20.2).
|
Рисунок 1.20.2. Один из проектов «вечного двигателя». Почему эта машина не будет работать? |
История хранит немалое число проектов «вечного двигателя». В некоторых из них ошибки «изобретателя» очевидны, в других эти ошибки замаскированы сложной конструкцией прибора, и бывает очень непросто понять, почему эта машина не будет работать. Бесплодные попытки создания «вечного двигателя» продолжаются и в наше время. Все эти попытки обречены на неудачу, так как закон сохранения и превращения энергии «запрещает» получение работы без затраты энергии.
10.2.1.4. Закон сохранения энергии в механических процессах
Механическая энергия подразделяется на два вида: потенциальную и кинетическую. Потенциальная энергия характеризует взаимодействующие тела, а кинетическая — движущиеся. И потенциальная и кинетическая энергии изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля.
Рассмотрим теперь вопрос об изменении энергии при взаимодействии тел, образующих замкнутую систему. Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы не действуют, то при любых взаимодействиях тел сумма кинетической и потенциальной энергий тел остается постоянной. Это утверждение называется законом сохранения энергии в механических процессах.
Сумма кинетической и потенциальной энергий тел называется полной механической энергией. Поэтому закон сохранения энергии можно сформулировать так: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается постоянной.
Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергий в равной количественной мере при взаимодействии тел.
Закон сохранения полной механической энергии в процессах с участием сил упругости и гравитационных сил является одним из основных законов механики. Знание этого закона упрощает решение многих задач, имеющих большое значение в практической жизни.
Например, для получения электроэнергии широко используется энергия рек. С этой целью строят плотины, перегораживают реки. Под действием сил тяжести вода из водохранилища за плотиной движется вниз по колодцу ускоренно и приобретает некоторую кинетическую энергию. При столкновении быстро движущегося потока воды с лопатками гидравлической турбины происходит преобразование кинетической энергии поступательного движения воды в кинетическую энергию вращательного движения роторов турбины, а затем с помощью электрического генератора — в электрическую энергию.
Механическая энергия не сохраняется, если между телами действуют силы трения. Автомобиль, двигавшийся по горизонтальному участку дороги после выключения двигателя, проходит некоторый путь и под действием сил трения останавливается. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. В результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.
Таким образом, при любых физических взаимодействиях энергия не возникает, а только превращается из одной формы в другую. Этот экспериментально установленный факт называется законом сохранения и превращения энергии.
Источники энергии на земле велики и разнообразны. Когда-то в древности люди знали только один источник энергии — мускульную силу и силу домашних животных. Энергия возобновлялась за счет пищи. Теперь большую часть работы делают машины, источником энергии для них служат различные виды ископаемого топлива: каменный уголь, торф, нефть, а также энергия воды и ветра.
Если проследить «родословную» всех этих разнообразных видов энергии, то окажется, что все они являются энергией солнечных лучей. Энергия окружающего нас космического пространства аккумулируется Солнцем в виде энергии атомных ядер, химических элементов, электромагнитных и гравитационных полей. Солнце, в свою очередь, обеспечивает Землю энергией, проявляющейся в виде энергии ветра и волн, приливов и отливов, в форме геомагнетизма, различного вида излучений (в том числе и радиоактивности недр и т.д.), мускульной энергии животного мира.
Геофизическая энергия высвобождается в виде природных стихийных явлений (вулканизм, землетрясения, грозы, цунами и т.д.), обмена веществ в живых организмах (составляющих основу жизни), полезной работы по перемещению тел, изменению их структуры, качества, передачи информации, запасения энергии в различного рода аккумуляторах, конденсаторах, в упругой деформации пружин, мембран.
Любые формы энергии, превращаясь друг в друга посредством механического движения, химических реакций и электромагнитных излучений, в конце концов переходят в тепло и рассеиваются в окружающее пространство. Это явление проявляется в виде взрывных процессов, горения, гниения, плавления, испарения, деформации, радиоактивного распада. Происходит круговорот энергии в природе, характеризующийся тем, что в космическом пространстве реализуется не только хаотизация, но и обратный ей процесс — упорядочивание структуры, которые наглядно прослеживаются прежде всего в звездообразовании, трансформации и возникновении новых электромагнитных и гравитационных полей, и они снова несут свою энергию новым «солнечным системам». И все возвращается на круги своя.
Закон сохранения механической энергии был сформулирован немецким ученым А. Лейбницем. Затем немецкий ученый Ю.Р. Майер, английский физик Дж. Джоуль и немецкий ученый Г. Гельмгольц экспериментально открыли законы сохранения энергии в немеханических явлениях.
Таким образом, к середине XIX в. оформились законы сохранения массы и энергии, которые трактовались как законы сохранения материи и движения. В начале XX в. оба эти закона сохранения подверглись коренному пересмотру в связи с появлением специальной теории относительности: при описании движений со скоростями, близкими к скорости света, классическая ньютоновская механика была заменена релятивистской механикой. Оказалось, что масса, определяемая по инерциальным свойствам тела, зависит от его скорости и, следовательно, характеризует не только количество материи, но и ее движение. Понятие энергии тоже подверглось изменению: полная энергия оказалась пропорциональна массе (Е = mс2). Таким образом, закон сохранения энергии в специальной теории относительности естественным образом объединил законы сохранения массы и энергии, существовавшие в классической механике. По отдельности эти законы не выполняются, т.е. невозможно охарактеризовать количество материи, не принимая во внимание ее движение и взаимодействие.
Эволюция закона сохранения энергии показывает, что законы сохранения, будучи почерпнутыми из опыта, нуждаются время от времени в экспериментальной проверке и уточнении. Нельзя быть уверенным, что с расширением пределов человеческого познания данный закон или его конкретная формулировка останутся справедливыми. Закон сохранения энергии, все более уточняясь, постепенно превращается из неопределенного и абстрактного высказывания в точную количественную форму.
Закон сохранения энергии в механических процессах — Мегаобучалка
БОУ ОО СПО «Орловский технический колледж»
РЕФЕРАТ
По физике
На тему:
Энергия. Виды энергии.
Выполнил: студент 1 курса
Группы 13-а Матвеев К.В.
Проверил: преподаватель
Физики Гнеушев Е.А.
Содержание:
1.Определение энергии;
2.Виды энергии;
3.Закон сохранения энергии в механических процессах;
4.Источники энергии;
5.Потребление энергии;
6.Вывод;
7.Список используемой литературы и сайтов.
Определения энергии.
Существует много определений энергии. Рассмотрим некоторые из них:
Энергия– общая мера различных форм движения материи, рассматриваемых в физике.
Энергия – скалярная физическая величина, являющаяся мерой способности тела (или системы тел) осуществить работу вследствие изменения своего состояния.
Энергия – это то, что необходимо для движения и роста.
Энергия — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие.
Энергия— это способность совершать работу.
Энергия — количественная мера различных форм движения материи.
Энергия — физическая величина, показывающая, какую работу может совершить тело (или несколько тел).
Все эти определения в той или иной степени верны.
Термин «энергия» впервые появился в работах Аристотеля
Лейбниц в своих трактатах 1686 и 1695 годов ввёл понятие «живой силы», которую он определил как произведение массы объекта и квадрата его скорости (в современной терминологии — кинетическая энергия, только удвоенная).
Маркиза Эмили дю Шатле в книге «Учебник физики» объединила идею Лейбница с практическими наблюдениями Виллема Гравезанда.
В 1807 году Томас Юнг первым использовал термин «энергия» в современном смысле этого слова взамен понятия живая сила. Гаспар-Гюстав Кориолис раскрыл связь между работой и кинетической энергией в 1829 году. Уильям Томсон (будущий лорд Кельвин) впервые использовал термин «кинетическая энергия» не позже 1851 года, а в 1853 году Уильям Ренкин впервые ввёл понятие «потенциальная энергия».
Несколько лет велись споры, является ли энергия субстанцией (теплород) или только физической величиной.
Автомобили и самолеты тепловозы и теплоходы, работают, расходуя энергию сгорающего топлива, гидротурбины — энергию падающей с высоты воды. Да и сами мы, чтобы жить, учиться и работать, возобновляем свой запас энергии при помощи пищи, которую мы едим.
Слово «энергия» употребляется нередко и в быту. Так, например, людей, которые могут быстро выполнять большую работу, мы называем энергичными, обладающими большой энергией.
Приведем примеры энергии:
Сжатая пружина, распрямляясь, может совершить работу, например, поднять на высоту груз, или заставить двигаться тележку.
Поднятый над землей неподвижный груз не совершает работы, но если этот груз упадет, он может совершить работу (например, может забить в землю сваю).
Энергия обычно обозначается символом Е (действие, деятельность,мощь).
Для обозначения тепловой энергии обычно используется символ Q (количество тепла).
Для обозначения потенциальной энергии обычно используется символ U (происхождение символа подлежит уточнению).
В отдельных случаях может использоваться символ W (работа, труд), как способность выполнять работу.
Виды энергии.
Существует много видов энергии как в физике, так и в других научных отраслях.
Раздел физики механика подразделяет энергию на два вида: потенциальнаяи кинетическая. Их сумма называется полной механической энергией.
Энергией обладают все виды полей. По этому признаку различают: электромагнитную, гравитационную (тяготения) и атомную (ядерную) энергии (также может быть разделена на энергию слабого и сильного взаимодействий).
В термодинамике различают внутреннюю энергию и иные термодинамические потенциалы.
В химии рассматриваются такие величины, как энергия связи и энтальпия, имеющие размерность энергии, отнесённой к количеству вещества.
Также существует энергия взрыва.
Кинетическая энергия. Ек=m*v^2/2Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек. Когда тело не движется, кинетическая энергия равна нулю. Впервые понятие кинетической энергии было введено в трудах Готфрида Лейбница (1695 г.). Кинетическая энергия имеет такие свойства, как аддитивность, инвариантность по отношению к повороту системы отсчета, сохранение. Аддитивность — свойство кинетической энергии механической системы, состоящей из материальных точек, которая равна сумме кинетических энергий всех материальных точек, входящих в систему. Инвариантность по отношению к повороту системы отсчета, это когда кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости. Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы.
Потенциальная энергия. Потенциальная энергия — скалярная физическая величина, характеризует запас энергии некоего тела (или материальной точки), находящегося в потенциальном силовом поле, который идет на приобретение (изменение) кинетической энергии тела за счет работы сил поля. Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными (потенциальными).Также, потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля. Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии. Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.
Энергия электромагнитного поля — энергия, заключенная в электромагнитном поле.Сюда же относятся частные случаи чистого электрического и чистого магнитного поля. Факт существования потоков энергии в постоянных электрических и магнитных полях может выглядеть странно, но не приводит к каким-либо парадоксам; более того, такие потоки обнаруживаются в эксперименте.
Гравитационная энергия — потенциальная энергия системы тел (частиц), обусловленная их взаимным гравитационным тяготением. Для любой системы тел, находящихся на конечных расстояниях, гравитационная энергия отрицательна, а для бесконечно удалённых, то есть для гравитационно не взаимодействующих тел, гравитационная энергия равна нулю. Полная энергия системы, равная сумме гравитационной и кинетической энергии, постоянна. Для изолированной системы гравитационная энергия является энергией связи. Системы с положительной полной энергией не могут быть стационарными.
Ядерная энергия (атомная энергия) — это энергия, содержащаяся в атомных ядрах и выделяемая при ядерных реакциях. Обычно для получения ядерной энергии используют цепную ядерную реакцию деления ядер урана-235 или плутония, реже других тяжёлых ядер (уран-238, торий-232).
Внутренняя энергия тела — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутреннюю энергию тела нельзя измерить напрямую. Свойства внутренней энергии: внутренняя энергия задаётся с точностью до постоянного слагаемого, зависящего от выбранного нуля отсчёта и не сказывающегося на экспериментальных замерах изменения внутренней энергии; внутренняя энергия есть величина аддитивная, т. е. внутренняя энергия системы равна сумме энергий её подсистем; внутренняя энергия есть индифферентный скаляр, т. е. во внутреннюю энергию не входит кинетическая энергия системы как единого целого и кинетическая энергия среды внутри системы (энергия смещения элементарных областей при деформации твёрдых тел и энергия потоков жидкостей и газов в среде).
Энергия взрыва.Взрыв — физический или/и химический быстропротекающий процесс с выделением значительной энергии в небольшом объёме за короткий промежуток времени, приводящий к ударным, вибрационным и тепловым воздействиям на окружающую среду и высокоскоростному расширению газов.При химическом взрыве, кроме газов, могут образовываться и твёрдые высокодисперсные частицы, взвесь которых называют продуктами взрыва. Энергию взрыва иногда измеряют в тротиловом эквиваленте — мере энерговыделения высокоэнергетических событий, выраженной в количестве тринитротолуола (ТНТ), выделяющем при взрыве равное количество энергии.
Закон сохранения энергии в механических процессах.
И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля.
Рассмотрим теперь вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему. Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:
А = — (Ер2 – Ер1). (1)
Вместе с тем по теореме о кинетической энергии работа тех же сил равна изменению кинетической энергии:
А = Ек2 – Ек1 (2)
Из сравнения равенств (1) и (2) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:
Ек2 – Ек1 = — (Ер2 – Ер1)
Или
Ек1 + Ер1 = Ек2 + Ер2 (3)
Из равенства (3) следует, что сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается постоянной.Это утверждение называется законом сохранения энергии в механических процессах.
Сумма кинетической и потенциальной энергии тел называется полной механической энергией.
Для полной механической энергии закон сохранения энергии имеет следующее выражение: полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения и упругости, остается неизменной.
Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергии тел в равной количественной мере при взаимодействии тел.
Источники энергии
Условно источники энергии можно поделить на два типа: невозобновляемые и постоянные. К первым относятся газ, нефть, уголь, уран и т. д. Технология получения и преобразования энергии из этих источников отработана, но, как правило, неэкологична, и многие из них истощаются. К постоянным источникам можно отнести энергию солнца, энергию, получаемую на ГЭС и т. д.
5.Потребление энергии
Существует довольно много форм энергии, большинство из которых так или иначе используются в энергетике и различных современных технологиях.
Темпы энергопотребления растут во всем мире, поэтому на современном этапе развития цивилизации наиболее актуальна проблема энергоэффективности и энергосбережения.
Вывод
Таким образом, энергия – понятие относительное. Существует много видов энергии, которые важны по-своему. Разные энергии выполняют свои особые функции и имеют свои неповторимые свойства.
В настоящее время тема потребления и сбережения энергии очень актуальна. Мы должны экономить энергию, не растрачивать её по пусту.
В физическом смысле энергия тоже очень важна.
Список используемой литературы и сайтов
1.О. Ф. Кабардин «Физика. Справочные материалы»;
2.Издательство «Росмэн» №Большая иллюстрированная энцикопедия»;
3.Веб-сайт ru.wikipedia.org
§2.8 Закон сохранения энергии в механике
В 1018 г.Эмми Нётер, немецкий физик и математик, доказал фундаментальную теорему физики, которую в упрощённом виде можно сформулировать так: каждому свойству симметрии пространства и времени соответствует свой закон сохранения. В частности, как следует из теоремы (теоремы Нётер) однородности времени должен соответствовать закон сохранения энергии: при любых процессах, происходящих в замкнутой консервативной системе, её полная механическая энергия не изменяется.
Элементарная работа потенциальных сил равна взятому с обратным знаком элементарному изменению потенциальной энергии dA= -dEп . Так как иных сил в системе нет, то та же элементарная работа равна элементарному изменению кинетической энергии dA= dEк. Поэтому можем записать
-dEп = dEк
dEк + dEп = 0,
d(Ек + Еп) = 0. (2.34) Обозначим
Ек + Еп = Е (2.35)
здесь Е — полная механическая энергия. Из (2.39) видим, что полная механическая энергия остается постоянной:
E=const (2.36)
При решении задач в механике удобно пользоваться законом сохранения энергии в виде
ΔEк = ΔEп или Ек1 + Еп1 = Ек2 + Еп2. (2.37) здесь Ек1 и Еп1, — соответственно кинетическая и потенциальная энергии тела (системы) в начальном положении; Ек2 и Еп2 — то же для конечного положения тела (системы).
Закон сохранения энергии в механике является частным случаем более общего закона сохранения и превращения энергии, который является одним из основных законов природы.
В земных условиях невозможно указать консервативную систему, хотя бы потому, что всегда действуют силы трения и сопротивления (диссипативные силы), происходит уменьшение механической энергии (диссипация энергии). В этом случае механическая энергия уже не будет оставаться постоянной; она будет изменяться, и её изменение, как это видно из формулы (2.38) будет складываться из изменения кинетической энергии ΔEк, и изменения потенциальной энергии ΔEп :
ΔЕ= ΔEк,+ ΔEп.. (2.38)
Учитывая соотношения (2.27) и (2.32), выражающие теорему о кинетической и потенциальной энергиях, последнее равенство можно переписать так:
ΔЕ= Апот+Адис-Апот= Адис. (2.39)
Изменение полной механической энергии неконсервативной системы равно сумме работы диссипативных сил.
Так как диссипативные силы направлены противоположно перемещению, то работа этих сил отрицательна и, следовательно, механическая энергия системы уменьшается.
§2.9 Столкновение тел
Столкновение тел – одно из наиболее часто встречающихся явлений в жизни. При столкновении происходит их кратковременное взаимодействие, сопровождающееся как деформацией, так и изменением направления их движения. Особый интерес представляют два вида столкновений – абсолютно упругий и абсолютно неупругий удары.
Простейшим видом соударения является центральный удар тел. При этом ударе тела движутся только поступательно, их скорость направлена по прямой, соединяющей центры масс.
Абсолютно неупругий удар. Так называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно целое. Например, столкновение слипающихся пластилиновых шариков; попадание ружейной пули в ящик с песком и т.д.
П
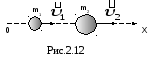 усть
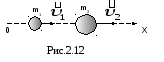
один из шаров массойm1 догоняет другой массой m2 (рис. 2.12).
усть
один из шаров массойm1 догоняет другой массой m2 (рис. 2.12).
Можно записать
m1υ1+m2υ2=(m1+m2)υ (2.40)
откуда 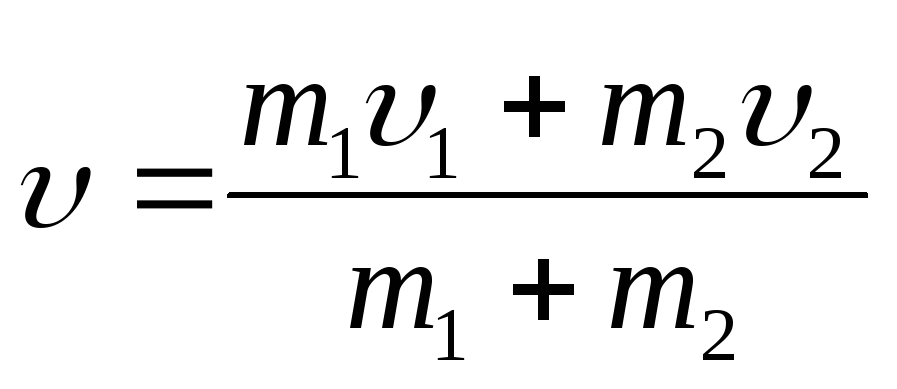 (2.41)
(2.41)
здесь υ1 и υ2 — скорости взаимодействующих шаров до удара; υ — их скорость после удара.
Направления векторов скоростей в общем случае определяются правилом: скорости положительны, если направлены вдоль оси ОХ, и отрицательны, если направлены противоположно.
Рассмотрим несколько частных случаев.
1. Если массы шаров равны (m1 = m2), то из (2.45) получим
 (2.42)
(2.42)
2. Удар шара о стенку. Неподвижное тело (стенка) (υ2 = 0) значительно массивнее шара (m2 » m1), тогда
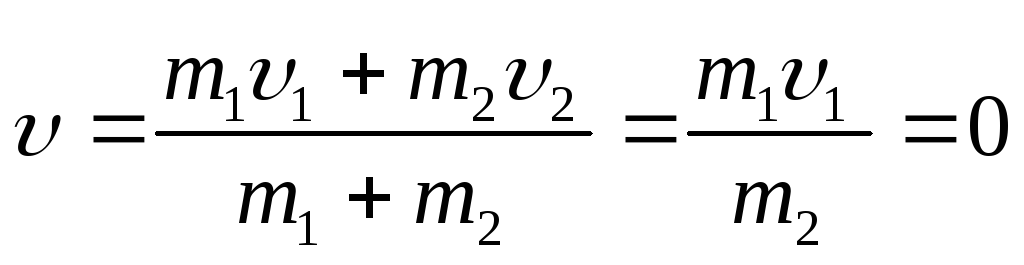 (2.43)
(2.43)
т.е. налетевшее тело остановится после абсолютно неупругого удара, при этом υ2 считаем не слишком большой.
При абсолютно неупругом ударе механическая энергия шаров не сохраняется, так как в системе действуют диссипативные силы и происходит потеря кинетической энергии, в результате чего механическая энергия системы уменьшается, переходя во внутреннюю энергию ΔЕ сталкивающихся тел (которые при этом нагреваются). Но закон сохранения полной энергии выполняется, т.е. сумма всех видов энергии замкнутой системы тел до и после столкновений остаётся неизменной:
 (2.44)
(2.44)
Абсолютно упругий удар. Так называется столкновение тел, в результате которого не происходит соединения тел в одно целое и их внутренние энергии остаются неизменными. При абсолютно упругом ударе сохраняется не только импульс, но и механическая энергия системы.
К абсолютно упругому удару можно применить закон сохранения механической энергии:
 (2.45)
(2.45)
где m1 и m2 — массы взаимодействующих шаров; υ1, υ2 – их скорости до удара; u1, u2— после удара.
По тем же причинам, которые были изложены для абсолютно неупругого удара, к этому случаю можно применить и закон сохранения импульса:
m1υ1+ m2υ2 = m1 u1+ m2 u2 (2.46)
Решая совместно уравнения (2.49) и (2.50), получим
 (2.47)
(2.47)
 (2.48)
(2.48)
§2.8 Закон сохранения энергии в механике
В 1018 г.Эмми Нётер, немецкий физик и математик, доказал фундаментальную теорему физики, которую в упрощённом виде можно сформулировать так: каждому свойству симметрии пространства и времени соответствует свой закон сохранения. В частности, как следует из теоремы (теоремы Нётер) однородности времени должен соответствовать закон сохранения энергии: при любых процессах, происходящих в замкнутой консервативной системе, её полная механическая энергия не изменяется.
Элементарная работа потенциальных сил равна взятому с обратным знаком элементарному изменению потенциальной энергии dA= -dEп . Так как иных сил в системе нет, то та же элементарная работа равна элементарному изменению кинетической энергии dA= dEк. Поэтому можем записать
-dEп = dEк
dEк + dEп = 0,
d(Ек + Еп) = 0. (2.34) Обозначим
Ек + Еп = Е (2.35)
здесь Е — полная механическая энергия. Из (2.39) видим, что полная механическая энергия остается постоянной:
E=const (2.36)
При решении задач в механике удобно пользоваться законом сохранения энергии в виде
ΔEк = ΔEп или Ек1 + Еп1 = Ек2 + Еп2. (2.37) здесь Ек1 и Еп1, — соответственно кинетическая и потенциальная энергии тела (системы) в начальном положении; Ек2 и Еп2 — то же для конечного положения тела (системы).
Закон сохранения энергии в механике является частным случаем более общего закона сохранения и превращения энергии, который является одним из основных законов природы.
В земных условиях невозможно указать консервативную систему, хотя бы потому, что всегда действуют силы трения и сопротивления (диссипативные силы), происходит уменьшение механической энергии (диссипация энергии). В этом случае механическая энергия уже не будет оставаться постоянной; она будет изменяться, и её изменение, как это видно из формулы (2.38) будет складываться из изменения кинетической энергии ΔEк, и изменения потенциальной энергии ΔEп :
ΔЕ= ΔEк,+ ΔEп.. (2.38)
Учитывая соотношения (2.27) и (2.32), выражающие теорему о кинетической и потенциальной энергиях, последнее равенство можно переписать так:
ΔЕ= Апот+Адис-Апот= Адис. (2.39)
Изменение полной механической энергии неконсервативной системы равно сумме работы диссипативных сил.
Так как диссипативные силы направлены противоположно перемещению, то работа этих сил отрицательна и, следовательно, механическая энергия системы уменьшается.
§2.9 Столкновение тел
Столкновение тел – одно из наиболее часто встречающихся явлений в жизни. При столкновении происходит их кратковременное взаимодействие, сопровождающееся как деформацией, так и изменением направления их движения. Особый интерес представляют два вида столкновений – абсолютно упругий и абсолютно неупругий удары.
Простейшим видом соударения является центральный удар тел. При этом ударе тела движутся только поступательно, их скорость направлена по прямой, соединяющей центры масс.
Абсолютно неупругий удар. Так называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно целое. Например, столкновение слипающихся пластилиновых шариков; попадание ружейной пули в ящик с песком и т.д.
П
 усть
один из шаров массойm1 догоняет другой массой m2 (рис. 2.12).
усть
один из шаров массойm1 догоняет другой массой m2 (рис. 2.12).
Можно записать
m1υ1+m2υ2=(m1+m2)υ (2.40)
откуда 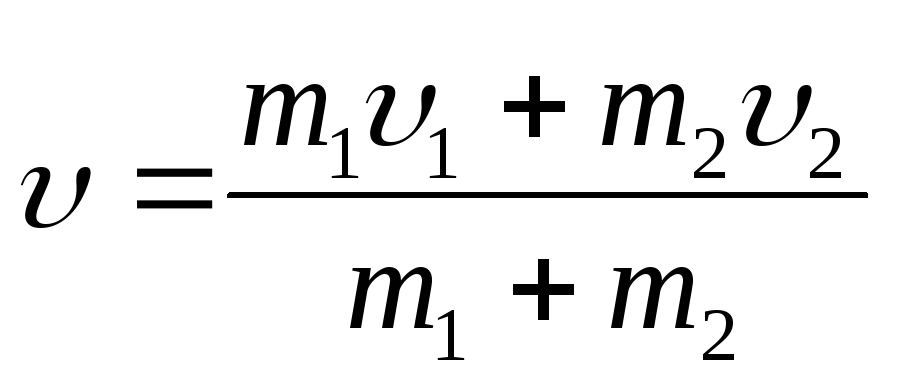 (2.41)
(2.41)
здесь υ1 и υ2 — скорости взаимодействующих шаров до удара; υ — их скорость после удара.
Направления векторов скоростей в общем случае определяются правилом: скорости положительны, если направлены вдоль оси ОХ, и отрицательны, если направлены противоположно.
Рассмотрим несколько частных случаев.
1. Если массы шаров равны (m1 = m2), то из (2.45) получим
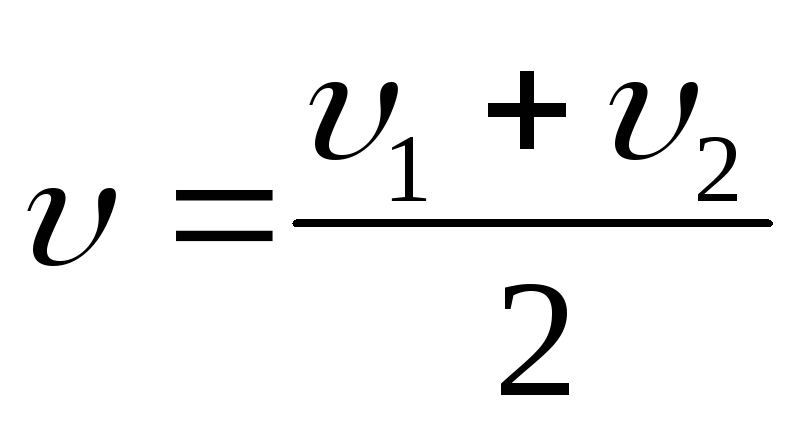 (2.42)
(2.42)
2. Удар шара о стенку. Неподвижное тело (стенка) (υ2 = 0) значительно массивнее шара (m2 » m1), тогда
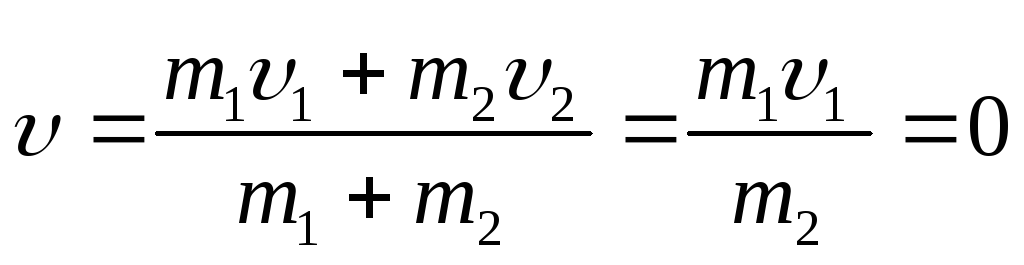 (2.43)
(2.43)
т.е. налетевшее тело остановится после абсолютно неупругого удара, при этом υ2 считаем не слишком большой.
При абсолютно неупругом ударе механическая энергия шаров не сохраняется, так как в системе действуют диссипативные силы и происходит потеря кинетической энергии, в результате чего механическая энергия системы уменьшается, переходя во внутреннюю энергию ΔЕ сталкивающихся тел (которые при этом нагреваются). Но закон сохранения полной энергии выполняется, т.е. сумма всех видов энергии замкнутой системы тел до и после столкновений остаётся неизменной:
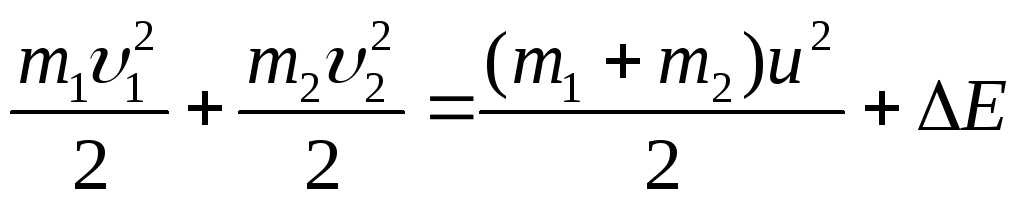 (2.44)
(2.44)
Абсолютно упругий удар. Так называется столкновение тел, в результате которого не происходит соединения тел в одно целое и их внутренние энергии остаются неизменными. При абсолютно упругом ударе сохраняется не только импульс, но и механическая энергия системы.
К абсолютно упругому удару можно применить закон сохранения механической энергии:
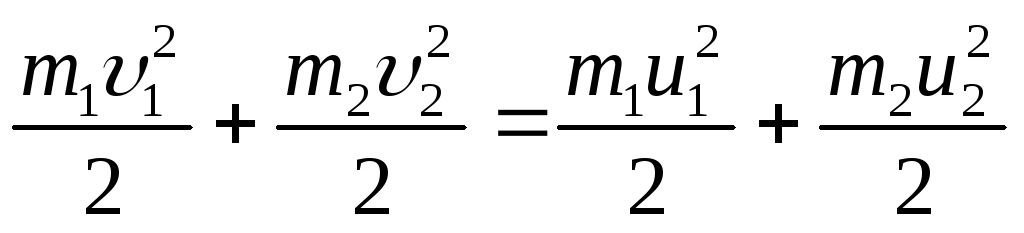 (2.45)
(2.45)
где m1 и m2 — массы взаимодействующих шаров; υ1, υ2 – их скорости до удара; u1, u2— после удара.
По тем же причинам, которые были изложены для абсолютно неупругого удара, к этому случаю можно применить и закон сохранения импульса:
m1υ1+ m2υ2 = m1 u1+ m2 u2 (2.46)
Решая совместно уравнения (2.49) и (2.50), получим
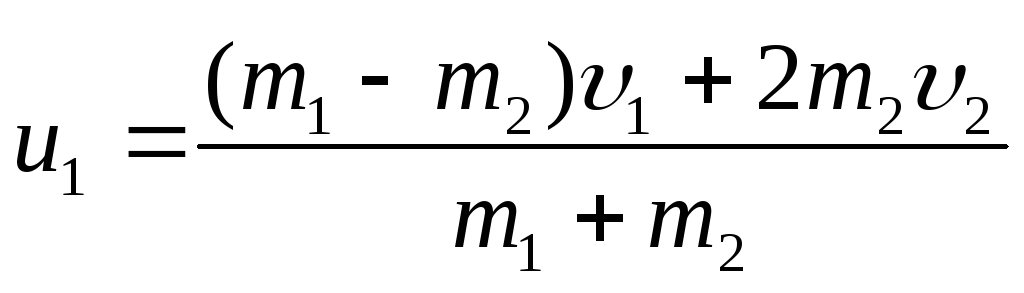 (2.47)
(2.47)
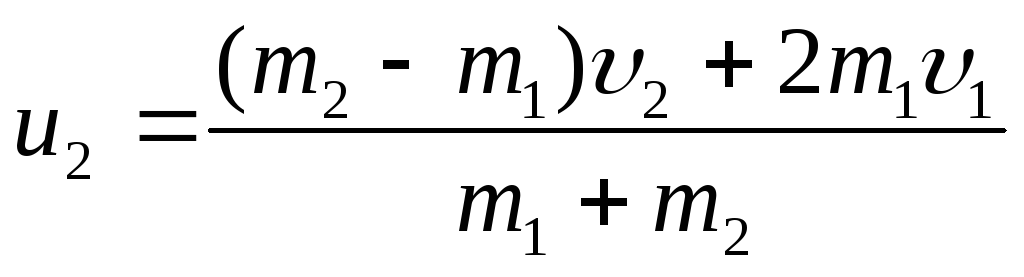 (2.48)
(2.48)

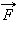 –
сила натяжения нити в нижней точке
траектории.
–
сила натяжения нити в нижней точке
траектории.