Числовые выражения; действия с дробными числами (В.А. Тарасов)
Основное свойство дроби заключается в том, что и числитель, и знаменатель можно умножить или разделить на одно и то же число, не равное нулю.
Пример 1: Домножить дробь 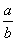 на k.
на k.
Дробь 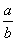 не изменится, если числитель
не изменится, если числитель  и знаменатель
и знаменатель 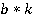 , при условии
, при условии 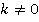 . Значит:
. Значит:
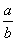
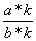
Пример 2: Разделить числитель и знаменатель дроби на число n.
При делении числителя и знаменателя на число nзначение дроби 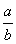 не изменится в случае, если
не изменится в случае, если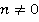 .
.
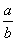 =
= 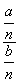
Пример 3: Домножить дробь 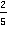
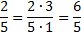
Ответ: 
Пример 4: Сократить дробь 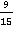 .
.
Для этого разложим и числитель, и знаменатель на простые множители.
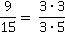
Разделим и числитель, и знаменатель на 3 и получим несократимую дробь:
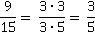
Ответ: 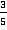
Пример 5: Сократить дробь 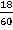 .
.
Разложим и числитель, и знаменатель на простые множители.

Разделим числитель и знаменатель на 2 и на 3 и получим несократимую дробь.
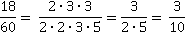
Ответ: 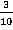 .
.
Пример 6: Сократить дробь 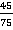
Разложим и числитель, и знаменатель на простые множители и сократим одинаковые.
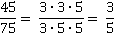
Ответ: 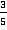 .
.
Пример 7: Найти значение выражения  .
.
Разложим каждый знаменатель на простые множители и найдем их НОК, который и является общим знаменателем.
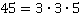 ;
;

НОК(45;75) = 
Дополнительный множитель дроби находится по формуле:

Значит, получаем: 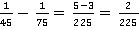
Ответ: 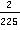 .
.
Правило умножения дроби на дробь.
При умножении дроби 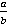 на дробь
на дробь 

Правило деления дроби на дробь.
Существует два способа деления дроби на дробь.
1-й способ: Для того, чтобы разделить дробь 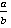 на дробь
на дробь  , надо дробь
, надо дробь  умножить на обратную дробь
умножить на обратную дробь 
 .
.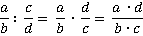
2-й способ: Для того чтобы разделить дробь 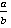 на дробь
на дробь  , надо числитель
, надо числитель  первой дроби умножить на знаменатель
первой дроби умножить на знаменатель 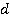 второй дроби и получить числитель
второй дроби и получить числитель 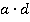
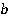 первой дроби умножить на числитель
первой дроби умножить на числитель 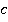 второй дроби и получить знаменатель
второй дроби и получить знаменатель 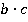 искомой дроби:
искомой дроби: 
Правило умножения дроби на число.
При умножении дроби 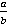 на число
на число 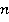
 умножить на число
умножить на число 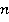 , а знаменатель
, а знаменатель 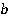 оставить неизменным. Данное правило подтверждается еще тем, что любое число
оставить неизменным. Данное правило подтверждается еще тем, что любое число 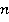 можно представить в виде дроби
можно представить в виде дроби  .
.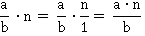
Пример 8: Умножить дробь  на число 7.
на число 7.
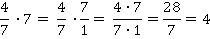
Ответ: 4.
Правило деления дроби на число.
При делении дроби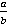 на число
на число 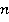 необходимо число
необходимо число 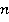 представить в виде дроби
представить в виде дроби 
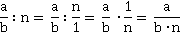
Пример 9: Разделить дробь  на число 7.
на число 7.
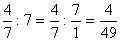 .
.
Ответ: .
.
Правило деления числа на дробь.
При делении числа n на дробь 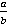 необходимо помнить, что n – это дробь
необходимо помнить, что n – это дробь 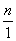 . И в результате использовать правило деления дроби на дробь.
. И в результате использовать правило деления дроби на дробь.

Пример 10: Решить уравнение 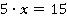 .
.
Для того чтобы найти х, следует и числитель, и знаменатель разделить на одно и то же число – коэффициент перед х.
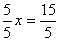 ,
,
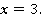
Ответ: 3.
Пример 11: Решить уравнение  .
.
Данное уравнение можно решить двумя способами – в одно и в два действия. В одно действие – надо разделить обе части на коэффициент 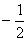 перед х.
перед х.


Для решения уравнения в 2 действия, можно сначала умножить на 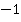 обе части уравнения и получить
обе части уравнения и получить 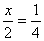 . Дальше, чтобы получить х, необходимо и левую, и правую часть умножить на 2.
. Дальше, чтобы получить х, необходимо и левую, и правую часть умножить на 2.



Ответ: .
.
Пример 12: Решить уравнение 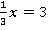 .
.
1-ый способ: Разделим правую и левую часть на коэффициент перед 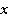 , т.е. на
, т.е. на  .
.
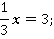
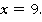
2-ой способ: Умножим обе части на 3. Получается тот же результат.
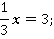
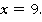
Ответ: 9.
Пример 13: Найти значение алгебраического выражения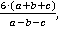 если
если 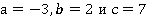 .
.
Первым действием необходимо вычислить данное выражение, подставив значения переменных.
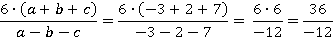
Вторым действием проверим, является ли набор значений 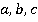 допустимым для данного алгебраического выражения.
допустимым для данного алгебраического выражения.
Напомним, что набор будет допустимым, если при значениях а, b и с выражение можно вычислить.
Подставив значения, видим, что знаменатель выражения не равен нолю, значит, выражение можно вычислить.
Третьим действием необходимо сократить дробь. Исходя из основного свойства дроби, при делении положительного числа на отрицательное получается отрицательное число.
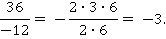
Ответ: 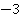 .
.
Итак, в данном уроке мы рассмотрели действия с числовыми и алгебраическими дробями. Также вспомнили основные правила сложения, вычитания, умножения и деления дробей. И мы видим, что вот эти действия и правила полностью переносятся на действия с алгебраическими дробями.
Список рекомендованной литературы
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Интернет-портал podelise.ru (Источник).
- Интернет-портал Павла Бердова (Источник).
Рекомендованное домашнее задание
1. № 20-23-7 стр. 10-11. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Выполнить умножение или деление:
а) 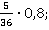 б)
б)  в)
в)  г)
г)
3. Сократить дробь:
а) 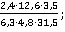 б)
б)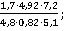
4. Найти значение выражения:
а) 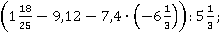
б)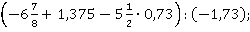
Как решать выражения с буквами? – boeffblog.ru

Чтобы научиться решать этот вид заданий, необходимо запомнить несколько нехитрых вещей.
Во-первых, если видно, что пример небольшой, и проще сразу подставить число вместо буквы, то так и надо делать.
Например:
Упростите выражение
и найдите его значение при y = 0,4.
В этом задании можно сразу сделать замену, и вместо “игрека” подставить 0,4:  .
.
И при помощи нехитрых действий это превращается в  .
.
Таким образом, первая заповедь при решении таких заданий – “Не перемудри”. Видите, что проще подставить сразу – подставляйте и считайте.
Во-вторых, если не сработала первая заповедь, то запомните – фраза “Упростите выражение” означает, что там многое должно сократиться. Для этого могут применяться 3 способа:
1. Вынести общий множитель за скобку: 3x + 3 = 3 (x + 1).
2. Применить формулу квадрата суммы: (a + b)2 = a2 + 2ab + b2, или квадрата разности: (a – b)2 = a2 – 2ab + b2 .
3. Применить формулу разности квадратов: a2 – b2 = (a + b)(a – b).
После этого многое должно сократиться. Остается что-то простое, куда подставляются значения наших переменных (буквы меняются на цифры). И все!
Рассмотрим несколько примеров.
Упростите выражение
и найдите его значение при a = 3, b = 0,2.
В этом примере работает первый способ, вынесение общего множителя и в числителе, и в знаменателе дроби:  .
.
Теперь можно сократить на (2 – a).
Остается простая дробь:  . Подставляем и считаем.
. Подставляем и считаем.
Найдите значение выражения:
при x = -13
Можно увидеть, что числитель первой дроби можно свернуть по формуле квадрат разности. Таким образом выражение перепишется в виде:  .
.
Затем, по правилу деления дробей переворачиваем вторую дробь:  .
.
Эту дробь можно сократить на (x – 7), и получится:  .
.
Далее подставляем вместо икса его численное значение (-13) и считаем.
Найдите значение выражения:
Первым делом, приведем к общему знаменателю разность дробей, которая записана в скобках. Общий знаменатель (как проводить математические операции с дробями смотрите здесь) 7xy, а в числителе получим x2 – 49y2.
Затем производим умножение, не забывая ставить скобки там, где это необходимо:
НЕВЕРНО
ВЕРНО
Теперь вспоминаем, что многое должно сократиться, и видим в числителе выражение в скобках, которое можно разложить по формуле разности квадратов на (x – 7y)(x + 7y).
Получаем: 
Сначала сокращаем на 7xy, а затем на (x + 7y):
Остается от этого всего выражение, которое решается очень просто: x – 7y.
Это были основные типы заданий на выражения с буквами. Задания, как видите, основываются всего лишь на трех операциях, поэтому должны легко решаться. Главное внимательнее читать условие и стараться упростить выражение. И запомните, что в них всегда что-то должно сократиться!
Найдите значение алгебраического выражения – как решать
Формулировка задачи: Найдите значение алгебраического выражения.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 5 (Вычисления и преобразования).
Рассмотрим, как решаются подобные задачи на примерах.
Пример задачи 1:
Найдите значение выражения:
Решение:
Приведем разность в скобках к общему знаменателю:
Преобразуем первый множитель по формуле разности квадратов и сократим получившуюся дробь:
Ответ: 6
Пример задачи 2:
Найдите значение выражения
Решение:
Преобразуем числитель по формуле разности квадратов, приведем подобные и сократим дробь:
Ответ: -12
Пример задачи 3:
Найдите значение выражения 2x + y + 6z, если 4x + y = 5, а 12z + y = 7.
Решение:
Легко заметить, что если мы сложим 2 приведенных равенства, то получим удвоенное значение выражения, которое нужно найти:
4x + y + 12z + y = 4x + 2y + 12z = 5 + 7 = 12
Поэтому нам достаточно разделить получившееся значение пополам:
4x + 2y + 12z = 12
2x + y + 6z = 6
Ответ: 6
Пример задачи 4:
Найдите значение выражения 5(p(2x) – 2p(x + 5)), если p(x) = x – 10.
Решение:
Найдем, чему равно p(2x), для этого в функцию p(x) подставим в качестве аргумента 2x:
Найдем, чему равно p(x + 5), для этого в функцию p(x) подставим в качестве аргумента x + 5:
p(x + 5) = x + 5 – 10 = x – 5
Подставим полученные значения в выражение и вычислим его значение:
5(p(2x) – 2p(x + 5)) = 5 ⋅ (2x – 10 – 2 ⋅ (x – 5)) = 5 ⋅ (2x – 10 – 2x + 10) = 5 ⋅ 0 = 0
Ответ: 0
Пример задачи 5:
Найдите значение выражения (√10 – 2√3)(√10 + 2√3)
Решение:
Преобразуем выражение по формуле разности квадратов, чтобы избавиться от корней, и вычислим значение выражения:
(√10 – 2√3)(√10 + 2√3) = (√10)2 – (2√3)2 = 10 – 4 ⋅ 3 = 10 – 12 = -2
Ответ: -2
Пример задачи 6:
Найдите значение выражения
при b = 345
Решение:
Приведем разность в скобках к общему знаменателю и упростим числитель:
Преобразуем первый множитель по формуле разности квадратов и заменим упрощенную разность:
Осталось подставить значение b и вычислить результат:
Ответ: 346
Пример задачи 7:
Найдите
если
при b ≠ 0
Решение:
Найдем значение p(1/b), для этого в функцию p(b) подставим в качестве аргумента 1/b:
Поскольку p(1/b) равно p(b), частное от их деления будет равно 1:
Ответ: 1
Пример задачи 8:
Найдите p(x) + p(6 – x), если
при x ≠ 3
Решение:
Найдем значение p(6 – x), для этого в функцию p(x) подставим в качестве аргумента 6 – x:
Тогда значение выражения равно:
p(x) + p(6 – x) = p(x) – p(x) = 0
Ответ: 0
Пример задачи 9:
Найдите a/b, если
Решение:
Разделим и числитель и знаменатель на b:
Таким образом среди неизвестных осталась только дробь a/b, которую и нужно найти. Вычислим ее значение из равенства:
Ответ: 1
Пример задачи 10:
Найдите
если a/b = 3.
Решение:
Разделим числитель и знаменатель на b и заменим a/b на 3, после чего упростим выражение:
Ответ: 2
Найти значение выражения. Задание 1 ГИА (ОГЭ)

Найти значение выражения обычно предлагают школьникам в первой части ОГЭ (ГИА) и они достаточно просты. Для решения такого задания нужно уметь вычислять, то есть знать таблицу умножения, уметь умножать десятичные числа, понимать смысл дроби и уметь работать со степенями. Таким образом, первое задание проверяет сразу несколько умений школьника. Найти значение выражения, не умея работать с числами и степенями, невозможно.
Найти значение выражения
Решение: Перемножим 6,8 на 2, получим 13,6. Теперь умножим на основания степеней одинаковые, значит, складываем показатели степеней.
Получим В итоге получим
Ответ:
Найти значение выражения
Решение: тогда
Ответ: -30.
Найти значение выражения
Решение: перепишем данное выражение в следующем виде
Почему мы смогли так записать? Потому что мы использовали свойство степени:
Тогда в нашем задании мы получаем или
или
или
Итак, имеем:
Ответ: 0,3054.
Найти значение выражения 
Решение: Можно просто перемножить 6,8 на 7,5, а затем, полученное число разделить столбиком на 8,5. А можно перевести десятичные дроби в обыкновенные и попробовать упростить.
68 и 10 сократим на 2, а 75 и 85 на 5, тогда получим:
Ответ: 6.
Найти значение выражения
Решение:
Ответ:
Следующая запись »
 и найдите его значение при y = 0,4.
и найдите его значение при y = 0,4. и найдите его значение при a = 3, b = 0,2.
и найдите его значение при a = 3, b = 0,2. при x = -13
при x = -13
 НЕВЕРНО
НЕВЕРНО ВЕРНО
ВЕРНО
