План-конспект урока по алгебре (10 класс) на тему: 10 класс алгебра » Корень n-ой степени»
Урок по теме «Корень n-й степени, арифметический корень n-й степени и его свойства»
Цели урока:
Образовательная: Создать условия для формирования у обучающихся целостного представления о корне n-ой степени, навыков сознательного и рационального использования свойств корня при решении различных задач.
Развивающая: Создать условия для развития алгоритмического, творческого мышления, развивать навыки самоконтроля.
Воспитательные: способствовать развитию интереса к предмету, активности, воспитывать аккуратность в работе, умение выражать собственное мнение, давать рекомендации.
Ход урока
1. Организационный момент.
Добрый день! Добрый час!
Как я рада видеть вас.
Прозвенел уже звонок
Начинается урок.
Улыбнулись. Подровнялись.
Друг на друга поглядели
И тихонько дружно сели.
2. Мотивация урока.
Выдающийся французский философ, ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя. Девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса:
— Что есть больше всего на свете? – Пространство.
— Что быстрее всего? – Ум.
— Что мудрее всего? – Время.
— Что приятнее всего? – Достичь желаемого.
Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого результата.
3.Актуализация знаний.
1. Назовите взаимообратные алгебраические операции над числами
(сложение и вычитание, умножение и деление).
2. Всегда ли можно выполнить такую алгебраическую операцию, как
деление?
(нет, делить на нуль нельзя)
3. Какую еще операцию вы можете выполнять с числами?
(возведение в степень)
4. Какая операция будет ей обратной?
(извлечение корня)
5. Корень какой степени вы можете извлекать?
(корень второй степени)
6. Какие свойства квадратного корня вы знаете?
(извлечение квадратного корня из произведения, из частного, из
корня, возведение в степень)
7. Найдите значения выражений:
…, т.к. …2 = 4, …, т.к. …2 = 9, …, т.к. …2 = 144,
…, т.к. …… …, т.к. …2 = 0,25, ……..
Квадратным корнем из числа а называют число, квадрат которого равен а. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Запись читается «квадратный корень из а», опуская при этом слово «арифметический». , а- подкоренное выражение, а знак-радикал (от латинского — корень).
Из истории. Ещё 4000 лет назад вавилонские ученые составили наряду с таблицами умножения и таблицами обратных величин ( при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней чисел. При этом они умели находить приблизительное значение квадратного корня из любого целого числа.
4. Изучение нового материала.
Корнем n-й степени из числа а называется такое число b, n-я степень которого равна а, т. е. b – корень n-й степени из |
Очевидно, что в соответствии с основными свойствами степеней с натуральными показателями, из любого положительного числа существует два противоположных значения корня четной степени, например, числа 4 и -4 являются корнями квадратными из 16, так как (-4)2 = 42 = 16, а числа 3 и -3 являются корнями четвертой степени из 81, так как (-3)4 = З4 = 81.
Кроме того, не существует корня четной степени из отрицательного числа, поскольку четная степень любого действительного числа неотрицательна. Что же касается корня нечетной степени, то для любого действительного числа существует только один корень нечетной степени из этого числа. Например, 3 есть корень третьей степени из 27, так как З3 = 27, а -2 есть корень пятой степени из -32, так как (-2)5 = 32.
В связи с существованием двух корней четной степени из положительного числа, введем понятие арифметического корня, чтобы устранить эту двузначность корня.
Неотрицательное значение корня n-й степени из неотрицательного числа называется арифметическим корнем.
Обозначение: – корень n-й степени.
Число n называется степенью арифметического корня. Если n=2, то степень корня не указывается и пишется . Корень второй степени принято называть квадратным, а корень третьей степени – кубическим.
= в, в2 == а, а ≥ 0, в ≥ 0
= в, вп = а
- п — четное
а ≥ 0, в ≥ 0 ()2 = а, а ≥ 0
- п — нечетное
а,в — любые ()п = а
=
а, если а ≥ 0 — а, если а
=
а — в. если а ≥ в в — а, если а
, а ≥ 0, в ≥ 0
., а ≥ 0, в ≥ 0
, а ≥ 0, в > 0
, а ≥ 0, в > 0
а ≥ 0
m, n, k — натуральные числа
5. Закрепление нового материала.
Устная работа
а) Какие выражения имеют смысл?
; ; ; ;
; ; ; ;
; ; ; ;
; ; ; .
б) при каких значениях переменной а имеет смысл выражение?
в) Вычислите:
; ; ; ; ; ; ; .
г) Верно ли равенство (устно):
= 2; = 2; ()2 = 2;
= — 2; = а; = — а;
= ; а — = 0; а — = 2а;
а — = а -; = 3; = — 2;
= 2; = 3; = .
Решить № 3, 4, 7, 9, 11.
6. Самостоятельная работа.
Работа в парах: с. 178.№1,2.
7. Итоги урока. Д/з. Рефлексия деятельности.
Достиг ли урок своей цели?
Чему вы научились?
Оцените свою деятельность на уроке в виде написания синквейна.
Спасибо всем за урок!
Примеры синквейнов:
Корень.
Квадратный, кубический.
Извлекали, возводили в степень, обобщали.
Было интересно. Я молодец.
Алгебра | ||||||||
Семестр: 1 семестр | Курс: 1, (класс:10) | |||||||
Тема: | Технология вычисления корня n-й степени | |||||||
Тип занятия: | Урок овладения новым материалом. | |||||||
Вид занятия: | Аудиторное теоретическое занятие | |||||||
Цели занятия: | ||||||||
Образовательные: | — ввести понятие арифметического корня натуральной степени; — ввести понятие корня нечетной степени из отрицательного числа; — рассмотреть свойства арифметического корня натуральной степени; — сформировать умения вычислять арифметические корни натуральной степени; — сформировать умения вычислять корни нечетной степени из отрицательного числа; — сформировать желание самостоятельно изучать материал; | |||||||
Воспитательные: | — воспитывать положительное отношение к приобретению новых знаний; — воспитывать ответственность за свои действия и поступки; — вызвать заинтересованность новым для студентов подходом изучения математики. | |||||||
Развивающие: | — формировать навыки познавательного мышления; — формировать умения и навыки учебного труда. | |||||||
Методы обучения: | Лекция объяснительно — иллюстрированная | |||||||
Планируемый результат: | Студент знает: Определение арифметического корня натуральной степени. Свойства арифметического корня натуральной степени. Владеет основными принципами вычисления арифметического корня натуральной степени. | |||||||
Структура занятия: | 1. Введение в тему «Арифметический корень натуральной степени» | |||||||
2. Определение арифметического корня натуральной степени. | ||||||||
Решение уравнения . Проверка уровня освоенности темы. Решение уравнения | ||||||||
3. Введение корня нечетной степени из отрицательного числа. | ||||||||
4. Решение тренировочных упражнений. | ||||||||
5.Разбор ключевого примера | ||||||||
6. Свойства арифметического корня натуральной степени. | ||||||||
7. Решение тренировочных упражнений | ||||||||
8.Решение упражнений (нечетные пункты) из учебника «Алгебра и начала анализа 10-11» на закрепление темы (№30 — 38) | ||||||||
9. Домашнее задание. | Введение в тему «Арифметический корень натуральной степени» | |||||||
2 | Определение арифметического корня натуральной степени | |||||||
Решение уравнения | Проверка уровня освоенности темы | |||||||
Решение уравнения | ||||||||
3 | Введение корня нечетной степени из отрицательного числа | |||||||
4 | ||||||||
5 | Решение ключевого примера | |||||||
6 | Свойства арифметического корня натуральной степени | |||||||
7 | Решение тренировочных упражнений | |||||||
8 | Решение упражнений из учебника «Алгебра и начала анализа 10-11» (нечетные пункты) на закрепление изученной темы. | |||||||
Ответы:
| ||||||||
Ответы:
| ||||||||
Ответы:
| ||||||||
Ответы: 3) 4 4) -11 | ||||||||
Ответы: 5) 1/30 | ||||||||
Ответы:
| ||||||||
Ответы:
| ||||||||
Ответы: 1)10 2) 0,2 3) 6 4) 2 | ||||||||
Ответы:
| Ответы:
| |||||||
Ответы:
| ||||||||
Ответы:
| ||||||||
9 | Домашнее задание | |||||||
Решение упражнений №30, 31, 32, 33,34, 35, 36, 37, 38 из учебника «Алгебра и начала анализа 10-11» (четные пункты). | ||||||||
10 | Литература
| |||||||
Свойства корня n-ой степени. Видеоурок. Алгебра 11 Класс
При доказательстве свойств корня n-й степени мы будем опираться на его определение.
Определение:
Корнем n-й степени из неотрицательного числа а называется такое неотрицательное число b, которое при возведении в степень n дает число а.
Приведем математическую запись определения:
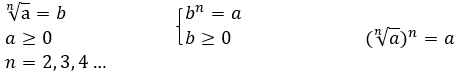
Например, 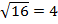 , т. к.
, т. к. 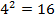 ;
; 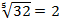 , т. к.
, т. к. 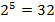 ;
;
Обратим внимание, что под знаком корня может стоять отрицательное число, но только в том случае, если корень – нечетной степени. В этом случае следует вынести минус из-под знака корня, и мы получим корень из неотрицательного числа: 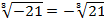
Напомним геометрическую интерпретацию корня n-й степени и дадим пояснения к определению.
Рассмотрим функцию 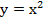 на множестве всех действительных значений. Рис. 1.
на множестве всех действительных значений. Рис. 1.
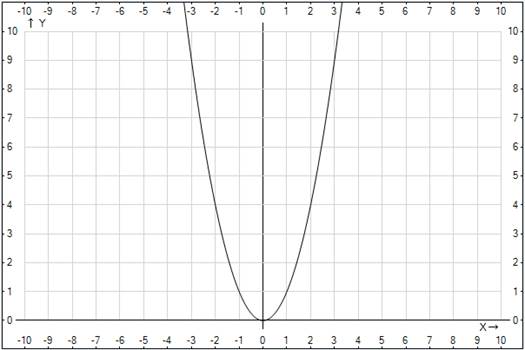
Рис. 1. График функции 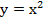
Значение 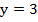 функция принимает при двух различных значениях аргумента:
функция принимает при двух различных значениях аргумента: 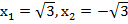
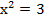 имеет два решения, положительное и отрицательное,
имеет два решения, положительное и отрицательное, 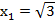 – неотрицательное значение – носит название арифметического корня.
– неотрицательное значение – носит название арифметического корня.Рассмотрим функцию 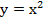 на множестве
на множестве 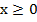 . Рис. 2.
. Рис. 2.
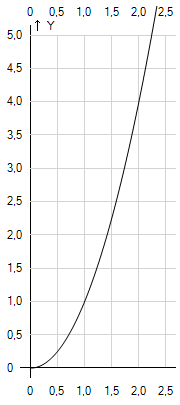
Рис. 2. График функции 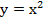 на множестве
на множестве 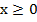
Данная функция принимает значение 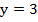 при единственном значении аргумента
при единственном значении аргумента 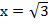 . Система
. Система
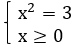
имеет единственное решение 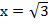 .
.
Корень n-й степени (n=2, 3, 4…) из произведения двух неотрицательных чисел равен произведению корней n-й степени из этих чисел.
Дано: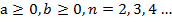
Доказать: 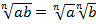
Доказательство:
Обозначим исходные выражения через х, у и z:
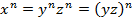
Так как все выражения неотрицательные и возводятся в натуральную степень, имеем право записать:
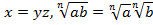
Теорема доказана.
Рассмотрим несколько примеров на применение доказанной теоремы.
Пример 1 – вычислить:

Теорема удобна тем, что не нужно выполнять трудоемкое умножение, а иногда, наоборот, раскладывать большие числа на множители.
Пример 2 – вычислить:
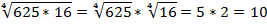
Теорема 1 допускает обобщение, например, для произведения трех сомножителей.
Обобщение:
Дано: 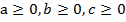 ,
, 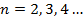
Доказать: 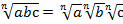
Доказательство:
Согласно условию 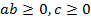 , если рассматривать ab как один множитель, а с как второй, можем применить к выражению теорему 1:
, если рассматривать ab как один множитель, а с как второй, можем применить к выражению теорему 1:
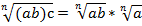
Теперь можем применить теорему 1 к корню из ab:
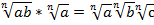
Обобщение доказано.
Пример 3 – вычислить:
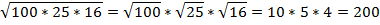
Пример 4 – вычислить:
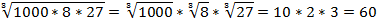
Если 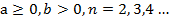 , то справедливо равенство:
, то справедливо равенство:
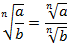
Дано: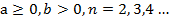
Доказать: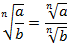
Доказательство:
Введем новые переменные:
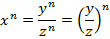
Так как все выражения неотрицательные и возводятся в натуральную степень, имеем право записать:
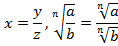
Теорема доказана.
Теорему 2 можно доказать непосредственно через теорему 1:
Дано: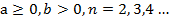
Доказать (используя теорему 1):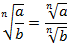
Доказательство:
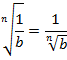
Если вышеуказанное равенство верно, то, возведя его правую часть в степень n, мы должны получить подкоренное выражение:
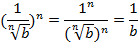
Рассмотрим заданное выражение:
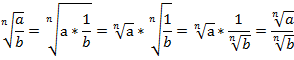
Теорема доказана.
Пример 5 – вычислить:

Пример 6 – вычислить:

Докажем теорему 1 вторым способом:
Дано: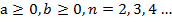
Доказать: 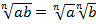
Доказательство:
Для доказательства будем использовать только определение корня.
Рассмотрим заданное выражение 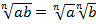 . Согласно определению корня, если правую часть выражения возвести в n-ю степень, мы должны получить подкоренное выражение, т. е.
. Согласно определению корня, если правую часть выражения возвести в n-ю степень, мы должны получить подкоренное выражение, т. е. 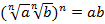
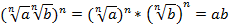
Теорема доказана.
Итак, мы рассмотрели и доказали важные теоремы о корне n-й степени из произведения и частного. На следующих уроках мы продолжим изучение свойств корня n-й степени.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Terver.ru (Источник).
- Pm298.ru (Источник).
- School.xvatit.com (Источник).
Домашнее задание
1. Алгебра и начала анализа, 10–11 класс (А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын) 1990, № 381–384;
2. Вычислить:
а) 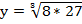 ; б)
; б) 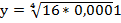 ; в)
; в) 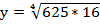 ; г)
; г) 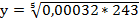 ;
;
3. Вычислить:
а) 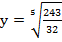 ; б)
; б) 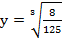 ; в)
; в) 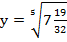 ; г)
; г) 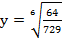
Урок по теме: «Свойства корня степени п»
Жученко Ирина Николаевна
Учитель математики
Квалификационная категория: высшая
Урок по алгебре и началам анализа в 10 классе (информационно-технологический профиль)
Тема урока: «Свойства корня степени п»
Цель деятельности учителя: создать условия для проверки знаний, умений и навыков обучающихся по усвоению и применению изученного материала.
Планируемые результаты:
Предметные: демонстрируют знание определения и свойств корня степени п, применяют эти знания для вычисления корней степени п, упрощения выражений, содержащих корни степени п, решения иррациональных уравнений, нахождения области допустимых значений выражений, содержащих корни степени п.
Познавательные: проводят анализ, конкретизацию;
Регулятивные: вносят необходимые коррективы в действие после его завершения, осуществляют самоанализ и самоконтроль, проводят рефлексию.
Коммуникативные: координируют различные позиции в сотрудничестве, учитывают разные мнения при работе в группе.
Личностные: осознают важность математических знаний для человека.
Тип урока: урок развивающего контроля.
Формы работы: фронтальная, групповая, индивидуальная.
Оборудование: мультимедийный проектор,карточки для индивидуальной и групповой работы, листы самооценки.
Ход урока.
. Организационный момент.
. Математическая разминка.
Задания проектируются на экран. Обучающиеся работают индивидуально. Затем сообщаются правильные ответы. Ученики выполняют самопроверку.
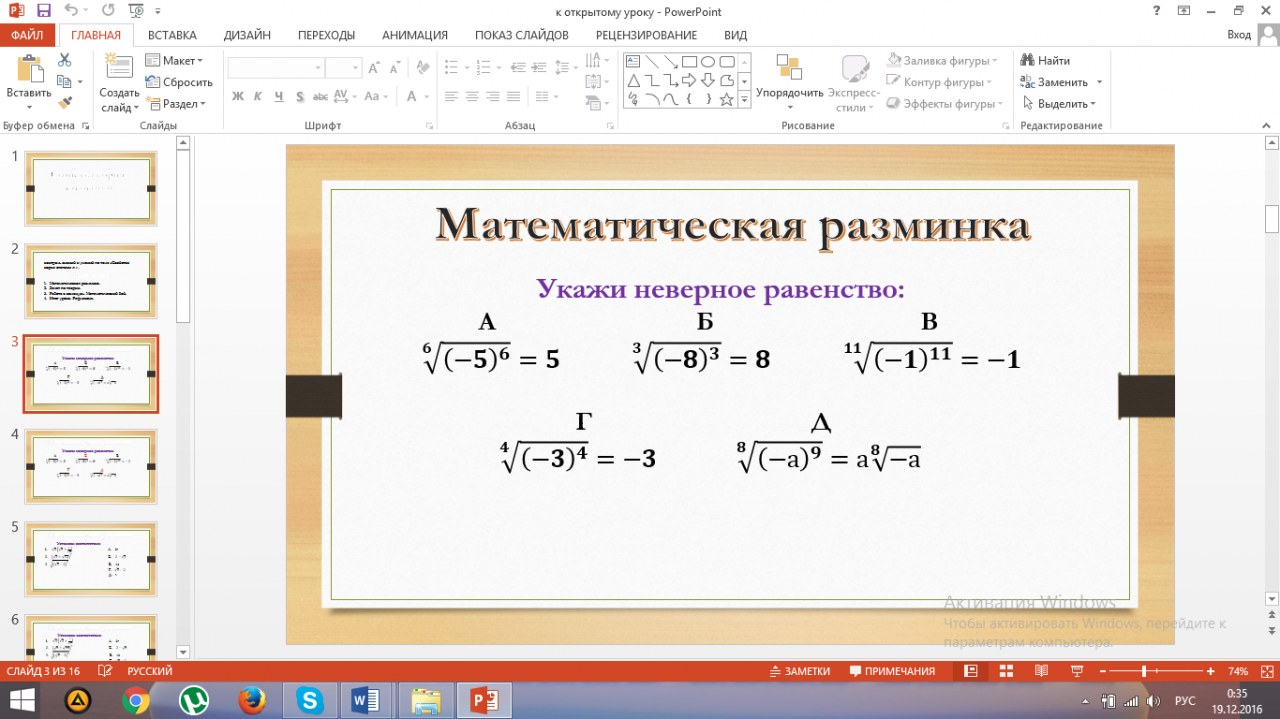
Ответ: Б, Г, Д.
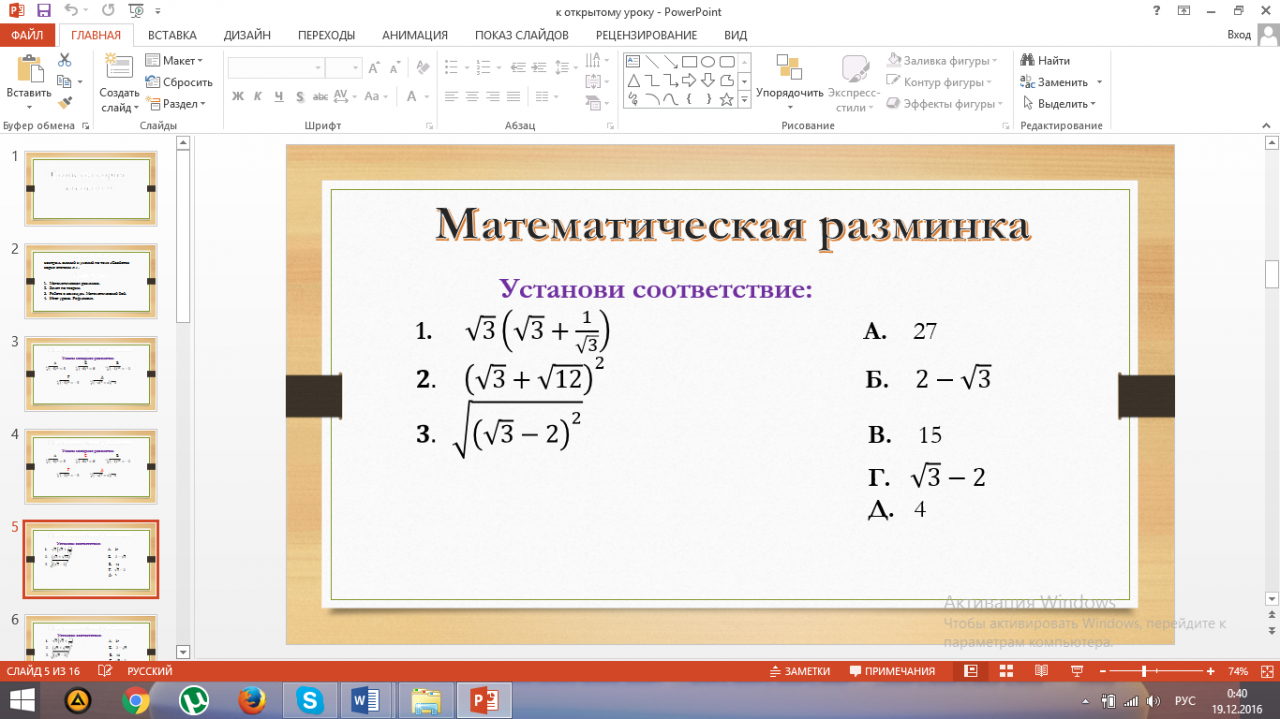
Ответ:1 – Д 2 – А 3 – Б
По окончании разминки ученики выставляют в лист самооценки отметки о правильно выполненных заданиях («+», «–»).
. Зачет по теории.
Ученики получают карточки, в которых они должны продолжить формулу. Все формулы описывают свойства корня степени п.
Фамилия Имя _______________________________________ Свойства корня степени п Для произвольного п ϵ N, п ≠ 1 При а ≥ 0, При а ≥ 0,b ≥ 0, При а ≥ 0,b> 0, При а ≥ 0, При а ≥ 0, ип – нечетном При а ≥ 0, ип – четном |
На экран выводятся правильные ответы. Ученики выполняют самопроверку.
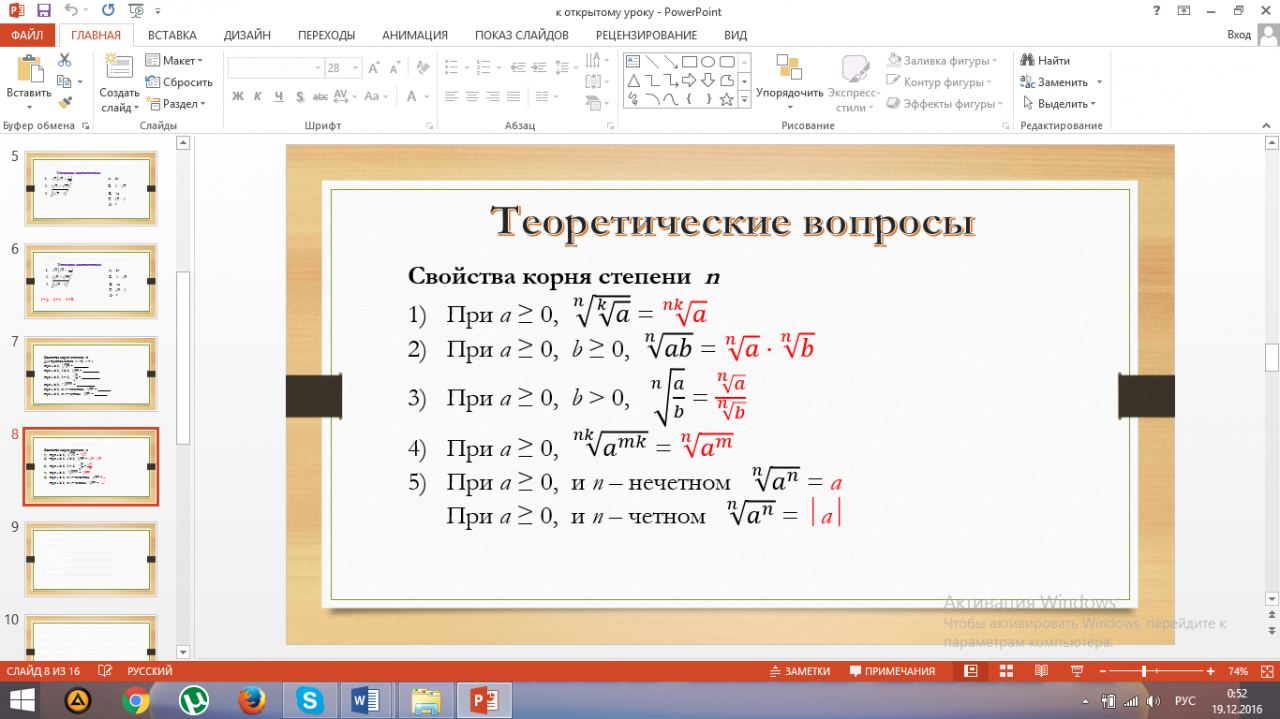
Затем выставляют в лист самооценки отметки о правильно выполненных заданиях («+», «–»).
V. Основной блок.
Учитель фронтально работает с классом.
— на доске написаны глаголы, что они означают?
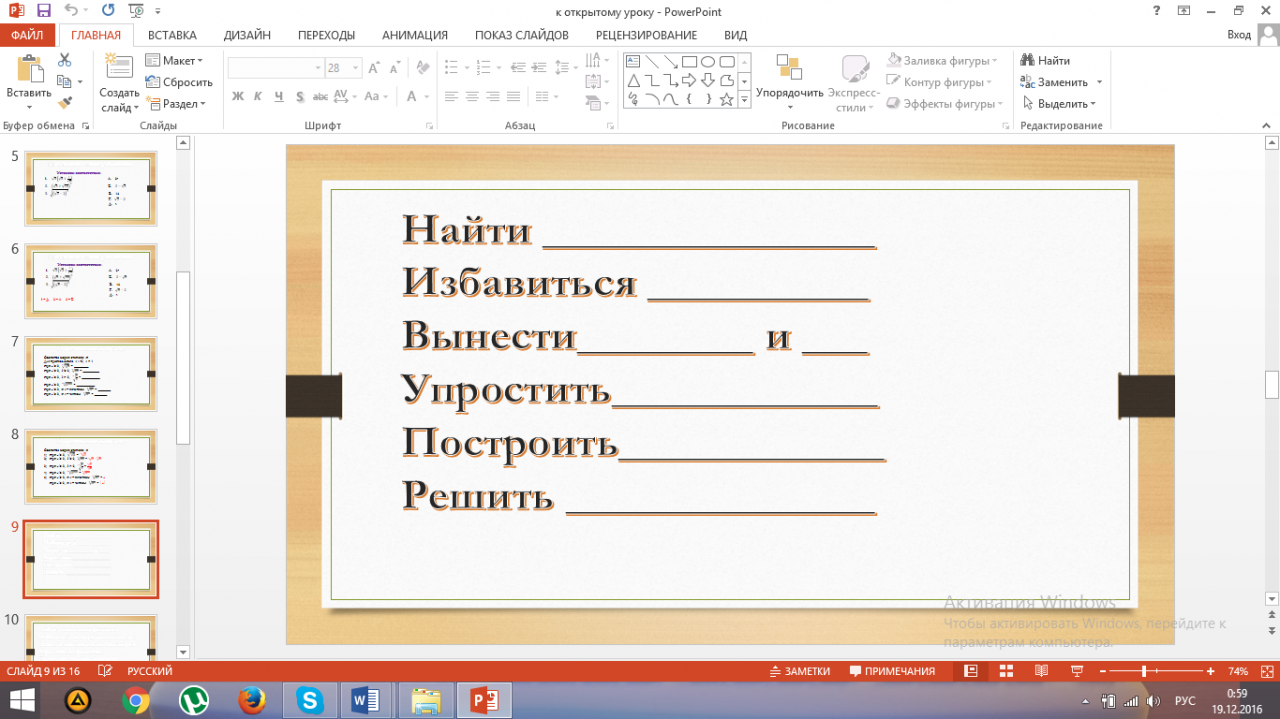
(основные типы заданий по теме «Корень степени п»)
— сформулируйте их.
(найти значение выражения, избавиться от иррациональности в знаменателе дроби, вынести множитель из-под знака корня и внести множитель под знак корня, упростить выражение, построить график функции, решить иррациональное уравнение)
— одного типа не хватает, какого?
(найти область допустимых значений выражения).
— сегодня на уроке будем проверять умения решать именно эти типы заданий.
Работа в группах. Игра «Математический бой».
Правила игры: Команды получают одинаковые карточки с заданиями.
Найти значение выражения:
а) 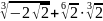 ;б)
;б) 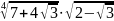
Избавьтесь от иррациональности в знаменателе:
а) 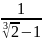 ; б)
; б) 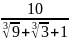 .
.
Вынесите множитель из-под знака корня:
a)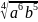 ,еслиа ≤ 0;
,еслиа ≤ 0;
б) 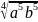 ,если а ≤ 0;
,если а ≤ 0;
в) 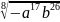 ,если b≤ 0
,если b≤ 0
Найдите произведение натуральных значений х, при которых имеет смысл выражение 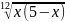 .
.
Упростите выражение
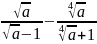
Постройте график функции y =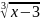
Решите уравнение 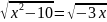
Представьте в виде корня выражение 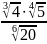
На решение всех заданий дается 15 минут. Затем команды в порядке очереди задают другой команде номер задания, решение которого они хотели бы услышать. Член команды соперников выступает с защитой своего способа решения. Члены других команд могут задавать ему вопросы по решению. Жюри оценивает ответ и вопросы соперников. Если команда не решила задание, она теряет столько баллов, во сколько оценено задание. Один раз за всю игру команда вправе отказаться отвечать по предложенной задаче без потери баллов и попросить другой номер.
В конце игры жюри подводит итоги. Ученики отмечают свой результат в листе самооценки.
V. Итоги урока. Рефлексия.
ЛИСТ САМООЦЕНКИ
Я убедился, что умею решать все типы заданий по данной теме или знаю, как это делать. Я увидел, что допускаю ошибки в заданиях типа_______ или не знаю, как их решать. К сожалению, я понял, что мне еще надо много работать, чтобы получить хороший результат на контрольной работе. Моя работа на уроке была продуктивной. |
В листе самооценки указаны задачи ЕГЭ. Это резерв на случай, если останется время.
Задать домашнее задание. Выставить оценки в журнал и дневники.
Презентация к уроку по алгебре (10 класс): Презентация по алгебре для 10 класса «Корень н-ной степени»
Слайд 1
Корень n -ной степениСлайд 2
Повторение Квадратный корень. Арифметический квадратный корень.
Слайд 3
Решите задачу Площадь квадрата равна 144 . Чему равна длина стороны этого квадрата? x Квадратные корни 12 см – длина стороны квадрата Арифметический квадратный корень
Слайд 4
Арифметический квадратный корень числа 144 = 12 Арифметическим квадратным корнем из числа a называется неотрицательное число b , квадрат которого равен a . При a 0 выражение не имеет смысла — не имеет смысла
Слайд 5
2 4 5 7 Не имеет смысла 11 25 21 14 28
Слайд 6
= 4 = 25 Основное свойство арифметического квадратного корня = 64
Слайд 7
Уравнения
Слайд 9
ОПРЕДЕЛЕНИЕ КОРНЯ Корнем n -ой степени из числа а называется такое число, n -ая степень которого равна а . ОБОЗНАЧАЮТ : — знак корня n — показатель корня а — подкоренное выражение
Слайд 10
Замечания :
Слайд 11
Замечание: Корень четной степени имеет смысл только для неотрицательного подкоренного числа; корень нечетной степени имеет смысл для любого подкоренного числа
Слайд 12
Имеет ли смысл выражения
Слайд 13
Свойства корня n- ой степени
Слайд 14
1.Корень n- степени ( n =2,3,4,5, …) из произведения двух неотрицательных чисел равен … произведению корней n- степени из этих чисел: = = = 2·3=6
Слайд 15
2. Если a ≥ 0, b> 0 и n =2,3,4,5,… то справедливо равенство = = =
Слайд 16
3. Если a ≥ 0, n =2,3,4,5,… и k любое натуральное число, то справедливо равенство
Слайд 17
4. Если a ≥ 0, n и k — натуральные числа, большие 1, то справедливо равенство
Слайд 18
5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то… значение корня не изменится
Слайд 19
Найдите значение числового выражения 1, 5 2 2 ) 3 ) 2 1 )
Слайд 20
4 ) 5 ) 6 )
Слайд 21
сравните 2 ) > 1 )
Слайд 22
Задания открытого банка задач . Найдите значение выражения . Решение. Найдите значение выражения . Решение.
Слайд 23
Решение. Задания открытого банка задач Найдите значение выражения . Найдите значение выражения при х 2. Решение. Т.к. при х 2
Слайд 24
? – мне есть над чем работать – всё понял (а) – Ура! Всё супер
Слайд 26
«Вы — талантливые дети! Когда – нибудь вы сами приятно поразитесь, какие вы умные, как много вы сумеете, если будете постоянно работать над собой…» Жан-Жак Руссо
Урок 16. арифметический корень натуральной степени — Алгебра и начала математического анализа — 10 класс
Урок Конспект Дополнительные материалыАрифметический корень натуральной степени
Выберите соответствие:
ПодсказкаПеренесите числа в левую часть уравнения, разложите каждую левую часть на простые множители, обратите внимание на количество множителей и показатель корня, а также – на знак перед числом; помним, что корень чётной степени нельзя извлечь из отрицательного числа.
Арифметический корень натуральной степени
Выберите верные утверждения:
ПодсказкаПримените определение арифметического корня: Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a.
Арифметический корень натуральной степени
Вычислите и запишите ответ:
ПодсказкаВоспользуйтесь свойством арифметического корня $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$, а затем каждое подкоренное выражение разложите на простые множители и обратите внимание на показатель корня.
$\sqrt[4]{\frac{16}{81}}=$
Варианты ответа (введите порядковый номер):
1) $\frac{3}{4}$
2) $\frac{2}{3}$
3) $\frac{1}{3}$
Арифметический корень натуральной степени
Выберите верные утверждения:
ПодсказкаВоспользуйтесь определением арифметического корня. Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна а. Воспользуйтесь свойством корня $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$.
Арифметический корень натуральной степени
ПодсказкаДля решения примеров можно применить следующие свойства: $\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}$; $\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$; $(\sqrt[n]{a})^{m}=\sqrt[n]{a^{m}}$.
$\sqrt[3]{\frac{-729}{125}}$= 1,8 -3,5 -1,9
$\sqrt[3]{9}⋅\sqrt[3]{24}$= 3 6 4
$\sqrt[3]{7^{6}}$= 49 48 42
$\sqrt[4]{0,0048⋅27}$= 0,3 0,9 0,6
Арифметический корень натуральной степени
ПодсказкаПредставьте подкоренные выражения в виде произведения одинаковых множителей, посчитайте количество множителей и обратите внимание на показатель корня.
Арифметический корень натуральной степени
Подчеркните верные ответы для уравнения:
x4 = 256
ПодсказкаПредставьте правую часть уравнения в виде произведения четырех одинаковых множителей.
Арифметический корень натуральной степени
Вычислите
Варианты ответов (введите порядковый номер):
1) -4
2) 3
3) 49
4) 0
5) 4
6) 16
ПодсказкаВоспользуйтесь определением арифметического корня. Арифметическим корнем натуральной степени из неотрицательного числа a называется неотрицательное число, n-я степень которого равна a и одним из его свойств $\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}$.
Арифметический корень натуральной степени
Установите соответствие между выражениями и ответами:
ПодсказкаВоспользуйтесь свойством $\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}$.
Арифметический корень натуральной степени
Найдите значение выражения и запишите ответ:
$\frac{7\sqrt{x}-5}{\sqrt{x}}+\frac{5\sqrt{x}}{x}+3x-4$, при x = 3.
ПодсказкаПредставьте х как произведение $\sqrt{x}\cdot\sqrt{x}$, приведите все к общему знаменателю, домножив на $\sqrt{x}$.
Арифметический корень натуральной степени
Установите соответствие между примерами и ответами:
ПодсказкаВоспользуйтесь свойством арифметического корня: $\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}$.
Арифметический корень натуральной степени
Запишите множитель, который можно вынести из-под знака корня (степени записывайте обычными цифрами после букв, например, а8):
ПодсказкаВоспользуйтесь свойствами арифметического корня: $\sqrt[n]{ab}=\sqrt[n]{a}\sqrt[n]{b}$, $\sqrt[n]{\sqrt[m]{a}}=\sqrt[mn]{a}$.
Арифметический корень натуральной степени
Выберите верный ответ:
$\sqrt[3]{1-\sqrt{3}}\cdot \sqrt{\sqrt[3]{4+2\sqrt{3}}}=$
Варианты ответа (введите порядковый номер):
1) $-\sqrt[3]{2}$
2) $\sqrt[3]{2}$
3) $\sqrt[6]{4}$
4) $-\sqrt[6]{4}$
ПодсказкаВсе выражение стоит представить под корнем 6-й степени, для этого надо $1-\sqrt{3}$ возвести в квадрат, тогда получим выражение: $\sqrt[6]{(1-\sqrt{3})^{2}\cdot (4+2\sqrt{3})}$. Далее следует применить формулы квадрата разности и разности квадратов.
Арифметический корень натуральной степени
Установите соответствие между примерами и ответами:
ПодсказкаВ первом и втором примерах избавьтесь от корней четвертой степени, а затем воспользуйтесь формулами квадрата суммы и квадрат разности, в третьем примере избавьтесь от корня четвертой степени и выполните действия сложения и вычитания.
Презентация к уроку по алгебре (10 класс) на тему: Свойства корня степени n
Слайд 1
МБОУ «Гимназия №6» г. Брянска Кривенкова Т.Ф. Свойства корней степени nСлайд 2
1. =0 2. =1 3. ( ) =a – по определению, причем ( ) =a для любых а ( ) =a только при а≥0 4. =a 5. = 6.( ) = — для всех а из области определения выражения 7. Корень из корня = — для всех а из области определения выражения 8.Корень из степени = при a
Слайд 3
9. Корень из произведения и частного Область применения формул Формулы Примеры Для неотрицательных a и b (a = (b = =3 = = Для любых a и b Корень нечетной степени = = (b = ab = = = Корень четной степени = где ab = , где = = 9. Корень из произведения и частного Область применения формул Формулы Примеры Для любых a и b Корень нечетной степени Корень четной степени
Слайд 4
10. Основное свойство корней При а 0 и, наоборот, Значение корня из степени неотрицательного числа не изменится, если показатель корня и показатель подкоренного выражения умножить (или разделить) на одно и то же число Особенности использования основного свойства при любых значениях а Умножение показателей Область применения формул Формулы Примеры m и n – оба нечетные, k — четное = = ; = — = — = — В остальных случаях ; . 10. Основное свойство корней Особенности использования основного свойства при любых значениях а Умножение показателей Область применения формул Формулы Примеры m и n – оба нечетные, k — четное В остальных случаях
Слайд 5
Деление показателей Хотя бы одно из чисел n и k — четное В частности, Если k — четное, то = = = = ; = = n и k – оба нечетные = = Деление показателей Хотя бы одно из чисел n и k — четное n и k – оба нечетные
Слайд 6
11.Вынесение множителя из-под знака корня Для неотрицательных a и b (a =a = ; =2 Для произвольного a Корень нечетной степени = = =(1 ) Корень четной степени , где b = = = =( 1) 11.Вынесение множителя из-под знака корня Для произвольного a Корень нечетной степени Корень четной степени
Слайд 7
12 .Внесение множителя под знак корня Для неотрицательных a и b (a a = 2 = = ; 2 = = Для произвольного a Корень нечетной степени = ) = Корень четной степени a = где = = ; (1 = = 12 .Внесение множителя под знак корня Для произвольного a Корень нечетной степени Корень четной степени
Слайд 8
Литература 1.С.М. Никольский, М. К .Потапов, Н . Н. Р ешетников, А. В.Шевкин «Алгебра и начала математического анализа» учебник для 10 класса 2.Е.П.Нелин «Алгебра 7-11 классы»
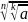 = ________
= ________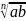 = _________
= _________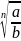 = __________
= __________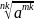 = __________
= __________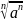 = _______
= _______