Угол. Градусная мера угла.
Понятие угла является одним из наиболее важных определений в геометрии. У́гол — геометрическая фигура, образованная двумя лучами, сторонами угла, выходящими из одной точки, которая называется вершиной угла. Понятия равенства и суммы углов часто используется в тригонометрии. Например, углы \(15,30,45\) градусов.
Наиболее распространенными единицами измерения угла являются градус и радиан. Один градус — это «\(\frac{1}{360}\)» полного круга. \(90\) градусов — это четверть круга, \(180\) – половина круга, \(270\) — три четверти круга и \(360\) это целый круг. Прямой угол равен \(90\) градусов, острый угол больше \(0\) и меньше \(90\) градусов и тупой угол больше \(90\) градусов и меньше \(180\) градусов. Развернутый угол равен \(180\) градусам.
Мы изучаем углы от \(0\)° до \(360\)°, но есть углы больше \(360\)° и отрицательные углы.
Градусы могут быть разделены на минуты и секунды.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявку Репетитор по математике
Ереванский госпединститут русского и иностранных языков им.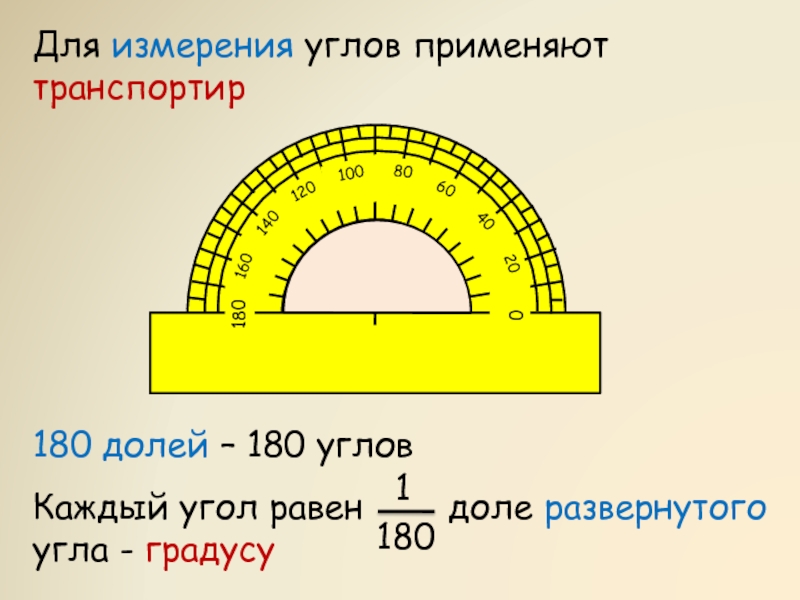 В.Я.Брюсова
В.Я.Брюсова
Форма обучения:
Дистанционно (Скайп)
Репетитор русского языка 1-11 классов. Давно влюблена в русский язык! Считаю, что языки призваны развивать интеллект, а языковое мышление — первая ступень в развитии логического мышления. Имея богатый опыт преподавательской и репетиторской деятельности, смогу передать свои знания и помогу в решении учебных задач. Оставить заявку
Давно влюблена в русский язык! Считаю, что языки призваны развивать интеллект, а языковое мышление — первая ступень в развитии логического мышления. Имея богатый опыт преподавательской и репетиторской деятельности, смогу передать свои знания и помогу в решении учебных задач. Оставить заявкуРоссийский университет дружбы народов
Проведенных занятий:
Форма обучения:Дистанционно (Скайп)
Репетитор 1-9 классов.
Репетитор по математике
Саратовский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 4-11 классов. Имею большой опыт работы с детьми. Готовлю к ОГЭ и ЕГЭ. Повышаю успеваемость. Помогаю в подготовке домашнего задания. Доходчиво объясняю ребенку даже сложные вещи на примерах. Всегда нахожу общий язык с учениками. Математика развивает интеллект, тренирует память, учит считать. За это я и люблю математику!
Имею большой опыт работы с детьми. Готовлю к ОГЭ и ЕГЭ. Повышаю успеваемость. Помогаю в подготовке домашнего задания. Доходчиво объясняю ребенку даже сложные вещи на примерах. Всегда нахожу общий язык с учениками. Математика развивает интеллект, тренирует память, учит считать. За это я и люблю математику!
Решение уравнений
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Математика 11 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Что такое угол? Определение, виды, как обозначают, примеры
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
Что такое вершина и стороны угла
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре.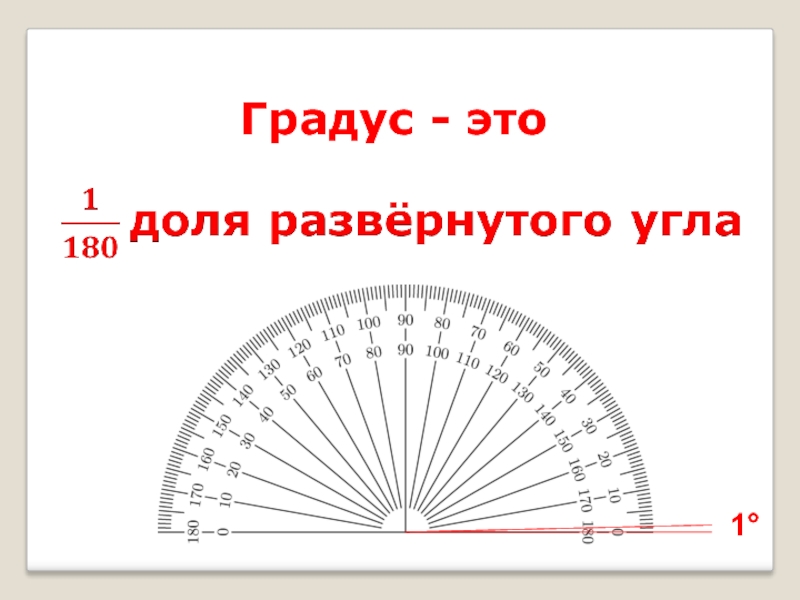 При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB − ∠COB,
- ∠COB = ∠AOB − ∠AOC.
Запоминаем!
Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
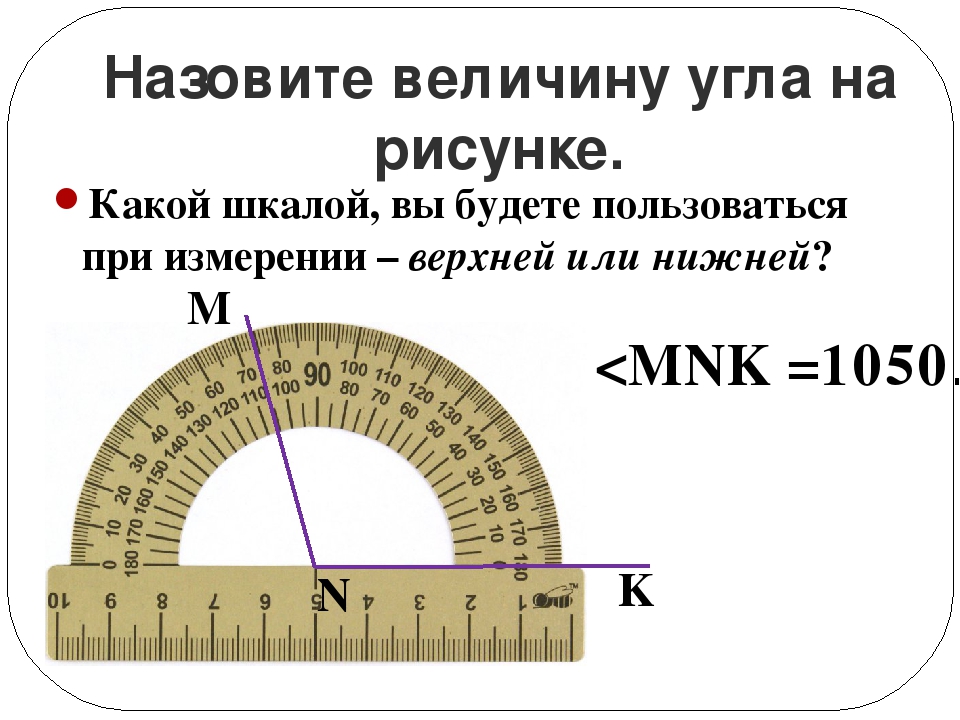
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Развернутый угол. Прямой, тупой, острый и развернутый угол
В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно.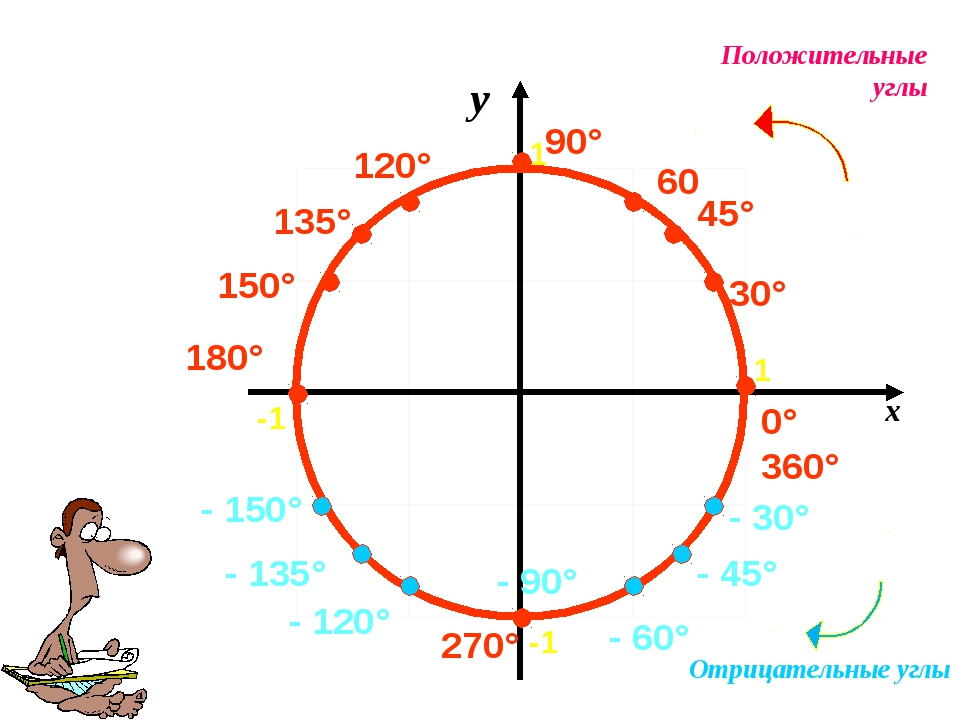 Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла — это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4.
 Вычислите полученные углы.
Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х. Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚.
 Ответ: 36˚ и 144˚.
Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
В этой статье мы всесторонне разберем одну из основных геометрических фигур – угол. Начнем со вспомогательных понятий и определений, которые нас приведут к определению угла. После этого приведем принятые способы обозначения углов. Далее подробно разберемся с процессом измерения углов. В заключении покажем как можно отметить углы на чертеже. Все теорию мы снабдили необходимыми чертежами и графическими иллюстрациями для лучшего запоминания материала.
Навигация по странице.
Определение угла.
Угол является одной из важнейших фигур в геометрии. Определение угла дается через определение луча. В свою очередь представление о луче невозможно получить без знания таких геометрических фигур как точка, прямая и плоскость. Поэтому, перед знакомством с определением угла, рекомендуем освежить в памяти теорию из разделов и .
Итак, будем отталкиваться от понятий точки, прямой на плоскости и плоскости.
Дадим сначала определение луча.
Пусть нам дана некоторая прямая на плоскости. Обозначим ее буквой a . Пусть O – некоторая точка прямой a . Точка O разделяет прямую a на две части. Каждая из этих частей вместе с точкой О называется лучом , а точка О называется началом луча . Еще можно услышать, что луч называют полупрямой .
Для краткости и удобства ввели следующие обозначения для лучей: луч обозначают либо малой латинской буквой (например, луч p или луч k ), либо двумя большими латинскими буквами, первая из которых соответствует началу луча, а вторая обозначает некоторую точку этого луча (например, луч ОА или луч СD ). Покажем изображение и обозначение лучей на чертеже.
Теперь мы можем дать первое определение угла.
Определение.
Угол – это плоская геометрическая фигура (то есть целиком лежащая в некоторой плоскости), которую составляют два несовпадающих луча с общим началом. Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Каждый из лучей называют стороной угла , общее начало сторон угла называют вершиной угла .
Возможен случай, когда стороны угла составляют прямую линию. Такой угол имеет свое название.
Определение.
Если обе стороны угла лежат на одной прямой, то такой угол называется развернутым .
Предлагаем Вашему вниманию графическую иллюстрацию развернутого угла.
Для обозначения угла используют значок угла «». Если стороны угла обозначены малыми латинскими буквами (например, одна сторона угла k
, а другая h
), то для обозначения этого угла после значка угла записывают подряд буквы, соответствующие сторонам, причем порядок записи значения не имеет (то есть, или ). Если стороны угла обозначены двумя большими латинскими буквами (к примеру, одна сторона угла OA
, а вторая сторона угла OB
), то угол обозначают следующим образом: после значка угла записывают три буквы, участвующие в обозначении сторон угла, причем буква, отвечающая вершине угла, располагается посередине (в нашем случае угол будет обозначен как или ).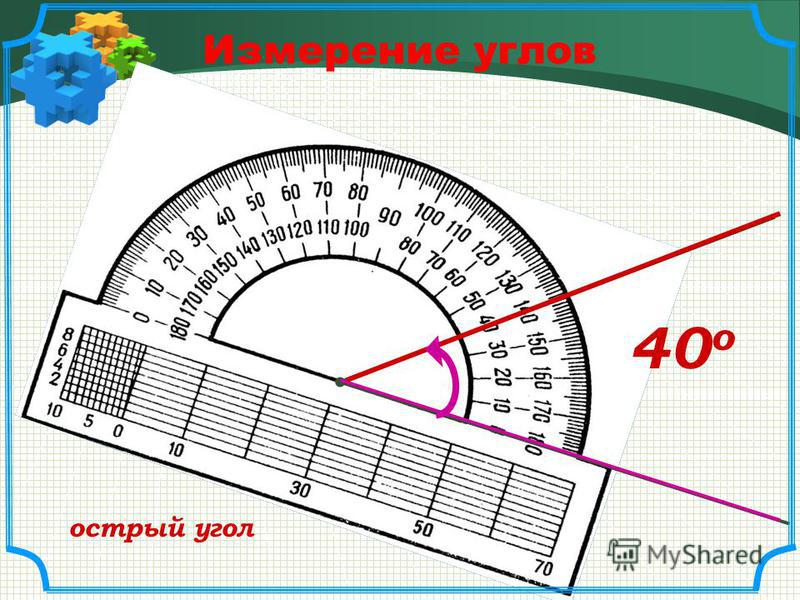 Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Если вершина угла не является вершиной еще какого-нибудь угла, то такой угол можно обозначать буквой, соответствующей вершине угла (например, ). Иногда можно видеть, что углы на чертежах отмечают цифрами (1
, 2
и т.д.), обозначают эти углы как и так далее. Для наглядности приведем рисунок, на котором изображены и обозначены углы.
Любой угол разделяет плоскость на две части. При этом если угол не развернутый, то одну часть плоскости называют внутренней областью угла , а другую – внешней областью угла . Следующее изображение разъясняет, какая часть плоскости отвечает внутренней области угла, а какая — внешней.
Любую из двух частей, на которые развернутый угол разделяет плоскость, можно считать внутренней областью развернутого угла.
Определение внутренней области угла приводит нас ко второму определению угла.
Определение.
Угол – это геометрическая фигура, которую составляют два несовпадающих луча с общим началом и соответствующая внутренняя область угла.
Следует отметить, что второе определение угла строже первого, так как содержит больше условий. Однако не следует отметать первое определение угла, также не следует рассматривать первое и второе определения угла по отдельности. Поясним этот момент. Когда речь идет об угле как о геометрической фигуре, то под углом понимается фигура, составленная двумя лучами с общим началом. Если же возникает необходимость провести какие-либо действия с этим углом (например, измерение угла), то под углом уже следует понимать два луча с общим началом и внутренней областью (иначе возникла бы двоякая ситуация из-за наличия как внутренней так и внешней области угла).
Дадим еще определения смежных и вертикальных углов.
Определение.
Смежные углы – это два угла, у которых одна сторона общая, а две другие образуют развернутый угол.
Из определения следует, что смежные углы дополняют друг друга до развернутого угла.
Определение.
Вертикальные углы – это два угла, у которых стороны одного угла являются продолжениями сторон другого.
На рисунке изображены вертикальные углы.
Очевидно, что две пересекающиеся прямые образуют четыре пары смежных углов и две пары вертикальных углов.
Сравнение углов.
В этом пункте статьи мы разберемся с определениями равных и неравных углов, а также в случае неравных углов разъясним, какой угол считается большим, а какой меньшим.
Напомним, что две геометрические фигуры называются равными, если их можно совместить наложением.
Пусть нам даны два угла. Приведем рассуждения, которые помогут нам получить ответ на вопрос: «Равны эти два угла или нет»?
Очевидно, что мы всегда можем совместить вершины двух углов, а также одну сторону первого угла с любой из сторон второго угла. Совместим сторону первого угла с той стороной второго угла, чтобы оставшиеся стороны углов оказались по одну сторону от прямой, на которой лежат совмещенные стороны углов. Тогда, если две другие стороны углов совместятся, то углы называются равными .
Если же две другие стороны углов не совместятся, то углы называются неравными , причем меньшим считается тот угол, который составляет часть другого (большим является тот угол, который полностью содержит другой угол).
Очевидно, что два развернутых угла равны. Также очевидно, что развернутый угол больше любого неразвернутого угла.
Измерение углов.
Измерение углов основывается на сравнении измеряемого угла с углом, взятым в качестве единицы измерения. Процесс измерения углов выглядит так: начиная от одной из сторон измеряемого угла, его внутреннюю область последовательно заполняют единичными углами, плотно укладывая их один к другому. При этом запоминают количество уложенных углов, которое и дает меру измеряемого угла.
Фактически, в качестве единицы измерения углов может быть принят любой угол. Однако существует множество общепринятых единиц измерения углов, относящихся к различным областям науки и техники, они получили специальные названия.
Одной из единиц измерения углов является градус .
Определение.
Один градус – это угол, равный одной сто восьмидесятой части развернутого угла.
Градус обозначают символом «», следовательно, один градус обозначается как .
Таким образом, в развернутом угле мы можем уложить 180 углов в один градус. Это будет выглядеть как половинка круглого пирога, разрезанная на 180 равных кусочков. Очень важно: «кусочки пирога» плотно укладываются один к другому (то есть, стороны углов совмещаются), причем сторона первого угла совмещается с одной стороной развернутого угла, а сторона последнего единичного угла совпадет с другой стороной развернутого угла.
При измерении углов выясняют, сколько раз градус (или другая единица измерения углов) укладывается в измеряемом угле до полного покрытия внутренней области измеряемого угла. Как мы уже убедились, в развернутом угле градус укладывается ровно 180 раз. Ниже приведены примеры углов, в которых угол в один градус укладывается ровно 30 раз (такой угол составляет шестую часть развернутого угла) и ровно 90 раз (половина развернутого угла).
Для измерения углов, меньших одного градуса (или другой единицы измерения углов) и в случаях, когда угол не удается измерить целым числом градусов (взятых единиц измерения), приходится использовать части градуса (части взятых единиц измерения). Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определенные части градуса получили специальные названия. Наибольшее распространение получили, так называемые, минуты и секунды.
Определение.
Минута – это одна шестидесятая часть градуса.
Определение.
Секунда – это одна шестидесятая часть минуты.
Иными словами, в минуте содержится шестьдесят секунд, а в градусе – шестьдесят минут (3600 секунд). Для обозначения минут используют символ «», а для обозначения секунд – символ «» (не путайте со знаками производной и второй производной). Тогда при введенных определениях и обозначениях имеем , а угол, в котором укладываются 17 градусов 3 минуты и 59 секунд, можно обозначить как .
Определение.
Градусной мерой угла называется положительное число, которое показывает сколько раз градус и его части укладываются в данном угле.
Например, градусная мера развернутого угла равна ста восьмидесяти, а градусная мера угла равна .
Для измерения углов существуют специальные измерительные приборы, наиболее известным из них является транспортир.
Если известно и обозначение угла (к примеру, ) и его градусная мера (пусть 110 ), то используют краткую запись вида и говорят: «Угол АОВ равен ста десяти градусам».
Из определений угла и градусной меры угла следует, что в геометрии мера угла в градусах выражается действительным числом из интервала (0, 180] (в тригонометрии рассматривают углы с произвольной градусной мерой, их называют ). Угол в девяносто градусов имеет специальное название, его называют прямым углом . Угол меньший 90 градусов называется острым углом . Угол больший девяноста градусов называется тупым углом . Итак, мера острого угла в градусах выражается числом из интервала (0, 90) , мера тупого угла – числом из интервала (90, 180) , прямой угол равен девяноста градусам. Приведем иллюстрации острого угла, тупого угла и прямого угла.
Из принципа измерения углов следует, что градусные меры равных углов одинаковы, градусная мера большего угла больше градусной меры меньшего, а градусная мера угла, который составляют несколько углов, равна сумме градусных мер составляющих углов. На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
На рисунке ниже показан угол АОВ
, который составляют углы АОС
, СОD
и DОВ
, при этом .
Таким образом, сумма смежных углов равна ста восьмидесяти градусам , так как они составляют развернутый угол.
Из этого утверждения следует, что . Действительно, если углы АОВ и СОD – вертикальные, то углы АОВ и ВОС — смежные и углы СОD и ВОС также смежные, поэтому, справедливы равенства и , откуда следует равенство .
Наряду с градусом удобна единица измерения углов, называемая радианом . Радианная мера широко используется в тригонометрии. Дадим определение радиана.
Определение.
Угол в один радиан – это центральный угол , которому соответствует длина дуги, равная длине радиуса соответствующей окружности.
Дадим графическую иллюстрацию угла в один радиан. На чертеже длина радиуса OA (как и радиуса OB ) равна длине дуги AB , поэтому, по определению угол AOB равен одному радиану.
Для обозначения радианов используют сокращение «рад». Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Например, запись 5 рад означает 5 радианов. Однако на письме обозначение «рад» часто опускают. К примеру, когда написано, что угол равен пи, то имеется в виду пи рад.
Стоит отдельно отметить, что величина угла, выраженная в радианах, не зависит от длины радиуса окружности. Это связано с тем, что фигуры, ограниченные данным углом и дугой окружности с центром в вершине данного угла, подобны между собой.
Измерение углов в радианах можно выполнять так же, как и измерение углов в градусах: выяснить, сколько раз угол в один радиан (и его части) укладываются в данном угле. А можно вычислить длину дуги соответствующего центрального угла, после чего разделить ее на длину радиуса.
Для нужд практики полезно знать, как соотносятся между собой градусная и радианная меры, так как довольно часть приходится осуществлять . В указанной статье установлена связь между градусной и радианной мерой угла, и приведены примеры перевода градусов в радианы и обратно.
Обозначение углов на чертеже.
На чертежах для удобства и наглядности углы можно отмечать дугами, которые принято проводить во внутренней области угла от одной стороны угла до другой. Равные углы отмечают одинаковым количеством дуг, неравные углы – различным количеством дуг. Прямые углы на чертеже обозначают символом вида «», который изображают во внутренней области прямого угла от одной стороны угла до другой.
Если на чертеже приходится отмечать много различных углов (обычно больше трех), то при обозначении углов кроме обычных дуг допустимо использование дуг какого-либо специального вида. К примеру, можно изобразить зубчатые дуги, или нечто подобное.
Следует отметить, что не стоит увлекаться с обозначением углов на чертежах и не загромождать рисунки. Рекомендуем обозначать только те углы, которые необходимы в процессе решения или доказательства.
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.

- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Погорелов А.В., Геометрия. Учебник для 7-11 классов общеобразовательных учреждений.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Yandex.RTB R-A-339285-1 Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение 6Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Что такое угол?
Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160).
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины.
Например, вместо «угол АОВ» пишут короче: «угол О».
Вместо слова «угол» пишут знак .
Например, AОВ, O.
На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла.
Как и все геометрические фигуры, углы сравниваются с помощью наложения.
Если один угол можно наложить на другой так, что они совпадут, то эти углы равны.
Например, на рисунке 162 ABC = MNK.
Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.
Пишут: COP
Прямой и развернутый угол
Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164).
Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165).
Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166).
Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми.
Прямым углом называют половину развернутого угла.
Чертежный треугольник
Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо:
а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА;
б) провести вдоль второй стороны треугольника луч ОВ.
В результате получим прямой угол АОВ.
Вопросы к теме
1.Что такое угол?
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.
Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О.
Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных.
Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла.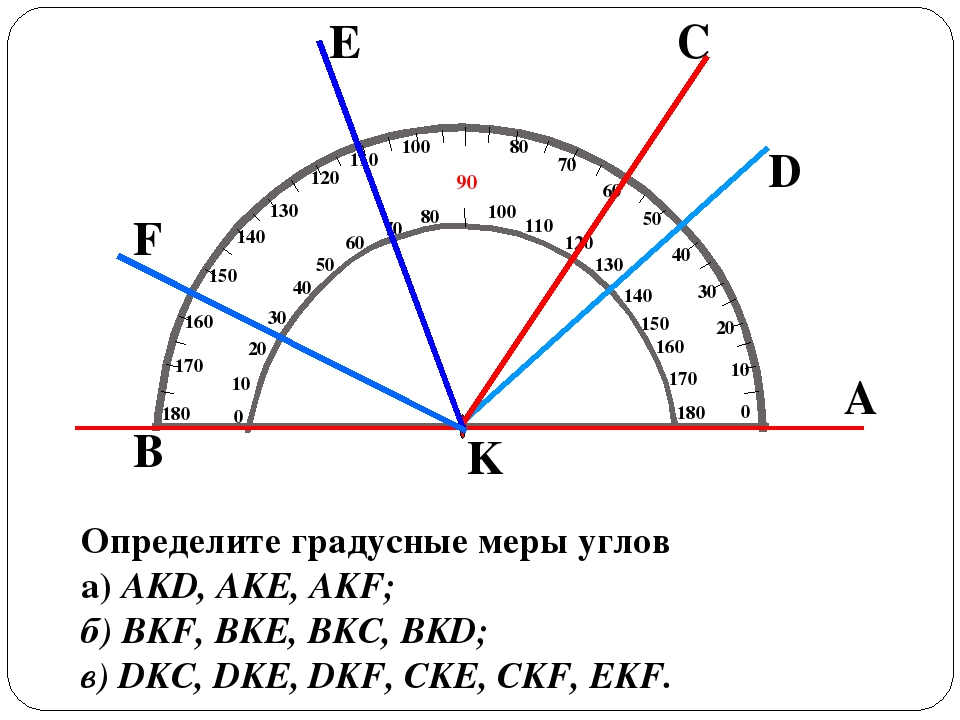
А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым.
Свойства развернутого угла
Развернутый угол обладает такими свойствами:
Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую;
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.
Измерение углов
Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам.
То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид: « ° ».
Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным.
А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол.
Практическое задание
1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения.
1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ?
На сколько частей эти лучи делят плоскость ?
1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD.
1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170).
1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях.
1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения.
1620. Укажите прямые углы в классной комнате.
а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1.
1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600?
1630. Найдите пропущенное число:
а) 2 5 3 б) 2 3 5
13 6 12 1
2 3? 42?
1631.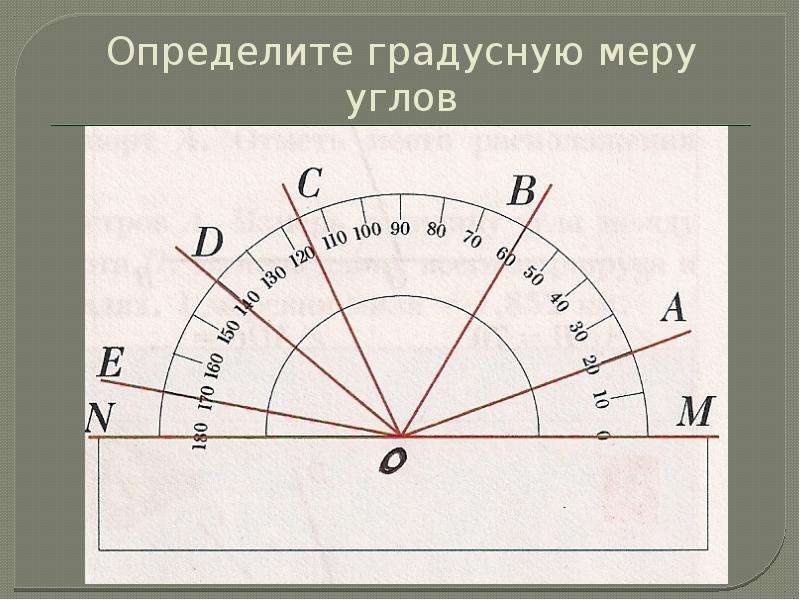 Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года?
1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди?
1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
1635. Найдите с помощью микрокалькулятора:
а) 4,5% от 168; в) 28,3% от 569,8;
б) 147,6% от 2500; г) 0,09% от 456 800.
1636. Решите задачу:
1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось?
1637. Выполните действия:
1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85;
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла.
1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК?
1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь.
1642. Найдите значение выражения:
а) 14,791: а + 160,961: b, если а = 100, b = 10;
б) 361,62с + 1848: d, если с = 100, d =100.
1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день?
1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке?
1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики?
1646. Найдите, сколько составляют:
а) 1% от тонны; в) 5% от 7 т;
б) 1% от литра; г) 6% от 80 км.
1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т?
1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат?
Н. Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам .
В морской терминологии углы обозначаются румбами .
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation . 2010 .
Смотреть что такое «Развернутый угол» в других словарях:
Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
Развертка кривой см. Эвольвента … Большой Энциклопедический словарь
угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… …
Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия
Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь
Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия
поперек — ▲ под углом максимум, косой угол поперечный. поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языка
градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка
Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия
Очень важной с практической точки зрения является проблема о конформном… … Википедия
Радиан, Углы больше 360 градусов, Положительные и отрицательные углы
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.
На картинке видны 4 разных угла, образованных пересечением прямых AB и CD
Обычно углы измеряются в градусах, что обозначается как °.
Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°).
Таким образом, градус — это $\frac{1}{360}$ круга.
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°. {\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
{\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
Объект описал $2\frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.
Пример 3
1. Найти соответствующий положительный угол
Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга. {\circ}$
{\circ}$
c) 1 рад = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$
Отрицаетльные углы и углы больше, чем $2\pi$ радиан
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.
Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.
Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$
Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.
Пример 6
1. Найти количество кругов пройденных объектом при данных углах
Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$
Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.
b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки
c) $\frac{7}{2}\pi=3,5\pi=2\pi+1,5\pi$, $1,5\pi$ равно три четверти цикла $(\frac{1,5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки
Почему в развернутом угле получилось 180 градусов? | Думай, как инженер!
Вспомним школьные дни. Уже в младшей школе дети сейчас начинают изучать основы геометрии. И одна из основ это измерение плоских углов. Мы все принимаем, что прямой угол — это 90 градусов, полный развернутый угол — 180 градусов, а вся окружность, соответственно, 360. Вы не задавались вопросом – почему так? Почему не 100 или 1000, а странное число 360? Сейчас расскажем Вам одну из обоснованных гипотез на этот счет…
Перенесемся же в древнюю Месопотамия на несколько тысяч лет назад. Именно там была одна из колыбелей человеческой цивилизации – шумерское государство, на месте которого впоследствии возникло Аккадское царство, а далее сам знаменитый Вавилон. Так вот, именно из тех давних времен, и происходит множество современных культурных, научных и других традиций, включая, например такие естественные для нас вещи, как семь дней в неделе или двенадцать месяцев в году. И измерение углов в градусах тоже происходит оттуда же.
Именно там была одна из колыбелей человеческой цивилизации – шумерское государство, на месте которого впоследствии возникло Аккадское царство, а далее сам знаменитый Вавилон. Так вот, именно из тех давних времен, и происходит множество современных культурных, научных и других традиций, включая, например такие естественные для нас вещи, как семь дней в неделе или двенадцать месяцев в году. И измерение углов в градусах тоже происходит оттуда же.
Сразу стоит отметить, что шумеры чрезвычайно увлекались астрономией и ее легкомысленно-глуповатой сестрицей астрологией. Для наблюдений за небесными светилами они как раз и строили свои знаменитые многоэтажные башни – зиккураты. И вот как-то раз древние ученые решили измерить на небе путь солнца… И в чем же его измерять, спросите Вы?
Древнешумерский бог Солнца ШамашДревнешумерский бог Солнца Шамаш
Ну уж точно не в попугаях! Солнце – это священный объект и измерять его путь нужно такой же священной величиной. И измерили они это расстояние самими солнечными дисками! Уложили их один за другим и оказалось, что от рассвета до заката их укладывается ровно 180! Но это всего полдороги небесного светила. Ведь, как это известно любому образованному шумеру, ночью солнце движется под земле обратно к точке рассвета. Наверное, та дорога такая же по длине, предположили шумеры, и получили длину суточного пути нашей звезды равную трехсотшестидесяти солнечным дискам!
И измерили они это расстояние самими солнечными дисками! Уложили их один за другим и оказалось, что от рассвета до заката их укладывается ровно 180! Но это всего полдороги небесного светила. Ведь, как это известно любому образованному шумеру, ночью солнце движется под земле обратно к точке рассвета. Наверное, та дорога такая же по длине, предположили шумеры, и получили длину суточного пути нашей звезды равную трехсотшестидесяти солнечным дискам!
Ну а дальше все уже очевидно. Мерой измерения углов и окружности стал размер того самого диска, как теперь мы их называем градусы. За много тысячелетий это шумерское геометрическое решение никак не изменилось. Как и многие другие, кстати. Множество знаний шумеров были подхвачены и приписаны себе другими древними народами. Даже часть Ветхого Завета заимствована из их легенд. Но это уже совсем другая история…
180 угол: 180 градусов угол какой? Тупой, прямой или острый? — ЭкоДом: Дом своими руками
Brennenstuhl датчик движения PIR 180, угол обзора 180 градусов, белый (1170900)
В современном мире одним из немногих необходимых устройств в офисах, на строительных площадках, придомовых территорий и любых других помещениях является датчик движения. Модель инфракрасного датчика PIR Brennenstuhl отлично подойдет для такого использования. Это применяют для того, чтобы привести в действие лампы. Угол обнаружения данной модели 180 °на дистанции около 12 м. Данная модель обладает возможностью регулировки яркости света. Датчик можно устанавливать как в горизонтальном положении, так и в вертикальном. Классический белый цвет данного датчика станет замечательной составляющей любого интерьера.
Модель инфракрасного датчика PIR Brennenstuhl отлично подойдет для такого использования. Это применяют для того, чтобы привести в действие лампы. Угол обнаружения данной модели 180 °на дистанции около 12 м. Данная модель обладает возможностью регулировки яркости света. Датчик можно устанавливать как в горизонтальном положении, так и в вертикальном. Классический белый цвет данного датчика станет замечательной составляющей любого интерьера.
Особенности:
- Датчик движения PlR 180 с защитой IP 44.
- Автоматически включает и выключает лампы (лампы накаливания, галогеновые лампы, энергосберегающие лампы и светодиодные лампы), когда кто-то входит в зону обнаружения.
- Для использования внутри/вне помещений.
- Угол обнаружения 180 °. Максимальная дальность работы 12 м.
- Рабочий цикл регулируется в пределах от 10 сек. до 4 мин.
- Яркость отклика регулируется от 10 до 150 люкс.
- Коммутационная способность — макс.
 1000 Вт (лампочки), макс. 300 Вт (энергосберегающая лампа), макс. 100 Вт (светодиод).
1000 Вт (лампочки), макс. 300 Вт (энергосберегающая лампа), макс. 100 Вт (светодиод). - Регулируется вертикально и горизонтально.
- Красочная упаковка.
Дальность действия:
12 м
Угол обнаружения:
180 °
Номинальное напряжение:
230 В
Материал корпуса:
пластик
Степень защиты
IP 20: для внутренних работ; IP 44: для наружных работ; IP 54: для недлительного использования под открытым небом
:
IP 44
Производитель:
Hugo Brennenstuhl GmbH & Co. KG
Поворотное крепление (угол 180 градусов) для светильников Айрон (V4-I0-70.0087.IR0-0001)
Код товара
7378123
Артикул
V4-I0-70.0087.IR0-0001
Страна
Россия
Наименование
Поворотное крепление (угол 180 градусов) для светильников Айрон
Упаковки
Сертификат
ПИСЬМО 051-OC-30-07-2015
Тип изделия Поворот
Высота, мм 80
Ширина, мм 45
Длина, мм 192
Масса, кг 0. 35
35
Способ подключения Поворотное крепление
Материал изделия Сталь
Способ монтажа Накладной
Цвет Металлик
Диапазон рабочих температур от -40 до +45
Сфера применения Промышленные и влажные помещения, совместим со светильниками серии Iron
Гарантийный срок, мес 60
Все характеристики
Характеристики
Код товара
7378123
Артикул
V4-I0-70.0087.IR0-0001
Страна
Россия
Наименование
Поворотное крепление (угол 180 градусов) для светильников Айрон
Упаковки
Сертификат
ПИСЬМО 051-OC-30-07-2015
Тип изделия Поворот
Высота, мм 80
Ширина, мм 45
Длина, мм 192
Масса, кг 0.35
Способ подключения Поворотное крепление
Материал изделия Сталь
Способ монтажа Накладной
Цвет Металлик
Диапазон рабочих температур от -40 до +45
Сфера применения Промышленные и влажные помещения, совместим со светильниками серии Iron
Гарантийный срок, мес 60
Все характеристики
Всегда поможем:
Центр поддержки
и продаж
Скидки до 10% +
баллы до 10%
Доставка по городу
от 150 р.
Получение в 150
пунктах выдачи
Угол открытия стеклянной двери Eurorack 180°, высота 43 U, ширина 600 мм
Поставщики в вашем регионе
Ниже приведен список местных поставщиков, которые в настоящее время имеют этот товар на складе:
| Дистрибьютор | Количество | Дата наличия на складе | Цена | |
|---|---|---|---|---|
| Информация отсутствует. |
Комплектность поставки
В комплект поставки этого изделия входят следующие позиции:
| Изделие | Описание | Количество | |
|---|---|---|---|
| 1 | Стеклянная дверь, закаленное стекло «Sekurit», 6 мм, дымчато-серое | 1 | |
| 2 | Английский замок с заглушкой | 1 | |
| 3 | Шарнир, сталь, 3 мм, RAL 9005 | 2 | |
| 4 | Монтажный комплект | 1 |
Острый, тупой, прямой и правый
Угол измеряет величину поворота
Названия углов
По мере увеличения угла название меняется:
Попробуйте сами:
В одной схемеЭта диаграмма может помочь вам запомнить: Также: Acute, Obtuse и Reflex расположены в алфавитном порядке. |
Также: буква «А» имеет острый угол.
Будьте осторожны при измерении
| Меньший угол — тупой угол , , но больший угол — угол отражения |
Поэтому при именовании углов убедитесь, что
что вы знаете , какой угол
просил !
Положительные и отрицательные углы
При измерении от линии:
- положительный угол идет против часовой стрелки (направление, противоположное движению часов)
- отрицательный угол идет по часовой стрелке
Пример: −67 °
Части угла
Угловая точка угла называется вершиной
И две прямые стороны называются руками
Угол равен повороту между каждым плечом.
Как маркировать углы
Есть два основных способа маркировать углы:
1. дайте углу имя, обычно строчную букву, например a или b , или иногда греческую букву, например α (альфа) или θ (тета)
2. или тремя буквами на форме, которые определяют угол, при этом средняя буква указывает на то, где на самом деле угол (его вершина).
или тремя буквами на форме, которые определяют угол, при этом средняя буква указывает на то, где на самом деле угол (его вершина).
Пример угла « a » равен « BAC », а угол « θ » равен « BCD »
.
Угол 180 градусов — Как его измерить и начертить
В этом мини-уроке мы узнаем об углах 180 градусов.При этом мы также обсудим создание угла 180 градусов с помощью компаса и шаги, которые необходимо выполнить, чтобы построить угол 180 градусов. Вы можете проверить интерактивные симуляции, чтобы узнать больше об уроке и попробовать свои силы в решении нескольких интересных практических вопросов в конце страницы.
Прежде чем мы начнем, замечали ли вы когда-нибудь угол между двумя стрелками часов в положении «6 часов»?
Угол между двумя стрелками на часах выше 180 °, потому что они образуют прямую линию.
Давайте подробнее рассмотрим угол 180 °.
План урока
Что такое угол 180 градусов?
Мы знаем, что угол образуется, когда два луча встречаются в вершине.
Если угол, образованный в вершине O, равен 180 °, мы называем это углом 180 градусов.
Прямой угол называется углом 180 градусов.
Его еще называют полукругом.Это похоже на прямую линию.
Как построить угол 180 градусов с помощью транспортира?
В этом разделе давайте рассмотрим, как построить угол 180 градусов с помощью транспортира.
Выполните следующие действия:
- Шаг 1. Нарисуйте отрезок линии \ (OA \)
- Шаг 2: Поместите транспортир в точку \ (O \)
- Шаг 3: Найдите во внешнем круге транспортира значение 180 °, отметьте карандашом точку и назовите ее \ (C \)
- Шаг 4: Соедините \ (O \) и \ (C \).\ circ \)
Все еще запутались? Посмотрите на симуляцию ниже.
Нажмите кнопку «Перейти», чтобы понять процесс построения угла 180 градусов с помощью транспортира.
Что такое углы 180 градусов в реальной жизни?
Углы 180 ° широко используются в реальной жизни.
В быту используются углы 180 градусов. При возведении конструкций, шоссе, домов и спортивных сооружений инженеры и архитекторы используют углы.Плотники делают из уголков скамейки, столы и диваны.
Обратите внимание на то, где вы можете видеть углы 180 ° в окружающем пространстве.
- Сколько 180-градусных углов в полном угле?
Решенные примеры
Можете ли вы помочь Алексу узнать разницу между углом 180 ° и углом 90 °?
Решение
Угол 180 градусов — это прямая линия, известная как полукруг.
Угол 90 градусов — это четверть круга или квадрант.
| 180 градусов — прямая линия или полукруг, а 90 градусов — квадрант |
Алина хочет построить угол 180 ° с помощью транспортира. Вы можете помочь ей построить?
Решение
Шаг 1: Нарисуйте луч (часть линии, у которой есть вершина на одном конце и острие стрелки на другом). Отметьте вершину как точку O.
Отметьте вершину как точку O.
Шаг 2: Точка O обозначает вершину угла.
Шаг 3: Теперь поместите транспортир над вершиной точки O и совместите базовую линию транспортира с плечом угла.
Шаг 4: Отметьте точкой угол 180 градусов.
Шаг 5: Теперь соедините эту новую вершину с точкой O. Это образует еще одно плечо угла.
Теперь у нас прямой угол.
- Угол 180 градусов также называется прямым углом, полукругом или полукругом.
- Угол 180 градусов можно построить с помощью транспортира или компаса.
Интерактивные вопросы
Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мы надеемся, что вам понравилось изучать угол 180 градусов с помощью моделирования и практических вопросов.Теперь вы сможете легко решать задачи на треугольнике с углом 180 градусов, строить угол 180 градусов с помощью компаса и другие связанные приложения с углом 180 градусов.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим.
Часто задаваемые вопросы об угле 180 градусов
1. Как выглядит угол 180 градусов?
180 градусов выглядят как прямая линия.
2. Как найти угол без транспортира?
Угол можно определить без транспортира с помощью циркуля или наклонной формы.
3. Сколько углов на 180 градусов нужно, чтобы сделать полный поворот?
Для полного поворота необходимы два угла 180 градусов.
4. Какой угол равен 180 градусам?
Угол 180 градусов — это прямой угол, потому что он образует прямую линию.
5. Угол 180 градусов тупой?
Тупой угол больше 90 °, но меньше 180 °, поэтому угол 180 градусов не является тупым углом.
8.1: Измерение угла — Математика LibreTexts
Угол — это мера размера отверстия двух пересекающихся линий. VERTEX является точкой пересечения, а линии, образующие проем, называются СТОРОНАМИ .
Угол можно назвать по
3 буквы с вершиной посередине: \ (\ angle ABC \) или только вершиной \ (\ angle B \), либо числом или буквой внутри угла.
В круге 360 градусов. Углы измеряются в градусах.
A Прямой угол составляет 90 градусов или 1/4 окружности. Right Angle будет выглядеть следующим образом.
Острый угол — это угол меньше 90 градусов.Ниже приведены примеры острых углов
.
Тупой угол — это угол больше 90 градусов и меньше 180 градусов. Ниже приведены примеры тупых углов.
A Прямой угол — это угол, равный 180 градусам.
Вертикальные углы
При пересечении двух прямых линий они образуют четыре угла.
Предположим, что \ (\ angle A \) равен 65 градусам, \ (\ angle B \) равен 115 градусам, \ (\ angle C \) равен 65 градусам, а \ (\ angle D \) равен 115 градусам
Вы заметили, что противоположные углы равны при измерении? Противоположные углы также называются Вертикальными углами .Когда две прямые линии пересекаются или пересекаются, вертикальные углы равны и всегда равны . Прямой угол — 180 градусов.
Углы W и X образуют прямую линию, вместе они составляют 180 градусов.
Они также известны как Смежные углы . Смежные углы в сумме составляют 180 градусов. Смежные углы также равны
.
- \ (\ angle Y \) и \ (\ angle Z \),
- \ (\ угол W \) и \ (\ угол Y \)
- \ (\ угол X \) и \ (\ угол Z \).

Сумма трех углов треугольника всегда составляет 180 градусов.
Линии Z и Y параллельны друг другу. Линия P, пересекающая обе линии, называется Transversal .
\ (\ angle C \) и \ (\ angle F \) называются Альтернативными внутренними углами ; Они равны по размеру.
\ (\ angle D \) и \ (\ angle E \) также называются Альтернативными внутренними углами .
Если угол равен 70 градусам, то \ (\ angle P \) будет равен 110 градусам, их сумма равна 180 градусам.
- \ (\ angle P \) и \ (\ angle Q \) — противоположные углы, поэтому они равны 110 градусам, потому что вертикальные углы равны друг другу.
- \ (\ angle P \) и \ (\ angle T \) и соответствующие углы, поэтому оба они равны 110 градусам.
- \ (\ angle W \) равняется 70 градусам, потому что \ (\ angle T \) плюс \ (\ angle W \) должно равняться в сумме 180 градусам.
Геометрия: линии и углы — Magoosh Math
Линии и углы составляют почти все геометрические формы. Итак, давайте погрузимся в геометрию, обсудив эти самые основные элементы форм.
Итак, давайте погрузимся в геометрию, обсудив эти самые основные элементы форм.
Теперь мы можем поговорить о геометрии. И, конечно же, геометрия — это изучение форм. Теперь для некоторых людей, ориентированных на зрение, геометрия приходит очень естественно. А другим людям, которые не развили свои визуальные навыки, с геометрией может быть посложнее.
Вот что я скажу специально для людей, для которых геометрия немного сложнее.
Недостаточно просто посмотреть эти ролики.После того, как вы посмотрите их, возьмите бумагу и линейку и нарисуйте эти разные формы, фактически физически нарисуйте их на бумаге. И создавайте формы и физические объекты. Вы можете использовать карандаши, зубочистки, соломку и все такое. На самом деле строите треугольники, строите прямоугольники, смотрите на них.
НАРИСИМ!
Изображение Aaron Amat
Используйте свои руки!
Используйте свои руки, наши руки на самом деле являются частью нашего интеллекта. Вы используете руки, вы задействуете каждую часть мозга.Так будет намного легче понять все эти отношения.
Итак, начнем с линий. Линии прямые и продолжаются вечно в обоих направлениях. Здесь у нас есть несколько разных прямых линий, направленных в разные стороны. Вы должны представить, что в конце каждой строки есть стрелки или что-то в этом роде. Это указывает на то, что линии действительно продолжаются вечно в обоих направлениях.
Линии и углы: все прямые прямые
Очень важно не путать прямую с горизонтальной.Эти два слова имеют очень разные значения, но иногда некоторые студенты путают их. Все линии прямые. Итак, все линии, которые у нас были на предыдущем слайде, линии, идущие в разных направлениях, все это прямые линии.
И вы всегда можете предположить, что линия на тесте прямая. Если смотрит прямо, то прям. Это всегда верно на тесте. Но некоторые линии для удобства нарисованы горизонтально. Однако вы никогда не можете предположить, что линии являются точно горизонтальными или вертикальными просто потому, что они кажутся таковыми.Теперь люди действительно запутались в этом. Вы сбиты с толку, если думаете, что горизонтальное и прямое означают одно и то же.
Если смотрит прямо, то прям. Это всегда верно на тесте. Но некоторые линии для удобства нарисованы горизонтально. Однако вы никогда не можете предположить, что линии являются точно горизонтальными или вертикальными просто потому, что они кажутся таковыми.Теперь люди действительно запутались в этом. Вы сбиты с толку, если думаете, что горизонтальное и прямое означают одно и то же.
Итак, мы говорим, что вы можете предположить из теста, что линии прямые. Люди ошибочно полагают, что это также означает, что они могут считать линии горизонтальными, а это неверно. Отрезок линии — это конечный отрезок линии.
Пример
Так, например, здесь у нас есть отрезок прямой, у него две конечные точки. И когда эти конечные точки помечены, это упрощает обсуждение.
Это отрезок AB. И для целей теста AB может означать фактическую форму самого отрезка линии. Или это может означать длину отрезка линии, числовую длину. Угол возникает между двумя линиями или двумя сегментами. Например, здесь у нас есть угол.
Линии и углы: понимание углов
Изображение Radu Bercan
Это происходит между одной линией и одним сегментом. Лучший способ понять угол — это думать о нем динамически, как об акте поворота или вращения.Другими словами, идем отсюда сюда. Вот что такое угол, это динамическое пространство между двумя линиями. Если мы помечаем точки, мы можем говорить об угле.
Уголки для этикеток
Мы могли бы назвать этот угол либо CDE, либо EDC, точка D, вершина угла. Здесь острие угла должно быть посередине имени. Итак, мы можем вызвать либо CDE, либо EDC, если вершина находится посередине. Иногда в этих видео я также использую одно название ракурса, если нет двусмысленности.Например, на этой диаграмме только один угол.
Я мог бы назвать это углом D. Теоретически это могло произойти на тесте. Хотя тест часто бывает достаточно осторожным, чтобы всегда использовать трехбуквенное имя для угла. Измеряем размер угла в градусах. Тест может указать это прямо, так что 50 градусов.
В качестве альтернативы тест может пометить диаграмму и указать меру угла в тексте. Итак, угол GFH = 50 градусов, потому что они ставят буквы в точках на диаграмме.Мы можем просто использовать это, чтобы говорить об этой мере, в количестве градусов в тексте. На самом деле, наверное, самое любимое занятие — это просто указать угол с переменным числом градусов.
Гибкий формат тестирования
Этот гибкий формат позволяет им либо указать угол, поскольку в тексте они могут сказать x = 50, либо задать вопрос по этому поводу. Они могут дать нам другую информацию и сказать «найди x». Итак, они хотели бы это сделать. Мы сделаем быстрый обзор основных фактов о степени.У прямого угла 180 градусов, и, конечно же, помните, что прямая линия может идти в любом направлении.
Но если есть какая-нибудь точка на прямой, от одной стороны до другой. То есть 180 градусов, есть 90 градусов под прямым углом. Итак, у нас есть две линии, пересекающиеся под прямым углом. На самом деле на этом пересечении есть четыре прямых угла. Если две линии или сегменты встречаются под прямым углом, они называются перпендикулярными, это термин, который вам следует знать.
Если две линии или сегменты встречаются под прямым углом, они называются перпендикулярными, это термин, который вам следует знать.
Перпендикулярные линии и прямые углы
Тест может либо нарисовать этот маленький квадрат, перпендикулярный знак, который является этим маленьким квадратом, либо он может указать, что угол равен 90 градусам. Он может обозначать 90 градусов на диаграмме или X градусов и сообщать нам в тексте, что X равно 90. Есть множество способов, которыми они могут сказать нам, что это угол 90 градусов. Не думайте, что две линии перпендикулярны, если вам не сказали об этом явно, это часто бывает ловушкой.
Изображение Анара Бабаева
Предположим, что эти точки появляются как часть большей диаграммы, и никакой дополнительной информации не дается.Конечно, похоже, что они могут быть расположены под прямым углом, и это очень заманчиво предположить. Тесту хотелось бы, чтобы вы допустили ошибку, предположив, что линии перпендикулярны, а угол равен точно 90 градусам.
На самом деле это не так, я нарисовал это так, что угол составляет 89,6 градуса. Итак, это почти прямой угол, и невооруженным глазом он может выглядеть как прямой. Но ни одно из особых свойств прямого угла не является истинным.
В следующих видеороликах мы поговорим больше о специальных свойствах прямого угла.Ни одно из специальных свойств прямого угла не является истинным, если угол близок к 90, но не точно 90.
Очень важно, поэтому вы не можете предполагать, что две линии перпендикулярны, если у вас нет какого-либо основания для этого.
Линии и углы: конгруэнтные формы
Один термин, который я представлю, который, вероятно, не появится в тесте, является конгруэнтным. Конгруэнтность подобна равенству форм. Мы используем концепцию равенства для числа и очень похожую концепцию «конгруэнтности» для форм.
Две формы являются конгруэнтными, если они имеют одинаковую форму и одинаковый размер.
Они не обязательно должны иметь одинаковую ориентацию. Так, например, фиолетовая и зеленая формы здесь совпадают, одна перевернута. Можно сказать, что одна версия для правшей, а другая — для левшей, но в основном это та же форма.
Так, например, фиолетовая и зеленая формы здесь совпадают, одна перевернута. Можно сказать, что одна версия для правшей, а другая — для левшей, но в основном это та же форма.
Эти двое совпадают, хотя имеют разную ориентацию.
Биссектриса
Биссектриса разрезает что-то на две равные части.Биссектриса угла разрезает угол на два меньших равных угла. Так, например, у нас есть биссектриса угла. Если нам говорят, например, что большой угол PNM равен 40 градусам и что NQ делит угол пополам, то мы можем сделать вывод, что каждый из двух меньших углов должен составлять 20 градусов.
Каждый из них должен быть ровно наполовину равен друг другу, потому что угол был разделен пополам. Точно так же биссектриса сегмента может быть точкой, другим сегментом или линией. Биссектриса делит отрезок на две равные половины.Обратите внимание, что здесь сегмент ST делит PQ пополам. Также обратите внимание, что PQ не делит пополам ST, потому что SR явно больше RT.
Итак, тот факт, что ST делит PQ пополам, означает, что R является средней точкой PQ, и что PR = RQ. Мы разделили его на две равные половины, и, опять же, это всегда означает деление пополам. Иногда линия будет делить сегмент пополам и также быть перпендикулярна ему. Прямая называется серединным перпендикуляром отрезка.
Мы разделили его на две равные половины, и, опять же, это всегда означает деление пополам. Иногда линия будет делить сегмент пополам и также быть перпендикулярна ему. Прямая называется серединным перпендикуляром отрезка.
Линия VW перпендикулярна, это серединный перпендикуляр к ТУ.Каждая точка на серединном перпендикуляре сегмента равноудалена от двух конечных точек сегмента. И это действительно полезный факт, который проявляется по-разному. Серединный перпендикуляр на самом деле представляет собой набор всех возможных точек, которые равноудалены от двух конечных точек отрезка.
Линии и углы: давайте посмотрим на углы
Теперь несколько основных фактов об углах. Мы уже говорили, что прямая содержит 180 градусов. Это означает, что если два или более угла лежат на прямой линии, сумма их углов составляет 180 градусов.Так, например, мы можем предположить, что эта длинная линия прямая. На этом этапе у него нет небольшого изгиба.
Тест нам этого не сделает, если смотрит прямо, то прям. И поэтому мы знаем, что эти два угла вместе составляют 180. Итак, x + y = 180. Если два угла в сумме дают 180, то они называются дополнительными. Два угла на прямой всегда дополняют друг друга. Итак, p + q = 180.
И поэтому мы знаем, что эти два угла вместе составляют 180. Итак, x + y = 180. Если два угла в сумме дают 180, то они называются дополнительными. Два угла на прямой всегда дополняют друг друга. Итак, p + q = 180.
Изображение: BlueRingMedia
Когда пересекаются две линии
При пересечении двух линий образуются четыре угла.Итак, у нас есть две линии, которые продолжаются вечно в обоих направлениях, они должны пересекаться, и эти четыре угла образуются. Пары углов напротив друг друга, имеющие общую вершину, называются вертикальными углами, а вертикальные углы всегда совпадают. Так, например, A и C, у них нет общих сторон.
Все, что есть у a и c, — это то, что они касаются одной вершины. Они касаются вершины, b и d также касаются вершины. Вот почему они называются вертикальными углами, потому что они встречаются в вершине.Итак, мы знаем, что вертикальные углы совпадают, мы знаем, что a = c и b = d. Конечно, пары углов, расположенных рядом друг с другом, a + b, b + c, все они являются дополнительными.
Все они в сумме дают 180 градусов, потому что у нас есть пары углов на линии. Следовательно, если на этой диаграмме нам дан один угол, мы сможем найти остальные три. Например, если a = 35, мы знаем, что c должно быть равно. Это тоже должно быть 35 градусов. А b и d должны быть дополнительным углом в 145 градусов. Таким образом, любые две пары вместе, любые два угла вместе в паре дают в сумме 180 градусов.
Линии и углы: практическая задача первая
Вот практическая задача, поставьте видео на паузу, а потом мы поговорим об этом.
Изображение Евгении Илюхиной
Хорошо. На диаграмме x = 40 градусов и RT делит пополам большой угол SRU, который является очень большим углом. Что ж, SRU — это дополнительный угол к этому углу в 40 градусов, поэтому SRU должно быть 180 минус 40, что будет 140. Итак, SRU равно 140.
И этот угол делится пополам, потому что он разрезан на две равные половины.Итак, есть две половины, каждая из которых должна быть под углом 70 градусов. SRT = 70 градусов, TRU = 70 градусов. Это две равные половины угла, который был разделен пополам. А теперь обратите внимание, что угол TRV, этот угол состоит из TRU и угла x, который мы знаем.
SRT = 70 градусов, TRU = 70 градусов. Это две равные половины угла, который был разделен пополам. А теперь обратите внимание, что угол TRV, этот угол состоит из TRU и угла x, который мы знаем.
Мы знаем, что TRU равен 70 градусам, мы знаем, что угол X равен 40 градусам, поэтому складываем их вместе. TRV должен быть под углом 110 градусов. Теперь обратите внимание, что TRV — это вертикальный угол SRW, поэтому эти два значения должны быть равны. Это означает, что SRW также должен быть под углом 110 градусов, поэтому Y равно 110.Наконец, мы рассмотрим параллельные линии.
Линии и углы: параллельные линии
Если две прямые параллельны, они никогда не пересекаются и всегда находятся на одинаковом расстоянии друг от друга. И опять же, это еще одно из этих свойств, например, перпендикулярность, близость к параллельности, не учитывается для бобов. Вы должны знать, что две линии точно параллельны. Очевидно, поскольку параллельные линии никогда не пересекаются, они никогда не образуют друг с другом углов.
Поперечные линии
Мы получаем много углов, если третья непараллельная линия пересекает две параллельные линии.Эта третья линия называется поперечной. Трансверсаль — это линия, пересекающая две параллельные линии. Итак, здесь мы имеем поперечный разрез по параллельным линиям WX и YZ. И у нас там восемь ангелов.
Итак, четыре больших ангела равны. И все четыре маленьких ангела равны. Другими словами, a = d = e = h и b = c = f = g, это большая идея. Вы, конечно, можете вспомнить из геометрии, что среди них есть всевозможные особые имена.
Альтернативный интерьер и такой же боковой внешний вид и соответствующие углы.Если вы хотите запомнить все эти особенные имена, это прекрасно, в этом нет необходимости. Все, что вам нужно запомнить, это то, что все большие углы равны, все маленькие углы равны. Итак, вот диаграмма, и теперь я пометил ее так, чтобы было ясно, что все равно.
Линии и углы: дополнительные углы
Также обратите внимание, что p и q являются дополнительными. Итак, любой большой угол плюс любой маленький угол равняется 180 градусам, это действительно отличная идея. Таким образом, если нам здесь дана степень любого из углов, мы сможем найти остальные семь.Подводя итог, мы говорили о прямых и линейных сегментах, мы говорили об углах и градусах.
Итак, любой большой угол плюс любой маленький угол равняется 180 градусам, это действительно отличная идея. Таким образом, если нам здесь дана степень любого из углов, мы сможем найти остальные семь.Подводя итог, мы говорили о прямых и линейных сегментах, мы говорили об углах и градусах.
Мы указали, что в прямом угле 180 градусов, а в прямом — 90 градусов. Мы говорили о биссектрисах и перпендикулярах. Биссектриса угла делит угол на два равных меньших угла. Серединный перпендикуляр перпендикулярен отрезку и делит его на две равные половины.
Мы говорили о том, что два угла на линии дополняют друг друга. Вертикальные углы совпадают.И мы говорили об углах, образованных трансверсалью, пересекающей пару параллельных прямых. И мы поговорим о многих приложениях этих фундаментальных идей в следующих видео.
Как рисовать под углом 180 градусов
Углы измеряются в градусах (или радианах), и в геометрии существует много типов углов; острый, тупой, прямой угол, полукруг, полное вращение и т. д. Полный круг равен 360 градусам, и все углы лежат внутри него.
д. Полный круг равен 360 градусам, и все углы лежат внутри него.
Угол, который составляет точно 180 градусов, называется прямым углом. Другое название угла 180 градусов — полукруг. Если прямая линия разделена на две части, и мы знаем один угол, мы всегда можем вычислить другой, поскольку прямая линия всегда равна 180 градусам, поэтому сумма углов будет равна 180 градусам.
В радианах угол 180 градусов представлен как π (пи).
Вы можете найти изображение с углом 180 градусов ниже:
[Изображение будет загружено в ближайшее время]
В этой статье мы увидим детали углов 180 и того, как рисовать углы 180 градусов.
Типы углов
Давайте кратко рассмотрим все возможные типы углов, которые могут существовать внутри круга, и их размеры.
[Изображение будет загружено в ближайшее время]
Любой угол больше 0 градусов и меньше 90 градусов является острым.
[Изображение будет загружено в ближайшее время]
Прямой угол равен 90 градусам.
Любой угол больше 90 градусов и меньше 180 градусов является тупым углом.
[Изображение будет загружено в ближайшее время]
Прямой угол равен точно 180 градусам.
Угол, который больше 180 градусов и меньше полного оборота или 360 градусов, является углом отражения.
[Изображение будет загружено в ближайшее время]
Полное вращение точно на 360 градусов.
Вы можете легко найти все углы в одном месте на диаграмме ниже:
[Изображение будет загружено в ближайшее время]
Шаги построения угла 180 градусов
Чтобы построить любой угол, нам понадобятся две вещи:
Перед мы расскажем, как нарисовать угол 180 градусов, давайте познакомимся с основами работы с компасом.
[Изображение будет загружено в ближайшее время]
Компас — это инструмент, который помогает находить направления. У него есть магнитная стрелка, которая всегда указывает на магнитный север. Направление можно определить по углу, который образует желаемое направление объекта и магнитная стрелка.
У него есть магнитная стрелка, которая всегда указывает на магнитный север. Направление можно определить по углу, который образует желаемое направление объекта и магнитная стрелка.
Теперь рассмотрим этапы построения угла 180 градусов:
[Изображение будет загружено в ближайшее время]
[Изображение будет загружено в ближайшее время]
Угол BOA — это прямой угол или 180 градусов.
Вы можете проверить, является ли угол 180 или нет, с помощью транспортира. Держите транспортир в верхней части точки O и затем измерьте угол BOA. Он должен отображаться как 180 градусов.
Примеры прямого угла
В повседневной жизни вы замечаете много прямых линий, некоторые из распространенных примеров:
Плоская поверхность — она имеет угол 180 градусов.

Качели — это пример прямого угла.
Рукоять повернута на 180 градусов по центру.
Прямая и прямой угол — это не одно и то же. Прямой угол составляет 180 градусов, а прямая линия соединяет две точки.
Теорема о прямом угле
Согласно теореме о прямом угле, все прямые углы составляют 180 градусов. В углу, если его ноги направлены в противоположные стороны, он образует прямой угол или 180 градусов. Сегмент линии в геометрии является хорошим примером прямого угла, поскольку его концы проходят в противоположных направлениях.
[Изображение будет загружено в ближайшее время]
Свойства прямого угла
Мы перечислили здесь несколько ключевых свойств прямого угла:
Прямой угол — это величина, равная половине оборота.

Мы можем получить прямой угол, повернув один луч линейного сегмента точно на 180 градусов относительно другого луча.
Плечи прямого угла проходят в противоположных направлениях.
Прямой угол изменяет направление точки.
Прямой угол можно получить, соединив два прямых угла.
Положительные и отрицательные углы
Угол можно измерить, начиная с линии, двумя способами: по часовой стрелке и против часовой стрелки.
Направление положительного угла — против часовой стрелки, т.е. противоположно направлению хода часов.
Измеряется по часовой стрелке.
[Изображение будет загружено в ближайшее время]
Когда вы измеряете и называете угол, чтобы быть уверенным в том, какой угол вас просили, и измерьте его против часовой стрелки (положительный угол)
[Изображение будет загружено в ближайшее время]
На рисунке выше меньший угол тупой, а больший — угол отражения.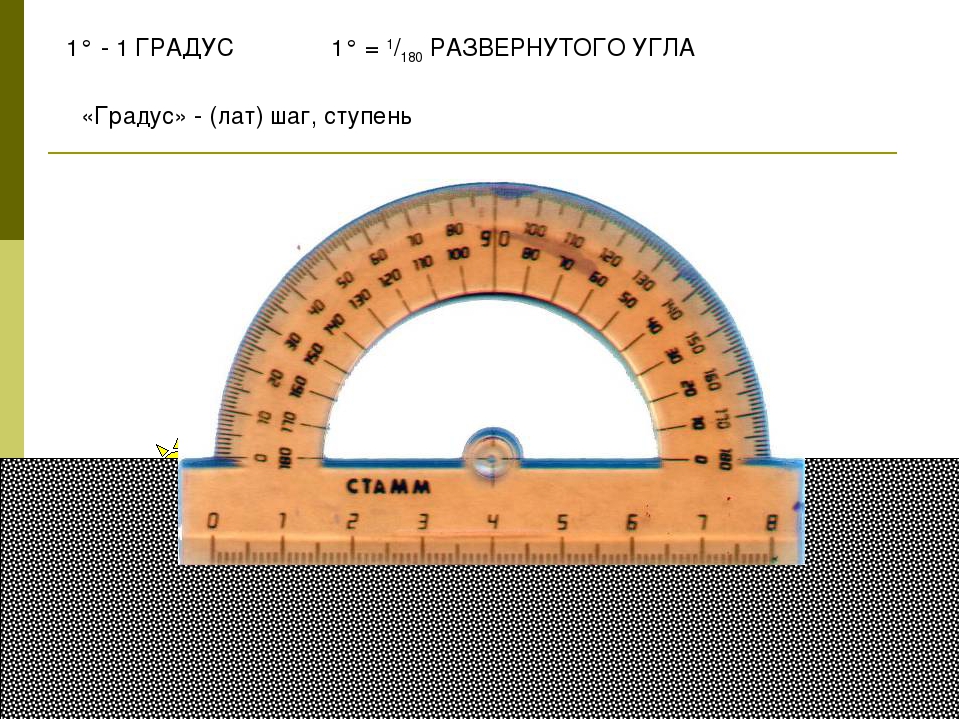
Почему треугольники в сумме составляют 180 градусов?
Вы знаете, как сумма углов треугольника всегда равна 180 0 ? Это почему? В конце концов, 180 0 — это угол, который простирается от одной стороны прямой линии до другой, поэтому странно, что это количество градусов в углах треугольника.
Какое отношение треугольник имеет к единственной прямой? Оказывается, довольно много. Треугольники также имеют прямое отношение к прямоугольникам, пятиугольникам, шестиугольникам и всему семейству многосторонних форм, известных как многоугольники.
Мы увидим, что я имею в виду, в ближайшие несколько недель. Но сегодня мы начнем с выяснения, почему именно углы треугольника всегда в сумме составляют 180 0 . Или вы так думали … потому что мы также увидим, что иногда они этого не делают.
Купить сейчас
Будучи партнером Amazon и партнером Bookshop.org, QDT зарабатывает на соответствующих покупках.
Виды треугольников
Напоминаем: есть три различных типа основных треугольников. Они бывают равносторонними, равнобедренными и разносторонними.
Они бывают равносторонними, равнобедренными и разносторонними.
- Равносторонний треугольник имеет три стороны одинаковой длины
- Равнобедренный треугольник имеет две стороны одинаковой длины и одну сторону разной длины
- Разносторонний треугольник имеет три стороны разной длины
Длина стороны треугольника напрямую влияет на его углы.
СВЯЗАННЫЙ: Что такое треугольник Паскаля?
Уголки внутренние и внешние
Прежде чем мы зайдем слишком далеко в наш рассказ о треугольниках и общем количестве градусов в их трех углах, есть один небольшой геометрический словарь, о котором мы должны поговорить. И в этом разница между внутренним и внешним углом.
Самый простой способ описать разницу между этими двумя вещами — это на примере. Поскольку сегодняшняя тема — треугольник, давайте поговорим о внутреннем и внешнем углах треугольника.Короче говоря, внутренние углы — это все углы в пределах границ треугольника. Другими словами, это те углы, о которых мы говорили все время.
Другими словами, это те углы, о которых мы говорили все время.
Внешние углы треугольника — это все углы между одной стороной треугольника и линией, которую вы получаете, расширяя соседнюю сторону за пределы границ треугольника. Если вы подумаете об этом, то увидите, что когда вы добавляете любой из внутренних углов треугольника к его соседнему внешнему углу, вы всегда получаете 180 0 — прямую линию.
Сколько градусов в треугольнике?
Это подводит нас к главному вопросу на сегодня: почему внутренние углы треугольника всегда в сумме составляют 180 0 ? Оказывается, вы можете понять это, подумав о внутреннем и внешнем углах треугольника. Чтобы понять, что я имею в виду, возьмите свое воображение или лист бумаги, потому что пришло время для небольшого математического проекта по рисованию в области декоративно-прикладного искусства.
Начните с рисования прямоугольного треугольника с одним горизонтальным участком, одним вертикальным участком и гипотенузой, идущей от верхнего левого угла к нижнему правому. Теперь сделайте копию этого треугольника, поверните ее вокруг 180 0 и поместите гипотенузу в гипотенузу с оригиналом (точно так же, как мы это делали, когда выясняли, как найти площадь треугольника). Наконец, сделайте еще одну копию исходного треугольника и сдвиньте ее вправо, чтобы она располагалась прямо рядом с только что сформированным прямоугольником. Со мной так далеко? В таком случае ваше изображение должно выглядеть так:
Теперь сделайте копию этого треугольника, поверните ее вокруг 180 0 и поместите гипотенузу в гипотенузу с оригиналом (точно так же, как мы это делали, когда выясняли, как найти площадь треугольника). Наконец, сделайте еще одну копию исходного треугольника и сдвиньте ее вправо, чтобы она располагалась прямо рядом с только что сформированным прямоугольником. Со мной так далеко? В таком случае ваше изображение должно выглядеть так:
В чем смысл этой фотографии? Взгляните на внутренний угол в правом нижнем углу исходного треугольника (помеченного буквой «A»).Теперь взгляните на два угла, которые составляют внешний угол этого угла треугольника (обозначенные буквами «B» и «C»). Как мы знаем, если сложить внутренние и внешние углы одного угла треугольника, мы всегда получим 180 0 . И наш маленький рисунок показывает, что рассматриваемый внешний угол равен сумме двух других углов в треугольнике. Другими словами, два других угла в треугольнике (те, которые в сумме образуют внешний угол) должны объединиться с углом в правом нижнем углу, чтобы образовать угол 180 0 .
СВЯЗАННЫЙ: Мир тригонометрии
Для простоты мы использовали прямоугольный треугольник. Но оказывается, что вы можете сделать точно такой же рисунок, используя любой треугольник, который вам нравится, и всегда будете приходить к одному и тому же выводу. Попробуйте сделать несколько рисунков, начиная с разных треугольников по вашему выбору, чтобы убедиться в этом сами. В качестве примера вот еще один, который я сделал:
Неизбежный вывод этой игры состоит в том, что внутренние углы треугольника всегда должны составлять 180 0 .Наш милый и изящный маленький рисунок доказывает, что так и должно быть.
Или нет?
Все ли треугольники равны 180 градусам? Может у треугольников больше?
Может быть, у нашего рисунка есть какие-то ограничения, которые не позволяют нам увидеть другую, более экзотическую возможность? Вот что вам стоит подумать или попробовать. Возьмите ненадутый воздушный шар, положите его на плоскую поверхность и нарисуйте на нем как можно более точный треугольник. Если у вас есть транспортир, было бы здорово измерить и сложить внутренние углы треугольника и убедиться, что они довольно близки к 180 0 .
Если у вас есть транспортир, было бы здорово измерить и сложить внутренние углы треугольника и убедиться, что они довольно близки к 180 0 .
Теперь надуйте воздушный шар и посмотрите на свой треугольник. Что случилось с этим? Если у вас есть транспортир, попробуйте еще раз просуммировать его внутренние углы. Что случилось с этой суммой? Вы все еще получаете 180 0 ? Что все это означает, когда дело доходит до вопроса о том, всегда ли внутренние углы треугольника в сумме составляют 180 0 , как мы, кажется, обнаружили?
К счастью, у меня есть ответ. Перейдите к статье на следующей неделе, в которой мы начали исследовать странный и удивительный мир, известный как неевклидова геометрия.
Доказательство того, что треугольник равен 180 градусам [Видео]
Доказательство того, что треугольник равен 180 градусам
Одна из первых вещей, которые мы все узнали о треугольниках, это то, что сумма внутренних углов равна 180 градусам .
Вы могли бы использовать эти знания, чтобы найти недостающий угол в треугольнике, когда вы знали два других, и все было хорошо. Но затем могло закрасться зерно сомнения или любопытства. Откуда мы знаем, что сумма углов всегда равна , всегда 180? Есть ли способ окончательно доказать это? Ответ положительный!
Чтобы математически доказать, что сумма углов треугольника всегда равна 180 градусам, нам нужно установить некоторые основные факты об углах.Первый факт, который нам нужно рассмотреть, — это определение прямого угла :
Прямой угол — это просто прямая линия, отсюда и название. Мы разместили на нем три точки, чтобы представить три угла треугольника. Размер этого прямого угла ABC составляет 180 градусов. Это будет важно позже.
Чтобы увидеть наши следующие углы, возьмем два прямых угла и пересечем их еще одной линией:
Это то, что мы называем поперечными. Мы можем видеть, что в этом случае используются только две разные угловые меры. Если мы посмотрим между параллельными линиями , мы увидим, что два угла на каждой стороне поперечной линии в сумме составляют 180 градусов.
Если мы посмотрим между параллельными линиями , мы увидим, что два угла на каждой стороне поперечной линии в сумме составляют 180 градусов.
Это потому, что поперечная линия разрезает каждую из параллельных линий на две части. Поскольку прямая линия представляет собой прямой угол, когда она разрезается пополам, сумма двух ее половинок должна составлять исходный размер. Это похоже на то, как если вы в любой момент отрежете метровую палку, когда вы снова сложите две части палки, они все равно получат в сумме один метр.
Если мы проведем еще одну линию, пересекающую параллельные линии, мы получим треугольник.
Наша верхняя группа углов была изменена с группы из четырех на группу из шести, потому что каждый из больших углов был разрезан новой линией.
Группа углов в нижнем левом углу не изменилась, и появилась новая группа углов, созданная новой линией, пересекающей нижнюю параллельную линию.
Давайте добавим метки углов ко всем углам между параллельными линиями:
Мы видим, что углы A, B и C вместе образуют прямой угол, а это означает, что их сумма должна составлять 180 градусов.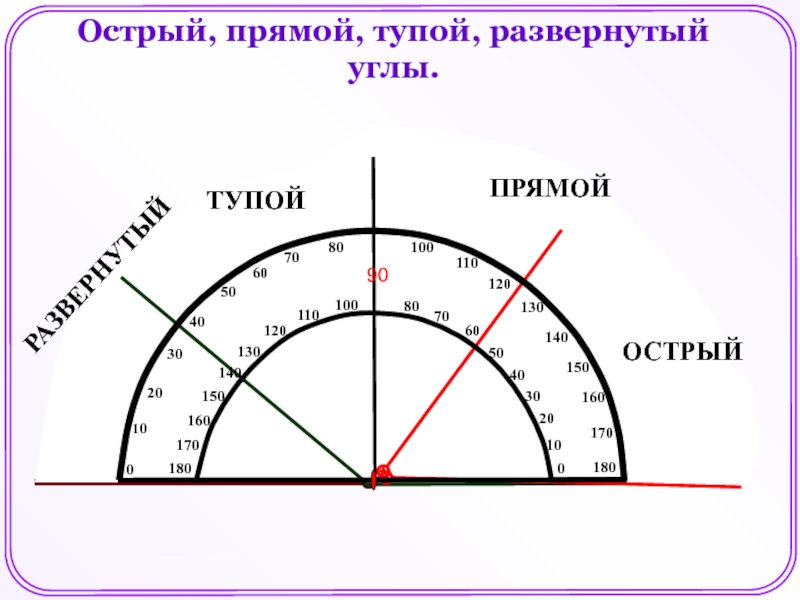 Теперь мы можем установить, что три угла внутри треугольника (B, E и F) также составляют 180. Углы A и E равны конгруэнтных углов, что означает, что они имеют одинаковую меру, потому что они представляют собой альтернативных внутренних угла трансверсали с параллельными линиями. Угол C и угол F совпадают по той же причине.
Теперь мы можем установить, что три угла внутри треугольника (B, E и F) также составляют 180. Углы A и E равны конгруэнтных углов, что означает, что они имеют одинаковую меру, потому что они представляют собой альтернативных внутренних угла трансверсали с параллельными линиями. Угол C и угол F совпадают по той же причине.
Угол B совпадает с самим собой. Следовательно, сумма углов A, B и C должна быть равна сумме углов B, E и F. А поскольку сумма углов A, B и C, как известно, равна 180, тогда сумма углов углы B, E и F также должны быть 180.Вот таблица, в которой все изложено для нас:
Определение прямого угла: «Мера угла A плюс мера угла B плюс мера угла C равна 180 градусам». «Мера угла A равна мере угла E» истинно, потому что эти два угла являются конгруэнтными, чередующимися внутренними углами. То же самое относится к углам C и F.
Давайте теперь посмотрим на это с установленными углами:
Когда мы посмотрим на три угла под линией 1, мы увидим, что они в сумме составляют 180 градусов, как мы знаем.![]()
Градусная мера угла / Начальные геометрические сведения / Справочник по геометрии 7-9 класс
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Градусная мера угла
Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения. Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения — с градусом.
Градус — это угол, который равен части развернутого угла,обозначается знаком
часть градуса называется минутой, обозначается знаком
часть минуты называется секундой, обозначается знаком
Пример: (двадцать градусов пятнадцать минут сорок семь секунд)
Градусная мера угла — это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.
Пример:
Градусная мера угла ABC равна . Говорят: «Угол ABC равен 120 градусам». Пишут: .
Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.
Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .
Свойства:
- Равные углы имеют равные градусные меры.
- Меньший угол имеет меньшую градусную меру.
- Развернутый угол равен .
- Неразвернутый угол меньше .
- Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Основные типы углов:
- Острый угол — угол, градусная мера которого меньше 90°.
- Прямой угол — угол, градусная мера которого равна 90°.
- Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.

- Развернутый угол — угол, градусная мера которого равна 180°.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Длина отрезка
Единицы измерения длины, расстояний
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 42, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 145, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 17, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 228, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 299, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 598, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 646, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 896, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1167, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
© budu5. com, 2021
com, 2021
Пользовательское соглашение
Copyright
Угол 180 градусов — конструкция, определение, шаги для рисования и измерения, примеры
Угол 180 градусов — это прямой угол, так как он образует прямую линию. Это ровно половина полного угла (угол 360 градусов). Если мы говорим о реальном примере угла 180 градусов, то идеальным примером является угол между двумя стрелками часов в положении «6 часов». Угол между двумя стрелками часов составляет 180 °, потому что они образуют прямую линию.
Что такое угол 180 градусов?
Угол 180 градусов — это прямой угол, составляющий ровно половину оборота.Его еще называют углом полукруга. Прямой угол получается из прямой линии. Два плеча угла, составляющие 180 градусов, прямо противоположны друг другу от общей вершины. Угол 180 градусов изменяет направление точки. Угол 90 градусов составляет половину угла 180 градусов, и он известен как прямой угол. Посмотрите на изображение, приведенное ниже, показывает, как выглядит угол в 180 градусов.
Угол 90 градусов составляет половину угла 180 градусов, и он известен как прямой угол. Посмотрите на изображение, приведенное ниже, показывает, как выглядит угол в 180 градусов.
На этом изображении лучи AO и OB имеют общую точку O. Лучи AO и OB противоположны друг другу.AB — прямая линия, образующая угол 180 градусов.
Название угла 180 градусов
Угол, который составляет 180 градусов, называется прямым углом . Когда мы строим угол в 180 градусов, он всегда образует прямую линию, поэтому он известен как прямой угол. Есть разные названия для углов разных измерений. Например, половина угла в 180 градусов, то есть угол в 90 градусов, в геометрии называется прямым углом. Точно так же двойной угол 180 градусов, то есть угол в 360 градусов, известен как полный угол.Углы меньше 180 градусов делятся на острые и тупые.
Два угла, которые вместе составляют 180 градусов, известны как дополнительные углы. В то время как два или более угла, соединяющиеся вместе в точке на линии, образующей 180 градусов, известны как линейные пары углов.
Как нарисовать угол 180 градусов?
Угол 180 градусов можно нарисовать с помощью транспортира и циркуля.
Построение угла 180 градусов с помощью транспортира
Чтобы построить угол 180 градусов с помощью транспортира, выполните следующие действия:
- Шаг 1. Нарисуйте луч OA.
- Шаг 2. Поместите транспортир в точку О.
- Шаг 3: Найдите во внутреннем круге транспортира угол 180 °, отметьте карандашом точку и назовите ее C.
- Шаг 4: Соедините O и C. Теперь ∠AOC = угол 180 градусов.
Построение угла 180 градусов с помощью компаса
Следуйте приведенным ниже инструкциям, чтобы построить угол 180 градусов с помощью компаса.
- Шаг 1. С помощью линейки нарисуйте прямую линию и назовите ее AB.
- Шаг 2: Отметьте точку O где-нибудь между A и B.
- Шаг 3: Возьмите O в качестве центральной точки, нарисуйте дугу любого радиуса с помощью циркуля, дуга должна проходить слева от точки O справа от O, или наоборот, касаясь линии AB.

- Шаг 4: Дуга пересекает прямую в двух точках. Отметьте разрезы точками C и D.
- Шаг 5: Таким образом, угол COD составляет 180 градусов.
Важные примечания
- Угол 180 градусов также называется прямым углом, полукругом или полукругом.
- Угол 180 градусов можно построить с помощью транспортира или компаса.
Статьи по теме об угле 180 градусов
Прочтите эти интересные статьи, чтобы узнать больше об углах 180 градусов и связанных с ними темах.
Часто задаваемые вопросы об угле 180 градусов
Что такое углы 180 градусов в реальной жизни?
Углы 180 ° широко используются в реальной жизни. В повседневной жизни 180-градусные углы используются инженерами и архитекторами при строительстве сооружений, дорог, домов и спортивных сооружений.Плотники делают скамейки, столы и диваны, используя прямые углы.
Как выглядит угол 180 градусов?
180 градусов выглядит как прямая линия, потому что лучи или стороны угла, составляющего 180 градусов, полностью противоположны друг другу. Общая точка, соединяющая линии, совершает половину оборота, то есть угол 180 градусов.
Общая точка, соединяющая линии, совершает половину оборота, то есть угол 180 градусов.
Сколько углов на 180 градусов нужно, чтобы совершить полный поворот?
Для полного поворота нам понадобятся два угла по 180 градусов.Угол 360 градусов — это полный оборот или полный оборот. Половина 360 градусов равна 180 градусам, таким образом, два или два раза угол 180 градусов дает полный поворот.
Что такое угол 180 градусов?
Угол 180 градусов известен как прямой угол. Стороны угла противоположны друг другу и составляют прямой угол на прямой, проходящей через вершину. Угол в 180 градусов выглядит как прямая линия.
Угол 180 градусов тупой?
Размер тупого угла больше 90 °, но меньше 180 °, таким образом, угол 180 градусов не является тупым углом.Это называется прямым углом.
Сколько углов 90 градусов в углу 180 градусов?
Есть два угла 90 градусов в углу 180 градусов, так как сумма двух углов 90 градусов равна 180 градусам.
Что такое 180 градусов для треугольника?
Сумма всех внутренних углов в треугольнике всегда равна 180 градусам. Кроме того, пара внутреннего угла и последующего внешнего угла в треугольнике дает прямой угол, составляющий 180 градусов.
Как называется угол 180 градусов?
Солнечная система состоит из Солнца и небесных тел, вращающихся вокруг него.Исследуйте Солнечную систему и узнайте о Солнце, планетах, лунах, астероидах, кометах и метеороидах.
Узнайте интересные факты о прямых углах. Откройте для себя измерение, определяющее прямой угол, формы, которые имеют прямые углы для их внутренних углов, и веселые занятия с использованием прямых углов.
Откройте для себя измерение, определяющее прямой угол, формы, которые имеют прямые углы для их внутренних углов, и веселые занятия с использованием прямых углов.
Что такое прямой угол? — Определение и формула
Прямые углы — это все углы, которые составляют ровно 90 градусов, и наиболее очевидным в геометрии является треугольник.Изучите определение прямого угла и изучите обозначения и формулы для прямых углов, используя теорему Пифагора, которая связывает все стороны треугольника друг с другом.
Определение параллельных линий в геометрических формах
Пара линий геометрической формы, которые не пересекаются, даже если они продолжены, называются параллельными линиями.Узнайте больше о параллельных линиях и о том, как определять их в геометрических фигурах, таких как квадраты, прямоугольники и параллелограммы.
вопросов о высшем мышлении для учителей математики
Вопросы для мышления высшего порядка — это вопросы, которые применяют понятые принципы в одной области к вопросам, ответ на которые не всегда предоставляется явно. Посмотрите, как эти вопросы появляются на разных уровнях обучения и как они применяются к математическому материалу.
Посмотрите, как эти вопросы появляются на разных уровнях обучения и как они применяются к математическому материалу.
Что такое точные существительные? — Определение и примеры
Письмо становится более мощным, если используется точный и информативный язык.Точные существительные превращают общее предложение в ясное и уникальное предложение, передающее конкретное значение. В этом уроке мы узнаем о точных существительных на различных примерах.
Диаметр и окружность, связанные с числом Пи
В математике пи — это константа, равная примерно 3. 14, хотя на самом деле число бесконечно. Узнайте об определении числа пи и исследуйте его связь с диаметром и длиной окружности круга, формулой для вычисления окружности, а также попрактикуйтесь в нахождении окружности или диаметра круга.
14, хотя на самом деле число бесконечно. Узнайте об определении числа пи и исследуйте его связь с диаметром и длиной окружности круга, формулой для вычисления окружности, а также попрактикуйтесь в нахождении окружности или диаметра круга.
Что такое прямая линия? — Определение и примеры
В геометрии прямая линия — это просто линия без кривых.Узнайте больше об определении прямой линии и ознакомьтесь с некоторыми примерами. Кроме того, узнайте об измерениях прямой линии и о том, как назвать эту линию, отрезки линии и лучи.
Что такое десятичные дроби? — Определение и примеры
Эквивалентные десятичные дроби создаются путем добавления нулей справа от десятичной точки или после нее, а полученные числа равны по значению. Этот урок определит и обсудит полезность эквивалентных десятичных знаков и предоставит реальный пример.
Этот урок определит и обсудит полезность эквивалентных десятичных знаков и предоставит реальный пример.
углов и градусов. Объяснение 1. 7. — 9. класс.
Геометрия — углы и градусы. Объяснение 1. 7. — 9. класс.Июль 2003 г. Rasmus ehf.
Геометрия — Углы и степени
Урок 1.
Углы измеряются в градусах.А
круг (полный оборот) составляет 360 градусов.
Посмотрите на 1/4 круга.
Некоторые общие углы
А Угол 90 называется прямым углом . | |
Угол между
90 и 180 называется тупым углом . | |
Угол, который меньше 90 называется острым углом . |
Подробнее об углах, градусах и аналогичные фигурки
Половина окружность равна 180 градусам (прямой угол). | |
Дополнительный углы — это углы, которые имеют общее плечо и имеют сумму 180 градусов. Сумма зеленого и синего углов равна 180 градусам. |
Пример:
Сколько градусов составляет угол X?
Вычислить: |
Похожие цифры
Фигурки
с точно такой же формой находятся аналогичных фигур . Соответствующие углы в
одинаковые треугольники равны по размеру. Это правило относится ко всем
полигоны.
Соответствующие углы в
одинаковые треугольники равны по размеру. Это правило относится ко всем
полигоны.
Подобные цифры | ||
Подобные цифры | ||
Подобные цифры | ||
не похож | ||
не похож |
Сумма углов
Попрактикуйтесь в этих методах и попробуйте Тест 1 по геометрии. Не забудьте использовать Контрольный список, чтобы отслеживать свою работу.
Не забудьте использовать Контрольный список, чтобы отслеживать свою работу.
типов углов — Бесплатная математическая справка
Типы углов
Вы, конечно, использовали слово «угол» в повседневной жизни, но оно также имеет важное значение в математике. Одна из тем, с которой вы захотите познакомиться, — это различные типы или классификации углов, определяемые величиной угла. Эта страница представляет собой простое и понятное руководство для начинающих по различным типам углов.
Три основных типа углов
Acute — любой угол менее 90 градусов. Эти углы кажутся «острыми», как лезвие ножа.
Пример: угол ABC составляет 40 градусов. Угол ABC острый.
Справа — любой угол, равный 90 градусам. Это как края деревянного бруска.
Пример: Угол CAT составляет 90 градусов. Угол КПП — это прямой угол.
Тупой — любой угол, который составляет более 90 градусов, но менее 180 градусов. Это «толстые» углы, очень широкие.
Это «толстые» углы, очень широкие.
Пример: угол DEF составляет 125 градусов. Тогда угол DEF тупой.
Особый случай
Прямой — любой угол, равный 180 градусам. Это даже не совсем угол … это просто прямая линия!
Пример: Точки ABC лежат на линии L, образуя ПРЯМОЙ ЛИНИЙ.Тогда линия L — прямая.
Взаимосвязь нескольких углов
Вертикальные углы — Два угла, образованные пересекающимися линиями. Они не могут быть смежными, но всегда равны по размеру. Они находятся напротив друг друга в углах буквы «X», образованной линиями.
На рисунке выше углы 1 и 3 и углы 2 и 4 вертикальны, потому что они расположены напротив друг друга. Теперь углы 1 и 2 и углы 3 и 4 НЕ являются вертикальными углами.
Дополнительные углы — Два угла, сумма которых составляет 90 градусов.
Пример: угол A = 30 градусов и угол B = 60 градусов.
Тогда угол A + угол B = 90 градусов. Можно сказать, что углы A и B дополняют друг друга.
Можно сказать, что углы A и B дополняют друг друга.
Дополнительные углы — Два угла, сумма которых составляет 180 градусов. Дополнительные углы можно разместить так, чтобы они образовывали прямую линию.
Пример: угол A = 80 градусов и угол B = 100 градусов.Тогда угол A + угол B = 180 градусов. Можно сказать, что углы A и B дополнительные.
связанные страницы
8.1: Измерение угла — Математика LibreTexts
Угол — это мера размера отверстия двух пересекающихся линий. VERTEX является точкой пересечения, а линии, образующие проем, называются SIDES .
Угол можно вызвать по
3 буквы с вершиной посередине: \ (\ angle ABC \) или только вершиной \ (\ angle B \), либо числом или буквой внутри угла.
В круге 360 градусов. Углы измеряются в градусах.
A Прямой угол составляет 90 градусов или 1/4 окружности. Прямоугольный будет выглядеть следующим образом.
Прямоугольный будет выглядеть следующим образом.
Острый угол — это угол менее 90 градусов. Ниже приведены примеры острых углов
.Тупой угол — это угол больше 90 градусов и меньше 180 градусов. Ниже приведены примеры тупых углов.
A Straight Angle — угол, равный 180 градусам.
Вертикальные углы
При пересечении двух прямых линий они образуют четыре угла.
Предположим, что \ (\ angle A \) равен 65 градусам, \ (\ angle B \) равен 115 градусам, \ (\ angle C \) равен 65 градусам, а \ (\ angle D \) равен 115 градусам
Вы заметили, что противоположные углы равны при измерении? Противоположные углы также называются Вертикальными углами .Когда две прямые линии пересекаются или пересекаются, вертикальные углы равны и всегда равны . Прямой угол — 180 градусов.
Углы W и X образуют прямую линию, вместе они составляют 180 градусов.
Они также известны как Смежные углы . Смежные углы в сумме составляют 180 градусов. Смежные углы также равны
.- \ (\ angle Y \) и \ (\ angle Z \),
- \ (\ угол W \) и \ (\ угол Y \)
- \ (\ угол X \) и \ (\ угол Z \).
Сумма трех углов треугольника всегда составляет 180 градусов.
Линии Z и Y параллельны друг другу. Линия P, пересекающая обе линии, называется Transversal .
\ (\ angle C \) и \ (\ angle F \) называются Альтернативными внутренними углами ; Они равны по размеру.
\ (\ angle D \) и \ (\ angle E \) также называются Альтернативными внутренними углами .
Если угол равен 70 градусам, то \ (\ angle P \) будет равен 110 градусам, их сумма равна 180 градусам.
- \ (\ angle P \) и \ (\ angle Q \) — противоположные углы, поэтому они равны 110 градусам, потому что вертикальные углы равны друг другу.

- \ (\ angle P \) и \ (\ angle T \) и соответствующие углы, поэтому оба они равны 110 градусам.
- \ (\ angle W \) равняется 70 градусам, потому что \ (\ angle T \) плюс \ (\ angle W \) должно равняться в сумме 180 градусам.
Разница между упражнениями 180 и 360
Вы можете вспомнить, когда изучали геометрию в средней школе, что круг состоит из 360 градусов.Углы измеряются в градусах, вершина находится в центре круга. Это означает, что прямой угол, образующий четверть круга, равен 90 градусам, а горизонтальная линия, образующая основу теоретического полукруга, равна 180 градусам.
(Неизвестно, как древние математики определяли 360 как число градусов в круге, но некоторые историки отметили, что это приблизительно соответствует количеству дней в календарном году и что круг нечетко совпадает с эллиптической орбитой земной шар. Тот факт, что многие числа делятся на 360, тоже может иметь какое-то отношение к этому.)
Тот факт, что многие числа делятся на 360, тоже может иметь какое-то отношение к этому.)
Градусы выражают углы поворота, поэтому мы говорим о них, когда говорим о шарнирах, наклонах, трюках со скейтбордом, маневрах на сноуборде и баскетбольных данках. Полный оборот по краю круга составляет 360 градусов, а это означает, что если бы вы завершили вращение вокруг центральной оси своего тела, вы бы оказались в том же направлении, что и в начале.
Половращение составляет 180 градусов, что приведет к тому, что вокруг той же центральной оси вы окажетесь лицом, противоположным тому месту, где вы смотрели изначально.Чарльз Линдберг в 1927 году использовал один-восемьдесят и три-шестьдесят для описания воздушных маневров, которые использовали половинный и полный оборот, соответственно.
Это была вторая половина 20-го века, когда идиоматическое использование one-восемьдесят для описания любого изменения направления, аналогично с поворотом на или его французскому эквиваленту, с поворотом на .
Я ввел «Пинто» в скоростной занос на четырех колесах, пересекая поток машин и выезжая на грунтовую дорогу, ведущую на кладбище, затем проехал один-восемьдесят , чтобы увидеть, что меня преследует в другом направлении.
— Дж. Гордон Лидди, Уилл , 1980
Естественно, фраза (иногда обозначаемая как поворот на 180 градусов ) может относиться к переносному изменению направления, которое делает противоположное тому, что делали раньше:
«У иранского режима есть выбор. Он может или развернуться на 180 градусов на от своего незаконного курса действий и действовать как нормальная страна, или он может увидеть, как его экономика рушится … Мы надеемся, что новое соглашение с Ираном возможно.”
— Майк Помпео, цитируется в New York Magazine , 6 ноября 2018 г.Они делают работу, и это непросто, не быстро. Но когда лампочка горит, они делают один восемьдесят .
Внезапно они начинают говорить о том, чтобы платить вперед и когда-нибудь вернуться, и сами стать наставниками.
— Кен Морган, цитируется в Macomb Daily (Clinton Township, Mich.), 25 сентября 2015 г.14 сентября Тигры проиграли DeSales 40-14. Это было их четвертое поражение подряд, в каждом из которых было не менее 19 очков.Три из этих поражений произошли дома. С тех пор команда Джоша Абелла совершила поворотов на 180 градусов на , одержав семь побед подряд.
— Джейсон Фрейкс и Стив Биттенбендер, The Courier Journal (Луисвилл, Кентукки), 10 ноября 2018 г.
Когда три-шестьдесят используется с точки зрения физических движений, это относится к полному вращению:
«Сделайте три-шестьдесят !» кто-то крикнул с трибуны, и Кори побледнел: « три-шестьдесят ? Я убью себя.Но ладно. «И он исполнил великолепный, вращающийся данк.
— Дарси Фрей, Последний выстрел , 1994Он сломал одного игрока, выполняющего прыжки, сломал левый, и сделал вращение на 360 градусов, чтобы сбить с толку другого игрока, выполняющего прыжки из Небраски.

— Аарон МакМанн, MLive.com , 22 сентября 2018 г.
Но иногда писатели забывают то, что они узнали в геометрии, и переходят на все 360 , хотя на самом деле они имеют в виду, конечно, обратное, то есть 180 :
Тайгер Вудс неудачно стартовал на чемпионате PGA, пройдя по первым двум лункам пугающий дабл-богги.Но после этого состояние Тайгера увеличилось на 360 , возможно, благодаря смене рубашки. То есть, если вы верите тому, что читаете в Твиттере.
— Golf.com , 9 августа 2018 г.
Если бы Тайгер Вудс совершил физическое вращение на 360 градусов, он бы смотрел в том же направлении, что и при старте. Если распространить это на фигуральное направление, его судьба не изменилась бы, и он все еще был бы пугающим. Вместо этого 180 предполагает изменение фортуны, которое автор предлагает здесь.
«« Сделать сто восемьдесят »подразумевает поворот, например:« С тех пор, как она начала использовать Прозак, ее личность в целом сделала сто восемьдесят ».
Я думаю, это не относится к гардеробу … Конечно, «три шестьдесят» намного хуже. «Volte face» намного лучше, но его больше никто не использует ».
— Кейт Кристенсен, Джереми Трейн , 2001
Есть несколько объяснений этой простой ошибки. Один из них — это соблазн думать, что удвоение числа — это просто подчеркивание или преувеличение, а не изменение его значения, как если бы кто-то выдавал невозможные 110 процентов.Другой заключается в том, что писатели могут не делать различия между вращением по оси и путешествием по окружности. Если вы представите машину, которая движется по кругу, проходит полный периметр на 360 градусов, а затем выходит, тогда автомобиль действительно будет двигаться в направлении, противоположном тому, с которого он стартовал. Но это не тот тип механизма, о котором изначально сообщалось в 360 .
Это такая логика, которая заставляет вас развернуться, и тогда вы не знаете, куда направляетесь.
Доказательство того, что треугольник равен 180 градусам [Видео]
Одна из первых вещей, которые мы все узнали о треугольниках, это то, что сумма внутренних углов равна 180 градусам.
Вы могли использовать это знание, чтобы найти недостающий угол угол в треугольнике, когда вы знали два других, и все было хорошо.Но затем могло закрасться зерно сомнения или любопытства. Как мы узнаем, что сумма углов всегда равна , 180? Есть ли способ окончательно доказать это? Ответ положительный!
Чтобы математически доказать, что сумма углов треугольника всегда равна 180 градусам, нам нужно установить некоторые основные факты об углах. Первый факт, который нам необходимо рассмотреть, — это определение прямого угла.
Прямой угол — это прямая линия, отсюда и название.
Мы разместили на нем три точки, чтобы представить три угла треугольника. Размер этого прямого угла ABC составляет 180 градусов. Это будет важно позже.
Чтобы увидеть наши следующие углы, возьмем два прямых угла и пересечем их еще одной линией:
Это то, что мы называем поперечными. Мы видим, что когда это происходит, есть только две разные угловые меры. Если мы посмотрим между параллельными линиями , мы увидим, что два угла на каждой стороне поперечной линии в сумме составляют 180 градусов.
Если мы посмотрим между параллельными линиями , мы увидим, что два угла на каждой стороне поперечной линии в сумме составляют 180 градусов.
Это потому, что поперечная линия разрезает каждую из параллельных линий на две части. Поскольку прямая линия представляет собой прямой угол, когда она разрезается пополам, сумма двух половинок должна составлять исходный размер. Это похоже на то, как если вы в любой момент отрежете метровую палку, когда вы снова сложите две части палки, они все равно получат один метр.
Если мы проведем еще одну линию, пересекающую параллельные линии, мы получим треугольник.
Наша верхняя группа углов была изменена с группы из четырех на группу из шести, потому что каждый из больших углов был разрезан новой линией.
Группа углов в нижнем левом углу не изменилась, и появилась новая группа углов, созданная новой линией, пересекающей нижнюю параллельную линию.
Давайте добавим метки углов ко всем углам между параллельными линиями:
Мы видим, что углы A, B и C вместе образуют прямой угол, так что их сумма должна составлять 180 градусов. Теперь мы можем установить, что три угла внутри треугольника (B, E и F) также дают в сумме 180. Углы A и E равны , совпадающим углам , что означает, что они имеют одинаковую величину, потому что они представляют собой внутренние переменные углов трансверсали с параллельными линиями.Угол C и угол F совпадают по той же причине.
Теперь мы можем установить, что три угла внутри треугольника (B, E и F) также дают в сумме 180. Углы A и E равны , совпадающим углам , что означает, что они имеют одинаковую величину, потому что они представляют собой внутренние переменные углов трансверсали с параллельными линиями.Угол C и угол F совпадают по той же причине.
Угол B совпадает с самим собой. Следовательно, сумма углов A, B и C должна быть равна сумме углов B, E и F. А поскольку сумма углов A, B и C, как известно, равна 180, тогда сумма углов углы B, E и F также должны быть 180. Вот таблица, в которой все изложено для нас:
Определение прямого угла: «Мера угла A плюс мера угла B плюс мера угла C равен 180 градусам.«Мера угла A равна мере угла E» истинно, потому что два угла совпадают, внутренние чередующиеся углы. То же самое относится к углам C и F.
Давайте посмотрим на это теперь с установленными углами:
Когда мы посмотрим на три угла под линией 1, мы увидим, что они в сумме составляют 180 градусов, как мы знаем. они должны.
они должны.
И три угла в треугольнике имеют те же три угла. Это всегда будет правдой. Если мы повернем добавленную линию и снова посмотрим на меры, мы увидим, что она все еще работает:
У нас есть 55, 75 и 50 внутри треугольника и 55, 75 и 50 под первой линией.Сложите их вместе, и вы получите, к удивлению, 180 градусов.
Review
Хорошо, прежде чем мы продолжим, давайте ответим на пару вопросов для быстрого обзора!
1. Какова мера прямого угла?
- 360 °
- 180 °
- 90 °
- 0 °
Правильный ответ — B, 180 градусов!
2. Если два угла являются чередующимися внутренними углами трансверсали с параллельными линиями, это означает, что углы также равны
- Конгруэнтный
- Острый
- Неконгруэнтный
- Параллельный
Правильный ответ — A , конгруэнтно!
Вот и все! Спасибо за просмотр и удачной учебы!
.
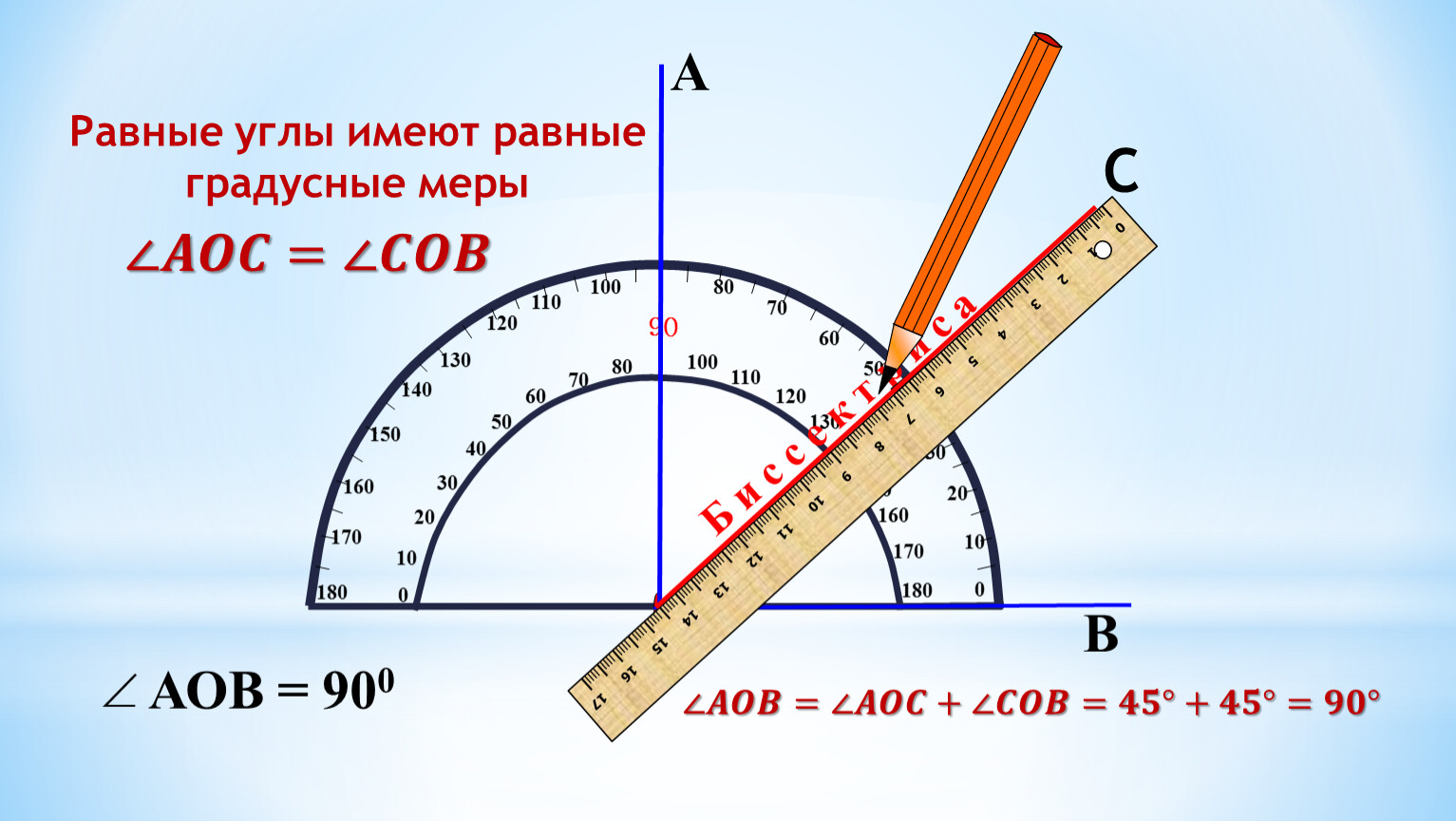 Вычислите полученные углы.
Вычислите полученные углы. Ответ: 36˚ и 144˚.
Ответ: 36˚ и 144˚.
 1000 Вт (лампочки), макс. 300 Вт (энергосберегающая лампа), макс. 100 Вт (светодиод).
1000 Вт (лампочки), макс. 300 Вт (энергосберегающая лампа), макс. 100 Вт (светодиод).






 Внезапно они начинают говорить о том, чтобы платить вперед и когда-нибудь вернуться, и сами стать наставниками.
Внезапно они начинают говорить о том, чтобы платить вперед и когда-нибудь вернуться, и сами стать наставниками. 
 Я думаю, это не относится к гардеробу … Конечно, «три шестьдесят» намного хуже. «Volte face» намного лучше, но его больше никто не использует ».
Я думаю, это не относится к гардеробу … Конечно, «три шестьдесят» намного хуже. «Volte face» намного лучше, но его больше никто не использует ».