Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней
Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет 6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для решения задач по теории вероятности, геометрии и математике! Также на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1 | 21=2 22=4 23=8 24=16 25=32 26=64 27=128 28=256 29=512 210=1024 | 31=3 32=9 3 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049 | 41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576 | 51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=39062559=1953125 510=9765625 |
61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176 | 71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249 | 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824 | 91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910=3486784401 | 101=10 102=100 103=1000 104=10000 105=100000106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000 |
Остались вопросы?
Здесь вы найдете ответы.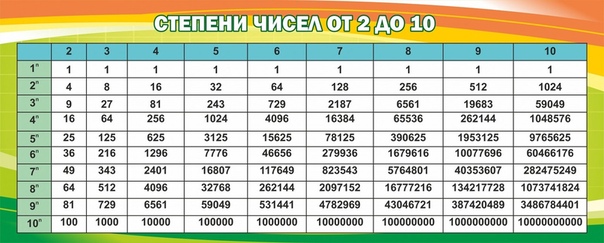 x=3
log2(3)=x
x=3
log2(3)=x
90 в 10 степени
90 в 10 =34867844009999998976.00000
12 в степени 1/3
Сложная формула но в кратце ответ — 6
Слишком сложно?
Таблица степеней не по зубам? Тебе ответит эксперт через 10 минут!
Таблица степеней 🆕
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
- an = a × a × … × a, где a — основание степени,
- n — натуральный показатель степени.
Запись читается, как «a» в степени «n».
Вот пример для наглядности:
- 35 = 3 × 3 × 3 × 3 × 3 = 243
Эту запись можно прочитать тремя способами:
- 3 в 5 степени;
- пятая степень числа три;
- возвести число три в пятую степень.

Свойства степеней
Свойства степеней обычно используют, чтобы сократить или упростить сложные примеры. Удобно использовать вместе с таблицей степеней и таблицей умножения.
a1 = а a0 = 1 (a ≠ 0) a−n = 1 : an am × an = am+n am : an = am-n (a × b)n = an × bn (am)n = am×n (a : b)n = an : bn |
Подготовка к ЕГЭ по математике онлайн поможет снять стресс перед экзаменом и повысит шансы на высокий балл.
Таблица степеней от 1 до 10
Таблица степеней — это перечень чисел от 1 до 10, возведенных в степень от 1 до 10. Ниже приведены два вида таблиц: выберите ту, которая удобнее для вас, скачайте на телефон или распечатайте и положите в учебник.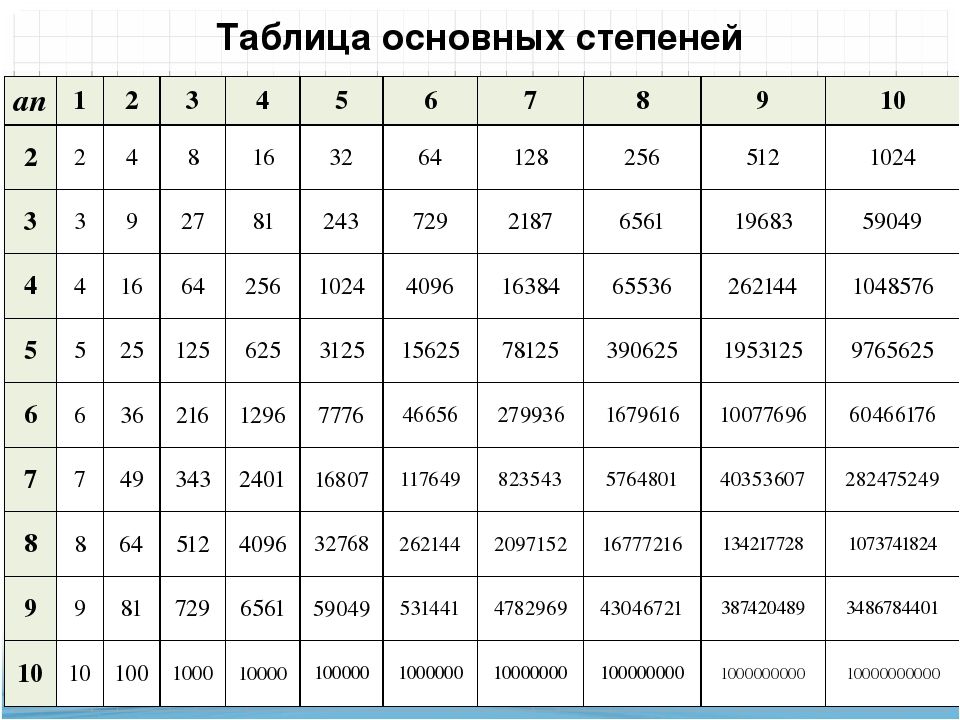
Как найти необходимые значения в этой таблице:
- В первом столбце находим число, которое обозначает степень. Запомним номер этой строки.
- В первой строке находим показатель степени. Запомним найденный столбец.
- На пересечении строки и столбца находится ответ.
В этой табличке мы просто ищем нужное нам число в степени и получаем ответ.
А если ответ нужно получить как можно быстрее, можно использовать онлайн-калькулятор степеней.
Решение задач
Задание 1. Упростить и решить выражение 52 × 53.
Как решаем:
52 × 53 = 52+3 = 55 = 3125
Задание 2. Упростить и решить выражение 24 × 33 × 25.
Как решаем:
24 × 33 × 25 = 24+5 × 33 = 29 × 33 = 512 × 27 = 13 824
Задание 3.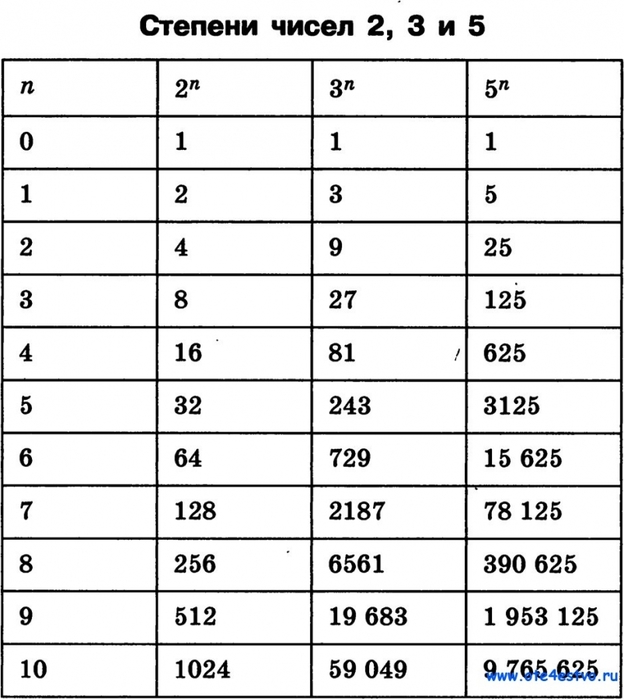 Найти 364.
Найти 364.
Как решаем:
При условии, что у нас есть только таблица до 10, разложим основание степени на множители:
364 = 64 × 64 = 1296 × 1296 = 1 679 616
364 = 64 × 64 = 68 = 1 679 616
Степени и возведение в степень, вторая, третья, четвёртая степени
Когда число умножается само на себя, произведение называется степенью.
Так 2.2 = 4, квадрат или вторая степень 2-х
2.2.2 = 8, куб или третья степень.
2.2.2.2 = 16, четвёртая степень.
Также, 10.10 = 100, вторая степень 10.
10.10.10 = 1000, третья степень.
10.10.10.10 = 10000 четвёртая степень.
И a.a = aa, вторая степень a
a.a.a = aaa, третья степень a
a.a.a.a = aaaa, четвёртая степень a
Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.
Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель. Это число или буква называется показателем степени или степенью числа. Так, а2 равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a3 означает aaa, то есть здесь a повторяется три раза как множитель.
Показатель первой степени есть 1, но он обычно не записывается. Так, a1 записывается как a.
Вы не должны путать степени с коэффициентами. Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a. Но a4 = a.a.a.a
Но a4 = a.a.a.a
Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква. В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении ax, показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень. Так, bm и dn возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда bm = b3; но если m = 5, тогда bm=b5.
Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d)3 есть (a + b + d). (a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a3 + 3a2b + 3a2d + 3ab2 + 6abd + 3ad2 + b3 + d3.
Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель, и этот множитель или делитель есть первоначальным числом, которое возводится в степень.
Так, в ряде aaaaa, aaaa, aaa, aa, a;
или a5, a4, a3, a2, a1;
показатели , если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножатьна a, мы успешно получим несколько значений.
Tак a.a = a2, второй член. И a3.a = a4
a2.a = a3, третий член. a4.a = a5.
a4.a = a5.
Если мы начнем слева делить на a,
мы получим a5:a = a4 и a3:a = a2.
a4:a = a3 a2:a = a1
Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.
Так, a:a = a/a = 1. (1/a):a = 1/aa
1:a = 1/a (1/aa):a = 1/aaa.
Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.
Или a5, a4, a3, a2, a, 1, 1/a, 1/a2, 1/a3.
Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.
Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a3) = a3.
Тот же самый план записи может применяться к многочленам. Так, для a + b, мы получим множество,
Так, для a + b, мы получим множество,
(a + b)3, (a + b)2, (a + b), 1, 1/(a + b), 1/(a + b)2, 1/(a + b)3.
Для удобства используется еще одна форма записи обратных степеней.
Согласно этой форме, 1/a или 1/a1 = a-1. И 1/aaa или 1/a3 = a-3.
1/aa или 1/a2 = a-2. 1/aaaa или 1/a4 = a-4.
А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a0.
Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать a4, a3, a2, a1, a0, a-1, a-2, a-3, a-4.
Или a+4, a+3, a+2, a+1, a0, a-1, a-2, a-3, a-4.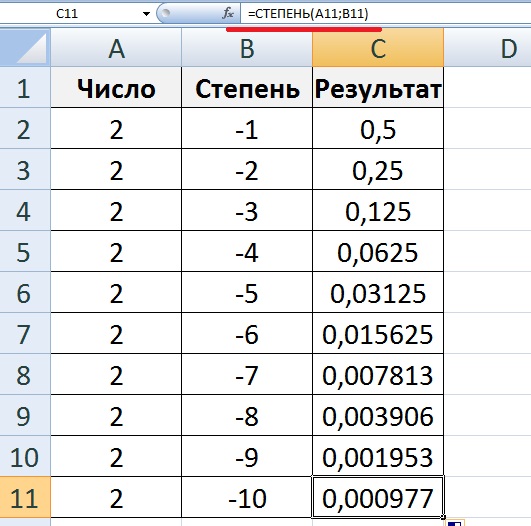
А ряд только отдельно взятых степеней будет иметь вид:
+4,+3,+2,+1,0,-1,-2,-3,-4.
Корень степени может выражен более чем одной буквой.
Так, aa.aa или (aa)2 есть второй степенью aa.
И aa.aa.aa или (aa)3 есть третьей степенью aa.
Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.
Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:
Умножайте величину саму на себя столько раз, сколько указано в степени числа.
Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.
Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.
Четвертая степень a есть a4 или aaaa. (Art. 195.)
Шестая степень y есть y6 или yyyyyy.
N-ая степень x есть xn или xxx….. n раз повторенное.
Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.
Tак (ay)2 =a2y2; (ay)2 = ay.ay.
Но ay.ay = ayay = aayy = a2y2.
Так, (bmx)3 = bmx.bmx.bmx = bbbmmmxxx = b3m3x3.
Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.
Пример 1. Четвертая степень dhy есть (dhy)4, или d4h4y4.
Пример 2. Третья степень 4b, есть (4b)3, или 43b3, или 64b3.
Пример 3. N-ая степень 6ad есть (6ad)n или 6nandn.
Пример 4. Третья степень 3m.2y есть (3m.2y)3, или 27m3.8y3.
Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,
(a + b)1 = a + b, первая степень.(a + b)1 = a2 + 2ab + b2, вторая степень (a + b).
(a + b)3 = a3 + 3a2b + 3ab2 + b3, третья степень.
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4, четвертая степень.
Квадрат a — b, есть a2 — 2ab + b2.
3 + 3a2 + 3a + 1.Квадрат a + b + h есть a2 + 2ab + 2ah + b2 + 2bh + h2
Упражнение 1. Найдите куб a + 2d + 3
Упражнение 2. Найдите четвертую степень b + 2.
Упражнение 3. Найдите пятую степень x + 1.
Упражнение 4. Найдите шестую степень 1 — b.
Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.
Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a2 + 2ah + h2 также, (a — h)(a — h) = a2 — 2ah + h2.
Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.
Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.
Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.
Пример 1. Квадрат 2a + b, есть 4a2 + 4ab + b2.
Пример 2. Квадрат ab + cd, есть a2b2 + 2abcd + c2d2.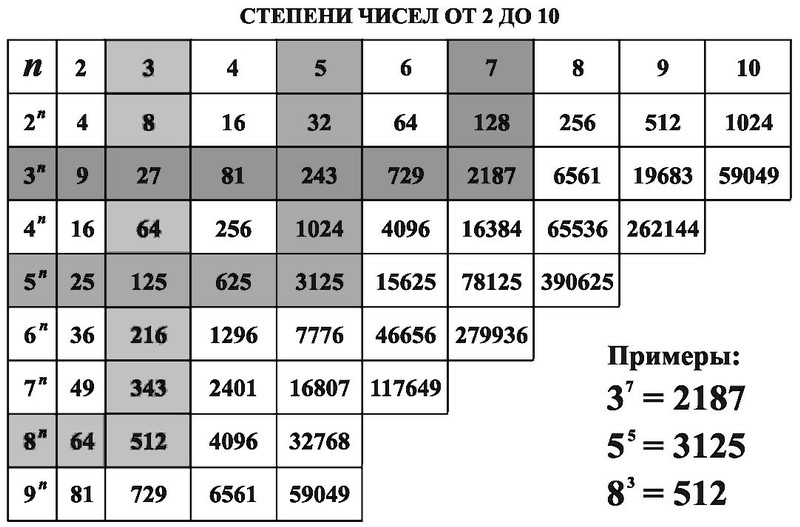
Пример 3. Квадрат 3d — h, есть 9d2 + 6dh + h2.
Пример 4. Квадрат a — 1 есть a2 — 2a + 1.
Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.
Во многих случаях является эффективным записывать степени без умножения.
Так, квадрат a + b, есть (a + b)2.
N-ая степень bc + 8 + x есть (bc + 8 + x)n
В таких случаях, скобки охватывают все члены под степенью.
Но если корень степени состоит из нескольких множителей, скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.
Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)]2 или (a + b)2.(c + d)2.
Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.
Куб a. (b + d), есть [a.(b + d)]3, или a3.(b + d)3.
(b + d), есть [a.(b + d)]3, или a3.(b + d)3.
Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.
Вторая степень (- a) есть +a2
Третья степень (-a) есть -a3
Четвёртая степень (-a) есть +a4
Пятая степень (-a) есть -a5
Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a2
И -a.-a = +a2
Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.
Третья степень a2 есть a2. 3 = a6.
3 = a6.Для a2 = aa; куб aa есть aa.aa.aa = aaaaaa = a6; что есть шестой степенью a, но третьей степенью a2.
Четвертая степень a3b2 есть a3.4b2.4 = a12b8
Третья степень 4a2x есть 64a6x3.
Пятая степень (a + b)2 есть (a + b)10.
N-ая степень a3 есть a3n
N-ая степень (x — y)m есть (x — y)mn
(a3.b3)2 = a6.b6
(a3b2h4)3 = a9b6h12
Правило одинаково применяется к отрицательным степеням.
Пример 1. Третья степень a-2 есть a-3.3=a-6.
Для a-2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a6 = a-6
Четвертая степень a2b-3 есть a8b-12 или a8/b12.
Квадрат b3x-1, есть b6x-2.
N-ая cтепень ax-m есть x-mn или 1/x.
Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.
Пример 1. Квадрат -a3 есть +a6. Квадрат -a3 есть -a3.-a3, которое, согласно правилам знаков при умножении, есть +a6.
2. Но куб -a3 есть -a9. Для -a3.-a3.-a3 = -a9.
3. N-ая степень -a3 есть a3n.
Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.
Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.
Квадрат a/b есть a2/b2. Согласно правилу умножению дробей,
(a/b)(a/b) = aa/bb = a2b2
Вторая, третья и n-ая степени 1/a есть 1/a2, 1/a3 и 1/an.
Примеры двочленов, в которых один из членов является дробью.
1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2)2 = x2 + 2.x.(1/2) + 1/22 = x2 + x + 1/4
(x — 1/2)2 = x2 — 2.x.(1/2) + 1/22 = x2 — x + 1/4
2. Квадрат a + 2/3 есть a2 + 4a/3 + 4/9.
3. Квадрат x + b/2 = x2 + bx + b2/4.
4 Квадрат x — b/m есть x2 — 2bx/m + b2/m2.
Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени.
Так, в дроби ax-2/y, мы можем переместить x из числителя в знаменатель.
Тогда ax-2/y = (a/y).x-2 = (a/y).(1/x2 = a/yx2. {5 i p} = 1$$
{5 i p} = 1$$
Используя формулу Эйлера, найдём корни для p
$$i \sin{\left(5 p \right)} + \cos{\left(5 p \right)} = 1$$
значит
$$\cos{\left(5 p \right)} = 1$$
и
$$\sin{\left(5 p \right)} = 0$$
тогда
$$p = \frac{2 \pi N}{5}$$
где N=0,1,2,3,…
Перебирая значения N и подставив p в формулу для z
Значит, решением будет для z:
$$z_{1} = 2$$
$$z_{2} = — \frac{1}{2} + \frac{\sqrt{5}}{2} — 2 i \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$z_{3} = — \frac{1}{2} + \frac{\sqrt{5}}{2} + 2 i \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$z_{4} = — \frac{\sqrt{5}}{2} — \frac{1}{2} — 2 i \sqrt{\frac{5}{8} — \frac{\sqrt{5}}{8}}$$
$$z_{5} = — \frac{\sqrt{5}}{2} — \frac{1}{2} + 2 i \sqrt{\frac{5}{8} — \frac{\sqrt{5}}{8}}$$
делаем обратную замену
$$z = x + 2$$
$$x = z — 2$$
Тогда, окончательный ответ:
$$x_{1} = 0$$
$$x_{2} = — \frac{5}{2} + \frac{\sqrt{5}}{2} — 2 i \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$x_{3} = — \frac{5}{2} + \frac{\sqrt{5}}{2} + 2 i \sqrt{\frac{\sqrt{5}}{8} + \frac{5}{8}}$$
$$x_{4} = — \frac{5}{2} — \frac{\sqrt{5}}{2} — 2 i \sqrt{\frac{5}{8} — \frac{\sqrt{5}}{8}}$$
$$x_{5} = — \frac{5}{2} — \frac{\sqrt{5}}{2} + 2 i \sqrt{\frac{5}{8} — \frac{\sqrt{5}}{8}}$$
Аденоиды у ребенка — откуда берутся, признаки и симптомы
“Кажется, у нашего ребёнка аденоиды!”– с такими сомнениями чаще всего приходят родители с малышом на прием к оториноларингологу, начитавшись статей в интернете, или после разговора с «всезнающими» мамами в песочнице/садике/школе. В этой статье мы постараемся разобрать наиболее частые вопросы об аденоидных вегетациях и попробуем понять, настолько ли все страшно.
В этой статье мы постараемся разобрать наиболее частые вопросы об аденоидных вегетациях и попробуем понять, настолько ли все страшно.
Что такое аденоиды и откуда они берутся
Аденоидные вегетации (носоглоточная миндалина) – это лимфоидная ткань в своде носоглотки. Она имеется у всех без исключения детей и является периферическим органом иммунной системы, частью лимфоидного глоточного кольца. Главной функцией данного анатомического образования является борьба с проникающими в организм ребёнка бактериями или вирусами. Главное ее отличие от остальных миндалин — поверхность покрыта особым эпителием, который продуцирует слизь. Увеличение (гипертрофию) аденоидной ткани провоцируют частые аллергические и респираторные заболевания вирусной или бактериальной этиологии. Поэтому пик гипертрофии аденоидной ткани приходится как раз на возраст 3-7 лет. Затем лимфоидная ткань постепенно редуцируется в возрасте 10–12 лет. К 17 годам нередко остаются только фрагменты ткани, у здоровых же взрослых людей аденоидная ткань отсутствует. Гипертрофию аденоидной ткани принято делить на несколько степеней по ее объёму в носоглотке от первой, где аденоиды закрывают носовые ходы (хоаны) на 1/3 , до третьей-четвертой степени, когда происходит полная обтурация носоглотки с невозможностью носового дыхания.
Гипертрофию аденоидной ткани принято делить на несколько степеней по ее объёму в носоглотке от первой, где аденоиды закрывают носовые ходы (хоаны) на 1/3 , до третьей-четвертой степени, когда происходит полная обтурация носоглотки с невозможностью носового дыхания.
Клинические проявления
Воспаление аденоидной ткани называется аденоидит. Течение его бывает острым, подострым и хроническим. Коснемся кратко основных симптомов, на которые стоит обращать внимание родителям:
1. Насморк, чаще всего он имеет затяжное течение.
2. Преимущественное дыхание через рот. Обусловлено затрудненным носовым дыханием. Степень затруднения напрямую зависит от степени гипертрофии аденоидной ткани. Часто появляется гнусавость. При длительном течении хронического аденоидита и дыхании через рот, возможно изменение лицевого скелета, что в дальнейшем проявляется стойким нарушением произношения речи.
3. Ночной храп, беспокойный сон.
Ночной храп, беспокойный сон.
4. Утренний кашель, обусловленный поперхиванием слизью, стекающей из носоглотки за ночь.
5. Снижение слуха, рецидивирующие отиты из-за механической обтурации слуховых труб аденоидными вегетациями. При этом гипертрофия может быть и 1-2 степени, при расположении аденоидов возле устьев слуховых труб, которые отвечают за вентиляцию среднего уха через слуховую трубу. Ребенок начинает постоянно переспрашивать или смотреть мультики слишком громко.
6. Быстрая утомляемость, апатия. Обусловлены постоянным кислородным голоданием головного мозга, особенно при хроническом аденоидите. Возможно отставание от сверстников в умственном и физическом развитии.
Методы исследования аденоидных вегетаций
В обычном состоянии без дополнительных оптических приспособлений эту миндалину увидеть невозможно. Существует ряд исследований, которые помогают установить степень аденоидных вегетаций: пальцевое исследование, задняя риноскопия зеркалом, рентгенография носоглотки, эндоскопия носоглотки, трёхмерное рентгенологическое исследование или КТ носоглотки. Наиболее современными методами на сегодняшний день являются:
Наиболее современными методами на сегодняшний день являются:
- эндоскопия носоглотки и полости носа. Процедура выполняется в нашей клинике под местной анестезией на приеме ЛОР врача. Полностью безболезненна, позволяет оценить не только степень аденоидных вегетаций, но и характер воспаления, состояние устьев слуховых труб, а также осмотреть задние отделы полости носа.
- трёхмерное рентгенологическое исследование / КТ носоглотки. Методы по информативности значительно превосходят обычный рентген носоглотки, так как позволяют определить не только размер, но и соотношение аденоидных вегетаций к остальным структурам носоглотки (устья слуховых труб, хоаны и др). Лучевая нагрузка практически в 3 раза меньше (0,009м3в), а длительность исследования не более 2 мин. Пройти данное исследование можно в клинике на Усачева.
Лечение аденоидита
Лечение аденоидита принято разделять на консервативное и оперативное. Консервативное лечение требует от родителей, в первую очередь, большого терпения (надо научить малыша правильно высмаркиваться, проводить с ним туалет полости носа иногда несколько раз в день!), посещения процедур (промывание носа ЛОР врачом, физиолечение и др.), четкого выполнения всех назначений врача. Это далеко не быстрый процесс, но если родители и врач заодно, и действуют сплоченной командой, то результат не заставляет себя ждать! Но бывают случаи, когда консервативное лечение неэффективно, тогда врач принимает решение об оперативном вмешательстве, и не всегда это зависит только от степени аденоидов. Чаще всего показаниями к оперативному лечению являются: полное отсутствие носового дыхания, рецидивирующие отиты (тубоотиты), ночное апное, стойкое снижение слуха.
Консервативное лечение требует от родителей, в первую очередь, большого терпения (надо научить малыша правильно высмаркиваться, проводить с ним туалет полости носа иногда несколько раз в день!), посещения процедур (промывание носа ЛОР врачом, физиолечение и др.), четкого выполнения всех назначений врача. Это далеко не быстрый процесс, но если родители и врач заодно, и действуют сплоченной командой, то результат не заставляет себя ждать! Но бывают случаи, когда консервативное лечение неэффективно, тогда врач принимает решение об оперативном вмешательстве, и не всегда это зависит только от степени аденоидов. Чаще всего показаниями к оперативному лечению являются: полное отсутствие носового дыхания, рецидивирующие отиты (тубоотиты), ночное апное, стойкое снижение слуха.
«Если они участвуют в иммунном ответе, зачем их удалять? Ничего лишнего в организме нет!»
Действительно, аденоидная ткань является частью лимфоидного кольца глотки, как было сказано выше, но только частью! Здесь важно оценивать соотношение вреда и пользы для организма. В случае хронического аденоидита сама миндалина становится местом обитания и размножения патогенных микроорганизмов, что явно не приносит пользы ребёнку, а частые обострения приводят к увеличению аденоидной ткани в размере, вызывая параллельно заболевание ушей, с последующим стойким снижением слуха.
В случае хронического аденоидита сама миндалина становится местом обитания и размножения патогенных микроорганизмов, что явно не приносит пользы ребёнку, а частые обострения приводят к увеличению аденоидной ткани в размере, вызывая параллельно заболевание ушей, с последующим стойким снижением слуха.
«Если их удалить — они вырастут заново!»
На данном этапе развития медицины это мнение является ошибочным. Операция аденотомия выполняется под общим наркозом, с использованием эндоскопической техники. Современное оснащение позволяет удалять аденоидную ткань полностью под визуальным контролем, тем самым гарантируя отсутствие рецидивов. При аденотомии под местной анестезией, как выполнялось ранее повсеместно, действительно высок риск повторных аденотомий, так как чаще всего часть миндалины не удаляется с первого раза, что и вызывает рецидив.
Совет от доктора
Как обобщение, хочу сказать, что всем известная шутка про лечение насморка за 7 дней и за неделю с детьми не работает! Те, кто относятся к насморку ребенка как к «обычным соплям, которые и сами пройдут», сталкиваются чаще всего в дальнейшем с целой кипой осложнений. Поэтому, чем раньше вы обратитесь к ЛОР врачу и начнете грамотное лечение, тем выше вероятность, что проблема аденоидов обойдет вас стороной!
Поэтому, чем раньше вы обратитесь к ЛОР врачу и начнете грамотное лечение, тем выше вероятность, что проблема аденоидов обойдет вас стороной!
Запишитесь к детскому врачу-оториноларингологу по телефону единого контакт-центра в Москве +7 (495) 775 75 66, заполните форму онлайн записи или обратитесь в регистратуру клиники «Семейный доктор».
Здоровья вам и вашим малышам!
Астигматизм — Мой офтальмолог
Что такое астигматизм и его симптомы
Астигматизм – одно из наиболее распространенных нарушений рефракции. Слабый астигматизм (≤0,5 диоптрии) встречается практически у всех людей, считается физиологическим. Как правило, он никак не проявляет себя, не влияет на зрение и человек его просто не замечает. Он может дать знать о себе с возрастом при возникновении тех или иных дополнительных факторов. В случае, когда нарушение составляет более 0,5 диоптрии, данная патология зрения существенно осложняет жизнь человека. При астигматизме человек видит предметы размыто и искаженно, ровные линии могут казаться кривыми, возникают проблемы с определением расстояния до предметов, глаза быстро устают, могут появиться жжение и резь в глазах, покраснение, двоение, «ощущение песка», головные боли и боль в области надбровных дуг и, естественно, падает острота зрения. Часто астигматизм возникает на фоне близорукости или дальнозоркости. Если вовремя не предпринять меры по лечению астигматизма, это может привести к амблиопии, косоглазию, резкому падению остроты зрения.
При астигматизме человек видит предметы размыто и искаженно, ровные линии могут казаться кривыми, возникают проблемы с определением расстояния до предметов, глаза быстро устают, могут появиться жжение и резь в глазах, покраснение, двоение, «ощущение песка», головные боли и боль в области надбровных дуг и, естественно, падает острота зрения. Часто астигматизм возникает на фоне близорукости или дальнозоркости. Если вовремя не предпринять меры по лечению астигматизма, это может привести к амблиопии, косоглазию, резкому падению остроты зрения.
Как возникает астигматизм – физиология процесса
Само название данного дефекта зрения происходит от греческого слова stigmate (точка) и приставки-отрицания «а». Это точно определяет суть астигматизма, которая заключается в следующем. В нормальном состоянии роговица и хрусталик обеспечивают фокусировку лучей на сетчатке в одной точке и, соответственно, четкое изображение. При астигматизме роговица (изредка хрусталик) имеют неправильную форму, преломляющая сила роговицы (хрусталика) отличается в разных плоскостях (по горизонтали и вертикали). В результате лучи проецируются на сетчатку не в одной, а в нескольких точках, образуя несколько фокусов, иногда в форме эллипса, отрезка, восьмерки. Как результат – нечеткое и расплывчатое изображение предметов, причем как вблизи, так и вдали.
В результате лучи проецируются на сетчатку не в одной, а в нескольких точках, образуя несколько фокусов, иногда в форме эллипса, отрезка, восьмерки. Как результат – нечеткое и расплывчатое изображение предметов, причем как вблизи, так и вдали.
Причины астигматизма
Астигматизм может быть врожденным и приобретенным. Основная причина врожденного астигматизма – наследственность. Причем выявить его можно сразу даже у грудных детей – современные методы диагностики позволяют сделать это, начиная с трехмесячного возраста. Среди причин приобретенного астигматизма: травмы, операции на глазах, роговичные рубцы после перенесенных воспалительных или инфекционных заболеваний, кератоконус.
Виды астигматизма
Астигматизм может быть прямым, когда преломляющая сила в вертикальной плоскости больше, чем в горизонтальной, и обратным (преломляющая сила в вертикальной плоскости меньше, чем в горизонтальной).
В случае, когда в одной из плоскостей нормальное зрение сочетается с близорукостью или дальнозоркостью, различают астигматизм простой близорукий и простой дальнозоркий соответственно. Если же близорукость или дальнозоркость имеется в обеих плоскостях (по горизонтали и вертикали), и при этом степень близорукости/дальнозоркости в этих плоскостях разная, то такой астигматизм называют сложный близорукий и сложный дальнозоркий соответственно. Существует также смешанный астигматизм, когда в одной из плоскостей роговицы присутствует близорукость, в другой – дальнозоркость.
Если же близорукость или дальнозоркость имеется в обеих плоскостях (по горизонтали и вертикали), и при этом степень близорукости/дальнозоркости в этих плоскостях разная, то такой астигматизм называют сложный близорукий и сложный дальнозоркий соответственно. Существует также смешанный астигматизм, когда в одной из плоскостей роговицы присутствует близорукость, в другой – дальнозоркость.
Степени астигматизма
Различают следующие степени астигматизма:
- слабая – до 2,0 – 2,5 диоптрий,
- средняя – от 2,5 до 5,0 диоптрий,
- сильная – свыше 5,0 диоптрий.
Диагностика и лечение астигматизма
Выявить астигматизм, определить его причины, вид, степень может только офтальмолог при осмотре пациента при помощи специального оборудования. В зависимости от состояния здоровья человека врач порекомендует подходящий метод лечения, например, очки или контактные линзы. Однако нужно помнить, что при коррекции астигматизма используется особая оптика: цилиндрические линзы для очков и торические мягкие контактные линзы. Подобрать и изготовить их могут только высококвалифицированные офтальмологи и оптометристы. Поэтому нужно приобретать такую корригирующую оптику в медицинских оптиках и специализированных офтальмологических центрах, где есть необходимое оборудование и хорошие специалисты. Но даже качественная и хорошо подобранная оптика не всегда решает проблему астигматизма полностью. У пациентов с высокой степенью астигматизма очки иногда приходится часто менять, линзы могут вызывать неприятные ощущения. Поэтому наиболее эффективным современным способом избавиться от астигматизма навсегда является процедура лазерной коррекции зрения, которая при отсутствии противопоказаний будет лучшим выбором для хорошего 100%-ного зрения.
Подобрать и изготовить их могут только высококвалифицированные офтальмологи и оптометристы. Поэтому нужно приобретать такую корригирующую оптику в медицинских оптиках и специализированных офтальмологических центрах, где есть необходимое оборудование и хорошие специалисты. Но даже качественная и хорошо подобранная оптика не всегда решает проблему астигматизма полностью. У пациентов с высокой степенью астигматизма очки иногда приходится часто менять, линзы могут вызывать неприятные ощущения. Поэтому наиболее эффективным современным способом избавиться от астигматизма навсегда является процедура лазерной коррекции зрения, которая при отсутствии противопоказаний будет лучшим выбором для хорошего 100%-ного зрения.
Близорукость у детей — причины, симптомы, виды и степени детской миопии, диагностика, профилактика и методы лечения
Подавляющее большинство детей (по разным данным — до 80%) рождается гиперметропами (хорошее зрение вдали, плохое вблизи), что обусловлено короткой переднезадней осью глазного яблока новорожденного (16-18 мм). В дальнейшем, по мере роста и самого ребенка и глазного яблока гиперметропия постепенно уменьшается, и у некоторых детей переходит в миопию.
В дальнейшем, по мере роста и самого ребенка и глазного яблока гиперметропия постепенно уменьшается, и у некоторых детей переходит в миопию.
Врожденная близорукость (миопия) у детей
Врожденная миопия может быть связана с недоношенностью, обусловлена наследственностью, или вызвана патологическими процессами. Следует заметить, что в большинстве случаев врожденная близорукость характеризуется слабыми изменениями на глазном дне.
Врожденная близорукость, как правило, носит стабильный характер, хотя, в некоторых случаях, возможно ее прогрессирование. Естественно, дети с врожденной близорукостью требуют к себе пристального внимания врача-офтальмолога с постоянным динамичным наблюдением. Необходимо как можно раньше назначать оптическую коррекцию и проводить профилактику возможной амблиопии.
Детская близорукость
Близорукость (миопия) — заболевание, при котором дети плохо различают предметы, расположенные на дальнем расстоянии. Это происходит из-за того, что параллельные лучи света, идущие от предметов расположенных вдали, сводятся в фокус в плоскости перед сетчаткой, а не на ней самой, вследствие чего снижается острота зрения у ребенка. Зачастую это связано с тем, что переднезадняя ось глаза оказывается слишком длинной. В результате вытянутой формы глазного яблока происходит неправильное преломление света, и острота зрения снижается, прежде всего, вдаль.
Зачастую это связано с тем, что переднезадняя ось глаза оказывается слишком длинной. В результате вытянутой формы глазного яблока происходит неправильное преломление света, и острота зрения снижается, прежде всего, вдаль.
Врачи-офтальмологи разделяют миопию на слабую (до 3,0 D включительно), среднюю (от 3,25 до 6,0 D) и высокую (более 6 D). Высокая миопия может достигать весьма значительных величин: 15,20,30 D и более.
Близорукие дети нуждаются в очках для дали, а многие и для зрения вблизи (когда миопия превышает 5-6 диоптрий). Но очки, увы, не всегда корректируют зрение до высокого уровня, что связано с дистрофическими и др. изменениями в оболочках близорукого глаза.
Причины возникновения близорукости (миопии) у детей могут быть разные: наследственный фактор, ослабление склеры, первичная слабость аккомодации, длительная работа на близком расстоянии (сидение у компьютера, телевизора), условия внешней среды, нарушение гигиены зрения, ослабление организма в результате неправильного питания, переутомление, различные заболевания. Но чаще всего близорукость (миопия) обусловлена видоизменением формы глазного яблока (удлинением его переднезадней оси).
Но чаще всего близорукость (миопия) обусловлена видоизменением формы глазного яблока (удлинением его переднезадней оси).
Лечение близорукости у детей
Для лечения близорукости применяются многочисленные средства и методы. Прежде всего, лечение близорукости у детей направлено не на ликвидацию или уменьшение степени миопии, а на остановку или замедление ее дальнейшего прогрессирования и профилактику ее осложнений.
Благоприятным течением для детской и подростковой близорукости считается снижение зрения со скоростью не более 0,5 диоптрии в год. Тогда ее лечат консервативными методами. Нужно носить очки или линзы, давать глазам больше отдыха, делать зрительную гимнастику, нормально высыпаться и питаться, соблюдать зрительную гигиену.
В детском отделении клиники «Эксимер» по итогам диагностики ребенку подбирают способ контактной коррекции и проводят лечение при помощи различных терапевтических методов. Кроме того, составляется программа индивидуальных занятий на дому, родителям объясняют, как тестировать зрение в домашних условиях. Врач следит за происходящими изменениями и, при необходимости, корректирует программу.
Врач следит за происходящими изменениями и, при необходимости, корректирует программу.
Для лечения близорукости в детском отделении клиники «Эксимер» работает: целый комплекс современного оборудования. Диагностика зрения, и лечение проходят по специальным игровым программам. Применяются такие терапевтические процедуры, как: лазерная, ультразвуковая и инфракрасная лазерная терапия, лазерная стимуляция, вакуумный массаж, магнитотерапия, электростимуляция — их эффективность признана на российском и международном уровнях.
-
Процедура инфракрасной лазерной терапии
Ввоздействие на глаз инфракрасным излучением с близкого расстояния позволяет улучшить питание тканей глаза, снять спазм аккомодации, который является одной из основных причин развития близорукости. Аппарат для инфракрасной лазерной терапии обеспечивает «физиологический массаж» цилиарной мышцы, которая отвечает за нормальную аккомодацию.
-
Вакуумный массаж
При вакуумном массаже в качестве лечебного фактора используется переменный вакуум.
 Данная процедура значительно улучшает гидродинамику глаза, обеспечивает увеличение кровообращения и, в результате, улучшается работа цилиарной мышцы.
Данная процедура значительно улучшает гидродинамику глаза, обеспечивает увеличение кровообращения и, в результате, улучшается работа цилиарной мышцы. -
Лазерная терапия
Сеансы лазерной терапии применяются для улучшения пространственного зрения, функций аккомодации. Лазерное излучение подается на экран, который расположен на расстоянии 8–10 см. от глаза пациента. Лечебное действие лазерной терапии оказывается за счет наблюдения за изменениями объемов и структуры изображения, появляющихся на экране, что стимулируют работу рецепторных (нервных) клеток сетчатки.
-
Электростимуляция
Это стимуляция дозированным электрическим током малой интенсивности. Она способствует повышению проводимости импульсов в зрительном нерве. Эта процедура абсолютно безболезненна.
-
Реамед
Кроме того, в детском отделении клиники «Эксимер» для лечения близорукости работает комплекс «Реамед», разработанный ведущими специалистами Института головного мозга.
 В основе действия прибора лежит метод видеокомпьютерного аутотренинга. Пока ребенок смотрит мультфильм, прибор с помощью датчиков снимает информацию о работе глаз, одновременно фиксируя энцефалограмму мозга. При этом изображение на экране сохраняется только во время «правильного» зрения и исчезает, как только оно перестает быть четким. Таким образом, прибор как бы заставляет мозг подсознательно сокращать периоды неконтрастного зрения. Подобный подход оптимизирует работу нейронов зрительной коры, а зрение при этом существенно улучшается.
В основе действия прибора лежит метод видеокомпьютерного аутотренинга. Пока ребенок смотрит мультфильм, прибор с помощью датчиков снимает информацию о работе глаз, одновременно фиксируя энцефалограмму мозга. При этом изображение на экране сохраняется только во время «правильного» зрения и исчезает, как только оно перестает быть четким. Таким образом, прибор как бы заставляет мозг подсознательно сокращать периоды неконтрастного зрения. Подобный подход оптимизирует работу нейронов зрительной коры, а зрение при этом существенно улучшается.
Для каждого ребенка лечебная программа составляется индивидуально, с учетом его возраста, состояния здоровья и общего психоэмоционального статуса. Очень важно относиться к лечению серьезно, не пропускать обязательные осмотры и процедуры по назначениям лечащего врача. Такой подход позволяет не просто устранить проблему, а дать гарантию пациенту и его родителям, что когда ребенок вырастет, болезнь не вернется.
Родителям на заметку
Количество близоруких детей в разных государствах мира, а часто и в пределах одной и той же страны, значительно варьируется. В разных регионах России близорукость выявляется от 2,3% до 13,8% школьников, а среди выпускников средних школ — от 3,5% до 32,2%. Пиковым возрастным периодом развития близорукости считается 10–12 лет, хотя в последнее время стремительно увеличивается количество близоруких детей среди учеников младших классов.
В разных регионах России близорукость выявляется от 2,3% до 13,8% школьников, а среди выпускников средних школ — от 3,5% до 32,2%. Пиковым возрастным периодом развития близорукости считается 10–12 лет, хотя в последнее время стремительно увеличивается количество близоруких детей среди учеников младших классов.
Специалистами было установлено увеличение числа близоруких в северных широтах по сравнению с южными и меньшее распространение миопии среди детей сельской местности по сравнению с городской. Объяснение этим факторам можно найти в особенностях светового режима, условиях питания, времени пребывания детей на свежем воздухе, в степени зрительной нагрузки, в занятиях спортом и т. д.
Как определить близорукость у ребенка?
Как известно, на ранних стадиях развития многие заболевания поддаются лечению гораздо лучше, это касается и близорукости. Ребенок не может пожаловаться вам на то, что он плохо видит, потому что он просто не знает разницу между «видеть плохо» и «видеть хорошо». Поэтому, если вы заметили, что ваш ребенок быстро устает при чтении, низко склоняется над книгой или тетрадью, периодически жалуется на головные боли, часто моргает, трет глаза кулачками — срочно обратитесь к врачу-офтальмологу! Помните, что только специалист может вовремя диагностировать заболевания и назначить необходимое лечение!
Поэтому, если вы заметили, что ваш ребенок быстро устает при чтении, низко склоняется над книгой или тетрадью, периодически жалуется на головные боли, часто моргает, трет глаза кулачками — срочно обратитесь к врачу-офтальмологу! Помните, что только специалист может вовремя диагностировать заболевания и назначить необходимое лечение!
Профилактика неправильных зрительных привычек
Но помимо всего родителям стоит заниматься профилактикой неправильных зрительных привычек у своих детей. Учите их правильно сидеть за рабочим столом. Следите за тем, чтобы во время работы свет падал на книгу или тетрадь равномерно, в то же время голова и лицо должны оставаться в тени. Лучше всего заниматься с настольной лампой, оставляя при этом общее освещение. Особенно это важно в темное время суток. Нужно избегать наклона головы ребенка близко к предмету работы, лучше расстояние для зрительной деятельности — 30–35 см. Желательно исключить из поля зрения ребенка во время работы различные бликующие или отражающие поверхности. Вредная привычка читать лежа может явиться еще одним из провоцирующих близорукость факторов. Необходимо делать перерывы после каждых 30–35 минут работы за письменным столом (для младших школьников — 20–25 минут), во время которых можно перекусить, выполнить гимнастику для глаз, упражнения–разминку или просто отдохнуть.
Вредная привычка читать лежа может явиться еще одним из провоцирующих близорукость факторов. Необходимо делать перерывы после каждых 30–35 минут работы за письменным столом (для младших школьников — 20–25 минут), во время которых можно перекусить, выполнить гимнастику для глаз, упражнения–разминку или просто отдохнуть.
Имеются противопоказания. Проконсультируйтесь со специалистом. | В подарок нашим маленьким пациентам скидка 20%:
скидка предоставляется на программы «Стандарт», «Эффект», «Максимум» при оплате полного курса. |
Запишитесь в клинику «эксимер»
и узнайте больше о своём здоровье!
Вы можете позвонить по телефону: +7 (831) 202-25-55
Или нажать кнопку и заполнить форму заявки
и получить 5% скидку на полную диагностику зрения
Лицензии клиники
| 1 | Найдите производную — d / dx | натуральное журнал x | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d / dx | е ^ х | |
| 4 | Оцените интеграл | интеграл e ^ (2x) относительно x | |
| 5 | Найдите производную — d / dx | 1 / х | |
| 6 | Найдите производную — d / dx | х ^ 2 | |
| 7 | Найдите производную — d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную — d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную — d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную — d / dx | соз (х) ^ 2 | |
| 14 | Оцените интеграл | интеграл от 1 / x по отношению к x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную — d / dx | х ^ 3 | |
| 17 | Найдите производную — d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную — d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную — d / dx | грех (2x) | |
| 23 | Найдите производную — d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную — d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную — d / dx | cos (2x) | |
| 28 | Найдите производную — d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл от 2x относительно x | |
| 30 | Найдите производную — d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную — d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную — d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную — d / dx | 2e ^ x | |
| 35 | Найдите производную — d / dx | натуральное бревно 2x | |
| 36 | Найдите производную — d / dx | -sin (х) | |
| 37 | Найдите производную — d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную — d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную — d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл от e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл от cos (2x) относительно x | |
| 42 | Найдите производную — d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную — d / dx | х / 2 | |
| 46 | Найдите производную — d / dx | -cos (x) | |
| 47 | Найдите производную — d / dx | грех (3x) | |
| 48 | Найдите производную — d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл от tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 по x | |
| 51 | Найдите производную — d / dx | х ^ х | |
| 52 | Найдите производную — d / dx | x натуральное бревно x | |
| 53 | Найдите производную — d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл x ^ 2 натуральный логарифм x относительно x | |
| 56 | Найдите производную — d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную — d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную — d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную — d / dx | у = х ^ 2 | |
| 62 | Найдите производную — d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную — d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную — d / dx | е ^ 2 | |
| 67 | Найдите производную — d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную — d / dx | арксин (х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную — d / dx | х ^ 5 | |
| 73 | Найдите производную — d / dx | 2 / х | |
| 74 | Найдите производную — d / dx | натуральное бревно из 3х | |
| 75 | Найдите производную — d / dx | х ^ (1/2) | |
| 76 | Найдите производную — d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную — d / dx | соз (х ^ 2) | |
| 78 | Найдите производную — d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную — d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную — d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 по x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную — d / dx | журнал x | |
| 86 | Найдите производную — d / dx | арктан (x) | |
| 87 | Найдите производную — d / dx | натуральное бревно 5x | |
| 88 | Найдите производную — d / dx | 5e ^ x | |
| 89 | Найдите производную — d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл от x ^ 2e ^ x относительно x | |
| 92 | Найдите производную — d / dx | 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 93 | Найдите производную — d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную — d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную — d / dx | 2sin (х) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную — d / dx | натуральный логарифм x ^ 2 |
Измерение углов
Измерение угловПонятие угла
Понятие угла — одно из важнейших понятий в геометрии. Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .
Понятия равенства, суммы и разности углов важны и используются во всей геометрии, но предмет тригонометрии основан на измерении углов .Есть две обычно используемые единицы измерения углов. Более знакомая единица измерения — это градусы. Круг делится на 360 равных градусов, так что прямой угол равен 90 °. В настоящее время мы будем рассматривать только углы между 0 ° и 360 °, но позже, в разделе о тригонометрических функциях, мы будем рассматривать углы больше 360 ° и отрицательные углы. Градусы можно разделить на минуты и секунды, но это деление не так универсально, как раньше. Каждый градус делится на 60 равных частей, называемых минут. Итак, семь с половиной градусов можно назвать 7 градусами и 30 минутами, записанными как 7 ° 30 ‘. Каждая минута далее делится на 60 равных частей, называемых секунд, и, например, 2 градуса 5 минут 30 секунд записывается как 2 ° 5 ’30 «. Деление градусов на минуты и угловые секунды аналогично делению на часы в минуты и секунды. |
Части градуса теперь обычно обозначаются десятичной дробью. Например, семь с половиной градусов теперь обычно пишут как 7,5 & deg.
Когда один угол нарисован на плоскости xy для анализа, мы нарисуем его в стандартной позиции с вершиной в начале координат (0,0), одна сторона угла вдоль x ось, а другая сторона выше оси x .
Радианы
Другое распространенное измерение углов — радианы.Для этого измерения рассмотрим единичный круг (круг радиуса 1), центр которого является вершиной рассматриваемого угла. Затем угол отсекает дугу окружности, и длина этой дуги является мерой угла в радианах. Легко переходить между градусами и радианами. Окружность всего круга равна 2 π , следовательно, 360 ° равняется 2 π радиан. Следовательно, 1 ° равняется π /180 радиани 1 радиан равен 180/ π градусов Большинство калькуляторов можно настроить на использование углов, измеряемых в градусах или радианах. |
Краткая записка по истории радианов
Хотя слово «радиан» было придумано Томасом Мьюром и / или Джеймсом Томпсоном около 1870 года, математики долгое время измеряли углы таким способом. Например, Леонард Эйлер (1707–1783) в своей работе Elements of Algebra явно сказал, что углы следует измерять по длине дуги, отрезанной в единичной окружности.Это было необходимо, чтобы дать его знаменитую формулу, включающую комплексные числа, которая связывает функции знака и косинуса с экспоненциальной функцией. e iθ = cos θ + i sin θгде θ — это то, что позже было названо измерением угла в радианах. К сожалению, объяснение этой формулы выходит далеко за рамки этих заметок. Но для получения дополнительной информации о комплексных числах см. Мой Краткий курс комплексных чисел.
Радианы и длина дуги
Альтернативное определение радианов иногда дается как отношение. Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, тогда мера в радианах равна 1.5.
Вместо того, чтобы брать единичную окружность с центром в вершине угла θ , возьмите любую окружность с центром в вершине угла. Тогда радианная мера угла — это отношение длины вытянутой дуги к радиусу r окружности. Например, если длина дуги равна 3, а радиус круга равен 2, тогда мера в радианах равна 1.5.Причина, по которой это определение работает, заключается в том, что длина вытянутой дуги пропорциональна радиусу круга. В частности, определение в терминах отношения дает ту же цифру, что и приведенная выше с использованием единичного круга. Однако это альтернативное определение более полезно, поскольку вы можете использовать его для соотнесения длин дуг с углами. Длина дуги равна радиусу r, умноженному на угол θ , где угол измеряется в радианах.
Например, дуга θ = 0,3 радиана в окружности радиуса r = 4 имеет длину 0,3 умноженную на 4, то есть 1,2.
Радианы и площадь сектора
Сектор круга — это часть круга, ограниченная двумя радиусами и дугой окружности, соединяющей их концы. Площадь этого сектора легко вычислить по радиусу r круга и углу θ между радиусами, если он измерен в радианах.Так как площадь всего круга равна πr 2 , а сектор относится к всей окружности, так как угол θ равен 2 π , поэтому
Площадь этого сектора легко вычислить по радиусу r круга и углу θ между радиусами, если он измерен в радианах.Так как площадь всего круга равна πr 2 , а сектор относится к всей окружности, так как угол θ равен 2 π , поэтомуУглы общие
Ниже приведена таблица общих углов как в градусах, так и в радианах. Обратите внимание, что измерение в радианах дано в терминах π . Его, конечно, можно было бы указать в десятичной дроби, но радианы часто появляются с коэффициентом π . .| Уголок | градусов | Радианы |
|---|---|---|
| 90 ° | π /2 | |
| 60 ° | π /3 | |
| 45 ° | π /4 | |
| 30 ° | π /6 |
Упражнения
Эдвин С.Кроули написал книгу Тысяча упражнений в плоской и сферической тригонометрии, Университет Пенсильвании, Филадельфия, 1914. Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на утомительных вычислениях.
Задачи этого короткого курса взяты из этого текста (но не все 1000 из них!). пять знаков точности, поэтому студентам пришлось потрудиться, чтобы решить их, и они использовали таблицы логарифмов, чтобы помочь в умножении и делении. Студенты должны были уметь пользоваться таблицей синус-косинусов, таблицей касательных, таблицей логарифмов, таблицей log-sin-cos и таблицей log-tan.Теперь мы можем пользоваться калькуляторами! Это означает, что вы можете сосредоточиться на концепциях, а не на утомительных вычислениях.Кроули использовал не десятичные дроби для дробей градуса, а минуты и секунды.
Каждый комплекс упражнений включает в себя, во-первых, формулировку упражнений, во-вторых, некоторые подсказки для решения упражнений, а в-третьих, ответы на упражнения.
1. Выразите следующие углы в радианах.
(а). 12 градусов, 28 минут, то есть 12 ° 28 ‘.
(б). 36 ° 12 ‘.
2. Сократите следующие числа радианов до градусов, минут и секунд.
(а). 0,47623.
(б). 0,25412.
3. Учитывая угол a и радиус r, , чтобы найти длину проходящей дуги.
(а). a = 0 ° 17 ’48 дюймов, r = 6,2935.
(б). a = 121 ° 6 ’18 дюймов, r = 0,2163.
4. Учитывая длину дуги l и радиус r, , чтобы найти угол, стянутый в центре.
(а). l = 0,16296, r = 12,587.
(б). l = 1,3672, r = 1,2978.
5. Зная длину дуги l и угол a , который она проходит в центре, найти радиус.
(а). a = 0 ° 44 ’30 дюймов, l = 0,032592.
(б). a = 60 ° 21 ‘6 дюймов, l = 0,4572.
6. Найдите длину с точностью до дюйма дуги окружности 11 градусов 48,3 минуты, если радиус составляет 3200 футов.
7. Кривая железной дороги образует дугу окружности 9 градусов 36,7 минут, радиус до центральной линии пути составляет 2100 футов. Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
Если калибр 5 футов, найдите разницу в длине двух рельсов с точностью до полудюйма.
9. Насколько можно изменить широту, идя на север на одну милю, если предположить, что Земля представляет собой сферу радиусом 3956 миль?
10. Вычислите длину в футах одной угловой минуты на большом круге Земли. Какова длина дуги в одну секунду?
14. На окружности радиусом 5,782 метра длина дуги составляет 1,742 метра. Какой угол он образует в центре?
23. Воздушный шар, известный как 50 футов в диаметре, сужается к глазу под углом 8 1/2 минут.Как далеко это?
Подсказки
1. Чтобы преобразовать градусы в радианы, сначала преобразуйте количество градусов, минут и секунд в десятичную форму. Разделите количество минут на 60 и прибавьте к количеству градусов. Так, например, 12 ° 28 ‘равно 12 + 28/60, что равно 12,467 °. Затем умножьте на π и разделите на 180, чтобы получить угол в радианах.
2. И наоборот, чтобы преобразовать радианы в градусы, разделите на π и умножьте на 180.Таким образом, 0,47623, деленное на π и умноженное на 180, дает 27,286 °. Вы можете преобразовать доли градуса в минуты и секунды следующим образом. Умножьте дробь на 60, чтобы получить количество минут. Здесь 0,286 умножить на 60 равно 17,16, поэтому угол можно записать как 27 ° 17,16 ‘. Затем возьмите любую оставшуюся долю минуты и снова умножьте на 60, чтобы получить количество секунд. Здесь 0,16 умножить на 60 равно примерно 10, поэтому угол также можно записать как 27 ° 17 ’10 «.
3. Чтобы найти длину дуги, сначала преобразуйте угол в радианы. Для 3 (a) 0 ° 17’48 «равно 0,0051778 радиана. Затем умножьте его на радиус, чтобы найти длину дуги.
4. Чтобы найти угол, разделите его на радиус. Это дает вам угол в радианах. Это можно преобразовать в градусы, чтобы получить ответы Кроули.
5. Как упоминалось выше, радиан умноженный на радиус = длина дуги, поэтому, используя буквы для этой задачи, ar = l, , но необходимо сначала преобразовать из градусного измерения в радиан . Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
Итак, чтобы найти радиус r, сначала преобразует угол a в радианы, а затем разделит его на длину l дуги.
6. Длина дуги равна радиусу, умноженному на угол в радианах.
7. Помогает нарисовать фигуру. Радиус внешнего рельса равен 2102,5, а радиус внутреннего рельса — 2097,5.
9. У вас есть круг радиусом 3956 миль и дуга этого круга длиной 1 милю.Какой угол в градусах? (Средний радиус Земли был известен довольно точно в 1914 году. Посмотрим, сможете ли вы узнать, каким, по мнению Эратосфена, был радиус Земли, еще в III веке до н. Э.)
10. Угловая минута равна 1/60 градуса. Преобразовать в радианы. Радиус — 3956. Какова длина дуги?
14. Поскольку длина дуги равна радиусу, умноженному на угол в радианах, отсюда следует, что угол в радианах равен длине дуги, деленной на радиус.Радианы легко преобразовать в градусы.
23. Представьте, что диаметр воздушного шара является частью дуги окружности с вами в центре. (Это не совсем часть дуги, но довольно близко.) Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
(Это не совсем часть дуги, но довольно близко.) Длина дуги составляет 50 футов. Вы знаете угол, так каков радиус этого круга?
ответы
1. (а). 0,2176. (б). 0,6318.2. (а). 27 ° 17 ’10 «. (B). 14,56 ° = 14 ° 33,6′ = 14 ° 33’36».
3. (а). 0,03259 (б). 2,1137 умножить на 0,2163 равно 0,4572.
4. (а). 0,16296 / 12,587 = 0,012947 радиан = 0 ° 44 ’30 дюймов.
(б). 1,3672 / 1,2978 = 1,0535
радианы = 60,360 ° = 60 ° 21,6 ‘= 60 ° 21’ 35 «.
5. (а). л / год = 0,032592 / 0,01294 = 2,518.
(б). л / год = 0,4572 / 1,0533 = 0,4340.
6. ra = (3200 ‘) (0.20604) = 659,31 ‘= 659’ 4 дюйма.
7. Угол a = 0,16776 радиана. Разница в длине составляет 2102,5 a –1997,5 a , что составляет 5 a. Таким образом, ответ составляет 0,84 фута, что с точностью до дюйма составляет 10 дюймов.
9. Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
Угол = 1/3956 = 0,0002528 радиан = 0,01448 ° = 0,8690 ‘= 52,14 дюйма.
10. Одна минута = 0,0002909 радиан. 1.15075 миль = 6076 футов.Следовательно, одна секунда будет соответствовать 101,3 фута.
14. a = л / об = 1,742 / 5,782 = 0,3013 радиан = 17,26 ° = 17 ° 16 ‘.
23. Угол a равен 8,5 ‘, что составляет 0,00247 радиана. Таким образом, радиус равен r = л / год = 50 / 0,00247 = 20222 ‘= 3,83 мили, почти четыре мили.
Насчет цифр точности.
Кроули старается давать свои ответы примерно с той же точностью, что и данные в вопросах.Это важно, особенно теперь, когда у нас есть калькуляторы. Например, в задаче 1 точка отсчета равна 12 ° 28 ‘, что соответствует примерно четырем знакам точности, поэтому ответ 0,2176 также должен быть дан только с точностью до четырех знаков. (Обратите внимание, что ведущие нули не учитываются при вычислении цифр точности.) Ответ 0,21758438 предполагает восьмизначную точность, и это может ввести в заблуждение, поскольку данная информация не была такой точной.
Другой пример см. В задаче 3 (a). Данные 0 ° 17’48 «и 6.2935, с точностью до 4 и 5 знаков соответственно. Следовательно, ответ должен быть дан только с точностью до 4 цифр, так как ответ не может быть более точным, чем наименее точные данные. Таким образом, ответ, который может дать калькулятор, а именно 0,032586547, следует округлить до четырех цифр (не включая ведущие нули) до 0,03259.
Хотя окончательные ответы должны быть выражены с соответствующим числом цифр точности, вы все равно должны сохранять все цифры для промежуточных вычислений.
радиан в градус Мера
Мера угла определяется величиной поворота от начальной стороны к конечной стороне. В радианах один полный оборот против часовой стрелки равен 2 π а в градусах один полный оборот против часовой стрелки равен 360 ° . Так, степень меры и радианная мера связаны уравнениями
360 ° знак равно 2 π радианы и
180 ° знак равно π радианы
Из последнего получаем уравнение
1
радиан =
(
180
π
)
о
. Это приводит нас к правилу преобразования радианов в градусы. Чтобы преобразовать радианы в градусы, умножьте радианы на
180
°
π
радианы
.
Это приводит нас к правилу преобразования радианов в градусы. Чтобы преобразовать радианы в градусы, умножьте радианы на
180
°
π
радианы
.
Пример 1:
Конвертировать π 4 радианы в градусы.
( π 4 рад ) ( 180 ° π рад ) знак равно ( 180 4 ) о знак равно 45 °
Пример 2:
Конвертировать
9
π
5
радианы в градусы.
( 9 π 5 рад ) ( 180 ° π рад ) знак равно 9 ( 36 ) о знак равно 324 °
Пример 3:
Конвертировать 3 радианы в градусы.
( 3 рад ) ( 180 ° π рад ) знак равно ( 540 π ) о ≈ 171,89 °
Этот рисунок объясняет, почему 2 градуса глобального потепления будут намного хуже, чем 1.
 5
5Примечание редактора: эта статья была первоначально опубликована в начале 2018 года и была переиздана для выпуска в воскресенье в специальном отчете IPCC о глобальном потеплении на 1,5 ° C .
Стороны, подписавшие Парижское соглашение по климату — все страны мира, если и до тех пор, пока США не выйдут из состава 2020 года, — согласились с уже известной целью: «сдерживать повышение средней глобальной температуры до уровня значительно ниже 2 ° C. выше доиндустриальных уровней и прилагает усилия, чтобы ограничить повышение температуры до 1.5 ° C ».
Но насколько важна эта разница? Насколько будет 2 градуса хуже 1,5? Стоит ли дополнительных усилий — и это было бы поистине героическим усилием — ограничить повышение температуры до этой более низкой цели?
Было трудно ответить на эти вопросы, отчасти потому, что они ценны и невероятно сложны, но также из-за недостаточного количества исследований. Несмотря на то, что было проделано много работы над разницей, скажем, между потеплением на 2 и 4 градуса (что было бы катастрофой), меньше работ по моделированию в районе 1.5 и нет исчерпывающего сравнения 1.5 и 2.
Несмотря на то, что было проделано много работы над разницей, скажем, между потеплением на 2 и 4 градуса (что было бы катастрофой), меньше работ по моделированию в районе 1.5 и нет исчерпывающего сравнения 1.5 и 2.
К счастью, исследование 2016 года, опубликованное в журнале Earth System Dynamics , напрямую занимается этим. В CarbonBrief Роз Пидкок кратко излагает исследование, которое уходит в прошлое, и некоторые выводы.
Лучше всего то, что команда CarbonBrief (которую вы действительно должны добавить в закладки) собрала соответствующие сравнения в исследовании в один четкий, эстетически приятный рисунок:
CarbonBriefЭто как прогноз погоды! Из ада.
2 градуса будет намного хуже 1.5 местами
Что касается экстремальной жары, как пишут авторы, «дополнительное повышение средней глобальной температуры на 0,5 ° C отмечает разницу между событиями на верхнем пределе современной естественной изменчивости и новым климатическим режимом, особенно в тропических регионах».
В районе Средиземного моря доступность пресной воды при 2 градусах упадет почти вдвое больше, чем на 1,5–17 процентов по сравнению с 9 процентами.
В некоторых высокоширотных регионах может быть полезна разница между 1.5 и 2 градуса (хотя такие преимущества будут сведены на нет, если температура в дальнейшем продолжит расти). Но даже при повышении температуры до 2 градусов «тропические регионы, такие как Западная Африка, Юго-Восточная Азия, а также Центральная и северная часть Южной Америки, по прогнозам, столкнутся со значительным снижением урожайности на местном уровне, особенно пшеницы и кукурузы».
TXX измеряет крайние температуры; WSDI измеряет количество длительных (6 с лишним дней) приступов. Earth Systems Dynamics Что касается повышения уровня моря относительно 1.5 градусов, 2 градуса означают, что уровни на 10 сантиметров выше и на 30 процентов выше , скорость увеличения к 2100 году.
А вот с коралловыми рифами все в порядке, несмотря ни на что. В сценарии с 1,5 градусом процент коралловых рифов в мире, подвергающихся риску, достигнет 90 процентов в 2050 году, но снизится до 70 процентов в 2100 году. По сценарию с двумя градусами риску подвергаются все они.
Отчет IPCC и исследование Earth System Dynamics подтверждают то, что многие ученые предупреждали годами: 2 градуса — это не «безопасный» порог.Негативные воздействия уже начались и будут только ухудшаться.
Чтобы остановить потепление на 1,5 градуса, потребуются серьезные и продолжительные глобальные действия.
У нас не так много времени, чтобы принимать решения. Окно для попадания на 1,5 градуса стремительно закрывается. Вот еще один ужасающий график от CarbonBrief, показывающий, сколько лет осталось до того, как «углеродный бюджет» для различных температур будет израсходован:
CarbonBrief При нашем нынешнем уровне выбросов, наш углеродный бюджет с хорошей (66%) вероятностью ограничения потепления до 1. 5 степеней будут израсходованы за шесть лет. Только вот этому графику два года назад, так что теперь осталось четыре года.
5 степеней будут израсходованы за шесть лет. Только вот этому графику два года назад, так что теперь осталось четыре года.
Чтобы притормозить на 1,5 градуса, глобальные выбросы углерода должны немедленно начать сокращаться, быстрее, чем когда-либо, и достичь нуля к 2050 году (а затем стать отрицательным):
OCIДля этого потребуется мобилизация, эквивалентная мобилизации США для Второй мировой войны, только глобальная и продолжающаяся до конца века.Шансы на это кажутся … маловероятными. Насколько нам известно, Трамп все еще будет у власти, когда бюджет в 1,5 градуса будет израсходован.
Но мы должны четко представлять себе решение, которое мы принимаем, даже если мы принимаем его, просто не принимая решения.
Откладывая необходимые работы по декарбонизации, мы обрекаем миллионы людей в тропических регионах на меньшее количество продуктов питания, а в Средиземноморье — на меньшее количество воды — со всеми сопутствующими проблемами со здоровьем и конфликтами. Мы допускаем больше волн жары и более высокого уровня моря.Мы отказываемся от коралловых рифов мира, а вместе с ними и от сотен видов, которые на них полагаются.
Мы допускаем больше волн жары и более высокого уровня моря.Мы отказываемся от коралловых рифов мира, а вместе с ними и от сотен видов, которые на них полагаются.
И даже тогда решение все равно будет стоять перед нами: 2 градуса или 3? Опять же, это будет означать больше волн тепла, больше потерь урожая, больше нехватки воды, больше затопленных прибрежных городов, больше болезней и конфликтов, миллионы страданий.
И даже тогда решение: 3 градуса или 4?
Чем дольше мы ждем, тем больше человеческих страданий и необратимого ущерба экосистемам мы вписываем в наше коллективное будущее.Но здесь нельзя спрятаться и избежать необходимости обезуглероживания. Это необходимо сделать, если у нашего вида есть надежный дом на Земле.
Похоже, что умнее всего было бы с этим справиться.
2,5 C в F Калькулятор преобразования (Цельсия в Фаренгейт)
Преобразование из 2,5 C в F (2,5 градусов Цельсия в Фаренгейт)
Изучите преобразование температуры из 2,5 C в F (Градусы Цельсия в Фаренгейты) прямо сейчас! Преобразовать градусы из метрических в британские легко с помощью нашего простого в использовании калькулятора преобразования или продолжайте читать, чтобы узнать, как преобразовать эти единицы самостоятельно!
2. 5 градусов Цельсия (C) равны 36,5 градусам Фаренгейта (F)
5 градусов Цельсия (C) равны 36,5 градусам Фаренгейта (F)
или 2,5 C = 36,5 F
Как преобразовать 2,5 C в F (Цельсия в Фаренгейта)
Узнайте, как легко преобразовать Цельсий в Фаренгейт, ниже . Общее уравнение для преобразования C в F состоит в том, чтобы умножить C на 1,8 (или 9/5), а затем прибавить 32.
Расчет C к F:
1 C = (1 C * 1,8) + 32 = 33,8 F
- Уравнение преобразования 2,5 C в F
2.5 C = (2,5 C * 1,8) +32 = 36,5 F
Быстрое преобразование температуры в духовке
Ознакомьтесь с нашей простой в использовании таблицей преобразования температуры в духовке, которая поможет вам в выпечке.
Обычное преобразование Цельсия в Фаренгейта
| Цельсия | Фаренгейта | Цельсия | Фаренгейта | Фаренгейта 9000 00 Фаренгейта 9000 00 00 | |
| 1 С | 33. 8 F 8 F | 60 C | 140 F | ||
| 2 C | 35,6 F | 70 C | 158 F | ||
| 3 C | 37,4 F | 80 C | |||
| 176 F | 80 C | ||||
| 176 F | |||||
| 176 F 4 C | 39,2 F | 90 C | 194 F | ||
| 5 C | 41 F | 100 C | 212 F | ||
| 6 C | 42,8 F | 0004 1254 1254 C||||
| 7 С | 44.6 F | 150 C | 302 F | ||
| 8 C | 46,4 F | 175 C | 347 F | ||
| 9 C | 48,2 F | 200 C | 0004 392 10 C50 F | 250 C | 482 F |
| 15 C | 59 F | 500 C | 932 F | ||
| 20 C | 68 F | 7504 13000 C | 750 C 9000 | ||
| 30 C | 86 F | 1000 C | 1832 F | ||
| 40 C | 104 F | 1500 C | 2732 F |
Конвертировать 2.
 5 C в другие единицы измерения температуры
5 C в другие единицы измерения температурыХотите преобразовать 2,5 C в другие единицы измерения температуры? Вот еще несколько полезных преобразований температуры:
| Единица | 2,5 Цельсия (C) = |
| Кельвина (K) | 275,65 K |
| R0004 496,175 | |
| Rømer (Rø) | 8,812 Rø |
| Ньютон (Н) | 0,825 N |
Что такое Цельсия (C)?
Цельсий (C), который также может называться градусом Цельсия, — это единица измерения температуры в метрической системе измерения.Эта шкала температур основана на температуре замерзания воды, равной 0 ° C, и температуре кипения воды, равной 100 ° C.
Аббревиатура для обозначения Цельсия — «C». Например, 2,5 градуса Цельсия можно записать как 2,5 C.
См. Определение словаря здесь.
Что такое Фаренгейт (F)?
Фаренгейт (F) — это единица измерения температуры в имперской системе измерения. Эта система основана на температурной шкале физика Даниэля Габриэля Фаренгейта.В системе по Фаренгейту точка замерзания воды составляет 32 градуса по Фаренгейту, а точка кипения воды — 212 градусов по Фаренгейту.
Эта система основана на температурной шкале физика Даниэля Габриэля Фаренгейта.В системе по Фаренгейту точка замерзания воды составляет 32 градуса по Фаренгейту, а точка кипения воды — 212 градусов по Фаренгейту.
Условное обозначение Фаренгейта — «F». Например, 2,5 градуса по Фаренгейту можно записать как 2,5 F.
Щелкните здесь, чтобы узнать больше об единицах измерения по Фаренгейту.
Степени свободы: что это такое?
При проверке гипотез используются степеней свободы.
Содержание (щелкните, чтобы перейти к этому разделу):
- Что такое степени свободы?
- DF: два образца
- степени свободы в ANOVA
- Почему критические значения снижаются при увеличении DF?
Посмотрите видео, чтобы узнать о степенях свободы и о том, почему мы вычитаем 1:
Не можете посмотреть видео? Кликните сюда.

Степени свободы в левом столбце таблицы t-распределения.
степеней свободы оценки — это количество независимых частей информации, которые использовались при вычислении оценки . Это не совсем то же самое, что количество элементов в выборке. Чтобы получить df для оценки, вы должны вычесть 1 из количества элементов. Допустим, вы определили среднюю потерю веса при низкоуглеводной диете. Вы можете использовать 4 человека, что дает 3 степени свободы (4 — 1 = 3), или вы можете использовать сто человек с df = 99.
В математическом выражении (где «n» — количество элементов в вашем наборе):
степеней свободы = n — 1
Почему мы вычитаем 1 из количества элементов?
Еще один способ взглянуть на степени свободы — это число значений, которые могут изменяться в наборе данных. Что значит «свободно варьироваться»? Вот пример с использованием среднего (среднего):
Q . Выберите набор чисел со средним (средним) значением 10.
Выберите набор чисел со средним (средним) значением 10.
А . Некоторые наборы чисел, которые вы можете выбрать: 9, 10, 11 или 8, 10, 12 или 5, 10, 15.
После того, как вы выбрали первые два числа в наборе, третье фиксируется. Другими словами, нельзя выбрать третий элемент в наборе . Единственные числа, которые могут изменяться, — это первые два. Вы можете выбрать 9 + 10 или 5 + 15, но как только вы примете это решение, вы должны выбрать конкретное число, которое даст вам то значение, которое вы ищете. Итак, степень свободы для набора из трех чисел равна ДВА.
Например: если вы хотите найти доверительный интервал для выборки, степень свободы равна n — 1. «N’ также может быть количеством классов или категорий. См .: Пример критического значения хи-квадрат.
В начало
Если у вас есть две выборки и вы хотите найти параметр, например среднее значение, у вас есть два «n», которые следует учитывать (выборка 1 и выборка 2). Степеней свободы в этом случае:
Степеней свободы в этом случае:
степеней свободы (два образца): (N 1 + N 2 ) — 2.
К началу
Степени свободы становятся немного сложнее в тестах ANOVA. Вместо простого параметра (например, нахождения среднего) тесты ANOVA включают сравнение известных средних значений в наборах данных. Например, в одностороннем дисперсионном анализе вы сравниваете два средних значения в двух ячейках. Общее среднее (среднее из средних) будет:
Среднее 1 + среднее 2 = большое среднее.
Что, если бы вы выбрали среднее значение 1 и знали большое среднее значение? У вас не было бы выбора относительно Среднее 2 , поэтому ваша степень свободы для двухгруппового дисперсионного анализа равна 1.
Двухгрупповой дисперсионный анализ df1 = n — 1
Для трехгруппового дисперсионного анализа вы можете варьировать два средних значения, так что степень свободы равна 2.
На самом деле это маленький более сложный, потому что в ANOVA есть две степеней свободы: df1 и df2. Приведенное выше объяснение относится к df1. Df2 в ANOVA — это общее количество наблюдений во всех ячейках — степени свободы, потерянные из-за того, что установлены средние значения ячеек.
Двухгрупповой дисперсионный анализ df2 = n — k
Буква «k» в этой формуле — это количество значений ячеек или групп / условий.
Например, предположим, что у вас есть 200 наблюдений и четыре средних значения ячейки. Степени свободы в этом случае будут: Df2 = 200 — 4 = 196.
К началу
Спасибо Мохаммеду Гезму за этот вопрос.
Давайте посмотрим на формулу t-показателя при проверке гипотез:
Когда n увеличивается, t-показатель увеличивается. Это из-за квадратного корня в знаменателе: по мере того, как он становится больше, дробь s / √n становится меньше, а t-показатель (результат другой дроби) становится больше. Поскольку степени свободы определены выше как n-1, можно подумать, что критическое значение t тоже должно увеличиться, но это не так: они уменьшаются на , на . Это кажется нелогичным.
Поскольку степени свободы определены выше как n-1, можно подумать, что критическое значение t тоже должно увеличиться, но это не так: они уменьшаются на , на . Это кажется нелогичным.
Однако, подумайте о том, что на самом деле представляет собой t-тест для . Вы используете t-тест, потому что вам неизвестно стандартное отклонение вашей совокупности и, следовательно, вы не знаете форму своего графика. У него могли быть короткие толстые хвосты. У него могли быть длинные тонкие хвосты. Вы просто не представляете.Степени свободы влияют на форму графика в t-распределении; по мере увеличения df площадь в хвостах распределения уменьшается. Когда df приближается к бесконечности, t-распределение будет выглядеть как нормальное распределение. Когда это происходит, вы можете быть уверены в своем стандартном отклонении (которое равно 1 при нормальном распределении).
Допустим, вы взяли повторную выборку весов у четырех человек, взятых из совокупности с неизвестным стандартным отклонением. Вы измеряете их вес, вычисляете среднюю разницу между парами образцов и повторяете этот процесс снова и снова.Крошечный размер выборки, равный 4, приведет к t-распределению с толстыми хвостами. Жирные хвосты говорят о том, что в вашей выборке вероятнее всего будут экстремальные значения. Вы проверяете свою гипотезу на уровне альфа 5%, который отсекает последние 5% вашего распределения . На графике ниже показано t-распределение с отсечкой 5%. Это дает критическое значение 2,6. ( Примечание : я использую здесь гипотетическое t-распределение в качестве примера — CV не является точным).
Вы измеряете их вес, вычисляете среднюю разницу между парами образцов и повторяете этот процесс снова и снова.Крошечный размер выборки, равный 4, приведет к t-распределению с толстыми хвостами. Жирные хвосты говорят о том, что в вашей выборке вероятнее всего будут экстремальные значения. Вы проверяете свою гипотезу на уровне альфа 5%, который отсекает последние 5% вашего распределения . На графике ниже показано t-распределение с отсечкой 5%. Это дает критическое значение 2,6. ( Примечание : я использую здесь гипотетическое t-распределение в качестве примера — CV не является точным).
Теперь посмотрим на нормальное распределение.У нас меньше шансов получить экстремальные значения при нормальном распределении. Наш 5% -ный альфа-уровень отсекает при CV 2.
Вернуться к исходному вопросу «Почему критические значения снижаются, а DF увеличивается?» Вот краткий ответ:
Степени свободы связаны с размером выборки (n-1).
Если df увеличивается, это также означает, что размер выборки увеличивается; график t-распределения будет иметь более узкие хвосты, что приведет к приближению критического значения к среднему.
Вернуться к началу
Ссылка :
Джерард Даллал.Маленький справочник по статистической практике. Получено 26 декабря 2015 г. отсюда.
Алистер В. Керр, Ховард К. Холл, Стивен А. Козуб. (2002). Выполнение статистики с помощью SPSS. Публикации Sage. стр.68. Доступно здесь.
Левин, Д. (2014). Даже вы можете изучить статистику и аналитику: простое для понимания руководство по статистике и аналитике, 3-е издание. Пресс Pearson FT
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в этой области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Загар 5 градусов — Найдите значение загара 5 градусов
Значение тангенса угла 5 градусов составляет 0,0874886. . . . Tan 5 градусов в радианах записывается как tan (5 ° × π / 180 °), то есть tan (π / 36) или tan (0,087266 …). В этой статье мы обсудим методы определения значения тангенса угла 5 градусов с примерами.
- Tan 5 ° в десятичной системе счисления: 0,0874886. . .
- Tan (-5 градусов): -0,0874886. . .
- Tan 5 ° в радианах: tan (π / 36) или tan (0,0872664…)
Что такое 5 градусов загара?
Значение тангенса угла 5 в десятичной системе счисления составляет 0,087488663. . .. Tan 5 градусов можно также выразить с помощью эквивалента заданного угла (5 градусов) в радианах (0,08726 …)
Мы знаем, используя преобразование градусов в радианы, θ в радианах = θ в градусах × (пи / 180 °)
⇒ 5 градусов = 5 ° × (π / 180 °) рад = π / 36 или 0. 0872. . .
0872. . .
∴ загар 5 ° = загар (0,0872) = 0,0874886. . .
Пояснение:
Для загара 5 градусов угол 5 ° находится между 0 ° и 90 ° (первый квадрант). Поскольку в первом квадранте функция тангенса положительна, значение tan 5 ° = 0,0874886. . .
Поскольку касательная функция является периодической функцией, мы можем представить tan 5 ° как, tan 5 градусов = tan (5 ° + n × 180 °), n ∈ Z.
⇒ загар 5 ° = загар 185 ° = загар 365 ° и так далее.
Примечание: Поскольку тангенс является нечетной функцией, значение tan (-5 °) = -tan (5 °).
Методы определения значения танка 5 градусов
Функция касательной положительна в 1-м квадранте. Значение tan 5 ° принимается как 0,08748. . .. Мы можем найти значение загара в 5 градусов по:
- Использование Unit Circle
- Использование тригонометрических функций
Желто-коричневый 5 градусов с использованием единичной окружности
Чтобы найти значение тангенса угла 5 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 5 ° с положительной осью x.

- Загар в 5 градусов равен координате y (0,0872), деленной на координату x (0,9962) точки пересечения (0,9962, 0,0872) единичной окружности и r.
Следовательно, значение tan 5 ° = y / x = 0,0875 (приблизительно).
Tan 5 ° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить загар в 5 градусов как:
- sin (5 °) / cos (5 °)
- ± sin 5 ° / √ (1 — sin² (5 °))
- ± √ (1 — cos² (5 °)) / cos 5 °
- ± 1 / √ (косек² (5 °) — 1)
- ± √ (сек² (5 °) — 1)
- 1 / детская кроватка 5 °
Примечание. Поскольку 5 ° находится в 1-м квадранте, окончательное значение тангенса угла 5 ° будет положительным.
Мы можем использовать тригонометрические тождества, чтобы представить загар 5 ° как,
- детская кроватка (90 ° — 5 °) = детская кроватка 85 °
- -детская кроватка (90 ° + 5 °) =-детская кроватка 95 °
- -тан (180 ° — 5 °) = -тан 175 °
☛ Также проверьте:
Часто задаваемые вопросы о 5 градусах загара
Что такое загар 5 градусов?
Тан 5 градусов — значение тригонометрической функции касательной для угла, равного 5 градусам. Значение тангенса угла наклона 5 ° составляет 0,0875 (приблизительно).
Значение тангенса угла наклона 5 ° составляет 0,0875 (приблизительно).
Какова ценность 5 градусов загара в переводе на 5 ° Cot?
Поскольку функция тангенса обратна функции котангенса, мы можем записать тангенс 5 ° как 1 / cot (5 °). Значение детской кроватки 5 ° равно 11,43005.
Какое значение Tan 5 ° в терминах Cosec 5 °?
Поскольку функцию касательной можно представить с помощью функции косеканса, мы можем записать tan 5 ° как 1 / √ (cosec² (5 °) — 1). Значение cosec 5 ° равно 11,47371.
Как определить значение 5-градусного загара?
Значение tan 5 градусов можно рассчитать, построив угол 5 ° с осью x, а затем найдя координаты соответствующей точки (0.9962, 0,0872) на единичной окружности. Значение tan 5 ° равно координате y (0,0872), деленной на координату x (0,9962). ∴ загар 5 ° = 0,0875
Как найти Tan 5 ° с помощью других тригонометрических функций?
Используя формулу тригонометрии, значение тангенса угла наклона 5 ° может быть выражено в терминах других тригонометрических функций как:
- sin (5 °) / cos (5 °)
- ± sin 5 ° / √ (1 — sin² (5 °))
- ± √ (1 — cos² (5 °)) / cos 5 °
- ± 1 / √ (косек² (5 °) — 1)
- ± √ (сек² (5 °) — 1)
- 1 / детская кроватка 5 °
☛ Также проверьте: тригонометрическая таблица
.

 Данная процедура значительно улучшает гидродинамику глаза, обеспечивает увеличение кровообращения и, в результате, улучшается работа цилиарной мышцы.
Данная процедура значительно улучшает гидродинамику глаза, обеспечивает увеличение кровообращения и, в результате, улучшается работа цилиарной мышцы. В основе действия прибора лежит метод видеокомпьютерного аутотренинга. Пока ребенок смотрит мультфильм, прибор с помощью датчиков снимает информацию о работе глаз, одновременно фиксируя энцефалограмму мозга. При этом изображение на экране сохраняется только во время «правильного» зрения и исчезает, как только оно перестает быть четким. Таким образом, прибор как бы заставляет мозг подсознательно сокращать периоды неконтрастного зрения. Подобный подход оптимизирует работу нейронов зрительной коры, а зрение при этом существенно улучшается.
В основе действия прибора лежит метод видеокомпьютерного аутотренинга. Пока ребенок смотрит мультфильм, прибор с помощью датчиков снимает информацию о работе глаз, одновременно фиксируя энцефалограмму мозга. При этом изображение на экране сохраняется только во время «правильного» зрения и исчезает, как только оно перестает быть четким. Таким образом, прибор как бы заставляет мозг подсознательно сокращать периоды неконтрастного зрения. Подобный подход оптимизирует работу нейронов зрительной коры, а зрение при этом существенно улучшается.
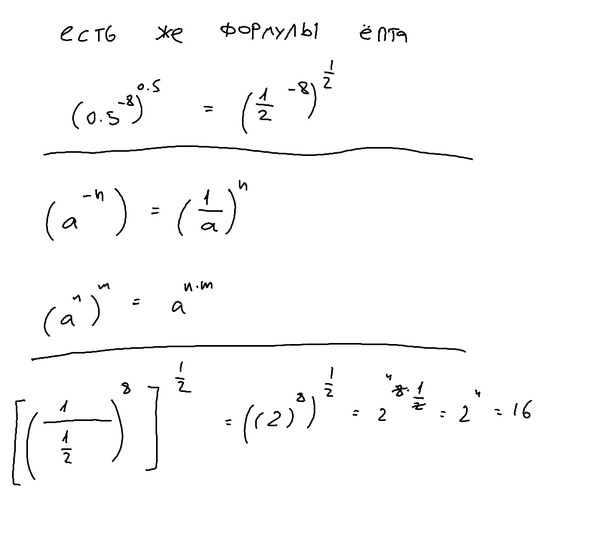
 Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор.
Убедитесь, что вы знаете, в каком режиме работает ваш калькулятор. Если df увеличивается, это также означает, что размер выборки увеличивается; график t-распределения будет иметь более узкие хвосты, что приведет к приближению критического значения к среднему.
Если df увеличивается, это также означает, что размер выборки увеличивается; график t-распределения будет иметь более узкие хвосты, что приведет к приближению критического значения к среднему.