Конспект обобщающего урока по алгебре в 9-м классе по теме «Решение уравнений высших степеней»
Цели урока:
- Образовательные:
— привести в систему знания учащихся по теме «Решение уравнений третьей и четвёртой степеней»;
— повторить теорию решения уравнений;
— выработать умение определять вид уравнения;
— выбирать наиболее рациональные способы решения данного уравнения.
— развитие аналитического мышления;
— развитие умения производить классификацию фактов;
— выработка желания глубины проникновения в предмет.
- Воспитательные:
— воспитание потребности в знаниях;
— воспитание культуры общения.
Методическая цель урока: реализация вариативной части учебного плана.
Тип урока: Урок обобщения и систематизации знаний.
Эпиграф к уроку:
Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду. Л.Н.Толстой.
Или
Уравнение представляет собой наиболее серьёзную и важную вещь в математике. О.Лодж.
Ход урока
I. Мотивация учебной деятельности (постановка перед учащимися целей урока, сообщение плана урока)
II. Актуализация опорных знаний
а) Повторение теории решения уравнений:
— что называется уравнением?
— что значит решить уравнение?
— что называется корнем уравнения?
— какие виды уравнений вы знаете?
— способы решения уравнений?
Для работы можно использовать таблицу «Классификация уравнений». (Приложение)
— Какие уравнения относятся к целым, дробным, иррациональным?
— А уравнения с модулем, параметром к каким уравнениям можно отнести?
б) Повторение методов решения уравнений.
Аналитический.
Приёмы:
1) простейшие(приведение подобных слагаемых, раскрытие скобок, приведение дробей к общему знаменателю, перенос слагаемых из одной части уравнения в другую, решение квадратных уравнений по формуле, умножение (деление) обеих частей уравнения на одно и то же не равное нулю число).
Пример 1.
х(х-6)=х
Решение:
х(х-6)=х | : х≠0
х-6=1
х=7
Обосновать ошибку. Что произошло? Решить уравнение правильно.
Пример 2.
=-1
Решение:
()2=(-1)2
х+3=1
х=-2
Обосновать ошибку. Что произошло? Решить уравнение правильно.
2) разложение на множители (формулы сокращённого умножения, группировка, теорема Безу).
3) введение вспомогательной переменной (следует помнить об ОДЗ самого уравнения и ОДЗ новой переменной).
4) Нетрадиционные приёмы решения:
- функционально-графический;
- смешанный.

в) Устная работа по группам.
Задание: классифицировать уравнения по виду и по способу решения.
1. =
2. у2-5у+6=0
3. (х-2)2-2(х-2)-4=0
4. +1=6
5. =х
6. Указать количество корней уравнения 2+|х|=а
7. х3+3х2-4х=0
8. (х-1)2-х2=4-3х
III. Решение уравнений 3 и 4 степени, т.е. решение уравнений
а0 х4+а1х3+а2
х2+а3 х+а4=0а0 х3+а1х2+а2х+а3 =0
Исторический экскурс
Вы знаете, что алгебра возникла в связи с решением разнообразных задач при помощи уравнений. XVи XVI столетия вошли в историю Европы под названием «эпоха Возрождения». Для неё характерен расцвет науки и культуры. В Европе появились компас, часы, порох, дешёвая бумага, книгопечатание. Развивалась промышленность, требующая технических усовершенствований и изобретений, появляются стимулы для развития науки. Расцвет науки происходит главным образом в Италии, Франции, Германии. Итальянские математики XVI в. сделали крупное математическое открытие. Они нашли формулы для решения уравнений 3 и 4 степеней. Николо Тарталья (ребёнок из очень бедной семьи, мать не могла платить за образование, поэтому мальчик в школе узнал только половину азбуки, всеми остальными знаниями он овладел самостоятельно). В 6 лет он получил удар мечом в гортань от французского воина и с тех пор говорил с трудом, отсюда и прозвище Тарталья (заика). Он вывел формулы для решения уравнений 3-ей степени, но своё открытие держал в тайне.
Развивалась промышленность, требующая технических усовершенствований и изобретений, появляются стимулы для развития науки. Расцвет науки происходит главным образом в Италии, Франции, Германии. Итальянские математики XVI в. сделали крупное математическое открытие. Они нашли формулы для решения уравнений 3 и 4 степеней. Николо Тарталья (ребёнок из очень бедной семьи, мать не могла платить за образование, поэтому мальчик в школе узнал только половину азбуки, всеми остальными знаниями он овладел самостоятельно). В 6 лет он получил удар мечом в гортань от французского воина и с тех пор говорил с трудом, отсюда и прозвище Тарталья (заика). Он вывел формулы для решения уравнений 3-ей степени, но своё открытие держал в тайне.
Джироламо Кардано (медик) занимался астрологией, составлял гороскопы. Кардано неоднократно обращался к Тарталье с просьбой сообщить ему формулу для решения кубических уравнений и обещал хранить её в секрете. Он не сдержал слово и опубликовал формулу, указав, что Тарталье принадлежит честь открытия «такого прекрасного и удивительного, превосходящего все таланты человеческого духа». Ученик Кардано Луиджи Феррари нашёл формулы для решения уравнений 4 степени.
Ученик Кардано Луиджи Феррари нашёл формулы для решения уравнений 4 степени.
Решение уравнений
№ 1.
х3-9х+х2–9=0
Способ решения данного уравнения — разложение на множители способом группировки.
(х3+х2)-(9х+9)=0
х2(х+1)-9(х+1)=0
(х+1)(х2-9)=0
(х+1)(х-3)(х+3)=0 Ответ: -3; -1; 3.
№ 2. х3-6х2+11х-6=0
Способ решения данного уравнения – разложение на множители с помощью теоремы Безу.
Один корень найдём подбором. Их следует искать среди делителей свободного члена данного многочлена ±1, ±2, ±3, ±6. Но т.к. сумма коэффициентов многочлена равна 0, то его корнем является 1.По теореме Безу (остаток от деления многочлена Р(х) на двучлен (х-а)равен Р(а). Если а- корень многочлена Р(х), то многочлен делится на (х-а)без остатка). Разделим многочлен 3 степени на двучлен (х-1).
х3-6х2+11х-6=(х-1)(х2
(х-1)(х2-5х+6)=0
Ответ: 1, 2, 3.
№ 3. х4 +5х3+6х2+5х+1=0
(Возвратное или симметричное уравнение – это уравнение, в котором коэффициенты, равностоящие от концов равны.)
Способ решения данного уравнения – деление правой и левой частей уравнения на х2.
Вопрос — почему это можно сделать? Не происходит ли потеря корня?
х2+5х+6++ = 0
(х2 +)+5(х+) = 0
х+=у (ОДЗ для вспомогательной переменной?)
х2 +=(х+)2-2 = у2-2
у2-2+5у+6=0
у1=-4; у2=-1
х+=-4, х=-2
х +=-1, корней нет.
Ответ: -2 -; -2+.
№ 4. х5+6х4+11х3+11х2+6х+1=0
Возвратное уравнение нечётной степени имеет корень х=-1 (применим теорему Безу), после деления многочлена, стоящего в левой части этого уравнения на двучлен (х+1) приводится к возвратному уравнению чётной степени.
(х+1)(х4+5х3+6х2+5х+1)=0 (см. предыдущий пример)
№ 5. (х+1)(х+2)(х+4)(х+5)=40
Уравнение сводится к квадратному, если сумма чисел любых двух скобок равна сумме чисел двух других скобок.
(х2+6х+5)(х2+6х+8)=40
ух2+6х
(у+5)(у+8)=40
у2+13у=0
х2+6х=0 х2+6х=-13, корней нет, т.к. D<0
Ответ: -6, 0.
IV. Домашнее задание
2х3+8х-х2-4=0
2х3-12х2+22х-12=0
6х4-35х3+62х2-35х+6=0
V. Подведение итогов урока
Список литературы
1. М.И. Сканави «Сборник задач по математике для поступающих в ВУЗы», Москва «ОНИКС 21 век », «Мир и Образование», 2002.
2. В. М. Говоров, П.Т. Дыбов, Н.В. Мирошин, С.Ф. Смирнова «Сборник конкурсных задач поматематике для поступающих в ВУЗы», Москва «ОНИКС 21 век », «Мир и Образование», 2003.
3. А.Г. Цыпкин, А.И. Пинский «Справочник по методам решения задач по математике», Москва «Наука», Главная редакция физико-математической литературы, 1989.
“Методы решения уравнений четвертой степени”
Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №1 г. Южи Ивановской области
Педагогический проект по теме:
“Методы решения уравнений четвертой степени”
Выполнила Чурина
Елена Вениаминовна,
учитель математики первой
квалификационной категории
Г. Южа
2021 год
Содержание
Актуальность
Цель и задачи работы:………………………………
1. Исторические сведения об уравнениях четвёртой степени……стр.
Исторические сведения об уравнениях четвёртой степени……стр.
2. Определение уравнения 4 степени………………………….стр.
3. Способы решения уравнений 4 степени……………………………стр.
3.1. Схема метода Феррари……………………….стр.
3.2. Разложение на множители. Кубическая резольвента……………стр.
3.3. Теорема Виета для уравнения 4 степени……………………..стр.
3.4. Решение уравнений 4 степени по схеме Горнера……………………стр.
4.Решение некоторых уравнений 4 степени……………………………стр.
4.1. Решение биквадратного уравнения………………………………стр.
4.2. Решение уравнения способом группировки………………….стр.
4.3. Решение уравнения по свободному члену……………………стр.
4.4. Графический метод………………………………………..стр.
4.5. Применение формул сокращенного умножения. Выделение полного квадрата………………………………………………..стр.
5. Исследование………………………………………………стр.
6. Выводы
7. Заключение
8. Тренировочные задания для отработки различных способов решения уравнений высших степеней……………………………………………стр.
Список литературы
Актуальность
Как все знают, в математике одна из важнейших вещей — это уравнения. Чаще всего решаются линейные либо квадратные уравнения, но не мало важны уравнения 4 степени, которые решить сможет не каждый учащийся 9 класса. Чтобы решать такие уравнения было проще, нужно выбрать тот способ, который тебе более понятен.
Задания с уравнениями высших степеней есть в контрольных измерительных материалах при проведении государственной итоговой аттестации. Значит, ученики должны уметь решать уравнения не только 2 степени, но и выше. А это умеет делать далеко не каждый.
Цель работы: узнать и разобрать методы решения уравнений высших степеней.
Задачи:
Изучить литературу по истории приемов решения уравнений 4-й стпени
Обобщить накопленные знания об уравнениях4-й степени и способах их решения.
Сделать выводы.
Разработать дидактический материал для проведения практикума по решению уравнений 4-й степени с использованием новых приемов в помощь ученикам, увлеченным математикой и учителям, ведущим факультативные занятия.
Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать уравнения 4-й степени?
Гипотеза: существует универсальный способ для решения всех видов уравнений 4-степеней.
Объект исследования: уравнения 4-й степени
Предмет изучения: методы и приемы решениях уравнений 4-й степени, в том числе
1.Исторические сведения об уравнениях четвёртой степени
Решение уравнений высших степеней – история полная драматизма, разочарования и радости открытия. В течение почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.
Необходимость решать уравнения не только первой, но и второй и высших степеней ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне.
Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне.
Однако уже при решении уравнений третей степени математики столкнулись с большими трудностями. История открытия способа решения кубических уравнений полна тайн, так как в древности учёные часто на открытых диспутах соревновались в решении трудных задач. От исхода этих состязаний зависела их научная репутация и материальное благополучие.
Тот, кто первым овладел решением кубических уравнений, мог легко победить своих соперников давая им задачи, сводящиеся к кубическим уравнениям. Поэтому способы решения уравнения тщательно скрывались. Историки полагают, что первым нашёл способ решения кубических уравнений известный итальянский алгебраист Специна дель Ферро (1465-1576), но впервые опубликовал общую формулу решения кубических уравнений итальянский математик Джераламо Кордано (1501-1576г.). Эта формула носит теперь название формулы Кордано, хотя предполагают, что эту формулу ему передал итальянский математик Николо Тарталья ( 1500-1557). С именами этих же математиков связано открытие способов решения уравнений четвёртой степени.
С именами этих же математиков связано открытие способов решения уравнений четвёртой степени.
В дальнейшем математики активно пытались найти формулы вычисления корней уравнений пятой и более степени. И только почти через три столетия впервые итальянский учёный Паоло Руффини (1765-1822), а затем норвежский математик Нильс Хенрих Абель (1802-1829г.) доказали, что не существует формулы, выражающей корни любого целого уравнения пятой степени через конечное число алгебраических операций над его коэффициентами. Да и найденные формулы вычисления корней для уравнений третьей и четвёртой степени столь сложны, что ими практически не пользуются. Поэтому в современной математике разработаны методы, позволяющие находить с любой степенью точности приближенные значения корней уравнений. Использование компьютеров значительно облегчают эту работу.
2. Определение уравнения 4 степени
Уравнение четвёртой степени —алгебраическое уравнение вида:
,
при этом a≠0 и где a,b,c,d,e- любые числа.
Четвёртая степень для алгебраических уравнений является наивысшей, при которой существует аналитическое решение в радикалах в общем виде (то есть при любых значениях коэффициентов).
3. Способы решения уравнений 4 степени.
3.1 Схема метода Феррари
a0x4 + a1x3 + a2x2 + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
Тогда оно примет вид
x4 + ax3 + bx2 + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
(3) |
где y – новая переменная.
Тогда, поскольку
то уравнение (2) принимает вид
(4) |
Если ввести обозначения
то уравнение (4) примет вид
y4 + py2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
3.2.Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
2sy2 + s2,
где s – некоторое число, которое мы определим чуть позже, из (5) получим
Следовательно, уравнение (5) принимает вид
(6) |
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
(7) |
то уравнение (6) примет вид
(8) |
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
или, раскрыв скобки, — в виде
(9) |
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Действительно,
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
(10) |
а также квадратное уравнение
(11) |
Вывод метода Феррари завершен.
Пример решения уравнения 4-ой степени
Пример. Решить уравнение
x4 + 4×3 – 4×2 – 20x – 5 = 0. | (12) |
Решение. В соответствии с (3) сделаем в уравнении (12) замену
В соответствии с (3) сделаем в уравнении (12) замену
Поскольку
x4 + 4×3 – 4×2 – 20x – 5 = (y – 1)4 + 4(y – 1)3 – 4(y – 1)2 – 20(y – 1)– 5 =
= y4 – 4y3 + 6y2 – 4y + 1 + 4y3 – 12y2 + 12y – 4 – 4y2 + 8y – 4 – 20y + 20 – 5 =
= y4 – 10y2 – 4y + 8,
то в результате замены (13) уравнение (12) принимает вид
y4 – 10y2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
2s3 + 10s2 – 16s – 84 = 0,
которое при сокращении на 2 принимает вид:
s3 + 5s2 – 8s – 42 = 0. | (16) |
Проверяя, какой из делителей свободного члена уравнения (16) является целым корнем этого уравнения, находим, что целым корнем кубической резольвенты является число
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
y2 – 2y – 4 = 0,
корни которого имеют вид:
(18) |
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
y2 + 2y – 2 = 0,
корни которого имеют вид:
(19) |
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
Ответ.
Но эти способы очень сложны. Рассмотрю более простые способы, с помощью которых можно решить некоторые уравнения 4-й четверти.
3.3Теорема Виета для уравнения четвёртой степениКорни уравнения четвёртой степени {\displaystyle x_{1},\,x_{2},\,x_{3},\,x_{4}} связаны с коэффициентами {\displaystyle a,\,b,\,c,\,d,\,e}следующим образом:
{\displaystyle x_{1}+x_{2}+x_{3}+x_{4}=-{\frac {b}{a}},}
3.4.Решение уравнений четвертой степени по схеме Горнера
2x4 + 5x3 — 11x2 — 20x + 12 = 0
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:
1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1 не является корнем многочлена
-1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена
Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления.
Они считаются так:
Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки. | |
2 ∙ 2 + 5 = 9 | |
2 ∙ 9 — 11 = 7 | |
2 ∙ 7 — 20 = -6 | |
2 ∙ (-6) + 12 = 0 | |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.
Если он равен 0, значит мы все верно посчитали.
Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению.
(х-2)(2х3+9х2+7х-6)=0
Многочлен, являющийся вторым множителем попробуем разложить на множители подобным образом.
Отыщем опять делители свободного члена. В данном случае делителями числа -6: ±1, ±2, ±3, ±4, ±6.
Число -2 является корнем многочлена. Напишем найденный корень в схему Горнера и начнем заполнять ячейки:
Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки. |
-2 ∙ 2 + 9 = 5 |
-2 ∙ 5 + 7 = -3 |
-2 ∙ (-3) — 6 = 0 |
Таким образом, мы исходный многочлен разложили на множители и переходим к уравнению. {2}-4ac}}}{2a}}}.}
{2}-4ac}}}{2a}}}.}
Пример.
Решить уравнение
Замена
из этого следует, что уравнение имеет два корня.
Обратная замена
т.е. невозможно
Ответ: .
4.2. Решение уравнения способом группировки
Способом группировки можно решить уравнение 4 степени.
Чтобы разложить уравнение на множители, надо сгруппировать слагаемые по парам. Мы должны сгруппировать слагаемые по парам таким образом, чтобы при вынесении общего множителя за скобки у слагаемых был одинаковый множитель.
Решим на примере.
2х4-5х3+2х2-5х=0
(2х4-5х3)+( 2х2-5х)=0
х3(2х-5)+х(2х-5)=0
(2х-5)(х3-х)=0
х(2х-5)(х2-1)=0
х(2х-5)(х-1)(х+1)=0
х=0 или 2х-5=0 или х-1=0 или х+1=0
х1=0 х2=2,5 х3=1 х4=-1
4.3. Решение уравнения по свободному члену
Любое уравнение вида можно свести к приведенному уравнению той же степени, домножив обе его части на и выполнив замену переменной вида :
Полученные коэффициенты тоже будут целыми.
Таким образом, будем решать приведенное уравнение степени n с целыми коэффициентами вида .
Алгоритм решения.
Находим целые корни уравнения.
Целые корни уравнения , i=1, 2, …, m (m – количество целых корней уравнения) находятся среди делителей свободного члена . То есть, первым делом выписываем делители свободного члена и подставляем их по очереди в исходное равенство для проверки. Перебираем их по очереди, пока не получим тождество. Как только тождество получено, то первый целый корень уравнения найден и уравнение предстает в виде , где — корень уравнения, а — частное от деления на .
Продолжаем подставлять выписанные ранее делители в уравнение , начиная с (так как корни могут повторяться). Как только получаем тождество, то корень найден и уравнение предстает в виде , где — частное от деления на .
И так продолжаем перебор делителей, начиная с . В итоге найдем все m целых корней уравнения и оно представится в виде , где — многочлен степени n-m. Весь этот процесс удобно проводить по схеме Горнера.
Весь этот процесс удобно проводить по схеме Горнера.
Дробных корней приведенное уравнение с целыми коэффициентами иметь не может.
Находим оставшиеся корни (иррациональные и/или комплексные) из уравнения любым способом.
Решить уравнение .
Во-первых, найдем все целые корни данного уравнения.
Свободным членом является -3. Его делителями являются числа 1, -1, 3 и -3.
Будем подставлять их по очереди в исходное равенство до получения тождества.
При х=1 имеем . То есть х=1 является корнем уравнения.
Разделим многочлен на (х-1) столбиком:
Следовательно, .
Продолжим перебор делителей, но уже для равенства :
При х = -1 получили верное равенство, следовательно, -1 является корнем уравнения.
Разделим на (х+1) столбиком:
Таким образом,
Продолжаем перебор делителей для равенства , начиная с х = -1:
Получили неверные равенства, следовательно, целых корней уравнение больше не имеет.
Оставшиеся корни исходного уравнения являются корнями квадратного трехчлена .
, то есть, действительных корней трехчлен не имеет, но имеет пару комплексно сопряженных.
4.4.Графический метод.
Иногда полезно рассмотреть эскизы графиков функций у=ƒ(x) и у=g(x), входящих в уравнение ƒ(x) = g(x). Это может помочь выяснить:
1) на какие множества надо разбить числовую ось, чтобы на каждом из этих множеств использовать свой способ решения;
2) наличие или отсутствие корней, их количество.
Пример: (материал взят из ОГЭ 2016г.)
x4=(3x-10)2
Решение №3: x4=(3x-10)2
1) Рассмотрим две функции: у = х4 и у =(3х-10)2.
2) Построим график функции у = х4 — график парабола ветви направлены вверх.
3) Построим график линейной функции у = (3х-10)2. Это парабола ветви, которой направлены вверх.
4) В данном примере наглядно видна только одна точка пересечения В(2;16) (см. приложение рис.3), хотя очевидно, что графики пересекаются еще в одной точке (т.е. имеется еще одно решение).
Как видим, что графический способ в данном случае не удобен, так как ограниченный размер листа тетради не позволяет увидеть все точки пересечения.
Графическое решение уравнения- наглядный способ, он хорош при необходимости определения наличия или отсутствия корней и их количества.
4.5. Применение формул сокращенного умножения. Выделение полного квадрата.
Этот метод основан на использовании формул:
а2-b2=(а-b)(а+b)a2+2ab+b2=(a+b)2a2−2ab+b2=(a−b)2
а3+b3=(а+b)(а2-аb+b2)а3-b3=(а-b)(а2+аb+b2)(а+b)3=а3+3а2b+3аb2+b3
(а-b)3= а3-3а2b+3аb2-b3,
Пример: х4=(3х-10)2
Способ 1: Используем формулу сокращенного умножения х4-(3х-10)2=0
(х2-3х+10)(х2+3х-10)=0
х2-3х+10=0 или х2+3х-10=0
D=9-40=-31 D=9+40=49
корней нет х1=-5, х2=2.
Ответ: х1=-2, х2=5.
6. Выводы:
1. Уравнения высших степеней решали еще более 500 тыс. лет назад.
2. Есть много способов решения уравнений 4-й степеней. Некоторые из них довольно сложные, а некоторые помогут быстро решить задания на ОГЭ.
3. Уравнения 4-й степеней играют немалую роль в развитии математики. Лишь немногие из учащихся умеют решать такие уравнения. Эти методы решения уравнений высших степеней непросты в применении, но они всё равно могут заинтересовать увлекающихся математикой учеников.
7. Заключение
В данной работе рассмотрены способы решения уравнений 4-й степени.
А также рассмотрены приёмы решения уравнений 4-й степени, которые позволяют быстрее и проще решить такие уравнения.
Данные приёмы решения заслуживают внимания, поскольку каждые из них интересны и уникальны. Овладение данными приёмами поможет экономить время и эффективно решать уравнения. Потребность в быстром и упрощенном решении обусловлена применением этих навыком на экзаменах.
Таким образом, цель работы — узнать и разобрать методы решения уравнений высших степеней- достигнуты. Гипотеза доказана, существует универсальный способ решения уравнений 4-й степени. Это способ Феррари.
Источники:
Алгебра. 9 класс:учебник для общеобразовательных организаций / А45 Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под редакцией С. А. Теляковского. – 4-е издание – М.: Просвещение, 2017. – 287 с.: ил. – ISBN 978-5-09-046396-6.
. М.Л. Галицкий, А.М. Гольдман, Л.М. Звавич «Сборник задач по алгебре для 8-9 классов». Учебное пособие для учащихся школ и классов с углубленным изучением математики -Москва «Просвещение», 1999.
В.В. Бардушкин, И.Б. Кожухов, А.А. Прокофьев, А.М. Ревякин,
А.М. Терещенко «Письменный вступительный экзамен по математике» — Москва «Лист», 1998.
Н.В. Бурмистрова, Н.Г. Старостенкова «Функции и их графики». Учебное пособие — Саратов «Лицей», 2003.
М. А.Еремин «Уравнения высших степеней» — Арзамас, 2003.
А.Еремин «Уравнения высших степеней» — Арзамас, 2003.
А.Г.Курош «Алгебраические уравнения произвольных степеней» — М.:Наука, 1975.
Л.М.Лоповок «1000 проблемных задач по математике» — М.: Просвящение, 1995.
И.Р.Шафаревич «Популярные лекции по математике. О решении уравнений высших степеней» Вып.15 – М.: Наука, 1954.
10.https://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/
11. http://www.cleverstudents.ru/equations/equations_of_higher_degree.html
12. https://ru.wikipedia.org/wiki/Уравнение_четвёртой_степени
Приложение 1
Тренировочные задания для отработки различных способов решения уравнений 4-й степени.
№1 Решите уравнения способом замены: , б) X4-2×2-8=0,
в) x4-8×2-9=0, г) x4-7×2+12=0, д) 3×4-13×2+4=0, е) 2×4-19×2+9=0,
ж) 3×4-13×2+4=0, з) (x2+4x)(x2+4x-17)=60=0, и) (x2-5x)(x2-5x+10)+24=0,
к)(x2-3x)2-2(x2-3x)=8, л) (x2+x)2-11(x2+x)=12, 1
м) ()+10=0, н) ()=3; о)
№2 Решите уравнения, раскладывая левую часть на множители способом группировки:
а) 2×4-5×3+2×2-5x=0,
б) 6×4-3×3+12×2-6x=0,
в) 2×4+3×3-8×2-12x=0,
г) 2×4-5×3-18×2+45x=0.
№3 Решите уравнения по свободному члену
а) 2×4 – 3×3 – 7×2 –15x + 50 =0 б)х4-4х2 +3х+2=0
в) х4+2х3-7х2 -8х+12=0
№4 Решить уравнения, применения формулы сокращенного умножения
а) б).
Об уравнениях высших степеней / Хабр
Как правило в физике, информатике и экономике мы сталкиваемся с простейшими линейными, или дробно-рациональными уравнениями, реже с квадратными. А что до уравнений третьей и четвёртой степени? Если вам интересно, то прошу под кат.
Для начала рассмотрим понятие уравнения высшей степени. Уравнением высшей степени, называется уравнение вида:
В этой статье я рассмотрю:
1. Кубические уравнения.
2. Возвратные кубические.
3. Применение схемы Горнера и теоремы Безу.
4. Возвратные биквадратные уравнения.
Кубические уравнения
Кубические уравнения, это уравнения, в которых у неизвестной при старшем члене степень равна 3. Кубические уравнения имеют следующий вид:
Решать такие уравнения можно по разному, однако мы воспользуемся знаниями базовой школы, и решим кубическое уравнение методом группировки:
В данном примере используется метод группировки, группируем первые два и последние два члена, получая равные скобки, снова выносим, получая уравнение из двух скобок.
Произведение равно нулю тогда, и только тогда, если хотя бы один из множителей равен нулю, на основании этого мы каждый множитель (скобку) приравниваем к нулю, получая неполное квадратное и линейное уравнения.
Также стоит отметить, что максимальное количество корней уравнения, равно степени неизвестной при главном члене, так в кубическом уравнении может быть не более трёх корней, в биквадратном (4-ой степени) не более четырёх корней и. т. д.
Возвратные кубические уравнения
Возвратные кубические уравнения имеют вид:
Возвратными они называются потому что коэффициенты будут зеркально повторяться. Подобные уравнения тоже решаются школьными методами, но чуть хитрее:
Сначала производится группировка, потом при помощи формул сокращённого умножения мы раскладываем получаемое на множители. Снова получаем 2 равные скобки, «выносим их». Получаем два множителя (скобки) и решаем их как два различных уравнения.
Теорема Безу и схема Горнера
Теорема Безу была открыта, как ни удивительно, Этьеном Безу, французским математиком, занимавшимся в основном алгеброй. Теорему Безу, можно сформулировать следующим образом:
Теорему Безу, можно сформулировать следующим образом:
Давайте разберёмся. P(x) — это какой-либо многочлен от x, (x — a) — это двучлен в котором a — это один из целых корней уравнения, который мы находим среди делителей свободного члена.
Три точки, это оператор обозначающий что одно выражение делится на другое. Из этого следует что найдя хотя бы один корень данного уравнения, мы сможем применить к нему эту теорему. Но зачем нужна эта теорема, каково её действие? Теорема Безу — это универсальный инструмент, если вы хотите понизить степень многочлена. Например, при её помощи, кубическое уравнение, можно превратить в квадратное, биквадратное, в кубическое и т. д.
Но одно дело понять, а как поделить? Можно конечно, делить и в столбик, однако этот метод доступен далеко не всем, да и вероятность ошибиться очень высока. Поэтому есть и иной путь, это схема Горнера. Её работу я поясню на примере. Предположим:
И так, нам дан многочлен, и мы возможно заранее нашли один из корней. Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:
Теперь мы рисуем небольшую табличку из 6 столбцов и 2 строк, в каждый столбец первой строки (кроме первого), мы вносим коэффициенты уравнения. А в первый столбец 2 строки мы вносим значение a (найденный корень). Потом первый коэффициент, в нашем случае 5, мы просто сносим вниз. Значения последующих столбиков мы рассчитываем так:
(Картинка позаимствована здесь)
Далее поступаем точно так же и с остальными столбцами. Значение последнего столбца (2 строки) будет остатком от деления, в нашем случае 0, если получается число отличное от 0, значит надо избрать другой подход. Пример для кубического уравнения:
Возвратные биквадратные уравнения
Выше мы так же рассматривали возвратные кубические уравнения, а теперь разберём биквадратные. Их общий вид:
В отличие от кубического возвратного уравнения, в биквадратном пары, относительно коэффициентов, есть не у всех, однако в остальном они очень схожи. Вот алгоритм решения таких уравнений:
Как видно, решать такие уравнения совсем не просто. 2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).
2, группируем, сворачиваем в полный квадрат, выполняем подстановку переменной и решаем квадратное уравнение. После этого полученные корни подставляем обратно, и решаем ещё 2 квадратных уравнения (с умножением на x).
Область применения
В виду своей громоздкости и специфичности уравнения высших степеней редко находят себе применение. Однако примеры всё же есть, уравнение Пуассона для адиабатических процессов в Физике.
Заключение
В этой статье я рассмотрел только кубические и биквадратные уравнения. Однако рассмотренная теорема Безу (и схема Горнера) могут быть задействованы и для решения уравнений 5, 6, 7 и других степеней, даже несмотря на ограниченность их применения.
Решение уравнений третьей степени различными способами
1. Проект по алгебре: «Решение уравнений третьей степени различными способами».
Выполнила ученица 9 классаЗингейской СОШ
Пушкарева Марина
2. Цель проекта:
• Совершенствовать свои умения и навыкипри решении уравнений;
• Познакомиться с историческими
сведениями о решении уравнений;
• Представить материал в виде презентации.

3. Омар Хайям (ок. 1048- ок. 1123)
Описал всевозможные видыуравнений третьей степени и
рассмотрел сложные и
красивые способы
геометрических построений
для отыскания их решения.
3
2
аx bx cx d 0
• В начале XVI века в крупных
торговых городах Северной Италии
были популярны математические
состязания. Математики публично
вызывали соперников на поединок,
причем на победителя обычно
делались денежные ставки. В это
время быстро распространялось
преподавание арифметики,
необходимой в торговле, и
публичные состязания обеспечивали
соперничающим преподавателям
известность и привлекали учеников.
Задачи формулировались для
числовых значений, но иногда
требовали решения алгебраических
уравнений более высокого порядка.
Результаты состязаний
обнародовались, но методы
решения математических задач —
оружие в борьбе за репутацию и
доходы — каждый из участников
противоборства предпочитал
держать в секрете.

• Николо Тарталья (ребёнок
из очень бедной семьи,
мать не могла платить за
образование, поэтому
мальчик в школе узнал
только половину азбуки,
всеми остальными
знаниями он овладел
самостоятельно). В 6 лет
он получил удар мечом в
гортань от французского
воина и с тех пор говорил
с трудом, отсюда и
прозвище Тарталья
(заика). Он вывел
формулы для решения
уравнений 3-ей степени,
но своё открытие держал
в тайне.
Никколо Тарталья
(1499-1557)
• Джероламо Кардано (медик)
занимался астрологией,
составлял гороскопы.
Кардано неоднократно
обращался к Тарталье с
просьбой сообщить ему
формулу для решения
кубических уравнений и
обещал хранить её в
секрете. Он не сдержал
слово и опубликовал
формулу, указав, что
Тарталье принадлежит честь
открытия «такого
прекрасного и
удивительного,
превосходящего все таланты
человеческого духа».

Джероламо Кардано
(1501-1576)
7. x³-3x-2=0 1) Разложение на множители:
x³-3x-2=x³+x²-x²-x-2x-2=0
x²(x+1)-x(x+1)-2(x+1)=0
(x+1)(x²-x-2)=0
x=-1
D=1+8=9
x₁=2
x₂=-1
Ответ: -1; 2.
8. 2) Решение с помощью теоремы Безу: x³-3x-2=0
x³-3x-2=0
(-1)³ -3(-1)-2=0
x=-1
x³-3x-2 x+1
x³+x²
x²-x-2
-x²-3x
-x²-x
-2x-2
-2x-2
0
• x³-3x-2 =(x+1)(x²-x-2)=0
Ответ: -1; 2.
9. 3) Графический способ решения:
• x³-3x-2=0• Ответ: -1; 2.
10. x³-7x+6=0 1) Разложение на множители:
x³-7x+6=0
x(x²-1)-6(x-1)=0
x(x-1)(x+1)-6(x-1)=0
(x²+x-6)(x-1)=0
D=1+24=25
x-1=0
x₁=2
x=1
x₂=3
Ответ: -3; 1; 2.
11. 2) Решение с помощью теоремы Безу: 1³-7+6=0
• 1³-7+6=0• x³-7x+6 x-1
• x³-x²
x²+x-6
x²-7x
-x²+x
-6x+6
-6x+6
0
x³-7x+6=(x-1)(x²+x-6)
x=1
x²+x-6=0
D=1+24=25
x₁=2
x₂=-3
Ответ: -3; 1; 2.

12. 3) Графический способ решения:
• Ответ: -3; 1; 2.13. x³-13x+12=0 1) Разложение на множители:
x³-13x+12=0
x³-x-12x+12=0
x(x²-1)-12(x-1)=0
x(x-1)(x+1)-12(x-1)=0
(x²+x-12)(x-1)=0
D=1+48=49
x=1
x₁=3
x₂=-4
Ответ: -4; 1; 3.
14. 2) Решение с помощью теоремы Безу: x³-13x+12=0
x³-13x+12=0
1-13+12=0
x=1
x³-13x+12 x-1
x³-x²
x²+x-12
x²-13x
x²-x
-12x+12
-12x+12
0
• x³-13x+12=(x-1)(x²+x12)=0
• x=1
D=1+48=49
x₁=3
x₂=-4
Ответ: -4; 1; 3.
15. 3) Графический способ решения:
• Ответ: -4; 1; 3.16. 2x³+x²-3=0 1) Разложение на множители:
2x³+x²-3=0
3x³-x³+x²-3=0
3(x³-1)-x²(x-1)=0
3(x-1)(x²+x+1)-x²(x-1)=0
(x-1)(3x²+3x+3-x²)=0
(x-1)(2x²+3x+3)=0
x=1
2x²+3x+3=0
D=9-24=-15
Ответ: 1.
17. 2) Решение с помощью теоремы Безу: 2x³+x²-3=0
• 2x³+x²-3 x-1• 2x³-2x² 2x²+3x+3
3x²-3
3x²-3x
3x-3
3x-3
0
• (x-1)(2x²+3x+3)=0
• x=1 или 2x²+3x+3=0
D=9-24=-15
Ответ: 1.

18. 3) Графический способ решения:
• Ответ: 1.Урок по теме «Решение уравнений и неравенств » 9 класс.
Чернышова Светлана Леонидовна
Тема урока «Решение уравнений и неравенств » (9 класс)
Цели : 1) Обобщить и систематизировать материал по теме «Уравнения и неравенства »;способствовать развитию умений и навыков в решении уравнений различными способами; организовать работу по отработке способов решения уравнения: введение новой переменной, разложение на множители так, чтобы каждый ученик научился решать целые уравнения высших степеней хотя бы одним способом, наиболее приемлемым для него;
Выявить степень усвоения материала каждым учеником.
2) развивать математическую культуру в чтении и оформлении записи решения уравнения; развивать интерес к решению уравнений различными способами;
3) воспитывать чувство товарищества, деликатности и дисциплинированности, умение работать в группах.
Оборудование: проектор, презентация, карточки с дифференцированным д/з, заготовки для рефлексии, индивидуального листа ,исследовательской карты, листа диагностики.
УМК: Учебник Ю. Н. Макарычев и др. «Алгебра 9класс», Москва., «Просвещение», 2009., Ю.Н. Макарычев. Дидактические материалы., Москва., «Просвещение».
Ход урока.
1.Организационный этап.
Приветствие учащихся. «Здравствуйте, ребята!
Вопрос – Чему вы сегодня хотите научиться на уроке?..
— какие качества в себе хотите сегодня развить?..
— что воспитать ? …
На сегодняшнем уроке нам будет необходимо трудолюбие и терпение, так как мы обобщаем способы решения уравнений. Тема имеет практическую значимость при последующем изучении математики . Без уравнений мы не сможем решить много практических задач ,систем уравнений. Задача нашего урока обобщить материал по теме «Уравнения » и выявить степень усвоения материала каждым из вас.
Эта тема занимает ведущее место при подготовке к ГИА и к ЕГЭ. Мы будем работать сегодня и в парах, по группам и индивидуально. Пусть девизом урока будут слова Сухомлинского: « Сегодня мы учимся вместе – я ваш учитель , и вы мои ученики ,но в будущем ученик должен превзойти учителя ,иначе в науке не будет прогресса». Результаты своей работы ребята будете отмечать в и индивидуальных листах.(Приложение 1)
Этап «Найди ошибку» (1-3 группа) , тест (2-4 группа)
Цель : проверка вычислительных навыков, умений переключаться с одного типа заданий на другое ,что у нас и требуется в вариантах ГИА, умение анализировать ситуацию.
Х – 5(х-4) = 6х+5 2. 2х² +32=0 3. 2х² -3х -5 =0 4. = 1
Х – 5х — 4= 6х +5 2х²= — 32 D= 49 >0 , 2 корня
-4х -4 = 6х +5 х² = — 16 х =
-4х-6х=5+4 х = ± 4
— 10х =9
Х = — 0,9
5.( х-8)(х+9) =0
Х -8 =0 или х+9 =0
Х=8 или х = -9 Ответы
Одновременно тест (2-4 группа)
Формуладискриминанта
4х²+4х=0
49m²-m
1)в²+4ас
2) 4ас -в²
3) в²-4ас
1) -1 и 4
2) 0 и -1
3) -2 и 2
1) )(7-m²)(7+m²)
2)(49m- m² )(49+m²)
3) m
1)
2)
3)
1) – 6 и 1
2) 6 и 1
3) – 6 и -1
Критерии 1 ) За тест: если правильно решены все задания , то 5 баллов.
2) «Найди ошибку» ;если правильно нашёл 1 ошибку ,то 3б,если нашёл
2 ошибки -4б,3ошибки – 5 баллов.
Сразу же проверка решений
Одновременно у доски 3человека для решения уравнений:
1-й
2-й
3-й
Дети оценивают друг друга работая в парах (взаимообмен тетрадями) и отмечают результаты в индивидуальных листах
Микровывод : Что для вас показалось наиболее трудным? На что надо обратить внимание ?Что удалось? Что не удалось? Какими навыками и умениями надо обладать, что успешно справляться данными заданиями?
Опрос по теории
Какие типы уравнений вы знаете?
Какой вид имеет полное квадратное уравнение?
Определение приведённого квадратного уравнения.
От чего зависит число корней квадратного уравнения ?
Общий вид дробно-рационального уравнения?
Какие методы решения уравнений ,вы знаете ? (биквадратные, с помощью подстановки, метод разложения на множители, метод группировки)
Микровывод : Что вам показалось наиболее трудным?
2-й этап . «Классификация» .
«Классификация» .
Цель: распределить уравнения по типам и результаты занести в исследовательскую карту. Причём ,обращаю ваше внимание в конце урока надо в данную карту записать общие виды уравнений.(Приложения 2)
Уравнения записаны на слайде
Даны уравнения : квадратные, линейные, дробно-рациональные ,целые, биквадратные ,метод группировки, вынесение множителя за скобки.
Критерии :если правильно сделана классификация ,то в лист учёта ставим 5 баллов, если 1-2 ошибки ,то 4 балла, если 3-4 ошибки, то ставим3 балла ,в остальных случаях 2б.
Дети оценивают друг друга работая в парах (взаимообмен тетрадями) и отмечают результаты в индивидуальных листах.
Микровывод ; Что для вас показалось наиболее трудным? На что надо обратить внимание ?Что удалось? Что не удалось? Какими навыками и умениями надо обладать ,что успешно справляться данными заданиями?
3-й этап :На 20-й минуте : (слайд10)
РАЗВИВАЮЩИЙ КАНОН D>0 2
D=0 ?
D<0 ?
Найти закономерность и сказать по какому признаку уравнения находятся в одной группе?
А) х² -7х+6 =0 Б) 20х² +100=0 в)
х² — 5х +4=0 4х²+16=0
х²-9х+8=0 х²+7=0
(у всех корень 1) (нет корней)
Дети оценивают друг друга работая в парах (взаимообмен тетрадями) и отмечают результаты в индивидуальных листах
Упражнения для глаз
4-й этап . После того как проведена классификация уравнений по видам. Мы переходим к следующему этапу урока; Индивидуально- дифференцированная работа в группах с консультантами. (Приложение 3)
После того как проведена классификация уравнений по видам. Мы переходим к следующему этапу урока; Индивидуально- дифференцированная работа в группах с консультантами. (Приложение 3)
Цель : выявить степень овладения каждым из вас ,ребята способами решения уравнений. Здесь у вас будут разные типы уравнений ,которые мы изучали с 5 класса по 9 класс. .Они у нас встречаются в ГИА и в ЕГЭ.
Проведём эту работу в виде «Силового многоборья» Задания подобраны разных уровней .
Каждое уравнение со своим номером написано на отдельной карточке. Это всё находится у вас на столах. Вам раздаются макеты гирь. На ручках этих макетов пишете свою фамилию. Объясняю правила многоборья : Каждый из вас, ребята выбирает тот вес ,который хотите поднять (каждое уравнение оценено определённым количеством баллов , т.к трудность разная) И приступаете к решению. После того как уравнение решено .ученик подходит к консультанту или к любому из арбитров и арбитр проверяет ответ. Если «вес » взят , то арбитр на гире спортсмена рядом с номером уравнения пишет его вес. Если «вес не взят» ,т.е уравнение решено неверно, арбитр или консультант консультирует ученика. Спортсмен ,который «взял вес» и зафиксировал это у арбитра, выбирает себе новое уравнение. Таким образом все спортсмены в течение урока пытаются поднять как можно больше веса, чтобы получить оценку за урок в соответствии с нормативами. В конце урока каждый ученик считает общий поднятый вес ,соотносит этот вес с нормативами и сдаёт гирю арбитрам. Разрешается демонстрировать свои достижения у доски ,решая уравнения.
Если «вес не взят» ,т.е уравнение решено неверно, арбитр или консультант консультирует ученика. Спортсмен ,который «взял вес» и зафиксировал это у арбитра, выбирает себе новое уравнение. Таким образом все спортсмены в течение урока пытаются поднять как можно больше веса, чтобы получить оценку за урок в соответствии с нормативами. В конце урока каждый ученик считает общий поднятый вес ,соотносит этот вес с нормативами и сдаёт гирю арбитрам. Разрешается демонстрировать свои достижения у доски ,решая уравнения.
Критерии :
Классификация заданий
- Решить уравнение ,предварительно,
упростив го
№1-5
Вес 2кг
№6-10
Вес 3кг
№11-15
Вес 5кг
№16-20
Вес 4кг
№21-25
Вес 7кг
- 26-30
Вес 10 кг
№31-35
Вес 9кг
№36-40
Вес 12кг
№40-45
Вес 15кг
Нормативы а) мастер спорта (свыше 50 кг) — 5 баллов
Б) кандидат в мастера спорта ( 0т 30 до 49кг) – 4 балла
В) первый юношеский разряд (от 11 до 29 кг) – 3 балла
Микровывод ; Что для вас показалось наиболее трудным? На что надо обратить внимание ?Что удалось? Что не удалось? Какими навыками и умениями надо обладать ,что успешно справляться данными заданиями?
Ребята отмечают результаты в индивидуальных листах
5-й этап Подведение итогов работы . Подсчёт баллов в листах учёта.
Подсчёт баллов в листах учёта.
Анализ работы учителем. Спрашиваю учеников : Чему мы сегодня научились? Что в себе воспитали ?Что развивали? … Урок закончим словами:
6-й этап.
Домашнее задание.
1. Составить тест по уравнениям, используя Открытый банк заданий.
2.Написать сочинение на тему «Уравнения в моей жизни»
7-й этап. Рефлексия.+ Заполнение диагностического листа.
Урок закончим словами : «Через математические знания, полученные в школе, лежит широкая дорога к огромным, почти необозримым областям труда и открытий.
А. Маркушевич.
Приложения 2
Исследовательская карта ученика(цы) 9 кл ________________________________________
Приложение3
III, IV группа
2 часть
(х² -5х)( х² -5х +10 ) +24 =0
Найдите область определения выражения :
При каких значениях параметра а уравнение 4х² — 4ах +1 =0 не имеет корней.

Не решая уравнения 3х² +3х -1 =0 найдите
Найдите все значения параметра р ,при которых разность корней уравнения
х² +рх+12 =0 равна 1.
Найдите корень уравнения ,удовлетворяющий неравенству — (5 -2х) > — (6,5 -3x)
(х² -7х +13)² — (х-3)(х-4) =1
(х-2)(х-1)(х+2)(х+3) =60
2
3х²(2х-1) +х(2х-1) +2(1-2х)=0
Приложение 1
Индивидуальный лист ученика(цы) 9б класса ____________________________________________________
- правильно нашёл 1 ошибку — 3б,
ошибки -4б, 3 ошибки – 5 баллов
Тест
правильно решены все 5 заданий- 5 баллов ;4 задания – 4б; 3 задания – 3б.

3.Работа у доски
Правильное решение 5б
4.Работа с определениями.
Правильный ответ 1б
5.«Классификация»
Если правильно ,без ошибок сделана классификация – 5б; 1,2 ошибки — 4б;
Если 3-4 ошибки-3б; Более 5 ошибок -2б.
6.«Развивающий канон»
Правильное решение 2б
7. «Силовое многоборье» — работа в группах
Каждое правильно выполненное задание 1 части – 3б ; второй части – 4б
Критерии «5» — 19 и более Итого :
« 4» — от 14 до 18б
«3» — от 8 до 13б
Приложение 4
Продолжите фразу
Мне понравилось на уроке ………………………..………………………………………………………
Я хорошо понял ……………………………………………………………………………………………
Мне очень трудно разобраться в …………………………………………………………………………
Мне нужна помощь в ……………………………………………………………………………………….
У меня хорошо получается решать способом………………………………………………………
Мне нужно ещё поработать над …………………. ……………………………………………………….
……………………………………………………….
На следующих уроках мне бы хотелось………….……………………………………………………….
Решение систем уравнений второй степени и решение задач с помощью таких систем 9 класс онлайн-подготовка на Ростелеком
Тема 8.
Решение систем уравнений второй степени и решение задач с помощью таких систем.
Какие основные способы решения систем уравнений вы знаете? (методы сложения, подстановки, графический)
Каким способом можно решить систему, одно из уравнений которой – уравнение второй степени?
Такие системы всегда можно решить способом подстановки. Для этого поступают следующим образом:
- Выражают из уравнения первой степени одну переменную через другую;
- Подставляют полученное выражение в уравнение второй степени, в результате чего приходят к уравнению с одной переменной;
- Решают получившееся уравнение с одной переменной;
-
Находят соответствующие значения второй переменной.

Рассмотрим пример:
Решим систему уравнений:
x2+y=14,y-x=8;
Выразим из первого уравнения переменную y и подставим во второе:
y=14-x2,14-x2-x=8;
Решим второе уравнение, относительно х:
x2 + x — 6 = 0, корни которого равны (– 3) и 2.
Вернемся к системе:
x1=-3,y1=14—32;
x1=-3,y1=14—32;
x1=-3,y1=5;
x2=2,y2=10;
Рассмотрим еще один пример, решим систему
x2-y2=17,x-y=2;
Эту систему так же можно решить методом подстановки, выразив переменную x, но можно упростить первое уравнение.
Заметим, что левую часть первого уравнения можно разложить на множители по формуле разности квадратов, получим:
x-yx+y=17,x-y=2;
Из второго уравнения разность x — y = 2. Поэтому вместо первой скобки в первое уравнение подставим число 2, получим:
Поэтому вместо первой скобки в первое уравнение подставим число 2, получим:
2x+y=17,x-y=2;
2x+y=17,x-y=2;
Разделим обе части первого уравнения на 2, получим:
x+y=8,5,x-y=2;
А эту систему давай решим методом сложения, сложим два уравнения, а затем из первого уравнения вычтем второе, получим:
2x=10,5,2y=6,5;
x=5,25,y=3,25.
А теперь решим несколько задач с помощью систем: уравнений второй системы:
Сумма двух чисел равна 12, а их произведение равно 35. Найдите эти числа.
Пусть число x – первое число, а y – второе число. Тогда получим:
x+y=12,x∙y=35;
Выразим из первого уравнения переменную х и подставим во второе, получим:
x=12-y,x∙y=35;
x=12-y,12-yy=35;
Решим уравнение:
12y — y2 — 35 = 0
y2 — 12y + 35 = 0
Получим корни 5 и 7.
Возвращаемся к нашей системе:
y1=55x=35
y2=7,7x=35;
y1=5×1=7
y2=7×2=5
Ответ: (7;5) и (5;7)
Рассмотрим еще одну задачу:
Площадь прямоугольного треугольника равен 24 см2, а его гипотенуза равна 10 см. Каковы катеты треугольника?
Пусть a – длина одного катета, а b – длина второго катета.
Вспомним формулу площади прямоугольного треугольника и теорему Пифагора:
Итак, площадь равна половине произведения катетов.
А квадрат гипотенузы равен сумме квадратов катетов:
12ab=24a2+b2=100
Решим эту систему, первое уравнение домножим на 2, получим:
ab=48a2+b2=100
Выразим переменную а из первого уравнения и подставим во второе, получим:
a=48b48b2+b2=100
Решим второе уравнение системы:
2304b2+b2-100=0,
b4-100b2+2304=0, решим это биквадратное уравнение:
Пусть b2 = t, тогда получим:
t2 — 100t + 2304 = 0, отсюда
t1 = 64, t2 = 36
Возвращаемся к нашей замене, получим:
b1,2=±8,b3,4=±6, так как b – это длина катета, то она не может быть отрицательной, следовательно, b равно 6 или 8, тогда второй катет равен 8 или 6 соответственно.
3.1.2. Разложение выражений на множители
Глава 3. Решение уравнений и неравенств
3.1.
3.1.2.
Изучение приёмов преобразования уравнений начнём с обсуждения того, как можно разлагать на множители выражения, входящие в данное уравнение. Вообще представление уравнения f (x) = g (x) в виде
| F1 (x) · F2 (x) · … · Fn (x) = 0, | (5) |
где выражения Fk (x), k = 1, …, n «проще» функций f (x) и g (x), представляет собой несомненное продвижение в решении уравнения. В самом деле, представление вида (5) позволяет сразу приравнивать множители Fk (x) нулю и решать более простые уравнения. Представление уравнения (1) в виде (5) иногда называют факторизованным видом уравнения (1) (от английского слова «factor» – множитель).
В самом деле, представление вида (5) позволяет сразу приравнивать множители Fk (x) нулю и решать более простые уравнения. Представление уравнения (1) в виде (5) иногда называют факторизованным видом уравнения (1) (от английского слова «factor» – множитель).
Перечислим теперь некоторые наиболее распространённые приёмы разложения многочленов, как наиболее простых алгебраических функций, на множители.
1. Вынесение общего множителя за скобку
В том случае, когда все члены многочлена имеют один и тот же общий множитель, его можно вынести за скобку, получая тем самым разложение многочлена.
Пример 1Разложить на множители многочлен x5 – 2x3 + x2.
|
Каждое слагаемое этого многочлена содержит множитель x2. Вынесем его за скобку и получим ответ: x5 – 2x3 + x2 = x2(x3 – 2x + 1). |
2. Применение формул сокращённого умножения
Формулы сокращения довольно эффективно применяются при разложении многочлена на множители. Полезно помнить следующие формулы:
Разложить на множители многочлен (x – 2)4 – (3x + 1)4.
|
Разложим разность четвёртых степеней по формуле, приведённой выше:
|
3. Применение выделения полного квадрата
Без преувеличения можно сказать, что метод выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов. Поясним сказанное на примере.
Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов. Поясним сказанное на примере.
Разложить на множители многочлен x4 + 4x2 – 1.
|
Имеем |
4. Группировка
Метод группировки слагаемых, как правило, применяется совместно с другими методами разложения на множители и чаще всего с методом вынесения за скобки. Суть метода состоит в том, что все слагаемые данного многочлена перегруппировываются таким образом, чтобы в каждой группе, возможно после вынесения общего множителя за скобки, образовалось бы одно и то же выражение. Это выражение можно также вынести за скобки как общий для всех групп множитель.
5. Метод неопределённых коэффициентов
Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной.
Теоретической основой метода являются следующие утверждения.
- Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
- Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
- Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.
Для доказательства второго утверждения вспомним, как выглядит график степенной функции с нечетной целой степенью (§ 2.2.5). Действительно, из его вида следует, что значение многочлена имеет разные знаки при x → +∞ и x → –∞. Многочлен степени n – непрерывная функция, значит, найдется хотя бы одна точка, в которой график этой функции пересечет ось Ox.
Пример 4Разложить на множители многочлен 3x3 – x2 – 3x + 1.
|
Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax2 + bx + c такие, что справедливо равенство
Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырёх уравнений для определения четырёх неизвестных коэффициентов:
Итак, многочлен 3x3 – x2 – 3x + 1 разлагается на множители:
|
6. Теорема о корнях многочлена
Разложение многочлена на множители иногда удаётся провести, если один из его корней угадан с помощью теоремы о рациональных корнях, доказанной в § 2.1.4. После того, как корень x = α угадан, многочлен Pn (x) представим в виде Pn (x) = (x – α) · Pn – 1 (x), где Pn – 1 (x) − многочлен степени на 1 меньше, чем Pn (x).
Разложить на множители многочлен x3 – 5x2 – 2x + 16.
|
Данный многочлен имеет целые коэффициенты. По следствию теоремы о рациональных корнях (см. § 2.1.4) если целое число является корнем этого многочлена, то оно является делителем числа 16, то есть если у данного многочлена есть целые корни, то это могут быть только числа ±1, ±2, ±4, ±8, ±16. Проверкой убеждаемся, что число 2 является корнем этого многочлена, то есть
|
7. Разложение относительно параметра
Разложение относительно параметра
Суть этого метода легче всего понять на примере.
Пример 6Разложить на множители многочлен x4 – 10x2 – x + 20.
|
Преобразуем данный многочлен:
Рассмотрим теперь многочлен a2 – a(1 + 2x2) + x4 – x, который при a = 5 совпадает с данным. Полученный многочлен является квадратным, его корни легко найти по теореме Виета:
|
Решение кубических уравнений — методы и примеры
Решение полиномиальных уравнений высшего порядка — важный навык для любого, кто изучает естественные науки и математику. Однако понять, как решать такие уравнения, довольно сложно.
Однако понять, как решать такие уравнения, довольно сложно.
В этой статье обсуждается, как решать кубические уравнения, используя различные методы, такие как метод деления, теорема о множителях и разложение на множители по группировке.
Но прежде чем перейти к этой теме, давайте обсудим , что такое полиномиальное и кубическое уравнение.
Многочлен — это алгебраическое выражение с одним или несколькими членами, в которых знак сложения или вычитания разделяет константу и переменную.
Общая форма многочлена: ax n + bx n-1 + cx n-2 +…. + kx + l, где у каждой переменной есть постоянная, сопровождающая ее в качестве коэффициента. Различные типы полиномов включают в себя; двучлены, трехчлены и четырехчлены. Примеры полиномов: 3x + 1, x 2 + 5xy — ax — 2ay, 6x 2 + 3x + 2x + 1 и т. Д.
Кубическое уравнение — это алгебраическое уравнение третьей степени.
Общий вид кубической функции: f (x) = ax 3 + bx 2 + cx 1 + d. Кубическое уравнение имеет вид ax 3 + bx 2 + cx + d = 0, где a, b и c — коэффициенты, а d — постоянная.
Как решать кубические уравнения?
Традиционный способ решения кубического уравнения состоит в том, чтобы свести его к квадратному уравнению, а затем решить его либо факторизацией, либо квадратной формулой.
Подобно тому, как квадратное уравнение имеет два действительных корня , кубическое уравнение может иметь три действительных корня. Но в отличие от квадратного уравнения, которое может не иметь реального решения, кубическое уравнение имеет по крайней мере один действительный корень.
Два других корня могут быть действительными или мнимыми.
Всякий раз, когда вам задают кубическое уравнение или какое-либо уравнение, вы всегда должны сначала преобразовать его в стандартную форму.
Например, если вам дано что-то вроде этого, 3x 2 + x — 3 = 2 / x, вы перегруппируете в стандартную форму и запишете это как, 3x 3 + x 2 — 3х — 2 = 0.Тогда вы сможете решить эту проблему любым подходящим способом.
Давайте рассмотрим несколько примеров ниже для лучшего понимания:
Пример 1
Определите корни кубического уравнения 2x 3 + 3x 2 — 11x — 6 = 0
Решение
Так как d = 6, то возможными множителями являются 1, 2, 3 и 6.
Теперь примените теорему о факторах, чтобы проверить возможные значения методом проб и ошибок.
f (1) = 2 + 3 — 11 — 6 ≠ 0
f (–1) = –2 + 3 + 11 — 6 ≠ 0
f (2) = 16 + 12 — 22 — 6 = 0
Следовательно, x = 2 — первый корень.
Мы можем получить другие корни уравнения, используя метод синтетического деления.
= (x — 2) (ax 2 + bx + c)
= (x — 2) (2x 2 + bx + 3)
= (x — 2) (2x 2 + 7x + 3 )
= (x — 2) (2x + 1) (x +3)
Следовательно, решения следующие: x = 2, x = -1/2 и x = -3.
Пример 2
Найдите корни кубического уравнения x 3 — 6x 2 + 11x — 6 = 0
Решение
x 3 — 6x 2 + 11x — 6
(x — 1) — один из факторов.
Разделив x 3 — 6x 2 + 11x — 6 на (x — 1),
⟹ (x — 1) (x 2 — 5x + 6) = 0
⟹ (x — 1) (x — 2) (x — 3) = 0
Это решение кубического уравнения: x = 1, x = 2 и x = 3.
Пример 3
Решить x 3 — 2x 2 — x + 2
Решение
Факторизуйте уравнение.
x 3 — 2x 2 — x + 2 = x 2 (x — 2) — (x — 2)
= (x 2 — 1) (x — 2)
= (x + 1) (x — 1) (x — 2)
x = 1, -1 и 2.
Пример 4
Решите кубическое уравнение x 3 — 23x 2 + 142x — 120
Решение
Сначала разложите полином на множители.
x 3 — 23x 2 + 142x — 120 = (x — 1) (x 2 — 22x + 120)
Но x 2 — 22x + 120 = x 2 — 12x — 10x + 120
= x (x — 12) — 10 (x — 12)
= (x — 12) (x — 10)
Следовательно, x 3 — 23x 2 + 142x — 120 = ( x — 1) (x — 10) (x — 12)
Приравнять каждый множитель к нулю.
x — 1 = 0
x = 1
x — 10 = 10
x — 12 = 0
x = 12
Корни уравнения: x = 1, 10 и 12.
Пример 5
Решите кубическое уравнение x 3 — 6 x 2 + 11x — 6 = 0.
Решение
Чтобы решить эту задачу методом деления, возьмите любой множитель константы 6 ;
let x = 2
Разделим полином на x-2 до
(x 2 — 4x + 3) = 0.
Теперь решите квадратное уравнение (x 2 — 4x + 3) = 0, чтобы получить x = 1 или x = 3
Следовательно, решениями являются x = 2, x = 1 и x = 3.
Пример 6
Решите кубическое уравнение x 3 — 7x 2 + 4x + 12 = 0
Решение
Пусть f (x) = x 3 — 7x 2 + 4x + 12
Поскольку d = 12, возможные значения: 1, 2, 3, 4, 6 и 12.
Методом проб и ошибок мы находим, что f (–1) = –1 — 7 — 4 + 12 = 0
Итак, (x + 1) является множителем функции.
x 3 — 7x 2 + 4x + 12
= (x + 1) (x 2 — 8x + 12)
= (x + 1) (x — 2) (x — 6)
Следовательно, x = –1, 2, 6
Пример 7
Решите следующее кубическое уравнение:
x 3 + 3x 2 + x + 3 = 0.
Решение
x 3 + 3x 2 + x + 3
= (x 3 + 3x 2 ) + (x + 3)
= x 2 (x + 3) + 1 (x + 3 )
= (x + 3) (x 2 + 1)
Следовательно, x = -1, 1-3.
Пример 8
Решить x 3 — 6x 2 + 11x — 6 = 0
Решение
Разложить на множители
x 3 — 6x 2 + 11x — 6 = 0 ⟹ (x — 1) (x — 2) (x — 3) = 0
Приравнивание каждого множителя к нулю дает;
x = 1, x = 2 и x = 3
Пример 9
Решить x 3 — 4x 2 — 9x + 36 = 0
Решение
Разложите каждый набор два срока.
x 2 (x — 4) — 9 (x — 4) = 0
Извлеките общий множитель (x — 4), чтобы получить
(x 2 — 9) (x — 4) = 0
Теперь разложите разность двух квадратов на множители
(x + 3) (x — 3) (x — 4) = 0
Приравнивая каждый множитель к нулю, мы получаем;
x = −3, 3 или 4
Пример 10
Решите уравнение 3x 3 −16x 2 + 23x — 6 = 0
Решение
Divide 3x 3 −16x 2 + 23x — 6 на x -2, чтобы получить 3x 2 — 1x — 9x + 3
= x (3x — 1) — 3 (3x — 1)
= (x — 3) ( 3x — 1)
Следовательно, 3x 3 −16x 2 + 23x — 6 = (x- 2) (x — 3) (3x — 1)
Приравняем каждый множитель к нулю, чтобы получить,
x = 2, 3 и 1/3
Пример 11
Найдите корни 3x 3 — 3x 2 — 90x = 0
Решение
разложите на множители 3x
3x 3 — 3x 2 — 90x ⟹3x (x 2 — x — 30)
Найдите пару множителей, произведение которых равно −30, а сумма равна −1.
⟹- 6 * 5 = -30
⟹ −6 + 5 = -1
Перепишите уравнение, заменив член «bx» на выбранные множители.
⟹ 3x [(x 2 — 6x) + (5x — 30)]
Разложите уравнение на множители;
⟹ 3x [(x (x — 6) + 5 (x — 6)]
= 3x (x — 6) (x + 5)
Приравнивая каждый множитель к нулю, получаем;
x = 0, 6, -5
Решение кубических уравнений с помощью графического метода
Если вы не можете решить кубическое уравнение ни одним из вышеперечисленных методов, вы можете решить его графическим способом.Для этого вам необходимо иметь точный набросок данного кубического уравнения.
Точка (точки), где его график пересекает ось x, является решением уравнения. Количество реальных решений кубических уравнений равно количеству пересечений его графиком оси абсцисс.
Пример 12
Найдите корни x 3 + 5x 2 + 2x — 8 = 0 графически.
Решение
Просто нарисуйте график следующей функции, подставив случайные значения x:
f (x) = x 3 + 5x 2 + 2x — 8
. График отсекает ось абсцисс в 3 точках, следовательно, существует 3 реальных решения.
График отсекает ось абсцисс в 3 точках, следовательно, существует 3 реальных решения.
На графике решения следующие:
x = 1, x = -2 & x = -4.
Предыдущий урок | Главная страница | Следующий урокСтепень (выражения)
«Степень» в математике может означать несколько вещей:
- В геометрии градус (°) — это способ измерения углов,
- Но здесь мы посмотрим, что означает степень в Алгебра .
В алгебре «Степень» иногда называют «Порядком»
Степень полинома (с одной переменной)
Полином выглядит так:
| пример полинома , у этого есть 3 члена |
Степень (для многочлена с одной переменной, например, x ) составляет:
— наибольший показатель этой переменной.
Еще примеры:
| 4x | Степень равна 1 (переменная без показателя степени фактически имеет показатель степени 1) | |
| 4x 3 — x + 3 | Степень 3 (наибольший показатель x) | |
| x 2 + 2x 5 — x | Степень 5 (наибольший показатель x) | |
| z 2 — z + 3 | Степень 2 (наибольший показатель z) |
Названия степеней
Когда мы знаем степень, мы можем дать ей имя!
| степень | Имя | Пример |
|---|---|---|
| 0 | Константа | 7 |
| 1 | линейный | х + 3 |
| 2 | Квадратичная | x 2 −x + 2 |
| 3 | Кубический | x 3 −x 2 +5 |
| 4 | Quartic | 6x 4 −x 3 + x − 2 |
| 5 | Квинтик | x 5 −3x 3 + x 2 +8 |
Пример: y = 2x + 7 имеет степень 1, поэтому это линейное уравнение
Пример: 5w 2 — 3 имеет степень 2, поэтому квадратичная
Уравнения высшего порядка обычно труднее решить :
- Линейные уравнения легко решить
- Квадратные уравнения немного сложнее решить
- Кубические уравнения снова сложнее, но есть формулы для помощи
- Уравнения четвертой степени также могут быть решены, но формулы очень сложные
- Уравнения пятой степени не имеют формул, а иногда бывает неразрешимым !
Степень многочлена с более чем одной переменной
Когда многочлен имеет более одной переменной, нам нужно посмотреть на каждый член . Термины разделены знаком + или -:
Термины разделены знаком + или -:
| Пример полинома с более чем одной переменной |
На каждый член :
- Найдите градус по , сложив экспоненты каждой переменной ,
наибольшая такая степень — это степень многочлена.
Пример: какова степень этого многочлена:
Проверка каждого термина:
- 5xy 2 имеет степень 3 (x имеет показатель 1, y имеет 2 и 1 + 2 = 3)
- 3x имеет степень 1 (x имеет показатель степени 1)
- 5y 3 имеет степень 3 (y имеет показатель степени 3)
- 3 имеет степень 0 (без переменной)
Наибольшая степень из них равна 3 (на самом деле два члена имеют степень 3), поэтому многочлен имеет степень 3
Пример: какова степень этого многочлена:
4z 3 + 5y 2 z 2 + 2yz
Проверка каждого термина:
- 4z 3 имеет степень 3 (z имеет показатель степени 3)
- 5y 2 z 2 имеет степень 4 (y имеет показатель степени 2, z имеет 2 и 2 + 2 = 4)
- 2yz имеет степень 2 (y имеет показатель 1, z имеет 1 и 1 + 1 = 2)
Наибольшая степень из них равна 4, поэтому полином имеет степень 4
Записываем
Вместо того, чтобы говорить «, степень (любого) равна 3 », мы пишем это так:
Когда выражение представляет собой дробь
Мы можем вычислить степень рационального выражения (того, которое имеет форму дроби), взяв степень вершины (числитель) и вычтя степень основания (знаменатель).
Вот три примера:
../algebra/images/degree-example.js?mode=x0
../algebra/images/degree-example.js?mode=x1
../algebra/images/degree-example.js?mode=xm1
Вычисление других типов выражений
Предупреждение: впереди новые идеи!
Иногда мы можем определить степень выражения, разделив …
- логарифм функции по
- логарифм переменной
… затем сделайте это для все больших и больших значений, чтобы увидеть, где находится ответ «заголовок».
(Точнее, мы должны определить предел до бесконечности ln (f (x)) ln (x) , но я просто хочу, чтобы это было просто).
Вот пример:
Пример: степень 3 + √x
Попробуем увеличить значения x:
| x | лин (3 + √x) | лин (x) | лин (3 + √x) лин (x) |
|---|---|---|---|
| 2 | 1. 48483 48483 | 0,69315 | 2,1422 |
| 4 | 1.60944 | 1,38629 | 1,1610 |
| 10 | 1,81845 | 2.30259 | 0,7897 |
| 100 | 2,56495 | 4.60517 | 0,5570 |
| 1000 | 3,54451 | 6. | 0,5131 |
| 10 000 | 4,6 3473 | 9,2 1034 | 0,5032 |
| 100 000 | 5.76590 | 11,51293 | 0,5008 |
| 1 000 000 | 6.9 1075 | 13,81551 | 0,5002 |
Глядя на таблицу:
- по мере того, как x становится больше, чем ln (3 + √x) ln (x) становится все ближе и ближе к 0.5
Итак, степень 0,5 (другими словами 1/2)
(Примечание: это хорошо согласуется с x ½ = квадратный корень из x, см. Дробные экспоненты)
Дробные экспоненты)
Некоторые значения степени
| Выражение | градусов |
|---|---|
| журнал (x) | 0 |
| e x | ∞ |
| 1 / х | -1 |
| √x | 1/2 |
462, 4003, 2092, 4004 463, 1108, 2093, 4005, 1109, 4006
полиномов
Проект «Улучшение математического образования в школах» (TIMES)
вернуться к индексу
Предполагаемые знания
Мотивация
Многочлены представляют следующий уровень алгебраической сложности после квадратичных.В самом деле, квадратичный — это многочлен степени 2. Мы можем разложить квадратные выражения на множители, решить квадратные уравнения и построить график квадратичных функций, возникает очевидный вопрос,
как эти вещи могут быть выполнены с помощью алгебраических выражений более высокой степени.
Квадратичный x2 — 5x + 6 множится как (x — 2) (x — 3). Следовательно, уравнение x2 — 5x + 6 = 0
Следовательно, уравнение x2 — 5x + 6 = 0
имеет решения x = 2 и x = 3.
Аналогичным образом мы можем разложить на множители кубику x3 — 6×2 + 11x — 6 как (x — 1) (x — 2) (x — 3), что позволяет нам показать, что решения x3 — 6×2 + 11x — 6 = 0 являются х = 1, х = 2 или х = 3.В этом модуле мы увидим, как прийти к этой факторизации.
Полиномы во многих отношениях ведут себя как целые или целые числа. Мы можем складывать, вычитать и умножать два или более полинома вместе, чтобы получить еще один полином. Так же, как мы можем разделить одно целое число на другое, получая частное и остаток, мы можем разделить один многочлен на другой и получить частное и остаток, которые также являются многочленами.
Квадратное уравнение вида ax2 + bx + c имеет 0, 1 или 2 решения, в зависимости от того, какой дискриминант отрицательный, нулевой или положительный.Количество решений этого уравнения помогло нам построить график квадратичной функции y = ax2 + bx + c. Точно так же информация о корнях полиномиального уравнения позволяет нам дать грубый набросок соответствующей полиномиальной функции.
Многочлены являются не только интересными объектами, но и важными приложениями в реальном мире. Одно из таких приложений для кодов исправления ошибок обсуждается в Приложении к этому модулю.
Содержимое
Терминология
Многочлен — это такое выражение, как x5 — 2×3 + 8x + 3 или x4 — x2 + 1.Может быть любое количество терминов, но каждый член должен быть кратным целому числу в степени x. Таким образом, 2×3 — x не является многочленом.
Член с наибольшей степенью называется старшим членом, а его коэффициент — старшим коэффициентом. Если старший коэффициент равен 1, то многочлен называется моническим. Индекс главного члена называется степенью многочлена. Термин, не зависящий от, называется постоянным членом.
Таким образом, x5 — 2×3 + 8x + 3 является моническим многочленом степени 5 с постоянным членом 3, а
x4 — x2 + 1 является немоническим многочленом степени 4 со старшим коэффициентом и постоянным членом 1.
В первом полиноме все коэффициенты являются целыми числами, а во втором полиноме есть иррациональный коэффициент. По большей части мы будем рассматривать только многочлены первого типа, но многое из того, что следует ниже, одинаково хорошо применимо и ко второму.
По большей части мы будем рассматривать только многочлены первого типа, но многое из того, что следует ниже, одинаково хорошо применимо и ко второму.
Для именования полиномов мы будем использовать обозначение функций, например p (x) или q (x). Таким образом, мы можем записать p (x) = x5 — 2×3 + 8x + 3 или q (x) = x4 — x2 + 1. Это позволяет нам удобно подставлять значения x, когда это необходимо.
Общий многочлен имеет вид
p (x) = тревога — an — 1xn — 1 + … + a1x + a0,
, где 0, а n — целое число. Коэффициенты, как правило, являются действительными числами.
УПРАЖНЕНИЕ 1
Запишите главный член, старший коэффициент, степень и постоянный член в приведенном выше общем полиноме.
Для полиномов малой степени мы используем следующие имена.
- полином степени 1 называется линейным
- полином степени 2 называется квадратичным
- полином степени 3 называется кубикой
- полином степени 4 называется квартикой
- полином степени 5 называется квинтикой
Многочлен, состоящий только из ненулевой константы, называется постоянным многочленом и имеет степень 0. Многочлен p (x) = 0 называется нулевым многочленом.В нем нет терминов, и поэтому нет ведущего термина. Лучше не определять степень нулевого многочлена. В некоторых книгах его степень обозначается как −1 или −∞.
Многочлен p (x) = 0 называется нулевым многочленом.В нем нет терминов, и поэтому нет ведущего термина. Лучше не определять степень нулевого многочлена. В некоторых книгах его степень обозначается как −1 или −∞.
Сложение, вычитание и умножение многочленов
Чтобы сложить или вычесть два многочлена, мы собираем одинаковые члены.
Обратите внимание, что мы обычно пишем члены многочлена от наибольшей к наименьшей степени. Иногда это называют стандартной формой многочлена.
Чтобы умножить два полинома, мы умножаем каждый член в первом полиноме на второй полином и собираем похожие члены.
ПРИМЕР
Многочлены P (x), Q (x) и R (x) задаются формулами P (x) = x3 — 2×2 + x — 1, Q (x) = 3×3 — 2×2 и R (x) = −x4 + 2×3 — 3×2. Найти:
а P (x) Q (x) b Q (x) R (x)
Решение
| P (x) Q (x) | = (x3 — x2 + x — 1) (3×3 — 2×2) | ||
| = x3 (3×2 — 2×2) — x2 (3×3 — 2×2) + x (3×3 — 2×2) — (3×3 — 2×2) | |||
| = 3×6 — 2×5 — 3×5 + 2×4 + 3×4 — 2×3 — 3×3 + 2×2 | |||
| = 3×6 — 5×5 + 5×4 — 5×3 + 2×2 | |||
| б | Q (x) R (x) | = (3×3 — 2×2) (- x4 + 2×3 — 3×2) | |
| = 3×3 (−x4 + 2×3 — 3×2) — 2×2 (−x4 + 2×3 — 3×2) | |||
| = −3×7 + 6×6 — 9×5 + 2×6 — 4×5 + 6×4 | |||
| = −3×7 + 8×6 — 13×5 + 6×4 |
Делительные многочлены
При делении одного целого числа на другое образуется частное и остаток. Таким образом дает 7 остаток 2. Есть разные способы записать этот результат.
Таким образом дает 7 остаток 2. Есть разные способы записать этот результат.
- 37 ÷ 5 равно 7 остаток 2
- 37 ÷ 5 = 7
- 37 = 7 × 5 + 2
В выписке 37 ÷ 5 равно 7, остаток 2
- число 5, на которое мы делим, называется делителем
- число 37, на которое мы делим, называется делимым
- число 7 называется частным
- число 2 называется остатком
Ключевым моментом в отношении остатка является то, что он неотрицателен, но строго меньше делителя.Таким образом, используя третье представление, когда мы разделим два целых числа p и d> 0, мы можем написать
p = dq + r, где 0 ≤ r ≤ d.
Если остаток равен нулю, то мы говорим, что d является множителем p.
Эти основные утверждения, касающиеся арифметики, имеют аналоги, когда мы начинаем делить один многочлен на другой. Мы будем использовать ту же терминологию при обсуждении полиномиального деления. Это делается по образцу деления в столбик.
Деление многочлена p (x) на многочлен d (x) также дает частное q (x) и остаток r (x), поэтому мы можем написать
п (х) = d (х) q (х) + г (х).
Ключевой идеей при выполнении деления является продолжение работы с ведущими терминами, как показано в следующем примере.
ПРИМЕР
Мы разделим многочлен p (x) = 5×4 −7×3 + 2x — 4 на многочлен d (x) = x — 2, а затем выразим деление в виде p (x) = d (x) q (x ) + г (х).
Решение
| 5×3 | + | 3×2 | + | 6x | + | 14 | |||||
| х — 2 | 5×4 | – | 7×3 | + | 2x | – | 4 | (Разделите x на 5×4, получив 5×3. ) ) | |||
| 5×4 | – | 10×3 | (Умножьте x — 2 на 5×3, а затем вычтите.) | ||||||||
| 3×3 | + | 2x | – | 4 | (Разделите x на 3×3, получив 3×2.) | ||||||
| 3×3 | – | 6×2 | (Умножьте x — 2 на 3×2 и затем вычтите. ) ) | ||||||||
| 6×2 | + | 2x | – | 4 | (Разделите x на 6×2, получится 6x.) | ||||||
| 6×2 | – | 12x | (Умножьте x — 2 на 6x, а затем вычтите.) | ||||||||
| 14x | – | 4 | (Разделите x на 14x, получим 14. ) ) | ||||||||
| 14x | – | 28 | (Умножьте x — 2 на 14 и затем вычтите.) | ||||||||
| 24 | (Это последний остаток.) |
Отсюда 5×4 — 7×3 + 2x — 4 = (x — 2) (5×3 + 3×2 + 6x + 14) + 24. (1)
(1)
В этом примере мы видим, что частное q (x) = 5×3 + 3×3 + 6x — 14, а остаток равен r (x) = 24.
Мы можем выполнить частичную проверку, подставив x = 2 в последнюю строку.
Из приведенного выше примера видно, что степень остатка меньше степени делителя, иначе мы могли бы продолжить деление.Таким образом, в случае, когда множитель является линейным, остаток будет константой, и поэтому мы можем записать его как.
В общем, теперь мы можем написать p (x) = d (x) q (x) + r (x), где r (x) = 0, или, 0 ≤ степень (r (x)) <степень (d (Икс)).
УПРАЖНЕНИЕ 3
Разделите p (x) = 5×4 — 7×3 + 2x — 4 на d (x) = x2 — 2. Выразите результат в виде
p (x) = d (x) q (x) + r (x) где степень r (x) меньше степени d (x).
Обратите внимание, что в этом случае, поскольку делитель имеет степень 2, остаток будет либо равен 0, либо иметь степень не выше 1.
Теорема об остатке
Деление многочленов в длину — громоздкий процесс, и в некоторых случаях нас интересует только остаток. Это не появляется до конца вычислений. Когда мы делим многочлен p (x) на линейный множитель (x — a), мы можем довольно легко найти остаток.
Это не появляется до конца вычислений. Когда мы делим многочлен p (x) на линейный множитель (x — a), мы можем довольно легко найти остаток.
Поскольку делитель линейный, p (x) = (x — a) q (x) + r, где r — постоянная. Подставляя x = a в обе части, получаем r = p (a).
Таким образом, остаток равен полиному, вычисленному при x = a.
Этот удивительный результат называется теоремой об остатке. Мы должны иметь в виду, что он вообще ничего не говорит о частном q (x) и работает только тогда, когда мы делим на линейный множитель (x — a).
УПРАЖНЕНИЕ 4
Многочлен p (x) = x5 — 7×3 + ax + 1 имеет остаток 13 после деления на x — 1. Найдите значение коэффициента a.
Факторная теорема
Факторинг квадратичного уравнения — важный метод, который мы использовали для решения квадратных уравнений.Подобным образом мы хотели бы разработать некоторые методы факторизации многочленов.
Если линейный многочлен (x — a) является множителем многочлена p (x), то мы можем записать
p (x) = q (x) (x — a) и, таким образом, остаток от деления p (x) by (x — a) равно 0.
Используя теорему об остатке, мы доказали:
Теорема
(x — a) является множителем многочлена p (x), если p (a) = 0. Если p (a) ≠ 0, то
(x — a) не является множителем p (x).
Число a, которое дает p (a) = 0, называется нулем многочлена.
Обратите внимание, что, поскольку (x — 2) и (x — 1) являются множителями p (x), то же самое и их произведение
(x — 2) (x — 1) = x2 — 3 x + 2. Таким образом, мы могли бы найти третий множитель методом длинного деления.
Разделение p (x) на x2 — 3x + 2 дает (x — 3) в качестве третьего множителя, и поэтому мы получаем
после факторизации,
p (x) = x3 — 6×2 + 11x — 6 = (x — 1) (x — 2) (x — 3).
Альтернативный метод
Поскольку p (2) = 0 и p (1) = 0, а p (x) имеет степень 3, мы можем записать p (x) = (x — 2) (x — 1) (x — a)
Где a — число, которое предстоит определить. Поскольку p (0) = −6, имеем −2a = −6, поэтому a = 3.
Поскольку p (0) = −6, имеем −2a = −6, поэтому a = 3.
УПРАЖНЕНИЕ 5
Многочлен p (x) = 3×6 — 5×3 + ax2 + bx + 10 делится на x + 1 и x — 2. Найдите значения коэффициентов a и b.
Факторинговые многочлены
Наша цель — взять многочлен с целыми коэффициентами и записать его как произведение многочленов меньшей степени, которые также имеют целые коэффициенты. Этот процесс называется факторингом по целым числам.
Теорема о факторах позволяет нам проверить, имеет ли многочлен p (x) линейный фактор (x — a). Если это так, то мы можем использовать длинное деление, чтобы найти многочлен q (x) такой, что p (x) = (x — a) q (x) и q (x) имеет степень на единицу меньше, чем степень p (x ). Таким образом, мы сможем повторять процесс над q (x) и так далее как можно чаще, чтобы получить полную факторизацию p (x).
Например,
Начнем с полинома p (x) = x3 + 4×2 — 7x — 10.
- Мы систематически ищем один линейный фактор, проверяя числа a = 1, — 1, 2, −2,… до тех пор, пока не найдем целое значение a такое, что p (a) = 0.

p (1) = −12 ≠ 0, p (−1) = 0, поэтому (x + 1) является множителем.
- Затем мы используем длинное деление, чтобы разделить p (x) на (x + 1), чтобы получить p (x) = (x + 1) (x2 + 3x — 10).
Теперь квадратичный q (x) = x2 + 3x — 10 может быть разложен на множители, используя наши знания о квадратиках, как (x + 5) (x — 2), и поэтому полное разложение p (x) на множители равно
.п (х) = (х + 1) (х + 5) (х — 2).
Чтобы помочь нам найти целое число ноль многочлена, мы используем следующий результат.
Теорема
Если многочлен
p (x) = тревога + an − 1xn − 1 +… + a1x + a0
имеет целое число ноль a, тогда a является множителем постоянного члена a0.
Таким образом, в приведенном выше примере единственными возможными целыми нулями являются ± 1, ± 2, ± 5 или ± 10.
УПРАЖНЕНИЕ 6
Объясните, почему приведенная выше теорема верна.
ПРИМЕР
Разложите многочлен p (x) = x4 — 2×3 — 8x + 16 на множители.
Решение
- Нам нужно проверить только положительный и отрицательный множители 16.
P (1) = 1-2-8 + 16 ≠ 0, поэтому x — 1 не является множителем p (x).
P (−1) = 1 + 2 + 8 + 16 ≠ 0, поэтому x + 1 не является множителем p (x).
P (2) = 16-16-16 + 16 = 0, поэтому x — 2 является множителем.
После деления p (x) на x — 2, p (x) = (x — 2) (x3 — 8) - Пусть Q (x) = x3 — 8.
x — 1 и x + 1 не являются факторами Q (x), поскольку P (x) = (x — 2) Q (x), и они не являются факторами P (Икс).
Однако Q (2) = 8-8 = 0, поэтому x — 2 также является множителем Q (x).
После деления Q (x) на x — 2, Q (x) = (x — 2) (x2 + 2x + 4). - Квадратичный x2 + 2x + 4 не может быть разложен на множители, см. Ниже.
Следовательно, P (x) = (x — 2) 2 (x2 + 2x + 4) — полная факторизация P (x).
Обратите внимание, что квадратичный x2 + 2x + 4 = (x + 1) 2 + 3, который всегда больше или равен 3, следовательно, квадратичный не имеет множителей.
УПРАЖНЕНИЕ 7
Сначала удалите очевидный общий множитель, разложите на множители многочлен
p (x) = 2×5 — 22×4 + 78×3 — 90×2.
Полиномиальные уравнения
Одним из основных методов решения квадратных уравнений был метод факторизации. Точно так же одно из основных приложений факторизации многочленов — решение полиномиальных уравнений.
ПРИМЕР
Решить x3 + 4 x2 — 7x — 10 = 0
Решение
В предыдущем примере мы разложили многочлен
p (x) = x3 + 4 x2 — 7x — 10 = 0 как (x + 1) (x + 5) (x — 2).
Таким образом, уравнение x3 + 4 x2 — 7x — 10 = 0 принимает вид (x + 1) (x + 5) (x — 2) = 0
Поскольку произведение трех множителей равно нулю, мы можем приравнять каждый множитель к нулю, чтобы найти решения. Таким образом, x + 1 = 0 или x — 2 = 0, или x + 5 = 0, что дает x = −1, x = 2 или x = −5.
Примечание: полином p (x) = (x — 1) (x — 2) 2 (x — 4) 3 имеет степень 6, но полиномиальное уравнение (x — 1) (x — 2) 2 (x — 4) 3 = 0 имеет только 3 (различных) решения x = 1 или x = 2 или x = 4.Таким образом, количество (различных) решений может быть меньше степени, но никогда не может превышать степень.
УПРАЖНЕНИЕ 8
Воспользуйтесь факторизацией p (x) = 2×5 — 22×4 + 78×3 −90×2 из приведенного выше упражнения, чтобы решить уравнение 2×5 — 22×4 + 78×3 — 90×2 = 0.
В некоторых ситуациях факторизация приводит к квадратному уравнению без реальных решений или без иррациональных решений. В этом случае нам может потребоваться завершить задачу, используя формулу корней квадратного уравнения.
ПРИМЕР
Решить x4 + 7×3 — 2×2 — 7x + 1 = 0
Решение
Многочлен x4 + 7×3 — 2×2 — 7x + 1 имеет факторизацию (x — 1) (x + 1) (x2 + 7x — 1).
Следовательно, уравнение принимает вид (x — 1) (x + 1) (x2 + 7x — 1) = 0.
Таким образом, решения x = 1, x = −1 и решения x2 + 7x — 1 = 0.
Используя формулу корней квадратного уравнения, b2 — 4ac = 49 + 4 = 53, поэтому квадратичная формула имеет решения
x = и x =.
Следовательно, квартика имеет четыре решения x = 1, −1 и x =.
Обратите внимание, что существуют полиномиальные уравнения с иррациональными корнями, которые нельзя решить с помощью описанной выше процедуры. Например, многочлен p (x) = x5 — 3×3 — 2×2 + 6 множится как
(x2 — 3) (x3 — 2), и поэтому уравнение x5 — 3×3 — 2×2 + 6 = 0 имеет решения, x =, x = — и x =.
В общем, факторизация многочленов по целым числам является сложной задачей. Например, многочлен
x3-2 не может быть разложен на целые числа, но у него есть одно действительное решение, x =.
Построение полиномиальных функций
Полиномиальная функция — это функция вида y = p (x), где p (x) — полином.
В модуле Квадратичные функции мы увидели, как нарисовать график квадратичного
, указав
- перехватчики
- нахождение вершины.
Вершина — это пример точки поворота.
Для многочленов степени больше 2 поиск точек поворота не является элементарной процедурой и обычно требует использования исчисления:
- Чтобы найти точку пересечения оси y, положим x = 0.
- Чтобы найти точки пересечения по оси x, мы полагаем y = 0 и решаем соответствующее полиномиальное уравнение, если это возможно.
Возьмем многочлен y = x3 + x2 — 6x = x (x — 2) (x — 3).
Перехват по оси Y равен 0, а пересечение по оси x происходит, когда x (x — 2) (x — 3) = 0, то есть когда x = 0, 2 и 3.
Чтобы получить представление об общей форме кривой, мы можем подставить несколько контрольных точек.
Мы можем представить знак y с помощью диаграммы знаков:
Обладая этой информацией, мы можем начать набросок графика y = x (x — 2) (x + 3).
Знаковая диаграмма говорит нам, что график пересекает ось x в точках x = −3, 0 и 2, а также находится ли график выше или ниже оси a с каждой стороны этих точек. Он не сообщает нам максимальное и минимальное значения y между нулями.
Обратите внимание, что если x — большое положительное число, то p (x) также большое и положительное число. Например, если x = 10, тогда y = 1040. Если x — большое отрицательное число, то p (x) также является большим отрицательным числом. Например, если x = −10, то y = −840.
УПРАЖНЕНИЕ 9
Нарисуйте график y = (x + 2) (x + 1) (x — 1) (x — 2).
Графики многочленов с повторяющимися множителями
Полиномиальные функции, такие как p (x) = 3 (x — 1) 2 (x + 3) 5 (x — 4), которые содержат повторяющиеся множители, требуют особой осторожности.
Если мы рассмотрим, например, размер x4 для различных значений x, мы заметим
- x4 положительно как для положительного, так и для отрицательного значения x
- для значений x от -1 до 1 размер x4 меньше, чем значение x.

Графически это говорит нам, что график y = x4 имеет минимум при x = 0 и что около x = 0 график довольно плоский, но начинает резко увеличиваться при x> 1 и x <−1.
Графики y = x2 и y = x4 показаны для сравнения.
Оба этих графа имеют минимум при x = 0. В случае параболы мы называем это вершиной, но обычно мы не используем это слово для многочленов более высокой степени. Вместо этого мы говорим о поворотной точке и далее классифицируем ее как максимум или минимум.
Каждый график y = −x2 и y = −x4 имеет максимум при x = 0.
Четные степени
То же самое происходит для всех положительных четных степеней x и для четных степеней (x — a). Следовательно, около нуля многочлена, который возникает из множителя с четной степенью, график имеет минимум или максимум и является «плоским» около этого нуля.
Нечетные степени
График y = (x — 2) срезает ось x в точке x = 2, но не имеет там максимума или минимума. Так как это прямая линия, график в этой точке не плоский, он действительно имеет градиент 45 °. С другой стороны, график y = (x — 2) 3 ведет себя немного иначе при
Так как это прямая линия, график в этой точке не плоский, он действительно имеет градиент 45 °. С другой стороны, график y = (x — 2) 3 ведет себя немного иначе при
x = 2. В Далее мы будем рассматривать нечетные степени, большие или равные 3.
Поскольку нечетная степень отрицательного числа отрицательна, знаковая диаграмма показывает, что значения
y графика y = x3 меняются от отрицательного к положительному, когда значения x перемещаются от -1 к 1. Как и выше, график имеет вид квартира возле начала координат.
Отсюда график y = x3 выглядит так:
В начале координат у нас нет ни максимума, ни минимума. Точка x = 0 называется точкой заражения кривой.
ПРИМЕР
Постройте график y = 2×3 (x — 2) 2.
Решение
График проходит через начало координат и срезает ось x в точках x = 0 и x = 2. При x = 0 график имеет точку перегиба, а при x = 2 — минимум. Знаковая схема есть.
Знаковая схема есть.
График:
УПРАЖНЕНИЕ 10
Нарисуйте график полиномиальной функции p (x) = (x + 3) 3 (x — 1) 3. (Вы должны обнаружить, что график симметричен относительно x = −1, вы понимаете, почему?)
Ссылки вперед
Основная теорема алгебры
Нули полинома также называют корнями соответствующего полиномиального уравнения.
Полиномиальное уравнение x2− 4 = 0 имеет два целых корня, x = 2, x = −2, а уравнение x2-2 = 0 имеет два действительных корня, x =, x = -. С другой стороны, уравнение x2 + 2 = 0 не имеет действительных корней. Кроме того, уравнение x3 — 1 = 0, которое множится как (x — 1) (x2 + x + 1 = 0), имеет только один действительный корень, поскольку квадратное уравнение x2 + x + 1 = 0 не имеет решений.
Чтобы правильно понять, сколько решений может иметь полиномиальное уравнение, нам нужно ввести комплексные числа. Комплексное число — это число в форме a + ib, где a, b — действительные числа, а i2 = — 1. Комплексное число i часто называют мнимым числом. Обратите внимание: если мы положим b = 0, мы получим действительное число, поэтому комплексные числа содержат набор всех действительных чисел.
Комплексное число — это число в форме a + ib, где a, b — действительные числа, а i2 = — 1. Комплексное число i часто называют мнимым числом. Обратите внимание: если мы положим b = 0, мы получим действительное число, поэтому комплексные числа содержат набор всех действительных чисел.
Таким образом, хотя уравнение x2 + 1 = 0 не имеет вещественных решений, у него есть два комплексных решения, x = i и x = −i, и многочлен x2 + 1 может быть разложен на множители как (x — i) (x + i).
Великий математик Гаусс (1777–1855) дал первое доказательство следующего удивительного результата, который стал известен как Основная теорема алгебры.
Теорема
Каждое полиномиальное уравнение степени больше 0 имеет хотя бы одно комплексное решение.
Учитывая этот результат, нетрудно показать, что:
Следствие
Каждое полиномиальное уравнение степени n больше 0 имеет ровно n решений над комплексными числами с учетом кратности.
УПРАЖНЕНИЕ 11
Объясните, как следствие можно вывести из теоремы.
Следовательно, каждый многочлен степени n, больше 0, можно разложить на n линейных множителей, используя комплексные числа.
Обратите внимание, что выражение, учитывающее кратность, означает, что при заданном полиномиальном уравнении (x — 2) 3 (x + 1) 2 = 0, например, мы говорим, что корни равны x = 2, 2, 2, −1, −1 . Таким образом, мы говорим, что x = 2 — корень кратности 3, а x = −1 — корень кратности 2. Однако уравнение имеет только два (различных) корня.
Поворотные точки
Вершина параболы — пример точки поворота.Координата x точки поворота параболы y = ax2 + bx + c задается как x = -. Координаты x точек поворота многочлена не так просто найти и требуют использования дифференциального исчисления, которое изучается в высшей математике.
Корни многочлена
Предположим, что мы можем разложить на множители моническую квадратичную x2 + bx + c как (x — α) (x — β). Раскрывая его, мы видим, что сумма корней α + β равна −b, а произведение корней ab равно c.
Аналогичное упражнение можно выполнить на монических кубиках. То есть, если корни кубики
x3 + bx2 + cx + d равны α, β, γ, то можно показать, что
α + β + γ = −b, αβ + αγ + βγ = c и αβγ = −d,
Эти тождества определяют отношения между корнями многочлена и его коэффициентами.
УПРАЖНЕНИЕ 12
Выведите приведенные выше формулы.
История
Изучение уравнений степени больше двух восходит к арабской математике.Омар Хайям (1048–1141 гг.) Большую часть своей жизни провел, пытаясь решить различные случаи кубического уравнения. Только в эпоху Возрождения было получено общее решение кубики. Точные детали отрывочны, но итальянский математик Кардано (1501–1576) сумел раскрыть секрет решения кубической схемы своего соотечественника Тартальи и включил его в свою работу Ars Magna (Великое искусство), опубликованную в 1545 году.
Кубик
Кардано показал, как привести любое кубическое уравнение к виду x3 + px + c = 0, а затем, сделав замену x = u — v, свести задачу к решению квадратичного. На практике проще положить x = u + v.
На практике проще положить x = u + v.
УПРАЖНЕНИЕ 13
Положите x = y — в уравнение x3 + ax2 + bx + c = 0, чтобы показать, что полученное уравнение не содержит членов степени 2.
ПРИМЕР
Решите x3 + 3x — 1 = 0, используя замену x = u + v.
Решение
Переставляя уравнение и подставляя, получаем
(u + v) 3 = −3 (u + v) + 1.
Теперь мы расширяем левую часть и множим 3uv из двух членов, чтобы получить
u3 + v3 + 3uv (u + v) = 1 −3 (u + v).
Приравнивая коэффициенты при (u + v) с обеих сторон и приравнивая оставшиеся члены,
получаем
u3 + v3 = 1, 3uv = −3.
Обработка второго уравнения дает
u3 + v3 = 1, u3v3 = -1,
На этом этапе у нас есть два числа u3, v3, сумма и произведение которых нам известны. Следовательно,
Следовательно,
они будут удовлетворять квадратному уравнению z2 — z — 1 = 0, которое имеет решения z = или
z =. Эти решения представляют числа u3 + v3 в любом порядке, поэтому, взяв кубические корни, мы получим следующее решение исходного уравнения
х = и + v = +.
Это единственное реальное решение уравнения.
УПРАЖНЕНИЕ 14
Воспользуйтесь калькулятором, чтобы выразить это в десятичной форме, и убедитесь, что оно удовлетворяет исходному уравнению
.
Квартик
Решение общего уравнения четвертой степени было вскоре найдено учеником Кардано и протеже Феррари. Он открыл метод, позволяющий свести задачу решения
квартики к задаче решения кубики.
В обоих случаях можно выразить решение данного уравнения, используя квадратные и более высокие корни, а также обычные арифметические операции (сложение, вычитание, умножение и деление). Такой раствор часто называют раствором с использованием радикалов.Решениями квадратного уравнения ax2 + bx + c = 0 являются x = и x = -, поэтому квадратное уравнение также может быть решено с использованием радикалов.
Такой раствор часто называют раствором с использованием радикалов.Решениями квадратного уравнения ax2 + bx + c = 0 являются x = и x = -, поэтому квадратное уравнение также может быть решено с использованием радикалов.
Потребовалось несколько сотен лет, прежде чем Абель (1802–1829) и Галуа (1811–1832) понял, что невозможно найти решение общего уравнения пятой степени или общего уравнения более высокой степени с использованием радикалов. . Очевидно, что некоторые уравнения более высокой степени могут быть решены с использованием радикалов, например x5 — 32 = 0, но в общем случае это невозможно.
Корни многочленов
Хотя работа Кардано была большим прорывом, по-прежнему оставалось много безответных вопросов, касающихся полиномов. В 17 веке Декарт нашел тест, известный как правило знаков Декарта, для определения числа положительных действительных корней многочлена, в то время как Ньютон открыл так называемые тождества Ньютона, которые находят и связывают формулы для суммы k-х степеней корней многочлена. В XVIII и XIX веках великие математики Эйлер, Лагранж, Эйзенштейн и Гаусс еще больше расширили наше понимание полиномов и полиномиальных уравнений.Это привело к развитию того, что сегодня называют современной алгеброй, которая занимается изучением алгебраических структур.
В XVIII и XIX веках великие математики Эйлер, Лагранж, Эйзенштейн и Гаусс еще больше расширили наше понимание полиномов и полиномиальных уравнений.Это привело к развитию того, что сегодня называют современной алгеброй, которая занимается изучением алгебраических структур.
Факторинговые полиномы
Выше мы видели, что когда мы изучаем многочлен, нам нужно указать, какие решения / факторы мы ищем. В частности, предположим, что p (x) — многочлен со степенью больше 0 и действительными коэффициентами
- над комплексными числами p (x) делится на линейные множители
- над действительными числами p (x) имеет все свои множители либо линейные, либо квадратичные
- над рациональными числами, можно найти полиномы сколь угодно большой степени
, которые являются неприводимыми, то есть они не могут быть выражены как произведение
двух полиномов с рациональными коэффициентами, каждый меньшей степени.
Основная теорема алгебры используется для доказательства первого из этих утверждений. Чтобы получить второе, нам нужно знать тот факт, что, когда у нас есть многочлен с действительными коэффициентами, любые комплексные корни будут встречаться парами, известными как сопряженные пары. То есть, если a + ib является корнем, то a — ib тоже. Этот факт можно использовать для доказательства второго утверждения.
Чтобы получить второе, нам нужно знать тот факт, что, когда у нас есть многочлен с действительными коэффициентами, любые комплексные корни будут встречаться парами, известными как сопряженные пары. То есть, если a + ib является корнем, то a — ib тоже. Этот факт можно использовать для доказательства второго утверждения.
УПРАЖНЕНИЕ 15
(Для этого нужно немного знать комплексные числа.)
Предположим, что все коэффициенты многочлена p (x) = dancingn — an — 1xn — 1 + … + a1x + a0 действительны.
- a
- Если α = a + ib является решением полиномиального уравнения, p (x) = dancingn — an — 1xn — 1 + … + a1x + a0 = 0, покажите, что = a — ib также является решением.
- б
- Покажите, что если x — α является множителем p (x), где α = a + ib — комплексное число, то квадратичный (x — α) (x -) также является множителем p (x) и что (x — α) (x -) имеет действительные коэффициенты.

- c
- Выведите, что каждый многочлен с действительными коэффициентами теоретически может быть разложен на множители как произведение линейных и / или квадратичных множителей с действительными коэффициентами. (Обратите внимание, что на практике это может быть очень сложной задачей.)
Эйзенштейн (ок. 1850 г.) придумал следующий гениальный тест на несводимость многочленов над рациональными числами.
Рассмотрим многочлен p (x) = тревогу — an — 1xn — 1 + … + a1x + a0, где все коэффициенты являются целыми числами.Предположим, что мы можем найти простое число p, которое не делит старший коэффициент an, но которое делит все остальные коэффициенты. Тест говорит, что если квадрат того же простого числа не делит постоянный член, то есть p2 + a0, то p (x) неприводимо по рациональным числам.
ПРИМЕР
Многочлен p (x) = 5×7 + 6×6 — 15x 4 + 12x — 21 удовлетворяет критерию Эйзенштейна с простым p = 3, и поэтому p (x) не может быть выражено как произведение двух многочленов меньшей степени с целыми коэффициентами. То есть p (x) неприводимо.
То есть p (x) неприводимо.
УПРАЖНЕНИЕ 16
Объясните, как построить многочлен сколь угодно большой степени, который нельзя разложить на рациональные числа.
Серия Maclaurin
В 17-м и 18-м веках математики сделали замечательное открытие, что такие функции, как y = sin x и y = cos x, могут быть выражены с помощью «бесконечных многочленов», то есть многочленов, чьи степени x продолжаются бесконечно.Это называется степенным рядом. Так, например,
sin x = x — + — +…,
, где очевидная закономерность продолжается вечно. Обозначение n! (читается как факториал n) — это сокращение от n (n — 1) (n — 2)… 3.2.1. Таким образом 5! = 5 × 4 × 3 × 2 × 1 = 120. Эти бесконечные ряды часто называют рядами Маклорена и имеют очень широкое применение как в математике, так и в физике.
На сегодняшний день остаются нерешенными проблемы, связанные с многочленами. В приложении ниже в общих чертах обсуждается замечательное применение полиномов в современных телекоммуникациях.
Приложение
Применение полиномов к кодам, исправляющим ошибки
Оцифровка информации
Информация обычно оцифровывается путем преобразования ее в последовательность нулей и единиц. Например, код ASCII для цифры 1 и буквы A — «1» 1000110 и «A» 1000001. Здесь мы предположим, что все рассматриваемые сообщения представляют собой конечные последовательности нулей и единиц.
Когда ваш мобильный телефон отправляет или принимает сообщения или данные отправляются со спутников в глубоком космосе, информация может быть потеряна или повреждена по пути к месту назначения.
Поскольку информация отправляется как последовательности из 0 и 1, «поврежденный» 0 становится 1 и наоборот.
Простая проверка на наличие ошибок — это добавить контрольную цифру, чтобы в строке было четное число единиц, и, следовательно, сумма цифр была четной.
Таким образом, мы кодируем 1 как 10001101 и A как 10000010.
Теперь, если байт передан и один из битов поврежден, то количество единиц становится нечетным, и получатель может запросить повторную передачу.
Этот код может обнаружить одну ошибку, но не может ее исправить.
Полиномы по модулю 2
Полином по модулю 2 — это полином, коэффициенты которого равны 0 или 1. Затем арифметические операции выполняются по модулю 2, так что 0 + 1 = 1 + 0 = 1 и 1 + 1 = 2 = 0.
Производим сложение по модулю 2.
ПРИМЕР
Если p (t) = t3 + 1 + 1, q (t) = t4 + t3 + t2 + 1
Тогда p (t) + q (t) = t4 + 2t3 + t2 + 2t + 2 = t4 + t2.
Умножение производится аналогично.
Решение
p (t) = t3 + 1 + 1, q (t) = t + 1, тогда
p (t) × q (t) = (t3 + t + 1) (t + 1) = t4 + t3 + t2 + 2t + 1 = t4 + t3 + t2 + 1
Кодировка
Зафиксируем многочлен m1 (t) = t3 + t + 1.
Этот многочлен не может быть разложен на множители по модулю 2, поскольку единственными возможными корнями являются 0 и 1, и ни один из них не работает.
Предположим, что многочлен m1 (t) имеет корень a. То есть a имеет свойство
α3 + α + 1 = 0 или α3 = α + 1 (напомним, что по модулю 2, −1 = 1)
Это число α очень интересно, и, используя приведенное выше уравнение, мы можем составить таблицу его степеней.
Мощность | Упрощенная форма
| α | | α | |
| α2 | | α2 | |
| α3 | | α + 1 | |
| α4 | | α2 + α | |
| α5 | | α2 + α + 1 | |
| α6 | | α2 + 1 | |
| α7 | | 1 |
Например, чтобы получить α5, мы умножаем α4 = α2 + α на α5 = α3 + α2 и заменяем α3 на α + 1, чтобы получить α5 = α + 1 + α2.
Таким образом, мы можем записать все степени α в виде комбинаций 1, α и α2 (!!)
Теперь о кодах.
Мы начинаем с сообщения (a, b, c, d) в двоичном формате длиной 4, добавляем 3 контрольных цифры, чтобы получить
(a, b, c, d, x, y, z). Мы используем их как коэффициенты многочлена
Мы используем их как коэффициенты многочлена
p (t) = at6 + bt5 + ct4 + dt3 + xt2 + yt + z.
Цифры x, y, z выбраны так, чтобы p (t) делилось на многочлен m1 (t) = t3 + t + 1
Поскольку a является корнем m1 (t), он также является корнем p (t), и поэтому p (a) = 0.
ПРИМЕР
Возьмите сообщение (1, 0, 0, 1) и закодируйте его как (1, 0, 0, 1, x, y, z). Преобразуя в полином, получаем
| п (т) | знак равно t6 + t3 + xt2 + yt + z. | |
| Подставляя t = a и используя таблицу для упрощения, получаем | ||
| п (а) | = a6 + a3 + xa2 + ya + z. | |
| = (a2 + 1) + (a + 1) + xa2 + ya + z | ||
= а2 (х + 1) + а (у + 1) + z. | ||
Теперь, если мы возьмем x = 1, y = 1, z = 0, тогда p (a) будет равно нулю.Следовательно, мы кодируем сообщение
(1, 0, 0, 1) как (1, 0, 0, 1, 1, 1, 0). Мы будем называть многочлен, соответствующий отправленному сообщению, C (t), поэтому C (a) = 0.
Исправление ошибок
Предположим, что одна ошибка возникает в пятом числе слева, поэтому мы получаем сообщение (1, 0, 1, 1, 1, 1, 0).
Таким образом, коэффициент t4 неверен и полином для полученного сообщения равен
R (t) = C (t) + t4
Подставляя t = α, получаем
R (α) = C (α) + α4 = α4
и поэтому мы знаем, где ошибка.
В общем, если бы была ровно одна ошибка в -й цифре, мы получили бы
R (t) = C (t) + ti.
Тогда R (α) = C (α) + αi = αi, и поэтому вычисление R (a) дает позицию неправильной цифры.
Если R (α) = 0, то ошибок не было. Этот процесс, конечно, предполагает, что произошло не более 1 ошибки
.
ПРИМЕР
Предполагая, что не более одной ошибки, исправьте и расшифруйте сообщение (1, 0, 0, 1, 0, 0, 1).
Решение
Преобразуя в полиномы, получаем
R (t) = t6 + t3 + 1
и так
R (α) = α6 + α3 + 1 = α2 + 1 + α + 1 + 1 = α2 + α + 1 = α5
Итак, исправленное сообщение было (1, 1, 0, 1, 0, 0, 1), которое декодируется как (1, 1, 0, 1).
Исправление более одной ошибки
Процедура кодирования и исправления, описанная выше, работает только в том случае, если при передаче возникла не более одной ошибки.
Полиномиальный метод может быть расширен для обнаружения и исправления более чем одной ошибки.
Детали этих кодов немного сложнее, но в них используются те же идеи, которые были развиты выше.
Коды, используемые для исправления множественных ошибок, называются кодами BCH и были открыты (независимо) Бозом и Чаудхури (в 1960 г. ) и Хоккенгемом (в 1959 г.) — отсюда и название BCH.
) и Хоккенгемом (в 1959 г.) — отсюда и название BCH.
В то время как арифметика теперь становится очень сложной, она легко выполняется компьютером, и могут быть созданы коды, которые могут обнаруживать и исправлять произвольное количество ошибок.
Современные коды исправления ошибок, используемые в технологии мобильных телефонов, снова более сложны, но в основном используют те виды оборудования, которые я описал выше.
В последнее время коды Рида-Соломона, которые представляют собой тип кода BCH, использовались в таких приложениях, как спутниковая связь, проигрыватели компакт-дисков, DVD-диски и дисководы.
ОТВЕТЫ НА УПРАЖНЕНИЯ
УПРАЖНЕНИЕ 1
Ведущий термин: тревога
Ведущий коэффициент:
Степень: n
Постоянный член: a0
УПРАЖНЕНИЕ 2
а 4×6 — 4×4 + 4×3 + x2 — 2x + 1
b i….сумма степеней полиномов
ii… произведение констант
УПРАЖНЕНИЕ 3
5×4 — 7×3 + 2x — 4 = (x2 — 2) (5×2 — 7x + 10) + (−12x + 16)
УПРАЖНЕНИЕ 4
а = 18
УПРАЖНЕНИЕ 5
a = -33 и b = -15
УПРАЖНЕНИЕ 6
Если P (a) = 0, то a0 = — anan — an − 1an − 1…. − A1a. Следовательно, a делит a0.
− A1a. Следовательно, a делит a0.
УПРАЖНЕНИЕ 7
2×2 (x — 3) 2 (x — 5)
УПРАЖНЕНИЕ 8
x = 0 или x = 3 или x = 5
УПРАЖНЕНИЕ 9
УПРАЖНЕНИЕ 10
УПРАЖНЕНИЕ 11
Для полиномиального уравнения P (x) = 0 существует решение x = a по теореме.Следовательно, x — a является фактором P (x) и P (x) = (x — a) Q (x). Уравнение Q (x) = 0 также имеет решение, поэтому с помощью теоремы можно найти новый линейный множитель.
УПРАЖНЕНИЕ 12
(x — α) (x — β) (x — γ) = x3 — (α + β + γ) x2 + (αβ + αγ + βγ) x + αβγ = x3 + bx2 + cx + d
Следовательно, результат b = — (α + β + γ), c = (αβ + αγ + βγ) и d = αβγ
УПРАЖНЕНИЕ 13
y3 — + — + d
УПРАЖНЕНИЕ 14
- a
- Возьмите конъюгаты с обеих сторон.Сопряжение с действительным — это то же самое с действительным.
- б
- Непосредственное следствие a и теоремы о факторах, а также того факта, что сумма и произведение комплексного числа и его сопряженного действительны.

- c
- Основная теорема и b дает результат
Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Департамента образования, занятости и трудовых отношений Австралийского правительства.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Непортированная лицензия.
https://creativecommons.org/licenses/by-nc-nd/3.0/
Уравнения, неравенства первой степени … Пошаговое решение математических задач
7. 1 Уравнения первой степени
1 Уравнения первой степени
Уравнения являются первой степенью, когда их можно записать в форме ax + b = c, где x — переменная, а a, b и c — известные константы и a a! = 0. Мы обсудили методы решения уравнений первой степени в разделе 3.4 и снова в разделе 3.5, когда речь идет о формулах. Кроме того, поиск решений пропорций, обсуждаемых в разделах 6.6 и 6.7, включал решение уравнений первой степени.
Эта тема является одной из самых основных и важных для любого начинающего изучающего алгебру и снова представлена здесь для положительного подкрепления и для подготовки к решению разнообразных приложений в разделах 7.3, 7.4 и 7.5.
Существует ровно одно решение уравнения первой степени с одной переменной.Это утверждение можно доказать методом противоречия. Доказательства здесь не приводятся. Уравнения, которые имеют более одного решения, будут рассмотрены в главах 8, 9 и 10.
Примеры
Решите следующие уравнения.
1. 3x + 14 = x-2 (x + 1) Напишите уравнение.
3x + 14 = x-2x-2 Используйте свойство distributive для удаления скобок.
3x + 14 = -x-2 Упростить.
4x + 14 = -2 Добавьте x к обеим сторонам.
4x = -16 Добавьте -14 к обеим сторонам.
x = -4 Разделим обе стороны на 4.
2. 1 + 2x + 3-3x = 20-x + 6x Напишите уравнение.
4-x = 20 + 5x Упростить.
4 = 20 + 6x Прибавьте x к обеим сторонам.
-16 = 6x Добавьте -20 к обеим сторонам.
-8 / 3 = x Разделите обе стороны на 6 и уменьшите.
3. (3x) / 4-7 = -1 Напишите уравнение.
(3x) / 4 = 6 Добавьте +7 к обеим сторонам.
3x = 24 Умножаем обе стороны на 4.
x = 8 Разделите обе стороны на 3 и уменьшите.
Поскольку (3x) / 4 = 3/4 * x / 1 = 3 / 4x, мы могли бы решить такое уравнение, как (3x) / 4 = 6 за один шаг, умножив обе части на 4/3, обратную величину 3 / 4, а именно:
(3x) / 4 = 6
(4/3 * 3/4) х = 4/3 * 6
х = 8
Пример 3 также может быть решен путем умножения первого числа на 4 вместо первого прибавления +7. Однако в этой процедуре мы должны обязательно умножить каждый член на 4 в обеих частях уравнения.
Однако в этой процедуре мы должны обязательно умножить каждый член на 4 в обеих частях уравнения.
(3x) / 4-7 = -1 Напишите уравнение.
(3x) / 4 * 4-7 * 4 = -1 * 4 Умножьте каждый член на 4.
3x-28 = -4 Упростите.
3x = 24 Добавьте +28 к обеим сторонам.
x = 8 Разделите обе стороны на 3 и уменьшите.
Этот последний метод имеет то преимущество, что он оставляет только целочисленные коэффициенты и константы. Если дробей больше одной, то каждый член следует умножить на НОК знаменателей дробей.
Давайте посмотрим, как наш математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
Пример
(2x) / 5 + 1/4 = — (1/2)
(2x) / 5 * 20 + 1/4 * 20 = — (1/2) * 20 Умножьте каждый член на 20, чтобы получить НОК 5, 4 и 2.
8x + 5 = -10
8x = -15
х = — (15/8)
7.2 Линия вещественных чисел и неравенства первой степени
Мы обсудили целые числа, которые включают в себя целые числа и их противоположности,
. .., — 4, -3, -2, -1,0,1,2,3,4 … (Целые числа)
.., — 4, -3, -2, -1,0,1,2,3,4 … (Целые числа)
и дроби, образованные с использованием целых чисел в числителе и знаменателе без знаменателя, равного 0. Формальное название таких дробей — рациональные числа. Рациональное число — это любое число, которое можно записать в виде
.a / b, где a и b — целые числа, а b! = 0
В десятичной форме все рациональные числа могут быть записаны как повторяющиеся десятичные дроби. Например,
1/3 = 0,33333 …
1/4 = 0,2500000.2 = 4/9
Символ √ называется знаком корня, а число под знаком корня — подкоренным выражением.
Не все корни являются целыми или рациональными числами. Такие числа, как корень (5), корень (7), корень (39) и -корень (10), называются иррациональными числами. В десятичной форме все иррациональные числа могут быть записаны как неповторяющиеся десятичные дроби. Другие примеры иррациональных чисел:
корень (2) = 1,4142136 … (квадратный корень из 2)
корень (3,4) = 1,5874011 . .. (кубический корень из 4)
.. (кубический корень из 4)
PI = 3.1415
E = 2,718281828459045 … (основание натурального логарифма)
Иррациональные числа так же важны, как и рациональные числа, и столь же полезны при решении уравнений, как мы увидим в главе 10. Числовые линии имеют точки, соответствующие иррациональным числам, а также рациональным числам (см. Рисунок 7.1).
Рисунок 7.1
Рассмотрим круг диаметром 1 единицу, катящийся по прямой.Если круг касается линии в точке 0, в какой точке линии эта же точка на круге снова коснется линии?
Точка будет в точке PI на числовой прямой, потому что PI — это длина окружности круга. (См. Рисунок 7.2.)
Вместе рациональные числа и иррациональные числа образуют действительные числа. То есть каждое рациональное число и каждое иррациональное число также является действительным числом. Свойства действительных чисел при сложении и умножении перечислены ниже на рисунке 7. 2 на странице 181.
2 на странице 181.
Рисунок 7.2
Свойства вещественных чисел
Для действительных чисел a, b и c:
| Дополнение | Недвижимость | Умножение |
| a + b действительное число | закрытие | a * b — действительное число |
| а + Ь = Ь + а | коммутативный | а * б = Ь * а |
| a + (b + c) = (a + b) + c | ассоциативный | а * (б * в) = (а * б) * в |
| а + 0 = а | идентичность | а * 1 = |
| а + (- а) = 0 | обратное | а * 1 / а = 1 (а! = 0) |
Распределительное свойство: a (b + c) = ab + ac
Числовые линии теперь называются вещественными числовыми линиями, потому что для каждого действительного числа есть одна соответствующая точка на строке, а для каждой точки на строке есть одно соответствующее действительное число.
Теперь нас интересует решение неравенств первой степени и отображение их решений на числовой прямой. Неравенство, которое можно записать в виде ac + bor ax + b <= c, где x - переменная, a, b и c - константы, а a! = 0, называется неравенством первой степени.
Решение неравенства типа 2x + 1 <7 аналогично решению уравнения первой степени. Цель состоит в том, чтобы найти эквивалентное неравенство (с теми же решениями), более простое по форме.
2x + 1 <7
2x + 1-1 <7-1
2x <6
(2x) / 2 <6/2
х <3
Затенением показаны все действительные числа меньше 3.Открытый кружок вокруг 3 означает, что 3 не включены в график.
Важное различие между решением уравнений и решением неравенств заключается в умножении или делении на отрицательные числа. Умножение или деление обеих сторон неравенства на отрицательное число меняет смысл неравенства на противоположный; «Меньше чем» становится «больше чем» и наоборот. Например (стрелки указывают на обратное неравенство)
Решение неравенства первой степени зависит от следующей аксиомы:
1. Если к обеим сторонам неравенства добавить ненулевую константу, новое неравенство эквивалентно исходному неравенству.
Если к обеим сторонам неравенства добавить ненулевую константу, новое неравенство эквивалентно исходному неравенству.
2. Если обе части неравенства умножаются на положительную константу (или делятся на нее), новое неравенство того же смысла эквивалентно исходному неравенству.
3. Если обе части неравенства умножаются на отрицательную константу (или делятся на нее), новое неравенство противоположного смысла эквивалентно исходному неравенству.
Примеры
Решите следующие неравенства и нанесите решения на график
1.5x + 4 <= - 1 Запишите неравенство.
5x + 4-4 <= - 1-4 Добавьте -4 к обеим сторонам.
5x <= - 5 Упростить.
(5x) / 5 <= - 5/5 Разделите обе стороны на 5.
x <= - 1 Упростить.
(Примечание: сплошная точка означает -1.)
Давайте посмотрим, как наш решатель неравенства решает эту и подобные проблемы. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
2. x + 1> = 3-2x
х + 1-х> = 3-2x-х
1> = 3-3x
1-3> = 3-3x-3
-2> = — 3x
-2 / -3 <= (- 3x) / - 3
2/3 <= х
Альтернативная процедура.
x + 1> = 3-2x
x + 1 + 2x> = 3-2x + 2x
3x + 1> = 3
3x + 1-1> = 3-1
3x> = 2
(3x) / 3> = 2/3
x> = 2/3 Обратите внимание, что два неравенства, 2/3 <= x и x> = 2/3, идентичны по смыслу.
Мы также можем использовать числовую линию для построения графиков чисел, удовлетворяющих более чем одному неравенству. Например, 3
Давайте посмотрим, как наш математический решатель решает эту и подобные задачи. Нажмите кнопку «Решить похожие», чтобы увидеть больше примеров.
Примеры
Изобразите на графике решения каждого из следующих неравенств
1. 3
3
2. x> = 2 или x <0
(Закрашивание круга вокруг 2 означает, что 2 включены.)
3. -корень (3)
7.3 Приложения (расстояние, геометрия)
Сложность или легкость решения конкретной проблемы зависит от многих факторов, в том числе от вашего личного опыта и общих способностей к рассуждению. Например, предположим, что вам дали следующую задачу:
«Автомобиль проезжает 170 миль за 3 часа. Какая была средняя скорость? »
Проблема не говорит напрямую о MULTIPLY, DIVIDE, ADD или SUBTRACT.Вы должны знать, что скорость, умноженная на время, равна расстоянию или, r * t = d. Вам дается расстояние (170 миль) и время (3 часа). Вам нужно найти среднюю скорость. Нужный вам инструмент — это формула r * t = d.
Пусть r = средняя скорость. Затем
3 * г = 170
r = 56 * 2/3 миль / ч
Пример 1: Расстояние
Мужчина уезжает в командировку, а его жена одновременно забирает детей в гости к бабушке и дедушке. Машины, движущиеся в противоположных направлениях, через 3 часа разделяют 360 миль.Если средняя скорость мужчины на 10 миль в час больше, чем у его жены, какова ее средняя скорость?
Машины, движущиеся в противоположных направлениях, через 3 часа разделяют 360 миль.Если средняя скорость мужчины на 10 миль в час больше, чем у его жены, какова ее средняя скорость?
Пусть x = средняя скорость жены
скорость * время = расстояние
| Жена | х | 3 | 3x |
| человек | (х + 10) | 3 | 3 (х + 10) |
| дистанция для жены | + | дистанция для мужчин | = | расстояние между собой |
| 3x | + | 3 (х + 10) | = | 360 |
3x + 3x + 30 = 360
6x = 330
x = 55 миль / ч
Средняя скорость жены — 55 миль в час.
Пример 2: Расстояние
Два поезда, A и B, находятся на расстоянии 540 километров друг от друга и едут навстречу друг другу по параллельным путям. Поезд A движется со скоростью 40 километров в час, а поезд Btravels — 50 километров в час. Через сколько часов они встретятся?
Поезд A движется со скоростью 40 километров в час, а поезд Btravels — 50 километров в час. Через сколько часов они встретятся?
Пусть x = время
скорость * время = расстояние
| поезд А | 40 | х | 40x |
| поезд B | 50 | х | 50x |
40x + 50x = 540
90x = 540
x = 6 часов
Поезда соберутся через 6 часов.
Пример 3: Геометрия
Прямоугольник с периметром 140 метров имеет длину на 20 метров меньше, чем удвоенную ширину. Найдите размеры прямоугольника.
Нарисуйте диаграмму и используйте формулу P = 2l + 2w.
Пусть w = ширина
2w-20 = длина
2 (вес) +2 (2w-20) = 140
2w + 4w-40 = 140
6 Вт = 180
w = 30 метров
2w-20 = 40 метров
Ширина 30 метров, длина 40 метров.
7.4 Заявки (интерес, работа)
Деловые люди знают несколько формул, включающих основную сумму (сумма вложенных денег), ставку (процент или процентную ставку) и проценты (фактическую прибыль или полученные проценты). Эти формулы могут зависеть от таких связанных тем, как способ выплаты процентов по ссуде (ежемесячно, ежедневно, ежегодно и т. прибыль.
В этом разделе мы будем использовать только базовую формулу для расчета процентов на годовой основе: P * R = {Iota}, или основная сумма, умноженная на ставку, равна проценту.
Пример 1: Проценты
Мужчина инвестирует в определенную облигацию с доходностью 9%, а затем инвестирует 500 долларов в высокорисковые акции с доходностью 12%. Через год его общая сумма процентов от двух инвестиций составит 240 долларов. Какую сумму он вложил в облигацию?
Пусть Pprincipal вложился под 9%.
основная сумма * ставка = проценты
| связка | -П | 0. 09 09 | 0,09P |
| акции высокого риска | 500 | 0,12 | 0,12 (500) |
| проценты по облигации | + | проценты по акциям | = | общий доход |
| 0,09P | + | 0,12 (500) | = | 240 |
0.09П + 60 = 240
0,09P = 180
(0,09P) / (0,09) = (180) / (0,09)
P = 2000 долларов США
Он вложил 2000 долларов в облигацию с доходностью 9%.
Пример 2: Проценты
У женщины 7000 долларов. Она решает разделить свои средства на два вложения. Один дает процентную ставку 6%, а другой — 10%. Если она хочет, чтобы годовой доход от инвестиций составлял 580 долларов, как ей разделить деньги?
Поскольку мы знаем, что общая сумма инвестиций составляет 7000 долларов, если одна инвестиция составляет x долларов, другая должна составлять от 7000 до x долларов.
Пусть x = сумма инвестиций под 10%
7000 — x = сумма инвестиций под 6%
основная сумма * ставка = проценты
| 10% инвестиций | х | 0,10 | 0,10x |
| 6% инвестиций | (7000-х) | 0,06 | 0,06 (7000-х) |
| проценты на 10% инвестиции | + | проценты по вложению 6% | = | общий доход |
| 0.10x | + | 0,06 (7000-х) | = | 580 |
10x + 6 (7000-x) = 5800 Умножьте каждый член на 100, чтобы исключить десятичные дроби.
10x + 42000-6x = 5800
4x = 16000
x = 4000 долларов США при 10%
7000-x = 3000 долл. США при 6%
Ей следует вложить 4000 долларов при 10% и 3000 долларов при 6%.
Задачи, связанные с «работой», могут быть очень сложными и требовать исчисления и физики. Проблемы, которые нас будут интересовать, связаны со временем, затраченным на выполнение конкретной работы. Эти проблемы связаны только с представлением о том, какая часть работы выполняется за одну единицу времени (часы, минуты, дни, недели и т. Д.). Например, если человек может выкопать канаву за 4 часа, какую часть (рытье канавы) он проделал за один час? Ответ — 1/4. Если работа длилась 5 часов, он бы сделал 1/5 за час. Если работа длилась x часов, он бы выполнил 1 / x за один час.
Проблемы, которые нас будут интересовать, связаны со временем, затраченным на выполнение конкретной работы. Эти проблемы связаны только с представлением о том, какая часть работы выполняется за одну единицу времени (часы, минуты, дни, недели и т. Д.). Например, если человек может выкопать канаву за 4 часа, какую часть (рытье канавы) он проделал за один час? Ответ — 1/4. Если работа длилась 5 часов, он бы сделал 1/5 за час. Если работа длилась x часов, он бы выполнил 1 / x за один час.
Пример 3: Работа
Майк может очистить бассейн своей семьи за 2 часа.Его младшая сестра Стейси может сделать это за 3 часа. Если они будут работать вместе, сколько времени им потребуется, чтобы очистить бассейн?
Пусть x = количество часов совместной работы
| часов | часть за 1 час | |
| Майк | 2 | 1/2 |
| Стейси | 3 | 1/3 |
| вместе | х | 1 / х |
| Часть сделана за 1 час Майком | + | Часть сделана за 1 час Stacey | = | часть делается за 1 час вместе |
| 1/2 | + | 1/3 | = | 1 / х |
1/2 (6x) +1/3 (6x) = 1 / x (6x) Умножьте каждый член в обеих частях уравнения на 6x НОК знаменателей.
3x + 2x = 6
5x = 6
x = 6/5 часов
Вместе они могут очистить бассейн за 6/5 часов или за 1 час 12 минут.
Пример 4: Работа
Мужчине сказали, что его новый бассейн с джакузи заполнится через впускной клапан за 3 часа. Он понял, что что-то не так, когда на заполнение бассейна ушло 8 часов. Он обнаружил, что оставил сливной клапан открытым. Сколько времени потребуется, чтобы осушить бассейн?
Пусть t = время слить воду из пула.
(Примечание: в этом случае впускной и выпускной клапаны работают друг против друга.)
| часов | часть за 1 час | |
| впуск | 3 | 1/3 |
| выход | т | 1 / т |
| вместе | 8 | 1/8 |
| часть заполнена входом | – | часть опорожняется выпускным отверстием | = | часть заполнена вместе |
| 1/3 | – | 1 / т | = | 1/8 |
1/3 (24т) -1 / т (24т) = 1/8 (24т)
8т-24 = 3т
5т = 24
т = 24/5
Вода из бассейна осушится через 24/5 часов или 4 часа 48 минут.
7.5 Приложения (смесь, неравенства)
Проблемы, связанные со смесями, возникают в физике и химии, а также в таких местах, как кондитерская или табачная лавка. Необходимо смешать два или более элемента с различным процентным содержанием химического вещества, такого как соль, хлор или антифриз; или два или более типа табака должны быть смешаны с образованием конечной смеси, которая удовлетворяет определенным условиям процентной концентрации.
Основной план состоит в том, чтобы написать уравнение, которое касается только одной части смеси.Следующие ниже примеры объясняют, как это можно сделать.
Пример 1: Смесь
Для конкретного химического эксперимента требуется 10% раствор кислоты. Если у лаборанта есть 9 унций 5% раствора, сколько кислоты нужно добавить, чтобы получить 10% раствор? (Подсказка: напишите уравнение, которое касается только количества кислоты.)
Пусть x = количество добавляемой кислоты.
количество раствора ⋅ процент кислоты = количество кислоты
| оригинальное решение | 9 | 0.05 | 0,05 (9) |
| добавленный раствор | х | 1,00 | 1,00 (х) |
| окончательное решение | (х + 9) | 0,10 | 0,10 (х + 9) |
| кислота в 9 унциях | + | кислота добавлена | = | кислота в конечном растворе |
| 0.05 (9) | + | 1,00 (х) | = | 0,10 (х + 9) |
5 (9) +100 (x) = 10 (x + 9)
45 + 100x = 10x + 90 Умножьте каждый член на 100.
90x = 45
х = 45/90
x = 0,5 унции кислоты
Чек:
| кислота в 9 унциях | + | кислота добавлена | = | кислота в конечном растворе |
0. 05 (9) 05 (9) | + | 0,5 | = | 0,10 (0,5 + 9) |
0,45 + 0,5 = 0,10 (9,5)
0,95 = 0,95
10% раствор можно получить, добавив 0,5 унции кислоты.
Пример 2: Смесь
Сколько галлонов 20% раствора соли следует смешать с 30% раствором соли, чтобы получить 50 галлонов 23% раствора? (Подсказка: напишите уравнение, касающееся только количества соли.)
Пусть x количество 20% раствора Примечание: Так как общее количество галлонов известно. одна сумма находится путем вычитания другой суммы из общей суммы.
50-х = количество 30% раствора
количество раствора ⋅ процент соли = количество соли
| 20% раствор | х | 0,20 | 0,20x |
| 30% раствор | 50-х | 0,30 | 0.30 (50-х) |
| 23% раствор | 50 | 0,23 | 0,23 (50) |
| Соль в 20% растворе | + | Соль в 30% растворе | = | Соль в 23% растворе |
| 0,20 х | + | 0,30 (50-х) | = | 0. 23 (50) 23 (50) |
20x + 30 (50-x) = 23 (50)
20x + 1500-30x = 1150
-10x = 1150-1500
-10x = -350
x = 35 гель 20% раствора
Чек:
| Соль в 20% растворе | + | Соль в 30% растворе | = | Соль в 23% растворе |
| 0,20 (35) | + | 0.30 (50-35) | = | 0,23 (50) |
7,0 + 0,30 (15) = 11,5
7,0 + 4,5 = 11,5
11,5 = 11,5
Тридцать пять галлонов 20% раствора следует добавить к 15 галлонам 30% раствора.
Следующий пример использования неравенств не требует пояснений. Внимательно изучите это.
Пример 3: Неравенства
Студент-физик получает оценки 85, 98, 93 и 90 на четырех экзаменах.Если он должен в среднем 90 или выше, чтобы получить пятерку за курс, какие баллы он может получить на заключительном экзамене и получить пятерку?
Пусть x = балл на заключительном экзамене.
(Среднее значение получается сложением баллов и делением на 5.)
(85 + 98 + 93 + 90 + x) / 5> = 90
(366 + x) / 5> = 90
366 + х> = 450
х> = 450-366
х> = 84
Если ученик наберет 84 или больше баллов на заключительном экзамене, он получит в среднем 90 или больше и получит пятерку по физике.
Полиномиальные уравнения — определение, формулы и решение полиномиальных уравнений
Полиномиальное уравнение — одно из основополагающих понятий алгебры в математике. Четкое и логическое представление о том, как решить полиномиальную задачу, позволит студентам более эффективно сдавать экзамены, а также послужит прочной базой для учебы в высших учебных заведениях. Полиномиальные уравнения представлены в виде чисел и переменных. Полиномиальное уравнение — это форма алгебраического уравнения.Между полиномиальным и полиномиальным уравнением есть небольшая разница. Полиномы — это выражения, тогда как полиномиальные уравнения — это выражения, приравненные к нулю.
Мы постараемся подробно разобраться в полиномиальных уравнениях. Мы узнаем о степени полинома, типах полиномиального уравнения и, самое главное, о том, как решить полиномиальное уравнение.
Что такое полиномиальное уравнение?
Полиномиальное уравнение — это выражение, состоящее из переменных, коэффициентов и показателей.Полиномиальная функция — это функция, имеющая единственную независимую переменную. Показатели в полиномиальном уравнении могут быть только в виде положительных целых чисел, поэтому любой отрицательный целочисленный показатель не может считаться полиномиальным уравнением.
Степень полинома
Независимая переменная может встречаться в полиноме несколько раз. Эти разные вхождения переменной разделяются операциями сложения, вычитания и умножения. Степень полинома определяется как наивысшая степень экспоненты, которая существует в уравнении.{2} + 5x = 0 \]
Здесь полином 2x 2 + 5x, приравненный к нулю, дает нам полиномиальное уравнение F (x) = 2x 2 + 5x = 0 со степенью 2.
Типы полиномиального уравнения
Полиномиальные уравнения классифицируются по степени полинома. Из практических соображений мы разделяем полиномиальные уравнения на четыре типа.
Мономиальное / линейное уравнение
Полиномиальное уравнение только с одним переменным членом называется мономиальным уравнением.Его еще называют линейным уравнением. Алгебраическая форма линейного уравнения имеет вид:
ax + b = 0, где a — коэффициент, b — константа, а степень полинома равна 1.
Примеры:
2x + 10 = 0
x — 5 = 0
Биномиальное / квадратное уравнение
Полином с двумя переменными членами называется биномиальным уравнением. Его также можно назвать квадратным уравнением. Алгебраическая форма квадратного уравнения имеет вид:
ax 2 + bx + c = 0, где a и b — коэффициенты, c — постоянная, а степень полинома равна 2.
Примеры:
2x 2 + 2x + 2 = 0
x 2 — 4 = 0
Трехчленное / кубическое уравнение
Полином с тремя переменными членами называется трехчленным уравнением. Его еще называют кубическим уравнением. Алгебраическая форма квадратного уравнения имеет вид:
ax 3 + bx 2 + cx + d = 0, где a, b и c — коэффициенты, d — постоянная, а степень полинома равна 3. .{n-2} +. . . + a_ {1} x + a_ {1} = 0 \].
Примеры,
4x 4 + 2x 3 + x 2 + 5 = 0
10x 5 + 2x — 10 = 0
Решение полиномиальных уравнений
Полиномиальные уравнения обычно решаются с помощью хит и пробный метод. Мы подставляем значение независимой переменной и пытаемся получить значение выражения равным нулю.
В случае линейного уравнения получить значение независимой переменной просто.Решаем уравнение относительно нулевого значения.
Для полинома 2x — 4 = 0
2x = 4
x = 2
Однако это решение не легко применимо к полиномам более высоких степеней, поэтому мы используем метод поиска и проб.
Алгебра 2 (Решение уравнений, глава 4) (Математические классы миссис Бенке)
Раздел 3: Алгебра 2 (Решение уравнений, глава 4) (Математические классы миссис Бенке)БЛОК 3 ОПИСАНИЕ:
U3D0 — Схема решения уравнений Это версия для печати схемы установки
MPM 1DI БЛОК 3 — РЕШЕНИЕ УРАВНЕНИЙ Учебная цель (я буду):
В этом блоке мы будем решать уравнения первой степени, а задачи со словами можно моделировать уравнениями первой степени.
Критерии успеха (я могу…):
- Решите простые уравнения
- Решите многоступенчатые уравнения
- Решите уравнения с дробями
- Переставить формулы с переменными первой степени
- Решите задачи со словами, которые можно смоделировать с помощью уравнения с одной переменной
- Решить проблемы с применением процента, соотношения, ставки и соотношения
День
| Урок
| Текст Арт. | Назначить. / Домашнее задание
|
| 1 | Диагностическая викторина U3D1 Решение простых уравнений U3D1_T_ Решение простых уравнений | 4,1 | стр. |
| 2 | U3D2_S_ Решение многоступенчатых уравнений U3D2_T_ Решение многоступенчатых уравнений | 4.2 | стр. 200-202 # 2, 4 («корень» просто означает «решение»), 5a, 6a, 8, 9, 10, 13 Вызов Страница 203 # 18-21 Дополнительный рабочий лист решения уравнений Тест №1 ПРАКТИКА Практика для решения викторины №1 |
| 3 | ВИКТОРИНА № 1 U3D3_S — Решение уравнений с дробями, часть 1 U3D3_T — Решение уравнений с дробями I (перекрестное умножение) | 4.3 | стр. 208-209 # 1, 3ac, 4ac, 5-8 |
| 4 | U3D4_S — Решение уравнений с дробями, часть 2 U3D4_T — Решение уравнений с дробями II | 4,3 | стр. Рабочий лист 3.3 Решение уравнений с дробями Рабочий лист 3.3 Решения Страница вызова 210 # 13 U3D4 Quiz # 2 ПРАКТИКА U3D4_Quiz # 2 PRACTICE Solutions |
| 5 | ВИКТОРИНА № 2 U3D5_S — Моделирование с помощью формул (перестановка уравнений) U3D5_T — Моделирование с помощью формул | 4.4 | стр. 215-219 № 1-3, 6-8, 10-12, 15, 16а Вызов Страница 219 # 18, 19 U3D5_W — Рабочий лист — Дополнительная практика с уравнениями |
| 6 | U3D6_S Number Story Вопросы U3D6_T Номер История Вопросы | 4,5 | стр. 226-227 № 1-11 Дополнительная практика: Рабочий лист 3.4 Число Рассказ Вопросы Дополнительная практика Рабочий лист 3. |
| 7 | U3D7_S История вопроса о расценке единицы U3D7_T Расценки на единицу продукции Вопросы | 4,5 | Рабочий лист 3.5 Вопросы для рассказа о расценках на единицу Рабочий лист 3.5 Решения |
| 8 | Блок 3 Обзор U3D8_S Обзорная информация См. Старый тест в Google Classroom, чтобы понять, чего ожидать. | Pg 230-231 # 2, 5, 7, 8, 9, 11, 12-16, Finish U3D5_W — Рабочий лист — Дополнительная практика с уравнениями для большей практики Дополнительная практика: Стр. 232-233 № 1-10 U3D8_W_Extra Review Story Questions U3D8_W_Extra Review РЕШЕНИЯ История вопросов | |
| 9 | ТЕСТ |
Срок действия этой информации истекает после печати. Пожалуйста, всегда обращайтесь к онлайн-версии для получения самой последней информации.
Пожалуйста, всегда обращайтесь к онлайн-версии для получения самой последней информации.
Решение уравнений
| Линейные уравнения также называются уравнениями первой степени , как
наивысшая степень переменной (или местоимения) в этих уравнениях равна 1. Например, x + 5 = 9 — уравнение первой степени, которое часто называют линейным уравнением. Многие проблемы можно решить с помощью линейных уравнений. Напомним, что:Уравнения ведут себя как весы. Поэтому нам нужно применить ту же операцию к обеим сторонам уравнения, чтобы сохранить баланс. Это означает, что мы можем:
Уравнения, включающие одну операцию Пример 1Решение:Примечание:Мы можем проверить решение следующим образом: Итак, наше решение, x = 5, является правильным. Пример 2 Решение:Чек:Итак, наше решение, x = 10, является правильным. Пример 3 Решение:Чек:Итак, наше решение, x = 3, является правильным. Пример 4 Решение:Чек: Итак, наше решение, x = 15, является правильным. |







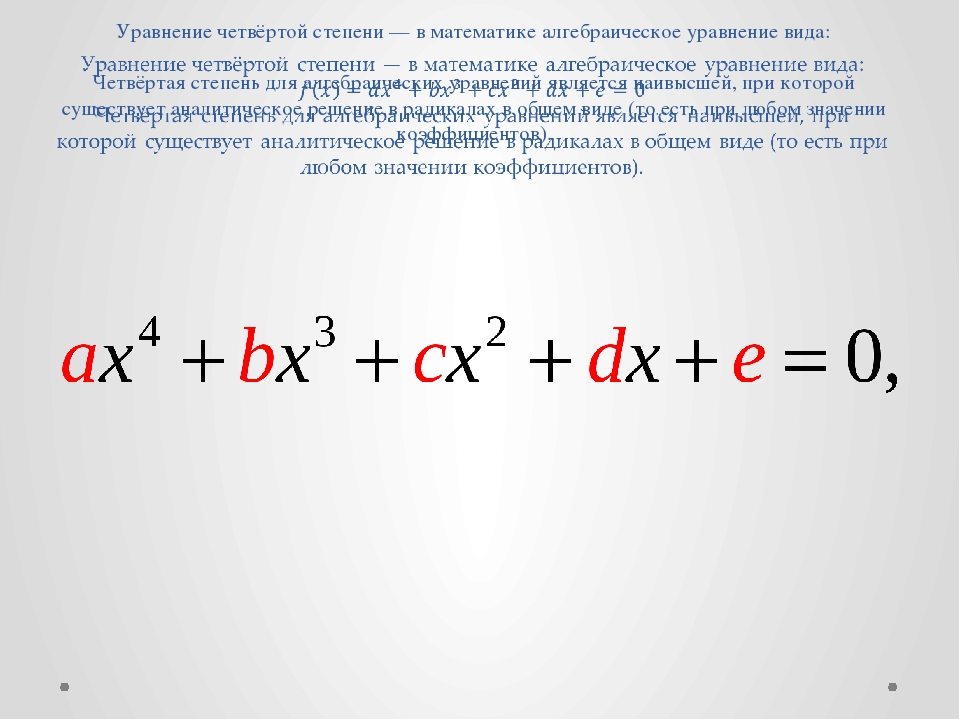
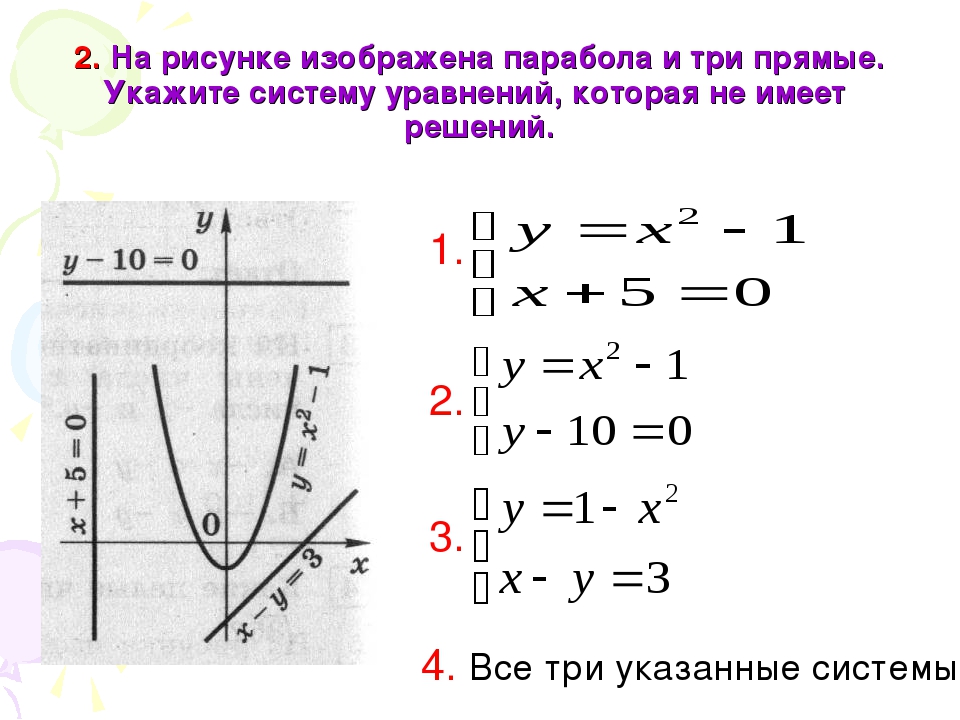



 193-195 № 3, 5, 6, 8-13, 16, 18, 20
193-195 № 3, 5, 6, 8-13, 16, 18, 20 208-210 # 3bd, 4bd, 11, 12,
208-210 # 3bd, 4bd, 11, 12, 4 Решения
4 Решения
