Калькулятор степеней онлайн | umath.ru

Калькулятор степеней поможет просто и быстро возвести число в степень онлайн. При этом показатель степени может быть как положительным, так и отрицательным!

Что такое степень числа?

Как возвести число в степень?

Чтобы понять, как возводить число в степень, рассмотрим несколько простых примеров.

Возведём в пятую степень число 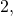то есть вычислим значение выражения 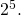По определению, данному выше,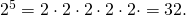

Вычислим, чему равно 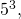то есть чему равно число 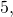возведённое в третью степень.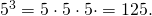

Отрицательный показатель степени

Показатели степени могут быть не только положительными, но и отрицательными.

   

Например,

   

а

   

Как пользоваться калькулятором степеней

Калькулятор помогает возводить число в степень онлайн. Основанием степени могут быть любые целые числа и десятичные дроби. Показатель степени тоже может быть любой десятичной дробью, однако следует помнить о том, что для отрицательных чисел не определена операция возведения в нецелую степень.

При записи дробных чисел можно использовать как точку, так и запятую. В ответе большие числа записываются в так называемом «научном формате», то есть число выглядит как <число>e<количество нулей>. Например, 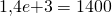, а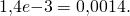

umath.ru

Решите уравнение 2^x+2=(1/2)^x (2 в степени х плюс 2 равно (1 делить на 2) в степени х)

Найду корень уравнения: 2^x+2=(1/2)^x

Решение

$$2^{x} + 2 = \left(\frac{1}{2}\right)^{x}$$

Подробное решение

[LaTeX]

Дано уравнение:
$$2^{x} + 2 = \left(\frac{1}{2}\right)^{x}$$
или
$$2^{x} + 2 — 2^{- x} = 0$$
Сделаем замену
$$v = \left(\frac{1}{2}\right)^{x}$$
получим
$$- v + 2 + \frac{1}{v} = 0$$
или
$$- v + 2 + \frac{1}{v} = 0$$
делаем обратную замену
$$\left(\frac{1}{2}\right)^{x} = v$$
или
$$x = — \frac{\log{\left (v \right )}}{\log{\left (2 \right )}}$$
Тогда, окончательный ответ
$$x_{1} = \frac{1}{\log{\left (\frac{1}{2} \right )}} \log{\left (\frac{1}{\log{\left (2 \right )}} \left(\log{\left (1 + \sqrt{2} \right )} + i \pi\right) \right )} = — \frac{1}{\log{\left (2 \right )}} \log{\left (\frac{1}{\log{\left (2 \right )}} \left(\log{\left (1 + \sqrt{2} \right )} + i \pi\right) \right )}$$
$$x_{2} = \frac{1}{\log{\left (\frac{1}{2} \right )}} \log{\left (\frac{\log{\left (-1 + \sqrt{2} \right )}}{\log{\left (2 \right )}} \right )} = \frac{1}{\log{\left (2 \right )}} \left(\log{\left (\log{\left (2 \right )} \right )} — \log{\left (- \log{\left (-1 + \sqrt{2} \right )} \right )} — i \pi\right)$$

Быстрый ответ

[LaTeX]

        /       ___\
     log\-1 + \/ 2 /
x1 = ---------------
          log(2)    

$$x_{1} = \frac{\log{\left (-1 + \sqrt{2} \right )}}{\log{\left (2 \right )}}$$

        /      ___\         
     log\1 + \/ 2 /    pi*I 
x2 = -------------- + ------
         log(2)       log(2)

$$x_{2} = \frac{\log{\left (1 + \sqrt{2} \right )}}{\log{\left (2 \right )}} + \frac{i \pi}{\log{\left (2 \right )}}$$

Численный ответ

[LaTeX]

x1 = 1.27155330316361 + 4.53236014182719*i

www.kontrolnaya-rabota.ru

Решите неравенство 2^(2*x+1)-5*2^x+2>=0 (2 в степени (2 умножить на х плюс 1) минус 5 умножить на 2 в степени х плюс 2 больше или равно 0)

Дано неравенство:
$$- 5 \cdot 2^{x} + 2^{2 x + 1} + 2 \geq 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$- 5 \cdot 2^{x} + 2^{2 x + 1} + 2 = 0$$
Решаем:
Дано уравнение:
$$- 5 \cdot 2^{x} + 2^{2 x + 1} + 2 = 0$$
или
$$- 5 \cdot 2^{x} + 2^{2 x + 1} + 2 = 0$$
Сделаем замену
$$v = 2^{x}$$
получим
$$2^{1} v^{2} — 5 v + 2 = 0$$
или
$$2 v^{2} — 5 v + 2 = 0$$
Это уравнение вида

a*v^2 + b*v + c = 0

Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$v_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$v_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 2$$
$$b = -5$$
$$c = 2$$
, то

D = b^2 - 4 * a * c = 

(-5)^2 - 4 * (2) * (2) = 9

Т.к. D > 0, то уравнение имеет два корня.

v1 = (-b + sqrt(D)) / (2*a)

v2 = (-b - sqrt(D)) / (2*a)

или
$$v_{1} = 2$$
$$v_{2} = \frac{1}{2}$$
делаем обратную замену
$$2^{x} = v$$
или
$$x = \frac{\log{\left (v \right )}}{\log{\left (2 \right )}}$$
$$x_{1} = \frac{1}{2}$$
$$x_{2} = 2$$
$$x_{1} = \frac{1}{2}$$
$$x_{2} = 2$$
Данные корни
$$x_{1} = \frac{1}{2}$$
$$x_{2} = 2$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} \leq x_{1}$$
Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$\frac{2}{5}$$
=
$$\frac{2}{5}$$
подставляем в выражение
$$- 5 \cdot 2^{x} + 2^{2 x + 1} + 2 \geq 0$$

 2*2                      
 --- + 1                  
  5           2/5         
2        - 5*2    + 2 >= 0

       2/5      4/5     
2 - 5*2    + 2*2    >= 0
     

но

       2/5      4/5    
2 - 5*2    + 2*2    
Тогда
$$x \leq \frac{1}{2}$$
не выполняется
значит одно из решений нашего неравенства будет при:
$$x \geq \frac{1}{2} \wedge x \leq 2$$
         _____  
        /     \  
-------•-------•-------
       x1      x2

www.kontrolnaya-rabota.ru