23 число нечетное: Четные и нечетные числа в математике

Posted on by alexxlab

Содержание

Четные и нечетные числа в математике

Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.

Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.

Четное число — это число, которое делится нацело на 2.


4 : 2 = 2
Это значит, что 4 — четное число.

Нечетное число — это число, которое не делится на 2 без остатка.


5 не делится на 2 без остатка — значит, 5 это нечетное число.

Если число оканчивается на 0, 2, 4, 6, 8, то это число четное.

Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное.

Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа.

Свойства четных и нечетных чисел

  • Если сложить два четных числа, получится четное число:
    8 + 8 = 16
    16 : 2 = 8
  • Если сложить два нечетных числа, получится четное число:
    3 + 3 = 6
    6 : 2 = 3
  • Если сложить четное число с нечетным, получится нечетное число:
    4 + 5 = 9
    9 : 2 = 4 (остаток 1)
  • Если четное число умножить на четное число, получится четное число:
    2 × 2 = 4
    4 : 2 = 2
  • Если четное число умножить на нечетное число, получится четное число:
    4 × 3 = 12
    12 : 2 = 6
  • Если нечетное число умножить на нечетное, получится нечетное:
    3 × 3 = 9

Четные и нечетные числа чередуются друг с другом

1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.

Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.

1112131415161718191
2122232425262728292
3132333435363738393
4
14		2434445464748494
5152535455565758595
6162636465666768696
7172737475767778797
8182838485868788898
9192939495969798999
102030405060708090100

Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.

  • Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
  • Однозначные числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
  • Натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13…
  • Четные числа: 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26…
  • Нечетные числа: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25…
  • Круглые числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120…

Онлайн-курсы по математике для детей помогут быстрее освоить новую тему при поддержке опытного преподавателя.

Задачи для практики

Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.

Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?

1♥17
210♥
♥1119
4
♥		20
513♥
♥1422
71523
8♥♥

Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.

Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.

X246810
X × 2     
X : 2  
 		  
X246810
X × 248121620
X : 212345

Как решаем:

2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
10 : 2 = 5 — нечетное

Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?

Как решаем:

  1. Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
    15 + 12 = 27 (к)

  2. Отнимем от общего количества конфет получившееся число:
    44 — 27 = 17 (к)

Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.

Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?

Как решаем:

51 — 5 = 46 (ф)
46 — четное число.

Ответ: изначально у Маши в инстаграме было 46 фотографий.

Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.

1☆3☆5
6☆☆910
☆1213☆15
16☆☆1920
☆2223☆25

Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.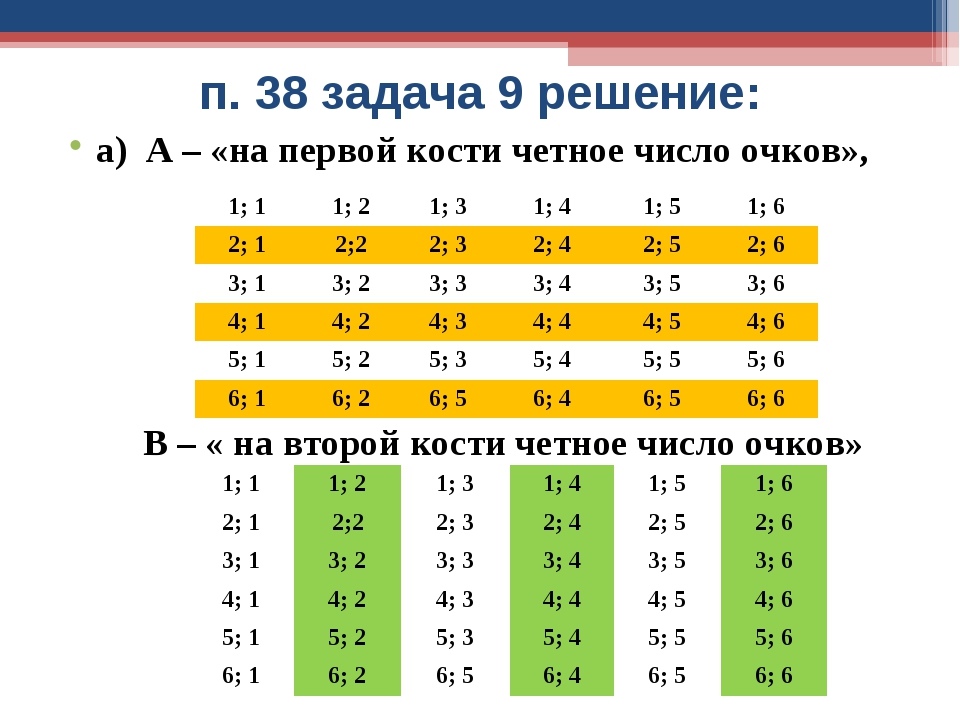

Как решаем:

Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70

Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
Число 126 оканчивается на четную цифру 6. Значит, число 126 — четное.

Ответ: 126 — четное.

от литературных затей до шахмат»

Сайт «Занимательные и методические материалы из книг Игоря Сухина: от литературных затей до шахмат»

 

 

Сайт «Занимательные и методические материалы из книг Игоря Сухина: от литературных затей до шахмат»

 

Избранные страницы из книги И.Г.Сухина «800 новых логических и математических головоломок» (часть 2)

 

 

ЧАСТЬ 1 РАСПОЛОЖЕНА ЗДЕСЬ

 

И.Г. СУХИН

НАТУРАЛЬНЫЕ, ПРОСТЫЕ, СОСТАВНЫЕ, ЧЁТНЫЕ, НЕЧЁТНЫЕ, КРУГЛЫЕ

 

Шпаргалка

Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Однозначные числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13…

Простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41…

Составные числа: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22…

Чётные числа: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26…

Нечётные числа: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25…

Круглые числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120…

 

Примечание: в задачах на вычитание уменьшаемое не должно быть меньше вычитаемого.

 

И.Г. СУХИН

Задачи из тетради гнома Загадалки

ОТ НУЛЯ ДО ДЕВЯТИ

(однозначные числа)

1. Что больше: наименьшее натуральное число или наименьшее простое?

2. Что меньше: самое маленькое натуральное число или самое маленькое однозначное?

3. Что больше: наименьшее чётное число или наименьшее нечётное?

4. Какое однозначное число не является натуральным?

5. Сумма двух неких однозначных чисел равна их разности. Назови одно из них.

6. Сумма двух слагаемых равна первому слагаемому. Назови второе слагаемое.

7. Сумма трёх одинаковых однозначных чисел равна их произведению. Что это за числа?

8. Какое из натуральных чисел наименьшее?

9. Произведение двух натуральных чисел равно частному от их деления. Назови один из сомножителей и делитель.

10. Произведение двух натуральных чисел меньше их суммы. Назови одно из чисел.

11. Если произведение двух натуральных чисел – простое число, то чему равен меньший сомножитель?

12. Сумма девяти натуральных чисел – однозначное число. Что это за числа?

13. Произведение двух неких натуральных чисел не является ни простым, ни составным числом. Что это за числа?

14. Какое натуральное число в 4 раза меньше самого маленького составного числа?

15. Сумма двух однозначных чисел в 2 раза больше их произведения. Какие это числа?

16. Какое чётное число является простым?

17. Чему равна наименьшая разность неодинаковых нечётных чисел?

18. Назови все чётные простые числа.

19. Сумма двух неких простых чисел есть нечётное число. Назови одно из слагаемых.

20. Произведение трёх простых чисел – однозначное число. Что это за числа?

21. Сумма четырёх чётных чисел – однозначное число. Какие это числа?

22. Произведение двух простых чисел равно их сумме. Что это за числа?

23. Сумма двух чётных чисел – однозначное число. Чему равно меньшее слагаемое?

24. Подсчитай сумму двух простых чётных чисел.

25. Вычти из наибольшего однозначного числа наименьшее простое. Сколько получилось?

26. Какое однозначное простое число больше 5?

27. Вычти из самого большого однозначного числа самое маленькое натуральное. Каков ответ?

28. Сумма двух однозначных чисел равна 1. Назови эти числа.

29. Разность двух однозначных чисел равна 9. Что это за числа?

30. Сумма двух натуральных чисел равна 3. Назови слагаемые.

31. Сумма двух чисел равна 4, а разность – в 2 раза меньше. Что это за числа?

32. Частное от деления двух однозначных чисел равно 5. Назови эти числа.

33. Произведение двух однозначных чисел равно 7. Что это за числа?

34. Сумма двух натуральных чисел равна 9, а произведение есть число однозначное. Найди эти числа.

35. Разность двух неодинаковых однозначных чисел равна 8. Назови эти числа.

36. Разность двух нечётных однозначных чисел равна 8. Какие это числа?

37. Произведение каких различных простых чисел будет числом однозначным?

38. Если сумма двух чётных чисел равна 6, то каковы слагаемые?

39. Если произведение двух неодинаковых чётных однозначных чисел – также число однозначное, то что это за числа?

40. Произведение двух однозначных чисел в 4 раза больше их разности. Вычисли эти числа.

41. Сумма каких двух простых чисел равна наибольшему однозначному простому числу?

42. Разность двух чисел равна 4, а сумма – в 2 раза больше. Что это за числа?

43. Сумма двух простых чисел равна 9. Назови эти числа.

44. Разность двух однозначных чётных чисел равна 6. Что это за числа?

45. Сумма двух простых чисел равна 8. Какие это числа?

46. Какие два соседних числа натурального ряда надо сложить, чтобы получить наибольшее однозначное число?

47. Сумма каких трёх последовательных чисел натурального ряда равна их произведению?

48. Каким натуральным числам не может равняться сумма нескольких простых чисел?

49. Какие три последовательных числа натурального ряда надо сложить, чтобы получить наибольшее однозначное число?

50. Если частное от деления двух неодинаковых однозначных чётных чисел будет числом нечётным, то чему равны частное и эти чётные числа?

 

И.Г. СУХИН

ОТ НУЛЯ ДО ДВАДЦАТИ

(однозначные и двузначные числа)

51. Если сумма двух неодинаковых однозначных чисел равна 16, то чему равна их разность?

52. Разность двух чётных однозначных чисел равняется 6. Вычисли их сумму.

53. Если разность двух нечётных однозначных чисел равна 8, то чему равна их сумма?

54. Подсчитай сумму самого маленького простого числа и самого большого однозначного.

55. Найди наибольшую сумму двух однозначных чисел.

56. Произведение однозначного и двузначного чисел равно 15. Найди эти числа.

57. Произведение двух неодинаковых однозначных чисел равно 16. Что это за числа?

58. Произведение двух однозначных чисел равняется 15. Каковы сомножители?

59. Сумма двух неодинаковых простых чисел равна 14. Назови слагаемые.

60. Произведение двух однозначных чисел равно 20. Что это за числа?

61. Сумма двух разных чётных однозначных чисел равна 12. Какие это числа?

62. Сумма двух простых чисел равна 12. Каковы слагаемые?

63. Сумма двух разных нечётных однозначных чисел равна 14. Назови их.

64. Сумма двух однозначных чисел равна 15, а разность – 3. Вычисли эти числа.

65. Сумма двух однозначных чисел равна 17. Что это за числа?

66. Разность двузначного и однозначного чисел равна единице. Каковы уменьшаемое и вычитаемое?

67. Даны 4 разных однозначных числа. Первое – 9. Если умножить 9 на второе, то получим столько же, сколько и при умножении третьего на четвёртое. Назови неизвестные числа.

68. Даны 4 неодинаковых однозначных числа. Известно, что первое – 2, а числа 9 среди них нет. Если умножить 2 на второе, то получим столько же, сколько и при перемножении третьего и четвёртого. Каковы неизвестные числа?

69. Какие последовательные числа натурального ряда надо сложить, чтобы получить наименьшее двузначное число?

70. Сумма нескольких разных простых чисел равна 17. Назови эти числа.

71. Что меньше: сумма чётных однозначных чисел или сумма простых однозначных чисел?

 

И. Г. СУХИН

СЮЖЕТНЫЕ ЗАДАЧИ

156. Какую отметку впервые в жизни получил по математике Фома, если известно, что она является числом не простым, а составным?

157. Таня послала Игорю некоторое чётное число писем, а Игорь Тане – на 2 письма больше. При этом общее число писем есть число однозначное. Какое?

158. Сколько всего мячей оказалось на поле во время матча между командами «Зубило» и «Шайба», когда старик Хоттабыч наколдовал каждому футболисту по одному мячу?

159. Сколько яиц снесла за месяц курочка ряба, если известно, что число их не составное, а простое, больше 19, но меньше 29?

160. Сколько лет сиднем просидел на печи Илья Муромец? Известно, что если бы он просидел ещё 2 раза по столько, то его возраст составил бы наибольшее двузначное число.

161. В какой известной сказке богатырей можно было бы выстроить несколькими равными рядами по 11 в каждом ряду? Каково число богатырей?

162. Барон Мюнхгаузен по секрету сообщил нам, что он пересчитал число волшебных волос в бороде старика Хоттабыча. Оно оказалось равным сумме наименьшего трёхзначного числа и наибольшего двузначного. Что это за число?

163. Если наибольшее двузначное число ты умножишь на 4 и прибавишь 4, то узнаешь, сколько муравьёв послал Артемон, чтобы перегрызть верёвку, на которой разбойники повесили за ноги главного героя сказки А.Толстого «Золотой ключик, или Приключения Буратино».

164. Раздели самое маленькое четырёхзначное число на наименьшее простое и узнаешь, сколько лет не умывалась, не чистила зубы и даже пальцем не прикасалась к воде злая волшебница Гингема из повести-сказки А.Волкова «Волшебник Изумрудного города».

165. В русской народной сказке «Притворная болезнь» у трёх чудищ было разное однозначное число голов, кратное трём. Какое?

166. В русской народной сказке «Хрустальная гора» Иван-царевич сражался по очереди с тремя змеями. У первого из них было в 2 раза меньше голов, чем у второго, а у второго – в 2 раза меньше, чем у третьего. Общее число голов у змеев – 21. Сколько голов было у каждого змея до встречи с Иваном-царевичем?

167. Сколько голов у каждого чуда-юда из русской народной сказки «Иван – коровий сын», если известно, что у второго чуда-юда на три головы больше, чем у первого, а у третьего – на 3 больше, чем у второго, причём всего голов было – 27?

 

И.Г. СУХИН

ИСПРАВЛЕНИЕ, ЗАЧЁРКИВАНИЕ, ПРЕВРАЩЕНИЕ, ОТГАДЫВАНИЕ ЦИФР И ЧИСЕЛ

Задачи из тетради гнома Загадалки

 

1. Зачеркни одинаковые цифры. Какое число осталось?

5 3 7 1 8 3 5 8 7

 

2. Какую цифру надо зачеркнуть в числе 621, чтобы оставшееся число делилось на 3?

 

3. Это число от 2 до 10, но не 5; кроме того, оно нечётное и не делится на 3. Назови его.

 

4. Перед тобой однозначные числа. Вычеркни нечётные. Какая цифра осталась?

7 9 3 1 9 5 8 7

 

5. Зачеркни в следующем числе цифры, которые встречаются только один раз. Остальные цифры соедини. Что за число получилось?

7290342615

6. Угадай число от 1 до 28, если в его написание не входят цифры 1, 5 и 7; кроме того, оно нечётное и не делится на 3.

 

7. Отгадай число от 1 до 58, если в его написание не входят цифры 1, 2 и 3; кроме того, оно нечётное и не делится на 3, 5 и 7.

 

8. Угадай число от 1 до 88, если в его написание не входят цифры 1, 2, 3 и 7; кроме того, оно нечётное и не делится на 3, 5 и 7.

 

9. Отгадай число от 1 до 408, если в его написание не входят цифры 1, 2, 3, 5, 7; кроме того, оно нечётное и не делится на 3 и 7.

 

10. Перед тобой однозначные числа. Зачеркни чётные. Оставшиеся цифры соедини. Какое число осталось?

4 2 6 4 8 2 9 6 5

11. Преврати в числе 123 одну цифру в пятёрку так, чтобы получившееся число делилось на 9. Каково оно?

 

12. Исправь в числе 982 одну цифру на четвёрку так, чтобы получившееся число делилось на 3. Назови новое число.

 

13. Вычти из произвольного двузначного числа сумму его цифр. Всегда ли разность разделится на 3? А на 9?

 

И.Г. СУХИН

РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ

 

И.Г. СУХИН

КАК ВСЕГДА ВЫИГРЫВАТЬ В ПОПУЛЯРНЫХ ИГРАХ МАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ

 

ИГРА В ДЕСЯТЬ

По очереди играют двое. Начинающий игру называет 1 или 2. Его товарищ прибавляет в уме к исходному числу 1 или 2 и сообщает сумму партнёру. Последний также увеличивает её на 1 или 2 и называет свой результат. Так игра продолжается, и побеждает тот, кто скажет число 10.

Чтобы выиграть, тебе нужно начать игру и независимо от ответов партнёра называть числа 1, 4, 7. Когда произнесено число 7, противнику приходится назвать 8 или 9. Ты говоришь: «Десять!» – и побеждаешь.

В другом варианте этой игры тот, кто скажет: «Десять», – проигрывает. Чтобы всегда выигрывать, здесь предложи товарищу начать игру. Как бы он ни играл, ты должен называть числа 3, 6, 9. Тут товарищу придётся сказать: «Десять». И снова ты победитель.

 

ИГРА В ПЯТНАДЦАТЬ

Массовики-затейники часто играют с желающими не в «Десять», а в «Пятнадцать», причём прибавляют также не больше двух. В первом варианте игры (сказавший 15 побеждает) предложи товарищу начать и называй числа 3, 6, 9, 12, 15. Во втором варианте игры (сказавший 15 проигрывает) первое число должно быть твоё. Ты называешь числа 2, 5, 8, 11, 14.

 

ИГРА В СТО

Играют в эту игру и до 100 (сказавший 100 выигрывает). Здесь первое число должно быть от 1 до 10, затем игроки по очереди прибавляют к предыдущему числу от 1 до 10. Чтобы победить, надо начать игру и называть 1, 12, 23, 34, 45, 56, 67, 78, 89, 100.

Конечно, можно запомнить все «выигрышные» числа в этих играх, но лучше установи закономерность, чтобы успешно играть не только в «Десять», «Пятнадцать» и «Сто», но и в другие варианты игры до любого числа, набавляя иные числа. Это пригодится тебе при решении заданий из тетради гнома Загадалки. Играй и побеждай!

 

И.Г. СУХИН

Задания гнома Загадалки

В следующих играх тот, кто скажет последнее число, выигрывает. Ты начинаешь. Какое первое число ты назовёшь, чтобы победить, если:

1. Вы с приятелем играете в «Десять», набавляете от 1 до 3?

2. Играете в «Десять», набавляете от 1 до 5?

3. Играете в «Десять», набавляете от 1 до 6?

4. Вы с другом играете в «Пятнадцать», набавляете от 1 до 3?

5. Играете в «Пятнадцать», набавляете от 1 до 5?

6. Играете в «Пятнадцать», набавляете от 1 до 6?

7. Играете в «Пятнадцать», набавляете от 1 до 7?

8. Играете в «Пятнадцать», набавляете от 1 до 8?

9. Вы с другом играете в «Сто», набавляете от 1 до 2?

10. Играете в «Сто», набавляете от 1 до 5?

11. Играете в «Сто», набавляете от 1 до 20?

12. Вы с товарищем играете в «Сто», набавляете от 1 до 30?

13. Играете в «Сто», набавляете от 1 до 40?

14. Играете в «Сто», набавляете от 1 до 50?

 

В следующих играх тот, кто скажет последнее число, проигрывает. Ты начинаешь. Какое первое число ты назовёшь, чтобы победить, если:

15. Вы с приятелем играете в «Десять», набавляете от 1 до 3?

16. Играете в «Десять», набавляете от 1 до 4?

17. Играете в «Десять», набавляете от 1 до 5?

18. Играете в «Десять», набавляете от 1 до 6?

19. Вы с другом играете в «Пятнадцать», набавляете от 1 до 3?

20. Играете в «Пятнадцать», набавляете от 1 до 4?

21. Играете в «Пятнадцать», набавляете от 1 до 5?

22. Играете в «Пятнадцать», набавляете от 1 до 7?

23. Играете в «Пятнадцать», набавляете от 1 до 8?

24. Вы с другом играете в «Сто», набавляете от 1 до 3?

25. Играете в «Сто», набавляете от 1 до 4?

26. Играете в «Сто», набавляете от 1 до 5?

27. Играете в «Сто», набавляете от 1 до 20?

28. Вы с товарищем играете в «Сто», набавляете от 1 до 30?

29. Играете в «Сто», набавляете от 1 до 40?

30. Играете в «Сто», набавляете от 1 до 50?

 

ИГРА В ШЕСТЬ ФАНТИКОВ

Ты и твой товарищ выкладываете на столе 2 горизонтальных ряда фантиков, по 3 фантика в каждом ряду. Вместо фантиков могут быть камешки, конфеты, копейки, пуговицы, спички или счётные палочки.

I I I

I I I

Пусть начинает партнёр-товарищ. Он должен взять любое число фантиков из первого или из второго ряда. Нельзя брать фантики одновременно из обоих рядов. Затем ты берёшь фантики – тоже из одного ряда (первого или второго). Так по очереди продолжаете игру. Кто возьмёт последний фантик, тот проиграл.

Условия игры просты, но, чтобы победить, нужно проявить смекалку.

Предположим, противник берёт все 3 фантика из любого ряда. Тогда ты возьмёшь 2 из другого ряда. На столе останется последний фантик.

Партнёр проиграет, ведь пропускать очередь хода нельзя.

Если же первым ходом он возьмёт 2 фантика из одного ряда, то ты выберешь все 3 из другого. Опять твоя победа.

Твоему товарищу лучше всего первым ходом взять 1 фантик. Чтобы не проиграть, ты тоже возьмёшь 1, но из другого ряда. Теперь в обоих рядах останется по 2 фантика. Поражение твоего противника неизбежно.

Ведь если он берёт 2 фантика, то ты возьмёшь 1.

А если он выберет 1, ты возьмёшь 2.

В обоих случаях перед товарищем останется лежать 1 фантик. Победа за тобой.

Запомни: в этой игре тот, кто начинает, проигрывает (при точной игре обоих противников).

 

ИГРА В ДЕВЯТЬ ФАНТИКОВ

Здесь фантики расположены в 3 ряда. В первом ряду – 1 фантик, во втором – 3, в третьем – 5.

I

I I I

I I I I I

Это расположение можно записать так: 1 3 5.

Условия игры такие же, как и в предыдущей игре.

При безошибочной игре партнёров здесь побеждает тот, кто начинает. Договорись с другом, чтобы первый ход был твоим, и возьми 3 фантика из третьего ряда. Оставшиеся фантики будут расположены так: 1 3 2.

Теперь, если твой товарищ заберёт единственный фантик из первого ряда, то ты возьмёшь 1 фантик из следующего ряда и получится расположение: 2 2, которое мы проанализировали в предыдущей игре. Ход за противником, и он проигрывает.

Твой партнёр терпит поражение и при других взятиях.

Если он возьмёт все 3 фантика из второго ряда, то ты заберёшь оба из третьего.

Если соперник выберет 2 фантика из второго ряда, ты возьмёшь 1 из третьего и получится положение: 1 1 1. Победа останется за тобой.

Если он возьмёт 1 фантик из второго ряда, ты заберёшь единственный фантик из первого ряда и снова получится выгодное для тебя положение: 2 2.

Если противник заберёт 2 фантика из третьего ряда, ты возьмёшь все 3 из второго.

Если он заберёт 1 фантик из третьего ряда, ты возьмёшь 2 из второго, и снова получится выигрышное для тебя положение: 1 1 1.

Всё, твоя победа, других вариантов нет.

 

И.Г. СУХИН

Положения для игры в девять фантиков из тетради гнома Загадалки

Представь, что игру начинает твой товарищ и своим ходом в исходном положении 1 3 5 берёт:

31. Единственный фантик из первого ряда: 3 5. Сколько фантиков и из какого ряда сейчас надо взять, чтобы победить?

32. 3 фантика из второго ряда: 1 5. Как выиграть?

33. 2 фантика из второго ряда: 1 1 5. Как сыграть теперь?

34. 1 фантик из второго ряда: 1 2 5. Сколько фантиков из какого ряда ты возьмёшь?

35. Все 5 фантиков из третьего ряда: 1 3. Как победить?

36. 4 фантика из третьего ряда: 1 3 1. Как сыграть?

37. 3 фантика из третьего ряда: 1 3 2. Можно ли тебе избежать поражения?

38. 2 фантика из третьего ряда: 1 3 3. Что делать?

39. 1 фантик из третьего ряда: 1 3 4. Каков твой ответ?

 

Итак, проанализировав игры в шесть и девять фантиков, мы установили 4 важных расположения, к которым должны стремиться. В них очередь хода за противником, но он неизбежно проигрывает. Запомни их!

N1: 2 2.

N2: 3 3.

N3: 1 1 1.

N4: 1 2 3.

Чтобы побеждать в этих играх, нельзя забывать: если остался всего один ряд с числом фантиков не менее двух, то своим ходом тебе надо забрать все фантики, кроме одного. А если осталось 2 ряда, в первом из которых находится 1 фантик, а во втором – любое количество фантиков, то нужно взять все фантики из второго ряда.

Всё это пригодится тебе в следующей игре.

 

ИГРА В ШЕСТНАДЦАТЬ ФАНТИКОВ

Мы постепенно подвели тебя к одной из самых интересных игр на свете, которую иногда называют «Мариенбад».

Здесь фантики расположены в 4 ряда. В первом ряду – 1 фантик, во втором – 3, в третьем – 5, в четвёртом – 7.

I

I I I

I I I I I

I I I I I I I

Это расположение можно записать так: 1 3 5 7.

Условия игры такие же, как и в предыдущих играх.

Проанализировать все варианты игры «Мариенбад» гораздо сложнее, чем для случаев с меньших числом фантиков.

Кроме положений: N1 – N4 своим ходом надо создавать ещё и такие: N5: 4 4, N6: 5 5 (эти 2 положения сводятся к: 2 2), N7: 1 4 5, N8: 2 4 6, N9: 2 5 7, N10: 3 4 7, N11: 3 5 6, N12: 1 1 х х (где х>1), N13: 1 2 4 7, N14: 1 2 5 6, N15: 1 3 4 6.

И наконец N16: 1 3 5 7. То есть в «Мариенбаде»тот, кто начинает, проигрывает!

Итак, если ты хочешь наверняка победить в этой игре, начать её должен твой товарищ. Чтобы быстро не проиграть, ему лучше всего взять один фантик из любого ряда. Теперь у тебя 3 равноценных ответа: надо взять один фантик в любом из трёх остальных рядов, получив расположения N9 – N11 или N13 – N15. Затем партнёр возьмёт фантик в одном из двух рядов, из которых фантики ещё не брали. А ты выберешь фантик из последнего такого ряда, и получится положение N8. Далее в зависимости от хода партнёра ты создашь расположения N1, N4, N5 или N7 и быстро выиграешь.

Всё это не так-то уж и трудно. Приобретя игровой опыт, ты убедишься: достаточно помнить 4 важных положения: N4, N7, N8 и N12, чтобы быстро находить лучший ход.

 

И.Г. СУХИН

Положения для игры в «Мариенбад» из тетради гнома Загадалки

Представь, что игру начинает твой товарищ и своим ходом в исходном положении 1 3 5 7 берёт:

40. 2 фантика из второго ряда: 1 1 5 7. Сколько фантиков и из какого ряда сейчас надо взять, чтобы победить?

41. 3 фантика из второго ряда: 1 5 7. Как выиграть?

42. 2 фантика из третьего ряда: 1 3 3 7. Как сыграть теперь?

43. 3 фантика из третьего ряда: 1 3 2 7. Сколько фантиков из какого ряда ты возьмёшь?

44. 4 фантика из третьего ряда: 1 3 1 7. Как победить?

45. Все 5 фантиков из третьего ряда: 1 3 7. Как сыграть?

46. 2 фантика из четвёртого ряда: 1 3 5 5. Твой ход?

47. 3 фантика из четвёртого: 1 3 5 4. Что делать?

48. 4 фантика из четвёртого: 1 3 5 3. Каков твой ответ?

49. 5 фантиков из четвёртого: 1 3 5 2. Как сыграть?

50. 6 фантиков из четвёртого: 1 3 5 1. Что делать?

51. Все 7 фантиков из четвёртого: 1 3 5. Каков твой ответ?

 

ИГРА В ДВАДЦАТЬ ПЯТЬ ФАНТИКОВ

Здесь фантики в пяти рядах. Это расположение можно записать так: 1 3 5 7 9.

Условия игры такие же, как и в предыдущих играх.

Чтобы выиграть, тебе надо начать и первым ходом забрать все 9 фантиков из последнего ряда. Получается игра «Мариенбад», в которой тот, кто начинает, проигрывает.

 

И.Г. СУХИН

ИГРЫ, ГДЕ ВЗЯВШИЙ ПОСЛЕДНИЙ ФАНТИК ВЫИГРЫВАЕТ

В игры с фантиками можно играть и иначе: тот, кто берёт последний фантик, считается победителем. Самое интересное здесь то, что тебе всё равно нужно стремиться в основном к тем же промежуточным положениям, которые мы уже рассмотрели. Т.е. старайся, чтобы после твоего хода создавались положения: N1 – N2, N4 – N16. Если сможешь сделать это, выиграешь. Стратегическое различие проявляется в самом конце. К примеру, если в положении: 2 2 партнёр возьмёт один фантик, то здесь и ты выберешь не два фантика, как в первом варианте игры, а 1 из другого ряда и получится: 1 1, что обеспечит тебе победу. А если соперник возьмёт 2 фантика, то и ты заберёшь оба оставшихся и выиграешь.

Что теперь? Научи товарища правилам игры в такие фантики и обыгрывай. Можешь провести чемпионат класса, турнир во дворе.

 

МАТЕМАТИЧЕСКИЕ ФОКУСЫ

Старинные фокусы из тетради гнома Загадалки

1. Напиши такое трёхзначное число, чтобы первая цифра была по крайней мере на 2 больше, чем третья. Например: 311. Запиши его цифрами в обратном порядке: 113. Из первого вычти второе: получится 198. Это число снова напиши наоборот: 891. И два последние числа сложи.

891 + 198 = 1089.

Удивительное дело: какие бы числа мы ни брали, в ответе всегда будет 1089!

Теперь предложи провести все эти действия с числами кому-то из друзей. Представляешь, как он удивится, когда ты, не спрашивая у него, сколько получилось в результате (как это бывает в других математических фокусах), сам назовёшь ответ! Для эффекта можешь сообщить его не сразу, а через несколько секунд, как-бы что-то подсчитывая в уме.

2. Попроси товарища задумать какое-нибудь двузначное число, вычесть из него сумму его цифр, зачеркнуть в полученном результате одну цифру и сообщить, какое число осталось. После этого ты тотчас скажешь, какая цифра зачёркнута! Для этого ты всего навсего из 9 вычтешь оставшееся однозначное число.

Пример: 97 – 16 = 81, 8 зачёркивается и друг говорит, что осталось 1. Ты выполняешь в уме вычитание и получаешь в результате зачёркнутую цифру: 9 – 1 = 8.

 

Для информации: СОДЕРЖАНИЕ КНИГИ

Предисловие для учителя

РАЗДЕЛ 1. ГНОМЫ ЗАГАДАЛКА, ПУТАЛКА И ЗАБЫВАЛКА

Знакомство с гномами Математические приключения гномов (в шутку и всерьёз) Говорят гномы Зачёркиваем буквы – получаем числа Задачи из тетради гнома Загадалки Переставляем буквы – получаем числа Задачи из тетради гнома Забывалки Числа прячутся в предложениях Задачи из тетради гнома Загадалки Задачи-шутки из тетради гнома Загадалки

РАЗДЕЛ 2. ЧИСЛА В КЛЕТКАХ

Шпаргалка Числовая горизонталь гнома Забывалки (задачи с дополнительными условиями и подсказками) Задачи из тетради гнома Забывалки Задачи на вычитание Задачи на сложение Задачи на умножение Задачи на деление Сочетание арифметических действий Числовая горизонталь гнома Путалки (задачи с дополнительными условиями и подсказками) Задачи из тетради гнома Путалки Математические дорожки Задачи из тетради гнома Забывалки Цифры в буквах Задачи из тетради гнома Забывалки Цифры в цифрах Задачи из тетради гнома Забывалки Волшебные квадраты Задачи из тетради гнома Загадалки

РАЗДЕЛ 3. НЕОБЫЧНЫЕ ЗАДАЧИ И ГОЛОВОЛОМКИ

Подумай и ответь Задачи из тетради гнома Загадалки Натуральные, простые, составные, чётные, нечётные, круглые Шпаргалка Задачи из тетради гнома Загадалки От нуля до девяти (однозначные числа) От нуля до двадцати (однозначные и двузначные числа) От нуля до девяноста девяти (однозначные и двузначные числа) От нуля до тысячи Чётные и нечётные числа Круглые числа Сюжетные задачи Исправление, зачёркивание, превращение, отгадывание цифр и чисел Задачи из тетради гнома Загадалки

РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ

Как всегда выигрывать в популярных играх математического содержания Игра в десять Игра в пятнадцать Игра в сто Задания гнома Загадалки Игра в шесть фантиков Игра в девять фантиков Положения для игры в девять фантиков из тетради гнома Загадалки Игра в шестнадцать фантиков Положения для игры в «Мариенбад» из тетради гнома Загадалки Игра в двадцать пять фантиков Игры, где взявший последний фантик выигрывает Математические фокусы Старинные фокусы из тетради гнома Загадалки

ОТВЕТЫ

 

ОТВЕТЫ

РАЗДЕЛ 1. ГНОМЫ ЗАГАДАЛКА, ПУТАЛКА И ЗАБЫВАЛКА

МАТЕМАТИЧЕСКИЕ ПРИКЛЮЧЕНИЯ ГНОМОВ

1. Двух. 2. У Забывалки одна, а у Путалки две. 3. У Забывалки две, у Загадалки одна, у Путалки три. 4. По две у Загадалки и Путалки и одна у Забывалки. 5. У Загадалки – 2, у Забывалки – 1, у Путалки – 3 (он 2 носка натянул на одну ногу). 6. За 11 секунд. 7. 12+3+45 = 60. 8. 54+3+2+1 = 60. 9. Одна. 10. Две. 17. Ни одного. 18. Он забил гол в свои ворота. 19. Это был тренер команды соперника. 20. Его товарищи играли за команду «Дырка». 23. Потому что, возвращаясь из магазина, Путалка снова свернул направо. Загадалка и Забывалка пошли по дороге прямо, не сворачивая у перекрёстка. 24. Он перепутал рубашки, надел без колокольчиков. 25. Он забыл надеть рубашку. 26. Забывалка зачитался в доме книгой о Мюнхгаузене и забыл пойти за грибами. 27. Ни от одной. 28. Трое (гномов).

ГОВОРЯТ ГНОМЫ

5. Две и четыре. 6. Нет, 15.

ЗАЧЁРКИВАЕМ БУКВЫ – ПОЛУЧАЕМ ЧИСЛА

1. Нуль. 2. Один. 3. Два. 4. Три. 5. Пять. 13. Тысяча.

ПЕРЕСТАВЛЯЕМ БУКВЫ – ПОЛУЧАЕМ ЧИСЛА

1. Три. 2. Нуль. 3. Сорок. 4. Один. 5. Два. 13-15. Двенадцать. 19. Тридцать. 22. Пятьдесят. 25. Семьдесят. 28. Восемьдесят. 71. Миллиард.

ЗАДАЧИ-ШУТКИ ИЗ ТЕТРАДИ ГНОМА ЗАГАДАЛКИ

1. Один. 2. Двадцать. 3. Нуль, потому что у осла нет рогов. 4. Одна. 5. Ни одного. 6. В норе Кролика. 7. Стон.

 

НАТУРАЛЬНЫЕ, ПРОСТЫЕ, СОСТАВНЫЕ, ЧЁТНЫЕ, НЕЧЁТНЫЕ, КРУГЛЫЕ

1. Простое. 2. Однозначное. 3. Чётное. 4-7. 0. 8-15. 1. 16-23. 2. 24. 4. 25-26. 7. 27. 8. 28. 1 и 0. 29. 9 и 0. 30. 1 и 2. 31. 3 и 1. 32. 5 и 1. 33. 1 и 7. 34. 8 и 1. 35-36. 9 и 1. 37. 2 и 3. 38-40. 4 и 2. 41. 2 и 5. 42. 6 и 2. 43. 2 и 7. 44. 8 и 2. 45. 3 и 5. 46. 4 и 5. 47-48. 1, 2, 3. 49. 2, 3 и 4. 50. 3, 6 и 2. 51. 2; (9 – 7). 52. 10; (8 + 2). 53. 10; (9 + 1). 54. 11. 55. 18. 56. 1 и 15. 57. 2 и 8. 58. 3 и 5. 59. 3 и 11. 60. 4 и 5. 61. 4 и 8. 62. 5 и 7. 63. 5 и 9. 64. 9 и 6. 65. 8 и 9. 66. 10 и 9. 67. 2, 3 и 6. 68. 6, 3 и 4. 69. 1, 2, 3 и 4. 70. 2, 3, 5, 7. 71. Простых.

156. Четвёрку. 157. 6; (2 + 4). 158. 23 (1 уже был, а 22 упали с неба). 159. 23. 160. 33. 161. А.Пушкин «Сказка о царе Салтане…»; 33. 162. 199. 163. 400. 164. 500. 165. 3, 6, 9. 166. 3, 6, 12. 167. 6, 9, 12.

ИСПРАВЛЕНИЕ, ЗАЧЁРКИВАНИЕ, ПРЕВРАЩЕНИЕ,

ОТГАДЫВАНИЕ ЦИФР И ЧИСЕЛ

1. 1. 2. 6. 3. 7. 4. 8. 5. 22. 6. 23. 7. 47. 8. 59. 9. 89. 10. 95. 11. 153. 12. 942. 13. Да.

РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ

КАК ВСЕГДА ВЫИГРЫВАТЬ В ПОПУЛЯРНЫХ ИГРАХ МАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ

1. 2. 2. 4. 3-5. 3. 6. 1. 7. 7. 8. 6. 9. 1. 10. 4. 11. 16. 12. 7. 13. 18. 14. 49. 15. 1. 16. 4. 17. 3. 18-19. 2. 20. 4. 21. 2. 22. 6. 23. 5. 24. 3. 25. 4. 26. 3. 27. 15. 28. 6. 29. 17. 30. 48. 31. 2 из последнего ряда. 32. Взять все 5 фантиков из последнего ряда. 33. Забрать 4 из третьего ряда. 34. 2 из третьего. 35. Взять все 3 из второго ряда. 36. Забрать 2 из второго ряда. 37. Нет. 38. Взять 1 фантик из любого ряда. 39. Забрать 2 из третьего ряда. 40. 2 из четвёртого ряда. 41. Взять 3 фантика из последнего ряда. 42. Забрать 6 из четвёртого ряда. 43. Все 7 из четвёртого. 44. Взять 4 из четвёртого ряда. 45. Забрать 5 из последнего ряда. 46. Взять 2 из второго ряда. 47. Взять все 3 фантика из второго ряда. 48. Взять 4 из третьего ряда. 49. Взять все 5 фантиков из третьего ряда. 50. Взять 2 из третьего ряда. 51. Взять 3 из третьего ряда.

 

О ЛИТЕРАТУРНЫХ ПРИКЛЮЧЕНИЯХ ГНОМОВ МОЖНО ПРОЧИТАТЬ ЗДЕСЬ

 

 

ОСНОВНЫЕ РУБРИКИ САЙТА

 

ЛИТЕРАТУРНЫЕ ЗАТЕИ

Лучшие книги:

«Литературные викторины, тесты и сказки-загадки для дошкольников и младших школьников» (1998) и «Незнайка, Хоттабыч, Карлсон и все-все-все: литературные викторины, кроссворды и чайнворды для детей».

 

ЗАГАДКИ, ЗАГАДКИ-ШУТКИ, СКАЗКИ-ЗАГАДКИ, ЗАНИМАТЕЛЬНЫЕ ЗАДАНИЯ

Лучшая книга:

«Новые 500 загадок – 70 кроссвордов».

 

ЛОГОПЕДИЯ И СКОРОГОВОРКИ

Лучшие книги:

«Чистоговорки, наоборотки, запрятки на звук «С» и «Весёлые скороговорки для «непослушных» звуков».

 

ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА

Лучшие книги:

«800 новых логических и математических головоломок» и «Весёлая математика: 1500 головоломок для математических олимпиад, уроков, досуга: 1-7 класс».

 

ШАХМАТЫ ДЛЯ ДЕТЕЙ

Лучшие книги:

«Волшебные фигуры, или Шахматы для детей 2–5 лет» и «Удивительные приключения в Шахматной стране» (для детей 5-–8 лет).

 

ЗАНИМАТЕЛЬНАЯ БИБЛИОГРАФИЯ

Занимательная библиография

 

ЧТО УЖЕ РАЗМЕЩЕНО НА САЙТЕ КНИГИ, РУКОПИСИ, СТАТЬИ И.Г.СУХИНА КТО ЗАЩИТИТ АВТОРА, ИЛИ ОХОТА НА ПЛАГИАТОРА ИЗ ПЕРЕПИСКИ С ЧИТАТЕЛЯМИ Калейдоскоп интересных ссылок

 

НА ГЛАВНУЮ СТРАНИЦУ

 

 

mailto:[email protected]

Home Page URL: http://suhin.narod.ru

© 2001-2006 Сухин И.Г. Все права защищены.

Обновление от 13 марта 2006 года.

Сайт управляется системой uCoz

Четное или нечетное число

Больше онлайн заданий по математике для детей от 2 до 11 лет. Начните прямо сейчас!

Уже в дошкольном возрасте ребята узнают, что бывают четные и нечетные числа. Определить абстрактно, четное число или нечетное, бывает непросто. Зато каждому понятно, получится ли некоторое количество разделить на двоих без остатка, или нет. Объяснить ребенку четные и нечетные числа помогут занимательные упражнения.

Что такое четные и нечетные числа

Четные числа — те, которые делятся на два без остатка. Но как же объяснить ребенку деление на два, если сложные математические операции осваивать еще рано? Самый простой способ — запомнить наизусть: на два делятся числа 2, 4, 6, 8 и все многозначные числа, которые оканчиваются на них же, а также на 0. Нечетные числа на 2 ровно не делятся , это числа 1, 3, 5, 7, 9 и те многозначные числа, которые оканчиваются на них же.

Таблица четных и нечетных чисел

Чтобы быстро определить, четным или нечетным является число, можно воспользоваться таблицей до 100. В ней четные и нечетные числа будут чередоваться. В нашей таблице выделены четные числа.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89

90

91

92

93

94

95

96

97

98

99

100

 

Определяем, четный или нечетный

Сначала расскажите ребенку, что такое четные и нечетные числа.

Проиллюстрируйте это на примерах – раскладывайте перед ребенком разное количество карандашей и попытайтесь разделить на две равные части. Если так получилось сделать, то число карандашей является четным. Если остался лишний карандаш – число нечетное.

Наглядно показать четность или нечетность можно на любых предметах — игрушках, фишках, ложечках. Если получились две равные группы и не осталось лишних предметов, то общее количество является четным. Если остался лишний предмет – число нечетное.

Закрепляем знание о четных и нечетных числах

Запоминание приходит с практикой. Вначале пусть ребенок продолжает ряды четных или нечетных чисел, начиная с указанного вами числа.  В этом упражнении пригодится навык счета через один. Следующим этапом предлагайте определить четность или нечетность любого числа. Поиграйте в игру: вы загадываете число в небольшом диапазоне и сообщаете, что оно находится между 4 и 7. А ребенок, используя вопрос: «Это четное или нечетное число?», пытается угадать задуманное число. Если ребенок угадал, то следующий вопрос задает он.

Выполните развивающие упражнения от Айкьюши

Правила сложения четных и нечетных чисел


Даже если ребенок не умеет складывать числа в уме, он может запомнить несколько простых правил:

  • при сложении двух четных чисел всегда получится тоже четное число. 24+32=56 — четное

  • при сложении двух нечетных чисел получается четное число. 13+17=30 — четное

  • при сложении одного четного и одного нечетного числа всегда получится нечетное число. 43+32=65 — нечетное

Какое число 0 – четное или нечетное?

Ноль – это четное число.

Некоторые взрослые до сих пор затрудняются правильно ответить на этот вопрос. Как же это доступно объяснить детям?

Во-первых, чтобы определить четность или нечетность, нужно вспомнить какие числа называются четными – те, которые делятся на 2 без остатка. Ноль делится на 2 без остатка. Значит, ноль – четное число.

Во-вторых, мы уже знаем, что четные и нечетные числа чередуются. После ноля стоит нечетное число 1. Значит ноль – четное число.

Также поможет запомнить четность ноля тот факт, что все числа, которые заканчиваются на 0 – четные. Значит и ноль тоже четное число.

Игры с четными и нечетными числами


Для того чтобы знания о четных и нечетных числах закрепились у малыша в памяти, регулярно используйте эти понятия в игре.

Например, в игре в магазин вы можете “печатать” для товаров ценники только с нечетными числами, выдумывая двузначные или трёхзначные числа из головы. Остается только вспомнить, на какие цифры должны оканчиваться эти числа.

Поиграйте в подвижную игру: если ты услышишь четное число, хлопни в ладоши. А если нечетное — топни ногой. 37, 18, 24, 53, 22, 95, 38, 14…

Еще можно играть в шпионов, которые передают друг другу информацию четными числами. Если каждое число ассоциировать с каким-то словом, то можно играть в сочинение предложений. Например, один шпион получил радиограмму: 2 8 4 6 10. А у него в ключе написано: 2 — апельсин, 4 — радость, 6 — бежит, 8 — красный, 10 — немедленно. Какое предложение можно составить, если по порядку расположить Апельсин Красный Радость Бежит Немедленно?

Напомнить знания о четных и нечетных поможет обычное русское лото. Когда вы с ребенком заполняете фишками карточки лото, проговаривайте вслух, является ли число четным.

Айкьюша поможет легко и в игровой форме познакомиться с математикой для детей 6-7 лет. Раздел включает задания и игры по арифметике для дошкольников: счет, сложение, вычитание, сравнение, умножение, деление, изучение геометрических фигур. Познавательные уроки и занятия для развития мальчиков и девочек.

Материалы для самостоятельных занятий по математике с дошкольником


Предложите ребенку раскрасить предметы с четными числами в зеленый цвет, а с нечетными – в красный.Распечатайте картинку и предложите ребенку продолжить последовательность четных и нечетных чисел, начиная с шеи жирафа.

Превратите изучение четных и нечетных чисел в увлекательное занятие – и ребенок без труда освоит эту непростую тему!

Больше онлайн заданий по математике для детей от 2 до 11 лет. Начните прямо сейчас!

Признаки делимости на 10, на 5 и на 2

Признаки делимости на 10, на 5 и на 2

Вопрос: что такое признаки делимости чисел ?

Ответ: признаки делимости чисел — это особенности чисел, которые помогают быстро определить, делится ли данное число на другое.

Знать эти признаки необходимо при решении многих арифметических задач.

 

Признак делимости на 10

Рассмотрим несколько чисел, запись которых оканчивается цифрой 0, например,

60, 130, 2340

Каждое из этих чисел делится без остатка на 10

Чтобы получить частное, достаточно отбросить цифру 0.

60 : 10 = 6

130 : 10 = 13

2340 : 10 = 234

Вывод: любое натуральное число, запись которого оканчивается цифрой 0, делится без остатка на 10

 

Если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10 

Проверим это утверждение, например, на числе 234

234 : 10 = 23 целых в остатке 4

(неполное частное 23 и остаток 4 — последняя цифра в записи числа 234)

Вывод: если последняя цифра в записи натурального числа отлична от нуля, то это число не делится без остатка на 10.

 

Определение

Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.

Если запись натурального числа оканчи­вается другой цифрой, то оно не делится без остатка на 10.

Остаток в этом случае равен последней цифре в записи числа.

 

Обратим внимание на то, что число 10 = 2 · 5 (число 10 делится без остатка и на 2, и на 5).

Вывод: число, запись которого оканчивается цифрой 0, делится без остатка и на 5, и на 2.

Например, 70 = 7 · 10 = 7 · (2 · 5) = (7 · 2) · 5 = 14 · 5, значит, 70 : 5 = 14.

А из того что 70 = 7 · (5 · 2) = (7 · 5) · 2 = 35 · 2, получаем, что 70 : 2 = 35.

 

Полные десятки

Существует такое понятие, как «круглое» число — это целое число, запись которого оканчивается одним или несколькими нулями. 

Такие числа принято называть «круглыми» («полными«) десятками.

Например, числа 40, 530, 3270, 3200 являются полными десятками.

40 — четыре десятка

530 — пятьдесят три десятка

3270 — триста двадцать семь десятков

3200 — триста двадцать десятков

Полные десятки делятся и на 10, и на 5, и на 2.

 

Признак делимости на 5

Каждое число можно представить в виде суммы полных десятков и еди­ниц, например, 

46 = 40 + 6, 539 = 530 + 9, 3278 = 3270 + 8.

Так как полные десятки делятся на 5, то и всё число делится на 5 лишь в том случае, когда на 5 делится число единиц.

Это возможно только тогда, когда в разряде единиц стоит цифра 0 или 5.

 

Определение

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.

Например, числа 270 и 275 делятся без остатка на 5

 

Если же запись числа оканчи­вается другой цифрой, то число без остатка на 5 не делится.

Например, числа 272 и 273 на 5 без остатка не делятся.

 

Четные и нечетные числа

Определение

Числа, делящиеся без остатка на 2, называют чётными, а числа, которые при делении на 2 дают остаток 1, называют нечётными.

 

Из однозначных чи­сел числа 0, 2, 4, 6 и 8 чётные, а числа 1, 3, 5, 7 и 9 нечётные

Цифры 0, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными.

 

Все полные десятки делятся на 2 без остатка (т. е. они чётны).

Вывод: любое на­туральное число чётно, когда в разряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра.

 

Определение

Если запись натурального числа оканчивается чётной цифрой, то это число чётно (делится без остатка на 2), а если запись числа оканчивается нечётной цифрой, то это число нечётно.

Например, числа 2, 30, 74, 56, 108 чётные, а числа 3, 31, 75, 57, 109 не­чётные.

 

Это интересно

Древнегреческий философ (профессиональный мыслитель), математик и мистик (верил в существование сверхъестественных сил) Пифагор Самосский, чётные числа считал женскими, а нечётные — мужскими

На рисунке числа от 1 до 100 (чётные и нечётные числа разного цвета)

В старину люди верили в магию чисел, где всё хорошее ассоциировалось с нечётными цифрами, а плохое – с чётными. Поэтому, например, в Рождество на стол всегда ставили нечётное количество блюд. Люди верили, что нечётные числа символизируют постоянное продолжение жизни, незавершенность. А чётные, наоборот, означают конечность всего живого, остановку движения.

Таблица признаков делимости чисел

Нумерация недель

1нечётная1 сентября – 5 сентября
2чётная6 сентября – 12 сентября
3нечётная13 сентября – 19 сентября
4чётная20 сентября – 26 сентября
5нечётная27 сентября – 3 октября
6чётная4 октября – 10 октября
7нечётная11 октября – 17 октября
8чётная18 октября – 24 октября
9нечётная25 октября – 31 октября
10чётная1 ноября – 7 ноября
11нечётная8 ноября – 14 ноября
12чётная15 ноября – 21 ноября
13нечётная22 ноября – 28 ноября
14чётная29 ноября – 5 декабря
15нечётная6 декабря – 12 декабря
16чётная13 декабря – 19 декабря
17нечётная20 декабря – 26 декабря
18чётная27 декабря – 2 января
19нечётная3 января – 9 января
20чётная10 января – 16 января
21нечётная17 января – 23 января
22чётная24 января – 30 января
23нечётная31 января – 06 февраля
24чётная07 февраля – 13 февраля
25нечётная14 февраля — 20 февраля
26чётная21 февраля — 27 февраля
27нечётная28 февраля — 06 марта
28чётная07 марта — 13 марта
29нечётная14 марта — 20 марта
30чётная21 марта — 27 марта
31нечётная28 марта — 03 апреля
32чётная04 апреля — 10 апреля
33нечётная11 апреля — 17 апреля
34чётная18 апреля — 24 апреля
35нечётная25 апреля — 01 мая
36чётная02 мая — 08 мая
37нечётная09 мая — 15 мая
38чётная16 мая — 22 мая
39нечётная23 мая — 29 мая
40чётная30 мая — 05 июня
41нечётная06 июня — 12 июня
42чётная13 июня — 19 июня
43нечётная20 июня — 26 июня
44чётная27 июня — 03 июля

Натуральные числа /qualihelpy

Числа, запись которых оканчивается четной цифрой, называют четными числами.  

Числа, запись которых оканчивается нечетной цифрой, называют нечетными числами. 

Над натуральными числами можно производить арифметические действия: 

Чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое. 

Чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое. 

Чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность. 

Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель. 

Чтобы найти неизвестное делимое, необходимо частное умножить на делитель. 

Чтобы найти неизвестный делитель, необходимо делимое разделить на частное. 

Если число  кратно числу , то записывают:  .5. Число делится на   , если его запись оканчивается цифрой  . Например, число  делится на  . 

Деление с остатком

Если же остаток равен нулю, то говорят, что число  делится нацело на число  .

Простые и составные числа

Числа, которые имеют только два различных делителя (делятся только сами на себя и на число 1), называют простыми.

Например, простыми являются числа  ,  ,  ,  ,  ,  ,  ,  , , …. . 

Числа, которые имеют более двух различных делителей, называют составными. Составные числа можно представить в виде произведения двух и более простых множителей. 

Например, число  составное, так как  . Натуральные числа называются взаимно простыми, если они не имеют общих делителей, за исключением числа  . Например, числа  и  взаимно простые; 

Наибольший общий делитель и наименьшее общее кратное

Общим делителем нескольких чисел называют число, которое является делителем каждого из этих чисел. Среди всех общих делителей всегда имеется наибольший. Это число называется наибольшим общим делителем (НОД). 

Общим кратным нескольких чисел называют число, которое является кратным каждого из этих чисел. Среди всех общих кратных всегда есть наименьшее. Это число называется наименьшим общим кратным (НOК). 

Чтобы найти НОД нескольких чисел, необходимо разложить их на простые множители и найти произведение только тех множителей, которые имеются в разложениях всех чисел. 

Чтобы найти НOК нескольких чисел, необходимо разложить их на простые множители, найти произведение всех множителей, входящих в разложение одного из чисел и недостающих множителей из разложений оставшихся чисел. 

ТРЕХМЕРНЫЙ КРОССНАМБЕР | Наука и жизнь

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

‹

›

#1#

Куб 3х3х3 сложен из 27 пронумерованных кубиков. На верхней грани каждого кубика вам надлежит написать по одной цифре (от 1 до 9). Их надо отыскать, соблюдая некоторые условия. Получатся трехзначные числа.

Изображенные здесь квадраты представляют соответственно три слоя кубиков — верхний, средний и нижний. Маленькие квадратики (кубики кросснамбера) пронумерованы. Разумеется, эти номера не имеют никакого отношения к тем числам, которые вам предстоит отыскать. Цепочки цифр могут быть заданы по горизонтали (например, 11, 14, 17), по вертикали (например, 3, 12, 21) или по диагонали (например, 7, 17, 27).

Верхний слой кубиков

#2#

(1, 4, 7) — число делится на 3.

(1, 2, 3) — сумма цифр — 17.

(3, 6, 9) — точный квадрат некоторого числа.

(7, 8, 9) — четное число. Сумма цифр его на 2 больше суммы цифр числа (3, 6, 9).

Средний слой кубиков

#3#

(13, 14) — точный квадрат некоторого числа.

(10, 13, 16) — сумма цифр — 12.

(10, 11, 12) — каждая последующая цифра меньше предыдущей.

(12, 15, 18) — нечетное число.

(16, 17, 18) — число делится на 3.

Нижний слой кубиков

#4#

(21, 23, 25) — четное число.

(22, 23, 24) — каждая последующая цифра больше предыдущей на одну и ту же величину.

(20, 23, 26) — каждая последующая цифра больше предыдущей. Сумма цифр такая же, как сумма цифр числа (21, 24, 27).

Дополнительные условия

(7, 16, 25) — точный куб некоторого числа.

(3, 12, 21) — произведение некоторого числа на число (13, 14). Сумма цифр произведе ния — 13.

(4, 13, 22) — каждая последующая цифра больше предыдущей. Частное от деления третьей цифры на вторую равно частному от деления второй цифры на первую.

(5, 14, 23) — все цифры различны. Их сумма — 19.

(9, 18, 27) — каждая последующая цифра меньше предыдущей.

(3, 15, 27) — точный квадрат некоторого числа.

(7, 17, 27) — нечетное число. Сумма его цифр — 11.

(3, 14, 25) — каждая последующая цифра больше предыдущей.

(7, 13, 19) — разность между первой и второй цифрами равна разности между второй и третьей цифрами.

Этих сведений вполне достаточно, чтобы расставить цифры на все 27 кубиков кросснамбера. Попробуйте это сделать.

ОТВЕТ

Список нечетных чисел — ChiliMath

Не стесняйтесь пересматривать понятие нечетного числа. Щелкните изображение ниже, чтобы перейти к моему уроку о нечетных числах.

Если вы ищете полный список нечетных чисел от 1 до 1000 , это место для вас!

Я разбил нечетные числа на десять (10) групп.

Нечетные числа от 1 до 100

1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
35
37
39
41
43
45
47
49
51
53
55
57
55
61
63
65
67
69
71
73
75
77
79
81
83
85
87
89
91
93
95
97
99

Нечетные числа от 101 до 200

101
103
105
107
109
111
113
115
117
119
121
123
125
127
129
131
133
135
137
139
141
143
145
147
149
151
153
155
157
159
161
163
165
167
169
171
173
175
177
179
181
183
185
187
189
191
193
195
197
199

Нечетные числа от 201 до 300

201
203
205
207
209
211
213
215
217
219
221
223
225
227
229
231
233
235
237
239
241
243
245
247
249
251
253
255
257
259
261
263
261
267
269
267
269
271
273
279
271
279
281
283
285
287
289
291
293
295
297
299

Нечетные числа от 301 до 400

301
303
305
307
309
311
313 ​​
315
317
319
317
319
321
327
325
327
329
331
333
335
337
339
341
343
345
347
349
351
353
355
357
359
361
363
365
367
369
371
377
375
377
379
381
383
385
387
389
391
393
395
397
399

Нечетные числа от 401 до 500

401
403
405
407
409
411
413
419
421
423
425
427
429
427
429
431
433
435
437
439
441
443
445
447
449
451
453
455
457
459
465
467
465
471
473
475
477
479
471
483
485
487
489
491
493
495
497
499

Нечетные числа от 501 до 600

501
503
505
507
509
511
517
515
517
519
525
527
525
527
529
531
533
535
537
539
541
543
545
547
549
551
553
555
557
559
561
563
565
567
569
571
573
575
577
579
581
583
585
587
589
591
593
595
597
599

Нечетные числа от 601 до 700

601
603
605
607
605
611
613
619
617
623
621
627
625
627
629
631
633
635
637
639
641
643
645
647
649
651
653
655
657
659
661
663
665
667
669
671
673
675
677
679
681
683
685
687
689
691
693
695
697
699

Нечетные числа от 701 до 800

701
707
705
707
709
711
717
715
717
723
725
727
729
731
733
735
737
739
741
743
745
747
749
751
753
755
757
759
761
763
765
767
769
771
773
775
777
779
781
783
785
787
789
791
793 По
795
797
799

Нечетные числа от 801 до 900

801
807
805
807
809
811
813
819
817
823
821
827
825
827
829
831
833
835
837
839
841
843
845
847
849
851
853
855
857
859
861
863
865
867
869
871
873
875
877
879
881
883
885
887
889
891
893
895
897
899

Нечетные числа от 901 до 1000

901
9001
9001
905
911
913
911
917
919
921
923
925
927
929
931
933
935
937
939
941
943
945
947
949
951
953
955
957
959
961
963
965
967
969
971
973
975
977
979
981
983
985
987
989
991
993
995
997
999

Вас также может заинтересовать:

Список четных чисел

Что такое нечетное число?

Что такое четное число?

Что такое четные и нечетные числа?

Четные и нечетные числа

Число, которое делится на 2 и дает в остатке 0, называется четным числом. Нечетное число — это число, которое не делится на 2. Остаток в случае нечетного числа всегда равен «1».

Свойство, по которому мы классифицируем целое число в математике как четное или нечетное, также известно как четность.

Идентификация четного или нечетного числа

1. Поняв число в разряде единиц

В этом подходе мы анализируем число в разряде единиц в целом числе, чтобы проверить, является ли число четным или нечетным.

Все числа, оканчивающиеся на 1,3,5,7 и 9, являются нечетными.Например, такие числа, как 11, 23, 35, 47 и т. д., являются нечетными числами.

Все числа, оканчивающиеся на 0,2,4,6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами.

25, 32, 38, 87, 95, 64, 76, 53
Четный Нечетный
32, 38, 64, 76 25, 87, 95, 53

 

2. По группировке

Если мы разделим число на две группы с равным количеством элементов в каждой, то число будет четным числом. В случае нечетных чисел мы получаем остаток 1 при группировке.

  • В виде групп по два в каждой

Для числа, если оно образует несколько групп «два» без остатка, это четное число. В случае остатка число является нечетным числом.

Данная таблица объясняет результат, когда мы применяем различные операции над набором из двух чисел.

 

Применение

Элементарные навыки понимания чисел пригодятся в старших классах для изучения математики, естественных наук и систем связи. Мы применяем эту концепцию при разработке схем с использованием логических вентилей и двоичных кодов. В древней математике изучение геометрических фигур началось с классификации фигур по количеству сторон на четные и нечетные.

Интересные факты

  • Каждое альтернативное число в счете является четным числом, начинающимся с 2, и нечетным числом, начинающимся с 1.

  • Ноль — четное число

  • Древние греки использовали формы и фигуры с нечетным числом сторон для обозначения «нечетных» чисел

  • Пифагорейцы использовали термин «гномон» для нечетных чисел

 

нечетных и четных чисел

Нечетные и четные числа являются только натуральными числами. См. следующую числовую строку.

Из приведенной выше диаграммы видно, что для четных чисел диаграмма полная, а для нечетных чисел на 1 клетку меньше.Четные числа можно разделить на две группы. Например, четыре можно разделить на две группы по два ( …. , эти 4 точки можно разделить как ..|.. ). Но нечетные числа нельзя разделить одинаково, как четные числа.

Таким образом, четные числа начинаются с 0, а нечетные числа начинаются с 1.

Четные числа: 0,2,4,6,8,10,…

Таким образом, в целом мы можем сказать, что числа, с указанными выше цифрами являются четными числами.

Нечетные числа: 1,3,5,7,9,…
Числа, разряд единиц которых отличен от 0,2,4,6,8, являются нечетными числами.
Наименьшее четное натуральное число равно 2, а наименьшее нечетное натуральное число равно 1.
______________________________________________________________

Практика

Q.1 Запишите все четные числа от 22 до 60.
22,___,___,___,___ ,___,___,___,___,___,___,___,___,___,___,___,___,___ ,___,___,60.

Q.2 Запишите все нечетные числа от 61 до 99.
61,___,___,___,___,___,___,___,___,___,___,___,___,___,___,___,___,___, ___,___,99

Q.3 Запишите следующее четное число.
1) 98 ,___ 2) 26,___ 3) 58, ___ 4) 52,___ 5) 48,___ 6) 34,___ 7) 88,___
8) 66,___ 9) 78,___ 10) 66,___

Q.4 Запишите следующее нечетное число.
1) 53,___ 2) 81,___ 3) 17,___ 4) 63,___ 5) 27,___ 6) 87,___ 7) 99,___
8) 49,___ 9) 95,___ 10) 33,___

В.5 Обведите четные числа.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
29 30 1 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77
78 79 80 81 82 83 84 85 86 87 83 84 95 86 87 88 89 90 91 92 93 94 95 96 97 98 99 94 95 96 97 98 99 100

нечетных и четных номеров

2-й класс Math

Главная Page

COVID-19 привел мир, чтобы пройти через феноменальный переход.

Электронное обучение — это будущее уже сегодня.

Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться!!!

Covid-19 повлиял на физическое взаимодействие между людьми.

Не позволяйте этому влиять на ваше обучение.

Нечетные и четные числа

Что такое четные и нечетные числа?

Целое число, которое можно разделить на 2, является четным числом, а целое число, которое нельзя разделить на 2, является нечетным числом. Они могут быть как положительными, так и отрицательными.Нечетные числа всегда находятся между четными числами и наоборот.

Чтобы различать нечетные и четные числа, вы всегда ищете их конечную цифру. Последняя цифра четного числа всегда 0, 2, 4, 6 или 8, а последняя цифра нечетного числа всегда 1, 3, 5, 7 или 9.

Примеры


Вот несколько примеров четных чисел:

-22, -10, 0, 6, 18, 234.

Приведенные выше числа четные, потому что они заканчиваются на 0, 2, 4, 6 или 8.

Несколько примеры нечетных чисел:

-101, -17, 1, 9, 23, 985.

Приведенные выше числа нечетные, так как они заканчиваются на 1, 3, 5, 7 или 9.

Свойства

Нечетные и четные числа обладают особыми свойствами относительно алгебраических операций (сложение, вычитание и умножение). Всякий раз, когда мы применяем алгебраические операции к двум четным или нечетным числам, мы всегда получаем четное или нечетное число. Мы исключаем деление здесь, потому что деление иногда дает вам результат в дробях, когда речь идет об особых свойствах.

  • Когда мы складываем или вычитаем два четных числа, результатом всегда будет четное число. Например, 6 + 4 = 10

    6 – 4 = 2

  • Когда мы складываем или вычитаем четное число и нечетное число, результат всегда будет нечетным. Например, 7 + 4 = 11

    7 – 4 = 3

  • Когда мы складываем или вычитаем два нечетных числа, результатом всегда будет четное число. Например, 7 + 3 = 10

    7 – 3 = 4

  • При умножении двух четных чисел всегда получается четное число. Например,
    6 × 4 = 24
  • Когда мы умножаем четное число на нечетное, всегда получается четное число. Например,
    7 × 4 = 28
  • При умножении двух нечетных чисел всегда получается нечетное число. Например,
    7 × 3 = 21

Обобщение нечетных и четных чисел

Мы также можем обобщать четные и нечетные числа. Например, если «n» — четное число, то следующее нечетное число — «n + 1», следующее четное число — «n + 2» и так далее. Точно так же, если «n» — нечетное число, то следующее четное число — «n + 1», следующее нечетное число — «n + 2» и так далее.

Например, если мы хотим написать ряд из пяти нечетных чисел, начиная с 73, мы можем написать это как:

73, 73 + 2, 73 + 4, 73 + 6, 73 + 7

73, 75 , 77, 79, 81

Таблица чисел

Следующая таблица представляет собой таблицу чисел от 1 до 100, где нечетных чисел выделены желтым цветом , а четных чисел выделены зеленым цветом .

Быстрый ответ: что такое нечетные числа?

Какие нечетные числа от 1 до 100?

нечетных чисел от 1 до 100 : 1 , 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69, 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99.

Какие все нечетные числа?

1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31 — это нечетных чисел .

Что такое нечетные числа и примеры?

Любое целое число, которое нельзя разделить точно на 2, является нечетным числом . Последняя цифра — 1, 3, 5, 7 или 9. Пример : −3, 1, 7 и 35 — все нечетных чисел .

Что такое нечетное четное число?

Четное число — это число , которое можно разделить на две равные группы.Нечетное число — это число , которое нельзя разделить на две равные группы. Четные числа оканчиваются на 2, 4, 6, 8 и 0 независимо от того, сколько в них цифр (мы знаем, что число 5 917 624 равно даже , потому что оно заканчивается на 4!). Нечетные числа заканчиваются на 1, 3, 5, 7, 9.

Является ли 27 нечетным числом?

Нечетные числа всегда заканчиваются цифрой 1, 3, 5, 7 или 9. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27 , 29, 31 — это нечетных чисел .

Является ли число 1 нечетным?

нечетное число является целым числом, которое при делении на два либо оставляет остаток, либо получается дробь. Один первый нечетный положительный число но он не оставляет остатка 1 . Некоторыми примерами нечетных чисел являются 1 , 3, 5, 7, 9 и 11. Целое число, не являющееся нечетным числом , является четным числом .

45 нечетно или четно?

45 — это нечетное число .

52 четно или нечетно?

52 — это четное число .

Чему равна сумма всех нечетных чисел от 1 до 1000?

Число ряд 1 , 3, 5, 7, 9,…., 1999. Таким образом, 1000000 это сумма первых 1000 нечетных чисел .

Почему нечетные числа выглядят лучше?

нечетное число деталей более эффективно захватывает ваш взгляд. Нечетные числа заставляют ваши глаза перемещаться по группе и, соответственно, по комнате.Это вынужденное движение является сердцевиной визуального интереса. Именно по этой причине набор из трех более привлекательный и запоминающийся, чем что-то в паре из двух.

Чему равна сумма нечетных чисел?

Сумма любого набора последовательных нечетных чисел, начинающихся с 1, всегда равна квадрату числа цифр, сложенных вместе. Если 1,3,5,7,9,11,…, (2n-1) нечетные числа, то; Сумма первого нечетного числа = 1. Сумма первых двух нечетных чисел = 1  + 3  = 4 (4 = 2 x 2).

Как вы представляете нечетные числа?

Множество нечетных с учетом чисел есть {x: x = 2n – 1, где n ∈ N}. Множество четных целых чисел равно {x: x = 2n, где n ∈ W}. Набор из нечетных целых чисел равен {x: x = 2n + 1, где n ∈ W}.

59 нечетное или четное?

A: Да, число 59 является нечетным числом .

0 четное или нечетное число?

Так что же это такое — нечетное , четное или ни то, ни другое? Для математиков ответ прост: ноль — это четное число .

67 нечетное или четное?

A: Да, число 67 является нечетным числом .

23 | Простые числа вики

23

Кардинальный номер

двадцать три

Порядковый номер

двадцать третий

Стандартная форма

2,3 x 10 1

Предыдущий Текущий Следующий
19 23 29

23 — простое число от 1 до 100.Число 23 имеет два делителя: 1 и 23. Говорят, что число 23 также является одним из тех чисел, сложение которых дает простое число. Это девятое простое число и девятое простое число от 1 до 100.

Доказательства

  • — 23 можно разделить на 1.
  • — 23 нельзя разделить на 2-22.
  • — 23 можно разделить на 23.
  • Следовательно, 23 имеет 2 делителя.

Как показатель числа Мерсенна

2 23 — 1, то есть число 8 388 607, можно разложить на 47 x 178 481, и поэтому оно не является простым числом.

Связь с другими нечетными числами

Цифры до

  • Предыдущее нечетное число 21 не является простым числом. Оно делится на 3 и 7.
  • Нечетное число, предшествующее 21, равно 19. 19 — простое число.
    • 19 и 23 разделены четырьмя числами; следовательно, они двоюродные простые числа.
  • Нечетное число, предшествующее 19, равно 17. 17 — простое число.
    • 17 и 23 разделены шестью числами; следовательно, они сексуальные простые числа.

Номера после

  • Следующее нечетное число 25 не является простым числом. Это квадратное число, равное 5 2  = 25,
    • .
  • 27, нечетное число после 25, не является простым числом. Это число в кубе: 3 3 = 27,
    • .
  • 29, нечетное число после 27, является простым числом.
    • 23 и 29 разделены шестью числами; следовательно, они сексуальные простые числа.
  • Из-за того, что 23 не является частью каких-либо чисел-близнецов, оно считается изолированным простым числом.

Иллюстративная математика

Комментарий IM

Это задание предназначено для обучения. Часть (b) этой задачи намеренно оставлена ​​открытой, чтобы побудить учащихся выработать привычку искать закономерности, которые могут намекать на некоторую основную структуру, как описано в Стандарте для математических занятий 7, Ищите и используйте структуру.

Этот вид работы также связан с выдвижением предположений и определением того, верны ли эти предположения или нет, как описано в Стандарте математической практики 1, Разбираться в задачах и настойчиво решать их. Некоторые вещи, которые учащиеся могут заметить в числах в таблице, на самом деле никуда не денутся; на самом деле такова природа предположений: они не всегда оказываются правдой.

Часть (c) предназначена для того, чтобы вовлечь учащихся в то, что должно естественным образом следовать после того, как они заметят закономерность, а именно: выяснить, всегда ли она выполняется, и если да, то объяснить, почему. Таким образом, в этом задании учащиеся также участвуют в Стандарте для математической практики 3, Создают жизнеспособные аргументы и критикуют рассуждения других.

Вариант выполнения этой задачи — удаление строительных лесов из части (c). В любом случае небольшие предметы, такие как фишки или монеты, могут помочь учащимся развить свои объяснения.

Представлено Шерри Мартини и Мелисой Хэнкок из Университета штата Канзас, Манхэттен, штат Канзас, на первый конкурс по написанию иллюстративных задач по математике.

Стандарты математической практики сосредоточены на характере учебного опыта, обращая внимание на процессы мышления и привычки ума, которые учащиеся должны развивать, чтобы достичь глубокого и гибкого понимания математики. Некоторые задания поддаются демонстрации студентами конкретных практик. Практики, наблюдаемые во время изучения задачи, зависят от того, как обучение разворачивается в классе. Возможные связи со вторичной практикой могут быть обсуждены, но не с такой же степенью детализации.

Несмотря на то, что это задание иллюстрирует несколько математических упражнений, оно используется для выделения стандарта математических упражнений 7. По мере того, как учащиеся будут следовать заданному правилу, они должны начать видеть, что все элементы нечетные (MP.8). Чтобы понять, почему все они нечетные, учащиеся должны использовать структуру четных и нечетных чисел, и именно в этот момент в игру вступает MP.7. Затем задание просит их объяснить, что они видят, чтобы они могли участвовать в MP.3.

.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *