Закон сложения скоростей и решение задачи. Кинематика — 10 класс

Закон сложения скоростей и решение задачи. Кинематика — 10 класс

Подробности

Просмотров: 1319

Закон сложения скоростей

Кинематика — это просто!

Формулировка закона:

Как в учебнике Буховцева для 10 класса:

Если тело движется относительно системы отсчета К₁ со скоростью V₁,
а сама система отсчета К₁ движется относительно другой системы отсчета К₂ со скоростью V,
то скорость тела (V₂) относительно второй системы отсчета К₂
равна геометрической сумме векторов V₁ и V.

Упрощаем форммулировку, не меняя смысла:

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.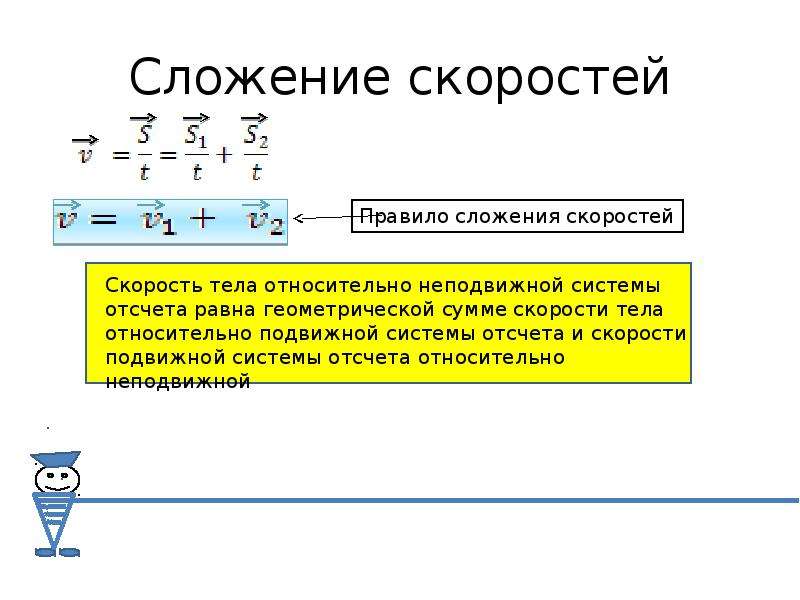

Вторая формулировка запоминается проще, какой ползоваться решайте сами!

где всегда
К₂ — неподвижная система отсчета
V₂ — скорость тела относительно неподвижной системы отсчета (К₂)

К₁ — подвижная система отсчета
V₁ — скорость тела относительно подвижной системы отсчета (К₁)

V — скорость подвижной системы отсчета (К₁) относительно неподвижной системы отсчета (К₂)

Алгоритм решения задачи на закон сложения скоростей

Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!

1. Определить тело — обычно это тело, о скорости которого спрашивается в задаче.
2. Выбрать неподвижную систему отсчета (дорога, берег) и подвижную систему отсчета (обычно это второе движущееся тело).

P.S. В условиях задачи скорости тел заданы обычно относительно неподвижной системы отсчета (например, дороги или берега)

3. Ввести обозначения скоростей (V₁, V₂, V).
4. Сделать чертеж, на котором показать координатную ось ОХ и векторы скорости.
Лучше, если ОХ будет совпадать по направлению с вектором скорости выбранного тела.
5. Записать формулу закона сложения скоростей в векторном виде.
6. Выразить из формулы искомую скорость в векторном виде.

7. Выразить искомую скорость в проекциях.
8. Определить по чертежу знаки проекций.
9. Расчет в проекциях.
10. В ответе не забыть перейти от проекции к модулю.

Пример решения простейшей задачи на закон сложения скоростей

Задача

Два автомобиля движутся равномерно по шоссе навстречу друг другу. Модули их скоростей равны 10 м/с и 20 м/с.
Определить скорость первого автомобиля относительно второго.

Решение:

Еще раз! Если вы внимательно прочитали пояснения к формуле, то решение любой задачи, пойдет «на автомате»!

1. В задаче спрашивается о скорости первого автомобиля — значит тело — первый автомобиль.
2. По условию задачи выбираем:
K₁ — подвижная система отсчета сязана со вторым автомобилем
К₂ — неподвижная система отсчета связана с дорогой

3. Вводим обозначения скоростей:
V₁ — скорость тела (первого авто) относительно подвижной системы отсчета (второго авто) — найти!
V₂ — скорость тела (первого авто) относительно неподвижной систеы отсчета (дороги) — дано 10м/с
V — скоростьь подвижной системы отсчета (второго авто) относительно неподвижной системы отсчета (дороги) — дано 20двух уравнений:м/с

Теперь понятно, что в задаче надо определить V₁.
4. Делаем чертеж, выписываем формулу:

5. далее по алгоритму …..

Всё, все отдыхают!)))

P.S. Если движение происходит не по пряммой, а на плоскости, то при переводе формулы векторного вида в проекции добавляется еще одно уравнение в прекциях относительно оси OY, далее решаем систему двух уравнений:

V_2x = V_1x + V_x
V_2y = V_1y + V_y

Кинематика — Класс!ная физика

Прямолинейное равномерное движение и решение задач — Закон сложения скоростей и решение задач — Движение с постоянным ускорением и решение задач — Свободное падение — Движение тела, брошенного под углом к горизонту — Решение задач. Тело, брошенное под углом к горизонту — Криволинейное движение

Сложение скоростей

Литература

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика 10. Учебник М.: Просвещение 2001.

Цель урока

Ввести понятие относительности движения, рассмотреть движение тела в разных системах отсчета, вывести закон сложения скоростей.

№ п/п Этапы урока Время, мин Приемы и методы 1 Организационный момент 2 2 Проверка знаний учащихся по теме «Равномерное движение» 20 Тест 3 Объяснение нового материала по теме «Сложение скоростей» 20 Лекция 4 Объяснение домашнего задания 3

 

Домашнее задание: § 12, № 42, 43 (Рымкевич А. П., Москва: Дрофа, 2001).

 

На данном уроке удобно использовать компьютерную модель «Относительность движения» для объяснения нового материала.

Рассмотрим движение лодки в разных системах отсчета.

1 случай

Лодка движется в стоячей воде перпендикулярно берегу. Для демонстрации этого движения задаем скорость течения реки υ₀ = 0 м/с, угол между векторами скоростей 90°. В этом случае лодка относительно воды и относительно берега движется с собственной скоростью υ (которую вы задаете сами, например 5 м/с). Так как ширина реки 150 м (это видно на схеме), то для того чтобы переплыть реку лодке понадобилось 30 с. С учащимися устно вычисляется данный результат, он же показан на модели.

2 случай

Вода в реке движется с какой-либо скоростью (пусть 2 м/с). На схеме видно, что характер движения лодки относительно берега изменился. Пока лодка переплывала реку, течением ее снесло на 60 м.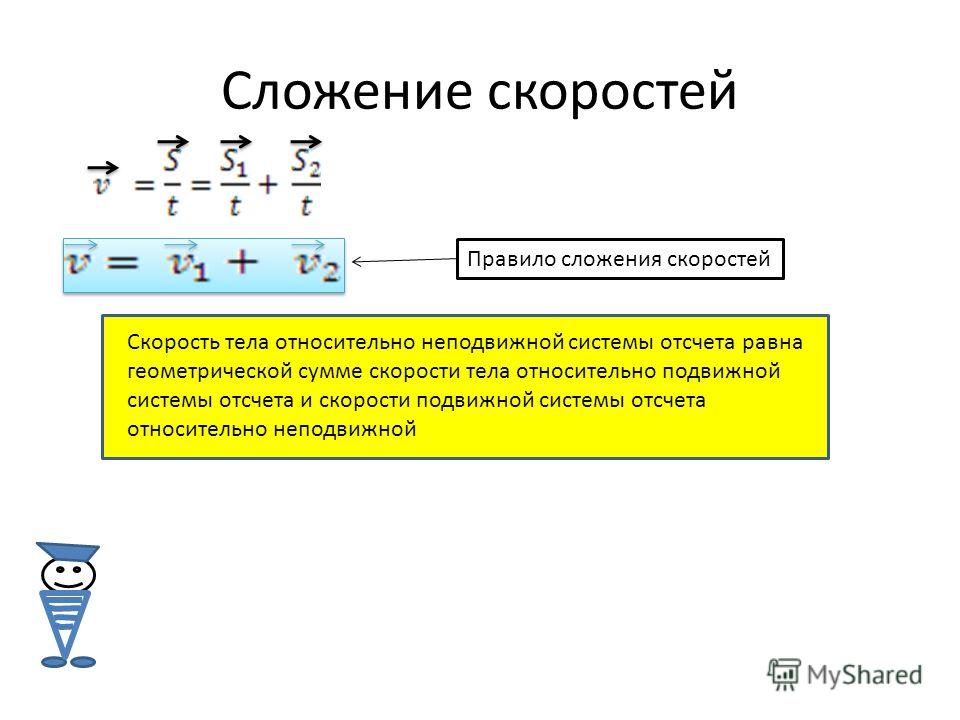 На этом этапе урока нужно ввести понятие неподвижной системы отсчета, подвижной системы отсчета, физического тела. После этого рассмотреть перемещение тела относительно подвижной системы отсчета, перемещения подвижной системы отсчета относительно неподвижной, перемещение тела относительное неподвижной системы отсчета. Выяснить, как графически можно найти перемещение лодки относительно берега и получить формулу для сложения перемещений. Далее, разделив данное выражение на время движения, получить закон сложения скоростей. Рассмотреть сложение скоростей на компьютерной модели. Рассчитать скорость лодки относительно берега по закону сложения скоростей, сравнить с тем, что показано в модели.

3 случай

Как должна двигаться лодка, что бы переплыть на другой берег точно напротив места отплытия? На модели наглядно можно показать, что для выполнения этой задачи нужно выбрать курс (обсудить, что понимаем под этим термином, в модели это угол между векторами скорости лодки и течения реки). Курс зависит от скорости течения реки и скорости движения лодки. Это тоже можно продемонстрировать на модели.

 

Решить задачи № 32, 34 (Рымкевич А.П. Москва: Дрофа, 2001).

Скорость

Скорость – это количественная характеристика движения тела.

Средняя скорость – это физическая величина, равная отношению вектора перемещения точки к промежутку времени Δt, за который произошло это перемещение. Направление вектора средней скорости совпадает с направлением вектора перемещения . Средняя скорость определяется по формуле:

Мгновенная скорость, то есть скорость в данный момент времени – это физическая величина, равная пределу, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Иными словами, мгновенная скорость в данный момент времени – это отношение очень малого перемещения к очень малому промежутку времени, за который это перемещение произошло.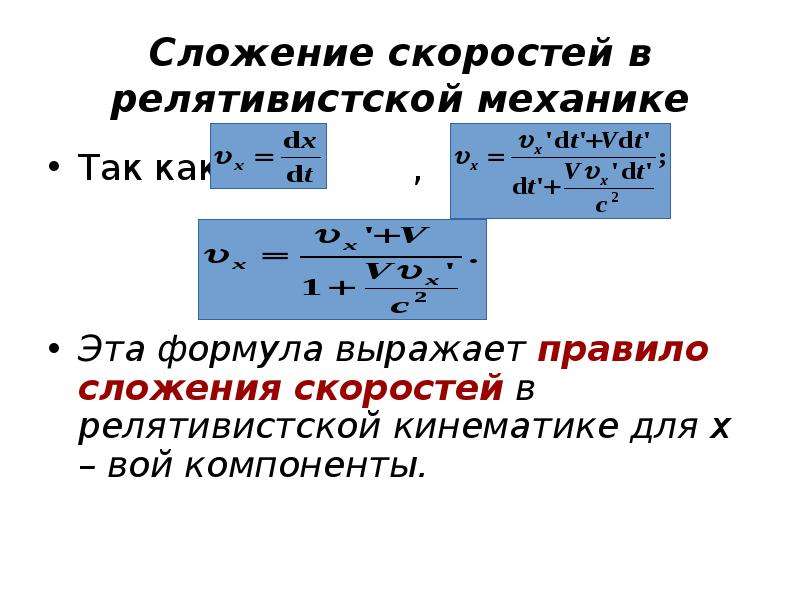

Вектор мгновенной скорости направлен по касательной к траектории движения тела (рис. 1.6).

Рис. 1.6. Вектор мгновенной скорости.

В системе СИ скорость измеряется в метрах в секунду, то есть единицей скорости принято считать скорость такого равномерного прямолинейного движения, при котором за одну секунду тело проходит путь в один метр. Единица измерения скорости обозначается м/с. Часто скорость измеряют в других единицах. Например, при измерении скорости автомобиля, поезда и т.п. обычно используется единица измерения километр в час:

1 км/ч = 1000 м / 3600 с = 1 м / 3,6 с

или

1 м/с = 3600 км / 1000 ч = 3,6 км/ч

Сложение скоростей

Скорости движения тела в различных системах отсчёта связывает между собой классический закон сложения скоростей.

Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и самой подвижной системы отсчёта относительно неподвижной.

Например, пассажирский поезд движется по железной дороге со скоростью 60 км/ч. По вагону этого поезда идет человек со скоростью 5 км/ч. Если считать железную дорогу неподвижной и принять её за систему отсчёта, то скорость человека относительно системы отсчёта (то есть относительно железной дороги), будет равна сложению скоростей поезда и человека, то есть

60 + 5 = 65, если человек идёт в том же направлении, что и поезд

и

60 – 5 = 55, если человек и поезд движутся в разных направлениях

Однако это справедливо только в том случае, если человек и поезд движутся по одной линии. Если же человек будет двигаться под углом, то придётся учитывать этот угол, вспомнив о том, что скорость – это векторная величина.

А теперь рассмотрим описанный выше пример более подробно – с деталями и картинками.

Итак, в нашем случае железная дорога – это неподвижная система отсчёта. Поезд, который движется по этой дороге – это подвижная система отсчёта.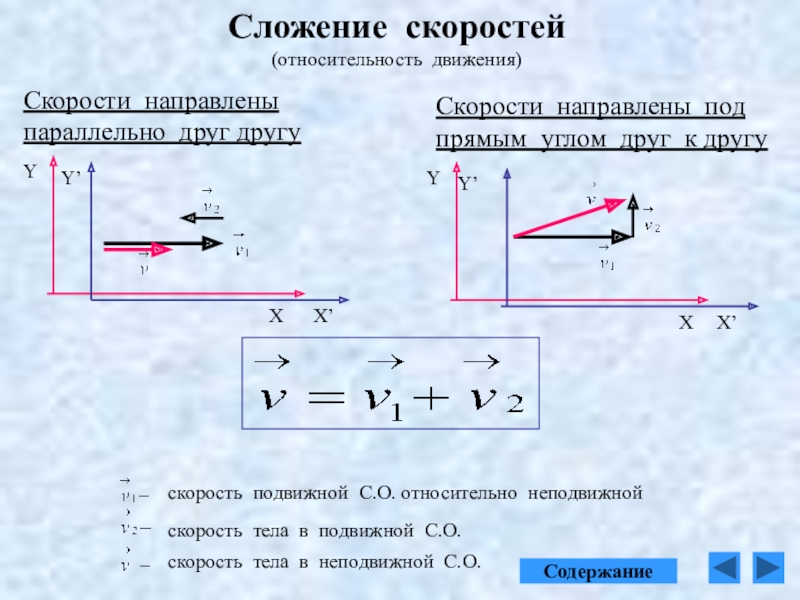 Вагон, по которому идёт человек, является частью поезда.

Скорость человека относительно вагона (относительно подвижной системы отсчёта) равна 5 км/ч. Обозначим её буквой _Ч.

Скорость поезда (а значит и вагона) относительно неподвижной системы отсчёта (то есть относительно железной дороги) равна 60 км/ч. Обозначим её буквой _В. Иначе говоря, скорость поезда – это скорость подвижной системы отсчёта относительно неподвижной системы отсчёта.

Скорость человека относительно железной дороги (относительно неподвижной системы отсчёта) нам пока неизвестна. Обозначим её буквой .

Свяжем с неподвижной системой отсчёта (рис. 1.7) систему координат ХОY, а с подвижной системой отсчёта – систему координат X_ПО_ПY_П (см. также раздел Система отсчёта). А теперь попробуем найти скорость человека относительно неподвижной системы отсчёта, то есть относительно железной дороги.

За малый промежуток времени Δt происходят следующие события:

• Человек перемещается относительно вагона на расстояние _Ч
• Вагон перемещается относительно железной дороги на расстояние _B

Тогда за этот промежуток времени перемещение человека относительно железной дороги:

= _Ч + _B

Это закон сложения перемещений. В нашем примере перемещение человека относительно железной дороги равно сумме перемещений человека относительно вагона и вагона относительно железной дороги.

Рис. 1.7. Закон сложения перемещений.

Закон сложения перемещений можно записать так:

= Δ_Ч • Δt + Δ_B • Δt

Скорость человека относительно железной дороги равна:

 =  / Δt

Так как

= _Ч + _B

то

Скорость человека относительно вагона:

ΔЧ = Ч / Δt

Скорость вагона относительно железной дороги:

ΔB = B / Δt

Поэтому скорость человека относительно железной дороги будет равна:

 = ΔЧ + ΔB

Это закон сложения скоростей:

Скорость тела относительно неподвижной системы отсчёта равна сумме скоростей тела в подвижной системе отсчёта и скорости самой подвижной системы отсчёта относительно неподвижной.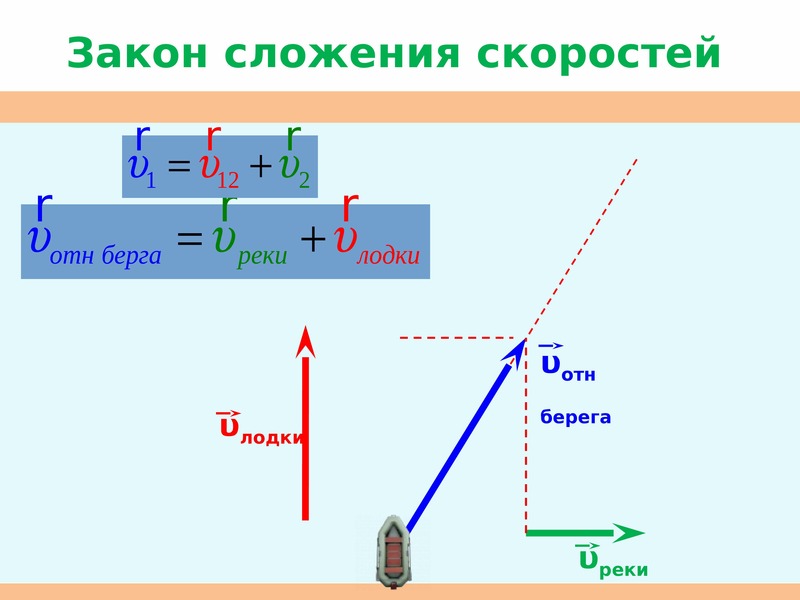

Закон сложения скоростей

Механическим движением называют изменение положения тела в пространстве относительно других тел с течением времени.

В этом определении ключевой является фраза «относительно других тел». Каждый из нас относительно какой-либо поверхности неподвижен, но относительно Солнца мы совершаем вместе со всей Землей орбитальное движение со скоростью 30 км/с, то есть движение зависит от системы отсчета.

Система отсчета – совокупность системы координат и часов, связанных с телом, относительно которого изучается движение.

Например, описывая движения пассажиров в салоне автомобиля, систему отсчета можно связать с придорожным кафе, а можно с салоном автомобиля или с движущимся встречным автомобилем, если мы оцениваем время обгона

Преобразование координат и времени

Закон сложения скоростей является следствием преобразований координат и времени.

Пусть частица в момент времени t’ находится в точке (x’, y’, z’), а через малое время Δt’ в точке (x’ + Δx’, y’ + Δy’, z’ + Δz’) системы отсчета K’. Это два события в истории дви­жущейся частицы. Имеем:

Δx’ = v_x’Δt’,

где
v_x’ — x-я компонента скорости частицы в системе K’.

Аналогичные соотношения имеют место для остальных компонент.

Разности координат и промежутки времени (Δx, Δy, Δz, Δt) преобразуются так же, как координаты:

Δx = Δx’ + VΔt’,

Δy = Δу’,

Δz = Δz’,

Δt = Δt’.

Отсюда следует, что скорость той же частицы в системе K будет иметь компоненты:

v_x = Δx / Δt = (Δx’ + VΔt’) / Δt = v_x’ + V,

v_y = v_y’,

v_z = v_z’.

Это закон сложения скоростей. Его можно выразить в векторной форме:

v̅ = v̅’ + V

(координатные оси в системах K и K’ параллельны).

Закон сложения скоростей

Если тело движется относительно системы отсчета К₁ со скоростью V₁, а сама система отсчета К₁ движется относительно другой системы отсчета К₂ со скоростью V, то скорость тела (V₂) относительно второй системы отсчета К₂ равна геометрической сумме векторов V₁ и V.

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета.

\( \vec{V_2} = \vec{V_1} + \vec{V} \)

где всегда
К₂ — неподвижная система отсчета
V₂ — скорость тела относительно неподвижной системы отсчета (К₂)

К₁ — подвижная система отсчета
V₁ — скорость тела относительно подвижной системы отсчета (К₁)

V — скорость подвижной системы отсчета (К₁) относительно неподвижной системы отсчета (К₂)

Закон сложения ускорений для поступательного движения

При поступательном движении тела относительно подвижной системы отсчёта и подвижной системы отсчёта относительно неподвижной, вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта $\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\ {\overrightarrow{a}}_{АБС}$ (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета ${\overrightarrow{a}}_r=\frac{d{\overrightarrow{v}}_r}{dt}={\overrightarrow{a}}_{ОТН}$ (относительного ускорения) и вектора ускорения подвижной системы отсчёта относительно неподвижной ${\overrightarrow{a}}_е=\frac{d{\overrightarrow{v}}_е}{dt}={\overrightarrow{a}}_{ПЕР}$ (переносного ускорения):

\[{\overrightarrow{a}}_{АБС}={\overrightarrow{a}}_{ОТН}+{\overrightarrow{a}}_{ПЕР}\]

В общем случае, когда движение материальной точки (тела) является криволинейным, его в каждый момент времени можно представить как комбинацию поступательного движения материальной точки (тела) относительно подвижной системы отсчёта со скоростью \( {\overrightarrow{v}}_r \), и вращательного движения подвижной системы отсчёта относительно неподвижной с угловой скоростью \( {\overrightarrow{\omega }}_e \). В этом случае, при сложении ускорений, наряду с относительным и переносным ускорением необходимо учитывать и ускорение Кориолиса \( a_c=2{\overrightarrow{\omega }}_e\times {\overrightarrow{v}}_r \), которое характеризует изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением.

Теорема Кориолиса

Вектор ускорения материальной точки (тела) относительно неподвижной системы отсчёта \( \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\ {\overrightarrow{a}}_{АБС} \) (абсолютное ускорение) является суммой вектора ускорения тела относительно подвижной системы отсчета \( {\overrightarrow{a}}_r=\frac{d{\overrightarrow{v}}_r}{dt}={\overrightarrow{a}}_{ОТН} \) (относительного ускорения), вектора ускорения подвижной системы отсчёта относительно неподвижной \( {\overrightarrow{a}}_е=\frac{d{\overrightarrow{v}}_е}{dt}={\overrightarrow{a}}_{ПЕР} \) (переносного ускорения), и кориолисова ускорения \( a_c=2{\overrightarrow{{\mathbf \omega }}}_e\times {\overrightarrow{v}}_r={\overrightarrow{a}}_{КОР} \):

\[{\overrightarrow{a}}_{АБС}={\overrightarrow{a}}_{ОТН}+{\overrightarrow{a}}_{ПЕР}+{\overrightarrow{a}}_{КОР}\]

 

Абсолютное перемещение равно сумме относительного и переносного перемещений.

Перемещение тела в неподвижной системе отсчета равно сумме перемещений: тела в подвижной системе отсчета и самой подвижной системы отсчета относительно неподвижной.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox

Физические основы механики

Мы говорили, что скорость света — максимально возможная скорость распространения сигнала. Но что будет, если свет испускается движущимся источником в направлении его скорости V ? Согласно закону сложения скоростей, следующему из преобразований Галилея, скорость света должна быть равна c + V. Но в теории относительности это невозможно. Посмотрим, какой закон сложения скоростей следует из преобразований Лоренца. Для этого запишем их для бесконечно малых величин:

По определению скорости ее компоненты в системе отсчета K находятся как отношения соответствующих перемещений к временным интервалам:

Аналогично определяется скорость объекта в движущейся системе отсчета K’, только пространственные расстояния и временные интервалы надо взять относительно этой системы:

Следовательно, разделив выражение dx на выражение dt, получим:

Разделив числитель и знаменатель на dt’, находим связь x-компонент скоростей в разных системах отсчета, которая отличается от галилеевского правила сложения скоростей:

Кроме того, в отличие от классической физики, меняются и компоненты скоростей, ортогональные направлению движения. Аналогичные вычисления для других компонент скоростей дают:

Таким образом, получены формулы для преобразования скоростей в релятивистской механике. Формулы обратного преобразования получаются при замене штрихованных величин на нештрихованные и обратно и заменой V на –V.

Теперь мы можем ответить на вопрос, поставленный в начале данного раздела. Пусть в точке 0′ движущейся системы отсчета K’ установлен лазер, посылающий импульс света в положительном направлении оси 0’х’. Какой будет скорость импульса для неподвижного наблюдателя в системе отсчета К? В этом случае скорость светового импульса в системе отсчета К’ имеет компоненты

Применяя закон релятивистского сложения скоростей, находим для компонент скорости импульса относительно неподвижной системы К :

Мы получаем, что скорость светового импульса и в неподвижной системе отсчета, относительно которой источник света движется, равна

Тот же результат получится при любом направлении распространения импульса. Это естественно, так как независимость скорости света от движения источника и наблюдателя заложена в одном из постулатов теории относительности. Релятивистский закон сложения скоростей — следствие этого постулата.

Действительно, когда скорость движения подвижной системы отсчета V << c, преобразования Лоренца переходят в преобразования Галилея, мы получаем обычный закон сложения скоростей

При этом ход течения времени и длина линейки будут одинаковы в обеих системах отсчета. Таким образом, законы классической механики применимы, если скорости объектов много меньше скорости света. Теория относительности не зачеркнула достижения классической физики, она установила рамки их справедливости.

Пример. Тело со скоростью v₀ налетает перпендикулярно на стенку, двигающуюся ему навстречу со скоростью v. Пользуясь формулами для релятивистского сложения скоростей, найдем скорость v₁ тела после отскока. Удар абсолютно упругий, масса стенки намного больше массы тела.

Воспользуемся формулами, выражающими релятивистский закон сложения скоростей.

Направим ось х вдоль начальной скорости тела v₀ и свяжем систему отсчета K’ со стенкой. Тогда v_x = v₀ и V = –v. В системе отсчета, связанной со стенкой, начальная скорость v’₀ тела равна

Поскольку стенку можно считать бесконечно массивной, по закону сохранения энергии после упругого удара тело отскочит в обратном направлении с тем же (относительно стенки) абсолютным значением скорости:

Вернемся теперь назад в лабораторную систему отсчета К. Подставляя в релятивистский закон сложения скоростей v’₁ вместо v’_x и учитывая опять же V = –v, находим после преобразований:

Проанализируем теперь предельные случаи.

• Если скорости тела и стенки малы (v₀ << с, v << с), то можно пренебречь всеми членами, где эти скорости и их произведение делятся на скорость света. Получаем тогда из найденной формулы результат классической механики

  Скорость шара после отскока увеличивается на удвоенную скорость стенки; направлена она, естественно, противоположно начальной. Ясно, что в релятивистском случае этот результат не годится. В частности, при v₀ =  v = с/3 из него следует, что скорость тела после отскока будет равна v₁ = –с, чего не может быть.

• Пусть теперь на стенку налетает тело, двигающееся со скоростью света (например, лазерный луч отражается от двигающегося зеркала). Подставляя v₀ = с в найденное соотношение, получаем

  Иными словами, скорость лазерного луча изменила направление, но не свою абсолютную величину, как и должно быть.

• Рассмотрим теперь случай, когда стенка движется с релятивистской скоростью. В этом случае найденное соотношение дает нам

  Тело после отскока также будет двигаться со скоростью, близкой к скорости света.

• Наконец, подставим в найденное соотношение значения v₀ = v = с/3 :

  В отличие от классической механики, теория относительности дает для скорости после отскока значение, меньшее скорости света.

• Напоследок посмотрим, что случится, если стенка удаляется от тела с той же скоростью (v = –v₀). Имеем в этом случае:

  Как и в классической механике, тело стенку не догонит, и его скорость не изменится.

Релятивистский Мир: Сложение скоростей

Рассмотрим инерциальные системы отсчёта $S$ и $S’$. Пусть их оси $x$ и $x’$ направлены параллельно к относительной скорости. Скорость системы $S’$ относительно $S$ равна $v$, а скорость $S$ относительно $S’$: «$-v$»:

Ключевым понятием кинематики является событие. Предполагается, что оно имеет сколь угодно малую длительность и локализацию в пространстве. Событие характеризуется временем $t$ и положением $\{x,\,y\}$. Наблюдатели в каждой системе отсчета регистрируют это событие по своим приборам, получая значения $\{t,\,x,\,y\}$ для $S$ и $\{t’,\,x’,\,y’\}$ для $S’$. Напомним, что наблюдатели способны проводить измерения только в своей непосредственной окрестности. Поэтому каждую систему отсчета мы представляем «заполненной» наблюдателями. Событие регистрируют два наблюдателя в $S$ и $S’$, находящихся там, где оно произошло. Благодаря процедуре синхронизации времени, полученные ими наблюдения будут непротиворечиво восприняты и другими собратьями из их систем отсчета. Эффекты теории относительности проявляются при больших скоростях и, для получения заметных отличий от классической кинематики, часто потребуется изучать большие расстояния. Поэтому введение множества наблюдателей оказывается полезным.

Аналогично сравниваются результаты наблюдений некоторого процесса. Пусть он состоит из двух последовательных событий: начала в момент времени $t_1$ (в системе $S$) и конца в момент $t_2$. 2}},~~~~~\Delta y’=\Delta y \end{equation} (часто мы будем ограничиваться 2-мерным пространством $\{x,\,y\}$, так как, в силу симметрии, ось $z$ аналогична оси $y$).

✦ Рассмотрим движущийся объект. Можно измерить его положение, т.е. координаты $\{x_1,\,y_1\}$ в момент времени $t_1$, а затем положение $\{x_2,\,y_2\}$ в момент времени $t_2$. По определению, проекции его скорости ${\bf u}=\{u_x, u_y\}$ в системе $S$ равны $$ u_x=\frac{\Delta x}{\Delta t},~~~~~~~~~~~~~u_y=\frac{\Delta y}{\Delta t},$$ и, аналогично, со штрихами в $S’$. Если скорость объекта постоянна, то значение $\Delta t$ роли не играет. Для движения с переменной скоростью предполагается, что $\Delta t$ сколь угодно мало и скорость является производной координаты по времени.

Из преобразований для приращений (\ref{delta_lorenz}) несложно найти связь между скоростями объекта для наблюдателей в системах $S$ и $S’$: \begin{equation}\label{speed_add0} u’_x =\frac{u_x-v}{1-u_x\,v},~~~~~~~~~~~~~~~u’_y=\frac{u_y\,\sqrt{1-v^2}}{1-u_x\,v}. *$ Запишем при помощи векторных преобразований Лоренца, преобразование для скорости в векторном виде. Разделив $\Delta\mathbf{r}’$ на $\Delta t’$, получаем: \begin{equation}\label{transf_u_vec0} \mathbf{u}’ = \frac{\mathbf{u}-\gamma\,\mathbf{v} + \Gamma\,{\mathbf v}\,({\mathbf v}{\mathbf u})} {\gamma\,(1-\mathbf{u}\mathbf{v})}. \end{equation} При помощи двойного векторного произведения («бац минус цаб»), это преобразование можно переписать в таком виде (см. определение $\Gamma$)): \begin{equation}\label{transf_u_vec} \mathbf{u}’ = \frac{\mathbf{u}-\mathbf{v} + [\mathbf{v}\times [\mathbf{v}\times\mathbf{u}]]\,\Gamma/\gamma }{1-\mathbf{u}\mathbf{v}}. \end{equation} Если скорость системы отсчёта $S’$ параллельна скорости тела, то произведение $\mathbf{v}\times\mathbf{u}=0$ и (\ref{transf_u_vec}) совпадает с одномерным преобразованием скорости вдоль оси $x$ (\ref{speed_add0}).

---

Фундаментальная инвариантная скорость «$c$» является предельно возможной скоростью движения «материального» объекта. В самом деле, пусть наблюдатель в системе $S$ создаёт своего клона и отправляет его в полет со скоростью $v$ (система $S_1$). Первый клон создает второго и «отправляет» его с той же скоростью относительно себя (система $S_2$), и т.д. до бесконечности. В классической физике $n$-тый клон относительно системы $S$ имел бы скорость $u_n=n\,v$, которая при $n\to\infty$ стремилась бы к бесконечности. В релятивистском мире скорость $n$-того и $(n-1)$-го клонов относительно системы отсчета $S$ связаны следующим образом:

$$ u_{n}=\frac{u_{n-1}+v}{1+u_{n-1}\,v} $$

Если протабулировать это соотношение, начиная с $u_0=0$, $v=1/2$, то получится график, приведенный на рисунке справа. Скорость $u_n$ при $n\to\infty$ стремится к $c=1$. Хотя $u_n$ постоянно увеличивается, относительно наблюдателя в $S$ каждая добавка становится всё меньше. При $n\to\infty$ можно положить $u_{n}=u_{n-1}=u_\infty$ и получить асимптотическое значение, не зависящее от $v$: $u_\infty = (u_\infty + v)/(1+u_\infty \,v),$ откуда $u_\infty = 1. n},~~~~~~~~~~~~w=\frac{1-v}{1+v}

Кроме мысленного эксперимента с клонами, существуют также веские энергетические причины предельности скорости «$c$», которые также рассматриваются чуть позже.

ЗАКОНЫ СЛОЖЕНИЯ СКОРОСТЕЙ | Наука и жизнь

Наука и жизнь // Иллюстрации

Схема эксперимента итальянских физиков, который якобы продемонстрировал распростране ние радиоволны в воздухе со сверхсветовой скоростью.

‹

›

Невозможность передать сигнал со сверхсветовой скоростью непосредственно следует из эйнштейновской формулы сложения скоростей — релятивистской формулы (от англ. relativity — относительность). Задача о сложении скоростей возникает при наличии двух движущихся одна относительно другой инерциальных (то есть движущихся равномерно и прямолинейно) систем отсчета. Состоит она в следующем: если движение некоторого тела или распространение сигнала происходит со скоростью V‘ в системе S‘, движущейся в том же направлении относительно системы S со скоростью U, то какова будет скорость V тела (сигнала) для наблюдателя, покоящегося в системе S? В классической кинематике ответ прост: V = V‘ + U. Например, если поезд (система S‘) движется относительно платформы (системы S) со скоростью U = 60 км/ч, а в поезде бежит человек в направлении движения поезда со скоростью V ‘ = 10 км/ч, то скорость перемещения человека относительно платформы будет V = 10 + 60 = 70 км/ч. Релятивис тская же формула сложения скоростей выглядит следующим образом:

V = (V‘ + U)/(1 + V‘U/c²). Когда величина скоростей V‘ и U значительно меньше c (что обычно бывает в привычных нам земных условиях), она переходит в обычную формулу классической механики. Нетрудно также убедиться, что даже если V‘ = c, то и V = c, то есть ни в какой инерциальной системе невозможно движение со скоростью, превышающей скорость света в вакууме.

СВЕРХСВЕТОВАЯ РАДИОВОЛНА

В эксперименте Д. Мугнаи, А. Ранфагни и Р. Руггери измерялось время распространения прямоугольных импульсов, которыми модулировались радиоволны длиной 3,5 см на дистанциях от 0,3 до 1,4 м при двух различных значениях угловой ширины 2q выходящего из передающей антенны радиолуча (32^о и 46^о). Экспериментаторы считают, что скорость распространения V подчиняется соотношению V = c/cos, и поскольку cos меньше единицы, то V > c. Заметим, что приведенное соотношение хорошо известно в волноводной технике и выражает собой фазовую скорость распростра нения электромагнитного поля в волноводе, а групповая скорость равна произведению с.cosq, которое меньше с. В воздухе же для радиоволн сантиметрового диапазона дисперсия практически отсутству ет, то есть V_гр=V_ф =V. Вот для этого случая авторы и получили значение V > с. Однако внимательный анализ этого эксперимента порождает большие сомнения в корректности вывода авторов. Не вдаваясь в подробности, отметим лишь, что полученный ими результат относится к так называемой ближней зоне, где сильно проявляется дифракция на краях зеркала передающей антенны. Это существенно искажает измерения и приводит к тому, что, вообще говоря, можно получить самые разные результаты. При удалении же от ближней зоны (уже на расстоянии 1,2-1,3 м от передающей антенны), как следует из графиков, приводимых в статье, получается V=c.

Статья об эксперименте с подробным его описанием опубликована в выпуске журнала Physical Review Letters от 22 мая 2000 года (т. 84, № 21).

См. в номере на ту же тему

Доктор технических наук А. ГОЛУБЕВ — Возможна ли сверхсветовая скорость?

дополнительных трюков для увеличения скорости | Бретт Берри | Математические лайфхаки

Серия математических вычислений в уме, часть 2

Сегодня мы рассмотрим несколько простых методов, которые помогут улучшить вашу способность складывать числа в уме. Давайте начнем наш урок с некоторых специальных пар чисел.

Q: Что общего у этих пар чисел?

A: Все они добавляют к 10.

Это может показаться очевидным, но это важный первый шаг. Мы будем использовать эти пары чисел для тестов и методов перегруппировки. Поэтому всякий раз, когда вы видите одну из этих пар, я хочу, чтобы вы автоматически думали «10».

При сложении однозначного числа с другим числом мне нравится использовать метод эталонных показателей. Тест — это удобное число, которое мы можем использовать в качестве точки отсчета в середине проблемы, обычно кратное десяти.

Предположим, мы хотим сложить 15 + 8.

Мы будем использовать число 20 в качестве эталона, поэтому разобьем 8 на 5 + 3.

Объедините сначала 15 + 5, чтобы получить наш контрольный показатель 20.

Затем завершите сложение.

Давайте попробуем решить другую задачу, используя эталонные тесты.

В этой задаче 70 будет эталоном, так как это следующее кратное десяти после 63. Нам нужно добавить 7 к 63, чтобы получить эталон 70. Итак, разбейте 9 на 7 + 2 и добавьте их в время.

Теперь мы тест.

Наконец, добавьте 2.

Другой пример:

В этой задаче 120 является эталоном.Поскольку 7 + 3 = 10, разобьем 6 на 3 + 3.

Чтобы решить эту задачу, мы разобьем числа по разрядности. Помните, что десятичная система разрядов — это структура под каждым числом.

Двенадцать соответствует 1 десятку и 2 единицам, а восемьдесят восемь соответствует 8 десяткам и 8 единицам. Используя разрядные значения, мы можем представить сложение в развернутом виде.

Сложение коммутативно , что означает, что мы можем изменить порядок, не меняя ответа. Это позволяет нам перемещать числа по мере необходимости.

Сгруппируйте десятки и единицы соответственно.

Примечание 8 + 2 = 10.

Теперь вы можете считать на десятки.

Конечно, это не единственный способ разбить числа. Мы также можем отрезать 2 от 12 и сначала добавить их к 88.

Или мы могли бы отколоть 8 от 88 и объединить сначала с 12.

Не существует «правильного» или лучшего способа разбить числа на части. Просто сочетается с тем, что имеет для вас смысл и кажется наиболее подходящим для данных чисел.

Попробуем еще.

Снова разбейте числа, используя их разрядность.

Используйте свойство коммутативности, чтобы преобразовать их в десятки и единицы.

Объединить десятки и единицы соответственно.

Этот метод использует возможность перераспределения номеров. Математический эквивалент числа «украсть у богатых и отдать бедным». Например, сложим 49 + 86.

Превратим 49 в 50, украв 1 из 86.

Эти числа проще сложить: 50 + 80 = 130 + 5 = 135.

В последнем примере давайте объединим техники.

Начните с разделения сотен.

Затем переставьте члены и добавьте сотни.

Затем украдите 1 из 62 и отдайте 79, чтобы 79 стало 80.

Что эквивалентно расширенной версии:

Теперь я буду добавлять слева направо, сгущая по мере продвижения.

Поэтому

Эти приемы могут показаться громоздкими на бумаге, но когда вы освоите их, вы обнаружите, что можете быстро и эффективно добавлять их в уме.

Следующий урок: Легкие методы вычитания

Спасибо за чтение!

Пожалуйста, нажмите ❤, чтобы сообщить мне, что вы узнали что-то новое!

7 игр для тренировки математических фактов

1. Гонщики на скорость

Что они будут практиковать: Определение нечетных и четных чисел

Что им понадобится: Одна колода карт на пару

Как играть: Учащиеся должны убрать все лицевые карты и разделить колоду пополам.Учащиеся переворачивают карточки одну за другой, чтобы получились две стопки: нечетная и четная. После того, как самый быстрый флиппер кладет свою последнюю карту, он кричит: «Стой!» и его противник замирает. Противник чекает обе стопки. Если обнаружена ошибка, противник может закончить складывать свои карты в стопки, пока она не закончит или не совершит ошибку (после чего она вернется к другому игроку). Игра продолжается до тех пор, пока все стопки не будут правильными, и гонщик не пересечет финишную черту!

2. Бирка для фонарика

Что они будут практиковать: Основные математические факты

Что им потребуется: Классная доска или интерактивная доска, два фонарика (один с цветным целлофаном, обернутым вокруг верхней части, чтобы различать команды)

Как играть:  Перед началом урока запишите несколько чисел на доске (рядом или в случайном порядке). Разделите свой класс на две команды. По одному игроку от каждой команды должны выйти перед классом.Выключите свет и задайте ученикам математическую задачу. Первый учащийся, который фонариком отметит правильный ответ, получает балл для своей команды. Измените эту игру в соответствии со своими потребностями, изменив символы на доске, чтобы они соответствовали тому, что вы изучаете.

3. Вычитание Салют

Что они будут практиковать: Сложение, вычитание

Что им понадобится: Одна колода карт на каждые три ученика (лицевые карты равны 11)

Как играть: Два игрока — «солдаты», а один игрок — «генерал». Раздайте по половине колоды каждому солдату. В начале игры оба солдата приветствуют генерала, поднося одну из своих карт ко лбу (они не могут видеть карту, которую держат, но два других игрока могут).

Генерал (единственный, кто может видеть обе карты) складывает два числа и громко произносит сумму. Затем каждый солдат берет эту сумму, вычитает число, которое держит его противник, и называет значение карты, которое он не может видеть. Тот, кто первым назовет правильный номер, получает обе карточки.Игра заканчивается, когда время истекает или кто-то выигрывает все карты.

4. Подбрасывание монеты

Что они будут практиковать: Значение монет, сложение, вычитание

Что им понадобится: Маленькие ведерки, много монет (фальшивые — хорошо, но настоящие веселее!)

Как играть : Расставить ведра под доской. Примерно в шести футах от доски, полосы на полу. Разделите учащихся на группы по четыре человека и дайте каждой команде по мешку, полному монет номиналом в один доллар (две четверти, три десятицентовика, два пятака и десять пенни подойдут).

Когда вы говорите «иди», ученики первой линии бросают монеты одну за другой в ведро своей команды. Когда первый игрок делает это, он пишет количество монет на доске, и следующий человек в очереди бросает. Если она получает монету в ведре, она добавляет сумму к сумме на доске. Если она промахивается, она поднимает его, вычитает и идет в конец строки. (Следующему игроку не разрешается бросать, пока не будут подсчитаны числа.) Побеждает команда, первой набравшая доллар!

5.Двойной пух

Что они будут практиковать: Добавление двойников

Что им понадобится: Два игральных кубика, один лист бумаги и один карандаш на ученика

Как играть: Попарно рассчитайте учеников так, чтобы каждый раунд игры длился пять минут. Когда вы говорите: «Бросьте их!» каждый бросает два своих кубика одновременно. Каждый раз, когда кто-то выбрасывает удвоение, он говорит: «Удвоить ставку!» Оба ученика в этой паре должны прекратить броски, затем сложить значение костей и записать сумму под именем игрока, который ее бросил.

Пока игра продолжается, учащиеся отслеживают оба набора очков. Побеждает тот, кто наберет больше всего очков по истечении пяти минут.

 

6. Слэм Десять

Что они будут практиковать: Сложение кратных 10

Что им понадобится: Одна колода карт на пару

Как играть: Удалите лицевые карты и раздайте каждому игроку половину оставшихся карт. По очереди игроки переворачивают карты лицом вверх одну за другой. Когда открывается первая карта, оба игрока умножают указанное число на 10 и произносят значение вслух.Например, если кто-то переворачивает тройку треф, обе говорят: «Тридцать».

Игроки продолжают переворачивать карты по одной, всегда прибавляя значение, умноженное на 10, и произнося это вслух. Например, если следующей картой была четверка червей, они оба сказали бы «Семьдесят», потому что 30 плюс 40 равно 70.

Каждый раз, когда общее значение карт достигает 50, 100, 150 и т. д., любой из игроков может «хлопнуть» по колоде рукой. Самый быстрый слэммер сохраняет все карты. Когда время истекло, каждый игрок подсчитывает стоимость своих карт в десятках (не количество карт!), чтобы определить победителя.

7. Петарда

Что они будут практиковать: Сложение, вычитание

Что им понадобится: Две колоды карточек, один шумодав

Как играть: Расставьте учеников по прямой линии. Определите, где находится середина линии. Вот тут-то и взорвется «фейерверк». Поместите туда маракасу, трещотку или что-нибудь, что производит шум.

Теперь вы и еще один ученик начинаете на противоположных концах очереди и показываете карточки участникам.Когда факты даны правильно, учащиеся садятся и игра переходит к следующему игроку на «предохранителе». Когда последний человек (ближайший к петарде) отвечает правильно, он включает шумогенератор, объявляя о победе своей команды.

В эту игру также можно играть с несколькими предохранителями меньшего размера для еще более захватывающего взрыва!

Подключено: практика математики онлайн

• Математические игры Мэгги
  В этих двух интерактивных играх дети могут помочь исследователю Мэгги путешествовать по миру или спасти ее пса Чувака, используя сложение, вычитание, умножение или деление.(Выберите, что вы хотите, чтобы дети практиковали).
  
• Математические приключения Макса
  Предложите детям прослушать сценарий с участием Макса и его друзей, а затем попрактиковаться в соответствующих математических понятиях, начиная от фигур и заканчивая простым построением графиков. Идеально подходит для интерактивной доски!

Добавление релятивистской скорости. Почему, даже подведя относительные… | by Ujjwal Singh

Необходимость специальной теории относительности

Главной заботой физиков конца 19 века было выяснить, в какой среде распространяются световые волны. Тогда было немыслимо, чтобы волна могла распространяться в отсутствие какой-либо среды. Итак, физики выдвинули гипотезу о среде, которая пронизывает всю Вселенную и несет световые волны — эфир . Естественно, первым препятствием было — доказать, что эфир действительно существует!

Ранее физики полагали, что для распространения световых волн требуется среда, и назвали ее Эфир . Фото Кейси Хорнер на Unsplash.

Были проведены многочисленные опыты по установлению присутствия эфира.Ключевым фактом, использованным в этих экспериментах, было то, что «скорость световых волн была бы c в системе отсчета эфира, но изменялась бы в системах отсчета, движущихся относительно эфира». Чтобы объяснить это схематически, предположим, что эфир покоился относительно земли. Тогда верны следующие сценарии —

Случай 1: Когда наблюдатель покоится относительно эфира. Случай 2: Когда наблюдатель движется против эфира.

Самым известным среди этих экспериментов был эксперимент Майкельсона-Морли, проведенный в 1887 году. Его результат был глубоко поразительным! Эксперимент фактически отбросил возможность существования эфира, установив тот факт, что скорость света остается неизменной в каждой инерциальной (неускоренной) системе отсчета . Излишне говорить, что это был один огромный результат для переваривания!

Это означало, что скорость света остается неизменной даже для наблюдателей, находящихся в движении относительно друг друга, что было немыслимо на тот момент времени, ибо нарушает классическое галилеевское уравнение преобразования скорости! Давайте разберемся с этим на примере —

Случай 1: И A, и B покоятся относительно Земли.Здесь, как и ожидалось, оба видят световую волну, приближающуюся к ним со скоростью c. Случай 2 (i): A покоится относительно Земли, а B движется со скоростью 0,2c против набегающей световой волны. Здесь, в соответствии с добавлением скорости Галилея, B должен видеть световую волну, приближающуюся со скоростью (c + 0,2c) = 1,2c. Случай 2 (ii): Однако в действительности B также видит световую волну, приближающуюся только со скоростью c, независимо от ее относительное движение!

Итак, как это возможно? Разумеется, господствовавшая в то время теория превращений Галилея не имела на это ответов. Эта теория, как и следовало ожидать читателю, носила интуитивный характер и требовала, чтобы скорости складывались, когда наблюдатель движется против наблюдаемого объекта. Но, согласно вышеизложенному, кажется, что преобразования Галилея не работают, по крайней мере, когда рассматриваемый субъект является светом.

Прежде чем двигаться дальше, давайте подробно рассмотрим, как преобразования Галилея работают для самых простых случаев — когда у нас есть две параллельные системы отсчета, движущиеся с постоянной скоростью относительно друг друга.

Допустим, кадры промаркированы —

• S — (x, y, z, t)
• S’ — (x’, y’, z’, t’)

Также, предположим (ради простоты), что два кадра совпадают в t = t’ = 0 . И S’ движется со скоростью v вправо от S (или S движется со скоростью v влево от S’). Если представить это схематически —

Два кадра совпадают в момент времени t = t’ = 0. В общий момент времени показано, что S’ движется вправо от S со скоростью v. Или, альтернативно, мы можем сказать, что S движется со скоростью v влево от S’.

Теперь классические (галилеевские) уравнения преобразования координат задаются формулой —

. В этот момент читатель может удивиться, почему мы явно назвали последнее равенство, т. е. t’ = t . Разве это не очевидно? Оказывается, это не так, как мы скоро увидим!

Но перед этим давайте посмотрим, как приведенный выше набор преобразований подразумевает, что наш наблюдатель B (на рисунках выше) должен измерить скорость света как 1.2в. Для этого заметьте, что мы можем представить, что наблюдатель А находится в состоянии покоя в кадре S, а В — в состоянии покоя в кадре S’. Здесь у нас есть v = 0,2c . Теперь —

Здесь мы добавили отрицательный знак к c , потому что световая волна распространяется в отрицательном направлении x. Продолжая, получаем —

То есть согласно преобразованиям Галилея наблюдатель Б должен измерить скорость света как 1,2с. Конечно, это несовместимо с упомянутыми выше экспериментальными данными о том, что скорость света остается одной и той же для каждого наблюдателя, независимо от его/ее движения.

Таким образом, классические уравнения преобразования явно не могут объяснить инвариантность скорости света. Вот почему нужна была новая теория — такая, которая согласовывалась бы с экспериментальными истинами.

Вступай, специальная теория относительности!

Контрольные математические факты: почему важна скорость письма

Упражнения по математике используются, чтобы помочь учащимся усвоить основные математические факты с однозначными числами. Цель состоит в том, чтобы помочь учащимся ответить на основные математические факты из памяти и развить автоматизм.Единственный способ узнать, вспоминает ли учащийся ответ, а не выясняет его, — использовать математические упражнения в качестве эталона. Но ученики не могут научиться вспоминать целую страницу математических фактов, тренируя их. Упражнения, вероятно, вызовут беспокойство и разочарование у студентов. Вот несколько распространенных ошибок, которых следует избегать при обучении студентов основным фактам, касающимся однозначных чисел.

Распространенные проблемы с математическими тестами

Школы обычно устанавливают «контрольные показатели» для оценки того, достигли ли учащиеся своих образовательных целей.Когда дело доходит до запоминания математических фактов, школы устанавливают контрольные точки, чтобы отличить знание ответов путем быстрого припоминания от медленного процесса выяснения фактов. У этих тестов есть две основные проблемы.

Учились по одному.

Первая проблема заключается в том, что математические факты изучаются индивидуально, и учащиеся решают одну задачу за раз. Контрольный показатель должен заключаться в том, чтобы решить проблему менее чем за секунду. Если бы они могли, то было бы ясно, какие математические факты студент запомнил, а какие нет. В школах чаще проводят тесты по всем фактам операции, и эти тесты не могут сказать школам, какие факты запоминаются. Более содержательным отчетом было бы то, какие факты в операции студент может ответить мгновенно.

 

Время написать ответ.

Вторая основная проблема заключается в том, что как бы хорошо учащиеся ни знали факты, они не могут писать ответы на факты быстрее, чем пишут. Учащиеся начальной школы различаются по скорости и могут писать ответы от 10 до 50 ответов в минуту.Если учащийся может ответить на 40 задач в минуту, он достиг мастерства в математических фактах. Но если они не могут писать ответы так быстро, они не могут соответствовать требованиям своей школы. Чтобы установить разумный стандарт, учителя должны знать, насколько быстро учащиеся могут писать, и тест на скорость письма поможет определить это.

Общее базовое знание математических фактов не должно вызывать страданий

Общая основная идея гласит, что учащиеся должны быстро запоминать математические факты, чтобы успешно продвигаться по математике. Почему-то почти все дети запомнили 2+2=4 и могут ответить на эту задачу по памяти. Это не напряжно, не сложно и не вызовет математической фобии. Итак, мы знаем, что научиться решать математическую задачу мгновенно по памяти выполнимо, и это можно сделать без стресса. Сложность в том, что есть много фактов, которые нужно изучить, но, если брать их понемногу, все они могут быть изучены одинаково легко.

Однако для этого требуются систематические усилия, ежедневная практика и тщательный контроль.Учителям нужна какая-то программа по сбору фактов, чтобы помочь ученикам запоминать большое количество фактов. До разработки принципов проектирования, лежащих в основе Rocket Math, я думал, что это почти невыполнимая задача. Но за последние 20 лет я видел, как Rocket Math успешно использовался для обучения студентов математическим фактам. Имея достаточно времени, терпения и поддержки, учащиеся могут научиться вспоминать математические факты по памяти, а с помощью Rocket Math они могут делать это, развлекаясь.

Тест скорости письма по математике

 Тест скорости письма для Rocket Math

Вот простой и удобный в использовании тест на скорость письма, который поможет выяснить, насколько быстро учащийся может ответить, когда он запоминает все факты операции.Тест представляет собой смесь однозначных и двузначных чисел, поэтому он работает со сложением и умножением.

Просто дайте тест своим ученикам и попросите их в течение одной минуты написать числа, которые они видят в каждой клетке. Вы сможете узнать, сколько ящиков они могут заполнить за одну минуту. Это число является верхним пределом задач по математике, на которые вы можете ожидать, что они смогут ответить, если они отвечают на припоминание, а не на их вычисление.

Скорость записи определяется количеством заполненных ящиков.  

Когда учащийся закончит тест, у вас будет количество коробок, которые он может заполнить за минуту. Вы можете ожидать, что учащийся сможет закончить не менее 80% этого числа, если он сможет мгновенно вспомнить факты. Если студент может ответить на 90%, ему не нужна работа с фактами. Если они составляют от 80 до 90% от этого числа, они хороши, но больше фактов поможет им. Что-нибудь ниже 80%, и они должны остановиться, чтобы выяснить некоторые факты и нуждаются в дополнительной работе.

Если вам не интересно снова и снова заниматься математикой, вот таблица целей для предварительных тестов, в которой цифры рассчитаны для вас. Вы можете распечатать его по этой ссылке.

Контрольные показатели должны основываться на скорости записи.  

Контрольные показатели, не учитывающие скорость, с которой дети могут писать, оставляют у многих детей невыполнимые ожидания. Просьба детей сделать что-то, на что они физически не способны, вызовет много ненужных страданий.

 

 

Тесты по математике для детского сада

Учеников следует учить правильно и эффективно писать числительные в детском саду. Способы рисования цифр, которые дети изобретают самостоятельно, могут быть медленными, громоздкими и неэффективными, что впоследствии приводит к снижению скорости письма.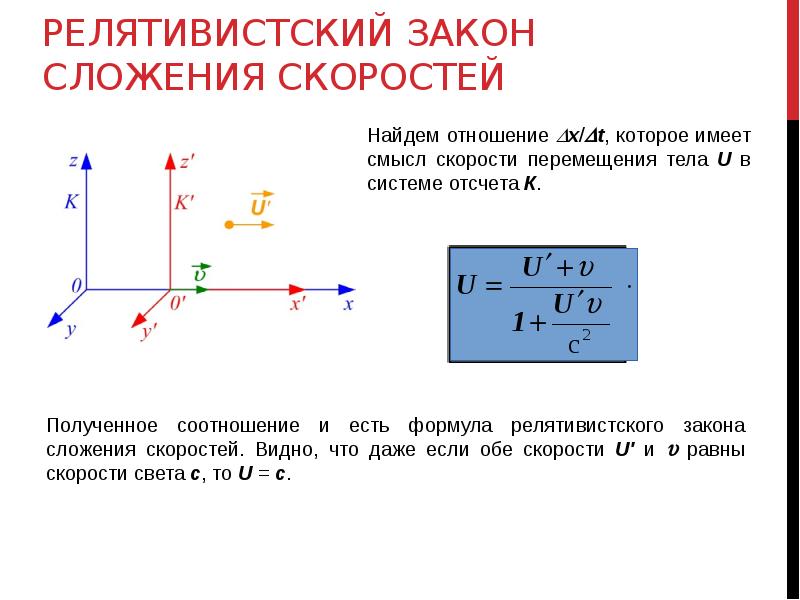 Rocket Math Writing for Numerals — это систематический метод, который поможет учащимся научиться составлять свои числительные. Контрольные показатели для дошкольников должны быть сосредоточены на скорости написания числительных, что требует большого количества практики и обучения.

Показатели беглости письма в детском саду (цифры)

• • Середина года       
    • 20 цифр в минуту        
  • Конец года     
    • 40 цифр в минуту        

Тесты по математике для первоклассников

Первоклассники должны свободно писать числительные.Не каждый детский сад делает это, поэтому учителя должны тестировать и давать какую-то программу для письма с цифрами ученикам, которые не соответствуют этим стандартам письма.

Контрольные показатели беглости письма для первого класса (цифры)

• • Начало года   
    • 40 цифр в минуту               
  •   Середина года    
    • 60 цифр в минуту                        
  •   Конец года     

Мы также хотим, чтобы первоклассники научились добавлять факты к уровню мгновенного запоминания. Скорость письма учащегося — это количество клеток, которые он может заполнить за одну минуту.

Контрольные показатели беглости чтения математических фактов для первого класса (задачи)

• • Начало года   
    • Дополнение 20% от скорости записи   
  •   Полугодие  
    • Добавление 40% скорости записи    
  • Конец года  
    • Добавление 80% скорости записи  
    • Вычитание 20 % скорости записи

Тесты по математике для второго класса

Во втором классе мы хотим, чтобы учащиеся освоили не только сложение, но и вычитание.

• • Начало года  
    • Добавление 80% скорости записи  
  • Середина года
    • Добавление 80% скорости записи
    • Вычитание 40% скорости записи
  • Конец года
    
    • Добавление 80% скорости записи
    • Вычитание 80% скорости записи

Тесты по математике для третьего класса

В третьем классе важно, чтобы учащиеся освоили вычитание и начали работать над умножением.

• • Начало года
    • Добавление 80% скорости записи  
    • Вычитание 80% скорости записи
  • Середина года
    • Добавление 80% скорости записи
    • Вычитание 80% скорости записи
    • Умножение 40% от скорости записи
  • Конец года  
    • Добавление 80% скорости записи  
    • Вычитание 80% скорости записи
    • Умножение 80% скорости записи

Тесты по математике для четвертого класса

В четвертом классе учащимся важно освоить умножение и начать деление.

• • Начало года
    • Добавление 80% скорости записи
    • Вычитание 80% скорости записи
    • Умножение 80% скорости записи
  • Середина года
    • Добавление 80% скорости записи
    • Вычитание 80% скорости записи
    • Умножение 80% скорости записи
    • Деление 40% от скорости записи
  • Конец года
    • Добавление 80% скорости записи  
    • Вычитание 80% скорости записи
    • Умножение 80% скорости записи
    • Деление 80% скорости записи

Тесты математических фактов для пятого класса (и выше)

В пятом классе важно, чтобы учащиеся усвоили основные математические факты, а также сложение, вычитание, умножение и деление.

• • Начало года  
    • Добавление 80% скорости записи  
    • Вычитание 80% скорости записи
    • Умножение 80% скорости записи
    • Деление 80% скорости записи
  •  
  •  
  • Середина года  
    •   Добавление 80% скорости записи
    • Вычитание 80% скорости записи
    • Умножение 80% скорости записи
    • Деление 80% скорости записи  
  • Конец года
    • Добавление 80% скорости записи
    • Вычитание 80% скорости записи
    • Умножение 80% скорости записи
    • Деление 80% скорости записи                      

Все 1-минутные предварительные тесты, тесты на скорость письма и лист целей можно найти на этой странице https://rocketmath.com/предварительные тесты/.

 

 

 

 

 

 

 

 

 

 

 

 

 

Ракетная математика — увлекательный способ изучения учащимися

Rocket Math использует систематический подход к обучению учащихся тому, как свободно владеть основными математическими фактами и при этом получать удовольствие от изучения математики. Математика может показаться сложной для изучения, и если ее не преподавать должным образом, используя хорошую математическую программу, у учащихся может развиться математическая фобия.Учителя используют Rocket Math уже более 20 лет и считают его бесценным инструментом, помогающим их ученикам изучать математику.

 

Подпишитесь на нас и поставьте лайк:

Фрукты10

Хватай десятки бананов!

Положите колоду круглых карт лицевой стороной вверх в центр стола — это кладовая с разноцветными грушами, бананами, ананасами и клубникой. Игроки превращаются в подлых енотов и ежей, задача которых — украсть со склада как можно больше кусочков фруктов.Выбирая фрукты по их типу или цвету, вам нужно найти число на вашей карточке и число на карточке склада, которые в сумме составляют ровно 10 (в сумке есть место для 10 штук). Само собой разумеется, что это должно быть сделано как можно быстрее!

Развлечение для всех!

Эта игра предназначена для развития навыков сложения скорости, внимательности и концентрации внимания и никого не оставит равнодушным! Правила предлагают несколько вариантов игры, которые могут быть очень простыми или довольно сложными.

Например, в версии под названием «три пятнадцать» игроки должны составлять комбинации, используя как сложение, так и вычитание. При этом требуемая комбинация меняется с 3 до 15 с каждым игровым ходом с шагом в единицу. Эта постоянная смена условий игры стимулирует енотов к сверхбыстрому мышлению и делает игру в хорошем смысле увлекательной и напряженной.

Карточки оригинально проиллюстрированы — мы уделяем этому процессу много времени и сил! Карты изготовлены из плотного переплетного картона и ламинированы полимерной пленкой.Вы можете играть где угодно и когда угодно — испачканные карты легко очищаются влажными салфетками.

«Фруи5» для детей младшего возраста

В набор входят дополнительные 15 карточек для игры с детьми младшего возраста. На этих карточках есть фрукты с цифрами от 1 до 4. Правила игры такие же, как и для «Frui10», только вместо суммы 10 нужно искать сумму 5.

Содержимое:

• 35 карт для игры Frui10,
• 15 карточек для игры Frui5,
• Иллюстрированные правила игры.

 

Еще одна игра для развития навыков сложения и вычитания — Numberloor. Эта красивая и увлекательная игра поможет вашему ребенку освоить процесс счета в уме.

 

Добавление скорости: подход слева направо

Большинство из нас учат считать на бумаге справа налево. И это нормально для математических расчетов на бумаге. Но если мы хотим посчитать в уме (даже быстрее , чем на бумаге), есть много веских причин, почему лучше работать слева направо.В конце концов, мы читаем числа слева направо, мы произносим числа слева направо, поэтому более естественно думать (и вычислять) числа слева направо. Когда мы вычисляем ответ справа налево (как мы, вероятно, делаем на бумаге), мы генерируем ответ в обратном порядке. Вот почему нам так трудно производить математические расчеты в уме.

Кроме того, если мы хотим оценить наш ответ, важнее знать, что наш ответ «чуть больше 1200», чем знать, что ответ «оканчивается на 8».Таким образом, работая слева направо, мы начинаем со старших цифр нашей задачи. Если мы привыкли работать на бумаге справа налево, работа с числами слева направо может показаться неестественной. На самом деле наш мозг уже запрограммирован на решение математических задач слева направо; мы потратили годы на чтение слева направо, верно? Но с практикой вы обнаружите, что это самый естественный и эффективный способ вычислений в уме.

С первым набором задач — сложением двух цифр — метод слева направо может показаться не таким выгодным.Но будьте терпеливы. Если вы будете придерживаться его, вы увидите, что единственный простой способ решения трехзначных и более крупных задач на сложение, всех задач на вычитание и, безусловно, всех задач на умножение и деление — слева направо. Чем раньше вы привыкнете к таким вычислениям, тем лучше.

Самые простые задачи на сложение двух цифр — это те, которые не требуют от вас переноса любых чисел, когда сумма первых цифр равна 9 или меньше, а сумма последних цифр равна 9 или меньше.Например:
               45

           +  34  

                ?

Обычно вы сначала суммируете 4 до 45, а затем прибавляете к результату 30. Но, используя подход слева направо, вы сначала суммируете 30 до 45, а затем добавляете к результату 4. После добавления 30 у вас есть более простая задача 75 + 4, что равняется 79.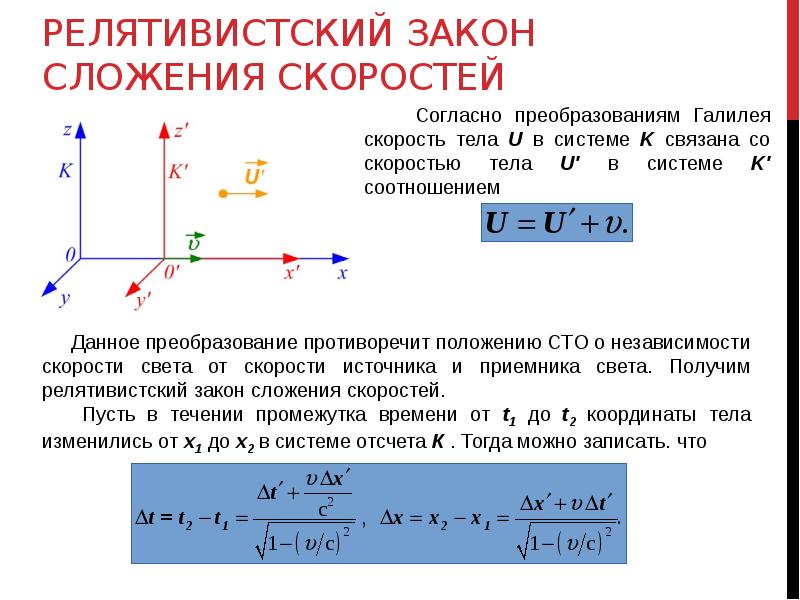

Давайте проиллюстрируем это следующим образом:

45 + 34 = (45 + 30=>) 75 + 4 = 79

(сначала добавьте 30)                (затем добавьте 4)

Хотя этот пример очень прост, вы увидите преимущества этого метода, когда начнете его использовать.

Теперь давайте попробуем рассчитать, для чего вам нужно иметь при себе число:

.

  84

+   57         => 84 + 57 = (84 + 50=>) 134 + 7 = 141

              ? (сначала добавьте 50)                    (затем добавьте 7)

Так как 57 = 50 + 7, вы сначала суммируете 84 с 50, а затем добавляете к результату 7.

Если вы работаете с трехзначными числами, процесс такой же.После каждого шага вы приходите к новой (и более простой ) задаче на сложение. Давайте попробуем следующее:

  759

      + 237    

            ?

Этот пример немного сложнее предыдущего, но его очень легко решить, используя подход слева направо.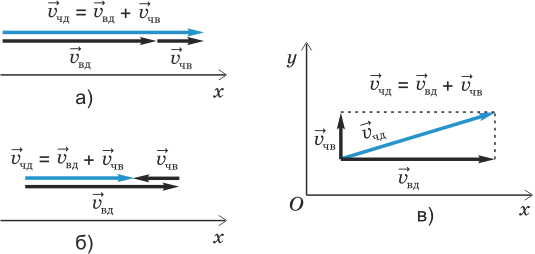 Начиная с 759, мы прибавляем 200, затем прибавляем 30, затем прибавляем 7. После прибавления 200 (759 + 200 = 959) задача становится 959 + 37.После прибавления 30 (959 + 30 = 989) задача упрощается до 989 + 7 = 996. Этот мыслительный процесс можно представить следующим образом:

759 + 237    =    959 + 37       =    989 + 7          =   996

(сначала добавьте 200)        (затем добавьте 30)         (в конце добавьте 7)

Все задачи на умственное сложение можно решить с помощью этого метода. Цель состоит в том, чтобы продолжать упрощать задачу до тех пор, пока вы просто не добавите однозначное число. Обратите внимание, что 759 + 237 требует, чтобы вы удерживали в уме шесть цифр, тогда как 959 + 37 и 989 + 7 требуют только пяти и четырех цифр соответственно. Когда вы упрощаете задачу, она становится проще!

Другой пример:

  858

      + 634    

            ?

858 плюс 634 будет 1458 плюс 34 будет 1488 плюс 4 будет 1492.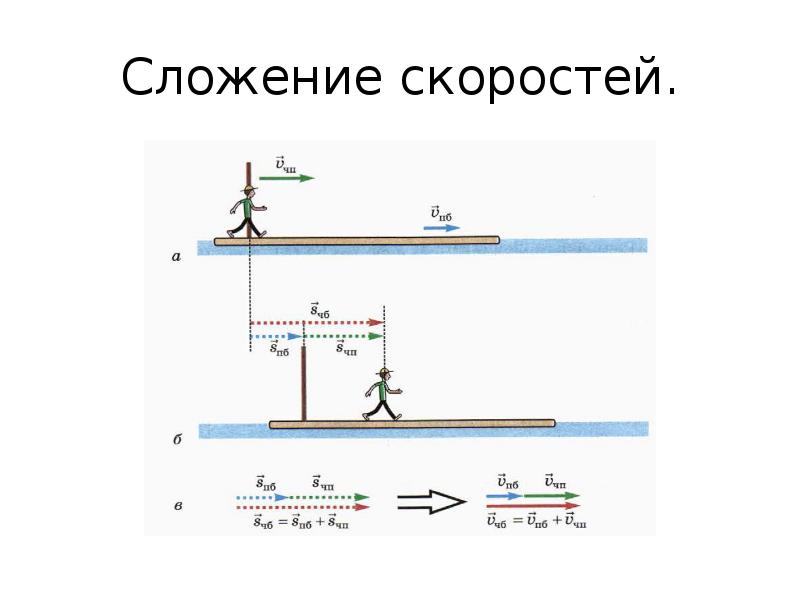

Вы можете разделить и решить таким же образом:

858 + 634 = (800 + 600) + (50 + 30) + (8 + 4) = 1400 + 80 + 12 = 1492

2785

      + 634    

            ?

2785 плюс 634 будет 3385 плюс 34 будет 3415 плюс 4 будет 3419.

Или 2785 + 634 = (2700 + 600) + (80 + 30) + (5 + 4) = 3300 + 110 + 9 = 3419

Пример длинного сложения:

326 + 678 + 245 + 567 = 900, 1100, 1600, 1620, 1690, 1730, 1790, 1804 и 1816

Ищите возможности комбинировать числа, чтобы сократить количество шагов к решению. Это было сделано с 6 + 8 = 14 и 5 + 7 = 12 выше. Ищите возможности составить 10, 100, 1000 и т. д. между числами, которые не обязательно находятся рядом друг с другом.

Если хотите, попрактикуйтесь сами, пока не научитесь мысленно выполнять сложение слева направо.

Проектирование высокоскоростных сумматоров для эффективных цифровых блоков проектирования

Ядром каждого микропроцессора и процессора цифровых сигналов является его тракт данных. Сердцем блоков пути данных и адресации, в свою очередь, являются арифметические блоки, в состав которых входят сумматоры. Сумматоры с параллельным префиксом предлагают высокоэффективное решение проблемы двоичного сложения и хорошо подходят для реализаций СБИС.В этой статье рассматриваются разработка и сравнение высокоскоростных сумматоров с параллельными префиксами, таких как сумматоры Когге-Стоуна, Брента-Кунга, Склански и Когге-Стоуна-Линга. Обнаружено, что сумматор Когге-Стоуна Линга работает намного эффективнее по сравнению с другими сумматорами. Здесь сумматоры Kogge-Stone Ling и сумматоры пульсаций включены как часть решетчатого фильтра, чтобы доказать их функциональность. Видно, что рабочая частота решетчатого фильтра увеличивается при использовании параллельного префиксного сумматора Когге-Стоуна-Линга вместо пульсационных сумматоров, поскольку комбинационная задержка сумматора Когге-Стоуна-Линга меньше.Кроме того, проектирование и сравнение различных структур древовидного сумматора выполняются с использованием как логики КМОП, так и логики шлюза передачи. С помощью этих сумматоров беззнаковые и знаковые компараторы разрабатываются в качестве примера приложения и сравниваются с их рабочими параметрами, такими как площадь, задержка и потребляемая мощность. Проектирование и моделирование выполняются с использованием библиотеки проектирования 65-нм CMOS.

1. Введение

Двоичное сложение является одним из самых примитивных и наиболее часто используемых приложений в компьютерной арифметике.Для бинарного сложения было предложено большое разнообразие алгоритмов и реализаций [1–3]. Структуры дерева сумматоров с параллельным префиксом, такие как Kogge-Stone [4], Sklansky [5], Brent-Kung [6], Han-Carlson [7] и Kogge-Stone с использованием сумматоров Ling [8, 9], могут использоваться для получить более высокие рабочие скорости. Сумматоры с параллельным префиксом подходят для реализации СБИС, поскольку они основаны на использовании простых ячеек и поддерживают регулярные соединения между ними. Целочисленные сумматоры СБИС являются важными элементами процессоров общего назначения и цифровых сигналов, поскольку они используются при разработке арифметико-логических устройств, трактов арифметических данных с плавающей запятой и в устройствах генерации адресов. Кроме того, цифровая обработка сигналов широко использует дополнение при реализации цифровых фильтров либо непосредственно в аппаратных средствах, либо в специализированных процессорах цифровых сигналов (DSP). При целочисленном сложении любое уменьшение задержки будет напрямую связано с увеличением пропускной способности. В нанометровом диапазоне очень важно разработать алгоритмы сложения, обеспечивающие высокую производительность при снижении энергопотребления. Требования к сумматору заключаются в том, что он должен быть в первую очередь быстрым и во вторую очередь эффективным с точки зрения энергопотребления и площади кристалла.Для широких сумматоров () задержка упреждающих сумматоров переноса становится доминирующей задержкой прохождения переноса через этапы упреждения. Эту задержку можно уменьшить, просматривая блоки упреждения вперед. В общем, мы можем построить многоуровневое дерево упреждающих структур для достижения задержки, которая растет с увеличением log . Такие сумматоры по-разному называются сумматорами дерева или сумматорами параллельных префиксов.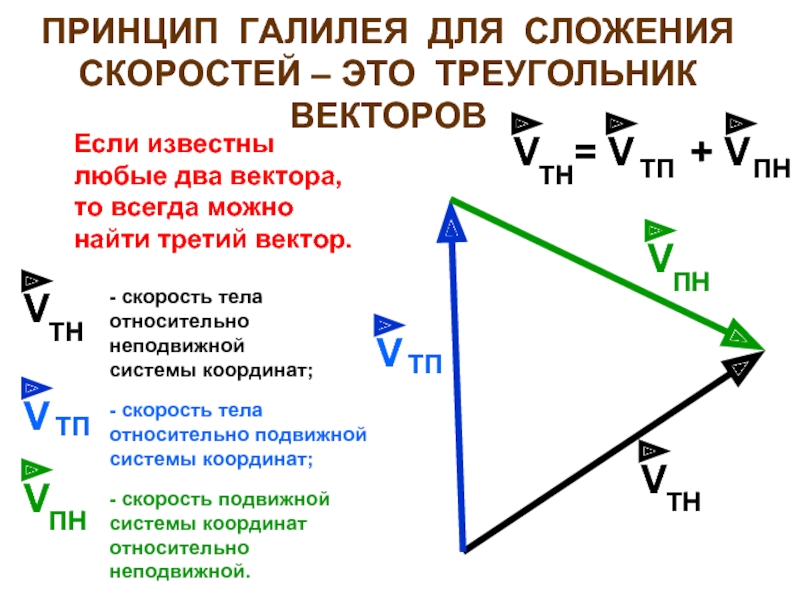 В литературе описано множество параллельных префиксных сетей, особенно в контексте сложения.Классические сети включают сумматоры Брент-Кунга, Склански, Когге-Стоуна и Хана-Карлсона. Основные компоненты сумматоров могут быть разработаны разными способами. Первоначально комбинационную задержку и функциональность можно проверить с помощью HDL, а оптимизацию можно увидеть на уровне архитектуры. На втором уровне оптимизация также может быть достигнута за счет использования в проекте определенных семейств логики. В этой статье компоненты сумматора спроектированы, проанализированы и сравнены с использованием вентилей CMOS и вентилей передачи с использованием файла технологии 130 nm.Это файл глубокой субмикронной технологии. Было представлено несколько вариантов упреждающих уравнений переноса, таких как переносы Линга [9], которые упрощают вычисление переноса и могут привести к более быстрым структурам. Большинство высокоскоростных сумматоров зависят от предыдущего переноса для генерации текущей суммы. 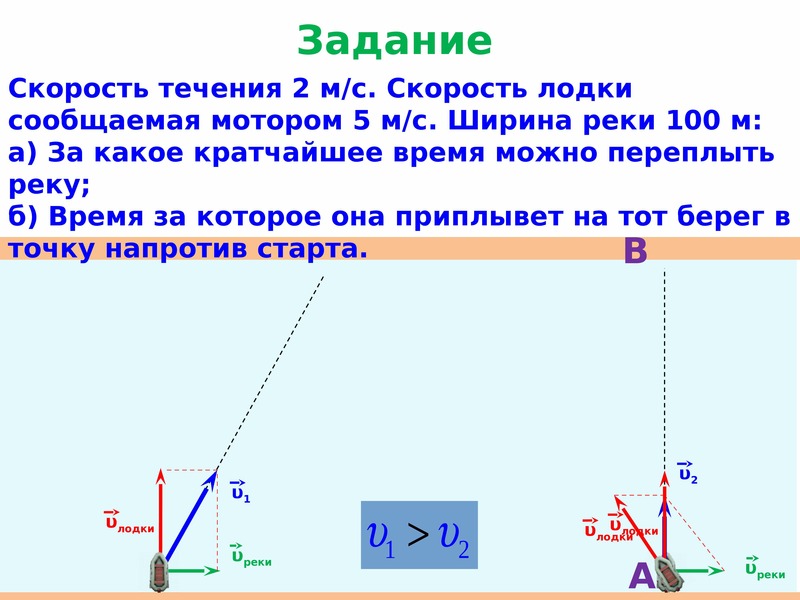С другой стороны, сумматоры Линга [8, 9] используют биты переноса и распространения Линга для вычисления бита суммы. В результате снижается зависимость от предыдущего добавления битов; то есть волновой эффект снижается.В данной статье проводится сравнительное исследование реализации вышеупомянутых высокоскоростных сумматоров. Разрабатывая и внедряя высокоскоростные сумматоры, мы обнаружили, что энергопотребление и занимаемая площадь резко сократились, когда вентили были реализованы с использованием передающих вентилей. Это происходит без ущерба для скорости. Позже в качестве примера приложения, такого как компаратор величин, был разработан сумматор Когге-Стоуна Линга для проверки эффективности.

2. Сумматоры

2.1. Сумматоры с опережением переноса

Рассмотрим -битное сложение двух чисел: и в результате получается сумма, и перенос, . Первый этап в CLA вычисляет генерацию и распространение битов следующим образом: где бит генерируется, а бит распространяется. Схема и использование стиля дизайна КМОП и вентилей передачи показана на рисунке 1.

Затем они используются для вычисления окончательной суммы и битов переноса на последнем этапе следующим образом: где , + и представляют собой операции AND, OR и XOR.Из (2) видно, что первый и последний этапы внутренне быстры, потому что они включают только простые операции над сигналами, локальными для каждой битовой позиции. Однако промежуточные этапы представляют собой распространение переносов на большие расстояния, в результате чего производительность сумматора зависит от этой части [10]. Эти промежуточные этапы вычисляют групповое генерирование и групповое распространение, чтобы избежать ожидания пульсаций, что, в свою очередь, уменьшает задержку. Эти группы генерируют и распространяют Существует много способов разработки этих промежуточных этапов, наиболее распространенным из которых является параллельный префикс.В литературе описано множество параллельных префиксных сетей, особенно в контексте сложения. В этой статье мы использовали реализацию Когге-Стоуна, реализацию Ганса-Карлсона, Склански, Брент-Кунга CLA и реализацию Когге-Стоуна сумматора Линга. Логика PG во всех сумматорах обычно представлена ​​в виде ячеек. Эти диаграммы, известные как диаграммы ячеек, будут использоваться для сравнения различных архитектур сумматоров в следующих разделах. Здесь для реализации всех сумматоров используются две ячейки: серая ячейка и черная ячейка.Основные блок-схемы показаны на рисунке 2.

3. Анализ сумматоров

В этой статье проводится математический анализ сумматоров Линга. Аналогичный анализ можно провести и для всех других сумматоров.

3.1. Реализация Брента-Кунга

Дерево Брента-Кунга вычисляет префиксы для 2-битных групп. Они используются для поиска префиксов для 4-битных групп, которые, в свою очередь, используются для поиска префиксов для 8-битных групп и так далее. Затем префиксы прокручиваются обратно вниз, чтобы вычислить переносы для каждого бита.Для дерева требуется   этапов. Разветвление ограничено двумя на каждом этапе. На диаграмме показаны буферы, используемые для минимизации разветвления и нагрузки на вентили, но на практике буферы обычно не используются. Базовыми блоками, используемыми в этом случае, являются серые и черные ячейки, которые объясняются в разделе 2. Этот сумматор реализован на 8, 16 и 32 бита с использованием логики CMOS и логики вентиля передачи.

3.2. Реализация Sklansky

Дерево Sklansky или по принципу «разделяй и властвуй» сокращает задержку до этапов, вычисляя промежуточные префиксы вместе с префиксами больших групп.Это происходит за счет ответвлений, которые удваиваются на каждом уровне. Ворота разветвляются на , соответственно. Эти высокие разветвления вызывают плохую производительность на широких сумматорах, если только вентили с высоким разветвлением не имеют соответствующего размера или критические сигналы не буферизуются перед использованием для промежуточных префиксов. Размер транзистора может нарушить регулярность компоновки, поскольку требуется несколько размеров каждой ячейки, хотя большие затворы могут распространяться на соседние столбцы.

3.3. Han-Carlson Adder

Деревья Han-Carlson представляют собой семейство сетей между Kogge-Stone и Brent-Kung.Логика выполняет метод Когге-Стоуна для битов с нечетными номерами, а затем использует еще один этап, чтобы перейти к четным позициям.

3.4. Сумматоры Когге-Стоуна

Основным отличием сумматоров Когге-Стоуна от других сумматоров является высокая производительность. Он вычисляет переносы, соответствующие каждому биту, с помощью группового создания и группового распространения. В этом сумматоре логические уровни обозначаются знаком  , а разветвление равно 2.

3.5. Ling Adders

Линг [8] предложил более простую форму уравнений CLA, которые полагаются на соседние пары битов () и ().Наряду с генерацией и распространением битов мы вводим еще один бит префикса, бит половинной суммы, заданный формулой Теперь, вместо использования традиционных переносов, создается новый тип переноса, известный как перенос Линга, где перенос Линга в [11] определяется как где Таким образом, каждый может быть, в свою очередь, представлен Из (5) видно, что Ling-перенос можно вычислить намного быстрее, чем булев перенос. Рассмотрим случай и Если мы предположим, что все входные вентили имеют только два входа, мы увидим, что для вычисления требуется 5 логических уровней, тогда как для вычисления for требуется только четыре. Хотя вычисление переноса упрощается, вычисление суммы битов с использованием переносов Ling намного сложнее. Бит суммы при расчете с использованием традиционного переноса равен Подставляя (5) в (9), получаем, что Однако согласно [12] вычисление битов может быть преобразовано следующим образом: Уравнение (11) может быть реализовано с использованием мультиплексора с линией выбора, которая выбирает либо или ().Переносы Ling не добавляют дополнительную задержку для вычисления суммы, поскольку задержка, генерируемая вентилем XOR, почти равна задержке, генерируемой мультиплексором, и что время, необходимое для вычисления входных данных мультиплексора, меньше, чем время, необходимое для вычисления Ling. нести. В [9] была разработана методология разработки параллельных префиксных сумматоров Линга с использованием алгоритмов Когге-Стоуна [4] и Ноулза [8]. Здесь для -битного сложения Линг переносит и задается выражением где Чтобы объяснить приведенные выше уравнения, рассмотрим перенос 3-го и 4-го Линга, заданный выражением Это можно еще уменьшить, используя (13) к Затем это можно уменьшить, используя оператор «» для Это позволяет параллельно вычислять префикс сумматоров Линга, используя отдельное дерево [9] для четных и нечетных индексированных позиций.Используя эту методологию, мы реализовали 16-битный сумматор с использованием дерева Когге-Стоуна, а затем использовали этот блок для разработки 32- и 64-битных сумматоров. Затем вентили и блоки, используемые для этой реализации, были изменены с помощью вентилей передачи. Ячейки, отличные от серых и черных ячеек, которые используются в качестве компонентов сумматора Линга, и они показаны на рисунках 3 и 4.

Рисунок 3 образует первую ступень сумматора. Он генерирует биты генерации, распространения битов и битов половинной суммы (для сумматоров Линга), то есть , , и , соответственно, которые широко используются на следующих этапах для генерации генерирования и распространения блоков.

Рисунок 5 используется для генерации переноса Ling, который представляет собой не что иное, как генерацию блока. Затем это используется для нахождения последующей группы генерации и распространения с помощью блока, показанного на рисунке 6. на рисунках 7 и 8.

Сумматоры широко используются в составе фильтров. Структуры решетчатых фильтров используются в различных приложениях обработки сигналов, и они рассматриваются в настоящей работе.Блок-схема решетчатого фильтра третьего порядка показана на рисунке 9. Сумматоры пульсаций в решетчатом фильтре заменены сумматором Когге-Стоуна-Линга с использованием экземпляров компонентов в VHDL. Здесь первоначально сумматор Kogge-Stone Ling реализован в VHDL для наблюдения за функциональностью и комбинационной задержкой. Установлено, что комбинационная задержка 32 сумматоров Когге-Стоуна-Линга составляет 12,492 нс, что намного меньше по сравнению с пульсационным сумматором 15,504 нс. Если компоненты с меньшей комбинационной задержкой используются в последовательных схемах, период синхронизации будет уменьшен, что внутренне увеличит тактовую частоту. Обнаружено, что реализация сумматора Линга привела к уменьшению задержки на 15% по сравнению с сумматорами пульсации после синтеза.

Для каскадного решетчатого фильтра, показанного на рисунке 9, с сумматором пульсаций мы получаем следующие результаты после синтеза: (i) минимальный период: 13,058  нс (максимальная частота: 76,579  МГц), (ii) минимальное время поступления на вход перед тактовой частотой : 2,680  нс, и (iii) максимальное требуемое время выхода после тактовой частоты: 21,707   нс. Аналогично для решетчатого фильтра с сумматором Когге-Стоуна-Линга результаты постсинтеза следующие: (i) минимальный период: 11.097  нс (максимальная частота: 90,112  МГц), (ii) минимальное время поступления на вход до тактовой частоты: 2,697   нс и (iii) максимальное требуемое время на выходе после тактовой частоты: 13,476   нс. Следовательно, тактовая частота любых блоков цифрового фильтра увеличивается. если используется сумматор Kogge-Stone Ling. Это может быть использовано для любых цифровых блоков, где требуется высокая скорость работы.

4. Моделирование и результаты

Схема построена для 8-битного и 32-разрядного сумматоров с использованием КМОП и вентилей передачи, как показано на рисунках 10, 11, 12, 13 и 14.В каждой цепи производится измерение мощности, площади и задержки. Это можно сделать, разработав основные компоненты, такие как черные и серые ячейки, с использованием КМОП и вентилей передачи. Параметры производительности получены для всех этих файлов с использованием 65-нм технологии, и различные параметры производительности сравниваются для сумматоров, использующих вентили CMOS, и сумматоров, использующих вентили передачи. Результат Резюме всех дополнений приведен в Таблице 1.

9112 9112 81125 Количество битов CMOS Logic Логическая логика Область (нет транзисторов) Power в W Задержка в SEC Область (нет транзисторов) 13 м 432 1,8799 м 16 1140 7,694 м тысячи пятьдесят-шести 5,2718 м 32 2658 13,648 м 2345 10. 314 м 7 8 415 415 17.88 м 323 8.92 м 16 1047 36,34 м 763 18,73 м 32 2199 65,13 м 1659 40,2 м Brent-Kung 8 598 0. 18 470 0.13 16 1126 9119 1268 0.4 1012 0,3 32 2494 12,5 1982 0,614 Хан-Карлсона 8 440 10.81 м 312 1.9178 m 16 992 992 13,54 м 736 6. 411 м 32 2208 13,99 м 1696 9,825 м Лин 8 742 0,313 530 0.139 16 1655 0.6 1250 0.3104 32 3382 13.3 м 2690 0,4105

5.

Пример применения

Здесь знаком и без знака величины компаратора [13, 14 ] разработан с использованием сумматора Kogge-Stone Ling. Компаратор величин определяет большее из двух двоичных чисел. Чтобы сравнить два числа без знака и , вычислите . Если есть перенос, ; в противном случае, .Детектор нуля указывает, что числа равны. На рис. 15(а) показан 8-битный беззнаковый компаратор, построенный из сумматора пульсаций переноса и двух блоков дополнения. Относительная величина определяется из сигналов переноса (C) и нуля (Z). Для более широких входов можно использовать любую из более быстрых архитектур сумматора. На рис. 15(b) показан 8-битный компаратор со знаком. Сравнение двух дополнительных чисел со знаком немного сложнее из-за возможности переполнения при вычитании двух чисел с разными знаками.Вместо того, чтобы просто проверять перенос, мы должны определить, является ли результат отрицательным (N, на что указывает старший бит результата) и выходит ли он за пределы диапазона возможных чисел со знаком. Сигнал переполнения V истинен, если входы имели разные знаки (старшие значащие биты), а выходной знак отличается от знака . Фактический знак разницы — XOR V, потому что переполнение меняет знак. Если этот скорректированный знак отрицательный (), мы знаем, что . Опять же, другие отношения могут быть получены из скорректированного знака и сигнала Z.Сигнал переноса также используется здесь для целей сравнения. Сумматор Когге-Стоуна-Линга как базовый блок компаратора работает намного лучше, так как его комбинационная задержка меньше.

6. Выводы

Из приведенной выше работы видно, что тактовая частота для БИХ-фильтра с использованием сумматора Линга была больше, чем тактовая частота для того же БИХ-фильтра с использованием простого сумматора пульсаций. Было обнаружено, что задержка комбинационного пути для сумматора Линга на 15% меньше, чем для сумматора пульсаций.Использование вентилей передачи уменьшило площадь сумматора и, следовательно, компаратора, построенного с использованием сумматора, по сравнению с площадью, потребляемой при использовании логики CMOS для реализации.