| 1 | Найти производную — d/dx | квадратный корень x | |
| 2 | Найти производную — d/dx | натуральный логарифм x | |
| 3 | Вычислить | интеграл натурального логарифма x по x | |
| 4 | Найти производную — d/dx | e^x | |
| 5 | Вычислить | интеграл e^(2x) относительно x | |
| 6 | Найти производную — d/dx | 1/x | |
| 7 | Найти производную — d/dx | x^2 | |
| 8 | Вычислить | интеграл e^(-x) относительно x | |
| 9 | Найти производную — d/dx | 1/(x^2) | |
| 10 | Найти производную — d/dx | sin(x)^2 | |
| 11 | Найти производную — d/dx | sec(x) | |
| 12 | Вычислить | интеграл e^x относительно x | |
| 13 | Вычислить | интеграл x^2 относительно x | |
| 14 | Вычислить | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Найти производную — d/dx | cos(x)^2 | |
| 19 | Вычислить | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислить | интеграл sin(x)^2 относительно x | |
| 22 | Найти производную — d/dx | x^3 | |
| 23 | Найти производную — d/dx | sec(x)^2 | |
| 24 | Найти производную — d/dx | 1/(x^2) | |
| 25 | Вычислить | интеграл arcsin(x) относительно x | |
| 26 | Вычислить | интеграл cos(x)^2 относительно x | |
| 27 | Вычислить | интеграл sec(x)^2 относительно x | |
| 28 | Найти производную — d/dx | e^(x^2) | |
| 29 | Вычислить | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Найти производную — d/dx | sin(2x) | |
| 31 | Вычислить | интеграл натурального логарифма x по x | |
| 32 | Найти производную — d/dx | tan(x)^2 | |
| 33 | Вычислить | интеграл e^(2x) относительно x | |
| 34 | Вычислить | интеграл 1/(x^2) относительно x | |
| 35 | Найти производную — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислить | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Найти производную — d/dx | cos(2x) | |
| 41 | Найти производную — d/dx | xe^x | |
| 42 | Вычислить | интеграл 1/x относительно x | |
| 43 | Вычислить | интеграл 2x относительно x | |
| 44 | Найти производную — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Найти производную — d/dx | натуральный логарифм (x)^2 | |
| 46 | Найти производную — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислить | интеграл xe^(2x) относительно x | |
| 49 | Найти производную — d/dx | 2e^x | |
| 50 | Найти производную — d/dx | натуральный логарифм 2x | |
| 51 | Найти производную — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Найти производную — d/dx | 4x^2-x+5 | |
| 54 | Найти производную — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Найти производную — d/dx | 2x^2 | |
| 56 | Вычислить | интеграл e^(3x) относительно x | |
| 57 | Вычислить | интеграл cos(2x) относительно x | |
| 58 | Вычислить | интеграл cos(x)^2 относительно x | |
| 59 | Найти производную — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислить | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Найти производную — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Найти производную — d/dx | -cos(x) | |
| 67 | Найти производную — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислить | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Найти производную — d/dx | 1/(x^3) | |
| 72 | Вычислить | интеграл e^x относительно x | |
| 73 | Вычислить | интеграл tan(x)^2 относительно x | |
| 74 | Вычислить | интеграл 1 относительно x | |
| 75 | Найти производную — d/dx | x^x | |
| 76 | Найти производную — d/dx | x натуральный логарифм x | |
| 77 | Вычислить | интеграл sin(x)^2 относительно x | |
| 78 | Найти производную — d/dx | x^4 | |
| 79 | Вычислить | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислить | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Найти производную — d/dx | f(x) = square root of x | |
| 82 | Найти производную — d/dx | x^2sin(x) | |
| 83 | Вычислить | интеграл sin(2x) относительно x | |
| 84 | Найти производную — d/dx | 3e^x | |
| 85 | Вычислить | интеграл xe^x относительно x | |
| 86 | Найти производную — d/dx | y=x^2 | |
| 87 | Найти производную — d/dx | квадратный корень x^2+1 | |
| 88 | Найти производную — d/dx | sin(x^2) | |
| 89 | Вычислить | интеграл e^(-2x) относительно x | |
| 90 | Вычислить | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Найти производную — d/dx | e^2 | |
| 93 | Найти производную — d/dx | x^2+1 | |
| 94 | Вычислить | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Найти производную — d/dx | arcsin(x) | |
| 97 | Вычислить | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислить | интеграл e^(-x) относительно x | |
| 100 | Вычислить | интеграл 1/x относительно x |
www.mathway.com
1. Определение первообразной.
Первообразной
функции f(x) на
промежутке (a;
b) называется
такая функция F(x),
что выполняется равенство  для
любогох из
заданного промежутка.
для
любогох из
заданного промежутка.
Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.
Определение неопределенного интеграла.
Все
множество первообразных функции f(x) называется
неопределенным интегралом этой функции
и обозначается 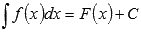 .
.
Выражение  называютподынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
называютподынтегральным
выражением,
а f(x) – подынтегральной
функцией.
Подынтегральное выражение представляет
собой дифференциал функции f(x).
Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.
Геометрический смысл неопределенного интеграла. График первообразной Д(х) называют интегральной кривой. В системе координат х0у графики всех первообразных от данной функции представляют семейство кривых, зависящих от величины постоянной С и получаемых одна из другой путем параллельного сдвига вдоль оси 0у. Для примера, рассмотренного выше, имеем:

J 2 х^х = х2 + C.
Семейство первообразных (х + С) геометрически интерпретируется совокупностью парабол.
Если из семейства первообразных нужно найти одну, то задают дополнительные условия, позволяющие определить постоянную С. Обычно с этой целью задают начальные условия: при значении аргумента х = х0 функция имеет значение Д(х0) = у0.
Пример. Требуется найти ту из первообразных функции у = 2 х, которая принимает значение 3 при х0 = 1.
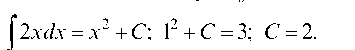
Искомая первообразная: Д(х) = х2 + 2.
Решение. ^2х^х = х2 + C; 12 + С = 3; С = 2.
2. Основные свойства неопределенного интеграла
1. Производная неопределенного интеграла равна подинтегральной функции:
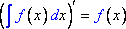
2. Дифференциал неопределенного интеграла равен подинтегральному выражению:

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме самой этой функции и произвольной постоянной:
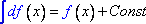
4. Постоянный множитель можно выносить за знак интеграла:
 ,
причем
,
причем 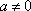
5. Интеграл суммы (разности) равен сумме (разности) интегралов:
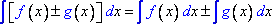
6. Свойство является комбинацией свойств 4 и 5:
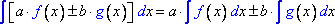 ,
причем
,
причем 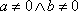
7. Свойство инвариантности неопределенного интеграла:
Если 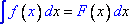 ,
то
,
то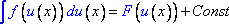
8. Свойство:
Если 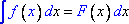 ,
то
,
то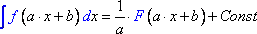
Фактически данное свойство представляет собой частный случай интегрирования при помощи метода замены переменной, который более подробно рассмотрен в следующем разделе.
Рассмотрим пример:
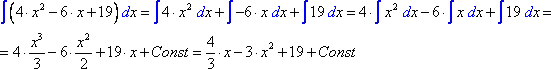
3. Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведения под знак дифференциала»):
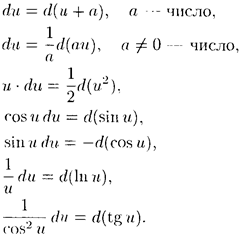 Вообще, f’(u)du
= d(f(u)). эта
(формула очень часто используется при
вычислении интегралов.
Вообще, f’(u)du
= d(f(u)). эта
(формула очень часто используется при
вычислении интегралов.
Пример:
Найти
интеграл 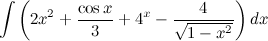
Решение. Воспользуемся свойствами интегралаи приведем данный интеграл к нескольким табличным.

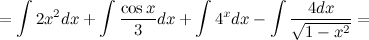
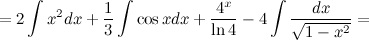
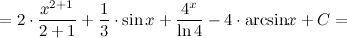
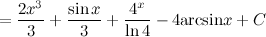
4. Интегрирование методом подстановки.
Суть метода заключается в том, что мы вводим новую переменную, выражаем подынтегральную функцию через эту переменную, в результате приходим к табличному (или более простому) виду интеграла.
Очень часто метод подстановки выручает при интегрировании тригонометрических функций и функций с радикалами.
Пример.
Найти
неопределенный интеграл 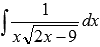 .
.
Решение.
Введем
новую переменную 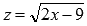 .
Выразимх через z:
.
Выразимх через z: 
Выполняем
подстановку полученных выражений в
исходный интеграл: 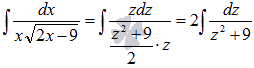
Из
таблицы первообразных имеем  .
.
Осталось
вернуться к исходной переменной х: 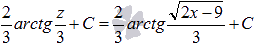
Ответ:

5. Интегрирование по частям.
Интегрирование
по частям основано на представлении
подынтегрального выражения в виде
произведения 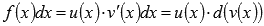
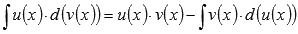 .
Этот метод является очень мощным
инструментом интегрирования. В зависимости
от подынтегральной функции, метод
интегрирования по частям иногда
приходится применять несколько раз
подряд до получения результата. Для
примера найдем множество первообразных
функции арктангенс.
.
Этот метод является очень мощным
инструментом интегрирования. В зависимости
от подынтегральной функции, метод
интегрирования по частям иногда
приходится применять несколько раз
подряд до получения результата. Для
примера найдем множество первообразных
функции арктангенс.Пример.
Вычислить
неопределенный интеграл 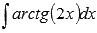 .
.
Решение.
Пусть 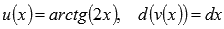 ,
тогда
,
тогда
Следует отметить, что при нахождении функции v(x) не прибавляют произвольную постоянную С.
Теперь
применяем формулу интегрирования по
частям: 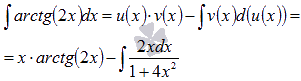
Последний интеграл вычислим по методу подведения под знак дифференциала.
Так
как 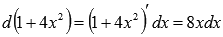 ,
то
,
то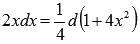 .
Поэтому
.
Поэтому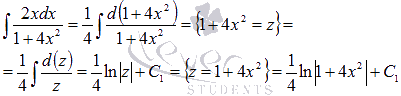
Следовательно, 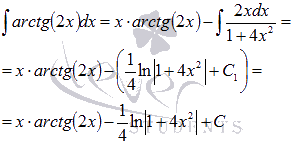 где
где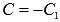 .
.
Ответ:
 .
.
studfile.net
| 1. |
| ||||
| 2. |
| ||||
| 3. |
| ||||
| 4. |
| ||||
| 5. |
| ||||
| 6. |
| ||||
| 7. |
| ||||
| 8. |
| ||||
| 9. |
| ||||
| 10. |
| ||||
| 11. |
| ||||
| 12. |
| ||||
| 13. |
| ||||
| 14. |
| ||||
| 15. |
| ||||
| 16. |
| ||||
| 17. |
| ||||
| 18. |
| ||||
| 19. |
| ||||
| 20. |
| ||||
| 21. |
| ||||
| 22. |
| ||||
| 23. |
| ||||
| 24. |
| ||||
| 25. |
| ||||
| 26. |
| ||||
| 27. |
| ||||
| 28. |
| ||||
| 29. |
| ||||
| 30. |
| ||||
| 31. |
|
ru.onlinemschool.com
| 1 | Найти производную — d/dx | квадратный корень x | |
| 2 | Найти производную — d/dx | натуральный логарифм x | |
| 3 | Вычислить | интеграл натурального логарифма x по x | |
| 4 | Найти производную — d/dx | e^x | |
| 5 | Вычислить | интеграл e^(2x) относительно x | |
| 6 | Найти производную — d/dx | 1/x | |
| 7 | Найти производную — d/dx | x^2 | |
| 8 | Вычислить | интеграл e^(-x) относительно x | |
| 9 | Найти производную — d/dx | 1/(x^2) | |
| 10 | Найти производную — d/dx | sin(x)^2 | |
| 11 | Найти производную — d/dx | sec(x) | |
| 12 | Вычислить | интеграл e^x относительно x | |
| 13 | Вычислить | интеграл x^2 относительно x | |
| 14 | Вычислить | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Найти производную — d/dx | cos(x)^2 | |
| 19 | Вычислить | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислить | интеграл sin(x)^2 относительно x | |
| 22 | Найти производную — d/dx | x^3 | |
| 23 | Найти производную — d/dx | sec(x)^2 | |
| 24 | Найти производную — d/dx | 1/(x^2) | |
| 25 | Вычислить | интеграл arcsin(x) относительно x | |
| 26 | Вычислить | интеграл cos(x)^2 относительно x | |
| 27 | Вычислить | интеграл sec(x)^2 относительно x | |
| 28 | Найти производную — d/dx | e^(x^2) | |
| 29 | Вычислить | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Найти производную — d/dx | sin(2x) | |
| 31 | Вычислить | интеграл натурального логарифма x по x | |
| 32 | Найти производную — d/dx | tan(x)^2 | |
| 33 | Вычислить | интеграл e^(2x) относительно x | |
| 34 | Вычислить | интеграл 1/(x^2) относительно x | |
| 35 | Найти производную — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислить | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Найти производную — d/dx | cos(2x) | |
| 41 | Найти производную — d/dx | xe^x | |
| 42 | Вычислить | интеграл 1/x относительно x | |
| 43 | Вычислить | интеграл 2x относительно x | |
| 44 | Найти производную — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Найти производную — d/dx | натуральный логарифм (x)^2 | |
| 46 | Найти производную — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислить | интеграл xe^(2x) относительно x | |
| 49 | Найти производную — d/dx | 2e^x | |
| 50 | Найти производную — d/dx | натуральный логарифм 2x | |
| 51 | Найти производную — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Найти производную — d/dx | 4x^2-x+5 | |
| 54 | Найти производную — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Найти производную — d/dx | 2x^2 | |
| 56 | Вычислить | интеграл e^(3x) относительно x | |
| 57 | Вычислить | интеграл cos(2x) относительно x | |
| 58 | Вычислить | интеграл cos(x)^2 относительно x | |
| 59 | Найти производную — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислить | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Найти производную — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Найти производную — d/dx | -cos(x) | |
| 67 | Найти производную — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислить | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Найти производную — d/dx | 1/(x^3) | |
| 72 | Вычислить | интеграл e^x относительно x | |
| 73 | Вычислить | интеграл tan(x)^2 относительно x | |
| 74 | Вычислить | интеграл 1 относительно x | |
| 75 | Найти производную — d/dx | x^x | |
| 76 | Найти производную — d/dx | x натуральный логарифм x | |
| 77 | Вычислить | интеграл sin(x)^2 относительно x | |
| 78 | Найти производную — d/dx | x^4 | |
| 79 | Вычислить | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислить | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Найти производную — d/dx | f(x) = square root of x | |
| 82 | Найти производную — d/dx | x^2sin(x) | |
| 83 | Вычислить | интеграл sin(2x) относительно x | |
| 84 | Найти производную — d/dx | 3e^x | |
| 85 | Вычислить | интеграл xe^x относительно x | |
| 86 | Найти производную — d/dx | y=x^2 | |
| 87 | Найти производную — d/dx | квадратный корень x^2+1 | |
| 88 | Найти производную — d/dx | sin(x^2) | |
| 89 | Вычислить | интеграл e^(-2x) относительно x | |
| 90 | Вычислить | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Найти производную — d/dx | e^2 | |
| 93 | Найти производную — d/dx | x^2+1 | |
| 94 | Вычислить | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Найти производную — d/dx | arcsin(x) | |
| 97 | Вычислить | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислить | интеграл e^(-x) относительно x | |
| 100 | Вычислить | интеграл 1/x относительно x |
www.mathway.com
Внеклассный урок — Первообразная. Интегрирование
Первообразная. Интегрирование.
Первообразная.
Первообразную легко понять на примере.
Возьмем функцию у = х3. Как мы знаем из предыдущих разделов, производной от х3 является 3х2:
(х3)’ = 3х2.
Следовательно, из функции у = х3 мы получаем новую функцию: у = 3х2.
Образно говоря, функция у = х3 произвела функцию у = 3х2 и является ее «родителем». В математике нет слова «родитель», а есть родственное ему понятие: первообразная.
То есть: функция у = х3 является первообразной для функции у = 3х2.
Определение первообразной:
Если F‘(x) = f(x), то функцию у = F(x) называют первообразной для функции у = f(x). |
В нашем примере (х3)’ = 3х2, следовательно у = х3 – первообразная для у = 3х2.
Интегрирование.
Как вы знаете, процесс нахождения производной по заданной функции называется дифференцированием. А обратная операция называется интегрированием.
Интегрирование – это процесс нахождения функции по заданной производной. |
Приведенный выше пример как раз является примером интегрирования: по производной (х3)’ мы вычислили функцию у = 3х2.
Правила и формулы для первообразной.
(1)
Первообразная суммы равна сумме первообразных. |
Пример-пояснение:
Найдем первообразную для функции у = 3х2 + sin x.
Решение:
Мы знаем, что первообразной для 3х2 является х3.
Первообразной для sin x является –cos x.
Складываем два первообразных и получаем первообразную для заданной функции:
у = х3 + (–cos x),
у = х3 – cos x.
Ответ:
для функции у = 3х2 + sin x первообразной является функция у = х3 – cos x.
(2)
kF(x) является первообразной для kf(x), если F(x) является первообразной для f(x). |
Пример-пояснение:
Найдем первообразную для функции у = 2 sin x.
Решение:
Замечаем, что k = 2. Первообразной для sin x является –cos x.
Следовательно, для функции у = 2 sin x первообразной является функция у = –2 cos x.
Коэффициент 2 в функции у = 2 sin x соответствует коэффициенту первообразной, от которой эта функция образовалась.
(3)
Если у = F(x) является первообразной для функции y = f(x), то для функции y = f(kx + m) первообразной является функция: 1 |
Пример-пояснение:
Найдем первообразную для функции y = sin 2x.
Решение:
Замечаем, что k = 2. Первообразной для sin x является –cos x.
Применяем нашу формулу при нахождении первообразной для функции y = cos 2x:
1
y = — · (–cos 2x),
2
cos 2x
y = – ————
2
cos 2x
Ответ: для функции y = sin 2x первообразной является функция y = – ————
2
(4)
Если у = F(x) является первообразной для функции y = f(x), то функция y = f(x) имеет бесконечное множество первообразных, имеющих вид: y = F(x) + C |
Пример-пояснение.
Возьмем функцию из предыдущего примера: y = sin 2x.
Для этой функции все первообразные имеют вид:
cos 2x
y = – ———— + C.
2
Пояснение.
Возьмем первую строчку. Читается она так: если функция y = f(x) равна 0, то первообразной для для нее является 1. Почему? Потому что производная единицы равна нулю: 1′ = 0.
В таком же порядке читаются и остальные строчки.
Как выписывать данные из таблицы? Возьмем восьмую строчку:
(-cos x)’ = sin x
Пишем вторую часть со знаком производной, затем знак равенства и производную.
Читаем: первообразной для функции sin x является функция -cos x.
Или: функция -cos x является первообразной для функции sin x.
raal100.narod.ru
Лекция «Первообразная. Понятие первообразной. Основное свойство первообразной функции» (11-й класс)
Цель:
- Формирование понятия первообразной.
- Подготовка к восприятию интеграла.
- Формирование вычислительных навыков.
- Воспитание чувства прекрасного (умение видеть красоту в необычном).
Математический анализ — совокупность разделов математики, посвященных исследованию функций и их обобщений методами дифференциального и интегрального исчислений.
Если до настоящего времени мы изучали раздел математического анализа, называемого диффренциальным исчислением, суть которого заключается в изучении функции в “малом”.
Т.е. исследование функции в достаточно малых окрестностях каждой точки определения. Одна из операций дифференцирования- нахождение производной (дифференциала) и применении к исследованию функций.
Не менее важной является обратная задача. Если известно поведение функции в окрестностях каждой точки ее определения, то как восстановить функцию в целом, т.е. во всей области ее определения. Эта задача составляет предмет изучения так называемого интегрального исчисления.
Интегрированием называется действие обратное дифференцированию. Или восстановление функции f(х) по данной производной f`(х). Латинское слово “integro” означает – восстановление.
Пример №1.
Пусть (х)`=3х2.
Найдем f(х).
Решение:
Опираясь на правило дифференцирования, нетрудно догадаться, что f(х)=х3, ибо (х3)`=3х2
Однако, легко можно заметить, что f(х) находится неоднозначно.
В качестве f(х) можно взять
f(х)= х3+1
f(х)= х3+2
f(х)= х3-3 и др.
Т.к.производная каждой из них равно 3х2. (Производная постоянной равна 0). Все эти функции отличаются друг от друга постоянным слагаемым. Поэтому общее решение задачи можно записать в виде f(х)= х3+С, где С — любое постоянное действительное число.
Любую из найденных функций f(х) называют ПЕРВООБРАЗНОЙ для функции F`(х)= 3х2
Определение. Функция F(х) называется первообразной для функции
f(х) на заданном промежутке J, если для всех х из этого промежутка F`(х)= f(х). Так функция F(х)=х3 первообразная для f(х)=3х2 на (- ∞
; ∞ ).
Так как, для всех х ~R справедливо равенство: F`(х)=(х3)`=3х2
Как мы уже заметили, данная функция имеет бесконечное множество первообразных (смотри пример № 1).
Пример № 2. Функция F(х)=х есть первообразная для всех f(х)= 1/х на
промежутке ( 0; + ), т.к. для всех х из этого промежутка, выполняется равенство.
F`(х)= (х 1/2)`=1/2х-1/2=1/2х
Пример № 3. Функция F(х)=tg3х есть первообразная для f(х)=3/cos3х на
промежутке (-п/2; п/2),
т.к. F`(х)=(tg3х)`= 3/cos23х
Пример № 4.Функция F(х)=3sin4х+1/х-2 первообразная для f(х)=12cos4х-1/х2
на промежутке (0;∞)
т.к. F`(х)=(3sin4х)+1/х-2)`= 4cos4х-1/х2
Лекция 2.
Тема: Первообразная. Основное свойство первообразной функции.
При изучении первообразной будем опираться на следующее утверждение. Признак постоянства функции: Если на промежутке J производная Ψ(х) функции равна 0, то на этом промежутке функция Ψ(х) постоянна.
Это утверждение можно продемонстрировать геометрически.
Известно, что Ψ`(х)=tgα, γде α-угол наклона касательной к графику функции Ψ(х) в точке с абсциссой х0. Если Ψ`(υ)=0 в любой точке промежутка J, то tgα=0 δля любой касательной к графику функции Ψ(х). Это означает, что касательная к графику функции в любой его точке параллельна оси абсцисс. Поэтому на указанном промежутке график функции Ψ(х) совпадает с отрезком прямой у=С.
Итак, функция f(х)=с постоянна на промежутке J, если f`(х)=0 на этом промежутке.
Действительно, для произвольного х1 и х2 из промежутка
J по теореме о среднем значении функции можно записать:
f(х2)- f(х1)=f`(с) (х2— х1), т.к.
f`(с)=0, то f(х2)= f(х1)
Теорема: (Основное свойство первообразной функции)
Если F(х) одна из первообразных для функции f(х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С — любое действительное число.
Доказательство:
Пусть F`(х) = f (х), тогда (F(х)+С)`= F`(х)+С`= f (х), для х Є J.
Допустим существует Φ(х)- другая
первообразная для f (х) на промежутке J, т.е. Φ`(х) = f (х),
тогда (Φ(х)- F(х))` = f (х) – f (х) = 0,
для х Є J.
Это означает, что Φ(х)- F(х) постоянна на
промежутке J.
Следовательно, Φ(х)- F(х) = С.
Откуда Φ(х)= F(х)+С.
Это значит, что если F(х) — первообразная для функции f (х) на промежутке J, то множество всех первообразных этой функции имеет вид: F(х)+С, где С — любое действительное число.
Следовательно, любые две первообразные данной функции отличаются друг от друга постоянным слагаемым.
Пример: Найти множество первообразных функции f (х) = cos х. Изобразить графики первых трех.
Решение: Sin х — одна из первообразных для функции f (х) = cos х
F(х) = Sin х+С –множество всех первообразных.
F1 (х) = Sin х-1
F2 (х) = Sin х
F3 (х) = Sin х+1
Геометрическая иллюстрация: График любой первообразной F(х)+С можно получить из графика первообразной F(х) при помощи параллельного переноса r (0;с).
Пример: Для функции f (х) = 2х найти первообразную, график которой проходит через т.М (1;4)
Решение: F(х)=х2+С – множество всех первообразных, F(1)=4 — по условию задачи.
Следовательно, 4 = 12+С
С = 3
F(х) = х2+3
urok.1sept.ru