Построение графиков функций по заданным параметрам»
Цели урока:
- научить строить графики элементарных математических функций с помощью табличного процессора Excel;
- показать возможности использования программы Excel для решения задач по математике;
- закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с основными приемами построения графиков функций в программе Excel;
- развивающие – формирование у учащихся логического и алгоритмического мышления; развитие познавательного интереса к предмету; развитие умения оперировать ранее полученными знаниями; развитие умения планировать свою деятельность;
- воспитательные – воспитание умения самостоятельно мыслить, ответственности за выполняемую работу, аккуратности при выполнении работы.
Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока.
 Домашнее задание – 7
мин.
Домашнее задание – 7
мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный опрос)
Вопросы для проверки
- Что представляет собой рабочая область программы Excel?
- Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она задается?
- Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как изменить ориентацию бумаги?
- Что такое функциональная зависимость у = f(х)? Какая переменная является зависимой, а какая независимой?
- Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.
Программа будет строить график по точкам: точки
с известными значениями будут плавно
соединяться линией. Эти точки нужно указать
программе, поэтому, сначала создается таблица
значений функции у = f(х).
Эти точки нужно указать
программе, поэтому, сначала создается таблица
значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться график.
- шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.
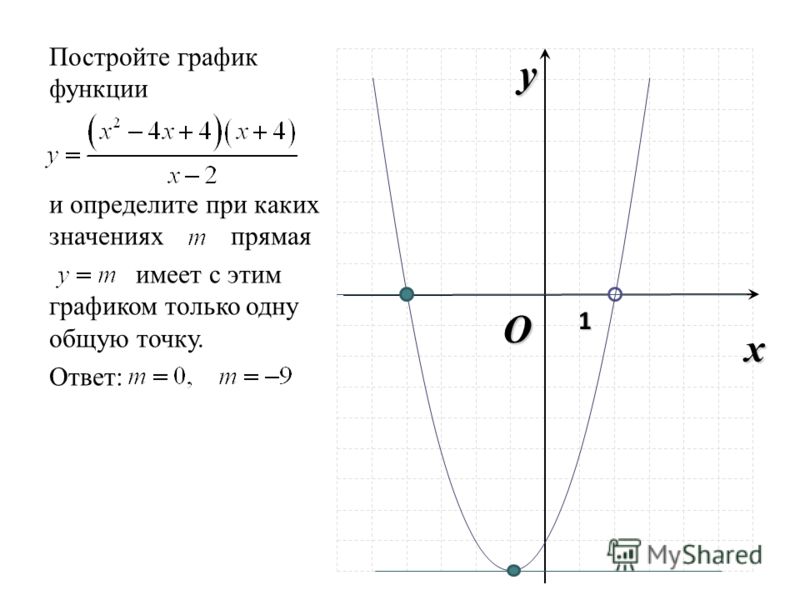
Задача 1.Построить график функции у = sin x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2.4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 |
6.
Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
В поле Подписи оси Х нажать на кнопку. Выделить в таблице ячейки со значениями х и нажмите на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем пункт Формат оси…. Во вкладке Шкала установим: цена основного деления: 1. Во вкладке Шрифт установим размер шрифта 8пт.
- Вызовем контекстное меню оси ОХ. Выберем пункт Формат оси….
Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и сформулировать следующую задачу.
Задача 2. Построить график функции у = х3 на отрезке [– 3; 3] с шагом h = 0,5.
1.
3
6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х3 на отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7. Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики.
8. На втором шаге во вкладке Ряд выполнить:
- В поле Ряд выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
- В поле Подписи оси Х нажать на кнопку .
Выделить в таблице ячейки со значениями х и
нажать на кнопку . Подписи по горизонтальной оси
станут такими, как у нас в таблице.

9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид Колонтитулы…):
14. Верхний колонтитул слева: график функции у = x3
Сохранить документ своей папке под именем График.
Самостоятельная работа.
Работа по карточкам с индивидуальными заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c
2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный график”
5. Вывести документ на печать.
После выполнения задания правильность каждого варианта проверяется с помощью проектора.
Подведение итогов.
Домашнее задание.
Оценки за урок.
Прогноз конъюнктуры мирового рынка нефти на основе тенденций
Нефтяная отрасль пережила трудные времена развития пандемии коронавируса Covid-19 и мирового экономического кризиса. Это понятно потому, что обрушившиеся цены нефти восстановились. Правительства стран поддерживали экономическую активность большими монетарными вливаниями для экономических субъектов разного типа.
 Появляются прогнозы восстановления международной экономики, которые обещают завершить масштабную помощь, укрепить денежно-кредитную политику, провести вакцинацию населения максимум к 2024 году. В таких условиях появляются вопросы относительно дальнейшего развития нефтяной отрасли в мире. Ответы на такие вопросы можно получить, опираясь на исследования тенденций нефтяной индустрии. Прежде всего, стоит спрогнозировать спрос на нефть до начала 2024 года на основе данных за I квартал 2008 года — IV квартал 2020 года — экономический цикл, построив уравнение линейной тенденции: y=0,264∙x+84,24, где y – мировой спрос на нефть (миллионы баррелей в день), x – номер даты периода исследования. Очевидно, что спрос на нефть после мирового экономического кризиса должен вырасти (рисунок 1).
Появляются прогнозы восстановления международной экономики, которые обещают завершить масштабную помощь, укрепить денежно-кредитную политику, провести вакцинацию населения максимум к 2024 году. В таких условиях появляются вопросы относительно дальнейшего развития нефтяной отрасли в мире. Ответы на такие вопросы можно получить, опираясь на исследования тенденций нефтяной индустрии. Прежде всего, стоит спрогнозировать спрос на нефть до начала 2024 года на основе данных за I квартал 2008 года — IV квартал 2020 года — экономический цикл, построив уравнение линейной тенденции: y=0,264∙x+84,24, где y – мировой спрос на нефть (миллионы баррелей в день), x – номер даты периода исследования. Очевидно, что спрос на нефть после мирового экономического кризиса должен вырасти (рисунок 1).Общее мировое предложение нефти существенно превышало мировой спрос на нефть в период экономического кризиса, что послужило причиной обвала нефтяных цен. Важно, чтобы соблюдался баланс спроса и предложения нефти в мире. Поэтому производители нефти приходили к решению ограничения добычи нефти во время экономического кризиса. В настоящее время планируется увеличение производства нефти. Целесообразно сделать прогноз общего предложения нефти в мире до 2024 года. С этой целью с использованием данных за I квартал 2008 года — IV квартал 2020 года — экономический цикл, построено уравнение линейной тенденции: y=0,294∙x+84,08, где y – мировое предложение нефти (миллионы баррелей в день), x – номер даты периода исследования. Очевидно, что предложение нефти после мирового экономического кризиса должно тоже вырасти (рисунок 2).
Соединенные Штаты успешно развивают нефтяную промышленность и к настоящему моменту времени являются крупным экспортером нефти. Экспансия нефтяной отрасли Соединенных Штатов на этом не должна остановиться, поскольку недорогая нефть необходима самим Соединенным Штатам, нефтяная отрасль приносит дополнительные доходы стране, страна становится менее зависимой в политической и экономической сфере. Производство нефти на месторождениях Соединенных Штатов имеет тенденцию роста и существенно увеличится к 2024 году. Рассчитано уравнение линейной тенденции производства нефти на месторождениях Соединенных Штатов (y, миллионы баррелей в день) за I квартал 2008 года — IV квартал 2020 года: y=0,155∙x+4,107, где x — номер даты периода исследования. Таким образом, большая часть дополнительно произведенной нефти принадлежит Соединенным Штатам (рисунок 3).
Производство нефти на месторождениях Соединенных Штатов имеет тенденцию роста и существенно увеличится к 2024 году. Рассчитано уравнение линейной тенденции производства нефти на месторождениях Соединенных Штатов (y, миллионы баррелей в день) за I квартал 2008 года — IV квартал 2020 года: y=0,155∙x+4,107, где x — номер даты периода исследования. Таким образом, большая часть дополнительно произведенной нефти принадлежит Соединенным Штатам (рисунок 3).
Поскольку Соединенные Штаты завоевывают дополнительные рынки сбыта нефти, вызывает интерес производства нефти без участия Соединенных Штатов. Предложение нефти без доли нефтяной отрасли Соединенных Штатов позволяет понять в большей степени и определить, насколько сильна конкурентная позиция упомянутых производителей нефти. Рассчитано уравнение линейной тенденции мирового предложения нефти без доли нефтяной отрасли Соединенных Штатов (y, миллионы баррелей в день) за I квартал 2008 года — IV квартал 2020 года: y=0,139∙x+79,98, где x — номер даты периода исследования. Таким образом, становится понятно, что другие страны в совокупности наращивают производство нефти менее быстрыми темпами, чем Соединенные Штаты (рисунок 4).
Для того, чтобы сопоставить объемы спроса и предложения на рынке энергетических ресурсов с ценами нефти, необходимо построить уравнение тенденции цен нефти марки за исследуемый временной отрезок I квартал 2008 года — IV квартал 2020 года. Такое действие поможет обосновать прогноз цен на нефть марки Brent до конца 2023 года – максимальный период, в течение которого будет сохраняться мягкая денежно-кредитная политика Федеральной резервной системы США. Возможно, будет расширен диапазон процентных ставок. Даже если Федеральная резервная система США будет повышать процентные ставки раньше указанного периода, они все равно будут достаточно низкими. Построено уравнение тенденции: y=-1,016∙x+103,8; где y – прогнозные цены нефти марки Brent, доллары США за баррель; x — номер даты периода исследования. Таким образом, прошлый экономический цикл указывает на тенденции снижения цен на нефть, вероятно, благодаря научно-техническому прогрессу (рисунок 5).
Итак, изучение краткосрочного периода формирования конъюнктуры мирового рынка энергетических ресурсов (I квартал 2008 года — IV квартал 2020 года) позволило выявить и сопоставить между собой тенденции спроса, предложения и цен нефти. Результаты исследования показали, что по мере восстановления экономики и спроса на нефть предложение нефти должно увеличиваться, в особенности, в Соединенных Штатах. График демонстрирует, что в процессе увеличения добычи нефти на довольно-таки небольшую величину, цены нефти реагируют существенным снижением (рисунок 6).
Существует другой тренд цен на нефть, который является долгосрочным (основан на периоде исследования июле 1988 года – апреле 2021 года; данный период исследования включает максимальное количество значений изучаемого показателя, что можно было получить в организации, предоставляющей статистические данные) и носит восходящую направленность. Уравнение долгосрочной тенденции цен на нефть марки Brent выглядит следующим образом: y=0,197∙x+8,967; где y – прогнозные цены нефти марки Brent, доллары США за баррель; x — номер даты периода исследования. Восходящая тенденция цен нефти является тоже устойчивой в связи со своим длительным временным интервалом и основана на редкости и ограниченности нефтяных ресурсов. Это действительно так, потому что многие месторождения нефти уже выработаны, например, в некоторых странах при существующих технологиях нефти может хватить на несколько десятилетий, но не больше (рисунок 7).
Далее для полноценного долгосрочного прогноза цен на нефть марки Brent нужно объединить тенденции краткосрочного и долгосрочного периодов. Как уже известно, в краткосрочном периоде цены нефти марки Brent должны снижаться. В данном случае краткосрочный период – это период длиною в один экономический цикл (I квартал 2008 года — IV квартал 2020 года), который включает в себя кризис, восстановление экономики и характеризуется снижением цен на нефть на фоне роста производства нефти на месторождениях Соединенных Штатов.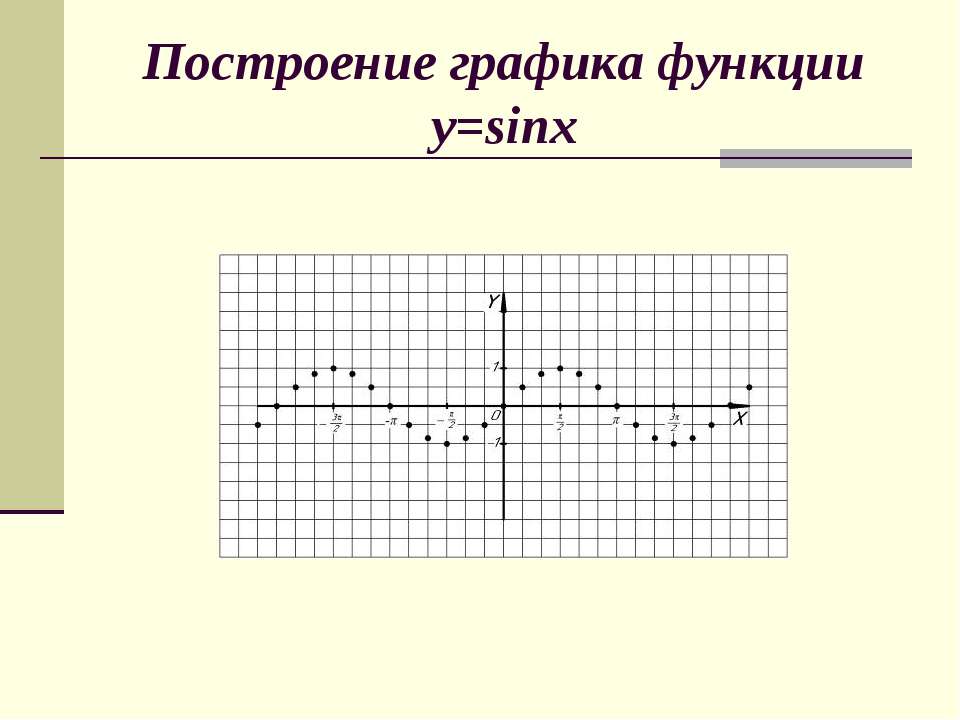 Тенденции краткосрочного периода продолжаются в настоящее время, поскольку существует большая вероятность дальнейшего роста производства нефти в Соединенных Штатах. Однако исследования долгосрочного периода говорят о том, что нефть как экономический ресурс ограничена, дополнительная добыча нефти может привести к дополнительному росту цен на нее. В итоге в краткосрочном периоде в процессе увеличения производства нефти и конкуренции за рынки сбыта цены нефти могут значительно снизиться; в долгосрочном периоде можно будет наблюдать рост цен на нефть как следствие активной добычи и менее рационального использования ограниченной нефти (рисунок 8).
Тенденции краткосрочного периода продолжаются в настоящее время, поскольку существует большая вероятность дальнейшего роста производства нефти в Соединенных Штатах. Однако исследования долгосрочного периода говорят о том, что нефть как экономический ресурс ограничена, дополнительная добыча нефти может привести к дополнительному росту цен на нее. В итоге в краткосрочном периоде в процессе увеличения производства нефти и конкуренции за рынки сбыта цены нефти могут значительно снизиться; в долгосрочном периоде можно будет наблюдать рост цен на нефть как следствие активной добычи и менее рационального использования ограниченной нефти (рисунок 8).
Почему именно в настоящее время существует вероятность конкурентной борьбы за рынки сбыта продукции, в частности нефти, указано на схеме (рисунок 9).
Таким образом, на мировом рынке нефти существует два типа тенденции: краткосрочная – указывает на снижение цен нефти; долгосрочная – указывает на рост цен нефти. Краткосрочная тенденция снижения цен на нефть обоснована тем, что в период восстановления экономик стран мира первичное значение принадлежит завоеванию и удержанию рынков сбыта продукции, вторичное значение принадлежит повышению цен на продукцию. Поэтому последовательность формирования конъюнктуры мирового рынка нефти сводится сначала к конкурентной борьбе и снижению цен на нефть, а затем – к повышению цен на нефть.
Теньковская Л.И., кандидат экономических наук, доцент
ГДЗ по алгебре 9 класс Дорофеев, Суворова Учебник Решебник
Алгебра в школьной программе начинается с 7 класса и так как это основной предмет при сдаче главных экзаменов, ему стоит уделить особое внимание. Если экзамен будет провален, речь об университете не может идти. Так как вступительное испытание в институт тоже предполагает сдачу этого предмета.
Конечно, такая наука развивает кругозор каждого, в будущем ребенок, владеющий аналитическим складом ума, быстро выполняя вычисления в уме, с развитой логикой будет намного востребован на рынке труда. Например, ему подойдут такие профессии как, инженер, архитектор, дизайнер. Казалось бы, технические знания и творческие специальности несовместимы, но с этим можно поспорить, вычисления и быстрое мышление очень пригодятся в такой деятельности.
Например, ему подойдут такие профессии как, инженер, архитектор, дизайнер. Казалось бы, технические знания и творческие специальности несовместимы, но с этим можно поспорить, вычисления и быстрое мышление очень пригодятся в такой деятельности.
Как может помочь онлайн-решебник по алгебре для 9 класса (авторы: Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович)?
Пособие издано компанией «Просвещение» в 2015 г. В онлайн-формате есть все готовые правильные ответы, как и в оригинале. Задача взрослого объяснить все плюсы использования ГДЗ и важность того, что нельзя просто бездумно списывать ответы, нужно разбираться и понимать приведенное решение задания. Иначе позора у доски не избежать, так как преподаватель сразу же раскусит заядлого списывальщика. Преимущества пособия:
- доступ к сайту круглосуточный;
- работает на любых гаджетах;
- легко найти правильные ответы;
- нужен только доступ в интернет.
У родителей, скорее всего, нет времени объяснять пропущенные темы, поэтому такой способ выработает самостоятельность при выполнении домашнего задания. И не придется нанимать дорогостоящего репетитора.
Из каких тем решебник по алгебре под авторством Дорофеева Г.В.?
- неравенства;
- квадратичная функция;
- уравнения;
- линейные неравенства;
- графики;
- уравнения с параметром.
Существует такая проблема как нежелание учить конкретный предмет, да, ребенок может знать теорию и основы, но углубляться в науку он не хочет. Может быть, у ребенка просто рвение к гуманитарным наукам и это тоже похвально. Заставлять ребенка зубрить правила и задачи не приведет к повышению оценок, а лишь вызовет негатив.
Учителя могут пользоваться учебником, как и родители при проверке домашнего задания, это намного сэкономит время и облегчит жизнь всем. Ведь его можно будет потратить на любимые развлечения и хобби. 2 — 4*x + 13 = 0 are 2 + 3*%i and 2 — 3*%i.
2 — 4*x + 13 = 0 are 2 + 3*%i and 2 — 3*%i.
Polar contour plot in Maxima. Ask Question Asked 7 years, 3 months ago. Active 4 days ago. Viewed 1k times 2. 1. How can I make a polar contour plot in Maxima? Given an expression such as. exp(-r) * cos(phi) I’d like to plot contours in the x-y plane which have the same value of the expression at all points along the contour. …
Polar contour plot in Maxima. Ask Question Asked 7 years, 3 months ago. Active 4 days ago. Viewed 1k times 2. 1. How can I make a polar contour plot in Maxima? Given an expression such as. exp(-r) * cos(phi) I’d like to plot contours in the x-y plane which have the same value of the expression at all points along the contour. …
Maximaをベースにした種類 † wxmaxima, 12.04.0(win7) ├ maxima, 5.27.0(win7) └ xmaxima, テキストベースらしい imaxima, wxmaximで十分のようだ texmacs, 1.99.1.8496(win7), maximaとの連携がうまくいかない。それ以外は単なるエディタ。 mac版のwxmaximaはファイル保存できない。
maxima: Maxima plots the frequency of the values, and not the values themselves. Non-positive values cannot be represented. horizontal bar chart. A bar chart in which zero is the y-axis and the bars extend to the right. grouped bar chart. stacked bar chart. pie chart. maxima: Note that Maxima plots the frequency of the values, and not the …
Maxima. Графики Построить простейший график в Maxima не трудно, достаточно записать plot2d ( функция, интервал ), где интервал задаётся в виде [ переменная, начало, конец ].
The Openmath viewer is in the distribution, and is based on tcl/tk. The executable is `maxima/bin/omplotdata’. The viewer lets you zoom in, slide around, and rotate (if 3 dimensional). This format is also the one used by netmath, for making plots with Netmath. (see `http://www.ma.utexas.edu/users/wfs/netmath.html’)
The Openmath viewer is in the distribution, and is based on tcl/tk. The executable is `maxima/bin/omplotdata’. The viewer lets you zoom in, slide around, and rotate (if 3 dimensional). This format is also the one used by netmath, for making plots with Netmath. (see `http://www.ma.utexas.edu/users/wfs/netmath.html’)
(see `http://www.ma.utexas.edu/users/wfs/netmath.html’)
The Openmath viewer is in the distribution, and is based on tcl/tk. The executable is `maxima/bin/omplotdata’. The viewer lets you zoom in, slide around, and rotate (if 3 dimensional). This format is also the one used by netmath, for making plots with Netmath. (see `http://www.ma.utexas.edu/users/wfs/netmath.html’)
En la clase de hoy hemos retomado el tema 7 (Gráficos y Animaciones), profundizando en los paquetes básicos para generación de gráficos desde Maxima, haciendo uso de las funciones plot2d/wxplot2d y plot3d/wxplot3d.
wxMaxima is a user interface for the computer algebra system Maxima. The interface al- lows the user to build, edit and save a document (a.wxm le) containing many calculations and graphics, and most operations can be accessed through the GUI if desired.
Учебное пособие поPyplot — документация Matplotlib 3.4.1
Введение в интерфейс pyplot.
Введение в pyplot
matplotlib.pyplot — это набор функций
которые заставляют matplotlib работать как MATLAB.
Каждая функция pyplot делает
некоторые изменения в фигуре: например, создает фигуру, создает область построения
на рисунке рисует несколько линий в области рисования, украшает сюжет
с этикетками и пр.
В matplotlib.pyplot сохраняются различные состояния
между вызовами функций, чтобы отслеживать такие вещи, как
текущий рисунок и область построения, а также график
функции направлены на текущие оси (обратите внимание, что здесь «оси»
и в большинстве мест в документации упоминается ось часть фигуры
а не строгий математический термин для более чем одной оси).
Примечание
API pyplot обычно менее гибок, чем объектно-ориентированный API.
Большинство вызовов функций, которые вы видите здесь, также можно вызывать как методы.
от объекта Axes . Мы рекомендуем просмотреть учебные пособия и
примеры, чтобы увидеть, как это работает.
Создание визуализаций с помощью pyplot выполняется очень быстро:
Вам может быть интересно, почему по оси X находятся значения от 0 до 3, а по оси Y
с 1-4. Если вы предоставите один список или массив для участок , matplotlib предполагает, что это
последовательность значений y, и автоматически генерирует значения x для
ты.Поскольку диапазоны Python начинаются с 0, вектор x по умолчанию имеет
той же длины, что и y, но начинается с 0. Следовательно, данные x [0, 1, 2, 3] .
plot — это универсальная функция, которая принимает произвольное количество
аргументы. Например, чтобы построить график зависимости x от y, вы можете написать:
Ушел:
[<объект matplotlib.lines.Line2D в 0x7f5effdf1760>]
Форматирование стиля вашего сюжета
Для каждой пары аргументов x, y существует необязательный третий аргумент. это строка формата, указывающая цвет и тип линии сценарий.Буквы и символы строки формата взяты из MATLAB, и вы объединяете строку цвета со строкой стиля линии. Строка формата по умолчанию — «b-», которая представляет собой сплошную синюю линию. Для Например, чтобы отобразить вышеупомянутое с красными кружками, вы должны ввести
plt.plot ([1, 2, 3, 4], [1, 4, 9, 16], 'ro') plt.axis ([0, 6, 0, 20]) plt.show ()
См. Документацию plot для полной
список стилей линий и форматных строк. В
Ось Функция в приведенном выше примере принимает
список [xmin, xmax, ymin, ymax] и определяет область просмотра
топоры.
Если бы matplotlib был ограничен работой со списками, было бы справедливо бесполезен для обработки чисел. Как правило, вы будете использовать массивы numpy. Фактически, все последовательности преобразованы в массивы numpy внутренне. Пример ниже иллюстрирует построение нескольких строк с разными стилями формата за один вызов функции с использованием массивов.
импортировать numpy как np # время с равномерной выборкой с интервалом 200 мс t = np.') plt.показывать()
Построение со строками ключевых слов
В некоторых случаях у вас есть данные в формате, который позволяет вам
доступ к определенным переменным с помощью строк. Например, с numpy.recarray или панд.DataFrame .
Matplotlib позволяет предоставить такой объект с помощью
аргумент ключевого слова data . Если предоставлено, вы можете создавать графики с помощью
строки, соответствующие этим переменным.
График с категориальными переменными
Также возможно построить график с использованием категориальных переменных.Matplotlib позволяет передавать категориальные переменные напрямую в множество функций построения графиков. Например:
Свойства управляющей линии
Линии имеют множество атрибутов, которые вы можете установить: ширину линии, стиль штриха,
сглаживание и т. д .; см. matplotlib.lines.Line2D . Есть
несколько способов установить свойства линии
Использовать аргументы ключевого слова:
Используйте методы установки экземпляра
Line2D.сюжетвозвращает списокобъектов Line2D; е.г.,строка1, строка2 = график (x1, y1, x2, y2). В коде ниже мы предположим, что у нас есть только одна строка, чтобы возвращаемый список имел длину 1. Мы используем распаковку кортежей сстрока,, чтобы получить первый элемент этого списка:Используйте
setp. Пример ниже использует функцию в стиле MATLAB для установки нескольких свойств в списке строк.setpпрозрачно работает со списком объектов или отдельный объект. Вы можете использовать аргументы ключевого слова python или Пары строка / значение в стиле MATLAB:строк = plt.сюжет (x1, y1, x2, y2) # используйте ключевые слова args plt.setp (линии, цвет = 'r', ширина линии = 2,0) # или пары строковых значений стиля MATLAB plt.
 setp (линии, 'цвет', 'r', 'ширина линии', 2.0)
setp (линии, 'цвет', 'r', 'ширина линии', 2.0)
Вот доступные свойства Line2D .
| Имущество | Тип значения |
|---|---|
| альфа | поплавок |
| анимированный | [Верно | Ложь] |
| сглаживание или AA | [Верно | Ложь] |
| clip_box | матплотлиб.transform.Bbox экземпляр |
| клипса_он | [Верно | Ложь] |
| clip_path | экземпляр Path и экземпляр Transform, патч |
| цвет или c | любой цвет matplotlib |
| содержит | функция проверки попадания |
| dash_capstyle | [ 'стык' | «круглый» | «проектирующий» ] |
| dash_joinstyle | [ 'митра' | «круглый» | 'bevel' ] |
| штрихов | последовательность включения / выключения чернил в точках |
| данные | (нп.массив xdata, np.array ydata) |
| рисунок | — экземпляр matplotlib.figure.Figure |
| этикетка | любая строка |
| linestyle или ls | [ '-' | '-' | '-.' | ':' | ступеней | …] |
| ширина линии или lw | значение с плавающей запятой в пунктах |
| маркер | [ '+' | ',' | '.' | '1' | '2' | '3' | '4' ] |
| markeredgecolor или mec | любой цвет matplotlib |
| markeredgewidth или mew | значение с плавающей запятой в пунктах |
| markerfacecolor или mfc | любой цвет matplotlib |
| размер маркера или мс | поплавок |
| markevery | [Нет | целое | (начало, шаг)] |
| подборщик | используется в интерактивном выборе линии |
| радиус обзора | радиус выбора линии выбора |
| solid_capstyle | [ 'стык' | «круглый» | «проектирующий» ] |
| solid_joinstyle | [ 'митра' | «круглый» | 'bevel' ] |
| преобразование | матплотлиб. transforms.Transform instance transforms.Transform instance |
| видимый | [Верно | Ложь] |
| xdata | нп. Массив |
| ярдов | нп. Массив |
| zorder | любой номер |
Чтобы получить список настраиваемых свойств линии, вызовите setp функция со строкой или строками в качестве аргумента
В [69]: lines = plt.plot ([1, 2, 3]) В [70]: plt.setp (строки) альфа: плавать анимированные: [True | Ложь] сглаживание или aa: [True | Ложь] ...щипнуть
Работа с несколькими фигурами и осями
MATLAB и pyplot имеют концепцию текущего рисунка
и текущие оси. Все функции построения графика применяются к текущему
топоры. Функция gca возвращает текущие оси (a matplotlib.axes.Axes instance), а gcf возвращает текущий
figure (экземпляр matplotlib.figure.Figure ). Обычно вам не нужно
беспокоиться об этом, потому что все это делается за кулисами.Ниже
сценарий для создания двух подзаговоров.
def f (t):
вернуть np.exp (-t) * np.cos (2 * np.pi * t)
t1 = np.arange (0,0; 5,0; 0,1)
t2 = np.arange (0,0; 5,0; 0,02)
plt.figure ()
plt.subplot (211)
plt.plot (t1, f (t1), 'bo', t2, f (t2), 'k')
plt.subplot (212)
plt.plot (t2, np.cos (2 * np.pi * t2), 'r--')
plt.show ()
цифра здесь не является обязательной, потому что цифра будет создана
если ничего не существует, так же будут созданы оси (эквивалентно явному subplot () call), если его нет.Вызов подзаговора определяет номеров,
numcols, plot_number , где plot_number находится в диапазоне от 1 до чисел * число . Запятые в подзаговоре обозначают
необязательно, если numrows * numcols <10 . Итак, подзаголовок (211) идентичен
на участок (2, 1, 1) .
Вы можете создать произвольное количество подзаговоров
и топоры. Если вы хотите разместить оси вручную, т.е. не на
прямоугольная сетка, использовать осей ,
что позволяет указать местоположение как осей ([слева, снизу,
ширина, высота]) , где все значения в дробном (от 0 до 1)
координаты.См. Демонстрацию Axes для примера
размещение осей вручную и демонстрация базового подсюжета для
пример с большим количеством сюжетов.
Вы можете создать несколько фигур, используя несколько цифра звонков с возрастающей цифрой
номер. Конечно, каждая фигура может содержать столько осей и подзаголовков.
как душе угодно:
Вы можете очистить текущую цифру с помощью clf и текущие оси с cla . Если ты найдешь
раздражает то, что состояния (в частности, текущее изображение, фигура и оси)
поддерживаются за кулисами, не отчаивайтесь: это всего лишь тонкая
оболочка с отслеживанием состояния вокруг объектно-ориентированного API, которую вы можете использовать
вместо этого (см. руководство художника)
Если вы делаете много фигур, вам нужно знать об одной
еще: память, необходимая для фигуры, не полностью
выпущен до тех пор, пока фигура не будет явно закрыта с помощью закрыть .Удаление всех ссылок на
рисунок и / или с помощью оконного менеджера, чтобы убить окно, в котором
фигура появляется на экране, этого недостаточно, потому что pyplot
поддерживает внутренние ссылки до закрыть называется.
Работа с текстом
текст можно использовать для добавления текста в произвольном месте и xlabel , ylabel и title используются для добавления
текст в указанных местах (см. Текст в графиках Matplotlib для
более подробный пример)
мю, сигма = 100, 15 х = му + сигма * нп.random.randn (10000) # гистограмма данных n, ячейки, участки = plt.hist (x, 50, плотность = 1, цвет лица = 'g', альфа = 0,75) plt.xlabel ("Умные") plt.ylabel ('Вероятность') plt.title ('Гистограмма IQ') plt.text (60, 0,025, r '$ \ mu = 100, \ \ sigma = 15 $') plt.axis ([40, 160, 0, 0,03]) plt.grid (Истина) plt.show ()
Все функции text возвращают matplotlib.text.Text пример. Как и в случае со строками выше, вы можете настроить свойства,
передача аргументов ключевого слова в текстовые функции или использование setp :
Эти свойства более подробно описаны в разделе «Свойства текста и макет».
Использование математических выражений в тексте
matplotlib принимает выражения уравнений TeX в любом текстовом выражении. Например, чтобы написать выражение \ (\ sigma_i = 15 \) в заголовке, вы можете написать выражение TeX, окруженное знаками доллара:
Значение r перед строкой заголовка важно - оно означает
что строка является необработанной строкой и не обрабатывает обратную косую черту как
питон ускользает. matplotlib имеет встроенный анализатор выражений TeX и
механизм компоновки и поставляет собственные математические шрифты - подробности см.
Написание математических выражений.Таким образом, вы можете использовать математический текст на разных платформах.
без установки TeX. Для тех, у кого есть LaTeX и
dvipng, вы также можете использовать LaTeX для форматирования текста и
включить вывод непосредственно в отображаемые цифры или сохранить
постскриптум - см. Рендеринг текста с помощью LaTeX.
Аннотирующий текст
Использование основной функции text выше
разместить текст в произвольной позиции на осях. Обычное использование для
текст должен аннотировать некоторые особенности сюжета, а annotate метод предоставляет помощника
функциональность для упрощения аннотаций.В аннотации есть
два момента, которые следует учитывать: аннотируемое местоположение, представленное
аргумент xy и расположение текста xytext . Оба
эти аргументы - (x, y) кортежей.
ax = plt.subplot ()
t = np.arange (0,0; 5,0; 0,01)
s = np.cos (2 * np.pi * t)
линия, = plt.plot (t, s, lw = 2)
plt.annotate ('локальный максимум', xy = (2, 1), xytext = (3, 1.5),
arrowprops = dict (цвет лица = 'черный', усадка = 0,05),
)
plt.ylim (-2, 2)
plt.показывать()
В этом базовом примере и xy (кончик стрелки), и xytext местоположения (расположение текста) находятся в координатах данных. Есть
множество других систем координат, которые можно выбрать - см.
Основные аннотации и расширенные аннотации для
подробности. Больше примеров можно найти в
Аннотирование сюжетов.
Логарифмические и прочие нелинейные оси
matplotlib.pyplot поддерживает не только линейные шкалы осей, но и
логарифмическая и логитовая шкалы.Это обычно используется, если данные охватывают много заказов.
величины. Изменить масштаб оси очень просто:
plt.xscale ('журнал')
Пример четырех графиков с одинаковыми данными и разными масштабами для оси y показано ниже.
# Исправление случайного состояния для воспроизводимости
np.random.seed (19680801)
# составляем данные в открытом интервале (0, 1)
y = np.random.normal (loc = 0,5, масштаб = 0,4, размер = 1000)
y = y [(y> 0) & (y <1)]
y.sort ()
x = np.arange (len (y))
# график с различными масштабами осей
plt.фигура()
# linear
plt.subplot (221)
plt.plot (x, y)
plt.yscale ('линейный')
plt.title ('линейный')
plt.grid (Истина)
# бревно
plt.subplot (222)
plt.plot (x, y)
plt.yscale ('журнал')
plt.title ('журнал')
plt.grid (Истина)
# симметричный бревно
plt.subplot (223)
plt.plot (x, y - y.mean ())
plt.yscale ('символический журнал', linthresh = 0,01)
plt.title ('символический журнал')
plt.grid (Истина)
# логит
plt.subplot (224)
plt.plot (x, y)
plt.yscale ('логит')
plt.title ('логит')
plt.grid (Истина)
# Отрегулируйте макет подзаголовка, потому что логит может занять больше места
# чем обычно, из-за меток y-галочки, таких как "1 - 10 ^ {- 3}"
plt. subplots_adjust (вверху = 0,92, внизу = 0,08, слева = 0,10, справа = 0,95, hspace = 0,25,
wspace = 0,35)
plt.show ()
subplots_adjust (вверху = 0,92, внизу = 0,08, слева = 0,10, справа = 0,95, hspace = 0,25,
wspace = 0,35)
plt.show ()
Также можно добавить свой собственный масштаб, см. Руководство разработчика по созданию масштабов и преобразований для подробности.
Общее время работы скрипта: (0 минут 3,431 секунды)
Ключевые слова: пример кода matplotlib, кодекс, график python, pyplot Галерея создана Sphinx-Gallery
График уравнений
Описание :: Все функции
Введите уравнение, используя переменные x и / или y и знак =, нажмите Go:
Описание
Он может построить уравнение, в котором x и y как-то связаны (а не только y =.2
Если вы не включите знак равенства, будет считаться, что вы имеете в виду « = 0 »
Он не был хорошо протестирован, поэтому развлекается с ним , но ему не доверяют .
Если возникнут проблемы, дайте мне знать.
Примечание: для завершения может потребоваться несколько секунд, потому что для этого требуется много вычислений.
Если вы просто хотите построить график функции в стиле «y = ...», вы можете предпочесть Function Grapher и Calculator
Масштабирование
Используйте ползунок масштабирования (влево увеличивает масштаб, вправо уменьшает).
Чтобы сбросить масштаб до исходных границ, нажмите кнопку Сбросить .
Перетаскивание
Щелкните и перетащите, чтобы переместить график. Если вы просто щелкнете и отпустите (без перетаскивания), то место, на котором вы щелкнули, станет новым центром
.Примечание: на графиках использовано компьютерных расчетов . Округление может вызвать ошибки или значения могут быть полностью упущены.
Все функции
Операторы
| + | Оператор сложения | |
|---|---|---|
| – | Оператор вычитания | |
| * | Оператор умножения | |
| / | Оператор отдела | |
| ^ | Оператор экспоненты (степени) |
Функции
| sqrt | Квадратный корень значения или выражения. | |
|---|---|---|
| грех | синус значения или выражения | |
| cos | Косинус значения или выражения | |
| желто-коричневый | тангенс значения или выражения | |
| asin | обратный синус (арксинус) значения или выражения | |
| acos | обратный косинус (arccos) значения или выражения | |
| атан | арктангенс (арктангенс) значения или выражения | |
| синх | Гиперболический синус (sinh) значения или выражения | |
| куш | Гиперболический косинус (cosh) значения или выражения | |
| танх | Гиперболический тангенс (tanh) значения или выражения | |
| эксп. | e (Константа Эйлера) в степени значения или выражения | |
| пер. | Натуральный логарифм значения или выражения | |
| журнал | Логарифм по основанию 10 значения или выражения | |
| этаж | Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу. | |
| потолок | Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и равно математическому целому числу. | |
| круглый | Округлить до ближайшего целого числа. Примеры: округление (−2,5) = −2, округление (-0,1) = 0, округление (0,1) = 0, округление (2,5) = 3 | |
| абс | Абсолютное значение (расстояние от нуля) значения или выражения | |
| знак | Знак (+1 или -1) значения или выражения | |
Константы
| пи | Константа π (3. 141592654 ...) 141592654 ...) | |
|---|---|---|
| и | Число Эйлера (2,71828 ...), основание натурального логарифма |
Отрисовка данных с помощью gnuplot
Отрисовка данных с помощью gnuplotЭто руководство предназначено как дополнение к информации содержится на сайте физического факультета: Графики и данные подгонки и данные графика с Калейдаграфом. Он показывает, как выполнять те же функции. описано в этих руководствах с использованием gnuplot, управляемого из командной строки программа построения графиков, обычно доступная на машинах Unix (хотя и и для других платформ).Возможно, вам будет полезно посмотреть на а также другие учебные пособия; этот предназначен для того, чтобы следовать за ними совсем внимательно.
Приведенные инструкции и примеры соответствуют работающей версии 3.7. под Linux, но результаты должны быть везде одинаковыми. Если ты однако при использовании более старой версии вы можете найти некоторые из отсутствуют расширенные функции.
gnuplot кажется почти полной противоположностью Калейдаграфа: В учебном пособии по калейдаграфу калейдаграф называется "простым в использовании, хотя и несколько ограниченная графическая программа ".gnuplot не так прост в использовании, хотя и чрезвычайно мощная программа для построения графиков из командной строки.
Запустить gnuplot просто: в командной строке любой системы введите gnuplot. Это можно сделать даже через telnet или ssh. подключение и предварительный просмотр графиков в текстовом режиме! Для лучших результатов, однако вы должны запускать gnuplot из X Window, чтобы вы могли увидеть лучшие превью ваших сюжетов.
Все наборы данных, которые вы используете в gnuplot, должны быть введены в текстовый файл.
первый.В каждой строке должна быть одна точка данных. Каждая точка данных будет
состоят из нескольких чисел: независимая переменная, зависимая
переменная и, при необходимости, планки погрешностей. Каждое из этих полей должно быть
разделенные табуляцией.
На самом деле, в каждой строке можно указать любое количество полей; это полезно, если у вас есть несколько измерений для каждой точки данных, для пример. Для получения информации о том, как получить доступ к этому дополнительному информацию о ваших графиках см. (fixme: add section) ниже.
Вы можете включить в файл любую дополнительную информацию, такую как описание данных, заголовки для каждого из столбцов данных и т. д. на, если каждая такая строка начинается с символа комментария, #.. Так после запустив gnuplot, в приглашении gnuplot> вы должны тип:
сюжет ехр (-x ** 2/2)
Обычно вам нужно немного больше контроля над своим сюжетом, по крайней мере указание диапазонов для осей x и y. Вы можете указать их в Форма [минимум: максимум] перед функцией. Сначала укажите диапазон x, затем диапазон y. Вы можете оставить y диапазон, или оба. Мы можем изменить нашу предыдущую команду построения графика на:
сюжет [-4: 4] exp (-x ** 2/2)
Здесь автоматически определяется диапазон y.
Отображение дополнительных функций
Если вы хотите построить более одной функции, просто перечислите все функции, разделенные запятыми. Например:
сюжет [-4: 4] exp (-x ** 2/2), x ** 2/16
Вы также можете переименовать независимую переменную, если хотите. Это выполняется совместно с указанием диапазона участка:
сюжет [t = -4: 4] exp (-t ** 2/2), t ** 2/16
Определение функций
Иногда бывает удобно определить функцию, чтобы она не нужно каждый раз набирать заново.Сделать это легко. Создадим функция f (x), чтобы представить нашу кривую колокола, а затем использовать ее в участок:
f (x) = ехр (-x ** 2/2) сюжет [t = -4: 4] f (t), t ** 2/16
Заголовки, метки и легенды
Вы могли заметить, что когда вы создавали свои сюжеты, легенда
был автоматически создан в правом верхнем углу графика. От
по умолчанию имя каждой кривой - это просто введенная вами формула. может дать им другие имена, используя заголовок
атрибут.Просто следуйте формуле функции с заголовком «Заголовок». Мы можем изменить наши предыдущие
команда на:
может дать им другие имена, используя заголовок
атрибут.Просто следуйте формуле функции с заголовком «Заголовок». Мы можем изменить наши предыдущие
команда на:
сюжет [t = -4: 4] f (t) название "Bell Curve", t ** 2/16 название "Parabola"
Обратите внимание, что запятые никогда не используются, кроме как для разделения отдельных функции. Если вы хотите, чтобы кривая не отображалась в легенде, установите его название "".
Мы также можем добавить заголовок к нашему графику и несколько меток на осях. Используется команда set. Вот пример:
установить заголовок "Некоторые образцы сюжетов" установить xlabel «Независимая переменная (без единиц)» установите ylabel "Зависимая переменная (без единиц измерения)"
Эти изменения не действуют, пока вы не перерисовываете график.Этот можно сделать, набрав команду plot еще раз, но если сам сюжет не меняется, достаточно набрать:
переделывать
, чтобы воспроизвести последние данные функции.
Другие приятные штрихи
Часто бывает приятно добавить к сюжету сетку, чтобы было легче увидеть где функции и данные попадают на график. Для этого наберите
установить сетку
После того, как вы научились строить функции, теперь пора научиться данные графика. Синтаксис почти такой же, за исключением того, что вместо указав функцию, вы должны указать имя файла, содержащего данные для построения, заключенные в двойные кавычки.
Во-первых, поскольку мы играли с графиками выше, мы очистим метки на осях и другие настройки:
сброс настроек
Вы также можете выйти из gnuplot и перезапустить его с тем же эффектом. Сейчас, мы построим наши образцы данных. Избавимся от записи в легенде для наши точки данных, используя заголовок "", а также настроить осей на участке:
установить заголовок "Данные Кавендиша" установить xlabel "Время (с)" установить ylabel "Угол (мрад)" установить сетку сюжет "cavendish.data" title ""
При построении данных обычно нет необходимости указывать диапазоны для независимые и зависимые переменные, поскольку они могут быть вычислены со входа.При необходимости, конечно, всегда можно их подарить.
, включая шкалы ошибок
Поскольку наши входные данные содержат неопределенности для измеренных (зависимое) количество, мы можем создать y полос погрешностей. Еще раз, gnuplot упрощает это:
сюжет "cavendish.data" title "" с yerrorbars
Можно построить x полос ошибок с помощью xerrorbars или и того, и другого. x и y шкалы ошибок с использованием xyerrorbars. Когда обе ошибки x и y используются столбцы, должно быть четыре столбца, а столбцы погрешностей x должны быть указанным первым в файле данных.Возможны другие варианты; видеть интерактивную справку для получения дополнительной информации.
Обратите внимание, что gnuplot может быть очень разборчивым в заказе, который вы даете. модификаторы сюжетов. Если бы вы вместо этого набрали
сюжет "cavendish.data" с заголовком yerrorbars ""
Вы получите довольно странное сообщение об ошибке: undefined variable: заглавие. Если вы видите подобные сообщения об ошибках, проверьте порядок в ваши сюжетные команды. Если вы не уверены, напечатайте график справки. выправить вас.
Ни одна программа построения графиков не будет полной без возможности соответствовать нашему данные в кривую.Для эксперимента Кавендиша нам нужно будет подогнать данные в синусоидальную кривую с экспоненциальным затуханием. gnuplot поддерживает эта нелинейная кривая подходит и может даже принимать экспериментальные учтены неопределенности точек данных.
Во-первых, необходимо определить форму функции, которую мы попытаемся подходит для. Определите это так же, как и любую другую функцию в gnuplot, но оставьте переменные для подгоночных параметров. Мы будем использовать
тета (т) = тета0 + а * ехр (-т / тау) * грех (2 * пи * т / Т + фи)
Различные параметры подгонки:
- а: амплитуда колебаний
- тау: период колебания
- фи: начальная фаза
- T: время экспоненциального затухания
- theta0: сдвиг из положения равновесия
Для подобной аппроксимации нелинейной кривой часто необходимо
предоставить первоначальное предположение для каждого из параметров подгонки или
попытка подгонки может потерпеть неудачу. Для простых уравнений, таких как многочлены,
в этом нет необходимости (но никогда не повредит).
Для простых уравнений, таких как многочлены,
в этом нет необходимости (но никогда не повредит).
а = 40 тау = 15 фи = -0,5 Т = 15 theta0 = 10
Наконец, мы выполним аппроксимацию кривой. Синтаксис для этого:
соответствовать theta (x) "cavendish.data" с использованием 1: 2: 3 через a, tau, phi, T, theta0
Вот как интерпретируется команда: fit сообщает gnuplot мы делаем аппроксимацию кривой. Следующая часть, theta (x), должна быть функция, которую мы используем для соответствия данным. Здесь мы должны использовать x как независимая переменная.Следующая часть, cavendish.data, должна быть файл данных, содержащий данные, которые мы хотим уместить. Использование 1: 2: 3 сообщает gnuplot взять столбцы 1, 2 и 3 из файла данных и использовать их как x, y и неопределенности соответственно. Если эта часть осталась out, то экспериментальные неопределенности не будут использоваться для кривой соответствовать. См. Ниже более подробное обсуждение чрезвычайно мощного квалификатора using. Наконец, мы должны сказать gnuplot какие переменные он может регулировать, чтобы лучше соответствовать. В этом случае мы говорим через a, tau, phi, T, theta0.
gnuplot будет производить вывод по мере прохождения подгонки, и если Подгонка успешна, вы должны увидеть что-то вроде этого:
степени свободы (ndf): 34
среднеквадратичное значение остатков (stdfit) = sqrt (WSSR / ndf): 1.07102
дисперсия остатков (приведенный числовой квадрат) = WSSR / ndf: 1.14708
Окончательный набор параметров Асимптотическая стандартная ошибка
======================= ==========================
а = 44,5389 +/- 2,127 (4,776%)
тау = 57.5667 +/- 8,132 (14,13%)
фи = -0,377254 +/- 0,04235 (11,22%)
Т = 13,1026 +/- 0,06465 (0,4934%)
theta0 = 2,45704 +/- 0,6081 (24,75%)
корреляционная матрица подгоночных параметров:
а тау фи T theta0
1.000
тау -0,844 1.000
фи -0,100 0,088 1,000
Т -0,072 0,072 0,806 1,000
тета0 -0,166 0,127 -0,182 -0,166 1,000
Важные величины, на которые следует обратить внимание, - это уменьшенный хи-квадрат (дисперсия
остатки), который в данном случае равен 1. 15, а значения для каждого из
подгоночные параметры. У каждого подгоночного параметра также есть неопределенность.
перечисленные. Корреляционную матрицу в конце обычно можно игнорировать.
15, а значения для каждого из
подгоночные параметры. У каждого подгоночного параметра также есть неопределенность.
перечисленные. Корреляционную матрицу в конце обычно можно игнорировать.
gnuplot также сохранил параметры подгонки в переменных, поэтому построить график с соответствующей кривой наилучшего соответствия так же просто, как:
заговор "cavendish.data" title "" с yerrorbars, theta (x) title "Best-Fit Curve"
Использование с использованием
Квалификатор using, используемый в приведенной выше команде подгонки, является чрезвычайно мощный инструмент в gnuplot.С его помощью вы можете тренироваться почти безграничный контроль над вашими данными во время их построения.
gnuplot обычно ожидает определенное количество столбцов данных при использовании файл данных (для построения графика или подгонки). Обычно всего два используются столбцы: независимая переменная и зависимая переменная. С планками погрешностей можно использовать еще один или два столбца. Обычно эти столбцы берутся напрямую из файла данных. Иногда это необходимо проявить немного больше контроля. Вот где использование входит.
Допустим, вам нужно поменять местами два столбца данных, так как зависимые сначала идет переменная, а затем независимая переменная в данных файл. Вы можете создать этот график с помощью команды:
график "reverse.data" с использованием 2: 1
Команда using ожидает несколько значений, по одному для каждого столбец требуемых данных, каждое значение которого отделено двоеточием. Если значение - это просто число, gnuplot возьмет этот фрагмент данных из указанный столбец в файле данных. В этом случае мы говорим gnuplot взять независимая переменная из столбца 2 и зависимая переменная из столбец 1.
Предыдущий пример был немного надуманным. Но есть очень распространенный
случай, когда используется использование: когда есть несколько наборов данных в
вход. Предположим, у вас есть файл данных с тремя столбцами:
независимая переменная и две зависимые переменные. Вы хотите построить
обе зависимые переменные как отдельный набор точек. Вы можете использовать:
Вы хотите построить
обе зависимые переменные как отдельный набор точек. Вы можете использовать:
построить график "double.data" с использованием заголовка 1: 2 "Серия 1", "double.data" с использованием заголовка 1: 3 "Серия 2"
В приведенном выше примере подгонки, указав 1: 2: 3, мы заставляли команду fit принимать в качестве входных данных три столбца вместо обычные два (чтобы включить информацию об ошибке), но мы не выполнили любой повторный заказ на них.
Это еще только верхушка того, что с помощью банки делать. Вместо того, чтобы указывать номер столбца, вы также можете указать полный выражение, которое должно быть заключено в круглые скобки. В рамках этого выражение, значения из столбцов можно получить как $ 1, $ 2, $ 3 и т. Д. В качестве примера, если бы мы хотели построить график натуральный логарифм нашей зависимой переменной, мы могли бы использовать:
построить "log.data", используя 1: (log ($ 2))
Обратите внимание, что как часть квалификатора using ($ 2) в точности эквивалентно 2.
Другой пример см. В следующем разделе: построение остатков.
Построение остатков
Чтобы понять этот раздел, вы должны понимать раздел «Использование с использованием» выше.
Сначала мы построим график разницы между каждой точкой данных. и подобранная кривая:
построить "cavendish.data", используя 1: (theta ($ 1) - $ 2): 3 заголовок "Остатки" с yerrorbars
Возможно, уместно небольшое пояснение к выражению using.Мы создаем график с полосами ошибок y, поэтому нам нужно три столбца данных.
Следовательно, квалификатор using состоит из трех частей, разделенных
двоеточия. Первая, 1, говорит первая часть, независимая
переменная, это просто первый столбец из входного файла. Второй
часть - это выражение: мы вычислим разницу между нашей функцией
(тета), оцениваемый по значению независимой переменной
($ 1 - первый столбец файла данных) и измеренное значение
($ 2 - второй столбец файла данных или зависимая переменная) для
этот момент. В третьем столбце 3 просто говорится об использовании
существующая неопределенность хранится в столбце 3 файла данных без
модификация.
В третьем столбце 3 просто говорится об использовании
существующая неопределенность хранится в столбце 3 файла данных без
модификация.
Было бы даже лучше, если бы мы могли положить остатки на такие же график как подобранная кривая. Чтобы это выглядело хорошо, мы будем использовать различный масштаб для остатков, поэтому их можно отделить от остальная часть графика. gnuplot позволяет использовать две разные шкалы для каждая ось: есть независимые шкалы x и x2 для оси x, y и y2 масштабируется для оси y и т. д.
Есть другой синтаксис для определения диапазонов для каждой из осей, что необходимо для одновременного использования более одной шкалы. Первый, давайте немного сдвинем график наших данных и подогнанную кривую, чтобы номер.
установить диапазон [-80: 60] сюжет "cavendish.data" title "" с yerrorbars, theta (x) title ""
Это похоже на указание диапазона как часть команды построения, но настройки останутся неизменными до тех пор, пока они не будут отменены, и мы сможем укажите диапазон y без диапазона x.
Теперь мы создадим вторую шкалу для оси Y справа. боковая сторона. Это можно сделать с помощью:
установить y2range [-20: 120] установить границу y2tics
Команда set y2tics border указывает gnuplot отображать это шкала на границе участка. Без него новая шкала была бы установлен, но он не будет отображаться в правой части графика.
Теперь пришло время добавить наши остатки. Добавляем их в команду plot, и укажите, что они должны использовать новую шкалу y.Они будут использовать та же шкала x, что и раньше:
сюжет "cavendish.data" title "" с yerrorbars, theta (x) title "", "cavendish.data" с использованием 1: (theta ($ 1) - $ 2): 3 оси x1y2 title "" с yerrorbars
Здесь оси x1y2 означают использование нормальной оси x, а новая ось y, которую мы только что определили.
Наконец, для небольшого дополнительного прикосновения нарисуем ось x для остатки:
установить x2zeroaxis lt -1 установить y2label "Остатки" переделывать
Здесь lt -1 означает "тип линии -1", где -1 - стиль
обычно используется для границ участка.
Если вы следовали всему руководству, теперь вы должны есть окно графика, которое выглядит примерно так:
gnuplot очень не зависит от устройства: при создании ваших графиков он может не заботьтесь о том, производит ли он предварительный просмотр на дисплее X Window, Версия ASCII-art для терминала или любая другая форма вывода. Сценарий все команды будут работать одинаково. Получив свой сюжет так, как вы нравится, однако вы хотите сохранить или распечатать. Для этого вы захотите изменить выходной формат, что можно сделать с помощью команда set term.
При работе в X тип терминала по умолчанию - x11. Если, после сохранения вывода в другом месте вы хотите снова просмотреть вывод в X, вы хотите ввести
установить срок x11
Если вы работаете через Telnet или где графика недоступна, вы можете набрать
установить термин немой
, чтобы выбрать тупой терминал. Хотя это и не красиво, но часто можно получить Представьте, как выглядит ваш сюжет с этим. Данные Кавендиша выглядят так: это на тупом терминале:
Кавендиш Данные
Угол (мрад) Остаточные
60 ++ ------ + -------- + ------- + -------- + ------- + ------ - + ------- + ------- ++ 120
+ * * + + + + + + + +
| A # A # *:::::: |
40 ++... # .. # AA ............... # * # ......................... * .......... ++ 100
| A: # *:: A AA ##:: * # A # ** A: |
20 ++. # ...... ## ............. A # * .. *. A # .............. * A. ..AA. * .......... ++ 80
| *: #: * * A: #A: # *: |
| #A: A: #: # *: A #: # *: |
0 + # ........... # ......... A ........... # A ........ # ... ........ А # ........ ++ 60
* #: A: * #:: #: A #: * # |
-20 А +............ ** .... A # A .............. * # ... A # .......... ..... A # ** # A .. ++ 40
| : A #: * #:: A # A # A *:: AA * |
| : # A # A:: *::: |
-40 ++ ............... *. * ............................ ................... ++ 20
| ::: $: $:: $ $ $$ |
-60 B + $ - $ - $ - B - B - $$ - BB - BB - $ - B-BB-B --- $ B - $ - $$ - $ - $ - BB - $ - B --- $ - B-BB-B - ++ 0
$ B BB B: $ $$ BB $ $ B $ B $ B B B BB B B $$ B B $ B: $ |
+ $ + B + $ + + $ + + B + +
-80 ++ ------ + - $ ----- + ------- + -------- + ------- + ----- --- + ---- $ - + ------- ++ - 20
0 5 10 15 20 25 30 35 40
Время (с)
R plot () Функция (добавление заголовков, меток, изменение цветов и наложение горшков)
Из этой статьи вы научитесь использовать функцию построения графика в R. Он используется для построения графиков в соответствии с типом переданного объекта.
Он используется для построения графиков в соответствии с типом переданного объекта.
Наиболее часто используемой функцией построения графиков в программировании на R является функция
plot () . Это общая функция, то есть у нее есть много методов, которые вызываются в соответствии с типом объекта, переданного в plot () .В простейшем случае мы можем передать вектор и получить диаграмму разброса величины и индекса. Но обычно мы передаем два вектора и строим диаграмму рассеяния этих точек.
Например, команда plot (c (1,2), c (3,5)) построит точки (1,3) и (2,5) .
Вот более конкретный пример, где мы строим график синусоидальной функции в диапазоне от -pi до pi .
x <- seq (-pi, pi, 0,1)
сюжет (x, sin (x))
Добавление заголовков и осей надписей
Мы можем добавить заголовок к нашему графику с помощью параметра main . Точно так же xlab и ylab можно использовать для маркировки оси x и оси y соответственно.
участок (x, sin (x),
main = "Функция синуса",
ylab = "грех (х)")
Изменение цвета и типа графика
Выше мы видим, что график состоит из круглых точек и имеет черный цвет. Это цвет по умолчанию.
Мы можем изменить тип графика с помощью аргумента типа . Он принимает следующие строки и имеет заданный эффект.
"p" - баллов "l" - линии «б» - и точки, и линии «c» - пустые точки, соединенные линиями «о» - точки и линии, нанесенные поверх черточки «s» и «S» - ступеньки лестницы "h" - вертикальные линии в виде гистограммы «n» - не создает точек или линий
Точно так же мы можем определить цвет, используя col .
участок (x, sin (x),
main = "Функция синуса",
ylab = "грех (х)",
type = "l",
col = "синий")
Наложение графиков с помощью функции легенды ()
Вызов plot () несколько раз приведет к построению текущего графика в том же окне вместо предыдущего.
Однако иногда мы хотим наложить графики, чтобы сравнить результаты.
Это стало возможным с помощью функций линий () и точек () для добавления линий и точек соответственно к существующему графику.
участок (x, sin (x),
main = "Наложение графиков",
ylab = "",
type = "l",
col = "синий")
строки (x, cos (x), col = "red")
легенда ("верхний край",
с («грех (х)», «соз (х)»),
fill = c ("синий", "красный")
)
Мы использовали функцию legend () , чтобы правильно отобразить легенду. Посетите функцию legend (), чтобы узнать больше.
Также посетите функцию plot (), чтобы узнать больше о различных аргументах. Функция plot () может принимать и другие примеры.
Понять df.сюжет в пандах
Построить хорошую графику с помощью matplotlib непросто! Лучший способ - создать несколько непривлекательная визуализация с помощью matplotlib, затем экспортируйте ее в PDF и откройте его в Illustrator. Но если вы хотите сначала доставить его в хорошее место?
Давай сделаем это.
Наши данные
Мы собираемся работать с данными ОЭСР, в частности безработица с 1980 по подарок для Японии, Австралии, США и Германии. Я отредактировал данные, чтобы они выглядит немного чище, и с ним немного легче работать.
% встроенный матplotlib
импортировать панды как pd df = pd.read_csv ("../ безработица.csv")
df.head () | страна | год | безработица | |
|---|---|---|---|
| 0 | Австралия | 1980 | 6.106246 |
| 1 | Австралия | 1981 | 5.783571 |
| 2 | Австралия | 1982 | 7. 156132 156132 |
| 3 | Австралия | 1983 | 9.96 1594 |
| 4 | Австралия | 1984 | 8.989680 |
панды против matplotlib
Под капотом pandas строит графики с помощью библиотеки matplotlib .Это
обычно довольно удобно, так как это позволяет вам только . построить ваших графиков, но
поскольку matplotlib - это , вид , панды-крушители поезда наследуют эту путаницу.
Какой
.plot мне использовать? Когда вы используете .plot на фрейме данных, вы иногда передаете ему вещи и иногда нет.
-
.plotотображает индекс для каждого столбца -
.plot (x = 'col1')строит графики против одного определенного столбца -
.plot (x = 'col1', y = 'col2')отображает один конкретный столбец против другого конкретного столбец
Давайте посмотрим, когда вы можете использовать то или другое!
Версия 1:
. Plot отображает индекс по каждому столбцуДавайте посмотрим на срез где-то посередине наших данных. Ничего особенного захватывающие, просто страны, годы и уровень безработицы.
df [35:40] | страна | год | безработица | |
|---|---|---|---|
| 35 | Австралия | 2015 | 6.063658 |
| 36 | Австралия | 2016 | 5,72 3454 |
| 37 | США | 1980 | 7.141667 |
| 38 | США | 1981 | 7.600000 |
| 39 | США | 1982 | 9,708333 |
Видите крайний левый столбец? Это индекс .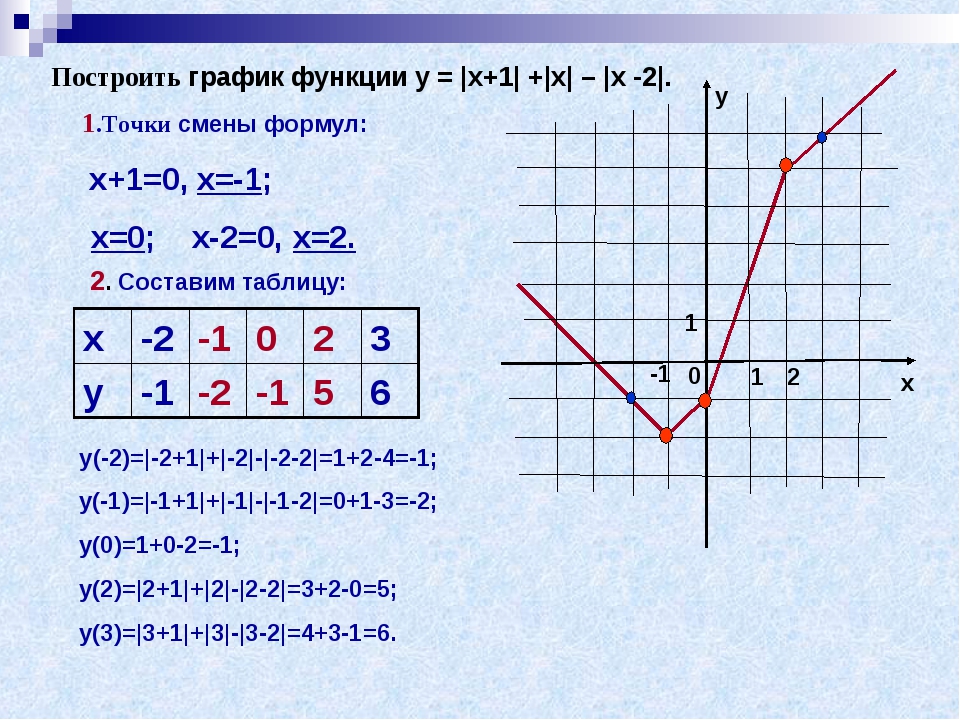 В данном случае это просто
номер строки. Первая строка - это индекс
В данном случае это просто
номер строки. Первая строка - это индекс 0 , 40-я строка - это индекс 39 и т. Д.
Если мы построим график, используя только .plot , он будет использовать этот номер строки в качестве оси X
на нашем графике. Как это будет выглядеть?
df.plot ()
Странно, правда? Ось x просто «эй, это 20-я строка, это 40-я». ряд, это 140 ряд »- ничего особенного.Посмотри, где маленький провалы в синей линии? Первая капля - это данные, которые мы только что рассмотрели: index 36 - это данные Австралии за 2016 год, затем индекс 37 - данные США за 1980 год. падает!
Он также отображает безработицу и за год. Что за крушение!
Основные варианты использования .plot () - это когда у вас есть значимый индекс, который
обычно бывает в двух ситуациях:
- Вы только что выполнили
.value_counts ()или.groupby () - Вы использовали
.set_index, вероятно, с датами
Давайте посмотрим, как это работает.
df.groupby ("страна") ["безработица"]. Mean () страна
Австралия 6.954607
Германия 6.926593
Япония 3.515090
США 6.379730
Имя: безработица, dtype: float64
Когда вы выполняете группировку и суммируете столбец, вы получаете Series , а не фрейм данных. Важно посмотреть на данные слева - индекс - и пойми, что на этот раз это что-то значит! Это название страны! И в из «прочих» строк только один - средний уровень безработицы.Так что если строим его…
df.groupby ("страна") ['безработица']. Mean (). Plot (kind = 'bar')
Это поразительно уродливо, но, по крайней мере, на этот раз имеет смысл!
Версия 2 для построения графиков:
. plot (x = 'col1')
plot (x = 'col1') строит графики против одного определенного столбцаЯ ... пропущу это и скажу вам просто использовать версию 3.
Версия графика 3:
.plot (x = 'col1', y = 'col2') отображает один конкретный столбецпротив другого конкретного столбца
Однако мы знаем, чего хотим - нам нужен год на оси x и
уровень безработицы по оси y. Если мы дадим . График и x = , и y = мы сможем об этом позаботиться, верно?
df.plot (x = 'год', y = 'безработица')
ну это вроде работало, по крайней мере!
Когда pandas строит графики, предполагается, что каждая точка данных должна быть подключена, aka pandas понятия не имеет, что мы не хотим, чтобы строка 36 (Австралия в 2016 году) подключалась
к строке 37 (США в 1980 г.).Чтобы исправить это, нам просто нужно добавить группа по . После того, как мы сгруппируем данные по странам, панды построят график
каждая группа в отдельности.
df.groupby ('страна'). График (x = 'год', y = 'безработица') страна
Топоры Австралии (0,125, 0,125; 0,775x0,775)
Топоры Германии (0,125,0,125; 0,775x0,775)
Японские топоры (0,125,0,125; 0,775x0,775)
Топоры США (0,125,0,125; 0,775x0,775)
dtype: объект
Ой, может быть, это было слишком отдельно! Мы поговорим об этом подробнее, когда мы обсуждаем такие вещи matplotlib-y, как фигуры , оси и подзаголовки , но основные идея в том, что сначала нам нужно создать график , а затем мы скажем пандам сохранить рисование поверх одного и того же графика для каждой отдельной диаграммы.
импортировать matplotlib. pyplot как plt
fig, ax = plt.subplots ()
df.groupby ('country'). plot (x = 'год', y = 'безработица', ax = ax, legend = False)
pyplot как plt
fig, ax = plt.subplots ()
df.groupby ('country'). plot (x = 'год', y = 'безработица', ax = ax, legend = False) country
Топоры Австралии (0,125, 0,125; 0,775x0,775)
Топоры Германии (0,125,0,125; 0,775x0,775)
Японские топоры (0,125,0,125; 0,775x0,775)
Топоры США (0,125,0,125; 0,775x0,775)
dtype: объект
Итого
В целом, вам просто нужно знать, есть ли у вас значимый индекс .
- Вы выполнили groupby или value_counts ()? Вы можете использовать
.plot () - У вас есть нормальный фреймворк? Вероятно, вам следует установить
xиy.
Далее мы поговорим о том, как настраивать графику, и о большой роли, которую matplotlib играет в графике с пандами.
3.2 Производная как функция - Объем исчисления 1
Цели обучения
- Определите производную функцию заданной функции.
- Постройте производную функцию от графика заданной функции.
- Укажите связь между производными финансовыми инструментами и непрерывностью.
- Опишите три условия, когда функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы дифференцируем функцию положения в данный момент времени, мы получаем скорость в этот момент.Кажется разумным заключить, что знание производной функции в каждой точке может дать ценную информацию о поведении функции. Однако процесс нахождения производной даже для нескольких значений с использованием методов предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная. Мы можем формально определить производную функцию следующим образом.
Мы можем формально определить производную функцию следующим образом.
Определение
Позвольте быть функцией. Производная функция , обозначенная как, - это функция, область определения которой состоит из таких значений, что существует следующий предел:
. Говорят, что функция дифференцируема на , если
существует. В более общем смысле говорят, что функция дифференцируема на , если она дифференцируема в каждой точке открытого набора, а дифференцируемая функция - это функция, в которой существует в своей области.
В следующих нескольких примерах мы используем (рисунок), чтобы найти производную функции.
Нахождение производной функции квадратного корня
Найдите производную от.
Решение
Начните непосредственно с определения производной функции. Используйте (рисунок).
Нахождение производной квадратичной функции
Найдите производную функции.
Решение
Выполните здесь ту же процедуру, но без умножения на конъюгат.
Найдите производную от.
Решение
Мы используем множество различных обозначений для выражения производной функции. На (Рисунок) мы показали, что если, то. Если бы мы выразили эту функцию в форме, мы могли бы выразить производную как или. Мы могли бы передать ту же информацию письменно. Таким образом, для функции каждое из следующих обозначений представляет собой производную от:
. Вместо мы также можем использовать. Использование обозначений (так называемых обозначений Лейбница) довольно распространено в инженерии и физике.Чтобы лучше понять это обозначение, напомним, что производная функции в точке - это предел наклона секущих линий, когда секущие линии приближаются к касательной. Наклоны этих секущих линий часто выражаются в виде где - разница значений, соответствующая разнице значений, которые выражаются как ((Рисунок)). Таким образом, производная, которую можно представить как мгновенную скорость изменения относительно, выражается как
Таким образом, производная, которую можно представить как мгновенную скорость изменения относительно, выражается как
Мы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение производной функции, мы можем построить график. Учитывая и то, и другое, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку дает скорость изменения функции (или наклон касательной к).
На (рис.) Мы обнаружили, что для. Если мы построим график этих функций на тех же осях, что и на (Рисунок), мы сможем использовать графики, чтобы понять взаимосвязь между этими двумя функциями.Во-первых, мы замечаем, что он увеличивается по всей своей области, что означает, что наклон его касательных во всех точках положительный. Следовательно, мы ожидаем для всех значений в его области. Кроме того, по мере увеличения наклон касательных к уменьшается, и мы ожидаем увидеть соответствующее уменьшение. Мы также замечаем, что это не определено и соответствует вертикальной касательной к точке 0.
Рис. 2. Производная везде положительна, потому что функция возрастает.На (рис.) Мы обнаружили, что для. Графики этих функций показаны на (Рисунок). Обратите внимание, что для. Для этих же значений. Для значений увеличивается и. Кроме того, имеет горизонтальную касательную в точках и.
Построение производной с помощью функции
Используйте следующий график, чтобы нарисовать график.
Нарисуйте график. На каком интервале находится график выше оси?
Решение
Теперь, когда мы можем построить график производной, давайте рассмотрим поведение графиков.Во-первых, мы рассматриваем взаимосвязь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в какой-то точке, не обязательно должна быть дифференцируемой в этой точке.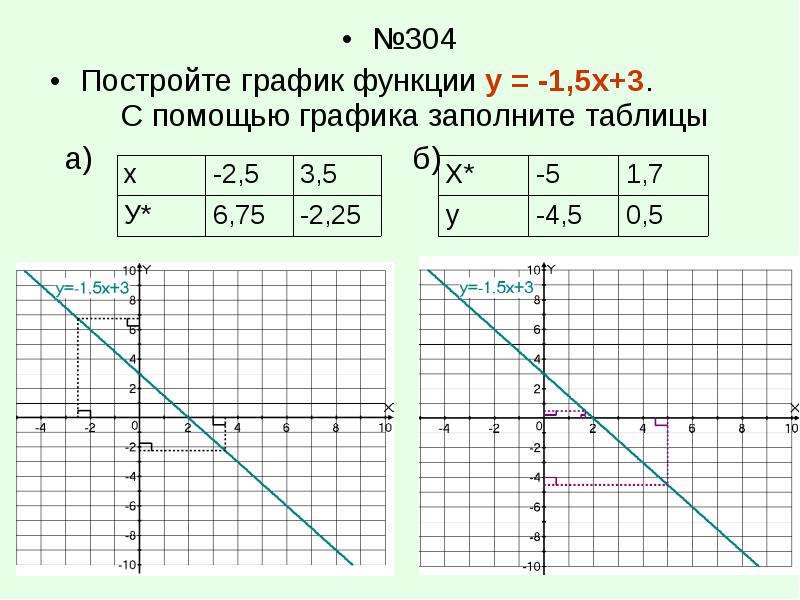 Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин.
Фактически, функция может быть непрерывной в точке и не дифференцируемой в этой точке по одной из нескольких причин.
Проба
Если дифференцируем в, то существует и
.Мы хотим показать, что это непрерывно, показав это.Таким образом,
Следовательно, поскольку определено и, заключаем, что непрерывно в точке.
Мы только что доказали, что дифференцируемость предполагает непрерывность, но теперь мы рассмотрим, подразумевает ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, исследуем функцию. Эта функция всюду непрерывна; однако не определено. Это наблюдение приводит нас к мысли, что непрерывность не предполагает дифференцируемости. Давайте изучим дальше. Для,
.Этот предел не существует, потому что
.См. (Рисунок).
Рисунок 4. Функция непрерывна в 0, но не дифференцируема в 0.Рассмотрим некоторые дополнительные ситуации, в которых непрерывная функция не дифференцируема. Рассмотрим функцию:
.Таким образом не существует. Беглый взгляд на график проясняет ситуацию. Функция имеет вертикальную касательную в точке 0 ((рисунок)).
Рисунок 5. Функция имеет вертикальную касательную в точке. Он непрерывен в 0, но не дифференцируем в 0.У функции также есть производная, которая демонстрирует интересное поведение при 0. Мы видим, что
.Этот предел не существует, в основном потому, что наклон секущих линий непрерывно меняет направление по мере приближения к нулю ((Рисунок)).
Рисунок 6. Функция не дифференцируема в 0.Итого:
- Заметим, что если функция не является непрерывной, она не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Однако, если функция непрерывна, она все равно не может быть дифференцируемой.
- Мы видели, что это невозможно дифференцировать в 0, потому что предел наклона касательных линий слева и справа не был одинаковым. Визуально это привело к появлению острого угла на графике функции в 0.
 Отсюда мы заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке.
Отсюда мы заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке. - Как мы видели в примере, функция не может быть дифференцируемой в точке, где есть вертикальная касательная.
- Как мы видели, функция может быть не дифференцируемой в точке и более сложными способами.
Непрерывная и дифференцируемая кусочная функция
Производная функции сама по себе является функцией, поэтому мы можем найти производную от производной. Например, производная функции положения - это скорость изменения положения или скорости. Производная скорости - это скорость изменения скорости, которая является ускорением. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать использовать производные для получения третьей производной, четвертой производной и так далее.В совокупности они называются производными более высокого порядка . Обозначения для производных высшего порядка от могут быть выражены в любой из следующих форм:
.Интересно отметить, что обозначение для можно рассматривать как попытку выразить более компактно. Аналогично.
Поиск второй производной
Для, найдите.
В поисках ускорения
Положение частицы вдоль оси координат в момент времени (в секундах) определяется выражением (в метрах).Найдите функцию, описывающую его ускорение во времени.
- Производная функция
В следующих упражнениях используйте определение производной для поиска.
1.
2.
3.
4.
Решение
5.
6.
Решение
7.
8.
Решение
9.
10.
Решение
Для следующих упражнений используйте график, чтобы нарисовать график его производной.
11. 12.Решение
13. 14.Решение
Для следующих упражнений данный предел представляет собой производную функции в.Найти и .
15.
16.
Решение
17.
18.
Решение
19.
20.
Решение
Для следующих функций:
- набросок графика и
- использует определение производной, чтобы показать, что функция не дифференцируема в.
21.
23.
Для следующих графиков
- ,
- определяет, для каких значений существует, но не является непрерывным, и
- определяет, для каких значений функция является непрерывной, но не дифференцируемой в.
Для следующих функций используйте, чтобы найти.
28.
29.
30.
Решение
Для следующих упражнений используйте калькулятор для построения графиков. Определите функцию, затем используйте калькулятор для построения графика.
31. [Т]
33. [Т]
35. [Т]
Для следующих упражнений опишите, что представляют собой эти два выражения в терминах каждой из данных ситуаций. Обязательно укажите единицы измерения.
37. обозначает население города во время в годах.
38. обозначает общую сумму денег (в тысячах долларов), потраченную клиентами на концессии в парке развлечений.
Решение
а. Средняя ставка, с которой клиенты потратили на уступки, в тысячах на одного клиента.
г. Скорость (в тысячах на одного покупателя), по которой покупатели тратили деньги на уступки, в тысячах на одного покупателя.
39. обозначает общую стоимость (в тысячах долларов) производства радиочасов.
40. обозначает оценку (в процентных пунктах), полученную по тесту с учетом часов обучения.
Решение
а. Средняя оценка, полученная за тест, при среднем времени обучения между двумя суммами.
г. Скорость (в процентных пунктах в час), с которой оценка по тесту повышалась или понижалась за данное среднее время обучения в часах.
41. обозначает стоимость (в долларах) учебника социологии в университетских книжных магазинах США с 1990 года.
42. обозначает атмосферное давление на высоте футов.
Решение
а. Среднее изменение атмосферного давления между двумя разными высотами.
г. Скорость (торр на фут), с которой атмосферное давление увеличивается или уменьшается на высоте.
Решение
а. Скорость (в градусах на фут), с которой температура повышается или понижается для данной высоты.
г. Скорость изменения температуры при изменении высоты на высоте 1000 футов составляет -0.1 градус на фут.
Решение
а. Скорость, с которой число людей, заболевших гриппом, меняется через несколько недель после первоначальной вспышки.
г. Скорость резко увеличивается до третьей недели, после чего она замедляется, а затем становится постоянной.
Для следующих упражнений используйте следующую таблицу, в которой показана высота ракеты Saturn V для миссии Apollo 11 через несколько секунд после запуска.
| Время (секунды) | Высота (метры) |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 2 | 4 |
| 3 | 13 |
| 4 | 25 |
| 5 | 32 |
47. В чем физический смысл? Какие единицы?
48. [T] Создайте таблицу значений для обоих графиков и на том же графике. (Подсказка : для внутренних точек, оцените оба предела слева и справа и усредните их.)
Решение
| Время (секунды) | (м / с) |
|---|---|
| 0 | 2 |
| 1 | 2 |
| 2 | 5.5 |
| 3 | 10,5 |
| 4 | 9,5 |
| 5 | 7 |
Matlab plot function 3d
Итак, мне нравится рисовать более толстые линии, примерно на 1,5–2,0 точки. Вы можете делать это при каждом вызове построения графика с помощью параметра LineWidth, например: plot (x, y1, x, y2, 'LineWidth', 2. 0) Но тогда вы должны не забывать добавлять параметр LineWidth все время. Оказывается, есть способ заставить MATLAB рисовать все построенные линии толще по умолчанию.Здесь ... Полезно строить комплексные числа как точки на комплексной плоскости, а также строить график функции комплексных переменных, используя контурные или поверхностные графики. Построение комплексных чисел Если входными данными для команды Matlab plot является вектор комплексных чисел, действительные части используются как координаты x, а мнимые части - как координаты y.
0) Но тогда вы должны не забывать добавлять параметр LineWidth все время. Оказывается, есть способ заставить MATLAB рисовать все построенные линии толще по умолчанию.Здесь ... Полезно строить комплексные числа как точки на комплексной плоскости, а также строить график функции комплексных переменных, используя контурные или поверхностные графики. Построение комплексных чисел Если входными данными для команды Matlab plot является вектор комплексных чисел, действительные части используются как координаты x, а мнимые части - как координаты y.
Вычислить и построить график функции и ее лапласиана Затем мы хотим вычислить лапласиан данной скалярной функции поля и построить соответствующие трехмерные графики каждого распределения в интересующей области.Скалярная функция задается x2 y2 в области 4 (x, y) 4. Код MATLAB дается в рамке. 3D-графики Matlab предоставляет множество полезных инструкций для визуализации 3D-данных. Предоставляемые инструкции включают инструменты для построения каркасных объектов, трехмерных графиков, кривых, поверхностей и т. Д. И могут автоматически генерировать контуры, отображать объемные данные, интерполировать цвета затенения и даже отображать изображения, созданные не в Matlab.
Как построить трехмерные точки с помощью функции Plot3 в ... Узнайте больше о трехмерных графиках MATLAB Построение нескольких наборов данных вместе помогает коррелировать тенденции между ними.Существует множество способов представления данных на графике, включая использование отдельных маркеров для представления уникальных точек данных или соединение каждой точки данных линией. Узнайте, как представлять данные, используя отдельные маркеры на графике MATLAB.
3 ноября 2008 г. · function [h] = plot3d_errorbars (x, y, z, e)% эта функция Matlab строит трехмерные данные с помощью функции plot3. % он добавляет вертикальные полосы ошибок к каждой точке, симметричной относительно z. % Я немного поэкспериментировал с созданием стандартного горизонтального хеша.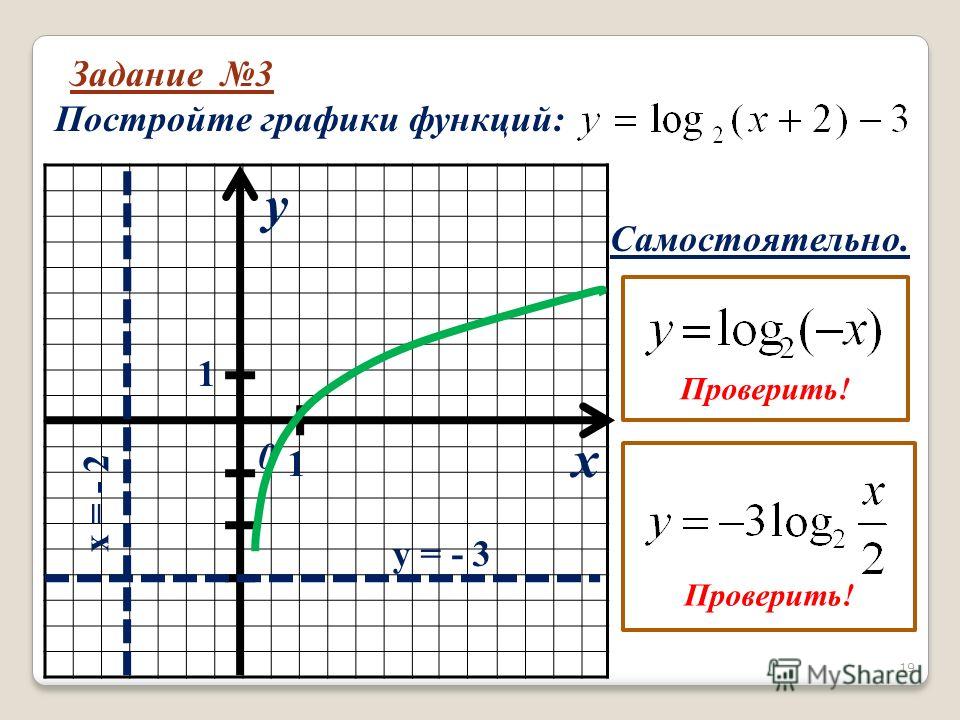
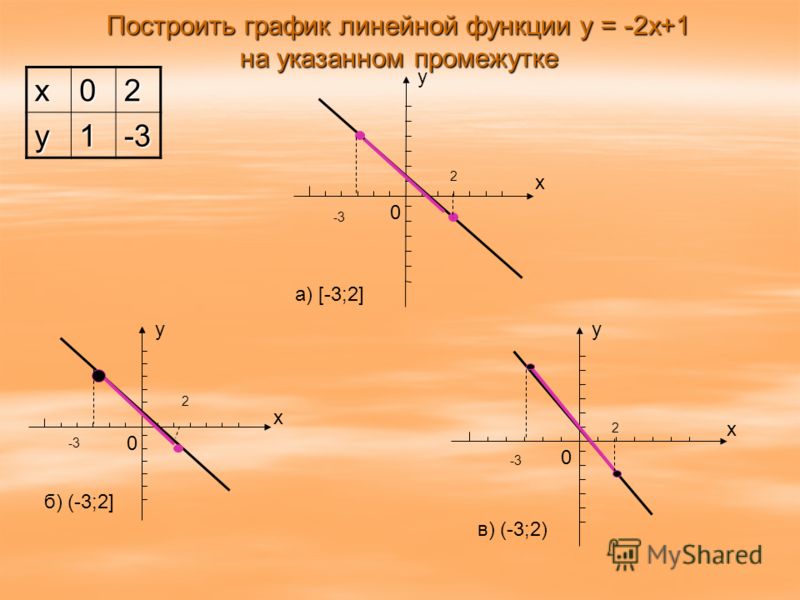 Домашнее задание – 7
мин.
Домашнее задание – 7
мин. Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики. 3
3
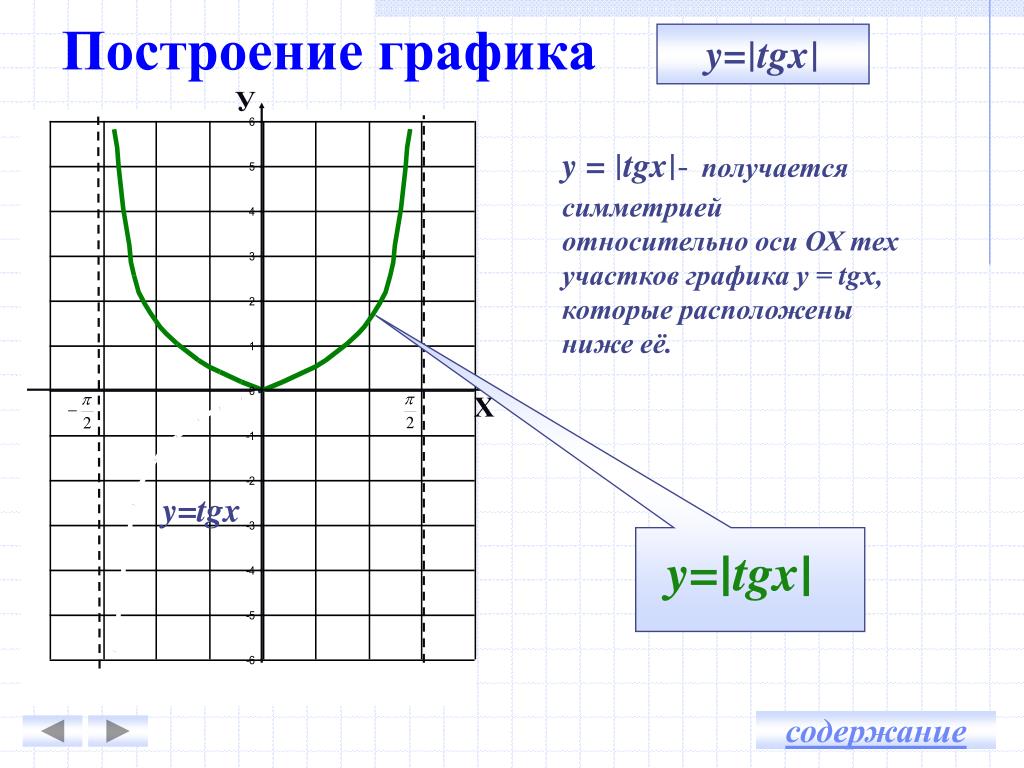 ')
plt.показывать()
')
plt.показывать()
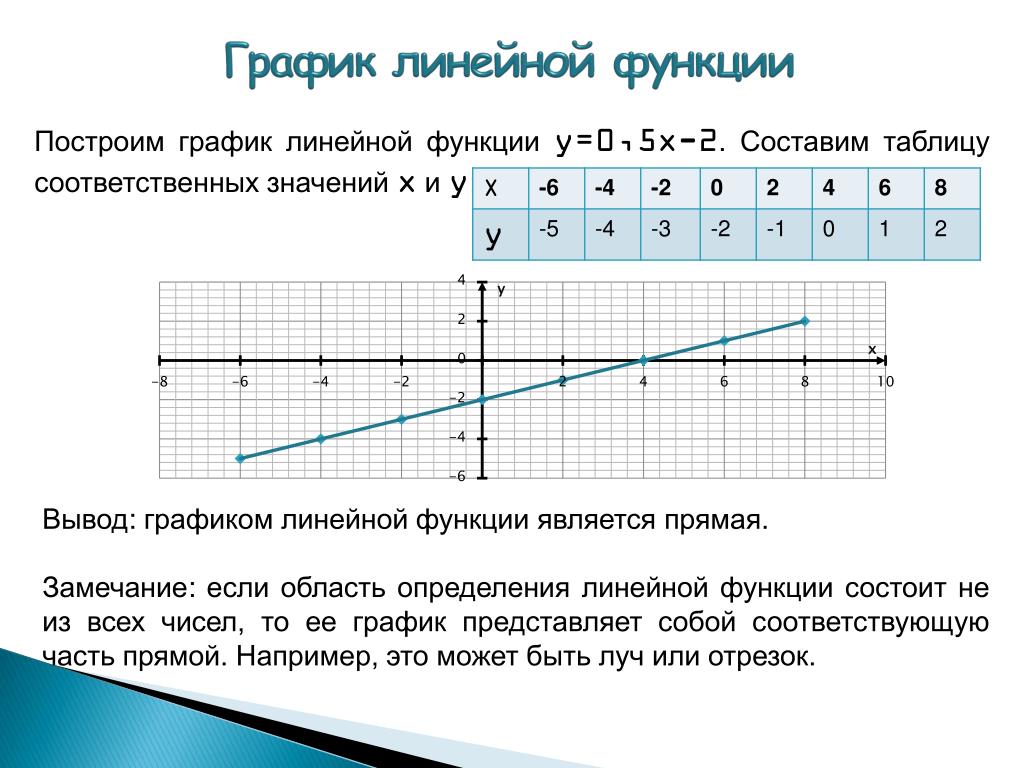 setp (линии, 'цвет', 'r', 'ширина линии', 2.0)
setp (линии, 'цвет', 'r', 'ширина линии', 2.0)
 xlabel ("Умные")
plt.ylabel ('Вероятность')
plt.title ('Гистограмма IQ')
plt.text (60, 0,025, r '$ \ mu = 100, \ \ sigma = 15 $')
plt.axis ([40, 160, 0, 0,03])
plt.grid (Истина)
plt.show ()
xlabel ("Умные")
plt.ylabel ('Вероятность')
plt.title ('Гистограмма IQ')
plt.text (60, 0,025, r '$ \ mu = 100, \ \ sigma = 15 $')
plt.axis ([40, 160, 0, 0,03])
plt.grid (Истина)
plt.show ()
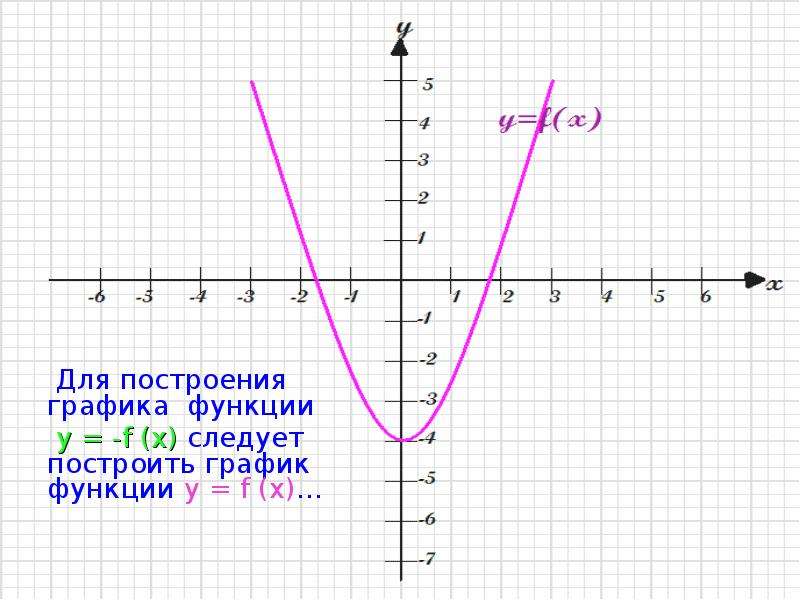 subplots_adjust (вверху = 0,92, внизу = 0,08, слева = 0,10, справа = 0,95, hspace = 0,25,
wspace = 0,35)
plt.show ()
subplots_adjust (вверху = 0,92, внизу = 0,08, слева = 0,10, справа = 0,95, hspace = 0,25,
wspace = 0,35)
plt.show ()
 data" title ""
data" title ""
 plot (x = 'col1')
plot (x = 'col1')  pyplot как plt
fig, ax = plt.subplots ()
df.groupby ('country'). plot (x = 'год', y = 'безработица', ax = ax, legend = False)
pyplot как plt
fig, ax = plt.subplots ()
df.groupby ('country'). plot (x = 'год', y = 'безработица', ax = ax, legend = False) 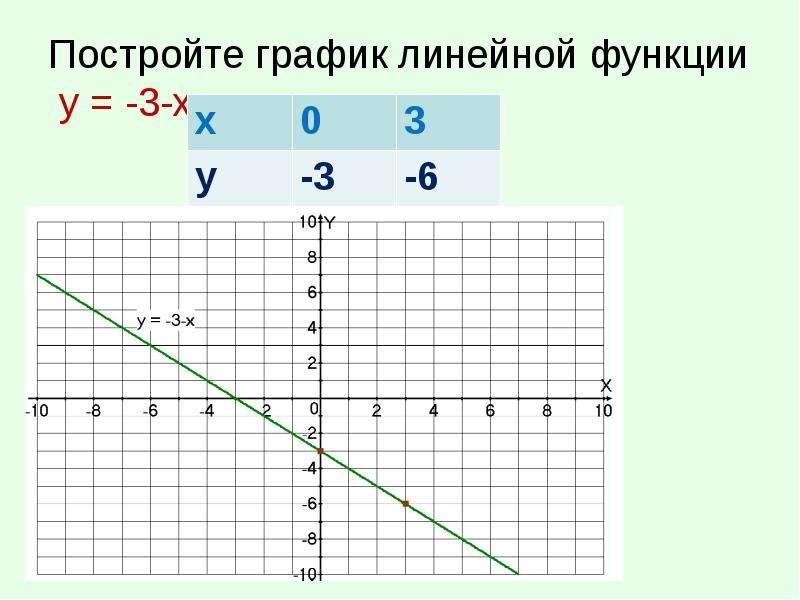 Отсюда мы заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке.
Отсюда мы заключаем, что для того, чтобы быть дифференцируемой в точке, функция должна быть «гладкой» в этой точке.