Свойства корней и степеней / Блог
Формулы корней n-ой степени и их свойства
- Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение:
(\sqrt[n] { a } )^k =\sqrt[n] { a^k } - Чтобы извлечь корень из корня, достаточно перемножить показатели корней:
\sqrt[n] { \sqrt[k] { a } ) } =\sqrt[n*k] { a } - Значение корня не изменится, если одновременно его показатель увеличить в k раз и подкоренное значение возвести в степень k:
\sqrt[n] { a^m } = \sqrt[n*k] { a^ { m*k } } - Корень из произведения равен произведению корней:
\sqrt[n] { a*b } = \sqrt[n] { a } * \sqrt[n] { b } - Корень из дроби — это корень из числителя и корень из знаменателя:
\sqrt[n] { \frac { a } { b } } = \frac { \sqrt[n] { a } } { \sqrt[n] { b } } - Корень из n-ой степени в степени n
(\sqrt[n] { a } )^n =a - Корень из квадрата:
(\sqrt { a^2 } ) = |a|
Формулы степеней и их свойства
- Возведение в нулевую степень:
a^0 = 1 - Произведение степеней:
a^m * a^n = a^ { m+n } - Деление степеней:
a^m : a^n = a^ { m — n } - Возведение степени в степень:
(a^m)^n = a^ { m*n } - При возведении в степень произведения каждый из множителей возводится в степень и результаты перемножают:
(a*b)^m = a^m * b^m - При возведении в степень частного возводят в эту степень и делимое, и делитель, результаты делят:
(\frac { a } { b } )^m = \frac { a^m } { b^m } - Степень с отрицательным рациональным показателем:
a^ { -n } = \frac { 1 } { a^n }
Обыкновенная дробь с отрицательным показателем заменяется на обратную ей дробь с положительным показателем:
(\frac { a } { b } )^ { -m } =(\frac { b } { a } )^ { m } - Степень с рациональным показателем:
a^ { \frac { 1 } { n } } = \sqrt[n] { a }
a^ { \frac { m } { n } } = \sqrt[n] { a^m }
Смотри также: Основные формулы по математике
Решай с разбором:
bingoschool.ru
Основные свойства степеней, корней, формулы
Основные свойства степеней.
a0 = 1 для любого числа a.
a1 = a для любого числа a.
(– a)n = an, если n — четное
(– a)n = – an, если n — нечетное
(ab)n = anbn



anam=an+m

Основные свойства корней
 для
любого
для
любого  .
. для
любого числа а. Здесь |a| — модуль числа
а, который равен а, если
для
любого числа а. Здесь |a| — модуль числа
а, который равен а, если  ,
и равен –а, если а < 0.
,
и равен –а, если а < 0. для
для
 и
и  .
. для
для  ,
,  и
и  .
. для
для  ,
,  и
и  .
. для
для 
 и
и  .
. для
для  ,
,  и
и  .
.
. для
для  ,
,  и
и 
 для
для  и
и  .
. для
для  и
и  .
. для
любого числа а и нечетного числа
для
любого числа а и нечетного числа  .
.
Формулы сокращенного умножения.
Для любых a, b и с верны следующие равенства:
 ;
;
 ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;
 ;
;
 где
x1 и x2 — корни квадратного трехчлена
где
x1 и x2 — корни квадратного трехчлена  .
.
studfile.net
Свойства степени с натуральным показателем
Свойства степени с натуральным показателем 7 класс
Свойство 1, формулаЕсли степени умножать ( при одинаковый основания), то показатели
степени сложить, основание остается неизменным.
am • an = am + n
Пример 33 • 3 4 = 37 = 2 187;42 • 43 = 45 = 1 024;
y3 • y5 = y8.
Свойство 2, формула Пример
(- 2)10 : (- 2)7 = (- 2)3 = 8;
Пример
(- 2)10 : (- 2)7 = (- 2)3 = 8;(0,1)101 : (0,1)101 = 1;
57 : 59 = 152 = 1 25.
Свойство 3, формулаЕсли основание не равно нулю, то любое основание в степени нуль,
равно единице.
a0 = 1
Пример 30 = 0;(? 5)0 = 1;
(- 2,5)0 = 1.
Свойство 4, формулаЕсли степень возвести в степень, то показатели — перемножить.
(am)n = amn
Пример (32)3 = 36 = 729.
Свойство 5, формулаЕсли произведение требуется возвести в степень, то каждый
множитель возводят в степень, и полученные результаты перемножают.
(ab)n = anbn
ПримерПример (0,9 • 2)2 = 0,92 • 22 = 0,81 • 4 = 1,62;
(3z)3 = 33z3=27z3.
Свойство 6, формулаЕсли требуется возвести в степень дробь, то возводят в степень
числитель и знаменатель.

При возведении отрицательного числа в степень, все зависит от
четности степени. Если степень четная, то и число получится четное,
если степень нечетная, то число останется со знаком «минус».

(- x)2 = x2;
(- z)3 = -z3;
(- 2ab)2 = (2ab)2 = 22a2b2 = 4a2b2.
formula-xyz.ru
Формулы степеней и их свойства
Любое ненулевое число в степени нуль равно единице:
При умножении степеней с одинаковым основанием их показатели складываются:
При делении степеней с одинаковым основанием их показатели вычитаются:
При возведении степени в степень их показатели перемножаются:
Степень произведения двух сомножителей равна произведению степеней этих сомножителей:
Отметим, что количество сомножителей может быть больше двух, тогда, аналогично, степень произведения нескольких сомножителей равна произведению степеней этих сомножителей:
Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
Степень некоторого числа с отрицательным показателем равна единице, деленной на степень того же числа с показателем противоположным по знаку:
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Свойства степеней | Алгебра
Основные свойства степеней задаются формулами:
(При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают).
(При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя).
(При возведении степени в степень основание оставляют прежним, а показатели перемножают).
(При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают).
(При возведении в степень частного возводят в эту степень и делимое, и делитель, результаты делят).
Кроме того,
(где a≠0)
Если n — натуральное число, то
в частности,
в частности,
Для a>0
В частности,
В школьном курсе алгебры свойства степеней изучаются на протяжении нескольких лет: сначала для степени с натуральным показателем, затем — для степени с целым показателем, далее — для степени с рациональным и иррациональным показателем.
Свойства степеней с натуральным и целым показателем верны и для степеней с рациональными и иррациональными показателем, но накладывается дополнительное условие: основания степеней в этом случае должны быть положительными.
По определению, для любого α
www.algebraclass.ru
Обобщение понятия степени и решение примеров со степенями
Здравствуйте. Многие ученики испытывают сложности при решении заданий, в которых встречаются выражения с корнями. В данной статье я попытаюсь обобщить материал по темам «Радикал» и «Степень». Покажу как решать некоторые задания. Если у Вас во время прочтения статьи появятся вопросы, Вы можете записаться ко мне на занятие, я с радостью помогу Вам во всем разобраться, помогу с решением именно Ваших задач!
1. Свойства степеней и корней
Степенью числа а с натуральным показателем n называется произведение n множителей, каждый из которых равняется а.
Степень числа а с показателем n обозначают an, например:
В общем случае при n > 1 имеем
Число a называется основой степени, число n — показателем степени.
Приведем основные свойства действий со степенями.
Приведенные свойства обобщаются для любых показателей степени
Часто в вычислениях используются степени с рациональным показателем. При этом удобным оказалось такое обозначение:
Корнем n— ой степени из числа а называется число b, n— я степень которого равняется a:
Корень также называется радикалом.
Корень нечетной степени n всегда существует. Корень четной степени 2n из отрицательного числа не существует. Существуют два противоположных числа, которые являются корнями четной степени из положительного числа а > 0. Положительный корень n— ой степени из положительного числа называют арифметическим корнем.
Из формул (3), (4) вытекают такие свойства радикалов
Если степень корня n = 2, то показатель корня обычно не пишется.
Пример 1.1. Найти значение выражения
Подкоренное выражение разложим на простые множители:
Пример 1.2. Упростить выражение
Имеем:
Пример 1.3. Извлечь корень
Имеем:
Пример 1.4. Упростить выражение
Поскольку при
2. Действия с радикалами
1) Преобразование корня по формуле называется внесением множителя под знак радикала.
Пример 2.1. Внести множитель под знак корня 5√2.
Исходя из формулы (7) получим
Пример 2.2. Внести множитель под знак радикала x√y при x< 0.
Имеем равенство
2) Преобразование корня исходя из формулы называется вынесением множителя из-под знака радикала.
Пример 2.3. Вынести множитель из-под знака корня в выражении
Получим:
Пример 2.4. Вынести множитель из-под знака корня
Имеем:
Пример 2.5. Вынести множитель из-под знака корня:
Радикалы вида , где a, b — рациональные числа, называются подобными. Их можно прибавлять и отнимать:
Пример 2.6. Упростить:
Пример 2.7. Сложить радикалы:
Пример 2.8. Выполнить действие:
Заметим, что равенство не выполняется. В этом можно убедиться на таком примере:
Приведем примеры умножения радикалов.
Пример 2.9.
Аналогично освобождаются от кубических иррациональностей в знаменателе:
Рассмотрим более сложные примеры рационализации знаменателей:
Чтобы перемножить радикалы с разными степенями, их сначала превращают в радикалы с одинаковыми степенями.
Пример 2.10. Перемножим радикалы:
Во время умножения радикалов можно использовать формулы сокращенного умножения. Например:
Если радикалы находятся в знаменателе дроби, то, используя свойства радикалов, можно избавиться от иррациональности.
Пример 2.11. Рационализируем знаменатели дробей
Выражения называются сопряженными. Произведение сопряженных выражений не содержит радикалов:
Это свойство используется для рационализации знаменателей.
Пример 2.12. Избавиться от иррациональности в знаменателе:
Избавимся от иррациональности в знаменателе дроби:
3. Вычисление иррациональных выражений
С помощью свойств корней можно упрощать и вычислять иррациональные выражения.
Пример 3.1. Вычислить
Выполним последовательно действия:
Пример 3.2. Вычислить:
Выполним действия.
Часто используется формула двойного радикала:
Пример 3.3. Исходя из формулы (8) находим:
Пример 3.4. Вычислить
Исходя из формулы (8) находим:
Окончательно получаем:
Аналогично вычисляются кубические корни. Имеем:
Возводим обе части равенства в куб:
Сравнивая выражения при √с, получаем однородную систему уравнений:
Поделив уравнение почленно, приходим к уравнению для z = y/x:
Пример 3.5. Вычислить значение радикала
После возведения в куб уравнения приходим к системе уравнений:
Поделив почленно первое уравнение на второе, получим уравнение для z= y/x:
По схеме Горнера находим корень z = — ½
Из системы уравнений и уравнения y/x = — ½ находим x = 2, y = -1. Итак,
Пример 3.6. Вычислить .
Возьмем .
Возведя обе части уравнения в куб, получаем откуда вытекает система уравнений
Система уравнений имеет очевидное решение x= 1, y= 1.
Поэтому .
Вычисляем радикал
Окончательно имеем a = — 1.
Пример 3.7. Вычислить
Поскольку
Дальше имеем:
Итак, a = — 2.
Пример 3.8. Вычислить
Возведем уравнение в куб, воспользовавшись равенством .
Получили для x кубическое уравнение
или x3 – 3x – 18 = 0,
имеет корни
Во множестве действительных чисел имеем корень x = 3.
4. Оценки для радикалов
Если
Это неравенство можно использовать для доведения неровностей, которые содержат радикалы.
Пример 4.1. Доказать, что .
Возведя неравенство в шестую степень, получим очевидное неравенство
Можно приводить радикалы к одной и то й же самой степени :
Пример 4.2. Оценим .
Поскольку
При преобразовании неравенств можно использовать символ V, понимая под ним знаки « > », « < », или « ».
Пример 4.3. Какое число больше
.
Поскольку
На этом все. Напоминаю, что Вы можете записываться ко мне на занятия в расписании, я с радостью помогу Вам с любыми вопросами по математике или высшей математике.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Свойства степеней
Свойства степеней. Разъяснения
\begin{align} & 1-3.\ x^1=x,\ x^0=1,\ x^{-1}=\frac{1}{x}\ \end{align}
Рассмотрим первые 3 свойства на примере числа 5.
| Пример | ||
|---|---|---|
\begin{align} & 5^2\\ \end{align} |
\begin{align} & 1×5×5\\ \end{align} |
\begin{align} & 25\\ \end{align} |
\begin{align} & 5^1\\ \end{align} |
\begin{align} & 1×5\\ \end{align} |
\begin{align} & 5\\ \end{align} |
\begin{align} & 5^0\\ \end{align} |
\begin{align} & 1\\ \end{align} |
\begin{align} & 1\\ \end{align} |
\begin{align} & 5^{-1}\\ \end{align} |
\begin{align} & 1÷5\\ \end{align} |
\begin{align} & \frac{1}{5}\\ \end{align} |
\begin{align} & 5^{-2}\\ \end{align} |
\begin{align} & 1÷5÷5\\ \end{align} |
\begin{align} & \frac{1}{25}\\ \end{align} |
\begin{align} & 4.\ x^m x^n=x^{m+n}\ \end{align}
xmxn сколько раз мы должны умножить x? Ответ: вначале m-раз, потом n-раз, итого m+n раз
\begin{align} & x^2 x^3=(xx)(xxx)=xxxxx=x^5\ \end{align}
\begin{align} & 5.\ \frac{x^m}{x^n}=x^{m-n}\ \end{align}
xm/xn сколько раз мы должны умножить x? Ответ: вначале m-раз умножить, затем n-раз поделить, итого m-n раз умножить
\begin{align} & \frac{x^5}{x^2}=\frac{xxxxx}{xx}=xxx=x^3\ \end{align}
\begin{align} & 6.\ (x^m)^n=x^{mn}\ \end{align}
xmxn сколько раз мы должны умножить x? Ответ: вначале m-раз, потом полученный результат n-раз, итого m×n раз
\begin{align} & (x^3)^4=(xxx)^4=(xxx)(xxx)(xxx)(xxx)=xxxxxxxxxxxx=x^12\ \end{align}
\begin{align} & 7.\ (xy)^n=x^n y^n\ \end{align}
Рассмотрим свойство на примере:
\begin{align} & (xy)^3=(xy)(xy)(xy)=xyxyxy=xxxyyy=(xxx)(yyy)=x^3 y^3\ \end{align}
\begin{align} & 8.\ \left ( \frac{x}{y} \right )^n=\frac{x^n}{y^n}\ \end{align}
Рассмотрим свойство на примере:
\begin{align} & \left ( \frac{x}{y} \right )^3=\left ( \frac{x}{y} \right )\left ( \frac{x}{y} \right )\left ( \frac{x}{y} \right )=\frac{(xxx)}{(yyy)}=\frac{x^3}{y^3}\ \end{align}
calcs.su
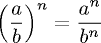



 для
любого
для
любого  .
. для
любого числа а. Здесь |a| — модуль числа
а, который равен а, если
для
любого числа а. Здесь |a| — модуль числа
а, который равен а, если  ,
и равен –а, если а < 0.
,
и равен –а, если а < 0. для
для
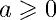 и
и 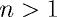 .
. для
для  ,
,  и
и 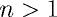 .
. для
для  ,
,  и
и  .
. для
для 
 и
и  .
. для
для  ,
,  и
и  .
. для
для  ,
,  и
и 
 для
для  и
и  .
. для
для  и
и  .
.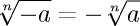 для
любого числа а и нечетного числа
для
любого числа а и нечетного числа  .
.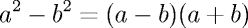 ;
;
 ;
;
 ;
;  ;
;
 ;
;  ;
;
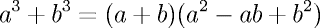 ;
;
 ;
;
 где
x1 и x2 — корни квадратного трехчлена
где
x1 и x2 — корни квадратного трехчлена  .
.