Сложение и вычитание смешанных чисел

Сегодня на уроке мы научимся складывать и вычитать смешанные числа.

Напомним, сумму натурального числа и правильной дроби принято записывать без знака «+». Такую сумму называют смешанным числом. То есть «смешали» натуральное число и правильную дробь, и назвали эту запись смешанным числом.

Натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа.

То есть запись  является сокращённым вариантом записи .

Складывать смешанные числа помогают свойства сложения: переместительное и сочетательное.

Пример

Найдём сумму чисел  и .

При выполнении записи в тетрадях, не нужно записывать смешанное число как сумму натурального числа и дроби, затем подробно расписывать, как вы складываете целые и дробные части смешанных чисел.

Пример

Найдём сумму смешанных чисел  и .

Таким образом, если при сложении дробных частей получилась неправильная дробь, выделяют целую часть этой дроби и добавляют к уже имеющейся целой части.

Пример

Теперь найдём сумму чисел  и .

Задача

На столе лежало  пиццы. Если принести ещё  пиццы. Сколько пицц окажется на столе?

Чтобы решить задачу, надо сложить числа  и .

Чтобы найти разность смешанных чисел, нужно найти отдельно разность целых частей и отдельно разность дробных частей.

Пример

Вычтем из дроби  дробь .

Есть в вычитании «коварные» примеры.

Пример

Запомните! Не начинайте выполнять вычитание, пока не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби.

А вот если вычесть нельзя, «занимаем» у целой части уменьшаемого одну целую единицу.

Иногда в примерах нужно вычесть из натурального числа смешанную дробь.

Пример

Найдём значение выражения .

Итоги

Чтобы сложить смешанные числа, надо: привести дробные части этих чисел к наименьшему общему знаменателю; отдельно выполнить сложение целых частей и отдельно дробных частей.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части.

Чтобы выполнить вычитание смешанных чисел, надо: привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить вычитание целых частей и отдельно дробных частей.

3.

Сложение и вычитание смешанных чисел (одинаковые знаменатели)

Рассмотрим на практических примерах, как складывать и вычитать смешанные числа.

Задача 1. В магазине лежали 238 коробки апельсинов. К ним добавили ещё 128 коробки. Сколько теперь коробок апельсинов в магазине?

 

Решение. Чтобы ответить на вопрос задачи, надо сложить числа 238 и 128.
Так как 238=2+38;128=1+28,  то

238+128=2+38+1+28=2+1+38+28=3+3+28=3+58=358.

Можно записать коротко: 238+128=358.

Ответ: 358 коробки апельсинов.

 

Задача 2. В магазине лежали 238 коробки апельсинов. Продали 128 коробки. Сколько осталось коробок апельсинов в магазине?

Решение. Чтобы ответить на вопрос задачи, надо из 238 вычесть 128.

 

Тогда:

 

238−128=2+38−1+28=2+38−1−28=2−1+38−28==1+3−28=1+18=118.

 

Промежуточные вычисления обычно не записывают: 238−128=118.

Ответ: 118 коробки апельсинов.

 

Обрати внимание!

Для сложении смешанных чисел надо сложить отдельно целые части и дробные части.

Для вычитания смешанных чисел надо вычесть отдельно целые части и  дробные части.

В результате сложения смешанных дробей может в дробной части получиться неправильная дробь. Тогда из неё нужно выделить целую часть и прибавить к целой части.

 

Пример 1.
15711+3611=181311=18+1311=18+1211=19211.

 

Рассмотрим пример, в котором при вычитании смешанных дробей нужно увеличить дробную часть уменьшаемого.

 

Пример 2.

713−523=7+13−523=6+1+13−523=6+113−523==6+43−523=643−523=123.

 

Обычно пишут короче: 713−523=643−523=123.

Так же вычитают дробь или смешанное число из натурального числа.

25−713=241313−713=2413−713=24613.

 

Пример 4.

12−857=1177−857=37−57=327.

Образование смешанного числа — математика, уроки

Конспект урока математики 6 класс в специальной(коррекционной) школе для детей с ОВЗ

Тема урока: « Образование смешанного числа»

Тип урока: получение новых знаний

Цель урока: познакомить со смешанным числом, научить записи, чтению смешанного числа, дать название компонентам смешанного числа.

Задачи:

Образовательные: дать понятие «смешанное число», учить записывать, читать, соотносить дробь с ее названием, уметь показать на геометрической фигуре, уметь заштриховывать заданную часть, определять место целой и дробной части, дать определение компонентам смешанного числа.

Коррекционно-развивающая: коррекция и развитие мыслительной деятельности, внимания через работу с дидактическим пособием; навыков устного счета, самостоятельной работы при решении арифметической задачи;

 Воспитательная: воспитывать интерес к предмету, к учебе.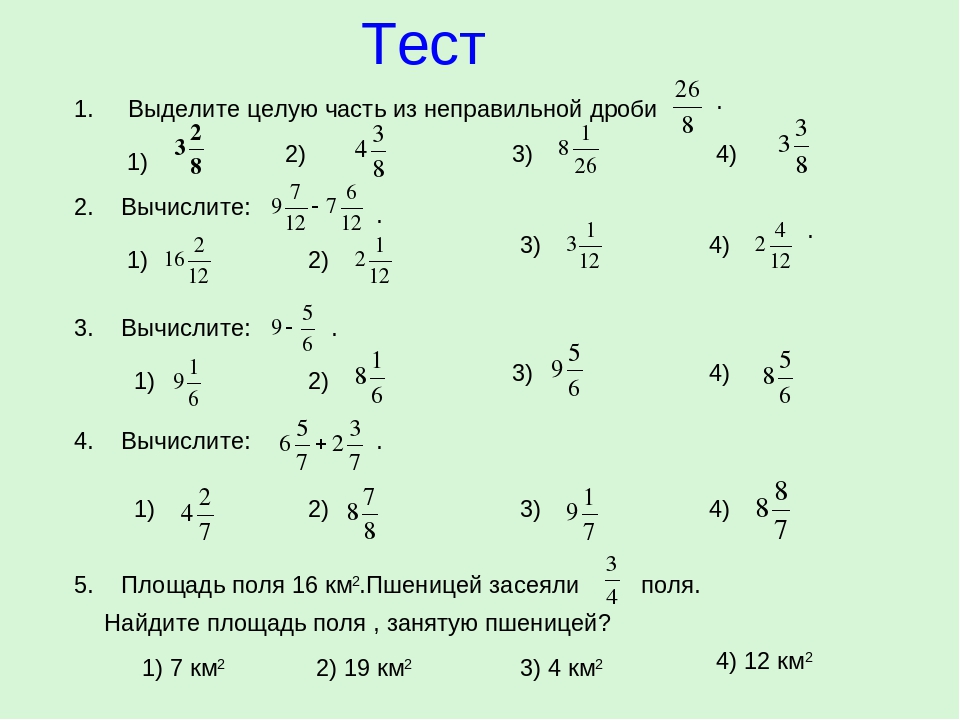

Ожидаемые (планируемые) результаты

Предметные: используют полученные знания при выполнении заданий

Познавательные: получат возможность научиться произвольно и осознанно владеть навыком работы со смешанным числом

Регулятивные: научатся планировать свое действие в соответствии с поставленной задачей и условиями ее реализации, в том числе во внутреннем плане.

Коммуникативные: получат возможность научиться аргументировать свою позицию и координировать ее с позициями партнеров в сотрудничестве при выработке общего решения в совместной деятельности

Личностные: получат возможность адекватного понимания причин успешности/неуспешности учебной деятельности.

Дидактические средства: учебник, памятки, карточки с заданиями для групповой работы.

Ход урока:

1. Организационный момент.

Проверка готовности учащихся к уроку. Приветствие.

II . Актуализация и систематизация знаний, умений и навыков.

Коррекционное задание, направленное на развитие внимания

— Постарайтесь найти среди написанных букв тему сегодняшнего урока.

ВЛВЛВРВОБРАЗОВАНИЕСМЕШАННОГОЧИСЛАЛОВГНУСАРП

— Сообщение темы урока.

— сегодня мы с вами познакомимся со смешанным числом, научимся записывать и читать его, узнаем компоненты смешанного числа.

III Устный счет

1)Прочитать обыкновенные дроби: ; ( правильные и неправильные вперемешку)

— назвать все правильные дроби

— все неправильные дроби

— все дроби, равные 1.

2)

3) Расположи дроби в порядке возрастания:

4) Коррекционное задание:

-Назвать все фигуры. Назвать лишнюю фигуру. Назвать лишнюю дробь в ней. Убрать картинку и предложить по памяти вспомнить, какого цвета был квадрат и т. д.

— Давайте эту лишнюю дробь запишем к себе в тетрадь.

IV Изучение нового.

_ Сделаем к этой дроби рисунок

— А сколько целых закрашенных фигур? ( 1) Запишем рядом с изображением 1(одна целая). Какая дробная часть осталась? ( ) Запишем после целой части. Получившееся число называют смешанным. Как вы думаете, почему?

Повторите название числа. Аналогично разобрать дроби

— Числа 1, 2,3 в смешанном числе называются целой частью. Как вы думаете, почему? Все остальное – это дробная часть.

— Записать и назвать компоненты следующих смешанных чисел: 9 18 7

V Первичное закрепление изученного – работа с учебником с. 82 № 315

— Коррекционное задание — возвращаемся к заданию с фигурами: Какого цвета был круг?квадрат, прямоугольник? В какой фигуре была неправильная дробь?

— VI Самостоятельная работа на карточке

VI Подведение итогов, рефлексия

VII домашнее задание с. 83 № 316(3)

Открытый урок для 6 класса «Сложение и вычитание смешанных чисел и дробей» (с преобразованием и без преобразования) | План-конспект урока по математике (6 класс) по теме:

6 класс

3 четверть

Урок № 98/16

Тема: Сложение и вычитание смешанных чисел  и дробей

(с преобразованием и без преобразования)

Тип урока: урок сообщения новых знаний и умений

Цель: закрепить знание алгоритмов выполнения сложения и вычитания смешанных чисел  и дробей (без преобразования и с преобразованием)

Задачи:

Образовательные: закрепить умение выполнять сложение и вычитание смешанных чисел и дробей (с преобразованием и без преобразования). Отрабатывать умение складывать и вычитать дроби с одинаковыми знаменателями, вычитать дроби из 1, вычитать смешанные числа из целого числа. Отрабатывать умение преобразовывать обыкновенные дроби (сокращать и заменять неправильные дроби смешанным или целым числом). Закрепить знание элементов дроби и их значение.

Коррекционно-развивающие: корригировать мышление посредством развития умения рассуждать (на примере решения задачи и примеров и выполнения задания на преобразование дробей).

Воспитательные: развивать умения и навыки работать в коллективе и самостоятельно; воспитывать у учащихся стремление к знаниям, упорство в достижении цели, уважение к другим людям, к их мнению.

Оборудование: учебник, опорные таблицы  «Сокращение дробей», «Замена неправильной дроби целым числом», «Замена неправильной дроби смешанным числом», набор цифр (шкаф №10, коробка №11), индивидуальные альбомы с опорными таблицами, карточка с числами для устного счета.

Ход урока

№	Содержание урока	Оборудование
1	Организационный  момент      Организация рабочего места, правильная посадка, настрой на урок       Кинезиологическое  упражнение       «Колечко» Поочередно перебирать пальцы рук, соединяя в кольцо большой палец и последовательно указательный, средний, безымянный и мизинец. Упражнения выполнять, начиная с указательного пальца и в обратном порядке от мизинца к указательному. Выполнять нужно каждой рукой отдельно, затем обеими руками вместе.
2	Устный счет Таблица умножения и деления на 7, на 9 Назвать две дроби и два смешанных числа меньше 5 со знаменателями 9 Сократить дроби: ;  ;  ;
3	Основная часть урока Вспомнить алгоритмы выполнения и записи действий сложения и  вычитания смешанных чисел и дробей с преобразованием  Чтобы сложить смешанные числа и дроби, надо сначала сложить целые части, потом сложить числители, а знаменатель оставить тот же  Чтобы вычесть смешанные числа и дроби (с преобразованием), нужно занять единицу у целого числа,   записать ее в виде неправильной дроби и прибавить к ней дробную часть смешанного числа. Далее  выполнить вычитание смешанных чисел или дробей. Если нужно, выполнить сокращение. Примеры № 445    2)   Взаимопроверка	Тетради, опорные таблицы  «Сокращение дробей», «Замена неправильной дроби целым числом», «Замена неправильной дроби смешанным числом» Учебники, тетради
4	Физкультминутка      Упражнения на коррекцию осанки Выполнять двигательные упражнения, сопровождая их проговариванием таблицы деления на 5
5	Закрепление материала Задача № 478   Фронтальное  решение 2)  Примеры № 473   Взаимопроверка Примеры № 471   3)  4) Фронтальное решение	Учебники, тетради Учебники, тетради Учебники, тетради
6	Физкультминутка      Упражнения для глаз «Горизонтальная восьмерка» Вытянуть перед собой правую руку на уровне глаз, пальцы сжать в кулак, оставив средний и указательный пальцы вытянутыми. Нарисовать в воздухе горизонтальную восьмерку как можно большего размера. Рисовать начинать с центра и следить глазами за кончиками пальцев, не поворачивая головы.      Дыхательная гимнастика «Свеча» Исходное положение – сидя за партой. Представьте, что перед вами стоит большая свеча. Сделайте глубокий вдох на пальчики, изображающие горящую свечу, и постарайтесь одним выдохом задуть свечу. А теперь представьте перед собой 5 маленьких свечек. Сделайте глубокий вдох и задуйте эти свечи маленькими порциями выдоха.
7	Итог  урока Как сложить обыкновенные дроби и смешанные числа? Как вычесть смешанные числа и дроби? Как вычесть смешанные числа с преобразованием? Примеры  № 480   1я стр.   Индивидуальная  проверка	Учебники, тетради
8	Домашнее задание Примеры № 480   2я стр.	Учебники, дневники
9	Выставление  оценок	Дневники

   

     

Мерзляк 5 класс — § 29. Смешанные числа

Вопросы к параграфу

1. В виде какого числа можно представить сумму натурального числа и правильной дроби?

В виде смешанного числа.

2. Как в записи смешанного числа называют натуральное число? Правильную дробь?

• Натуральное число называют целой частью смешанного числа.
• Правильную дробь называют дробной частью смешанного числа.

3. Какой дробью является дробная часть смешанного числа?

Правильной дробью.

4. В каком случае неправильная дробь равна натуральному числу?

Неправильная дробь равна натуральному числу в том случае, если числитель нацело делится на знаменатель.

5. Как неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число?

Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.

6. Как смешанное число преобразовать в неправильную дробь?

Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а её знаменатель записать в знаменатель дробной части смешанного числа.

7. Сформулируйте правило сложения двух смешанных чисел.

Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.

8. Как найти разность двух смешанных чисел?

Чтобы найти разность двух смешанных чисел, надо из целой и дробной части уменьшаемого вычесть целую и дробную части вычитаемого.

Решаем устно

1. Сравните значения выражений:

1)

  +     >     — 

   >  

   >  

2)

+    —      >     — + 

  > 

 > 

3)

+     >      —   

  > 

 > 

4)

+    +    <     + 

  <

  <  

2. Ответом к каким из следующих задач является число ?

1) Сколько килограммов конфет получил каждый из шести отрядов, между которыми поделили поровну 5 кг конфет?

5 : 6 = ( кг) — получил каждый из шести отрядов.

2) С какой скоростью шёл пешеход, если за 6 ч он прошёл 5 км?

5 : 6 = (км/ч) — скорость пешехода.

3) Из 6 м ткани сшили пять фартуков. Сколько метров ткани пошло на один фартук?

6 : 5 =   ( м) — пошло на 1 фартук.

4) Решите уравнение 6x = 5.

6х = 5

х = .

Ответ: является ответом к задаче № 1, №2 и №4.

3. Решите уравнение:

1)

  = 3

y : 6 = 3

y = 3 • 6

y = 18

2)

  = 3

6 : y = 3

y = 6 : 3

y = 2

3)

3y = 6

y = 6 : 3

y = 2

4)

6y = 3

y = 3 : 6

y =

4. Назовите все пары правильных дробей со знаменателем 9, сумма которых равна .

  +    =    и    +    = 

+    =     и    +    = 

+    =     и    +    = 

5. На обед Пончик съел 42 вареника, из которых    составляли вареники с творогом, — вареники с картофелем, а остальные — вареники с вишней. Сколько вареников с вишней съел Пончик?

1)   +    = ( вареников) — с творогом и с картофелем.

2) 42 : 7 • 5 = 6 • 5 = 30 (шт) — вареники с творогом и картофелем.

3) 42 — 30 = 12 (шт) — вареники с вишней.

Ответ: 12 шт.

Упражнения

769. Преобразуйте неправильную дробь в смешанное число:

1)   =  =   +  =

2)   =    =    +    =

3)   =    =    +    = 

4)   =    =    +    = 

5)   =    =    +    = 

6)   =    =    +    = 

770. Преобразуйте неправильную дробь в смешанное число:

1)   =    =    +    = 

2)   =    =    +    = 

3)   =    =    +    = 

4)   =    =    +    = 

5)   =    =    +    = 

6)   =    =    +    = 

771. Запишите частное в виде дроби и выделите из полученной дроби целую и дробную части:

1) 10 : 6 =    =    = 

2) 18 : 5 =    =   = 

3) 23 : 11 =    =    = 

4) 19 : 6 =   =    =

5) 425 : 50 =    =    = 

6) 55 : 6 =    =    = 

772. Запишите частное в виде дроби и выделите из полученной дроби целую и дробную части:

1) 7 : 2 =    =    = 

2) 9 : 4 =    =    = 

3) 25 : 8 =    =    = 

4) 110 : 20 =    =    = 

5) 327 : 10 =    =    = 

6) 812 : 81 =    =    = 

773. Запишите число в виде неправильной дроби:

1)   =    =    = 

2)   =    =    = 

3)   =    =    = 

4)   =  =   = 

5)   =    =    = 

6)   =    =    = 

774. Запишите число в виде неправильной дроби:

1)   =    =    = 

2)   =    =    = 

3)   =    =    = 

4)   =    =    = 

5)   =    =    = 

6)   =    =    = 

775. Выполните действия:

1) +    = 

2)   +    =  + =   =   =   =

3) = =   =   = 

4)   =  =   =   = 

776. Выполните действия:

1) = 

2)   = =   =    = 

3)   = =   =   = 

4)   = =   =    = 

777. Вычислите:

1)

2)   =    =    =    =    =    = 

3)   =    =    =    =    =    =

4)   =    =    =    =    =    = 

5)   =    =    = 

6)   =    =    = 

7)   =    =    =    = 

8)   =    =    =    = 

9)   =    =    =    =    =

10) =   =    =    =    =    = 

11)   =    =   =    =    =    = 

12)   =    =    =    =    =    = 

13)   =    =    = 

14)   =    =    =    =    =    =    =    = 

778. Вычислите:

1)   =    =    = 

2)   =    =   =   =    = 

3)   =    = 

4)   =    =    =    = 

5)   =    =    =    = 

6)   =    =   =    =    = 

7)   =    =   =    =    = 

8)   =    =   =    =    = 

9)   =    =    = 

10)   =    =    =    =    =    =    =    =    =

779. Решите уравнение:

1)

2)

3)

780. Решите уравнение:

1)

2)

781. Решите уравнение:

1)

2)

782. Степан, Иван и Андрей съели арбуз. Степан съел арбуза, Иван — . Какую часть арбуза съел Андрей?

1)   +    =    (часть) — арбуза съели Степан и Иван.

2) (часть) — арбуза съел Андрей.

Ответ:    часть арбуза.

783. Мария, Ирина, Елена и Ольга съели торт. Мария съела торта, Ирина — , Елена — . Какую часть торта съела Ольга?

1)   +    +    =    =    (часть) — торта съели Мария, Ирина и Елена.

2) (часть) — торта съела Ольга.

Ответ: часть торта.

784. Три тракториста вспахали вместе поле. Бригадир записал, что один из них вспахал поля, второй — , а третий — . Не ошибся ли бригадир.

1)   +    +    =    =    =  (части) — поля вспахано по записям бригадира.

2) >  , значит бригадир ошибся, так как трактористы не могли вспахать больше, чем всё поле, равное 1.

Ответ: Бригадир ошибся.

785. Фермер решил выделить под морковь огорода, под свёклу — , под лук — , под горох — , под картофель — . Сможет ли он реализовать свой план?

1)   +    +    +    +    =    =  (части) — решил выделить фермер.

2)  >  , значит не сможет реализовать свой план.

Ответ: нет, не сможет.

786. 1) Какое наибольшее натуральное число удовлетворяет неравенству:

а)

, наибольшее натуральное число, при котором неравенство верно — 4.

Ответ: n = 4.

б)  

, наибольшее натуральное число, при котором неравенство верно — 13.

Ответ: n = 13.

2) Какое наименьшее натуральное число удовлетворяет неравенству:

а)  

, наименьшее натуральное число, при котором неравенство верно — 3.

Ответ: m = 3.

б)  

, наименьшее натуральное число, при котором неравенство верно — 28.

Ответ: m = 28.

787. 1) Какое наибольшее натуральное число удовлетворяет неравенству:

а)  

, наибольшее натуральное число, при котором неравенство верно — 15.

Ответ: n = 15.

б)  

, наибольшее натуральное число, при котором неравенство верно — 20.

Ответ: n = 20.

2) Какое наименьшее натуральное число удовлетворяет неравенству:

а)

, наименьшее натуральное число, при котором неравенство верно — 6.

Ответ: m = 6.

б)

, наименьшее натуральное число, при котором неравенство верно — 27.

Ответ: m = 27.

788. Найдите все натуральные значения х, при которых верно неравенство:

1)

Неравенство верно при х = 8, 9 и 10.

2)

Неравенство верно при х = 9, 10 и 11.

789. Найдите все натуральные значения х, при которых верно неравенство:

1)

Неравенство верно при х = 57, 58 и 59.

2)

Неравенство верно при х =4, 5, 6 и 7.

790. При каких натуральных значениях a является верным неравенство, левая часть которого — неправильная дробь:

1)

Неравенство будет верным при а = 11, 12, 13, 14, 15, 16, 17, 18, 19 и 20.

2) 

Неравенство будет верным при а = 1.

791. При каких натуральных значениях a является верным неравенство , левая часть которого — неправильная дробь?

Неравенство будет верным при а = 1, 2 и 3.

Упражнения для повторения

792. Одна из сторон треугольника в 2 раза меньше второй и на 7 см меньше третьей. Найдите стороны треугольника, если его периметр равен 39 см.

Пусть длина первой стороны треугольника — х см. Тогда длина второй стороны — 2х см, а длина третьей стороны — (х + 7) см. Мы знаем, что периметр треугольника равен 39 см.

Составим уравнение:

х + 2х + (х + 7) = 39
(х + 2х + х) + 7 = 39
4х + 7 = 39
4х = 39 — 7
4х = 32
х = 32 : 4
х = 8 (см) — длина первой стороны треугольника.

2х = 2 • 8 = 16 (см) — длина второй стороны треугольника.

х + 7 = 8 + 7 = 15 (см) — длина третьей стороны треугольника.

Ответ: 8 см, 16 см и 15 см.

793. Общая площадь трёх крупнейших волжских водохранилищ Куйбышевского, Рыбинского и Волгоградского составляет 14 197 км². Площадь Волгоградского водохранилища на 1 463 км² меньше площади Рыбинского водохранилища и на 3 383 км² меньше площади Куйбышевского водохранилища. Найдите площадь каждого водохранилища.

Пусть х км² — площадь Волгоградского водохранилища. Тогда площадь Рыбинского водохранилища (х + 1 463) км², а площадь Куйбышевского водохранилища — (х + 3 383) км². Мы знаем, что общая площадь трёх водохранилищ 14 197 км².

Составим уравнение:

х + (х + 1 463) + (х + 3 383) = 14 197
(х + х + х) + (1 463 + 3 383) = 14 197
3х + 4 846 = 14 197
3х = 14 197 — 4 846
3х = 9 351
х = 9 351 : 3
х = 3 117 (км²) — площадь Волгоградского водохранилища.

х + 1 463 = 3 117 + 1 463 = 4 580 (км²) — площадь Рыбинского водохранилища.

х + 3 383 = 3 117 + 3 383 = 6 500 (км²) — площадь Куйбышевского водохранилища.

Ответ: Волгоградское — 3 117 км², Рыбинское — 4 580 км², Куйбышевское — 6 500 км².

794. Пакет кефира стоит 68 р. У Кати есть 200 р. Какое наибольшее количество пакетов кефира она может купить? Сколько денег останется у Кати?

200 = 68 • 2 + 64 

Значит Катя сможет купить 2 пакета молока и у неё ещё останется 64 рубля.

Ответ: 2 пакета молока, 64 рубля.

795. По дороге в одном направлении идут два пешехода. В 12 ч 54 мин расстояние между ними было 540 м. Скорость пешехода, который идёт впереди, равна 25 м/мин, что составляет  скорости пешехода, который идёт сзади. В котором часу второй пешеход догонит первого?

1) 25 : 5 • 8 = 5 • 8 = 40 (м/мин) — скорость движения второго пешехода.

2) 40 — 25 = 15 (м/мин) — скорость сближения пешеходов.

3) 540 : 15 = 36 (мин) — потребуется второму пешеходу, чтобы догнать первого.

4) 12 ч 54 мин + 36 мин = 12 ч 90 мин = 13 ч 30 мин — время, в которое второй пешеход догонит первого.

Ответ: в 13 часов 30 минут.

Задача от мудрой совы

796. Ученики Фёдоров, Сидоров и Петров входили в сборную школы по шахматам. Имена этих учеников были Фёдор, Сидор и Пётр. Известно, что фамилия Фёдора не Петров, волосы у Сидора рыжего цвета и учится он в 6 классе; Петров учится в 7 классе, а волосы у Фёдорова чёрного цвета. Укажите фамилию и имя каждого мальчика.

Занесём в таблицу данные, которые нам известны:

• «фамилия Фёдорова не Петров»
• «волосы Сидора рыжего цвета»
• «Сидор учится в 6 классе».

Теперь начнём рассуждать:

• «Петров учится в 7 классе» — мы уже знаем, что «фамилия Фёдорова не Петров», значит Петровым может быть только Пётр
• «волосы Фёдорова чёрного цвета» — по условию у Сидора волосы рыжие, значит чёрные волосы у Фёдора, а его фамилия — Фёдоров.
• оставшийся мальчик Сидор носит фамилию Сидоров.

Ответ: Фёдор Фёдоров, Сидор Сидоров и Пётр Петров.

Онлайн калькулятор дробей. Вычисления с дробями. Сложение, вычитание, умножение и деление дробей.

Инструкция использования калькулятора дробей

Для решения вашей задачи выполните следующие действия:

• введите ваш пример в калькулятор;
• нажмите кнопку  для выполнения вычислений.

Ввод данных в калькулятор дробей

В калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.

Целые числа. Для ввода целых чисел используйте цифровые клавиши калькулятора или цифровые клавиши вашего компьютера. 1 2 3 4 5 6 7 8 9 0

Десятичные дроби. Десятичные дроби вводятся также как и целые числа, в качестве десятичного разделителя рекомендуется использовать точку .

Обыкновенные дроби: Для ввода обыкновенной дроби нажмите клавишу на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши. 3)

N.B. Калькулятор поддерживает только целые степени!

N.B. Буквенные выражения, операции извлечения корня калькулятор не поддерживает!

Дополнительные возможности калькулятора дробей — старая версия

• С — полностью очистить поле ввода.
•  — удалить один символ.
•   для перемещения между полями калькулятора.

правила, примеры, решения, вычитание из целого числа смешанной дроби

В данной статье рассмотрим правила, согласно которым выполняется действие вычитания смешанных чисел. Разберем конкретные примеры и некоторые нюансы при их решении. Изучим вычитание обыкновенной дроби и натурального числа из смешанного числа, а также — вычитание смешанного числа из дроби и натурального числа. Рассматривать вычитание мы будем при условии вычитания из большего числа меньшее.

Вычитание смешанных чисел

Пусть в качестве исходных данных даны два смешанных числа: abc и def , необходимо выполнить вычитание данных смешанных чисел.

Нам известно, что любое смешанное число возможно представить, как сумму его целой и дробной части, тогда получим:

abc-def=a+bc-d+ef

Свойства действий сложения и вычитания дают возможность выполнить вычисление полученного выражения различными способами. Опираясь на значения дробных частей смешанных чисел

abc и def , необходимо придерживаться следующих схем вычисления:

• если дробная часть уменьшаемого больше, чем дробная часть вычитаемого:

bc>ef, то вычитание оптимально будет произвести так:

abc-def=(a-d)+bc-ef

Пример 1

Произвести вычитание смешанных чисел: 356-249 .

Решение

Сравним дробные части смешанных чисел, т.е. 56 и 49 . Чтобы определить, какая из дробей больше, приведем их к общему наименьшем знаменателю или наименьшему общему кратному: НОК (6, 9) = 18. При этом дополнительным множителем для дроби 56 станет 18 : 6 = 3; а для дроби 49 – 18 : 9 = 2, поэтому : 56=5·36·3=1518 и 49=4·29·2=818 .

Оценим полученный результат: 1518>818, что означает 56>49. Т.е. дробная часть уменьшаемого больше дробной части вычитаемого, и тогда действие вычитания производится путем раздельного вычитания целых и дробных частей заданных смешанных чисел:

3-2=156-49=1518-818=15-818=718

Т.е.: (3-2)+56-49=1+718=1718

Ответ: 356-249=1718

 

• если дробные части заданных смешанных чисел равны: bc=ef , а, соответственно разность их равна нулю, то результатом вычитания таких смешанных чисел будет разность их целых частей:

abc-def=(a-d)+bc-ef=a-d+0=a-d

Пример 2

Произвести вычитание смешанных чисел 15710 и 2710 .

Решение

Мы видим, что дробные части заданных чисел равны, т.е. их разность есть нуль. Таким образом, действие вычитания заданных чисел сводится к нахождению разности их целых частей: 15710-2710=15+710-2+710=15-2+710-710=15-2+0=13

Ответ: 15710-2710=13

• если дробная часть уменьшаемого меньше дробной части вычитаемого: bc<ef , то действие вычитания оптимально произвести так:

abc-def=a-d-ef+bc

Пример 3

Произвести вычитание смешанных чисел: 2625-81415 .

Решение

Проведем сравнение дробных частей заданных чисел, определив для начала наименьший общий знаменатель: НОК (5, 15) = 15, тогда 25=2·35·3=615 .

Следовательно: 615<1415, т.е. дробная часть уменьшаемого меньше дробной части вычитаемого. Таким образом, находить разность заданных смешанных чисел будем так: 2625-81415=26615-81415=26+615-8+1415==26-8-1415+615=18-1415+615

Для начала вычтем дробь из натурального числа (в скобках): 18-1415=(17+1)-1415=17+1+1415=17+11+1415==17+1515-1415=17+115

Тогда 18-1415+615=17+115+615=17+115+615==17+715=17715

Ответ: 2625-81415=17715 .

Вычитание обыкновенной дроби из смешанного числа

Схема вычитания правильной дроби из смешанного числа такая же, как при действии вычитания смешанных чисел.

Пример 4

Найти разницу: 356-415

Решение:

Приведем дробные части заданных чисел к единому наименьшему общему кратному: НОК (6, 15) = 30, тогда 65=5·56·5=2530 и 415=4·215·2=830 .

Таким образом, 56>415 .

В итоге вычитание возможно произвести так: 356-415=3+56-415=3+56-415=3+2530-830=3+1730=31730

Ответ: 356-415=31730

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 5

Произвести действие вычитания: 127-37

Решение

Дробные части исходных чисел имеют одинаковый знаменатель, что дает возможность их легко сравнить. Понятно, что 27 меньше, чем 37.

Тогда находить разницу будем так:

127-37=1+27-37=1-37+27=11-37+27==77-37+27=47+27=67

Ответ: 127-37=67.

Добавим еще одну, в общем очевидную деталь вычислений: если дробная часть смешанного числа равна вычитаемой дроби, то итогом вычисления будет число, равное целой части уменьшаемого смешанного числа. К примеру:

16311-311=16+311-311=16+311-311=16+0=16

Чтобы вычесть неправильную дробь из смешанного числа, необходимо выделить целую часть из неправильной дроби, а затем производить вычисление.

Пример 6

Вычислить значение разности: 7512-199 .

Решение: вычитаемая дробь является неправильной, выделим из нее целую часть и получим: 199=219

Приведем к общему знаменателю дробные части заданных чисел и согласно указанным выше схемам произведем вычитание смешанных чисел:

7512-219=7+512-2+19=7-2+512-19==5+1536-436=5+1136=51136

Ответ: 7512-199=51136 .

Вычитание натурального числа из смешанного

Определение 1

Для совершения действия вычитания натурального числа из смешанного, необходимо вычесть заданное натуральное число из целой части смешанного числа, а дробную часть оставить без изменений: abc-n=a-n+bc

Пример 7

Необходимо вычесть из смешанного числа 1511528 натуральное число 44.

Решение: 1511528-44=151+1528-44=151-44+1528=107+1528=1071528

Ответ: 1511528-44=1071528

Вычитание смешанного числа из обыкновенной дроби

Очевидно, что любое заданное смешанное число будет больше единицы. Уменьшаемая дробь должна быть больше вычитаемого, тогда эта дробь – неправильная. Необходимо выделить целую часть из неправильной дроби, и далее выполнение действия вычитания смешанного числа из обыкновенной дроби сведется к вычитанию смешанных чисел.

Пример 8

Необходимо выполнить вычитание: 749-612

Решение 

В первую очередь выделим целую часть неправильной уменьшаемой дроби: 749=829 , тогда заданный пример примет вид: 749-612=829-612

Найдем наименьший общий знаменатель: НОК (9, 2) = 18.

Получим: 29=2·29·2=418 и 12=1·92·9=918.

Тогда:

829-612=8418-6918=8+418-6+918=8-6-918+418==2-918+418=1+1-918+418=1+1-918+418==1+1-918+418=1+918+418=1+918+418==1+9+418=1+1318=11318

Ответ: 749-612=11318

Вычитание смешанного числа из натурального

Чтобы произвести действие вычитания смешанного числа из натурального, сначала от натурального числа отнимаем целую часть смешанного, после чего из полученного результата вычитаем дробную часть:

n-abc=n-a+bc=n-a-bc

Пример 9

Необходимо вычесть из натурального числа 18 смешанное число.

Решение

18-535=18-5+35=18-5-35=13-35=12+1-35==12+1-35=12+11-35=12+55-35=12+5-35==12+25=1225

Ответ: 18-535=1225

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Что такое смешанные числа? — Определение, факты и пример

Что такое смешанные числа?

Смешанное число — это целое число и правильная дробь, представленные вместе. Обычно представляет собой число между любыми двумя целыми числами.

Посмотрите на данное изображение, оно представляет собой дробь, которая больше 1, но меньше 2. Таким образом, это смешанное число.

Некоторые другие примеры смешанных чисел:

Части смешанного числа

Смешанное число образуется путем объединения трех частей: целого числа, числителя и знаменателя.Числитель и знаменатель являются частью правильной дроби, составляющей смешанное число.

Свойства смешанных чисел

Преобразование неправильных дробей в смешанные.

Шаг 1 : Разделите числитель на знаменатель.

Шаг 2 : Запишите частное как целое число.

Шаг 3 : Запишите остаток в числителе и делитель в знаменателе.

Например, мы следуем указанным шагам, чтобы преобразовать 7/3 в смешанную числовую форму.

Шаг 1 : разделить 7 на 3

Шаг 2 : Запишите частное, делитель и остаток в форме, как на шагах 2 и 3 выше.

Сложение смешанных чисел

Можно складывать смешанные числа, переставляя целые числа, складывая их по отдельности и добавляя оставшиеся дроби по отдельности и, в конце концов, расчесывая их все.

1 ¹ ⁄ ₂ + 3 ³ ⁄ ₄

Сложение целых чисел отдельно и дробей отдельно.

Для целых чисел:

1 + 3 = 4

Для дробей: найдите НОК и прибавьте

.

В конце складываем обе части вместе.

4 + 1 ¹ ⁄ ₄ = 5 ¹ ⁄ ₄

Примеры из жизни

Мы можем проверить наше понимание смешанных дробей, выразив части целого как смешанные дроби, подавая пиццу или пирог дома.Образцы смешанных фракций образуют остатки пиццы, наполовину заполненные стаканы молока.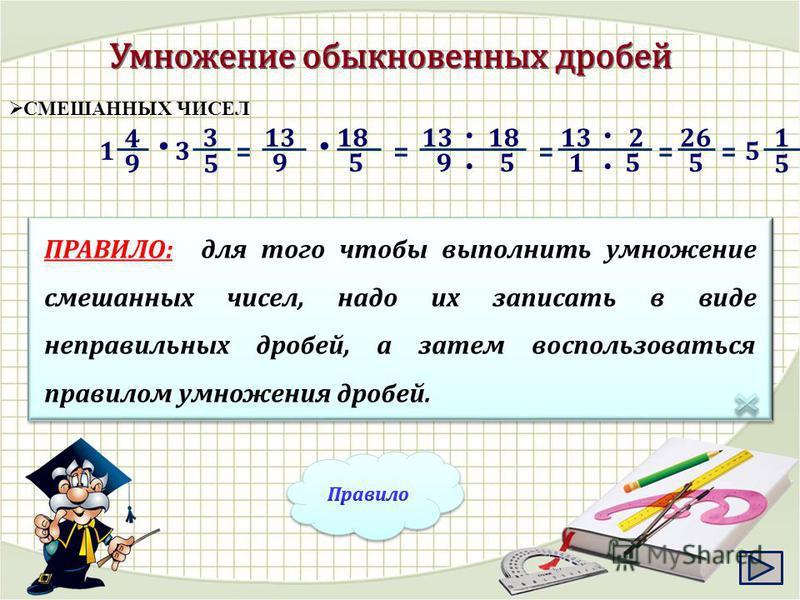

Интересные факты

Урок 6: Смешанные числа — IntoMath

Мы рассмотрели концепцию простой дроби в одном из предыдущих уроков.

Дроби могут быть правильными (когда значение числа в числителе ниже значения в знаменателе) или неправильным (когда значение числа в числителе больше или равно значению в знаменателе).Неправильная дробь всегда равна 1 или больше 1.

Неправильная дробь может быть преобразована в смешанные числа (также называемые смешанными дробями) путем выделения целого в неправильную дробь.

Что такое смешанный номер?

Смешанное число — это комбинация целого числа и правильной дроби. Может оказаться полезным перезапись неправильной дроби как смешанного числа. Это помогает нам легче определить, сколько целых компонентов имеется.

Смешанные числа можно визуально представить как несколько целых и частей чего-либо.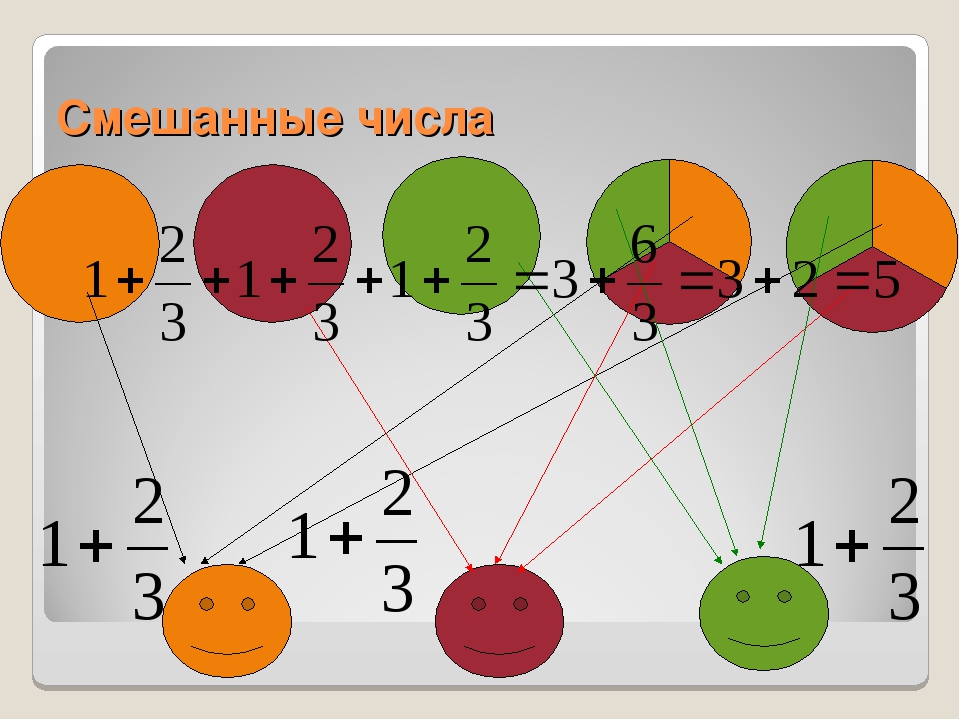 Например, в короткой анимации ниже мы используем пиццу, чтобы продемонстрировать концепцию. Важно понимать, как связать визуальное представление смешанных чисел и их арифметическое представление на бумаге (планшете).

Мы можем складывать и вычитать смешанные числа, сначала складывая и вычитая их целые части, а затем их дробные части. Если сумма дробей является неправильной дробью, мы меняем ее на смешанное число. Когда знаменатели дробей различаются, нам нужно найти эквивалентные дроби с общим знаменателем перед сложением или вычитанием.

Посмотреть видеоурок

Запись неправильных дробей в виде смешанных чисел

1. Разделите знаменатель на числитель

2. Частное — это целое число смешанного числа, которое идет впереди

3. Число остаток попадает в числитель дробной части смешанного числа

4. Если в числителе уже есть другое число, прибавьте к нему остаток

5. Знаменатель дробной части останется прежним

Смешанные числа Краткое Анимация

Пройдите тест

Обзор дробей: смешанные числа и неправильные дроби

Purplemath

Если у вас большая вечеринка с пиццей и после этого у вас осталась одна пицца с ананасом и половина пиццы с анчоусами, вы бы сказали, что у вас есть «полторы» пиццы.«Полтора» — это стандартный разговорный английский способ выражения этого числа, он записывается как «1 ¹ / ₂ ». Этот символ, «1 ¹ / ₂ », называется «смешанным числом», потому что он объединяет «обычное» число «1» с дробью « ¹ / ₂ ».

Хотя смешанные числа являются естественным выбором для разговорного английского (и поэтому хорошо подходят для ответов на словесные задачи), они, как правило, не самые простые дроби для вычисления. В алгебре вы почти всегда предпочитаете, чтобы дроби , а не были смешанными числами.

MathHelp.com

Вместо этого вы будете использовать так называемые «неправильные» дроби (также иногда называемые «вульгарными» дробями), когда верхнее число больше нижнего числа.

Стандартный способ преобразовать смешанное число в неправильную дробь — это умножить нижнее число на «обычное» число, добавить верхнее число, а затем поместить его поверх исходного нижнего числа как новую дробь.

Например, чтобы преобразовать 1 ¹ / ₂ в неправильную дробь, выполните следующие действия:

Я умножил нижние 2 на «обычную» 1, а затем добавил 1 сверху, получив 3. Затем я положил эти 3 поверх 2 снизу.

• Преобразовать в неправильную дробь.

Чтобы выполнить преобразование, я умножу знаменатель (16) на целое число (2), чтобы получить 32. Затем я добавлю числитель (3) к 32, чтобы получить новый числитель (35). Знаменатель останется прежним; а именно, 16.

---

• Преобразовать в неправильную дробь.

Чтобы выполнить преобразование, я умножу знаменатель (5) на целое число (6), чтобы получить 30. Затем я добавлю числитель (2) к 30, чтобы получить новый числитель (32). Знаменатель останется прежним; а именно 5.

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании процентов в десятичные числа. Попробуйте выполнить указанное упражнение или введите свое собственное.Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)

---

Чтобы перейти от неправильной дроби к смешанному числу, вы помните, что «дроби — это деление», и применяете длинное деление, чтобы найти частное целого числа плюс остаток.Другими словами, вы делите верхнее число на нижнее число. Все, что вы видите поверх символа деления, является частным и является частью вашего «обычного числа» смешанного числа. Каким бы ни был ваш остаток, положите это число поверх числа, на которое вы делили; это дробная часть вашего смешанного числа.

Примечание. При преобразовании неправильной дроби в смешанные числа не продолжайте деление числа после запятой на , а не на .Просто найдите частное и остаток. Тогда остановись.

• Преобразовать в смешанное число.

Сначала я делаю в столбик, чтобы найти целую часть (являющуюся частным) и остаток:

Частное сверху — 11, так что это будет целая часть смешанного числа.Поскольку остаток равен 1, а я делю на 4, дробная часть будет равна ¹ / ₄ .

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании неправильной дроби в смешанное число. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)

---

Эта процедура отлично работает с рациональными выражениями (полиномиальные дроби). Вы можете увидеть это в примере ниже (или же можете сразу перейти к умножению обычных дробей):

• Преобразовать в смешанное число.

Сначала проделайте длинное деление, чтобы найти правильную часть многочлена и остаток:

Полином сверху равен « x + 1», а остаток равен –1. Поскольку вы делите на « x + 2», дробная часть будет «(–1) / ( x + 2)»:

---

URL: https: // www.