Разложение многочлена на множители способом группировки
Основные понятия
Мы знаем, что слово «множитель» происходит от слова «умножать».
Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.
Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:
Так выглядит пошаговое разложение на множители. Числа, которые обведены в кружок на картинке — это множители, которые дальше разложить уже нельзя.
Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.
5 способов разложения многочлена на множители
- Вынесение общего множителя за скобки.
- Формулы сокращенного умножения.
- Метод группировки.
- Выделение полного квадрата.
- Разложение квадратного трехчлена на множители.

Способ группировки множителей
Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.
Разложить на множители методом группировки можно в три этапа:
- Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
- Вынести общий множитель за скобки.
- Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.
Объединить члены многочлена в группы можно по-разному. И не всегда группировка может быть удачной для последующего разложения на множители.
Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.
Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.
Как решаем:
1 способ | 2 способ |
up — bp + ud — bd = (up — bp) + (ud — bd) Заметим, что в первой группе повторяется p, а во второй — d. Вынесем в первой группе общий множитель p, а во второй общий множитель d. Получим: p(u — b) + d(u — b). Заметим, что общий множитель (u — b). Вынесем его за скобки: (u — b)(p + d). Группировка множителей выполнена. | up — bp + ud — bd = (up + ud) — (bp + bd) Заметим, что в первой группе повторяется u, а во второй — b. Вынесем в первой группе общий множитель u, а во второй общий множитель b. Получим: u(p + d) — b(p + d). Заметим, что общий множитель (p + d). Вынесем его за скобки: (p + d) (u — b). Группировка множителей выполнена. |
От перестановки мест множителей произведение не меняется, поэтому оба ответа верны:
(u — b)(p + d) = (p + d)(u — b).
Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.
Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).
Как решаем:
- Найдем общий множитель: (m — n)
- Вынесем общий множитель за скобки: (m — n)(c + d).
Ответ: c(m — n) + d(m — n) = (m — n)(c + d).
Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.
Как решаем:
5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)
Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).
Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные. |
Проверим как это на следующем примере.
Пример 4. Произвести разложение многочлена на множители способом группировки: ax2 — bx2 + bx — ax + a — b.
Как решаем:
- Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:
ax2 — bx2 + bx — ax + a — b = (ax2 — bx2) + (bx — ax) + (a — b) = x2(a — b) — x(a — b) + (a — b)
Получили три слагаемых, в каждом из которых есть общий множитель (a — b).
- Теперь вынесем за скобку (a — b), используя распределительный закон умножения:
x2(a — b) + x(b — a) + (a — b) = (a — b)(x2 + x + 1)
Ответ: ax2 — bx2 + bx — ax + a — b = (a — b)(x2 + x + 1)
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Вынесение общего множителя за скобку. Урок алгебры
В этой статье мы остановимся на вынесении за скобки общего множителя . Для начала разберемся, в чем состоит указанное преобразование выражения. Дальше приведем правило вынесения общего множителя за скобки и подробно рассмотрим примеры его применения.
Навигация по странице.
Например, слагаемые в выражении 6·x+4·y имеют общий множитель 2 , который не записан явно. Его можно увидеть лишь после того, как представить число 6 в виде произведения 2·3 , а 4 в виде произведения 2·2 . Итак, 6·x+4·y=2·3·x+2·2·y=2·(3·x+2·y) . Еще пример: в выражении x 3 +x 2 +3·x слагаемые имеют общий множитель x , который становится явно виден после замены x 3 на x·x 2 (при этом мы использовали ) и x 2 на x·x . После вынесения его за скобки получим x·(x 2 +x+3) .
Отдельно скажем про вынесение минуса за скобки. Фактически вынесение минуса за скобки означает вынесение за скобки минус единицы. Для примера вынесем за скобки минус в выражении −5−12·x+4·x·y
. Исходное выражение можно переписать в виде (−1)·5+(−1)·12·x−(−1)·4·x·y
, откуда отчетливо виден общий множитель −1
, который мы и выносим за скобки. В результате придем к выражению (−1)·(5+12·x−4·x·y)
, в котором коэффициент −1
заменяется просто минусом перед скобками, в итоге имеем −(5+12·x−4·x·y)
. Отсюда хорошо видно, что при вынесении минуса за скобки в скобках остается исходная сумма, в которой изменены знаки всех ее слагаемых на противоположные.
Исходное выражение можно переписать в виде (−1)·5+(−1)·12·x−(−1)·4·x·y
, откуда отчетливо виден общий множитель −1
, который мы и выносим за скобки. В результате придем к выражению (−1)·(5+12·x−4·x·y)
, в котором коэффициент −1
заменяется просто минусом перед скобками, в итоге имеем −(5+12·x−4·x·y)
. Отсюда хорошо видно, что при вынесении минуса за скобки в скобках остается исходная сумма, в которой изменены знаки всех ее слагаемых на противоположные.
В заключение этой статьи заметим, что вынесение за скобки общего множителя применяется очень широко. Например, с его помощью можно более рационально вычислять значения числовых выражений . Также вынесение за скобки общего множителя позволяет представлять выражения в виде произведения, в частности, на вынесении за скобки основан один из методов разложения многочлена на множители .
Список литературы.
- Математика. 6 класс: учеб. для общеобразоват. учреждений / [Н. Я. Виленкин и др.]. — 22-е изд., испр. — М.
 : Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.
: Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.
Урок алгебры в 7 классе.
Тема « Вынесение общего множителя за скобки».
Учебник Макарычев Ю.Н., Миндюк Н.Г. и др.
Цели урока:
Образовательная –
выявить уровень овладения учащимися комплекса знаний и умений по применению навыков умножения и деления степеней;
формировать умение применять разложение многочлена на множители с помощью вынесения общего множителя за скобки;
применять вынесение общего множителя за скобки при решении уравнений.
Развивающая –
способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы;
развивать навыки самоконтроля при выполнении заданий.
Воспитательная —
воспитание ответственности, активности, самостоятельности, объективной самооценки.
Тип урока: комбинированный.
Основные результаты обучения:
уметь выносить общий множитель за скобки;
уметь применять данный способ при решении упражнений.
Ход урока.
1 модуль (30 мин).
1. Организационный момент.
2. Проверка домашнего задания.
Проверка наличия (дежурные), обсуждение возникших вопросов.
3 . Актуализация опорных знаний.
Н айдите НОД (15,6), (30,60), (24,8), (4,3), (20,55) , (16, 12).
Что такое НОД?
Как выполняется деление степеней с одинаковыми основаниями?
Как выполняется умножение степеней с одинаковыми основаниями?
Для данных степеней (c 3) 7 ,b 45 ,c 5 , a 21 , a 11 b 7 ,d 5 Назовите степень с наименьшим показателем, одинаковыми основаниями, одинаковыми показателями
Повторим распределительный закон умножения. Запишите его в буквенной форме
а (в + с)= ав + ас
* — знак умножения
Выполнить устные задания на применение распределительного свойства. (Подготовить на доске).
1) 2*(а + в) 4) (х – 6)*5
2) 3*(х – у) 5) -4*(у + 5)
3) а*(4 + х) 6) -2*(в – а)
На закрытой доске записаны задания, ребята решают и записывают на доске результат. Задания на умножения одночлена на многочлен.
Задания на умножения одночлена на многочлен.
Для начала я предлагаю вам пример на умножение одночлена на многочлен:
2 х (х 2 +4 х у – 3)= 2х 3 + 8х 2 у – 6х Не стираем!
Написать правило умножения одночлена на многочлен в виде схемы.
На доске появляется запись:
Я могу написать это свойство в виде:
В таком виде мы уже использовали запись для простого способа вычисления выражений.
а) 23 * 15 + 15 * 77 = (23 + 77) * 15 = 100 * 15 = 1500
Остальные устно, проверить ответы:
е) 55*682 – 45*682 = 6820
ж) 7300*3 + 730*70 = 73000
з) 500*38 – 50*80 = 15000
Какой закон помог вам найти простой способ вычислений? (Распределительный)
Действительно – распределительный закон помогает упрощать выражения.
4 . Постановка цели и темы урока. Устный счет. Отгадайте тему урока.
Работа в парах.
Карточки для пар.
Оказывается, что разложение на множители выражения – это операция, обратная почленному умножению одночлена на многочлен.
Рассмотрим тот же самый пример, который решал учащийся, но в обратном порядке. Разложить на множители – значит вынести за скобки общий множитель.
2 х 3 + 8 х 2 у – 6 х = 2 х (х 2 + 4 ху – 3).
Сегодня на уроке мы рассмотрим понятия разложение многочлена на множители и вынесение общего множителя за скобки, научимся применять эти понятия при выполнении упражнений.
Алгоритм вынесения общего множителя за скобки
Наибольший общий делитель коэффициентов.
Одинаковые буквенные переменные.
Проставить наименьшую степень к вынесенным переменным.
Затем в скобках записывается оставшиеся одночлены многочлена.
Наибольший общий делитель находили в младших класса, общую переменную в наименьшей степени можно сразу увидеть. А чтобы быстро находить оставшийся в скобках многочлен надо потренироваться по номеру №657.
5. Первичное усвоение с проговариванием вслух.
№657 (1 столбик)
2 модуль (30 мин).
1. Итог первой 30-минутки.
Итог первой 30-минутки.
А) Какое преобразование называется разложением многочлена на множители?
Б) На каком свойстве основано вынесение общего множителя за скобки?
В) Как выносится общий множитель за скобки?
2. Первичное закрепление.
На доске записаны выражения. Найти в этих равенствах ошибки, если они имеются и исправить.
1) 2 х 3 – 3 х 2 – х =х (2 х 2 – 3 х).
2) 2 х + 6 = 2 (х + 3).
3) 8 х + 12 у = 4 (2 х — 3у).
4) а 6 – а 2 = а 2 (а 2 – 1).
5) 4 -2а = – 2 (2 – а).
3. Первичная проверка понимания.
Работа с самопроверкой. 2 чел на обратной стороне
Вынесите общий множитель за скобки:
Устно сделать проверку умножением.
4. Подготовка учащихся к обобщенной деятельности.
Выносим многочленный множитель за скобки (объяснение учителя).
Разложите на множители многочлен .
В данном выражении мы видим, присутствует один и тот же множитель , который можно вынести за скобки. Итак, получим:
Итак, получим:
Выражения и являются противоположными, поэтому в некоторых случаях можно пользоваться данным равенством . Два раза меняем знак! Разложите на множители многочлен
Здесь присутствуют противоположные выражения и , воспользовавшись предыдущим тождеством мы получим следующую запись: .
А теперь мы видим, что общий множитель можно вынести за скобки.
На этом уроке мы познакомимся с правилами вынесения за скобки общего множителя, научимся находить его в различных примерах и выражениях. Поговорим о том, как простая операция, вынесение общего множителя за скобки, позволяет упростить вычисления. Полученные знания и навыки закрепим, рассмотрев примеры разных сложностей.
Что такое общий множитель, зачем его искать и с какой целью выносить за скобки? Ответим на эти вопросы, разобрав простейший пример.
Решим уравнение . Левая часть уравнения является многочленом, состоящим из подобных членов. Буквенная часть является общей для данных членов, значит, она и будет общим множителем. Вынесем за скобки:
Вынесем за скобки:
В данном случае вынесение за скобки общего множителя помогло нам преобразовать многочлен в одночлен. Таким образом, мы смогли упростить многочлен и его преобразование помогло нам решить уравнение.
В рассмотренном примере общий множитель был очевиден, но будет ли так просто найти его в произвольном многочлене?
Найдём значение выражения: .
В данном примере вынесение общего множителя за скобки значительно упростило вычисление.
Решим еще один пример. Докажем делимость на выражения .
Полученное выражение делится на , что и требовалось доказать. И снова вынесение общего множителя позволило нам решить задачу.
Решим еще один пример. Докажем, что выражение делится на при любом натуральном : .
Выражение является произведением двух соседних чисел натурального ряда. Одно из двух чисел обязательно будет четным, значит, выражение будет делиться на .
Мы разобрали разные примеры, но применяли один и тот же метод решения: выносили общий множитель за скобки. Мы видим, что эта простая операция значительно упрощает вычисления. Было легко найти общий множитель для этих частных случаев, а что делать в общем случае, для произвольного многочлена?
Мы видим, что эта простая операция значительно упрощает вычисления. Было легко найти общий множитель для этих частных случаев, а что делать в общем случае, для произвольного многочлена?
Вспомним, что многочлен — сумма одночленов.
Рассмотрим многочлен . Данный многочлен является суммой двух одночленов. Одночлен — произведение числа, коэффициента, и буквенной части. Таким образом, в нашем многочлене каждый одночлен представлен произведением числа и степеней, произведение множителей. Множители могут быть одинаковыми для всех одночленов. Именно эти множители нужно определить и вынести за скобку. Сначала находим общий множитель для коэффициентов, причем целочисленных.
Было легко найти общий множитель, но давайте определим НОД коэффициентов: .
Рассмотрим ещё один пример: .
Найдем , что позволит нам определить общий множитель для данного выражения: .
Мы вывели правило для целых коэффициентов. Нужно найти их НОД и вынести за скобку. Закрепим это правило, решив ещё один пример.
Мы рассмотрели правило вынесения общего множителя для целочисленных коэффициентов, перейдем к буквенной части. Сначала ищем те буквы, которые входят во все одночлены, а потом определяем наибольшую степень буквы, которая входит во все одночлены: .
В этом примере была всего одна общая буквенная переменная, но их может быть несколько, как в следующем примере:
Усложним пример, увеличив количество одночленов:
После вынесения общего множителя мы преобразовали алгебраическую сумму в произведение.
Мы рассмотрели правила вынесения для целых коэффициентов и буквенных переменных отдельно, но чаще всего для решения примера нужно применять их вместе. Рассмотрим пример:
Иногда бывает сложно определить, какое выражение остается в скобках, рассмотрим легкий прием, который позволит вам быстро решить эту проблему.
Общим множителем также может быть искомое значение :
Общим множителем может быть не только число или одночлен, но и любое выражение, как, например, в следующем уравнении.
>>Математика: Вынесение общего множителя за скобки
Прежде чем начинать изучение этого параграфа, вернитесь к § 15. Там мы уже рассмотрели пример, в котором требовалось представить многочлен в виде произведения многочлена и одночлена. Мы установили, что эта задача не всегда корректна. Если все же такое произведение удалось составить, то обычно говорят, вынесение что многочлен разложен на множители с помощью общего вынесения общего множителя за скобки. Рассмотрим несколько примеров.
Пример 1. Разложить на множители многочлен:
А) 2х + 6у, в) 4а 3 + 6а 2 ; д) 5а 4 — 10а 3 + 15а 8 .
б) а 3 + а 2 ; г) 12аЬ 4 — 18а 2 b 3 с;
Р е ш е н и е.
а) 2х + 6у = 2 (x + Зу). За скобки вынесли общий делитель коэффициентов членов многочлена.
б) а 3 + а 2 = а 2 (а + 1). Если одна и та же переменная входит во все члены многочлена, то ее можно вынести за скобки в степени, равной наименьшей из имеющихся (т. е. выбирают наименьший из имеющихся показателей).
в) Здесь используем тот же прием, что и при решении примеров а) и б): для коэффициентов находим общий делитель (в данном случае число 2), для переменных — наименьшую степень из имеющихся (в данном случае а 2). Получаем:
4а 3 + 6а 2 = 2а 2 2а + 2а 2 3 = 2а 2 (2а + 3).
г) Обычно для целочисленных коэффициентов стараются найти не просто общий делитель, а наибольший общий делитель. Для коэффициентов 12 и 18 им будет число 6. Замечаем, что переменная а входит в оба члена многочлена, при этом наименьший показапоказатель равен 1. Переменная b также входит в оба члена многочлена, причем наименьший показатель равен 3. Наконец, переменная с входит только во второй член многочлена и не входит в первый член, значит, эту переменную нельзя вынести за скобки ни в какой степени. В итоге имеем:
12аb 4 — 18а 2 Ь 3 с = 6аЬ 3 2b — 6аЬ 3 Зас = 6аb 3 (2b — Зас).
д) 5а 4 -10а 3 +15а 8 = 5а 3 (а-2 + За 2).
Фактически в этом примере мы выработали следующий алгоритм.
Замечание . В ряде случаев полезно выносить за скобку в качестве общего множителя и дробный коэффициент.
Например:
Пример 2. Разложить на множители:
Х 4 у 3 -2х 3 у 2 + 5х 2 .
Решение. Воспользуемся сформулированным алгоритмом.
1) Наибольший общий делитель коэффициентов -1, -2 и 5 равен 1.
2) Переменная х входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки х 2 .
3) Переменная у входит не во все члены многочлена; значит, ее нельзя вынести за скобки.
В ы в о д: за скобки можно вынести х 2 . Правда, в данном случае целесообразнее вынести за скобки -x 2 .
Получим:
-х 4 у 3 -2х 3 у 2 + 5х 2 = — х 2 (х 2 у 3 + 2ху 2 — 5).
Пример 3 . Можно ли разделить многочлен 5а 4 — 10а 3 + 15а 5 на одночлен 5а 3 ? Если да, то выполнить деление .
Решение. В примере 1д) мы получили, что
5а 4 — 10а 3 + 15а 8 — 5а 3 (а — 2 + За 2).
Значит, заданный многочлен можно разделить на 5а 3 , при этом в частном получится а — 2 + За 2 .
Подобные примеры мы рассматривали в § 18; просмотрите их, пожалуйста, еще раз, но уже с точки зрения вынесения общего множителя за скобки.
Разложение многочлена на множители с помощью вынесения общего множителя за скобки тесно связано с двумя операциями, которые мы изучали в § 15 и 18, — с умножением многочлена на одночлен и с делением многочлена на одночлен .
А теперь несколько расширим наши представления о вынесении общего множителя за скобки. Дело в том, что иногда алгебраическое выражение задается в таком виде, что в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов.
Пример 4. Разложить на множители:
2x(x-2) + 5(x-2) 2 .
Решение. Введем новую переменную у = х — 2. Тогда получим:
2x (x — 2) + 5 (x — 2) 2 = 2ху + 5у 2 .
Замечаем, что переменную у можно вынести за скобки:
2ху + 5у 2 — у (2х + 5у). А теперь вернемся к старым обозначениям:
А теперь вернемся к старым обозначениям:
у(2х + 5у) = (х- 2)(2x + 5(х — 2)) = (x — 2)(2x + 5x-10) = (x-2)(7x:-10).
В подобных случаях после приобретения некоторого опыта можно не вводить новую переменную, а использовать следующую
2х(х — 2) + 5(х — 2) 2 = (х — 2)(2x + 5(x — 2))= (х — 2)(2х + 5х~ 10) = (х — 2)(7x — 10).
Календарно-тематичне планування з математики, відео з математики онлайн , Математика в школі скачати
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиСреди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. 3 \)
3 \)
Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.
Обычно пользуются следующим правилом.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.
Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов
С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто
встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.
Рекомендуем также
Примеры где надо вынести общий множитель за. » вынесение общего множителя за скобки»
В этой статье мы остановимся на вынесении за скобки общего множителя . Для начала разберемся, в чем состоит указанное преобразование выражения. Дальше приведем правило вынесения общего множителя за скобки и подробно рассмотрим примеры его применения.
Навигация по странице.
Например, слагаемые в выражении 6·x+4·y
имеют общий множитель 2
, который не записан явно. Его можно увидеть лишь после того, как представить число 6
в виде произведения 2·3
, а 4
в виде произведения 2·2
. Итак, 6·x+4·y=2·3·x+2·2·y=2·(3·x+2·y)
. Еще пример: в выражении x 3 +x 2 +3·x
слагаемые имеют общий множитель x
, который становится явно виден после замены x 3
на x·x 2
(при этом мы использовали ) и x 2
на x·x
. После вынесения его за скобки получим x·(x 2 +x+3)
.
Итак, 6·x+4·y=2·3·x+2·2·y=2·(3·x+2·y)
. Еще пример: в выражении x 3 +x 2 +3·x
слагаемые имеют общий множитель x
, который становится явно виден после замены x 3
на x·x 2
(при этом мы использовали ) и x 2
на x·x
. После вынесения его за скобки получим x·(x 2 +x+3)
.
Отдельно скажем про вынесение минуса за скобки. Фактически вынесение минуса за скобки означает вынесение за скобки минус единицы. Для примера вынесем за скобки минус в выражении −5−12·x+4·x·y . Исходное выражение можно переписать в виде (−1)·5+(−1)·12·x−(−1)·4·x·y , откуда отчетливо виден общий множитель −1 , который мы и выносим за скобки. В результате придем к выражению (−1)·(5+12·x−4·x·y) , в котором коэффициент −1 заменяется просто минусом перед скобками, в итоге имеем −(5+12·x−4·x·y) . Отсюда хорошо видно, что при вынесении минуса за скобки в скобках остается исходная сумма, в которой изменены знаки всех ее слагаемых на противоположные.
В заключение этой статьи заметим, что вынесение за скобки общего множителя применяется очень широко. Например, с его помощью можно более рационально вычислять значения числовых выражений . Также вынесение за скобки общего множителя позволяет представлять выражения в виде произведения, в частности, на вынесении за скобки основан один из методов разложения многочлена на множители .
Например, с его помощью можно более рационально вычислять значения числовых выражений . Также вынесение за скобки общего множителя позволяет представлять выражения в виде произведения, в частности, на вынесении за скобки основан один из методов разложения многочлена на множители .
Список литературы.
- Математика. 6 класс: учеб. для общеобразоват. учреждений / [Н. Я. Виленкин и др.]. — 22-е изд., испр. — М.: Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.
В рамках изучений тождественных преобразований очень важна тема вынесения общего множителя за скобки. В данной статье мы поясним, в чем именно заключается такое преобразование, выведем основное правило и разберем характерные примеры задач.
Yandex.RTB R-A-339285-1
Понятие вынесения множителя за скобки
Чтобы успешно применять данное преобразование, нужно знать, для каких выражений оно используется и какой результат надо получить в итоге. Поясним эти моменты.
Вынести общий множитель за скобки можно в выражениях, представляющих собой суммы, в которых каждое слагаемое является произведением, причем в каждом произведении есть один множитель, общий (одинаковый) для всех. Он так и называется – общим множителем. Именно его мы будем выносить за скобки. Так, если у нас есть произведения 5 · 3 и 5 · 4 , то мы можем вынести за скобки общий множитель 5 .
Он так и называется – общим множителем. Именно его мы будем выносить за скобки. Так, если у нас есть произведения 5 · 3 и 5 · 4 , то мы можем вынести за скобки общий множитель 5 .
В чем состоит данное преобразование? В ходе него мы представляем исходное выражение как произведение общего множителя и выражения в скобках, содержащего сумму всех исходных слагаемых, кроме общего множителя.
Возьмем пример, приведенный выше. Вынесем общий множитель 5 в 5 · 3 и 5 · 4 и получим 5 (3 + 4) . Итоговое выражение – это произведение общего множителя 5 на выражение в скобках, которое является суммой исходных слагаемых без 5 .
Данное преобразование базируется на распределительном свойстве умножения, которое мы уже изучали до этого. В буквенном виде его можно записать как a · (b + c) = a · b + a · c . Поменяв правую часть с левой, мы увидим схему вынесения общего множителя за скобки.
Правило вынесения общего множителя за скобки
Используя все сказанное выше, выведем основное правило такого преобразования:
Определение 1
Чтобы вынести за скобки общий множитель, надо записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.
Пример 1
Возьмем простой пример вынесения. У нас есть числовое выражение 3 · 7 + 3 · 2 − 3 · 5 , которое является суммой трех слагаемых 3 · 7 , 3 · 2 и общего множителя 3 . Взяв за основу выведенное нами правило, запишем произведение как 3 · (7 + 2 − 5) . Это и есть итог нашего преобразования. Запись всего решения выглядит так: 3 · 7 + 3 · 2 − 3 · 5 = 3 · (7 + 2 − 5) .
Мы можем выносить множитель за скобки не только в числовых, но и в буквенных выражениях. Например, в 3 · x − 7 · x + 2 можно вынести переменную x и получить 3 · x − 7 · x + 2 = x · (3 − 7) + 2 , в выражении (x 2 + y) · x · y − (x 2 + y) · x 3 – общий множитель (x 2 + y) и получить в итоге (x 2 + y) · (x · y − x 3) .
Определить сразу, какой множитель является общим, возможно не всегда. Иногда выражение нужно предварительно преобразовать, заменив числа и выражения тождественно равными им произведениями.
Пример 2
Так, к примеру, в выражении 6 · x + 4 · y можно вынести общий множитель 2 , не записанный в явном виде. Чтобы его найти, нам нужно преобразовать исходное выражение, представив шесть как 2 · 3 , а четыре как 2 · 2 . То есть 6 · x + 4 · y = 2 · 3 · x + 2 · 2 · y = 2 · (3 · x + 2 · y) . Или в выражении x 3 + x 2 + 3 · x можно вынести за скобки общий множитель x , который обнаруживается после замены x 3 на x · x 2 . Такое преобразование возможно благодаря основным свойствам степени. В итоге мы получим выражение x · (x 2 + x + 3) .
Чтобы его найти, нам нужно преобразовать исходное выражение, представив шесть как 2 · 3 , а четыре как 2 · 2 . То есть 6 · x + 4 · y = 2 · 3 · x + 2 · 2 · y = 2 · (3 · x + 2 · y) . Или в выражении x 3 + x 2 + 3 · x можно вынести за скобки общий множитель x , который обнаруживается после замены x 3 на x · x 2 . Такое преобразование возможно благодаря основным свойствам степени. В итоге мы получим выражение x · (x 2 + x + 3) .
Еще один случай, на котором следует остановиться отдельно, – это вынесение за скобки минуса. Тогда мы выносим не сам знак, а минус единицу. Например, преобразуем таким образом выражение − 5 − 12 · x + 4 · x · y . Перепишем выражение как (− 1) · 5 + (− 1) · 12 · x − (− 1) · 4 · x · y , чтобы общий множитель был виден более отчетливо. Вынесем его за скобки и получим − (5 + 12 · x − 4 · x · y) . На этом примере видно, что в скобках получилась та же сумма, но с противоположными знаками.
В выводах отметим, что преобразование путем вынесения общего множителя за скобки очень часто применяется на практике, например, для вычисления значения рациональных выражений. 3 \)
3 \)
Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.
Этот результат обычно формулируют в виде правила.
Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.
Мы уже неоднократно использовали это правило для умножения на сумму.
Произведение многочленов. Преобразование (упрощение) произведения двух многочленов
Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.
Обычно пользуются следующим правилом.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.
Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов
С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто
встречаются выражения \((a + b)^2, \; (a — b)^2 \) и \(a^2 — b^2 \), т. 2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
2 = (a — b)(a + b) \) — разность квадратов равна произведению разности на сумму.
Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.
Продолжаем разбираться с основами алгебры. Сегодня мы поработаем с , а именно рассмотрим такое действие, как вынесение общего множителя за скобки .
Содержание урокаОсновной принцип
Распределительный закон умножения позволяет умножить число на сумму (или сумму на число). Например, чтобы найти значение выражения 3 × (4 + 5) можно умножить число 3 на каждое слагаемое в скобках и сложить полученные результаты:
3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15
Число 3
и выражение в скобках можно поменять местами (это следует из переместительного закона умножения). Тогда каждое слагаемое, которое в скобках, будет умножено на число 3
Тогда каждое слагаемое, которое в скобках, будет умножено на число 3
(4 + 5) × 3 = 4 × 3 + 5 × 3 = 12 + 15
Пока не будем вычислять конструкцию 3 × 4 + 3 × 5 и складывать полученные результаты 12 и 15 . Оставим выражение в виде 3 (4 + 5) = 3 × 4 + 3 × 5 . Ниже оно нам потребуется именно в таком виде, чтобы понять суть вынесения общего множителя за скобки.
Распределительный закон умножения иногда называют внесением множителя во внутрь скобок. В выражении 3 × (4 + 5) множитель 3 был за скобками. Умножив его на каждое слагаемое в скобках, мы по сути внесли его во внутрь скобок. Для наглядности можно так и записать, хоть и не принято так записывать:
3 (4 + 5) = (3 × 4 + 3 × 5)
Поскольку в выражении 3 × (4 + 5) число 3 умножается на каждое слагаемое в скобках, это число является общим множителем для слагаемых 4 и 5
Как говорилось ранее, умножив этот общий множитель на каждое слагаемое в скобках, мы вносим его во внутрь скобок. Но возможен и обратный процесс — общий множитель можно обратно вынести за скобки. В данном случае в выражении 3
× 4 + 3
× 5
общий множитель виден, как на ладони — это множитель 3
. Его и нужно вынести за скобки. Для этого сначала записывается сам множитель 3
В данном случае в выражении 3
× 4 + 3
× 5
общий множитель виден, как на ладони — это множитель 3
. Его и нужно вынести за скобки. Для этого сначала записывается сам множитель 3
и рядом в скобках записывается выражение 3 × 4 + 3 × 5 но уже без общего множителя 3 , поскольку он вынесен за скобки
3 (4 + 5)
В результате вынесения общего множителя за скобки получается выражение 3 (4 + 5) . Это выражение тождественно равно предыдущему выражению 3 × 4 + 3 × 5
3(4 + 5) = 3 × 4 + 3 × 5
Если вычислить обе части полученного равенства, то получим тождество:
3(4 + 5) = 3 × 4 + 3 × 5
27 = 27
Как происходит вынесение общего множителя за скобки
Вынесение общего множителя за скобки по сути является обратной операцией внесению общего множителя во внутрь скобок.
Если при внесении общего множителя внутрь скобок, мы умножаем этот множитель на каждое слагаемое в скобках, то при вынесении этого множителя обратно за скобки, мы должны разделить каждое слагаемое в скобках на этот множитель.
В выражении 3 × 4 + 3 × 5 , которое было рассмотрено выше, так и происходило. Каждое слагаемое было разделено на общий множитель 3 . Произведения 3 × 4 и 3 × 5 и являются слагаемыми, поскольку если их вычислить, мы получим сумму 12 + 15
Теперь мы можем детально увидеть, как происходит вынесение общего множителя за скобки:
Видно, что общий множитель 3 сначала вынесен за скобки, затем в скобках происходит деление каждого слагаемого на этот общий множитель.
Деление каждого слагаемого на общий множитель можно выполнять не только разделяя числитель на знаменатель, как это было показано выше, но и сокращая эти дроби. В обоих случаях получится один и тот же результат:
Мы рассмотрели простейший пример вынесения общего множителя за скобки, чтобы понять основной принцип.
Но не всё так просто, как кажется на первый взгляд. После того, как число умножено на каждое слагаемое в скобках, полученные результаты складывают, и общий множитель пропадает из виду.
Вернёмся к нашему примеру 3 (4 + 5) . Применим распределительный закон умножения, то есть умножим число 3 на каждое слагаемое в скобках и сложим полученные результаты:
3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15
После того, как вычислена конструкция 3 × 4 + 3 × 5 , мы получаем новое выражение 12 + 15 . Видим, что общий множитель 3 пропал из виду. Теперь в полученном выражении 12 + 15 попробуем обратно вынести общий множитель за скобки, но чтобы вынести этот общий множитель его сначала нужно найти.
Обычно при решении задач встречаются именно такие выражения, в которых общий множитель сначала нужно найти, прежде чем его выносить.
Чтобы в выражении 12 + 15 вынести общий множитель за скобки, нужно найти наибольший общий делитель (НОД) слагаемых 12 и 15. Найденный НОД и будет общим множителем.
Итак, найдём НОД для чисел 12 и 15. Напомним, что для нахождения НОД необходимо разложить исходные числа на простые множители, затем выписать первое разложение и убрать из него множители, которые не входят в разложение второго числа. Оставшиеся множители нужно перемножить и получить искомый НОД. Если испытываете затруднения на этом моменте, обязательно повторите .
Оставшиеся множители нужно перемножить и получить искомый НОД. Если испытываете затруднения на этом моменте, обязательно повторите .
НОД для 12 и 15 это число 3. Данное число является общим множителем для слагаемых 12 и 15. Его и нужно выносить за скобки. Для этого сначала записываем сам множитель 3 и рядом в скобках записываем новое выражение, в котором каждое слагаемое выражения 12 + 15 разделено на общий множитель 3
Ну и дальнейшее вычисление не составляет особого труда. Выражение в скобках легко вычисляется — двенадцать разделить на три будет четыре , а пятнадцать разделить на три будет пять :
Таким образом, при вынесении общего множителя за скобки в выражении 12 + 15 получается выражение 3(4 + 5) . Подробное решение выглядит следующим образом:
В коротком решении пропускают запись в которой показано, как каждое слагаемое разделено на общий множитель:
Пример 2. 15 + 20
Найдём НОД для слагаемых 15 и 20
НОД для 15 и 20 это число 5. Данное число является общим множителем для слагаемых 15 и 20. Его и вынесем за скобки:
Данное число является общим множителем для слагаемых 15 и 20. Его и вынесем за скобки:
Получили выражение 5(3 + 4). Получившееся выражение можно проверить. Для этого достаточно умножить пятёрку на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 15 + 20
Пример 3. Вынести общий множитель за скобки в выражении 18+24+36
Найдём НОД для слагаемых 18, 24 и 36. Чтобы найти , нужно разложить эти числа на простые множители, затем найти произведение общих множителей:
НОД для 18, 24 и 36 это число 6. Данное число является общим множителем для слагаемых 18, 24 и 36. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим число 6 на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 18+24+36
Пример 4. Вынести общий множитель за скобки в выражении 13 + 5
Слагаемые 13 и 5 являются простыми числами. Они раскладываются только на единицу и самих себя:
Это значит, что у слагаемых 13 и 5 нет общих множителей, кроме единицы. Соответственно, нет смысла выносить эту единицу за скобки, поскольку это ничего не даст. Покажем это:
Соответственно, нет смысла выносить эту единицу за скобки, поскольку это ничего не даст. Покажем это:
Пример 5. Вынести общий множитель за скобки в выражении 195+156+260
Найдём НОД для слагаемых 195, 156 и 260
НОД для 195, 156 и 260 это число 13. Данное число является общим множителем для слагаемых 195, 156 и 260. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим 13 на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 195+156+260
Выражение в котором требуется вынести общий множитель за скобки может быть не только суммой чисел, но и разностью. Например, вынесем общий множитель за скобки в выражении 16 − 12 − 4. Наибольшим общим делителем для чисел 16, 12 и 4 это число 4. Данное число и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим четвёрку на каждое число в скобках. Если мы всё сделали правильно, то должны получить выражение 16 − 12 − 4
Пример 6. Вынести общий множитель за скобки в выражении 72+96−120
Вынести общий множитель за скобки в выражении 72+96−120
Найдём НОД для чисел 72, 96 и 120
НОД для 72, 96 и 120 это число 24. Данное число является общим множителем для слагаемых 195, 156 и 260. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим 24 на каждое число в скобках. Если мы всё сделали правильно, то должны получить выражение 72+96−120
Общий множитель, выносимый за скобки, может быть и отрицательным. Например, вынесем общий множитель за скобки в выражении −6−3. Вынести общий множитель за скобки в таком выражении можно двумя способами. Рассмотрим каждый из них.
Способ 1.
Заменим вычитание сложением:
−6 + (−3)
Теперь находим общий множитель. Общим множителем данного выражения будет наибольший общий делитель слагаемых −6 и −3.
Модуль первого слагаемого это 6. А модуль второго слагаемого это 3. НОД(6 и 3) равен 3. Данное число является общим множителем для слагаемых 6 и 3. Его и вынесем за скобки:
Выражение полученное таким способом получилось не очень аккуратным. Много скобок и отрицательных чисел не придают выражению простоту. Поэтому можно воспользоваться вторым способом, суть которого заключается в том, чтобы вынести за скобки не 3, а −3.
Много скобок и отрицательных чисел не придают выражению простоту. Поэтому можно воспользоваться вторым способом, суть которого заключается в том, чтобы вынести за скобки не 3, а −3.
Способ 2.
Как и в прошлый раз заменяем вычитание сложением
−6 + (−3)
В этот раз мы вынесем за скобки не 3, а −3
Выражение полученное в этот раз выглядит намного проще. Запишем решение покороче, чтобы сделать его ещё проще:
Разрешать выносить отрицательный множитель за скобки связано с тем, что разложение чисел −6 и (−3) можно записать двумя видами: сначала сделать множимое отрицательным, а множитель положительным:
−2 × 3 = −6
−1 × 3 = −3
во втором случае множимое можно сделать положительным, а множитель отрицательным:
2 × (−3) = −6
1 × (−3) = −3
А значит мы вольны выносить за скобки тот сомножитель, который захотим.
Пример 8. Вынести общий множитель за скобки в выражении −20−16−2
Заменим вычитание сложением
−20−16−2 = −20 + (−16) + (−2)
Наибольшим общим делителем для слагаемых −20, −16 и −2 является число 2. Это число является общим множителем для этих слагаемых. Посмотрим, как это выглядит:
Это число является общим множителем для этих слагаемых. Посмотрим, как это выглядит:
−10 × 2 = −20
−8 × 2 = −16
−1 × 2 = −2
Но приведенные разложения можно заменить на тождественно равные разложения. Различие будет в том, что общим множителем будет не 2 , а −2
10 × (−2) = −20
8 × (−2) = −16
1 × (−2) = −2
Поэтому для удобства за скобки можно вынести не 2 , а −2
Запишем приведенное решение покороче:
А если бы вынесли за скобки 2 , то получилось бы не совсем аккуратное выражение:
Пример 9. Вынести общий множитель за скобки в выражении −30−36−42
Заменим вычитание сложением:
−30 + (−36) + (−42)
Наибольшим общим делителем слагаемых −30, −36 и −42 это число 6. Данное число является общим множителем для этих слагаемых. Но за скобки мы вынесем не 6, а −6 поскольку числа −30, −36 и −42 можно представить так:
5 × (−6) = −30
6 × (−6) = −36
7 × (−6) = −42
Вынесение минуса за скобки
При решении задач иногда может быть полезным вынесение минуса за скобки. Это позволяет упростить выражение и привести его в порядок.
Это позволяет упростить выражение и привести его в порядок.
Рассмотрим следующий пример. Вынести минус за скобки в выражении −15+(−5)+(−3)
Для наглядности заключим данное выражение в скобки, ведь речь идёт о том, чтобы вынести минус за эти скобки
(−15 + (−5) + (−3))
Итак, чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые, но с противоположными знаками
Мы вынесли минус за скобки в выражении −15+(−5)+(−3) и получили −(15+5+3). Оба выражения равны одному и тому же значению −23
−15 + (−5) + (−3) = −23
−(15 + 5 + 3) = −(23) = −23
Поэтому между выражениями −15+(−5)+(−3) и −(15+5+3) можно поставить знак равенства, потому что они несут одно и то же значение:
−15 + (−5) + (−3) = −(15 + 5 + 3)
На самом деле при вынесении минуса за скобки опять же срабатывает распределительный закон умножения:
a(b+c) = ab + ac
Если поменять местами левую и правую часть этого тождества, то получится, что сомножитель a вынесен за скобки
ab + ac = a(b+c)
Тоже самое происходит, когда мы выносим общий множитель в других выражениях и когда выносим минус за скобки.
Очевидно, что при вынесении минуса за скобки, выносится не минус, а минус единица. Мы уже говорили, что коэффициент 1 принято не записывать.
Поэтому и образуется перед скобками минус, а знаки слагаемых которые были в скобках меняют свой знак на противоположный, поскольку каждое слагаемое разделено на минус единицу.
Вернёмся к предыдущему примеру и детально увидим, как на самом деле минус выносился за скобки
Пример 2. Вынести минус за скобки в выражении −3 + 5 + 11
Ставим минус и рядом в скобках записываем выражение −3 + 5 + 11 с противоположным знаком у каждого слагаемого:
−3 + 5 + 11 = −(3 − 5 − 11)
Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица. Подробное решение выглядит следующим образом:
Сначала получилось выражение −1(3 + (−5) + (−11))
, но мы раскрыли в нем внутренние скобки и получили выражение −(3 − 5 − 11)
. Раскрытие скобок это тема следующего урока, поэтому если данный пример вызывает у вас затруднения, можете пока пропустить его.
Вынесение общего множителя за скобки в буквенном выражении
Выносить общий множитель за скобки в буквенном выражении намного интереснее.
Для начала рассмотрим простейший пример. Пусть имеется выражение 3 a + 2 a . Вынесем общий множитель за скобки.
В данном случае, общий множитель виден невооруженным глазом — это множитель a . Его и вынесем за скобки. Для этого записываем сам множитель a и рядом в скобках записываем выражение 3a + 2a , но уже без множителя a поскольку он вынесен за скобки:
Как и в случае с числовым выражением, здесь происходит деление каждого слагаемого на вынесенный общий множитель. Выглядит это так:
В обеих дробях переменные a были сокращены на a .
Вместо них в числителе и в знаменателе получились единицы. Единицы получились по причине того, что вместо переменной a может стоять любое число. Эта переменная располагалась и в числителе и в знаменателе. А если в числителе и в знаменателе располагаются одинаковые числа, то наибольший общий делитель для них будет само это число.
А если в числителе и в знаменателе располагаются одинаковые числа, то наибольший общий делитель для них будет само это число.
Например, если вместо переменной a подставить число 4 , то конструкция примет следующий вид: . Тогда четвёрки в обеих дробях можно будет сократить на 4:
Получается то же самое, что и раньше, когда вместо четвёрок стояла переменная a .
Поэтому не следует пугаться при виде сокращения переменных. Переменная это полноправный множитель, пусть даже выраженный буквой. Такой множитель можно выносить за скобки, сокращать и выполнять другие действия, которые допустимы к обычным числам.
Буквенное выражение содержит не только числа, но и буквы (переменные). Поэтому общий множитель, который выносится за скобки часто бывает буквенным множителем, состоящим из числа и буквы (коэффициента и переменной). К примеру, следующие выражения являются буквенными множителями:
3a, 6b, 7ab, a, b, c
Прежде чем выносить такой множитель за скобки, нужно определиться, какое число будет в числовой части общего множителя и какая переменная будет в буквенной части общего множителя. Другими словами, нужно узнать какой коэффициент будет у общего множителя и какая переменная будет в него входить.
Другими словами, нужно узнать какой коэффициент будет у общего множителя и какая переменная будет в него входить.
Рассмотрим выражение 10a + 15a . Попробуем вынести в нём общий множитель за скобки. Сначала определимся из чего будет состоять общий множитель, то есть узнаем его коэффициент и какая переменная будет в него входить.
Коэффициентом общего множителя должен быть наибольший общий делитель коэффициентов буквенного выражения 10a + 15a . 10 и 15 , а их наибольший общий делитель это число 5 . Значит число 5 будет коэффициентом общего множителя, выносимого за скобки.
Теперь определимся какая переменная будет входить в общий множитель. Для этого нужно посмотреть на выражение 10a + 15a и найти буквенный сомножитель, который входит во все слагаемые. В данном случае, это сомножитель a . Этот сомножитель входит в каждое слагаемое выражения 10a + 15a . Значит переменная a будет входить в буквенную часть общего множителя, выносимого за скобки:
Теперь осталось вынести общий множитель 5a за скобки. Для этого разделим каждое слагаемое выражения 10a + 15a на 5a . Для наглядности коэффициенты и числа будем отделять знаком умножения (×)
Для этого разделим каждое слагаемое выражения 10a + 15a на 5a . Для наглядности коэффициенты и числа будем отделять знаком умножения (×)
Проверим получившееся выражение. Для этого умножим 5a на каждое слагаемое в скобках. Если мы всё сделали правильно, то получим выражение 10a + 15a
Буквенный множитель не всегда можно вынести за скобки. Иногда общий множитель состоит только из числа, поскольку ничего подходящего для буквенной части в выражении не находится.
Например, вынесем общий множитель за скобки в выражении 2a − 2b . Здесь общим множителем будет только число 2 , а среди буквенных сомножителей общих множителей в выражении нет. Поэтому в данном случае будет вынесен только множитель 2
Пример 2. Вынести общий множитель выражении 3x + 9y + 12
Коэффициентами данного выражения являются числа 3, 9 и 12, их НОД равен 3 3 . А среди буквенных сомножителей (переменных) нет общего множителя. Поэтому окончательный общий множитель это 3
Поэтому окончательный общий множитель это 3
Пример 3. Вынести общий множитель за скобки в выражении 8x + 6y + 4z + 10 + 2
Коэффициентами данного выражения являются числа 8, 6, 4, 10 и 2, их НОД равен 2 . Значит коэффициентом общего множителя, выносимого за скобки, будет число 2 . А среди буквенных сомножителей нет общего множителя. Поэтому окончательный общий множитель это 2
Пример 4. Вынести общий множитель 6ab + 18ab + 3abc
Коэффициентами данного выражения являются числа 6, 18 и 3, их НОД равен 3 . Значит коэффициентом общего множителя, выносимого за скобки, будет число 3 . В буквенную часть общего множителя будут входить переменные a и b, поскольку в выражении 6ab + 18ab + 3abc эти две переменные входят в каждое слагаемое. Поэтому окончательный общий множитель это 3ab
При подробном решении выражение становится громоздким и даже непонятным. В данном примере это более чем заметно. Это связано с тем, что мы сокращаем множители в числителе и в знаменателе. Лучше всего делать это в уме и сразу записывать результаты деления. Тогда выражение станет коротким и аккуратным:
В данном примере это более чем заметно. Это связано с тем, что мы сокращаем множители в числителе и в знаменателе. Лучше всего делать это в уме и сразу записывать результаты деления. Тогда выражение станет коротким и аккуратным:
Как и в случае с числовым выражением в буквенном выражении общий множитель может быть и отрицательным.
Например, вынесем общий за скобки в выражении −3a − 2a .
Для удобства заменим вычитание сложением
−3a − 2a = −3a + (−2a )
Общим множителем в данном выражении является множитель a . Но за скобки можно вынести не только a , но и −a . Его и вынесем за скобки:
Получилось аккуратное выражение −a (3+2). Не следует забывать, что множитель −a на самом деле выглядел как −1a и после сокращения в обеих дробях переменных a , в знаменателях остались минус единицы. Поэтому в итоге и получаются положительные ответы в скобках
Пример 6. Вынести общий множитель за скобки в выражении −6x − 6y
Заменим вычитание сложением
−6x−6y = −6x+(−6y)
Вынесем за скобки −6
Запишем решение покороче:
−6x − 6y = −6(x + y)
Пример 7. Вынести общий множитель за скобки в выражении −2a − 4b − 6c
Вынести общий множитель за скобки в выражении −2a − 4b − 6c
Заменим вычитание сложением
−2a-4b-6c = −2a + (−4b) + (−6c)
Вынесем за скобки −2
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Урок алгебры в 7 классе.
Тема « Вынесение общего множителя за скобки».
Учебник Макарычев Ю.Н., Миндюк Н.Г. и др.
Цели урока:
Образовательная –
выявить уровень овладения учащимися комплекса знаний и умений по применению навыков умножения и деления степеней;
формировать умение применять разложение многочлена на множители с помощью вынесения общего множителя за скобки;
применять вынесение общего множителя за скобки при решении уравнений.
Развивающая –
способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы;
развивать навыки самоконтроля при выполнении заданий.
Воспитательная —
воспитание ответственности, активности, самостоятельности, объективной самооценки.
Тип урока: комбинированный.
Основные результаты обучения:
уметь выносить общий множитель за скобки;
уметь применять данный способ при решении упражнений.
Ход урока.
1 модуль (30 мин).
1. Организационный момент.
2. Проверка домашнего задания.
Проверка наличия (дежурные), обсуждение возникших вопросов.
3 . Актуализация опорных знаний.
Н айдите НОД (15,6), (30,60), (24,8), (4,3), (20,55) , (16, 12).
Что такое НОД?
Как выполняется деление степеней с одинаковыми основаниями?
Как выполняется умножение степеней с одинаковыми основаниями?
Для данных степеней (c 3) 7 ,b 45 ,c 5 , a 21 , a 11 b 7 ,d 5 Назовите степень с наименьшим показателем, одинаковыми основаниями, одинаковыми показателями
Повторим распределительный закон умножения. Запишите его в буквенной форме
Запишите его в буквенной форме
а (в + с)= ав + ас
* — знак умножения
Выполнить устные задания на применение распределительного свойства. (Подготовить на доске).
1) 2*(а + в) 4) (х – 6)*5
2) 3*(х – у) 5) -4*(у + 5)
3) а*(4 + х) 6) -2*(в – а)
На закрытой доске записаны задания, ребята решают и записывают на доске результат. Задания на умножения одночлена на многочлен.
Для начала я предлагаю вам пример на умножение одночлена на многочлен:
2 х (х 2 +4 х у – 3)= 2х 3 + 8х 2 у – 6х Не стираем!
Написать правило умножения одночлена на многочлен в виде схемы.
На доске появляется запись:
Я могу написать это свойство в виде:
В таком виде мы уже использовали запись для простого способа вычисления выражений.
а) 23 * 15 + 15 * 77 = (23 + 77) * 15 = 100 * 15 = 1500
Остальные устно, проверить ответы:
е) 55*682 – 45*682 = 6820
ж) 7300*3 + 730*70 = 73000
з) 500*38 – 50*80 = 15000
Какой закон помог вам найти простой способ вычислений? (Распределительный)
Действительно – распределительный закон помогает упрощать выражения.
4 . Постановка цели и темы урока. Устный счет. Отгадайте тему урока.
Работа в парах.
Карточки для пар.
Оказывается, что разложение на множители выражения – это операция, обратная почленному умножению одночлена на многочлен.
Рассмотрим тот же самый пример, который решал учащийся, но в обратном порядке. Разложить на множители – значит вынести за скобки общий множитель.
2 х 3 + 8 х 2 у – 6 х = 2 х (х 2 + 4 ху – 3).
Сегодня на уроке мы рассмотрим понятия разложение многочлена на множители и вынесение общего множителя за скобки, научимся применять эти понятия при выполнении упражнений.
Алгоритм вынесения общего множителя за скобки
Наибольший общий делитель коэффициентов.
Одинаковые буквенные переменные.
Проставить наименьшую степень к вынесенным переменным.
Затем в скобках записывается оставшиеся одночлены многочлена.
Наибольший общий делитель находили в младших класса, общую переменную в наименьшей степени можно сразу увидеть. А чтобы быстро находить оставшийся в скобках многочлен надо потренироваться по номеру №657.
А чтобы быстро находить оставшийся в скобках многочлен надо потренироваться по номеру №657.
5. Первичное усвоение с проговариванием вслух.
№657 (1 столбик)
2 модуль (30 мин).
1. Итог первой 30-минутки.
А) Какое преобразование называется разложением многочлена на множители?
Б) На каком свойстве основано вынесение общего множителя за скобки?
В) Как выносится общий множитель за скобки?
2. Первичное закрепление.
На доске записаны выражения. Найти в этих равенствах ошибки, если они имеются и исправить.
1) 2 х 3 – 3 х 2 – х =х (2 х 2 – 3 х).
2) 2 х + 6 = 2 (х + 3).
3) 8 х + 12 у = 4 (2 х — 3у).
4) а 6 – а 2 = а 2 (а 2 – 1).
5) 4 -2а = – 2 (2 – а).
3. Первичная проверка понимания.
Работа с самопроверкой. 2 чел на обратной стороне
Вынесите общий множитель за скобки:
Устно сделать проверку умножением.
4. Подготовка учащихся к обобщенной деятельности.
Выносим многочленный множитель за скобки (объяснение учителя).
Разложите на множители многочлен .
В данном выражении мы видим, присутствует один и тот же множитель , который можно вынести за скобки. Итак, получим:
Выражения и являются противоположными, поэтому в некоторых случаях можно пользоваться данным равенством . Два раза меняем знак! Разложите на множители многочлен
Здесь присутствуют противоположные выражения и , воспользовавшись предыдущим тождеством мы получим следующую запись: .
А теперь мы видим, что общий множитель можно вынести за скобки.
Разложение многочлена на множители
Разложить многочлен на множители означает представить его в виде произведения двух или нескольких многочленов.
Примером разложения многочлена на множители является вынесение общего множителя за скобки, поскольку исходный многочлен обращается в произведение двух сомножителей, один из которых является одночленом, а другой многочленом.
Разложение многочлена на множители способом вынесения общего множителя за скобки
При вынесении общего множителя за скобки образуется произведение из двух сомножителей, один из которых является одночленом, а другой многочленом. Например:
6x + 3xy = 3x(2 + y)
В рамках изучения многочленов, одночлен принято считать многочленом, состоящим из одного члена. Поэтому, когда в многочлене выносится за скобки общий множитель, то говорят что исходный многочлен представлен в виде произведения многочленов.
В нашем примере многочлен 6x + 3xy был представлен в виде произведения многочленов 3x и (2 + y). По-другому говорят, что многочлен 6x + 3xy разложен на множители 3x и (2 + y)
Существуют также многочлены, в которых можно вынести за скобки такой общий множитель, который является двучленом. Например, рассмотрим многочлен 5a(x + y) + 7a(x + y). В этом многочлене общим множителем является двучлен (x + y). Вынесем его за скобки:
В этом многочлене общим множителем является двучлен (x + y). Вынесем его за скобки:
Разложение многочлена на множители способом группировки
Некоторые многочлены содержат группу членов, имеющих общий множитель. Такие группы можно заключать в скобки и далее выносить общий множитель за эти скобки. В результате получается разложение исходного многочлена на множители, которое называют разложением на множители способом группировки.
Рассмотрим следующий многочлен:
ax + ay + 3x + 3y
Члены ax и ay имеют общий множитель a. Выпишем эти члены и заключим их в скобки:
(ax + ay)
Далее в многочлене ax + ay + 3x + 3y члены 3x и 3y имеют общий множитель 3. Выпишем эти члены и тоже заключим их в скобки:
(3x + 3y)
Теперь соединим выражения (ax + ay) и (3x + 3y) знаком «плюс»
(ax + ay) + (3x + 3y)
В многочлене (ax + ay) вынесем за скобки общий множитель a, а в многочлене (3x + 3y) вынесем за скобки общий множитель 3. Делать это нужно в исходном выражении:
Делать это нужно в исходном выражении:
Далее замечаем, что двучлен (x + y) является общим множителем. Вынесем его за скобки. Продолжаем решение в исходном примере. В результате получим:
Запишем решение покороче, не расписывая подробно, как каждый член был разделен на общий множитель. Тогда решение получится более компактным:
Чтобы проверить правильно ли мы разложили многочлен на множители, выполним умножение (x + y)(a + 3). Если мы всё сделали правильно, то получим многочлен ax + ay + 3x + 3y
(x + y)(a + 3) = ax + ay + 3x + 3y
Пример 2. Разложить многочлен 9x + ax − 9y − ay на множители способом группировки.
Члены 9x и −9y имеют общий множитель 9. А члены ax и −ay имеют общий множитель a. Сгруппируем их с помощью скобок, и объединим с помощью знака «плюс»
(9x − 9y) + (ax − ay)
В первой группе (9x − 9y) вынесем за скобки общий множитель 9. Во второй группе (ax − ay) вынесем за скобки за скобки общий множитель a
Во второй группе (ax − ay) вынесем за скобки за скобки общий множитель a
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y)
Далее вынесем за скобки двучлен (x − y)
(9x − 9y) + (ax − ay) = 9(x − y) + a(x − y) = (x − y)(9 + a)
Пример 3. Разложить многочлен ab − 3b + b2 − 3a на множители способом группировки.
Сгруппируем первый член ab с четвёртым членом −3a. А второй член −3b сгруппируем с третьим членом b2. Не забываем, что объединять группы нужно с помощью знака «плюс»
(ab − 3a) + (−3b + b2)
В первой группе вынесем за скобки общий множитель a, во второй группе — общий множитель b
(ab − 3a) + (−3b + b2) = a(b − 3) + b(−3 + b)
Во втором произведении b(−3 + b) в сомножителе (−3 + b) изменим порядок следования членов. Тогда получим b(b − 3)
Тогда получим b(b − 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3)
Теперь вынесем за скобки общий множитель (b − 3)
(ab − 3a) + (−3b + b2) = a(b − 3) + b(b − 3) = (b − 3)(a + b)
Пример 4. Разложить многочлен x2y + x + xy2 + y + 2xy + 2 на множители способом группировки.
Сгруппируем первый член многочлена со вторым, третий с четвёртым, пятый с шестым:
В первой группе вынесем за скобки общий множитель x, во второй группе — общий множитель y, в третьей группе — общий множитель 2
Далее замечаем, что многочлен (xy + 1) является общим множителем. Вынесем его за скобки:
Разложение многочлена на множители по формуле квадрата суммы двух выражений
Формулы сокращённого умножения, которые мы рассматривали в прошлом уроке, можно применять для разложения многочленов на множители.
Вспомним, как выглядит формула квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Поменяем местами левую и правую часть, получим:
a2 + 2ab + b2 = (a + b)2
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)2 представляет собой перемножение двух сомножителей, каждый из которых равен многочлену (a + b).
Стало быть, если нам встретится выражение вида a2 + 2ab + b2, то мы можем представить его в виде произведения (a + b)(a + b). Иными словами, разложить на множители (a + b) и (a + b).
a2 + 2ab + b2 = (a + b)(a + b)
Пример 1. Разложить на множители многочлен 4x2 + 12xy + 9y2
Разложить на множители многочлен 4x2 + 12xy + 9y2
Чтобы воспользоваться формулой a2 + 2ab + b2 = (a + b)2, нужно узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член многочлена 4x2 + 12xy + 9y2 является результатом возведения в квадрат одночлена 2x, поскольку (2x)2 = 4x2. Третий член 9y2 является результатом возведения в квадрат одночлена 3y, поскольку (3y)2 = 9y2, а член 12xy это есть удвоенное произведение членов 2x и 3y, то есть 2 × 2x × 3y = 12xy.
Очевидно, что переменная a в данном случае равна 2x, а переменная b равна 3y
a = 2x
b = 3y
Тогда можно сделать вывод, что когда-то выражение 4x2 + 12xy + 9y2 выглядело в виде квадрата суммы (2x + 3y)2, но в результате применения формулы квадрата суммы оно обратилось в многочлен 4x2 + 12xy + 9y2. Наша задача — вернуть ему былую форму, то есть представить в виде (2x + 3y)2
Наша задача — вернуть ему былую форму, то есть представить в виде (2x + 3y)2
4x2 + 12xy + 9y2 = (2x + 3y)2
А поскольку (2x + 3y)2 это произведение двух сомножителей, каждый из которых равен многочлену (2x + 3y), то исходный многочлен 4x2 + 12xy + 9y2 можно представить в виде разложения на множители (2x + 3y) и (2x + 3y)
4x2 + 12xy + 9y2 = (2x + 3y)(2x + 3y)
Полностью решение можно записать так:
4x2 + 12xy + 9y2 = (2x)2 + 2 × 2x × 3y + (3y)2 = (2x + 3y)2 = (2x + 3y)(2x + 3y)
Пример 2. Разложить на множители многочлен x2 + 12x + 36
Разложить на множители многочлен x2 + 12x + 36
Первый член данного многочлена является результатом возведения в квадрат одночлена x, поскольку x2 = x2, третий член — результатом возведения в квадрат числа 6, поскольку 62 = 36, а член 12x это удвоенное произведение членов x и 6, поскольку 2 × x × 6 = 12x.
Воспользуемся формулой a2 + 2ab + b2 = (a + b)2. Роль переменной a играет одночлен x, а роль переменной b играет одночлен 6. Отсюда:
x2 + 12x + 36 = (x + 6)2
А поскольку (x + 6)2 это произведение двух сомножителей, каждый из которых равен многочлену (x + 6), то исходный многочлен x2 + 12x + 36 можно представить в виде разложения на множители (x + 6) и (x + 6)
x2 + 12x + 36 = (x + 6)(x + 6)
Разложение многочлена на множители по формуле квадрата разности двух выражений
Как и по формуле квадрата суммы двух выражений, многочлен можно разложить на множители по формуле квадрата разности двух выражений.
Формула квадрата разности двух выражений выглядит так:
(a − b)2 = a2 − 2ab + b2
Если в этой формуле поменять местами левую и правую часть, то получим:
a2 − 2ab + b2 = (a − b)2
Поскольку правая часть это произведение двух сомножителей, каждый из которых равен (a − b), то многочлен вида a2 − 2ab + b2 можно разложить на множители (a − b) и (a − b).
a2 − 2ab + b2 = (a − b)(a − b)
Пример 1. Разложить на множители многочлен 9x2 − 12xy + 4y2
Чтобы воспользоваться формулой a2 − 2ab + b2 = (a − b)2, нужно узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в квадрат одночлена 3x, поскольку (3x)2 = 9x2. Третий член 4y2является результатом возведения в квадрат одночлена 2y, поскольку (2y)2 = 4y2, а член 12xy это удвоенное произведение членов 3x и 2y, то есть 2 × 3x × 2y = 12xy.
Очевидно, что переменная a в данном случае равна 3x, а переменная b равна 2y
a = 3x
b = 2y
Тогда можно сделать вывод, что когда-то выражение 9x2 − 12xy + 4y2 выглядело в виде квадрата разности (3x − 2y)2, но в результате применения формулы квадрата разности оно обратилось в многочлен 9x2 − 12xy + 4y2. Наша задача — вернуть ему былую форму, то есть представить в виде (3x − 2y)2
9x2 − 12xy + 4y2 = (3x − 2y)2
А поскольку (3x − 2y)2 это произведение двух сомножителей, каждый из которых равен многочлену (3x − 2y), то исходный многочлен 9x2 − 12xy + 4y2 можно представить в виде разложения на множители (3x − 2y) и (3x − 2y)
9x2 − 12xy + 4y2 = (3x − 2y)(3x − 2y)
Полностью решение можно записать так:
9x2 − 12xy + 4y2 = (3x)2 − 2 × 3x × 2y + (2y)2 = (3x − 2y)2 = (3x − 2y)(3x − 2y)
Пример 2. Разложить на множители многочлен x2 − 4x + 4
Разложить на множители многочлен x2 − 4x + 4
Воспользуемся формулой квадрата разности двух выражений:
x2 − 4x + 4 = x2 − 2 × x × 2 + 22 = (x − 2)2 = (x − 2)(x − 2)
Разложение многочлена на множители по формуле куба суммы двух выражений
Вспомним, как выглядит формула куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Поменяем местами левую и правую часть, получим:
a3 + 3a2b + 3ab2 + b3 = (a + b)3
Левая часть этого равенства является многочленом, а правая часть — произведением многочленов, поскольку выражение (a + b)3 представляет собой перемножение трёх сомножителей, каждый из которых равен многочлену (a + b).
Стало быть, если нам встретится выражение вида a3 + 3a2b +3ab2 + b3, то мы можем представить его в виде произведения (a + b)(a + b)(a + b). Иными словами, разложить на множители (a + b), (a + b) и (a + b).
a3 + 3a2b + 3ab2 + b3 = (a + b)(a + b)(a + b)
Пример 1. Разложить на множители многочлен m3 + 6m2n + 12mn2 + 8n3
Прежде чем применять формулу куба суммы, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб суммы двух выражений.
Чтобы убедиться, что исходное выражение является кубом суммы двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в куб одночлена m
m3 = m3
Последний член 8n3 является результатом возведения в куб одночлена 2n
(2n)3 = 8n3
Второй член 6m2n является утроенным произведением квадрата первого выражения m и последнего 2n
3 × m2 × 2n = 6m2n
Третий член 12mn2 является утроенным произведением первого выражения m и квадрата последнего выражения 2n
3 × m × (2n)2 = 3 × m × 4n2 = 12mn2
То есть исходный многочлен m3 + 6m2n + 12mn2 + 8n3 по всем параметрам соответствует кубу суммы двух выражений. Переменной a в данном многочлене соответствует m, а переменной b соответствует 2n
Переменной a в данном многочлене соответствует m, а переменной b соответствует 2n
a = m
b = 2n
Тогда можно сделать вывод, что когда-то выражение m3 + 6m2n + 12mn2 + 8n3 выглядело в виде куба суммы (m + 2n)3, но в результате применения формулы куба суммы оно обратилось в многочлен m3 + 6m2n + 12mn2 + 8n3. Наша задача — вернуть ему былую форму, то есть представить в виде (m + 2n)3
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)3
А поскольку (m + 2n)3 это произведение трёх сомножителей, каждый из которых равен многочлену (m + 2n), то исходный многочлен m3 + 6m2n + 12mn2 + 8n3 можно представить в виде разложения на множители (m + 2n), (m + 2n) и (m + 2n)
m3 + 6m2n + 12mn2 + 8n3 = (m + 2n)(m + 2n)(m + 2n)
Пример 2. Разложить на множители многочлен 125x3 + 75x2 + 15x + 1
Разложить на множители многочлен 125x3 + 75x2 + 15x + 1
Первый член данного многочлена является результатом возведения в куб одночлена 5x
(5x)3 = 125x3
Последний член 1 является результатом возведения в куб одночлена 1
13 = 1
Второй член 75x2 является утроенным произведением квадрата первого выражения 5x и последнего 1
3 × (5x)2 × 1 = 3 × 25x2 = 75x2
Третий член 15x является утроенным произведением первого выражения 5x и квадрата второго выражения 1
3 × 5x × 12 = 15x
Воспользуемся формулой a3 + 3a2b + 3ab2 + b3 = (a + b)3. Роль переменной a играет одночлен 5x, а роль переменной b играет одночлен 1
a = 5x
b = 1
Поэтому,
125x3 + 75x2 + 15x + 1 = (5x + 1)3
А поскольку (5x + 1)3 это произведение трёх сомножителей, каждый из которых равен многочлену (5x + 1), то исходный многочлен 125x3 + 75x2 + 15x + 1 можно представить в виде разложения на множители (5x + 1), (5x + 1) и (5x + 1)
125x3 + 75x2 + 15x + 1 = (5x + 1)(5x + 1)(5x + 1)
Разложение многочлена на множители по формуле куба разности двух выражений
Как и по формуле куба суммы двух выражений, многочлен можно разложить на множители по формуле куба разности двух выражений.
Вспомним, как выглядит формула куба разности двух выражений:
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Если в этой формуле поменять местами левую и правую часть, то получим:
a3 − 3a2b + 3ab2 − b3 = (a − b)3
Поскольку правая часть это произведение трёх сомножителей, каждый из которых равен (a − b), то многочлен вида a3 − 3a2b + 3ab2 − b3 можно разложить на множители (a − b), (a − b) и (a − b).
a3 − 3a2b + 3ab2 − b3 = (a − b)(a − b)(a − b)
Пример 1. Разложить на множители многочлен 64 − 96x + 48x2 − 8x3
Разложить на множители многочлен 64 − 96x + 48x2 − 8x3
Прежде чем применять формулу куба разности, следует проанализировать данный многочлен. А именно, убедиться что перед нами действительно куб разности двух выражений.
Чтобы убедиться, что исходное выражение является кубом разности двух выражений, следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член данного многочлена является результатом возведения в куб одночлена 4
43 = 64
Последний член 8x3 является результатом возведения в куб одночлена 2x
(2x)3 = 8x3
Второй член 96x является утроенным произведением квадрата первого выражения 4 и последнего 2x
3 × 42 × 2x = 3 × 16 × 2x = 96x
Третий член 48x2 является утроенным произведением первого выражения 4 и квадрата второго выражения 2x
3 × 4 × (2x)2 = 3 × 4 × 4x2 = 48x2
Видим, что исходный многочлен 64 − 96x + 48x2 − 8x3 по всем параметрам соответствует кубу разности двух выражений. Переменной a в данном многочлене соответствует 4, а переменной b соответствует 2x
Переменной a в данном многочлене соответствует 4, а переменной b соответствует 2x
a = 4
b = 2x
Тогда можно сделать вывод, что когда-то выражение 64 − 96x + 48x2 − 8x3 выглядело в виде куба разности (4 − 2x)3, но в результате применения формулы куба разности оно обратилось в многочлен 64 − 96x + 48x2 − 8x3. Наша задача — вернуть ему былую форму, то есть представить в виде (4 − 2x)3
64 − 96x + 48x2 − 8x3 = (4 − 2x)3
А поскольку (4 − 2x)3 это произведение трёх сомножителей, каждый из которых равен (4 − 2x), то исходный многочлен 64 − 96x + 48x2 − 8x3 можно представить в виде разложения на множители (4 − 2x), (4 − 2x) и (4 − 2x)
64 − 96x + 48x2 − 8x3 = (4 − 2x)(4 − 2x)(4 − 2x)
Пример 2. Разложить на множители многочлен 27 − 135x + 225x2 − 125x3
Разложить на множители многочлен 27 − 135x + 225x2 − 125x3
Первый член данного многочлена является результатом возведения в куб одночлена 3
33 = 27
Последний член 125 является результатом возведения в куб одночлена 5x
(5x)3 = 125x3
Второй член 135x является утроенным произведением квадрата первого выражения 3 и последнего 5x
3 × 32 × 5x = 3 × 9 × 5x = 135x
Третий член 225x2 является утроенным произведением первого выражения 3 и квадрата второго выражения 5x
3 × 3 × (5x)2 = 3 × 3 × 25x2 = 225x2
Воспользуемся формулой a3 − 3a2b + 3ab2 − b3 = (a − b)3. Роль переменной a играет одночлен 3, а роль переменной b играет одночлен 5x
a = 3
b = 5x
Поэтому,
27 − 135x + 225x2 − 125x3 = (3 − 5x)3
А поскольку (3 − 5x)3 это произведение трёх сомножителей, каждый из которых равен многочлену (3 − 5x), то исходный многочлен 27 − 135x + 225x2 − 125x3 можно представить в виде разложения на множители (3 − 5x), (3 − 5x) и (3 − 5x)
125x3 + 75x2 + 15x + 1 = (3 − 5x)(3 − 5x)(3 − 5x)
Разложение многочлена на множители по формуле разности квадратов двух выражений
Вспомним, как выглядит формула умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
Если в этой формуле поменять местами левую и правую часть, то получим:
a2 − b2 = (a − b)(a + b)
Эту формулу называют разностью квадратов. Она позволяет разложить выражение вида a2 − b2 на множители (a − b) и (a + b).
Она позволяет разложить выражение вида a2 − b2 на множители (a − b) и (a + b).
Пример 1. Разложить на множители многочлен 16x2 − 25y2
Чтобы воспользоваться формулой a2 − b2 = (a − b)(a + b), следует узнать чему в данном случае равна переменная a и чему равна переменная b.
Первый член 16x2 является результатом возведения в квадрат одночлена 4x
(4x)2 = 16x2
Второй член 25y2 является результатом возведения в квадрат одночлена 5y
(5y)2 = 25y2
То есть в данном случае переменной a соответствует одночлен 4x, а переменной b соответствует одночлен 5y
a = 4x
b = 5y
Теперь можно воспользоваться формулой a2 − b2 = (a − b)(a + b). Подставим в неё наши значения a и b
Подставим в неё наши значения a и b
(4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
Полностью решение можно записать так:
16x2 − 25y2 = (4x)2 − (5y)2 = (4x − 5y)(4x + 5y)
Для проверки можно выполнить умножение (4x − 5y)(4x + 5y). Если мы всё сделали правильно, то должны получить 16x2 − 25y2
(4x − 5y)(4x + 5y) = 16x2 − 20xy + 20xy − 25y2 = 16x2 − 25y2
Пример 2. Разложить на множители многочлен x2 − y2
В данном случае переменной a соответствует x, а переменной b соответствует y. Тогда по формуле квадрата разности имеем:
Тогда по формуле квадрата разности имеем:
x2 − y2 = (x − y)(x + y)
Случай как в данном примере является наиболее простым, поскольку здесь сразу видно чему равно a и чему равно b.
Чаще всего члены, из которых состоит исходная разность, являются результатами возведения во вторую степень каких-нибудь одночленов. Чтобы узнать чему в таком случае равны a и b, нужно как в первом примере представить члены исходной разности в виде одночленов возведённых в квадрат.
Например, чтобы разложить многочлен 4x4 − 9y6 на множители, нужно исходные члены представить в виде одночленов возведённых в квадрат. Первый член в виде одночлена, возведенного в квадрат, можно записать как (2x2)2, поскольку вычисление этого выражение даёт в результате 4x4
(2x2)2 = 4x4
А член 9y6 в виде одночлена, возведенного в квадрат, можно записать как (3y3)2, поскольку вычисление этого выражение даёт в результате 9y6
(3y3)2 = 9y6
Теперь мы знаем, чему равны a и b. Они равны 2x2 и 3y3 соответственно. Подставим их в формулу a2 − b2 = (a − b)(a + b)
Они равны 2x2 и 3y3 соответственно. Подставим их в формулу a2 − b2 = (a − b)(a + b)
(2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Полностью решение можно записать так:
4x4 − 9y6 = (2x2)2 − (3y3)2 = (2x2 − 3y3)(2x2 + 3y3)
Несмотря на простоту разложения по формуле разности квадратов, частые ошибки приходятся именно на эти задачи. Чтобы убедиться, что задача решена правильно, не мешает выполнить умножение в получившемся разложении. Если задача решена правильно, то должен получиться изначальный многочлен.
Проверим умножением данный пример. У нас должен получиться многочлен 4x4 − 9y6
У нас должен получиться многочлен 4x4 − 9y6
(2x2 − 3y3)(2x2 + 3y3) = 2x2(2x2 + 3y3) − 3y3(2x2 + 3y3)
= 4x4 + 6x2y3 − 6x2y3 − 9y6 = 4x4 − 9y6
Пример 4. Разложить на множители многочлен 81 − 64
Представим члены исходной разности в виде одночленов возведенных в квадрат. Далее воспользуемся формулой разности квадратов:
81 − 64 = 92 − 82 = (9 − 8)(9 + 8)
Разложение многочлена на множители по формуле сумме кубов двух выражений
Мы помним, что произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений:
(a + b)(a2 − ab + b2) = a3 + b3
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую суммой кубов двух выражений:
a3 + b3 = (a + b)(a2 − ab + b2)
Эта формула позволяет разложить выражение вида a3 + b3 на множители (a + b) и (a2 − ab + b2).
Пример 1. Разложить на множители многочлен 27x3 + 64y3
Представим члены 27x3 и 64y3 в виде одночленов, возведённых в куб
27x3 + 64y3 = (3x)3 + (4y)3
Теперь воспользуемся формулой суммы кубов. Переменная a в данном случае равна 3x, переменная b равна 4y
27x3 + 64y3 = (3x)3 + (4y)3 = (3x + 4y)((3x)2 − 3x × 4y + (4y)2) =
(3x + 4y)(9x2 − 12xy + 16y2)
Пример 2. Разложить на множители многочлен 125 + 8
Представим члены 125 и 8 в виде одночленов, возведённых в куб:
125 + 8 = 53 + 23
Далее воспользуемся формулой суммы кубов:
125 + 8 = 53 + 23 = (5 + 2)(25 − 10 + 4)
Разложение многочлена на множители по формуле разности кубов двух выражений
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений:
(a − b)(a2 + ab + b2) = a3 − b3
Если в этой формуле поменять местами левую и правую часть, то получим формулу, называемую разностью кубов двух выражений:
a3 − b3 = (a − b)(a2 + ab + b2)
Эта формула позволяет разложить выражение вида a3 − b3 на множители (a − b) и (a2 + ab + b2).
Пример 1. Разложить на множители многочлен 64x3 − 27y3
Представим члены 64x3 и 27y3 в виде одночленов, возведённых в куб:
64x3 − 27y3 = (4x)3 − (3y)3
Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 4x, переменная b равна 3y
64x3 − 27y3 = (4x)3 − (3y)3 = (4x − 3y)((4x)2 + 4x × 3y + (3y)2) =
(4x − 3y)(16x2 + 12xy + 9y2)
Пример 2. Разложить на множители многочлен 64 − 27
Представим члены 64 и 27 в виде одночленов, возведённых в куб:
64 − 27 = 43 − 33 = (4 − 3)(16 + 12 + 9)
Пример 3. Разложить на множители многочлен 125x3 − 1
Разложить на множители многочлен 125x3 − 1
Представим члены 125x3 и 1 в виде одночленов, возведённых в куб:
125x3 − 1 = (5x)3 − 13
Теперь воспользуемся формулой разности кубов. Переменная a в данном случае равна 5x, переменная b равна 1
125x3 − 1 = (5x)3 − 13 = (5x − 1)((5x)2 + 5x × 1 + 12) =
(5x − 1)(25x2 + 5x + 1)
Разложение многочлена на множители различными способами
К некоторым многочленам можно применять различные способы разложения на множители. Например, к одному многочлену можно применить способ вынесения общего за скобки, а затем воспользоваться одной из формул сокращённого умножения.
Пример 1. Разложить на множители многочлен ax2 − ay2
В данном многочлене содержится общий множитель a. Вынесем его за скобки:
Вынесем его за скобки:
ax2 − ay2 = a(x2 − y2)
При этом в скобках образовался многочлен, который является разностью квадратов. Применив формулу разности квадратов. Тогда получим:
ax2 − ay2 = a(x2 − y2) = a(x − y)(x + y)
Пример 2. Разложить на множители многочлен 3x2 + 6xy + 3y2
Вынесем за скобки общий множитель 3
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2)
В скобках образовался многочлен, который является квадратом суммы двух выражений, а именно выражений x и y. Тогда этот квадрат суммы можно представить как (x + y)2 и далее записать в виде двух сомножителей, каждый из которых равен (x + y)
3x2 + 6xy + 3y2 = 3(x2 + 2xy + y2) = 3(x + y)2 = 3(x + y)(x + y)
Задания для самостоятельного решения
Задание 1. Следующий многочлен разложите на множители способом группировки:
Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 2. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 3. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 4. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 5. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 6. Следующий многочлен разложите на множители способом группировки:
Решение:
Задание 7. Разложите на множители многочлен:
x2 + 12x + 36
Решение:
x2 + 12x + 36 = x2 + 2 × x × 6 + 62 = (x + 6)2 = (x + 6)(x + 6)
Задание 8. Разложите на множители многочлен:
8xy + y2 + 16x2
Решение:
8xy + y2 + 16x2 = 16x2 + 8xy + y2 = (4x)2 + 2 × 4x × y + y2 = (4x + y)2 = (4x + y)(4x + y)
Задание 9. Разложите на множители многочлен:
Разложите на множители многочлен:
Решение:
Задание 10. Разложите на множители многочлен:
Решение:
Задание 11. Разложите на множители многочлен:
Решение:
Задание 12. Разложите на множители многочлен:
Решение:
Задание 13. Разложите на множители многочлен:
Решение:
Задание 14. Разложите на множители многочлен:
Решение:
Задание 15. Разложите на множители многочлен:
Решение:
Задание 16. Разложите на множители многочлен:
Решение:
Задание 17. Разложите на множители многочлен:
Решение:
Задание 18. Разложите на множители многочлен:
Решение:
Задание 19. Разложите на множители многочлен:
Решение:
Задание 20. Разложите на множители многочлен:
Решение:
Задание 21. Разложите на множители многочлен:
Решение:
Задание 22. Разложите на множители многочлен:
Решение:
Задание 23. Разложите на множители многочлен:
Разложите на множители многочлен:
Решение:
Задание 24. Разложите на множители многочлен:
Решение:
Задание 25. Разложите на множители многочлен:
Решение:
Задание 26. Разложите на множители многочлен:
Решение:
Задание 27. Разложите на множители многочлен:
Решение:
Задание 28. Разложите на множители многочлен:
Решение:
Задание 29. Разложите на множители многочлен:
Решение:
Задание 30. Разложите на множители многочлен:
Решение:
Задание 31. Разложите на множители многочлен:
Решение:
Задание 32. Разложите на множители многочлен:
Решение:
Задание 33. Разложите на множители многочлен:
Решение:
Задание 34. Разложите на множители многочлен:
Решение:
Задание 35. Разложите на множители многочлен:
Решение:
Задание 36. Разложите на множители многочлен:
Решение:
Задание 37. Разложите на множители многочлен:
Разложите на множители многочлен:
Решение:
Задание 38. Разложите на множители многочлен:
Решение:
Задание 39. Разложите на множители многочлен:
Решение:
Задание 40. Разложите на множители многочлен:
Решение:
Задание 41. Разложите на множители многочлен:
Решение:
Задание 42. Разложите на множители многочлен:
Решение:
Задание 43. Разложите на множители многочлен:
Решение:
Задание 44. Разложите на множители многочлен:
Решение:
Задание 45. Разложите на множители многочлен:
Решение:
Задание 46. Разложите на множители многочлен:
Решение:
Задание 47. Разложите на множители многочлен:
Решение:
Задание 48. Разложите на множители многочлен:
Решение:
Задание 49. Разложите на множители многочлен:
Решение:
Задание 50. Разложите на множители многочлен:
Решение:
Задание 51. В следующем выражении вынесите за скобки общий множитель 2a, затем выражение в скобках разложите на множители:
В следующем выражении вынесите за скобки общий множитель 2a, затем выражение в скобках разложите на множители:
Решение:
Задание 52. В следующем выражении вынесите за скобки общий множитель 4, затем выражение в скобках разложите на множители:
Решение:
Задание 53. В следующем выражении вынесите за скобки общий множитель 2x2y2, затем выражение в скобках разложите на множители:
Решение:
Задание 54. В следующем выражении вынесите за скобки общий множитель 4x3y3, затем выражение в скобках разложите на множители:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Найдите наибольший общий делитель
Быстрый! Мне нужна помощь с:
Выберите элемент справки по математике . .. Исчисление, Исчисление производных, Исчисление интеграции, Правило частного, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Расчет с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование длины, Преобразование массы, Преобразование мощности, Преобразование скорости, Преобразование температуры , Анализ объемных данных, Поиск среднего анализа данных, Поиск стандартного отклонения Анализ данных, Гистограммы Десятичные числа, Преобразование в дробь Электричество, Стоимость факторинга, Целые коэффициенты, Наибольшие общие коэффициенты, Наименьшие общие дроби, Добавление дробей, Сравнение дробей, Преобразование дробей, Преобразование в десятичные дроби, Разделение дробей, Умножение дробей, Сокращение дробей, ВычитаниеДроби, Что это такоеГеометрия, КоробкиГеометрия, КругиГеометрия, ЦилиндрыГеометрия, ПрямоугольникиГеометрия, Прямоугольные треугольникиГеометрия, СферыГеометрия, КвадратыГрафика, ЛинииГрафика, Любая функцияГрафика, КругиГрафика hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x,y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Уравнение из точки и наклонных линий, Уравнение из наклона и y-intLines, Уравнение из двух точек, Кредит, График платежей, Лотерея , Нахождение коэффициентовМатематика, Практика полиномовМатематика, Практика Основыметрической системы, Преобразование чисел, Сложение чисел, Расчет с числами, Расчет с переменными числами, Деление чисел, Умножение чисел, Сравнение чисел в ряду, Числовые числа в ряду, Размещение значений чисел, Произношение чисел, Округление чисел, Вычитание парабол, Вычисление полиномов, Сложение полиномов, Сложение КвадратМногочлены, РазделениеМногочленов, Разложение на множители КвадратовМногочлены, Разложение на множители ТрехчленовМногочлены, Факторизация с помощью GCFМногочлены, УмножениеМногочленов, Возведение в степеньПрактика, Математические задачиПропорции, Что они собой представляютКвадратные уравнения, Квадратное F ormulaКвадратные уравнения, Решить факторингомРадикалы, Другие корниРадикалы, Соотношения квадратных корней, Что они представляют собойВыход на пенсию, Сбережение для продажной цены, Вычисление научной нотации, Преобразование научной нотации, Разделение научной нотации, Умножение фигур, Прямоугольники, Упрощение всего, Экспоненты, Упрощение, Как термины, Упрощение, ПродуктыВремя, Размышление о совете, Вычисление , Прямоугольные треугольникиWindchill, Фигура
.. Исчисление, Исчисление производных, Исчисление интеграции, Правило частного, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Расчет с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование длины, Преобразование массы, Преобразование мощности, Преобразование скорости, Преобразование температуры , Анализ объемных данных, Поиск среднего анализа данных, Поиск стандартного отклонения Анализ данных, Гистограммы Десятичные числа, Преобразование в дробь Электричество, Стоимость факторинга, Целые коэффициенты, Наибольшие общие коэффициенты, Наименьшие общие дроби, Добавление дробей, Сравнение дробей, Преобразование дробей, Преобразование в десятичные дроби, Разделение дробей, Умножение дробей, Сокращение дробей, ВычитаниеДроби, Что это такоеГеометрия, КоробкиГеометрия, КругиГеометрия, ЦилиндрыГеометрия, ПрямоугольникиГеометрия, Прямоугольные треугольникиГеометрия, СферыГеометрия, КвадратыГрафика, ЛинииГрафика, Любая функцияГрафика, КругиГрафика hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x,y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Уравнение из точки и наклонных линий, Уравнение из наклона и y-intLines, Уравнение из двух точек, Кредит, График платежей, Лотерея , Нахождение коэффициентовМатематика, Практика полиномовМатематика, Практика Основыметрической системы, Преобразование чисел, Сложение чисел, Расчет с числами, Расчет с переменными числами, Деление чисел, Умножение чисел, Сравнение чисел в ряду, Числовые числа в ряду, Размещение значений чисел, Произношение чисел, Округление чисел, Вычитание парабол, Вычисление полиномов, Сложение полиномов, Сложение КвадратМногочлены, РазделениеМногочленов, Разложение на множители КвадратовМногочлены, Разложение на множители ТрехчленовМногочлены, Факторизация с помощью GCFМногочлены, УмножениеМногочленов, Возведение в степеньПрактика, Математические задачиПропорции, Что они собой представляютКвадратные уравнения, Квадратное F ormulaКвадратные уравнения, Решить факторингомРадикалы, Другие корниРадикалы, Соотношения квадратных корней, Что они представляют собойВыход на пенсию, Сбережение для продажной цены, Вычисление научной нотации, Преобразование научной нотации, Разделение научной нотации, Умножение фигур, Прямоугольники, Упрощение всего, Экспоненты, Упрощение, Как термины, Упрощение, ПродуктыВремя, Размышление о совете, Вычисление , Прямоугольные треугольникиWindchill, Фигура
Математика (алгебра) Решения для 9 класса Math Chapter 3
Страница № 42:
Вопрос 1:
Добавьте следующее выражение.
(i) 2 а + б + 7 ; 4 a + 2 b + 3
(ii) 3 x + y — 8; y + 4 -7 x
(iii) 3 x 2 + 5 x — 4 ; 8 x — 2 x 2 + 11
(iv) 5x — 4y + 2; 2x + 7 лет — 5
Ответ:
(i)
2 a + b + 7
4 a + 2 b + 3
———————
6 A + 3 B + 10
(II)
3 x + Y — 8
— 7 x + y + 4
——— ————-
-4 x + 2 y — 4
(iii)
3 x 2 + 5 1 9-012 x 90 x 2 + 8 x + 11
———————
x 2 + 13 x + 7
(iv)
5x – 4y + 2 2x + 7y — 5 7x +3y — 3
Страница № 42:
Вопрос 2:
Вычесть второе выражение из первого:
(i) 5 x 2 — 6 xy + 2; 3 x 2 + 10 xy -8
(ii) м 2 n — 8 + mn
(III) 5 x 2 + 4 y 2 — 6 y + 8; x 2 — 5 у 2 + 2 xy + 3 у — 10
Ответ:
I 5×2 — 6xy + 2 3×2 + 10xy — 8 — + 2×2 + 10xy — 8 — + 2×2 — 16xy +10
II M2n — 8 + Mn2 -M2n + 7-Mn2 + — + 2M2N — 15 + 2MN2
III 5×2 + 4Y2 — 6Y + 8 x2 — 5y2 + 2xy + 3y — 10 — + — + 4×2 + 9y2 — 2xy — 9y + 18
Страница № 42:
Вопрос 3:
Что нужно прибавить к 5 x 2 + 2 xy + y 2 , чтобы получить 3 x 2 + 3 x 42y?
Ответ:
.
5 x 2 + 2 xy + y 2
— — —
—————— ———-
— 2 x 2 + 2 xy — y 2
Страница № 42:
Вопрос 4:
Что нужно вычесть из 2 a + 6 b — 5, чтобы получить — 3 a + 2 b + 3?
Ответ:
Мы можем получить требуемое выражение, вычитая — 3 a + 2 b + 3 из 2 a + 6 b — 5 следующим образом: — 3 a + 2 b + 3
+ — —
—————————
5 a + 4 б — 8
Страница № 42:
Вопрос 5:
Вычесть 4 х + y + 2 из суммы 3 х — 2 y + 7 и 5 х — 3 y — 8.
Ответ:
сумма 3 x — 2 Y + 7 и 5 x — 3 y — 8:
3 x — 2 y + 7
5 x — 3 y — 8
———————
8 x — 5 y — 1
Теперь, вычитание 8 x — 5 y — 1 и 4 x + y + 2:
8 x — 5 y — 1
4 x + y + 2
— — —
——— —————
4 x — 6 y — 3
Страница № 42:
Вопрос 6:
Упрости:
(I) 5 x (2 x + 3 y )
(II) (2 x — y ) (3 x + 5 y )
(III ) (3 xy 2 + 4 x 2 ) ( xy — 3 x 2 )
Ответ:
i 5x2x+3y= 5x×2x + 5x×3y= 10×2 + 15xy
ii 2x-y3x+5y=2x3x+5y – y3x+5y= 6×2 + 10xy — 3xy — 5y2= 6×2 + 7y2 — 0 3xy2 + 4x2xy — 3×2=3xy2xy — 3×2 + 4x2xy — 3×2= 3x2y3 — 9x3y2 + 4x3y — 12 x4
Страница № 42:
Вопрос 7:
Разделите первое выражение на второе. Напишите частное и остаток.
Напишите частное и остаток.
(i) а 2 — b ; a — b
(ii) x 2 -14×2; х — 12x
Ответ:
(i)
∴ Частное = a + b и остаток = 0
(ii)
∴ Частное = x + 12x и остаток = 0
Страница № 44:
Вопрос 1:
Факторизируйте следующее:
1.4 х — 8 у
Ответ:
4x — 8y= 4x — 2y
Страница № 44:
Ответ:
5т + 25т2= 5т1 + 5т
Страница № 44:
Ответ:
x4y5 — 3x5y4= x4y4y — 3x
Страница № 44:
Вопрос 4:
x 2 + xy -3 x — 3 y
Ответ:
x2 + xy — 3x — 3y= xx+y — 3x+y= x+yx-3
Страница № 44:
Вопрос 5:
6 ax — 6 by — 4 ay + 9 bx
Ответ:
6ax — 6by -4ay + 9bx=6ax + 9bx-4ay- 6by = 3x2a+3b — 2y2a+3b= 2a+3b3x-2y
Страница № 44:
Вопрос 6:
7 x 2 — 21 x + 2 xy — 6 у
Ответ:
7×2 – 21x + 2xy – 6y=7xx-3 + 2yx-3= x-37x+2y
Страница № 44:
Вопрос 7:
2 x 2 — 3 xy — 8 xy 2 + 12 y 3
Ответ:
2×2 – 3xy – 8xy2 + 12y3=x2x-3y — 4y22x-3y= 2x-3yx-4y2
Страница № 44:
Ответ:
81×2 — 64y2= 9×2 — 8y2= 9x+8y9x-8y
Страница № 44:
Ответ:
27a2 – 75b2= 39a2 – 25b2= 33a2 – 5b2= 33a + 5b3a — 5b
Страница № 44:
Ответ:
3a3 – 3a= 3aa2 – 1= 3aa2 – 12= 3aa + 1a — 1
Страница № 44:
Вопрос 11:
x 2 — у 2 — 6 x — 6 у
Ответ:
x2 — y2 -6x — 6y= x+y x-y — 6 x+y= x+y x — y — 6
Страница № 44:
Вопрос 12:
( а + б ) ( в + г ) — а 2 + б 2
3Ответ:
а + b c + d — a2 + b2= a + b c + d — a2 — b2= a + b c + d — a + b a — b= a + b c + da — b= a + b c + д-а+ б
Страница № 44:
Вопрос 13:
x 2 + 8 x + 24 у — 9 у 2
Ответ:
x2 + 8x + 24y – 9y2=x2 – 9y2 +8x + 24y =x2 – 3y2 +8x + 3y = x + 3yx – 3y +8x + 3y = x + 3y x — 3y + 8
Страница № 44:
Вопрос 14:
а 2 — 12 аб + 36 б 2 — 25
Ответ:
a2 — 12ab + 36b2 — 25= a2 — 2×a×6b + 6b2 — 25= a — 6b2 — 52= — 6b + 5a — 6b — 5
Страница № 44:
Вопрос 15:
x 2 + 9 Y 2 — 25 м 2 — 16 N 2 + 6 XY + 40 MN
Ответ:
x2 + 9y2 -25м2 — 16n2 + 6xy + 40mn=x2 + 9y2 + 6xy -25m2 — 16n2 + 40mn= x2 + 6xy+ 9y2 -25m2 — 40mn×5×3m+16n2-2 x2 xy 2 + 2 x2 3 5m×4n + 4n2 =x + 3y2 — 5m — 4n2=x + 3y+5m — 4nx + 3y-5m — 4n=x + 3y+5m — 4n x + 3y-5m + 4n
Страница № 46:
Вопрос 1:
Факторизируйте следующее.
8 x 3 + 125 у 3
Ответ:
8×3 + 125y3= 2×3 + 5y3= 2x + 5y 2×2 — 2x×5y + 5y2= 2x + 5y 4×2 — 10xy + 25y2
Страница № 46:
Ответ:
2a3 — 54b3= 2a3 — 27b3= 2a3 — 3b3= 2a — 3b a2 + a×3b + 3b2= 2a — 3b a2 + 6ab + 9b2
Страница № 46:
Ответ:
a + b3 — 8= a + b3 — 23=a + b — 2a + b2 + a + b×2 + 22= a + b — 2 a2 +2ab + b2 + 2a + 2b + 4
Страница № 46:
Вопрос 4:
m364 + n327
Ответ:
m364 + n327=m43 + n33=m4 + n3m42 -m4×n3+n32= m4 + n3m216 -mn12+n29
Страница № 46:
Ответ:
8y3 — 125y3= 2y3 — 5y3=2y — 5y2y2 + 2y×5y + 5y2=2y — 5y4y2 + 10 + 25y2
Страница № 46:
Вопрос 6:
( а + б ) 3 — ( а — б ) 3
Ответ:
a+b3 – a-b3= a+b – a-ba+b2 + a+ba-b + a-b2= 2ba2 + 2ab + b2 + a2 — b2 + a2 — 2ab + b2= 2b3a2 + b2
Страница № 46:
Вопрос 7:
(2 м + 3 н ) 3 — (3 м + 2 н ) 3
Ответ:
2m + 3n3 — 3m + 2n3=2m + 3n -3m + 2n 2m + 3n2 + 2m + 3n3m + 2n +3m + 2n2=-m+n4m2 + 12mn + 9n2 + 6m2 + 4+n + 9mn + 12m2 + 4n2=-m+n19m2 + 37mn + 19n2
Страница № 46:
Вопрос 8:
(3 x + 5 y ) 3 — (2 x — y ) 3
Ответ:
3x + 5y3 — 2x — y3=3x + 5y-2x — y3x + 5y2 +3x + 5y2x — y + 2x — y2=x +6y9x2 + 25y2 + 30xy + 6×2 -3xy + 10+xy -5y2 — + 4×2 =x +6y19x2 + 33xy + 21y2
Страница № 46:
Вопрос 9:
27( x -1) 3 + у 3
Ответ:
27x-13 + y3=3x-13 + y3=3x-1 + y3x-12 — 3x-1×y + y2=3x + y -33x-32-3xy + 3y + y2=3x + y -39×2-18x + 9-3xy + 3y + y2
Страница № 46:
Ответ:
a6 — b6= a23 — b23= a2 — b2 a22 + a2b2 + b22=a + ba — ba4 + a2b2 + b4
Страница № 47:
Вопрос 1:
Разложите на множители:
2 x 2 + 3 x — 5
Ответ:
2×2 + 3x — 5 = 2×2 + 5x -2x — 5 ∵ 2×-5 = -10 5×-2 = -10 и 5 + -2 = 3= x 2x + 5 — 12x + 5= 2x + 5x — 1
Страница № 47:
Ответ:
3×2 — 14x + 8 = 3×2 — 12x -2x + 8 ∵ 3×8 = 24 -12x-2 = 24 и -12+ -2 =-14= 3x x — 4 — 2x — 4= x — 43x — 2
Страница № 47:
Вопрос 3:
6 x 2 + 11 x — 10
Ответ:
6×2 + 11x — 10=6×2 + 15x -4x — 10 ∵ 6×-10 = -60, 15×-4 =-60 и 15+ -4 =11= 3x 2x + 5 — 22x +5= 2x + 53x — 2
Страница № 47:
Ответ:
У нас есть 2x + 3x -5Страница № 47:
Вопрос 5:
x 2 + 9 xy + 18 y 2
Ответ:
x2 +9xy + 18y2=x2 + 6xy + 3xy +18y2 ∵ 1×18 = 18, 6×3 =18 и 6+3 =9= x x + 6y +3yx +6y= x + 6yx +3y
Страница № 47:
Вопрос 6:
а 2 — 5 аб — 36 б 2
Ответ:
a2 -5ab — 36b2=a2 + 4ab — 9ab -36b2 ∵ 1×-36 =-36, 4×-9 =-36 и 4+-9 =-5= a + 4b -9ba +4b= a + 4ba -9б
Страница № 47:
Вопрос 7:
а 2 + 14 аб — 51 б 2
Ответ:
a2 +14ab — 51b2=a2 + 17ab — 3ab -51b2 ∵ 1×-51 =-51 17×-3 =-51 и 17+-3 =14= а а + 17b -3ba +17b= a + 17ba -3b
Страница № 47:
Вопрос 8:
2 м 2 + 19 мин + 30 п 2
Ответ:
2м2 +19мн + 30n2=2м2 + 15мн + 4мн + 30н2 ∵ 2×30 =60 15×4 =60 и 15+4 =19= м
Страница № 47:
Вопрос 9:
3 а 2 — 11 аб + 6 б 2
Ответ:
3a2 -11ab + 6b2=3a2 -9ab — 2ab +6b2 ∵ 3×6 =18 -9×-2 =18и -9+-2 =-11= 3a a — 3b -2ba -3b= a — 3b3a -2b
Страница № 47:
Вопрос 10:
6 x 2 + 7 xy — 13 y 2
Ответ:
6×2 -7xy — 13y2=6×2 + 6xy — 13xy -13y2 ∵ 6×-13 = -78 6×-13 =-78 и 6+-13 =-7= 6x x + y -13yx +y= x + y6x — 13 лет
Страница № 47:
Вопрос 11:
2×2 + 3x + 2
Ответ:
2 x2 + 3x + 2 = 2 x2 + 2x + x +2 ∵ 2×2 = 2, 2×1 = 2 и 2+1 =3=2 x x +2 + 1x +2= x +22 x + 1
Страница № 48:
Вопрос 1:
Разложите на множители:
x 4 — 8 x 2 y 2 + 12 y 3
Ответ:
У нас есть x4 – 8x2y2 + 12y4. Пусть x2 = a и y2 = bi.e., x4 = a2, y4 = b2 и x2y2 = ab∴ x4 — 8x2y2 + 12y4 = A2 — 8ab + 12b2 = A2 — 6ab- 2ab + 12b2 = Aa — 6b -2BA — 6B =a — 6ba — 2b. Подставляя значения a и b, мы получаем: x4 — 8x2y2 + 12y4 =x2 — 6y2x2 — 2y2
Пусть x2 = a и y2 = bi.e., x4 = a2, y4 = b2 и x2y2 = ab∴ x4 — 8x2y2 + 12y4 = A2 — 8ab + 12b2 = A2 — 6ab- 2ab + 12b2 = Aa — 6b -2BA — 6B =a — 6ba — 2b. Подставляя значения a и b, мы получаем: x4 — 8x2y2 + 12y4 =x2 — 6y2x2 — 2y2
Страница № 48:
Вопрос 2:
2 x 4 — 13 x 2 у 2 + 15 у 4
Ответ:
У нас есть 2×4 — 13x2y2 + 15y4.Пусть x2 = a и y2 = bi.e., x4 = a2 = y4 = b2 и x2y2 = ab∴2 x4 — 13x2y2 + 15y4 = 2a2 — 13ab + 15b2 = 2A2 — 10ab-3ab + 15b2 = 2AA — 5b -3ba — 5b =a — 5b2a — 3b.
Страница № 48:
Вопрос 3:
6 а 4 + 11 а 2 2 б 2 — 10 б 4
Ответ:
У нас есть 6a4 + 11a2b2 — 10b4. Пусть a2 = m и b2 = ni.e., a4 = m2, b4 = n2 и a2b2 = mn∴6a4 + 11a2b2 — 10b4 = 6m2 + 11mn — 10n2 = 6m2 + 15mn -4mn- 10n2 = 3m2m + 5n -2n2m + 5n =2m + 5n3m — 2n.
Пусть a2 = m и b2 = ni.e., a4 = m2, b4 = n2 и a2b2 = mn∴6a4 + 11a2b2 — 10b4 = 6m2 + 11mn — 10n2 = 6m2 + 15mn -4mn- 10n2 = 3m2m + 5n -2n2m + 5n =2m + 5n3m — 2n.
Страница № 48:
Вопрос 4:
3( x 2 -5 x ) 2 — 2( x 2 -5 x + 5) — 6
Ответ:
У нас есть 3×2 — 5×2 — 2×2 — 5x + 5 — 6.Пусть x2 -5x = a∴3×2 — 5×2 — 2×2 — 5x + 5 — 6 = 3A2 — 2a + 5-6 = 3A2 — 2a-16 = 3A2 — 8A + 6A-16 = A3A — 8 + 23A — 8 = 3A — 8 A + 2RESUBSTITUTING Значение A, мы получаем: 3×2 — 5×2 — 2×2 — 5x + 5 — 6 = 3×2 — 5x — 8 x2 — 5x + 2 = 3×2 -15x -8×2 -5x +2
Страница № 48:
Вопрос 5:
( у 2 + 5 у ) ( у 2 + 5 у — 2) — 24
Ответ:
У нас есть y2 + 5yy2 + 5y — 2 — 24. Пусть y2 + 5y = a∴y2 + 5yy2 + 5y — 2 — 24 = Aa-2 — 24 = A2 — 2A-24 = A2 — 6A + 4A-24 = Aa — 6 + 4a — 6 = A — 6 A + 4RESUBSTITITING Значение A, мы получаем: Y2 + 5YY2 + 5Y — 2 — 24 = Y2 + 5Y -6 Y2 + 5Y + 4 = Y2 + 6Y -Y-6 Y2 + 4Y + Y + 4 = YY + 6 — 1Y +6 yy+4 + 1y+4 =y+6 y-1 y+4 y+1
Пусть y2 + 5y = a∴y2 + 5yy2 + 5y — 2 — 24 = Aa-2 — 24 = A2 — 2A-24 = A2 — 6A + 4A-24 = Aa — 6 + 4a — 6 = A — 6 A + 4RESUBSTITITING Значение A, мы получаем: Y2 + 5YY2 + 5Y — 2 — 24 = Y2 + 5Y -6 Y2 + 5Y + 4 = Y2 + 6Y -Y-6 Y2 + 4Y + Y + 4 = YY + 6 — 1Y +6 yy+4 + 1y+4 =y+6 y-1 y+4 y+1
Страница № 51:
Вопрос 1:
Разложите на множители:
x 3 — 27 y 3 + 125 + 45 xy
Ответ:
x3 — 27y3 + 125 + 45xy=x3 + -3y3 + 53 — 3×x-3y5=x+-3y+5×2 + -3y2 + 52-x×-3y—3y×5 — 5×x=x-3y +5×2 + 9y2 + 25 + 3xy + 15y -5x
Страница № 51:
Вопрос 2:
а 3 — б 3 + 8 в 3 + 6 абв
Ответ:
a3 – b3 + 8c3 + 6abc= a3 + -b3 + 2c3 — 3×a×-b×2c=a+-b+2c a2 + -b2 + 2c2 -a×-b — -b×2c — 2c×a = a-b+2c a2 + b2 + 4c2 +ab + 2bc — 2ca
Страница № 51:
Вопрос 3:
8 а 3 + 27 б + 64 в 3 — 72 абв
Ответ:
8a3 + 27b3 + 64c3 — 72abc= 2a3 + 3b3 + 4c3 — 3×2a×3b×4c=2a+3b+4c 2a2 + 3b2 + 4c2 -2a×3b — 3b×4c — 4c×2a= 2a+3b+ 4c 4a2 + 9b2 + 16c2 — 6ab — 12bc -8ca
Страница № 51:
Вопрос 4:
-27 x 3 + y 3 — z 3 — 9 xyz
Ответ:
-27×3 + y3 -z3 -9xyz=-3×3 + y3 + -z3 — 3×-3xy-z=-3x+y+-z-3×2 + y2 + -z2—3x×yy×-z — -z× -3x=-3x+y-z9x2 + y2 +z2 + 3xy + yz -3zx
Страница № 51:
Вопрос 5:
г 6 + 32 г 3 — 64
Ответ:
У нас есть y6 + 32y3 — 64. Здесь 32y3 нельзя записать в кубической форме, поэтому 32y3 будет разбито на 8y3 + 24y3. y6 + 8y3 + 24y3 — 64=y6 + 8y3 — 64 + 24y3=y23 + 2y3 +-43 — 3×y2×2y×-4=y2 + 2y + -4 y22 + 2y2 + -42 — y2×2y -2y ×-4—4×y2=y2+2y-4y4+4y2+16-2y3+8y+4y2=y2+2y-4y4-2y3+8y2+8y+16
Здесь 32y3 нельзя записать в кубической форме, поэтому 32y3 будет разбито на 8y3 + 24y3. y6 + 8y3 + 24y3 — 64=y6 + 8y3 — 64 + 24y3=y23 + 2y3 +-43 — 3×y2×2y×-4=y2 + 2y + -4 y22 + 2y2 + -42 — y2×2y -2y ×-4—4×y2=y2+2y-4y4+4y2+16-2y3+8y+4y2=y2+2y-4y4-2y3+8y2+8y+16
Страница № 51:
Ответ:
У нас есть x6-10×3-27. Здесь -10×3 нельзя записать в кубической форме, поэтому мы разделим -10×3 на -9×3 -x3.x6 -9×3 -x3 -27=x6 -x3 -27 -9×3=x23 + -x3 +-33 — 3×x2×-x×-3=x2 + -x + -3 x22 + -x2 + -32 — x2 ×-x—x×-3—3×x2=x2-x-3×4+x2+9+x3-3x+3×2=x2-x-3×4+x3+4×2-3x+9
Страница № 51:
Ответ:
У нас есть a3+4 -1a3. Здесь 4 нельзя записать в кубической форме, поэтому мы разделим 4 на 1+3. a3+1+3-1a3=a3+1-1a3+3=a3+13+-1a3-3×a×1×-1a=a+1+-1aa2 +12 + -1a2-a×1-1× -1a—1a×a=a+1-1aa2+1+1a2-a+1a+1=a+1-1aa2+2+1a2-a+1a
Страница № 51:
Вопрос 8:
( p — 3 q ) 3 + (3 q — 7 r ) 3 + (7 r 003 9013 — 32) 390 Имеем p-3q3+3q-7r3+ 7r-p3Пусть p-3q=a, 3q-7r=b и 7r-p=c∴p-3q3+3q-7r3+7r-p3=a3+b3+c3Здесь, a +b+c=p-3q+3q-7r+7r-p=0Однако мы знаем, что если a+b+c=0, то a3+b3+c3=3abc∴p-3q3 + 3q-7r3 + 7r- p3 = 3p-3q3q-7r 7r-p (5 x — 6 y ) 3 Ответ:
Страница № 51:
Вопрос 9:
Ответ:
Имеем 5x-6y3+7z-5×3+6y-7z3Пусть 5x-6y=a, 7z-5x=b и 6y-7z=c∴5x-6y3 + 7z-5×3 + 6y-7z3=a3+ b3+c3Здесь, a +b+c=5x-6y+7z-5x+6y-7z=0Однако мы знаем, что если a+b+c=0, то a3+b3+c3=3abc∴5x-6y3+7z-5×3+6y-7z3 = 35x-6y7z-5x 6y-7z
Страница № 51:
Вопрос 10:
27 ( A — B ) 3 + (2 A — B ) 3 ) 3 + (4 B — 5 A ) 3
Ответ:
Имеем 27a-b3+2a-b3+4b-5a3=3a-b3 + 2a-b3 +4b-5a3. Пусть 3a-b=x, 2a-b=y и 4b-5a=z∴3a-b3+2a- b3+4b-5a3 = x3 + y3 + z3Здесь x + y + z = 3a-b + 2a-b + 4b-5a= 0 Однако мы знаем, что если x + y + z = 0, то x3+y3+z3 =3xyz∴3a-b3+2a-b3+4b-5a3=33a-b2a-b4b-5a
Пусть 3a-b=x, 2a-b=y и 4b-5a=z∴3a-b3+2a- b3+4b-5a3 = x3 + y3 + z3Здесь x + y + z = 3a-b + 2a-b + 4b-5a= 0 Однако мы знаем, что если x + y + z = 0, то x3+y3+z3 =3xyz∴3a-b3+2a-b3+4b-5a3=33a-b2a-b4b-5a
Страница № 52:
Вопрос 1:
Какие из следующих выражений являются полиномами?
(i) 5 x 2 — 7 x — 7 x + 4
(II) 5
(III) 5 A 2
6 + A + 4
(IV) 78x — 4×4 + 5×3
(V) T2 + 2 T -7
(VI) 3 x 2 + 7x- 7 x x 38 38 — 4
(VIII) 3 x -2 + x -1 + 5
(ix) y23 + 7y — 8
(x) 1 5×3
Ответ:
i 5×2 – 7x + 4 – это полиномиальное выражение, поскольку степени переменной x — положительные целые числа.
ii 24 — ненулевая константа, а каждая ненулевая константа — полиномиальное выражение. Следовательно, это полиномиальное выражение.
iii У нас есть 5a2 + a + 4 =5a2 + a12 + 4 5a2 + a + 4 не является полиномиальным выражением, так как одна из степеней переменной a равна 12, что не является целым числом.
iv 78x-4×4+5×3 — это полиномиальное выражение, поскольку все степени переменной x являются целыми положительными числами.
v t2 + 2 t — 7 является полиномиальным выражением, так как все степени переменной t являются целыми положительными числами.
vi У нас есть 3×2+7 x-7x=3×2+7x-1-7x 3×2 + 7 x- 7x не является полиномиальным выражением, так как одна из степеней переменной x равна -1, что не является положительным целым числом.
vii x38-4 — полиномиальное выражение, так как все степени переменной x — положительное целое число.
viii 3x-2+x-1+5 не является полиномиальным выражением, так как степени переменной x равны -2 и -1, которые не являются положительными целыми числами.
ix y23+7y-8 не является полиномиальным выражением, так как одна из степеней переменной y равна 23, что не является целым числом.
x У нас x35-1=x35-1 x35-1 не является полиномиальным выражением, поскольку степень переменной x равна 35, что не является целым числом.
Страница № 52:
Вопрос 3:
Напишите степень каждого из следующих полиномов:
(i) 5
(ii) -32
(iii) 4p — 5
(iv) 3 y + 4
y 2(v) x 9 — x 4 + _ x 12 + x — 2
(VI) 5 M 2 N — 3
(vii) 2 xy + 4 x 3
(VIII) 7
(VIII) 7 P 2 Q 3 T — 11 P 4 T + 2 P 8 8
(IX) 5 x 2 Y Z 3 + XY 4 Z 2
(x) ab 2 CD — 3 a 2 bcd 3 + 2 ac 4
Ответ:
i 5 – ненулевой постоянный термин. Степень отличного от нуля постоянного члена равна 0 нулю. ∴ Степень 5=0
Степень отличного от нуля постоянного члена равна 0 нулю. ∴ Степень 5=0
ii -32 – ненулевой постоянный член. Степень отличного от нуля постоянного члена равна 0 нулю. ∴ Степень -32=0
iii 4p — 5 – многочлен от переменной p. Наибольшая степень числа p в данном выражении равна 1. ∴ Степень 4p-5=1
iv 3y + 4y2 – многочлен от переменной y. Наивысшая степень y в данном выражении равна 2. ∴ Степень 3y+4y2=2
v x9-x4+x12+x-2 – многочлен от переменной x.Наибольшая степень x в данном выражении равна 12. ∴ Степень x9-x4+x12+x-2=12
vi 5m2n – это полином от переменных m и n. Сумма степеней m и n в данном выражении=2+1=3 ∴Степень 5m2n=3
vii 2xy+4×3 является многочленом от переменных x и y. Максимальная сумма степеней x и y в данном выражении равна 3.∴. Степень 2xy+4×3=3
viii 7p2q3t-11p4t+2p8 является полиномом от переменных p, q и t. Максимальная сумма степеней p, q и t в данном выражении равна 8.∴ Степень 7p2q3t-11p4t+2p8=8
ix 5x2yz3+xy4z2 — многочлен от переменных x, y и z. Максимальная сумма степеней переменных x, y и z в данном выражении равна 7. Максимальная сумма степеней a, b, c и d в данном выражении равна 7. ∴ Степень ab2cd-3a2bcd3+2ac4=7
Максимальная сумма степеней переменных x, y и z в данном выражении равна 7. Максимальная сумма степеней a, b, c и d в данном выражении равна 7. ∴ Степень ab2cd-3a2bcd3+2ac4=7
Страница № 53:
Вопрос 2:
Написать следующие полиномы в стандартной форме (тип по убыванию):
(i) 3 x — x 4 + 5 x 3 + 2 x 2 — 5
( II) 3 x + 5 + x 3
(III) 7 + 4 T 2 + 5 T
(IV) 118×2 + 2 — 7x
(V) 7 x + 4 x 2 + 3×3 — 14
Ответ:
i Стандартная форма нисходящего типа уравнения 3x – x4 + 5×3 + 2×2 — 5 будет -x4 + 5×3 + 2×2 + 3x — 5.
ii Стандартный тип нисходящей формы уравнения 3x + 5 + x3 будет x3 + 3x + 5.
iv Тип стандартного уравнения по убыванию 118×2 + 2 — 7x будет 118×2 — 7x + 2. 14.
Страница № 54:
Вопрос 1:
Найдите сумму следующих полиномов и запишите степень полученной суммы
(i) 2 x 3 — 7 x 2 + 3 x + 4 ; 2 x 3 — 3 — 3 x 2 + 4 x + 1
(II) 3 x 2
(iii) x 4 + 5 x 3 + 7 x 9; 4 x 3 — 3 x 2 + 5
(iv) у 2 + 2 у 9001; у 3 + 2 у 2 + 3 у + 4 ; у 3 + 7 у — 2
(v) 5 м 2 + 3 м + 8 ; м 3 — 6 м 2 + 4 м ; м 3 — м 2 — м + 5
Ответ:
Я требовал Polynomial = 2×3-7×2 + 3x + 4 + 2×3-3×2 + 4x + 1 = 2×3-7×2 + 3x + 4 + 2×3-3×2 + 4x + 1 = 2×3 + 2×3-7×2-3×2 + 3x + 4x + 4 +1 =4×3-10×2+7x+5Здесь наибольшая степень равна 3. ∴ Степень полиномина = 3
∴ Степень полиномина = 3
IIrequired Polynomial = 3×2 + 5x-x7 + -3×2 + 5x + 8 = 3×2 + 5x-x7-3×2 + 5x + 8 = -x7 + 3×2-3×2 + 5x + 5x + 8 = — x7 + 10x + 8 и высокая мощность составляет 7. ∴ Степень полинома = 7
III требуемая полиномиал = x4 + 5×3 + 7x + 4×3-3×2 + 5 = x4 + 5×3 + 7x + 4×3-3×2 + 5 = x4 +5×3+4×3-3×2+7x+5 = x4+9×3-3×2+7x+5. Здесь наибольшая степень равна 4.∴ Степень полинома = 4
IV требуется полиномиал = Y2 + 2Y-5 + Y3 + 2Y2 + 3Y + 4 + Y3 + 7Y-2 = Y2 + 2Y-5 + Y3 + 2Y2 + 3Y + 4 + Y3 + 7Y -2 = Y3 + Y3 + Y2 + 2Y2 + 2Y + 3Y + 7Y-5 + 4-2 = 2Y3 + 3Y2 + 12Y-3, самая высокая мощность 3. +8+m3-6m2+4m+m3-m2-m+5 =5m2+3m+8+m3-6m2+4m+m3-m2-m+5 -m+8+5 =2m3-2m2+6m+13Здесь наибольшая степень равна 3.∴ Степень полинома = 3
Страница № 54:
Вопрос 2:
Вычтите второй многочлен из первого и запишите степень полученного многочлена.
(i) x 4 + x 2 + x — 1 ; x 4 — x 3 — x 2 n 2 n 3 — 5 N 2 + 6; n 2 — 3 n + 8
(iii) 2 a + 3 a 2 — 7 ; 3 а 2 — 12 + 2 а
Ответ:
I требовала Polynomial = x4 + x2 + x-1-x4-x3-x2 + 1 = x4 + x2 + x — 1-x4 + x3 + x2-1 = x4-x4 + x3 + x2 + x2 + x — 1 -1 =x3+2×2+x-2Здесь наивысшая степень равна 3.∴ Степень полинома = 3
II Требуется полиномиал = N3-5N2 + 6-N3-3N + 8 = N3-5N2 + 6-N3 + 3N-8 = N3-N3-5N2 + 3N + 6-8 = — 5n2 + 3n-2, самая высокая мощность 2.∴ Степень полинома = 2
III требуемая полиномиал = 2А + 3А2-7-3А2-12 + 2А = 2А + 3А2-7-3А2 + 12-2А = 3А2 -3a2+2a-2a-7+12 =5Здесь полином – ненулевая константа. Мы знаем, что степень отличной от нуля константы равна 0.∴ Степень многочлена = 0
Мы знаем, что степень отличной от нуля константы равна 0.∴ Степень многочлена = 0
Страница № 54:
Вопрос 3:
Упростите:
(I) (3 x 2 — 2 x + 1) + ( x 2 + 5 x — 3) + (4 x 2 + 8)
(ii) (2 у 3 + 3 у — 7) — (8 у — 6) + (4 у 3 — 1 2
у) iii) 5 м 3 — м + 6 м 2 — (3 м 2 — 2 + м )
Ответ:
i 3×2-2x+1+x2+5x-3+4×2+8=3×2-2x+1+x2+5x-3+4×2+8=3×2+x2+4×2-2x+5x+1-3+8= 8×2+3x+6
ii 2y3+3y-7-8y-6+4y3-2y+1=2y3+3y-7 -8y+6+4y3-2y+1=2y3+4y3+3y-8y-2y- 7 +6+1=6y3-7y
iii 5м3-м+6м2-3м2-2+м=5м3-м+6м2-3м2+2-м=5м3+6м2-3м2-м-м+2=5м3+ 3м2-2м+2
Страница № 54:
Вопрос 4:
Какой многочлен нужно прибавить к 2 х 4 — 3 х 2 + 5 х + 8, чтобы получить 2 х 2 3 х 9041 — 2 5?
Ответ:
Пусть добавляемый многочлен равен p(x). Тогда 2×4-3×2+5x+8+ p(x)=2×2-5x+4⇒p(x) = 2×2-5x+4-2×4-3×2+5x+8 = 2×2-5x+4-2×4+3×2-5x -8 = -2×4+ 2×2+3×2-5x-5x+4-8 = -2×4+5×2-10x-4∴-2×4+5×2-10x-4 следует добавить к 2×4-3×2+5x+8, чтобы получить 2×2-5x +4.
Тогда 2×4-3×2+5x+8+ p(x)=2×2-5x+4⇒p(x) = 2×2-5x+4-2×4-3×2+5x+8 = 2×2-5x+4-2×4+3×2-5x -8 = -2×4+ 2×2+3×2-5x-5x+4-8 = -2×4+5×2-10x-4∴-2×4+5×2-10x-4 следует добавить к 2×4-3×2+5x+8, чтобы получить 2×2-5x +4.
Страница № 54:
Вопрос 5:
Какой полином нужно вычесть из y 3 + 2 y 2 + 5 y − 1, чтобы получить 2 y 3 2 9003?
Ответ:
Пусть многочлен, который нужно вычесть, равен p(x).Тогда y3+2y2+5y-1- p(x) = 2y2+12⇒p(x) = y3+2y2+ 5y-1 -2y2+12 = y3+ 2y2+ 5y-1-2y2-12 = y3+ 2y2-2y2+ 5y- 1- 12 = y3+ 5y-13∴ y3+ 5y-13 следует вычесть из y3+2y2+5y-1, чтобы получить 2y2+12.
Страница № 54:
Вопрос 6:
из суммы Z 3 + 3 Z 2 + 5 Z + 8 и 4 Z + 8 и 4 Z 3 + 2 Z 2 — 7 Z — 2 Вычтите 2 x 3 — 3 z 2 + z — 4.
Ответ:
Требуемый полином = z3+3z2+5z+8+4z3+2z2-7z-2-2z3-3z2+z-4 =z3+3z2+5z+8+4z3+2z2-7z-2-2z3+3z2-z+ 4 =z3+4z3-2z3+3z2+2z2+3z2+5z-7z-z+8-2+4 = 3z3+ 1z2-0z+
Страница № 56:
Вопрос 1:
Найдите произведение следующих полиномов и укажите степень их произведения.
(i) х 2 + 3 х + 1; 2 x — 3
(ii) 3 x 2 + 5 x ; x 2 + 2 x + 1
(iii) x 3 + 4 x + 2 ; x 2 + x + 5
(iv) x 3 — 1 ; x 2 — x + 4
(v) 2 y 2 + 3 ; 3 г 3 + 1
Ответ:
i У нас есть x2+3x+12x-3=x22x-3+3x2x-3+12x-3=2×3-3×2+6×2-9x+2x-3=2×3+3×2-7x-3∴Градус = 3
ii У нас есть 3×2+5xx2+2x+1=3x2x2+2x+1+5xx2+2x+1=3×4+6×3+3×2+5×3+10×2+5x=3×4+11×3+13×2+5x∴Степень = 4
iii У нас есть х3+4х+2х2+х+5=х3х2+х+5+4хх2+х+5+2х2+х+5=х5+х4+5х3+4х3+4х2+20х+2х2+2х+10=х5+х4+ 9×3+6×2+22x+10∴Градус = 5
iv У нас есть x3-1×2-x+4=x3x2-x+4-1×2-x+4=x5-x4+4×3-x2+x-4∴Градус = 5
v У нас 2y2+33y3+1=2y23y3+1+33y3+1=6y5+2y2+9y3+3=6y5+9y3+2y2+3∴степень = 5
Страница № 56:
Вопрос 2.
 1:
1:В каждом из следующих случаев разделите первый многочлен на второй многочлен и выразите как Делитель = Делитель ✕ Частное + Остаток.
(i) x 3 — 5 x 2 + 4 x + 8 ; х + 2
Ответ:
Здесь частное = x 2 — 7 x + 18
и остаток = -28
∴x3-5×2+4x+8=x+2×2-7x+900-38
Страница № 56:
Вопрос 2.2:
г 3 — 6 г 2 + 6 г + 1 ; г — 1
Ответ:
Здесь частное = y 2 — 5y + 1
и остаток = 2
∴y3-6y9+6y+3=y-1y
Страница № 56:
Вопрос 2.
 3:
3:г 3 — 64 ; г — 4
Ответ:
Здесь частное = y 2 + 4 y + 16
и остаток = 0
∴y3-64=y-41y2+4y
Страница № 56:
Вопрос 2.4:
6 x 3 + 5 x 2 — 21 x + 10, 3 x — 2
Ответ:
Здесь, частное = 2 x 2 + 3 x — 5
и остаток = 0
∴6×3+5×2-21×20=3+0+90×2-21×20=3
Страница № 56:
Вопрос 2.5:
3 x 5 — 4 x 4 + 3 x 3 + 2 x ; х 2 — 3
Ответ:
здесь, Quicent = 3 x 3 — 4 x 2 + 12 x — 12
и остаток = 38 x — 36
∴3×5-4×4 + 3×3 + 2x=x2-33×3-4×2+12x-12+38x-36
Страница № 59:
Вопрос 1:
Экспресс следующие многочлены в коэффициент Форма:
(I) 2 x 2
6 + 5 + 12
(II) y 4 — 3 Y 2 + 2 Y — 7
(III) x 5 + 3 x + 3 x 2
(IV) y 4
6 — 3
(V) 9 x
Ответ:
(i) Степень данного многочлена равна 2.
∴ Количество членов в индексной форме многочлена = 2 + 1 = 3
Многочлен 2×2+5x+12 можно записать в индексной форме как 2×2+5x+12.
∴ Форма коэффициентов данного многочлена: (2, 5, 12).
(ii) Степень данного многочлена равна 4.
∴ Количество членов в индексной форме полинома = 4 + 1 = 5
Многочлен y4-3y2+2y-7 можно записать в индексной форме как у4+0 у3-3у2+2у-7.
∴ Форма коэффициентов данного многочлена: (1, 0, — 3, 2, — 7).
(iii) Степень данного многочлена равна 5.
∴ Количество членов в индексной форме полинома = 5 + 1 = 6
Многочлен x5+3×2 может быть записан в индексной форме как x5+0 x4 +0 x3+3×2+0 x+0.
∴ Форма коэффициента данного многочлена: (1, 0, 0, 3, 0, 0).
(iv) Степень данного полинома равна 4.
∴ Количество членов в индексной форме полинома = 4 + 1 = 5
Многочлен y4-3 можно записать в индексной форме как y4+0 y3 +0 y2+0 y-3.
∴ Форма коэффициента данного многочлена: (1, 0, 0, 0, -3).
(v) Степень данного многочлена равна 1.
∴ Количество членов в индексной форме полинома = 1 + 1 = 2
Многочлен 9x можно записать в индексной форме как 9x+0
∴ коэффициентная форма данного полинома (1, 0).
Страница № 59:
Вопрос 2:
Выразите следующие многочлены в индексной форме, взяв ‘x’ в качестве переменной.
(i) (3, 2, 7)
(ii) (2, 0, 0, -4)
(iii) (1, 0, -3, 1, 5)
(iv) (-2, 3, -5, 6)
(в) ( 1, 0, 0, 0, 0, 0, 64)
Ответ:
(i) Многочлен (3, 2, 7) содержит 3 коэффициента.
т. е. степень полинома = 3 — 1 = 2
∴ Индексная форма данного полинома: 3 x 2 + 2 x + 7. 0,- 4) содержит 4 коэффициента.
т. е. степень полинома = 4 — 1 = 3
∴ Индексная форма данного полинома: ) Многочлен (1, 0, — 3, 1, 5) содержит 5 коэффициентов.
IE, степень полинома = 5 — 1 = 4
∴ Индекс форма данного полинома x 4 + 0 x 3 -3 x 2 + x 5.
(iv) Многочлен (-2, 3, — 5, 6) содержит 4 коэффициента.
т. е. степень полинома = 4 — 1 = 3
∴ Индексная форма данного полинома: v) Многочлен (1, 0, 0, 0, 0, 0, 64) содержит 7 коэффициентов.
IE, степень полиномина = 7 — 1 = 6
∴ Индексная форма данного полинома x 6 + 0 x 5 + 0 x 4 + 0 x 3 + 0 х 2 + 0 х + 64.
Страница № 59:
Вопрос 3.1:
Используйте метод синтетического деления для выполнения следующих делений. Запишите результат в виде
Делитель = Делитель × Частное + Остаток.
(i) ( x 3 — 4 x 2 — 2 x + 1) ÷ ( x — 3)
Ответ:
Делимое=x3-4×2-2x+1Форма индекса=x3-4×2-2x+1Форма коэффициента=1,-4,-2,1Сравнивая делитель x-3 с xa, получаем a=3
Теперь частное в виде коэффициента равно 1, -1, -5∴Частное=x2-x-5 в переменной xRemainder=-14∴x3-4×2-2x+1 = x-3×2-x-5 -14
Страница № 59:
Вопрос 3.
 2:
2:(2 x 3 — 3 x 2 + 4 x + 2) ÷ ( x — 1)
Ответ:
Делимое = 2 x3-3×2+4x+2Форма индекса=2 x3-3×2+4x+2Форма коэффициента=2, -3, 4, 2 Сравнивая делитель x-1 с xa, мы получаем a=1
Теперь, частное в форме коэффициента = 2, -1, 3∴ Частное = 2×2-x+3 в переменной xRemainder = 5∴ 2×3-3×2+4x+2 = x-12×2-x+3 +5
Страница № 59:
Вопрос 3.3:
( г 3 + 343) ÷ ( г + 7)
Ответ:
Дивиденд=y3+343Форма индекса=y3+0 y2+0 y+343Форма коэффициента=1, 0, 0, 343Сравнивая делитель y+7 с ya, мы получаем a=-7
Теперь частное в форме коэффициента =1, -7, 49∴Частное=y2-7y+49 в переменной yRemainder=0∴ y3+343=y+7y2-7y+49 +0
Страница № 59:
Вопрос 3.
 4:
4:( x 5 + x 3 + x 2 — 2 x + 4) ÷ ( x 0
Ответ:
Дивиденд=x5+x3+x2-2x+4Форма индекса=x5+0 x4+x3+x2-2x+4Форма коэффициента=1, 0, 1, 1, -2, 4 Сравнивая делитель x+3 с xa, получаем a=-3
Теперь частное в форме коэффициента=1, -3, 10, -29, 85∴Частное=x4-3×3+10×2-29x+85 в переменной xRemainder = -251∴ x5+x3+ x2-2x+4 = x+3×4-3×3+10×2-29x+85 -251
Страница № 59:
Вопрос 3.5:
( x 3 + 2 x 2 + x + 2) ÷ ( x — 1)
Ответ:
Дивиденд=x3+2×2+x+2Форма индекса=x3+2×2+x+2Форма коэффициента=1, 2, 1, 2Сравнивая делитель x-1 с xa, получаем a=1
Теперь частное в коэффициенте form=1, 3, 4∴Частное = x2+3x+4 в переменной xRemainder = 6∴ x3+2×2+x+2 = x-1×2+3x+4 +6
Страница № 59:
Вопрос 3.
 6:
6:( г 2 — 11 г + 30) ÷ ( г — 5)
Ответ:
Дивиденд=y2-11y+30Форма индекса=y2-11y+30Форма коэффициента=1,-11,30Сравнивая делитель y-5 с ya, получаем a=5
Теперь частное в форме коэффициента=1,- 6∴Частное = y-6 в переменной yRemainder = 0∴ y2-11y+30 = y-5y-6 +0
Страница № 59:
Вопрос 3.7:
( x 3 — 3 x 2 — 12 x + 4) ÷ ( x — 2)
Ответ:
Делимое=x3-3×2-12x+4Форма индекса=x3-3×2-12x+4Форма коэффициента=1, -3, -12, 4Сравнивая делитель x-2 с xa, получаем a=2
Теперь частное в форме коэффициента=1, -1, -14∴ Частное = x2-x-14 в переменной xRemainder = -24∴ x3-3×2-12x+4 = x-2×2-x-14 -24
Страница № 59:
Вопрос 3.
 8:
8:(2 x 4 + 3 x 2 + 5) ÷ ( x + 2)
Ответ:
Делимое=2×4+3×2+5Форма индекса=2×4+0x3+3×2+0x+5Форма коэффициента=2,0,3,0,5Сравнивая делитель x+2 с xa, получаем a=-2
Теперь частное в виде коэффициента равно 2, -4, 11, -22.∴ Частное=2×3-4×2+11x-22 в переменной xRemainder=49∴2×4+3×2+5=x+22×3-4×2+11x-22 +49
Страница № 60:
Вопрос 1:
Найдите значение многочлена х 2 + 2 х + 5, когда 1
(iv) x = — 3
(v) x = a
Ответ:
Пусть p ( x ) = x 2 + 2 x + 5
i Чтобы найти значение px при xial=0, положим x=0 в поном.px=x2+2x+5⇒p0=02+2×0+5 =5⇒p0=5∴Значение многочлена равно 5, когда x=0
ii Чтобы найти значение px, когда x=3, положим x=3 в заданном многочлене. px=x2+2x+5⇒p3=32+2×3+5 =9 + 6 + 5 =20⇒p3=20∴Значение многочлена равно 20, когда x=3
px=x2+2x+5⇒p3=32+2×3+5 =9 + 6 + 5 =20⇒p3=20∴Значение многочлена равно 20, когда x=3
iii Чтобы найти значение px когда x=-1, подставить x=-1 в заданный многочлен. px=x2+2x+5⇒p-1=-12+2×-1+5 =1-2 + 5 =4⇒p-1=4∴Значение многочлена равно 4, когда x=-1
iv Чтобы найти значение px при x=-3, подставьте x=-3 в заданный многочлен.px=x2+2x+5⇒p-3=-32+2×-3+5 =9-6 + 5 =8⇒p-3=8∴ Значение полинома равно 8, когда x=-3
v Чтобы найти значение px при x=a, подставьте x=a в заданный полином. px=x2+2x+5⇒pa=a2+2×a+5 =a2+2a+5⇒pa=a2+2a+5∴Значение многочлена равно a2+2a+5, когда x=a
Страница № 60:
Вопрос 2:
Найти значение полинома y 3 — 5 y — 2 y 2 + 3 когда.
(i) y = 1
(II) y = 2
(III) y = — 2
(iv) y = 4
(v) y = — b
Ответ:
Пусть p ( y ) = y3-5y-2y2+3
i Чтобы найти значение py при y=1, подставьте y=1 в заданный многочлен. py=y3-5y-2y2+3⇒p1=13-5×1-2×12+3 =1-5-2+3 =-3⇒p1=-3∴ Значение многочлена равно -3 при y =1
py=y3-5y-2y2+3⇒p1=13-5×1-2×12+3 =1-5-2+3 =-3⇒p1=-3∴ Значение многочлена равно -3 при y =1
ii Чтобы найти значение py при y=2, подставьте y=2 в заданный полином.py=y3-5y-2y2+3⇒p2=23-5×2-2×22+3 =8-10-8+3 =-7⇒p2=-7∴Значение многочлена равно -7, когда y =2
iii Чтобы найти значение py при y=-2, подставьте y=-2 в заданный многочлен. py=y3-5y-2y2+3⇒p-2=-23-5×-2-2×-22+3 =-8+10-8+3 =-3⇒p-2=-3∴ Значение многочлена равно -3, когда y=-2
ivЧтобы найти значение py, когда y=4, подставьте y=4 в заданный многочлен. py=y3-5y-2y2+3⇒p4=43-5×4-2×42+3 =64-20-32+3 =15⇒p4=15∴Значение многочлена равно 15, когда y=4
v Чтобы найти значение py при y=-b, подставьте y=-b в заданный многочлен.py=y3-5y-2y2+3⇒pb=-b3-5×-b-2×-b2+3 =-b3+5b-2b2+3 =-b3-2b2+5b+3⇒pb=-b3- 2b2+5b+3∴Значение полинома равно -b3-2b2+5b+3, когда y=-b
Страница № 60:
Вопрос 3:
Если значение полинома x 2 — m x + 7 равно 35 при x = 2, то найдите m .
Ответ:
Пусть px=x2-mx+7Тогда p2=22-m×2+7 = 4-2m+7∴p2=-2m+11Но p2=35 Гивень.е.,-2м+11=35⇒-2м=35-11⇒-2м=24∴м=-12
Страница № 60:
Вопрос 4:
Значение полинома ay 2 + 2 y — 6 для y = — 3 равно 15, найдите a .
Ответ:
Пусть py=ay2+2y-6 Тогда p-3=a-32+2-3-6 = 9a-6-6∴p-3=9a-12 Но p-3=15 Giveni, т. е. 9a-12= 15⇒9а=15+12⇒9а=27∴ а=3
Страница № 63:
Вопрос 1:
Найдите ноль полинома в каждом из следующих:
(i) p ( x ) = x + 2
(ii) q ( x x 90 ) = 0 4 4 12
(III) R ( r ( x ) = 5 — 6 x
(IV) p ( y ) = y + 1
(v) p ( м ) = м
(vi) q ( y ) = 4 y
Ответ:
i Чтобы найти ноль px, решим уравнение px=0. Имеем x+2=0⇒x=-2∴-2 – это ноль заданного многочлена.
Имеем x+2=0⇒x=-2∴-2 – это ноль заданного многочлена.
ii Чтобы найти ноль qx, решим уравнение qx=0. У нас есть 4x-12=0 ⇒4x=12 ⇒ x=3∴3 – это ноль заданного многочлена.
iii Чтобы найти ноль rx, решим уравнение rx=0. У нас 5-6x=0 ⇒ -6x=-5 ⇒x=-5-6=56∴56 – это ноль заданного многочлена.
iv Чтобы найти ноль числа py, мы решим уравнение py=0. Имеем y+1=0 ⇒y=-1∴-1 – это ноль заданного многочлена.
v Чтобы найти ноль pm, решим уравнение pm=0. Имеем m=0∴0 — ноль заданного многочлена.
vi Чтобы найти ноль qy, решим уравнение qy=0. Имеем 4y=0 ⇒y=0∴0 – это ноль заданного многочлена.
Страница № 63:
Вопрос 2:
Убедитесь, что:
(i) 2 является нулем многочлена p ( x ) = ( x — 2).
(ii) 2 и 9 являются нулями полинома p ( x ) = ( x — 2) ( x — 9).
(iii) 4 и — 3 являются нулями полинома p ( x ) = x 2 — x — 12.
Ответ:
i У нас есть px=x-2⇒p2 = 2-2⇒ p2 = 0∴2 – это ноль заданного многочлена.
ii У нас есть px=x-2x-9⇒p2=2-22-9⇒p2=0×-7⇒p2=0 и p9=9-29-9⇒p9=7×0⇒p9 = 0∴2 9 — нули заданного многочлена.
iii У нас есть px=x2-x-12⇒p4=42-4-12⇒p4 = 16-4-12⇒p4=0 и p-3=-32—3-12 ⇒p-3 = 9+ 3-12⇒p-3 = 0∴2 и -3 – нули данного многочлена.
Страница № 63:
Вопрос 3:
Найдите нули следующих квадратных многочленов и проверьте связь между нулями и коэффициентами:
(i) x 2 + 10 x + 16
(ii) x 2 — 1 1 х — 5
Ответ:
I У нас есть x2 + 10x + 16 = x2 + 8x + 2x + 16 = xx + 8 + 2x + 8 = x + 8x + 2-х полиномиал имеет zeroes, когда px = 0i. например, x+8=0 или x+2=0⇒x=-8 или x=-2∴Нули многочлена x2+10x+16 равны -8 и -2. Теперь сумма нулей=- 8+-2=-10=-101=-baи произведение нулей=-8×-2=16=161=caСледовательно, проверено.
например, x+8=0 или x+2=0⇒x=-8 или x=-2∴Нули многочлена x2+10x+16 равны -8 и -2. Теперь сумма нулей=- 8+-2=-10=-101=-baи произведение нулей=-8×-2=16=161=caСледовательно, проверено.
II У нас есть x2-4x-5 = x2-5x + x-5 = xx-5 + 1x-5 = x-5x + 1-й полиномиальный имеет Zeroes, когда px = 0i.e., X-5 = 0 или x +1=0⇒x=5 или x=-1∴Нули многочлена x2+10x+16 равны 5 и -1. Теперь сумма нулей=5+-1=4=—41=-ba и произведение нулей= 5×-1=-5=-51=caСледовательно, проверено.
Страница № 63:
Вопрос 4:
Найдите квадратный многочлен, сумма и произведение нулей которого равны соответственно:
(i) 5 и — 50
(ii) — 11 и 10
Ответ:
i Мы знаем, что квадратичный многочлен a имеет вид x2-α+βx+αβ. Здесь α+β – сумма нулей, а αβ – произведение нулей. 50∴Требуемый квадратичный многочлен =x2-5x+-50=x2-5x-50
ii Мы знаем, что квадратичный многочлен a имеет вид x2-α+βx+αβ. Здесь α+β – сумма нулей, а αβ – произведение нулей. Учитывая: α+β =-11 и αβ =10∴Требуемый квадратичный многочлен =x2—11x+10=x2+11x+10
Здесь α+β – сумма нулей, а αβ – произведение нулей. Учитывая: α+β =-11 и αβ =10∴Требуемый квадратичный многочлен =x2—11x+10=x2+11x+10
Страница № 64:
Вопрос 1:
Используя теорему об остатках, найдите остаток, если: х — 10 делится на х — 3.
(iii) x 3 — ax 2 + 2 x — a делится на x — a
Ответ:
i Пусть, px=3×2+x+7 Здесь, divisor=x+2 Когда x+2=0 ⇒x=-2По теореме об остатках, подставляя x=-2 в px, мы получаем, Остаток =p-2=3-22 + -2 + 7 = 3 × 4-2 + 7 = 12-2 + 7 = 17∴remainder = 17
II Пусть px = 4×3 + 5x-10 здесь, divisor = x-3, когда x — 3 = 0, имеем x=3. Подставив x=3 в px, получим:p3=433+53-10 =4×27+15-10 =108+15-10 =113∴Остаток = 113
iii Позвольте 2 px=x3-ax +2x-a Здесь, divisor=xa Когда xa=0, мы имеем x=a.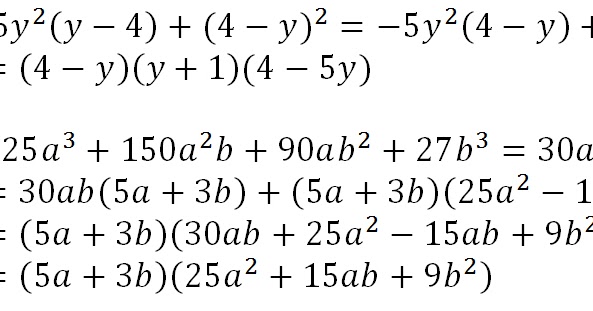 Подставив x=a в px, мы получим: pa=a3-aa2+2a-a =a3-a×a2+2a-a =a3- a3+2a-a =a∴Остаток=a
Подставив x=a в px, мы получим: pa=a3-aa2+2a-a =a3-a×a2+2a-a =a3- a3+2a-a =a∴Остаток=a
Страница № 64:
Вопрос 2:
Если р ( х ) = 2 х 3 — 3 х 2 + 4 х — 5.Найдите остаток от деления на ( x ).
(i) x — 2
(ii) x + 3
(iii) x — 1
Ответ:
i У нас есть px=2×3-3×2+4x-5 Здесь, divisor=x-2 Когда x-2=0, мы имеем x=2. Подставив x=2 в px, мы получим: p2=223-322+42-5 =2×8-3×4+8-5 =16-12+8-5 =7∴Остаток= 7
ii У нас есть px=2×3-3×2+4x-5 Здесь divisor=x+3 Когда x+ 3=0, у нас есть x=-3. Подставив x=-3 в px, мы получим:p-3=2-33-3-32+4-3-5 =2×-27-3×9-12-5 =-54-27-12-5 =-98∴Остаток =-98
iii У нас есть px=2×3-3×2+4x-5 Здесь, divisor=x-1 Когда x-1=0, мы имеем x=1. x=1 в пикселях, мы получаем: p1=213-312+41-5 =2×1-3×1+4-5 =2-3+4-5 =-2∴Остаток=-2
x=1 в пикселях, мы получаем: p1=213-312+41-5 =2×1-3×1+4-5 =2-3+4-5 =-2∴Остаток=-2
Страница № 64:
Вопрос 3:
Когда х 3 + х 2 + 4 х — 5 делится на х + 1, остаток равен 14.Найдите и .
Ответ:
Пусть px=x3+ax2+4x-5Здесь, divisor=x+1 Когда x+1=0, мы имеем x=-1 Подставляя x=-1 в px, получаем: Остаток =p-1=-13+a -12+4-1-5 = 1+a-4-5 =a-10Дано: Остаток=14, т.е.
Страница № 65:
Вопрос 1:
Используя теорему о множителях, покажите, что:
(i) ( x + 2) является множителем x 2 — 4.
(ii) ( x — 3) является коэффициентом x 3 — 27.
(iii) ( x — 1) является коэффициентом 2 x 4 0 3 2 3 90 90 90 3 + 6 x 2 — 11 x — 6.
(IV) ( x + 4) — это фактор x 2 + 10 x + 24.
Ответ:
i Пусть px=x2-4. Когда x+2=0, имеем x=-2. Подставив x=-2 в px, получим: p-2=-22-4 =4-4 =0∴ По теореме о факторах x +2 — это коэффициент x2-4.27-27 коэффициент x3-27.
iii Пусть px=2×4+9×3+6×2-11x-6Когда x-1=0, мы имеем x=1. Подставив x=3 в px, получим: p1=214+913+612-111-6 =2+9 +6-11-6 =0∴ По теореме о множителях x-1 является множителем 2×4+9×3+6×2-11x-6.
iv. Пусть, px=x2+10x+24Когда x+4=0, мы имеем x=-4. Положим x=-4 в px, получим, p-4=-42+10-4+24 =16-40+ 24 =0∴ Согласно теореме о множителях x+4 является множителем x2+10x+24.
Страница № 65:
Вопрос 2:
Используйте теорему о факторах, чтобы определить, является ли ( x — 2) множителем x 3 — 3 x 2 + 4 x + 4.
Ответ:
Пусть px=x3-3×2+4x+4При x-2=0 имеем x=2. Подставив x=2 в px, получаем: p2=23-322+42+4 =8-12+8+4 =8We имеют p2 ≠ 0i.т. е. 2 не является нулем px.∴ По теореме о факторах x-2 не является множителем x3-3×2+4x+4.
Страница № 65:
Вопрос 3:
Найдите значение « a », если ( x — 2) является коэффициентом 2 x 3 — 6 x 2 + 5 x 9,0012 +
Ответ:
Пусть px=2×3-6×2+5x+aКогда x-2=0, имеем x=2. Подставив x=2 в px, получим:p2=223-622+52+a =16-24+10+a =a +2x-2 – это ноль пикселей.По теореме о факторах имеем:p2=0⇒a+2=0∴a=-2
Страница № 173:
Вопрос 1:
Добавить следующие выражения:
(i) 5 м + 0,3 n — 1,2 t ; 0,23 м — 2,8 t + 4 n
(ii) a2-7b3+3c4 ; 5a2-2b3-7c4
Ответ:
i У нас есть 5m+0. 3n-1.2t+0,23м-2,8t+4n = 5м+0,3n-1,2t+0,23м-2,8t+4n = 5м+0,23м+0,3n+4n-1,2t-2,8t = 5,23м+4,3n-4t
3n-1.2t+0,23м-2,8t+4n = 5м+0,3n-1,2t+0,23м-2,8t+4n = 5м+0,23м+0,3n+4n-1,2t-2,8t = 5,23м+4,3n-4t
ii У нас есть a2-7b3+3c4+5a2-2b3-7c4 =a2-7b3+3c4+5a2-2b3-7c4 =a2+5a2-7b3-2b3+3c4-7c4=6a2-9b3-4c4 =3a-3b- с
Страница № 173:
Вопрос 2:
Вычесть второе выражение из первого:
(i) m3+ n2; m6 + n 4
(ii) 0,07p2q+3,6pq2-p2q2-0,003pq2+2p2q-8,5p2q2
Ответ:
i У нас есть m3+n2-m6+n4=m3+n2-m6-n4=m3-m6+n2-n4=2m6-m6+2n4-n4=m6+n4
ii У нас 0.07p2q+3,6pq2-p2q2-0,003pq2-2p2q+8,5p2q2= 0,07p2q+3,6pq2-p2q2-0,003pq2+2p2q-8,5p2q2=0,07p2q+2p2q+3,6pq2-0,003pq2-p2q2-8,5p2q2=2,5p2q2=2,5p2q2 3,597pq2-9,5p2q2
Страница № 173:
Вопрос 3:
Упрощение:
(i) 3c (2b-2a) + 2a (b+3c) — 2b (3c + a)
(ii) mm3-m2+1-2m4-m3-1+m2m2-m+2
(iii) 2×2+y-3+7×2-y+2-3y-3×2-1
(iv) x+yx-y+2x-y3x+y
(v) 2a+bc-2d+a -b2c+3d+4ac+bd
Ответ:
i У нас 3c2b-2a+2ab+3c-2b3c+a =6bc-6ac+2ab+6ac-6bc-2ab =6bc-6bc-6ac+6ac+2ab-2ab =0
ii У нас mm3-m2+ 1-2m4-m3-1+m2m2-m+2 =m4-m3+m-2m4+2m3+2+m4-m3+2m2 =m4-2m4+m4-m3+2m3-m3+2m2+m+2 = 2m2+m+2
iii У нас 2×2+y-3+7×2-y+2-3y-3×2-1 =2×2+2y-6+7×2-7y+14-3y+9×2+3 =2×2+7×2+ 9×2+2y-7y-3y-6+14+3 =18×2-8y+11
iv У нас есть x+yx-y+2x-y3x+y =xx-y+yx-y+2x3x+y-y3x+ y =x2-xy+xy-y2+6×2+2xy-3xy-y2 =x2+6×2-xy+xy+2xy-3xy-y2-y2 =7×2-xy-2y2
v У нас есть 2a+bc-2d+ a-b2c+3d+4ac+bd =2ac-2d+bc-2d+a2c+3d-b2c+3d+4ac+bd =2ac-4ad+bc-2bd+2ac+3ad-2bc-3bd+4ac+4bd = 2ac+2ac+4ac-4ad+3ad+bc-2bc-2bd-3bd+4bd =8ac-ad-bc-bd
Страница № 173:
Вопрос 4.
 1:
1: Факторизация:
x216 — y225
Ответ:
У нас есть x216-y225=x42-y52=x4+y5x4-y5
Страница № 173:
Вопрос 4.2:
x 2 — (2 y + 3 z ) 2
Ответ:
У нас есть x2-2y+3z2=x+2y+3zx-2y+3z=x+2y+3zx-2y-3z
Страница № 173:
Вопрос 4.3:
16a-b2-4c-d2
Ответ:
У нас есть 16a-b2-4c-d2=44a-b2-c-d2=4 2a-b2-c-d2=42a-b+c-d2a-bcd=42a-2b+c-d2a-2b-c+ д
Страница № 173:
Вопрос 4.4:
( а — б ) 2 + 8( а — б ) + 15
Ответ:
У нас есть a-b2+8a-b+15=a-b2+5a-b+3a-b+15=a-ba-b+5+3a-b+5=a-b+5a-b+3 =а-б+5а-б+3
Страница № 173:
Вопрос 4.
 5:
5:9 a 2 — 18 ab — 4 ab 2 + 8 b 3
Ответ:
У нас есть 9a2-18ab-4ab2+8b3=9aa-2b-4b2a-2b=a-2b9a-4b2
Страница № 173:
Вопрос 4.6:
6 x 2 + 4 xy — 9 xy 2 — 6 y 3
Ответ:
У нас есть 6×2+4xy-9xy2-6y3=2x3x+2y-3y23x+2y=3x+2y2x-3y2
Страница № 173:
Вопрос 4.7:
а2+4аб+4б2-9м2+6мн-н2
Ответ:
Имеем a2+4ab+4b2-9m2+6mn-n2= a2+4ab+4b2-9m2-6mn+n2= a2+2×a×2b+2b2-3m2-2×3m×n+n2=a+2b2 -3m-n2=a+2b+3m-na+2b-3m-n=a+2b+3m-na+2b-3m+n
Страница № 173:
Вопрос 4.
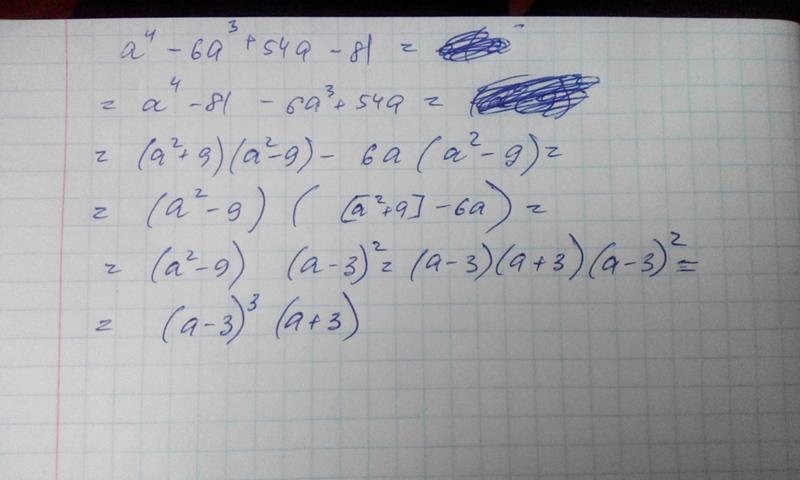 8:
8:(2 a + b ) 3 — ( a + 3 b ) 3
Ответ:
У нас есть 2a+b3-a+3b3=2a+b-a+3b2a+b2+2a+ba+3b+a+3b2= a-2b4a2+b2+4ab+2a2+7ab+3b2+a2+9b2+6ab =a-2b4a2+2a2+a2+b2+3b2+9b2+4ab+7ab+6ab=a-2b7a2+13b2+17ab
Страница № 173:
Вопрос 4.9:
8a3+b3+12a2b+6ab2
Ответ:
У нас есть 8a3+b3+12a2b+6ab2=2a3+b3+6ab2a+b=2a3+b3+3×2a×b2a+b=2a+b3=2a+b2a+b2a+b
Страница № 173:
Вопрос 4.10:
2×2-6×2-8×2-6x+3-40
Ответ:
у нас есть 2×2-6×2-8×2-6x + 3-40субституток x2-6x = A, мы получаем: 2×2-6×2-8×2-6x + 3-40 = 2a2-8a + 3-40 = 2a2-8a-24-40 = 2A2-8A-64 = 2A2-4A-32 = 2A2-8A + 4A-32 = 2ААА-8 + 4А-8 = 2ААА-8 + 4А-8 = 2А-8А + 4А-8 = 2А-8А + 4A-8 = 2A-8A + 4RESUBSTITIONTION Значение A, мы получаем: 2×2-6×2-8×2-6x + 3-40= 2×2-6x-8×2-6x+4
Страница № 173:
Вопрос 4.
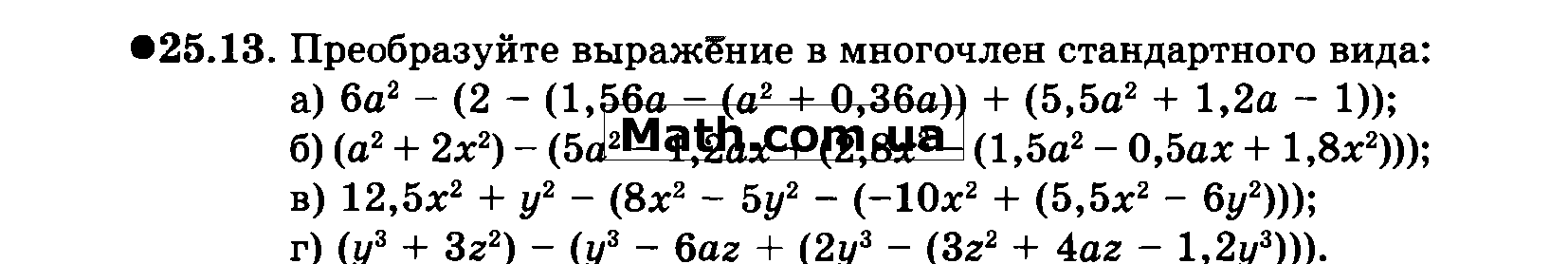 11:
11:а2-2а+3а2-2а+5-35
Ответ:
Имеем a2-2a+3a2-2a+5-35. Подставляя a2-2a=x, получаем: a2-2a+3a2-2a+5-35=x+3x+5-35 -35 = x2 + 8x-20 = x2 + 10x-2x-20 = xx + 10-2x + 10 = x + 10x-2RESUBSTITUTION Значение A, мы получаем: A2-2a + 3A2-2a + 5-35 = а2-2а+10а2-2а-2
Страница № 173:
Вопрос 4.12:
x3-8y3-64z3-24xyz
Ответ:
У нас есть x3-8y3-64z3-24xyz=x3+-2y3+-4z3-3×x×-2y×-4z=x+-2y+-4zx2+-2y2+-4z2-x-2y—2y-4z—4zx=x -2y-4zx2+4y2+16z2+2xy-8yz+4xz
Страница № 173:
Вопрос 4.13:
p3-10+27p3
Ответ:
Имеем p3-10+27p3= p3+8-18+27p3= p3+8+27p3-18= p3+23+3p3-3× p×2×3p=p+2+3pp2+22+3p2-p ×2-2×3р-3р×р=р+2+3рр2+4+9р2-2р-6р-3
Страница № 173:
Вопрос 4.
 14:
14:8×6+95×3+1
Ответ:
Имеем 8×6+95×3+1= 8×6+125×3-30×3+1= 8×6+125×3+1-30×3=2×23+5×3+13-3×2×2×5x×1=2×2+5x+12×22+5×2+12-2×2 ×5x-5x×1-1×2×2=2×2+5x+14×4+25×2+1-10×3-5x-2×2=2×2+5x+14×4-10×3+25×2-2×2-5x+1=2×2+5x+14×4-10×3 +23×2-5x+1
Страница № 173:
Вопрос 4.15:
8×3+27y3+125z3-90xyz
Ответ:
У нас есть 8×3+27y3+125z3-90xyz=2×3+3y3+5z3-3×2x×3y×5z=2x+3y+5z2x2+3y2+5z2-2x×3y-3y×5z-5z×2x=2x+3y +5z4x2+9y2+25z2-6xy-15yz-10xz
Страница № 173:
Вопрос 5:
Что нужно добавить к 6×2 — 3xy + 4y2, чтобы получить 2y2 + xy — 4×2?
Ответ:
Пусть px прибавляется к 6×2-3xy+4y2, чтобы получить 2y2+xy-4×2. т. е. 6×2-3xy+4y2+px=2y2+xy-4×2⇒px=2y2+xy-4×2-6×2-3xy+4y2⇒px=2y2+xy-4×2-6×2+3xy-4y2⇒px=2y2-4y2+ xy+3xy-4×2-6×2⇒px=-2y2+4xy-10×2⇒px=-10×2-2y2+4xy∴-10×2-2y2+4xy можно добавить к 6×2-3xy+4y2, чтобы получить 2y2+xy-4×2.
т. е. 6×2-3xy+4y2+px=2y2+xy-4×2⇒px=2y2+xy-4×2-6×2-3xy+4y2⇒px=2y2+xy-4×2-6×2+3xy-4y2⇒px=2y2-4y2+ xy+3xy-4×2-6×2⇒px=-2y2+4xy-10×2⇒px=-10×2-2y2+4xy∴-10×2-2y2+4xy можно добавить к 6×2-3xy+4y2, чтобы получить 2y2+xy-4×2.
Страница № 173:
Вопрос 6:
Что нужно вычитаться из 3 м 2 N + 5 MN + 5 MN 2 — 2 м 2 N 2 для получения -3 м 2 N + 7 мн 2 + 4 м 2 п 2 ?
Ответ:
Пусть px вычитается из 3m2n+5mn2-2m2n2, чтобы получить -3m2n+7mn2+4m2n2.∴3m2n+5mn2-2m2n2 -px=-3m2n+7mn2+4m2n2⇒px=3m2n+5mn2-2m2n2 —3m2n+7mn2+4m2n2⇒px=3m2n+5mn2-2m2n2 +3m2n-7mn2-4m2n2⇒px=3n2n+3m2n2 +5mn2-7mn2-2m2n2 -4m2n2⇒px=6m2n-2mn2-6m2n2∴6m2n-2mn2-6m2n2 можно вычесть из 3m2n+5mn2-2m2n2, чтобы получить -3m2n+7mn2+4m2n2.
Страница № 173:
Вопрос 7:
Вычесть 6 х + 8 у + 4 от солнца из 4 х — 2 у + 3 и 2 у — х + ?
Ответ:
Требуемое Polynomial = 4x 2Y + 3 + 2Y-X + 3-6x + 8Y + 4 = 4x-2Y + 3 + 2Y-X + 3-6x-8Y-4 = 4x-X-6x-2y + 2y- 8y+3+3-4 = -3x-8y+2
Страница № 173:
Вопрос 8:
Найдите периметр прямоугольника, две смежные стороны которого равны
5 x 2 + 2 xy — 13 ; 2 х 2 — 6 ху + 11.
Ответ:
Две смежные стороны прямоугольника представляют собой ее длину и широту. 25×2+2×2+2xy-6xy-13+11 =27×2-4xy-2 =14×2-8xy-4
Страница № 173:
Вопрос 9:
Периметр треугольника 9 м 2 — 2 N + 8 и его две стороны 4 м 2 + 3 N и 7 м 2 + 5 N — 12. Найдите третью сторону треугольника.
Найдите третью сторону треугольника.
Ответ:
Пусть первая сторона треугольника равна 4м2+3n.Вторая сторона треугольника=7м2+5n-12Третья сторона=pxПериметр=9м2-2n+8Теперь, 4м2+3n+7м2+5n-12+ px=9м2-2n+8 ⇒ px=9м2-2n+8-4м2+3n+7м2+5n-12⇒px=9м2-2n+8-4м2-3n-7м2-5n+12⇒px=9м2-4м2-7м2-2n-3n-5n +8+12⇒px=-2m2-10n+20∴ Третья сторона треугольника=-2m2-10n+20
Страница № 173:
Вопрос 10:
Ежемесячная зарплата Рахула составляет рупий.2 p 3 + p — 3. Его ежегодные расходы составляют 14 p 2 + 6 p — 10. Найдите его годовую экономию.
Ответ:
Учитывая: ежемесячная заработная плата Rahul = 2P2 + P-3ANEALAWALAWAL = 12 Ежемесячная заработная плата = RS 122P2 + P-3 = 24P2 + 12P — 36 и его ежегодные расходы = rs 14p2 + 6p-10ance Aseature = Годовая заработная плата — годовые расходы = 24P2 + 12P-36-RS 14P2 + 12P-36-RS 14P2 + 6P-10 = 24P2 + 12P — 36- 14P2 + 6P-10 = 24P2 + 12P-36-12-6P + 10 = 24P2-6P + 10 = 24P- 14P2 + 12P-6P- 36+10 = Rs 10p2+6p-26
Страница № 173:
Вопрос 11.
 1:
1:Используйте метод синтетического деления для выполнения следующих делений. Напишите, является ли делитель делимым. Оправдывать.
(i) (3 p 4 — 4 p 3 — 3 p — 1) ÷ ( p — 1)
Ответ:
Дивиденд=3p4-4p3-3p-1Форма индекса=3p4-4p3+0p2-3p-1Форма коэффициента=3, -4, 0, -3, -1 Сравнивая делитель p-1 с pa, получаем a=1
∴ Частное в форме коэффициента=3, -1, -1, -4i.например, частное = 3p3-p2-p-4 в переменной pЗдесь остаток равен -5, отличному от нуля. ∴p-1 не является множителем 3p4-4p3-3p-1.
Страница № 173:
Вопрос 11.2:
(ii) ( x 3 — 8) ÷ ( x — 2)
Ответ:
Делимое=x3-8Форма индекса=x3+0 x2 +0 x-8Форма коэффициента=1, 0, 0, -8Сравнивая делитель x-2 с xa, мы получаем a=2
∴ Частное в форме коэффициента= 1, 2, 4и. т. е., частное=x2+2x+4 в переменной xЗдесь остаток равен 0 нулю. ∴x-2 – это множитель x3-8.
т. е., частное=x2+2x+4 в переменной xЗдесь остаток равен 0 нулю. ∴x-2 – это множитель x3-8.
Страница № 173:
Вопрос 11.3:
(4 x 4 + 10 x 3 — 3 x 2 + 2 x — 21) ÷ ( x + 3)
Ответ:
Делимое=4×4+10×3-3×2+2x-21Форма индекса=4×4+10×3-3×2+2x-21Форма коэффициента=4, 10, -3, 2, -21 Сравнивая делитель x+3 с xa, получаем a=-3
∴ Частное в виде коэффициента = 4, -2, 3, -7i.т. е., частное = 4×3-2×2+3x-7 в переменной xЗдесь остаток равен 0 нулю. ∴x+3 – это множитель 4×4+10×3-3×2+2x-21.
Страница № 173:
Вопрос 11.4:
(3 м 2 + м — 10) ÷ ( м + 2)
Ответ:
Дивиденд=3m2+m-10Форма индекса=3m2+m-10Форма коэффициента=3, 1, -10Сравнивая делитель m+2 с ma, получаем a=-2
∴ Частное в виде коэффициента=3,- 5и. т. е., частное=3m-5 в переменной m Остаток =0Здесь остаток равен 0 ноль.∴m+2 – множитель 3m2+m-10.
т. е., частное=3m-5 в переменной m Остаток =0Здесь остаток равен 0 ноль.∴m+2 – множитель 3m2+m-10.
Страница № 174:
Вопрос 12:
Найдите ноль в каждом из полиномов, приведенных ниже:
(i) p ( x ) = 9 x — 3
(ii) p ( y ) = 5 y
Ответ:
i Чтобы найти ноль px, решим уравнение px=0.Имеем 9x-3=0 ⇒9x=3 ∴x=39=13∴Нуль данного полинома равен 13.
ii Чтобы найти ноль py, решим уравнение py=0. Имеем 5y+25=0 ⇒ 5y=-25 ∴ y=-255=-5∴Нуль заданного полинома равен -5.
Страница № 174:
Вопрос 13:
Найти значение полинома 2 a 2 — 5 a 3 + 7 a — 3 для a = 0, 2 и — 3
Ответ:
Пусть P ( A ( A ) = 2 A 2 — 5 2 — 5 A 3 + 7 A — 32 A — 3
Для поиска значения PA при A = 0, поставьте A = 0 в заданном многочлене. т. е. p0=202-503+70-3 =-3∴Когда a=0, значение многочлена равно -3.
т. е. p0=202-503+70-3 =-3∴Когда a=0, значение многочлена равно -3.
Аналогично, когда a=2, мы имеем:p2=222-523+72-3 =2×4-5×8+14-3⇒p2=-21∴При a=2 значение полинома равно -21.
Опять же, когда a=-1, мы имеем:p-1=2-12-5-13+7-1-3 =2+5-7-3⇒p-1=-3∴ Когда a=- 1, значение многочлена равно -3.
Страница № 174:
Вопрос 14:
Если значение многочлена x 3 + 2 x 2 — x + 1 при x = 2 равно 11, найдите a .
Ответ:
Пусть px=x3+2×2-ax+1Тогда p2=23+222-a2+1 =8+8-2a+1∴p2=-2a+17Но p2=11 Дано сейчас, -2a+17=11⇒-2a= 11-17⇒-2а=-6∴а=3
Страница № 174:
Вопрос 15:
Если a — 2 y + 5 y 2 разделить на ( y — 2) остаток равен 7, то найдите значение a .
Ответ:
Пусть py=a-2y+5y2Здесь, divisor=y-2Когда y-2=0, мы имеем y=2. Подставив y=2 в py, мы получим: Остаток =p2=a-22+522 =a-4+20 =a+16Дано: Остаток=7Теперь, a+16=7⇒a=7-16∴a=-9
Страница № 174:
Вопрос 16:
Когда 2 х 2 — х + 7 и ах 2 + 7 х + 12 делятся на ( х + — 1) 02 соответственно остаток такой же.Найдите и .
Ответ:
Пусть px=2×2-ax+7Здесь, divisor=x-3Когда x-3=0, имеем x=3. Подставив x=3 в px, получим: Остаток =p3=232-a3+7 =18-3a+7 =-3a+25Аналогично, пусть qx=ax2+7x+12Здесь, divisor=x+1Когда x+1=0, мы имеем x=-1Подставив x=-1 в qx, получим: Остаток=q-1=a- 12+7-1+12 =a-7+12 =a+5Дано, что остатки в обоих случаях одинаковы. т. е. -3a+25=a+5⇒-3a-a=5-25⇒-4a=-20∴a=5
т. е. -3a+25=a+5⇒-3a-a=5-25⇒-4a=-20∴a=5
Страница № 174:
Вопрос 17:
Если 2x + 1 является коэффициентом (3b + 2)x 3 + (b — 1), то найдите b.
Ответ:
Пусть px=3b+2×3+b-1Дано: 2x+1 — это множитель px.∴ Когда мы разделим px на 2x+1, остаток будет равен нулю. Здесь divisor=2x+1 Когда 2x+1=0, мы имеем x=-12∴Остаток=p-12=0 ⇒3b+2-123+b-1 =0 ⇒3b+2-18+b-1 =0 ⇒- 3b+2+8b-18 =0 ⇒- 3b+2+8b-1=0 ⇒- 3b-2+8b-8=0 ⇒5b-10=0 ⇒5b=10 ∴b=2
Страница № 174:
Вопрос 18:
R 1 и R 2 и R 2 остатки, когда полиномиальный AX 3 + 3 x 2 — 3 и 2 x 3 — 5 x + 2 и делятся на ( x — 4) соответственно. Если 2R 1 — R 2 = 0, то найдите значение a .
Если 2R 1 — R 2 = 0, то найдите значение a .
Ответ:
Пусть px=ax3+3×2-3Здесь, делитель=x-4Когда x-4=0, мы имеем x=4Дано: когда px делится на x-4, остаток равен R1.∴Остаток=R1=p4 ⇒ R1= a43+342-3 ⇒R1=64a+48-3 ⇒ R1=64a+45 …1 Опять же, пусть qx=2×3-5x+2aЗдесь, divisor=x-4Когда x-4=0, имеем x=4 Учитывая: Когда qx делится на x-4, остаток равен R2.∴remainder = R2 = q4 ⇒R2 = 243-54 + 2a ⇒ R2 = 128-20 + 2a ⇒R2 = 2A + 108 … 2IT приведен, что 2R1-R2 = 0 и мощность значения R1 и R2 от 1 до 2 , получаем: 264a+45-2a+108=0⇒128a+90-2a-108=0⇒126a-18=0⇒126a=18⇒a=18126=17∴a=17
Посмотреть решения NCERT для всех глав класса 9
Архивы полиномов— Экзамен SAM
Добавление полиномов – примеры
Чтобы увидеть примеры и решения для многочленов, прокрутите страницу вниз. Тогда попробуйте свои силы в сложении многочленов, выполнив приведенные ниже упражнения. Ответы и пояснения даны после последнего упражнения.
Тогда попробуйте свои силы в сложении многочленов, выполнив приведенные ниже упражнения. Ответы и пояснения даны после последнего упражнения.
Добавление многочленов — упражнения
1) (6x 2 + 9xy + 7y 2 ) + (8x 2 + 2xy + 5y 2 ) = ?
2) (2x 2 + 3xy + 5y 2 ) + (2x 2 – 6xy – 7y 2 ) = ?
3) (3x 3 – 5xy – 2y + 3y 2 ) + (2x 3 + 4x 2 + 5x + 3y – 8xy – 9y 2 ) 900 ?
4) (3a 2 + 4ab + 2b 2 ) + (7a 2 – ab – 6b 2 ) + (8a 2 – 5ab – 4b 2 3?
5) (4x 2 + 3xy + 6y + 7y 2 ) + (3x 2 + 7xy + 5x – 9y 2 ) + (6x 2 ) + (6x 2 9003 )
Добавление полиномов – ответы
Ответ 1
1) Ответ: 14x 2 + 11xy + 12y 2
Шаг 1: Удалите скобки.
(6x 2 + 9xy + 7y 2 ) + (8x 2 + 2xy + 5y 2 ) =
6x 2 + 9xy + 7y 2 + 8x 2 + 2xy + 5y 2
Шаг 2: Затем сложите одинаковые термины вместе.
6x 2 + 8x 2 + 9xy + 7y 2 + 8x 2 + 2xy + 3 0 0
6x 2 + 8x 2 + 9xy + 7y 2 + 2xy + 5y 2 =
6x 2 + 8x 2 + 9xy + 2xy + 7y 2 + 2xy + 5y 2 3 = 9000
6x 2 + 8x 2 + 9xy + 2xy + 7y 2 + 5y 2
Шаг 3: Затем выполните операции для решения.
(6x 2 + 8x 2 ) + (9xy + 2xy) + (7y 2 + 5y 2 ) =
14x 2 + 11xy + 12y 2
Ответ 2
2) Ответ: 4x 2 – 3xy – 2y 2
(2x 2 + 3xy + 5y 2 ) + (2x 2 — 6xy — 7y 2 ) =
2x 2 + 3xy + 5y 2 + 2x 2 – 6xy – 7y 2
Шаг 2: Затем сложите одинаковые термины вместе.
2x 2 + 2X 2 + 3xy + 5Y 2 + 2x 2 — 6xy — 77 2 =
2x 2 + 2x 2 + 3xy + 5y 2 – 6xy – 7y 2 =
2x 2 + 2x 2 + 3xy – 6xy + 5y 2 2x 2 + 2x 2 + 3xy – 6xy + 5y 2 – 7y 2 Шаг 3: Затем выполните операции для решения. (2x 2 + 2x 2 ) + (3xy – 6xy) + (5y 2 – 7y 2 ) = 4x 2 – 3xy – 2y 2 3) Ответ: 5x 3 + 4x 2 + 5x – 13xy – 6y 2 + y Шаг 1: Удалите скобки. (3x 3 – 5xy – 2y + 3y 2 ) + (2x 3 + 4x 2 + 5x + 3y – 8xy – 9y 2 3 ) = 3 3x 3 – 5xy – 2y + 3y 2 + 2x 3 + 4x 2 + 5x + 3y – 8xy – 9y 2 Шаг 2: Затем сложите одинаковые термины вместе. 3X 3 + 2x 3 3 — 5xy — 2y + 3y 2 3x 3 + 2x 3 – 5xy – 2y + 3y 2 + 4x 2 + 5x + 3y – 8xy – 9y 2 0 3= 2 0 3= – 6xy – 7y 30 2 9 Ответ 3

+ 2x 3 + 4x 2 + 5x + 3Y — 8xy — 2 2 =
3x 3 + 2x 3 + 4x 2 — 5xy — 2y + 3Y 2 + 4x 2 + 5x + 3Y — 8xy — 9- 2 =
3x 3 + 2x 3 + 4x 2 – 5xy – 2y + 3y 2 + 5x + 3y – 8xy – 9y 2 3 = 3x 3 + 2x 3 + 4x 2 + 5x — 5xy — 2y + 3Y 2 3x 3 + 2x 3 + 4x 2 + 5x – 5xy – 2y + 3y 2 + 3y – 8xy – 9y 2 3 0 = 3X 3 + 2x 3 + 4x 2 + 5x — 5xy — 8xy — 2Y + 3Y 2 + 3Y 3x 3 + 2x 3 + 4x 2 + 5x – 5xy – 8xy – 2y + 3y 2 + 3y – 9y 2 3 = 3x 3 + 2x 3 + 4x 2 + 5x — 5xy — 8xy 3x 3 + 2x 3 + 4x 2 + 5x – 5xy – 8xy + 3y 2 + 3y – 2y – 9y 2 3 0 = 3x 3 + 2x 3 + 4x 2 + 5x — 5xy — 8xy + 3Y 2 — 91 2 2 + 3Y — 2Y 3x 3 + 2x 3 + 4x 2 + 5x – 5xy – 8xy + 3y 2 – 9y 2 + 3y – 03 y Шаг 3: Затем выполните операции для решения. (3x 3 + 2x 3 ) + 4x 2 + 5x + (–5xy – 8xy) + (3y 2 – 9y 2 ) + (3y – 9y 2 2 ) + (3y – 9 200) 5x 3 + 4x 2 + 5x – 13xy – 6y 2 + y 4) Ответ: 18a 2 – 2ab – 8b 2 Шаг 1: Удалите скобки. (3a 2 + 4ab + 2b 2 ) + (7a 2 – ab – 6b 2 ) + (8a 2 – 5ab – 4b 3 0 0 3a 2 + 4ab + 2b 2 + 7a 2 – ab – 6b 2 + 8a 2 – 5ab – 4b 2 3 0 Шаг 2: Затем сложите одинаковые термины вместе. 3A 2 2 + 7A 2 + 4AB + 2B + 4AB + 2B 2 3a 2 + 7a 2 + 4ab + 2b 2 – ab – 6b 2 + 8a 2 – 5ab – 4b 3 0 90 90 3A 2 + 7A 2 + 8A 3a 2 + 7a 2 + 8a 2 + 4ab + 2b 2 – ab – 6b 2 – 5ab – 4b 30 3 9= 3A 2 + 7A 2 + 8A 2 + 8A 2 + 4AB — AB + 2b 2 3а 2 + 7а 2 + 8а 2 + 4аб – аб + 2б 2 – 6б 2 – 5аб – 4б 30 0 3 0 9= 3A 2 + 7A 2 + 8A 2 + 8A 2 + 4AB — AB — 5ab + 2b 2 — 6B 2 — 6B 2 3а 2 + 7а 2 + 8а 2 + 4аб – аб – 5аб + 2б 2 – 6б 2 – 4б 3 9 9 Шаг 3: Затем выполните операции для решения. (3а 2 + 7а 2 + 8а 2 ) + (4аб – аб – 5аб) + (2б 2 – 6б 2 – 90 3 0 18а 2 – 2аб – 8б 2 5) Ответ: 13x 2 + 5x + 12xy – 2y 2 – 2y Шаг 1: Удалите скобки. (4x 2 + 3xy + 6y + 7y 2 ) + (3x 2 + 7xy + 5x – 9y 2 ) + (6x 2 0 – 0332x 8y = 903 )8y 4x 2 + 3xy + 6y + 7y 2 + 3x 2 + 7xy + 5x – 9y 2 + 6x 2 0 x 3 9 8y Шаг 2: Затем сложите одинаковые термины вместе. 4x 2 + 3x 2 + 3xy + 6y + 7y 2 4x 2 + 3x 2 + 3xy + 6y + 7y 2 + 7xy + 5x – 9y 4x 2 9003 + 3x 2 + 6x 2 2 + 3xy + 6y + 7y 2 + 7xy + 5x — 9Y 2 4x 2 + 3x 2 + 6x 2 + 3xy + 6y + 7y 2 + 7xy + 5x – 9y = 2 x – 8y + 020y 4x 2 + 3x 2 + 6x 2 + 5x + 3xy + 6y + 7y 2 + 7y 2 + 7xy 4x 2 + 3x 2 + 6x 2 + 5x + 3xy + 6y + 7y 2 + 7xy – 9y 2 2xy 3 = 9 0 – 8y 4X 2 + 3x 2 + 6x 2 + 5x + 3xy + 7xy + 6y + 7y 2 4x 2 + 3x 2 + 6x 2 + 5x + 3xy + 7xy + 6y + 7y 2 – 9y 2 2xy 3 = 9 0 0033 – 8y 4x 2 + 3x 2 + 6x 2 + 5x + 3xy + 7xy + 2xy + 6y + 7Y 2 — 9Y 2 — 8Y 4x 2 + 3x 2 + 6x 2 + 5x + 3xy + 7xy + 2xy + 6y + 7y 2 – 9y 2 0 0 9 0 8 3 3 4x 2 + 3x 2 + 6x 2 + 5x + 3xy + 7xy + 2xy 4x 2 + 3x 2 + 6x 2 + 5x + 3xy + 7xy + 2xy + 7y 2 – 9y 2 – 6y 8y 0 0 0 Шаг 3: Затем выполните операции для решения. (4x 2 + 3x 2 + 6x 2 ) + 5x + (3xy + 7xy + 2xy) + (7y 2 – 9y 2 ) + 0 (0 = + 5x + 3Y — 8xy — 9y 2 = — 8xy — 9Y 2 = — 2Y + 3Y 2 + 3Y — 2y — 9728 — 2Y — 2 2 = — 9Y 2 =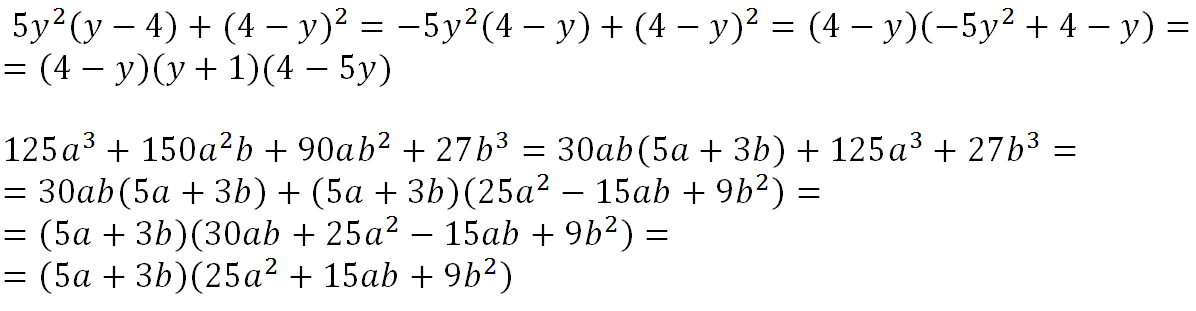
Ответ 4
3 ) + 7A 2 — AB — 6B 2 + 8A 2 — 5AB — 4B 2 = + 8A 2 — 5ab — 4b 2 = — AB — 6B 2 — 5ab — 4b 2 = — 5ab — 4b 2 =
Ответ 5
+ 3x 2 + 7xy + 5x — + 7xy + 5x — 9Y 2 + 6x 2 — 8Y + 2xy = + 6x 2 — 8Y + 2xy = + 5x — 9Y 2 — 8Y + 2xy = + 7xy + 2xy = + 6y + 2xy + 6y + 7y 2 — 97 0928 2 
13x 2 + 5x + 12xy – 2 года 2 – 2 года
Сложение полиномов – примеры сложения полиномов
Для задач на сложение многочленов нужно сгруппировать одинаковые члены вместе.
Нажмите здесь, чтобы увидеть наш пост о группировке похожих терминов.
Теперь посмотрите на приведенный ниже пример сложения многочленов.
Инструкции: Изучите следующий пример сложения многочленов.
(x 2 + xy + y 2 ) + (3x 2 – 4xy + 2y 2 ) = ?
Ответ: 4x 2 – 3xy + 3y 2
ШАГ 1: Удалите скобки, обращая внимание на все минусы.
(х 2 + ху + у 2 ) + (3х 2 – 4ху + 2у 2 ) =
x 2 + xy + y 2 + 3x 2 – 4xy + 2y 2
ШАГ 2: Сгруппируйте похожие термины, используя скобки.
x 2 + xy + y 2 + 3x 2 – 4xy + 2y 2 =
x 2 + 3x 2 + xy + y 2 + 3x 2 – 4xy + 2y 2 3
x 2 + 3x 2 + xy + y 2 – 4xy + 2y 2 =
x 2 + 3x 2 + xy – 4xy + y 2 – 4xy + 2y 2 =
x 2 + 3x 2 + xy – 4xy + y 2 + 2y 2 =
(x 2 + 3x 2 ) + (xy – 4xy) + (y 2 + 2y 2 )
ШАГ 3: Выполните сложение или вычитание членов внутри каждого набора скобок для решения.
(x 2 + 3x 2 ) + (xy – 4xy) + (y 2 + 2y 2 ) =
(4x 2 ) + (–3xy) + (3y 2 ) =
4x 2 – 3xy + 3y 2
Добавление полиномов к экзамену
Вы увидите несколько проблем при добавлении многочленов на экзамене.
Если вам понравился этот пост с примерами сложения полиномов, вы также должны посмотреть наш пост о вычитании полиномов, чтобы просмотреть этот навык.
Также обратите внимание, что проблемы со сложением полиномов могут включать сложение выражений, содержащих отрицательное число.
Сложение полиномов – дополнительная практика
Если вы нашли эти вопросы и примеры по добавлению полиномов полезными, вы также можете просмотреть другие наши сообщения о полиномах:
Умножение многочленов
Разделение многочленов
Подпишитесь на нас на YouTube
frac 6a2+5ab-6b212a2-11ab+2b2 / frac 4a2-12ab+9b28
Gauthmathier6443
12 класс · 2021-11-22
Ответ
a.3 bdfrac2 Ответ: 1{2}))Фактор выражения:\dfrac{2 a + 3 b}{4 a — b} \div (4 a (2 a — 3 b) — b (2 a — 3 b))
Фактор выражение:\dfrac{2 a + 3 b}{4 a — b} \div (2 a — 3 b) (4 a — b)
Уменьшить дробь:\dfrac{2 a + 3 b}{4 a — b} \div \dfrac{2 a — 3 b}{4 a — b}
Разделить дробь, умножив ее обратную:\dfrac{2 a + 3 b}{4 a — b} \times \dfrac{4 a — b}{2 a — 3 b}
Вычеркните общий множитель: (2 a + 3 b) \times \dfrac{1}{2 a — 3 b}
Запишите в виде одной дроби :\dfrac{2 a + 3 b}{2 a — 3 b}
Ответ: \dfrac{2 a + 3 b}{2 a — 3 b}
Помог ли вам ответ? Оцените это!
Фактор по группировке – методы и примеры
Теперь, когда вы научились разлагать многочлены на множители, используя различные методы, такие как; Наибольший общий множитель (GCF, сумма или разность двух кубов, метод разности двух квадратов и трехчленный метод.
Какой метод вы считаете самым простым среди них?
Все эти методы разложения многочленов на множители просты как азбука, только если их правильно применять.
В этой статье мы изучим еще один простейший метод, известный как факторинг по группировке, но прежде чем перейти к теме факторинга по группировке, давайте обсудим, что такое факторинг многочлена.
Многочлен — это алгебраическое выражение с одним или несколькими членами, в котором знак сложения или вычитания разделяет константу и переменную.
Общая форма полинома: + kx + l, где каждой переменной соответствует константа в качестве коэффициента. Различные типы полиномов включают в себя; двучлены, трехчлены и четырехчлены.
Примеры полиномов: 12x + 15, 6x 2 + 3xy – 2ax – ay, 6x 2 + 3x + 20x + 10 и т. д.
Как факторизовать по группировке?
Фактор по группировке полезен, когда нет общего множителя среди терминов, и вы разбиваете выражение на две пары и факторизуете каждую из них отдельно.
Разложение полиномов на множители — это операция, обратная умножению, поскольку она выражает полиномиальное произведение двух или более множителей. Вы можете факторизовать многочлены, чтобы найти корни или решения выражения.
Как разложить трехчлены на множители по группам?
Чтобы разложить на множители трехчлен формы ax 2 + bx + c с помощью группировки, мы выполняем процедуру, как показано ниже:
- Найдите произведение старшего коэффициента «a» и константы «c.
⟹ a * c = ac
- Найдите множители «ac», которые складываются с коэффициентом «b».
- Перепишите bx как сумму или разность множителей ac, которые добавляются к b.
⟹ ax 2 + bx + c = ax 2 + (a + c) x + c
⟹ ax 2 + ax + cx + c
+ (c) 1 ax (x + 1)
⟹ (AX + C) (x + 1)
2 Пример 1
Фактор X 2 — 15x + 50
Решение
Найти два числа, сумма которой равно -15, а произведение равно 50.
⟹ (-5) + (-10) = -15
⟹ (-5) x (-10) = 50
Перепишите данный многочлен в виде;
x 2 -15x + 50⟹ x 2 -5x – 10x + 50
Разложить на множители каждый набор групп;
⟹ x(x – 5) – 10(x – 5)
⟹ (x – 5) (x – 10)
Пример 2 по группировке.
Решение
6Y 2 + 11y + 4 ⟹ 6Y 2 + 3Y + Y + 4
⟹ (6y 2 + 3Y) + (8Y + 4)
⟹ 3Y (2Y + 1) + 4(2y + 1)
= (2y + 1) (3y + 4)
Решение
2x 2 — 5x — 12
= 2x 2 + 3x — 8x — 12
= X (2x + 3) — 4 (2x + 3)
= (2x + 3) (x — 4)
Пример 4
фактора 3Y 2 + 14Y + 8
Решение
3Y 2 + 14Y + 8 ⟹ 3Y 2 + 12Y + 2Y + 8
⟹ (3у 2 + 12у) + (2у + 8)
= 3у (у + 4) + 2(у + 4)
Следовательно,
3у 2 + + 14у + 4) (3y + 2)
Пример 5
Коэффициент 6x 2 – 26x + 28
Решение
Умножить на последний коэффициент.
⟹ 6 * 28 = 168
Найдите два числа, произведение которых равно 168, а сумма -26
⟹ -14 + -12 = -26 и -14 * -12 = 168
Запишите выражение, заменив bx на два числа.
⟹ 6x 2 – 26x + 28 = 6x 2 + -14x + -12x + 28
6x 2 + -14x + -12x + 28 = (6x x 2 + -12432) +-14x 2
= 2x (3x + -7) + -4(3x + -7)
Следовательно, 6x 2 – 26x + 28 = (3x -7) (2x – 4)
Как разложить биномы на множители по группировке?
Бином — это выражение, состоящее из двух членов, объединенных знаком сложения или вычитания.Чтобы разложить бином, применяются следующие четыре правила:
- ab + ac = a (b + c)
- a 2 – b 2 = (a – b) (a + b)
- a 3 – б 3 = (а – б) (а 2 +аб + б 2 )
- а 3 + б 3 3 = (2 9 3 0 ) (2 9 3 0) AB + B 2 )
Пример 6
фактора XYZ — x 2 Z
Решение
xyz — x 2 Z = xz (y — x)
Пример 7
Фактор 6А 2 B + 4BC
Раствор
6A 2 B + 4BC = 2B (3A 2 + 2C)
Пример 8
Фактор полностью: x 6 – 64
Раствор
x 6 – 64 = (x 3 ) 2 – 8 2 (x 3 + 8) (x 3 – 8) = (x+2) (x 2 − 2x + 4) (x − 2) (x 2 + 2x + 4)
Пример 9
Коэффициент: x 6 – y 6 .
Решение
х 6 – у 6 = (х + у) (х 2 – ху + у 2 ) (х – 3 х 3 х + у) (х 29003 2 )
Как разложить многочлены на множители по группировке?
Как следует из названия, разложение по группам — это просто процесс группировки терминов с общими факторами перед разложением на множители.
Чтобы разложить многочлен по группам, выполните следующие действия:
- Проверьте, имеют ли члены многочлена наибольший общий делитель (GCF).Если это так, вычеркните это и не забудьте включить в свой окончательный ответ.
- Разбейте многочлен на наборы по два.
- Учтите GCF каждого набора.
- Наконец, определите, можно ли еще разложить оставшиеся выражения на множители.
Пример 10
Факторизация 2ax + AY + 2BX + на
Решение
2AX + AY + 2BX + BY
= A (2x + Y) + B (2x + Y)
= (2x + Y) (A + B)
Пример 11
фактор AX 2 — BX 2 + AY 2 — BY 2 + AZ 2 — BZ 2
Решение Solution
AX 2 — BX 2 + AY 2 — BY 2 + AZ 2 — BZ 2
= X 2 (A — B) + Y 2 (A — B) + Z 2 (A — B)
= (A — B) (x 2 + Y 2 + Z 2 )
Пример 12
Фактор 6x 2 + 3xy – 2ax – ay
Решение
6x 2 + 3xy – 2ax – y
= 3x (2x + 2xy) + – a (2×0 + 1) (3x – а)
x 3 + 3x 2 + X + 3
x 3 + 3x 2 + x + 3
= (x 3 + Пример 14
6x + 3xy + y + 2
Решение
6x + 3xy + y + 2 (2 + у)
= 3х (у + 2) + 1(у + 2)
= (у + 2) (3х + 1)
= (3х + 1) (у + 2)
Пример 15
AX 2 — BX 2 + AY 2 + AY 2 — BY 2 + AZ 2 — BZ 2 Вынести из каждой группы двух слагаемых Пример 16 Коэффициент 6x + 1203x 2 Решение Вынесите GCF в каждом наборе из двух членов. ⟹ 3x (2x + 1) + 10(2x + 1) = (3x + 10) (2x + 1) Равносторонний треугольник имеет ? Для определения длины окружности используйте ? Круг содержит? Линия, проведенная из центра окружности, называется ? 15,4/2 — 2*(6,2 — 15,6) ? Что такое разносторонний треугольник? Вычислите следующую сумму: 4 {2 (5-1) -3} + 8 ? 4 3/8 – 2 1/4 + 1/8 = ? Площадь прямого кругового конуса с радиусом основания r и высотой l равна ? Сколько сантиметров в дюйме? Найдите квадратный корень из 1600 ? Вычислить 5[ 3 + 6(7-4)-2] ? Чему равен кубический корень из -64? 3 + 4-5(4-2) = ? Если 20% от 120 равно 24, чему равно 24% от 20? Самолет проходит 1400 морских миль за 1 час 45 минут. Какой тип уравнения y = x2 + 9x + 14 ? Сколько градусов в π радианах? (х + у + г) (х + у + г) = ? Упростить 3a-2b +6a-3b-2a ? Сделать P объектом формулы I = PRT/100 ? Вычислить (3a + 2b)(2a-3b) ? 100000 в двоичном формате какое число в десятичном? 101012 +110012 = ? А+В)4 равно (А+В)2 ? журнал 9-лог 3= ? Если 2x-8y=14 и 4x+8y=16; тогда х = ? Что такое 0111000012 в Octal? Характеристика Log 0.
Решение
AX 2 — BX 2 + ау 2 – по 2 + аз 2 – бз 2
⟹ x 2 (a – b) + y 2 (a – b) + z 2 (a – b)
= (a – b) ( x 2 + y 2 + z 2 )
M-1 Итоговый практический тест по математике [32 вопроса и 40 минут] ~ Часть 66 Подготовка
 25
25 Какова средняя скорость самолета?
Какова средняя скорость самолета?


 : Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.
: Мнемозина, 2008. — 288 с.: ил. ISBN 978-5-346-00897-2.