8 x в 3 степени 1: Упростите выражение: 1)х(в 3 степени) * х(в 7 степени) : х(в 8 степени) — Детская игровая комната «Волшебный лес»

Posted on 06.07.201916.04.2021 by alexxlab

Содержание

Перевод корней в степени и обратно: объяснение, примеры

Часто преобразование и упрощение математических выражений требует перехода от корней к степеням и наоборот. Данная статья рассказывает о том, как осуществлять перевод корня в степень и обратно. Рассматривается теория, практические примеры и наиболее распространенные ошибки.

Переход от степеней с дробными показателями к корням

Допустим, мы имеем число с показателем степени в виде обыкновенной дроби — amn. Как записать такое выражение в виде корня?

Ответ вытекает из самого определения степени!

Определение

Положительное число a в степени mn — это корень степени n из числа am.

amn=amn.

При этом, обязательно должно выполнятся условие:

a>0; m∈ℤ; n∈ℕ.

Дробная степень числа нуль определяется аналогично, однако в этом случае число m принимается не целым, а натуральным, чтобы не возникло деления на 0:

0mn=0mn=0.

В соответствии с определением, степень amn можно представить в виде корня amn.

Например: 325=325, 123-34=123-34.

Однако, как уже было сказано, не следует забывать про условия: a > 0 ; m ∈ ℤ ; n ∈ ℕ .

Так, выражение -813 нельзя представить в виде -813, так как запись -813 попросту не имеет смысла — степень отрицательных чисел на определена.При этом, сам корень -813 имеет смысл.

Переход от степеней с выражениями в основании и дробными показателями осуществляется аналогично на всей области допустимых значений (далее — ОДЗ) исходных выражений в основании степени.

Например, выражение x2+2x+1-412 можно представить в виде квадратного корня x2+2x+1-4.Выражение в степени x2+x·y·z-z3-73 переходит в выражение x2+x·y·z-z3-73 для всех x, y, z из ОДЗ данного выражения.

Как представить корень в виде степени?

Обратная замена корней степенями, когда вместо выражения с корнем записывается выражения со степенью, также возможна. Просто перевернем равенство из предыдущего пункта и получим:

amn=amn

Опять же, переход очевиден для положительных чисел a. Например, 764=764, или27-53=27-53.

Для отрицательных a корни имеют смысл. Например -426, -23. Однако, представить эти корни в виде степеней -426 и -213 нельзя.

Можно ли вообще преобразовать такие выражения со степенями? Да, если произвести некоторые предварительные преобразования. Рассмотрим, какие.

Используя свойства степеней, можно выполнить преобразования выражения -426.

-426=-12·426=426.

Так как 4>0, можно записать:

426=426.

В случае с корнем нечетной степени из отрицательного числа, можно записать:

-a2m+1=-a2m+1.

Тогда выражение -23 примет вид:

-23=-23=-213.

Разберемся теперь, как корни, под которыми содержатся выражения, заменяются на степени, содержащие эти выражения в основании.

Обозначим буквой A некоторое выражение. Однако не будем спешить с представлением Amn в виде Amn. Поясним, что здесь имеется в виду. Например, выражение х-323, основываясь на равенстве из первого пункта, хочется представить в виде x-323. Такая замена возможна только при x-3≥0, а для остальных икс из ОДЗ она не подходит, так как для отрицательных a формула amn=amn не имеет смысла.

Таким образом, в рассмотренном примере преобразование вида Amn=Amn является преобразованием, сужающим ОДЗ, а из-за неаккуратного применения формулы Amn=Amn нередко возникают ошибки.

Чтобы правильно перейти от корня Amn к степени Amn, необходимо соблюдать несколько пунктов:

В случае, если число m — целое и нечетное, а n — натуральное и четное, то формула Amn=Amn справедлива на всей ОДЗ переменных.
Если m — целое и нечетное, а n — натуральное и нечетное,то выражение Amn можно заменить:
— на Amn для всех значений переменных, при которых A≥0;
— на —Amn для для всех значений переменных, при которых A<0;
Если m — целое и четное, а n — любое натуральное число, то Amn можно заменить на Amn.

Сведем все эти правила в таблицу и приведем несколько примеров их использования.

Вернемся к выражению х-323. Здесь m=2 — целое и четное число, а n=3 — натуральное число. Значит, выражение х-323 правильно будет записать в виде:

х-323=x-323.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Приведем еще один пример с корнями и степенями.

Пример. Перевод корня в степень

x+5-35=x+5-35, x>-5—x-5-35, x<-5

Обоснуем результаты, приведенные в таблице. Если число m — целое и нечетное, а n — натуральное и четное, для всех переменных из ОДЗ в выражении Amn значение A положительно или неотрицательно (при m>0). Именно поэтому Amn=Amn.

Во втором варианте, когда m — целое, положительное и нечетное, а n — натуральное и нечетное, значения Amn разделяются. Для переменных из ОДЗ, при которых A неотрицательно, Amn=Amn=Amn. Для переменных, при которых A отрицательно, получаем Amn=-Amn=-1m·Amn=-Amn=-Amn=-Amn.

Аналогично рассмотрим и следующий случай, когда m — целое и четное, а n — любое натуральное число. Если значение Aположительно или неотрицательно, то для таких значений переменных из ОДЗ Amn=Amn=Amn. Для отрицательных A получаем Amn=-Amn=-1m·Amn=Amn=Amn.

Таким образом, в третьем случае для всех переменных из ОДЗ можно записать Amn=Amn.

Урок 12. решение алгебраических уравнений разложением на множители — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №12. Решение алгебраических уравнений разложением на множители.

Перечень вопросов, рассматриваемых в теме

1) типы алгебраических уравнений;

2) решение алгебраические уравнения методом разложения на множители;

3) методы решения алгебраических уравнений.

Глоссарий по теме

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого множества F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над множеством F.

Степенью алгебраического уравнения называют степень многочлена P.

Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Биквадратными называются уравнения вида ах⁴ + bх² + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Симметрическим уравнением 3-ей степени называют уравнение вида: ax³ + bx² + bx + a = 0, где a, b – заданные числа.

Уравнение вида aⁿxⁿ₊a^n-1x^n-1+…+a¹x+a⁰=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a^n-1=a^k, при k=0, 1, …, n.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Дополнительная литература:

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Давайте вспомним, что такое алгебраическое уравнение?

Алгебраическое уравнение (полиномиальное уравнение) — уравнение вида P(x₁, x₂, …, x_n)=0, где P — многочлен от переменных x₁, x₂, …, x_n, которые называются неизвестными.

Коэффициенты многочлена P обычно берутся из некоторого поля F, и тогда уравнение P(x₁, x₂, …, x_n)=0 называется алгебраическим уравнение над полем F.

Степенью алгебраического уравнения называют степень многочлена P.

Например, уравнение

является алгебраическим уравнением седьмой степени от трёх переменных (с тремя неизвестными) над полем вещественных чисел.

Связанные определения. Значения переменных x₁, x₂, …, x_n, которые при подстановке в алгебраическое уравнение обращают его в тождество, называются корнями этого алгебраического уравнения.

Примеры и разбор решения заданий тренировочного модуля

Алгебраические уравнения, решаемые разложением на множители:

Пример 1.

x³ – 3x – 2 = 0.

Решение: I способ

D(–2) : ,

Можно догадаться, что число х₁ = –1 является корнем этого уравнения, так как –1 + 3 – 2 = 0.

(х + 1)( х² –х–2) = 0;

х + 1 = 0 или х² –х–2 = 0;

х₁= –1 х_2,3 = ;

х_2,3 = ;

х₂= –1, х₃ = 2

Ответ: –1; 2.

II способ

x³ + х² – х²– х – 2x – 2 = 0;

(x³ + х²) – (х² + х) – 2(x + 1) = 0;

х²(х + 1) – х(х + 1) – 2(х + 1) = 0;

(х + 1) (х² –х–2) = 0;

(х + 1) (х + 1) (х –2) = 0;

(х –2) = 0;

х₁= –1, х₂ = 2

Ответ: –1; 2.

Уравнения, сводящиеся к алгебраическим
1. Биквадратные уравнения

На прошлом уроке мы познакомились с данным видом уравнений

Определение. Биквадратными называются уравнения вида ах⁴ + bх² + с = 0, где а, b, с – заданные числа, причем, а ≠ 0.

Метод решения

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки у=х².

Новое квадратное уравнение относительно переменной у: ay²+by+c=0.

Решая это уравнение, мы получаем корни квадратного уравнения

y₁ и y₂.

Решая эти два уравнения (y₁=x₁² и y

2=x₁²) относительно переменной x, мы получаем корни данного биквадратного уравнения.

Порядок действий при решении биквадратных уравнений

Ввести новую переменную у=х²
Подставить данную переменную в исходное уравнение
Решить квадратное уравнение относительно новой переменной
После нахождения корней (y₁; y₂) подставить их в нашу переменную у=х² и найти исходные корни биквадратного уравнения

Пример 2.

х⁴ – 8х² – 9 = 0.

Решение: Пусть у = х², где у 0; у² – 8у – 9 = 0;

По формулам Виета:

у₁ = –1; у₂ = 9;

Первое решение отбрасываем ( у 0),

а из второго находим х₁ = –3; х₂ = 3.

Ответ: х₁ = –3; х₂ = 3.

2 Симметрические уравнения

Решение симметрических уравнений рассмотрим на примере симметрических уравнений третьей степени.

Симметрическим уравнением 3-ей степени называют уравнение вида ax³ + bx² + bx + a = 0, где a, b – заданные числа.

Для того, чтобы успешно решать уравнения такого вида, полезно знать и уметь использовать следующие простейшие свойства симметрических уравнений:

1⁰. У любого симметрического уравнения нечетной степени всегда есть корень, равный -1.

Действительно, если сгруппировать в левой части слагаемые следующим образом: а(х³ + 1) + bx(х + 1) = 0, то есть возможность вынести общий множитель, т.е.

(х + 1)(ах² + (b – а)x + а) = 0, поэтому,
х + 1 = 0 или ах² + (b – а)x + а = 0,

первое уравнение и доказывает интересующее нас утверждение.

2⁰. У симметрического уравнения корней, равных нулю, нет.

3⁰. При делении многочлена нечетной степени на (х + 1) частное является снова симметрическим многочленом.

Пример 3.

х³ + 2x² + 2х + 1 = 0.

Решение: У исходного уравнения обязательно есть корень х = –1.

Разлагая далее левую часть на множители, получим

(х + 1)(x² + х + 1) = 0.

Квадратное уравнение

x² + х + 1 = 0 не имеет корней.

Ответ: –1.

2 Возвратные уравнения

Уравнение вида aⁿxⁿ₊a^n-1x^n-1+…+a¹x+a⁰=0 называется возвратным, если его коэффициенты, стоящие на симметричных позициях, равны, т.е. a^n-1=a^k, при k=0, 1, …, n.

Рассмотрим возвратное уравнение четвёртой степени вида

ax⁴ + bx³ + cx² + bx + a = 0, где a, b и c — некоторые числа, причём a ≠ 0. Оно является частным случаем уравнения ax⁴ + bx³ + cx² + kbx + k²a = 0 при k = 1.

Порядок действий при решении возвратных уравнений вида ax⁴ + bx³ + cx² + bx + a = 0:

разделить левую и правую части уравнения на . При этом не происходит потери решения, так как x = 0 не является корнем исходного уравнения;
группировкой привести полученное уравнение к виду

ввести новую переменную , тогда выполнено
, то есть ;

в новых переменных рассматриваемое уравнение является квадратным: at² +bt+c–2a=0;

решить его относительно t, возвратиться к исходной переменной.

Пример 4

2x⁴ – 3x³ – 7x² –15x + 50 = 0.

Решение: Разделим на x², получим:

Введем замену:
Пусть

тогда 2t² – 3t – 27 = 0

t=-3

x2+3x+5=0

D<0

2×2-9x+10=0

x=2; x=2,5

Ответ: .

Урок 13. многочлены от нескольких переменных — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №13. Многочлены от нескольких переменных.

Перечень вопросов, рассматриваемых в теме

1) определение многочлена от нескольких переменных;

2) понятие симметрических многочленов;

3) формулы сокращенного умножения для старших степеней;

4) бином Ньютона;

5) метод неопределенных коэффициентов.

Глоссарий по теме

Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.

Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х.

Уравнение Р(x;y) = а, где , называютсимметрическим, если Р(х;y) — симметрический многочлен.

Треугольник Паскаля —бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

Основная литература:

Дополнительная литература:

Теоретический материал для самостоятельного изучения

Многочлены от нескольких переменных можно складывать, вычитать, перемножать, возводить в натуральную степень, разлагать на множители — это вам известно из курса алгебры 7—9-го классов. Этот урок позволит нам несколько расширить знания о многочленах.

Пример 1. Разложить на множители многочлен: 2x²-5xy+2y².

Воспользуемся методом группировки

2x²-5xy+2y²⁼2x²-4xy-xy+2y²= 2x(x-2y) –y(x-2y)=

(x-2y)(2x+2y).

Пример 2. Выведем формулу сокращенного умножения для «квадрата суммы» (x+y+z+u)².

(x+y+z+u)²=((x+y)+(z+u))²= (x+y)²+2(x+y)(z+u)+(z+u)²= x²+y²+z²+u²+2(xy+xz+xu+yz+yu+zu).

Итак, мы получили (x+y+z+u)²= x²+y²+z²+u²+2(xy+xz+xu+yz+yu+zu).

Среди многочленов от двух переменных выделяют однородные и симметрические многочлены.

Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.

Приведем примеры.

1) р(х; у)=2х+3у – однородный многочлен первой степени; соответственно 2х+3у=0 – однородное уравнение первой степени.

2) р(х; у)=3х²+5ху-7у² — однородный многочлен второй степени; соответственно 3х²+5ху-7у² =0 — однородное уравнение второй степени.

3) p(x; y)= x³+4xy²-5y³ — однородный многочлен третьей степени; x³+4xy²-5y³ =0 соответственно — однородное уравнение третьей степени.

4) p(x; y)= a_nxⁿ+a_n-1x^n-1y+a_n-2x^n-2y²₊…+a₁xy^n-1+a₀yⁿ — общий вид однородного многочлена n-й степени.

Рассмотрим еще один метод разложения многочленов на множители-

метод неопределенных коэффициентов. Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения

Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.
Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.

Пример 3. Разложить на множители многочлен

3 x ³ – x ² – 3 x + 1.

Решение. Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и ax ² + bx + c такие, что справедливо равенство 3 x ³ – x ² – 3 x + 1 = ( x – p )( ax ²+ bx + c ) = ax ³ + ( b – ap ) x ² + ( c – bp ) x – pc . Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырех уравнений для определения четырех неизвестных коэффициентов:

Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен 3 x ³ – x ² – 3 x + 1 разлагается на множители: 3 x ³ – x ² – 3 x + 1 = ( x – 1)(3 x ² + 2 x – 1).

Стоит отметить, что существует достаточно изящный способ решения однородных уравнений. Поясним его суть на примере.

Пример 4. Решим уравнение x³+4xy²-5y³ =0

Заметим, что если в заданном уравнении взять х=0, то получится у=0; это означает, что пара (0; 0) является решением однородного уравнения. Пусть теперь х. Разделим почленно обе части заданного однородного уравнения на х³, получим:

Введем новую переменную . Тогда уравнение примет вид 1+4z²-5z³=0.

Далее последовательно находим:

5z³-4z²-1=0

(5z³-5z²)+(z²-1)=0

5z²(z-1)+(z-1)(z+1)=0

(z-1)(5z²+z+1)=0

Из уравнения z-1=0 находим z=1, уравнение 5z³-4z²-1=0 действительных корней не имеет.

Если z=1, то , т.е. у=х. Это значит, что любая пара вида (t; t) является решением заданного однородного уравнения. Между прочим, и отмеченная нами ранее пара (0; 0) также входит в указанный перечень решений.

Ответ: (t; t), где t- любое действительное число.

Теперь поговорим о симметрических многочленах. Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х. Например, симметрическим является двучлен x²y+xy². В самом деле, при одновременной замене х на у и у на х получится двучлен y²x+yx², но это то же самое, что x²y+xy² . Другие примеры симметрических многочленов: xy, x+y, x²+y², x³+y³, x⁴+y⁴ и т.д. Первые два из записанных многочленов считаются основными в том смысле, что любые другие симметрические многочлены можно представить в виде некоторой комбинации многочленов х + у и ху.

Теорема. Любой симметрический многочлен Р(х;у) можно представить в виде многочлена от ху и х+у.

Например,

x²+y²=(x+y)²-2xy

x³+y³=(x+y)³-3xy(x+y)

x⁴+y⁴= 2xy(x²+y²)-(x⁴+y⁴)+3(xy)² и т.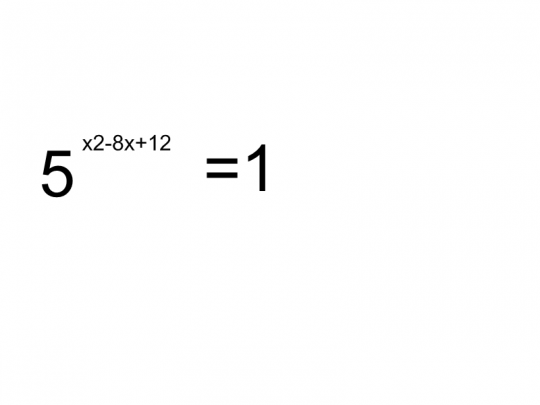 д.

Уравнение Р(x;y) = а, где , называют симметрическим, если Р(х;y) — симметрический многочлен. Мы с вами рассматривали его на предыдущем уроке.

А теперь перейдем к такому понятию как бином Ньютона.

Слово бином означает «Два числа». В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных». Бином Ньютона — название формулы, выражающей степень двучлена в виде суммы одночленов.

Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.

Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.

(a+b)²=a²+2ab+b²

(a+b)³=a³+3a²b+3ab²+b³

Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах

(a+b)²=(a+b)(a+b)

(a+b)³=(a+b)(a+b)(a+b)

Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?

Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):

(a+b)⁴=(a+b)³(a+b)=(a³+3a²b+3ab²+b³)(a+b)=a⁴+4a³b+6a²b²+4ab³+b⁴

(a+b)⁵=(a+b)⁴(a+b)=(a⁴+4a³b+6a²b²+4ab³+b⁴)(a+b)=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵

Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:

n=2 1,2,1

n=3 1,3,3,1

n=4 1,4,6,4,1

n=5 1,5,10,5,1

Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):

n=0, (a+b)⁰=1

n=1, (a+b)¹=a+b

Окончательно получим:

n=0 1

n=1 1,1

n=2 1,2,1

n=3 1,3,3,1

n=4 1,4,6,4,1

n=5 1,5,10,5,1

Общая формула бинома Ньютона:

Правая часть формулы называется разложением степени бинома.

— называется биномиальными коэффициентами, а все слагаемые — членами бинома.

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

На самом деле, о треугольнике Паскаля было известно задолго до Паскаля — его знал живший в XI-XII вв. среднеазиатский математик и поэт Омар Хайям (к сожалению, его сочинение об этом до нас не дошло). Первое, дошедшее до нас описание формулы бинома Ньютона содержится в появившейся в 1265 г. книге среднеазиатского математика ат-Туси, где дана таблица чисел (биномиальных коэффициентов) до n=12 включительно.

Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.

В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.

Пример 5.

Доказать, что значение выражения 5ⁿ+28n-1, где n – натуральное число, делится на 16 без остатка.

Решение: представим первое слагаемое выражение как 5ⁿ= (4+1)ⁿ и воспользуемся формулой бинома Ньютона:

Полученное произведение доказывает делимость исходного выражения на 16.

Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница

Примеры и разборы решения заданий тренировочного модуля

№1.

Из данных многочленов выделите симметрические:

2х²-5ху+2у²-6
6x⁴-16xy²-6y³+19
-3ху+6х²-5у²+8
16x⁴y²+16x²y⁴-x⁴-y⁴

Решение: к данному заданию применим определение симметрических многочленов (Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х). Получим, что нам подходят 1 и 4 пункты.

Верный ответ:

2х²-5ху+2у²-6
6x⁴-16xy²-6y³+19
-3ху+6х²-5у²+8
16x⁴y²+16x²y⁴-x⁴-y⁴

№2.

(а+b)⁵= __a⁵ +___a⁴b+___a³b²+___a²b³+___ab⁴+__b⁵

Решение: для решения данного задания воспользуемся треугольником Паскаля

1
1    1
1    2    1
1    3    3    1
1    4    6    4    1
1    5    10    10    5    1

Нас интересует последняя строчка.

Применив ее, получим ответ:

(а+b)⁵= 1a⁵ +5a⁴b+10a³b²+10a²b³+5ab⁴+1b⁵

Возведение в степень | Кодкамп

Квадратный корень: math.sqrt () и cmath.sqrt

math модуль содержит math.sqrt() -функции , который может вычислить квадратный корень из любого числа (которые могут быть преобразованы в float ) , и результат всегда будет float :

import math

math.sqrt(9)                # 3.0
math.sqrt(11.11)            # 3.3331666624997918
math.sqrt(Decimal('6.25'))  # 2.5

math.sqrt() функция вызывает ValueError , если результат будет complex :

math.sqrt(-10)

ValueError: ошибка математического домена

math.sqrt(x) быстрее , чем math. pow(x, 0.5) или x ** 0.5 , но точность результатов является то же самое. cmath модуль очень похож на math модуля, за исключением того , что можно вычислить комплексные числа , и все его результаты в виде + би исключением. Он может также использовать .sqrt() :

import cmath

cmath.sqrt(4)  # 2+0j
cmath.sqrt(-4) # 2j

Что с j ? j является эквивалентом квадратного корня из -1. Все числа можно записать в виде a + bi или в этом случае a + bj. реальная часть числа , как 2 в 2+0j . Так как она не имеет мнимую часть, b равно 0. b представляет собой часть мнимой части числа , как 2 — в 2j . Поскольку нет никакой реальной части в этом, 2j также можно записать в виде 0 + 2j .

Экспонирование с использованием встроенных функций: ** и pow ()

Возведение может быть использован с помощью встроенного pow -функции или ** оператора:

2 ** 3    # 8
pow(2, 3) # 8

Для большинства (все в Python 2.x) арифметических операций тип результата будет типом более широкого операнда. Это не верно для ** ; следующие случаи являются исключениями из этого правила:

Основание: int , показатель: int < 0 :

2 ** -3
# Out: 0.125 (result is a float)

Это также верно для Python 3.x.

Перед Python 2.2.0, это поднял ValueError .

Основание: int < 0 или float < 0 , показатель: float != int

(-2) ** (0.5)  # also (-2.) ** (0.5)# Out: 0.125 (result is a float) 
Out: (8.659560562354934e-17+1.4142135623730951j) (result is complex)

operator модуль содержит две функции, которые эквивалентны ** -оператора:

import operator
operator.pow(4, 2)      # 16
operator.__pow__(4, 3)  # 64

или можно напрямую вызвать __pow__ метод:

val1, val2 = 4, 2
val1. ------------

Магические методы и возведение в степень: построение, математика и математика

Предположим, у вас есть класс, который хранит чисто целочисленные значения:

class Integer(object):
    def __init__(self, value):
        self.value = int(value) # Cast to an integer

    def __repr__(self):
        return '{cls}({val})'.format(cls=self.__class__.__name__,
                                     val=self.value)

    def __pow__(self, other, modulo=None):
        if modulo is None:
            print('Using __pow__')
            return self.__class__(self.value ** other)
        else:
            print('Using __pow__ with modulo')
            return self.__class__(pow(self.value, other, modulo))

    def __float__(self):
        print('Using __float__')
        return float(self.value)

    def __complex__(self):
        print('Using __complex__')
        return complex(self.value, 0)

Использование встроенной pow функции или ** оператор всегда вызывает __pow__ :

Integer(2) ** 2                 # Integer(4)
# Prints: Using __pow__
Integer(2) ** 2.5               # Integer(5)
# Prints: Using __pow__
pow(Integer(2), 0.5)            # Integer(1)
# Prints: Using __pow__  
operator.pow(Integer(2), 3)     # Integer(8)
# Prints: Using __pow__
operator.__pow__(Integer(3), 3) # Integer(27)
# Prints: Using __pow__

Второй аргумент __pow__() метод может подаваться только с помощью builtin- pow() или путем непосредственного вызова метода:

pow(Integer(2), 3, 4)           # Integer(0)
# Prints: Using __pow__ with modulo
Integer(2).__pow__(3, 4)        # Integer(0) 
# Prints: Using __pow__ with modulo

В то время как math -функции всегда преобразовать его в float и использовать флоат-вычисления:

import math

math.pow(Integer(2), 0.5) # 1.4142135623730951
# Prints: Using __float__

cmath -функции попытаться преобразовать его в complex , но может также Откат к float , если нет явного преобразования в complex :

import cmath

cmath. exp(Integer(2))     # (7.38905609893065+0j)
# Prints: Using __complex__

del Integer.__complex__   # Deleting __complex__ method - instances cannot be cast to complex

cmath.exp(Integer(2))     # (7.38905609893065+0j)
# Prints: Using __float__

Ни math , ни cmath будет работать , если также __float__() -метод отсутствует:

del Integer.__float__  # Deleting __complex__ method

math.sqrt(Integer(2))  # also cmath.exp(Integer(2))

Ошибка типа: требуется плавающее число

Модульное возведение в степень: pow() с 3 аргументами

Обеспечение pow() с аргументами 3 pow(a, b, c) оценивает модульного возведения в степень а б мод C:

pow(3, 4, 17)   # 13

# equivalent unoptimized expression:
3 ** 4 % 17     # 13

# steps:
3 ** 4          # 81
81 % 17         # 13

Для встроенных типов использование модульного возведения в степень возможно только в том случае, если:

Первый аргумент является int
Второй аргумент является int >= 0
Третий аргумент является int != 0

Эти ограничения также присутствуют в Python 3.x

Например, можно использовать 3-аргумент форму pow определить модульную обратную функцию:

def modular_inverse(x, p):
    """Find a such as  a·x ≡ 1 (mod p), assuming p is prime."""
    return pow(x, p-2, p)

[modular_inverse(x, 13) for x in range(1,13)]
# Out: [1, 7, 9, 10, 8, 11, 2, 5, 3, 4, 6, 12]

Корни: n-корень с дробными показателями

В то время как math.sqrt функция предусмотрена для конкретного случая квадратных корней, это часто бывает удобно использовать оператор возведения в степень ( ** ) с дробными показателями для выполнения п-корневые операции, как кубические корни.

Обратное возведение в степень является возведением в степень по взаимности экспоненты. Таким образом, если вы можете кубизировать число, указав его в показателе степени 3, вы можете найти корень куба в числе, указав его в показателе 1/3.

>>> x = 3
>>> y = x ** 3
>>> y
27
>>> z = y ** (1.0 / 3)
>>> z
3.0
>>> z == x
True

Вычисление больших целочисленных корней

Несмотря на то, что Python изначально поддерживает большие целые числа, получение n-го корня очень больших чисел может привести к сбою в Python.

 x = 2 ** 100
cube = x ** 3
root = cube ** (1.0 / 3)

OverflowError: long int слишком велико для преобразования в float

При работе с такими большими целыми числами вам нужно будет использовать пользовательскую функцию для вычисления n-го корня числа.

def nth_root(x, n):
    # Start with some reasonable bounds around the nth root.
    upper_bound = 1
    while upper_bound ** n <= x:
        upper_bound *= 2
    lower_bound = upper_bound // 2
    # Keep searching for a better result as long as the bounds make sense.
    while lower_bound < upper_bound:
        mid = (lower_bound + upper_bound) // 2
        mid_nth = mid ** n
        if lower_bound < mid and mid_nth < x:
            lower_bound = mid
        elif upper_bound > mid and mid_nth > x:
            upper_bound = mid
        else:
            # Found perfect nth root.
            return mid
    return mid + 1

x = 2 ** 100
cube = x ** 3
root = nth_root(cube, 3)
x == root
# True

Свойства показателей степени с примерами: умножение, деление

Степень aⁿ равняется произведению числа a на само себя n-ое количество раз.

aⁿ = a * a * a… a (n раз)

В данном случае a – это основание, а n – показатель степени.

Примеры:

3¹ = 3
3² = 3 × 3 = 9
3³ = 3 × 3 × 3 = 27
3⁴ = 3 × 3 × 3 × 3 = 81
3⁵ = 3 × 3 × 3 × 3 × 3 = 243

Произошение:

Число a² следует произносить как “a в квадрате”. Например, 4² – это “четыре в квадрате”.
Число a³ произносится как “a в кубе”. Например, 4³ – это “четыре в кубе”.
Во всех остальных случаях aⁿ говорится как “a в n-ой степени”. Например, 4⁶ – это “четыре в шестой степени”.

Правила операций с показателями степени

#1. Умножение степеней (одинаковые основания)

aⁿ ⋅ a^m = a^n+m

Пример: 2² ⋅ 2³ = 2²⁺³ = 2⁵ = 32

#2. Степень произведения

(a ⋅ b)ⁿ = aⁿ ⋅ bⁿ

Пример: (2 ⋅ 3)⁴ = 2⁴ ⋅ 3⁴ = 1296

#3. Деление степеней (одинаковые основания)

aⁿ / a^m = a^n-m

Пример: 2⁵ ⋅ 2³ = 2^5-3 = 2² = 4

#4. Степень частного

(a / b)ⁿ = aⁿ / bⁿ

Пример: (12 / 4)³ = 12³ / 4³ = 27

#5. Возведение степени в степень

(aⁿ)^m = a^{n · m}

Пример: (5²)³ = 5^{2 · 3} = 3125

#6. Степень, возведенная в степень

a^{n^m} = a^{(n^m)}

Пример: 2^4² = 2^(4²) = 2^{(4 · 4)} = 2⁽¹⁶⁾ = 65536

#7. Извлечение степени из числа в степени

^m√(aⁿ) = aⁿ^/m

Пример: ³√(2⁶) = 2^6/3 = 2² = 2⋅2 = 4

#8. Возведение в отрицательную степень

b^-n = 1 / bⁿ

Пример: 2^-4 = 1 / 2⁴ = 1 / (2⋅2⋅2⋅2) = 1/16 = 0,0625

#9. .

Если еще остались вопросы, пишите, пожалуйста, комментарии!

Поделитесь нашей статьей в ваших соцсетях:
Похожие статьи
Функция РАНГ в Excel Факториал в Excel
Основы программирования в R
Установка библиотек
Очень часто (на самом деле, всегда) для работы с данными предустановленных библиотек – тех, которые были автоматически установлены вместе с R – бывает недостаточно. Поэтому необходимые библиотеки нужно устанавливать самостоятельно. Для этого используется функция install.packages(). Для примера установим библиотеку foreign.
install.packages("foreign")
Важно: название библиотеки нужно всегда указывать в кавычках. Если ввести название без кавычек, R не найдет библиотеку и выдаст ошибку (Error in install.packages : объект ‘foreign’ не найден).
Иногда при установке библиотек можно столкнуться с проблемой: R пишет, что не может сохранить установочные файлы, так как нет доступа к нужной папке. Это обычно возникает в случае, если мы работаем в учетной записи, которая не является учетной записью администратора. Например, на компьютере есть пользователь Administrator (с неограниченными правами, в том числе по установке программ) и Student (с ограничениями). Решить проблему можно следующим образом: закрыть RStudio, щелкнуть по значку RStudio правой клавишей и выбрать “Запуск от имени администратора”. После этого библиотеки должны устанавливаться нормально.
Для того чтобы использовать функционал установленной библиотеки, надо сначала к ней обратиться –иначе R не будет понимать, откуда брать запрашиваемые функции и писать “Ошибка: не могу найти функцию …”. Сделать это можно так:
library(foreign)
Здесь уже можно вводить название библиотеки без кавычек.
Ориентирование на местности
Рано или поздно при работе в R у нас появится необходимость загружать или сохранять данные. 2
## [1] 7.389056
log(exp(1)) # log - натуральный логарифм
## [1] 1
log10(100) # log10 - десятичный логарифм
## [1] 2
log(4, base = 2) # можем указать основание логарифма (base)
## [1] 2
Кто забыл про логарифмы: см. здесь.
Переменные в R
Названия переменных в R могут содержать буквы, цифры, точки и знаки подчеркивания, при этом название переменной не может начинаться с цифры. Название переменной не должно совпадать со служебными словами (операторами) в R: if, else, for, while и другимим.
Оба оператора <- и = используются для присваивания, но <- является основным в R и используется чаще. А точнее, всегда 🙂
x <- 3 x
## [1] 3
Мы можем изменить значение переменной и сохранить ее под тем же именем:
x <- x + 3 x
## [1] 6
Типы переменных
Основными типами переменных в R являются:
числовой (numeric)
целочисленный (integer)
текстовый (character)
логический (logical) — только два значения: TRUE и FALSE
Важно: В дробных числах в R в качестве разделителя используется точка.
Создадим переменную x1 и присвоим ей значение 9.5.
x1 <- 9.5 is.numeric(x1) # проверим, является ли числом
## [1] TRUE
is.integer(x1) # проверим, является ли целым числом
## [1] FALSE
is.character(x1) # проверим, является ли текстовой переменной
## [1] FALSE
is.logical(x1) # проверим, является ли логической переменной
## [1] FALSE
Создадим переменную x2:
x2 <- "welcome"
Узнаем, какого она типа:
class(x2)
## [1] "character"
Важно: Если забыли, что делает та или иная функция, можно спросить это у R:
?class # так
Или так:
help(class)
Тип переменной можно менять. {20}\). Если, напротив, R нужно было бы выдать очень маленькое число, 10 стояло бы в отрицательной степени:
2/23789
## [1] 8.407247e-05
Tекстовые переменные (строки)
Что можно делать с текстовыми переменными? Например, в текстовых переменных можно заменять одни символы на другие. Для этого существует функция sub().
group <- "group#1 group#2 group#3" sub("#","-", group) # (что заменяем, на что заменяем, где заменяем)
## [1] "group-1 group#2 group#3"
Однако функция sub() позволяет изменить только первое совпадение. Для того, чтобы заменить все встречающиеся в тексте символы, нужно воспользоваться gsub():
gsub("#","-", group) # gsub - от global sub
## [1] "group-1 group-2 group-3"
Логические выражения
Необходимы для проверки или формулировки условий.
x <- 2 y <- 10
Привычные выражения:
x > y
## [1] FALSE
x < y
## [1] TRUE
x <= y
## [1] TRUE
x == y # для проверки условия равенства - двойной знак =
## [1] FALSE
Менее привычные:
x != y # отрицание равенства
## [1] TRUE
x & y < 5 # и (одновременно x и y)
## [1] FALSE
x | y < 10 # или (хотя бы один из x и y)
## [1] TRUE
Тем по алгебре: Показатели
/ ru / algebra-themes / order-of-operations / content /
Что такое экспоненты?
Показатели — это числа, которые были умножены сами на себя. Например, 3 · 3 · 3 · 3 может быть записано как показатель степени 3 ⁴: число 3 было умножено само на себя 4 раз. 3.Не волнуйтесь, это точно такое же число: основание — это число слева, а степень — это число справа. В зависимости от типа калькулятора, который вы используете, и особенно если вы используете калькулятор на своем телефоне или компьютере, вам может потребоваться ввести показатель степени таким образом, чтобы вычислить его.
Показатели в 1-й и 0-й степени
Как бы вы упростили эти показатели?
7 ¹ 7 ⁰
Не расстраивайтесь, если вы запутались. Даже если вы чувствуете себя комфортно с другими показателями, непонятно, как вычислить их со степенями 1 и 0.К счастью, эти показатели следуют простым правилам:
Показатели степени 1
Любой показатель степени 1 равен основанию , поэтому 5 ¹ равно 5, 7 ¹ равно 7, а x ¹ равно x .
Показатели степени 0
Любой показатель степени со степенью 0 равен 1 , поэтому 5 ⁰ равно 1, а также 7 ⁰, x ⁰ и любой другой показатель степени со степенью 0 вы можете придумать.
Операции с показателями
Как бы вы решили эту проблему?
2 ² ⋅ 2 ³
Если вы думаете, что вам нужно сначала решить экспоненты, а затем перемножить полученные числа, вы правы. (Если вы не уверены, ознакомьтесь с нашим уроком по порядку действий).
Как насчет этого?
x ³ / x ²
Или этот?
2x ² + 2x ²
Хотя точно решить эти проблемы без дополнительной информации невозможно, можно упростить, их.В алгебре вас часто просят выполнить вычисления экспонент с переменными в качестве основы. К счастью, эти показатели легко складывать, вычитать, умножать и делить.
Сложение экспонент
Когда вы добавляете два показателя степени, вы не добавляете фактические полномочия — вы добавляете основания. Например, чтобы упростить это выражение, вы просто добавите переменные. У вас есть два xs, которые можно записать как 2x . Итак, x ² + x ² будет 2x ² .
x ² + x ² = 2x ²
Как насчет этого выражения?
3 года ⁴ + 2 года ⁴
Вы добавляете 3y к 2y. Поскольку 3 + 2 равно 5, это означает, что 3 года ⁴ + 2 года ⁴ = 5 лет ⁴.
3 года ⁴ + 2 года ⁴ = 5 лет ⁴
Вы могли заметить, что мы рассматривали только те задачи, в которых добавляемые показатели имели одинаковую переменную и мощность.Это потому, что вы можете добавлять экспоненты только в том случае, если их основания и экспоненты точно такие же . Таким образом, вы можете добавить их ниже, потому что оба члена имеют одинаковую переменную ( r ) и одинаковую мощность (7):
4к ⁷ + 9 ⁷
Вы не можете никогда добавлять что-либо из них в том виде, в каком они написаны. В этом выражении есть переменные с двумя разными степенями:
4к ³ + 9 ⁸
У этого есть те же возможности, но разные переменные, поэтому вы также не можете добавить его:
4к ² + 9с ²
Вычитание показателей
Вычитание экспонент работает так же, как их сложение.Например, вы можете придумать, как упростить это выражение?
5x ² — 4x ²
5-4 равно 1, поэтому, если вы сказали 1 x ² или просто x ², вы правы. Помните, что, как и при сложении показателей, вы можете вычитать только показатели с одинаковой степенью и основанием .
5x ² — 4x ² = x ²
Показатели умножения
Умножение экспонент — это просто, но способ, которым вы это делаете, может вас удивить. Чтобы умножить степень, сложите степени . Например, возьмите это выражение:
x ³ ⋅ x ⁴
Степени: 3 и 4 . Поскольку 3 + 4 равно 7, мы можем упростить это выражение до x ⁷.
x ³ ⋅ x ⁴ = x ⁷
А как насчет этого выражения?
3x ² ⋅ 2x ⁶
Степени равны 2 и 6 , поэтому наша упрощенная экспонента будет иметь степень 8.В этом случае нам также потребуется умножить коэффициенты. Коэффициенты равны 3 и 2. Нам нужно умножить их, как и любые другие числа. 3⋅2 равно 6 , поэтому наш упрощенный ответ: 6x ⁸ .
3x ² ⋅ 2x ⁶ = 6x ⁸
Вы можете упростить умножение экспоненты только с той же переменной. Например, выражение 3x ² ⋅2x ³ ⋅4y ² будет упрощено до 24x ⁵ ⋅y ².Для получения дополнительной информации перейдите к нашему уроку «Упрощение выражений».
Показатели деления
Деление показателей аналогично их умножению. Вместо того, чтобы складывать степени, вы вычитаете из . Возьмите это выражение:
х ⁸ / х ²
Поскольку 8-2 равно 6, мы знаем, что x ⁸ / x ² равно x ⁶.
x ⁸ / x ² = x ⁶
Что насчет этого?
10x ⁴ / 2x ²
Если вы думаете, что ответ — 5x ², вы правы! 10/2 дает нам коэффициент 5, а вычитание степеней ( 4-2 ) означает, что степень равна 2.
Возведение власти в степень
Иногда можно увидеть такое уравнение:
(х ⁵) ³
Показатель степени на другой экспоненте может сначала показаться запутанным, но у вас уже есть все навыки, необходимые для упрощения этого выражения. Помните, что показатель степени означает, что вы умножаете основание само на себя столько раз. Например, 2 ³ равно 2⋅2⋅2. Это означает, что мы можем переписать (x ⁵) ³ как:
x ⁵ x ⁵ ⋅x ⁵
Чтобы умножить экспоненты с одинаковым основанием, просто прибавьте показателей.Следовательно, x ⁵ ⋅x ⁵ ⋅x ⁵ = x ^{5 + 5 + 5} = x ¹⁵.
На самом деле есть еще более короткий способ упростить подобные выражения. Взгляните еще раз на это уравнение:
(x ⁵) ³ = x ¹⁵
Вы обратили внимание, что 5⋅3 тоже равно 15? Помните, умножение — это то же самое, что и добавление чего-либо более одного раза. Это означает, что мы можем думать о 5 + 5 + 5, как мы делали раньше, как о 5 умноженных на 3.Следовательно, когда вы возводите степень в степень , вы можете умножить степень .
Рассмотрим еще один пример:
(х ⁶) ⁴
Так как 6⋅4 = 24, (x ⁶) ⁴ = x ²⁴
х ²⁴
Рассмотрим еще один пример:
(3x ⁸) ⁴
Во-первых, мы можем переписать это как:
3x ⁸ ⋅3x ⁸ ⋅3x ⁸ ⋅3x ⁸
Помните, что при умножении порядок не имеет значения.Следовательно, мы можем переписать это снова как:
3⋅3⋅3⋅3⋅x ⁸ ⋅x ⁸ ⋅x ⁸ ⋅x ⁸
Поскольку 3⋅3⋅3⋅3 = 81 и x ⁸ ⋅x ⁸ ⋅x ⁸ ⋅x ⁸ = x ³², наш ответ:
81x ³²
Обратите внимание, что это также было бы то же самое, что и 3 ⁴ ⋅x ³².
Все еще не знаете, как умножать, делить или возводить экспоненты в степень? Посмотрите видео ниже, чтобы узнать, как запомнить правила:
<noscript><img src='/800/600/https/ru-static.z-dn.net/files/dc7/38ece061eb529789cd5774bd8dfbbe18.jpg' /></noscript> youtube.com/embed/8oLYEFGM0N0?rel=0&showinfo=0″ allowfullscreen=»» frameborder=»0″/>
/ ru / algebra-themes / negative-numbers / content /
Решение экспоненциальных уравнений из определения
Purplemath
Чтобы решить экспоненциальные уравнения без логарифмов, вам необходимо иметь уравнения со сравнимыми экспоненциальными выражениями по обе стороны от знака «равно», чтобы вы могли сравнивать степени и решать.Другими словами, у вас должно быть «(некоторая основа) к (некоторой степени) равняется (та же основа) (некоторой другой степени)», где вы устанавливаете две степени равными друг другу и решаете полученное уравнение. Например:
Так как основания («5» в каждом случае) одинаковы, то единственный способ, при котором два выражения могут быть равны, — это одинаковые степени. То есть:
MathHelp.com
Это решение демонстрирует логическую основу того, как решается весь этот класс уравнений: если основания одинаковы, то мощности также должны быть равны; это единственный способ, чтобы две части уравнения были равны друг другу.Поскольку степени должны быть одинаковыми, мы можем установить две степени равными друг другу и решить полученное уравнение.
Поскольку основания одинаковы, то я могу приравнять силы и решить:
1 — x = 4
1–4 = x
–3 = x
Тогда мое решение:
Не все экспоненциальные уравнения даны с одинаковым основанием по обе стороны от знака «равно». Иногда нам сначала нужно преобразовать одну или другую сторону (или обе) в какую-то другую базу, прежде чем мы сможем установить степени равными друг другу. Например:
Поскольку 9 = 3 ², это действительно просит меня решить:
Преобразовав 9 в 3 ², я преобразовал правую часть уравнения в то же самое основание, что и левая часть. Поскольку базы теперь такие же, я могу установить две степени равными друг другу:
В данном случае у меня экспонента с одной стороны от знака «равно» и число с другой.Я могу решить уравнение, если могу выразить «27» как степень 3. Поскольку 27 = 3 ³, я могу преобразовать и продолжить решение:
3 ^{2 x –1} = 27
3 ^{2 x –1} = 3 ³
2 x — 1 = 3
2 х = 4
х = 2
Если я не уверен в своем ответе или если я хочу проверить его перед тем, как сдать его (скажем, на тест), я могу проверить его, снова подключив его к исходному упражнению.Степень в левой части исходного уравнения упростится как:
И 3 ³ = 27, что является правой частью исходного уравнения. Тогда мое (подтвержденное) решение:
Как вы, вероятно, догадались, вам нужно будет хорошо освоить свои числовые степени, такие как степени от 2 до 2 ⁶ = 64, степени от 3 p до 3 ⁵ = 243, степени От 4 до 4 ⁴ = 256, от 5 до 5 ⁴ = 625, от 6 до 6 ³ = 216, и все квадраты.
Не планируйте полагаться на свой калькулятор во всем, потому что необходимость находить каждое значение в вашем калькуляторе может потратить много времени. К тому времени, как вы дойдете до теста, вы захотите иметь определенную степень удобства (то есть определенную степень осведомленности и скорости), поэтому ознакомьтесь с меньшими способностями сейчас.
Примечание по форматированию: HTML обычно не «любит» вложенные надстрочные индексы, поэтому выше для обозначения степени используется нотация «каратов».2–3 x = 3 ⁴
x ²-3 x = 4
x ²-3 x -4 = 0
( x -4) ( x + 1) = 0
x = –1, 4
Итак, мой ответ:
Это уравнение похоже на предыдущие два, но не совсем то же самое, потому что 8 не является степенью 4.2 + 4 x = 2 ³
4 x ² + 4 x = 3
4 x ² + 4 x — 3 = 0
(2 x — 1) (2 x + 3) = 0
x = ¹/₂, ^–3/₂
Отрицательные показатели степени могут использоваться, чтобы указать, что основание принадлежит другой стороне дробной линии.Поскольку 64 = 4 ³, то я могу использовать отрицательные показатели для преобразования дроби в экспоненциальное выражение:
Используя это, я могу решить уравнение:
4 ^{x +1} = ¹/₆₄
4 ^{x +1} = 4 ^–3
x + 1 = –3
x = –4
Чтобы решить эту задачу, мне сначала нужно напомнить, что квадратные корни — это то же самое, что и половинные степени, и преобразовать радикал в экспоненциальную форму. Тогда я могу решить уравнение:
8 ^{x –2} = sqrt [8]
8 ^{x –2} = 8 ^1/2
x — 2 = 1/2
x = 2 + ¹/₂ = ⁵/₂
Тогда мой ответ:
Ниже приводится пример распространенного типа вопроса с подвохом:
Подумайте об этом: какая мощность на положительном числе «2» может дать , возможно, , дать отрицательное число ? Число никогда не может перейти от положительного к отрицательному, принимая полномочия; Я никогда не смогу превратить положительные два в отрицательные , любые , четыре или другие, умножая два на себя, независимо от того, сколько раз я делаю это умножение.Возведение в степень просто не работает. Итак, ответ здесь:
URL: https://www.purplemath.com/modules/solvexpo.htm
Правила экспонент
5.1 Правила экспонент
Цели обучения
Упростите выражения, используя правила экспонент.
Упростите выражения, содержащие круглые скобки и показатели степени.
Упростите выражения, содержащие 0 в качестве показателя степени.
Правило произведения, коэффициента и степени для экспонент
Если коэффициент повторяется несколько раз, то произведение может быть записано в экспоненциальной форме Эквивалентное выражение, записанное с использованием рациональной экспоненты. xn. Положительное целое число экспонента n указывает, сколько раз в качестве множителя повторяется основание x .4 = 5 * 5 * 5 * 5.
Затем рассмотрим произведение 23 и 25,
Расширение выражения с использованием определения дает несколько множителей основания, что довольно громоздко, особенно когда n велико. По этой причине мы разработаем несколько полезных правил, которые помогут нам упростить выражения с показателями степени. В этом примере обратите внимание, что мы можем получить тот же результат, добавив экспоненты.
В общем, это описывает правило произведения для показателей xm⋅xn = xm + n; произведение двух выражений с одинаковым основанием можно упростить, добавив показатели степени.. Если m и n — положительные целые числа, то
Другими словами, при умножении двух выражений с одним и тем же основанием следует складывать экспоненты.
Пример 1: Упростить: 105⋅1018.
Решение:
Ответ: 1023
Обратите внимание, что в предыдущем примере мы не умножили основание в 10 раз.При применении правила продукта добавьте экспоненты и оставьте базу без изменений.
Пример 2: Упростить: x6⋅x12⋅x.
Решение: Напомним, что предполагается, что переменная x имеет показатель степени 1: x = x1.
Ответ: x19
Основанием может быть любое алгебраическое выражение.
Пример 3: Упростить: (x + y) 9 (x + y) 13.
Решение: Считать выражение (x + y) основанием.
Ответ: (x + y) 22
Коммутативное свойство умножения позволяет нам использовать правило произведения для показателей, чтобы упростить множители алгебраического выражения.
Пример 4: Упростить: 2x8y⋅3x4y7.
Решение: Умножьте коэффициенты и сложите экспоненты переменных факторов с одинаковым основанием.
Ответ: 6x12y8
Затем мы разработаем правило деления, сначала посмотрев на частное 27 и 23.
Здесь мы можем отменить факторы после применения определения показателей. Обратите внимание, что тот же результат может быть получен путем вычитания показателей степени.
Это описывает правило частного для показателей xmxn = xm − n; частное двух выражений с одинаковым основанием можно упростить, вычитая показатели степени.. Если m и n — натуральные числа и x ≠ 0, то
Другими словами, когда вы делите два выражения с одинаковым основанием, вычтите экспоненты.
Пример 5: Упростить: 12y154y7.
Решение: Разделите коэффициенты и вычтите экспоненты переменной y .
Ответ: 3y8
Пример 6: Упростить: 20×10 (x + 5) 610×9 (x + 5) 2.
Решение:
Ответ: 2x (x + 5) 4
Теперь возведем 23 в четвертую степень следующим образом:
Записав основание 23 как множитель четыре раза, разложите его, чтобы получить 12 множителей 2. Мы можем получить тот же результат, умножив показатели степени.
В общем, это описывает правило степени для показателей (xm) n = xmn; степень, возведенную в степень, можно упростить, умножив степень. . Учитывая положительные целые числа m и n , тогда
Другими словами, возведя степень в степень, умножьте степень.
Пример 7: Упростить: (y6) 7.
Решение:
Ответ: y42
Подводя итог, мы разработали три очень полезных правила экспонент, которые широко используются в алгебре.Если даны положительные целые числа m и n , то
Правило продукта: xm⋅xn = xm + n
Правило частного: xmxn = xm − n, x ≠ 0
Правило силы: (xm) n = xm⋅n
Попробуй! Упростить: y5⋅ (y4) 6.
Ответ: y29
Правила мощности для продуктов и коэффициентов
Теперь мы рассматриваем возведение сгруппированных продуктов в степень. Например,
После расширения у нас есть четыре фактора продукта xy . Это эквивалентно возведению каждого из исходных множителей в четвертую степень. В общем, это описывает правило мощности для продукта (xy) n = xnyn; если продукт возведен в степень, то примените эту мощность к каждому коэффициенту в продукте.. Если n — целое положительное число, то
Пример 8: Упростить: (2ab) 7.
Решение: Мы должны применить показатель степени 7 ко всем факторам, включая коэффициент 2.
Если коэффициент возведен в относительно небольшую степень, то представьте эквивалент действительного числа, как мы сделали в этом примере: 27 = 128.
Ответ: 128a7b7
Во многих случаях процесс упрощения выражений, включающих экспоненты, требует использования нескольких правил экспонент.
Пример 9: Упростить: (3xy3) 4.
Решение:
Ответ: 81x4y12
Пример 10: Упростить: (4x2y5z) 3.
Решение:
Ответ: 64x6y15z3
Пример 11: Упростить: [5 (x + y) 3] 3.
Решение:
Ответ: 125 (x + y) 9
Затем рассмотрим частное в степени.
Здесь мы получаем четыре множителя частного, что эквивалентно числителю и знаменателю в четвертой степени. В общем, это описывает правило мощности для частного (xy) n = xnyn; если частное возводится в степень, то применить эту степень к числителю и знаменателю. Если n является положительным целым числом и y 0, то
Другими словами, если дана дробь в степени, мы можем применить этот показатель к числителю и знаменателю.Это правило требует, чтобы знаменатель был ненулевым. Мы сделаем это предположение до конца раздела.
Пример 12: Упростить: (3ab) 3.
Решение: Сначала примените правило мощности для частного, а затем правило мощности для продукта.
Ответ: 27a3b3
На практике мы часто объединяем эти два шага, применяя показатель степени ко всем множителям в числителе и знаменателе.
Пример 13: Упростить: (ab22c3) 5.
Решение: Примените показатель степени 5 ко всем множителям в числителе и знаменателе.
Ответ: a5b1032c15
Пример 14: Упростить: (5×5 (2x − 1) 43y7) 2.
Решение:
Ответ: 25×10 (2x − 1) 89y14
Перед использованием правил мощности рекомендуется заключить упрощение в скобки; это соответствует порядку операций.
Пример 15: Упростить: (−2x3y4zxy2) 4.
Решение:
Ответ: 16x8y8z4
Подводя итог, мы разработали два новых правила, которые полезны, когда символы группировки используются вместе с показателями степени. Если задано положительное целое число n , где y ненулевое число, то
Правило мощности для продукта: (ху) п = xnyn
Правило степени для частного: (ху) п = xnyn
Попробуй! Упростить: (4×2 (x − y) 33yz5) 3.
Ответ: 64×6 (x − y) 927y3z15
Ноль как экспонента
Используя правило частного для показателей степени, мы можем определить, что значит иметь 0 в качестве показателя степени. Рассмотрим следующий расчет:
Восемь, разделенная на 8, явно равна 1, и когда применяется правило частного для показателей степени, мы видим, что в результате получается показатель степени 0. Это приводит нас к определению нуля как показателя x0 = 1; любая ненулевая база, возведенная в степень 0, определяется как 1., где x ≠ 0:
Важно отметить, что 00 не определено. Если основание отрицательное, то результат все равно +1. Другими словами, любая ненулевая база, возведенная в степень 0, определяется как 1. В следующих примерах предполагается, что все переменные ненулевые.
Пример 16: Упростить:
а. (−5) 0
г. −50
Решение:
а.Любая ненулевая величина, возведенная в нулевую степень, равна 1.
г. В примере -50 основание 5, а не -5.
Ответы: а. 1; б. −1
Пример 17: Упростить: (5x3y0z2) 2.
Решение: Рекомендуется сначала упростить в круглых скобках.
Ответ: 25x6z4
Пример 18: Упростить: (−8a10b55c12d14) 0.
Решение:
Ответ: 1
Попробуй! Упростить: 5×0 и (5x) 0.
Ответ: 5×0 = 5 и (5x) 0 = 1
Ключевые выводы
Правила экспонент позволяют упростить выражения, включающие экспоненты.
При умножении двух величин с одинаковым основанием сложите экспоненты: xm⋅xn = xm + n.
При делении двух величин с одинаковым основанием вычтите показатели: xmxn = xm − n.
При возведении степеней в степени умножьте показатели: (xm) n = xm⋅n.
Когда сгруппированная величина, включающая умножение и деление, возводится в степень, примените эту степень ко всем множителям в числителе и знаменателе: (xy) n = xnyn и (xy) n = xnyn.
Любая ненулевая величина, возведенная в степень 0, определяется как равная 1: x0 = 1.
Тематические упражнения
Часть A: Правило произведения, коэффициента и степени для экспонентов
Запишите каждое выражение в экспоненциальной форме.
1. (2x) (2x) (2x) (2x) (2x)
2. (−3y) (- 3y) (- 3y)
3. −10⋅a⋅a⋅aaaa⋅a
4. 12⋅x⋅x⋅y⋅y⋅y⋅y⋅y⋅y
5. −6⋅ (x − 1) (x − 1) (x − 1)
6.(9ab) (9ab) (9ab) (a2 − b) (a2 − b)
Упростить.
7. 27⋅25
8. 393
9. −24
10. (−2) 4
11. −33
12. (−3) 4
13. 1013⋅105⋅104
14. 108⋅107⋅10
15. 51252
16. 10710
17. 1012109
18.(73) 5
19. (48) 4
20. 106⋅ (105) 4
Упростить.
21. (−x) 6
22. a5⋅ (−a) 2
23. x3⋅x5⋅x
24. y5⋅y4⋅y2
25. (a5) 2⋅ (a3) 4⋅a
26. (x + 1) 4 (y5) 4⋅y2
27. (х + 1) 5 (х + 1) 8
28. (2a − b) 12 (2a − b) 9
29. (3x − 1) 5 (3x − 1) 2
30.(а-5) 37 (а-5) 13
31. xy2⋅x2y
32. 3x2y3⋅7xy5
33. −8a2b⋅2ab
34. −3ab2c3⋅9a4b5c6
35. 2a2b4c (−3abc)
36. 5a2 (b3) 3c3⋅ (−2) 2a3 (b2) 4
37. 2×2 (x + y) 5⋅3×5 (x + y) 4
38. −5xy6 (2x − 1) 6⋅x5y (2x − 1) 3
39. x2y⋅xy3⋅x5y5
40. −2x10y⋅3x2y12⋅5xy3
41.32x4y2z⋅3xy4z4
42. (−x2) 3 (x3) 2 (x4) 3
43. a10⋅ (a6) 3a3
44. 10×9 (x3) 52×5
45. a6b3a2b2
46. m10n7m3n4
47. 20x5y12z310x2y10z
48. −24a16b12c36a6b11c
49. 16 x4 (x + 2) 34x (x + 2)
50. 50y2 (x + y) 2010y (x + y) 17
Часть B: Правила мощности для продуктов и коэффициентов
Упростить.
51. (2x) 5
52. (−3y) 4
53. (−xy) 3
54. (5xy) 3
55. (−4abc) 2
56. (72x) 2
57. (−53y) 3
58. (3abc) 3
59. (−2xy3z) 4
60. (5у (2x − 1) x) 3
61. (3х2) 3
62. (−2×3) 2
63. (xy5) 7
64.(x2y10) 2
65. (3х2г) 3
66. (2x2y3z4) 5
67. (−7ab4c2) 2
68. [x5y4 (x + y) 4] 5
69. [2y (x + 1) 5] 3
70. (ab3) 3
71. (5a23b) 4
72. (−2x33y2) 2
73. (−x2y3) 3
74. (ab23c3d2) 4
75. (2x7y (x − 1) 3z5) 6
76. (2×4) 3⋅ (x5) 2
77.(x3y) 2⋅ (xy4) 3
78. (−2a2b3) 2⋅ (2a5b) 4
79. (−a2b) 3 (3ab4) 4
80. (2×3 (x + y) 4) 5⋅ (2×4 (x + y) 2) 3
81. (−3x5y4xy2) 3
82. (−3x5y4xy2) 2
83. (−25x10y155x5y10) 3
84. (10x3y55xy2) 2
85. (−24ab36bc) 5
86. (−2x3y16x2y) 2
87. (30ab33abc) 3
88.(3с3т22с2т) 3
89. (6xy5 (x + y) 63y2z (x + y) 2) 5
90. (−64a5b12c2 (2ab − 1) 1432a2b10c2 (2ab − 1) 7) 4
91. Вероятность подбросить честную монету и получить n орла подряд определяется формулой P = (12) n. Определите вероятность выпадения 5 голов подряд в процентах.
92. Вероятность прокатки одной честной шестигранной кости и получения n одинаковых граней вверх в ряду определяется формулой P = (16) n.Определите вероятность получения одной и той же лицевой стороной вверх два раза подряд в процентах.
93. Если каждая сторона квадрата имеет размер 2×3 единицы, то определите площадь с помощью переменной x .
94. Если каждое ребро куба имеет размер 5×2 единиц, то определите объем с помощью переменной x .
Часть C: Нулевые экспоненты
Упростить. ( Предположим, что переменные не равны нулю .)
95. 70
96. (−7) 0
97. −100
98. −30⋅ (−7) 0
99. 86753090
100. 52⋅30⋅23
101. −30⋅ (−2) 2⋅ (−3) 0
102. 5x0y2
103. (−3) 2x2y0z5
104. −32 (x3) 2y2 (z3) 0
105. 2x3y0z⋅3x0y3z5
106. −3ab2c0⋅3a2 (b3c2) 0
107.(−8xy2) 0
108. (2x2y3) 0
109. 9x0y43y3
Часть D. Темы дискуссионной доски
110. Рене Декарт (1637) установил использование экспоненциальной формы: a2, a3 и так далее. Как до этого обозначали экспоненты?
111. Обсудите достижения Аль-Кариси.
112. Почему 00 не определено?
113. Объясните начинающему студенту, почему 34⋅32 ≠ 96.
ответов
1: (2x) 5
3: −10a7
5: −6 (x − 1) 3
7: 212
9: −16
11: −27
13: 1022
15: 510
17: 103
19: 432
21: x6
23: x9
25: a23
27: (x + 1) 13
29: (3x − 1) 3
31: x3y3
33: −16a3b2
35: −6a3b5c2
37: 6×7 (x + y) 9
39: x8y9
41: 27x5y6z5
43: a25
45: a4b
47: 2x3y2z2
49: 4×3 (х + 2) 2
51: 32×5
53: −x3y3
55: 16a2b2c2
57: −12527y3
59: 16x4y481z4
61: 27×6
63: x7y35
65: 27x6y3
67: 49a2b8c4
69: 8y3 (x + 1) 15
71: 625a881b4
73: −x6y9
75: 64x42y6 (x − 1) 18z30
77: x9y14
79: −81a10b19
81: −27x12y6
83: −125x15y15
85: −1024a5b10c5
87: 1000b6c3
89: 32x5y15 (x + y) 20z5
91: 318%
93: A = 4×6
95: 1
97: -1
99: 1
101: −4
103: 9x2z5
105: 6x3y3z6
107: 1
109: 3 года
Ввод математических задач на этом сайте
Быстро! Мне нужна помощь с: Выберите пункт справки по математике. ..Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DividingFractions, MultiplyingFractions, SubplicationFractions are, SubplicationFractions , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основМетрическая система, преобразование чисел, сложение чисел, вычисление с числами, вычисление с переменными Числа, деление чисел, умножение чисел, сравнение числовой строки, числовые строки, размещение значений чисел, произнесение чисел, округление чисел, вычитание частичных / параболических чисел, графическое построение чисел , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Методы Правые треугольники, Ветер, рисунок
Калькулятор дробей

Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное в дробное: 0.625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в задачах:
следующие математические задачи »
Что такое экспонента?

наверх
MATH ОБЗОР: ПОЛЕЗНАЯ МАТЕМАТИКА ДЛЯ ВСЕХ
РАЗДЕЛ 3. ЧТО ТАКОЕ ДОКАЗАТЕЛЬ?
Показатель степени относится к количеству раз, когда число умножается само на себя.Например, 2 до 3-го (написано так: 2 ³) означает:
2 х 2 х 2 = 8 .
2 ³ не то же самое, что 2 x 3 = 6.
Помните, что число в степени 1 само по себе. Например,
a ¹ = a
5 ¹ = 5 .
Есть несколько особых случаев:
1. a ⁰ = 1
Когда показатель равен нулю, как и в 6 ⁰, выражение всегда равно 1.
a ⁰ = 1
6 ⁰ = 1
14 356 ⁰ = 1
2.а ^-м = 1 / а ^м
Когда показатель степени отрицательный число, результат всегда дробь. Дроби состоят из числителя над знаменателем. В этом случае числитель всегда равен 1. Чтобы найти знаменатель, представьте, что отрицательная экспонента положительна, и возвести число в эту степень, например:
a ^-м = 1 / a ^м
6 ^-3 = 1/6 ³
У вас может быть переменная заданной мощности, например ³, что будет означать a x a x a.Вы также можете указать число переменной мощности, например 2 ^m, что означает умножение 2 на себя m раз. Мы будем разберутся с этим через некоторое время.
в экспоненты, стр. 2
Для подробнее об этом сайте свяжитесь с Distance Координатор по образованию.
Авторские права © 2004 г. регентами Миннесотского университета, равные возможности работодатель и педагог.
Уроки по упрощению экспонент | Ресурсы Wyzant
Прежде чем мы углубимся в упрощение экспоненты, давайте потратим некоторое время, чтобы узнать, что именно такое экспонента. Показатель степени — это верхний индекс, или небольшое число, написанное в правом верхнем углу числа, переменной или набора круглых скобок. Пример одного показан ниже.
2 ³
Это говорит вам умножить 1 на число столько раз, сколько указано в экспоненте.В приведенном выше примере 2 в третьей степени (в третьей степени означает, что показатель степени равен 3). Это эквивалентно задаче умножения ниже, потому что 1 умножается на 2 три раз.
1 * 2 * 2 * 2
8
Как видите, 1 * 2 * 2 * 2 можно упростить до 8, что является ответом на проблему.
Экспоненты
Изучите следующую проблему:
-3 ⁶
Эта задача заменена на задачу умножения, описанную ниже.Из-за порядка операций (объяснено на следующем уроке) сначала упрощается показатель степени, а затем к ответу добавляется отрицательный знак.
1 * 3 * 3 * 3 * 3 * 3 * 3
-729
Как видите, умножение упрощается до числа -729. Вы можете проделать работу для этого в уме, на полях. бумаги или с помощью калькулятора, если это возможно.
Экспоненты
Следующая проблема показана ниже:
(-3) ⁶
На этот раз -3 заключен в круглые скобки.Вместо того, чтобы переносить отрицательный знак, каждые 3 становятся отрицательными.
1 * -3 * -3 * -3 * -3 * -3 * -3
729
Как видите, умножение упрощается до 729. Обратите внимание, что помимо результат предыдущего примера отрицательный, результат вот то же самое. Обратите особое внимание на поиск экспонентов, когда они отрицательны. присутствуют знаки, так как это частый источник ошибок.
Особые случаи
Нулевой показатель
Каждая из этих проблем решается умножением единицы на число, количество раз, указываемое экспонентой. Если показатель равен 0, то 1 не умножить на число вообще. Следовательно, ответ — 1. Это важное правило, о котором следует помнить.
51 ⁰
1
Ноль с показателем степени:
В большинстве случаев ноль с показателем степени можно вычислить как любое другое число. и показатель степени.
0 ⁴
1 * 0 * 0 * 0 * 0
0
Обратите внимание, что до тех пор, пока 1 умножается хотя бы на один 0, конечный результат равен 0. Следовательно, мы можем заключить, что 0 для любого положительного показателя всегда равен нулю.
Другой особый случай — 0 ⁰. Ноль с показателем ноль не определен и не может быть вычислен.
Будьте осторожны, не соблюдайте правила для нулевых показателей! От нуля до любой положительной силы всегда равен нулю, потому что сколько бы раз вы ни умножали 1 на ноль ответ всегда будет ноль.Но 0 ⁰ не определено.
1 показатель степени:
Рассмотрим этот пример, в котором число rasies возведено в первую степень.
51 ¹
1 * 51
51
Если вы попробуете любой аналогичный пример, например 10 ¹ или 100 ¹, вы обнаружит, что результатом всегда будет исходное число или основание. Это потому что 1, умноженное на любое другое число, всегда равно второму числу.
Итак, чтобы упростить случай, когда число возводится в первую степень, мы можем просто удалите показатель степени.
Экспоненты
От десяти до любой степени
Этот совет поможет вам сэкономить много времени: десять в любой степени — это просто цифра 1. за которым следует количество нулей, обозначенных показателем степени. Пример показан ниже.
10 ⁵
100 000
Обратите внимание, что результатом является единица с пятью нулями, потому что показатель степени на 10 было 5.
Показатели чтения
В общем проблема типа
5 ¹⁰
читается как «пять в десятой степени».
Специальные случаи для чтения экспонент
У некоторых экспонентов есть особые способы произнесения. Это делает его Сказать немного проще, но совсем не обязательно, чтобы вы их использовали.
Вторая степень: 3 ² — может читаться как «тройка во второй степени» или «тройка в квадрате».»
Третья степень: 10 ³ — может читаться как «Десять в третьей степени» или «10 в кубе».
Показатели числа ресурсов
Подпишитесь бесплатно для доступа к дополнительным ресурсам по алгебре, например. Ресурсы Wyzant содержат блоги, видео, уроки и многое другое по алгебре и более чем 250 другим предметам. Прекратите бороться и начните учиться сегодня с тысячами бесплатных ресурсов! .