Трапеция
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие;
— прямоугольные
.Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У равнобокой трапеции боковые стороны равны, а основания параллельны.
У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапецииПрямыми бывают только два угла.
У прямоугольной трапеции два угла прямые, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник, у которого линия сечения параллельна основанию треугольника.
Важно. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
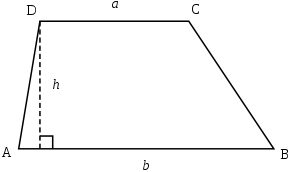
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
h1h2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
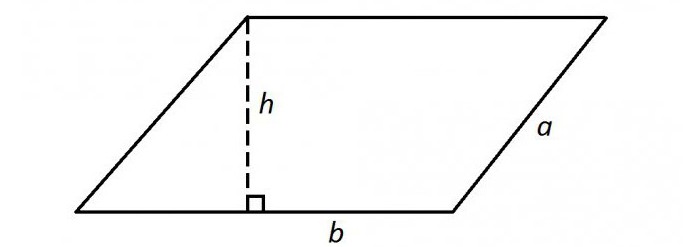
Площадь трапеции
где
a и b — параллельные основания трапеции
c и d — боковые стороны трапеции
m — средняя линия трапеции
r — радиус вписанной в трапецию окружности
S — площадь трапеции Содержание главы:
Ромб | Описание курса | Площадь трапеции
profmeter.com.ua
Трапеция — это… Что такое Трапеция?
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого
Связанные определения
Элементы трапеции
- Параллельные стороны называются основаниями трапеции.
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
Виды трапеций
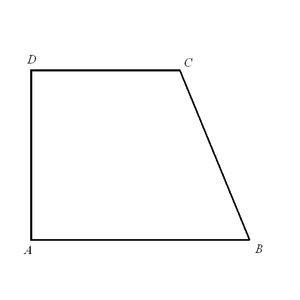 Прямоугольная трапеция
Прямоугольная трапеция 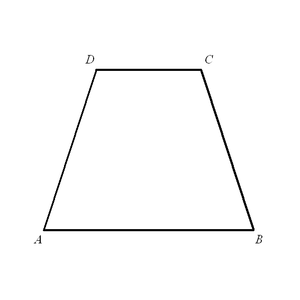 Равнобедренная трапеция
Равнобедренная трапеция- Трапеция, у которой боковые стороны равны, называется равнобокой или равнобедренной.
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Общие свойства
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей, равен полуразности оснований.
- (Обобщённая теорема Фалеса). Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
Свойства и признаки равнобедренной трапеции
- Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
- Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
- В равнобедренной трапеции углы при любом основании равны.
- В равнобедренной трапеции длины диагоналей равны.
- Если трапецию можно вписать в окружность, то она равнобедренная.
- Около равнобедренной трапеции можно описать окружность.
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная и описанная окружность
Площадь
- Здесь приведены формулы, свойственные именно трапеции. См. также формулы для площади произвольных четырёхугольников.
- В случае, если и — основания и — высота, формула площади:
- В случае, если — средняя линия и — высота, формула площади:
ɴʙ Эти формулы — одинаковы, так как полусумма оснований равняется средней линии трапеции:
- Формула, где , — основания, и — боковые стороны трапеции:
- Площадь равнобедренной трапеции с радиусом вписанной окружности, равным , и углом при основании :
- В частности, если угол при основании равен 30°, то:
- .
См. также
Примечания
dic.academic.ru
Трапеция
Трапеция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара противолежащих сторон параллельна.
Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон трапеции.
Элементы трапеции
- Параллельные стороны называются
- Две другие стороны называются боковыми сторонами.
- Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
- Расстояние между основаниями называется высотой трапеции.
Виды трапеций
- Трапеция, у которой боковые стороны равны, называется равнобедренной.
- Трапеция, у которой один из углов «прямой», называется прямоугольной.
Основные свойства трапеции
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
\[ AB + CD = BC + AD \]
Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
\[ AK = KB, AM = MC, BN = ND, CL = LD \]
Средняя линия трапеции параллельна основаниям и равна их полусумме:
\[ m = \dfrac{a + b}{2} \]
Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
\[ \dfrac{BC}{AD} = \dfrac{OC}{AO} = \dfrac{OB}{DO} \]
Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
\[ d_1^2 + d_2^2 = 2ab + c^2 + d^2 \]
Формулы длин сторон трапеции
Формула длины оснований трапеции через среднюю линию и другую основу:
\[ a = 2m — b , b = 2m — a \]
Формулы длины основ трапеции через высоту и углы при нижнем основании:
\[ a = b + h · (ctg \alpha + ctg \beta) , b = a — h · (ctg \alpha + ctg \beta)\]
Формулы длины основ трапеции через боковые стороны и углы при нижнем основании:
\[ a = b + c·cos \alpha + d·cos \beta, b = a — c·cos \alpha — d·cos \beta \]
Формулы боковых сторон трапеции через высоту и углы при нижнем основании:
\[ с = \dfrac{h}{sin \alpha } , d = \dfrac{h}{sin \beta } \]
Формулы длины средних линий трапеции
Формула определения длины средней линии через длины оснований:
\[ m = \dfrac{a + b}{2} \]
Формула определения длины средней линии через площадь и высоту:
\[ m = \dfrac{S}{h} \]
Формулы длины высоты трапеции
Формула высоты трапеции через сторону и прилегающий угол при основании:
\[ h = c·sin α = d·sin β \]
Формула высоты трапеции через диагонали и углы между ними:
\[ h = sin γ \cdot \dfrac{d_1\cdot d_2}{a + b} = sin δ \cdot \dfrac{d_1\cdot d_2}{a + b} \]
Формула высоты трапеции через диагонали, углы между ними и среднюю линию:
\[ h = sin γ \cdot \dfrac{d_1 \cdot d_2}{2m 2m} = sin δ · \dfrac{d_1}{d_2} \]
Формула высоты трапеции через площадь и длины оснований:
\[ h = \dfrac{2S}{a + b} \]
Формула высоты трапеции через площадь и длину средней линии:
\[ h = \dfrac{2S}{m} \]
Формулы длин диагоналей трапеции
Формулы длин диагоналей трапеции по теореме косинусов:
\[ d_1 = \sqrt{a^2 + d^2 — 2ad·cos β} \]
\[ d_2 = \sqrt{a^2 + c^2 — 2ac·cos β} \]
Формулы длин диагоналей трапеции через четыре стороны:
\[ d_1 = \sqrt{d^2 + ab — \dfrac{a(d^2 — c^2)}{a — b} } \]
\[ d_2 = \sqrt{c^2 + ab — \dfrac{ a(c^2 — d^2) }{a — b} } \]
Формулы длин диагоналей трапеции через высоту:
\[ d_1 = \sqrt{h^2 + (a — h · ctg β)^2} = \sqrt { h^2 + (b + h · ctg α)^2} \]
\[ d_2 = \sqrt{h^2 + (a — h · ctg α)^2} = \sqrt{h^2 + (b + h · ctg β)^2} \]
Формулы длин диагоналей трапеции через сумму квадратов диагоналей:
\[ d_1 = \sqrt{c^2 + d^2 + 2ab — d_2^2} \]
\[ d_2 = \sqrt{c^2 + d^2 + 2ab — d_1^2} \]
Формулы площади трапеции
Формула площади трапеции через основания и высоту:
\[ S = \dfrac{ (a + b) · h }{2} \]
Формула площади трапеции через среднюю линию и высоту:
\[ S = m · h \]
Формула площади трапеции через диагонали и угол между ними:
\[ S = \dfrac{d_1d_2}{2} · sin γ = \dfrac{d_1d_2}{2} · sin δ \]
Формула площади трапеции через четыре стороны:
\[ S = \dfrac{a + b}{2}\sqrt{c^2 — \left\lgroup\dfrac{(a — b)^2 + c^2 — d^2)}{2\cdot (a — b)} \right\rgroup ^2 } \]
Формула Герона для площади трапеции
\[ S = \frac{a + b}{\left|a-b\right| } \sqrt{(p — a)(p — b)(p — a — c)(p — a — d)} \]
где \( p = \dfrac{a + b + c + d}{2} \) — полупериметр трапеции.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Источник информации
×Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
calcsbox.com
Конспект занятия «В стране геометрических фигур».
Государственное бюджетное образовательное учреждение школа № 982
Конспект НОД по математике в старшей группе:
«Занимательная страна геометрических фигур»
Составила:
Воспитатель
Осипова
Татьяна
Викторовна
Москва, 2018
Конспект НОД по математике «Занимательная страна геометрических фигур» для старшей группы.
Интеграция образовательных областей: «Познавательное развитие»; «Социально- коммуникативное развитие»; «Физическое развитие».
Цель: учить классифицировать фигуры по разным признакам; познакомить с трапецией и ромбом.
Задачи:
Образовательные:
— упражнять детей в умении различать и называть знакомые геометрические фигуры: круг, треугольник, квадрат, прямоугольник;
— познакомить с новыми геометрическими фигурами – трапеция и ромб;
— учить находить в окружении предметы четырехугольной формы;
-упражнять в счете в пределах 6.
Развивающие:
— закреплять умение детей составлять фигуры из счетных палочек;
— способствовать развитию мелкой моторики рук;
— развивать слуховое и зрительное внимание, память, наблюдательность, любознательность и воображение;
— развивать способность у детей отгадывать загадки;
— развивать умения выполнять движения в соответствии с текстом.
Воспитательные:
— Воспитывать самостоятельность, умение планировать свою работу
— Воспитывать стремление оказывать помощь другим;
— Воспитывать дружеские взаимоотношения между детьми.
Предварительная работа: рассмотреть плакат «Геометрические фигуры», разгадывание загадок о геометрических фигурах.
Материалы: счетные палочки на каждого ребенка, плакат «Геометрические фигуры», фишки, 2 обруча, набор геометрических фигур разной формы, магнитная доска, карточки с цифрами, набор цифр на каждого ребенка.
Ход НОД:
Организационный момент:
Мы построим ровный круг,
Справа друг и слева друг.
Дружно за руки возьмемся,
И друг другу улыбнемся!
У всех хорошее настроение?
Все забыты огорчения?
Я прошу вас мне сказать
Готовы вы сейчас играть?
(ответы детей).
Воспитатель: Ну тогда вы готовы отгадать мои загадки?
Дети: Да!
Загадки про геометрические фигуры:
Каждый ребенок знает,

Что это напоминает:
Яркое солнышко,
Подсолнуха донышко,
Колеса у машины
И новый мяч у Нины! (круг).
Все четыре стороны – все ,как близнецы, равны,
И прямых угла четыре,
Как у рамки на картине.
К четырехугольникам фигуру отнесем
И …(квадратом) назовем.
Если три стороны и три угла

Вместе соединить,
То сможем тогда очень легко
(Треугольник)… получить.
Велика ли фигура или мала,
Но прямые смотри все четыре угла, 
И напротив друг друга две стороны
Меж собою до миллиметра равны,-
Значит это- ….(прямоугольник),
Знает об этом каждый дошкольник!
Воспитатель: Молодцы, ребята! Все загадки отгадали! И сегодня мы отправимся в страну Геометрических фигур и познакомимся с новыми геометрическими фигурами. Послушайте стихотворения.
(Воспитатель показывает новые фигуры на плакате и зачитывает стихотворение).
Трапеция больше на крышу похожа,
Юбку трапецией рисуют тоже,
Взять треугольник и верх удалить,
Трапецию можно так получить.
Ромб -фигура непростая, 
Две в себе объединяет:
Треугольник раз и два –
Фигура стала вдруг одна!
Воспитатель: Ребята, а на что похожа трапеция? А ромб? (ответы детей)
-Сколько углов у этих фигур? Подумайте и скажите, как их можно назвать одним словом?(если дети не смогут ответить, предложить им пересчитать все углы и стороны).
— Четырехугольники! Правильно! А теперь, ребята, давайте сядем за столы и выложим из счетных палочек сначала треугольник, затем квадрат, прямоугольник. (Дети выполняют задание).
Воспитатель: Из скольких палочек получился треугольник? (из трех).
А квадрат? (из четырех). А прямоугольник? (из шести). А сейчас, давайте попробуем построить из палочек новые фигуры – трапецию и ромб. Сколько нам понадобится палочек, чтобы построить трапецию? (пять палочек). А чтобы построить ромб? (четыре палочки). (Воспитатель проверяет как дети выполняют задание, помогает).
Воспитатель: Ребята, а скажите какая фигура здесь лишняя? (треугольник). Почему? (потому что у треугольника три угла, а у всех остальных фигур по четыре угла).
Воспитатель: Ребята, пока мы с вами строили фигуры, налетел ветер и перепутал все геометрические фигуры. Поможете мне найти домики для каждой фигуры? (Проводится игра «Разложи фигуры» — треугольники, круги, квадраты лежат на ковре в беспорядке, рядом лежат три обруча – зеленый, красный и желтый). Давайте треугольники положим в красный обруч, круги – в желтый, а квадраты в зеленый. Берем по одной фигуре и несем в «домик» (Дети выполняют задание под музыку).
-Молодцы, ребята! Справились отлично! А теперь немного отдохнем и превратимся в геометрические фигуры.
Физимнутка: В математику играю
Вас в фигуры превращаю,
Раз, два, три, раз, два, три!
Геометрические фигуры на месте замри!
(игра проводится три раза).
Воспитатель: Ребята, пока мы с вами играли, цифры на нашей доске поссорились!
Случай странный, случай редкий
Цифры в ссоре! Вот те на!
Со своей стоять соседкой
Не желает ни одна!
Помири скорей ты всех,
А то будет просто смех!
(Дети выполняют задание за столами, расставляют цифры по порядку, воспитатель проверяет, как дети выполнили задание, отмечает тех детей, которые справились, помогает остальным).
Рефлексия:
Воспитатель:
Мы фигуры различали,
Мы узоры собирали,
И играли, и считали,
И совсем мы справились!
А теперь спрошу у вас:
«Задания вам понравились?»
(ответы детей)
Воспитатель: Ребята, чем мы занимались сегодня? С какими новыми фигурами познакомились? Что делали? Что было самым трудным? А что больше всего запомнилось?
infourok.ru
Картинки названия геометрических фигур (30 фото)
 Геометрические фигуры нужно знать для лучшего понимания предмета. Смотрите далее красивые картинки про названия геометрических фигур.
Геометрические фигуры нужно знать для лучшего понимания предмета. Смотрите далее красивые картинки про названия геометрических фигур.  Прямоугольник, ромб, круг.
Прямоугольник, ромб, круг.  Параллелепипед, шар, конус.
Параллелепипед, шар, конус.  Круг, квадрат, овал.
Круг, квадрат, овал.
 Сложные геометрические фигуры с названием.
Сложные геометрические фигуры с названием.  Ломанная, многоугольник, отрезок.
Ломанная, многоугольник, отрезок.  Конус, цилиндр, сфера.
Конус, цилиндр, сфера.  Картинка про название геометрических фигур.
Картинка про название геометрических фигур.  Полукруг, треугольник, трапеция.
Полукруг, треугольник, трапеция.  Квадраты, круги, овалы.
Квадраты, круги, овалы.  Разные фигуры из геометрии.
Разные фигуры из геометрии.  Параллелограмм, восьмиугольник.
Параллелограмм, восьмиугольник.  Квадрат, шестиугольник, семиугольник.
Квадрат, шестиугольник, семиугольник.  Звезда, призма, сфера.
Звезда, призма, сфера.  Предметная картинка про геометрические фигуры.
Предметная картинка про геометрические фигуры.  Большой красный конус.
Большой красный конус.  Оранжевый ромб.
Оранжевый ромб.  Синий куб.
Синий куб. 
 Геометрические тела.
Геометрические тела.  Разные пирамиды.
Разные пирамиды.  Простая картинка названия геометрических фигур.
Простая картинка названия геометрических фигур.  Фиолетовый ромб.
Фиолетовый ромб.  Красивый конус.
Красивый конус.  Овал, трапеция, ромб.
Овал, трапеция, ромб.  Много фигур из учебника геометрии.
Много фигур из учебника геометрии.  Куб, сфера.
Куб, сфера. 
Сердце, звезда, овал.
 Геометрические фигуры и их названия.
Геометрические фигуры и их названия. 
klike.net
Проектная работа Геометрическая фигура трапеция страница 2
Гипотеза:Трапеция обладает рядом интересных и полезных для решения задач свойствами. Если овладеть ими и рассмотреть их на примере задач, то при решении подобных задач на ГИА, вы сможете гарантировать себе дополнительные баллы.
Теоретическая часть.
Происхождение слова трапеция
Трапеция – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две не параллельны
Трапе́ция. Не знаю, как вас, а меня радуют внезапно открываемые этимологией связи между совсем далекими друг от друга словами. Что общего между «трапеция», «трапеза» (еда) и именем турецкого города Трапезунд? А оно есть.
По-гречески «trapedza» значило «стол», «trapezion» — «столик». Из второго слова создалось наше «трапеция» — известная математическая фигура с двумя равными и двумя параллельными сторонами: именно такой формы столы бывали в Греции.
Первое слово — по тем столам, за которыми вкушали пищу монахи византийских монастырей, — начало обозначать и самый этот процесс, еду, — «трапезу»; говорим же мы: «хороший стол», «плохой стол» о еде в каком-нибудь пансионате или доме отдыха. Вы, конечно, сами сообразили, почему «трапецией» называется определенный гимнастический снаряд: конечно, за «трапецеидальную» форму.
А Трапезунд? Над этим приморским городом высится гора, принадлежащая к типу «столовых». Основателями Трапезунда были греки; они и дали ему такое имя: «Город столовой горы».
Происхождение слова трапеция в этимологическом Успенского Л. В.:
Трапе́ция Через нов.-в.-н. Тrареzium — то же из ср.-лат. Trapezium, греч. Τραπέζιον, буквально «столик» (см. Хайзе; Даль 4, 823).
Происхождение слова трапеция в этимологическом Фасмера М.:
ТРАПЕЦИЯ. Заимств. В XVIII в. Из лат. Яз., где trapezium < греч. Trapezion, уменьшит.-ласкат. Суф. Производного от trapeza «стол». Трапеция буквально — «столик». Геометрическая фигура была названа так по внешнему сходству с маленьким столом.
Трапеция, в повседневной жизни
Слово «трапеция» присутствует не только в геометрии, она имеет более широкое применение в повседневной жизни.
Это необычное слово мы можем встретить, просматривая спортивные соревнования гимнастов, выполняющих акробатические упражнения на трапеции. В гимнастике трапецией называют спортивный снаряд, который состоит из перекладины, подвешенной на двух веревках.
Также это слово можно услышать, занимаясь в спортивном зале или в среде людей, которые занимаются бодибилдингом, так как трапеции – это не только геометрическая фигура или спортивный акробатический снаряд, но и мощные мышцы спины, которые расположены сзади за шеей.
www.prodlenka.org
Плоские и объемные геометрические фигуры :: SYL.ru
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
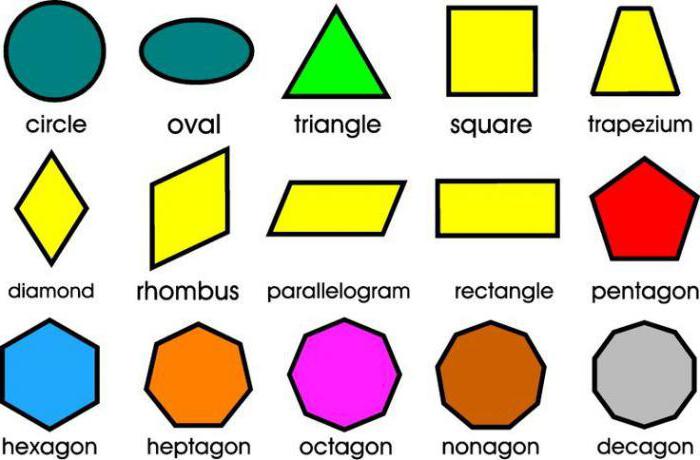
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.

Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат – это четырехугольник с равными сторонами и углами.
Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
К этой категории стоит отнести геометрические фигуры разнообразных форм, ломаная линия контуров которых замыкается.
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
К этой категории причисляют следующие конструкции:
- куб;
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
- тор.
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.

Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
www.syl.ru

